简单几何图形的面积计算

几何图形的面积计算几何图形的面积计算是数学中非常重要的一部分，它涉及到了诸多的几何知识和计算方法。

在几何学中，面积是用来描述平面图形所占的空间大小的一个指标。

不同的几何图形有不同的面积计算公式，下面将会一一介绍各个常见几何图形的面积计算方法。

一、矩形的面积计算矩形是最简单的几何图形之一，它的面积计算公式是：面积 = 长 ×宽。

例如，一个矩形的长为5cm，宽为3cm，那么它的面积 = 5cm ×3cm = 15cm²。

二、三角形的面积计算三角形也是常见的几何图形，它的面积计算公式是：面积 = 1/2 ×底边长 ×高。

例如，一个三角形的底边长为4m，高为6m，那么它的面积 = 1/2 ×4m × 6m = 12m²。

三、圆形的面积计算圆形是一种特殊的几何图形，其面积计算公式是：面积= π × 半径²。

其中，π是一个无理数，约等于3.14159。

半径是圆的半径长度。

例如，一个圆的半径为5cm，那么它的面积 = 3.14159 × 5cm × 5cm= 78.54cm²。

四、正方形的面积计算正方形是边长相等的矩形，因此它的面积计算公式与矩形相同，即：面积 = 边长 ×边长。

例如，一个正方形的边长为7cm，那么它的面积 = 7cm × 7cm =49cm²。

五、梯形的面积计算梯形也是一种常见的几何图形，它的面积计算公式是：面积 = 1/2 ×(上底 + 下底) ×高。

例如，一个梯形的上底为4cm，下底为8cm，高为5cm，那么它的面积 = 1/2 × (4cm + 8cm) × 5cm = 30cm²。

六、圆环的面积计算圆环是由两个同心圆围成的区域，它的面积计算公式是：面积= π× (外圆半径² - 内圆半径²)。

小学五年级数学解析：几何图形的面积计算一、常见几何图形的面积公式1. 长方形的面积公式：长方形的面积 = 长×宽。

例题解析：例题1：一个长方形的长为8米，宽为5米，求其面积。

解答：面积 = 8米× 5米 = 40平方米。

2. 正方形的面积公式：正方形的面积 = 边长×边长。

例题解析：例题2：一个正方形的边长为6厘米，求其面积。

解答：面积 = 6厘米× 6厘米 = 36平方厘米。

3. 三角形的面积公式：三角形的面积 = 底×高÷ 2。

例题解析：例题3：一个三角形的底为10米，高为4米，求其面积。

解答：面积 = 10米× 4米÷ 2 = 20平方米。

4. 平行四边形的面积公式：平行四边形的面积 = 底×高。

例题解析：例题4：一个平行四边形的底为9米，高为5米，求其面积。

解答：面积 = 9米× 5米 = 45平方米。

5. 梯形的面积公式：梯形的面积 = （上底 + 下底）×高÷ 2。

例题解析：例题5：一个梯形的上底为6米，下底为10米，高为4米，求其面积。

解答：面积 = （6米 + 10米）× 4米÷ 2 = 32平方米。

6. 圆的面积公式：圆的面积 = π×半径²。

例题解析：例题6：一个圆的半径为3厘米，求其面积。

解答：面积 = π× 3²厘米²≈ 3.14 × 9厘米² = 28.26平方厘米。

二、复合图形的分割与面积计算1. 复合图形的定义与分割方法定义：复合图形是由多个简单图形组合而成的图形。

要计算复合图形的面积，可以将其分割成多个简单图形，然后分别计算面积，再将这些面积相加。

例题解析：例题1：计算一个由两个长方形组合而成的L形图形的面积。

解答：将L形图形分割为两个长方形，分别计算面积，再将两部分面积相加。

面积的基本概念和计算面积是几何学中的一个重要概念，用来描述平面图形所覆盖的面积大小。

在日常生活和学习中，我们经常会遇到需要计算或比较面积的情况，比如房屋的面积、学校的操场面积等。

因此，了解面积的基本概念和计算方法对我们的生活和学习都非常有帮助。

一、面积的基本概念面积是用来衡量平面图形所占空间的大小的一个数值。

在数学中，面积通常用单位平方来表示，如平方米、平方厘米等。

不同的平面图形有各自的面积计算方法，下面我们来介绍几种常见的平面图形及其面积计算方法。

1. 矩形的面积计算矩形是最常见的平面图形之一，其面积计算非常简单，只需要将矩形的长和宽相乘即可。

例如，一块长为5米，宽为3米的矩形地毯的面积为5米 × 3米 = 15平方米。

2. 正方形的面积计算正方形是特殊的矩形，其四条边长度相等。

因此，正方形的面积计算也非常简单，只需要将正方形的边长平方即可。

例如，一个边长为4厘米的正方形的面积为4厘米 × 4厘米 = 16平方厘米。

3. 三角形的面积计算三角形是由三条边和三个内角组成的平面图形。

计算三角形的面积需要用到高和底边的概念。

具体计算方法为将底边长度乘以高，然后除以2。

例如，一个底边长为6厘米，高为4厘米的三角形的面积为（6厘米 × 4厘米）÷ 2 = 12平方厘米。

二、面积的计算公式除了上述的基本面积计算方法外，还有一些更为复杂的图形的面积计算公式，下面我们来介绍几个常见的图形及其对应的面积计算公式。

1. 圆的面积计算圆是一个没有边界的几何图形，其面积计算需要用到圆周率π。

圆的面积计算公式为面积等于半径的平方乘以圆周率。

例如，一个半径为3厘米的圆的面积为3厘米 × 3厘米× π ≈ 28.27平方厘米。

2. 梯形的面积计算梯形是由两条平行的边和两条斜边组成的平面图形。

计算梯形的面积需要用到上底、下底和高的概念。

具体计算方法为将上底与下底之和乘以高，然后除以2。

EXCEL自动求得常用面积体积计算公式Excel是一款功能强大的电子表格软件，可以用于各种计算和数据分析任务。

在面积和体积计算方面，Excel提供了许多自动计算公式，可以帮助用户快速计算各种图形的面积和体积。

本文将介绍Excel中常用的面积和体积计算公式，并提供一些实际应用示例。

矩形是最简单的几何形状之一，其面积和体积可以通过以下公式计算：面积（A）=长（L）×宽（W）体积（V）=长（L）×宽（W）×高（H）在Excel中，可以使用乘法运算符“*”来计算面积和体积。

例如，如果矩形的长为10，宽为5，高为3，可以使用以下公式计算面积和体积：面积：=10*5体积：=10*5*3圆是一种常见的二维和三维几何形状，其面积和体积可以通过以下公式计算：面积（A）=π×半径（R）^2体积（V）=4/3×π×半径（R）^3在Excel中，可以使用内置的PI函数（=PI(）来获取圆周率π的值，并使用幂运算符“^”来计算面积和体积。

例如，如果圆的半径为5，可以使用以下公式计算面积和体积：面积：=PI(*5^2体积：=4/3*PI(*5^3三角形是另一个常见的二维几何形状，其面积可以通过以下公式计算：面积（A）=1/2×底边（B）×高（H）在Excel中，可以使用除法运算符“/”来计算面积。

例如，如果三角形的底边为10，高为8，可以使用以下公式计算面积：面积：=1/2*10*8由于三角形是一个二维形状，没有体积的概念。

正方形是一种特殊的矩形，其面积可以通过以下公式计算：面积（A）=边长（S）^2在Excel中，可以使用幂运算符“^”来计算面积。

例如，如果正方形的边长为6，可以使用以下公式计算面积：面积：=6^2由于正方形是一个二维形状，没有体积的概念。

以上是常见的几何形状的面积和体积计算公式。

除了这些基本的公式之前，在Excel中还可以使用一些其他功能来进行更复杂的计算，并将计算结果应用于实际问题中。

初中几何等面积法
初中几何等面积法是指通过计算几何图形的各个部分的面积来求解整个图形的面积的方法。

这些方法包括了矩形的面积公式、平行四边形的面积公式、三角形的面积公式、梯形的面积公式等。

对于矩形，它的面积可以通过长乘以宽来计算，公式为面积=长×宽。

平行四边形的面积可以通过底边乘以高度来计算，公式为面积=底×高。

三角形的面积可以通过底边乘以高度再除以2来计算，公式为面积=（底×高）÷2。

梯形的面积可以通过上底加下底再乘以高度再除以2来计算，公式为面积=（上底+下底）×高÷2。

另外，圆的面积计算稍有不同，它的面积可以通过半径的平方乘以π（圆周率）来计算，公式为面积=半径²×π。

使用这些等面积法，我们可以方便地计算出各种不规则形状的图形的面积，进而应用于实际生活中的问题。

这些公式是初中几何学习中的基础，能够帮助我们更好地理解和应用几何知识。

专题训练。

几何图形的面积计算专题训练: 几何图形的面积计算本文档旨在提供关于几何图形面积计算的相关指导和训练题目。

一、矩形的面积计算矩形的面积可以通过将矩形的长和宽相乘来计算。

公式如下：面积 = 长 ×宽以下是一个面积计算的示例：问题：一个矩形的长为10cm，宽为5cm，求其面积。

解答：根据公式，面积 = 10cm × 5cm = 50cm²二、三角形的面积计算三角形的面积可以通过将三角形的底边长度乘以对应的高，再除以2来计算。

公式如下：面积 = 底边长度 ×高 / 2以下是一个面积计算的示例：问题：一个三角形的底边长度为6cm，高为8cm，求其面积。

解答：根据公式，面积 = 6cm × 8cm / 2 = 24cm²三、圆的面积计算圆的面积可以通过将圆的半径的平方乘以π（圆周率）来计算。

公式如下：面积 = 半径² × π以下是一个面积计算的示例：问题：一个圆的半径为5cm，求其面积（取π ≈ 3.14）。

解答：根据公式，面积= 5cm² × 3.14 ≈ 78.5cm²四、其他几何图形的面积计算除了矩形、三角形和圆之外，还有其他各种几何图形的面积计算方法。

每种图形都有不同的计算公式，请根据具体图形的特点选择合适的计算方式。

例如，正方形的面积计算方法与矩形相同，等边三角形的面积计算方法与普通三角形相同，梯形的面积计算方法需要确定上下底边长度、高和平行边长度等。

注意。

在计算过程中，请确保使用相同单位进行计算，并按照题目要求进行精确和适当的取舍。

注意。

在计算过程中，请确保使用相同单位进行计算，并按照题目要求进行精确和适当的取舍。

注意。

在计算过程中，请确保使用相同单位进行计算，并按照题目要求进行精确和适当的取舍。

注意。

在计算过程中，请确保使用相同单位进行计算，并按照题目要求进行精确和适当的取舍。

几何图形计算公式大全在几何学中，我们经常会遇到各种各样的几何图形，如三角形、矩形、圆形等等。

对于这些几何图形，我们需要掌握它们的计算公式，以便能够准确地计算它们的各种属性。

本文将为大家总结几何图形的计算公式大全，希望能对大家有所帮助。

一、三角形。

1. 面积公式。

三角形的面积可以用以下公式计算：\[ S = \frac{1}{2} \times 底 \times 高 \]其中，S代表三角形的面积，底代表三角形的底边长，高代表三角形的高。

2. 周长公式。

三角形的周长可以用以下公式计算：\[ 周长 = 边1 + 边2 + 边3 \]其中，边1、边2、边3分别代表三角形的三条边长。

3. 三角形内角和公式。

三角形的内角和为180度，即：\[ 内角和 = 角1 + 角2 + 角3 = 180度 \]其中，角1、角2、角3分别代表三角形的三个内角。

二、矩形。

1. 面积公式。

矩形的面积可以用以下公式计算：\[ S = 长 \times 宽 \]其中，S代表矩形的面积，长代表矩形的长，宽代表矩形的宽。

2. 周长公式。

矩形的周长可以用以下公式计算：\[ 周长 = 2 \times (长 + 宽) \]其中，长代表矩形的长，宽代表矩形的宽。

三、圆形。

1. 面积公式。

圆形的面积可以用以下公式计算：\[ S = \pi \times 半径^2 \]其中，S代表圆形的面积，π代表圆周率，半径代表圆形的半径。

2. 周长公式。

圆形的周长可以用以下公式计算：\[ 周长 = 2 \times \pi \times 半径 \]其中，π代表圆周率，半径代表圆形的半径。

四、正方形。

1. 面积公式。

正方形的面积可以用以下公式计算：\[ S = 边长^2 \]其中，S代表正方形的面积，边长代表正方形的边长。

2. 周长公式。

正方形的周长可以用以下公式计算：\[ 周长 = 4 \times 边长 \]其中，边长代表正方形的边长。

以上就是几何图形的计算公式大全，希望对大家有所帮助。

面积公式大全面积是数学中一个基础的概念，广泛应用于几何学和物理学等领域。

在解决问题和计算物体表面或图形面积时，掌握各种不同形状的面积公式是非常重要的。

本文将为你介绍一些常见的面积公式及其应用。

1. 矩形面积公式矩形是最简单的几何图形之一，其面积公式非常直观和简单。

对于矩形而言，其面积公式为：面积 = 长 ×宽。

例如，如果矩形的长为5个单位，宽为3个单位，则其面积为15个单位。

2. 正方形面积公式正方形是一种特殊的矩形，它的四条边相等且四个角都为直角。

正方形的面积公式为：面积 = 边长 ×边长，也可以写作面积 = 边长²。

假设一个正方形的边长为4个单位，则其面积为16个单位。

3. 三角形面积公式三角形是几何学中最重要的形状之一，有多种计算面积的公式，其中最常用的是“底乘高除以二”的公式。

假设三角形的底为b，高为h，则其面积可以表示为：面积 = (底 ×高) / 2。

举例而言，如果一个三角形的底长是6个单位，高度为3个单位，则它的面积为9个单位。

另外，还有一个常用的三角形面积公式叫做海伦公式，用于计算任意三角形的面积。

根据海伦公式，三角形的面积可以表示为：面积 =√[s(s-a)(s-b)(s-c)]，其中a、b、c为三角形的三边长度，s为三边长度的一半。

4. 圆的面积公式圆是平面上距离圆心相等的一组点的集合，其面积公式由著名的数学常数π（pi）决定。

圆的面积公式为：面积= π × 半径²。

假设一个圆的半径为r个单位，则其面积为πr²。

5. 椭圆的面积公式椭圆是另一种重要的几何图形，其形状介于圆和矩形之间。

椭圆的面积公式为：面积= π × 长半轴 ×短半轴。

假设一个椭圆的长半轴为a，短半轴为b，则它的面积为πab。

6. 梯形的面积公式梯形是一个有四边的几何图形，其中两边平行而另外两边不平行。

梯形的面积公式为：面积 = (上底 + 下底) ×高度 / 2。

几何图形的面积计算方法一、平面几何图形的面积概念及计算方法1.面积的概念：面积是用来表示平面图形占据平面空间大小的量。

2.计算方法：（1）矩形的面积计算：矩形的面积等于长乘以宽。

（2）平行四边形的面积计算：平行四边形的面积等于底乘以高。

（3）三角形的面积计算：三角形的面积等于底乘以高除以2。

（4）梯形的面积计算：梯形的面积等于上底加下底的和乘以高除以2。

（5）圆的面积计算：圆的面积等于π乘以半径的平方。

（6）扇形的面积计算：扇形的面积等于π乘以半径的平方乘以圆心角除以360°。

二、立体图形的体积及表面积计算方法1.体积的概念：体积是用来表示立体图形占据空间大小的量。

2.表面积的概念：表面积是用来表示立体图形各表面大小之和的量。

3.计算方法：（1）长方体的体积计算：长方体的体积等于长乘以宽乘以高。

（2）长方体的表面积计算：长方体的表面积等于（长乘以宽+长乘以高+宽乘以高）乘以2。

（3）正方体的体积计算：正方体的体积等于棱长的三次方。

（4）正方体的表面积计算：正方体的表面积等于棱长的平方乘以6。

（5）圆柱体的体积计算：圆柱体的体积等于π乘以底面半径的平方乘以高。

（6）圆柱体的表面积计算：圆柱体的表面积等于底面圆的周长乘以高加上底面圆的面积乘以2。

（7）圆锥体的体积计算：圆锥体的体积等于π乘以底面半径的平方乘以高除以3。

（8）圆锥体的表面积计算：圆锥体的表面积等于底面圆的周长乘以母线除以2加上底面圆的面积。

三、面积单位及换算1.面积单位：平方米（m²）、平方分米（dm²）、平方厘米（cm²）、公顷（hm²）、平方千米（km²）等。

2.面积单位换算：（1）1平方米（m²）=100平方分米（dm²）（2）1平方米（m²）=10000平方厘米（cm²）（3）1公顷（hm²）=10000平方米（m²）（4）1平方千米（km²）=100公顷（hm²）=1000000平方米（m²）四、面积的实际应用1.计算土地面积：如农田、住宅区、公园等。

表面积计算公式大全以下是一些常见的表面积计算公式大全，涵盖了不同几何图形的表面积计算：
1. 矩形表面积：矩形的表面积等于长度乘以宽度。

公式为
A = l ×w，其中A 表示表面积，l 表示长度，w 表示宽度。

2. 正方形表面积：正方形的表面积等于边长的平方。

公式为 A = a^2，其中 A 表示表面积，a 表示边长。

3. 圆的表面积：圆的表面积等于圆的半径的平方乘以π。

公式为 A = πr^2，其中 A 表示表面积，r 表示半径，π是一个近似于3.14159的常数。

4. 圆环的表面积：圆环的表面积等于外半径的平方减去内半径的平方，再乘以π。

公式为 A = π(R^2 - r^2)，其中A 表示表面积，R 表示外半径，r 表示内半径，π是一个近似于3.14159的常数。

5. 三角形的表面积：三角形的表面积可以通过海伦公式或直角三角形的半边积公式来计算，具体取决于已知的边长和高。

海伦公式为 A = √[s(s-a)(s-b)(s-c)]，其中 A 表示表面积，s 表示三角形的半周长，a、b、c 分别表示三角形的三边长。

这些公式适用于计算二维几何图形的表面积。

对于三维几何图形，例如立方体、圆柱体、球体等，其表面积计算涉及更多参数和公式。

具体的计算方法可以根据几何图形的特点和属性进行查阅相关的数学资料或参考几何学教科书。

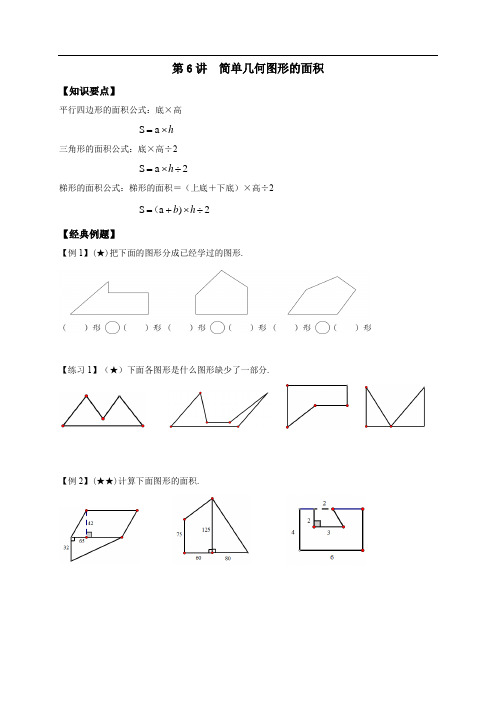
第6讲简单几何图形的面积【知识要点】平行四边形的面积公式：底×高S=a⨯h三角形的面积公式：底×高÷2=h⨯2aS÷梯形的面积公式：梯形的面积＝（上底＋下底）×高÷2+=h（bS÷⨯)2a【经典例题】【例1】(★)把下面的图形分成已经学过的图形.【练习1】（★）下面各图形是什么图形缺少了一部分.【例2】(★★)计算下面图形的面积.【练习2】（★★）计算下面图形的面积.【例3】（★★）计算下面图形的面积，你有几种方法？【练习3】（★★）计算下面图形的面积，你有几种方法？【例4】（★★）“六一”儿童节那天，英华小学在校门口用花盆摆成如下图所示的图案，你能算出这个图案的面积吗？【练习4】（★★）某块菜地的形状如图，这块菜地的占地面积是多少平方米？【例5】（★★）一块梯形草地中间有一条长8米，宽1米的长方形小路(如图，单位：m)，这块草地的面积是多少平方米？【练习5】（★★）下图是一块长方形的草地，长是16米，宽是10米，中间有两条道路，一条是长方形，一条是平行四边形，那么有草部分的面积有多大？【例6】（★★）从下面的梯形中剪去一个最大的三角形，剩下部分的面积是多少？【练习6】（★★）美术课上，黄老师让小雯在一张上底是30厘米、下底是40厘米、高是30厘米的直角梯形白纸上，画一幅最大的正方形水彩画，剩下的白纸的面积是多少？【例7】（★★）下图中梯形的面积是9平方米，求阴影部分的面积.【练习7】（★★）求下面图形中阴影部分的面积.（梯形面积为8平方米）【例8】（★★★）如图是一个平行四边形，它包含了三个三角形，其中两个白三角形的面积15平方厘米和25平方厘米，中间涂色的三角形面积是____平方厘米.【练习8】（★★★）如图，AD=DC，AE=EB.若阴影部分的面积是20cm2，则三角形ABC的面积是( ) cm2.【课后练习】1.（★）计算下面图形的面积.2.（★★）求阴影部分的面积(单位：米).3.（★★）图中长方形的面积是220cm，那么，空白的两个三角形①、②面积的和是( ) 2cm.4.（★★）如图，边长相等的两个正方形中，画了甲、乙两个三角形(用阴影表示)，它们的面积相比：甲乙.（填“大于”“小于”或“等于”）5.（★★）一把雨伞的伞面是由8块相同的三角形布料拼成的.每个三角形的底是37厘米，高是48厘米.做这把雨伞至少要用多少平方米的布料？(得数保留两位小数)6.（★★）一块平行四边形麦田，中间有一条宽1.5m的小路.（1）这块麦田的面积是多少平方米？（2）如果每平方米收小麦约0.75kg，这块地大约能收小麦多少千克？7.（★★）公园里有两块空地，计划分别种玫瑰和牡丹.占地面积价格①②（1）玫瑰园占地多少平方米？种玫瑰一共需要多少元？（2）你还能提出什么数学问题？并尝试解答.8.（★★）这是小东在计算下面图形的面积的方法，请你判断下：他做的对吗？如果不对，请改正过来.9.（★★★）如图，是一张长方形卡纸和一张三角形卡纸重叠在一起的图形.已知长方形卡纸的面积比三角形卡纸的面积小16cm2，三角形底边CE的长是多少厘米？(单位：cm)10.（★★★）如图，直角梯形的上下底分别是6cm、10cm，高为8cm，如果用虚线把梯形分成面积相等的两部分，那么AB的长度是多少cm？cm. 11.（★★★）大正方形的边长是9cm，小正方形的边长是5cm.阴影部分的面积是____212.（★★★）计算下图阴影部分的面积.。

计算几何体的表面积计算几何体的表面积是数学中的一个重要概念，它用于确定三维物体的曲面总面积。

在几何学中，几何体可以是由平面图形延伸而成的立体图形。

它们的表面积可用于计算物体的涂料用量、包装尺寸以及其他与表面积相关的问题。

在计算几何体的表面积时，我们需要根据几何体的形状和性质选择相应的计算公式。

下面将介绍几种常见几何体的表面积计算方法。

一、立方体的表面积计算立方体是一种具有六个相等正方形面的几何体。

它的表面积计算公式为：表面积 = 6 ×边长^2，其中边长指立方体的任意相邻边的长度。

二、长方体的表面积计算长方体也是一种常见的几何体，它具有六个面，其中有两个面是相等的长方形。

长方体的表面积计算公式为：表面积 = 2 × (长 ×宽 + 长×高 + 宽 ×高)，其中长、宽和高分别表示长方体的长度、宽度和高度。

三、圆柱体的表面积计算圆柱体由一个圆和一个平行于其底面的矩形组成。

圆柱体的表面积计算公式为：表面积= 2 × π × 半径^2 + 2 × π × 半径 ×高，其中半径是圆柱体底面圆的半径，高为圆柱体的高度。

四、球体的表面积计算球体是一个完全由曲面组成的几何体，其表面积计算公式为：表面积= 4 × π × 半径^2，其中半径为球体半径。

除了上述常见几何体外，还存在着许多其他几何体，每个几何体的表面积计算方法都是独特的。

对于不规则几何体，我们可以通过将其分解为多个规则几何体的组合，然后分别计算每个几何体的表面积，最后将它们相加来获得整个几何体的表面积。

在实际应用中，计算几何体表面积十分重要。

例如，在建筑工程中，需要准确计算出墙壁、天花板和地板的表面积，以确定所需的建材数量。

同样，在包装设计中，需要计算产品的表面积以确定包装纸张的使用量。

因此，掌握计算几何体表面积的方法对于解决一系列实际问题至关重要。

面积计算公式怎么做出来的面积是我们在日常生活中经常会用到的一个概念，无论是在建筑、土地、农田还是其他领域，都需要对面积进行计算。

面积计算公式是通过对图形的特征和属性进行分析，推导出来的数学表达式。

本文将从几何图形的角度出发，介绍面积计算公式是如何推导出来的。

1. 矩形和正方形的面积计算公式。

首先我们来看矩形和正方形的面积计算公式。

矩形的面积计算公式是长乘以宽，即S=长×宽。

正方形是特殊的矩形，其四边长度相等，因此面积计算公式为S=边长×边长。

这两个公式的推导非常简单，只需要将矩形或正方形分割成小正方形，然后计算小正方形的面积，再将所有小正方形的面积相加即可得到矩形或正方形的面积。

2. 三角形的面积计算公式。

接下来我们来推导三角形的面积计算公式。

假设三角形的底边长为a，高为h，根据三角形的性质，可以将三角形分割成两个等腰直角三角形。

这样，三角形的面积就可以表示为S=1/2×a×h。

这个公式的推导过程其实是利用了三角形的特性和分割成两个简单图形进行计算的方法。

3. 圆的面积计算公式。

圆是一个非常特殊的几何图形，其面积计算公式是通过对圆的特性进行推导得到的。

圆的面积计算公式为S=πr^2，其中π是一个无理数，约等于3.14，r是圆的半径。

这个公式的推导过程需要使用一些高等数学知识，主要是通过对圆的弧长和扇形面积的分析，最终得到了圆的面积计算公式。

4. 多边形的面积计算公式。

对于其他多边形，其面积计算公式的推导也是通过对多边形的特性进行分析得到的。

例如，梯形的面积计算公式是通过将梯形分割成两个三角形和一个矩形，然后计算这三个图形的面积相加得到的。

对于其他多边形，也可以通过类似的方法进行推导。

总结。

通过以上的介绍，我们可以看到面积计算公式是通过对几何图形的特性和属性进行分析和推导得到的。

在日常生活中，我们可以利用这些面积计算公式来计算各种图形的面积，从而更好地应用数学知识解决实际问题。

专题28 求几何图形面积及面积法解题的问题一、几何图形面积公式1.三角形的面积:设三角形底边长为a ，底边对应的高为h ，则面积S=ah/22.平行四边形的面积:设平行四边形的底边长为a ，高为h ，则面积S=ah3.矩形的面积:设矩形的长为a ，宽为b ，则面积S=ab4.正方形的面积:设正方形边长为a ，对角线长为b ，则面积S=222b a = 5.菱形的面积:设菱形的底边长为a ，高为h ，则面积S=ah若菱形的两条对角线长分别为m 、n ，则面积S=mn/2也就是说菱形的面积等于两条对角线乘积的一半。

6.梯形的面积:设梯形的上底长为a,下底长为b ，高为h ，则面积S=（a+b ）h/27.圆的面积:设圆的半径为r,则面积S=πr 28.扇形面积计算公式9．圆柱侧面积和表面积公式（1）圆柱的侧面积公式S 侧=2πrh2360r n s π⋅=lr s 21=或（2）圆柱的表面积公式：S 表=2S 底+S 侧=2πr 2+2πrh10.圆锥侧面积公式从右图中可以看出，圆锥的母线L 即为扇形的半径，而圆锥底面的周长是扇形的弧长2πr ，这样，圆锥侧面积计算公式:S 圆锥侧=S 扇形=πrL注意：有时中考题还经常考查圆的周长、扇形的弧长的公式的应用。

（1）圆的周长计算公式为：C=2πr（2）扇形弧长的计算公式为：（3）其他几何图形周长容易计算，不直接给出。

二、用面积法解题的理论知识1.面积方法：运用面积关系来证明或计算平面几何题的方法，称为面积方法，它是几何中的一种常用方法。

2.面积法解题的特点：把已知量和未知量用面积公式联系起来，通过运算达到求证的结果。

所以用面积法来解几何题，几何元素之间关系变成数量之间的关系，只需要计算，有时可以不添置补助线，即使需要添置辅助线，也很容易考虑到。

三、面积方法问题主要涉及以下两部分内容1.证明面积相等的理论依据（1）三角形的中线把三角形分成两个面积相等的部分。

简单几何图形的面积计算第二讲简单几何图形的面积计算一．常用的基本公式：1．正方形的边长为a，则正方形的面积是S=a2；2．长方形的长与宽分别是a、b，则长方形的面积是S=a×b。

3．平行四边形的底边长为a，高为h，则面积是S=a ×h。

4．三角形的三条边长分别为a、b、c，在它们上的高分别是h a、h b、h c，则三角形的面积S=a×h a÷2= b×h b÷2= c×h c÷2。

5．梯形的上底为a，下底为b，高为h，则梯形的面积是(a+b)×h÷2。

6．圆的半径为r，则圆的面积是S=π×r2。

其中π=3.14159265…。

二．几种常用的求面积的方法：1．直接利用公式计算；2．列出方程求图形的面积；3．添加辅助线计算图形面积；4．利用割补的办法变化图形，计算图形的面积。

5．用相等面积变换计算图形的面积。

（同底等高问题，等底等高问题）三．例题讲解：例1．如图，一块长方形耕地，它由四个小长方形拼合而成，其中三个长方形的面积分别是15、18、30公顷，则图中阴影部分的面积是 公顷。

解：由题意知，a ×c =15，b ×c =18，b ×d =30，所以a ×d =(a ×c )×(b ×d )÷(b ×c )=15×30÷18=25(公顷)。

例2．如图所示，三角形ABC 是直角三角形，ACD 是以A 圆心，AC 为半径的扇形，图中阴影部分的面积是 。

（π取3.14）6cm6cm D C B A解：阴影部分的面积是三角形面积减去扇形的面积， 三角形ABC 的面积=6×6÷2=18，扇形的面积是圆的面积的八分之一，所以扇形面积是π×6×6÷8=4.5×π=14.13，所以阴影部分的面积是18–14.13=3.87（平方厘米）。

基本图形的面积计算方法面积是研究几何学中的一个重要概念，它描述了一个物体或图形所占据的平面范围的大小。

在几何学中，面积的计算方法与图形的形状有关，在本文中，我将介绍一些常见基本图形的面积计算方法。

一、三角形的面积计算方法三角形是最简单的平面图形之一，其面积计算公式为：面积 = 底边长度 ×高 / 2其中，底边长度是指三角形的底边的长度，高是指从底边到与之平行的顶点的垂直距离。

二、矩形的面积计算方法矩形是一个拥有四个直角的四边形，其面积计算公式为：面积 = 长 ×宽其中，长代表矩形的长边的长度，宽代表矩形的短边的长度。

三、正方形的面积计算方法正方形是一种特殊的矩形，其四条边相等，且都是直角形成的。

正方形的面积计算公式为：面积 = 边长 ×边长其中，边长指正方形的任意一条边的长度。

四、圆的面积计算方法圆是一个几何学中重要的图形，其面积计算公式为：面积= π × 半径 ×半径其中，π是一个无理数，可以近似取为3.14或22/7，半径代表圆的半径长度。

五、椭圆的面积计算方法椭圆是一个具有两个焦点的几何图形，其面积计算公式为：面积= π × 长半径 ×短半径其中，长半径代表椭圆的长轴的一半长度，短半径代表椭圆的短轴的一半长度。

六、正多边形的面积计算方法正多边形是一个具有相等边长和相等内角的多边形，例如正三角形、正四边形等。

对于正多边形的面积计算，我们可以使用以下公式：面积 = (边长 ×边长) × (边数/ 4 × tan(π / 边数))其中，边长代表正多边形的任意一条边的长度，边数代表正多边形的边的数量。

通过以上的介绍，我们可以看到不同基本图形的面积计算方法是不同的，但都可以通过找到合适的公式来求解。

掌握这些方法对于几何学的学习和实际应用都具有重要意义。

最后，需要注意的是，在应用这些面积计算方法时，要确保所使用的长度单位一致，以求得准确的面积值。