西南交通大学限修课数学实验题目及答案四

数值分析上机实习报告学号：姓名：专业：联系电话：任课教师：序 (3)一、必做题 (4)1、问题一 (4)1.1 问题重述 (4)1.2 实验方法介绍 (4)1.3 实验结果 (5)2、问题二 (7)2.1 问题重述 (7)2.2 实验原理 (7)雅各比算法：将系数矩阵A分解为：A=L+U+D，则推到的最后迭代公式为： (8)2.3 实验结果 (8)二、选做题 (10)3、问题三 (10)3.1 问题重述 (10)3.2 实验原理 (10)3.3 实验结果 (11)总结 (11)序伴随着计算机技术的飞速发展，所有的学科都走向定量化和准确化，从而产生了一系列的计算性的学科分支，而数值计算方法就是解决计算问题的桥梁和工具。

数值计算方法，是一种研究并解决数学问题的数值近似解方法，是在计算机上使用的解数学问题的方法。

为了提高计算能力，需要结合计算能力与计算效率，因此，用来解决数值计算的软件因为高效率的计算凸显的十分重要。

数值方法是用来解决数值问题的计算公式，而数值方法的有效性需要根据其方法本身的好坏以及数值本身的好坏来综合判断。

数值计算方法计算的结果大多数都是近似值，但是理论的严密性又要求我们不仅要掌握将基本的算法，还要了解必要的误差分析，以验证计算结果的可靠性。

数值计算一般涉及的计算对象是微积分，线性代数，常微分方程中的数学问题，从而对应解决实际中的工程技术问题。

在借助MA TLAB、JA V A、C++ 和VB软件解决数学模型求解过程中，可以极大的提高计算效率。

本实验采用的是MATLAB软件来解决数值计算问题。

MA TLAB是一种用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境，其对解决矩阵运算、绘制函数/数据图像等有非常高的效率。

本文采用MATLAB对多项式拟合、雅雅格比法与高斯－赛德尔迭代法求解方程组迭代求解，对Runge-Kutta 4阶算法进行编程，并通过实例求解验证了其可行性，使用不同方法对计算进行比较，得出不同方法的收敛性与迭代次数的多少，比较各种方法的精确度和解的收敛速度。

西南交通大学高等数学练习题答案详解精品文档西南交通大学高等数学练习题答案详解高等数学1. 函数y?xcos2? A. 奇函数x3?x是1?xB. 偶函数C. 非奇非偶函数D. 有界函数2. 函数y?2cos的周期是B.?C.?D. 0an?2，. 设数列an,bn及cn满足:对任意的n,an?bn?cn，且limn??lim?0，则limbn?n??n??A. 0B. 1C.D. -21 / 32精品文档x2?2x?14. lim=x?ix3?xA.1B. 0C.1D. ?5. 在抛物线y?x2上点M的切线的倾角为 A. 1124tan2x?，则点M的坐标为11B. C. D.426.limx?0e?1?sinxB.2 / 32精品文档1xA. 0 C. 1 D. -27. A.limx?012B. eC.1D. ?8. 设曲线y?x与直线x=2的交点为P，则曲线在P点的切线方程是 A x-y-4=0B x+y-1=0C x+y-3=0D x-y+2=09. y?x?3?sinx,则y?? A. xx?1xx?3x?cosx1B. x?3ln3?cosxxxC. xlnx?3ln3?cosxxxD. x?3ln3?cosx3 / 32精品文档xx10. f在点x0可微是f在点x0连续的 A. 充分条件B. 必要条件C. 充分必要条件D. 无关条件11. 函数y?2x3?6x2?18x?7单调减少的区间是 A.B. x? D.C. ,12.?sin3xdx?11cos3x?c B. ?cos3x?C C. ?cos3x?C D. cos3x?C3 21dt，则??? 13. 设??? sinx1?t21cosxcosx1?? A.B.C.D.1?sin2x1?sin2x1?sin2x1?sin2xA.14. 函数5e的一个原函数为 A.e5x5xB.e4 / 32精品文档5xC.15xeD. ?e5x15.??2??2xcos3xdx= B.A.2???4C. 0D.216. 下列广义积分收敛的是 A.5 / 32精品文档??dxx1B.dx? 022C.??11dx 1?xD.?adxa?x2217. 下列集合可作为一条有向直线在空间直角坐标系中的方向角?,?,?的是 A. 5?，45?，60?C. 0?，45?，60?，18. 设函数f?xy? A. 06 / 32精品文档B. 12B.5?，60?，60? D.5?，60?，90? y，则f?=xxC. ?1D.2219. 设函数u?ln，则du2=A.1C. dx?dy?dz 0.24D.3B.7 / 32精品文档23x ??xA?2xcos2x B xsinx2C sinxDsin2x2. 当D?{|x2?y2?1} 时,则??dx?DA ?B 1C 0D ?a23. 设a?0,则?? A.?B.?C.发散D.?4225. 曲面z?x2?y2在点处的切平面方程是A.?4??0 B ?4??0 C. ?2??0，D.?4??0?26. 判断级数?n?118 / 32精品文档n?12n2?n是 A绝对收 . B条件收敛. C 发散 . D 以上都不正确 . ?g27. f???x,x?0其中g?=2要使f在x?0处连续，则a?A. 0B. 1C.D. e28. 方程y???4y?0的通解是 A. y?Ce2x?Ce?2xC.y?C1e2x?C2e?2x?B. y?C1e2x?e?2x D. y?e2x?C2e?2xn?1x2n?129. ?内的和函数是n?1!AsinxB cosx Cex30. 设f?3??x9 / 32精品文档20tdt,，则f=西南交通大学网络教育2010年秋季入学考试模拟题高等数学1.函数y?x2sinx?ln,则y?? A. xx?1x3?3x?cosx2B. x?3ln3?cosx D. x?3ln3?cosxxxxxC. x?3x?sinxx7. f在点x0可导是f在点x0连续的 A. 充分条件B. 必要条件C. 充分必要条件D. 无关条件8. 函数y?2x3?6x2?18x?7单调减少的区间是 A.B. x? D.10 / 32精品文档C. ,1x9. 曲线y?e?1的水平渐近线方程为 A. x?1B. y?1C. x?0D.y?0210.?5一、填空题: 1(设函数z?z是由?nxz?lnzy所确定，则dz?0,1,1??dx?dy (?2(设幂级数?anx的收敛区间为??3,3?，则幂级数?an?x?1?的收11 / 32精品文档n?0n?0n敛区间为 ??2,4? ((设函数??x,f???0,y???x?00?x??的付氏级数的和函数为S，则S??2(4(设z?f，其中f具有连续的二阶偏导数，则x??z?x?y2=1x???f121x12 / 32精品文档2f2??yx3?? ( f225(设幂级数?an?x?1?在x?0处收敛，而在x?2处发散，则幂级数?anxn的n?0n?0n?收敛域为 [?1,1)((函数?n?1?n关于x的幂级数展开式为 ? ( f??1??x,x?2n?1x?x?2n?0?2?3?y7(设函数z?x，则dz? dx?2ln2dy8(曲线x?t,y??t2,z?t3的切线中，与平面x?2y?3z?6垂直的切线方程是13 / 32精品文档x?11?y?1?2?z?13z(9(设z?z是由方程e?zsin?lna a?0为常数所确定的二元函数，则 dz? yzcose?sin2zdx?xzcose?sinzdy(10.旋转抛物面z?x?y的切平面:x?4y?8z?1?0，2平行与已知平面x?y?2z?1.111(微分方程2y???y??y?0的通解为 Y?C1e2x?C2e14 / 32精品文档?x，1x2y???y??y?e的通解为 y?C1e2?C2ex?x?12e(x12.曲线?:x??tecosudu,y?2sint?cost,z?1?eu3t在点?0,1,2?处的切线方程为3(函数f?1x?4的麦克劳林级数的第5项为?x44515 / 32精品文档，收敛域为.14.(已知函数f?2x?3y?x?y,有一个极值点，则a?2, b?3，此时函数f 的极大值为 .ab15.试写出求解下列条件极值问题的拉格朗日函数:分解已知正数a为三个正数x,y,z之和，使x,y,z的倒数之和最小L?x,y,z??1x?1y?1z???x?y?z?a?16函数f?xln?1?x?的麦克劳林级数的收敛域为x???1,1?，f?二、单项选择题:请将正确结果的字母写在括号内。

西交大少年班备考专题（四）几何初步（测试题）试卷简介:整张试卷共四道选择题，共100分，针对我们专题一种的三种类型，希望同学们能独立认真地做一遍，争取把这四种类型题全面掌握。

学习建议:几何初步在考试中往往以选择、填空等小题出现，对同学们的要求是又快又准，大家注意我们课程讲解的四种类型，掌握每一种类型的解题套路和方法。

一、单选题(共4道，每道25分)1.已知△ABC为等腰三角形，BC边上的高等于BC长的一半，∠BAC的度数不可能为（）A.90°B.75°C.30°D.15°答案：C解题思路：（1）若BC为等腰三角形的底，作AH⊥BC于H，则H为BC的中点，且，故△AHB和△AHC都是等腰直角三角形，故∠BAC=90°；（2）BC为等腰三角形中的一腰：①当∠ABC为锐角时，，故∠B=30°，∠BAC=75°；②当∠ABC=90°时，AB=BC=AH，这与矛盾；③当∠ABC为钝角时，，故∠ABH=30°，∠BAC=∠C=15°综上所述，∠BAC的度数可能为90°、75°或15°.易错点：分类标准不清晰，漏掉若干情况。

试题难度：三颗星知识点：等腰三角形的性质2.在△ABC中，最大角∠A是最小角∠C的2倍，且AB=7，AC=8.则BC=（）A.B.C.D.答案：C解题思路：如图，延长CA至点D，使AD=AB则∠D=∠ABD==∠C故△CBD∽△DAB则，又因为∠C=∠D，则BC=BD=，答案为C.易错点：没有注意到“二倍角”这个几何特征，构造不出相似三角形试题难度：三颗星知识点：相似三角形的判定与性质3.如图，设E、F分别是△ABC边AC、AB上的点，线段BE、CF交于点D.已知△BDF、△BCD、△CDE的面积分别为3、7、7.则四边形AEDF的面积为（）A.15B.10C.14D.18答案：D解题思路：易错点：没有注意到三角形的面积与线段比之间的两种常用思路，设未知数表达也是非常重要的方法。

西南交大线性代数习题参考答案第一章 行列式§1 行列式的概念1． 填空(1) 排列6427531的逆序数为 ，该排列为 排列。

(2) i = ，j = 时， 排列1274i 56j 9为偶排列。

(3) n 阶行列式由 项的代数和组成，其中每一项为行列式中位于不同行不同列的 n 个元素的乘积，若将每一项的各元素所在行标按自然顺序排列，那么列标构成一个n 元排列。

若该排列为奇排列，则该项的符号为 号；若为偶排列，该项的符号为 号。

(4) 在6阶行列式中， 含152332445166aa a a a a 的项的符号为 ，含324314516625a a a a a a的项的符号为 。

2． 用行列式的定义计算下列行列式的值(1)1122233233000a a a a a解： 该行列式的3!项展开式中，有 项不为零，它们分别为 ，所以行列式的值为 。

(2)12,121,21,11,12,100000n n n nn n n n n n n n nna a a a a a a a a a ------解：该行列式展开式中唯一不可能为0的项是 ，而它的逆序数是 ，故行列式值为 。

3． 证明：在全部n 元排列中，奇排列数与偶排列数相等。

证明：n 元排列共有!n 个，设其中奇排列数有1n 个，偶排列数为2n 个。

对于任意奇排列，交换其任意两个元的位置，就变成偶排列，故一个奇排列与许多偶排列对应，所以有1n 2n ，同理得2n1n ，所以1n 2n 。

4． 若一个n 阶行列式中等于0的元素个数比nn-2多，则此行列式为0，为什么？5． n 阶行列式中，若负项的个数为偶数，则n 至少为多少？（提示：利用3题的结果）6． 利用对角线法则计算下列三阶行列式 （1）21141183---（2）222111a b c a b c§2 行列式的性质1．利用行列式的性质计算系列行列式。

(1) 2141 3121 1232 5062-(2)100 110 011 001abcd ---(3)ab ac ae bd cd de bf cf ef ---2． 证明下列恒等式 (1)()33ax byay bzaz bxxy z D ay bz az bx ax by a b yz x az bx ax by ay bz zxy+++=+++=++++（提示：将行列式按第一列分解为两个行列式之和，再利用性质证明）(2) ()()()()()()()()()()()()22222222222222221231230123123a a a a b b b b cc c cd d d d ++++++=++++++(3)1111221100001000001n n n nnn n xx x a x a x a x a a a a x a ------=++++-+(提示：从最后一列起，后列的x 倍加到前一列)3． 已知四阶行列式D 的第三行元素分别为：1,0,2,4-；第四行元素的对应的余子式依次是2，10，a ，4，求a 的值。

数学建模精讲_西南交通大学中国大学mooc课后章节答案期末考试题库2023年1.Lingo软件是常用的优化问题的求解软件。

参考答案:正确2.0-1规划是整数规划。

参考答案:正确3.求解整数规划一定能得到最优解。

参考答案:错误4.整数规划是指规划问题中的全部变量限制为整数。

参考答案:错误5.所有决策变量均要求为整数的整数规划称为纯整数规划。

参考答案:正确6.整数规划与线性规划不同之处在于增加了整数约束。

参考答案:正确7.分枝定界法是整数规划的常见算法。

参考答案:正确8.原线性规划有最优解，当自变量限制为整数后，其整数规划也一定有最优解。

参考答案:错误9.整数规划最优解常可以按照实数最优解简单取整而获得。

参考答案:错误10.与线性规划连续的可行域不同，整数规划的可行域是离散的。

参考答案:正确11.整数规划由于限制变量是整数，增加了求解难度，但整数解是有限个，所以有时候可以采用枚举法。

参考答案:正确12.非线性规划已经有一般的适合所有问题的成熟的解法。

参考答案:错误13.非线性规划的局部最优解和全局最优解等价。

参考答案:错误14.多目标规划的目标函数多于1个。

参考答案:正确15.非线性规划是指规划模型的目标函数或者约束条件中至少有一个为非线性表达式。

参考答案:正确16.多目标规划的解法包括分枝定界法，单纯形法。

参考答案:错误17.根据地球上任意两点的经纬度就可以计算这两点间的距离。

参考答案:正确18.如果可能，把非线性规划转换为线性规划是非常好的一个思路，原因是线性规划有比较成熟的算法。

参考答案:正确19.Lingo软件求解非线性规划的结果都是全部最优解。

参考答案:错误20.求解多目标规划的线性加权和法，在确定权系数之前，一般要对目标函数值做统一量纲处理，其目的是避免出现大数吃小数、权系数失去其作用的问题。

参考答案:正确21.哥尼斯堡七桥问题由欧拉证明了是可以走通的。

参考答案:错误22.“健康中国2030”规划纲要其中一项主要指标是将我国人均预期寿命提升至79岁左右。

西交大数学试题及答案解析一、选择题（每题5分，共20分）1. 函数$f(x) = x^2 - 4x + 3$的零点个数是：A. 0B. 1C. 2D. 3解析：函数$f(x) = x^2 - 4x + 3$可以通过因式分解为$f(x) = (x-1)(x-3)$，因此函数有两个零点，即$x=1$和$x=3$。

正确答案为C。

2. 以下哪个选项是$\sin(\frac{\pi}{6})$的值：A. $\frac{1}{2}$B. $\frac{\sqrt{2}}{2}$C. $\frac{\sqrt{3}}{2}$D. $\frac{\sqrt{5}}{2}$解析：根据三角函数的定义，$\sin(\frac{\pi}{6})$等于$\frac{1}{2}$。

正确答案为A。

3. 直线$y = 2x + 3$与x轴的交点坐标是：A. $(-\frac{3}{2}, 0)$B. $(\frac{3}{2}, 0)$C. $(0, 3)$D. $(0, -3)$解析：要找到直线与x轴的交点，需要令$y=0$，解方程$0 = 2x +3$得到$x = -\frac{3}{2}$。

因此，交点坐标为$(-\frac{3}{2}, 0)$。

正确答案为A。

4. 以下哪个选项是$e^{\ln 2}$的值：A. 1B. 2C. $\ln 2$D. $\ln e$解析：根据对数的定义，$e^{\ln 2}$等于2。

正确答案为B。

二、填空题（每题5分，共20分）1. 函数$f(x) = \sqrt{x}$的定义域是 $[0, +\infty)$。

2. 函数$f(x) = \cos x$的周期是 $2\pi$。

3. 函数$f(x) = \log_2 x$的反函数是 $f^{-1}(x) = 2^x$。

4. 函数$f(x) = x^3 - 3x^2 + 2$的导数是 $f'(x) = 3x^2 - 6x$。

三、解答题（每题15分，共40分）1. 求函数$f(x) = x^3 - 6x^2 + 9x + 1$的极值点。

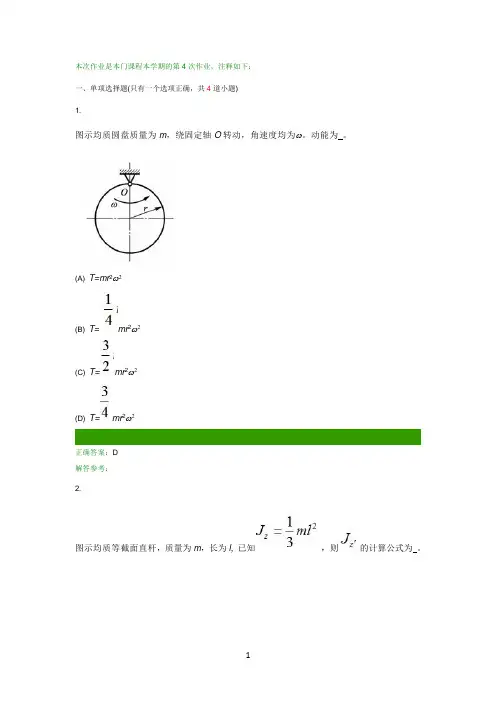
本次作业是本门课程本学期的第4次作业，注释如下：一、单项选择题(只有一个选项正确，共4道小题)1.图示均质圆盘质量为m，绕固定轴O转动，角速度均为ω。

动能为。

(A) T=mr2ω2(B) T=mr2ω2(C) T=mr2ω2(D) T=mr2ω2正确答案：D解答参考：2.图示均质等截面直杆，质量为m，长为l, 已知，则的计算公式为。

(A)(B)(C)正确答案：C解答参考：3.设弹簧的原长为l0，弹簧系数为k，物块由M1运动至M2 ，弹性力的功为。

(A)(B)(C)(D)正确答案：A解答参考：4.图a、b中所示的两个滑轮O1和O2完全相同，在图a所示情况中绕在滑轮上的绳的一端受拉力作用，在图b所示情况中绳的一端挂有重物A，其重量等于，且P=F。

设绳重及轴承摩擦均可不计。

则两轮的角加速度。

(A) 相同(B) 不相同(C) 不能确定正确答案：B解答参考：二、判断题(判断正误，共9道小题)5.只要知道作用在质点上的力，那么质点在任一瞬时的运动状态就完全确定了。

（）正确答案：说法错误解答参考：6.作用于质点上的力越大，质点运动的速度也越大。

（）正确答案：说法错误解答参考：7.牛顿定律适用于任意参考系。

（）正确答案：说法错误解答参考：8.一个质点只要运动，就一定受力的作用，而且运动的方向就是它受力的方向。

（）正确答案：说法错误解答参考：9.若系统的总动量为零，则系统中每个质点的动量必为零。

（）正确答案：说法错误解答参考：10.冲量的量纲与动量的量纲相同。

（）正确答案：说法正确解答参考：11.质点系的内力不能改变质点系的动量与动量矩。

（）正确答案：说法错误解答参考：12.质点系内力所做功之代数和总为零。

（）正确答案：说法错误解答参考：13.如果某质点系的动能很大，则该质点系的动量也很大。

（）正确答案：说法错误解答参考：（注意：若有主观题目，请按照题目，离线完成，完成后纸质上交学习中心，记录成绩。

在线只需提交客观题答案。

习题1—71．指出下列各函数的间断点以及所属的类型。

如果是可去间断点，则重新定义函数值使函数在该点连续（1）23x -x 1-x y 22+=解：1x 023x -x 2=→=+，2x =22-x 1x lim 23x -x 1-x lim y lim 1x 221x 1x -=+=+=→→→，y lim 2x →不存在 所以1x =，是函数的第一类间断点，且是可去间断点 定义当1x =，-2y =可使函数在1x = 点连续。

2x =是函数的第二类间断点（2）2x x xy 2-+=解：→⎩⎨⎧≥=-+0x 02x x 21x =，y lim 1x →不存在，所以1x =是函数的第二类间断点 （3）x x 1x -1limy 2n2nn +=∞→ 解：1x >时，x x 1x11x 1lim x x 1x -1limy 2n 2nn 2n2nn -=+-=+=∞→∞→1x =时，0x x 1x -1limy 2n 2nn =+=∞→ 1x <时，x x x 1x -1limy 2n2nn =+=∞→ -1y lim 01x =+→，1y lim 01x =-→，0y 1x ==，所以1x =是函数的第一类间断点-1y lim 01x =+-→，1y lim 01x =--→，0y 1x =-=，所以1x -=是函数的第一类间断点（4）x 1x)1(y +=解：e x )1(lim y lim x10x 0x =+=→→，0x =时，x1无意义，x 1x)1(y +=无意义，所以0x =是函数的第一类间断点。

定义0x =时，e y =可使函数在0x =处连续 2．写出函数在点x 0连续的ε—δ定义。

解：设函数x)(f 在点x 0的某邻域内有定义，0>∀ε，0>∃δ，x ∀：δ<0x -x ，使ε<)x (-(x)0f f 成立，则x)(f 在点x 0处连续3．（1）函数x)(f 在点x 0连续，而函数x)(g 在点x 0不连续，问此两函数之和在点x 0是否连续？那么此两函数的积呢？（2）在点x 0，x)(f 与x)(g 都不连续，则两函数的积是否必不连续？ 解：（1）①(x)x)(g f +在x 0处不连续证明：设(x)x)(g f +在x 0处连续，则0>∀ε，01>∃δ，x ∀：10x -x δ<，2/)x ()x (-(x)x)(00ε<-+g f g f2/)x ()x (-(x )x )(2/00εε<-+<-g f g f)]x (-x )([2/)x ((x ))]x (-x )([2/000f f g g f f -<-<--εε由于x)(f 在x 0处连续，所以0>∀ε，02>∃δ，x ∀：20x -x δ<，2/)x (-x)(0ε<f f ，2/)x (-x )(2/0εε<<-f fεεεε=--<-<-]2/[2/)]x (-x )([2/)x ((x )00f f g g εεεε-=-->-->-2/2/)]x (-x )([2/)x ((x )00f f g g故： ε<-)x ((x)0g g所以0>∀ε，},m in{21δδδ=∃，x ∀：δ<0x -x ，使ε<-)x ((x)0g g 成立。

西南交通大学2019－2020学年第2学期半期测试课程代码 MATH011512 课程名称 高等数学II 考试时间 60 分钟注意：本试卷共9道大题，需要详细解答过程，将答案写在答题纸上，考试结束前拍照上传。

要求独立完成，诚信参考！考试诚信承诺书。

我郑重承诺：我愿意服从学校本次考试的安排，承认考试成绩的有效性，并已经认真阅读、了解了《西南交通大学考试考场管理办法》和《西南交通大学本科生考试违规处理办法》，我愿意在本次考试过程中严格服从监考教师的相关指令安排，诚信考试。

如果在考试过程中违反相关规定，我愿意接受《西南交通大学本科生考试违规处理办法》的规定处理。

您是否同意：A. 同意B. 不同意选择B 选项，本次考试无效。

一（10分） 、判断直线1212:012+--==-x y z L 与222:2+=⎧⎨+-=⎩x y L x y z 的位置关系，并给出理由。

解 法一 化2L 为对称方程12:121-==--x y zL （不唯一） 故12、L L 方向向量分别为()()120,1,21,2,1=-=--、s s ，（不唯一）分别过点()()122,1,20,2,0=-=、M M计算121201212110212-⎡⎤=--=-⎣⎦-，，s s M M （8分）（不唯一，只要最终表明混合积不为零即可）这表明直线异面（而且12⊥s s 表明其异面垂直）法二 1L 的参数为2122=-⎧⎪=+⎨⎪=-⎩x y t z t ，（不唯一）代入2L 得41221222-++=⎧⎨-++-+=⎩t t t （*），（*）无解，这表明12、L L 无交点，故它们要么平行要么异面，注意到12、L L 方向向量分别为()()120,1,21,2,1=-=--、s s ，它们不平行，这表明12、L L 异面。

二 （10分）、 设函数()22,=z f xy x y ，其中f 具有二阶连续偏导数，求d z 及22∂∂z x。

本文部分内容来自网络整理，本司不为其真实性负责，如有异议或侵权请及时联系，本司将立即删除！== 本文为word格式，下载后可方便编辑和修改！ ==西南交大,数字电路,实验报告篇一：数字电子技术实验报告数字电子技术实验报告姓名：尚朝武学号：201X0123400044 实验时间：201X-12-24实验一（一） 1、实验内容：（1用静态法测试74LS00与非门电路的逻辑功能 2、实验原理图如图1.113、实验步骤：1) 用万用表测量双路跟踪稳压电源中的+5V电源电压； 2) 检查无误后引用通用接插板；3) 在芯片盒中找到74LS00芯片并插入通用接插板上； 4) 测试与非门的逻辑功能A. 按图1.1接线，检查接线无误后通电；；B. 设置输入变量A、B的高（H）、低（L）电平，并分别测量与非门的输出电压U；（U>3.6V时，则Y=H(1)；反之，Y=L(0)）。

5）用万用表测量输出电压，并将结果填入表1.1.1中 4、实验结果见表1.1.1表1.1.1（二 1、实验内容用动态测试法验证图（a）、（b）、（c）的输入输出波形。

2、实验原理图图图图（表）d74ls86管脚图和引脚图及真值表3、实验步骤1）利用实验一——（一）的双路跟踪稳压电源中的+5V电源电压； 2）检查无误后引用通用接插板；3）在芯片盒中分别找到74LS86、74LS60芯片并分别插入通用接插板上； 4）分次按图a、b、c、d接线，检查接线无误后通电；设置输入变量A的信号为100kHz 5）分别记下数字显示器显示的波形。

4、实验结果见下图图a的输入（图上）、输出（图下）波形图b的输入（图上）、输出（图下）波形三)图c的输入（图上）、输出（图下）波形1、实验内容：（1用静态法测试74LS139静态译码器的逻辑功能 2、实验原理图如图A、B 3、实验步骤：1) 利用实验一——（一）的双路跟踪稳压电源中的+5V电源电压； 2) 检查无误后引用通用接插板；3) 在芯片盒中找到74LS139芯片并插入通用接插板上； 4) 测试74LS139译码器的逻辑功能a) 按图1.1接线，检查接线无误后通电；；b) 设置输入变量A、B及E的高（H）、低（L）电平，并分别测量74LS139的输出电压U；（U>3.6V时，则Y=H(1)；反之，Y=L(0)）； 5）用万用表测量输出电压，并将结果填入表1.2中 4、实验结果见表1.2图A 74LS139的管脚图篇二：201X-201X西南交大数字电路第1次作业（注意：若有主观题目，请按照题目，离线完成，完成后纸质上交学习中心，记录成绩。

一、选择题1．已知对任意实数m ，直线1:3232l x y m +=+和直线2:2323l x y m -=-分别与圆22:(1)()1C x y m -+-=相交于,A C 和,B D ，则四边形ABCD 的面积为（ ）A ．1B ．2C ．3D ．42．若过点(1,2)总可以作两条直线和圆2222150x y kx y k ++++-=相切，则实数k 的取值范围是( )A ．8333k k ⎧⎪-<<-⎨⎪⎩或8323k ⎫⎪<<⎬⎪⎭B ．()(),32,-∞-⋃+∞C ．()3,2-D ．8333k k ⎧⎪-≤<-⎨⎪⎩或8323k ⎫⎪<≤⎬⎪⎭3．已知圆2129:x C y ＋＝,圆2226811:0x y x C y ＋＋－－＝,则圆1C 、圆2C 的公切线有 A ．1条B ．2条C ．3条D ．4条4．圆22460x y x y +-+=和圆2260x y y +-=交于A B 、两点，则直线AB 的方程是（ ）A ．30x y +=B ．30x y -=C ．390x y --=D ．390x y ++=5．圆22:4210A x y x y ++++=与圆22:2610B x y x y +--+=的位置关系是（ ）．A ．相交B ．相离C ．相切D ．内含6．已知圆的方程为x 2＋y 2－6x －8y ＝0.设该圆过点（3，5）的最长弦和最短弦分别为 AC 和BD ，则四边形ABCD 的面积为 （ ） A ．10B ．20C ．30D ．407．若圆22:(5)(1)4C x y -++=上有n 个点到直线4320x y +-=的距离为1，则n 等于（ ） A ．2B ．1C ．4D ．38．已知点(0,2)A 为圆22:220(0)C x y ax ay a +--=>外一点，圆C 上存在点使得45CAP ∠=，则实数a 的取值范围是（ ）A.(0,1)B.[31,1)C.31]D.[3131]-9．直线:1l y kx =-与圆221x y +=相交于A 、B 两点，则OAB ∆的面积最大值为（ ） A ．14 B ．12 C ．1 D ．3210．直线0ax by a b +++=与圆222x y +=的位置关系为（ ） A ．相交 B ．相切 C ．相离 D ．相交或相切11．已知圆C ：1)1(22=++y x 与圆O ：1)1(22=+-y x 关于某直线对称，则直线的方程为 （ ）A 、x y -=B 、1+-=x yC 、x y =D 、1-=x y12．从原点O 引圆m kx y m y m x 当的切线,1)2()(222=+=-+-变化时，切点P 的轨迹方程是 A ．322=+y x B ．2)1(22=+-y x C ．3)1()1(22=-+-y x D ．222=+y x二、填空题13．已知0a >，0b >，0c >，且222c a b =+，()1,0A a -，()2 ,0A a ，()0,B b ，() ,0F c ．若在线段BF 上（不含端点）存在不同的两点()1,2i P i =，使得i 1i 2PA PA ⊥，则实数ca的取值范围是___． 14．已知点P 是直线20x y ++=上的动点，过P 引圆221x y +=的切线，则切线长的最小值为____. 15．若点在圆上，点在圆上，则的最小值是__________．16．已知()()1,0,5,0A B -，若在圆()222:22290C x y mx my m m R +-++-=∈上存在点P 使得2220PA PB +=成立，则m 的取值范围为_____． 17．过点()2,0A与圆221x y +=相切的直线方程为__________________.18．如图所示，过点P 的直线与⊙O 相交于A ，B 两点．若PA ＝1，AB ＝2，PO ＝3，则⊙O 的半径r ＝________.19．如图，已知AB 是圆O 的直径，4AB =，C 为圆上任意一点，过C 点做圆的切线分别与过,A B 两点的切线交于,P Q 点，则CP CQ ⋅=________________．20．已知极坐标系的极点在直角坐标系的原点处,极轴与轴的正半轴重合,曲线的参数方程为4cos {3sin x y θθ==（θ为参数）,直线l 的极坐标方程为.点在曲线上,则点到直线l 的距离的最小值为 .三、解答题21．如图，已知圆22:4O x y +=与y 轴交于,A B 两点（A 在B 的上方），直线:4l y kx =-．（1）当2k =时，求直线l 被圆O 截得的弦长；（2）若0k =，点C 为直线l 上一动点（不在y 轴上），直线,CA CB 的斜率分别为12,k k ，直线,CA CB 与圆的另一交点分别,P Q ．①问是否存在实数m ，使得12k mk =成立？若存在，求出m 的值；若不存在，说明理由；②证明：直线PQ 经过定点，并求出定点坐标．22．如图，CD 是圆O 的切线，切点为D ，CA 是过圆心O 的割线且交圆O 于点B ，过B 作圆O 的切线交CD 于点E ，12DE EC =. 求证：3CA CD =.23．已知ABC ∆的三个顶点(1,0)A -，(1,0)B ，(3,2)C ，其外接圆为H .若直线l 过点C ，且被H 截得的弦长为2，求直线l 的方程.24．已知ABC △的顶点A B ，在圆224x y +=上，C 在直线2l y x =+：上，且AB l ∥．（1）当AB 边通过坐标原点O 时，求AB 的长及ABC △的面积； （2）当90ABC ∠=，且斜边AC 的长最大时，求AB 所在直线的方程．25．（12分）已知圆C 过点A （13+，0）、B （31-，0），半径为2,且圆心在X 轴上方。

西南交通大学限修课数学实验题目及答案六313-+=x x f 实验课题六一元微积分第一大题函数运算1.用程序集m 文件中定义函数：键盘输入自变量x ,由下列函数求函数值：f 1 (12) f 1 (-32) function y=f1(x) if x>0y=4*x^3+5*sqrt(x)-7 else y=x^2+sin(x) end end2. 用函数m 文件定义函数f 2<+≥+=06)5sin(03232x x x x x e f x 求f 2(-6) f 2(11) function y=f2(x) if x<0y=sin(5*x)+6*x^3 else y=exp(2*x)+3*x end end3.已知求其反函数 syms xf3=(1+x)/(x-3); g=finverse(f3)%g =(3*x + 1)/(x - 1)≤+>-+=0)sin(0754123x x x x x x f4.已知：92847653423234-++=+-+=x x x g x x x f做函数运算：u1 = f 4+ g 4 ; u2 = f 4 – g 4 ; u3 = f 4 * g 4 ; u4 = f 4 / g 4u5=)(4)(4x g x f ,u6=()()x g f 44syms xf4=3*x^4+5*x^3-6*x^2+7 g4=8*x^3+2*x^2+x-9 u1=f4+g4 u2=f4-g4 u3=f4*g4 u4=f4/g4 u5=f4^g4u6=compose(f4,g4)%u1 =3*x^4 + 13*x^3 - 4*x^2 + x - 2 %u2 =3*x^4 - 3*x^3 - 8*x^2 - x + 16%u3 =(3*x^4 + 5*x^3 - 6*x^2 + 7)*(8*x^3 + 2*x^2 + x - 9) %u4 =(3*x^4 + 5*x^3 - 6*x^2 + 7)/(8*x^3 + 2*x^2 + x - 9) %u5 =(3*x^4 + 5*x^3 - 6*x^2 + 7)^(8*x^3 + 2*x^2 + x - 9)%u6 =5*(8*x^3 + 2*x^2 + x - 9)^3 - 6*(8*x^3 + 2*x^2 + x - 9)^2 + 3*(8*x^3 + 2*x^2 + x - 9)^4 + 75.已知32029660224452)(5432+-++-=x x x x x f (1)定义函数(2)给出排版形式的函数 (3)因式分解函数 (4)转换成嵌套形式(5)求解代数方程f 5( x )=0 syms xf5=-452*x^2+224*x^3+60*x^4-296*x+320 pretty(f5) factor(f5) horner(f5) solve(f5)% 4 3 2% 60 x + 224 x - 452 x - 296 x + 320 %ans =4*(3*x - 2)*(5*x - 8)*(x + 5)*(x + 1) %ans=x*(x*(x*(60*x + 224) - 452) - 296) + 320 %ans =-5 -1 2/3 8/56.求52)(62+-=x xe x g x在[-2,2]上的零点 g6='x*exp(x)-2*x^2+5'; x=fzero(g6,[-2,2])第二大题一元微积分1. 定义函数-+=-233112x x x y 计算：y y x ∞→=lim 1syms xy=x^2*(3^(1/x)+3^(-1/x)-2); y1=limit(y,x,inf) %y1 =log(3)^2 2. .求极限x x x y xx y x x /)sin 1(sin lim 22sin ln lim 21200-+==∞→+→syms xb1=x*log(sin(x));b2=sin(sqrt(x^2+1)-sin(x))/x; y21=limit(b1,x,0,'right') y22=limit(b2,x,inf) %y21 =0 %y22 =03. 对本大题第1小题定义的函数y 求导，dxdy y =3 y3=diff(y)%y3 =2*x*(3^(1/x) + 1/3^(1/x) - 2) + x^2*(log(3)/(3^(1/x)*x^2) - (3^(1/x)*log(3))/x^2) 4. 求 y 对x 的不定积分：?=dx x y y )(4 y4=int(y)5. 求y 在[3,5]上的定积分：?=53)(5dx x y yy5=int(y,3,5)6. 将函数f=sin(x)在x=0点展开成泰勒展式7项。

一、选择题1．在直角坐标系xOy 中，以O 为极点，x 轴正半轴为极轴，建立极坐标系，直线l 的参数方程为1cos sin x t y t αα=-+⎧⎨=⎩，（t 为参数），曲线C 的方程为4cos 02πρθθ⎛⎫= ⎪⎝⎭，(2,0)C 直线l 与曲线C 相交于A B ，两点，当ABC∆的面积最大时，tan α=( )A．3B．2CD ．72．在参数方程cos sin x a t y b t θθ=+⎧⎨=+⎩，(0θπ<，t 为参数)所表示的曲线上有,B C 两点，它们对应的参数值分别为1t ，2t ，则线段BC 的中点M 对应的参数值是（ ） A ．122t t - B ．122t t + C ．122t t - D ．122t t + 3．已知(,)P x y 是椭圆sin x y αα⎧=⎪⎨=⎪⎩上任意一点，则点P 到40x -=的距离的最大值为（ ） A．42+B．2C．42- D ．24．在极坐标系中，点()M 1,0关于极点的对称点为( ) A ．()1,0B ．()1,π-C ．()1,πD ．()1,2π5．记椭圆221441x ny n +=+围成的区域（含边界）为n Ω（12n =，，），当点()x y ，分别在1Ω，2Ω，…上时，x y +的最大值分别是1M ，2M ，…，则lim n n M →+∞=（ ） A ．0B ．14C ．2D ．6．已知M 为曲线3sin :cos x C y θθ=+⎧⎨=⎩（θ为参数）上的动点，设O 为原点，则OM 的最大值是 A ．1 B ．2 C ．3 D ．4 7．参数方程2cos sin x y θθ=⎧⎨=⎩（θ为参数）和极坐标方程6cos ρθ=-所表示的图形分别是（ ）A ．圆和直线B ．直线和直线C ．椭圆和直线D ．椭圆和圆8．在平面直角坐标系中以原点为极点，以x 轴正方向为极轴建立的极坐标系中，直线:20l y kx ++=与曲线2:cos C ρθ=相交，则k 的取值范围是( )A ．k ∈RB ．34k ≥-C ．34k <-D ．k ∈R 但0k ≠9．直线22{x ty t=+=-（t 为参数）被曲线4cos p θ=所截的弦长为( )A ．4 BCD ．810．直线1sin 70{2cos70x t y t =+=+(t 为参数)的倾斜角为 ( )A ．70°B ．20°C ．160°D ．110°11．椭圆221169x y +=上的点到直线34x y += ）A ．0B．5C．D．245- 12．已知圆()22:11M x y -+=,圆()22:11N x y ++=,直线12,l l 分别过圆心,M N ,且1l 与圆M 相交于,A B 两点,2l 与圆N 相交于,C D 两点,点P 是椭圆22149x y+=上任意一点,则PA PB PC PD ⋅+⋅的最小值为（ ） A ．7B ．8C ．9D ．10二、填空题13．在平面直角坐标系xOy 中，以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，已知曲线C 的参数方程是1cos 1sin x y θθ=+⎧⎨=+⎩（θ为参数，0θπ≤≤），直线l 的极坐标方程是sin 4πρθ⎛⎫-= ⎪⎝⎭，若曲线C 与直线l 有交点，则a 的取值范围是_______. 14．在平面直角坐标系xOy 中，直线l 的参数方程为5,4x t y t =+⎧⎨=--⎩（t 为参数），圆C 的参数方程是cos ,sin x y θθ=⎧⎨=⎩，（θ为参数），直线l 与圆C 交于两个不同的点A 、B ，当点P 在圆C 上运动时，PAB ∆面积的最大值为__________.15．设P 、Q 分别为直线1,82x t y t =-⎧⎨=-⎩（t 为参数，t R ∈）和曲线1,:2x C y θθ⎧=⎪⎨=-⎪⎩（θ为参数，R θ∈）上的点，则PQ 的取值范围是______．16．若直线{1232(x ty t t =+=+为参数)与直线41x ky +=垂直，则常数k =______17．在直角坐标系xOy 中，曲线C 的参数方程为2cos ,4sin x y θθ=⎧⎨=⎩（θ为参数），则曲线C 的直角坐标方程为__________18．已知曲线C ：2x cos y sin θθ=+⎧⎨=⎩(θ为参数)，与直线l ：1324x t y t =+⎧⎨=-⎩(t 为参数)，交于A B ，两点，则AB =___________．19．内接于半径为R 的半圆的周长最大的矩形的宽和长分别为_____________20．直线3,423x t y t =⎧⎪⎨=+⎪⎩（t 为参数），点C 在椭圆2214x y +=上运动，则椭圆上点C 到直线l 的最大距离为______.三、解答题21．选修4-4：坐标系与参数方程以直角坐标系的原点O 为极点，x 轴的正半轴为极轴，且两个坐标系取相等的长度单位， 已知曲线1C 的参数方程为2cos sin x y αα=⎧⎨=⎩（α为参数），曲线2C 的极坐标方程为()cos 2sin 20ρθθ++=.曲线2C 的图象与x 轴、y 轴分别交于,A B 两点.（1）判断,A B 两点与曲线1C 的位置关系；（2）点M 是曲线1C 上异于,A B 两点的动点，求MAB ∆面积的最大值.22．在直角坐标系xOy 中，曲线C 的参数方程为2cos (22sin x y θθθ=⎧⎨=+⎩为参数).以坐标原点为极点，以x 轴的正半轴为极轴，建立极坐标系．()1写出曲线C 的极坐标方程；()2设点M的极坐标为4π⎫⎪⎭，过点M 的直线l 与曲线C 相交于A ，B 两点，若2MA MB =，求AB 的弦长．23．在平面直角坐标系中，直线l 的参数方程为cos sin x t y t αα=⎧⎨=⎩（t 为参数，0απ≤<）．以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 的极坐标方程为244cos 2sin ρρθρθ-=-．（1）写出曲线C 的直角坐标方程；（2）若直线l 与曲线C 交于A 、B 两点，且AB的长度为l 的普通方程． 24．在平面直角坐标系xOy 中，以原点O 为极点，x 轴正半轴为极轴建立极坐标系．已知直线l的极坐标方程为sin 4πρθ⎛⎫-= ⎪⎝⎭C 的极坐标方程为2sin cos ρθθ=． （1）写出直线l 和曲线C 的直角坐标方程；（2）过动点20000()(),P x y y x <且平行于l 的直线交曲线C 于,A B 两点，若2PA PB ⋅=，求动点P 到直线l 的最近距离．25．在平面直角坐标系xOy 中，以坐标原点为极点，x 轴的非负半轴为极轴且取相同的单位长度建立极坐标系．直线l的参数方程为12x y t ⎧=⎪⎪⎨⎪=⎪⎩（t 为参数），圆C 的参数方程为22cos 2sin x y αα=+⎧⎨=⎩（α为参数）．（1）写出直线l 的普通方程和圆C 的极坐标方程；（2）已知点()1,0M ，直线l 与圆C 交于A ，B 两点，求MA MB -的值．26．在直角坐标系xOy 中，已知直线l 过点P （2，2）.以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线C 的极坐标方程为ρ﹣ρcos 2θ﹣4cos θ＝0. （1）求C 的直角坐标方程； （2）若l 与C 交于A ，B 两点，求PA PB PA PB-⋅的最大值.【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】先将直线直线l 与曲线C 转化为普通方程，结合图形分析可得，要使ABC ∆的面积最大，即要ACB ∠为直角，从而求解出tan α． 【详解】解：因为曲线C 的方程为4cos 02πρθθ⎛⎫= ⎪⎝⎭， 两边同时乘以ρ，可得24cos ρρθ=，所以曲线C 的普通方程为22(2)4(02)x y y -+=， 曲线C 是以(2,0)C 为圆心，2为半径的上半个圆. 因为直线l 的参数方程为1cos sin x t y t αα=-+⎧⎨=⎩，（t 为参数），所以直线l 的普通方程为tan tan 0x y αα-+=， 因为1sin 2sin 2ABCS CA CB ACB ACB ∆，所以当ACB ∠为直角时ABC ∆的面积最大，此时C 到直线l 的距离22222AB CA CB d +=== ，因为直线l 与x 轴交于()1,0D -， 所以3CD =，于是7DE = 所以214tan 7α==， 故选D ． 【点睛】本题考查了曲线的参数方程、极坐标方程与普通方程之间的互化，同时考查了直线与圆的位置关系，数形结合是本题的核心思想．2．D解析：D 【解析】 【分析】根据参数的几何意义求解即可。

西南交通大学限修课数学实验题目及答案三实验课题三向量与曲线绘图第一大题：向量的创建与运算用元素输入法创建向量x11=(2 �C5 8 �C1 7 1 -8 3 2 5 9)x11=[2 -5 8 -1 7 1 -8 3 2 5 9]用冒号输入法创建向量x12=(2 4 6 8 10 12 14 16 18 20 22)x12=2:2:22用等分取值法创建向量x13，其初值为0，终值为2π，共20个元素.x13=linspace(0,2*pi,20) 用随机输入法创建8维行向量x14 x14=rand(1,8)用随机输入法创建6维整数列向量x15 x15=fix(rand(6,1)*100)取向量x11的绝对值大于3的元素构成向量x16. x16=x11(abs(x11)>3)求空间两点间距离M 1(5,?4,?9)、M2(8,?6,?3) d=norm([8 6 3]-[5 4 9])做向量的线性运算：x18=4十x11+7x12. x18=4+x11+7*x12做向量的数量积 x19=x11・x12.x19=dot(x11,x12)分别取x11与x12的前三个元素做向量的叉积赋给x10.x10=cross(x11([1:3]),x12([1:3])) 第二大题：曲线绘图：构造坐标向量绘出‘田’字的图形（先给出构成字的数据点坐标） figureaxis([0,6,0,6])x=[1 1 5 5 1 1 5 5 3 3]; y=[1 5 5 1 1 3 3 5 5 1]; line(x,y)绘制向量y=[4 5 5 3 2 3 5 6 7 8]的图形。

y=[4 5 5 3 2 3 5 6 7 8]; plot(y)数据数组x23=(0.1 0.11 0.12…10)，函数y23=30/x23，绘出函数曲线图形。

x23=0.1:0.01:10; y23=30./x23; plot(x23,y23)数据数组x24为区间[-5,5]上等分的30个点列，绘出函数y24= 5・x24・cos(x24) 的曲线图。

一、选择题1．已知点G 是ABC 的重心，(),AG AB AC R λμλμ=+∈，若120,2,A AB AC ∠=︒⋅=-则AG 的最小值是（ ）A ．33B ．22C ．12D ．232．已知向量()2,3a =，()4,2b =，那么向量a b -与a 的位置关系是（ ） A ．平行B ．垂直C ．夹角是锐角D ．夹角是钝角3．已知O 为正三角形ABC 内一点，且满足()10OA OB OC λλ+++=，若OAB 的面积与OAC 的面积之比为3，则λ=（ ） A ．12B ．14C ．34D ．324．已知函数()sin (0)2f x x a a π⎛⎫=>⎪⎝⎭，点A ，B 分别为()f x 图象在y 轴右侧的第一个最高点和第一个最低点，O 为坐标原点，若OAB 为钝角三角形，则a 的取值范围为（ ）A ．10,(2,)2⎛⎫+∞ ⎪⎝⎭ B ．30,(1,)3⎛⎫⋃+∞ ⎪⎝⎭C ．3,13⎛⎫ ⎪ ⎪⎝⎭D ．(1,)+∞5．已知非零向量a →，b →夹角为45︒，且2a =，2a b -=,则b →等于（ ）A ．22B ．2C ．3D ．26．已知圆C 的方程为22(1)(1)2x y -+-=，点P 在直线3y x上，线段AB 为圆C的直径，则PA PB ⋅的最小值为（） A ．2B ．52C ．3D ．727．如下图，四边形OABC 是边长为1的正方形，点D 在OA 的延长线上，且2OD =，点P 为BCD 内(含边界)的动点，设(,)OP OC OD R αβαβ=+∈，则αβ+的最大值等于( )A ．3B ．2C ．52D ．328．在边长为2的正方形ABCD 中，E ，F 分别为BC 和DC 的中点，则AE AF ⋅=（ ）A ．52B ．52-C ．4D ．4-9．在ABC ∆中，D 为BC 边上一点，且AD BC ⊥，向量AB AC +与向量AD 共线，若10AC =，2BC =，0GA GB GC ++=，则AB CG=（ ）A ．3B ．5C ．2D ．10210．如图，已知点D 为ABC 的边BC 上一点，3BD DC =，*()∈n E n N 为AC 边的一列点，满足11(32)4n n n n n E A a E B a E D +=-+，其中实数列{}n a 中，10,1n a a >=，，则{}n a 的通项公式为（ ）A ．1321n -⋅-B ．21n -C ．32n -D ．1231n -⋅-11．已知等边ABC 的边长为2，若3BC BE =，AD DC =，则BD AE ⋅等于（ ） A ．103B ．103-C ．2D ．2-12．如图所示，在ABC 中，点D 在线段BC 上，且3BD DC =，若AD AB AC λμ=+，则λμ=（ ）A ．12B．13C．2D．23二、填空题13．已知向量(9,6),(3,)a b x==，若//a b，则()b a b⋅-=___________.14．已知向量a，b及实数t满足|(1)(1)|1t a t b++-=，若22||||1a b-=，则t的最大值是________．15．圆O为△ABC的外接圆，半径为2，若2AB AC AO+=，且OA AC=，则向量BA在向量BC方向上的投影为_____.16．已知平面向量a，b，c满足45a b⋅=，4a b-=，1c a-=，则c的取值范围为________．17．如图，设圆M的半径为2，点C 是圆M上的定点，A，B是圆M上的两个动点，则CA CB⋅的最小值是________.18．在ABC中，22AC AB==，120BAC∠=，O 是BC的中点，M是AO上一点，且3AO MO=，则MB MC⋅的值是______.19．在ABC△中，已知4CA=，3CP=23ACBπ∠=，点P是边AB的中点，则CP CA⋅的值为_____.20．已知点O是ABC∆内部一点，并且满足230OA OB OC++=，BOC∆的面积为1S，ABC∆的面积为2S，则12SS=______.三、解答题21．三角形ABC中，D为BC上一点，2BD DC=，设AD a=，AC b=，可以用a，b来表示出AD，方法如下：方法一：23AD AB AD BCBB==++，∵BC AC AB=-，∴21212()33333AD AB AC AB AB AC a b=+-=+=+.方法二：13AC CD ACAD CB=+=+，∵CB AB AC=-，∴11212()33333AD AC AB AC AB AC a b=+-=+=+.方法三：如图所示，过点D作AC的平行线，交AB于点E，过点D作AB的平行线，交AC 于点F ，则四边形AEDF 为平行四边形.∵//DF AB 且2BD DC =，∴13FD CD AB CB ==，13FD AE AB ==.∵//ED AC ，2BD DC =.∴23ED BD AC BC ==，得23ED AF AC ==.∴12123333AD AE ED AE AF AB AC a b =+=+=+=+. 请参照上述方法之一(用其他方法也可)，解决下列问题：（1）三角形ABC 中，D 为BC 的中点，设AB a =，AC b =，试用a ，b 表示出AD ；（2）设D 为直线BC 上任意一点(除B ､C 两点)，BD kDC =.点A 为直线BC 外任意一点，AB a =，AC b =，证明：存在唯一实数对λ，μ，使得：AD a b λμ=+，且1λμ+=.22．已知12,e e 是平面内两个不共线的非零向量，12122,,AB e e BE e e EC λ=+=-+=122e e -+，且A ，E ，C 三点共线．（1）求实数λ的值；（2）若()()122,1,2,2e e ==-，求BC 的坐标；（3）已知()3,5D ，在（2）的条件下，若,,,A B C D 四点按逆时针顺序构成平行四边形，求点A 的坐标．23．已知向量()sin ,cos a x x =，()3,1b =-，[]0,x π∈.（1）若a b ⊥，求x 的值；（2）记()f x a b =⋅，求()f x 的最大值和最小值以及对应的x 的值. 24．已知||6a =，||4=b ，(2)(3)72a b a b -⋅+=-. （1）求向量a ，b 的夹角θ； （2）求|3|a b +.25．已知向量()1,2a =，(),1b x =. （1）若|2|||a b a b -=+，求实数x 的值； （2）若2x =，求2a b -与a b +的夹角.26．设非零向量a ，b 不共线.（1）若(),1a t =，()5,b t =，且//a b ，求实数t 的值；（2）若OA a b =+，2OB a b =+，3OC a b =+.求证：A ，B ，C 三点共线.【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】先根据重心得到()13AG AB AC =+，设0,0AB x AC y =>=>，利用数量积计算4xy =，再利用重要不等式求解()2219A AGB AC =+的最小值，即得结果.【详解】点G 是ABC 的重心，设D 为BC 边上的中点，则()2133AG AD AB AC ==+， 因为120,2,A AB AC ∠=︒⋅=-设0,0AB x AC y =>=>，则cos1202xy ︒=-，即4xy =，故()()()222211144249999AG x y x B AC y A =+-≥-=+=，即23AG ≥， 当且仅当2x y ==时等号成立，故AG 的最小值是23. 故选：D. 【点睛】 关键点点睛：本题的解题关键在于通过重心求得向量关系()13AG AB AC =+，利用数量积得到定值，才能利用重要不等式求最值，突破难点，要注意取条件的成立.2．D解析：D 【分析】首先根据题中所给的向量的坐标，结合向量数量积运算法则，求得其数量积为负数，从而得到其交集为钝角. 【详解】因为()2,3a =，()4,2b =，222()23(2432)131410a b a a a b -⋅=-⋅=+-⨯+⨯=-=-<，所以向量a b -与a 的位置关系是夹角为钝角， 故选：D. 【点睛】该题考查的是有挂向量的问题，涉及到的知识点有向量数量积的运算律，数量积坐标公式，根据数量积的符号判断其交集，属于简单题目.3．A解析：A 【分析】分别取AC 、BC 的中点D 、E ，连接DE 、AE ，由平面向量的线性运算可得OD OE λ=-，进而可得13OAC AEC S S =△△，即可得解. 【详解】分别取AC 、BC 的中点D 、E ，连接DE 、AE ，如图，所以DE 是ABC 的中位线，因为()10OA OB OC λλ+++=，所以()OA OC OB OC λ+=-+， 所以OD OE λ=-，所以D 、E 、O 三点共线，所以111363OAC OAB ABC AEC S S S S ===△△△△，所以13OD ED =即12OD OE =-，所以12λ-=-即12λ=.故选：A. 【点睛】本题考查了平面向量共线、线性运算及基本定理的应用，考查了运算求解能力与转化化归思想，属于中档题.4．B解析：B 【分析】首先根据题的条件，将三角形三个顶点的坐标写出来，之后根据三角形是钝角三角形，利用向量夹角为钝角的条件，从而转化为向量的数量积0OA OB ⋅<或0AB AO ⋅<，找出a 所满足的条件，最后求得结果. 【详解】 由题意得24,(0,0),(,1),(3,1)2T a O A a B a aππ==-，因为OAB 为钝角三角形，所以0OA OB ⋅<或0AB AO ⋅<，即2310a -<，或2220a -+<，从而0a <<或1a >． 故选：B. 【点睛】该题考查的是有关利用钝角三角形求对应参数的取值范围，涉及到的知识点有正弦型函数图象上的特殊点的坐标，钝角三角形的等价转化，向量的数量积坐标公式，属于中档题.5．A解析：A 【分析】根据数量积的运算，2a b →→-=两边平方即可求解. 【详解】2a b →→-=,=2a →,a →，b →夹角为45︒,2222()24a b a b a a b b →→→→→→→→∴-=-=-⋅+=,2422||cos||44b b π→→∴-⨯+=,解得：||b →= 故选：A 【点睛】本题主要考查了向量数量积的运算性质，数量积的定义，属于中档题.6．B解析：B 【分析】将PA PB ⋅转化为2||2PC -，利用圆心到直线的距离求得||PC 的取值范围求得PA PB ⋅的最小值. 【详解】()()()()PA PB PC CA PC CB PC CA PC CA ⋅=+⋅+=+⋅-22223||||||222PC CA PC ⎛⎫=-=-≥- ⎪⎝⎭52=.故选B. 【点睛】本小题主要考查向量的线性运算，考查点到直线距离公式，考查化归与转化的数学思想方法，属于中档题.7．D解析：D 【分析】以O 为原点，边OA 和OC 所在的直线分别为x 和y 轴建立如图所示的平面直角坐标系，设(),P x y ，易得1,2y x αβ==，则12x y αβ+=+，再将原问题转化为线性规划问题，求目标函数12x y +在可行域BCD 内(含边界)的最大值，即可求出结果． 【详解】以O 为原点，边OA 和OC 所在的直线分别为x 和y 轴建立如图所示的平面直角坐标系， 则()()0,1,2,0C D ，如下图所示：设(),P x y ，∵ (,)OP OC OD R αβαβ=+∈， ∴()()(),0,12,0)2,(x y αββα=+=， ∴2,x y βα==，即1,2y x αβ==，∴12x y αβ+=+，令1,2z x y =+则12y x z =-+，其中z 为直线12y x z =-+在y 轴上的截距，由图可知，当该直线经过点()1,1B 时，其在y 轴上的截距最大为32，∴αβ+的最大值为32． 故选：D ． 【点睛】本题考查平面向量在几何中的应用，建立坐标系后，可将原问题转化为线性规划中的最值问题，考查学生的转化思想、逻辑推理能力和运算能力，属于中档题．8．C解析：C 【分析】建立直角坐标系，利用向量的坐标运算求解即可. 【详解】以点A 为坐标原点，建立如下图所示的直角坐标系(0,0),(2,1),(1,2)A E F(2,1),(1,2)AE AF ∴== 21124AE AF ∴⋅=⨯+⨯= 故选：C【点睛】本题主要考查了求平面向量的数量积，属于中档题.9．B解析：B 【解析】取BC 的中点E ，则2AB AC AE +=与向量AD 共线，所以A 、D 、E 三点共线，即ABC ∆中BC 边上的中线与高线重合，则10AB AC ==因为0GA GB GC ++=，所以G 为ABC ∆的重心，则2222() 2.32BC GA GE AC ==-=所以22101,112, 5.2AB CE CG CG==+===本题选择B 选项.10．D解析：D 【分析】以BA 和BC 为基底，表示n BE ，根据n E ，A ，C 三点共线，可得1193331442+-++=++n n n a a a ，构造等比数列，即可求出通项公式. 【详解】113(32),44+=-+=-=-n n n n n n n n E A a E B a E D E D BD BE BC BE , 113(32)()44n n n n n E A a E B a BC BE +∴=-+- 113(32)(32)44n n n n a a E B a BC +=---+ 又=-n n E A BA BE113(32)(32=)44+∴---+-n n n n n a a E B a BC BA BE113(33)(32)44+-∴++=++n n n n a a BE a BC BA因为n E ，A ，C 三点共线113(33)1(32)44+-++=++∴n n n a a a ，即1=32++n n a a ，即1+1=3(1)++n n a a ，所以数列{1}n a +是等比数列，首项为2，公比为3．1+1=23-∴⋅n n a ，即1=23-1-⋅n n a ， 故选：D ． 【点睛】本题考查了平面向量基本定理和等比数列的通项公式，考查了运算求解能力和逻辑推理能力，属于中档题.11．D解析：D 【分析】 根据题意得出()12BD BA BC =+，13AE BC BA =-，运用数量积求解即可． 【详解】解：等边△ABC 的边长为2，3BC BE =，AD DC =， ∴()12BD BA BC =+，1313A AB BE AB B E BC A C B =+=+=-，∴()221111223233BD AE BA BC BC BA BC BA BC BA ⎛⎫⎛⎫+-=--⋅ ⎪ ⎪⎝=⎭⎝⎭， 112144222332⎛⎫=⨯⨯--⨯⨯⨯ ⎪⎝⎭， 2=-．故选：D ．【点睛】本题考查了平面向量的运算，数量积的求解，关键是分解向量，属于中档题． 12．B解析：B【分析】 由向量的运算法则，化简得1344AD AB AC =+,再由AD AB AC λμ=+，即可求得,λμ 的值，即可求解. 【详解】 由向量的运算法则， 可得34=+=+AD AB BD AB BC 313()444AB AC AB AB AC =+-=+, 因为AD AB AC λμ=+，所以13,44λμ==，从而求得13λμ=， 故选:B ．【点睛】该题考查的是有关向量的基本定理，在解题的过程中，需要利用向量直角的关系，结合三角形法则，即可求得结果，属于基础题. 二、填空题13．26【分析】先由求出求出再进行的计算【详解】因为所以解得所以故答案为：26【点睛】向量类问题的常用处理方法——向量坐标化利用坐标运算比较简单解析：26【分析】先由//a b 求出2x =，求出b ，再进行()b a b ⋅-的计算.【详解】因为//a b ，所以9180x -=，解得2x =，所以(6,4),()362426a b b a b -=⋅-=⨯+⨯=.故答案为：26【点睛】向量类问题的常用处理方法——向量坐标化，利用坐标运算比较简单．14．【分析】根据整理为再两边平方结合得到然后利用基本不等式求解【详解】因为所以两边平方得因为即所以而所以解得当且仅当时等号成立所以的最大值是故答案为：【点睛】关键点点睛：本题关键是由这一信息将转化为再遇 解析：14【分析】根据|(1)(1)|1t a t b ++-=，整理为()()||1t a b a b ++-=，再两边平方结合22||||1a b -=，得到()()22212t a ba b t ++-=-，然后利用基本不等式求解.【详解】因为|(1)(1)|1t a t b ++-=， 所以()()||1t a b a b ++-=， 两边平方得()()()()22221t a b t a b a b a b +++-+-=，因为22||||1a b -=，即()()1a b a b +-=，所以()()22212t a b a b t ++-=-，而()()()()22222t a b a b t a b a b t ++-≥+⋅-=， 所以122t t -≥，解得14t ≤，当且仅当()()t a b a b +=-时等号成立， 所以t 的最大值是14 故答案为：14【点睛】 关键点点睛：本题关键是由22||||1a b -=这一信息，将|(1)(1)|1t a t b ++-=，转化为()()||1t a b a b ++-=，再遇模平方，利用基本不等式从而得解. 15．3【分析】根据向量关系即可确定的形状再根据向量投影的计算公式即可求得结果【详解】因为圆O 为△ABC 的外接圆半径为2若故可得是以角为直角的直角三角形又因为且外接圆半径是故可得则故向量在向量方向上的投影 解析：3【分析】根据向量关系，即可确定ABC 的形状，再根据向量投影的计算公式，即可求得结果.【详解】因为圆O 为△ABC 的外接圆，半径为2，若2AB AC AO +=，故可得ABC 是以角A 为直角的直角三角形. 又因为OA AC =，且外接圆半径是2，故可得224BC OA AC ===，则AB =AB cos ABC BC ∠== 故向量BA 在向量BC方向上的投影为3AB cos ABC ⨯∠==. 故答案为：3.【点睛】本题考查向量数量积的几何意义，属中档题. 16．【分析】结合已知条件画出图象由的几何意义求得的取值范围【详解】如图所示设设是线段的中点依题意可知由于所以即解得所以即所以根据向量模的几何意义可知点在以为圆心为半径的圆上所以所以即的取值范围为故答案为 解析：[]4,10 【分析】 结合已知条件画出图象，由c 的几何意义求得c 的取值范围.【详解】如图所示，设,,OA a OB b OC c ===，设D 是线段AB 的中点. 依题意可知4,1,2AB AC AD BD ====，由于45a b ⋅=所以45OA OB ⋅=，即()()()()222224544OA OB OA OB OD BA +---==222441644OD BA OD --==，解得7OD =. 所以59OD AD OA OD AD =-≤≤+=, 即59OA ≤≤， 所以418,6110OA OA ≤-≤≤+≤ 根据向量模的几何意义可知，点C 在以A 为圆心，1为半径的圆上， 所以()()min max 11OA OC OA -≤≤+，所以410OC ≤≤，即c 的取值范围为[]4,10.故答案为：[]4,10【点睛】本小题主要考查向量数量积的运算，考查向量模的几何意义，属于中档题.17．【分析】延长BC 作圆M 的切线设切点为A1切线与BD 的交点D 结合数量积的几何意义可得点A 运动到A1时在上的投影最小设将结果表示为关于的二次函数求出最值即可【详解】如图延长BC 作圆M 的切线设切点为A1切 解析：2-【分析】延长BC ，作圆M 的切线，设切点为A 1，切线与BD 的交点D ，结合数量积的几何意义可得点A 运动到A 1时，CA 在CB 上的投影最小，设CP x =，将结果表示为关于x 的二次函数，求出最值即可.【详解】如图，延长BC ，作圆M 的切线，设切点为A 1，切线与BD 的交点D ，由数量积的几何意义，CA CB ⋅等于CA 在CB 上的投影与CB 之积，当点A 运动到A 1时，CA 在CB 上的投影最小；设BC 中点P ，连MP ，MA 1，则四边形MPDA 1为矩形；设CP =x ，则CD =2-x ，CB =2x ，CA CB ⋅=()()222224212x x x x x --⋅=-=--，[]02x ∈，， 所以当1x =时，CA CB ⋅最小，最小值为2-，故答案为：2-.【点睛】本题考查平面向量数量积的几何意义，考查了学生的作图能力以及分析问题解决问题的能力，属于中档题.18．【分析】用表示向量然后利用平面向量数量积的运算律可求得的值【详解】为的中点故答案为：【点睛】本题考查平面向量数量积的计算解答的关键就是选择合适的基底表示向量考查计算能力属于中等题 解析：53- 【分析】用AB 、AC 表示向量MB 、MC ，然后利用平面向量数量积的运算律可求得MB MC ⋅的值.【详解】 O 为BC 的中点，()12AO AB AC ∴=+， 3AO MO =，()1136MO AO AB AC ∴==+，()2133AM AO AB AC ==+， ()()11233MB AB AM AB AB AC AB AC ∴=-=-+=-， ()()11233MC AC AM AC AB AC AC AB ∴=-=-+=-， 22AC AB ==，120BAC ∠=，()()()22112252299MB MC AB AC AC AB AB AC AB AC ∴⋅=-⋅-=⋅--221155122122923⎡⎤⎛⎫=⨯⨯⨯--⨯-⨯=- ⎪⎢⎥⎝⎭⎣⎦. 故答案为：53-. 【点睛】 本题考查平面向量数量积的计算，解答的关键就是选择合适的基底表示向量，考查计算能力，属于中等题.19．6【分析】根据平方处理求得即可得解【详解】在中已知点是边的中点解得则故答案为：6【点睛】此题考查平面向量的基本运算关键在于根据向量的运算法则求出模长根据数量积的运算律计算求解解析：6【分析】 根据()12CP CA CB =+，平方处理求得2CB =，()12CP CA CA CB CA ⋅=+⋅即可得解.【详解】在ABC △中，已知4CA =，3CP 23ACB π∠=，点P 是边AB 的中点， ()12CP CA CB =+ ()222124CP CA CB CA CB =++⋅ 211316842CB CB ⎛⎫⎛⎫=++⨯- ⎪ ⎪⎝⎭⎝⎭， 解得2CB =则()()21111162462222CP CA CA CB CA CA CB CA ⎛⎫⎛⎫⋅=+⋅=+⋅=+⨯⨯-= ⎪ ⎪⎝⎭⎝⎭. 故答案为：6【点睛】 此题考查平面向量的基本运算，关键在于根据向量的运算法则求出模长，根据数量积的运算律计算求解. 20．【分析】将化为再构造向量和得出比例关系最后求解【详解】因为所以分别取的中点则所以即三点共线且如图所示则由于为中点所以所以故答案为：【点睛】本题考查向量的线性运算但是在三角形中考查又和三角形面积综合在解析：16【分析】将230OA OB OC ++=化为()2OA OC OB OC +=-+，再构造向量()12OA OC +和()12OB OC +，得出比例关系，最后求解12.S S 【详解】因为230OA OB OC ++=，所以()2OA OC OB OC +=-+，分别取AC ，BC 的中点D ，E ，则2OA OC OD +=，2OB OC OE +=.所以2OD OE =-，即O ，D ，E 三点共线且2OD OE =.如图所示，则13OBC DBC S S ∆∆=，由于D 为AC 中点，所以12DBC ABC S S ∆∆=，所以16OBC ABC S S ∆∆=. 故答案为：16【点睛】 本题考查向量的线性运算，但是在三角形中考查，又和三角形面积综合在一起，属于中档题.三、解答题21．（1）1122AD a b =+；（2）证明过程见详解. 【分析】（1）根据题干中所给的方法，结合向量的线性运算，可分别求解；（2）根据题干中所给的方法，由向量的线性运算，用a ，b 表示出AD ，即可得出结论成立.【详解】（1）因为D 为BC 的中点，方法一： 12AD AB BD AB BC =+=+，∵BC AC AB =-， ∴11221)22(221AD AB AC AB AB AC a b =+-=+=+； 方法二： 21AC CD AC AD CB =+=+，∵CB AB AC =-， ∴111221)2(221AD AC AB AC AB AC a b =+-=+=+； 方法三：如图所示，过点D 作AC 的平行线，交AB 于点E ，过点D 作AB 的平行线，交AC 于点F ，则四边形AEDF 为平行四边形.∵//DF AB 且BD DC =，∴21FD CD AB CB ==，21FD AE AB ==. ∵//ED AC ，BD DC =.∴12ED BD AC BC ==，得12ED AF AC ==. ∴11212212AD AE ED AE AF AB AC a b =+=+=+=+； （2）因为D 为直线BC 上任意一点(除B ､C 两点)，BD kDC =，显然1k ≠-； 所以1k BD BC k =+，11CB k CD =+， 方法一： 1AD AB BD AB BC k k =+++=，∵BC AC AB =-， ∴1111111()k k k AD AB AC AB AB AC a b k k k k k +++++=+-=+=+； 即存在唯一实数对1k k λ=+，11k μ=+，使得：AD a b λμ=+，且1λμ+=； 方法二：11A AC CD AC CB D k =++=+，∵CB AB AC =-， ∴11111111()k k k k AD AC AB AC A k k B AC a b k ++=+-=+++=++； 即存在唯一实数对11k λ=+，1k k μ=+，使得：AD a b λμ=+，且1λμ+=； 方法三：若点D 位于点B 左侧，如图，过点D 作//DM AB ，过点A 作//AM BC ，交DM 于点M ，则AMDB 为平行四边形，1k AM BD BC k ==+，所以11()AD AB AM AB BC AB k k k k AC AB =++=-+++=111111k k AB AC a b k k k k ++++=+=+； 即存在唯一实数对1k k λ=+，11k μ=+，使得：AD a b λμ=+，且1λμ+=； 若点D 位于点C 右侧，如图，过点D 作//DN AC ，过点A 作//AN BC ，交DN 于点N ，则ANDC 为平行四边形， 11AN CD BC k ==+，因此11A AC AN AC CB D k =++=+111111(1)k k k AB AC AB AB AC a b k k k k k +++=+++-+=+=， 即存在唯一实数对1k k λ=+，11k μ=+，使得：AD a b λμ=+，且1λμ+=； 若点D 位于BC 之间，则0k >；如图所示，过点D 作AC 的平行线，交AB 于点P ，过点D 作AB 的平行线，交AC 于点Q ，则四边形APDQ 为平行四边形.∵//DQ AB 且BD DC =，∴11QD CD AB C k B =+=，11Q k D AP AB =+=， ∵//PD AC ，BD DC =.∴1PD BD AC BC k k =+=，得1k k PD AQ AC =+=. ∴111111AD AP AQ AB AC k k a b k k k k =+=++=++++； 即存在唯一实数对1k k λ=+，11k μ=+，使得：AD a b λμ=+，且1λμ+=； 综上，存在唯一实数对λ，μ，使得：AD a b λμ=+，且1λμ+=. 【点睛】思路点睛：利用平面向量的一组基底表示向量时，只需根据向量的线性运算法则，结合平面向量基本定理，逐步求解即可.22．（1）32λ=-；（2）(－7，－2)；（3）(10，7)． 【分析】 （1）AE =k EC ， 得到()()12121k e k e λ+=--.由12,e e 不共线，得到12010k k λ+=⎧⎨--=⎩，求解得到λ的值；（2）利用平面向量的坐标运算计算即可；（3）设A (x ，y )，由AD BC =，利用向量的坐标运算求解即可.【详解】（1）()()()12121221AE AB BE e e e e e e λλ=+=++-+++＝.因为A ，E ，C 三点共线，所以存在实数k ，使得AE =k EC ，即()()121212e e k e e λ++=-+，得()()12121k e k e λ+=--.因为12,e e 是平面内两个不共线的非零向量，所以12010k k λ+=⎧⎨--=⎩解得13,λ22k =-=-. （2）()()()12136,31,17,22BE EC e e +=--=--+-=--． （3）因为A ，B ，C ，D 四点按逆时针顺序构成平行四边形，所以AD BC =.设A (x ，y )，则()35AD x y =--，， 因为()7,2BC =--，所以3752x x -=-⎧⎨-=-⎩解得107x y =⎧⎨=⎩ 即点A 的坐标为(10，7)．【点睛】本题考查平面向量的基本定理的应用，平面向量的坐标运算，属基础题. 根据平面向量的基本定理中的唯一性可得若12,e e 不共线，由12xe ye =，则0x y ==.这是在已知三点共线或向量共线求参数值的常用方法.23．（1）6x π=；（2）23x π=时，()f x 取到最大值2，0x =时，()f x 取到最小值1-.【分析】（1）利用向量垂直的坐标表示可求得tan x =x 的范围可求得x 的值；（2）将函数化简为()2sin 6f x x π⎛⎫=- ⎪⎝⎭，根据x 的范围可求得6x π-的范围，结合正弦函数图象可确定最大值和最小值取得的点，进而求得结果.【详解】解:（1）因为a b ⊥， 所以sin co 30s b x x a =-=⋅，于是sin tan s co x x x == 又[]0,x π∈，所以6x π=；（2）()())sin ,1cos f x a x b x =⋅=⋅-cos x x =-2sin 6x π⎛⎫=- ⎪⎝⎭. 因为[]0,x π∈，所以5,666x πππ⎡⎤-∈-⎢⎥⎣⎦， 从而12sin 26x π⎛⎫-≤-≤ ⎪⎝⎭ 于是，当62x ππ-=，即23x π=时，()f x 取到最大值2； 当66x ππ-=-，即0x =时，()f x 取到最小值1-.【点睛】本题考查平面向量垂直的坐标表示、平面向量与三角函数的综合应用，涉及到三角函数最值的求解问题；求解三角函数最值的关键是能够利用整体对应的方式，结合正弦函数的图象来进行求解.24．（1）23πθ=（2）【分析】 ()1利用平面向量数量积的分配律求出a b ⋅,然后代入夹角公式求解即可; ()2结合()1中a b ⋅的值,利用平面向量数量积的性质：()22222a ba b a a b b +=+=+⋅+进行运算，求出23a b +的值,然后再开方即可. 【详解】∵(2)(3)72a b a b -⋅+=-,∴22672a a b b +⋅-=-，∵6a =，4b =,∴3661672a b +⋅-⨯=-,解得12a b ⋅=-,由平面向量数量积的夹角公式得,∴121cos 642a ba b θ⋅-===-⨯, ∵0θπ≤≤∴23πθ=. （2）因为222369a b a a b b +=+⋅+， 所以()2336612916a b +=+⨯-+⨯108= ∴363a b +=.【点睛】本题考查平面向量数量积的性质及其夹角公式;考查运算求解能力;属于中档题、常考题型. 25．（1）12；（2）4π． 【分析】（1）求出向量2a b -与a b +的坐标，然后由模的坐标运算列出方程可求得x ； （2）求出向量2a b -与a b +的坐标，由向量夹角的坐标运算计算．【详解】（1）因为()1,2a =，(),1b x =，所以()22,3a b x -=-，()1,3a b x +=+.因为|2|||a b a b -=+，= 解得12x =. （2）当2x =时，()20,3a b -=，()3,3a b +=， 所以()()203339a b a b -⋅+=⨯+⨯=， 23a b -=，32a b +=.设2a b -与a b +的夹角为θ.则(2)()cos 2|2|||332a b a b a b a b θ-⋅+===-⋅+⋅. 又[]0,θπ∈，所以4πθ=，即2a b -与a b +的夹角为4π.【点睛】本题考查向量模的坐标运算，考查向量夹角的坐标运算，掌握向量的坐标运算是解题基础．26．（1）2）证明见解析.【分析】（1）利用平面向量的坐标运算和共线定理列方程求出t 的值；（2）根据条件得到2AC AB =且有公共点A ,即可得到结论.【详解】解：（1）∵(),1a t =，()5,b t =，且//a b ，故250t t -=⇒=，即实数t 的值为：5±；（2）证明：∵OA a b =+，2OB a b =+，3OC a b =+.∴AB OB OA b =-=，2AC OC OA b =-=，即2AC AB =且有公共点A ，故A ，B ，C 三点共线．【点睛】本题考查向量平行的坐标表示，用向量法证明三点共线，属于基础题．。

一、填空题： 1．设函数(,)z z x y =是由ln x zz y=所确定，则()0,1,1dz =dx dy + ． 2．设幂级数0nn n a x ∞=∑的收敛区间为()3,3-，则幂级数()01nn n a x ∞=-∑的收敛区间为 ()2,4- ．3．设函数,0()0,0x x f x x ππ--<≤⎧=⎨<≤⎩的付氏级数的和函数为()S x ，则(5)S π=2π．4．设),(xyx f z =，其中f 具有连续的二阶偏导数，则y x z∂∂∂2= 223221211f xy f x f x ''-'-'' ． 5．设幂级数()01nn n a x ∞=-∑在0x =处收敛，而在2x =处发散，则幂级数0n n n a x ∞=∑的收敛域为 [1,1)-．6．函数23)(2-+=x x x f 关于x 的幂级数展开式为 110(1)1,(1,1)2n n n n x x +∞+=⎡⎤--∈-⎢⎥⎣⎦∑ ． 7．设函数y z x =，则(2,1)dz = 2ln 2dx dy +8．曲线23,,x t y t z t ==-=的切线中，与平面236x y z -+=垂直的切线方程是111123x y z -+-==-． 9．设),(y x z z=是由方程sin()ln z e z xy a -= 0a >为常数所确定的二元函数，则 =dz cos()cos()sin()sin()z zyz xy xz xy dx dy e xy e xy +--． 10.旋转抛物面22zx y =+的切平面： 44810x y z -++=，平行与已知平面21x y z -+=.11．微分方程20y y y '''+-=的通解为 1212x x YC eC e -=+，2x y y y e '''+-=的通解为 121212x x x yC eC e e -=++．12.曲线：Γt tu e z t t y udu e x 301,cos sin 2,cos +=+==⎰在点()2,1,0处的切线方程为 3．函数41)(-=x x f 的麦克劳林级数的第5项为544x -，收敛域为)4,4(-.14.．已知函数(,)23a b f x y x y x y =+--（其中,a b 是大于1的实数）,有一个极值点(1,1)， 则3,2==b a ， 此时函数(,)f x y 的极大值为 3.15.试写出求解下列条件极值问题的拉格朗日函数：分解已知正数a 为三个正数z y x ,,之和，使z y x ,,的倒数之和最小()()a z y x zy x z y x L -+++++=λ111,, 16函数()x x x f -=1ln )(的麦克劳林级数的收敛域为[)1,1-∈x ，=)0()5(f-30二、单项选择题：请将正确结果的字母写在括号内。

四川省遂宁市西南交通大学附属实验中学高三数学理月考试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 已知i为虚数单位,复数z满足：，则在复平面上复数z对应的点位于（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限参考答案：D【分析】先求出并化简，从而确定复数对应的点的坐标为，进而判断其位于第四象限.【详解】因为，所以复平面上复数对应的点为，位于第四象限，故选.【点睛】本题主要考查了复数的运算，以及复数的几何意义，属于基础题.2. 定义运算：，则的值是( )A． B． C． D．参考答案：D由定义运算得，选D.3. 若曲线C1：y=ax2（a＞0）与曲线C2：y=e x存在公共切线，则a的取值范围为( )A．B．C．[，+∞）D．参考答案：C考点：利用导数研究曲线上某点切线方程．专题：导数的综合应用．分析：求出两个函数的导函数，由导函数相等列方程，再由方程有根转化为两函数图象有交点求得a 的范围．解答：解：由y=ax2（a＞0），得y′=2ax，由y=e x，得y′=e x，∵曲线C1：y=ax2（a＞0）与曲线C2：y=e x存在公共切线，则设公切线与曲线C1切于点（），与曲线C2切于点（），则，将代入，可得2x2=x1+2，∴a=，记，则，当x∈（0，2）时，f′（x）＜0．∴当x=2时，．∴a的范围是[）．故选：C．点评：本题考查了利用导数研究过曲线上某点处的切线方程，考查了方程有根的条件，是中档题．4. 若则下列不等式:①;②;③;④中正确的是（）A．①②B．②③ C．①④ D．③④参考答案：C略5. 如图，在矩形ABCD中，，，两个圆的半径都是1，且圆心，均在对方的圆周上，在矩形ABCD内随机取一点，则此点取自阴影部分的概率为（）A．B． C．D．参考答案：D如图所示，分别连接，则分别为边长为的等边三角形，所以其面积分别为，其中拱形的面积为，所以阴影部分的面积为，所以概率为，故选D．6. 设变量z，y满足约束条件，则目标函数的最大值为(A) (B)2 (C)3 (D) 4参考答案：C7. 已知复数z满足z=1+i（i为虚数单位），则复数z的共轭复数的虚部为（）A．﹣1 B．1 C．﹣i D．i参考答案：A【考点】A5：复数代数形式的乘除运算．【分析】由已知求得，则答案可求．【解答】解：∵z=1+i，∴，则复数z的共轭复数的虚部为﹣1．故选：A．8. 已知数列{a n}的前n项和为S n，且满足，，则（）A．1009 B．1008 C．2 D．1参考答案：A，、,,∴故选：A9. 已知定义在R上的函数f(x)的图象关于点(－,0)对称，且满足f(x)＝－f(x＋)，f(－1)＝1，f(0)＝－2，则f(1)＋f(2)＋…＋f(2008)的值为 ( ）A．－2B．－1 C．0D．1参考答案：D10. 已知复数z，“z+=0”是“z为纯虚数”的（）A．充分非必要条件B．必要非充分条件C．充要条件D．既非充分也不必要条件参考答案：B【考点】复数的基本概念；必要条件、充分条件与充要条件的判断．【专题】阅读型；对应思想；分析法；数系的扩充和复数．【分析】由充分必要条件的判断方法，结合两复数和为纯虚数的条件判断．【解答】解：对于复数z，若z+=0，z不一定为纯虚数，可以为0，反之，若z为纯虚数，则z+=0．∴“z+=0”是“z为纯虚数”的必要非充分条件．故选：B．【点评】本题考查复数的基本概念，考查了充分必要条件的判断方法，是基础题．二、填空题:本大题共7小题,每小题4分,共28分11. 已知函数，若函数f（x）在区间[﹣2，a]上单调递增，则实数a的取值范围是．参考答案：[1，+∞）【考点】利用导数研究函数的单调性．【专题】分类讨论；转化思想；综合法；函数的性质及应用；导数的综合应用．【分析】f′（x）=x2+2x+a，由于函数f（x）在区间[﹣2，a]上单调递增，可得：f′（x）≥0在区间[﹣2，a]上恒成立．令g（x）=（x+1）2+a﹣1，x∈[﹣2，a]．对a分类讨论即可得出．【解答】解：f′（x）=x2+2x+a，∵函数f（x）在区间[﹣2，a]上单调递增，∴f′（x）=x2+2x+a≥0在区间[﹣2，a]上恒成立．令g（x）=x2+2x+a，x∈[﹣2，a]．g（x）=（x+1）2+a﹣1，①当﹣2＜a＜﹣1时，函数g（x）在x∈[﹣2，a]单调递减，∴必有g（a）=a2+3a≥0，解得a≤﹣3或a≥0，舍去．②当﹣1≤a时，函数g（x）在x=﹣1时取得最小值，∴必有g（x）≥g（﹣1）=1﹣2+a≥0，解得a≥﹣1，满足条件．综上可得：a≥﹣1．∴实数a的取值范围是[﹣1，+∞）．故答案为：[﹣1，+∞）．【点评】本题考查了利用导数研究函数的单调性极值与最值、二次函数的单调性、恒成立转化问题，考查了分类讨论方法、推理能力与计算能力，属于难题．12. 有编号依次为1，2，3，4，5，6的6名学生参加数学竞赛选拔赛，今有甲、乙、丙、丁四位老师在猜谁将得第一名，甲猜不是3号就是5号；乙猜6号不可能；丙猜2号，3号，4号都不可能；丁猜是1号，2号，4号中的某一个.若以上四位老师中只有一位老师猜驿，则猜对者是_____________.参考答案：丙13. 已知实数满足约束条件若恒成立，则实数的取值范围为.参考答案：略14. 已知函数的定义域［-1，5］，部分对应值如表，的导函数的图象如图所示，下列关于函数的命题:①函数的值域为［1，2］；②函数在［0，2］上是减函数；③当时，函数最多有4个零点；④如果当时，的最大值是2，那么的最大值为4.其中正确命题的序号是(写出所有正确命题的序号)参考答案：①②③15. 为满足人民群众便利消费、安全消费、放心消费的需求，某社区农贸市场管理部门规划建造总面积为2400m2的新型生鲜销售市场．市场内设蔬菜水果类和肉食水产类店面共80间．每间蔬菜水果类店面的建造面积为28 m2，月租费为x万元；每间肉食水产店面的建造面积为20 m2，月租费为0.8万元．全部店面的建造面积不低于总面积的80%，又不能超过总面积的85%．①两类店面间数的建造方案为_________种．②市场建成后所有店面全部租出，为保证任何一种建设方案平均每间店面月租费不低于每间蔬菜水果类店面月租费的90%，则x的最大值为_________万元．参考答案：16；1【分析】（1）设蔬菜水果类和肉食水产类店分别为，根据条件建立不等关系和相等关系，求解，确定解的个数；（2）平均每间店的收入不低于每间蔬菜水果类店面月租费的90%建立不等式，根据不等式恒成立求的最大值即可.【详解】设蔬菜水果类和肉食水产类店分别为, （1）由题意知，，化简得：，又，所以，解得：，共种；（2）由题意知，，，，，即的最大值为1万元，故答案为：16；1【点睛】本题主要考查了不等式在实际问题中的应用，不等式的性质，属于难题.16. 某电视台夏日水上闯关节目中的前三关的过关率分别为0.8,0.7,0.6，只有通过前一关才能进入下一关，且通过每关相互独立．一选手参加该节目，则该选手只闯过前两关的概率为______________．参考答案：0.224【分析】依据题意可知，该选手过了前两关，没过第三关，利用相互独立事件概率乘法公式即可求出。