平行线与三角形内角和的综合应用每日一题目及答案word版

平行线与三角形内角和过程训练综合测试（二）

（人教版）

一、单选题(共6道，每道16分)

1.请根据过程示范完成下题．

例题：已知：如图，直线AB，CD被直线EF所截，AB∥CD，∠2=50°，求∠1的度数．

过程示范如下：

解：如图，

∵AB∥CD（已知）

∴∠1=∠2（两直线平行，同位角相等）

∵∠2=50°（已知）

∴∠1=50°（等量代换）

问题：

已知：如图，在△ABC中，点D，E分别在AB，AC边上，DE∥BC，∠1=60°，求∠B的度数．

解：如图，

∵_____________（已知）

∴_____________（________________）

∵∠1=60°（已知）

∴_____________（________________）

①DE∥BC；②∠1=∠B；③∠AED=∠C；④同位角相等，两直线平行；⑤两直线平行，同位角相等；⑥等量代换；⑦同位角相等；⑧∠B=60°．

以上空缺处依次所填正确的是( )

A.①②⑤⑧⑥

B.①③⑤⑧⑦

C.①②④⑧⑦

D.②③⑤⑧⑥

答案：A

解题思路：

试题难度：三颗星知识点：平行线的性质

2.请根据过程示范，完成下题．

例题：

已知：如图，在△ABC中，∠A=30°，∠C=100°，求∠B的度数．

解：如图，

在△ABC中，∠A=30°，∠C=100°（已知）

∴∠B=180°-∠A-∠C

=180°-30°-100°

=50°（三角形的内角和等于180°）

问题：

已知：如图，AB与CD交于点E，连接BC，∠1=75°，∠C=50°，求∠B的度数．

解：如图，

∵∠1=75°（已知）

∠CEB=∠1（对顶角相等）

三角形真题汇编及答案解析

一、选择题

1．如图，11∥l2，∠1＝100°，∠2＝135°，则∠3的度数为()

A．50°B．55°C．65°D．70°

【答案】B

【解析】

【分析】

如图，延长l2，交∠1的边于一点，由平行线的性质，求得∠4的度数，再根据三角形外角性质，即可求得∠3的度数．

【详解】

如图，延长l2，交∠1的边于一点，

∵11∥l2，

∴∠4＝180°﹣∠1＝180°﹣100°＝80°，

由三角形外角性质，可得∠2＝∠3+∠4，

∴∠3＝∠2﹣∠4＝135°﹣80°＝55°，

故选B．

【点睛】

本题考查了平行线的性质及三角形外角的性质，熟练运用平行线的性质是解决问题的关键．

2．把一副三角板如图甲放置，其中∠ACB=∠DEC=90°，∠A-45°，∠D=30°，斜边AB=6，DC=7，把三角板DCE绕着点C顺时针旋转15°得到△D1CE1（如图乙），此时AB与CD1交于点O，则线段AD1的长度为（）

A．32B．5 C．4 D．31

【答案】B

【解析】

【分析】

【详解】

由题意易知：∠CAB=45°，∠ACD=30°，

若旋转角度为15°，则∠ACO=30°+15°=45°．

∴∠AOC=180°－∠ACO－∠CAO=90°．

在等腰Rt△ABC中，AB=6，则AC=BC=32．

同理可求得：AO=OC=3．

在Rt△AOD1中，OA=3，OD1=CD1－OC=4，

由勾股定理得：AD1=5．故选B．

3．如图，已知△ABC是等腰直角三角形，∠A＝90°，BD是∠ABC的平分线，DE⊥BC于E，若BC＝10cm，则△DEC的周长为（）

相交线与平行线、三角形及尺规作图

1.【辽宁沈阳2015年中考数学试卷】如图，在△ABC中，点D是边AB上一点，点E是边AC上一点，且DE∥BC，∠B=40°，∠AED=60°，则∠A的度数是（）

A．100° B．90° C．80° D．70°

【答案】C．

【解析】

考点：1．平行线的性质；2．三角形内角和定理．

2.【湖北荆门2015年中考数学试卷】如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，BM，下面结论：①△ABE≌△DBC；②∠DMA=60°；③△BPQ为等边三角形；④MB平分∠AMC，其中结论正确的有（）

A．1个 B．2个 C．3个 D．4个

【答案】D．

【解析】

在△ABP 和△DBQ 中，∵∠BAP =∠BDQ ，AB =DB ，∠ABP =∠ADBQ =60°，∴△ABP ≌△DBQ （ASA ），∴BP =BQ ，∴△BPQ 为等边三角形，∴③正确；

∵∠DMA =60°，∴∠AMC =120°，∴∠AMC +∠PBQ =180°，∴P 、B 、Q 、M 四点共圆，∵BP =BQ ，∴BP BQ =，∴∠BMP =∠BMQ ，即MB 平分∠AMC ，∴④正确；

综上所述：正确的结论有4个，故选D ．

考点：1．全等三角形的判定与性质；2．等边三角形的判定与性质．

3.【2015届湖北省黄冈市启黄中学中考模拟】如图，已知∠MON=60°，OP 是∠MON 的角平分线，点A 是OP 上一点，过点A 作ON 的平行线交OM 于点B ，AB=4．则直线AB 与ON 之间的距离是（ ）

专题4.1三角形内角和定理的运用【八大题型】

【北师大版】

【题型1运用三角形内角和定理直接求角的度数】 (1)

【题型2三角形内角和定理与角平分线、高线综合】 (4)

【题型3三角形内角和定理与平行线的性质综合】 (9)

【题型4三角形内角和定理与折叠性质综合】 (13)

【题型5三角形内角和定理与新定义问题综合】 (18)

【题型6运用三角形内角和定理探究角的数量关系】 (23)

【题型7判断直角三角形】 (30)

【题型8运用直角三角形两锐角互余的性质倒角】 (35)

【知识点1三角形的内角及内角和定理】

三角形内角的概念：三角形内角是三角形三边的夹角．每个三角形都有三个内角，且每个内角均大于0°且

小于180°．三角形内角和定理：三角形内角和是180°．

【题型1运用三角形内角和定理直接求角的度数】

【例1】（2021秋•涡阳县期末）在△ABC中，已知∠B＝∠A+10°，∠C＝∠B+25°，求∠A的度数．

【分析】将第一个等式代入第二等式用∠A表示出∠C，再根据三角形的内角和等于180°

列方程求出∠A，然后求解即可．

【解答】解：∵∠B＝∠A+10°，∠C＝∠B+25°，

∴∠C＝∠A+10°+25°＝∠A+35°，

由三角形内角和定理得，∠A+∠B+∠C＝180°，

所以，∠A+∠A+10°+∠A+35°＝180°，

解得∠A＝45°．

【变式1-1】（2022春•武侯区校级期中）如图，点E、D分别在AB、AC上．若∠B＝30°，∠C＝50°，则∠1+∠2＝°．

【分析】根据三角形的内角和定理列式整理可得∠1+∠2＝∠B+∠C，从而可求解．【解答】解：∵∠1+∠2+∠A＝180°，∠B+∠C+∠A＝180°，

七上数学每日一练：平行线的性质练习题及答案_2020年综合题版

答案解析2020年七上数学：图形的性质_相交线与平行线_平行线的性质练习题

1.

(2019南关.七上期末)

（1） 感知：如图①，若AB ∥CD ，点P 在A

B 、CD 内部，则∠P 、∠A 、∠

C 满足的数量关系是．

（2） 探究：如图②，若AB ∥CD ，点P 在AB 、CD 外部，则∠APC 、∠A 、∠C 满足的数量关系是．

请补全以下证明过程：

证明：如图③，过点P 作PQ ∥AB

∴∠A ＝

∵AB ∥CD ，PQ ∥AB

∴∥CD

∴∠C ＝∠

∵∠APC ＝∠﹣∠

∴∠APC ＝

（3） 应用：

① 如图④，为北斗七星的位置图，如图⑤，将北斗七星分别标为A 、B 、C 、D 、E 、F 、G ，其中B 、C 、D 三点在一条直线上，AB ∥EF ，则∠

B 、∠D 、∠E 满足的数量关系是．

② 如图⑥，在（1）问的条件下，延长AB 到点M ，延长FE 到点N ，过点B 和点E 分别作射线BP 和EP ，交于点P ，使得B D 平分∠MBP ，EN 平分∠DEP ，若∠MBD ＝25°，则∠D ﹣∠P ＝°．

考点： 角的平分线;平行线的性质;2.

(2019德惠.七上期末) 三角板是学习数学的重要工具，将一副三角板中的两块直角三角板的直角顶点C 按如图方式叠放在一起，当0°＜∠ACE ＜90°且点E 在直线AC 的上方时，解决下列问题：（友情提示：∠A ＝60°，∠D ＝30°，∠B ＝∠E ＝45°）．

答案解析答案解析

答案解析（1） ①若∠DCE ＝45°，则∠ACB 的度数为；

三角形的内角和与外角的性质（含答案）

一个零件的形状如图所示，按规定∠90°, ∠21°, ∠20°,检验工人量得∠130°，就断定这个零件不合格，你能运用所学的知识说出其中的道理吗？

C

D

A B

2、将一副直角三角板如图所示放置，使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边重合，则∠1的度数为（）

A、45°

B、60°

C、75°

D、85°

3、如图，已知∥，∠60°，∠25°，则∠E等于（）

A、60°

B、25°

C、35°

D、45°

4、如图所示，∥，∠37°，∠20°，则∠的度数为（）

A、57°

B、60°

C、63°

D、123°

5、直角三角形中两锐角平分线所交成的角的度数是（）

A、45°

B、135°

C、45°或135°

D、都不对

6、如图，△中，∠90°，∠50°，将其折叠，使点A落在边上A′处，折痕为，则∠A′（）

A、40°

B、30°

C、20°

D、10°

7、如图，、都是△的角平分线，且∠110°，则∠（）

A、50°

B、40°

C、70°

D、35°

8、如图，将等边三角形剪去一个角后，则∠1+∠2的大小为（）

A、120°

B、180°

C、200°

D、240°

13、如图在△中，∠50°，∠80°，平分∠，平分∠，则∠的大小是（）

A、B、 C、 D、

18、如图，∠31°，又∠的平分线与∠的平分线相交于E点，则∠为（）

A、14.5°

B、15.5°

C、16.5°

D、20°

20、（2010?聊城）如图，l∥m，∠1=115°，∠2=95°，则∠3=（）

A、120°

B、130°

C、140°

D、150°

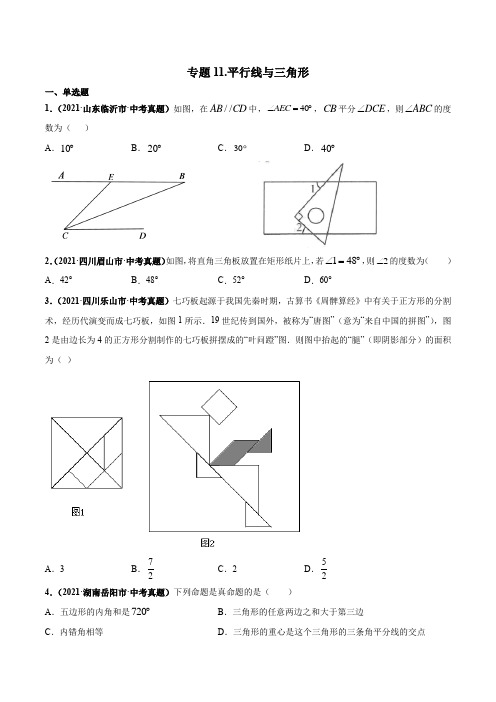
专题11.平行线与三角形

一、单选题

1．（2021·山东临沂市·中考真题）如图，在//AB CD 中，40AEC ∠=︒，CB 平分DCE ∠，则ABC ∠的度数为（ ）

A ．10︒

B ．20︒

C ．30

D ．40︒

2．（2021·四川眉山市·中考真题）如图，将直角三角板放置在矩形纸片上，若148∠=︒，则2∠的度数为（ ）

A ．42°

B ．48°

C ．52°

D ．60°

3．（2021·四川乐山市·中考真题）七巧板起源于我国先秦时期，古算书《周髀算经》中有关于正方形的分割术，经历代演变而成七巧板，如图1所示．19世纪传到国外，被称为“唐图”（意为“来自中国的拼图”），图2是由边长为4的正方形分割制作的七巧板拼摆成的“叶问蹬”图．则图中抬起的“腿”（即阴影部分）的面积为（ ）

A ．3

B ．72

C ．2

D ．52

4．（2021·湖南岳阳市·中考真题）下列命题是真命题的是（ ）

A ．五边形的内角和是720︒

B ．三角形的任意两边之和大于第三边

C ．内错角相等

D ．三角形的重心是这个三角形的三条角平分线的交点

5．（2021·安徽中考真题）两个直角三角板如图摆放，其中90BAC EDF ∠=∠=︒，45E ∠=︒，30C ∠=︒，AB 与DF 交于点M ．若//BC EF ，则BMD ∠的大小为（ ）

A ．60︒

B ．67.5︒

C ．75︒

D ．82.5︒

6．（2021·浙江金华市·中考真题）某同学的作业如下框，其中※处填的依据是（ ）

A ．两直线平行，内错角相等

B ．内错角相等，两直线平行

C ．两直线平行，同位角相等

三角形内角和定理练习题

1.在△ABC中，∠A＝∠B＝∠C，则△ABC是三角形.

2.如图，在△ABC中，BE、CF分别是∠ABC和∠ACB的角平分线，它们相交于点I，已知∠A＝56°，则∠BIC＝.

3.如图，在△ABC中，∠B＝25°，延长BC至E，过点E作AC的垂线ED，垂足为O，且∠E＝40°，则∠A＝.

4.如图，若AB＝AC，BG＝BH，AK＝KG，则∠BAC的度数为.

5.若等腰三角形一腰上的高和另一腰上的高的夹角为58°，则这个等腰三角形顶角的度数是.

6.如图，将三角形纸片ABC的一角折叠，折痕为EF，若∠A＝80°，∠B＝68°，∠CFB＝22°，则∠CEA ＝.

7.在一个三角形中，三个内角中至少有个锐角，最多有个直角或钝角.

8.如图，AB∥CD，若∠ABE＝135°，∠CDE＝110°，则∠DEF＝.

9.如图，在△ABC中，∠B＝∠C，FD⊥BC，DE⊥AB，∠AFD＝158°，则∠EDF等于( )

A.64°

B.65°

C.67°

D.68°

10.如图，已知AB∥CD，BE平分∠ABD，DE平分∠BDC，则∠E是( )

A.锐角

B.直角

C.钝角

D.无法确定

11.如图，已知在△ABC中，AD平分外角∠EAC，AD∥BC，则△ABC的形状是( ) A.等边三角形 B.

直角三角形 C.等腰三角形 D.任意三角形

12.如图，在△ABC中，∠ABC和∠ACB的外角平分线交于点D，设∠BAC＝∠α，则∠D等于( )

A.180°-2∠α

B.180°-∠α

C.90°-∠α

D.90°-2∠α

13.如果三角形的一个外角等于与它相邻的内角，那么这个三角形的形状是( )

人教版八年级数学上册第一单元

《三角形的内角和》同步练习2

（含参考答案）

一．选择题

1．已知在Rt△ABC中，∠B＝90°，∠C＝35°，则∠A等于（）A．35°B．45°C．55°D．65°

2．如右图，已知AB⊥BD，AC⊥CD，∠A＝40°，则∠D的度数为（）A．40°B．50°C．60°D．70°

3．如右图，Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，则下列结论不一定成立的是（）

A．∠1+∠2＝90°B．∠2＝∠3 C．∠1＝∠4 D．∠1＝30°

4．直角三角形两个锐角平分线相交所成的钝角的度数为（）

A．90°B．135°C．120°D．45°或135°5．如右图△ABC中，∠BAC＝90°，AD⊥BC，AE平分∠BAC，∠B＝2∠C，∠DAE的度数是（）

A．45°B．20°C．30°D．15°

二．填空题

6．若直角三角形的一个锐角为15°，则另一个锐角等于．

7．如右图，直线a∥b，在Rt△ABC中，点C在直线a上，若∠1＝54°，∠2＝24°，则∠B的度数为．

8．在直角三角形中，两个锐角的度数比为2：3，那么较小锐角的度数是．9．如右图，在△ABC中，∠ACB＝90°，AD平分∠CAB，交边BC于点D，过点D作DE⊥AB，垂足为E．若∠CAD＝20°，则∠EDB的度数是．

10．将两张矩形纸片如图所示摆放，使其中一张矩形纸片的一个顶点恰好落在另一张矩形纸片的一条边上，则∠1+∠2＝．

三．解答题

11．AD、BE为△ABC的高，AD、BE相交于H点，∠C＝50°，求∠BHD．12．解方程组：．

规律方法指导

1．三角形内角和为180°，三角形三个外角的和是360°，这是在做题时题设不用加以说明的已知条件;

在三个角中已知其中两个角的度数便能求第三个角的大小。

2．在一个三角形中最多只能有一个钝角或者一个直角，最少有两个锐角。

3．三角形内角和定理和三角形外角的性质是求角度数及有关的推理论证时经常使用的理论依据．

外角的性质应用：①证明一个角等于另两个角的和；②作为中间关系式证明两角相等；③证明角的不等关系。

4．利用作辅助线求解问题，会使问题变得简便。

经典例题透析

类型一：三角形内角和定理的应用

1．已知一个三角形三个内角度数的比是1:5：6，则其最大内角的度数为( ）A．60° B．75° C．90° D．120°

举一反三:

【变式1】在△ABC中，∠A=55°，∠B比∠C大25°,则∠B的度数为（ )

A．50° B．75°C．100° D．125°

【变式2】三角形中至少有一个角不小于________度。

类型二：利用三角形外角性质证明角不等

2．如图所示，已知CE是△ABC外角∠ACD的平分线，CE交BA延长线于点E。求证：∠BAC ＞∠B。

举一反三：

【变式】如图所示,用“＜”把∠1、∠2、∠A联系起来________。

类型三：三角形内角和定理与外角性质的综合应用

3．如图,求∠A+∠B+∠C+∠D+∠E的度数.

举一反三：

【变式】如图所示,五角星ABCDE中，试说明∠A+∠B+∠C+∠D+∠E=180°。

类型四:与角平分线相关的综合问题

4．如图9，△ABC中，∠ABC、∠ACB的平分线相交于点Ｄ．（1）若∠ABC＝70°，∠ACB＝50°，则∠BDC＝________;

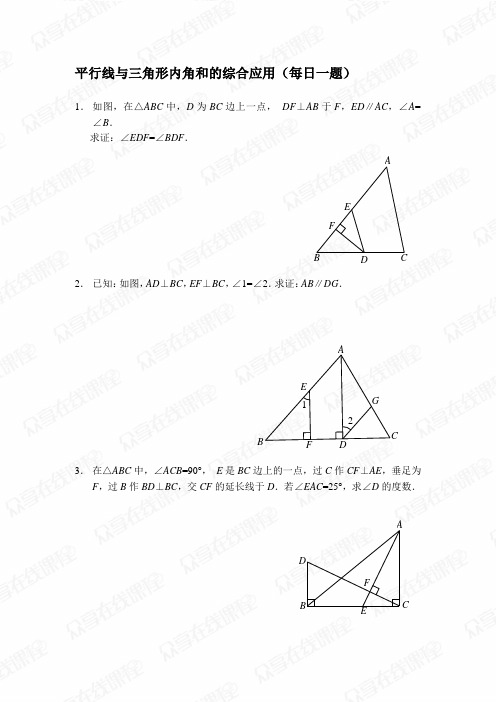
平行线与三角形内角和的综合应用（每日一题）

1． 如图，在△ABC 中，D 为BC 边上一点， DF ⊥AB 于F ，ED ∥AC ，∠A =

∠B ．

求证：∠EDF =∠BDF ．

F E D

C

B

A

2． 已知：如图，AD ⊥BC ，EF ⊥BC ，∠1=∠2．求证：AB ∥DG ．

2

1

G

F E D

C

B

A

3． 在△ABC 中，∠ACB =90°， E 是BC 边上的一点，过C 作CF ⊥AE ，垂足为

F ，过B 作BD ⊥BC ，交CF 的延长线于D ．若∠EAC =25°，求∠D 的度数．

F

E

D

C

B

A

4． 已知：如图，AC 、EF 相交于点O ，∠E =∠F ，∠1=∠2．

求证：AB ∥DG ．

O

2

1

C

G

D

F

E

B

A

5． 已知：如图，AD ∥EF ，BF ∥DG ，∠A =∠B =∠G =35°．

求∠EFG 的度数．

G

F

E

D

C

B

A

【参考答案】

1.证明：如图，

∵DE∥AC （已知）∴∠A＝∠FED （两直线平行，同位角相等）∵∠A=∠B（已知）∴∠B＝∠FED （等量代换）∵DF⊥AB（已知）∴∠FED +∠EDF =∠B+∠BDF=90°（直角三角形两锐角互余）∴∠EDF=∠BDF（等角的余角相等）2.证明：如图，

∵EF⊥BC （已知）

∴∠B+∠1=90°（直角三角形两锐角互余）

∵AD⊥BC（已知）

∴∠2+∠CDG=90°（垂直的性质）

∵∠1=∠2 （已知）

∴∠B=∠CDG （等角的余角相等）

∴AB∥DG（同位角相等，两直线平行）

3.解：如图，

∵CF⊥AE（已知）

∴∠EAC +∠ACD=90°（直角三角形两锐角互余）

第五章相交线与平行线单元试卷试卷（word 版含答案）

一、选择题

1．下列命题是真命题的是（ ）

A ．直角三角形中两个锐角互补

B ．相等的角是对顶角

C ．同旁内角互补，两直线平行

D ．若a b =，则a b = 2．如图，给出下列条件：①∠3=∠4；②∠1=∠2；③∠5=∠B ；④AD ∥B

E ，且∠D =∠B ．其

中能说明AB ∥DC 的条件有（ ）

A ．4个

B ．3个

C ．2个

D ．1个 3．如图，直线l 1，l 2，l 3交于一点，直线l 4∥l 1，若∠1=124°，∠2=88°，则∠3的度数为

（ ）

A ．26°

B ．36°

C ．46°

D ．56° 4．如果A ∠与B 的两边分别平行，A ∠比B 的3倍少36，则A ∠的度数是( )

A ．18

B ．126

C ．18或126

D ．以上都不对 5．①如图1,AB∥CD,则∠A +∠

E +∠C=180°；②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E－∠1=180° ； ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )

A ．、1个

B ．2个

C ．3个

D ．4个 6．下列命题中，假命题的个数为（ ） （1）“是任意实数，

”是必然事件； （2）抛物线的对称轴是直线；

（3）若某运动员投篮2次，投中1次，则该运动员投1次篮，投中的概率为

；

（4）某件事情发生的概率是1，则它一定发生；

（5）某彩票的中奖率为10%，则买100张彩票一定有1张会中奖；

（6）函数与轴必有两个交点．

A ．2

B ．3

《7.5 三角形内角和定理》

一、选择题

1、一个多边形的每个内角都等于156°，则此多边形是（）

A.十五边形

B.十六边形

C.十七边形

D.十八边形

2、具备下列条件的△ABC中，不是直角三角形的是（）

A.∠A+∠B=∠C

B.∠A-∠B=∠C

C.∠A:∠B:∠C=1:2:3

D.∠A=∠B=3∠C

3、一个三角形的三个外角中，钝角的个数最少为（）

A.0个

B.1个

C.2个

D.3个

4、若一个三角形三个内角度数的比为2：7：4，那么这个三角形是（）

A．直角三角形 B．锐角三角形 C．钝角三角形 D．等边三角形

5、已知△ABC的三个内角∠A、∠B、∠C满足关系式∠B+∠C=∠A，则此三角形（）

A．一定有一个内角为45° B．一定有一个内角为60°

C．一定是直角三角形 D．一定是钝角三角形

6、在△ABC中，∠A﹣∠B=35°，∠C=55°，则∠B等于（）

A．50°B．55°C．45°D．40°

7、如图，在△ABC中，∠B=46°，∠C=54°，AD平分∠BAC，交BC于D，DE∥AB，交AC于E，则∠ADE的大小是（） A．45°B．54°C．40°D．50°

第7题第8题第10题第11题

8、如图，△ABC中，∠C=70°，若沿图中虚线截去∠C，则∠1+∠2=（）

A．360°B．250°C．180°D．140°

9、关于三角形内角的叙述错误的是（）

A．三角形三个内角的和是180° B．三角形两个内角的和一定大于60°

C．三角形中至少有一个角不小于60° D．一个三角形中最大的角所对的边最长

10、如图，点O是△ABC内一点，∠A=80°，∠1=15°，∠2=40°，则∠BOC等于（）

平行线与三角形内角和的综合应用（讲义）➢课前预习

1.如图，在△ABC中，如果∠C=90°，∠A=30°，则∠B=_______，∠A+

∠B=_______，也就是∠A与∠B________（填“互余”、“互补”）．

2.在下面的括号内，填上推理的根据．

（1）如图，已知直线AB，CD相交于点O，∠1=30°，求∠2

的度数．

解：如图，

∵∠1=∠2 （_______________________）

∠1=30° （已知）

∴∠2=______ （_______________________）

（2）如图，已知∠AOC=∠BOD=90°，求证：∠AOD=∠BOC．

解：如图，

∵∠AOC=∠BOD=90° （_______________________）

∴∠AOD=∠BOC （_______________________）

➢知识点睛

1.三角形的内角和等于__________．

已知：如图，△ABC．

求证：∠BAC+∠B+∠C=180°．

证明：_______，_____________________________________．

∵MN∥BC （已作）

∴∠B=∠1，∠C=∠2（_______________________）

∵∠BAC+∠1+∠2=180°（_______________________）

∴∠BAC+∠B+∠C=180°（_______________________）

2.直角三角形两锐角___________．

➢精讲精练

1.如图，在△ABC中，∠A=50°，∠C=72°，BD是△ABC的一条角平分线，