数字电子技术基础康华光第五版答案
- 格式:docx
- 大小:527.45 KB
- 文档页数:20
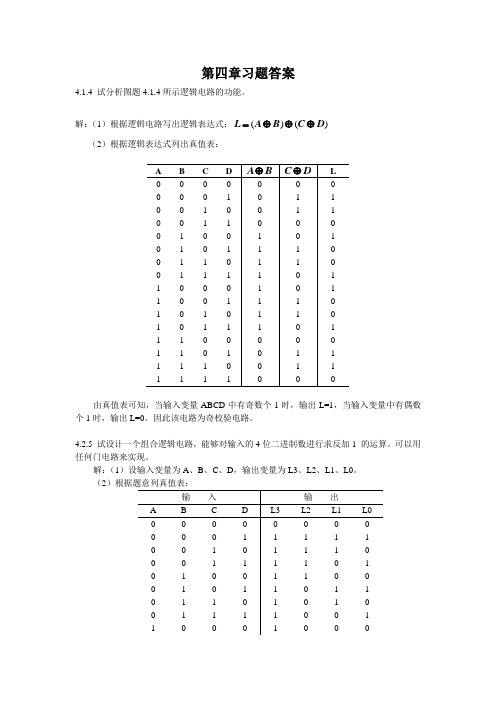
第四章习题答案4.1.4 试分析图题4.1.4所示逻辑电路的功能。
解:(1)根据逻辑电路写出逻辑表达式:()()L A B C D =⊕⊕⊕ (2)根据逻辑表达式列出真值表:由真值表可知,当输入变量ABCD 中有奇数个1时,输出L=1,当输入变量中有偶数个1时,输出L=0。
因此该电路为奇校验电路。
4.2.5 试设计一个组合逻辑电路,能够对输入的4位二进制数进行求反加1 的运算。
可以用任何门电路来实现。
解:(1)设输入变量为A 、B 、C 、D ,输出变量为L3、L2、L1、L0。
(2)根据题意列真值表:(3)由真值表画卡诺图(4)由卡诺图化简求得各输出逻辑表达式()()()3L AB A C AD ABCD A B C D A B C D A B C D =+++=+++++=⊕++ ()()()2L BC BD BCD B C D B C D B CD =++=+++=⊕+ 1L CD CD C D =+=⊕0L D =(5)根据上述逻辑表达式用或门和异或门实现电路,画出逻辑图如下:A B CDL 3L 2L 1L 04.3.1判断下列函数是否有可能产生竞争冒险,如果有应如何消除。
(2)(,,,)(,,,,,,,)2578910111315L A B C D m =∑ (4)(,,,)(,,,,,,,)4024612131415L A B C D m =∑解:根据逻辑表达式画出各卡诺图如下:(2)2L AB BD =+,在卡诺图上两个卡诺圈相切,有可能产生竞争冒险。
消除办法:在卡诺图上增加卡诺圈(虚线)包围相切部分最小项,使2L AB BD AD =++,可消除竞争冒险。
(4)4L AB AD =+,在卡诺图上两个卡诺圈相切,有可能产生竞争冒险。
消除办法:在卡诺图上增加卡诺圈(虚线)包围相切部分最小项,使4L AB AD BD =++,可消除竞争冒险。
4.3.4 画出下列逻辑函数的逻辑图,电路在什么情况下产生竞争冒险,怎样修改电路能消除竞争冒险。

第一章习题答案一周期性信号的波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比0121112(ms)图题1.1.4解: 周期T=10ms 频率f=1/T=100Hz占空比q=t w /T ×100%=1ms/10ms ×100%=10%将下列十进制数转换为二进制数、八进制数和十六进制数,要求误差不大于2-4:(1)43(2)127(3)(4)解:1. 转换为二进制数:(1)将十进制数43转换为二进制数,采用“短除法”,其过程如下:2 43 ………………………余1……b 02 21 ………………………余1……b 12 1 ………………………余1……b 52 2 ………………………余0……b 42 5 ………………………余1……b 32 10 ………………………余0……b 2高位低位从高位到低位写出二进制数,可得(43)D =(101011)B(2)将十进制数127转换为二进制数,除可用“短除法”外,还可用“拆分比较法”较为简单: 因为27=128,因此(127)D =128-1=27-1=(1000 0000)B -1=(111 1111)B(3)将十进制数转换为二进制数,整数部分(254)D =256-2=28-2=(1 0000 0000)B -2=(1111 1110)B 小数部分()D =()B()D=(1111 )B(4)将十进制数转换为二进制数整数部分(2)D=(10)B小数部分()D=()B演算过程如下:0.718×2=1.436……1……b-1 0.436×2=0.872……0……b-2 0.872×2=1.744……1……b-3 0.744×2=1.488……1……b-4 0.488×2=0.976……0……b-5 0.976×2=1.952……1……b-6高位低位要求转换误差小于2-4,只要保留小数点后4位即可,这里算到6位是为了方便转换为8进制数。

第一章数字逻辑习题1.1数字电路与数字信号1.1.2 图形代表的二进制数0101101001.1.4一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSB LSB0 1 2 11 12 (ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/0.01s=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%1.2数制2 1.2.2将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于4(2)127 (4)2.718解:(2)(127)D=72-1=(10000000)B-1=(1111111)B=(177)O=(7F)H(4)(2.718)D=(10.1011)B=(2.54)O=(2.B)H1.4二进制代码1.4.1将下列十进制数转换为8421BCD码:(1)43 (3)254.25解:(43)D=(01000011)BCD1.4.3试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+ (2)@ (3)you (4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+”的ASCⅡ码为0101011,则(00101011)B=(2B)H(2)@的ASCⅡ码为1000000,(01000000)B=(40)H(3)you的ASCⅡ码为本1111001,1101111,1110101,对应的十六进制数分别为79,6F,75(4)43的ASCⅡ码为0110100,0110011,对应的十六紧张数分别为34,331.6逻辑函数及其表示方法1.6.1在图题1. 6.1中,已知输入信号A,B`的波形,画出各门电路输出L的波形。
解: (a)为与非, (b)为同或非,即异或第二章 逻辑代数 习题解答2.1.1 用真值表证明下列恒等式 (3)A B AB AB ⊕=+(A ⊕B )=AB+AB 解:真值表如下A B A B ⊕ABAB A B ⊕AB +AB0 0 0 1 0 1 1 0 1 1 0 0 0 0 1 0 1 0 0 0 0 11111由最右边2栏可知,A B ⊕与AB +AB 的真值表完全相同。

第1章 数字逻辑概论1.1 复习笔记一、模拟信号与数字信号 1.模拟信号和数字信号 (1)模拟信号在时间上连续变化,幅值上也连续取值的物理量称为模拟量,表示模拟量的信号称为模拟信号,处理模拟信号的电子电路称为模拟电路。
(2)数字信号 与模拟量相对应,在一系列离散的时刻取值,取值的大小和每次的增减都是量化单位的整数倍,即时间离散、数值也离散的信号。
表示数字量的信号称为数字信号,工作于数字信号下的电子电路称为数字电路。
(3)模拟量的数字表示①对模拟信号取样,通过取样电路后变成时间离散、幅值连续的取样信号; ②对取样信号进行量化即数字化;③对得到的数字量进行编码,生成用0和1表示的数字信号。
2.数字信号的描述方法(1)二值数字逻辑和逻辑电平在数字电路中,可以用0和1组成的二进制数表示数量的大小,也可以用0和1表示两种不同的逻辑状态。
在电路中,当信号电压在3.5~5 V 范围内表示高电平;在0~1.5 V 范围内表示低电平。
以高、低电平分别表示逻辑1和0两种状态。
(2)数字波形①数字波形的两种类型非归零码:在一个时间拍内用高电平代表1,低电平代表0。
归零码:在一个时间拍内有脉冲代表1,无脉冲代表0。
②周期性和非周期性周期性数字波形常用周期T 和频率f 来描述。
脉冲波形的脉冲宽度用W t 表示,所以占空比100%t q T=⨯W③实际数字信号波形在实际的数字系统中,数字信号并不理想。
当从低电平跳变到高电平,或从高电平跳到低电平时,边沿没有那么陡峭,而要经历一个过渡过程。
图1-1为非理想脉冲波形。
图1-1 非理想脉冲波形④时序图:表示各信号之间时序关系的波形图称为时序图。
二、数制 1.十进制以10为基数的计数体制称为十进制,其计数规律为“逢十进一”。
任意十进制可表示为:()10iDii N K ∞=-∞=⨯∑式中,i K 可以是0~9中任何一个数字。
如果将上式中的10用字母R 代替,则可以得到任意进制数的表达式:()iR ii N K R ∞=-∞=⨯∑2.二进制(1)二进制的表示方法以2为基数的计数体制称为二进制,其只有0和1两个数码,计数规律为“逢二进一”。

第一章数字逻辑习题1.1 数字电路与数字信号图形代表的二进制数1.1.4 一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSB LSB0 1 2 11 12 (ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%数制将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于24(2)127 (4)解:(2)(127)D= 27 -1=()B-1=(1111111)B=(177)O=(7F)H(4)()D=B=O=H二进制代码将下列十进制数转换为 8421BCD 码:(1)43 (3)解:(43)D=(01000011)BCD试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+ (2)@ (3)you (4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+”的ASCⅡ码为 0101011,则(00101011)B=(2B)H(2)@的ASCⅡ码为 1000000,(01000000)B=(40)H(3)you 的ASCⅡ码为本 1111001,1101111,1110101,对应的十六进制数分别为 79,6F,75(4)43 的ASCⅡ码为 0110100,0110011,对应的十六紧张数分别为 34,33 逻辑函数及其表示方法在图题 1. 中,已知输入信号 A,B`的波形,画出各门电路输出 L 的波形。
解: (a)为与非, (b)为同或非,即异或第二章逻辑代数习题解答用真值表证明下列恒等式(3)A⊕ =B AB AB+(A⊕B)=AB+AB用逻辑代数定律证明下列等式(3)A+ABC ACD C D E A CD E+ + +( ) = + + 解:A+ABC ACD C D E+ + +( )=A(1+BC ACD CDE)+ += +A ACD CDE+= +A CD CDE+ = +A CD+ E用代数法化简下列各式(3) ABC B( +C) 解:ABC B( +C)= + +(A B C B C)( + )=AB AC BB BC CB C++ + + +=AB C A B B+ ( + + +1)=AB C+(6)(A+ + + +B A B AB AB) ( ) ()( ) 解:(A+ + + +B A B ABAB) ( ) ( )( )= A B + A B+(A+ B A)(+ B)=AB(9)ABCD ABD BCD ABCBD BC+ + + + 解:ABCD ABD BCD ABCBD BC+ + + + =ABC D D ABD BC D C( + +) + ( + ) =B AC AD C D( + + + ) =B A C A D( + + + ) =B A C D( + + ) =AB BC BD+ +画出实现下列逻辑表达式的逻辑电路图,限使用非门和二输入与非门B AB AB = + + AB B = + A B= + (1) L AB AC= + (2) ( ) L DAC= +已知函数L (A ,B ,C ,D )的卡诺图如图所示,试写出函数L 的最简与或表达式用卡诺图化简下列个式(3)( )() L ABCD=+ + 解: ( , , , ) L ABCDBCDBCDBCDABD= + + +(1)ABCD ABCD AB AD ABC++ + + 解:ABCD ABCD AB AD ABC+ + + +=ABCD ABCD ABC C D D AD B B C C ABC D D+ + ( + )( + +) ( + )( + +) ( + ) =ABCD ABCD ABCD ABCD ABCD ABCD ABCD+ + ++ + +(6)L A B C D( , , , ) =∑m (0,2,4,6,9,13)+∑d(1,3,5,7,11,15)L= +A D(7)L A B C D( , , , ) =∑m (0,13,14,15)+∑d(1,2,3,9,10,11)L AD AC AB=+ +解:解:已知逻辑函数L AB BC CA= + +,试用真值表,卡诺图和逻辑图(限用非门和与非门)表示解:1>由逻辑函数写出真值表A B C L0 0 0 00 0 1 10 1 0 10 1 1 11 0 0 11 0 1 11 1 0 11 1 1 0用摩根定理将与或化为与非表达式L = AB + BC + AC = AB BC AC4>由已知函数的与非-与非表达式画出逻辑图2>由真值表画出卡诺图3>由卡诺图,得逻辑表达式LABBCAC=++第三章习题MOS 逻辑门电路根据表题所列的三种逻辑门电路的技术参数,试选择一种最合适工作在高噪声环境下的门电路。
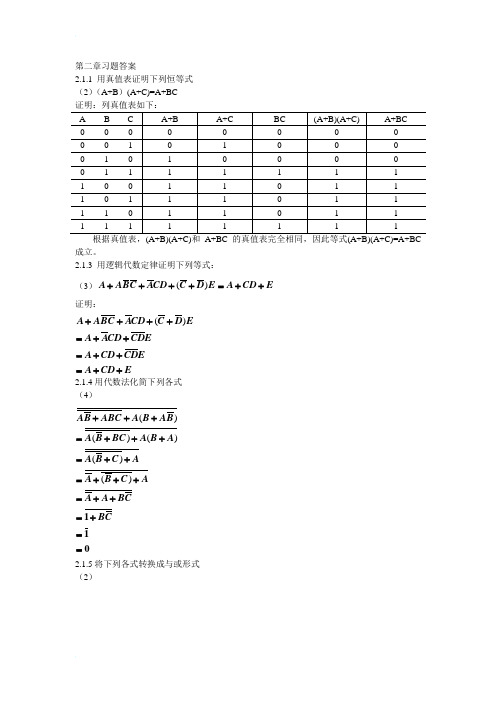
第二章习题答案2.1.1 用真值表证明下列恒等式 (2)(A+B )(A+C)=A+BC 证明:列真值表如下:成立。
2.1.3 用逻辑代数定律证明下列等式:(3)()A ABC ACD C D E A CD E ++++=++ 证明:()A ABC ACD C D E A ACD CDE A CD CDE A CD E++++=++=++=++2.1.4用代数法化简下列各式 (4)()()()()()110AB ABC A B AB A B BC A B A A B C A A B C A A A BC BC +++=+++=++=+++=++=+==2.1.5将下列各式转换成与或形式 (2)()()()()A B C D C D A DA B C D C D A D AC AD BC BD AC CD AD D AC BC AD BD CD D AC BC D+++++++=+++++=+++++++=+++++=++2.1.7 画出实现下列逻辑表达式的逻辑电路图,限使用非门和二输入与非门。
(1)L=AB+AC解:先将逻辑表达式化为与非-与非式:L AB AC AB AC AB AC =+=+=根据与非-与非表达式,画出逻辑图如下:LA B C2.1.8 已知逻辑函数表达式为L AB AC =+,画出实现该式的逻辑电路图,限使用非门和二输入或非门。
解:先将逻辑函数化为或非—或非表达式L AB A C AB A C A B A C =+=+=+++根据或非—或非表达式,画出逻辑图如下:A B CL另一种做法:用卡诺图化简变换为最简或与式A+B()()()()L A C A B A C A B A C A B =++=++=+++根据或非—或非表达式,画出逻辑图如下:AC BL2.2.1将下列函数展开为最小项表达式 (1)()()(,,,,)29101315L ACD BC D ABCD A B B CD ABCD A A BC D ABCD ABCD ABCD ABC D ABC D ABCD m =++=+++++=++++=∑(2)()L A B C =+()()()(,,)023L A B C AB AC AB C C A B B CABC ABC ABC ABC ABC ABC ABC m =+=+=+++=+++=++=∑(,,,,)14567L L m ==∑2.2.3用卡诺图化简下列各式(1) ABCD ABCD AB AD ABC ++++ 解:由逻辑表达式作卡诺图如下:ABAD由卡诺图得到最简与或表达式如下:L AB AC AD =++(5)(,,,)(,,,,,,,,,)0125689101314L A B C D m =∑解:由逻辑表达式作卡诺图如下:由卡诺图得到最简与或表达式如下:(,,,)L A B C D BD CD C D =++(7) (,,,)(,,,)(,,,,,)013141512391011L A B C D m d =+∑∑解:由逻辑表达式作卡诺图如下:A BAD AC由卡诺图得到最简与或表达式如下:=++(,,,)L A B C D AB AC AD。

第一章习题答案一周期性信号的波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比012(ms)图题1.1.4解:周期T=10ms频率f=1/T=100Hz占空比q=t w/T×100%=1ms/10ms×100%=10%将下列十进制数转换为二进制数、八进制数和十六进制数,要求误差不大于2-4:(1)43 (2)127 (3)(4)解:1. 转换为二进制数:(1)将十进制数43转换为二进制数,采用“短除法”,其过程如下:2 43 ………………………余1……b 02 21 ………………………余1……b 12 1 ………………………余1……b 52 2 ………………………余0……b 42 5 ………………………余1……b 32 10 ………………………余0……b20高位低位从高位到低位写出二进制数,可得(43)D =(101011)B(2)将十进制数127转换为二进制数,除可用“短除法”外,还可用“拆分比较法”较为简单: 因为27=128,因此(127)D=128-1=27-1=(1000 0000)B -1=(111 1111)B(3)将十进制数转换为二进制数,整数部分(254)D =256-2=28-2=(1 0000 0000)B -2=(1111 1110)B小数部分()D =()B ()D =(1111 )B(4)将十进制数转换为二进制数 整数部分(2)D =(10)B 小数部分()D =()B演算过程如下:0.718×2=1.436……1……b-1 0.436×2=0.872……0……b-2 0.872×2=1.744……1……b-3 0.744×2=1.488……1……b-4 0.488×2=0.976……0……b-5 0.976×2=1.952……1……b-6高位低位要求转换误差小于2-4,只要保留小数点后4位即可,这里算到6位是为了方便转换为8进制数。



第三章作业答案3.1.2(2)求74LS 门驱动74ALS 系列门电路的扇出数解:首先分别求出拉电流工作时的扇出数N OH 和灌电流工作时的扇出数N OL ,两者中的最小值就是扇出数。
从教材附录A 可查得74LS 系列门电路的输出电流参数为I OH =0.4mA,I OL =8mA ,74ALS 系列门电路的输入电流参数为I IH =0.02mA,I IL =0.1mA拉电流工作时的扇出数..0420002OH OH IH I mAN I mA===灌电流工作时的扇出数.88001OL OL IL I mAN I mA===因此,74LS 门驱动74ALS 系列门电路的扇出数N O 为20。
3.1.4已知图题3.1.4所示各MOSFET 管的∣V T ∣=2V ,忽略电阻上的压降,试确定其工作状态(导通或截止)。
解:图(a )和(c )为N 沟道场效应管,对于图(a ),V GS =5V>V T ,因此管子导通对于图(c ),V GS =0V<V T ,因此管子截止图(b )和(d )为P 沟道场效应管,对于图(b ),V GS =5V-5V=0>V T ,因此管子截止对于图(d ),V GS =0V-5V=-5V<V T ,因此管子导通3.1.7写出图题3.1.7所示电路的输出逻辑表达式.解:L AB BC D E=A A A 3.1.12试分析图题3.1.12所示的CMOS 电路,说明他们的逻辑功能。
解:从图上看,这些电路都是三态门电路,分析这类电路要先分析使能端的工作情况,然后再分析逻辑功能。
(a )当=0时,T P2和T N2均导通,由T P1和T N1组成的反相器正常工作,;EN L A =当=1时,T P2和T N2均截止,此时无论输入端A 为高电平还是低电平,输出端均EN 为高阻态;因此该电路为低电平使能三态非门。
(b )当=0时,或门的输出为,T P2导通,由T P1和T N1组成的反相器正常工作,EN A ;L A =当=1时,或门的输出为0,T P2和T N1均截止,此时无论输入端A 为高电平还是低EN 电平,输出端均为高阻态;因此该电路为低电平使能三态缓冲器。

第一章数字逻辑习题1.1 数字电路与数字信号图形代表的二进制数1.1.4 一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSB LSB0 1 2 11 12 (ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%数制将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于24(2)127 (4)解:(2)(127)D= 27 -1=()B-1=(1111111)B=(177)O=(7F)H(4)()D=B=O=H二进制代码将下列十进制数转换为 8421BCD 码:(1)43 (3)解:(43)D=(01000011)BCD试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+ (2)@ (3)you (4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+”的ASCⅡ码为 0101011,则(00101011)B=(2B)H(2)@的ASCⅡ码为 1000000,(01000000)B=(40)H(3)you 的ASCⅡ码为本 1111001,1101111,1110101,对应的十六进制数分别为 79,6F,75(4)43 的ASCⅡ码为 0110100,0110011,对应的十六紧张数分别为 34,33逻辑函数及其表示方法在图题 1. 中,已知输入信号 A,B`的波形,画出各门电路输出 L 的波形。
解: (a)为与非, (b)为同或非,即异或第二章逻辑代数习题解答用真值表证明下列恒等式(3)A⊕ =B AB AB+ (A⊕B)=AB+AB由最右边2栏可知,与+AB的真值表完全相同。
用逻辑代数定律证明下列等式(3)A+ABC ACD C D E A CD E++ +( ) = + +解:A+ABC ACD C D E++ +( )=A(1+BC ACD CDE)+ += +A ACD CDE+= +A CD CDE+ = +A CD+ E用代数法化简下列各式 (3)ABC B( +C)解:ABCB( +C)= + +(A B C B C)( + )=AB AC BB BC CB C+ + + + +=AB C A B B+ ( + + +1)=AB C+(6)(A+ + + +B A B AB AB) ( ) ( )()解:(A+ + + +B A B AB AB) () ( )( )= A B?+ A B?+(A+ B A)(+ B)=AB(9)ABCD ABD BCD ABCBD BC+ + + + 解:ABCD ABD BCD ABCBD BC+ + + +=ABC D D ABD BC D C( + +) + ( + ) =B AC AD C D( + + + ) =B A C A D( + + + ) =B A C D( + + ) =AB BC BD+ +画出实现下列逻辑表达式的逻辑电路图,限使用非门和二输入与非门( ))ABCD AB AC+已知函数L(A,B,C,D)的卡诺图如图所示,试写出函数L的最简与或表达式用卡诺图化简下列个式(1)ABCD ABCD AB AD ABC+ + + +解:ABCD ABCD AB AD ABC+ + + +=ABCD ABCD ABC C D D AD B B C C ABC D D++ ( + )( + +)( + )( + +)( + )=ABCD ABCD ABCD ABCD ABCD ABCD ABCD+ + + + + + (6)L A B C D( , , , )=∑m(0,2,4,6,9,13)+∑d(1,3,5,7,11,15)L= +A D(7)L A B C D( , , , )=∑m(0,13,14,15)+∑d(1,2,3,9,10,11)L AD AC AB= + +已知逻辑函数L AB BC CA=+ + ,试用真值表,卡诺图和逻辑图(限用非门和与非门)表示解:1>由逻辑函数写出真值表A B C L0 0 0 00 0 1 10 1 0 10 1 1 11 0 0 11 0 1 11 1 0 11 1 1 02>由真值表画出卡诺图LABBCAC用摩根定理将与或化为与非表达式L = AB + BC + AC = AB BC AC? ?4>由已知函数的与非-与非表达式画出逻辑图第三章习题MOS 逻辑门电路根据表题所列的三种逻辑门电路的技术参数,试选择一种最合适工作在高噪声环境下的门电路。
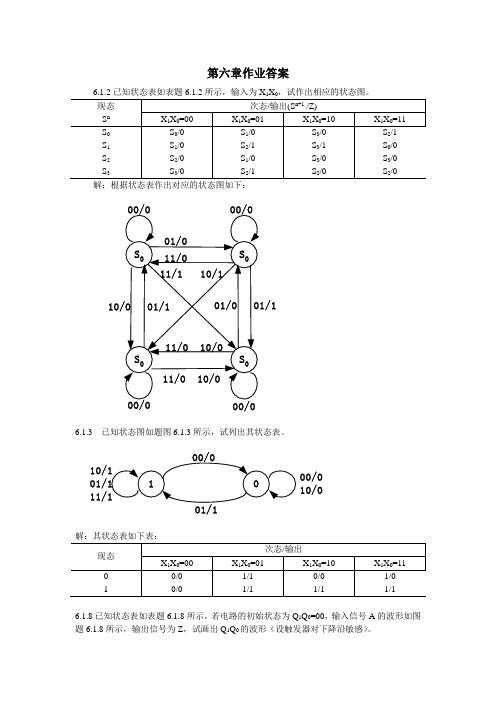
第六章作业答案解:根据状态表作出对应的状态图如下:6.1.3 已知状态图如题图6.1.3所示,试列出其状态表。
00/010/06.1.8已知状态表如表题6.1.8所示,若电路的初始状态为Q 1Q 0=00,输入信号A 的波形如图题6.1.8所示,输出信号为Z ,试画出Q 1Q 0的波形(设触发器对下降沿敏感)。
解:根据已知的状态表及输入信号A=011001,该电路将从初始状态Q1Q0=00开始,按照下图所示的顺序改变状态:Q1Q0的波形图如下:CPAQQ16.2.1试分析图题6.2.1(a)所示时序电路,画出其状态表和状态图。
设电路的初始状态为0,试画出在图题6.2.1(b)所示波形的作用下,Q和Z的波形图。
CP AZ解:由电路图可写出该电路的状态方程和输出方程分别为:1n n Q A Q Z AQ+=⊕=状态图如下所示:0/1Q 和Z 的波形如下所示:CP A Q Z6.2.4分析图题6.2.4所示电路,写出它的激励方程组、状态方程组和输出方程,画出状态表和状态图。
A CPZ解:电路的激励方程组为:10101011J Q K AQ J Q K ==== 状态方程组为:()11101101100nn n nnnnnn n Q Q Q QQ Q AQ Q Q Q A ++==+=+输出方程为: 10Z AQ Q =根据状态方程组和输出方程可列出状态表如下:状态图如下:6.3.2 某同步时序电路的状态图如图题6.3.2所示,试写出用D 触发器设计时的最简激励方程组。
解:由状态图可知,要实现该时序电路需要用3个D 触发器。
(2)画出各激励信号的卡诺图,在状态转换真值表中未包含的状态为不可能出现的,可作无关项处理。
(3)由卡诺图得到各激励信号的最简方程如下:22110nnnD Q D Q D Q === 6.3.5试用下降沿触发的JK 触发器和最少的门电路实现图6.3.5所示的Z 1和Z 2输出波形。
Z Z解:从Z 1和Z 2输出波形可以看出,对于每一个Z 1或Z 2周期,均可等分为4段时间间隔相等的状态,即Z 2 Z 1=00、Z 2 Z 1=01、Z 2 Z 1=11和Z 2 Z 1=01,因此要设计的时序电路可以有4个状态,分别用00、01、10、11来表示。

第一章数字逻辑习题1.1 数字电路与数字信号1.1.2 图形代表的二进制数0101101001.1.4 一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSB LSB0 1 2 11 12 (ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/0.01s=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%1.2 数制1.2.2 将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于2−4(2)127 (4)2.718 解:(2)(127)D= 27 -1=(10000000)B-1=(1111111)B=(177)O=(7F)H(4)(2.718)D=(10.1011)B=(2.54)O=(2.B)H1.4 二进制代码1.4.1 将下列十进制数转换为 8421BCD 码:(1)43 (3)254.25 解:(43)D=(01000011)BCD1.4.3 试用十六进制写书下列字符繁荣 ASCⅡ码的表示:P28(1)+ (2)@ (3)you (4)43解:首先查出每个字符所对应的二进制表示的 ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+”的 ASCⅡ码为 0101011,则(00101011)B=(2B)H(2)@的 ASCⅡ码为 1000000,(01000000)B=(40)H(3)you 的 ASCⅡ码为本 1111001,1101111,1110101,对应的十六进制数分别为 79,6F,75(4)43 的 ASCⅡ码为 0110100,0110011,对应的十六紧张数分别为 34,331.6 逻辑函数及其表示方法1.6.1 在图题 1. 6.1 中,已知输入信号 A,B`的波形,画出各门电路输出 L 的波形。
解: (a)为与非, (b)为同或非,即异或第二章逻辑代数习题解答2.1.1 用真值表证明下列恒等式(3)A⊕ =B AB AB+ (A⊕B)=AB+AB解:真值表如下由最右边2栏可知,A⊕B与AB+AB的真值表完全相同。

第二章习题答案2.1.1 用真值表证明下列恒等式 (2)(A+B )(A+C)=A+BC 证明:列真值表如下:根据真值表,(A+B)(A+C)和A+BC 的真值表完全相同,因此等式(A+B)(A+C)=A+BC 成立。
2.1.3 用逻辑代数定律证明下列等式:(3)()A ABC A CD C D E A CD E ++++=++ 证明:()A ABC ACD C D E A ACD CDE A CD CDE A CD E++++=++=++=++2.1.4用代数法化简下列各式 (4)()()()()()110AB ABC A B AB A B BC A B A A B C A A B C A A A BC BC +++=+++=++=+++=++=+==2.1.5将下列各式转换成与或形式 (2)()()()()A B C D C D A D A B C D C D A D AC AD BC BD AC CD AD D AC BC AD BD CD D AC BC D+++++++=+++++=+++++++=+++++=++2.1.7 画出实现下列逻辑表达式的逻辑电路图,限使用非门和二输入与非门。
(1)L=AB+AC解:先将逻辑表达式化为与非-与非式:L AB AC AB AC AB AC =+=+=根据与非-与非表达式,画出逻辑图如下:LA B C2.1.8 已知逻辑函数表达式为L AB A C =+,画出实现该式的逻辑电路图,限使用非门和二输入或非门。
解:先将逻辑函数化为或非—或非表达式L AB A C AB A C A B A C =+=+=+++根据或非—或非表达式,画出逻辑图如下:A B CL另一种做法:用卡诺图化简变换为最简或与式A+B()()()()L A C A B A C A B A C A B =++=++=+++根据或非—或非表达式,画出逻辑图如下:AC BL2.2.1将下列函数展开为最小项表达式 (1)()()(,,,,)29101315L ACD BC D ABCD A B B CD ABCD A A BC D ABCD ABCD ABCD ABC D ABC D ABCD m =++=+++++=++++=∑(2)()L A B C =+()()()(,,)023L A B C AB AC AB C C A B B CABC ABC ABC ABC ABC ABC ABC m =+=+=+++=+++=++=∑(,,,,)14567L L m ==∑2.2.3用卡诺图化简下列各式(1) ABCD ABCD AB AD ABC ++++ 解:由逻辑表达式作卡诺图如下:ABAD由卡诺图得到最简与或表达式如下:L AB AC AD =++(5)(,,,)(,,,,,,,,,)0125689101314L A B C D m =∑解:由逻辑表达式作卡诺图如下:由卡诺图得到最简与或表达式如下:(,,,)L A B C D BD CD CD =++(7) (,,,)(,,,)(,,,,,)013141512391011L A B C D m d =+∑∑解:由逻辑表达式作卡诺图如下:A BAD AC由卡诺图得到最简与或表达式如下:=++L A B C D AB AC AD(,,,)友情提示:部分文档来自网络整理,供您参考!文档可复制、编制,期待您的好评与关注!。
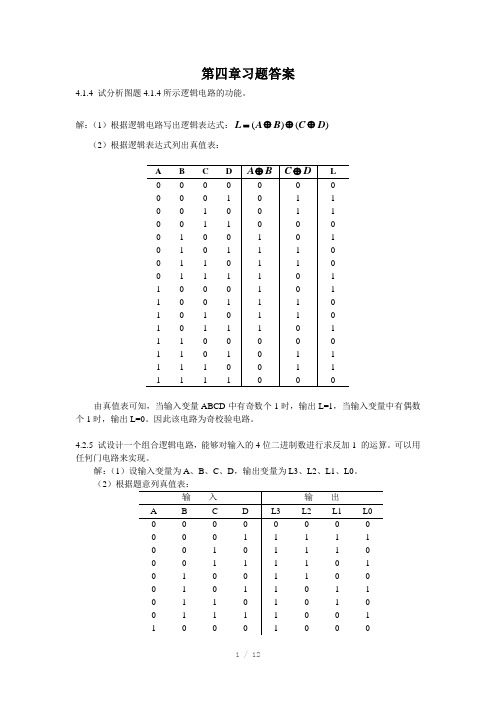
第四章习题答案4.1.4 试分析图题4.1.4所示逻辑电路的功能。
解:(1)根据逻辑电路写出逻辑表达式:()()L A B C D =⊕⊕⊕ (2)根据逻辑表达式列出真值表:由真值表可知,当输入变量ABCD 中有奇数个1时,输出L=1,当输入变量中有偶数个1时,输出L=0。
因此该电路为奇校验电路。
4.2.5 试设计一个组合逻辑电路,能够对输入的4位二进制数进行求反加1 的运算。
可以用任何门电路来实现。
解:(1)设输入变量为A 、B 、C 、D ,输出变量为L3、L2、L1、L0。
(2)根据题意列真值表:(3)由真值表画卡诺图(4)由卡诺图化简求得各输出逻辑表达式()()()3L AB A C AD ABCD A B C D A B C D A B C D =+++=+++++=⊕++ ()()()2L BC BD BCD B C D B C D BC D =++=+++=⊕+ 1L CD CD C D =+=⊕0L D=(5)根据上述逻辑表达式用或门和异或门实现电路,画出逻辑图如下:A B CDL 3L 2L 1L 04.3.1判断下列函数是否有可能产生竞争冒险,如果有应如何消除。
(2)(,,,)(,,,,,,,)2578910111315L A B C D m =∑ (4)(,,,)(,,,,,,,)4024612131415L A B C D m =∑解:根据逻辑表达式画出各卡诺图如下:(2)2L AB BD =+,在卡诺图上两个卡诺圈相切,有可能产生竞争冒险。
消除办法:在卡诺图上增加卡诺圈(虚线)包围相切部分最小项,使2L AB BD AD =++,可消除竞争冒险。
(4)4L AB AD =+,在卡诺图上两个卡诺圈相切,有可能产生竞争冒险。
消除办法:在卡诺图上增加卡诺圈(虚线)包围相切部分最小项,使4L AB AD BD =++,可消除竞争冒险。
4.3.4 画出下列逻辑函数的逻辑图,电路在什么情况下产生竞争冒险,怎样修改电路能消除竞争冒险。

第二章运算放大器2.1 集成电路运算放大器2.1.1答;通常由输入级,中间级,输出级单元组成,输入级由差分式放大电路组成,可以提高整个电路的性能。
中间级由一级或多级放大电路组成,主要是可以提高电压增益。
输出级电压增益为1,可以为负载提供一定的功率。
2.1.2答:集成运放的电压传输曲线由线性区和非线性区组成,线性区的直线的斜率即Vvo 很大,直线几乎成垂直直线。
非线性区由两条水平线组成,此时的Vo达到极值,等于V+或者V-。
理想情况下输出电压+Vom=V+,-Vom=V-。
2.1.3答:集成运算放大器的输入电阻r约为10^6欧姆,输出电阻r约为100欧姆,开环电压增益Avo约为10^6欧姆。
2.2 理想运算放大器2.2.1答:将集成运放的参数理想化的条件是:1.输入电阻很高,接近无穷大。
2.输出电阻很小,接近零。
3.运放的开环电压增益很大。
2.2.2答:近似电路的运放和理想运放的电路模型参考书P27。
2.3 基本线性运放电路2.3.1答:1.同相放大电路中,输出通过负反馈的作用,是使Vn自动的跟从Vp,使Vp≈Vn,或Vid=Vp-Vn≈0的现象称为虚短。
2.由于同相和反相两输入端之间出现虚短现象,而运放的输入电阻的阻值又很高,因而流经两输入端之间Ip=In≈0,这种现象称为虚断。
3.输入电压Vi通过R1作用于运放的反相端,R2跨接在运放的输出端和反相端之间,同相端接地。
由虚短的概念可知,Vn≈Vp=0,因而反相输入端的电位接近于地电位,称为虚地。
虚短和虚地概念的不同:虚短是由于负反馈的作用而使Vp≈Vn,但是这两个值不一定趋向于零,而虚地Vp,Vn接近是零。
2.3.2答:由于净输入电压Vid=Vi-Vf=Vp-Vm,由于是正相端输入,所以Vo为正值,Vo等于R1和R2的电压之和,所以有了负反馈电阻后,Vn增大了,Vp不变,所以Vid变小了,Vo 变小了,电压增益Av=Vo/Vi变小了。
由上述电路的负反馈作用,可知Vp≈Vn,也即虚短。
第一章数字逻辑习题1.1 数字电路与数字信号图形代表的二进制数1.1.4 一周期性数字波形如图题所示,试计算:(1)周期;(2)频率;(3)占空比例MSB LSB0 1 2 11 12 (ms)解:因为图题所示为周期性数字波,所以两个相邻的上升沿之间持续的时间为周期,T=10ms 频率为周期的倒数,f=1/T=1/=100HZ占空比为高电平脉冲宽度与周期的百分比,q=1ms/10ms*100%=10%数制将下列十进制数转换为二进制数,八进制数和十六进制数(要求转换误差不大于24(2)127 (4)解:(2)(127)D= 27 -1=()B-1=(1111111)B=(177)O=(7F)H(4)()D=B=O=H二进制代码将下列十进制数转换为 8421BCD 码:(1)43 (3)解:(43)D=(01000011)BCD试用十六进制写书下列字符繁荣ASCⅡ码的表示:P28(1)+ (2)@ (3)you (4)43解:首先查出每个字符所对应的二进制表示的ASCⅡ码,然后将二进制码转换为十六进制数表示。
(1)“+”的ASCⅡ码为 0101011,则(00101011)B=(2B)H(2)@的ASCⅡ码为 1000000,(01000000)B=(40)H(3)you 的ASCⅡ码为本 1111001,1101111,1110101,对应的十六进制数分别为 79,6F,75(4)43 的ASCⅡ码为 0110100,0110011,对应的十六紧张数分别为 34,33逻辑函数及其表示方法在图题 1. 中,已知输入信号 A,B`的波形,画出各门电路输出 L 的波形。
解: (a)为与非, (b)为同或非,即异或第二章逻辑代数习题解答用真值表证明下列恒等式(3)A⊕ =B AB AB+ (A⊕B)=AB+AB由最右边2栏可知,与+AB的真值表完全相同。
用逻辑代数定律证明下列等式(3)A+ABC ACD C D E A CD E++ +( ) = + +解:A+ABC ACD C D E++ +( )=A(1+BC ACD CDE)+ += +A ACD CDE+= +A CD CDE+ = +A CD+ E用代数法化简下列各式 (3)ABC B( +C)解:ABCB( +C)= + +(A B C B C)( + )=AB AC BB BC CB C+ + + + +=AB C A B B+ ( + + +1)=AB C+(6)(A+ + + +B A B AB AB) ( ) ( )()解:(A+ + + +B A B AB AB) () ( )( )= A B?+ A B?+(A+ B A)(+ B)=AB(9)ABCD ABD BCD ABCBD BC+ + + + 解:ABCD ABD BCD ABCBD BC+ + + +=ABC D D ABD BC D C( + +) + ( + ) =B AC AD C D( + + + ) =B A C A D( + + + ) =B A C D( + + ) =AB BC BD+ +画出实现下列逻辑表达式的逻辑电路图,限使用非门和二输入与非门( ))ABCD AB AC+已知函数L(A,B,C,D)的卡诺图如图所示,试写出函数L的最简与或表达式用卡诺图化简下列个式(1)ABCD ABCD AB AD ABC+ + + +解:ABCD ABCD AB AD ABC+ + + +=ABCD ABCD ABC C D D AD B B C C ABC D D++ ( + )( + +)( + )( + +)( + )=ABCD ABCD ABCD ABCD ABCD ABCD ABCD+ + + + + + (6)L A B C D( , , , )=∑m(0,2,4,6,9,13)+∑d(1,3,5,7,11,15)L= +A D(7)L A B C D( , , , )=∑m(0,13,14,15)+∑d(1,2,3,9,10,11)L AD AC AB= + +已知逻辑函数L AB BC CA=+ + ,试用真值表,卡诺图和逻辑图(限用非门和与非门)表示解:1>由逻辑函数写出真值表A B C L0 0 0 00 0 1 10 1 0 10 1 1 11 0 0 11 0 1 11 1 0 11 1 1 02>由真值表画出卡诺图LABBCAC用摩根定理将与或化为与非表达式L = AB + BC + AC = AB BC AC? ?4>由已知函数的与非-与非表达式画出逻辑图第三章习题MOS 逻辑门电路根据表题所列的三种逻辑门电路的技术参数,试选择一种最合适工作在高噪声环境下的门电路。
电平噪声容限分别为:V=V(min) —V(min) =—2V=V=V—V=—=同理分别求出逻辑门 B 和 C 的噪声容限分别为:V=1VV=V=1V V=电路的噪声容限愈大,其抗干扰能力愈强,综合考虑选择逻辑门 C根据表题所列的三种门电路的技术参数,计算出它们的延时-功耗积,并确定哪一种逻辑门性能最好DP= t P根据上式可以计算出各逻辑门的延时-功耗分别为DP = t+t P= (1 +ns *16mw=* 1012 J=2 2同理得出: DP=44PJ DP=10PJ,逻辑门的 DP 值愈小,表明它的特性愈好,所以逻辑门 C 的性能最好.为什么说 74HC 系列 CMOS 与非门在+5V 电源工作时,输入端在以下四种接法下都属于逻辑 0: (1)输入端接地; (2)输入端接低于的电源; (3)输入端接同类与非门的输出低电压 ; (4)输入端接10kΩ的电阻到地.解:对于 74HC 系列 CMOS 门电路来说,输出和输入低电平的标准电压值为:V=, V L =,因此有:(1)Vi =0< V L =,属于逻辑门 0(2)Vi <=V L ,属于逻辑门 0(3)Vi <<V L =,属于逻辑门 0(4)由于 CMOS 管的栅极电流非常小,通常小于 1uA,在10kΩ电阻上产生的压降小于 10mV 即Vi <<V L =,故亦属于逻辑 0.求图题所示电路的输出逻辑表达式.解:图解所示电路中 L1= AB ,L2= BC ,L3=D ,L4 实现与功能,即 L4=L1? L2? L3,而L= L4 E ,所以输出逻辑表达式为 L= AB BC D E图题表示三态门作总线传输的示意图,图中 n 个三态门的输出接到数据传输总线,D1,D2,……Dn 为数据输入端,CS1,CS2……CSn 为片选信号输入端.试问:(1) CS信号如何进行控制,以便数据D1,D2, ……Dn通过该总线进行正常传输; (2)CS信号能否有两个或两个以上同时有效?如果出现两个或两个以上有效,可能发生什么情况? (3)如果所有 CS 信号均无效,总线处在什么状态?解: (1)根据图解可知,片选信号 CS1,CS2……CSn 为高电平有效,当 CSi=1 时第 i 个三态门被选中,其输入数据被送到数据传输总线上,根据数据传输的速度,分时地给 CS1,CS2……CSn 端以正脉冲信号,使其相应的三态门的输出数据能分时地到达总线上.(2)CS 信号不能有两个或两个以上同时有效,否则两个不同的信号将在总线上发生冲突,即总线不能同时既为 0 又为 1.(3)如果所有 CS 信号均无效,总线处于高阻状态.试分析所示的 CMOS 电路,说明它们的逻辑功能解:对于图题(a)所示的 CMOS 电路,当EN =0 时,T P2和均导通,和T N2 T P1 T N1构成的反相器正常工作,L= A,当EN =1 时,和均截止,无论T P2 T N2 A 为高电平还是低电平,输出端均为高阻状态,其真值表如表题解所示,该电路是低电平使能三态非门,其表示符号如图题解(a)所示。
图题(b)所示 CMOS 电路,EN =0 时,导通,或非门打开,和构成反T P2 T P1 T N1相器正常工作,L=A;当EN =1 时,截止,或非门输出低电平,使截止,输出端T P2 T N1 处于高阻状态,该电路是低电平使能三态缓冲器,其表示符号如图题解(b)所示。
同理可以分析图题(c)和图题(d)所示的 CMOS 电路,它们分别为高电平使能三态缓冲器和低电平使能三态非门,其表示符号分别如图题(c)和图题(d )所示。
A L0 0 10 1 01 0高阻1 1(a)A L0 0 00 1 11 0 高阻1 1 高阻(b)EN A L0 0 高阻0 1 高阻1 0 01 1 1(cA L0 0 10 1 01 0 高阻1 1 高阻(d)为什么说 TTL 与非门的输入端在以下四种接法下,都属于逻辑 1:(1)输入端悬空;(2)输入端接高于 2V 的电源;(3)输入端接同类与非门的输出高电压;(4)输入端接10kΩ的电阻到地。
解:(1)参见教材图电路,当输入端悬空时,T1 管的集电结处于正偏,Vcc 作用于 T1 的集电结和T2 ,T3 管的发射结,使T2 ,T3 饱和,使T2 管的集电极电位Vc2=Vc E s2+V BE3=+=,而 T4 管若要导通 V B2=V c2≥V BE4+V D=+=,故 T4 截止。
又因 T3 饱和导通,故与非门输出为低电平,由上分析,与非门输入悬空时相当于输入逻辑 1。
(2)当与非门输入端接高于 2V 的电源时,若 T1 管的发射结导通,则 V BE1≥,T1 管的基极电位 V B≥2+ C1=。
而 V B1≥ 时,将会使 T1 的集电结处于正偏,T2,T3 处于饱和状态,使 T4 截止,与非门输出为低电平。
故与非门输出端接高于 2V 的电源时,相当于输入逻辑 1。
(3)与非门的输入端接同类与非门的输出高电平输出时,若 T1 管导通,则 V B1=+=。
而若 V B1> 时,将使 T1 的集电结正偏,T2,T3 处于饱和状态,这时V B1 被钳位在,即 T1 的发射结不可能处于导通状态,而是处于反偏截止。
由(1)(2),当V B1≥,与非门输出为低电平。
(4)与非门输入端接10kΩ的电阻到地时,教材图的与非门输入端相当于解图所示。
这时输入电压为 V I=(Vcc-V BE)=10()/(10+4)=。
若 T1 导通,则 V BI=+ V BE=+= V。
但 V BI 是个不可能大于的。
当 V BI= 时,将使 T1 管的集电结正偏,T2,T3 处于饱和,使 V BI 被钳位在,因此,当 R I=10kΩ时,T1 将处于截止状态,由( 1 )这时相当于输入端输入高电平。
设有一个 74LS04 反相器驱动两个 74ALS04 反相器和四个 74LS04 反相器。