MXT-高三函数复习专题

高考数学-函数值域、定义域、解析式本专题有四部分：壹， 函数值域的求法 貳， 函数定义域 參， 解析式的求法肆，基础练习题&&高考题第一部分：函数值域的求法1、直接法：例1：求函数y例2：求函数1y =的值域。

2、配方法：例1：求函数242y x x =-++（[1,1]x ∈-）的值域。

例2：求 函 数]2,1[x ,5x 2x y 2-∈+-= 的 值域。

例3：求函数2256y x x =-++的值域。

3、分离常数法： 例1：求函数125xy x -=+的值域。

例2：求函数122+--=x x xx y 的值域．例3：求函数132x y x -=-得值域.4、换元法：例1：求函数2y x =+例2： 求 函 数1x x y -+=的 值 域。

5、函数的单调性法：确定函数在定义域（或某个定义域的子集）上的单调性，求出函数的值域。

例1：求函数y x =-例2：求函数()x x x f -++=11的值域。

例3：求 函 数1x 1x y --+=的 值 域。

6、数型结合法：函数图像是掌握函数的重要手段，利用数形结合的方法，根据函数图像求得函数值域，是一种求值域的重要方法。

当函数解析式具有某种明显的几何意义（如两点间距离，直线的斜率、截距等）或当一个函数的图象易于作出时，借助几何图形的直观性可求出其值域。

例1：求函数|3||5|y x x =++-的值域。

7、非负数法根据函数解析式的结构特征，结合非负数的性质，可求出相关函数的值域。

例1、(1)求函数216x y -=的值域。

(2)求函数1322+-=x x y 的值域。

第二部分：函数定义域例1：已知函数()f x 的定义域为[]15-，，求(35)f x -的定义域．例2：若()f x 的定义域为[]35-，，求()()(25)x f x f x ϕ=-++的定义域． 例3：求下列函数的定义域：① 21)(-=x x f ； ② 23)(+=x x f ；③ xx x f -++=211)( 例4：求下列函数的定义域：④ 14)(2--=x x f⑤ ②2143)(2-+--=x x x x f⑥ 373132+++-=x x y ④xx x x f -+=0)1()(第三部分：解析式的求法1、配凑法例1：已知 ：23)1(2+-=+x x x f ，求f(x)；例2 ：已知221)1(xx xx f +=+ )0(>x ，求 ()f x 的解析式． 2、换元法（注意：使用换元法要注意t 的范围限制，这是一个极易忽略的地方。

高三数学《反函数》专题训练班级 姓名 学号一、选择题：1．函数b ax y +=与它的反函数是同一个函数，则（ ）Ａ．0,1==b a Ｂ．0,1=-=b aＣ．0,1=±=b a Ｄ．0,1==b a 或R b a ∈-=,12．函数31xy =的反函数是)(x g ，则（ ） Ａ．)3()1()2(->->g g g Ｂ．)1()3()2(->->g g gＣ．)2()3()1(g g g >->- Ｄ．)2()1()3(g g g >->-3．若函数)(x f 的图象上经过点)1,0(-，则函数)4(+x f 的反函数的图象上必经过点（ ）Ａ．)4,1(- Ｂ．)1,4(-- Ｃ．)4,1(-- Ｄ．)4,1(4．已知函数)(x f y =有反函数，则方程a x f =)(（a 为常数）（ ）Ａ．有且只有一个实根 Ｂ．至多有一个实根Ｃ．至少有一个实根 Ｄ．实根的个数无法确定5．函数)(x f y =存在反函数)(1x fy -=，把)(x f y =的图象在直角坐标系内绕原点顺时针转动ο90后是另一个函数的图象，这个函数是（ ）Ａ．)(1x f y -=- Ｂ．)(1x f y -= Ｃ．)(1x f y --= Ｄ．)(1x f y --=-二、填空题：6．函数)0)(2(≥+-=x x x y 的反函数的定义域是______________．7．设1)1(+=+x x x f ，则=+-)1(1x f ______________．8．关于反函数有下列命题：①二次函数一定有反函数；②反比例函数一定有反函数；③若函数)(x f y =与其反函数)(1x f y -=有公共点，则该点一定在直线x y =上；④单调函数在其单调区间上一定有反函数．以上命题，正确的命题的序号是______________．三、解答题：9．已知函数)1()(2≤+=x ax x x f ，且函数)(x f 具有反函数，求常数a 的取值范围．设0a是满足上述条件的a 的最大值，当0a a =时，求)(x f 的反函数．10．若x x f 21)(+=，且)(x g y =的图象与)1(1+=-x f y 的图象关于直线x y =对称，求)3(g 的值．11．给定实数)1,0(≠≠a a a ，设函数)1,(11ax R x ax x y ≠∈--=且． （１）求证这个函数的图象关于直线x y =成轴对称图形；（２）若函数图象与直线x y =无公共点，求a 的取值范围．12．已知函数)1(12≥-=x x y 的图象为1C ，)(x g y =的图象为2C ，1C 与2C 关于直线x y =对称．又)(x g y =的定义域为M ，对于M x x ∈21,，且21x x ≠，试比较|)()(|21x g x g -与||21x x -的大小．13．已知函数)(x f y =在其定义域D 内是减函数，且存在反函数，求证：)(x f y =的反函数)(1x fy -=在它的定义域E 内也是减函数（E 是)(x f y =的值域）．贵州省晴隆一中09-10学年高三数学《反函数》专题训练答案一、选择题：1－5．DBCBC二、填空题：6．]0,(-∞；7．x 1-；8．②④． 三、解答题：9．解：二次函数ax x x f +=2)(对称轴为2a x -=，∵函数)(x f 具有反函数， ∴12≥-a ，解得常数a 的取值范围为2-≤a ．∴20-=a ． 令1)1(2)(22--=-==x x x x f y ，∴2)1(1-=+x y ，∵1≤x ，∴11+-=-y x ，11++-=y x ．∴)(x f 的反函数为11)(1++-=-x x f ．10．解：令x y 21+=，得12-=y x ，∴12)(1-=-x x f ，∴xx f 2)1(1=+-． ∵)(x g y =的图象与)1(1+=-x fy 的图象关于直线x y =对称， ∴令x y 2=，得y x 2=，∴x x g 2)(=，33232)3(==g ． 11．（１）由11--=ax x y ，得1-=-x y axy ，∴1)1(-=-y x ay ， 11--=ay y x ． 即函数11--=ax x y 的反函数就是它本身．∴这个函数的图象关于直线x y =成轴对称图形． （２）由题意知，即求使方程11--=ax x x 无解的a 的取值范围． 方程可化为0122=+-x ax ，∴只需⎩⎨⎧<-=∆≠0440a a ，解得a 的取值范围是1>a ．12．解：∵1C 与2C 关于直线x y =对称，故函数)(x g y =是函数)1(12≥-=x x y 反函数．∵)1(12≥-=x x y ，∴12+=y x ． ∴1+=y x ，或1+-=y x （舍），故x x g +=1)(． 于是2121212111|||11||)()(|x x x x x x x g x g +++-=+-+=-． ∵当0≥x 时，012≥-=x y ，∴函数)1(12≥-=x x y 的值域为),0[+∞，∴)(x g y =的定义域),0[+∞=M ，∴0,021≥≥x x ． ∴||11||11|||)()(|2121212121x x x x x x x x x g x g -<+-≤+++-=-， 即|)()(|21x g x g -＜||21x x -．13．证明：∵)(x f y =在其定义域D 内是减函数，∴设D x x ∈21,，且21x x <，有)()(21x f x f >．令)(),(2211x f y x f y ==，有E y y ∈21,，且21y y >．∵函数)(x f y =在上D 存在反函数E x x f y ∈=-),(1，∴)(),(212111y f x y f x --==．由题意，)()(21112121y f y fx x y y --<⇔<⇔>，且E y y ∈21,， ∴)(1x fy -=在定义域E 内是减函数．。

学习有方法，考题有规律，解题有技巧第一节 事件与概率一、选择题1．(2008年广州模拟)下列说法：①频率反映事件发生的频繁程度，概率反映事件发生的可能性大小；②做n 次随机试验，事件A 发生m 次，则事件A 发生的频率mn 就是事件的概率；③百分率是频率，但不是概率；④频率是不能脱离n 次的试验的试验值，而概率是具有确定性的不依赖于试验次数的理论值；⑤频率是概率的近似值，概率是概率的稳定值． 其中正确的是( )A ．①②③④B ．①④⑤C ．①②③④⑤D ．②③2．某班有3位同学分别做抛硬币试验20次，那么下面判断正确的是( ) A ．3位同学都得到10次正面朝上，10次反面朝上 B ．3位同学一共得到30次正面朝上，30次反面朝上 C ．3位同学得到正面朝上的次数为10次的概率是相同的 D ．3位同学中至少有一人得到10次正面朝上，10次反面朝上 3．同时掷3枚硬币，那么互为对立事件的是( ) A ．至少有1枚正面和最多有1枚正面 B ．最多1枚正面和恰有2枚正面 C ．至多1枚正面和至少有2枚正面 D ．至少有2枚正面和恰有1枚正面4．从一篮鸡蛋中取1 个，如果其质量小于30克的概率是0.30，重量在[30,40]克的概率是0.50，那么重量不小于30克的概率是( )A ．0.30B ．0.50C ．0.80D ．0.705．(2009年福建)已知某运动员每次投篮命中的概率都为40%，现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率：先由计算器产生0到9之间取整数值的随机数，指定1,2,3,4表示命中，5,6,7,8,9,0表示不命中；再以每三个随机数为一组，代表三次投篮的结果．经随机模拟产生了如下20组随机数：907 966 191 925 271 932 812 458 569 683431 257 393 027 556 488 730 113 537 989据此估计，该运动员三次投篮恰有两次命中的概率为( )A．0.35 B．0.25 C．0.20 D．0.15二、填空题6．给出下列事件：①物体在只受重力的作用下会自由下落；②方程x2＋2x＋8＝0有两个实根；③某信息台每天的某段时间收到信息咨询的请求次数超过10次；④下周六会下雨．其中随机事件的是________．(把所有正确的序号填上)．7．现有2008年奥运会志愿者7名，其中4名为男性，3名为女性，从中任选2名志愿者为游客做向导，其中下列事件：①恰有1名女性与恰有2名女性；②至少有1名女性与全是女性；③至少有1名男性与至少有1名女性；④至少有1名女性与全是男性．是互斥事件的组数有________．8．(2009年台州第一次调研)一堆除颜色外其他特征都相同的红白两种颜色的球若干个，已知红球的个数比白球多，但比白球的2倍少，若把每一个白球都记作数值2，每一个红球都记作数值3，则所有球的数值的总和等于60.现从中任取一个球，则取到红球的概率等于________．三、解答题9．某射手在一次射击训练中，射中10环、9环、8环、7环的概率分别为0.21,0.23,0.25,0.28，计算该射手在一次射击中：(1)射中10环或9环的概率；(2)少于7环的概率．10．假设人的某一特征(如眼睛大小)是由他的一对基因所决定的，以d表示显性基因，r表示隐性基因，则具有dd基因的人为纯显性，具有rr基因的人是纯隐性，具有rd基因的人为混合性．纯显性与混合性的人都表露显性基因决定的某一特征，孩子从父母身上各得到一个基因，假定父母都是混合性．求：(1)一个孩子有显性基因决定的特征的概率是多少？(2)两个孩子中至少有一个有显性基因决定的特征的概率是多少？参考答案1．解析：对于②，频率mn ，只是概率的估计值，②错误；对于③，百分率可以是频率，也可以是概率，③错误．答案：B2．解析：理解频率的随机性和概率的稳定性． 答案：C 3．C4．解析：不小于30克的对立事件是小于30克，其概率为1－0.30＝0.70. 答案：D5．解析：20组数中恰有两次命中的共有5组，因此所求概率为520＝0.25.答案：B6．解析：①是必然事件，②是不可能事件，③④是随机事件． 答案：③④7．解析：①、④互斥，②、③不互斥． 答案：28．解析：设白球x 个，红球y 个，则2x ＋3y ＝60. ∵x＜y<2x ，∴3x<3y<6x.∴5x<2x＋3y<8x ，即⎩⎪⎨⎪⎧5x<60，8x>60.∴608<x<12. 又x∈N *，∴x＝8,9,10,11.又y∈N *，易知，x ＝9时，y ＝14，适合． ∴取到红球的概率为1414＋9＝1423. 答案：14239．解析：(1)该射手射中10环与射中9环的概率是射中10环的概率与射中9环的概率的和，即为0.21＋0.23＝0.44.(2)射中不少于7环的概率恰为射中10环、9环、8环、7环的概率的和，即为0.21＋0.23＋0.25＋0.28＝0.97，而射中少于7环的事件与射中不少于7环的事件为对立事件，所以射中少于7环的概率为1－0.97＝0.03.10．解析：孩子的一对基因为dd ，rr ，rd 的概率分别为14，14，12，孩子由显性基因决定的特征是具有dd ，rd ，所以(1)一个孩子由显性基因决定的特征的概率为14＋12＝34.(2)因为两个孩子如果都不具有显性基因决定的特征，即两个孩子都具有rr 基因的纯隐性特征，其概率为14×14＝116，所以两个孩子中至少有一个显性基因决定特征的概率为1－116＝1516.第二节 古典概型一、选择题1．(2009年金华模拟)同时抛掷三枚均匀的硬币，出现一枚正面，二枚反面的概率等于( )A.14B.13 C.38 D.122．(2008年重庆)(理)从编号为1,2，…，10的10个大小相同的球中任取4个，则所取4个球的最大号码是6的概率为( )A.184 B.121 C.25 D.352．(文)盒中有10个铁钉，其中8个是合格的，2个是不合格的，从中任取一个恰为合格铁钉的概率是( )A.15B.14C.45D.1103．(文)设x ，y 是0,1,2,3,4,5中任意两个不同的数，那么复数x ＋y i 恰好是纯虚数的概率为( )A.16B.13C.15D.1304．(2009西安第三次统考)(理)从4名男同学，3名女同学中任选3名参加体能测试，则选到的3名同学中既有男同学又有女同学的概率为( )A.1235 B.1835 C.67 D.784．(文)设集合A ＝{1,2}，B ＝{1,2,3}，分别从集合A 和B 中随机取一个数a 和b ，确定平面上的一个点P (a ，b )，记“点P (a ，b )落在直线x ＋y ＝n 上”为事件C n (2≤n ≤5，n ∈N )，若事件C n 的概率最大，则n 的所有可能值为( )A ．3B ．4C ．2和5D ．3和45．(2009年重庆)(理)锅中煮有芝麻馅汤圆6个，花生馅汤圆5个，豆沙馅汤圆4个，这三种汤圆的外部特征完全相同．从中任意舀取4个汤圆，则每种汤圆至少取到1个的概率为( )A.891 B.2591 C.4891 D.60915．(文)一袋中装有大小相同，编号分别为1,2,3,4,5,6,7,8的八个球，从中有放回地每次取一个球，共取2次，则取得两个球的编号和不小于15的概率为( )A.132B.164C.332 D.364二、填空题6．(2009年上海奉贤区模拟)(理)在1,2,3,4,5这五个数字中任取不重复的3个数字组成一个三位数，则组成的三位数是奇数的概率是________．(用分数表示)6．(文)(2008年江苏卷)一个骰子连续投2次，点数和为4的概率为________． 7．(2009年安徽卷)从长度分别为2、3、4、5的四条线段中任意取出三条，则以这三条线段为边可以构成三角形的概率是________．8．(2009年江苏卷)现有5根竹竿，它们的长度(单位：m)分别为2.5,2.6,2.7,2.8,2.9，若从中一次随机抽取2根竹竿，则它们的长度恰好相差0.3 m 的概率为________． 三、解答题9．(理)(2008年浙江)一个袋中装有大小相同的黑球、白球和红球．已知袋中共有10个球．从袋中任意摸出1个球，得到黑球的概率是25；从袋中任意摸出2个球，至少得到1个白球的概率是79.求：(1)从中任意摸出2个球，得到的都是黑球的概率； (2)袋中白球的个数.9．(文)(2008年海南宁夏卷)为了了解《中华人民共和国道路交通安全法》在学生中的普及情况，调查部门对某校6名学生进行问卷调查，6人得分情况如下：5,6,7,8,9,10.把这6名学生的得分看成一个总体．(1)求该总体的平均数；(2)用简单随机抽样方法从这6名学生中抽取2名，他们的得分组成一个样本．求该样本平均数与总体平均数之差的绝对值不超过0.5的概率．10．(2009年滨海新区五校联考)某商场举行抽奖活动，从装有编号0,1,2,3四个小球的抽奖箱中，每次取出后放回，连续取两次，取出的两个小球号码相加之和等于5中一等奖，等于4中二等奖，等于3中三等奖．(1)求中三等奖的概率； (2)求中奖的概率．参考答案1．解析：(理)共23＝8种情况，符合要求的有C 13＝3种，所以概率等于38.(文)同时抛三枚硬币，所有可能出现的结果为：(正，正，正)，(正，正，反)，(正，反，正)，(正，反，反)，(反，正，正)，(反，正，反)，(反，反，正)，(反，反，反)；其中符合要求的只有3种，所以概率为：P ＝38.答案：C2．解析：本小题主要考查组合的基本知识及古典概型的概率．P ＝C 35C 410＝121，故选B .答案：B2．解析：法一：从盒中任取一个铁钉包含基本事件总数为10，其中抽到合格铁订(记为事件A)包含8个基本事件，所以，所求概率为P(A)＝810＝45.法二：本题还可以用对立事件的概率公式求解，因为从盒中任取一个铁钉，取到合格品(记为事件A)与取到不合格品(记为事件B)恰为对立事件，因此，P(A)＝1－P(B)＝1－210＝45.答案：C3．解析：从中任取三个数共有C 39＝84种取法，没有同行、同列的取法有C 13C 12C 11＝6，至少有两个数位于同行或同列的概率是1－684＝1314，故选D .答案：D3．解析：x 取到0的概率为1/6. 答案：A4．解析：其对立事件的概率为C 34＋C 33C 37＝535＝535＝17，所以P ＝1－17＝67. 答案：C4．解析：事件C n 的总事件数为6.只要求出当n ＝2,3,4,5时的基本事件个数即可． 当n ＝2时，落在直线x ＋y ＝2上的点为(1,1)； 当n ＝3时，落在直线x ＋y ＝3上的点为(1,2)、(2,1)； 当n ＝4时，落在直线x ＋y ＝4上的点为(1,3)、(2,2)； 当n ＝5时，落在直线x ＋y ＝5上的点为(2,3)； 显然当n ＝3,4时，事件C n 的概率最大为13.答案：D 5．解析：P ＝C 26C 15C 14＋C 16＋C 25C 14＋C 16C 15C 24C 415＝15×20＋6×40＋18015×13×7＝4891，故选C .答案：C5．解析：从中有放回地取2次，所取号码共有8×8＝64种，其中和不小于15的有3种，分别是(7,8)，(8,7)，(8,8)，故所求概率为P ＝364.故选D . 答案：D 6．解析：P ＝C 13A 24A 35＝3660＝35. 答案：356．解析：基本事件共6×6个，点数和为4的有(1,3)、(2,2)、(3,1)共3个，故P ＝36×6＝112. 答案：1127．解析：四条线段中任意取出三条的可能有：2,3,4或2,3,5或2,4,5或3,4,5共4种．能构成三角形的可能情况：2,3,4或2,4,5或3,4,5，∴P＝34.答案：348．解析：(理)从5根竹竿中，一次随机抽取2根竹竿的方法数为C 25＝10. 而满足它们的长度恰好相差0.3 m 的方法数为2个，即2.5和2.8,2.6和2.9. 由古典概型的求法得P ＝210＝15.解析：(文)从5根竹竿中，一次随机抽取2根竹竿的方法数有(2.5,2.6)，(2.5,2.7)，(2.5,2.8)，(2.5,2.9)，(2.6,2.7)，(2.6,2.8)，(2.6,2.9)，(2.7,2.8)，(2.7,2.9)，(2.8,2.9)共10种．而满足它们的长度恰好相差0.3 m 的方法数为2种，即2.5和2.8,2.6和2.9.由古典概型的求法得P ＝210＝15.答案：159．解析：(1)由题意知，袋中黑球的个数为10×25＝4.记“从袋中任意摸出两个球，得到的都是黑球”为事件A ，则P(A)＝C 24C 210＝215.设袋中白球的个数为x ，则P(B)＝1－P(B )＝1－C 2n －1C 2n ＝79，解得x ＝5.答案：(1)215 (2)59．解析：(1)总体平均数为16()5＋6＋7＋8＋9＋10＝7.5. (2)设A 表示事件“样本平均数与总体平均数之差的绝对值不超过0.5”．从总体中抽取2个个体全部可能的基本结果有：(5,6), (5,7), (5,8), (5,9), (5,10), (6,7), (6,8), (6,9), (6,10), (7,8), (7,9), (7,10), (8,9), (8,10), (9,10)，共15个基本结果．事件A 包含的基本结果有：(5,9), (5,10), (6,8), (6,9)， (6,10), (7,8), (7,9)，共有7个基本结果； 所以所求的概率为P ()A ＝715.10．解析：设“中三等奖”的事件为A ，“中奖”的事件为B ，从四个小球中有放回的取两个共有4×4＝16种可能．(1)两个小球号码相加之和等于3的取法有4种：0＋3,1＋2,2＋1,3＋0，所以P(A)＝416＝14. (2)法一：①两个小球号码相加之和等于3的取法有4种． ②两个小球相加之和等于4的取法有3种：1＋3,2＋2,3＋1； ③两个小球号码相加之和等于5的取法有2种：2＋3,3＋2. 所以P(B)＝416＋316＋216＝916.法二：考虑问题的对立事件，即不中奖的概率． ①等于6的取法有1种：3＋3；②等于2的取法有3种：0＋2,1＋1,2＋0； ③等于1的取法有2种：0＋1,1＋0； ④等于0的取法有1种：0＋0. 所以P(B －)＝116＋316＋216＋116＝716，于是P(B)＝1－P(B －)＝1－716＝916.第三节 几何概型一、选择题1．有一杯2升的水，其中含有一个细菌，用一个小杯从这杯水中取出0.1升水，则小杯水中含有细菌的概率是( )A ．0.5B ．0.05C ．0.1D ．0.012．(2008年佛山一模)如右图所示，矩形长为6，宽为4，在矩形内随机地撒300颗黄豆，数得落在椭圆外的黄豆数为96颗，以此实验数据为依据可以估计出椭圆的面积约为( )A ．7.68B ．16.32C ．17.32D ．8.683．(2009年辽宁)ABCD 为长方形，AB ＝2，BC ＝1，O 为AB 的中点．在长方形ABCD 内随机取一点，取到的点到O 的距离大于1的概率为( )A.π4 B ．1－π4 C.π8 D ．1－π84．(2009年福建上杭)已知函数f(x)＝x 2＋bx ＋c ，其中0≤b≤4,0≤c≤4.记函数f(x)满足条件⎩⎪⎨⎪⎧f2≤12，f －2≤4为事件A ，则事件A 发生的概率为( )A.14B.58C.12D.385．(2009年山东卷)在区间[－1,1]在随机取一个数x ，cos πx 2的值介于0到12之间的概率为( )A.13B.2π C.12 D.23 二、填空题6．两根相距8 m 的木杆上系一根绳子，并在绳子上挂一盏灯，则灯与两端距离都大于2 m 的概率是________．7．(2009年福建卷)点A 为周长等于3的圆周上的一个定点．若在该圆周上随机取一点B ，则劣孤AB 的长度小于1的概率为________．8．(2009年浙江杭州模拟)在边长为2的正三角形ABC 内任取一点P ，则使点P 到三个顶点的距离至少有一个小于1的概率是________． 三、解答题9．(2009年厦门一中质检)投掷一个质地均匀的、每个面上标有一个数字的正方体玩具，它的六个面中，有两个面标的数字是0，两个面标的数字是2，两个面标的数字是4，将此玩具连续抛掷两次，以两次朝上一面的数字分别作为点P 的横坐标和纵坐标．(1)求点P 落在区域C ：x 2＋y 2≤10内的概率；(2)若以落在区域C 上的所有点为顶点作面积最大的多边形区域M ，在区域C 上随机散一粒豆子，求豆子落在区域M 上的概率．10．(2009年深圳第二次调研改编)设M 点的坐标为(x ，y)．(1)设集合P ＝{－4，－3，－2,0}，Q ＝{0,1,2}，从集合P 中随机取一个数作为x ，从集合Q 中取随机取一个数作为y ，求M 点落在y 轴的概率；(2)设x∈[0,3]，y∈[0,4]，求点M 落在不等式组： ⎩⎪⎨⎪⎧x ＋2y －3≤0x≥0y≥0，所表示的平面区域内的概率．参考答案1．解析：P ＝0.12＝120＝0.05.答案：B2．解析：∵S 椭S 矩＝300－96300，∴S 椭＝204300×24＝16.32.答案：B3．解析：根据几何概率公式得概率为P ＝S 阴影部分S 长方形ABCD ＝2－12π·122＝1－π4. 答案：B4．解析：由题意，⎩⎪⎨⎪⎧2b ＋c －8≤0，2b －c≥0表示的区域的面积为8，所以概率为12，故选C.答案：C5．解析：在区间[－1,1]上随机取一个实数x ，cos πx 2的值位于[0,1]区间，若使cosπx2的值位于⎣⎢⎡⎦⎥⎤0，12区间，取到的实数x 应在区间⎣⎢⎡⎦⎥⎤－1，－23∪⎣⎢⎡⎦⎥⎤23，1内，根据几何概型的计算公式可知P ＝2×132＝13，故选A.答案：A6．解析：P(A)＝8－2－28＝12.答案：127．解析：如右图，设A 、M 、N 为圆周的三等分点，当B 点取在优孤MAN 上时，对劣弧AB 来说，其长度小于1，故其概率为23.答案：23.8.解析：以A 、B 、C 为圆心，以1为半径作圆，与△ABC 交出三个扇形， 当P 落在其内时符合要求． ∴P＝3×12×π31234×22＝3π6.答案：3π69．解析：(1)以0,2,4为横、纵坐标的点P 的可能共3×3＝9个， 而这些点中，落在区域C 的点有：(0,0)、(0,2)、(2,0)、(2,2)4个 ，∴所求概率为P ＝49.(2)∵区域M 的面积为4，而区域C 的面积为10π， ∴所求概率P ＝410π＝25π. 10．解析：(1)记“M 点落在y 轴”为事件A.M 点的组成情况共4×3＝12种，且每种情况出现的可能性相等，属于古典概型． 其中事件A 包含的基本事件有(0,0)，(0,1)，(0,2)共3处． ∴P(A)＝312＝14.(2)依条件可知，点M 均匀地分布在不等式组⎩⎪⎨⎪⎧0≤x≤30≤y≤4所表示的平面区域内，属于几何概型．该平面区域的图形为右图中矩形OABC 围成的区域，面积为S ＝3×4＝12.而所求事件构成的平面区域由不等式组⎩⎪⎨⎪⎧x ＋2y －3≤0x≤0y≤0表示的区域，其图形如右图中的三角形OAD(阴影部分)．又直线x ＋2y －3＝0与x 轴、y 轴的交点分别为A(3,0)、D ⎝ ⎛⎭⎪⎫0，32，∴三角形OAD 的面积为 S 1＝12×3×32＝94.∴ 所求事件的概率为P ＝S 1S ＝9412＝316.第四节 条件概率与事件的独立性一、选择题1．一个口袋中有黑球和白球各5个，从中连摸两次球，每次摸一个且每次摸出后不放回，用A 表示第一次摸得白球，B 表示第二次摸得白球，则A 与B 是( )A ．互斥事件B ．不相互独立事件C ．对立事件D ．相互独立事件解析：第一次摸得白球和第二次摸得白球有可能同时发生，∴A、B 不是互斥事件，自然也不是对立事件；第一次摸得白球与否会影响第二次摸得白球的概率，∴A、B 是不相互独立事件．答案：B2．甲、乙两人独立地解同一问题，甲解决这个问题的概率是p 1，乙解决这个问题的概率是p 2，那么恰好有1人解决这个问题的概率是( )A ．p 1p 2B ．p 1(1－p 2)＋p 2(1－p 1)C ．1－p 1p 2D ．1－(1－p 1)(1－p 2)解析：恰有一人解决这个问题包括两种情况：一种是甲解决了问题乙没有解决，概率为p 1(1－p 2)，另一种是乙解决了问题甲没有解决，概率为p 2(1－p 1)，所以恰有一人解决这个问题的概率是p 1(1－p 2)＋p 2(1－p 1)．答案：B3．在一段时间内，甲去某地的概率是14，乙去此地的概率是15，假定两人的行动相互之间没有影响，那么在这段时间内至少有1人去此地的概率是( )A.320 B.15 C.25 D.920解析：考虑对立事件A －没有人去此地，概率为34×45＝35，所以P(A)＝1－35＝25.答案：C4．在某段时间内，甲地不下雨的概率为0.3，乙地不下雨的概率为0.4，假设在这段时间内两地是否下雨相互无影响，则这段时间内两地都下雨的概率是( )A ．0.12B ．0.88C ．0.28D ．0.42 解析：P ＝(1－0.3)(1－0 .4)＝0.42. 答案：D5．将三颗骰子各掷一次，设事件A ＝“三个点数都不相同”，B ＝“至少出现一个6点”，则概率P(A | B＝()A.6091 B.12 C.518 D.91216解析：∵B －为一个6点都没有出现，其概率为P(B －)＝56×56×56＝125216，∴P(B)＝1－125216＝91216，而AB 表示“三个点数都不相同且至少出现一个6点”，其概率为16×56×46×3＝518，所以P(A|B)＝P ABP B ＝51891216＝216×591×18＝6091.答案：A 二、填空题6．甲、乙两个袋子中均装有红、白两种颜色的小球，这些小球除颜色外完全相同，其中甲袋装有4个红球、2个白球，乙袋装有1个红球、5个白球．现分别从甲、乙两袋中各随机抽取1个球，则取出的两球是红球的概率为________(答案用分数表示)解析：46×16＝19.答案：197．(2008年湖北卷)明天上午李明要参加义务劳动，为了准时起床，他用甲、乙两个闹钟叫醒自己，假设甲闹钟准时响的概率是0.80，乙闹钟准时响的概率是0.90，则两个闹钟至少有一准时响的概率是________．解析：法一： 两个闹钟一个也不准时响的概率是(1－0.8)×(1－0.9)＝0.02，所以要求的结果是1－0.02＝0.98.法二：要求的概率是(1－0.8)×0.9＋0.8×(1－0.9)＋0.8×0.9＝0.98. 答案：0. 988．(2009年冠龙中学月考)甲、乙两人各进行一次射击，如果两人击中目标的概率都是0.6，则其中恰有一人击中目标的概率是________．解析：0.6×0.4＋0.4×0.6＝0.48. 答案：0.48 三、解答题9．(2009年金陵模拟改编)某地区试行高考考试改革：在高三学年中举行5次统一测试，学生如果通过其中2次测试即可获得足够学分升上大学继续学习，不用参加其余的测试，而每个学生最多也只能参加5次测试．假设某学生每次通过测试的概率都是13，每次测试时间间隔恰当，每次测试通过与否互相独立．(1)求该学生考上大学的概率；(2)求该学生经过4次测试考上大学的概率．解析：(1)记“该学生考上大学”为事件A ，其对立事件为A －，则P(A －)＝C15⎝ ⎛⎭⎪⎫13⎝ ⎛⎭⎪⎫234＋⎝ ⎛⎭⎪⎫235＝112243， ∴P(A)＝1－[C15·⎝ ⎛⎭⎪⎫13⎝ ⎛⎭⎪⎫234＋⎝ ⎛⎭⎪⎫235]＝131243.(2)∵该学生经过4次测试考上大学∴该学生第4次考试通过测试，前3次考试只有一次通过测试，所以概率为 P(B)＝13×⎝ ⎛⎭⎪⎫13×23×23＋23×13×23＋23×23×13＝427. 10．(2009年全国卷Ⅰ改编)甲、乙二人进行一次围棋比赛，约定先胜3局者获得这次比赛的胜利，比赛结束．假设在一局中，甲获胜的概率为0.6，乙获胜的概率为0.4，各局比赛结果相互独立．已知前2局中，甲、乙各胜1局．(1)求甲获得这次比赛胜利的概率； (2)求经过5局比赛，比赛结束的概率．解析：记A i 表示事件：第i 局甲获胜，i ＝3,4,5，B j 表示事件：第j 局乙获胜，j ＝3,4. (1)记B 表示事件：甲获得这次比赛的胜利．因前两局中，甲、乙各胜一局，故甲获得这次比赛的胜利当且仅当在后面的比赛中，甲先胜2局，从而B ＝A 3·A 4＋B 3·A 4·A 5＋A 3·B 4·A 5， 由于各局比赛结果相互独立，故P(B)＝P(A 3·A 4)＋P(B 3·A 4·A 5)＋P(A 3·B 4·A 5) ＝P(A 3)P(A 4)＋P(B 3)P(A 4)P(A 5)＋P(A 3)P(B 4)P(A 5) ＝0.6×0.6＋0.4×0.6×0.6＋0.6×0.4×0.6＝0.648. (2)经过5局比赛，甲获胜的概率为P(B 3·A 4·A 5)＋P(A 3·B 4·A 5)＝0.4×0.6×0.6＋0.6×0.4×0.6＝0.288； 经过5局比赛，乙获胜的概率为P(A 3·B 4·B 5)＋P(B 3·A 4·B 5)＝0.6×0.4×0.4＋0.4×0.6×0.4＝0.192. 所以经过5局比赛，比赛结束的概率为0.288＋0.192＝0.48.第五节 离散型随机变量的分布列一、选择题1．抛掷两颗骰子，所得点数之和为ξ，那么ξ＝4表示的随机试验结果是( ) A ．两颗都是2点B 一颗是3点，一颗是1点C ．两颗都是4点D ．一颗是3点，一颗是1点或两颗都是2点解析：对A 、B 中表示的随机试验的结果，随机变量均取值4，而D 是 ξ＝4代表的所有试验结果．掌握随机变量的取值与它刻画的随机试验的结果的对应关系是理解随机变量概念的关键．答案：D2．下列分布列中，是离散型随机变量分布列的是( ) A.B.C.D.解析：只有选项C 答案：C3．设某项试验的成功率是失败率的2倍，用随机变量ξ描述一次该项试验的成功次数，则P(ξ＝0)等于( )A ．0 B.13 C.12 D.23解析：1－P(ξ＝0)＝2P(ξ＝0)，即P(ξ＝0)＝13.答案：B4．在15个村庄中有7个村庄交通不方便，现从中任意选10个村庄，用X 表示这10个村庄中交通不方便的村庄数，下列概率中等于C47C68C1015的是( )A ．P(X ＝2)B ．P(X≤2)C ．P(X ＝4)D ．P(X≤4)解析：由分子C47C68可知是从7个不方便的村庄中选4个，从8个方便的村庄中选6个，∴X＝4，∴是P(X ＝4)的概率．答案：C5．若离散型随机变量X 的分布列为：则常数q 的值为( ) A ．1 B. 1±22 C. 1＋22 D. 1－22解析：由12＋(1－2q)＋q 2＝1，解得q ＝1－22或q ＝1＋22，又∵q 2∈[0,1]，∴q＝1＋22舍去．∴q＝1－22. 答案：D 二、填空题6．随机变量X 等可能取值为1,2,3，……，n ，如果P(X ＜4)＝0.3，那么n ＝________. 解析：∵P(X＜4)＝ P(X ＝1)＋P(X ＝2)＋P(X ＝3)＝3n ＝0.3，∴n＝10. 答案：107．随机变量ξ的分布列为若a ＋c ＝2b ，则P(|ξ|＝解析：∵a＋c ＝2b ，又∵a＋b ＋c ＝1，∴b＝13，a ＋c ＝23，于是P(|ξ|＝1)＝P(ξ＝1)＋P(ξ＝－1)＝a ＋c ＝23.答案：238．若离散型随机变量X 的分布列为P(X ＝k)＝c2k ，k ＝1,2,3,4,5,6.其中c 为常数，则P(X≤2)的值是________．解析：由c 2＋c 4＋c 8＋c 16＋c 32＋c 64＝1，可得c ＝6463.∴P(X≤2)＝P(X ＝1)＋P(X ＝2)＝3263＋1663＝4863＝1621.答案：1621三、解答题9．(2009年广州调研)一厂家向用户提供的一箱产品共10件，其中有2件次品，用户先对产品进行抽检以决定是否接收．抽检规则是这样的：一次取一件产品检查(取出的产品不放回箱子)，若前三次没有抽查到次品，则用户接收这箱产品；若前三次中一抽查到次品就立即停止抽检，并且用户拒绝接收这箱产品．(1)求这箱产品被用户接收的概率；(2)记抽检的产品件数为ξ，求ξ的分布列． 解析：(1)设“这箱产品被用户接收”为事件A ，P(A)＝8×7×610×9×8＝715，即这箱产品被用户接收的概率为715.(2)ξ的可能取值为1,2,3.P(ξ＝1)＝210＝15，P(ξ＝2)＝810×29＝845，P(ξ＝3)＝810×79＝2845，∴ξ的分布列为10.(2009年广州模拟)50名一线教师参加，使用不同版本教材的教师人数如下表所示：(1)从这(2)若随机选出2名使用人教版的教师发言，设使用人教A 版的教师人数为ξ，求随机变量ξ的分布列．解析：(1)从50名教师中随机选出2名的方法数为C250＝1225. 选出2人使用版本相同的方法数为 C 220＋C 215＋C 25＋C 210＝350，故2人使用版本相同的概率为：P ＝3501225＝27.(2)∵P(ξ＝0)＝C215C235＝317，P(ξ＝1)＝C120C115C235＝60119，P(ξ＝2)＝C220C235＝38119，∴ξ的分布列为第六节 二项分布、超几何分布、正态分布一、选择题1．设随机变量ξ～B ⎝ ⎛⎭⎪⎫6，12，则P (ξ＝3)的值为( ) A.516 B.316 C.58 D.716解析：P (ξ＝3)＝C36⎝ ⎛⎭⎪⎫123⎝ ⎛⎭⎪⎫1－123＝516.答案：A2．设随机变量ξ ～ B (2，p )，随机变量η ～ B (3，p )，若P (ξ ≥1) ＝59，则P (η≥1)＝( )A.13B.59C.827D.1927解析：∵P (ξ≥1) ＝2p (1－p )＋p 2＝59， ∴p ＝13，∴P (η≥1) ＝C 13⎝ ⎛⎭⎪⎫13⎝ ⎛⎭⎪⎫232＋C 23⎝ ⎛⎭⎪⎫132⎝ ⎛⎭⎪⎫23＋C 33⎝ ⎛⎭⎪⎫133＝1927，故选D.答案：D3．一袋中有5个白球，3个红球，现从袋中往外取球，每次任取一个记下颜色后放回，直到红球出现10次时停止，设停止时共取了ξ次球，则P (ξ＝12)＝( )A ．C 1012⎝ ⎛⎭⎪⎫3810·⎝ ⎛⎭⎪⎫582B ．C 911⎝ ⎛⎭⎪⎫389⎝ ⎛⎭⎪⎫582·38C ．C 911⎝ ⎛⎭⎪⎫589·⎝ ⎛⎭⎪⎫382D ．C 911⎝ ⎛⎭⎪⎫389·⎝ ⎛⎭⎪⎫582解析：P (ξ＝12)表示第12次为红球，前11次中有9次为红球，从而P (ξ＝12)＝C 911·⎝ ⎛⎭⎪⎫389⎝ ⎛⎭⎪⎫582×38. 答案：B4．在4次独立重复试验中，随机事件A 恰好发生1次的概率不大于其恰好发生2次的概率，则事件A 在一次试验中发生的概率p 的取值范围是( )A ．[0.4,1)B ．(0,0.6]C ．(0,0.4]D ．[0.6,1)解析：C14p (1－p )3≤C24p 2(1－p )2，即2(1－p )≤3p ， ∴p ≥0.4.又∵p <1，∴0.4≤p <1. 答案：A5．(2009年湖南四市联考)已知随机变量ξ服从正态分布N (2，σ2)，P (ξ≤4)＝0.84，则P (ξ＜0)＝( )A ．0.16B ．0.32C ．0.68D ．0.84 解析：∵P (ξ≤4)＝0.84，μ＝2，∴P (ξ＜0) ＝P (ξ＞4)＝1－0.84＝0.16.故选A. 答案：A 二、填空题6．某篮运动员在三分线投球的命中率是12，他投球10次，恰好投进3个球的概率________．(用数值作答)解析：由题意知所求概率P ＝C 310⎝ ⎛⎭⎪⎫123⎝ ⎛⎭⎪⎫127＝15128.答案：151287．从装有3个红球，2个白球的袋中随机取出两个球，设其中有X 个红球，则X 的分布列为________．解析：这是超几何分布，P (X ＝0)＝C 03C 22C 25＝0.1；P (X ＝1)＝C 13C 12C 25＝0.6; P (X ＝2)＝C 23C 02C 25＝0.3，分布列如下表：答案：8.1000件零件中随机抽查一件，测得它的外径为5.7 cm.则该厂生产的这批零件是否合格________．解析：根据3σ原则，在4－3×0.5＝2.5——4＋3×0.5＝5.5之外为异常，所以这批零件不合格．答案：不合格 三、解答题9．(2008年四川延考)一条生产线上生产的产品按质量情况分为三类：A 类、B 类、C 类．检验员定时从该生产线上任取2件产品进行一次抽检，若发现其中含有C 类产品或2件都是B 类产品，就需要调整设备，否则不需要调整．已知该生产线上生产的每件产品为A 类品，B 类品和C 类品的概率分别为0.9,0.05和0.05，且各件产品的质量情况互不影响．(1)求在一次抽检后，设备不需要调整的概率；(2)若检验员一天抽检3次，以ξ表示一天中需要调整设备的次数，求ξ的分布列． 解析：(1)设A i 表示事件“在一次抽检中抽到的第i 件产品为A 类品”，i ＝1,2.B i 表示事件“在一次抽检中抽到的第i 件产品为B 类品”， i ＝1,2.C 表示事件“一次抽检后，设备不需要调整”．则C ＝A 1·A 2＋A 1·B 2＋B 1·A 2.由已知P (A i )＝0.9，P (B i )＝0.05 i ＝1,2. 所以，所求的概率为P (C )＝P (A 1·A 2)＋P (A 1·B 2)＋P (B 1·A 2)＝0.92＋2×0.9×0.05＝0.9.(2)由(1)知一次抽检后，设备需要调整的概率为p ＝P (C )＝1－0.9＝0.1，依题意知ξ～B (3,0.1)，ξ的分布列为10.(2009算采用现场答题的方式来进行，已知在备选的10道试题中，甲能答对其中的6题，乙能答对其中的8题．规定每次考试都从备选题中随机抽出3题进行测试，至少答对2题才能入选．(1)求甲答对试题数ξ的概率分布； (2)求甲、乙两人至少有一人入选的概率．解析：(1)依题意，甲答对试题数ξ的可能取值为0、1、2、3，则 P (ξ＝0)＝C 34C 310＝130，P (ξ＝1)＝C 16·C 24C 310＝310，P (ξ＝2)＝C 26·C 14C 310＝12，P (ξ＝3)＝C 36C 310＝16，其分布列如下：(2)P (A )＝C 26C 14＋C 36C 310＝60＋20120＝23， P (B )＝C 28C 12＋C 38C 310＝56＋56120＝1415. 因为事件A 、B 相互独立，∴甲、乙两人考试均不合格的概率为 P()A ·B ＝P ()A ·P ()B ＝⎝ ⎛⎭⎪⎫1－23⎝ ⎛⎭⎪⎫1－1415＝145， ∴甲、乙两人至少有一人考试合格的概率为P ＝1－P()A ·B ＝1－145＝4445. 答：甲、乙两人至少有一人考试合格的概率为4445.法二：甲、乙两人至少有一个考试合格的概率为P ＝P ()A ·B＋P ()A ·B ＋P ()A ·B＝23×115＋13×1415＋23×1415＝4445. 答：甲、乙两人至少有一人考试合格的概率为4445。

高中数学--函数的性质二壹、填空题 1、函数1y x x=+在区间[]2,5上的最大值为 2、已知()(),f x g x 分别是定义在R 上的偶函数和奇函数，且()()321f x g x x x -=++，则()()11f g +=3、已知函数()()2231lg 11x x x f x x x ⎧+-≥⎪=⎨⎪+<⎩，()f x 的最小值是4、已知函数()()()21201lg 11x x f x a a x x -≤⎧⎪=>≠⎨+<⎪⎩且的最大值为1，则a 的取值范围是5、已知函数y =M ，最小值为m ，则mM的值是 6、已知函数()()ln 1f x x =+()()21f x f x >-的x 的范围是7、设12,x x 为方程24420x mx m -++=的两个实根，2212x x +的最小值为8、若函数()12f x x x a =++-的最小值为5，则实数a 的取值范围是9、若函数()12log 414x x f x ax x ≥⎧⎪=⎨⎪-<⎩为单调函数，则实数a 的取值范围是10、设()01x a x f x x x x -+≤⎧⎪=⎨+>⎪⎩若()0f 是()f x 的最小值，则a 的取值范围为11、设函数()()221sin 1x xf x x ++=+的最大值为M ，最小值为m ，则M m += 12、已知非空集合M R ⊆，定义域为R 的函数()10M x M f x x M∈⎧=⎨∉⎩，若,A B 是R 的两个非空真子集，函数()()()()11A B A B f x F x f x f x ⋃+=++的值域为贰、解答题17、判断函数()211f x x =-在区间()1,0-上的单调性，并用定义加以证明。

18、已知函数()2220x xx f x x mxx ⎧-+≥=⎨+<⎩是奇函数 （1）求实数m 的值；（2）若函数()f x 在区间[]1,2a --上单调递增，求实数a 的取值范围19、求函数()()20a x f x a x+=>在[]1,2上的最小值20、设a 为实数，函数()21,f x x x a x R =+-+∈（1）求当a 分别取-1,0,1时()f x 的最小值；（2）求()f x 的最小值()h a 的函数解析式21、设()22f x x a x=-+，其中a R ∈ （1）判断函数()f x 的奇偶性，并说明理由；（2）若不等式()1f x ≥对一切()0,x ∈+∞恒成立，求实数a 的取值范围叁、选择题 13、函数22lg2x y x x -=+的图像（ ） A.关于x 轴对称 B.关于原点对称 C.关于直线y x =对称 D.关于y 轴对称14、函数()2log 21f x x x =+-的零点必落在区间（ ） A. 11,84⎛⎫ ⎪⎝⎭ B. 11,42⎛⎫ ⎪⎝⎭ C. 1,12⎛⎫⎪⎝⎭D. ()1,215、设函数()f x 的定义域为R ，有下列三个命题：（1）若存在常数M ，使得对任意x R ∈，都有()f x M ≤，则M 是()f x 函数的最大值； （2）若存在0x R ∈，使得对任意x R ∈，都有()()0f x f x ≤，则()0f x 是函数()f x 的最大值；（3）若存在0x R ∈，使得对任意x R ∈，且0x x ≠，都有()()0f x f x <，则()0f x 是函数()f x 的最大值。

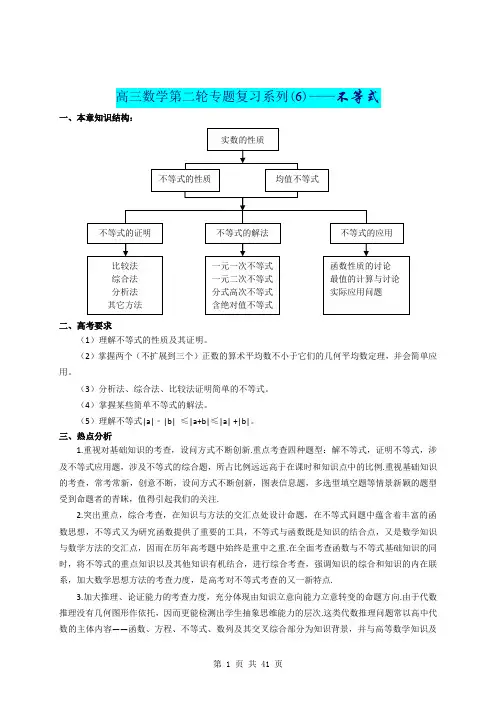
高三数学第二轮专题复习系列(6)——不等式一、本章知识结构：二、高考要求（1）理解不等式的性质及其证明。

（2）掌握两个（不扩展到三个）正数的算术平均数不小于它们的几何平均数定理，并会简单应用。

（3）分析法、综合法、比较法证明简单的不等式。

（4）掌握某些简单不等式的解法。

（5）理解不等式|a|﹣|b| ≤|a+b|≤|a| +|b|。

三、热点分析1.重视对基础知识的考查，设问方式不断创新.重点考查四种题型：解不等式，证明不等式，涉及不等式应用题，涉及不等式的综合题，所占比例远远高于在课时和知识点中的比例.重视基础知识的考查，常考常新，创意不断，设问方式不断创新，图表信息题，多选型填空题等情景新颖的题型受到命题者的青眯，值得引起我们的关注.2.突出重点，综合考查，在知识与方法的交汇点处设计命题，在不等式问题中蕴含着丰富的函数思想，不等式又为研究函数提供了重要的工具，不等式与函数既是知识的结合点，又是数学知识与数学方法的交汇点，因而在历年高考题中始终是重中之重.在全面考查函数与不等式基础知识的同时，将不等式的重点知识以及其他知识有机结合，进行综合考查，强调知识的综合和知识的内在联系，加大数学思想方法的考查力度，是高考对不等式考查的又一新特点.3.加大推理、论证能力的考查力度，充分体现由知识立意向能力立意转变的命题方向.由于代数推理没有几何图形作依托，因而更能检测出学生抽象思维能力的层次.这类代数推理问题常以高中代数的主体内容——函数、方程、不等式、数列及其交叉综合部分为知识背景，并与高等数学知识及思想方法相衔接，立意新颖，抽象程度高，有利于高考选拔功能的充分发挥.对不等式的考查更能体现出高观点、低设问、深入浅出的特点，考查容量之大、功能之多、能力要求之高，一直是高考的热点.4.突出不等式的知识在解决实际问题中的应用价值，借助不等式来考查学生的应用意识.不等式部分的内容是高考较为稳定的一个热点,考查的重点是不等式的性质、证明、解法及最值方面的应用。

高考数学专题复习 导数的应用黄冈第二轮复习新思维)(5)(')(.62.1.1.2.))1(,1()(,12)21()1(lim )(.5),(3.),(3.),(.),(.5)(.4)3,.(),3.(),3.[),3.[12)(.3.0.8.4.3)(32lim ,2)3(',2)3(.2)2,0.()0,.()2,.(),2.(13)(.1022233323x f x f R x f D C B A f x f y x x f f x f t s D t s C B A tx sx x x f R t s D C B A a ax x x f D C B A x x f x f f D C B A x x x f x x 所示，则函数的图象如图，导函数的定义域为函数处切线的斜率为上点则过曲线为可导函数，且设单调递减时，在当单调递增时，在当单调递减在单调递增在，则、若的取值范围为）内为增函数，则实数，在（不存在的值为已知是减函数的区间为函数一、选择题--=-=--+∞-∞<+∞-∞<+∞-∞+∞-∞+-+-=∈--∞+∞-+∞-+∞∞+-+=----==-∞-∞+∞+-=→→abb a b a x f xxx x f xk x x f x x f y x x y a ax x x y x y e x f x e x f b bf a af D b af a bf C b af a af B b af a bf A b a b a x f x xf x x f y s cm D s cm C s cm B s cm A cm cm y x D y x C y x B y A M xx x y D C B A cm D C B A x x x ->->>+-+==≠=--==+-===--=<<>>>>>>==-+=-+=+-=-+-=→1ln ln 0,02)(11)1ln()(.1521,1)0)((,()(.14]22[|3|.133.121('lim,2)(.11)()(.)()(.)()(.)()(.0)()('0)(.10/32./21./1./41.10100.9012.022.012.0.0121ln .812.10.8.6.45.7....23230232，求证：）若（的极小值；）求（已知函数三、解答题），则次曲线方程为，此曲线过点（处切线斜率为在一曲线上的最大值是，在闭区间函数的切线，则是曲线直线则设二、填空题的是则下列不等式一定成立满足、恒成立，又知常数上可导，且满足不等式在若函数径增加的速度为时，气球半气球半径为气体压力不变，那么当的常速注入气体，假设设气球以每秒）处的切线方程为，（在点曲线为截去的小正方形的边长盒容积最大，则在四角焊成铁盒，若所做的铁然后把四边折起，就能的小正方形四各截去一个面积相等盖的铁盒时，在铁皮的的正方形铁皮做一个无用边长为小值点有四个极大值点，无极极小值点有两个极大值点，两个极小值点有三个极大值点，两个小值点无极大值点，有四个极ππππ).,2,1(2,,,,)0()()3(1)]([)()2(,sin 2)()2()1()(sin )(.171|)()(|),,[2)()1(21],[)1()1()(.16121240200212122ΛΛΛ=<-<∞++==-+∈=<-∈≤<≤-+-=+n a a a a a x f x x x f x f x k x k x f k x f R x x x x f x f x f n m x x x f n m n m xnm x x f nn n ππππ证明，到大的顺序排列为内的全部极值点按从小，在设的一个极值点，证明为设为整数；其中证明设函数恒成立不等式、）证明：对任意（的单调性讨论且的定义域为已知专题三 导数的应用（答案）一、1.D 2.B 3.B 4.D 5.B 6.C 7.B 8.D 9.A 10.A 二、 31.142.134131.124.11+-=xy 或三、.144)()1(2)1(|)()(|),[,)1()(,)1(2)(],[)(12),[],[)(0)('),[0)('),[,0)('0,0)(,0221))(()(2)(22222)('222)1()1()(1.160,01ln ln 11111,0111)1ln(,0)0()()(0)2(0)0()(00)('01;0)('01)(,)1()(',1)1ln()(1.15222212122232232232243223222222222-+⋅-=---≤-∈-=-=∴>∈<∈==>+∴>+-=+->∴≤<≤≤∴-++-=+--=+--=∴+--+=-+-=>>-≥--=+-=+>=+->+≥+=≥===<<<->>->+=+-+=mn m n m n m n m n x f x f n m x x mnm f mnmn f n m x f n mn mn m x f x f n mn x x f mn m x mn x x f mn x mn m x x mn mx x xm n x m mn x mn x mn mx x xm nx m mx n m x x m x n m x n m x x f x n m x xn m x x n m x x f b a a bb a abx x x b a x x x xx f x f x f x f x f x x f x x f x x x f x xx f x x x x f 对任意最大值为上的最小值为：在）可知）证明：由（（内为增函数内为减函数，在在时，②当时，①当得令）解：（时成立在于是则时恒成立，令在从而于是值，取得极小值，而且最小时，证明：在取得极小值，时，因此在时在时，在的定义域为：而求导数得）解：（Θ中的符号可列表如下：在第二象限或第四象限由①式，在第二或第四象限内，即数，使则存在一个非负任意正实根，即是设因此得：由一定满足的极值点有解如图所示，此方程一定上述方程化简为有程的显然，对于满足上述方得令①上可导，在定义域函数有：的定义，对任意整数）证明：由函数解（恒成立不等式故对任意和上是增函数在即令)(tan cos )('),,2(:tan 0)('0)3(1sin )]([,tan 1tan sin ,tan 1tan cos sin sin sin tan )(,,tan ,0cos 0cos sin ,0)('cos sin )(')()2(sin 2sin sin )2(sin )2sin()2()()2()(1.171|)()(|),,[,152412484)2()(]2,1()(,0)215)(215()1(4484)('21,21,21144)(,0000240022020020202222222002121323x x x x f x k k k x x x f x x x x x x f x x x xx x x x x x x x x f x x x x x x x x f x x x x f R x f xk x x x k x x k x k x x f k x f k x f x f x f n m x x h u u h u u u u u u h u mnn m u u u u h mnu +=++∈-==>+==+=+=+=-=-=≠=+=+==-+=-++=-+<-∈<-=-+-=≤∴∴>++---=+-=≤<≤<∴≤<≤∴-+-==πππππππππΘπππππππππππππ<-<<--<->⋅<-<+<<+-+<<-+-⋅+-=--=-=ΛΛ-=ΛΛ=++++++-++++n n n n n n n n n n n n n n n n n n n n n n n n a a a a a a a a a a a a n a n n a n a a a a a a a a n a a a x x a a a x f x x f 11111111111212102,0)tan(,0tan tan 232,2,)1()1(2)tan()tan tan 1()tan (tan ,2,1,,,,tan ,,,,.)(0)('综上，即必在第二象限由此可知由②式知由于则由于②，那么对于，的全部正实根且满足为方程由题设条件，的极值点都为的正根所以满足Λ。

难点36 函数方程思想函数与方程思想是最重要的一种数学思想，高考中所占比重较大，综合知识多、题型多、应用技巧多.函数思想简单，即将所研究的问题借助建立函数关系式亦或构造中间函数，结合初等函数的图象与性质，加以分析、转化、解决有关求值、解（证）不等式、解方程以及讨论参数的取值范围等问题；方程思想即将问题中的数量关系运用数学语言转化为方程模型加以解决.●难点磁场1.（★★★★★）关于x 的不等式2·32x –3x +a 2–a –3＞0，当0≤x ≤1时恒成立，则实数a 的取值范围为 .2.（★★★★★）对于函数f (x )，若存在x 0∈R ,使f (x 0)=x 0成立，则称x 0为f (x )的不动点.已知函数f (x )=ax 2+(b +1)x +(b –1)(a ≠0)（1）若a =1,b =–2时，求f (x )的不动点；（2）若对任意实数b ，函数f (x )恒有两个相异的不动点，求a 的取值范围；（3）在（2）的条件下，若y =f (x )图象上A 、B 两点的横坐标是函数f (x )的不动点，且A 、B 关于直线y =kx +1212+a 对称，求b 的最小值.●案例探究［例1］已知函数f (x )=log m33+-x x (1)若f (x )的定义域为［α，β］，（β＞α＞0），判断f (x )在定义域上的增减性，并加以说明；(2)当0＜m ＜1时，使f (x )的值域为［log m ［m (β–1)］，log m ［m (α–1)］］的定义域区间为［α,β］(β＞α＞0)是否存在？请说明理由.命题意图：本题重在考查函数的性质，方程思想的应用.属★★★★级题目.知识依托：函数单调性的定义判断法；单调性的应用；方程根的分布；解不等式组. 错解分析：第(1)问中考生易忽视“α＞3”这一关键隐性条件；第(2)问中转化出的方程，不能认清其根的实质特点，为两大于3的根.技巧与方法：本题巧就巧在采用了等价转化的方法，借助函数方程思想，巧妙解题.解：（1）⇔>+-033x x x ＜–3或x ＞3. ∵f (x )定义域为［α,β］,∴α＞3 设β≥x 1＞x 2≥α，有0)3)(3()(6333321212211>++-=+--+-x x x x x x x x 当0＜m ＜1时，f (x )为减函数，当m ＞1时，f (x )为增函数.（2）若f (x )在［α,β］上的值域为［log m m (β–1),log m m (α–1)］ ∵0＜m ＜1, f (x )为减函数.∴⎪⎪⎩⎪⎪⎨⎧-=+-=-=+-=)1(log 33log )()1(log 33log )(ααααββββm f m f m m m m即3,0)1(3)12(0)1(3)12(22>>⎪⎩⎪⎨⎧=---+=---+αβααββ又m m m m m m即α,β为方程mx 2+(2m –1)x –3(m –1)=0的大于3的两个根∴⎪⎪⎪⎩⎪⎪⎪⎨⎧>>-->+-=∆<<0)3(3212011616102mf m m m m m ∴0＜m ＜432-故当0＜m ＜432-时，满足题意条件的m 存在. ［例2］已知函数f (x )=x 2–(m +1)x +m (m ∈R ) (1)若tan A ,tan B 是方程f (x )+4=0的两个实根，A 、B 是锐角三角形ABC 的两个内角.求证：m ≥5;(2)对任意实数α,恒有f (2+cos α)≤0，证明m ≥3;(3)在(2)的条件下，若函数f (sin α)的最大值是8，求m .命题意图：本题考查函数、方程与三角函数的相互应用；不等式法求参数的范围.属 ★★★★★级题目.知识依托：一元二次方程的韦达定理、特定区间上正负号的充要条件，三角函数公式. 错解分析：第(1)问中易漏掉Δ≥0和tan(A +B )＜0，第(2)问中如何保证f (x )在［1,3］恒小于等于零为关键.技巧与方法：深挖题意，做到题意条件都明确，隐性条件注意列.列式要周到，不遗漏. （1）证明：f (x )+4=0即x 2–(m +1)x +m +4=0.依题意：⎪⎩⎪⎨⎧>+=⋅>+=+≥+-+=∆04tan tan 01tan tan 0)4(4)1(2m B A m B A m m 又A 、B 锐角为三角形内两内角 ∴2π＜A +B ＜π ∴tan(A +B )＜0，即031tan tan 1tan tan )tan(<--+=-+=+m m B A B A B A∴⎪⎪⎪⎩⎪⎪⎪⎨⎧>++>+>+≥--031040101522m m m m m m ∴m ≥5 (2)证明：∵f (x )=(x –1)(x –m )又–1≤cos α≤1，∴1≤2+cos α≤3，恒有f (2+cos α)≤0 即1≤x ≤3时，恒有f (x )≤0即(x –1)(x –m )≤0 ∴m ≥x 但x max =3，∴m ≥x max =3(3)解：∵f (sin α)=sin 2α–(m +1)sin α+m =4)1()21(sin 22+-++-m m m α 且21+m ≥2,∴当sin α=–1时，f (sin α)有最大值8. 即1+(m +1)+m =8，∴m =3 ●锦囊妙计函数与方程的思想是最重要的一种数学思想，要注意函数，方程与不等式之间的相互联系和转化.考生应做到：（1）深刻理解一般函数y =f (x )、y =f –1(x )的性质（单调性、奇偶性、周期性、最值和图象变换），熟练掌握基本初等函数的性质，这是应用函数思想解题的基础.（2）密切注意三个“二次”的相关问题，三个“二次”即一元二次函数、一元二次方程、一元二次不等式是中学数学的重要内容，具有丰富的内涵和密切的联系.掌握二次函数基本性质，二次方程实根分布条件，二次不等式的转化策略.●歼灭难点训练 一、选择题1.（★★★★★）已知函数f (x )=log a ［x –(2a )2］对任意x ∈［21,+∞］都有意义，则实数a 的取值范围是( )A.(0,41] B.(0,41) C.［41,1) D.(41,21） 2.（★★★★★）函数f (x )的定义域为R ，且x ≠1，已知f (x +1)为奇函数，当x ＜1时，f (x )=2x 2–x +1，那么当x ＞1时，f (x )的递减区间是( )A.［45，+∞) B.(1,45] C.［47,+∞) D.(1,47］二、填空题3.（★★★★）关于x 的方程lg(ax –1)–lg(x –3)=1有解，则a 的取值范围是 .4.（★★★★★）如果y =1–sin 2x –m cos x 的最小值为–4，则m 的值为 . 三、解答题5.（★★★★）设集合A ={x ｜4x –2x +2+a =0,x ∈R }. （1）若A 中仅有一个元素，求实数a 的取值集合B ；（2）若对于任意a ∈B ，不等式x 2–6x ＜a (x –2)恒成立，求x 的取值范围.6.（★★★★）已知二次函数f (x )=ax 2+bx (a ,b 为常数，且a ≠0)满足条件:f (x –1)=f (3–x )且方程f (x )=2x 有等根.（1）求f (x )的解析式；（2）是否存在实数m ，n (m ＜n ＝，使f (x )定义域和值域分别为［m ,n ］和［4m ,4n ］，如果存在，求出m 、n 的值；如果不存在，说明理由.7.（★★★★★）已知函数f (x )=6x –6x 2，设函数g 1(x )=f (x ), g 2(x )=f ［g 1(x )］, g 3(x )=f ［g 2(x )］, …g n (x )=f ［g n –1(x )］,…（1）求证：如果存在一个实数x 0，满足g 1(x 0)=x 0，那么对一切n ∈N ，g n (x 0)=x 0都成立； （2）若实数x 0满足g n (x 0)=x 0，则称x 0为稳定不动点，试求出所有这些稳定不动点； （3）设区间A =（–∞,0）,对于任意x ∈A ，有g 1(x )=f (x )=a ＜0, g 2(x )=f ［g 1(x )］=f (0)＜0， 且n ≥2时，g n (x )＜0.试问是否存在区间B （A ∩B ≠∅），对于区间内任意实数x ，只要n ≥2，都有g n (x )＜0.8.（★★★★）已知函数f (x )=xa 11- (a ＞0,x ＞0). （1）求证:f (x )在(0,+∞)上是增函数；（2）若f (x )≤2x 在(0,+∞)上恒成立，求a 的取值范围；（3）若f (x )在［m ,n ］上的值域是［m ,n ］(m ≠n )，求a 的取值范围.参 考 答 案●难点磁场1.解析：设t =3x ，则t ∈［1,3］，原不等式可化为a 2–a –3＞–2t 2+t ,t ∈［1,3］. 等价于a 2–a –3大于f (t )=–2t 2+t 在［1,3］上的最大值. 答案：(–∞,–1)∪(2,+∞)2.解：（1）当a =1,b =–2时，f (x )=x 2–x –3，由题意可知x =x 2–x –3，得x 1=–1,x 2=3. 故当a =1,b =–2时，f (x )的两个不动点为–1,3.（2）∵f (x )=ax 2+(b +1)x +(b –1)(a ≠0)恒有两个不动点，∴x =ax 2+(b +1)x +(b –1)，即ax 2+bx +(b –1)=0恒有两相异实根 ∴Δ=b 2–4ab +4a ＞0(b ∈R )恒成立. 于是Δ′=(4a )2–16a ＜0解得0＜a ＜1故当b ∈R ，f (x )恒有两个相异的不动点时，0＜a ＜1.（3）由题意A 、B 两点应在直线y =x 上，设A (x 1,x 1),B (x 2,x 2) 又∵A 、B 关于y =kx +1212+a 对称.∴k =–1.设AB 的中点为M (x ′,y ′)∵x 1,x 2是方程ax 2+bx +(b –1)=0的两个根. ∴x ′=y ′=a b x x 2221-=+，又点M 在直线1212++-=a x y 上有 121222++=-a a b a b ，即aa a ab 121122+-=+-= ∵a ＞0，∴2a +a 1≥22当且仅当2a =a1即a =22∈(0,1)时取等号，故b ≥–221，得b 的最小值–42. ●歼灭难点训练一、1.解析：考查函数y 1=x 和y 2=(2a )x的图象，显然有0＜2a ＜1.由题意21)2(21a =得a =41，再结合指数函数图象性质可得答案. 答案：A 2.解析：由题意可得f (–x +1)=–f (x +1).令t =–x +1，则x =1–t ，故f (t )=–f (2–t )，即f (x )=–f (2–x ).当x ＞1,2–x ＜1，于是有f (x )=–f (2–x )=–2(x –47)2–87，其递减区间为［47，+∞). 答案：C3.解析：显然有x ＞3，原方程可化为1031=--x ax 故有(10–a )·x =29,必有10–a ＞0得a ＜10又x =a -1029＞3可得a ＞31. 答案：31＜a ＜104.解析：原式化为4)2(cos 22m m x y --=.当2m＜–1,y min =1+m =–4⇒m =–5. 当–1≤2m≤1,y min =42m -=–4⇒m =±4不符.当2m＞1，y min =1–m =–4⇒m =5. 答案：±5二、5.解：(1)令2x =t (t ＞0)，设f (t )=t 2–4t +a .由f (t )=0在(0,+∞)有且仅有一根或两相等实根，则有 ①f (t )=0有两等根时，Δ=0⇒16–4a =0⇒a =4 验证：t 2–4t +4=0⇒t =2∈(0,+∞)，这时x =1 ②f (t )=0有一正根和一负根时,f (0)＜0⇒a ＜0③若f (0)=0，则a =0，此时4x –4·2x =0⇒2x =0（舍去），或2x =4,∴x =2，即A 中只有一个元素综上所述，a ≤0或a =4，即B ={a ｜a ≤0或a =4}（2）要使原不等式对任意a ∈(–∞,0］∪｛4｝恒成立.即g (a )=(x –2)a –(x 2–6x )＞0恒成立.只须175081020)4(022-⇒⎩⎨⎧<+-≤⇒⎩⎨⎧>≤-x x x g x ＜x ≤2 6.解：（1）∵方程ax 2+bx =2x 有等根，∴Δ=(b –2)2=0,得b =2. 由f (x –1)=f (3–x )知此函数图象的对称轴方程为x =–ab2=1得a =–1，故f (x )=–x 2+2x . （2）f (x )=–(x –1)2+1≤1，∴4n ≤1，即n ≤41 而抛物线y =–x 2+2x 的对称轴为x =1 ∴n ≤41时，f (x )在［m ,n ］上为增函数. 若满足题设条件的m ,n 存在，则⎩⎨⎧==nn f mm f 4)(4)(⎩⎨⎧-==-==⇒⎪⎩⎪⎨⎧=+-=+-2020424222n n m m nn n m m m 或或即 又m ＜n ≤41,∴m =–2,n =0，这时定义域为［–2,0］，值域为［–8,0］. 由以上知满足条件的m 、n 存在，m =–2,n =0. 7.(1)证明：当n =1时，g 1(x 0)=x 0显然成立；设n =k 时，有g k (x 0)=x 0(k ∈N )成立， 则g k +1(x 0)=f ［g k (x 0)］=f (x 0)=g 1(x 0)=x 0 即n =k +1时，命题成立.∴对一切n ∈N ,若g 1(x 0)=x 0，则g n (x 0)=x 0.（2）解：由（1）知，稳定不动点x 0只需满足f (x 0)=x 0 由f (x 0)=x 0，得6x 0–6x 02=x 0,∴x 0=0或x 0=65 ∴稳定不动点为0和65. (3)解：∵f (x )＜0，得6x –6x 2＜0⇒x ＜0或x ＞1.∴g n (x )＜0⇔f ［g n –1(x )］＜0⇔g n –1(x )＜0或g n –1(x )＞1要使一切n ∈N ,n ≥2，都有g n (x )＜0，必须有g 1(x )＜0或g 1(x )＞1. 由g 1(x )＜0⇔6x –6x 2＜0⇔x ＜0或x ＞1 由g 1(x )＞0⇔6x –6x 2＞1⇔633633+<<-x 故对于区间(633,633+-)和(1,+∞)内的任意实数x ,只要n ≥2,n ∈N ，都有g n (x )＜0. 8.(1)证明：任取x 1＞x 2＞0,f (x 1)–f (x 2)=2121122111)11()11(x x xx x x x a x a -=-=--- ∵x 1＞x 2＞0,∴x 1x 2＞0，x 1–x 2＞0,∴f (x 1)–f (x 2)＞0，即f (x 1)＞f (x 2)，故f (x )在(0,+∞)上是增函数. （2）解：∵xa 11-≤2x 在(0,+∞)上恒成立，且a ＞0, ∴a ≥xx 121+在（0，+∞）上恒成立，令421221121)(=⋅≤+=xx xx x g （当且仅当2x =x1即x =22时取等号），要使a ≥xx 121+在(0,+∞)上恒成立，则a ≥42.故a 的取值范 围是［42,+∞).(3)解：由（1）f (x )在定义域上是增函数. ∴m =f (m ),n =f (n )，即m 2–a 1m +1=0，n 2–a1n +1=0 故方程x 2–a 1x +1=0有两个不相等的正根m ，n ，注意到m ·n =1，故只需要Δ=(a1)2–4＞0,由于a ＞0，则0＜a ＜21.。

116难点33 函数的连续及其应用函数的连续性是新教材新增加的内容之一.它把高中的极限知识与大学知识紧密联在一起.在高考中，必将这一块内容溶入到函数内容中去，因而一定成为高考的又一个热点.本节内容重点阐述这一块知识的知识结构体系.●难点磁场(★★★★)已知函数f (x )=⎪⎩⎪⎨⎧≤<-≤≤-+-<)51( )1(log )11( )1()1( 32x x x x x x(1)讨论f (x )在点x =－1,0,1处的连续性； (2)求f (x )的连续区间. ●案例探究［例1］已知函数f (x )=242+-x x ,(1)求f (x )的定义域，并作出函数的图象； (2)求f (x )的不连续点x 0;(3)对f (x )补充定义，使其是R 上的连续函数.命题意图：函数的连续性，尤其是在某定点处的连续性在函数图象上有最直观的反映.因而画函数图象去直观反映题目中的连续性问题也就成为一种最重要的方法.知识依托：本题是分式函数，所以解答本题的闪光点是能准确画出它的图象.错解分析：第(3)问是本题的难点，考生通过自己对所学连续函数定义的了解.应明确知道第(3)问是求的分数函数解析式.技巧与方法：对分式化简变形，注意等价性，观察图象进行解答. 解：(1)当x +2≠0时，有x ≠－2因此，函数的定义域是(－∞,－2)∪(－2,+∞)当x ≠－2时，f (x )=242+-x x =x －2,其图象如上图(2)由定义域知，函数f (x )的不连续点是x 0=－2.(3)因为当x ≠－2时，f (x )=x －2,所以)2(lim )(lim 22-=-→-→x x f x x =－4.因此，将f (x )的表达式改写为f (x )=⎪⎩⎪⎨⎧-=--≠+-2)( 4)2( 242x x x x则函数f (x )在R 上是连续函数.［例2］求证：方程x =a sin x +b (a ＞0,b ＞0)至少有一个正根，且它不大于a +b .命题意图：要判定方程f (x )=0是否有实根.即判定对应的连续函数y =f (x )的图象是否与x 轴有交点，因此根据连续函数的性质，只要找到图象上的两点，满足一点在x 轴上方，另一点在x 轴下方即可.本题主要考查这种解题方法.知识依托：解答本题的闪光点要找到合适的两点，使函数值其一为负，另一为正.错解分析：因为本题为超越方程，因而考生最易想到画图象观察，而忽视连续性的性质在解这类题目中的简便作用.117证明：设f (x )=a sin x +b －x ,则f (0)=b ＞0,f (a +b )=a ·sin(a +b )+b －(a +b )=a ［sin(a +b )－1］≤0, 又f (x )在(0,a +b ］内是连续函数，所以存在一个x 0∈(0,a +b ］，使f (x 0)=0,即x 0是方程f (x )=0的根，也就是方程x =a ·sin x +b 的根.因此，方程x =a sin x +b 至少存在一个正根，且它不大于a +b . ●锦囊妙计1.深刻理解函数f (x )在x 0处连续的概念：等式lim 0x x →f (x )=f (x 0)的涵义是：(1)f (x 0)在x =x 0处有定义，即f (x 0)存在；(2)lim 0x x →f (x )存在，这里隐含着f (x )在点x =x 0附近有定义；(3)f (x )在点x 0处的极限值等于这一点的函数值，即lim 0x x →f (x )=f (x 0).函数f (x )在x 0处连续，反映在图象上是f (x )的图象在点x =x 0处是不间断的. 2.函数f (x )在点x 0不连续，就是f (x )的图象在点x =x 0处是间断的.其情形：(1)lim 0x x →f (x )存在；f (x 0)存在，但lim 0x x →f (x )≠f (x 0);(2)lim 0x x →f (x )存在，但f (x 0)不存在.(3)lim 0x x →f (x )不存在.3.由连续函数的定义，可以得到计算函数极限的一种方法：如果函数f (x )在其定义区间内是连续的，点x 0是定义区间内的一点，那么求x →x 0时函数f (x )的极限，只要求出f (x )在点x 0处的函数值f (x 0)就可以了，即lim 0x x →f (x )=f (x 0).●歼灭难点训练 一、选择题 1.(★★★★)若f (x )=11113-+-+x x 在点x =0处连续，则f (0)等于( )A.23B.32 C.1 D.02.(★★★★)设f (x )=⎪⎪⎩⎪⎪⎨⎧<<=<<21 11 2110 x x x x 则f (x )的连续区间为( )A.(0，2)B.(0，1)C.(0，1)∪(1，2)D.(1，2)二、填空题3.(★★★★)xx x x arctan 4)2ln(lim 21--→ =_________.4.(★★★★)若f (x )=⎪⎩⎪⎨⎧≥+<--0 0 11x bx a x xx处处连续，则a 的值为_________. 三、解答题1185.(★★★★★)已知函数f (x )=⎪⎪⎩⎪⎪⎨⎧=≠+-)0( 1)0( 121211x x xx(1)f (x )在x =0处是否连续？说明理由；(2)讨论f (x )在闭区间［－1,0］和［0,1］上的连续性.6.(★★★★)已知f (x )=⎪⎩⎪⎨⎧≥+<--)0()0(11x bx a x xx(1)求f (－x );(2)求常数a 的值，使f (x )在区间(－∞,+∞)内处处连续.7.(★★★★)求证任何一个实系数一元三次方程a 0x 3+a 1x 2+a 2x +a 3=0(a 0,a 1,a 2,a 3∈R ,a 0≠0)至少有一个实数根.8.(★★★★)求函数f (x )=⎪⎩⎪⎨⎧>-≤)1( )21(log )1( 2x x x x 的不连续点和连续区间.参考答案难点磁场解：(1)lim 1--→x f (x )=3, lim 1+-→x f (x )=－1,所以lim 1-→x f (x )不存在，所以f (x )在x =－1处不连续，但lim 1-→x f (x )=f (－1)=－1, lim 1--→x f (x )≠f (－1),所以f (x )在x =－1处右连续，左不连续lim 1-→x f (x )=3=f (1), lim 1+→x f (x )不存在，所以lim 1→x f (x )不存在，所以f (x )在x =1不连续，但左连续，右不连续.又lim 0→x f (x )=f (0)=0,所以f (x )在x =0处连续.(2)f (x )中，区间(－∞,－1),［－1,1］,(1,5］上的三个函数都是初等函数，因此f (x )除不连续点x =±1外，再也无不连续点，所以f (x )的连续区间是(－∞,－1),［－1,1］和(1,5].歼灭难点训练 一、1.解析：]11][11)1()[11(]11)1()[11)(11()(3332332-+++++++++++-+++=x x x x x x x x x f2311111)0(1111)1(323=+++=++++++=f x x x答案：A2.解析：11lim )(lim 11==++→→x x x f11921)1(1)(lim ,1lim )(lim 111=≠===→→→--f x f x x f x x x即f (x )在x =1点不连续，显知f (x )在(0,1)和(1,2)连续. 答案：C二、3.解析：利用函数的连续性，即)()(lim 00x f x f x x =→,π=--=--∴→11arctan 4)12sin(11arctan 4)2sin(lim 221x x x 答案：π121,0)(lim )(lim 21111lim 11lim)(lim :.400000=∴=+==-+=--=++---→→→→→a bx a x f x x x x f x x x x x 解析答案：21三、5.解：f (x )=⎪⎩⎪⎨⎧=≠+-)0( 1)0(12111x x x(1) lim 10-→x f (x )=－1, lim 0+→x f (x )=1,所以lim 0→x f (x )不存在，故f (x )在x =0处不连续.(2)f (x )在(－∞,+∞)上除x =0外，再无间断点，由(1)知f (x )在x =0处右连续，所以f (x )在［－1，0］上是不连续函数，在［0,1］上是连续函数.6.解：(1)f (－x )=⎪⎩⎪⎨⎧≥-<-+)0( )0( 11x bx a x xx (2)要使f (x )在(－∞,+∞)内处处连续，只要f (x )在x =0连续，lim 0-→x f (x )= lim-→x x x--11=21111lim )11(lim00=-+=-+--→→xx x x x x lim 0+→x f (x )=lim 0+→x (a +bx )=a ,因为要f (x )在x =0处连续，只要lim 0+→x f (x )= lim 0+→x f (x )= lim 0+→x f (x )=f (0),所以a =217.证明：设f (x )=a 0x 3+a 1x 2+a 2x +a 3,函数f (x )在(－∞,+∞)连续，且x →+∞时，f (x )→+∞;x →－∞时，f (x )→－∞,所以必存在a ∈(－∞,+∞),b ∈(－∞,+∞),使f (a )·f (b )＜0,所以f (x )的图象至少在(a ,b )上穿过x 轴一次，即f (x )=0至少有一实根.8.解：不连续点是x =1,连续区间是(－∞,1),(1,+∞)120。

高考数学总复习资料高三数学第三轮总复习分类讨论押题针对训练复习目标:1．掌握分类讨论必须遵循的原则 2．能够合理，正确地求解有关问题 命题分析:分类讨论是一种重要的逻辑方法，也是一种常用的数学方法，这可以培养学生思维的条理性和概括性，以及认识问题的全面性和深刻性，提高学生分析问题，解决问题的能力.因此分类讨论是历年数学高考的重点与热点.而且也是高考的一个难点.这次的一模考试中，尤其是西城与海淀都设置了解答题来考察学生对分类讨论问题的掌握情况.重点题型分析: 例1．解关于x 的不等式:)()(232R a x a a a x ∈+<+解:原不等式可分解因式为:(x-a)(x-a 2)<0 （下面按两个根的大小关系分类）（1）当a>a 2⇒a 2-a<0即 0<a<1时，不等式的解为 x ∈(a 2, a).（2）当a<a 2⇒a 2-a>0即a<0或a>1时，不等式的解为:x ∈(a, a 2)（3）当a=a 2⇒a 2-a=0 即 a=0或 a=1时，不等式为x 2<0或(x-1)2<0 不等式的解为 x ∈∅.综上，当 0<a<1时，x ∈(a 2, a)当a<0或a>1时，x ∈(a,a 2) 当a=0或a=1时，x ∈∅.评述:抓住分类的转折点，此题分解因式后，之所以不能马上写出解集，主要是不知两根谁大谁小，那么就按两个根之间的大小关系来分类.例2．解关于x 的不等式 ax 2+2ax+1>0(a ∈R) 解:此题应按a 是否为0来分类.（1）当a=0时，不等式为1>0, 解集为R. （2）a ≠0时分为a>0 与a<0两类①10)1(00440002>⇒⎩⎨⎧>->⇒⎪⎩⎪⎨⎧>->⇒⎩⎨⎧>>a a a a a a a a ∆时，方程ax 2+2ax+1=0有两根aa a a aa a a a a a x )1(12442222,1-±-=-±-=-±-=.则原不等式的解为),)1(1())1(1,(+∞-+-----∞aa a a a a Y . ②101000440002<<⇒⎩⎨⎧<<>⇒⎪⎩⎪⎨⎧<->⇒⎩⎨⎧<>a a a a a a a ∆时， 方程ax 2+2ax+1=0没有实根，此时为开口向上的抛物线，则不等式的解为（-∞，+∞）.③ 11000440002=⇒⎩⎨⎧==>⇒⎪⎩⎪⎨⎧=->⇒⎩⎨⎧=>a a a a a a a a 或∆时， 方程ax 2+2ax+1=0只有一根为x=-1，则原不等式的解为(-∞,-1)∪(-1,+∞).④01000440002<⇒⎩⎨⎧><<⇒⎪⎩⎪⎨⎧>-<⇒⎩⎨⎧><a a a a a a a a 或∆时，方程ax 2+2ax+1=0有两根，aa a a a a a x )1(12)1(22,1-±-=-±-=此时，抛物线的开口向下的抛物线，故原不等式的解为:))1(1,)1(1(aa a a a a ----+-. ⑤φ∈⇒⎩⎨⎧≤≤<⇒⎪⎩⎪⎨⎧≤-<⇒⎩⎨⎧≤<a a a a a a a 1000440002∆综上:当0≤a<1时，解集为（-∞，+∞）.当a>1时，解集为),)1(1())1(1,(+∞-+-----∞aa a a a a Y . 当a=1时，解集为(-∞,-1)∪(-1,+∞). 当a<0时，解集为))1(1,)1(1(aa a a a a ----+-. 例3．解关于x 的不等式ax 2-2≥2x-ax(a ∈R)(西城2003’一模 理科）解:原不等式可化为⇔ ax 2+(a-2)x-2≥0, (1)a=0时，x ≤-1，即x ∈(-∞,-1]. (2)a ≠0时，不等式即为(ax-2)(x+1)≥0. ① a>0时， 不等式化为0)1)(2(≥+-x ax ， 当⎪⎩⎪⎨⎧->>120a a ，即a>0时，不等式解为),2[]1,(+∞--∞a Y .当⎪⎩⎪⎨⎧-≤>120aa ，此时a 不存在.② a<0时，不等式化为0)1)(2(≤+-x ax ，当⎪⎩⎪⎨⎧-<<120a a ，即-2<a<0时，不等式解为]1,2[-a当⎪⎩⎪⎨⎧-><120a a ，即a<-2时，不等式解为]2,1[a -.当⎪⎩⎪⎨⎧-=<120aa ，即a=-2时，不等式解为x=-1.综上:a=0时，x ∈(-∞,-1).a>0时，x ∈),2[]1,(+∞--∞aY .-2<a<0时，x ∈]1,2[-a .a<-2时，x ∈]2,1[a-.a=-2时，x ∈{x|x=-1}.评述:通过上面三个例题的分析与解答，可以概括出分类讨论问题的基本原则为: 10:能不分则不分； 20:若不分则无法确定任何一个结果； 30:若分的话，则按谁碍事就分谁.例4．已知函数f(x)=cos 2x+asinx-a 2+2a+5.有最大值2，求实数a 的取值. 解:f(x)=1-sin 2x+asinx-a 2+2a+5.6243)2(sin 22++---=a a a x 令sinx=t, t ∈[-1,1]. 则6243)2()(22++---=a a a t t f (t ∈[-1,1]). (1)当12>a即a>2时，t=1，2533max =++-=a a y 解方程得:22132213-=+=a a 或（舍）. (2)当121≤≤-a 时，即-2≤a ≤2时，2a t =,262432max =++-=a a y ,解方程为:34-=a 或a=4（舍）.(3)当12-<a 即a<-2时， t=-1时，y max =-a 2+a+5=2即 a 2-a-3=0 ∴ 2131±=a , ∵ a<-2, ∴ 2131±-=a 全都舍去.综上，当342213-=+=a a 或时，能使函数f(x)的最大值为2. 例5．设{a n }是由正数组成的等比数列，S n 是其前n 项和，证明:15.025.05.0log 2log log ++>+n n n S S S .证明:（1）当q=1时，S n =na 1从而0)1()2(2121211212<-=+-+⋅=-⋅++a a n a n na S S S n n n（2）当q ≠1时，qq a S n n --=1)1(1， 从而.0)1()1()1)(1(2122121221212<-=-----=-⋅++++nn n n n n n q a q q a q q a S S S由（1）（2）得:212++<⋅n n n S S S . ∵ 函数xy 5.0log =为单调递减函数.∴15.025.05.0log 2log log ++>+n n n S S S .例6．设一双曲线的两条渐近线方程为2x-y+1=0, 2x+y-5=0，求此双曲线的离心率. 分析:由双曲线的渐近线方程，不能确定其焦点位置，所以应分两种情况求解.解:（1）当双曲线的焦点在直线y=3时，双曲线的方程可改为1)3()1(222=---b y a x ，一条渐近线的斜率为2=ab， ∴ b=2.∴ 555222==+==a a a b a c e . （2）当双曲线的焦点在直线x=1时，仿（1）知双曲线的一条渐近线的斜率为2=ba，此时25=e . 综上（1）（2）可知，双曲线的离心率等于255或. 评述:例5，例6，的分类讨论是由公式的限制条件与图形的不确定性所引起的，而例1-4是对于含有参数的问题而对参数的允许值进行的全面讨论.例7．解关于x 的不等式 1512)1(<+--x x a .解:原不等式 012)1(55<⇔+--x x a0)]2()1)[(2(022)1(012)1(<----⇔<--+-⇔<+--⇔a x a x x a x a x x a⎪⎩⎪⎨⎧>----<-⎪⎩⎪⎨⎧<---->-⎩⎨⎧<--=-⇔0)12)(2(01)3(0)12)(2(01)2(0)21)(2(01)1(a ax x a a a x x a x a 或或 由(1) a=1时，x-2>0, 即 x ∈(2,+∞). 由(2)a<1时，012>--aa，下面分为三种情况. ①⎩⎨⎧<<⇒⎪⎩⎪⎨⎧>--<012121a a aa a 即a<1时，解为)12,2(a a --. ②0012121=⇒⎩⎨⎧=<⇒⎪⎩⎪⎨⎧=--<a a a a a a 时，解为∅.③ ⎪⎩⎪⎨⎧<--<2121aa a ⇒ ⎩⎨⎧><01a a 即0<a<1时，原不等式解为:)2,12(a a --.由（3）a>1时，aa--12的符号不确定，也分为3种情况.①⎩⎨⎧≤>⇒⎪⎩⎪⎨⎧≥-->012121a a aa a ⇒ a 不存在.② ⇒⎩⎨⎧>>⇒⎪⎩⎪⎨⎧<-->012121a a aa a 当a>1时，原不等式的解为:),2()12,(+∞---∞Y a a .综上:a=1时，x ∈(2,+∞). a<1时，x ∈)12,2(aa-- a=0时，x ∈∅.0<a<1时，x ∈)2,12(a a-- a>1时，x ∈),2()12,(+∞---∞Y aa.评述:对于分类讨论的解题程序可大致分为以下几个步骤: 10:明确讨论的对象，确定对象的全体； 20:确定分类标准，正确分类，不重不漏； 30:逐步进行讨论，获得结段性结记； 40:归纳总结，综合结记. 课后练习:1．解不等式2)385(log 2>+-x x x2．解不等式1|)3(log ||log |3121≤-+x x3．已知关于x 的不等式052<--ax ax 的解集为M. （1）当a=4时，求集合M:（2）若3∈M ，求实数a 的取值范围.4．在x0y 平面上给定曲线y 2=2x, 设点A 坐标为(a,0), a ∈R ，求曲线上点到点A 距离的最小值d ，并写成d=f(a)的函数表达式.参考答案:1. ），（），（∞+235321Y 2.]4943[，3. (1) M 为），（），（2452Y ∞- (2)),9()35,(+∞-∞∈Y a 4. ⎪⎩⎪⎨⎧<≥-==时当时当1||112)(a a a a a f d .2006年高三数学第三轮总复习函数押题针对训练复习重点：函数问题专题，主要帮助学生整理函数基本知识，解决函数问题的基本方法体系，函数问题中的易错点，并提高学生灵活解决综合函数问题的能力。

难点35 导数的应用问题利用导数求函数的极大(小)值，求函数在连续区间［a ,b ］上的最大最小值，或利用求导法解决一些实际应用问题是函数内容的继续与延伸，这种解决问题的方法使复杂问题变得简单化，因而已逐渐成为新高考的又一热点.本节内容主要是指导考生对这种方法的应用.●难点磁场(★★★★★)已知f (x )=x 2+c ,且f ［f (x )］=f (x 2+1)(1)设g (x )=f ［f (x )］,求g (x )的解析式；(2)设φ(x )=g (x )－λf (x ),试问：是否存在实数λ,使φ(x )在(－∞,－1)内为减函数，且在 (－1，0)内是增函数.●案例探究［例1］已知f (x )=ax 3+bx 2+cx (a ≠0)在x =±1时取得极值，且f (1)=－1.(1)试求常数a 、b 、c 的值；(2)试判断x =±1是函数的极小值还是极大值，并说明理由.命题意图：利用一阶导数求函数的极大值和极小值的方法是导数在研究函数性质方面的继续深入.是导数应用的关键知识点，通过对函数极值的判定，可使学生加深对函数单调性与其导数关系的理解.属★★★★★级题目.知识依托：解题的成功要靠正确思路的选择.本题从逆向思维的角度出发，根据题设结构进行逆向联想，合理地实现了问题的转化，使抽象的问题具体化.这是解答本题的闪光点.错解分析：本题难点是在求导之后，不会应用f ′(±1)=0的隐含条件，因而造成了解决问题的最大思维障碍.技巧与方法：考查函数f (x )是实数域上的可导函数，可先求导确定可能的极值，再通过极值点与导数的关系，建立由极值点x =±1所确定的相等关系式，运用待定系数法求值.解：(1)f ′(x )=3ax 2+2bx +c∵x =±1是函数f (x )的极值点，∴x =±1是方程f ′(x )=0,即3ax 2+2bx +c =0的两根. 由根与系数的关系，得⎪⎪⎩⎪⎪⎨⎧-==-13032ac a b又f (1)=－1,∴a +b +c =－1, ③由①②③解得a =23,0,21==c b , (2)f (x )=21x 3－23x , ∴f ′(x )=23x 2－23=23(x －1)(x +1) 当x ＜－1或x ＞1时，f ′(x )＞0当－1＜x ＜1时，f ′(x )＜0∴函数f (x )在(－∞,－1)和(1,+∞)上是增函数，在(－1，1)上是减函数.∴当x =－1时，函数取得极大值f (－1)=1,当x =1时，函数取得极小值f (1)=－1.［例2］在甲、乙两个工厂，甲厂位于一直线河岸的岸边A 处，乙厂与甲厂在河的同侧，① ②乙厂位于离河岸40 km 的B 处，乙厂到河岸的垂足D 与A 相距50 km ，两厂要在此岸边合建一个供水站C ，从供水站到甲厂和乙厂的水管费用分别为每千米3a 元和5a 元，问供水站C 建在岸边何处才能使水管费用最省？命题意图：学习的目的，就是要会实际应用，本题主要是考查学生运用导数知识解决实际问题的意识，思想方法以及能力.知识依托：解决实际应用问题关键在于建立数学模型和目标函数.把“问题情景”译为数学语言，找出问题的主要关系，并把问题的主要关系近似化，形式化，抽象成数学问题，再划归为常规问题，选择合适的数学方法求解.错解分析：本题难点是如何把实际问题中所涉及的几个变量转化成函数关系式.技巧与方法：根据题设条件作出图形，分析各已知条件之间的关系，借助图形的特征，合理选择这些条件间的联系方式，适当选定变化，构造相应的函数关系.解法一：根据题意知，只有点C 在线段AD 上某一适当位置，才能使总运费最省，设C 点距D 点x km,则∵BD =40,AC =50－x ,∴BC =222240+=+x CD BD 又设总的水管费用为y 元，依题意有：y =30(5a －x )+5a 2240+x (0＜x ＜50)y ′=－3a +22405+x ax,令y ′=0,解得x =30在(0,50)上，y 只有一个极值点，根据实际问题的意义，函数在x =30(km)处取得最小值，此时AC =50－x =20(km)∴供水站建在A 、D 之间距甲厂20 km 处，可使水管费用最省.解法二：设∠BCD =Q ,则BC =θsin 40,CD =40cot θ,(0＜θ＜2π),∴AC =50－40cot θ 设总的水管费用为f (θ),依题意，有f (θ)=3a (50－40·cot θ)+5a ·θsin 40 =150a +40a ·θθsin cos 35- ∴f ′(θ)=40a ·θθθθθθθ22sin cos 5340sin )(sin )cos 35(sin )cos 35(-⋅='⋅--⋅'-a 令f ′(θ)=0,得cos θ=53 根据问题的实际意义，当cos θ=53时，函数取得最小值，此时sin θ=54,∴cot θ=43, ∴AC =50－40cot θ=20(km),即供水站建在A 、D 之间距甲厂20 km 处，可使水管费用最省.●锦囊妙计1.f (x )在某个区间内可导，若f ′(x )＞0,则f (x )是增函数；若f ′(x )＜0,则f (x )是减函数.2.求函数的极值点应先求导，然后令y ′=0得出全部导数为0的点，(导数为0的点不一定都是极值点，例如：y =x 3,当x =0时，导数是0，但非极值点)，导数为0的点是否是极值点，取决于这个点左、右两边的增减性，即两边的y ′的符号，若改变符号，则该点为极值点；若不改变符号，则非极值点，一个函数的极值点不一定在导数为0的点处取得，但可得函数的极值点一定导数为0.3.可导函数的最值可通过(a ,b )内的极值和端点的函数值比较求得，但不可导函数的极值有时可能在函数不可导的点处取得，因此，一般的连续函数还必须和导数不存在的点的函数值进行比较，如y =|x |,在x =0处不可导，但它是最小值点.●歼灭难点训练一、选择题1.(★★★★)设f (x )可导，且f ′(0)=0,又xx f x )(lim0'→=－1,则f (0)( )A.可能不是f (x )的极值B.一定是f (x )的极值C.一定是f (x )的极小值D.等于02.(★★★★)设函数f n (x )=n 2x 2(1－x )n (n 为正整数)，则f n (x )在［0,1］上的最大值为( )A.0B.1C.n n )221(+-D.1)2(4++n n n 二、填空题3.(★★★★)函数f (x )=log a (3x 2+5x －2)(a ＞0且a ≠1)的单调区间_________.4.(★★★★)在半径为R 的圆内，作内接等腰三角形，当底边上高为_________时它的面积最大.三、解答题5.(★★★★★)设f (x )=ax 3+x 恰有三个单调区间，试确定a 的取值范围，并求其单调区间.6.(★★★★)设x =1与x =2是函数f (x )=a ln x +bx 2+x 的两个极值点.(1)试确定常数a 和b 的值；(2)试判断x =1,x =2是函数f (x )的极大值还是极小值，并说明理由.7.(★★★★)已知a 、b 为实数，且b ＞a ＞e ,其中e 为自然对数的底，求证：a b ＞b a .8.(★★★★)设关于x 的方程2x 2－ax －2=0的两根为α、β(α＜β),函数f (x )=142+-x a x . (1)求f (α)·f (β)的值；(2)证明f (x )是［α，β］上的增函数；(3)当a 为何值时，f (x )在区间［α，β］上的最大值与最小值之差最小？［科普美文］新教材中的思维观点数学科学具有高度的综合性、很强的实践性，不断的发展性，中学数学新教材打破原教材的框架体系，新增添了工具性、实践性很强的知识内容，正是发展的产物.新教材具有更高的综合性和灵活多样性，更具有朝气与活力，因此，把握新教材的脉搏，培养深刻严谨灵活的数学思维，提高数学素质成为燃眉之需.新教材提升与增添的内容包括简易逻辑、平面向量、空间向量、线性规划、概率与统计、导数、研究型课题与实习作业等，这使得新教材中的知识内容立体交叉，联系更加密切，联通的渠道更多，并且富含更高的实用性.因此在高考复习中，要通过总结、编织科学的知识网络，求得对知识的融会贯通，揭示知识间的内在联系.做到以下几点：一、深刻领会数学思想方法，把立足点放在提高数学素质上.数学的思想方法是数学的精髓，只有运用数学思想方法，才能把数学的知识与技能转化为分析问题与解决问题的能力，才能形成数学的素质.知识是能力的载体，领悟并逐步学会运用蕴含在知识发生发展和深化过程中，贯穿在发现问题与解决问题过程中的数学思想方法，是从根本上提高素质，提高数学科能力的必由之路，只有通过对数学思想方法的不断积累，不断总结经验，才能从知识型向能力型转化，不断提高学习能力和学习水平.二、培养用化归（转化）思想处理数学问题的意识.数学问题可看作是一系列的知识形成的一个关系链.处理数学问题的实质，就是实现新问题向旧问题的转化，复杂问题向简单问题的转化，实现未知向已知的转化。

高三数学复习：函数第一节 函数的概念一、选择题1．下列对应中是映射的是 ()A ．(1)、(2)、(3)B ．(1)、(2)、(5)C ．(1)、(3)、(5)D ．(1)、(2)、(3)、(5) 2．下面哪一个图形可以作为函数的图象 ()3．已知f ：A →B 是从集合A 到集合B 的一个映射，∅是空集，那么下列结论可以成立的是 ( ) A ．A ＝B ＝∅ B ．A ＝B ≠∅C ．A 、B 之一为∅D ．A ≠B 且B 的元素都有原象4．已知集合M ＝{}x ，y |x ＋y ＝1，映射f ：M →N ，在f 作用下点(x ，y)的元素是(2x,2y )， 则集合N ＝ ( ) A.{}(x ，y )|x ＋y ＝2，x >0，y >0 B.{}(x ，y )|xy ＝1，x >0，y >0 C.{}(x ，y )|xy ＝2，x <0，y <0 D.{}(x ，y )|xy ＝2，x >0，y >0 5．现给出下列对应：(1)A ＝{x|0≤x ≤1}，B ＝R －，f ：x →y ＝ln x ； (2)A ＝{x|x ≥0}，B ＝R ，f ：x →y ＝±x ；(3)A ＝{平面α内的三角形}，B ＝{平面α内的圆}，f ：三角形→该三角形的内切圆； (4)A ＝{0，π}，B ＝{0,1}，f ：x →y ＝sin x. 其中是从集A 到集B 的映射的个数( )A ．1B ．2C ．3D ．4 二、填空题6．已知函数f(x)＝1122+-x x ，则2)1()2(f f ＝________.7．设f：A→B是从集合A到B的映射，A＝B＝{(x，y)|x∈R，y∈R}，f：(x，y)→(kx，y ＋b)，若B中元素(6,2)在映射f下的元素是(3,1)，则k，b的值分别为________．8．集合A＝{a，b}，B＝{1，－1,0}，那么可建立从A到B的映射个数是________．从B到A的映射个数是________．三、解答题9．已知f满足f(ab)＝f(a)＋f(b)，且f(2)＝p，f(3)＝q，求f(72)的值．10.集合M＝{a，b，c}，N＝{－1,0,1}，映射f：M→N满足f(a)＋f(b)＋f(c)＝0，那么映射f：M→N的个数是多少？参考答案1．解析：(4)中元素c 没有象，不符合映射定义中的“集A 中的任意一个元素在集B 中都有 元素与之对应”；(5)中，与元素a 对应的元素有两个，不符合映射定义中的“对于集A 中的任意一个元素，在集B 中都有唯一确定的元素与之对应”；而(1)(2)(3)中的对应都 符合映射定义．故本题正确答案为A.答案：A 2．解析：A 、C 、D 中的对应法则都是“一对多”，故它们不是函数的图象，正确答案为B. 答案：B 3．B4．解析：因为x ＋y ＝1，所以2x ·2y ＝2x ＋y ＝2.这就是说，集合N 中的元素，其横坐标与 其纵坐标之积为常数2，又显然集合N 中横、纵坐标都是正数，故本题正确答案为D. 答案：D5．解析：(1)的对应中，对于集A 中值0，在集合B 中，没有元素与之对应，故(1)的对应 不是从A 到B 的映射；(2)的对应中，对于集A 中的任意一个非零x 的值，在集合B 中， 都有两个元素与之对应(不满足唯一性)，故(2)的对应不是从A 到B 的映射；(3)、(4) 的对应都满足映射的定义，故(3)、(4)的对应都是从A 到B 的映射．故选B. 答案：B 6．－17．解析：依题意，(3,1)→(6,2)，则⎩⎪⎨⎪⎧3k ＝61＋b ＝2，∴k ＝2，b ＝1. 答案：k ＝2，b ＝18．9 89．解析：∵f(ab)＝f(a)＋f(b)， ∴f(72)＝f(8×9)＝f(8)＋f(9) ＝f(4×2)＋f(3×3)＝f(4)＋f(2)＋2f(3)＝f(2×2)＋ f(2)＋2f(3)＝3f(2)＋2f(3)＝3p ＋2q.10．解析：∵f(a)∈N ，f(b)∈N ，f(c)∈N ，且f(a)＋f(b)＋f(c)＝0，∴有0＋0＋0＝0＋1＋(－1)＝0.当f(a)＝f(b)＝f(c)＝0时，只有一个映射；当f(a)、 f(b)、f(c)中恰有一个为0，而另两个分别为1，－1时，有2213A C ⋅＝6个映射．因此所 求的映射的个数为1＋6＝7.第二节 函数的解析式与定义域一、选择题1．函数f(x)＝xx -132＋lg(3x ＋1)的定义域是 ( )A.⎝ ⎛⎭⎪⎫－13，＋∞B.⎝ ⎛⎭⎪⎫－13，1C.⎝ ⎛⎭⎪⎫－13，13D.⎝⎛⎭⎪⎫－∞，－13 2．已知22111)1(x x x x f +-=+-，则f(x)的解析式可取为 ( ) A.21x x + B. 212x x +- C.212x x + D ．21xx+- 3．汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，若把这一过程中汽车的行驶 路程s 看作时间t 的函数，其图象可能是 ( )4．设函数f(x)＝,1,2),1,1(22>-+≤-x x x x x 则)2()1(f f的值为 ( ) A.1516 B ．－2716 C.89D ．185．(2009年北京卷)若函数f(x)＝1,(0)1,(0)3xx xx <≥则不等式|f(x)|≥13的解集为( )A ．(－3,1)B ．[－1,3]C ．(－1,3]D ．[－3,1]二、填空题6．已知函数f(x)＝1222-+-a ax x 的定义域为A,2∉A ，则a 的取值范围是____________． 7．如果f[f(x)]＝2x －1，则一次函数f(x)＝_____________.8．为了保证信息安全传输必须使用加密方式，有一种方式其加密、解密原理如下：明文――→加密密文――→发送密文――→解密明文已知加密为y ＝a x－2(x 为明文、y 为 密文)，如果明文“3”通过加密后得到密文为“6”，再发送，接受方通过解密得到明文 “3”，若接受方接到密文为“14”，则原发的明文是_______．三、解答题9．如右图所示，在边长为4的正方形ABCD上有一点P，沿着折线BCDA由B点(起点)向A点(终点)移动，设P点移动的路程为x，△ABP的面积为y＝f(x)．(1)求△ABP的面积与P移动的路程间的函数关系式；(2)作出函数的图象，并根据图象求y的最大值．10.已知二次函数f(x)＝ax2＋bx＋c，(a<0)不等式f(x)>－2x的解集为(1,3)．(1)若方程f(x)＋6a＝0有两个相等的实根，求f(x)的解析式；(2)若f(x)的最大值为正数，求实数a的取值范围．参考答案1．解析：由⎩⎪⎨⎪⎧1－x>03x ＋1>0⇒－13<x<1，故选B. 答案：B2．解析：令1－x 1＋x ＝t ，则x ＝1－t 1＋t ，∴f(t)＝122+t t ，∴f(x)＝122+x x. 答案：C3．A 4.A5．解析：(1)由|f(x)|≥13⇒⎩⎪⎨⎪⎧x ＜0⎪⎪⎪⎪⎪⎪1x ≥13⇒－3≤x ＜0.(2)由|f (x )|≥13⇒⎩⎪⎨⎪⎧x ≥0⎪⎪⎪⎪⎝⎛⎭⎫13x ≥13⇒⎩⎪⎨⎪⎧x ≥0⎝⎛⎭⎫13x ≥13⇒0≤x ≤1. ∴不等式|f(x)|≥13的解集为{x|－3≤x ≤1}．答案：D6．解析：∵2∉A ，∴4－4a ＋a 2－1<0，即a 2－4a ＋3<0，解得1<a<3. 答案：1<a<37．解析：设f(x)＝kx ＋b ，则f[f(x)]＝kf(x)＋b ＝k(kx ＋b)＋b ＝k 2x ＋kb ＋b. 由于该函数与y ＝2x －1是同一个函数， ∴k 2＝2且kb ＋b ＝－1，∴k ＝± 2. 当k ＝2时，b ＝1－2； 当k ＝－2时，b ＝1＋ 2.答案：2x ＋1－2或－2x ＋1＋ 2 8．49．解析：(1)这个函数的定义域为(0,12)， 当0＜x ≤4时，S ＝f(x)＝12·4·x ＝2x ；当4＜x ≤8时，S ＝f(x)＝8；当8＜x ＜12时，S ＝f(x)＝12·4·(12－x)＝24－2x.∴这个函数的解析式为f(x)＝⎩⎪⎨⎪⎧2x ， x ∈0，4]，8， x ∈4，8]，24－2x ， x ∈8，12.(2)其图形如右，由图知，[f(x)]max ＝8.10．解析：(1)∵不等式f(x)>－2x 的解集为(1,3)，∴x ＝1和x ＝3是方程ax 2＋(b ＋2)x ＋c ＝0(a<0)的两根， ∴⎩⎪⎨⎪⎧b ＋2a ＝－4ca ＝3，∴b ＝－4a －2，c ＝3a ，又方程f(x)＋6a ＝0有两个相等的实根．∴ Δ＝b 2－4a(c ＋6a)＝0，∴4(2a ＋1)2－4a ×9a ＝0. ∴(5a ＋1)(1－a)＝0，∴a ＝－15或a ＝1(舍)．∴a ＝－15，b ＝－65，c ＝－35，∴f(x)＝－15x 2－65x －35.(2)由(1)知f(x)＝ax 2－2(2a ＋1)x ＋3a ＝a ⎝⎛⎭⎫x －2a ＋1a 2－(2a ＋1)2a ＋3a＝a ⎝⎛⎭⎫x －2a ＋1a 2＋－a 2－4a －1a∵a<0，∴f(x)的最大值为－a 2－4a －1a ，∵f(x)的最大值为正数． ∴⎩⎪⎨⎪⎧a <0－a 2－4a －1a >0∴⎩⎪⎨⎪⎧a <0a 2＋4a ＋1>0 解得a<－2－3或－2＋3<a<0.∴所求实数a 的取值范围是()－∞，－2－3∪(－2＋3，0)．第三节 函数的值域与最值一、选择题1．函数y ＝x 2－2x 的定义域为{0,1,2,3}，那么其值域为 ( ) A ．{－1,0,3} B ．{0,1,2,3} C ．{y|－1≤y ≤3} D ．{y|0≤y ≤3} 2．函数y ＝log 2x ＋log x (2x)的值域是 ( )A ．(－∞，－1]B ．[3，＋∞)C ．[－1,3]D ．(－∞，－1]∪[3，＋∞)3．设f(x)＝⎩⎨⎧x 2， ||x ≥1x ， ||x <1，g(x)是二次函数，若f(g(x))的值域是[)0，＋∞，则g(x)的值域是( )A.(]－∞，－1∪[)1，＋∞B.(]－∞，－1∪[)0，＋∞ C ．[0，＋∞) D.[)1，＋∞ 4．设函数f(x)＝⎩⎪⎨⎪⎧－1，x>01，x<0，则2)()()(b a f b a b a ---+(a ≠b)的值是( )A ．aB ．bC ．a ，b 中较小的数D ．a ，b 中较大的数5．(2008年重庆卷)已知函数y ＝1－x ＋x ＋3的最大值为M ，最小值为m ，则mM 的值为( )A.14B.12C.22D.32二、填空题6．函数y ＝a x在[0,1]上的最大值与最小值的和为3，则a ＝________.7．若f ⎝ ⎛⎭⎪⎫12＋x ＋f ⎝ ⎛⎭⎪⎫12－x ＝2对任意的非负实数x 成立，则f ⎝ ⎛⎭⎪⎫12010＋f ⎝ ⎛⎭⎪⎫22010＋f ⎝ ⎛⎭⎪⎫32010＋…＋f ⎝⎛⎭⎪⎫20092010＝________. 8．(2009年福州模拟)对a ，b ∈R ，记max{a ，b}＝⎩⎪⎨⎪⎧a ，a ≥bb ，a ＜b，函数f(x)＝max{|x ＋1|，|x －2|}(x ∈R)的最小值是________.三、解答题9．若函数y ＝f(x)＝12x 2－2x ＋4的定义域、值域都是闭区间[2,2b]，求b 的值．10．某企业生产一种产品时，固定成本为5000元，而每生产100台产品时直接消耗成本要增加2500元，市场对此商品年需求量为500台，销售的收入函数为R(x)＝5x －12x 2(万元)(0≤x ≤5)，其中x 是产品售出的数量(单位：百台) (1)把利润表示为年产量的函数；(2)年产量多少时，企业所得的利润最大？ (3)年产量多少时，企业才不亏本？参考答案1．A 2.D3．解析：要f(μ)的值域是[)0，＋∞，则μ可取(－∞，－1]∪[)0，＋∞.又g(x)是二次函数，定义域连续，故g(x)不可能同时取(－∞，－1]和[)0，＋∞.结合选项只能选C. 答案：C4．解析：按a>b ，a<b 两种情形分类讨论．答案：D 5．C 6.2 7.20098．解析：由||x ＋1≥||x －2⇒()x ＋12≥()x －22⇒x ≥12，故f ()x ＝⎩⎪⎨⎪⎧||x ＋1⎝ ⎛⎭⎪⎫x ≥12||x －2⎝ ⎛⎭⎪⎫x<12，其图象如下，则f min ()x ＝f ⎝ ⎛⎭⎪⎫12＝⎪⎪⎪⎪⎪⎪12＋1＝32.答案：329．解析：∵y ＝f(x)＝12(x 2－4x ＋8)＝12(x －2)2＋2，∴其图象的对称轴是x ＝2.因此y ＝f(x)在[2,2b]上是递增函数，且2b>2，即b>1.又函数y ＝f(x)＝12x 2－2x ＋4的定义域、值域都是闭区间[2,2b]，所以有f(2b)＝2b ，即12(2b)2－2×2b ＋4＝2b ，∴b 2－3b ＋2＝0，∴b ＝1(舍去)，b ＝2.10.解析：(1)利润y 是指生产数量x 的产品售出后的总收入R(x)与其总成本C(x)之差，由 题意，当x ≤5时，产品能全部售出，当x>5时，只能销售500台，所以 ))50)(25.05.0(215()5)(25.05.0()52155(22≤≤+-->+-⨯-⨯=x x x x x x y ))50(5.02175.4()5(25.0122≤≤-->-=x x x x x . (2)在0≤x ≤5时，y ＝－12x 2＋4.75x －0.5，当x ＝－b2a ＝4.75(百台)时，y max ＝10.78125(万元)；当x>5(百台)时，y ＜12－0.25×5＝10.75(万元)， 所以当生产475台时，利润最大． (3)要使企业不亏本，即要求)50(05.075.4212≤≤≥-+-x x x 或⎩⎪⎨⎪⎧x>512－0.25x ≥0，解得5≥x ≥4.75－21.5625≈0.1(百台)或5＜x ＜48(百台)时，即企业年产量在10台 到4800台之间时，企业不亏本．。

：三角函数专题1、 三角函数化简与性质1、已知函数2()2sin cos 2cos f x x x x ωωω=-（0x ω∈>R ，），相邻两条对称轴之间的距离等于2π． （Ⅰ）求()4f π的值；（Ⅱ）当0,2x π⎡⎤∈⎢⎥⎣⎦时，求函数)(x f 的最大值和最小值及相应的x 值． 解：（Ⅰ）()sin 2cos 212)14f x x x x ωωωπ=--=--．因为22T π=，所以 T =π，1ω=． 所以 ()2)14f x x π=--．所以 ()04f π=（Ⅱ）()2)14f x x π=--当 0,2x π⎡⎤∈⎢⎥⎣⎦时， 32444x πππ-≤-≤， 所以 当242x ππ-=，即8x 3π=时，max ()21f x =， 当244x ππ-=-，即0x =时，min ()2f x =-．2、已知函数()sin()f x A x ωϕ=+(0,0,,)2A x ωϕπ>><∈R 的图象的一部分如下图所示.(1)求函数()f x 的解析式;(2)当2[6,]3x ∈--时,求函数()(2)y f x f x =++的最大值与最小值及相应的x 的值.2、解:(1)由图像知2A =,2284T T ωπ=⇒==,∴4ωπ=,得()2sin()4f x x ϕπ=+. 由对应点得当1x =时,1424ϕϕπππ⨯+=⇒=.∴()2sin()44f x x ππ=+;……………5分(2)2sin()2sin[(2)]2sin()2cos()44444444y x x x x ππππππππ=++++=+++=sin()424x x πππ+=,……………9分∵2[6,]3x ∈--,∴3[,]426x πππ∈--,………………10分∴当6x ππ=-,即23x =-时,y ;当4x π=-π,即4x =-时,y 的最小值-.………………12分2、三角函数与向量综合1、已知平面向量(cos ,sin )a ϕϕ=r ，(cos ,sin )b x x =r ，(sin ,cos )c ϕϕ=-r，其中0ϕπ<<，且函数()()cos ()sin f x a b x b c x =⋅+⋅r r r r 的图象过点)1,6(π．（1）求ϕ的值；（2）将函数)(x f y =图象上各点的横坐标变为原来的的2倍，纵坐标不变，得到函数)(x g y =的图象，求函数)(x g y =在[0,]2π上的最大值和最小值．1、解：（1）cos cos sin sin cos()a b x x x ϕϕϕ⋅=+=-r rQcos sin sin cos sin()b c x x x ϕϕϕ⋅=-=-r r()()cos ()sin f x a b x b c x ∴=⋅+⋅r r r rcos()cos sin()sin x x x x ϕϕ=-+-cos()x x ϕ=--cos(2)x ϕ=-，即()cos(2)f x x ϕ=-∴()cos()163f ππϕ=-=，而0ϕπ<<，∴3πϕ=．（2）由（1）得，()cos(2)3f x x π=-，于是1()cos(2())23g x x π=-，即()cos()3g x x π=-． 当[0,]2x π∈时，336x πππ-≤-≤， 所以1cos()123x π≤-≤，即当0x =时，()g x 取得最小值12，当3x π=时，()g x 取得最大值1．3、三角函数与解三角形1、已知△ABC 中，2sin cos sin cos cos sin A B C B C B =+. （Ⅰ）求角B 的大小；（Ⅱ）设向量(cos , cos 2)A A =m ，12(, 1)5=-n ，求当⋅m n 取最小值时，)4tan(π-A 值.解：（Ⅰ）因为2sin cos sin cos cos sin A B C B C B =+，所以2sin cos sin()sin()sin A B B C A A =+=π-=. …………………… 3分 因为0A p <<，所以sin 0A ¹.所以1cos 2B =. 因为0B p <<，所以3B π=.（Ⅱ）因为12cos cos 25A A ⋅=-+m n ，所以2212343cos 2cos 12(cos )5525A A A ⋅=-+-=--m n .所以当3cos 5A =时，⋅m n 取得最小值.此时4sin 5A =（0A p <<），于是4tan 3A =.所以tan 11tan()4tan 17A A A π--==+.2、在△ABC 中，角A ，B ，C 所对的边分别是,,a b c ，且cos A B =（Ⅰ）求角C ；（Ⅱ）若1a b -，求边c ．解：(Ⅰ)∵cos 0A A π<<，∴sin A =.又∵sin B =sin sin A B >，∴a b >，∴A B >，∴(0 )2B π∈，，∴cos B =． ……………………… 3分∴cos cos()C A B =-+cos cos sin sin A B A B =-+=，∴34C π=．(Ⅱ)由正弦定理sin sin a b A B =得，sin sin a Ab B==a =.又∵1a b -，∴1a b ==． ………………………9分又∵sin sin b cB C=，∴c .(用余弦定理也可) ………………………12分 10、在ABC ∆中，已知45A =o，4cos 5B =. (Ⅰ)求cos C 的值；(Ⅱ)若10,BC D =为AB 的中点，求CD 的长.解：（Ⅰ）4cos ,5B =Q 且(0,180)B ∈o o ，∴3sin 5B ==． cos cos(180)cos(135)C A B B =--=-o o43cos135cos sin135sin 55B B =+=o o =（Ⅱ）由（Ⅰ）可得sin C===由正弦定理得sin sinBC ABA C=7AB=，解得14AB=．在BCD∆中，7BD=，22247102710375CD=+-⨯⨯⨯=，所以CD=3、在△ABC中，内角A，B，C对边的边长分别是cba,,，已知3,2π==Cc．（1）若△ABC的面积等于3，求a，b；（2）若AABC2sin2)sin(sin=-+，求△ABC的面积．3、解：（1）由余弦定理及已知条件，得422=-+abba．又因为△ABC的面积等于3，所以3sin21=Cab，得4=ab．联立方程组⎩⎨⎧==-+,4,422ababba解得⎩⎨⎧==.2,2ba（2）由题意，得AAABAB cossin4)sin()sin(=-++，即AAAB cossin2cossin=．当0cos=A，即2π=A时，6π=B，334=a，332=b，此时△ABC的面积123S bc==．当0cos≠A时，得AB sin2sin=，由正弦定理，得ab2=．联系方程组⎩⎨⎧==-+,2,422ababba解得⎪⎪⎩⎪⎪⎨⎧==.334,332ba此时△ABC的面积332sin21==CabS面积332sin21==CabS．。

高考数学复习专题专题一集合、逻辑与不等式集合概念及其基本理论，是近代数学最基本的内容之一，集合的语言、思想、观点渗透于中学数学内容的各个分支．有关简易逻辑的常识与原理始终贯穿于数学的分析、推理与计算之中，学习关于逻辑的有关知识，可以使我们对数学的有关概念理解更透彻，表达更准确．不等式是高中数学的重点内容之一，是工具性很强的一部分内容，解不等式、不等式的性质等都有很重要的应用．关注本专题内容在其他各专题中的应用是学习这一专题内容时要注意的．§1－1 集合【知识要点】1．集合中的元素具有确定性、互异性、无序性．2．集合常用的两种表示方法：列举法和描述法，另外还有大写字母表示法，图示法(韦恩图)，一些数集也可以用区间的形式表示．3．两类不同的关系：(1)从属关系——元素与集合间的关系；(2)包含关系——两个集合间的关系(相等是包含关系的特殊情况)．4．集合的三种运算：交集、并集、补集．【复习要求】1．对于给定的集合能认识它表示什么集合．在中学常见的集合有两类：数集和点集．2．能正确区分和表示元素与集合，集合与集合两类不同的关系．3．掌握集合的交、并、补运算．能使用韦恩图表达集合的关系及运算．4．把集合作为工具正确地表示函数的定义域、值域、方程与不等式的解集等．【例题分析】例1 给出下列六个关系：(1)0∈N*(2)0∉{－1，1} (3)∅∈{0}(4)∅∉{0} (5){0}∈{0，1} (6){0}⊆{0}其中正确的关系是______．解答：(2)(4)(6)【评析】1．熟悉集合的常用符号：不含任何元素的集合叫做空集，记作∅；N表示自然数集；N＋或N*表示正整数集；Z表示整数集；Q表示有理数集；R表示实数集．2．明确元素与集合的关系及符号表示：如果a是集合A的元素，记作：a∈A；如果a 不是集合A的元素，记作：a∉A．3．明确集合与集合的关系及符号表示：如果集合A中任意一个元素都是集合B的元素，那么集合A叫做集合B的子集．记作：A⊆B或B⊇A．如果集合A是集合B的子集，且B中至少有一个元素不属于A，那么，集合A叫做集合B的真子集．A B或B A．4．子集的性质：①任何集合都是它本身的子集：A⊆A；②空集是任何集合的子集：∅⊆A；提示：空集是任何非空集合的真子集．③传递性：如果A⊆B，B⊆C，则A⊆C；如果A B，B C，则A C．例2 已知全集U ＝{小于10的正整数}，其子集A ，B 满足条件(U A )∩(U B )＝{1，9}，A ∩B ＝{2}，B ∩(U A )＝{4，6，8}．求集合A ，B ．解：根据已知条件，得到如图1－1所示的韦恩图，图1－1于是，韦恩图中的阴影部分应填数字3，5，7．故A ＝{2，3，5，7}，B ＝{2，4，6，8}．【评析】1、明确集合之间的运算对于两个给定的集合A 、B ，由既属于A 又属于B 的所有元素构成的集合叫做A 、B 的交集．记作：A ∩B ．对于两个给定的集合A 、B ，把它们所有的元素并在一起构成的集合叫做A 、B 的并集．记作：A ∪B ． 如果集合A 是全集U 的一个子集，由U 中不属于A 的所有元素构成的集合叫做A 在U中的补集．记作U A ．2、集合的交、并、补运算事实上是较为复杂的“且”、“或”、“非”的逻辑关系运算，而韦恩图可以将这种复杂的逻辑关系直观化，是解决集合运算问题的一个很好的工具，要习惯使用它解决问题，要有意识的利用它解决问题．例3 设集合M ＝{x ｜－1≤x ＜2}，N ＝{x ｜x ＜a }．若M ∩N ＝∅，则实数a 的取值范围是______．答：(－∞，－1]． 【评析】本题可以通过数轴进行分析，要特别注意当a 变化时是否能够取到区间端点的值．象韦恩图一样，数轴同样是解决集合运算问题的一个非常好的工具．例4 设a ，b ∈R ，集合},,0{},,1{b a b a b a =+，则b －a ＝______．【分析】因为},,0{},,1{b a b a b a =+，所以a ＋b ＝0或a ＝0(舍去，否则a b 没有意义)， 所以，a ＋b ＝0，ab ＝－1，所以－1∈{1，a ＋b ，a }，a ＝－1， 结合a ＋b ＝0，b ＝1，所以b －a ＝2．练习1－1一、选择题1．给出下列关系：①R ∈21；②2∉Q ；③｜－3｜∉N *；④Q ∈-|3|．其中正确命题的个数是( )(A)1 (B)2 (C)3 (D)42．下列各式中，A 与B 表示同一集合的是( )(A)A ＝{(1，2)}，B ＝{(2，1)} (B)A ＝{1，2}，B ＝{2，1}(C)A＝{0}，B＝∅(D)A＝{y｜y＝x2＋1}，B＝{x｜y＝x2＋1} 3．已知M＝{(x，y)｜x＞0且y＞0}，N＝{(x，y)｜xy＞0}，则M，N的关系是( )(A)M N(B)N M(C)M＝N(D)M∩N＝∅4．已知全集U＝N，集合A＝{x｜x＝2n，n∈N}，B＝{x｜x＝4n，n∈N}，则下式中正确的关系是( )(A)U＝A∪B(B)U＝(U A)∪B(C)U＝A∪(U B) (D)U＝(U A)∪(U B)二、填空题5．已知集合A＝{x｜x＜－1或2≤x＜3}，B＝{x｜－2≤x＜4}，则A∪B＝______．6．设M＝{1，2}，N＝{1，2，3}，P＝{c｜c＝a＋b，a∈M，b∈N}，则集合P中元素的个数为______．7．设全集U＝R，A＝{x｜x≤－3或x≥2}，B＝{x｜－1＜x＜5}，则(U A)∩B＝______. 8．设集合S＝{a0，a1，a2，a3}，在S上定义运算⊕为：a i⊕a j＝a k，其中k为i＋j被4除的余数，i，j＝0，1，2，3．则a2⊕a3＝______；满足关系式(x⊕x)⊕a2＝a0的x(x∈S)的个数为______．三、解答题9．设集合A＝{1，2}，B＝{1，2，3}，C＝{2，3，4}，求(A∩B)∪C．10．设全集U＝{小于10的自然数}，集合A，B满足A∩B＝{2}，(U A)∩B＝{4，6，8}，(U A)∩(U B)＝{1，9}，求集合A和B．11．已知集合A＝{x｜－2≤x≤4}，B＝{x｜x＞a}，①A∩B≠∅，求实数a的取值范围；②A∩B≠A，求实数a的取值范围；③A∩B≠∅，且A∩B≠A，求实数a的取值范围．§1－2 常用逻辑用语【知识要点】1．命题是可以判断真假的语句．2．逻辑联结词有“或”“且”“非”．不含逻辑联结词的命题叫简单命题，由简单命题和逻辑联结词构成的命题叫做复合命题．可以利用真值表判断复合命题的真假．3．命题的四种形式原命题：若p则q．逆命题：若q则p．否命题：若⌝p，则⌝q．逆否命题：若⌝q，则⌝p．注意区别“命题的否定”与“否命题”这两个不同的概念．原命题与逆否命题、逆命题与否命题是等价关系．4．充要条件如果p⇒q，则p叫做q的充分条件，q叫做p的必要条件．如果p⇒q且q⇒p，即q⇔p则p叫做q的充要条件，同时，q也叫做p的充要条件．5．全称量词与存在量词【复习要求】1．理解命题的概念．了解“若p，则q”形式的命题的逆命题、否命题与逆否命题，会分析四种命题的相互关系．理解必要条件、充分条件与充要条件的意义．2．了解逻辑联结词“或”、“且”、“非”的含义．3．理解全称量词与存在量词的意义．能正确地对含有一个量词的命题进行否定．【例题分析】例1 分别写出由下列命题构成的“p∨q”“p∧q”“⌝p”形式的复合命题，并判断它们的真假．(1)p：0∈N，q：1∉N；(2)p：平行四边形的对角线相等，q：平行四边形的对角线相互平分．解：(1)p∨q：0∈N，或1∉N；p∧q：0∈N，且1∉N；⌝p：0∉N．因为p真，q假，所以p∨q为真，p∧q为假，⌝p为假．(2)p∨q：平行四边形的对角线相等或相互平分．p∧q：平行四边形的对角线相等且相互平分．⌝p：存在平行四边形对角线不相等．因为p假，q真，所以p∨q为真，p∧q为假，⌝p为真．【评析】判断复合命题的真假可以借助真值表．例2 分别写出下列命题的逆命题、否命题和逆否命题，并判断其真假．(1)若a2＋b2＝0，则ab＝0；(2)若A∩B＝A，则A B．解：(1)逆命题：若ab＝0，则a2＋b2＝0；是假命题．否命题：若a2＋b2≠0，则ab≠0；是假命题．逆否命题：若ab≠0，则a2＋b2≠0；是真命题．(2)逆命题：若A B，则A∩B＝A；是真命题．否命题：若A∩B≠A，则A不是B的真子集；是真命题．逆否命题：若A不是B的真子集，则A∩B≠A．是假命题．评述：原命题与逆否命题互为逆否命题，同真同假；逆命题与逆否命题也是互为逆否命题．例3 指出下列语句中，p是q的什么条件，q是p的什么条件．(1)p：(x－2)(x－3)＝0；q：x＝2；(2)p：a≥2；q：a≠0．【分析】由定义知，若p⇒q且q p，则p是q的充分不必要条件；若p q且q⇒p，则p是q的必要不充分条件；若p⇒q且q⇒p，p与q互为充要条件．于是可得(1)中p是q的必要不充分条件；q是p的充分不必要条件．(2)中p是q的充分不必要条件；q是p的必要不充分条件．【评析】判断充分条件和必要条件，首先要搞清楚哪个是条件哪个是结论，剩下的问题就是判断p与q之间谁能推出谁了．例4设集合M＝{x｜x＞2}，N＝{x｜x＜3}，那么“x∈M或x∈N”是“x∈M∩N”的( )(A)充分非必要条件(B)必要非充分条件(C)充要条件(D)非充分条件也非必要条件解：条件p：x∈M或x∈N，即为x∈R；条件q：x∈M∩N，即为{x∈R｜2＜x＜3}．又R{x∈R｜2＜x＜3}，且{x∈R｜2＜x＜3}⊆R，所以p是q的必要非充分条件，选B．【评析】当条件p和q以集合的形式表现时，可用下面的方法判断充分性与必要性：设满足条件p的元素构成集合A，满足条件q的元素构成集合B，若A⊆B且B A，则p是q 的充分非必要条件；若A B且B⊆A，则p是q的必要非充分条件；若A＝B，则p与q互为充要条件．例5命题“对任意的x∈R，x3－x2＋1≤0”的否定是( )(A)不存在x∈R，x3－x2＋1≤0，(B)存在x∈R，x3－x2＋1≤0(C)存在x∈R，x3－x2＋1＞0 (D)对任意的x∈R，x3－x2＋1＞0【分析】这是一个全称命题，它的否定是一个特称命题．其否定为“存在x∈R，x3－x2＋1＞0．”答：选C．【评析】注意全(特)称命题的否定是将全称量词改为存在量词(或将存在量词改为全称量词)，并把结论否定．练习1－2一、选择题1．下列四个命题中的真命题为( )(A)∃x∈Z，1＜4x＜3 (B)∃x∈Z，3x－1＝0(C)∀x∈R，x2－1＝0 (D)∀x∈R，x2＋2x＋2＞02．如果“p或q”与“非p”都是真命题，那么( )(A)q一定是真命题(B)q不一定是真命题(C)p不一定是假命题(D)p与q的真假相同3．已知a为正数，则“a＞b”是“b为负数”的( )(A)充分不必要条件(B)必要不充分条件(C)充要条件(D)既不充分也不必要条件4．“A是B的子集”可以用下列数学语言表达：“若对任意的x∈A⇒x∈B，则称A⊆B”．那么“A不是B的子集”可用数学语言表达为( )(A)若∀x∈A但x∉B，则称A不是B的子集(B)若∃x∈A但x∉B，则称A不是B的子集(C)若∃x∉A但x∈B，则称A不是B的子集(D)若∀x∉A但x∈B，则称A不是B的子集二、填空题5．“⌝p 是真命题”是“p ∨q 是假命题的”__________________条件．6．命题“若x ＜－1，则｜x ｜＞1”的逆否命题为_________．7．已知集合A ，B 是全集U 的子集，则“A ⊆B ”是“U B ⊆U A ”的______条件．8．设A 、B 为两个集合，下列四个命题：①AB ⇔对任意x ∈A ，有x ∉B ②A B ⇔A ∩B ＝∅ ③A B ⇔A B ④A B ⇔存在x ∈A ，使得x ∉B其中真命题的序号是______．(把符合要求的命题序号都填上)三、解答题9．判断下列命题是全称命题还是特称命题并判断其真假：(1)指数函数都是单调函数；(2)至少有一个整数，它既能被2整除又能被5整除；(3)∃x ∈{x ｜x ∈Z }，log 2x ＞0；(4).041,2≥+-∈∀x x x R10．已知实数a ，b ∈R ．试写出命题：“a 2＋b 2＝0，则ab ＝0”的逆命题，否命题，逆否命题，并判断四个命题的真假，说明判断的理由．§1－3 不等式(含推理与证明)【知识要点】1．不等式的性质．(1)如果a ＞b ，那么b ＜a ；(2)如果a ＞b ，且b ＞c ，那么a ＞c ；(3)如果a ＞b ，那么a ＋c ＞b ＋c (如果a ＋c ＞b ，那么a ＞b －c )；(4)如果a ＞b ，c ＞d ，那么a ＋c ＞b ＋d ；(5)如果a ＞b ，c ＞0，那么ac ＞bc ；如果a ＞b ，c ＜0，那么ac ＜bc ；(6)如果a ＞b ＞0，c ＞d ＞0，那么ac ＞bd ；(7)如果a ＞b ＞0，那么a n ＞b n (n ∈N ＋，n ＞1)；(8)如果a ＞b ＞0，那么)1,N (>∈>+n x b a n n ；2．进行不等式关系判断时常用到的实数的性质：若a ∈R ，则)R (0.0||;02+∈≥≥≥a a a a ．3．会解一元一次不等式，一元二次不等式，简单的分式不等式、绝对值不等式．简单的含参数的不等式．4．均值定理：如果a 、b ∈R ＋，那么.2ab b a ≥+当且仅当a ＝b 时，式中等号成立． 其他常用的基本不等式：如果a 、b ∈R ，那么a 2＋b 2≥2ab ，(a －b )2≥0．如果a 、b 同号，那么.2≥+ba ab 5．合情推理之归纳推理与类比推理；演绎推理；综合法、分析法与反证法．【复习要求】1．运用不等式的性质解决以下几类问题：(1)根据给定的条件，判断给出的不等式能否成立；(2)利用不等式的性质，实数的性质以及函数的有关性质判断实数值的大小关系；(3)利用不等式的性质等判断不等式变换中条件与结论间的充分必要关系．2．熟练掌握一元一次不等式，一元二次不等式、简单的分式不等式、绝对值不等式的解法．并会解简单的含参数的不等式．3．了解合情推理和演绎推理的含义，能利用归纳和类比等进行简单的推理．了解演绎推理的重要性，掌握演绎推理的基本模式，并能运用它们进行一些简单推理．能较为灵活的运用综合法、分析法与反证法证明数学问题．熟练运用比较法比较数与式之间的大小关系．比较法：常有“作差比较法”和“作商比较法”；综合法：从已知推导致结果的思维方法；分析法：从结果追溯到产生这一结果的原因的思维方法；反证法：由证明p ⇒q 转向证明⌝q ⇒r ⇒…⇒t ，而t 与假设矛盾，或与某个真命题矛盾，从而判定⌝q 为假，进而推出q 为真的方法，叫做反证法．一般来讲，由分析法得到的证明思路往往用综合法的方式来书写．【例题分析】例1 若a ＞b ＞c ，则一定成立的不等式是( )A ．a ｜c ｜＞b ｜c ｜B ．ab ＞acC ．a －｜c ｜＞b －｜c ｜D ．cb a 111<< 【分析】关于选项A ．当c ＝0时，a ｜c ｜＞b ｜c ｜不成立．关于选项B ．当a ＜0时，ab ＞ac 不成立．关于选项C ．因为a ＞b ，根据不等式的性质a －｜c ｜＞b －｜c ｜，正确．关于选项D ．当a ＞b ＞0＞c 时，cb a 111<<不成立．所以，选C ． 例2 a ，b ∈R ，下列命题中的真命题是( ) A ．若a ＞b ，则｜a ｜＞｜b ｜ B ．若a ＞b ，则ba 11< C ．若a ＞b ，则a 3＞b 3D ．若a ＞b ，则1>b a 【分析】关于选项A ．当a ＝－1，b ＝－2时，｜a ｜＞｜b ｜不成立．关于选项B ．当a ＞0，b ＜0时，ba 11<不成立． 关于选项C ．因为a ＞b ，根据不等式的性质a 3＞b 3，正确．关于选项D ．当b ＜0时，1>ba 不成立．所以，选C ． 【评析】判断不等关系的正误，其一要掌握判断的依据，依据相关的理论判断，切忌仅凭感觉进行判断；其二要掌握判断的方法．判断不等式的理论依据参看本节的知识要点，另外，后面专题讲到的函数的相关知识尤其是函数的单调性也是解决不等式问题的非常重要的方法．判断一个不等式是正确的，就应该给出一个合理的证明(或说明)，就像例1、例2对正确的选项判断那样．判断一个不等式是不正确的，应举出反例．例3 解下列不等式：(1)x 2－x －1＞0；(2)x 2－3x ＋2＞0；(3)2x 2－3x ＋1≤0； (4);021>--x x (5)｜2x －1｜＜3；(6).1212≤--x x 解：(1)方程x 2－x －1＝0的两个根是251,21±=x x 结合函数y ＝x 2－x －1的图象，可得不等式x 2－x －1＞0的解集为}.251251|{+>-<x x x 或 (2)不等式x 2－3x ＋2＞0等价于(x －1)(x －2)＞0，易知方程(x －1)(x －2)＝0的两个根为x 1＝1，x 2＝2，结合函数y ＝x 2－3x ＋2的图象，可得不等式x 2－3x ＋2＞0的解集为{x ｜x ＜1或x ＞2}．(3)不等式2x 2－3x ＋1≤0等价于(2x －1)(x －1)≤0，以下同(2)的解法， 可得不等式的解集为}.121|{≤≤x x (4)021>--x x 等价于(x －1)(x －2)＞0，以下同(2)的解法，可得不等式的解集为{x ｜x ＜1或x ＞2}．(5)不等式｜2x －1｜＜3等价于－3＜2x －1＜3，所以－2＜2x ＜4，即－1＜x ＜2，所以不等式｜2x －1｜＜3的解集为{x ｜－1≤x ＜2}．(6)不等式1212≤--x x 可以整理为,021≤-+x x ,021≤-+x x 等价于.021021=-+<-+x x x x 或以下同(4)的解法，可得不等式的解集为{x ｜－1≤x ＜2}．【评析】一元一次不等式、一元二次不等式的解法要熟练掌握．其他不等式的解法适当掌握．1．利用不等式的性质可以解一元一次不等式．2．解一元二次不等式要注意函数、方程、不等式三者之间的联系，通过研究与一元二次不等式相对应的一元二次方程的根的情况、进而结合相应的二次函数的图象就可以解决一元二次不等式解集的问题了．所以，解一元二次不等式的步骤为：计算二次不等式相应的方程的判别式；求出相应的一元二次方程的根(或根据判别式说明无根)；画出相应的二次函数的简图；根据简图写出二次不等式的解集．3、不等式0>--bx a x 与(x －a )(x －b )＞0同解；不等式0<--b x a x 与(x －a )(x －b )＜0同解； 4*、不等式｜f (x )｜＜c 与－c ＜f (x )＜c 同解；不等式｜f (x )｜＞c 与“f (x )＞c 或f (x )＜－c ”同解．在解简单的分式不等式时要注意细节，例如(5)题关于“≤”号的处理．例4 解下列关于x 的不等式；(1)ax ＋3＜2；(2)x 2－6ax ＋5a 2≤0．解：(1)由ax ＋3＜2得ax ＜－1，当a ＝0时，不等式解集为∅；当a ＞0时，不等式解集为}1|{ax x -<；当a ＜0时，不等式解集为}1|{a x x ->．(2)x 2－6ax ＋5a 2≤0等价于不等式(x －a )(x －5a )≤0，当a ＝0时，不等式解集为{x ｜x ＝0}；当a ＞0时，不等式解集为{x ｜a ≤x ≤5a }；当a ＜0时，不等式解集为{x ｜5a ≤x ≤a }．【评析】含参数的不等式的解法与不含参数的不等式的解法、步骤是完全一致的．要注意的是，当进行到某一步骤具有不确定性时，需要进行分类讨论．如(2)的解决过程中，当解出方程(x －a )(x －5a )＝0的两根为x 1＝a ，x 2＝5a 之后，需要画出二次函数y ＝x 2－6ax ＋5a 2的草图，这时两根a 与5a 的大小不定，需要讨论，当分a ＝0，a ＞0，a ＜0三种情况之后，就可以在各自情况下确定a 与5a 的大小，画出二次函数y＝x 2－6ax ＋5a 2的草图写出解集了．例5 已知a ＞b ＞0，c ＜d ＜0，m ＜0．求证：⋅->-db mc a m 证明：方法一(作差比较) ,))(()]()[())(()]()[(d b c a d c a b m d b c a c a d b m d b m c a m ---+-=-----=--- 由已知b －a ＜0，c －d ＜0，又m ＜0，所以m [(b －a )＋(c －d )]＞0，因为a ＞b ＞0，c ＜d ＜0，所以a －c ＞0，b －d ＞0， 所以0))(()]()[(>---+-d b c a d c a b m ，所以⋅->->---db mc a md b m c a m 即,0 方法二因为c ＜d ＜0，所以c －d ＜0，又a ＞b ＞0，所以a －b ＞0，所以a －b ＞c －d ，所以a －c ＞b －d ＞0， 所以d b c a -<-11，又因为m ＜0，所以⋅->-db mc a m 例6 已知a ＋b ＋c ＝0，a ＞b ＞c ，求证：(1)a ＞0；(2).2->ac 证明：(1)假设a ≤0，因为a ＞b ＞c ，所以b ＜0，c ＜0．所以a ＋b ＋c ＜0，与a ＋b ＋c ＝0矛盾．(2)因为b ＝－a －c ，a ＞b ，所以，所以2a ＞－c ，又a ＞0，所以a c ->2，所以.2->ac 例7 已知a ，b ，c ∈(0，1)，求证：(1－a )b ，(1－b )c ，(1－c )a 中至少有一个不大于41. 证明：假设(1－a )b ，(1－b )c ，(1－c )a 均大于41， 即,41)1(,41)1(,41)1(>->->-a c c b b a ,21)1(,21)1(,21)1(>->->-a c c b b a 因为a ，b ，c ∈(0，1)，所以1－a ，1－b ，1－c ∈(0，1)，所以1)1(2)1(>-≥+-b a b a ，同理(1－b )＋c ＞1，(1－c )＋a ＞1， 所以(1－a )＋b ＋(1－b )＋c ＋(1－c )＋a ＞3，即0＞0，矛盾． 所以(1－a )b ，(1－b )c ，(1－c )a 中至少有一个不大于41． 【评析】证明常用的方法有比较法、综合法、分析法与反证法等．证明不等式也是如此． 1、例5中的方法一所用到的比较法从思维、书写的角度都较为容易，也相对易于把握，要熟练掌握．2、例5中的方法二所用到的综合法是一般证明题常用的方法，其书写方法简明、易读，但要注意的是，这样的题的思路常常是分析法．比如，例5中的方法二的思路我们可以认为是这样得到的：欲证,db mc a m ->-只需证明m (b －d )＞m (a －c )(因为b －d ＞0，a －c ＞0)，即只需证明b －d ＜a －c ，即只需证明a －b ＞c －d ，而由已知a －b ＞0，c －d ＜0，所以可以循着这个思路按照相反的顺序书写．所以，在很多情况下，分析法更是思考问题的方法，而综合法更是一种书写方法．3、适合用反证法证明的常见的命题一般是非常显而易见的问题(如例6(1))、否定式的命题、存在性的命题、含至多至少等字样的命题(如例7)等等．证明的步骤一般是：(1)假设结论的反面是正确的；(2)推出矛盾的结论；(3)得出原来命题正确的结论．例8 根据图中图形及相应点的个数找规律，第8个图形相应的点数为______．【分析】第一个图有1行，每行有1＋2个点； 第二个图有2行，每行有2＋2个点； 第三个图有3行，每行有3＋2个点； ……第八个图有8行，每行有8＋2个点，所以共有8×10＝80个点． 答：80．练习1－3一、选择题 1．若011>>ba 则下列各式正确的是( ) (A)a ＞b(B)a ＜b(C)a 2＞b 2(D)2211ba < 2．已知a ，b 为非零实数，且a ＜b ，则下列命题成立的是( )(A)a 2＜b 2(B)a 2b ＜ab 2(C)ba ab 2211< (D)b a a b < 3．已知A ＝{x ｜｜x ｜＜a }，B ＝{x ｜x ＞1}，且A ∩B ＝∅，则a 的取值范围是( )(A){a ｜a ≤1} (B){a ｜0≤a ≤1} (C){a ｜a ＜1} (D){a ｜0＜a ＜1} 4．设集合M ＝{1，2，3，4，5，6}，S 1，S 2，…，S k 都是M 的含有两个元素的子集，且满足：对任意的S i ＝{a i ，b i }、S j ＝{a j ，b j }(i ≠j ，i ，j ∈{1，2，3，…，k })都有},min{},min{jj j j i ii i a b b a a b b a =/，(min{x ，y }表示两个数x ，y 中的较小者)，则k 的最大值是( ) (A)10 (B)11(C)12(D)13二、填空题5．已知数列{a n }的第一项a 1＝1，且),3,2,1(11Λ=+=+n a a a nnn ，请计算出这个数列的前几项，并据此归纳出这个数列的通项公式a n ＝______． 6．不等式x 2－5x ＋6＜0的解集为____________． 7．设集合A ＝{x ∈R ｜｜x ｜＜4}，B ＝{x ∈R ｜x 2－4x ＋3＞0}，则集合{x ∈R ｜x ∈A ，且x ∉A ∩B }＝____________．8．设a ∈R 且a ≠0，给出下面4个式子： ①a 3＋1；②a 2－2a ＋2；③a a 1+；④⋅+221aa 其中恒大于1的是______．(写出所有满足条件式子的序号)三、解答题9．解下列不等式：(1)2x 2＋x ＞0；(2)x 2＋3x ＋1＜0；(3)032<-x x ；(4)｜2－x ｜＜3；(5)21>-x x.10．已知a ＋b ＋c ＝0，求证：ab ＋bc ＋ca ≤0．11．解下列关于x 的不等式：(1)x 2－2ax －3a 2＜0；(2)ax 2－x ＞0；习题1一、选择题1．命题“若x 是正数，则x ＝｜x ｜”的否命题是( ) (A)若x 是正数，则x ≠｜x ｜ (B)若x 不是正数，则x ＝｜x ｜ (C)若x 是负数，则x ≠｜x ｜ (D)若x 不是正数，则x ≠｜x ｜ 2．若集合M 、N 、P 是全集U 的子集，则图中阴影部分表示的集合是( )(A)(M ∩N )∪P (B)(M ∩N )∩P (C)(M ∩N )∪(U P )(D)(M ∩N )∩(U P )3．“81=a ”是“对任意的正数12,≥+xa x x ”的( ) (A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既不充分也不必要条件 4．已知集合P ＝{1，4，9，16，25，…}，若定义运算“&”满足：“若a ∈P ，b ∈P ，则a &b ∈P ”，则运算“&”可以是( ) (A)加法 (B)减法 (C)乘法 (D)除法 5．已知a ，b ，c 满足c ＜b ＜a ，且ac ＜0，那么下列选项中不一定．．．成立的是( ) (A)ab ＞ac (B)c (b －a )＜0(C)cb 2＜ab 2(D)ac (a －c )＜0二、填空题6．若全集U ＝{0，1，2，3}且U A ＝{2}，则集合A ＝______． 7．命题“∃x ∈A ，但x ∉A ∪B ”的否定是____________．8．已知A ＝{－2，－1，0，1}，B ＝{y ｜y ＝｜x ｜，x ∈A }，则B ＝____________． 9．已知集合A ＝{x ｜x 2－3x ＋2＜0}，B ＝{x ｜x ＜a }，若AB ，则实数a 的取值范围是____________．10．设a ，b 是两个实数，给出下列条件：①a ＋b ＞1；②a ＋b ＝2；③a ＋b ＞2； ④a 2＋b 2＞2；⑤ab ＞1，其中能推出“a ，b 中至少有一个大于1”的条件是______．(写出所有正确条件的序号) 三、解答题 11．解不等式.21<x12．若0＜a ＜b 且a ＋b ＝1．(1)求b 的取值范围；(2)试判断b 与a 2＋b 2的大小．13．设a ≠b ，解关于x 的不等式：a 2x ＋b 2(1－x )≥[ax ＋b (1－x )]2．14．设数集A 满足条件：①A ⊆R ；②0∉A 且1∉A ；③若a ∈A ，则.11A a∈- (1)若2∈A ，则A 中至少有多少个元素； (2)证明：A 中不可能只有一个元素．专题一 集合、逻辑与不等式参考答案练习1－1一、选择题1．B 2．B 3．A 4．C 提示：4．集合A 表示非负偶数集，集合B 表示能被4整除的自然数集，所以{正奇数}(U B )，从而U ＝A ∪(U B )． 二、填空题5．{x ｜x ＜4} 6．4个 7．{x ｜－1＜x ＜2} 8．a 1；2个(x 为a 1或a 3)． 三、解答题9．(A ∩B )∪C ＝{1，2，3，4}10．分析：画如图所示的韦恩图：得A ＝{0，2，3，5，7}，B ＝{2，4，6，8}．11．答：①a ＜4；②a ≥－2；③－2≤a ＜4提示：画数轴分析，注意a 可否取到“临界值”．练习1－2一、选择题1．D 2．A 3．B 4．B 二、填空题5．必要不充分条件 6．若｜x ｜≤1，则x ≥－1 7．充要条件 8．④ 提示：8．因为A B ，即对任意x ∈A ，有x ∈B ．根据逻辑知识知，AB ，即为④．另外，也可以通过文氏图来判断． 三、解答题9．答：(1)全称命题，真命题．(2)特称命题，真命题． (3)特称命题，真命题；(4)全称命题，真命题．10．略解：答：逆命题：若ab ＝0，则a 2＋b 2＝0；是假命题；例如a ＝0，b ＝1否命题：若a 2＋b 2≠0，则ab ≠0；是假命题；例如a ＝0，b ＝1逆否命题：若ab ≠0，则a 2＋b 2≠0；是真命题；因为若a 2＋b 2＝0，则a ＝b ＝0，所以ab ＝0，即原命题是真命题，所以其逆否命题为真命题．练习1－3一、选择题1．B 2．C 3．A 4．B 二、填空题 5．n16．{x ｜2＜x ＜3} 7．{x ∈R ｜1≤x ≤3｜ 8．④ 三、解答题9．答：(1)}210|{-<>x x x 或；(2)}253253|{+-<<--x x ； (3)}230|{<<x x ；(4){x ｜－1＜x ＜5}；(5)}310|{<<x x ． 10．证明：ab ＋bc ＋ca ＝b (a ＋c )＋ac ＝－(a ＋c )(a ＋c )＋ac ＝－a 2－ac －c 20]43)2[(]434[22222≤++-=+++-=c c a c c ac a所以ab ＋bc ＋ca ≤0．11．解：(1)原不等式⇔(x ＋a )(x －3a )＜0．分三种情况讨论：①当a ＜0时，解集为{x ｜3a ＜x ＜－a }；②当a ＝0时，原不等式⇔x 2＜0，解集为∅； ③当a ＞0时，解集为{x ｜－a ＜x ＜3a }． (2)不等式ax 2－x ＞0⇔x (ax －1)＞0． 分三种情况讨论：①当a ＝0时，原不等式⇔－x ＞0，解集为{x ｜x ＜0}；②当a ＞0时，x (ax －1)＞0⇔x (x －a 1)＞0，解集为}10|{ax x x ><或； ③当a ＜0时，x (ax －1)＞0⇔x (x －a 1)＜0，解集为}01|{<<x ax ．习题1一、选择题1．D 2．D 3．A 4．C 5．C 提示：5．A 正确．B 不正确．D ．正确．当b ≠0时，C 正确；当b ＝0时，C 不正确，∴C 不一定成立． 二、填空题6．{0，1，3} 7．∀x ∈A ，x ∈A ∪B 8．{0，1，2} 9．{a ｜a ≥2} 10．③． 提示：10、均可用举反例的方式说明①②④⑤不正确．对于③：若a 、b 均小于等于1．即，a ≤1，b ≤1，则a ＋b ≤2，与a ＋b ＞2矛盾，所以③正确． 三、解答题 11．解：不等式21<x 即,021,021<-<-xx x 所以012>-xx ，此不等式等价于x (2x －1)＞0，解得x ＜0或21>x ，所以，原不等式的解集为{x ｜x ＜0或21>x }．12．解：(1)由a ＋b ＝1得a ＝1－b ，因为0＜a ＜b ，所以1－b ＞0且1－b ＜b ，所以.121<<b(2)a 2＋b 2－b ＝(1－b )2＋b 2－b ＝2b 2－3b ＋1＝⋅--81)43(22b 因为121<<b ，所以,081)43(22<--b 即a 2＋b 2＜b ．13．解：原不等式化为(a 2－b 2)x ＋b 2≥(a －b )2x 2＋2b (a －b )x ＋b 2，移项整理，得(a －b )2(x 2－x )≤0．因为a ≠b ，故(a －b )2＞0，所以x 2－x ≤0． 故不等式的解集为{x ｜0≤x ≤1}． 14．解：(1)若2∈A ，则.22111,21)1(11,1211A A A ∈=-∴∈=--∴∈-=-∴A 中至少有－1，21，2三个元素．(2)假设A 中只有一个元素，设这个元素为a ，由已知A a∈-11，则a a -=11．即a 2－a ＋1＝0，此方程无解，这与A 中有一个元素a 矛盾，所以A 中不可能只有一个元素．专题二 函 数函数是中学数学中的重点内容，是描述变量之间依赖关系的重要数学模型．本章内容有两条主线：一是对函数性质作一般性的研究，二是研究几种具体的基本初等函数——一次函数、二次函数、指数函数、对数函数、幂函数．研究函数的问题主要围绕以下几个方面：函数的概念，函数的图象与性质，函数的有关应用等．§2－1 函 数【知识要点】要了解映射的概念，映射是学习、研究函数的基础，对函数概念、函数性质的深刻理解在很多情况下要借助映射这一概念．1、设A ，B 是两个非空集合，如果按照某种对应法则f ，对A 中的任意一个元素x ，在B 中有一个且仅有一个元素y 与x 对应，则称f 是集合A 到集合B 的映射．记作f ：A →B ，其中x 叫原象，y 叫象．2、设集合A 是一个非空的数集，对A 中的任意数x ，按照确定的法则f ，都有唯一确定的数y 与它对应，则这种映射叫做集合A 上的一个函数．记作y ＝f (x )，x ∈A ．其中x 叫做自变量，自变量取值的范围(数集A )叫做这个函数的定义域．所有函数值构成的集合{y ｜y ＝f (x )，x ∈A }叫做这个函数的值域．函数的值域由定义域与对应法则完全确定．3、函数是一种特殊的映射．其定义域和值域都是非空的数集，值域中的每一个元素都有原象．构成函数的三要素：定义域，值域和对应法则．其中定义域和对应法则是核心． 【复习要求】1．了解映射的意义，对于给出对应关系的映射会求映射中指定元素的象与原象． 2．能根据函数三要素判断两个函数是否为同一函数．3．掌握函数的三种表示法(列表法、图象法和解析法)，理解函数符号f (x )(对应法则)，能依据一定的条件求出函数的对应法则．4．理解定义域在三要素的地位，并会求定义域． 【例题分析】例1 设集合A 和B 都是自然数集合N ．映射f ：A →B 把集合A 中的元素x 映射到集合B 中的元素2x ＋x ，则在映射f 作用下，2的象是______；20的原象是______．【分析】由已知，在映射f 作用下x 的象为2x ＋x ． 所以，2的象是22＋2＝6；设象20的原象为x ，则x 的象为20，即2x ＋x ＝20．由于x ∈N ，2x ＋x 随着x 的增大而增大，又可以发现24＋4＝20，所以20的原象是4．例2 设函数⎩⎨⎧>++-≤-=,0,22,0,1)(2x x x x x x f 则f (1)＝______；若f (0)＋f (a )＝－2，则a的所有可能值为______．【分析】从映射的角度看，函数就是映射，函数解析式就是映射的法则． 所以f (1)＝3．又f (0)＝－1，所以f (a )＝－1，当a ≤0时，由a －1＝－1得a ＝0；当a ＞0时，由－a 2＋2a ＋2＝－1，即a 2－2a －3＝0得a ＝3或a ＝－1(舍)． 综上，a ＝0或a ＝3．例3 下列四组函数中，表示同一函数的是( )(A)22)(,t y x y ==(B)2|,|t y x y ==(C)1,112+=--=x y x x y (D)x x y x y 2,==【分析】(A)(C)(D)中两个函数的定义域均不同，所以不是同一函数．(B)中两个函数的定义域相同，化简后为y ＝｜x ｜及y ＝｜t ｜，法则也相同，所以选(B)．【评析】判断两个函数是否为同一函数，就是要看两个函数的定义域与法则是否完全相同．一般有两个步骤：(1)在不对解析式进行变形的情况下求定义域，看定义域是否一致．(2)对解析式进行合理变形的情况下，看法则是否一致．例4 求下列函数的定义域(1);11--=x y(2);3212-+=x x y(3);)1()3lg(0-+-=x xx y(4);2|2|12---=x x y解：(1)由｜x －1｜－1≥0，得｜x －1｜≥1，所以x －1≥1或x －1≤－1，所以x ≥2或x ≤0．所以，所求函数的定义域为{x ｜x ≥2或x ≤0}． (2)由x 2＋2x －3＞0得，x ＞1或x ＜－3．所以，所求函数的定义域为{x ｜x ＞1或x ＜－3}．(3)由⎪⎩⎪⎨⎧=/-=/>-,01,0,03x x x 得x ＜3，且x ≠0，x ≠1， 所以，所求函数的定义域为{x |x ＜3，且x ≠0，x ≠1}(4)由⎩⎨⎧=/=/≤≤-⎩⎨⎧=/-≥-⎩⎨⎧≠--≥-,4,0,112|2|01,02|2|0122x x x x x x x 且即，，得，所以－1≤x ≤1，且x ≠0．所以，所求函数定义域为{x ｜－1≤x ≤1，且x ≠0}．例5 已知函数f (x )的定义域为(0，1)，求函数f (x ＋1)及f (x 2)的定义域．【分析】此题的题设条件中未给出函数f (x )的解析式，这就要求我们根据函数三要素之间的相互制约关系明确两件事情：①定义域是指x 的取值范围；②受对应法则f 制约的量的取值范围在“已知”和“求”当中是一致的．那么由f (x )的定义域是(0，1)可知法则f 制约的量的取值范围是(0，1)，而在函数f (x ＋1)中，受f 直接制约的是x ＋1，而定义域是指x 的范围，因此通过解不等式0＜x ＋1＜1得－1＜x ＜0，即f (x ＋1)的定义域是(－1，0)．同理可得f (x 2)的定义域为{x ｜－1＜x ＜1，且x ≠0}．例6 如图，用长为l 的铁丝弯成下部为矩形，上部为半圆形的框架，若矩形的底边长为2x ，求此框架围成的面积y 与x 的函数关系式，并指出定义域．解：根据题意，AB ＝2x ．⋅--==2π2,πxx l AD x 所以，.)2π2(π212π2222lx x x x x l x y ++-=+--=⋅⋅根据问题的实际意义．AD ＞0，x ＞0．解.π20,02π2,0+<<⎪⎩⎪⎨⎧>-->l x xx l x 得 所以，所求函数定义域为⋅+<<}π20|{lx x 【评析】求函数定义域问题一般有以下三种类型问题．(1)给出函数解析式求定义域(如例4)，这类问题就是求使解析式有意义的自变量的取值范围．正确的解不等式或不等式组在解决这类问题中是重要的．中学数学中常见的对变量有限制的运算法则有：①分式中分母不为零；②偶次方根下被开方数非负；③零次幂的底数要求不为零；④对数中的真数大于零，底数大于零且不等于1；⑤y ＝tan x ，则2ππ+≠k x ，k ∈Z ． (2)不给出f (x )的解析式而求定义域(如例5)．其解决办法见例5的分析．(3)在实际问题中求函数的定义域(如例6)．在这类问题中除了考虑解析式对自变量的限制，还应考虑实际问题对自变量的限制．另外，在处理函数问题时要有一种随时关注定义域的意识，这是极其重要的．比如在研究函数单调性、奇偶性、最值等问题时，首先要考虑的就是函数的定义域．例7 (1)已知21)1(x xxf -=，求f (x )的解析式； (2)已知221)1(xx x x f +=+，求f (3)的值；(3)如果f (x )为二次函数，f (0)＝2，并且当x ＝1时，f (x )取得最小值－1，求f (x )的解析式；(4)*已知函数y ＝f (x )与函数y ＝g (x )＝2x 的图象关于直线x ＝1对称，求f (x )的解析式． 【分析】(1)求函数f (x )的解析式，从映射的角度看就是求对应法则，于是，我们一般有下面两种方法解决(1)这样的问题．方法一．⋅-=-=1)1(111)1(2xxx xxf 通过这样“凑型”的方法，我们可以明确看到法则f 是“原象对应于原象除以原象的平方减1”．所以，⋅-=1)(2x xx f。

函 数 练 习 题班级 姓名一、 求函数的定义域1、求下列函数的定义域：⑴y =⑵y =⑶01(21)111y x x =+-++-2、设函数f x ()的定义域为[]01，，则函数f x ()2的定义域为_ _ _；函数f x ()-2的定义域为________； 3、若函数(1)f x +的定义域为[]-23，，则函数(21)f x -的定义域是 ；函数1(2)f x+的定义域为 。

4、 知函数f x ()的定义域为 [1,1]-，且函数()()()F x f x m f x m =+--的定义域存在，求实数m 的取值范围。

二、求函数的值域5、求下列函数的值域：⑴223y x x =+- ()x R ∈ ⑵223y x x =+- [1,2]x ∈ ⑶311x y x -=+ ⑷311x y x -=+ (5)x ≥⑸ y = ⑹ 225941x x y x +=-＋ ⑺31y x x =-++ ⑻2y x x =-⑼ y ⑽ 4y = ⑾y x =-6、已知函数222()1x ax b f x x ++=+的值域为[1，3]，求,a b 的值。

三、求函数的解析式1、 已知函数2(1)4f x x x -=-，求函数()f x ，(21)f x +的解析式。

2、 已知()f x 是二次函数，且2(1)(1)24f x f x x x ++-=-，求()f x 的解析式。

3、已知函数()f x 满足2()()34f x f x x +-=+，则()f x = 。

4、设()f x 是R 上的奇函数，且当[0,)x ∈+∞时， ()(1f x x =，则当(,0)x ∈-∞时()f x =____ _ ()f x 在R 上的解析式为5、设()f x 与()g x 的定义域是{|,1}x x R x ∈≠±且，()f x 是偶函数，()g x 是奇函数，且1()()1f xg x x +=-，求()f x 与()g x 的解析表达式四、求函数的单调区间6、求下列函数的单调区间：⑴ 223y x x =++ ⑵y = ⑶ 261y x x =--7、函数()f x 在[0,)+∞上是单调递减函数，则2(1)f x -的单调递增区间是8、函数236x y x -=+的递减区间是 ；函数y =的递减区间是 五、综合题9、判断下列各组中的两个函数是同一函数的为 （ ）⑴3)5)(3(1+-+=x x x y ， 52-=x y ； ⑵111-+=x x y ， )1)(1(2-+=x x y ；⑶x x f =)(， 2)(x x g = ； ⑷x x f =)(， ()g x =； ⑸21)52()(-=x x f ， 52)(2-=x x f 。

导数与函数的极值、最值◆高考导航·顺风启程◆最新考纲常见题型1.了解函数在某点取得极值的必要条件和充分条件；会用导数求函数的高考必考题，既有选极大值、极小值(其中多项式函数不超过三次)．择，也有填空，还有2.会求闭区间上函数的最大值、最小值(其中多项式函数不超过三次)．解答题，为中、高档3.会利用导数解决实际问题.题型，占5～13分.[知识梳理]1．函数的极值与导数2．函数的最值f ( b(1)在闭区间[a ，b ]上连续的函数 f (x )在[a ，b ]上必有最大值与最小值．(2)若函数 f (x )在[a ，b ]上单调递增，则 f (a ) 为函数的最小值， f (b ) 为函数的最大值；若函数 f (x )在[a ，b ]上单调递减，则f (a ) 为函数的最大值， f (b ) 为函数的最小值．(3)求函数 y ＝f (x )在[a ，b ]上的最大值与最小值的步骤为①求函数 y ＝f (x )在(a ，b )内的 极值 ；②将函数 y ＝f (x )的各 极值 与端点处的 f (a )、 b ) 比较，其中最大的一个是最大值，最小的一个是最小值，得出函数 f (x )在[a ，b ]上的最值．[知识感悟]1．导数与函数单调性的关系(1)f ′(x )＞0(或 f ′(x )＜0)是 f (x )在(a ，b )内单调递增(或递减)的充分不必要条件；(2)f ′(x )≥0(或 f ′(x )≤0)是 f (x )在(a ，)内单调递增(或递减)的必要不充分条件(f ′(x )＝0不恒成立)．2．求函数 f (x )极值的方法求函数的极值应先确定函数的定义域，再解方程 f ′(x )＝0，再判断 f ′(x )＝0 的根是否是极值点，可通过列表的形式进行分析，若遇极值点含参数不能比较大小时，则需分类讨论．3．求函数 f (x )在区间[a ，b ]上的最值的方法(1)若函数在区间[a ，b ]上单调递增或递减，f (a )与 f (b )一个为最大值，一个为最小值； (2)若函数在闭区间[a ，b ]内有极值，要先求出[a ，b ]上的极值，与 f (a )，f (b )比较，最大的是最大值，最小的是最小值，可列表完成；(3)函数 f (x )在区间(a ，b )上有唯一一个极值点，这个极值点就是最大(或小)值点，此结论在导数的实际应用中经常用到．[知识自测]1．函数 f (x )的定义域为 R ，导函数 f ′(x )的图象如图所示，则函数 f (x )()22．函数f(x)＝＋x－3x－4在[0,2]上的最小值是________.[解析]f′(x)＝x2＋2x－3，f′(x)＝0，x∈[0,2]，得x＝1.比较f(0)＝－4，f(1)＝－，f(2)＝－.可知最小值为－.[答案]－[解析]设矩形的一边边长为x，则另一边边长为，其周长为l＝2x＋，x＞0，l′＝2－2.xA．无极大值点、有四个极小值点B．有三个极大值点、一个极小值点C．有两个极大值点，两个极小值点D．有一个极大值点，两个极小值点[解析]设f′(x)的图象与x轴的4个交点从左至右依次为x1、x2、x3、x4.当x＜x1时，f′(x)＞0，f(x)为增函数，当x1＜x＜x2时，f′(x)＜0，f(x)为减函数，则x＝x1为极大值点，同理，x＝x3为极大值点，x＝x2，x＝x4为极小值点，故选C.[答案]Cx33173 1017331733．面积为S的矩形中，其周长最小时的边长是________.S2Sx x2S令l′＝0，解得x＝S.易知，当x＝S时，其周长最小．[答案]S题型一函数的极值问题(高频考点题，多角突破)考向一根据函数图象判断极值1．(1)(2018·青岛模拟)设f′(x)是函数f(x)的导函数，y＝f′(x)的图象如图所示，则y＝f(x)的图象最有可能是()(2)设函数f(x)在R上可导，其导函数为f′(x)，且函数y＝(1－x)f′(x)的图象如图所示，则下列结论中一定成立的是()A．函数f(x)有极大值f(2)和极小值f(1)B．函数f(x)有极大值f(－2)和极小值f(1)C．函数f(x)有极大值f(2)和极小值f(－2)D．函数f(x)有极大值f(－2)和极小值f(2)[解析](1)由f′(x)图象可知，x＝0是函数f(x)的极大值点，x＝2是f(x)的极小值点，故选C.(2)由题图可知，当x＜－2时，f′(x)＞0；当－2＜x＜1时，f′(x)＜0；当1＜x＜2时，f′(x)＜0；当x＞2时，f′(x)＞0.由此可以得到函数f(x)在x＝－2处取得极大值，在x＝2处取得极小值．2．(2017·山东)已知函数 f (x )＝ x 3－ ax 2，a ∈R ，(1)当 a ＝2 时，求曲线 y ＝f (x )在点(3， g (x )取到极大值，极大值是 g (a )＝－ a 3－sin a ，[答案] (1)C (2)D考向二 已知函数求极值1 1 3 2f (3))处的切线方程；(2)设函数 g (x )＝f (x )＋(x －a )cos x －sin x ，讨论 g (x )的单调性并判断有无极值，有极值时求出极值．[解析] (1)由题意 f ′(x )＝x 2－ax ，所以，当 a ＝2 时，f (3)＝0，f ′(x )＝x 2－2x ， 所以 f ′(3)＝3，因此，曲线 y ＝f (x )在点(3，f (3))处的切线方程是 y ＝3(x －3)，即 3x －y －9＝0.(2)因为 g (x )＝f (x )＋(x －a )cos x －sin x ，所以 g ′(x )＝f ′(x )＋cos x －(x －a )sin x －cos x ，＝x (x －a )－(x －a )sin x ＝(x －a )(x －sin x )令 h (x )＝x －sin x ，则 h ′(x )＝1－cos x ＞0，所以 h (x )在 R 上单调递增，因为 h (0)＝0，所以，当 x ＞0 时，h (x )＞0；当 x ＜0 时，h (x )＜0. (1)当 a ＜0 时，g (x )＝(x －a )(x －sin x )，当 x ∈(－∞，a )时，x －a ＜0，g (x )＞0，g (x )单调递增；当 x ∈(a,0)时，x －a ＞0，g ′(x )＜0，g (x )单调递减；当 x ∈(0，＋∞)时，x －a ＞0，g ′(x )＞0，g (x )单调递增．所以，当 x ＝a 时，16当 x ＝0 时，g (x )取到极小值，极小值是 g (0)＝－a .(2)当 a ＝0 时，g ′(x )＝x (x －sin x )，当 x ∈(－∞，＋∞)时，g ′(x )≥0，g (x )单调递增；所以，g (x )在(－∞，＋∞)上单调递增， g (x )无极大值也无极小值．(3)当 a ＞0 时，g ′(x )＝(x －a )(x －sin x )，当 x ∈(－∞，0)时，x －a ＜0，g ′(x )＞0，g (x )单调递增；当 x ∈(0，a )时，x －a ＜0，g ′(x )＜0，g (x )单调递减；当 x ∈(a ，＋∞)时，x －a ＞0，g ′(x )＞0，(2)(2018·福州质检)若函数 f (x )＝ － x 2＋x ＋1 在区间⎛⎝2，3⎫⎭上有极值点，则实数 a 的取 A.⎛⎝2，2⎫⎭ B.⎣2，2⎭ C.⎛⎝2， 3 ⎫⎭D.⎡⎣2， 3 ⎫⎭(2)若函数 f (x )在区间⎛⎝2，3⎫⎭上无极值， 则当 x ∈⎝2，3⎭时，f ′(x )＝x 2－ax ＋1≥0 恒成立或当 x ∈⎝2，3⎭时，f ′(x )＝x 2－ax ＋1≤0当 x ∈⎝2，3⎭时，y ＝x ＋x 的值域是⎣2， 3 ⎭；当 x ∈⎝2，3⎭时，f ′(x )＝x 2－ax ＋1≥0，⎪ ⎪ ⎪⎩ ⎩ ⎩g (x )单调递增．所以，当 x ＝0 时，g (x )取到极大值，极大值是 g (0)＝－a ；当 x ＝a 时，g (x )取到极小值，1极小值是 g (a )＝－6a 3－sin a .综上所述：当 a ＜0 时，函数 g (x )在(－∞，a )和(0，＋∞)上单调递增，在(a,0)上单调递减，函数既1有极大值，又有极小值，极大值是 g (a )＝－6a 3－sin a ，极小值是 g (0)＝－a .当 a ＝0 时，函数 g (x )在(－∞，＋∞)上单调递增，无极值；当 a ＞0 时，函数 g (x )在(－∞，0)和(a ，＋∞)上单调递增，在(0，a )上单调递减，函数1既有极大值，又有极小值，极大值是 g (0)＝－a ，极小值是 g (a )＝－6a 3－sin a .考向三 已知极值求参数(范围)3．(1)(2018·广州模拟)已知 f (x )＝x 3＋3ax 2＋bx ＋a 2 在 x ＝－1 时有极值 0，则 a －b ＝________ .x 3 a 1 3 2值范围是()510 ⎡ 5⎫10[解析] (1)由题意得 f ′(x )＝3x 2＋6ax ＋b ，则⎧a 2＋3a －b －1＝0， ⎧a ＝1， ⎧a ＝2， ⎨解得⎨ 或⎨ ⎪b －6a ＋3＝0， ⎪b ＝3 ⎪b ＝9， 经检验当 a ＝1，b ＝3 时，函数 f (x )在 x ＝－1 处无法取得极值，而 a ＝2，b ＝9 满足题意，故 a －b ＝－7.1⎛1 ⎫ ⎛1 ⎫恒成立．⎛1 ⎫ 1 ⎡ 10⎫⎛1 ⎫当 x ∈⎝2，3⎭时，f ′(x )＝x 2－ax ＋1≤0， 因此要使函数 f (x )在⎝2，3⎭上有极值点，实数 a 的取值范围是⎝2， 3 ⎭.2．(2018·济宁模拟节选)已知函数 f (x )＝ (k ≠0)．求函数 f (x )的极值．1即 a ≤x ＋x 恒成立，a ≤2；⎛1 ⎫1 10 即 a ≥x ＋x 恒成立，a ≥ 3 .⎛1 ⎫⎛ 10⎫[答案] (1)－7 (2)C方法感悟利用导数研究函数极值的一般流程【针对补偿】1．(2017·课标Ⅱ)若 x ＝－2 是函数 f (x )＝(x 2＋ax －1)e x －1 的极值点，则 f (x )的极小值为()A ．－1C ．5e －3B ．－2e －3D ．1[解析] 由题可得 f ′(x )＝(2x ＋a )e x －1＋(x 2＋ax －1)e x －1＝[x 2＋(a ＋2)x ＋a －1]e x －1. 因为 f ′(－2)＝0，所以 a ＝－1，f (x )＝(x 2－x －1)e x －1，故 f ′(x )＝(x 2＋x －2)e x －1令 f ′(x )＞0，解得 x ＜－2 或 x ＞1，所以 f (x )在(－∞，－2)，(1，＋∞)单调递增，在(－2,1)单调递减，所以 f (x )极小值为 f (1)＝(1－1－1)e 1－1＝－1，故选 A.[答案] A1＋ln xkx[解] f (x )＝ ，其定义域为(0，＋∞)， (2)求函数 f (x )在区间⎡⎣0，2⎤⎦上的最大值和最小值． 当 x ∈⎝0，2⎭时，h ′(x )＜0，所以 h (x )在区间⎣0，2⎦上单调递减．所以对任意 x ∈⎝0，2⎦有 h (x )＜h (0)＝0，1＋ln xkxln x则 f ′(x )＝－ kx 2 .令 f ′(x )＝0，得 x ＝1，当 k ＞0 时，若 0＜x ＜1，则 f ′(x )＞0；若 x ＞1，则 f ′(x )＜0，1∴f (x )在(0,1)上单调递增，在(1，＋∞)上单调递减，即当 x ＝1 时，函数 f (x )取得极大值k .当 k ＜0 时，若 0＜x ＜1，则 f ′(x )＜0；若 x ＞1，则 f ′(x )＞0，∴f (x )在(0,1)上单调递减，在(1，＋∞)上单调递增，即当 x ＝11时，函数 f (x )取得极小值k .题型二 函数的最值问题(重点保分题，共同探讨)(2017·北京)已知函数 f (x )＝e x cos x －x .(1)求曲线 y ＝f (x )在点(0，f (0))处的切线方程；π[解] (1)因为 f (x )＝e x cos x －x ，所以 f ′(x )＝e x (cos x －sin x )－1，f ′(0)＝0.又因为 f (0)＝1，所以曲线 y ＝f (x )在点(0，f (0))处的切线方程为 y ＝1.(2)设 h (x )＝e x (cos x －sin x )－1，则 h ′(x )＝e x (cos x －sin x －sin x －cos x )＝－2e x sin x .⎛ π⎫⎡ π⎤⎛ π⎤即 f ′(x )＜0.所以函数 f (x )在区间⎣0，2⎦上单调递减．因此 f (x )在区间⎣0，2⎦上的最大值为 f (0)＝1，最小值为 f ⎝2⎭＝－2.，x 2＝∴f (x )在 －∞， ⎪和 －1＋ 4＋3a ，＋∞⎪上单调递减，在( ， )上单调递增．－1－ 4＋3a ⎫ ⎛ 3 3⎡ π⎤⎡ π⎤ ⎛π⎫ π方法感悟求函数 f (x )在[a ，b ]上的最大值和最小值的步骤(1)求函数在(a ，b )内的极值；(2)求函数在区间端点处的函数值 f (a )，f (b )；(3)将函数 f (x )的各极值与 f (a )，f (b )比较，其中最大的一个为最大值，最小的一个为最小值．【针对补偿】3．设函数 f (x )＝1＋(1＋a )x －x 2－x 3，其中 a >0. (1)讨论 f (x )在其定义域上的单调性；(2)当 x ∈[0,1]时，求 f (x )取得最大值和最小值时的 x 的值．[解] (1)f (x )的定义域为 (－∞，＋∞)，f ′(x )＝1＋a －2x －3x 2，令 f ′(x )＝0 得 x 1＝－1－ 4＋3a －1＋ 4＋3a3 3，且 x 1<x 2.∴f ′(x )＝－3(x －x 1)(x －x 2)，当 x <x 1 或 x >x 2 时， f ′(x )<0；当 x 1<x <x 2 时，f ′(x )>0，⎛ ⎫ ⎝ ⎭ ⎝ ⎭－1－ 4＋3a －1＋ 4＋3a3 3(2)∵a >0，∴x 1<0，x 2>0，①当 a ≥4 时，x 2≥1，由(1)知 f (x )在[0,1]上单调递增，∴f (x )在 x ＝0 和 x ＝1 处分别取得最小值和最大值．②当 0<a <4 时，x 2<1，由(1)知 f (x )在[0，x 2]上单调递增，在[x 2,1]上单调递减，－1＋ 4＋3a∴f (x )在 x ＝x 2＝ 3处取得最大值．又 f (0)＝1，f (1)＝a ，∴当 0<a <1 时，f (x )在 x ＝1 处取得最小值；当 a ＝1 时，f (x )在 x ＝0 和 x ＝1 处同时取得最小值；当 1<a <4 时，f (x )在 x ＝0 处取得最小值．题型三 利用导数研究生活中的最优化问题(重点保分题，共同探讨)．＝ ·A 1B 12·PO 1＝ ×62×2＝ 3 32 1 1(2016·江苏卷 )现需要设计一个仓库，它由上下两部分组成，上部分的形状是正四棱锥P A 1B 1C 1D 1，下部分的形状是正四棱柱ABCD A 1B 1C 1D 1(如图所示)，并要求正四棱柱的高 O 1O 是正四棱锥的高 PO 1 的 4 倍． (1)若 AB ＝6 ，PO 1＝2 m ，则仓库的容积是多少；(2)若正四棱锥的侧棱长为 6 m ，当 PO 1 为多少时，仓库的容积最大？ [解] (1)由 PO 1＝2 知 O 1O ＝4PO 1＝8.因为 A 1B 1＝AB ＝6，所以正四棱锥 P A 1B 1C 1D 1 的体积 V锥 1 124(m 3)；正四棱柱 ABCD A 1B 1C 1D 1 的体积 V 柱＝AB 2·O 1O ＝62×8＝288(m 3)．所以仓库的容积 V ＝V 锥＋V 柱＝24＋288＝312(m 3)． (2)设 A 1B 1＝a (m)，PO 1＝h (m)， 则 O <h <6，O 1O ＝4 h ．连结 O 1B 1.因为在 Rt △PO 1B 1 中，O 1B 1＋PO 2＝PB 2，于是仓库的容积 V ＝V 柱＋V 锥＝a 2·4h ＋ a2·h 3 ＝ a 2h ＝ (36h －h 3)，3 3 0<h <6，从而 V ′＝ (36－3h 2)＝26(12－h 2)．所以 h ＝ (300－4r 2)，5r 从而 V (r )＝πr 2h ＝ (300r －4r 3)．5 ⎛ 2a ⎫2＋h 2＝36.即 a 2＝2(36－h 2)．所以⎝ 2 ⎭113 26263令 V ′＝0，得 h ＝2 3或 h ＝－2 3(舍)．当 0<h <2 3时，V ′>0，V 是单调增函数；当 2 3<h <6 时，V ′<0，V 是单调减函数．故 h ＝2 3时，V 取得极大值，也是最大值．因此，当 PO 1＝2 3 m 时，仓库的容积最大．方法感悟利用导数解决生活中的优化问题的一般步骤(1)分析实际问题中各量之间的关系，列出实际问题的数学模型，写出实际问题中变量之间的函数关系式 y ＝f (x )；(2)求函数的导数 f ′(x )，解方程 f ′(x )＝0；(3)比较函数在区间端点和 f ′(x )＝0 的点的函数值的大小，最大(小)者为最大(小)值； (4)回归实际问题作答．【针对补偿】4．(重庆高考)某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度)．设该蓄水池的底面半径为 r 米，高为 h 米，体积为 V 立方米．假设建造成本仅与表面积有关，侧面的建造成本为100 元/平方米，底面的建造成本为 160 元/平方米，该蓄水池的总建造成本为 12 000π 元(π为圆周率)．(1)将 V 表示成 r 的函数 V (r )，并求该函数的定义域；(2)讨论函数 V (r )的单调性，并确定 r 和 h 为何值时该蓄水池的体积最大．[解] (1)因为蓄水池侧面的总成本为 100·2πrh ＝200πrh (元)，底面的总成本为 160πr 2 元，所以蓄水池的总成本为(200πrh ＋160πr 2)元．又根据题意 200πrh ＋160πr 2＝12 000π，1π因为 r ＞0，又由 h ＞0 可得 r ＜5 3，故函数 V (r )的定义域为(0,5 3)．5 时 上 成岳xx 2．(2018· 尔滨调研)函数 f(x)＝ x 2－lnx 的最小值为( )2x x 且 x ＞0.f(1)＝ －ln 1＝ .π(2)因为 V (r )＝ (300r －4r 3)，π所以 V ′(r)＝5(300－12r 2)．令 V ′(r)＝0，解得 r 1＝5，r 2＝－5(因为 r 2＝－5 不在定义域内，舍去)．当 r ∈(0,5) ，V ′(r)＞0，故 V (r)在(0,5) 为增函数；当 r ∈(5,5 3)时，V ′(r)＜0，故 V (r)在(5,5 3)上为减函数．由此可知，V (r )在 r ＝5 处取得最大值，此时 h ＝8.即当 r ＝5，h ＝8 时，该蓄水池的体积最大．◆牛刀小试· 功靠岸◆课堂达标(十五)[A 基础巩固练]1．(2018· 阳一模)下列函数中，既是奇函数又存在极值的是( )A ．y ＝x 3C ．y ＝xe －B ．y ＝ln(－x)2D ．y ＝x ＋[解析] 由题可知，B 、C 选项中的函数不是奇函数，A 选项中，函数 y ＝x 3 单调递增(无极值)，而 D 选项中的函数既为奇函数又存在极值．[答案] D121 A.C ．0B ．1D ．不存在1 x 2－1[解析] f′(x)＝x － ＝令 f′(x)＞0，得 x ＞1.令 f′(x)＜0，得 0＜x ＜1.∴f(x)在 x ＝1 处取得极小值也是最小值，1 12 2[答案] A3．设函数 f(x)＝ax 2＋bx ＋c(a ，b ，c ∈R )．若 x ＝－1 为函数 f(x)e 的一个极值点，则下列图象不可能为 y ＝f(x)图象的是( )2C. 55．(2018·山西省太原五中二模)正项等比数列{a n }中的 a 1，a 4033 是函数 f (x )＝ x 3－4x 2＋3 2 [解析]∵f (x )＝ x 3－4x 2＋6x －3，[解析] 因为[f (x )e x ]′＝f ′(x )e x ＋f (x )(e x )′＝[f (x )＋f ′(x )]e x ，且 x ＝－1 为函数 f (x )e x 的一个极值点，e x ＞0，所以 f (－1)＋f ′(－1)＝0；选项 D 中，f (－1)＞0，f ′(－1)＞0，不满足f ′(－1)＋f (－1)＝0.[答案] D4．设直线 x ＝t 与函数 h (x )＝x 2，g (x )＝ln x 的图象分别交于点 M ，N ，则当|MN |最小时t 的值为()A ．11 B.22 D. 2[解析] 由已知条件可得|MN |＝t 2－ln t ，1设 f (t )＝t 2－ln t (t ＞0)，则 f ′(t )＝2t － t ，2 2令 f ′(t )＝0，得 t ＝ 2 ，当 0＜t ＜ 2 时，f ′(t )＜0，2 2当 t ＞ 2 时，f ′(t )＞0，∴当 t ＝ 2 时，f (t )取得最小值．[答案] D16x －3 的极值点，则 log 6a 2017＝()A ．11 C.13B ．2D ．－1∵正项等比数列{a n }中的 a 1，a 4033 是函数 f (x )＝3x 3－4x 2＋6x －3 的极值点，∴a 1×a 4033 ＝6，∴a 2017＝ a 1×a 4033＝ 6，∴log 6a 2017＝log 6 6＝2.6．若函数 f (x )＝ x 3＋x 2－ 在区间(a ，a ＋5)上存在最小值，则实数 a 的取值范围是( )示，令3x 3＋x 2－3＝－3得，x ＝0 或 x ＝－3，则结合图象可知，⎨ ，解得 a ∈[－⎩ 则 V ＝3π(400－h 2)h ＝3π(400h －h 3)， ∴V ′＝3π(400－3h 2)，由 V ′＝0，得 h ＝ 3 ，∴f ′(x )＝x 2－8x ＋6，11故选：C.[答案] C1 23 3A ．[－5,0)C ．[－3,0)B ．(－5,0)D ．(－3,0)[解析] 由题意，f ′(x )＝x 2＋2x ＝x (x ＋2)，故 f (x )在(－∞，－2)，(0，＋∞)上是增函数，在(－2,0)上是减函数，作出其图象如图所1 2 2 ⎧⎪－3≤a ＜0 ⎪a ＋5＞03,0)，故选 C.[答案] C7．要做一个圆锥形漏斗，其母线长为 20 cm ，要使体积最大，则其高为______cm. [解析] 设圆锥的体积为 V cm 3，高为 h cm ，1 11 20 320 3所以当 h ＝3cm 时，V 最大．[答案]20 ⎪ ⎪ ⎩ ⎩ ⎧(－ a )3－3a (－ a )＋b ＝6， ⎧a ＝1， [解] (1)f (x )的定义域为(0，＋∞)，f ′(x )＝ －a .若 a ＞0，则当 x ∈⎝0，a ⎭时，f ′(x )＞0；当 x ∈⎝a ，＋∞⎭时，f ′(x )＜0. 所以 f (x )在⎝0，a ⎭上单调递增，在⎝a ，＋∞⎭上单调递减．⎩ 3 38．(2018·东北八校月考)已知函数 y ＝f (x )＝x 3＋3ax 2＋3bx ＋c 在 x ＝2 处有极值，其图象在 x ＝1 处的切线平行于直线 6x ＋2y ＋5＝0，则 f (x )的极大值与极小值之差为______．[解析] ∵f ′(x )＝3x 2＋6ax ＋3b ，⎧f ′(2)＝3×22＋6a ×2＋3b ＝0， ⎧a＝－1， ∴⎨ ⎨ ⎪f ′(1)＝3×12＋6a ×1＋3b ＝－3，⎪b ＝0，∴f ′(x )＝3x 2－6x ，令 3x 2－6x ＝0，得 x ＝0 或 x ＝2，∴f (x )极大值－f (x )极小值＝f (0)－f (2)＝4. [答案] 49．函数 f (x )＝x 3－3ax ＋b (a ＞0)的极大值为 6，极小值为 2，则 f (x )的单调递减区间是________ .[解析] 令 f ′(x )＝3x 2－3a ＝0，得 x ＝± a ，则 f (x )，f ′(x )随 x 的变化情况如下表：x (－∞，－－ a (－ a ， a ) a( a ，＋∞)a )f ′(x )f (x )＋ 0极大值－极小值＋从而⎨ 解得⎨⎩( a )3－3a a ＋b ＝2， ⎪b ＝4.所以 f (x )的单调递减区间是(－1,1)．[答案] (－1,1)10．(新课标全国卷Ⅱ)已知函数 f (x )＝ln x ＋a (1－x )． (1)讨论 f (x )的单调性；(2)当 f (x )有最大值，且最大值大于 2a －2 时，求 a 的取值范围．1x若 a ≤0，则 f ′(x )＞0，所以 f (x )在(0，＋∞)上单调递增．⎛ 1⎫⎛1 ⎫⎛ 1⎫ ⎛1 ⎫(2)由(1)知，当 a ≤0 时，f (x )在(0，＋∞)上无最大值；当 a ＞0 时，f (x )在 x ＝ 处取得最大值，最大值为 f ⎝a ⎭＝ln ⎝a ⎭＋a ⎝1－a ⎭＝－ln a ＋a －1.因此 f ⎝a ⎭＞2a －2 等价于 ln a ＋a －1＜0. 2．(2018·郑州第三次质检) 设函数 f (x )满足 2x 2f (x )＋x 3f ′(x )＝e x ，f (2)＝ ，则 x ∈[2， 2 [解析]对于等式 x 2f ′(x )＋2xf (x )＝ e x －2x 2f (x ) x ，因为 x ＞0，故此等式可化为：f ′(x )＝ 且 f ′(2)＝ ＝0.令 g (x )＝e x －2x 2f (x )，g (2)＝0，g ′(x )＝e x －2[x 2f ′(x )＋2xf (x )]＝e x －2 ＝ (x －2)．当 x ≥2 时，g ′(x )＞0， g (x )单调递增，故 min{g (x )}＝g (2)＝0，因此当 x ≥2 时，g (x )≥0 恒成立．因为 f ′(x )＝ 3 ，x所以 f ′(x )≥0 恒成立．因此，f (x )在[2，＋∞)上单调递增，f (x )的最小值为 f (2)＝ 8 .故本题正41a⎛1⎫ ⎛1⎫ ⎛ 1⎫⎛1⎫令 g (a )＝ln a ＋a －1，则 g (a )在(0，＋∞)上单调递增，g (1)＝0.于是，当 0＜a ＜1 时，g (a )＜0；当 a ＞1 时，g (a )＞0.因此，a 的取值范围是(0,1)．[B 能力提升练]1．(2018·吉大附中第七次模拟)已知函数 f (x )满足 f (x )＋xf ′(x )＝ln x ，且 f (1)＝0，则函数 f (x )()A. 有极大值，无极小值B. 有极小值，无极大值C. 既有极大值，又有极小值D. 既无极大值，也无极小值[解析] 因为 f (x )＋xf ′(x )＝ln x ，即[xf (x )]′＝ln x ，所以 xf (x )＝x ln x －x ＋c ，其中 c 为1 1 1 x －1常数，又因为 f (1)＝0，所以 xf (x )＝x ln x －x ＋1，f (x )＝ln x －1＋x ，f ′(x )＝x －x 2＝ x 2 ，当0＜x ＜1 时，f ′(x )＜0，当 x ＞1 时，f ′(x )＞0，所以函数 f (x )在 x ＝1 时取得极小值，无极大值．[答案] Be 28＋∞)时，f (x )的最小值为()e 2 A. 3e 2B. 2e 2 e 2 C. D. 8e x ，x 3e 2－8f (2)8e x e xx xg (x)e 21 ax －1 1 1⎫ [解析]易知 a >0，由 f ′(x )＝a － ＝ ＝0，得 x ＝a ，当 x ∈⎝0，a ⎭时，f ′(x )<0，f (x )单调递减；当 x ∈⎛⎝a ，＋∞⎫⎭时，f ′(x )>0，f (x )单调递增．①当 0< ≤e ，即 a ≥ 时，f (x )在(0，e]上的最小值为 f ⎝a ⎭，即 1－ln a ＝3，得 a ＝e 2，符合题意；②当a >e 即 a <e 时，f (x )在(0，e]上的最小值为 f (e)，即 a e －ln e ＝3，得 a ＝ > ，舍去．综上，a ＝e 2.确答案为 D.[答案] D3．(2018·广西三市调研)已知函数 f (x )＝ax －ln x ，当 x ∈(0，e](e 为自然常数)时，函数 f (x )的最小值为 3，则 a 的值为______．⎛ x x1 1 1 a e⎛1⎫ 1 1 14 1e e[答案] e 24．已知 f (x )＝x 3－6x 2＋9x －abc ，a <b <c ，且 f (a )＝f (b )＝f (c )＝0.现给出如下结论：①f (0)f (1)>0；②f (0)f (1)<0；③f (0)f (3)>0；④f (0)f (3)<0.其中正确结论的序号是______．[解析] ∵f ′(x )＝3x 2－12＋9＝3(x －1)(x －3)，由 f ′(x )<0，得 1<x <3，由 f ′(x )>0，得 x <1 或 x >3，∴f (x )在区间(1,3)上是减函数，在区间(－∞，1)，(3，＋∞)上是增函数．又 a <b <c ，f (a )＝f (b )＝f (c )＝0，∴y 极大值＝f (1)＝4－abc >0，y 极小值＝f (3)＝－abc <0.∴0<abc <4.∴a ，b ，c 均大于零，或者 a <0，b <0，c >0.又 x ＝1，x ＝3 为函数 f (x )的极值点，后一种情况不可能成立，如图．∴f (0)<0.∴f (0)f (1)<0，f (0)f (3)>0.∴正确结论的序号是②③.f ′(x )＝ －1，令 f ′(x )＝0 解得 x ＝1. ln c(2)证明当 x ∈(1，＋∞)时，1<<x ；[答案] ②③5．(2016·全国Ⅲ卷)设函数 f (x )＝ln x －x ＋1. (1)讨论 f (x )的单调性；x －1ln x(3)设 c >1，证明当 x ∈(0,1)时，1＋(c －1)x >c x .[解] (1)由题设，f (x )的定义域为(0，＋∞)，1x当 0<x <1 时，f ′(x )>0，f (x )单调递增；当 x >1 时，f ′(x )<0，f (x )单调递减．(2)由(1)知 f (x )在 x ＝1 处取得最大值，最大值为 f (1)＝0.所以当 x ≠1 时，ln x <x －1.1 1故当 x ∈(1，＋∞)时，ln x <x －1，ln x <x －1，x －1 即 1< ln x <x .(3)由题设 c >1，设 g (x )＝1＋(c －1)x －c x ，c －1 ln 则 g '(x )＝c －1－c x ln c ，令 g '(x )＝0，解得 x 0＝ ln c .当 x <x 0 时，g ′(x )>0，g (x )单调递增； 当 x >x 0 时，g ′(x )<0，g (x )单调递减． c －1由(2)知 1< ln c <c ，故 0<x 0<1.又 g (0)＝g (1)＝0，故当 0<x <1 时，g (x )>0.所以当 x ∈(0,1)时，1＋(c －1)x >c x .[C 尖子生专练](2017·课标Ⅰ)已知函数 f (x )＝a e 2x ＋(a －2)e x －x .(1)讨论 f (x )的单调性；(2)若 f (x )有两个零点，求 a 的取值范围． [解] (1)f (x )的定义域为(－∞，＋∞)，f ′(x )＝2a e 2x ＋(a －2)e x －1＝(a e x －1)(2e x ＋1)， (ⅰ)若 a ≤0，则 f ′(x )＜0，所以 f (x )在(－∞，＋∞)单调递减．(ⅱ)若 a ＞0，则由 f ′(x )＝0 得 x ＝－ln a .当 x ∈(－∞，－ln a )时，f ′(x )＜0；当 x ∈(－ln a ，＋∞)时，f ′(x )＞0，(ⅱ)若 a ＞0，由(1)知，当 x ＝－ln a 时，f (x )取得最小值，最小值为 f (－ln a )＝1－ ＋ln a .设正整数 n 0 满足 n 0＞ln ⎝a －1⎭，由于 ln ⎝a －1⎭＞－ln a ，所以 f (x )在(－∞，－ln a )单调递减，在(－ln a ，＋∞)单调递增．(2)(ⅰ)若 a ≤0，由(1)知，f (x )至多有一个零点．1a①当 a ＝1 时，由于 f (－ln a )＝0，故 f (x )只有一个零点；1②当 a ∈(1，＋∞)时，由于 1－a ＋ln a ＞0，即 f (－ln a )＞0，故 f (x )没有零点；1③当 a ∈(0,1)时，1－a ＋ln a ＜0，即 f (－ln a )＜0.又 f (－2)＝a e －4＋(a －2)e －2＋2＞－2e －2＋2＞0， 故 f (x )在(－∞，－ln a )有一个零点．⎛3 ⎫则 f (n 0)＝e n 0(a e n 0＋a －2)－n 0＞e n 0－n 0＞2n 0－n 0＞0.⎛3 ⎫因此 f (x )在(－ln a ，＋∞)有一个零点．综上，a 的取值范围为(0,1)．。

二次函数与幂函数◆高考导航·顺风启程◆[知识梳理]1．幂函数(1)幂函数的定义形如y＝xα(α∈R)的函数称为幂函数，其中x是自变量，α为常数.(2)五种幂函数的图象(3)五种幂函数的性质2．二次函数(1)二次函数的图象和性质(2)二次函数表达式的三种形式 ①一般式： y ＝ax 2＋bx ＋c (a ≠0) .②顶点式： y ＝a (x ＋h )2＋k (其中a ≠0，顶点坐标为(－h ，k ))．③两根式：y ＝ a (x －x 1)(x －x 2) (其中a ≠0，x 1、x 2是二次函数的图象与x 轴的两个交点的横坐标)．[知识感悟]1．对于函数y ＝ax 2＋bx ＋c ，要认为它是二次函数，就必须满足a ≠0，当题目条件中未说明a ≠0时，就要讨论a ＝0和a ≠0两种情况．2．幂函数的图象一定会出现在第一象限内，一定不会出现在第四象限，至于是否出现在第二、三象限内，要看函数的奇偶性；幂函数的图象最多只能同时出现在两个象限内；如果幂函数图象与坐标轴相交，则交点一定是原点．3．函数y ＝f (x )对称轴的判断方法(1)对于二次函数y ＝f (x )对定义域内所有x ，都有f (x 1)＝f (x 2)，那么函数y ＝f (x )的图象关于x ＝x 1＋x 22对称．(2)对于二次函数y ＝f (x )对定义域内所有x ，都有f (a ＋x )＝f (a －x )成立的充要条件是函数y ＝f (x )的图象关于直线x ＝a 对称(a 为常数)．4．与二次函数有关的不等式恒成立的两个条件(1)ax 2＋bx ＋c ＞0，a ≠0恒成立的充要条件是⎩⎪⎨⎪⎧a ＞0，b 2－4ac ＜0.(2)ax 2＋bx ＋c ＜0，a ≠0恒成立的充要条件是⎩⎪⎨⎪⎧a ＜0，b 2－4ac ＜0.5．会用两种数学思想(1)数形结合是讨论二次函数问题的基本方法．特别是涉及二次方程、二次不等式的时候常常要结合图形寻找思路．(2)含字母系数的二次函数问题经常使用的方法是分类讨论．比如讨论二次函数的对称轴与给定区间的位置关系，讨论二次方程根的大小等．[知识自测]1．判断下面结论是否正确(请在括号中打“√”或“×”) (1)函数y ＝2x 12是幂函数．( )(2)如果幂函数的图象与坐标轴相交，则交点一定是原点．( ) (3)当n ＜0时，幂函数y ＝x n 是定义域上的减函数．( ) (4)二次函数y ＝ax 2＋bx ＋c ，x ∈[m ，n ]的最值一定是4ac －b 24a.( ) (5)关于x 的不等式ax 2＋bx ＋c ＞0恒成立的充要条件是⎩⎪⎨⎪⎧a ＞0，b 2－4ac ＜0.( ) [答案] (1)× (2)√ (3)× (4)× (5)×2．已知函数y ＝ax 2＋bx ＋c ，如果a ＞b ＞c 且a ＋b ＋c ＝0，则它的图象可能是( )[解析] 由a ＋b ＋c ＝0和a ＞b ＞c 知a ＞0，c ＜0，由c ＜0，排除A ，B ，又a ＞0，排除C. [答案] D3．若幂函数y ＝(m 2－3m ＋3)xm 2－m －2的图象不经过原点，则实数m 的值为 ________ .[解析] 由⎩⎪⎨⎪⎧m 2－3m ＋3＝1m 2－m －2≤0，解得m ＝1或2.经检验m ＝1或2都适合． [答案] 1或2题型一 幂函数的图象与性质(基础保分题，自主练透)(1)幂函数y ＝f (x )的图象过点(4,2)，则幂函数y ＝f (x )的图象是( )(2)(2018·江西临川模拟)已知幂函数y ＝xm 2－2m －3(m ∈N *)的图象与x 轴、y 轴无交点且关于原点对称，则m ＝ ________ .(3)(2018·安庆三模)若(a ＋1)－13＜(3－2a )－13，则实数a 的取值范围是 ________ .[解析] (1)∵幂函数y ＝f (x )的图象过点(4,2)，∴f (x )＝x 12.(2)由题意知：m 2－2m －3＜0，∴(m －3)(m ＋1)＜0，∴－1＜m ＜3，∵m ∈N *，m ＝1时不符题意，∴m ＝0,2.(3)不等式(a ＋1)－13＜(3－2a )－13等价于a ＋1＞3－2a ＞0或3－2a ＜a ＋1＜0或a ＋1＜0＜3－2a .解得a ＜－1或23＜a ＜32.[答案] (1)C (2)0,2 (3)(－∞，－1)∪⎝⎛⎭⎫23，32方法感悟幂函数y ＝x α的性质和图象由于α的取值不同而比较复杂，一般可从三方面考查： 1．α的正负：α＞0时图象经过(0,0)点和(1,1)点，在第一象限的部分“上升”；α＜0时图象不过(0,0)点，经过(1,1)点，在第一象限的部分“下降”；2．曲线在第一象限的凹凸性：α＞1时曲线下凹，0＜α＜1时曲线上凸，α＜0时曲线下凹；3．函数的奇偶性：一般先将函数式化为正指数幂或根式形式，再根据函数定义域和奇偶性定义判断其奇偶性．【针对补偿】1．下面给出4个幂函数的图象，则图象与函数的大致对应是( )A ．①y ＝x 13，②y ＝x 2，③y ＝x 12，④y ＝x －1B ．①y ＝x 3，②y ＝x 2，③y ＝x 12，④y ＝x －1C ．①y ＝x 2，②y ＝x 3，③y ＝x 12，④y ＝x －1D ．①y ＝x 13，②y ＝x 13，③y ＝x 2，④y ＝x －1[解析] 图象①对应的幂函数的幂指数必然大于1，排除A ，D ，图象②中幂函数是偶函数，幂指数必为正偶数，排除C.故选B.[答案] B2．(2016·全国Ⅲ卷)已知a ＝243，b ＝425，c ＝2513，则( )A ．b ＜a ＜cB ．a ＜b ＜cC ．b ＜c ＜aD ．c ＜a ＜b[解析] 因为a ＝243＝423＞425＝b ，c ＝2513＝523＞423＝a ，所以b ＜a ＜c ，故选A.[答案] A3．已知幂函数f (x )＝(n 2＋2n －2)xn 2－3n (n ∈Z )的图象关于y 轴对称，且在(0，＋∞)上是减函数，则n 的值为( )A ．－3B ．1C ．2D ．1或2[解析] 由于f (x )为幂函数，所以n 2＋2n －2＝1，解得n ＝1或n ＝－3，经检验只有n ＝1适合题意，故选B.[答案] B题型二 求二次函数的解析式(重点保分题，共同探讨)已知二次函数f (x )满足f (2)＝－1，f (－1)＝－1，且f (x )的最大值是8，试确定此二次函数的解析式．[解] 法一：(利用一般式)： 设f (x )＝ax 2＋bx ＋c (a ≠0)．由题意得⎩⎪⎨⎪⎧4a ＋2b ＋c ＝－1，a －b ＋c ＝－1，4ac －b 24a ＝8，解得⎩⎪⎨⎪⎧a ＝－4，b ＝4，c ＝7.∴所求二次函数的解析式为f (x )＝－4x 2＋4x ＋7. 法二：(利用顶点式)：设f (x )＝a (x －m )2＋n .∵f (2)＝f (－1)， ∴抛物线的对称轴为x ＝2＋(－1)2＝12.∴m ＝12.又根据题意函数有最大值8，∴n ＝8.∴y ＝f (x )＝a ⎝⎛⎭⎫x －122＋8. ∵f (2)＝－1，∴a ⎝⎛⎭⎫2－122＋8＝－1，解得a ＝－4， ∴f (x )＝－4⎝⎛⎭⎫x －122＋8＝－4x 2＋4x ＋7. 法三：(利用零点式)：由已知f (x )＋1＝0两根为x 1＝2，x 2＝－1， 故可设f (x )＋1＝a (x －2)(x ＋1)， 即f (x )＝ax 2－ax －2a －1.又函数有最大值y max ＝8， 即4a (－2a －1)－a 24a ＝8.解得a ＝－4或a ＝0(舍)．∴所求函数的解析式为f (x )＝－4x 2＋4x ＋7.方法感悟求二次函数解析式的方法根据已知条件确定二次函数的解析式，一般用待定系数法，但所给条件不同选取的求解方法也不同，选择规律如下：【针对补偿】4．已知二次函数图象的对称轴为x ＝－2，截x 轴所得的弦长为4，且过点(0，－1)，求函数的解析式．[解] 因为二次函数图象的对称轴为x ＝－2， 所以可设所求函数的解析式为f (x )＝a (x ＋2)2＋b . 因为二次函数f (x )的图象截x 轴所得的弦长为4， 所以f (x )过点(－2＋2,0)和(－2－2,0)． 又二次函数f (x )的图象过点(0，－1)，所以⎩⎪⎨⎪⎧4a ＋b ＝0，2a ＋b ＝－1，解得⎩⎪⎨⎪⎧a ＝12，b ＝－2.所以f (x )＝12(x ＋2)2－2＝12x 2＋2x －1.题型三 二次函数的图象与性质(高频考点题，多角突破) 考向一 二次函数的图象与识别1．(2018·黄岛月考)两个二次函数f (x )＝ax 2＋bx ＋c 与g (x )＝bx 2＋ax ＋c 的图象可能是( )[解析] 函数f (x )图象的对称轴为x ＝－b 2a ，函数g (x )图象的对称轴为x ＝－a 2b ，显然－b2a 与－a2b同号，故两个函数图象的对称轴应该在y 轴的同侧．只有D 满足．[答案] D考向二 二次函数的单调性问题2．若函数f (x )＝x 2＋a |x －2|在(0，＋∞)上单调递增，则实数a 的取值范围是 ________ . [解析] ∵f (x )＝x 2＋a |x －2|，∴f (x )＝⎩⎪⎨⎪⎧x 2＋ax －2a ，x ≥2，x 2－ax ＋2a ，x ＜2.又∵f (x )在(0，＋∞)上单调递增，∴⎩⎨⎧－a2≤2，a2≤0，解得－4≤a ≤0，即实数a 的取值范围是[－4,0]．[答案] [－4,0]考向三 二次函数的最值3．已知函数f (x )＝ax 2－2x (0≤x ≤1)，求函数f (x )的最小值． [解] (1)当a ＝0时，f (x )＝－2x 在[0,1]上单调递减， ∴f (x )min ＝f (1)＝－2.(2)当a ＞0时，f (x )＝ax 2－2x 的图象开口向上 且对称轴为x ＝1a.①当0＜1a ≤1，即a ≥1时，f (x )＝ax 2－2x 的对称轴在[0,1]内，∴f (x )在⎣⎡⎦⎤0，1a 上单调递减，在⎣⎡⎦⎤1a ，1上单调递增． ∴f (x )min ＝f ⎝⎛⎭⎫1a ＝1a －2a ＝－1a. ②当1a ＞1，即0＜a ＜1时，f (x )＝ax 2－2x 的对称轴在[0,1]的右侧，∴f (x )在[0,1]上单调递减． ∴f (x )min ＝f (1)＝a －2.(3)当a ＜0时，f (x )＝ax 2－2x 的图象开口向下 且对称轴x ＝1a ＜0，在y 轴的左侧，∴f (x )＝ax 2－2x 在[0,1]上单调递减， ∴f (x )min ＝f (1)＝a －2.综上所述，f (x )min ＝⎩⎪⎨⎪⎧a －2，a ＜1，－1a ，a ≥1.考向四 二次函数中恒成立问题4．已知函数f (x )＝x 2－x ＋1，在区间[－1,1]上不等式f (x )＞2x ＋m 恒成立，则实数m 的取值范围是 ________ .[解析] f (x )＞2x ＋m 等价于x 2－x ＋1＞2x ＋m ，即x 2－3x ＋1－m ＞0，令g (x )＝x 2－3x ＋1－m ，要使g (x )＝x 2－3x ＋1－m ＞0在[－1,1]上恒成立，只需使函数g (x )＝x 2－3x ＋1－m 在[－1,1]上的最小值大于0即可． ∵g (x )＝x 2－3x ＋1－m 在[－1,1]上单调递减， ∴g (x )min ＝g (1)＝－m －1. 由－m －1＞0，得m ＜－1. [答案] m <－1考向五 二次函数的零点问题5．已知关于x 的二次函数f (x )＝x 2＋(2t －1)x ＋1－2t . (1)求证：对于任意t ∈R ，方程f (x )＝1必有实数根；(2)若12＜t ＜34，求证：函数f (x )在区间(－1,0)及⎝⎛⎭⎫0，12上各有一个零点． [证明] (1)∵f (x )＝x 2＋(2t －1)x ＋1－2t ， ∴f (x )＝1⇔(x ＋2t )(x －1)＝0，(*)∴x ＝1是方程(*)的根，即f (1)＝1.因此x ＝1是f (x )＝1的实根，即f (x )＝1必有实根． (2)当12＜t ＜34时，f (－1)＝3－4t ＞0，f (0)＝1－2t ＝2⎝⎛⎭⎫12－t ＜0，f ⎝⎛⎭⎫12＝14＋12(2t －1)＋1－2t ＝34－t ＞0. 又函数f (x )的图象连续不间断．因此f (x )在区间(－1,0)及⎝⎛⎭⎫0，12上各有一个零点． 方法感悟1．识别二次函数的图象主要从开口方向、对称轴、特殊点对应的函数值这几个方面入手．2．而用数形结合法解决与二次函数图象有关的问题时，要尽量规范作图，尤其是图象的开口方向、顶点、对称轴及与两坐标轴的交点要标清楚，这样在解题时才不易出错．3．当二次函数的对称轴不确定时，应分类讨论，分类讨论的标准就是对称轴在区间的左、中、右三种情况．求解过程中，求出的参数的值或范围并不一定符合题意，因此要检验结果是否符合要求． 【针对补偿】5．设abc ＞0，二次函数f (x )＝ax 2＋bx ＋c 的图象可能是( )[解析] (1)由A ，C ，D 知，f (0)＝c ＜0.∵abc ＞0，∴ab ＜0，∴对称轴x ＝－b2a ＞0，知A ，C 错误，D 符合要求．由B 知f (0)＝c ＞0，∴ab ＞0，∴x ＝－b2a＜0，B 错误．[答案] D6．已知函数f (x )＝x 2＋mx －1，若对于任意x ∈[m ，m ＋1]，都有f (x )＜0成立，则实数m 的取值范围是 ________ .[解析] 作出二次函数f (x )的草图，对于任意x ∈[m ，m ＋1]，都有f (x )＜0，则有⎩⎪⎨⎪⎧ f (m )＜0，f (m ＋1)＜0，即⎩⎪⎨⎪⎧m 2＋m 2－1＜0，(m ＋1)2＋m (m ＋1)－1＜0，解得－22＜m ＜0.[答案] ⎝⎛⎭⎫－22，07．已知a 是实数，函数f (x )＝2ax 2＋2x －3在x ∈[－1,1]上恒小于零，求实数a 的取值范围．[解] 2ax 2＋2x －3＜0在[－1,1]上恒成立． 当x ＝0时，适合；当x ≠0时，a ＜32⎝⎛⎭⎫1x －132－16，因为1x ∈(－∞，－1]∪[1，＋∞)，当x ＝1时，右边取最小值12，所以a ＜12.综上，实数a 的取值范围是⎝⎛⎭⎫－∞，12. ◆牛刀小试·成功靠岸◆课堂达标(九)[A 基础巩固练]1．(2018·吉林东北二模)已知幂函数f (x )＝x n ，n ∈{－2，－1,1,3}的图象关于y 轴对称，则下列选项正确的是( )A ．f (－2)＞f (1)B ．f (－2)＜f (1)C ．f (2)＝f (1)D ．f (－2)＞f (－1)[解析] 由于幂函数f (x )＝x n 的图象关于y 轴对称，可知f (x )＝x n 为偶函数，所以n ＝－2，即f (x )＝x －2，则有f (－2)＝f (2)＝14，f (－1)＝f (1)＝1，所以f (－2)＜f (1)．[答案] B2．幂函数y ＝xm 2－4m (m ∈Z )的图象如图所示，则m 的值为( )A ．0B ．1C ．2D ．3[解析] ∵y ＝xm 2－4m (m ∈Z )的图象与坐标轴没有交点，∴m 2－4m ＜0，即0＜m ＜4， 又∵函数的图象关于y 轴对称，且m ∈Z ， ∴m 2－4m 为偶数，因此m ＝2. [答案] C3．设函数f (x )＝x 2－23x ＋60，g (x )＝f (x )＋|f (x )|，则g (1)＋g (2)＋…＋g (20)＝( ) A ．56 B ．112 C ．0D ．38[解析] 由二次函数图象的性质得，当3≤x ≤20时，f (x )＋|f (x )|＝0，∴g (1)＋g (2)＋…＋g (20)＝g (1)＋g (2)＝112.[答案] B4．已知函数f (x )＝x 12，若0＜a ＜b ＜1，则下列各式中正确的是( )A ．f (a )＜f (b )＜f ⎝⎛⎭⎫1a ＜f ⎝⎛⎭⎫1b B ．f ⎝⎛⎭⎫1a ＜f ⎝⎛⎭⎫1b ＜f (b )＜f (a ) C ．f (a )＜f (b )＜f ⎝⎛⎭⎫1b ＜f ⎝⎛⎭⎫1a D ．f ⎝⎛⎭⎫1a ＜f (a )＜f ⎝⎛⎭⎫1b ＜f (b )[解析] 因为函数f (x )＝x 12在(0，＋∞)上是增函数，又0＜a ＜b ＜1b ＜1a ，故f (a )＜f (b )＜f ⎝⎛⎭⎫1b ＜f ⎝⎛⎭⎫1a .[答案] C5．(2018·吉林松原调研)设函数f (x )＝x 2＋x ＋a (a ＞0)，已知f (m )＜0，则( ) A ．f (m ＋1)≥0 B ．f (m ＋1)≤0 C ．f (m ＋1)＞0D ．f (m ＋1)＜0[解析] ∵f (x )的对称轴为x ＝－12，f (0)＝a ＞0，∴f (x )的大致图象如图所示． 由f (m )＜0，得－1＜m ＜0， ∴m ＋1＞0， ∴f (m ＋1)＞f (0)＞0. [答案] C6．(2018·安徽皖北片高三第一次联考)已知函数f (x )＝－x 2＋2ax ＋1－a 在区间[0,1]上的最大值为2，则a 的值为( )A ．2B ．－1或－3C ．2或－3D ．－1或2[解析] 函数f (x )＝－x 2＋2ax ＋1－a 的对称轴为x ＝a ，图象开口向下， ①当a ≤0时，函数f (x )＝－x 2＋2ax ＋1－a 在区间[0,1]是减函数， ∴f max (x )＝f (0)＝1－a ， 由1－a ＝2，得a ＝－1，②当0＜a ≤1时，函数f (x )＝－x 2＋2ax ＋1－a 在区间[0，a ]是增函数，在[a,1]上是减函数，∴f max (x )＝f (a )＝－a 2＋2a 2＋1－a ＝a 2－a ＋1， 由a 2－a ＋1＝2，解得a ＝1＋52或a ＝1－52，∵0＜a ≤1，∴两个值都不满足；③当a ＞1时，函数f (x )＝－x 2＋2ax ＋1－a 在区间[0,1]是增函数， ∴f max (x )＝f (1)＝－1＋2a ＋1－a ＝a ，∴a ＝2. 综上可知，a ＝－1或a ＝2.故选：D. [答案] D7．当0＜x ＜1时，函数f (x )＝x 1.1，g (x )＝x 0.9，h (x )＝x －2的大小关系是 ________ .[解析] 如图所示为函数f (x )，g (x )，h (x )在(0,1)上的图象，由此可知，h (x )＞g (x )＞f (x )． [答案] h (x )＞g (x )＞f (x )8．对于任意实数x ，函数f (x )＝(5－a )x 2－6x ＋a ＋5恒为正值，则a 的取值范围是 ________ .[解析] 由题意可得⎩⎪⎨⎪⎧5－a ＞0，36－4(5－a )(a ＋5)＜0，解得－4＜a ＜4. [答案] (－4,4)9．(2018·长沙模拟)若函数f (x )＝x 2－3x －4的定义域为[0，m ]，值域为⎣⎡⎦⎤－254，－4，则m 的取值范围是______．[解析] 函数f (x )图象的对称轴为x ＝32，且f ⎝⎛⎭⎫32＝－254，f (3)＝f (0)＝－4，由二次函数的图象知m 的取值范围为⎣⎡⎦⎤32，3.[答案] ⎣⎡⎦⎤32，310．已知函数f (x )＝ax 2－2ax ＋2＋b (a ≠0)，若f (x )在区间[2,3]上有最大值5，最小值2. (1)求a ，b 的值；(2)若b ＜1，g (x )＝f (x )－mx 在[2,4]上单调，求m 的取值范围． [解] (1)f (x )＝a (x －1)2＋2＋b －a . 当a ＞0时，f (x )在[2,3]上为增函数，故⎩⎪⎨⎪⎧ f (3)＝5，f (2)＝2⇒⎩⎪⎨⎪⎧ 9a －6a ＋2＋b ＝5，4a －4a ＋2＋b ＝2⇒⎩⎪⎨⎪⎧a ＝1b ＝0.当a ＜0时，f (x )在[2,3]上为减函数，故⎩⎪⎨⎪⎧f (3)＝2，f (2)＝5⇒⎩⎪⎨⎪⎧9a －6a ＋2＋b ＝2，4a －4a ＋2＋b ＝5⇒⎩⎪⎨⎪⎧a ＝－1，b ＝3.(2)∵b ＜1，∴a ＝1，b ＝0，即f (x )＝x 2－2x ＋2. g (x )＝x 2－2x ＋2－mx ＝x 2－(2＋m )x ＋2， ∵g (x )在[2,4]上单调，∴2＋m 2≤2或m ＋22≥4.∴m ≤2或m ≥6.故m 的取值范围为(－∞，2]∪[6，＋∞)．[B 能力提升练]1．已知f (x )＝3－2|x |，g (x )＝x 2－2x ，F (x )＝⎩⎪⎨⎪⎧g (x )，f (x )≥g (x )，f (x )，f (x )＜g (x )，则F (x )的最值情况为( )A ．最大值为3，最小值为－1B ．最大值为7－27，无最小值C ．最大值为3，无最小值D ．既无最大值，又无最小值 [解析] 作出F (x )的图象，如图实线部分．由图象知F (x )有最大值无最小值，且最大值不是3. [答案] B2．关于x 的二次方程(m ＋3)x 2－4mx ＋2m －1＝0的两根异号，且负根的绝对值比正根大，那么实数m 的取值范围是( )A ．－3＜m ＜0B ．0＜m ＜3C ．m ＜－3或m ＞0D ．m ＜0或m ＞3[解析] 由题意知⎩⎨⎧Δ＝16m 2－4(m ＋3)(2m －1)＞0， ①x 1＋x 2＝4m m ＋3＜0， ②x 1·x 2＝2m－1m ＋3<0，③由①②③得－3＜m ＜0，故选A. [答案] A3．若函数f (x )＝x 2－a |x －1|在[0，＋∞)上单调递增，则实数a 的取值范围是 ________ .[解析] f (x )＝⎩⎪⎨⎪⎧x 2－ax ＋a ，x ∈[1，＋∞)，x 2＋ax －a ，x ∈(－∞，1)，x ∈[1，＋∞)时，f (x )＝x 2－ax ＋a ＝⎝⎛⎭⎫x －a 22＋a －a 24，x ∈(－∞，1)时，f (x )＝x 2＋ax －a ＝⎝⎛⎭⎫x ＋a 22－a －a 24.①当a2＞1，即a ＞2时，f (x )在⎣⎡⎭⎫1，a 2上单调递减， 在⎝⎛⎭⎫a 2，＋∞上单调递增，不合题意；②当0≤a2≤1，即0≤a ≤2时，符合题意；③当a2＜0，即a ＜0时，不符合题意，综上，a 的取值范围是[0,2]． [答案] [0,2]4．设f (x )与g (x )是定义在同一区间[a ，b ]上的两个函数，若函数y ＝f (x )－g (x )在x ∈[a ，b ]上有两个不同的零点，则称f (x )和g (x )在[a ，b ]上是“关联函数”，区间[a ，b ]称为“关联区间”．若f (x )＝x 2－3x ＋4与g (x )＝2x ＋m 在[0,3]上是“关联函数”，则m 的取值范围是 ________ .[解析] 由题意知，y ＝f (x )－g (x )＝x 2－5x ＋4－m 在[0,3]上有两个不同的零点．在同一直角坐标系下作出函数y ＝m 与y ＝x 2－5x ＋4(x ∈[0,3])的图象如图所示，结合图象可知，当x ∈[2,3]时，y ＝x 2－5x ＋4∈⎣⎡⎦⎤－94，－2，故当m ∈⎝⎛⎦⎤－94，－2时，函数y ＝m 与y ＝x 2－5x ＋4(x ∈[0,3])的图象有两个交点．[答案] ⎝⎛⎦⎤－94，－2 5．已知函数f (x )＝ax 2－2x ＋1. (1)试讨论函数f (x )的单调性．(2)若13≤a ≤1，且f (x )在[1,3]上的最大值为M (a )，最小值为N (a )，令g (a )＝M (a )－N (a )，求g (a )的表达式．(3)在(2)的条件下，求证：g (a )≥12.[解] (1)当a ＝0时，函数f (x )＝－2x ＋1在(－∞，＋∞)上为减函数；当a ＞0时，抛物线f (x )＝ax 2－2x ＋1开口向上，对称轴为x ＝1a ，所以函数f (x )在⎝⎛⎦⎤－∞，1a 上为减函数，在⎣⎡⎭⎫1a ，＋∞上为增函数； 当a ＜0时，抛物线f (x )＝ax 2－2x ＋1开口向下，对称轴为x ＝1a ，所以函数f (x )在⎝⎛⎦⎤－∞，1a 上为增函数，在⎣⎡⎭⎫1a ，＋∞上为减函数． (2)因为f (x )＝a ⎝⎛⎭⎫x －1a 2＋1－1a ， 由13≤a ≤1得1≤1a ≤3， 所以N (a )＝f ⎝⎛⎭⎫1a ＝1－1a . 当1≤1a ＜2，即12＜a ≤1时，M (a )＝f (3)＝9a －5， 故g (a )＝9a ＋1a－6；当2≤1a ≤3，即13≤a ≤12时，M (a )＝f (1)＝a －1，故g (a )＝a ＋1a－2.所以g (a )＝⎩⎨⎧a ＋1a－2，a ∈⎣⎡⎦⎤13，12，9a ＋1a －6，a ∈⎝⎛⎦⎤12，1.(3)证明：当a ∈⎣⎡⎦⎤13，12时g ′(a )＝1－1a 2<0， 所以函数g (x )在⎣⎡⎦⎤13，12上为减函数； 当a ∈⎝⎛⎦⎤12，1时，g ′(a )＝9－1a 2＞0， 所以函数g (a )在⎝⎛⎦⎤12，1上为增函数， 所以当a ＝12时，g (a )取最小值，g (a )min ＝g ⎝⎛⎭⎫12＝12.故g (a )≥12.[C 尖子生专练](2018·浙江瑞安四校联考)已知函数f (x )＝x 2－1，g (x )＝a |x －1|. (1)若当x ∈R 时，不等式f (x )≥g (x )恒成立，求实数a 的取值范围；(2)求函数h (x )＝|f (x )|＋g (x )在区间[0,2]上的最大值．[解] (1)不等式f (x )≥g (x )对x ∈R 恒成立，即x 2－1≥a |x －1|(*)对x ∈R 恒成立．①当x ＝1时，(*)显然成立，此时a ∈R ；②当x ≠1时，(*)可变形为a ≤x 2－1|x －1|， 令φ(x )＝x 2－1|x －1|＝⎩⎪⎨⎪⎧x ＋1，x ＞1，－(x ＋1)，x ＜1. 因为当x ＞1时，φ(x )＞2，当x ＜1时，φ(x )＞－2，所以φ(x )＞－2，故此时a ≤－2. 综合①②，得所求实数a 的取值范围是(－∞，－2]．(2)h (x )＝⎩⎪⎨⎪⎧ －x 2－ax ＋a ＋1，0≤x ＜1，0，x ＝1，x 2＋ax －a －1，1＜x ≤2.①当－a 2≤0时，即a ≥0，(－x 2－ax ＋a ＋1)max ＝h (0)＝a ＋1， (x 2＋ax －a －1)max ＝h (2)＝a ＋3.此时，h (x )max ＝a ＋3.②当0＜－a 2≤1时，即－2≤a ＜0，(－x 2－ax ＋a ＋1)max ＝h ⎝⎛⎭⎫－a 2＝a 24＋a ＋1， (x 2＋ax －a －1)max ＝h (2)＝a ＋3.此时h (x )max ＝a ＋3.③当1＜－a 2≤2时，即－4≤a ＜－2， (－x 2－ax ＋a ＋1)max ＝h (1)＝0，(x 2＋ax －a －1)max ＝max{h (1)，h (2)}＝max{0,3＋a }＝⎩⎪⎨⎪⎧ 0，－4≤a ＜－3，3＋a ，－3≤a ＜－2. 此时h (x )max ＝⎩⎪⎨⎪⎧0，－4≤a ＜－3，3＋a ，－3≤a ＜－2. ④当－a 2＞2时，即a ＜－4， (－x 2－ax ＋a ＋1)max ＝h (1)＝0，(x 2＋ax －a －1)max ＝h (1)＝0.此时h (x )max ＝0.综上：h (x )max ＝⎩⎪⎨⎪⎧3＋a ，a ≥－3，0，a ＜－3.。

上海市高三数学理一轮复习专题突破训练函数一、填空、选择题1、（2016年上海高考）已知点(3,9)在函数xa x f +=1)(的图像上，则________)()(1=-x f x f 的反函数2、（2016年上海高考）设()f x 、()g x 、()h x 是定义域为R 的三个函数，对于命题：①若()()f x g x +、()()f x h x +、()()g x h x +均为增函数，则()f x 、()g x 、()h x 中至少有一个增函数；②若()()f x g x +、()()f x h x +、()()g x h x +均是以T 为周期的函数，则()f x 、()g x 、()h x 均是以T为周期的函数，下列判断正确的是（ ）A 、①和②均为真命题B 、①和②均为假命题C 、①为真命题，②为假命题D 、①为假命题，②为真命题3、（2015年上海高考）方程log 2（9x ﹣1﹣5）=log 2（3x ﹣1﹣2）+2的解为 ．4、（2015年上海高考）设f ﹣1（x ）为f （x ）=2x ﹣2+，x ∈[0，2]的反函数，则y=f （x ）+f ﹣1（x ）的最大值为 ．5、（2014年上海高考）设2,(,),(),[,).x x a f x x x a ∈-∞⎧=⎨∈+∞⎩ 若(2)4f =，则a 的取值范围为 .6、（2014年上海高考）若2132()f x x x-=-，则满足()0f x <的x 的取值范围是 .7、（虹口区2016届高三三模）若函数()()()f x x a x a R =-∈存在反函数1()f x -，则1(1)(4)f f -+-= _________.8、（虹口区2016届高三三模）若函数()y f x =的图像与函数3x ay +=的图像关于直线y x =-对称，且(1)(3)3f f -+-=，则实数a 等于 ( )（A ）-1 ( B) 1 （C ） 2 (D) 4 9、（杨浦区2016届高三三模）函数2log (1)y x =+的反函数为10、（崇明县2016届高三二模）已知函数22,0(),0x a x f x x ax x ⎧+⎪=⎨-<⎪⎩≥，若()f x 的最小值是a ，则a = ．11、（奉贤区2016届高三二模）函数21x y =-的定义域是_______．(用区间表示) 12、（虹口区2016届高三二模）已知函数()f x 的对应关系如下表：x2-1- 01 2()f x 32-15m若函数()f x 不存在反函数，则实数m 的取值集合为___________.13、（静安区2016届高三二模）若函数()()2F x f x x =+为奇函数，且g (x )= f (x )＋2，已知 f (1) =1，则g (－1)的值为（ ）A ．－1B ．1C ．－2D ．214、（浦东新区2016届高三二模）方程22log (97)2log (31)x x+=++的解为15、（徐汇、金山、松江区2016届高三二模）定义在R 上的奇函数(),f x 当0x ≥时，[)[)12log (1),0,1,()13,1,,x x f x x x ⎧+∈⎪=⎨⎪--∈+∞⎩则关于x 的函数()()(01)F x f x a a =-<<的所有零点之和为________________（结果用a 表示）．16、（闸北区2016届高三二模）设函数()(01x xf x a a a a -=+>≠且），且(1)3f =，则(0)(1)(2)f f f ++的值是17、（长宁、青浦、宝山、嘉定四区2016届高三二模）设0>a 且1≠a ，若函数2)(1+=-x a x f 的反函数的图像经过定点P ，则点P 的坐标是___________．18、（崇明县2016届高三二模）已知函数()f x 是定义在[)1,+∞上的函数，且123,12()11,222x x f x f x x ⎧--<⎪=⎨⎛⎫⎪⎪⎝⎭⎩≤≥，则函数2()3y x f x =-在区间(1,2016)上的零点个数为 ． 19、（闸北区2016届高三上学期期末）函数ln(1),0()1ln,01x x f x x x⎧+≥⎪=⎨<⎪-⎩的单调性为 ；奇偶性为 ；20、（长宁区2016届高三上学期期末）方程9x ＋3x －2 ＝ 0的解是___________. 21、（闵行区2016届高三上学期期末）若函数()2x af x -=()a ∈R 满足(1)(1)f x f x +=-，且()f x在[,)m +∞上单调递增，则实数m 的最小值等于 .22、（青浦区2016届高三上学期期末）函数()lg(23)xxf x =-的定义域为 . 23、（金山区2016届高三上学期期末）如图，AB 为定圆O 的直径，点P 为半圆AB 上的动点．过点P 作AB 的垂线，垂足为Q ，过Q 作OP 的垂线，垂足为M ．记 弧AP 的长为x ，线段QM 的长为y ，则函数y =f (x )的大致图像是( )．24、（静安区2016届高三上学期期末）函数213(10)x y x -=-≤<的反函数是 ( )A ．311log ()3y x x =-+≥B ．311log (1)3y x x =-+<≤C ．311log (1)3y x x =+<≤ D ．311log ()3y x x =+≥25、（闵行区2016届高三上学期期末）设2345()2510105f x x x x x x =+++++，则其反函数的解析式为（ ）.(A) 511y x =+- (B) 511y x =--(C) 511y x =-+- (D) 511y x =---二、解答题1、（2016年上海高考） 已知a R ∈，函数21()log ()f x a x=+. （1）当5a =时，解不等式()0f x >；（2）若关于x 的方程2()log [(4)25]0f x a x a --+-=的解集中恰好有一个元素，求a 的取值范围；（3）设0a >，若对任意1[,1]2t ∈，函数()f x 在区间[,1]t t +上的最大值与最小值的差不超过1，求a 的取值范围.2、（2014年上海高考）设常数0a ≥，函数2()2x x af x a+=-.(1) 若4a =，求函数()y f x =的反函数1()y fx -=；(2) 根据a 的不同取值，讨论函数()y f x =的奇偶性，并说明理由.3、（浦东新区2016届高三三模）已知函数()212af x ax =-+，()ag x x x=+ （1）()0f x >在[)1,2x ∈上恒成立，求a 的取值范围；（2）当0a >时，对任意的[]11,3x ∈，存在[]21,3x ∈，使得()()12f x g x ≥恒成立，求a 的取值范围。