大学本科语音信号处理实验讲义8学时

语音信号处理
一、实验课程名称：语音信号处理
二、实验课程英文名称： Speech signal processing
三、实验课程编号： 0451714
四、实验课程性质：非独立设课
五、学时安排：理论课程学时42 实验课程学时12
六、实验课程学分：0学分
七、实验课程类型：专业课
八、实验课程要求：必修课
九、课程适用专业：电子信息科学与技术
十、教学目的：
使学生掌握语音信号各种处理方法的原理、算法、用matlab的编程方法和仿真。

通过实际应用和亲身体验，加深对所学知识的理解，增强动手能力。

十一、实验教学项目表
实验课教学内容项目表（必做）
十一、实验报告要求：
1．编写程序；
2．验证调试实验并写出调试结果，需指导教师确认。

十二、实验成绩评定：
分数分配：
预习：10%，操作：60%，实验报告：60%，创新能力：10%；
实验总计6个，满分20分，第一和第二个实验每个4分，第三、四、五、六个实验每个3分。

十三、教材及参考书：
１．《语音信号处理》．胡航编著．哈尔滨工业大学出版社
２．《语音信号处理实验指导书》自编
学院签署意见表。

《语音数字信号处理》课程简介课程编号：06044008课程名称：语音数字信号处理/ Speech Digital Signal Processing学分：2学时：32 （实验：0 上机：0 课外实践：0 ）适用专业：电子信息工程建议修读学期：7开课单位：电气与信息工程学院电子信息与通信工程系先修课程：《数字信号处理》、《MATLAB及应用》、《随机信号处理》考核方式与成绩评定标准：作业、考试（闭卷）教材与主要参考书目：主要教材：《语音信号处理》主编：赵力机械工业出版社2011-6T参考书目：《离散时间语音信号处理》主编：夸特尔瑞电子工业出版社2004-87内容概述：《语音数字信号处理》是电子信息工程专业本科生的专业必修课程。

它系统地介绍了语音信号处理涉及的主要内容和方法，讲述语音信号的应用前景、语音信号处理流程及流程中涉及到的相关知识点，每个知识点通过案例仿真讲述其应用的结果。

主要内容分四部分：（1）基础部分：语音信号基础知识、人的发音原理、人的听觉原理、语音的数学模型；（2）语音信号分析方法：时域分析、频域分析、同态处理和线性预测分析；（3）语音信号涉及的新技术：矢量量化和隐马尔可夫模型；（4）语音的四个方面应用：语音编码、语音识别、语音合成和语音增强；通过《语音数字信号处理》学习，使学生掌握语音信号发音和听觉原理、语音信号的数字模型; 语音的时域、频域、倒谱、线性预测的分析方法；矢量量化；隐马尔可夫模型；语音波形编码、参数编码、混合编码；语音的合成；语音识别和语音增强的原理和技术，为学生毕业后从事语音处理工作和进一步研究相关课题打下一定的基础。

《嵌入式系统及应用》教学大纲课程编号：06044008课程名称：语音数字信号处理/ Speech Digital Signal Processing学分：2学时：32 （实验：0 上机：0 课外实践：0 ）适用专业：电子信息工程建议修读学期：7开课单位：电气与信息工程学院电子信息与通信工程系先修课程：《数字信号处理》、《MATLAB及应用》、《随机信号处理》一、课程性质、目的与任务《语音数字信号处理》是电子信息工程专业本科生的专业必修课程。

语音信号处理实验讲义时间：2011-12目录实验一语音信号生成模型分析 (3)实验二语音信号时域特征分析 (7)实验三语音信号频域特征分析 (12)实验四语音信号的同态处理和倒谱分析 (16)实验一 语音信号生成模型分析一、实验目的1、了解语音信号的生成机理，了解由声门产生的激励函数、由声道产生的调制函数和由嘴唇产生的辐射函数。

2、编程实现声门激励波函数波形及频谱，与理论值进行比较。

3、编程实现已知语音信号的语谱图，区分浊音信号和清音信号在语谱图上的差别。

二、实验原理语音生成系统包含三部分：由声门产生的激励函数()G z 、由声道产生的调制函数()V z 和由嘴唇产生的辐射函数()R z 。

语音生成系统的传递函数由这三个函数级联而成，即()()()()H z G z V z R z =1、激励模型发浊音时，由于声门不断开启和关闭，产生间隙的脉冲。

经仪器测试它类似于斜三角波的脉冲。

也就是说，这时的激励波是一个以基音周期为周期的斜三角脉冲串。

单个斜三角波的频谱表现出一个低通滤波器的特性。

可以把它表示成z 变换的全极点形式121()(1)cT G z e z --=-⋅这里c 是一个常数，T 是脉冲持续时间。

周期的三角波脉冲还得跟单位脉冲串的z 变换相乘：1121()()()1(1)v cT A U z E z G z z e z ---=⋅=⋅--⋅ 这就是整个激励模型，v A 是一个幅值因子。

2、声道模型当声波通过声道时，受到声腔共振的影响，在某些频率附近形成谐振。

反映在信号频谱图上，在谐振频率处其谱线包络产生峰值，把它称为共振峰。

一个二阶谐振器的传输函数可以写成12()1i i i i A V z B z C z--=-- 实践表明，用前3个共振峰代表一个元音足够了。

对于较复杂的辅音或鼻音共振峰要到5个以上。

多个()i V z 叠加可以得到声道的共振峰模型012111()()11R r r M M i r i Nki i i i k k b z A V z V z B z C z a z -=---======---∑∑∑∑ 3、辐射模型从声道模型输出的是速度波，而语音信号是声压波。

数字语音信号处理实验指导书北方学院信息科学与工程学院电子教研室2014年1月前言语音信号处理是研究用数字信号处理技术和语音学知识对语音信号进行处理的新兴的学科，是目前发展最为迅速的信息科学研究领域的核心技术之一。

通过语音传递信息是人类最重要、最有效、最常用和最方便的交换信息形式。

同时，语言也是人与机器之间进行通信的重要工具，它是一种理想的人机通信方式，因而可为信息处理系统建立良好的人机交互环境，进一步推动计算机和其他智能机器的应用，提高社会的信息化程度。

语音信号处理是一门新兴的学科，同时又是综合性的多学科领域和涉及面很广的交叉学科。

虽然从事这一领域研究的人员主要来自信号与信息处理及计算机应用等学科，但是它与语音学、语言学、声学、认知科学、生理学、心理学等许多学科也有非常密切的联系。

20世纪60年代中期形成的一系列数字信号处理的理论和算法，如数字滤波器、快速傅立叶变换（FFT）等是语音信号数字处理的理论和技术基础。

随着信息科学技术的飞速发展，语音信号处理取得了重大的进展：进入70年代之后，提出了用于语音信号的信息压缩和特征提取的线性预测技术（LPC），并已成为语音信号处理最强有力的工具，广泛应用于语音信号的分析、合成及各个应用领域，以及用于输入语音与参考样本之间时间匹配的动态规划方法；80年代初一种新的基于聚类分析的高效数据压缩技术—矢量量化（VQ）应用于语音信号处理中；而用隐马尔可夫模型（HMM）描述语音信号过程的产生是80年代语音信号处理技术的重大发展，目前HMM已构成了现代语音识别研究的重要基石。

近年来人工神经网络(ANN)的研究取得了迅速发展，语音信号处理的各项课题是促进其发展的重要动力之一，同时，它的许多成果也体现在有关语音信号处理的各项技术之中。

为了深入理解语音信号数字处理的基础理论、算法原理、研究方法和难点，根据数字语音信号处理教学大纲，结合课程建设的需求，我们编写了本实验参考书。

本参考书针对教学大纲规定的八个研究设计型实验，每个实验给出了参考程序，目的是起一个抛砖引玉的作用，学生在学习过程中，可以针对某一个实验进行延伸的创新学习，比如说，语音端点的检测、语音共振峰提取、基于HMM或DTW的有限词汇或大词汇的特定人、非特定人的语音识别、识别率的提高（如何提高有噪环境下的识别率）、以及编码问题等，同时在学习中还可深入思考如何将有关的方法在嵌入式系统或DSP下的实现问题等。

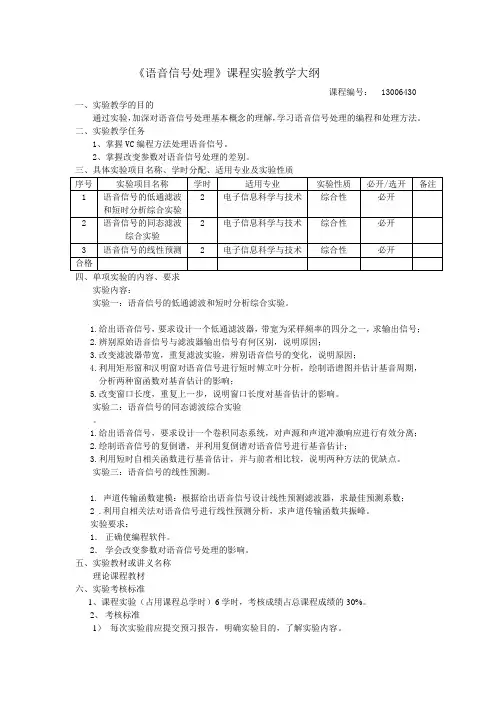
《语音信号处理》课程实验教学大纲课程编号： 13006430 一、实验教学的目的通过实验，加深对语音信号处理基本概念的理解，学习语音信号处理的编程和处理方法。

二、实验教学任务1、掌握VC编程方法处理语音信号。

2、掌握改变参数对语音信号处理的差别。

三、具体实验项目名称、学时分配、适用专业及实验性质四、单项实验的内容、要求实验内容：实验一：语音信号的低通滤波和短时分析综合实验。

1.给出语音信号，要求设计一个低通滤波器，带宽为采样频率的四分之一，求输出信号；2.辨别原始语音信号与滤波器输出信号有何区别，说明原因；3.改变滤波器带宽，重复滤波实验，辨别语音信号的变化，说明原因；4.利用矩形窗和汉明窗对语音信号进行短时傅立叶分析，绘制语谱图并估计基音周期，分析两种窗函数对基音估计的影响；5.改变窗口长度，重复上一步，说明窗口长度对基音估计的影响。

实验二：语音信号的同态滤波综合实验。

1.给出语音信号，要求设计一个卷积同态系统，对声源和声道冲激响应进行有效分离；2.绘制语音信号的复倒谱，并利用复倒谱对语音信号进行基音估计；3.利用短时自相关函数进行基音估计，并与前者相比较，说明两种方法的优缺点。

实验三：语音信号的线性预测。

1. 声道传输函数建模：根据给出语音信号设计线性预测滤波器，求最佳预测系数；2 .利用自相关法对语音信号进行线性预测分析，求声道传输函数共振峰。

实验要求：1．正确使编程软件。

2．学会改变参数对语音信号处理的影响。

五、实验教材或讲义名称理论课程教材六、实验考核标准1、课程实验（占用课程总学时）6学时，考核成绩占总课程成绩的30%。

2、考核标准1）每次实验前应提交预习报告，明确实验目的，了解实验内容。

2）实验中遵守实验纪律，听从老师指导，爱护仪器设备，遵守操作规程。

3）课程实验完成时，应对学生实验技能进行检查，提出问题能说明清楚。

4）实验报告应及时完成，字要整洁、图表要规范，记录和处理的数据应准确。

语音信号处理实验指导书实验一：语音信号的采集与播放实验目的：了解语音信号的采集与播放过程，掌握采集设备的使用方法。

实验器材：1. 电脑2. 麦克风3. 扬声器或耳机实验步骤：1. 将麦克风插入电脑的麦克风插孔。

2. 打开电脑的录音软件（如Windows自带的录音机）。

3. 在录音软件中选择麦克风作为录音设备。

4. 点击录音按钮开始录音，讲话或唱歌几秒钟。

5. 点击停止按钮停止录音。

6. 播放刚刚录制的语音，检查录音效果。

7. 将扬声器或耳机插入电脑的音频输出插孔。

8. 打开电脑的音频播放软件（如Windows自带的媒体播放器）。

9. 选择要播放的语音文件，点击播放按钮。

10. 检查语音播放效果。

实验二：语音信号的分帧与加窗实验目的：了解语音信号的分帧和加窗过程，掌握分帧和加窗算法的实现方法。

实验器材：1. 电脑2. 麦克风3. 扬声器或耳机实验步骤：1. 使用实验一中的步骤1-5录制一段语音。

2. 将录制的语音信号进行分帧处理。

选择合适的帧长和帧移参数。

3. 对每一帧的语音信号应用汉明窗。

4. 将处理后的语音帧进行播放，检查分帧和加窗效果。

实验三：语音信号的频谱分析实验目的：了解语音信号的频谱分析过程，掌握频谱分析算法的实现方法。

实验器材：1. 电脑2. 麦克风3. 扬声器或耳机实验步骤：1. 使用实验一中的步骤1-5录制一段语音。

2. 将录制的语音信号进行分帧处理。

选择合适的帧长和帧移参数。

3. 对每一帧的语音信号应用汉明窗。

4. 对每一帧的语音信号进行快速傅里叶变换（FFT）得到频谱。

5. 将频谱绘制成图像，观察频谱的特征。

6. 对频谱进行谱减法处理，去除噪声。

7. 将处理后的语音帧进行播放，检查频谱分析效果。

实验四：语音信号的降噪处理实验目的：了解语音信号的降噪处理过程，掌握降噪算法的实现方法。

实验器材：1. 电脑2. 麦克风3. 扬声器或耳机实验步骤：1. 使用实验一中的步骤1-5录制一段带噪声的语音。

《数字语音处理》课程教学大纲课程代码：ABJD0626课程中文名称：数字语音处理课程英文名称：Dig让a1AudioProcessing课程性质：选修课程学分数：2.5课程学时数：40（32学时论课时+8学时实验）授课对象：电子信息工程本课程的前导课程：信号与系统、数字信号处理一、课程简介本课程是通信工程专业、电子信息类专业、电气工程及其自动化等专业的任选课。

它是基于信号处理基础之上理论性和应用性较强的专业课程，其任务是：通过本课程的学习，学生掌握语音信号处理的基本原理；通过试验加深学生对语音信号处理方法的认识。

同时向学生介绍该学科领域近年取得的新成果、新发展及新技术，同时培养学生的独立研究和思考的能力二、教学基本内容和要求（-）语音信号处理的基础知识教学内容：一、语音信号处理的发展二、语音信号处理的过程的总体结构三、语音的发声机理和听觉机理四、语音的感知和信号模型课程的重点、难点：重点：语音的发生原理以及信号模型。

难点：语音信号的数字模型。

教学要求：1.了解本课程的性质和任务，理解掌握语音、语音信号处理的基本概念，了解语音信号的发展概况及其应用。

2.理解语音信号处理的基本过程，了解语音信号的特性和语音信号产生的数字模型，了解语音感知的概念；掌握语音信号产生的数字模型，了解人类的听觉系统的特性。

（二）语音信号的时域分析和短时傅里叶分析教学内容：一、语音信号的预处理二、语音信号的时域分析三、傅里叶变换的解释四、语音信号的频域分析课程的重点、难点：重点：语音信号的短时时域分析和短时频域分析。

难点：短时自相关函数和短时谱的时域及频域采样率。

教学要求：1.了解语音信号的时域分析的基本概念，理解并掌握语音信号的数字化和预处理过程。

2.理解短时能量分析，短时过零分析和短时相关分析的基本概念，掌握语音信号的能量、过零、相关各种时域分析方法。

3.理解语音信号的短时傅里叶分析的基本概念，理解短时傅里叶变换的取样率，掌握语音信号的短时综合方法，掌握语谱图的基本概念。

语音信号处理实验讲义时间：2011-12目录实验一语音信号生成模型分析 (3)实验二语音信号时域特征分析 (7)实验三语音信号频域特征分析 (12)实验四语音信号的同态处理和倒谱分析 (16)实验一 语音信号生成模型分析一、实验目的1、了解语音信号的生成机理，了解由声门产生的激励函数、由声道产生的调制函数和由嘴唇产生的辐射函数。

2、编程实现声门激励波函数波形及频谱，与理论值进行比较。

3、编程实现已知语音信号的语谱图，区分浊音信号和清音信号在语谱图上的差别。

二、实验原理语音生成系统包含三部分：由声门产生的激励函数()G z 、由声道产生的调制函数()V z 和由嘴唇产生的辐射函数()R z 。

语音生成系统的传递函数由这三个函数级联而成，即()()()()H z G z V z R z =1、激励模型发浊音时，由于声门不断开启和关闭，产生间隙的脉冲。

经仪器测试它类似于斜三角波的脉冲。

也就是说，这时的激励波是一个以基音周期为周期的斜三角脉冲串。

单个斜三角波的频谱表现出一个低通滤波器的特性。

可以把它表示成z 变换的全极点形式121()(1)cTG z ez --=-⋅这里c 是一个常数，T 是脉冲持续时间。

周期的三角波脉冲还得跟单位脉冲串的z 变换相乘：1121()()()1(1)v cT A U z E z G z z e z ---=⋅=⋅--⋅这就是整个激励模型，v A 是一个幅值因子。

2、声道模型当声波通过声道时，受到声腔共振的影响，在某些频率附近形成谐振。

反映在信号频谱图上，在谐振频率处其谱线包络产生峰值，把它称为共振峰。

一个二阶谐振器的传输函数可以写成12()1ii i i A V z B z C z--=-- 实践表明，用前3个共振峰代表一个元音足够了。

对于较复杂的辅音或鼻音共振峰要到5个以上。

多个()i V z 叠加可以得到声道的共振峰模型12111()()11Rrr MMir i N ki i i ik k b zA V z V zB zC z a z -=---======---∑∑∑∑3、辐射模型从声道模型输出的是速度波，而语音信号是声压波。

语音信号处理课程教学大纲课程编码：08052课程名称：语音信号处理Speech Signal Processing先修课程：电子技术基础、数字信号处理、信号与系统总学时：40 （授课学时：34 上机学时：4 实验学时：2）一、课程的性质和任务本课程是通信、电子信息类的一门重要的专业选修课。

《语音信号处理》是计算机信息处理的一个重要分支，其发展十分迅速，它包含着众多新思想、新技术、新器件、新应用。

它主要介绍的内容是语音学基础知识、语音信号处理四大分支--语音识别、说话人识别、语音合成和语音编码，通过该门课程的学习，可以对数字语音信号处理的基本理论和方法有一个较为系统的掌握。

二、课程教学内容的基本要求、重点和难点及学时分配1．语音学概要、语音处理基础理论（8学时）基本要求：通过学习，使学生了解语音学基本知识、语音产生机制及语音处理基础理论。

重点与难点：语音产生机制、语音信号的特点和语音信号的源滤波模型。

2．语音信号的时域处理方法（2学时）基本要求：通过学习，使学生了解语音信号的时域处理方法，掌握短时能量测量方法及基音频率分析方法，熟悉短时自相关的计算、短时平均过零率及端点检测方法。

重点与难点：基音频率分析方法、短时平均过零率。

3．语音信号的频域处理方法（4学时）基本要求：通过学习，使学生了解语音信号的频域处理方法，掌握短时付氏变换的基本理论及其性质、语音信号的加窗处理及其效应。

重点与难点：短时付氏变换的基本理论及其性质。

4．语音编码（6学时）基本要求：通过学习，使学生了解语音编码的基本方法及有关标准，熟悉常用语音编码方法，如波形编码、源编码、线性预测编码。

重点与难点：波形编码、线性预测编码。

5．语音识别（6学时）基本要求：通过学习，使学生了解语音识别的基本问题，熟悉隔离字的识别方法、语者识别方法，掌握模式匹配识别方法，了解语音的HMM模型。

重点与难点：语音识别的基本问题、模式匹配识别方法。

6．语音合成（4学时）基本要求：通过学习，使学生了解语音合成的基本过程，熟悉语音合成系统的基本构成，掌握文语转换的波形合成方法。

语音信号处理实验讲义王艳芬李剑编中国矿业大学信电学院学生实验守则一、学生进入实验室必须遵守实验室的规章制度，遵守课堂纪律，保持实验室的安静和整洁，爱护实验室的一切设施。

二、实验课前要认真预习实验指导书，写出实验预习报告，并经教师批阅后方可进行实验。

三、实验课中要遵守操作规程，不要带电连接、更改或拆除线路。

线路接好后，经指导老师检查后，方可接通电源进行实验。

对于软件上机实验，不得随意删改计算机中原有的文件。

四、学生实验前对实验所用仪器设备要了解其操作规程和使用方法，凡因不预习或不按使用方法进行操作而造成仪器设备损坏者，除书面检查外，按学校规定进行赔偿。

五、实验中主意安全，遇到事故应立即关断电源并报告教师检查处理。

六、实验完毕后要做好整理工作，实验数据必须经指导教师签阅后，才能拆除线路，并将仪器、设备、凳子等按规定放好，经同意后方可离开实验室。

七、因故缺课的学生可向实验室申请一次补做机会。

无故缺课或无故迟到（15分钟以上）的不予补做，该次实验无成绩；累计三次者，该实验课以不及格论，并不得参加该门理论课程的考试。

八、实验室仪器设备不能擅自搬动调换，更不能擅自带出实验室。

信电学院专业实验中心二零一一年九月目录实验一语音信号得基音参数提取 (1)实验二语音信号的谱分析 (7)实验三基于DTW算法的孤立字识别 (11)《语音信号处理实验讲义》是为了配合“语音信号处理”课程教学而编写的，适用于信息工程、电子科学与技术等专业。

前修课程为“数字信号处理”。

该课程总学时数为40学时，其中实验学时为8学时。

实验内容及参考学时安排如下：实验一语音信号的基音参数提取（3个学时）实验二语音信号的谱分析（3个学时）实验三基于DTW算法的孤立字识别（2个学时）实验一 语音信号的基音参数提取一、实验目的1.了解基音的基本概念以及清音与浊音的区别。

2.掌握几种基本的基音提取方法，熟悉自相关法、倒谱法和简化逆滤波法进行基音提取的matlab 编程。