数列求和——裂项相消法

例析数列求和的裂项相消法多数数学问题中都要求求出一个数列的某一个总和，这种推导过程通常是重复加法，涉及到大量的运算时间和工作量，特别是当数列项数很大时，传统的累加法就会遇到非常大的困难。

裂项相消法便是为了解决这一问题而出现的。

它是将正负型数列按照规律因式分解，以减少运算量，从而达到较快求和的目的。

将数列分解为正、负两种类型，正数加上负数可以使其和为0，也就是把问题转化为查找不同正、负数的有效组合。

求和公式：S=a1+a2-a3+a4-a5+a6-a7+...现在引入另一种折叠方法裂项相消法，它是一种数学方法，将一个正数与一个负数相加，让这两个数的和等于0，可以使用更简便的直接求和方法，使时间和空间复杂度更低，从而提高效率。

该方法的实现可以从两个角度进行:1.正数与负数相邻对消，此时正数和负数的组合要满足：两两之和等于0。

2.正数、负数以不等长度分组，此时组内的和相加的和需要等于0。

以上两种方法实现时，关键在于分组和求和的方式，解决方案有很多种，以下将介绍其中一种实现方式。

假设有一个数列S={S1,S2,S3,S4,…,Sn}，其中n为未知数，需要求和。

可以用裂项相消法将这个数列分解成三步：步骤1：先把数列分组，每一组包括两个数：第一个数是数列中正数的和，第二个数是数列中负数的和。

步骤2:每一组数的和缩小为单个数，因为每一组的和的计算，我们可以等价的将每一组的两个数相加，把它们减小到一个数，这个数就是最后的求和结果。

步骤3：最后再将每一个单个数相加，就得到了最终的求和结果。

以上就是裂项相消法的具体操作过程，它主要用于求和数列中正负数的组合，以更快的时间求出该数列的总和。

因此，裂项相消法是一种简便有效的求和方法。

不过，引入裂项相消法也有其局限性，因为它比累加法要慢，而且它只适用于数列的求和，并不能应用于其它的数学问题，而且在求和过程中，如果不正确求出最终的结果，就会影响最终的结果。

总之，裂项相消法是一种较为简单灵活的求和方法，可以在计算算式上带动效率，减少时间和空间复杂度。

1．已知数列{a n}的前n项的积记为T n，且满足．（1）证明：数列{T n}为等差数列；（2）设，求数列{b n}的前n项和S n．2．已知等差数列{a n}的公差为正数，且a1＝1，若a2，a6﹣2a1，a14分别是等比数列{b n}的前三项．（1）分别求数列{a n}、{b n}的通项公式；（2）求数列的前n项之和S n．3．已知数列{a n}的首项a1＝4，且a n+1＝2a n﹣3．（1）求数列{a n}的通项公式；（2）记b n＝log2（a n+1﹣3），求数列的前n项和T n．4．在①a8＝9，②S5＝20，③a2+a9＝13这三个条件中选择两个，补充在下面问题中，并进行解答．已知等差数列{a n}的前n项和为S n，n∈N*，_____，_____．（1）求数列{a n}的通项公式；（2）设，证明数列{b n}的前n项和解析1．已知数列{a n}的前n项的积记为T n，且满足．（1）证明：数列{T n}为等差数列；（2）设，求数列{b n}的前n项和S n．分析：（1）根据数列的递推式和等差数列的定义，即可证明结论；（2）由（1）得T n＝2n+1，则，利用裂项相消法，即可得出答案．解答：解：（1）证明：∵，∴当n＝1时，，解得T1＝a1＝3，当n≥2时，，∴，即T n﹣T n﹣1＝2，∴数列{T n}是以3为首项，2为公差的等差数列；（2）由（1）得T n＝2n+1，则，∴．点评：本题考查数列的求和，考查转化思想，考查逻辑推理能力和运算能力，属于中档题．2．已知等差数列{a n}的公差为正数，且a1＝1，若a2，a6﹣2a1，a14分别是等比数列{b n}的前三项．（1）分别求数列{a n}、{b n}的通项公式；（2）求数列的前n项之和S n．分析：（1）设等差数列{a n}的公差为d（d＞0），由已知可得（5d﹣a1）2＝（a1+d）（a13+13d），可求d；（2）由（1）得，可求数列的前n项之和S n．解答：解：（1）设等差数列{a n}的公差为d（d＞0），因为a2，a6﹣2a1，a14是等比数列{b n}的前三项，所以（a6﹣2a1）2＝a2a14，即（5d﹣a1）2＝（a1+d）（a13+13d），化简得d＝2a1，又a1＝1，所以d＝2．得a n＝1+2（n﹣1）＝2n﹣1．由（1）可得数列{b n}的前三项分别为b1＝3，b2＝9，b3＝27，显然该等比数列{b n}的公比为3，首项为3，所以．综上，两数列的通项公式分别为a n＝2n﹣1，．（2）由（1）得．．点评：本题考查数列的通项公式和前n项和公式的求法，注意裂项求和法的合理运用，属中档题．3．已知数列{a n}的首项a1＝4，且a n+1＝2a n﹣3．（1）求数列{a n}的通项公式；（2）记b n＝log2（a n+1﹣3），求数列的前n项和T n．分析：（1）由递推关系构造等比数列{a n﹣3}，利用等比数列通项公式求解即可；（2）求出b n，再由裂项相消法求解．解答：解：（1）由a n+1＝2a n﹣3得a n+1﹣3＝2（a n﹣3），且a1﹣3＝1≠0，则数列{a n﹣3}是以1为首项，以2为公比的等比数列，可得，从而；（2），故，故．点评：本题考查由数列的递推式求数列的通项公式，利用裂项相消法求数列的前n项和，属中档题．4．在①a8＝9，②S5＝20，③a2+a9＝13这三个条件中选择两个，补充在下面问题中，并进行解答．已知等差数列{a n}的前n项和为S n，n∈N*，_____，_____．（1）求数列{a n}的通项公式；（2）设，证明数列{b n}的前n项和．分析：（1）利用等差数列的通项公式及求和公式直接求解；（2）利用裂项相消法求和即可得证．解答：解：（1）由于{a n}是等差数列，设公差为d，当选①②时：a8＝a1+7d＝9，S5＝5a1+10d＝20，解得a1＝2，d＝1，所以{a n}的通项公式a n＝2+（n﹣1）×1＝n+1，n∈N*．选①③时，a8＝a1+7d＝9，a2+a9＝2a1+9d＝13，解得a1＝2，d＝1，所以{a n}的通项公式a n＝2+（n﹣1）×1＝n+1，n∈N*．选②③时，S5＝5a1+10d＝20，a2+a9＝2a1+9d＝13，解得a1＝2，d＝1，所以{a n}的通项公式a n＝2+（n﹣1）×1＝n+1，n∈N*．（2）证明：由（1）知a n＝n+1，n∈N*，所以，所以，∵n∈N*，∴．点评：本题主要考查数列的通项公式的求法，数列的求和，裂项求和法的应用，考查运算求解能力，属于中档题．。

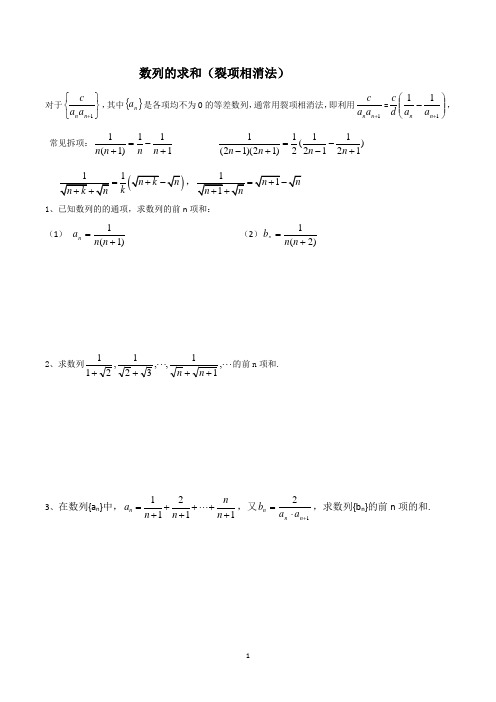
数列的求和（裂项相消法）对于⎭⎬⎫⎩⎨⎧+1n n a a c ，其中{}n a 是各项均不为0的等差数列，通常用裂项相消法，即利用1+n n a a c =⎪⎪⎭⎫⎝⎛-+111n n a a d c ， 常见拆项：111)1(1+-=+n n n n)121121(21)12)(12(1+--=+-n n n n1k==1、已知数列的的通项，求数列的前n 项和： （1） )1(1+=n n a n （2）)2(1+=n n b n2、求数列⋅⋅⋅++⋅⋅⋅++,11,,321,211n n 的前n 项和.3、在数列{a n }中，11211++⋅⋅⋅++++=n nn n a n ，又12+⋅=n n n a a b ，求数列{b n }的前n 项的和.4、等比数列{a n}的各项均为正数，且2a1+3a2=1，a32=9a2a6，（1）求数列{an}的通项公式；（2）设bn =log3a1+log3a2+…+log3an，求数列{}的前n项和．5、正项数列{an }满足﹣（2n﹣1）an﹣2n=0．（1）求数列{an }的通项公式an；（2）令bn=，求数列{bn}的前n项和Tn．6、已知等差数列{an }满足：a3=7，a5+a7=26．{an}的前n项和为Sn．（1）求an 及Sn；（2）令（n∈N*），求数列{bn}的前n项和Tn．7. 已知数列{}n a 的前n 项和为n S ，点),(n s n n 在直线21121+=x y 上，数列{}n b 满足0212=+-++n n n b b b ，()*N n ∈，113=b，且其前9项和为153.（1）求数列{}n a ，{}n b 的通项公式； （2）设)12)(112(3--=n n n b a c ，求数列{}n c 前n 项的和n T .8、已知等差数列{a n }的前n 项和S n 满足5,053-==S S (1)求{a n }的通项公式； (2)求数列21211n n a a -+⎧⎫⎨⎬⎩⎭的前n 项和．9、S n 为数列{a n }的前n 项和.已知a n >0，(Ⅰ)求{a n }的通项公式： (Ⅱ)设 ，求数列}的前n 项和10、已知公差不为零的等差数列{}n a 中，37a =，且1413,,a a a 成等比数列． （1）求数列{}n a 的通项公式； （2）令211n n b a =-（n N *∈），求数列{}n b 的前n 项和n S ．11、已知各项均为正数的等比数列{}n a 的首项12a =，n S 为其前n 项和，且312253S S S =+. （1）求数列{}n a 的通项公式； （2）设2log n n b a =，11n n n c b b +=，记数列{}n c 的前n 项和n T ，求4n Tn +的最大值.12. 已知数列{}n a 的前n 项和为n S ，且22n n S a =-，(1,2,3)n =⋅⋅⋅；数列{}n b 中，11,b = 点1(,)n n P b b +在直线20x y -+=上．（1）求数列{}n a 和{}n b 的通项公式； （2）设数列12n b +⎧⎫⎨⎬⎩⎭的前n 和为n S ，求12111nS S S +++；答案：1（1）1n n +（2）3111-)4212n n +++（21-；3、81n n +；4、（1）13n n a =（2）21n n S n =-+；5、（1）2n a n =（2）21n n T n =+（）;6、（1）2+1n a n =22n S n n =+（2）1n n T n =+4（）；7、（1）5;32n n a n b n =+=+（2）21n n T n =+；8、（1）2-n a n =（2）1-2n nT n=；9、（1）2+1n a n =（2）323)n n T n =+（10、（1）2+1n a n =（2）1)n n S n =+4（;11、、（1）2nn a =（2）1n n T n =+，最大值为19;12、（1）2nn a =；21n b n =-（2）21n nT n =+，。

《数列求和--裂项相消法》考查内容：主要考查裂项相消法进行数列求和一．选择题(在每小题给出的四个选项中，只有一项是符合题目要求的） 1．数列{}n b 中，若()11n b n n =+，数列{}n b 的前n 项和n T ，则2020T 的值为（ ）A ．20202021B ．12021 C ．12020D ．199920202．11111447710(32)(31)n n ++++=⨯⨯⨯-+（ ）A ．31+nn B ．331nn + C ．111n -+ D ．1331n -+ 3．已知在等差数列{}n a 中，5=5a ，3=3a ，则数列11n n a a +⎧⎫⎨⎬⎩⎭的前2019项和是（ ） A ．20202019B ．20192020C ．20182019D ．201920184．已知数列{}n a ：112,233+，123444++，12345555+++，…，又1114n n n b a a +=⋅，则数列{}n b 的前n 项的和n S 为（ ） A ．1411n ⎛⎫-⎪+⎝⎭B ．11421n ⎛⎫-⎪+⎝⎭C ．111n -+ D ．1121n -+ 5．已知222n a n n=+，则6S =（ ） A ．6956B ．78C ．6928D ．7166．设数列2141n ⎧⎫⎨⎬-⎩⎭的前n 项和为n S ，则10S =（ ） A ．1021 B ．2021 C ．919D ．18197．求和111112123123n +++++++++++的值为（ ）A ．12n-B ．111n -+ C ．221n n -D ．221n -+ 8．已知n a =*n N ∈.记数列{}n a 的前n 项和为n S ，则2020S =（ ）A1 B1C1D1-9．已知数列{}n a 为:12，1233+，123444++，12345555+++，…，那么数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和为（ ） A ．1411n ⎛⎫-⎪+⎝⎭ B ．11421n ⎛⎫- ⎪+⎝⎭C ．111n -+ D ．1121n -+ 10．已知函数()a f x x 的图象过点()4,2，令*1,(1)()n a n f n f n =∈++N .记数列{}n a 的前n 项和为n S ，则2021S =（）A1-BCD111．已知数列{}n a 与{}n b 前n 项和分别为n S ，n T ，且20,2,n n n n a S a a n >=+∈*N ,1121(2)(2)n n n n n n b a a +++=++，对任意的*,n n N k T ∈>恒成立，则k 的最小值是（ ） A ．13B ．12C ．16D ．112．已知数列{}n a ，对任意*n N ∈，总有123232n a a a na n +++⋯+=成立，设()128(1)41n n nb n a +=--，则数列{}n b 的前10项的和为（ ）A ．2221B ．4041C ．2021D ．4241二．填空题13．设数列{}n a 满足11a =，且()*11n n a a n n N +-=+∈，则数列1n a ⎧⎫⎨⎬⎩⎭前2020项的和为________．14．已知数列{}n a的通项公式为n a =，则数列{}n a 的前n 项和n S =__15．设正项数列{}n a 的前n 项和n S 满足2+1441n n S a n =--，*n N ∈，且2a ，5a ，14a 成等比数列，则1111++⋅⋅⋅++=______.16．已知数列{}n a 与{}n b 前n 项和分别为n S ，n T ，且0n a >，22n n n S a a =+，n *∈N ，()()112122n n n n n n b a a +++=++，对任意的n *∈N ，n k T >恒成立，则k 的取值范围是_____.三．解答题(解答应写出文字说明、证明过程或演算步骤)17．已知数列{}n a 的前n 项和为n S ，且12a =，()()*21n n S n a n N =+∈．（1）求{}n a 的通项公式； （2）令()()1422n n n b a a +=++，求数列{}n b 的前n项和n T ．18．已知等差数列{}n a 的前n 项和为n S ，且23a =，636S =. （1）求数列{}n a 的通项公式； （2）若数列{}n b 满足2142n n b a n =+-（*n N ∈），求数列{}n b 的前n 项和n T .19．正项数列{}n a 的前项和n S 满足：242n n n S a a =+，()*n ∈N，（1）求数列{}n a 的通项公式； （2）令()2212n nn b n a+=+，数列{}n b 的前n 项和为n T ，证明：对于任意的*n ∈N 都有564n T <.20．已知等差数列{}n a 中，13212a a +=，12421a a a +=+. （1）求数列{}n a 的通项公式；（2）记数列{}n a 的前n 项和为n S ，证明：121112123n S S S n +++<+++.21．已知数列{}n a 满足15a =，2123n n a a n +=+-.（1）求证：数列{}22n a n n --为等比数列；（2）若数列{}n b 满足2nn n b a =-，求12111n nT b b b =++⋅⋅⋅+.22．在数列{}n a 中，1114,340n n a a a +=-+=． （1）证明：数列{}2n a -是等比数列．（2）设()()1(1)3131n nn n n a b +-=++，记数列{}n b 的前n 项和为n T ，若对任意的*,n n N m T ∈≥恒成立，求m 的取值范围．《数列求和--裂项相消法》解析1.【解析】因为111n b n n =-+， 所以20201111112020112232020202120212021…T ⎛⎫⎛⎫⎛⎫=-+-++-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故选：A 2.【解析】由题得1111()(32)(31)32313n n n n =-⨯-+-+所以11111447710(32)(31)n n ++++⨯⨯⨯-+11111111(1)34477103231n n =-+-+-++--+1113(1)=33133131n nn n n =-⨯=+++.故选：A. 3.【解析】设{}n a 的公差为d ，由5353a a =⎧⎨=⎩得114523a d a d +=⎧⎨+=⎩解得111a d =⎧⎨=⎩，则n a n =．则()1111n n a a n n +==+111n n -+． 故前2019项和2019111111112232018201920192020S =-+-++-+-12019120202020=-=，故选：B ． 4.【解析】因为数列{}n a 为:12，1233+，123444++，12345555+++，… 所以(1)1232112n n n n n a n n +++++===++， 所以1111114(1)1n n n b a a n n n n +=⋅==-++， 所以{}n b 的前n 项和为11111111112233411n n n -+-+-++-=-++故选：C. 5.【解析】由题意()21221222n a n n n n n n ===-+++，所以612611111111111132435465768S a a a =++⋅⋅⋅+=-+-+-+-+-+-6.【解析】()()21111141212122121n n n n n ⎛⎫==- ⎪--+-+⎝⎭，因此，101111111012335192121S ⎛⎫=-+-++-= ⎪⎝⎭.故选：A. 7.【解析】()()1121121123112n n nn n n n ⎛⎫∴===- ⎪+++++++⎝⎭， 因此，111112123123n+++++++++++111111121222223341n n ⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++- ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭1221211n n ⎛⎫=-=- ⎪++⎝⎭.故选：D.8.【解析】由题意na===所以20201S ==. 故选：D.9.【解析】因为数列{}n a 为:12，1233+，123444++，12345555+++，… 所以(1)1232112n n n n n a n n +++++===++，所以114114()(1)1n n a a n n n n +==-++ 所以11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和为111111114(1)412233411n n n ⎛⎫-+-+-++-=- ⎪++⎝⎭故选：A10.【解析】由()42f =，可得42a =，解得12a =，则12()f x x =.∴1(1)()n a fn f n ===++，202111S ∴==，故选：D11.【解析】因为22n n n S a a =+，所以当2,n n N *≥∈时，21112n n n S a a ---=+，两由0n a > 知，10n n a a -+≠，从而110n n a a ---=，即当2,n n N *≥∈时，11n n a a --=，当1n =时，21112a a a =+，解得11a =或0（舍），则{}n a 首项为1，公差为1的等差数列，则()111n a n n =+-⨯=.所以112111(2)(21)221n n n n n n b n n n n +++==-++++++，则1211111111111 (366112213213)n n n n n T b b b n n n ++=+++=-+-++-=-<+++++，所以13k ≥.则k 的最小值是13.故选:A12.【解析】数列{}n a ，对任意*n N ∈，总有123232n a a a na n +++⋯+=成立. 当1n =时，12a =.当2n ≥时，()()123123121n a a a n a n -+++⋯+-=-. 又123232n a a a na n +++⋯+=，两式相减可得2n na =， 即2n a n=，当1n =时也成立. ()()()11122288(1)(1)(1)24141414n n n n n n b n a n n n+++=-=-=----⋅111212(1)1n n n +=-⎛⎫+ ⎪-+⎝⎭所以数列{}n b 的前10项的和为123101111111+1+335571921b b b b ⎛⎫⎛⎫⎛⎫⎛⎫+++=+-+++-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. 12012121=-=，故选：C 13.【解析】因为()*11n n a a n n N+-=+∈,所以1122321,1,2,...,2------=-=--=--=n n n n n n a a n a a n a a n a a ， 左右分别相加得()()112234 (2)-+=++++=-n n n n a a ，所以2n n a +=，所以1211=2⎛⎫=-，所以20201111111140402 (2122320202021120212021)⎛⎫⎛⎫=-+-++-=-=⎪ ⎪⎝⎭⎝⎭S ， 故答案为：4040202114.【解析】由题可知：n a =，则2n a =所以12n n S a a a =+++，则122n n S =++，所以112n S=，故答案为：11215.【解析】由2+1441n n S a n =--,可得21443(2)n n S a n n -=-+≥,以上两式相减可得:22144n n n a a a +=--,即222144(2)n n n n a a a a +=++=+,又∵{}n a 为正项数列,∴12n n a a +-=,由等差数列的定义可知数列{}n a 从第二项开始是公差为2的等差数列,又2a ,5a ,14a 成等比数列,所以22514a a a =,即()()2222624a a a +=+,∴23a =,∴()212n a n n =-≥,当1n =时,2112445S a a ==-,∴11a =,满足通项公式,∴21n a n =-,∴122320182019201920201111a a a a a a a a ++⋅⋅⋅++1111111201921335403740394039⎛⎫=⨯-+-+⋅⋅⋅+-= ⎪⎝⎭ 16.【解析】因为22n n n S a a =+，所以当2,n n N *≥∈时，21112n n n S a a ---=+， 两式相减得:22112n n n n n a a a a a --=+-- ，整理得，()()1101n n n n a a a a --+--=，由0n a > 知，10n n a a -+≠，从而110n n a a ---=，当1n =时，21112a a a =+，解得11a =或0（舍），则{}n a 首项为1，公差为1的等差数列， 则()111n a n n =+-⨯=.所以112111(2)(21)221n n n n n n b n n n n +++==-++++++，则121111111 (36611221)n n n n T b b b n n +=+++=-+-++-+++ 11311213n n +=<++-，所以13k ≥.故答案为：13k ≥. 17.【解析】（1）因为()()*21n n S n a n N=+∈，所以112n n S na --=()2n ≥，两式作差可得()()1212n n n a n a na n -=+-≥，整理得()()112n n n a na n -=-≥，则()121n n a nn a n -=≥-， 故()32112123222121n n n a a a na a n n a a a n -=⨯⨯⨯⨯=⨯⨯⨯⨯=≥-， 当1n =时，12a =满足上式，故2n a n =． （2）由（1）可知()()()()()()1441112222241212n n n b a a n n n n n n +====-++++++++，则1231111111123344512n n T b b b b n n ⎛⎫⎛⎫⎛⎫⎛⎫=++++=-+-+-++- ⎪ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎝⎭． 112224nn n =-=++． 18.【解析】（1）设等差数列{}n a 的公差为d ，因为23a =，636S =，所以113656362a d a d +=⎧⎪⎨⨯+=⎪⎩，解得112a d =⎧⎨=⎩， 所以()()1112121n a a n d n n =+-=+-=-； （2）由题意()()()221114221212142n n b a n n n n n ===+-+--+-所以1231111111233557112121n n T b b b b n n ⎛⎫=+++⋅⋅⋅+=-+-+-⋅⋅⋅+ ⎪⎝-+⎭-11122121n n n ⎛⎫=-= ⎪++⎝⎭. 19.【解析】（1）解：∵正项数列{}n a 的前项和n S 满足：242n n n S a a =+，()*n ∈N ① 则211142n n n S a a ---=+，()2n ≥②①-②得()22114222n n n n n a a a a a n --=-+≥-即()2211222n n n n a a a a n --+=-≥即()()()()11122n n n n n n a a a a a a n ---+=+-≥ 又10n n a a ->+，12n n a a --=，()2n ≥.又12a =，所以数列{}n a 是以2为首项2为公差的等差数列.所以2n a n =. （2）证明：由于2n a n =，()2212n nn b n a +=+则()()2222111116422n n b n n n n ⎡⎤+==-⎢⎥++⎢⎥⎣⎦()()()222222222111111111111632435112n T n n n n ⎡⎤=-+-+-+⋅⋅⋅+-+-⎢⎥-++⎢⎥⎣⎦()()22221111115111621626412n T n n ⎡⎤⎛⎫=+--<+=⎢⎥ ⎪⎝⎭++⎢⎥⎣⎦. 20.【解析】（1）设数列{}n a 的公差为d ，由题意得()()111112212231a a d a a d a d ⎧++=⎪⎨++=++⎪⎩，解得12a =，3d =，故数列{}n a 的通项公式为()23131n a n n =+-=-.（2）由（1）知()2313222n n n n nS n -+=+=， 所以()231322n n n n n S n n +++=+=，所以()122113131nS n n n n n ⎛⎫==- ⎪+++⎝⎭，所以1211121111111232231n S S S n n n ⎡⎤⎛⎫⎛⎫⎛⎫+++=-+-++- ⎪ ⎪ ⎪⎢⎥++++⎝⎭⎝⎭⎝⎭⎣⎦2121313n ⎛⎫=-< ⎪+⎝⎭. 21.【解析】（1）设22n n c a n n =-- ，2123n n a a n +=+-，则()()21121212n n n n a n n cc a n n++-+-+=-- ()2222222212222223n n n n a n n n n n a n n a a n nn -------===--+---， 所以{}22n a n n --是以2为首项，以2为公比的等比数列.（2）由（1）可得222nn a n n --=，所以222n n a n n =++所以()2222nn n b a n n n n =-=+=+，所以()1211111111324352n n T b b b n n =++⋅⋅⋅+=+++⨯⨯⨯+11111111111112324352112n n n n n n ⎛⎫=-+-+-+-+-+- ⎪--++⎝⎭()()211113512212412n n n n n n +⎛⎫=+--=⎪++++⎝⎭. 22.【解析】（1）证明：因为1340n n a a +-+=， 所以134n n a a +=-，所以()1232n n a a +-=-，即()*1232n n a n N a +-=∈-．因为114a =，所以1212a -=，故数列{}2n a -是以12为首项，3为公比的等比数列． （2）解：由（1）可得1212343n n n a --=⨯=⨯，即432n n a =⨯+，则()()()()()111(1)432(1)11(1)313131313131n n n n n n n n n n n n a b +++-⨯+-⎛⎫===-+ ⎪++++++⎝⎭． 当n 为偶数时，22311111111113131313131313131n n n n n T -+⎛⎫⎛⎫⎛⎫⎛⎫=--++++--++ ⎪ ⎪ ⎪ ⎪++++++++⎝⎭⎝⎭⎝⎭⎝⎭1111113131431n n ++=-+=-++++，因为111431n n T +=-++是递减的，所以13414n T -<≤-． 当n 为奇数时，22311111111113131313131313131n n n n n T -+⎛⎫⎛⎫⎛⎫⎛⎫=--++++++-- ⎪ ⎪ ⎪ ⎪++++++++⎝⎭⎝⎭⎝⎭⎝⎭1111113131431n n ++=--=--+++， 因为11031n +>+，所以14nT <-． 要使对任意的*,n n N m T ∈≥恒成立，只需()max n m T ≥，即314m ≥-， 故m 的取值范围是3,14⎡⎫-+∞⎪⎢⎣⎭．。

高中数列裂项相消公式
数列裂项相消公式是指在一个数列中删除相邻的两项后，将删除项的和加到相邻的另一项上，这一操作称为裂项相消。

对于一个等差数列和等比数列，裂项相消后得到的结果仍然是一个等差数列或等比数列。

等差数列的裂项相消公式：设一个等差数列为a1，a2，a3，…，an，公差为d，则有
an-1 + a1 = 2an-d
an-2 + a2 = 2an-2d
an-3 + a3 = 2an-3d
…
a(n-m-1) + a(m+1) = 2an-(m+1)d
其中 m = n/2, n为偶数时，m = n/2-1。

等比数列的裂项相消公式：设一个等比数列为a1，a2，a3，…，an，公比为q，则有：
an-1 + a1 = 2anq^-1
an-2 + a2 = 2an-1q^-1
an-3 + a3 = 2an-2q^-1
…
a(n-m-1) + a(m+1) = 2an-(m+1)q^-1
其中 m = n/2, n为偶数时，m = n/2-1。

裂项相消公式可以用来简化一些复杂的求和计算，也可以用来证明一些数学定理。

创作编号：GB8878185555334563BT9125XW创作者：凤呜大王*对于本题通项公式类型的数列，采用的“求前n项和”的方法叫“裂项相消法”——就是把通项拆分成“两项的差”的形式，使得恰好在求和时能够“抵消”多数的项而剩余少数几项。

很多题目要善于进行这种“拆分”请看几例：（1）本题：()()2211111nn n n nan n n n++===-++-+（变形过程中用了“分子有理化”技巧）得12233411111 11111 nn n nS n++ =++++==+ -----…【往下自己求吧！答案C 】（2）求和1111122334(1)nSn n=++++⨯⨯⨯+…解：通项公式：()()()1111111n n n a n n n n n n +-===-+++ 所以 111111*********n S n n ⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++- ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭…1111n n n =-+=+（3）求和 1111377111115(41)(43)n S n n =++++⨯⨯⨯-+… 解：()()()()()()43411111141434414344143n n n a n n n n n n +--⎛⎫===- ⎪-+-+-+⎝⎭得 1111377111115(41)(43)n S n n =++++⨯⨯⨯-+ (11111111)143771111154143n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++- ⎪ ⎪ ⎪ ⎪⎢⎥-+⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦… 1114343n ⎛⎫=- ⎪+⎝⎭ ()343nn =+（4）求和 1111132435(2)n S n n =++++⨯⨯⨯+… ()()()21111122222n n n a n n n n n n +-⎛⎫===- ⎪+++⎝⎭()()()()1111111113243546572112n S n n n n n n =++++++++⨯⨯⨯⨯⨯--++… 1111111111111112132435462112n n n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-+-++-+-+- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥--++⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦…11111212n n =+--++ （仔细看看上一行里边“抵消”的规律 ） 311212n n =--++ 最后这个题，要多写一些项，多观察，才可能看出抵消的规律来。