简单物体的三视图专项练习

小学数学三视图练习题三视图是指物体在正投影面上的三个视图分别为正视图、左视图和顶视图。

它是学习立体几何的基础，并且在工程制图中也有广泛的应用。

下面是一些小学数学的三视图练习题，帮助大家巩固相关知识。

题目一：根据下图的正视图、左视图和顶视图，确定物体的形状。

（插入图片，显示正视图、左视图和顶视图）要求：根据正视图、左视图和顶视图确定物体的形状，然后用文字描述出这个物体的形状。

注意描述要准确，并包括物体的名称和各个面的特征。

解答：根据正视图，我们可以看到物体是一个长方体形状的容器，其中有两个相对的长方形面。

根据左视图，我们可以看到物体的侧面有两个边相等的正方形面。

根据顶视图，我们可以看到物体的上面是一个定位的长方形，而下面则无法确定。

综合以上三个视图，我们可以确定这个物体是一个长方体形状的容器，上面和下面都是长方形面，两侧是正方形面。

题目二：根据下图的正视图、左视图和顶视图，求这个物体的体积，并单位是立方米。

（插入图片，显示正视图、左视图和顶视图）要求：根据三个视图计算出物体的体积，并将结果用文字描述出来，并附上计算过程。

解答：根据正视图和左视图，我们可以得出这个物体的长、宽、高分别为5米、3.5米和2米。

根据三个值，我们可以利用体积的计算公式V=长×宽×高来计算该物体的体积。

计算过程如下：V = 5米 × 3.5米 × 2米 = 35立方米。

综上所述，这个物体的体积为35立方米。

题目三：根据下图的正视图、左视图和顶视图，求这个物体的表面积，并单位是平方米。

（插入图片，显示正视图、左视图和顶视图）要求：根据三个视图计算出物体的表面积，并将结果用文字描述出来，并附上计算过程。

解答：根据正视图和左视图，我们可以得出物体的长、宽、高同题目二中一样，即5米、3.5米和2米。

根据这三个值，我们可以利用表面积的计算公式表面积=2×(长×宽+长×高+宽×高)来计算该物体的表面积。

三视图（一）1（2011西城一模理12）.一个棱锥的三视图如图所示，则这个棱锥的体积为_____.2（2011西城一模文5）．一个棱锥的三视图如图所示，则这个棱锥的体积是（A）6（B）12（C）24（D）363．（2011朝阳一模理6）已知某个三棱锥的三视图如图所示，其中正视图是等边三角形，侧视图是直角三角形，俯视图是等腰直角三角形，则此三棱锥的体积等于（）（A ）612（B ）33（C ）64（D ）2334（2011门头沟一模理3）．一几何体的三视图如右图所示，则该几何体的体积是(A) 2 (B) 4 3(C)312+(D)316+正(主)视图俯视图侧(左)视图3443 33正(主)视图俯视图侧(左)视图3443 33侧视图正视图1俯视图2主视图左视图111ABC DO EA 1B 1C 1D 1 5（2011石景山一模理4）．一个空间几何体的三视图及部分数据如图所示（单位：cm ），则这个几何体的体积是（ ） A ． 33cm B ．352cm C ． 32cm D ．332cm6（2011朝阳一模文6.）已知三棱锥的三视图如图所示，其中侧视图为直角三角形，俯视图为等腰直角三角形，则此三棱锥的体积等于（）（A ）23（B ）33（C ）223 （D ）2337（2011丰台文5）．如图所示，O 是正方体ABCD -A 1B 1C 1D 1对角线A 1C 与AC 1的交点，E 为棱BB 1的中点，则空间四边形OEC 1D 1在正方体各面上的正投影不可能．．．是( )8（2011海淀一模文11）. 如图，在正方体1111ABCD A B C D -中，点P 是上底面1111A B C D 内一动点，则三棱锥P ABC -的主视图与左视图的面积的比值为_____.(A) (B) (C) (D)正视图俯视图侧视图13PDCBA1A 1D 1B 1C 左视主视9(2011门头沟一模文10).一几何体的三视图如左下图所示，则该几何体的体积是10（2011石景山一模文4）．一个空间几何体的三视图及部分数据如图所示 （单位：cm ），则这个几何体的表面积是（ ） A ．29πcm B ．212πcm C ．215πcm D ．224πcm参考答案：1.122.B3.B4.B5.D6.B7.A _8._1__9. 3710.D俯视23主视左视11（第10题（二）1(10。

三视图练习题及答案三视图是工程设计、制图等领域中常用的表达方式之一，它能够以三个不同的视角展示一个物体的外观和内部结构，帮助人们更好地理解和分析物体的形状和构造。

为了提高对三视图的理解和应用能力，下面将给出一些三视图练习题及答案，希望对读者有所帮助。

1. 请根据给出的三视图，画出物体的立体图。

答案：根据三视图，我们可以确定物体的形状和尺寸，然后利用透视法将其转化为立体图。

在绘制过程中，需要注意比例和透视关系，以保证立体图的准确性。

2. 给出一个物体的立体图，请根据立体图绘制出相应的三视图。

答案：在绘制三视图时，我们需要观察立体图中的各个面，然后根据其相对位置和大小来绘制对应的正视图、俯视图和侧视图。

在绘制过程中，需要注意比例和尺寸的准确性，以确保三视图能够准确地表达立体图的形状和结构。

3. 请根据给出的三视图，判断物体的形状是什么？答案：通过观察三视图中的线条和面，我们可以判断物体的形状。

例如，如果正视图中的线条是直的，侧视图中的线条是弯曲的，那么物体可能是一个圆柱体。

通过观察三视图中的特征，我们可以逐步推断出物体的形状。

4. 给出一个物体的形状，请根据形状绘制出相应的三视图。

答案：在绘制三视图时，我们需要观察物体的形状和结构，然后根据其特征来绘制对应的正视图、俯视图和侧视图。

在绘制过程中，需要注意线条的粗细和长度，以确保三视图能够准确地表达物体的形状和结构。

通过以上的练习题和答案，我们可以提高对三视图的理解和应用能力。

练习三视图不仅可以帮助我们更好地理解和分析物体的形状和结构，还可以提高我们的制图能力和空间想象力。

在实际工程设计和制图中，三视图是非常重要的表达方式，掌握好三视图的绘制和解读技巧对于工程师和设计师来说是非常必要的。

总之，通过不断地练习和应用，我们可以提高对三视图的掌握程度，为工程设计和制图提供更准确、更有效的表达方式。

希望以上的练习题和答案能够对读者有所帮助，进一步提高对三视图的理解和应用能力。

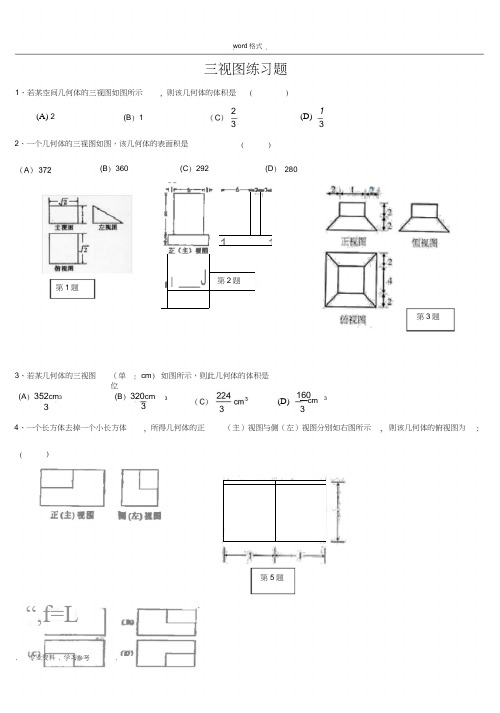
word 格式三视图练习题则该几何体的体积是()(D)()(D ) 280第3题（单位cm ) 16033(D) 所得几何体的正则该几何体的俯视图为()1 3第5题(A) 2（主）视图与侧（左）视图分别如右图所示(B ) 1(C ) 292第1题(B ) 3603、若某几何体的三视图 如图所示，则此几何体的体积是 1、若某空间几何体的三视图如图所示—cm 34、一个长方体去掉一个小长方体 2、一个几何体的三视图如图，该几何体的表面积是(B ) 320cm 3“,f=L23(A ) 352cm 3 33r — 1111I ___J第2题1'1-T P5、 若一个底面是正三角形的三棱柱的正视图如图所示，则其侧.面积等于（A . . 3B . 2C . 2 3D . 66、 图2中的三个直角三角形是一个体积为20cm 2的几何体的三视图，则h=7、 一个几何体的三视图如图所示 ，则这个几何体的体积为 _____________AA // BB // CC , CC 丄平面 ABC3且3 AA = 3 BB = CC =AB,则多面体△ ABC - ABC 的正视图（也称主视图）是（）8、如图，网格纸的小正方形的边长是1 ,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为9、如图1 , △ ABC 为正三角形，)S 2a.俯视图正（主）视图侧（左）视图A. 9 nB. 10 nC. 11 n D . 12 n10、一空间几何体的三视图如图所示，则该几何体的体积为（）.A.2 2.3B. 4 2 . 3侧（左）视图C. 2D. 4第11题第10题11、上图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是12、一个棱锥的三视图如图,则该棱锥的全面积（单位：c m2）为(A) 48+12 . 2 (B) 48+24 . 2 ( C) 36+12 2 (D)36+24 213、若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是cm3第12题正视图侧视图俯视图15题14、设某几何体的三视图如上图所示。

三视图练习1.一个几何体的三视图如右图所示，它的正视图和侧视图均为半圆，俯视图为圆，则这个空间几何体的体积是（ ） A ．32π B ．34π C ．π4 D ．π32.有一个几何体的三视图及其尺寸如下图(单位：cm)，则该几何体的表面积为( )A ．12πcm 2B ．15πcm 2C ．24πcm 2D ．36πcm 23.某几何体的三视图如图所示，根据图中标出的数据．可得这个几何体的表面积为( )A.错误！未找到引用源。

B.错误！未找到引用源。

C.错误！未找到引用源。

D.124.如图，网格纸上小正方形边长为1，粗线是一个棱锥的三视图，则此棱锥的体积为（ ）． （A ）38 （B ）34（C ）34 （D）325.一个简单几何体的三视图如图所示，其正视图和俯视图均为正三角形，侧视图为腰长是2的等腰直角三角形则该几何体的体积为（ ）A ．B ．1C ．D ．36.某几何体的三视图如图所示（单位：cm ），则该几何体的侧面PAB 的面积是（ ） A ．7B ．2C ．1D ．37.说出下列三视图(依次为主视图、左视图、俯视图)表示的几何体是（ ）A ．六棱柱B ．六棱锥C ．六棱台D ．六边形8.一个空间几何体的三视图如图所示，则该几何体的体积为（ ）A ．56πcm 3 B ．3πcm 3 B ．C ．32πcm 3 D ．37πcm 3 9.右图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是( ) (A)9π （B ）10π (C)11π (D)12π10.用若干单位正方体搭一个几何体，使它的正视图和俯视图如图所示，则它的体积的最大值和最小值分别为( )A. 9,14B.7,13C. 8,14D. 9,13 11.已知某几何体的三视图如上图所示，其中正视图，侧视图均是由三角形与半圆构成，视图由圆与内接三角形构成，根据图中的数据可得此几何体的体积为( ) (A)2132π+(B)4136π+ （C）132+(D) 166+12.一个几何体的三视图如图所示，则该几何体的体积为( )(A)92 (B)72(C)3 (D)4 13.右图是一个几何体的三视图，根据图中数据，可得该几何体的体积是( )(A) 9π (B)1333π- （C ）103π (D)133π 14.一个几何体的三视图如图所示，则该几何体的体积是（ ） （A ）64 （B ）72 （C ）80（D ）11215.一个几何体的三视图如图所示，则该几何体的体积是（ ）A ．64B ．72C ．80D ．11216.已知一个几何体的三视图如下图所示(单位：cm)，其中正视图是直角梯形，侧视图和俯视图都是矩形，则这个几何体的体积是________cm 3.17.如图为一个几何体的三视图，其中俯视为正三角形，A 1B 1=2,AA 1=4，则该几何体的表面积为_______。

几何体的三视图练习题1、若某空间几何体的三视图如图所示，则该几何体的体积是 （ ）（A ）2（B ）1（C ）23（D ）132、一个几何体的三视图如图，该几何体的表面积是 （ ） （A ）372 （B ）360 （C ）292 （D ）2803、若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 （A ）3523cm 3 （B ）3203cm 3 （C ）2243cm 3 （D ）1603cm 34、一个长方体去掉一个小长方体，所得几何体的正（主）视图与侧（左）视图分别如右图所示，则该几何体的俯视图为： （ ）5、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积．．．等于 ( ) A．2 C．．66、图2中的三个直角三角形是一个体积为20cm 2的几何体的三视图，则h= cm第2题第5题7、一个几何体的三视图如图所示，则这个几何体的体积为 。

8、如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.9、如图1，△ ABC 为正三角形，AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图（也称主视图）是（ ）10、一空间几何体的三视图如图所示,的体积为().A.2π+B. 4π+C. 23π+D. 43π+11、上图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（ ）A ．9πB ．10πC ．11πD ．12π12、一个棱锥的三视图如图，则该棱锥的全面积（单位：c 2m ）为 （ ）第7题侧(左)视图正(主)视俯视图俯视图 正(主)视图 侧(左)视图（A ）（B ）（C ）（D ）13、若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 3cm ．14、设某几何体的三视图如上图所示。

四年级数学三视图练习题三视图是在工程制图中常用的表示物体外观的方法，通过绘制物体的正视图、左视图和顶视图，可以清晰地展示物体的形状和结构。

对于四年级的学生来说，掌握三视图的绘制方法是非常重要的。

本文将介绍一些常见的四年级数学三视图练习题，帮助学生巩固相关知识。

练习题一：绘制物体的正视图和左视图请根据下面给出的物体的三视图图纸绘制物体的正视图和左视图。

（插入题目一的图纸图片）（插入题目一的答案图片）练习题二：根据三视图确定物体形状请根据下面给出的物体的三视图图纸，确定物体的形状并回答问题。

（插入题目二的图纸图片）问题一：物体的底面是什么形状？答：根据顶视图可以得知物体的底面是一个矩形。

问题二：物体的高度是多少？答：根据左视图可以测量得知物体的高度为5厘米。

练习题三：根据物体外部条件确定三视图请根据下面给出的物体的正视图和左视图，确定物体的外部条件并回答问题。

（插入题目三的正视图和左视图图片）问题一：物体的底面是否有孔洞？答：根据正视图可以看到物体底面有一个圆形孔洞。

问题二：物体的宽度是多少？答：根据左视图可以看到物体的宽度为6厘米。

练习题四：绘制物体的三视图请根据下面给出的物体的外部条件绘制物体的三视图。

物体的外部条件：底面是一个正方形，边长为3厘米；高度为4厘米。

（插入题目四的外部条件图片）（插入题目四的三视图答案图片）通过以上练习题，希望同学们能够掌握基本的三视图绘制方法，并能够根据给定的三视图进行问题的解答。

在实际生活中，工程制图和三视图的应用非常广泛，掌握这些知识对同学们的未来学习和职业发展都将有很大的帮助。

希望同学们能够认真练习，提高自己的数学素养。

三视图练习题编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（三视图练习题）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为三视图练习题的全部内容。

29.2 三视图一、选择题（共15小题；共75分）1. 下列物体的主视图、俯视图和左视图不全是圆的是（）A。

橄榄球B。

兵乓球C。

篮球D。

排球2. 如图,几何体的俯视图是A。

B。

C. D.3。

长方体的主视图与左视图如图所示（单位：)，则其俯视图的面积是A。

B。

C. D.4. 如图所示，几何体的俯视图是A. B.C. D.5。

如图是有几个相同的小正方体组成的一个几何体．它的左视图是A. B.C。

D.6。

如图是由八个相同小正方体组成的几何体，则其主视图是A. B。

C。

D。

7. 桌面上放着个长方体和个圆柱体，按下图所示的方式摆放在一起，其左视图是A。

B。

与原题图不一样C. D.8. 下列几何体中，有一个几何体的俯视图的形状与其它三个不一样，这个几何体是( ）A. B.C。

D。

9. 图中三视图所对应的直观图是A。

B.C。

D。

10. 如图是常用的一种圆顶螺杆,它的俯视图正确的是A。

B。

C。

D. 11. 如图的几何体的三视图是A。

B.C. D。

12。

如图是由一些相同的小正方体搭成的几何体的三视图，则构成这个几何体的小正方体的个数为A. 个B. 个C. 个D。

个13. 一个几何体由大小相同的小方块搭成，从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数，则从正面看到几何体的形状图是A。

B。

C. D.14。

一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为．A. B. C. D.15. 如图所示是某几何体的三视图，根据图中数据，求得该几何体的体积为A. B. C。

立体几何三视图同步练习1.一个几何体的三视图如图所示，则该几何体的表面积为 22侧视图俯视图A ．．．．2.一条线段长为25，其侧视图长这5，俯视图长为34，则其正视图长为（ ）A ．5B ．34C ．6D ．413.如图三棱锥,,,30o V ABC VA VC AB BC VAC ACB -∠=∠=⊥⊥，若侧面VAC ⊥底面ABC ，则其主视图与左视图面积之比为（ ）A ．4B．4CD4.某几何体的三视图如图所示，则该几何体的体积为（ ）A ．5603B ．5803C ．200D ．2405.已知某几何体的三视图如图所示，其中正（主）视图中半圆的半径为1，则该几何体的体积为（）CVA ．243π- B ．242π-C ．24π-D ． 3242π- 6.一个几何体的三视图如右图所示，其中正视图和侧视图是腰长为5的两个全等的等腰直角三角形.用多少个这样的几何体可以拼成一个棱长为5的正方体（ ）A.2个 B ．3个 C ．4个 D ．5个7.某几何体是由直三棱柱与圆锥的组合体，其直观图和三视图如图所示，正视图为正方形，其中俯视图中椭圆的离心率为 （ ）A ．2B ．21C ．42D ．22 8.一个几何体的三视图如图所示，则该几何体的表面积与体积分别为( ) A ．7＋2，3 B ．7＋2，23 直观图俯视图侧视图正视图C ．8＋2，3D ．8＋2，239.如图所示是某一容器的三视图，现向容器中匀速注水，容器中水面的高度h 随时间t 变化的可能图象是（ ）C为1V ，俯视图绕底边所在直线旋转一周形成的几何体的体积记为2V ,则12:V V （ ）A ．B ．C ．D ．11.某几何体的三视图如图所示，则该几何体的体积为（ ）A. 73B.92C. 72D.9412.已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为A B C D13.将正方体（如图1所示）截去两个三棱锥，得到图2所示的几何体，则该几何体的左视图为（）A． B． C． D．14.一个几何体的三视图及其尺寸如图所示，则该几何体的侧面积 ( )。

简单物体的三视图专题复习练习题1．如图是一个正方体被截去一个直三棱柱得到的几何体，则该几何体的左视图( )2．如图所示的几何体的主视图是( )3．如图所示的几何体的三视图是( )4．如图是一个正方体截去一角后得到的几何体，它的主视图是( )5．由一个圆柱体与一个长方体组成的几何体如图所示，这个几何体的左视图是( )6．如图所示的三通管的立体图，则这个几何体的俯视图是( )7. 如图所示的零件的左视图是( )8. 如图，从不同方向看一只茶壶，你认为其俯视图可能是( )9. 在生活和生产实践中，我们经常需要运用三视图来描述物体的形状和大小．小亮在观察如图所示的热水瓶时，得到的左视图是( )10. 如图是由若干个大小相同的小正方体堆砌而成的几何体，那么其三视图中面积最小的是___________．11. 如图，图①是一个水平摆放的小正方体木块，图②③是由这样的小正方体木块按一定的规律叠放而成．其中图①的主视图有1个正方形，图②的主视图有4个正方形，图③的主视图有9个正方形，按照这样的规律继续叠放下去，则图⑩的主视图有_________个正方形．12. 两个正方体形状的积木摆成如图所示的塔形平放于桌面上，上面正方体下底面的四个顶点恰好是正面相邻正方体的上底面各边的中点，并且下面正方体的棱长为1，则能被看到部分的面积为______．13. 已知某几何体的主视图和俯视图如图所示．(1)画出该几何体的左视图；(2)该几何体是几面体？它有多少条棱？多少个顶点？(3)该几何体的表面有哪些你熟悉的平面图形？14. 如图，一个工件是由大长方体上面中间部位挖去一个小长方体后形成的，主视图是凹字形的轴对称图形．(1)请补画该工件的俯视图；(2)若该工件的前侧面(即主视图部件)需涂油漆，根据图中尺寸(单位：cm)，计算需涂油漆部位的面积．15．墙角处有若干个大小相同的小正方体堆成如图所示的立体图形，如果你打算搬走其中部分小正方体，但希望搬完后该立体图形的主视图、左视图和俯视图都不变，那么你最多可以搬走____个小正方体？16．如图，上、下底面为全等的正六边形礼盒，其主视图与左视图均由矩形构成，主视图中大矩形边长如图所示，左视图中包含两个全等的矩形，如果用彩色胶带按如图所示的方式包扎礼盒，那么所需胶带长度至少为多少厘米？(结果精确到1 cm)答案：1---9 ADCCD ABAB 10. 左视图 11. 100 12. 713. 解：(1)略 (2)六 12 8 (3)梯形，正方形 14. 解：(1)俯视图如图(2)57 cm 215. 解：搬走最多的小正方体方案不唯一，如：第1列最多可以搬走9个小正方体；第2列最多可以搬走8个小正方体；第3列最多可以搬走3个小正方体；第4列最多可以搬走5个小正方体；第5列最多可以搬走2个小正方形．最多可以搬9＋8＋3＋5＋2＝27(个)16. 解：根据题意，作出实际图形的上底面，如解图．AC ，CD 是上底面的两边，过点C 作CB ⊥AD 于点B .易得∠ACD ＝120°，AC ＝CD ，CB ⊥AD ，∴∠CDB ＝30°，∴CB ＝12CD .∵最长对角线长60 cm ，∴2CB ＋CD ＝60 cm ，∴CB ＝15 cm ，CD ＝30 cm ，∴BD ＝153，∴AD ＝30 3 cm.∴胶带的长至少为303×6＋20×6≈432(cm)。

三视图习题50道（含答案）三视图练习题1、若某空间⼏何体的三视图如图所⽰，则该⼏何体的体积是（）（A）2 （B）1 （C）23（D）132、⼀个⼏何体的三视图如图，该⼏何体的表⾯积是（）（A）372 （B）360 （C）292 （D）2803、若某⼏何体的三视图（单位：cm）如图所⽰，则此⼏何体的体积是（A）3523cm3（B）3203cm3 （C）2243cm3（D）1603cm34、⼀个长⽅体去掉⼀个⼩长⽅体，所得⼏何体的正（主）视图与侧（左）视图分别如右图所⽰，则该⼏何体的俯视图为：（）5、若⼀个底⾯是正三⾓形的三棱柱的正视图如图所⽰,则其侧⾯积．．．等于 ( )A．2 C．．66、图2中的三个直⾓三⾓形是⼀个体积为20cm2的⼏何体的三视图，则h= cm第2题第5题7、⼀个⼏何体的三视图如图所⽰，则这个⼏何体的体积为。

8、如图，⽹格纸的⼩正⽅形的边长是1，在其上⽤粗线画出了某多⾯体的三视图，则这个多⾯体最长的⼀条棱的长为______.9、如图1，△ ABC 为正三⾓形，AA '//BB ' //CC ' , CC ' ⊥平⾯ABC 且3AA '= 32BB '=CC '=AB,则多⾯体△ABC -A B C '''的正视图（也称主视图）是（）10、⼀空间⼏何体的三视图如图所⽰,则该⼏何体的体积为( ).A.2π+B. 4π+C. 23π+D. 43π+ 11、上图是⼀个⼏何体的三视图，根据图中数据，可得该⼏何体的表⾯积是（）A ．9πB ．10πC ．11πD ．12π第7题侧(左)视图正(主)视图俯视图俯视图正(主)视图侧(左)视图12、⼀个棱锥的三视图如图，则该棱锥的全⾯积（单位：c2m）为（）（A）（B）（C）（D）13、若某⼏何体的三视图（单位：cm）如图所⽰，则此⼏何体的体积是3cm．14、设某⼏何体的三视图如上图所⽰。

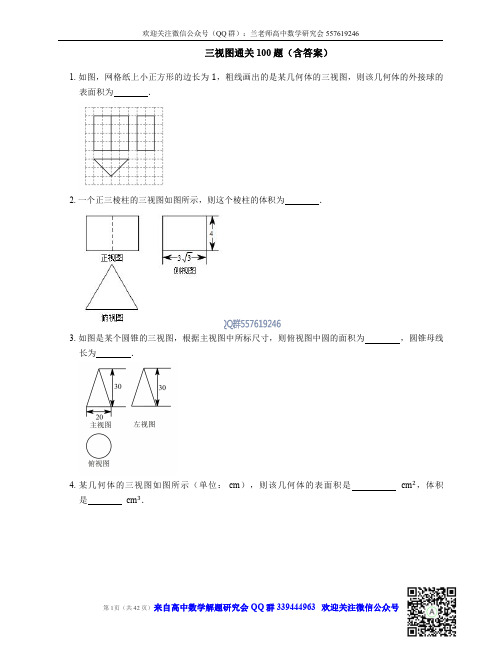
三视图练习题六年级在学习图学的过程中，三视图是一个非常重要的概念。

通过观察物体的正视图、侧视图和俯视图，我们可以更好地理解和描述物体的形状和结构。

本文将为六年级的学生提供一些三视图练习题，帮助他们加深对三视图的理解和运用。

练习题一：绘制三视图请你根据下面的描述，用适当比例绘制物体的三视图。

物体描述：这个物体是一个立方体，所有的边长都相等。

正视图上，你能看到正方形的轮廓，左上角有一个小正方形，表示开放的一面。

侧视图上，你能看到一个竖直方向的线段，表示物体的高度。

俯视图上，你能看到一个水平方向的线段，表示物体的宽度。

练习题二：识别物体下面是三个物体的正视图、侧视图和俯视图，请你根据给出的视图，识别物体的形状并写下对应的名称。

正视图：（图片描述）侧视图：（图片描述）（图片描述）练习题三：推测三视图下面是一个物体的正视图和侧视图，请你根据这两个视图，推测物体的俯视图，并画出来。

正视图：（图片描述）侧视图：（图片描述）练习题四：绘制三视图（进阶）请你使用适当比例，根据下面的描述绘制物体的三视图。

物体描述：这个物体是一个长方体，长边是短边的2倍。

正视图上，你能看到一个长方形的轮廓，短边朝向左侧。

侧视图上，你能看到一个竖直方向的线段，表示物体的高度。

俯视图上，你能看到一个水平方向的线段，表示物体的宽度。

练习题五：识别物体（进阶）下面是三个物体的三视图，请你根据给出的视图，识别物体的形状并写下对应的名称。

（图片描述）侧视图：（图片描述）俯视图：（图片描述）练习题六：推测三视图（进阶）下面是一个物体的正视图和俯视图，请你根据这两个视图，推测物体的侧视图，并画出来。

正视图：（图片描述）俯视图：（图片描述）以上是六年级的三视图练习题，希望对你们的学习有所帮助。

通过练习，相信你们能够更加熟练地观察和绘制物体的三视图，提高对图学的理解和运用能力。

加油！。

1、下面几何体的俯视图是（ D ）2、如图是一个由相同的小正方体组成的立体图形，它的主视图是（ D ）3. 如图是由6个相同的正方体搭成的一个几何体，则它的俯视图是( A )4.、如左下图所示几何体的主视图是（ D ）5．如图是某几何体的三视图，则该几何体的侧面展开图是（A）A ．B ．C ．D ．6．如图1，四个几何体中，主视图、俯视图、左视图都相同的有( B )A．1个B．2个C．3个D．4个7．如图是每个面上都有一个汉字的正方体的一种平面展开图，那么在原正方体中和“国”字相对的图1面是（ C ）A．中 B．钓C．鱼D．岛8、左下图是由3个完全相同的小正方体组成的立体图形，它的主视图是（ B ）DCBA正面9、在下列几何体中，各自的三视图中只有两种视图相同的几何体是（ C ）A. B. C. D.10．某几何体的三视图如图所示，则这个几何体是（ D ）A．圆柱B．正方体C．球D．圆锥11．由5个完全相同的正方体组成的立体图形如图所示，则它的俯视图是（ C ）A．B．C．D．12．如图是一个六角螺栓，它的主视图和俯视图都正确的是（ C ）中国的钓鱼岛A．B．C．D、13．若一个几何体的主视图、左视图、俯视图是半径相等的圆，则这个几何体是（ C ）A．圆柱 B．圆锥C．球D．正方体14．下列几何体的左视图为长方形的是（ C ）A．B． C．D．15．如图所示的支架（一种小零件）的两个台阶的高度和宽度相等，则它的左视图为（ D ）A．B．C．D．16、正面是由7个小立方块所搭成的几何体的俯视图，小正方形中的数字表示该位置小立方块的个数，这个几何体的左视图是（ C ）17、如图所示的几何体是由一个圆锥和一个长方体组成的，则它的俯视图是（C）A ．B ．C ．D ．18、我国古代数学家刘徽用“牟合方盖”找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体.如图所示的几何体是可以形成“牟合方盖”的一种模型，它的俯视图是（ A ）19、下列立体图形中，俯视图是三角形的是（ A ）20、如图是由6个完全相同的小正方体组成的立体图形，它的左视图是（D）21、下列几何体中，主视图是三角形的是（ C ）A B C D第20题图A B CD。

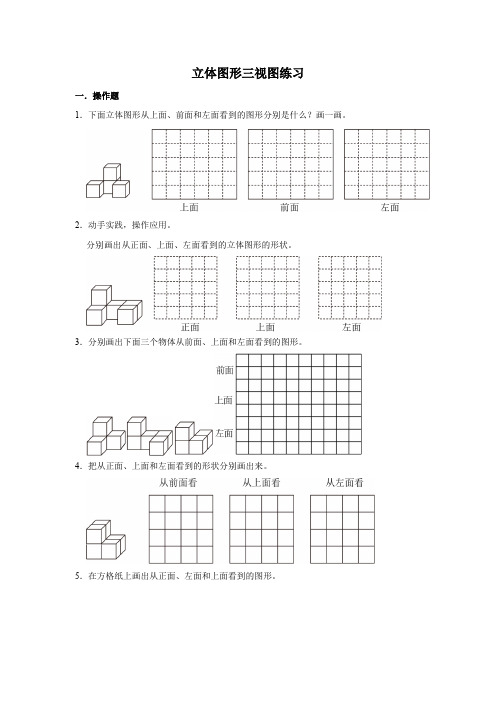
立体图形三视图练习一．操作题1．下面立体图形从上面、前面和左面看到的图形分别是什么？画一画。

2．动手实践，操作应用。

分别画出从正面、上面、左面看到的立体图形的形状。

3．分别画出下面三个物体从前面、上面和左面看到的图形。

4．把从正面、上面和左面看到的形状分别画出来。

5．在方格纸上画出从正面、左面和上面看到的图形。

6．下面的图形从上面，左面和正面看到的分别是什么形状？请画在方格纸上。

7．如图是由8个同样大小的正方体摆成的几何体，请在方格纸中画出从正面、左面和上面看到的图形。

8．画图题。

9．下列立体图形从上面、正面和左面看到的形状分别是什么？画一画。

10．在方格纸上画出从不同位置看到的图形。

11．在方格图中分别画出右边两个几何体从前面和左面看到的图形。

12．分别画出从前面、上面和左面看到的图形。

13．分别画出如图所示的立体图形从前面，左面和上面看到的形状。

14．分别画出从正面、上面、右面看到的立体图形的形状。

15．分别画出下面这个立体图形从正面、左面、上面看到的图形。

16．画出如图从前面、上面和左面看到的图形。

17．在方格纸上画出右上图从上面、左面和前面看到的平面图形。

18．下面的物体分别从正面、左面、上面看到的形状分别是什么？请你在方格纸上画出来。

19．动手实践，操作应用。

分别画出下图从正面、左面、上面看到的图形。

20．把下面的几何体从正面、上面、左面观察到的图形在方格纸上画出来。

21．在方格纸上分别画出下面物体从前面、上面、左面看到的图形。

22．分别画出下面立体图形从不同位置观察到的图形。

2017届高三三视图专练例1. 一个四面体的顶点都在球面上，它们的正视图、侧视图、俯视图都是右图．图中圆内有一个以圆心为中心边长为1的正方形．则这个四面体的外接球的表面积是（）A．π B．3πC．4πD．6π【分析】由三视图可知：该四面体是正方体的一个内接正四面体．此四面体的外接球的半径为正方体的对角线长为．利用球的表面积计算公式即可得出．解：由三视图可知：该四面体是正方体的一个内接正四面体．∴此四面体的外接球的直径为正方体的对角线长为．∴此四面体的外接球的表面积为表面积为=3π．故选：B．例2. 如图是某几何体的三视图，则该几何体的体积为（）A ．6B ．9C ．12D ．18【分析】根据几何体的三视图知该几何体是长方体和三棱柱的组合体，结合图中数据求出它的体积即可．解：根据几何体的三视图知，该几何体是上部为长方体，下部为三棱柱的组合体，画出几何体的直观图如图所示，根据图中数据，计算其体积为V 组合体=V 三棱柱+V 长方体=． 选C ． 例3. 如图为某几何体的三视图，则该几何体的外接球的表面积为A ．B ．C ．D 272π27π【点睛拨窍】空间几何体与球接、切问题的求解方法(1)求解球与棱柱、棱锥的接、切问题时，一般过球心及接、切点作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．(2)若球面上四点P，A，B，C构成的三条线段PA，PB，PC两两互相垂直，且PA＝a，PB＝b，PC＝c，一般把有关元素“补形”成为一个球内接长方体，利用4R2＝a2＋b2＋c2求解．例4. 一个几何体的三视图如图，则该几何体的体积为A．π B．C．D．【分析】由已知的三视图可得：该几何体是一个以俯视图为底面的半圆锥，代入锥体体积公式，可得答案．解：由已知的三视图可得：该几何体是一个以俯视图为底面的半圆锥，其底面面积S==，高h=1，故半圆锥的体积V= =，故选：D【点评】本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．例5. 如图所示，网格纸上小正方形的边长为1，粗线画出的是某一无上盖几何体的三视图，则该几何体的表面积等于（）A．39πB．48πC．57πD．63π【分析】由已知中的三视图可得：该几何体为圆柱中挖去一个圆锥，画出直观图，数形结合可得答案．解：该几何体直观图为圆柱中挖去一个圆锥，如图所示，∴该几何体的表面积为S==48π，故选B．【点评】本题考查的知识点是圆柱的体积和表面积，圆锥的体积和表面积，简单几何体的三视图，难度中档．例6. 某几何体的三视图如图所示，则该几何体的体积是（）A．B．C．D．【分析】几何体为半球与半圆柱的组合体．解：几何体半球与半圆柱的组合体，半球的半径为1，半圆柱的底面半径为1，高为2，∴几何体的体积V=+=．故选B．例7. 若一个底面是正三角形的三棱柱的正视图如图所示，其顶点都在一个球面上，则该球的表面积为（）A．B．C．D．【分析】根据由已知底面是正三角形的三棱柱的正视图，我们可得该三棱柱的底面棱长为2，高为1，进而求出底面外接圆半径r，球心到底面的球心距d，球半径R，代入球的表面积公式．即可求出球的表面积．解：由已知底面是正三角形的三棱柱的正视图可得该三棱柱的底面棱长为2，高为1，则底面外接圆半径r=，球心到底面的球心距d=，则球半径R2==，则该球的表面积S=4πR2=。

一、 三视图考点⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧画图邻关系判断几何体各个面的相个数，判断几何体给出某一视图和几何体判断几何体个数体形状给出三视图，判断几何图给出几何体，判断三视例题1：如图所示的几何体的俯视图是（ ）．A ．B ．C ．D ．例题2：下图是由几个相同的小正方体搭成的一个几何体,它的俯视图是( )例题3：一个物体的三视图如图所示，该物体是（ ） A ．圆柱 B ．圆锥 C ．棱锥 D ．棱柱例题5：下图是由几个相同的小正方体搭成的几何体的三视图， 则搭成这个几何体的小正方体的个数是A ．5B ．6C ．7D ．8例题6：如图是由大小相同的小正方体组成的简单几何体的主视图和左视图，那么组成这个几何体的小正方体的个数最多为 .左视图主视图俯视图第1题图B C D A例题7：在如图所示的正方体的三个面上，分别画了填充不同的圆，下面的4个图中，是这个正方体展开图的有( )．例题8：如图是正方体的展开图，则原正方体相对两个面上的数字和最小的是( ).A. 4B. 6C. 7D.8例题9：骰子是一种特别的数字立方体，它符合规则：相对两面的点数之和总是7.下面四幅图中可以折成符合规则的骰子的是例题10主视图 左视图 俯视图 例题11：由一些大小相同的小正方体组成的几何体的主视图和俯视图（1）请你画出这个几何体的一种左视图；1 42 5 36第8题图从正面看 从左面看 从上面看（2）若组成这个几何体的小正方形的块数n，请你写出n的所有可能值。

例题12：一个画家有14个边长为1m的正方体，他在地面上把它们摆成如图所示的形式，然后他把露出的表面都涂上颜色，那么被涂上颜色的总面积为（）A. 19m2B. 21m2C. 33m2D. 34m2。

简单三视图练习题航空航天工程是一个非常庞大而复杂的行业，设计和制造飞行器需要各种各样的技术和工具。

其中，简单三视图是一种非常重要的设计工具，通过绘制飞行器的正视图、俯视图和侧视图来展示飞行器的外形和结构。

简单三视图练习题可以帮助工程师和学生熟悉这一工具，并提高他们的设计能力。

绘制简单三视图是学习航空航天工程的基础。

正视图通常是从前方观察飞行器，俯视图是从上方观察，侧视图则是从侧面观察。

通过绘制这三个视图，我们可以清楚地了解飞行器的形状、尺寸和结构。

练习题一：绘制一个简单的长方形盒子的三视图。

首先，我们可以从正视图开始。

在纸上绘制一个长方形，表示盒子的前视图。

确保长度和宽度的比例正确，并标记好尺寸。

接下来，绘制一个顶视图。

从盒子的上方观察，绘制一个和前视图一样的长方形，但是没有前视图上的高度。

最后，绘制一个侧视图，从盒子的一侧观察，绘制一个和前视图一样的长方形，但是没有前视图上的宽度。

确保三个视图都符合比例和尺寸标记。

练习题二：绘制一个简单的飞机的三视图。

这个练习题更加复杂，但是非常有趣。

首先，从正视图开始。

绘制一个较长的矩形表示机身。

接下来，在机身前端绘制两个小矩形，表示机头。

在机身后端绘制一个小矩形，表示机尾。

绘制一个较大的矩形表示机翼，连接在机身上。

在机翼前部和后部绘制一个小矩形，表示机翼的前缘和后缘。

最后，绘制两根直线表示垂直尾翼和水平尾翼。

然后，绘制飞机的俯视图。

在纸上绘制一个矩形，表示飞机的顶部。

继续绘制直线连接机头和机尾，表示机身。

在机身两侧绘制两根曲线，表示机翼的外形。

最后，用两个小圆圈表示垂直尾翼和水平尾翼。

最后，绘制飞机的侧视图。

在纸上绘制一个长方形，表示飞机的高度和宽度。

绘制一个小圆圈表示机头。

在长方形上方绘制一个类似三角形的形状，表示机翼的外形。

在长方形下方绘制一个小圆圈表示机尾。

在长方形的后方绘制两个小曲线，表示垂直尾翼和水平尾翼。

通过完成这些练习题，我们可以更好地理解和运用简单三视图的知识。