锐角三角函数(特殊值)

【基础知识回顾】一、锐角三角函数定义：1.在Rt △ABC 中，∠C=900, ∠A 、∠B 、∠C 的对边分别为a 、b 、c ，则∠A 的正弦可表示为： sinA= ，∠A 的余弦可表示为cosA= ∠A 的正切：tanA= ， 它们统称为∠A 的锐角三角函数二、特殊角的三角函数值：2、正弦和正切值随着角度的增大而 余弦值随着角度的增大而3、几个特殊关系：⑴sin 2A+cos 2A= , tanA =sin A （ ） ⑵若∠A+∠B=900，则sinA= ，tanA.tanB =三、解直角三角形：1、定义：由直角三角形中除直角外的 个已知元素，求出另外 个未知元素的过程叫解直角三角形。

2、解直角三角形的依据：Rt ∠ABC 中，∠C=900 三边分别为a 、b 、c⑴三边关系：⑵两锐角关系⑶边角之间的关系：sinA cosA tanAsinB cosB tanB3、解直角三角形应用中的有关概念 ⑴仰角和俯角：如图：在图上标上仰角和俯角⑵坡度坡角：如图： 斜坡AB 的垂直度h 和水平宽度l 的比叫做坡度，用i 表示，即i= 坡面与水平面得夹角为 用字母α表示，则i=tanα=h l。

经典例题1.如图，将∠AOB 放置在5×5的正方形网格中，则tan ∠AOB 的值是（ ）A ．23B ．32C ．21313D ．313132.计算6tan45°-2cos60°的结果是（ ）A ．43B ．4C ．53D ．5αsinα cosα tanα 300450600铅直水平线 视线3.如图，四边形ABCD的对角线AC，BD相交于点O，且BD平分AC．若BD=8，AC=6，∠BOC=120°，则四边形ABCD的面积为．（结果保留根号）4.河堤横断面如图所示，堤高BC=6米，迎水坡AB的坡比为1：3，则AB的长为（）A．12 B．43米C．53米D．63米5.一渔船在海岛A南偏东20°方向的B处遇险，测得海岛A与B的距离为20海里，渔船将险情报告给位于A处的救援船后，沿北偏西80°方向向海岛C靠近，同时，从A处出发的救援船沿南偏西10°方向匀速航行，20分钟后，救援船在海岛C处恰好追上渔船，那么救援船航行的速度为（）A．103海里/小时B．30海里/小时C．203海里/小时D．303海里/小时6.某校研究性学习小组测量学校旗杆AB的高度，如图在教学楼一楼C处测得旗杆顶部的仰角为60°，在教学楼三楼D处测得旗杆顶部的仰角为30°，旗杆底部与教学楼一楼在同一水平线上，已知每层楼的高度为3米，则旗杆AB的高度为米．7.如图，某海监船向正西方向航行，在A处望见一艘正在作业渔船D在南偏西45°方向，海监船航行到B处时望见渔船D在南偏东45°方向，又航行了半小时到达C处，望见渔船D在南偏东60°方向，若海监船的速度为50海里/小时，则A，B之间的距离为（取3≈1.7，结果精确到0.1海里）．D8.如图，一艘海上巡逻船在A地巡航，这时接到B地海上指挥中心紧急通知：在指挥中心北偏西60°方向的C地，有一艘渔船遇险，要求马上前去救援．此时C地位于北偏西30°方向上，A地位于B地北偏西75°方向上，A、B两地之。

锐角三角函数的定义•锐角三角函数：锐角角A的正弦（sin）,余弦（cos）和正切（tan）,余切（cot）以及正割（sec），余割（csc）都叫做角A的锐角三角函数。

初中学习的锐角三角函数值的定义方法是在直角三角形中定义的，所以在初中阶段求锐角的三角函数值，都是通过构造直角三角形来完成的，即把这个角放到某个直角三角形中。

所谓锐角三角函数是指：我们初中研究的都是锐角的三角函数。

初中研究的锐角的三角函数为：正弦（sin），余弦（cos），正切（tan）。

正弦：在直角三角形中，锐角A的对边与斜边的比叫做∠A的正弦，记作sinA，即；余弦：在直角三角形中，锐角A的邻边与斜边的比叫做∠A的余弦，记作cosA，即；正切：在直角三角形中，锐角A的对边与邻边的比叫做∠A的正切，记作tanA，即，锐角A的正弦、余弦、正切都叫做A的锐角三角函数。

•锐角三角函数的增减性：°～90°°≤A≤90°间变化时，0≤sinA≤1, 1≥cosA≥0；当角度在0°<A0, cotA>0。

•锐角三角函数的关系式：同角三角函数基本关系式tanα·cotα=1sin2α·cos2α=1cos2α·sin2α=1sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα(sinα)2+(cosα)2=11+tanα=secα1+cotα=cscα诱导公式sin（－α）=－sinαcos（－α）=cosαtan（－α）=－tanαcot（－α）=－cotαsin（π/2－α）=cosαcos（π/2－α）=sinαtan（π/2－α）=cotαcot（π/2－α）=tanαsin（π/2+α）=cosαcos（π/2+α）=－sinαtan（π/2+α）=－cotαcot（π/2+α）=－tanαsin（π－α）=sinαcos（π－α）=－cosαtan（π－α）=－tanαcot（π－α）=－cotαsin（π+α）=－sinαcos（π+α）=－cosαtan（π+α）=tanαcot（π+α）=cotαsin（3π/2－α）=－cosαcos（3π/2－α）=－sinαtan（3π/2－α）=cotαcot（3π/2－α）=tanαsin（3π/2+α）=－cosαcos（3π/2+α）=sinαtan（3π/2+α）=－cotαcot（3π/2+α）=－tanαsin（2π－α）=－sinαcos（2π－α）=cosαtan（2π－α）=－tanαcot（2π－α）=－cotαsin（2kπ+α）=sinαcos（2kπ+α）=cosαtan（2kπ+α）=tanαcot（2kπ+α）=cotα(其中k∈Z)二倍角、三倍角的正弦、余弦和正切公式Sin(2α)=2sinαcosαCos(2α)=（cosα）2－(sinα)2=2(cosα)2－1=1－2(sinα)2Tan(2α)=2tanα/(1tanα)sin(3α)=3sinα4sin3α=4sinα·sin(60°+α)sin(60°α)cos(3α)=4cos3α3cosα=4cosα·cos(60°+α)cos(60°α)tan(3α)=(3tanαtan3α)/(13tan2α)=tanαtan(π/3+α)tan(π/3α) 和差化积、积化和差公式sinα+sinβ=2sin[(α+β)/2]·cos[(αβ)/2]sinαsinβ=2cos[(α+β)/2]·sin[(αβ)/2]cosα+cosβ=2cos[(α+β)/2]·cos[(αβ)/2]cosαcosβ=2sin[(α+β)/2]·sin[(αβ)/2]sinαcosβ=[sin（α+β）+sin（α－β）]sinαsinβ=[1][cos（α+β）cos（αβ）]/2cosαcosβ=[cos（α+β）+cos（αβ）]/2sinαcosβ=[sin（α+β）+sin（αβ）]/2cosαsinβ=[sin（α+β）sin（αβ）]/2。

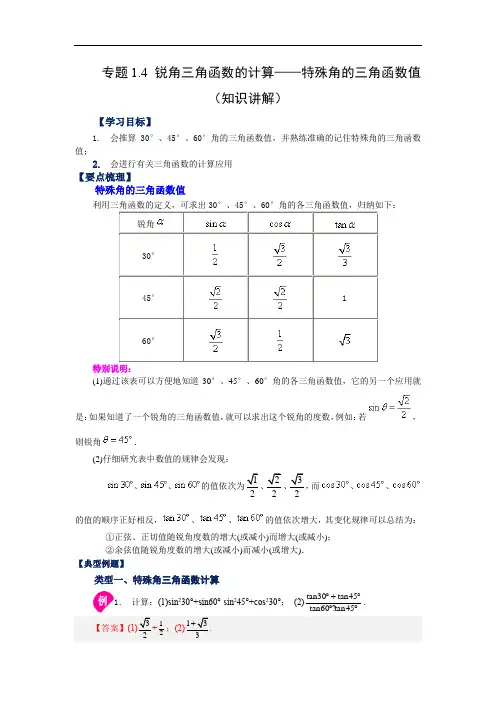
专题1.4 锐角三角函数的计算——特殊角的三角函数值（知识讲解）【学习目标】1.会推算30°、45°、60°角的三角函数值，并熟练准确的记住特殊角的三角函数值；2.会进行有关三角函数的计算应用【要点梳理】特殊角的三角函数值锐角30°45° 160°特别说明：(1)通过该表可以方便地知道30°、45°、60°角的各三角函数值，它的另一个应用就是：如果知道了一个锐角的三角函数值，就可以求出这个锐角的度数，例如：若，则锐角．(2)仔细研究表中数值的规律会发现：、、的值依次为12、22、32，而、、的值的顺序正好相反，、、的值依次增大，其变化规律可以总结为：①正弦、正切值随锐角度数的增大(或减小)而增大(或减小)；②余弦值随锐角度数的增大(或减小)而减小(或增大)．【典型例题】类型一、特殊角三角函数计算1．计算：(1)sin230°+sin60°-sin245°+cos230°；(2)tan30tan45 tan60?tan45︒+︒︒︒.【答案】(1)32+12；(2)133+.【分析】（1）将特殊角的三角函数值代入求解；（2）将特殊角的三角函数值代入求解．特殊值：sin 30° =12；sin 60° = 32；sin 45° = 22；cos 30° = 32；tan 60° = 3；tan 45° = 1解：(1)原式=1342+-12+34=32 + 12； 3133?1+（2）原式= =133+. 【点拨】本题考查了特殊角的三角函数值，解答本题的关键是掌握几个特殊角的三角函数值．举一反三：【变式1】计算：222sin 60cos 60︒︒︒︒-﹣sin45°•tan45° 【答案】3232+ 【分析】把特殊角的三角函数值代入计算即可．解：222sin 60cos 60tan 604cos 45︒︒︒︒--﹣sin45°•tan45° ()22312222122342⎛⎫⨯- ⎪⎝⎭=-⨯-⨯ 122322=-- 23222=+-=3232+． 【点拨】本题考查了特殊角的三角函数值及分母有理化、二次根式的化简，牢记特殊角的三角函数值，是解决本题的关键．【变式2】计算：2cos45°﹣tan60°+sin30°﹣12tan45°【答案】2-3【分析】将各特殊角的三角函数值代入即可得出答案．解：原式=2×22﹣3+12﹣12×1 =2-3【点拨】此题考查特殊角的三角函数值，属于基础题，熟练记忆一些特殊角的三角函数值是关键．类型二、特殊角三角函数计算2．计算：()2012sin 451220202π-︒⎛⎫----+- ⎪⎝⎭ 【答案】-2【分析】直接利用特殊角的三角函数值、绝对值的性质、零指数幂的性质、负整数指数幂的性质分别代入化简即可．解：原式＝24121-+-+=-2【点拨】此题主要考查了实数运算，正确化简各数是解题关键．举一反三：【变式1】计算：0113tan 30(2014π)32()3-︒---． 【答案】-2试题分析：分别计算033tan3033=⨯，(2014-π)0=1，32-=2﹣11333-⎛⎫= ⎪⎝⎭，，再用实数的混合运算法则计算.解：原式=3×33﹣1+2﹣3﹣3=﹣2. 【变式2】计算：()()2(31)3tan3052522sin60+--++． 【答案】3试题分析：用完全平方公式、平方差公式去括号，计算出特殊角三角函数值，再进行乘法运算，最后进行加减运算即可.解：(3－1)2+3tan 30°－(5－2)( 5+2)+2sin 60°=4－23+3×33－(5－4)+2×32=4－23+3－1+3=3.【点拨】掌握二次根式的加减乘除运算法则.类型三、三角函数计算3． 已知A ∠为锐角，且24sin 30A -=，则A ∠=______． 【答案】60︒【分析】计算，并结合A ∠是个锐角，即可求解．解：∵24sin 30A -=，∵23sin 4A =， ∵3sin 2A =±， ∵A ∠为锐角，∵3sin 2A =， ∵60A ∠=︒故答案是：60°【点拨】本题主要考察计算和锐角三角函数与角度关系，属于基础的计算题，难度不大．解题的关键是结合角度范围确定三角函数值范围．举一反三：【变式1】已知矩形ABCD 的周长为()232cm ，对角线2cm AC =，求BAC ∠与DAC ∠的度数． 【答案】30BAC ∠=︒，60=︒∠DAC 或60BAC ∠=︒，30DAC ∠=︒．【分析】设AB=x,将BC 表示出来，再利用勾股定理可求出x=1或x=3,再利用三角函数求出一个角为30°，另一个角为60°.解：∵矩形ABCD 的周长为232+，∵AB+BC= 3+1,∵对角线AC=2,∵设AB=x,则BC=3+1-x,∵AB 2+BA 2=AC 2,∵x 2+(3+1-x)2=22,解得：x 1=1,x 2=3,∵当AB=1,则BC=3,∵tan∵BAC=3,∵∵BAC=60°,∵DAC=30°,当AB=3,则BC=1,∵tan∵BAC= 33, ∵∵BAC=30°,∵DAC=60°,故30BAC ∠=︒，60=︒∠DAC 或60BAC ∠=︒，30DAC ∠=︒． 【点拨】此题主要考查了勾股定理和特殊角的三角函数值，解答本题的关键是掌握特殊角的三角函数值．【变式2】计算(1)23602cos 30tan 45︒-︒+︒(2)已知α是锐角，且()1sin 152α-︒=84cos α的值． 【答案】(1)1 (2)0【分析】（1）把特殊角的三角函数值代入代数式进行计算即可；（2）先利用锐角的正弦求解α的大小，再代入代数式进行计算即可．(1)解：23sin 602cos 30tan 45︒-︒+︒ 23332122331122(2) α是锐角，且()1sin 152α-︒=，1530,=45,∴ 84cos α-2224222220=-=【点拨】本题考查的是特殊角的三角函数值的混合运算，已知三角函数值求解锐角的大小，熟记特殊角的三角函数值是解本题的关键．类型四、三角函数计算4．（1）计算：21122cos453-⎛⎫--︒+-⎪⎝⎭．（2）如图，在△ABC中，∵ACB=90°，角平分线AE与高CD交于点F，求证：CE=CF．【答案】（1）8；（2）见分析【分析】（1）计算绝对值、特殊角的三角函数值、负整数指数幂，再合并即可；（2）根据直角三角形两锐角互余求得∵B=∵ACD，然后根据三角形外角的性质求得∵CEF=∵CFE，根据等角对等边求得CE=CF．（1）解：21 122cos453-⎛⎫--︒+-⎪⎝⎭221292=--⨯+2129=--+=8；（2）证明：∵在△ABC中，∵ACB=90°，∵∵B+∵BAC=90°，∵CD是AB边上的高，∵∵ACD+∵BAC=90°，∵∵B=∵ACD，∵AE是∵BAC的角平分线，∵∵BAE=∵EAC，∵∵B +∵BAE =∵ACD +∵EAC ，即∵CEF =∵CFE ，∵CE =CF ．【点拨】本题考查了特殊角的三角函数值，负整数指数幂，直角三角形的性质，三角形外角的性质，等腰三角形的判定等，熟练掌握性质定理是解题的关键．举一反三：【变式1】如图，将∵ABC 沿射线AB 平移4cm 后能与∵BDE 完全重合，连接CE 、CD 交BE 于点O ，OB ＝OC ．(1)求证：四边形CBDE 为矩形；(2)若S △BOC 432，求∵ACD 的度数． 【答案】(1)见分析(2)120°【分析】（1）由平移的性质及ASA判定定理可证得OCE ODB ≌，根据全等三角形的性质即可求证结论．（2）根据矩形的性质及面积公式即可求得BC ，进而可利用特殊三角函数值可求得60BCD ∠=︒，根据垂直平分线的性质即可求解．（1）证明：由题意可知：△BDE 由△ABC 平移后得到，∵//BC DE ，且BC DE =，∵四边形CBDE 是平行四边形，∵//CE BD ，且CE BD =，∵ECD CDB ∠=∠，CEB EBD ∠=∠，在OCE 和ODB △中 ECD CDB CE BDCEB EBD ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∵ ()OCE ODB ASA ≌∵OC OD =，OB OE =，又∵OB OC =，∵CD BE =，∵ 平行四边形CBDE 为矩形．（2）由（1）可知四边形CBDE 为矩形，∵90CBD ∠=︒，且4BD =cm ，在OBC 中过点O 作BC 的垂线，垂足为F ，则2OF =，∵143223BOC S BC =⨯⨯=，∵433BC =cm ， ∵在Rt CBD △，43433BD tan BCD CB ∠===，∵60BCD ∠=︒，又∵在△ACD 中，BC 是AD 的垂直平分线，∵60ACB BCD ∠=∠=︒，∵120ACD ∠=︒，∴∵ACD 的度数为120︒．【点拨】本题考查了平移的性质、全等三角形的判定及性质、矩形的判定及性质、特殊三角函数值求角度，熟练掌握相关性质及判定定理是解题的关键．【变式2】将矩形ABCD 对折，使AD 与BC 重合，得到折痕EF ，展开后再一次折叠，使点A 落在EF 上的点A '处，并使得折痕经过点B ，得到折痕BG ，连接AA '，如图1，问题解决：(1)试判断图1中ABA '△是什么特殊的三角形？并说明理由；(2)如图2，在图1的基础上，AA '与BG 相交于点N ，点P 是BN 的中点，连接AP 并延长交BA '于点Q ，求BQ BA '的值．【答案】(1)ABA '△是等边三角形，理由见分析(2)13BQ BA =' 【分析】（1）等边三角形，解法一利用垂直平分线性质得出AA ′=BA ′，利用折叠得出BA BA '=即可，解法二：根据折叠得出12BE BA =，BA BA '=，90A EB '∠=︒然后利用锐角三角函数定义得出1cos 2BE A BE BA '∠==' ，求出60A BE '∠=︒即可； （2）解法一：过点N 作NH A B '∥交AP 于H ，先证PHN PQB ≌△△（AAS ），再证AHN AQA '∽△△，得出12BQ QA =' 即可 解法二：由折叠可知A N AN '=，由点P 是BN 的中点 ，得出BP PN =，利用平行线等分性质得出1A M A N QM AN ''==，1BQ BP QM PN ==，证出BQ QM A M '==即可．(1)解：ABA '△是等边三角形．解法一：理由是：由折叠可知EF 垂直平分AB ；∵AA ′=BA ′，∵∵ABG 折叠得△A ′BG ，∵BA BA '=，∵AA BA BA ''==；∵ABA '△是等边三角形；解法二：理由是：由折叠可知12BE BA =，BA BA '=，90A EB '∠=︒， ∵1cos 2BE A BE BA '∠==' ， ∵60A BE '∠=︒，∵ABA '△是等边三角形；(2)解法一：过点N 作NH A B '∥交AP 于H ，∵HNP QBP ∠=∠，NHP BOP ∠=∠， 又∵点P 是BN 的中点 ， ∵BP NP =，在△PHN 和△PQB 中， HNP QBP NHP BQP PN PB ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∵PHN PQB ≌△△（AAS ）， ∵HN BQ =，又∵NH A B '∥，∵ANH AA Q '∠=∠，AHN AQA '∠=∠， ∵AHN AQA '∽△△， 由折叠可知12A N AN AA ''==， ∵12HN AN QA AA =='' ， ∵12BQ QA ='， ∵13BQ BA ='； 解法二：由折叠可知A N AN '=， 又∵点P 是BN 的中点 ， ∵BP PN =，过点N 作NM AQ ∥交BA '于M ， ∵1A M A N QM AN''==，1BQ BP QM PN ==， ∵BQ QM A M '==， ∵13BQ BA ='．【点拨】本题考查一题多解，等边三角形的判定，折叠性质，线段垂直平分线性质，平行线等分线段定理，三角形相似判定与性质，锐角三角函数值求角，掌握一题多解，等边三角形的判定，折叠性质，线段垂直平分线性质，平行线等分线段定理，三角形相似判定与性质是解题关键．。

锐角三角形必背知识点1 定义直角三角形中角A的正弦（sin）,余弦（cos）和正切（tan）叫做角A的三角函数。

正弦（sin）等于对边比斜边；sinA=a/c余弦（cos）等于邻边比斜边；cosA=b/c正切（tan）等于对边比邻边；tanA=a/b锐角三角函数值的定义方法是在直角三角形中定义的，所以求锐角的三角函数值，要通过构造直角三角形来完成的，即把这个角放到某个直角三角形中。

2 特殊角的三角函数值角度30°45°60°正弦(sin) 1/2 √2/2 √3/2余弦(cos) √3/2 √2/2 1/2正切(tan) √3/3 1 √3（注θ是锐角：0<sinθ<1 0<cosθ<1 tanθ>0）3锐角三角函数值的符号及其变化规律1）锐角三角函数值都是正值。

2）当角度在0°~90°间变化时，正弦值随着角度的增大（或减小）而增大（或减小）；余弦值随着角度的增大（或减小）而减小（或增大）；正切值随着角度的增大（或减小）而增大（或减小）；4同角三角函数基本关系式a a a tan cos sin ⋅=5互为余角的三角函数间的关系a a cos )90sin(=-a a sin )90cos(=-6 解直角三角形的基础知识在Rt ABC ∆中， 90=∠C ，A ∠，B ∠，C ∠所对的边分别为a ，b ，c（1） 三边之间的关系：222c b a =+（2） 锐角之间的关系：A ∠+B ∠=C ∠= 90（3） 边角之间的关系：c a A =sin ；c b A =cos ；ba A =tan ； c a B =cos ；c b B =sin ；ab B =tan （4） 面积公式：ch ab S 2121==∆（h 为斜边上的高） 7 解直角三角形的基本类型及其解法如下表：解直角三角形的思路可概括为“有斜（斜边）用弦（正弦、余弦），无斜用切（正切），宁乘勿除，取原避中”。

锐角三角函数知识点总结一、引言锐角三角函数是数学中的基础知识点，它在解决与直角三角形相关的问题中扮演着重要角色。

本文将总结锐角三角函数的基本概念、性质和公式，以及它们在实际问题中的应用。

二、基本概念1. 锐角：角度小于90度的角。

2. 直角三角形：一个角为90度的三角形。

3. 边的命名：- 对边（Opposite side）：锐角所对的边。

- 邻边（Adjacent side）：锐角旁边的边，但不包括斜边。

- 斜边（Hypotenuse）：直角三角形中最长的边，对直角的两边进行闭合。

4. 锐角三角函数：- 正弦（Sine, sin）：锐角的对边与斜边的比值。

- 余弦（Cosine, cos）：锐角的邻边与斜边的比值。

- 正切（Tangent, tan）：锐角的对边与邻边的比值。

三、基本公式1. 定义公式：- sin(θ) = 对边 / 斜边- cos(θ) = 邻边 / 斜边- tan(θ) = 对边 / 邻边2. 互余关系：- sin(90° - θ) = cos(θ)- cos(90° - θ) = sin(θ)- tan(90° - θ) = cot(θ)3. 基本恒等式：- sin²(θ) + cos²(θ) = 1- 1 + tan²(θ) = sec²(θ)- 1 + cot²(θ) = csc²(θ)4. 特殊角的三角函数值：- sin(30°) = 1/2, cos(30°) = √3/2, tan(30°) = √3/3 - sin(45°) = √2/2, cos(45°) = √2/2, tan(45°) = 1- sin(60°) = √3/2, cos(60°) = 1/2, tan(60°) = √3四、应用1. 解直角三角形问题：- 利用三角函数求解边长。

三角函数值大全(总7页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--三角函数值大全（1）特殊角三角函数值sin0=0,sin15=（√6-√2)/4 ,sin30=1/2,sin45=√2/2,sin60=√3/2,sin75=(√6+√2)/2 ,sin90=1,sin105=√2/2*(√3/2+1/2)sin120=√3/2sin135=√2/2sin150=1/2sin165=（√6-√2)/4sin180=0sin270=-1sin360=0cos0=1cos30= 二分之根号3cos45= 二分之根号2cos60=cos90=0tan0=0tan30= 三分之根号3tan45=1tan60= 根号3tan90=无cot0=无cot30= 根号3cot45=1cot60= 三分之根号3cot90=0（2）0°～90°的任意角的三角函数值，查三角函数表。

（3）锐角三角函数值的变化情况（i）锐角三角函数值都是正值（ii）当角度在0°～90°间变化时，正弦值随着角度的增大（或减小）而增大（或减小）余弦值随着角度的增大（或减小）而减小（或增大）正切值随着角度的增大（或减小）而增大（或减小）余切值随着角度的增大（或减小）而减小（或增大）（iii）当角度在0°≤α≤90°间变化时，0≤sinα≤1, 1≥cosα≥0,当角度在0°<α<90°间变化时，tanα>0, cotα>0.附：三角函数值表sin1= sin2= sin3=sin4= sin5= sin6=sin7= sin8= sin9=sin10= sin11= sin12=sin13= sin14= sin15=sin16= sin17= sin18=sin19=0. sin20=0. sin21= sin22= sin23= sin24=sin25= sin26= sin27=sin28= sin29= sin30=sin31= sin32= sin33=sin34= sin35= sin36=0. sin37= sin38= sin39=0. sin40=0. sin41=0. sin42= sin43= sin44= sin45=sin46= sin47= sin48=sin49= sin50= sin51=sin52= sin53= sin54=sin55= sin56=0. sin57=0. sin58= sin59= sin60=0.sin61= sin62=0. sin63=sin64= sin65=0. sin66=sin67=0. sin68= sin69=0. sin70= sin71= sin72=sin73=0. sin74= sin75=0. sin76=0. sin77=0. sin78= sin79= sin80= sin81=sin82=0. sin83= sin84=sin85= sin86= sin87=0.sin88=0. sin89=0.sin90=1cos1=0. cos2=0. cos3=0. cos4= cos5= cos6=cos7= cos8=0. cos9=cos10= cos11= cos12=cos13=0. cos14=0. cos15=0. cos16= cos17=0. cos18=cos19= cos20= cos21=0.cos22= cos23=0. cos24=cos25=0. cos26= cos27=cos28= cos29= cos30=0.cos31= cos32= cos33=cos34=0. cos35= cos36=cos37= cos38= cos39=cos40= cos41= cos42=cos43= cos44= cos45=cos46= cos47= cos48=cos49=0. cos50=0. cos51=0. cos52= cos53= cos54=0.cos55=0. cos56= cos57=0. cos58= cos59= cos60=cos61= cos62= cos63=0.cos64= cos65= cos66=0.cos67= cos68=0. cos69=cos70=0. cos71= cos72=cos73= cos74= cos75=cos76= cos77= cos78=cos79= cos80= cos81=cos82= cos83= cos84=cos85= cos86= cos87=cos88= cos89=cos90=0tan1= tan2= tan3=tan4= tan5= tan6=tan7= tan8= tan9=tan10= tan11= tan12=tan13=0. tan14= tan15=0. tan16=0. tan17= tan18=tan19= tan20= tan21=0.tan22=0. tan23=0. tan24=0. tan25=0. tan26=0. tan27=0. tan28= tan29= tan30=0.tan31=0. tan32=0. tan33=0. tan34=0. tan35=0. tan36=0. tan37= tan38= tan39=0.tan40=0. tan41=0. tan42=0. tan43= tan44=0. tan45=0. tan46= tan47= tan48=tan49= tan50= tan51=tan52= tan53=1. tan54=tan55= tan56=1. tan57=1. tan58=1. tan59=1. tan60=1. tan61=1. tan62=1. tan63= tan64= tan65= tan66=tan67= tan68=2. tan69=2. tan70=2. tan71= tan72=tan73=3. tan74= tan75=3. tan76= tan77= tan78=tan79= tan80= tan81=tan82= tan83= tan84=tan85= tan86= tan87=tan88= tan89=tan90=无取值。