第三次数模作业

第一次作业1、光电检测技术有何特点？光电检测系统的基本组成是怎样的？答：光电检测技术是将光学技术与现代技术相结合，以实现对各种量的测量，它具有如下特点：（1）高精度，光电测量是各种测量技术中精度最高的一种。

（2）高速度，光电检测以光为媒介，而光是各种物质中传播速度最快的，因此用光学方法获取和传递信息的速度是最快的。

（3）远距离、大量程，光是最便于远距离传递信息的介质，尤其适用于遥控和遥测。

（4）非接触式测量，不影响到被测物体的原始状态进行测量。

光电检测系统通过接收被测物体的光辐射，经光电检测器件将接收到的光辐射转换为电信号，再通过放大、滤波等电信号调理电路提取有用信息，经数模转换后输入计算机处理，最后显示，输出所需要的检测物理量等参数。

2、什么是能带、允带、禁带、满带、价带和导带？绝缘体、半导体、导体的能带情况有何不同？答:晶体中电子所能具有的能量范围，在物理学中往往形象化地用一条条水平横线表示电子的各个能力值，能量愈大,线的位置愈高,一定能量范围内的许多能级（彼此相隔很近）形成一条带,称为能带。

其中允许被电子占据的能带称为允带。

允带之间的范围是不允许电子占据的，称为禁带。

在晶体中电子的能量状态遵守能量最低原理和泡利不相容原理，晶体最外层电子壳层分裂所形成的能带称为价带。

价带可能被电子填满也可能不被填满，其中被填满的能带称为满带。

半导体的价带收到光电注入或热激发后，价带中的部分电子会越过禁带进入能量较高的空带，空带中存在电子后即成为导电的能带--导带。

对绝缘体和半导体，它的电子大多数都处于价带，不能自由移动，但是热，光等外界因素的作用下，可以少量价带中的电子越过禁带，跃迁到导带上去成为载流子。

绝缘体和半导体的区别主要是禁的宽度不同。

半导体的禁带很窄，绝缘体的禁带宽一些，电子的跃迁困难的多，因此，绝缘体的载流子的浓度很小。

导电性能很弱。

实际绝缘体里，导带里电子不是没有，并且总有一些电子会从价带跃迁到导带，但数量极少，所以，在一般情况下，可以忽略在外场作用下他们移动所形成的电流。

院系：数学学院专业：信息与计算科学年级：2014级学生姓名：***学号：************ 教师姓名：徐霞6.6 习题3.一个慢跑者在平面上沿着他喜欢的路径跑步，突然一只狗攻击他，这只狗以恒定速率跑向慢跑者，狗的运动方向始终指向慢跑者，计算并画出狗的轨迹。

解：（1）模型分析建立:狗的轨迹：在任意时刻，狗的速度向量都指向它的目标慢跑者。

假设1：慢跑者在某路径上跑步，他的运动由两个函数X(t)和Y(t)描述。

假设2：当t=0时，狗是在点(x0,y0)处，在时刻t时，它的位置是(x(t),y(t))那么下列方程成立：(1)狗以恒定速率跑: X’2+y’2=w2(2) 狗的速度向量平行于慢跑者与狗的位置的差向量：将上述方程带入等式：,可得：再将λ代入第二个方程，可得狗的轨迹的微分方程：（2）程序及结果dog函数[dog.m]function [zs,isterminal,direction] = dog(t,z,flag)global w;% w=speed of the dogX=jogger(t);h = X-z;nh=norm(h);if nargin<3 || isempty(flag)zs=(w/nh)*h;elseswitch(flag)case'events'zs = nh-1e-3;isterminal = 1;direction = 0;otherwiseerror(['Unknow flag:' flag]);end慢跑者的运动轨迹方程，水平向右[jogger.m]function s = jogger(t);s = [8*t;0];标记的函数[cross.m]function cross(Cx,Cy,v)Kx = [Cx Cx Cx Cx-v Cx+v];Ky = [Cy Cy+2.5*v Cy+1.5*v Cy+1.5*v Cy+1.5*v] plot(Kx,Ky);plot(Cx,Cy,'o');主程序：静态显示[main1.m]global wy0 = [60;70];w=10;options = odeset('RelTol',1e-5,'Events','on'); [t,Y] = ode23('dog',[0,20],y0,options);clf;hold on;axis([-10,100,-10,70]);plot(Y(:,1),Y(:,2));J=[];for h=1:length(t),w = jogger(t(h));J=[J;w'];endplot(J(:,1),J(:,2),':');p = max(size(Y));cross(Y(p,1),Y(p,2),2)hold off;动态显示[main2.m]global w;y0=[60;70];w=10;options = odeset('RelTol',1e-5,'Events','on'); [t,Y]=ode23('dog',[0,20],y0,options); J=[]; for h=1:length(t);w= jogger(t(h));J=[J;w'];xmin = min(min(Y(:,1)),min(J(:,1)));xmax = max(max(Y(:,1)),max(J(:,1)));ymin = min(min(Y(:,2)),min(J(:,2)));ymax = max(max(Y(:,2)),max(J(:,2)));clf;hold on;axis([xmin-10 xmax ymin-10 ymax]);title('The jogger and the Dog');for h = 1:length(t)-1,plot([Y(h,1),Y(h+1,1)],[Y(h,2),Y(h+1,2)],'-','Color','red','EraseMode ','none');plot([J(h,1),J(h+1,1)],[J(h,2),J(h+1,2)],'-','Color','green','EraseMo de','none');drawnow;pause(0.1);endplot(J(:,1),J(:,2),':');p = max(size(Y));cross(Y(p,1),Y(p,2),2)hold off;结果t=12.2761812635281，在12.27秒后狗追上慢跑者。

数据的插值和拟合一：拉格朗日插值多项式拉格朗日插值函数function y=lagrange(x0,y0,x);n=length(x0);m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif j~=kp=p*(z-x0(j))/(x0(k)-x0(j));endends=p*y0(k)+s;endy(i)=s;end>> x=[1800 2700];>> y=[32 112];>> x1=[1800 1890 1950 2020 2100 2130 2230 2470 2600 2700]; >> y1=lagrange(x,y,x1);>> p lot(x,y,'co')>> hold on>> plot(x1,y1,'y-*')>> x=[1800 2400 2650];>> y=[32 98 108];>> x1=[1800 1860 1920 2040 2130 2240 2310 2470 2550 2600]; >> y1=lagrange(x,y,x1);>> plot(x,y,'r+')>> plot(x1,y1,'g-s')>> x=[1800 2100 2400 2700];>> y=[32 75 98 112];>> x1=[1800 1890 1950 2090 2140 2230 2380 2470 2550 2650]; >> y1=lagrange(x,y,x1);>> plot(x,y,'bx')>> plot(x1,y1,'m-d')>> x=[1800 1900 2200 2400 2650];>> y=[32 60 85 98 108];>> x1=[1800 1845 1990 2080 2145 2350 2450 2500 2580 2650];>> y1=lagrange(x,y,x1);>> plot(x,y,'go')>> plot(x1,y1,'r-p')>> x=[1800 1900 2100 2300 2400 2700];>> y=[32 60 75 90 98 112];>> x1=[1800 1945 2034 2170 2225 2370 2470 2564 2620 2700];>> y1=lagrange(x,y,x1);>> plot(x,y,'cs')>> plot(x1,y1,'b:h')>> x=[1800 1900 2100 2200 2300 2500 2650];>> y=[32 60 75 85 90 100 108];>> x1=[1800 1910 1978 2098 2130 2265 2370 2400 2550 2650];>> y1=lagrange(x,y,x1);>> plot(x,y,'rx')>> plot(x1,y1,'c:o')>> x=[1800 1900 2100 2200 2300 2400 2600 2650];>> y=[32 60 75 85 90 98 102 108];>> x1=[1800 1878 1920 2067 2165 2230 2400 2540 2600 2650];>> y1=lagrange(x,y,x1);>> plot(x,y,'cs')>> plot(x1,y1,'g-.*')>> x=[1800 1900 2100 2200 2300 2400 2600 2650 2700];>> y=[32 60 75 85 90 98 102 108 112];>> x1=[1800 1930 2060 2265 2300 2470 2500 2580 2680 2700];>> y1=lagrange(x,y,x1);>> plot(x,y,'m<')>> plot(x1,y1,'b--o')>> x=[1800 1900 2100 2200 2300 2400 2500 2600 2650 2700];>> y=[32 60 75 85 90 98 100 102 108 112];>> x1=[1800 1940 2050 2100 2240 2370 2400 2560 2640 2700];>> y1=lagrange(x,y,x1);>> plot(x,y,'b>')>> plot(x1,y1,'c--s')>> hold off>> title('1-9次拉格朗日插值多项式曲线图及散点图')>> legend('1次散点','1次','2次散点','2次','3次散点','3次','4次散点','4次','5次散点','5次','6次散点','6次','7次散点','7次','8次散点','8次','9次散点','9次',4)二：牛顿插值多项式牛顿插值多项式函数function [p2,z]=newton(x,y,t)n=length(x);chaS(1)=y(1);for i=2:nx1=x;y1=y;x1(i+1:n)=[];y1(i+1:n)=[];n1=length(x1);s1=0;for j=1:n1t1=1;for k=1:n1if k==jcontinue;elset1=t1*(x1(j)-x1(k));endends1=s1+y1(j)/t1;endchaS(i)=s1;endb(1,:)=[zeros(1,n-1) chaS(1)];cl=cell(1,n-1);for i=2:nu1=1;for j=1:i-1u1=conv(u1,[1 -x(j)]);cl{i-1}=u1;endcl{i-1}=chaS(i)*cl{i-1};b(i,:)=[zeros(1,n-i),cl{i-1}];endp2=b(1,:);for j=2:np2=p2+b(j,:);endif length(t)==1rm=0;for i=1:nrm=rm+p2(i)*t^(n-i);endz=rm;elsek1=length(t);rm=zeros(1,k1);for j=1:k1for i=1:nrm(j)=rm(j)+p2(i)*t(j)^(n-i);endz=rm;endend>> x=[1800 2700];>> y=[32 112];>> x1=[1800 1890 1950 2020 2100 2130 2230 2470 2600 2700]; >> [p2,y1]=newton(x,y,x1);>> plot(x,y,'co')>> hold on>> plot(x1,y1,'y-*')>> x=[1800 2400 2650];>> y=[32 98 108];>> x1=[1800 1860 1920 2040 2130 2240 2310 2470 2550 2600]; >> [p2,y1]=newton(x,y,x1);>> plot(x,y,'r+')>> plot(x1,y1,'g-s')>> x=[1800 2100 2400 2700];>> y=[32 75 98 112];>> x1=[1800 1890 1950 2090 2140 2230 2380 2470 2550 2650]; >> [p2,y1]=newton(x,y,x1);>> plot(x,y,'bx')>> plot(x1,y1,'m-d')>> x=[1800 1900 2200 2400 2650];>> y=[32 60 85 98 108];>> x1=[1800 1845 1990 2080 2145 2350 2450 2500 2580 2650]; >> [p2,y1]=newton(x,y,x1);>> plot(x,y,'go')>> plot(x1,y1,'r-p')>> x=[1800 1900 2100 2300 2400 2700];>> y=[32 60 75 90 98 112];>> x1=[1800 1945 2034 2170 2225 2370 2470 2564 2620 2700]; >> [p2,y1]=newton(x,y,x1);>> plot(x,y,'cs')>> plot(x1,y1,'b:h')>> x=[1800 1900 2100 2200 2300 2500 2650];>> y=[32 60 75 85 90 100 108];>> x1=[1800 1910 1978 2098 2130 2265 2370 2400 2550 2650]; >> [p2,y1]=newton(x,y,x1);>> plot(x,y,'rx')>> plot(x1,y1,'c:o')>> x=[1800 1900 2100 2200 2300 2400 2600 2650];>> y=[32 60 75 85 90 98 102 108];>> x1=[1800 1878 1920 2067 2165 2230 2400 2540 2600 2650]; >> [p2,y1]=newton(x,y,x1);>> plot(x,y,'cs')>> plot(x1,y1,'g-.*')>> x=[1800 1900 2100 2200 2300 2400 2600 2650 2700];>> y=[32 60 75 85 90 98 102 108 112];>> x1=[1800 1930 2060 2265 2300 2470 2500 2580 2680 2700]; >> [p2,y1]=newton(x,y,x1);>> plot(x,y,'m<')>> plot(x1,y1,'b--o')>> x=[1800 1900 2100 2200 2300 2400 2500 2600 2650 2700]; >> y=[32 60 75 85 90 98 100 102 108 112];>> x1=[1800 1940 2050 2100 2240 2370 2400 2560 2640 2700]; >> [p2,y1]=newton(x,y,x1);>> plot(x,y,'b>')>> plot(x1,y1,'c--s')>> hold off>> title('1-9次牛顿插值多项式曲线图及散点图')>> legend('1次散点','1次','2次散点','2次','3次散点','3次','4次散点','4次','5次散点','5次','6次散点','6次','7次散点','7次','8次散点','8次','9次散点','9次',4)三：三次样条插值(csapi)>> x=[1800 2700];>> y=[32 112];>> x1=[1800 1890 1950 2020 2100 2130 2230 2470 2600 2700];>> plot(x1,csapi(x,y,x1),'y-*',x,y,'co')>> hold on>> x=[1800 2400 2650];>> y=[32 98 108];>> x1=[1800 1860 1920 2040 2130 2240 2310 2470 2550 2600];>> plot(x1,csapi(x,y,x1),'g-s',x,y,'r+')>> x=[1800 2100 2400 2700];>> y=[32 75 98 112];>> x1=[1800 1890 1950 2090 2140 2230 2380 2470 2550 2650];>> plot(x1,csapi(x,y,x1),'m-d',x,y,'bx')>> x=[1800 1900 2200 2400 2650];>> y=[32 60 85 98 108];>> x1=[1800 1845 1990 2080 2145 2350 2450 2500 2580 2650];>> plot(x1,csapi(x,y,x1),'r-p',x,y,'go')>> x=[1800 1900 2100 2300 2400 2700];>> y=[32 60 75 90 98 112];>> x1=[1800 1945 2034 2170 2225 2370 2470 2564 2620 2700];>> plot(x1,csapi(x,y,x1),'b:h',x,y,'cs')>> x=[1800 1900 2100 2200 2300 2500 2650];>> y=[32 60 75 85 90 100 108];>> x1=[1800 1910 1978 2098 2130 2265 2370 2400 2550 2650];>> plot(x1,csapi(x,y,x1),'c:o',x,y,'rx')>> x=[1800 1900 2100 2200 2300 2400 2600 2650];>> y=[32 60 75 85 90 98 102 108];>> x1=[1800 1878 1920 2067 2165 2230 2400 2540 2600 2650];>> plot(x1,csapi(x,y,x1),'g-.*',x,y,'cs')>> x=[1800 1900 2100 2200 2300 2400 2600 2650 2700];>> y=[32 60 75 85 90 98 102 108 112];>> x1=[1800 1930 2060 2265 2300 2470 2500 2580 2680 2700];>> plot(x1,csapi(x,y,x1),'b--o',x,y,'m<')>> x=[1800 1900 2100 2200 2300 2400 2500 2600 2650 2700];>> y=[32 60 75 85 90 98 100 102 108 112];>> x1=[1800 1940 2050 2100 2240 2370 2400 2560 2640 2700];>> plot(x1,csapi(x,y,x1),'c--s',x,y,'b>')>> plot(x,y,'b>')>> plot(x1,y1,'c--s')>> hold off>> title('2-10组数据的三次样条插值多项式曲线图及散点图')>> legend('2组数据','2组数据散点','3组数据','3组数据散点','4组数据','4组数据散点','5组数据','5组数据散点','6组数据','6组数据散点','7组数据','7组数据散点','8组数据','8组数据散点','9组数据','9组数据散点','10组数据','10组数据散点',4)三次样条插值多项式（spline）x=[1800 2700];y=[32 112];x1=[1800 1890 1950 2020 2100 2130 2230 2470 2600 2700]; y1=interp1(x,y,x1,'spline');plot(x,y,'co')hold onplot(x1,y1,'y-*')x=[1800 2400 2650];y=[32 98 108];x1=[1800 1860 1920 2040 2130 2240 2310 2470 2550 2600]; y1=interp1(x,y,x1,'spline');plot(x,y,'r+')plot(x1,y1,'g-s')x=[1800 2100 2400 2700];y=[32 75 98 112];x1=[1800 1890 1950 2090 2140 2230 2380 2470 2550 2650]; y1=interp1(x,y,x1,'spline');plot(x,y,'bx')plot(x1,y1,'m-d')x=[1800 1900 2200 2400 2650];y=[32 60 85 98 108];x1=[1800 1845 1990 2080 2145 2350 2450 2500 2580 2650]; y1=interp1(x,y,x1,'spline');plot(x,y,'go')plot(x1,y1,'r-p')x=[1800 1900 2100 2300 2400 2700];y=[32 60 75 90 98 112];x1=[1800 1945 2034 2170 2225 2370 2470 2564 2620 2700]; y1=interp1(x,y,x1,'spline');plot(x,y,'cs')plot(x1,y1,'b:h')x=[1800 1900 2100 2200 2300 2500 2650];y=[32 60 75 85 90 100 108];x1=[1800 1910 1978 2098 2130 2265 2370 2400 2550 2650]; y1=interp1(x,y,x1,'spline');plot(x,y,'rx')plot(x1,y1,'c:o')x=[1800 1900 2100 2200 2300 2400 2600 2650];y=[32 60 75 85 90 98 102 108];x1=[1800 1878 1920 2067 2165 2230 2400 2540 2600 2650]; y1=interp1(x,y,x1,'spline');plot(x,y,'cs')plot(x1,y1,'g-.*')x=[1800 1900 2100 2200 2300 2400 2600 2650 2700];y=[32 60 75 85 90 98 102 108 112];x1=[1800 1930 2060 2265 2300 2470 2500 2580 2680 2700];y1=interp1(x,y,x1,'spline');plot(x,y,'m<')plot(x1,y1,'b--o')x=[1800 1900 2100 2200 2300 2400 2500 2600 2650 2700];y=[32 60 75 85 90 98 100 102 108 112];x1=[1800 1940 2050 2100 2240 2370 2400 2560 2640 2700];y1=interp1(x,y,x1,'spline');plot(x,y,'b>')plot(x1,y1,'c--s')hold offtitle('2-10组数据三次样条插值多项式曲线图及散点图')legend('2组数据散点','2组数据','3组数据散点','3组数据','4组数据散点','4组数据','5组数据散点','5组数据','6组数据散点','6组数据','7组数据散点','7组数据','8组数据散点','8组数据','9组数据散点','9组数据','10组数据散点','10组数据',4)四：分段线性插值多项式（linear）>> x=[1800 2700];>> y=[32 112];>> x1=[1800 1890 1950 2020 2100 2130 2230 2470 2600 2700];>> y1=interp1(x,y,x1,'linear');>> plot(x,y,'co')>> hold on>> plot(x1,y1,'y-*')>> x=[1800 2400 2650];>> y=[32 98 108];>> x1=[1800 1860 1920 2040 2130 2240 2310 2470 2550 2600]; >> y1=interp1(x,y,x1,'linear');>> plot(x,y,'r+')>> plot(x1,y1,'g-s')>> x=[1800 2100 2400 2700];>>y=[32 75 98 112];>> x1=[1800 1890 1950 2090 2140 2230 2380 2470 2550 2650]; >> y1=interp1(x,y,x1,'linear');>> plot(x,y,'bx')>> plot(x1,y1,'m-d')>> x=[1800 1900 2200 2400 2650];>> y=[32 60 85 98 108];>> x1=[1800 1845 1990 2080 2145 2350 2450 2500 2580 2650]; >> y1=interp1(x,y,x1,'linear');>> plot(x,y,'go')>> plot(x1,y1,'r-p')>> x=[1800 1900 2100 2300 2400 2700];>> y=[32 60 75 90 98 112];>> x1=[1800 1945 2034 2170 2225 2370 2470 2564 2620 2700]; >> y1=interp1(x,y,x1,'linear');>> plot(x,y,'cs')>> plot(x1,y1,'b:h')>> x=[1800 1900 2100 2200 2300 2500 2650];>> y=[32 60 75 85 90 100 108];>> x1=[1800 1910 1978 2098 2130 2265 2370 2400 2550 2650]; >> y1=interp1(x,y,x1,'linear');>> plot(x,y,'rx')>> plot(x1,y1,'c:o')>> x=[1800 1900 2100 2200 2300 2400 2600 2650];>> y=[32 60 75 85 90 98 102 108];>> x1=[1800 1878 1920 2067 2165 2230 2400 2540 2600 2650]; >> y1=interp1(x,y,x1,'linear');>> plot(x,y,'cs')>> plot(x1,y1,'g-.*')>> x=[1800 1900 2100 2200 2300 2400 2600 2650 2700];>> y=[32 60 75 85 90 98 102 108 112];>> x1=[1800 1930 2060 2265 2300 2470 2500 2580 2680 2700]; >> y1=interp1(x,y,x1,'linear');>> plot(x,y,'m<')>> plot(x1,y1,'b--o')>> x=[1800 1900 2100 2200 2300 2400 2500 2600 2650 2700]; >> y=[32 60 75 85 90 98 100 102 108 112];>> x1=[1800 1940 2050 2100 2240 2370 2400 2560 2640 2700]; >> y1=interp1(x,y,x1,'linear');>> plot(x1,y1,'c--s')>> hold off>> title('2-10组数据分段线性插值多项式曲线图及散点图')>> legend('2组数据散点','2组数据','3组数据散点','3组数据','4组数据散点','4组数据','5组数据散点','5组数据','6组数据散点','6组数据','7组数据散点','7组数据','8组数据散点','8组数据','9组数据散点','9组数据','10组数据散点','10组数据',4)分段线性插值函数（ppval）x=[1800 2700];y=[32 112];x1=[1800 1890 1950 2020 2100 2130 2230 2470 2600 2700];y1=interp1(x,y,x1,'ppval');plot(x,y,'co')hold onplot(x1,y1,'y-*')x=[1800 2400 2650];y=[32 98 108];x1=[1800 1860 1920 2040 2130 2240 2310 2470 2550 2600];y1=interp1(x,y,x1,'ppval');plot(x,y,'r+')plot(x1,y1,'g-s')x=[1800 2100 2400 2700];y=[32 75 98 112];x1=[1800 1890 1950 2090 2140 2230 2380 2470 2550 2650];y1=interp1(x,y,x1,'ppval');plot(x,y,'bx')x=[1800 1900 2200 2400 2650];y=[32 60 85 98 108];x1=[1800 1845 1990 2080 2145 2350 2450 2500 2580 2650];y1=interp1(x,y,x1,'ppval');plot(x,y,'go')plot(x1,y1,'r-p')x=[1800 1900 2100 2300 2400 2700];y=[32 60 75 90 98 112];x1=[1800 1945 2034 2170 2225 2370 2470 2564 2620 2700];y1=interp1(x,y,x1,'ppval');plot(x,y,'cs')plot(x1,y1,'b:h')x=[1800 1900 2100 2200 2300 2500 2650];y=[32 60 75 85 90 100 108];x1=[1800 1910 1978 2098 2130 2265 2370 2400 2550 2650];y1=interp1(x,y,x1,'ppval');plot(x,y,'rx')plot(x1,y1,'c:o')x=[1800 1900 2100 2200 2300 2400 2600 2650];y=[32 60 75 85 90 98 102 108];x1=[1800 1878 1920 2067 2165 2230 2400 2540 2600 2650];y1=interp1(x,y,x1,'ppval');plot(x,y,'cs')plot(x1,y1,'g-.*')x=[1800 1900 2100 2200 2300 2400 2600 2650 2700];y=[32 60 75 85 90 98 102 108 112];x1=[1800 1930 2060 2265 2300 2470 2500 2580 2680 2700];y1=interp1(x,y,x1,'ppval');plot(x,y,'m<')plot(x1,y1,'b--o')x=[1800 1900 2100 2200 2300 2400 2500 2600 2650 2700];y=[32 60 75 85 90 98 100 102 108 112];x1=[1800 1940 2050 2100 2240 2370 2400 2560 2640 2700];y1=interp1(x,y,x1,'ppval');plot(x,y,'b>')plot(x1,y1,'c--s')hold offtitle('2-10组数据分段线性插值多项式曲线图及散点图')legend('2组数据散点','2组数据','3组数据散点','3组数据','4组数据散点','4组数据','5组数据散点','5组数据','6组数据散点','6组数据','7组数据散点','7组数据','8组数据散点','8组数据','9组数据散点','9组数据','10组数据散点','10组数据',4)五：2点3次哈密特插值多项式哈密特插值函数function y=hermite(x0,y0,y1,x);n=length(x0);m=length(x);for k=1:myy=0.0;for i=1:nh=1.0;a=0.0;for j=1:nif j~=ih=h*((x(k)-x0(j))/(x0(i)-x0(j)))^2;a=1/(x0(i)-x0(j))+a;endendyy=yy+h*((x0(i)-x(k))*(2*a*y0(i)-y1(i))+y0(i));endy(k)=yy;end分段哈密特插值多项式（pchip）>> x=[1800 2700];>> y=[32 112];>> x1=[1800 1890 1950 2020 2100 2130 2230 2470 2600 2700]; >> y1=interp1(x,y,x1,'pchip');>> plot(x,y,'co')>> hold on>> plot(x1,y1,'y-*')>> x=[1800 2400 2650];>> y=[32 98 108];>> x1=[1800 1860 1920 2040 2130 2240 2310 2470 2550 2600]; >> y1=interp1(x,y,x1,'pchip');>> plot(x,y,'r+')>> plot(x1,y1,'g-s')>> x=[1800 2100 2400 2700];>> y=[32 75 98 112];>> x1=[1800 1890 1950 2090 2140 2230 2380 2470 2550 2650]; >> y1=interp1(x,y,x1,'pchip');>> plot(x,y,'bx')>> plot(x1,y1,'m-d')>> x=[1800 1900 2200 2400 2650];>> y=[32 60 85 98 108];>> x1=[1800 1845 1990 2080 2145 2350 2450 2500 2580 2650]; >> y1=interp1(x,y,x1,'pchip');>> plot(x,y,'go')>> plot(x1,y1,'r-p')>> x=[1800 1900 2100 2300 2400 2700];>> y=[32 60 75 90 98 112];>> x1=[1800 1945 2034 2170 2225 2370 2470 2564 2620 2700]; >> y1=interp1(x,y,x1,'pchip');>> plot(x,y,'cs')>> plot(x1,y1,'b:h')>> x=[1800 1900 2100 2200 2300 2500 2650];>> y=[32 60 75 85 90 100 108];>> x1=[1800 1910 1978 2098 2130 2265 2370 2400 2550 2650]; >> y1=interp1(x,y,x1,'pchip');>> plot(x,y,'rx')>> plot(x1,y1,'c:o')>> x=[1800 1900 2100 2200 2300 2400 2600 2650];>> y=[32 60 75 85 90 98 102 108];>> x1=[1800 1878 1920 2067 2165 2230 2400 2540 2600 2650]; >> y1=interp1(x,y,x1,'pchip');>> plot(x,y,'cs')>> plot(x1,y1,'g-.*')>> x=[1800 1900 2100 2200 2300 2400 2600 2650 2700];>> y=[32 60 75 85 90 98 102 108 112];>> x1=[1800 1930 2060 2265 2300 2470 2500 2580 2680 2700]; >> y1=interp1(x,y,x1,'pchip');>> plot(x,y,'m<')>> plot(x1,y1,'b--o')>> x=[1800 1900 2100 2200 2300 2400 2500 2600 2650 2700];>> y=[32 60 75 85 90 98 100 102 108 112];>> x1=[1800 1940 2050 2100 2240 2370 2400 2560 2640 2700];>> y1=interp1(x,y,x1,'pchip');>> plot(x,y,'b>')>> plot(x1,y1,'c--s')>> hold off>> title('2-10组数据两点三次哈密特插值多项式曲线图及散点图')>> legend('2组数据散点','2组数据','3组数据散点','3组数据','4组数据散点','4组数据','5组数据散点','5组数据','6组数据散点','6组数据','7组数据散点','7组数据','8组数据散点','8组数据','9组数据散点','9组数据','10组数据散点','10组数据',4)六：多项式拟合>> x=[1800 1900 2100 2200 2300 2400 2500 2600 2650 2700];>> y=[32 60 75 85 90 98 100 102 108 112];>> p=polyfit(x,y,1);>> x1=[1800 1940 2050 2100 2240 2370 2400 2560 2640 2700];>> y1=polyval(p,x1);>> plot(x,y,'co')>> hold on>> plot(x1,y1,'y-*')>> p=polyfit(x,y,2);>> y1=polyval(p,x1);>> plot(x,y,'r+')>> plot(x1,y1,'g-s')>> p=polyfit(x,y,3);>> y1=polyval(p,x1);>> plot(x,y,'bx')>> plot(x1,y1,'m-d')>> p=polyfit(x,y,4);>> y1=polyval(p,x1);>> plot(x,y,'go')>> plot(x1,y1,'r-p')>> p=polyfit(x,y,5);>> y1=polyval(p,x1);>> plot(x,y,'cs')>> plot(x1,y1,'b:h')>> p=polyfit(x,y,6);>> y1=polyval(p,x1);>> plot(x,y,'rx')>> plot(x1,y1,'c:o')>> p=polyfit(x,y,7);>> y1=polyval(p,x1);>> plot(x,y,'cs')>> plot(x1,y1,'g-.*')>> p=polyfit(x,y,8);>> y1=polyval(p,x1);>> plot(x,y,'m<')>> plot(x1,y1,'b--o')>> p=polyfit(x,y,9);>> y1=polyval(p,x1);>> plot(x,y,'b>')>> plot(x1,y1,'c--s')>> hold off>> title('10组数据1-9阶多项式拟合曲线图及散点图')>> legend('1阶拟合散点','1阶拟合','2阶拟合散点','2阶拟合','3阶拟合散点','3阶拟合','4阶拟合散点','4阶拟合','5阶拟合散点','5阶拟合','6阶拟合散点','6阶拟合','7阶拟合散点','7阶拟合','8阶拟合散点','8阶拟合','9阶拟合散点','9阶拟合',4)插值信息如下表所示：>> x=0:0.5*pi:3*pi;>> y=[4 5 4 3 4 5 4];>> x1=0:pi/10:3*pi;>> y1=lagrange(x,y,x1);>> plot(x1,y1,'g-s')>> s1=trapz(x1,y1)s1 =39.4886>> s=39.6991;>> s1=s-s1s1 =0.2105>> hold on>> di=[1 0 -1 0 1 0 -1];>> y1=hermite(x,y,di,x1);>> plot(x1,y1,'r-p')>> s2=trapz(x1,y1)s2 =39.6826>> s2=s-s2s2 =0.0165>> y1=interp1(x,y,x1,'spline') ;>> plot(x1,y1,'m-d')>> s3=trapz(x1,y1)s3 =39.9162>> s3=s-s3s3 =-0.2171>> hold off>> legend('拉格朗日曲线图','两点三次哈密特曲线图','三次样条曲线图')用拉格朗日插值多项式计算的面积为：S1= 39.4886拉格朗日插值多项式的误差为：S1(误差)=0.2105用两点三次哈密特插值多项式计算的面积为：S2= 39.6826两点三次哈密特插值多项式的误差为：S2(误差)=0.0165用三次样条插值多项式计算的面积为：S3= 39.9162三次样条插值多项式的误差为：S3(误差)=0.2171所以综上所述：与断面真实面积误差最小的是用两点三次哈密特插值多项式计算出来的面积误差大小为0.0165。

《数学模型》作业解答第一章（2008年9月9日）4．在“椅子摆放问题”的假设条件中，将四脚的连线呈正方形改为呈长方形，其余条件不变.试构造模型并求解.解：设椅子四脚连线呈长方形ABCD. AB 与CD 的对称轴为x 轴，用中心点的转角θ表示椅子的位置.将相邻两脚A 、B 与地面距离之和记为)(θf ;C 、D 与地面距离之和记为)(θg .并旋转0180.于是，设,0)0(,0)0(=g f 就得到()()0,0=ππf g .数学模型：设()()θθg f 、是[]π2,0上θ的非负连续函数.若[]πθ2,0∈∀,有()()0=θθg f ,且()()()()0,0,00,00==ππf g f g ,则[]πθ2,00∈∃,使()()000==θθg f .模型求解:令)()()(θθθg f h -= .就有,0)0( h 0)(0)()()( ππππg g f h -=-=.再由()()θθg f ,的连续性,得到()θh 是一个连续函数. 从而()θh 是[]π,0上的连续函数.由连续函数的介值定理：()πθ,00∈∃,使()00=θh .即()πθ,00∈∃,使()()000=-θθg f .又因为[]πθ2,0∈∀,有()()0=θθg f .故()()000==θθg f .8. 假定人口的增长服从这样的规律：时刻t 的人口为)(t x ,单位时间内人口的增量与)(t x x m -成正比（其中m x 为最大容量）.试建立模型并求解.作出解的图形并与指数增长模型、阻滞增长模型的结果比较.解：现考察某地区的人口数，记时刻t 的人口数为()t x （一般()t x 是很大的整数）,且设()t x 为连续可微函数.又设()00|x t x t ==.任给时刻t 及时间增量t ∆,因为单位时间内人口增长量与)(t x x m -成正比, 假设其比例系数为常数r .则t 到t t ∆+内人口的增量为：()()()t t x x r t x t t x m ∆-=-∆+)(. 两边除以t ∆,并令0→∆t ,得到⎪⎩⎪⎨⎧=-=0)0()(x x x x r dtdxm 解为rtm m e x x x t x ---=)()(0如图实线所示，当t 充分大时 m x 它与Logistic 模型相近.0x t9．为了培养想象力、洞察力和判断力，考察对象时除了从正面分析外，还常常需要从侧面 或反面思考.试尽可能迅速回答下面问题：（1） 某甲早8：00从山下旅店出发，沿一条路径上山，下午5：00到达山顶并留宿. 次日早8：00沿同一路径下山，下午5：00回到旅店.某乙说，甲必在两天中的同一时刻经 过路径中的同一地点.为什么？（2） 37支球队进行冠军争夺赛，每轮比赛中出场的每两支球队中的胜者及轮空者 进入下一轮，直至比赛结束.问共需进行多少场比赛，共需进行多少轮比赛.如果是n 支球队比赛呢？（3） 甲乙两站之间有电车相通，每隔10分钟甲乙两站相互发一趟车，但发车时刻 不一定相同.甲乙之间有一中间站丙，某人每天在随机的时刻到达丙站，并搭乘最先经过丙站的那趟车，结果发现100天中约有90天到达甲站，仅约10天到达乙站.问开往甲乙两站的电车经过丙站的时刻表是如何安排的？（4） 某人家住T 市在他乡工作，每天下班后乘火车于6：00抵达T 市车站，他的 妻子驾车准时到车站接他回家，一日他提前下班搭早一班火车于5：30抵T 市车站，随即步行回家，他的妻子象往常一样驾车前来，在半路上遇到他，即接他回家，此时发现比往常 提前了10分钟.问他步行了多长时间？（5） 一男孩和一女孩分别在离家2 km 和1 km 且方向相反的两所学校上学，每天 同时放学后分别以4 km/h 和2 km/h 的速度步行回家.一小狗以6 km/h 的速度由男孩处奔向女孩，又从女孩处奔向男孩，如此往返直至回到家中，问小狗奔波了多少路程？如果男孩和女孩上学时小狗也往返奔波在他们之间，问当他们到达学校时小狗在何处？解：（1）方法一：以时间t 为横坐标，以沿上山路径从山下旅店到山顶的行程x 为纵坐标， 第一天的行程)(t x 可用曲线（I ）表示 ，第二天的行程)(t x 可用曲线（I I ）表示，（I ）（I I ）是连续曲线必有交点),(000d t p ,两天都在0t 时刻经过0d 地点.方法二：设想有两个人， 一人上山，一人下山，同一天同 时出发，沿同一路径,必定相遇. 0d t早8 0t 晚5方法三：我们以山下旅店为始点记路程,设从山下旅店到山顶的路程函数为)(t f (即t 时刻走的路程为)(t f ),同样设从山顶到山下旅店的路函数为)(t g ,并设山下旅店到山顶的距离为a (a >0).由题意知：,0)8(=f a f =)17(,a g =)8(,0)17(=g .令)()()(t g t f t h -=,则有0)8()8()8(<-=-=a g f h ，0)17()17()17(>=-=a g f h ，由于)(t f ,)(t g 都是时间t 的连续函数,因此)(t h 也是时间t 的连续函数,由连续函数的介值定理,]17,8[0∈∃t ,使0)(0=t h ,即)()(00t g t f =.（2）36场比赛，因为除冠军队外，每队都负一场；6轮比赛，因为2队赛1轮，4队赛2轮，32队赛5轮. n 队需赛1-n 场，若k k n 221≤- ，则需赛k 轮.（3）不妨设从甲到乙经过丙站的时刻表是8：00，8：10，8：20，…… 那么从乙到甲经过丙站的时刻表应该是8：09，8：19，8：29……（4）步行了25分钟.设想他的妻子驾车遇到他后，先带他前往车站，再回家，汽车多行驶了10分钟，于是带他去车站这段路程汽车多跑了5分钟，而到车站的时间是6：00，所以妻子驾车遇到他的时刻应该是5：55.（5）放学时小狗奔跑了3 km .孩子上学到学校时小狗的位置不定（可在任何位置），因为设想放学时小狗在任何位置开始跑，都会与孩子同时到家.之所以出现位置不定的结果，是由于上学时小狗初始跑动的那一瞬间，方向无法确定.10*. 某人第一天上午9：00从甲地出发，于下午6：00到达乙地.第二天上午9：00他又从乙地出发按原路返回，下午6：00回到甲地.试说明途中存在一点，此人在两天中同一时间到达该处.若第二天此人是下午4：00回到甲地，结论将如何？答：（方法一）我们以甲地为始点记路程,设从甲地到乙地的路程函数为)(t f (即t 时刻走的路程为)(t f ),同样设从乙地到甲地的路函数为)(t g ,并设甲地到乙地的距离为a (a >0).由题意知：,0)9(=f a f =)18(,a g =)9(,0)18(=g . 令)()()(t g t f t h -=,则有0)9()9()9(<-=-=a g f h ，0)18()18()18(>=-=a g f h 由于)(t f ,)(t g 都是时间t 的连续函数,因此)(t h 也是时间t 的连续函数,由连续函数的介值定理,]18,9[0∈∃t ,使0)(0=t h ,即)()(00t g t f =. 若第二天此人是下午4：00回到甲地,则结论仍然正确,这是因为0)9()9()9(<-=-=a g f h ，0)16()16()16()16(>=-=f g f h .（方法二）此题可以不用建模的方法,而变换角度考虑：设想有两个人，一人从甲地到乙地,另一人从乙地到甲地,同一天同时出发,沿同一路径,必定相遇.若第二天此人是下午4：00回到甲地,则结论仍然正确.《数学模型》作业解答第二章(1)（2008年9月16日）1． 学校共1000名学生，235人住在A 宿舍，333人住在B 宿舍，432人住在C 宿舍.学生们要组织一个10人的委员会，试用下列办法分配各宿舍的委员数：（1）. 按比例分配取整数的名额后,剩下的名额按惯例分给小数部分较大者; （2）. §1中的Q 值方法；（3）.d ’Hondt 方法：将A 、B 、C 各宿舍的人数用正整数n=1,2,3,……相除，其商数如下表：将所得商数从大到小取前10个（10为席位数），在数字下标以横线，表中A 、B 、C 行有横线的数分别为2，3，5，这就是3个宿舍分配的席位.你能解释这种方法的道理吗？如果委员会从10个人增至15人，用以上3种方法再分配名额，将3种方法两次分配的结果列表比较.解：先考虑N=10的分配方案，,432 ,333 ,235321===p p p ∑==31.1000i ip方法一（按比例分配） ,35.23111==∑=i ipNp q ,33.33122==∑=i ipNp q 32.43133==∑=i ipNp q分配结果为： 4 ,3 ,3321===n n n 方法二（Q 值方法）9个席位的分配结果（可用按比例分配）为：4 ,3 ,2321===n n n第10个席位：计算Q 值为,17.92043223521=⨯=Q ,75.92404333322=⨯=Q 2.93315443223=⨯=Q3Q 最大，第10个席位应给C.分配结果为 5 ,3 ,2321===n n n方法三（d ’Hondt 方法）此方法的分配结果为：5 ,3 ,2321===n n n此方法的道理是：记i p 和i n 为各宿舍的人数和席位（i=1,2,3代表A 、B 、C 宿舍）.iin p 是每席位代表的人数，取,,2,1 =i n 从而得到的i i n p 中选较大者，可使对所有的,i ii n p尽量接近.再考虑15=N 的分配方案，类似地可得名额分配结果.现将3种方法两次分配的结果列表如下：2． 试用微积分方法，建立录像带记数器读数n 与转过时间的数学模型. 解： 设录像带记数器读数为n 时，录像带转过时间为t.其模型的假设见课本.考虑t 到t t ∆+时间内录像带缠绕在右轮盘上的长度，可得,2)(kdn wkn r vdt π+=两边积分，得⎰⎰+=ntdn wkn r k vdt 0)(2π)22 2n wk k(r n πvt +=∴ .2 22n vk w n v rk t ππ+=∴第二章(2)（2008年10月9日）15．速度为v 的风吹在迎风面积为s 的风车上，空气密度是ρ ，用量纲分析方法确定风车获得的功率P 与v 、S 、ρ的关系.解: 设P 、v 、S 、ρ的关系为0),,,(=ρs v P f ， 其量纲表达式为: [P]=32-TML , [v ]=1-LT,[s ]=2L ,[ρ]=3-ML ,这里T M L ,,是基本量纲.量纲矩阵为：A=)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---ρ()()()()()()(001310013212s v P T M L齐次线性方程组为：⎪⎩⎪⎨⎧=--=+=-++030032221414321y y y y y y y y 它的基本解为)1,1,3,1(-=y由量纲i P 定理得 1131ρπs v P -=， 113ρλs v P =∴ ， 其中λ是无量纲常数. 16．雨滴的速度v 与空气密度ρ、粘滞系数μ和重力加速度g 有关，其中粘滞系数的定义是：运动物体在流体中受的摩擦力与速度梯度和接触面积的乘积成正比，比例系数为粘滞系数，用量纲分析方法给出速度v 的表达式.解：设v ,ρ,μ,g 的关系为(f v ,ρ,μ,g )=0.其量纲表达式为[v ]=LM 0T -1，[ρ]=L -3MT 0，[μ]=MLT -2（LT -1L -1）-1L -2=MLL -2T -2T=L -1MT -1，[g ]=LM 0T -2,其中L ，M ，T 是基本量纲.量纲矩阵为A=)()()()()()()(210101101131g v T M L μρ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----- 齐次线性方程组Ay=0 ，即⎪⎩⎪⎨⎧==+=+02y -y - y -0y y 0y y -3y -y 431324321 的基本解为y=(-3 ,-1 ,1 ,1)由量纲i P 定理 得 g v μρπ13--=. 3ρμλgv =∴，其中λ是无量纲常数. 16*．雨滴的速度v 与空气密度ρ、粘滞系数μ、特征尺寸γ和重力加速度g 有关，其中粘滞系数的定义是：运动物体在流体中受的摩擦力与速度梯度和接触面积的乘积成正比，比例系数为粘滞系数，用量纲分析方法给出速度v 的表达式.解：设v ,ρ,μ,γ，g 的关系为0),,,,(=g v f μργ.其量纲表达式为[v ]=LM 0T -1，[ρ]=L -3MT 0，[μ]=MLT -2（LT -1L -1）-1L -2=MLL -2T -2T=L -1MT -1，[γ]=LM 0T 0 ，[g ]=LM 0T -2其中L ，M ，T 是基本量纲. 量纲矩阵为A=)()()()()()()()(21010110011311g v T M L μργ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----齐次线性方程组Ay=0 即⎪⎩⎪⎨⎧=---=+=+--+020035414354321y y y y y y y y y y 的基本解为⎪⎩⎪⎨⎧---=--=)21,1,1,23,0()21,0,0,21,1(21y y得到两个相互独立的无量纲量⎩⎨⎧==-----2/112/322/12/11g g v μργπγπ 即 1212/12/31,--==πμργπγg g v . 由0),(21=Φππ , 得 )(121-=πϕπ∴ )(12/12/3-=μργϕγυg g , 其中ϕ是未定函数.20.考察阻尼摆的周期，即在单摆运动中考虑阻力，并设阻力与摆的速度成正比.给出周期的表达式，然后讨论物理模拟的比例模型，即怎样由模型摆的周期计算原型摆的周期. 解：设阻尼摆周期t ,摆长l , 质量m ,重力加速度g ，阻力系数k 的关系为0),,,,(=k g m l t f其量纲表达式为：112120000000)(]][[][,][,][,][,][-----======LT MLT v f k T LM g MT L m T LM l T M L t 10-=MT L ， 其中L ，M ，T 是基本量纲.量纲矩阵为A=)()()()()()()()(120011010001010k g m l t T M L ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-- 齐次线性方程组⎪⎩⎪⎨⎧=--=+=+02005415342y y y y y y y 的基本解为⎪⎩⎪⎨⎧--=-=)1,21,1,21,0()0,21,0,21,1(21Y Y 得到两个相互独立的无量纲量∴g l t =1π, )(21πϕπ=, 2/12/12mg kl =π ∴)(2/12/1mg kl g l t ϕ=，其中ϕ是未定函数 . 考虑物理模拟的比例模型，设g 和k 不变，记模型和原型摆的周期、摆长、质量分别为t ,'t ；l ,'l ;m ,'m . 又)(2/12/1g m l k g l t '''='ϕ 当无量纲量l l mm '='时， 就有 ll l g g l tt '=⋅'='. 《数学模型》作业解答第三章1（2008年10月14日）1. 在3.1节存贮模型的总费用中增加购买货物本身的费用,重新确定最优订货周期和订货批量．证明在不允许缺货模型中结果与原来的一样，而在允许缺货模型中最优订货周期和订货批量都比原来结果减少．解：设购买单位重量货物的费用为k ,其它假设及符号约定同课本．01 对于不允许缺货模型，每天平均费用为：kr rTc T c T C ++=2)(212221r c Tc dT dC+-= 令0=dTdC， 解得 rc c T 21*2= ⎩⎨⎧==---22/112/112/12/1ππk g m l g tl由rT Q = ， 得212c rc rT Q ==** 与不考虑购货费的结果比较，Ｔ、Ｑ的最优结果没有变．02 对于允许缺货模型，每天平均费用为：⎥⎦⎤⎢⎣⎡+-++=kQ Q rT r c r Q c c T Q T C 23221)(221),(2223322221222T kQ rT Q c r c rT Q c T c T C--+--=∂∂Tk rT Q c c rT Qc Q C ++-=∂∂332 令⎪⎪⎩⎪⎪⎨⎧=∂∂=∂∂00Q CTC， 得到驻点：⎪⎪⎩⎪⎪⎨⎧+-+-+=-+=**323222233232132233221)(22c c krc c c r k c c c c c r c Q c c k c c c rc c T与不考虑购货费的结果比较，Ｔ、Ｑ的最优结果减少．2．建立不允许缺货的生产销售存贮模型．设生产速率为常数k ，销售速率为常数r ，r k >．在每个生产周期Ｔ内，开始的一段时间()00T t <<一边生产一边销售，后来的一段时间)(0T t T <<只销售不生产，画出贮存量)(t g 的图形.设每次生产准备费为1c ，单位时间每件产品贮存费为2c ，以总费用最小为目标确定最优生产周期，讨论r k >>和r k ≈的情况.解：由题意可得贮存量)(t g 的图形如下：贮存费为 ∑⎰=→∆⋅-==∆ni Ti i t TT r k c dt t g c t g c 1022022)()()(limξ又 )()(00T T r T r k -=- ∴ T k r T =0 , ∴ 贮存费变为 kTT r k r c 2)(2⋅-=于是不允许缺货的情况下，生产销售的总费用（单位时间内）为kTr k r c T c kT T r k r c T c T C 2)(2)()(21221-+=-+=k r k r c Tc dT dC 2)(221-+-=. 0=dT dC令, 得)(221r k r c k c T -=* 易得函数处在*T T C )(取得最小值，即最优周期为： )(221r k r c kc T -=*rc c ，Tr k 212≈>>*时当 . 相当于不考虑生产的情况. ∞→≈*，Tr k 时当 . 此时产量与销量相抵消，无法形成贮存量.第三章2（2008年10月16日）3．在3.3节森林救火模型中，如果考虑消防队员的灭火速度λ与开始救火时的火势b 有关，试假设一个合理的函数关系，重新求解模型.解：考虑灭火速度λ与火势b 有关，可知火势b 越大，灭火速度λ将减小，我们作如下假设: 1)(+=b kb λ， 分母∞→→+λ时是防止中的011b b 而加的. 总费用函数()xc b kx b x t c b kx b t c t c x C 3122121211)1()(2)1(2+--++--++=βββββββ最优解为 []k b k c b b b c kbc x ββ)1(2)1()1(223221+++++=5．在考虑最优价格问题时设销售期为T ，由于商品的损耗，成本q 随时间增长，设t q t q β+=0)(，为增长率β.又设单位时间的销售量为)(为价格p bp a x -=.今将销售期分为T t TT t <<<<220和两段，每段的价格固定，记作21,p p .求21,p p 的最优值，使销售期内的总利润最大.如果要求销售期T 内的总售量为0Q ，再求21,p p 的最优值. 解：按分段价格，单位时间内的销售量为⎪⎩⎪⎨⎧<<-<<-=T t T bp a T t bp a x 2,20,21又 t q t q β+=0)(.于是总利润为[][]⎰⎰--+--=22221121)()()()(),(TTT dt bp a t q p dt bp a t q p p p=22)(022)(20222011T Tt t q t p bp a T t t q t p bp a ⎥⎦⎤⎢⎣⎡---+⎥⎦⎤⎢⎣⎡---ββ=)8322)(()822)((20222011T t q T p bp a T T q T p bp a ββ---+--- )(2)822(12011bp a T T T q T p b p -+---=∂∂β )(2)8322(22022bp a TT t q T p b p -+---=∂∂β 0,021=∂∂=∂∂p p 令, 得到最优价格为: ⎪⎪⎩⎪⎪⎨⎧⎥⎦⎤⎢⎣⎡++=⎥⎦⎤⎢⎣⎡++=)43(21)4(210201T q b a b p T q b a b p ββ 在销售期T 内的总销量为⎰⎰+-=-+-=20221210)(2)()(T TT p p bTaT dt bp a dt bp a Q 于是得到如下极值问题：)8322)(()822)((),(m ax 2022201121T t q T p bp a T T q T p bp a p p ββ---+---=t s . 021)(2Q p p bTaT =+-利用拉格朗日乘数法，解得：⎪⎩⎪⎨⎧+-=--=880201TbT Q b a p T bT Q b a p ββ 即为21,p p 的最优值.第三章3（2008年10月21日）6. 某厂每天需要角钢100吨，不允许缺货.目前每30天定购一次，每次定购的费用为2500元.每天每吨角钢的贮存费为0.18元.假设当贮存量降到零时订货立即到达.问是否应改变订货策略？改变后能节约多少费用？解：已知：每天角钢的需要量r=100(吨);每次订货费1c ＝2500（元）; 每天每吨角钢的贮存费2c ＝0.18（元）.又现在的订货周期T 0＝30（天） 根据不允许缺货的贮存模型：kr rT c T c T C ++=2121)( 得：k T TT C 10092500)(++=令0=dTdC， 解得：35092500*==T 由实际意义知：当350*=T （即订货周期为350）时，总费用将最小. 925002+-=TdT dC又k T C 10035095025003)(*+⨯+⨯=＝300＋100k k T C 100309302500)(0+⨯+==353．33＋100k)(0T C －)(*T C ＝（353.33＋100k ）－（300＋100k ）32＝53．33.故应改变订货策略.改变后的订货策略（周期）为T *=350，能节约费用约53．33元.《数学模型》作业解答第四章（2008年10月28日）1. 某厂生产甲、乙两种产品,一件甲产品用A 原料1千克, B 原料5千克；一件乙产品用A 原料2千克,B 原料4千克.现有A 原料20千克, B 原料70千克.甲、乙产品每件售价分别为20元和30元.问如何安排生产使收入最大？ 解：设安排生产甲产品x 件,乙产品y 件，相应的利润为S 则此问题的数学模型为：max S=20x+30ys.t. ⎪⎩⎪⎨⎧∈≥≤+≤+Z y x y x y x y x ,,0,7045202这是一个整线性规划问题，现用图解法进行求解可行域为：由直线1l ：x+2y=20, 2l :5x+4y ＝702l以及x=0,y=0组成的凸四边形区域. 直线l ：20x+30y=c 在可行域内 平行移动.易知：当l 过1l 与2l 的交点时， x S 取最大值. 由⎩⎨⎧=+=+7045202y x y x 解得⎩⎨⎧==510y x此时 m ax S ＝2053010⨯+⨯＝350（元）2. 某厂拟用集装箱托运甲乙两种货物，每箱的体积、重量以及可获利润如下表：货物 体积（立方米/箱）重量 （百斤/箱）利润 （百元/箱）甲 5 2 20 乙4510已知这两种货物托运所受限制是体积不超过24立方米，重量不超过13百斤.试问这两种货物各托运多少箱，使得所获利润最大，并求出最大利润.解:设甲货物、乙货物的托运箱数分别为1x ,2x ,所获利润为z .则问题的数学模型可表示为211020 m ax x x z +=⎪⎩⎪⎨⎧∈≥≤+≤+Z y x x x x x x x st ,,0,13522445212121这是一个整线性规划问题. 用图解法求解. 可行域为：由直线2445:211=+x x l1352:212=+x x l 及0,021==x x 组成直线 c x x l =+211020:在此凸四边形区域内平行移动.易知：当l 过l 1与l 2的交点时，z 取最大值 由⎩⎨⎧=+=+135224452121x x x x 解得 ⎩⎨⎧==1421x x90110420max =⨯+⨯=z .3．某微波炉生产企业计划在下季度生产甲、乙两种型号的微波炉.已知每台甲型、乙型微波炉的销售利润分别为3和2个单位.而生产一台甲型、乙型微波炉所耗原料分别为2和32ll1x1l2x个单位,所需工时分别为4和2个单位.若允许使用原料为100个单位,工时为120个单位,且甲型、乙型微波炉产量分别不低于6台和12台.试建立一个数学模型,确定生产甲型、乙型微波炉的台数,使获利润最大．并求出最大利润.解：设安排生产甲型微波炉x 件,乙型微波炉y 件,相应的利润为S. 则此问题的数学模型为：max S=3x +2ys.t. ⎪⎩⎪⎨⎧∈≥≥≤+≤+Z y x y x y x y x ,,12,61202410032这是一个整线性规划问题 用图解法进行求解可行域为：由直线1l ：2x+3y=100, 2l :4x+2y ＝120 及x=6,y=12组成的凸四边形区域.直线l ：3x+2y=c 在此凸四边形区域内平行移动. 易知：当l 过1l 与2l 的交点时, S 取最大值.由⎩⎨⎧=+=+1202410032y x y x 解得⎩⎨⎧==2020y x .m ax S ＝320220⨯+⨯＝100.《数学模型》作业解答第五章1（2008年11月12日）1.对于5.1节传染病的SIR 模型，证明：（1）若处最大先增加，在则σσ1)(,10=s t i s ，然后减少并趋于零；)(t s 单调减少至.∞s（2）.)()(,10∞s t s t i s 单调减少至单调减少并趋于零，则若σ解：传染病的SIR 模型（14）可写成⎪⎩⎪⎨⎧-=-=i s dtds s i dt diλσμ)1(.)(lim 0.(t) .)( .0,t 存在而单调减少知由∞∞→=∴≥-=s t s s t s dtdsi s dt ds λ.)(∞s t s 单调减少至故（1）.s s(t) .s(t) .100≤∴单调减少由若σs;)(,0 .01,10单调增加时当t i dtdis s s ∴-σσ.)(,0 .01,1单调减少时当t i dtdis s ∴-σσ.0)(lim .0)18(t ==∞→∞t i i 即式知又由书上.)( .0,1m i t i dtdis 达到最大值时当∴==σ（2）().0 0.1-s ,1,10 dtdit s s σσσ从而则若()().0.0lim ==∴∞∞→i t i t i t 即单调减少且4．在5.3节正规战争模型（3）中，设乙方与甲方战斗有效系数之比为.4=ba初始兵力00y x 与相同.(1) 问乙方取胜时的剩余兵力是多少,乙方取胜的时间如何确定.(2) 若甲方在战斗开始后有后备部队以不变的速率r 增援,重新建立模型,讨论如何判断双方的胜负.解:用()()t y t x ,表示甲、乙交战双方时刻t 的士兵人数,则正规战争模型可近似表示为:()()()⎪⎪⎩⎪⎪⎨⎧==-=-=000,01 ,yy x x bx dtdyay dt dx现求(1)的解: (1)的系数矩阵为⎥⎦⎤⎢⎣⎡--=00b a Aab ab b aA E ±=∴=-==-1,22 .0λλλλλ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛-1212,21，对应的特征向量分别为λλ ()()()tab t ab eC e C t y t x -⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛∴1212121的通解为.再由初始条件，得()()2 220000 tab tab e y x ey x t x -⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛-=又由().1aybx dx dy =可得其解为 ()3 ,202022 bx ay k k bx ay -==-而(1) ()().231000202011y a b y a bx ay ak t y t x =-=-===时，当 即乙方取胜时的剩余兵力数为.230y又令().0222,01100001=-⎪⎭⎫⎝⎛++⎪⎭⎫⎝⎛-=t ab t ab e y x e y x t x ）得由（注意到000020022,1x y y x ey x t ab -+==得. .43ln ,3121bt et ab =∴=∴ (2) 若甲方在战斗开始后有后备部队以不变的速率r 增援.则()()⎪⎪⎩⎪⎪⎨⎧==-=+-=000,)0(4 yy x x bx dtdyr ay dt dx().,4rdy aydy bxdx bxray dy dx -=-+-=即得由 相轨线为,222k bx ry ay =-- .222220.020k a r bx a r y a bx ry ay k =--⎪⎭⎫ ⎝⎛---=或 此相轨线比书图11中的轨线上移了.a r 乙方取胜的条件为.,0222020a r x a b a r y k +⎪⎭⎫ ⎝⎛- 亦即 第五章2（2008年11月14日）6. 模仿5.4节建立的二室模型来建立一室模型（只有中心室），在快速静脉注射、恒速静脉滴注（持续时间为τ）和口服或肌肉注射3种给药方式下求解血药浓度，并画出血药浓度曲线的图形.解: 设给药速率为(),0t f()()()()().,,0/t VC t x t f t kx t x k ==+则排除速率为常数(1)快速静脉注射: 设给药量为,0D 则()()().,0,0000t k e VDt C V D C t f -===解得 (2)恒速静脉滴注(持续时间为τ): 设滴注速率为()(),00,000==C k t f k ，则解得()()()()⎪⎩⎪⎨⎧-≤≤-=----τττ t e e Vkk t e Vkk t C t k kt kt,10 ,10(3) 口服或肌肉注射: ()()，解得）式节（见134.5010010tk eD k t f -=()()()⎪⎪⎩⎪⎪⎨⎧=≠--=---010101001 ,,01k k te VkD k k e e k k V D k t C kt t k kt3种情况下的血药浓度曲线如下：第五章3（2008年11月18日）8. 在5.5节香烟过滤嘴模型中,(1) 设3.0,/50,08.0,02.0,20,80,80021=======a s mm b mm l mm l mg M νβ求./21Q Q Q 和(2) 若有一支不带过滤嘴的香烟,参数同上,比较全部吸完和只吸到1l 处的情况下，进入人体毒物量的区别.解)(857563.229102.07.050103.01508002.07.0502008.0/01/2毫克≈⎪⎪⎭⎫ ⎝⎛-⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛-=⨯⨯-⨯---e e e eba v aw Q v bl a vl β ()10/10==l M w 其中，()()97628571.0502002.008.0212===⨯----ee Q Q vl b β(2) 对于一支不带过滤嘴的香烟,全部吸完的毒物量为⎪⎪⎭⎫⎝⎛-=-vbl a e b a v aw Q '103‘ 只吸到1l 处就扔掉的情况下的毒物量为⎪⎪⎭⎫ ⎝⎛-=--vbl a v ble e b a v aw Q 1'21'04 .256531719.1110096.0032.0012.004.0508002.03.0508002.05010002.03.05010002.043111'1'≈--=--=--=⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=⨯⨯⨯⨯⨯⨯--e e e e e e e e e e e e e e e e Q Q v abl v bl v abl v bl v bl a v bl v bl a vbl 44.235,84.29543≈≈　ＱQ4．在5.3节正规战争模型（3）中，设乙方与甲方战斗有效系数之比为.4=ba初始兵力00y x 与相同.(1) 问乙方取胜时的剩余兵力是多少,乙方取胜的时间如何确定.(2) 若甲方在战斗开始后有后备部队以不变的速率r 增援,重新建立模型,讨论如何判断双方的胜负.解:用()()t y t x ,表示甲、乙交战双方时刻t 的士兵人数,则正规战争模型可近似表示为:()()()⎪⎪⎩⎪⎪⎨⎧==-=-=000,01 ,yy x x bx dtdyay dt dx现求(1)的解: (1)的系数矩阵为⎥⎦⎤⎢⎣⎡--=00b a Aab ab b aA E ±=∴=-==-1,22 .0λλλλλ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛-1212,21，对应的特征向量分别为λλ ()()()tab t ab eC e C t y t x -⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛∴1212121的通解为.再由初始条件，得()()2 220000 tab tab e y x ey x t x -⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛-=又由().1aybx dx dy =可得其解为 ()3 ,202022 bx ay k k bx ay -==-而(1) ()().231000202011y a b y a bx ay ak t y t x =-=-===时，当 即乙方取胜时的剩余兵力数为.230y 又令().0222,01100001=-⎪⎭⎫⎝⎛++⎪⎭⎫⎝⎛-=t ab t ab e y x e y x t x ）得由（注意到000020022,1x y y x ey x t ab -+==得. .43ln ,3121bt et ab =∴=∴ (2) 若甲方在战斗开始后有后备部队以不变的速率r 增援.则()()⎪⎪⎩⎪⎪⎨⎧==-=+-=000,)0(4 yy x x bx dtdyr ay dt dx().,4rdy aydy bxdx bxray dy dx -=-+-=即得由 相轨线为,222k bx ry ay =-- .222220.02k a r bx a r y a bx ry ay k =--⎪⎭⎫ ⎝⎛---=或 此相轨线比书图11中的轨线上移了.a r 乙方取胜的条件为.,0222020a r x a b a r y k +⎪⎭⎫ ⎝⎛- 亦即《数学模型》作业解答第六章（2008年11月20日）1.在6.1节捕鱼模型中，如果渔场鱼量的自然增长仍服从Logistic 规律，而单位时间捕捞量为常数h ．(1)分别就4/rN h >，4/rN h <，4/rN h =这3种情况讨论渔场鱼量方程的平衡点及其稳定状况．(2)如何获得最大持续产量，其结果与6.1节的产量模型有何不同．解：设时刻t 的渔场中鱼的数量为()t x ，则由题设条件知：()t x 变化规律的数学模型为h Nxrx dt t dx --=)1()( 记h Nxrx x F --=)1()( (1).讨论渔场鱼量的平衡点及其稳定性： 由()0=x F ，得0)1(=--h Nxrx ． 即()102=+-h rx x Nr )4(42Nhr r N rh r -=-=∆ ， (1)的解为：2412,1N rNhN x -±=①当4/rN h >，0<∆，(1)无实根，此时无平衡点； ②当4/rN h =，0=∆，(1)有两个相等的实根，平衡点为20N x =. Nrxr N rx N x r x F 2)1()('-=--=，0)(0'=x F 不能断定其稳定性. 但0x x ∀ 及0x x 均有04)1()( rNN x rx x F --= ，即0 dtdx ．∴0x 不稳定；③当4/rN h <，0>∆时，得到两个平衡点：2411N rNhN x --=， 2412N rNh N x -+=易知：21N x <， 22N x > ，0)(1'>x F ，0)(2'<x F ∴平衡点1x 不稳定，平衡点2x 稳定.(2)最大持续产量的数学模型为⎩⎨⎧=0)(..max x F t s h即 )1(max Nxrx h -=， 易得 2*0N x = 此时 4rN h =，但2*0N x =这个平衡点不稳定．这是与6.1节的产量模型不同之处．要获得最大持续产量，应使渔场鱼量2N x >，且尽量接近2N ，但不能等于2N ． 2.与Logistic 模型不同的另一种描述种群增长规律的是Gompertz 模型：()xNrx t x ln '=．其中r 和N 的意义与Logistic 模型相同．设渔场鱼量的自然增长服从这个模型，且单位时间捕捞量为Ex h =．讨论渔场鱼量的平衡点及其稳定性，求最大持续产量m h 及获得最大产量的捕捞强度m E 和渔场鱼量水平*0x ．解：()t x 变化规律的数学模型为()Ex xNrx dt t dx -=ln 记 Ex xNrx x F -=ln)( ① 令()0=x F ，得0ln =-Ex xNrx ∴r ENe x -=0，01=x ．∴平衡点为1,0x x . 又 ()E r xNr x F --=ln'，()()∞=<-=1'0',0x F r x F ． ∴ 平衡点o x 是稳定的，而平衡点1x 不稳定.②最大持续产量的数学模型为：⎪⎩⎪⎨⎧≠=-=.0,0ln ..max x Ex x N rx t s Ex h Ex()x f由前面的结果可得 rE ENeh -=r Er Ee r EN Ne dE dh ---=，令.0=dEdh 得最大产量的捕捞强度r E m =．从而得到最大持续产量e rN h m /=，此时渔场鱼量水平eNx =*0． 3．设某渔场鱼量)(t x (时刻t 渔场中鱼的数量)的自然增长规律为：)1()(Nxrx dt t dx -= 其中r 为固有增长率,`N 为环境容许的最大鱼量. 而单位时间捕捞量为常数h .10．求渔场鱼量的平衡点,并讨论其稳定性;20．试确定捕捞强度m E ,使渔场单位时间内具有最大持续产量m Q ,求此时渔场鱼量水平*0x . 解：10．)(t x 变化规律的数学模型为h Nxrx dt t dx --=)1()( 记h N x rx x f --=)1()(,令 0)1(=--h N x rx ，即 02=+-h rx x Nr ----（1）)4(42Nhr r N rh r -=-=∆ ， （1）的解为：2412,1N rNhN x -±=① 当0 ∆时，（1）无实根，此时无平衡点； ② 当0=∆时，（1）有两个相等的实根，平衡点为20Nx =. Nrx r N rx N x r x f 2)1()('-=--= ，0)(0'=x f 不能断定其稳定性. 但0x x ∀ 及0x x 均有04)1()( rN N x rx x f --= ，即0 dt dx∴0x 不稳定； ③ 当0 ∆时，得到两个平衡点：2411rNhN N x --=， 2412rNh N N x -+=易知 21N x， 22N x ∴0)('1 x f ， 0)('2 x f ∴平衡点1x 不稳定 ，平衡点2x 稳定.20．最大持续产量的数学模型为： ⎩⎨⎧=0)(..max x f t s h即 )1(max Nx rx h -=，易得 2*0N x = 此时 4rN h =，但2*0N x =这个平衡点不稳定. 要获得最大持续产量，应使渔场鱼量2N x ,且尽量接近2N ,但不能等于2N.《数学模型》第七章作业（2008年12月4日）1．对于7.1节蛛网模型讨论下列问题：（1）因为一个时段上市的商品不能立即售完，其数量也会影响到下一时段的价格，所以第1+k 时段的价格1+k y 由第1+k 和第k 时段的数量1+k x 和k x 决定，如果仍设1+k x 仍只取决于k y ，给出稳定平衡的条件，并与7.1节的结果进行比较.2．已知某商品在k 时段的数量和价格分别为k x 和k y ，其中1个时段相当于商品的一个生产周期.设该商品的需求函数和供应函数分别为)(k k x f y =和)2(11-++=k k k y y g x .试建立关于商品数量的差分方程模型，并讨论稳定平衡条件.3． 已知某商品在k 时段的数量和价格分别为k x 和k y ，其中1个时段相当于商品的一个生产周期.设该商品的需求函数和供应函数分别为)2(11kk k x x f y +=++和)(1k k y g x =+.试建立关于商品数量的差分方程模型，并讨论稳定平衡条件.《数学模型》作业解答第七章（2008年12月4日）2． 对于7.1节蛛网模型讨论下列问题：（1）因为一个时段上市的商品不能立即售完，其数量也会影响到下一时段的价格，所以第1+k 时段的价格1+k y 由第1+k 和第k 时段的数量1+k x 和k x 决定，如果仍设1+k x 仍只取决于k y ，给出稳定平衡的条件，并与7.1节的结果进行比较.（2）若除了1+k y 由1+k x 和k x 决定之外，1+k x 也由前两个时段的价格k y 和1-k y 确定.试分析稳定平衡的条件是否还会放宽.解：（1）由题设条件可得需求函数、供应函数分别为：⎪⎩⎪⎨⎧=+=+++)()2(111k k k k k y h x x x f y 在),(000y x P 点附近用直线来近似曲线h f ,，得到⎪⎩⎪⎨⎧>-=->-+-=-+++)2( 0, )()1( 0),2(0010101 ββααy y x x x x x y y k k k k k 由（2）得 )3( )(0102 y y x x k k -=-++β （1）代入（3）得 )2(0102x x x x x kk k -+-=-++αβ0012222 x x x x x k k k αβαβαβ+=++∴++对应齐次方程的特征方程为 02 2=++αβαβλλ特征根为48)(22,1αβαβαβλ-±-=当8≥αβ时，则有特征根在单位圆外，设8<αβ，则248)()4(2222,1αβαβαβαβλ=+-+= 2 12,1<⇔<∴αβλ即平衡稳定的条件为2<αβ与207P 的结果一致. （2）此时需求函数、供应函数在),(000y x P 处附近的直线近似表达式分别为：⎪⎩⎪⎨⎧>-+=->-+-=--+++)5( 0 , )2()4( 0),2(01010101ββααy y y x x x x x y y k k k k k k 由（5）得，)( ) y y y β(y )x (x k k k 62010203 -+-=-+++ 将（4）代入（6），得 ⎥⎦⎤⎢⎣⎡-+--+-=-++++)2()2()(20101203x x x x x x x x k k k k k ααβ 001234424 x x x x x x k k k k αβαβαβαβ+=+++∴+++对应齐次方程的特征方程为(7) 024 23=+++αβαβλαβλλ 代数方程（7）无正实根，且42 ,αβαβ---, αβ不是（7）的根.设（7）的三个非零根分别为321,,λλλ，则⎪⎪⎪⎩⎪⎪⎪⎨⎧-==++-=++424321133221321αβλλλαβλλλλλλαβλλλ 对（7）作变换：,12αβμλ-=则,03=++q p μμ其中 )6128(41 ),122(412233322αββαβαβααβ+-=-=q p 用卡丹公式：⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+--+++-=+--+++-=+--+++-=33233223332233223323321)3()2(2)3()2(2)3()2(2)3()2(2)3()2(2)3()2(2p q q w p q q w p q q w p q q w pq q p q q μμμ 其中,231i w +-=求出321,,μμμ，从而得到321,,λλλ，于是得到所有特征根1<λ的条件.2．已知某商品在k 时段的数量和价格分别为k x 和k y ，其中1个时段相当于商品的一个生产周期.设该商品的需求函数和供应函数分别为)(k k x f y =和)2(11-++=k k k y y g x .试建立关于商品数量的差分方程模型，并讨论稳定平衡条件.解：已知商品的需求函数和供应函数分别为)(k k x f y =和)2(11-++=k k k y y g x . 设曲线f 和g 相交于点),(000y x P ，在点0P 附近可以用直线来近似表示曲线f 和g ：0,)(00 ααx x y y k k --=- ----------------------（1）0,)2(0101 ββy y y x x k k k -+=--+ --------------------（2） 从上述两式中消去k y 可得,2,1,)1(22012=+=++++k x x x x k k k αβαβαβ， -----------（3） 上述（3）式是我们所建立的差分方程模型，且为二阶常系数线性非齐次差分方程. 为了寻求0P 点稳定平衡条件，我们考虑（3）对应的齐次差分方程的特征方程：022=++αβαβλλ容易算出其特征根为48)(22,1αβαβαβλ-±-=---------------（4） 当αβ 8时，显然有448)(22αβαβαβαβλ----= -----------（5） 从而2λ 2，2λ在单位圆外．下面设8 αβ，由(5)式可以算出 22,1αβλ=要使特征根均在单位圆内，即2,1λ1 ，必须 2 αβ．故0P 点稳定平衡条件为 2 αβ．3． 已知某商品在k 时段的数量和价格分别为k x 和k y ，其中1个时段相当于商品的一个生产周期.设该商品的需求函数和供应函数分别为)2(11k k k x x f y +=++和)(1k k y g x =+.试建立关于商品数量的差分方程模型，并讨论稳定平衡条件.解：已知商品的需求函数和供应函数分别为)2(11k k k x x f y +=++和)(1k k y g x =+. 设曲线f 和g 相交于点),(000y x P ，在点0P 附近可以用直线来近似表示曲线f 和g ：0,)2(0101 ααx x x y y k k k -+-=-++ --------------------（1） 0,)(001 ββy y x x k k -=-+ --- ----------------（2）由（2）得 )(0102y y x x k k -=-++β --------------------（3）（1）代入（3），可得)2(0102x x x x x k k k -+-=-++αβ ∴ ,2,1,2220012=+=++++k x x x x x k k k αβαβαβ， --------------（4）上述（4）式是我们所建立的差分方程模型，且为二阶常系数线性非齐次差分方程.为了寻求0P 点稳定平衡条件，我们考虑（4）对应的齐次差分方程的特征方程：022=++αβαβλλ容易算出其特征根为 48)(22,1αβαβαβλ-±-= ---------------（4） 当αβ≥8时，显然有448)(22αβαβαβαβλ-≤---= -----------（5） 从而2λ 2，2λ在单位圆外．下面设8 αβ，由(5)式可以算出 22,1αβλ=要使特征根均在单位圆内，即 2,1λ1 ，必须 2 αβ．故0P 点稳定平衡条件为 2 αβ．。

数学建模作业题目1、深圳杯数学建模夏令营题目（3）A题计划生育政策调整对人口数量、结构及其影响的研究B题基因组组装C题垃圾焚烧厂的经济补偿问题2、吉林省第五届数学建模竞赛试题（2）E题汽车租赁调度问题F题：阶梯电价的效用分析3、西北工业大学校数模竞赛试题（2）A题西安市经开区公共自行车服务系统设计B题食品价格变动分析4、浙江大学城市学院第八届数学建模竞赛题目（2）A题：外汇交易策略算法设计B题：雾霾时空分布研究5、井冈山大学第七届“井冈杯”数学建模竞赛试题（2）A题：课表编排问题B题：客房预定的价格和数量问题6、第十一届五一数学建模联赛(原苏北) （1）B题：能源总量控制问题7、第七届华中数学建模邀请赛赛题发布（2）A题：加速度检测仪数据校正B题：互联网搜索引擎的排名与设计8、第十六届华东杯大学生数学建模邀请赛试题（3）A电力网络出租车打车模式的现状和未来污水排放问题9、南京信息工程大学第八届数学建模竞赛赛题（2）A 污染气体的传播扩散B 乳腺癌病因分析10、北京交通大学数学建模校赛赛题（1）电梯运输策略问题11、武汉科技大学（2）A题：装配线平衡问题的随机算例生成B题：研究生研究水平的成因分析12、广州六校数学建模联赛题目（2）A题：中国GDP是否超过美国B题：反服贸团体游行的人数13、同济大学数学建模竞赛本科组赛题（2）A题经济金三角C题基因重排14、甘肃农业大学第十届数学建模竞赛试题（1）B题石油资源的开发与储备15江西理工大学数学建模竞赛题目（1）高层建筑火灾中的烟雾扩散建模与仿真以上为2014年各校试题。

从以上题目或者自行收集2014各高校的数学建模比赛试题（与我院数学建模选拔赛相同的不算，自己收集以上题目的信息)中选一作一篇不少于15页的论文。

论文格式如下●论文用白色A4纸单面打印；上下左右各留出至少2.5厘米的页边距；从上面装订。

●论文第一页为搜索的高校姓名与学号、班级。

●论文题目和摘要写在论文第二页上，从第三页开始是论文题目内容与论文正文。

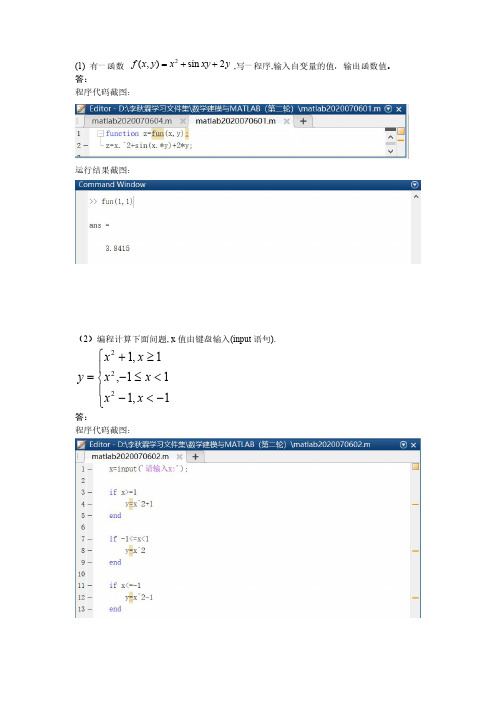
一、单项选择题(只有一个选项正确，共27道小题）1。

计算机具有逻辑判断能力，主要取决于___。

(C）编制的软件2。

计算机的通用性使其可以求解不同的算术和逻辑问题,这主要取决于计算机的___. （C) 可编程性3。

用来表示计算机辅助设计的英文缩写是___。

(C）CAD4. 计算机系统由两大部分组成，它们是___。

（C) 硬件系统和软件系统5。

冯·诺依曼计算机的基本原理是____ (D) 程序存储6. 与二进制数11111110等值的十进制数是____ （D）2547. 计算机存储单元中存储的内容____ (A）可以是数据和指令8. 计算机中用来表示内存储器容量大小的基本单位是____ （B) 字节（byte)9。

为解决某一特定的问题而设计的指令序列称为____ （D) 程序10. 十进制数向二进制数进行转换时，十进制数91相当于二进制数____ （D) 101101l11. 己知英文字母m的ASCII码值为109，那么英文字母p的ASCII码值为____ (B）11212. 微型计算机的微处理器芯片上集成了____ （B）控制器和运算器13。

在文件系统的树形目录结构中，从根目录到任何数据文件，其通路_____ (B) 唯一条15。

在查找文件时,通配符＊与？的含义是_____ （A) *表示任意多个字符，?表示任意一个字符19。

在Word的编辑状态,要将该文档复制到软盘，应当使用___ （A）"文件"菜单中的”另存为"命令20。

在Word的编辑状态，可以显示页面四角的视图方式是___ (B) 页面视图方式22。

用来给电子工作表中的列标进行编号的是___ (B) 字母27. 在PowerPoint中，对幻灯片的重新排序,添加和删除幻灯片都特别有用的视图是____. (B）幻灯片浏览视图2。

Intel公司使用LSI率先推出微处理器4004,宣布第四代计算机问世是在____. (D) 1 971年3. 某型计算机峰值性能为数千亿次／秒,主要用于大规模数据处理，它属于____。

1、P179题2. 要求建模过程完整考虑美国大学生就餐于各类型的餐厅人数的长期趋势，以了解美国大学生的就餐习惯。

增加披萨饼外卖作为就餐的一种选择，根据一项学生调查，表6—3给出了转移的百分比，确定学生在每个地方就餐的百分比。

表6—3美国大学生就餐调查下一状态当前状态Grease餐厅Sweet餐厅披萨饼外卖Grease餐厅Sweet餐厅披萨饼外卖0.250.25 0.500.10 0.30 0.60 0.05 0.15 0.80问题分析：增加披萨饼外卖作为就餐的一种选择，在三种不同类型的餐厅就餐条件下，预测该选择是否具有长期选择性。

关键字：离散概率模型，动力系统模型，马尔可夫链，预测模型假设：学会就餐不按严格规定方向选择，利用以上表格数据建立一个假想的转移。

由上数据可得三个餐厅的就餐问题的三种状态的马尔可夫链模型建立定义如下变量：P(1):Grease 餐厅就餐的初始人数所占百分比.P(n):第n 状态美国大学生在Grease 餐厅就餐的人数所占百分比。

q(1):Sweet 餐厅就餐的初始人数所占百分比.q(n): 第n 状态美国大学生在Sweet 餐厅就餐的人数所占百分比a(1):比萨饼外卖就餐的初始人数所占百分比.a(n): 第n 状态美国大学生在Sweet 餐厅就餐的人数所占百分比。

模型预测：这个动力系统模型，清晰的描述了随着时间的推移，到各个餐厅就餐人数的百分比（概率）。

只要给定时间n ，就可计算出p(n+1),q(n+1),a(n+1).那么，经过若干个时间后，系统就会出现平稳状态，系统的各个子系统的长期行为就会固定Sweet 餐厅Grease 餐厅 比萨饼外卖 0.250.1 0.15 0.6 0.300.50.05 0.25 0.80下来，下面是具体的求解及计算结果。

构造概率模型：p(1)=1;q(1)=0;a(1)=0;p(n+1)=0.25.*p(n)+0.1.*q(n)+0.05.*a(n);q(n+1)=0.25.*p(n)+0.3.*q(n)+0.15.*a(n)a(n+1)=0.5.*p(n)+0.6.*q(n)+0.8.*a(n);模型求解:p(1)=1;q(1)=0;a(1)=0;for n=1:15p(n+1)=0.25.*p(n)+0.1.*q(n)+0.05.*a(n);q(n+1)=0.25.*p(n)+0.3.*q(n)+0.15.*a(n);a(n+1)=0.5.*p(n)+0.6.*q(n)+0.8.*a(n); endformat short gp,q,an=1:16;plot(n,p,'c-')hold onplot(n,q,'m--')hold onplot(n,a,'r*')legend('Grease 餐厅-','Sweet 餐厅--','披萨饼外卖*')xlabel('某状态')ylabel('餐厅类型所占比例') 024681012141600.10.20.30.40.50.60.70.80.91某状态餐厅类型所占比例Grease 餐厅-Sweet 餐厅--披萨饼外卖*模型解释:由图可清楚的看出，如果总的学生就餐人数为n 人，那么在下一状态为4时，比萨饼外卖人数大约占75%，Sweet 餐厅大约占20%，Grease餐厅大约占10%。

一、历年全国数学建模试题及解法赛题解法93A 非线性交调的频率设计拟合、规划93B 足球队排名图论、层次分析、整数规划94A 逢山开路图论、插值、动态规划94B 锁具装箱问题图论、组合数学95A 飞行管理问题非线性规划、线性规划95B 天车与冶炼炉的作业调度动态规划、排队论、图论96A 最优捕鱼策略微分方程、优化96B 节水洗衣机非线性规划97A 零件的参数设计非线性规划97B 截断切割的最优排列随机模拟、图论98A 一类投资组合问题多目标优化、非线性规划98B 灾情巡视的最灾情巡视的最佳佳路线图论、组合优化99A 自动化车动化车床床管理随机优化、计随机优化、计算算机模拟99B 钻井布局0-1规划、图论00A DNA 序列分类模式识别式识别、、Fisher 判别判别、、人工神经网络00B 钢管订购和运输组合优化、组合优化、运输运输运输问题问题01A 血管三维重建曲线拟合、线拟合、曲面重建曲面重建01B 工交车调度问题多目标规划02A 车灯线光源光源的优化的优化非线性规划02B 彩票彩票问题问题问题 单目标目标决决策 03A SARS 的传播传播 微分方程、微分方程、差差分方程分方程03B 露天矿生产矿生产的车的车的车辆安辆安辆安排排 整数规划、整数规划、运输运输运输问题问题问题 04A 奥运会临时超市网点奥运会临时超市网点设计设计设计 统计分析、数计分析、数据处据处据处理、优化理、优化理、优化 04B 电力市场电力市场的的输电阻塞输电阻塞管理管理管理 数据拟合、优化拟合、优化 05A 长江长江水水质的评价和预测评价和预测 预测评价预测评价、数、数、数据处据处据处理理 05B DVD 在线租赁租赁 随机规划、整数规划随机规划、整数规划二、赛题发展的特点1.对选手对选手的计的计的计算算机能力提出了更高能力提出了更高的的要求：要求：赛题的解赛题的解赛题的解决依赖决依赖决依赖计计算机，题目的数题目的数据较据较据较多多，手工，手工计计算不能完成，如03B ，某些，某些问题问题问题需要需要需要使用使用使用计计算机软件，01A 。

第 1 页 共2页 第 1 页 共2页《数学建模》课程试卷适用专业： 考试日期：试卷类型：闭卷 考试时间：120分钟 试卷总分：100分一． 怎样解决下面的实际问题，包括需要哪些数据资料、观察、试验以及建立什么样的数学模型（10分） （1）估计一个人体内血液的总量 （2）估计一批日光灯管的寿命二.对于技术革新的推广，在下列几种情况下分别建立模型（10分）1．推广工作通过已经采用新技术的人进行，推广速度与已采用新技术的人数成正比，推广是无限的。

2．总人数有限，因而推广速度还会随着尚未采用新技术人数的减少而降低。

3.在（2）的前提下考虑广告等媒介的传播作用三.报童每天清晨从报社购进报纸零售，晚上将没有卖掉的报纸退回，设报纸每份的购进价 为b ，零售价为a ，退回价为c,应该自然地假设为a>b>c,这就是说，报童售出一份报纸赚a-b ，退回一份赔b-c 。

报童每天如果购进的报纸太少，不够卖的，会少赚钱；如果购进太多，卖不完，将要赔钱。

请你为报童筹划一下，他应如何确定每天购进报纸的数量，以获得最大的收入（10分）四．试建立正规战争模型，并进一步分析双方战平、甲方或乙方获胜得条件(10分))(),(t y t x 甲乙兵力)(),(t v t u 甲乙增援率a,b 乙甲射伤率 u cx ay dt dx +--= v dy bx dtdy +--= 不考虑非战斗减员和增援ay dt dx -=，bx dtdy-= 相轨线aybx dx dy =，k bx ay =-22，k bx ay =-2020 双方战平k=0甲方获胜得条件k<0 乙方获胜得条件K>0第 2 页 共2页 第 2 页 共2页60分）一家保姆服务公司专门向顾主提供保姆服务。

根据估计，下一年的需求是：6000人日，夏季7500人日，秋季5500人日，冬季9000人日。

公司新招5天的培训才能上岗，每个保姆每季工作65天，保姆从该公每人每月工资800元，春季开始时公司拥有12015%的保姆自动离职，（1）如果公司不允许2）如果公司在每个季度结束后请你为公司制定下一年的招聘计划（程序计算结果可自由确定）第 3 页 共2页 第 3 页 共2页《数学建模》课程试卷 答案适用专业： 考试日期：试卷类型：闭卷 考试时间：120分钟 试卷总分：100分二． 怎样解决下面的实际问题，包括需要哪些数据资料、观察、试验以及建立什么样的数学模型（10分） （1）估计一个人体内血液的总量 （2）估计一批日光灯管的寿命（1）注射一定量的葡萄糖，采取一定容积的血样，测量注射前后葡糖糖含量的变化，即可估计人体的血液总量 (5)（2）从一批灯管中取一定容量的样本，测的取平均寿命，可作为该批灯管寿命的平均值，为衡量估计的精度，需要从样本寿命确定该批灯管寿命的概率分布，即可得估计值的置信区间。

院系: 数学学院专业: 信息与计算科学年级: 2014级学生姓名: 王继禹学号: 2教师姓名: 徐霞6、6 习题3、一个慢跑者在平面上沿着她喜欢的路径跑步,突然一只狗攻击她,这只狗以恒定速率跑向慢跑者,狗的运动方向始终指向慢跑者,计算并画出狗的轨迹。

解:(1)模型分析建立:狗的轨迹:在任意时刻,狗的速度向量都指向它的目标慢跑者。

假设1:慢跑者在某路径上跑步,她的运动由两个函数X(t)与Y(t)描述。

假设2:当t=0时,狗就是在点(x0,y0)处,在时刻t时,它的位置就是(x(t),y(t))那么下列方程成立:(1)狗以恒定速率跑: X’2+y’2=w2(2) 狗的速度向量平行于慢跑者与狗的位置的差向量:将上述方程带入等式:,可得:再将λ代入第二个方程,可得狗的轨迹的微分方程:(2)程序及结果dog函数[dog、m]function [zs,isterminal,direction] = dog(t,z,flag) global w;% w=speed of the dogX=jogger(t);h = X-z;nh=norm(h);if nargin<3 || isempty(flag)zs=(w/nh)*h;elseswitch(flag)case'events'zs = nh-1e-3;isterminal = 1;direction = 0;otherwiseerror(['Unknow flag:' flag]);endend慢跑者的运动轨迹方程,水平向右[jogger、m]function s = jogger(t);s = [8*t;0];标记的函数[cross、m]function cross(Cx,Cy,v)Kx = [Cx Cx Cx Cx-v Cx+v];Ky = [Cy Cy+2、5*v Cy+1、5*v Cy+1、5*v Cy+1、5*v] plot(Kx,Ky);plot(Cx,Cy,'o');主程序:静态显示[main1、m]global wy0 = [60;70];w=10;options = odeset('RelTol',1e-5,'Events','on');[t,Y] = ode23('dog',[0,20],y0,options);clf;hold on;axis([-10,100,-10,70]);plot(Y(:,1),Y(:,2));J=[];for h=1:length(t),w = jogger(t(h));J=[J;w'];endplot(J(:,1),J(:,2),':');p = max(size(Y));cross(Y(p,1),Y(p,2),2)hold off;动态显示[main2、m]global w;y0=[60;70];w=10;options = odeset('RelTol',1e-5,'Events','on');[t,Y]=ode23('dog',[0,20],y0,options); J=[];for h=1:length(t);w= jogger(t(h));J=[J;w'];endxmin = min(min(Y(:,1)),min(J(:,1)));xmax = max(max(Y(:,1)),max(J(:,1)));ymin = min(min(Y(:,2)),min(J(:,2)));ymax = max(max(Y(:,2)),max(J(:,2)));clf;hold on;axis([xmin-10 xmax ymin-10 ymax]);title('The jogger and the Dog');for h = 1:length(t)-1,plot([Y(h,1),Y(h+1,1)],[Y(h,2),Y(h+1,2)],'-','Color','red','EraseMode ','none');plot([J(h,1),J(h+1,1)],[J(h,2),J(h+1,2)],'-','Color','green','EraseMo de','none');drawnow;pause(0、1);endplot(J(:,1),J(:,2),':');p = max(size(Y));cross(Y(p,1),Y(p,2),2)hold off;结果t=12、2761812635281,在12、27秒后狗追上慢跑者。

新疆乌鲁木齐地区2021届高三数学第三次质量监测试题 文（含解析）一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中只有一.项是符合题目要求的. 1.()21i i +=（ ） A. 22i +B. 22i -+C. 22i -D.22i --【答案】B 【解析】 【分析】直接按照复数的乘法法则运算即可. 【详解】()2122i i i +=-+. 故选：B【点睛】本题考查复数的运算，属于基础题.2.已知集合()(){}|220A x x x =-+<，{}2,1,0,1,2,3B =--，则A B =( )A. ∅B. {}0,1,2C. {}1,0,1-D.{}2,1,0,1,2--【答案】C 【解析】 【分析】先解不等式得集合A ，再根据交集定义求结果. 【详解】()(){}|220(2,2)A x x x =-+<=-,{}2,1,0,1,2,3B =--A B ∴={}1,0,1-故选：C【点睛】本题考查集合交集以及一元二次不等式解法，考查基本分析求解能力，属基础题. 3.设命题p ：x R ∀∈，211x +≥，则p⌝（ ）A. x R ∀∈，211x +<B. x R ∀∈，211x +≤C. 0x R ∃∈，2011x +<D. 0x R ∃∈，2011x +≤【答案】C 【解析】 【分析】根据全称命题的否定是特征命题进行解答即可. 【详解】因为命题p ：x R ∀∈，211x +≥，所以p ⌝为：0x R ∃∈，2011x +<.故选：C【点睛】本题考查了全称命题的否定，属于基础题. 4.已知等差数列{}n a 满足13518a a a ++=，35730a a a ++=，则246a a a ++=( )A. 20B. 24C. 26D. 28【答案】B 【解析】 【分析】直接根据等差数列的性质求解即可．【详解】解：∵等差数列{}n a 满足13518a a a ++=，35730a a a ++=，∴35351748a a a a a a +++=++，即()()()33571548a a a a a a +++=++， ∴24622482a a a ++=， ∴24624a a a ++=， 故选：B ．【点睛】本题主要考查等差数列的性质，属于基础题． 5.若角α的终边过点()3,4P -，则sin 2α的值为( )A.1225B. 1225-C.2425D. 2425-【答案】D【解析】 【分析】根据三角函数的定义求出sin ,cos αα，即可求出结论. 【详解】角α的终边过点()3,4,||5P OP -∴=， 43sin ,cos 55αα∴=-=，24sin 22sin cos 25ααα==-. 故选：D.【点睛】本题考查三角函数定义以及二倍角公式求三角函数值，考查计算求解能力，属于基础题.6.某校有甲、乙两个数学建模兴趣班.其中甲班有40人，乙班有50人.现分析两个班的一次考试成绩，算得甲班的平均成绩是90分，乙班的平均成绩是81分，则这两个数学建模兴趣班所有同学的平均成绩是( ) A. 85 B. 85.5C. 86D. 86.5【答案】A 【解析】 【分析】本题是一个加权平均数的问题，求出甲和乙两个班的总分数，再除以两个班的总人数，就是这两个班的平均成绩．【详解】解：由题意，这两个数学建模兴趣班所有同学的平均成绩是40905081854050⨯+⨯=+，故选：A ．【点睛】本题主要考查加权平均数的求法，属于基础题．7.如图，正方体1111ABCD A B C D -中，AB 的中点为M ，1DD 的中点为N ，则异面直线1B M 与CN 所成角的大小为( )A. 30B. 45︒C. 60︒D. 90︒【答案】D 【解析】 【分析】取CD 中点E ，连1,C E ME ，可证11//C E B M ，转化为求1,C E CN 所成的角，利用平面几何关系，证明1C E CN ⊥即可.【详解】取CD 中点E ，连1,C E ME ，在正方体1111ABCD A B C D -中，M 为AB 中点，1111////ME BC B C ME BC B C ∴,==，四边形11B C EM 为平行四边形，11//C E B M ∴，∴异面直线1B M 与CN 所成角为直线1,C E CN 所成的角，在正方形11CC D D 中，1Rt C CE Rt CDN ≅△△，1111,90CC E DCN CC E C EC DCN C EC ∴∠=∠∠+∠=∠+∠=︒， 1,C E CN ∴⊥∴直线1B M 与CN 所成角的大小为90︒.故选：D..【点睛】本题考查空间线、面位置关系，证明异面直线垂直，考查直观想象、逻辑推理能力，属于基础题.8.在Rt ABC 中，1AB AC ==，点D 满足2BD DC =，则AB AD ⋅=（ ） A.13B.23C. 1D. 2【答案】A 【解析】 【分析】由题意可知A ∠为直角，以A 为原点，AB 为x 轴，AC 为y 轴，建立平面直角坐标系，设(),D x y ，利用向量共线求出点D ，从而再根据向量数量积的坐标运算即可求解.【详解】在Rt ABC 中，1AB AC ==， 所以A ∠为直角，以A 为原点，AB 为x 轴，AC 为y 轴，建立平面直角坐标系，则()10B ,，()0,1C ，设(),D x y ，()1,BD x y =-，(),1DC x y =--， 由2BD DC =，可得()1,x y -()2,1x y =--，即1222x x y y-=-⎧⎨=-⎩，解得13x =，23y =，所以12,33D ⎛⎫⎪⎝⎭，由()1,0AB = ，12,33AD ⎛⎫= ⎪⎝⎭所以12110333AB AD ⋅=⨯+⨯=. 故选：A【点睛】本题考查了平面向量的线性坐标运算、向量数量积的坐标表示，考查了基本运算能力，属于基础题.9.直线2y x =-与抛物线()220y px p =>交于A ，B 两点，若OA OB ⊥，则p 的值为( ) A.12B. 1C.32D. 2【答案】B 【解析】 【分析】设()11,A x y ，()22,B x y ，联立222y x y px=-⎧⎨=⎩并消元得，()22440x p x -++=，得韦达定理结论，由题意得0OA OB ⋅=，由此根据数量积的坐标表示求解即可． 【详解】解：设()11,A x y ，()22,B x y ， 联立222y x y px=-⎧⎨=⎩并消元得，()22440x p x -++=， ∴1224x x p +=+，124x x =， 又OA OB ⊥，∴1212OA OB x x y y ⋅=+()()121222x x x x =+--()1212224x x x x =-++()82244p =-++440p =-=，∴1p =， 故选：B ．【点睛】本题主要考查直线与抛物线的位置关系，考查韦达定理的应用，属于基础题．10.在四面体ABCD 中，AB =，1DA DB CA CB ====，则四面体ABCD 的外接球的表面积为( ) A. πB. 2πC. 3πD. 4π【答案】B 【解析】 【分析】取AB 的中点O ，连接OC ，OD ，由题意可得O 为外接球的球心，利用球的表面积公式即可求解. 【详解】由2AB =，1DA DB CA CB ====，所以222CA CB AB +=，222AD BD AB +=可得90ACB ADB ∠=∠=，所以22OA OB OC OD ====， 即O 为外接球的球心，球的半径2R =所以四面体ABCD 的外接球的表面积为：214422S R πππ==⨯= 故选：B【点睛】本题考查了多面体的外接球的表面积，需熟记球的表面积公式，属于基础题.11.M 是双曲线C ：()222210,0x y a b a b-=>>上位于第二象限的一点，1F ，2F 分别是左、右焦点，112MF F F ⊥.x 轴上的一点N 使得290NMF ∠=︒，A ，B 两点满足MA AN =，12MB BF =，且A ，B ，2F 三点共线，则双曲线C 的离心率为( )A. 21+B. 31+C. 22+D.32+【答案】A 【解析】 【分析】由题意，先求出2,b M c a ⎛⎫- ⎪⎝⎭，再根据290NMF ∠=︒，求出442,02a c N a c ⎛⎫-- ⎪⎝⎭，再求出()22222,42a c b A a c a ⎛⎫-+ ⎪ ⎪⎝⎭，再求出2,3b B c a ⎛⎫- ⎪⎝⎭，根据A ，B ，2F 三点共线，利用向量平行，找到,a c 的关系即可求解. 【详解】解：如图，()1,0F c -，()2,0F c把x c =-代入()222210,0x y a b a b -=>>，得2by a =±，2,b M c a ⎛⎫- ⎪⎝⎭设(),0N n ，222+,,2,b b MN n c MF c a a ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭因为290NMF ∠=︒，所以20MN MF ⋅=，所以()422+0b c n c a += ，4422a c n a c--=， 即442,02a c N a c ⎛⎫-- ⎪⎝⎭，因为MA AN =，所以是A 线段MN 的中点，所以44222,22a c c b a c A a ⎛⎫--- ⎪⎪ ⎪ ⎪⎝⎭， 即()22222,42a c b A a c a ⎛⎫-+ ⎪ ⎪⎝⎭，设(),B x y ，则2,b MB x c y a ⎛⎫=+- ⎪⎝⎭，()1,BF c x y =---因为12MB BF =，所以2222x c c x b y y a +=--⎧⎪⎨-=-⎪⎩，23x c b y a =-⎧⎪⎨=⎪⎩，所以2,3b B c a ⎛⎫- ⎪⎝⎭， 222,3b BF c a ⎛⎫=- ⎪⎝⎭，()2222442222226,,4242a c b a c a c b AF c a c a a c a ⎛⎫+⎛⎫++ ⎪=+-=- ⎪ ⎪⎝⎭⎝⎭ 因为A ，B ，2F 三点共线，所以22//BF AF ，所以24422226243b a c a c b c a a c a ⎛⎫⎛⎫++⨯-=⨯- ⎪ ⎪⎝⎭⎝⎭， 442260a c a c +-=，42610e e -+=，23e =±因为1e >，所以)2231e =+=，所以e =，故选：A.【点睛】结合向量考查用解析法求双曲线的离心率，对于学生的运算求解能力是挑战，计算量大，容易出错；中档题.12.定义在R 上的函数()y f x =，当[]0,2x ∈时，()2144x f x --=-，且对任意实数122,22(,2)k k x k N k +⎡⎤∈--∈≥⎣⎦，都有1()122x f x f ⎛⎫=- ⎪⎝⎭，若()()log a g x f x x =-有且仅有5个零点，则实数a 的取值范围是( )A.B.C.D.【答案】C 【解析】 【分析】由()()log 0a g x f x x =-=，可得()log a f x x =，分别作出函数()f x 和log a y x =的图像，利用数形结合即可得出结果. 【详解】当[]0,2x ∈时，()2144x f x --=-，当2k =时，[]2,6x ∈，此时[]10,22x-∈， 则1()122x f x f ⎛⎫=- ⎪⎝⎭211222211444422x x-----⎛⎫⎛⎫=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，当3k =时，[]6,14x ∈，此时[]12,62x-∈，则1()122x f x f ⎛⎫=- ⎪⎝⎭12225224211444422xx -----⎛⎫ ⎪⎛⎫ ⎪=-=- ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪⎝⎭，当4k =时，[]14,30x ∈，此时[]16,142x-∈，则1()122x f x f ⎛⎫=- ⎪⎝⎭1522114228411444422xx -----⎛⎫ ⎪⎛⎫ ⎪=-=- ⎪ ⎪ ⎪⎝⎭ ⎪ ⎪⎝⎭，由()()log 0a g x f x x =-=，可得()log a f x x =， 分别作出函数()f x 和log ay x =的图像：若01a <<时，此时两个函数图像只有1个交点，不满足条件； 若1a >时，当对数函数经过点A 时，两个图像有4个交点， 经过点时B 有6个交点，则要使两个函数有有且仅有5个零点，则对数函数图像必须在点A 以下，在点B 以上，()103f =，()3222f =， ()10,3A ∴，322,2B ⎛⎫ ⎪⎝⎭，即满足log 1033log 222a a <⎧⎪⎨>⎪⎩，解得3321022a a ⎧>⎪⎨⎪<⎩3310484a <<. 故选：C【点睛】本题考查了由函数的零点个数求参数的取值范围，考查了数形结合以及转化与化归的思想，属于难题.二、填空题：本大题共4小题，每小题5分.13. 将2本不同的数学书和1本语文书在书架上随机排成一行，则2本数学书相邻的概率为________. 【答案】23【解析】2本不同的数学书和1本语文书在书架上随机排成一行，所有的基本事件有（数学1，数学2，语文），（数学1，语文，数学2），（数学2，数学1，语文），（数学2，语文，数学1），（语文，数学1，数学2），（语文，数学2，数学1）共6个，其中2本数学书相邻的有（数学1，数学2，语文），（数学2，数学1，语文），（语文，数学1，数学2），（语文，数学2，数学1）共4个，故2本数学书相邻的概率42=63．14.已知定义在R 上的奇函数()f x 满足：当0x <时，()()3log 1f x x =-，则()8f =______.【答案】-2 【解析】 【分析】根据()f x 定义在R 上的奇函数，则()()88f f =--，然后再由0x <时，()()3log 1f x x =-求解.【详解】因为()f x 定义在R 上的奇函数，且当0x <时，()()3log 1f x x =-， 所以()()233log 9lo 8g 328f f =---===--.故答案为：-2【点睛】本题主要考查函数的奇偶性的应用以及对数运算，还考查了运算求解的能力，属于基础题.15.f (x )＝2sin ωx (0<ω<1)，在区间0,3π⎡⎤⎢⎥⎣⎦，则ω＝________. 【答案】34【解析】【详解】函数f (x )的周期T ＝2πω，因此f (x )＝2sin ωx 在0,πω⎡⎤⎢⎥⎣⎦上是增函数， ∵0<ω<1，∴0,3π⎡⎤⎢⎥⎣⎦是0,πω⎡⎤⎢⎥⎣⎦的子集，∴f (x )在0,3π⎡⎤⎢⎥⎣⎦上是增函数，∴3f π⎛⎫⎪⎝⎭，即2sin 3πω⎛⎫ ⎪⎝⎭∴3πω＝4π， ∴ω＝34，故答案为34.16.在正项等比数列{}n a 中，464a a +=，12a ，312a ，2a成等差数列，则数列{}1n n a a +的前n 项之积的最小值为______. 【答案】202- 【解析】 【分析】设公比为q ，由题意0q >.根据464a a +=，12a 、312a 、2a成等差数列，求出1,a q ，写出n a .令1n n n b a a +=，可得数列{}n b 的前n 项之积n T ，即求n T 的最小值. 【详解】由题意等比数列{}n a 中，0n a >.设公比为q ，则0q >.12a ，312a ，2a 成等差数列，3122a a a ∴=+，即2211112,0,20a q a a q a q q =+∴>∴--=，解得2q或1-（舍）.464a a +=，35114a q q a ∴+=5111322432a a a +=∴=⨯⨯，116122n n n n a a q ---∴===.651210222n n n n n a a --+-==∴.令1n n n b a a +=，则数列{}n b 的前n 项之积()()22211021210211022102109212981242222222n n n n nn nnn n n T b b b +-++-⨯-⨯---⎛⎫-- ⎪⎝⎭==⨯⨯⨯====，∴当4n =或5时，()20min 2n T -=.故答案为：202-.【点睛】本题考查等比数列的通项公式、等差数列的前n 项和公式，属于中档题. 三、解答题：第17~21题每题12分，解答应在答卷的相应各题中写出文字说明，证明过程或演算步骤.17.在ABC 中，a ，b ，c 是A ∠，B ，C ∠所对的边，a =1c =，cos 0A A +=.（Ⅰ）求b ；（Ⅱ）若D 为BC 边上一点，且AD AB ⊥，求ACD 的面积.【答案】. 【解析】 【分析】（Ⅰ）由题意求得150A =︒，再根据余弦定理即可求出答案；（Ⅱ）根据正弦定理可得sin 14B =，从而求得tan B =，则5AD =，再根据三角形的面积公式即可求出答案．详解】解：cos 0A A +=，得tan 3A =-， ∴150A =︒，又∵a =1c =，又2222cos a b c bc A =+-，即260b -=，解得b =(负值舍去)；（Ⅱ）由（Ⅰ）得sin sin a b A B=，∴13si 21sin 14n 27B ab A⋅===，∴21si 57co 1n s 4B B ==-， ∴3tan 5B =，∵AD AB ⊥， ∴3tan AD c B ==，且60=︒∠DAC ， ∴ACD 的面积133sin 602ACD S AD AC ︒=⋅⋅=△． 【点睛】本题主要考查正弦定理、余弦定理的应用，考查三角形的面积公式的应用，属于基础题．18.在疫情这一特殊时期，教育行政部门部署了“停课不停学”的行动，全力帮助学生在线学习.复课后进行了摸底考试，某校数学教师为了调查高三学生这次摸底考试的数学成绩与在线学习数学时长之间的相关关系，对在校高三学生随机抽取45名进行调查.知道其中有25人每天在线学习数学的时长是不超过1小时的，得到了如下的等高条形图：（Ⅰ）将频率视为概率，求学习时长不超过1小时但考试成绩超过120分的概率； （Ⅱ）是否有99%的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”.()20P K k ≥ 0.050 0.010 0.0010k3.841 6.635 10.828()()()()()22n ad bc K a b c d a c b d -=++++ 【答案】（Ⅰ）29；（Ⅱ）没有99%的把握认为“高三学生的这次摸底成绩与其在线学习时长有关” 【解析】 【分析】（Ⅰ）根据等高条形图求出学习时长不超过1小时但考试成绩超过120分的人数为225105⨯=人，由古典概型的概率计算公式即可求解. （Ⅱ）根据题意列出列联表，计算出观测值，根据独立性检验的基本思想即可求解. 【详解】（Ⅰ）从等高条形图中看出，学习时长不超过1小时， 但考试成绩超过120分的人数为225105⨯=人，∴其概率为102459=； （Ⅱ）依题意，得22⨯列联表：数学成绩 在线学习时长120≤分120>分合计1≤小时15 10 25 1>小时515 20 合计 202545∵2245(1515510)4415.51256.6352025252080K ⨯-⨯===<⨯⨯⨯，∴没有99%的把握认为“高三学生的这次摸底成绩与其在线学习时长有关”.【点睛】本题主要考查了独立性检验的基本思想、古典概型的概率计算公式、列联表，属于基础题.19.如图，将直角边长为2的等腰直角三角形ABC ，沿斜边上的高AD 翻折，使二面角B ADC --的大小为3π，翻折后BC 的中点为M .（Ⅰ）证明BC ⊥平面ADM ； （Ⅱ）求点D 到平面ABC 的距离. 【答案】（Ⅰ）见解析；（Ⅱ）217【解析】 【分析】（Ⅰ）证出DM BC ⊥，AM BC ⊥，然后利用线面垂直的判定定理即可证出. （Ⅱ）设点D 到平面ABC 的距离为d ，利用等体法，由三棱锥的体积公式即可求解. 【详解】（Ⅰ）∵折叠前AB AC =，AD 是斜边上的高， ∴D 是BC 的中点，∴BD CD =， 又因为折叠后M 是BC 的中点， ∴DM BC ⊥，折叠后AB AC =， ∴AM BC ⊥，AM DM M =，∴BC ⊥平面ADM ；（Ⅱ）设点D 到平面ABC 的距离为d ， 由题意得A BCD D ABC V V --=，∵113A BCD V -==∴13412D ABC V d -=⨯=，∴7d =. 【点睛】本题考查了线面垂直的判定定理、等体法求点到面的距离、三棱锥的体积公式，考查了逻辑推理能力，属于基础题.20.已知椭圆C ：()222210x y a b a b+=>>右焦点为()2,0F ，P 为椭圆上异于左右顶点A ，B 的一点，且PAB △面积的最大值为.（Ⅰ）求椭圆C 的标准方程；（Ⅱ）若直线AP 与直线x a =交于点Q ，线段BQ 的中点为M ，证明直线FM 平分PFB ∠.【答案】（Ⅰ）22195x y +=；（Ⅱ）证明见解析. 【解析】 【分析】（Ⅰ）由题意得2222ab a b ⎧=⎪⎨-=⎪⎩，解出即可； （Ⅱ）设直线AP 的方程为3x my =-，与椭圆方程联立求得点222152730,5959m m P m m ⎛⎫- ⎪++⎝⎭，求出点63,Q m ⎛⎫ ⎪⎝⎭，从而得中点33,M m ⎛⎫⎪⎝⎭，利用斜率的计算公式与正切的定义即可证明结论．【详解】解：（Ⅰ）由题意得2222ab a b ⎧=⎪⎨-=⎪⎩，解得2295a b ⎧=⎨=⎩， ∴椭圆C 的标准方程为22195x y +=；（Ⅱ）设直线AP 的方程为3x my =-，代入22195x y +=，得()2259300m y my +-=， 解得0y =，或23059my m =+，∴222230152735959P m m x m m -=-=++， ∴222152730,5959m m P m m ⎛⎫- ⎪++⎝⎭， 易知直线AP 与3x =的交点63,Q m ⎛⎫ ⎪⎝⎭， ∴线段BQ 的中点33,M m ⎛⎫ ⎪⎝⎭， 设MFB α∠=，则33tan 1m mα==， ∴22326tan 2991m m m mα⨯==--，222223030659tan 15275459259PF mm m m PFB k m m m m +∠====----+，∵()20,απ∈，()0,PFB π∠∈，tan 2tan PFB α=∠， ∴2PFB α∠=，即直线FM 平分PFB ∠．【点睛】本题主要考查直线与椭圆的位置关系，考查计算能力，考查转化与化归思想，属于中档题．21.已知()()ln 20xf x e a x a a =-+>.（Ⅰ）当a e =时，求()f x 的单调区间；（Ⅱ）设0x 是()f x 的极小值点，求()0f x 的最大值.【答案】（Ⅰ）()f x 在()0,1上单调递减，在()1,+∞上单调递增；（Ⅱ）2e e【解析】 【分析】（Ⅰ）当a e =时，对函数()f x 求导，再对导函数'()f x 进行求导，判断导函数'()f x 的单调性，最后利用导函数'()f x 的单调性进行判断'()f x 的正负性，最后确定()f x 的单调性； （Ⅱ）对函数()f x 求导，再对导函数'()f x 进行求导，判断导函数'()f x 的单调性，根据极值的定义，结合构造新函数，对新函数进行求导，结合新函数的单调性进行求解即可.【详解】（Ⅰ）当a e =时，()ln 2xf x e e x e =-+，()'xef x e x=-，显然()'10f =， 设()'()xef x h x e x==-，(1)0h =， ∵2'()0xeh x e x=+>，∴()'f x 在()0,∞+上是增函数， 当01x <<时，()()''10f x f <=，当1x >时，()()''10f x f >=， ∴()f x 在()0,1上单调递减，在()1,+∞上单调递增； （Ⅱ）由()'xa e f x x=-，设()()'xm x f x a e x ==-，则2'()0xm x e ax=+>，∴()'f x 在()0,∞+上单调递增， ∴存在极小值点0x 满足()0'0f x =，即0x a e x =， ∴()000000000ln 2ln 2xxxx f x e a x a e x e x x e=-+=-+()00001ln 2x e x x x =-+，令()(1ln 2)xg x e x x x =-+，则()()'1ln 21ln x g x e x x x x =-++-()1(2ln )x x x e =+-，当2x e >时，'()0,()g x g x <单调递减，当20x e <<时，'()0,()g x g x >单调递增， 所以当2x e =时，()g x 有最大值，即()()22max e g x g e e ==，所以()0f x 的最大值为2e e .【点睛】本题考查了利用导数求函数的单调区间，考查了利用导数求函数的最值问题，考查了数学运算能力.选考题：共10分，请考生在22、23两题中任选一题作答， 如果多做，则按所做的第一题计分.作答时用2B 铅笔在答题卡上把所选题目的题号涂黑.22.已知曲线1C的参数方程为23x t y t⎧=+⎪⎨=+⎪⎩（t 为参数），以坐标原点O 为极点，x 轴的正半轴为极轴建立极坐标系，曲线2C 的极坐标方程为2sin ρθ=.（Ⅰ）求曲线1C 的极坐标方程；（Ⅱ）设1C 与2C 交点为A ，B ，求AOB 的面积.【答案】（Ⅰ）24cos 6sin 80ρρθρθ--+=；（Ⅱ）1.【解析】【分析】（Ⅰ）先根据曲线1C 的参数方程，消去参数t 化为直角坐标方程，然后将 cos ,sin x y ρθρθ==代入求解.（Ⅱ）先把曲线2C 的极坐标方程化为直角坐标方程，然后与曲线1C 的直角坐标方程联立，求得A ，B 的坐标，再求面积.【详解】（Ⅰ）因为曲线1C的参数方程为23x t y t⎧=+⎪⎨=+⎪⎩（t 为参数），消去参数t 得：()()22235x y -+-=，即：224680x y x y +--+=，又因为cos ,sin x y ρθρθ==，代入上式得曲线1C ：24cos 6sin 80ρρθρθ--+=；（Ⅱ）因为曲线2C 的极坐标方程为2sin ρθ=，所以22sin ρρθ=，所以2220x y y +-=， 联立方程2222468020x y x y x y y ⎧+--+=⎨+-=⎩，解得02x y =⎧⎨=⎩或11x y =⎧⎨=⎩， ∴()0,2A ，()1,1B ， ∴12112AOB S =⨯⨯=. 【点睛】本题主要考查参数方程，极坐标方程，直角坐标方程的转化以及曲线的位置关系，还考查了运算求解的能力，属于中档题.23.设a ，b 均为正数，且222a b +=，证明：（Ⅰ）()33()4a b a b ++≥；2≤.【答案】（Ⅰ）证明见解析；（Ⅱ）证明见解析.【解析】【分析】（Ⅰ）利用分析法、作差法即可证明不等式.（Ⅱ）将不等式两边平方，利用分析法即可证明.【详解】（Ⅰ）∵222a b +=，要证()33()4a b a b ++≥，只需要证明，()2443322a b ab ba a b +++≥+，也就是要证明4433442220a b ab ba a b a b +++---≥，即证()20ab a b -≥，∵a ，b 均为正数，∴()20ab a b -≥，∴()33()4a b a b ++≥；（Ⅱ）∵a ，b 均为正数，∴a b +≥，∴22()a b +≥，≤≤，又∵222a b +=2≤.【点睛】本题考考查了分析法、作差法、基本不等式证明不等式，属于基础题.。

雨中行走淋雨量问题分析芮雪（数科院数创2班）A班刘倩冰（数科院数创2班）姜勇（计科院软工1班）摘要人在雨中奔跑时的淋雨量与很多因素有关，主要分析人的跑步速度、降雨方向和雨速大小与淋雨量之间的关系。

本文讨论了在给定降雨条件下，分别建立相应的数学模型，探究淋雨量与跑步速度、降雨方向和雨速大小之间的量化关系，分析总淋雨量最小时对应的跑步速度大小。

针对问题一，在不考虑雨方向的条件下，淋雨总面积为人体前后左右及头顶面积之和，结合雨速大小与淋雨时间，进一步得到跑完全程的总淋雨量。

针对问题二，根据雨线与跑步方向在同一平面内，可分析出雨速在某一方向上没有分量，又由雨迎面吹来，可知淋雨面积为人体前方和头顶面积之和。

进而借鉴数学分析中曲面积分的通量概念，建立雨从迎面吹来的淋雨量模型，运用图解法分析淋雨量最小时对应的跑步速度，有以下结论：当雨从迎面吹来，即雨在人跑步水平方向上的分速度与人跑步速度方向相反时，人跑得越快，总淋雨量越少。

针对问题三，按照问题二的建模思想，建立雨从背面吹来的淋雨量模型，通过图解法探究淋雨量最小时对应的跑步速度。

结果表明：雨速在人跑步方向上的分速度大于某一常量的情况下，人跑步速度等于雨速在跑步方向上的分速度时，总淋雨量最小；雨速在人跑步方向上的分速度小于这一常量的情况下，人跑的越快淋雨量越少；雨速在人跑步方向上的分速度等于这一常量的情况下，人跑步速度为这一常量的两倍时，总淋雨量最小为零，在理论上即人的速度为合理值时，可以不淋雨，但是不具有实际的指导意义。

针对问题四，根据雨线方向与跑步方向不再同一平面内，分析出雨速在三个方向上都有分量，同样利用通量概念，建立此时跑步速度与总淋雨量之间的模型，探究模型的变化。

通过综合对比各模型给出结论：当雨速在人跑步方向上的分速度大于某一正常数的情况下，只要人跑步速度等于雨速在人跑步方向上的分速度时，总淋雨量最小，其他情况下，人跑得越快，淋雨量越小，显然这符合人们的生活常识。

第三次线性规划建模作业1、公共交通司机排班班次时间需要人数1 6： 00-10： 00 222 10： 00-14： 00 283 14： 00-18： 00 254 18： 00-22： 00 205 22： 00-2： 00 156 2： 00-6： 00 101）每个人上两个连续的班（8小时），最少需要多少人？2）每个人可以上两个连续的班（8小时）或者一个4小时的班，最少需要多少人？3）如果连续两个班的工资为64元，只上4小时班的工资为36元，如何排班为好？1、！设乂1是第一班开始时上班的人数, .. X2是第二班....，X6是第六班开始上班的人数!所有人上连续8小时班MIN X1+X2+X3+X4+X5+X6STX6+X1 >=22X1+X2 >=28X2+X3 >=25X3+X4 >=20X4+X5 >=15X5+X6 >=10END2、设XI是第一班开始时上上连续8小时班的人数,X6是第六班开始上上连续8小时班的人数 !设丫1是第一班开始时上4小时班的人数,Y6是第六班开始上4小时班的人数。

!为了使得到的解都是整数（人数），用GIN 12表示“要求前面12个变量是非负整数。

MIN X+ YSTX1+X2+X3+X4+X5+X6-X二0Y1+Y2+Y3+Y4+Y5+Y6-Y二0X6+X1+Y1〉=22X1+X2+Y2〉=28X2+X3+Y3〉=25X3+X4+Y4〉=20X4+X5+Y5X15X5+X6+Y6>=10ENDGIN 123、！设乂1是第一班开始时上上连续8小时班的人数,X6是第六班开始上上连续8小时班的人数 !设丫1是第一班开始时上4小时班的人数,Y6是第六班开始上4小时班的人数。

!为了使得到的解都是整数（人数），用GIN 12表示“要求前面12个变量是非负整数。

MIN 64X+ 36YSTX1+X2+X3+X4+X5+X6-X二0Y1+Y2+Y3+Y4+Y5+Y6-Y二0X6+X1+Y1〉=22X1+X2+Y2〉=28X2+X3+Y3〉=25X3+X4+Y4〉=20X4+X5+Y5X15X5+X6+Y6>=10ENDGIN 122、某商场对售货人员的需求经过统计分析如下所示:续的，问应该如何安排售货人员的休息，既满足了工作需要，又使配备的售货人员的人数最少？解：设XI为星期一开始休息的人数，X2为星期二开始休息的人数， ........ ，X6为星期六开始休息的人数，X7为星期日开始休息的人数。

江西省景德镇市2023届高三第三次质量检测理科数学试题学校:___________姓名：___________班级：___________考号：___________A．3 285．一个几何体的三视图如图所示，则该几何体的体积为（A．2π3B．π6．互相垂直且有公共原点的两条数轴构成平面直角坐标系，但如果平面坐标系中两条坐标轴不垂直，则这样的坐标系称为“斜坐标系轴的平行线，其在x轴和y轴上的截距(),P a b.若斜坐标系中，x轴正方向和y()4,1NA．2B．17．首钢滑雪大跳台是冬奥史上第一座与工业旧址结合再利用的竞赛场馆，它的设计创造性地融入了敦煌壁画中飞天的元素，建筑外形优美流畅，飘逸灵动，被形象地称为雪飞天.中国选手谷爱凌和苏翊鸣分别在此摘得女子自由式滑雪大跳台和男子单板滑雪大A ．5459．中国古代十进位制的算筹记数法在世界数学史上是一个伟大的创造筹最晚出现在春秋晚期战国初年，算筹记数的方法是数码摆出：十位､千位､1-9这9个数字的纵式与横式的表示数码如上图所示，则()πcos d x x ⎰可用算筹表示为（ ）．．．．．某地举办数学建模大赛，本次大赛的冠军奖杯由一个铜球和一个托盘组成，如图A ．733B ．833C ．33D ．11．已知1F ，2F 分别是双曲线()2222:10,0x yC a b a b-=>>的左、右焦点，直线且与C 左支交于P ，Q 两点，P 在以12F F 为直径的圆上，2:3:PQ PF =率是（ ）A ．17B ．217C ．215D ．二、填空题(1)证明：面PAC⊥面ACD；(2)若M为PD上的一点，点P到面ACM的距离为25，求二面角519．部分高校开展基础学科招生改革试点工作（强基计划）的校考由试点高校自主命题，校考过程中达到笔试优秀才能进入面试环节.已知,A B两所大学的笔试环节都设有三门(1)若2π3O ON ∠=，求点N 的极坐标；(2)若点K 是射线(π3θρ=≥23．设a ，b ，c 均为正数，且10ab <<参考答案：半圆锥的体积111π23V=⨯⨯∴几何体体积122 3V V V=+=故选：A.用算筹记数表示为面ADE，面CDF，面BEF都与面∴≌，ABC MNG的边长为2，则其外接圆半径MNG∴球心到平面ABC的距离d R=//BC AD Q ，1BC AN ==12CN AD ∴=，CD AC ∴⊥PA CD ⊥ ，PA AC =则()0,0,1P ，()3,0,0A，(C -()3,2,1DP ∴=- ，(23,0,0AC =- 设()(3,2,0DM DP λλλλ==-< 则(323,AM AD DM λ=+=-）设直线:1MN x ty =-，()()1122,,,M x y N x y ，则22113ty y =-+=得：()2234690t y ty +--=，0∆>，122634t y y t ∴+=+，122934y y t =-+()3ty y y y =+，又21y y k -=，∴点N 的极角为π112π66-=（2）由题意知：2OK =，2sin OM =1sin 2MOK OK OM MOK =⋅∠答案第15页，共15页。