第四讲-综合分析题

第四讲韵母习题一．基础知识填空1.普通话共有（）个辅音声母，有（）个韵母。

2.普通话中有一些音节的开头没有辅音，这叫做（）。

3.韵母是（）。

韵母的结构可以由（）、（）、（）三部分组成。

4.由（）充当的韵母叫单韵母，普通话的单韵母共有（）个。

5.普通话共有（）个韵母，按照构成成分分为（）、（）、（）三类。

6.复韵母是（）。

7.韵腹是韵母的（），又叫（）；位置在韵腹前面的是（），在韵腹后面的是（），一个韵母可以没有（）、（），但是一定要有韵腹。

8.所有的元音都可以充当韵腹，而能作韵头的只有（）；能作韵尾的只有（）三个元音和（）两个辅音。

9.汉语拼音方案中的e代表两个元音，它们是________________。

10. ɑi、ei、ɑo、ou是（）韵母，它们的特点是：前一个元音充当（）；后一个元音充当（）。

11.iɑ、ie、uɑ、uo、ue是（）韵母，它们的特点是：前一个元音充当（）；后一个元音充当（）。

12.ie、üe中的e实际是单韵母中的（）。

13.iɑo、iou、uɑi、uei是（）韵母。

14. ɑnɡ、enɡ、inɡ、onɡ等韵母的韵腹分别是（）。

15.iɑnɡ、uɑnɡ、uenɡ、ionɡ等韵母的韵腹分别是（），韵头分别是（），韵尾是（）。

16.没有韵头，而韵腹又不是i、u、ü的韵母，叫做（），韵头或韵腹是i的韵母，叫做（），韵头或韵腹是u的韵母，叫做（），韵头或韵腹是ü的韵母，叫做（）。

17.普通话的韵母除了按照韵腹的特点分类外，还可以按照韵头的情况分类，这叫做（）。

18.在普通话中，音节与汉字基本是（）的关系，但是（）例外。

19.普通话音节可以分为（）、（）、（）。

20.对普通话音节结构作深层次分析，一般一个完整的音节应该具备（）、（）、（）、（）、（）五个部分。

21.《汉语拼音分案》规定iou、uei、uen三个韵母前面加辅音声母时，写成（）。

22.声调的调号应该标在（）。

解答题王阿姨买了3千克梨和3千克苹果共付19.8元，李阿姨买了1千克梨和3千克苹果共付14.8元。

每千克苹果和每千克梨各多少元？【答案】每千克苹果：4.1元；每千克梨：2.5元【解析】已知3千克梨和3千克苹果一共19.8元，那么用19.8除以3即是1千克梨和1千克苹果的钱数，用1千克梨和3千克苹果的钱数减去1千克梨和1千克苹果的钱数即是2千克苹果的钱数，然后除以2，就是1千克苹果的钱数，从而解答此题。

1千克梨＋1千克苹果＝19.8÷3＝6.6（元）1千克苹果：（14.8－6.6）÷2＝8.2÷2＝4.1（元）1千克梨：6.6－4.1＝2.5（元）答：每千克苹果4.1元，每千克梨2.5元。

解答题用边长是15厘米的方砖给实验室铺地,需要4000块，如果改用边长25厘米的方砖铺地,需要多少块砖？【答案】1440块【解析】根据正方形面积公式：边长×边长，先求出边长15厘米的方砖面积，然后乘以块数即是实验室铺地面积，接着除以边长25厘米的方砖面积即可解答。

15×15×4000÷（25×25）＝225×4000÷625＝900000÷625＝1440（块）答：需要1440块砖。

解答题用一部收割机收大豆，5天可以收割20.8公顷．照这样计算，7天可以收割多少公顷？62.4公顷大豆需要多少天才能收完？【答案】29.12公顷．15天【解析】试题分析：（1）根据题意，每天收割小麦20.8÷5公顷，那么7天可以收割20.8÷5×7公顷，解决问题；（2）每天收割小麦20.8÷5=4.16公顷，收割62.4公顷的大豆需要的时间为62.4÷（20.8÷5），计算即可．解：（1）20.8÷5×7=4.16×7=29.12（公顷）；答：7天可以收割29.12公顷．（2）62.4÷（20.8÷5）=62.4÷4.16=15（天）；答：62.4公顷的大豆需要15天才能收完．解答题做一套成人服装用布2.6米，用120米布可以做多少套成人服装？【答案】46套【解析】根据题意可知，直接用布总米数÷一套衣服的用布米数即可解答。

第四讲组织形象分析一、单项选择题1．组织形象最基本的构成因素是（）A 实力形象B 文化形象C 社会形象D 产品形象2．品牌形象是属于（）A 有形形象B 无形形象C 实际形象D 单一形象3．万宝路香烟，最初是一种女士香烟，由于市场销售不畅，公司决定以新的西部牛仔的粗狂形象定位，最终获得成功，这是根据哪一要素进行成功定位的？（）A 主体个性B传达方式C 公众认知D 媒体特征4．组织形象的基础是（）A 员工形象B 管理形象C 机构形象D 产品形象5．高美誉度、低知名度属于公共关系的（）状态。

A 最佳B 较为稳定、安全C 不良D 恶劣6．分析组织的自我形象与实际形象之间的现实距离时使用（）A 组织形象象限图B 形象要素调查表C 语义差异分析法D 形象要素差距图7．高美誉度低知名度的企业在组织形象地位图中处在（）。

A 第Ⅰ象限B 第Ⅱ象限C 第Ⅲ象限D 第Ⅳ象限二、判断题（）1 产品形象是整个组织形象的基础。

（）2 组织的自我期待形象，是一个组织自我希望具有的社会形象。

（）3 知名度高的企业其美誉度一定是好的。

（）4 知名度高美誉度好的企业是处在一个公共关系的最佳状态，企业可以高枕无忧了。

三、多选题1．组织形象分析的三个环节是（）A 自我形象分析B 实际形象分析C 历史形象分析D 形象差距分析E 公众评议分析2．进行组织形象要素分析时，其通常的步骤有（）。

A 确定组织形象要素B 制作调查表格C 分发表格D 进行实际调查E 汇总定位3．组织自我期望形象的调查包括（）。

A 组织状态和条件的调查分析B 员工阶层的调查与分析C 管理阶层的调查与分析D 决策层的调查与分析E 公众的调查与分析四、问答题1．组织形象的具体内容有哪些？2．组织的自我期望形象调查包括哪些方面？3．为什么要对组织进行形象差距分析？参考答案：一、单选题DBCDB；DB二、判断题√√××三、多选题1．ABD 2．ABCDE 3．ABCD。

第四讲组合日常生活中有很多“分组”问题.如在体育比赛中,把参赛队分为几个组,从全班同学中选出几人参加某项活动等等.这种“分组”问题,就是我们将要讨论的组合问题,这里,我们将着重研究有多少种分组方法的问题.例如某客轮航行于天津、青岛、大连三个城市之间.那么,船票共有几种价格（往返票价相同）？注意到由天津到青岛的票价与从青岛到天津的票价是一样的,所以问题实际上就是计算从三个城市中取两个城市,有多少种不同的取法,即这时只与考虑的两个城市有关而与两个城市的顺序无关.由枚举法知,共有下面的三种票价：天津←→青岛青岛←→大连大连←→天津我们把研究对象（如天津、青岛、大连）看作元素,那么上面的问题就是从3个元素中取出2个,组成一组的问题,我们把每一组叫做一个组合,把所有的组合的个数叫做组合数,上面的问题就是要求组合数.一般地,从n个不同元素中取出m个（m≤n）元素组成一组不计较组内各元素的次序,叫做从n个不同元素中取出m个元素的一个组合.由组合的定义可以看出,两个组合是否相同,只与这两个组合中的元素有关,而与取到这些元素的先后顺序无关.只有当两个组合中的元素不完全相同时,它们才是不同的组合.从n个不同元素中取出m个元素（m≤n）的所有组合的个数,叫做从n个不同元素中取出m个不同元素的组合数.记作C mn.如上面的例子,就是要计算从3个城市中取2个城市的组合数C23,由枚举法得出的结论知：C23＝3.那么它是怎样计算出来的呢？从第三讲开头的例子,即准备天津、青岛、大连三个城市之间的船票的问题发现,这个问题实际上可以这样分两步完成：第一步是从三个城市中选两个城市,是一个组合问题,由组合数公式,有取C23法.第二步是将取出的两个城市进行排列,由全排列公式,有P23种排法,所以,由乘法原理得到P23＝C23×P23.故有：C23＝P23÷P22＝（3×2）÷2＝3.一般地,求从n个不同元素中取出m个元素排成一列的排列数Pmn可以分两步求得：第一步：从n个不同元素中取出m个元素组成一组,共有C mn种方法；第二步：将每一个组合中的m个元素进行全排列,共有P mm种排法.故由乘法原理得到：P mm ＝C mn•P mm种因此这就是组合数公式.例1 计算：①C26,C46；②C27,C57.注意到上面的结果中,有C26= C46,C27= C57.一般地,组合数有下面的重要性质：C m n＝C n-m n（m≤n）这个公式是很容易理解的,它的直观意义是：C m n表示从n个元素中取出m 个元素组成一组的所有分组方法. C n-m n表示从n个元素中取出（n—m）个元素组成一组的所有分组方法.显然,从n个元素中选出m个元素的分组方法恰是从n个元素中选m个元素剩下的（n-m）个元素的分组方法.例如,从5人中选3人开会的方法和从5人中选出2人不去开会的方法是一样多的,即C35=C25.规定C n n＝1, C0n＝1.例2 计算：①C198200；②C5556；③C98100-2C100100.例3 从分别写有1、3、5、7、9的五张卡片中任取两张,作成一道两个一位数的乘法题,问：①有多少个不同的乘积？②有多少个不同的乘法算式？分析①中,要考虑有多少个不同乘积.由于只要从5张卡片中取两张,就可以得到一个乘积,所以,有多少个乘积只与所取的卡片有关,而与卡片取出的顺序无关,所以这是一个组合问题.②中,要考虑有多少个不同的乘法算式,它不仅与两张卡片上的数字有关,而且与取到两张卡片的顺序有关,所以这是一个排列问题.解：①由组合数公式,共有个不同的乘积.②由排列数公式,共有P25＝5×4＝20种不同的乘法算式.例4 在一个圆周上有10个点,以这些点为端点或顶点,可以画出多少不同的①直线段,②三角形,③四边形？分析由于10个点全在圆周上,所以这10个点没有三点共线,故只要在10个点中取2个点,就可以画出一条线段；在10个点中取3个点,就可以画出一个三角形；在10个点中取4个点,就可以画出一个四边形,三个问题都是组合问题.解：由组合数公式.例5 如下图,问：①下左图中,共有多少条线段？②下右图中,共有多少个角？分析①中,在线段AB上共有7个点（包括端点A、B）.注意到,只要在这七个点中选出两个点,就有一条以这两个点为端点的线段,所以,这是一个组合问题,而C27表示从7个点中取两个不同点的所有取法,每种取法可以确定一条线段,所以共有C27条线段.②中,从O点出发的射线一共有11条,它们是OA, OP1,OP2,OP3,…,OP9,OB.注意到每两条射线可以形成一个角,所以,只要看从11条射线中取两条射线有多少种取法,就有多少个角.显然,是组合问题,共有C211种不同的取法,所以,可组成C211个角.解：①由组合数公式知,共有条不同的线段；②由组合数公式知,共有例6 某校举行排球单循环赛,有12个队参加.问：共需要进行多少场比赛？分析因为比赛是单循环制的,所以,12个队中的每两个队都要进行一场比赛,并且比赛的场次只与两个队的选取有关而与两个队选出的顺序无关.所以,这是一个在12个队中取2个队的组合问题.解：由组合数公式知,共需进行场比赛.例7 某班要在42名同学中选出3名同学去参加夏令营,问共有多少种选法？如果在42人中选3人站成一排,有多少种站法？分析要在42人中选3人去参加夏令营,那么,所有的选法只与选出的同学有关,而与三名同学被选出的顺序无关.所以,应用组合数公式,共有C342种不同的选法.要在42人中选出3人站成一排,那么,所有的站法不仅与选出的同学有关,而且与三名同学被选出的顺序有关.所以,应用排列数公式,共有P342种不同的站法.解：由组合数公式,共有种不同的选法；由排列数公式,共有P342＝42×41×40＝68880种不同的站法.习题四1.计算：①C315；②C19982000；③C34×C28；④P28-C68.2.从分别写有1、2、3、4、5、6、7、8的八张卡片中任取两张作成一道两个一位数的加法题.问：①有多少种不同的和？②有多少个不同的加法算式？3.某班毕业生中有10名同学相见了,他们互相都握了一次手,问这次聚会大家一共握了多少次手？4.在圆周上有12个点.①过每两个点可以画一条直线,一共可以画出多少条直线？②过每三个点可以画一个三角形,一共可以画出多少个三角形？5.如右图,图上一共有六个点,且六个点中任意三个点不共线,问：①从这六个点中任意选两点可以连成一条线段,这些点一共可以连成多少条线段？②从这六个点中任意选两点可以作一条射线,这些点一共可以作成多少条射线？（射线是一端固定,经另一点可以无限延长的.）。

第四讲测验（三）1单选(0.25分)在小组讨论要接近尾声时，小组开始商议让谁上去代表小组做汇报总结。

成员A准备好了之前记录的稿子刚说完“我来吧”，另外一位成员B就表达了不满的意见“每次都是你，能不能换一换其他的同学”。

结果，成员A感到非常尴尬，把稿子往桌上一拍，看了一眼成员A说道，“那好，我不去了，你们谁想去谁去”。

上述场景描述了哪种类型的冲突？（D）A.目标冲突B.程序冲突C.逻辑冲突D.人际冲突2单选(0.25分)有研究人员从自信和协作程度两个维度区分了应对冲突的五种模式，分别为竞争模式，回避模式，适应模式，妥协模式与合作模式。

其中，回避模式和适应模式各自对应着怎样的自信程度与协作程度?（B）A.回避模式—较高的自信程度与较低的协作程度；适应模式——较低的自信程度与中等的协作程度B.回避模式——较低的自信程度与较低的协作程度；适应模式——较低的自信程度与较高的协作程度C.回避模式——较低的自信程度与中等的协作程度；适应模式——较低的自信程度与较高的协作程度D.回避模式——较低的自信程度与较低的协作程度；适应模式——较低的自信程度与中等的协作程度3单选(0.25分)有时候幽默与玩笑在冲突管理中也有特殊的效果，但是在使用的时候要避免出现以下哪种情况？（B）A.在开玩笑的同时，通过重新组织问题的呈现方式来避免对峙情况的出现B.将某位成员当成了取笑的对象，特别是取笑的内容涉及到该成员敏感的话题C.当冲突双方产生了不必要的争论和分歧时，利用幽默和玩笑来转移关注的焦点D.利用幽默和玩笑来缓和已经非常紧张的气氛4单选(0.25分)在一次讨论中，学生就最终以何种形式汇报合作的成果产生了冲突。

一位学生认为不需要呈现调查结果的全貌，因为这样会弱化大家对最有价值的发现的印象。

另一位学生认为如果不将整体的全貌呈现出来，调查的逻辑可能遭到质疑，而且小组的整个工作量不能体现出来。

下列那个选项最有可能是引发上述争论的原因？（C）A.学生不清楚完成任务的要求B.学生不清楚各自承担的角色C.学生不清楚具体的评价标准D.学生不清楚教师期待的合作行为5单选(0.25分)在下列哪种情况下，教师可以不用立刻介入？（A）A.某位成员还没有完全理解题目的意思B.小组中出现了主导了整个合作进程的支配者，一些学生被排除在主要任务之外C.小组的讨论陷入了泥沼，由于缺乏突破性的思路，整个组的情绪都比较的沮丧D.学生在自顾自的完成任务，没有进行合作沟通，也没有相互的帮助6单选(0.25分)下列哪个选项不是学生不敢或不愿表达自己的想法的原因？（B）A.学生不知道如何表述清楚自己的观点B.说话的人太多了，学生没有机会表达自己的观点C.学生担心自己说出了不符合教师期望的观点D.在许多人面前表达自己的观点会让学生感到紧张7多选(0.25分)与其他类型的冲突相比，人际关系的冲突可能更难解决的原因描述正确的是：（BCD）A.与其他类型的冲突相比，人际关系冲突会激发更多的讨论，从梳理讨论的线索到形成一致的认识的过程中，冲突的双方很容易迷失B.人际关系的冲突可能导致双方更少的互动，沟通渠道的封闭使得冲突的缓解变得更加的困难C.人际关系的冲突更多的来自与个人的，内在的一种状态。

第四讲固体压强知识点一压力（1）定义：垂直压在物体表面上的力（2）压力的三要素：①作用点必在被压物体的表面上②方向应与被压物体的接触面垂直③压力的有无要看是否有相互挤压作用（3）压力大小的几种情况①单独放在水平面上的物体，如图甲所示②叠放在一起的物体，放在水平面上，如图乙所示③放在斜面上的物体对斜面压力与重力大小关系，与斜面的坡角有关，物体对斜面压力的大小小于物体的重力，如图丙所示④被压在竖直墙壁上的物体对墙的压力，如图丁所示⑤被压在屋顶下的物体对屋顶的压力，如图戊所示【例1】按要求画图（1）在图甲中，物体放在水平桌面上静止，画出物体对桌面的压力示意图；（2）在图乙中，物体放在斜面上静止，画出物体对斜面压力的示意图；（3）在图丙中，用力F将物体压在竖直的墙壁上，画出物体对墙壁的压力的示意图。

【例2】如图所示，各物体的大小、形状、材料相同，重都为30N，施加的压力F=60N，垂直于物体表面，其中对支持面压力最大和最小的分别是（）A．甲、乙B．甲、丙C．甲、丁D．丙、丁【例3】关于压力，下列说法正确的是（）A．压力的方向一定垂直于受力面B．压力的大小一定等于物体的重量C．压力的方向有时垂直于物体间接触表面，有时不垂直于物体间接触表面D．无法确定【例4】 放在水平桌面上的茶杯，对桌面有压力，下列有关“茶杯对桌面压力”的说法，正确的是（）A ．茶杯对桌面的压力是由于茶杯发生形变而产生的B ．茶杯对桌面的压力是作用在茶杯上的C ．茶杯对桌面的压力就是重力D ．茶杯对桌面的压力是由于桌面发生形变而产生的【例5】 一个重力为G 的书包放在倾斜的木板上，则书包对木板的压力（）A ．一定大于GB ．一定小于GC ．一定等于GD ．可能等于G知识点二 压强1．定义：物体单位面积上受到的压力叫 ，是一个反映压力的作用效果的物理量，压强越大，其作用效果越大；压强越小，其作用效果越小，物理学中用 来表示压强，其单位是 ，简称帕，用 表示。

小升初奥数常考题第四讲 几何综合内容概述勾股定理，多边形的内角和，两直线平行的判别准则，由平行线形成的相似三角形中对应线段和面积所满足的比例关系．与上述知识相关的几何计算问题．各种具有相当难度的几何综合题．典型问题1．如图30-2，已知四边形ABCD 和CEFG 都是正方形，且正方形ABCD 的边长为10厘米，那么图中阴影三角形BFD 的面积为多少平方厘米?【分析与解】 方法一：因为CEFG 的边长题中未给出，显然阴影部分的面积与其有关．设正方形CEFG 的边长为x ，有：=1010=100,ABCD S ⨯正方形2=x ,S 正方形CEFG 21110x-x =DG GF=(10-x)x=,222DGF S ∆⨯ 又1=1010=50,2ABD S ∆⨯⨯2110x+x =(10+x)x=.22BEF S ∆ 阴影部分的面积为:DGF ABD BEF ABCD CEFG S S S S S ∆∆∆++--正方形正方形2221010100505022x x x x x -+=++--=(平方厘米). 方法二：连接FC ，有FC 平行与DB ，则四边形BCFD 为梯形．有△DFB 、△DBC 共底DB ，等高，所以这两个三角形的面积相等，显然,△DBC 的面积11010502⨯⨯=(平方厘米)．阴影部分△DFB 的面积为50平方厘米．2.如图30-4，∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I等于多少度?【分析与解】为了方便所述，如下图所示，标上数字，有∠I=1800 -(∠1+∠2),而∠1=1800-∠3, ∠2=1800-∠4,有∠I=∠3+∠4-1800同理, ∠H=∠4+∠5-1800, ∠G=∠5+∠6-1800, ∠F=∠6+∠7-1800, ∠E=∠7+∠8-1800,∠D=∠8+∠9-1800, ∠C=∠9+∠10-1800, ∠B=∠10+∠11-1800, ∠A=∠11+∠3-1800则∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=2×(∠3+∠4+∠5+∠6+∠7+∠8+∠9+∠10+∠11)-9×1800而∠3+∠4+∠5+∠6+∠7+∠8+∠9+∠10+∠11正是9边形的内角和为(9-2)×1800=12600．所以∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=2×12600-9×1800=90003．长边和短边的比例是2：1的长方形称为基本长方形．考虑用短边互不相同的基本长方形拼图，要求任意两个基本长方形之间既没有重叠，也没有空隙.现在要用短边互不相同且最小短边长为1的5个基本长方形拼接成一个更大的长方形．例如，短边长分别是1，2，5，6，12的基本长方形能拼接成大长方形，具体案如图30-6所示．请给出这5个基本长方形所有可能的选择方式.设a1=1<a2<a3<a4<a5分别为5条短边的长度,则我们将这种选择方式记为(a1,a2,a3,a4,a5),这里无需考虑5个基本长方形的拼图方案是否惟一．【分析与解】我们以几个不同的基本长方形作为分类依据，并按边长递增的方式一一列出．第一类情况：以为特征的有7组：第二类情况：以 为特征的有6组：第三类情况有如下三组：共有16组解，它们是：(1，2，2.5，5，7.25)，(1，2，2．5，5，14.5)．(1，2，2.25，2.5，3.625)，(1，2，2.25，2.5，7.25)．(1，2，5，5.5，6)，(1，2，5，6，11)，(1，2，2.5，4.5，7)，(1，2，2.5，4.5，14)，(1，2，5，12，14.5)，(1，2，5，12，29)，(1，2，2.25，2.5，4.5)，(1，2，5，6，12).1020251,,2,,,999⎛⎫ ⎪⎝⎭(1,2,2.4,4.8,5), 131025147813101,,,,,1,,,,636333313⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭.4.如图30-8，ABCD 是平行四边形，面积为72平方厘米，E ，F 分别为边AB,BC 的中点．则图形中阴影部分的面积为多少平方厘米?【分析与解】 如下图所示，连接EC ，并在某些点处标上字母，因为AE 平行于DC ，所以四边形AECD 为梯形，有AE:DC=1:2，所以:1:4AEG DCG S S ∆∆=,AGD ECG AEG DCG S S S S ∆∆∆∆⨯=⨯,且有AGD ECG S S ∆∆=,所以:1:2AEG ADG S S ∆∆=,而这两个三角形高相同，面积比为底的比，即EG ：GD=1:2，同理FH ：HD=1:2．有AED AEG AGD S S S ∆∆∆=+,而111822AED ABCD S S ∆=⨯⨯=(平方厘米) 有EG:GD=:AEG AGB S S ∆∆, 所以1612AEG AED S S ∆∆=⨯=+(平方厘米) 21212AGD AED S S ∆∆=⨯=+(平方厘米) 同理可得6HFC S ∆=(平方厘米), 12DCH S ∆=(平方厘米) ,44624DCG AEG S S ∆∆==⨯= (平方厘米)又GHD DCG DCH S S S ∆∆∆=-=24-12=12(平方厘米)所以原题平行四边形中空白部分的面积为6+6+12=24(平方厘米)，所以剩下的阴影部分面积为72-24=48(平方厘米)．5．图30-10是一个正方形，其中所标数值的单位是厘米．问：阴影部分的面积是多少平方厘米?【分析与解】 如下图所示，为了方便所叙，将某些点标上字母，并连接BG ．设△AEG 的面积为x ，显然△EBG 、△BFG 、△FCG 的面积均为x ，则△ABF 的面积为3x ，120101002ABF S ∆=⨯⨯=即1003x =，那么正方形内空白部分的面积为40043x =. 所以原题中阴影部分面积为400800202033⨯-= (平方厘米)．6．如图30-12，若图中的圆和半圆都两两相切，两个小圆和三个半圆的半径长都是1．求阴影部分的面积．【分析与解】 如下图所示，左图中的3个阴影部分面积相等，右图中的3个阴影部分的面积也相等．我们把左下图中的每一部分阴影称为A ，右下图中的每一部分阴影称为B ． 大半圆的面积为13332A B ++小圆的面积219322ππ=⨯⨯=.而小圆的面积为π，则9133223A B πππ⎛⎫+=-÷= ⎪⎝⎭， 原题图中的阴影部分面积为小半圆面积与阴影A 、B 的面积和，即为5236πππ+=7.如图30-14，将长方形ABCD 绕顶点C 顺时针旋转90度，若AB=4，BC=3，AC=5，求AD 边扫过部分的面积．(π取3.14)【分析与解】 如下图所示，如下图所示，端点A 扫过的轨迹为AA A '''，端点D 扫过轨迹为DD D '''，而AD 之间的点，扫过的轨迹在以A 、D 轨迹，AD ，A D ''所形成的封闭图形内，且这个封闭图形的每一点都有线段AD 上某点扫过，所以AD 边扫过的图形为阴影部分．显然有阴影部分面积为A D C ACA ACD S S S S ''''∆∆+--直角扇形直角扇形CD D ,而直角三角形A D C ''、ACD 面积相等． 所以=A D C ACA ACD ACA S S S S S S ''''''∆∆+---直角扇形直角扇形CD D 扇形扇形CD D222290909=(54)7.065()36036044AC CD ππππ-=-==平方厘米即AD 边扫过部分的面积为7．065平方厘米．。

第四讲补充：写出p2组态的光谱项教材第三章：3.5、3.7、3.8、3.9、3.11补充：写出p2组态的光谱项p2：l = 1，m l= ±1, 0；m s= ±1/2微观状态数为：N=6!/2!(6-2)!=6⨯5/2=15（L SL=2, S=0；简并度：(2S+1)(2L+1)=51D（2）M L =±1, 0；M S=±1, 0L=1, S=1；简并度：(2S+1)(2L+1)=93P（3）M L = 0；M S= 0L=0, S=0；简并度：(2S+1)(2L+1)=11Sp2组态的光谱项为：3P，1D，1S3.5 写出下列电子组态的基谱项。

(1) 2p1(2) 2p2(3) 2d1(4) 2d3(5) 3d5(6) 3d9（1）2p1L=1，12S=，基谱项2P（2）2p2L=1，S=1，基谱项3P（3）3d 1L=2， 12S =， 基谱项 2D （4）3d 3 L=3， 32S =， 基谱项 4F（5）3d 5 L=0， 52S =， 基谱项 6S（6）3d 9 L=2， 12S =， 基谱项 2D3.7 已知1017600cm -∆=，1918cm B -=，用Tanabe-Sugano 图预言Cr(H 2O)63+吸收光谱中自旋允许的两个四重态谱带。

Cr(H 2O)63+中Cr 3+为d 3组态，且0/17600/91819.2B ∆==从T －S 图上得到：可能的两个允许跃迁为4A 2g →4T 2g 4A 2g →4T 1g在横轴上找到19.2的点，作垂线与4T 1g 和4T 2g 分别相交于E/B=28.5和E/B=19.5两点。

∴E 1/B=28.5 E 1=28.5×918=26200（cm -1） E 2/B=19.5E 2=19.5×918=17901(cm -1)3.8 用Tanabe-Sugano 图确定基态能级：（1）低自旋[Rh(NH 3)6]3+；（2）[Ti(H 2O)6]3+；（3）[Fe(H 2O)6]3+。

第四讲真题选讲及检测1、（小数报02届）王大伯从家（A点处）去河边挑水，然后把水挑到积肥潭里（B点处）。

请帮他找一条最短的路线，在右图表示出来，并写出过程。

2、（小数报06届）下面5个图形都具有两个特点：（1）由4个连在一起的同样大小的正方形组成；（2）每个小正方形至少和另一个小正方形有一条公共边。

我们把具有以上两个特点的图形叫做“俄罗斯方块”。

3、如果把某个俄罗斯方块在平面上旋转后与另一个俄罗斯方块相同（比如上面图中的B与E），那么这两个俄罗斯方块只算一种。

除上面4种外，还有好几种俄罗斯方块，请你把这几种都画出来。

4、（第12届迎春杯）比赛用的足球是由黑、白两色皮子缝制的，其中黑色皮子为正五边形，白色皮子为正六边形，并且黑色正五边形与白色正六边形的边长相等。

缝制的方法是：每块黑色皮子的5条边分别与5块白色皮子的边缝在一起；每块白色皮子的6条边中，有3条边与黑色皮子的边缝在一起，另3条边则与其他白色皮子的边缝在一起。

如果一个足球表面上共有12块黑色正五边形皮子，那么，这个足球应有正六边形皮子块。

5、（第13届迎春杯）在一张四边形的纸上共有10个点，如果把四边形的顶点算在一起，则一共有14个点，已知这些点中的任意三个点都不在同一直线上。

按下面规定把这张纸剪成一些三角形：（1）每个三角形的顶点都是这14个点中的3个；（2）每个三角形内，都不再有这些点。

那么，这张四边形的纸最多可以剪出个三角形。

6、（第2届希望杯）如图2，正方形每条边上的三个点（端点除外）都是这条边的四等分点，则阴影部分的面积是正方形面积的 。

图27、（第二届两岸四地华罗庚金杯少年数学精英邀请赛）如图，房间里有一只老鼠，门外有一只小猫，如果每块正方形地砖的边长为50厘米，那么老鼠在地面上能避开小猫视线的活动范围为______平方厘米。

（将小猫和老鼠分别看作两个点，墙的厚度忽略不计）8、（第2届希望杯）下图中的（A ）、（B ）、（C ）是三块形状不同的铁皮，将每块铁皮沿虚线弯折后焊接成一个无盖的长方体铁桶。

第四讲行程问题之平均速度1、概念物体的路程和通过这段路程所用时间的比，叫做这段路程的平均速率。

(对运动的物体，平均速率不可能为零）平均速率=路程/时间平均速率在习惯上称平均速度.2、典型例题【例1】、从山顶到山脚的路长36千米，一辆汽车上山，需要4小时到达山顶，下山沿原路返回，只用了2小时到达山脚。

求这辆汽车往返的平均速度。

【例2】、12个人拿了8把铁锹去挖花池，采取“歇人不歇马”的办法一共干了6小时，平均每人挖了几小时？【例3】、金瑟往返于相距36里的东西两地，由东地去西地每小时走7.2里，从西地回东地比来时少用一小时，他往返的平均速度是多少？【例4】、赵兵骑自行车去某地，一天平均每小时行36里。

已知他上午平均每小时行40里，骑了3小时就休息了；下午平均每小时行33里，他下午骑了几小时？【例5】、小宁去爬山,上山时每小时行3千米,原路返回时每小时行5千米.求小宁往返的平均速度。

【例6】、在300 米的环形跑道上，甲乙两人并行起跑，甲速是每秒5 米，乙速是每秒4.2 米，以这样的平均速度计算，再次相遇时经过几秒钟？相遇地点在起跑线前面多少米？【例7】、车要走2英里的路，上山及下山各1英里，上山时平均速度每小时15英哩问当它下山走第二个英里的路时要多快才能达到每小时30英里？分析：这是平均速度的题目。

而我一再强调，平均速度和速度的平均数是两个不同的概念。

速度的平均数是指：这些速度整体水平。

它的公式是：把这些速度加起来除以他们的个数，求出的是平均值而已！而平均速度是指，在整个过程中的快慢程度，它的公式是：总路程除以总时间！这道题路程已经告诉你了，而整个过程的平均速度也告诉你了，你完全可以求出整个时间然后根据时间，可以求出走第二个英里的时间，从而求出下山的速度！【例8】、一个车队以4米/秒的速度缓缓通过一座长200米的大桥，共用115秒。

已知每辆车长5米，两车间隔10米。

问：这个车队共有多少辆车？分析与解：求车队有多少辆车，需要先求出车队的长度，而车队的长度等于车队115秒行的路程减去大桥的长度。

第四讲 曲线形问题综合提高本讲知识点汇总：一、 基本曲线形计算1. 圆：2ππC r d =⨯⨯=⨯；222ππ44πd C S r =⨯==． 2. 扇形：2π360nl r =⨯⨯⨯； 2π3602n l r S r ⨯=⨯⨯=． 3. 圆柱体：V S h =⨯底．4. 圆锥体：13V S h =⨯⨯底．二、 曲线形计算技巧：1. 割补法2. 平移、旋转3. 重叠（容斥）例1． （1）如图1，有一个长是10、宽是6的长方形，那么两个阴影部分的面积之差为多少？（π取3.14）（2）如图2，三角形ABC 是直角三角形，AB 长40厘米，以AB 为直径做半圆，阴影部分①比阴影部分②的面积小28平方厘米．求AC 的长度．（π取3.14）「分析」（1）阴影是不规则图形，无法直接求出面积，需要进行割补整体法求解；（2）阴影分别加上空白部分均会变成规则图形直接求出面积．练习1、如图，扇形AOB 的圆心角是90度，半径是2，C 是弧AB 的中点．求两个阴影部分的面积差．（π取3.14）例2． （1）如下左图，两个相同的直角扇形放在一起，重叠部分恰好是一个长方形，且长和宽分别为15和5．那么阴影部分的面积是多少？（π取3.14）（2）如下右图，以直角三角形ABC 的三条边为直径做半圆，已知6AB =，8AC =，那么，图中阴影部分的面积是多少？（π取3.14）「分析」（1）正方形的对角线刚好是扇形的半径；（2）这道题目可能会用到勾股定理．BC图1图2练习2、（1）如下左图，三角形ABC 是等腰直角三角形，以AC 为直径画半圆，以BC 为半径画扇形．已知10ACBC ==，那么阴影部分的面积是多少？（π取3.14）（2）如下右图，由一个长方形与两个直角扇形构成，其中阴影部分的面积是多少？（π取3.14）例3． 如图，一只小狗被拴在建筑物的一角，四周都是空地．建筑物是一个边长为10米的正方形，绳长是20米，那么小狗的活动范围能有多少平方米？（建筑外墙不可逾越，小狗身长忽略不计，π取3）「分析」首先画出小狗活动范围的图形，然后根据每块扇形的半径求出面积．练习3、如图，一只小狗被拴在建筑物的一角，四周都是空地．建筑物是一个边长为2米的等边三角形，绳长是3米，那么小狗的活动范围是多少？（建筑外墙不可逾越，小狗身长忽略不计，π取3）狗A 狗例4．一个半径为1的圆绕着边长为4的正方形滚动一周又回到原来的位置，扫过的面积是多少？（π取3.14）「分析」注意拐角处扇形的半径．练习4、一个半径为1的圆绕着边长为4的正六边形滚动一周又回到原来的位置，扫过的面积是多少？（π取3.14）例5．面上有7个大小相同的圆，位置如图所示．如果每个圆的面积都是10，那么阴影部分的面积是多少？（π取3.14）「分析」这道题目较难，需要进行巧妙的割补求解．例6．（1）如下左图，将对角线长度为6的正方形，按照如图所示的方式旋转一周，那么得到的旋转体的体积是多少？（π取3.14）（2）如下右图，将上底是2，下底是4，高是4的梯形，按照图中所示的方式旋转一周，那么得到的旋转体的体积是多少？（π取3.14）「分析」求出必要数据，结合公式即可得出答案．作业1. 如下图所示，如果正方形的边长为2，那么阴影部分的面积为多少？（π取3.14）2. 在下图中大圆的面积为30，三个小圆完全相同，那么图中阴影部分的面积为多少？3. 如图，阴影部分的面积是多少？（π取3.14）4. 一个半径为1的圆绕着边长为4的等边三角形滚动一周又回到原来的位置时，扫过的面积是多少？（π取近似值3.14）5. 如图，一只小狗被拴在建筑物的一角，四周都是空地．建筑物是一个边长为4米的等边三角形，绳长是6米，那么小狗的活动范围是多少？（建筑外墙不可逾越，小狗身长忽略不计，π取3）4狗第四讲 曲线形问题综合提高例7． 答案：（1）18.5；（2）32.8．解答：(1)大块“阴影+空白”刚好构成直角扇形，小块“阴影+空白”刚好构成长方形，所以直角扇形与长方形的面积差即是两块阴影面积的差21106018.54π⨯⨯-=． （2）“阴影①+空白”刚好构成半圆，“阴影②+空白”刚好等于直角三角形，半圆面积为21206282π⨯⨯=，所以，直角三角形面积为62828656+=，另一条直角边32.8AC =．例8． 答案：242.5；24．解答：（1）两个直角扇形面积之和减去长方形面积即为阴影面积： ()221515752242.52π⨯⨯+-⨯=．例9． 答案：1050．解答：狗的活动范围如图，分为A 、B 、C 三部分， 求面积得：22312010350105042πππ⨯⨯+⨯⨯==平方米．例10． 答案：44.56．解答：四个半径为2的直角扇形+四个相同的长方形 即为该圆扫过的面积，212424444.564π⨯⨯⨯+⨯⨯=．例11． 答案：20．解答：阴影包括中间的一个圆和周围六个花瓣状的小小图形．这个图形可以割补成一个顶角60°的扇形，因此六个这样的图形面积和正好等于一个圆；阴影部分的面积等于两个圆的面积，为20．例12． 答案：56.52；879275． 解答：（1）可以把得到的立体图形看做两个锥体，体积为2133256.523π⨯⨯⨯⨯=；可以把得到的立体图形看做两个锥体体积之差，体积为： 2211879248243375ππ⨯⨯⨯-⨯⨯⨯=． 练习：练习1、答案：0．简答：两个阴影分别加上下部的空白部分可得到扇形和半圆，而扇形和半圆面积相等，所以，面积之差是0．练习2、答案：28.5；12.765．简答：（1）半圆+圆心角是45度的扇形面积之和减去直角三角形面积：22111510101028.5282ππ⨯⨯+⨯⨯-⨯⨯=；（2）阴影面积为两个直角扇形面积之和减去长方形面积，2211521012.76544ππ⨯⨯+⨯⨯-=．练习3、答案：24.5．简答：解法同例3，首先画出小狗活动的范围图，然后把活动范围分成几个扇形来求解，2230024031=24.5360360ππ⨯⨯+⨯⨯．练习4、答案：60.56．简答：圆所扫过的面积可以分成6个长方形和6个扇形，面积之和为24262=60.56π⨯⨯+⨯．作业1.答案：0.86．简答：正方形的面积是4，圆的面积是3.14，所以，阴影的面积是0.86．2.答案：20．简答：大圆的半径是小圆的三倍，所以，大圆的面积是小圆面积的9倍，那么，阴影面积是整个面积的三分之二，即阴影面积为20．3.答案：4.56．简答：阴影面积为两个半圆的面积之和减去直角形的面积，两个半圆的面积之和为12.56，直角三角形的面积是8，所以，阴影面积为4.56．4.答案：36.56．简答：扫过的面积为三个相同的长方形，加三个相同的圆心角为120度的扇形，长方形总面积2×4×3=24，扇形总面积为12.56，所以，扫过的整个面积是36.56．5.答案：98．简答：活动范围由三个扇形构成，最大的扇形面积为半径是6的圆的四分之三，即90，两个小扇形的面积之和为18，总面积为98．。

第四讲应用题综合（下）1、巩固包含与排除和抽屉原理的解题方式。

2、复习前一讲内容。

3、培养学员发现数学中的美，激发学员学习探索的意识。

有重叠部分的若干对象的计数问题。

能利用文氏图进行辅助分析，弄清文氏图中每部分的含义；结合文氏图理解两个对象和三个对象的容斥原理；灵活处理具有一些不确定性的计数问题，以及其他形式酌重复计数问题。

抽屉原理：把多于n个的苹果放进n个抽屉里，那么至少有一个抽屉里有两个或两个以上的苹果。

讲演者：得分：森林里住着一群小白兔，每只小白兔都爱吃萝卜，白菜和青草中的一种或者几种，爱吃萝卜的小白兔中有12只不爱吃白菜；爱吃白菜的小白兔中有23只不爱吃青草；爱吃青草的小白兔中有34只不爱吃萝卜，如果三种食物都爱吃的小白兔又有五只，那么这群小白兔共有多少只？【解析】萝卜①②③④⑤⑥⑦白菜青草爱吃萝卜的小白兔中不爱吃白菜的部分是①③，共12只。

爱吃白菜的小白兔中有23只不爱吃青草，所以②⑤是23只。

爱吃青草的小白兔中有34只不爱吃萝卜，所以⑥⑦是34只。

三种都喜欢的小白兔有5只，所以④是5只。

以上4部分正好构成小白兔的全部，所以将它们相加即可，共有12＋23＋34＋5=74只。

解答：这群小白兔共有74只。

讲演者：得分：从1到99这99个自然数中，最多可以取出多少个数，使得其中每两个数的和都不等于100？最多可以取出多少个数，使得其中每两个数的差不等于5？【解析】解析：（1）将99个自然数分成50组：（1，99），（2，98），（3，97），……，（49，51），50，每组中取出一个数，则这50个数中每两个数的和都不等于100，满足要求。

（2）将99个自然数如下分组：（1，6），（2，7），（3，8），（4，9），（5，10）；（11，16），（12，17），（13，18），（14，19），（15，20），……，（91，96），（92，97），（93，98），（94，99），95；在每组中选取一个数，满足题目的要求。

浓度问题专题综合卷答案解析1、有浓度为10%的盐水170 克，加入多少克盐后，盐水的浓度为15%?浓度为 10%的盐⽔中的⽔：170×（1-10%）=153（克）由于前后两个溶液的⽔不变，根据量率对应可知：新的溶液总质量为：153÷（1-15%）＝180（克）加⼊的盐：180-170=10（克）答：加⼊10克盐后,盐⽔的浓度为 15%.2、有浓度为2.5%的盐水700 克，为了制成浓度为3.5%的盐水，从中要蒸发掉多少克水?分析：将题意转化为3.5%的盐⽔加⼊⼀部分⽔配制成浓度为 2.5%的盐⽔ 700 克，根据浓度配比可知：3.5% 0%2.5％2.5% 1%5 ： 2则蒸发掉的⽔：700×$=200)克*%&$答： 要蒸发掉200克⽔3、一种35%的新农药，如稀释到1.75%时，治虫最有效。

用多少千克浓度为35%的农药加多少千克水，才能配成1.75%的农药800 千克?分析：将35%的农药加⼊⼀部分⽔配制成浓度为 1.75%的农药 800千克，根据浓度配比可知：35% 0%1.75％1.75% 33.25%1 ： 19=40)千克*则需要35%的农药：800×,,&,-需要的⽔：800×,-=760)千克*,&,-答：用40千克浓度为 35%的农药加760千克⽔ 4、仓库运来含水量为90%的一种水果100 千克。

一星期后再测，发现含水量降低到80%。

现在这批水果的质量是多少千克?分析：将题意转化为含⽔量80%的⽔果加⼊⼀部分⽔变成含⽔量为 90%的⽔果 100千克，根据浓度配比可知：80% 100%90％10% 10%1 ： 1现在的⽔果质量：100×,=50)千克*,&,答： 现在的这批⽔果质量是50千克。

5、有含盐率为10%的盐水300 克,和含盐率为15%的盐水200 克。

将这两种浓度的盐水混合，混合之后的盐水的浓度是多少?含盐率为 10%的盐⽔的盐：300×10%=30（克）含盐率为 15%的盐⽔的盐：200×15%=30（克）混合后的盐⽔的浓度：（30＋30）÷（300+200）×100%＝12%答：混合之后的盐⽔的浓度是12%。

第四讲 四点共圆问题“四点共圆”问题在数学竞赛中经常出现，这类问题一般有两种形式：一是以“四点共圆”作为证题的目的，二是以“四点共圆”作为解题的手段，为解决其他问题铺平道路.判定“四点共圆”的方法，用得最多的是统编教材《几何》二册所介绍的两种（即P 89定理和P 93例3），由这两种基本方法推导出来的其他判别方法也可相机采用. 1 “四点共圆”作为证题目的例1．给出锐角△ABC ，以AB 为直径的圆与AB 边的高CC ′及其延长线交于M ，N .以AC 为直径的圆与AC 边的高BB ′及其延长线将于P ，Q .求证：M ，N ，P ，Q 四点共圆.(第19届美国数学奥林匹克)分析：设PQ ，MN 交于K 点，连接AP ，AM .欲证M ，N ，P ，Q 四点共圆，须证 MK ·KN ＝PK ·KQ ，即证(MC ′-KC ′)(MC ′+KC ′) ＝(PB ′-KB ′)·(PB ′+KB ′)或MC ′2-KC ′2=PB ′2-KB ′2 . ①不难证明 AP =AM ，从而有 AB ′2+PB ′2=AC ′2+MC ′2. 故 MC ′2-PB ′2=AB ′2-AC ′2ABCK M NPQ B ′C ′=(AK 2-KB ′2)-(AK 2-KC ′2)=KC ′2-KB ′2. ②由②即得①，命题得证.例2．A 、B 、C 三点共线，O 点在直线外，O 1，O 2，O 3分别为△OAB ，△OBC ， △OCA 的外心.求证：O ，O 1，O 2， O 3四点共圆.(第27届莫斯科数学奥林匹克)分析：作出图中各辅助线.易证O 1O 2垂直平分OB ，O 1O 3垂直平分OA .观察△OBC 及其外接圆，立得∠OO 2O 1=21∠OO 2B =∠OCB .观察△OCA 及其外接圆，立得∠OO 3O 1=21∠OO 3A =∠OCA .由∠OO 2O 1=∠OO 3O 1 O ，O 1，O 2，O 3共圆.利用对角互补，也可证明O ，O 1，O 2，O 3四点共圆，请同学自证.2 以“四点共圆”作为解题手段这种情况不仅题目多，而且结论变幻莫测，可大体上归纳为如下几个方面. (1)证角相等例3．在梯形ABCD 中，AB ∥DC ，AB ＞CD ，K ，M 分别在AD ，BC 上，∠DAM ＝∠CBK .A BCOO O O 123？？求证：∠DMA ＝∠CKB .（第二届袓冲之杯初中竞赛）分析：易知A ，B ，M ，K 四点共圆.连接KM ，有∠DAB ＝∠CMK .∵∠DAB +∠ADC ＝180°，∴∠CMK +∠KDC ＝180°.故C ，D ，K ，M 四点共圆 ∠CMD ＝∠DKC . 但已证∠AMB ＝∠BKA ， ∴∠DMA ＝∠CKB .(2)证线垂直例4．⊙O 过△ABC 顶点A ，C ，且与AB ， BC 交于K ，N (K 与N 不同).△ABC 外接圆和△BKN 外接圆相交于B 和 M .求证：∠BMO =90°. (第26届IMO 第五题)分析：这道国际数学竞赛题，曾使许多选手望而却步.其实，只要把握已知条件和图形特点，借助“四点共圆”，问题是不难解决的. 连接OC ，OK ，MC ，MK ，延长BM 到G .易得∠GMC =∠BAC =∠BNK =∠BMK .而∠COK =2·∠BAC =∠GMC +A BC D K M ··ABO K N CMG∠BMK =180°-∠CMK ，∴∠COK +∠CMK =180°⇒C ，O ，K ，M 四点共圆. 在这个圆中，由OC =OK ⇒ OC =OK ⇒∠OMC =∠OMK . 但∠GMC =∠BMK ， 故∠BMO =90°. (3)判断图形形状例5．四边形ABCD 内接于圆，△BCD ，△ACD ，△ABD ，△ABC的内心依次记为I A ，I B ，I C ，I D .试证：I A I B I C I D 是矩形.(第一届数学奥林匹克国家集训选拔试题) 分析：连接AI C ，AI D ，BI C ，BI D 和DI B .易得∠AI C B =90°+21∠ADB =90°+21 ∠ACB =∠AI D B ⇒A ，B ，I D ，I C 四点 共圆.同理，A ，D ，I B ，I C 四点共圆.此时 ∠AI C I D =180°-∠ABI D =180°-21∠ABC ， ∠AI C I B =180°-∠ADI B =180°-21∠ADC ， ABCDI C I DAI I B∴∠AI C I D +∠AI C I B =360°-21(∠ABC +∠ADC ) =360°-21×180°=270°. 故∠I B I C I D =90°.同样可证I A I B I C I D 其它三个内角皆为90°.该四边形必为矩形. (4)计算例6．正方形ABCD 的中心为O ，面积为1989㎝2.P 为正方形内一点，且∠OPB =45°，P A :PB =5:14.则PB =__________ (1989，全国初中联赛)分析：答案是PB =42㎝.怎样得到的呢？连接OA ，OB .易知O ，P ，A ，B四点共圆，有∠APB =∠AOB =90°. 故P A 2+PB 2=AB 2=1989. 由于P A :PB =5:14，可求PB . (5)其他例7．设有边长为1的正方形，试在这个正方形的内接正三角形中找出面积最大的和一个面积最小的，并求出这两个面积(须证明你的论断).··P OA BCD(1978，全国高中联赛)分析：设△EFG 为正方形ABCD 的一个内接正三角形，由于正三角形的三个顶点至少必落在正方形的三条边上，所以不妨令F ，G 两点在正方形的一组对边上. 作正△EFG 的高EK ，易知E ，K ，G ，D 四点共圆⇒∠KDE =∠KGE =60°.同 理，∠KAE =60°.故△KAD 也是一个正 三角形，K 必为一个定点.又正三角形面积取决于它的边长，当KF 丄AB 时，边长为1，这时边长最小，而面积S =43也最小.当KF 通过B 点时，边长为2·32-，这时边长最大，面积S =23-3也最大. 例8．NS 是⊙O 的直径，弦AB 丄NS 于M ，P 为ANB 上异于N 的任一点，PS 交AB 于R ，PM 的延长线交⊙O 于Q .求证：RS ＞MQ .(1991，江苏省初中竞赛)分析：连接NP ，NQ ，NR ，NR 的延长线交⊙O 于Q ′.连接MQ ′，SQ ′.易证N ，M ，R ，P 四点共圆，从而，∠SNQ ′=∠MNR =∠MPR =∠SPQ =∠SNQ .根据圆的轴对称性质可知Q 与Q ′关于NS 成轴对称⇒MQ ′=MQ .A BCDEF KG ······又易证M，S，Q′，R四点共圆，且RS是这个圆的直径(∠RMS=90°)，MQ′是一条弦(∠MSQ′＜90°)，故RS ＞MQ′.但MQ=MQ′，所以，RS＞MQ.练习题1.⊙O1交⊙O2于A，B两点，射线O1A交⊙O2于C点，射线O2A交⊙O1于D点.求证：点A是△BCD的内心.(提示：设法证明C，D，O1，B四点共圆，再证C，D，B，O2四点共圆，从而知C，D，O1，B，O2五点共圆.)2.△ABC为不等边三角形.∠A及其外角平分线分别交对边中垂线于A1，A2；同样得到B1，B2，C1，C2.求证：A1A2=B1B2=C1C2.(提示：设法证∠ABA1与∠ACA1互补造成A，B，A1，C四点共圆；再证A，A2，B，C四点共圆，从而知A1，A2都是△ABC的外接圆上，并注意∠A1AA2=90°.)3.设点M在正三角形三条高线上的射影分别是M1，M2，M3(互不重合).求证：△M1M2M3也是正三角形.4.在Rt△ABC中，AD为斜边BC上的高，P是AB上的点，过A 点作PC的垂线交过B所作AB的垂线于Q点.求证：PD丄QD.(提示：证B，Q，E，P和B，D，E，P分别共圆)5.AD，BE，CF是锐角△ABC的三条高.从A引EF的垂线l1，从B引FD的垂线l2，从C引DE的垂线l3.求证：l1，l2，l3三线共点.(提示：过B作AB的垂线交l1于K，证：A，B，K，C四点共圆)。

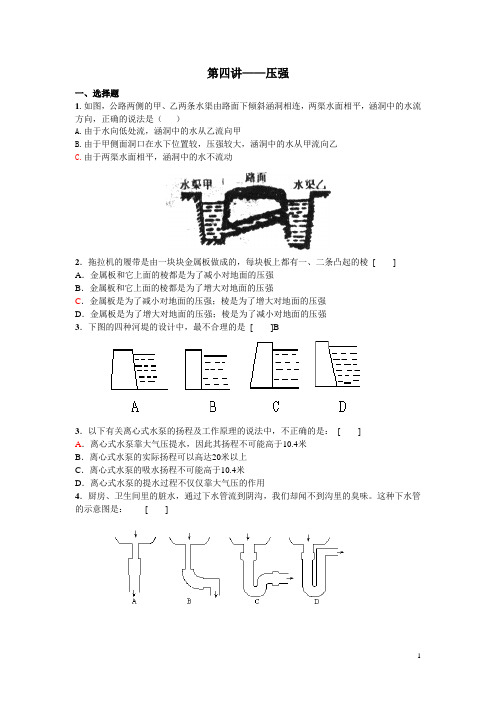
第四讲——压强一、选择题1.如图，公路两侧的甲、乙两条水渠由路面下倾斜涵洞相连，两渠水面相平，涵洞中的水流方向，正确的说法是（）A.由于水向低处流，涵洞中的水从乙流向甲B.由于甲侧面洞口在水下位置较，压强较大，涵洞中的水从甲流向乙C.由于两渠水面相平，涵洞中的水不流动2．拖拉机的履带是由一块块金属板做成的，每块板上都有一、二条凸起的棱[ ] A．金属板和它上面的棱都是为了减小对地面的压强B．金属板和它上面的棱都是为了增大对地面的压强C．金属板是为了减小对地面的压强；棱是为了增大对地面的压强D．金属板是为了增大对地面的压强；棱是为了减小对地面的压强3．下图的四种河堤的设计中，最不合理的是[ ]B3．以下有关离心式水泵的扬程及工作原理的说法中，不正确的是：[ ]A．离心式水泵靠大气压提水，因此其扬程不可能高于10.4米B．离心式水泵的实际扬程可以高达20米以上C．离心式水泵的吸水扬程不可能高于10.4米D．离心式水泵的提水过程不仅仅靠大气压的作用4．厨房、卫生间里的脏水，通过下水管流到阴沟，我们却闻不到沟里的臭味。

这种下水管的示意图是：[ ]图105．由于长期的河道淤塞，黄河下游的河床已被抬高。

沿河农民通常采用如图3所示的方式，引黄河水来灌溉农田。

有关这种引水灌溉方式，下列说法中错误的是 ( )A ．这种取水灌溉方式利用了连通器原理B ．使用时B 端管口必须低于A 处水面C ．使用时先将管道中灌满水D ．高度差B 越大，管道中的水流得就越快二、填空题6．如下图所示的三个容器中分别装有酒精、清水与盐水，它们对容器底部的压力相等，则所装三种液体中，质量最大的是________，质量最小的是_______。

7．如图10内径均匀的U 形管内盛有密度不同的两种液体．其中一种液体的密度是ρ1；另一种液体的密度是ρ2，体积是V ．且ρ2>ρ1．静止时，两种液体不混合．若U 形管的横截面积为S ，则两边液面的高度差h 等于 ． 答案：8.如图3所示，在某科技馆内陈列着一个模拟“风洞实验室”，一架重1 5 N 的模型飞机固定在台秤的秤盘上，当迎风吹向飞机的风速V 达到2 0 m ／s 时．台秤的读数为7 N ，则模型飞机得到的升力为____N 。

第四讲中国革命的三大法宝本文档由【中文word文档库】提供，转载分发敬请保留本信息；中文word文档库免费提供海量范文、教育、学习、政策、报告和经济类word文档。

一、单项选择题（下列每题的选项中，有一项是最符合题意的）1.毛泽东提出的“工农武装割据”的基本思想包括三个不可分割的部分是（）。

A.武装斗争、统一战线、党的建设B.武装斗争、土地革命、根据地建设C.实事求是、群众路线、自我批评D.游击战争、红色政权、党的建设2.中国共产党在民主革命中战胜敌人的三大法宝是（）。

A.土地革命、党的建设、武装斗争B.统一战线、党的建设、武装斗争C.工农运动、党的建设、武装斗争D.武装斗争、土地革命、统一战线3.正确处理党内矛盾，进行马克思主义教育的一个好的形式是（）。

A.密切联系群众B.批评与自我批评C.理论联系实际D.整风4.坚持统一战线中独立自主原则的实质是（）。

A.建立抗日民族统一战线的政权B.保持党在政治上的自主权C.无产阶级对统一战线的领导权D.保持对同盟者的自由批评5.人民军队建设的根本原则是（）。

A.战略上藐视敌人B.游击战的战略战术C.战术上重视敌人D.党对军队的绝对领导6.人民军队的惟一宗旨是（）。

A.打仗消灭敌人B.三大纪律C.八项注意D.全心全意为人民服务7.毛泽东指出：统一战线建立的依据之一是因为中国是一个“两头小中间大”的社会，这个“中间大”是指（）。

A.大资产阶级B.工业无产阶级C.大地主阶级D.农民、城市小资产阶级和其他中间阶级8.中国共产党在统一战线中坚持的原则是（）。

A.武装斗争B.独立自主C.土地革命D.实事求是9.中国共产党在统一战线中的最基本的政策是（）。

A.开展武装斗争B.坚持独立自主C.既团结又斗争D.发展进步势力10.中国共产党发展统一战线不可缺少的基本原则是（）。

A.坚持独立自主B..原则性与灵活性的统一C.有理有利有节D.争取中间势力的支持11.中国革命的特点和优点指的是（）。

爱学习第四讲应用题综合二日积月累
【日积月累】
（关于帮助的名言）
1、予人玫瑰，手有余香。

2、平时肯帮人，急时有人帮。

3、与其锦上添花，不如雪中送炭。

（十二生肖）子鼠丑牛寅虎卯兔
辰龙巳蛇午马未羊
申猴酉鸡戌狗亥猪
《弟子规》
冠必正，纽必结，袜与履，俱紧切。

置冠服，有定位，勿乱顿，致污秽。

惟德学，惟才艺，不如人，当自砺。

若衣服，若饮食，不如人，勿生戚。

微笑、狂笑、傻笑、笑眯眯、笑呵呵
眉开眼笑、破涕为笑、哈哈大笑、捧腹大笑
教诲、寻找、伙伴、灾难、明亮、柔软
洞穴、窟窿、窑洞、窄小部首是“穴”的字多与洞穴有关
博物馆、展览馆、科技馆、体育馆、研究所、派出所、哨所、诊所
扫帚、抹布、拖把、水桶、簸箕、扫地、擦玻璃、倒垃圾、摆桌椅
春天的风像妈妈的手似的软软的。

小鸟害怕极了，慌慌张张地飞走了。