Andreev-reflection and Point-Contact Spectroscopy of Superconducting Rare Earth Transition
- 格式:pdf
- 大小:562.33 KB
- 文档页数:19

TARGE1703-D Target SegmentMP ME ST PR PRN DS DSS <> EM <> <> PP <> EME MFSProduct RestrictionsTARGE170 Element DescriptionTARGE170 is used to represent various 3-D "target" surfaces for the associated contact elements (CONTA173, CONTA174, CONTA175, CONTA176, and CONTA177). The contact elements themselves overlay the solid, shell, or line elements describing the boundary of a deformable body and are potentially in contact with the target surface, defined by TARGE170. This target surface is discretized by a set of target segment elements (TARGE170) and is paired with its associated contact surface via a shared real constant set. You can impose any translational or rotational displacement, temperature, voltage, and magnetic potential on the target segment element. You can also impose forces and moments on target elements. SeeTARGE170 in the Theory Reference for the Mechanical APDL and Mechanical Applications for more details about this element. To represent 2-D target surfaces, use TARGE169, a 2-D target segment element.For rigid target surfaces, these elements can easily model complex target shapes. For flexible targets, these elements will overlay the solid, shell, or line elements describing the boundary of the deformable target body.Figure 170.1: TARGE170 GeometryTARGE170 Input DataThe target surface is modeled through a set of target segments, typically, several target segments comprise one target surface.The target surface can either be rigid or deformable. For modeling rigid-flexible contact, the rigid surface must be represented by a target surface. For flexible-flexible contact, one of the deformable surfaces must be overlayed by a target surface. See the Contact Technology Guide for more information about designating contact and target surfaces.The target and associated contact surfaces are identified via a shared real constant set. This real constant set includes all real constants for both the target and contact elements.Each target surface can be associated with only one contact surface, and vice-versa. However, several contact elements could make up the contact surface and thus come in contact with the same target surface. Likewise, several target elements could make up the target surface and thus come in contact with the same contact surface. For either the target or contact surfaces, you can put many elements in a single target or contact surface, or you can localize the contact and target surfaces by splitting the large surfaces into smaller target and contact surfaces, each of which contain fewer elements.If a contact surface may contact more than one target surface, you must define duplicate contact surfaces that share the same geometry but relate to separate targets, that is, that have separate real constant set numbers.Figure 170.2: TARGE170 Segment Types shows the available segment types for TARGE170. The general 3-D surface segments (3-node and 6-node triangles, and4-node and 8-node quadrilaterals) and the primitive segments (cylinder, cone, and sphere) can be paired with 3-D surface-to-surface contact elements, CONTA173 and CONTA174, the 3-D node-to-surface contact element, CONTA175, and the 3-Dline-to-surface contact element, CONTA177. The line segments (2-node line and3-node parabola) can only be paired with the 3-D line-to-line contact element, CONTA176, to model 3-D beam-to-beam contact.For any target surface definition, the node ordering of the target segment element is critical for proper detection of contact. For the general 3-D surface segments (triangle and quadrilateral segment types), the nodes must be ordered so that the outward normal to the target surface is defined by the right hand rule (seeFigure 170.2: TARGE170 Segment Types). Therefore, for the surface target segments, the outward normal by the right hand rule is consistent to the external normal. For 3-D line segments (straight line and parabolic line), the nodes must be entered in a sequence that defines a continuous line. For a rigid cylinder, cone, or sphere, contact must occur on the outside of the elements; internal contacting of these segments is not allowed.Considerations for Rigid Target SurfacesEach target segment of a rigid surface is a single element with a specific shape, or segment type.The segment types are defined by several nodes and a target shape code, TSHAP, and are described in Table 170.1: TARGE170 3-D Segment Types, Target Shape Codes, and Nodes. The TSHAP command indicates the geometry (shape) of the element. The segment radii are defined by real constants (R1 and R2), and the segment location is determined by the nodes. ANSYS supports eleven 3-D segmenttypes; see Table 170.1: TARGE170 3-D Segment Types, Target Shape Codes, and Nodes.Table 170.1 TARGE170 3-D Segment Types, Target Shape Codes, and Nodes1.The DOF available depends on the setting of KEYOPT(1) of the associatedcontact element. Refer to the element documentation for either CONTA173,CONTA174, or CONTA175 for more details.2.When creating a cylinder, cone, or sphere via direct generation, define the realconstant set before creating the element.3.Only pilot nodes have rotational degrees of freedom (ROTX, ROTY, ROTZ).4.Input the target radius as a negative value when modeling internal pipe-to-pipecontact (a pipe contacting/sliding inside another pipe). Input a positive valueto model external 3-D beam-to-beam contact.5.Input a positive contact radius when modeling internal pipe-to-pipe contact orexternal 3-D beam-to-beam contact.6.Rigid surface node. This segment type is only used to apply boundaryconditions to rigid target surfaces.Figure 170.2: TARGE170 Segment Types shows the 3-D segment shapes.Figure 170.2: TARGE170 Segment TypesFor simple rigid target surfaces (including line segments), you can define the target segment elements individually by direct generation. You must first specify the SHAPE argument on the TSHAP command. When creating cylinders, cones, or spheres through direct generation, you must also define the real constant R1 (and R2 for cones) before creating the element. Real constants R1 and R2 (seeTable 170.1: TARGE170 3-D Segment Types, Target Shape Codes, and Nodes) define the dimensions of the target shape.For general 3-D rigid surfaces, target segment elements can be defined by area meshing (AMESH). Set KEYOPT(1) = 0 (the default) to generate low order target elements (3-node triangles and/or 4-node quadrilaterals) for rigid surfaces. Set KEYOPT(1) = 1 to generate target elements with midside nodes (6-node triangles and/or 8-node quadrilaterals).For 3-D rigid lines, target segment elements can be defined by line meshing (LMESH). Set KEYOPT(1) = 0 (the default) to generate low order target elements (2-node straight lines). Set KEYOPT(1) = 1 to generate target elements with midside nodes (3-node parabolas).You can also use keypoint meshing (KMESH) to generate the pilot node.If the TARGE170 elements will be created via program meshing (AMESH, LMESH, or KMESH commands), then the TSHAP command is ignored and ANSYS chooses the correct shape automatically.For rigid-to-flexible contact, by default, ANSYS automatically fixes the structural degree of freedom for rigid target nodes if they aren't explicitly constrained (KEYOPT(2) = 0). If you wish, you can override the automatic boundary condition settings by setting KEYOPT(2) = 1 for the target elements. For flexible-to-flexible contact, no special boundary conditions treatment is performed, and the KEYOPT(2) = 0 setting should be used.For each rigid-flexible contact pair, you can assign only one pilot node to an entire rigid target surface (or none if it is not needed). The pilot node, unlike the other segment types, is used to define the degrees of freedom for the entire target surface. This node can be any of the target surface nodes, but it does not have to be. All possible rigid motions of the target surface will be a combination of a translation and a rotation around the pilot node. The pilot node provides a convenient and powerful way to assign boundary conditions such as rotations, translations, moments, temperature, voltage, and magnetic potential on an entire rigid target surface. By default (KEYOPT(2) = 0), you can assign the boundary conditions only to the pilot node, eliminating the need to assign boundary conditions to individual target nodes, thus reducing the chance of errors. ANSYS will also automatically fix the structural degrees of freedom on the pilot node if they aren't explicitly constrained.By setting KEYOPT(2) = 1 for the target elements, you can apply boundary conditions on any rigid target nodes rather than only on the pilot node. It is your responsibility to make sure the rigid target surface is not under-constrained orover-constrained. It is still recommended that you apply all boundary conditions on the pilot node, even when KEYOPT(2) = 1.Considerations for Deformable Target SurfacesFor general deformable surfaces, use the ESURF command to overlay the target elements on the boundary of the existing mesh. By default, the command generates a target element with an external surface that has the same shape as the underlying element. You can issue ESURF,,,LINE to generate 3-D line or parabola segments on an exterior of selected 3-D elements (e.g., shell edges). While not recommended, you may select to split the external surface into triangle facet elements by issuing the ESURF,,,TRI command (see Figure 170.3: TARGE170 Triangle Facet Elements). The cylinder, cone, sphere, point, or pilot node target segments should not be used for deformable target surfaces.Figure 170.3: TARGE170 Triangle Facet ElementsNote: Segment types (TSHAP command) should not be used for this caseConsiderations for Fluid Penetration LoadingTo model fluid penetration loads, use the SFE command to specify the fluid pressure and fluid penetration starting points. For more information, see Applying Fluid Pressure-Penetration Loads in the Contact Technology Guide.Considerations for Thermal Contact AnalysisBy default, the temperature is set to the value of TUNIF, and if this has no explicit value the temperature is set to zero. For thermal contact analysis, such as convection and radiation modeling, the behavior of a thermal contact surface (whether a“near-field” or“free” surface) is usually based on the contact status. Contact status affects the behavior of the contact surface as follows:•If the contact surface is outside the pinball region, its behavior is as a far-field of free surface. In this instance, convection/radiation occurs with the ambienttemperature.•If the contact surface is inside the pinball region, the behavior is as a near-field surface.However, the thermal contact surface status is ignored if KEYOPT(3) = 1 is set, and the surface is always treated as a free surface (see CONTA173, CONTA174, or CONTA175 for details).A summary of the element input is given in "TARGE170 Input Summary". A general description of element input is given in Element Input.TARGE170 Input SummaryNodesI, J, K, L, M, N, O, P (J - P are not required for all segment types)Degrees of FreedomUX, UY, UZ, TEMP, VOLT, MAG (ROTX, ROTY, ROTZ for pilot nodesonly)Real ConstantsR1, R2, [the others are defined through the associated CONTA173,CONTA174, CONTA175, CONTA176, or CONTA177 elements]Material PropertiesNoneSurface LoadsPressure, Face 1 (I-J-K-L) (opposite to target normal direction) Body LoadsNoneSpecial FeaturesNonlinearBirth and deathFluid pressure penetration loadKEYOPT(1)Element order (used by AMESH and LMESH commands only):0 --Low order elements1 --High order elementsKEYOPT(2)Boundary conditions for rigid target nodes:0 --Automatically constrained by ANSYS1 --Specified by userKEYOPT(3)Behavior of thermal contact surface:0 --Based on contact status1 --Treated as free-surfaceKEYOPT(4)DOF set to be constrained on dependent DOF for internally-generatedmultipoint constraints (MPCs). This option is used for these situations:solid-solid and shell-shell assemblies; surface-based constraints that use asingle pilot node for the target element; and rigid target surfaces that use theKEYOPT(2) = 1 setting.n --Enter a six digit value that represents the DOF set to be constrained. The firstto sixth digits represent ROTZ, ROTY, ROTX, UZ, UY, UX, respectively.The number 1 (one) indicates the DOF is active, and the number 0 (zero)indicates the DOF is not active. For example, 100011 means that UX, UY, and ROTZ will be used in the multipoint constraint. Leading zeros may be omitted;for example, you can enter 11 to indicate that UX and UY are the only activeDOF. If KEYOPT(4) = 0 (which is the default) or 111111, all DOF areconstrained.KEYOPT(5)DOF set to be used in internally-generated multipoint constraints (MPCs),with the MPC algorithm and no separation or bonded behavior (KEYOPT(2) =2 and KEYOPT(12) = 4, 5, or 6 on the contact element). Note that this keyoption is not used for surface-based constraints. (See "Multipoint Constraintsand Assemblies" in the Contact Technology Guide for more information):0 --Automatic constraint type detection (default)1 --Solid-solid constraint (no rotational DOFs are constrained)2 --Shell-shell constraint (both translational and rotational DOFs are constrainedindependently). Also used with penalty based shell-shell assembly(KEYOPT(2) = 0 or 1 and KEYOPT(12) = 5 or 6 on the contact element); seeBonded Contact for Shell-Shell Assemblies in the Contact Technology Guidefor more information.3 --Shell-solid constraint - contact normal direction (both translational androtational DOFs from the contact surface are included in the constraint set;only translational DOFs from the target surface are included in the constraintset).4 --Shell-solid constraint - all directions. This option acts the same as KEYOPT(5) = 3 if an intersection is found from the contact normal to the target surface.Otherwise, constraint equations are still built as long as contact node(s) andtarget segments are inside the pinball region.5 --Shell-solid constraint - anywhere inside pinball region. Constraint equationsare always built as long as contact node(s) and target segments are inside thepinball region, regardless of whether an intersection exists between the contact normal and the target surface.Note: When the no separation option (KEYOPT(12) = 4 on the contactelement) is used with the MPC approach, only the KEYOPT(5) = 0 and1 options (auto detection or solid-solid constraint) described above arevalid. If the auto detection option is set and the program finds ashell-shell or shell-solid constraint in this situation, the solution willterminate.TARGE170 Output DataThe solution output associated with the element is shown in Table 170.2: TARGE170 Element Output Definitions.The Element Output Definitions table uses the following notation:A colon (:) in the Name column indicates that the item can be accessed by the Component Name method (ETABLE, ESOL). The O column indicates the availability of the items in the file Jobname.OUT. The R column indicates the availability of the items in the results file.In either the O or R columns, “Y” indicates that the item is always available, a number refers to a table footnote that describes when the item is conditionally available, and “-” indicates that the item is not available.Table 170.2 TARGE170 Element Output Definitions1.An internal segment number determined by ANSYS. ISEG for the targetelement has a different meaning than ISEG reported for the contact element. You can display or list the actual fluid pressure applied to the target element through several POST1 postprocessing commands, as shown below:PLESOL,CONT,FPRSPLNSOL,CONT,FPRSPRESOL,CONTPRNSOL,CONTNote that only the FPRS (fluid penetration pressure) output item is meaningful when the PRESOL and PRNSOL commands are used for target elements.Table 170.3: TARGE170 Item and Sequence Numbers lists output available through the ETABLE command using the Sequence Number method. See Creating an Element Table in the Basic Analysis Guide and The Item and Sequence Number Table in this manual for more information. The following notation is used inTable 170.3: TARGE170 Item and Sequence Numbers:Nameoutput quantity as defined in the Table 170.2: TARGE170 Element OutputDefinitionsItempredetermined Item label for ETABLE commandEsequence number for single-valued or constant element dataI,J,K,Lsequence number for data at nodes I, J, K, LTable 170.3 TARGE170 Item and Sequence NumbersTARGE170 Assumptions and Restrictions•Generally speaking, you should not change real constants R1 or R2, either between load steps or during restart stages; otherwise ANSYS assumes theradii of the primitive segments varies between the load steps. When usingdirect generation, the real constants for cylinders, cones, and spheres may bedefined before the input of the element nodes. If multiple rigid primitives aredefined, each having different radii, they must be defined by different targetsurfaces.•For each pilot node, ANSYS automatically defines an internal node and an internal constraint equation. The rotational DOF of the pilot node is connected to the translational DOF of the internal node by the internal constraintequation. ANSYS recommends against using external constraint equations orcoupling on pilot nodes; if you do, conflicts may occur, yielding incorrectresults.•For rotation of a rigid body constrained only by a bonded, rigid-flexible contact pair with a pilot node, use the MPC algorithm or a surface-basedconstraint as described in "Multipoint Constraints and Assemblies" in theContact Technology Guide. Penalty-based algorithms can create undesirablerotational energies in this situation.TARGE170 Product RestrictionsThere are no product-specific restrictions for this element.Release 12.0 - © 2009 SAS IP, Inc. All rights reserved.。

Abelian group 阿贝尔群,又称Abel群ablation 烧蚀abnormal dispersion 反常色散Abrikosov vortex lattice 阿布里科索夫涡旋线格子Abrikocov vortex state 阿布里科索夫涡旋态absorber 吸收体absorption spectroscopy 吸收光谱abundance 丰度acceptor doping 受主掺杂acceptor impurity 受主杂质accumulation layer 累积层achromatic phase matching 消色差相位匹配achromatic wave plate 消色差波片achromatism 消色差[性]ac Josephson effect 交流约瑟夫森效应,又称交流Josephson效应acoustic compliance 声顺acoustic ohm 声欧[姆]acoustic stiffness 声劲[度]acoustic-optic tensor 声光系数张量acousto-optic effect 声光效应acousto-optic Q-switch 声光Q-开关acousto-optic signal processor 声光信号处理器acousto-optical tunable filter 声光可调滤波器actinide element 锕系元素activated tunneling 激活隧穿active device 有源器件active region 激活区addressing electrode 寻址电极adiabatic theorem,绝热定理adiabatic transformation 绝热变换adiabatic transport,绝热输运adiabaton 浸渐子,绝热子advection 平流aerodynamic sound 空气动力声aersol 气溶胶affinity potential 亲和势aggregate 聚集体aggregation 聚集Aharonov-Bohm (AB) effect AB效应,又称Aharonov-Bohm (AB) 效应Aharonov-Bohm (AB) flux AB磁通,又称Aharonov-Bohm (AB)磁通allowed state 容许态alpha decay ( -decay) 衰变alpha particle ( -particle) 粒子Altshular-Aronov-Spivak (AAS) effect AAS效应,又称Altshular-Aronov-Spivak效应amplification without inversion 无反转放大amplitude limiting 限幅amplitude transformer 变幅杆Andreev reflection 安德列也夫反射,又称Andreev反射Andreev mirror 安德列也夫镜[子],又称Andreev镜[子] Andreev scattering 安德列也夫散射,又称Andreev散射angular resolved photoemission spectroscopy 角分辨光电子谱[学] anisotropic confinement 各向异性限域anisotropic scatterer, 各向异性散射体anisotropy energy 各向异性能anomalon 反常子anomalous power laws 反常幂[次]率anomalous proximity effect,反常临近效应anomaly 反常antidot 同quantum antidot 反量子点antidodal point 腹点antigravity 反引力antihyperon 反超子anti-localization, 反局域化antimeson 反介子anti-exclusive principle 反不相容原理antiferromagnetic interaction 反铁磁相互作用antiferromagnetic semiconductor 反铁磁半导体anti-Stokes scattering 反斯托克斯散射anti-time ordered function, 反时序函数anyon 任意子aphelion 近日点, 远核点areal density 面密度armchair nanotube 扶手椅型纳米管arrayed waveguide gratings 阵列波导光栅artificial atom,人[工]构[造]原子artificial barrier 人工势垒artificial elment 人造元素atom laser 原子凝射器atom optics 原子光学atom trapping 原子陷俘,原子捕获atom waveguide 原子波导atomic clock原子钟atomic diffraction 原子衍射atomic fountain 原子喷泉atomic form factor 原子形状因子atomic time 原子时attenuation 衰减attosecond X-ray pulse 阿秒X射线脉冲Auger process 俄歇过程,又称Auger过程avalanche counter 雪崩计数器avalanche effect 雪崩效应avalanche photodiodes,apd 雪崩光电二极管azimuth 方位角back-action evasion 非干扰[测量]background radiation 本底辐射,背景辐射background temperature 本底温度, 背景温度balanced homodyne detection平衡零拍探测ballistic aggregate 弹道聚集体ballistic aggregation 弹道聚集ballistic electron injection 弹道电子注入ballistic transport弹道输运ballistics 弹道学band bending 带弯曲band index 带指标band of rotation-vibration 振转[谱]带band offset 带阶band repulsion 带排斥band theory 能带论bar 巴(压强单位),杆Barkhausen noise 巴克豪森噪声,又称Barkhausen噪声barn 巴恩(截面单位,10-24厘米2)barrier 势垒barrier curvature 势垒曲率barrier height 势垒高度barrier state 势垒态barrier tunneling 势垒隧穿base-centered orthorhombic lattice 底心正交格[子] base line 基线base material 基质base metal 碱金属basis vector 基矢beam 束,梁beam dump 束流捕集器beam focusing 束流聚焦behaviour 行为,性能Bell inequality贝尔不等式,又称Bell不等式bend resistance,弯曲电阻bent crystal 弯晶Berry phase 贝里相位,又称Berry相位βdecay β衰变βradioactivity β放射性βray β射线βspectum β谱βstability line β稳定线bevatron 吉伏质子加速器(高能质子同步稳相加速器)bicritical point 双临界点bicrystal junction 双晶结big bang model 大爆炸模型binary diffractive optical element 二元衍射光学元件bioastrophysics 天体生物物理学biochip 生物芯片bipolar junction transistor 双极[结]晶体管bit rate 比特率blackness 黑度blaze line 闪耀角bleaching effect 漂白效应blob 团迹,链滴Bloch electron 布洛赫电子,又称Bloch电子Bloch frequency,布洛赫频率,又称Bloch频率Bloch oscillation,布洛赫振荡,又称Bloch振荡Bloch theorem 布洛赫定理,又称Bloch定理blockade 阻塞Blonder-Tinkham-Klapwijk [BTK] model BTK模型body-centered cubic lattice 体心立方格[子]body-centered orthorhombic lattice 体心正交格[子]Bogoliubov [-de Gennes] equations 博戈留波夫[-得简斯]方程,又称Bogoliubov [-de Gennes]方程Boltzmann distribution 玻尔兹曼分布Boltzmann transport equation,玻尔兹曼输运方程bond-angle order 键角有序bond-orientational order 键取向有序bond polarizability 键极化性bond valence 键价boojum 布经(超流氦3中的取向织构)bosonization of field operators 场算符的波色化Bragg peak 布拉格峰,又称Bragg峰Bragg plane 布拉格平面,又称Bragg平面Bragg reflection 布拉格反射,又称Bragg 反射Bragg reflectors 布拉格反射器,又称Bragg 反射器Bragg waveguide 布拉格波导,又称Bragg 波导break junction 断裂结breathing mode呼吸模breeder 增殖反应堆breakup reaction 崩裂反应bright state 亮态brittleness 脆性buffer amplifier 缓冲放大器buffer gas 缓冲气体buffer layer, 缓冲层burn-up 燃耗Büttiker formula, 比特克公式,又称Büttiker公式buzzer 蜂鸣器C-15 structure C-15结构C[a]esium clock 铯钟calorie 卡【洛里】candle 烛光candescence 白热,又称白炽canonical commutation relation 正则对易关系canonical variable 正则变量cantact angle 接触角canted spin order倾斜自旋有序cantilever 悬臂(原子力显微镜中的)canthotaxie眼角[式]排列(另文说明)carbon cycle 碳循环(恒星内部的)carbon nanotube 碳纳米管carrier 载流子carrier concentration 载流子浓度carrier diffuse 载流子扩散carrier reservoir 载流子库Cartesian coordinates 笛卡儿坐标Cauchu-Schwarz inequality Cauchu-Schwarz不等式cavity dark state 腔暗态cavity dumping 腔倒空cavity quantum electrodynamics 腔量子电动力学cavity resonator [谐振]腔共振器14C dating 碳14测年celestial X-ray source 宇宙X 射线源center of inversion 反演中心center of moment 矩心central collision中心碰撞center-of-mass energy 质心系能量centrifuge 离心机centrifugal separation 离心分离ceramic 陶瓷chain folding 链折叠chain statistics 链统计学chalcogenide 硫属化物channel waveguide 沟道波导chaos synchronization 混沌同步chaotic communication 混沌通讯chaotic noise 混沌噪声characteristic impedance 特性阻抗characteristic curve 特征曲线charge-separated plasma 电荷分离等离子体(正负电荷在空间不同区域的等离子体) charge imbalance 电荷不平衡charge ordering 电荷有序charge parity effect,电荷宇称效应charge qubit 电荷量子比特(超导量子比特的一种)charge-phase qubit 电荷-相位量子比特(超导量子比特的一种)charge reservoir 电荷库charge stiffness 电荷劲度(衡量外场作用下电荷被自由加速的难易程度)charge-spin coupling电荷自旋耦合(用于自旋电子学)charge stripe phase 电荷条纹相charge-to-mass ratio 荷质比charge transfer insulator 电荷转移绝缘体charge transfer salt 电荷转移盐charge velocity 电荷速度(见于电荷-自旋分离现象)charging energy,充电能chemical shift 化学位移chiral liquid crystal 手征液晶chiral molecule手征分子,又称手性分子chiral symmetry broken 手征对称[性]破缺chirp啁啾chirped Gaussian pulse 啁啾高斯脉冲chirp filter 啁啾滤波器,又称线性调频滤波器,或色散延迟线chopper 斩波器circumlunar orbit 环月轨道circumsolar orbit 环日轨道circumterrestrial orbit 环地轨道cis-lunar space 月地空间clad 覆盖clamping 箝位classical fluid 经典液体clean limit [干]净极限cleaved coupling cavity 解理耦合腔cloning fidelity克隆保真度closed shell 满壳层,又称闭壳层,英文又称closure shellcluster state簇态CNO cycle 碳氮氧循环coalescence 聚合, 并合code 1,[代]码;2,密码;3,符号coding 编码codirectional coupling 同向耦合coefficient of correlation 关联系数coefficient of elasticity 弹性系数coexistence line 共存线(相图中的)coexisting phase 共存相coherence factor 相干因子coherence length,相干长度coherent atomic recoil 相干原子反冲coherent electron tunneling 相干电子隧道coherent peak 相干峰coherent photoassociation 相干光缔合coherent population oscillation相干布居振荡coherent population trapping相干布居囚禁coherent population transfer相干布居迁移coherent structure 拟序结构coherent terahertz waves相干太赫波coherent transient effects 相干暂态效应coherent trap 相干捕获cold finger 冷头cold fusion 冷聚变collective coordinate 集体坐标collective mode 集体模collective motion 集体运动collective pinning model 集体钉扎模型collinear phase matching 共线相位匹配colloid 胶体,胶质colloidal metal 胶体金属colored noise 色噪声colossal magnetoresistance [CMR] 庞磁电阻commensurate lattice 公度格子compact star 致密星compensated impurity 补偿杂质complementary metal oxide semiconductor [CMOS] 互补金属氧化物半导体complex 1,复合体;2,络合物complex analytical signal theory 复解析信号理论complex-conjugate pulses 复共轭脉冲compliance 1,柔度;2,顺度composite Fermion 复合费米子compression of ultrashort pulses 超短脉冲压缩compressor 压缩器,压机concurrence并发纠缠,又称量子并发condensate 凝聚体condensation energy 凝聚能condenser 冷凝器conductance fluctuation, 电导涨落conductance quantization 电导量子化conduction electron 传导电子confinement 1,约束(等离子);2,限域(凝聚态);3,禁闭(高能)congregating effect 聚集效应conjugate variable 共轭变量conservation of angular momentum 角动量守恒conservation of crystal momentum 晶体动量守恒conservative dislocation motion 保守位错运动(位错沿滑移面平行于Burgers矢量运动无净质量流)conservation of energy 能量守恒conservation law of flux 磁通守恒律conservation of momentum 动量守恒conservation of particle number粒子数守恒contact angle 接触角contact potential 接触势contact resistance 接触电阻continuation 延拓continuous group 连续群contour line 等值线contour map 等值线图contradirectional coupling反向耦合conventional unit cell 惯用单胞,简称单胞convergence factor 收敛因子conversion electron 内转换电子coolant moderator 载热减速剂cooperative diffusion 合作扩散Cooperon, 库珀子Cooper pair box 库珀对盒子coplanar waveguide 共面波导copolymer 共聚物core energy 芯能core nucleus 核芯[核]correlated spontaneous emission 关联自发发射correlation exponent 关联指数cosmic aerodynamics 宇宙气体动力学cosmic age 宇宙年龄cosmic constant 宇宙常量cosmic [microwave] background radiation [CMBR] 宇宙[微波]背景辐射cosmic microwave background 宇宙微波背景cosmic string 宇宙弦cosmochemistry 宇宙化学,天体化学cosmological nucleosynthesis 宇宙核合成cosmos 宇宙co-tunneling 共隧穿Couette flow 库埃特流Coulomb blockade 库仑阻塞Coulomb gap 库仑隙Coulomb interaction 库仑[相互]作用Coulomb island 库仑岛,又称单电子岛(single electron island)Coulomb potential 库仑势Coulomb repulsion 库仑斥力Coulomb staircase 库仑台阶counter telescope 计数器望远镜coupled-channels model 耦合道模型coupled mode theory 耦合模理论coupled waveguides,耦合波导coupled wells耦合阱coupling energy 耦合能coupling strength 耦合强度covalent bond 共价键creep wave蠕波,又称爬波critical assembly [核反应堆]临界装置critical density 临界密度critical dimension 临界维度cross-phase-modulation 交叉相位调制cross field 交叉场cross junction, 十字结crosstalk attenuation 串扰衰减crystal-field splitting 晶[体]场劈裂crystalline anisotropy晶态各向异性crystal symmetry class 晶体对称类cubic lattice 立方格子cuprate 铜氧化物curie 居里(非国际制放射性活度单位)current bias 电流偏置current operator 电流算符cutoff energy,截止能量cyclone 气旋cyclotron effective mass 回旋有效质量D/A converter 等于digital to analog converter 数模转换器damping radiation 阻尼辐射dark current 暗电流dark energy 暗能量dark state 暗态dark-state polariton 暗态光极化子date line 日界线dc Josephson effect 直流约瑟夫森效应,直流Josephson效应dc SQUID (superconducting quantum interference device) 直流超导量子干涉器Debye wave vector 德拜波矢decay heat 衰变热decay time,衰减时间deceleration 减速度decibel 分贝decoherence 退相干,又称消相干decoherence-free 无退相干,又称无消相干decontamination factor 去污因子decoupling epoch 退耦期decoy state 诱骗态deformation potential,形变势degeneracy collapse 简并塌缩degenerate pressure 简并压degenerate star 简并星de Gennes-Taupin length de Gennes-Taupin长度degree of order 有序度de Haas-Shubnikov effect de Haas-Shubnikov效应delay time,延迟时间demultiplexer 解复用器dendrite 1,枝晶;2,枝蔓;3,枝蔓体dense coding 密集编码dense wavelength division multiplexing 密集波分复用density correlation function,密度关联函数density distribution 密度分布density wave 密度波depairing 拆对dephasing length,退相位长度depinning 脱钉[扎]depleted Uranium 贫化铀deplation force 排空力(胶体物理用语)depletion layer 耗尽层descreening 去屏蔽deterministic equation 确定(论)的方程deuterium 氘, 即重氢deuterium oxide 重水dextrorotation 右旋diabatic approach 非绝热近似diagnostics 诊断学diagonal element 对角元diagonal matrix 对角矩阵diagonalization 对角化diamond structure 金刚石结构diblock copolymer 双嵌段共聚物dielectric response function 介电响应函数dielectric function,介电函数dielectric microcavity 介电[质]微腔dielectric reflector 介[电]质反射器differential conductance 微分电导differential input 差分输入differential rotation 较差自转(天文学用语)differential scanning calorimetry 差分扫描量热术diffraction-free beam 消衍射光束diffractive binary optics 衍射二元光学diffuseness [parameter] 弥散参数diffusion constant,扩散常数diffusion current 扩散电流diffusion region 扩散区diffusive transport,扩散输运digit 数字digital circuit 数字电路digital cross connect 数字交叉连接digit[al] to analog converter (DAC) 数模转换器digital micromirror device 数字微镜器件dilation 膨胀dilute phase 稀相dilation symmetry 伸缩对称dimensionless conductance 无量纲电导dimer 二聚体dimerization 二聚化dipole interaction 偶极相互作用dipole giant resonance 偶极巨共振Dirac braket 狄拉克括号Dirac picture 狄拉克绘景, 即相互作用绘景directed diffusion 定向扩散directional bond 定向键directional coupler 定向耦合器directional ordering 取向有序directional quantization 方向量子化direction of magnetization 磁化方向direct lattice 正格子,又称正点阵direct transition 直接跃迁dirty limit 脏极限dirty-metal regime,脏金属区discontinuity 1,不连续[性];2,突变[性] dislocation network 位错网络disordered alloy 无序合金disordered system 无序系统dispersion compensation 色散补偿dispersion-managed solitons 调控色散孤子dissipationless flow 无耗散流dissociation energy 离解能distillable entanglement 可萃取纠缠distinguishable states可区分态distributed Bragg reflector 分布布拉格反射器domain 1,畴;2,[定义]域;3,区域donor level 施主能级dopant 掺杂物doping 掺杂dosimetry 剂量学double-barrier tunneling,双势垒隧穿double exchange interaction 双交换相互作用double heterostructure DH 双异质结doublet state 双重态dressed atom 着衣原子,又称缀饰原子droplet model 小液滴模型Drude model,德鲁德模型duty ratio 占空比d-wave pairing d波配对dyad 并矢dynamical mass 动力学质量(08.02dynamic random access memory [DRAM] 动态随机存储器dynamic screening,动态屏蔽dynamically induced coherence 动态诱导相干dynamo theory 发动机理论dyne 达因early universe 早期宇宙eccentricity 偏心率eclipse 1,食;2,交食edge channel,边缘通道edge dislocation 刃[型]位错edge state,边缘态effective field theory 有效场理论effective Hamiltonian 有效哈密顿量effective mass approximation,有效质量近似Einstein-Podolsky-Rosen thought experiment EPR思想实验Einstein-Podolsky-Rosen effect EPR效应Einstein-Podolsky-Rosen pair EPR对Einstein-Podolsky-Rosen paradox EPR佯谬elastic compliance 弹性顺度elastic deformation 弹性形变electrical isolation 电绝缘electric breakdown 电击穿electric capacity 电容electric resistance 电阻electrical quadrupole moment 电四极矩electrochemical potential 电化学势electromagnetic absorption 电磁吸收electromagnetically induced absorption 电磁感生吸收electromagnetically induced transparency 电磁感生透明electromagnetic-environment effect,电磁环境效应electron backscattering pattern 电子背散射图样electron-beam lithography 电子束刻蚀electron configuration 电子组态electron density 电子密度electron-doped high temperature superconductor 电子掺杂的高温超导体electronegativity 电负性electron-electron interaction,电子-电子相互作用electron-hole pair 电子空穴对electron-hole recombination 电子-空穴复合electron hologram 电子全息术electron transition 电子跃迁electron pair 电子对electron pair tunneling 电子对隧穿electron-phonon coupling 电子声子耦合electron temperature,电子温度electron tunneling 电子隧穿electron waveguide,电子波导electron volt (eV) 电子伏electrorheological effect 电流变效应electrorheological fluid 电流变液Eliashberg equations Eliashberg方程Eliashberg theory of strong coupling Eliashberg强耦合理论elliptical orbit 椭圆轨道elliptic flow 椭圆流emittance 发射度empirical pseudopotential method 经验赝势方法empty lattice approximation 空晶格近似endohedral fullerene 内嵌原子富勒烯end-butt coupling 端面对接耦合energy relaxation length,能量弛豫长度energy transport velocity 能量传输速度ensemble average,系综平均entangled state 纠缠态entanglement 1,纠缠;2,纠缠度entanglement concentration 纠缠浓缩entanglement measure 纠缠度量entanglement monotone 单调纠缠量entanglement of formation 生成纠缠entanglement purification 纠缠纯化entanglement witness 纠缠见证entropy force 熵力envelope function,包络函数epithermal neutron 超热中子epoxy 环氧树脂erbium-doped fiber amplifier 掺饵光纤放大器error correction 纠错Esaki diode 江崎二极管evanescent state,衰逝态even-odd nucleus 偶奇核even parity 偶宇称evolution of inflation 暴涨演化Ewald construction Ewald作图法Ewald sphere Ewald球excess current 过剩电流excess neutron 过剩中子exchange-correlation hole 交换关联空穴exchange-correlation functional 交换关联泛函exchange hole 交换空穴exchange integral 交换积分excitation spectrum 激发谱excluded volume 排除体积exclusion of flux 磁通排斥exclusion principle 不相容原理exotic nucleus 奇特核expanding universe 膨胀宇宙extended [Brillouin] zone scheme 扩展[布里渊]区图式extraterrestrial life 地外生命extravehicular activity(EV A) [太空]舱外活动f-sum rule f求和规则face-centered orthorhombic lattice 面心正交格[子] face-on 正向facsimile 传真,英文简写为faxfacula 光斑Fahrenheit thermometer 华氏温度计faint object 暗天体fan diagram 扇形图F-center F中心Feno lineshape Feno线型Feno resonance Feno共振fan spin order 扇状自旋有序farad (F) 法拉(电容单位)Faraday depolarization 法拉第退偏振Faraday law of electrolysis 法拉第电解定律far-from-equilibrium system,远离平衡态系统far-side 背面(far-side of the moon, 月球背面)far-ultraviolet (FUV) 远紫外fast fission 快裂变fatigue crack 疲劳裂纹fatigue fracture 疲劳断裂fatigue strength 疲劳强度feed [source] 馈源feeder 馈线femto (f) 飞(=10-15)(01)femtosecond pulse shaping 飞秒脉冲成形Fermi age 费米[中子]年龄Fermi age-diffusion equation 费米年龄扩散方程Fermi arc 费米弧Fermi coupling constant 费米耦合常数Fermi energy 费米能量Fermi gas 费米气体Fermi golden rule 费米黄金定则Fermi liquid 费米液体Fermi liquid parameter 费米液体参数Fermi loop 费米环Fermi point 费米点Fermi transition费米跃迁Fermi vacuum 费米真空Fermi velocity 费米速度Fermi wavelength 费米波长Fermi wave vector,费米波矢Fermi’s golden rule费米黄金规则ferrielectric crystal 亚铁电晶体ferrimagnet 亚铁磁体ferroelectric 铁电体ferroelectric crystal 铁电晶体ferromagnet 铁磁体few-cycle pulse少周[期]脉冲few nucleon transfer 少[数]核子转移Feynman path,费曼路径Feynman path integral,费曼路径积分fiber cross connect 光纤交叉连接fiber grating 光纤光栅Fibonacci sequence 斐波那契序列fiducial confidence bar 置信棒fiducial point 基准点field intensity 场强field quantization 场量子化field quantum 场量子field strength 场强figure of merit,又称qualityfactor 品质因数filament 1,丝;2,丝极finite-amplitude wave 有限振幅波,又称大振幅波finite-difference method 有限差分方法finite element method 有限元法finite size effect 有限尺寸效应finite-size scaling 有限尺寸标度first approximation 一级近似first Brillouin zone 第一布里渊区first point of Aries 春分点,英文又称:vernal equinoxfirst point of Cancer 夏至点,英文又称:summer solsticefirst point of Capricornus 冬至点,英文又称:winter solsticefirst point of Libra 秋分点,英文又称:autumnal equinoxFiske steps 费斯克台阶,又称自感应台阶fissility 易裂变性fission 1,裂变;2,分裂fission isomer 裂变同质异能素fission nuclide 裂变核素fission reactor 裂变反应堆fission-spectrum neutron 裂变谱中子fission track dating 裂变径迹年代测定fitting curve 拟合曲线five-fold symmetry 5重对称fixed-range hopping 定程跳跃flash memory 闪速存储器,简称闪存flat spectrum 平谱flattening factor 扁率floating probe 浮置电极,又称浮置探针floating phase 浮置相Floquest theorem 弗洛开定理flow resistance 流阻fluctuating wall 涨落壁fluctuation 涨落(统计物理〕,又称起伏(声学〕fluence 注量fluorescence probe 荧光探剂flux,通量flux 1通量,又称流量;2,注量率;3,焊料;4 助熔剂flux bundle 磁通束flux flow amplifier (FFA) 磁通流放大器flux flow oscillator (FFO) 磁通流振荡器flux flow transistor(FFT)磁通流三极管,又称涡旋流三极管(vortex flow transistor) flux-line lattice 磁通线格子flux line 磁通线flux tube 磁流管flux quantum 磁通量子flux quantization 磁通量子化foam 泡沫focal point 焦点focal ratio 焦比focus 1,焦点;2,震源folding Brillouin zone 折叠布里渊区forbidden beta decay 禁戒b衰变forecast 预报forward bias 正向偏压four-Josephson junction logic (4JL) 四约瑟夫森结逻辑门Fourier analysis 傅里叶分析Fourier transform 傅里叶变换Fourier [transform] nuclear magnetic resonance 傅里叶[变换]核磁共振Fourier [transform] Raman spectroscopy 傅立叶[变换]拉曼谱学four probe method 四探针法four-terminal resistance,4端电阻fractional chain yield 相对链产额fractional cumulative yield 分积累产额fractional distillation 分馏fractional independent yield 分独立产额fractional statistics 分数统计法fragment 1,碎片;2,片段Franck-Condon principle弗兰克-康登原理free electron approximation 自由电子近似free electron gas 自由电子气体free energy 自由能free –free transition 自由-自由跃迁,又称自由态间跃迁freely falling body 自由落体free radical 自由基free spectral range 自由光谱范围freezing point 凝固点Frenkel exciton 弗仑克尔激子frequency conversion 频率转换Frequency division multiplexing 频分复用frequency jitter 频率抖动frequency multiplication 倍频friction 摩擦Friedel oscillation,Friedel振荡Friedel sum rule Friedel求和规则Frohlich interaction Frohlich相互作用front velocity波前速度frustrated magnet 窘组磁体fuel cell 燃料电池Fulde-Ferrell state Fulde-Ferrell态fullerene 富勒烯full moon 满月function 函数functional (1)泛函(2)功能(的)fundamental interaction 基本相互作用fundamental space-filling mode 基本空间填充模fuse (1)熔解(2)保险丝fused silica熔融石英fusion reactor 聚变[核反应]堆fuzzy information 模糊信息fussy mathematics 模糊数学gain-clamping 增益箝位gain efficiency 增益效率Galton plate 伽尔顿板-陈gamma(γ)伽马(地磁场强单位γ=nT)gamma rayγ射线gap 1,隙;2,能隙gap anisotropy 能隙各向异性gap parameter 能隙参数gaseous state 气态gate1,门;2,栅(极)gate voltage 门电压gauge symmetry 规范对称性gauss (G) 高斯(磁感应强度单位G=10-4T)Gaussian fluctuation 高斯涨落Gauss law 高斯定理Gauss surface 高斯面generalized Balmer formula 广义巴尔末公式generalized work 广义功general refractive index 广义折射率(量子信息)geomagnetic declination 地磁偏角geomagnetic inclination 地磁倾角geometrical structure factor 几何结构因子geometrization of gravitation 引力几何化German silver 德银g-factor g因子g-factor of electrons 电子的g因子g shift g移位ghost imaging 鬼成像giant magnetoresistance (GMR) 巨磁电阻Giaever tunneling 盖沃尔隧穿(单电(粒)子隧穿)Gibbs ensemble 吉布斯系综gilbert 吉尔(磁通势单位)Ginzburg-Landau coherence length 金兹堡-朗道(GL)相干长度Ginzburg-Landau equation 金兹堡-朗道(GL)方程Ginzburg-Landau-Abrikosov Go’rkov theory(GLAG)金兹堡-朗道-阿布里科索夫-高里科夫理论Glan-Thompson prism 格兰-汤普森棱镜Glan-Taylor prism 格兰-泰勒棱镜glass phase 玻璃相glassy ceramics 微晶玻璃glassy metal 玻璃态金属Glauber state Glauber态glide axis 滑移轴glide line 滑移线global phase 整体相位(量子信息)goniometer 测角器graded bandgap layer 缓变带隙层Gorter-Casimir two-fluid model 高特-卡西米尔二流体模型Graded index lens (GRIN) 梯度折射率透镜gradient of electric potential 电势梯度gram-molecule 克分子,摩尔(mole)grand free energy 巨自由能granular matter 颗粒物质granular superconductor 颗粒超导体granule 颗粒granularity 颗粒性granular metal 颗粒金属graphite 石墨graphite structure 石墨结构graph [线]图graph state 图态(量子信息)gravitational deflection of light 光线的引力偏折gravity acceleration 重力加速度Gray code 格雷码grazing angle 1,掠射角;2,擦边角greenhouse effect 温室效应group index of refraction 群折射率group theory 群论group velocity dispersion 群速度色散growth 生长growth model 生长模型guest host liquid crystal 宾主型液晶guided wave optics 导波光学gyroscopic effect 回转效应half metal 半金属half metallic magnet 半金属磁体half wave filter 半波滤波器half wave oscillator 半波振子half- wave zone method 半波带法half-wave voltage 半波电压Hall angle 霍尔角Hall coefficient 霍尔系数Hall field 霍尔电场[强度]Hall plateau 霍尔平台Hall resistance 霍尔电阻Hall voltage 霍尔电压halo nucleus 晕核halogen 卤素Hamiltonian matrix哈密顿[量]矩阵hard sphere 硬球hard sphere approximation 硬球近似harmonic generation 谐波产生Hartree-Fock electron 哈特里-福克电子H-center H心health physics 保健物理heat conductivity 1,导热性;2,热导率heat flow vector 热流矢量heat flux 热通量heat switch 热开关heavy electron 重电子heavy element 重元素heavy fermion superconductor 重费米子超导体heavy [fission] fragment 重【裂变】碎片heavy hole 重空穴heavy wall 重壁heavy water 重水hedgehog 猬缺陷height of potential barrier 势垒高度Heisenberg Hamiltonian 海森伯哈密顿量Heisenberg operators 海森伯算符Heisenberg uncertainty principle 海森伯不确定【性】原理Heitler-London theory 海特勒-伦敦理论Helfrich spontaneous curvature model 黑弗里希自发曲率模型helical spin order螺旋自旋有序helium liquefier 氦液化器heptahgedron 七面体Hermite polynomial 厄米多项式Hermitian matrix 厄米矩阵hertz (Hz) 赫兹, 频率单位heterotic superstring theory 杂化超弦理论Heusler alloy 霍伊斯勒合金hexadecapole 十六极hexahedron 六面体hexatic phase 六角相high coherence model 高相干模型high electron mobility transistor 高电子迁移率晶体管(简写:HEMT)high energy particle 高能粒子high-field domain 强场畴high-order dispersion 高阶色散high-order harmonic generation 高阶谐波产生high pass filter 高通滤波器high temperature reservoir 高温热源high temperature superconductor(HTS)高温超导体high vacuum 高真空high voltage electron microscopy 高压电子显微术Hohenberg-Kohn energy functional 霍恩伯格-科恩能量泛函hole-electron recombination 空穴-电子复合hole surface 空穴面(k空间中未占据态区的表面)hole-type high temperature superconductor 空穴型高温超导体holey fiber 多孔光纤hollow core optical fibers 空心光纤holon 空穴子homodyne零拍homodyne detection 零拍探测homolog[ue] 同系物homopolymer 单聚合物honeycomb photonic band gap fiber 蜂窝型光子带隙光纤hopping conductance 跳跃电导hopping energy,跳跃能hopping probability 跳跃概率hopping transport 跳跃输运host 基质host crystal 基质晶体,又称主晶hot carrier 热载流子h/e oscillation h/e振荡h/2e oscillation h/2e振荡Huang equations 黄[昆]方程组Huang-Rhys factor 黄昆-里斯因子Hubbard Hamiltonian 哈勃德哈密顿量Hubbard model 哈勃德模型Hubble time 哈勃时间hybrid bond 杂化键hybrid field effect 混合场效应hydrodynamics 流体[动]力学hydrodynamic mode 流体[动]力学模hydromagnetic disturbance 磁流体扰动hydromagnetic instability 磁流体不稳定性hydrophilic force 亲水力hydrophobic association 疏水缔合hydrophobic force 疏水力hyperbolic point 双曲点hypernucleus 超核hyper-Rayleigh scattering 超瑞利散射hyperspherical coordinate 超球座标hysteresis loop 1,滞后回线;2,磁滞回线hysteresis loss 1,滞后损失;2,磁滞损耗。

Abelian group 阿贝尔群,又称Abel群ablation 烧蚀abnormal dispersion 反常色散Abrikosov vortex lattice 阿布里科索夫涡旋线格子Abrikocov vortex state 阿布里科索夫涡旋态absorber 吸收体absorption spectroscopy 吸收光谱abundance 丰度acceptor doping 受主掺杂acceptor impurity 受主杂质accumulation layer 累积层achromatic phase matching 消色差相位匹配achromatic wave plate 消色差波片achromatism 消色差[性]ac Josephson effect 交流约瑟夫森效应,又称交流Josephson效应acoustic compliance 声顺acoustic ohm 声欧[姆]acoustic stiffness 声劲[度]acoustic-optic tensor 声光系数张量acousto-optic effect 声光效应acousto-optic Q-switch 声光Q-开关acousto-optic signal processor 声光信号处理器acousto-optical tunable filter 声光可调滤波器actinide element 锕系元素activated tunneling 激活隧穿active device 有源器件active region 激活区addressing electrode 寻址电极adiabatic theorem,绝热定理adiabatic transformation 绝热变换adiabatic transport,绝热输运adiabaton 浸渐子,绝热子advection 平流aerodynamic sound 空气动力声aersol 气溶胶affinity potential 亲和势aggregate 聚集体aggregation 聚集Aharonov-Bohm (AB) effect AB效应,又称Aharonov-Bohm (AB) 效应Aharonov-Bohm (AB) flux AB磁通,又称Aharonov-Bohm (AB)磁通allowed state 容许态alpha decay ( -decay) 衰变alpha particle ( -particle) 粒子Altshular-Aronov-Spivak (AAS) effect AAS效应,又称Altshular-Aronov-Spivak效应amplification without inversion 无反转放大amplitude limiting 限幅amplitude transformer 变幅杆Andreev reflection 安德列也夫反射,又称Andreev反射Andreev mirror 安德列也夫镜[子],又称Andreev镜[子] Andreev scattering 安德列也夫散射,又称Andreev散射angular resolved photoemission spectroscopy 角分辨光电子谱[学] anisotropic confinement 各向异性限域anisotropic scatterer, 各向异性散射体anisotropy energy 各向异性能anomalon 反常子anomalous power laws 反常幂[次]率anomalous proximity effect,反常临近效应anomaly 反常antidot 同quantum antidot 反量子点antidodal point 腹点antigravity 反引力antihyperon 反超子anti-localization, 反局域化antimeson 反介子anti-exclusive principle 反不相容原理antiferromagnetic interaction 反铁磁相互作用antiferromagnetic semiconductor 反铁磁半导体anti-Stokes scattering 反斯托克斯散射anti-time ordered function, 反时序函数anyon 任意子aphelion 近日点, 远核点areal density 面密度armchair nanotube 扶手椅型纳米管arrayed waveguide gratings 阵列波导光栅artificial atom,人[工]构[造]原子artificial barrier 人工势垒artificial elment 人造元素atom laser 原子凝射器atom optics 原子光学atom trapping 原子陷俘,原子捕获atom waveguide 原子波导atomic clock原子钟atomic diffraction 原子衍射atomic fountain 原子喷泉atomic form factor 原子形状因子atomic time 原子时attenuation 衰减attosecond X-ray pulse 阿秒X射线脉冲Auger process 俄歇过程,又称Auger过程avalanche counter 雪崩计数器avalanche effect 雪崩效应avalanche photodiodes,apd 雪崩光电二极管azimuth 方位角back-action evasion 非干扰[测量]background radiation 本底辐射,背景辐射background temperature 本底温度, 背景温度balanced homodyne detection平衡零拍探测ballistic aggregate 弹道聚集体ballistic aggregation 弹道聚集ballistic electron injection 弹道电子注入ballistic transport弹道输运ballistics 弹道学band bending 带弯曲band index 带指标band of rotation-vibration 振转[谱]带band offset 带阶band repulsion 带排斥band theory 能带论bar 巴(压强单位),杆Barkhausen noise 巴克豪森噪声,又称Barkhausen噪声barn 巴恩(截面单位,10-24厘米2)barrier 势垒barrier curvature 势垒曲率barrier height 势垒高度barrier state 势垒态barrier tunneling 势垒隧穿base-centered orthorhombic lattice 底心正交格[子] base line 基线base material 基质base metal 碱金属basis vector 基矢beam 束,梁beam dump 束流捕集器beam focusing 束流聚焦behaviour 行为,性能Bell inequality贝尔不等式,又称Bell不等式bend resistance,弯曲电阻bent crystal 弯晶Berry phase 贝里相位,又称Berry相位βdecay β衰变βradioactivity β放射性βray β射线βspectum β谱βstability line β稳定线bevatron 吉伏质子加速器(高能质子同步稳相加速器)bicritical point 双临界点bicrystal junction 双晶结big bang model 大爆炸模型binary diffractive optical element 二元衍射光学元件bioastrophysics 天体生物物理学biochip 生物芯片bipolar junction transistor 双极[结]晶体管bit rate 比特率blackness 黑度blaze line 闪耀角bleaching effect 漂白效应blob 团迹,链滴Bloch electron 布洛赫电子,又称Bloch电子Bloch frequency,布洛赫频率,又称Bloch频率Bloch oscillation,布洛赫振荡,又称Bloch振荡Bloch theorem 布洛赫定理,又称Bloch定理blockade 阻塞Blonder-Tinkham-Klapwijk [BTK] model BTK模型body-centered cubic lattice 体心立方格[子]body-centered orthorhombic lattice 体心正交格[子]Bogoliubov [-de Gennes] equations 博戈留波夫[-得简斯]方程,又称Bogoliubov [-de Gennes]方程Boltzmann distribution 玻尔兹曼分布Boltzmann transport equation,玻尔兹曼输运方程bond-angle order 键角有序bond-orientational order 键取向有序bond polarizability 键极化性bond valence 键价boojum 布经(超流氦3中的取向织构)bosonization of field operators 场算符的波色化Bragg peak 布拉格峰,又称Bragg峰Bragg plane 布拉格平面,又称Bragg平面Bragg reflection 布拉格反射,又称Bragg 反射Bragg reflectors 布拉格反射器,又称Bragg 反射器Bragg waveguide 布拉格波导,又称Bragg 波导break junction 断裂结breathing mode呼吸模breeder 增殖反应堆breakup reaction 崩裂反应bright state 亮态brittleness 脆性buffer amplifier 缓冲放大器buffer gas 缓冲气体buffer layer, 缓冲层burn-up 燃耗Büttiker formula, 比特克公式,又称Büttiker公式buzzer 蜂鸣器C-15 structure C-15结构C[a]esium clock 铯钟calorie 卡【洛里】candle 烛光candescence 白热,又称白炽canonical commutation relation 正则对易关系canonical variable 正则变量cantact angle 接触角canted spin order倾斜自旋有序cantilever 悬臂(原子力显微镜中的)canthotaxie眼角[式]排列(另文说明)carbon cycle 碳循环(恒星内部的)carbon nanotube 碳纳米管carrier 载流子carrier concentration 载流子浓度carrier diffuse 载流子扩散carrier reservoir 载流子库Cartesian coordinates 笛卡儿坐标Cauchu-Schwarz inequality Cauchu-Schwarz不等式cavity dark state 腔暗态cavity dumping 腔倒空cavity quantum electrodynamics 腔量子电动力学cavity resonator [谐振]腔共振器14C dating 碳14测年celestial X-ray source 宇宙X 射线源center of inversion 反演中心center of moment 矩心central collision中心碰撞center-of-mass energy 质心系能量centrifuge 离心机centrifugal separation 离心分离ceramic 陶瓷chain folding 链折叠chain statistics 链统计学chalcogenide 硫属化物channel waveguide 沟道波导chaos synchronization 混沌同步chaotic communication 混沌通讯chaotic noise 混沌噪声characteristic impedance 特性阻抗characteristic curve 特征曲线charge-separated plasma 电荷分离等离子体(正负电荷在空间不同区域的等离子体) charge imbalance 电荷不平衡charge ordering 电荷有序charge parity effect,电荷宇称效应charge qubit 电荷量子比特(超导量子比特的一种)charge-phase qubit 电荷-相位量子比特(超导量子比特的一种)charge reservoir 电荷库charge stiffness 电荷劲度(衡量外场作用下电荷被自由加速的难易程度)charge-spin coupling电荷自旋耦合(用于自旋电子学)charge stripe phase 电荷条纹相charge-to-mass ratio 荷质比charge transfer insulator 电荷转移绝缘体charge transfer salt 电荷转移盐charge velocity 电荷速度(见于电荷-自旋分离现象)charging energy,充电能chemical shift 化学位移chiral liquid crystal 手征液晶chiral molecule手征分子,又称手性分子chiral symmetry broken 手征对称[性]破缺chirp啁啾chirped Gaussian pulse 啁啾高斯脉冲chirp filter 啁啾滤波器,又称线性调频滤波器,或色散延迟线chopper 斩波器circumlunar orbit 环月轨道circumsolar orbit 环日轨道circumterrestrial orbit 环地轨道cis-lunar space 月地空间clad 覆盖clamping 箝位classical fluid 经典液体clean limit [干]净极限cleaved coupling cavity 解理耦合腔cloning fidelity克隆保真度closed shell 满壳层,又称闭壳层,英文又称closure shellcluster state簇态CNO cycle 碳氮氧循环coalescence 聚合, 并合code 1,[代]码;2,密码;3,符号coding 编码codirectional coupling 同向耦合coefficient of correlation 关联系数coefficient of elasticity 弹性系数coexistence line 共存线(相图中的)coexisting phase 共存相coherence factor 相干因子coherence length,相干长度coherent atomic recoil 相干原子反冲coherent electron tunneling 相干电子隧道coherent peak 相干峰coherent photoassociation 相干光缔合coherent population oscillation相干布居振荡coherent population trapping相干布居囚禁coherent population transfer相干布居迁移coherent structure 拟序结构coherent terahertz waves相干太赫波coherent transient effects 相干暂态效应coherent trap 相干捕获cold finger 冷头cold fusion 冷聚变collective coordinate 集体坐标collective mode 集体模collective motion 集体运动collective pinning model 集体钉扎模型collinear phase matching 共线相位匹配colloid 胶体,胶质colloidal metal 胶体金属colored noise 色噪声colossal magnetoresistance [CMR] 庞磁电阻commensurate lattice 公度格子compact star 致密星compensated impurity 补偿杂质complementary metal oxide semiconductor [CMOS] 互补金属氧化物半导体complex 1,复合体;2,络合物complex analytical signal theory 复解析信号理论complex-conjugate pulses 复共轭脉冲compliance 1,柔度;2,顺度composite Fermion 复合费米子compression of ultrashort pulses 超短脉冲压缩compressor 压缩器,压机concurrence并发纠缠,又称量子并发condensate 凝聚体condensation energy 凝聚能condenser 冷凝器conductance fluctuation, 电导涨落conductance quantization 电导量子化conduction electron 传导电子confinement 1,约束(等离子);2,限域(凝聚态);3,禁闭(高能)congregating effect 聚集效应conjugate variable 共轭变量conservation of angular momentum 角动量守恒conservation of crystal momentum 晶体动量守恒conservative dislocation motion 保守位错运动(位错沿滑移面平行于Burgers矢量运动无净质量流)conservation of energy 能量守恒conservation law of flux 磁通守恒律conservation of momentum 动量守恒conservation of particle number粒子数守恒contact angle 接触角contact potential 接触势contact resistance 接触电阻continuation 延拓continuous group 连续群contour line 等值线contour map 等值线图contradirectional coupling反向耦合conventional unit cell 惯用单胞,简称单胞convergence factor 收敛因子conversion electron 内转换电子coolant moderator 载热减速剂cooperative diffusion 合作扩散Cooperon, 库珀子Cooper pair box 库珀对盒子coplanar waveguide 共面波导copolymer 共聚物core energy 芯能core nucleus 核芯[核]correlated spontaneous emission 关联自发发射correlation exponent 关联指数cosmic aerodynamics 宇宙气体动力学cosmic age 宇宙年龄cosmic constant 宇宙常量cosmic [microwave] background radiation [CMBR] 宇宙[微波]背景辐射cosmic microwave background 宇宙微波背景cosmic string 宇宙弦cosmochemistry 宇宙化学,天体化学cosmological nucleosynthesis 宇宙核合成cosmos 宇宙co-tunneling 共隧穿Couette flow 库埃特流Coulomb blockade 库仑阻塞Coulomb gap 库仑隙Coulomb interaction 库仑[相互]作用Coulomb island 库仑岛,又称单电子岛(single electron island)Coulomb potential 库仑势Coulomb repulsion 库仑斥力Coulomb staircase 库仑台阶counter telescope 计数器望远镜coupled-channels model 耦合道模型coupled mode theory 耦合模理论coupled waveguides,耦合波导coupled wells耦合阱coupling energy 耦合能coupling strength 耦合强度covalent bond 共价键creep wave蠕波,又称爬波critical assembly [核反应堆]临界装置critical density 临界密度critical dimension 临界维度cross-phase-modulation 交叉相位调制cross field 交叉场cross junction, 十字结crosstalk attenuation 串扰衰减crystal-field splitting 晶[体]场劈裂crystalline anisotropy晶态各向异性crystal symmetry class 晶体对称类cubic lattice 立方格子cuprate 铜氧化物curie 居里(非国际制放射性活度单位)current bias 电流偏置current operator 电流算符cutoff energy,截止能量cyclone 气旋cyclotron effective mass 回旋有效质量D/A converter 等于digital to analog converter 数模转换器damping radiation 阻尼辐射dark current 暗电流dark energy 暗能量dark state 暗态dark-state polariton 暗态光极化子date line 日界线dc Josephson effect 直流约瑟夫森效应,直流Josephson效应dc SQUID (superconducting quantum interference device) 直流超导量子干涉器Debye wave vector 德拜波矢decay heat 衰变热decay time,衰减时间deceleration 减速度decibel 分贝decoherence 退相干,又称消相干decoherence-free 无退相干,又称无消相干decontamination factor 去污因子decoupling epoch 退耦期decoy state 诱骗态deformation potential,形变势degeneracy collapse 简并塌缩degenerate pressure 简并压degenerate star 简并星de Gennes-Taupin length de Gennes-Taupin长度degree of order 有序度de Haas-Shubnikov effect de Haas-Shubnikov效应delay time,延迟时间demultiplexer 解复用器dendrite 1,枝晶;2,枝蔓;3,枝蔓体dense coding 密集编码dense wavelength division multiplexing 密集波分复用density correlation function,密度关联函数density distribution 密度分布density wave 密度波depairing 拆对dephasing length,退相位长度depinning 脱钉[扎]depleted Uranium 贫化铀deplation force 排空力(胶体物理用语)depletion layer 耗尽层descreening 去屏蔽deterministic equation 确定(论)的方程deuterium 氘, 即重氢deuterium oxide 重水dextrorotation 右旋diabatic approach 非绝热近似diagnostics 诊断学diagonal element 对角元diagonal matrix 对角矩阵diagonalization 对角化diamond structure 金刚石结构diblock copolymer 双嵌段共聚物dielectric response function 介电响应函数dielectric function,介电函数dielectric microcavity 介电[质]微腔dielectric reflector 介[电]质反射器differential conductance 微分电导differential input 差分输入differential rotation 较差自转(天文学用语)differential scanning calorimetry 差分扫描量热术diffraction-free beam 消衍射光束diffractive binary optics 衍射二元光学diffuseness [parameter] 弥散参数diffusion constant,扩散常数diffusion current 扩散电流diffusion region 扩散区diffusive transport,扩散输运digit 数字digital circuit 数字电路digital cross connect 数字交叉连接digit[al] to analog converter (DAC) 数模转换器digital micromirror device 数字微镜器件dilation 膨胀dilute phase 稀相dilation symmetry 伸缩对称dimensionless conductance 无量纲电导dimer 二聚体dimerization 二聚化dipole interaction 偶极相互作用dipole giant resonance 偶极巨共振Dirac braket 狄拉克括号Dirac picture 狄拉克绘景, 即相互作用绘景directed diffusion 定向扩散directional bond 定向键directional coupler 定向耦合器directional ordering 取向有序directional quantization 方向量子化direction of magnetization 磁化方向direct lattice 正格子,又称正点阵direct transition 直接跃迁dirty limit 脏极限dirty-metal regime,脏金属区discontinuity 1,不连续[性];2,突变[性] dislocation network 位错网络disordered alloy 无序合金disordered system 无序系统dispersion compensation 色散补偿dispersion-managed solitons 调控色散孤子dissipationless flow 无耗散流dissociation energy 离解能distillable entanglement 可萃取纠缠distinguishable states可区分态distributed Bragg reflector 分布布拉格反射器domain 1,畴;2,[定义]域;3,区域donor level 施主能级dopant 掺杂物doping 掺杂dosimetry 剂量学double-barrier tunneling,双势垒隧穿double exchange interaction 双交换相互作用double heterostructure DH 双异质结doublet state 双重态dressed atom 着衣原子,又称缀饰原子droplet model 小液滴模型Drude model,德鲁德模型duty ratio 占空比d-wave pairing d波配对dyad 并矢dynamical mass 动力学质量(08.02dynamic random access memory [DRAM] 动态随机存储器dynamic screening,动态屏蔽dynamically induced coherence 动态诱导相干dynamo theory 发动机理论dyne 达因early universe 早期宇宙eccentricity 偏心率eclipse 1,食;2,交食edge channel,边缘通道edge dislocation 刃[型]位错edge state,边缘态effective field theory 有效场理论effective Hamiltonian 有效哈密顿量effective mass approximation,有效质量近似Einstein-Podolsky-Rosen thought experiment EPR思想实验Einstein-Podolsky-Rosen effect EPR效应Einstein-Podolsky-Rosen pair EPR对Einstein-Podolsky-Rosen paradox EPR佯谬elastic compliance 弹性顺度elastic deformation 弹性形变electrical isolation 电绝缘electric breakdown 电击穿electric capacity 电容electric resistance 电阻electrical quadrupole moment 电四极矩electrochemical potential 电化学势electromagnetic absorption 电磁吸收electromagnetically induced absorption 电磁感生吸收electromagnetically induced transparency 电磁感生透明electromagnetic-environment effect,电磁环境效应electron backscattering pattern 电子背散射图样electron-beam lithography 电子束刻蚀electron configuration 电子组态electron density 电子密度electron-doped high temperature superconductor 电子掺杂的高温超导体electronegativity 电负性electron-electron interaction,电子-电子相互作用electron-hole pair 电子空穴对electron-hole recombination 电子-空穴复合electron hologram 电子全息术electron transition 电子跃迁electron pair 电子对electron pair tunneling 电子对隧穿electron-phonon coupling 电子声子耦合electron temperature,电子温度electron tunneling 电子隧穿electron waveguide,电子波导electron volt (eV) 电子伏electrorheological effect 电流变效应electrorheological fluid 电流变液Eliashberg equations Eliashberg方程Eliashberg theory of strong coupling Eliashberg强耦合理论elliptical orbit 椭圆轨道elliptic flow 椭圆流emittance 发射度empirical pseudopotential method 经验赝势方法empty lattice approximation 空晶格近似endohedral fullerene 内嵌原子富勒烯end-butt coupling 端面对接耦合energy relaxation length,能量弛豫长度energy transport velocity 能量传输速度ensemble average,系综平均entangled state 纠缠态entanglement 1,纠缠;2,纠缠度entanglement concentration 纠缠浓缩entanglement measure 纠缠度量entanglement monotone 单调纠缠量entanglement of formation 生成纠缠entanglement purification 纠缠纯化entanglement witness 纠缠见证entropy force 熵力envelope function,包络函数epithermal neutron 超热中子epoxy 环氧树脂erbium-doped fiber amplifier 掺饵光纤放大器error correction 纠错Esaki diode 江崎二极管evanescent state,衰逝态even-odd nucleus 偶奇核even parity 偶宇称evolution of inflation 暴涨演化Ewald construction Ewald作图法Ewald sphere Ewald球excess current 过剩电流excess neutron 过剩中子exchange-correlation hole 交换关联空穴exchange-correlation functional 交换关联泛函exchange hole 交换空穴exchange integral 交换积分excitation spectrum 激发谱excluded volume 排除体积exclusion of flux 磁通排斥exclusion principle 不相容原理exotic nucleus 奇特核expanding universe 膨胀宇宙extended [Brillouin] zone scheme 扩展[布里渊]区图式extraterrestrial life 地外生命extravehicular activity(EV A) [太空]舱外活动f-sum rule f求和规则face-centered orthorhombic lattice 面心正交格[子] face-on 正向facsimile 传真,英文简写为faxfacula 光斑Fahrenheit thermometer 华氏温度计faint object 暗天体fan diagram 扇形图F-center F中心Feno lineshape Feno线型Feno resonance Feno共振fan spin order 扇状自旋有序farad (F) 法拉(电容单位)Faraday depolarization 法拉第退偏振Faraday law of electrolysis 法拉第电解定律far-from-equilibrium system,远离平衡态系统far-side 背面(far-side of the moon, 月球背面)far-ultraviolet (FUV) 远紫外fast fission 快裂变fatigue crack 疲劳裂纹fatigue fracture 疲劳断裂fatigue strength 疲劳强度feed [source] 馈源feeder 馈线femto (f) 飞(=10-15)(01)femtosecond pulse shaping 飞秒脉冲成形Fermi age 费米[中子]年龄Fermi age-diffusion equation 费米年龄扩散方程Fermi arc 费米弧Fermi coupling constant 费米耦合常数Fermi energy 费米能量Fermi gas 费米气体Fermi golden rule 费米黄金定则Fermi liquid 费米液体Fermi liquid parameter 费米液体参数Fermi loop 费米环Fermi point 费米点Fermi transition费米跃迁Fermi vacuum 费米真空Fermi velocity 费米速度Fermi wavelength 费米波长Fermi wave vector,费米波矢Fermi’s golden rule费米黄金规则ferrielectric crystal 亚铁电晶体ferrimagnet 亚铁磁体ferroelectric 铁电体ferroelectric crystal 铁电晶体ferromagnet 铁磁体few-cycle pulse少周[期]脉冲few nucleon transfer 少[数]核子转移Feynman path,费曼路径Feynman path integral,费曼路径积分fiber cross connect 光纤交叉连接fiber grating 光纤光栅Fibonacci sequence 斐波那契序列fiducial confidence bar 置信棒fiducial point 基准点field intensity 场强field quantization 场量子化field quantum 场量子field strength 场强figure of merit,又称qualityfactor 品质因数filament 1,丝;2,丝极finite-amplitude wave 有限振幅波,又称大振幅波finite-difference method 有限差分方法finite element method 有限元法finite size effect 有限尺寸效应finite-size scaling 有限尺寸标度first approximation 一级近似first Brillouin zone 第一布里渊区first point of Aries 春分点,英文又称:vernal equinoxfirst point of Cancer 夏至点,英文又称:summer solsticefirst point of Capricornus 冬至点,英文又称:winter solsticefirst point of Libra 秋分点,英文又称:autumnal equinoxFiske steps 费斯克台阶,又称自感应台阶fissility 易裂变性fission 1,裂变;2,分裂fission isomer 裂变同质异能素fission nuclide 裂变核素fission reactor 裂变反应堆fission-spectrum neutron 裂变谱中子fission track dating 裂变径迹年代测定fitting curve 拟合曲线five-fold symmetry 5重对称fixed-range hopping 定程跳跃flash memory 闪速存储器,简称闪存flat spectrum 平谱flattening factor 扁率floating probe 浮置电极,又称浮置探针floating phase 浮置相Floquest theorem 弗洛开定理flow resistance 流阻fluctuating wall 涨落壁fluctuation 涨落(统计物理〕,又称起伏(声学〕fluence 注量fluorescence probe 荧光探剂flux,通量flux 1通量,又称流量;2,注量率;3,焊料;4 助熔剂flux bundle 磁通束flux flow amplifier (FFA) 磁通流放大器flux flow oscillator (FFO) 磁通流振荡器flux flow transistor(FFT)磁通流三极管,又称涡旋流三极管(vortex flow transistor) flux-line lattice 磁通线格子flux line 磁通线flux tube 磁流管flux quantum 磁通量子flux quantization 磁通量子化foam 泡沫focal point 焦点focal ratio 焦比focus 1,焦点;2,震源folding Brillouin zone 折叠布里渊区forbidden beta decay 禁戒b衰变forecast 预报forward bias 正向偏压four-Josephson junction logic (4JL) 四约瑟夫森结逻辑门Fourier analysis 傅里叶分析Fourier transform 傅里叶变换Fourier [transform] nuclear magnetic resonance 傅里叶[变换]核磁共振Fourier [transform] Raman spectroscopy 傅立叶[变换]拉曼谱学four probe method 四探针法four-terminal resistance,4端电阻fractional chain yield 相对链产额fractional cumulative yield 分积累产额fractional distillation 分馏fractional independent yield 分独立产额fractional statistics 分数统计法fragment 1,碎片;2,片段Franck-Condon principle弗兰克-康登原理free electron approximation 自由电子近似free electron gas 自由电子气体free energy 自由能free –free transition 自由-自由跃迁,又称自由态间跃迁freely falling body 自由落体free radical 自由基free spectral range 自由光谱范围freezing point 凝固点Frenkel exciton 弗仑克尔激子frequency conversion 频率转换Frequency division multiplexing 频分复用frequency jitter 频率抖动frequency multiplication 倍频friction 摩擦Friedel oscillation,Friedel振荡Friedel sum rule Friedel求和规则Frohlich interaction Frohlich相互作用front velocity波前速度frustrated magnet 窘组磁体fuel cell 燃料电池Fulde-Ferrell state Fulde-Ferrell态fullerene 富勒烯full moon 满月function 函数functional (1)泛函(2)功能(的)fundamental interaction 基本相互作用fundamental space-filling mode 基本空间填充模fuse (1)熔解(2)保险丝fused silica熔融石英fusion reactor 聚变[核反应]堆fuzzy information 模糊信息fussy mathematics 模糊数学gain-clamping 增益箝位gain efficiency 增益效率Galton plate 伽尔顿板-陈gamma(γ)伽马(地磁场强单位γ=nT)gamma rayγ射线gap 1,隙;2,能隙gap anisotropy 能隙各向异性gap parameter 能隙参数gaseous state 气态gate1,门;2,栅(极)gate voltage 门电压gauge symmetry 规范对称性gauss (G) 高斯(磁感应强度单位G=10-4T)Gaussian fluctuation 高斯涨落Gauss law 高斯定理Gauss surface 高斯面generalized Balmer formula 广义巴尔末公式generalized work 广义功general refractive index 广义折射率(量子信息)geomagnetic declination 地磁偏角geomagnetic inclination 地磁倾角geometrical structure factor 几何结构因子geometrization of gravitation 引力几何化German silver 德银g-factor g因子g-factor of electrons 电子的g因子g shift g移位ghost imaging 鬼成像giant magnetoresistance (GMR) 巨磁电阻Giaever tunneling 盖沃尔隧穿(单电(粒)子隧穿)Gibbs ensemble 吉布斯系综gilbert 吉尔(磁通势单位)Ginzburg-Landau coherence length 金兹堡-朗道(GL)相干长度Ginzburg-Landau equation 金兹堡-朗道(GL)方程Ginzburg-Landau-Abrikosov Go’rkov theory(GLAG)金兹堡-朗道-阿布里科索夫-高里科夫理论Glan-Thompson prism 格兰-汤普森棱镜Glan-Taylor prism 格兰-泰勒棱镜glass phase 玻璃相glassy ceramics 微晶玻璃glassy metal 玻璃态金属Glauber state Glauber态glide axis 滑移轴glide line 滑移线global phase 整体相位(量子信息)goniometer 测角器graded bandgap layer 缓变带隙层Gorter-Casimir two-fluid model 高特-卡西米尔二流体模型Graded index lens (GRIN) 梯度折射率透镜gradient of electric potential 电势梯度gram-molecule 克分子,摩尔(mole)grand free energy 巨自由能granular matter 颗粒物质granular superconductor 颗粒超导体granule 颗粒granularity 颗粒性granular metal 颗粒金属graphite 石墨graphite structure 石墨结构graph [线]图graph state 图态(量子信息)gravitational deflection of light 光线的引力偏折gravity acceleration 重力加速度Gray code 格雷码grazing angle 1,掠射角;2,擦边角greenhouse effect 温室效应group index of refraction 群折射率group theory 群论group velocity dispersion 群速度色散growth 生长growth model 生长模型guest host liquid crystal 宾主型液晶guided wave optics 导波光学gyroscopic effect 回转效应half metal 半金属half metallic magnet 半金属磁体half wave filter 半波滤波器half wave oscillator 半波振子half- wave zone method 半波带法half-wave voltage 半波电压Hall angle 霍尔角Hall coefficient 霍尔系数Hall field 霍尔电场[强度]Hall plateau 霍尔平台Hall resistance 霍尔电阻Hall voltage 霍尔电压halo nucleus 晕核halogen 卤素Hamiltonian matrix哈密顿[量]矩阵hard sphere 硬球hard sphere approximation 硬球近似harmonic generation 谐波产生Hartree-Fock electron 哈特里-福克电子H-center H心health physics 保健物理heat conductivity 1,导热性;2,热导率heat flow vector 热流矢量heat flux 热通量heat switch 热开关heavy electron 重电子heavy element 重元素heavy fermion superconductor 重费米子超导体heavy [fission] fragment 重【裂变】碎片heavy hole 重空穴heavy wall 重壁heavy water 重水hedgehog 猬缺陷height of potential barrier 势垒高度Heisenberg Hamiltonian 海森伯哈密顿量Heisenberg operators 海森伯算符Heisenberg uncertainty principle 海森伯不确定【性】原理Heitler-London theory 海特勒-伦敦理论Helfrich spontaneous curvature model 黑弗里希自发曲率模型helical spin order螺旋自旋有序helium liquefier 氦液化器heptahgedron 七面体Hermite polynomial 厄米多项式Hermitian matrix 厄米矩阵hertz (Hz) 赫兹, 频率单位heterotic superstring theory 杂化超弦理论Heusler alloy 霍伊斯勒合金hexadecapole 十六极hexahedron 六面体hexatic phase 六角相high coherence model 高相干模型high electron mobility transistor 高电子迁移率晶体管(简写:HEMT)high energy particle 高能粒子high-field domain 强场畴high-order dispersion 高阶色散high-order harmonic generation 高阶谐波产生high pass filter 高通滤波器high temperature reservoir 高温热源high temperature superconductor(HTS)高温超导体high vacuum 高真空high voltage electron microscopy 高压电子显微术Hohenberg-Kohn energy functional 霍恩伯格-科恩能量泛函hole-electron recombination 空穴-电子复合hole surface 空穴面(k空间中未占据态区的表面)hole-type high temperature superconductor 空穴型高温超导体holey fiber 多孔光纤hollow core optical fibers 空心光纤holon 空穴子homodyne零拍homodyne detection 零拍探测homolog[ue] 同系物homopolymer 单聚合物honeycomb photonic band gap fiber 蜂窝型光子带隙光纤hopping conductance 跳跃电导hopping energy,跳跃能hopping probability 跳跃概率hopping transport 跳跃输运host 基质host crystal 基质晶体,又称主晶hot carrier 热载流子h/e oscillation h/e振荡h/2e oscillation h/2e振荡Huang equations 黄[昆]方程组Huang-Rhys factor 黄昆-里斯因子Hubbard Hamiltonian 哈勃德哈密顿量Hubbard model 哈勃德模型Hubble time 哈勃时间hybrid bond 杂化键hybrid field effect 混合场效应hydrodynamics 流体[动]力学hydrodynamic mode 流体[动]力学模hydromagnetic disturbance 磁流体扰动hydromagnetic instability 磁流体不稳定性hydrophilic force 亲水力hydrophobic association 疏水缔合hydrophobic force 疏水力hyperbolic point 双曲点hypernucleus 超核hyper-Rayleigh scattering 超瑞利散射hyperspherical coordinate 超球座标hysteresis loop 1,滞后回线;2,磁滞回线hysteresis loss 1,滞后损失;2,磁滞损耗。

Progressive Simplicial Complexes Jovan Popovi´c Hugues HoppeCarnegie Mellon University Microsoft ResearchABSTRACTIn this paper,we introduce the progressive simplicial complex(PSC) representation,a new format for storing and transmitting triangu-lated geometric models.Like the earlier progressive mesh(PM) representation,it captures a given model as a coarse base model together with a sequence of refinement transformations that pro-gressively recover detail.The PSC representation makes use of a more general refinement transformation,allowing the given model to be an arbitrary triangulation(e.g.any dimension,non-orientable, non-manifold,non-regular),and the base model to always consist of a single vertex.Indeed,the sequence of refinement transforma-tions encodes both the geometry and the topology of the model in a unified multiresolution framework.The PSC representation retains the advantages of PM’s.It defines a continuous sequence of approx-imating models for runtime level-of-detail control,allows smooth transitions between any pair of models in the sequence,supports progressive transmission,and offers a space-efficient representa-tion.Moreover,by allowing changes to topology,the PSC sequence of approximations achieves betterfidelity than the corresponding PM sequence.We develop an optimization algorithm for constructing PSC representations for graphics surface models,and demonstrate the framework on models that are both geometrically and topologically complex.CR Categories:I.3.5[Computer Graphics]:Computational Geometry and Object Modeling-surfaces and object representations.Additional Keywords:model simplification,level-of-detail representa-tions,multiresolution,progressive transmission,geometry compression.1INTRODUCTIONModeling and3D scanning systems commonly give rise to triangle meshes of high complexity.Such meshes are notoriously difficult to render,store,and transmit.One approach to speed up rendering is to replace a complex mesh by a set of level-of-detail(LOD) approximations;a detailed mesh is used when the object is close to the viewer,and coarser approximations are substituted as the object recedes[6,8].These LOD approximations can be precomputed Work performed while at Microsoft Research.Email:jovan@,hhoppe@Web:/jovan/Web:/hoppe/automatically using mesh simplification methods(e.g.[2,10,14,20,21,22,24,27]).For efficient storage and transmission,meshcompression schemes[7,26]have also been developed.The recently introduced progressive mesh(PM)representa-tion[13]provides a unified solution to these problems.In PM form,an arbitrary mesh M is stored as a coarse base mesh M0together witha sequence of n detail records that indicate how to incrementally re-fine M0into M n=M(see Figure7).Each detail record encodes theinformation associated with a vertex split,an elementary transfor-mation that adds one vertex to the mesh.In addition to defininga continuous sequence of approximations M0M n,the PM rep-resentation supports smooth visual transitions(geomorphs),allowsprogressive transmission,and makes an effective mesh compressionscheme.The PM representation has two restrictions,however.First,it canonly represent meshes:triangulations that correspond to orientable12-dimensional manifolds.Triangulated2models that cannot be rep-resented include1-d manifolds(open and closed curves),higherdimensional polyhedra(e.g.triangulated volumes),non-orientablesurfaces(e.g.M¨o bius strips),non-manifolds(e.g.two cubes joinedalong an edge),and non-regular models(i.e.models of mixed di-mensionality).Second,the expressiveness of the PM vertex splittransformations constrains all meshes M0M n to have the same topological type.Therefore,when M is topologically complex,the simplified base mesh M0may still have numerous triangles(Fig-ure7).In contrast,a number of existing simplification methods allowtopological changes as the model is simplified(Section6).Ourwork is inspired by vertex unification schemes[21,22],whichmerge vertices of the model based on geometric proximity,therebyallowing genus modification and component merging.In this paper,we introduce the progressive simplicial complex(PSC)representation,a generalization of the PM representation thatpermits topological changes.The key element of our approach isthe introduction of a more general refinement transformation,thegeneralized vertex split,that encodes changes to both the geometryand topology of the model.The PSC representation expresses anarbitrary triangulated model M(e.g.any dimension,non-orientable,non-manifold,non-regular)as the result of successive refinementsapplied to a base model M1that always consists of a single vertex (Figure8).Thus both geometric and topological complexity are recovered progressively.Moreover,the PSC representation retains the advantages of PM’s,including continuous LOD,geomorphs, progressive transmission,and model compression.In addition,we develop an optimization algorithm for construct-ing a PSC representation from a given model,as described in Sec-tion4.1The particular parametrization of vertex splits in[13]assumes that mesh triangles are consistently oriented.2Throughout this paper,we use the words“triangulated”and“triangula-tion”in the general dimension-independent sense.Figure 1:Illustration of a simplicial complex K and some of its subsets.2BACKGROUND2.1Concepts from algebraic topologyTo precisely define both triangulated models and their PSC repre-sentations,we find it useful to introduce some elegant abstractions from algebraic topology (e.g.[15,25]).The geometry of a triangulated model is denoted as a tuple (K V )where the abstract simplicial complex K is a combinatorial structure specifying the adjacency of vertices,edges,triangles,etc.,and V is a set of vertex positions specifying the shape of the model in 3.More precisely,an abstract simplicial complex K consists of a set of vertices 1m together with a set of non-empty subsets of the vertices,called the simplices of K ,such that any set consisting of exactly one vertex is a simplex in K ,and every non-empty subset of a simplex in K is also a simplex in K .A simplex containing exactly d +1vertices has dimension d and is called a d -simplex.As illustrated pictorially in Figure 1,the faces of a simplex s ,denoted s ,is the set of non-empty subsets of s .The star of s ,denoted star(s ),is the set of simplices of which s is a face.The children of a d -simplex s are the (d 1)-simplices of s ,and its parents are the (d +1)-simplices of star(s ).A simplex with exactly one parent is said to be a boundary simplex ,and one with no parents a principal simplex .The dimension of K is the maximum dimension of its simplices;K is said to be regular if all its principal simplices have the same dimension.To form a triangulation from K ,identify its vertices 1m with the standard basis vectors 1m ofm.For each simplex s ,let the open simplex smdenote the interior of the convex hull of its vertices:s =m:jmj =1j=1jjsThe topological realization K is defined as K =K =s K s .The geometric realization of K is the image V (K )where V :m 3is the linear map that sends the j -th standard basis vector jm to j 3.Only a restricted set of vertex positions V =1m lead to an embedding of V (K )3,that is,prevent self-intersections.The geometric realization V (K )is often called a simplicial complex or polyhedron ;it is formed by an arbitrary union of points,segments,triangles,tetrahedra,etc.Note that there generally exist many triangulations (K V )for a given polyhedron.(Some of the vertices V may lie in the polyhedron’s interior.)Two sets are said to be homeomorphic (denoted =)if there ex-ists a continuous one-to-one mapping between them.Equivalently,they are said to have the same topological type .The topological realization K is a d-dimensional manifold without boundary if for each vertex j ,star(j )=d .It is a d-dimensional manifold if each star(v )is homeomorphic to either d or d +,where d +=d:10.Two simplices s 1and s 2are d-adjacent if they have a common d -dimensional face.Two d -adjacent (d +1)-simplices s 1and s 2are manifold-adjacent if star(s 1s 2)=d +1.Figure 2:Illustration of the edge collapse transformation and its inverse,the vertex split.Transitive closure of 0-adjacency partitions K into connected com-ponents .Similarly,transitive closure of manifold-adjacency parti-tions K into manifold components .2.2Review of progressive meshesIn the PM representation [13],a mesh with appearance attributes is represented as a tuple M =(K V D S ),where the abstract simpli-cial complex K is restricted to define an orientable 2-dimensional manifold,the vertex positions V =1m determine its ge-ometric realization V (K )in3,D is the set of discrete material attributes d f associated with 2-simplices f K ,and S is the set of scalar attributes s (v f )(e.g.normals,texture coordinates)associated with corners (vertex-face tuples)of K .An initial mesh M =M n is simplified into a coarser base mesh M 0by applying a sequence of n successive edge collapse transforma-tions:(M =M n )ecol n 1ecol 1M 1ecol 0M 0As shown in Figure 2,each ecol unifies the two vertices of an edgea b ,thereby removing one or two triangles.The position of the resulting unified vertex can be arbitrary.Because the edge collapse transformation has an inverse,called the vertex split transformation (Figure 2),the process can be reversed,so that an arbitrary mesh M may be represented as a simple mesh M 0together with a sequence of n vsplit records:M 0vsplit 0M 1vsplit 1vsplit n 1(M n =M )The tuple (M 0vsplit 0vsplit n 1)forms a progressive mesh (PM)representation of M .The PM representation thus captures a continuous sequence of approximations M 0M n that can be quickly traversed for interac-tive level-of-detail control.Moreover,there exists a correspondence between the vertices of any two meshes M c and M f (0c f n )within this sequence,allowing for the construction of smooth vi-sual transitions (geomorphs)between them.A sequence of such geomorphs can be precomputed for smooth runtime LOD.In addi-tion,PM’s support progressive transmission,since the base mesh M 0can be quickly transmitted first,followed the vsplit sequence.Finally,the vsplit records can be encoded concisely,making the PM representation an effective scheme for mesh compression.Topological constraints Because the definitions of ecol and vsplit are such that they preserve the topological type of the mesh (i.e.all K i are homeomorphic),there is a constraint on the min-imum complexity that K 0may achieve.For instance,it is known that the minimal number of vertices for a closed genus g mesh (ori-entable 2-manifold)is (7+(48g +1)12)2if g =2(10if g =2)[16].Also,the presence of boundary components may further constrain the complexity of K 0.Most importantly,K may consist of a number of components,and each is required to appear in the base mesh.For example,the meshes in Figure 7each have 117components.As evident from the figure,the geometry of PM meshes may deteriorate severely as they approach topological lower bound.M 1;100;(1)M 10;511;(7)M 50;4656;(12)M 200;1552277;(28)M 500;3968690;(58)M 2000;14253219;(108)M 5000;029010;(176)M n =34794;0068776;(207)Figure 3:Example of a PSC representation.The image captions indicate the number of principal 012-simplices respectively and the number of connected components (in parenthesis).3PSC REPRESENTATION 3.1Triangulated modelsThe first step towards generalizing PM’s is to let the PSC repre-sentation encode more general triangulated models,instead of just meshes.We denote a triangulated model as a tuple M =(K V D A ).The abstract simplicial complex K is not restricted to 2-manifolds,but may in fact be arbitrary.To represent K in memory,we encode the incidence graph of the simplices using the following linked structures (in C++notation):struct Simplex int dim;//0=vertex,1=edge,2=triangle,...int id;Simplex*children[MAXDIM+1];//[0..dim]List<Simplex*>parents;;To render the model,we draw only the principal simplices ofK ,denoted (K )(i.e.vertices not adjacent to edges,edges not adjacent to triangles,etc.).The discrete attributes D associate amaterial identifier d s with each simplex s(K ).For the sake of simplicity,we avoid explicitly storing surface normals at “corners”(using a set S )as done in [13].Instead we let the material identifier d s contain a smoothing group field [28],and let a normal discontinuity (crease )form between any pair of adjacent triangles with different smoothing groups.Previous vertex unification schemes [21,22]render principal simplices of dimension 0and 1(denoted 01(K ))as points and lines respectively with fixed,device-dependent screen widths.To better approximate the model,we instead define a set A that associates an area a s A with each simplex s 01(K ).We think of a 0-simplex s 00(K )as approximating a sphere with area a s 0,and a 1-simplex s 1=j k 1(K )as approximating a cylinder (with axis (j k ))of area a s 1.To render a simplex s 01(K ),we determine the radius r model of the corresponding sphere or cylinder in modeling space,and project the length r model to obtain the radius r screen in screen pixels.Depending on r screen ,we render the simplex as a polygonal sphere or cylinder with radius r model ,a 2D point or line with thickness 2r screen ,or do not render it at all.This choice based on r screen can be adjusted to mitigate the overhead of introducing polygonal representations of spheres and cylinders.As an example,Figure 3shows an initial model M of 68,776triangles.One of its approximations M 500is a triangulated model with 3968690principal 012-simplices respectively.3.2Level-of-detail sequenceAs in progressive meshes,from a given triangulated model M =M n ,we define a sequence of approximations M i :M 1op 1M 2op 2M n1op n 1M nHere each model M i has exactly i vertices.The simplification op-erator M ivunify iM i +1is the vertex unification transformation,whichmerges two vertices (Section 3.3),and its inverse M igvspl iM i +1is the generalized vertex split transformation (Section 3.4).Thetuple (M 1gvspl 1gvspl n 1)forms a progressive simplicial complex (PSC)representation of M .To construct a PSC representation,we first determine a sequence of vunify transformations simplifying M down to a single vertex,as described in Section 4.After reversing these transformations,we renumber the simplices in the order that they are created,so thateach gvspl i (a i)splits the vertex a i K i into two vertices a i i +1K i +1.As vertices may have different positions in the different models,we denote the position of j in M i as i j .To better approximate a surface model M at lower complexity levels,we initially associate with each (principal)2-simplex s an area a s equal to its triangle area in M .Then,as the model is simplified,wekeep constant the sum of areas a s associated with principal simplices within each manifold component.When2-simplices are eventually reduced to principal1-simplices and0-simplices,their associated areas will provide good estimates of the original component areas.3.3Vertex unification transformationThe transformation vunify(a i b i midp i):M i M i+1takes an arbitrary pair of vertices a i b i K i+1(simplex a i b i need not be present in K i+1)and merges them into a single vertex a i K i. Model M i is created from M i+1by updating each member of the tuple(K V D A)as follows:K:References to b i in all simplices of K are replaced by refer-ences to a i.More precisely,each simplex s in star(b i)K i+1is replaced by simplex(s b i)a i,which we call the ancestor simplex of s.If this ancestor simplex already exists,s is deleted.V:Vertex b is deleted.For simplicity,the position of the re-maining(unified)vertex is set to either the midpoint or is left unchanged.That is,i a=(i+1a+i+1b)2if the boolean parameter midp i is true,or i a=i+1a otherwise.D:Materials are carried through as expected.So,if after the vertex unification an ancestor simplex(s b i)a i K i is a new principal simplex,it receives its material from s K i+1if s is a principal simplex,or else from the single parent s a i K i+1 of s.A:To maintain the initial areas of manifold components,the areasa s of deleted principal simplices are redistributed to manifold-adjacent neighbors.More concretely,the area of each princi-pal d-simplex s deleted during the K update is distributed toa manifold-adjacent d-simplex not in star(a ib i).If no suchneighbor exists and the ancestor of s is a principal simplex,the area a s is distributed to that ancestor simplex.Otherwise,the manifold component(star(a i b i))of s is being squashed be-tween two other manifold components,and a s is discarded. 3.4Generalized vertex split transformation Constructing the PSC representation involves recording the infor-mation necessary to perform the inverse of each vunify i.This inverse is the generalized vertex split gvspl i,which splits a0-simplex a i to introduce an additional0-simplex b i.(As mentioned previously, renumbering of simplices implies b i i+1,so index b i need not be stored explicitly.)Each gvspl i record has the formgvspl i(a i C K i midp i()i C D i C A i)and constructs model M i+1from M i by updating the tuple (K V D A)as follows:K:As illustrated in Figure4,any simplex adjacent to a i in K i can be the vunify result of one of four configurations in K i+1.To construct K i+1,we therefore replace each ancestor simplex s star(a i)in K i by either(1)s,(2)(s a i)i+1,(3)s and(s a i)i+1,or(4)s,(s a i)i+1and s i+1.The choice is determined by a split code associated with s.Thesesplit codes are stored as a code string C Ki ,in which the simplicesstar(a i)are sortedfirst in order of increasing dimension,and then in order of increasing simplex id,as shown in Figure5. V:The new vertex is assigned position i+1i+1=i ai+()i.Theother vertex is given position i+1ai =i ai()i if the boolean pa-rameter midp i is true;otherwise its position remains unchanged.D:The string C Di is used to assign materials d s for each newprincipal simplex.Simplices in C Di ,as well as in C Aibelow,are sorted by simplex dimension and simplex id as in C Ki. A:During reconstruction,we are only interested in the areas a s fors01(K).The string C Ai tracks changes in these areas.Figure4:Effects of split codes on simplices of various dimensions.code string:41422312{}Figure5:Example of split code encoding.3.5PropertiesLevels of detail A graphics application can efficiently transitionbetween models M1M n at runtime by performing a sequence ofvunify or gvspl transformations.Our current research prototype wasnot designed for efficiency;it attains simplification rates of about6000vunify/sec and refinement rates of about5000gvspl/sec.Weexpect that a careful redesign using more efficient data structureswould significantly improve these rates.Geomorphs As in the PM representation,there exists a corre-spondence between the vertices of the models M1M n.Given acoarser model M c and afiner model M f,1c f n,each vertexj K f corresponds to a unique ancestor vertex f c(j)K cfound by recursively traversing the ancestor simplex relations:f c(j)=j j cf c(a j1)j cThis correspondence allows the creation of a smooth visual transi-tion(geomorph)M G()such that M G(1)equals M f and M G(0)looksidentical to M c.The geomorph is defined as the modelM G()=(K f V G()D f A G())in which each vertex position is interpolated between its originalposition in V f and the position of its ancestor in V c:Gj()=()fj+(1)c f c(j)However,we must account for the special rendering of principalsimplices of dimension0and1(Section3.1).For each simplexs01(K f),we interpolate its area usinga G s()=()a f s+(1)a c swhere a c s=0if s01(K c).In addition,we render each simplexs01(K c)01(K f)using area a G s()=(1)a c s.The resultinggeomorph is visually smooth even as principal simplices are intro-duced,removed,or change dimension.The accompanying video demonstrates a sequence of such geomorphs.Progressive transmission As with PM’s,the PSC representa-tion can be progressively transmitted by first sending M 1,followed by the gvspl records.Unlike the base mesh of the PM,M 1always consists of a single vertex,and can therefore be sent in a fixed-size record.The rendering of lower-dimensional simplices as spheres and cylinders helps to quickly convey the overall shape of the model in the early stages of transmission.Model compression Although PSC gvspl are more general than PM vsplit transformations,they offer a surprisingly concise representation of M .Table 1lists the average number of bits re-quired to encode each field of the gvspl records.Using arithmetic coding [30],the vertex id field a i requires log 2i bits,and the boolean parameter midp i requires 0.6–0.9bits for our models.The ()i delta vector is quantized to 16bitsper coordinate (48bits per),and stored as a variable-length field [7,13],requiring about 31bits on average.At first glance,each split code in the code string C K i seems to have 4possible outcomes (except for the split code for 0-simplex a i which has only 2possible outcomes).However,there exist constraints between these split codes.For example,in Figure 5,the code 1for 1-simplex id 1implies that 2-simplex id 1also has code 1.This in turn implies that 1-simplex id 2cannot have code 2.Similarly,code 2for 1-simplex id 3implies a code 2for 2-simplex id 2,which in turn implies that 1-simplex id 4cannot have code 1.These constraints,illustrated in the “scoreboard”of Figure 6,can be summarized using the following two rules:(1)If a simplex has split code c12,all of its parents havesplit code c .(2)If a simplex has split code 3,none of its parents have splitcode 4.As we encode split codes in C K i left to right,we apply these two rules (and their contrapositives)transitively to constrain the possible outcomes for split codes yet to be ing arithmetic coding with uniform outcome probabilities,these constraints reduce the code string length in Figure 6from 15bits to 102bits.In our models,the constraints reduce the code string from 30bits to 14bits on average.The code string is further reduced using a non-uniform probability model.We create an array T [0dim ][015]of encoding tables,indexed by simplex dimension (0..dim)and by the set of possible (constrained)split codes (a 4-bit mask).For each simplex s ,we encode its split code c using the probability distribution found in T [s dim ][s codes mask ].For 2-dimensional models,only 10of the 48tables are non-trivial,and each table contains at most 4probabilities,so the total size of the probability model is small.These encoding tables reduce the code strings to approximately 8bits as shown in Table 1.By comparison,the PM representation requires approximately 5bits for the same information,but of course it disallows topological changes.To provide more intuition for the efficiency of the PSC repre-sentation,we note that capturing the connectivity of an average 2-manifold simplicial complex (n vertices,3n edges,and 2n trian-gles)requires ni =1(log 2i +8)n (log 2n +7)bits with PSC encoding,versus n (12log 2n +95)bits with a traditional one-way incidence graph representation.For improved compression,it would be best to use a hybrid PM +PSC representation,in which the more concise PM vertex split encoding is used when the local neighborhood is an orientableFigure 6:Constraints on the split codes for the simplices in the example of Figure 5.Table 1:Compression results and construction times.Object#verts Space required (bits/n )Trad.Con.n K V D Arepr.time a i C K i midp i (v )i C D i C Ai bits/n hrs.drumset 34,79412.28.20.928.1 4.10.453.9146.1 4.3destroyer 83,79913.38.30.723.1 2.10.347.8154.114.1chandelier 36,62712.47.60.828.6 3.40.853.6143.6 3.6schooner 119,73413.48.60.727.2 2.5 1.353.7148.722.2sandal 4,6289.28.00.733.4 1.50.052.8123.20.4castle 15,08211.0 1.20.630.70.0-43.5-0.5cessna 6,7959.67.60.632.2 2.50.152.6132.10.5harley 28,84711.97.90.930.5 1.40.453.0135.7 3.52-dimensional manifold (this occurs on average 93%of the time in our examples).To compress C D i ,we predict the material for each new principalsimplex sstar(a i )star(b i )K i +1by constructing an ordered set D s of materials found in star(a i )K i .To improve the coding model,the first materials in D s are those of principal simplices in star(s )K i where s is the ancestor of s ;the remainingmaterials in star(a i )K i are appended to D s .The entry in C D i associated with s is the index of its material in D s ,encoded arithmetically.If the material of s is not present in D s ,it is specified explicitly as a global index in D .We encode C A i by specifying the area a s for each new principalsimplex s 01(star(a i )star(b i ))K i +1.To account for this redistribution of area,we identify the principal simplex from which s receives its area by specifying its index in 01(star(a i ))K i .The column labeled in Table 1sums the bits of each field of the gvspl records.Multiplying by the number n of vertices in M gives the total number of bits for the PSC representation of the model (e.g.500KB for the destroyer).By way of compari-son,the next column shows the number of bits per vertex required in a traditional “IndexedFaceSet”representation,with quantization of 16bits per coordinate and arithmetic coding of face materials (3n 16+2n 3log 2n +materials).4PSC CONSTRUCTIONIn this section,we describe a scheme for iteratively choosing pairs of vertices to unify,in order to construct a PSC representation.Our algorithm,a generalization of [13],is time-intensive,seeking high quality approximations.It should be emphasized that many quality metrics are possible.For instance,the quadric error metric recently introduced by Garland and Heckbert [9]provides a different trade-off of execution speed and visual quality.As in [13,20],we first compute a cost E for each candidate vunify transformation,and enter the candidates into a priority queueordered by ascending cost.Then,in each iteration i =n 11,we perform the vunify at the front of the queue and update the costs of affected candidates.4.1Forming set of candidate vertex pairs In principle,we could enter all possible pairs of vertices from M into the priority queue,but this would be prohibitively expensive since simplification would then require at least O(n2log n)time.Instead, we would like to consider only a smaller set of candidate vertex pairs.Naturally,should include the1-simplices of K.Additional pairs should also be included in to allow distinct connected com-ponents of M to merge and to facilitate topological changes.We considered several schemes for forming these additional pairs,in-cluding binning,octrees,and k-closest neighbor graphs,but opted for the Delaunay triangulation because of its adaptability on models containing components at different scales.We compute the Delaunay triangulation of the vertices of M, represented as a3-dimensional simplicial complex K DT.We define the initial set to contain both the1-simplices of K and the subset of1-simplices of K DT that connect vertices in different connected components of K.During the simplification process,we apply each vertex unification performed on M to as well in order to keep consistent the set of candidate pairs.For models in3,star(a i)has constant size in the average case,and the overall simplification algorithm requires O(n log n) time.(In the worst case,it could require O(n2log n)time.)4.2Selecting vertex unifications fromFor each candidate vertex pair(a b),the associated vunify(a b):M i M i+1is assigned the costE=E dist+E disc+E area+E foldAs in[13],thefirst term is E dist=E dist(M i)E dist(M i+1),where E dist(M)measures the geometric accuracy of the approximate model M.Conceptually,E dist(M)approximates the continuous integralMd2(M)where d(M)is the Euclidean distance of the point to the closest point on M.We discretize this integral by defining E dist(M)as the sum of squared distances to M from a dense set of points X sampled from the original model M.We sample X from the set of principal simplices in K—a strategy that generalizes to arbitrary triangulated models.In[13],E disc(M)measures the geometric accuracy of disconti-nuity curves formed by a set of sharp edges in the mesh.For the PSC representation,we generalize the concept of sharp edges to that of sharp simplices in K—a simplex is sharp either if it is a boundary simplex or if two of its parents are principal simplices with different material identifiers.The energy E disc is defined as the sum of squared distances from a set X disc of points sampled from sharp simplices to the discontinuity components from which they were sampled.Minimization of E disc therefore preserves the geom-etry of material boundaries,normal discontinuities(creases),and triangulation boundaries(including boundary curves of a surface and endpoints of a curve).We have found it useful to introduce a term E area that penalizes surface stretching(a more sophisticated version of the regularizing E spring term of[13]).Let A i+1N be the sum of triangle areas in the neighborhood star(a i)star(b i)K i+1,and A i N the sum of triangle areas in star(a i)K i.The mean squared displacement over the neighborhood N due to the change in area can be approx-imated as disp2=12(A i+1NA iN)2.We let E area=X N disp2,where X N is the number of points X projecting in the neighborhood. To prevent model self-intersections,the last term E fold penalizes surface folding.We compute the rotation of each oriented triangle in the neighborhood due to the vertex unification(as in[10,20]).If any rotation exceeds a threshold angle value,we set E fold to a large constant.Unlike[13],we do not optimize over the vertex position i a, but simply evaluate E for i a i+1a i+1b(i+1a+i+1b)2and choose the best one.This speeds up the optimization,improves model compression,and allows us to introduce non-quadratic energy terms like E area.5RESULTSTable1gives quantitative results for the examples in thefigures and in the video.Simplification times for our prototype are measured on an SGI Indigo2Extreme(150MHz R4400).Although these times may appear prohibitive,PSC construction is an off-line task that only needs to be performed once per model.Figure9highlights some of the benefits of the PSC representa-tion.The pearls in the chandelier model are initially disconnected tetrahedra;these tetrahedra merge and collapse into1-d curves in lower-complexity approximations.Similarly,the numerous polyg-onal ropes in the schooner model are simplified into curves which can be rendered as line segments.The straps of the sandal model initially have some thickness;the top and bottom sides of these straps merge in the simplification.Also note the disappearance of the holes on the sandal straps.The castle example demonstrates that the original model need not be a mesh;here M is a1-dimensional non-manifold obtained by extracting edges from an image.6RELATED WORKThere are numerous schemes for representing and simplifying tri-angulations in computer graphics.A common special case is that of subdivided2-manifolds(meshes).Garland and Heckbert[12] provide a recent survey of mesh simplification techniques.Several methods simplify a given model through a sequence of edge col-lapse transformations[10,13,14,20].With the exception of[20], these methods constrain edge collapses to preserve the topological type of the model(e.g.disallow the collapse of a tetrahedron into a triangle).Our work is closely related to several schemes that generalize the notion of edge collapse to that of vertex unification,whereby separate connected components of the model are allowed to merge and triangles may be collapsed into lower dimensional simplices. Rossignac and Borrel[21]overlay a uniform cubical lattice on the object,and merge together vertices that lie in the same cubes. Schaufler and St¨u rzlinger[22]develop a similar scheme in which vertices are merged using a hierarchical clustering algorithm.Lue-bke[18]introduces a scheme for locally adapting the complexity of a scene at runtime using a clustering octree.In these schemes, the approximating models correspond to simplicial complexes that would result from a set of vunify transformations(Section3.3).Our approach differs in that we order the vunify in a carefully optimized sequence.More importantly,we define not only a simplification process,but also a new representation for the model using an en-coding of gvspl=vunify1transformations.Recent,independent work by Schmalstieg and Schaufler[23]de-velops a similar strategy of encoding a model using a sequence of vertex split transformations.Their scheme differs in that it tracks only triangles,and therefore requires regular,2-dimensional trian-gulations.Hence,it does not allow lower-dimensional simplices in the model approximations,and does not generalize to higher dimensions.Some simplification schemes make use of an intermediate vol-umetric representation to allow topological changes to the model. He et al.[11]convert a mesh into a binary inside/outside function discretized on a three-dimensional grid,low-passfilter this function,。
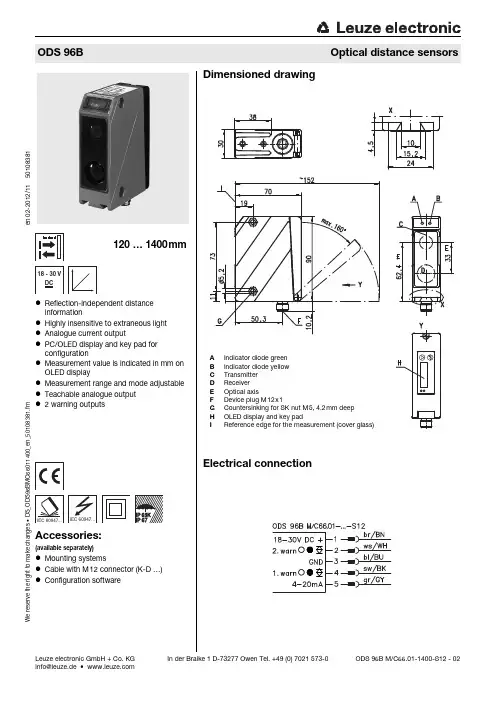
Leuze electronic GmbH + Co. KG In der Braike 1 D-73277 Owen Tel. +49 (0) 7021 573-0*************•W e r e s e r v e t h e r i g h t t o m a k e c h a n g e s • D S _O D S 96B M C 66011400_e n _50108381.f m●Reflection-independent distance information●Highly insensitive to extraneous light ●Analogue current output●PC/OLED display and key pad for configuration●Measurement value is indicated in mm on OLED display●Measurement range and mode adjustable ●Teachable analogue output ●2 warning outputs120…1400mm18 - 30 VDCAccessories:(available separately)●Mounting systems●Cable with M12 connector (K-D …)●Configuration softwareDimensioned drawingA Indicator diode greenB Indicator diode yellowC TransmitterD ReceiverE Optical axisF Device plug M12x1G Countersinking for SK nut M5, 4.2mm deep H OLED display and key padI Reference edge for the measurement (cover glass)Electrical connectionODS 96BOptical distance sensorsODS 96B M/C66.01-1400-S12 - 02e n 02-2012/1150108381ODS 96B M/C66.01-1400-S12 - 022012/11SpecificationsOptical dataMeasurement range 1)1)Luminosity coefficient 6%…90%, complete measurement range, at 20°C, medium range of U B , measurement object ≥50x50mm²120…1400mm Resolution 2)2)Minimum and maximum value depend on measurement distance0.1…0.5mm Light source LEDWavelength 880nm (infrared light)Light spotapprox. 15 x 15mm 2 at 600mmError limits (relative to measurement distance)Absolute measurement accuracy 1)±1.5% up to 800mm, ±2% up to 1400mm Repeatability 3)3)Same object, identical environmental conditions, measurement object ≥50x50mm²±0.5% up to 800mm, ±1% up to 1400mm b/w detect. thresholds (6…90% rem.)≤1% up to 800mm, ≤2% up to 1400mm Temperature compensationyes 4)4)Typ. ± 0.02 %/KTimingMeasurement time 1…51)ms Response time 1)≤15ms Delay before start-up≤300msElectrical dataOperating voltage U B 18…30VDC (incl. residual ripple)Residual ripple≤15% of U B Open-circuit current ≤150mASwitching output 2 push-pull warning outputs 5),PNP light switching, NPN dark switching, respectively 5)The push-pull switching outputs must not be connected in parallelSignal voltage high/low ≥(U B -2V)/≤2VAnalogue outputcurrent 4…20mA, R L ≤500ΩIndicatorsteach-in on GNDteach-in on +U BGreen LED continuous lightready flashing fault teaching procedure offno voltageYellow LED continuous lightobject inside teach-in measurement distanceflashing teaching procedureoffobject outside teach-in measurement distanceMechanical dataMetal housingHousing diecast zinc Optics cover glassWeight 380g Connection type M12 connector Environmental dataAmbient temp. (operation/storage)-20°C …+50°C / -30°C …+70°C Protective circuit 6)6)1=transient protection, 2=polarity reversal protection, 3=short circuit protection for all outputs 1,2,3VDE safety class 7)7)Rating voltage 250VAC, with cover closedII, all-insulated Protection class IP 67, IP 69K 8)8)IP 69K test acc. to DIN 40050 part 9 simulated, high pressure cleaning conditions without the use of additives.Acids and bases are not part of the test.LED class1 (acc. to EN 60825-1)Standards appliedIEC 60947-5-2A Area not definedB Linearity not definedC Measurement rangeD Object presentE No object detected FMeasurement distanceOrder guideDesignationPart No.With M12 connector Current outputODS 96B M/C66.01-1400-S1250106727TablesDiagramsODS 96BRemarks●Measurement timedepends on the reflectivity of the measurement object and on the mea-surement mode.●Coding of the warning outputs:●Approved purpose : The ODS 96B distance sensors are optical elec-tronic sensors for the opti-cal, contactless measure-ment of distance to objects.Warning outputMeaning1200Distance measurement is impossible01Object below measure-ment range (short range)10Object beyond the mea-surement range (distant range)11Optimum function。

散粒噪声用于研究超导体性质的实例综述1北京大学物理学院本科毕业论文作者崔治权指导老师危健散粒噪声用于研究超导体性质的实例综述【摘要】 : 散粒噪声是一类重要的噪声信号 , 主要由载流子的离散性造成 ,在载流子通过隧道结时表现得最为明显, 人们可以通过对它的分析获得关于介观系统某些性质的信息, 这些信息往往又是从电导等物理量的平均值测量中不易获得的。
本文将主要介绍近年来在常规以及高温超导体中 , 利用散粒噪声信号研究其性质的典型实例 , 以期对于散粒噪声的特性及其用于研究凝聚态特别是超导体性质的思路和手段进行全面准确的把握 , 从而为实验室下一步研究高温超导体 YBCO 隧道结中散粒噪声信号提供一定的帮助。
【关键词】 :散粒噪声,常规超导体, 高温超导体, 隧道结 ,电输运性质 2北京大学物理学院本科毕业论文作者崔治权指导老师危健目录一、引言 (4)二、散粒噪声的性质及表征..…………………………………………… 51.噪声信号的一般数学描述..................................................................... 52. 热噪声简介 (7)3. 闪烁噪声简介 (7)4. 散粒噪声的产生机制及数学描述 (8)4.1 单电子隧穿一维势垒.................................................................................9 4.2 单电子随机入射一维势垒 (9)4.3 多电子随机入射 (9)三、应用散粒噪声信号研究半导体性质的几个范例........................ 101. 分数量子霍尔效应 (10)2.SNT (shot noise thermometer )标准低温温度计.................................... 133. 量子混沌微腔中的电子散射...............................................................144.小结 (16)四、利用隧道结中散粒噪声研究常规超导体特性的实例............... 171. 超导简介 (17)2. 超导隧道结中电流散粒噪声应用的两个实例....................................17 2.1 无序金属- 超导体隧道结中散粒噪声的特性 (18)2.2 SNS 隧道结中 MARMultiple Andreev Reflection 效应引起的散粒噪声激增 (21)3. 常规超导体中其他未及说明的实例................................................234.小结 (23)五、利用隧道结中散粒噪声研究高温超导体特性的实例……… 241. 高温超导简介…………………………………………………………………… 242. 高温超导隧道结中的散粒噪声………………………………………………… 25 2.1 d- 波超导体 SN 结中散粒噪声与 s- 波超导体中散粒噪声的区别………………………… 25 2.2 YBCO 双晶结中散粒噪声的研究..................................................................283.小结 (29)六、总结与讨论………………………………………………………… 29 3北京大学物理学院本科毕业论文作者崔治权指导老师危健七、参考文献 (30)八、致谢 (31)九、原创性和使用授权说明……………………………………………… 32 4北京大学物理学院本科毕业论文作者崔治权指导老师危健【正文】 :一、引言半导体器件中的噪声信号, 实际上就是指半导体中所通电流或两端测得的电压不会一直保持一个不变的值, 而是会随时间围绕着平均值发生一定的上下波动,这种波动有时甚至会比较剧烈。

APPLIED PHYSICS REVIEWS–FOCUSED REVIEWPlasmonics:Localization and guiding of electromagnetic energy in metal/dielectric structuresStefan A.Maier a ͒and Harry A.AtwaterThomas J.Watson Laboratories of Applied Physics,California Institute of Technology,Pasadena,California 91125͑Received 17September 2004;accepted 23March 2005;published online 11July 2005͒We review the basic physics of surface-plasmon excitations occurring at metal/dielectric interfaces with special emphasis on the possibility of using such excitations for the localization of electromagnetic energy in one,two,and three dimensions,in a context of applications in sensing and waveguiding for functional photonic devices.Localized plasmon resonances occurring in metallic nanoparticles are discussed both for single particles and particle ensembles,focusing on the generation of confined light fields enabling enhancement of Raman-scattering and nonlinear processes.We then survey the basic properties of interface plasmons propagating along flat boundaries of thin metallic films,with applications for waveguiding along patterned films,stripes,and nanowires.Interactions between plasmonic structures and optically active media are also discussed.©2005American Institute of Physics .͓DOI:10.1063/1.1951057͔TABLE OF CONTENTSI.INTRODUCTION............................1II.LOCALIZED PLASMON RESONANCES IN METAL NANOPARTICLES...................2A.Optical properties of single metalnanoparticles (2)B.Interacting particle ensembles as a basis for applications of metal nanoparticles inoptical devices (4)C.Local field enhancement around metal nanoparticle structures for sensing andnonlinear applications ....................5III.INTERFACE PLASMON POLARITONS ATMETAL/DIELECTRIC BOUNDARIES.........6A.Surface-plasmon polaritons at metalinterfaces ..............................6B.Metal stripes and nanowires:Two-dimensional confinement .............8C.Apertures in a metallic screen .............8D.Interactions with optically active media .....9IV .OUTLOOK.. (9)I.INTRODUCTIONThe electromagnetic properties of metal/dielectric inter-faces have attracted a vast amount of research effort ever since the work of Mie 1and Ritchie 2for small particles and flat interfaces,respectively.The ability of such structures tosustain coherent electron oscillations known as surface-plasmon polaritons ͑SPPs ͒leading to electromagnetic fields confined to the metallic surface has been intensively investigated 3,4both in light of the fundamental physics in-volved and for applications such as surface-enhanced spec-troscopy and enhancement of nonlinear light generation.Af-ter initial studies of the physics of these excitations,in the 1980s SPPs started to attract the attention of chemists,as the electric-field enhancement around metal nanostructures was found to be crucial for surface-enhanced Raman spectros-copy.More recently,the development of nanofabrication tech-niques such as electron-beam lithography,ion-beam milling,and self-assembly,together with modern nanocharacteriza-tion techniques such as dark-field and near-field optical mi-croscopies and the emergence of quantitative electromag-netic simulation tools,has lead to a resurgence of interest in this field,5partly due to potential applications for creating subwavelength optical devices enabling the miniaturization of optical components to size dimensions of their electronic counterparts,i.e,to the sub-100-nm-size regime.The unify-ing physical processes enabling light localization and guid-ing in such structures are the above-mentioned SPP excita-tions,and the name “plasmonics”for the subfield of modern optics studying such processes has been proposed.6Due to the vast amount of research in this exploding field,5we naturally had to select a rather small amount of topics for this review,leading to the omission of important applications of SPPs,for example,their use in integrated biological sensors based on multilayer structures,7investiga-tions from a more chemical viewpoint,8as well as an in-depth treatment of fabrication techniques.9Here,we limit ourselves to a discussion of the fundamental physics ofa ͒Present address:Department of Physics,University of Bath,Bath BA27AY ,U.K.;electronic mail:s.maier@JOURNAL OF APPLIED PHYSICS 98,011101͑2005͒0021-8979/2005/98͑1͒/011101/10/$22.50©2005American Institute of Physics98,011101-1surface-plasmon excitations both for localized plasmons in metallic nanoparticles and for interface plasmons at metall-odielectric film boundaries.A special focus has been put on the localization and guiding properties for electromagnetic radiation in light of applications of plasmon excitations for surface-enhanced spectroscopy such as sensing and higher harmonic generation and for the creation of a planar wave-guide technology that can beat the diffraction limit.II.LOCALIZED PLASMON RESONANCES IN METAL NANOPARTICLESA.Optical properties of single metal nanoparticlesThe strong interaction of microscopic metal particles of dimensions below 1m with visible light has been em-ployed for beautiful applications long before Gustav Mie’s seminal 1908paper Beiträge zur Optik trüber Medien,spez-iell kolloidaler Metallösungen ͑contributions to the optics of turbid media,particularly solution of colloidal metals ͒.1His-torically,one prominent use of metal nanoparticles has been the staining of glass windows and ceramic pottery as seen in Fig.1͑a ͒by example of the Lycurgus cup ͑Byzantine empire,4th century A.D.͒.The glass cup,on display in the British Museum,shows a striking red color when viewed in trans-mitted light,while appearing green in reflection.This pecu-liar behavior is due to small Au nanoparticles embedded in the glass ͓Fig.1͑b ͔͒,which show a strong optical absorption of light in the green part of the visible spectrum ͓Fig.1͑c ͔͒.Indeed,the optical properties of metal nanoparticles,es-pecially those of the noble metals Au,Ag,and Cu,show striking differences relative to their bulk or thin-film optical responses.As an example,Fig.1͑c ͒shows the calculated absorption of a thin Au film ͑blue dots ͒,as well as that of 30-nm Au spheres immersed in water ͑red dots ͒,where the dispersion properties of Au have been modeled using mea-sured dielectric data for bulk Au.10For the nanoparticles,the optical-absorption spectrum has been obtained by directlysolving Maxwell’s equations for the scattering of electro-magnetic waves by spherical objects as carried out by Mie,1and retaining only the dipolar term,which is suitable for nanoparticles with a diameter d Ӷ,where is the wave-length of light in the surrounding medium.As shown,this quasistatic approximation is in good agreement with mea-surements ͑black dots ͒,which has been confirmed via a plethora of studies of the optical response of metallic nano-particles with a diameter well below in solid,liquid,and gaseous environments.4Figure 1͑c ͒further demonstrates a striking difference between the optical response of the thin film and the nanoparticles.Whereas the film absorbs light throughout the near-infrared and visible regions due to free-electron absorption,for the nanoparticles this process is strongly quenched for energies lower than 2eV ͑correspond-ing to wavelengths larger than 620nm ͒.Indeed,all the free-electron oscillator strength for absorption is pulled into a dipolar absorption peak around 2.25eV,the dipolar surface-plasmon particle resonance.This modified optical response leads to the bright colors of noble-metal nanoparticles,a nice discussion of which can be found in Ref.11.For higher energies above the dipole resonance,the optical absorption of particles and films is similar,due to the dominance of d –sp electronic interband transitions,which are prominent for Au and Cu in the vicinity of the dipole plasmon reso-nance,but less so for Ag.The resonant electromagnetic behavior of noble-metal nanoparticles is due to the confinement of the conduction electrons to the small particle volume.For particles with a diameter d Ӷ,the conduction electrons inside the particle move all in phase upon plane-wave excitation with radiation of wavelength ,leading to the buildup of polarization charges on the particle surface.These charges act as an ef-fective restoring force,allowing for a resonance to occur at a specific frequency—the particle dipole plasmon frequency-,where the response of the electrons shows a /2phase lag with respect to the driving field.Thus,a resonantly enhanced field builds up inside the particle,which in the small particle limit is homogeneous throughout its volume,producing a dipolar field outside the particle.This leads to enhanced ab-sorption and scattering cross sections for electromagnetic waves,as well as to a strongly enhanced near field in the immediate vicinity of the particle surface.It is this reso-nantly enhanced near field from which most of the promising applications of metal nanoparticles stem.For larger particles,the spectral response is modified due to retardation effects and the excitation of higher-order ͑quadrupole and higher ͒modes,the spectral signature of which can be calculated by retaining higher orders of the Mie theory scattering coefficients.1In general,the spectral position,damping,and strength of the dipole as well as of the higher-order plasmon reso-nances of single metal nanoparticles depend on the particle material,size,geometry,and the dielectric function of the surrounding host.4For theoretical considerations,the large variety of naturally occurring or synthesized shapes of nano-particles is often approximated via spheres or spheroids,for which analytically exact solvable solutions exist to all orders.1,4,12,13The analysis is further facilitated forparticlesFIG.1.͑Color online ͒͑a ͒The Lycurgus glass cup,demonstrating the bright red color of gold nanocrystals in transmitted light.͑b ͒scanning electron microscopy ͑SEM ͒image of a typical nanocrystal embedded in the glass ͑courtesy of the British museum ͒.͑c ͒Calculated absorption spectrum of a thin gold film ͑blue dots ͒and of 30-nm Au nanoparticles in water ͑red dots ͒using classical electromagnetic theory.A measured absorption spectrum of an aqueous solution of 30-nm Au colloids ͑black dots ͒shows good agree-ment with the theory.much smaller than the wavelength of light,where only the lowest ͑dipolar ͒order of the modal expansion of the scat-tered fields has to be retained.In this case,a quasistatic ap-proach serves well to describe the spectral position,width,and strength of the dipolar plasmon resonance,as pointed out in the discussion of Fig.1.For a spherical metal nanoparticle of radius a Ӷembedded in a nonabsorbing surrounding me-dium of dielectric constant m ,the quasistatic analysis gives the following expression for the particle polarizability ␣:␣=4a 3−m+2m,͑1͒with the complex =͑͒describing the dispersive dielectric response of the metal.The polarizability and thus the in-duced homogeneous polarization inside the particle are reso-nantly enhanced at the Fröhlich frequency where the de-nominator shows a minimum,limited by the imaginary part of describing Ohmic heating losses within the particle.These losses are due to the creation of electron-hole pairs,the energy of which is subsequently coupled to the phonon bath.14The spectral position of this resonance is seen to red-shift with increasing dielectric constant of the surrounding host due to the buildup of polarization charges on the dielec-tric side of the interface,thus weakening the total restoring force.For ellipsoidal particles with principal axes a ,b ,and c ,an analogous expression can be found in the quasistatic ap-proximation via introducing geometrical depolarization fac-tors L i along these axes,4,12leading to␣=43abc−m m +L i ͑−m ͒,͚L i =1.͑2͒For spherical particles,L 1=L 2=L 3=1/3.For spheroidal par-ticles ͑L 1=L 2͒,the plasmon resonance thus splits into astrongly redshifted long-axis mode ͑polarization parallel to the long axis ͒and a slightly blueshifted short axis mode ͑polarization perpendicular to the long axis ͒.12For larger particles beyond the Rayleigh approximation,the dipolar resonance redshifts while at the same time suffer-ing substantial broadening.The redshift is due to a reduction of the depolarization field due to retardation effects 15—the conduction electrons do not all move in phase anymore,leading to a reduced depolarization field at the particle centergenerated by the surrounding polarized matter.Additionally,radiative losses 16begin to significantly contribute to the plas-mon damping,dominating the total damping of Au and Ag nanoparticles for particle sizes in excess of 100nm.The de-polarization field and radiation damping effect can be seen as lowest-order corrections to the quasistatic theory,leading to additional real and imaginary parts of the denominator of the polarizability.A generalization of the quasistatic approach to particles of arbitrary shape has been suggested,with surpris-ingly good results 17͓see Fig.2͑a ͔͒.For particles with a di-ameter smaller than the free-electron scattering length,scat-tering processes at the particle surface are thought to begin to contribute to the total damping.4These additional damping mechanisms for large and small particles lead to respective decreases in the total enhancement of the exciting field via a decrease of the plasmon dephasing time T 2.4Generally,numerical methods such as the T -matrix method,18the discrete dipole approximation 19͓Fig.2͑b ͔͒,or finite-difference time-domain simulations 20have to be used to calculate the resonance frequencies and mode profiles of more complex shapes.Such simulations have especially been employed to determine the local-field enhancement at the particle surface,in conjunction with discussions of enhance-ments of nonlinear processes and surface-enhanced Raman scattering ͑SERS ͒as discussed below.Experimentally,sophisticated modern fabrication meth-ods allow for the fabrication of metal nanoparticles and other nanostructures of a variety of shapes using both colloidal synthesis methods 21and top-down nanofabrication tech-niques such as electron-beam lithography,22and a wide vari-ety of methods for the fabrication of metallic nanoparticles and ensembles thereof have recently been described in a dif-ferent review article.9The good control over the size and shape of the particles provided by these methods method allows one generally to observe homogeneously broadened line shapes of dipolar 23and multipolar 24plasmon modes in particle ensembles using conventional far-field spectroscopy.The direct examination of single particles has been demon-strated using both dark-field 25and near-field optical microscopies.26The former method allows for a dramatic visualization of the spectral properties of single particles,as can be seen by the example in Fig.2͑a ͒.FIG.2.͑Color online ͒͑a ͒Dark-field microcopy image ͑top ͒and light-scattering spectra ͑bottom ͒of Au nanocrystals of different shapes ͑adapted from Ref.17͒.The measured spectra ͑black curves ͒show good agreement with predictions from a simple analytical extension of quasi-static Mie theory ͑open circles ͒.͑b ͒Electric near-field profile of the lowest-order modes of Ag nanoprisms calculated using the discrete dipole ap-proximation formalism ͑adapted from Ref.54͒.B.Interacting particle ensembles as a basis forapplications of metal nanoparticles in optical devicesAdvances in particle synthesis and fabrication tech-niques ͑for example,Refs.22,27,and 28͒have recently allowed for studies of ordered arrays of noble-metal nano-particles.In such arrays,each nanoparticle with a diameter much smaller than the wavelength of the exciting light acts as an electric dipole.Thus,two types of electromagnetic in-teractions between the particles can be distinguished,de-pending on the spacing d between adjacent nanoparticles.For particle spacings on the order of the exciting wavelength ,far-field dipolar interactions with a d −1dependence domi-nate.Work on regular two-dimensional arrays of Au nano-particles has indeed confirmed the existence of such interac-tions,and quantified their influence on both the spectral position of the collective dipolar extinction peak and the plasmon damping characteristics.29Figures 3͑a ͒and 3͑b ͒show an example of the dependence of both extinction peak and plasmon decay time on the grating constant d for a regu-lar square array of 150-nm-diameter Au nanoparticles.Both the variation of the spectral position and width of the reso-nances can be explained by assuming far-field dipolar interactions—the ensemble acts effectively as a grating,lead-ing to increased radiation damping of the collective reso-nances for grating constants where grating orders change from evanescent to radiative in character.29Applications of such ordered arrays lie,for example,in the possibility of maximizing surface-enhanced Raman scattering of adsorbed molecules by careful spectral tuning of the plasmon resonance.30For particle spacings much smaller than the wavelength of light,near-field dipolar interactions between adjacent par-ticles with a distance dependence of d −3dominate.23,31These strongly distance-dependent interactions lead to a splitting of the plasmon dipolar peak for regular one-dimensional arrays of metal nanoparticles as seen in Fig.3͑c ͒for ordered arrays of 50-nm Au particles.The spectral position of the extinction peak for far-field excitation shows a blueshift for polarization perpendicular to the chain axis ͑T ͒,and a redshift for longi-tudinal polarization ͑L ͒,which can easily be understood by analyzing Coulombic force interactions between the elec-trons in neighboring particles.The near-field interactions be-tween such particles have been directly visualized using near-field optical microscopy,32confirming a strongly en-hanced field between the particles ͓Fig.3͑d ͔͒,indicative of near-field coupling.One application of near-field coupling between particles in ordered arrays is the use of such structures as waveguides for electromagnetic energies at optical frequencies with a lateral mode profile below the diffraction limit of light.6,33Indeed,it has been shown both theoretically 34and experimentally 35that such arrays can guide electromagnetic energy over distances of several hundred nanometers via near-field particle interactions.Such structures could poten-tially be used in nanoscale all-optical networks,contributing to a class of functional optical devices below the diffraction limit of light.5,6,36Localized plasmon excitations mediated by particle in-teractions also occur in randomly nanostructured metallic surfaces.37In this case,multiple-scattering processes can lead to “hot spots”of extremely large field enhancement ͑on the order of 1000͒,which has enabled the use of such struc-tures for single-molecule spectroscopy.38FIG.3.͑Color online ͒͑a,b ͒Measured extinction spectrum ͑a ͒and plasmon decay time ͑b ͒for regular two-dimensional ͑2D ͒square arrays of Au nanoparticles ͑adapted from Ref.29,copyright by the American Physical Society ͒.Both the spectral position and the decay time of the collective dipolar plasmon mode show a marked variation with grating constant due to far-field dipolar interactions.͑c ͒Mea-sured spectral position of the collec-tive plasmon resonances of one-dimensional arrays of closely spaced Au nanoparticles for longitudinal ͑L ͒and transverse polarizations ͑T ͒.Also shown are results of a simple near-field point-dipolar coupling model ͑solid lines ͒and finite-difference time-domain simulations ͑stars ͒.͑d ͒Optical near-field around such a chain ob-tained using collection mode near-field optical microscopy ͑left ͒and numeri-cal simulations ͑right ͒,adapted from Ref.32.C.Localfield enhancement around metal nanoparticle structures for sensing and nonlinear applications The enhanced nearfields around metallic nanostructures induced by illumination at visible and near-infrared frequen-cies allow for a variety of intriguing applications apart from energy guiding in ordered particle arrays discussed above. Since the enhancedfields are localized to the surface of the nanostructures,they serve as a local probe of the dielectric environment within a few nanometers of the particle surface. This fact has,for example,been employed in studying varia-tions of the local refractive index in light of biological ͑mass͒sensing applications.39–41Also,the local response of metallic nanostructures can serve so as to enhance the in-coming and generatedfields for nonlinear processes and de-cay rate enhancements of emissive species.For nonlinear applications and surface-enhanced Raman sensing,the local-field E Local close to the metal surface should be maximized so as to maximize the respective higher-order processes,neglecting the possibility of absorption-induced damage of the optically active medium. The local-field enhancement factor L=E Local/E0,with E0be-ing the amplitude of the incomingfield,can for a single nanoparticle be written as the product of two factors L =L SP͑͒L LR,highlighting two possible enhancement processes—the surface-plasmon resonance of the whole par-ticle͑L SP͒and the lightning rod effect͑L LR͒.For larger par-ticles,surface roughness and crevices can lead to additional localized resonances forming hot spots on the particle sur-face.For a perfectly spherical particle in the Rayleigh limit, only the dipole surface-plasmon resonance contributes to the enhancement process,with L SPϰQϰT2in the absorption-dominated regime,where T2and Q are the dephasing time, limited by the decay of the particle plasmon into electron-hole pairs and photons and by phase-destroying elastic scat-tering processes,and the quality factor of the resonance,re-spectively.The origins of plasmon decay and dephasing have been extensively discussed in the literature,14,42and T2has been determined both using time-resolved pump-probe measurements43–46and higher harmonic generation.47For small Au nanospheres in air and low-index matrixes,plas-mon excitation competes with interband transitions,leading to low Q factorsϳ10,while radiation damping dominates for larger spheres with diameters of about100nm.16Higher Q factorsϳ20have been reported for spheroidal Au par-ticles,due to a redshift of the long-axis dipolar resonance away from the interband transition edge.42For Ag nanopar-ticles,the respectivefield enhancements at visible frequen-cies are higher,partly due to a larger spectral separation of the plasmon resonance from the interband transition edge. Another promising route to larger quality factors are metallic nanoshells,where Q factors up to150have been estimated for Ag.48For nonspherical shapes,the geometric and only weakly frequency-dependent lightning rod effect L LR of the electric field at sharp surface protrusions,leading to an increased surface charge and thus a crowding of the electric-field lines, serves as an additional enhancement process.49–51This way,highly localizedfields can be generated at the tips of elon-gated spheroids or rough surfaces.For very rough or veryhigh-aspect ratio particles,additionally local-plasmon reso-nances at specific parts on the particle surface can be excited,leading to an additional enhancement.For the case of sphe-roids with aspect ratiosϾ10:1,the overall particle resonancecan be interpreted as an antenna effect,where thefield isfurther enhanced at the tip due to lightning rod and localplasmon resonances.13,52Fully analytical53and a variety ofnumerical models54have been used to quantify thefield en-hancement at sharp points on a variety of single-metal par-ticles,predicting highest-field enhancement factors of about100for Ag particles.The heightened opticalfields near metal nanostructuresmanifest themselves in the enhancement of higher harmonicgeneration and local spectroscopy.For example,the total en-hancement of second-harmonic generation on a rough silversurface is expected to scale as L͑͒4L͑2͒2upon resonance, whereas for Raman spectroscopy the enhancement scales asL͑exc͒2L͑RS͒2.Note that due to the small Stokes shift in Raman scattering,usually thefields at both the excitationfrequency and the Stokes frequency are enhanced.Forsecond-harmonic generation on the other hand,usually onlyone of the two processes shows enhancement due to the largespectral separation between the two lines.Also,due to thesignificant absolute value of͉͉͑͒at visible frequencies,the field inside the particle͑where second harmonic generation from the particle itself occurs͒is smaller than thefield out-side͑where SERS occurs͒.Thus,the observed SERS en-hancements are usually significantly larger than those of second-and higher harmonic processes.Note that for calcu-lations offield enhancement with metallic nanoparticles,the enhancement is usually evaluated for the peak power at a specific Stokes or higher harmonic output frequency,i.e.,not integrated over the total resonance line shape.Experimentally,the enhancement of second-harmonicgeneration at rough metal surfaces has been observed usingboth far-field55–58and near-field59,60spectroscopic tech-niques,with measured enhancements of second-harmonicgeneration on Au and Ag islandfilms up to1000.58While themagnitude of the reported enhancement varies considerably,recently direct observations of localized second-harmonicenhancements of order1000have been reported on Au sur-faces coated with random scatterers using laser scanningmicroscopy.61,62The highest enhancement of an optical process on arough metal surface so far reported is that of Raman Stokesscattering͑surface-enhanced Raman scattering͒,where emis-sion from single molecules63,64with an enhancement factorof the Raman cross section up to1014has been observed,although the interpretation of these experiments is somewhatcontroversial.At this point,it is believed that this huge in-crease in the cross section is due to both local-field enhance-ments up to a factor of1000on roughened Ag surfaces,leading to a Raman enhancement of1012,and to chemicaleffects due to adsorbate binding at the metal surface,65mak-ing up for the additional factor of100in the total enhance-ment.Sincefield enhancements of a factor of1000canhardly be achieved for single particles,with the possible ex-ception of gap modes in surface crevices,it is believed that field localization in small gaps between metal particles due to geometric effects and multiple photon scattering on rough surfaces contributes to this high-field enhancement in nanometer-sized volumes,so-called hot spots,53,54,62and re-cently a detailed analytical description of the enhancement using a simple resonator model has been given.66These lo-calized resonances tend to show very different strengths,po-larization,and localization characteristics.The importance of multiple scattering for the creation of hot spots for field en-hancement has been highlighted via many studies showing the significance of fractal-like character of the silver surface.37,67III.INTERFACE PLASMON POLARITONS AT METAL/DIELECTRIC BOUNDARIESA.Surface-plasmon polaritons at metal interfacesCoherent electron oscillations leading to enhanced local fields at the surface of metallic structures cannot only be excited in metallic nanoparticles,but also at flat interfaces such as metallic films.As is well known,the interface be-tween a metallic film and a dielectric can sustain SPPs in the form of coherent longitudinal charge oscillations of the con-duction electrons,thus leading to a surface wave confined within one dimension perpendicular to the surface.3At flat interfaces,these charge oscillations were observed in energy loss spectra obtained via bombardment of the film with fast electrons,revealing “low-lying plasma losses”at energies lower than the characteristic bulk-plasmon energy p of the respective metal.2,68At a metal/air boundary,these low-lying plasma losses for electrons occur at a frequency p /ͱ2.This lowering of the plasmon resonance is due to the depolarizing effect of the flat surface,analogous to the case of localizedplasmons in metallic nanoparticles.However,while for exci-tation with fast electrons plasma waves at flat interfaces do not propagate ͑group-velocity g =0͒,SPPs at lower energies exhibit a significant dispersion with wave vector k due to retardation effects.Figure 4͑a ͒shows the dispersion relation for surface-plasmon polaritons propagating at a flat interface between Ag and air,glass,and silicon,respectively,calcu-lated using a simple boundary condition analysis for electro-magnetic surface waves,3yieldingk x =c ͫ͑͒2͑͒+2ͪ,͑3͒where ͑͒are the ͑complex ͒dielectric function of the metal and 2the dielectric constant of the adjacent dielectric half-space.As can be seen,the dispersion relations of the SPPs al-ways lie to the right of the respective light line,approaching sp =p /ͱ1+2for large wave vectors,the magnitude of the wave vector at sp being limited by dissipation.While ex-periments with fast electrons mainly probe this high wave-vector regime where dispersion is absent,3for lower wave vectors surface-plasmon polaritons can be excited by TM-polarized light,providing that the retardation-induced mo-mentum mismatch is compensated.The main techniques for achieving this momentum matching are prism coupling,cou-pling via surface grating or roughness ͑defects ͒,and using highly focused optical excitation.3Recently,excitation of surface plasmons using regular hole arrays created via shad-owed metal evaporation has been achieved.69This work has provided a beautiful demonstration of the transition between localized surface plasmons of nontouching particles to dis-persive surface-plasmon polaritons propagating along the hole film ͓Figs.4͑b ͒–4͑d ͔͒.FIG.4.͑a ͒Calculated dispersion of surface plasmon-polaritons propagating at a Ag/air,Ag/glass,and Ag/Si interface,respectively.͑b ͒–͑d ͒Measured transmittance as a function of in-plane wave vector and frequency for p -polarized light incident upon an array of nontouching nanoparticles ͑b ͒,an intermediate array of bigger particles with some coalescence ͑c ͒,and a periodic array of holes formed by touching nanoparticles ͑d ͒,showing the transition from localized to dispersive behavior ͑adapted from Ref.69͒.。


MPI Probe Selection GuideWith a critical understanding of the numerous measurement challenges associated with today’s RF ap-plications, MPI Corporation has developed TITAN™ RF Probes, a product series specifically optimized for these complex applications centered upon the requirements of advanced RF customers.TITAN™ Probes provide the latest in technology and manufacturing advancements within the field of RF testing. They are derived from the technology transfer that accompanied the acquisition of Allstron, then significantly enhanced by MPI’s highly experienced RF testing team and subsequently produced utilizing MPI’s world class MEMS technology. Precisely manufactured, the TITAN™ Probes include matched 50 Ohm MEMS contact tips with improved probe electrical characteristics which allow the realization of unmat -ched calibration results over a wide frequency range. The patented protrusion tip design enables small passivation window bond pad probing, while significantly reducing probe skate thus providing the out -standing contact repeatability required in today’s extreme measurement environments. TITAN TM Probes with all their features are accompanied by a truly affordable price.The TITAN™ Probe series are available in single-ended and dual tip configurations, with pitch range from 50 micron to 1250 micron and frequencies from 26 GHz to 110 GHz. TITAN™ RF Probes are the ideal choice for on-wafer S-parameter measurements of RF, mm-wave devices and circuits up to 110 GHz as well as for the characterization of RF power devices requiring up to 10 Watts of continuous power. Finally, customers can benefit from both long product life and unbeatable cost of ownership which they have desired foryears.Unique design of the MEMS coplanar contacttip of the TITAN™ probe series.DC-needle-alike visibility of the contact point and the minimal paddamage due to the unique design of the tipAC2-2 Thru S11 Repeatability. Semi-Automated System.-100-80-60-40-200 S 11 E r r o r M a g n i t u d e (d B )Frequency (GHz)Another advantage of the TITAN™ probe is its superior contact repeatability, which is comparable with the entire system trace noise when measured on the semi-automated system and on gold contact pads.CROSSTALKCrosstalk of TITAN™ probes on the short and the bare ceramic open standard of 150 micron spacing compared to conventional 110 GHz probe technologies. Results are corrected by the multiline TRL calibration. All probes are of GSG configuration and 100 micron pitch.-80-60-40-200Crosstalk on Open. Multiline TRL Calibration.M a g (S21) (d B )Frequency (GHz)-80-60-40-200Crosstalk on Short. Multiline TRL Calibration.M a g (S21) (d B )Frequency (GHz)The maximal probe c ontac t repeatability error of the c alibrate S11-parameter of the AC2-2 thru standard by T110 probes. Semi-automated system. Ten contact circles.Cantilever needle material Ni alloy Body materialAl alloy Contact pressure @2 mils overtravel 20 g Lifetime, touchdowns> 1,000,000Ground and signal alignment error [1]± 3 µm [1]Planarity error [1] ± 3 µm [1]Contact footprint width < 30 µm Contact resistance on Au < 3 mΩThermal range-60 to 175 °CMechanical CharacteristicsAC2-2 Thru S21 Repeatability. Manual TS50 System.-100-80-60-40-200S 21 E r r o r M a g n i t u d e (d B )Frequency (GHz)MECHANICAL CHARACTERISTICSThe maximal probe c ontac t repeatability error of the c alibrate S21-parameter of the AC2-2 thru standard by T50 probes. Manual probe system TS50.26 GHZ PROBES FOR WIRELESS APPLICATIONSUnderstanding customer needs to reduce the cost of development and product testing for the high competitive wireless application market, MPI offers low-cost yet high-performance RF probes. The specifically developed SMA connector and its outstanding transmission of electro-magnetic waves through the probe design make these probes suitable for applications frequencies up to 26 GHz. The available pitch range is from 50 micron to 1250 micron with GS/SG and GSG probe tip configurations. TITAN™ 26 GHz probes are the ideal choice for measurement needs when developing components for WiFi, Bluetooth, and 3G/4G commercial wireless applications as well as for student education.Characteristic Impedance 50 ΩFrequency rangeDC to 26 GHz Insertion loss (GSG configuration)1< 0.4 dB Return loss (GSG configuration)1> 16 dB DC current ≤ 1 A DC voltage ≤ 100 V RF power, @10 GHz≤ 5 WTypical Electrical Characteristics26 GHz Probe Model: T26Connector SMAPitch range50 µm to 1250 µm Standard pitch step from 50 µm to 450 µm from 500 µm to 1250 µm25 µm step 50 µm stepAvailable for 90 µm pitch Tip configurations GSG, GS, SG Connector angleV-Style: 90-degree A-Style: 45-degreeMechanical CharacteristicsT26 probe, A-Style of the connectorTypical Electrical Characteristics: 26 GHz GSG probe, 250 micron pitchPROBES FOR DEVICE AND IC CHARACTERIZATION UP TO 110 GHZTITAN™ probes realize a unique combination of the micro-coaxial cable based probe technology and MEMS fabricated probe tip. A perfectly matched characteristic impedance of the coplanar probe tips and optimized signal transmission across the entire probe down to the pads of the device under test (DUT) result in excellent probe electrical characteristics. At the same time, the unique design of the probe tip provides minimal probe forward skate on any type of pad metallization material, therefo -re achieving accurate and repeatable measurement up to 110 GHz. TITAN™ probes are suitable for probing on small pads with long probe lifetime and low cost of ownership.The TITAN™ probe family contains dual probes for engineering and design debug of RF and mm-wave IC’s as well as high-end mm-wave range probes for S-parameter characterization up to 110 GHz for modeling of high-performance microwave devices.Characteristic Impedance 50 ΩFrequency rangeDC to 40 GHz Insertion loss (GSG configuration)1< 0.6 dB Return loss (GSG configuration)1> 18 dB DC current ≤ 1 A DC voltage ≤ 100 V RF power, @10 GHz≤ 5 WTypical Electrical Characteristics40 GHz Probe Model: T40Connector K (2.92 mm)Pitch range50 µm to 500 µmStandard pitch step For GSG configuration:from 50 µm to 450 µm from 500 µm to 800 µmFor GS/SG configuration:from 50 µm to 450 µm 25 µm step 50 µm stepAvailable for 90 µm pitch25 µm stepAvailable for 90/500 µm pitch Tip configurations GSG, GS, SG Connector angleV-Style: 90-degree A-Style: 45-degreeMechanical CharacteristicsTypical Electrical Characteristics: 40 GHz GSG probe, 150 micron pitchT40 probe, A-Style of the connectorCharacteristic Impedance50 ΩFrequency range DC to 50 GHz Insertion loss (GSG configuration)1< 0.6 dB Return loss (GSG configuration)1> 17 dBDC current≤ 1 ADC voltage≤ 100 VRF power, @10 GHz≤ 5 W Typical Electrical Characteristics Connector Q (2.4 mm)Pitch range50 µm to 250 µm Standard pitch stepFor GSG configuration: from 50 µm to 450 µm For GS/SG configuration: from 50 µm to 450 µm 25 µm stepAvailable for 90/500/550 µm pitch 25 µm stepAvailable for 90/500 µm pitchTip configurations GSG, GS, SG Connector angle V-Style: 90-degreeA-Style: 45-degreeMechanical CharacteristicsT50 probe, A-Style of the connectorTypical Electrical Characteristics: 50 GHz GSG probe, 150 micron pitchCharacteristic Impedance50 ΩFrequency range DC to 67 GHz Insertion loss (GSG configuration)1< 0.8 dB Return loss (GSG configuration)1> 16 dBDC current≤ 1 ADC voltage≤ 100 VRF power, @10 GHz≤ 5 W Typical Electrical Characteristics Connector V (1.85 mm)Pitch range50 µm to 250 µm Standard pitch stepFor GSG configuration: from 50 µm to 400 µm For GS/SG configuration: from 50 µm to 250 µm 25 µm step Available for 90 µm pitch25 µm step Available for 90 µm pitchTip configurations GSG Connector angle V-Style: 90-degreeA-Style: 45-degreeMechanical CharacteristicsT67 probe, A-Style of the connectorTypical Electrical Characteristics: 67 GHz GSG probe, 100 micron pitchCharacteristic Impedance 50 ΩFrequency rangeDC to 110 GHz Insertion loss (GSG configuration)1< 1.2 dB Return loss (GSG configuration)1> 14 dB DC current ≤ 1 A DC voltage ≤ 100 V RF power, @10 GHz≤ 5 WTypical Electrical CharacteristicsMechanical CharacteristicsTypical Electrical Characteristics: 110 GHz GSG probe, 100 micron pitchT110 probe, A-Style of the connectorCharacteristic impedance50 ΩFrequency range DC to 220 GHz Insertion loss (GSG configuration)1< 5 dB Connector end return loss(GSG configuration)1> 9 dBTip end return loss(GSG configuration)1> 13 dBDC current≤ 1.5 ADC voltage≤ 50 V Typical Electrical CharacteristicsConnector Broadband interface Pitch range50/75/90/100/125 µm Temperature range -40 ~ 150 ºC Contact width15 µmquadrant compatible(allowing corner pads)Yes recommended pad size20 µm x 20 µm recommended OT (overtravel)15 µmcontact resistance(on Al at 20 ºC using 15 µm OT)< 45 mΩlifetime touchdowns(on Al at 20 ºC using 15 µm OT)> 200,000Mechanical CharacteristicsT220 probe, broadband interface Typical Performance (at 20 ºC for 100 µm pitch)BODY DIMENSIONS PROBES Single-Ended V-StyleT220 GHz Probe1.161.1628.328437.455.6512.5527.73Single-Ended A-StyleCALIBRATION SUBSTRATESAC-series of calibration standard substrates offers up to 26 standard sets for wafer-level SOL T, LRM probe-tip cali -bration for GS/SG and GSG probes. Five coplanar lines provide the broadband reference multiline TRL calibration as well as accurate verification of conventional methods. Right-angled reciprocal elements are added to support the SOLR calibration of the system with the right-angled configuration of RF probes. A calibration substrate for wide-pitch probes is also available.Material Alumina Elements designCoplanarSupported calibration methods SOLT, LRM, SOLR, TRL and multiline TRL Thickness 635 µmSizeAC2-2 : 16.5 x 12.5 mm AC3 : 16.5 x 12.5 mm AC5 : 22.5 x 15 mm Effective velocity factor @20 GHz0.45Nominal line characteristic impedance @20 GHz 50 ΩNominal resistance of the load 50 ΩTypical load trimming accuracy error ± 0.3 %Open standardAu pads on substrate Calibration verification elements Yes Ruler scale 0 to 3 mm Ruler step size100 µmCalibration substrate AC2-2Probe Configuration GSGSupported probe pitch100 to 250 µm Number of SOL T standard groups 26Number of verification and calibration lines5Calibration substrate AC-3Probe Configuration GS/SG Supported probe pitch50 to 250 µm Number of SOL T standard groups 26Number of verification and calibration lines5Calibration substrate AC-5Probe Configuration GSG, GS/SG Supported probe pitch250 to 1250 µm Number of SOL T standard groups GSG : 7GS : 7SG : 7Open standardOn bare ceramic Number of verification and calibration linesGSG : 2GS : 1Typical characteristics of the coplanar line standard of AC2-2 calibration substrate measured using T110-GSG100 probes, and methods recommended by the National Institute of Standard and Technologies [2, 3].2468(d B /c m )F requency (G Hz)α-6-4-202I m a g (Z 0) ()F requency (G Hz)AC2-2 W#006 and T110A-GSG100Ω2.202.222.242.262.282.30 (u n i t l e s s )F requency (G Hz)β/βо4045505560R e a l (Z 0) ()F requency (G Hz)ΩTypical Electrical CharacteristicsMPI QAlibria® RF CALIBRATION SOFTWAREMPI QAlibria® RF calibration software has been designed to simplify complex and tedious RF system calibration tasks. By implementing a progressive disclosure methodology and realizing intuitive touch operation, QAlibria® provides crisp and clear guidance to the RF calibration process, minimizing con-figuration mistakes and helping to obtain accurate calibration results in fastest time. In addition, its concept of multiple GUI’s offers full access to all configuration settings and tweaks for advanced users. QAlibria® offers industry standard and advanced calibration methods. Furthermore, QAlibria® is integrated with the NIST StatistiCal™ calibration packages, ensuring easy access to the NIST mul-tiline TRL metrology-level calibration and uncertainty analysis.MPI Qalibria® supports a multi-language GUI, eliminating any evitable operation risks and inconvenience.SpecificationsRF AND MICROWAVE CABLESMPI offers an excellent selection of flexible cables and acces-sories for RF and mm-wave measurement applications forcomplete RF probe system integration.CablesHigh-quality cable assemblies with SMA and 3.5 mm connectorsprovide the best value for money, completing the entry-level RFsystems for measurement applications up to 26 GHz. Phase stab-le high-end flexible cable assemblies with high-precision 2.92, 2.4, 1.85 and 1 mm connectors guarantee high stability, accuracy and repeatability of the calibration and measurement for DC applications up to 110 GHz.MPI offers these cable assemblies in two standard lengths of 120 and 80 cm, matching the probe system’s footprint and the location of the VNA.Cables Ordering InformationMRC-18SMA-MF-80018 GHz SMA flex cable SMA (male) - SMA (female), 80 cmMRC-18SMA-MF-120018 GHz SMA flex cable SMA (male) - SMA (female), 120 cmMRC-26SMA-MF-80026 GHz SMA flex cable SMA (male) - SMA (female), 80 cmMRC-26SMA-MF-120026 GHz SMA flex cable SMA (male) - SMA (female), 120 cmMRC-40K-MF-80040 GHz flex cable 2.92 mm (K) connector, male-female, 80 cm longMRC-40K-MF-120040 GHz flex cable 2.92 mm (K) connector, male-female, 120 cm longMRC-50Q-MF-80050 GHz flex cable 2.4 mm (Q) connector, male-female , 80 cm longMRC-50Q-MF-120050 GHz flex cable 2.4 mm (Q) connector, male-female , 120 cm longMRC-67V-MF-80067 GHz flex cable 1.85 mm (V) connector, male-female, 80 cm longMRC-67V-MF-120067 GHz flex cable 1.85 mm (V) connector, male-female, 120 cm longMMC-40K-MF-80040 GHz precision flex cable 2.92 mm (K) connector, male-female, 80 cm long MMC-40K-MF-120040 GHz precision flex cable 2.92 mm (K) connector, male-female, 120 cm long MMC-50Q-MF-80050 GHz precision flex cable 2.4 mm (Q) connector, male-female , 80 cm long MMC-50Q-MF-120050 GHz precision flex cable 2.4 mm (Q) connector, male-female , 120 cm long MMC-67V-MF-80067 GHz precision flex cable 1.85 mm (V) connector, male-female, 80 cm long MMC-67V-MF-120067 GHz precision flex cable 1.85 mm (V) connector, male-female, 120 cm long MMC-110A-MF-250110 GHz precision flex cable 1 mm (A) connector, male-female, 25 cm longMPI Global PresenceDirect contact:Asia region: ****************************EMEA region: ******************************America region: ********************************MPI global presence: for your local support, please find the right contact here:/ast/support/local-support-worldwide© 2023 Copyright MPI Corporation. All rights reserved.[1] [2][3] REFERENCESParameter may vary depending upon tip configuration and pitch.R. B. Marks and D. F. Williams, "Characteristic impedance determination using propagation constant measu -rement," IEEE Microwave and Guided Wave Letters, vol. 1, pp. 141-143, June 1991.D. F. Williams and R. B. Marks, "Transmission line capacitance measurement," Microwave and Guided WaveLetters, IEEE, vol. 1, pp. 243-245, 1991.AdaptersHigh-In addition, high-quality RF and high-end mm-wave range adapters are offered to address challenges ofregular system reconfiguration and integration with different type of test instrumentation. MRA-NM-350F RF 11 GHz adapter N(male) - 3.5 (male), straight MRA-NM-350M RF 11 GHz adapter N(male) - 3.5 (female), straightMPA-350M-350F Precision 26 GHz adapter 3.5 mm (male) - 3.5 mm (female), straight MPA-350F-350F Precision 26 GHz adapter 3.5 mm (female) - 3.5 mm (female), straight MPA-350M-350M Precision 26 GHz adapter 3.5 mm (male) - 3.5 mm (male), straight MPA-292M-240F Precision 40 GHz adapter 2.92 mm (male) - 2.4 mm (female), straight MPA-292F-240M Precision 40 GHz adapter 2.92 mm (female) - 2.4 mm (male), straight MPA-292M-292F Precision 40 GHz adapter 2.92 mm (male) - 2.92 mm (female), straight MPA-292F-292F Precision 40 GHz adapter 2.92 mm (female) - 2.92 mm (female), straight MPA-292M-292M Precision 40 GHz adapter 2.92 mm (male) - 2.92 mm (male), straight MPA-240M-240F Precision 50 GHz adapter 2.4 mm (male) - 2.4 mm (female), straight MPA-240F-240F Precision 50 GHz adapter 2.4 mm (female) - 2.4 mm (female), straight MPA-240M-240M Precision 50 GHz adapter 2.4 mm (male) - 2.4 mm (male), straight MPA-185M-185F Precision 67 GHz adapter 1.85 mm (male) -1.85 mm (female), straight MPA-185F-185F Precision 67 GHz adapter 1.85 mm (female) -1.85 mm (female), straight MPA-185M-185M Precision 67 GHz adapter 1.85 mm (male) -1.85 mm (male), straight MPA-185M-100FPrecision 67 GHz adapter 1.85 mm (male) -1.00 mm (female), straightDisclaimer: TITAN Probe, QAlibria are trademarks of MPI Corporation, Taiwan. StatistiCal is a trademark of National Institute of Standards and Technology (NIST), USA. All other trademarks are the property of their respective owners. Data subject to change without notice.。

H38 | INCREMENTAL OPTICAL ENCODERSPECIFICATIONSThe H38 is an explosion proof version of the field-proven H25 encoder series. The H38 is UL certified for NEMA Class 4X and 6 (outdoor nonhazardous locations) and Class 4X and 13 (indoor non-hazardous locations). It is available with single and triple certifications for use in hazardous locations and includes a standard shaft seal, double bearing seals, and a cast aluminum housing with hard anodized and dichromate sealed finish. The H38 is suitable for use in petroleum service industries, solvent refining operations, spray painting applications, and explosive dust environments.IntroductionMechanicalSPECIFICATIONS (CONTINUED)Notes & Tables:All notes and tables referred to in the text can be found on pages 4 and 5.ElectricalEnvironmentalDIMENSIONS Dimensions in mm1. Non-standard index widths and multiple indices are available by special order. Consult factory.2. Complementary outputs are recommended for use with line driver type (source/sink) outputs. When used with differential receivers, this combination provides a high degree of noise immunity.3. Output IC’s: Output IC’s are available as either Line Driver (LD) or NPN Open Collector (OC) types. Open Collectors require pull-up resistors, resulting in higher output source impedance (sink impedance is similar to that of line drivers). In general, use of a Line Driver style output is recommended. Line Drivers source or sink current and their lower impedance means better noise immunity and faster switching times. Warning: Do not connect any line driver outputs directly to circuit common/OV. Those may damage the driver. Unused outputs should be isolated and left floating. Our applications specialists would be pleased to discuss your system requirements and the compatibility of your receiving electronics with Line Driver type outputs. 28V/V: Multi-voltage Line Driver (7272*): 100 mA source/sink. Input voltage 5 to 28 VDC +/- 5% standard (Note: Vout = Vin). This driver is TTL compatible when used with 5 volt supply. Supply lines are protected against overvoltage to 60 volts and reverse voltage. Outputs are short circuit protected for one minute. Supply current is 120 mA typical (plus load current). This is the recommended replacement for 3904R and 7406R open collector outputs with internal pullup resistors. It is also a direct replacement for any 4469, 88C30, 8830 or 26LS31 line driver 28V/5: Multi-voltage Line Driver (7272*): 100 mA source/sink. Input voltage 5 to 28 VDC +/- 5% standard, internally regulated with 5V (TTL compatible) logic out. Supply lines are protected against overvoltage to 60 volts and reverse voltage. Outputs are short circuit protected for one minute. Supply current is 90 mA typical (plus load current). 15V/V: Multi-voltage Line Driver (4469*): 100 mA source/sink. Input voltage 5 to 15 VDC +/- 5% standard (Note: Vout = Vin). TTL compatible when used with 5 volt. Supply lines are protected against overvoltage to 60 volts and reverse voltage. Outputs are short circuit protected for one minute. Supply current is 90 mA typical (plus load current). This is a direct replacement for the 4469 Line Driver. 28V/OC: NPN Open Collector (3904*, 7273*). Current sink of 80 mA max. Current sourced by external pull- up resistor. Output can be pulled up to voltage other than supply voltage (30 V max). Input voltage 5 to 28 VDC +/- 5% standard. Supply current is 120 mA typical. This replaces prior IC’s with designations of 3904, 7406, 3302, 681 and 689. 5V/OCR, 15V/OCR, 24V/OCR: Open Collector (3904R*, 7406R*, 7273R*): Current sink of 70 mA max. Includes internal pull-ups sized at approximately 100 ohms/ volt. Max current source is 10 mA. Supply current is 100 mA typical, 120 mA with internal pull-ups. The 5V/OCR, 15V/OCR and 24V/OCR are often replaced by the 28V/V in system upgrades.4. Special –S at the end of the model number is used to define a variety of non-standard features such as special shaft lengths, voltage options, or special testing. Please consult the factory to discuss your special requirements.5. Higher frequency response may be available. Please consult with the factory.6. Extended temperature ratings are available. Consult with factory for more specific information.7. For interpolation options, contact factory. See Doc. 01059-000 supplied with encoders for Important Installation and Usage notes summarized here.1. Environment: Hazardous Locations — UL Complies with UL and cUL requirements; CEN Shall comply with UL requirements plus CENELAC/ATEX plus IECEx standards2. WARNING: Open all circuits prior to connecting this product to power and controller.3. The installation must comply with NEC Class 2 circuits or with the regulations of the country of use.4. AWG 14 - 22 stranded wire stripped to .25” [6.3mm} is recommended.5. Use agency approved 105° C minimum rated cable/conductors housed within an approved rigid conduit.6. Conduit runs must have a sealing fitting certified to 60079-0 Ex d IIB immediately at the entrance to the device.7. Tightly close terminal block access cover prior to applying power.8. For maximum bearing life, a flexible coupling is recommended between encoder shaft and driving shaft.Encoder Installation1. Keep terminal block access tightly secured during use.2. DO NOT loosen two 5/16” set screws at opposite face.1. There are no user serviceable parts inside. Encoder must be returned to factory for service.2. WARNING: Open all circuits to this product prior to opening access cover to disconnect wires.During UseMaintenance and Service*AB or ABC output only.NOTE: Resolutions up to 72,000 are available. See Note 7.ORDERING OPTIONSS = Special features specified on purchase order (consult factory) See note 4Page 7CONTACT USAmericas+1 (800) 350 2727 – Option 1****************************Europe, Middle East & Africa +33 (3) 88 20 8080****************************Asia Pacific*************************.com China +86 (21) 2306 1500Japan +81 (45) 277 7117Korea +82 (31) 601 2004India +91 (80) 67920890Rest of Asia +886 (2) 27602006 ext 2808Sensata Technologies, Inc. (“Sensata”) data sheets are solely intended to assist designers (“Buyers”) who are developing systems that incorporate Sensata products (also referred to herein as “components”). Buyer understands and agrees that Buyer remains responsible for using its independent analysis, evaluation and judgment in designing Buyer’s systems and products. Sensata data sheets have been created using standard laboratory conditions and engineering practices. Sensata has not conducted any testing other than that specifically described in the published documentation for a particular data sheet. Sensata may make corrections, enhancements, improvements and other changes to its data sheets or components without notice.Buyers are authorized to use Sensata data sheets with the Sensata component(s) identified in each particular data sheet. HOWEVER, NO OTHER LICENSE, EXPRESS OR IMPLIED, BY ESTOPPEL OR OTHERWISE TO ANY OTHER SENSATA INTELLECTUAL PROPERTY RIGHT, AND NO LICENSE TO ANY THIRD PARTY TECHNOLOGY OR INTELLECTUAL PROPERTY RIGHT, IS GRANTED HEREIN. SENSATA DATA SHEETS ARE PROVIDED “AS IS”. SENSATA MAKES NO WARRANTIES OR REPRESENTATIONS WITH REGARD TO THE DATA SHEETS OR USE OF THE DATA SHEETS, EXPRESS, IMPLIED OR STATUTORY, INCLUDING ACCURACY OR COMPLETENESS. SENSATA DISCLAIMS ANY WARRANTY OF TITLE AND ANY IMPLIED WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE, QUIET ENJOYMENT, QUIET POSSESSION, AND NON-INFRINGEMENT OF ANY THIRD PARTY INTELLECTUAL PROPERTY RIGHTS WITH REGARD TO SENSATA DATA SHEETS OR USE THEREOF.All products are sold subject to Sensata’s terms and conditions of sale supplied at SENSATA ASSUMES NO LIABILITY FOR APPLICATIONS ASSISTANCE OR THE DESIGN OF BUYERS’ PRODUCTS. BUYER ACKNOWLEDGES AND AGREES THAT IT IS SOLELY RESPONSIBLE FOR COMPLIANCE WITH ALL LEGAL, REGULATORY AND SAFETY-RELATED REQUIREMENTS CONCERNING ITS PRODUCTS, AND ANY USE OF SENSATA COMPONENTS IN ITS APPLICATIONS, NOTWITHSTANDING ANY APPLICATIONS-RELATED INFORMATION AGENCY APPROVALS & CERTIFICATIONSEN 61000-6-4 and EN 61000-6-2Class I, Group C & D;Class II Group E,F & G;Class I, XXXXXII 2 G Ex d IIB T4 GbIECEx (Exd IIB T4)UL 14.0006XThe Mine Safety and Health Administration (MSHA) is an organization that operates in the United States and enforces compliance with safety and health standards in the Nation’s mines. Consult factory for MSHArated product.。

Laser nano-manufacturing–State of the art and challengesLin Li(1)a,*,Minghui Hong b,Michael Schmidt(3)c,Minlin Zhong d,Ajay Malshe(2)e, Bert Huis in’tVeld(3)f,Volodymyr Kovalenko(1)ga Laser Processing Research Centre,School of Mechanical,Aerospace and Civil Engineering,The University of Manchester,M139PL,UKb Department of Electrical and Computer Engineering,National University of Singapore,Singaporec Photonic Technologies,FAU Erlangen-Nuremberg,Germanyd Department of Mechanical Engineering,Tsinghua University,Chinae Department of Mechanical Engineering,University of Arkansas,USAf Department of Mechanical Engineering,University of Twente,The Netherlandsg National Technical University of Ukraine,Ukraine1.IntroductionThe need for nano-manufacturing is dictated not only by the requirement of increasingly sophisticated devices and structures with novel properties but also by the trend of decreasing component sizes,material usages and energy consumption of products.To meet the demand for product miniaturization and nano-material and structures enabled novel functionality,a logical step is to achieve the desired nano precision and resolution through the development and wide implementation of nano-fabrication technologies[78,119].Nano-scale manufacture refers to the production of structures,materials and components with at least one of lateral dimensions between1nm and100nm including surface and sub-surface patterns,3D nano structures, nanowires,nanotubes and sers have provided important opportunities in the realisation of nano-manufacturing.This paper reviews the progress in the development of laser based nano-manufacturing technologies and associated sciences in order to understand the state of the art and challenges.Fig.1shows the scope of the paper with three main areas of focus:(1)laser fabrication technologies for surface and subsurface nano struc-tures including nearfield and farfield techniques,(2)laser synthesis of nano materials including nanoparticles,nanowires and nanotubes,(3)laser fabrication of3D nano structures and devices primarily based on additive or bottom-up nano-manu-facturing techniques.Their industrial applications and scientific/ technological challenges are ser fabrication of surface nano-structures2.1.Diffraction limits to laser beamsLaser materials processing has been successfully applied in industry for several decades for cutting,welding,drilling,cleaning, additive manufacturing,surface modification and micro-machin-ing.In most cases,the feature size and resolution of machining are above1m m.One of the reasons for the limited resolution is the diffraction limit of the laser beams in the farfield(where the target surface from the optical element is greater than the optical wavelength)governed by:d¼l2n sin a(1) where d is the minimum beam spot diameter,l is the laser wavelength,n is the refractive index of the medium of beam delivery to the target material and a is the beam divergence angle. The best theoretical resolution is therefore around half of the laser wavelength.For most high power engineering lasers the optical wavelengths are within248nm–10.6m m.Therefore,there are considerable challenges to achieve nano-scale(100nm)resolu-tion in direct laser fabrication of surface structures.To improve the fabrication resolution a number of approaches have been considered including the use of high numerical aperture optics and shorter wavelength light sources.For example,deep ultra-violet(DUV,ArF193nm)laser sources have been used in producing lines of130nm and90nm lithography(32nm and 45nm with optics immersed a high refractive index liquid).To achieve smaller surface patterning feature sizes,F2lasers of 157nm wavelength and extreme ultraviolet(EUV)Xe or Sn plasma systems with a13nm wavelength are used for nanolithography. However,these sources are costly,low output power and unstableCIRP Annals-Manufacturing Technology60(2011)735–755A R T I C L E I N F OKeywords:LaserNano manufacturing Material A B S T R A C TThis paper provides an overview of advances in laser based nano-manufacturing technologies including surface nano-structure manufacturing,production of nano materials(nanoparticles,nanotubes and nanowires)and3D nano-structures manufacture through multiple layer additive techniques and nano-joining/forming.Examples of practical applications of laser manufactured nano-structures,materials and components are given.A discussion on the challenges and outlooks in laser nano-manufacturing is presented.ß2011CIRP.*Corresponding author.Contents lists available at ScienceDirectCIRP Annals-Manufacturing Technology journal homepage:/cirp/default.asp0007-8506/$–see front matterß2011CIRP. doi:10.1016/j.cirp.2011.05.005in light intensity.Strong absorption of the UV light by air molecules requires the nanolithography to be carried out in a vacuum or dry high purity N 2gas protection chamber.How to overcome the optical diffraction limit with stable UV or visible,IR light sources is attracting much research interests in the world.Near field optics utilizing evanescent waves at the close proximity (within the length of the light wavelength)from the focusing optics have been recently applied for laser based nano-fabrications beyond the diffraction limits.In addition,femto second pulsed lasers have been used to achieve far field nano-resolution fabrication based on ablation threshold setting of the Gaussian beam profile of the lasers and non-linear light absorption ser radiation on scanning probe tips for nano-fabrication is not included in this paper as it was reported elsewhere [111].In the following sections,recent developments in near field laser nano-fabrication techni-ques,far field femto second laser nano-fabrication and laser induced self-organising nano-ripple formations are summarised.2.2.Scanning near field photolithography (SNP)using laser coupled near field scanning optical microscopy (NSOM)SNP is based on the coupling of a laser beam (e.g.a frequency doubled argon ion laser at l =244nm)with an optical fibre based Near-field Scanning Optical Microscope (NSOM,first demonstrated in 1992)with a very fine tip (typically 50nm)and very close (10–20nm)tip to target surface distance.A high resolution (beyond diffraction limit)evanescent energy field generates at the tip and decays exponentially with increasing distance.The nanometer distance between the tip and target ensures that the evanescent wave arrives at the target surface with sufficient energy density.The patterned photo-resist is further treated by chemical etching,plasma etching or UV light radiation to create nano-scale patterns on the substrate.The technique was first reported by Lo and Wang in 2001to demonstrate 128nm resolution fabrications [100].Sun and Legget from Sheffield University,UK [172,173]selectively oxidized a strongly bound self-assembled nanolayer (SAM)photo resist on a gold substrate using the SNP technique (the terminology of SNP was first proposed in 2002)followed by chemical etching to realise 20–55nm resolution in surface patterning.This is matching the resolution by electron beam lithography but without the use of a vacuum chamber.The technique was further developed by scientists at Singapore Data Storage Institute and National University of Singapore,using a frequency-doubled Ti:Sapphire femto-second laser at l =400nm,coupled into an NSOM fibre probe to achieve 20mm resolution surface patterning on a UV photo resist (around 40–120nm thickness)spin coated on a Si substrate for data storage applications [21,56,93–95,217].The laser etched depth was 20–100nm.The tip/sample distance was regulated by a tuning-fork-based shear-force feedback.Typical writing speed is 8–12m m/s.In the coupled laser and NSOM nano-fabrication technique,the probe-to-sample distance is a critical parameter to control both the nano-feature size and shape.At a small probe diameter and probe-to-substrate distance,the NSOM overcomes the traditional far-field diffraction limit and can be used to obtain sub-wavelength-size patterns.Fig.2shows an example of nano-line arrays created at different incident laser powers.In addition,higher writing speed leads to shorter exposure time and thus lower exposure dose,resulting in a narrower line width and shallower depth.Considering that there is a melting threshold of the NSOM tip metal coating,a low power (<1mW)laser source is typically used to avoid damaging theNSOM tip.For the photo-resist exposure process,exposure energy dose is another important parameter,which is decided by exposure UV light energy and exposure time.The high resolution of the SNP technique is comparable to electron beam lithography.Furthermore,as the nano-features can be fabricated in air,with a multi-NSOM fibre tip design,parallel nanolithography can be realised for high speed surface nano-structuring.The drawbacks of the technique include the requirement of high precision nano-distance control between the fibre tip and the target,and potential contamination or damage to the fibre tip.If the target surface is rough (>50nm Rz)then it is difficult to apply the technique for uniform pattern writing.A recent development has enabled a nano-second laser NSOM technique (200nm probe diameter)to be applied for direct fabrication of nano-scale features on Si without the use of subsequent photo or chemical etching [165].2.3.Nano ridge aperture (bowtie)beam transmission enhanced nano-fabricationThe amount of light transmission through a small aperture of an object depends on the aperture size,d a ,relative to the wavelength,l ,of the light source.For an aperture smaller than the laser wavelength,light transmission is restricted.For example,for a circular aperture,the transmission efficiency is on the order of (d a /l )4due to the optical diffraction effect [11].Researchers in Perdue University,USA,found that,with a specific aperture geometry such as a bowtie or H,high energy laser beams can be delivered through the aperture with much less attenuation than a circular aperture and the energy is sufficient to produce nano-scale patterns on a surface through contact lithography [29,226].The enhancement was found to be due to near field surface plasmonic effect [29,227].Fig.3a shows a typical bowtie aperture used for nano-fabrication.The aperture was made of atomic force microscope cantilever probe (Si 3N 4coated with an Al film)with the gold coating removed from the back side and the bowtie geometry milled using a focused ion beam.The aperture had 180nm Â180nm outline dimension and a 30nm gap.When a laser beam of 800nm wavelength and 50fs pulse width at 1.5–7.9mW power passed through the aperture,lines with widths down to 62nm and 2nm depth were produced on a photoresist material at a scanning speed of 2.5m m/s as shown in Fig.3b.The distance between the bowtie aperture tip and the target surface was 30nm.The laser beam intensity at the tip of the bowtie aperture was found 39.8times that of the incoming beam due to plasmonic enhancement.As this phenom-enon only occurs at the near field,some researchers also classify this technique as the NSOM based nano-fabrication.2.4.Optically trapped micro-sphere assisted nano-writing (OTAN)Scientists at Princeton University recently developed a laser nano-patterning technique based on laser tweezers [118].AFig.1.Illustration of the scope of thepaper.Fig.2.Nano-lines created by the coupled fs laser/NSOM SNP technique at different incident laser powers [55].L.Li et al./CIRP Annals -Manufacturing Technology 60(2011)735–755736transparent sphere (polystyrene)was held by a focused continuous wave laser beam (converted to a Bessel beam using an axicon lens)as in a typical laser tweezers setup in a liquid environment.At the same time,another pulsed laser (355nm wavelength,15nm pulse length,15nJ–8mJ pulse energy)passes through the sphere and produces a focused energy spot at the bottom of the sphere based on the near field evanescence wave effect.By traversing the sphere over a surface,nano-scale patterns have been generated.Due to the balance of the laser beam radiation pressure with the electrostatic repulsion from the target surface [211],which develops due to ionic groups on the surfaces,the distance between the sphere and the target surface can be maintained constant even for a curved surface without any additional feedback control systems.Fig.4shows a typical process set up and an example of a nano-pattern fabricated using the technique.Arbitrary patterns with the line width around 100nm were demonstrated with 15nm feature size variation.The scientists at the Princeton group further developed the technique by splitting the sphere trapping beam into multiple beams using beam splitters to hold and move several micro-spheres (0.76–3m m diameters)simultaneously,while firing a pulsed power beam to them.Such a system enabled them to write a number of parallel nano-patterns on a polyimide film coated on a glass substrate [118].An advantage of the technique compared with other near field direct writing techniques is that for OTAN there is no need for distance control and it can work on rough surfaces [186].A limitation of the technique is that it can only operate in a liquid environment.2.5.Femtosecond (fs)laser direct writingThe process involved in the formation of nano-scale features by fs lasers is different from the conventional lasers.In fs laserinteraction with materials,the laser interaction time (10À15–10À13s)is shorter than the time for electrons to pass the energy to the lattice (around 10À11s).As a result,the material remains cool while absorbing the laser energy.The use of ultra-short pulse durations of the fs laser pulses restricts the heat diffusion,and improves surface roughness,and also minimizes damage to the adjacent areas.Due to the above mentioned advantages,fs lasers are used for writing couplers [120],waveguide amplifiers [162],diffraction gratings and memory bits [24].To achieve nano-scale resolution,the tip of Gaussian beam is used (setting the laser fluence low enough so that only the tip of laser beam is above the ablation or phase change threshold of the material).In this way,far field laser nano-fabrication beyond diffraction limit can be realised.Typical pulse energy of fs laser nano-fabrication is between 0.1and 100m J and power densities above 1TW/cm 2.Tight focusing of the light by a high NA telecentric lens is essential for fs laser nanofabrication.Another advantage of telecentric lens is that every successive scanning beam is parallel to the optical axis.Due to this,the beam is incident normally on the entire surface area and symmetrical features can thus be written.Minimal variation in laser focus energy and accuracy of focal spot/sample scanning ensure fabrication with high precision.The charge-coupled device (CCD)camera assists in optical adjustment and in situ fabrication monitoring [236].Three critical factors that govern the fs laser writing mechanism are chemical nonlinearity,material nonlinearity,and optical nonlinearity.When a high power density from a fs laser is incident on a target surface,photons are absorbed by either one-photon absorption (OPA),two-photon absorption (TPA),or the multi-photon absorption (MPA).Photon absorption caused by fs-laser beam irradiation leads to different processes such as ionization,electron excitation,and phase transitions.The electrons are agitated and their oscillatory energy is converted into thermal energy of the plasma by collisions with ions by the linear damping mechanism referred to as inverse Bremsstrahlung heating .This raises the temperature and the laser energy is absorbed by the plasma by OPA.These phenomena can occur only in a localized region around the focal point due to the high peak intensity.The separation between the high energetic electron cloud and the positively charged ions in the bulk causes a high voltage (known as Dember voltage)close to the surface which results in the repelling of materials in a process known as Coulomb Explosion.For this reason,the fs laser processing is also termed as cold laser processing and it is possible to write features even in transparent materials [109,121,126].In summary,the formation of nano-features is attributed to the interaction between the fs laser beam and laser-induced electron plasma and matter [159].Two photon absorption mechanisms are illustrated in Fig.5[84].In the figure,S 0,S 1,and S 2are ground state,one-photon allowed and two-photon allowed excited states,respectively.The incident light frequencies are v 1and v 2while the fluorescent emission frequency is v 3.It should be noted that in standard optical lithography,the materials respond to light excitation to the first order effect.For TPA and MPA in fs laser writing,the response is limited to two and higher orders and the square light intensity is also narrower than a linear one.This makes the photon energy of TPA less than thatofFig. 3.Nano bowtie aperture (a)and nano surface patterns produced by transmitting a laser beam through it (b)[29].Fig.4.Illustration of laser trapped micro-sphere nano-patterning.(a)Experimental set up and (b)an example of optically trapped micro-sphere nano writing.The scale bars on the larger picture and the zoomed-in pictures are 2m m and 250nm,respectively [118].Fig. 5.Schematic energy diagram of a TPA process [84](reproduced with permission from Elsevier).L.Li et al./CIRP Annals -Manufacturing Technology 60(2011)735–755737OPA.As a consequence,the volume involved in beam-material interaction reduces and this leads to better resolution in writing the features.The volume in which this energy is absorbed is less than the third order of the laser wavelength (l 3)and hence high spatial resolution of the writing process ( 100nm)beyond the optical diffraction limit is possible [176].For nanoscale writing,it is essential that the laser energy penetrates into the bulk material without any significant losses.For this purpose,a light source with near-infrared wavelength (such as l =800nm)is selected for surface,sub-surface and in-bulk writing.Due to the high transient power density,fs lasers can excite a wide range of materials and induce irreversible processes such as photopolymerisation,photoisomerization,and photoreduction.Femtosecond lasers have numerous advantages over longer pulsed lasers for materials processing [179,195–197]due to which they have been used for writing nano-features in a wide variety of materials such as metals,polymers and ceramics.Examples of the material,and dimensions of the nanofeatures ( 100nm)written by fs lasers are presented in Table 1and Fig.6.2.6.Micro-lens array for fabricating periodic nano-structuresPeriodic nanostructures are useful for plasmonic structures,photonic crystals,high density data storage,miniaturized radio frequency (RF)oscillators and optical gratings.Micro-lens array (MLA)lithography is a laser-based technique being developed for rapid fabrication of large-scale periodic nanostructures.MLA consists of a series of miniaturized lenses of identical sizes and focal lengths,typically arranged hexagonally or squarely packed.When used in a typical optical system,an MLA can focus an incident light beam to form a series of parallel light spots in the focal plane.Downscaling of the diameter,D ,and the focal length,f ,of a lens improves its optical performance [52].For a fixed F number F =f /D ,the diffraction-limited resolution is given by d x %l F 2which is independent of the lens scale.However,the wave aberrations which describe the deviation of the actual wave front from a perfect spherical wave front,are less for smaller lenses for the same F number and wavelength.On the other hand,small lenses have a shorter focal length [200].The early studies of micro-lens array based photolithography were for the manufacturing of periodic micro-scale features [58,200].As the micro-lens array production technology improves,the size of micro-lenses get smaller and so are the feature sizes.For example,scientists at Singapore Data Storage Institute and National University of Singapore used an 800nm wavelength,100fs laser to irradiate a 30nm-thick GeSbTe layer sputtered onto a polycarbonate substrate.It created thousands of field emission transistor structures in a few minutes with a gate line width of 200nm.In addition,using an alkaline solution to etch the material after laser radiation,nanostructures down to 55nm on the thin film were produced [96].To achieve further reduction in feature sizes,they manufactured a micro lens array on a quartz substrate with a diameter and pitch of 1m m each,which consists of 2500Â2500(6.25million)lenses covering an area of 5mm Â5mm.UV light-sensitive photoresist irradiated by a 248nm wavelength,23ns pulse width KrF excimer laser through the MLA created nano-dots as small as 78nm in diameter,at a resolution of one-third the operating wavelength [92].Fig.7shows an example of periodic patterns produced by a micro-lens array system.A critical requirement of the micro-lens array lithography fabrication technology is that the lens must be horizontal to the target surface within the entire radiated area to ensure the beams are vertical to the surface so that the feature sizes are identical.The lens to target surface is also needed to be controlled precisely.For a non-flat surface,it is difficult to fabricate uniform nano-structures using this technique.2.7.Far field laser interference lithography (LIL)Laser-interference lithography is a large-area,maskless,and noncontact nanofabrication technique suitable for repeatable structures such as periodic lines and 2D shapes.It is based on the interference of two or more coherent light beams that form a horizontal standing-wave pattern.The minimum spacing,d L ,between the lines is determined by the laser wavelength,l ,and angle,a ,between the laser beams as in:d L ¼l2n sin ða =2Þ(2)This interference pattern is then recorded on the exposed ser-interference lithography can be used to fabricate micro-and nano-surface structures in large areas.By overlapping exposures at different angles,various patterns (e.g.circular,square,and hexagonal geometry)can be produced.Table 1Examples of nano-features written by fs lasers.Base materialNano-featuresReferences Copper thin film Pits of 75nm[195]Amorphous silicaGratings of 15nm width[57]Urethane acrylate resin,SCR 500Wires of 65nm lateral width at central portion [177]Glass Hillocks of 40–70nm height [193,194]TeO 2Voids of 30nm width [158]SiO 2Stripes of 20nm width[159]Bulk aluminium Irregular nanoentities with average size of 100nm [170]Lithium niobateThick layer of 100nm[24,109,110,169]CVD diamond surfaceRipples with periodicity of 50–100nm[136]AAO matrix (Au deposited into anodized aluminium oxide)Nanorods of diameter 20–40nm and length of $50nm [147]Commercial resin,SCR 500Lines with width of 23nm[180]Gallium nitride Craters of depth varying from 26to 40nm[126]Silica glass Wires of width of 15nm and holes of 20nm diameter [70]TiO 2Ripples with depth of 100nm[23]Fig.6.Nanofeatures developed in (a)amorphous silica [57](reproduced with permission from Elsevier),(b)urethane acrylate resin,SCR 500[176](reproduced with permission from the Optical Society of America),(c)commercial resin,SCR 500[180](reproduced with permission from American Institute of Physics),(d)glass [193],(e)TeO 2[158],(f)photoresist thin film [94],(g)CVD diamond surface [136](reproduced with permission from American Institute of Physics).L.Li et al./CIRP Annals -Manufacturing Technology 60(2011)735–755738Examples include nano-cone arrays on Ni–Cr alloy (Fig.8)and Au/Ag bi-metallic plasmonic structures on quartz ing this approach,after only a few minutes of UV light exposure,followed by photoresist development and chemical etching,periodic nano-lines and nano-dot arrays can be created over a centimetre scale area.To further improve the resolution,immersion laser interference lithography was developed at Max-Planck Institute of Micro-structure Physics,Germany [18].This is to increase ‘‘n ’’in Eq.(2)by introducing a Littrow prism and water as the immersion liquid.In this case,n =1.51.Line patters with a period less than 100nm and a width of 45nm were demonstrated with a 244nm wavelength laser (Fig.9).Another way of increasing the resolution is by reducing the laser wavelength,such as the use of an extreme ultraviolet laser source (e.g.an A +8laser at a 46.9nm wavelength).A great advantage of this method is the increase of ablation depth to over 120nm on Si based photo-resist [112].By combining an EUV laser and Lloyd’s mirror interferometer (Fig.10),nanostructures of 60nm feature size were produced on PMMA (Fig.11).The ablation depth is 20–30nm.Also lines with 95nm width were produced on Au substrates using the technique by the same group.A drawback of the EUV technology is that the process will need a vacuum chamber to operate due to the use of EUV system which can easily ionize gases if it is operated in non-vacuum conditions.2.8.Near field interference lithographyNear field interference lithography is based on evanescent (non-propagating)wave or surface plasmon wave interferences.The purpose is to defeat the diffraction limit of the lasers to fabricate smaller nano-structures.Evanescent interferometric lithography (EIL)or evanescent near field optical lithography (ENFOL),or evanescent wave interference lithography (EWIL)was first demonstrated using a mercury arc lamp in 1999by Blackie et al.at University of Canterbury,New Zealand [3,14].Laser based evanescent wave near field lithography using total internal reflection (TIR)was first reported in 2006by Martinez-Anton of University Complutense Madrid,Spain [115].A typical TIR configuration is shown in Fig.12with two intersecting beams at an angle to enable the total reflection to occur to create periodic evanescent waves.Theprismrge area micro/nanostructures fabricated by laser MLA [92].Fig.8.A nano-cone structure fabricated by laser interference lithography (height 40nm and width 30nm)[152].Fig.9.Photoresist patterns created by immersion laser interference lithography.(a)Low magnification and (b)high magnification images of the pattern;the width of the resist lines is 43.4nm.(c)Silver lines after evaporation of 15nm Ag and lift-off [18].Fig.10.A typical optical configuration for Lloyd’s mirror interferometer laser interference lithography,where u =a /2[112].Fig.12.Illustration of a typical TIR optical configuration to generated evanescent waves through interference of tow intersecting beams [115].Fig.11.Two dimensional nano patterns on PMMA produced by EUV laser interference lithography using Lloyd’s mirror interferometer with two exposures at different angles,(a)dots with 60nm FWHM feature size and a period of 150nm,(b)regular shapes dots,(c)elongated dots [112].L.Li et al./CIRP Annals -Manufacturing Technology 60(2011)735–755739was irradiated with split 405nm wavelength laser beams.Periodic surface relief gratings of around 100nm period were produced on photoresists using this technique [115].More complicated 2D nano-structures can be fabricated using multiple (more than 2)beam interference through polarization tuning,based on TIR evanescence wave near field lithography,as demonstrated by Chua and Murukeshan [22].The photoresist in optical contact with the TIR prism (rectangular)has a lower refractive index than the prism.Patterns of 70nm feature size had been produced using this method (Fig.13).A drawback of this method is that the depth is shallow due to the non-propagating nature of the evanescent wave.The energy transmission through the masks is also very low.Surface Plasmon Interference Lithography (SPIL)is another near field lithographic technique developed recently to improve energy transmission and fabrication depth over the evanescent wave lithography.It is based on energy field enhancement by the interaction of light with surface Plasmon (SP,collective electron oscillation)waves induced around the nano-scale metallic struc-tures and a dielectric interface.If the metallic mask is very thin (e.g.50nm),surface Plasmon waves can be generated on both surfaces,even the structures are not through the full thickness of the metallic film.The enhancement,through the coupling between the surface plasma waves and the evanescent waves,can be several orders of magnitude in intensity compared with the incoming beam.The wavelength of the excited surface Plasmon wave is shorter than that of the exciting laser at the same frequency.Therefore higherresolution is expected.The wavelength of the exciting laser,l (i ,j ),needs to match the materials and the structures of the mask.Their relationships can be found from [168]:l ði ;j Þ¼affiffiffiffiffiffiffiffiffiffiffiffiffiffii 2þj 2q ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffie d e m e d þe mr (3)where a is the metallic mask periodic nanostructure period,e a and e m are the dielectric constants of the mask metal and the surrounding dielectric medium,respectively and i ,j are mode indices.For example,a UV light can excite surface Plasmon waves on Al with a nanostructure period of 220nm.A green or blue light can excite surface Plasmon waves on a silver mask with a period of 400–500nm.A larger period allows longer exciting wavelengths.The SPIL technique for the fabrication of periodic surface nanostructures was first reported independently by two separate groups (University of California in USA and RIKEN in Japan)in 2004[103,168]using an Al or a silver mask.An example of a typical configuration for the SPIL technique is shown in Fig.14.For an 80nm thick Al mask of 20nm diameter holes and 220nm period (fabricated using a focused ion beam)and 30nm spacer (PMMA)and irradiated with an arc lamp with a peak intensity at 365nm,90nm periodic structures were produced on a photoresist [168].The RIKEN group fabricated periodic 100nm lines using a silver mask radiated with a 436nm light.They termed the method as SPRINT (Surface Plasmon Resonance Interference Nanolithography Technique)and proposed to use imperforated metallic marks which have corrugated surfaces on both sides of the metallic mask.The illuminated side collects the light and induces the SP waves on the other side of the target material through SP coupling.Sreekanth et al.at Nanyang Technological University of Singapore compared standard far field laser interference lithography,near field evanescent wave lithography and the SPLIT techniques in nano fabrication of period surface structures [167].They found that that the SPIL technique can produce deeper features than the evanescent wave lithography technique and both near field lithography techniques have a better resolution than the far field lithography technique.Fig.15shows an example of periodic dot arrays fabricated on a Si wafer using the SPIL technique with a UV Argon ion laser at 364nm wavelength,which has a 82Æ11nm feature size,164Æ11nm period and an average height of 180nm [167].2.9.Contact particle lens array nano-fabrication (CPLA)This technique is based on the use of transparent micro spherical particles spread onto the target surface byself-assemblyFig.13.Two dimensional features fabricated using evanescent wave interference lithography generated by TIR of four p-polarized incident beams.(a)Theoretical inverse positional photoresist development rate at the interface between the prism and photoresist,(b)SEM image of hexagonal arrayed 2D features.Inset:Enlarged region showing the peak (P),valley (V)and saddle (S)regions (top right),(c)AFM image of the nano-structures [22].Fig.14.A typical process configuration for SPIL and an optical mask,(A)schematic drawing of the SPIL set up and (B)an Al mask for the SPIL experiment (fabricated using FIB)with a hole size of 160nm and a period of 500nm [168].L.Li et al./CIRP Annals -Manufacturing Technology 60(2011)735–755740。
专利名称:Method for high precision optical distance measurement using an adjustable pointlightsource and multi-channel ccd sensor arraysbased on optical triangulation and point bypoint scanning, especially contactlessmeasurement of three dimens ional objects 发明人:KARL-HEINZ NAUSCHUTZ,NORBERTROSENKRANZ,ALFRED SONTAG申请号:AU9628598申请日:19980928公开号:AU9628598A公开日:19991129专利内容由知识产权出版社提供摘要:The invention relates to a method for high precision optical distance measurement using an adjustable point light source and multi-channel CCD sensor arrays based on optical triangulation and point by point scanning, especially contactless measurement of three dimensional objects. According to the invention, measurement values exceeding a given threshold value with respect to a measuring point are centrally and simultaneously captured in all channels. Said values form an initial local measurement pulse value, whereby peripheral data indicates in each case a measurement pulse. The measurement pulses are subsequently evaluated with respect to pulse form, amplitude, width, multi-pulses or the like, together with pulse location in order to output assembled, averaged measurement data that corresponds solely to given test criteria for external data storage and further processing.申请人:INTECU GESELLSCHAFT FUR INNOVATION, TECHNOLOGIE UND UMWELT MBH更多信息请下载全文后查看。
专利名称:METHOD FOR MEASURING THEMICRORELIEF OF AN OBJECT AND OPTICALCHARACTERISTICS OF NEAR-SURFACELAYER, MODULATION INTERFERENCEMICROSCOPE FOR CARRYING OUT SAIDMETHOD发明人:Andreev, Vladimir Andreevich,Indukaev,Konstantin Vasilievich,Osipov, PavelAlbertovich申请号:EP01922153.0申请日:20010123公开号:EP1359451A1公开日:20031105专利内容由知识产权出版社提供摘要:The invention relates to optical engineering, in particular to methods for measuring a microrelief, the distribution of optical material constants of a near-surface layer and can be used for microelectronic engineering, nanotechnology, material science, medicine and biology. The aim of the invention is to improve spatial resolution for measuring geometrical parameters of the relief and the distribution of the optical material constants, extend the range of defined constants including optical anisotropy constants, significantly increasing the accuracy of definition of the material constant and extending the number of objects studied. The inventive method for measuring microrelief and optical characteristics of the near-surface layer and a modulation interference microscope for carrying out said method are also disclosed.申请人:Andreev, Vladimir Andreevich,Indukaev, Konstantin Vasilievich,Osipov, Pavel Albertovich地址:ul. Akademika Vargi, 2-252 Moscow, 117133 RU,Prospekt Mira, 52-43 Moscow RU,ul. Festicalnaya, 63-2-147 Moscow, 123502 RU国籍:RU,RU,RU代理机构:Andrae, Steffen, Dr.更多信息请下载全文后查看。
VL53L0X Distance SensorUser ManualOVERVIEWVL53L0X Distance Sensor is a Time-of-Flight (ToF) ranging module based on the VL53L0X from ST, with accurate ranging up to 2m, it is controlled through I2C interface, and pretty low power consumption.The VL53L0X is a ToF sensor which embeds the ST’s second generation FlightSense patented technology.Unlike conventional ranging sensors, the VL53L0X is able to provide accurate distance measurement whatever the target color and reflectance, achieves better anti-interference capability.FEATURES⚫I2C communication interface, control the module on/off via IO pins⚫Onboard voltage translator, compatible with 3.3V/5V operating voltage⚫Comes with development resources and manual (examples for Raspberry Pi/Arduino/STM32)SPECIFICATIONS➢Operating voltage: 3.3V/5V➢Dimension: 20mm × 24mm➢Mounting holes size: 2.0mm➢Ranging distance: 30 ~ 2000mm➢Ranging accuracy: ±5% (high speed mode), ±3% (high accuracy mode)➢Ranging time (min): 20ms (high speed mode), 200ms (high accuracy mode) ➢Field of view: 25°➢Laser wavelength: 940nm➢Operating temperature: -20 ~ 70°CPINOUTSVCC: 3.3V/5V power inputGND:groundSDA: I2C data pinSCL:I2C clock pinSHUT:shutdown control, connects to IO pinINT:interrupt output, connects to IO pinHARDWAREVL53L0XVL53L0X Time-of-Flight (ToF) ranging sensor is ST’s second generation laser-ranging module housed in the smallest package on the market today. The VL53L0X is a fully integrated miniature module which integrates embedded infrared ranging sensor, VCSEL (Vertical Cavity Surface-Emitting Laser), couples with internal physical infrared filters and a leading-edge SPAD array (Single Photon Avalanche Diodes). The VL53L0x embeds ST’s second generation FightSense TM patented technology, has longer ranging distance, higher rate and accuracy, opening the door to various new applicationVL53L0X can measure absolute distances up to 2m t whatever the target reflectances unlike conventional technologies. It’s ultra-Low designs supports for wireless and IOT application.Features:⚫Fully integrated miniature module–940 nm laser VCSEL–VCSEL driver–Ranging sensor with advanced embedded micro controller–4.4 x 2.4 x 1.0 mm⚫Fast, accurate distance ranging–Measures absolute range up to 2 m–Reported range is independent of the target reflectance–Advanced embedded optical cross-talk compensation to simplify cover glass selection⚫Eye safe–Class 1 laser device compliant with latest standard IEC 60825-1:2014 - 3rd edition⚫Easy integration–Single reflowable component–No additional optics–Single power supply–I2C interface for device control and data transfer–Xshutdown (reset) and interrupt GPIO–Programmable I2C addressPictures:For more details, please read the datasheetUSING WITH DEMO CODESWORKING WITH RASPBERRY PIThe demo code is based on open-source project on github:https:///cassou/VL53L0X_raspHARDWARE CONNECTIONThe connection is based on Raspberry Pi 3 Mode B+VL53L0X Distance Sensor Raspberry PiVCC 3.3VGND GNDSDA SDA.1SCL SCL.1 COMPILING AND RUNGING1.Download demo code from Wiki2.Unzip and copy the code of Raspberry Pi to your Pi (Recommend put on/home/pi/)3.Enter the path of the demo code on Terminal and run this compiling commandsudo make clean && sudo make && sudo make examples4.After compiling, enter bin folder and list the files as below:5.Execute command to run the code vl53l0x_SingleRanging_Long_Range_Example:6.Execute the command to run code vl53l0x_ContinuousRanging_Example:WORKING WITH ARDUINOHARDWARE CONNECTIONThe connection is based on Waveshare UNO PLUSVL53L0X Distance Sensor ArduinoVCC 3.3VGND GNDSDA SDASCL SCLRUNINGCopy the VL53L0X-Arduino-Library folder which is under Arduino demo code directory to Arduino IDE’s Libraries directory which is under the installation directory of your IDE. Then Open Arduino IDE, and choose File->Examples-> VL53L0X-Arduino-LibraryCompiling and run 5 examples for test as below:1.high_accuracy_ranging: High accuracy ranging which will cost more times2.high_speed_ranging: Fast ranging, cost less time and low accuracy3.long_distance_ranging: Long distance ranging, with bigger measure rang4.single_ranging: Single ranging mode5.continuous_ranging: Continuous ranging modeFor more information about different ranging modes, please read VL53L0X APIWORKING WITH STM32HARDWARE CONNECTIONThis connection is based on XNUCLEO-F411RE/ NUCLEO-F401RE:VL53L0X Distance Sensor XNUCLEO-F411RE/NUCLEO-F401REVCC 3.3VGND GNDSDA SDASCL SCLRUNNING VL53L0X_GUI1.Connecting sensor to NUCLEO-F401RE board as Hardware connection above2.Install ST’s VL53L0X_GUI software and run it. The software will write the testfirmware to NUCLEO board automatically. (Note: for this example, you need to use the NUCLEO-F401RE development board, and it is not an open-source code)3.Switch to Low-Power Automous, Distance Mode choose Short, then click Start.Distance curve will be showed on the softwareFor more information about STM32 examples VL53L0X, please visit ST website.。
a r X i v :c o n d -m a t /0008030v 1 [c o n d -m a t .s u p r -c o n ] 2 A u g 2000ANDREEV-REFLECTION AND POINT-CONTACT SPECTROSCOPY OF SUPERCONDUCTING RARE EARTH TRANSITION METAL BOROCARBIDES.I.K.YANSON B.Verkin Institute for Low Temperature Physics and Engineering National Academy of Sciences,61164Kharkiv,Ukraine keywords:rare earth transition metal borocarbides,Andreev-reflection and point-contact spectroscopy 1.Introduction The recently discovered [1],superconducting compounds R Ni 2B 2C,where R is rare earths (Lu,Tm,Er,Ho and Dy)and Y,still remain a hot topic of intensive research.Their crystallographic structure resembles that of high-T c materials,albeit being 3D in electronic properties.The mechanism of Cooper pairing in these compounds is not known in detail although they are commonly believed to be mediated by the ordinary electron-phonon interaction,like A15.The boron isotope effect [2,3]clearly points that the phonons are involved in superconductivity .Whether these compounds are s −or d −wave superconductors [4]is still under debate.The important sub-class in these materials is presented by the magnetic compounds (R =Tm,Er,Ho,and Dy),with the antiferromagnetic (AFM)order [5]and weak ferromagnetism (Er)[6]coexisting with superconductivity.The measurements of the quasiparticle density of states (DOS)by tun-neling spectroscopy encounters experimental difficulties,especially these re-fer to the magnetic superconductors.To our knowledge,no information is available about the electron-quasiparticle-interaction (EQI)spectral func-tion measured by tunneling spectroscopy in the superconducting state,which unambiguously allows one to determine the mechanism of Cooper pairing.An investigation of point contacts between a normal metal and a su-perconductor can partially solve these problems.The superconducting en-ergy gap and DOS can be measured by Andreev-reflection spectroscopy[7],and EQI spectral function can be obtained by inelastic point-contact2spectroscopy(PCS)both in the normal[9]and in the superconducting[10] paring the tunneling junction with point contacts,we can see that the boundary between R Ni2B2C-superconductor and vacuum(dielec-tric)in tunnel devices constitutes much stronger discontinuity than the interface between R Ni2B2C and a normal metal in point contacts,since in the latter case there is a Fermi-sea of electrons at both sides around the interface with no additional dielectric layer introduced.This discontinuity may severely influence the measurements making them different from the bulk properties.The schematic experimental setup is shown in Fig.1.A small noble metal(Ag,Cu)rod with sharp edges touches the(a−b)-plane edge of aflat R Ni2B2C single crystal or a sharp edge of a polycrystal with an a priory unknown orientation.Many spots can be tried both on the rod and along the R Ni2B2C edge for investigating the point contacts.The temperature and magneticfield can be varied,the latter,in case of a single crystal,is oriented either or⊥to the a−b plane.The I−V characteristics and theirfirst,R(V)=dV/dI(V),and second,dR/dV(V),derivatives are recordedby means of a standard lock-in technique.The latter equals dR/dV(V)=√2R0where d is in nm,the nominator is the average of the noble metal and R Ni2B2C[11],and R0is the zero-bias normal-state resistance of a contact inΩ.2.Superconducting energy gap measurements by Andreev-reflection spectroscopy.2.0.1.BCS-like DOS in paramagnetic and antiferromagnetic state ofR Ni2B2C(R=Dy,Tm)Recently the temperature dependence of quasiparticle DOS has been mea-sured in the DyNi2B2C-Ag point contacts[11]by means of Andreev-reflection spectroscopy.The R(V)-curves normalized by the normal-state R(V)de-pendences arefitted very well with the Blonder-Tinkham-Klapwijk(BTK) theory[7]with a zero smearing parameterΓ[8].This evidences that the quasiparticle DOS is BCS-like in this material.The superconducting en-ergy gap extrapolated to zero temperature equals(3.63±0.05)k B T c which evidences that on the average DyNi2B2C is a moderately strong coupling superconductor.The only disagreement with the BTK theory is that the decrease of the differential resistance around zero bias in the supercon-ducting state is typically a few percentage,instead of the order of one-halfof a normal resistance[7].This can be due either to microscopic inho-mogeneity of the material under the contact where only a small part re-3 veals the unperturbed superconducting properties,or to the intrinsicallydecreased Andreev reflection from an AFM superconductor with ferromag-netically ordered DyC planes.It should be stressed that DyNi2B2C is theonly R Ni2B2C compound which has T c<T N.Hence,one might think thatthe molecularfield due to the AFM order averages to zero on the scale ofsuperconducting coherence length except of very narrow directions almostparallel to the a−b planes.The situation is different in TmNi2B2C where incommensurate spinwave ordering occurs at temperatures much below the superconductingtransition(T c≫T m)and the superconductivity develops in the paramag-netic state.Preliminary results[12]show that the overall behavior of R(V)-curves alsofits the BTK predictions.That means that this compound alsohas the BCS form of quasiparticle DOS.2.0.2.Fine structure in temperature dependence of superconductingenergy gap in ErNi2B2C near T m.The overall temperature dependence of the Andreev-reflection spectra inErNi2B2C(Fig.2)also follows the BTK model.In this material T c>T m and around T m=6.5K spinfluctuations depress the superconducting order parameter which manifested as the lowering of H c2near T m[13].Recently, this depression has been measured using the temperature dependence of the superconducting penetration depthλ(T)[14]which together with supercon-ducting coherence lengthξ(T)permits determination of the temperature√dependence of the thermodynamic criticalfield H c=φ0/[24the incommensurate helical state with wave vector q∗c=0.91c∗.Moreover,the incommensurate a-axis modulation with q∗a=0.55a∗also exists over thesame temperature range along with the spiral-AFM transition.Both ofthese states collapse near the commensurate AFM transition with q∗=c∗and T N≈5K[5].The Andreev-reflection spectra of HoNi2B2C vividly mirror these transformations(Fig.4)[16].Below T c and down to T N theR(V)-spectra cannot befitted by the BTK model.The shallow dip whichappears around zero bias has an order of magnitude larger width than thatexpected for the given T c.We emphasize that for T c≥T≥6.5K the Andreev spectra are completely different from those in the paramagnetic state of Dy,Tm and Er compounds.Hence,in HoNi2B2C we observed the magnetic transition at the same temperature as the superconducting one, but not at T m=6.5K as in the single crystals[17].It is probable that the uncompensated internal magneticfield along the a−b plane for the spiral structure leads to the gapless behavior of DOS in the temperature region discussed.Below the AFM transition(T<T N=6.6K),the spectra reveal the ordinary BTK behavior.Interestingly,the temperature dependence of the spectra follows the BCS law albeit with a new T∗c≈6.6K.The BTK fits yield a zero-temperature energy gap∆0=1.04±0.06meV which gives2∆0/k B T∗c=3.7±0.2for lower”T∗c”,i.e.the same as for other R Ni2B2C[18].Using the upper T c=8.5K,one obtains unreasonably low 2∆0/k B T c=2.8.3.Point-contact spectroscopy of electron-quasiparticle-interaction spectral function.3.0.4.Principles of PCS.The point-contact spectroscopy(PCS)involves studies of the nonlinearities of the I−V characteristics of metallic constrictions in the normal state, with the size d smaller than the inelastic electron mean free path(m.f.p.) [19,20].In contrast to a tunneling junction,an ideal point contact has no barrier.PCS has the advantage that the material is probed into the depth of the current spreading region,which is of the order of the constriction size.This size should not be too large in order not to violate the conditions of the spectroscopic regime of the currentflow:d≤min(l in,√dV (V)=4¯h v Fg P C(ω)|¯hω=eV;(T≃0)5 Here g P C(ω)is the EQI or EPI spectral function with kinematic restric-tions imposed by the contact geometry.The factor4(instead of8as inhomocontacts)is due to weak EPI coupling and much greater v F for thenoble metal,as compared to R Ni2B2C.Correspondingly,the noble-metalEPI function is not seen in the spectrum.For the same reason,in the two-band model of R Ni2B2C[21],only the EQI spectral function for the bandwith the lowest Fermi velocity and largest EQI is seen in the spectrum.In the spectroscopic regime no heating of the contact area occurs since the energy dissipation length,Λε,is much larger than the contact size.How-ever,if the contact size is large compared toΛε,then there is local heatingand the temperature rises up to T0≃eV/3.63k B.The thermal feature in the PC spectra can be quite large if at a particular temperature T cr a sharp in-crease in resistivity occurs like,for example,for the superconducting-normalor AFM-paramagnetic transitions.The voltage position of such transitionon the I−V curve should depend on the input power V/R2,which meanson the contact resistance.parison between phonon DOS and EQI spectral function forsuperconducting YNi2B2C and non-superconducting LaNi2B2C.It is very instructive to compare the phonon density of states,measuredby inelastic neutron scattering,and the EPI(EQI)spectral function,ob-tained by PCS,for superconducting and non-superconducting compounds(Fig.5).For these we choose the nonmagnetic superconducting compoundYNi2B2C and non-superconducting homologue LaNi2B2C[22,23].Thephonon spectra measured by neutrons contain three groups of peaks:low-frequency modes(0–30meV),middle-frequency group(40–60meV)and boron high-frequency modes(100–160meV)[22].For point-contact spec-tra,the high-frequency modes cannot be seen as separate peaks because of non-spectroscopic(thermal)regime of currentflow where the m.f.p. becomes shorter than the contact size.For the same reason,the middle-size peaks are smeared,approaching the thermal regime.On the contrary, the low-frequency peaks are well resolved and can be compared with the phonon spectra.It should be noted that the neutron spectra are taken at room temperature while the PC spectra at liquid helium temperature.For non-superconducting LaNi2B2C the positions of the low-frequency peaks are very close in both spectra(a)and(b)whereas for YNi2B2C the whole low-frequency group in PC spectrum(d)is shifted appreciably below the neutron one(c).This substantial softening of the low-frequency peaks with decreasing temperature was thoroughly studied in Ref.[24]by neutron scat-tering.A special problem arises with the low-frequency peak at≈4meV, which is not resolved yet.In neutron scattering,the emergence of this peak coincides with the transition to the superconducting state and it is observed6within a narrow solid angle of phonon wave vectors.In PCS it is seen both in the superconducting and sometimes in the normal state whereas in the latter case its intensity is greatly diminished by the magneticfield.Here we remind that in order to measure the PCS spectra the requisite mag-neticfield should be applied to suppress superconductivity.One should also take into account that the lowest-frequency peak is clearly seen in the EPI spectrum which is the phonon DOS weighted by the averaged EPI matrix element within a relatively large(∼45◦)solid angle.Summarizing the PCS study of EQI function,one can argue that the low frequency modes are characteristic of the superconducting compounds while the behaviour of high energy part of the spectra does not differ appreciably for superconducting and non-superconducting compounds[25,23,18]. 3.0.6.Low-frequency phonon and crystal-electric-field excitation peaks in ErNi2B2CIn the R Ni2B2C compound where magnetic and superconducting orders coexist(i.e.R-ion is magnetic),the new branches of excitations appear which can interact with an electron.These are the magnons at tempera-tures below the characteristic magnetic transition temperatures(T m,T N) and crystal-electric-field(CEF)excitations.Neutron scattering experiments and magnetization measurements show that the characteristic energies in the latter case are absent in the range2-10meV in Ho-,and possibly,Dy-compounds[26,27].In Fig.6the PC EQI spectra are shown for two different ErNi2B2C-Ag point contacts.Along with the second harmonic curves1,2, V2(V),taken in the magneticfield needed to destroy superconductivity,the Fig.6shows(insets)the Andreev-reflection spectra R(V)for the same junc-tions.These curves serve as a”passport”evidencing that there is an intact material under the contact.Both PC spectra have a large low-frequency peak at about8-9meV confirming that this low-frequency phonon feature is necessary for observation of the superconducting state.There is an ad-ditional structure at about6meV which most probably corresponds to the CEF-excitation determined in ErNi2B2C by neutrons[28,29].There is also a non-identified structure(maximum of R(V))at zero bias which does not belong to superconductivity.3.0.7.Low-energy peaks in HoNi2B2C and DyNi2B2C compounds.The low-energy parts of the EQI spectra of HoNi2B2C and DyNi2B2C are shown in Fig.7.These compounds possess the same ground state(commen-surate AFM order with magnetic moments aligned ferromagnetically along the[110]direction on the R C planes[5])though with different T N.Their spectra are very similar in overall shape while the positions of peaks are different.The characteristic energies are hardly due only to the differences7 between the phonon branches since the masses of the constituent atoms are nearly the same.Quite definitely,the magnetic excitations should be involved.This follows from the strong temperature and magneticfield de-pendences of the intensity and energy position in HoNi2B2C[25,23].It is difficult to interpret these dependences,since the magnetic phase diagram in HoNi2B2C is very complicated.Fortunately,it is simpler in DyNi2B2C. The unexpected temperature dependence of the lowest-peak for the latter compound is shown in Fig.8[30].At lowering the temperature,the lowest-frequency peak appears at about15K,much above the superconducting order T c=6K and even the magnetic order T N=10.6K.Its height and area grow linearly with T(see the lower inset),which means that its width remains approximately constant.It can also be seen in the superconducting state as a strong feature superimposed on the rapidly changing background due to the superconducting DOS.The other phonon lines(eV=10−30 meV in Fig.8)are smeared due to the large background in the PC spectra without any noticeable overall change of intensity with temperature.We are inclined to relate the lowest-lying peak with magnetic excitations(like the same peak at eV=3.5meV,Fig,7,in HoNi2B2C).It should not be the true magnon density of state peak,since it is observed above T N in DyNi2B2C, neither it is due to the CEF excitation,since no peak at this energy is expected.Its origin still remains a puzzle.Perhaps it may be attributed to the spinfluctuations which,judging from the neutron measurement,have a large tail at higher temperatures[5].In HoNi2B2C,the lowest-frequency peak mentioned above exists starting at T=12K,which is also above the magnetic transition temperature T m=8.5K in this material.4.DiscussionIn literature[31,32]one can encounter a statement that at least the non-magnetic compounds R Ni2B2C(Y,Lu)are similar to A15superconductors in that they have enhanced electron density of state at the Fermi energy and their Cooper-pairing mechanism involves phonons[2,3].Still,despite several attempts,no phonon structure was observed above the energy gap in the tunneling characteristics[35,36,37,38].In the tunneling characteristics of A15,a distinct phonon structure is observed with a proper value of the electron-phonon parameterλ[40].For magnetic R Ni2B2C,the situation is even worse,since the superconducting energy gap is not safely measured [35],to say nothing about the above the gap spectroscopic structure.This situation is disturbing and similar to that in high-T c superconductors where no structure is seen above the gap,yet[33,34].Contrary to tunneling,the PC spectra show strong electron-quasiparticles interactions both with phonons and magnetic excitations.In principle,they8can be studied both in normal and superconducting[10]states.Inter-pretation of these spectra is not straightforward,since several electron-quasiparticles interactions can interfere with each other.The magnetic structure can hinder the electron-phonon interaction responsible for Cooper pairing[41,42].On the other hand,the superconducting transition may lead to a change in magnetic order[43]since it affects the RKKY interaction. Even in the non-magnetic compounds,the proximity of the superconduct-ing energy gap to nonadiabatic softening of phonon modes may lead to drastic changes in the phonon spectrum and electron-phonon interaction. Only the systematic study of PC spectra,both in non-magnetic and mag-netic compounds in different magneticfields and at various temperatures, can shed light on the peculiarities of Cooper pairing in these compounds. In this respect,the use of high quality single crystals is invaluable,since the properties of these compounds are often very anisotropic. References1.Nagarajan,R.,Mazumdar, C.,Hossain,Z.,Dhar,S.K.,Gopalakrishnan,K.V.,Gupta,L.C.,Godart,C.,Padalia,B.D.,and Vijayaraghavan,R.(1994)Bulk Su-perconductivity at an Elevated Temperature(T c≈12K)in a Nickel Containing Alloy System Y-Ni-B-C,Phys.Rev.Lett.72,274-277.wrie,D.D.,Franck,J.P.(1995)Boron isotope effect in Ni and Pd based borocar-bide superconductors,Physica C245,159-163.3.Cheon,K.O.,Fisher,I.R.,and Canfield,P.C.(1999)Boron isotope effect in single-crystal YNi2B2C and LuNi2B2C superconductors,Physica C312,35-39.4.Maki,K.(2000)Possible Unconventional Superconductivity in Borocarbides,in-vited talk in NATO ARW”Rare Earth Transition Metal Borocarbides(Nitrides): Superconducting,Magnetic and Normal State Properties”,14-17June2000,Dres-den,Germany.5.Lynn,J.W.,Skanthakumar,S.,Huang,Q.,Sinha,S.K.,Hossain,Z.,Gupta,L.C.,Nagarajan,R.,and Godart,C.(1997)Magnetic order and crystal structure in the superconducting R Ni2B2C materials,Phys.Rev.B55,6584-6598.6.Canfield,P.C.,Bud’ko,S.L.,and Cho,B.K.(1996)Possible co-existence of super-conductivity and weak ferromagnetism in ErNi2B2C,Physica C(Amsterdam)262, 249-254.7.Blonder,G.E.,Tinkham,M.and Klapwijk,T.M.(1982)Transition from metallicto tunneling regimes in superconducting microconstrictions:Excess current,charge imbalance,and supercurrent conversion,Phys.Rev.B25,4515-4532.8.Dynes,R.C.,Narayanamurti,V.,and Garno,J.P.(1978)Direct Measurements ofQuasiparticle-Lifetime Broadening in Strong-Coupled Superconductor Phys.Rev.Lett.41,1509-1512.9.Yanson,I.K.(1974)Non-linear effects in electrical conductivity of point contactsand electron-phonon interaction in normal metals,Zh.Exper.Theor.Phys.66, 1035-1050[Sov.Phys.JETP39,506].10.Yanson,I.K.(2000)Point-contact Spectroscopy of Superconductors,in I.O.Kulikand R.Ellialtioglu(eds.),Proceedings of NATO ASI:”Quantum Mesoscopic Phe-nomena and Mesoscopic Devices in Microelectronics”,Kluwer Academic Publishers, Bilkent-Antalya.11.Yanson,I.K.,Bobrov,N.L.,Tomy,C.V.,and Paul,D.McK(2000)Point-contactspectroscopy of superconducting energy gap in DyNi2B2C,Physica C334,33-43.9 12.Yanson,I.K.,Bobrov,N.L.et al.(2000)Temperature dependence of superconduct-ing energy gap in ErNi2B2C(to be published).13.Eisaki,H.,Takagi,H.,Cava,R.J.,Batlogg,B.,Krajewski,J.J.,Peck,Jr.,W.F.,Mizuhashi,K.,Lee,J.O.,and Uchida,S.(1994)Competition between magnetism and superconductivity in rare-earth nickel boride carbides,Phys.Rev.B50,647-650.14.Gammel,P.L.,Barber,B.,Ramirez,A.P.,Varma,C.M.,Bishop,D.J.,Canfield,P.C.,Kogan,V.G.,Eskildsen,M.R.,Andersen,N.H.,Mortensen,K.,and Harada, K.(2000)Effects of Magnetic Order on the Superconducting Length Scales and Critical Fields in Single Crystal ErNi2B2C,Phys.Rev.Lett.82,1756-1759.15.Rybaltchenko,L.F.,Yanson,I.K.,Jansen,A.G.M.,Mandal,P.,Wyder,P.,Tomy,C.V.and Paul,D.McK.(1996)Andreev-reflection study of superconductingRNi2B2C compounds,Physica B218,189-192.16.Rybaltchenko,L.F.,Yanson,I.K.,Jansen,A.G.M.,Mandal,P.,Wyder,P.,Tomy,C.V.,and Paul,D.McK.(1996)Two superconducting states of HoNi2B2C as seenby Andreev reflection in point-contacts,Europhys.Lett.33,483-488.17.Du Mar,A.C.,Rathnayaka,K.D.D.,Naugle,D.G.,Canfield,P.C.,and Cho,B.K.(1996)Magnetic and Superconducting Phase Diagrams of Single Crystal HoNi2B2C, Czechoslovak Journal of Physics,46,Suppl.S2,843-844.18.Yanson,I.K.(1999)Point-Contact Spectroscopy of Superconducting R Ni2B2C(R=rare earth,Y),in M.Ausloos and S.Kruchinin(eds.),Symmetry and Pair-ing in Superconductors,Kluwer Academic Publishers,printed in the Netherlands, pp.271-28519.Kulik,I.O.,Omel’yanchuk,A.N.and Shekhter,R.I.(1977)Electrical conductivity ofpoint microcontacts and spectroscopy of phonons and impurities in normal metals, Fiz.Nizk.Temp.3,1543-1558[Sov.J.Low Temp.Phys.3,740].20.I.K.Yanson and A.V.Khotkevich,Atlas of Point Contact Spectra of Electron-Phonon Interaction in Metals,1980,Nauka Publish,Kiev[Engl.transl.: A.V.Khotkevich and I.K.Yanson,Kluwer Academic,New York,1995)].21.Shulga,S.V.,Drechsler,S.-L.,Fuchs,G.,M¨u ller,K.-H.,Winzer,K.,Heinecke,M.,and Krug,K.(1998)Upper Critical Field Peculiarities of Superconducting YNi2B2C and LuNi2B2C,Phys.Rev.Lett.80,1730-1733.‘22.Gompf,F.,Reichardt,W.,Schober,H.,Renker,B.,and Buhgeister,M.(1997)Lattice vibrations and electron-phonon coupling in superconducting quarternary borocarbides:An inelastic neutron-scattering investigation,Phys.Rev.B55,9058-9066.23.Yanson,I.K.,Fisun,V.V.,Jansen,A.G.M.,Wyder,P.,Canfield,P.C.,Cho,B.K.,Tomy,C.V.,and Paul,D.McK.(1997)Observation of Electron-phonon Interaction with Soft Phonons in Superconducting R Ni2B2C,Phys.Rev.Lett.78,935-938.24.Bullock,M.,Zarestky,J.,Stassis,C.,Goldman,A.,Canfield,P.,Honda,Z.,Shirane,G.,and Shapiro,S.M.(1998)Low-energy phonon excitations in superconductingR Ni2B2C(R=Lu,Y),Phys.Rev.B57,7916-7921.25.Yanson,I.K.,Fisun,V.V.,Jansen,A.G.M.,Wyder,P.,Canfield,P.C.,Cho,B.K.,Tomy,C.V.,and Paul,D.McK.(1997)Point-contact-spectroscopy evidence of quasi-particle interactions in RNi2B2C(R=Ho,Y),Fiz.Nizk.Temp.23,951-964[Low Temp.Phys.23,712-723].26.Cho,B.K.,Harmon,B.N.,Johnston,D.C.,and Canfield,P.C.(1996)Crystallineelectric-field effects in single-crystal HoNi2B2C,Phys.Rev.B53,2217-2220.27.Gasser,U.,Allenspach,P.,Buchgeister,M.,Fauth, F.,Henggeler,W.,Mesot,J.,Rosenkranz,S.,Vorderwisch,P.,and Furrer,A.(1996)Neutron crystal-field spectroscopy of RNi2B2C(R=Ho,Er,Tm),Czechoslovak Journal of Physics46, Suppl.S2,821-822.28.Allenspach,P.(2000)Crystal Electric Field Effects in Borocarbide Superconductors,invited talk in NATO ARW”Rare Earth Transition Metal Borocarbides(Nitrides): Superconducting,Magnetic and Normal State Properties”,14-17June2000,Dres-10den,Germany.29.Loewenhaupt,M.(2000)Crystal Field Effects in Borocarbides Studied by Inelas-tic Neutron Scattering,invited talk in NATO ARW”Rare Earth Transition Metal Borocarbides(Nitrides):Superconducting,Magnetic and Normal State Properties”, 14-17June2000,Dresden,Germany.30.Yanson,I.K.,Bobrov,N.L.,Tomy, C.V.and Paul, D.McK.(2000)Electron-quasiparticle interaction in DyNi2B2C measured by point-contact spectroscopy, Physica C.31.Carter,S.A.,Batlogg,B.,Cava,R.J.,Krajewski,J.J.,Peck,Jr.,W.F.,and Takagi,H.(1994)Electron density of states in the borocarbide intermetallic superconduc-tors,Phys.Rev.B50,R4216-R4219.32.Vaglio,R.,Andreone,A.,Aruta,C.,Cassinese,A.,Fontana,F.,Crabtree,G.W.,Iavarone,M.,Y.De Wilde,Maritato,L.,Attanasio,C.,Coccorese,C.,Salluzzo,M., and Salvato,M.(1997)Properties of YNi2B2C superconducting thinfilms,Phys.Rev.B56,934-939.33.Tao,H.J.,Chang,A.,Lu,F.,and Wolf,E.L.(1992)Electron tunneling spectroscopyof single-crystal Bi2Sr2CaCu2O8,Phys.Rev.B45,10622-10632.34.Chen,J.,Zasadzinski,J.F.,Gray,K.E.,Wagner,J.L.,and Hinks,D.G.(1994)Point-contact tunneling study of HgBa2CuO4+δ:BCS-like gap structure,Phys.Rev.B49, 3683-3686.35.Watanabe,T.,Hasegawa,T.,Kitazawa,K.,and Gupta,L.C.(1999)Magnetismand superconductivity in ErNi2B2C,Proceedings of LT-22,Helsinki’99,preprint submitted to Physica B9July199936.Hasegawa,T.,Ogino,M.,Takagi,A.,Watanabe,E.,Nantoh,M.,Takagi,H.,Uchida,S.,Cava,R.J.,and Kitazawa,K.(1994)Tunneling spectroscopic Measurements on Boride Carbide Superconductors,Physica C235-240,1859-1860.37.Ekino,T.,Fujii,H.,Kosugi,M.,Zenitani,Yu.,and Akimitsu,J.(1996)Tunnelingspectroscopy of the superconducting energy gap in R Ni2B2C(R=Y and Lu),Phys.Rev.B53,5640-5649.38.De Wilde,Y.,Iavarone,M.,Welp,U.,Metlushko,V.,Koshelev,A.E.,Aranson,I.,Crabtree,G.W.and Canfield,P.C.(1997)Scanning Tunneling Microscopy Obser-vation of a Square Abrikosov Lattice in LuNi2B2C,Phys.Rev.Lett.78,4273-4276.39.Sakata,H.,Oosawa M.,Matsuba K.,Nishida,N.,Takeya,H.,and Hirata K.(2000)Imaging of a Vortex Lattice Transition in YNi2B2C by Scanning Tunneling Spec-troscopy,Phys.Rev.Lett.84,1583-1586.40.Wolf,E.L.(1985)Principles of Electron Tunneling Spectroscopy,Oxford UniversityPress,New York.41.Morozov,A.I.(1996)Helical magnetic ordering and superconductivity in HoNi2B2C,JETP83,1048-1054.42.Amici.A.,Thalmeier,P.,and Fulde,P.(2000)Theoretical Model for the Supercon-ducting and Magnetically Ordered Borocarbides,Phys.Rev.Lett.841800-1803.43.Nørgaard,K.,Eskildsen,M.R.,Andersen,N.H.,Jensen,J.,Hedeg˚ard,P.,Klausen,S.N.,and Canfield,P.C.(2000)Interdependence of Magnetism and Superconduc-tivity in the Borocarbide TmNi2B2C,Phys.Rev.Lett.84,4982-4985.11 Figure1.Schematic presentation of a sample holder.Figure2.Differential resistance of polycrystalline ErNi2B2C-Ag point contact at differ-ent temperatures:T=4.2,4.6,5.0,5.6,6.2,6.8,7.4,8.2,and9.0K from bottom to top. The experimental curves(dots)are shifted vertically for clarity and normalized for each curve separately.The BTKfits are shown with thin straight lines.H=0.Resistance in the normal state:R N=16.5Ω.Figure3.(a)Temperature dependence of the superconducting energy gap in ErNi2B2C (solid square dots)determined by BTKfitting shown in Fig.2.The dashed vertical straight line points to the magnetic ordering temperature T m.(b)and(c)are smear-ing parameterΓand barrier strength Z for the same point contact,respectively.Note the dip of the gap at T m.Figure4.Temperature dependence of Andreev-reflection spectra for HoNi2B2C.The curves represented by dots are shifted vertically for clarity after subtraction of a poly-nomialfit of the8.6K data[16].Near each curve the temperature is indicated.T c and T∗c stand for superconducting transition temperature and the”BCS-like”transition tem-perature,respectively.BTKfits are shown as thin solid lines.R N=2.65Ω.The Y-scale is shown by a vertical bar of0.1Ω.Note that the BCS-like Andreev-reflection spectra appear only below T∗c.parison of phonon densities of states measured by incoherent scattering of neutrons at room temperatures[22](curves(a)and(c))and electron-quasiparticle spec-tral functions obtained by point-contact spectroscopy at liquid helium temperatures[23] for non-superconducting LaNi2B2C and superconducting YNi2B2C,respectively.Note the substantial softening of low-frequency phonons in YNi2B2C due to lowering temper-ature[24].Figure6.The second harmonic signal for two different ErNi2B2C-Ag point contacts proportional to the EQI spectral function.Resistance of junctions1and2are8.25 and14.4Ω,modulation voltages0.975and1.94mV,and magneticfield1.95and2.6 T,respectively.Correspondingly,for each junction their Andreev-reflection spectra are presented in the inserts.Note the low-frequency peaks at energies below10meV and the feature at eV≃6meV which is tentatively ascribed to crystal-field excitation.parison between the PC spectra of HoNi2B2C and DyNi2B2C.The parameters are R N=2.3and27Ω,T=4.2and1.8K,and H=0.5and0.65T,for HoNi2B2C and DyNi2B2C,respectivelyFigure8.The temperature dependence of the EQI PC spectra of DyNi2B2C with R N=4.8Ω,V1=0.76mV.The temperatures are6,7,9,11,and15K for different curves,respectively.Either the area or the height defined as is shown in the upper inset for T=6K are used for the intensity of the lowest-lying peak.The lower inset displays the temperature dependence of these parameters(squares-area,dots-heights)normalized at T=7K.Three more pairs of dots are added which correspond to the other contact (not shown)whose characteristic is presented in Ref.[30].Note the onset temperature ≈15K which is substantially higher than T N=10.5K and T c=6K.H=0.。