第三章刚体力学
- 格式:ppt
- 大小:1.69 MB
- 文档页数:93


第三章 刚体力学习题答案3-1 如图3-1示,一轻杆长度为2l ,两端各固定一小球,A 球质量为2m ,B 球质量为m ,杆可绕过中心的水平轴O 在铅垂面内自由转动,求杆与竖直方向成θ角时的角加速度.解:系统受外力有三个,即A ,B 受到的重力和轴的支撑作用力,轴的作用力对轴的力臂为零,故力矩为零,系统只受两个重力矩作用. 以顺时针方向作为运动的正方向,则A 球受力矩为正,B 球受力矩为负,两个重力的力臂相等为sin d l θ=,故合力矩为2sin sin sin M mgl mgl mgl θθθ=-=系统的转动惯量为两个小球(可视为质点)的转动惯量之和22223J ml ml ml =+=应用转动定律 M J β=有:2sin 3mgl ml θβ= 解得sin 3g lθβ=3-2 计算题3-2图所示系统中物体的加速度.设滑轮为质量均匀分布的圆柱体,其质量为M ,半径为r ,在绳与轮边缘的摩擦力作用下旋转,忽略桌面与物体间的摩擦,设1m =50kg,2m =200kg,M =15kg,r =0.1m.解: 分别以1m ,2m 滑轮为研究对象,受力图如图(b)所示.对 1m ,2m 运用牛顿定律,有a m T g m 222=- ① a m T 11= ②对滑轮运用转动定律,有图3-1 图3-2β)21(212Mr r T r T =- ③又, βr a = ④ 联立以上4个方程,得2212s m 6.721520058.92002-⋅=++⨯=++=M m m g m a3-3 飞轮质量为60kg,半径为0.25m,当转速为1000r/min 时,要在5s 内令其制动,求制动力F ,设闸瓦与飞轮间摩擦系数μ=0.4,飞轮的转动惯量可按匀质圆盘计算,闸杆尺寸如图所示.解:以飞轮为研究对象,飞轮的转动惯量212J mR =,制动前角速度为1000260ωπ=⨯rad/s ,制动时角加速度为tωβ-=- 制动时闸瓦对飞轮的压力为N F ,闸瓦与飞轮间的摩擦力f N F F μ=,运用转动定律,得 212f F R J mR ββ-== 则 2N mR F tωμ=以闸杆为研究对象,在制动力F 和飞轮对闸瓦的压力N F -的力矩作用下闸杆保持平衡,两力矩的作用力臂分别为(0.500.75)l =+m 和1l =0-50m ,则有10N Fl F l -=110.50600.252100015720.500.7520.4560N l l mR F F l l t ωπμ⨯⨯⨯===⨯=+⨯⨯⨯N 图3-33-4 设有一均匀圆盘,质量为m ,半径为R ,可绕过盘中心的光滑竖直轴在水平桌面上转动. 圆盘与桌面间的滑动摩擦系数为μ,若用外力推动它使其角速度达到0ω时,撤去外力,求:(1) 此后圆盘还能继续转动多少时间? (2) 上述过程中摩擦力矩所做的功.解:(1)撤去外力后,盘在摩擦力矩f M 作用下停止转动- 设盘质量密度为2mRσπ=,则有20223Rf Mg r dr mgR μπσμ==⎰ 根据转动定律 21,2f M J mR Jα-==43g Rμα-= 034R t gωωαμ-==(2)根据动能定理有 摩擦力的功2220011024f W J mR ωω=-=-3-5 如题3-6图所示,一匀质细杆质量为m ,长为l ,可绕过一端O 的水平轴自由转动,杆于水平位置由静止开始摆下.求: (1)初始时刻的角加速度; (2)杆转过θ角时的角速度.解: (1)由转动定律,有β)31(212ml mg= ∴ lg23=β(2)由机械能守恒定律,有图3-622)31(21sin 2ωθml l mg =∴ lg θωsin 3=3-6 固定在一起的两个同轴均匀圆柱体可绕其光滑的水平对称轴O O '转动.设大小圆柱体的半径分别为R 和r ,质量分别为M 和m .绕在两柱体上的细绳分别与物体1m 和2m 相连,1m 和2m 则挂在圆柱体的两侧,如3-8图所示.设R =0.20m, r =0.10m,m =4 kg,M =10 kg,1m =2m =2 kg,且开始时1m ,2m 离地均为h =2m .求:(1)柱体转动时的角加速度; (2)两侧细绳的张力.解: 设1a ,2a 和β分别为1m ,2m 和柱体的加速度及角加速度,方向如图(如图b).(a)图 (b)图(1) 1m ,2m 和柱体的运动方程如下:2222a m g m T =- ① 1111a m T g m =- ②βI r T R T ='-'21 ③式中 ββR a r a T T T T ==='='122211,,,而 222121mr MR I += 由上式求得22222222121s rad 13.68.910.0220.0210.042120.0102121.022.0-⋅=⨯⨯+⨯+⨯⨯+⨯⨯⨯-⨯=++-=gr m R m I rm Rm β(2)由①式8.208.9213.610.02222=⨯+⨯⨯=+=g m r m T βN由②式1.1713.6.2.028.92111=⨯⨯-⨯=-=βR m g m T N3-7 一风扇转速为900r/min,当马达关闭后,风扇均匀减速,止动前它转过了75转,在此过程中制动力做的功为44.4J,求风扇的转动惯量和摩擦力矩.解:设制动摩擦力矩为M ,风扇转动惯量为J ,止动前风扇的角位移2N θπ=,摩擦力矩所做的功为2A M M N θπ=-=-摩擦力所做的功应等于风扇转动动能的增量,即2102A J ω=-2222(44.4)0.01(9002/60)AJ ωπ⨯-=-=-=⨯kg ⋅m 2 44.40.09422275A M N ππ-=-=-=⨯N ⋅m 3-8 一质量为M 、半径为r 的圆柱体,在倾斜θ角的粗糙斜面上从距地面h 高处只滚不滑而下,试求圆柱体滚止地面时的瞬时角速度ω.解: 在滚动过程中,圆柱体受重力Mg 和斜面的摩擦力F 作用,设 圆柱体滚止地面时,质心在瞬时速率为v ,则此时质心的平动动能为212Mv ,与此同时,圆柱体以角速度ω绕几何中心轴转动,其转动动能为212J ω.将势能零点取在地面上,初始时刻圆柱体的势能为Mgh ,由于圆柱体只滚不滑而下,摩擦力为静摩擦力,对物体不做功,只有重力做功,机械能守恒,于是有221122Mgh Mv J ω=+ 式中 21,2J Mr v r ω==,代入上式得 22211()22Mgh Mr Mr ω=+即 23gh r ω=3-9 一个轻质弹簧的倔强系数 2.0k =N/m,它的一端固定,另一端通过一条细绳绕过一个定滑轮和一个质量为m =80g 的物体相连,如图所示. 定滑轮可看作均匀圆盘,它的质量为M =100g,半径r =0.05m. 先用手托住物体m ,使弹簧处于其自然长度,然后松手.求物体m 下降h =0.5m 时的速度为多大?忽略滑轮轴上的摩擦,并认为绳在滑轮边缘上不打滑.解:由于只有保守力(弹性力、重力)做功,所以由弹簧、滑轮和物体m 组成的系统机械能守恒,故有222111222mgh kh I mv ω=++21,2v r I Mr ω==所以 22 1.4812mgh kh v M m -==+m/s3-10 有一质量为1m 、长为l 的均匀细棒, 静止平放在滑动摩擦系数为μ的水平桌面上,它可绕通过其端点O 且与桌面垂直的固定光滑轴转动. 另有一水平运动的质量为2m 的小滑块, 从侧面垂直于棒与棒的另一端A 相碰撞, 设碰撞时间极短. 已知小滑块在碰撞前后的速度分别为1V 和2V ,如图示,求碰撞后从细棒开始转动到停止转动的过程所需的时间(已知棒绕O点的转动惯量2113J m l =).图3-11图3-12解:对棒和滑块组成的系统,因为碰撞时间极短,所以棒和滑块所受的摩擦力矩远小于相互间的冲量矩,故可认为合外力矩为零,所以系统的角动量守恒,且碰撞阶段棒的角位移忽略不计,由角动量守恒得22122113m v l m v l m l ω=-+碰撞后在在转动过程中棒受到的摩擦力矩为 11012tf m M gdx m gl l μμ=-=-⎰由角动量定理得转动过程中210103tfM dt m l ω=-⎰ 联立以上三式解得:12212V V t m m gμ+= 3-11 哈雷彗星绕太阳运动的轨道是一个椭圆.它离太阳最近距离为1r =8.75×1010m 时的速率是1v =5.46×104m ·s -1,它离太阳最远时的速率是2v =9.08×102m ·s -1,这时它离太阳的距离2r 为多少?(太阳位于椭圆的一个焦点.)解: 哈雷彗星绕太阳运动时受到太阳的引力——即有心力的作用,所以角动量守恒;又由于哈雷彗星在近日点及远日点时的速度都与轨道半径垂直,故有 2211mv r mv r =∴ m 1026.51008.91046.51075.81224102112⨯=⨯⨯⨯⨯==v v r r 3-12 平板中央开一小孔,质量为m 的小球用细线系住,细线穿过小孔后挂一质量为1M 的重物.小球做匀速圆周运动,当半径为0r 时重物达到平衡.今在1M 的下方再挂一质量为2M 的物体,如3-14图.试问这时小球做匀速圆周运动的角速度ω'和半径r '为多少?图3-14解: 在只挂重物时1M ,小球作圆周运动的向心力为g M 1,即201ωmr g M =①挂上2M 后,则有221)(ω''=+r m g M M②重力对圆心的力矩为零,故小球对圆心的角动量守恒. 即 v m r mv r ''=00ωω''=⇒2020r r ③联立①、②、③得10021123011213212()M g mr M g M M mr M M M M r g r m M M ωωω=+'=+'==⋅'+3-13 如图示, 长为l 的轻杆, 两端各固定质量分别为m 和2m 的小球, 杆可绕水平光滑轴在竖直平面内转动, 转轴O 距两端的距离分别为/3l 或2/3l . 原来静止在竖直位置. 今有一质量为m 的小球, 以水平速度0v 与杆下端的小球m 做对心碰撞, 碰后以0/2v 的速度返回, 试求碰撞后轻杆所获得的角速度ω.解:将杆与两端的小球视为一刚体,水平飞来的小球m 与刚体视为一系统,在碰撞过程中,外力包括轴O 处的作用力和重力,均不产生力矩,故合外力矩为零,系统角动量守恒- 选逆时针转动为正方向,则由角动量守恒得 0022323v ll mv m J ω=-+ 222()2()33l l J m m =+图3-13解得 032v lω=3-14 圆盘形飞轮A 质量为m , 半径为r , 最初以角速度0ω转动, 与A 共轴的圆盘形飞轮B质量为4m ,半径为2r , 最初静止, 如图所示, 两飞轮啮合后, 以同一速度ω转动, 求ω及啮合过程中机械能的损失.解:以两飞轮组成的系统为研究对象,由于运动过程中系统无外力矩作用,角动量守恒,有22201114(2)222mr mr m r ωωω=+ 得 0117ωω=初始机械能为 2222100111224W mr mr ωω==啮合后机械能为222222201111114(2)2222174W mr m r mr ωωω=+=则机械能损失为 221201611617417W W W mr W ω∆=-==3-15 如图示,一匀质圆盘半径为r ,质量为1m ,可绕过中心的垂轴O 转动.初时盘静止,一质量为2m 的子弹一速度v 沿与盘半径成160θ︒=的方向击中盘边缘后以速度/2v 沿与半径方向成230θ︒=的方向反弹,求盘获得的角速度.解:对于盘和子弹组成的系统,撞击过程中轴O 的支撑力的力臂为零,不提供力矩,其他外力矩的冲量矩可忽略不计,故系统对轴O 的角动量守恒,即12L L =,初时盘的角动量为零,只有子弹有角动量,故图3-14 图3-1512sin 60L m vr ︒=末态中盘和子弹都有角动量,设盘的角速度为ω,则22211sin 3022v L m r m r ω︒=+ 故有 22211sin 60sin 3022v m vr m r m r ω︒︒=+可解得:1ω=3-16 一人站在一匀质圆板状水平转台的边缘,转台的轴承处的摩擦可忽略不计,人的质量为'm ,转台的质量为10'm ,半径为R .最初整个系统是静止的,这人把一质量为m 的石子水平地沿转台的边缘的切线方向投出,石子的速率为v (相对于地面).求石子投出后转台的角速度与人的线速度.解:以人、转台和石子组成的系统为研究对象,由于系统无外力矩作用,角动量守恒,设转台角速度ω的转向与投出的石子速度v 方向一致,初始时系统角动量为零,得0J mRv ω+= 人和转台的转动惯量'2'21102J m R m R =+,代入上式后得 '6mvm Rω=-人的线速度为'6mvv R mω==-其中负号表示转台角速度转向和人的线速度方向与假设方向相反-3-17 一人站在转台上,两臂平举,两手各握一个4m =kg,哑铃距转台轴00.8r =m,起初转台以02ωπ=rad/s 的角速度转动,然后此人放下两臂,使哑铃与轴相距r =0.2m,设人与转台的转动惯量不变,且5J =kg ⋅m 2,转台与轴间摩擦忽略不计,求转台角速度变为多大?整个系统的动能改变了多少?解:以人、转台和哑铃组成的系统为研究对象,由于系统无外力矩作用,角动量守恒,有2200(2)(2)J mr J mr ωω+=+22002225240.8212.025240.2J mr J mr ωωπ++⨯⨯==⨯=++⨯⨯rad/s 动能的增量为222200011(2)(2)22W W W J mr J mr ωω∆=-=+-+222211(5240.2)12(5240.8)(2)22π=⨯+⨯⨯⨯-⨯+⨯⨯⨯ =183J3-18 如3-20图所示,质量为M ,长为l 的均匀直棒,可绕垂直于棒一端的水平轴O 无摩擦地转动,它原来静止在平衡位置上.现有一质量为m 的弹性小球飞来,正好在棒的下端与棒垂直地相撞.相撞后,使棒从平衡位置处摆动到最大角度=θ30°处.(1)设这碰撞为弹性碰撞,试计算小球初速0v 的值; (2)相撞时小球受到多大的冲量?解: (1)设小球的初速度为0v ,棒经小球碰撞后得到的初角速度为ω,而小球的速度变为v ,按题意,小球和棒做弹性碰撞,所以碰撞时遵从角动量守恒定律和机械能守恒定律,可列式:mvl I l mv +=ω0 ①2220212121mv I mv +=ω ② 上两式中231Ml I =,碰撞过程极为短暂,可认为棒没有显著的角位移;碰撞后,棒从竖直位置上摆到最大角度o30=θ,按机械能守恒定律可列式:)30cos 1(2212︒-=lMg I ω ③ 由③式得2121)231(3)30cos 1(⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡︒-=lg I Mgl ω由①式mlI v v ω-=0 ④ 由②式mI v v 2202ω-= ⑤所以22001)(2ωωmv ml I v -=-图18求得glmM m m M l ml I l v +-=+=+=31232(6)311(2)1(220ωω(2)相碰时小球受到的冲量为⎰-=∆=0d mvmv mv t F由①式求得ωωMl l I mv mv t F 31d 0-=-=-=⎰ gl M 6)32(6--=负号说明所受冲量的方向与初速度方向相反.3-19如图示,一个转动惯量为I ,半径为R 的定滑轮上面绕有细绳,并沿水平方向拉着一个质量为M 的物体 A. 现有一质量为m 的子弹在距转轴2R 的水平方向以速度0v 射入并固定在定滑轮的边缘,使滑轮拖住A 在水平面上滑轮.求(1)子弹射入并固定在滑轮边缘后,滑轮开始转动时的角速度ω.(2)若定滑轮拖着物体A 刚好转一圈而停止,求物体A 与水平面间的摩擦系数μ(轴上摩擦力忽略不计).解:(1)子弹射入定滑轮前后,子弹、定滑轮及物体A 构成的系统角动量守恒220[]2Rmv mR I MR ω=++ 解得 0222()mv RmR I MR ω=++(2)定滑轮转动过程中物体A 受的摩擦力所做的功等于系统动能的增量 2221()22I mR MR Mg R ωμπ-++=-⨯ 解得 202216()m v RMg mR MR I μπ=++ 3-20 行星在椭圆轨道上绕太阳运动,太阳质量为1m ,行星质量为2m ,行星在近日点和远日点时离太阳中心的距离分别为1r 和2r ,求行星在轨道上运动的总能量.解:将行星和太阳视为一个系统,由于只有引力做功,系统机械能守恒,设行星在近日点图3-19和远日点时的速率分别为1v 和2v ,有2212121122121122m m m m m v G m v G r r -=- 行星在轨道上运动时,受太阳的万有引力作用,引力的方向始终指向太阳,以太阳为参考点,行星所受力矩为零,故行星对太阳的角动量守恒 111222m rv m r v =行星在轨道上运动时的总能量为2212121122121122m m m m E m v G m v G r r =-=- 联立以上三式得:1212Gm m E r r =-+3-21 半径为R 质量为'm 的匀质圆盘水平放置,可绕通过圆盘中心的竖直轴转动. 圆盘边缘及/2R 处设置了两条圆形轨道,质量都为m 的两个玩具小车分别沿两轨道反向运行,相对于圆盘的线速度值同为v . 若圆盘最初静止,求两小车开始转动后圆盘的角速度.解: 设两小车和圆盘运动方向如图所示,以圆盘转动方向为正向,外轨道上小车相对于地面的角动量为()mR R v ω-,内轨道上小车相对于地面的角动量为11()22m R R v ω+,圆盘的角动量为'212J m R ωω=,由于两小车和圆盘组成的系统,外力对转轴的力矩为零,角动量守恒,得 '2111()()0222mR R v m R R v m R ωωω-+++= '2(52)mvm m Rω=+ 3-22 如图示,一匀质圆盘A 作为定滑轮绕有轻绳,绳上挂两物体B 和C,轮A 的质量为1m ,半径为r ,物体B 、C 的质量分别为2m 、3m ,且2m >3m . 忽略轴的摩擦,求物体B 由静止下落到t 时刻时的速度.图3-21图3-22解:把滑轮和两个物体作为一个系统,其运动从整体上看对定轴O 是顺时针方向的,即轮A 沿顺时针方向转动物体B 向下运动物体C 向上运动,故以顺时针方向的运动作为系统运动的正方向,根据角动量定理,得00tMdt L L =-⎰(1)(1)式左边为系统受到的合外力矩对轴O 的冲量矩,由于轮A 所受重力和轴的作用力对轴O 的力矩为零,故只有两物体所受重力提供力矩,注意到两个重力矩的方向相反,故合力矩为2121()M m gr m gr m m gr =-=- (2)(1)式右边为系统对轴O 的角动量的增量- 0t =时系统静止,角动量00L = (3)到t 时刻,A 、B 、C 三个物体均沿顺时针方向运动,角动量均为正- 设此时轮A 的角速度ω,B 、C 两物体速率相同设为v ,则有212312A B C L L L L m r m vr m vr ω=++=++ (4)把(2)、(3)、(4)式代入(1)式有2211231()2m m grt m r m vr m vr ω-=++由于系统为一连接体,两物体的速率与轮边缘的速率相同,即有v r ω= 把此式代入(5)式即可求得物体下落t 时的速度 211232()23m m gtv m m m -=++。









第三章刚体力学本章介绍刚体运动状态的描述(§3.1-§3.2)以及刚体受力与运动状态的关系(§3.3-§3.10)。
其内容包括:刚体运动学、刚体静力学和刚体动力学,重点掌握刚体运动学和刚体动力学。
刚体是指在任何情况下形状、大小都不发生变化的力学体系,它是一种理想物理模型,只要一个物体中任意两点的距离不因受力而改变,它就可以称为刚体。
§3.1 刚体运动的分析一、描述刚体位置的独立变量刚体的特性是任意两点距离不因受力而变。
这种特性决定了确定刚体的位置并不需要许多变量,而只要少数变量就行。
能完全确定刚体位置的,彼此独立的变量个数叫刚体的自由度。
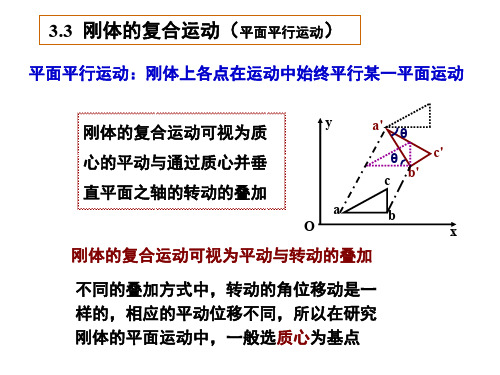
二、刚体运动的分类及其自由度1、平动:自由度3,可用其中任一点的坐标x、y、z描述;2、定轴转动:自由度1,用对轴的转角φ描述;3、平面平行运动:自由度3,用基点的坐标(x o,y o)及其对垂直平面过基点的轴的转角φ描述。
4、定点转动:自由度3,用描述轴的方向的θ,ψ角和轴线的转角ψ描述。
5、一般运动:自由度6,用描述质心位置的坐标(x c,y c,z c)和通过的定点的轴的三个角(θ,φ,ψ)描述。
§3.2 角速度矢量、角速度矢量及其与刚体中任本节重点是:掌握角位移矢量一点的线位移、线速度的相互关系。
理解有限转动时角位移不是矢量,只有无限小角位移才是矢量。
一、有限转动与无限小转动1、有限转动不是矢量,不满足对易律2、无限小转动是矢量,它满足矢量对易律。
①线位移△r与无限小角位移△n的关系设转轴OM,有矢量△n,其大小等于很小的转角Δθ,方向沿转轴方向,转轴的方向与刚体转动方向成右手螺旋,则△n称为角位移矢量。
由图3.2.1很容易求得即线位移△r=角位移△n与位矢r的矢量积。
②角位移和△n满足矢量对易律利用两次位移的可交换性,可证得该式表明:微小转动的合成遵循平行四边形加法的对易律,从而无限小角位移△n是一个矢量。





