七年级求代数式的值习题

4.3代数式的值一、选择题1.已知|x|=3，|y|=2，且xy>0，则x−y的值等于()A. 5或−5B. 1或−1C. 5或1D. −5或−12.若|a|=8，|b|=5，且ab<0，那么a−b的值为()A. 3或13B. 13或−13C. 8或−8D. −3或−133.已知m是√15的整数部分，n是√10的小数部分，则m2−n的值是()A. 6−√10B. 6C. 12−√10D. 134.已知|2m+n+1|+(3y+1)2=0，则3y+2m+n的值是()A. 1B. 0C. −2D. 25.已知代数式x−5y的值是100，则代数式−2x+10y+5的值是()A. 205B. −200C. −195D. 2006.已知a+b=12，则代数式2a+2b−3的值是()A. 2B. −2C. −4D. −3127.若a，b互为相反数，c，d互为倒数，则代数式(a+b−1)(cd+1)的值是()A. 1B. 0C. −1D. −28.已知a2+3a=1，则代数式2a2+6a−1的值为()A. 0B. 1C. 2D. 39.已知a+b=4，则代数式1+a2+b2的值为()A. 3B. 1C. 0D. −110.若x2−3x−5=0，则6x−2x2+5的值为()A. 0B. 5C. −5D. −10二、填空题11.如果m−n=3，那么2m−2n−3的值是______．12.在一次智力竞赛中，主持人问了这样的一道题目：“a是最小的正整数，b是最大的负整数的相反数，c是绝对值最小的有理数，请问：a、b、c三数之和为多少？”你能回答主持人的问题吗？其和应为______．13.若|x−5|+(y+1)2=0，则xy的值是_______14.有理数2，+7.5，−0.03，−300%，0，中，非负整数有a个，负数有b个，正分数有c个，则a−b+c=__________．三、解答题15.已知a，b互为相反数，m，n互为倒数，c的绝对值为2，求代数式a+b+mn−c的值．16.某班为了开展乒乓球比赛活动，准备购买一些乒乓球和乒乓球拍，通过去商店了解情况，甲乙两家商店出售同样品牌的乒乓球和乒乓球拍，乒乓球拍每副定价48元，乒乓球每盒定价12元，经商谈，甲乙两家商店给出了如下优惠措施：甲店每买一副乒乓球拍赠送一盒乒乓球，乙店全部按定价的9折优惠．现该班急需乒乓球拍5副，乒乓球x盒(不少于5盒)．(1)请用含x的代数式分别表示去甲、乙两店购买所需的费用；(2)当需要购买40盒乒乓球时，通过计算，说明此时去哪家商店购买较为合算；(3)当需要购买40盒乒乓球时，你能给出一种更为省钱的方法吗？试写出你的购买方法和所需费用．17.分别用a,b,c,d表示有理数，a是最小的正整数，b是最大的负整数，c是绝对值最小的有理数，d是数轴上到原点距离为5的点表示的数，求|3a−b+2c−d|的倒数.答案和解析1.【答案】B【解析】解：∵|x|=3，|y|=2，∴x=±3，y=±2．又xy>0，∴x=3，y=2或x=−3，y=−2．∴x−y=±1．故选：B．绝对值的性质：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．有理数的乘法法则：同号得正，异号得负．本题考查了代数式求值、绝对值的性质：互为相反数的绝对值相等．能够根据两个数的乘积的符号判断两个数的符号的关系．2.【答案】B【解析】【分析】本题主要考查的是绝对值，有理数的乘法，有理数的减法，代数式求值的有关知识，先根据ab<0可以得到a，b异号，然后求出a，b，再代入代数式求值即可．【解答】解：∵ab<0，∴a，b异号，∵|a|=8，|b|=5，∴a=8，b=−5或a=−8，b=5，∴a−b=8−(−5)=13或a−b=−8−5=−13．故选B．3.【答案】C【解析】略4.【答案】C【解析】【分析】本题主要考查了绝对值，完全平方的非负性，令2m+n+1=0，3y+1=0，运用整体代入可以求出2m+n=−1，3y=−1的值代入即可求出结果．【解答】解：∵|2m+n+1|+(3y+1)2=0∴2m+n+1=0，3y+1=0∴2m+n=−1，3y=−1∴3y+2m+n=−2．故选C．5.【答案】C【解析】【分析】此题考查了代数式求值，熟练掌握运算法则是解本题的关键．原式前两项提取−2变形后，把已知x−5y=100代入计算即可求出值．【解答】解：∵x−5y=100，∴原式=−2(x−5y)+5=−200+5=−195故选C．6.【答案】B【解析】【分析】本题主要考查的是代数式求值，运用了整体代入法的有关知识，将给出的代数式进行变形，然后整体代入求值即可．【解答】解：∵a+b=12，∴原式=2(a+b)−3=2×12−3=1−3=−2，故选B．7.【答案】D【解析】【分析】本题主要考查的是代数式求值，相反数，倒数的有关知识，先利用相反数，倒数的定义得到a+b=0，cd=1，然后代入代数式求值即可．解：∵a，b互为相反数，c，d互为倒数，∴a+b=0，cd=1，∴原式=(−1)×(1+1)=−2，故选D．8.【答案】B【解析】【分析】此题主要考查了代数式求值，正确将原式变形是解题关键．直接利用已知将原式变形，然后整体代入计算即可求出答案．【解答】解：∵a2+3a=1，∴2a2+6a=2(a2+3a)=2∴2a2+6a−1=2−1=1．故选B．9.【答案】A【解析】解：当a+b=4时，原式=1+12(a+b)=1+12×4=1+2=3，故选：A．将a+b的值代入原式=1+12(a+b)计算可得．本题主要考查代数式求值，解题的关键是得出待求代数式与已知等式间的特点，利用整体代入的办法进行计算．10.【答案】C【解析】本题考查了代数式求值，整体代入法，关键是由x2−3x−5=0，得x2−3x=5把x2−3x看作一个整体，代入计算的值即可．【解答】解：6x−2x2+5，=−2x2+6x+5=−2(x2−3x)+5=−2×5+5=−5.故选C．11.【答案】3【解析】解：∵m−n=3，∴原式=2(m−n)−3=2×3−3=6−3=3．故答案为：3．原式前两项提取公因式变形后，把已知等式代入计算即可求出值．此题考查了代数式求值，利用了整体代入的思想，熟练掌握运算法则是解本题的关键．12.【答案】2【解析】解：∵a是最小的正整数，b是最大的负整数的相反数，c是绝对值最小的有理数，∴a=1，b=1，c=0，∴a+b+c=1+1+0=2．故答案是2．先根据已知条件求出a、b、c的值，再代入代数式求值即可．解题的关键是先求出a、b、c的值，然后再求代数式的值．13.【答案】−514.【答案】2【解析】【分析】本题考查了有理数的分类，解题的关键是分类的标准要不重不漏的找到符合条件的a，b，c的值．根据有理数的分类标准把给出的非负整数有a个，负数有b个，正分数有c 个，，即可求出a−b+c的值．【解答】解：有理数2，+7.5，−0.03，−300%，0中，非负整数有3个，负数有2个，正分数有1个，则a−b+c=3−2+1=2．故答案为2．15.【答案】解：∵a，b互为相反数，m，n互为倒数，c的绝对值为2，∴a+b=0，mn=1，c=±2，当c=2时，a+b+mn−c=0+1−2=−1；当c=−2时，a+b+mn−c=0+1−(−2)=0+1+2=3；由上可得，代数式a+b+mn−c的值是−1或3．【解析】本题考查的是相反数定义，倒数定义和绝对值的性质以及代数式的值，根据a，b互为相反数，m，n互为倒数，c的绝对值为2，可以求得a+b，mn、c的值，从而可以求得所求式子的值．16.【答案】解：(1)甲店购买需付款48×5+(x−5)×12=(12x+180)元；乙店购买需付款48×90%×5+12×90%×x=(10.8x+216)元；(2)当x=40时，甲店需12×40+180=660元；乙店需10.8×40+216=648元；所以乙店购买合算；(3)先甲店购买5副球拍，送5盒乒乓球240元，另外35盒乒乓球再乙店购买需378元，共需618元．【解析】(1)按照对应的方案的计算方法分别列出代数式即可；(2)把x=40代入求得的代数式求得数值，进一步比较得出答案即可；(3)根据两种方案的优惠方式，可得出先甲店购买5副球拍，送5盒乒乓球，另外35盒乒乓球再乙店购买即可．此题考查列代数式，理解两种方案的优惠方案，得出运算的方法是解决问题的关键．17.【答案】解：∵a是最小的正整数，∴a=1，∵b是最大的负整数，∴b=−1，∵c是绝对值最小的有理数，∴c=0，∵d是数轴上到原点距离为5的点表示的数，∴d=±5，∴|3a−b+2c−d|=|3+1+0−5|=1或|3a−b+2c−d|=|3+1+0+5|=9∴|3a−b+2c−d|的倒数为1或19【解析】本题主要考查了有理数的加减混合运算，有理数、绝对值，数轴及倒数，熟练掌握各自的定义是解决本题的关键.根据最小的正整数为1，最大的负整数为−1，绝对值最小的有理数为0，以及数轴上到原点距离的定义，确定出a，b，c，d的值，即可求出|3a−b+2c−d|的值，再求出其倒数即可．。

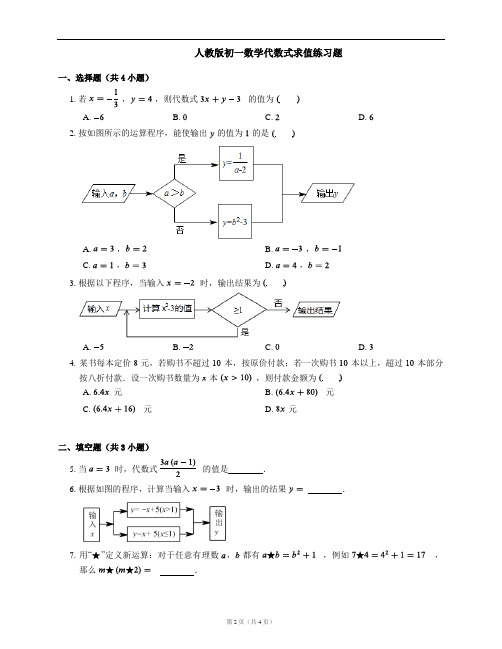
人教版初一数学代数式求值练习题一、选择题（共4小题）1. 若，，则代数式的值为B. C. D.2. 按如图所示的运算程序，能使输出的值为的是A. ，B. ，C. ，D. ，3. 根据以下程序，当输入时，输出结果为C. D.4. 某书每本定价元，若购书不超过本，按原价付款；若一次购书本以上，超过本部分按八折付款．设一次购书数量为本，则付款金额为A. 元B. 元C. 元D. 元二、填空题（共3小题）5. 当时，代数式的值是．6. 根据如图的程序，计算当输入时，输出的结果．7. 用“”定义新运算：对于任意有理数，都有，例如，那么．三、解答题（共3小题）8. “”代表一种新运算，已知，求的值．其中和满足．9. 为解决沙区拥堵问题，政府在三峡广场附近拟建一个地下长方形车库，图案设计如图所示，已知长方形长为米，宽为米，在长方形内部修等宽为米的安全通道，四角修完全一样的正方形临时停车位，且正方形临时停车位的边长为米，若安全通道铺红色地胶，临时停车位铺黄色地胶，其余部分铺绿色地胶．（1）请用含的代数式表示铺绿色地胶部分的面积，并将所得式子化简；（2）如果铺红色地胶的费用为每平方米元，铺黄色地胶的费用为每平方米元，铺绿色地胶的费用为每平方米元，设铺地下车库地面的总费用为元，请用含的代数式表示，并将所得式子化简；（3）在（）的条件下，求当时，求铺地下车库地面的总费用．10. 小王购买了一套经济适用房，他准备将地面铺上地砖，地面结构如图所示．根据图中的数据（单位：），解答下列问题：（1）用含，的代数式表示地面总面积；（2）已知客厅面积比卫生间面积多平方米，且地面总面积是卫生间面积的倍．若铺平方米地砖的平均费用为元，那么铺地砖的总费用为多少元?答案第一部分1. B2. A 【解析】A．当，时，，符合题意；B．当，时，，不符合题意；C．当，时，，不符合题意；D．当，时，，不符合题意．3. B 【解析】当时，；当时，；，当输入时，输出结果为4. C 【解析】设一次购书数量为本，则付款金额为：．第二部分5.6.【解析】，．7.【解析】因为，所以．第三部分8. 由知，，则．9. （1）（2）（3）当时，10. （1）．（2）由题意得：且解得。

初一数学代数式的值练习题精选1.化简代数式322(2x-1+x)-x-1，可以先将括号内的项合并得到322(3x-1)-x-1，再将常数项合并得到966x-325.2.代数式(a+b)2-(a-b)2可以展开得到4ab，代入a=-2、b=-3得到结果12.3.将2(x-y)2+3x-3y+1展开得到2x2-7xy+6y2+3x+1，代入x-y=3得到2y2+15.4.将x(2x-y+3z)展开得到2x3-xy+3xz的值，代入x=7、y=4、z=0得到126.5.将3a-a-a+1化简得到-a-1，代入a=-3得到结果2.6.将b-4ac代入a=2、b=-3、c=4得到-59.7.代数式(1/2-x-y)+5ab可以化简得到(5/2)-x-y+5ab，但没有给出具体的求值。

8.将3x-1+2y+3化简得到3x+2y+2，代入3x-2y得到-x+2.9.将2a+3a+1=6代入得到a=1，代入6a+9a+5得到35.10.将x=-2、y=-5代入得到-9/8，将x=2、y=5代入得到23/8.11.将x=2代入4x2-2xy+2y2得到20-4y+2y2，y的绝对值最小为0，代入得到20.12.将x+3=5-y化简得到y=2-x，代入a/b=b/a得到a=-1，b=-1，代入得到-5/2.13.将2x2+3x+5=6代入得到x=-1或x=5/2，代入6x2+9x-3得到33/2或-3/2.14.将2x-y=5化简得到y=2x-5，代入2y-4x+5得到-3x+5，没有给出具体的求值。

15.将x=11/2代入得到121/4.16.将a=4、b=12代入得到44.17.将x=1、y=-6代入得到(1)37，(2)49，(3)49.18.用代数式10a+(a+5)表示这个两位数，当a=3时得到35.19.用代数式100a+b表示这个四位数，没有给出具体的求值。

20.将x=1、y=-1代入得到-1/2.。

求代数式的值专项练习60题（有答案）1．当x=﹣1时，代数式2﹣x的值是_________ ．2．若a2﹣3a=1，则代数式2a2﹣6a+5的值是_________ ．3．若a2+2a=1，则（a+1）2= _________ ．4．如图是一个数值转换机，若输入a值为2，则输出的结果应为_________ ．5．若x+y=﹣1，且（x+y）2﹣3（x+y）a=7，则a2+2= _________ ．6．若a、b互为相反数，x、y互为倒数，则式子2（a+b）+5xy的值为_________ ．7．若a+b=2，则2a+2b+1= _________ ．8．当a=1，|a﹣3|= _________ ．9．若x=﹣3，则= _________ ，若x=﹣3，则﹣x= _________ ．10．若a，b互为相反数，且都不为零，则（a+b﹣1）（+1）的值为_________ ．11．若a﹣b=，则10（b﹣a）= _________ ．12．如果m﹣n=，那么﹣3（n﹣m）= _________ ．13．a、b互为相反数，m，n互为倒数，则（a+b）2+= _________ ．14．a，b互为相反数，a≠0，c、d互为倒数，则式子的值为_________ ．15．若a﹣b=1，则代数式a﹣（b﹣2）的值是_________ ；若a+b=1，则代数式5﹣a﹣b的值是_________ ．16．d是最大的负整数，e是最小的正整数，f的相反数等于它本身，则d﹣e+2f的值是_________ ．17．当x= _________ 时，代数式2009﹣|2008﹣x|有最大值，最大值为_________ ．18．若|m|=3，则m2= _________ ．19．若代数式2a+2b的值是8，则代数式a+b的值是_________ ．20．若m=n﹣5，则5m﹣5n+5等于_________ ．21．已知x=﹣，则代数式1﹣x3的值等于_________ ．22．当x=2时，x3﹣x﹣8= _________ ．23．若代数式a﹣b的值是1，那么代数式2a﹣（3+2b）的值等于_________ ．24．若x2﹣2x的值是6，则﹣3x2+6x+5的值是_________ ．25．已知x﹣y=5，代数式x﹣2﹣y的值是_________ ．26．已知：a2+ab=5，b2+ab=2，则a2+2ab+b2= _________ ．27．若2x+3=5，则6x+10等于_________ ．28．若m2+2m﹣2=0，则2m2+4m﹣9= _________ ．29．已知多项式3x2﹣4x+6的值为9，则多项式的值为_________ ．30．若3a2﹣a﹣3=0，则6a2﹣2a+9= _________ ．31．若（3+a）2+|b﹣2|=0，则3a﹣2b﹣2012的值为_________ ．32．在数轴上，点A、B分别表示有理数 a、b，原点O恰好是AB的中点，则（a+b）2004+（）2005的值是_________ ．33．如果x2+3x﹣1的值是4，则代数式2x2+6x+5的值是_________ ．34．已知a、b互为相反数，c、d互为倒数，m的绝对值为2，求m2+a+b+的值．35．求代数式的值：（1）当，b=5时，求8a+3b的值；（2）已知a=|﹣4|，b=（﹣2）3，求b2﹣ab的值．36．已知a2+5ab=76，3b2+2ab=51，求代数式a2+11ab+9b2的值．37．当x=2，y=﹣4时，求代数式x2+2xy+y2的值．38．如果有理数a、b满足|a﹣1|+（b+1）2=0，求a101+b100的值．39．当x=﹣，y=﹣3时，求代数式x2﹣2xy+y2的值．40．已知，|a|=3，|b|=5，且a2＞0，b3＜0，求2a+b的值．41．当x=7时，代数式ax3+bx﹣5的值为7；当x=﹣7时，代数式ax3+bx﹣5的值为多少？42．求代数式的值：（1）当a=﹣2，b=5时，求2a+5b的值；（2）已知a=|﹣3|，b=（﹣2）3，求a2+b2的值．43．有理数m，n为相反数，x，y互为负倒数，z的绝对值等于7，求3m+3n+5xy+z的值．44．三个有理数a，b，c的积是负数，其和为正数，当x=++时，试求x2011﹣2010x+2009 的值．45．已知a是最小的正整数，b是a的相反数，c的绝对值为9，试求2a+2b﹣3c的值．46．已知2x2+3x=5，求代数式﹣4x2﹣6x+6的值．47．当a=3，b=﹣2，c=﹣5时，代数式b2﹣4ac的值是_________ ．48．若|a|=4，b是绝对值最小的数，c是最大的负整数，求a+b﹣c的值．49．已知a与b互为相反数，c与d互为倒数，|x|=5，求x2+（a+b）2012+（﹣cd）2013的值．50．若|x﹣4|+（2y﹣x）2=0，求代数式x2﹣2xy+y2的值．51．已知|m|=3，n2=16，且mn＜0，求2m﹣3n的值．52．若a、b互为相反数，c、d互为倒数，|m|=3，求+m2﹣3cd+5m的值．53．己知：|x|=4，y2=；且x＞0，y＜0，求2x﹣7y的值．54．已知m2﹣mn=21，mn﹣n2=﹣12．求下列代数式的值：（1）m2﹣n2（2）m2﹣2mn+n2．55．a※b是新规定的这样一种运算法则：a※b=a2+2ab，例如3※（﹣2）=32+2×3×（﹣2）=﹣3（1）试求（﹣2）※3的值（2）若1※x=3，求x的值（3）若（﹣2）※x=﹣2+x，求x的值56．已知a是最小的正整数，b、c是有理数，且有|2+b|+（3a+2c）2=0，求代数式的值．57．如果4a﹣3b=7，并且3a+2b=19，求14a﹣2b的值．58．已知，求代数式的值．59．已知a、b互为相反数，c、d互为倒数，x的绝对值是5．试求﹣x2+[a+b+cd2﹣（d﹣1）]﹣（a+b﹣4）3﹣|cd ﹣3|的值．60．已知当x=2时，多项式ax5+bx3+cx+3的值为100，那么当x=﹣2时，求多项式ax5+bx3+cx+3的值．求代数式的值60题参考答案：1．∵x=﹣1∴2﹣x=2﹣（﹣1）=2+1=3．2．∵a2﹣3a=1，∴原式=2×1+5=7．3．等式两边同时加1，等式即可转换为a2+2a+1=2，即为（a+1）2=2．故答案为：24．﹣3a2+1=﹣3×4+1=﹣11．5．∵x+y=﹣1，∴（x+y）2﹣3（x+y）a=7，1+3a=7，即a=2，则a2+2=4+2=66．∵a、b互为相反数，x、y互为倒数，∴a+b=0，xy=1，∴2（a+b）+5xy=0+5=57．2a+2b+1=2（a+b）+1=2×2+1=5．8．当a=1时，|a﹣3|=|1﹣3|=|﹣2|=2．9．（1）∵x=﹣3，∴=﹣；（2）∵x=﹣3，∴﹣x=﹣（﹣3）=3．10．由题意得：a+b=0且a≠0、b≠0，∴原式=﹣1×0=0．11．当a﹣b=时，原式=10×（﹣）=﹣4．故填﹣4．12．当m﹣n=时，原式=﹣3×[﹣（m﹣n）]=﹣3×（﹣）=．故填．13．∵a、b互为相反数∴a+b=0∵m，n互为倒数∴mn=1∴（a+b）2+=02+=3故此题应该填3．14．∵a，b互为相反数，a≠0，c、d互为倒数，∴a+b=0，cd=1，∴式子=+（﹣1）2007﹣12008=0﹣1﹣1=﹣2，故答案为﹣2 将a﹣b=1代入得：所求的结果为1+2=3．同理，整理代数式得，5﹣a﹣b=5﹣（a+b），将a+b=1代入得，所求结果为5﹣1=4．故本题答案为：3、4．16．由题意知，d=﹣1，e=1，f=0，所以d﹣e+2f=﹣1﹣1+0=﹣2．故应填﹣217．∵代数式2009﹣|2008﹣x|有最大值，∴2008﹣x=0，即x=2008．当x=2008时，代数式2009﹣|2008﹣x|=2009．故当x=2008时，代数式2009﹣|2008﹣x|有最大值，最大值为200918．∵|m|=3，∴m=﹣3或3，∴m2=（±3）2=919．由题意得：2a+2b=8∴a+b=4．20．∵m=n﹣5，∴m﹣n=﹣5，∴5m﹣5n+5=5（m﹣n）+5=﹣25+5=﹣20．21．∵x=﹣，∴1﹣x3=1﹣（﹣）3=1+=4，故答案为422．当x=2时，x3﹣x﹣8=23﹣2﹣8=﹣2．故答案为：﹣223．∵a﹣b=1，∴原式=2a﹣3﹣2b=2（a﹣b）﹣3=2×1﹣3=﹣1．故答案为﹣124．∵x2﹣2x=6，∴﹣3x2+6x+5=﹣3（x2﹣2x）+5=﹣3×6+5=﹣13．故答案为﹣1325．原式=x﹣y﹣2，当x﹣y=5时，原式=5﹣2=3．故答案为326．∵a2+ab=5，b2+ab=2，∴a2+ab+b2+ab=7，∴a2+2ab+b2=7．故答案为：727．6x+10=3（2x+3）+1=15+1=16．故答案是：16∴m2+2m=2，∴2m2+4m﹣9=2（m2+2m）﹣9=2×2﹣9=﹣5．故答案为﹣5．29．由已知得：3x2﹣4x+6=9，即3x2﹣4x=3，，=（3x2﹣4x）+6，=×3+6=7．故答案为：730．∵3a2﹣a﹣3=0，∴3a2﹣a=3，∴6a2﹣2a+9=2（3a2﹣a）+9=2×3+9=15．故答案为15．31．根据题意得，3+a=0，b﹣2=0，解得a=﹣3，b=2，所以，3a﹣2b﹣2012=3×（﹣3）﹣2×2﹣2012=﹣9﹣4﹣2012=﹣2025．故答案为：﹣202532．∵点A、B分别表示有理数 a、b，原点O恰好是AB 的中点，∴a+b=0，即a=﹣b，∴（a+b）2004+（）2005=0﹣1=﹣133．由x2+3x﹣1=4得x2+3x=5，∴2x2+6x+5=2（x2+3x）+5=2×5+5=15．故本题答案为：15．34．a，b互为相反数，则a+b=0，c，d互为倒数，则cd=1，m的绝对值是2，则m=±2，当m=2时，原式=4+0+=；当m=﹣2时，原式=4+0﹣=．35．（1）∵，b=5，∴8a+3b=﹣4+15=11；（2）∵a=|﹣4|，b=（﹣2）3，∴a=4，b=﹣8时，∴b2﹣ab=64+32=96．（3分）36．a2+11ab+9b2=a2+5ab+6ab+9b2=a2+5ab+3（2ab+3b2）∵a2+5ab=76，3b2+2ab=51，37．∵x=2，y=﹣4，∴x+y=2﹣4=﹣2，x2+2xy+y2=（x+y）2=（﹣2）2=4．38．∵|a﹣1|+（b+1）2=0，∴a﹣1=0，b+1=0，∴a=1，b=﹣1，当a=1，b=﹣1时，原式=1101+（﹣1）100=239．当时，原式==﹣3+9=．40．∵|a|=3，且a2＞0，∴a=±3，∵|b|=5，b3＜0，∴b=﹣5，∴当a=3，b=﹣5时，2a+b=6﹣5=1；当a=﹣3，b=﹣5时，2a+b=﹣6﹣5=﹣11；答：2a+b的值为1或﹣1141．∵x=7时，代数式ax3+bx﹣5的值为7，∴a×73+7b﹣5=7，即a×73+7b=12，∴当x=﹣7时，a×（﹣7）3﹣7x﹣5=﹣（a×73+7b）﹣5=﹣12﹣5=﹣17．42．（1）当a=﹣2，b=5时，2a+5b=2×（﹣2）+5×5=21；（2）∵a=|﹣3|=3，b=（﹣2）3=﹣8，∴a2+b2=9+64=7343．∵m，n为相反数，x，y互为负倒数，z的绝对值等于7，∴m+n=0，xy=﹣1，z=±7，∴3m+3n+5xy+z=3（m+n）+5xy+z=3×0+5×（﹣1）+z=﹣5+z，当z=7时，3m+3n+5xy+z=﹣5+7=2；当z=﹣7时，3m+3n+5xy+z=﹣5﹣7=﹣12．∴3m+3n+5xy+z的值为2或﹣1244．∵三个有理数a，b，c的积是负数，其和为正数，∴三个有理数a，b，c中有两个正数、一个负数，∴、、中有两个1和一个﹣1，∴x=++=1，∴x2011﹣2010x+2009=12011﹣2010×1+2009=045．∵a是最小的正整数，∴a=1，∴b=﹣1，∵c的绝对值为9，∴c=9或﹣9，当c=9时，2a+2b﹣3c=2×1+2×（﹣1）﹣3×9=﹣27，当c=﹣9时，2a+2b﹣3c=2×1+2×（﹣1）﹣3×（﹣9）=27，所以，代数式的值是27或﹣2746．∵2x2+3x=5，∴（2x2+3x）×（﹣2）=5×（﹣2），即：﹣4x2﹣6x=﹣10，∴﹣4x2﹣6x+6=﹣10+6=﹣447．当a=3，b=﹣2，c=﹣5时，原式=（﹣2）2﹣4×3×（﹣5）=64．故答案是6448．由|a|=4，得a=4或a=﹣4，∵b是绝对值最小的数，∴b=0，又∵c是最大的负整数，∴c=﹣1，∴a+b﹣c=4+0﹣（﹣1）=4+1=5，或a+b﹣c=﹣4+0﹣（﹣1）=﹣4+1=﹣3，即a+b﹣c的值为﹣3或549．∵a与b互为相反数，∴a+b=0，∵c与d互为倒数∴cd=1，∵|x|=5，∴x2=25，∴x2+（a+b）2012+（﹣cd）2013=25+0+（﹣1）=24．50．因为|x﹣4|+（2y﹣x）2=0，所以x﹣4=0，2y﹣x=0，解得：x=4，y=2，x2﹣2xy+y2=（x﹣y）2，把x=4，y=2代入得：（4﹣2）2=4，所以代数式x2﹣2xy+y2的值为：451．∵|m|=3，n2=16，∴m=±3，n=±4，又∵mn＜0，∴（1）当m=3，n=﹣4时，2m﹣3n=2×3﹣3×（﹣4），=6+12，=18；（2）当m=﹣3，n=4时，2m﹣3n=2×（﹣3）﹣3×4，=﹣6﹣12，=﹣18．综上所述，2m﹣3n的值为18或﹣1852．∵a、b互为相反数，c、d互为倒数，|m|=3，∴a+b=0，cd=1，m=±3，①m=3时，原式=0+9﹣3+15=21；∴+m2﹣3cd+5m的值是21或﹣953．∵|x|=4，y2=；且x＞0，y＜0，∴x=4，y=﹣，∴2x﹣7y=2×4﹣7×（﹣）=8+1=954．（1）∵m2﹣mn=21，mn﹣n2=﹣12，∴m2﹣n2=（m2﹣mn）+（mn﹣n2）=21﹣12=9；（2）∵m2﹣mn=21，mn﹣n2=﹣12，∴m2﹣2mn+n2=（m2﹣mn）﹣（mn﹣n2）=21﹣（﹣12）=21+12=3355．（1）（﹣2）※3=（﹣2）2+2×（﹣2）×3=4﹣12=﹣8；（2）∵1※x=3，∴12+2x=3，∴2x=3﹣1，∴x=1；（3）﹣2※x=﹣2+x，（﹣2）2+2×（﹣2）x=﹣2+x，4﹣4x=﹣2+x，﹣4x﹣4=﹣2﹣4，﹣5x=﹣6，x=56．由已知得a=1，又因为|2+b|+（3a+2c）2=0，所以2+b=0，3a+2c=0，所以b=﹣2，c=．把a=1，b=﹣2，c=代入原式求得：57．∵4a﹣3b=7，并且3a+2b=19，∴14a﹣2b=2（7a﹣b）=2[（4a+3a）+（﹣3b+2b）]=2[（4a﹣3b）+（3a+2b）]=2（7+19）=52，答：14a﹣2b的值为52∴xy=2（x+y）∴原式===59．∵a、b互为相反数，c、d互为倒数，x的绝对值是5．∴a+b=0，cd=1，x2=25，∴﹣x2+[a+b+cd2﹣（d﹣1）]﹣（a+b﹣4）3﹣|cd﹣3| =﹣25+（0+d﹣d+1）﹣（0﹣4）3﹣|1﹣3|=﹣25+1+64﹣2=3860．x=2时，25a+23b+2c+3=100，∴25a+23b+2c=97，x=﹣2时，ax5+bx3+cx+3=﹣25a﹣23b﹣2c+3=﹣97+3=﹣94。

代数式求值（习题）➢ 例题示范例1：若23a b -=，则代数式2(2)422000b a a b --++的值是_______．思路分析观察已知，发现字母a ，b 的值无法确定，所以考虑整体代入．对比已知及所求，把2a -b 当作一个整体，对所求式子进行变形．原式=2(2)2(2)2000a b a b ---+最后整体代入，化简➢ 巩固练习1. 关于x 的代数式222(28)4(21)x x kx x x ⎡⎤+---+⎣⎦，当k 为何值时，代数式的值是常数？2. 若关于x 的代数式2214(45)64x mx x x mx mx ⎛⎫+---+- ⎪⎝⎭的值与x 无关，求代数式2223(21)363m m m m ⎡⎤-+-+⎢⎥⎣⎦的值． 3. 若232a b a b -=+，则代数式2(2)15(2)22a b a b a b a b-+-+-+的值是_______． 4. 若代数式2346x x -+的值是9，则代数式2463x x -+的值是___________． 5. 若2x y =，则代数式45x y x y-+的值是___________． 6. 已知当5x =时，代数式25ax bx +-的值是10，则当5x =时，代数式25ax bx ++的值是____________．7. 已知当3x =-时，代数式535ax bx cx ++-的值是7，则当3x =时，代数式535ax bx cx ++-的值是__________．8. 若m 表示一个两位数， n 表示一个两位数，把m 放在n 的右边，则这个四位数可用代数式表示为_____________．9. 若a 表示一个一位数，b 表示一个两位数，c 表示一个三位数，把c 放在a的左边，b 放在a 的右边，组成一个六位数，则这个六位数可用代数式表示为__________________．➢ 思考小结1. 已知3240x x --=，则代数式3361x x -++的值是_______．通过本讲的学习，小明的做法：①把含有字母的项“32x x -”作为整体，则324x x -=；②在所求的代数式中找整体，对比系数解决：小刚的做法：①把最高次项“3x ”作为整体，则324x x =+；②在所求的代数式中找整体，对比系数解决：小聪的做法：①把“324x x --”作为整体；②在所求的代数式中找整体，对比系数解决：对比小明、小刚、小聪的做法，我们发现无论把“32x x -”， “3x ”还是“324x x --”作为整体，代入，目标都是把所求的代数式降次，这种转化的思想是“高次降次”．【参考答案】➢巩固练习1.当k=6时，代数式的值为常数2.m=-1，原式=-m-3，当m=-1时，原式=-23.114.75.16.207.-178.100n+m9. 1 000c+100a+b➢思考小结-11。

初中数学代数式求值精选练习题及答案1、已知3a-b+2c=7,5a+4b-3c=6，求代数式a+11b-12c的值；2、已知2m6+ m4= 3，求m的值；3、已知x2 −3x−27=0，求代数式1（x+4）2+（x+4）2的值；4、已知x，y，z为正数，且xy=28，yz=48，xz=84，求代数式x+2y+3z值；5、已知a= 2b−3，求代数式6ab+3a（2-3b）+3a+7的值；6、已知m a=2，m a+b=14，求代数式√m a + m b的值；7、已知x，y，z为整数，若x+y+z=3，x2+ y2+z2=5，求代数式x3+y3+ z3-10的值；8、已知m2-n2=12，（m+n）2= 16，求代数式8mn+9的值；9、已知x=√2+√3，求代数式x2−2√3x-4的值；10、已知m +n =-5，求代数式m2- 10n- n2的值。

参考答案1、已知3a-b+2c=7,5a+4b-3c=6，求代数式a+11b-12c的值；解：已知3a-b+2c=7将上式变换一下，得b=3a+2c-7---------------①将①代入5a+4b-3c=6，得5a+4（3a+2c-7）-3c =6整理，得17a+5c=34---------------②代数式a+11b-12c将①代入=a+11（3a+2c-7）-12c=34a+10c-77=2（17a+5c）-77将②代入=2×34-77=-92、已知2m6+ m4= 3，求m的值；解：2m6+ m4= 32（m2）3+ （m2）2= 3令m2=t，原式则为2t3 + t2 =32t3 + t2 -3 =02t3 + t2 -2-1 =0（2t3 - 2）+（t2 -1）=02（t3 -1）+（t2 -1）=02（t-1）（t2 +t+1）+（t+1）（t-1）=0 （t-1）〔2（t2 +t+1）+（t+1）〕=0（t-1）（2t2 +3t+3）=0因为2t2 +3t+3 =2（t+34）2+ 158>0所以2t2 +3t+3≠0故：只有t-1=0即t=1又m2=t所以m2=1，得m=±1故：m的值为±13、已知x2 −3x−27=0，求代数式1（x+4）2+（x+4）2解：x2 −3x−27=0x2 −3x−27−1= -1x2 −3x−28= -1（x+4）（x-7）= -1等号两边同时除以（x+4），得X -7= −1x+4等号两边同时乘以-1，得7-x = 1x+4-----------------①代数式1（x+4）2+（x+4）2=（1x+4）2+2×1x+4×（x+4）+（x+4）2-2=〔1x+4+（x+4）〕2-2将①带入，用7-x替换1x+4=〔（7−x）+（x+4）〕2-2 =（11）2-2=1094、已知x，y，z为正数，且xy=28，yz=48，xz=84，求代数式x+2y+3z值；解：xy=28-------------------①yz=48-------------------②xz=84-------------------③三个等式相乘，得（xyz）2= 28*48*84=（4*7）*（4*12）*（7*12）（xyz）2=（4∗7∗12）2因为x，y，z为正数所以xyz =4∗7∗12 -----④④÷①，得：z=12④÷②，得：x=7④÷③，得：y=4代数式x+2y+3z将x=7，y=4，z=12代入=7+2*4+3*12=515、已知a= 2b−3，求代数式6ab+3a（2-3b）+3a+7的值；解：a= 2b−3等式两边同时乘以b-3，得ab-3a=2上式变换一下，得ab=3a+2--------------①代数式6ab+3a（2-3b）+3a+7=6ab+6a-9ab+3a+7=-3ab+9a+7将①代入=-3（3a+2）+9a+7=-9a-6+9a+7=16、已知m a=2，m a+b=14，求代数式√m a + m b的值；解：m a+b=14m a×m b=14已知m a=2--------------①即：2 ×m b=14m b= 7-------------②代数式√m a + m b将①②代入=√2+7=37、已知x，y，z为整数，若x+y+z=3，x2+ y2+z2=5，求代数式x3+y3+ z3-10的值；解：因为x，y，z为整数且x2+ y2+z2=5若其中一个数为±3，它的平方为9，显然大于5所以：x，y，z只能取±2，±1, 0 -------------------①（A）设x= -2，因为x+y+z=3，所以y+z=5，这时y或z必定有一个取±3或±4或±5，不符合①，所以舍去；（B）设x= 2因为x+y+z=3，所以y+z=1即：y=1-z--------------------------②又x2+ y2+z2=5，所以y2+z2=1-------③将②代入③（1−z）2+z2=12z2-2z=0解得：z=0，或z=1对应的y=1或0整理得：{x=2y=0x=1或{x=2y=1z=0求代数式（x3+y3+ z3）-10=（23+03+ 13）-10=-1（C）设x= -1因为x+y+z=3，所以y+z=4，因为x，y，z只能取±2，±1, 0所以，这时只能是：y=z=2整理得：{x=−1 y=2 x=2求代数式（x3+y3+ z3）-10=（−13+23+ 23）-10=5（D）设x= 1因为x+y+z=3，所以y+z=2，即y=2- z又x2+ y2+z2=5，所以y2+z2=4将y=2- z代入（2−z）2+z2=4化简，得2z2-4z=0解得：z=0，或z=2对应y=2或y=0整理得：{x=1y=0x=2或{x=1y=2z=0求代数式（x3+y3+ z3）-10=（13+23+ 03）-10= -1（E）设x= 0因为x+y+z=3，所以y+z=3，即y=3- z又x2+ y2+z2=5，所以y2+z2=5将y=3- z代入（3−z）2+z2=5化简，得2z2-6z+4=0，即z2-3z+2=0即（z-2）（z-1）=0解得：z=2或z=1对应：y=1或y=2整理得：{x=0y=2x=1或{x=0y=1z=2求代数式（x3+y3+ z3）-10=（03+23+ 13）-10= -18、已知m2-n2=12，（m+n）2= 16，求代数式8mn+9的值；解：m2-n2=12（m +n）（m -n）=12两边同时平方，得（m + n）2（m−n）2=144将（m+n）2= 16代入16*（m−n）2=144（m−n）2=9等号左边展开：m2-2mn + n2=9------------①又（m+n）2= 16等号左边展开：m2+2mn + n2=16-----------②②-①，得4mn=7代数式8mn+9=2*4mn+9=2*7+9=239、已知x=√2+√3，求代数式x2−2√3x-4的值；解：x=√2+√3x= √2−√3（√2+√3）（√2−√3）= √2−√32−3=√2−√3−1=√3-√2--------------①x2 = （√3 − √2）2 =3+2-2√6=5-2√6---------------------②代数式x2−2√3x−4将①②代入=（5-2√6）-2√3（√3-√2）+4=5-2√6-6+2√6+4=310、已知m +n =-5，求代数式m2- 10n- n2的值。

求代数式的值练习目的：能用具体的数值代替代数式中的字母，求出代数式的值。

什么是代数式的值：通常我们将代数式中的字母用具体指代的数字代替，并按照代数式的运算法则运算出具体的数值结果，就成作为代数式的值。

例1学校为了开展校体育活动，需要购进一批篮球，要求每班能分配2个，学校后备余留15个。

那么学校需要购进多少个篮球？解：设前学校共有n个班级，那么学校需要购进的篮球总数为：n.2+15假设，现在学校有20个班级（即20n），那么篮球总数=就是：2=+20⨯.2+15n=5515进一步假设，现在学校有班级25个（即25n），那么篮=球总数就是：+⨯+2==n.651515225由例题可以看出，当n取值不同是，代数式15n的计算2+结果也不同。

当20=n时，n的值是55；当25=n时，代数式152+代数式15n的值是65.2+例2当375===,z ,y x 时，求代数式z)y x x(462-+的值. 解：z)y x x(462-+=）（3476525⨯-⨯+⨯⨯=12)42(105-+⨯=405⨯=200.例3根据下面a,b 的值，求代数式ab a -2的值： （1）205==,b a ；（2）24==,b a .解:（1）当205==,b a 时，代数式ab a -2的值为： a b a -2=52052-=425-=21. （2）当24==,b a 时，代数式ab a -2的值为： a b a -2=4242-=2116-=2115. 练一练：1、求下列代数式的值.（1）当2=x 时，求代数式12-x 的值. 解：当2=x 时，求代数式12-x 的值为：12-x =122-=3.（2）当3143==,y x 时，求代数式y)x(x -的值. 解：当3143==,y x 时，求代数式y)x(x -的值为： y)x(x -=）（314343-⨯=12543⨯=165. 2、当213==,b a 时，求下列代数式的值.（1）（b a +）2；（2）（b a -）2. 解：（1）当213==,b a 时，代数式（b a +）2的值为： （b a +）2=（3+21）2=2)27(=449. （2）当213==,b a 时，代数式（b a -）2的值为： （b a -）2=（213-）2=2)25(=425. 3、当25==，y x 时，求代数式yx y x 4354--的值. 解：当25==，y x 时，求代数式y x y x 4354--的值为： y x y x 4354--=24532554⨯-⨯⨯-⨯=8151020--=710. 4、当2085===c ，b a ，时，求下列代数式的值：（1）b ）a)(c (c c --+；（2）b a a c +-.解：（1）当2085===c ，b a ，时，代数式b ）a)(c (c c --+的值为：b ）a)(c (c c --+=)820()520(20-⨯-+=20+1215⨯=20+180=200. （2）当2085===c ，b a ，时，代数式ba a c +-的值为：b a ac +-=85520+-=1315.。

初中数学代数式求值经典练习题及答案根据已知，求下列代数式的值。

，求代数式x3的值；1、已知已知x＞0，且x2=10+2√214的值；2、已知x2 +4x2= 5 ，xy=1，求代数式xx3、已知2x+1·3x= 24，2x·3x+1= 54，求代数式√（x+y）xx的值；4、已知x2= x+1，x2= y+1，且x≠y，求求代数式√x5+x5+5的值；= 4 ，求代数式x7−14x5+x3的值；5、已知x + 1x的的值；6、已知x2= √234x +1 ，求代数式x2 + 1x27、已知（x+y）3-2（x+y）2-3xy（x+y） +3xy +2（x+y） -1= 0，求代数式x+y的值；8、已知13x·9x= 4 ，求代数式1x+ 1x的值；9、已知（x2+2x）（x+y）=60，且x2 +3x+y=19，求代数式 x-y 的值；10、已知x2+2x+4=0，求代数式x4 +1的值。

参考答案1、已知已知x＞0，且x2=10+2√214，求代数式x3的值。

解：x2=10+2√214x2=7 +2√21+34x2=（√7）2+ 2√21+ （√3）222x2=（√7 + √32）2因为x＞0，所以 x = √7 + √32x3=x2·x= 10+2√214·√7 + √32x3= 10√7 + 10√3 + 14√3 + 6√78x3= 16√7 + 24√38x3= 2√7 +3√3故代数式x3的值是：2√7 +3√3。

2、已知x2 +4x2= 5 ，xy=1，求代数式xx的值。

解：x2 +4x2= 5可将5写为：5×1，所以上式为x2 +4x2= 5 ×1又xy=1，将式中的1用xy代替，则有x2 +4x2= 5xyx2-5xy+ 4x2=0等式两边同时除以x2，得（xy ）2-5·xx+ 4 =0（xx -4）（xx-1）=0当xx -4=0 时，xx= 4当xx -1=0 时，xx= 1故代数式x3的值是：4或1。

代数式及代数式的值练习题第一讲 代数式及代数式的值知识点：1、代数式：用运算符号和括号把数或表示数的字母连接而成的式子.2、代数式的值：用数值代替代数式里的字母，按照代数式中的运算关系计算得出的结果.例题精讲：例题1：设某数为x ，用x 表示下列各数：（1）比某数的一半还多2的数；（2）某数减去3的差与5的积；（3）某数与3的和除以某数所得的商；（4）某数的0060除以m 的商.练习1：用代数式表示：（1）比a 的3倍还多2的数；（2）b 的34倍的相反数； （3）X 的平方的倒数减去21的差； （4）9减去y 的31的差； （5）X 的立方与2的和.例题2：某次数学测验，班级中男生20名平均得a 分，女生25名平均得b 分，此次测验全班的平均分是多少？练习2：一个长方形周长是L ，长为a ，求该长方形的宽？练习3：买一本笔记本需8元，一支圆珠笔需3元，现买了a 本笔记本，b 支圆珠笔，付给售货员100元，可找回多少钱？练习4：小明从家到学校要走1000米，上学时速度为每小时a 米，放学回家速度为每小时b 米，问小明该天上学与放学路上共花了几小时？例题3：当a 分别取下列值时，求代数式2)1(3+a a 的值. （1）a=2； （2）a=-3； （3）a=21练习5：当x=-2，y=-21时，求下列各代数式的值： （1）22463y xy x +-； （2）x y +6例题4：若20132=-a a ，求()201522014--a a 的值.练习6：已知：164232=+-y x ，则代数式2232+-y x 的值是多少？例题5：已知：()02322=-+-x y x ，求2y x 的值.练习7：若()0242=-+-x y x ，求代数式222y xy x +-的值.练习8：已知：422=+-ba b a ，求代数式b a b a b a b a 2)2(3)2(4)2(3-+++-的值.拓展练习： 1．当x=-12，y=-3时，求代数式xy y x xy ++-的值.2．当x=1时，代数式13++bx ax 的值为2014，求当x=-1时代数式13++bx ax 的值.3. 当x ＝3时，代数式px 2＋qx ＋1的值为2002，则当x ＝－3时，代数式px 2－qx ＋1的值为多少？课堂巩固练习：一、选择题1、下列选项错误的是 （ ）A 、3＞2是代数式B 、式子2－5是代数式C 、x ＝2不是代数式D 、0是代数式2、下列代数式书写规范的是（ ） A 、a ×2 B 、2a 2 C 、112a D 、()5÷3 a 3、“a 的相反数与a 的2倍的差”，用代数式表示为（ ） A 、a －2a B 、a ＋2a C 、－a －2a D 、－a ＋2a4、用代数式表示与2a －1的和是8的数是 （ ）A 、8－(2a －1)B 、(2a －1)＋8C 、8－2a －1D 、2a －1－85、已知2x －1＝0，则代数式x 2＋2x 等于 （ ）A 、2B 、114C 、212D 、1126. 某班的男生人数比女生人数的 多16人，若男生人数是a ，则女生人数为 （ ）A. a+16B. a －16C. 2（a+16）D. 2（a －16）7. 原产量n 千克增产20%之后的产量应为 （ ）A.（1－20%）n 千克B.（1+20%）n 千克C. n+20%千克D. n ×20%千克8. 甲乙两人的年龄和等于甲乙两人年龄差的3倍，甲x 岁，乙y 岁，则他们的年龄和如何用年龄差表示 （ ）A.（x+3y ）B.（x －y ）C. 3（x －y ）D. 3（x+y ）A. 2n －1 ，2n+1B. 2n+1，2n+3C. 2n －1，2n+3D. 2n －1，3n+19. 若a 是一个两位数，b 是一个一位数，如果把b 放在a 左边，组成一个三位数，则这个三位数可表示为（ ）A. baB. b+aC. 10b+aD. 100b+a10． 当21=x 时，代数式)1(512+x 的值为 （ ）A.51 B. 41 C. 1 D. 5311． 当a ＝5时，下列代数式中值最大的是（ ）A.2a ＋3B.12a -C.212105a a -+D.271005a -12．已知3a b =，a b a -的值是（ ）A.43B.1C.23 D.013．如果代数式22m nm n -+的值为0，那么m 与n 应该满足 （ ）A.m ＋nB.mn ＝0C.m ＝n ≠0D.mn ≠114．求下列代数式的值，计算正确的是 （ ）当x ＝0时，3x ＋7＝0 B.当x ＝1时，3x 2－4x ＋1＝0当x ＝3，y ＝2时，x 2－y 2＝1 C.当x ＝0.1，y ＝0.01时，3x 2＋y ＝0.31二、填空题1. 一个正方体边长为a ，则它的表面积是_______.2. 鸡，兔同笼，有鸡a 只，兔b 只，则共有头_______个，脚_______只.3. 代数式2x 2+3x+7的值为12，则代数式4x 2+6x －10=___________.4.当x ＝_______时，代数式53x -的值为0。

初一数学代数式练习题一、选择题（每题2分，共20分）1. 已知 \( a = 3 \)，\( b = 2 \)，求 \( a^2 - b \) 的值。

A. 7B. 5C. 9D. 32. 若 \( x + y = 5 \)，\( x - y = 1 \)，求 \( x \) 和 \( y \) 的值。

A. \( x = 3, y = 2 \)B. \( x = 2, y = 3 \)C. \( x = 4, y = 1 \)D. \( x = 1, y = 4 \)3. 代数式 \( 3x + 5y \) 与 \( 4x - 7y \) 的和是：A. \( 7x - 2y \)B. \( 7x + 2y \)C. \( 7x + 12y \)D. \( 7x - 12y \)4. 计算 \( (3x - 2)^2 \) 的结果中 \( x^2 \) 的系数。

A. 3B. 9C. 4D. 15. 若 \( 2x = 3y \)，求 \( 4x^2 - 9y^2 \) 的值。

A. 0B. 1C. 2D. 3二、填空题（每题2分，共20分）6. 代数式 \( ax + b \) 中，当 \( a = 4 \)，\( b = -1 \) 时，代数式变为 ________。

7. 当 \( x = -2 \) 时，代数式 \( x^2 + 3x + 2 \) 的值为________。

8. 若 \( a = 5 \)，\( b = -3 \)，求 \( a^2 - b^2 \) 的值为________。

9. 代数式 \( (x + y)(x - y) \) 可以化简为 ________。

10. 若 \( 2x + 3y = 7 \)，\( 3x - 2y = 8 \)，求 \( 5x + y \) 的值为 ________。

三、解答题（每题10分，共60分）11. 已知 \( x = 1 \)，\( y = -2 \)，求代数式 \( (x - y)^2 + xy \) 的值。

初中《代数式求值》精选练习题及答案根据已知，求代数式的值：1、已知：x=√3 + √3 ，求代数式（x+1）（x-1）的值；2、已知x 2 +1= x ，求代数式x 1001 -x 1000的值；3、已知m =√493 +√563 +√643，求代数式 m - 1m 2 的值；4、已知a 2 = √2 √1+a 2 -1，求代数式a 2024 + a −2024的值；5、已知t ≠0，且 1t - t =1，求代数式t 3 +2t 2 +3003的值；6、已知9x2 +30x+23=0，求代数式（3x +4）2 + 1（3x+4）2 的值；7、已知m 2 -13m =n ，n 2 -13n =m ，求代数式√m 2+n 2+1 的值；8、已知2t +√2 =√3 ，求代数式t 6 -2t 4的值；9、已知3m 2 +5m -11=0，求代数式（4m+7）（2m-5）+m （m+21）+3 的值；10、已知x+√3 =2，求代数式4x 2-〔6x-（5x-8）-x 2〕+3x-〔5x-2（2x-1）〕的值。

参考答案1、已知：x=√3+√3，求代数式（x+1）（x-1）的值；解：已知x=√3+√3=√3+ √33=4√33那么x2=（4√33）2= 163----------①代数式（x+1）（x-1）=x2 -1将①代入= 163-1= 1332、已知x2 +1=x，求代数式x1001 -x1000的值；解：已知x2 +1=x变换一下，得x2-x= -1----------①再变换，得x2 =x -1------------②又x3=x2·x将②代入x3=（x -1）·x=x2-x将①代入故：x3= -1------------③代数式x1001 -x1000=x999+2 -x999+1=x999·x2 -x999·x=x 999（x 2 -x ）将①代入=x 999·（-1）= -x 999= -（x 3）333将③代入= -（−1）333 = -（-1）= 13、已知m =√493 +√563 +√643，求代数式 m - 1m 2 的值； 解：m =√493 +√563 +√643m=（√73）2 +√73 √83 + （√83）2-------------------① 将①等号两边同时取分母为1，得 m 1 =（√73）2 +√73 √83 + （√83）21等号右边分子分母同时乘以√83 -√73，得m 1 =[（√73）2 +√73 √83 + （√83）2]（√83 −√73）√83 −√73m 1 = √83）3√73）3√83 −√73 = √83 −√73 = √83 −√73 等号两边同时取倒数所以：1m = √83 -√73故： 1m 2 = （√73）2 -2√73 √83 + （√83）2-----------② 由① -②，得m - 1m 2 = 3√73 √833·2= 3√73=6√74、已知a2=√2√1+a2 -1，求代数式a2024+ a−2024的值；解：已知a2=√2√1+a2 -1变换一下，得a2+1=√2√1+a2等号两边同时平方，得a4+2a2+1= 2（1+a2）a4+2a2+1= 2+2a2化简，得a4=1代数式a2024+ a−2024=a4×506+ a4×（−506）=（a4）506+（a4）−506将a4=1代入= 1506+ 1−506=1+1=25、已知t≠0，且1- t =1，求代数式t3 +2t2 +3003的值；t解：已知t≠01- t =1t等号两边同时乘以t，得1 -t2=t变换一下，得t2=1 - t---------------------①代数式t3 +2t2 +3003=t2·t +2t2 +3003将①待入=（1 - t）·t +2（1 - t）+3003 =t -t2 +2-2t +3003再将①待入=t -（1- t） +2-2t +3003= t -1 +t +2 -2t +3003=（t +t -2t）+（-1 +2 +3003）=30046、已知9x2+30x+23=0，求代数式（3x+4）2+1（3x+4）2的值；解：设3x+4 =t则x= 13（t -4）---------------①已知9x2+30x+23=0将①代入9×[13（t−4）]2+30×[ 13（t−4）]+23=0（t−4）2+10（t -4）+23=0t2 -8t +16 +10t -40 +23=0 t2 +2t -1=0等号两边同时除以t，得t +2 - 1t=0变化一下，得1t- t =2等号两边同时平方，得1t2-2 + t2=4整理，得1t2+ t2= 6因为3x+4 =t故：（3x+4）2+1（3x+4）2=67、已知m2 -13m =n，n2 -13n =m，求代数式√m2+n2+1的值；解：m2 -13m=n，n2 -13n=m则变换一下，得m2 =13m +n----------------①n2 =m +13n----------------②① -②，得m2 -n2 =12（m-n）（m +n）（m -n）=12（m-n）（m +n）（m -n）-12（m-n）=0（m -n）〔（m +n）-12〕=0则有：m -n =0，或（m +n）-12=0即：m = n 或m +n =12（1）当m = n时已知m2 =13m +nm2 =13m +m=14m解得m=0，或m=14第一种情况：m=n=0代数式√m2+n2+1将m=n=0代入=√1=1第二种情况：m=n=14代数式√m2+n2+1将m=n=0代入=√142+142+1=√393（2）当m +n =12时① +②，得m2 +n2 =14（m+n）=14×12代数式√m2+n2+1=√14×12+1=√（13+1）（13−1）+1= √132−1+1=138、已知2t +√2=√3，求代数式t6 -2t4的值；解：2t +√2=√3t = √3−√22所以：t2= 5−2√64----------------①①两边同时平方，得t4= 49−20√616------------------------②代数式t6 -2t4=t4（t2 -2）将①，②代入= 49−20√616（5−2√64-2）= 49−20√616×−3−2√64=−3×49+（−20√6）×（−2√6）+（60√6−98√6）64= 93−38√6649、已知3m2 +5m -11=0，求代数式（4m+7）（2m-5）+m（m+21）+3 的值；解：3m2 +5m -11=0变换一下，得3m2 +5m =11------------①代数式（4m+7）（2m-5）+m（m+21）+3=8m2 -20m+14m -35 +m2 +21m+3=9m2 +15m -32=3（3m2 +5m）-32将①代入=3×11-32=110、已知x+√3=2，求代数式4x2-〔6x-（5x-8）-x2〕+3x-〔5x-2（2x-1）〕的值。

代数式的值练习题近年来，随着数学教育的发展，代数式的知识在学生们的学习中越来越重要。

代数式的值练习题是帮助学生巩固知识、培养逻辑思维能力的重要方法之一。

本文将介绍一些常见的代数式的值练习题，并提供详细的解答步骤，供学生参考。

题目一：计算代数式的值已知 x = 2，y = 3，计算以下代数式的值：1) 2x + 3y2) x^2 + y^2 - xy3) (x + y)^2 - x^2 - y^2解答：1) 2x + 3y = 2(2) + 3(3) = 4 + 9 = 132) x^2 + y^2 - xy = 2^2 + 3^2 - 2(3) = 4 + 9 - 6 = 73) (x + y)^2 - x^2 - y^2 = (2 + 3)^2 - 2^2 - 3^2 = 5^2 - 4 - 9 = 25 - 4 - 9 = 12题目二：代数式的展开将以下代数式展开：1) (x + y)(x - y)2) (2x + 3y)^23) (a - b)(a^2 + ab + b^2)解答：1) (x + y)(x - y) = x^2 - xy + xy - y^2 = x^2 - y^22) (2x + 3y)^2 = (2x + 3y)(2x + 3y) = 4x^2 + 6xy + 6xy + 9y^2 = 4x^2 + 12xy + 9y^23) (a - b)(a^2 + ab + b^2) = a^3 - a^2b + a^2b - ab^2 + ab^2 - b^3 = a^3 - b^3题目三：代数式的简化将以下代数式简化：1) 2x + 3x - x2) (a + b)^2 - (a - b)^23) a^2 - 2ab + b^2 - (a^2 - b^2)解答：1) 2x + 3x - x = 5x - x = 4x2) (a + b)^2 - (a - b)^2 = a^2 + 2ab + b^2 - (a^2 - 2ab + b^2) = a^2 + 2ab + b^2 - a^2 + 2ab - b^2 = 4ab3) a^2 - 2ab + b^2 - (a^2 - b^2) = a^2 - 2ab + b^2 - a^2 + b^2 = -2ab + 2b^2通过以上几道代数式的值练习题，希望能够帮助学生们更好地理解和掌握代数式的运算方法。

代数式的值练习题代数式的值练习题数学作为一门抽象而又精确的学科，代数是其中的重要分支之一。

代数式的值是代数学习中的基础概念之一，也是学习代数的关键。

在这篇文章中，我们将探讨一些代数式的值练习题，帮助读者更好地理解和掌握这一概念。

1. 求值练习题：(1) 已知a = 2，求代数式3a - 5的值。

解析：将a的值代入代数式中，得到3 * 2 - 5 = 6 - 5 = 1。

所以代数式3a - 5的值为1。

(2) 已知b = -3，求代数式2b^2 + 5b的值。

解析：将b的值代入代数式中，得到2 * (-3)^2 + 5 * (-3) = 2 * 9 - 15 = 18 - 15 = 3。

所以代数式2b^2 + 5b的值为3。

2. 求解方程练习题：(1) 求解方程2x + 3 = 9。

解析：首先将方程转化为代数式形式，得到2x + 3 - 9 = 0。

化简得到2x - 6 = 0。

然后移项得到2x = 6。

最后除以系数2，得到x = 3。

所以方程2x + 3 = 9的解为x = 3。

(2) 求解方程x^2 + 5x + 6 = 0。

解析：首先尝试因式分解，得到(x + 2)(x + 3) = 0。

根据乘积为零的性质，可以得到x + 2 = 0或者x + 3 = 0。

解得x = -2或者x = -3。

所以方程x^2 + 5x + 6 = 0的解为x = -2或者x = -3。

3. 运用代数式的值解决实际问题练习题：(1) 一个长方形的长是x + 3，宽是2x - 1，求其面积。

解析：长方形的面积等于长乘以宽，即(x + 3)(2x - 1)。

将代数式展开得到2x^2 + 5x - 3。

所以该长方形的面积为2x^2 + 5x - 3。

(2) 一个正方形的边长是2a + 1，求其周长。

解析：正方形的周长等于4倍边长，即4(2a + 1)。

将代数式展开得到8a + 4。

所以该正方形的周长为8a + 4。

通过以上的练习题，我们可以看到代数式的值在数学中扮演着重要的角色。

●、已知;，012=-+a a 求1999223++a a 的值●、已知032=-+x x 求243+-x x 的值． ●、若21=+xx 则221x x +＝ ●、已知8xy =满足2256x y xy x y --+=。

求22x y +的值。

●、如果x ＋y ＝6, xy ＝7, 那么x 2＋y 2＝______●、已知：49)(,52=+=-y x y x ，求22y x +的值． ●、已知31=+x x ，求⑴ 221xx + ，⑵ 2)1(x x - ●、如果x ＋y ＝6, xy ＝7, 那么x 2＋y 2＝ ●、a+b=5, ab=3，求：(1) (a-b)2 ；(2) a 2+b 2 ；(3) a 4+b4 ●、已知6)(,18)(22=-=+y x y x ，求：①的值；22y x + ②xy 的值.●、已知a 2－3a ＋1＝0．①、求aa 1+和221a a +的值； ②、a 3与8a －3的值是否一定相等？若相等，请说明理由；若不相等，请举例说明．●、若321x y z -=-=-，求222x y z xy yz zx ++---的值。

●、已知4m ＋n ＝90，2m －3n ＝10，求(m ＋2n )2－(3m －n )2的值．●、已知：2c a ,3b a =-=-，求：()()()()()[]22c a c a b a b a b c -+--+--的值。

●、已知a ＋b=0，求a 3－2b 3＋a 2b －2ab 2的值．●、若x 2＋mx ＋n=(x －3)(x ＋4)，求(m ＋n)2的值．●、已知：a=10000，b=9999，求a 2+b 2－2ab －6a+6b+9的值。

●、已知(4x -2y -1)2+2-xy =0，求4x 2y -4x 2y 2-2xy 2的值. ●、已知10m =20,10n =51,的值求n m 239÷. ●、已知5922=-+y x y x ，求yx 的值。

勾文六州方火为市信马学校 代数式的值一、根底达标1.当x ＝32时，代数式2x+x 2的值是( ) A.312 B.928 C.38 D.916 2.假设代数式23+x 的值为5，那么x 取( ) A.2 B.5 C.7 D.113.n 表示整数，那么代数式2n-1的值是( )A.自然数B.偶数C.奇数D.质数4．n 是正整数，那么当a=-1时，代数式n n a a2+的值是 〔 〕A.0B.2C.1或-1D.0或25.以下求代数式的值的计算，正确的选项是( )A.当a ＝1时，代数式a 2-2a+1＝0B.当a ＝3时，代数式a 2-2a+1＝16 C.当a ＝2，b ＝1时，代数式a 2-b 2＝1 D.当a ＝5，b ＝4时，代数式(a+b)2＝9 6.假设a ＝21，b ＝2，那么b 2－a b 的值是 .7.假设2m-1的值为0，那么m 的值是 ，此时代数式m 2-m+41的值是 .8.重量为a 千克的食盐，售价为b 元，那么单价d ＝ 元/千克；假设a ＝，b ＝，那么d ＝ 元/千克.9.代数式x211-中的x 的值不能等于 . 10.当a ＝5，b ＝3时，代数式(a+b)2＝ ，a 2+2ab+b 2＝ ，知(a+b)2 a 2+2ab+b 2.11.假设m ＝21，n ＝31时，代数式m 2-n 2＝ ，(m+n)(m-n)＝ ，知m 2-n 2(m+n)(m-n). 12.当x ＝4，y ＝2时，代数式y x y x 5423+-的值是 .13.礼堂有长椅x 条，每5名学生坐一条，其中有一条坐3人，这时长椅还剩7条，那么学生人数为 ，当x ＝95时，学生有人.14.某班有学生a 人，假设再增加5名男生，那么女生人数为男生人数的80%.(1)写出表示原有男生人数的代数式.(2)当a ＝58时，求原有男生人数.15.邮购一批书，每册定价a 元，另加书价5%的邮费，现购书y 册，共计金额b ，用代数式表示 b ，当a ＝，y ＝80时，求b 的值.16.〔1〕代数式x 2-2y 的值为5，求代数式3x 2-6y+2的值. 〔2〕代数式3x 2-4x+6的值为9，求代数式x 2-34x+6的值. 二、自主选择 17.当b a b a +-＝2时，求代数式)(3)(4b a b a +--b a b a -+)(2的值.。