反比例函数练习题及答案最新
- 格式:doc
- 大小:207.17 KB
- 文档页数:8

反比例函数专题练习(含答案)
一.选择题(共10小题)
1.关于x的函数y=k(x+1)和y=(k≠0)在同一坐标系中的图象大致是()
A.B.C.D.
2.如图,在平面直角坐标系中,A(﹣3,1),以点O为顶点作等腰直角三角形AOB,双曲线y1=在第一象限内的图象经过点B.设直线AB的解析式为y2=k2x+b,当y1>y2时,x的取值范围是()
A.﹣5<x<1 B.0<x<1或x<﹣5 C.﹣6<x<1 D.0<x<1或x<﹣6
3.如图,直线y=﹣x+3与y轴交于点A,与反比例函数y=(k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=3BO,则反比例函数的解析式为()
A.y=B.y=﹣C.y=D.y=﹣
4.如图,已知点A是双曲线y=在第一象限的分支上的一个动点,连接AO并延长交另一分支于点B,过点A作y
轴的垂线,过点B作x轴的垂线,两垂线交于点C,随着点A的运动,点C的位置也随之变化.设点C的坐标为(m,n),则m,n满足的关系式为()
A.n=﹣2m B.n=﹣C.n=﹣4m D.n=﹣
5.如果点A(﹣2,y1),B(﹣1,y2),C(2,y3)都在反比例函数的图象上,那么y1,y2,y3的大小关
系是()
A.y1<y3<y2B.y2<y1<y3C.y1<y2<y3D.y3<y2<y1
6.如图,是反比例函数y=和y=(k1<k2)在第一象限的图象,直线AB∥x轴,并分别交两条曲线于A、B两点,若S△AOB=4,则k2﹣k1的值是()
A.1 B.2 C.4 D.8
7.如图:等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两

反比例函数练习题集锦(含答案)
1、综合题
1、如图,已知直线与双曲线交于两点,且点的横坐标为.
(1)求的值;
(2)若双曲线上一点的纵坐标为8,
求的面积;
(3)过原点的另一条直线交双曲线于
两点(点在第一象限),若由点为顶点组成的四边形面积为,求点的坐标.
2、已知一次函数与双曲线在第一象限交于A、B两点,A点横坐
标为1.B点横坐标为4
(1)求一次函数的解析式;
(2)根据图象指出不等式的解集;
(2) 点P是x轴正半轴上一个动点,过P点作x轴的垂线分别交直线和双曲线于M、N,设P点的横坐标是t(t>0),△OMN的面积为S,求S和t的函数关系式,并指出t的取值范围。
二、简答题
3、.已知:如图,在平面直角坐标系中,直线AB 分别与轴交于点B、A,与反比例函数的图象分别交
(1)求该反比例函数的解析式;
(2)求直线AB的解析式.
4、如图,已知正比例函数与反比例函数的图象交于两点.
(1)求出两点的坐标;
的范围;
(2)根据图象求使正比例函数值大于反比例函数值的
三、计算题
5、为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒。已知药物释放过程中,室内每立方米空气中含药
量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t 的函数关系为(为常数)。如下图所示,据图中提供的信息,解答下列问题:
(1)写出从药物释放开始,y与t之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米和含药量降低到0.25毫克以下时,学生方可进入教室,那么从药物释放开始,至
少需要经过多少小时后,学生才能进入教室?

一、选择题(每小题3分,共36分)
1.(2022河口模拟)下列关系式中,y是x的反比例函数的是( C )
A.x(y-1)=1
B.y=1
x+1
C.y=1
3x D.y=1
x3
2.对于反比例函数y=-5
x
,下列说法不正确的是( D )
A.图象分布在第二、四象限
B.当x<0时,y随x的增大而增大
C.图象经过点(5,-1)
D.若点A(x1,y1),B(x2,y2)都在图象上,且x1
3.若点A(-1,y1),B(1,y2),C(3,y3)在反比例函数y=-3
x
的图象上,则y1,y2,y3的大小关系是( B )
A.y1
B.y2
C.y3
D.y2
4.若A(2,4)与B(-2,a)都是反比例函数y=k
x
(k≠0)图象上的点,则a 的值是( B )
A.4
B.-4
C.2
D.-2
5.在一个可以改变容积的密闭容器内,装有质量为m的某种气体,当改变容积V时,气体的密度ρ也随之改变,ρ与V在一定范围内满足,它的图象如图所示,则该气体的质量m为( C )
ρ=m
V
第5题图
A.1.4 kg
B.5 kg
C.7 kg
D.6.4 kg
6.正比例函数y=6x的图象与反比例函数y=6
的图象的交点位于
x
( D )
A.第一象限
B.第二象限
C.第三象限
D.第一、三象限
(k≠0)与一次函数y=kx+k(k≠0)在同一平面直角7.反比例函数y=k
x
坐标系内的图象可能是( D )
A B C D
的图象相交于点M(1,m),N(-2,n).
8.如图所示,函数y1=x+1与函数y2=2
x
若y1>y2,则x的取值范围是( D )
第8题图
A.x<-2或0

一、判断题
1.当x 与y 乘积一定时,y 就是x 的反比例函数,x 也是y 的反比例函数( ) 2.如果一个函数不是正比例函数,就是反比例函数 ( ) 3.y 与2x 成反比例时y 与x 并不成反比例( ) 二.填空题
4.已知三角形的面积是定值S ,则三角形的高h 与底a 的函数关系式是h =__________,这时h 是a 的__________;
5.如果y 与x 成反比例,z 与y 成正比例,则z 与x 成____ ___; 6.如果函数
2
22-+=k k kx
y 是反比例函数,那么k =________,此函数的解析式是____ ____;
7.有一面积为60的梯形,其上底长是下底长的3
1,若下底长为x ,高为y ,则y 与x 的函数关系是______________ 三、选择题:
8.如果函数12-=m x y 为反比例函数,则m 的值是 ( ) A 1- B 0 C 2
1 D 1
9.李老师骑自行车上班,最初以某一速度匀速行进,中途由于自行车故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,结果准时到校。在课堂上,李老师请学生画出自行车行进路程s 千米与行进时间t 的函数图像的示意图,同学们画出的示意图如下,你认为正确的是( )
10、下列函数中,y 是x 反比例函数的是( ) §5.1
反比例函数
四.辨析题
(1)兄弟二人分吃一碗饺子,每人吃饺子的个数如下表:
①写出兄吃饺子数y 与弟吃饺子数x 之间的函数关系式(不要求写xy 的取值范围). ②虽然当弟吃的饺子个数增多时,兄吃的饺子数(y )在减少,但y 与x 是成反例吗?
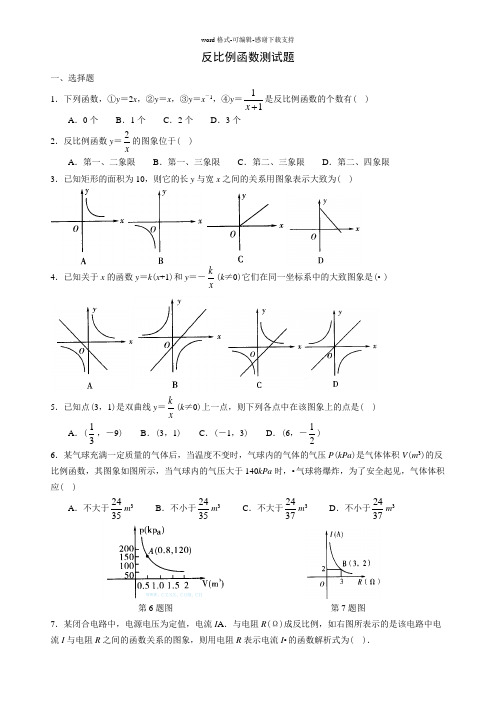
反比例函数测试题一、选择题
1.下列函数,①y=2x,②y=x,③y=x-1,④y=
1
1
x
是反比例函数的个数有()
A.0个B.1个C.2个D.3个
2.反比例函数y=2
x
的图象位于()
A.第一、二象限B.第一、三象限C.第二、三象限D.第二、四象限3.已知矩形的面积为10,则它的长y与宽x之间的关系用图象表示大致为()
4.已知关于x的函数y=k(x+1)和y=-k
x
(k≠0)它们在同一坐标系中的大致图象是(• )
5.已知点(3,1)是双曲线y=k
x
(k≠0)上一点,则下列各点中在该图象上的点是()
A.(1
3
,-9)B.(3,1)C.(-1,3)D.(6,-
1
2
)
6.某气球充满一定质量的气体后,当温度不变时,气球内的气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于140kPa时,•气球将爆炸,为了安全起见,气体体积应()
A.不大于24
35
m3B.不小于
24
35
m3C.不大于
24
37
m3D.不小于
24
37
m3第6题图第7题图
7.某闭合电路中,电源电压为定值,电流I A.与电阻R(Ω)成反比例,如右图所表示的是该电路中电流I与电阻R之间的函数关系的图象,则用电阻R表示电流I•的函数解析式为().
A .I =
6R B .I =-6R C .I =3R D .I =2R 8.函数y =1
x
与函数y =x 的图象在同一平面直角坐标系内的交点个数是( ).
A .1个
B .2个
C .3个
D .0个 9.若函数y =(m +2)|m |
-3
是反比例函数,则m 的值是( ).
Word 格式
反比率函数综合
一.选择题(共23 小题)
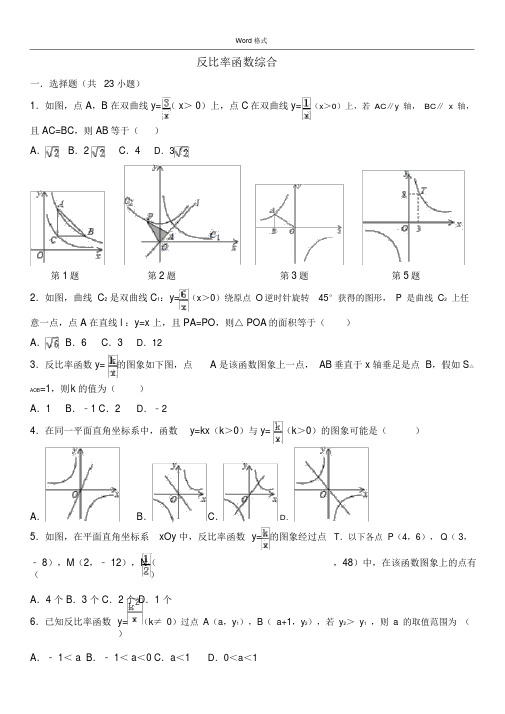
1.如图,点 A,B 在双曲线 y= ( x> 0)上,点 C在双曲线 y=(x>0)上,若AC∥y轴,BC∥ x轴,且 AC=BC,则 AB等于()
A.B.2C.4D.3
第1题第2题第3题第5题
2.如图,曲线 C2是双曲线 C1:y=(x>0)绕原点O逆时针旋转45°获得的图形,P是曲线C2上任意一点,点 A 在直线 l :y=x 上,且 PA=PO,则△ POA的面积等于()
A.B.6C.3D.12
3.反比率函数 y=的图象如下图,点 A 是该函数图象上一点, AB垂直于 x 轴垂足是点 B,假如 S△
AOB=1,则k 的值为()
A.1B.﹣1 C.2D.﹣2
4.在同一平面直角坐标系中,函数y=kx(k>0)与 y=(k>0)的图象可能是()
A.B.C.D.
5.如图,在平面直角坐标系xOy 中,反比率函数y=的图象经过点T.以下各点 P(4,6), Q( 3,﹣ 8),M(2,﹣ 12),N(,48)中,在该函数图象上的点有()
A.4 个 B.3 个 C.2 个 D.1 个
6.已知反比率函数y=(k≠ 0)过点A(a,y1),B(a+1,y2),若y2>y1,则a的取值范围为()
A.﹣ 1< a B.﹣ 1< a<0 C.a<1D.0<a<1
完满整理
Word 格式
7.如图,双曲线 y=与直线y=kx+b交于点M,N,而且点M的坐标为(1,3),点N的纵坐标为﹣1.根据图象信息可得对于x 不等式<kx+b的解为()
A.x<﹣ 3 B .﹣ 3<x<0 C .﹣ 3<x<1 D .﹣ 3< x<0 或 x > 1

反比例函数》测试题(含答案)
1、选择题(每小题5分,共50分)
1、若点(x1.-1)、(x2.-2)、(x3.1)都在反比例函数y= k/x 上,则它们之间的大小关系是()
A.x1
B.x2
C.x1
D.x2
2、若反比例函数y=k/x的图象经过点(m,3m),其中
m≠0,则此反比例函数的图象在()
A.第一、二象限;
B.第一、三象限;
C.第二、四象限;
D.第三、四象限
3、在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线y=3/x上的一个动点,当点B的横坐标逐渐增大时,△OAB的面积将会()
A.逐渐增大
B.不变
C.逐渐减小
D.先增大后减小
4、函数y=-kx与函数y=k/x的图象的交点个数是()
A。0
B。1
C。2
D.不确定
5、函数y=6-x与函数y=k/x的图象交于A、B两点,设点A的坐标为(x1,y1),则边长分别为x1、y1的矩形面积和周长分别为()
A。4,12
B。4,6
C。8,12
D。8,6
6、已知y1+y2=y,其中y1与x成反比例,且比例系数为
k1,而y2与x2成正比例,且比例系数为k2,若x=-1时,y=0,
则k1,k2的关系是( )
A.k1+k2=0
B.k1k2=1
C.k1-k2=0
D.k1k2=-1
7、正比例函数y=2kx与反比例函数y=k/(x-1)在同一坐标
系中的图象不可能是()
18、如图,直线y=mx与双曲线y=k/(x-1)交与A、B两点,过点A作AM⊥x轴,垂足为M,连接BM,若S△ABM=2,
则k的值是()
A、2
B、m-2
C、m
D、4
9、如图,点A在双曲线y=6/x上,且OA=4,过A作

反比例函数测试题
一、选择题(每题3分,共30分)
n + 5
1反比例函数y = —— 图象经过点(2, 3),则n 的值是(
).
x
A 、一 2
B 、一 1
C 、0
D 、1
k
2、 若反比例函数y =上(k M 0)的图象经过点(一1, 2),则这个函数的图象
x
一定经过点( ).
1
1
A 、(2,— 1)
B 、( -- , 2)
C 、(一 2, — 4)
D 、( — , 2)
2
2
3、 已知甲、乙两地相距s (km ),汽车从甲地匀速行驶到乙地,则汽车行驶的
时间t (h )与行驶速度v (km/h )的函数关系图象大致是(
)
k 4、一次函数y = kx — k ,y 随x 的增大而减小,那么反比例函数y = 满足( ).
x
B 、在每个象限内,y 随x 的增大而减小 D 、图
象分布在第二、四象限
5、如图,点P 是x 轴正半轴上一个动点,过点 P 作x 轴的垂
1
线PQ 交双曲线y =丄于点Q ,连结0Q ,点P 沿x 轴正方向运动
x
时,Rt △ QOP 的面积( ).
A 、逐渐增大
B 、逐渐减小
C 、保持不变
D 、无法确定
A 、当 x >0 时,y >0 C 、图象分布在第一、三象限
1
6、在一个可以改变容积的密闭容器内,装有一定质量
m的某种气体,当改变容积V时,气体的密度p也随之改变. p与V在一定范围内满足p = m,它的图象如图所示,则该
V
1
二、填空题(每题3分,共27分)
11、 对于双曲线本身来说,它的两个分支关于直角坐标系原点 ______________ ; 12、
某种灯的使用寿命为1000小时,它的可使用天数y 与平均每天使用的小时 数x 之间的函数关系式为 __________ . _________

反比例函数定义专项练习30题(有答案)
1.下列函数中,是反比例函数的为()
A.y=2x+1 B.y=C.
y=
D.2y=x
2.下列关系式中,y是x反比例函数的是()
A.
y=B.
y=
C.y=﹣D.
y=
3.下列函数关系中,成反比例函数的是()
A.矩形的面积S一定时,长a与宽b的函数关系
B.矩形的长a一定时,面积S与宽b的函数关系
C.正方形的面积S与边长a的函数关系
D.正方形的周长L与边长a的函数关系
4.如果函数y=x2m﹣1为反比例函数,则m的值是()
A.﹣1 B.0C.D.1
5.下列函数,①y=2x,②y=x,③y=x﹣1,④y=是反比例函数的个数有()A.0个B.1个C.2个D.3个
6.若y与成反比例,x与成正比例,则y是z的()
A.正比例函数B.反比例函数C.一次函数D.二次函数
7.下列关系式中,y是x的反比例函数的是()
A.x(y﹣1)=1 B.
y=C.y=D.
y=
8.下列两个变量x、y不是反比例的关系是()
A.书的单价为12元,售价y(元)与书的本数x(本)
B.xy=7
C.当k=﹣1时,式子y=(k﹣1)x k2﹣2中的y与x
D.小亮上学用的时间x(分钟)与速度y(米/分钟)
9.下列各问题中,变量间是反比例函数关系的是()
①三角形的面积S一定时,它的底a与这个底边上的高h的关系;
②正三角形的面积与边长之间的关系;
③直角三角形中两锐角间的关系;
④当路程s一定时,时间t与速度v的关系.
A.①②B.②③C.③④D.①④10.下列函数中,不是反比例函数的是()
A.
x=B.
y=(k≠0)

完整版)反比例函数练习题含答案测试1 反比例函数的概念
一、填空题
1.一般的,形如 y=k/x 的函数称为反比例函数,其中x是
自变量,y是因变量。自变量x的取值范围是x≠0.
2.写出下列各题中所要求的两个相关量之间的函数关系式,并指出函数的类别。
1) 商场推出分期付款购电脑活动,每台电脑元,首付
4000元,以后每月付y元,x个月全部付清,则y=(8000+)/x,是反比例函数。
2) 某种灯的使用寿命为1000小时,它的使用天数y与平
均每天使用的小时数x之间的关系式为 y=1000/x,是反比例
函数。
3) 设三角形的底边、对应高、面积分别为a、h、S。当
a=10时,S与h的关系式为 S=10h/2,是正比例函数;当S=18时,a与h的关系式为 h=36/a,是反比例函数。
4) 某工人承包运输粮食的总数是w吨,每天运x吨,共
运了y天,则 y=w/x,是反比例函数。
3.下列各函数 y=1/(k2+1)、y=x/(x5+x12)、y=14-3x、y=2x
和y=3x-1 中,是y关于x的反比例函数的有:①y=1/(k2+1)、② y=x/(x5+x12)、③ y=2x。
4.若函数 y=m/(x-1) (m是常数) 是反比例函数,则 m=1,
解析式为 y=1/(x-1)。
5.近视眼镜的度数y(度)与镜片焦距x(m)成反比例,已知400度近视眼镜片的焦距为0.25m,则 y=1000/x。
二、选择题
6.已知函数 y=3x/(kx+1),当x=1时,y=-3,那么这个函数的解析式是 y=3x/(3k+1)。(解析:由 y=-3=3/(3k+1) 可得 k=-

初中反比例函数练习题及答案初中反比例函数知识训练
初中反比例函数练习题及答案初中反比例函数知识训练一般地,如果两个变量x、y之间的关系可以表示成y=k/x(k为常数,k≠0)的形式,那么称y是x的反比例函数。下面是为大家的初中反比例函数练习题及答案,欢迎阅读!希望对大家有所帮助!
初中反比例函数练习题及答案
一、选择题(每小题3分,共30分)
1、反比例函数y=图象经过点(2,3),则n的值是( ).
A、-2
B、-1
C、0
D、1
2、若反比例函数y=(k≠0)的图象经过点(-1,2),则这个函数的图象一定经过点( ).
A、(2,-1)
B、(-,2)
C、(-2,-1)
D、(,2)
3、(08双柏县)已知甲、乙两地相距(km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间(h)与行驶速度(km/h)的函数关系图象大致是()
4、若y与x成正比例,x与z成反比例,则y与z之间的关系是( ).
A、成正比例
B、成反比例
C、不成正比例也不成反比例
D、无法确定
5、一次函数y=kx-k,y随x的增大而减小,那么反比例函数y=满足( ).
A、当x>0时,y>0
B、在每个象限内,y随x的增大而减小
C、图象分布在第一、三象限
D、图象分布在第二、四象限
6、如图,点P是x轴正半轴上一个动点,过点P作x轴的垂
线交双曲线y=于点Q,连结OQ,点P沿x轴正方向运动时,Rt△QOP的面积( ).
A、逐渐增大
B、逐渐减小
C、保持不变
D、无法确定
7、在一个可以改变容积的密闭容器内,装有一定质量
m的某种气体,当改变容积V时,气体的密度ρ也随之改变.

中考数学总复习《反比例函数》练习题(附答案)
班级:___________姓名:___________考号:_____________
一、单选题
1.一次函数y1=k1x+b(k1≠0)与反比例函数y
2=
k2
x(k2≠0)
的图象交于点A(−1,−2),点
B(2,1).当y1
A.x<−1B.−12 C.0
2.关于函数y=−2
x,下列说法中正确的是()
A.图像位于第一、三象限B.图像与坐标轴没有交点
C.图像是一条直线D.y的值随x的值增大而减小
3.如图,在直角坐标系中,点A是双曲线y= 3x(x>0)上的一个动点,点B是x轴正半轴上的一个定点,当点A的横坐标逐渐增大时,△OAB的面积将会()
A.逐渐减小B.不变
C.逐渐增大D.先减小后增大
4.在同一平面直角坐标系中,反比例函数y=-8x与一次函数y=-x+2交于A,B两点,O为坐标原点,则△AOB的面积为()
A.2B.6C.10D.8
5.如图,△ABC的三个顶点分别为A(1,2),B(4,2),C(4,4).若反比例函数y= k x在第一象限内的图象与△ABC有交点,则k的取值范围是()
A.1≤k≤4B.2≤k≤8C.2≤k≤16D.8≤k≤16
6.如图,过反比例函数y= 1x(x>0)的图象上任意两点A、B分别作x轴的垂线,垂足分别为C、
D,连接OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2,比较它们的大小,可得()
A.S1>S2B.S1=S2
C.S l<S2D.大小关系不能确定
7.某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是()

反比例函数综合
一.选择题(共23小题)
1.如图,点A,B在双曲线y=(x>0)上,点C在双曲线y=(x>0)上,若AC∥y轴,BC∥x 轴,且AC=BC,则AB等于()
A.B.2C.4 D.3
第1题第2题第3题第5题
2.如图,曲线C2是双曲线C1:y=(x>0)绕原点O逆时针旋转45°得到的图形,P是曲线C2上任意一点,点A在直线l:y=x上,且PA=PO,则△POA的面积等于()
A.B.6 C.3 D.12
3.反比例函数y=的图象如图所示,点A是该函数图象上一点,AB垂直于x轴垂足是点B,如果S△AOB=1,则k的值为()
A.1 B.﹣1 C.2 D.﹣2
4.在同一平面直角坐标系中,函数y=kx(k>0)与y=(k>0)的图象可能是()
A.B.C.D.
5.如图,在平面直角坐标系xOy中,反比例函数y=的图象经过点T.下列各点P(4,6),Q(3,﹣8),M(2,﹣12),N(,48)中,在该函数图象上的点有()
A.4个B.3个C.2个D.1个
6.已知反比例函数y=(k≠0)过点A(a,y1),B(a+1,y2),若y2>y1,则a的取值范围为()A.﹣1<a B.﹣1<a<0 C.a<1 D.0<a<1
7.如图,双曲线y=与直线y=kx+b交于点M,N,并且点M的坐标为(1,3),点N的纵坐标为﹣1.根据图象信息可得关于x不等式<kx+b的解为()
A.x<﹣3 B.﹣3<x<0 C.﹣3<x<1 D.﹣3<x<0 或x>1
第7题第9题第11题第12题
8.点A(x1,y1),B(x2,y2),C(x3,y3)在反比例函数y=的图象上,若x1<x2<0<x3,则y1,y2,y3的大小关系是()

第17章《反比例函数》单元测试题
(满分100分,时间40分钟)
班级: __________ 姓名:__________学号: __________
一、选择题(每题4分,共24分)
1.下列函数中, y 是x 的反比例函数的是( )
A 、2
1x y =
B 、52+=x y
C 、xy=8
D 、53+=x y
2. 已知反比例函数)0(≠=k x
k
y 上有一个点(-4,-2),则点( )在此函数图象上。
A 、A(3,4)
B 、B(2,4)
C 、C(-4,2)
D 、D(4,-2)
3. 若反比例函数y =x
k 3
-的图像在每一个象限内,y 随x 的增大而增大,则有( ) A 、 k 0≠ B 、k 3≠ C 、k<3 D 、k>3
4.设A( 1x ,1y ) B (2x ,2y )是反比例函数x
y 5
= 图像上的两点, 若1x <2x <0 则1y 与 2y
之间的关系是( )。
A 、1y <2y <0
B 、2y <1y <0
C 、1y >2y >0
D 、2y >1y >0 5.一次函数y=kx —1 与 反比例函数)0(≠=
k x
k
y 的图像的形状大致是( )
A B C D
6.如图2,双曲线上两点A、B,AP垂直x轴,垂足为P,BD垂直于x 轴,垂足为D。连接OA、OB,设△AOP 的面积为S 1,△BOD 面积为
S 2,则S 1与S 2的大小关系是( )。
A 、S 1=S 2
B 、S 1<S 2
C 、S 1>S 2

反比例函数综合-题集
一、反比例函数与一次函数交点
1.已知一次函数的图象与反比例函数的图象相交,其中一个交点的纵坐标为,求
一次函数的图象与轴的交点坐标(,).
【答案】或
【解析】令一次函数和中的.
,
∴,
∴与轴的交点坐标.
【标注】【知识点】反比例函数与方程、不等式
2.如图,双曲线与直线交于点、,关于的方程的解为().
A.,
B.,
C.,
D.,
【答案】A
【解析】由点坐标可得,
∴
又∵方程的解对应两函数图像交点的横坐标,
故为,.
故选.
【标注】【知识点】求反比例函数与一次函数交点坐标
A. B.
C. D.
3.反比例函数的图象与直线有两个交点,且两交点横坐标的积为负数,则的取值
范围是().
【答案】B
【解析】将代入到反比例函数中,
得:,
整理,得.
∵反比例函数的图象与直线有两个交点,且两交点横坐标的积为负
数,
∴,
解得.
故选.
【标注】【知识点】反比例函数与一次函数综合
二、反比例函数与不等式
A.或
B.
C. D.或
4.已知关于的方程的解为和,则不等式的解集为().
【答案】D
【解析】由题意可得:
令,
∵的解为和.
即函数和的图象交点横坐标为和
又函数为一次函数,为反比例函数.
∴可画出大致图象为:
由图象关系可得:
若,则或
即解集为或.
故选.
【标注】【知识点】反比例函数与方程、不等式
5.如图,直线经过和两点,在反比例函数的图象上,则不等式组
的解集为.
y
x
O
【答案】
【解析】由题意得:,
解得,,
把,代入得,
,
解得.
故答案为:.
【标注】【知识点】反比例函数与一次函数综合
【知识点】反比例函数与方程、不等式
【能力】运算能力【思想】数形结合思想

反比例函数综合测试题
一、选择题(每小题3分,共24分)
1.已知点M (- 2,3 )在反比例函数
x
k
y=的图象上,下列各点也在该函数图象上的是( ).A
A. (3,- 2)
B. (- 2,- 3)
C. (2,3)
D. (3,2)
2. 反比例函数(0)
k
y k
x
=≠的图象经过点(- 4,5),则该反比例函数的图象位于( ).B
A. 第一、三象限
B. 第二、四象限
C. 第二、三象限
D. 第一、二象限
3. 在同一平面直角坐标系中,函数
x
y
2
-
=与x
y2
=的图象的交点个数为( ). D
A. 3个
B. 2个
C. 1个
D. 0个
4. 如图1,点A是y轴正半轴上的一个定点,点B是反比例函数y = 2 x(x> 0)图象上的一个动点,当点B的纵坐标逐渐减小时,△OAB的面积将( ). A
A.逐渐增大B.逐渐减小C.不变D.先增大后减小
5. (2009年恩施市)如图2,一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,设小矩形的长和宽分别为x,y,剪去部分的面积为20,若2 ≤x≤ 10,则y与x的函数图象是( ). A
6. 已知点A(x1,y1),B(x2,y2)是反比例函数
x
k
y=(k > 0)的图象上的两点,若x1 < 0 < x2,则( ).A
A. y1 < 0 < y2
B. y2 < 0 < y1
C. y1 < y2 < 0
D. y2 < y1 < 0
7. 如图3,反比例函数
3
y
x
=的图象与一次函数y = x + 2的图象交于A,B两点,那么△AOB 的面积是( ).C
A. 2
B. 3