当前位置：文档之家 › 3.5希尔伯特空间的自伴算子酉算子和正规算子

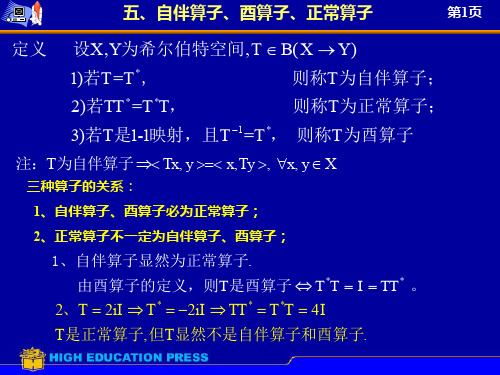
3.5希尔伯特空间的自伴算子酉算子和正规算子

  • 格式：ppt
  • 大小：85.50 KB
  • 文档页数：13

下载文档原格式

  / 13

合集下载

第一章 希尔伯特空间

第一章 希尔伯特空间

第二个例子 取数学对象为三维位形空间中由一点引
出的不同方向不同长短的线段的全体，即理论力学中
位置矢量全体。规定加法服从平行四边形法则；数乘
中的数是实数，以a数乘的结果是方向不变，长度乘
以a；内积是两矢量的点乘积。这是一个实数域上的
内积空间。
第三个例子 取数学对象为一组有次序的复数，例如四个数， 可以把它们写成一个一列矩阵：
高等量子力学
主讲人：顾运厅
参考教材：《高等量子力学》（第二版），喀兴林，
高等教育出版社
第一章 希尔伯特空间
本章讨论量子力学的主要数学工具——希尔伯特空间，即 满足一定要求的多维矢量空间。 主要内容： §1 矢量空间 §2 算符 §3 本征矢量和本征值 §4 表象理论 §5 矢量空间的直和与直积
§1 矢量空间
下面我们举出矢量空间的一些简单性质。 （1）在矢量空间中，零矢量是唯一的。
证明：
设在空间中有 1 和 2 ，对所有矢量 都满足
1 , 2
取第一式的 为 2 ，第二式中的 为 1 ，分别得
2 1 2 , 1 2 1



* * * （，）（ 2 （ ，） ， （ （（ 1） （，）（，） ，），* ，） ） ，） 2 （ ） 0 ，） ， 2，） ，） 22 （，） （ （ （，） （ 0 （ （ ，） 2 （ 2 2 2 2 2
2 2

2

1

2
1 2 2 2 ， ） 2（，） （ 2

由于
0 ，所以有 （，）
2
2

2
即 （，）

Hilbert空间中的线性算子

Hilbert空间中的线性算子
Hilbert空间中的线性算子
共轭（伴随）算子
• 定理 T B( H1 , H 2 ) 1 S B( H 2 , H1 )
s.t., (Tx, y) ( x, Sy), x H1 , y H 2 .
唯一的有界线性算子S 称为T 的共轭 * 算子记为 T 。
i.e., (Tx, y) (x, T y), x H1, y H2
b

a
a
x(t ) K ( s, t ) y ( s ) ds dt
a a
b
( x(t ),
*

b
a
K ( s, t ) y ( s ) ds )
( x, T y ) L2 [ a ,b ]
(T y )( t )


b a
K ( s , t ) y ( s ) ds
自伴算子
H R
n
n
U U UU I
T
T
T
正交矩阵
酉矩阵Βιβλιοθήκη H CU U UU I
T
投影算子
• 定义 L是Hilbert空间H中的一个闭子空 间，定义算子P：
x H ,Px是x在L上的投影，
则称P为H到L的投影算子。 投影算子的范数或是0或是1
• 定理
线性算子 P：HH，则P
* 2
2 2
求T的共轭算子。
(Tx, y ) ( K (t , s ) x( s )ds, y (t ) )
a
b
L2 [ a ,b ]

b
a

b
b
a
K (t , s ) x( s ) y (t ) ds dt

为Hilbert空间.

为Hilbert空间.

（3） 因 U 为一一到上，故U 1也一一到上，并 1 1 * ** 1 1 且由于(U ) U U (U ) ，所以 U 仍为酉 算子。 （4） 因U 及 V 为酉算子，故为一一到上映射， 所以U V 仍为一一到上映射，且
(U V ) V U V U (U V )
T
9.5自伴算子、酉算子和正常算子
在矩阵理论中，我们已经研究过 Hermitian 阵，酉阵和正常阵，下面我们要在Hilbert空间中 建立起相应的自伴算子、酉算子和正常算子的概 念，并讨论这些算子的一些基本性质。
定义 1 设 T 为 Hilbert 空间 X 到 X 中的有 * 界线性算子，若 T T ，则称 T 为 X 上的自伴 * * 算子；若 TT T T，则称 T 为 X 上正常算子； 若 T 是 X 到 X 的一对一映射，且 T * T 1 ，则 称 T 为 X 上的酉算子。
但 Tn自伴，故 lim Tn* T ，因此由极限的唯一
n
性，成立 T T 。证毕。 定理4 设U 及 V 是Hilbert空间 X 上两个酉 算子，那么
*
x X ，成立|| Ux |||| x ||； （1） U 是保范算子，即对任意
（2）当X {0} 时， || U || 1 ；
（3）U 1是酉算子；
UV 是酉算子； （4）
{U n }收 （5）若U n , n 1, 2, 是 X 上一列酉算子，且 敛于有界算子 A ，则 A 也为酉算子。
证明 （1）由酉算子定义
|| Ux ||2 Ux,Ux x,U *Ux x, x || x ||2
（2） 由（1）立即可得。
证明 若 T 为自伴算子，则对所有 x X ，

希尔伯特空间

希尔伯特空间

希尔伯特空间在数学中，希尔伯特空间（以大卫·希尔伯特命名）允许将线性代数和微积分的方法从二维和三维欧几里得空间推广到可能具有无限维数的空间。

希尔伯特空间是一个具有内积运算的向量空间，它允许定义距离函数和垂直度（称为正交性）。

此外，对于这个距离，希尔伯特空间是完备的，这意味着空间中有足够的限制，可以使用微积分技术。

希尔伯特空间在数学和物理中自然而频繁地出现，典型的是无穷维函数空间。

在偏微分方程、量子力学、傅立叶分析（包括信号处理和传热的应用）和遍历理论（形成热力学的数学基础）中，它们是不可或缺的工具。

约翰·冯·诺伊曼创造了希尔伯特空间这个术语，用来描述这些不同应用的抽象概念。

希尔伯特空间方法的成功开创了一个非常富有成果的泛函分析时代。

除了经典的欧几里得空间外，希尔伯特空间的例子还包括平方可积函数空间、序列空间、由广义函数组成的索伯列夫空间和全纯函数的哈代空间。

几何直觉在希尔伯特空间理论的许多方面都起着重要的作用。

毕达哥拉斯定理和平行四边形定律在希尔伯特空间中有确切的类比。

在更深层次上，在子空间上的垂直投影在优化问题和理论的其他方面起着重要的作用。

希尔伯特空间理论是代数、拓扑和几何的融合。

在这个意义上，代数和几何之间的“相互作用”是相当平滑的。

不过，只要考虑到无限维线性空间，情况就会发生变化，这也是拓扑学出现的地方。

对于无限维线性空间，所有的线性算子都是连续的，算子的收敛具有单一的含义，任何线性空间都与它的双重对偶自然同构，而且封闭单位球是紧凑的。

这些便利条件在无限维的情况下并不存在。

虽然基数确实存在，但其存在的证明是非结构性的，而且往往不能明确地给出基数。

因此，依靠坐标和矩阵的技术通常是不合适的。

线性算子不一定是连续的，事实上，许多感兴趣的线性算子都不是连续的。

由两个线性空间之间的所有线性算子组成的空间带有两种不同的拓扑结构，因此也有两种不同的收敛概念。

对偶空间的正确概念是所有连续线性算子进入地五十度的空间，即使如此，原空间也只嵌入其双重对偶中。

《实变函数与泛函分析基础》目录简介

《实变函数与泛函分析基础》目录简介

《实变函数与泛函分析基础》目录简介内容简介本次修订是在第二版的基础上进行的，作者根据多年来的使用情况以及数学的近代发展，做了部分但是重要的修改。

《实变函数与泛函分析基础(第3版)》共11章：实变函数部分包括集合、点集、测度论、可测函数、积分论、微分与不定积分；泛函分析则主要涉及赋范空间、有界线性算子、泛函、内积空间、泛函延拓、一致有界性以及线性算子的谱分析理论等内容。

这次修订继续保持简明易学的风格，力图摆脱纯形式推演的论述方式，着重介绍实变函数与泛函分析的基本思想方法，尽量将枯燥的数学学术形态呈现为学生易于接受的教育形态；同时，补充了一些现代化的内容，如“分形”的介绍。

《实变函数与泛函分析基础(第3版)》可作为高等院校数学类专业学生的教学用书，也可作为自学参考书。

目录第一篇实变函数第一章集合1 集合的表示2 集合的运算3 对等与基数4 可数集合5 不可数集合第一章习题第二章点集1 度量空间，n维欧氏空间2 聚点，内点，界点3 开集，闭集，完备集4 直线上的开集、闭集及完备集的构造5 康托尔三分集第二章习题第三章测度论1 外测度2 可测集3 可测集类4 不可测集第三章习题第四章可测函数1 可测函数及其性质2 叶果洛夫定理3 可测函数的构造4 依测度收敛第四章习题第五章积分论1 黎曼积分的局限性，勒贝格积分简介2 非负简单函数的勒贝格积分3 非负可测函数的勒贝格积分4 一般可测函数的勒贝格积分5 黎曼积分和勒贝格积分6 勒贝格积分的几何意义·富比尼定理第五章习题第六章微分与不定积分1 维它利定理2 单调函数的可微性3 有界变差函数4 不定积分5 勒贝格积分的分部积分和变量替换6 斯蒂尔切斯积分7 L-S测度与积分第六章习题第二篇泛函分析第七章度量空间和赋范线性空间1 度量空间的进一步例子2 度量空间中的极限，稠密集，可分空间3 连续映射4 柯西点列和完备度量空间5 度量空间的完备化6 压缩映射原理及其应用7 线性空间8 赋范线性空间和巴拿赫空间第七章习题第八章有界线性算子和连续线性泛函1 有界线性算子和连续线性泛函2 有界线性算子空间和共轭空间3 广义函数第八章习题第九章内积空间和希尔伯特(Hilbert)空间1 内积空间的基本概念2 投影定理3 希尔伯特空间中的规范正交系4 希尔伯特空间上的连续线性泛函5 自伴算子、酉算子和正常算子第九章习题第十章巴拿赫空间中的基本定理1 泛函延拓定理2 C[a，b]的共轭空间3 共轭算子4 纲定理和一致有界性定理5 强收敛、弱收敛和一致收敛6 逆算子定理7 闭图像定理第十章习题第十一章线性算子的谱1 谱的概念2 有界线性算子谱的基本性质3 紧集和全连续算子4 自伴全连续算子的谱论5 具对称核的积分方程第十一章习题附录一内测度，L测度的另一定义附录二半序集和佐恩引理附录三实变函数增补例题参考书目。

几类算子

几类算子

由条件得
0 Tv , v Tx Ty, x y
| |2 Tx , x Ty , y Tx , y Ty , x Tx , y Ty , x
令
(4)
i ，则 i ，此时由（4）式
(5)
Tx , y Ty , x 0
又若令
二 自伴算子、酉算子和正常算子的性质
引理1 设 T 为复内积空间 X上有界线性算 子,那么T 0 的充要条件为对一切 x X ,有
Tx, x 0
证明
(3)
若 T 0，显然有 Tx, x 0 ；
反之，如果（3）式对一切 x X 成立，对 任意 x, y X 及数 ，令 v x y ，由
U 是保范算子,即对任意 xX，有
U
证明 （1）由酉算子定义,有
|| Ux || Ux ,Ux x ,U Ux x , x || x ||
2 *
2
（2） 由（1）立即可得. （3） 因 U 为一一到上,故 U 1 也一一到上，
1 * ** 1 1 ( U ) U U ( U ) ，所以 并且由于 1 U 仍为酉算子. （4） 因 U 及 V 为酉算子，故为一一到上 映射，所以 U V 仍为一一到上映射，且


由自伴算子定义可知,若 T1 和 T 2 是 X上的 两个自伴算子，则 T1 T 2 也是自伴算子. 并且 有下列定理 定理2 设 T1 和 T2是Hilbert空间 X上两个自 伴算子,则 T1 T 2 自伴的充要条件为 T1 T2 T2 T1. 证明 由共轭算子性质，
(T1 T2 ) T2 T T2 T1 ,
Tx , x x , Tx Tx , x ,

酉算子的谱定理

酉算子的谱定理

酉算子的谱定理酉算子的谱定理是泛函分析中的一个重要定理，它涉及到线性算子和谱理论的概念。

在介绍酉算子的谱定理之前，我们首先需要了解一些相关的背景和术语。

1.酉算子：在数学中，特别是在泛函分析和线性代数中，酉算子（或称为幺正算子）是一种保持内积不变的线性算子。

对于复数域上的希尔伯特空间H，一个线性算子U: H → H被称为酉算子，如果对于H中的所有向量x和y，都有<Ux, Uy> = <x, y>。

2.谱定理：谱定理是数学中的一个基本结果，它描述了某些类型的自伴算子（或更一般地，正规算子）可以通过其谱（即特征值的集合）来完全描述。

对于自伴算子，谱定理表明存在一组正交的特征向量，它们构成希尔伯特空间的一个完备正交基，并且算子可以表示为这些特征向量的线性组合，其中系数是对应的特征值。

然而，酉算子的谱定理与自伴算子的谱定理有所不同。

酉算子的谱定理主要关注算子的谱性质和分解，而不是通过特征向量来表示算子。

具体来说，酉算子的谱定理表明，对于给定的酉算子U，存在一组正交投影算子（这些投影算子对应于U的特征子空间），使得U可以表示为这些投影算子的线性组合。

此外，这些投影算子的系数是复数域上的单位圆上的点，它们构成了U的谱。

酉算子的谱定理的一个关键结果是：酉算子的谱（即特征值的集合）都在单位圆上。

我们可以通过一个简单的例子来说明这一点。

考虑二维复数空间C^2，并定义一个线性算子U如下：U((x, y)) = (a x + b y, c x + d y)其中a, b, c, d是复数。

为了使U成为酉算子，它必须满足<U(x,y), U(z,w)> = <(x,y), (z,w)>对所有(x,y)和(z,w)成立。

这导致了一些限制条件，特别是矩阵[a b; c d]必须是酉矩阵，即它的共轭转置矩阵等于它的逆矩阵。

现在，假设U是一个酉算子，并且它有一个特征值λ。

那么存在一个非零向量(x, y)使得U((x, y)) = λ*(x, y)。

自伴算子酉算子和正常算子ppt课件

自伴算子酉算子和正常算子ppt课件
12
(U V )* V * U * V 1 U 1 (U V )1
所以 U V 仍为酉算子.
（5）当 n 时，因 Un A ，
所以
||
U
* n
A*
|||| Un
A
||
0
即
U
* n
A* ,
因此
A* A
limU
n
n*U
n
I
.
同理可证 AA* I . 故 A 为酉算子.证毕.
13
定理4中的（1）的逆命题不一定成立， 即保范算子不一定为酉算子.
11
U
证明 （1）由酉算子定义,有
||Ux ||2 Ux,Ux x,U*Ux x, x || x ||2
（2） 由（1）立即可得.
（3） 因U 为一一到上,故U 1也一一到上， 并且由于 (U 1)* U ** U (U 1)1，所以 U 1仍为酉算子.
（4） 因U 及V 为酉算子，故为一一到上 映射，所以 U V 仍为一一到上映射，且
反之,如果对所有 x X ，Tx, x 都为实数,则
Tx , x Tx , x x , T x T x , x , 所以 (T T )x, x 0 . 由引理1，T T* ， 即 T 自伴算子，证毕.
8
由自伴算子定义可知,若T1 和 T2 是 X上的
两个自伴算子，则 T1 T2 也是自伴算子. 并且 有下列定理
16
下面介绍正常算子的一些基本性质.
设 T是复 Hilbert 空间 X 上的有界算子,令
T T*
T T*
A
,B
2
2i
容易证明 A和 B是自伴算子,并且有 T A iB
称 A和 B分别为算子 T 的实部和虚部，并称

希伯特空间上的算子理论及应用

希伯特空间上的算子理论及应用

希伯特空间上的算子理论及应用算子理论是函数分析的重要分支领域之一，它在各个科学领域中都有着广泛的应用。

其中，希伯特空间上的算子理论尤为重要，它是通过研究希伯特空间中的线性算子性质和运算规律，来深入了解和应用算子的性质和特点。

一、希伯特空间的基本概念在介绍算子理论之前，我们首先来了解一下希伯特空间的基本概念。

希伯特空间是指一个具有内积的完备线性空间，它是由一组满足特定条件的向量所组成的。

希伯特空间具有以下几个重要性质：1. 连续性：希伯特空间中的向量和算子都是连续的，这也是它在计算和分析问题中的重要性。

2. 完备性：希伯特空间是一个完备的空间，也就是说，它中的柯西序列都能收敛于某一点。

3. 内积：希伯特空间中的向量之间定义了内积，这决定了向量的长度和夹角。

二、希伯特空间上的算子理论希伯特空间上的算子理论主要研究在希伯特空间中定义的线性算子的性质和运算规律。

线性算子是将一个希伯特空间映射到另一个希伯特空间的操作。

对于希伯特空间上的线性算子，我们有以下几个重要概念：1. 自伴算子：如果一个算子与其共轭转置相等，那么它就是一个自伴算子。

自伴算子在量子力学中具有重要的应用。

2. 酉算子：如果一个算子的逆等于其共轭转置，那么它就是一个酉算子。

酉算子在正交变换和傅里叶变换中有广泛应用。

3. 压缩算子：如果一个算子将希尔伯特空间中的向量映射到一个子空间中，且保持其长度不变，那么它就是一个压缩算子。

算子理论研究了以上概念的性质和运算规律，可以通过分析算子的特征值和特征向量来了解算子的行为和性质。

通过研究这些性质，我们可以更好地掌握希伯特空间上的算子理论，为实际问题的求解提供有力的工具和方法。

三、希伯特空间上算子理论的应用希伯特空间上的算子理论在许多不同的科学领域中都有广泛的应用，下面以几个具体领域为例进行介绍：1. 量子力学：希伯特空间上的算子理论是量子力学的重要基础，通过研究自伴算子和酉算子的性质，可以描述量子体系中的能量和态的演化规律。

3.5希尔伯特空间的自伴算子酉算子和正规算子

3.5希尔伯特空间的自伴算子酉算子和正规算子

定义3.5.7（正规算子）
设 H 为希尔伯特空间，T：H→H 是
有界线性算子，若T T* = T* T，则称 T 为
正规算子。
3.5.3 正算子
自伴算子可以比较大小：
定义3.5.8（正算子）设 H 为复希尔伯特
空间， T：H→H 为自伴算子，如果 T ≥
0，即
< T x， x > ≥ 0 任意 x ∈ H
定理3.5.2（自伴性）
设 H 为复希尔伯特空间，T 为 H 到自
身的有界线性算子，则 T 为自伴的充分必
要条件是，对任意的 x ∈ H ，< T x , x >
为实数。 证明：板书。
定理3.5.3（算子积的自伴性）
设 T1 和 T2 是希尔伯特空间 H 上的有
界自伴线性算子，则其乘积也自伴的充分
必要条件是其乘积可交换，即有
T1 T2 = T2 T1
定理 3.5.4
设 T 为希尔伯特空间 H 的自伴算子，
I 为恒等算子，λ 为实数，则 λ I - T 也 是自伴算子。
3.5.2 酉算子和正规算子
定义3.5.5（酉算子）设 H 为希尔伯特空 间，T：H → H 是有界线性算子，若 T 是
一双射且 T* = T-1，则称 T 为酉算子。
3.5 希尔伯特空间的自伴算子酉算子和 正规算子
3.5.1 自伴算子 定义3.5.1（自伴算子）设 H 为希尔伯特 空间，子 T* 满足 T* = T ，即 有关系
< T x , y > = < x , T y > （x，y ∈ H ）
则称 T 为自伴算子或厄米特算子。
则称 T 为正算子或非负算子。
定义3.5.10（正定算子）

泛函分析23

泛函分析23

主要教学内容
（3） U
1
是酉算子；
（4） UV 是酉算子； （5）若 U n 是 X 上一列酉算子,且 U n A ,则 A 是酉算子. 由上面定可知,酉算子一定是保范的,但保范的线性算子不一定是酉算子. 三、正常算子 定理 5 设 T 为复 Hilbert 空间 X 上有界线性算子, A iB 为 T 的笛卡尔分 解，则 T 为正常算子充分必要是 AB =BA . 定理 6 设 T 为复 Hilbert 空间 X 上有界线性算子, A iB 为 T 的笛卡尔分 解，则 T 为正常算子充分必要是对于任意 x X ,有 || T * x |||| Tx || . 教学重点与难点 教学方法 课后作业与 下次课预习内容 正规算子的性质. 讲空间和希尔伯特空间 §5 自伴算子、酉算子和正常算子 月 日星期 课 型 第 讲授课 节
授课时间 课 次
教学目的
掌握自伴算子,酉算子和正规算子的定义 Ⅰ 引入 在实际应用中比较重要的算子是自伴算子,酉算子和正常算子. Ⅱ 新课 三、酉算子 酉算子也具有一些较好的性质. 定理 4 设 U 和 V 为复 Hilbert 空间 X 上两个酉算子,那么 （1） U 是保范算子，对于任意 x X ,有 || Ux |||| x || ； （2）当 X 0 时， || U || 1

9-5自伴算子、酉算子和正常算子

9-5自伴算子、酉算子和正常算子

由条件得
0 = Tv , v = αTx + Ty, α x + y
=| α |2 Tx , x + Ty , y +α Tx , y +α Ty , x
= α Tx , y +α Ty , x
令α
(4)
= i ，则 α = −i ，此时由（4）式 此时由（
(5)
则由（ α = 1 ，则由（4）式
*
自伴算子； 自伴算子；若 TT * = T *T ,则称 T 为 X 上的 正常算子； 的一对一映射, 正常算子；若 T 是 X 到 X 的一对一映射,且
1 上的酉算子. T * = T −，则称 T 为 X 上的酉算子.
是自伴算子时， 的定义， 当 T 是自伴算子时，由 T * 的定义， 对一切 x, y ∈ X ，有
−1
仍为酉算子. 所以 U ⋅ V 仍为酉算子. （5 ）当 n → ∞ 时，因 U n → A ， 所以
|| U n − A ||=|| U n − A ||→ 0
* *
即 U n → A , 因此 A A = limU Un = I . n→∞
* *
*
* n
AA* = I . 故 A 为酉算子.证毕. 同理可证 为酉算子.证毕.
Tx , y − Ty , x = 0
又若令
Tx , y + Ty , x = 0
(6)
将（5）式与（6）式相加,得到 Tx , y = 0 , 式与（ 式相加, 中的任意向量， 由于x, y是 X 中的任意向量，所以 T = 0 . 定理1 为复Hilbert Hilbert空间 定理1 设 T 为复Hilbert空间 X 上有界 有界线性算子， 有界线性算子，则 T 为自伴算子的充要条件 是实数. 为对一切 x ∈ X ， Tx , x 是实数. 为自伴算子, 证明 若T为自伴算子,则对所有 x ∈ X,有

泛函分析课程教学大纲

泛函分析课程教学大纲

泛函分析课程教学大纲一、课程的基本信息适应对象：数学与应用数学本科专业课程代码：14E01525学时分配：54赋予学分：3先修课程：数学分析、高等代数、实变函数等后续课程：数学物理方程二、课程性质与任务泛函分析是数学与应用数学专业的专业选修课程。

本课程综合了函数论、几何和代数的观点与方法研究无穷维空间上的函数、算子理论，解决了分析学中的诸多问题，是学生进入现代数学学习和研究的最重要专业基础课。

课程的主要任务是：使学生掌握空间和算子的基本概念和理论，进一步提高抽象思维能力和逻辑推理能力，引导学生学会数学研究问题的思想和方法，使用泛函分析的理论解决分析、代数中的问题，培养学生综合运用分析、代数、几何手段处理问题的方法和能力。

三、教学目的与要求通过泛函分析课程的教学，使学生掌握度量空间和赋范线性空间、有界线性算子与连续线性泛函、内积空间和HilberI空间理论、线性算子的谱的基本概念、思想和方法，以及巴拿赫空间中的基本定理。

通过泛函分析课程的教学，应注意培养学生学会数学研究问题的思想和方法，使用泛函分析的理论解决分析、几何和代数中的问题，培养学生综合运用分析、代数、几何手段处理问题的方法和能力。

要求学生对泛函分析方法在数学、物理、经济等学科领域的应用有所了解。

四、教学内容与安排第一章度量空间和赋范线性空间（16学时）1.1度量空间的进一步例子12度量空间中的极限，稠密集，可分空间1.3连续映射1.4柯西点列和完备度量空间1.5度量空间的完备化1.6压缩映射原理及其应用1.7线性空间1.8赋范线性空间和巴拿赫空间第二章有界线性算子与连续线性泛函（6学时）2.1有界线性算子和连续线性泛函2.2有界线性算子空间和共规空间2.3广义函数大意第三章内积空间和希尔伯特空间（12学时）3.1内积空间的基本概念3.2投影定理3.3希尔伯特空间中的规范正交系3.4希尔特空间上的连续线性泛函3.5自伴算子、酉算子和正常算子第四章巴拿赫空间中的基本定理（14学时）4.1泛函延拓定理4.2 C [a, b]的共枕空间4.3共扼算子4.4纲定理和一致有界性定理4.5强收敛、弱收敛和一致收敛4.6逆算子定理4.7闭图像定理*第五章线性算子的谱（6学时）5.1谱的概念5.2有界线性算子谱的基本性质5.3紧集和全连续算子5.4自伴全连续算子的谱论*可根据学生实际情况选讲五、附录教学参考文献目录1.程其襄张奠宙等编，《实变函数与泛函分析基础》下册，高等教育出版社，2010年2.夏道兴等编，《实变函数论与泛函分析》（第二版）上册，高等教育出版社，1984年3.张恭庆等著，《泛函分析讲义》，北京大学出版社，1990年。

论希尔伯特空间

论希尔伯特空间

论希尔伯特空间前言：在数学领域，希尔伯特空间是欧几里德空间的一个推广，其不再局限于有限维的情形。

与欧几里德空间相仿，希尔伯特空间也是一个内积空间，其上有距离和角的概念（及由此引伸而来的正交性与垂直性的概念）。

此外，希尔伯特空间还是一个完备的空间，其上所有的柯西列等价于收敛列，从而微积分中的大部分概念都可以无障碍地推广到希尔伯特空间中。

希尔伯特空间为基于任意正交系上的多项式表示的傅立叶级数和傅立叶变换提供了一种有效的表述方式，而这也是泛函分析的核心概念之一。

希尔伯特空间是公式化数学和量子力学的关键性概念之一。

希尔伯特空间以大卫·希尔伯特的名字命名，他在对积分方程的研究中研究了希尔伯特空间。

冯·诺伊曼在其1929年出版的关于无界厄米算子的著作中，最早使用了“希尔伯特空间”这个名词。

冯·诺伊曼可能是最早清楚地认识到希尔伯特空间的重要性的数学家之一，他在进行对量子力学的基础性和创造性地研究的时候认识到了这一点。

此项研究由冯·诺伊曼与希尔伯特和朗道展开，随后由尤金·维格纳（Template:Lang）继续深入。

“希尔伯特空间”这个名字迅速被其他科学家所接受，例如在外尔1931年出版的著作《群与量子力学的理论》（Template:Lang）中就使用这一名词，此书的英文平装版ISBN编号为0486602699。

一个抽象的希尔伯特空间中的元素往往被称为向量。

在实际应用中，它可能代表了一列复数或是一个函数。

例如在量子力学中，一个物理系统可以被一个复希尔伯特空间所表示，其中的向量是描述系统可能状态的波函数。

详细的资料可以参考量子力学的数学描述相关的内容。

量子力学中由平面波和束缚态所构成的希尔伯特空间，一般被称为装备希尔伯特空间（rigged Hilbert space）。

定义在一个复向量空间H上的给定的内积 < .,. > 可以按照如下的方式导出一个范数（norm）：此空间称为是一个希尔伯特空间，如果其对于这个范数来说是完备的。

酉算子的谱定理

酉算子的谱定理

酉算子的谱定理全文共四篇示例，供读者参考第一篇示例：酉算子的谱定理是量子力学中一个非常重要的定理，它是描述酉算子特征值和特征向量的定理。

酉算子是一个特殊的线性算子，它是保持内积不变的单位ary 矩阵。

在量子力学中，酉算子描述了一个系统的演化，它是量子门操作的数学表示。

谱定理是说每个酉算子都可以被对角化为一组特征值和特征向量的乘积。

在这篇文章中，我们将详细探讨酉算子的谱定理。

让我们来了解一下酉算子的定义。

酉算子U是指满足以下条件的复数矩阵：U*U = I，其中U*是U的共轭转置，I是单位矩阵。

这意味着对于任意向量x，有||Ux|| = ||x||，即U保持向量的长度不变。

根据酉算子的定义，我们可以知道它是保持内积不变的，即对于任意向量x和y，有⟨Ux, Uy⟨ = ⟨x, y⟨。

具体来说，对于一个酉算子U，我们可以将它表示为：其中V是一个酉矩阵，Λ是一个对角矩阵，V*是V的共轭转置。

Λ的对角线上的元素就是U的特征值，V的列向量是U的特征向量。

通过谱定理，我们可以将一个复杂的酉算子表示为一组简单的特征值和特征向量的乘积，这更方便我们进行计算和分析。

在量子力学中，谱定理提供了一种便捷的方法来研究酉算子的性质和演化。

除了谱定理外，我们还可以利用酉算子的性质来研究量子系统的演化。

酉算子描述了量子门操作的数学表示，通过对酉算子进行研究，我们可以了解系统的量子态是如何随着时间演化的。

通过谱定理，我们可以将一个酉算子表示为一组特征值和特征向量，这使得我们可以更清晰地理解系统的演化轨迹。

第二篇示例：酉算子的谱定理，是量子力学中一个非常重要的定理，其深刻地揭示了酉算子在量子系统中的作用和性质。

酉算子是量子力学中描述时间演化的关键操作符，在量子力学的各个领域都有广泛的应用。

谱定理则是指对于一个酉算子，其本征值的集合以及对应的本征态构成了完备的正交基底，从而可以将任意态在该基底下展开。

这个定理的重要性在于它为量子系统的研究提供了一个非常有效的数学工具，使得我们能够更深入地理解量子力学的奇妙之处。

9.5 自伴算子、酉算子、正常算子

9.5 自伴算子、酉算子、正常算子
五、自伴算子、酉算子、正常算子
第1页
定义 设X ,Y 为希尔伯特空间,T B( X Y )
1)若T =T *,
则称T 为自伴算子；
2)若TT *=T *T，
则称T 为正常算子；
3)若T是1-1映射，且T 1=T *， 则称T为酉算子
注：T为自伴算子 Tx, y x,Ty , x, y X
|| T (1,2,3,
所以T 是保范算子.

) ||2 | i |2 ||(1,2,
i 1
) ||2 ，
但T的像为l 2中第一个坐标为0的向量全体.故?T 不映射到上,
因此不是酉算子.称T 为l 2上单向移位算子.
第8页
定理5 设T 为复Hilbert空间 X上有界线性算子，那么T是酉算子的 充要条件T 为是映射到上的保范算子.
(6)

第3页
定理1 设T为复Hilbert空间X上有界线性算子，则T为自伴算子 的充要条件为对一切x X， Tx , x 是实数.
证明 若T为自伴算子,则对所有x X ,有 Tx , x x , Tx Tx , x Tx , x 是实数.
反之,如果对所有x X ,? Tx , x 都为实数,则 Tx , x Tx , x x , T x T x , x (T T )x , x 0 T T 0 T T T为自伴算子.
证明：由定理4，只要证明充分性即可. 设T为 X到 X上的保范算子，所以T是一对一的，并且对x X，有 T *Tx , x Tx , Tx x , x ,
所以 (T *T I )x , x 0. 由引理1， T *T I , 又因T是映射到X 上的，故T 1在全空间X 上有定义，由于T *T I ,

9-5自伴算子、酉算子与正常算子

9-5自伴算子、酉算子与正常算子
（2） 由（1）立即可得.
（3） 因U 为一一到上,故U 1也一一到上， 并且由于 (U 1)* U ** U (U 1)1，所以 U 1仍为酉算子.
（4） 因U 及V 为酉算子，故为一一到上 映射，所以 U V 仍为一一到上映射，且
(U V )* V * U * V 1 U 1 (U V )1
（2） 当 X {0} 时，||U ||1 ； （3） U 1 是酉算子； （4） UV 是酉算子； （5） 若 Un , n 1, 2, 是 X 上一列酉算子， 且{Un} 收敛于有界算子 A，则 A也为酉算子.
U
证明 （1）由酉算子定义,有
||Ux ||2 Ux,Ux x,U*Ux x, x || x ||2
lim
n
Tn*
T*
，
但 Tn 自伴，故
lim
n
Tn*

T
，因此由极限的唯
一性，有 T* T .证毕.
上述三个定理是研究自伴算子,特别是 研究自伴算子谱理论的基础.
定理4 设U 及V 是Hilbert空间 X上两个
酉算子，则
（1） U是保范算子,即对任意 x X ，有
||U x |||| x || ;
所以 U V 仍为酉算子.
（5）当 n 时，因 Un A ，
所以
||
U
* n

A*
|||| Un

A
||
0
即
U
* n

A*
,
因此
A* A

limU
n
n*U n

I
.
同理可证 AA* I . 故 A 为酉算子.证毕.

数学物理方法希尔伯特

数学物理方法希尔伯特

数学物理方法希尔伯特希尔伯特是德国数学家大卫·希尔伯特（David Hilbert）的姓氏，在数学和物理学领域有很多与之相关的方法和定理。

本文将介绍希尔伯特运算法则和希尔伯特空间这两个与数学物理相关的方法。

首先，希尔伯特运算法则是指希尔伯特在数学中提出的运算法则，这个法则主要包括加法和乘法两种运算。

希尔伯特运算法则在数学中起到了很重要的作用，可以用来推导和证明很多重要的定理和命题。

在代数学中，希尔伯特法则可以用来求解线性方程组，矩阵求逆，矩阵求特征值等问题。

同时，希尔伯特运算法则也可以应用于物理学中的一些问题，例如量子力学中的矩阵表示法和算符表示法等。

其次，希尔伯特空间（Hilbert space）是指在一个Hilbert空间中定义了内积运算的向量空间。

希尔伯特空间是数学中的一个重要概念，也是量子力学中描述物理系统状态的数学工具之一。

在希尔伯特空间中，向量可以表示为具有无穷个分量的列向量，而内积运算可以表示为两个向量之间的内积积分。

希尔伯特空间中的基矢量是正交归一的，可以用于展开任意向量，类似于傅里叶级数展开。

希尔伯特空间的另一个重要性质是完备性，即任何收敛的序列在这个空间中都有极限。

这个概念在量子力学中很重要，例如薛定谔方程就是在希尔伯特空间中描述量子体系的运动。

总之，希尔伯特方法是一个重要的数学物理方法，在数学和物理学中都有广泛的应用。

希尔伯特运算法则可以用来推导和验证数学定理和命题，也可以在物理学中解决一些问题。

希尔伯特空间是描述量子力学问题的重要工具，可以用来描述物理系统的状态和运动。

通过研究希尔伯特运算法则和希尔伯特空间，我们可以更深入地理解数学和物理学中的一些基本概念和原理。

希尔伯特方法的研究和应用对于数学物理学的发展具有重要的意义。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3.5 希尔伯特空间的自伴算子酉算子和 正规算子
3.5.1 自伴算子 定义3.5.1（自伴算子）设 H 为希尔伯特 空间， T：H → H 为有界线性算子，若 T 的希尔伯特伴随算子 T* 满足 T* = T ，即 有关系
< T x , y > = < x , T y > （x，y ∈ H ）
则称 T 为自伴算子或厄米特算子。
定义3.5.7（正规算子）
设பைடு நூலகம்H 为希尔伯特空间，T：H→H 是
有界线性算子，若T T* = T* T，则称 T 为
正规算子。
3.5.3 正算子
自伴算子可以比较大小：
定义3.5.8（正算子）设 H 为复希尔伯特
空间， T：H→H 为自伴算子，如果 T ≥
0，即
< T x， x > ≥ 0 任意 x ∈ H
必要条件是其乘积可交换，即有
T1 T2 = T2 T1
定理 3.5.4
设 T 为希尔伯特空间 H 的自伴算子，
I 为恒等算子，λ 为实数，则 λ I - T 也 是自伴算子。
3.5.2 酉算子和正规算子
定义3.5.5（酉算子）设 H 为希尔伯特空 间，T：H → H 是有界线性算子，若 T 是
一双射且 T* = T-1，则称 T 为酉算子。
定理3.5.2（自伴性）
设 H 为复希尔伯特空间，T 为 H 到自
身的有界线性算子，则 T 为自伴的充分必
要条件是，对任意的 x ∈ H ，< T x , x >
为实数。 证明：板书。
定理3.5.3（算子积的自伴性）
设 T1 和 T2 是希尔伯特空间 H 上的有
界自伴线性算子，则其乘积也自伴的充分
则称 T 为正算子或非负算子。
定义3.5.10（正定算子）
设 T 是希尔伯特空间 H 上的正算子，
若存在常数 C ＞ 0，使得
< T x，x > ≥ C‖x‖
x∈H
则称 T 为 H 上的正定算子。