几何证明选讲习题附答案

几何证明选讲专题1．如图所示，在四边形ABCD 中，//,//EF BC FG AD ，则EF FGBC AD+=1 由平行线分线段成比例可知,EF AF FG FC BC AC AD AC ==，所以1EF FG AF FCBC AD AC++==2．在平行四边形ABCD 中，点E 在边AB 上，且:1:2,AE EB DE =与AC 交于点F ，若AEF ∆的面积为6cm 2，则ABC ∆的面积为 cm 272 不妨设,AEF ABC ∆∆,AE AB 边上的高分别为12,h h ，因为四边形ABCD 为平行四边 形，:1:2,AE EB =，所以12:1:3,:1:3,:1:4AE AB EF FD h h ===，所以:1:12AEF ABC S S ∆∆=，从而ABC ∆的面积为72 cm 23．如图，圆O 上一点C 在直径AB 上的射影为D ，4,8CD BD ==，则圆O 的半径等于5 由直角三角形射影定理2CD BD DA =⋅可知2DA =，10AB =，即半径为5 4．如图，从圆O 外一点P 作圆O 的割线,,PAB PCD AB 是圆O 的直径，若4,5,3PA PC CD ===，则CBD ∠=30 由割线定理知PA PB PC PD ⋅=⋅，即4(4)5(53)AB ⨯+=⨯+，得6AB =即圆O 的半径为3，因为弦3CD =，所以60COD ∠=，从而1302CBD COD ∠=∠= 5．已知PA 是圆O 的切线，切点为A ，2,PA AC =是圆O 的直径，PC 与圆O 交于点B ，1PB =，则圆O 的半径R =由切割线定理知2PA PB PC =⋅，即221PC =⨯，4PC =，所以AC =6．如图，PC 切圆O 于点C ，割线PAB 经过圆心O ，弦C D A B ⊥于E ，4,8PC PB ==，则CD =245由切割线定理知2PC PA PB =⋅得2,826PA AB ==-=，圆O 半径为3，连接CO ，则在直角三角形PCO 中，有3512,235CO CP OP CE CE ⨯⋅=⋅==+，从而245CD = 7．如图，,AB CD 是圆O 的两条弦，交点为E 且AB 是线段CD 的中垂线，已知6,AB CD ==AD 的长度为由条件可知AB 为圆O 的直径，所以3r =，连接OD ，则2OE ==，所以5,AE AD ===8．如图，在梯形ABCD 中，////AD BC EF ，E 是AB 的中点，EF 交BD 于G ，交AC 于H ，若5,7AD BC ==，则GH =1 由条件可知EF 为梯形ABCD 的中线，且1(57)62EF =+=；由相似三角形的相似比可知,57EG BG GF DG BD BD ==，从而6157EG EG -+=，解得52EG =，同理可解得52HF =，所以1GH =9．如图，圆的内接ABC ∆的C ∠的平分线CD 延长后交圆于点E ，连接BE ，已知3BD =，7,5CE BC ==，则线段BE =215因为CD 为C ∠的平分线，所以BCE ECA ∠=∠，又圆周角EBA ECA ∠=∠，所以BCE EBA ∠=∠，又E E ∠=∠，所以EBC EBD ∆∆ ，从而BE BD EC BC =，即375BE =，所以215BE =10．如图，四边形ABCD 内接于圆O ，BC 是直径，MN 切圆O 于A ，25MAB ∠=， 则D ∠=115 连接AC ，由条件可知25C MAB ∠=∠= ，又BC 为直径，所以90BAC ∠= ，、从而180902565B ∠=--= ，又180B D ∠+∠= ，所以115D ∠=11．如图，在ABC ∆中，D 是AC 的中点，E 是BD 的中点，AE 交BC 于F ，则BFBC=12过E 作//EG DC 交BC 于G ，因为E 是BD 的中点，D 是AC 的中点，所以1124EG DC AC ==，BG GC =，又1143FG FC GC ==，所以2132BF BG FG GC FC =-==12．如图，圆'O 和圆O 相交于A 和B ，PQ 切圆O 于P ，交圆'O 于,Q M ，交AB 的延长线于N ，3,15,MN NQ ==则PN =由割线定理、切割线定理，有2NM NQ NB NA NP ⋅=⋅=，所以2315PN =⨯，即PN =13．如图，,EB EC 是圆O 的两条切线，,B C 是切点，,A D 是圆上两点，如果46E ∠=32DCF ∠= ，则A ∠的度数是因为,EB EC 是圆O 的两条切线，所以EB EC =，又46E ∠=，所以1(18046)672EBC ECB ∠=∠=-= ，又32DCF ∠= ，所以180673281BCD ∠=--= ，从而1808199A ∠=-=14．已知圆O 的半径为3，从圆O 外一点A 引切线AD 和割线ABC ，圆心O 到AC 的距离为3AB =，则切线AD 的长为依题意，2BC ==，所以5AC =，由215AD AB AC =⋅=，得AD =15．如图，已知P 是O 外一点，PD 为O 的切线，D 为切点，割线PEF 经过圆心O ，若12,PF PD ==则EFD ∠的度数为30由切割线定理得2PD PE PF =⋅2163412PD PE PF ⨯⇒===8EF ⇒=,4OD =, ∵OD PD ⊥,12OD PO =∴30P ∠= ,60,30POD PDE EFD ∠=∠=∠=。

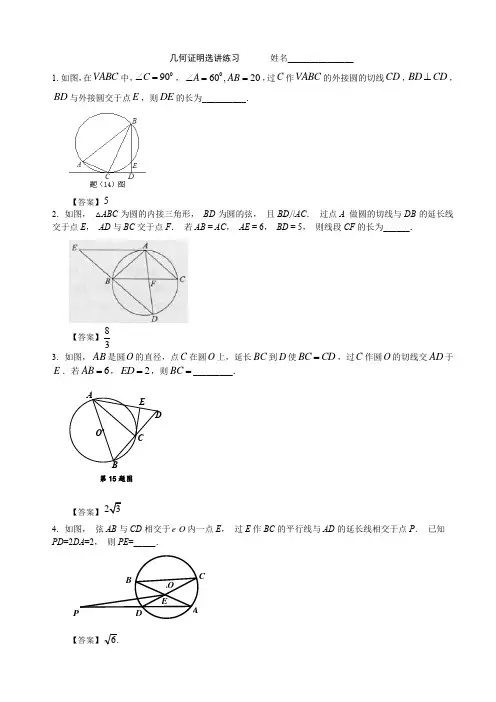
几何证明选讲练习 姓名_______________1．如图，在中，，，过作的外接圆的切线，，与外接圆交于点，则的长为__________．【答案】2．如图， △ABC 为圆的内接三角形， BD 为圆的弦， 且BD //AC ． 过点A 做圆的切线与DB 的延长线交于点E ， AD 与BC 交于点F ． 若AB = AC ， AE = 6， BD = 5， 则线段CF 的长为______．【答案】833．如图，AB 是圆O 的直径，点C 在圆O 上，延长BC 到D 使BC CD =，过C 作圆O 的切线交AD 于E ．若6AB =，2ED =，则BC =_________．【答案】4．如图， 弦AB 与CD 相交于O 内一点E ， 过E 作BC 的平行线与AD 的延长线相交于点P ． 已知PD =2DA =2， 则PE =_____．【答案】.6 ABC 090C ∠=060,20A AB ∠==C ABC CD BD CD ⊥BD EDE5.A ED CB O 第15题图5．如图2，O 中，弦,AB CD 相交于点,2P PA PB ==，1PD =，则圆心O 到弦CD 的距离为____________．【答案】23 6．如图，圆O 上一点C 在直线AB 上的射影为D ，点D 在半径OC 上的射影为E ．若3AB AD =，则CEEO的值为___________．【答案】8 7．如图，AB 为圆O 的直径，P A 为圆O 的切线，PB 与圆O 相交于D ．若PA=3，916PD DB =：：，则PD=_________；AB=___________．【答案】95；4 解三角形练习1．如图，△ABC 中，AB=AC=2，BC=点D在BC 边上，∠ADC=45°，则AD 的长度等于______．【命题意图】本题考查运用正余弦定理解三角形，是中档题．【解析】（法1）过A 作AE ⊥BC,垂足为E ，∵AB=AC=2，BC=∴E 是BC 的中点，且EC=O D EBACRt AEC ∆中，AE=又∵∠ADE=45°，∴DE=1，∴AD=（法2） ∵AB=AC=2，BC=由余弦定理知，cos C =2222AC BC AB AC BC +-⨯∴C=30°， 在△ADC 中，∠ADE=45°，由正弦定理得，sin sin AD AC C ADC=∠， ∴AD=sin sin AD C ADC ∠=12⨯2．如图，在△ABC 中，D 是边AC 上的点，且AB AD =，2AB =，2BC BD =，则sin C 的值为（ ）A．3 B．6 C3 D6【答案】D【解析】设BD a =,则由题意可得:2,BC a =2AB AD a ==,在ABD ∆中,由余弦定理得： 222cos 2AB AD BD A AB AD +-==⋅2232a a ⨯-=13，所以sin A=，在△ABC 中，由正弦定理得，sin sin AB BC C A =，所以2sin C =，解得sin CD ． 3．,EF 是等腰直角ABC ∆斜边AB 上的三等分点，则tan ECF ∠=（ ）A ．1627B ．23 CD ．34【答案】D4．在△ABC 中， 4ABC π∠=，AB 3BC =，则sin BAC ∠ =（ ） （A ）（B ）（C ）（D ）【答案】C5．ABC ∆中，90C ∠=，M 是BC 的中点，若31sin =∠BAM ，则=∠BAC sin ________．【答案】36．在△ABC 中，已知AB=4，AC=7，BC 边的中线27=AD ，求边BC 的长．7．如图，在四边形ABCD 中，AC 平分∠DAB ，∠ABC=60°，AC=7，AD=6，S △ADC =2315，求AB 的长．排列组合练习题1．有6位同学在毕业聚会活动中进行纪念品的交换，任意两位同学之间最多交换一次，进行交换的两位同学互赠一份纪念品，已知6位同学之间共进行了13次交换，则收到份纪念品的同学人数为（ ） 或 或 或 或【解析】选①设仅有甲与乙，丙没交换纪念品，则收到份纪念品的同学人数为人②设仅有甲与乙，丙与丁没交换纪念品，则收到份纪念品的同学人数为人．2．将字母排成三行两列，要求每行的字母互不相同，每列的字母也互不相同，则不同的排列方法共有A ．12种B ．18种C ．24种D ．36种答案A【命题意图】本试题考查了排列组合的用用．4()A 13()B 14()C 23()D 24D 261315132C -=-=4244,,,,,a a b b c c【解析】利用分步计数原理，先填写最左上角的数，有3种，再填写右上角的数为2种，在填写第二行第一列的数有2种，一共有．3．现有16张不同的卡片，其中红色、黄色、蓝色、绿色卡片各4张，从中任取3张，要求这些卡片不能是同一种颜色，且红色卡片至多1张，不同取法的种数为（A ）232 (B)252 (C)472 (D)484解析：,答案应选C ． 另解：． 4． 两人进行乒乓球比赛，先赢三局着获胜，决出胜负为止，则所有可能出现的情形（各人输赢局次的不同视为不同情形）共有（ ）A ．10种B ．15种C ．20种D ．30种【解析】甲赢和乙赢的可能情况是一样的，所以假设甲赢的情况如下：若两人进行3场比赛，则情况只有是甲全赢1种情况；若两人进行4场比赛，第4场比赛必为甲赢前3场任选一场乙赢为种情况；若两人进行5场比赛，第5场比赛必为甲赢前4场任选一场乙赢为种情况；综上，甲赢有10种情况，同理，乙赢有10种情况，则所有可能出现的情况共20种，故选C ．5．若从1，2，2，…，9这9个整数中同时取4个不同的数，其和为偶数，则不同的取法共有A ．60种B ．63种C ．65种D ．66种【解析】1，2，2，…，9这9个整数中有5个奇数，4个偶数．要想同时取4个不同的数其和为偶数，则取法有：4个都是偶数：1种；2个偶数，2个奇数：种； 4个都是奇数：种．∴不同的取法共有66种．【答案】D6．某艺校在一天的6节课中随机安排语文、数学、外语三门文化课和其他三门艺术课个1节，则在课表上的相邻两节文化课之间最多间隔1节艺术课的概率为 （用数字作答）．【解析】概率为 语文、数学、英语三门文化课间隔一节艺术课，排列有种排法，语文、数学、英语三门文化课相邻有种排法，语文、数学、英语三门文化课两门相邻有种排法． 32212⨯⨯=472885607216614151641122434316=-=--⨯⨯=--C C C C 472122642202111241261011123212143431204=-+=⨯⨯+-⨯⨯=+-C C C C C 313=C 624=C 225460C C =455C =3____53344A A 3312122223A C C A C3故所有的排法种数有在课表上的相邻两节文化课之间最多间隔1节艺术课的概率为5。

高中数学选修4-1《几何证明选讲》练习题（三）一、选择题：本大题共12小题，每小题5分，共60分，在每个小题给出的四个选项中，只有一项是符合题目要求的．1．已知三角形的3条中位线分别为3cm 、4cm 、6cm ，则这个三角形的周长是（ ）．A ．3cmB ．26cmC ．24cmD ．65cm2．要做甲、乙两个形状相同(相似)的三角形框架,已知三角形框架甲的三边分别为50cm 、60cm 、80cm ，三角形框架乙的一边长为20cm ，那么符合条件的三角形框架乙共有（ ）．A ．1种B ．2种C ．3种D ．4种3．在Rt ΔABC 中，CD 是斜边上的高线，AC∶BC=3∶1，则S ΔABC ∶S ΔACD 为（ ）．A ．4∶3 B．9∶1 C．10∶1 D．10∶94．如图，在正方形ABCD 中，E 为AB 中点，BF⊥CE 于F ，那么S △BFC :S 正方形ABCD =（ ）．A ．1：3B ．1：4C ．1：5D ．1：65．在△ABC 中，∠A∶∠B∶∠C＝1∶2∶3，CD⊥AB 于D ，AB ＝a ，则DB ＝（ ）A ．4aB ．3aC ．2aD ．43a6．若梯形的中位线被它的两条对角线三等分，则梯形的上底a 与下底b(a<b)的比是（）． A ．12 B ．13 C ．23 D ．257．如图，在正方形ABCD 中，E 是BC 的中点，F 是CD 上一点，且14CF CD =， 下列结论：①30BAE ∠=，②ABE AEF △∽△，③AE EF ⊥，④ADF ECF △∽△． 其中正确的个数为（ ） A ．1 B ．2 C ．3 D ．48．直角梯形的一条对角线把梯形分成两个三角形，其中一个是边长为30的等边三角形，则这个梯形的中位线长是（ ）．A ．15B ．22.5C ．45D ．909．如图所示，在△ABC 中，AC=5，中线AD=4，则AB 边的取值范围是（ ）．A ．19<<AB B ．313<<ABC ．513<<ABD ．913<<ABA B D CE F10．如图，平行四边形ABCD 中，::AE EB m n =，若AEF ∆的面积等于a ，则CDF ∆的面积等于（ ）．A BCFDEA ．22m a n B ．22n a m C ．22()m n a m + D ．22()m n a n +11．如图，在梯形ABCD 中，AD//BC ，对角线AC ⊥BD ，且AC=12，BD=9，则此梯形的中位线长是（ ）．A ．10B ．212C ．152D ．12 12．如图，设P 为ABC ∆内一点，且5152+=， 则ABP ∆的面积与ABC ∆的面积之比等于（ ）．A ．15B ．25C ．35D ．12二、填空题：本大题共4小题，每小题5分，共20分，把答案填在题中横线上．13．若两个相似三角形的周长比为3:4，则它们的三角形面积比是____________．14．如图，在梯形ABCD 中，AD//BC ，AC ⊥BA ，AD=DC=5，则BC 的长是__________．15．已知：△ABC 中，AD 是BC 边上的中线，E 是AD 的中点，BE 的延长线交AC 于点F ，则AF AC=____________． 16．在△ABC中，AB AC ==96，，点M 在AB 上且AM =3，点N 在AC 上，联结MN ，使△AMN 与原三角形相似，则AN ＝___________三、解答题：本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤．17．如图，在ABC ∆中，AD 为BC 边上的中线，F 为AB 上任意一点，CF 交AD 于点E ，求证：2AE BF DE AF ⋅=⋅．（ 10分）18．如图，正方形DEMF 内接于△ABC，若1=∆ADE S ，4=D EFM S 正方形，求ABC S ∆（ 12分）例2图 Q P M F ED CB AA BC P A DB19．已知：如图，△ＡＢＣ中，ＡＤ平分∠ＢＡＣ，ＡＤ的垂直平分线交ＡＢ于点Ｅ，交ＡＤ于点Ｈ，交ＡＣ于点Ｇ，交ＢＣ的延长线于点Ｆ，求证：ＤＦ２＝ＣＦ•ＢＦ．（ 12分）20．如图，CD 是Rt△ABC 的斜边AB 上的高，E 是BC 上任意一点，EF⊥AB 于F ．求证：EF CD AF AD AC ⋅+⋅=2．（ 12分）21．如图，在Rt ABC △中，90ACB =∠，CD AB ⊥，垂足为D ，设BC a =，AC b =，AB c =．CD b =，试说明：222111a b h +=．（ 12分）22．如图，在ABC △中，90BAC ∠=，AD 是BC 边上的高，E 是BC 边上的一个动点（不与B C ，重合），EF AB ⊥，EG AC ⊥，垂足分别为F G ，．（1）求证：EG CG AD CD=； （2）FD 与DG 是否垂直？若垂直，请给出证明；若不垂直，请说明理由；（3）当AB AC =时，FDG △为等腰直角三角形吗？并说明理由．（ 12分）B答案与解析：1-5 BCCCA 6-10AABBC 11-12 CA13．9:16 14．10 15．13 16．2，或9217．证明：过D 作//DG AB ，交CF 于G ，∴AEF DEG ∆∆，CDG CBF ∆∆，∴AE DE AF DG =，DG CD BF CB=， ∵D 为BC 的中点，12CD CB =， 12DG BF =，12DG BF =， 2AE DE AF BF =，即2AE BF DE AF ⋅=⋅． 18．解：∵正方形的面积为4，∴DE＝MF ＝2,过A 点作AQ⊥BC 于Q ，交DE 于P ，∵1=∆ADE S ，∴AP＝1，∵DE∥BC，∴△ADE∽△ABC， ∴BCDE AQ AP =，即BC 231= ∴BC＝6，故ABC S ∆＝919．证明：连ＡＦ， ∵ＦＨ垂直平分ＡＤ，∴ＦＡ＝ＦＤ， ∠ＦＡＤ＝∠ＦＤＡ，∵ＡＤ平分∠ＢＡＣ，∴∠ＣＡＤ＝∠ＢＡＤ， ∴∠ＦＡＤ－∠ＣＡＤ＝∠ＦＤＡ－∠ＢＡＤ， ∵∠Ｂ＝∠ＦＤＡ－∠ＢＡＤ，∴∠ＦＡＣ＝∠Ｂ，又∠ＡＦC 公共，∴△ＡＦＣ∽△ＢＦＡ，∴ＢＦＡＦ＝ＡＦC Ｆ， ∴ＡＦ２＝ＣＦ•ＢＦ，∴ＤＦ２＝ＣＦ•ＢＦ．20．证明：2AC AD AB =, 2()AC AD AF AD AB AF AD BF -⋅=-=因为Rt ADC Rt EFB ,所以AD EF CD BF=, 则AD BF CD EF =，2AC AD AF CD EF -⋅=⋅,即EF CD AF AD AC ⋅+⋅=2．21．解：等式222111h b a =+成立．理由如下： ∵AB CD ACB ⊥=∠,90 ，∴1122ab AB h =⋅ ， 222AB a b =+， ∴h c ab ⋅=， ∴2222h c b a ⋅=，∴22222)(h b a b a +=， ∴22222222222)(hb a h b a h b a b a +=， ∴222221b a b a h +=， ∴222111b a h +=． 22．证明：在四边形AFEG 中，∵90FAG AFE AGE ∠=∠=∠=，∴四边形AFEG 为矩形，∴AF EG =，（1）易证EG CG AD CD=，而AF EG =， ∴AF CG AD CD=； （2）ABC △为直角三角形，AD BC ⊥，∴FAD C ∠=∠，即AFD CGD △∽△，∴ADF CDG ∠=∠，又90CDG ADG ∠+∠=，∴90ADF ADG ∠+∠=，即90FDG ∠=，∴FD DG ⊥；（3）当AB AC =时，FDG △为等腰直角三角形，理由如下：AB AC =，90BAC ∠=，∴AD DC =又因为AFD CGD △∽△ ∴1FD AD GD DC==，FD DG = 又90FDG ∠=∴FDG △,FDG △为等腰直角三角形．。

第十一章⎪⎪⎪几何证明选讲(选修4－1)第一节 相似三角形的判定及有关性质1．平行线的截割定理 (1)平行线等分线段定理定理：如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等．推论1：经过三角形一边的中点与另一边平行的直线必平分第三边． 推论2：经过梯形一腰的中点，且与底边平行的直线平分另一腰． (2)平行线分线段成比例定理定理：三条平行线截两条直线，所得的对应线段成比例．推论：平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例． 2．相似三角形的判定定理(1)判定定理1：两角对应相等，两三角形相似．(2)判定定理2：两边对应成比例且夹角相等，两三角形相似． (3)判定定理3：三边对应成比例，两三角形相似． 3．相似三角形的性质定理(1)性质定理：相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．(2)推论：相似三角形外接圆的直径比、周长比等于相似比，外接圆的面积比等于相似比的平方．4．直角三角形相似的判定定理(1)判定定理1：如果两个直角三角形有一个锐角对应相等，那么它们相似． (2)判定定理2：如果两个直角三角形的两条直角边对应成比例，那么它们相似． (3)判定定理3：如果一个直角三角形的斜边和一条直角边与另一个三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似．5．直角三角形射影定理直角三角形斜边上的高是两直角边在斜边上射影的比例中项；两直角边分别是它们在斜边上射影与斜边的比例中项．[小题体验]1.(教材习题改编)如图，AB ∥EM ∥DC ，AE ＝ED ，EF ∥BC ，EF＝12 cm ，则BC 的长为________ cm.解析：由⎭⎪⎬⎪⎫AB ∥EM ∥DC AE ＝ED ⇒E 为AD 中点，M 为BC 的中点， 又EF ∥BC ⇒EF ＝MC ＝12 cm. ∴BC ＝2MC ＝24 cm. 答案：242.(教材习题改编)如图，D ，E 分别是△ABC 的边AB ，AC 上的点，DE ∥BC 且ADDB＝2，那么△ADE 与四边形DBCE 的面积比是________．解析：∵DE ∥BC ，∴△ADE ∽△ABC ， ∴S △ADE S △ABC ＝AD 2AB 2. ∵AD DB ＝2，∴AD AB ＝23，∴S △ADE S △ABC ＝49，故S △ADE S 四边形DBCE ＝45. 答案：451．在使用平行线截割定理时易出现对应边的对应顺序混乱，导致错误． 2．在解决相似三角形的判定或应用时易出现对应边和对应角的对应失误．3．射影定理是直角三角形中的一个重要结论，其实质就是三角形的相似．但要注意满足直角三角形射影定理结论的三角形不一定是直角三角形，所以要搞清楚定理中的条件和结论之间的关系，不能乱用．[小题纠偏]1.(2016·鞍山模拟)如图，在▱ABCD 中，E 是BC 上一点，BE ∶EC ＝2∶3，AE 交BD 于点F ，则BF ∶FD 的值为________．解析：因为AD ＝BC ，BE ∶EC ＝2∶3， 所以BE ∶AD ＝2∶5，因为AD ∥BC ， 所以BF ∶FD ＝BE ∶AD ＝2∶5， 所以BF ∶FD 的值为25.答案：252.如图，在Rt △ABC 中 ，∠BAC ＝90°，AD 是斜边BC 上的高，若AB ∶AC ＝2∶1，则AD ∶BC 为________．解析：设AC ＝k ，则AB ＝2k ，BC ＝5k ， ∵∠BAC ＝90°，AD ⊥BC ， ∴AC 2＝CD ·BC ， ∴k 2＝CD ·5k ，∴CD ＝55k ， 又BD ＝BC －CD ＝455k ， ∴AD 2＝CD ·BD ＝55k ·455k ＝45k 2， ∴AD ＝255k ，∴AD ∶BC ＝2∶5. 答案：2∶5考点一 平行线分线段成比例定理的应用(基础送分型考点——自主练透)[题组练透]1．如图，在梯形ABCD 中，AD ∥BC ，BD 与AC 相交于点O ，过点O 的直线分别交AB ，CD 于E ，F ，且EF ∥BC ，若AD ＝12，BC ＝20，求EF 的值．解：∵AD ∥BC ， ∴OB OD ＝BC AD ＝2012＝53， ∴OB BD ＝58.∵OE ∥AD ，∴OE AD ＝OB BD ＝58.∴OE ＝58AD ＝58×12＝152，同理可求得OF ＝38BC ＝38×20＝152，∴EF ＝OE ＋OF ＝15.2．如图，在△ABC 中，点D 是AC 的中点，点E 是BD 的中点，AE 交BC 于点F ，求BFFC 的值．解：如图，过点D 作DM ∥AF 交BC 于点M . ∵点E 是BD 的中点，∴在△BDM 中，BF ＝FM . 又点D 是AC 的中点， ∴在△CAF 中，CM ＝MF ， ∴BF FC ＝BF FM ＋MC ＝12.[谨记通法]平行线分线段成比例定理及推论的应用的一个注意点及一种转化(1)一个注意点：利用平行线分线段成比例定理来计算或证明，首先要观察平行线组，再确定所截直线，进而确定比例线段及比例式，同时注意合比性质、等比性质的运用．(2)一种转化：解决此类问题往往需要作辅助的平行线，要结合条件构造平行线组，再应用平行线分线段成比例定理及其推论转化比例式解题．考点二 相似三角形的判定及性质 (重点保分型考点——师生共研)[典例引领]如图，在△ABC 中，AB ＝AC ，∠BAC ＝90°，D ，E ，F 分别在AB ，AC ，BC 上，AE ＝13AC ，BD ＝13AB ，且CF ＝13BC .求证：(1)EF ⊥BC ； (2)∠ADE ＝∠EBC . 证明：设AB ＝AC ＝3a ， 则AE ＝BD ＝a ，CF ＝2a . (1)CE CB ＝2a 32a ＝23，CF CA ＝2a 3a ＝23. 又∠C 为公共角， 故△BAC ∽△EFC ，由∠BAC ＝90°，得∠EFC ＝90°， 故EF ⊥BC .(2)由(1)得EF ＝FC AC ·AB ＝2a ， 故AE EF ＝a 2a ＝22，AD BF ＝2a 22a ＝22，∴AE EF ＝AD BF， ∴△ADE ∽△FBE ， 所以∠ADE ＝∠EBC .[由题悟法]证明相似三角形的一般思路(1)先找两对内角对应相等．(2)若只有一个角对应相等，再判定这个角的两邻边是否对应成比例． (3)若无角对应相等，就要证明三边对应成比例．[即时应用]如图，已知在△ABC 中，D 是BC 边的中点，且AD ＝AC ，DE ⊥BC ，DE 与AB 相交于点E ，EC 与AD 相交于点F .(1)求证：△ABC ∽△FCD ；(2)若S △FCD ＝5，BC ＝10，求DE 的长．解：(1)证明：因为DE ⊥BC ，D 是BC 的中点，所以EB ＝EC ，所以∠B ＝∠BCE .又因为AD ＝AC ，所以∠ADC ＝∠ACB.所以△ABC ∽△FCD.(2)如图，过点A 作AM ⊥BC ， 垂足为点M .因为△ABC ∽△FCD ，BC ＝2CD ， 所以S △ABC S △FCD ＝⎝⎛⎭⎫BC CD 2＝4.又因为S △FCD ＝5，所以S △ABC ＝20. 因为S △ABC ＝12BC ·AM ，BC ＝10，所以20＝12×10×AM ，所以AM ＝4.因为DE ∥AM ，所以DE AM ＝BDBM . 因为DM ＝12DC ＝52，BM ＝BD ＋DM ，所以DE 4＝55＋52，解得DE ＝83.考点三 直角三角形中的射影定理 (重点保分型考点——师生共研)[典例引领]如图所示，CD 垂直平分AB ，点E 在CD 上，DF ⊥AC ，DG ⊥BE ，F ，G 分别为垂足．求证：AF ·AC ＝BG ·BE . 证明：因为CD 垂直平分AB ， 所以∠ADC ＝∠BDC ＝90°，AD ＝D B.在Rt △ADC 中，因为DF ⊥AC ， 所以AD 2＝AF ·AC . 同理BD 2＝BG ·BE . 所以AF ·AC ＝BG ·BE .[由题悟法]对射影定理的理解和应用(1)利用直角三角形的射影定理解决问题首先确定直角边与其射影．(2)要善于将有关比例式进行适当的变形转化，有时还要将等积式转化为比例式或将比例式转化为等积式，并且注意射影定理的其他变式．(3)注意射影定理与勾股定理的结合应用．[即时应用]在Rt △ACB 中，∠C ＝90°，CD ⊥AB 于D ，若BD ∶AD ＝1∶9，求tan ∠BCD 的值． 解：由射影定理得CD 2＝AD ·BD ， 又BD ∶AD ＝1∶9， 令BD ＝x ，则AD ＝9x (x >0)． ∴CD 2＝9x 2， ∴CD ＝3x .Rt △CDB 中，tan ∠BCD ＝BD CD ＝x 3x ＝13.1.如图，在四边形ABCD 中，EF ∥BC ，FG ∥AD ，求EF BC ＋FGAD 的值．解：由平行线分线段成比例定理得 EF BC ＝AF AC ，FG AD ＝FC AC ，故EF BC ＋FG AD ＝AF AC ＋FC AC ＝AC AC ＝1.2.如图，等边三角形DEF 内接于△ABC ，且DE ∥BC ，已知AH ⊥BC 于点H ，BC ＝4，AH ＝3，求△DEF 的边长．解：设DE ＝x ，AH 交DE 于点M ，显然MH 的长度与等边三角形DEF 的高相等，又DE ∥BC ，则DE BC ＝AM AH ＝AH －MH AH ， 所以x4＝3－32x 3＝2－x 2，解得x ＝43.故△DEF 的边长为43.3.如图，M 是平行四边形ABCD 的边AB 的中点，直线l 过点M 分别交AD ，AC 于点E ，F ，交CB 的延长线于点N .若AE ＝2，AD ＝6，求AFAC的值． 解：∵AD ∥BC ， ∴△AEF ∽△CNF ， ∴AF CF ＝AE CN ， ∴AF AF ＋CF ＝AEAE ＋CN.∵M 为AB 的中点，∴AE BN ＝AMBM ＝1，∴AE ＝BN ， ∴AF AC ＝AF AF ＋CF ＝AE AE ＋BN ＋BC ＝AE 2AE ＋BC. ∵AE ＝2，BC ＝AD ＝6， ∴AF AC ＝22×2＋6＝15.4.如图，AD ，BE 是△ABC 的两条高，DF ⊥AB ，垂足为F ，交BE 于点G ，交AC 的延长线于H ，求证：DF 2＝GF ·HF .证明：在△AFH 与△GFB 中， 因为∠H ＋∠BAC ＝90°， ∠GBF ＋∠BAC ＝90°，所以∠H ＝∠GBF .因为∠AFH ＝∠BFG ＝90°， 所以△AFH ∽△GFB ， 所以HF BF ＝AF GF ， 所以AF ·BF ＝GF ·HF .因为在Rt △ABD 中，FD ⊥AB ， 所以DF 2＝AF ·BF . 所以DF 2＝GF ·HF .5.(2016·大连模拟)如图，已知D 为△ABC 中AC 边的中点，AE ∥BC ，ED 交AB 于G ，交BC 延长线于F ，若BG ∶GA ＝3∶1，BC ＝8，求AE 的长．解：因为AE ∥BC ，D 为AC 的中点， 所以AE ＝CF ，AE BF ＝AG BG ＝13.设AE ＝x ，又BC ＝8， 所以x x ＋8＝13，所以x ＝4. 所以AE ＝4.6.(2016·大连模拟)如图，在△ABC 中，D 是AC 的中点，E 是BD 的中点，AE 的延长线交BC 于F .(1)求BFFC 的值；(2)若△BEF 的面积为S 1，四边形CDEF 的面积为S 2，求S 1∶S 2的值． 解：(1)过点D 作DG ∥BC ，并交AF 于点G ，因为E 是BD 的中点，所以BE ＝DE . 又因为∠EBF ＝∠EDG ，∠BEF ＝∠DEG ， 所以△BEF ≌△DEG ，则BF ＝DG ， 所以BF ∶FC ＝DG ∶FC .又因为D 是AC 的中点，则DG ∶FC ＝1∶2， 则BF ∶FC ＝1∶2，即BF FC ＝12.(2)若△BEF 以BF 为底，△BDC 以BC 为底， 则由(1)知BF ∶BC ＝1∶3，又由BE ∶BD ＝1∶2，可知h 1∶h 2＝1∶2， 其中h 1，h 2分别为△BEF 和△BDC 的高， 则S △BEF S △BDC ＝13×12＝16， 则S 1∶S 2＝1∶5. 故S 1∶S 2的值为15.7.如图，在△ABC 中，AB ＝AC ，过点A 的直线与其外接圆交于点P ，交BC 的延长线于点D.(1)求证：PC AC ＝PDBD ；(2)若AC ＝3，求AP ·AD 的值．解：(1)证明：因为∠CPD ＝∠ABC ，∠PDC ＝∠PDC ， 所以△DPC ∽△DBA ，所以PC AB ＝PD BD . 又AB ＝AC ，所以PC AC ＝PD BD. (2)因为∠ABC ＋∠APC ＝180°，∠ACB ＋∠ACD ＝180°， ∠ABC ＝∠ACB ， 所以∠ACD ＝∠APC .又∠CAP ＝∠DAC ，所以△APC ∽△ACD ， 所以AP AC ＝AC AD. 所以AP ·AD ＝AC 2＝9.8.△ABC 中，D ，E ，F 分别是BC ，AB ，AC 上的点，AD ，EF 交于点P ，若BD ＝DC ，AE ＝AF .求证：AB AC ＝PF PE .证明：过F 作MN ∥AD 交BA 的延长线及DC 于M ，N .对△MEF ，有PF PE ＝AMAE ，因为AE ＝AF ，所以PF PE ＝AM AF. 对△MBN ，有AB AM ＝BDDN ， 因为BD ＝DC ，所以AB AM ＝DCDN . 对△ADC ，有AC AF ＝DC DN ，所以AB AM ＝ACAF . 所以AB AC ＝AM AF ，所以AB AC ＝PF PE .第二节 直线与圆的位置关系1．圆周角(1)定理：圆上一条弧所对的圆周角等于它所对的圆心角的一半． (2)推论1：①同弧或等弧所对的圆周角相等； ②同圆或等圆中，相等的圆周角所对的弧也相等． (3)推论2：①半圆(或直径)所对的圆周角是直角； ②90°的圆周角所对的弦是直径． 2．圆的切线(1)判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线． (2)性质定理：圆的切线垂直于经过切点的半径．(3)切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角．3．弦切角定理及其推论(1)定理：弦切角等于它所夹的弧所对的圆周角． (2)推论：弦切角的度数等于它所夹的弧的度数的一半． 4．圆中的比例线段(1)相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等．(2)割线定理：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等．(3)切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项．[小题体验]1.(教材习题改编)如图，已知AB ，BC 是⊙O 的两条弦，AO ⊥BC ，AB ＝3，BC ＝22，则⊙O 的半径等于________．解析：设垂足为D ，⊙O 的半径等于R ， ∵AB ，BC 是⊙O 的两条弦， AO ⊥BC ，AB ＝3，BC ＝22， ∴AD ＝1，∴R 2＝2＋(R －1)2， ∴R ＝1.5.故⊙O 的半径为1.5. 答案：1.52.如图，AC 为⊙O 的直径，OB ⊥AC ，弦BN 交AC 于点M .若OC ＝3，OM ＝1，则MN 的长为________．解析：由题意得： CM ＝CO ＋OM ＝3＋1， AM ＝AO －OM ＝3－1， BM 2＝OB 2＋OM 2＝4，BM ＝2， 根据相交弦定理有CM ·AM ＝BM ·MN ，代入数值可解得MN ＝CM ·AM BM ＝(3＋1)(3－1)2＝1.答案：13.如图，⊙O 的直径AB ＝6 cm ，P 是AB 延长线上的一点，过P 点作⊙O 的切线，切点为C ，连接AC ，若∠CPA ＝30°，PC ＝________ cm.解析：连接OC ，则OC ⊥PC .又OC ＝3，∠CPA ＝30°， ∴CP ＝OCtan 30°＝3 3.答案：3 31．解决圆周角、圆心角及弦切角问题时，角之间关系易于混淆导致错误．2．使用相交弦定理与切割线定理时，注意对应线段成比例及相似三角形知识的应用．[小题纠偏]1.如图所示，CD 是圆O 的切线，切点为C ，点B 在圆O 上，BC ＝2，∠BCD ＝30°，则圆O 的面积为________．解析：设圆O的半径为r，过B作⊙O的直径BA，连接AC，则∠ACB＝90°.又由弦切角定理得∠CAB＝∠BCD＝30°，∴AB＝2BC＝4.∴r＝2，∴S＝πr2＝4π.答案：4π2.如图所示，已知⊙O的割线PAB交⊙O于A，B两点，割线PCD经过圆心，若PA＝3，AB＝4，PO＝5，则⊙O的半径为________．解析：设⊙O的半径为r.由割线定理得PA·PB＝PC·PD,3×7＝(PO－r)(PO＋r)，即21＝25－r2，∴r2＝4，∴r＝2.答案：2考点一圆周角、弦切角和圆的切线问题(基础送分型考点——自主练透)[题组练透]1.(2016·黄冈模拟)已知点C在圆O的直径BE的延长线上，直线CA与圆O相切于A，∠ACB的平分线分别交AB，AE于D，F两点，求∠AFD的大小．解：因为AC为圆O的切线，由弦切角定理，得∠B＝∠EAC.又因为CD平分∠ACB，则∠ACD＝∠BCD，所以∠B＋∠BCD＝∠EAC＋∠ACD.根据三角形外角定理，∠ADF＝∠AFD.因为BE是圆O的直径，则∠BAE＝90°，所以△ADF是等腰直角三角形．所以∠ADF＝∠AFD＝45°.2．(2015·广东高考改编)如图，已知AB是圆O的直径，AB＝4，EC是圆O的切线，切点为C，BC＝1.过圆心O作BC的平行线，分别交EC和AC于点D和点P，求OD的长．解：由题意得OP ＝12BC ＝12，OA ＝2，于是PA ＝CP ＝22－⎝⎛⎭⎫122＝152. 因为∠DCP ＝∠B ＝∠POA ，又∠DPC ＝∠APO ，所以△DCP ∽△AOP ， 故PD PA ＝PCPO， 即PD ＝15212×152＝152，所以OD ＝152＋12＝8.[谨记通法]1．圆周角定理及其推论与弦切角定理及其推论多用于推出角的关系，从而证明三角形全等或相似，可求线段或角的大小．2．涉及圆的切线问题时要注意弦切角的转化；关于圆周上的点，常作直径(或半径)或向弦(弧)两端作圆周角或弦切角．考点二 圆内接四边形的性质及判定 (重点保分型考点——师生共研)[典例引领](2016·昆明模拟)如图所示，已知D 为△ABC 的BC 边上一点，⊙O 1经过点B ，D ，交AB 于另一点E ，⊙O 2经过点C ，D ，交AC 于另一点F ，⊙O 1与⊙O 2的另一交点为G .(1)求证：A ，E ，G ，F 四点共圆；(2)若AG 切⊙O 2于G ，求证：∠AEF ＝∠ACG . 证明：(1)如图，连接GD ，四边形BDGE ，四边形CDGF 分别内接于⊙O 1，⊙O 2， ∴∠AEG ＝∠BDG ， ∠AFG ＝∠CDG ，又∠BDG ＋∠CDG ＝180°， ∴∠AEG ＋∠AFG ＝180°，∴A，E，G，F四点共圆．(2)∵A，E，G，F四点共圆，∴∠AEF＝∠AGF，∵AG与⊙O2相切于点G，∴∠AGF＝∠ACG，∴∠AEF＝∠ACG.[由题悟法]证明四点共圆的常用方法(1)若四个点到一定点等距离，则这四个点共圆．(2)若一个四边形的一组对角的和等于180°，则这个四边形的四个顶点共圆．(3)若一个四边形的一个外角等于它的内对角，则这个四边形的四个顶点共圆．(4)若两个点在一条线段的同旁，并且和这条线段的两端连线所夹的角相等，那么这两个点和这条线段的两个端点共圆．[即时应用](2016·吉林实验中学)如图，圆周角∠BAC的平分线与圆交于点D，过点D的切线与弦AC的延长线交于点E，AD交BC于点F.(1)求证：BC∥DE；(2)若D，E，C，F四点共圆，且AC＝BC，求∠BAC.解：(1)证明：因为DE为圆的切线，所以∠EDC＝∠DAC.又因为∠DAC＝∠DAB，∠DAB＝∠DCB，所以∠EDC＝∠DCB，所以BC∥DE.(2)因为D，E，C，F四点共圆，所以∠CFA＝∠CED，由(1)知∠ACF＝∠CED，所以∠CFA＝∠ACF.设∠DAC＝∠DAB＝x，因为AC＝BC，所以∠CBA＝∠BAC＝2x，所以∠CFA＝∠FBA＋∠FAB＝3x，在等腰△ACF中，180°＝∠CFA＋∠ACF＋∠CAF＝7x，则x≈25.7°，所以∠BAC＝2x≈51.4°.考点三 与圆有关的比例线段 (重点保分型考点——师生共研)[典例引领](2015·陕西高考)如图，AB 切⊙O 于点B ，直线AO 交⊙O 于D ，E 两点，BC ⊥DE ，垂足为C .(1)证明：∠CBD ＝∠DBA;(2)若AD ＝3DC ，BC ＝2，求⊙O 的直径． 解：(1)证明：因为DE 为⊙O 的直径， 所以∠BED ＋∠EDB ＝90°.又BC ⊥DE ，所以∠CBD ＋∠EDB ＝90°， 从而∠CBD ＝∠BED.又AB 切⊙O 于点B ，得∠DBA ＝∠BED ， 所以∠CBD ＝∠DBA . (2)由(1)知BD 平分∠CBA ， 则BA BC ＝ADCD＝3. 又BC ＝2，从而AB ＝3 2. 所以AC ＝AB 2－BC 2＝4， 所以AD ＝3.由切割线定理得AB 2＝AD ·AE ， 即AE ＝AB 2AD ＝6，故DE ＝AE －AD ＝3， 即⊙O 的直径为3.[由题悟法]与圆有关的比例线段解题思路(1)见到圆的两条相交弦就要想到相交弦定理． (2)见到圆的两条割线就要想到割线定理． (3)见到圆的切线和割线就要想到切割线定理．[即时应用]1．(2015·天津高考改编)如图，在圆O 中，M ，N 是弦AB 的三等分点，弦CD ，CE 分别经过点M ，N ，若CM ＝2，MD ＝4，CN ＝3，求线段NE 的长．解：由题意可得CM ·MD ＝AM ·MB ， 则2×4＝2AM 2，AM ＝2. 又CN ·NE ＝AN ·NB ， 即3NE ＝4×2，解得NE ＝83.2．(2015·湖北高考改编)如图，PA 是圆的切线，A 为切点，PBC 是圆的割线，且BC ＝3PB ，求ABAC的值． 解：因为PA 是圆的切线， A 为切点，PBC 是圆的割线，由切割线定理，知PA 2＝PB ·PC ＝PB (PB ＋BC )， 因为BC ＝3PB ，所以PA 2＝4PB 2，即PA ＝2PB. 由弦切角定理，得∠PAB ＝∠PCA ， 又∠APB ＝∠CPA ，故△PAB ∽△PCA ， 所以AB AC ＝PB PA ＝12.1．(2015·重庆高考改编)如图，圆O 的弦AB ，CD 相交于点E ，过点A 作圆O 的切线与DC 的延长线交于点P ，若PA ＝6，AE ＝9，PC ＝3，CE ∶ED ＝2∶1，求BE 的长．解：由切割线定理，知PA 2＝PC ·PD ， 即62＝3PD ， 解得PD ＝12，所以CD ＝PD －PC ＝9， 所以CE ＝6，ED ＝3.由相交弦定理，知AE ·EB ＝CE ·ED ，即9BE ＝6×3，解得BE ＝2.2．(2016·兰州双基测试)如图，在正△ABC 中，点D ，E 分别在BC ，AC 上，且BD ＝13BC ，CE ＝13CA ，AD ，BE 相交于点P .求证：(1)P ，D ，C ，E 四点共圆； (2)AP ⊥CP .证明：(1)在正△ABC 中，由BD ＝13BC ，CE ＝13CA ，知：△ABD ≌△BCE ，∴∠ADB ＝∠BEC ，即∠ADC ＋∠BEC ＝180°， ∴P ，D ，C ，E 四点共圆．(2)连接DE ，在△CDE 中，CD ＝2CE ，∠ACD ＝60°， 由正弦定理知∠CED ＝90°，由P ，D ，C ，E 四点共圆知，∠DPC ＝∠DEC ， ∴AP ⊥CP .3．(2016·陕西一检)如图，设AB 为⊙O 的任一条不与直线l 垂直的直径，P 是⊙O 与l 的公共点，AC ⊥l ，BD ⊥l ，垂足分别为C ，D ，且PC ＝PD.(1)求证：l 是⊙O 的切线；(2)若⊙O 的半径OA ＝5，AC ＝4，求CD 的长．解：(1)证明：连接OP ， ∵AC ⊥l ，BD ⊥l ， ∴AC ∥BD.又OA ＝OB ，PC ＝PD ， ∴OP ∥BD ，从而OP ⊥l .∵点P 在⊙O 上，∴l 是⊙O 的切线． (2)由(1)可得OP ＝12(AC ＋BD )，∴BD ＝2OP －AC ＝10－4＝6. 过点A 作AE ⊥BD ，垂足为E ， 则BE ＝BD －AC ＝6－4＝2. ∴在Rt △ABE 中，AE ＝AB 2－BE 2＝102－22＝4 6. ∴CD ＝4 6.4.(2015·全国卷Ⅰ)如图，AB 是⊙O 的直径，AC 是⊙O 的切线，BC交⊙O 于点E .(1)若D 为AC 的中点，证明：DE 是⊙O 的切线； (2)若OA ＝3CE ，求∠ACB 的大小． 解：(1)证明：如图，连接AE ，由已知得AE ⊥BC ，AC ⊥AB. 在Rt △AEC 中，由已知得DE ＝DC ，故∠DEC ＝∠DCE . 连接OE ，则∠OBE ＝∠OEB. 又∠ACB ＋∠ABC ＝90°， 所以∠DEC ＋∠OEB ＝90°，故∠OED ＝90°，即DE 是⊙O 的切线． (2)设CE ＝1，AE ＝x .由已知得AB ＝23，BE ＝12－x 2. 由射影定理可得AE 2＝CE ·BE ， 所以x 2＝12－x 2，即x 4＋x 2－12＝0. 解得x ＝3，所以∠ACB ＝60°.5．(2015·沈阳一模)如图所示，已知AB 为圆O 的直径，C ，D 是圆O 上的两个点，CE ⊥AB 于E ，BD 交AC 于G ，交CE 于F ，CF ＝FG .(1)求证：C 是劣弧BD 的中点； (2)求证：BF ＝FG .证明：(1)∵CF ＝FG ，∴∠CGF ＝∠FCG . ∵AB 是圆O 的直径，∴∠ACB ＝∠ADB ＝π2.∵CE ⊥AB ，∴∠CEA ＝π2.∵∠CBA ＝π2－∠CAB ，∠ACE ＝π2－∠CAB ，∴∠CBA ＝∠ACE .∵∠CGF ＝∠DGA ，∠DGA ＝∠ABC ， ∴π2－∠DGA ＝π2－∠ABC ， ∴∠CAB ＝∠DAC ， ∴C 为劣弧BD 的中点．(2)∵∠GBC ＝π2－∠CGB ，∠FCB ＝π2－∠GCF ，∴∠GBC ＝∠FCB ，∴CF ＝FB ，∴BF ＝FG .6．(2016·贵州七校联考)如图，⊙O 1和⊙O 2的公切线AD 和BC 相交于点D ，A ，B ，C 为切点，直线DO 1交⊙O 1于E ，G 两点，直线DO 2交⊙O 2于F ，H 两点．(1)求证：△DEF ∽△DHG ；(2)若⊙O 1和⊙O 2的半径之比为9∶16，求DEDF 的值． 解：(1)证明：∵AD 是两圆的公切线， ∴AD 2＝DE ·DG ，AD 2＝DF ·DH ， ∴DE ·DG ＝DF ·DH ，∴DE DH ＝DF DG ， 又∵∠EDF ＝∠HDG ， ∴△DEF ∽△DHG .(2)连接O 1A ，O 2A ， ∵AD 是两圆的公切线， ∴O 1A ⊥AD ，O 2A ⊥AD ， ∴O 1，A ，O 2共线，∵AD 和BC 是⊙O 1和⊙O 2的公切线， DG 平分∠ADB ，DH 平分∠ADC ， ∴DG ⊥DH ，∴AD 2＝O 1A ·O 2A .设⊙O 1和⊙O 2的半径分别为9x 和16x ，则AD ＝12x ， ∵AD 2＝DE ·DG ，AD 2＝DF ·DH ，∴144x 2＝DE (DE ＋18x )，144x 2＝DF (DF ＋32x )， ∴DE ＝6x ，DF ＝4x ， ∴DE DF ＝32.7．(2016·沈阳模拟)如图，已知圆O 1与圆O 2外切于点P ，直线AB 是两圆的外公切线，分别与两圆相切于A ，B 两点，AC 是圆O 1的直径，过C 作圆O 2的切线，切点为D.(1)求证：C ，P ，B 三点共线； (2)求证：CD ＝CA .证明：(1)连接PC ，PA ，PB ，BO 2，∵AC是圆O1的直径，∴∠APC＝90°.连接O1O2必过点P，∵AB是两圆的外公切线，A，B为切点，∴设∠BAP＝∠ACP＝α，∴∠AO1P＝2α.由于O1A⊥AB，O2B⊥AB，∴∠BO2P＝π－2α，∴∠O2BP＝α.又∠ABP＋∠O2BP＝90°，∴∠ABP＋∠BAP＝90°，∴C，P，B三点共线．(2)∵CD切圆O2于点D，∴CD2＝CP·CB.在△ABC中，∠CAB＝90°，又∵AP⊥BC，∴CA2＝CP·CB，故CD＝CA.8．(2015·全国卷Ⅱ)如图，O为等腰三角形ABC内一点，⊙O与△ABC的底边BC交于M，N两点，与底边上的高AD交于点G，且与AB，AC分别相切于E，F两点．(1)证明：EF∥BC；(2)若AG等于⊙O的半径，且AE＝MN＝23，求四边形EBCF的面积．解：(1)证明：由于△ABC是等腰三角形，AD⊥BC，所以AD是∠CAB的平分线．又因为⊙O分别与AB，AC相切于点E，F，所以AE＝AF，故AD⊥EF，从而EF∥BC.(2)由(1)知，AE＝AF，AD⊥EF，故AD是EF的垂直平分线．又EF为⊙O的弦，所以O在AD上．连接OE，OM，则OE⊥AE.由AG等于⊙O的半径得AO＝2OE，所以∠OAE ＝30°.因此△ABC 和△AEF 都是等边三角形． 因为AE ＝23，所以AO ＝4，OE ＝2.因为OM ＝OE ＝2，DM ＝12MN ＝3， 所以OD ＝1.于是AD ＝5，AB ＝1033. 所以四边形EBCF 的面积为12×⎝⎛⎭⎫10332×32－12×(23)2×32＝1633.。

高中数学选修 4-1《几何证明选讲》练习题（二）1． (2010 ·津卷天 )如图，四边形 ABCD 是圆 O 的内接四边形，延伸 AB 和 DC订交于点P.若PB ＝ 1， PD ＝ 3，则 ADBC 的值为 ________．分析：∵∠P ＝∠ P ，∠ A ＝∠ PCB ，∴△ PCB ∽△ PAD .PB BC 1∴ PD ＝ AD ＝3.答案：132．(2010 湖·南卷 )如下图，过⊙ O 外一点 P 作一条直线与⊙ O 交于 A ，B 两点，已知 PA ＝ 2，点 P 到⊙ O 的切线长 PT ＝4，则弦 AB 的长为 ______．分析： 由切割线定理知 PT 2＝PA ·PB ，2∴ PB ＝ 4＝ 8.∴弦 AB 的长为 PB －PA ＝ 8－ 2＝ 6. 2答案： 63．如下图，已知PC 、 DA 为⊙ O 的切线， C 、A 分别为切点， AB 为⊙ O 的直径，若 DA ＝ 2， CD ＝ 1，则 AB ＝ ________.DP 2分析： 由 CD ＝DA ＝2，∴ DP ＝ 4.2 2在 Rt △ADP 中， AP ＝ 4 － 2 ＝ 2 3.2由切割线定理： PC ＝ PA ·PB ，∴ 62＝ 2 3(2 3＋ AB)，∴ AB ＝ 4 3. 答案：4 34． (2010 ·西卷陕 )如图，已知 Rt △ ABC 的两条直角边AC ， BC 的长分别为 3 cm ，BD4 cm ，以 AC 为直径的圆与 AB 交于点 D ，则 DA ＝ ________. 分析： ∵∠ C ＝ 90°， AC 为圆的直径，∴ BC 为圆的切线， AB 为圆的割线．∴ BC 2＝ BD ·BA ，即 16＝BD ·5，解得 BD ＝16.5∴ DA ＝ BA － BD ＝5－ 16 9BD ＝ 16. 5 ＝ .∴DA 916 5 答案：95． (2010 ·东东莞广 )如图，已知 PA 、PB 是圆 O 的切线， A 、B 分别为切点， C 为圆 O 上不与 A 、 B 重合的另一点，若∠ ACB ＝ 120°，则∠ APB ＝ ________.分析： 连结 OA 、OB ，∠ PAO ＝∠ PBO ＝90°，∵∠ ACB ＝ 120°，∴∠ AOB ＝ 120°.又 P 、 A 、O 、 B 四点共圆，故∠ APB ＝ 60°.答案：60°PC 6． (2010切圆 O 于·东佛山广 )如图，点 C 点， CD ⊥AB 于 D P 在圆点，则 O 直径 AB 的延伸线上，且CD ＝ ________.PB ＝ OB ＝ 2，2分析：由切割线定理知， PC ＝PA ·PB ，又 OC ⊥PC ，故 CD ＝PC ·OC ＝2 3×2＝ 3.PO4答案：37．如图， AB 为⊙ O 的直径， AC 切⊙ O 于点 A ，且 AC ＝ 2 2 cm ，过 C 的割线 CMN交 AB 的延伸线于点 D ， CM ＝MN ＝ ND ，则 AD 的长等于 ________cm.分析： 由切割线定理知 |CA |2＝ |CM | ·|CN|＝ 2|CM |2，由于 |CA |＝2 2，因此 |CM|＝ 2， |CD |＝ 6，22答案：2 78． (2010 广·东卷 )如图， AB ，CD 是半径为 a 的圆 O 的两条弦，它们订交于AB 的中点 P ， PD ＝2a，∠ OAP ＝ 30°，则 CP ＝______. 3分析： ∵ AP ＝ PB ，∴ OP ⊥AB .3又∵∠ OAP ＝ 30°，∴ AP ＝ 2 a.由订交弦定理得 CP ·PD ＝AP 2，∴ CP ＝ AP 2 3 2 3 9＝ a × ＝ a.PD 4 2a 8答案：98a9．(2010 北·京卷 )如图， ⊙ O 的弦 ED ，CB 的延伸线交于点 A.若 BD ⊥ AE ，AB ＝ 4， BC ＝ 2， AD ＝ 3，则 DE ＝ ______， CE ＝ ______.分析： 由圆的割线定理知：∴ AE ＝ 8，∴ DE ＝ 5.连结 EB ，∵∠ EDB ＝90°，∴ EB 为直径．∴∠ ECB ＝ 90°.由勾股定理，得2 222 22＝ 16－ 9＋ 25＝ 32.EB＝DB＋ ED＝AB －AD ＋ED 在 Rt △ECB 中， EB 2＝ BC 2＋ CE 2＝ 4＋ CE 2，∴ CE 2＝ 28，∴ CE ＝ 2 7. 答案： 5 2 710．如图， PC 切⊙ O 于点 C ，割线 PAB 经过圆心 O ，弦 CD ⊥AB 于点 E ，已知⊙O 的半径为 3，PA ＝ 2，则 PC ＝________， OE ＝ ________.分析： 由于 PB ＝ PA ＋ AB ＝ 8，因此在⊙ O 中，由切割线定理得：2PC ＝ PA ·PB ＝ 2×8＝ 16，故 PC ＝ 4；在 Rt △OCP 中，由射影定理得：PC 2＝ PE ·PO ，2则 PE ＝PC＝ 169PO5 .故 OE ＝ PO － PE ＝ 5.答案：4511．如图，自圆 O外一点P 引切线与圆切于点A ，M为PA 的中点，过M 引割线交圆于 B 、 C 两点．求证：∠ MCP ＝∠ MPB.证明： ∵ PA 与圆相切于 A ， ∴ MA 2＝ MB ·MC.∵ M 为 PA 的中点，∴ PM ＝ MA ， ∴PM 2＝MB ·MC ，∴PM ＝MBMC PM .∵∠ BMP ＝∠ PMC ，∴△ BMP ∽△ PMC ， ∴∠ MCP ＝∠ MPB.12．如图，已知在△ ABC 中，∠ ABC ＝ 90°，O 是 AB 上一点，以 O 为圆心， OB为半径的圆与 AB 交于点 E ，与 AC 切于点 D ，连结 DB 、DE 、OC.若 AD ＝ 2，AE ＝ 1，求 CD 的长．2分析：由切割线定理得 AD ＝ AE ·AB ，又∵∠ OCD ＝∠ ADE ＝ 90°－∠ CDB ，∠ A ＝∠ A ，∴△ ADE ∽△ ACO ，∴ AD ＝AC ，即 2＝CD ＋2，CD ＝3.AE AO12.5答： CD 的长等于 3.13． (2010 ·苏卷江 )如图， AB 是圆 O 的直径， D 为圆 O 上一点，过 D 作圆 O 的切线交 AB 的延伸线于点 C ，若 DA ＝ DC ，求证： AB ＝ 2BC.证明： 如下图，连结 OD ， BD ，由于 CD 为⊙ O 的切线， AB 为直径， 因此∠ ADB ＝∠ ODC ＝ 90°. 因此∠ ODA ＝∠ BDC . 又由于 DA ＝DC ， 因此∠ DAB ＝∠ DCB . 因此△ ADO ≌△ CDB .因此 OA ＝BC ，进而 AB ＝ 2BC.14．已知弦 AB 与⊙ O 半径相等，连结 OB 并延伸使 BC ＝ OB. (1)问 AC 与⊙ O 的地点关系是如何的； (2)试在⊙ O 上找一点 D ，使 AD ＝ AC. 分析： (1) ∵AB 与⊙ O 半径相等， ∴△ OAB 为正三角形，∠ OAB ＝ 60°＝∠ OBA ，又∵ BC ＝ OB ＝ AB ，∴∠ C ＝∠ BAC ＝ 30°，故∠ OAC ＝ 90°， ∴AC 与⊙ O 相切．(2)延伸 BO 交⊙ O 于 D ，则必有 AD ＝ AC.∵∠ BOA ＝ 60°， OA ＝ OD ，∴∠ D ＝ 30°， 又∵∠ C ＝ 30°，∴∠ C ＝∠ D ，得 AD ＝AC.15． (2010 ·宁卷辽 )如图，△ ABC 的角均分线 AD 的延伸线交它的外接圆于点 E.(1)证明：△ ABE ∽△ ADC ；1(2)若△ ABC 的面积 S ＝2AD ·AE ，求∠ BAC 的大小．分析： (1) 证明：由已知条件，可得∠ BAE ＝∠ CAD. 由于∠ AEB 与∠ ACB 是同弧所对的圆周角， 因此∠ AEB ＝∠ ACD . 故△ ABE ∽△ ADC .AB AD(2)由于△ ABE ∽△ ADC ，因此 AE ＝ AC ， 即 AB ·AC ＝ AD ·AE .1 1又 S ＝ AB ·ACsin ∠ BAC ，且 S ＝ AD ·AE ，2 2故 AB ·ACsin ∠BAC ＝ AD ·AE.则 sin ∠ BAC ＝ 1，又∠ BAC 为△ ABC 的内角，因此∠ BAC ＝ 90°.16．如图， AB 、 CD 是圆的两条平行弦， BE ∥AC ，并交 CD 于 E ，交圆于 F ，过 A 点的切线交 DC 的延伸线于 P ， PC ＝ED ＝ 1， PA ＝ 2.(1)求 AC 的长；(2)求证： EF ＝ BE.2分析： (1) ∵PA ＝PC ·PD ， PA ＝2， PC ＝ 1，∴ PD ＝ 4.∵∠ PAC ＝∠ CBA ，∠ PCA ＝∠ CAB ，∴△ PAC ∽△ CBA ，∴ PC ＝ AC，∴ AC 2＝ PC ·AB ＝ 2，∴ AC ＝ 2.AC AB(2)证明：∵ CE ·ED ＝ BE ·EF ， BE ＝ AC ＝ 2，∴ EF ＝ 2·1＝ 2，∴ EF ＝BE . 217．如图， PA 切⊙ O 于点 A ，割线 PBC 交⊙ O 于点 B ，C ，∠ APC 的角均分线分别与 AB ， AC 订交于点 D ， E ，求证：(1)AD ＝ AE ；(2)AD 2＝ DB ·EC.【分析方法代码 108001161】证明： (1) ∠AED ＝∠ EPC ＋∠ C ，∠ ADE ＝∠ APD ＋∠ PAB.由于 PE 是∠ APC 的角均分线，故∠ EPC ＝∠ APD ，又 PA 是⊙ O 的切线，故∠ C ＝∠ PAB. 因此∠ AED ＝∠ ADE .故 AD ＝AE .∠ PCE ＝∠ PADEC PC(2) ∠ CPE ＝∠ APD ? △ PCE ∽△ PAD ? AD ＝PA ； ∠ PEA ＝∠ PDB AE PA∠ APE ＝∠ BPD ? △ PAE ∽△ PBD ? DB ＝ PB .又 PA 是切线， PBC 是割线 ? PA2＝ PB ·PC? PB PA ＝PCPA .故EC＝AE，又 AD＝ AE，故 AD 2＝ DB ·EC. AD DB18．如图，已知AD 是△ ABC 的外角∠ EAC 的均分线，交BC 的延伸线于点 D ，延伸 DA 交△ ABC 的外接圆于点 F ，连结 FB 、FC .(1)求证： FB ＝ FC；(2)求证： FB 2＝ FA·FD ；(3)若 AB 是△ ABC 外接圆的直径，∠ EAC＝ 120 °，BC＝6 cm，求 AD 的长 . 【分析方法代码 108001162】分析：(1) 证明：∵ AD 均分∠ EAC，∴∠ EAD＝∠ DAC.∵四边形 AFBC 内接于圆，∴∠ DAC＝∠ FBC.∵∠ EAD ＝∠ FAB＝∠ FCB ，∴∠ FBC＝∠ FCB ，∴ FB＝ FC .(2)证明：∵∠ FAB＝∠ FCB＝∠ FBC，∠ AFB ＝∠ BFD ，FB FA∴△ FBA ∽△ FDB .∴FD＝FB，∴FB2＝ FA·FD .(3)∵ AB 是圆的直径，∴∠ACB＝ 90°.1∵∠ EAC＝ 120°，∴∠ DAC ＝∠ EAC＝ 60°，∴∠ BAC＝∠ BFC ＝60°，∠ FDB ＝30°，∴△ FBC 为正三角形，又 BC＝ 6，在 Rt△ ABC 中，∴ AC＝2 3，∴在 Rt△ ACD 中， AD ＝ 4 3.。

⼏何证明选讲知识点汇总与练习（内含答案）《⼏何证明选讲》知识点归纳与练习(含答案)⼀、相似三⾓形的判定及有关性质平⾏线等分线段定理平⾏线等分线段定理：如果⼀组平⾏线在⼀条直线上截得的线段相等，那么在其他直线上截得的线段也相等。

推理1：经过三⾓形⼀边的中点与另⼀边平⾏的直线必平分第三边。

推理2：经过梯形⼀腰的中点，且与底边平⾏的直线平分另⼀腰。

平分线分线段成⽐例定理平分线分线段成⽐例定理：三条平⾏线截两条直线，所得的对应线段成⽐例。

推论：平⾏于三⾓形⼀边的直线截其他两边（或两边的延长线）所得的对应线段成⽐例。

相似三⾓形的判定及性质相似三⾓形的判定：定义：对应⾓相等，对应边成⽐例的两个三⾓形叫做相似三⾓形。

相似三⾓形对应边的⽐值叫做相似⽐（或相似系数）。

由于从定义出发判断两个三⾓形是否相似，需考虑6个元素，即三组对应⾓是否分别相等，三组对应边是否分别成⽐例，显然⽐较⿇烦。

所以我们曾经给出过如下⼏个判定两个三⾓形相似的简单⽅法：（1）两⾓对应相等，两三⾓形相似；（2）两边对应成⽐例且夹⾓相等，两三⾓形相似；（3）三边对应成⽐例，两三⾓形相似。

预备定理：平⾏于三⾓形⼀边的直线和其他两边（或两边的延长线）相交，所构成的三⾓形与三⾓形相似。

判定定理1：对于任意两个三⾓形，如果⼀个三⾓形的两个⾓与另⼀个三⾓形的两个⾓对应相等，那么这两个三⾓形相似。

简述为：两⾓对应相等，两三⾓形相似。

判定定理2：对于任意两个三⾓形，如果⼀个三⾓形的两边和另⼀个三⾓形的两边对应成⽐例，并且夹⾓相等，那么这两个三⾓形相似。

简述为：两边对应成⽐例且夹⾓相等，两三⾓形相似。

判定定理3：对于任意两个三⾓形，如果⼀个三⾓形的三条边和另⼀个三⾓形的三条边对应成⽐例，那么这两个三⾓形相似。

简述为：三边对应成⽐例，两三⾓形相似。

引理：如果⼀条直线截三⾓形的两边（或两边的延长线）所得的对应线段成⽐例，那么这条直线平⾏于三⾓形的第三边。

定理：（1）如果两个直⾓三⾓形有⼀个锐⾓对应相等，那么它们相似；（2）如果两个直⾓三⾓形的两条直⾓边对应成⽐例，那么它们相似。

高中几何证明选讲课后练习及答案解析1、[选修4-1：几何证明选讲]如图，P是⊙O外一点，PA是切线，A为切点，割线PBC与⊙O相交于点B，C，PC=2PA，D为PC的中点，AD的延长线交⊙O于点E.证明：①BE=EC;②AD·DE=2PB2.证明：①∵PC=2PA，PD=DC，∴PA=PD，△PAD为等腰三角形.连接AB，那么∠PAB=∠DEB=β，∠BCE=∠BAE=α，∵∠PAB+∠BCE=∠PAB+∠BAD=∠PAD=∠PDA=∠DEB+∠DBE，∴β+α=β+∠DBE，即α=∠DBE，即∠BCE=∠DBE，所以BE=EC.②∵AD·DE=BD·DC，PA2=PB·PC，PD=DC=PA，BD·DC=(PA-PB)PA=PB·PC-PB·PA=PB·(PC-PA)，PB·PA=PB·2PB=2PB2.2、[选修4-4：坐标系与参数方程]在直角坐标系xOy中，曲线C1的参数方程为y=2+2sinα(x=2cosα)(α为参数)，M为C1上的动点，P点满足→(OP)=2→(OM)，点P的轨迹为曲线C2.①求C2的参数方程;②在以O为极点，x轴的正半轴为极轴的极坐标系中，射线θ=3(π)与C1的异于极点的交点为A，与C2的异于极点的交点为B，求|AB|.解：①设P(x，y)，那么由条件知M2(y).由于M点在C1上，所以=2+2sinα(y)，即y=4+4sinα(x=4cosα).从而C2的参数方程为y=4+4sinα(x=4cosα)(α为参数).②曲线C1的极坐标方程为=4sinθ，曲线C2的极坐标方程为=8sinθ.射线θ=3(π)与C1的交点A的极径为1=4s in3(π)，射线θ=3(π)与C2的交点B的极径为2=8sin3(π).所以|AB|=|2-1|=2.3、 [选修4-5：不等式选讲]函数f(x)=|x-m|+|x+6|(m∈R).①当m=5时，求不等式f(x)≤12的解集;②假设不等式f(x)≥7对任意实数x恒成立，求m的取值范围.解：①当m=5时，f(x)≤12即|x-5|+|x+6|≤12，当x<-6时，得-2x≤13，即x≥-2(13)，所以-2(13)≤x<-6;当-6≤x≤5时，得11≤12成立，所以-6≤x≤5;当x>5时，得2x≤11，即x≤2(11)，所以5故不等式f(x)≤12的解集为2(11).②f(x)=|x-m|+|x+6|≥|(x-m)-(x+6)|=|m+6|，由题意得|m+6|≥7，那么m+6≥7或m+6≤-7，解得m≥1或m≤-13，故m的取值范围是(-∞，-13]∪[1，+∞).三道题让你快速“吃透”几何选讲，你还在等什么呢?更多数学资讯，尽在数学网。

高中数学高考总复习几何证明选讲习题(附参考答案)一、选择题1．已知矩形ABCD ，R 、P 分别在边CD 、BC 上，E 、F 分别为AP 、PR 的中点，当P 在BC 上由B 向C 运动时，点R 在CD 上固定不变，设BP ＝x ，EF ＝y ，那么下列结论中正确的是( )A ．y 是x 的增函数B ．y 是x 的减函数C ．y 随x 的增大先增大再减小D ．无论x 怎样变化，y 为常数 [答案] D[解析] ∵E 、F 分别为AP 、PR 中点，∴EF 是△P AR 的中位线，∴EF ＝12AR ，∵R 固定，∴AR 是常数，即y 为常数．2．(2010·湖南考试院)如图，四边形ABCD 中，DF ⊥AB ，垂足为F ，DF ＝3，AF ＝2FB ＝2，延长FB 到E ，使BE ＝FB ，连结BD ，EC .若BD ∥EC ，则四边形ABCD 的面积为( )A ．4B ．5C ．6D ．7 [答案] C[解析] 由条件知AF ＝2，BF ＝BE ＝1， ∴S △ADE ＝12AE ×DF ＝12×4×3＝6，∵CE ∥DB ，∴S △DBC ＝S △DBE ，∴S 四边形ABCD ＝S △ADE ＝6.3．(2010·广东中山)如图，⊙O 与⊙O ′相交于A 和B ，PQ 切⊙O 于P ，交⊙O ′于Q 和M ，交AB 的延长线于N ，MN ＝3，NQ ＝15，则PN ＝( )A ．3 B.15 C ．3 2 D ．3 5 [答案] D[解析] 由切割线定理知：PN 2＝NB ·NA ＝MN ·NQ ＝3×15＝45， ∴PN ＝3 5.4．如图，Rt △ABC 中，CD 为斜边AB 上的高，CD ＝6，且AD BD ＝，则斜边AB 上的中线CE 的长为( )A ．5 6 B.562 C.15 D.3102[答案] B[解析] 设AD ＝3x ，则DB ＝2x ，由射影定理得CD 2＝AD ·BD ，∴36＝6x 2，∴x ＝6，∴AB ＝56，∴CE ＝12AB ＝562.5．已知f (x )＝(x －2010)(x ＋2009)的图象与x 轴、y 轴有三个不同的交点，有一个圆恰好经过这三个点，则此圆与坐标轴的另一个交点的坐标是( )A ．(0,1)B ．(0,2)C ．(0，20102009) D ．(0，20092010) [答案] A[解析] 由题意知圆与x 轴交点为A (2010,0)，B (－2009,0)，与y 轴交点为C (0，－2010×2009)，D (0，y 2)．设圆的方程为：x 2＋y 2＋Dx ＋Ey ＋F ＝0令y ＝0得x 2＋Dx ＋F ＝0，此方程两根为2010和－2009，∴F ＝－2010×2009 令x ＝0得y 2＋Ey －2010×2009＝0 ∴－2010×2009×y 2＝－2010×2009 ∴y 2＝1，故选A.[点评] 圆与x 轴交点A (2010,0)，B (－2009,0)与y 轴交点C (0，－2010×2009)，D (0，y 2)，∵A 、C 、B 、D 四点共圆，∴AO ·OB ＝OC ·OD ， ∴OD ＝1，∴y 2＝1.6．设平面π与圆柱的轴的夹角为β (0°<β<90°)，现放入Dandelin 双球使之与圆柱面和平面π都相切，若已知Dandelin 双球与平面π的两切点的距离恰好等于圆柱的底面直径，则截线椭圆的离心率为( )A.12B.22C.33D.32[答案] B[解析] ∵Dandelin 双球与平面π的两切点是椭圆的焦点，圆柱的底面直径恰好等于椭圆的短轴长，∴2b ＝2c ，∴e ＝c a ＝c b 2＋c 2＝c 2c ＝22.二、填空题7．如图，PT 切⊙O 于点T ，P A 交⊙O 于A 、B 两点，且与直径CT 交于点D ，CD ＝2，AD ＝3，BD ＝6，则PB ＝________.[答案] 15[解析] 由相交弦定理得DC ·DT ＝DA ·DB ，则DT ＝9.由切割线定理得PT 2＝PB ·P A ，即(PB ＋BD )2－DT 2＝PB (PB ＋AB )．又BD ＝6，AB ＝AD ＋BD ＝9，∴(PB ＋6)2－92＝PB (PB ＋9)，得PB ＝15.8．(09·天津)如图，AA 1与BB 1相交于点O ，AB ∥A 1B 1且AB ＝12A 1B 1.若△AOB 的外接圆的直径为1，则△A 1OB 1的外接圆的直径为______________．[答案] 2[解析] ∵AB ∥A 1B 1且AB ＝12A 1B 1，∴△AOB ∽△A 1OB 1，∴两三角形外接圆的直径之比等于相似比，∴△A 1OB 1的外接圆直径为2.9．如图，EB 、EC 是⊙O 的两条切线，B 、C 是切点，A 、D 是⊙O 上两点，如果∠E ＝46°，∠DCF ＝32°，则∠A 的度数是________．[答案] 99°[解析] 连接OB 、OC 、AC ，根据弦切角定理得， ∠EBC ＝∠BAC ，∠CAD ＝∠DCF ，可得∠A ＝∠BAC ＋∠CAD ＝12(180°－∠E )＋∠DCF ＝67°＋32°＝99°.[点评] 可由EB ＝EC 及∠E 求得∠ECB ，由∠ECB 和∠DCF 求得∠BCD ，由圆内接四边形对角互补求得∠A .10．PC 是⊙O 的切线，C 为切点，P AB 为割线，PC ＝4，PB ＝8，∠B ＝30°，则BC ＝________.[答案] 4 3[解析] (1)由切割线定理 PC 2＝P A ·PB ， ∴P A ＝2，∠ACP ＝∠B ＝30°，在△P AC 中，由正弦定理2sin30°＝4sin ∠P AC ，∴sin ∠P AC ＝1，∴∠P AC ＝90°，从而∠P ＝60°，∠PCB ＝90°， ∴BC ＝PB 2－PC 2＝82－42＝4 3.11．(2010·重庆文)如图中实线是由三段圆弧连接而成的一条封闭曲线C ，各段弧所在的圆经过同一点P (点P 不在C 上)且半径相等，设第i 段弧所对的圆心角为αi (i ＝1,2,3)，则cosα13cos α2＋α33－sin α13sin α2＋α33＝____________.[答案] －12[解析] 如图，O 1、O 2、O 3为三个圆的圆心，A 1、A 2、A 3分别是每两个圆的交点，则∠A 1P A 2＋∠A 2P A 3＋∠A 3P A 1＝12(α1＋α2＋α3)＝2π，∴α1＋α2＋α3＝4π，∴cos α13cos α2＋α33－sin α13sin α2＋α33＝cos α1＋α2＋α33＝cos 4π3＝cos ⎝⎛⎭⎫π＋π3 ＝－cos π3＝－12.12．(2010·广东中山市四校联考)如图，P A 切圆O 于点A ，割线PBC 经过圆心O ，OB ＝PB ＝1，OA 绕点O 逆时针旋转60°到OD ，则PD 的长为________．[答案]7[解析] 由图可知，P A 2＝PB ·PC ＝PB ·(PB ＋BC )＝3，∴P A ＝3，∴∠AOP ＝60°， 又∠AOD ＝60°，∴∠POD ＝120°，∵PO ＝2，OD ＝1， ∴cos ∠POD ＝22＋12－PD 22×2×1＝－12，∴PD ＝7.三、解答题13．(2010·南京市调研)如图，AB 是⊙O 的直径，点P 在AB 的延长线上，PC 与⊙O 相切于点C ，PC ＝AC ＝1，求⊙O 的半径．[解析] 连接OC .设∠P AC ＝θ.因为PC ＝AC ，所以∠CP A ＝θ，∠COP ＝2θ. 又因为PC 与⊙O 相切于点C ，所以OC ⊥PC . 所以3θ＝90°.所以θ＝30°.设⊙O 的半径为r ，在Rt △POC 中， r ＝CP ·tan30°＝1×33＝33. 14．(2010·江苏盐城调研)如图，圆O 的直径AB ＝8，C 为圆周上一点，BC ＝4，过C 作圆的切线l ，过A 作直线l 的垂线AD ，D 为垂足，AD 与圆O 交于点E ，求线段AE 的长．[解析] 连结OC 、BE 、AC ，则BE ⊥AE .∵BC ＝4，∴OB ＝OC ＝BC ＝4，即△OBC 为正三角形，∴∠CBO ＝∠COB ＝60°， 又直线l 切⊙O 于C ， ∴∠DCA ＝∠CBO ＝60°，∵AD ⊥l ，∴∠DAC ＝90°－60°＝30°，而∠OAC ＝∠ACO ＝12∠COB ＝30°，∴∠EAB ＝60°，在Rt △BAE 中，∠EBA ＝30°，∴AE ＝12AB ＝4.15．(2010·辽宁实验中学)如图，⊙O 的直径AB 的延长线与弦CD 的延长线相交于点P ，E 为⊙O 上一点，AE ＝AC ，DE 交AB 于点F ，且AB ＝2BP ＝4，(1)求PF 的长度．(2)若圆F 与圆O 内切，直线PT 与圆F 切于点T ，求线段PT 的长度． [解析] (1)连结OC ，OD ，OE ，由同弧对应的圆周角与圆心角之间的关系， 结合题中条件弧长AE 等于弧长AC 可得∠CDE ＝∠AOC ，又∠CDE ＝∠P ＋∠PFD ，∠AOC ＝∠P ＋∠OCP ， 从而∠PFD ＝∠OCP ，故△PFD ∽△PCO ， ∴PF PC ＝PDPO， 由割线定理知PC ·PD ＝P A ·PB ＝12， 故PF ＝PC ·PD PO ＝124＝3.(2)若圆F 与圆O 内切，设圆F 的半径为r ， 因为OF ＝2－r ＝1，即r ＝1，所以OB 是圆F 的直径，且过P 点的圆F 的切线为PT ， 则PT 2＝PB ·PO ＝2×4＝8，即PT ＝2 2.。

几何证明练习题及答案题目1：已知三角形ABC中，AB=AC，点D在BC上，且AD垂直于BC。

证明：三角形ABD与三角形ACD全等。

答案：由于AB=AC，所以三角形ABC是等腰三角形。

根据等腰三角形的性质，角BAD等于角CAD。

又因为AD垂直于BC，所以角ADB和角ADC都是直角。

因此，我们有：- AD=AD（公共边）- ∠BAD=∠CAD（等腰三角形的性质）- ∠ADB=∠ADC=90°（直角）根据SAS（边角边）全等条件，三角形ABD与三角形ACD全等。

题目2：已知三角形ABC中，AB=AC，点E在AB上，点F在AC上，且BE=CF。

证明：三角形AEF是等腰三角形。

答案：由于AB=AC，三角形ABC是等腰三角形。

根据等腰三角形的性质，角ABC等于角ACB。

又因为BE=CF，我们可以得出：- AB=AC（已知）- BE=CF（已知）- ∠ABC=∠ACB（等腰三角形的性质）根据SSS（边边边）全等条件，三角形BEC与三角形CFB全等。

因此，角BEC等于角CFB。

由于角AEF是三角形AEF的外角，根据外角定理，角AEF等于角BEC加角CFB。

因此：- ∠AEF=∠BEC+∠CFB- ∠AEF=2∠BEC（因为∠BEC=∠CFB）由于角AEF是三角形AEF的两个相等的角，所以三角形AEF是等腰三角形。

题目3：已知四边形ABCD中，AB平行于CD，BC平行于AD，且AB=CD。

证明：四边形ABCD是平行四边形。

答案：由于AB平行于CD且BC平行于AD，根据平行四边形的定义，我们可以推断出AD也平行于BC。

因此，四边形ABCD的对边都是平行的。

又因为AB=CD，根据平行四边形的判定条件，我们可以得出四边形ABCD是平行四边形。

题目4：已知三角形ABC中，角A等于角C，点D在BC上，且AD垂直于BC。

证明：三角形ABD与三角形CBD是等腰三角形。

答案：由于角A等于角C，根据三角形内角和定理，我们可以得出角A+角C+角B=180°。

相似三角形的判定及有关性质知识点1：比例线段的相关概念比例线段：对于四条线段a b c d 、、、，如果其中两条线段的长度的比与另两条线段的长度的比相等，即a cb d=（或:=a b c d :）那么这四条线段叫做成比例线段，简称比例线段． 注意：⑴在求线段比时，线段单位要统一，单位不统一应先化成同一单位．⑵当两个比例式的每一项都对应相同，两个比例式才是同一比例式．⑶比例线段是有顺序的，如果说a 是d c b ,,的第四比例项，那么应得比例式为：ad c b=． 知识点2：比例的性质基本性质：(1)bc ad d c b a =⇔=::；(2)b a c b c c a ⋅=⇔=2::．反比性质(把比的前项、后项交换)：cd a b d c b a =⇒=． 合比性质：ddc b b ad c b a ±=±⇒=．发生同样和差变化比例仍成立．如：⎪⎪⎩⎪⎪⎨⎧+-=+--=-⇒=dc dc b a b a c cd a a b d c b a 等． 等比性质：如果)0(≠++++====n f d b nmf e d c b a ΛΛ，那么ban f d b m e c a =++++++++ΛΛ．知识点3：比例线段的有关定理平行线等分线段定理：如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等.推论1：经过三角形一边的中点与另一边平行的直线必平分第三边.（三角形中位线定理的逆定理）推论2：经过梯形一腰的中点，且与底边平行的直线平分另一腰.（梯形中位线定理的逆定理）平行线等分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例．推论：(1)平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例．(2)平行于三角形一边并且和其它两边相交的直线，所截得的三角形的三边与原三角形三边对应成比例．定理：如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例，那么这条直线平行于三角形第三边． 知识点:4：黄金分割把线段AB 分成两条线段)(,BC AC BC AC >，且使AC 是BC AB 和的比例中项，叫做把线段AB 黄金分割，点C 叫做线段AB 的黄金分割点，其中AB AC 215-=0.618AB ≈．知识点5：相似图形1、相似图形的定义：把形状相同的图形叫做相似图形（即对应角相等、对应边的比也相等的图形）.相似三角形的定义：对应角相等，对应边成比例的两个三角形叫做相似三角形.相似三角形对应边的比值叫做相似比（或相似系数）2、相似三角形的判定方法预备定理：平行于三角形一边并且和其它两边相交的直线，所截得的三角形的三边与原三角形三边对应成比例．定理的基本图形语言：数学符号语言表述是：BC DE //Θ∴ADE ∆∽ABC ∆．判定定理1：如果一个三角形的两个角分别与另一个三角形的两个角对应相等，那么这两个三角形相似．简述为：两角对应相等，两三角形相似.判定定理2：如果一个三角的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似．简述为：两边对应成比例且夹角相等，两三角形相似.判定定理3：如果一个三角形的三条边分别与另一个三角形的三条边对应成比例，那么这两个三角形相似．简述为：三边对应成比例，两个三角形相似.判定定理4：直角三角形被斜边上的高分成的两个直角三角形与原三角形都相似．三角形相似的判定方法与全等的判定方法的联系列表如下：从表中可以看出只要将全等三角形判定定理中的“对应边相等”的条件改为“对应边成比例”就可得到相似三角形的判定定理，这就是我们数学中的用类比的方法，在旧知识的基础上找出新知识并从中探究新知识掌握的方法. 3、相似三角形的性质定理：（1）相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比； （2）相似三角形的周长比等于相似比； （3）相似三角形的面积比等于相似比的平方；（4）相似三角形内切圆与外接圆的直径比、周长比等于相似比，面积比等于相似比的平方. 4、相似三角形的等价关系(1)反身性：对于任一ABC ∆有ABC ∆∽ABC ∆． (2)对称性：若ABC ∆∽'''C B A ∆，则'''C B A ∆∽ABC ∆．(3)传递性：若ABC ∆∽C B A '∆''，且C B A '∆''∽C B A ''''''∆，则ABC ∆∽C B A ''''''∆． 5、相似直角三角形引理：如果一条直线截三角形的两边（或两边的延长线）所得的线段成比例，那么这两条直线平行于三角形的第三边.（与三角形的中位线定理类似）定理：如果两个直角三角形有一个锐角对应相等，那么这两个直角三角形相似.定理：如果两个直角三角形的两条直角边对应成比例，那么这两个直角三角形相似.定理：如果两个直角三角形的斜边和一直边对应成比例，那么这两个直角三角形相似. 6、直角三角形的射影定理从一定向一直线所引垂线的垂足，叫做这个点在这条直线上的正射影；一条线段在直线上的正射影，是指线段的两个端点在这条直线上的正射影间的线段.点和线段的正射影简称为射影直角三角形的射影定理：直角三角形斜边上的高是两直角边在斜边上射影的比例中项；两直角边分别是它们在斜边上的射影与斜边的比例中项.推论：直角三角形中其中一条直角边是该直角边在斜边上的射影与斜边的比例中项.经过归纳和总结，相似三角形有以下几种基本类型知识点6：与位似图形有关的概念1、如果两个图形不仅是相似图形，而且每组对应顶点的连线都交于一点，那么这样的两个图形叫做位似图形.这个点叫做位似中心，这时的相似比又称为位似比.2、位似图形的性质：位似图形上任意一对对应点到位似中心的距离之比等于相似比.3、画位似图形⑴画位似图形的一般步骤：①确定位似中心；②分别连接原图形中的关键点和位似中心，并延长（或截取）；③根据已知的位似比，确定所画位似图形中关键点的位置；④顺次连结上述得到的关键点，即可得到一个放大或缩小的图形.⑵位似中心的选取：①位似中心可以在图形外部，此时位似中心在两个图形中间，或在两个图形之外；②位似中心可取在多边形的一条边上；③位似中心可取在多边形的某一顶点上.说明：位似中心的选取决定了位似图形的位置，以上位似中心位置的选取中，每一种方法都能把一个图形放大或缩小.圆的章节知识点总结一、圆的概念集合形式的概念： 1、圆可以看作是到定点的距离等于定长的点的集合； 2、圆的外部：可以看作是到定点的距离大于定长的点的集合； 3、圆的内部：可以看作是到定点的距离小于定长的点的集合； 轨迹形式的概念： 1、圆：到定点的距离等于定长的点的轨迹就是以定点为圆心，定长为半径的圆；（补充）2、垂直平分线：到线段两端距离相等的点的轨迹是这条线段的垂直平分线（也叫中垂线）；3、角的平分线：到角两边距离相等的点的轨迹是这个角的平分线；4、到直线的距离相等的点的轨迹是：平行于这条直线且到这条直线的距离等于定长的两条直线；5、到两条平行线距离相等的点的轨迹是：平行于这两条平行线且到两条直线距离都相等的一条直线； 二、点与圆的位置关系1、点在圆内⇔d r <⇔点C 在圆内；2、点在圆上⇔d r =⇔点B 在圆上；3、点在圆外⇔d r >⇔点A 在圆外； 三、直线与圆的位置关系1、直线与圆相离⇔d r >⇔无交点；2、直线与圆相切⇔d r =⇔有一个交点；3、直线与圆相交⇔d r <⇔有两个交点；四、圆与圆的位置关系外离（图1）⇔ 无交点 ⇔d R r >+； 外切（图2）⇔ 有一个交点⇔d R r =+；AD相交（图3）⇔ 有两个交点⇔R r d R r -<<+； 内切（图4）⇔ 有一个交点⇔d R r =-； 内含（图5）⇔ 无交点 ⇔d R r <-；五、垂径定理弦：连接圆上任意两点之间的线段叫做弦.垂径定理：垂直于弦的直径平分弦且平分弦所对的两条弧.推论1：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧； 推论2：弦的垂直平分线经过圆心，并且平分弦所对的两条弧；推论3：平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧以上共4个定理，简称2推3定理：此定理中共5个结论中，只要知道其中2个即可推出其它3个结论.即：AB 是直径;②AB CD ⊥;③CE DE =;④ 弧BC =弧BD ( );⑤ ;中任意2个条件推出其他3个结论. 推论4：圆的两条平行弦所夹的弧相等.即：在⊙O 中，∵AB ∥CD ∴弧AC =弧BD 六、 圆心角定理圆心角的定义：顶点在圆心且两边与圆相交的角叫做圆心角.圆心角定理：圆心角的度数等于它所对弧的度数. （同圆或等圆中，相等的圆心角所对的弦相等，所对的弧相等，弦心距相等——也称一推三定理）即上述四个结论中，只要知道其中的1个相等，则可以推出其它的3个结论也即：①AOB DOE ∠=∠;②AB DE =;③图4图5»»BCBD =»»AC AD =DB AB AOOC OF=;④推论1：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等；推论2：在同圆或等圆中，相等的弧所对的圆心角相等，所对的弦也相等；推论3：在同圆或等圆中，相等的弦所对的圆心角相等，所对的弧也相等；七、圆周角定理圆周角的定义：顶点在圆上，并且两边都与圆相交的角叫做圆周角.圆周角定理：同弧或等弧所对的圆周角相等且都等于它所对的圆心的角的一半.符号语言：①∵在Oe中，C D∠∠、都是弧AB所对的圆周角∴C D∠=∠②∵AOB∠和ACB∠是弧AB所对的圆心角和圆周角∴2AOB ACB∠=∠图形语言：推论1：同圆或等圆中，相等的圆周角所对的弧相等.推论2：半圆或直径所对的圆周角是直角；（90︒的圆周角所对的弧是半圆，所对的弦是直径）符号语言：∵在Oe中，AB是直径∴=90C︒∠;或∵=90C︒∠∴AB是直径推论3：三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形符号语言：在△ABC中，∵OA OB OC==∴△ABC是直角三角形或=90C︒∠八、圆内接四边形圆内接四边形：如果多边形的所有顶点都在一个圆上，那么这个多边形叫做圆的内接多边形，这个圆叫做多边形的外接圆.圆的内接四边形的性质定理：圆的内接四边形的对角互补，圆的内接四边形的外角等于它的内角的对角.»»BA ED=符号语言：∵在O e 中，四边形ABCD 是内接四边形 ∴180180C BAD B D DAE C ︒︒∠+∠=∠+∠=∠=∠，， 图形语言：圆的内接四边形的判定定理1：如果一个四边形的对角互补，那么这个四边形四个顶点共圆.符号语言：∵在四边形ABCD 中，180180C BAD B D ︒︒∠+∠=∠+∠=， ∴A B C D 、、、四点共圆圆的内接四边形的判定定理2：如果四边形的一个外角等于它内角的对角，那么这个四边形的四个顶点共圆.符号语言：∵在四边形ABCD 中，DAE C ∠=∠ ∴A B C D 、、、四点共圆 九、 切线的性质与判定定理1、切线的定义：当直线和圆有且只有一个公共点时，我们把这条直线叫做圆的切线. （1）判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线.符号语言：∵MN OA ⊥且MN 过半径OA 外端∴MN 是O e 的切线 图形语言：（2）性质定理：圆的切线垂直于经过切点的半径. 推论1：经过圆心且垂直于切线的直线必经经过切点. 推论2：经过切点且垂直于切线的直线必经经过圆心.2、切线长的定义：经过圆外一点作圆的切线，该点和切点之间的线段的长叫做该点到圆的切线长.切线长定理: 从圆外一点引圆的两条切线，它们的切线长相等且该点和圆心的连线平分两条切线的夹角.符号语言：∵PA PB 、是的两条切线 ∴=PAPB 且PO 平分APB ∠图形语言：3、弦切角：顶点在圆上，且一边和圆相交而另一边和圆相切的角叫做弦切角.(弦与切线的夹角叫做弦切角)弦切角定理：弦切角等于它所夹弧所对的圆周角.符号语言：∵BAC ∠是圆的一个弦切角 ∴BAC APC ∠=∠4、相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的乘积相等. 符号语言： ∵在⊙O 中，弦AB 、CD 相交于点P ，∴PA PB PC PD ⋅=⋅ 图形语言：推论：如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项. 符号语言：∵在⊙O 中，直径AB CD ⊥， ∴2CE AE BE =⋅5、割线定理：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的乘积相等.符号语言：∵在⊙O 中，PB 、PE 是割线 ∴PC PB PD PE ⋅=⋅6、切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项.符号语言：∵在⊙O 中，PA 是切线，PB 是割线 ∴ 2PA PC PB =⋅图形语言：PO DC BA OE DCBADEC BPAO十、圆内正多边形的计算（1）正三角形：在O e 中，△ABC 是正三角形，有关计算在Rt △BOD 中进行，::2OD BD OB =（2）正四边形：同理，四边形的有关计算在Rt △OAE 中进行，::OE AE OA =（3）正六边形：同理，六边形的有关计算在Rt △OAB 中进行，::2AB OB OA =十一、圆的有关概念1、三角形的外接圆、外心. →用到：线段的垂直平分线及性质2、三角形的内切圆、内心. →用到：角的平分线及性质3、圆的对称性。

专题10 第1讲 几何证明选讲一、填空题1．(2011·广东理，15)如右图，过圆O 外一点P 分别作圆的切线和割线交圆于A ，B ，且PB ＝7，C 是圆上一点使得BC ＝5，∠BAC ＝∠APB ，则AB ＝________.[答案]35[解析] 由圆的切线性质可知∠PAB ＝∠ACB ， 又∠APB ＝∠BAC ，所以△P AB ∽△ACB ， 所以AB BC ＝PB AB ，而BC ＝5，PB ＝7，∴AB 5＝7AB， ∴AB 2＝35，AB ＝35.2．(2011·湖南理，11)如右图，A ，E 是半圆周上的两个三等分点，直径BC ＝4，AD ⊥BC ，垂足为D ，BE 与AD 相交于点F ，则AF 的长为________．[答案]233[解析] 如图，连结AE ，OA ，OE ，∠AOB ＝60°，OA ＝2，∴AD ＝ 3. 又∵△AFE ∽△DFB ，∴AF FD ＝AEBD，AE ＝2，BD ＝1，∴AF3－AF ＝2，∴AF ＝233.3．(2011·陕西理，15)如图，∠B ＝∠D ，AE ⊥BC ，∠ACD ＝90°，且AB ＝6，AC ＝4，AD ＝12，则BE ＝________.[答案] 4 2[解析] ∠B ＝∠D ，∠DCA ＝∠BEA ＝90°. ∴△DAC ∽△BAE ，∴AB AD ＝AE AC .∴AE ＝2，∴BE ＝AB 2－AE 2＝4 2.4．(2010·北京理，12)如图，⊙O 的弦ED ，CB 的延长线交于点A ，若BD ⊥AE ，AB ＝4，BC ＝2，AD ＝3，则DE ＝______；CE ＝________.[答案] 5 27[解析] 首先由割线定理不难知道AB ·AC ＝AD ·AE ， 于是AE ＝8，DE ＝5，又BD ⊥AE ，故BE 为直径， 因此∠C ＝90°，由勾股定理可知 CE 2＝AE 2－AC 2＝28， 故CE ＝27.5．如图：PA 与圆O 相切于点A ，PCB 为圆O 的割线，并且不过圆心O ，已知∠BPA ＝30°，PA ＝23，PC ＝1，则圆O 的半径等于________．[答案] 7[解析] 由已知可得，PA 2＝PC ·PB ，从而可得PB ＝12，连结OA 并反向延长，交圆于点E ，交BC 于D ，且∠BPA ＝30°，在直角三角形APD 中可以求得PD ＝4，DA ＝2，故CD ＝3，DB ＝8，记圆的半径为R ，由于ED ·DA ＝CD ·DB ，因此，(2R －2)×2＝3×8，解得R ＝7.6．(2011·广东东莞)如下图，圆O 是△ABC 的外接圆，过点C 的切线交AB 的延长线于点D ，CD ＝27，AB ＝3.则BD 的长为________．[答案] 4[解析] 由切割线定理得：DB ·DA ＝DC 2，即DB ·(DB ＋BA )＝DC 2，∴DB 2＋3DB －28＝0，∴DB ＝4.7．如图，AB 是半圆O 的直径，∠BAC ＝30°，BC 为半圆的切线，且BC ＝43，则点O 到AC 的距离OD ＝________.[答案] 3[解析] 由已知得∠CBA ＝90°，因为BC ＝43，∠BAC ＝30，所以AB ＝BC tan30°＝4333＝12，故AO ＝6，由于∠ODA ＝90°，所以OD ＝3.8．如图，已知在△ABC 中，CD⊥AB 于D ，BC 2＝BD ·AB ，则∠ACB ＝________.[答案] 90°[解析] 在△ABC 与△CBD 中，由BC 2＝BD ·AB ，得BC BD ＝ABBC ，且∠B ＝∠B ，所以△ABC ∽△CBD .则∠ACB ＝∠CDB ＝90°. 二、解答题9．(2011·江苏，21)如图，圆O 1与圆O 2内切于点A ，其半径分别为r 1与r 2(r 1>r 2)．圆O 1的弦AB 交圆O 2于点C (O 1不在AB 上)．求证：AB AC 为定值．[证明] 连结AO 1，并延长分别交两圆于点E 和点D ，连结BD ，SE .因为圆O 1与圆O 2内切于点A ，所以点O 2在AD 上．故AD ，AE 分别为圆O 1，圆O 2的直径．从而∠ABD ＝∠ACE ＝π2.所以BD ∥CE ， 于是AB AC ＝AD AE ＝2r 12r 2＝r 1r 2. 所以AB AC 为定值．10．(2011·新课标理，22)如图，D 、E 分别为△ABC 的边AB 、AC 上的点，且不与△ABC 的顶点重合，已知AE 的长为m ，AC 的长为n ，AD ，AB 的长是关于x 的方程x 2－14x ＋mn ＝0的两个根．(1)证明：C 、B 、D 、E 四点共圆；(2)若∠A ＝90°，且m ＝4，n ＝6，求C 、B 、D 、E 所在圆的半径． [解析] (1)证明：如图，连接DE ，在△ADE 和△ACB 中，AD ·AB ＝mn ＝AE ·AC ，即AD AC ＝AE AB .又∠DAE ＝∠CAB ，从而△ADE ∽△ACB .因此∠ADE ＝∠ACB .所以C ，B ，D ，E 四点共圆．(2)解：m ＝4，n ＝6时，方程x 2－14x ＋mn ＝0的两根为x 1＝2，x 2＝12.故AD ＝2，AB ＝12.如图，取CE 的中点G ，DB 的中点F ，分别过G ，F 作AC ，AB 的垂直，两垂线相交于H 点，连接DH .因为C ，B ，D ，E 四点共圆，所以C ，B ，D ，E 四点所在圆的圆心为H ，半径为DH .由于∠A ＝90°，故GH ∥AB ，HF ∥AC .从而HF ＝AG ＝5，DF ＝12(12－2)＝5.故C ，B ，D ，E 四点所在圆的半径为5 2.11．(2011·辽宁理，22)如图，A ，B ，C ，D 四点在同一圆上，AD 的延长线与BC 的延长线交于E 点，且EC ＝ED .(1)证明：CD∥AB;(2)延长CD到F，延长DC到G，使得EF＝EG，证明：A，B，G，F四点共圆．[解析](1)因为EC＝ED，所以∠EDC＝∠ECD.因为A，B，C，D四点在同一圆上，所以∠EDC＝∠EBA.故∠ECD＝∠EBA.所以CD∥AB.(2)由(1)知，AE＝BE.因为EF＝EG，故∠EFD＝∠EGC，从而∠FED＝∠GEC.连结AF，BG，则△EF A≌△EGB，故∠FAE＝∠GBE.又CD∥AB，∠EDC＝∠ECD，所以∠F AB＝∠GBA.所以∠AFG＋∠GBA＝180°.故A，B，G，F四点共圆．12．如图，AE、AF分别为△ABC的内、外角平分线，O为EF的中点．求证：OB OC＝AB2 AC2.[分析]OB OC等于△ABO与△ACO的面积之比(高相等)，自然想到证明△ABO∽△CAO.[证明]∵AE，AF为△ABC的内、外角平分线，∴AE⊥AF，又∵O为EF的中点，∴∠OEA＝∠OAE.∵∠OAE＝∠CAE＋∠OAC，∠OEA＝∠B＋∠BAE，而∠BAE＝∠CAE，∴∠OAC＝∠B.∵∠AOB为公共角，∴△OAC∽△OBA.S△OAC＝AB2 AC2.∴S△OBA又∵△OAB与△OCA有一个公共边OA.S△OAC＝OB OC，∴OB OC＝AB2 AC2.∴S△OBA[评析]利用三角形相似的判定定理来证明三角形相似，然后由面积比等于相似比的平方这一性质来解题．所以并非见到内外角平分线，就用角平分线定理．。

数学选修4-1几何证明选讲解答题第一篇：数学选修4-1几何证明选讲解答题选修4-1：几何证明选讲一、填空题1.(2011·陕西)如图，∠B＝∠D，AE⊥BC，∠ACD＝90°，且AB＝6，AC＝4，AD＝12，则BE＝________.2．(2011·湖南)如图，A，E是半圆周上的两个三等分点，直径BC＝4，AD⊥BC，垂足为D，BE与AD相交于点F，则AF的长为________．二、解答题3.如图所示，四边形ABCD是平行四边形，点E在边BA的延长线上，CE交AD于点F，∠ECA＝∠D.求证：AC·BE＝CE·AD.4．(2011·江苏)如图，圆O1与圆O2内切于点A，其半径分别为r1与r2(r1>r2)．圆O1的弦AB交圆O2于点C(O1不在AB 上)．求证：AB∶AC为定值．5．如图，在直角梯形ABCD中，DC∥AB，CB⊥AB，AB＝AD＝a，CD，点E，F分别为线段AB，AD的中点，求EF的长． a 26．如图所示，点P是圆O直径AB延长线上的一点，PC切圆O 于点C，直线PQ平分∠APC，分别交AC、BC于点M、N.求证：(1)CM＝CN；(2)MN2＝2AM·BN.7．如图，四边形ABCD内接于⊙O，AB＝AD.过A点的切线交CB的延长线于E点．求证：AB2＝BE·CD.8．如图，PA切⊙O于点A，割线PBC经过圆心O，OB＝PB＝1，OA绕点O逆时针旋转60°到OD，求PD的长．9.如图，已知△ABC的两条角平分线AD和CE相交于点H，∠ABC＝60°，F在AC上，且AE＝AF.求证：(1)B、D、H、E 四点共圆；(2)CE平分∠DEF.10．如图，已知AD是△ABC的外角∠EAC的平分线，交BC的延长线于点D，延长DA交△ABC的外接圆于点F，连结FB，FC.(1)求证：FB＝FC；(2)求证：FB2＝FA·FD；(3)若AB是△ABC外接圆的直径，∠EAC＝120°，BC＝6 cm，求AD的长．答案231．2 2.3CE3．证明因为四边形ABCD是平行四边形，所以AF∥BC，所以BE＝.又因为AE∥CD，所以△AFE∽△DFC，EFEAEAEFCFEFCE所以＝＝.CDCFCDEABE又因为∠ECA＝∠D，∠CAF＝∠DAC，ACCF所以△AFC∽△ACD，所以，ADDCACCE所以，ADBE所以AC·BE＝CE·AD.4.证明如图，连结AO1并延长，分别交两圆于点E和点D.连结BD，CE.因为圆O1与圆O2内切于点A，所以点O2在AD上，故AD，AE分别为圆O1，圆O2的直径．π从而∠ABD＝∠ACE.2所以BD∥CE，ABAD2r1r1于是＝＝.ACAE2r2r2所以AB∶AC为定值．5．解连结DE，由于E是AB的中点，故BE＝.又CD＝，AB∥DC，22CB⊥AB，∴四边形EBCD是矩形．在Rt△AED中，AD＝a，F是AD的中点，故EF26．证明(1)∵PC切圆O于点C，∴∠PCB＝∠PAC，又∵∠CPM＝∠APM，∴∠CNM＝∠CPM＋∠PCB＝∠APM＋∠PAM＝∠CMN，∴CM＝CN.(2)∵∠CPN＝∠APM，∠PCN＝∠PAM，aaaPCCN∴△PCN∽△PAM＝，①PAAM同理△PNB∽△PMCPBBN.② PCCM又∵PC2＝PA·PB，③由①②③可知CM·CN＝AM·BN，∵CM＝CN，∴CM2＝AM·BN.∵AB是圆O的直径，∴∠ACB＝90°.∴MN2＝2CM2，即MN2＝2AM·BN.7．证明连结AC.∵EA切⊙O于A，∴∠EAB＝∠ACB，∵AB ＝AD，∴∠ACD＝∠ACB，AB＝AD.∴∠EAB＝∠ACD.又四边形ABCD 内接于⊙O，所以∠ABE＝∠D.∴△ABE∽△CDA.ABBE，即AB·DA＝BE·CD.CDDA∴AB2＝BE·CD.8．解方法一连结AB，∵PA切⊙O于点A，B为PO中点，∴AB＝OB＝OA，∴∠AOB＝60°，∴∠POD＝120°.在△POD 中，由余弦定理得PD2＝PO2＋DO2－2PO·DO·cos∠POD＝4＋1－14×(－＝7.∴PD7.2方法二过D作DE⊥PC，垂足为E，∴∠POD＝120°，13∴∠DOE ＝60°，可得OE，DE＝，22在Rt△PED中，25322PDPE＋DE＝7.449．证明(1)在△ABC中，∵∠ABC＝60°，∴∠BAC＋∠BCA＝120°.∵AD，CE分别是△ABC的角平分线，∴∠HAC＋∠HCA＝60°，∴∠AHC＝120°.∴∠EHD＝∠AHC＝120°.∴∠EBD＋∠EHD＝180°.∴B，D，H，E四点共圆．(2)连结BH，则BH为∠ABC的平分线，∴∠EBH＝∠HBD＝30°.由(1)知B，D，H，E四点共圆，∴∠CED＝∠HBD＝30°，∠HDE＝∠EBH ＝30°.∴∠HED＝∠HDE＝30°.∵AE＝AF，AD平分∠BAC，∴EF⊥AD.∴∠CEF＝30°.∴CE平分∠DEF.10．(1)证明因为AD平分∠EAC，所以∠EAD＝∠DAC.因为四边形AFBC内接于圆，所以∠DAC ＝∠FBC.因为∠EAD＝∠FAB＝∠FCB，所以∠FBC＝∠FCB，所以FB＝FC.(2)证明因为∠FAB＝∠FCB＝∠FBC，∠AFB＝∠BFD，FBFA所以△FBA∽△FDB.所以＝ FDFB所以FB2＝FA·FD.(3)解因为AB是圆的直径，所以∠ACB＝90°.又∠EAC＝120°，所以∠ABC＝30°，1∠DAC＝EAC＝60°.因为BC＝6，2所以AC＝BCtan∠ABC＝23，AC所以AD＝＝43(cm)．cos∠DAC第二篇：2007-2012新课标数学几何证明选讲解答题汇总1、如图，已知AP是εO的切线，P为切点，AC是εO的割线，与εO交于B，C两点，圆心O在∠PAC的内部，点M是BC的中点．，P，O，M四点共圆；（Ⅰ）证明A（Ⅱ）求∠OAM+∠APM的大小．（2007新课标）A【解析】（Ⅰ）证明：连结OP，OM．因为AP与εO相切于点P，所以OP⊥AP．因为M是εO的弦BC 的中点，所以OM⊥BC．于是∠OPA+∠OMA=180°．，P，O，M四点共圆．由圆心O在∠PAC的内部，可知四边形APOM的对角互补，所以A，P，O，M四点共圆，所以∠OAM=∠OPM．（Ⅱ）解：由（Ⅰ）得A由（Ⅰ）得OP⊥AP．由圆心O在∠PAC的内部，可知∠OPM+∠APM=90°．所以∠OAM+∠APM=90°．A2、如图，过圆O外切点为A，过A点作直线AP垂直直线OM，垂足为P．一点M 作它的一条切线，OP=OA；（Ⅰ）证明：OMε（Ⅱ）N为线段AP上一点，直线NB垂直直线ON，且交圆O于B点．过B点的切线交直线ON于K．证明：∠OKM=90．（2008课标卷）ο23、如图,已知△ABC的两条角平分线AD和CE相交于H,∠B＝60°,F在AC上,且AE＝AF.（2009课标卷）(1)证明B,D,H,E四点共圆;(2)证明CE平分∠DEF.分析:此题考查平面几何知识,如四点共圆的充要条件,角平分线的性质等.证明:(1)在△ABC中，因为∠B＝60°,所以∠BAC+∠BCA＝120°.因为AD,CE是角平分线,所以∠HAC+∠HCA＝60°.故∠AHC＝120°.于是∠EHD＝∠AHC＝120°,因为∠EBD+∠EHD＝180°,所以B,D,H,E四点共圆.(2)连结BH,则BH为∠ABC的平分线,得∠HBD＝30°.由(1)知B,D,H,E四点共圆,所以∠CED＝∠HBD＝30°.又∠AHE＝∠EBD ＝60°,由已知可得EF⊥AD,可得∠CEF＝30°.所以CE平分∠DEF.4、如图，已经圆上的弧，过C点的圆切线与BA的延长线交于E点，证明：（Ⅰ）∠ACE=∠BCD；2（Ⅱ）BC=BF×CD。

第1页 （共4页）选修4-1 《几何证明选讲》一，几何证明选讲基础知识填空：1.平行线等分线段定理:如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段_________.推论1: 经过三角形一边的中点与另一边平行的直线必______________。

推论2: 经过梯形一腰的中点，且与底边平行的直线________________。

2.平行线分线段成比例定理：三条平行线截两条直线，所得的________________成比例。

推论：平行于三角形一边的直线截其他两边（或两边的延长线）所得的对应线段___________。

3.相似三角形的性质定理：相似三角形对应高的比、对应中线的比、对应角平分线的比都等于______； 相似三角形周长的比、外接圆的直径比、外接圆的周长比都等于_________________； 相似三角形面积的比、外接圆的面积比都等于____________________；4. 直角三角形的射影定理：直角三角形斜边上的高是______________________的比例中项；两直角边分别是它们在斜边上_______与_________的比例中项。

5.圆周角定理：圆上一条弧所对的圆周角等于它所对的____________的一半。

圆心角定理：圆心角的度数等于_______________的度数。

推论1：同弧或等弧所对的圆周角_________；同圆或等圆中，相等的圆周角所对的弧_______。

推论2：半圆（或直径）所对的圆周角是_______；90o的圆周角所对的弦是________。

弦切角定理：弦切角等于它所夹的弧所对的______________。

6.圆内接四边形的性质定理与判定定理：圆的内接四边形的对角_______；圆内接四边形的外角等于它的内角的_________。

如果一个四边形的对角互补，那么这个四边形的四个顶点__________；如果四边形的一个外角等于它的内角的对角，那么这个四边形的四个顶点_________。

数学几何选讲试题答案及解析1.（本小题满分10分）选修4－1：几何证明选讲如图，圆O的半径OB垂直于直径AC,M为AO上一点，BM的延长线交圆O于N，点是线段延长线上一点，连接PN,且满足（Ⅰ）求证：是圆O的切线；(Ⅱ)若圆O的半径为，OA=OM，求MN的长.【答案】（Ⅰ）见解析(Ⅱ) 2【解析】（Ⅰ）证明：如图，连接ON，∵，则，……2分又，则.,∴，……4分∴，故是圆O的切线．……5分(Ⅱ) .在△BOM中，，,延长BO交圆O于点D，连接DN，由条件知△BOM∽△BND,于是,，即MN=BN-BM=6-4=2.……10分【考点】本题考查切线的判定定理、三角形相似等基础知识，意在考查学生推理证明和逻辑思维能力.2.如图，，是圆的两条弦，它们相交于的中点，若，，,求圆的半径.【答案】1【解析】解：由，,，得 5分又为中点，，， 10分【考点】本题考查圆的基本性质，相交弦定理等知识，意在考查推理论证能力.3.（本小题满分10分）选修4－1：几何证明选讲如图，Δ是内接于圆，,直线切于点，弦，与相交于点．（1）求证：≌；（2）若求．【答案】（1）见解析（2）【解析】（1）在ΔABE和ΔACD中，∵，∠ABE=∠ACD．又∠BAE=∠EDC，∵BD∥MN，∴∠EDC=∠DCN，∵直线是圆的切线，∴∠DCN=∠CAD，∴∠BAE=∠CAD，∴Δ≌Δ（角、边、角）． 5分（2）∵∠EBC=∠BCM，∠BCM=∠BDC，∴∠EBC=∠BDC=∠BAC，BC=CD=4，又∠BEC=∠BAC+∠ABE=∠EBC+∠ABE=∠ABC=∠ACB，∴BC=BE=4．设AE=，易证ΔABE∽ΔDEC，∴，从而.又，，∴，解得.因此. 10分【命题意图】本题考察弦切角定理、等腰三角形的性质、三角形相似等基础知识，意在考察学生推理证明和逻辑思维能力.4.如图，已知△ABC的两条角平分线AD和CE相交于H，∠B＝60°，F在AC上，且AE＝AF.（1）证明：B、D、H、E四点共圆；（2）证明：CE平分∠DEF.【答案】（1）见解析（2）见解析【解析】（1）在△ABC中，因为∠ABC＝60°，所以∠BAC＋∠BCA＝120°.因为AD、CE是角平分线，所以∠HAC＋∠HCA＝60°，故∠AHC＝120°，于是∠EHD＝∠AHC＝120°.因为∠EBD＋∠EHD＝180°，所以B、D、H、E四点共圆．（2）连结BH，则BH为∠ABC的平分线，得∠HBD＝30°.由（1）知B、D、H、E四点共圆，所以∠CED＝∠HBD＝30°.又∠AHE＝∠EBD＝60°，由已知可得EF⊥AD.可得∠CEF＝30°.所以CE平分∠DEF.【点评】熟记圆的切线性质、圆周角定理、切割线定理、相交弦定理，这些知识点是解决有关圆的问题的关键，要好好理解．5.如图, 弦AB与CD相交于内一点E, 过E作BC的平行线与AD的延长线相交于点P. 已知PD＝2DA＝2, 则PE＝ .【答案】【解析】本题考查平面几何证明，利用三角形相似即可求解，属于容易题。