巧填算符

三年级奥数题及答案：巧填算符★这篇《三年级奥数题及答案：巧填算符》，是###特地为大家整理的，希望对大家有所协助！1.巧填算符在下面算式中合适的地方，只添两个加号和两个减号使等式成立。

1 2 3 4 5 6 7 8 9＝100分析在本题条件中，不但限制了所使用运算符号的种类，而且还限制了每种运算符号的个数。

因为题目中，一共能够添四个运算符号，所以，应把1 23 4 5 67 8 9分为五个数，又考虑最后的结果是100，所以应在这五个数中凑出一个较接近100的，这个数能够是123或89。

如果有一个数是123，就要使剩下的后六个数凑出23，且把它们分为四个数，应该是两个两位数，两个一位数.观察发现，45与67相差22，8与9相差1，加起来正巧是23，所以本题的一个答案是：123＋45-67＋8-9＝100如果这个数是89，则它的前面一定是加号，等式变为1 2 3 4 56 7＋89=100，为满足要求，1 2 3 4 5 6 7=11，在中间要添一个加号和两个减号，且把它变成四个数，观察发现，无论怎样都不能满足要求。

解：本题的一个答案是：123＋45-67＋8-9=100补充说明：一般在解题时，如果没有特别说明，只要得到一个准确的解答就能够了。

在例5这类限制比较多的题目的解决过程中，要时时注意按照题目的要求去做，因为题目的要求比较高，所以解决的方法比较少。

2.巧填算符在下面算式适当的地方添上加号，使算是成立。

1 1 1 1 1 1 1 1 = 1000分析：这道题，1000是大数，先找一个离1000最近的数，就是1111，那么多了111怎么办呢？那么就要"-111"这时已经是1000了，还有一个1怎么办呢？会想到：（1111－111）÷1 = 1000。

第五讲----巧填算符知识导航所谓填算符，就是指在一些数之间的适当地方填上适当的运算符号（包括括号），从而使这些数和运算符号构成的算式成为一个等式。

在填算符的问题中，所填的算符包括 +、-、×、÷、（）、[]、｛｝。

解决这类问题常用两种基本方法：一是凑数法，二是逆推法，有时两种方法并用。

凑数法是根据所给的数，凑出一个与结果比较接近的数，然后，再对算式中剩下的数字作适当的增加或减少，从而使等式成立。

逆推法常是从算式的最后一个数字开始，逐步向前推想，从而得到等式。

例1、在下列各题中的数字之间填上“+”、“—”、“×”或“÷”等运算符号，使等式成立。

（1）5 5 5 5 5=1 （2）5 5 5 5 5=2练一练（1）5 5 5 5 5=3 （2）5 5 5 5 5=4（3）5 5 5 5 5=10 （4）3 3 3 3 3=0（5）3 3 3 3 3=1 （6）3 3 3 3 3=2例2、把“+”、“—”、“×”或“÷”填入下面的方格中，使等式成立。

（1）4=41 （2）（3）2=10 （4）6=24练一练在下面两题的中填上“+”、“—”、“×”或“÷”，使等式成立。

1、（1）（2）4=242、（1）4=8 （2）7=453、=2例3填上合适的数。

（每次填的运算符号不要完全相同）=15练一练在下面算式里的中填上合适的运算符号，在填上合适的数。

（每次填的运算符号不要完全相同）1、8 =202、12 =303、请你在中填上和左边不同的符号，使等式成立。

（1）1×2×（2）4×2—（3）8÷ 1（4）3×2+2× 1例4中填上运算符号，使等式成立。

3 2=24练一练中填上运算符号，使等式成立。

1、2、3、（1）2=1 （2）2=6（3）例5、选用“+”、“—”、“×”、“÷”或( ),把下面的式子组成等式。

一年级奥数（竞赛班）7讲-第02讲：巧填算符巧qiǎo 填tián 算suàn 符fú课kè前qián 活huó动dòng画huà“数shù人rén ”闹nào 闹nào 最zuì近jìn 学xué会huì了le 用yòng 数shù字zì作zuò画huà。

他tā不bú但dàn 会huì用yòng 数shù字zì画huà动dòng 物wù，还hái 能néng 用yòng 数shù字zì画huà出chū各gè种zhǒng 各gè样yàng 的de 人rén 。

瞧qiáo ，这zhè就jiù是shì闹nào 闹nào 画huà的de“数shù人rén ”《快kuài 乐lè的de 一yì家jiā》，多duō有yǒu 趣qù！小xiǎo 朋péng 友yǒu ，你nǐ能néng 辨biàn 别bié出chū每měi 个gè“数shù人rén ”是shì由yóu 哪nǎ些xiē数shù字zì组zǔ成chéng 的de ？(乐yuè乐lè老lǎo 师shī温wēn 馨xīn 提tí示shì：6和hé9需xū要yào 正zhèng 着zhe 看kàn 哦ò！) 妈mā妈mā是shì由yóu ( )组zǔ成chéng 的de 。

第一讲巧填算符（总结-北京程雪）第一讲：巧填算符一、做题前准备：1、审题！（读清题目要求，可以用哪些符号，在哪里填符号）2、口算能力！（有很多试算的过程，如果有很强的口算能力，做题速度自然就快了）二、方法论1、试算法最基本、最常用的方法，考察、锻炼孩子的口算能力。

但切记：不要瞎试，而要动脑思考，边分析边尝试。

小练一在○内填上与等号左边不同的运算符号，使等式成立。

（1） 6－2＋2=6○2○2（2） 8＋2＋3=8○2○3（3） 16－8－3=16○8○3解析：要使等式成立，先要算出左边等于多少。

（1）左边-2+2用抵消法计算结果还是6，右边只能用×和÷，尝试发现6×2÷2=6，6÷2×2=6。

小结：加减同一个数，结果不变；乘除同一个数（0除外），结果也不变。

（2）左边=11，右边的数比11都小，那就要把它们变大点，哪些符号可以让数字变大呢？——＋或×，左边已经用过＋了，所以尝试填×，8×2-3=11。

（3）左边=5，右边的16太大，要把它变小，用什么符号呢？——÷或－，左边已经用过－了，所以尝试÷，得到结果16÷8＋3=5 小练二用运算符号把下面三个相同的数字连接起来，使等式成立。

（1） 5 5 5 = 30（2） 6 6 6 = 30解析：结果30比5、6大得多，显然要用到乘法，填上×后很容易试算出正确算式5 × 5 ＋ 5 = 306 × 6 － 6 = 302、倒推法（从最后一个符号往前填）适合于数字比较少，结果也比较小的问题。

例在下面每两个数字之间填上“＋”或“－”，使等式成立。

（1）1 2 3 4 5 6 = 1解析：用倒推法尝试。

6前面填什么符号呢？试想几+6=1，没有，所以6前面只能填－，而且7-6=1，所以前面的12345要等于7，那5前面只能填＋（因为若填－，1234就要等于12，不可能），2+5=7，所以1234要等于2，这时候就很容易填出来了1+2+3-4=2，所以最后结果是1+2+3-4+5-6=1。

第1讲巧填算符【知识要点】解决这类问题常用两种基本方法：一是凑数法，二是逆推法，有时两种方法并用。

凑数法：是根据所给的数，凑出一个与结果比较近的数，然后，再对算式中剩下的数字作适当的增加或减少，从而使等式成立。

逆推法：常是从算式的最后一个数字开始，逐步向前推想，从而得到等式。

【例题讲解】【例1】在下面算式适当的地方添上加号，使算式成立。

8 8 8 8 8 8 8 8 = 1000【例2】在下列算式中合适的地方添上＋、－、×，使等式成立。

① 9 8 7 6 5 4 3 2 1 = 1993② 1 2 3 4 5 6 7 8 9 = 1993【例3】在下面算式合适的地方添上＋、－、×号，使等式成立。

3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 = 1992【例4】在下面算式合适的地方添上＋、－、×，使等式成立。

1 2 3 4 5 6 7 8 = 1【例5】在下面算式合适的地方，只添两个加号和两个减号使等式成立。

1 2 3 4 5 6 7 8 9 = 100【例6】在下列算式中合适的地方，添上（），［］，使等式成立。

① 1＋2×3＋4×5＋6×7＋8×9 = 303② 1＋2×3＋4×5＋6×7＋8×9 = 1395③ 1＋2×3＋4×5＋6×7＋8×9 = 4455【例7】在＋、－、×、÷、（）中，挑出合适的符号，填入下面的数字之间，使算式成立。

① 9 8 7 6 5 4 3 2 1 = 1② 9 8 7 6 5 4 3 2 1 = 1000【例8】在下列算式中合适的地方，添上＋、－、×、÷、（）等运算符号，使算式成立。

① 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 = 1993② 2 2 2 2 2 2 2 2 2 2 2 2 = 1993【例9】在下面的式子里加上（）和［］，使它们成为正确的等式。

第一天在各个2 之间插入算术运算符号，使每个式子都成为等式。

（算术运算符号只包括＋、－、×、÷与括号）分析：9 个算式中，有难有易，而且填法大多不唯一，下面依次看一下。

结果为0：这个应该是比较简单的，4 个2，两两一组，每组分别相减，每组的差都是0然后把两组的结果相加、相减、相乘都可以得到0：2－2＋2－2＝0（2－2）－（2－2）＝0（2－2）×（2－2）＝0结果为1：两两一组，每组内部相除，每组的商都是1然后把两组的结果相乘或相除就可以得到1也可以两组内部相加或相乘，然后两组之间相除：（2÷2）×（2÷2）＝1（2÷2）÷（2÷2）＝1（2＋2）÷（2＋2）＝1（2×2）÷（2×2）＝1结果为2：在处理结果为1 的情形时，就会发现前面两种很容易就转换成2：（2÷2）＋（2÷2）＝2结果为3：最直接的方式：前面3 个2 相加，除以最后1 个2：（2＋2＋2）÷2＝3也可以：（2＋2）－（2÷2）＝3（2×2）－（2÷2）＝3结果为4：这个应该也比较容易看出来：（2＋2）＋（2－2）＝4（2×2）＋（2－2）＝4两组之间的加号换成减号也可以结果为5：可以通过结果为3 的后面两种填法转换得到：（2＋2）＋（2÷2）＝5（2×2）＋（2÷2）＝5结果为6：（2×2×2）－2＝6（2＋2）×2－2＝6结果为10：可以在6 的基础上转换得到：（2×2×2）＋2＝10（2＋2）×2＋2＝10结果为12：（2＋2＋2）×2＝12第二天在各个3 之间插入算术运算符号，使每个式子都成为等式。

（算术运算符号只包括＋、－、×、÷与括号）分析：结果为3：跟四个2 计算3 是一样的原理：（3＋3＋3）÷3＝3结果为4：可以在结果为3 的基础上稍作变动：（3×3＋3）÷3＝4结果为5：这个相对比较简单：3＋3－（3÷3）＝5结果为6：这个也比较直观：3＋3＋（3－3）＝63＋3－（3－3）＝6结果为7：可以在结果为5 的基础上稍作变动：3＋3＋（3÷3）＝7结果为8：可以利用结果为7 的填法稍作变动：3×3－3÷3＝8结果为9：比较直观：3×3＋3－3＝9结果为10：将结果为8 的填法稍作变动：3×3＋3÷3＝10第三天在各个4 之间插入算术运算符号，使每个式子都成为等式。

巧添算符与文字谜学会巧添算符和文字谜给算式添加运算符号，通常采用尝试探索法。

主要有两种：1、如果题目中的数字比较少，可以从算式的结果入手，推想哪些算式能得到这个结果，然后拼凑出所求的式子2、如果题目中的数字较多，结果也比较大，可以考虑先用多少个数字凑出比较接近算式结果的数，然后再进行调整，使算式成立注：通常情况下，根据题目的特点选择方法，有时将以上两种方法结合使用，更有助于问题的解决。

例1：在下面的算式中添上＋、－、×、÷或者（），使算式成立。

1 2 3 4 5 = 10例2：在下面的算式中添上＋、－、×、÷或者（），使算式成立。

（1）8 8 8 8 = 0（2）8 8 8 8 = 1（3）8 8 8 8 = 2（4）8 8 8 8 = 3练习2：在下面的算式中添上＋、－、×、÷或者（），使算式成立。

（1）4 4 4 4 = 0 （2）4 4 4 4 = 1 （3）4 4 4 4 = 2（4）4 4 4 4 = 3 （5）4 4 4 4 = 4 （6）4 4 4 4 = 5例:3：在下面的算式中添上＋、－、×、÷或者（），使算式成立。

5 5 5 5 5 5 5 5 5 5 5 5 =1000练习3：用12个3组成8个数，使它们的结果等于2000。

3 3 3 3 3 3 3 3 3 3 3 3 =2000例4：在下面算式中合适的地方添上＋或－，使算式成立。

9 8 7 6 5 4 3 2 1 =21练习4：在下面算式中合适的地方添上＋或－，使算式成立。

9 8 7 6 5 4 3 2 1 =21例5：改变下式中的一个运算符号，使算式成立。

1 +2 +3 +4 +5 +6 +7 +8 +9 =100练习5：王老师在批改作业时发现小林同学抄题时丢了符号，但结果仍然是正确的。

请你给小林的算式添上符号:4 + 28 ÷ 4 － 2 × 3 － 1 = 4练习6：自然数M N 满足：.410-=-=-N N M M 则=+N M （ ）例6：下式中，每个汉字各代表一个不同的数字，其中“心”代表9，请问其他汉字分别代表哪些数字？少 年 足 球 活 动 中 心× 心少 少 少 少 少 少 少 少 少练习7：下面每个汉字各代表一个不同的数字，这些汉字分别代表数字几？世 博 成 功 举 办× 办好 好 好 好 好 好例:7：下面每个汉字各代表一个不同的数字，相同的汉字代表相同的数字，这些汉字分别代表数字几？2 华 罗 庚 数 学× 3华 罗 庚 数 学 2练习8：下面每个汉字各代表一个不同的数字，这些汉字分别代表数字几？小 数 报× 学1 6 7 3练习9：下面A 、B 、C 、D 各代表数字几？A B C D× 9D C B A例8：下面算式中的“巨龙腾飞”四字分别代表不同的数字，当它们各代表什么数字时，下列算式成立。

第四讲巧填算符主要知识点：1.分组法适用范围：题目中让填入“+”、“-”号的问题减号组和=（左和-右数）÷2，但要注意第一个数不要选入减号组。

2.凑数法适用范围：题目中没有要求必须要在指定的地方填入，可以在适当的位置填入时步骤：首先选一个离结果最接近的数，然后找到这个数离结果差多少，利用差来填剩余的数。

3.逆推法适用范围：一般适用于数字比较少、结果比较小的，可以填加减乘除和括号的情况。

步骤：从等号左边最后一个数开始分四类进行讨论，最后一个数前面可以填入+、-、×、÷，然后逐步往前推。

一、分组法例题：在下面的圆圈内填入“+”、“-”号，使等号成立。

8=9解题步骤：1.先算出左边所有数的和：2+3+5+7+8=252. 利用公式算出减号组和=（左和-右数）÷2=（25-9）÷2=83.由减号组和等于8，可以选出两组属于减号组的数（3,5；8）写出答案：2-3-5+7+8=9或者2+3+5+7-8=9二、凑数法例题：在下面数字的适当位置填入“+”、“-”号，使等号成立。

1 2 3 4 5 6 7 8=50分析：可以看出，上式中8个数字之间填入+号后，和为36，无法达到50，所以要用凑数法，在适当的位置填入符号。

1. 先找出一个离50最近的数452. 除去45后，题目转化为1 2 3 6 7 8=5，即转化为第一种类型加减分组类题目。

左和=1+2+3+6+7+8=27，减号组和=（27-5）÷2=11，找出减号组的数2,3,6，3. 写出答案：1-2-3+45-6+7+8=50三、逆推法例题：在下式中填入“+”、“-”、“×”、“÷”号和（），使等号成立。

6 6 6 6=12分析：逆推法就是倒着推，从最后一个数字6开始，先写出所有情况1. +6=12 等于6，6+6-6=6；6×6÷6=62. -6=12 等于18，6+6+6=183. ×6=12 等于2，（6+6）÷6=24. ÷6=12 等于72，(6+6)×6=72写出所有答案： 6+6-6+6=12；6×6÷6+6=12；6+6+6-6=12；（6+6）÷6×6=12；(6+6)×6÷6=12.。

第十一讲巧填算符（一）所谓填算符，就是指在一些数之间的适当地方填上适当的运算符号（包括括号），从而使这些数和运算符号构成的算式成为一个等式。

在填算符的问题中，所填的算符包括+、-、×、÷、（）、[]、｛｝。

解决这类问题常用两种基本方法：一是凑数法，二是逆推法，有时两种方法并用。

凑数法是根据所给的数，凑出一个与结果比较接近的数，然后，再对算式中剩下的数字作适当的增加或减少，从而使等式成立。

逆推法常是从算式的最后一个数字开始，逐步向前推想，从而得到等式。

例1 在下面算式适当的地方添上加号，使算式成立。

8 8 8 8 8 8 8 8=1000分析要在八个8之间只添加号，使和为1000，可先考虑在加数中凑出一个较接近1000的数，它可以是888，而888＋88=976，此时，用去了五个8，剩下的三个8应凑成1000-976＝24，这只要三者相加就行了。

解：本题的答案是888+88+8+8+8=1000例2 在下列算式中合适的地方添上+、-、×，使等式成立。

① 9 8 7 6 5 4 3 2 1=1993② 1 2 3 4 5 6 7 8 9=1993分析本题的特点是所给的数字比较多，而得数比较大，这种题目一般用凑数法来做，在本题中应注意可使用的运算符号只有+、-、×。

①中，654×3=1962，与结果1993比较接近，而1993-1962=31，所以，如果能用9 8 72 1凑出31即可，而最后两个数合在一起是21，那么只需用9 8 7凑出10，显然，9+8-7=10，就有：9＋8-7＋654×3+21=1993②中，与1993比较接近的是345×6=2070.它比1993大77，现在，剩下的数是1 2 7 8 9，如果把7、8写在一起，成为78，则无论怎样，前面的1、2和最后的9都不能凑成1.注意到8×9=72，而7+8×9=79，1×2=2，79-2=77.所以这个问题可以如下解决：1×2+345×6-7-8×9=1993。

小学三年级奥数巧填算符【三篇】1 2 3 4 5 6 7 8 9=100分析在本题条件中，不但限制了所使用运算符号的种类，而且还限制了每种运算符号的个数。

因为题目中，一共能够添四个运算符号，所以，应把123456789分为五个数，又考虑最后的结果是100，所以应在这五个数中凑出一个较接近100的，这个数能够是123或89。

如果有一个数是123，就要使剩下的后六个数凑出23，且把它们分为四个数，应该是两个两位数，两个一位数.观察发现，45与67相差22，8与9相差1，加起来正巧是23，所以本题的一个答案是：123+45-67+8-9=100如果这个数是89，则它的前面一定是加号，等式变为1234567+89=100，为满足要求，1234567=11，在中间要添一个加号和两个减号，且把它变成四个数，观察发现，无论怎样都不能满足要求。

答案与解析：本题的一个答案是：123+45-67+8-9=100补充说明：一般在解题时，如果没有特别说明，只要得到一个准确的解答就能够了。

在例5这类限制比较多的题目的解决过程中，要时时注意按照题目的要求去做，因为题目的要求比较高，所以解决的方法比较少。

【第二篇】练习题：在下面算式适当的地方添上加号，使算是成立。

1 1 1 1 1 1 1 1=1000分析：这道题，1000是大数，先找一个离1000最近的数，就是1111，那么多了111怎么办呢？那么就要“-111”这时已经是1000了，还有一个1怎么办呢？会想到：(1111-111)÷1=1000【第三篇】练习题：在下面算式适当的地方添上加号，使算式成立。

8 8 8 8 8 8 8 8=1000分析要在八个8之间只添加号，使和为1000，可先考虑在加数中凑出一个较接近1000的数，它能够是888，而888+88=976，此时，用去了五个8，剩下的三个8应凑成1000-976=24，这只要三者相加就行了。

答案与解析：本题的答案是888+88+8+8+8=1000。

二年级奥数：《巧填算符》预习一．了解有哪些算符和功能1．算符+、-、×、÷、=、>、<、( )2．运算算符的功能变大：“+”和“×”变小：“-”和“÷”例题：将“+、-、×、÷”填入下面两个数之间，是等式成立.16 2 5=3解析：由左边的16到右边的3，数变小了，那么我们就应该考虑“-”或者“÷”，全“-”不够，而且“÷”只能填在16与2之间，所以答案为：16÷2-5=3二．添小括号( )改变运算顺序:括号里要先算例题：在下面式子中适当的地方添上括号使等式成立.36-12-10=34解析：括号添前面不行，前面本来就可以先算的，那么隐藏的括号就只能把12与10括起来.那么就先算括号里的12-10=2，然后再是36-2=34，所以答案为：36-(12-10)=34 三．称象法关键：找与结果最接近的那个数例题：在合适的地方填上”+”,使等式成立.1 2 3 4 5=60解析：等式左边与60最接近的数是45，剩下60-45=15，再考虑1 2 3=15，可以得出12+3=15.所以答案为：12+3+45=60.四．倒推法例题：在相邻的两个数之间填上“+ “，”- “，使等式成立.1 2 3 4 5=5解析:倒推法就是从最后的结果开始推起.如果最后一个数5，前面是“+“，那么需要1 2 3 4=0 ，在4 前面填”+”,不可以，在4 前面只能填”- “，则需要1 2 3=4 ，推导不出来，所以失败.如果最后一个数5 ，前面是“- “，那么需要1 2 3 4=10 （这里有厉害的小朋友可以一眼看出来，全加即可）；在4 前面填”-”,则需要1 2 3=14 ，不可行，在4 前面填”+”, 则需要1 2 3=6 ，1+2+3=6成立.所以结果为1+2+3+4-5=5 PS ：此题还有其他的答案，如1-2-3+4+5=5 .五．分组法全加求和分两组：一组加法，一组减法例题：在相邻的两个数之间填上“+ “，”- “，使等式成立.1 2 3 4 5=5解析：先将左边全部加起来：1+2+3+4+5=15，即为加法和减法的和，加法比减法多5，则加法为10，减法为5；凑减法，直接一个5或者2和3，所以答案为：1+2+3+4-5=5或者为1-2-3+4+5=5如何预习？为了保护孩子课前的好奇心和学习兴趣，以及保证课堂效果，家长在给孩子预习的时候，一定要把握好度.预习，切忌给孩子讲解书本上的例题和知识点，因为孩子容易先入为主，如果家长选取的方式方法不当，那么孩子很难转换思路了；另外，家长给孩子讲过例题后，孩子可能会觉得自己已经学会了，上课的时候就不愿意认真听了.我们预习的目的是回顾这一讲课前的铺垫知识，以及引起孩子的思考，因此家长可以把我们的这份预习资料打印出来，让孩子自己看一看，如果孩子有不明白的，您可以适当点拨.这节课主要还是涉及到了较多的+、-、×、÷四则混合运算，所以乘法、除法还不熟练的小朋友们赶紧抽时间练起来.计算是学好数学的基础，一起加油吧！《巧填算符》知识点精讲【知识点总结】一、算符＋、－、×、÷、＝、＞、＜、（）二、加减乘除混合时有括号先算括号没有括号先算乘除，后算加减三、填符号小技巧①凑数【例】：下面有4 张扑克牌，请你用这4 张扑克牌通过加减乘除算出24.3 6 7 8解析：凑数方法一：发现这四个数之和刚好为24.可得：3+6+7+8=24方法二：3×8＝24，7-6=1.可得：3×8×（7-6）＝24方法三：4×6＝24，3+8-7=4或8-7+3=4.可得：（3+8-7）×6=24或（3+8-7）×6=24.②遇到四种符号都要填时，先填÷【例】：在下面的算式中分别填上＋、－、×、÷，使等式成立.7 2 4 ＝10 2 5解析：先考虑“÷”的位置，发现只能填在10 和2 之间，先填÷，再考虑2 和5之间填什么，发现可以填＋，那么左边就可以根据右边的答案去填7×2-4.答案： 7×2-4 ＝10÷2+5③称象法（只填“+”）【例】：在下面算式中适当的地方填“＋“，使等号成立.1 2 3 4 5 6 ＝75答案一：用称象法先选择最接近75 的数，56，剩下75-56=19，就可以先选12，刚好还有3 和4，所以可得：12 ＋3 ＋4 ＋56 ＝75.答案二：用称象法的顺序思考，把最大的数变小，变成45，那么后面就有一个6，一共还差 24，刚好可以选23 和1 ，所以得答案二：1 ＋23 ＋45 ＋6 ＝75④倒推法和分组法【例】：在每两个数之间填上“＋“，使算式成立.1 2 3 4 5 6 ＝1倒推法：1 + 2 + 3 – 4 + 5 - 6 = 1=6 =2 =7分组法：1~6 总和为21，加法要比减法多1，加法总和为11，减法总和为10.【学习建议】本讲讲的是巧填算符，做这类题目首先要仔细读题，并注意以下几点：1.题目是否有提到用括号2.每种符号是否只能用一次3.符号填写的位置有没有规定《巧填算符》补充题1. 用下列四个数字算24 点游戏.3 ，3 ，5 ，6 2 ，2 ，4 ，81 ，4 ，4 ，5 6 ，8 ，8 ，92. 给算式添上括号，使等式成立.5×9+15÷3=703. 在两数中间加上运算符号+、-、×、÷，使等式成立.12 4 4 = 10 3 8 4 2 = 4 44. 在下面适当的地方填上“+”，使等式成立.（位置相邻的数可以组成一个数） 8 8 8 8 8 8 8 8 = 10005. 在下面相邻两数之间都填上“＋”或“－”使等式成立.9 8 7 6 5 4 3 2 1 =316. 在相邻两个数之间填上“+、-、×、÷和（）”使等式成立.5 5 5 5 = 1 8 8 8 8 = 3【答案】1.（6-3 ）×（3+5 ）=24 8÷2×（2+4 ）=24 4×5+4÷1=24 8×9-6×8 =242. 5×（9+15÷3 ）=703. 12 ＋4÷4 =10 ＋3 8 ＋4×2 =4×44. 8 8 8+8 8+8+8+8=10005. 9+8+7+6+5-4-3+2+1 =316. 5÷5×5÷5=1 （8 ＋8 ＋8 ）÷8=3注:上述有些题目一题有多解，答案只要写出一种就可以了。

三一文库（）/小学三年级〔三年级数学题及答案：巧填算符〕1.巧填算符在下面算式中合适的地方，只添两个加号和两个减号使等式成立。

1 2 3 4 5 6 7 8 9＝100分析在本题条件中，不仅限制了所使用运算符号的种类，而且还限制了每种运算符号的个数。

由于题目中，一共可以添四个运算符号，所以，应把1 23 4 5 6 7 8 9分为五个数，又考虑最后的结果是100，所以应在这五个数中凑出一个较接近100的，这个数可以是123或89。

如果有一个数是123，就要使剩下的后六个数凑出23，且把它们分为四个数，应该是两个两位数，两个一位数.观察发现，45与67相差22，8与9相差1，加起来正巧是23，所以本题的一个答案是：123＋45-67＋8-9＝100如果这个数是89，则它的前面一定是加号，等式变为1 2 3 4 5 6 7＋89=100，为满足要求，1 2 3 4 5 6 7=11，在中间要添一个加号和两个减号，且把它变成四个数，观察发现，无论怎样都不能满足要求。

解：本题的一个答案是：123＋45-67＋8-9=100补充说明：一般在解题时，如果没有特别说明，只要得到一个正确的解答就可以了。

在例5这类限制比较多的题目的解决过程中，要时时注意按照题目的要求去做，由于题目的要求比较高，所以解决的方法比较少。

2.巧填算符在下面算式适当的地方添上加号，使算是成立。

1 1 1 1 1 1 1 1 = 1000分析：这道题，1000是大数，先找一个离1000最近的数，就是1111，那么多了111怎么办呢？那么就要"-111"这时已经是1000了，还有一个1怎么办呢？会想到：（1111－111）÷1 = 1000。

消失的符号(巧填算符)知识图谱消失的符号知识精讲一．巧填算符1．一个加减法算式中，如果把某个数前的加号变为减号，那么最后的计算结果不但少加了一次这个数，还额外减了一次这个数，那么结果会变小该数的两倍．2．对于特定的两个数，之间填上“+”和“⨯”一般可以使结果变大，而如果填上“-”和“÷”一般可以使结果变小，但注意存在数字1时比较特殊．3．两个数字越大，那么填上“⨯”所得的结果要比“+”的结果大得多．4．在填写除号的时候，注意一定要让组成的算式可以整除．5．括号用来改变运算顺序，在原有算式的基础上添上括号会使整个计算结果发生变化．6．注意题意，数字间不填符号可以得到多位数．二．算符与数字1．除了和符号相关的问题外，还有许多有关数字的问题．两个一位数相加，所能得到的和最大是9918+=，最小为000+=．除了0、1、17、18外，其他的和都可以有多组数相加得到，而且离9越近，分拆的方法就越多．2．部分数字（0、1、6、8、9）颠倒后仍是数字，而其他则不行．3．各种算式的组成与修改问题．在已知数之间添加运算符号与括号，得出给定结果或取得最大、最小值．通过枚举、试算、顺推、逆推等方法解决算式的变化问题．要求学生有较强的心算和估算能力．三点剖析本讲主要培养学生的观察推理能力，其次培养学生的运算能力．本讲内容是在整数计算的基础上，学习算符与数字．课堂引入例题1、 柯小南对数学可以说是情有独钟，而且对于一些数学难题他会很轻松的解答出来，所以知道他的人都称他为数学家．一天，他的朋友唐小虎遇到一个数学难题，怎么也算不出来．于是，唐小虎带着这个疑问去找柯小南．当唐小虎刚说完题目，聪明的柯小南只是说这不是什么难题，同时在纸上马上添加了运算符号，唐小虎看了后豁然开朗．例题2、 下面有6个数，在每两个相邻的数之间都填上一个加号或减号，使得结果为18：6 5 4 3 2 118=算符与数字中的等式成立例题1、 （1）下面有6个数，在每两个相邻的数之间都填上一个加号或减号，使得结果为19： 65432119=（2）在下面相邻两数之间，填上“”或“”，使等式成立．3____4____5____610=． （3）在下面算式中合适的地方填入小括号，使等式成立： （4）在下面算式中合适的地方填入＋、－、×、÷或（），使等式成立：1234578=（5）请在下式中填入“+”和“⨯”，使等式成立（不要求每两个数之间都填入符号，但不能填“+”和“⨯”以外的符号）：．例题2、 改变下面算式中一个数字前的运算符号，就能使等式成立． （1）（只能加变减，减变加）：765432118++--+-=，（2）123456789100++++++++=，（3）1234567891011121314151617181920200+++++++++++++++++++=．⨯÷6812430⨯+÷=12345678910100=在3个9之间添加任意的运算符号，使其等于2．你知道柯小南是怎样添加运算符号的吗？说一说．我能不能先填一种运算符号呢？然后根据结果再调整？那是不是可以先看看原来的算式结果是多少呢？例题3、 在下面算式中合适的地方填入＋、－、×、÷或（），使等式成立： （1）999999102=（2）8888888888882016=随练1、 在下面算式中合适的地方填入＋、－、×、÷或（），使等式成立． （1），（2） 随练2、 在下面算式中合适的地方填入小括号，使等式成立：算符与数字中的最值问题例题1、 在下面的算式中填入一对括号，使得算式的结果最大，最大值是________．例题2、 （1）把＋、－、×、÷各一个填入下面的空格内，使得计算的结果最大，这个最大值是________．（2）在下面的一排数字之间添入一个加号和一个减号，组成的算式的最小值是________．（3）把＋、－、×、÷各一个填入下面的横线上，再添一对括号，要使计算的结果最大，那么能得到的最大的结果是________．例题3、 将1至8填入算式“”中，使得算式结果达到最大或最小．444420=9999919=578124220+⨯+÷-=108320++⨯97531□□□□5432110_____8_____4_____2_____1()()+⨯-□□□□□□□□注意仔细读题哦~是在合适的地方添符号哦~结果最大，那就应该乘数最大吧？什么时候才会有最大值呢？结果最大，相乘的两数要尽可能大；结果最小，相乘的两数要……随练1、 在下面的算式中填入一对括号，使得算式的结果最大，最大值是________． 随练2、 把从1到6这6个数字填入算式中，使得等式达到最大：．算符与数字的实际应用例题1、 有一类三位数，各数位上的数字之积是18，在所有这样的三位数中，最大的数与最小的数的差是______．例题2、 将一个多位数的相邻两个数字从左到右依次相加，得到的和分别为：2、0、4，那么这个多位数是________．例题3、 一张纸片上写着一个两位数，把纸片倒过来之后又变成了另一个两位数，且两个两位数的和为107，那么这两个两位数分别是________．例题4、 在下面的横线上填入2、3、8、9各一个，使得最后的结果等于24．随练1、 将一个多位数相邻两位数字依次相加，得到的和从左到右依次为：5、1、9、8、2、4、8、15，那么这个多位数是________．24点与36点例题1、 在下面各题中，请你用给出的四个数，适当进行加、减、乘、除运算，每个数恰好用一次，使得计算结果等于24：（1）1，4，5，6；（2）1，5，5，5；（3）3，3，7，7；（4）3，3，8，8． 例题2、 把＋、－、×、÷这4个运算符号，分别填入下面四个圆圈内，使等式成立：例题3、 用下面每小题给定的5个数凑36，数可以打乱顺序，每个数仅用一次，可用＋、－、×、÷或（）． （1）2，4，6，8，10 （2）1，3，5，7，9随练1、 在下面的横线上填入1、3、6、8各一个，使得最后的结果等于24．102310++⨯⨯+⨯□□□□□□()________________________________24÷⨯-=()()28418936=○○○○()________________________________24÷+⨯=三位数，各数位上的数字之积是18，那就是说……最后一步是乘法，是不是去凑两个数相乘等于24就可以了呢？易错纠改例题1、看完题目，唐小虎思考了一会，和姐姐唐小果有了以下的讨论：你能帮唐小虎解决这个问题吗？请写出计算过程．拓展1、 用运算符号将1、4、7、7组成一个算式，使结果等于24．__________2、 在下面算式中合适的地方填入＋、－、×、÷或（），使等式成立 （1）333310=，（2）55555500=3、 在下面的算式中填入一对括号，使得算式的结果最大，最大值是__________． 7523++⨯4、 在下面的算式中合适的地方填入小括号，使等式成立： （1）48123217-⨯÷+=；（2）3020105250+÷÷⨯=．5、 请将四个4用“＋、－、×、÷、（ ）”组成3个算式如：44449++÷=．使它们的结果分别等于5、6、7． （1）________________________=5（2）________________________=6 （3）________________________=7．6、 ()()÷⨯+-⨯+-□□□□□□□□从1至9这9个数中选出8个数，分别填在上面的8个□内，使算式的结果尽可能大，那么这个最大的结果是多少？7、 把＋、－、×、÷各一个填入下面的横线上，再添一对括号，要使计算的结果最大，那么能得到的最大的结果是多少？9_____7_____5_____3_____18、 将一个多位数相邻两位数字依次相加，得到的和分别为：6、2、4、9、5、8、11，那么这个多位数是多少？ 9、 分析并口述题目的做题思路及方法．请用4、5、7、9以及算符和括号组成一个算式，使得结果为24，至少用三种方法．姐姐，这节课的内容既好玩还容易哦~那是你没遇到，来看看这题吧．把0~9这十个数字倒过来看，其中0，1，8三个数字不变，6与9两个数字互换，而其余数字倒过来都没有意义．在一张纸片上写出一个两位数，把纸片倒过来看，恰好与原数相同，这样的两位数有几个？如果写的是一个三位数，倒过来看与原数相同，这样的三位数有几个？首先两位数肯定只能是由0、1、8、6、9组成．那就在这5个数中挑出2来组成两位数就可以了呀！按照你的方法，那10满足要求吗？注意题目中的意思哦~不行哎，倒过来就变成01，和10不想等了，姐姐，你等我再想想奥……。

巧填运算符号的技巧
运算符号在数学中起着至关重要的作用，它们用于表示数学运算的方式和结果。

在解决数学问题时，巧妙地运用运算符号可以更加高效地解决问题。

下面介绍一些巧填运算符号的技巧。

1. 利用括号：括号的作用是改变运算的顺序，可以用来改变优先级。

在填写运算符号时，可以先把括号填好，再填写括号外的运算符号。

这样可以避免优先级的错误，同时也更加清晰明了。

2. 利用等式：等式两边的值相等，因此可以在等式两边填写相同的运算符号。

这样可以减少填写的运算符号数量，提高填写的效率。

3. 利用数学规律：在填写运算符号时，可以根据数学规律来选择合适的运算符号。

例如，两个正数相乘得到的结果也是正数，因此可以用乘号表示；两个负数相乘得到的结果是正数，因此也可以用乘号表示。

4. 利用符号的可替换性：一些运算符号是可以相互替换的，例如加法和减法、乘法和除法。

因此，在填写运算符号时，可以根据需要进行替换，使运算更加简便。

巧填运算符号需要结合具体的数学问题来进行，需要不断地练习和掌
握才能达到熟练的水平。

同时也需要注意运算符号的优先级和规律，避免出现错误。

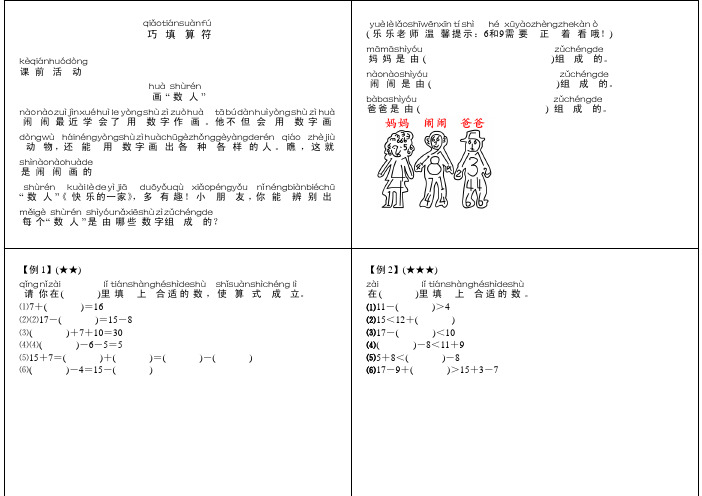
巧qiǎo 填tián 算suàn 符fú课kè前qián 活huó动dòng画huà“数shù人rén ”闹nào 闹nào 最zuì近jìn 学xué会huì了le 用yòng 数shù字zì作zuò画huà。

他tā不bú但dàn 会huì用yòng 数shù字zì画huà动dòng 物wù，还hái 能néng 用yòng 数shù字zì画huà出chū各gè种zhǒng 各gè样yàng 的de 人rén 。

瞧qiáo ，这zhè就jiù是shì闹nào 闹nào 画huà的de“数shù人rén ”《快kuài 乐lè的de 一yì家jiā》，多duō有yǒu 趣qù！小xiǎo 朋péng 友yǒu ，你nǐ能néng 辨biàn 别bié出chū每měi 个gè“数shù人rén ”是shì由yóu 哪nǎ些xiē数shù字zì组zǔ成chéng 的de ？(乐yuè乐lè老lǎo 师shī温wēn 馨xīn 提tí示shì：6和hé9需xū要yào 正zhèng 着zhe 看kàn 哦ò！) 妈mā妈mā是shì由yóu ( )组zǔ成chéng 的de 。