计量经济学第08章2.

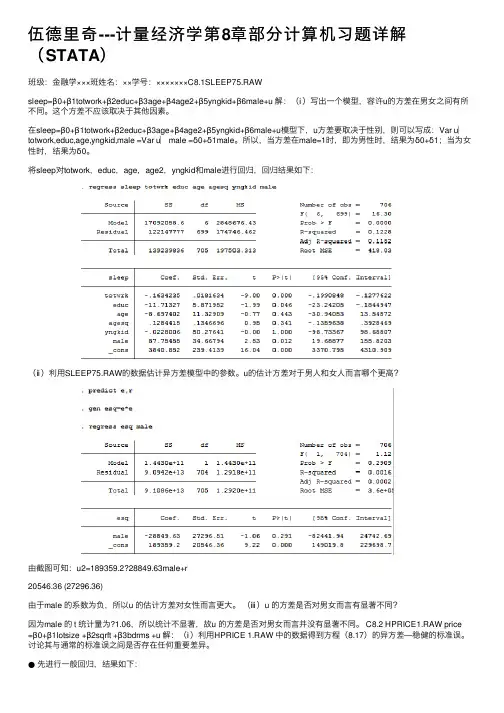
伍德⾥奇---计量经济学第8章部分计算机习题详解（STATA）班级：⾦融学×××班姓名：××学号：×××××××C8.1SLEEP75.RAWsleep=β0+β1totwork+β2educ+β3age+β4age2+β5yngkid+β6male+u 解：（ⅰ）写出⼀个模型，容许u的⽅差在男⼥之间有所不同。

这个⽅差不应该取决于其他因素。

在sleep=β0+β1totwork+β2educ+β3age+β4age2+β5yngkid+β6male+u模型下，u⽅差要取决于性别，则可以写成：Var u︳totwork,educ,age,yngkid,male =Var u︳male =δ0+δ1male。

所以，当⽅差在male=1时，即为男性时，结果为δ0+δ1；当为⼥性时，结果为δ0。

将sleep对totwork，educ，age，age2，yngkid和male进⾏回归，回归结果如下：（ⅱ）利⽤SLEEP75.RAW的数据估计异⽅差模型中的参数。

u的估计⽅差对于男⼈和⼥⼈⽽⾔哪个更⾼？由截图可知：u2=189359.2?28849.63male+r20546.36 (27296.36)由于male 的系数为负，所以u 的估计⽅差对⼥性⽽⾔更⼤。

（ⅲ）u 的⽅差是否对男⼥⽽⾔有显著不同？因为male 的 t 统计量为?1.06，所以统计不显著，故u 的⽅差是否对男⼥⽽⾔并没有显著不同。

C8.2 HPRICE1.RAW price =β0+β1lotsize +β2sqrft +β3bdrms +u 解：（ⅰ）利⽤HPRICE 1.RAW 中的数据得到⽅程（8.17）的异⽅差—稳健的标准误。

讨论其与通常的标准误之间是否存在任何重要差异。

●先进⾏⼀般回归，结果如下：●再进⾏稳健回归，结果如下：由两个截图可得：price =?21.77+0.00207lotsize +0.123sqrft +13.85bdrms29.48 0.00064 0.013 (9.01)37.13 0.00122 0.018 [8.48]n =88，R 2=0.672⽐较稳健标准误和通常标准误，发现lotsize 的稳健标准误是通常下的2倍，使得 t 统计量相差较⼤。

第八章虚拟变量模型1. 回归模型中引入虚拟变量的作用是什么?答:在模型中引入虚拟变量，主要是为了寻找某(些)定性因素对解释变量的影响。

加法方式与乘法方式是最主要的引入方式，前者主要适用于定性因素对截距项产生影响的情况，后者主要适用于定性因素对斜率项产生影响的情况。

除此外，还可以加法与乘法组合的方式引入虚拟变量，这时可测度定性因素对截距项与斜率项同时产生影响的情况。

2. 虚拟变量有哪几种基本的引入方式?它们各适用于什么情况?答:在模型中引入虚拟变量的主要方式有加法方式与乘法方式，前者主要适用于定性因素对截距项产生影响的情况，后者主要适用于定性因素对斜率项产生影响的情况。

除此外，还可以加法与乘法组合的方式引入虚拟变量，这时可测度定性因素对截距项与斜率项同时产生影响的情况。

3．什么是虚拟变量陷阱？答：根据虚拟变量的设置原则，一般情况下，如果定性变量有m个类别，则需在模型中引入m-1个变量。

如果引入了m个变量，就会导致模型解释变量出现完全的共线性问题，从而导致模型无法估计。

这种由于引入虚拟变量个数与类别个数相等导致的模型无法估计的问题，称为“虚拟变量陷阱”。

4．在一项对北京某大学学生月消费支出的研究中，认为学生的消费支出除受其家庭的每月收入水平外，还受在学校中是否得到奖学金，来自农村还是城市，是经济发达地区还是欠发达地区，以及性别等因素的影响。

试设定适当的模型，并导出如下情形下学生消费支出的平均水平：(1) 来自欠发达农村地区的女生，未得到奖学金；(2)来自欠发达城市地区的男生，得到奖学金；(3)来自发达地区的农村女生，得到奖学金；(4)来自发达地区的城市男生，未得到奖学金。

解答:记学生月消费支出为Y，其家庭月收入水平为X，则在不考虑其他因素的影响时，有如下基本回归模型：Y i=β0+β1X i+μi有奖学金1 来自城市无奖学金来自农村来自发达地区 1 男性0 来自欠发达地区0 女性Y i=β0+β1X i+α1D1i+α2D2i+α3D3i+α4D4i+μi由此回归模型，可得如下各种情形下学生的平均消费支出：(1)来自欠发达农村地区的女生，未得到奖学金时的月消费支出：E(Y i|=X i,D1i=D2i=D3i=D4i=0)=β0+β1X i(2)来自欠发达城市地区的男生，得到奖学金时的月消费支出：E(Y i|=X i,D1i=D4i=1,D2i=D3i=0)=(β0+α1+α4)+β1X i(3)来自发达地区的农村女生，得到奖学金时的月消费支出：E(Y i |=X i ,D 1i =D 3i =1,D 2i =D 4i =0)=(β0+α1+α3)+β1X i (4)来自发达地区的城市男生，未得到奖学金时的月消费支出： E(Y i |=X i ,D 2i =D 3i =D 4i =1,D 1i =0)=(β0+α2+α3+α4)+β1X i5. 研究进口消费品的数量Y 与国民收入X 的模型关系时，由数据散点图显示1979年前后Y 对X 的回归关系明显不同，进口消费函数发生了结构性变化：基本消费部分下降了，而边际消费倾向变大了。

计量经济学夏凡第八章动态计量模型基础第一节分布滞后模型第二节单位根检验第三节协整与误差修正模型计量经济学夏凡引言⏹传统的时序模型●一般先从已知相关理论出发设定模型形式，再由样本数据估计模型中的参数⏹这种方法使建模过程对相关理论有很强的依赖性⏹动态计量经济学模型●20世纪70年代末，以英国计量经济学家Hendry为代表，将理论和数据信息有效结合，提出了动态计量经济学模型的理论与方法●为时序模型带来了重要的发展量经济学夏凡第一节分布滞后模型⏹几何分布滞后模型⏹多项式分布滞后模型⏹自回归分布滞后模型量经济学夏凡基本概念⏹分布滞后模型●⏹如果p是有限数，称为有限分布滞后模型⏹如果p是无限数，称为无限分布滞后模型npptxxxytptpttt,,2,111++=+++++=--εβββα计量经济学夏凡基本概念（续）⏹分布滞后模型的两个问题●由于存在滞后值，则要损失若干个自由度⏹如果滞后时期长，而样本较小，自由度损失就较大，有时甚至无法进行估计●通常一个变量的滞后变量之间共线性问题严重，影响估计量的精度⏹解决方法●对系数施加约束条件，减少待估参数的数目计量经济学夏凡几何分布滞后模型⏹几何分布滞后模型●又称Koyck滞后模型●反映变量的影响程度随滞后期的延长而按几何级数递减⏹经济变量间的因果关系，往往随着时间间隔的延伸而逐渐减弱●模型⏹●()1221ti ititttttxxxxyελβαεβλλββα++=+++++=∑∞=---1<λ计量经济学夏凡几何分布滞后模型（续1）⏹模型的第二种表达形式●⏹对(1)式取一期滞后，并两边同乘λ得●⏹(1)式减去(2)式得●⏹令，即可得到模型的第二种表达式●用y t-1代替了x的滞后变量⏹减小了多重共线性的程度()ttttuyxy+++-=-11λβλα()212211----++++=ttttxxyλεβλλβλαλ()111---++-=-tttttxyyλεεβλαλ1--=tttuλεε计量经济学夏凡几何分布滞后模型（续2）⏹模型的估计●模型中的随机扰动项通常存在一阶负相关关系⏹参数估计变得较复杂●可采用工具变量法和广义差分法相结合的估计方法计量经济学夏凡多项式分布滞后模型⏹多项式分布滞后模型●为解决几何分布滞后模型存在的问题，Almon提出了多项式分布滞后(PDL：Polynomial Distributed Lag)模型⏹用多项式表示滞后变量系数βi和滞后长度i的关系⏹一般，多项式阶数不超过3次计量经济学夏凡多项式分布滞后模型（续1）⏹对于模型●其解释变量之间存在多重共线性，不能采用OLS估计●将βi分解为⏹●其中，且●即将每个参数用一个多项式表示()()()()pqpipipi qqi<-++-+-+=ααααβ221pi,,2,1,0=()()Nkkpkpppp∈⎩⎨⎧-==-=1222/12/()30tpi ititxyεβα++=∑=-计量经济学夏凡多项式分布滞后模型（续2）⏹模型的估计●(3)式可改写为⏹●其中●则(4)式实际上比(3)式少了p-q个参数●可对模型施加约束条件⏹近端(near end)约束和远端(far end)约束⏹应用时，可同时指定上述两种约束，或其中之一，也可不含约束条件()4110tqtqtttzzzyμαααα+++++=()()qjxpizitjpijt,,1,0=-=-=∑计量经济学夏凡多项式分布滞后模型（续3）⏹PDL模型的确定因素●滞后期p、多项式次数q和约束条件⏹PDL模型的特点●优点⏹减少了待估参数，因此减小了多重共线性的程度⏹方程的变换并没有改变干扰项的形式，没有引入自相关问题，可用OLS直接估计变换后的方程●缺点⏹样本损失没有减少●只有(n-q)个观测值可用于估计计量经济学夏凡多项式分布滞后模型（续4）⏹操作命令●ls y x1 x2pdl(series_name,lags,order,options)⏹lags：代表滞后期p⏹order：表示多项式阶数q⏹options：指定约束类型，没有约束条件时缺省●1：近端约束●2：远端约束●3：同时采用近端和远端两种约束计量经济学夏凡多项式分布滞后模型（续5）⏹[例8-1]某水库1998年至2000年各旬的流量、降水量数据如下所示。

计量经济学第二版第八章答案【篇一：庞皓计量经济学课后答案第八章】业1、①在给定的数据中可以看出人均收入的系数的t值t(?2)?0.857，di(lnxi?7)系数的t值t(?3)?2.42，在给定显著性水平??0.05下n=101，t0.025(101)?1.984。

所以人均收入对期望寿命并没有显著影响。

而di(lnxi?7)对期望寿命有显著影响。

当人均收入超过1097美元时，即di=1为富国时：???2.40?9.39lnx?3.36(lnx?7)?21.12?6.03lnx yiiii当人均收入未超过1097美元时，即di=0为穷国时：???2.40?9.39lnx yii②引入di(lnxi?7)的原因是从截距和斜率两个方面来考虑收入对期望寿命的影响。

③对穷国进行回归时，yi取xi?1097时的值。

对富国进行回归时，yi取xi?1097时的值④结论：富国的期望寿命高于穷国的期望寿命。

贫富国之间的期望寿命的确存在显著差异。

2、①d1t???1,t为1987年及以后?0,t为1987年以前 d2t??年及以后?1,t为1994年以前?0,t为1994年及以后年及以后?1,t为2006?1,t为2008 d3t?? d4t?? 0,t为2006年以前0,t为2008年以前??②从图形上看。

consume和income 及employment存在线性相关关系。

而与burden从图形上看不出线性关系。

所以对模型的设定保持怀疑态度。

③?umecons.16?0.63incomeconsume.51employmentt?1674t?0.0 86t?1?537t?202.50burden.27d2t?127.04d3t?172.2d4tt?7.22d1t?194r2?0.9998672?0.99979 2 f=13189.98 dw=2.921拟合效果好，且通过dw检验由回归可知consumet，d1td3t的系数未能通过显著性水平??0.05下的tt?1，burden检验。

第8章练习5证明:对方程εβtttX Y1+=两边同时减去Yt 1-，得：εβt t ttYX Y11+-=∆-然后对该式等号右边加上再减去一个Xt 1-β，得：εβββt t t t t t XXYX Y 1111+-+-=∆---()εββtt t tX YX 111+--=--∆将第二个方程εαt t tX X21+∆=∆-代入，得：()()εεβαβtt t t t t X Y X Y 11121+--+∆=∆--- ()εεβββαttt t t X Y X21111++--∆=---()εαβδtt t t X Y X +-+∆=---1111其中，βαα=1，1-=δ，εεεβt t t 21+=第8章练习8（1） 解：根据Eview 软件操作得：对1978-2007年中国货物进、出口额的自然对数系列LX ， LM 的单位根检验分别如下： 对LX 的单位根检验：Null Hypothesis: LX has a unit root Exogenous: NoneLag Length: 2 (Fixed)t-Statistic Prob.*Augmented Dickey-Fuller test statistic 3.660835 0.9998Test critical values: 1% level -2.6534015% level -1.95385810% level -1.609571*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test EquationDependent Variable: D(LX)Method: Least SquaresDate: 05/28/11 Time: 12:13Sample (adjusted): 1981 2007Included observations: 27 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.LX(-1) 0.022104 0.006038 3.660835 0.0012D(LX(-1)) 0.089362 0.198210 0.450844 0.6561D(LX(-2)) -0.056822 0.179525 -0.316512 0.7544R-squared 0.165948 Mean dependent var 0.155844Adjusted R-squared 0.096444 S.D. dependent var 0.094091S.E. of regression 0.089439 Akaike info criterion -1.886086Sum squared resid 0.191983 Schwarz criterion -1.742104Log likelihood 28.46216 Hannan-Quinn criter. -1.843273Durbin-Watson stat 2.075404根据上表得”Augmented Dickey-Fuller test statistics”的数值为 3.660835，大于5% critical values:的数值-1.953858，即3.660835>-1.953858。

第一章：绪论1．计量经济学的学科属性、计量经济学与经济学、数学、统计学的关系；2．计量经济研究的四个基本步骤（1）建立模型（依据经济理论建立模型，通过模型识别、格兰杰因果关系检验、协整关系检验建立模型）；（2）估计模型参数（满足基本假设采用最小二乘法，否则采用其他方法：加权最小二乘估计、模型变换、广义差分法等）；（3）模型检验：经济意义检验（普通模型、双对数模型、半对数模型中的经济意义解释，见例1、例2），统计检验（T 检验，拟合优度检验、F 检验，联合检验等）；计量经济学检验（异方差、自相关、多重共线性、在时间序列模型中残差的白噪声检验等）；（4）模型应用。

例1：在模型中，y 某类商品的消费支出，x 收入，P 商品价格，试对模型进行经济意义检验，并解释21,ββ的经济学含义。

t t t P x y 31.0ln 25.0213.0ln -+=∧,其中参数21,ββ都可以通过显著性检验。

经济意义检验可以通过（商品需求与收入正相关、与商品价格负相关）。

商品消费支出关于收入的弹性为0.25（)/ln(25.0)/ln(11-∧-=t t t t x x y y ）；价格增加一个单位，商品消费需求将减少31%。

例2：研究金融发展与贫富差距的关系，认为金融发展先使贫富差距加大（恶化），尔后会使贫富差距降低（好转），成为倒U 型。

贫富差距用GINI 系数表示，金融发展用（贷款余额/存款总额）表示。

回归结果为： 229.164.034.2t t t x x GINI -+=∧，模型参数都可以通过显著性检验。

在x 的有意义的变化范围内，GINI 系数的值总是大于1，细致分析后模型变的毫无意义；同样的模型还有：GINI 系数的值总是为负231.1412.734.13t t t x x GINI -+-=∧。

3．计量经济学中的一些基本概念数据的三种类型：横截面数据、时间序列数据、面板数据；线性模型的概念；模型的解释变量与被解释变量，被解释变量为随机变量（如 果一个变量为随机变量，并与随机扰动项相关，这个变量称为内生变量），被解释变量为内生变量，有些解释变量也为内生变量。

E8.1(1) (2) (3) (4)ahe lnahe lnahe lnahe age 0.585***0.0273***0.0814(0.0365) (0.00186) (0.0434) female -3.664***-0.186***-0.186***-0.186***(0.208) (0.0108) (0.0108) (0.0108) bachelor 8.083***0.428***0.428***0.428***(0.213) (0.0108) (0.0108) (0.0108) lnage 0.804***(0.0545)age2 -0.000915(0.000735) _cons -0.636 1.876***-0.0345 1.085(1.083) (0.0559) (0.185) (0.635) N7711 7711 7711 7711R20.200 0.201 0.201 0.201 adj. R20.1995 0.2003 0.2005 0.2004 Standard errors in parentheses （表1）*p < 0.05, **p < 0.01, ***p < 0.001（1）该问的回归结果如表第（1）列所示。

如果age从25增加到26岁，则预期收入每小时增加0.585美元。

如果age从33增加到34岁，则预期收入也是每小时增加0.585美元。

（2）该问的回归结果如表第（2）列所示。

如果age从25增加到26，则lnahe预计增加0.0273，即预期收入每小时增加2.73%。

如果age从33增加到34岁，则预期收入也是每小时增加2.73%。

（3）该问的回归结果如表第（3）列所示。

如果age从25增加到26岁，则lnage增加ln26-ln25≈0.04，预计lnahe增加0.04×0.804=0.03216，所以预期收入每小时增加3.216%。