中考数学专题训练：找规律、新概念(含答案)

初中数学找规律题（有答案）“有比较才有鉴别”。

通过比较，可以发现事物的相同点和不同点，更容易找到事物的变化规律。

找规律的题目，通常按照一定的顺序给出一系列量，要求我们根据这些已知的量找出一般规律。

揭示的规律，常常包含着事物的序列号。

所以，把变量和序列号放在一起加以比较，就比较容易发现其中的奥秘。

初中数学考试中，经常出现数列的找规律题，本文就此类题的解题方法进行探索：一、基本方法——看增幅（一）如增幅相等（实为等差数列）：对每个数和它的前一个数进行比较，如增幅相等，则第n个数可以表示为：a1+(n-1)b，其中a为数列的第一位数，b 为增幅，(n-1)b为第一位数到第n位的总增幅。

然后再简化代数式a+(n-1)b。

例：4、10、16、22、28……，求第n位数。

分析：第二位数起，每位数都比前一位数增加6，增幅都是6，所以，第n位数是：4+(n-1) 6＝6n－2（二）如增幅不相等，但是增幅以同等幅度增加（即增幅的增幅相等，也即增幅为等差数列）。

如增幅分别为3、5、7、9，说明增幅以同等幅度增加。

此种数列第n位的数也有一种通用求法。

基本思路是：1、求出数列的第n-1位到第n位的增幅；2、求出第1位到第第n位的总增幅；3、数列的第1位数加上总增幅即是第n位数。

此解法虽然较烦，但是此类题的通用解法，当然此题也可用其它技巧，或用分析观察的方法求出，方法就简单的多了。

（三）增幅不相等，但是增幅同比增加，即增幅为等比数列，如：2、3、5、9,17增幅为1、2、4、8.（四）增幅不相等，且增幅也不以同等幅度增加（即增幅的增幅也不相等）。

此类题大概没有通用解法，只用分析观察的方法，但是，此类题包括第二类的题，如用分析观察法，也有一些技巧。

二、基本技巧（一）标出序列号：找规律的题目，通常按照一定的顺序给出一系列量，要求我们根据这些已知的量找出一般规律。

找出的规律，通常包序列号。

所以，把变量和序列号放在一起加以比较，就比较容易发现其中的奥秘。

中考规律探索1以下为全部整理类型;规律探索共两套试题;供参考学习使用一．选择题1．观察下列等式：31＝3;32＝9;33＝27;34＝81;35＝243;36＝729;37＝2187… 解答下列问题：3＋32＋33＋34…＋32013的末位数字是 A ．0 B ．1 C ．3 D ．72. 把所有正奇数从小到大排列;并按如下规律分组：1;3;5;7;9;11;13;15;17;19;21;23;25;27;29;31;…;现用等式A M =i;j 表示正奇数M 是第i 组第j 个数从左往右数;如A 7=2;3;则A 2013= A ．45;77 B ．45;39 C ．32;46 D ．32;233.下表中的数字是按一定规律填写的;表中a 的值应是 ．4.下列图形都是由同样大小的矩形按一定的规律组成;其中第1个图形的面积为2cm 2;第2个图形的面积为8 cm 2;第3个图形的面积为18 cm 2;……;第10个图形的面积为 A ．196 cm 2B ．200 cm 2C ．216 cm 2D ． 256 cm 25．如图;动点P 从0;3出发;沿所示的方向运动;每当碰到矩形的边时反弹;反弹时反射角等于入射角;当点P 第2013次碰到矩形的边时;点P 的坐标为 A 、1;4 B 、5;0 C 、6;4 D 、8;36．如图;下列各图形中的三个数之间均具有相同的规律.根据此规律;图形中M 与m 、n 的关系是A ． M=mnB ． M=nm+1C ．M=mn+1D ．M=mn+17．我们知道;一元二次方程12-=x 没有实数根;即不存在一个实数的平方等于-1;若我们规定一个新数“”;使其满足12-=i 即方程12-=x 有一个根为;并且进一步规定: 一切实数可以与新数进行四则运算;且原有的运算律和运算法则仍然成立;于是有,1i i =12-=i ;,).1(23i i i i i -=-=⋅=.1)1()(2224=-==i i 从而对任意正整数n;我们可得到,.)(.4414i i i i i i n n n ===+同理可得,1,,143424=-=-=++n n n i i i i 那么;20132012432i i i i i i +⋅⋅⋅++++的值为A ．0B ．1C ．-1D ．8．下列图形都是由同样大小的棋子按一定的规律组成;其中第①个图形有1颗棋子;第②个图形一共有6颗棋子;第③个图形一共有16颗棋子;…;则第⑥个图形中棋子的颗数为A ．51B ．70C ．76D ．81图① 图②图③···第8题图二．填空题1．观察下列图形中点的个数;若按其规律再画下去;可以得到第n个图形中所有的个数为用含n的代数式表示．2．如图;在直角坐标系中;已知点A﹣3;0、B0;4;对△OAB连续作旋转变换;依次得到△1、△2、△3、△4…;则△2013的直角顶点的坐标为．3．如图;正方形ABCD的边长为1;顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1;由顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…;以此类推;则第六个正方形A6B6C6D6周长是．4．直线上有2013个点;我们进行如下操作：在每相邻两点间插入1个点;经过3次这样的操作后;直线上共有个点．5．如图;古希腊人常用小石子在沙滩上摆成各种形状来研究数．例如：称图中的数1;5;12;22…为五边形数;则第6个五边形数是．6 ．如图;是用火柴棒拼成的图形;则第n个图形需根火柴棒．7．观察规律：1=12；1+3=22；1+3+5=32；1+3+5+7=42；…;则1+3+5+…+2013的值是．8．如图12;一段抛物线：y＝－xx－30≤x≤3;记为C1;它与x轴交于点O;A1；将C1绕点A1旋转180°得C2;交x 轴于点A2；将C2绕点A2旋转180°得C3;交x 轴于点A3；……如此进行下去;直至得C13．若P37;m在第13段抛物线C13上;则m =_________．9.直线上有2013个点;我们进行如下操作：在每相邻两点间插入1个点;经过3次这样的操作后;直线上共有个点. 10．观察下列各式的计算过程：5×5=0×1×100+25;15×15=1×2×100+25;25×25=2×3×100+25;35×35=3×4×100+25;…………请猜测;第n个算式n为正整数应表示为____________________________．11．将连续的正整数按以下规律排列;则位于第7行、第7列的数x是__ __．12、如下图;每一幅图中均含有若干个正方形;第①幅图中含有1个正方形；第②幅图中含有5个正方形；……按这样的规律下去;则第6幅图中含有个正方形；••••••①②③13．将一些半径相同的小圆按如图所示的规律摆放：第1个图形有6个小圆; 第2个图形有10个小圆; 第3个图形有16个小圆; 第4个图形有24个小圆; ……;依次规律;第6个图形有 个小圆． 14.已知一组数2;4;8;16;32;…;按此规律;则第n 个数是 ． 15、我们知道;经过原点的抛物线的解析式可以是y ＝ax 2＋bxa ≠0 1对于这样的抛物线：当顶点坐标为1;1时;a ＝__________；当顶点坐标为m ;m ;m ≠0时;a 与m 之间的关系式是__________；2继续探究;如果b ≠0;且过原点的抛物线顶点在直线y ＝kxk ≠0上;请用含k 的代数式表示b ；3现有一组过原点的抛物线;顶点A 1;A 2;…;A n 在直线y ＝x 上;横坐标依次为1;2;…;n 为正整数;且n ≤12;分别过每个顶点作x 轴的垂线;垂足记为B 1;B 2;…;B n ;以线段A n B n 为边向右作正方形A n B n C n D n ;若这组抛物线中有一条经过D n ;求所有满足条件的正方形边长．16．如图;所有正三角形的一边平行于x 轴;一顶点在y 轴上;从内到外;它们的边长依次为2;4;6;8;…;顶点依次用1A 、2A 、3A 、4A 、…表示;其中12A A 与x 轴、底边12A A 与45A A 、45A A 与78A A 、…均相距一个单位;则顶点3A 的坐标是 ;22A 的坐标是 ．第16题图17．如图;已知直线l ：y=33x ;过点A 0;1作y 轴的垂线交直线l 于点B ;过点B 作直线l 的垂线交y 轴于点A 1；过点A 1作y 轴的垂线交直线l 于点B 1;过点B 1作直线l 的垂线交y 轴于点A 2；……按此作法继续下去;则点A 2013的坐标为 ．18、如图;在平面直角坐标系中;一动点从原点O 出发;按向上;向右;向下;向右的方向不断地移动;每移动一个单位;得到点A 1 0;1;A 21;1;A 31;0;A 42;0;…那么点A 4n ＋1n 为自然数的坐标为 用n 表示19．当白色小正方形个数n 等于1;2;3…时;由白色小正方形和和黑色小正方形组成的图形分别如图所示．则第n 个图形中白色小正方形和黑色小正方形的个数总和等于_____________．用n 表示;n 是正整数20. 2013 衢州4分如图;在菱形ABCD 中;边长为10;∠A=60°．顺次连结菱形ABCD 各边中点;可得四边形A 1B 1C 1D 1；顺次连结四边形A 1B 1C 1D 1各边中点;可得四边形A 2B 2C 2D 2；顺次连结四边形A 2B 2C 2D 2各边中点;可得四边形A 3B 3C 3D 3；按此规律继续下去…．则四边形A 2B 2C 2D 2的周长是 ；四边形A 2013B 2013C 2013D 2013的周长是 ．21.一组按规律排列的式子：ａ２;43a ;65a ;87a ;….则第n 个式子是________22.观察下面的单项式：a;﹣2a 2;4a 3;﹣8a 4;…根据你发现的规律;第8个式子是 ． 23.如图;已知直线l ：y=x;过点M2;0作x 轴的垂线交直线l 于点N;过点N 作直线l 的垂线交x 轴于点M 1；过点M 1作x轴的垂线交直线l 于N 1;过点N 1作直线l 的垂线交x 轴于点M 2;…；按此作法继续下去;则点M 10的坐标为 ．24.为庆祝“六一”儿童节;某幼儿园举行用火柴棒摆“金鱼”比赛．如图所示：按照上面的规律;摆第n图;需用火柴棒的根数为．答案：选择题：1、C 2、C 3、21 4、B 5、D 6、D 7、D 8、 C填空题：1、n+12 2、8052;0 3、0.5 4、16097 5、51 6、2n+1 7、1014049 8、 2 9、16097 10、10n-1+52=100nn-1+25 11、85 12、91 13、46 14、2n 15、1－1；a ＝－1m或am ＋1＝0；2解：∵a ≠0 ∴y ＝ax 2＋bx ＝ax ＋2b a2－24b a ∴顶点坐标为－2ba;－24b a∵顶点在直线y ＝kx 上∴k －2ba＝－24b a∵b ≠0 ∴b ＝2k3解：∵顶点A n 在直线y ＝x 上 ∴可设A n 的坐标为n ;n ;点D n 所在的抛物线顶点坐标为t ;t由12可得;点D n 所在的抛物线解析式为y ＝－1tx 2＋2x∵四边形A n B n C n D n 是正方形 ∴点D n 的坐标为2n ;n∴－1t2n 2＋2×2n ＝n∴4n ＝3t∵t 、n 是正整数;且t ≤12;n ≤12∴n ＝3;6或9∴满足条件的正方形边长为3;6或916、0;31-;－8;－8. 17、()()201340260,40,2或注：以上两答案任选一个都对18、2n;1 19、n 2+4n 20、20；21、221na n n 为正整数22、-128a 8 23、884736;0 24、6n+2规律探索21、 我们平常用的数是十进制数;如2639=2×103+6×102+3×101+9×100;表示十进制的数要用10个数码又叫数字：0;1;2;3;4;5;6;7;8;9..在电子数字计算机中用的是二进制;只要两个数码：0和1..如二进制中101=1×22+0×21+1×20等于十进制的数5;10111=1×24+0×23＋1×22＋1×21＋1×20等于十进制中的数23;那么二进制中的1101等于十进制的数 ..2、 从1开始;将连续的奇数相加;和的情况有如下规律：1=1=12；1+3=4=22；1+3+5=9=32；1+3+5+7=16=42；1+3+5+7+9=25=52；…按此规律请你猜想从1开始;将前10个奇数即当最后一个奇数是19时;它们的和是 .. 3、小王利用计算机设计了一个计算程序;输入和输出的数据如下表：输入 (1)2345… 输出……那么;当输入数据是8时;输出的数据是A 、618B 、638C 、658D 、6784、如下左图所示;摆第一个“小屋子”要5枚棋子;摆第二个要11枚棋子;摆第三个要17枚棋子;则摆第30个“小屋子”要 枚棋子.5、如下右图是某同学在沙滩上用石子摆成的小房子;观察图形的变化规律;写出第n 个小房子用了 块石子6、如下图是用棋子摆成的“上”字：第一个“上”字 第二个“上”字 第三个“上”字如果按照以上规律继续摆下去;那么通过观察;可以发现：1第四、第五个“上”字分别需用 和 枚棋子；2第n 个“上”字需用 枚棋子..7、如图一串有黑有白;其排列有一定规律的珠子;被盒子遮住一部分;则这串珠子被盒子遮住的部分有_______颗.(1)(2)(3)第4题第7题图⑴ ⑵ ⑶1 2 348、根据下列5个图形及相应点的个数的变化规律：猜想第6个图形有 个点;第n 个图形中有 个点.. 9、下面是按照一定规律画出的一列“树型”图：经观察可以发现：图2比图1多出2个“树枝”；图3比图2多出5个“树枝”；图4比图3多出10个“树枝”；照此规律;图7比图6多出 个“树枝”..10、观察下面的点阵图和相应的等式;探究其中的规律：1在④和⑤后面的横线上分别写出相应的等式；2通过猜想写出与第n 个点阵相对应的等式_____________________..11、用边长为1cm 的小正方形搭成如下的塔状图形;则第n 次所搭图形的周长是_______________cm 用含n 的代数式表示..12、如图;都是由边长为1例如第1个图形的表面积为6个平方单位;第2个图形的表面积为18个平方单位;第3个图形的表面积是36..个图形的表面积 个平方单位13、图1是一个水平摆放的小正方体木块;图2、3是由这样的小正方体木块叠放而成;按照这样的规律继续叠放下去;至第七个叠放的图形中;小正方体木块总数应是A 25B 66C 91D 12014、如图是由大小相同的小立方体木块叠入而成的几何体;图⑴中有1个立方体;图⑵中有4个立方体;图⑶中有9个立方体;……按这样的规律叠放下去;第8个图中小立方体个数是 .15、图1是棱长为a 的小正方体;图2、图3由这样的小正方体摆放而成．按照这样的方法继续摆放;由上而下分别叫第一层、第二层、…、第n 层;第n 层的小正方体的个数为s ．解答下列问题：1按照要求填表：2写出当n =10时;s= ．16、如图用火柴摆去系列图案;按这种方式摆下去;当每边摆10根时即10 n 时;需要的火柴棒总数为 根；n1 2 3 4… s 1 3 6……………①1=12； ②1+3=22；③1+3+5=32； ④ ；⑤ ；第 ··· ···图1 图2 图3B 17、用火柴棒按如图的方式搭一行三角形;搭一个三角形需3支火柴棒;搭2个三角形需5支火柴棒;搭3个三角形需7支火柴棒;照这样的规律下去;搭n 个三角形需要S 支火柴棒;那么用n 的式子表示S 的式子是 _______ n 为正整数．18、;请观察下图：则第n 个图形中需用黑色瓷砖 ____ 19题图19、如图;用同样规格的黑白两种正方形瓷砖铺设正方形地面;观察图形并猜想填空：当黑色瓷砖为20块时;白色瓷砖为 块；当白色瓷砖为n 2n 为正整数块时;黑色瓷砖为 块．20、观察下列由棱长为1的小立方体摆成的图形;寻找规律：如图1中：共有1 个小立方体;其中1个看得见;0个看不见；如图2中：共有8个小立方体;其中7个看得见;1个看不见；如图3中：共有27个小立方体;其中有19个看得8个看不见；……;则第6个图中;看不见的小立方体有 个..21、下面的图形是由边长为l 的正方形按照某种规律排列而组成的． 1观察图形;填写下表：2推测第n 个图形中;正方形的个数为________;周长为______________都用含n 的代数式表示．22、观察下图;我们可以发现：图⑴中有1个正方形；图⑵中有5个正方形;图⑶中共有14个正方形;按照这种规律继续下去;图⑹中共有_______个正方形..23、某正方形园地是由边长为1的四个小正方形组成的;现要在园地上建一个花坛阴影部分使花坛面积是园地面积的一半;以下图中设计不合要求．．．．的是 第22题图 24;25<1>、 <3>26、2次把第1次铺的完全围起来;如图2；第3次把第23；…依此方法;第n 次铺完后;用字母n 表示第n 次镶嵌所使用的木块块数为 . n 为正整数27、用黑白两种颜色的正六边形地面砖按如下所示的规律;拼成若干个图案： ⑴ 第4个图案中有白色地面砖 块； ⑵ 第n 个图案中有白色地面砖 块..28、分析如下图①;②;④中阴影部分的分布规律;按此规律在图③中画出其中的阴影部分.29、将一圆形纸片对折后再对折;得到图2;然后沿着图中的虚线剪开;得到两部分;其中一部分展开后的平面图形是30．如图1;小强拿一张正方形的纸;沿虚线对折一次得图2;再对折一次得图3;然后用剪刀沿图3中的虚线剪去一个角;再DCB打开后的形状是A B C D31、 用一条宽相等的足够长的纸条;打一个结;如图１所示;然后轻轻拉紧、压平就可以得到如图２所示的正五边形ＡＢＣＤＥ;其中∠ＢＡＣ＝ 度.32、如图;一张长方形纸沿AB 对折;以AB 中点O 为顶点将平角五等分;并沿五等分的折线折叠;再沿CD 剪开;使展开后为正五角星正五边形对角线所构成的图形.则∠OCD 等于A ．108°B ．144°C ．126°D ．129°33、如图;把一个正方形三次对折后沿虚线剪下则得到的图形是A B C D 第35题图34、将一张长方形的纸对折;如图5所示可得到一条折痕图中虚线. 继续对折;对折时每次折痕与上次的折痕保持平行;连续对折三次后;可以得到7条折痕;那么对折四次可以得到 条折痕 .如果对折n 次;可以得到 _____________条折痕 ..35、观察图形：图中是边长为1;2;3 …的正方形：当边长n ＝1时;正方形被分成2个大小相等的小等腰直角三角形；当边长n ＝2时;正方形被分成8个大小相等的小等腰直角三角形；当边长n ＝3时;正方形被分成18个大小相等的小等腰直角三角形；以此类推：当边长为n 时;正方形被分成大小相等的小等腰直角三角形的个数是 ..36、水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示.如右图;是一个正方体的平面展开图;若图中的“似”表示正方体的前面; “锦”表示右面; “程”表示下面.则“祝”、 “你”、“前”分别表示正方体的___________________.37、如图是一块长方形ABCD 的场地;长AB =102m;宽AD =51m;从A 、B 两处入口的中路宽都为1m;两小路汇合处路宽为2m;其余部分种植草坪;则草坪面积为A5050m 2 B4900m 2 Ｃ5000m 2Ｄ4998m 238、读一读;想一想;做一做：国际象棋、中国象棋和围棋号称为世界三大棋种.国际象棋中的“皇后”的威力可比中国象棋中的“车”大得多：“皇后”不仅能控制她所在的行与列中的每一个小方格;而且还能控制“斜”方向的两条直线上的每一个小方格.如图甲是一个4×4的小方格棋盘;图中的“皇后Q ”能控制图中虚线所经过的每一个小方格.① 在如图乙的小方格棋盘中有一“皇后Q ”;她所在的位置可用“2;3”来表示;请说明“皇后Q ”所在的位置“2;3”的意义;并用这种表示法分别写出棋盘中不能被该“皇后Q ”所控制的四个位置.②如图丙也是一个4×4的小方格棋盘;请在这个棋盘中放入四个“皇后Q ”;使这四个“皇后Q ”之间互不受对方控制在图丙中的某四个小方格中标出字母Q 即可._沿虚线剪开 程前 你 祝 似 锦 AS D S CSB S 图１DEBA图２3 甲行乙3丙参考答案1、132、1003、C4、1795、 3n+1-3+nn+1或n+12+2n-16、118、22 24n+27、278、31;n2-n-19、8010、1+3+5+7=42；1+3+5+7+9=52；1+3+5+……+2n-1=n2 11、 4n 12、9013、C 14、64 5、110 21+2+3+……+n=nn+1/2 16、16517、s=2n+1 18、4n+6 19、16;4n+420、125 21、113、18；28、38； 25n+3;10n+8 22 、9123、B 24、B 25、A 26、8n-6 27、118 ；24n+228、29、C30、 C31、3632、A 33、C34、15 ；2n-1 35、 2n2 36、后面、上面、左面 37、C38、1 1;1;3;1;4;2;4;4；2。

找规律题和新概念知识点讲解：1、顺等差数列，前⼀个数减去后⼀个数的差相等。

例如：1,3,5,7,9,…逆等差数列，后⼀个数减去前⼀个数的差相等。

例如：10,8,6,4, 2…;2、顺等⽐数列，即前⼀个数除以后⼀个数的商相等。

例如：2,4,8,16,32…;逆等⽐数列，即后⼀个数除以前⼀个数的商相等。

例如：1024,512,256,128,…;3、兔⼦数列，即单数序号的数字与双数序号的数分别形成规律。

例如8，15，10，13，12，11,(14),(9)这⾥8,10,12,14成规律，15,13,12,11,9成规律；4、质数数列规律，例如：2,3,5,7,11,(13),(17)....这些数学都为质数；注意：⼀般考试只有以下⼀种情况，⽽且容易出现到⼩升初考试，要特别注意。

5、“平⽅数列”、“⽴⽅数列”等，例如：平⽅数列：1、4、9、16、27、64、125、…⽴⽅数列：1、8、27、64、81、256、625、…6、相邻数字差呈现规律。

数字之间差呈现等差数列，例如：1、3、7、13、21、31、43、…数字之间差呈现等⽐数列，例如：1、3、7、15、31、63、…7、多个数字间呈现规律，（本题考查较少）裴波那契数列，即任意连续两个数字之和等于第三个数字，例如：1、1、2、3、5、8、13、21、34、…任意连续三个数字之和等于第四个数字，例如：1、1、1、3、5、9、17、31、57、105、…练习题：1. 如图，把同样⼤⼩的⿊⾊棋⼦摆放在正多边形的边上，按照这样的规律摆下去，则第五个图形需要⿊⾊棋⼦的个数是，第n 个图形需要⿊⾊棋⼦的个数是（1n ，且n为整数）．2.若“！”是⼀种数学运算符号，并且1！=1，2！=2×1=2，3！=3×2×1=6，4！=4×3×2×1，…，则10098！！的值为（）A. 5049B. 99！C. 9900D. 2！3.观察下⾯⼏个算式：1+2+1=4，1+2+3+2+1=9， 1+2+3+4+3+2+1=16， 1+2+3+4+5+4+3+2+1=25， ……根据你所发现的规律，请你直接写出下⾯式⼦的结果： 1+2+3+…+99+100+99+…+3+2+1=_________. 4.观察下⾯⼀列数，探究其中的规律：---,65,54,43,32,21,1（1）第11，12，13个数分别是，，（2）第2010个数是什么（3）第n 个数是（ n 为⼤于1的正整数） 5．观察：33221129234+==；33322112336344++==??；33332211234100454+++==??；……，⑴若n 为正整数，猜想3333123n ++++＝；⑵利⽤上题的结论来⽐较3333123100++++与2(5000)-的⼤⼩.6.有若⼲个数，第⼀个数记为a1，第⼆个数记为a2，…，第n 个数记为an.若a1=21，从第⼆个数起，每个数都等于“1与它前⾯那个数的差的倒数”.试计算：a2=______，a3=____，a4=_____，a5=______.这排数有什么规律吗？由你发现的规律，请计算a2043是多少？7.⽤“?”定义新运算：对于任意实数a, b , 都有a ?b=b2+1. 例如， 7?4= 42+1=17，那么5?3= ；当m 为实数时，m ? (m ?2) = ．8. 如图，在⼀个三⾓点阵中，从上向下数有⽆数多⾏，其中各⾏点数依次为2，4，6，…，2n ，…，请你探究出前n ⾏的点数和所满⾜的规律．若前n ⾏点数和为930，则n =（）．A ．29B ．30C ．31D ．32 9．下⾯是⼀列单项式2342,4,8x x x--观察它们的系数和指数的特点，则第7个单项式是，第n 个单项式是 .10．观察下列算式，⽤你所发现的规律得出20132的末位数字是（）21=2，22=4，23=8，24=16，25=32，26=64，27=128，28=256，… A ．2 B ．4 C ．6 D ．8 11．⼀组按规律排列的式⼦：()25811234,,,,0b b b b ab a a a a --≠其中第7个式⼦是，第n 个式⼦是（n 为正整数）． 12.（2011年）在右表中，我们把第i ⾏第j 列的数记为,i j a （其中i ，j 都是不⼤于5的正整数），对于表中的每个数,i j a 规定如下：当i ≥j 时，,1i j a =；当< i j 时，,0i j a =．例如：当i=2，j=1时，,2,11i j a a ==．按此规定，1,3a =_____；表中的25个数中，共有_____个1；计算1,1,11,2,21,3,31,4,41,5,5i i i i i a a a a a a a a a a ?+?+?+?+? 的值为_______．13. 刘谦的魔术表演风靡全国，⼩明也学起了刘谦，发明了⼀个魔术盒，当任意有理数对（a ，b ）进⼊其中时，会得到⼀个新的有理数：－a2＋b －1，例如：如果把（1，－2）放⼊其中，就会得到－12＋（－2）－1＝－4．现若将有理数对（－3，－2）放⼊其中，得到的有理数是．14. 定义计算“?”，对于两个有理数a ,b ，有a ?b =ab -（a +b ），例如：-3?2=516)23(23-=+-=+--?-，则[]4)1()1(?-?-m =___ __。

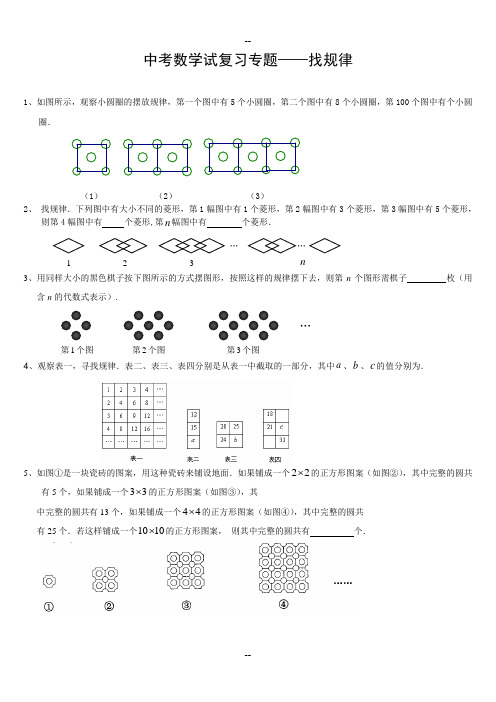
中考数学试复习专题——找规律1、如图所示，观察小圆圈的摆放规律，第一个图中有5个小圆圈，第二个图中有8个小圆圈，第100个图中有个小圆圈．（1） （2） （3）2、 找规律．下列图中有大小不同的菱形，第1幅图中有1个菱形，第2幅图中有3个菱形，第3幅图中有5个菱形，则第4幅图中有 个菱形,第n 幅图中有 个菱形．3、用同样大小的黑色棋子按下图所示的方式摆图形，按照这样的规律摆下去，则第n 个图形需棋子 枚（用含n 的代数式表示）.4、观察表一，寻找规律．表二、表三、表四分别是从表一中截取的一部分，其中a 、b 、c 的值分别为．5、如图①是一块瓷砖的图案，用这种瓷砖来铺设地面．如果铺成一个22⨯的正方形图案（如图②），其中完整的圆共有5个，如果铺成一个33⨯的正方形图案（如图③），其中完整的圆共有13个，如果铺成一个44⨯的正方形图案（如图④），其中完整的圆共有25个．若这样铺成一个1010⨯的正方形图案， 则其中完整的圆共有 个．1 2 3n … … 第1个图 第2个图 第3个图 …6、如下图,用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案，则第n个图案需要用白色棋子枚（用含有n的代数式表示，并写成最简形式）.○○○○○○○○○○○○○●●○○●●●○○●○○●●○○●●●○○○○○○○○○●●●○○○○○○7、用火柴棒按下图中的方式搭图形，按照这种方式搭下去，搭第334个图形需根火柴棒。

8、将正整数按如图5所示的规律排列下去，若有序实数对（n，m）表示第n排，从左到右第m个数，如（4，2）表示实数9，则表示实数17的有序实数对是．9、如图２，用n表示等边三角形边上的小圆圈，f(n)表示这个三角形中小圆圈的总数，那么f(n)和n的关系是10、观察图4的三角形数阵，则第50行的最后一个数是（）1-2 3-4 5 -67 -8 9 -10。

11、下列图案由边长相等的黑、白两色正方形按一定规律拼接而成，依此规律，第n个图案中白色正方形的个数为．12、观察下列各式：3211=332123+=33221236++=33332123410+++=……猜想：333312310++++=．第一个第二个第三个……第n个第一排第二排第三排第四排6┅┅10 9 8 73 2154答案解析：1解析：1时，5．n再每增加一个数时，m就增加3个数．解答：根据所给的具体数据，发现：8=5+3，11=5+3×2，14=5+3×3，…．以此类推，第n个圈中，5+3（1）=32．2解析：分析可得：第1幅图中有1×2-1=1个，第2幅图中有2×2-1=3个，第3幅图中有3×2-1=5个，…，故第n幅图中共有21个3解析：在4的基础上，依次多3个，得到第n个图中共有的棋子数．观察图形，发现：在4的基础上，依次多3个．即第n个图中有4+3（1）=31．当6时，即原式=19．故第6个图形需棋子19枚4解析：此题只要找出截取表一的那部分，并找出其规律即可解．解答：解：表二截取的是其中的一列：上下两个数字的差相等，所以15+3=18．表三截取的是两行两列的相邻的四个数字：右边一列数字的差应比左边一列数字的差大1，所24+25-20+1=30．表四中截取的是两行三列中的6个数字：18是3的6倍，则c应是4的7倍，即28．故选D．认真观察表格，熟知各个数字之间的关系：第一列是1，2，3，…；第二列是对应第一列的2倍；等三列是对应第一列的3倍5解析：据给出的四个图形的规律可以知道，组成大正方形的每个小正方形上有一个完整的圆，因此圆的数目是大正方形边长的平方，每四个小正方形组成一个完整的圆，从而可得这样的圆是大正方形边长减1的平方，从而可得若这样铺成一个10×10的正方形图案，则其中完整的圆共有102+（10-1）2=181个．解答：解：分析可得完整的圆是大正方形的边长减1的平方，从而可知铺成一个10×10的正方形图案中，完整的圆共有102+（10-1）2=181个．点评：本题难度中等，考查探究图形的规律．本题也只可以直接根据给出的四个图形中计数出的圆的个数，找出数字之间的规律得出答案．6解析：解：第1个正方形图案有棋子共32=9枚，其中黑色棋子有12=1枚，白色棋子有（32-12）枚；第2个正方形图案有棋子共42=16枚，其中黑色棋子有22=4枚，白色棋子有（42-22）枚；…由此可推出想第n个图案的白色棋子数为（2）22=4（1）．故第n个图案的白色棋子数为（2）22=4（1）．点评：根据图形提供的信息探索规律，是近几年较流行的一种探索规律型问题．解决这类问题首先要从简单图形入手，抓住随着“编号”或“序号”增加时，后一个图形与前一个图形相比，在数量上增加（或倍数）情况的变化，找出数量上的变化规律，从而推出一般性的结论7解析：根据题意分析可得：搭第1个图形需12根火柴；搭第2个图形需12+6×1=18根；搭第3个图形需12+6×2=24根；…搭第n个图形需12+6（1）=66根．解答：解：搭第334个图形需6×334+6=2010根火柴棒8解析：寻找规律，然后解答．每排的数字个数就是排数；且奇数排从左到右，从小到大，而偶数排从左到右，从大到小．解答：解：观察图表可知：每排的数字个数就是排数；且奇数排从左到右，从小到大，而偶数排从左到右，从大到小．实数15=1+2+3+4+5，则17在第6排，第5个位置，即其坐标为（6，5）．故答案填：（6，5）．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．9解析：根据题意分析可得：第n行有n个小圆圈．故f（n）和n的关系是ƒ（n）= （n2）．10解析：根据题意可得：第n行有n个数；且第n行第一个数的绝对值为+1，最后一个数的绝对值为；奇数为正，偶数为负；故第50行的最后一个数是1275．解答：解：第n行第一个数的绝对值为+1，最后一个数的绝对值为，奇数为正，偶数为负，第50行的最后一个数是1275第一个图中白色正方形的个数为3×3-1；第二个图中白色正方形的个数为3×5-2第三个图中白色正方形的个数为3×7-3；…当其为第n个时，白色正方形的个数为3（21）5312解析：根据所给的等式，可以发现右边的底数是前边的底数的和，指数是平方，则最后的底数是1+2+310=5×11=55，则原式=552．解答：解：根据分析最后的底数是1+2+310=5×11=55，则原式=552．故答案552。

======s a a a a a a 则.......,9926,6317,72,31,3253214111nnx x 第4讲：规律探究、新概念专项训练 1.(2015 广东省东莞市) 观察下列一组数：，…，根据该组数的排列规律，可推出第10个数是 ． 2.(2015 内蒙古包头市) 观察下列各数：1，，，，…，按你发现的规律计算这列数的第6个数为（ ）A ．B ．C ．D ．3.(2016年鄂尔多斯）请观察下列式子的规律：4.(2016 湖北省荆州市) 如图，用黑白两种颜色的菱形纸片，按黑色纸片数逐渐增加1的规律拼成下列图案，若第n 个图案中有2017个白色纸片，则n 的值为（ ）A ．671B ．672C ．673D ．6745. (2016 贵州省黔南州) 在平面直角坐标系中，对于平面内任一点（a ，b ），若规定以下三种变换：①△（a ，b ）=（﹣a ，b ）； ②○（a ，b ）=（﹣a ，﹣b ）； ③Ω（a ，b ）=（a ，﹣b ），按照以上变换例如：△（○（1，2））=（1，﹣2），则○（Ω（3，4））等于 ．6.(2016 贵州省黔南州) 】．阅读材料并解决问题： 求1+2+22+23+…+22014的值，令S=1+2+22+23+…+22014等式两边同时乘以2，则2S=2+22+23+…+22014+22015 两式相减：得2S ﹣S=22015﹣1所以，S=22015﹣1依据以上计算方法，计算1+3+32+33+ (32015)7.(2015 内蒙古通辽市) 一列数1x ，2x ，3x ，…，其中1x =12，（n 为不小于2的整数），则2015x= ．8.（2015 贵州省铜仁地区)．请看杨辉三角（1），并观察下列等式（2）：根据前面各式的规律，则（a+b ）6= ．9.(2016 青海省西宁市) 如图，下列各图形中的三个数之间均具有相同的规律，依此规律，那么第4个图形中的x= ，一般地，用含有m ，n 的代数式表示y ，即y= ．10.(2016 广东省梅州市) 】．如图，在平面直角坐标系中，将△ABO 绕点A 顺时针旋转到△AB 1C 1的位置，点B 、O 分别落在点B 1、C 1处，点B 1在x 轴上，再将△AB 1C 1绕点B 1顺时针旋转到△A 1B 1C 2的位置，点C 2在x 轴上，将△A 1B 1C 2绕点C 2顺时针旋转到△A 2B 2C 2的位置，点A 2在x 轴上，依次进行下去…．若点A （23，0），B （0，2），则点B 2016的坐标为______________．。

中考总复习专题之找规律与新定义型问题板块一：找规律1.有2019个数排成一行，对于任意相邻的三个数，都有中间的数等于前后两数的和．如果第一个数是0，第二个数是1，那么前6个数的和是，这2019个数的和是．2.观察下列各式：，，，设n表示正整数，用关于n的等式表示这个规律是．3.观察下列图形规律：当n= 时，图形“●”的个数和“△”的个数相等．4.如图图形都是由同样大小的菱形按照一定规律所组成的，其中第①个图形中一共有3个菱形，第②个图形中一共有7个菱形，第③个图形中一共有13个菱形，…，按此规律排列下去，第⑦个图形中菱形的个数为________．5.如图，将从1开始的自然数按下规律排列，例如位于第3行、第4列的数是12，则位于第45行、第7列的数是．6．如图所示，用相同的小正方形按照某种规律进行摆放，则第8个图形中小正方形的个数是( )A ．71B ．78C ．85D ．897.如图所示，下列每个图是由若干盆花组成的形如三角形的图案，每条边(包括两个顶点)有n 盆花，每个图案花盆总数是S ，按此推断S 与n 的关系式为( )A ．S=3nB ．S=3(n ﹣1)C ．S=3n ﹣1D ．S=3n+1板块二：新定义型问题1.定义新运算：a ※b =1()(0)a a b a a b b b-≤⎧⎪⎨->≠⎪⎩且，则函数y =3※x 的图象大致是( ) A ． B ．C ．D ．2.对于两个不相等的实数a 、b，定义一种新的运算如下，*0a b a b =+＞），如：3*232==﹣，那么6*(5*4)= ． 3.定义一种新运算：a ※b ＝()3()a b a b b a b -⎧⎨<⎩，则2※3﹣4※3的值______． 4.定义一种新运算：x*y=，如2*1==2，则(4*2)*(﹣1)= ．5.对于x y ，定义一种新运算“☆”，x y ax by =+☆，其中a b ，是常数，等式右边是通常的加法和乘法运算．已知3515=☆，4728=☆，则11☆的值为____．6.定义：对于实数a ，符号[a]表示不大于a 的最大整数．例如：[5.7]=5，[5]=5，[-π]=-4．(2)如果[]=3，求满足条件的所有正整数x ． 7.定义：三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角．(1)如图1，∠E 是△ABC 中∠A 的遥望角，若∠A ＝α，请用含α的代数式表示∠E ．(2)如图2，四边形ABCD 内接于⊙O ，AD ＝BD ，四边形ABCD 的外角平分线DF 交⊙O 于点F ，连结BF 并延长交CD 的延长线于点E ．求证：∠BEC 是△ABC 中∠BA C 的遥望角．(3)如图3，在(2)的条件下，连结AE ，AF ，若AC 是⊙O 的直径．①求∠AED 的度数；②若AB ＝8，CD ＝5，求△DEF 的面积．12x +8.定义：有一组邻边相等且对角互补的四边形叫做等补四边形．理解：(1)如图1，点A，B，C在⊙O上，∠ABC的平分线交⊙O于点D，连接AD，CD．求证：四边形ABCD是等补四边形；探究：(2)如图2，在等补四边形ABCD中，AB＝AD，连接AC，AC是否平分∠BCD？请说明理由．运用：(3)如图3，在等补四边形ABCD中，AB＝AD，其外角∠EAD的平分线交CD的延长线于点F，CD＝10，AF＝5，求DF的长．9.在平面直角坐标系中，我们定义直线y ＝ax －a 为抛物线y ＝ax 2＋bx ＋c (a 、b 、c 为常数，a ≠0)的“梦想直线”；有一个顶点在抛物线上，另一个顶点在y 轴上的三角形为其“梦想三角形”． 已知抛物线2234323yx x 与其“梦想直线”交于A 、B 两点(点A 在点B 的左侧)，与x 轴负半轴交于点C ．(1)填空：该抛物线的“梦想直线”的解析式为 ，点A 的坐标为 ，点B 的坐标为 ；(2)如图，点M 为线段CB 上一动点，将△ACM 以AM 所在直线为对称轴翻折，点C 的对称点为N ，若△AMN 为该抛物线的“梦想三角形”，求点N 的坐标；(3)当点E 在抛物线的对称轴上运动时，在该抛物线的“梦想直线”上，是否存在点F ，使得以点A 、C 、E 、F 为顶点的四边形为平行四边形？若存在，请直接写出点E 、F 的坐标；若不存在，请说明理由．。

初中数学中考复习专题：找规律专项练习及答案解析(50道)以下是为大家整理的初中数学中考复习专题：找规律专项练习及答案解析(50道)的相关范文，本文关键词为初中,数学,中考,复习,专题,规律,专项,练习,答案,解析,，您可以从右上方搜索框检索更多相关文章，如果您觉得有用，请继续关注我们并推荐给您的好友，您可以在中考初中中查看更多范文。

初中数学中考复习专题：找规律专项练习及答案解析（50道）一、选择题1、连结多边形不相邻的两个顶点的线段，叫做多边形的对角线．观察上述图形并阅读相关文字，思考回答问题：显然四边形对角线有2条；五边形的对角线有5条；对于六边形的对角线条数，光靠“数”数，也能数出来，但已感到较麻烦！需寻找规律！从一个顶点A 出发，显然有3条，同理从b出发也3条，每个顶点出发都是3条，但从c顶点出发，就有重复线段！用此方法算出六边形的对角线条数为a；且能归纳出n边形的对角线条数的计算方法；若一个n边形有35条对角线，则a和n的值分别为（）A．12，20b．12，15c．9，10D．9，122、寻找规律计算1-2+3-4+5-6+…+20XX-20XX等于()A．0b．-1c．-1008D．10083、观察下列各式并找规律，再猜想填空：，则______．4、观察一列数：是（），，，，，……根据规律，请你写出第10个数A．c．b．D．共20页，第1页二、填空题5、观察一下几组勾股数，并寻找规律：①3，4，5；②5，12，13；③7，24，25；④9，40，41；……请你写出有以上规律的第⑤组勾股数：6、找规律填空：……7、已知察上面的计算过程，寻找规律并计算：=．…，观8、观察分析下列数据，寻找规律：0，据应是_________.，，3，2，……那么第10个数9、找规律．一张长方形桌子可坐6人，按下图方式讲桌子拼在一起。

①2张桌子拼在一起可坐______人；（1分）3张桌子拼在一起可坐______人；（1分）n张桌子拼在一起可坐______人。

2024年中考数学复习重难点题型训练—规律探索题（含答案解析）类型一数式规律1．（2023·云南·统考中考真题）按一定规律排列的单项式：2345,a ，第n 个单项式是（）AB1n -CnD1n -【答案】Ca ，指数为1开始的自然数，据此即可求解．【详解】解：按一定规律排列的单项式：2345,a ，第nn ，故选：C ．【点睛】本题考查了单项式规律题，找到单项式的变化规律是解题的关键．2．（2023·山东·统考中考真题）已知一列均不为1的数123n a a a a ，，，，满足如下关系：1223121111a a a a a a ++==--，34131111n n na a a a a a +++==-- ，，，若12a =，则2023a 的值是（）A ．12-B ．13C ．3-D ．2【答案】A【分析】根据题意可把12a =代入求解23a =-，则可得312a =-，413a =，52a =……；由此可得规律求解．【详解】解：∵12a =，∴212312a +==--，3131132a -==-+，411121312a -==+，51132113a +==-，…….；由此可得规律为按2、3-、12-、13四个数字一循环，∵20234505.....3÷=，∴2023312a a ==-；故选A ．【点睛】本题主要考查数字规律，解题的关键是得到数字的一般规律．3．（2023·湖南常德·统考中考真题）观察下边的数表（横排为行，竖排为列），按数表中的规律，分数202023若排在第a 行b 列，则a b -的值为()11122113223114233241……A ．2003B ．2004C ．2022D ．2023【答案】C【分析】观察表中的规律发现，分数的分子是几，则必在第几列；只有第一列的分数，分母与其所在行数一致．【详解】观察表中的规律发现，分数的分子是几，则必在第几列；只有第一列的分数，分母与其所在行数一致，故202023在第20列，即20b =；向前递推到第1列时，分数为201912023192042-=+，故分数202023与分数12042在同一行．即在第2042行，则2042a =．∴2042202022.a b -=-=故选：C ．【点睛】本题考查了数字类规律探索的知识点，解题的关键善于发现数字递变的周期性和趋向性．4．（2023·四川内江·统考中考真题）对于正数x ，规定2()1xf x x =+，例如：224(2)213f ⨯==+，1212212312f ⨯⎛⎫== ⎪⎝⎭+，233(3)312f ⨯==+，1211313213f ⨯⎛⎫== ⎪⎝⎭+，计算：11111(1)1011009932f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++++++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭(2)(3)(99)(100)(101)f f f f f +++++= （）A ．199B ．200C ．201D ．202【答案】C【分析】通过计算11(1)1,(2)2,(3)223f f f f f ⎛⎫⎛⎫=+=+= ⎪ ⎪⎝⎭⎝⎭，⋯可以推出11111(1)(2)(3)(99)(100)(101)1011009932f f f f f f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++++++++++++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭结果．【详解】解：2(1)1,11f ==+ 12441212(2),,(2)2,112323212f f f f ⨯⎛⎫⎛⎫====+= ⎪ ⎪+⎝⎭⎝⎭+122331113(3),,(3)2,113232313f f f f ⨯⨯⎛⎫⎛⎫====+= ⎪ ⎪+⎝⎭⎝⎭+…2100200(100)1100101f ⨯==+，1212100()11001011100f ⨯==+，1(100)(2100f f +=，11111(1)(2)(3)(99)(100)(101)1011009932f f f f f f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++++++++++++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭21001=⨯+201=故选：C ．【点睛】此题考查了有理数的混合运算，熟练掌握运算法则，找到数字变化规律是解本题的关键．5.（2021·湖北鄂州市·中考真题）已知1a 为实数﹐规定运算：2111a a =-，3211a a =-，4311a a =-，5411a a =-，……，111n n a a -=-．按上述方法计算：当13a =时，2021a 的值等于（）A．23-B．13C．12-D．23【答案】D 【分析】当13a =时，计算出23421,,3,32a a a ==-=⋅⋅⋅⋅⋅⋅，会发现呈周期性出现，即可得到2021a 的值．【详解】解：当13a =时，计算出23421,,3,32a a a ==-=⋅⋅⋅⋅⋅⋅，会发现是以：213,,32-，循环出现的规律，202136732=⨯+ ，2021223a a ∴==，故选：D ．【点睛】本题考查了实数运算规律的问题，解题的关键是：通过条件，先计算出部分数的值，从中找到相应的规律，利用其规律来解答．6.（2021·湖北随州市·中考真题）根据图中数字的规律，若第n 个图中的143q =，则p的值为（）A．100B．121C．144D．169【答案】B 【分析】分别分析n 的规律、p 的规律、q 的规律，再找n 、p 、q 之间的联系即可．【详解】解：根据图中数据可知：1,2,3,4n =，……22221,2,3,4,p =……222221,31,41,51,q =----……则2p n =，2(1)1q n =+-，∵第n 个图中的143q =，∴2(1)1=143q n =+-，解得：11n =或13n =-(不符合题意，舍去)∴2=121p n =，故选：B ．【点睛】本题主要考查数字之间规律问题，将题中数据分组讨论是解决本题的关键．7.（2021·山东济宁市·中考真题）按规律排列的一组数据：12，35，□，717，926，1137，…，其中□内应填的数是（）A．23B．511C．59D．12【答案】D 【分析】分子为连续奇数，分母为序号的平方1+，根据规律即可得到答案．【详解】观察这排数据发现，分子为连续奇数，分母为序号的平方1+，∴第n 个数据为：2211n n -+当3n =时W 的分子为5，分母为23110+=∴这个数为51102=故选：D ．【点睛】本题考查了数字的探索规律，分子和分母分别寻找规律是解题关键．8.（2021·湖北十堰市·）将从1开始的连续奇数按如图所示的规律排列，例如，位于第4行第3列的数为27，则位于第32行第13列的数是（）A．2025B．2023C．2021D．2019【答案】B 【分析】根据数字的变化关系发现规律第n 行，第n 列的数据为：2n(n-1)+1，即可得第32行，第32列的数据为：2×32×(32-1)+1=1985，再依次加2，到第32行，第13列的数据，即可．解：观察数字的变化，发现规律：第n行，第n列的数据为：2n(n-1)+1，∴第32行，第32列的数据为：2×32×(32-1)+1=1985，根据数据的排列规律，第偶数行从右往左的数据一次增加2，∴第32行，第13列的数据为：1985+2×(32-13)=2023，故选：B．【点睛】本题考查了数字的变化类，解决本题的关键是观察数字的变化寻找探究规律，利用规律解决问题．9.（2020•天水）观察等式：2+22＝23﹣2；2+22+23＝24﹣2；2+22+23+24＝25﹣2；…已知按一定规律排列的一组数：2100，2101，2102，…，2199，2200，若2100＝S，用含S的式子表示这组数据的和是（）A．2S2﹣S B．2S2+S C．2S2﹣2S D．2S2﹣2S﹣2【分析】根据已知条件和2100＝S，将按一定规律排列的一组数：2100，2101，2102，…，2199，2200，求和，即可用含S的式子表示这组数据的和．【解析】∵2100＝S，∴2100+2101+2102+…+2199+2200＝S+2S+22S+…+299S+2100S＝S（1+2+22+…+299+2100）＝S（1+2100﹣2+2100）＝S（2S﹣1）＝2S2﹣S．10．（2023·湖南岳阳·统考中考真题）观察下列式子：21110-=⨯；22221-=⨯；23332-=⨯；24443-=⨯；25554-=⨯；…依此规律，则第n （n 为正整数）个等式是．【答案】()21n n n n -=-【分析】根据等式的左边为正整数的平方减去这个数，等式的右边为这个数乘以这个数减1，即可求解．【详解】解：∵21110-=⨯；22221-=⨯；23332-=⨯；24443-=⨯；25554-=⨯；…∴第n （n 为正整数）个等式是()21n n n n -=-，故答案为：()21n n n n -=-．【点睛】本题考查了数字类规律，找到规律是解题的关键．11．（2023·山东临沂·统考中考真题）观察下列式子21312⨯+=；22413⨯+=；23514⨯+=；……按照上述规律，2n =．【答案】()()111n n -++【分析】根据已有的式子，抽象出相应的数字规律，进行作答即可．【详解】解：∵21312⨯+=；22413⨯+=；23514⨯+=；……∴()()2211n n n ++=+，∴()()2111n n n -++=．故答案为：()()111n n -++【点睛】本题考查数字类规律探究．解题的关键是从已有的式子中抽象出相应的数字规律．12．（2023·四川成都·统考中考真题）定义：如果一个正整数能表示为两个正整数m ，n 的平方差，且1m n ->，则称这个正整数为“智慧优数”．例如，221653=-，16就是一个智慧优数，可以利用22()()m n m n m n -=+-进行研究．若将智慧优数从小到大排列，则第3个智慧优数是；第23个智慧优数是．【答案】1545【分析】根据新定义，列举出前几个智慧优数，找到规律，进而即可求解．【详解】解：依题意，当3m =，1n =，则第1个一个智慧优数为22318-=当4m =，2n =，则第2个智慧优数为224214-=当4m =，1n =，则第3个智慧优数为224115-=，当5m =，3n =，则第5个智慧优数为225316-=当5m =，2n =，则第6个智慧优数为225221-=当5m =，1n =，则第7个智慧优数为225324-=……6m =时有4个智慧优数，同理7m =时有5个，8m =时有6个，12345621+++++=第22个智慧优数，当9m =时，7n =，第22个智慧优数为2297814932-=-=，第23个智慧优数为9,6m n ==时，2296813645-=-=，故答案为：15，45．【点睛】本题考查了新定义，平方差公式的应用，找到规律是解题的关键．13．（2023·山东聊城·统考中考真题）如图，图中数字是从1开始按箭头方向排列的有序数阵．从3开始，把位于同一列且在拐角处的两个数字提取出来组成有序数对：()3,5；()7,10；()13,17；()21,26；()31,37…如果单把每个数对中的第一个或第二个数字按顺序排列起来研究，就会发现其中的规律．请写出第n 个数对：．【答案】()221,22n n n n ++++【分析】根据题意单另把每个数对中的第一个或第二个数字按顺序排列起来研究，可发现第n 个数对的第一个数为：()11n n ++，第n 个数对的第二个位：()211n ++，即可求解．【详解】解：每个数对的第一个数分别为3，7，13，21，31，…即：121⨯+，231⨯+，341⨯+，451⨯+，561⨯+，…则第n 个数对的第一个数为：()2111n n n n ++=++，每个数对的第二个数分别为5，10，17，26，37，…即：221+；231+；241+；251+；261+…，则第n 个数对的第二个位：()221122n n n ++=++，∴第n 个数对为：()221,22n n n n ++++，故答案为：()221,22n n n n ++++．【点睛】此题考查数字的变化规律，找出数字之间的排列规律，利用拐弯出数字的差的规律解决问题．14．（2023·内蒙古通辽·统考中考真题）点Q 的横坐标为一元一次方程37322x x +=-的解，纵坐标为a b +的值，其中a ，b 满足二元一次方程组2428a b a b -=⎧⎨-+=-⎩，则点Q 关于y 轴对称点Q '的坐标为___________．【答案】()5,4--【分析】先分别解一元一次方程37322x x +=-和二元一次方程组2428a b a b -=⎧⎨-+=-⎩，求得点Q的坐标，再根据直角坐标系中点的坐标的规律即可求解．【详解】解：37322x x +=-，移项合并同类项得，525x =，系数化为1得，5x =，∴点Q 的横坐标为5，∵2428a b a b -=⎧⎨-+=-⎩①②，由2+⨯①②得，3=12b -，解得：4b =-，把4b =-代入①得，24=4a +，解得：0a =，∴=04=4a b +--，∴点Q 的纵坐标为4-，∴点Q 的坐标为()5,4-，又∴点Q 关于y 轴对称点Q '的坐标为()5,4--，故答案为：()5,4--．【点睛】本题考查解一元一次方程和解二元一次方程组、代数值求值、直角坐标系中点的坐标的规律，熟练掌握解一元一次方程和解二元一次方程组的方法求得点Q 的坐标是解题的关键．15．（2023·湖北恩施·统考中考真题）观察下列两行数，探究第②行数与第①行数的关系：2-，4，8-，16，32-，64，……①0，7，4-，21，26-，71，……②根据你的发现，完成填空：第①行数的第10个数为；取每行数的第2023个数，则这两个数的和为．【答案】1024202422024-+【分析】通过观察第一行数的规律为(2)n -，第二行数的规律为(2)1n n -++，代入数据即可.【详解】第一行数的规律为(2)n -，∴第①行数的第10个数为10(2)1024-=；第二行数的规律为(2)1n n -++，∴第①行数的第2023个数为2023(2)-，第②行数的第2023个数为2023(2)2024-+，∴202422024-+，故答案为：1024；202422024-+．【点睛】本题主要考查数字的变化，找其中的规律，是今年考试中常见的题型.16.（2021·湖南怀化市·中考真题）观察等式：232222+=-，23422222++=-，2345222222+++=-，……，已知按一定规律排列的一组数：1002，1012，1022，……，1992，若1002=m ，用含m 的代数式表示这组数的和是___________．【答案】100(21)m -【分析】根据规律将1002，1012，1022，……，1992用含m 的代数式表示，再计算0199222+++ 的和，即可计算1001011011992222++++ 的和．【详解】由题意规律可得：2399100222222++++=- ．∵1002=m∴23991000222222=2m m +++++== ，∵22991001012222222+++++=- ，∴10123991002222222=++++++ 12=2m m m m =+=．102239910010122222222+=++++++ 224=2m m m m m =++=．1032399100101102222222222=++++++++ 3248=2m m m m m m =+++=．……∴1999922m =．故10010110110199992222222m m m ++++=+++ ．令012992222S ++++= ①12310022222S ++++= ②②-①，得10021S-=∴10010110110199992222222m m m ++++=+++ =100(21)m -故答案为：100(21)m -．【点睛】本题考查规律问题，用含有字母的式子表示数、灵活计算数列的和是解题的关键．17.（2022·湖南怀化）正偶数2，4，6，8，10，……，按如下规律排列，2468101214161820……则第27行的第21个数是______．【答案】744【分析】由图可以看出，每行数字的个数与行数是一致的，即第一行有1个数，第二行有2个数，第三行有3个数••••••••第n行有n个数，则前n行共有(1)2n n+个数，再根据偶数的特征确定第几行第几个数是几．【详解】解：由图可知，第一行有1个数，第二行有2个数，第三行有3个数，•••••••第n行有n个数．∴前n行共有1+2+3+⋯+n=(1)2n n+个数．∴前26行共有351个数，∴第27行第21个数是所有数中的第372个数．∵这些数都是正偶数，∴第372个数为372×2=744．故答案为：744．【点睛】本题考查了数字类的规律问题，解决这类问题的关键是先根据题目的已知条件找出其中的规律，再结合其他已知条件求解．18.（2021·四川眉山市·中考真题）观察下列等式：1311 212x===+⨯；2711623x ===+⨯；313111234x ===+⨯；……根据以上规律，计算12320202021x x x x ++++-= ______．【答案】12016-【分析】根据题意，找到第n 个等式的左边为1与1n(n 1)+的和；利用这个结论得到原式＝112+116+1112+…+1120202021⨯﹣2021，然后把12化为1﹣12，16化为12﹣13，120152016⨯化为12015﹣12016，再进行分数的加减运算即可．【详解】11(1)n n =++，20201120202021x =+⨯12320202021x x x x ++++- ＝112+116+1112+…+1120202021⨯﹣2021＝2020+1﹣12+12﹣13+…+12015﹣12016﹣2021＝2020+1﹣12016﹣2021＝12016-．故答案为：12016-．【点睛】本题考查了二次根式的化简和找规律，解题关键是根据算式找的规律，根据数字的特征进行简便运算．19.（2022·安徽）观察以下等式：第1个等式：()()()22221122122⨯+=⨯+-⨯，第2个等式：()()()22222134134⨯+=⨯+-⨯，第3个等式：()()()22223146146⨯+=⨯+-⨯，第4个等式：()()()22224158158⨯+=⨯+-⨯，……按照以上规律．解决下列问题：(1)写出第5个等式：________；(2)写出你猜想的第n 个等式（用含n 的式子表示），并证明．【答案】(1)()()()2222516101610⨯+=⨯+-⨯(2)()[][]22221(1)21(1)2n n n n n +=+⋅+-+⋅，证明见解析【分析】（1）观察第1至第4个等式中相同位置的数的变化规律即可解答；（2）观察相同位置的数变化规律可以得出第n 个等式为()[][]22221(1)21(1)2n n n n n +=+⋅+-+⋅，利用完全平方公式和平方差公式对等式左右两边变形即可证明．(1)解：观察第1至第4个等式中相同位置数的变化规律，可知第5个等式为：()()()2222516101610⨯+=⨯+-⨯，故答案为：()()()2222516101610⨯+=⨯+-⨯；(2)解：第n 个等式为()[][]22221(1)21(1)2n n n n n +=+⋅+-+⋅，证明如下：等式左边：()2221441n n n +=++，等式右边：[][]22(1)21(1)2n n n n +⋅+-+⋅[][](1)21(1)2(1)21(1)2n n n n n n n n =+⋅+++⋅⋅+⋅+-+⋅[](1)411n n =+⋅+⨯2441n n =++，故等式()[][]22221(1)21(1)2n n n n n +=+⋅+-+⋅成立．【点睛】本题考查整式规律探索，发现所给数据的规律并熟练运用完全平方公式和平方差公式是解题的关键．20.（2021·贵州铜仁市·中考真题）观察下列各项：112，124，138，1416，…，则第n 项是______________．【答案】12nn +【分析】根据已知可得出规律：第一项：1111122=+，第二项：2112242=+，第三项：3113382=+…即可得出结果．【详解】解：根据题意可知：第一项：1111122=+，第二项：2112242=+，第三项：3113382=+，第四项：41144162=+，…则第n 项是12n n +；故答案为：12nn +．【点睛】此题属于数字类规律问题，根据已知各项的规律得出结论是解决此类题目的关键．0.618≈这个数叫做黄金比，著名数学家华罗庚优选法中的“0.618法”就应用了黄金比．设12a =，b =11111S a b =+++，2222211S a b =+++，…，10010010010010011S a b=+++，则12100S S S +++= _______．【答案】5050【分析】利用分式的加减法则分别可求S 1=1，S 2=2，S 100=100，•••，利用规律求解即可．【详解】解： 12a =，b =11122ab =⨯=∴，1112211112a ba ba b b ba bS a a ++++=+==+++++++ ，222222222222222222221112a b a b S a b a b a b a b ++++=+=⨯=⨯=+++++++，…，10101001001001010101010010011100100111a b S a b a b a b +++=+=⨯=+++++∴12100S S S +++= 121005050++⋯⋯+=故答案为：5050【点睛】本题考查了分式的加减法，二次根式的混合运算，求得1ab =，找出的规律是本题的关键．22.（2021·江西中考真题）下表在我国宋朝数学家杨辉1261年的著作《详解九章算法》中提到过，因而人们把这个表叫做杨辉三角，请你根据杨辉三角的规律补全下表第四行空缺的数字是______．【答案】3【分析】通过观察每一个数字等于它上方相邻两数之和．【详解】解：通过观察杨辉三角发现每一个数字等于它上方相邻两数之和的规律，例如：第3行中的2，等于它上方两个相邻的数1，1相加，即：211=+；第4行中的3，等于它上方两个相邻的数2，1相加，即：321=+；⋅⋅⋅⋅⋅⋅由此规律：故空缺数等于它上方两个相邻的数1，2相加，即空缺数为：3，故答案是：3．【点睛】本题考查了杨辉三角数的规律，解题的关键是：通过观察找到数与数之间的关系，从来解决问题．23.（2022·山东泰安）将从1开始的连续自然数按以下规律排列：若有序数对(),n m 表示第n 行，从左到右第m 个数，如()3,2表示6，则表示99的有序数对是_______．【答案】()10,18【分析】分析每一行的第一个数字的规律，得出第n 行的第一个数字为211n +-（），从而求得最终的答案．【详解】第1行的第一个数字：()2111=+-1第2行的第一个数字：()22121=+-第3行的第一个数字：()25131=+-第4行的第一个数字：()210141=+-第5行的第一个数字：()217151=+-…..，设第n 行的第一个数字为x ，得()211x n =+-设第1n +行的第一个数字为z ，得21z n =+设第n 行，从左到右第m 个数为y 当99y =时221(1)991n n +-≤<+∴22(1)98n n -≤<∵n 为整数∴10n =∴21182x n =+-=（）∴9982118m =-+=故答案为：()10,18．【点睛】本题考查数字规律的性质，解题的关键是熟练掌握数字规律的相关性质．24.（2022·浙江舟山）观察下面的等式：111236=+，1113412=+，1114520=+，……(1)按上面的规律归纳出一个一般的结论（用含n 的等式表示，n 为正整数）(2)请运用分式的有关知识，推理说明这个结论是正确的．【答案】(1)1111(1)n n n n =+++(2)见解析【分析】（1）根据所给式子发现规律，第一个式子的左边分母为2，第二个式子的左边分母为3，第三个式子的左边分母为4，…；右边第一个分数的分母为3，4，5，…，另一个分数的分母为前面两个分母的乘积；所有的分子均为1；所以第（n+1）个式子为1111(1)n n n n =+++．（2）由（1）的规律发现第（n+1）个式子为1111(1)n n n n =+++，用分式的加法计算式子右边即可证明．(1)解：∵第一个式子()1111123621221=+=+++，第二个式子()11111341231331=+=+++，第三个式子()11111452041441=+=+++，……∴第（n+1）个式子1111(1)n n n n =+++；(2)解：∵右边=111111(1)(1)(1)(1)n n n n n n n n n n n n ++=+==+++++=左边，∴1111(1)n n n n =+++．【点睛】此题考查数字的变化规律，分式加法运算，解题关键是通过观察，分析、归纳发现其中各分母的变化规律．类型二图形规律25．（2023·重庆·统考中考真题）用长度相同的木棍按如图所示的规律拼图案，其中第①个图案用了9根木棍，第②个图案用了14根木棍，第③个图案用了19根木棍，第④个图案用了24根木棍，……，按此规律排列下去，则第⑧个图案用的木棍根数是（）A ．39B ．44C ．49D ．54【答案】B 【分析】根据各图形中木棍的根数发现计算的规律，由此即可得到答案．【详解】解：第①个图案用了459+=根木棍，第②个图案用了45214+⨯=根木棍，第③个图案用了45319+⨯=根木棍，第④个图案用了45424+⨯=根木棍，……，+⨯=根，第⑧个图案用的木棍根数是45844故选：B．【点睛】此题考查了图形类规律的探究，正确理解图形中木棍根数的变化规律由此得到计算的规律是解题的关键．25．（2023·重庆·统考中考真题）用圆圈按如图所示的规律拼图案，其中第①个图案中有2个圆圈，第②个图案中有5个圆圈，第③个图案中有8个圆圈，第④个图案中有11个圆圈，…，按此规律排列下去，则第⑦个图案中圆圈的个数为（）A．14B．20C．23D．26【答案】B【分析】根据前四个图案圆圈的个数找到规律，即可求解.=⨯-；【详解】解：因为第①个图案中有2个圆圈，2311=⨯-；第②个图案中有5个圆圈，5321=⨯-；第③个图案中有8个圆圈，8331=⨯-；第④个图案中有11个圆圈，11341…，⨯-=；所以第⑦个图案中圆圈的个数为37120故选：B.【点睛】本题考查了图形类规律探究，根据前四个图案圆圈的个数找到第n个图案的规律为31n -是解题的关键.27．（2023·山东日照·统考中考真题）数学家高斯推动了数学科学的发展，被数学界誉为“数学王子”，据传，他在计算1234100+++++ 时，用到了一种方法，将首尾两个数相加，进而得到100(1100)12341002⨯++++++= ．人们借助于这样的方法，得到(1)12342n n n ++++++= （n 是正整数）．有下列问题，如图，在平面直角坐标系中的一系列格点(),i i i A x y ，其中1,2,3,,,i n = ，且,i i x y 是整数．记n n n a x y =+，如1(0,0)A ，即120,(1,0)a A =，即231,(1,1)a A =-，即30,a = ，以此类推．则下列结论正确的是（）A ．202340a =B ．202443a =C ．2(21)26n a n -=-D ．2(21)24n a n -=-【答案】B 【分析】利用图形寻找规律()211,1n A n n ---，再利用规律解题即可．【详解】解：第1圈有1个点，即1(0,0)A ，这时10a =；第2圈有8个点，即2A 到()91,1A ；第3圈有16个点，即10A 到()252,2A ，；依次类推，第n 圈，()211,1n A n n ---；由规律可知：2023A 是在第23圈上，且()202522,22A ，则()202320,22A 即2023202242a =+=，故A 选项不正确；2024A 是在第23圈上，且()202421,22A ，即2024212243a =+=，故B 选项正确；第n 圈，()211,1n A n n ---，所以2122n a n -=-，故C 、D 选项不正确；故选B ．【点睛】本题考查图形与规律，利用所给的图形找到规律是解题的关键．28.（2022·江西）将字母“C”，“H”按照如图所示的规律摆放，依次下去，则第4个图形中字母“H”的个数是（）A．9B．10C．11D．12【答案】B 【分析】列举每个图形中H 的个数，找到规律即可得出答案．【详解】解：第1个图中H 的个数为4，第2个图中H 的个数为4+2，第3个图中H 的个数为4+2×2，第4个图中H 的个数为4+2×3=10，故选：B．【点睛】本题考查了规律型：图形的变化类，通过列举每个图形中H 的个数，找到规律：每个图形比上一个图形多2个H 是解题的关键．29.（2022·重庆）用正方形按如图所示的规律拼图案，其中第①个图案中有5个正方形，第②个图案中有9个正方形，第③个图案中有13个正方形，第④个图案中有17个正方形，此规律排列下去，则第⑨个图案中正方形的个数为（）A．32B．34C．37D．41【答案】C 【分析】第1个图中有5个正方形，第2个图中有9个正方形，第3个图中有13个正方形，……，由此可得：每增加1个图形，就会增加4个正方形，由此找到规律，列出第n 个图形的算式，然后再解答即可．【详解】解：第1个图中有5个正方形；第2个图中有9个正方形，可以写成：5+4=5+4×1；第3个图中有13个正方形，可以写成：5+4+4=5+4×2；第4个图中有17个正方形，可以写成：5+4+4+4=5+4×3；．．．第n 个图中有正方形，可以写成：5+4（n-1）=4n+1；当n=9时，代入4n+1得：4×9+1=37．故选：C．【点睛】本题主要考查了图形的变化规律以及数字规律，通过归纳与总结结合图形得出数字之间的规律是解决问题的关键．30.（2021·广西玉林市·中考真题）观察下列树枝分杈的规律图，若第n 个图树枝数用n Y 表示，则94Y Y -=（）A．4152⨯B．4312⨯C．4332⨯D．4632⨯【答案】B【分析】根据题目中的图形，可以写出前几幅图中树枝分杈的数量，从而可以发现树枝分杈的变化规律，进而得到规律21nn Y =-，代入规律求解即可．【详解】解：由图可得到：11223344211213217211521n n Y Y Y Y Y =-==-==-==-==-则：9921Y =-，∴944942121312Y Y -=--+=⨯，故答案选：B．【点睛】本题考查图形规律，解答本题的关键是明确题意，利用数形结合的思想解答31.（2021·黑龙江大庆市·中考真题）如图，3条直线两两相交最多有3个交点，4条直线两两相交最多有6个交点，按照这样的规律，则20条直线两两相交最多有______个交点【答案】190【分析】根据题目中的交点个数，找出n 条直线相交最多有的交点个数公式：1(1)2n n -．【详解】解：2条直线相交有1个交点；3条直线相交最多有1123322+==⨯⨯个交点；4条直线相交最多有11236432++==⨯⨯个交点；5条直线相交最多有1123410542+++==⨯⨯个交点；⋯20条直线相交最多有120191902⨯⨯=．故答案为：190．【点睛】本题考查的是多条直线相交的交点问题，解答此题的关键是找出规律，即n 条直线相交最多有1(1)2n n -．32．（2023·四川遂宁·统考中考真题）烷烃是一类由碳、氢元素组成的有机化合物，在生产生活中可作为燃料、润滑剂等原料，也可用于动、植物的养护．通常用碳原子的个数命名为甲烷、乙烷、丙烷、……、癸烷（当碳原子数目超过10个时即用汉文数字表示，如十一烷、十二烷……）等，甲烷的化学式为4CH ，乙烷的化学式为26C H ，丙烷的化学式为38C H ……，其分子结构模型如图所示，按照此规律，十二烷的化学式为．【答案】1226C H 【分析】根据碳原子的个数，氢原子的个数，找到规律，即可求解．【详解】解：甲烷的化学式为4CH ，乙烷的化学式为26C H ，丙烷的化学式为38C H ……，碳原子的个数为序数，氢原子的个数为碳原子个数的2倍多2个，十二烷的化学式为1226C H ，故答案为：1226C H ．【点睛】本题考查了规律题，找到规律是解题的关键．33．（2023·山西·统考中考真题）如图是一组有规律的图案，它由若干个大小相同的圆片组成．第1个图案中有4个白色圆片，第2个图案中有6个白色圆片，第3个图案中有8个白色圆片，第4个图案中有10个白色圆片，…依此规律，第n 个图案中有个白色圆片（用含n 的代数式表示）【答案】()22n +【分析】由于第1个图案中有4个白色圆片4221=+⨯，第2个图案中有6个白色圆片6222=+⨯，第3个图案中有8个白色圆片8223=+⨯，第4个图案中有10个白色圆片10224=+⨯，⋯，可得第(1)n n >个图案中有白色圆片的总数为22n +．【详解】解：第1个图案中有4个白色圆片4221=+⨯，第2个图案中有6个白色圆片6222=+⨯，第3个图案中有8个白色圆片8223=+⨯，第4个图案中有10个白色圆片10224=+⨯，⋯，∴第(1)n n >个图案中有()22n +个白色圆片．故答案为：()22n +．【点睛】此题考查图形的变化规律，通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．解题关键是总结归纳出图形的变化规律．34．（2023·黑龙江绥化·统考中考真题）在求123100++++ 的值时，发现：1100101+=，299101+= ，从而得到123100++++= 101505050⨯=．按此方法可解决下面问题．图（1）有1个三角形，记作11a =；分别连接这个三角形三边中点得到图（2），有5个三角形，记作25a =；再分别连接图（2）中间的小三角形三边中点得到图（3），有9个三角形，记作39a =；按此方法继续下去，则123n a a a a ++++= ．（结果用含n 的代数式表示）【答案】22n n -/22n n -+【分析】根据题意得出()14143n a n n =+-=-，进而即可求解．【详解】解：依题意，()1231,5,9,14143n a a a a n n ===⋅⋅⋅=+-=-，，∴123n a a a a ++++= ()21432122n n n n n n +-==-=-，故答案为：22n n -．【点睛】本题考查了图形类规律，找到规律是解题的关键．35.（2022·山东泰安）观察下列图形规律，当图形中的“○”的个数和“．”个数差为2022时，n 的值为____________．【答案】不存在【分析】首先根据n=1、2、3、4时，“•”的个数分别是3、6、9、12，判断出第n 个图形中“•”的个数是3n；然后根据n=1、2、3、4，“○”的个数分别是1、3、6、10，判断出第n 个“○”的个数是()12n n +；最后根据图形中的“○”的个数和“．”个数差为2022，列出方程，解方程即可求出n 的值是多少即可．【详解】解：∵n=1时，“•”的个数是3=3×1；n=2时，“•”的个数是6=3×2；n=3时，“•”的个数是9=3×3；n=4时，“•”的个数是12=3×4；……∴第n 个图形中“•”的个数是3n；又∵n=1时，“○”的个数是1=1(11)2⨯+；n=2时，“○”的个数是2(21)32⨯+=，n=3时，“○”的个数是3(31)62⨯+=，n=4时，“○”的个数是4(41)102⨯+=，……∴第n 个“○”的个数是()12n n +，由图形中的“○”的个数和“．”个数差为2022()1320222n n n +∴-=①，()1320222n n n +-=②解①得：无解解②得：12n n ==故答案为：不存在【点睛】本题考查了图形类规律，解一元二次方程，找到规律是解题的关键．36.（2022·四川遂宁）“勾股树”是以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程所画出来的图形，因为重复数次后的形状好似一棵树而得名．假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树，按照勾股树的作图原理作图，则第六代勾股树中正方形的个数为______．【答案】127【分析】由已知图形观察规律，即可得到第六代勾股树中正方形的个数．【详解】解：∵第一代勾股树中正方形有1+2=3（个），第二代勾股树中正方形有1+2+22=7（个），第三代勾股树中正方形有1+2+22+23=15（个），.....．∴第六代勾股树中正方形有1+2+22+23+24+25+26=127（个），故答案为：127．【点睛】本题考查图形中的规律问题，解题的关键是仔细观察图形，得到图形变化的规律．37.（2021·湖南常德市·中考真题）如图中的三个图形都是边长为1的小正方形组成的网格，其中第一个图形有11⨯个正方形，所有线段的和为4，第二个图形有22⨯个小正方形，所有线段的和为12，第三个图形有33⨯个小正方形，所有线段的和为24，按此规律，则第n 个网格所有线段的和为____________．(用含n 的代数式表示)【答案】2n 2+2n【分析】本题要通过第1、2、3和4个图案找出普遍规律，进而得出第n 个图案的规律为S n =4n+2n ×(n-1)，得出结论即可．【详解】解：观察图形可知：第1个图案由1个小正方形组成，共用的木条根数141221,S =⨯=⨯⨯第2个图案由4个小正方形组成，共用的木条根数262232,S =⨯=⨯⨯第3个图案由9个小正方形组成，共用的木条根数383243,S =⨯=⨯⨯第4个图案由16个小正方形组成，共用的木条根数4104254,S =⨯=⨯⨯…由此发现规律是：第n 个图案由n 2个小正方形组成，共用的木条根数()22122,n S n n n n =+=+ 故答案为：2n 2+2n．【点睛】本题考查了规律型-图形的变化类，熟练找出前四个图形的规律是解题的关键．38.（2021·黑龙江绥化市·中考真题）下面各图形是由大小相同的三角形摆放而成的，图①中有1个三角形，图②中有5个三角形，图③中有11个三角形，图④中有19个三角形…，依此规律，则第n 个图形中三角形个数是_______．【答案】21n n +-【分析】此题只需分成上下两部分即可找到其中规律，上方的规律为(n-1)，下方规律为n 2，结合两部分即可得出答案．【详解】解：将题意中图形分为上下两部分，则上半部规律为：0、1、2、3、4……n-1，下半部规律为：12、22、32、42……n 2，∴上下两部分统一规律为：21n n +-．故答案为：21n n +-．【点睛】本题主要考查的图形的变化规律，解题的关键是将图形分为上下两部分分别研究．类型三与函数有关规律39．（2023·山东烟台·统考中考真题）如图，在直角坐标系中，每个网格小正方形的边长均为1个单位长度，以点P 为位似中心作正方形123PA A A ，正方形456,PA A A ⋯，按此规律作下去，所作正方形的顶点均在格点上，其中正方形123PA A A 的顶点坐标分别为()()()123,0,2,1,1,0P A A ---，()32,1A --，则顶点100A 的坐标为（）。

初中数学中考复习专题：找规律专项练习及答案解析(50道) 初中数学中考复习专题：找规律专项练习及答案解析（50道）一、选择题1、连结多边形不相邻的两个顶点的线段，叫做多边形的对角线．观察上述图形并阅读相关文字，思考回答问题：显然四边形对角线有2条；五边形的对角线有5条；对于六边形的对角线条数，光靠“数”数，也能数出来，但已感到较麻烦！需寻找规律！从一个顶点A出发，显然有3条，同理从B出发也3条，每个顶点出发都是3条，但从C顶点出发，就有重复线段！用此方法算出六边形的对角线条数为a；且能归纳出n边形的对角线条数的计算方法；若一个n边形有35条对角线，则a和n的值分别为（）A．12，20 B．12，15C．9，10 D．9，122、寻找规律计算1 - 2+3 - 4+5 - 6+…+2021 - 2021等于 ( ) A．0 B．- 1 C．- 1008 D．10083、观察下列各式并找规律，再猜想填空：，则______ ．4、观察一列数：是（），，，，，……根据规律，请你写出第10个数A．C．B． D．共 20 页，第 1 页二、填空题5、观察一下几组勾股数，并寻找规律：① 3， 4， 5；② 5，12，13；③ 7，24，25；④ 9，40，41；……请你写出有以上规律的第⑤组勾股数：6、找规律填空：……7、已知察上面的计算过程，寻找规律并计算：= ．…，观8、观察分析下列数据，寻找规律：0，据应是_________.，，3，2，……那么第10个数9、找规律．一张长方形桌子可坐6人，按下图方式讲桌子拼在一起。

① 2张桌子拼在一起可坐______人；（1分） 3张桌子拼在一起可坐______人；（1分） n张桌子拼在一起可坐______人。

（3分）②一家餐厅有40张这样的长方形桌子，按照上图方式每5张桌子拼成1张大桌子，则40张桌子可拼成8张大桌子，共可坐______人。

（3分）共 20 页，第 2 页10、观察以下几组勾股数，并寻找规律：①3，4，5；②5，12，13；③7，24，25；④9，40，41；…，请你写出具有以上规律的第⑥组勾股数：_________________．11、找规律填上合适的数：-2，4，-8，16，，64，……………12、用火柴棒按以下方式搭“小鱼”．…………搭1条“小鱼”需用8根火柴棒，搭2条“小鱼”需用14根火柴棒，搭3条“小鱼”需用20根火柴棒……观察并找规律，搭10条“小鱼”需用火柴棒的根数为．13、观察分析下列数据，寻找规律：0，么第10个数据应是．，，3，2，，3，……，那14、填空找规律(结果保留四位有效数字)． (1)利用计算器分别求：＝________；(2)由(1)的结果，我们发现所得的结果与被开方数间的规律是________； (3)运用(2)中的规律，直接写出结果：＝________，＝________．＝________，＝________，＝________，15、观察表一，寻找规律．表二、表三、表四分别是从表一中截取的一部分，其中a+b+c的值为．共 20 页，第 3 页16、找规律填上合适的数：﹣2，4，﹣8，16，，64，…17、观察下列数据：0，，，，，……,寻找规律，第9个数据应是 .18、观察烟花燃放图形，找规律:依此规律，第9个图形中共有_________个★.19、观察并分析下列数据,寻找规律: 0，,-,3,-2,,-3,……那么第10个数据是___________ ；第n个数据是_______________ .20、观察一下几组勾股数，并寻找规律：①3，4，5；②5，12，13；③7，24，25；④9，40，41；……请你写出有以上规律的第⑤组勾股数:______________________.21、寻找规律，根据规律填空：，，，，，，…，第n个数是 .22、找规律,并按规律填上第五个数:.23、阅读下文，寻找规律．计算：（1﹣x）（1+x）=1﹣x，（1﹣x）（1+x+x）=1﹣x，（1﹣x）（1+x+x+x）=1﹣x…．（1）观察上式，并猜想：（1﹣x）（1+x+x+…+x）= ．（2）根据你的猜想，计算：1+3+3+3…+3= ．（其中n是正整数）23n2n42323共 20 页，第 4 页24、找规律，如图有大小不同的平行四边形，第1幅图中有1个，第2幅图中有3个，第3幅图中有5个，则第n幅图中有个。

中考数学专题讲座二：新概念型问题一、中考专题诠释所谓“新概念”型问题，主要是指在问题中概念了中学数学中没有学过的一些概念、新运算、新符号，要求学生读懂题意并结合已有知识、能力进行理解，根据新概念进行运算、推理、迁移的一种题型.“新概念”型问题成为近年来中考数学压轴题的新亮点.在复习中应重视学生应用新的知识解决问题的能力二、解题策略和解法精讲“新概念型专题”关键要把握两点：一是掌握问题原型的特点及其问题解决的思想方法；二是根据问题情景的变化，通过认真思考，合理进行思想方法的迁移．三、中考典例剖析考点一：规律题型中的新概念考点二：运算题型中的新概念整理得：x2+2x+1-（1-2x+x2）-8=0，即4x=8，解得：x=2．故答案为：2点评：此题考查了整式的混合运算，属于新概念的题型，涉及的知识有：完全平方公式，去括号、合并同类项法则，根据题意将所求的方程化为普通方程是解本题的关键．对应训练2．（株洲）若（x1，y1）•（x2，y2）=x1x2+y1y2，则（4，5）•（6，8）=．考点三：探索题型中的新概念例3（南京）如图，A、B是⊙O上的两个定点，P是⊙O上的动点（P不与A、B重合）、我们称∠APB是⊙O上关于点A、B的滑动角．（1）已知∠APB是⊙O上关于点A、B的滑动角，①若AB是⊙O的直径，则∠APB=°；②若⊙O的半径是1，AB=，求∠APB的度数；（2）已知O2是⊙O1外一点，以O2为圆心作一个圆与⊙O1相交于A、B两点，∠APB是⊙O1上关于点A、B的滑动角，直线PA、PB分别交⊙O2于M、N（点M与点A、点N与点B均不重合），连接AN，试探索∠APB与∠MAN、∠ANB之间的数量关系．思路分析：（1）①根据直径所对的圆周角等于90°即可求解；②根据勾股定理的逆定理可得∠AOB=90°，再分点P在优弧上；点P在劣弧上两种情况讨论求解；（2）根据点P在⊙O1上的位置分为四种情况得到∠APB与∠MAN、∠ANB之间的数量关系．解：（1）①若AB是⊙O的直径，则∠APB=90．②如图，连接AB、OA、OB．在△AOB中，∵OA=OB=1．AB=，∴OA2+OB2=AB2．∴∠AOB=90°．当点P在优弧上时，∠AP1B=∠AOB=45°；当点P在劣弧上时，∠AP2B=（360°﹣∠AOB）=135°…6分（2）根据点P在⊙O1上的位置分为以下四种情况．第一种情况：点P在⊙O2外，且点A在点P与点M之间，点B在点P与点N之间，如图①∵∠MAN=∠APB+∠ANB，∴∠APB=∠MAN﹣∠ANB；第二种情况：点P在⊙O2外，且点A在点P与点M之间，点N在点P与点B之间，如图②．∵∠MAN=∠APB+∠ANP=∠APB+（180°﹣∠ANB），∴∠APB=∠MAN+∠ANB﹣180°；第三种情况：点P在⊙O2外，且点M在点P与点A之间，点B在点P与点N之间，如图③．∵∠APB+∠ANB+∠MAN=180°，∴∠APB=180°﹣∠MAN﹣∠ANB，第四种情况：点P在⊙O2内，如图④，∠APB=∠MAN+∠ANB．点评：综合考查了圆周角定理，勾股定理的逆定理，点与圆的位置关系，本题难度较大，注意分类思想的运用．对应训练3．（陕西）如果一条抛物线y=ax2+bx+c（a≠0）与x轴有两个交点，那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”．（1）“抛物线三角形”一定是三角形；（2）若抛物线y=-x2+bx（b＞0）的“抛物线三角形”是等腰直角三角形，求b的值；（3）如图，△OAB是抛物线y=-x2+b′x（b′＞0）的“抛物线三角形”，是否存在以原点O为对称中心的矩形ABCD？若存在，求出过O、C、D三点的抛物线的表达式；若不存在，说明理由．考点四：开放题型中的新概念考点五：阅读材料题型中的新概念四、中考真题演练一、选择题1．（六盘水）概念：f（a，b）=（b，a），g（m，n）=（-m，-n）．例如f（2，3）=（3，2），g（-1，-4）=（1，4）．则g[f（-5，6）]等于（）A．（-6，5）B．（-5，-6）C．（6，-5）D．（-5，6）A．5B．6C．7D．8点评：本题考查的是实数的运算，根据题意得出输出数的式子是解答此题的关键．3．（丽水）小明用棋子摆放图形来研究数的规律．图1中棋子围城三角形，其棵数3，6，9，12，…称为三角形数．类似地，图2中的4，8，12，16，…称为正方形数．下列数中既是三角形数又是正方形数的是（）A．2010B．2012C．2014D．2016二、填空题4．（常德）规定用符号[m]表示一个实数m的整数部分，例如：[]=0，[3.14]=3．按此规定[]的值为．5．（随州）概念：平面内的直线1l与2l相交于点O，对于该平面内任意一点M，点M到直线1l、2l的距离分别为a、b，则称有序非实数对（a，b）是点M的“距离坐标”，根据上述概念，距离坐标为（2，3）的点的个数是（）三、解答题410．（无锡）对于平面直角坐标系中的任意两点到直线y=ax+b11．（厦门）如图，在平面直角坐标系中，已知点解：∵（x1，y1）•（x2，y2）=x1x2+y1y2，∴（4，5）•（6，8）=4×6+5×8=64，故答案为64．四、中考真题演练一、选择题1．A2．B．3．D解：∵3，6，9，12，…称为三角形数，∴三角数都是3的倍数，∵4，8，12，16，…称为正方形数，∴正方形数都是4的倍数，∴既是三角形数又是正方形数的是12的倍数，∵2010÷12=167…6，2012÷12=167…8，2014÷12=167…10，2016÷12=168，∴2016既是三角形数又是正方形数．故选D．二、填空题4．4解：∵3＜＜4，∴3+1＜+1＜4+1，∴4＜+1＜5，∴[+1]=4，故答案为：4．5．C解：如图所示，所求的点有4个，三、解答题22，。

中考数学总复习《规律问题》专题训练(附带答案)学校:___________班级：___________姓名：___________考号：___________一、单选题1．下列图形都是由几个黑色和白色的正方形按一定规律组成，图①中有2个黑色正方形，图①中有5个黑色正方形，图①中有8个黑色正方形，图①中有11个黑色正方形……依此规律，图10中黑色正方形的个数是( ) A ．32B ．27C ．28D ．292．在-44，-43，-42，…，2021，2022这一串连续的整数中，前100个连续整数的和为（ ） A ．465B ．550C ．560D ．6063．在平面直角坐标系中，一蚂蚁从原点O 出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位，其行走路线如下图所示．那么点2020A 的坐标是（ ）A ．()10100，B ．()10101，C ．()10110，D ．()10111，4．下列图形都是由同样大小的棋子按一定的规律组成，其中第①个图形有3颗棋子，第①个图形一共有9颗棋子，第①个图形一共有18颗棋子，…，则第①个图形中棋子的颗数为（ ）A ．84B ．108C ．135D ．1525．观察下列图形，图①中有7个空心点，图①中有11个空心点，图①中有15个空心点，…，按此规律排列下去，第50个图形中有（ ）个空心点．A ．196B ．199C ．203D ．2076．小红在课下用叠的五角星排成如下的形状若按照这种排法，则前10个图形中五角星的总个数为（ ） A ．145B ．155C ．165D ．1757．如图，已知正方形的边长为4，甲、乙两动点分别从正方形ABCD 的顶点A 、C 同时沿正方形的边开始移动，甲点依顺时针方向环行，乙点依逆时针方向环行，若乙的速度是甲的速度的3倍，则它们第2022次相遇在边（ ）上．A ．AB B ．BC C ．CD D ．DA8．根据图中数字的规律，则代数式()x y x --的值是（ ）A ．396-B ．398-C ．400-D ．402-二、填空题9．如图，矩形ABCD 的两边BC CD 、分别在x 轴、y 轴上，点C 与原点重合，点()1,2A -，将矩形ABCD 沿x 轴向右翻滚，经过一次翻滚点A 对应点记为1A ，经过第二次翻滚点A 对应点记为2A …依此类推，经过2022次翻滚后点A 对应点记为2022A 的坐标为 ．10．用同样大小的黑色棋子按如图表示的方式摆图形，按照这样的规律摆下去，则第100个图形需棋子 枚．11．如图，已知1AB A B = 112223334AC A A A D A A A E A A ===，，， …以此类推，若20B ∠=︒，则n A ∠= ．12．如图，在平面直角坐标系中，菱形OABC 中，已知()4,0A ，120OAB ∠=︒对角线AC BO 、交点D ，将菱形OABC 绕点D 顺时针方向旋转，每次旋转60°，则旋转2次后，点D 的坐标是 ，旋转2022次后，点D 的坐标是 ．13．有一列数按如下规律排列：则第2019个数是 ．14．如图，下面每个图形中的四个数都是按相同的规律填写的，根据此规律确定x 的值为 ．三、解答题17．观察下面三行数，回答下面的问题：﹣2，4，﹣8，16，﹣32，64，……；①0，6，﹣6，18，﹣30，66，……；①5，﹣1，11，﹣13，35，﹣61，……；①（1）第①行的第8个数是，第n个数是；（2）第①行的第8个数是，第n个数是；第①行的第8个数是；（3）取每行数中的第k个数，这三个数的和能否等于﹣507？如果能，请你求出k的值，如果不能，请说明理由；（4）若第①行连续三个数的和恰为﹣183，直接写出这三个数分别为．18．下列是用火柴棒拼出的一列图形．仔细观察，找出规律，解答下列各题：（1）第5个图中共有___________根火柴；（2）第n个图形中共有___________根火柴（用含n的式子表示）；（3）请计算第2021个图形中共有多少根火柴？19．动脑筋、找规律．邱老师给小明出了下面的一道题，如图所示，请根据数字排列的规律，探索下列问题：（1）在A处的数是正数还是负数？（2）负数排在A，B，C，D中的什么位置？（3）第2020个数是正数还是负数？排在对应于A，B，C，D中的什么位置？20．如图是用长度相等的小棒按一定规律摆成的一组图案，第1个图案中有6根小棒，第2个图案中有11根小棒，第3个图案中有16根小棒……（1）第8个图案中有根小棒；（2）如果第n个图案中有1011根小棒，那么n的值是多少？参考答案：20．（1）41；（2）202。

2024中考数学复习专题规律探索题类型一数式规律1. (2023鄂州)生物学中，描述、解释和预测种群数量的变化，常常需要建立数学模型．在营养和生存空间没有限制的情况下，某种细胞可通过分裂来繁殖后代，我们就用数学模型2n 来表示．即：21＝2，22＝4，23＝8，24＝16，25＝32，…，请你推算22023的个位数字是()A. 8B. 6C. 4D. 22. (2023泰安)将从1开始的连续自然数按以下规律排列：…若有序数对(n，m)表示第n行，从左到右第m个数，如(3，2)表示6，则表示99的有序数对是________．3. (2022怀化)观察等式：2＋22＝23－2，2＋22＋23＝24－2，2＋22＋23＋24＝25－2，…，已知按一定规律排列的一组数：2100，2101，2102，…，2199，若2100＝m，用含m的代数式表示这组数的和是________．4. (2023张家界)有一组数据：a1＝31×2×3，a2＝52×3×4，a3＝73×4×5，…，a n＝2n＋1n（n＋1）（n＋2）.记S n＝a1＋a2＋a3＋…＋a n，则S12＝________．5. (2023达州)人们把5－12≈0.618这个数叫做黄金比，著名数学家华罗庚优选法中的“0.618法”就应用了黄金比．设a＝5－12，b＝5＋12，记S1＝11＋a＋11＋b，S2＝21＋a2＋2 1＋b2，…，S100＝1001＋a100＋1001＋b100，则S1＋S2＋…＋S100＝________．6. (2023安徽)观察以下等式：第1个等式：(2×1＋1)2＝(2×2＋1)2－(2×2)2，第2个等式：(2×2＋1)2＝(3×4＋1)2－(3×4)2，第3个等式：(2×3＋1)2＝(4×6＋1)2－(4×6)2，第4个等式：(2×4＋1)2＝(5×8＋1)2－(5×8)2，…按照以上规律，解决下列问题：(1)写出第5个等式：____________________；(2)写出你猜想的第n个等式(用含n的式子表示)，并证明．类型二图形规律考向1累加型7. (2023重庆B卷)把菱形按如图所示的规律拼图案，其中第①个图案中有1个菱形，第①个图案中有3个菱形，第①个图案中有5个菱形，…，按此规律排列下去，则第①个图案中菱形的个数为()第7题图A. 15B. 13C. 11D. 98. (2023济宁)如图，用相同的圆点按照一定的规律拼出图形．第一幅图4个圆点，第二幅图7个圆点，第三幅图10个圆点，第四幅图13个圆点…按照此规律，第一百幅图中圆点的个数是()第8题图A. 297B. 301C. 303D. 4009. (2023青海省卷)木材加工厂将一批木料按如图所示的规律依次摆放，则第n个图中共有木料________根．第9题图源自人教七上P70第10题10. (2022常德)如图中的三个图形都是边长为1的小正方形组成的网格，其中第一个图形有1×1个小正方形，所有线段的和为4，第二个图形有2×2个小正方形，所有线段的和为12，第三个图形有3×3个小正方形，所有线段的和为24，按此规律，则第n个网格中所有线段的和为________．(用含n的代数式表示)第10题图11. (2023遂宁)“勾股树”是以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程所画出来的图形，因为重复数次后的形状好似一棵树而得名．假设下图分别是第一代勾股树、第二代勾股树、第三代勾股树，按照勾股树的作图原理作图，则第六代勾股树中正方形的个数为________．第11题图12. (2023德阳)古希腊的毕达哥拉斯学派对整数进行了深入的研究，尤其注意形与数的关系，“多边形数”也称为“形数”，就是形与数的结合物．用点排成的图形如下：第12题图其中：图①的点数叫做三角形数，从上至下第一个三角形数是1，第二个三角形数是1＋2＝3，第三个三角形数是1＋2＋3＝6，…图①的点数叫做正方形数，从上至下第一个正方形数是1，第二个正方形数是1＋3＝4，第三个正方形数是1＋3＋5＝9，……由此类推，图①中第五个正六边形数是________．考向2成倍递变型13. (2023威海)由12个有公共顶点O 的直角三角形拼成如图所示的图形，①AOB ＝①BOC ＝①COD ＝…＝①LOM ＝30°.若S ①AOB ＝1，则图中与①AOB 位似的三角形的面积为( )第13题图A. (43 )3B. (43 )7C. (43 )6D. (34)6 14. (2023荆州)如图，已知矩形ABCD 的边长分别为a ，b ，进行如下操作：第一次，顺次连接矩形ABCD 各边的中点，得到四边形A 1B 1C 1D 1；第二次，顺次连接四边形A 1B 1C 1D 1各边的中点，得到四边形A 2B 2C 2D 2；…如此反复操作下去，则第n 次操作后，得到四边形A n B n C n D n 的面积是( )A. ab 2nB. ab 2n －1C. ab 2n ＋1 D. ab22n第14题图15. (2023烟台)如图，正方形ABCD 边长为1，以AC 为边作第2个正方形ACEF ，再以CF 为边作第3个正方形FCGH ，…，按照这样的规律作下去，第6个正方形的边长为( ) A. (22 )5 B. (22 )6 C. (2 )5 D. (2 )6第15题图16. (2023广安)如图，四边形ABCD 是边长为12的正方形，曲线DA 1B 1C 1D 1A 2…是由多段90°的圆心角所对的弧组成的．其中，弧DA 1的圆心为A ，半径为AD ；弧A 1B 1的圆心为B ，半径为BA1；弧B1C1的圆心为C，半径为CB1；弧C1D1的圆心为D，半径为DC1….弧DA1、弧A1B1、弧B1C1、弧C1D1…的圆心依次按点A、B、C、D循环，则弧C2023D2023的长是________(结果保留π).第16题图17. (2023绥化)如图，①AOB＝60°，点P1在射线OA上，且OP1＝1，过点P1作P1K1①OA 交射线OB于K1，在射线OA上截取P1P2，使P1P2＝P1K1；过点P2作P2K2①OA交射线OB 于K2，在射线OA上截取P2P3，使P2P3＝P2K2；…；按照此规律，线段P2023K2023的长为________.第17题图考向3周期变化型18. (2023玉林)如图的电子装置中，红黑两枚跳棋开始放置在边长为2的正六边形ABCDEF 的顶点A处．两枚跳棋跳动规则是：红跳棋按顺时针方向1秒钟跳1个顶点，黑跳棋按逆时针方向3秒钟跳1个顶点，两枚跳棋同时跳动，经过2023秒钟后，两枚跳棋之间的距离是()A. 4B. 23C. 2D. 0第18题图19. (2023河南)如图，在平面直角坐标系中，边长为2的正六边形ABCDEF的中心与原点O 重合，AB①x轴，交y轴于点P.将①OAP绕点O顺时针旋转，每次旋转90°，则第2023次旋转结束时，点A的坐标为()A. (3，－1)B. (－1，－3)C. (－3，－1)D. (1，3)第19题图20. (2023毕节)如图，在平面直角坐标系中，把一个点从原点开始向上平移1个单位，再向右平移1个单位，得到点A1(1，1)；把点A1向上平移2个单位，再向左平移2个单位，得到点A2(－1，3)；把点A2向下平移3个单位，再向左平移3个单位，得到点A3(－4，0)；把点A3向下平移4个单位，再向右平移4个单位，得到点A4(0，－4)；…；按此做法进行下去，则点A10的坐标为________．第20题图类型三与函数图象结合21. (2023龙东地区)如图，在平面直角坐标系中，点A1，A2，A3，A4…在x轴上且OA1＝1，OA2＝2OA1，OA3＝2OA2，OA4＝2OA3…按此规律，过点A1，A2，A3，A4…作x轴的垂线分别与直线y＝3x交于点B1，B2，B3，B4…记①OA1B1，①OA2B2，①OA3B3，①OA4B4…的面积分别为S1，S2，S3，S4…则S2023＝________．第21题图22. (2022菏泽)如图，一次函数y ＝x 与反比例函数y ＝1x(x ＞0)的图象交于点A ，过点A 作AB ①OA ，交x 轴于点B ；作BA 1①OA ，交反比例函数图象于点A 1；过点A 1作A 1B 1①A 1B 交x 轴于点B 1；再作B 1A 2①BA 1，交反比例函数图象于点A 2，依次进行下去…，则点A 2022的横坐标为________．第22题图23. (2023盐城)《庄子·天下篇》记载“一尺之棰，日取其半，万世不竭”．如图，直线l 1：y ＝12x ＋1与y 轴交于点A ，过点A 作x 轴的平行线交直线l 2：y ＝x 于点O 1，过点O 1作y 轴的平行线交直线l 1于点A 1，以此类推，令OA ＝a 1，O 1A 1＝a 2，…，O n －1A n －1＝a n ，若a 1＋a 2＋…＋a n ≤S 对任意大于1的整数n 恒成立，则S 的最小值为________．第23题图类型四 与实际问题结合24. (2022安徽)某矩形人行道由相同的灰色正方形地砖与相同的白色等腰直角三角形地砖排列而成，图①表示此人行道的地砖排列方式，其中正方形地砖为连续排列．【观察思考】当正方形地砖只有1块时，等腰直角三角形地砖有6块(如图①)；当正方形地砖有2块时，等腰直角三角形地砖有8块(如图①)；以此类推．第24题图【规律总结】(1)若人行道上每增加1块正方形地砖，则等腰直角三角形地砖增加________块；(2)若一条这样的人行道一共有n(n为正整数)块正方形地砖，则等腰直角三角形地砖的块数为______(用含n的代数式表示)；【问题解决】(3)现有2022块等腰直角三角形地砖，若按此规律再建一条人行道，要求等腰直角三角形地砖剩余最少，则需要正方形地砖多少块？参考答案与解析1. C 【解析】21＝2，22＝4，23＝8，24＝16，25＝32，则2的1，2，3，4次方的个位上的数分别为2，4，8，6，每4个一次循环，而22022中2022÷4＝550……2，∴个位上的数为4.2. (10，18) 【解析】按照规律可得每一行的最后一个数为行数的平方，第n 行有(2n －1)个数．∵92＝81，102＝100，∴99是第10行，第18个数，∴表示99的有序数对是(10，18).3. m 2－m4.201182 【解析】∵a n ＝2n ＋1n （n ＋1）（n ＋2） ＝n ＋n ＋1n （n ＋1）（n ＋2） ＝n n （n ＋1）（n ＋2） ＋n ＋1n （n ＋1）（n ＋2） ＝1（n ＋1）（n ＋2） ＋1n （n ＋2） ＝1n ＋1 －1n ＋2 ＋12 (1n －1n ＋2)，∴S 12＝12 －13 ＋13 －14 ＋…＋113 －114 ＋12 ×(1－13 ＋12 －14 ＋…＋112 －114 )＝12 －114 ＋12 ×(1＋12 －113 －114 )＝12 ＋12 ＋14 －126 －114 －128 ＝201182. 5. 5050 【解析】∵a ＝5－12 ，b ＝5＋12 ，∴ab ＝1，∵S 1＝11＋a ＋11＋b ＝2＋a ＋b 1＋a ＋b ＋ab ＝2＋a ＋b 2＋a ＋b ＝1，S 2＝21＋a 2 ＋21＋b 2 ＝2（2＋a 2＋b 2）1＋a 2＋b 2＋a 2b 2 ＝2（2＋a 2＋b 2）2＋a 2＋b 2＝2，…，S 100＝1001＋a 100 ＋1001＋b 100 ＝100（2＋a 100＋b 100）1＋a 100＋b 100＋a 100b 100 ＝100（2＋a 100＋b 100）2＋a 100＋b 100＝100，∴S 1＋S 2＋…＋S 100＝1＋2＋…＋100＝100×（100＋1）2＝5050. 6. 解：(1)(2×5＋1)2＝(6×10＋1)2－(6×10)2；(2)(2n ＋1)2＝[2n (n ＋1)＋1]2－[2n (n ＋1)]2.证明：等式左边＝4n 2＋4n ＋1，等式右边＝4n 2(n ＋1)2＋1＋4n (n ＋1)－4n 2(n ＋1)2＝4n (n ＋1)＋1＝4n 2＋4n ＋1，∴左边＝右边，∴等式成立．7. C 【解析】经分析可得，第个图案的菱形个数为2n －1，∴第⑥个图案中菱形个数为2×6－1＝11(个).8. B 【解析】第一幅图中圆点的个数是4＝1×3＋1；第二幅图中圆点的个数是7＝2×3＋1；第三幅图中圆点的个数是10＝3×3＋1；第四幅图中圆点的个数是13＝4×3＋1；…；按照此规律，第n 幅图中圆点的个数是3n ＋1，∴第一百幅图中圆点的个数是3×100＋1＝301.9. n （n ＋1）2【解析】∵第1个图中有木料1根，第2个图中有木料1＋2＝3根，第3个图中有木料1＋2＋3＝6根，第4个图中有木料1＋2＋3＋4＝10根，…，∴第n 个图中有木料1＋2＋3＋4＋…＋n ＝n （n ＋1）2根． 10. 2n 2＋2n 【解析】观察图形可知：第一个图形由1个小正方形组成，所有线段的和为4×1＝2×2×1, 第二个图形由4个小正方形组成，所有线段的和为6×2＝2×3×2, 第三个图形由9个小正方形组成，所有线段的和为8×3＝2×4×3, 第4个图形由16个小正方形组成，所有线段的和为10×4＝2×5×4，…由此发现规律是：第n 个图形由n 2个小正方形组成，所有线段的和为2(n ＋1)·n ＝2n 2＋2n .11. 127 【解析】第一代勾股树中正方形个数＝20＋21；第二代勾股树中正方形个数＝20＋21＋22；第三代勾股树中正方形个数＝20＋21＋22＋23；第四代勾股树中正方形个数＝20＋21＋22＋23＋24，…，∴第六代勾股树中正方形个数＝20＋21＋22＋23＋24＋25＋26＝127.12. 45 【解析】由题图可知，题图④前三层点数分别是：1＝4×1－3，5＝4×2－3，9＝4×3－3，…，∴第n 层的点数是4n －3，∴第n 个正六边形数是1＋5＋9＋…＋4n －3＝4×1－3＋4×2－3＋4×3－3＋…＋4n －3＝2n 2－n ，∴题图④中第五个正六边形数是2×52－5＝45.13. C 【解析】在Rt △AOB 中，∠AOB ＝30°，∵cos ∠AOB ＝OA OB ，∴OB ＝23OA .同理可得OC ＝23 OB ，∴OC ＝(23 )2OA ，…，∴OG ＝(23)6OA ，由题图可知△GOH 与△AOB 位似且位似比为(23 )6.∵S △AOB ＝1，∴S △GOH ＝[(23 )6]2＝(43 )6. 14. A 【解析】第一次操作后S 四边形A 1B 1C 1D 1＝12 S 矩形ABCD ＝12ab ，第二次操作后S 四边形A 2B 2C 2D 2＝12 S 四边形A 1B 1C 1D 1＝12 ×12 ab ＝ab 22 ，第三次操作后S 四边形A 3B 3C 3D 3＝12S 四边形A 2B 2C 2D 2＝ab 23 ，…，第n 次操作后S 四边形A n B n C n D n ＝ab 2n . 15. C 【解析】∵正方形ABCD 边长为1，∴AB ＝BC ＝1，∴AC ＝2 ，∴以AC 为边作第2个正方形ACEF 的边长为2 ；∵CF 是正方形ACEF 的对角线，∴CF ＝2 ×2 ＝(2 )2＝2，∴以CF 为边作第3个正方形FCGH 的边长为2；又∵GF 是正方形FCGH 的对角线，∴GF ＝2 ×2 ×2 ＝(2 )3＝22 ，以GF 为边作第4个正方形FGMN 的边长为22 ，…∴依此规律可知下一个正方形的边长是原来正方形边长的2 倍，即第n 个正方形的边长为(2 )n －1，∴第6个正方形的边长为(2 )5.16. 2022π 【解析】由题图可知，题图中由一段90°的弧组成的，弧所在圆的半径每次增加12 ，则弧C 1D 1的半径＝12 ×4＝12 ×4×1，弧C 2D 2的半径＝12 ×8＝12×4×2，弧C 3D 3的半径＝12 ×12＝12 ×4×3…，弧C 2022D 2022的半径＝12×4×2022＝4044，∴弧C 2022D 2022的长＝90π180×4044＝2022π. 17. 3 (1＋3 )2022 【解析】∵∠AOB ＝60°，OP 1＝1，∴P 1K 1＝3 OP 1＝3 ，∴P 1P 2＝P 1K 1＝3 ，∴OP 2＝1＋3 .∵P 2K 2＝3 OP 2，∴P 2K 2＝3 (1＋3 )，∴OP 3＝(1＋3 )2，∴P 3K 3＝3 OP 3＝3 (1＋3 )2，…，∴依此规律可得P 2023K 2023＝3 (1＋3 )2022.18. B 【解析】根据两枚跳棋跳动规则可知，红跳棋每过6秒钟跳动回顶点A ，黑跳棋每过18秒钟跳动回顶点A ，∵2022÷6＝337，∴经过2022秒后，红跳棋在顶点A 处；∵2022÷18＝112……6，6÷3＝2，∴经过2022秒钟后，黑跳棋在顶点E 处．如解图，连接AE ，过点F 作FG ⊥AE 于点G ，∵六边形ABCDEF 是边长为2的正六边形，∴∠AFE ＝120°，FE ＝AF ，∴∠F AE ＝30°，∴AG ＝EG ＝AF ·cos 30°＝2×32 ＝3 ，∴AE ＝23 ，即两枚跳棋之间的距离是23 .第18题解图19. B 【解析】如解图，连接OB ，∵AB ∥x 轴，∴AB ⊥y 轴，∵六边形ABCDEF 是正六边形，点O 是中心，∴OB ＝OA ，∠AOB ＝60°，∴∠AOP ＝30°，AP ＝12AB ＝1，∴OP ＝3 ，∴点A (1，3 )，将△AOP 绕点O 顺时针每次旋转90°，则第1次结束点A 的坐标为(3 ，－1)，第2次结束点A 的坐标为(－1，－3 )，第3次结束点A 的坐标为(－3 ，1)，第4次结束点A 的坐标为(1，3 )，…，∴每4次一个循环，∵2022＝4×505＋2，∴第2022次旋转结束时，相当于第2次结束，∴点A 的坐标为(－1，－3 ).第19题解图20. (－1，11) 【解析】由图象可知，A 5(5，1)，将点A 5向左平移6个单位，再向上平移6个单位，可得A 6(－1，7)，将点A 6向左平移7个单位，再向下平移7个单位，可得A 7(－8，0)，将点A 7向右平移8个单位，再向下平移8个单位，可得A 8(0，－8)，将点A 8向右平移9个单位，再向上平移9个单位，可得A 9(9，1)，将点A 9向左平移10个单位，再向上平移10个单位，可得A 10(－1，11).21. 240433 【解析】∵S 1＝1×32 ＝ 20×32 ，S 2＝2×232 ＝ 22×32，… ，依此规律可得S n ＝ 22(n －1)×32 ，∴S 2023＝ 22×(2023－1)×32＝ 240433 . 22. 2021 ＋2022 【解析】∵点A 是函数y ＝x 与y ＝1x的图象在第一象限的交点，∴点A 的坐标为(1，1)，又∵AB 垂直于直线y ＝x ，∴点B 坐标为(2，0)，又∵BA 1∥OA ，∴BA 1的解析式为y ＝x －2，与y ＝1x 联立，解得x ＝1＋2 (负值已舍)，即点A 1的横坐标为1＋2 ；同理可得B 1的横坐标为22 ，∵B 1A 2∥BA 1，∴B 1A 2的解析式为y ＝x －22 ，与y ＝1x 联立，解得A 2的横坐标为2 ＋3 (负值已舍)；…；依此按规律可得A 2021的横坐标为2021 ＋2022 .23. 2 【解析】由题可得a 1＝OA ＝1，而y ＝x 与y 轴的正方向的夹角是45°，O 1A ⊥y 轴，∴O 1A ＝OA ＝1，∴ 点O 1的横坐标是1，对于y ＝12 x ＋1，当x ＝1时，y ＝32，∴a 2＝O 1A 1＝12 ，∴tan ∠A 1AO 1＝O 1A 1O 1A ＝12 ，依次得出A 1O 2＝A 1O 1＝12 ，a 3＝A 2O 2＝12 A 1O 2＝(12)2，…，可以得出A n －1O n －1＝(12 )n －1，∴a 1＋a 2＋…＋a n －1＋a n ＝1＋12 ＋…＋(12 )n －2＋(12)n －1①，①×2得2×(a 1＋a 2＋…＋a n －1＋a n )＝2＋1＋12 ＋…＋(12 )n －3＋(12)n －2②，②－①得a 1＋a 2＋…＋a n －1＋a n ＝2－(12 )n －1，∴S ≥2－(12)n －1，∴S 的最小值是2. 24. 解：(1)2；【解法提示】观察题图②与题图③，每增加1块正方形地砖，则增加2块等腰直角三角形地砖．(2)2n ＋4；【解法提示】在题图②中，正方形地砖1块，等腰直角三角形地砖(4＋2)块；在题图③中，正方形地砖2块，等腰直角三角形地砖(4＋2×2)块；正方形地砖若有3块，则等腰直角三角形地砖(4＋2×3)块；…；依此按规律可得正方形地砖若有n 块，则等腰直角三角形地砖有(4＋2n )块．(3)设需要正方形地砖n块，∴2n＋4≤2021，解得n≤1008.5，∵n为正整数，∴n最大取1008，答：需要正方形地砖1008块．。

初中数学找规律题(有标准答案)初中数学找规律题（有答案）有比较才有鉴别”。

通过比较，可以发现事物的相同点和不同点，更容易找到事物的变化规律。

找规律的题目，通常按照一定的顺序给出一系列量，要求我们根据这些已知的量找出一般规律。

揭示的规律，常常包含着事物的序列号。

所以，把变量和序列号放在一起加以比较，就比较容易发现其中的奥秘。

初中数学考试中，经常出现数列的找规律题，本文就此类题的解题方法进行探索。

一、基本方法——看增幅一）如增幅相等（实为等差数列）：对每个数和它的前一个数进行比较，如增幅相等，则第n个数可以表示为：a1+(n-1)b，其中a为数列的第一位数，b为增幅，(n-1)b为第一位数到第n位的总增幅。

然后再简化代数式a+(n-1)b。

例如，数列4、10、16、22、28……，求第n位数。

分析可得，第二位数起，每位数都比前一位数增加6，增幅都是6，所以，第n位数是：4+(n-1)6＝6n－2.二）如增幅不相等，但是增幅以同等幅度增加（即增幅的增幅相等，也即增幅为等差数列）。

如增幅分别为3、5、7、9，说明增幅以同等幅度增加。

此种数列第n位的数也有一种通用求法。

基本思路是：1、求出数列的第n-1位到第n位的增幅；2、求出第1位到第第n位的总增幅；3、数列的第1位数加上总增幅即是第n位数。

虽然此解法较繁琐，但是此类题的通用解法。

当然，此题也可用其它技巧或用分析观察的方法求出，方法就简单的多了。

三）增幅不相等，但是增幅同比增加，即增幅为等比数列，如：2、3、5、9、17增幅为1、2、4、8.四）增幅不相等，且增幅也不以同等幅度增加（即增幅的增幅也不相等）。

此类题大概没有通用解法，只能用分析观察的方法，但是，此类题包括第二类的题，如用分析观察法，也有一些技巧。

二、基本技巧一）标出序列号：找规律的题目，通常按照一定的顺序给出一系列量，要求我们根据这些已知的量找出一般规律。

找出的规律，通常包含序列号。

所以，把变量和序列号放在一起加以比较，就比较容易发现其中的奥秘。

2020年中考数学真题分项汇编(湖南专版)专题14 规律探索、新定义、阅读理解题1. (2020年湖南长沙中考)2020年3月4日，是人类第一个“国际数学日”，这个节日的昵称是“π(Day)”。

国际数学日之所以定在3月4日，是因为“3.14”是与圆周率数值最接近的数字。

在古代，一个国家所算得的圆周率的精确程度，可以作为衡量这个国家当时数学与科技发展水平的一个主要标志。

我国南北朝时的祖冲之是世界上最早把圆周率的精确值计算到小数点后第7位的科学巨匠，该成果领先世界一千多年。

以下对于圆周率的四个表述：①圆周率是一个有理数； ②圆周率是一个无理数；③圆周率是一个与圆的大小无关的常数，它等于该圆的周长与直径的比； ④圆周率是一个与圆的大小有关的常数，它等于该圆的周长与半径的比。

其中表述正确的是( )A. ②③B. ①③C. ①④D. ②④ 【答案】A【解析】本题考查圆周率的基本概念及无理数的定义，回溯到“知其所以然”的数学思想。

圆周率是一个无理数，并且是一个与圆的大小无关的常数，它等于该圆的周长与直径的比(π=dc)，②③正确。

故选A 。

2.(2020年湖南常德市中考)如图，将一枚跳棋放在七边形ABCDEFG 的顶点A 处，按顺时针方向移动这枚跳棋2020次．移动规则是：第k 次移动k 个顶点(如第一次移动1个顶点，跳棋停留在B 处，第二次移动2个顶点，跳棋停留在D 处)，按这样的规则，在这2020次移动中，跳棋不可能停留的顶点是( )A ．C 、EB ．E 、FC ．G 、C 、ED ．E 、C 、F【分析】设顶点A ，B ，C ，D ，E ，F ，G 分别是第0，1，2，3，4，5，6格，因棋子移动了k 次后走过的总格数是1+2+3+…+k ＝21k (k +1)，然后根据题目中所给的第k 次依次移动k 个顶点的规则，可得到不等式最后求得解．解：经实验或按下方法可求得顶点C ，E 和F 棋子不可能停到．设顶点A ，B ，C ，D ，E ，F ，G 分别是第0，1，2，3，4，5，6格， 因棋子移动了k 次后走过的总格数是1+2+3+…+k ＝21k (k +1)，应停在第21k (k +1)﹣7p 格， 这时P 是整数，且使0≤21k (k +1)﹣7p ≤6，分别取k ＝1，2，3，4，5，6，7时， 21k (k +1)﹣7p ＝1，3，6，3，1，0，0，发现第2，4，5格没有停棋， 若7＜k ≤2020，设k ＝7+t (t ＝1，2，3)代入可得，21k (k +1)﹣7p ＝7m +21t (t +1)， 由此可知，停棋的情形与k ＝t 时相同，故第2，4，5格没有停棋，即顶点C ，E 和F 棋子不可能停到． 故选：D ．3.(2020年湖南常德中考)阅读理解：对于x 3﹣(n 2+1)x +n 这类特殊的代数式可以按下面的方法分解因式： x 3﹣(n 2+1)x +n ＝x 3﹣n 2x ﹣x +n ＝x (x 2﹣n 2)﹣(x ﹣n )＝x (x ﹣n )(x +n )﹣(x ﹣n )＝(x ﹣n )(x 2+nx ﹣1)． 理解运用：如果x 3﹣(n 2+1)x +n ＝0，那么(x ﹣n )(x 2+nx ﹣1)＝0，即有x ﹣n ＝0或x 2+nx ﹣1＝0， 因此，方程x ﹣n ＝0和x 2+nx ﹣1＝0的所有解就是方程x 3﹣(n 2+1)x +n ＝0的解． 解决问题：求方程x 3﹣5x +2＝0的解为 ．【分析】将原方程左边变形为x 3﹣4x ﹣x +2＝0，再进一步因式分解得(x ﹣2)[x (x +2)﹣1]＝0，据此得到两个关于x 的方程求解可得． 解：∵x 3﹣5x +2＝0， ∴x 3﹣4x ﹣x +2＝0， ∴x (x 2﹣4)﹣(x ﹣2)＝0， ∴x (x +2)(x ﹣2)﹣(x ﹣2)＝0，则(x ﹣2)[x (x +2)﹣1]＝0，即(x ﹣2)(x 2+2x ﹣1)＝0， ∴x ﹣2＝0或x 2+2x ﹣1＝0， 解得x ＝2或x ＝﹣12 ，故答案为：x ＝2或x ＝﹣1+2或x ＝﹣1﹣2．4.(2020年湖南怀化中考)如图，11OB A △，122A B A △，233A B A △，…，1n n n A B A -△，都是一边在x 轴上的等边三角形，点1B ，2B ，3B ，…，n B 都在反比例函数(0)y x x=>的图象上，点1A ，2A ，3A ，…，n A ，都在x 轴上，则n A 的坐标为________．【答案】()【解析】如图，过点B 1作B 1C ⊥x 轴于点C ，过点B 2作B 2D ⊥x 轴于点D ，过点B 3作B 3E ⊥x 轴于点E ，先在△OCB 1中，表示出OC 和B 1C 的长度，表示出B 1的坐标，代入反比例函数，求出OC 的长度和OA 1的长度，表示出A 1的坐标，同理可求得A 2、A 3的坐标，即可发现一般规律．【详解】如图，过点B 1作B 1C ⊥x 轴于点C ，过点B 2作B 2D ⊥x 轴于点D ，过点B 3作B 3E ⊥x 轴于点E ，∵△OA 1B 1为等边三角形， ∴∠B 1OC=60°，∴11B Ctan B OC=OC∠B 1C= ，设OC 的长度为x ，则B 1的坐标为(x )2= 解得，x=1或x=-1(舍去)， ∴OA 1=2OC=2， ∴A 1(2，0)设A 1D 的长度为y ，同理，B 2D y ，B 2的坐标表示为()2y +，代入函数关系式可得(2y +=解得：1或y=1-(舍去)∴A 11，A 1A 2=2，OA 2=22+=∴A 2(0)设A 2E 的长度为z ，同理，B 3E ，B 3的坐标表示为()z ，代入函数关系式可得(z=解得：z=舍去)∴A 2，A 2A 3=OA 3==∴A 3(0)，综上可得：A n (0)，故答案为：()．5.(2020年湖南湘西中考)观察下列结论：(1)如图①，在正三角形ABC 中，点M ，N 是,AB BC 上的点，且AM BN =，则AN CM =，60NOC ∠=︒； (2)如图②，在正方形ABCD 中，点M ，N 是,AB BC 上的点，且AM BN =，则AN DM =，90NOD ∠=︒； (3)如图③，在正五边形ABCDE 中，点M ，N 是,AB BC 上的点，且AM BN =，则AN EM =，108NOE ∠=︒；……根据以上规律，在正n 边形1234n A A A A A 中，对相邻的三边实施同样的操作过程，即点M ，N 是1223,A A A A 上的点，且12A M A N =，1A N 与n A M 相交于O ．也会有类似的结论．你的结论是_________________．【答案】1A N =n A M ，(2)180n n NOA n-⋅︒∠=【解析】根据正多边形内角和定理结合全等三角形的判定和性质可得出(1)、(2)、(3)的结论，根据以上规律可得出正n 边形的结论．【详解】(1)∵正三角形ABC 中，点M 、N 是AB 、AC 边上的点，且AM=BN ， ∴AB=AC ，∠CAM=∠ABN=()()218032180603n n-⋅︒-⋅︒==︒，∵在△ABN 和△CAM 中，AB AC ABN CAM BN AM =⎧⎪∠=∠⎨⎪=⎩， ∴△ABN ≌△CAM(SAS)， ∴AN= CM ，∠BAN=∠MCA ，∴∠NOC=∠OAC+∠MCA =∠OAC+∠BAN =∠BAC=60°， 故结论为：AN= CM ，∠NOC=60︒；(2)∵正方形ABCD 中，点M 、N 是AB 、BC 边上的点，且AM=BN ， ∴AB=AD ，∠DAM=∠ABN=()()218042180904n n-⋅︒-⋅︒==︒，同理可证：Rt △ABN ≅Rt △DAM ， ∴AN= DM ，∠BAN=∠ADM ，∠NOD=∠OAD+∠ADM =∠OAD+∠BAN =∠BAC=90°， 故结论为：AN= DM ，∠NOD=90︒；(3)∵正五边形ABCDE 中，点M 、N 是AB 、BC 边上的点，且AM=BN ， ∴AB=AE ，∠EAM=∠ABN=()()2180521801085n n-⋅︒-⋅︒==︒，同理可证得：Rt △ABN ≅Rt △EAM ， ∴AN= EM ，∠BAN=∠AEM ，∠NOE=∠OAE+∠AEM =∠OAE+∠BAN =∠BAE=108°，故结论为：AN= EM ，∠NOE=108︒；∵正三角形的内角度数为：60°， 正方形的内角度数为：90°， 正五边形的内角度数为：108°， ∴以上所求的角恰好等于正n 边形的内角()2180n n-⋅︒，在正n 边形1234n A A A A A 中，点M ，N 是1223,A A A A 上的点，且12A M A N =，1A N 与n A M 相交于O ，结论为：1A N =n A M ，(2)180n n NOA n-⋅︒∠=．故答案为：1A N =n A M ，(2)180n n NOA n-⋅︒∠=．6.(2020年湖南省衡阳市中考)如图，在平面直角坐标系中，点1P 的坐标,22⎛ ⎝⎭，将线段1OP 绕点O 按顺时针方向旋转45°，再将其长度伸长为1OP 的2倍，得到线段2OP ；又将线段2OP 绕点O 按顺时针方向旋转45°，长度伸长为2OP 的2倍，得到线段3OP ；如此下去，得到线段4OP 、5OP ，……，n OP (n 为正整数)，则点2020P 的坐标是_________．【答案】(0，-22019)【解析】根据题意得出OP 1=1，OP 2=2，OP 3=4，如此下去，得到线段OP 3=4=22，OP 4=8=23…，OP n =2n -1，再利用旋转角度得出点P 2020的坐标与点P 4的坐标在同一直线上，进而得出答案．【详解】解：∵点P 1的坐标为22⎛⎫⎪ ⎪⎝⎭，将线段OP 1绕点O 按顺时针方向旋转45°，再将其长度伸长为OP 1的2倍，得到线段OP 1； ∴OP 1=1，OP 2=2，∴OP 3=4，如此下去，得到线段OP 4=23，OP 5=24…， ∴OP n =2n -1，由题意可得出线段每旋转8次旋转一周， ∵2020÷8=252…4，∴点P 2020的坐标与点P 4的坐标在同一直线上，正好在y 轴负半轴上， ∴点P 2020的坐标是(0，-22019)． 故答案为：(0，-22019)．5.(2020年湖南张家界市中考)观察下面的变化规律：212112112111,,,133353557577979=-=-=-=-⨯⨯⨯⨯，…… 根据上面的规律计算：222213355720192021++++=⨯⨯⨯⨯__________．【答案】20202021【解析】本题可通过题干信息总结分式规律，按照该规律展开原式，根据邻项相消求解本题． 【详解】由题干信息可抽象出一般规律：211a b a b=-•(,a b 均为奇数，且2b a =+)． 故222213355720192021++++=⨯⨯⨯⨯111111111111111202011()()()13355720192021335520192019202120212021-+-+-++-=+-+-++--=-=． 故答案：20202021． 7.(2020年湖南湘潭中考)阅读材料：三角形的三条中线必交于一点，这个交点称为三角形的重心．(1)特例感知：如图(一)，已知边长为2的等边ABC 的重心为点O ，求OBC 与ABC 的面积．(2)性质探究：如图(二)，已知ABC 的重心为点O ，请判断OD OA 、OBC ABCSS是否都为定值？如果是，分别求出这两个定值：如果不是，请说明理由．(3)性质应用：如图(三)，在正方形ABCD 中，点E 是CD 的中点，连接BE 交对角线AC 于点M ． ①若正方形ABCD 的边长为4，求EM 的长度； ②若1CMES=，求正方形ABCD 的面积．【答案】(2)都是定值，1=2OD OA ，13OBCABCS =S ；(3)①EM =12． 【解析】 【分析】(1)连接DE ，利用相似三角形证明12OD AO =，运用勾股定理求出AD 的长，运用三角形面积公式求解即可；(2)根据(1)的证明可求解； (3)①证明△CME ∽△ABM 得12EM BM =，再运用勾股定理求出BE 的长即可解决问题； ②分别求出S △BMC 和S △ABM 即可. 【详解】(1)连接DE ，如图，∵点O 是ABC 的重心，AD ∴，BE 是BC ，A C 边上的中线，D E ∴，为BC ，AC 边上的中点，DE ∴为ABC 的中位线，//DE AB ∴，12DE AB =， ~ODE OAB ∴，12OD DE OAAB ∴==，2AB ∴=，1BD =AD ∴=，OD =，1122233OBCSBC OD ∴=⨯⨯=⨯⨯=11222ABCSBC AD =⋅⋅=⨯= (2)由(1)可知，12OD OA =是定值；112132OBC OABC BC OD S OD S AD BC AD ⋅===⋅是定值； (3)①∵四边形ABCD 是正方形，//CD AB ∴，4AB BC CD ÷==，CMEAMB ∴EM CEBM AB∴=E 为CD 的中点，122CE CD ∴==BE ∴=12EM BM ∴= 13EM BE ∴=，即EM = ②1CME S ∴=，且12ME BM = ∴2BMCS=，12ME BM =， 214CME AMBS ME SBM ⎛⎫∴== ⎪⎝⎭，4S 4AMBCME S∆∴==，246ABCBMCABMSSS∴=+=+=，又ADC ABC S S =△△6ADCS∴=∴正方形ABCD 的面积为：6+6=12．8.(2020年湖南张家界市中考)阅读下面材料：对于实数,a b ，我们定义符号min{,}a b 的意义为：当a b <时，min{,}a b a =；当a b 时，min{,}a b b =，如：min{4,2}2,min{5,5}5-=-=． 根据上面的材料回答下列问题： (1)min{1,3}-=______； (2)当2322min ,233x x x -++⎧⎫=⎨⎬⎩⎭时，求x 的取值范围． 【答案】(1)﹣1 ；(2)x≥134【解析】 【分析】(1)比较大小，即可得出答案； (2)根据题意判断出2x 3x+223－≥ 解不等式即可判断x 的取值范围． 【详解】解：(1)由题意得min{1,3}-=﹣1 故答案为：﹣1； (2)由题意得：2x 3x+223－≥3(2x －3)≥2(x+2) 6x －9≥2x+4 4x≥13 x≥134∴x 的取值范围为x≥134． 的。

规律探索与定义新运算一、规律探索1.图形的变化2.数字的变化3.与代数知识相结合4.与几何知识相结合5.综合问题二、定义新运算一、规律探索1.图形的变化1.【易】（初二数学期末）如图，是一个装饰物品连续旋转闪烁所成的三个图形，照此规律闪烁，下一个呈现出来的图形是（）【答案】B2.【易】（2010深圳外国语初一上联合测）如图，一串有趣的图案按一定规律排列，请仔细观察，按此规律第2010个图案是（）A．B．C．D．【答案】B3.【易】（北京市西城区2011—2012学年度第一学期期末试卷）把全体自然数按下面的方式进行排列：按照这样的规律，从2010到2012，箭头的方向应为（）A．↓→B．→↑C．↑→D．→↓．【答案】C4. 【易】（2012届九年级第一模拟试题）将一些半径相同的小圆按如图所示的规律摆放：第1个图形有6个小圆，第2个图形有10个小圆，第3个图形有16个小圆，第4个图形有24个小圆，……，依次规律，第6个图形有________个小圆．【答案】465. 【易】（哈尔滨中考）观察下列图形：它们是按一定规律排列的，依照此规律，第9个图形中共有________个★【答案】206. 【易】(河南郑州市2009-2010年初一上期末)用同样大小的黑色五角星按图所示的方式摆图案，按照这样的规律摆下去，第99个图案需要的黑色五角星个．【答案】1507. 【易】(2009-2010年辽宁沈阳崇文中学初一上期末)一串有黑有白，其排列有一定规律的珠子，被盒子遮住一部分（如图所示），则这串珠子被盒子遮住的部分有________颗．【答案】278. 【易】（密云区一模）如图，将一张正方形纸片剪成四个小正方形，得到4个小方形，称为第一次操作；然后，将其中的一个正方形再剪成四个小正方形，共得到7个小正方形，称为第二次操作；再将其中的一个正方形再剪成四个小正方形，共得到10个第1个图形第2个图形第3个图形第4个图形…小正方形，称为第三次操作；……，根据以上操作，若要得到2011个小正方形，则需要操作的次数是（ ） A ．669 B ．670 C ．671 D ．672【答案】B9. 【易】（武汉二中广雅中学下学期期中七年级数学）如图，要使四边形木架（用4根木条钉成）不变形，至少要钉上1根木条；使五边形木架不变形，至少要钉上2根木条，使六边形木架不变形，至少要钉上3根木条；……，若要使十边形木架不变形，至少要钉上________根木条．【答案】710. 【易】（2012深圳外国语初三月考）如图，用小棒摆下面的图形，图形⑴需要3根小棒，图形⑵需要7根小棒……照这样的规律继续摆下去，第个图形需要________根小棒（用含的代数式表示）．【答案】41n －11. 【易】（漳州）用形状和大小相同的黑色棋子按下图所示的方式排列，按照这样的规律，第n 个图形需要棋子________枚．（用含n 的代数式表示）【答案】31n12. 【易】（2011-2012太原市七年级第二次测评）如图是一组有规律的图案，第1个图案由4个基础图形组成，第2个图案由7个基础图形组成，……，第n 个图案由（ ）个基础图形组成（n 为正整数）nn (3)(2)(1)……【答案】31n +找规律发现基础图形的个数是4710，，，总结出第n 个图案中基础图形的个数是31n +13. 【易】（广州中考）如图7-①，7-②，7-③，7-④，……是用围棋棋子按照某种规律摆成的一行“广”字，按照这种规律，第5个“广”字中的棋子个数是________，第个“广”字中的棋子个数是________．【答案】15,25n +14. 【易】（2011深圳中学初一期末）如图是用棋子摆成的“T”字．⑴摆成第一个“T”字需要________个棋子，第二个需________个棋子．⑵按这样的规律摆下去，摆成第10个“T”字需要________个棋子，第n 个需________个棋子．⑶是否存在这样的情况，使得其中一个图形的棋子是另一个图形棋子的k 倍，其中2011k =．若存在，请指出来，若不存在，请说明理由．【答案】⑴5，8⑵32，32n +⑶存在．设一个图形的棋子数为32n +，另一个图形的棋子数为32m +，（n m ＞）20111340n m =+．15. 【易】（2010年北京西城区期末）下图是按一定规律排列的一组图形，依照此规律，第n 个图形中★的个数为________．（n 为正整数）n 图7-① 图7-② 图7-③ 图7-④……【答案】3n16. 【易】（2011罗湖外国语初一下期中）用棋子摆出下列一组“口”字，按照这种方法摆下去，则摆第个“口”字需用棋了（ ）A ．枚B ．枚C ．枚D ．枚【答案】A17. 【易】（2009-2010武汉洪山去初一下期末）则当输入的下面是用棋子摆成的“上”字：第1个“上”字第2个“上”字第3个“上”字如果按照以上规律继续摆下去，那么通过观察，可以发现： ⑴第四、第五个“上”字分别需用________和________枚棋子； ⑵第n 个“上”字需用________枚棋子． 【答案】⑴18，22⑵42n +18. 【易】已知一个面积为S 的等边三角形，现将其各边n （n 为大于2的整数）等分，并以相邻等分点为顶点向外作小等边三角形（如图所示）．当8n =时，共向外作出了________个小等边三角形；当n k =时，共向外作出了________个小等边三角形，这些小等边三角形的面积和是________（用含k 的式子表示）．【答案】18，36k -，236k S k -⋅ …第5个图形第4个图形第3个图形第2个图形第1个图形★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★n 4n ()44n -()44n +2n n =3n =5……n=419. 【易】（2012河南中招模拟试卷）用边长为1cm 的小正方形搭如下的塔状图形，则第n 次所搭图形的周长是________cm （用含n 的代数式表示）．【答案】4n20. 【易】（2011-2012北京十四中初一下期中）观察下列图形，则第n 个图形中三角形的个数是________．【答案】4n21. 【易】（北京东直门七年级下期中）规律探索：连结图⑴中的三角形三边的中点得图⑵，再连结图⑵中间的三角形三边的中点得图，如此继续下去，那么在第n 个图形中共有多少个三角形？【答案】43n －22. 【易】（2011深圳中学初一上期中）用棋子摆出下列一组图形：⑴个图形棋子的枚数为________．⑶如果某一图形共有99枚棋子，你知道它是第几个图形吗？ 【答案】⑴36n(1) (2) (3)第1次 第2次 第3次 第4次······⑶3223. 【易】（郑州一中教育集团2010-2011学年上期期中考试）为参加“第十届中国开封菊展”，某单位想在步行街设计一座三角形展台，要求园林工人把它的每条边上摆放相等盆数的盆栽小菊花（如图所示的每个小圆圈表示一盆小菊花）．如果每条边上摆两盆小菊花，共需要3盆小菊花；如果每条边上摆3盆小菊花，共需要6盆小菊花；……，按此要求摆放下去：⑴________．⑶请你帮园林工人参考一下，能否用2003盆小菊花作出符合要求的摆放？如果能，请计算出每条边上应摆小菊花的盆数；如果不能，请简要说明理由．【答案】⑴⑵⑶不能．令332003n -=，解得26683n =，n 不是整数．24. 【易】（通州二模）根据如图所示的⑴，⑵，⑶三个图所表示的规律，依次下去第n个图中平行四边形的个数是（ ）A ．3nB ．()31n n +C ．6nD ．()61n n +【答案】B25. 【易】（2011山西中考）如图是用相同长度的小棒摆戍的一组有规律的图案，图案⑴需要4根小棒，图案⑵需要10根小棒……，按此规律摆下去，第n 个图案需要小棒________根(用含有n 的代数式表示)．……【答案】62n －26. 【易】（2010深圳外国语初一上联合测）用棋子按下列方式摆图案，依照此规律，第n 个图形比第()1n -个图形多________枚棋子．【答案】32n -27. 【易】（武汉二中初一下期中）某体育馆用大小相同的长方形木块镶嵌地面，第1次铺2块，如图，第2次把第1次铺的完全围起来，如图，第3次把第2次铺的完全围起来，如图；…．依此方法，第n 次铺完后，用字母n 表示第n 次镶嵌所使用的木块数________．【答案】86n －根据图形得到一列数2、10、18、26、…，这一个列数，从第二项起，每一项与它前面紧邻的一项的差，都等于一个常数8． 第2个数=第一个数+（2﹣1）个8； 第3个数=第一个数+（3﹣1）个8； 第4个数=第一个数+（4﹣1）个8； …由此猜想：第n 个数=第一个数+()1n －个8； 即第n 个数=2+8×()1n －=86n －；一般规律：()11n a a n d =+－，其中1a 为首项（第一个）、n a 为这一列数的第n 个，d 为每相邻两个数的差．28. 【易】（南平中考）观察下列各图形中小正方形的个数，依此规律，第（11）个图形中小正方形的个数为________第2个第1个……A ．78B ．66C ．55D ．50【答案】B29. 【易】（2012贵州毕节中考）在下图中，每个图案均由边长为1的小正方形按一定的规律堆叠而成，照此规律，第10个图案中共有________个小正方形．【答案】10030. 【易】（2011深圳中学初一上期末）小卫搭积木块，开始时用2块积木搭拼（第1步），然后用更多的积木块完全包围原来的积木块（第2步），如图反映提前3步的田径赛案，当第10步结束后，组成图案的积木块数为________．【答案】380（规律为242n n －）31. 【易】（2010初一期末）探索规律图⑴是一个正方形，依次连结这个正方形各边中点得到图⑵，再依次连结图⑵中间小正方形各边的中点得到图⑶，按以上的方法继续下去……①第1步第2步第3步（3）（2）（1）②按上面的方法继续下去，小明说：第101个图形中有100个正方形；小颖说：第101个图形中有401个三角形．请判断他们的说法是否正确，并说明理由． 【答案】①小颖的说法错误，第101个图形中有400个三角形．32. 【易】（天津市河西区2010-2011学年度第一学期七年级期中质量调查数学试卷）如图，用同样规格的黑白两色正方形瓷砖铺设矩形地面，请观察下列图形，探究问题在第n 个图中，共有白色瓷砖________块．【答案】2n n +33. 【易】（2010年初一下两部联考）古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”，而把1、4、9、16…这样的数称为“正方形数”．从右图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．下列等式中符合这一规律的是（ ）A ．13310=+ B ．25916=+ C ．361521=+ D ．491831=+ 【答案】C34.【易】（徐州市中考）如图，每个图案都由若干个棋子摆成．依照此规律，第n 个图案中棋子的总个数可用含n 的代数式表示为________．【答案】2n n +4=1+39=3+616=6+10…第1第2第3第435.【易】（2011•达州）用同样大小的小圆按下图所示的方式摆图形，第1个图形需要1个小圆，第2个图形需3个小圆，第3个图形需要6个小圆，第4个图形需要10个小圆，按照这样的规律摆下去，则第n个图形需要小圆________个（用含n的代数式表示）．【答案】()12 n n+36.【易】（2009-2010年太原市七年级第二次测评）根据下列五个图形及对应点的个数的变化规律，试猜测第n个图中有________个点．【答案】21n n-+如果没有公共交点，那么一共是n条线段，每条线上n个点，现在n条线有一个公共交点，所以总点数为21n n-+．37.【易】（郑州外国语中学第三次质量检测数学卷）如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第n个图形需要黑色棋子的个数是________．【答案】22n n+38.【易】（南山初一统考）如图，是用三角形摆成的图案，摆第一层图需要1个三角形，摆第二层图需要3个三角形，摆第三层图需要7个三角形，摆第四层图需要13个三角形，摆第五层图需要21个三角形摆第n层图需要________个三角形．……第1个图第2个图第3个图第4个图【答案】21n n +－观察可得，第1层三角形的个数为1， 第2层三角形的个数为22213+=－， 第3层三角形的个数为33317+=－， 第四层图需要244113+=－个三角形， 摆第五层图需要255121+=－．那么摆第n 层图需要21n n +－个三角形．39. 【易】（怀柔区一模）观察下列图形及所对应的算式，根据你发现的规律计算1816248n ++++⋅⋅⋅+(n 是正整数)的结果为（ ）A ．()221n +B ．18n +C ．18(1)n +-D ．244n n +【答案】A40. 【易】（2012年青羊区初一下期末）下图是用火柴棍摆成的边长分别是1，2，3根火柴棍时的正方形．当边长为n 根火柴棍时，设摆出的正方形所用的火柴棍的根数为S ，则S =________．（用n 的代数式表示S ）【答案】()21n n +41. 【易】（2010年北京怀柔区期末）小明在阅览时发现这样一个问题“在某次聚会中，共有6人参加，如果每两个人都握一次手，共握几次手？”小明通过努力得出了答案，同时为了解决的方法更具有一般性，小明设计了以下图表进行探究．n =1 n =2 n=3请你在图表右下角的横线上填上你归纳出的一般结论． 【答案】()12n n -42. 【易】（郑州一中教育集团2010-2011学年上期期中考试）图中是一幅“苹果排列图”，第一行有1个苹果，第二行有2个，第三行有4个，第四行有8个，你是否发现苹果的排列规律？猜猜看，第十行有________个苹果； 第n 行有________个苹果．（可用乘方形式表示）【答案】92，12n -43. 【易】（2010深圳外国语初一上联合测）在计算机程序中，二叉树是一种表示数据结构的方法，如图，一层二叉树的结点总数为1，二层二叉树的结点总数为3，三层二叉树的结点总数为7······照此规律，七层二叉树的结点总数为（ ）A ．63B ．64C ．127D ．128【答案】C （规律为21n -）44. 【易】（福建三明市中考）如图，直线l 上有2个圆点A ，B ．我们进行如下操作：第1次操作，在A ，B 两圆点间插入一个圆点C ，这时直线l 上有（2＋1）个圆点；第2次操作，在A ，C 和C ，B 间再分别插入一个圆点，这时直线l 上有（3＋2）个圆点；第3次操作，在每相邻的两圆点间再插入一个圆点，这时直线l 上有（5＋4）个圆点；…第n 次操作后，这时直线l 上有________个圆点．……三层二叉树二层二叉树一层二叉树【答案】21n +45. 【易】（2010年九年级第三次质量预测试题）观察下列图形（每幅图中最小的三角形都是全等的），请写出第n个图中最小的三角形的个数有________个．【答案】14n -46.【中】（2012广西桂林中考）下图是在正方形网格中按规律填成的阴影，根据此规律，则第n 个图中阴影部分小正方形的个数是________．【答案】22n n ++47. 【中】（2011年天津市河北区初中毕业生学业考试模拟试卷（三））如图，第1个多边形由正三角形“扩展”而来，边数记为3a ，且312a =；第2个多边形由正方形“扩展”而来，边数记为4a ，且420a =；…；依此类推，由正n 边形“扩展”而来的多边形的边数记为()3n a n ≥，则当3451111n a a a a ++++的结果是6702013时，n 的值为________．【解析】()1n a n n =+，则()111111n a n n n n ==++－， （第16题）l l l lA B A B C A B C 第1个图第2个图第3个图第4个图（第14题图）所以34511111131n a a a a n ++++=+－，则2012n =． 【答案】201248. 【中】（武汉）如图的图案均是用长度相同的小木棒按一定的规律拼搭而成，拼搭第一个图案需4根小木棒，拼搭第2个图案需10根小木棒，……，依此提出，拼搭第8个图案需小木棒________根．【答案】8849. 【中】（2011-2012年铁二中初一下期中）如图①是一块瓷砖的图案，用这种瓷砖来铺设地面，如果铺成一个22⨯的正方形图案（如图②），其中完整的圆共有5个，如果铺成一个33⨯的正方形图案（如图③），其中完整的圆共有13个，如果铺成一个44⨯的正方形图案（如图④），其中完整的圆共有25个，若这样铺成一个1010⨯的正方形图案，则其中完整的圆共有________个．【答案】18150. 【中】（荆州市中考）图①是一瓷砖的图案，用这种瓷砖铺设地面，图②铺成了一个2×2的近似正方形，其中完整菱形共有5个；若铺成3×3的近似正方形图案③，其中完整的菱形有13个；铺成4×4的近似正方形图案④，其中完整的菱形有25个；如此下去，可铺成一个n n ⨯的近似正方形图案．当得到完整的菱形共181个时，n 的值为（ ） A ．7 B ．8 C ．9 D ．10【答案】D51. 【中】按照如图所示的式样画下去，则第15个图形有________个黑方块．【解析】由已知所画图形，可得：依次图形的方块数是：1，9，25，49，…又：1=129=3225=5249=72…左边乘方的底数依次是：1，3，5，7，…1=1+2×（1﹣1）3=1+2×（2﹣1）5=1+2×（3﹣1）7=1+2×（4﹣1）…那么第15项可表示为：1+2×（15﹣1）=29．所以第15个图形的方块数为：292．又从图形上得知，所以黑方块数为22914212+=个．【答案】42152.【中】（武汉二中广雅七年级下期末模拟试卷）如图，是由同型号黑白两种颜色的正三角形瓷砖按一定规律铺设的图形，仔细观察图形可知：图⑴中黑色瓷砖与白色瓷砖块数之比为1:3；图⑵中黑色瓷砖与白色瓷砖块数之比为3:6；图⑶中黑色瓷砖与白色瓷砖块数之比为6:10；···；那么按这样的规律铺设，第6个图形黑色瓷砖与白色瓷砖块数之比为________．【答案】3:453.【中】（2013年安徽省初中毕业学业考试数学）我们把正六边形的顶点及其对称中心称作如图（1）所示基本图的特征点，显然这样的基本图共有7个特征点．将此基本图不断复制并平移，使得相邻两个基本图的一边重合，这样得到图（2）、图（3），……．⑴猜想：在图（）中，特征点的个数为（用表示）⑵ 如图，将图（n ）放在直角坐标系中，设其中第一个基本图的对称中心1O 的坐标为()12x ，，则1x =________；图（2013）的对称中心的横坐标为___________【答案】⑴22；52n +⑵1x =；54. 【中】（2012年安徽省初中毕业学业考试数学）在由()1m n m n ⨯⨯＞个小正方形组成的矩形网格中，研究它的一条对角线所穿过的小正方形个数f ，⑴当m 、n 互质（m 、n 除1外无其他公因数）时，观察下列图形并完成下表：图(3)图(2)图(1)……图(n )x⑵猜想：当m 、n 互质时，在m n ⨯的矩形网格中，一条对角线所穿过的小正方形的个数f 与m 、n 的关系式是________（不需要证明）；⑶当m 、n 不互质时，请画图验证你猜想的关系式是否依然成立； 根据题意，画出当m 、n 不互质时，结论不成立的反例即可． 【答案】⑴如表：⑵1f m n =+－⑶m 、n 不互质时，上述结论不成立，例如2×4，如下图：55. 【中】（初二上题型训练一）如图是某广场用地板铺设的部分图案，中央是一块正六边形的地板砖，周围是正三角形和正方形的地板砖．从里向外的第1层包括6个正方形和6个正三角形，第2层包括6个正方形和18个正三角形，依此递推，第8层中含有正三角形个数是（ ） A ．54个 B ．90个 C ．102个 D ．114个【答案】B56. 【中】（2011年南山二外初一下测试）观察下图，我们可以发现：第1个图中有1个正方形，第2个图中共有5个正方形，第3个图中共有14个正方形，按照这种规律下去的第5个图形共有________个正方形．【答案】5557. 【中】（2011深圳外国语分校初一下期末）某种树木的分枝生长规律如图所示，则预计到第6年时，树木的分枝数为（ ）A ．5B ．6C ．7D ．8【答案】D58. 【中】(2009年初一上期末)意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…，其中从第三个数起，每一个数都等于它前面两个数的和、现以这组数中的各个数作为正方形的边长值构造如下正方形：再分别依次从左到右取2个、3个、4个、5个…正方形拼成如下长方形并记为①、②、③、④、…相应长方形的周长如下表所示：________，________若按此规律继续作长方形，则序号为⑧的长方形周长是________ 【答案】16x =，26y =，周长是17859. 【中】（2012黑龙江绥化中考）长为20，宽为a 的矩形纸片（1020a ＜＜），如图那样折一下，剪下一个边长等于矩形宽度的正方形（称为第一次操作）；再把剩下的矩形如图那样折一下，剪下一个边长等于此时矩形宽度的正方形（称为第二次操作）；……第3个图第2个图第1个图如此反复操作下去，若在第n 次操作后，剩下的矩形为正方形，则操作停止．当3n =时，a 的值为________．【答案】12或152．数字的变化60. 【易】（2010-2011太原市七年级第二次测评）下面的正方形中都填有4个数，这些数之间有一定的规律，根据此规律，m 的值是（ ）A ．38B ．52C ．66D ．74【答案】D本题考察类似于“行列式”的交叉相乘规律： 24084622268444810674m⨯-=⨯-=⨯-=⨯-==61. 【易】（武汉二中广雅中学2010-2011下学期期末七年级数学）如图，填在各方格中的三个数之间均具有相同规律，根据此规律，n 的值是（ ）A ．36B ．49C ．63D ．64【答案】B62. 【易】（2013年福建省泉州市初中毕业、升学考试）有一数值转换器，原理如图所示，若开始输入x 的值是7，可发现第1次输出的结果是12，第2次输出的结果是6，第3次输出的结果是________，依次继续下去，第2013次输出的结果是_______．【答案】3；363. 【易】（2013年三明市初中毕业暨高级中等学校招生统一考试）观察下列各数，它们是按一定规律排列的，则第n 个数是_______．12，34，78，1516，3132，【答案】212n n -64. 【易】(2013年山东日照初中学业考试)如图，下列各图形中的三个数之间均具有相同的规律．根据此规律，图形中M 与m 、n 的关系是（ ）A ．M mn =B ．()1M n m =+C ．1M mn =+D ．()1M m n =+【答案】D65. 【易】（2013年南宁市初中毕业升学考试数学试卷）陈老师打算购买气球装扮学校“六一”儿童节活动会场，起球的种类有笑脸和爱心两种，两种气球的价格不同，但同一种气球的价格相同，由于会场布置需要，购买时以一束（4个气球）为单位，已知第一、二束气球的价格如图所示，则第三束气球的价格为：A ．19B ．18C ．16D ．15【答案】C66. 【易】(山西省2013中考数学试卷)一组按规律排列的式子：2a ，43a ，65a ，87a ，…，则第n 个式子是__________（n 为正整数）．【答案】221na n -67. 【易】（2010深圳外国语分校初一上期中）有若干个数，第一个数记为1a ，第二个数记为2a ，···，第n 个数记为n a ．若112a =-，从第二个数起，每个数都等于“1与…mnM 56353415321它前面那个数的差的倒数”．试计算：2a =________，3a =________，4a =________，6a =________．你发现这排数有什么规律吗？由你发现的规律，请计算2004a 是多少？【答案】223a =，33a =，412a =-，63a =．规律：每三个数一循环 20043a =68. 【易】（2011深圳外国语分校初一上期中）读题填空：等边ABC △在数轴上的位置如图所示，点A 、C 对应的数字分别是0和1-，若△ABC 绕顶点沿顺时针方向在数轴上连续翻转，翻转1次后，点B 所对应的数为1，则连续翻转2012次后，点B 对应的数字为________．【答案】201169. 【易】（2011深圳育才二中初一上期中）如下表，从左到右在每个小格子中都填入一个整数，使得其中任意三个相邻格子中所填整数之和都相等，则第2011个格子中的数70. 【易】（2011耀华实验初三四模）在很小的时候，我们就用手指练习过数数．一个小朋友按如图所示的规则练习数数，数到2010时对应的指头是________（填出指头的名称，各指头的名称依次为大拇指、食指、中指、无名指、小指）．【答案】无名指71. 【易】（杭州翠苑中学初一2011第一学期期中）让我们轻松一下，做一个数字游戏：第一步：取一个自然数12n =，计算211n +得1a ；第二步：算出1a 的各位数字之和得2n ，计算221n +得2a ； 第三步：算出2a 的各位数字之和得3n ，计算231n +得3a ； B…………以此类推则2011a =________． 【答案】12272. 【易】（石景山二模）有一列数1a ，2a ，3a ，，n a ，从第二个数开始，每一个数都等于1与它前面那个数的倒数的差，若12a =，则2009a 为（ ） A ．2009B ．2C ．12D ．1-【答案】C73. 【易】（2011•南京）甲、乙、丙、丁四位同学围成一圈依序循环报数，规定：①甲、乙、丙、丁首次报出的数依次为1、2、3、4，接着甲报5，乙报6…按此规律，后一位同学报出的数比前一位同学报出的数大1．当报到的数是50时，报数结束； ②若报出的数为3的倍数，则报该数的同学需拍手一次．在此过程中，甲同学需拍手的次数为________． 【答案】4解：∵甲、乙、丙、丁首次报出的数依次为1、2、3、4，接着甲报5，乙报6…按此规律，后一位同学报出的数比前一位同学报出的数大1．当报到的数是50时，报数结束； ∴504=122÷⋅⋅⋅⋅⋅⋅，∴甲共报数13次，分别为1，5，9，13，17，21，25，29，33，37，41，45，49，∴报出的数为3的倍数，则报该数的同学需拍手一次．在此过程中，甲同学需拍手的次数为：9，21，33，45时， 所以一共有4次．74. 【中】（2011深圳外国语分校初一下期末）“抢30”游戏的规则是：第一个人先说“1”或“1、2”，第二个人要接着往下说一个或两个数，然后又轮到第一个人，再接着往下说一个或两个数，这样两人反复轮流，每次每人说一个或两个数都可以，但是不可以连说三个数，谁先抢到30谁就获胜，那么采取适当策略，其结果是（ ） A ．先报数者胜 B ．后报数者胜 C ．两者都可能胜 D ．很难预料 【答案】B为了抢到30，那就必须抢到27，这样无论对方叫“28”或“29”，你都获胜．游戏的关键是报数先后顺序，并且每次报的个数和对方合起来是三个，即对方报a ()12a ≤≤个数字，你就报()3a －个数．抢数游戏，它的本质是一个是否被“3”整除的问题．75. 【中】（辽宁省中考题）计算：1234531431103128318231244+=+=+=+=+=，，；，，…归纳各计算结果中的个位数字的规律，猜测200931+的个位数字是（ ）． A ．0 B ．2 C ．4 D ．8【答案】C76. 【易】（2011年初一上期中）观察下列算式：122=，224=，328=，4216=，5232=，6264=，72128=，82256=，······根据上述算式中的规律，你认为302的个位数字是________． 【答案】477. 【易】（2010深圳外国语初一下期末）已知122=，224=，328=，，则20112的末位数字是（ ） A ．2 B ．4 C ．6 D ．8 【答案】D78. 【易】（2010深圳外国语分校初一下期中）已知122=，224=，328=，4216=，5232=，6264=，72128=，82256=，……结合计算估计一下：()()()()()24322121212121-++++的个位数字是________．【答案】579. 【易】（郑州四中2010-2011学年下期初三年级第五次月考）观察算式：133=，239=，3327=，4381=，53243=，63729=，732187=，836561=，···通过观察，用你所发现的规律确定32011的个位数字是（ ） A ．3 B ．9 C ．7 D ．1 【答案】C80. 【易】（2010-2011武汉青山区初一上期末）己知：41=4，42=16，43=64，44=256，45=1024…以上算式结果的个位数字分别为4，6，4，6…，按照上面的研究方法确定20062007+20072006的个位数字为（ ） A ．3 B ．4 C ．5 D ．6 【答案】C81. 【易】（2011深圳中学初一上期中）QQ 空间一个展示自我和沟通交流的网络平台，它既是网络日记本，又可以上传图片、视频等，QQ 空间等级是用户资料和身份的象征，按照空间积分划分不同的等级，当用户在10级以上，每个等级与对应的积分有一定的关系，现在知道第10级的积分是90，第11级的积分是160，第12级的积分是250，第13级的积分是360，第14级的积分是490······，若某用户的空间积分达到1000，则他的等级是（ ） A ．18 B ．17 C ．16 D ．15 【答案】B解：第10级到第11级，12级，13级，14级积分分别增加的值是70，90，110，130，15级增加150，16级增加170，17级增加190，18级增加210，则15级积分是640，16级积分是810，17级积分是1000，18级积分是1210， 所以他的等级是17级．82. 【易】（眉山市中考）一组按规律排列的多项式：，，，，···，其中第10个式子是（ ） A ． B ． C ． D ． 【答案】B83. 【易】（初一下期中）观察下列单项式：、、、、…，按此规律写出第13个单项式是________． 【答案】84. 【易】（石景山一模）一组按规律排列的式子：3579234,,,,x x x x y y y y--（0xy ≠），其中第6个式子是________，第n 个式子是________（n 为正整数）．【答案】136x y-，211(1)n n n xy ++-85. 【易】（怀柔一模）一组按规律排列的式子：52a b ，84a b -，118a b ，1416a b-，……（0ab ≠），其中第6个式子是________，第n 个式子是________（n 为正整数）．【答案】2064a b -；()32121n n n a b ++-⋅或()32121n n n ab+--⋅86. 【易】（2010年门头沟二模）一组按一定规律排列的式子：2a -，52a ，83a -，114a ，…，()0a ≠，则第n 个式子是________（n 为正整数）． 【答案】87. 【易】（门头沟初二上期末）一组按规律排列的分式：3b a ，522b a-，733b a ，944b a-，…（0b ≠），其中第8个分式是________，第n 个分式是________（n 为正整数）．a b +23a b -35a b +47a b -1019a b +1019a b -1017a b -1021a b -23x 38x 415x 524x 14195x 31(1)n na n--。

完整)初中数学找规律专项练习题(有答案)1、观察规律：1=1；1+3=4；1+3+5=9；1+3+5+7=16；…，则2+6+10+14+…+2014的值是多少？2、用四舍五入法对取近似数，并精确到千位，用科学计数法表示为多少？3、观察下面的一列数：-1，2，-3，4，-5，6…请找出其中排列的规律，并按此规律填空。

（1）第10个数是多少？第21个数是多少？（2）-40是第几个数？26是第几个数？4、一组按规律排列的数：1，3，6，10，15…请推断第9个数是多少？5、计算：（-100）+（-101）=多少？（-2）+（-2）=多少？6、若。

则等于多少？7、大肠杆菌每过20分钟便由1个分裂成2个，经过3小时后这种大肠杆菌由1个分裂成多少个？8、猜数字游戏中，XXX写出如下一组数：1，3，5，7，9…n个数是…，XXX猜想出第六个数字是多少？根据此规律，第9、10个数字分别是多少？9、若。

与｜b+5|的值互为相反数，则等于多少？10、在计数制中，通常我们使用的是“十进位制”，即“逢十进一”.而计数制方法很多，如60进位制：60秒化为1分，60分化为1小时；24进位制：24小时化为1天；7进位制：7天化为1周等…而二进位制是计算机处理数据的依据.已知二进位制与十进位制的比较如下表：十进位制二进制 1 1 2 10 3 11 4 100 5 101 6 110 …… 请将二进位制xxxxxxxx（二）写成十进位制数为多少？11、为求。

值，可令S=。

则2S=。

因此所以。

仿照以上推理计算出的值是多少？二、选择题13、的值是多少？【】A．-2 B．-1 C．0 D．114、已知8.62=73.96，若x=0.7396，则x的值等于（）A.86.2B.862C.±0.862D.±86215、计算：(-2)+(-2)的值是多少？A.2B.-1C.-2D.-416、计算等于多少？A． B． C． D．17、已知a、b互为相反数，c、d互为倒数，m的绝对值为1，p是数轴到原点距离为1的数，那么的值是多少？A．3 B．2 C．1 D．018、若。

中考数学找规律练习题（20道，后附答案）一：数式问题1.已知22223322333388+=⨯+=⨯，，244441515+=⨯，……，若288a ab b+=⨯（a 、b 为正整数）则a b +=．2.有一列数a 1，a 2，a 3，a 4，a 5，…，a n ，其中a 1＝5×2＋1，a 2＝5×3＋2，a 3＝5×4＋3，a 4＝5×5＋4，a 5＝5×6＋5，…，当a n ＝2009时，n 的值等于（）A．2010B．2009C．401D．3343.有一组单项式：a 2，－a 32，a 43，－a 54，…．观察它们构成规律，用你发现的规律写出第10个单项式为．4.有一列数1234251017--，，，…，那么第7个数是．5.观察下列等式：111122⨯=-，222233⨯=-，333344⨯=-，……（1）猜想并写出第n 个等式；（2）证明你写出的等式的正确性．6.将正整数依次按下表规律排成四列，则根据表中的排列规律，数2009应排的位置是第行第列．第1列第2列第3列第4列第1行123第2行654第3行789第4行121110……7.将正整数1，2，3，…从小到大按下面规律排列．若第4行第2列的数为32，则①n=；②第i行第j列的数为（用i，j表示）．第1列第2列第3列…第n列第1行123…n第2行1+n2+n3+n…n2第3行12+n22+n32+n…n3………………二：定义运算问题8、有一列数1a，2a，3a， ，n a，从第二个数开始，每一个数都等于1与它前面那个数的倒数的差，若12a=，则2007a为（）Ａ．2007Ｂ．2Ｃ．12Ｄ．1-三：剪纸问题9．如图（9），把一个正方形三次对折后沿虚线剪下则得到的图形是（）10题图四：数形结合问题10、已知,A、B、C、D、E 是反比例函数16y x=（x>0）图象上五个整数点（横、纵坐标均为整数），分别以这些点向横轴或纵轴作垂线段，由垂线段所在的正方形边长为半径作四分之一圆周的两条弧，组成如图5所示的五个橄榄形（阴影部分），则这五个橄榄形的面积总和是（用含π的代数式表示）11、阅读材料：设一元二次方程ax 2+bx +c ＝0(a ≠0)的两根为x 1，x 2，则两根与方程系数之间有如下关系：x 1+x 2＝－b a ，x 1·x 2＝c a.根据该材料填空：已知x 1、x 2是方程x 2+6x +3＝0的两实数根，则21x x +12x x 的值为．12、如图，在x 轴的正半轴上依次截取112233445OA A A A A A A A A ====，过点12345A A A A A 、、、、分别作x 轴的垂线与反比例函数()20y x x=≠的图象相交于点12345P P P P P 、、、、，得直角三角形1112233344455OP A A P A A P A A P A A P A 2、、、、，并设其面积分别为12345S S S S S 、、、、，则5S 的值为．四:图形问题13.如图所示，已知：点(00)A ，，3B ，，(01)C ，在ABC △内依次作yxO P 1P 2P 3P4P 5A 1A 2A 3A 4A 5（第12题图）2y x=第14题图C 2D 2C 1D 1CD AB等边三角形，使一边在x 轴上，另一个顶点在BC 边上，作出的等边三角形分别是第1个11AA B △，第2个122B A B △，第3个233B A B △，…，则第n 个等边三角形的边长等于（）14.如图，边长为1的菱形ABCD 中，︒=∠60DAB ．连结对角线AC ，以AC 为边作第二个菱形11D ACC ，使︒=∠601AC D ；连结1AC ，再以1AC 为边作第三个菱形221D C AC ，使︒=∠6012AC D ；……，按此规律所作的第n 个菱形的边长为．15.如图，已知Rt ABC △，1D 是斜边AB 的中点，过1D 作11D E AC ⊥于E 1，连结1BE 交1CD 于2D ；过2D 作22D E AC ⊥于2E ，连结2BE 交1CD 于3D ；过3D 作33D E AC ⊥于3E ，…，如此继续，可以依次得到点45D D ，，…，n D ，分别记112233BD E BD E BD E △，△，△，…，n n BD E △的面积为123S S S ，，，…n S .则n S =________ABC S △（用含n 的代数式表示）.16.用正三角形和正六边形按如图所示的规律拼图案，即从第二个图案开始，每个图案都比上一个图案多一个正六边形和两个正三角O yx(A )A 1C112B A 2A 3B 3B 2B 1第13题图BCAE 1E 2E 3D 4D 1D 2D 3（第15题）（第16题）形，则第n个图案中正三角形的个数为（用含n 的代数式表示）.17.如图，用同样大小的黑色棋子按图所示的方式摆图案，按照这样的规律摆下去，第100个图案需棋子枚．18.观察下列图形（每幅图中最小．．的三角形都是全等的），请写出第n 个图中最小．．的三角形的个数有个．19.观察下列图形：它们是按一定规律排列的，依照此规律，第16个图形共有个★．五：对称问题20.在平面直角坐标系中，已知3个点的坐标分别为1(11)A ，、2(02)A ，、3(11)A ，.一只电子蛙位于坐标原点处，第1次电子蛙由原点第1个图第2个图第3个图第4个图（第18题图）第17题图图案1图案2图案3……跳到以A为对称中心的对称点1P，第2次电子蛙由1P点跳到以2A为对1称中心的对称点P，第3次电子蛙由2P点跳到以3A为对称中心的对称2点P，…，按此规律，电子蛙分别以1A、2A、3A为对称中心继续跳下3去．问当电子蛙跳了2009次后，电子蛙落点的坐标是P（_______，2009_______）.参考答案1、8+63=712、D3、－a11104、－7505、（1）n×=n-；（2）证明见解析.【解析】试题分析：（1）等号左边第一个因数为整数，与第二个因数的分子相同，第二个因数的分母比分子多1；等号右边为等号左边的第一个数式-第二个因数，即n×=n-；（2）把左边进行整式乘法，右边进行通分．试题解析：（1）猜想：n×=n-；（2）证：右边==左边，即n×=n-考点：规律型：数字的变化类．6、670，第三列7、1010（i-1）+j8、D 9、C 10、13π-2611、1012、1/513、14、15、16、2n+217、30218、19、4920、（2，2）。

2020年中考数学试题分类汇编之十五新概念新规律题一、选择题1.（2020河南）定义运算：21m n mn mn =--☆．例如2:42424217=⨯-⨯-=☆．则方程10x =☆的根的情况为（ ） A. 有两个不相等的实数根 B. 有两个相等的实数根 C. 无实数根 D. 只有一个实数根【答案】A【详解】解：根据定义得：2110,x x x =--=☆1,1,1,a b c ==-=-()()22414115b ac ∴∆=-=--⨯⨯-=＞0, ∴ 原方程有两个不相等的实数根，故选.A2.（2020湖北武汉）下列图中所有小正方形都是全等的．图（1）是一张由4个小正方形组成的“L ”形纸片，图（2）是一张由6个小正方形组成的32⨯方格纸片．把“L ”形纸片放置在图（2）中，使它恰好盖住其中的4个小正方形，共有如图（3）中的4种不同放置方法，图（4）是一张由36个小正方形组成的66⨯方格纸片，将“L ”形纸片放置在图（4）中，使它恰好盖住其中的4个小正方形，共有n 种不同放置方法，则n 的值是（ ）A. 160B. 128C. 80D. 48解：由图可知，在66⨯方格纸片中，32⨯方格纸片的个数为5420⨯=（个） 则20480n =⨯= 故选：C ．③②①3.（2020重庆A 卷）把黑色三角形按如图所示的规律拼图案，其中第①个图案中有1个黑色三角形，第①个图案中有3个黑色三角形，第①个图案中有6个黑色三角形，…，按此规律排列下去，则第①个图案中黑色三角形的个数为（ ）A. 10B. 15C. 18D. 21解：∵第①个图案中黑色三角形的个数为1， 第①个图案中黑色三角形的个数3＝1+2， 第①个图案中黑色三角形的个数6＝1+2+3， ……∴第①个图案中黑色三角形的个数为1+2+3+4+5＝15， 故选：B ．4.（2020重庆B 卷）下列图形都是由同样大小的实心圆点按一定规律组成的，其中第①个图形一共有5个实心圆点，第②个图形一共有8个实心圆点，第③个图形一共有11个实心圆点，⋯，按此规律排列下去，第⑥个图形中实心圆点的个数为（ ）A.18B. 19C.20D.21 答案C.5．(2020山东枣庄)（3分）对于实数a 、b ，定义一种新运算“⊗”为：21a b a b=-⊗，这里等式右边是实数运算．例如：21113138==--⊗．则方程2(2)14x x -=--⊗的解是( ) A ．4x = B ．5x = C ．6x = D ．7x =【解答】解：根据题意，得12144x x =---， 去分母得：12(4)x =--， 解得：5x =，经检验5x =是分式方程的解．故选：B ．6．（3分）（2020•常德）如图，将一枚跳棋放在七边形ABCDEFG 的顶点A 处，按顺时针方向移动这枚跳棋2020次．移动规则是：第k 次移动k 个顶点（如第一次移动1个顶点，跳棋停留在B 处，第二次移动2个顶点，跳棋停留在D 处），按这样的规则，在这2020次移动中，跳棋不可能停留的顶点是（ ）A ．C 、EB ．E 、FC ．G 、C 、ED ．E 、C 、F【解答】解：经实验或按下方法可求得顶点C ，E 和F 棋子不可能停到． 设顶点A ，B ，C ，D ，E ，F ，G 分别是第0，1，2，3，4，5，6格，因棋子移动了k 次后走过的总格数是1+2+3+…+k =12k （k +1），应停在第12k （k +1）﹣7p格，这时P 是整数，且使0≤12k （k +1）﹣7p ≤6，分别取k ＝1，2，3，4，5，6，7时，12k （k +1）﹣7p ＝1，3，6，3，1，0，0，发现第2，4，5格没有停棋，若7＜k ≤2020，设k ＝7+t （t ＝1，2，3）代入可得，12k （k +1）﹣7p ＝7m +12t （t +1），由此可知，停棋的情形与k ＝t 时相同，故第2，4，5格没有停棋，即顶点C ，E 和F 棋子不可能停到． 故选：D ．7．（3分）（2020•烟台）如图，△OA 1A 2为等腰直角三角形，OA 1＝1，以斜边OA 2为直角边作等腰直角三角形OA 2A 3，再以OA 3为直角边作等腰直角三角形OA 3A 4，…，按此规律作下去，则OA n 的长度为（ ）A ．（√2）nB ．（√2）n ﹣1C ．（√22）nD ．（√22）n ﹣1【解答】解：∵△OA 1A 2为等腰直角三角形，OA 1＝1， ∴OA 2=√2；∵△OA 2A 3为等腰直角三角形， ∴OA 3＝2=(√2)2；∵△OA 3A 4为等腰直角三角形， ∴OA 4＝2√2=(√2)3． ∵△OA 4A 5为等腰直角三角形， ∴OA 5＝4=(√2)4， ……∴OA n 的长度为（√2）n ﹣1．故选：B ．8．（2020云南）（4分）按一定规律排列的单项式：a ，﹣2a ，4a ，﹣8a ，16a ，﹣32a ，…，第n 个单项式是（ ） A ．（﹣2）n ﹣1aB ．（﹣2）n aC ．2n ﹣1aD ．2n a解：∵a ＝（﹣2）1﹣1a ， ﹣2a ＝（﹣2）2﹣1a ，4a ＝（﹣2）3﹣1a ，﹣8a ＝（﹣2）4﹣1a ，16a ＝（﹣2）5﹣1a ，﹣32a ＝（﹣2）6﹣1a ，…由上规律可知，第n 个单项式为：（﹣2）n ﹣1a ． 选：A ．二、填空题9.（2020江西）公元前2000年左右，古巴比伦人使用的楔形文字中有两个符号（如图所示），一个钉头形代表1，一个尖头形代表10，在古巴比伦的记数系统中，人们使用的标记方法和我们当今使用的方法相同，最右边的数字代表个位，然后是十位，百位，根据符号记数的方法，右下面符号表示一个两位数，则这个两位数是 ．【解析】依题意可得，有两个尖头表示20102=⨯，有5个丁头表示15⨯，故这个两位数为2510．（2020贵州黔西南）（3分）如图，是一个运算程序的示意图，若开始输入x 的值为625，则第2020次输出的结果为 1 ．【分析】依次求出每次输出的结果，根据结果得出规律，即可得出答案． 【解答】解：当x ＝625时，15x ＝125，当x ＝125时，15x ＝25，当x ＝25时，15x ＝5，当x ＝5时，15x ＝1，当x ＝1时，x +4＝5， 当x ＝5时，15x ＝1，…依此类推，以5，1循环， （2020﹣2）÷2＝1010， 即输出的结果是1， 故答案为：111．（2020贵州黔西南）（3分）如图图形都是由同样大小的菱形按照一定规律所组成的，其中第①个图形中一共有3个菱形，第②个图形中一共有7个菱形，第③个图形中一共有13个菱形，…，按此规律排列下去，第⑦个图形中菱形的个数为 57 ．【解答】解：第①个图形中一共有3个菱形，即2+1×1＝3；第②个图形中一共有7个菱形，即3+2×2＝7；第③个图形中一共有13个菱形，即4+3×3＝13；…，按此规律排列下去，所以第⑦个图形中菱形的个数为：8+7×7＝57．故答案为：57．12．（2020齐齐哈尔）（（3分）如图，在平面直角坐标系中，等腰直角三角形①沿x轴正半轴滚动并且按一定规律变换，每次变换后得到的图形仍是等腰直角三角形．第一次滚动后点A1（0，2）变换到点A2（6，0），得到等腰直角三角形②；第二次滚动后点A2变换到点A3（6，0），得到等腰直角三角形③；第三次滚动后点A3变换到点A4（10，4√2），得到等腰直角三角形④；第四次滚动后点A4变换到点A5（10+12√2，0），得到等腰直角三角形⑤；依此规律…，则第2020个等腰直角三角形的面积是22020．【解答】解：∵点A1（0，2），∴第1个等腰直角三角形的面积=12×2×2=2，∵A2（6，0），∴第2个等腰直角三角形的边长为√2=2√2，∴第2个等腰直角三角形的面积=12×2√2×2√2=4＝22，∵A4（10，4√2），∴第3个等腰直角三角形的边长为10﹣6＝4， ∴第3个等腰直角三角形的面积=12×4×4=8＝23， …则第2020个等腰直角三角形的面积是22020； 故答案为：22020（形式可以不同，正确即得分）．13.(2020甘肃定西）已知5y x =+，当x 分别取1，2，3，…，2020时，所对应y 值的总和是_________. 答案：203214．（2020辽宁抚顺）（3分）如图，四边形ABCD 是矩形，延长DA 到点E ，使AE ＝DA ，连接EB ，点F 1是CD 的中点，连接EF 1，BF 1，得到△EF 1B ；点F 2是CF 1的中点，连接EF 2，BF 2，得到△EF 2B ；点F 3是CF 2的中点，连接EF 3，BF 3，得到△EF 3B ；…；按照此规律继续进行下去，若矩形ABCD 的面积等于2，则△EF n B 的面积为．（用含正整数n 的式子表示）解：∵AE ＝DA ，点F 1是CD 的中点，矩形ABCD 的面积等于2， ∴△EF 1D 和△EAB 的面积都等于1， ∵点F 2是CF 1的中点， ∴△EF 1F 2的面积等于， 同理可得△EF n ﹣1F n 的面积为，∵△BCF n 的面积为2×÷2＝，∴△EF n B 的面积为2+1﹣1﹣﹣…﹣﹣＝2﹣（1﹣）＝．故答案为：．15．（2020内蒙古呼和浩特）（3分）“书法艺术课”开课后，某同学买了一包纸练习软笔书法，且每逢星期几写几张，即每星期一写1张，每星期二写2张，……，每星期日写7张，若该同学从某年的5月1日开始练习，到5月30日练习完后累积写完的宣纸总数过120张，则可算得5月1日到5月28日他共用宣纸张数为 112 ，并可推断出5月30日应该是星期几 五、六、日 ．解：∵5月1日～5月30日共30天，包括四个完整的星期， ∴5月1日～5月28日写的张数为：4×＝112，若5月30日为星期一，所写张数为112+7+1＝120， 若5月30日为星期二，所写张数为112+1+2＜120， 若5月30日为星期三，所写张数为112+2+3＜120， 若5月30日为星期四，所写张数为112+3+4＜120， 若5月30日为星期五，所写张数为112+4+5＞120， 若5月30日为星期六，所写张数为112+5+6＞120， 若5月30日为星期日，所写张数为112+6+7＞120， 故5月30日可能为星期五、六、日． 故答案为：112；五、六、日．16．（2020黑龙江龙东）（3分）如图，直线AM 的解析式为1y x =+与x 轴交于点M ，与y 轴交于点A ，以OA 为边作正方形ABCO ，点B 坐标为(1,1)．过点B 作1EO MA ⊥交MA 于点E ，交x 轴于点1O ，过点1O 作x 轴的垂线交MA 于点1A ，以11O A 为边作正方形1111O A B C ，点1B 的坐标为(5,3)．过点1B 作12E O MA ⊥交MA 于1E ，交x 轴于点2O ，过点2O 作x 轴的垂线交MA 于点2A ．以22O A 为边作正方形2222O A B C ．⋯．则点2020B 的坐标 2020231⨯-，20203 ．解：点B 坐标为(1,1)， 11OA AB BC CO CO ∴=====，1(2,3)A ，111111123AO A B B C C O ∴====，1(5,3)B ∴，2(8,9)A ∴，222222239A O A B B C C O ∴====，2(17,9)B ∴，同理可得4(53,27)B ，5(161,81)B ，⋯由上可知，(231,3)Bn n n ⨯-，∴当2020n =时，(2320201,32020)Bn ⨯-．故答案为：2020(231⨯-，20203)．17．（2020黑龙江牡丹江）（3分）一列数1，5，11，19⋯按此规律排列，第7个数是() A ．37 B ．41 C ．55 D ．71解：1121=⨯-， 5231=⨯-， 11341=⨯-， 19451=⨯-，⋯第n 个数为(1)1n n +-， 则第7个数是：55． 故选：C ．18．（2020四川遂宁）（4分）如图所示，将形状大小完全相同的“▱”按照一定规律摆成下列图形，第1幅图中“▱”的个数为a1，第2幅图中“▱”的个数为a2，第3幅图中“▱”的个数为a3，…，以此类推，若2a1+2a2+2a3+⋯+2a n=n2020．（n为正整数），则n的值为4039．【解答】解：由图形知a1＝1×2，a2＝2×3，a3＝3×4，∴a n＝n（n+1），∵2a1+2a2+2a3+⋯+2a n=n2020，∴21×2+22×3+23×4+⋯+2n(n+1)=n2020，∴2×（1−12+12−13+13−14+⋯⋯+1n−1n+1）=n2020，∴2×（1−1n+1）=n2020，1−1n+1=n4040，解得n＝4039，经检验：n＝4039是分式方程的解，故答案为：4039．19．（2020广西南宁）（3分）如图，某校礼堂的座位分为四个区域，前区一共有8排，其中第1排共有20个座位（含左、右区域），往后每排增加两个座位，前区最后一排与后区各排的座位数相同，后区一共有10排，则该礼堂的座位总数是556个．解：因为前区一共有8排，其中第1排共有20个座位（含左、右区域），往后每排增加两个座位，所以前区最后一排座位数为：20+2（8﹣1）＝34，所以前区座位数为：（20+34）×8÷2＝216，以为前区最后一排与后区各排的座位数相同，后区一共有10排，所以后区的座位数为：10×34＝340，所以该礼堂的座位总数是216+340＝556个．故答案为：556个．20．（3分）（2020•常德）阅读理解：对于x3﹣（n2+1）x+n这类特殊的代数式可以按下面的方法分解因式：x3﹣（n2+1）x+n＝x3﹣n2x﹣x+n＝x（x2﹣n2）﹣（x﹣n）＝x（x﹣n）（x+n）﹣（x﹣n）＝（x﹣n）（x2+nx﹣1）．理解运用：如果x3﹣（n2+1）x+n＝0，那么（x﹣n）（x2+nx﹣1）＝0，即有x﹣n＝0或x2+nx﹣1＝0，因此，方程x﹣n＝0和x2+nx﹣1＝0的所有解就是方程x3﹣（n2+1）x+n＝0的解．解决问题：求方程x3﹣5x+2＝0的解为x＝2或x＝﹣1+√2或x＝﹣1−√2．【解答】解：∵x3﹣5x+2＝0，∴x3﹣4x﹣x+2＝0，∴x（x2﹣4）﹣（x﹣2）＝0，∴x（x+2）（x﹣2）﹣（x﹣2）＝0，则（x﹣2）[x（x+2）﹣1]＝0，即（x﹣2）（x2+2x﹣1）＝0，∴x﹣2＝0或x2+2x﹣1＝0，解得x＝2或x＝﹣1±√2，故答案为：x＝2或x＝﹣1+√2或x＝﹣1−√2．21．（3分）（2020•徐州）如图，∠MON＝30°，在OM上截取OA1=√3．过点A1作A1B1⊥OM，交ON于点B1，以点B1为圆心，B1O为半径画弧，交OM于点A2；过点A2作A2B2⊥OM，交ON于点B2，以点B2为圆心，B2O为半径画弧，交OM于点A3；按此规律，所得线段A20B20的长等于219．【解答】解：∵B1O＝B1A1，B1A1⊥OA2，∴OA1＝A1A2，∵B2A2⊥OM，B1A1⊥OM，∴B1A1∥B2A2，∴B1A1=12A2B2，∴A2B2＝2A1B1，同法可得A 3B 3＝2A 2B 2＝22•A 1B 1，…， 由此规律可得A 20B 20＝219•A 1B 1，∵A 1B 1＝OA 1•tan30°=√3×√33=1， ∴A 20B 20＝219， 故答案为219．22．（2020山西）（3分）如图是一组有规律的图案，它们是由边长相等的正三角形组合而成，第1个图案有4个三角形，第2个图案有7个三角形，第3个图案有10个三角形…按此规律摆下去，第n 个图案有 （3n +1） 个三角形（用含n 的代数式表示）．【分析】根据图形的变化发现规律，即可用含n 的代数式表示． 解：第1个图案有4个三角形，即4＝3×1+1 第2个图案有7个三角形，即7＝3×2+1 第3个图案有10个三角形，即10＝3×3+1 …按此规律摆下去，第n 个图案有（3n +1）个三角形． 故答案为：（3n +1）．23.（2020东莞）如图，等腰12Rt OA A ∆，1121OA A A ==，以2OA 为直角边作23Rt OA A ∆，再以3OA 为直角边作34Rt OA A ∆，以此规律作等腰89Rt OA A ∆，则89OA A ∆的面积是_________.答案：64（或62）24．（2020四川自贡）（4分）如图，直线y =−√3x +b 与y 轴交于点A ，与双曲线y =kx 在第三象限交于B 、C 两点，且AB •AC ＝16．下列等边三角形△OD 1E 1，△E 1D 2E 2，△E 2D 3E 3，…的边OE1，E1E2，E2E3，…在x轴上，顶点D1，D2，D3，…在该双曲线第一象限的分支上，则k＝4√3，前25个等边三角形的周长之和为60．【解答】解：设直线y=−√3x+b与x轴交于点D，作BE⊥y轴于E，CF⊥y轴于F．∵y=−√3x+b，∴当y＝0时，x=√33b，即点D的坐标为（√33b，0），当x＝0时，y＝b，即A点坐标为（0，b），∴OA＝﹣b，OD=−√33b．∵在Rt△AOD中，tan∠ADO=OAOD=√3，∴∠ADO＝60°．∵直线y=−√3x+b与双曲线y=kx在第三象限交于B、C两点，∴−√3x+b=k x，整理得，−√3x2+bx﹣k＝0，由韦达定理得：x1x2=√33k，即EB•FC=√33k，∵EBAB=cos60°=12，∴AB＝2EB，同理可得：AC＝2FC，∴AB•AC＝（2EB）（2FC）＝4EB•FC=4√33k＝16，解得：k＝4√3．由题意可以假设D1（m，m√3），∴m2•√3=4√3，∴m＝2∴OE1＝4，即第一个三角形的周长为12，设D2（4+n，√3n），∵（4+n）•√3n＝4√3，解得n＝2√2−2，∴E1E2＝4√2−4，即第二个三角形的周长为12√2−12，设D3（4√2+a，√3a），由题意（4√2+a）•√3a＝4√3，解得a＝2√3−2√2，即第三个三角形的周长为12√3−12√2，…，∴第四个三角形的周长为12√4−12√3，∴前25个等边三角形的周长之和12+12√2−12+12√3−12√2+12√4−12√3+⋯+12√25−12√24=12√25=60，故答案为4√3，60．25．（3分）（2020•怀化）如图，△OB1A1，△A1B2A2，△A2B3A3，…，△A n﹣1B n A n，都是一边在x轴上的等边三角形，点B1，B2，B3，…，B n都在反比例函数y=√3x（x＞0）的图象上，点A1，A2，A3，…，A n，都在x轴上，则A n的坐标为（2√n，0）．解：如图，过点B1作B1C⊥x轴于点C，过点B2作B2D⊥x轴于点D，过点B3作B3E⊥x轴于点E，∵△OA1B1为等边三角形，∴∠B1OC＝60°，OC＝A1C，∴B1C=√3OC，设OC的长度为t，则B1的坐标为（t，√3t），把B1（t，√3t）代入y=√3x得t•√3t=√3，解得t＝1或t＝﹣1（舍去），∴OA1＝2OC＝2，∴A1（2，0），设A1D的长度为m，同理得到B2D=√3m，则B2的坐标表示为（2+m，√3m），把B2（2+m，√3m）代入y=√3x得（2+m）×√3m=√3，解得m=√2−1或m=−√2−1（舍去），∴A1D=√2−1，A1A2=2√2−2，OA2=2+2√2−2=2√2，∴A2（2√2，0）设A2E的长度为n，同理，B3E为√3n，B3的坐标表示为（2√2+n，√3n），把B3（2√2+n，√3n）代入y=√3x得（2√2+n）•√3n=√3，∴A2E=√3−√2，A2A3=2√3−2√2，OA3=2√2+2√3−2√2=2√3，∴A3（2√3，0），综上可得：A n（2√n，0），故答案为：(2√n，0)．26．（2020青海）（2分）对于任意两个不相等的数a，b，定义一种新运算“⊕”如下：a⊕b ＝，如：3⊕2＝＝，那么12⊕4＝．解：12⊕4＝＝．故答案为：．27．（2020青海）（4分）观察下列各式的规律：①1×3﹣22＝3﹣4＝﹣1；②2×4﹣32＝8﹣9＝﹣1；③3×5﹣42＝15﹣16＝﹣1． 请按以上规律写出第4个算式 4×6﹣52＝24﹣25＝﹣1 ．用含有字母的式子表示第n 个算式为 n （n +2）﹣（n +1）2＝﹣1 ． 解：④4×6﹣52＝24﹣25＝﹣1．第n 个算式为：n （n +2）﹣（n +1）2＝﹣1．故答案为：4×6﹣52＝24﹣25＝﹣1；n （n +2）﹣（n +1）2＝﹣1． 28．（2020山东滨州）（5分）观察下列各式：123a =，235a =，3107a =，4159a =，52611a =，⋯，根据其中的规律可得n a =21(1)21n n n ++-+ （用含n 的式子表示）． 【解答】解：由分析可得21(1)21n n n a n ++-=+．故答案为：21(1)21n n n ++-+．29．（2020山东泰安）（4分）如表被称为“杨辉三角”或“贾宪三角”．其规律是：从第三行起，每行两端的数都是“1”，其余各数都等于该数“两肩”上的数之和．表中两平行线之间的一列数：1，3，6，10，15，…，我们把第一个数记为a 1，第二个数记为a 2，第三个数记为a 3，…，第n 个数记为a n ，则a 4+a 200＝ 20110 ．解：观察“杨辉三角”可知第n 个数记为a n ＝（1+2+…+n ）=12n （n +1）， 则a 4+a 200=12×4×（4+1）+12×200×（200+1）＝20110． 故答案为：20110．30．（2020海南）（4分）海南黎锦有着悠久的历史，已被列入世界非物质文化遗产名录．如图是黎锦上的图案，每个图案都是由相同菱形构成的，若按照第1个图至第4个图中的规律编织图案，则第5个图中有 41 个菱形，第n 个图中有 2n 2﹣2n +1 个菱形（用含n 的代数式表示）．解：∵第1个图中菱形的个数1＝12+02， 第2个图中菱形的个数5＝22+12， 第3个图中菱形的个数13＝32+22， 第4个图中菱形的个数25＝42+32， ∴第5个图中菱形的个数为52+42＝41，第n 个图中菱形的个数为n 2+（n ﹣1）2＝n 2+n 2﹣2n +1＝2n 2﹣2n +1， 故答案为：41，2n 2﹣2n +1．三、解答题31.（2020长沙）我们不妨约定：若某函数图像上至少存在不同的两点关于原点对称，则把该函数称之为“H 函数”，其图像上关于原点对称的两点叫做一对“H 点”，根据该约定，完成下列各题（1）在下列关于x 的函数中，是“H 函数”的，请在相应题目后面的括号中打“√”，不是“H 函数”的打“×”①2y x =（ ） ①my (m 0)x=≠（ ） ①31y x =-（ ） （2）若点()1,A m 与点(),4B n -关于x “H 函数” ()20y ax bx c a =++≠的一对“H 点”，且该函数的对称轴始终位于直线2x =的右侧，求,,a b c 的值域或取值范围；（3）若关于x 的“H 函数” 223y ax bx c =++（a ，b ，c 是常数）同时满足下列两个条件：①0a b c ++=，①(2)(23)0c b a c b a +-++<，求该H 函数截x 轴得到的线段长度的取值范围．【答案】（1）√；√；×；（2）-1＜a ＜0，b=4，0＜c ＜0；（3）2＜12x x -＜． 解：（1）①2y x =是 “H 函数”①my (m 0)x=≠是 “H 函数”①31y x =-不是 “H 函数”； 故答案为：√；√；×； （2）①A,B 是“H 点” ①A,B 关于原点对称， ①m=4,n=1①A(1,4），B （-1，-4） 代入223y ax bx c =++得44a b c a b c ++=⎧⎨-+=-⎩解得40b a c =⎧⎨+=⎩又①该函数的对称轴始终位于直线2x =的右侧，①-2ba ＞2 ①-42a＞2 ①-1＜a ＜0 ①a+c=0 ①0＜c ＜0，综上，-1＜a ＜0，b=4，0＜c ＜0；（3）①223y ax bx c =++是“H 函数”①设H 点为（p,q ）和（-p,-q ）,代入得222323ap bp c qap bp c q⎧++=⎨-+=-⎩ 解得ap 2+3c=0,2bp=q ①p 2＞0 ①a,c 异号， ①ac ＜0 ①a+b+c=0①b=-a -c ，①(2)(23)0c b a c b a +-++< ①(2)(23)0c a c a c a c a -----+< ①(2)(2)0c a c a -+< ①c 2＜4a 2①22c a＜4 ①-2＜c a ＜2 ①-2＜c a ＜0设t=ca，则-2＜t ＜0设函数与x 轴的交点为（x 1,0）（x 2,0） ①x 1, x 2是方程223ax bx c ++=0的两根①12x x -== 又①-2＜t ＜0①2＜12x x -＜．32.（2020山东青岛）实际问题：某商场为鼓励消费，设计了投资活动．方案如下：根据不同的消费金额，每次抽奖时可以从100张面值分别为1元、2元、3元、…、100元的奖券中（面值为整数），一次任意抽取2张、3张、4张、…等若干张奖券，奖券的面值金额之和即为优惠金额．某顾客获得了一次抽取5张奖券的机会，小明想知道该顾客共有多少种不同的优惠金额？ 问题建模：从1，2，3，…，n （n 为整数，且3n ≥）这n 个整数中任取()1a a n <<个整数，这a 个整数之和共有多少种不同的结果？ 模型探究：我们采取一般问题特殊化的策略，先从最简单的情形入手，再逐次递进，从中找出解决问题的方法． 探究一：（1）从1，2，3这3个整数中任取2个整数，这2个整数之和共有多少种不同的结果？ 表①如表①，所取的2个整数之和可以为3，4，5，也就是从3到5的连续整数，其中最小是3，最大是5，所以共有3种不同的结果．（2）从1，2，3，4这4个整数中任取2个整数，这2个整数之和共有多少种不同的结果？ 表①如表①，所取的2个整数之和可以为3，4，5，6，7，也就是从3到7的连续整数，其中最小是3，最大是7，所以共有5种不同的结果．（3）从1，2，3，4，5这5个整数中任取2个整数，这2个整数之和共有______种不同的结果．（4）从1，2，3，…，n （n 为整数，且3n ≥）这n 个整数中任取2个整数，这2个整数之和共有______种不同的结果．探究二：（1）从1，2，3，4这4个整数中任取3个整数，这3个整数之和共有______种不同的结果． （2）从1，2，3，…，n （n 为整数，且4n ≥）这n 个整数中任取3个整数，这3个整数之和共有______种不同的结果．探究三：从1，2，3，…，n （n 为整数，且5n ≥）这n 个整数中任取4个整数，这4个整数之和共有______种不同的结果．归纳结论：从1，2，3，…，n （n 为整数，且3n ≥）这n 个整数中任取()1a a n <<个整数，这a 个整数之和共有______种不同的结果．问题解决：从100张面值分别为1元、2元、3元、…、100元的奖券中（面值为整数），一次任意抽取5张奖券，共有______种不同的优惠金额．拓展延伸：（1）从1，2，3，…，36这36个整数中任取多少个整数，使得取出的这些整数之和共有204种不同的结果？（写出解答过程）（2）从3，4，5，…，3n +（n 为整数，且2n ≥）这()1n +个整数中任取()11a a n <<+个整数，这a 个整数之和共有______种不同的结果．解：探究一：（3）如下表：所取的2个整数之和可以为3，4，5，6，7，8，9也就是从3到9的连续整数，其中最小是3，最大是9，所以共有7种不同的结果．（4）从1，2，3，…，n （n 为整数，且3n ≥）这n 个整数中任取2个整数，这2个整数之和的最小值是3，和的最大值是21,n - 所以一共有()213123n n --+=-种． 探究二：（1）从1，2，3，4这4个整数中任取3个整数，如下表：从1，2，3，4这4个整数中任取3个整数，这3个整数之和共有4种，（2）从1，2，3，4，5这5个整数中任取3个整数，这3个整数之和的最小值是6，和的最大值是12,所以从1，2，3，4，5这5个整数中任取3个整数，这3个整数之和共有7种， 从而从1，2，3，…，n （n 为整数，且4n ≥）这n 个整数中任取3个整数， 这3个整数之和的最小值是6，和的最大值是33,n -所以一共有()336138n n --+=-种，探究三：从1，2，3，4，5这5个整数中任取4个整数， 这4个整数之和最小是10, 最大是14， 所以这4个整数之和一共有5种，从1，2，3，4，5，6这6个整数中任取4个整数， 这4个整数之和最小是10, 最大是18,， 所以这4个整数之和一共有9种，从1，2，3，…，n （n 为整数，且5n ≥）这n 个整数中任取4个整数，这4个整数之和的最小值是10，和的最大值是46n -，所以一共有()46101415n n --+=- 种不同的结果．归纳结论：由探究一，从1，2，3，…，n （n 为整数，且3n ≥）这n 个整数中任取2个整数，这2个整数之和共有()23n -种．探究二，从1，2，3，…，n （n 为整数，且4n ≥）这n 个整数中任取3个整数，这3个整数之和共有()38n -种，探究三，从1，2，3，…，n （n 为整数，且5n ≥）这n 个整数中任取4个整数，这4个整数之和共有()415n - 种不同的结果．从而可得：从1，2，3，…，n （n 为整数，且3n ≥）这n 个整数中任取()1a a n <<个整数，这a 个整数之和共有()21an a -+种不同的结果．问题解决：从100张面值分别为1元、2元、3元、…、100元的奖券中（面值为整数），一次任意抽取5张奖券，这5张奖券和的最小值是15，和的最大值是490，共有490151476-+=种不同的优惠金额．拓展延伸：（1） 从1，2，3，…，n （n 为整数，且3n ≥）这n 个整数中任取()1a a n <<个整数，这a 个整数之和共有()21an a -+种不同的结果． ∴ 当36,n = 有2361204,a a -+=236203,a a ∴-=-()218121,a ∴-= 1811a ∴-=或1811,a -=-29a ∴=或7.a =从1，2，3，…，36这36个整数中任取29个或7个整数，使得取出的这些整数之和共有204种不同的结果．（2）由探究可知：从3，4，5，…，3n +（n 为整数，且2n ≥）这()1n +个整数中任取()11a a n <<+个整数，等同于从1，2，3，…，1n +（n 为整数，且2n ≥）这()1n +个整数中任取()11a a n <<+个整数，所以：从3，4，5，…，3n +（n 为整数，且2n ≥）这()1n +个整数中任取()11a a n <<+个整数，这a 个整数之和共有()211a n a ⎡⎤+-+⎣⎦种不同的结果． 33．（2020四川遂宁）（9分）阅读以下材料，并解决相应问题：小明在课外学习时遇到这样一个问题：定义：如果二次函数y ＝a 1x 2+b 1x +c 1（a 1≠0，a 1、b 1、c 1是常数）与y ＝a 2x 2+b 2x +c 2（a 2≠0，a 2、b 2、c 2是常数）满足a 1+a 2＝0，b 1＝b 2，c 1+c 2＝0，则这两个函数互为“旋转函数”．求函数y ＝2x 2﹣3x +1的旋转函数，小明是这样思考的，由函数y ＝2x 2﹣3x +1可知，a 1＝2，b 1＝﹣3，c 1＝1，根据a 1+a 2＝0，b 1＝b 2，c 1+c 2＝0，求出a 2，b 2，c 2就能确定这个函数的旋转函数．请思考小明的方法解决下面问题：（1）写出函数y ＝x 2﹣4x +3的旋转函数．（2）若函数y ＝5x 2+（m ﹣1）x +n 与y ＝﹣5x 2﹣nx ﹣3互为旋转函数，求（m +n ）2020的值．（3）已知函数y ＝2（x ﹣1）（x +3）的图象与x 轴交于A 、B 两点，与y 轴交于点C ，点A 、B 、C 关于原点的对称点分别是A 1、B 1、C 1，试求证：经过点A 1、B 1、C 1的二次函数与y ＝2（x ﹣1）（x +3）互为“旋转函数”．【解答】解：（1）由y ＝x 2﹣4x +3函数可知，a 1＝1，b 1＝﹣4，c 1＝3，∵a 1+a 2＝0，b 1＝b 2，c 1+c 2＝0，∴a 2＝﹣1，b 2＝﹣4，c 2＝﹣3，∴函数y ＝x 2﹣4x +3的“旋转函数”为y ＝﹣x 2﹣4x ﹣3；（2）∵y ＝5x 2+（m ﹣1）x +n 与y ＝﹣5x 2﹣nx ﹣3互为“旋转函数”，∴{m −1=−n n −3=0， 解得：{m =−2n =3， ∴（m +n ）2020＝（﹣2+3）2020＝1．（3）证明：当x ＝0时，y ＝2（x ﹣1）（x +3））＝﹣6，∴点C 的坐标为（0，﹣6）．当y ＝0时，2（x ﹣1）（x +3）＝0，解得：x 1＝1，x 2＝﹣3，∴点A 的坐标为（1，0），点B 的坐标为（﹣3，0）．∵点A ，B ，C 关于原点的对称点分别是A 1，B 1，C 1，∴A1（﹣1，0），B1（3，0），C1（0，6）．设过点A1，B1，C1的二次函数解析式为y＝a（x+1）（x﹣3），将C1（0，6）代入y＝a（x+1）（x﹣3），得：6＝﹣3a，解得：a＝﹣2，过点A1，B1，C1的二次函数解析式为y＝﹣2（x+1）（x﹣3），即y＝﹣2x2+4x+6．∵y＝2（x﹣1）（x+3）＝2x2+4x﹣6，∴a1＝2，b1＝4，c1＝﹣6，a2＝﹣2，b2＝4，c2＝6，∴a1+a2＝2+（﹣2）＝0，b1＝b2＝4，c1+c2＝6+（﹣6）＝0，∴经过点A1，B1，C1的二次函数与函数y＝2（x﹣1）（x+3）互为“旋转函数”．34．（2020•怀化）定义：对角线互相垂直且相等的四边形叫做垂等四边形．（1）下面四边形是垂等四边形的是④；（填序号）①平行四边形；②矩形；③菱形；④正方形（2）图形判定：如图1，在四边形ABCD中，AD∥BC，AC⊥BD，过点D作BD垂线交BC的延长线于点E，且∠DBC＝45°，证明：四边形ABCD是垂等四边形．（3）由菱形面积公式易知性质：垂等四边形的面积等于两条对角线乘积的一半．应用：在图2中，面积为24的垂等四边形ABCD内接于⊙O中，∠BCD＝60°．求⊙O的半径．【解答】解：（1）①平行四边形的对角线互相平分但不垂直和相等，故不是垂等四边形；②矩形对角线相等但不垂直，故不是垂等四边形；③菱形的对角线互相垂直但不相等，故不是垂等四边形；④正方形的对角线互相垂直且相等，故正方形是垂等四边形；故选：④；（2）∵AC⊥BD，ED⊥BD，∴AC∥DE，又∵AD∥BC，∴四边形ADEC 是平行四边形，∴AC ＝DE ，又∵∠DBC ＝45°，∴△BDE 是等腰直角三角形，∴BD ＝DE ，∴BD ＝AC ，又∵BD ⊥AC ，∴四边形ABCD 是垂等四边形；（3）如图，过点O 作OE ⊥BD ，∵四边形ABCD 是垂等四边形，∴AC ＝BD ，又∵垂等四边形的面积是24，∴12AC •BD ＝24， 解得，AC ＝BD ＝4√3，又∵∠BCD ＝60°，∴∠DOE ＝60°，设半径为r ，根据垂径定理可得：在△ODE 中，OD ＝r ，DE =2√3，∴r =DE sin60°=2√332=4，∴⊙O 的半径为4．35．（2020浙江宁波）（14分）定义：三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角．（1）如图1，∠E 是△ABC 中∠A 的遥望角，若∠A ＝α，请用含α的代数式表示∠E ．（2）如图2，四边形ABCD 内接于⊙O ，AD ̂=BD ̂，四边形ABCD 的外角平分线DF 交⊙O于点F，连结BF并延长交CD的延长线于点E．求证：∠BEC是△ABC中∠BAC 的遥望角．（3）如图3，在（2）的条件下，连结AE，AF，若AC是⊙O的直径．①求∠AED的度数；②若AB＝8，CD＝5，求△DEF的面积．【解答】解：（1）∵BE平分∠ABC，CE平分∠ACD，∴∠E＝∠ECD﹣∠EBD=12（∠ACD﹣∠ABC）=12∠A=12α，（2）如图1，延长BC到点T，∵四边形FBCD内接于⊙O，∴∠FDC+∠FBC＝180°，又∵∠FDE+∠FDC＝180°，∴∠FDE＝∠FBC，∵DF平分∠ADE，∴∠ADF＝∠FDE，∵∠ADF＝∠ABF，∴∠ABF＝∠FBC，∴BE是∠ABC的平分线，̂=BD̂，∵AD∴∠ACD＝∠BFD，∵∠BFD+∠BCD＝180°，∠DCT+∠BCD＝180°，∴∠DCT＝∠BFD，∴∠ACD＝∠DCT，∴CE是△ABC的外角平分线，∴∠BEC是△ABC中∠BAC的遥望角．（3）①如图2，连接CF，∵∠BEC是△ABC中∠BAC的遥望角，∴∠BAC＝2∠BEC，∵∠BFC＝∠BAC，∴∠BFC＝2∠BEC，∵∠BFC＝∠BEC+∠FCE，∴∠BEC＝∠FCE，∵∠FCE＝∠F AD，∴∠BEC＝∠F AD，又∵∠FDE＝∠FDA，FD＝FD，∴△FDE≌△FDA（AAS），∴DE＝DA，∴∠AED＝∠DAE，∵AC是⊙O的直径，∴∠ADC＝90°，∴∠AED+∠DAE＝90°，∴∠AED＝∠DAE＝45°，②如图3，过点A 作AG ⊥BE 于点G ，过点F 作FM ⊥CE 于点M ，∵AC 是⊙O 的直径，∴∠ABC ＝90°，∵BE 平分∠ABC ，∴∠F AC ＝∠EBC =12∠ABC ＝45°，∵∠AED ＝45°，∴∠AED ＝∠F AC ，∵∠FED ＝∠F AD ，∴∠AED ﹣∠FED ＝∠F AC ﹣∠F AD ，∴∠AEG ＝∠CAD ，∵∠EGA ＝∠ADC ＝90°，∴△EGA ∽△ADC ，∴AE AC =AG CD ，∵在Rt △ABG 中，AG =√22AB =4√2，在Rt △ADE 中，AE =√2AD ，∴AD AC =45， 在Rt △ADC 中，AD 2+DC 2＝AC 2，∴设AD ＝4x ，AC ＝5x ，则有（4x ）2+52＝（5x ）2，∴x =53，∴ED ＝AD =203，∴CE ＝CD +DE =353，∵∠BEC＝∠FCE，∴FC＝FE，∵FM⊥CE，∴EM=12CE=356，∴DM＝DE﹣EM=5 6，∵∠FDM＝45°，∴FM＝DM=5 6，∴S△DEF=12DE•FM=259．36．（2020•株洲）如图所示，△OAB的顶点A在反比例函数y=kx（k＞0）的图象上，直线AB交y轴于点C，且点C的纵坐标为5，过点A、B分别作y轴的垂线AE、BF，垂足分别为点E、F，且AE＝1．（1）若点E为线段OC的中点，求k的值；（2）若△OAB为等腰直角三角形，∠AOB＝90°，其面积小于3．①求证：△OAE≌△BOF；②把|x1﹣x2|+|y1﹣y2|称为M（x1，y1），N（x2，y2）两点间的“ZJ距离”，记为d（M，N），求d（A，C）+d（A，B）的值．【解答】解：（1）∵点E为线段OC的中点，OC＝5，∴OE=12OC=52，即：E点坐标为(0，52)，又∵AE ⊥y 轴，AE ＝1，∴A(1，52)，∴k =1×52=52．（2）①在△OAB 为等腰直角三角形中，AO ＝OB ，∠AOB ＝90°，∴∠AOE +∠FOB ＝90°，又∵BF ⊥y 轴，∴∠FBO +∠FOB ＝90°，∴∠AOE ＝∠FBO ，在△OAE 和△BOF 中，{∠AEO =∠OFB =90°∠AOE =∠FBO AO =BO ，∴△OAE ≌△BOF （AAS ），②解：设点A 坐标为（1，m ），∵△OAE ≌△BOF ，∴BF ＝OE ＝m ，OF ＝AE ＝1，∴B （m ，﹣1），设直线AB 解析式为：l AB ：y ＝kx +5，将AB 两点代入得：则{k +5=m km +5=−1． 解得{k 1=−3m 1=2，{k 2=−2m 2=3． 当m ＝2时，OE ＝2，OA =√5，S △AOB =52＜3，符合；∴d （A ，C ）+d （A ，B ）＝AE +CE +（BF ﹣AE ）+（OE +OF ）＝1+CE +OE ﹣1+OE +1＝1+CE +2OE ＝1+CO +OE ＝1+5+2＝8，当m ＝3时，OE ＝3，OA =√10，S △AOB ＝5＞3，不符，舍去；综上所述：d （A ，C ）+d （A ，B ）＝8．。