材料力学能量法最经典解析

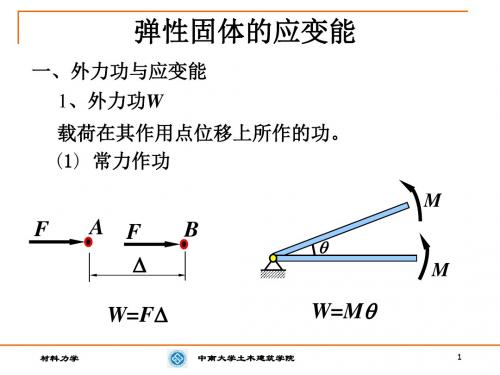
材料力学能量法材料力学能量法是材料力学中的一种重要分析方法，它通过能量原理来研究材料的力学性能和行为。

能量法在工程应用中具有广泛的意义，可以用于解决各种复杂的材料力学问题。

本文将对材料力学能量法进行详细介绍，包括其基本原理、应用范围和计算方法等内容。

首先，我们来看一下材料力学能量法的基本原理。

能量法是以能量守恒原理为基础的一种力学分析方法，它认为在任何力学系统中，系统的总能量始终保持不变。

在材料力学中，通过能量方法可以方便地求解结构的变形、应力分布和稳定性等问题。

能量法的基本原理为系统的总能量等于外力对系统做功的总和，即系统的内能和外力对系统做功的总和保持恒定。

其次，材料力学能量法的应用范围非常广泛。

它可以用于分析材料的弹性、塑性、断裂等力学性能，也可以用于研究材料的疲劳、蠕变、冷却等行为。

在工程实践中，能量法可以应用于各种材料的设计、优化和性能评估，如金属材料、复合材料、土木工程材料等。

通过能量法分析，可以更好地理解材料的力学行为，为工程设计和材料选型提供科学依据。

最后，我们来介绍一下材料力学能量法的计算方法。

能量法的计算方法主要包括弹性能量法、弹塑性能量法和断裂能量法等。

在应用中，需要根据具体问题选择合适的能量方法，并结合数值计算和实验验证进行分析。

在计算过程中，需要考虑材料的本构关系、加载条件和边界约束等因素，以确保计算结果的准确性和可靠性。

综上所述，材料力学能量法是一种重要的力学分析方法，具有广泛的应用前景和深远的理论意义。

通过能量法分析，可以更好地理解材料的力学性能和行为，为工程实践提供科学依据。

在今后的研究和应用中，我们需要进一步深入理解能量法的基本原理和计算方法，推动其在材料力学领域的发展和应用。

材料力学第10章能量法在材料力学这门学科中，能量法是一种重要的分析方法。

它可以帮助我们计算杆件受力、弯曲、扭转等方面的机械能量，以及计算受力杆件的变形和应力分布等方面的物理能量。

本文将对材料力学第10章中的能量法做一简要介绍和讲解。

第一节：能量法的基本概念能量法的基本概念是物理学中的能量守恒定律。

根据能量守恒定律，能量可以被转化为其他形式，但总能量守恒不变。

在材料力学中，能量法通过分析杆件的受力变形过程，计算机械能、变形能和应变能等不同形式的能量，来求解某些物理量，如杆件的应力、变形等。

第二节：能量法的应用能量法可以应用在杆件的弯曲、扭转、受力等方面。

其中，弯曲问题是最为常见的。

在弯曲分析中，我们需要计算杆件上各点的剪力和弯矩，使用能量法时，我们可以采用双曲线弧长法和曲率半径法来计算。

在扭转分析中，我们需要计算杆件上各点的切向力和扭矩，使用能量法时，我们可采用扭转角度法和扭转能的变化法来计算。

在受力分析中，我们需要计算杆件上各点的应力和应变，使用能量法时，我们可以用弹性能和破裂能来计算杆件的应力和应变等物理量。

第三节：能量法的计算过程在应用能量法进行分析时，需要进行以下步骤：1. 建立受力变形模型：根据杆件的几何形状和受力情况建立受力变形模型，确定受力分布和变形情况。

2. 确定杆件的位移和应变能量：计算杆件受力变形后的弹性能、变形能等物理能量。

3. 利用能量守恒定律：将机械能、弹性能、变形能和应变能等能量之和等于零，根据能量守恒定律和受力变形模型，求解杆件的位移、应力和应变等物理量。

4. 对解得的结果进行有效检验：通过检查应力、应变等物理量的分布情况，对解得的结果进行有效检验。

总而言之，能量法是材料力学分析领域中非常重要的分析方法。

它广泛应用于工程设计、科研和生产实践等领域。

通过掌握能量法的理论基础和实际应用方法，可以有效地分析和解决杆件受力、弯曲、扭转等方面的技术问题，推动材料力学学科的发展进步。