2018届广东省广州市高三毕业班综合测试(二)文科数学试

数学（文科）试题A 第 1 页 共 8 页2018届广州市高三年级调研测试 文科数学试题答案及评分参考评分说明:1．本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分参考制订相应的评分细则．2．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数． 4．只给整数分数．选择题不给中间分．一．选择题二．填空题13．10 14．21- 15．1ln 2+ 16．1三、解答题17． 解：（1）当1n =时，114a =．………………………………………………………………………1分 因为221*123-144+44,4n n n n n a a a a a n --++++=∈N L ， ①所以22123-1-1444,24n n n a a a a n -++++=≥L ． ②……………………………………3分①－②得1144n n a -=．……………………………………………………………………………………4分所以()*1=2,4n n a n n ≥∈N ．……………………………………………………………………………5分由于114a =也满足上式，故*1=()4n n a n ∈N ．…………………………………………………………6分（2）由（1）得421n n n a b n =+=121n +．………………………………………………………………………7分所以()()11111=212322123n n b b n n n n +⎛⎫=- ⎪++++⎝⎭．………………………………………………9分数学（文科）试题A 第 2 页 共 8 页故1111111235572123n T n n ⎛⎫=-+-++- ⎪++⎝⎭L ……………………………………………………10分 1112323n ⎛⎫=- ⎪+⎝⎭…………………………………………………………………………………11分 69nn +=．…………………………………………………………………………………………12分18．（1）证明：连接 BD ，交 AC 于点O ，设PC 中点为F ， 连接OF ，EF ．因为O ，F 分别为AC ，PC 的中点， 所以OF PA P ，且12OF PA =， 因为DE PA P ，且12DE PA =， 所以OF DE P ，且OF DE =．…………………………………………………………………………1分 所以四边形OFED 为平行四边形，所以OD EF P ，即BD EF P ．………………………………2分 因为PA ⊥平面ABCD ，BD ⊂平面ABCD ，所以PA BD ⊥． 因为ABCD 是菱形，所以BD AC ⊥．因为PA AC A =I ，所以BD ⊥平面PAC ．…………………………………………………………4分 因为BD EF P ，所以EF ⊥平面PAC ．………………………………………………………………5分 因为FE ⊂平面PCE ，所以平面PAC ⊥平面PCE ． ………………………………………………6分 （2）解法1：因为60ABC ∠=o ，所以△ABC 是等边三角形，所以2AC =．………………………7分又因为PA ⊥平面ABCD ，AC ⊂平面ABCD ，所以PA AC ⊥．所以122PAC S PA AC ∆=⨯=．……………………………………………………………………………8分 因为EF ⊥面PAC ，所以EF 是三棱锥E PAC -的高． ……………………………………………9分因为EF DO BO ===……………………………………………………………………………10分 所以13P ACE E PACPAC V VS EF --∆==⨯…………………………………………………………………11分1233=⨯=．………………………………………………………………………12分 解法2：因为底面ABCD 为菱形，且︒=∠60ABC ，所以△ACD 为等边三角形．………………7分 取AD 的中点M ，连CM ，则AD CM ⊥，且3=CM ．………………………………………8分数学（文科）试题A 第 3 页 共 8 页因为⊥PA 平面ABCD ，所以CM PA ⊥，又A AD PA =I ，所以CM ⊥平面PADE ，所以CM 是三棱锥C PAE -的高．………………………………………9分因为122PAE S PA AD ∆=⨯=．…………………………………………………………………………10分 所以三棱锥ACE P -的体积13P ACE C PAE PAE V V S CM --∆==⨯……………………………………11分1233=⨯=．…………………………………………12分19．解：（1）由已知数据可得2456855x ++++==，3444545y ++++==．…………………1分因为51()()(3)(1)000316ii i xx y y =--=-⨯-++++⨯=∑， ………………………………………2分，52310)1()3()(22222512=+++-+-=-∑=i ix x ………………………………………………3分==……………………………………………………4分所以相关系数()()0.95nii xx y y r --===≈∑．………………5分因为0.75r >，所以可用线性回归模型拟合y 与x 的关系． …………………………………………6分 （2）记商家周总利润为Y 元，由条件可得在过去50周里：当X >70时，共有10周，此时只有1台光照控制仪运行，周总利润Y =1×3000-2×1000=1000元． …………………………………………………………………8分 当50≤X ≤70时，共有35周，此时有2台光照控制仪运行，周总利润Y =2×3000-1×1000=5000元． …………………………………………………………………9分 当X<50时，共有5周，此时3台光照控制仪都运行，周总利润Y =3×3000=9000元． …………………………………………………………………………10分 所以过去50周周总利润的平均值10001050003590005460050Y ⨯+⨯+⨯==元，所以商家在过去50周周总利润的平均值为4600元． ………………………………………………12分数学（文科）试题A 第 4 页 共 8 页20． 解：（1）抛物线的准线方程为2p x =-， 所以点E ()2t ，到焦点的距离为232p+=．…………………………………………………………1分解得2p =．所以抛物线C 的方程为24y x =．………………………………………………………………………2分（2）解法1：设直线l 的方程为()10x my m =->．………………………………………………………3分将1x my =-代入24y x =并整理得2440y my -+=，………………………………………………4分 由()24160m ∆=->，解得1m >．……………………………………………………………………5分 设()11,A x y ， ()22,B x y ， ()11,D x y -，则124y y m +=， 124y y =，……………………………………………………………………………6分因为()()()2212121212·11(1)2484FA FB x x y y m y m y m y y =--+=+-++=-u u u r u u u r ，………………7分因为FA FB ⊥，所以0FA FB =u u u r u u u rg ．即2840m -=，又0m >，解得m =．…………………………………………………………8分所以直线l的方程为10x -+=． 设AB 的中点为()00,x y , ，0013x my =-=，……………………………………………………9分 所以直线AB的中垂线方程为)3y x -=-． 因为AD 的中垂线方程为0y =，所以△ABD 的外接圆圆心坐标为()5,0．……………………………………………………………10分因为圆心()5,0到直线l 的距离为AB ==……………………………………………………………11分 所以△ABD 的外接圆的方程为()22524x y -+=．…………………………………………………12分数学（文科）试题A 第 5 页 共 8 页解法2：依题意可设直线()():10l y k x k =+>．……………………………………………………3分 将直线l 与抛物线C 联立整理得0)42(2222=+-+k x k x k ．………………………………………4分 由04)42(422>--=∆k k ，解得10<<k ．………………………………………………………5分 设),,(),,(2211y x B y x A 则1,4221221=+-=+x x k x x ．…………………………………………………………………………6分 所以4)1(2121221=+++=x x x x k y y ，因为12121224()18FA FB x x x x y y k⋅=-+++=-u u u r u u u r ，…………………………………………………7分因为FA FB ⊥，所以0FA FB =u u u r u u u rg ．所以2480k-=，又0k > ，解得22=k ．…………………………………………………………8分 以下同解法1．21．解：（1）函数()f x 的定义域为()0,+∞．当2b =时，()2ln f x a x x =+，所以()222a x af x x x x+'=+=．………………………………1分① 当0a >时，()0f x '>，所以函数()f x 在()0,+∞上单调递增．………………………………2分 ② 当0a <时，令()0f x '=，解得x =当0x <<()0f x '<，所以函数()f x在⎛ ⎝上单调递减；当x >()0f x '>，所以函数()f x在⎫+∞⎪⎪⎭上单调递增．………………………3分 综上所述，当2b =，0a >时，函数()f x 在()0,+∞上单调递增；当2b =，0a <时，函数()f x在⎛ ⎝上单调递减，在⎫+∞⎪⎪⎭上单调递增．………4分（2）因为对任意1,e ex ⎡⎤∈⎢⎥⎣⎦，有()e 1f x ≤-成立，所以()max e 1f x ≤-．……………………………5分数学（文科）试题A 第 6 页 共 8 页当0a b +=即a b =-时，()ln b f x b x x =-+，()()11bb b x b f x bx x x---'=+=． 令()0f x '<，得01x <<；令()0f x '>，得1x >．所以函数()f x 在1,1e ⎡⎫⎪⎢⎣⎭上单调递减，在(]1,e 上单调递增，…………………………………………7分()max f x 为1e e b f b -⎛⎫=+ ⎪⎝⎭与()e e b f b =-+中的较大者．…………………………………………8分设()()1e e e 2e b b g b f f b -⎛⎫=-=-- ⎪⎝⎭()0b >， 则()e e220bbg b -'=+->=，所以()g b 在()0,+∞上单调递增，故()()00g b g >=所以()1e e f f ⎛⎫> ⎪⎝⎭，从而()max f x =⎡⎤⎣⎦()e e bf b =-+．………………………………………………………………………9分所以e e 1bb -+≤-即e e 10b b --+≤．设()=e e 1bb b ϕ--+()0b >，则()=e 10bb ϕ'->．…………………………………………………10分所以()b ϕ在()0,+∞上单调递增．又()10ϕ=，所以e e 10b b --+≤的解为1b ≤．……………………………………………………11分 因为0b >，所以b 的取值范围为(]0,1．………………………………………………………………12分22．解：（1）因为曲线1C 的参数方程为cos 2sin x y αα=⎧⎨=⎩（α为参数），因为2.x x y y '=⎧⎨'=⎩，，则曲线2C 的参数方程2cos 2sin .x y αα'=⎧⎨'=⎩，．………………………………………………2分所以2C 的普通方程为224x y ''+=．……………………………………………………………………3分 所以2C 为圆心在原点，半径为2的圆．…………………………………………………………………4分所以2C 的极坐标方程为24ρ=，即2ρ=．…………………………………………………………5分数学（文科）试题A 第 7 页 共 8 页（2）解法1：直线l 的普通方程为100x y --=．…………………………………………………………6分曲线2C 上的点M 到直线l的距离+)10|d απ-==．…………8分 当cos +=14απ⎛⎫⎪⎝⎭即()=24k k αππ-∈Z 时，d2-．……………9分 当cos +=14απ⎛⎫- ⎪⎝⎭即()3=24k k απ+π∈Z 时，d+10分 解法2：直线l 的普通方程为100x y --=．…………………………………………………………6分 因为圆2C 的半径为2，且圆心到直线l 的距离252|1000|=--=d ，…………………………7分因为225>，所以圆2C 与直线l 相离．………………………………………………………………8分 所以圆2C 上的点M 到直线l 的距离最大值为225+=+r d ，最小值为225-=-r d ．…10分23．解：（1）当1=a 时，()|1|=+f x x ．…………………………………………………………………1分①当1x ≤-时，原不等式可化为122x x --≤--，解得1≤-x ．…………………………………2分 ②当112x -<<-时，原不等式可化为122+≤--x x ，解得1≤-x ，此时原不等式无解．……3分 ③当12x ≥-时，原不等式可化为12+≤x x ，解得1≥x ．…………………………………………4分 综上可知，原不等式的解集为{1x x ≤-或}1≥x ．…………………………………………………5分（2）解法1：①当3a ≤时，()3,3,23,3,3,.a x g x x a x a a x a -≤-⎧⎪=----<<-⎨⎪-≥-⎩………………………………………6分所以函数()g x 的值域[]3,3A a a =--， 因为[2,1]-⊆A ，所以3231a a -≤-⎧⎨-≥⎩，，解得1a ≤．………………………………………………………7分②当3a >时，()3,,23,3,3, 3.a x a g x x a a x a x -≤-⎧⎪=++-<<-⎨⎪-≥-⎩…………………………………………………8分数学（文科）试题A 第 8 页 共 8 页所以函数()g x 的值域[]3,3A a a =--， 因为[2,1]-⊆A ，所以3231a a -≤-⎧⎨-≥⎩，，解得5a ≥．………………………………………………………9分综上可知，a 的取值范围是(][),15,-∞+∞U ．………………………………………………………10分 解法2：因为|+||+3|x a x -≤()+(+3)3x a x a -=-，……………………………………………7分 所以()g x =()|+3||+||+3|[|3|,|3|]-=-∈---f x x x a x a a ．所以函数()g x 的值域[|3|,|3|]A a a =---．…………………………………………………………8分因为[2,1]-⊆A ，所以|3|2|3|1a a --≤-⎧⎨-≥⎩，，解得1a ≤或5a ≥．所以a 的取值范围是(][),15,-∞+∞U ．………………………………………………………………10分。

2018年广州市普通高中毕业班综合测试（二）文科数学试题答案及评分参考评分说明:1．本解答给出了一种或几种解法供参考，如果考生的解法与本解答不同，可根据试题的主要考查内容比照评分参考制订相应的评分细则．2．对计算题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后继部分的解答有较严重的错误，就不再给分．3．解答右端所注分数，表示考生正确做到这一步应得的累加分数． 4．只给整数分数．选择题不给中间分． 一．选择题二．填空题13.14. 1 15. ① ③ ④ 16. (2,3-三、解答题17.（1）解:由sin 2sin b A a B =，得2sin cos sin b A A a B =， ……………………1分 由正弦定理得2sin sin cos sin sin B A A A B =， ………………………………2分 由于sin sin 0A B ≠，则1cos 2A =. ………………………………………………………3分 因为0A <<π， 所以A =3π. ………………………………………………………4分（2）解:由余弦定理得2222cos a b c bc A =+-， ………………………………………5分又2=a ，则224=+-b c bc .① ………………………………………………………6分又△ABC 则1sin 2=bc A …………………………………………7分即1sin 2bc 3π=4=bc .② …………………………………………………8分 由①②得228+=b c , …………………………………………………9分则()22228816+=++=+=b c b c bc , ……………………………………………10分得4+=b c . ………………………………………………………11分MNC 1B 1A 1CBA所以△ABC 的周长为6. ………………………………………………………12分 18. (1) 解: A 药店应选择乙药厂购买中药材 .……………………………………………2分 (2) 解: (ⅰ) 从乙药厂所抽取的每件中药材的质量的平均值为()17911121217182121221510x =+++++++++=, ………………4分 故A 药店所购买的100件中药材的总质量的估计值为100151500⨯=克. …5分(ⅱ) 乙药厂所提供的每件中药材的质量15n <的概率为50.510=,1520n ≤≤的概 率为20.210=,20n >的概率为30.310=,……………………………………8分 则A 药店所购买的100件中药材的总费用为()100500.50.21000.3a ⨯⨯++⨯.………………………………………9分 依题意得()100500.50.21000.3a ⨯⨯++⨯7000≤,………………………10分 解得75a ≤. ……………………………………………11分 所以a 的最大值为75. ……………………………………………12分19. (1) 证明: 连接11,A B AC , 依题意可得点M 是1A B 的中点, ……………………1分 因为点N 是BC 的中点,所以MN ∥1AC . ……………………2分 又1AC ⊂平面11AAC C , MN ⊄平面11AAC C , 所以MN ∥平面11AAC C .……………………4分 (2) 解法1: 连接1B N ,由于1AB AC ==, 点N 是BC 的中点, 则AN BC ⊥. ……………………5分 又90BAC ︒∠=,则12AN BC === 在直三棱柱111-ABC A B C 中, 可得平面ABC ⊥平面11BB C C , 又平面ABC平面11BB C C BC =, AN ⊂平面ABC ,所以AN ⊥平面11BB C C . …………………………………………6分 又1B N ⊂平面11BB C C , 则1AN B N ⊥. …………………………………………7分在Rt △1B BN 中, 12B N ===,则1111111222B C N S B C B B ∆=⋅⋅== ……………………8分11113224AB N S B N AN ∆=⋅⋅==. ……………………9分 依题意, 点1C 到平面AMN 的距离与它到平面1AB N 的距离相等, 设为h ,由1111C AB N A B C N V V --=, …………………………………………10分得113AB N h S ∆⋅⋅1113B C N AN S ∆=⋅⋅, 得34h = ……………………11分 得43h =. 所以棱锥1C AMN -的高为43. …………………………………………12分 解法2：设点1C 到平面AMN 的距离为h , 因为BC ∥11B C , 且11B C ⊂平面11AB C ,所以BC ∥平面11AB C . …………………………………………5分 所以点B 到平面11AB C 的距离等于点N 到平面11AB C 的距离. ………………………6分 所以111N AC M B AC M C ABM V V V ---==. …………………………………………7分 由于1111AC A B ⊥, 111AC A A ⊥,则11AC ⊥平面11AA B B . …………………………………………8分 所以11111111113326C ABM ABM V S AC ∆-=⋅⋅=⨯⨯⨯⨯=. …………………………………9分在△AMN 中, 112MN AC ==, 112AM AB ==, AN =所以13228AMN S ∆=⨯=. ……………………………………10分 由11163C ABM AMN V S h ∆-==⋅⋅, …………………………………………11分 得43h =. 所以棱锥1C AMN -的高为43. …………………………………………12分20.（1）解:依题意，设椭圆C 方程为22221(0)x y a b a b+=>>，由于椭圆C 的右焦点为()2,0F ，则2c =. ………………………………………1分 又由于椭圆C 的短轴长为4，则24b =，得2b =. ……………………………2分 所以2228a b c =+=， …………………………………………3分所以椭圆C 的方程为22184x y +=. …………………………………………4分 (2) 解法1: 设点11(,)M x y ，22(,)N x y , 00(,)P x y ，由221,84y kx x y ⎧=+⎪⎨+=⎪⎩消去y 得()2212280k x +++=, (*)则12x x +=, 1222812x x k =+. …………………………………………5分 由于点P 是线段MN 的中点,则1202212x x x k +==-+, 00212y kx k =+=+. …………………………6分 所以0012OP y k x k==-. …………………………………………7分 因为OP ∥FM , 所以12FM OP k k k==-. 所以直线FM 的方程为()122y x k=--. …………………………………………8分由()12,2y kx y x k ⎧=+⎪⎨=--⎪⎩解得22.12x k y k ⎧=⎪⎪⎨⎪=⎪+⎩则点2222,1212k M k k ⎛⎫- ⎪ ⎪++⎝⎭. …………………………………………9分由于点M 在椭圆C 上,则2228+=⎝⎭⎝⎭, 解得22k =. …………………………………………10分此时,(*)的判别式()()2242812160k ∆=-⨯+=>.则k = ………………………………………11分 所以直线l的方程为y =+y =+ ……………………12分 解法2: 设点11(,)M x y ，22(,)N x y , 00(,)P x y ，由于点P 是线段MN 的中点, 则120120,2.2x x x y y y +⎧=⎪⎪⎨+⎪=⎪⎩由于,M N 在椭圆C 上, 则221122221,841,84x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩ ……………………………………5分两式相减得()()()()12121212084x x x x y y y y -+-++=,即121212121222y y y y x x x x +-⋅=-+-, ……………………………………6分得12MN OP k k ⋅=-.故12OP k k=-. ……………………………………7分因为OP ∥FM , 所以12FM OP k k k ==-.所以直线FM 的方程为()122y x k=--. ……………………………………8分由()12,2y kx y x k ⎧=+⎪⎨=--⎪⎩解得22.12x k y k ⎧=⎪⎪⎨⎪=⎪+⎩则点2222,1212k M k k ⎛⎫- ⎪ ⎪++⎝⎭. …………………………………………9分 由于点M 在椭圆C 上,则2228+=⎝⎭⎝⎭, 解得22k =. …………………………………………10分由221,84y kx x y ⎧=+⎪⎨+=⎪⎩消去y 得()2212280k x +++=,则()()2242812160k ∆=-⨯+=>.则k = ………………………………………11分 所以直线l的方程为y =+y =+ ……………………12分21.(1) 解: 函数()f x 的定义域为()0,+∞. ………………………………………1分 由()f x =()1ln a x x --, 得()1f x a x'=-. 当0a >时, 令()1f x a x '=-0=, 得1x a=.则10,x a ⎛⎫∈ ⎪⎝⎭时, ()0f x '<; 1,x a ⎛⎫∈+∞ ⎪⎝⎭时, ()0f x '>; ………………………2分故函数()f x 在10,a ⎛⎫ ⎪⎝⎭上单调递减, 在1,a ⎛⎫+∞ ⎪⎝⎭上单调递增. 当1x a=时, 函数()f x 取得极小值, 其值为1111ln 1ln f a a a a a a ⎛⎫⎛⎫=--=-+ ⎪ ⎪⎝⎭⎝⎭.………………………………………………3分令()()1ln 0g a a a a =-+>, 则()111a g a a a-'=-+=-, 当01a <<时, ()0g a '>; 当1a >时, ()0g a '<. 故()g a 在()0,1上单调递增, 在()1,+∞上单调递减.当1a =时, ()g a 取得最大值, 其值为()10g =. ………………………………4分 由于函数()f x 的极小值不大于k 对任意0a >恒成立, 则0k ≥.所以k 的取值范围是[)0,+∞. ………………………………………………5分(2) 证明:由(1)可知, 当1a =时, 函数()f x 在()0,1上单调递减, 在()1,+∞上单调递增. 当1x =时, 函数()f x 取得最小值为()10f =.所以当0x >时, ()0f x ≥, 即1ln 0x x --≥, 得ln 1x x ≤-. ………………6分 ∀n ∈N *, 令12n n x =+, 得ln 122n n n n⎛⎫+≤ ⎪⎝⎭. ………………………7分 所以2323123123ln 1ln 1ln 1ln 122222222n n n n ⎛⎫⎛⎫⎛⎫⎛⎫++++++++≤++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. ………………………………………………8分令231232222n n nS =++++, ① 2341112322222n n nS +=++++ ② ①-②得23111111222222n n n nS +=++++-1111221212n n n +⎛⎫- ⎪⎝⎭=--1212n n ++=-. ………………………………………………9分 所以2222n n n S +=-<. ………………………………………………10分所以22123ln 111122222n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+⋅+⋅+⋅⋅+< ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦. ………………………11分 所以2212311112222n n ⎛⎫⎛⎫⎛⎫⎛⎫+⋅+⋅+⋅⋅+< ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭e 2. ………………………12分 另法: 令()()ln 1h x x x =+-, 则()1111x h x x x'=-=-++. 当0x >时, ()0h x '<, 则()h x 在()0,+∞上单调递减.故当0x >时, ()()00h x h <=, 即()ln 1x x +<. ………………………6分 ∀n ∈N *, 令2n n x =, 得ln 122n n n n⎛⎫+< ⎪⎝⎭. ………………………7分所以2323123123ln 1ln 1ln 1ln 122222222n n n n ⎛⎫⎛⎫⎛⎫⎛⎫++++++++<++++⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. ………………………………………………8分令231232222n n nS =++++, ① 2341112322222n n nS +=++++ ② ①-②得23111111222222n n n nS +=++++-1111221212n n n +⎛⎫- ⎪⎝⎭=--1212n n ++=-. ………………………………………………9分 所以2222n n n S +=-<. ………………………………………………10分所以22123ln 111122222n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+⋅+⋅+⋅⋅+< ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦. ………………………11分 所以2212311112222n n ⎛⎫⎛⎫⎛⎫⎛⎫+⋅+⋅+⋅⋅+< ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭e 2.………………………12分 22. (1) 解: 由11,2,2x t y ⎧=-⎪⎪⎨⎪=⎪⎩消去t , 得l 的普通方程为)1y x =-,0y +.……………………………………2分由()2212sin a ρθ+=, 得2222sin a ρρθ+=, …………………………………3分把222x y ρ=+, sin y ρθ=代入上式, 得223x y a +=,所以C 的直角坐标方程为223x y a +=. ……………………………………5分(2) 解法1: 把11,2x t y ⎧=-⎪⎪⎨⎪=⎪⎩代入223x y a +=, 得252220t t a -+-=, (*) ………6分设A , B 两点对应的参数分别为12,t t , 得 1225t t +=, 12225a t t -=, ………………………7分12AB t t =-2=9==, ………8分又AB ==, 解得65a =. ………………………………………………9分 此时, (*)式的判别式6445221205∆⎛⎫=-⨯⨯-⨯=> ⎪⎝⎭. 所以a 的值为65. ………………………………………………10分解法2: 由)221,3y x x y a⎧=-⎪⎨+=⎪⎩消去y ,得2101890x x a -+-=, (*) ………6分 设()()1122,,,A x y B x y , 得1295x x +=, 12910ax x -=, ………………………7分A B ===. ………………………8分又AB =5, 得55=, 解得65a =. ………………………9分 此时, (*)式的判别式6445221205∆⎛⎫=-⨯⨯-⨯=> ⎪⎝⎭. 所以a 的值为65. ………………………10分 23.(1)解: ()2f x ≤, 即21212x x ++-≤, ………………………1分 当12x ≤-时, 得()()21122x x -++-≤, 解得12x ≥-, 故12x =-; ………2分 当1122x -<<时, 得()()21212x x +--≤, 即22≤, 故1122x -<<; ………3分当12x ≥时, 得()()21212x x ++-≤, 解得12x ≤, 故12x =. ………………4分 所以不等式()2f x ≤的解集M 1122x x ⎧⎫=-≤≤⎨⎬⎭⎩. ………………5分 (2) 证明: 当,a b M ∈时, 即1111,2222a b -≤≤-≤≤, 得11,22a b ≤≤. 当()()0a b a b +-≥时, ()()21a b a b a b a b a ++-=++-=≤; …………7分 当()()0a b a b +-<时, ()()21a b a b a b a b b ++-=+--=≤; …………9分 所以1a b a b ++-≤. ………………………………10分 另法：当,a b M ∈时, 即1111,2222a b -≤≤-≤≤, 得11,22a b ≤≤.()()2222222a b a b a b a b ++-=++- ………………………………6分2222224,,4,.a ab b a b ⎧≥=⎨<⎩ ………………………………7分 由于2211,44a b ≤≤，则2241,41a b ≤≤. ………………………………8分 故()21a b a b++-≤. ………………………………9分所以1a b a b ++-≤. ………………………………10分。

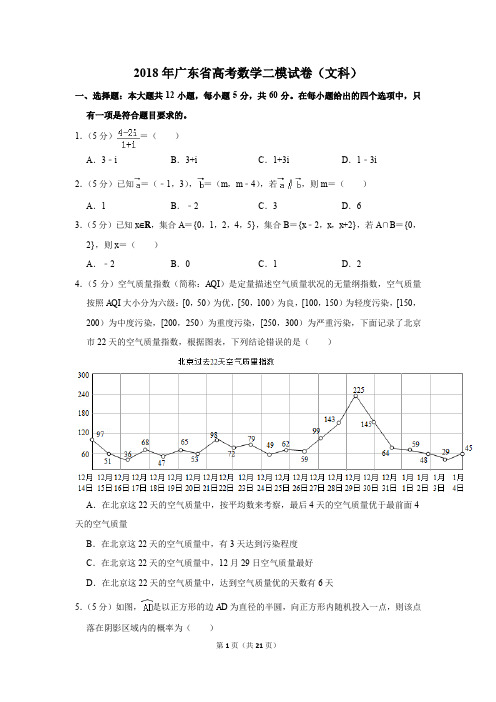
青霄有路终须到，金榜无名誓不还！2018-2019年高考备考2018年普通高等学校招生全国统一考试广东省文科数学模拟试卷（二）第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. （）A. B. C. D.2. 已知，，若，则（）A. B. C. D.3. 已知，集合，集合，若，则（）A. B. C. D.4. 空气质量指数（简称：）是定量描述空气质量状况的无量纲指数，空气质量按照大小分为六级：为优，为良，为轻度污染，为中度污染，为重度污染，为严重污染.下面记录了北京市天的空气质量指数，根据图表，下列结论错误的是（）A. 在北京这天的空气质量中，按平均数来考察，最后天的空气质量优于最前面天的空气质量B. 在北京这天的空气质量中，有天达到污染程度C. 在北京这天的空气质量中，12月29日空气质量最好D. 在北京这天的空气质量中，达到空气质量优的天数有天5. 如图，是以正方形的边为直径的半圆，向正方形内随机投入一点，则该点落在阴影区域内的概率为（ ）A. B. C. D.6. 已知等比数列的首项为，公比，且，则（ ）A. B. C. D.7. 已知双曲线的一个焦点坐标为，且双曲线的两条渐近线互相垂直，则该双曲线的方程为（ ）A. B. C. D. 或8. 已知某几何体的三视图如图所示，则该几何体的表面积为（ ）A. B. C. D.9. 在印度有一个古老的传说：舍罕王打算奖赏国际象棋的发明人——宰相宰相西萨•班•达依尔．国王问他想要什么，他对国王说：“陛下，请您在这张棋盘的第1个小格里，赏给我1粒麦子，在第2个小格里给2粒，第3小格给4粒，以后每一小格都比前一小格加一倍．请您把这样摆满棋盘上所有的64格的麦粒，都。

2018年广州市普通高中毕业班综合测试（二）文科综合2018．4 本试卷共12页，41小题，满分300分。

考试用时150分钟。

注意事项：1．答卷前，考生务必用2B铅笔在“考生号”处填涂考生号，用黑色字迹钢笔或签字笔将自己所在的市、县／区、学校，以及自己的姓名和考生号、试室号、座位号填写在答题忙上。

用2B铅笔将试卷类型（A）填涂在答题卡相应位置上。

2．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．考生必须保持答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

一、选择题：本题共35小题，每小题4分，共140分。

每小题给出的四个选项中，只有一个选项符合题目要求。

当地时间2018年3月11日14时46分，日本东北地区发生了里氏9级地震，引发了海啸和核泄漏危机。

回答1～3题。

1．右图是全球板块构造剖面示意图，日本的板块交界类型是A．①B．②C．③D．④2．世界核电站主要分布在沿海、沿江地区，影响其分布最主要的区位因子是A．交通B．地质构造C．铀矿资源D．水源3．核辐射危机具有全球性，影响其全球化的因素是A．大气环流和水循环B．水循环和生物循环C．生物循环和地壳物质循环D．地壳物质循环和大气环流下图是某地区某月平均气温分布示意图，完成4～5题。

4．此时，地球在公转轨道上运行到A．近日点附近B．远日点附近C．春分点附近D．秋分点附近5．M处比同纬度大陆（澳大利亚）气温高，其最主要影响因素是A．马达加斯加暖流B．海陆热力性质差异C．西风D．山地下图是我国某地区气温、降水量和蒸发量年内分布示意图，完成6～7题。

6．该地区位于我国A．华北地区B．华南地区C．青藏地区D．西南地区7．有关该地区自然环境的叙述，正确的是A．植被为常绿阔叶林B．河流以冰雪融水补给为主C．农业耕作制度一年一熟D．一年中春季最干旱下图是我国1978年～2018年东部沿海地区农业产值结构变化统计图，完成8～9题。

2018年高三数学二模文科试题（广州市附答案）
5
广州市∞，1)，则实数a的值为
A -2
B -1c 1D 2
3对于任意向量a、B、c,下列命题中正确的是
A |ab| = |a| |b|
B |a+b|=|a|+丨b丨
c (ab)c =a (b-c)D aa =|a|2
4直线=x +1与圆(x+1)2+2=0相交于A，B两点，则|AB|的值为A2B1c D与有关的数值
5若1-i(i是虚数单位）是关于x的方程x2+2px +q=0(p、q∈R)的一个解，则p+q=
A-3 B -1 c 1D 3
6执行如图l所示的程序框图，输出的S值为
A 225
B 196c 169D 144
(注框图中的赋值符号“=”也可以写成“←”或“=”）
7若函数的一个对称中心是( ，0),则ω的最小值为
A 2
B 3c 6D 9
8一个圆锥的正（主）视图及其尺寸如图2所示若一个平行于圆锥底面的平面将此圆锥截成体积之比为l7的上、下两部分，则截面的面积为
A B
c B
9已知0 a 1，0 x≤ 1,且lgaxlga=1，那么x的取值范围为
A (0，a2]
B (0，a] c D
10某校高三（1)班50个学生选择选修模块程，他们在A、B、c 三个模块中进行选择，R至少需要选择l个模块，具体模块选择的情况如下表。

2018年广东省广州市高考数学二模试卷（文科）一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A={﹣1，0，1，2，3，4，5}，B={b|b=n2﹣1，n∈Z}，则A∩B=（）A．{﹣1，3}B．{0，3}C．{﹣1，0，3}D．{﹣1，0，3，5}2．若复数z满足（3﹣4i+z）i=2+i，则z=（）A．4+6i B．4+2i C．﹣4﹣2i D．﹣2+2i．3．已知命题p：∀x∈R，x2+ax+a2≥0（a∈R），命题q：，，则下列命题中为真命题的是（）A．p∧q B．p∨q C．（¬p）∨q D．（¬p）∧（¬q）4．执行如图所示的程序图，则输出的S值为（）A．4 B．3 C．﹣2 D．﹣35．函数f（x）=ln（|x|﹣1）+x的大致图象是（）A．B．C．D．6．在区间[﹣1，5]上随机地取一个实数a，则方程x2﹣2ax+4a﹣3=0有两个正根的概率为（）A．B．C．D．7．已知三条直线2x﹣3y+1=0，4x+3y+5=0，mx﹣y﹣1=0不能构成三角形，则实数m的取值集合为（）A．{﹣， } B．{，﹣ } C．{﹣，， } D．{﹣，﹣， }8．已知两点A（﹣1，1），B（3，5），点C在曲线y=2x2上运动，则的最小值为（）A．2 B．C．﹣2 D．9．在棱长为2的正方体ABCD﹣A1B1C1D1中，M是棱A1D1的中点，过C1，B，M作正方体的截面，则这个截面的面积为（）A．B．C．D．10．数列{a n}满足a2=2，a n+（﹣1）n+1a n=1+（﹣1）n（n∈N*），S n为数列{a n}+2前n项和，S100=（）A．5100 B．2550 C．2500 D．245011．已知函数f（x）=2sin（ωx+）（ω＞0）的图象在区间[0，1]上恰有3个最高点，则ω的取值范围为（）A．[，）B．[，）C．[，）D．[4π，6π）12．如图，网格纸上小正方形的边长为1，粗线画出的是某三棱锥的三视图，则该三棱锥的体积为（）A．B．C．D．16二、填空题已知双曲线（a＞0）的离心率为2，则a的值为．14．在各项都为正数的等比数列{a n}中，已知a1=2，，则数列{a n}的通项公式a n=．15．《孙子算经》是我国古代重要的数学著作，约成书于四、五世纪，传本的《孙子算经》共三卷，其中下卷：“物不知数”中有如下问题：“今有物，不知其数，三三数之，剩二；五五数之，剩三；七七数之，剩二，问：物几何？”其意思为：“现有一堆物品，不知它的数目，3个3个数，剩2个，5个5个数，剩3个，7个7个数，剩2个，问这堆物品共有多少个？”试计算这堆物品至少有个．16．已知函数，若f（3a﹣1）≥8f（a），则实数a的取值范围为．三、解答题（本大题共5小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17．（12分）△ABC的内角A，B，C的对边分别为a，b，c，已知bcosC+bsinC=a．（Ⅰ）求角B的大小；（Ⅱ）若BC边上的高等于，求cosA的值．18．（12分）某中学为了解高中入学新生的身高情况，从高一年级学生中按分层抽样共抽取了50名学生的身高数据，分组统计后得到了这50名学生身高的频数分布表：（Ⅰ）在答题卡上作出这50名学生身高的频率分布直方图；（Ⅱ）估计这50名学生身高的方差（同一组中的数据用该组区间的中点值作代表）；（Ⅲ）现从身高在[175，185]这6名学生中随机抽取3名，求至少抽到1名女生的概率．19．（12分）如图，ABCD 是边长为a 的正方形，EB ⊥平面ABCD ，FD ⊥平面ABCD ，．（Ⅰ）求证：EF ⊥AC ；（Ⅱ）求三棱锥E ﹣FAC 的体积．20．（12分）已知定点F （0，1），定直线l ：y=﹣1，动圆M 过点F ，且与直线l 相切．（Ⅰ）求动圆M 的圆心轨迹C 的方程；（Ⅱ）过点F 的直线与曲线C 相交于A ，B 两点，分别过点A ，B 作曲线C 的切线l 1，l 2，两条切线相交于点P ，求△PAB 外接圆面积的最小值． 21．（12分）已知函数．（Ⅰ）求函数f （x ）的单调区间；（Ⅱ）若函数g （x ）=f （x ）+4x 存在极小值点x 0，且，求实数a 的取值范围．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．[选修4-4：坐标系与参数方程]22．（10分）在平面直角坐标系xOy中．已知直线l的普通方程为x﹣y﹣2=0，曲线C的参数方程为（θ为参数），设直线l与曲线C交于A，B 两点．（1）求线段AB的长（2）已知点P在曲线C上运动．当△PAB的面积最大时，求点P的坐标及△PAB 的最大面积．[选修4-5：不等式选讲]23．（I）已知a+b+c=1，证明（a+1）2+（b+1）2+（c+1）2≥；（Ⅱ）若对任总实数x，不等式|x﹣a|+|2x﹣1|≥2恒成立，求实数a的取值范围．2018年广东省广州市高考数学二模试卷（文科）参考答案与试题解析一、选择题：本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合A={﹣1，0，1，2，3，4，5}，B={b|b=n2﹣1，n∈Z}，则A∩B=（）A．{﹣1，3}B．{0，3}C．{﹣1，0，3}D．{﹣1，0，3，5}【考点】1E：交集及其运算．【分析】化简集合B，根据交集的定义写出A∩B．【解答】解：集合A={﹣1，0，1，2，3，4，5}，B={b|b=n2﹣1，n∈Z}={﹣1，0，3，8，15，…，}，∴A∩B={﹣1，0，3}．故选：C．【点评】本题考查了交集的定义与应用问题，是基础题．2．若复数z满足（3﹣4i+z）i=2+i，则z=（）A．4+6i B．4+2i C．﹣4﹣2i D．﹣2+2i．【考点】A5：复数代数形式的乘除运算．【分析】利用复数的运算法则、共轭复数的定义即可得出．【解答】解：（3﹣4i+z）i=2+i，则3﹣4i+z===﹣2i+1．∴z=﹣2+2i．故选：D．【点评】本题考查了复数的运算法则、共轭复数的定义，考查了推理能力与计算能力，属于基础题．3．已知命题p：∀x∈R，x2+ax+a2≥0（a∈R），命题q：，，则下列命题中为真命题的是（）A．p∧q B．p∨q C．（¬p）∨q D．（¬p）∧（¬q）【考点】2E：复合命题的真假．【分析】利用不等式的解法化简命题p，q，再利用复合命题的判定方法即可得出．【解答】解：命题p：∵△=a2﹣4a2=﹣3a2≤0，因此∀x∈R，x2+ax+a2≥0（a∈R），是真命题．命题q：由2x2﹣1≤0，解得≤x，因此不存在x0∈N*，使得，是假命题．则下列命题中为真命题的是p∨q．故选：B．【点评】本题考查了不等式的解法、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．4．执行如图所示的程序图，则输出的S值为（）A．4 B．3 C．﹣2 D．﹣3【考点】EF：程序框图．【分析】由已知中的程序语句可知该框图的功能是利用循环结构计算并输出变量S的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．【解答】解：s=0，i=2，s=2，i=3， s=﹣1．i=4， s=3，i=5， s=﹣2，i=6， s=4，i=7＞6， 结束循环，输出s=4， 故选：A ．【点评】本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，属于基础题．5．函数f （x ）=ln （|x |﹣1）+x 的大致图象是（ ）A ．B ．C ．D ．【考点】3O ：函数的图象．【分析】化简f （x ），利用导数判断f （x ）的单调性即可得出正确答案． 【解答】解：f （x ）的定义域为{x |x ＜﹣1或x ＞1}．f （x ）=，∴f′（x ）=，∴当x ＞1时，f′（x ）＞0，当x ＜﹣2时，f′（x ）＞0，当﹣2＜x ＜﹣1时，f′（x ）＜0，∴f（x）在（﹣∞，﹣2）上单调递增，在（﹣2，﹣1）上单调递减，在（1，+∞）上单调递增．故选A．【点评】本题考查了函数图象的判断，函数单调性的判断，属于中档题．6．在区间[﹣1，5]上随机地取一个实数a，则方程x2﹣2ax+4a﹣3=0有两个正根的概率为（）A．B．C．D．【考点】CF：几何概型．【分析】根据根与系数之间的关系，求出a的取值范围，结合几何概型的概率公式进行计算即可．【解答】解：若方程x2﹣2ax+4a﹣3=0有两个正根，则满足，即，得＜a≤1或a≥3，∵﹣1≤a≤5则对应的概率P=+=+=，故选：C【点评】本题主要考查几何概型的概率的计算，根据根与系数之间的关系求出a 的取值范围是解决本题的关键．7．已知三条直线2x﹣3y+1=0，4x+3y+5=0，mx﹣y﹣1=0不能构成三角形，则实数m的取值集合为（）A．{﹣， } B．{，﹣ } C．{﹣，， } D．{﹣，﹣， }【考点】IG：直线的一般式方程．【分析】三条直线若两两相交围成一个三角形，则斜率必不相同；否则，只要有两条直线平行，或三点共线时不能构成三角形．【解答】解：∵三条直线不能围成一个三角形，∴（1）l1∥l3，此时m=；l2∥l3，此时m=﹣；（2）三点共线时也不能围成一个三角形2x﹣3y+1=0与4x+3y+5=0交点是（﹣1，﹣）代入mx﹣y﹣1=0，则m=．故选：C．【点评】本题考查两直线平行的条件，当斜率相等且截距不相等时两直线平行．属于基础题．8．已知两点A（﹣1，1），B（3，5），点C在曲线y=2x2上运动，则的最小值为（）A．2 B．C．﹣2 D．【考点】9R：平面向量数量积的运算．【分析】设C（x，2x2），得出关于x的函数，根据函数性质求出最小值．【解答】解：设C（x，2x2），则=（4，4），=（x+1，2x2﹣1），∴=4（x+1）+4（2x2﹣1）=8x2+4x=8（x+）2﹣．∴当x=﹣时取得最小值﹣．故选D．【点评】本题考查了平面向量的数量积运算，函数最值得计算，属于中档题．9．在棱长为2的正方体ABCD﹣A1B1C1D1中，M是棱A1D1的中点，过C1，B，M作正方体的截面，则这个截面的面积为（）A．B．C．D．【考点】LA ：平行投影及平行投影作图法．【分析】由于截面被平行平面所截，所以截面为梯形，取AA 1的中点N ，可知截面为等腰梯形，利用题中数据可求．【解答】解：取AA 1的中点N ，连接MN ，NB ，MC 1，BC 1，由于截面被平行平面所截，所以截面为梯形，且MN=BC 1=，MC 1=BN ，=，∴梯形的高为，∴梯形的面积为（）×=，故选C ．【点评】本题的考点是棱柱的结构特征，主要考查几何体的截面问题，关键利用正方体图形特征，从而确定截面为梯形．10．数列{a n }满足a 2=2，a n +2+（﹣1）n +1a n =1+（﹣1）n （n ∈N *），S n 为数列{a n }前n 项和，S 100=（ ） A ．5100B ．2550C ．2500D ．2450【考点】8H ：数列递推式．【分析】数列{a n }满足a 2=2，a n +2+（﹣1）n +1a n =1+（﹣1）n （n ∈N *），n=2k （k ∈N *）时，a 2k +2﹣a 2k =2，因此数列{a 2k }为等差数列，首项为2，公差为2．n=2k ﹣1（k ∈N *）时，a 2k +1+a 2k ﹣1=0．通过分组求和，利用等差数列的求和公式即可得出．【解答】解：数列{a n }满足a 2=2，a n +2+（﹣1）n +1a n =1+（﹣1）n （n ∈N *），n=2k （k ∈N *）时，a 2k +2﹣a 2k =2，因此数列{a 2k }为等差数列，首项为2，公差为2．n=2k ﹣1（k ∈N *）时，a 2k +1+a 2k ﹣1=0．∴S 100=（a 1+a 3+…+a 97+a 99）+（a 2+a 4+…+a 100）=0+2×50+=2550．故选：B．【点评】本题考查了等差数列的通项公式与求和公式、数列递推关系、分类讨论方法、分组求和，考查了推理能力与计算能力，属于中档题．11．已知函数f（x）=2sin（ωx+）（ω＞0）的图象在区间[0，1]上恰有3个最高点，则ω的取值范围为（）A．[，）B．[，）C．[，）D．[4π，6π）【考点】H2：正弦函数的图象．【分析】根据区间[0，1]上，求出ωx+的范围，由于在区间[0，1]上恰有3个最高点，建立不等式关系，求解即可．【解答】解：函数f（x）=2sin（ωx+）（ω＞0），∵x∈[0，1]上，∴ωx+∈[，]，图象在区间[0，1]上恰有3个最高点，∴+，解得：．故选C．【点评】本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用，利用三角函数公式将函数进行化简是解决本题的关键．属于中档题．12．如图，网格纸上小正方形的边长为1，粗线画出的是某三棱锥的三视图，则该三棱锥的体积为（）A．B．C．D．16【考点】L!：由三视图求面积、体积．【分析】根据三视图可知三棱锥倒立放置，从而得出棱锥的高，根据俯视图找出三棱锥的底面，得出底面积，从而可求出棱锥的体积．【解答】解：由主视图和侧视图可知三棱锥倒立放置，棱锥的底面水平放置，故三棱锥的高为h=4，∵主视图为直角三角形，∴棱锥的一个侧面与底面垂直，=4，结合俯视图可知三棱锥的底面为俯视图中的左上三角形，∴S底=∴V==．故选：B．【点评】本题考查了棱锥的三视图和体积计算，根据三视图的特征找出棱锥的底面是关键，属于中档题．二、填空题（2018•广州二模）已知双曲线（a＞0）的离心率为2，则a的值为．【考点】KB：双曲线的标准方程．【分析】求得双曲线的b2=2，由c=和e=，解关于a的方程，即可得到所求值．【解答】解：由双曲线（a＞0）得到b2=2，则c=，所以=2，解得a=．故答案是：．【点评】本题考查双曲线的方程和性质，注意运用离心率公式和基本量a，b，c 的关系，考查方程思想和运算能力，属于基础题．14．在各项都为正数的等比数列{a n}中，已知a1=2，，则数列{a n}的通项公式a n=．【考点】8H：数列递推式．【分析】设等比数列{a n}的公比为q＞0，由a1=2，，可得+=4，化简解出q，再利用等比数列的通项公式即可得出．【解答】解：设等比数列{a n}的公比为q＞0，∵a1=2，，∴+=4，化为：q4﹣4q2+4=0，解得q2=2，q＞0，解得q=．则数列{a n}的通项公式a n==．故答案为：．【点评】本题考查了等比数列的通项公式、数列递推关系，考查了推理能力与计算能力，属于中档题．15．《孙子算经》是我国古代重要的数学著作，约成书于四、五世纪，传本的《孙子算经》共三卷，其中下卷：“物不知数”中有如下问题：“今有物，不知其数，三三数之，剩二；五五数之，剩三；七七数之，剩二，问：物几何？”其意思为：“现有一堆物品，不知它的数目，3个3个数，剩2个，5个5个数，剩3个，7个7个数，剩2个，问这堆物品共有多少个？”试计算这堆物品至少有23个．【考点】F4：进行简单的合情推理．【分析】根据“三三数之剩二，五五数之剩三，七七数之剩二”找到三个数：第一个数能同时被3和5整除；第二个数能同时被3和7整除；第三个数能同时被5和7整除，将这三个数分别乘以被7、5、3除的余数再相加即可求出答案．【解答】解：我们首先需要先求出三个数：第一个数能同时被3和5整除，但除以7余1，即15；第二个数能同时被3和7整除，但除以5余1，即21；第三个数能同时被5和7整除，但除以3余1，即70；然后将这三个数分别乘以被7、5、3除的余数再相加，即：15×2+21×3+70×2=233．最后，再减去3、5、7最小公倍数的整数倍，可得：233﹣105×2=23，或者105k+23（k为正整数）．∴这堆物品至少有23，故答案为：23．【点评】本题考查的是带余数的除法，简单的合情推理的应用，根据题意下求出15、21、70这三个数是解答此题的关键，属于中档题．16．已知函数，若f（3a﹣1）≥8f（a），则实数a的取值范围为．【考点】5B：分段函数的应用．【分析】根据条件判断函数f（x）的奇偶性和单调性即可．【解答】解：∵，∴f（﹣x）=f（x），即函数f（x）是偶函数，在[0，+∞）上为增函数，则不等式f（3a﹣1）≥8f（a），等价为f（|3a﹣1|）≥f（2|a|），∴|3a﹣1|≥2|a|，解得a∈．故答案为．【点评】本题主要考查不等式的求解，根据条件判断函数的奇偶性和单调性是解决本题的关键．综合考查函数的性质．三、解答题（本大题共5小题，共70分．解答应写出文字说明、证明过程或演算步骤．）17．（12分）（2018•广州二模）△ABC的内角A，B，C的对边分别为a，b，c，已知bcosC+bsinC=a．（Ⅰ）求角B的大小；（Ⅱ）若BC边上的高等于，求cosA的值．【考点】HT：三角形中的几何计算．【分析】（Ⅰ）利用正弦定理求和三角形的三角的关系，以及两角和的正弦公式sinB=cosB，即可求出B，（Ⅱ）设BC边上的高线为AD，运勾股定理和余弦定理，即可求得cosB，再由正弦定理，即可求出【解答】解：（Ⅰ）因为bcosC+bsinC=a，由正弦定理得，sinBcosC+sinBsinC=sinA．因为A+B+C=π，所以sinBcosC+sinBsinC=sin（B+C）．即sinBcosC+sinBsinC=sinBcosC+cosBsinC．因为sinC≠0，所以sinB=cosB．因为cosB≠0，所以tanB=1．因为B∈（0，π），所以．（Ⅱ）设BC边上的高线为AD，则．因为，则，．所以=，．由余弦定理得=．所以cosA=．【点评】本题考查正弦定理和余弦定理的运用，考查两角和的正弦公式的运用，考查运算能力，属于中档题．18．（12分）（2018•广州二模）某中学为了解高中入学新生的身高情况，从高一年级学生中按分层抽样共抽取了50名学生的身高数据，分组统计后得到了这50名学生身高的频数分布表：（Ⅰ）在答题卡上作出这50名学生身高的频率分布直方图；（Ⅱ）估计这50名学生身高的方差（同一组中的数据用该组区间的中点值作代表）；（Ⅲ）现从身高在[175，185]这6名学生中随机抽取3名，求至少抽到1名女生的概率．【考点】CC：列举法计算基本事件数及事件发生的概率；B8：频率分布直方图．【分析】（Ⅰ）由频率分布表能作出这50名学生身高的频率分布直方图．（Ⅱ）由频率分布直方图能估计这50名学生的平均身高，并能估计这50名学生身高的方差．（Ⅲ）记身高在[175，185]的4名男生为a，b，c，d，2名女生为A，B．利用列举法能求出从这6名学生中随机抽取3名学生，至少抽到1名女生的概率．【解答】解：（Ⅰ）这50名学生身高的频率分布直方图如下图所示：（Ⅱ）由题意可估计这50名学生的平均身高为=164．所以估计这50名学生身高的方差为s2==80．所以估计这50名学生身高的方差为80．（Ⅲ）记身高在[175，185]的4名男生为a，b，c，d，2名女生为A，B．从这6名学生中随机抽取3名学生的情况有：{a，b，c}，{a，b，d}，{a，c，d}，{b，c，d}，{a，b，A}，{a，b，B}，{a，c，A}，{a，c，B}，{a，d，A}，{a，d，B}，{b，c，A}，{b，c，B}，{b，d，A}，{b，d，B}，{c，d，A}，{c，d，B}，{a，A，B}，{b，A，B}，{c，A，B}，{d，A，B}共20个基本事件．其中至少抽到1名女生的情况有：{a，b，A}，{a，b，B}，{a，c，A}，{a，c，B}，{a，d，A}，{a，d，B}，{b，c，A}，{b，c，B}，{b，d，A}，{b，d，B}，{c，d，A}，{c，d，B}，{a，A，B}，{b，A，B}，{c，A，B}，{d，A，B}共16个基本事件．所以至少抽到1名女生的概率为．【点评】本题考查频率分布直方图的应用，概率的求法，是基础题，解题时要认真审题，注意列举法的合理运用．19．（12分）（2018•广州二模）如图，ABCD是边长为a的正方形，EB⊥平面ABCD，FD⊥平面ABCD，．（Ⅰ）求证：EF⊥AC；（Ⅱ）求三棱锥E﹣FAC的体积．【考点】LF：棱柱、棱锥、棱台的体积．【分析】（Ⅰ）连接BD，推导出AC⊥BD，AC⊥FD，从而AC⊥平面BDF．推导出EB∥FD，从而B，D，F，E四点共面，由此能证明EF⊥AC．（Ⅱ）设AC∩BD=O，连接EO，FO，由V E﹣FAC =V A﹣FEO+V C﹣FEO，能求出三棱锥E﹣FAC的体积．【解答】证明：：（Ⅰ）连接BD，因为ABCD是正方形，所以AC⊥BD．因为FD⊥平面ABCD，AC⊂平面ABCD，所以AC⊥FD．因为BD∩FD=D，所以AC⊥平面BDF．因为EB⊥平面ABCD，FD⊥平面ABCD，所以EB∥FD．所以B，D，F，E四点共面．因为EF⊂平面BDFE，所以EF⊥AC．解：（Ⅱ）设AC∩BD=O，连接EO，FO．由（Ⅰ）知，AC⊥平面BDFE，所以AC⊥平面FEO．因为平面FEO将三棱锥E﹣FAC分为两个三棱锥A﹣FEO和C﹣FEO，所以V E﹣FAC =V A﹣FEO+V C﹣FEO．因为正方形ABCD的边长为a，，所以，．取BE的中点G，连接DG，则FE=DG=．所以等腰三角形FEO的面积为=．所以V E﹣FAC =V A﹣FEO+V C﹣FEO====．所以三棱锥E﹣FAC的体积为．【点评】本题考查线线垂直的证明，考查三棱锥的体积的求法，考查空间中线线、线面、面面间的关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查化归与转化思想、数形结合思想，是中档题．20．（12分）（2018•广州二模）已知定点F（0，1），定直线l：y=﹣1，动圆M过点F，且与直线l相切．（Ⅰ）求动圆M的圆心轨迹C的方程；（Ⅱ）过点F的直线与曲线C相交于A，B两点，分别过点A，B作曲线C的切线l1，l2，两条切线相交于点P，求△PAB外接圆面积的最小值．【考点】KN：直线与抛物线的位置关系；J3：轨迹方程．【分析】（Ⅰ）利用直接法，即可求动圆M的圆心轨迹C的方程；（Ⅱ）证明△PAB的外接圆的圆心为线段AB的中点，线段AB是直径．得到当k=0时线段AB最短，最短长度为4，此时圆的面积最小，最小面积为4π．【解答】解：（Ⅰ）设点M到直线l的距离为d，依题意|MF|=d．设M（x，y），则有=|y+1|．化简得x2=4y．所以点M的轨迹C的方程为x2=4y．（Ⅱ）设l AB：y=kx+1，代入x2=4y中，得x2﹣4kx﹣4=0．设A（x1，y1），B（x2，y2），则x1+x2=4k，x1•x2=﹣4．所以．因为C：x2=4y，即，所以．所以直线l1的斜率为，直线l2的斜率为．因为，所以PA⊥PB，即△PAB为直角三角形．所以△PAB的外接圆的圆心为线段AB的中点，线段AB是直径．因为|AB|=4（k2+1），所以当k=0时线段AB最短，最短长度为4，此时圆的面积最小，最小面积为4π．【点评】本题考查轨迹方程，考查直线与抛物线位置关系的运用，考查学生的计算能力，属于中档题．21．（12分）（2018•广州二模）已知函数．（Ⅰ）求函数f（x）的单调区间；（Ⅱ）若函数g（x）=f（x）+4x存在极小值点x0，且，求实数a的取值范围．【考点】6D：利用导数研究函数的极值；6B：利用导数研究函数的单调性．【分析】（I）计算f′（x），讨论a判断f′（x）的符号得出f（x）的单调区间；（II）由导数和二次函数的性质得g′（x）=0在（0，+∞）上有两解列不等式组得出a的范围，根据得出a的范围，再取交集即可．【解答】解：（Ⅰ）因为函数，所以其定义域为（0，+∞）．所以=．当a≤0时，f'（x）＜0，函数f（x）在区间（0，+∞）上单调递减．当a＞0时，f'（x）=．当时，f'（x）＜0，函数f（x）在区间上单调递减．当时，f'（x）＞0，函数f（x）在区间上单调递增．综上可知，当a≤0时，函数f（x）的单调递减区间为（0，+∞）；当a＞0时，函数f（x）的单调递增区间为，单调递减区间为．（Ⅱ）因为g（x）=f（x）+4x=，所以=（x＞0）．因为函数g（x）存在极小值点，所以g'（x）在（0，+∞）上存在两个零点x1，x2，且0＜x1＜x2．即方程x2﹣4x﹣a=0的两个根为x1，x2，且0＜x1＜x2，所以，解得﹣4＜a＜0．则=．当0＜x＜x1或x＞x2时，g'（x）＜0，当x1＜x＜x2时，g'（x）＞0，所以函数g（x）的单调递减区间为（0，x1）与（x2，+∞），单调递增区间为（x1，x2）．所以x=x1为函数g（x）的极小值点x0．由，得．由于等价于．由，得，所以alnx0+a＞0．因为﹣4＜a＜0，所以有lnx0+1＜0，即．因为，所以．解得．所以实数a的取值范围为．【点评】本题考查了导数与函数单调性、极值的关系，函数最值得计算，属于中档题．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．[选修4-4：坐标系与参数方程]22．（10分）（2018•广州二模）在平面直角坐标系xOy中．已知直线l的普通方程为x﹣y﹣2=0，曲线C的参数方程为（θ为参数），设直线l 与曲线C交于A，B两点．（1）求线段AB的长（2）已知点P在曲线C上运动．当△PAB的面积最大时，求点P的坐标及△PAB 的最大面积．【考点】KL：直线与椭圆的位置关系；QL：椭圆的参数方程．【分析】（1）根据题意，将曲线C的参数方程变形为普通方程，将直线x﹣y ﹣2=0代入其中，可得x2﹣3x=0，解可得x的值，由弦长公式计算可得答案；（2）分析可得要使△PAB的面积最大，则必须使P到直线直线l的距离最大，设P的坐标为（2cosθ，2sinθ），其中θ∈[0，2π），由点到直线l的距离公式可得d=，由余弦函数的性质分析可得当θ+=π，即θ=时，d取得最大值，代入点的坐标（2cosθ，2sinθ）中可得P的坐标，进而计算可得△PAB的最大面积，即可得答案．【解答】解：（1）根据题意，曲线C的参数方程为，则其普通方程为： +=1，将直线x﹣y﹣2=0代入+=1可得：x2﹣3x=0，解可得x=0或3，故|AB|=|x1﹣x2|=3；（2）要求在椭圆+=1上求一点P，使△PAB的面积最大，则P到直线直线l的距离最大；设P的坐标为（2cosθ，2sinθ），其中θ∈[0，2π），则P到直线l的距离d==，又由θ∈[0，2π），则≤θ+＜，所以当θ+=π，即θ=时，d取得最大值，且d max=3，此时P（﹣3，1），△PAB的最大面积S=×|AB|×d=9．【点评】本题考查椭圆与直线的位置关系，涉及椭圆的参数方程，关键是正确将参数方程化为普通方程．[选修4-5：不等式选讲]23．（2018•广州二模）（I）已知a+b+c=1，证明（a+1）2+（b+1）2+（c+1）2≥；（Ⅱ）若对任总实数x，不等式|x﹣a|+|2x﹣1|≥2恒成立，求实数a的取值范围．【考点】R4：绝对值三角不等式；R6：不等式的证明．【分析】（I）利用柯西不等式，即可证明；（Ⅱ）分：①a=、②a＞、③a＜三种情况，分别化简不等式，根据函数y=|2x ﹣1|+|x﹣a|的最小值大于或等于2，求得a的范围．【解答】（I）证明：由柯西不等式可得（1+1+1）[（a+1）2+（b+1）2+（c+1）2]≥（a+1+b+1+c+1）2，∵a+b+c=1，∴（a+1）2+（b+1）2+（c+1）2≥；（Ⅱ）解：①当a=时，不等式即|x﹣|≥，显然不能任意实数x均成立．②当a＞时，|2x﹣1|+|x﹣a|=，此时，根据函数y=|2x﹣1|+|x﹣a|的单调性可得y的最小值为﹣3×+a+1．∵不等式|2x﹣1|+|x﹣a|≥2对任意实数x均成立，∴﹣3×+a+1≥2，解得a≥．③当a＜时，|2x﹣1|+|x﹣a|=，此时，根据函数y=|2x﹣1|+|x﹣a|的单调性可得y的最小值为﹣﹣a+1．∵不等式|2x﹣1|+|x﹣a|≥2对任意实数x均成立，∴﹣﹣a+1≥2，解得a≤﹣．综上可得，实数a的取值范围是（﹣∞，﹣]∪[，+∞）．【点评】本题主要考查绝对值不等式的解法，体现了转化以及分类讨论的数学思想，属于中档题．。

2018年广东省广州市高考数学二模试卷（文科）一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）已知集合M＝{﹣1，0，1，2}，N＝{x|x＜0或x＞1}，则M∩N中的元素个数为（）A．1B．2C．3D．42．（5分）若a为实数，且（1+ai）（a﹣i）＝2，则a＝（）A．﹣1B．0C．1D．23．（5分）执行如图的程序框图，若输出y＝，则输入x的值为（）A．log23﹣1或B．1﹣log23或C．1﹣log23D．4．（5分）若双曲线C：（a＞0，b＞0）的一条渐近线方程为y＝2x，则C的离心率为（）A．B．C．D．5．（5分）根据如图给出的2000年至2016年我国实际利用外资情况，以下结论正确的是实际利用外资规模实际利用外资同比增速（）A．2000年以来我国实际利用外资规模与年份负相关B．2010年以来我国实际利用外资规模逐年增加C．2008年我国实际利用外资同比增速最大D．2010年我国实际利用外资同比增速最大6．（5分）已知命题p：∀x∈R，x2+x﹣1＞0；命题q：∃x∈R，2x＞3x，则下列命题中为真命题的是（）A．p∧q B．p∨（￢q）C．（￢p）∨q D．（￢p）∧（￢q）7．（5分）设x，y满足约束条件，则z＝3x﹣y的取值范围是（）A．[﹣1，3]B．[1，3]C．[﹣7，1]D．[﹣7，3]8．（5分）若函数f（x）＝sin（ωx+φ）的部分图象如图所示，则f（x）的单调递增区间是（）A．[kπ﹣，kπ+]（k∈Z）B．[kπ，kπ+]（k∈Z）C．[2kπ﹣，2kπ+]（k∈Z）D．[2kπ，2kπ+]（k∈Z）9．（5分）设{a n}是公差不为零的等差数列，其前n项和为S n，若＝，S7＝﹣21，则a10＝（）A．8B．9C．10D．1210．（5分）某几何体由长方体和半圆柱体组合而成，如图，网格纸上小正方形的边长为1，粗线画出的是该几何体的三视图，则该几何体的表面积是（）A．18+πB．18+2πC．16+πD．16+2π11．（5分）已知直线l与曲线y＝x3﹣x+1有三个不同交点A（x1，y1），B（x2，y2），C（x3，y3），且|AB|＝|AC|，则（x i+y i）＝（）A．0B．1C．2D．312．（5分）体积为的三棱锥P﹣ABC的顶点都在球O的球面上，P A⊥平面ABC，P A＝2，∠ABC＝120°，则球O的体积的最小值为（）A．πB．πC．πD．π二、填空题：本题共4小题，每小题5分，共20分．13．（5分）已知向量与的夹角为，||＝2，||＝，则||＝．14．（5分）已知函数f（x）＝e x﹣x2的图象在点（1，f（1））处的切线过点（0，a），则a ＝．15．（5分）古希腊著名的毕达哥拉斯学派把1，3，6，10…这样的数称为“三角形数”，而把1，4，9，16…这样的数称为“正方形数”．如图，可以发现任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和，下列等式：①36＝15+21；②49＝18+31；③64＝28+36；④81＝36+45中符合这一规律的等式是．（填写所有正确结论的编号）16．（5分）设点P是抛物线x2＝4y上的动点，点P到x轴的距离为d，点P1是圆（x﹣2）2+（y+1）2＝1上的动点，当d+|PP1|最小时，点P的坐标为．三、解答题：共70分．解答应写出文字说明、证明过程和演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分．17．（12分）已知△ABC的内角A，B，C的对边分别是a，b，c，且b sin2A＝a sin B．（1）求A；（2）若a＝2，△ABC的面积为，求△ABC的周长．18．（12分）A药店计划从甲，乙两家药厂选择一家购买100件某种中药材，为此A药店从这两家药厂提供的100件该种中药材中随机各抽取10件，以抽取的10件中药材的质量（单位：克）作为样本，样本数据的茎叶图如图所示．已知A药店根据中药材的质量（单位：克）的稳定性选择药厂．（1）根据样本数据，A药店应选择哪家药厂购买中药材？（不必说明理由）（2）若将抽取的样本分布近似看作总体分布，药店与所选药厂商定中药材的购买价格如表：（ⅰ）估计A药店所购买的100件中药材的总质量；（ⅱ）若A药店所购买的100件中药材的总费用不超过7000元，求a的最大值．19．（12分）如图，在直三棱柱ABC﹣A1B1C1中，M，N分别是AB1和BC的中点．（1）证明：MN∥平面AA1C1C；（2）若AA1＝2，AB＝AC＝1，∠BAC＝90°，求棱锥C1﹣AMN的高．20．（12分）已知椭圆C的中心为坐标原点O，右焦点为F（2，0），短轴长为4．（1）求椭圆C的方程；（2）若直线l：y＝kx+3与椭圆C相交于不同的两点M，N，点P为线段MN的中点，OP∥FM，求直线l的方程．21．（12分）已知函数f（x）＝a（x﹣1）﹣lnx．（1）若函数f（x）的极小值不大于k对任意a＞0恒成立，求k的取值范围；（2）证明：∀n∈N*，（1+）•（1+）•（1+）…（1+）＜e2．（其中e为自然对数的底数）（二）选考题：共10分．请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]22．（10分）在直角坐标系xOy中，直线l的参数方程为（t为参数）．以坐标原点为极点，以x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ2（1+2sin2θ）＝a（a＞0）．（1）求l的普通方程和C的直角坐标方程；（2）若l与C相交于A，B两点，且|AB|＝，求a的值．[选修4-5：不等式选讲]23．已知函数f（x）＝|2x+1|+|2x﹣1|，不等式f（x）≤2的解集为M．（1）求M；（2）证明：当a，b∈M时，|a+b|+|a﹣b|≤1．2018年广东省广州市高考数学二模试卷（文科）参考答案与试题解析一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）已知集合M＝{﹣1，0，1，2}，N＝{x|x＜0或x＞1}，则M∩N中的元素个数为（）A．1B．2C．3D．4【解答】解：集合M＝{﹣1，0，1，2}，N＝{x|x＜0或x＞1}，则M∩N＝{﹣1，2}，∴集合M∩N中元素的个数为2．故选：B．2．（5分）若a为实数，且（1+ai）（a﹣i）＝2，则a＝（）A．﹣1B．0C．1D．2【解答】解：∵a为实数，且（1+ai）（a﹣i）＝2a+（a2﹣1）i＝2，∴2a＝2，即a＝1．故选：C．3．（5分）执行如图的程序框图，若输出y＝，则输入x的值为（）A．log23﹣1或B．1﹣log23或C．1﹣log23D．【解答】解：当x≤1时，由y＝2x＝得：x＝log23﹣1，当x＞1时，由y＝2﹣log2x＝得：x＝，综上可得：若输出y＝，则输入x的值为log23﹣1或，故选：A．4．（5分）若双曲线C：（a＞0，b＞0）的一条渐近线方程为y＝2x，则C的离心率为（）A．B．C．D．【解答】解：由已知双曲线C：（a＞0，b＞0）的一条渐近线方程为y＝2x，可得，，故选：B．5．（5分）根据如图给出的2000年至2016年我国实际利用外资情况，以下结论正确的是实际利用外资规模实际利用外资同比增速（）A．2000年以来我国实际利用外资规模与年份负相关B．2010年以来我国实际利用外资规模逐年增加C．2008年我国实际利用外资同比增速最大D．2010年我国实际利用外资同比增速最大【解答】从图表中可以看出，2000年以来我国实际利用外资规模基本上是逐年上升的，因此实际利用外资规模与年份正相关，选项A错误；我国实际利用外资规模2012年比2011年少，所以选项B错误；从图表中的折线可以看出，2008年实际利用外资同比增速最大，所以选项C正确；2008年实际利用外资同比增速最大，所以选项D错误；故选：C．6．（5分）已知命题p：∀x∈R，x2+x﹣1＞0；命题q：∃x∈R，2x＞3x，则下列命题中为真命题的是（）A．p∧q B．p∨（￢q）C．（￢p）∨q D．（￢p）∧（￢q）【解答】解：∵判别式△＝1﹣4（﹣1）＝5＞0，∴∀x∈R，x2+x﹣1＞0不成立，即命题p 是假命题，当x＝﹣1时，2﹣1＞3﹣1，即命题q：∃x∈R，2x＞3x，是真命题，则（￢p）∨q是真命题，其余为假命题，故选：C．7．（5分）设x，y满足约束条件，则z＝3x﹣y的取值范围是（）A．[﹣1，3]B．[1，3]C．[﹣7，1]D．[﹣7，3]【解答】解：由x，y满足约束条件作出可行域如图，可知A（﹣1，4），化目标函数z＝3x﹣y为y＝3x﹣z，由图可知，当直线y＝3x﹣z过点A时，直线在y轴上的截距最大，z有最小值为﹣7．B（1，0），由图可知，当直线y＝3x﹣z过点B时，直线在y轴上的截距最小，z有最大值为3．∴z＝3x﹣y的取值范围是[﹣7，3]．故选：D．8．（5分）若函数f（x）＝sin（ωx+φ）的部分图象如图所示，则f（x）的单调递增区间是（）A．[kπ﹣，kπ+]（k∈Z）B．[kπ，kπ+]（k∈Z）C．[2kπ﹣，2kπ+]（k∈Z）D．[2kπ，2kπ+]（k∈Z）【解答】解：根据函数f（x）＝sin（ωx+φ）的部分图象，可得•＝﹣，∴ω＝2，再根据五点法作图可得2×+φ＝0，求得φ＝﹣，∴f（x）＝sin（2x﹣）．令2kπ﹣≤2x﹣≤2kπ+，求得kπ﹣≤x≤kπ+，故函数f（x）的增区间为[kπ﹣，kπ+]（k∈Z），故选：A．9．（5分）设{a n}是公差不为零的等差数列，其前n项和为S n，若＝，S7＝﹣21，则a10＝（）A．8B．9C．10D．12【解答】解：设{a n}是公差d不为零的等差数列，∵＝，S7＝﹣21，∴+＝+，7a1+d＝﹣21，∴2a1+9d＝0，a1+3d＝﹣3，解得a1＝﹣9，d＝2．则a10＝﹣9+2×9＝9．故选：B．10．（5分）某几何体由长方体和半圆柱体组合而成，如图，网格纸上小正方形的边长为1，粗线画出的是该几何体的三视图，则该几何体的表面积是（）A．18+πB．18+2πC．16+πD．16+2π【解答】解：由三视图可知长方体的棱长为2，2，1，半圆柱的底面半径为1，高为1，∴长方体的表面积为（2×2+2×1+2×1）×2＝16，半圆柱的侧面积为π×1×1+2×1＝π+2，∴几何体的表面积为16+π+2＝18+π．故选：A．11．（5分）已知直线l与曲线y＝x3﹣x+1有三个不同交点A（x1，y1），B（x2，y2），C（x3，y3），且|AB|＝|AC|，则（x i+y i）＝（）A．0B．1C．2D．3【解答】解：∵y＝x3﹣x是奇函数，故y＝x3﹣x的图象关于原点对称，∴y＝x3﹣x+1的函数图象关于点（0，1）对称，∵直线l与曲线y＝x3﹣x+1有三个不同交点A（x1，y1），B（x2，y2），C（x3，y3），且|AB|＝|AC|，∴A为函数的对称点，即A（0，1），且B，C两点关于点A（0，1）对称，∴x1+x2+x3＝0，y1+y2+y3＝3．于是（x i+y i）＝3．故选：D．12．（5分）体积为的三棱锥P﹣ABC的顶点都在球O的球面上，P A⊥平面ABC，P A＝2，∠ABC＝120°，则球O的体积的最小值为（）A．πB．πC．πD．π【解答】解：∵V P﹣ABC＝S△ABC•P A＝＝，∴AB•BC＝6，∵P A⊥平面ABC，P A＝2，∴O到平面ABC的距离为d＝P A＝1，设△ABC的外接圆半径为r，球O的半径为R，R＝＝．由余弦定理可知AC2＝AB2+BC2﹣2AB•BC•cos120°＝AB2+BC2+6≥2AB•BC+6＝18，当且仅当AB＝BC＝时取等号．∴AC≥3．由正弦定理可得2r＝≥＝2，∴r≥．∴R≥．∴当R＝时，球O的体积取得最小值V＝＝．故选：B．二、填空题：本题共4小题，每小题5分，共20分．13．（5分）已知向量与的夹角为，||＝2，||＝，则||＝．【解答】解：∵向量与的夹角为，||＝2，||＝，∴•＝||•||•cos＝2××＝2，∴||2＝||2+||2﹣2•＝4+2﹣4＝2，∴||＝，故答案为：14．（5分）已知函数f（x）＝e x﹣x2的图象在点（1，f（1））处的切线过点（0，a），则a ＝1．【解答】解：函数f（x）＝e x﹣x2的导数为f′（x）＝e x﹣2x，函数f（x）＝e x﹣x2的图象在点（1，f（1））处的切线的斜率为e﹣2，切点为（1，e﹣1），由切线过点（0，a），可得：e﹣2＝，解得a＝1，故答案为：1．15．（5分）古希腊著名的毕达哥拉斯学派把1，3，6，10…这样的数称为“三角形数”，而把1，4，9，16…这样的数称为“正方形数”．如图，可以发现任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和，下列等式：①36＝15+21；②49＝18+31；③64＝28+36；④81＝36+45中符合这一规律的等式是①③④．（填写所有正确结论的编号）【解答】解：由已知条件可得如下规律等式4＝1+3，9＝3+6，16＝6+10，25＝10+15，36＝15+2149＝21+2864＝28+36，81＝36+45，．．故答案为①③④16．（5分）设点P是抛物线x2＝4y上的动点，点P到x轴的距离为d，点P1是圆（x﹣2）2+（y+1）2＝1上的动点，当d+|PP1|最小时，点P的坐标为（﹣2+2，3﹣2）．【解答】解：抛物线的焦点为F（0，1），准线方程为y＝﹣1．圆的圆心为M（2，﹣1），∴d＝PF﹣1，故当FP1PM四点共线且P，P1在M，F之间时，d+|PP1|取得最小值，此时直线MF的方程为：y＝﹣x+1，联立方程组，得：x2+4x﹣4＝0，解得x＝﹣2，或x＝﹣2﹣2（舍），∴y＝3﹣2．故答案为（﹣2+2，3﹣2）．三、解答题：共70分．解答应写出文字说明、证明过程和演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题：共60分．17．（12分）已知△ABC的内角A，B，C的对边分别是a，b，c，且b sin2A＝a sin B．（1）求A；（2）若a＝2，△ABC的面积为，求△ABC的周长．【解答】解：（1）知△ABC的内角A，B，C的对边分别是a，b，c，且b sin2A＝a sin B．则：2b sin A cos A＝a sin B，由于：sin A sin B≠0，则：cos A＝，由于：0＜A＜π，所以：A＝．（2）利用余弦定理得：a2＝b2+c2﹣2bc cos A，由于：a＝2，所以：4＝b2+c2﹣bc，△ABC的面积为，则：，解得：bc＝4．故：b2+c2＝8，所以：（b+c）2＝8+2•4＝16，则：b+c＝4．所以：三角形的周长为2+4＝6．18．（12分）A药店计划从甲，乙两家药厂选择一家购买100件某种中药材，为此A药店从这两家药厂提供的100件该种中药材中随机各抽取10件，以抽取的10件中药材的质量（单位：克）作为样本，样本数据的茎叶图如图所示．已知A药店根据中药材的质量（单位：克）的稳定性选择药厂．（1）根据样本数据，A药店应选择哪家药厂购买中药材？（不必说明理由）（2）若将抽取的样本分布近似看作总体分布，药店与所选药厂商定中药材的购买价格如表：（ⅰ）估计A药店所购买的100件中药材的总质量；（ⅱ）若A药店所购买的100件中药材的总费用不超过7000元，求a的最大值．【解答】解：（1）根据样本数据知，A药店应选择乙药厂购买中药材；（2）（ⅰ）从乙药厂所抽取的每件中药材的质量平均数为＝×（7+9+11+12+12+17+18+21+21+22）＝15；估计A药店所购买的100件中药材的总质量为100×15＝1500克；（ⅱ）乙药厂所提供的每件中药材的质量n＜15的概率为＝0.5，15≤n≤20的概率为＝0.2，n＞20的概率为＝0.3，则A药店所购买的100件中药材的总费用为100×（50×0.5+0.2a+100×0.3）；依题意得100×（50×0.5+0.2a+100×0.3）≤7000，解得a≤75，∴a的最大值为75．19．（12分）如图，在直三棱柱ABC﹣A1B1C1中，M，N分别是AB1和BC的中点．（1）证明：MN∥平面AA1C1C；（2）若AA1＝2，AB＝AC＝1，∠BAC＝90°，求棱锥C1﹣AMN的高．【解答】（1）证明：连结A1B，CA1，∵四边形ABB1A1是平行四边形，M是AB1的中点，∴M是A1B的中点，又N是BC的中点，∴MN∥A1C，又MN⊄平面ACC1A1，A1C⊂平面ACC1A1，∴MN∥平面AA1C1C．（2）解：以A1为原点，以A1B1，A1A，A1C1为坐标轴建立空间坐标系如图所示：则C1（0，0，1），A（0，2，0），M（，1，0），N（，2，），∴＝（，1，﹣1），＝（﹣，1，0），＝（，0，），设平面AMN的法向量为＝（x，y，z），则，＝0，∴，令y＝1，得＝（2，1，﹣2），∴cos＜，＞＝＝＝．设直线C1M与平面AMN的夹角为θ，则sinθ＝，∴C1到平面AMN的距离d＝|C1M|sinθ＝×＝．∴棱锥C1﹣AMN的高为．20．（12分）已知椭圆C的中心为坐标原点O，右焦点为F（2，0），短轴长为4．（1）求椭圆C的方程；（2）若直线l：y＝kx+3与椭圆C相交于不同的两点M，N，点P为线段MN的中点，OP∥FM，求直线l的方程．【解答】解：（1）设椭圆方程为＝1（a＞b＞0），由题意可知c＝2，2b＝4，即b＝2，∴a＝＝2．∴椭圆方程为＝1．（2）联立方程组，消去y得：（1+2k2）x2+12kx+28＝0，△＝288k2﹣112（1+2k2）＝64k2﹣112＞0，解得k2＞．设M（x1，y1），N（x2，y2），P（x0，y0），则x1+x2＝﹣，x1x2＝，x0＝＝﹣，y0＝kx0+3＝，∴k OP＝＝﹣，∵OP∥FM，∴k FM＝k OP＝﹣，∴直线FM的方程为y＝﹣（x﹣2），解方程组，得，即M（，），∵M在椭圆上，∴（）2+2（）2＝8，解得k2＝2，即k＝．∴直线l的方程为y＝x+3或y＝﹣x+3．21．（12分）已知函数f（x）＝a（x﹣1）﹣lnx．（1）若函数f（x）的极小值不大于k对任意a＞0恒成立，求k的取值范围；（2）证明：∀n∈N*，（1+）•（1+）•（1+）…（1+）＜e2．（其中e为自然对数的底数）【解答】解：（1）函数f（x）的定义域是（0，+∞），由f（x）＝a（x﹣1）﹣lnx，得f′（x）＝a﹣，当a＞0时，令f′（x）＝0，解得：x＝，则x∈（0，）时，f′（x）＜0，x∈（，+∞）时，f′（x）＞0，故函数f（x）在（0，）递减，在（，+∞）递增；当x＝时，函数f（x）取得极小值，其值为f（）＝a（﹣1）﹣ln＝1﹣a+lna，令g（a）＝1﹣a+lna（a＞0），则g′（a）＝﹣，当0＜a＜1时，g′（a）＞0，当a＞1时，g′（a）＜0，故g（a）在（0，1）递增，在（1，+∞）递减，当a＝1时，g（a）取最大值，其值为g（1）＝0，应用函数f（x）的极小值不大于k对任意a＞0恒成立，则k≥0，故k的范围是[0，+∞），（2）证明：由（1）可知，当a＝1时，函数f（x）在（0，1）递减，在（1，+∞）递增，当x＝1时，函数f（x）取最小值为f（1）＝0，故x＞0时，f（x）≥0，即x﹣1﹣lnx≥0，得lnx≤x﹣1，∀n∈N*，令x＝1+，得ln（1+）≤，故ln（（1+）+ln（1+）+ln（1+）+…+ln（1+）≤+++…+，令S n＝+++…+①，s n＝+++…+②，①﹣②得s n＝+++…+﹣，＝﹣＝1﹣故S n＝2﹣＜2，故ln[（1+）（1+）（1+）…（1+）]＜2，故（1+）（1+）（1+）…（1+）]＜e2．（二）选考题：共10分．请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]22．（10分）在直角坐标系xOy中，直线l的参数方程为（t为参数）．以坐标原点为极点，以x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ2（1+2sin2θ）＝a（a＞0）．（1）求l的普通方程和C的直角坐标方程；（2）若l与C相交于A，B两点，且|AB|＝，求a的值．【解答】（1）解：由消去参数t，得直线l的普通方程为y＝﹣（x﹣1）．即+y﹣＝0，由ρ2（1+2sin2θ）＝a，即ρ2+2ρ2sin2θ＝a，把ρ2＝x2+y2，ρsinθ＝y代入上式得x2+3y2＝a．所以C的直角坐标方程为x2+3y2＝a．（2）解：由消去y，得10x2﹣18x+9﹣a＝0（1），设A（x1，y1），B（x2，y2），得x1+x2═，x1x2＝．|AB|＝•|x2﹣x1|＝．又由已知|AB|＝，得＝，解得a＝，此时（1）式的判别式△＝4﹣4×5×（2﹣2×）＝12＞0．所以a的值为．[选修4-5：不等式选讲]23．已知函数f（x）＝|2x+1|+|2x﹣1|，不等式f（x）≤2的解集为M．（1）求M；（2）证明：当a，b∈M时，|a+b|+|a﹣b|≤1．【解答】解：（1）f（x）≤2，即|2x+1|+|2x﹣1|≤2，当x≤﹣时，得﹣（2x+1）+（1﹣2x）≤2，解得：x≥﹣，故x＝﹣，当﹣＜x＜时，得（2x+1）﹣（2x﹣1）≤2，即2≤2，故﹣＜x＜，当x≥时，得（2x+1）+（2x﹣1）≤2，解得：x≤，故x＝，故不等式f（x）≤2的解集M＝{x|﹣≤x≤}；（2）证明：法一：当a，b∈M时，即﹣≤a≤，﹣≤b≤，得|a|≤，|b|≤，当（a+b）（a﹣b）≥0时，|a+b|+|a﹣b|＝|a+b+a﹣b|＝2|a|≤1，当（a+b）（a﹣b）＜0时，|a+b|+|a﹣b|＝|a+b﹣a+b|＝2|b|≤1，故|a+b|+|≤1；法二：当a，b∈M时，即﹣≤a≤，﹣≤b≤，得|a|≤，|b|≤，（|a+b|+|a﹣b|）2＝2（a2+b2）+2|a2﹣b2|＝，由于a2≤，b2≤，则4a2≤1，4b2≤1，故（|a+b|+|a﹣b|）2≤1，故|a+b|+|a﹣b|≤1．。

2018年普通高等学校招生全国统一考试广东省文科数学模拟试卷（二）第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. （）A. B. C. D.【答案】D【解析】分析：本题利用复数的除法法则进行求解.详解：.故选D.点睛：复数的除法法则涉及的公式比较难记忆，搞清其实质（分子、分母同乘以分母的共轭复数）是解题的关键.2. 已知，，若，则（）A. B. C. D.【答案】A【解析】分析：利用“若，且，则”得到关于的方程，再通过解方程求得值.详解：由题意，得，解得.故选A.点睛：涉及平面向量的共线（平行）的判定问题主要有以下两种思路：（1）若且，则存在实数，使成立；（2）若，且，则.3. 已知，集合，集合，若，则（）A. B. C. D.【答案】B【解析】分析：先利用得到，由此得到值，再验证是否成立进行取舍. 详解：因为，，且，所以或，若时，,（舍）；若时，,；即.故选B.点睛：本题的易错点是由得到或后，就直接得到错误答案（或），忘记验证是否成立.4. 空气质量指数（简称：）是定量描述空气质量状况的无量纲指数，空气质量按照大小分为六级：为优，为良，为轻度污染，为中度污染，为重度污染，为严重污染.下面记录了北京市天的空气质量指数，根据图表，下列结论错误的是（）A. 在北京这天的空气质量中，按平均数来考察，最后天的空气质量优于最前面天的空气质量B. 在北京这天的空气质量中，有天达到污染程度C. 在北京这天的空气质量中，12月29日空气质量最好D. 在北京这天的空气质量中，达到空气质量优的天数有天【答案】C【解析】分析：通过题目所提供的图表得出22个数据，研究在各区间上的数据个数，对选项逐一验证得到答案.详解：因为，所以在北京这天的空气质量中，按平均数来考察，最后天的空气质量优于最前面天的空气质量，即选项A正确；不低于100的数据有3个：，所以在北京这天的空气质量中，有天达到污染程度，即选项B正确；因为12月29日的为225，为重度污染，该天的空气质量最差，即选项C错误；在的数据有6个：，即达到空气质量优的天数有天，即选项D正确.故选C.点睛：本题考查频率分布表的识别和应用，属于基础题，本题的技巧是判定选项A时，仅从各数据的大小关系上进行判定，避免了不必要的运算.5. 如图，是以正方形的边为直径的半圆，向正方形内随机投入一点，则该点落在阴影区域内的概率为（）A. B. C. D.【答案】D【解析】分析：先由圆的对称性得到图中阴影部分的面积，再用几何概型的概率公式进行求解.详解：连接，由圆的对称性得阴影部分的面积等于的面积，易知，由几何概型的概率公式，得该点落在阴影区域内的概率为.故选D..点睛：本题的难点是求阴影部分的面积，本解法利用了圆和正方形的对称性，将阴影部分的面积转化为求三角形的面积.6. 已知等比数列的首项为，公比，且，则（）A. B. C. D.【答案】B【解析】分析：先根据得到值，再利用等比数列的通项公式进行求解.详解：因为，所以，又因为，所以.故选B.点睛：本题考查了等比数列的基本运算，在记忆等比数列的通项公式时，既要熟记，还要注意的应用.7. 已知双曲线的一个焦点坐标为，且双曲线的两条渐近线互相垂直，则该双曲线的方程为（）A. B. C. D. 或【答案】A【解析】分析：先利用双曲线的渐近线相互垂直得出该双曲线为等轴双曲线，再利用焦点位置确定双曲线的类型，最后利用几何元素间的等量关系进行求解.详解：因为该双曲线的两条渐近线互相垂直，所以该双曲线为等轴双曲线，即，又双曲线的一个焦点坐标为，所以，即，即该双曲线的方程为.故选D.点睛：本题考查了双曲线的几何性质，要注意以下等价关系的应用：等轴双曲线的离心率为，其两条渐近线相互垂直.8. 已知某几何体的三视图如图所示，则该几何体的表面积为（）A. B. C. D.【答案】B【解析】分析：先利用三视图得到该组合体的结构特征，再分别利用球的表面积公式、圆柱的侧面积公式求出各部分面积，再求和即可.详解：由三视图可得该几何体是由圆柱的一半（沿轴截面截得，底面半径为1，母线长为3）和一个半径为1的半球组合而成（部分底面重合），则该几何体的表面积为.点睛：处理几何体的三视图和表面积、体积问题时，往往先由三视图判定几何体的结构特征，再利用相关公式进行求解.9. 在印度有一个古老的传说：舍罕王打算奖赏国际象棋的发明人——宰相宰相西萨•班•达依尔．国王问他想要什么，他对国王说：“陛下，请您在这张棋盘的第1个小格里，赏给我1粒麦子，在第2个小格里给2粒，第3小格给4粒，以后每一小格都比前一小格加一倍．请您把这样摆满棋盘上所有的64格的麦粒，都赏给您的仆人吧！”国王觉得这要求太容易满足了，就命令给他这些麦粒．当人们把一袋一袋的麦子搬来开始计数时，国王才发现：就是把全印度甚至全世界的麦粒全拿来，也满足不了那位宰相的要求．那么，宰相要求得到的麦粒到底有多少粒？下面是四位同学为了计算上面这个问题而设计的程序框图，其中正确的是（）A. B. C. D.【答案】C【解析】分析：先分析这个传说中涉及的等比数列的前64项的和，再对照每个选项对应的程序框图进行验证.详解：由题意，得每个格子所放麦粒数目形成等比数列，且首项，公比，所设计程序框图的功能应是计算，经验证，得选项B符合要求.故选B.学。

2018年广州市普通高中毕业班综合测试(二)文科数学含答案D数学（文科）试题第2页（共5页）数学（文科）试题第3页（共5页）数学（文科）试题第4页（共5页）数学（文科）试题第5页（共5页）数学（文科）试题 第6页 （共5页）C ．2008年我国实际利用外资同比增速最大D ．2010年我国实际利用外资同比增速最大6．已知命题:p x ∀∈R,210x x +->；命题:q x ∃∈R ，23x x >，则下列命题中为真命题的是A ．p q ∧B ．()p q ∨⌝C ．()p q ⌝∨D ．()()p q ⌝∧⌝7．设,x y 满足约束条件11,13,x x y -⎧⎨+⎩≤≤≤≤则3z x y =-的取值范围是A ．[]1,3-B ．[]1,3C ．[]7,1-D ．[]7,3-8．若函数()()sin f x x ωϕ=+的部分图象如图所示，则()f x 的单调递增区间是A ．,63k k ππ⎡⎤π-π+⎢⎥⎣⎦(k ∈Z )B ．5,36k k ππ⎡⎤π+π+⎢⎥⎣⎦(k ∈Z ) C ．2,263k k ππ⎡⎤π-π+⎢⎥⎣⎦ (k ∈Z )D ．52,236k k ππ⎡⎤π+π+⎢⎥⎣⎦ (k ∈Z ) 9．设{}na 是公差不为零的等差数列，其前n 项和为12π 7π12数学（文科）试题 第7页 （共5页）n S ，若22223478aa a a +=+，721S =-， 则10a =A ．8B ．9C ．10D ．1210．某几何体由长方体和半圆柱体组合而成，如图，网格纸上小正方形的边长为1，粗线画出的是该几何体的三视图，则该几何体的表面积是A ．18+πB ．182+πC ．16+πD ．162+π11．已知直线l 与曲线31y xx =-+有三个不同交点()11,A x y ，()()2233,,,B x y C x y ， 且AB AC =，则()31i ii x y =+=∑A ．0B ．1C ．2D ．312．体积为3的三棱锥P ABC -的顶点都在球O 的球面上，PA ⊥平面ABC ，2=PA ，数学（文科）试题 第8页 （共5页）120ABC ︒∠=，则球O 的体积的最小值为AB．C．3 D．3π二、填空题：本题共4小题，每小题5分，共20分．13．已知向量a 与b 的夹角为4π，2,==a b ，则-=a b .14．已知函数()f x =e 2x x -的图象在点()()1,1f 处的切线过点()0,a ，则a = .15．古希腊著名的毕达哥拉斯学派把1,3,6,10,…这样的数称为“三角形数”，而把1,4,9,16,…这样的数称为“正方形数”．如图，可以发现任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和，下列等式：①361521=+；②491831=+；③642836=+；④813645=+中符合这一规律的等式是 ．（填写所有正确结论的编号）数学（文科）试题 第9页 （共5页）……16．设点P 是抛物线24=xy 上的动点，点P 到x 轴的距离为d ，点1P 是圆()()22211x y -++=上的动点，当1d PP +最小时，点P 的坐标为 ．三、解答题：共70分．解答应写出文字说明、证明过程和演算步骤．第17～21题为必考题，每个试题考生都必须做答．第22、23题为选考题，考生根据要求做答．（一）必考题：共60分．17．（本小题满分12分）已知△ABC 的内角A ，B ，C 的对边分别是a ，b ，c ，且sin 2sin b A a B =.（1）求A ；（2）若2=a ，△ABC ABC 的周长.18．（本小题满分12分）A药店计划从甲，乙两家药厂选择一家购买100件某种中药材，为此A药店从这两家药厂提供的100件该种中药材中随机各抽取10件，以抽取的10件中药材的质量（单位：克）作为样本，样本数据的茎叶图如图所示．已知A药店根据中药材的质量（单位：克）的稳定性选择药厂．（1）根据样本数据，A药店应选择哪家药厂购买中药材？(不必说明理由)（2）若将抽取的样本分布近似看作总体分布，药店与所选药厂商定中药材的购买价格如下表：每件中药材的质量n（单位：克）购买价格（单位：元/件）15n<501520n≤≤a20n>100数学（文科）试题第10页（共5页）（ⅰ）估计A 药店所购买的100件中药材的总质量；（ⅱ）若A 药店所购买的100件中药材的总费用不超过7000元，求a 的最大值．19．（本小题满分12分）如图，在直三棱柱111-ABC A B C 中，,M N 分别是1AB 和BC的中点．（1）证明：MN ∥平面11AAC C ；（2）若12,1AA AB AC ===，90BAC ︒∠=，求棱锥1C AMN -的高．20．（本小题满分12分）已知椭圆C 的中心为坐标原点O ，右焦点为()2,0F ，短轴长为4.（1）求椭圆C 的方程； （2）若直线:l y =k x+C 相交于不同的两点,M N ，点P 为线段MN 的中点，OP FM ∥，求直线l 的方程.21．（本小题满分12分） 已知函数()f x =()1ln a x x --.（1）若函数()f x 的极小值不大于k 对任意0a >恒成立，求k 的取值范围；（2）证明：∀n ∈N *，2231231111e 2222n n ⎛⎫⎛⎫⎛⎫⎛⎫+⋅+⋅+⋅⋅+< ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭．（其中e 为自然对数的底数）（二）选考题：共10分．请考生在第22、23题中任选一题做答，如果多做，则按所做的第一题计分．22．（本小题满分10分）选修4－4：坐标系与参数方程在直角坐标系xOy 中，直线l的参数方程为11,2(,2x t t y t ⎧=-⎪⎪⎨⎪=⎪⎩为参数). 以坐标原点为极点，以x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为()()2212sin 0a a ρθ+=>．（1）求l 的普通方程和C 的直角坐标方程； （2）若l 与C 相交于A ，B 两点，且AB=，求a的值．23．（本小题满分10分）选修4－5：不等式选讲已知函数()2121f x x x =++-，不等式()2f x ≤的解集为M .（1）求M ；（2）证明：当,a b M ∈时，1a b a b ++-≤．2018年广州市普通高中毕业班综合测试（二）文科数学参考答案一．选择题二．填空题13. 2 14. 1 15.①③④ 16. )223,222(--三．解答题3,0,21cos 0sin sin sin sin cos sin sin 2:sin cos sin 2,sin sin )1(17.ππ=<<=≠===A A A A B B A A A B B a A A b B a A b 所以因为则由于由正弦定理得得解6,4162)(8)2)(1()2......(4,33sin 213sin 21,3)1.......(4,2cos 2)2(2222222222周长为所以得则得由得即则得面积为又则又解：由余弦定理得ABC c b bc c b c b c b bc bc A bc ABC bc c b a A bc c b a ∆=+=++=+=+===∆-+==-+=π75,757000)103100512150(100100A 10320,5110220152110515ii 150015100100A 15)222121181712121197(101(2)i 中药药药店应选择乙药厂购买A ）解：1（18.最大值为所以解得件中药材总费用为药店所购买的则的概率为的概率为的概率为中药材质量：乙药厂所提供的每件克件中药材质量估计值为药店所购买的故中药材质量的平均值为从乙药厂所抽取的每件a a a n n n x ≤≤⨯+⨯+⨯⨯<=≤≤=<=⨯=+++++++++=3422243432222321,22221223,,222121,90,1)2(//,//BC ,,)1(19.11111111122111111111111111122111111111111=⨯===⨯⨯==⨯⨯==+=∆⊥⊂⊥⊂=⋂⊥-=+===∠⊥==⊄⊂--∆∆h h V V h N AB AMN C S S BN BB N B BN B Rt NB ANC C BB N B CC BB AN ABC AN BC C C BB ABC C C BB ABC C B A ABC AC AB BC AN BAC BC AN BC N AC AB N B CC AA MN C C AA MN C C AA C A C A MN N B A M C A B A N c B A N AB c N AB N C B ，得到得由的距离相等设为的距离与它到平面到平面依题意，点则中，在所以平面又平面平面平面又平面平面中，可得平面在直三棱柱则又的中点，则是点，由于连接平面所以平面平面又中点，所以是因为的中点是依题意可得点证明：连接232,2322016)21(284)212()5(28)21223(2)21262()21223,21262(2122321262)2(2123)2(21:21,//,21)21(14,)21(26)21(28,)21(212)5......(028212)21(14823),(),,(),,()2(148:2,4242),0,2()0(1:)1(20.222222222220020202212212222002211222222+-=+=±=>=+⨯-=∆==++++-+++-⎪⎪⎩⎪⎪⎨⎧++=+-=⎪⎩⎪⎨⎧--=+=--=-==-==+=+-=+=+-=+=+++⎪⎩⎪⎨⎧=++==+===>>=+x y x y l k k k k kk k k kkk k M k ky k kx x k y kx y x ky FM k k k FM OP k x y k k y k x MN P k x x k x x kx x k y y x kx y y x P y x N y x M y x b b c F C b a by a x C OP FM OP 或方程为：所以直线则式判别式此时，解得带入椭圆方程得则点解得由得方程为所以直线所以因为中点，则是点得消去由设点椭圆方程为得，则又由于椭圆短轴长为则的右焦点为由于椭圆的方程为圆解：依题意可得，设椭),0[k 00)(0)1()()1()1,0()(0)(1,0)(101)(),0(ln 1)(ln 1)1()(1),1()1,0()(0)(),1(,0)()1,0(10)(01)(,ln )1()(),0()()1(21.max +∞≥>==∞+<'<>'<<--='>+-=+-==+∞>'+∞∈<'∈=='>-='--=+∞取值范围为所以，恒成立，则对于任意的极小值不大于由于函数上单调递减，上单调递增，在在故时，当时，当则令取得极小值，其值为时，函数当单调递增单调递减，在在故函数时，时，则，得时，令当得由得定义域为解：函数k a k x f g a g a g a g a a g a aa a g a a a a g aa af x f a x aa x f x f ax x f a x ax x f a x a x f x x a x f x f22213213222e )21ln()221ln()211ln(2)21ln()221ln()211ln(2,2222212121212122221212c 22221)21ln()221ln()211ln(2)21ln(,2,)1ln(,0)0()(0),0()(,0)(01)(,)1ln()()2(<+•••+++<+•••+++<+-=-+•••++=+•••+=+•••=+•••+<+•••+++<+=∈∀<+=<>+∞<'>+-='-+=++*n n n n n n n n n n nn nn nn n nnS n S nS n S nS nn n n n x N n xx h x h x x h x h x xx x h x x x h 所以所以整理化简得：上式减下式得令所以得令即时，故当上单调递减在则时，当令5612)5622(544)(56,53259102591024)(522,52,).....(022********)2(3,)sin 21()1(3,23211)1.(2221221212121212222222的值为所以式的判别式解得所以得亮点对应得参数分别是，设得带入把得由得消去解：由a a a a t t t t t t AB a t t t t t t B A a t t a y x t y t x ay x a x y t t y t x >=⨯-⨯⨯-=∆*==--=-+=-=-==+*=-+-=+⎪⎪⎩⎪⎪⎨⎧=-==+=+--=⎪⎪⎩⎪⎪⎨⎧=-=θρ。

秘密★启用前 试卷类型：A2018年广州市普通高中毕业班综合测试（二）文科数学2018．4本试卷共5页，23小题，满分150分。

考试用时120分钟。

注意事项：1．答卷前，考生务必将自己的姓名和考生号、试室号、座位号填写在答题卡上，并用2B 铅笔在答题卡的相应位置填涂考生号。

2．作答选择题时，选出每小题答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。

写在本试卷上无效。

3．作答填空题和解答题时，必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4．考生必须保持答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{}1,0,1,2M =-，{0N x x =<或}1x >，则M N 中的元素个数为A ．1B ．2C ．3D ．42．若a 为实数，且(1i)(i)=2a a +-，则=aA ．1-B ．0C ．1D ．23．执行如图的程序框图，若输出32y =，则输入x 的值为A ．2log 31-B ．21log 3-C ．21log 3-D4．若双曲线2222:1x y C a b-=()0,0a b >>的一条渐近线方程为2y x =，则C 的离心率为ABC ．2D ．25．根据下图给出的2000年至2016年我国实际利用外资情况，以下结论正确的是A ．2000年以来我国实际利用外资规模与年份负相关B ．2010年以来我国实际利用外资规模逐年增大C ．2008年我国实际利用外资同比增速最大D ．2010年我国实际利用外资同比增速最大6．已知命题:p x ∀∈R ,210x x +->；命题:q x ∃∈R ，23xx>，则下列命题中为真命题的是A ．p q ∧B ．()p q ∨⌝C ．()p q ⌝∨D ．()()p q ⌝∧⌝7．设,x y 满足约束条件11,13,x x y -⎧⎨+⎩≤≤≤≤则3z x y =-的取值范围是A ．[]1,3-B ．[]1,3C ．[]7,1-D ．[]7,3-8．若函数()()sin f x x ωϕ=+的部分图象如图所示，则()f x 的单调递增区间是A ．,63k k ππ⎡⎤π-π+⎢⎥⎣⎦(k ∈Z ) B ．5,36k k ππ⎡⎤π+π+⎢⎥⎣⎦(k ∈Z ) C ．2,263k k ππ⎡⎤π-π+⎢⎥⎣⎦(k ∈Z ) 12π 7π12实际利用外资规模 实际利用外资同比增速D ．52,236k k ππ⎡⎤π+π+⎢⎥⎣⎦(k ∈Z ) 9．设{}n a 是公差不为零的等差数列，其前n 项和为n S ，若22223478a a a a +=+，721S =-，则10a = A ．8B ．9C ．10D ．1210．某几何体由长方体和半圆柱体组合而成，如图，网格纸上小正方形的边长为1，粗线画出的是该几何体的三视图，则该几何体的表面积是 A ．18+π B ．182+π C ．16+π D ．162+π11．已知直线l 与曲线31y x x =-+有三个不同交点()11,A x y ，()()2233,,,B x y C x y ，且AB AC =，则()31iii x y =+=∑A ．0B ．1C ．2D ．312．体积为3的三棱锥P ABC -的顶点都在球O 的球面上，PA ⊥平面ABC ，2=PA ，120ABC ︒∠=，则球O 的体积的最小值为A ．773π B ．2873πC ．3π D ．3π二、填空题：本题共4小题，每小题5分，共20分．13．已知向量a 与b 的夹角为4π，2,==a b -=a b . 14．已知函数()f x =e 2xx -的图象在点()()1,1f 处的切线过点()0,a ，则a = .15．古希腊著名的毕达哥拉斯学派把1,3,6,10,…这样的数称为“三角形数”，而把1,4,9,16,…这样的数称为“正方形数”．如图，可以发现任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和，下列等式：①361521=+；②491831=+；③642836=+；④813645=+中符合这一规律的等式是 ．（填写所有正确结论的编号）……16．设点P 是抛物线24=x y 上的动点，点P 到x 轴的距离为d ，点1P 是圆()()22211x y -++=上的动点，当1d PP +最小时，点P 的坐标为 ．三、解答题：共70分．解答应写出文字说明、证明过程和演算步骤．第17～21题为必考题，每个试题考生都必须做答．第22、23题为选考题，考生根据要求做答． （一）必考题：共60分． 17．（本小题满分12分）已知△ABC 的内角A ，B ，C 的对边分别是a ，b ，c ，且sin 2sin b A a B =. （1）求A ；（2）若2=a ，△ABC 的面积为3，求△ABC 的周长.18．（本小题满分12分）A 药店计划从甲，乙两家药厂选择一家购买100件某种中药材，为此A 药店从这两家药厂提供的100件该种中药材中随机各抽取10件，以抽取的10件中药材的质量（单位：克）作为样本，样本数据的茎叶图如图所示．已知A 药店根据中药材的质量（单位：克）的稳定性选择药厂．（1）根据样本数据，A 药店应选择哪家药厂购买中药材？(不必说明理由)（2）若将抽取的样本分布近似看作总体分布，药 店与所选药厂商定中药材的购买价格如下表：（ⅰ）估计A 药店所购买的100件中药材的总质量；（ⅱ）若A 药店所购买的100件中药材的总费用不超过7000元，求a 的最大值．每件中药材的质量n （单位：克） 购买价格（单位：元/件）15n < 501520n ≤≤a20n >10019．（本小题满分12分）如图，在直三棱柱111-ABC A B C 中，,M N 分别是1AB 和BC 的中点． （1）证明：MN ∥平面11AAC C ；（2）若12,1AA AB AC ===，90BAC ︒∠=，求棱锥1C AMN -的高．20．（本小题满分12分）已知椭圆C 的中心为坐标原点O ，右焦点为()2,0F ，短轴长为4. （1）求椭圆C 的方程；（2）若直线:32l y =k x+与椭圆C 相交于不同的两点,M N ，点P 为线段MN 的中点，OP FM ∥，求直线l 的方程.21．（本小题满分12分）已知函数()f x =()1ln a x x --.（1）若函数()f x 的极小值不大于k 对任意0a >恒成立，求k 的取值范围；（2）证明：∀n ∈N *，2231231111e 2222n n ⎛⎫⎛⎫⎛⎫⎛⎫+⋅+⋅+⋅⋅+< ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭．（其中e 为自然对数的底数）（二）选考题：共10分．请考生在第22、23题中任选一题做答，如果多做，则按所做的第一题计分．22．（本小题满分10分）选修4－4：坐标系与参数方程在直角坐标系xOy 中，直线l 的参数方程为11,2(,2x t t y ⎧=-⎪⎪⎨⎪=⎪⎩为参数). 以坐标原点为极点，以x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为()()2212sin 0a a ρθ+=>．（1）求l 的普通方程和C 的直角坐标方程； （2）若l 与C 相交于A ，B 两点，且AB =，求a 的值．23．（本小题满分10分）选修4－5：不等式选讲已知函数()2121f x x x =++-，不等式()2f x ≤的解集为M . （1）求M ；（2）证明：当,a b M ∈时，1a b a b ++-≤．2015年初中毕业班综合测试（一）试卷参考答案及解析语文一、语文知识积累与运用（6小题，21分）二、古诗文积累与运用（2小题，15分）三、古诗文阅读与鉴赏（4小题，15分）四、现代文阅读（9小题，39分）（一）议论文阅读（18分）：《激发“到此一游”的文明耻感》五、按要求作文（1小题，60分）【作文要求】请以“惊喜”为题目写一篇文章。