湘教版解读-114逆命题

《命题与证明》知识全解教学目标1、知识与能力目标：①结合具体实例，了解原命题与逆命题的概念，会识别两个互逆命题；知道原命题成立但其逆命题不一定成立；了解定理、逆定理和互逆定理；②知道证明的意义和必要性，知道证明要合乎逻辑，知道证明的过程可以有不同的表达方式，掌握综合法证明的格式。

2、过程与方法：体验、理解证明的必要性。

3、情感态度与价值观：①培养学生树立科学严谨的学习方法；②体验、理解证明的必要性。

教学重点难点重点：说出命题、真命题、假命题、定义、定理、公理的的含义，能够区分命题的条件和结论。

表述反例的作用，知道利用反例可以说明一个命题是错误的．初步体会证明的基本步骤和书写格式。

难点：运用基本事实和相关定理进行简单的证明。

内容解析探究几何图形的性质可以通过观察、操作和实验的方法。

但这些方法得到的结论有时候是近似的、甚至是错误的。

要想结论使人信服就要用到推理、推理就需要思维、思维就需要作出判断，判断的语句就是命题。

1.定义对于一个概念特征特性性质的描述叫做这个概念的定义。

2.命题（1）叙述一件事情的句子（陈述句），要么是真的，要么是假的，那么称这个陈述句是一个命题。

（2）真命题与假命题：如果一个命题叙述的事情是真的，那么称它是真命题；如果一个命题叙述的事情事假的，那么她是假命题（3）证明及互逆命题的定义：从一个命题的条件出发，通过推理得出它的结论的成立，这个过程叫作证明。

注意：证明一个命题是假命题的方法是举反例，即找出一个例子，它符合命题条件但它不满足命题的结论，从而判断这个命题是假命题。

（4）一个命题的条件和结论分别是另一个命题的结论和条件，这两个命题称为互逆命题，其中一个命题叫作另一个命题的逆命题。

3.公理与定理（1）数学中有些命题的正确性是人们在长期实践中总结出来的，并把它们作为判断其它命题真假的原始依据，这样的真命题叫做公理。

（2）以基本定义和公理作为推理的出发点，去判断其它命题的真假，已经判断为真的命题称为定理。

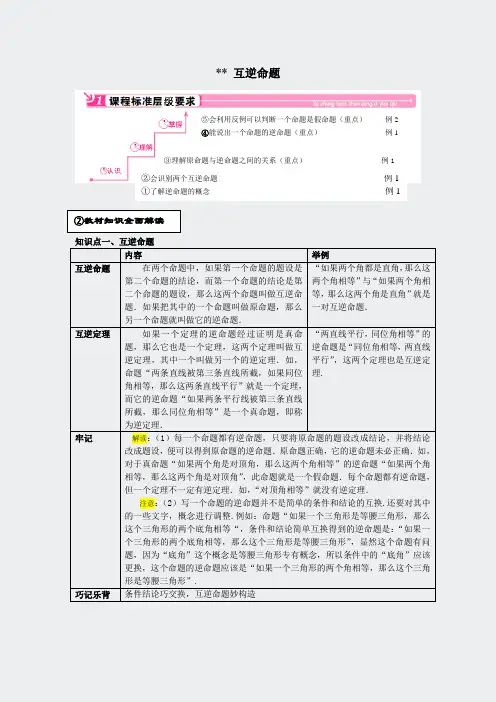
**互逆命题1 课程标准层次要求认识：①互逆命题例1理解：②举反例说明假命题的方法例2掌握：③判断两个命题是否是逆否命题和求一个命题的逆命题的方法（重点）例1 、例3、例62教材知识全面解读知识点1 互逆命题意义举例互逆命题在两个命题中，如果第一个的条件是第二个命题的结论，而第二个命题的条件又是第一个命题的结论，那么这两个命题称为互逆命题，其中一个命题叫另一个命题的逆命题．“若a b=，则a b=”的逆命题是“a b=，则a b=”．牢记解读：（1）互逆命题不是指一个命题，而是指两个命题之间的一种关系，它和互为倒数，互为相反数，互为余角，互为补角这些的含义类似．（2）原命题与逆命题是相对的，互逆命题是指两个命题之间的某种关系，这种关系体现在题设与结论的相互交换上．（3）每个命题都可以将它的条件和结论互换得到它的逆命题，因而每个命题都有逆命题．（4）写出一个命题的逆命题的方法：首先找出原命题的条件和结论，然后把结论作为条件，把条件作为结论就可以了．如：“对顶角相等”的条件是“两个角是对顶角”，结论是“这两个角相等”．互换题设与结论后是：“如果两个角相等，那么这两个角是对顶角”，即“相等的角是对顶角”．拓展：每个命题都有逆命题，但原命题正确，它的逆命题却不一定正确，原命题错误，逆命题不一定错误．巧记乐背互逆命题是两个命题之间的一种特殊关系，它们的条件、结论是互换的关系．基础题型一互逆命题【例1】给出下列命题：（1）直角都相等；（2）同位角相等，两直线平行；（3）如果a+b>0，那么a>0，b>0；（4）两直线平行，同位角相等；（5）相等的角都是直角；（6）如果a>0，b>0，那么ab>0，其中，互为逆命题的是：____________. 分析：根据逆命题的定义，只要找到条件和结论互换的两个命题即可．答案：（1）与（5）、（2）与（4）、（3）与（6）．方法点拨：判断互逆命题关键看在条件与结论有没有相互交换．变式练习：1．写出下列命题的逆命题：（1）两直线平行，内错角相等；逆命题是：_________________________. （2）如果a2=b2，那么a=b；逆命题是：__________________________. （3）内错角相等逆命题是：__________________________. 答案：（1）内错角相等，两直线平行；（2）如果a=b，那么a2=b2；（3）相等的两角是内错角．知识点2 反例内容举例反例举出一个符合命题的条件但命题结论不成立的例子来说明命题是假命题的例子称为反例．命题若xy=0,则x=0的反例是2x=，y=．牢记注意：数学中，判断一个命题是假命题，只需举出一个反例．巧记乐背反例，反例，反驳的例子，也就是条件成立结论不成立的例子．基础题型二用反例说明命题是假命题【例2】举反例说明下列命题是假命题：①如果a+b>0，那么a>0,b>0；②两个锐角的和大于90°分析：找出满足条件且结论不成立的例子解：①a=5，b=－2时，有a+b=5＋（－2）=3，但b=－2＜0；②30°的锐角与40°的锐角有30°＋40°=70°＜90°．方法点拨：注意满足条件的例子有多种可能，要在这几种可能中找出符合条件且结论不成立的例子．变式练习：2．举反例说明若a＞b则a2＞b2的逆命题为假命题．解：若a＞b，则a2＞b2的逆命题为：若a2＞b2，则a ＞b，反例：a=-2，b=-1，有a2＞b2，但a＜b．3 典型例题分类解读类型一逆命题的真假判断【例3】写出下列命题的逆命题，并指出其真假(1) 如果a2=b2，那么a=b；(2)对顶角相等．分析：先写出逆命题，再判断其真假．解：（1）如果a2=b2，那么a=b；的逆命题是：如果a=b，那么a2=b2．显然，其逆命题是真命题．(2) 对顶角相等的逆命题是相等的两角是对顶角，其逆命题是假命题，反例如下图的两个角∠AOB，∠BOC，尽管∠AOB=∠BOC，但∠AOB与∠BOC不是对顶角．图12-3-1方法点拨：解本题的前提是写对逆命题，再做出正确判断，注意运用恰当的反例来说明一个命题是假命题．要点总结：逆命题的真假情况与原命题的真假没有必然的联系，所以判断逆命题的真假步骤还是先写出逆命题，再判断其真假．变式练习3．下列定理中，逆命题不正确的是（）A．内错角相等，两直线平行；B．直角三角形中两锐角互余C．相反数的绝对值相等；D．同位角相等，两直线平行答案：C．类型二完成证明、寻找互逆命题【例4】已知，如图，∠1=∠ACB，∠2=∠3，FH⊥AB于H．（1）求证：CD⊥AB；（2）在上面的证明过程中应用了哪个互逆的真命题？图12-3-2分析：由∠1=∠ACB，利用同位角相等，两直线平行可得DE∥BC，根据平行线的性质和等量代换可得∠3=∠DCB，故推出CD∥FH，再结合已知FH⊥AB，易得CD⊥AB．⑴证明：∵∠1=∠ACB（已知），∴DE∥BC（同位角相等，两直线平行），∠2=∠DCB（两直线平行，内错角相等），又∵∠2=∠3（已知）∴∠3=∠DCB（等量代换），故CD∥FH（同位角相等，两直线平行），∴∠FHB=∠CDB（两直线平行，同位角相等），∵FH⊥AB（已知），∴∠FHB=90°（垂直的定义）∴∠CDB=90°，∴CD⊥AB（垂直的定义）．⑵应用了“同位角相等，两直线平行”与“两直线平行，同位角相等”这两个真命题．方法点拨：本题关键是由角的关系与直线的位置关系互相转化以及等量代换等变换．要点总结：先判定平行再用平行的性质，要判定平行先找角的特殊关系．变式练习4．如图，BD是∠ABC的平分线，ED∥BC，∠FED=∠BDE，求证：EF也是∠AED的平分线．图12-3-3证明：∵BD是∠ABC的平分线（已知），∴∠ABD=∠DBC（角平分线定义）；∵ED∥BC（已知），∴∠BDE=∠DBC（两直线平行，内错角相等），∴∠ABD=∠BDE（等量代换）；又∵∠FED=∠BDE（已知），∴EF∥BD（内错角相等，两直线平行），∴∠AEF=∠ABD（两直线平行，同位角相等），∴∠AEF=∠DEF（等量代换），∴EF是∠AED的平分线（角平分线定义）．4 拓展创新能力提升类型三：平行线性质与判定的综合应用【例5】已知，如图，∠1+∠2=180°，∠3=∠B，试证明∠AED=∠C，分析：先利用补角性质证明∠2=∠4，于是EF∥AB，因而可得∠ADE=∠B，再由DE∥BC，证得∠AED=∠C．证明：∵∠1+∠2=180°（已知），又∠1+∠4=180°（补角的性质），∴∠2=∠4（同角的补角相等），∴EF∥AB（内错角相等，两直线平行），∴∠3=∠ADE（两直线平行，内错角相等），又∵∠3=∠B（已知），∴∠ADE=∠B，∴DE∥BC（同位角相等，两直线平行），∴∠AED=∠C（两直线平行，同位角相等）．方法点拨：本题利用补角的性质证等角，从而证平行线，再利用平行线性质解决问题．易错点1 命题的真假性判断错误易错例1 下列说法中真命题的个数有（）（1）若a∥b，b∥c，则a∥c．（2）在同一平面内，不相交的两条线段必平行．（3）相等的角是对顶角．（4）两条直线被第三条直线所截，所得到同位角相等．（5）若a⊥b，b⊥c，则a⊥c．（6）两条平行线被第三条直线所截，一对内错角的角平分线互相平行．A．1个B．2个C．3个D．4个常见错解：C．【误区分析】产生错解的原因是误以为“两条直线被第三条直线所截，所得到同位角相等”是正确的，事实上，“两条直线被第三条直线所截，所得到同位角相等”是假命题，只有两条平行线被第三条直线所截取得的同位角才相等，（4）是假命题；而根据平行于同一直线的两条直线平行，（1）是真命题；∵如图：AB和CD不平行，∴（2）是假命题；∵在两条平行线被第三条直线所截的同位角相等，但不是对顶角，∴（3）错误；∵若在同一平面内，a⊥b，b⊥c，∴a∥c，∴（5）假命题；如图：∵AB∥CD，∴∠BEF=∠CFE，∵EN平分∠BEF，FM平分∠CFE，∴∠NEF=12∠BEF，∠MFE=12∠CFE，∴∠MFE=∠NEF，∴EN∥FM，∴（6）是真命题．故选B．正解：B．易错点2 误以为原命题与逆命题的真假性是一致的易错例2 下列说法中，正确的是（）A．每个命题不一定都有逆命题；B．每个定理都有逆定理C．真命题的逆命题仍是真命题；D．假命题的逆命题未必是假命题常见错解：C．【误区分析】误以为一个真命题的逆命题一定是真命题，一个假命题的逆命题一定是假命题．事实上，一个命题的真假与它逆命题的真假并无相关性，如命题“同位角相等，两直线平行”原命题和逆命题都是真命题；命题“对顶角相等”，原命题是真命题，逆命题是假命题；命题“同位角相等”，原命题与逆命题都错误．另外，每个定理的都是真命题，它的逆命题也可能是真命题，也可能是假命题，既是逆命题是真命题，并不一定把逆命题作为定理，故选D．正解：D．6 3年中考3年模拟中考命题方向本节内容在中考中以考察逆命题知识的题目较少，常以填空题、选择题形式出现，在今后的中考中，这部分知识大约考0-3分． 中考典型习题考点一 命题与逆命题真假判断1．(2012•内蒙古包头)已知下列命题：①若a ≤0，则｜a ｜=-a ②若ma 2>na 2，则m >n ; ③两组对角分别相等的四边形是平行四边形； ④垂直于弦的直径平分弦．其中原命题与逆命题均为真命题的个数是（ ） A. 1个 B ．2个 C ．3个 D ．4个 考点二 写出逆命题 2．（2011•凉山州）把命题“如果直角三角形的两直角边长分别为a 、b ，斜边长为c ，那么a 2+b 2=c 2”的逆命题改写成“如果…，那么…”的形式：考点三 平行线性质与判定的综合应用 3．（2012•恩施州）如图，AB ∥CD ，直线EF 交AB 于点E ，交CD 于点F ，EG 平分∠BEF ，交CD 于点G ，∠1=50°，则∠2等于（ ）A ．50°B ．60°C ．65°D ．90°参考解答：1、B 分析：四个命题的原命题均为真命题，①的逆命题为：若｜a ｜=－a ，则a ≤0，也为真命题；②的逆命题为：若m >n ，则ma 2>na 2，是假命题，当a =0时，结论就不成立；③的逆命题是平行四边形的两组对角分别相等，是真命题；④的逆命题是：平分弦的直径垂直于弦，这是个假命题，当这条弦为直径时，结论不一定成立。

1．1.2命题的四种形式1．了解命题的逆命题、否命题与逆否命题，会分析四种命题的相互关系．2．会判断四种命题的真假．下列四个命题：(1)若f(x)是正弦函数，则f(x)是周期函数；(2)若f(x)是周期函数，则f(x)是正弦函数；(3)若f(x)不是正弦函数，则f(x)不是周期函数；(4)若f(x)不是周期函数，则f(x)不是正弦函数．观察命题(1)与命题(2)(3)(4)的条件和结论之间分别有什么关系？答：命题(1)的条件是命题(2)的结论，且命题(1)的结论是命题(2)的条件．对于命题(1)和(3)．其中一个命题的条件和结论分别是另一个命题的条件的否定和结论的否定；对于命题(1)和(4)．其中一个命题的条件和结论分别是另一个命题的结论的否定和条件的否定．1．命题“若p则q”的四种形式原命题：若p则q；逆命题：若q则p；否命题：若¬p则¬q；逆否命题若¬q则¬p.2．四种命题间的关系3．四种命题的真假判断(1)原命题为真，它的逆命题可以为真，也可以为假．(2)原命题为真，它的否命题可以为真，也可以为假．(3)原命题为真，它的逆否命题一定为真．(4)互为逆否的两个命题是等价命题，它们同真同假，同一个命题的逆命题和否命题是一对互为逆否的命题，所以它们同真同假．要点一四种命题的概念例1分别写出下列命题的逆命题、否命题、逆否命题，并判断它们的真假：(1)实数的平方是非负数；(2)若x、y都是奇数，则x＋y是偶数．解(1)原命题是真命题逆命题：若一个数的平方是非负数，则这个数是实数．真命题．否命题：若一个数不是实数，则它的平方不是非负数．真命题．逆否命题：若一个数的平方不是非负数，则这个数不是实数．真命题．(2)原命题是真命题逆命题：若x＋y是偶数，则x、y都是奇数，是假命题．否命题：若x、y不都是奇数，则x＋y不是偶数，是假命题．逆否命题：若x＋y不是偶数，则x、y不都是奇数，是真命题．规律方法(1)写命题的四种形式时，首先要找出命题的条件和结论，然后写出命题的条件的否定和结论的否定，再根据四种命题的结构写出所求命题．(2)在写命题时，为了使句子更通顺，可以适当的添加一些词语，但不能改变条件和结论．跟踪演练1写出以下命题的逆命题、否命题和逆否命题．(1)如果一条直线垂直于平面内的两条相交直线，那么这条直线垂直于这个平面；(2)如果x>10，那么x>0；(3)当x＝2时，x2＋x－6＝0.解(1)逆命题：如果一条直线垂直于平面，那么该直线垂直于平面内的两条相交直线．否命题：如果一条直线不垂直于平面内的两条相交直线，那么这条直线不垂直于这个平面．逆否命题：如果一条直线不垂直于平面，那么这条直线不垂直于平面内的两条相交直线．(2)逆命题：如果x>0，那么x>10.否命题：如果x≤10，那么x≤0.逆否命题：如果x≤0，那么x≤10.(3)逆命题：如果x2＋x－6＝0，那么x＝2.否命题：如果x≠2，那么x2＋x－6≠0.逆否命题：如果x2＋x－6≠0，那么x≠2.要点二四种命题的关系例2下列命题：①“若xy＝1，则x、y互为倒数”的逆命题；②“四边相等的四边形是正方形”的否命题；③“梯形不是平行四边形”的逆否命题；④“若ac2>bc2，则a>b”的逆命题．其中是真命题的是________．答案①②③解析①“若xy＝1，则x，y互为倒数”的逆命题是“若x，y互为倒数，则xy＝1”，是真命题；②“四边相等的四边形是正方形”的否命题是“四边不都相等的四边形不是正方形”，是真命题；③“梯形不是平行四边形”本身是真命题，所以其逆否命题也是真命题；④“若ac2>bc2，则a>b”的逆命题是“若a>b，则ac2>bc2”，是假命题．所以真命题是①②③.规律方法要判断四种命题的真假：首先，要熟练四种命题的相互关系，注意它们之间的相互性；其次，利用其他知识判断真假时，一定要对有关知识熟练掌握．跟踪演练2有下列四个命题：①“若x＋y＝0，则x，y互为相反数”的否命题；②“若x≤－3，则x2－x－6>0”的否命题；③“同位角相等”的逆命题．其中真命题的个数是________．答案 1解析①“若x＋y≠0，则x，y不是相反数”，是真命题．②“若x>－3，则x2－x－6≤0”，解不等式x2－x－6≤0可得－2≤x≤3，而x＝4>－3不是不等式的解，故是假命题．③“相等的角是同位角”是假命题．要点三等价命题的应用例3判断命题“已知a，x为实数，若关于x的不等式x2＋(2a＋1)x＋a2＋2≤0的解集不是空集，则a≥1”的逆否命题的真假．解法一原命题的逆否命题：已知a，x为实数，若a<1，则关于x的不等式x2＋(2a＋1)x＋a2＋2≤0的解集为空集．真假判断如下：因为抛物线y＝x2＋(2a＋1)x＋a2＋2开口向上，判别式Δ＝(2a＋1)2－4(a2＋2)＝4a－7，若a<1，则4a－7<0.即抛物线y＝x2＋(2a＋1)x＋a2＋2与x轴无交点．所以关于x的不等式x2＋(2a＋1)x＋a2＋2≤0的解集为空集．故原命题的逆否命题为真．法二先判断原命题的真假．因为a，x为实数，且关于x的不等式x2＋(2a＋1)x＋a2＋2≤0的解集不是空集，所以Δ＝(2a＋1)2－4(a2＋2)≥0，即4a－7≥0，所以a≥1.所以原命题成立．又因为原命题与其逆否命题等价，所以逆否命题为真．规律方法由于原命题和它的逆否命题有相同的真假性，即互为逆否命题的命题具有等价性，所以我们在直接证明某一个命题为真命题有困难时，可以通过证明它的逆否命题为真命题，来间接地证明原命题为真命题．跟踪演练3判断命题“若m>0，则方程x2＋2x－3m＝0有实数根”的逆否命题的真假．解∵m>0，∴12m>0，∴12m＋4>0.∴方程x2＋2x－3m＝0的判别式Δ＝12m＋4>0.∴原命题“若m>0，则方程x2＋2x－3m＝0有实数根”为真．又因原命题与它的逆否命题等价，所以“若m>0，则方程x2＋2x－3m＝0有实数根”的逆否命题也为真．1．命题“若a∉A，则b∈B”的否命题是()A．若a∉A，则b∉B B．若a∈A，则b∉B C．若b∈B，则a∉A D．若b∉B，则a∉A 答案 B解析命题“若p，则q”的否命题是“若¬p，则¬q”，“∈”与“∉”互为否定形式．2．命题“若A∩B＝A，则A∪B＝B”的逆否命题是()A．若A∪B＝B，则A∩B＝AB．若A∩B≠A，则A∪B≠BC．若A∪B≠B，则A∩B≠AD．若A∪B≠B，则A∩B＝A答案 C解析注意“A∩B＝A”的否定是“A∩B≠A”．3．命题“若平面向量a，b共线，则a，b方向相同”的逆否命题是______________________________，它是________命题(填“真”或“假”)．答案若平面向量a，b的方向不相同，则a，b不共线假4．给出以下命题：①“若x2＋y2≠0，则x、y不全为零”的否命题；②“正多边形都相似”的逆命题；③“若m>0，则x2＋x－m＝0有实根”的逆否命题．其中为真命题的是________．答案①③解析①否命题是“若x2＋y2＝0，则x，y全为0”．真命题．②逆命题是“若两个多边形相似，则这两个多边形为正多边形”，假命题．③∵Δ＝1＋4m，若m>0时，Δ>0，∴x2＋x－m＝0有实根，即原命题为真．∴逆否命题为真．1．写四种命题时，可以按下列步骤进行：(1)找出命题的条件p和结论q；(2)写出条件p的否定¬p和结论q的否定¬q；(3)按照四种命题的结构写出所有命题．2．每一个命题都有条件和结论组成，要分清条件和结论．3．判断命题的真假可以根据互为逆否的命题真假性相同来判断，这也是反证法的理论基础．。

常用逻辑用语知识点归纳
1. 四种命题，（原命题、否命题、逆命题、逆否命题） （1）四种命题的关系，
（2）等价关系（互为逆否命题的等价性）
（a ）原命题与其逆否命题同真、同假.（b ）否命题与逆命题同真、同假. 2. 充分条件、必要条件、充要条件
（1）定义：若p 成立，则q 成立，即q p ⇒时，p 是q 的充分条件.同时q 是p 的必要条件.
若p 成立，则q 成立，且q 成立，则p 成立 ，即q p ⇒且p q ⇒，则p 与q 互为充要条件.
（2）判断方法： （i ）定义法，
（ii ）集合法：设使p 成立的条件组成的集合是A ，使q 成立的条件组成的集合为B ，若B A ⊆ 则p 是q 的充分条件.同时q 是p 的必要条件.
若A=B ，则p 与q 互为充要条件.
（iii ）命题法：假设命题：“若p 则q ”.当原命题为真时，p 是q 的充分条件. 当其逆命题也为真时，p 与q 互为充要条件. 注意：充分条件与充分非必要条件的区别：
用集合法判断看，前者：集合A 是集合B 的子集；后者：集合A 是集合B 的真子集. 3. 全称命题、特称命题（含有全称量词的命题叫全称命题，含有存在量词的命题叫特称命题）
（1）关系：全称命题的否定是特称命题，特称命题的否定是全称命题. （2）全称量词与存在量词的否定. 关键词 否定词 关键词 否定词 关键词 否定词 关键词 否定词 都是
不都是
至少一个
一个都没有
至多一个
至少两个
属于
不属于
（1）构造复合命题的方式：简单命题+逻辑连结词（或、且、非）+简单命题.
（2）复合命题的真假判断：
条件共同否定.。

** 互逆命题知识点一、互逆命题 内容举例互逆命题在两个命题中，如果第一个命题的题设是第二个命题的结论，而第一个命题的结论是第二个命题的题设，那么这两个命题叫做互逆命题．如果把其中的一个命题叫做原命题，那么另一个命题就叫做它的逆命题．“如果两个角都是直角，那么这两个角相等”与“如果两个角相等，那么这两个角是直角”就是一对互逆命题．互逆定理如果一个定理的逆命题经过证明是真命题，那么它也是一个定理，这两个定理叫做互逆定理，其中一个叫做另一个的逆定理．如，命题“两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行”就是一个定理，而它的逆命题“如果两条平行线被第三条直线所截，那么同位角相等”是一个真命题，即称为逆定理．“两直线平行，同位角相等”的逆命题是“同位角相等，两直线平行”，这两个定理也是互逆定理.牢记 解读：（1）每一个命题都有逆命题，只要将原命题的题设改成结论，并将结论改成题设，便可以得到原命题的逆命题．原命题正确，它的逆命题未必正确．如，对于真命题“如果两个角是对顶角，那么这两个角相等”的逆命题“如果两个角相等，那么这两个角是对顶角”，此命题就是一个假命题．每个命题都有逆命题，但一个定理不一定有逆定理．如，“对顶角相等”就没有逆定理．注意：（2）写一个命题的逆命题并不是简单的条件和结论的互换.还要对其中的一些文字，概念进行调整.例如：命题“如果一个三角形是等腰三角形，那么这个三角形的两个底角相等“，条件和结论简单互换得到的逆命题是：“如果一个三角形的两个底角相等，那么这个三角形是等腰三角形”，显然这个命题有问题，因为“底角”这个概念是等腰三角形专有概念，所以条件中的“底角”应该更换，这个命题的逆命题应该是“如果一个三角形的两个角相等，那么这个三角形是等腰三角形”.巧记乐背 条件结论巧交换，互逆命题妙构造②会识别两个互逆命题 例1 ①了解逆命题的概念 例1③理解原命题与逆命题之间的关系（重点） 例1⑤会利用反例可以判断一个命题是假命题（重点） 例2 ④能说出一个命题的逆命题（重点） 例1②教材知识全面解读基本题型一写逆命题【例1】“等腰三角形两腰上的高相等”的逆命题是.分析：把一个命题的条件和结论互换就得到它的逆命题．解：命题的条件是“一个三角形是等腰三角形”，结论是“两腰上的高相等”．将条件和结论互换得逆命题为：如果一个三角形两腰上的高相等，那么这个三角形是等腰三角形．概念解读：本题考查了互逆命题的知识，两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么这两个命题叫做互逆命题．其中一个命题称为另一个命题的逆命题．变式练习1. 命题“平行四边形的对角线互相平分”的逆命题是.“平行四边形对角线互相平分”的条件是：四边形是平行四边形，结论是：四边形的对角线互相平分．所以逆命题是：对角线互相平分的四边形是平行四边形．知识点二举反例内容举例反例要说明一个命题是假命题，通常可以举一个例子，使之具备命题的条件，而不具有命题的结论，这种例子称为反例. 命题“两个锐角的和一定是钝角”是假命题，我们可以举一反例：两个30°的角的和是60°．牢记解读：（1）反例的列举必须符合实际，举反例时，可以用文字语言来表述，也可以用数据来说明，还可以用图形来表示．注意：（2）举反例时要符合命题的条件，但不符合命题的结论巧记乐背这真命题需证明，假命题举反例基本题型二举反例【例2】对假命题“任何一个角的补角都不小于这个角”举反例，正确的反例是（）A．∠α=60°，∠α的补角∠β=120°，∠β＞∠αB．∠α=90°，∠α的补角∠β=900°，∠β=∠αC．∠α=100°，∠α的补角∠β=80°，∠β＜∠αD．两个角互为邻补角分析：熟记反证法的步骤，然后进行判断即可．解：举反例应该是证明原命题不正确，即要举出不符合叙述的情况；A、∠α的补角∠β＞∠α，符合假命题的结论，故A错误；B、∠α的补角∠β=∠α，符合假命题的结论，故B错误；C、∠α的补角∠β＜∠α，与假命题结论相反，故C正确；D、由于无法说明两角具体的大小关系，故D 错误．故选C．方法点拨：本题结合角的比较考查反证法，解此题关键要懂得反证法的意义及步骤．变式练习2.写出下列假命题的反例：（1）有两个角是锐角的三角形是锐角三角形；（2）相等的角是对顶角．（1）反例是：直角三角形有两个锐角；（2）反例是：两直线平行，同位角相等（等等）．类型一判定逆命题的真假【例3】写出下列各命题的逆命题，并判断其逆命题是真命题还是假命题，若是假命题，请举出一个反例说明：（1）两直线平行，同旁内角互补；（2）垂直于同一条直线的两直线平行；（3）相等的角是内错角；（4）有一个角是60°的三角形是等边三角形．分析：分别找出各命题的题设和结论将其互换即可．解：（1）同旁内角互补，两直线平行，真命题；（2）如果两条直线平行，那么这两条直线垂直于同一条直线，真命题；（3）内错角相等，假命题；例如：如图11-4-1，∠1与∠2是内错角，但不相等；图11-4-1（4）等边三角形有一个角是60°真命题．方法点拨：两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么这两个命题叫做互逆命题．其中一个命题称为另一个命题的逆命题．变式练习3.写出下列两个定理的逆命题，并判断真假（1）在一个三角形中，等角对等边．（2）四边形的内角和等于360°．3.分析：把一个命题的条件和结论互换就得到它的逆命题．分析是否为真命题，需要分别分析各题设是否能推出结论．解：（1）逆命题：在一个三角形中，等边对等角．真命题．（2）内角和等于360°的多边形是四边形．真命题．③典型例题分类解析类型二 构造逆命题并说理【例4】请写出“直角三角形斜边上的中线等于斜边的一半”的逆命题，并进行证明. 分析：先写出“直角三角形斜边上的中线等于斜边的一半”的逆命题，再根据等腰三角形的性质得出∠A=∠ACD ，∠BCD=∠B ，根据三角形的内角和定理得出∠BCD+∠B+∠A+∠ACD=180°，代入即可求出∠BCD+∠ACD=90°，即∠ACB=90°，即可推出答案．图11-4-2解：逆命题是：如果一个三角形一边上的中线等于这边的一半，那么这个三角是直角三角形． 已知，如图，△ABC 中，D 是AB 边的中点，且CD=21AB 求证：△ABC 是Rt 三角形 证明：∵D 是AB 边的中点，且CD=21AB ， ∴AD=BD=CD ， ∵AD=CD ， ∴∠ACD=∠A ， ∵BD=CD ， ∴∠BCD=∠B ，又∵∠ACD+∠BCD+∠A+∠B=180°， ∴2（∠ACD+∠BCD ）=180°， ∴∠ACD+∠BCD=90°， ∴∠ACB=90°，∴△ABC 是Rt 三角形． 方法点拨：这是一道逆命题构造的综合题，首先写出逆命题，再根据逆命题写出已知，求证，并写出证明过程.变式练习4.（1）若四边形ABCD 的对角线AC 将四边形分成面积相等的两个三角形，证明直线AC 必平分对角线BD ．（2）写出（1）的逆命题，这个逆命题是否正确？为什么？图11-4-3 分析：（1）证明BD 被AC 平分，即证明OB=OD ，结合同底等高的三角形面积相等这一性质，不难想到要证明线段相等，可以证明线段所在的三角形全等．（2）将（1）的思路进行倒推，不难解决本小题． 解：（1）证：S △ABC =S △ADC ′且△ABC 与△ADC 有同底AC ，∴两高线相等：BE=DF 设AC 与BD 交于点O ，则Rt △BOE ≌Rt △DOF ，∴OB=OD ，即AC 平分BD ． （2）逆命题：若四边形ABCD 的对角线AC 平分对角线BD ，则AC 必将四边形分成两个面积相等的三角形这个逆命题是正确的． 证明如下：在图中，由于OB=OD ，∠BOE=∠DOF ，∠BEO=∠DFO=Rt ∠，∴△BOE ≌△DOF ．∴BE=DF ，即两高线相等．∴S△ABC=21AC •BE=21AC •DF=S △ADC'．④综合创新能力提升类型四举反例证明命题【例5】已知△ABC，D是BC的中点，将三角板中的90°角的顶点绕D点在△ABC内旋转，角的两边分别与AB、AC交于E、F，且点E、F不与A、B、C三点重合．（1）如果∠A=90°，观察并探索，当E、F点位置变化时，BE、EF、CF三条线段中有否有一条线段始终最长？请指出，并给予证明．（2）请分别∠A＞90°、∠A＜90°两种情况考察BE、EF、CF三条线段中有否有一条线段始终最长？如果有，请指出最长的线段，但不需证明；如果没有，请画草图举出反例．图11-4-4分析：（1）根据旋转的性质，推理得出三角形全等，根据全等的性质及直角三角形斜边最大即可推理得出，（2）根据（1）中结论即可画图反例图示．解：（1）线段EF始终最大，证明如下：将△FDC绕点D顺时针方向旋转180°，如图，∵D是BC的中点，∴点C旋转后与点B重合，△FDC≌△F′DB，∠FCD=F′BD，DF=DF′，FC=F′B，连接EF、EF′，在△EDF和△EDF′中，∵∠EDF=90°=∠EDF，ED=ED，FD=F′D，∴△FDE≌△F′DE，∴EF=EF′，在△EBF′中，∠EBF′=∠EBD+∠F′BD=∠EBD+∠FCD=180°-∠A=90°，EF’是Rt△EBF′斜边EF′＞EB，EF′＞BF′，∴BE、EF、CF三条线段中，EF的长度始终最大，（2）当∠A＜90°，BE、EF、CF三条线段中，EF始终最长，（原因∠EBF′＞180°，当∠A＞90°，BE、EF、CF三条线段中，不存在始终最长的线段，反例如图11-4-5：图11-4-5易错点一 简单交换致错 【例6】“直角三角形斜边上的中线等于斜边的一半”的逆命题是 . 【误区分析】写出一个命题的逆命题，只需将命题的条件与结论交换一下，但不是简单的交换.本题中斜边是直角三角形特有的概念，在三角形未知的条件下不能说是斜边. 易错点一 审题不清致错【例7】请写出一个原命题是真命题，逆命题是假命题的命题 ． 【误区分析】本题有两个要求，首先原命题是真命题，其次它的逆命题是假命题.而本解答忽略了逆命题是假命题这个条件.中考命题方向图形与几何是新课标下的一个重要板块，在“图形与几何”的学习中，应帮助学生建立空间观念，注重培养几何直观与推理能力.推理是数学的基本思维方式，也是人们学习和生活中经常使用的思维方式.推理一般包括合情推理和演绎推理，合情推理是从已有的事实出发，凭借经验和直觉，通过归纳和类比等推测某些结果，演绎推理是从已有的事实（包括定义、公理、定理等）出发，按照规定的法则（包括逻辑和运算）证明结论，在解决问题的过程中，合情推理有助于探索解决问题的思路，发现结论；演绎推理用于证明结论的正确性.本章中是演绎推理的起步，是中考重点内容.这一部分在中考中各种图形都有体现，作为初中数学四大板块之一，这一部分仍将是中考重点. 中考典型习题1.（2010年包头）已知下列命题：①若a=b ，则a 2=b 2；②若x ＞0，则|x|=x ；③一组对边平行且对角线相等的四边形是矩形； ④一组对边平行且不相等的四边形是梯形．其中原命题与逆命题均为真命题的个数是（ ） A.1个 B.2个 C.3个 D.4个2.（2011年四川凉山）把命题“如果直角三角形的两直角边长分别为a 、b ，斜边长为c ，那么a 2＋b 2＝c 2”的逆命题改写成“如果……，那么……”的形式： .3. （2011年德州）下列命题中，其逆命题成立的是 ．（只填写序号） ①同旁内角互补，两直线平行；②如果两个角是直角，那么它们相等；③如果两个实数相等，那么它们的平方相等；④如果三角形的三边长a ，b ，c 满足a 2+b 2=c 2，那么这个三角形是直角三角形． 4.（2011年新疆建设兵团）请判断下列命题是否正确？如果正确，请给出证明；如果不正确，请举出反例．常见 错解 斜边上的中线等于斜边的一半的三角形是直角三角形.正确 解答如果一个三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形.常见 错解 答案不唯一，例如：两直线平行，同位角相等.正确 解答答案不唯一，例如：对顶角相等.⑥3年中考3年模拟⑤误区易错明析解读（1）一组对边平行且相等的四边形是平行四边形；（2）一组对角相等，一条对角线被另一条对角线平分的四边形是平行四边形．5. (2011年襄阳)如图11-4-，点D ，E 在△ABC 的边BC 上，连接AD ，AE ．①AB ＝AC ；②AD ＝AE ；③BD ＝CE ．以此三个等式中的两个作为命题的题设，另一个作为命题的结论，构成三个命题：①②→③：①③→②；②③→① (1)以上三个命题是真命题的为(直接作答)(2)请选择一个真命题进行证明(先写出所选命题，然后证明)．图11-4- 1.答案：A分析：①若a=b ，则a 2=b 2，其逆命题为若a 2=b 2，则a=b ，故本选项错误， ②若x ＞0，则|x|=x ，其逆命题为若|x|=x ，则x ＞0，故本选项错误，③例如等腰梯形，满足一组对边平行且两条对角线相等，但它不是矩形，故本选项错误， ④一组对边平行且不相等的四边形是梯形，其逆命题为若四边形是梯形，则它的对边平行且不相等，故本选项正确．故选A ．2.答案：如果三角形三边长a ，b ，c ，满足a 2＋b 2＝c 2，那么这个三角形是直角三角形．3. 答案：①④分析：A 、两直线平行，同旁内角互补，正确，B 、如果两个角相等，那么它们是直角，错误；C 、如果两个实数的平方相等，那么这两个实数相等，错误；D 、一个三角形是直角三角形，那么三角形的三边长a ，b ，c 满足a 2+b 2=c 2，正确.4. （1）已知：如图11-4-，在四边形ABCD 中，AB ∥CD ，AB ＝CD ， 求证：四边形ABCD 是平行四边形， 证明：连接BD ，∵AB ∥CD ， ∴∠ABD ＝∠BDC ，在△ABD 和△CDB 中，⎩⎪⎨⎪⎧AB ＝CD ∠ABD ＝∠BDC BD ＝BD，图11-4-∴△ABD ≌△CDB （SAS ），∴∠ADB ＝∠DBC （全等三角形对应角相等）， ∴AD ∥BC （内错角相等，两直线平行）， ∴四边形ABCD 是平行四边形；（2）一组对角相等，一条对角线被另一条对角线平分的四边形是平行四边形不正确． 如图11-4-，∠BAD ＝∠BCD ，对角线AC 被BD 平分，但四边形ABCD 不是平行四边形．图11-4-5.解：(1)①②→③，①③→②，②③→①， (2)选择①③→②， 证明：∵AB ＝AC ， ∴∠B ＝∠C ，∵⎪⎩⎪⎨⎧=∠=∠=CE BD C B AC AB ∴△ABD ≌△ACE ， ∴AD ＝AE ．·基础训练·1.下列命题的逆命题不正确的是（ ）A ．相等的角是对顶角B ．两直线平行，同旁内角互补C ．矩形的对角线相等D ．平行四边形的对角线互相平分 (知识点1例题1)2. 下列命题中，其逆命题是假命题的是（ ）A ．若a=b ，则a2=b2B ．若ab=1，则a 与b 互为倒数C ．直角三角形两个锐角互余D ．角平分线上的一点到角的两边距离相等3. 逆命题“两直线平行，同旁内角互补”的原命题是（ ） (知识点1例题1 )A ．两直线平行，同位角相等B ．两直线平行，内错角相等C ．同旁内角互补，两直线平行D ．同位角相等，两直线平行 (知识点1例题1 )4.对假命题举反例时，应注意使反例（ ）A ．满足命题的条件，并满足命题的结论B ．不满足命题的条件，但满足命题的结论⑦紧扣教材强化训练C．不满足命题的条件，也不满足命题的结论D．满足命题的条件，但不满足命题的结论(知识点2例题2 )5. “等角的补角相等”的逆命题是.(知识点1例题1 )6. 命题“四个角都是直角的四边形是矩形”的逆命题是.(知识点1例题1 )7. 命题“垂直于同一直线的两直线平行”的逆命题是.(知识点1例题1 )8. 命题“角平分线上的点到角的两边的距离相等”的逆命题是. (知识点1例题1 )9. 写出命题“若a2=b2，则a=b”是假命题的反例是.(知识点2例题2)10.判断下列命题是真命题还是假命题，如果是假命题举出反例．（1）有两个角和一边对应相等的两个三角形全等；（2）有两边和一角对应相等的两个三角形全等；（3）有两边和其中一边上的中线对应相等的两个三角形全等；（4）有一边对应相等的两个等边三角形全等．(知识点2例题2 )11. 已知四边形ABCD的对角线AC与BD交于点O，给出下列四个论断：①OA=OC，②AB=CD，③∠BAD=∠DCB，④AD∥BC．请你从中选择两个论断作为条件，以“四边形ABCD为平行四边形”作为结论，完成下列各题：①构造一个真命题，画图并给出证明；②构造一个假命题，举反例加以说明．(知识点2例题4 )·能力拓展·12.在△ABC中，若AD是∠BAC的角平分线，点E和点F分别在AB和AC上，且DE⊥AB，垂足为E，DF⊥AC，垂足为F（如图（1）），则可以得到以下两个结论：①∠AED+∠AFD=180°；②DE=DF．那么在△ABC中，仍然有条件“AD是∠BAC的角平分线，点E和点，分别在AB和AC 上”，请探究以下两个问题：（1）若∠AED+∠AFD=180°（如图（2）），则DE与DF是否仍相等？若仍相等，请证明；否则请举出反例．（2）若DE=DF，则∠AED+∠AFD=180°是否成立？（只写出结论，不证明）(知识点2例题4 )** 分析：A、逆命题是：对顶角相等．正确；B、逆命题是：同旁内角互补，两直线平行，正确；C、逆命题是：对角线相等的四边形是矩形，错误；D、逆命题是：对角线互相平分的四边形是平行四边形，正确．故选C．** 分析：A、错误，逆命题是“若a2=b2，则a=b”，因为当a2=b2时a，b可以相等，也可以互为相反数；B、正确，逆命题是“若a与b互为倒数，则ab=1”，是真命题；C、正确，逆命题是“两锐角互余的三角形是直角三角形”，是真命题；D、正确，逆命题是“到角两边距离相等的点在角的平分线上”，是真命题．故选A．3. C分析：逆命题“两直线平行，同旁内角互补”的题设是“两条直线平行”，结论是“同旁内角互补”，故原命题是“同旁内角互补，两直线平行”．故选C.** 分析：根据反证法的步骤，∵对假命题举反例，∴应注意使反例：满足命题的条件，但不满足命题的结论．故选D．5. “等角的补角相等”的题设是：两个角相等，结论是：这两个角的补角相等，所以逆命题是：如果两个角的补角相等，那么这两个角相等．6. 命题“四个角都是直角的四边形是矩形”的题设是“四个角都是直角的四边形”，结论是“矩形”故其逆命题是“矩形的四个角都是直角”．7. 把一个命题的条件和结论互换就得到它的逆命题．命题“垂直于同一直线的两直线平行”的条件是“两条直线垂直于同一直线”结论是“两条直线平行”，故命题“垂直于同一直线的两直线平行”的逆命题是如果两条直线平行，那么它们垂直于同一条直线．8.到角的两边的距离相等的是角平分线上的点分析：把一个命题的题设和结论互换即可得到其逆命题，“角平分线上的点到角的两边的距离相等”的条件是“到角两边距离相等的点”，结论是“角平分线上的点”．9. 22=（-2）2，但是2≠-2等分析：：∵命题是“若a2=b2，则a=b”∴假命题的反例是：∵22=（-2）2，但是2≠-2．故此命题是假命题．10. （1）真命题（2）假命题，如图11-4-，△ABC与△ABD中，AB=AB，∠B=∠B，AD=AC，但△ABC与△ABD不全等；（3）真命题；（4）真命题．11.（1）①④为论断时：∵AD∥BC，∴∠DAC=∠BCA，∠ADB=∠DBC．又∵OA=OC，∴△AOD≌△COB．∴AD=BC．∴四边形ABCD为平行四边形．（2）②④为论断时，此时一组对边平行，另一组对边相等，可以构成等腰梯形．12.解析：（1）DE=DF．理由如下：过点D作DM⊥AB于M，DN⊥AC于N，∵AD平分∠BAC，DM⊥AB，DN⊥AC，∴DM=DN，∵∠AED+∠AFD=180°，∠AFD+∠DFN=180°，∴∠DFN=∠AED∴△DME≌△DNF（AAS），∴DE=DF；（2）不一定成立．如图，若DE、DF在点D到角的两边的垂线段与顶点A的同侧则一定不成立，经过（1）的证明，若在垂线段上或两侧则成立，所以不一定成立．。

苏科版八年级下册数学第十一章**互逆命题I．知识技能达标版学习目标1、了解逆命题的概念，会识别两个互逆命题，通过具体例子理解反例的作用，会利用反例可以判断一个命题是假命题。

2、能使用合情推理和演绎推理证明一个命题；一、相关知识链接1.命题判断一件事情的句子叫做命题．这里强调了“判断”这个条件，也就是说命题是带有肯定或否定语气完整的陈述语句，其它形式的句子，如：疑问句、感叹句、祈使句等都不是命题．2.真、假命题命题有正确的（真命题），也有不正确的（假命题）．要注意，不一定肯定的就是真命题，否定的就是假命题．3.命题的组成命题是由题设和结论两部分组成．题设是命题的条件，结论则是命题中判断的结果．一般情况下，命题的条件是由“如果”、“若”、“已知”等字样表示，用“那么”、“则”、“求证” 等字样表示出命题的结论．二、教材知识详解(链接例1)【知识点1】互逆命题在两个命题中，如果第一个命题的题设是第二个命题的结论，而第一个命题的结论是第二个命题的题设，那么这两个命题叫做互逆命题．如果把其中的一个命题叫做原命题，那么另一个命题就叫做它的逆命题．如，“如果两个角都是直角，那么这两个角相等”与“如果两外角相等，那么这两个角是直角”就是一对互逆命题．可见每一个命题都有逆命题，只要将原命题的题设改成结论，并将结论改成题设，便可以得到原命题的逆命题．但原命题正确，它的逆命题未必正确．如，对于真命题“如果两个角都是直角，那么这两个角相等”的逆命题“如果两外角相等，那么这两个角是直角”，此命题就是一个假命题．【注意】互逆命题之间的关系：（1）、根据互逆命题的概念，可知每一个命题都有逆命题。

“互逆命题”只是说明两个命题之间的关系，而两个命题的地位可以互换，它们之中可以确定其中任何一个为原命题，但是一旦确定，另一个就是它的逆命题了．（2）、命题有真有假，其中正确的命题叫做真命题；错误的命题叫做假命题．原命题正确，但它的逆命题未必正确．如“如果两个角都是直角，那么这两个角相等”是真命题，但它的逆命题“如果两个角相等，那么这两个角是直角”却是一个假命题．（3）、有些命题的正确性是通过推理证实的，这样的真命题叫定理．定理是我们用来证明的依据。

11. 4互逆命题(1)设计：上会中学夏彪【设计意图】“互逆命题”是在学生学习“命题”概念基础上的新知识，本节课通过创设“等腰三角形等边对等角与等角对等边叩勺情境，让学牛对比两者Z间的联系与区别，从而得出互逆命题的概念。

在此基础上，让学生举出平吋遇到过的命题，并说出它的逆命题，口判定命题与它的逆命题的真假，使学生经历“探索一发现一猜想一证明''的过程，不断发展合乎逻辑的思考能力，最后通过具体例题巩固所学过的知识，体会反面思考问题的方法，让学生懂得任何事物都是正反两方面的对立统一体。

设计关于“反例”的力史故事，旨在让学生了解数学历史，渗透和传播数学文化，同时也引导学生学习数学家严谨治学、追求真理的科学精神。

设计的课堂作业现场反馈，及时巩固所学知识，及时了解学生掌握情况，同时也可有针对性的辅导后进生。

教师的主导作用和学生的主体地位贯穿整堂课始终，最大限度的发挥师生的创造力。

让学生真正成为课堂的主人。

【教学目标】1.了解逆命题的概念，会识别两个互逆命题，并知道原命题成立其逆命题不一定成立。

2.通过具体例了理解反例的作用，知道利用反例可以判断一个命题是假命题。

3.通过自学、探索、讨论等形式，体会反面思考问题的方法，渗透数学文化教育，培养有学生条理地表述事理的能力和自主学习的习惯。

【教学重、难点】重点：能熟练说出一个命题的逆命题。

难点：举反例说明一个命题是假命题。

【教学过程】(一)情境创设：1、引入情境：在三角形中，“等边对等角”和“等角对等边”的条件、结论2、知识回顾：(1)什么是命题？(2)命题由哪两部分组成？(3)命题有真有假3、考考你：多媒体投影片设计意图：创设情境，冋忆in知，引入新知，口然过渡。

(-)探索活动：1、学生自学(出示自学提示) 自学课本第142-143页的内容：(1)“两直线平行，同位角相等”与“同位角相等，两直线平行”这两个命题的条件和结论有何特点？(2)怎样给互逆命题下定义？(3)若原命题是真命题，则它的逆命题一定是真命题吗？(4)在数学中，如何判断一个命题是假命题？2、师生共同归纳归纳一：关于互逆命题的定义：两个命题中，如果第一个命题的条件是第二个命题的结论，而第一个命题的结论又是第二个命题的条件，那么这两个命题叫做互逆命题。

抽象问题情境化，新知无师自通1. 1.2命题的四种形式［读教材填要点］1. 四种命题结构逆命题:若4则p/原命题，若“则耳〜否命题;若「0则X逆否命题：若「小则「P2. 四种命题的相互关系3. 四种命题的真假性(1) 四种命题的真假性，有且仅有下面四种情况原命题逆命题否命题逆否命题真真真真真假假真假真真假假假假假(2) 四种命题的真假性之间的关系①两个命题互为逆否命题，它们有相同的真假性.②两个命题为互逆命题或互否命题，它们的真假性没有关________［小问题大思维］1. 命题a的否命题是b,命题b的逆否命题是c,命题c的逆命题是d,则命题a与命题d的关系是怎样的？提示：由四种命题间的关系可知a与d是一个命题.2. 如果一个命题的逆命题为真命题，这个命题的否命题一定为真命题吗？提示：一定为真命题.因为一个命题的逆命题和否命题互为逆否命题，所以它们的真假性相同.3. 在四种命题中，真命题的个数可能会有几种情况？提示：因为原命题与逆否命题，逆命题和否命题互为逆否命题，它们同真同假，所以真命题的个数可能为0,2,4.高额掉点题组化.名师一点就通'■-写出下列命题的逆命题、否命题和逆否命题：n n r(1) 若a+ 3= 2，贝V sin a= cos 3；⑵对任意非正数c,若有a w b+ c成立，则a < b.n［自主解答］逆命题：若sin a= cos 3,则a+ 3= 2"否命题：若a+ 3工2，贝y sin a^ cos 3 逆否命题：若sin a^ cos 3,贝y a+ 3工n(2) 逆命题：对任意非正数c,若有a w b成立，则a w b+ c.否命题：对任意非正数c,若有a>b+ c成立，则a>b.逆否命题：对任意非正数c,若有a>b成立，则a>b+ c.现障总结四种命题的转换方法(1) 交换原命题的条件和结论，所得命题是原命题的逆命题.(2) 同时否定原命题的条件和结论，所得命题是原命题的否命题.(3) 交换原命题的条件和结论，并且同时否定，所得命题是原命题的逆否命题.I szni. 写出下列命题的逆命题、否命题和逆否命题.(1) 负数的平方是正数；(2) 如果一条直线垂直于平面内的两条相交直线，那么这条直线垂直于平面.解：(1)原命题改写成“若一个数是负数，则它的平方是正数”.逆命题：若一个数的平方是正数，则它是负数.否命题：若一个数不是负数，则它的平方不是正数.逆否命题：若一个数的平方不是正数，则它不是负数.(2)逆命题：如果一条直线垂直于平面，那么这条直线垂直于平面内的两条相交直线;否命题：如果一条直线不垂直于平面内的两条相交直线，那么这条直线不垂直于平面; 逆否命题：如果一条直线不垂直于平面，那么这条直线不垂直于平面内的两条相交直 线.判断下列命题的真假，并说明理由.(1)"若X 2+『工0,贝y X , y 不全为零”的否命题; (2) “正三角形都相似”的逆命题；(3) “若m>0，贝U x 2+ x — m = 0有实根”的逆否命题； (4) “若x — 2是有理数，则x 是无理数”的逆否命题.［自主解答］⑴原命题的否命题为 “若x 2+ y 2 = 0，贝V x , y 全为零 (2) 原命题的逆命题为“若两个三角形相似，则这两个三角形是正三角形 ”. 假命题(3) 原命题的逆否命题为 “若x 2+ x — m = 0无实根，贝V m w 0”. •••方程无实根，•••判别式 △= 1 + 4m<0. 1• mv —-w 0. 真命题4(4) 原命题的逆否命题为 “若x 不是无理数，则x — .2不是有理数”. •/ x 不是无理数，• x 是有理数•又.2是无理数， • x — 2是无理数，不是有理数. 真命题話稱卧一变若本例(3)改为判断“若 m>0，则mx 2 + x — 1= 0有实根”的逆否命题的真假， 则结论如 何？ 解：原命题的逆否命题为 “若mx 2 + x — 1 = 0无实根，则 m w 0”.因为方程 mx 2 + x — 11 = 0无实根，则 m M 0，所以判别式 △= 1+ 4m<0，贝U m< — 4，故m w 0，为真命题.理偉总缰在判断一个命题的真假时，可以有两种方法：一是分清原命题的条件和结论，直接对 原命题的真假进行判断；二是不直接写出命题，而是根据命题之间的等价关系进行判断， 即原命题和逆否命题同真同假，逆命题和否命题同真同假.|变口之阵2. 把命题“平行于同一条直线的两条直线平行”改写成“若 出它的逆命题、否命题和逆否命题，同时判断它们的真假.解：“若p ,则q ”的形式：若两条直线平行于同一条直线，则这两条直线平行，是真 命题； 逆命题：若两条直线平行，则这两条直线平行于同一条直线，是真命题；真命题 p,贝U q ”的形式，并写否命题：若两条直线不平行于同一条直线，则这两条直线不平行，是真命题；逆否命题：若两条直线不平行，则这两条直线不平行于同一条直线，是真命题.证明：已知函数f(x)是(一R, )上的增函数，a, b€ R,若f(a) + f(b) >f(—a) + f( —b),贝V a+ b》0.［自主解答］法一：原命题的逆否命题为“已知函数f(x)是(—R, +^)上的增函数，a, b€ R，若 a + b<0，则f(a) + f(b)vf( —a) + f( —b)”.若 a + b<0，贝V a< —b, bv — a.又••• f(x)在(—g,+s)上是增函数，••• f(a)vf(—b), f(b)vf(—a),••• f(a) + f(b)vf( —a) + f( —b).即原命题的逆否命题为真命题.•原命题为真命题.法二：假设a+ bv0，贝U av —b, bv— a.又••• f(x)在(—g,+s)上是增函数，•f(a)vf(—b), f(b)vf(—a).•f(a) + f(b)vf( —a) + f( —b).这与已知条件f(a) + f(b)> f(—a)+ f(—b)相矛盾.因此假设不成立，故a+ b> 0.由于原命题和它的逆否命题有相同的真假性，所以在直接证明某一个命题为真命题有困难时，可以通过证明它的逆否命题为真命题，来间接地证明原命题为真命题.品N佬3.证明：若m2+ n2= 2,贝V m+ n< 2.证明：将“若m2+ n2= 2，则m+ n< 2”视为原命题，则它的逆否命题为“若m+ n>2, 则m2+ n2^ 2”.由于m+ n>2，则m2+ n2>$m + n)2>1x 22= 2,所以m2+ n2工2.故原命题的逆否命题为真命题，从而原命题也为真命题.解题高手|多解题条条大路通罗马，换一个思路试一试判断命题“已知a,x为实数，若关于x的不等式x2+ (2a+ 1)x+ a2+ 2< 0的解集非空，则a> 1 ”的逆否命题的真假.2［解］法一：逆否命题：已知a, x为实数，若a v 1，则关于x的不等式x + (2a + 1)x + a2+ 2W 0的解集为？.判断如下：抛物线y= x2+ (2a+ 1)x+ a2+ 2开口向上,令x2+ (2a + 1)x+ a2+ 2= 0,则△= (2a+ 1)2—4(a2+ 2)= 4a—7.因为a v 1,所以4a—7v 0,即抛物线y= x2+ (2a + 1)x+ a2+ 2< 0的解集为？.故逆否命题为真命题.法二：禾U用原命题的真假去判断逆否命题的真假.因为关于x的不等式x2+ (2a+ 1)x+ a2+ 2< 0的解集非空，所以△= (2a + 1)2—4(a2+2)>0.即4a —7>0,解得a> 1.所以原命题为真，故其逆否命题为真.4法三：利用集合的包含关系求解.命题p：关于x的不等式x2+ (2a + 1)x+ a2+ 2< 0的解集非空，命题q：a> 1,2 2 7所以p：A= {a|(2a+ 1)2—4(a2+ 2)>0} = a|a>4 ;q：B= {a|a> 1}.因为A? B,所以“若p,则q”为真命题.所以原命题的逆否命题为真.［点评］因为互为逆否命题的两个命题具有相同的真假性，所以判断某个命题真假时, 可以改为判断它的逆否命题的真假•当命题与不等式的解集有关时，也可以利用集合的包随堂练含关系.1.设m€ R，命题“若m>0，则方程x2+ x—m= 0有实根”的逆否命题是()A .若方程x2+ x—m= 0有实根，则m>0B. 若方程x2+ x —m= 0有实根，则m w 0C. 若方程x2+ x—m= 0没有实根，则m>0D .若方程x?+ x—m = 0没有实根，则m w 0解析：根据逆否命题的定义，命题“若m>0 ,则方程x2+ x—m= 0有实根”的逆否命题是“ 若方程x2＋x—m= 0 没有实根，则m w 0”. 故选D.答案：D2. 已知a, b, c€ R，命题“若a+ b+ c= 3，则a2+ b2+ c2>3”的否命题是()222A. 若a + b+ C M 3,贝U a + b + c <3B. 若a+ b+ c= 3,贝U a2+ b2+ c2<3222C .若a + b+ C M 3,贝U a + b + c > 3D .若a2+ b2+ c2> 3，贝V a+ b+ c= 3解析：a+ b+ c= 3 的否定是a + b+ C M 3, a? + b? + c?》3 的否定是a? + b? + c?v3. 答案：A 3．命题“若a>—3,则a>—6”以及它的逆命题、否命题、逆否命题这四个命题中, 真命题的个数为( )A．0 B．1C．2 D．4解析：“ 若a>—3,则a>—6”为真命题,所以其逆否命题亦为真命题．又逆命题、否命题为假命题,所以真命题的个数为 2.故选 C.答案：C4. ____________________________________________ 命题“若a>b,则2a>2b—1”的否命题为___________________________________________________ .解析：Ab”的否定是“a w b” , “2a>2b—1 ”的否定是“2a w 2b—1 ”.答案：若a w b,贝U 2a w 2b—15．有下列四个命题：①命题“若x+ y= 0,则x, y 互为相反数”的逆命题；②命题“面积相等的三角形全等”的否命题；③命题“若m w 1,则x2—2x+ m= 0 有实根”的逆否命题；④命题“若A H B= B,贝U A? B”的逆否命题.其中是真命题的是 _______________ (填上你认为正确的命题的序号)．解析：④中由A H B= B,应该得出B? A,原命题为假命题，所以逆否命题为假命题. 答案：①②③6．写出下列原命题的其他三种命题,并分别判断真假．⑴在厶ABC中，若a>b,则/ A>Z B;(2)若ab= 0,则a= 0；(3)若x€ A，贝U x€ A U B.解：(1)逆命题：在△ ABC中，若/ A>Z B，贝U a>b，真命题；否命题：在△ ABC中，若a w b,则/ A W / B,真命题；逆否命题：在△ ABC中，若/ A W / B,贝U a w b,真命题.⑵逆命题：若a= 0,贝U ab= 0，真命题；否命题：若ab z0，则a^0,真命题；逆否命题：若a z 0,则ab z 0，假命题.⑶逆命题：若x€ A U B,则x € A,假命题; 否命题：若x?A，则x?A U B，假命题；逆否命题：若x?A U B，则x?A，真命题.课下训练经典化，贵在触类育通一、选择题1.命题"若a>b，则a+ 1>b”的逆否命题是()A .若a + 1 w b,贝U a>bB .若a+ 1<b，贝U a>bC .若a + 1 w b,贝U a w bD .若a+ 1<b，贝U a<b解析：把条件与结论交换，再否定.答案：C2•命题“若f(x)是奇函数，贝U f(- x)是奇函数”的否命题是()A .若f(x)是偶函数，则f( —x)是偶函数B.若f(x)不是奇函数，则f( —x)不是奇函数C .若f( —x)是奇函数，则f(x)是奇函数D .若f( —x)不是奇函数，则f(x)不是奇函数解析：否命题是既否定题设又否定结论.因此否命题应为“若函数f(x)不是奇函数，则f(—x)不是奇函数”.答案：B3.下列说法中错误的是()A. 命题“ a, b, c中至少有一个等于0”的否命题是“ a, b, c中没有一个等于0”B. 命题“若x>1，则x—1>0”的否命题是“若xvl，则x—1<0”C .命题“ 0，- 2,0.4都是偶数”的否命题是“ 0，- 2,0.4不都是偶数”D .命题“ x=—4是方程x2+ 3x —4= 0的根”的否命题是“ x=—4不是方程x2+ 3x —4= 0的根”解析：命题"若x>1，则x—1>0”的否命题应该是 "若x w 1,贝U x—K 0”.答案：B4.命题“函数f(x)g(x)在定义R上，h(x)= f(x)g(x),若f(x), g(x)均为奇函数，则h(x) 为偶函数”的逆命题，否命题，逆否命题中正确的命题的个数是()A. 0B. 1C. 2D. 3解析：由f(x) g(x)均为奇函数可得h(x)= f(x) g(x)为偶函数，反之则不成立，如h(x)=2x2是偶函数，但函数f(x) = -2刍,g(x) = x2+ 1都不是奇函数，故逆命题不正确，故其否命题也不正确，即只有逆否命题正确.答案：B二、填空题5 . 命题“若A U B = B , 贝U A ? B” 的否命题是逆否命题是 ______________________________________________________________ .解析：命题“若A U B = B,则A? B”的否命题是“若A U B丰B,则A= B”，逆否命题是“若A E B，则A U B M B”.答案：若A U B M B，贝U A^B 若A B,贝U A U B工B6. 给定下列命题：①“若k> 0，则方程x2+ 2x —k = 0”有实根；②“若a> b,则a+ c> b+ c”的否命题.其中真命题的序号是 _________ .解析：◎△= 4 + 4k > 0,二是真命题.②否命题为“若a w b,则a+ c< b+ c”，是真命题.答案：①②7. 已知命题“若m —1<xvm+ 1,贝U 1<x<2”的逆命题为真命题，则m的取值范围是m—1 w 1,解析：由已知得，若1<x<2成立，贝U m—1vxvm+ 1也成立./• 1 w m w 2. m+ 1> 2.答案：[1,2]8.下列命题中：①若一个四边形的四条边不相等，则它不是正方形；②若一个四边形对角互补，则它内接于圆；③正方形的四条边相等；④圆内接四边形对角互补；⑤对角不互补的四边形不内接于圆；⑥若一个四边形的四条边相等，则它是正方形.其中互为逆命题的有 ____________ ；互为否命题的有_____________ ；互为逆否命题的有解析：命题③可改写为“若一个四边形是正方形，则它的四条边相等”；命题④可改写为“若一个四边形是圆内接四边形，则它的对角互补”；命题⑤可改写为“若一个四边形的对角不互补，则它不内接于圆”，再依据四种命题间的关系便不难判断.答案：③和⑥，②和④①和⑥，②和⑤①和③，④和⑤三、解答题9•写出下列命题的逆命题、否命题、逆否命题，并判断其真假.(1) 若X M 1 时，贝U x2—3x + 2工0；(2) 弦的垂直平分线平分弦所对的弧.解：(1)逆命题：若X2—3X + 2M0,则X M 1,是真命题；否命题：若X= 1，贝U X2—3X + 2 = 0,是真命题；逆否命题：若X2— 3x+ 2= 0,贝U X = 1,是假命题.(2)逆命题：若一条直线平分弦所对的弧，则这条直线是弦的垂直平分线，是假命题；否命题：若一条直线不是弦的垂直平分线，则这条直线不平分弦所对的弧，是假命题；逆否命题：若一条直线不平分弦所对的弧，则这条直线不是弦的垂直平分线，是真命题.10.已知集合A = {X|X2— 4mx+ 2m+ 6= 0}, B = {x|x<0}，若命题“ A n B= ? ” 是假命题，求实数m的取值范围.解：因为A n B= ?是假命题，所以A n B M?.设全集U = {m|A= (—4m)2—4(2m+ 6)>0},则U = Im m w —1 或m>3r .假设方程X2— 4mx+ 2m+ 6 = 0的两根X1 , X2都非负，则有m€ U, m€ U,X1+ X2> 0, 即4m》0,X1X2》0, 2m+ 6 > 0.3解得m>?. 又集合m m>2，在全集U中的补集是{m|m<- 1}, 所以实数m的取值范围是（一R,- 1].。

参考答案第七章 一元一次不等式第1节 生活中的不等式 [即时训练]**（点拨：判断是不是不等式，要把握两点：一是有不等号；二是表示不等关系．∴上面的式子中不等式有①、②、⑤、⑥共4个，选C ．） 2．B （点拨：不小于就是“≥”故选B ） 3.解：(1) 2x +1＜0；(2) 2a －4＞0；(3)102b +c ＜；(4)11x +≥． 4. 1＜x ＜7．（点拨：本例考查三角形三边之间的关系，作为第三边的x ，要满足两个关系：作为最长边时，要小于另两边之和，作为最短边，要大于另两边之差，∴4－3＜x ＜4+3，即1＜x ＜7．）5．2（点拨：由题意，得这罐饮料中蛋白质的含量≥500×0.4％，即这罐饮料中蛋白质的含量≥2．）**（点拨：最高气温是33℃是指气温不大于33℃，即t ≤33，最低气温24℃是指气温不小于24℃，即t ≥24．所以24≤t ≤33．） [牛刀小试]1．D （点拨：先算加法，然后求一半，∴表示为12(+5)x ；是非负数表示为≥0．） 2．D （点拨：无论a 取何值，20a ≥，∴210a +>．）3．C （点拨：左图A 大于2g ，右图A 小于3g ．）4．D （点拨：4－x 是x －4的相反数，绝对值等于其相反数的数是负数和0．） 5．(1) a －(－2)＜0；(2)23a ≥b －3 点拨：是负数表示为＜0，不小于表示为≥． 6．x ≥1000 点拨：满1000元是大于或等于1000元． 7．b m ba a+＞ 点拨：分别表示加糖前后的含糖率． 8．x +x －2＜100 点拨：乙班人数用x －2表示，不足100，表示为＜100． 9．解：3x ＞5． 点拨：由图上看出三个乒乓球的质量大于5g ． 10．解：2002.21000x -＞．点拨：剩余钱数可以购买的苹果质量不少于1000. 11．解：x ＞488.9－479.6，即x ＞9.3． [教材习题参考答案] 练习(P 7)1．(1)a ＜0；(2)x +5＞2；(3)x －a ＜2；(4)x －y ≥0． 2．(1)v ≤200；(2)h ≤1.74；(3)s ≤4． 习题7.1(P 7)1．(1)＞；(2)＞；(3)＜；(4)＜；(5)＞．2．(1)x ≤14；(2)t ≥30；(3)t ≥8；(4)h ＞1.75；(5)t ＜12．3．(1)x －6＞－1；(2)2x +5＜0；(3)3x －2＞0；(4)3a +b ≥0．第2节 不等式的解集 [即时训练]1． D （点拨：将各个数值代入不等式计算，使得不等式成立的是不等式的解．） 2．B （点拨：由大于方向向右，找到点－1，再由不小于是实心点，故选B ．） 3．－3＜x ≤2（点拨：根据数轴表示的不等式组解集，可知－3＜x ≤2．） 4．[牛刀小试]1．A 2．B 3．B4．B （点拨：不等式两边都加上6，得2x≥6，不等式两边都除以2，得x≥3．）5．9 (点拨：因为a≥1的最小值是m ，所以m=1，因为b≤8的最大值是n ，所以n=8，所以m+n=1+8=9．)6．5x+2（30－x ）≤100 ( 点拨：设能买钢笔x 支，则买笔记本（30－x ）本，依题意5x+2（30－x ）≤100．)7．15 （点拨：第三边的取值范围是4<x<10，所以第三边长的最小整数值为5，故这样的三角形的周长最小值是3+7+5=15．）8．（1）如图7.2－12所示，（2）如图7.2－13所示．点拨：在数轴上表示不等式的解集时应牢记：边界点含于解集用实心圆点，•不含于解集用空心圆圈；方向遵循“大于向右走，小于向左走”的原则．9.（1）这句话是正确的；（2）不正确，•因为不等式的解集是所有符合条件的解的集合，3只是其中之一；（3）不等式的解集是所有符合条件的解的集合，而x<3却丢掉了其中的一部分，所以说法（3）不正确，而（4）正确．10．解：(1)x ＜－1；(2)x ≥－1；(3)a ＞0；(4)b ≥0. 在数轴上表示为：11．解：t ＜12.87，在数轴上表示如下图． 点拨：打破记录是用时更少．图7.2－13图7.2－12[教材习题参考答案]练习(P10)1．3.4，4，5，6.2，9是不等式x+2＞4的解；－5，－3，－1.5，0，1，2不是不等式x+2＞4的解．2．(1)如图①；(2)如图②；(3)如图③；(4)如图④．3．不能．点拨：只能说明小于0的所有的数是不等式的解，不一定是全部的解．习题7.2(P11)1．(1)如图①；(2)如图②；(3)如图③；(4)如图④．2．(1)x＜3；(2)x＞14；(3)x≥－2；(4)x≤13．3．2，3，4，5，6都是不等式2x+1＞3的解，方程2x+1＝3的解是x＝1，不等式的解都大于方程的解．第3节不等式的性质[即时训练]1.<( 点拨：根据不等式的性质，在不等式的两边都加上y，得出x＜y．＝**（点拨：根据不等式性质1，A一定是成立的；根据不等式性质2，B、C一定不成立，D 不一定成立．）3. >（点拨：根据不等式的性质1，在不等式a－b>a两边都减去a，得出－b＞0，然后两边都乘－1，得出b＜0；在不等式a+b<b两边都减去b，得出a＜0；∴，得出ab＞0．）4. ＞，不等式的性质2．（点拨：不等式的左边系数是负数，变形成为x，要在不等式两边都除以34，∴不等号方向改变．）5. ○b＞○c．（点拨：由图中的天平得出不等式○a+○b+○c＞○a+○c+○c，在这个不等式的两边都减去○a+○c，根据不等式的性质1，不等号的方向不变，∴得出○b＞○c．）[牛刀小试]1．C(点拨：注意乘以－2时，不等号方向改变．)2．A(点拨：不等号方向改变，得出a＜0．)3．D(点拨：不等号方向改变，得出a－2＜0，∴a＜2．)4．C ( 点拨：根据不等式的性质，将各个不等式变形为x＞a或x＜a的形式．)5．＞，(不等式的性质1 点拨：不等式两边都加上2．)6．＜，(不等式的性质2 点拨：不等式两边都除以25．)7．解：(1) x＜－5 (点拨：不等式两边都减去x，不等号方向不变；)(2)x ＞－1 (点拨：不等式两边都除以110-，不等号方向改变．) 8．解：表示为x ≥－1，根据不等式的性质可以变形得出x +1≥0，2x ≥－2等． 9．解：∵a ＞1，∴a 1＜1．∵－1＜b ＜0，∴0b a a --1＜＜．∴b a a-1＜． 点拨：根据不等式的性质将不等式进行变形． 10．解：解方程，得263a x -=．∴根据题意，得2630a -≥，根据不等式的性质2，两边都乘3，得出260a -≥．根据不等式的性质1，两边都加上6，得出26a ≥．根据不等式的性质2，两边都除以2，得出3a ≥．11．解：3×4+2x ≤24．根据不等式的性质1，两边都减去12，得出2x ≤12．根据不等式的性质2，两边都除以2，得出x ≤6．∴最多可以买6根．[教材习题参考答案] 练习(P 13)1．(1)＞；(2)＞；(3)＞；(4)＜；(5)＞；(6)＞．2．(1)不等式的性质1；(2)不等式的性质2；(3)不等式的性质2；(4)不等式的性质1． 3．解：x ＞3．点拨：根据不等式的性质2，不等式两边都除以2，得出x ＞3． 习题7.3(P 14)1．(1)x ＞2．点拨：不等式两边都减去2； (2)x ＜－3．点拨：不等式两边都减去x ； (3)x ＜4．点拨：不等式两边都乘3； (4)x ＜43-．点拨：不等式两边都除以－6．2．解：x +4＜12，根据不等式的性质1，不等式两边都减去4，得到x ＜8．第4节 解一元一次不等式 [即时训练]1．A (点拨：采用排除法，排除B 、C 、D ．)2. m ＝3(点拨：先将字母m 看成是常数，解不等式得x ＞253-m ，再由解集为x ＞2可得到关于m 的方程2253=-m ，即可求出m 的值．)3. x ＜-1(点拨：移项得：3x ＜-3，两边同时除以3得：x ＜-1．)4. 1或2或3(点拨：这个不等式的解集是x ＜3.5，所以它的正整数解是1，2，3．)5. 解：去括号，得5x －10+8＜6x －6+7．移项、合并同类项，得－x ＜3． 系数化为1，得x ＞－3．∵大于－3的最小整数是－2，∴x ＝－2．把x ＝－2代入方程2x －ax ＝4，得－4+2a ＝4，a ＝4． 6.解：（1）32x x -≥21+ 得 x≥3[牛刀小试]1．C 2．C 3．A （点拨：设该数为x ，列不等式为4+7x ≥6-5x ） 4．C 5．x>-1 6．x ≤2 7．x>-438．9 9．（1）x<-1 （2）x>-3 （3）x ≥3 （4）x ≤2 10．解：根据题意，得3x －4＜0，解得43x ＜．11．解：解方程组32143 1.x y m x y m +++-⎧⎨⎩＝，＝得57.x m y m +--⎧⎨⎩＝，＝∵x ＞y ． ∴m +5＞－m －7．∴m ＞－6．[教材习题参考答案] 练习(P 16)1．(1)a ＞2，(图①)；(2)x ＞4，(图②)；(3)x ≤32，(图③)；(4)x ＜－6，(图④)．在数轴上表示如下：2．解：根据题意，得0.5×5+2a ≤5，解得a ≤1.25． 练习(P 17)1．(1)x ＞4，(图①)；(2)x ≥－3，(图②)；(3)x ≤8，(图③)；(4)x ＞6，(图④)． 在数轴上表示如下图：2．根据题意，得[]2(20)280x x +-≤，解得x ≤80．∴x 的最大值是80cm ． 习题7.4(P 18)1．(1) x ≥4，(图①)；(2)x ＜4，(图②)；(3)x ≤23，(图③)；(4)x ＜16，(图④)；(5)a ＞14，(图⑤)；(6)b ≥－113，(图⑥)．在数轴上表示如下：2．(1)y ＜1；(2)x ≤1；(3)x ≥1；(4)x ＜2．3．解：解不等式2x －3≤5，得x ≤4．∵小于等于4的正整数有1，2，3，4，∴不等式2x －3≤5的正整数解是1，2，3，4． 4．解：根据题意，得2132x x -4+＜，解得4x 11-＞．∴当4x 11-＞时，代数式3x -4的值比212x +的值小．5．解：设这块苗圃地的长最多为x m ，根据题意，得[]2(4)36x x +-≤，解得x ≤11．答：这块苗圃地的长最多为11m ．第5节 用一元一次不等式解决问题 [即时训练]1. B （点拨：题目中给出的不等关系是：此人应该交的车费≤19元．所以列出不等式7+2.4(x －3)≤19．解得x ≤8，能买x 的最大值是8．）**．4．（原样书第46页到第47页例2、例3、例4对应的随堂变式的解答））5. 解：由题意知单独用A 型车，需6辆，共要2100元费用，单独用B 型车，需5辆，共需2000元费用．设若用A 型车x 辆，用B 型车(x ＋1)辆，根据题意，得350x ＋400(x ＋1)＜2000．解得x ＜3215．∴x ＝1或x ＝2． 而当x ＝1时x ＋1＝2，所运台数为45×1＋60×2＝165＜270，不合题意，舍去；当x ＝2时，x ＋1＝3，且2×45+3×60＝270恰好符合题意． 此时所需费用为350×2+400×3＝1900(元)．答：这种方案需A 型汽车2辆，B 型汽车3辆，运费是1900元．[牛刀小试]1．B （点拨：可以设中间一个数是x ，则另两个数分别是x －1，x +1．根据题意，得(x －1)+x +(x +1)≤12，解得x ≤4．由于x 是正整数，∴x 有3个值．） 2．C （点拨：n 边形的内角和为(n －2)·180°，根据题意，得(n －2)·180°＜2009°，解得n ＜2918013，则n 得最大整数解是13．） 3．B （点拨：设售价为x 元，则利润为(x －800)元，根据题意，得(x －800)≥800·15％，解得x ≥920．∴至少为920元．）4．B （点拨：设张老师和他的学生至少有x 人，根据题意，得5x ＞50×5×80％．解得x ＞40．∵x 是大于40得正整数，∴x 至少是41．）5．7 (点拨：设最低打x 折，根据题意，得750×10％·x －500≥500×5％．解得x ≥7．) 6．3 (点拨：设乙最多输入x 页，根据题意，得2(5+x )＜26－5－x ．解得x ＜113．) 7．解：设从第7天起，每天找x 克，根据题意，得150+(15－6)x ≥600．解得x ≥50．答：从第7天起，每天平均找50克． 8．解：设以后每天至少加工x 个小板凳，根据题意，得24×3+(15－3)x ≥408．解得x ≥28．又∵x 是正整数，∴x 的最小值是28．答：以后每天至少加工28个小板凳才能在计划的日期内完成．9．解：设乙方的追击速度至少为x km ／h ，根据题意，得6x ＞14+4+4x ．解得x ＞9．答：乙方的追击速度至少为9km ／h ． 10．解：设李明第三次的得分至少是x 分，才能使平均分不低于85分，根据题意，得76+92+x≥85×3．解这个不等式，得x ≥87．答：李明第三次的得分至少是87分，才能使平均分不低于85分．11．解：设小明设置最长时间为x 分钟，根据题意，得36－0.9x ≥18．解这个不等式，得x≤20．∵x 是正整数，∴x 最大是20．答：小明最长设置的时间是20分钟．[教材习题参考答案] 练习(P 20)1．解：设参加合影的人数至少有x 人，根据题意，得1+0.6x ≤0.8x ．解得x ≥5． 答：参加合影的人数至少有5人．2．解：设导火索至少需要x cm ，根据题意，得0.85x 200＞，解得x ≥32． 答：导火索至少需要32cm ．3．解：设甲队至少胜了x 场，根据题意，得3x +(10－x )＞22，解得x ＞6．∵x 是整数，所以x 最小是7． 答：所以甲队至少胜7场． 习题7.5(P 20)1．解：根据题意，得(n －2)·180°－360≥120°，解得n ≥134．所以n 的最小值是5． 2．解：设40座的客车至少需租x 辆，根据题意，得44×2+40x ≥406，解得20x 159≥．所以x 的最小整数解为8，即40座的客车至少需租用8辆．第6节 一元一次不等式组 [即时训练] **（点拨：解不等式3x-1>-4得x>-1，解不等式2x ≤x+2，得x ≤2.所以不等式组的解集是-1<x ≤2.）2．解：3(2)1522x x x x --⎧⎪⎨-⎪⎩≤8　①＞ ② 解不等式①得：x ≥－1解不等式②得：x ＜2∴ 不等式组的解集为－1≤x ＜2 **4．解 (1)设商品进了x 件，则乙种商品进了(80-x )件，依题意得10x +(80-x )×30=1600解得：x =40，即甲种商品进了40件，乙种商品进了80-40=40件．(2)设购买甲种商品为x 件，则购买乙种商品为(80-x )件， 依题意可得：600≤(15-10)x +(40-30)(80-x )≤610 解得： 38≤x ≤40∵x 为整数，∴x 取38，39，40，∴80- x 为42，41，40即有三种方案，分别为甲38件，乙42件或甲39件，乙41件或甲40件，乙40件5. 解：根据题意，得2(70+)350707560x x ⎧⎨⎩＞，＜.解这个不等式组，得105＜x ＜108．∵国际足球比赛的足球场的长的标准为100～110m 之间，∴符合标准；宽为70m ，标准为64～75m 之间，∴宽符合标准．∴可以用作国际足球比赛．答：x 的范围是105＜x ＜108，可以用作国际足球比赛．[牛刀小试]1．B （点拨：4上是空心圆圈且向左画，是小于4；－1上是实心圆点且向右画，是大于等于－1．）2．C （点拨：解不等式①，得x ＞0，解不等式②，得x ≤3，∴0＜x ≤3．∴正整数解是1，2，3．）3．C （点拨：设最小边用了x 根火柴，则最长边用3x 根火柴．根据题意，得2x ＜120－4x ＜3x ．解得117207x ＜＜．∵x 是正整数，∴x 可以是18或19．）4．D （点拨：由图可以得出25262(82+52)45.x x x <+--⎧⎨⎩，≤解得7582x ≤＜．）5．6＜a ＜16 （ 点拨：根据两边之和大于第三边，两边之差小于第三边，得出不等式组9－5＜a －2＜9+5． 6．a ≤3 （点拨：解不等式组，得 3.x a x ⎧⎨⎩＞，＞∵解集是x ＞3，∴a ≤3．） 7．解：解不等式①，得x ＜2． 解不等式②，得x ＞－1．∴不等式的解集为 －1＜x ＜2．8．解：解不等式①，得x ＞－2，解不等式②，得x ≤2，∴不等式组的解集为－2＜x ≤2．∵大于－2且小于等于2的整数有－1，0，1，2，∴不等式组的整数解是－1，0，1，2． 9．解：设该小学有x 个班，则奥运福娃共有(10x +5)套．由题意，得10513(1)410513(1).x x x x +<-++>-⎧⎨⎩，解之，得1463x <<．∵x 只能取整数，∴x ＝5，此时10x +5＝55．答：该小学有5个班级，共有奥运福娃55套10．解：(1)解不等式组：9040(50)360030100(50)2900.x x x x +-+-⎧⎨⎩≤，≤解得30≤x ≤32．∵x 为整数，∴x 只取30，31，32．∴A 、B 造型的搭配方案有三种：搭配A 种造型30个，B 种造型20个； 或者搭配A 种造型31个，B 种造型19个； 或者搭配A 种造型32个，B 种造型18个． (2)y ＝1000 x ＋1200(50－x )＝－200 x ＋60000．∵y 随x 的增大而减小，∴当x ＝32时，y 取得最小值， 此时y ＝－200×32＋60000＝43600(元)．答：当A 中造型32个时成本最低，最低成本是43600元．11．解：设一盒饼干的价格是x 元，那么一袋牛奶的价格是 (9.2－0.9x )元．根据题意，得9.20.91010.x x x +-⎧⎨⎩＞，＜解得8＜x ＜10． ∵x 是整数，∴x ＝9，9.2－0.9x ＝1.1．答：一盒饼干的价格是9元，一袋牛奶的价格是1.1元．[教材习题参考答案] 练习(P 23)1．(1)1≤x ＜4；(2)x ＞－1；(3)x ＜－12；(4)0≤x ＜1．2．解：设一杯咖啡应该加糖xg ，根据题意，得0.5121.5.12xx ⎧⎪⎪⎨⎪⎪⎩≥，≤解得6≤x ≤18．所以一杯咖啡应该用糖6～18g ． 练习(P 24)1．解：设AB 长为x cm ，根据题意，得2103421044.x+x+⎧⎪⎨⎪⎩＞，＜解得12＜x ＜17．2．解：设污水抽完需x 分钟，根据题意，得202000201800.x x ⎧⎪⎨⎪⎩≤，≥解得，90≤x ≤100．答：将污水抽完至少需要90分钟，至多需要100分钟．3．解：设需用载重量20t 得货车不少于x 辆，根据题意，得360≤20x ≤400． 解得18≤x ≤20．答：需用载重量20t 得货车不少于18辆，不多于20辆． 习题7.6(P 25)1．(1)－4≤x ＜2；(2)3＜x ＜4；(3)x ＜－3；(4)x ＞13．2．解：根据题意，得90＜5x －35＜180，解得25＜x ＜43． 3．解：设小丽骑自行车的速度为x m/min ，根据题意得203400253400.x x ⎧⎪⎨⎪⎩≤，≥解得136≤x ≤170．答：小丽骑自行车的速度应不大于170m/min ，不小于136 m/min ． 4．解：设为x m ，根据题意，得6213212.x x ⎧⎪⎨⎪⎩+≤，≥解得2≤x ≤3.5．答：长方形土地的宽x 得取值范围是2≤x ≤3.5．5．解：设共有x 名学生，根据题意，得423523.x x ⎧⎪⎨⎪⎩＜，＞解得4.6＜x ＜5.75．∵x 取整数，∴x ＝5．答：共有5名学生．第7节 一元一次不等式与一元一次方程、一次函数 [即时训练]1．原样书第68页例1对应的随堂变式的解答 2．C3. 解：取点(0，12)，(4，0)，作出函数图像，如图7.7－6．(1)从图象上看出，当x ＜4时，y ＞0，即不等式－3x +12>0的解集是x ＜4； (2)从图象上看出，当x ≥4时，y ≤0，即不等式－3x +12≤0的解集是x ≥4； (3)由题意，得－6≤－3x +12≤6，解得2≤x ≤6．4. 解 (1) x x x w 2100)10(1012+=-+=，x x x y 202000)10(200240+=-+=.(2)⎩⎨⎧≥+≤+20402020001062100x x ，解得32≤≤x ，所以有两种方案：方案一：2台A 型设备、8台B 型设备，方案二：3台A 型设备、7台B 型设备，方案一需104万元资金，方案二需106万元资金，所以方案一最省钱，需要104万元资金[牛刀小试]1．A （ 点拨：根据题意，得x －1＞0，解得x ＞1．）2．D （点拨：将y =－x +4变形为x =－y +4．∵x >－2，∴－y +4>－2，解得y <6．）3．C （点拨：将y －2x －2=0变形为y =2x +2．求出此函数与x 轴、y 轴的交点，画出图象为C ．）4．D（点拨：∵ax+1>0(a≠0)的解集是x<1，可以得出当x＝1时，ax+1＝0，∴直线y=ax+1与x轴的交点是(1，0)．）5．x≤2 （点拨：根据题意，得2x－5≤－2x+3．解得x≤2．即当x≤2时，y1≤y2．）6．(2，3) （点拨：∵－x+5>3x－3的解集是x<2，∴交点的横坐标为x＝2，将x＝2代入其中一个函数解析式中，得出y＝3．∴交点坐标为(2，3)．）7．解：将方程化为3x－3＝0，在平面直角坐标系中画出函数y＝3x－3的图象，观察图象与x轴的交点的坐标是(1，0)，所以方程214x x+=-+的解为x＝1．图象如下．8．解：将不等式变形为2x－10＞0．在平面直角坐标系中画出函数y＝2x－10的图象，观察函数图象，当x＞5时，函数的图象在x轴的上方，所以得出当x＞5时，2x－10＞0，即5436x x->+．图象如图所示．9．解：(1)将x＝2，y＝―1分别代入两个函数中，得出k＝12，b＝5．图象如图所示；(2)观察函数图象，得出：①当x＜2时，y1<y2；②当x≥2时，y1≥y2；(3) ∵直线y1=12x－2与x轴的交点为B(4，0)，直线y2=－3x+5与x轴的交点为C(53，0)，∴从图象上可以看出：①当x<4时y1<0，当x>53时y2<0，所以当53<x<4时，y1<0且y2<0．②当x>4时，y1>0；当x>53时y2<0，∴当x>4时y1>0且y2<0．10．解：设甲公司的总费用为y1元，乙公司的总费用y2元．制作材料x份，则y1=3000+20x，y2=30x．(1)当y1<y2时，3000+20x<30x，10x>3000，x>300．当制作的材料大于300份时，选甲公司合算．(2)当y2<y1时，30x<3000+20x，10x<3000，x<300．当制作的材料小于300份时，选乙公司合算．(3)当y 2=y 1时，3000+20x =30x ，10x =3000，x =300，当制作的材料等于300份时，两家公司收费相同．11．解：(1)设小明的存款为y 1，从现在开始的月份数为x ，则y 1=12x +50． (2)设小丽的存款数为y 2，则y 2=18x ．图像略． 当x =6时，y 1=12×6+50=72+50=122，y 2=18×6=108．因108<122，所以半年后小丽的存款为108元，不能超过小明．当y 2>y 1时，18x >12x +50，x >813,∴至少9个月后小丽的存款数超过小明．[教材习题参考答案] 练习(P 27)1．解：x ＜1；x ＞1；x ≤1．2．解：(1)把x ＝340代入y ＝33315x +，的x ＝15．即音速为340m/s 时的气温为15℃． (2)解不等式33315x +＞340，得x ＞15．即音速超过340m/s 时的气温大于15℃． 习题7.7(P 27)1．解：解不等式－3x +1＞－2，解得x ＜1，即当x ＜1时函数值大于－2； 解不等式－3x +1＜－2，解得x ＞1，即当x ＞1时函数值小于－2； 解不等式－3x +1＝－2，解得x ＝1，即当x ＝1时函数值等于－2． 2．解：由x +2y ＝－5，得y ＝5212x --． 当1522x --＞0，即x ＜－5时，y 的值为正数； 当5212x --＜0，即x ＞－5时，y 的值为负数； 当5212x --≥0，即x ≤－5时，y 的值为非负数； 3．解：(1)设y 与x 的函数关系式为y ＝kx +b (k ≠0)，把x ＝10，y ＝0；x ＝60，y ＝10代入关系式后，得k ＝15，b ＝－2．所以y 与x 的函数关系式为y ＝15x －2． (2)旅客最多可免费携带的行李为10kg ．(3)根据题意，得1251215.5xx⎧⎪⎪⎨⎪⎪⎩--≥4，≤解得30≤x≤85．∴旅客所带行李质量范围为30kg≤x≤85kg．复习题(P29)1．(1)x≥3；(2)x≤－1；(3)x＜－3；(4)x＞－1；(5)x＜3；(6)x＜0．2．(1)解不等式，得x≤1，∴最大正数解为1；(2)解不等式，得x＜133，∴最大整数解为3．3．(1)解不等式，得x≥－4，∴最小整数解为－4；(2)解不等式，得x＞－3，∴最小整数解为－2．4．(1)解得35.xx⎧⎪⎨⎪⎩-＜，＜∴不等式组的解集为x＜－3；(2)解得9.xx⎧⎪⎨⎪⎩-14＞，＞∴不等式组的解集为x＞9．5．解：不等式组的解集为－2＜x＜12，∴不等式组的整数解为－1，0．6．解：不等式组的解集为x＜2.5，∴不等式组的自然数解为0，1，2．7．解：根据题意，得42(1).x x+x x⎧⎪⎨⎪⎩-2-3-＞，＜5解得2＜x＜4．8．解：由4x+y＝1，得x＝11+44y-，∴当x＞－1时，即11+44y-＞－1，解得y＜5．当x≤2时，11+44y-≤2，解得y≥－7．∴当－7≤y＜5时，－1＜x≤2．9．解：设至少销售x件衬衫，销售收入才超过总成本，则有95x＞50×80，解得x＞24219，∴x取43．答：至少销售超过43件，销售收入才超过总成本．10．解；设至少可以打x折出售，根据题意，得2800×10％·x≥2000×(1+5％)，解得x≥7.5．答：至少可以打7.5折出售．11．解：设车工平均每天加工x个零件，才能在规定时间内完成，则有24×3+12x≥408，解得x≥28．答：车工平均每天加工28个零件．12．解：设学生有x人，则1≤43－6(x－1)＜3，解得233＜x≤8，∵x取整数，∴x＝8．答：学生有8人．13．解：(1)设y＝kx+b，根据题意，得201600302000.k bk b⎧⎪⎨⎪⎩+=+=，解得40800.kb⎧⎪⎨⎪⎩==，∴y＝20x+800．(2)根据题意，得40x+800≤6250，解得x≤136.25．∴这场比赛最多可以邀请136名运动员参加．14．解：a＞2．点拨：根据题意，得a－2＞0．15．解：1.5＜a＜2．点拨：根据题意，得0.aa⎧⎪⎨⎪⎩2-3-2＞，＜或0.aa⎧⎪⎨⎪⎩2-3-2＜，＞16．解：根据题意，得(1)2(1)+(2)39.x x+x+x x+x+⎧⎪⎨⎪⎩++＞，≤解得12.xx⎧⎪⎨⎪⎩＞1，≤即1＜x≤12．17．根据题意，得4+3294+3+456.x x x+x x x+⎧⎪⎨⎪⎩+--7⨯3+-⨯3＞，＜解得.xx⎧⎪⎨⎪⎩＞15，＜17∵x为整数，∴x＝16．18．(1)①＜；②＝；③＜；(2)≤．19．解：根据题意，得3100()5100().x xx x⎧⎪⎨⎪⎩+13＞是偶数，＞是奇数解得29()20().x xx x⎧⎪⎨⎪⎩＞是偶数，＞是奇数∴x最小取21．20．解：(1)a≤1；(2)a＞1．21．解：答案不唯一，如：3x－2≥0，9x－6≥0等．(根据不等式性质将x≥23变形)培优实践1．D 2.A3.解（1）(2 420+1 980)×13%＝572 答：可以享受政府572元的补贴.（2）①设冰箱采购x台，则彩电采购(40－x)台，则根据题意，得()()232019004085000,540.6x xx x+-≤⎧⎪⎨≥-⎪⎩解不等式组，得18211≤x≤2137.因为x为正整数，所以x＝19，20，21.即该商场共有3种进货方案：方案一：冰箱购买19台，彩电购买21台；方案二：冰箱购买20台，彩电购买20台；方案三：冰箱购买21台，彩电购买19台.②设商场获得总利润y元，则根据题意，得y＝(2 420－2 320)x+(1 980－1900)(40－x)＝20x+3 200.因为20＞0，所以y随x的增大而增大.所以当x＝21时，y最大＝20×21+3 200＝3 620.答：方案三商场获得利润最大，最大利润是3 620元.第七章检测卷一、选择题（每小题6分，共48分）1. D（点拨：先算加法，然后求一半，∴表示为12(+5)x；是非负数表示为≥0．）2．D（点拨：无论a取何值，20a≥，∴210a+>．）3．D（点拨：小于向左，∴D不正确．）4．A（点拨：不等号方向改变，得出a＜0。