初中数学 第十一章 全等三角形(11.1~11.2)课课练
- 格式:doc
- 大小:495.94 KB
- 文档页数:11


图2BFECDE第十一章 《全等三角形》练习题一、选择题1、下列判断不正确的是( ) .A .形状相同的图形是全等图形B .能够完全重合的两个三角形全等C .全等图形的形状和大小都相同D .全等三角形的对应角相等2、如图:若△ABE ≌△ACF ,且AB=5,AE=2,则EC 的长为( )A .2B .3C .5D .2.53、如图:在△ABC 中,AB=AC ,∠BAD=∠CAD ,则下列结论:①△ABD ≌△ACD ,②∠B=∠C ,③BD=CD ,④AD ⊥BC 。
其中正确的个数有( )A .1个B .2个C .3个D .4个4、如图:AB=AD ,AE 平分∠BAD ,则图中有( )对全等三角形。
A .2 B .3 C .4 D.5 5、工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB 的边OA ,OB 上分别取OM=ON ,移动角尺,使角尺两边相同的刻度分别与M ,N 重合,得到∠AOB 的平分线OP ,做法中用到三角形全等的判定方法是( )A .SSSB .SASC .ASAD .HL 6、.如图,D 是∠BAC 的平分线上一点,DE ⊥AC 于E ,DF ⊥AB 于F ,下列结论中不正确的是( )A .DE=DFB .AE=AFC .△ADE ≌△ADFD .AD=DE+DF 7、如图:EA ∥DF ,AE=DF ,要使△AEC ≌△DBF ,则只要( ) A .AB=CD B .EC=BF C .∠A=∠D D .AB=BC8、的办法是( )A .带①去B .带②去C .带③去D .带①和②去9、如图:直线a ,b ,c 表示三条相互交叉环湖而建的公路,现在建立一个货物中转站,要求它到三条公距离相等,则可供选择的地址有( )A .1个B .2个C .3个D .4个10、如图:△ABC 中,∠C=90°,AC=BC ,AD 平分∠CAB 交BC 于D ,DE ⊥AB 于E ,且AB=6㎝,则△DEB 的周长是( ) A .6㎝ B .4㎝ C .10㎝ D .以上都不对二、填空题(每小题3分,共30分)11、如图:AB=AC ,BD=CD ,若∠B=28°则∠C= ;12、已知:ΔABE ≌ΔACD ,AC=8cm ,AD=5cm ,根据全等三角形的记法,则AE=_____。

11.1全等三角形◆随堂检测1.若两个三角形全等,猜想它们对应的高、中线、角平分线的关系是。
2.如图,△ABC≌△CDA,AC=7cm,AB=5cm,BC=8cm,则AD的长是()A、7cmB、5cmC、8cmD、6cm3.如果∆ABC≌∆ADC,AB=AD,∠B=70°,BC=3cm,那么∠D=____,DC=__cm4.如图,已知△ABE≌△ACD,∠B=∠C,∠ADE=∠AED,指出这两个三角形的其他相等的边或角.◆典例分析例:如图,若△OAD≌△OBC,且∠0=65°,∠BEA=135°,求∠C的度数.分析:全等三角形的对应角相等,根据该性质可得∠OAD=∠OBC.借助四边形和三角形的内角和(或三角形的外角性质)可求得∠C的度数.解:∵△OAD≌△OBC,∴∠OAD=∠OBC,∵∠0=65°,∠BEA=135°,∠O+∠OBE+∠OAE+∠BEA=360°,∴∠OBE=∠OAE=(360°-65°-135°)÷2=80°,∵∠BEA=135°,∴∠AEC=45°∴∠C=80°-45°=35°.提示:当已知两个三角形全等时,首先要考虑到全等三角形性质:全等三角形的对应边相等、全等三角形的A 'BDAC对应角相等.◆课下作业●拓展提高1.下列说法不正确的是( ) A 、全等三角形的周长相等; B 、全等三角形的面积相等; C 、全等三角形能重合;D 、全等三角形一定是等边三角形.2.已知△DEF ≌△ABC ,AB=AC ,且△ABC 的周长是23cm ,BC=4cm ,则△DEF 的边长中必有一边等于( ) A 、9.5cmB 、9.5cm 或9cmC 、9cmD 、4cm 或9cm3.△ABC ≌△DEF ,且△ABC 的周长为12,若AB=3,EF=4,则AC= . 4.如图,△ABC ≌△ADE ,若∠BAE=120°,∠BAD=40°,求∠BAC 的度数.5.如图,△ABC ≌△ADE ,BC 的延长线交DA 于F ,交DE 于G ,∠D=25°,∠E=105°,∠DAC=16°,求∠DGB 的度数 。

11.2.3三角形全等的条件(三)学习目标1.三角形全等的条件:角边角、角角边.2.三角形全等条件小结.3.掌握三角形全等的“角边角”“角角边”条件.4.能运用全等三角形的条件,解决简单的推理证明问题.学习重点已知两角一边的三角形全等探究.学习难点灵活运用三角形全等条件证明.学习过程Ⅰ.提出问题1.复习:(1)三角形中已知三个元素,包括哪几种情况?_________________(2)到目前为止,可以作为判别两三角形全等的方法有几种?各是什么?______________ 2.在三角形中,已知三个元素的四种情况中,我们研究了三种,今天我们接着探究已知两角一边是否可以判断两三角形全等呢?Ⅱ.学习新课问题1:三角形中已知两角一边有几种可能?________________________________________ 问题2:三角形的两个内角分别是60°和80°,它们的夹边为4cm,•你能画一个三角形同时满足这些条件吗?将你画的三角形剪下,与同伴比较,观察它们是不是全等,你能得出什么规律?提炼规律:___________________________________________________________问题3:我们刚才做的三角形是一个特殊三角形,随意画一个三角形ABC,•能不能作一个△A′B′C′,使∠A=∠A′、∠B=∠B′、AB=A′B′呢?步骤:_________________________________________________________________________ 由此得到:两角和它们的夹边对应相等的两三角形全等(可以简写成“角边角”或“ASA”).思考:在一个三角形中两角确定,第三个角一定确定.我们是不是可以不作图,用“ASA”推出“两角和其中一角的对边对应相等的两三角形全等”呢?探究问题4:如图,在△ABC 和△DEF 中,∠A=∠D ,∠B=∠E ,BC=EF ,△ABC 与△DEF 全等吗?能利用角边角条件证明你的结论吗?证明:两个角和其中一角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS ”). Ⅲ.随堂练习 课本练习1、2.3. 图中的两个三角形全等吗?请说明理由.Ⅳ.课时小结:请同学们举出所有的证两个三角形全等的方法__________________________________ Ⅴ.作业1.课本习题5、6、题.2. 如下图,D 在AB 上,E 在AC 上,AB=AC ,∠B=∠C .求证:AD=AE . 证明:DCABFE50︒50︒45︒45︒DCAB (1)29︒29︒DC A B(2)ED CABE。

11.1 《全等三角形》课后练习
1.如图(1),把△ABC 沿直线BC 翻折180,得△ABC ≌ , 对应边分别为 、 、 ,
对应角分别为 、 、 .
2.如图(2),将△ABC 绕点A 旋转180,得△ABC ≌ , 对应边分别为 、 、 ,
对应角分别为 、 、 .
(友情提示:对应顶点要写在相应的位置)
3.如图(3),△ABC 沿直线BC 向右平移线段BC 的长后与△ECD 重合,则△ABC ≌ ,
对应边分别为 、 、 ,
对应角分别为 、 、 .
图(3)
3.如图:△OCA ≌△OBD ,C 和B,A 和D 是对应点,写出这两个三角形中相等的边和角.
4.如图:△EFG ≌△NMH ,∠F 和∠M 是对应角.在△EFG 中,FG 是最长边.在△NMH 中,MH 是最长边. 2.1, 1.1, 3.3===EF cm EH cm NH cm .
(1)写出其他对应边及对应角.
(2)求线段NM 及线段HG 的长度.
图(1)
图(2)
5.如图:△ABC≌△DEC,CA和CD,CB和CE是对应边,∠ACD和∠BCE相等吗?为什么?
6.如图,△ABC≌△DEF,且A、D、B、E在同一直线上,试找出图中互相平行的线段,并说明理由.
7.如图,△AEC≌△ADB,点E和点D为对应点.试说明(1)BE =CD;(2)∠DCO =∠EBO.。
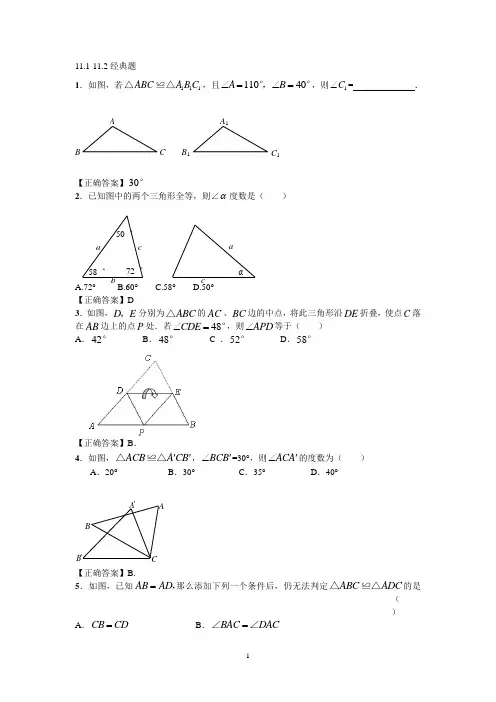
11.1-11.2经典题1.如图,若111ABC A B C △≌△,且11040A B ∠=∠=°,°,则1C ∠= .【正确答案】30°2.已知图中的两个三角形全等,则∠α度数是( )A.72°B.60°C.58°D.50° 【正确答案】D3.如图,D E ,分别为ABC △的AC 、BC 边的中点,将此三角形沿DE 折叠,使点C 落在AB 边上的点P 处.若48CDE ∠=°,则APD ∠等于( ) A .42° B .48° C .52° D .58°【正确答案】B .4.如图,ACB A CB ''△≌△,BCB ∠'=30°,则ACA '∠的度数为( ) A .20° B .30°C .35°D .40°【正确答案】B.5.如图,已知AB AD =,那么添加下列一个条件后,仍无法判定ABC ADC △≌△的是( )A .CB CD = B .BAC DAC =∠∠C A B B 'A 'ABC C 1A 1B 1a b c 50゜ 58゜ 72゜ ca αC .BCA DCA =∠∠D .90B D ==︒∠∠【正确答案】C .6.尺规作图作AOB ∠的平分线方法如下:以O 为圆心,任意长为半径画弧交OA 、OB 于C 、D ,再分别以点C 、D 为圆心,以大于12CD 长为半径画弧,两弧交于点P ,作射线OP ,由作法得OCP ODP △≌△的根据是( )A .SASB .ASAC .AASD .SSS【正确答案】D 7.如图,已知∠1=∠2,AO=BO.求证:AC=BC.【正确答案】证明:在△AOC 与△BOC 中∵AO =BO ,∠1=∠2,OC =OC ∴△AOC ≌△BOC ∴AC =BCOA B C DAB FOCDE8.如图,已知AC 平分∠BAD ,∠1=∠2,求证:AB =AD【正确答案】证明:∵AC 平分∠BAD ∴∠BAC =∠DAC . ∵∠1=∠2∴∠ABC =∠ADC .在△ABC 和△ADC 中,,BAC DAC ABC ADC AC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△ADC (AAS ). ∴AB =AD .9.如图,AB =DC ,AD =CB ,O 为AC 中点,过O 的直线分别交AB 、CD 的延长线于F 、E .求证:∠F =∠E . 【正确答案】 证明:,,,.,,,.ABC CDA AB CD AD CB AC CA ABC CDA BAC DCA AOF COE FAO ECO AO CO AOF COE AOF COE F E ∆∆=⎧⎪=⎨⎪=⎩∴∆∆∠=∠∆∆∠=∠⎧⎪=⎨⎪∠=∠⎩∴∆∆∴∠=∠在和中≌在和中≌A BDC1210.如图,已知AD AB =,DAC BAE ∠=∠,要使 ABC △≌ADE △,可补充的条件是 (写出一个即可).【正确答案】AE AC =(或填E C ∠=∠或D B ∠=∠)11.如图,在△ABE 中,AB =AE ,AD =AC ,∠BAD =∠EAC , BC 、DE 交于点O .求证: △ABC ≌△AED.【正确答案】 证明:BAD EAC BAC EAD ABC AED AB AEBAC EAD AC AD ABC AED∠=∠∴∠=∠∆∆=⎧⎪∠=∠⎨⎪=⎩∴∆∆ 在和中≌ 12.如图,点B 、E 、F 、C 在同一直线上. 已知∠A =∠D ,∠B =∠C ,要使△ABF ≌△DCE ,需要补充的一个条件是 (写出一个即可).【正确答案】AB = DC (填AF =DE 或BF =CE 或BE =CF 也对) 13.已知命题:如图,点A ,D ,B ,E 在同一条直线上,且AD =BE ,∠A =∠FDE ,则△ABC ≌△DEF .判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一.个.适当条件使它成为真命题,并加以证明.FEABCD AC E BD A B CEDOABEFCD【正确答案】解:是假命题.以下任一方法均可: ①添加条件:AC =DF . 证明:∵AD =BE ,∴AD +BD =BE +BD ,即AB =DE . 在△ABC 和△DEF 中,,,,AB DE A FDE AC DF =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△DEF (SAS). ②添加条件:∠CBA =∠E . 证明:∵AD =BE ,∴AD +BD =BE +BD ,即AB =DE . 在△ABC 和△DEF 中, ∠A =∠FDE , AB =DE , ∠CBA =∠E , ∴△ABC ≌△DEF (ASA). ③添加条件:∠C =∠F . 证明:∵AD =BE ,∴AD +BD =BE +BD ,即AB =DE . 在△ABC 和△DEF 中, ∠A =∠FDE , ∠C =∠F , AB =DE , ∴△ABC ≌△DE F(AAS)【正确答案】AE AC =(或填E C ∠=∠或D B ∠=∠) 14.已知:如图,在四边形ABCD 中,AB =CB ,AD =CD . 求证:∠C =∠A .【正确答案】 证明:连接BD .在△ABD 和△CBD 中,A BC D BC DA OB D∵AB =CB ,AD =CD ,BD =BD , ∴△ABD ≌△CBD . ∴∠C =∠A .15.如图,AC 、BD 相交于点O ,且AB =DC ,AC =DB .求证:∠A =∠D . 证明:连接BC.,,,.ABC DCB AB DC AC DB BC CB ABC DCBA D ∆∆=⎧⎪=⎨⎪=⎩∴∆∆∠=∠在和中≌16.已知Rt ABC △中,90AC BC C D ==︒,∠,为AB 边的中点,90EDF ∠=°,EDF ∠绕D 点旋转,它的两边分别交AC 、CB (或它们的延长线)于E 、F .当EDF ∠绕D 点旋转到DE AC ⊥于E 时(如图1),易证12DEF CEF ABC S S S +=△△△.当EDF ∠绕D 点旋转到DE AC 和不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,DEF S △、CEF S △、ABC S △又有怎样的数量关系?请写出你的猜想,不需证明.【正确答案】解:图2成立;图3不成立. 证明图2:过点D 作DM AC DN BC ⊥⊥, 则90DME DNF MDN ∠=∠=∠=°再证MDE NDF DM DN ∠=∠=, 有DME DNF △≌△AOBCDAEC F BD 图1 图3ADFECBA D BC E 图2 F图2ADBCE M NFD ME D NF S S ∴=△△D E FC EF D M C N D E C F S S SS∴==+△△四边形四边形由信息可知12ABC DMCN S S =△四边形 12D E F C E F A B CS S S ∴+=△△△ 图3不成立,DEF CEF ABC S S S △△△、、的关系是:12DEF CEF ABC S S S -=△△△ 11.1-11.2易错题1.如图,给出下列四组条件:①AB DE BC EF AC DF ===,,; ②AB DE B E BC EF =∠=∠=,,; ③B E BC EF C F ∠=∠=∠=∠,,; ④AB DE AC DF B E ==∠=∠,,.其中,能使ABC DEF △≌△的条件共有( ) A .1组 B .2组 C .3组 D .4组【错解】选D .【错解剖析】错选D 的原因是对全等三角形的判定方法理解不透,当两个三角形有两边及一边的对角对应相等时,两个三角形不一定全等.【正确答案】选C .2.已知△ABC 中,AB =BC ≠AC ,作与△ABC 只有一条公共边,且与△ABC 全等的三角形,这样的三角形一共能作出 个.【错解】所找三角形比7个多或比7个少.【错解剖析】不能够正确画出图形理解题意,并分多种情况进行讨论. 【正确答案】7.3.在△ABC 和△A /B /C /中,AB =A /B /,AC =A /C /,高AD =A /D /,则∠C 和∠C /的关系是( ) (A )相等. (B )互补. (C )相等或互补. (D )以上都不对. 【错解】A .【错解剖析】不能够正确画出图形理解题意,并分多种情况进行讨论. 【正确答案】C .TM北11.3经典题1.Rt 90ABC C BAC ∠∠在△中,=,的角平分线AD 交BC 于点D ,2CD =,则点D 到AB 的距离是( )A .1B .2C .3D .4 【正确答案】B 2.如图,点P 是∠BAC 的平分线AD 上一点,PE ⊥AC 于点E .已知PE =3,则点P 到AB 的距离是( )A .3B .4C .5D .6 【正确答案】A 3.如图,∠ACB=90度,AD 平分∠BAC ,BC=9,BD=5,则点D 到AB 的距离为 .【正确答案】4.4.如图,要在河流的南边,公路的左侧M 处建一个工厂,位置选在到河流和公路的距离相等,并且到河流与公路交叉A 点处的距离为1cm (指图上距离),则图中工厂的位置应在 ,理由是 .【正确答案】∠BAC 的平分线上且距A 点1cm 处,角的平分线上的点到角两边的距离相等. 5.三角形中,到三边距离相等的点是( )(A )三条高线交点. (B )三条中线交点. (C )三条角平分线交点. (D )三边垂直平分线交点. 【正确答案】C.6.如图,MP ⊥NP ,MQ 为△NMP 的角平分线,MT =MP ,连结TQ ,则下列结论中,不正确的是( )(A )TQ =PQ . (B )∠MQT =∠MQP .(C )∠QTN =90o . (D )∠NQT =∠MQT .A B C DF EDCB A FEO C A B 【正确答案】D.7.已知:如图,BE 、CF 是△ABC 的角平分线,BE 、CF 相交于D ,∠A =50o ,则∠BDC 的度数是( )(A )70o . (B )120o . (C )115o . (D )130o .【正确答案】C.8.已知:如图,△ABC 中,∠C =90o ,点O 为△ABC 的三条角平分线的交点,OD ⊥BC ,OE ⊥AC ,OF ⊥AB ,点D 、E 、F 分别是垂足,且AB =10cm ,BC =8cm ,CA =6cm ,则点O 到三边AB 、AC 和BC 的距离分别等于( )(A )2cm 、2cm 、2cm . (B )3cm 、3cm 、3cm . (C )4cm 、4cm 、4cm . (D )2cm 、3cm 、5cm .【正确答案】A.9.如图,OP 平分AOB ∠,PA OA ⊥,PB OB ⊥,垂足分别为A ,B .下列结论中不一定成立的是( ) A .PA PB = B .PO 平分APB ∠ C .OA OB = D .AB 垂直平分OP【正确答案】D 10.如图,BE ⊥AC,CF ⊥AB,且BE,CF 相交于点D ,若AB=AC ,求证:点D 在∠BAC 的平分线上.【正确答案】OBAPA BCEF DMDCB AONPCBA 证明:在△ABE 与△ACF 中,,,BEA CFA A A AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△ACF ∴AF AE =B C ∠=∠AB AC =,AF AE = ∴BF CE =在△DBF 与△DCE 中,,,FDB EDC B C FB EC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△ACF ∴DF=DE又BE ⊥AC,CF ⊥AB∴点D 在∠BAC 的平分线上. 11.如图,∠B =∠C =90o ,M 是BC 上一点,且∠AMD =90o ,DM 平分∠ADC ,求证:AM平分∠DAB .【正确答案】证明:∵∠B =∠C =90o ,∴∠ADC +∠DAB =180o , 又∵∠AMD =90o ,∴∠ADM +∠DAM =90o ,∠CDM +∠MAB =90o , ∵∠CDM =∠ADM , ∴∠DAM =∠MAB .12.如图,已知P A ⊥ON 于A ,PB ⊥OM 于B ,且P A =PB .∠MON =50o ,∠OPC =30o ,则∠PCA= .【正确答案】55o .N M D C B A A B C D F N P MO P Q C B A 13.如图,∠AOB 是直角,OP 平分∠AOB ,OQ 平分∠AOC ,∠POQ =70o ,则∠AOC = .【正确答案】140o .14.如图,AE 平分∠BAC ,BD =DC ,DE ⊥BC ,EM ⊥AB ,EN ⊥AC .求证:BM =CN .【正确答案】证明:连结BE 、CE ,∵AE 平分∠BACEM ⊥AB ,EN ⊥AC∴EM=EC在△DBE 与△DCE 中 ,,,DB DC BDE CDE DE DE =⎧⎪∠=∠⎨⎪=⎩∴△DBE ≌△DCE∴BE=NE在△BME 与△CNE 中,,ME NE BE CE =⎧⎨=⎩ ∴△BME ≌△CNE∴ BM =CN .15. 已知:如图,P A 、PC 分别是△ABC 外角∠MAC 与∠NCA 的平分线,它们交于P ,PD⊥BM 于M ,PF ⊥BN 于F .求证:BP 为∠MBN 的平分线.N ME D C BA【正确答案】作过点P 作PE ⊥AC 于E .∵AP 平分∠MACPE ⊥AC ,PD ⊥BM∴PE=PD同理可证PE=PC∴PD=PF 又PD ⊥BM ,PF ⊥BN∴BP 为∠MBN 的平分线.易错题1.已知点P 到△ABC 三边的距离相等,则符合条件的点P 有 个.【错解】1.【错解剖析】不能够正确画出图形理解题意,并分多种情况进行讨论.【正确答案】4.2.如图,在△ABC 中,AD 平分∠BAC ,DE ⊥AB 于E ,DF ⊥AC于F ,M 为AD 上任意一点,则下列结论错误的是( )(A )DE =DF . (B )ME =MF .(C )AE =AF . (D )BD =DC .【错解】A .【错解剖析】不能正确审题,本题是选错误的选项.【正确答案】D3.若一个三角形的最长边是10,最短边是5,其周长是奇数,则第三边长可取值有 个.【错解】4.【错解剖析】第三边c 的范围本应是510c <<,但由于没有注意到条件“最长边是10,最短边是5”,误认为第三边c 的范围本应是515c <<.【正确答案】2M F E D C B A A D NP M E。


矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。

§11.2.1 三角形全等的条件(一)学习目标1.三角形全等的“边边边”的条件.2.了解三角形的稳定性.3.经历探索三角形全等条件的过程,体会利用操作、•归纳获得数学结论的过程. 学习重点 三角形全等的条件.学习难点 寻求三角形全等的条件.学习过程一 回忆前面研究过的全等三角形.1已知△ABC ≌△A ′B ′C ′,说出其中相等的边与角.2画一画在纸上任意画一个三角形,你能画一个三角形与它全等吗?怎样画?那么是否一定需要六个条件呢?条件能否尽可能少呢?现在我们就来探究这个问题. 二.进入新课1.只给一个条件(一组对应边相等或一组对应角相等),•画出的两个三角形一定全等吗?2.给出两个条件画三角形时,有几种可能的情况,每种情况下作出的三角形一定全等吗?分别按下列条件做一做.①三角形一内角为30°,一条边为3cm .②三角形两内角分别为30°和50°.③三角形两条边分别为4cm 、6cm .同学们分组讨论、探索、归纳,最后以组为单位出示结果作补充交流.结果展示:1.只给定一条边时:___________________只给定一个角时:_________________2.给出的两个条件可能是:一边一内角、两内角、两边.可以发现按这些条件画出的三角形___________________.给出三个条件画三角形,你能说出有几种可能的情况吗?归纳:有4种可能.即:三内角、________、两边一内角、_______.在刚才的探索过程中,我们已经发现三内角不能保证三角形全等.下面我们就来逐一探索其C 'B 'A 'A余的三种情况.3画一画:已知一个三角形的三条边长分别为6cm 、8cm 、10cm .你能画出这个三角形吗?把你画的三角形剪下与同伴画的三角形进行比较,它们全等吗?由此得到证明三角形全等的一个依据____________.4 看课本例题三.随堂练习1.课本练习.2 如图,已知AC=FE 、BC=DE , AD=FB .证明△ABC ≌△FDE.四.课时小结五.作业1. 复习巩固1、2.2. 如图,一个六边形钢架ABCDEF 由6条钢管连结而成,为使这一钢架稳固,请你用三条钢管连接使它不能活动,你能找出几种方法?3 如图,△ABC 是一个钢架,AB=AC ,AD 是连结点A 与BC 中点D 的支架.求证:△ABD ≌△ACD .F DC BE AC。

全等三角形的性质练习题一、单选题(选择一个正确的选项)1 、已知△ABC≌△A′B′C′,若∠A=50°,∠B′=80°,则∠C的度数是()A、30°B、40C、50°D、60°2 、如图,△ABC≌△FDE,∠C=40°,∠F=110°,则∠B等于()A、20°B、30°C、40°D、150°3 、下列各组图形中是全等图形的是()A、B、C、D、4 、如图,△ABC≌△EFD且AB=EF,AE=10,CD=3,则AC=()A、3B、3.5C、5D、6.54 、如图,已知三角形ABC与三角形DEF是全等形,则相等的线段有()A、1组B、2组C、3组D、4组6 、如图,在△ABC中AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是()A、1B、2C、3D、47 、如图,在△ABC中,∠A=90°,P是BC上一点,且DB=DC,过BC上一点P,作PE⊥AB于E,PF⊥DC于F,已知:AD:DB=1:3,,则PE+PF的长是()A、B、6 C、D、8 、如图,∠ACB=90°,AC=BC,AE⊥CE于E,BD⊥CE于D,AE=5cm,BD=2cm,则DE的长是()A、8B、5C、3D、29 、如图已知:△ABE≌△ACD,AB=AC,BE=CD,∠B=50°,∠AEC=120°,则∠DAC的度数为()A、80°B、70°C、60°D、50°10 、下列说法中正确的是()A、面积相等的两个图形是全等图形B、周长相等的两个图形是全等图形C、所有正方形都是全等图形D、能够完全重合的两个图形是全等图形11 、下列说法错误的有()①只有两个三角形才能完全重合;②如果两个图形全等,它们的形状和大小一定都相同;③两个正方形一定是全等图形;④边数相同的图形一定能互相重合.A、4个B、3个C、2个D、1个12 、如图所示,△ABP与△CDP是两个全等的等边三角形,且PA⊥PD,有下列四个结论:①∠PBC=15°,②AD∥BC,③PC⊥AB,④四边形ABCD是轴对称图形,其中正确的个数为()A、1个B、2个C、3个D、4个13 、已知图中的两个三角形全等,则∠x的度数是()A、38°B、82°C、60°D、62°14 、下列每组中的两个图形,是全等图形的为()A、B、C、D、15 、下列说法:①相似多边形一定全等;②不相似多边形一定不全等;③全等多边形不一定相似;④全等多边形一定相似.其中正确的是()A、①②B、②③C、②④D、③④16 、如图,△ABC≌△CDA,∠BAC=∠DCA,则BC的对应边是()A、CDB、CAC、DAD、AB17 、如图,△ABC与△CDA是全等三角形,则一定是一组对应边的是()A、AB和DCB、AC和CAC、AD和CBD、AD和DC18 、下列四个几何体中,主视图、左视图与俯视图是全等图形的几何体是()A、球B、圆柱C、三棱柱D、圆锥19 、图中是大小相等的两个矩形,请你判断出哪一个阴影部分的面积较大()A、甲图的阴影面积大B、乙图的阴影面积大C、甲、乙图的阴影面积相等D、以上都不对20 、判断下列命题:①等腰三角形是轴对称图形;②若a>1且b>1,则a+b>2;③全等三角形对应角相等;④不可能事件的概率为0,其中逆命题正确的有()A、1个B、2个C、3个D、0个。
ABOCD第十一章全等三角形11.1 全等三角形一.填空题:1.如图所示,沿直线AC对折,△ABC与△ADC重合,则△ABC≌,AB的对应边是,BC的对应边是,∠BCA 的对应角是.第1题第2题2.如图所示,△ACB≌△DEF,其中A与D,C与E是对应顶点,则CB的对应边是,∠ABC的对应角是.3. 如图,AD、BC相交于点O,△AOB≌△DOC,A、D为对应顶点,则这两个三角形中,相等的边是____________ ________,相等的角是________________ ____.4.右图是用七巧板拼成的一艘帆船,其中全等的三角形共有对.5.由同一张底片冲洗出来的两张五寸照片的图案全等图形,而由同一张底片冲洗出来的五寸照片和七寸照片全等图形(填“是”或“不是”).6.如图,△ABC与△DBC能够完全重合,则△ABC与△DBC是____________,表示为△ABC____△DBC.7. 已知ABC MNP△≌△,48A∠=,62N∠=,则B∠=,C∠,M∠和P∠的度数分别为,,.二.选择题:8.下列说法:①全等图形的形状相同、大小相等;②全等三角形的对应边相等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等,其中正确的说法为()A.①②③④B.①③④C.①②④D.②③④9.一个正方形的侧面展开图有()个全等的正方形.A.2个B.3个C.4个D.6个10.全等三角形是()A.面积相等的三角形B.角相等的三角形C.周长相等的三角形D.完全重合的三角形11.下列说法中,错误的是().A.全等三角形的面积相等B.全等三角形的周长相等C.面积相等的三角形全等AB CD(第6题)D.面积不等的三角形不全等12.如图所示,△ABC≌△AEF,AB=AE,∠B=∠E,有以下结论:①AC=AE;②∠FAB=•∠EAB;③EF=BC;④∠EAB=∠FAC,其中正确的个数是().A.1个 B.2个C.3个 D.4个13.如图,若△ABC≌△DEF,则∠E等于(). A.30° B.50° C.60° D.100°三.解答题:14.(教材变式题)如图,已知△ABD≌△ACE,写出所有的对应边和对应角.15.如图,已知△ABC≌△ADE,写出所有的对应边和对应角.16.如图,△AOC≌△BOD,试证明AC∥BD.17.已知:△DEF≌△MNP,且EF=NP,∠F=∠P,∠D=48°,∠E=52°,MN=12cm,求:∠P的度数及DE的长.18.如图,已知△AEC≌△BFD,试说明AD 和BC的大小关系.D CB ADC BA EDC B AE11.2 三角形全等的判定(SSS)一.填空题:1.如图,已知AB=AC ,EB=EC ,AE 的延长线交BC 于D ,则图中全等的三角形共有对.2.只要三角形的三边的长度固定,这个三角形的________和________•就完全确定,三角形的这个性质叫做三角形的________. 3.如图,AB=DE ,AC=DF ,BF=CE . (1)若BC=18cm ,则FE=______;(2)若 ∠ACB=50°,∠D=70°,则∠E=_______.(3题) (4题) 4.如图,AB=CD ,若添加条件_______,则可根据_______公理证得△ABC ≌△CDA . 5.如图,AB=ED ,AC=EC ,C 是BD 的中点,若∠A=36°,则∠E= .(5题) (6题)6.如图, AB= AC,BE=CD ,要使△ABE ≌△ACD ,依据SSS ,则还需添加条件 . 二.选择题:7.下列判断两个三角形全等的条件中,正确的是( )A. 一条边对应相等;B. 两条边对应相等;C. 三个角对应相等;D. 三条边对应相等 8.如图1,在①AB=AC ②AD=AE ③∠B=∠C ④BD=CE 四个条件中,能证明△ABD 与△ACE全等的条件顺序是( )A. ① ② ③B. ② ③ ④C. ① ② ④D. ③ ② ④(8题) (9题) 9.如图,在△ABC 中,AB=AC,D 、E 两点在BC 上,且有AD=AE ,BD=CE.若∠BAD=30°,∠DAE=50°,则∠BAC 的度数为( ) A .130° B. 120° C.110° D.100° 10.如图,MP=MQ ,PN=QN ,MN 交PQ 于点Q ,则下列结论中不正确的是( ). A .△MPN ≌△MQN B .OP=OQ C .MO=NO D .∠MPN=∠MQN 三.解答题:11.如图,在△ABC 中,AB=AC ,D 是BC 边上的中点,连接AD.(1)求证:△ADB ≌△ADC ;(2)求证:∠ADB=∠ADC=90°;CB AED CAE DB AEDFCBAED F CBAEDC OA B12.已知:如图,C 是AB 的中点,AD=CE ,CD=BE ,求证:△ACD ≌△CBE .13.(2008年宜宾市)已知:如图,AD =BC,AC =BD.求证:∠C =∠D14.如图,AB=CD ,AE=DF ,BF=CE ,试判断AB 和CD ,AE 和FD 的位置关系.15.如图,已知在四边形ABCD 中,AD=AB ,CD=CB ,则∠D=∠B ,试说明理由.16.如图,AD=CB ,E 、F 是AC 上两动点,且有DE=BF.(1)若E 、F 运动至如图所示的位置,且有AF=CE ,求证:△ADE ≌△CBF.(2)若E 、F 运动至如图②所示的位置,仍有AF=CE ,那么△ADE ≌△CBF 还成立吗?为什么?(3)若E 、F 不重合,AD 和CB 平行吗?说明理由。
OEA BD C11.2 三角形全等的判定(SAS)一.填空题:1.如图,∠1=∠2,BC=EF ,那么需要补充一个直接条件________(•写出一个即可),才能使△ABC ≌△DEF .2.如图,AD=AE ,BE=CD ,∠1=∠2,则 ∠B=_____,图中有____对三角形全等,请写出来_____ __. 3.如图,已知AB ⊥BD 于B ,ED ⊥BD 于D ,点C 在BD 上,AB=CD ,BC=ED ,则 ∠ACE=_ _.(3题) (4题) 4.如图,点D 在AB 上,点E 在AC 上,且AD=AE ,AB=AC ,•若∠B=20•°,则∠C=_____. 二.选择题:5.如图,使△ABC ≌△ADC 成立的条件是( ). A .AB=AD ,∠B=∠DB .AB=AD ,∠ACB=∠ACDC .BC=DC ,∠BAC=∠DACD .AB=AD ,∠BAC=∠DAC6.如图,若AB 与CD 互相平分于O ,则下列结论中错误的是( ).A .∠C=∠DB .AD=BC C .AD ∥BC D .AB=CD(5题) (6题)(7题) (8题) 7.如图,已知AB=AC ,AD=AE ,欲证△ABD ≌△ACE ,须补充的条件是( ) A .∠B=∠C B .∠D=∠E C .∠1=∠2 D .∠CAD=∠DAC8.如图,∠1=∠2,若用“SAS ”证明△ACB ≌△BDA ,还需要加上条件( ) A .AD=BC B .BD=AC C .∠D=∠C D .OA=OB9.(2008年遵义市)如图,OA =OB ,OC =OD ,∠O =50°,∠D =35°,则∠AEC 等于( ) A .60° B .50° C .45° D .30°三.解答题:10.如图,已知AC=DB ,∠1=∠2,你能找出A BDC EADB CFE△ABC≌△DCB的理由吗?11.如图,已知:AB=AC,AE=AD,点D,E 分别在AB,AC上.求证:∠B=∠C.12.已知:如图,AE=CF,AD∥BC,AD=CB,求证:△ADF≌△CBE.13.(2008常州市) 已知:如图,AB=AD,AC=AE,∠BAD=∠CAE.求证:BC=DE. 14.(2008年泰安市)两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);(2)证明:DC⊥BE.15.(2009年南昌市)如图,在△ABC中,D 是AB上一点,DF交AC于点E,DE=FE,AE =CE,AB与CF有什么位置关系?证明你的结论.16.已知如图,AB=AD,BC=DC,E是AC上的一点,试证明:BE=DE.DCBA EDCBAEDCBA DCBAO11.2 三角形全等的判定(ASA 与AAS)一.填空题:1.如图,已知∠CAB=∠DBA 要使△ABC ≌△BAD,只要增加的一个条件是________ (只写一个)。
(1题) (2题) 2.如图,AE=AD, ∠B=∠C,BE=6,AD=4,则AC=______ .3.如图,AD=AB, ∠C=∠E, ∠CDE=55°,则∠ABE=_____. (3题) (4题)4.如图,AB 与CD 相交与点O ,∠A=∠B ,AO=BO ,因为 = ,所以△AOC ≌△BOD ,其理由是 。
二.选择题:5.已知AB=A ′B ′,∠A=∠A ′,∠B=∠B ′,则△ABC ≌△A ′B ′C ′的根据是( )A .SASB .SSSC .AASD .ASA 6.如图,李明同学把一块三角形玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,他最省事的办法是( ). A .带①去 B .带②去 C .带③去 D .带①和②去7.已知△ABC 的六个元素如图,则甲、乙、丙三个三角形中和△ABC 全等的图形是( ) A .甲、乙 B.乙、丙 C.只有乙 D.只有丙8.在△ABC 和△DEF 中,AB=DE ,∠A=∠D.若证△ABC ≌△DEF ,还需补充一个条件,错误的补充方法是( )A.∠B=∠EB.∠C=∠FC.BC=EFD.AC=DF 9.在△ABC 和△DEF 中,已知C D ∠=∠,B E ∠=∠,要判定这两个三角形全等,还需要条件( )A .AB ED = B .AB FD =C .AC FD= D .A F ∠=∠ 三.解答题:10.如图,D 是△ABC 的边BC 的中点,CE ∥AB ,E 在AD 的延长线上.DCBAO 1 234试证明△ABD•≌△ECD .11.如图,已知AB ∥CD ,AF=CE ,∠B=∠D ,证明BE 和DF 的关系.12.如图,AB ∥A ′B ′,AC ∥A ′C ′,且 BB ′=CC ′,你能说明AC=A ′C ′的理由吗?13.如图,在△AFD 和△BED 中,点A ,E ,F ,C 在同一直线上,有下面四个论断: (1)AD=CD ; (2)AE=CF ; (3)∠B=∠D ; (4)AD ∥BC .请用其中三个作为条件,余下一个作为结论,编一道数学问题,并写出解答过程.14.(2008年苏州)如图,四边形ABCD 的对角线AC 与BD 相交于O 点,∠1=∠2,∠3=∠4. 求证:(1)△ABC ≌△ADC ;(2)BO =DO .15.如图(1),在△ACB 中,∠ACB=90°,AC=BC ,直线L 经过点C ,AD ⊥L 于D ,BE ⊥L 于E . (1)求证:①△ADC ≌△CEB ;②DE=AD+BE . (2)当直线L 绕点C 旋转到图(2)的位置时,DE ,AD ,BE 具有怎样的等量关系?说出你的猜想,并证明你的猜想.DCBAEA D F C BE11.2 三角形全等的判定(HL )一.填空题:1.如图,△ABC 中,AB=AC ,AD ⊥BC 于D ,由_______可证明△ABD ≌△ACD ,从而有BD=______,∠B=________.(1题) (2题) 2.如图,已知∠ACB=∠BDA=90°,若要使△ACB ≌△BDA,还需要条件__ =____(只写1个即可)3.如图,在直角三角形ABC 中,∠C =90°,AC =10cm ,BC =5cm ,一条线段PQ=AB , P 、Q 两点分别在AC 和AC 的垂线AX 上移动,则当AP = 时,才能使△ABC 和△APQ 全等.(3题) (4题)4.(2009宿迁)如图,有一块边长为4的正方形塑料摸板 ABCD ,将一块足够大的直角三角板的直角顶点落在A 点,两条直角边分别与CD 交于点F ,与CB 延长线交于点E .则四边形AECF 的面积是 . 二.选择题:5.下面说法不正确的是( ) A .有一直角边和斜边对应相等的两个直角三角形全等B .有两直角边对应相等的两个直角三角形全等C .有两角对应相等的两个直角三角形全等D .有一锐角和其对边对应相等的两个直角三角形全等6.如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离BD 与CD 的距离间的关系是( )A.BD>CDB.BD<CDC.BD=CDD.不能确定(6题) (7题)7.如图,有两个长度相同的滑梯,左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等, 两个滑梯的倾斜角∠ABC 和∠DFE 的大小间的关系是( )A.∠ABC=∠DFEB.∠ABC >∠DFEC.∠ABC <∠DFED.∠ABC+∠DFE=90°.DCBAE8.在△ABC 和△A ′B ′C ′中,∠C=∠C ′= 90°,有下面几组条件:①AC=B ′C ′=3,BC=A ′C ′=4; ②AC=A ′C ′=3,AB=A ′B ′=4; ③AC=A ′B ′=3,AB=A ′C ′=4. 其中能判定两个三角形全等的有( ). A .1个 B .2个 C .3个 D .4个 三.解答题:9.如图,AC=AD ,∠C 和∠D 是直角,将上述条件标注在图中,线段BC 和BD 相等吗?请说明理由.10.如图,已知AB=CD ,DE ⊥AC ,BF ⊥AC ,DE=BF ,求证:AB ∥CD .11.如图,已知AE =DE ,AE ⊥DE ,AB ⊥BC ,DC ⊥BC. 求证:AB +CD =BC12.如图,已知DC ⊥AC ,DB ⊥AB ,点C ,B 为垂足,AC=AB ,AD 与BC 相交于点O . 求证:AD ⊥BC .13.如图,太阳光线AC 与A ′C ′是平行的,同一时刻两根高度相同的木杆在太阳光照射下的影子一样长吗?说说你的理由.14.(2008年南宁市)如图,在△ABC 中,D 是BC 的中点,DE ⊥AB ,DF ⊥AC ,垂足分别是E 、F ,BE=CF 。