用神经网络实现NURBS曲面重构

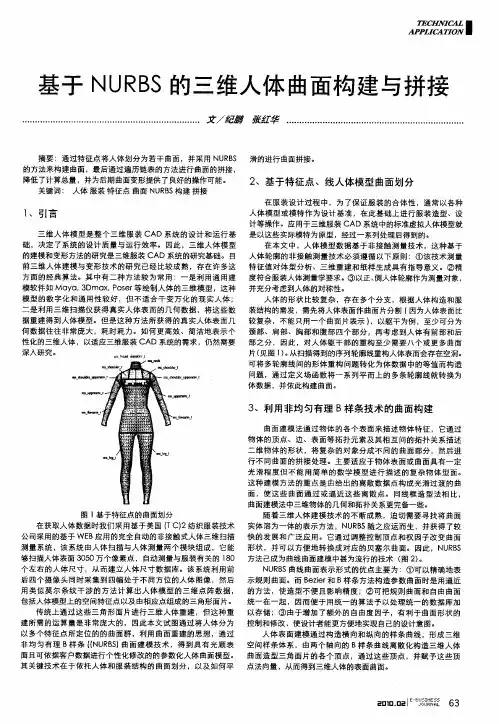
万方数据激光与红外Ｎｏ．３２０１０孟凡文等三维面部数据采集与ＮＵＲＢＳ曲面重构３３５程忙】，而三维ＣＡＤ模型的重构是逆向工程的核心和主要目的。

自从Ｐａｒｋｅ于２０世纪７０年代在计算机上建立了第一个人脸模型起”１，人脸的建模就一直是计算机图形学、计算机视觉、模式识别等领域最为活跃的研究热点ＨＪ。

对三维人脸的研究目前只有很少量的文献发表。

这主要是因为三维数据的获取基于多张二维图像的重构，需要复杂的硬件设备，比如标定好的同步的摄像机。

一些研究者尝试使用其他的数据提取方法，比如三维激光扫描仪，这种方法获得的三维数据非常精确，但是非常缓慢。

朱敏等Ｍ１采用工业用ＡＴＯＳ快速三维光学测量仪，对面部轮廓模型进行三维重建，改进了传统的投影光栅装置，应用２个ＣＣＤ摄像头接收信号，实现了对面部三维数据的快速精确采集。

但用于点云采集的ＡＴＯＳ三维测量仪价格昂贵。

ＡｒｍｉｎＧｒｕｅｎ等Ｍ１采用最小二乘法原理对点云数据进行拼接和三角化处理，利用高斯一马尔科夫模型减小不同曲面问的最小平方和，从而计算出目标曲面与基准曲面间的转换参数。

并将此方法用于面部点云拼接和曲目重构，但处理后的三角曲面无法转换为通用ＮＵＲＢＳ曲面。

人脸曲面具有无规律性和奇异性，它们的几何数据也很难获得，人脸曲面重构是利用获取的人脸散乱点云数据，通过差值和拟合，构建一个近似模型来逼近人脸原型。

对人脸模型的海量点云数据进行优化处理，获取高精度ＮＵＲＢＳ曲面是研究的难点。

该问题的研究和解决可为复杂对象的三维建模提供借鉴，在雕塑、美容和医疗等领域具有广阔的应用前景。

本文通过采用结构光的双光栅式三维扫描仪获取面部三维点云，将两组点云通过求取协方差矩阵的方法实现点云拼接，将点云处理后通过三角化处理生成三角面片，最后进行曲面成形处理生成高精度四边域ＮＵＲＢＳ曲面，并对重构后的三角面片和ＮＵＲＢＳ面片进行误差分析。

２三维面部点云数据采集２．１系统标定实物数字化点云是曲面模型重建及其加工制造、模拟仿真和特征分析的基础，扫描参数的设置直接影响扫描点云的精度和效果，需设置合适的扫描参数。

nurbs曲面算法流程
NURBS曲面是一种重要的三维曲面表示方法，其具备优良的数学性能和灵活性，被广泛应用于计算机动画、游戏开发、三维建模等领域。

下面介绍NURBS曲面的算法流程。

1.确定曲面控制点：通过给定的曲线或几何体，确定曲面的控制点，通常使用Bézier曲线、B样条曲线等方法。

2.构造NURBS基函数：根据控制点的坐标和权重，构造NURBS基函数。

基函数可以表示为权重函数和B样条基函数的乘积形式。

3.计算曲面点：使用NURBS基函数和控制点，计算曲面上的任意点。

通常使用逐步逼近法进行计算。

4.曲面细分：为了提高曲面的精度和美观度，通常需要对曲面进行细分操作。

可以使用均匀细分、自适应细分等不同的方法。

5.曲面编辑：通过修改控制点的坐标和权重，可以对曲面进行编辑。

常见的编辑操作包括平移、旋转、缩放等。

6.曲面切割和拼接：可以对曲面进行切割和拼接操作，以实现复杂的曲面形状。

通常使用布尔运算、交集运算等方法。

7.曲面评估：评估曲面的质量和性能，通常使用曲率、曲面平滑度等指标进行评估。

以上就是NURBS曲面的算法流程，需要注意的是，在实际应用中，不同的应用领域会有不同的具体实现方法和算法优化。

- 1 -。

基于RBF混合神经网络的自由曲面特征重构的研究的开题报告一、研究背景及意义：自由曲面是一种常见的曲面形态，在许多领域中应用广泛，如计算机辅助设计、制造和工艺控制，汽车、船舶和航空的车身、壳体和气动型面的设计等。

其中，曲面重构是自由曲面的重要应用之一。

传统的曲面重构方法，如B样条曲面、NURBS曲面等，存在着较大的限制，主要是几何限制和计算效率低的问题，对于大规模、高精度、复杂的曲面重构任务较难完成。

因此，如何有效地进行曲面特征重构，提高曲面重构的精度和效率，是当前自由曲面研究的热点和难点，也是本文研究的目标。

二、研究内容及目标：基于RBF混合神经网络的自由曲面特征重构研究，是一种新型的曲面重构算法。

本文将结合具体的应用案例，以自由曲面变形和识别为主要研究内容，重点研究以下几个方面：1.构建基于RBF混合神经网络的特征提取模型，实现曲面变形的特征提取和解析任务。

主要包括RBF网络的构建、参数调优、拓扑结构选择等内容。

2.设计基于RBF混合神经网络的曲面重构算法。

采用逐步优化的思想，将曲面重构任务划分为多个子任务，并针对不同的子任务进行特征提取和重构操作，最终实现曲面的高精度还原。

3.应用基于RBF混合神经网络的曲面重构算法进行曲面变形和识别任务，验证算法的有效性和实用性。

三、研究方法：1.文献调研：对当前自由曲面研究的相关文献进行综合调研和分析，深入理解自由曲面的特征和重构方法，为本文的研究提供理论支持和实验基础。

2.算法设计：基于RBF混合神经网络的曲面特征提取和重构算法的设计和实现，主要涉及到神经网络模型的构建、参数优化、模型融合等内容。

3.算法验证：应用所设计的算法进行曲面变形和识别任务，对算法的有效性和实用性进行验证，比较其与传统方法的优劣。

四、研究进度及计划：1.第一阶段：文献调研和数据收集，明确研究方向和目标，了解当前自由曲面研究的状况和发展趋势，定义问题和任务的具体内容。

时间安排：1个月。

用神经网络实现NURBS曲面重构
曾建江;丁秋林
【期刊名称】《计算机工程与应用》
【年(卷),期】2003(039)001
【摘要】曲面重构问题是几何逆向工程中的首要问题,为了获得物体的几何模型(某些物体可能发生部分损坏)需要从大量的测量点构造曲面.该文采用了一个神经网络模型和相应的快速学习算法应用于曲面重建.该模型可以有效地逼近曲面并剔除输入数据点中的"坏"点.
【总页数】3页(P69-71)
【作者】曾建江;丁秋林
【作者单位】南京航空航天大学航空宇航学院CAD中心,南京,210016;南京航空航天大学航空宇航学院CAD中心,南京,210016
【正文语种】中文
【中图分类】TP391
【相关文献】
1.基于Geomagic Studio实现自由曲面全逆向NURBS重构 [J], 马春宇;袁军平;郭文显
2.基于 NURBS 曲面插值的船体曲面重构 [J], 钱宏;刘敏;贺庆;刘朕明;荣焕宗
3.NURBS曲面与隐式曲面求交的计算机实现及应用 [J], 张明霞;纪卓尚;林焰
4.NURBS曲面重构与点云-曲面误差分析 [J], 吴禄慎;高红卫;孟凡文
5.基于C1连续的NURBS边界Gregory曲面片实现曲面拼接 [J], 贾超;聂绍珉;陈飞
因版权原因，仅展示原文概要，查看原文内容请购买。

25卷 第7期2008年7月微电子学与计算机M ICROELECTRONICS &COM PUTERVol.25 No.7July 2008收稿日期:2007-09-29基金项目:国家自然科学基金项目(60475021);河南省杰出青年基金(0412000400);洛阳市科技攻关计划项目(0701041A )基于RBF 神经网络的B 样条曲面重构张海朝1,黄 淼1,2(1河南科技大学电子信息工程学院,河南洛阳471003;2平顶山学院软件学院,河南平顶山467000)摘 要:采用RBF 神经网络模型进行自由曲面重构,建立了适合曲面重构的径向基函数网络模型,并在B 样条曲面上做了仿真试验.实验结果表明:该模型不仅能够有效地逼近不完善的、带有噪声的曲面,而且拟合精度高、网络的训练速度快.说明了径向基函数神经网络应用于曲面重构问题的可行性.关键词:曲面重构;径向基函数;B 样条中图分类号:T P39 文献标识码:A 文章编号:1000-7180(2008)07-0010-04B spline Surface Reconstruction Based on RBF Neural NetworkZHANG Hai chao 1,HUANG M iao 1,2(1Colleg e of Electronic Info rmat ion Eng ineering,Henan U niv ersity of Science &T echnolog y,Luoyang 471003,China;2College of So ftw are,Pingdingshan U niversity,Pingdingshan 467000,China)Abstract:T his paper use RBF NN mo del to reconstruct free surface.Surface Reconstruction established for the RBF net wo rk model,and has done a simulation test on the B spline sur face.T he r esults show t hat the model can not only effec tiv ely approach imperfect,w ith noise surface,and have a hig h precision netw ork training speed.Described the feasibility of RBFN N on sur face r econstruction.Key words:surface reconstruct ion;RBF ;B spline1 引言随着几何扫描仪应用的范围越来越广泛,相应的扫描实物模型的数量和复杂性也随着增长,稳健和有效的几何处理方法引起了人们的兴趣.即使高保真度扫描仪,所获得的3D 模型也不可避免地带有噪声,因此需要对获取的数据进行预处理以进行后序操作.如果零件表面部分损坏、磨损或不完整,则这部分曲面的拟合将更加困难.对于这类曲面的恢复和重构,必然采用智能推理来达到对部分损坏、磨损或不完整曲面进行重构的目的.随着神经网络(ANN)理论的发展[1 4],提出了神经网络曲面重建的方法,从新的角度提出了散乱数据云的曲面建模方法.文中根据径向基函数(RBF)神经网络[5 6]可以用任意精度逼近任何非线性函数,以及强大的抗噪、修复能力等优点,对散乱数据点进行曲面重构,所采用的训练方法无论是在逼近能力、分类能力、收敛速度,还是搜索的遍历性等方面均优于上述网络,因而得到了广泛的应用.2 B 样条曲面不同曲面重构问题需要不同类型的曲面,文中采用的是B 样条曲面[3](B Spline Surface).这主要因为B 样条方法不仅保留Bezier 曲面的优点,同时克服了Bezier 曲面由于整体表示带来不具有局部性质的缺点,而且B 样条曲面作为矩形域参数曲面的代表,B 样条具有统一、通用、有效的标准算法和强有力的配套技术,以及表示和设计自由曲线曲面的强大功能,因此是最广泛流行的形状数学描述主流方法之一,在曲面重构中被广泛采用.在实际运用中,给定参数轴u 和v 的节点矢量U =[u 0,u 1, ,u m+p ]和V =[v 1,v 2, ,v n+q ],p q 阶B 样条曲面定义如下:P (u ,v )=!m i=1!ni =1P ij N ip (u )N jq (v )式中,P ij (i =0,1, ,m ;j =0,1, ,n )是给定的空间(m +1)(n +1)个点列,构成一张控制网格,称为B 样条曲面的特征网格;N ip (u)和N j q (v )是B 样条基,分别由节点矢量U 和V 按deBoor Cox 递推公式决定.3 人工神经网络以及RBF 神经网络人工神经网络理论是20世纪80年代中后期世界范围内迅速发展起来的一个前沿研究领域.人工神经网络实质是一个带误差反馈的多约束、多变量方程迭代求解系统.网络中的节点即神经元之间按某种规律连接,相互传递信息和反馈误差测试的结果.神经网络具有强大的泛函逼近能力,三层前向网络能以任意精度逼近任意连续函数及其各阶导数,神经网络将表示曲面的映射关系存储于网络的连接权值和阈值中,使模型具有较强的容错性能和联想能力,故利用神经网络能够对重构的曲面进行局部修改和缺陷表面的局部修补.径向基函数网络起源于数值分析中多变量插值的径向基函数方法,是一种局部逼近的神经网络.RBF 网络应用需要一个训练集用于神经网络的学习阶段,同时还要有一个测试集用于评价工作网络的效果.训练集和测试集都是由输入和输出模式对组成的集合,其元素即模式对来源于同一数据集合.训练集用于训练网络,使网络能按照学习算法调整结构参数,以达到学习的目的;测试集则是用于评价已训练好的网络的性能即泛化能力.为了获得比较好的网络性能,必须满足两个基本前提,即训练集和测试集应使用典型的模式对;测试集应不同于训练集.RBF 神经网络已经被成功地应用于各种各样的领域,如插值、无序时间序列建模、控制工程、语音识别、图像恢复、3D 实物建模等领域.3.1 RBF 神经网络的工作原理和结构径向基函数神经网络是一种由输入层、隐层和输出层组成的三层前向网络.其结构简图如图1所示:输入层节点只传递输入信号到隐层.从输入层到隐层的变换是非线性的,隐层节点由一定的作用函数构成,从隐层到输出层的变换是线性的.输入层到隐层之间的权固定为1,只有隐层到输出层之间的权可调.图1 RBF 神经网络结构图隐层节点中的变换函数(基函数)对输入信号将在局部产生影响,也就是说,当输入信号靠近基函数的中央范围时,隐层节点将产生较大的输出,由此看出这种网络具有局部逼近能力,所以径向基函数网络也称为局部感知场网络.3.2 RBF 神经网络的训练学习方法由于RBF 神经网络是一种由输入层、隐层和输出层组成的三层前向网络,它可以实现任何的函数映射,隐层节点中的变换函数是一种局部分布的、对中心点径向对称衰减的非负线性函数.由于高斯基函数具备表示形式简单、径向对称、光滑性好、易于进行理论分析等优点,所以文中隐层变换函数采用高斯基函数,其表达形式如下所示:j (X )=exp [-∀X -c j E ∀2 2j],(j =1,2, ,h )(1)式中, j 为隐层第j 个单元输出;X =(x 1,x 2, ,x T )为输入矢量;∀#∀表示范数.通常取∀X -c j E ∀=(X -c j E )T (X -c j E )(2)式中,c j 为隐层第j 个高斯单元的中心,E 为n 1个单位矢量; j 为半径;网络的输出可表示为y k =!hj =1kj j (X ),(k =1,2,...,m )(3)写成矩阵形式为Y =W !式中,Y =(y 1,y 2, ,y m )T 为输出矢量;!=( 1(X ), 2(X ), , h (X ))T为隐层输出量.W =( 1, 2, , m )T ( k =( k 1, k 2, , kn ),k =1,2, ,m )为隐层到输出层的权矩阵.由于 j (x )为高斯函数,对任意x 均有 j (x )>0,从而失去了局部调整权值的优点.而事实上,当x 远离c j 时, j (X )已非常小,可作为0对待.因此实际上当 j (X )大于某一数值(文中采用0.01)时就对相应的权值进行修改,经这样处理后,RBF 网络11第7期张海朝,等:基于RBF 神经网络的B 样条曲面重构也同样具备局部逼近、网络学习收敛快的优点.同时这样近似的处理,可在一定程度上克服高斯基函数不具备紧密性的缺点.RBF 网络的学习过程分两步:一是根据输入样本确定隐层各节点的变换函数的中心c j 和半径 j ;二是采用误差校正学习算法,调节输出层的权W.网络具体学习的算法如下:(1)确定c j ;采用K 均值法[4]:首先,初始化所有的聚类中心c j (1∃j ∃h ∃P ,P 为样本总数),通常将其初始化为最初的N (文中取N =1000)个训练样本;然后将所有样本X 按最近的聚类中心分组,即:如果∀X p -c i E ∀=min pj=1∀(X p-c j E )∀(1∃p ∃P )(4)则将样本X p划归为类i ;再计算各类的样本均值c j =1N j !x p %jX p (5)式中,N j 为第j 类的样本数.重复以上步骤,直到所有聚类的中心不再变化,则可将其作为RBF 的中心.(2)确定 j ;对每个类中心c j ,可以令相应的半径 j 等于其与属于该类的训练样本之间的平均距离,即:j =1N j !x p %j(X p -c j E )T (X p-c j E )(6)(3)调节输出层的权W .定义网络的目标函数为J =12(U -Y )T (U -Y )(7)式中,U 为期望输出.采用误差梯度下降法调节W ,使得J 最小,则有W (t +1)=W (t )+∀(U -Y )!T(8)式中,t 为迭代次数,∀为步长.有时在完成第二阶段的学习后,需要再根据样本信号,同时校正隐层到输出层的参数,以进一步提高网络的精度.由于曲面重建过程对存储要求小,执行时间短,自动化程度高,所以可以根据这一特点,采用基于均方差最小准则的参数优化算法.定义如下目标函数:E =12N!Nn=1∀ d n - y n ∀2=12N !Nn=1!Ll=1X i (y d nl -y nl )2(9)可以通过调整隐层节点到输出层节点间的连接权值kj 和隐层节点中基函数的中心矢量C j 与宽度#j 来极小化E 值.通过研究发现权值的线性化属于一类特定的最小二乘法问题.可以使用Cholesky 平方根分解法等快速算法立刻得到全局最优解,只要网络输出和实际值之间的误差小于给定的最大误差后,就完成了网络的训练.这比基于误差回传的梯度下降法更迅速、更准确.3.3 基于RBF 网络的B 样条曲面重构用RBF 网络进行散乱测量数据点拟合的实质是对原型曲面p 进行精确映射的网络参数优化过程,映射形式为p (x ,y ,z )=p (u,v ).将测量点数据输入RBF 网络,网络采用上边的训练算法开始对已知信息进行学习,当网络输出和实际值之间的误差满足指定的阈值时,就完成了网络的训练,实现了RBF 网络对原型曲面p 的拟合.文中利用B 样条曲面进行仿真试验,曲面拟合模型如图2所示.输入层两节点分别对应测量数据点的u ,v 值,输出层节点对应测量数据点的x ,y ,z 值.图2 RBF 神经网络曲面拟合模型4 实验分析文中算法综合运用M atlab 仿真工具和VC 开发工具实现,机器配置为RAM 1G,AMD3400+GHz,文中提出的算法是通用的,输入是B 样条曲面中的u ,v 节点矢量,输出是将三维坐标连成网格后的三角网格模型.在实验中对多种数据集进行了表面重建.表1、图3给出它们的数据参数和算法运行参数.表1 数据集数据参数和算法运行参数表对象点集数目三角形数归一化时间/s CPU 时间/s 图3(a)1008020156154.77 3.98图3(b)79191583496.58 2.65图3(c)999520000146.56 3.82图3(d)51931037067.131.97可以看出,在点集数目较少时,归一化处理和重建速度比较快,随着点集数目的增大,相应的处理时12微电子学与计算机2008年间增加比较大,因此,文中算法比较适合于处理少量数据点的场合.重建的结果如图4所示.用本方法重建的三维网格结构与真实的表面形状基本一致,能够有效地逼近不完善的、带有噪声的曲面,达到了预期的效果.图4利用文中算法重建出三维网格模型图3 原始点云数据5 结束语根据径向基函数神经网络可以用任意精度逼近任何非线性函数,以及强大的抗噪、修复能力等优点,文中采用RBF 神经网络模型进行自由曲面重构,建立了适合曲面重构的径向基函数网络模型.并在B 样条曲面上做了仿真实验.对RBF 神经网络重构曲面在理论上的可行性和实践上的实用性进行了讨论和验证.结果表明:该模型不仅能够有效地逼近不完善的、带有噪声的曲面,而且拟合精度高、网络的训练速度快.说明了径向基函数神经网络应用于曲面重构问题的可行性.参考文献:[1]F rey P J.Generation and adaptation of computational surface meshes fro m di scr ete anatomical data[J].International Journal for Numer ical M ethods in Eng ineering,2004,60(2):1049-1074.[2]Hu Haifeng,Yang Zhi.3D reconst ruction appr oach basedon neural netwo rk[J].ISN N 2007,Part II(LN CS 4492):630-639.[3]L iu Xumin,Huang Houkuan,Xu Weix iang.Approx imateB-spline sur face based on RBF neural netw orks[J].ICCS 2005(LN CS 3514):995-1002.[4]朱根标,张凤鸣,董群立.基于核函数和相似度的动态聚类算法[J].微电子学与计算机,2006,23(3):178-184.[5]蒋春燕,王国良,尹宝才,等.由三维散乱点重建三角网格曲面方法的分类与评价[J].北京工业大学学报,2002,28(1):91-96.[6]鄢腊梅,袁友伟.点云数据重构三维网格形状的新方法[J].计算机工程,2005,23(31):2-4.作者简介:张海朝 男,(1963-),副教授,硕士生导师.研究方向为计算机图形图像处理、系统工程与智能控制系统等.黄 淼 女,(1982-),硕士研究生,教师.研究方向为计算机图形图像处理.13第7期张海朝,等:基于RBF 神经网络的B 样条曲面重构。

《NURBS 计算曲面插值在 Java 中的应用》1. 引言在计算机图形学中，NURBS（Non-Uniform Rational B-Splines）是一种重要的曲面表示方法，它能够高效地描述复杂的曲线和曲面。

而在 Java 编程中，通过对NURBS进行计算曲面插值，可以实现对曲面的平滑、高质量的生成。

本文将介绍 NURBS 计算曲面插值在 Java 中的应用，包括基本概念、算法原理和实际编程实践。

2. NURBS 概述NURBS 是一种数学曲线和曲面的表示方法，它通过控制点、权重、节点矢量和阶数来定义曲线和曲面的形状。

在NURBS中，控制点的位置和权重决定了曲线或曲面的几何形状，而节点矢量和阶数则控制了曲线或曲面的插值特性。

3. NURBS 算法原理在NURBS 计算曲面插值中，一般采用的算法是基于 De Boor 算法的B-spline 插值。

该算法通过对给定的控制点和权重进行插值计算，生成高质量的曲面表示。

在 Java 编程中，可以利用 B-spline 插值算法和相关数学库来实现 NURBS 计算曲面插值的操作。

4. 实际编程实践在 Java 编程实践中，实现 NURBS 计算曲面插值需要以下步骤：1) 定义控制点和权重：通过定义控制点的位置和权重来确定曲面的形状。

2) 定义节点矢量和阶数：确定曲面的插值特性，如平滑度和曲率。

3) 进行插值计算：利用 B-spline 插值算法对给定的控制点和权重进行插值计算，生成曲面的表示。

4) 可视化显示：通过图形库或相关工具，将计算得到的曲面表示在界面上显示出来，对曲面进行渲染和显示。

5. 个人观点和理解对于 NURBS 计算曲面插值在 Java 中的应用，我认为这是一种非常重要的技术，可以在计算机图形学、CAD 设计和虚拟现实等领域发挥巨大作用。

通过对 NURBS 的深入理解和实际编程实践，可以实现对复杂曲面的高效表示和处理，为相关领域的应用提供技术支持和解决方案。

nurbs曲面连续算法
NURBS曲面是一种常用的数学模型，它可以用来描述复杂的曲
面形状。

NURBS曲面连续性算法是一种用于确保曲面在连接点处平
滑过渡的方法。

在计算机图形学和计算机辅助设计领域，NURBS曲
面连续性算法扮演着重要的角色。

NURBS曲面是由一系列的控制点和权重构成的，通过对这些控
制点进行调整，可以得到各种不同形状的曲面。

然而，当需要将多
个NURBS曲面连接在一起时，通常需要确保它们在连接点处具有一
定的连续性，以避免出现明显的不连续或者突变。

NURBS曲面连续性算法的主要目标是在连接点处实现G1、G2或
者G3连续性。

G1连续性意味着曲面在连接点处具有相同的切线方向，而G2连续性则要求曲面在连接点处不仅具有相同的切线方向，
还要求曲率相同。

而G3连续性则要求曲面在连接点处不仅具有相同
的切线方向和曲率，还要求它们的二阶导数相同。

实现NURBS曲面连续性算法的关键在于对控制点和权重的调整。

通常情况下，需要通过一定的数学计算和优化方法来实现这一连续
性要求。

在实际的应用中，NURBS曲面连续性算法被广泛应用于汽
车设计、航空航天领域以及工程建模等领域。

总之，NURBS曲面连续性算法是一种重要的数学算法，它可以确保NURBS曲面在连接点处平滑过渡，从而在计算机图形学和计算机辅助设计领域发挥着重要作用。

曲面重构方法的研究摘要针对三维扫描数据点的曲面重构技术在实际系统中的应用，本文提出了一种NURBS曲面构造方法，该方法根据已知数据点逼近目标曲面。

通过实际系统应用验证，该方法是一种行之有效的曲面拟合方法。

关键词数据点曲线和曲面重构算法0 引言扫描设备使用某种有组织的方式频繁地扫描目标物体，产生多行数据点，这些行可能包含有相同或不同的数据点数，每行点的分布可能有较大的变化。

本文基于曲面逼近理论，给出了一种NURBS曲面构造方法，用来合成目标曲面，并在自行开发的曲面造型系统中得到了验证。

给出已知数据点的格式如下：Q i，j i=0…n，j=0…m i所求曲面为幂次（p，q）的NURBS曲面。

已知数据点既不保证具有一个矩形拓朴结构，也不保证沿着每行均匀分布，在曲面拟合的过程中，主要解决两个关键的问题，第一是：彼此独立的每行数据点的曲线逼近；第二是：通过合适的节点矢量的控制避免数据量的大量增加。

1 曲线曲面逼近的基本理论将NURBS曲面表示成有理基函数形式为：上式中，P i，j为控制顶点，N i，k（u）、N j，l（v）分别为u，v方向的k次和l次B样条基函数，W i，j为权因子。

权因子的加入虽然可以增加对曲面的局部控制能力，但权因子的选取缺乏明显的几何意义，为简化计算将权值赋1，使式（1）中的分母为1，消除有理式，简化求解过程。

对曲面的u，v方向的次数选取从使用和表示的效果两方面考虑，取k=l=3，即工程中常用的三次曲面。

曲面上u，v方向的节点序列的确定中，使每一序列的前端和后端的重复度为3，保证曲面的边缘控制点和型值点融合，中间内节点的选取上考虑数据点分布不均匀，采用了累积弦长法。

通过上述权值、节点、次数的赋值，式（1.1）改变为：2 曲线逼近构成曲面的前提是必需对构成曲面的曲线作逼近处理，该处理过程包括曲线的计算、参数的计算、节点的选择和节点矢量的控制几个方面：2.1 最小二乘曲线逼近曲线逼近问题可表述如下：给出一系列数据点r，r=0…m和预定义参数t 0，…，t m以及预定义节点矢量u，2.2 参数和节点的计算参数的计算与节点的选择是相互影响的，如果选择了不合适的参数，那么节点就不可能被正确地选择，在实际应用过程中，通常采用累积弦长参数化方法：为控制曲线误差在允差范围之内，常把最小二乘曲线拟合的过程使用作一个迭代过程，用来调整控制点的最大下标索引值n及参数值t。

收稿日期:2004210222基金项目:国家自然科学基金资助项目(50275024)・作者简介:赵宇明(1970-),男,黑龙江肇东人,东北大学博士研究生;张国忠(1936-),男,黑龙江哈尔滨人,东北大学教授,博士生导师・第26卷第7期2005年7月东北大学学报(自然科学版)Journal of Northeastern University (Natural Science )Vol 126,No.7J ul.2005文章编号:100523026(2005)0720680203汽车逆向设计中用NURBS曲面拟合点云数据赵宇明,张国忠,于哲峰(东北大学机械工程与自动化学院,辽宁沈阳　110004)摘 要:针对汽车的逆向设计,利用非接触测量方法中的CDD 相机拍照法得到一组点云数据・将Tritop ,Atos 和CA TIA 三种软件联合应用,对点云数据进行了筛选、划分,用曲线拟合的方法做出了点云的特征线网格,并在此网格的基础上,利用NURBS 曲面拟合技术,得出了点云的曲面造型・通过将拟合得到的曲面造型和原始点云数据的对比,对拟合曲面进行了误差分析・结果显示,只是在凹槽的边缘部位误差稍有增大,但也在很小的范围内变化,符合实际设计时的要求・由此证明,此种多软件联合应用的方法在处理曲面造型的逆向设计方面是可行的・关　键　词:汽车设计;逆向工程;NURBS 曲面;曲面拟合;点云中图分类号:TH 122 文献标识码:A基于计算机辅助技术的实物逆向工程是CAD/CAM 领域的一个研究热点,其技术方法和流程已实用化,并在产品开发中得到广泛应用,各流程也已形成专业生产商和软件开发商・但逆向工程技术仍存在许多问题有待解决[1,2],如对实物外形的测量仍然存在误差和遗漏;复杂曲面重建时,尤其是由多个子曲面拼合而成的组合曲面,由于其表面特征识别难度大,影响了后续的数据分割和造型处理;没有一个整体曲面光顺的方法;尽管现在已经有多种专用逆向软件进入市场,但软件的数据处理技术、造型技术仍不完善,没有一种令人得心应手的软件[3];专用逆向软件和其他计算机辅助技术的结合已经受到重视,但不同系统的数据传输仍需要采取通用数据格式:“在数字化设备与造型软件的集成上,目前进展甚微”[4]・本文针对复杂曲面重建过程中单一软件的数据处理技术、造型技术的不完善,试图寻求一种能够充分发挥不同逆向造型设计软件的特长和优势,联合应用多种软件的方法,力求得到一条新的曲面造型途径・1　曲面重构方法目前测量设备的发展趋势是向着高速度、高精度、系统化、集成化、智能化的方向发展,CDD相机、激光、CT 等非接触式方法越来越成为主要的测量方式[5,6]・本文将采用的汽车点云数据就是利用CDD 相机拍照的方法获得的・1.1　曲面重构方法简介曲面重构是实现快速成型制造(RPM )的核心技术之一・从点云数据到曲面模型的曲面重构过程的技术难点在于:曲面表示以及根据点云数据拟合的算法・从1946年Schoenberg 提出样条函数至今的近60年间,经历了Ferguson 曲线曲面、Coons 曲面、Bezier 曲线曲面、B 样条曲线曲面、均匀B 样条曲线曲面及NU RBS 曲线曲面等[7]・现在实际应用的主要有两种曲面重建方法:基于矩形参数作用域,以B 样条和NU RBS 曲面为代表的方法;基于三角参数域,以三角Bezier 曲面为代表的方法[8,9]・本文应用的是前者・1.2　NURBS 曲面重构的特点NU RBS 曲面的定义[10]:P (u ,w )=6n i =06mj =0B i ,k (u )B j ,l (u )W i ,j V i ,j6n i =06mj =0B i ,k (u )B j ,l (u )W i ,j,u ∈[0,1](1)式中,V i ,j (i =0,1,2,…,n ;j =0,1,2,…,m )为给定特征网格顶点的位置矢量;W i,j为对应顶点的权因子・其中,基函数递推公式为B i,0(u)=1,u i≤u≤u i+1, 0,其他・B i,k(u)=u-u iu i+k-u iB i,k-1(u)+u i+k+1-uu i+k+1-u i+1B i+1,k-1(u),k≥1・　(2)节点矢量两端各有k+1个节点相同,以使曲线通过控制多边形的首末端点,并与首末两边相切・其节点矢量分别为U=[u0　u1　…　u k　u k+1　…　u r-k-1　u r-k　u r-k+1　…　u r];(3) W=[w0　w1　…　w l　w l+1　…　w s-l-1　w s-l　w s-l+1　…　w s]・(4)式中,u0=u1=…=u k=0;u r-k=u r-k+1=…=u r=1;w0=w1=…=w l=0;w s-l=w s-l+1=…=w s=1・NU RBS曲面用统一的表达式精确地表示了标准的解析形体和自由曲面,为修改曲面形状,既可以调整控制顶点也可以利用权因子,具有计算稳定、线性变换时的几何不变性等特性・但也有不尽如人意的地方,如用来定义解析曲面时需要额外的存储空间,对设计人员和用户的要求提高了,某些算法可能导致数值计算不稳定等・2　应用实例2.1　点云数据的获得首先利用高分辨率数码相机拍照片的方法,应用宝力机械公司的数码测量设备和Tritop软件,通过数码照片得到单张的点云数据,然后再将单张点云数据输入Atos软件,将测量得到的单张点云数据拼接成整张点云数据・2.2　特征网格划分CA TIA软件具有强大的曲面设计和曲面造型功能,所以将拼接完成的点云数据加载到CA TIA软件的数字曲面编辑器中・由于整个的点云数据极其庞大,所以此处只截取了一小部分・由于点云数据过多,如果全部用来做曲面拟合很浪费机时,也是不必要的,因此先采取筛选方法利用部分点云数据划分出代表点云造型特征的曲线,继而再组成特征曲线网格・具体步骤是:首先以等距均布和过数据点的方式,将点云划分成具有20×18条经纬线的网格,如图1所示,然后每条经纬线再用样条曲线拟合,从而形成曲线网格,如图2所示・图1　在点云上划分网格Fig.1　Netting the point cloud data图2　曲线网格图Fig.2　Net surface s2.3　曲面重构根据图2的曲线网格,选用软件CA TIA中的数字曲面编辑器,利用软件中的NU RBS曲面拟合功能,最终得到的拟合结果如图3所示・图3　通过曲线网格拟合出曲面Fig.3　NURBS curved surface fitted from net surface s 为了对NU RBS曲面拟合结果有一个比较感性的认识,本文还在点云数据上直接铺设了一个拉伸曲面,结果如图4所示・两种方法得到的结果基本相同・图4　在点云上直接铺面Fig.4　Surface spreading directly on point cloud2.4　误差分析图3建立的曲面是拟合而成的,有一定的误差・将拟合曲面与原始的点云数据进行比较,得出了拟合曲面的误差分布彩图,如图5所示・可以看出,拟合曲面的误差很小,只是在有凹槽部位的边缘稍微有些增大,但也在±01005mm以内・186第7期 赵宇明等:汽车逆向设计中用NU RBS曲面拟合点云数据图5　曲面与点云数据的误差分析Fig.5　Error analysis of NURBS curved surface inaccordance to point cloud data3　结果分析本文利用CA TIA软件的点云处理功能,将点云数据经分网和铺面处理,用NU RBS曲面拟合得到了后围板弯角部位的造型,通过误差分析可以认为此造型方法是可行的,从而提出了一种多软件联合应用的曲面造型逆向设计方法・本文应用CA TIA软件的两种方法拟合点云数据分别得到了两种拟合曲面,从外观上看,用分网铺面拟合的NU RBS曲面不如直接在点云数据上铺设的曲面光滑,其误差也相对大一些,这主要和曲面形成的方法有关・前者在利用点云数据分网的过程中是有间隔地部分利用了点云数据,且拟合成NU RBS曲线的过程中也有误差,导致后面形成的曲面有误差,同时在曲率变化较大的凹槽边缘部位,拟合过程也会出现一定的误差・由于测量方法的限制,在点云图中出现三块圆形空白区,这是在测量过程中车身上贴的参照点标识符造成的,对拟合曲面影响不大・后者拟合出的是一种拉伸曲面,虽然在外观上更忠实于点云数据,但在工程上应用不大・4　结 语本文对点云数据的处理做出了新的尝试,将Tritop,Atos和CA TIA联合应用,利用CDD相机拍摄得到的点云数据,进行数据筛选、划分、组成特征网格,利用NU RBS曲面拟合功能获取了产品的数学模型,最后通过误差分析用实例说明了该方法的有效性,为应用多软件联合处理曲面造型的逆向设计提供了一种新的方法・参考文献:[1]刘之江・反求工程[M]・北京:机械工业出版社,1996.2-5・(Liu Z J.Reverse engi neeri ng[M].Beijing:China MachinePress,1996.2-5.)[2]Pal P.An easy rapid prototyping technique with point clouddata[J].Rapi d Prototypi ng Journal,2001,7(2):82-89.[3]Seo J,Lee H C,Park S.Reconstruction of a compositesurface by reverse engineering techniques[J].Int J ofA dvanced M anuf act uri ng Technology,2001,17(9):639-643.[4]金涛,童水光・逆向工程技术[M]・北京:机械工业出版社,2003.19-20・(Jin T,Tong S G.Reverse engi neeri ng technique[M].Beijing:China Machine Press,2003.19-20.)[5]Carbone V,Carocci M,Savio E,et bination ofvision system and a coordinate measuring machine for thereverse engineering of freedom surface[J].Int J ofA dvanced M anuf act uri ng Technology,2000,17(4):263-271.[6]Aoyama H,Suzuki Y.Autonomous measurement of physicalmodel shape for reverse engineering[J].J of M anuf act uri ngSystem,2001,19(6):375-382.[7]Piegl L,Tiller W.The N U RBS book[M].New Y ork:Springer,1995.15-20.[8]Wang L Z,Zhu X X.Local interpolation blended B2splinesurfaces and its conversion to NURBS surface[J].Com puterA i ded Draf ti ng,Design and M anuf act uri ng,1994,4(2):5-17.[9]G ero putational models of innovative and creativedesign processes[J].Technological Forecasti ng and SocialChange,2000,64(2-3):183-196.[10]朱心雄・自由曲线曲面造型技术[M]・北京:科学出版社,2000.152-154・(Zhu X X.Modeli ng technique f or f ree f orm curve surf ace[M].Beijing:Science Press,2000.152-154.)Point Cloud Fitting of NURBS Curved Surface in Reverse Design of AutomobilesZHA O Y u2ming,ZHA N G Guo2z hong,YU Zhe2f eng(School of Mechanical Engineering&Automation,Northeastern University,Shenyang110004,China.Corres pondent: ZHAO Yu2ming,E2mail:yvmingzhaoyan@)Abstract:A group of point cloud data is obtained by way of no contact CDD photogrammetry for reverse design of automobiles. The point cloud data are screened and classified with combinin g the three softwares together,i.e.,Tritop,Atos and CA TIA, thus making a characteristic curve net for the point cloud data by curve fitting technique.Then,a relevant curved surface is shaped using the fitting technique of NURBS curved paring the curved surface thus shaped with the original point cloud data,the errors of the curved surface are analyzed and the result shows that only the error at recess edge increases a bit in a very small range.It conforms with the actual requirement for design.The way applying several softwares in combination to curved surface shaping is therefore proved available to reverse design of automobiles.K ey w ords:automobile design;reverse engineering;NURBS;curved surface fitting;point cloud(Received October22,2004) 286东北大学学报(自然科学版) 第26卷。

基于BP神经网络的NURBS曲线插补方法研究的开题报告论文题目：基于BP神经网络的NURBS曲线插补方法研究一、研究背景及意义：随着现代制造业技术的不断发展，高精度加工技术对于产品质量的重要性不断增强。

而数控机床正是现代加工技术中的代表，其对于加工精度和效率的要求也越来越高。

而数控机床的高精度加工技术中，NURBS曲线插补技术是一种常用的加工方式。

在现有的数控机床加工技术中，常用的插补算法为多项式插值算法，但这种算法的精度与运算复杂度之间是一种矛盾，精度更高的算法可能会导致计算效率低下，因此需要寻求一种更加高效精准的NURBS曲线插补方法。

神经网络自20世纪以来，作为一种模仿生物神经系统的计算模型，逐渐成为了研究各个学科中常用的工具之一。

其中BP神经网络是目前应用最广泛的神经网络算法之一，其具有数据拟合、分类、预测等方面的能力。

因此，将BP神经网络应用于NURBS曲线插补算法的研究具有很高的研究价值。

二、研究内容和目标：本文旨在将BP神经网络应用于NURBS曲线插补算法中，基于BP神经网络的学习能力和非线性映射能力，通过对数据的拟合，提高NURBS 曲线插补算法的精度和效率，并且提供在不同加工条件下的预测能力。

具体研究内容如下：（1）通过BP神经网络拟合NURBS曲线控制点的坐标，实现曲线的插补。

（2）对于不同的加工条件，设计不同的NURBS曲线控制点坐标训练数据，应用BP神经网络进行训练，提供曲线插补的预测能力。

（3）对比多项式插值算法与基于BP神经网络的NURBS曲线插补算法的加工效率与精度，并且对算法进行优化。

三、研究方法和技术路线：本文的研究方法主要是基于BP神经网络算法进行。

首先需要采集不同加工条件下的实验数据，将实验数据进行处理，得到不同加工条件下的NURBS曲线控制点坐标数据。

接着将数据输入到BP神经网络中进行训练，并对训练效果进行评估。

在完成BP神经网络模型的搭建和训练之后，结合数控机床的实际加工情况，进行多项式插值算法与基于BP神经网络的NURBS曲线插补算法的效率与精度比较，并针对NURBS曲线插补算法进行优化。