第十章齿轮机构及其设计
- 格式:doc
- 大小:429.00 KB
- 文档页数:12

第十章 齿轮机构及其设计第一节 齿轮机构的应用和分类一、齿轮机构的应用1、功用:齿轮机构可用于传递空间任意两轴(平行、相交、交错)的旋转运动,或将转动转换为移动。
图10—1 图10—2 图10—32、优点:①传动比准确、传动平稳。
②圆周速度大,高达300 m/s 。
③传动功率范围大,从几瓦到10万千瓦。
④效率高(η→0.99)、使用寿命长、工作安全可靠。
3、缺点:加工成本高、不适宜远距离传动。
二、齿轮机构的分类图10—4非圆齿轮 图10—5斜齿圆锥齿轮图10—6曲线齿圆锥齿轮 图10—7准双曲面齿轮第二节 齿轮的齿廓曲线共轭齿廓:一对能实现预定传动比(i12=ω1/ω2)规律的啮合齿廓。
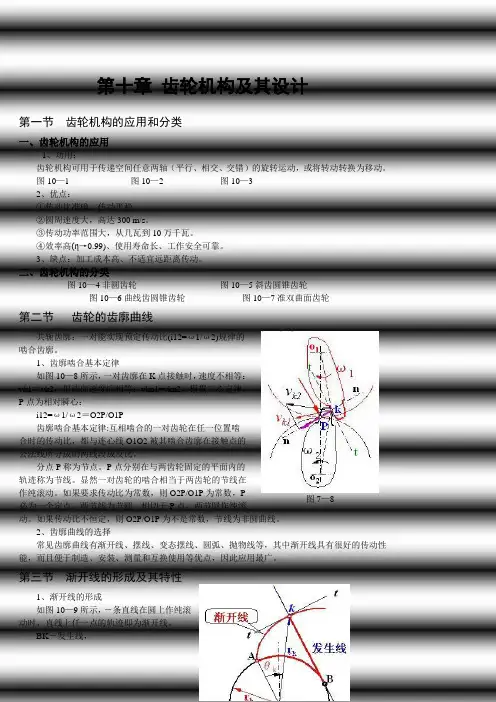
1、齿廓啮合基本定律如图10—8所示,一对齿廓在K 点接触时,速度不相等:vk1≠vk2,但法向速度应相等:vkn1=vkn2,根据三心定律,P 点为相对瞬心:i12=ω1/ω2=O2P/O1P齿廓啮合基本定律:互相啮合的一对齿轮在任一位置啮合时的传动比,都与连心线O1O2被其啮合齿廓在接触点的公法线所分成的两线段成反比。
分点P 称为节点。
P 点分别在与两齿轮固定的平面内的轨迹称为节线。
显然一对齿轮的啮合相当于两齿轮的节线在作纯滚动。
如果要求传动比为常数,则O2P/O1P 为常数,P 必为一个定点。
两节线为节圆,相切于P 点,两节圆作纯滚动。
如果传动比不恒定,则O2P/O1P 为不是常数,节线为非圆曲线。
2、齿廓曲线的选择常见齿廓曲线有渐开线、摆线、变态摆线、圆弧、抛物线等,其中渐开线具有很好的传动性能,而且便于制造、安装、测量和互换使用等优点,因此应用最广。
第三节 渐开线的形成及其特性1、渐开线的形成如图10—9所示,―条直线在圆上作纯滚动时,直线上任一点的轨迹即为渐开线。
BK -发生线, 图7—8基圆-rb,θk-AK段的展角。
2、渐开线的特性①AB =BK;如图7—10所示,发生线滚过基圆的长度等于基圆上被滚过的弧长。



第十章齿轮机构及其设计第十章齿轮机构及其设计基本要求了解齿轮机构的应用及其分类以及齿廓啮合的基本定律、共轭齿廓等概念。
熟练掌握渐开线直齿圆柱齿轮几何尺寸的计算以及一对轮齿的啮合过程、正确啮合条件、连续传动条件、渐开线齿轮传动的特点等。
了解渐开线齿轮的切制原理。
掌握标准齿轮不发生根切的最少齿数以及最小变位系数的计算和变位齿轮几何尺寸的计算。
了解斜齿圆柱齿轮传动的特点、齿廓的形成。
掌握端面和法面参数之间的关系转换及基本尺寸的计算。
了解圆锥齿轮和蜗轮蜗杆传动的特点以及主要几何尺寸的计算。
基本概念题和答案1.什么是齿廓啮合基本定律,什么是定传动比的齿廓啮合基本定律?齿廓啮合基本定律的作用是什么?答:一对齿轮啮合传动,齿廓在任意一点接触,传动比等于两轮连心线被接触点的公法线所分两线段的反比,这一规律称为齿廓啮合基本定律。
若所有齿廓接触点的公法线交连心线于固定点,则为定传动比齿廓啮合基本定律。
作用;用传动比是否恒定对齿廓曲线提出要求。
2.什么是节点、节线、节圆?节点在齿轮上的轨迹是圆形的称为什么齿轮?答:齿廓接触点的公法线与连心线的交点称为节点,一对齿廓啮合过程中节点在齿轮上的轨迹称为节线,节线是圆形的称为节圆。
具有节圆的齿轮为圆形齿轮,否则为非圆形齿轮。
3.什么是共轭齿廊?答:满足齿廓啮合基本定律的一对齿廓称为共轭齿廓。
4.渐开线是如何形成的?有什么性质?答:发生线在基圆上纯滚动,发生线上任一点的轨迹称为渐开线。
性质:(1)发生线滚过的直线长度等于基圆上被滚过的弧长。
(2)渐开线上任一点的法线必切于基圆。
(3)渐开线上愈接近基圆的点曲率半径愈小,反之则大,渐开线愈平直。
(4)同一基圆上的两条渐开线的法线方向的距离相等。
(5)渐开线的形状取决于基圆的大小,在展角相同时基圆愈小,渐开线曲率愈大,基圆愈大,曲率愈小,基圆无穷大,渐开线变成直线。
(6)基圆内无渐开线。
5.请写出渐开线极坐标方程。
答:r k = r b/ cos αk θk= inv αk= tgαk一αk6.渐开线齿廓满足齿廓啮合基本定律的原因是什么?答;(1)由渐开线性质中,渐开线任一点的法线必切于基圆(2)两圆的同侧内公切线只有一条,并且两轮齿廓渐开线接触点公法线必切于两基圆,因此节点只有一个,即i12=ω1/ ω2=O2P / O1P =r2′/ r1′= r b2/ r b1= 常数7.什么是啮合线?答:两轮齿廓接触点的轨迹。

第十章齿轮机构及其设计§10—1齿轮机构的应用及分类1.齿轮机构的应用及特点直接啮合:齿轮传动啮合传动中间件:链传动机械传动直接啮合:摩擦轮传动. 摩擦传动中间件:带传动齿轮用于空间任意两轴之间传递运动或动力。
(使用范围广泛、历史悠久)齿轮机构传动的特点(与链、带或其它传动比较)1)传递的功率大(可达10万千瓦)2)转速高(10万转/每分;线速度300米/秒)3)传动的效率高(0。
99);4)寿命长、工作可靠性高;5)可以保持恒定的传动比(或按某一规律变化);6)空间轴线位置不受限制7)制造、安装的成本较高,不宜作较远距离传动。
2.齿轮机构的分类§10—2 齿廓啮合基本定律若两轮的传动能实现预定的传动比(i12=ω1/ω2),则相互接触传动的一对齿廓称为共轭齿廓1)啮合的基本要求图示为齿轮1和齿轮2的两条齿廓曲线点任意K 啮合接触,两齿廓的公法线nn与连心线 O1O2 相交于点P。
即:啮合点处两齿廓在法线方向上的相对速度为零;设:n为法矢有:V K1K2·n=02)齿廓啮合基本定律齿廓啮合基本定律:两齿廓在任一位置啮合接触时,它们的传动比等于连心线O1O2被节点C 所分成的两条线段的反比。
讨论:1)如果要求两齿廓作定传动比传动,节点P为连心线上的一个定点。
2) 如果要求两齿廓作变定传动比传动,节点P应按给定的规律在O1O2线上移动。
3)在传动比和中心距的已知情况下,给定一个齿廓就能运用齿廓啮合基本定律求出与之共轭的另一齿廓;4)关于节点与节线:节线:节点在齿轮1、2运动平面上的轨迹。
对定比传动:节线→节圆齿轮传动→节圆作纯滚动对变比传动:节线→非圆曲线齿轮传动→非圆曲线作纯滚动3.齿廓曲线的选择理论上,共轭齿廓可以找出无限多;实际上,考虑设计、制造、测量、安装、强度、互换等方面,对于定传动比的齿轮机构,通常采用渐开线、圆弧、摆线等。
§10—3 渐开线齿廓的啮合特点一、渐开线的形成及性质1、形成方法:1)展开法1)纯滚动法AK——渐开线;基圆r b;BK:发生线;θK:渐开线AK段的展角2、性质(1)(2)BK为渐开线在K点的法线,且与基圆相切。
![机械原理课件:第10章 齿轮机构及其设计[优选内容]](https://uimg.taocdn.com/982da12365ce0508763213ed.webp)



第十章 齿轮机构及其设计一、齿轮的齿廓曲线1.共轭齿廓:一对能实现预定传动比(i 12=ω1/ω2)规律的啮合齿廓。
2.齿廓啮合基本定律齿廓啮合基本定律:互相啮合的一对齿轮在任一位置啮合时的传动比,都与连心线O 1O 2被其啮合齿廓在接触点的公法线所分成的两线段长成反比。
二、渐开线 1.特性:①发生线滚过基圆的长度等于基圆上被滚过的弧长。
②渐开线上任意点的法线切于基圆,渐开线上任意点的法线即渐开线的发生线。
③B 点为曲率中心,BK 为曲率半径。
渐开线起始点A 处曲率半径为0。
④渐开线形状取决于基圆,基圆越大,渐开线越平缓,当r b →∞,渐开线变成直线,齿轮变为齿条。
⑤基圆内无渐开线。
⑥同一基圆上任意两条渐开线公法线处处相等。
2.渐开线方程式压力角:啮合时K 点正压力方向与绝对速度方向所夹锐角为渐开线上该点之压力角αk 。
αk r b =r k cos αkcos αk= r b/ r k (渐开线离基圆愈远,其压力角越大)极坐标方程:tg αk = BK/r b =AB/r b = r b (θk +αk )/r bθk = tg αk -αk上式称为渐开线函数,用inv αk 表示:θk =inv αk =tg αk -αk由tg αk = BK/r b- ------得渐开线任一点的曲率半径 ρ=BK= r b tg αk ,则分度园上的曲率半径(*会计算)ρ=BK= r b tg α3、渐开线齿廓的啮合特性1)渐开线齿廓能保证定传动比传动两齿廓在任意点K 啮合时,过K 作两齿廓的法线N 1N 2,是基圆的切线,且为定直线;两轮中心连线也为定直线,故交点P 必为定点 i 12=ω1/ω2=O 2P/ O 1P=const2)齿廓间正压力方向不变N 1N 2是啮合点的轨迹,称为啮合线,该线又是接触点的法线,正压力总是沿法线方向,故正压力方向不变。
该特性对传动的平稳性有利。
3)运动可分性7—14传动比写成:i 12=ω1/ω2=O 2P/ O 1P = r b2 /r b1= r 2’ /r 1’传动比为基圆半径之反比。
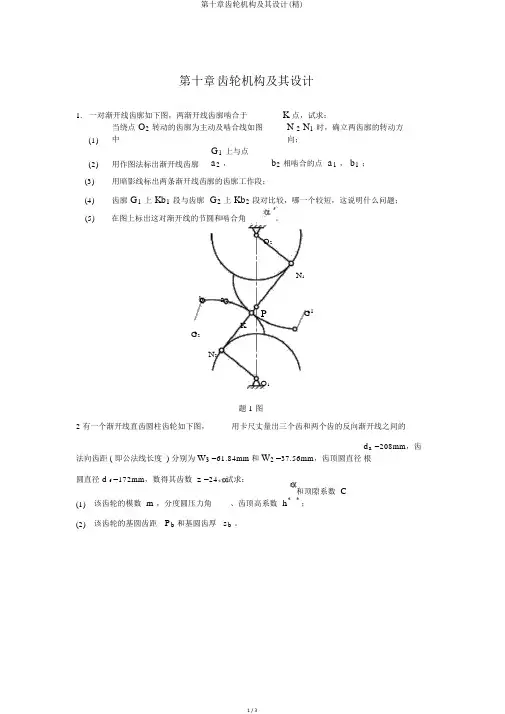
第十章齿轮机构及其设计1. 一对渐开线齿廓如下图,两渐开线齿廓啮合于K 点,试求:(1) 当绕点 O2转动的齿廓为主动及啮合线如图中N 2 N1时,确立两齿廓的转动方向;(2) 用作图法标出渐开线齿廓G1上与点a2,b2相啮合的点 a1, b1;(3)用暗影线标出两条渐开线齿廓的齿廓工作段;(4)齿廓 G1上 Kb1段与齿廓 G2上 Kb2段对比较,哪一个较短,这说明什么问题;(5)在图上标出这对渐开线的节圆和啮合角。
O2N1b2a2P G1KG2N2O1题 1 图2 有一个渐开线直齿圆柱齿轮如下图,用卡尺丈量出三个齿和两个齿的反向渐开线之间的法向齿距 ( 即公法线长度 ) 分别为W3 =61.84mm和W2 =37.56mm,齿顶圆直径d a=208mm,齿根圆直径 d f=172mm,数得其齿数 z =24,试求:(1) 该齿轮的模数 m ,分度圆压力角、齿顶高系数 h* 和顶隙系数 C *;(2) 该齿轮的基圆齿距 P b和基圆齿厚s b。
W3W2D BA Cr bO题 2 图3 已知一对渐开线外啮合标准直齿圆柱齿轮机构,=20°,h* =1,m =4mm,z1 =18,z2 =41。
试求:(1) 标准安装时的重合度;(2) 用作图法画出理论啮合线N1 N 2,在其上标出实质啮合线段B1B2,并标出单齿啮合区和双齿啮合区,以及节点P 的地点。
O1r a1r b1p b p b 1NB1 B2 N2 P8p b 2p b0.3 0.662p b b. p.6231r b2 r a2O2题3解图4丈量齿轮的公法线长度是查验齿轮精度的常用方法之一,试用图证明渐开线齿轮公法线长度 W 和卡尺跨的齿数 k 的计算公式:W m cos (k 0.5) zinv a 2xmsin ak ( z 0.5) z( tg x tg ) 2x tg式中 z 为被测齿轮的齿数,k 为卡尺跨的齿数,目的是为了卡尺一定卡在渐开线齿廓上。
第十章齿轮机构及其设计-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第十章齿轮机构及其设计10-1 填空题(1)渐开线齿廓的齿轮啮合的特点是。
(2)影响渐开线直齿圆柱齿轮齿廓形状的参数有、、。
(3)决定单个渐开线标准直齿圆柱齿轮几何尺寸的五个基本参数是,其中参数是标准值。
(4)一对外啮合渐开线直齿圆柱齿轮机构的正确啮合条件是和分别相等。
(5)渐开线斜齿圆柱齿轮的标准参数在面上,在几何尺寸计算时应按面参数代入直齿轮的几何计算公式。
(6)用标准齿条型刀具加工标准齿轮时,其刀具的线与轮坯圆相切并作纯滚动。
(7)斜齿圆柱齿轮的螺旋角对传动的主要影响有、、、,其常用的取值范围为。
(8)用标准齿条型刀具加工n=20°,h*an=1,=20°的标准斜齿轮时,其不根切的最少齿数是。
(9)一对渐开线直齿圆柱齿轮(=20°,h*a=1)啮合时,当安装的实际中心距a′大于标准中心距a时,啮合角′是变大还是变小;重合度是增大还是减小;传动比i又是如何变化的。
(10)一对正常齿制的渐开线标准直齿圆柱外啮合齿轮传动,其模数m=4mm,当两轮以标准中心距安装时,其顶隙为 mm,理论上侧隙为 mm;当中心距增大时,其顶隙变为mm,侧隙于零。
10-2 选择题(1)渐开线直齿圆柱齿轮传动的可分性是指不受中心距变化的影响。
A.节圆半径; B.传动比; C.啮合角。
(2)模数m=2mm, 压力角=20°,齿数z=20,齿顶圆直径d a=,齿根圆直径d f=正常齿制的渐开线直齿圆柱齿轮是齿轮。
A.标准; B. 变位; C. A、B皆不是。
(5)齿轮经过正变位修正后,其分度圆与标准齿轮的分度圆相比,是。
A.相同; B.减小; C.增大。
(6)等移距(高度)变位齿轮传动的中心距和啮合角必分别标准中心距和标准压力角。
A.大于; B.小于; C.等于。
(8)渐开线直齿圆柱外齿轮齿廓根切发生在的场合。
A.模数较大; B. 模数较小; C. 齿数较少。
(10)斜齿圆柱齿轮基圆柱上的螺旋角βb与分度圆上的螺旋角β相比。
A.b>; B.b<; C.b=。
(11)直齿圆锥齿轮的当量齿数z v其实际齿数。
A.大于; B.小于; C.等于。
(12)负变位齿轮的分度圆齿距应πm。
A.大于; B.小于; C.等于; D.等于或小于。
(14)标准渐开线外齿轮的齿数增加,齿顶圆压力角将。
A.不变; B.增大; C.减小; D.不确定。
(15)蜗杆传动的正确啮合条件中,应除去。
A.m a1=m t2; B.a1=t2; C.1=2; D.螺旋方向相同。
(16)在蜗杆传动中,用来计算传动比i12是错误的。
A.i12=1/2; B.i12=z2/z1; C.i12=n1/n2; D.i12=d2/d1。
(17)阿基米德圆柱蜗杆的标准模数是指模数。
A.端面; B.法面; C.轴面。
(18)平行轴渐开线斜齿圆柱外啮合齿轮传动的正确啮合条件中,应除去。
A.m n1=m n2; B. n1= n2; C.1= 2; D.1=- 2。
(19)渐开线斜齿圆柱齿轮的当量齿数是用来。
A.计算传动比; B.计算重合度; C.选择盘形铣刀。
(20)相同几何尺寸的渐开线斜齿圆柱齿轮传动的重合度直齿圆柱齿轮传动的重合度。
A.大于; B.小于; C.等于。
(22)在用标准齿条型刀具加工标准圆柱齿轮时,若被切齿轮的齿数z<z min时,为避免根切,应采用变位修正。
A.正; B.负; C.两者皆可。
10-3 在图中,已知基圆半径r b=50mm,现需求:1)当r K=65mm时,渐开线在该点的压力角K、曲率半径K、展角K。
2)当K=5°时,渐开线的压力角K及向径r K的值。
注:渐开线函数inv K (rad)表(摘录)次0′10′20′25′30′35′40′45′50′55′°3481097824288377784457851428583286525872238792588631解:10-4已知一渐开线正常齿制标准直齿圆柱齿轮在z=40,m=5mm,=20°,试分别求出其渐开线齿廓在分度圆、基圆及齿顶圆上的曲率半径、b及a和压力角、b及a。
解:想一想:渐开线上各点的曲率半径按什么规律变化10-5有一正常齿制的标准渐开线直齿圆柱齿轮,=20°,测量其顶圆直径d a=132mm,齿数z=20,求其模数、基圆直径、分度圆直径、齿根圆直径、齿距、分度圆上的齿厚和齿槽宽各是多少解:1、计算模数2、计算齿轮几何尺寸(将尺寸名称、计算公式、计算结果填写于表内,尺寸单位为mm)名称符号计算公式计算结果dd fd bpse10-6在技术革新中,拟使用现有的两个正常齿制的标准渐开线直齿圆柱齿轮,=20°,已测得两轮齿数分别为z1=22,z2=98,小齿轮齿顶圆直径d a1=240mm,大齿轮的全齿高h=(因大齿轮太大,不便测其齿顶圆直径),试判断这两个齿轮能否正确啮合传动解:想一想:渐开线齿轮传动的正确啮合条件是什么10-7已知一对渐开线外啮合标准直齿圆柱齿轮,z1=18,z2=41,m=10mm,=20°,h a*=1,c*=,试求:(1)两轮的分度圆直径d1、d2;基圆直径d b1、d b2;齿顶圆直径d a1、d a2;齿根圆直径d f1、d f2和中心距a;(2)重合度,并用长度比例尺l=mm绘出实际啮合线B1B2,在其上标出一齿对啮合区和两齿对啮合区。
解:1)计算两齿轮的几何尺寸(将尺寸名称、计算公式、计算结果填写于表内,尺寸单位为mm)名称符号计算公式计算结果d1d 2d a1d a2d f1d f2d b1d b2a2)计算重合度=a1=a2=3)绘制实际啮合线B1B2,在其上标出一齿对啮合区和两齿对啮合区P b= B1B2=10-8 用齿条刀具加工一直齿圆柱齿轮。
设已知被加工齿轮轮坯的角速度rad/s,刀具移动速度v2=s,刀具的模数m=10mm,压力角=20°。
求:(1)被加工齿轮的齿数z1;(2)若齿条分度线与被加工齿轮中心的距离为77mm,求被加工齿轮的齿厚;(3)若已知该齿轮与大齿轮相啮合时的传动比i12=4,当无侧隙标准安装时,中心距a′=377mm,求这两个齿轮的节圆直径d1′、d2′;及其啮合角′。
解:10-9 今有一对标准斜齿圆柱齿轮传动,已知斜齿轮的法面参数:m n=4mm,n=20°,h*an=1,c*n=,齿宽b=30mm,中心距a=,齿数z1=20,z2=40。
试求:(1)这对斜齿圆柱齿轮传动的螺旋角及重合度。
(2)如果将这对斜齿轮传动改为直齿圆柱齿轮传动,其模数、齿数、齿宽及中心距均与斜齿轮的参数相同,为了保证齿轮无侧隙啮合传动,这对齿轮是否可以采用标准直齿圆柱齿轮若不行,应采用何种传动类型(3)这对斜齿轮的分度圆直径d 1、d 2;齿顶圆直径d a1、d a2;基圆直径d b1、d b2;节圆直径d 1′、d 2′。
解:10-10 某传动中的一对正常齿制标准渐开线直齿圆柱齿轮,其模数m =5mm ,传动比i 12=3,中心距a =100mm ,试分析计算以下问题:(1)计算两齿轮的齿数z 1、z 2,这两个齿轮加工时是否发生根切(2)若已知条件不变,同时要求无根切,这对齿轮应采用何种类型的齿轮传动(3)当齿轮不发生根切时,应满足的条件为ααsin )(2sin *xm m h mz a-≥,试求出其最小变位系数x min 。
(4)选取齿轮1的变位系数,求出变位后齿轮1的主要几何尺寸基圆直径、分度圆直径、齿根圆直径、齿距、分度圆上的齿厚和槽宽。
解:1)计算两齿轮的齿数z 1、z 2,判断这两个齿轮加工时是否发生根切 2)这对齿轮的传动类型为: 3)最小变位系数:x min = =4)计算齿轮1的几何尺寸(将尺寸名称、计算公式、计算结果填写于表内,尺寸单位为mm )尺寸名称齿轮1(变位)的计算公式计算结果取x1=d1=d a1=d f1=d b1=p1=s1=10-11 如图所示,已知各齿轮的齿数z1=15,z2=53,z3=56,z4=14,中心距a12=a34=70mm,压力角n,模数m m n mm,正常齿。
试问:(1)如两对齿轮均采用直齿圆柱,采用何种传动类型,可以满足中心距a12=a34=70mm,此时啮合角各为多大(2)如果轮1、2采用斜齿圆柱齿轮,而轮3、4仍采用直齿圆柱齿轮,那么(a)轮1、2的螺旋角是多大(b)轮1是否根切(c)轮3、4不发生根切的最小变位系数(d)轮3、4的分度圆、齿顶圆、齿根圆有何变化解:10-12在一对外啮合的渐开线直齿圆柱齿轮传动中,已知:z1=12,z2=28,m=5mm,,h*a=1,c*=。
要求小齿轮刚好不发生根切,试问在无侧隙啮合条件下:(1)实际中心距a′=100mm时,应采用何种类型的齿轮传动并计算其主要几何尺寸。
(2)实际中心距a′=102mm时,应采用何种类型的齿轮传动并计算其主要几何尺寸。
(注:渐开线函数inv K (rad)表(摘录))°次0'10'20'25'30'35'40'45'50'55'20149041529315689158901609216296165201671016920171322220054205332101921266215142176522018222722252922788解:(1) 1)确定传动类型及变位系数a=传动类型为:x1=x2=2)计算两齿轮的几何尺寸(将尺寸名称、计算公式和结果填写于表内,尺寸单位为mm)尺寸名称小齿轮大齿轮x1=x2=y=y=d1=d2=h a1=h a2=h f1=h f2=d a1=d a 2=d f1=d f 2=d b1= d b2=p1=p2=s1=s2=e1=e2=(2)1)确定传动类型及变位系数传动类型为:′=x1+ x2=x2=2)计算两齿轮的几何尺寸(将尺寸名称、计算公式和结果填写于表内,尺寸单位为mm)尺寸名称小齿轮大齿轮x1=x2=y=y=d1=d2=h a1=h a2=h f1=h f2=d a1=d a 2=d f1=d f 2=d b1= d b2=p1=p2=s1=s2=e1=e2=10-13 已知一对等顶隙渐开线标准直齿圆锥齿轮传动,其轴交角=90°,齿数z1=15,z2=30,m=5mm。
求分度圆锥角、分度圆直径、齿顶圆直径、齿根圆直径、锥距、齿根角、顶锥角、根锥角和当量齿数。
解:计算两齿轮的几何尺寸(将尺寸名称、计算公式和结果填写于表内,尺寸单位为mm)尺寸名称小齿轮大齿轮=2=1d1=d2=d a2=d a2=d f1=d f 2=R==f=a2=a1=f2=f1z v1=z v2=10-14 已知阿基米德蜗杆传动的参数如下:z1=1,z2=40,1=°,m=10mm。