梅涅劳斯定理与塞瓦定理

梅涅劳斯定理和塞瓦定理一、梅涅劳斯定理定理1若直线l不经过∆ABC的顶点，并且与∆ABC的三边BC、CA、AB或它们的延长线分别交于P 、Q、R，则BPPC ∙CQQA∙ARRB=1证明：设ℎA、ℎB、ℎC分别是A、B、C到直线l的垂线的长度，则：BPPC ∙CQQA∙ARRB=ℎBℎC∙ℎCℎA∙ℎAℎB=1。

例1若直角∆ABC中，CK是斜边上的高，CE是∠ACK的平分线，E点在AK上，D是AC的中点，F是DE与CK的交点，证明：BF∥CE。

【解析】因为在∆EBC中，作∠B的平分线BH，则：∠EBC=∠ACK，∠HBC=∠ACE，∠HBC+∠HCB=∠ACK+∠HCB=90°，即BH⊥CE，所以∆EBC为等腰三角形，作BC上的高EP，则：CK=EP，对于∆ACK和三点D、E、F根据梅涅劳斯定理有：CDDA ∙AEEK∙KFFC=1，于是KFFC=EKAE=CKAC=EPAC=BPBC=BKBE，即KFFC =BKBE，根据分比定理有：KFKC=BKKE，所以∆FKB≅∆CKE，所以BF∥CE。

例2从点K引四条直线，另两条直线分别交直线与A、B、C、D和A1，B1，C1，D1，试证：ACBC :ADBD=A1C1B1C1:A1D1B1D1。

【解析】若AD∥A1D1，结论显然成立；若AD与A1D1相交于点L，则把梅涅劳斯定理分别用于∆A1AL和∆B1BL可得：ADLD ∙LD1A1D1∙A1KAK=1，LCAC∙AKA1K∙A1C1LC1=1，BCLC∙LC1B1C1∙B1KBK=1，LDBD∙BKB1K∙B1D1 LD1=1，将上面四个式子相乘，可得：ADAC∙BCBD∙A1C1A1D1∙B1D1B1C1=1，即：ACBC:ADBD=A1C1B1C1:B1D1B1C1定理2设P、Q、R 分别是∆ABC的三边BC、CA、AB上或它们延长线上的三点，并且P、Q、R三点中，位于∆ABC边上的点的个数为0或2，这时若BPPC ∙CQQA∙ARRB=1，求证P、Q、R三点共线。

梅涅劳斯定理和塞瓦定理
梅涅劳斯定理和塞瓦定理是数学和物理学中两个经典定理，它们对研究
热力学有重要意义，它们可以帮助我们理解不同物质体系的能量变化。

梅涅劳斯定理是一个数学定理，英国数学家弗朗西斯·梅涅劳斯在1850年提出的。

梅涅劳斯定理述说，一个“完整”的物理过程，当它完全
可逆时，它的总热力学功将等于零。

这种定理要求物理过程必须完全可逆，
且不会发生任何热量流出或流入，否则结果会不等于零。

塞瓦定理也是一个数学定理，意大利数学家Carlo Sévé于1870年
提出来的。

它述说：“当一个物理过程是完全可逆的，而且没有涉及有外力，如引力，牛顿力等外力，作用在物体上，则其工作量为零，即功等于能量变化。

”由于没有任何外力介入，这对于理解物理过程有着重要的意义。

梅涅劳斯定理和塞瓦定理在热力学研究中都有重要的意义，它们可
以帮助我们更好地理解物质体系的能量变化。

它们还有助于帮助我们认识物
理过程，是热力学研究中不可或缺的定理。

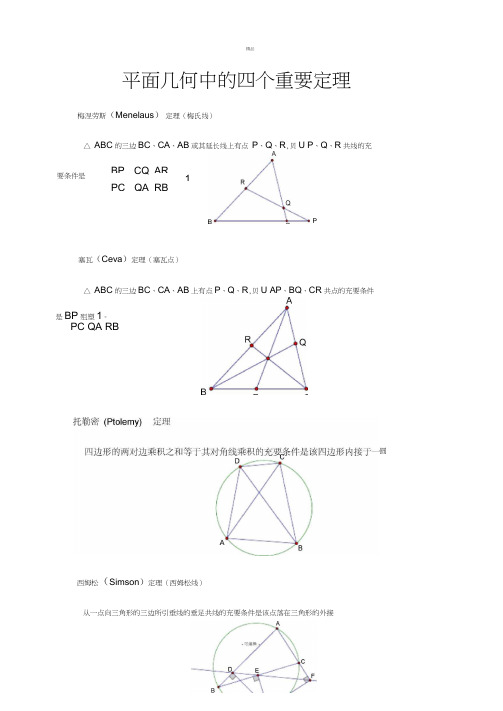
平面几何中的四个重要定理梅涅劳斯（Menelaus ） 定理（梅氏线）△ ABC 的三边BC 、CA 、AB 或其延长线上有点 P 、Q 、R ,贝U P 、Q 、R 共线的充塞瓦（Ceva ）定理（塞瓦点）△ ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ,贝U AP 、BQ 、CR 共点的充要条件西姆松（Simson ）定理（西姆松线）从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接要条件是 BP CQ AR1PC QA RB是BP 殂塑1。

PC QA RBP圆。

-可编辑-圆上。

例题:1、设AD 是厶ABC 的边BC 上的中线，直线CF 交AD 于F 。

求、 AE 2AF证：——ED FBAE DC BF【分析】CEF 截厶ABD T -------------------------- 1 （梅氏定理）ED CB FA【评注】也可以添加辅助线证明：过A 、B 、D 之一作CF 的平行线。

【分析】连结并延长 AG 交BC 于M ，贝U M 为BC 的中点。

BE CF GM (DB DC) = GM 2MD EA FA = AG MD 2GM MDAB 、AC 于 E 、F ,交 CB 于 D 。

求证： BE CF 1。

EA FADEG 截厶 ABM T DGF 截厶 ACM TBE AG MD EA GM DB CF AG MD FA GM DC1 （梅氏定理） 1 （梅氏定理）A2、过△ ABC 的重心G 的直线分别交5、已知△ ABC 中，/ B=2 / C 。

求证:【评注】梅氏定理【评注】梅氏定理CG 相交于一点。

【分析】【评注】塞瓦定理3、D 、E 、F 分别在△ ABC 的 BC 、匹圧些,AD 、BE 、DC FB EA【分析】4、以△ ABC 各边为底边向外作相似的等腰厶BCE 、△ CAF 、△ ABG 。

求证： AE 、BF 、-可编辑-【分析】过A 作BC 的平行线交△ ABC 的外接圆于D ，连结BD 。

设0是厶ABC内任意一点，AB、BO、CO 分别交对边于 D、E、F,贝U BD/DC*CE/EA*AF/FB=1(I)本题可利用梅内劳斯定理证明：•••△ ADC被直线BOE所截，CB/BD*DO/OA*AE/EC=1 ①而由△ ABD 被直线 COF 所截，••• BC/CD*DO/OA*AF/DF=1 ②①十②：即得：BD/DC*CE/EA*AF/FB=1(n)也可以利用面积关系证明•/ BD/DC=S △ ABD/S △ ACD=S △ BOD/S △ COD=(S △ ABD-S △ BOD)/(S △ ACD-S △ COD)=S △ AOB/S △ AOC③同理 CE/EA=S △ BOC/ S △ AOB ④ AF/FB=S △ AOC/S △ BOC ⑤③X④X⑤得 BD/DC*CE/EA*AF/FB=1塞瓦定理：设P、Q、R分别是MBC的BC、CA、AB边上的点，则AP、BQ、CR三线共点的充要条件是：氐杀詈」QC P C AB i证：先证必要性：设 AP 、BQ 、CR 相交于点M,贝V ：以上三式相乘，得：_BE.空=1PC QA RB再证充分性：若 =1，设AP 与BQ 相交于M ，且直线CM 交AB 于 R ， PC QA RB由塞瓦定理有： 拻.BP CQ ARAR AR‘ 1,于是：因为R 和R 都在线 PC QA R B R B RB 段AB 上，所以R ‘必与R 重合，故 AP 、BQ 、CR 相交于一点点 M ； 例1:证明：三角形的中线交于一点；证明：记 ABC 的中线秋，BB r CC,，我们只须证明也BA 1 CB 1=11 C 1B AC B 1A 而显然有：AG 二 GB, BA 二 AC ,CB j 二 B 1A 【练习1】证明：三角形的角平 分线交于一点; 【练习2】证明：锐角三角形的 高交于一点； 例2：在锐角 ABC 中,角.C 的平分线交 于AB 于L,从L 作边AC 和BC 的垂线，垂 足分别是M 和N,设AN 和BM 的交点是 P,证明：CP _ ABB例3设AD 是 ABC 的高，且D 在BC 边上，若P 是AD 上任一点，BP 、CP 分别与AC 、AB 交于 E 和 F ，贝U EDA = FDA证：过A 作AD 的垂线，与DE 、DF 的延长线分别 交于M 、N 。

四个重要定理梅涅劳斯(Menelaus)定理（梅氏线）△ABC的三边BC、CA、AB或其延长线上有点P、Q、R，则P、Q、R共线的充要条件是 。

塞瓦(Ceva)定理（塞瓦点）△ABC的三边BC、CA、AB上有点P、Q、R，则AP、BQ、CR共点的充要条件是。

托勒密(Ptolemy)定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。

西姆松(Simson)定理（西姆松线）从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。

例题：1． 设AD是△ABC的边BC上的中线，直线CF交AD于F。

求证：。

【分析】CEF截△ABD→（梅氏定理）【评注】也可以添加辅助线证明：过A、B、D之一作CF的平行线。

2． 过△ABC的重心G的直线分别交AB、AC于E、F，交CB于D。

求证：。

【分析】连结并延长AG交BC于M，则M为BC的中点。

DEG截△ABM→（梅氏定理）DGF截△ACM→（梅氏定理）∴===1【评注】梅氏定理3． D、E、F分别在△ABC的BC、CA、AB边上，，AD、BE、CF交成△LMN。

求S△LMN。

【分析】【评注】梅氏定理4． 以△ABC各边为底边向外作相似的等腰△BCE、△CAF、△ABG。

求证：AE、BF、CG相交于一点。

【分析】【评注】塞瓦定理5． 已知△ABC中，∠B=2∠C。

求证：AC2=AB2+AB·BC。

【分析】过A作BC的平行线交△ABC的外接圆于D，连结BD。

则CD=DA=AB，AC=BD。

由托勒密定理，AC·BD=AD·BC+CD·AB。

【评注】托勒密定理6． 已知正七边形A1A2A3A4A5A6A7。

求证：。

（第21届全苏数学竞赛）【分析】【评注】托勒密定理7． △ABC的BC边上的高AD的延长线交外接圆于P，作PE⊥AB于E，延长ED交AC延长线于F。

求证：BC·EF=BF·CE+BE·CF。

塞瓦定理与梅涅劳斯定理1、比尔逊原理：比尔逊原理又称“比尔逊想象定理”，是指假定有一组有限的事件，并且这些事件之间没有重叠或互斥，那么所有可能出现的各种情况的概率之和恒定为1。

比尔逊原理是事件系统中概率论的基础思想，它可以被应用于大部分的有限的实验，包括随机的事件序列，如随机选择、随机抽样、相似性和易受作用的概率。

2、泊松分布：泊松分布是描述多个事件的发生概率的分布，它是概率论的一种基本概念，用于描述在有限的时间段内某个随机变量发生的次数，又称“先验概率分布”。

在理论上，泊松分布也称为泊松分布和泊松实验，是一种特殊类型的事件/次数统计上的概率分布。

简单来说，泊松分布是以次数或事件数为变量的概率分布，可用来度量一段时间内某事件可能出现的次数。

3、贝叶斯定理：贝叶斯定理是一种基于概率的观点，它将概率视为某事件发生前后条件跳跃的函数，即“后验概率”。

根据贝叶斯定理，在获得新信息后，某事件出现的概率是先验概率（不含新信息前发生概率）乘以后验概率（含新信息后发生概率）再乘以新信息发生概率的总和。

是统计学方法和模型选择的根本原理。

4、高斯概率分布：高斯概率分布（又称正态分布）是数学特殊的概率分布，它可描述连续随机变量的分布特性，可用来表达均值的基本信息。

它的概率密度函数有一个平坦的顶峰，两个参数：平均值μ和标准差σ。

高斯函数可以用来描述一维正太分布，在多维空间中也能被应用。

一般而言，大多数服从正态分布的原始数据集被称为“正态数据”。

5、卡方分布：卡方分布是一种常见的多元概率分布，用于估计能够预测总体参数的把握程度。

在概率统计中，卡方分布是某种指定条件下的概率分布，用于表示实验中不同变量之间的关系，这些变量通常与特定的总体参数相关。

卡方检验可以用来比较两个给定的比较集中水平，以及检验是否存在某种相关性。

6、塞瓦定理：塞瓦定理也称为“互补定理”或“事件定理”，是指某一个事件A发生的概率等于一个二分事件A和B的总概率减去不发生A的概率，即P(A)=P(A+B)-P(B)。

第十讲：梅涅劳斯定理和塞瓦定理一、梅涅劳斯定理定理1若直线l不经过的顶点，并且与的三边或它们的延长线分别交于，则证明：设分别是A、B、C到直线l的垂线的长度，则：。

注：此定理常运用求证三角形相似的过程中的线段成比例的条件。

例1若直角中，CK是斜边上的高，CE是的平分线，E点在AK上，D是AC的中点，F是DE与CK的交点，证明：。

【解析】因为在中，作的平分线BH，则：，，即，所以为等腰三角形，作BC上的高EP，则：，对于和三点D、E、F根据梅涅劳斯定理有：，于是，即，根据分比定理有：，所以，所以。

例2从点K引四条直线，另两条直线分别交直线与A、B、C、D和，试证：。

【解析】若，结论显然成立；若AD与相交于点L，则把梅涅劳斯定理分别用于和可得：，，，，将上面四个式子相乘，可得：，即：定理2设P、Q、R分别是的三边BC、CA、AB上或它们延长线上的三点，并且P、Q、R 三点中，位于边上的点的个数为0或2，这时若，求证P、Q、R三点共线。

证明：设直线PQ与直线AB交于，于是由定理1得：，又因为，则，由于在同一直线上P、Q、R三点中，位于边上的点的个数也为0或2，因此R与或者同在AB线段上，或者同在AB的延长线上；若R 与同在AB线段上，则R 与必定重合，不然的话，设，这时，即，于是可得，这与矛盾，类似地可证得当R 与同在AB的延长线上时，R 与也重合，综上可得：P、Q、R三点共线。

注：此定理常用于证明三点共线的问题，且常需要多次使用再相乘；例3点P 位于的外接圆上；是从点P向BC、CA、AB 引的垂线的垂足，证明点共线。

【解析】易得：，，，将上面三个式子相乘，且因为，，，可得，根据梅涅劳斯定理可知三点共线。

例4设不等腰的内切圆在三边BC、CA、AB上的切点分别为D、E、F，则EF与BC，FD 与CA，DE与AB的交点X、Y、Z在同一条直线上。

【解析】被直线XFE所截，由定理1可得：，又因为，代入上式可得，同理可得，，将上面的式子相乘可得：，又因为X、Y、Z丢不在的边上，由定理2可得X、Y、Z三点共线。

初等几何五大ZB定理某日，燕尾模型讲毕，一六年级学霸级学生说，其可用燕尾模型证梅涅劳斯定理，大惊，问其如何得之，其说：一老师讲的。

六年级学生学梅涅劳斯定理，ZB大于实用。

既然学生感兴趣，咱就一装到底。

一、梅涅劳斯定理梅涅劳斯：古希腊数学家。

梅涅劳斯定理指的是：一条直线（红线）与一个三角形的三边或延长线相交，三角形的三个顶点按顺时针或逆时针方向，三条边顶点到交点的比值的积为1.其证明方法很多，相似三角形即可证明。

下面咱们用小学奥数的“燕尾模型”证明一下。

二、塞瓦定理塞瓦：意大利数学家、水利工程师，该定理于1678年发表于《直线论》一书。

塞瓦定理：可以简单记为三线共点的充要条件是：顺时针或逆时针的分线段的比值积为1.该定理可以用上面的梅涅劳斯定理证明。

三、斯坦纳定理斯坦纳：瑞士几何学家斯坦纳定理：两内角平分线相等的三角形必为等腰三角形。

早在2000多年前，《几何原本》就有定理：等腰三角形的两底角平分线的长相等。

可是它的逆定理书上却只字未提，估计作者也不会，呵呵。

直到1840年，莱默斯请求斯图姆给予纯几何证明，可斯图姆也不会，最后斯坦纳给出了证明，因此该定理也称作：斯坦纳——莱默斯定理。

现在很多高中生也能证明。

大家可以试试有没有难度。

四、托勒密定理托勒密定理:圆内接凸四边形的对边积的和等于对角线的积。

用相似可以证明五、西姆松定理西姆松定理：过三角形外接圆上异于三角形顶点的任意一点作三边所在直线垂线，则三垂足在一点直线上，这条直线我们称作西姆松线。

这些定理一般的中考都不考，一和四和中学的相似联系比较紧密，尽量掌握，培优课上可能会有，感兴趣的同学可以看看。

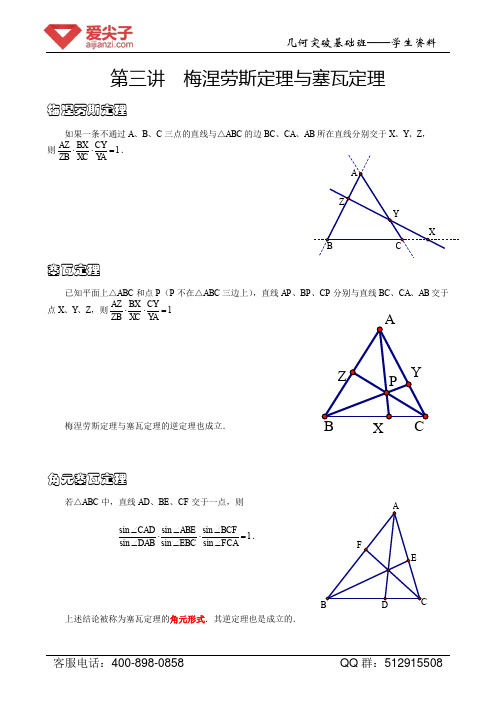
第三讲 梅涅劳斯定理与塞瓦定理梅涅劳斯定理如果一条不通过A 、B 、C 三点的直线与△ABC 的边BC 、CA 、AB 所在直线分别交于X 、Y 、Z ， 则1AZ BX CY ZB XC YA ⋅⋅=．塞瓦定理已知平面上△ABC 和点P （P 不在△ABC 三边上），直线AP 、BP 、CP 分别与直线BC 、CA 、AB 交于点X 、Y 、Z ，则1AZ BX CYZB XC YA⋅⋅=梅涅劳斯定理与塞瓦定理的逆定理也成立．角元塞瓦定理若△ABC 中，直线AD 、BE 、CF 交于一点，则sin sin sin 1sin sin sin CAD ABE BCFDAB EBC FCA∠∠∠⋅⋅=∠∠∠．上述结论被称为塞瓦定理的角元形式．其逆定理也是成立的．例1. 如图，已知△ABC 中，AD 、BE 、CF 交于一点P ．（1）已知54BP PE =，32CP PF =，求BDDC ． （2）已知31AP PD =，43BP PE =，求CPPF． （3）已知74AF FB =，32AE EC =，求APPD．例2. 已知BE 、CF 为△ABC 的两条内角平分线，A ∠的外角平分线与BC 的延长线相交于D ．求证：D 、E 、F 共线．例3. △ABC 中，40BAC ∠=︒，60ABC ∠=︒，点D 、E 分别在AC 、AB 上，40CBD ∠=︒，70BCE ∠=︒，BD 、CF 相交于点F ．求证：AF ⊥BC ．例4. 过△ABC 的顶点A 作外接圆的切线与对边相交于点1A ，类似定义1B 、1C ，证明：1A 、1B 、1C 三点共线．例5. 如图，在△ABC 中，P 为高AD 上一点．延长BP 交AC 于E ，延长CP 交AB 于F ．求证：ADE ADF ∠=∠． A 1C 1'''的三组对应边AB与A B''交于点X，AC与A C''交于点Y，BC与B C''交于例6.如图，△ABC和△A B C点Z，且X、Y、Z三点共线．求证：直线AA'、BB'、CC'相交于一点或相互平行．Array例7.圆内接六边形ABCDEF的三组对边AB和DE、BC和EF、CD和F A所在直线分别交于L、M、N，证明：L、M、N三点共线．L。

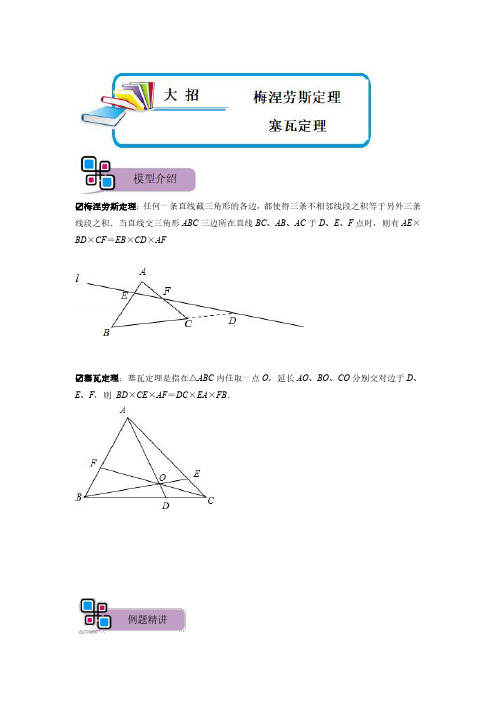
☑梅涅劳斯定理：任何一条直线截三角形的各边，都使得三条不相邻线段之积等于另外三条线段之积．当直线交三角形ABC三边所在直线BC、AB、AC于D、E、F点时，则有AE×BD×CF＝EB×CD×AF☑塞瓦定理：塞瓦定理是指在△ABC内任取一点O，延长AO、BO、CO分别交对边于D、E、F，则BD×CE×AF＝DC×EA×FB．例题精讲考点一：梅涅劳斯定理【例1】．如图，等边△ABC的边长为2，F为AB中点，延长BC至D，使CD＝BC，连接FD交AC于E，则四边形BCEF的面积为．解：∵DEF是△ABC的梅氏线，∴由梅涅劳斯定理得，••＝1，即••＝1，则＝，＝S△ABC，S△CEF＝S△ABC，连FC，S△BCF于是S BCEF＝S△BCF+S△CEF＝S△ABC＝××2×2sin60°＝×＝．故答案为．变式训练【变式1-1】．如图，D、E、F内分正△ABC的三边AB、BC、AC均为1：2两部分，AD、BE、CF相交成的△PQR的面积是△ABC的面积的（）A．B．C．D．解：对△ADC用梅涅劳斯定理可以得：••＝1，则＝．＝，S△BCQ＝S△BCE＝，S BPRF＝S△ABD＝，设S△BCF＝S△BCF﹣S△BCQ﹣S BPRF＝S△ABC．∴S△PQR故选：D．【变式1-2】．梅涅劳斯定理梅涅劳斯（Menelaus）是古希腊数学家，他首先证明了梅涅劳斯定理，定理的内容是：如图（1），如果一条直线与△ABC的三边AB，BC，CA或它们的延长线交于F、D、E三点，那么一定有••＝1．下面是利用相似三角形的有关知识证明该定理的部分过程：证明：如图（2），过点A作AG∥BC，交DF的延长线于点G，则有＝．任务：（1）请你将上述材料中的剩余的证明过程补充完整；（2）如图（3），在△ABC中，AB＝AC＝13，BC＝10，点D为BC的中点，点F在AB 上，且BF＝2AF，CF与AD交于点E，则AE＝6．解：（1）补充的证明过程如下：∵AG∥BD，∴△AGE∽△CDE．∴，∴；（2）根据梅涅劳斯定理得：．又∵，，∴DE＝AE．在Rt△ABD中，AB＝13，BD＝5，∠ADB＝90°，则由勾股定理知：AD＝＝＝12．∴AE＝6．故答案是：6．考点二：塞瓦定理【例2】．如图：P，Q，R分别是△ABC的BC，CA，AB边上的点．若AP，BQ，CR相交于一点M，求证：．证明：如图，由三角形面积的性质，有，，．以上三式相乘，得．变式训练【变式2-1】．请阅读下列材料，并完成相应任务如图，塞瓦定理是指在△ABC内任取一点O，延长AO，BO，CO分别交对边D，E，F 于，则××＝1．任务：（1）当点D，E分别为边BC，AC的中点时，求证：点F为AB的中点；（2）若△ABC为等边三角形，AB＝12，AE＝4，点D是BC边的中点，求BF的长．解：（1）证明：∵D，E分别为边BC，AC的中点，∴BD＝CD，EA＝CE，∴，由塞瓦定理，得，∴，∴AF＝BF，∴点F为AB的中点；（2）解：∵△ABC为等边三角形，AB＝12，∴AB＝AC＝BC＝12，∵AE＝4，∴EC＝12﹣4＝8，∵点D是BC的中点，∴BD＝CD＝6，∵AB＝12，∴AF＝AB﹣BF＝12﹣BF，由赛瓦定理，得，∴，∴BF＝8．【变式2-2】．请阅读下列材料，并完成相应任务塞瓦定理定理内容：如图1，塞瓦定理是指在△ABC内任取一点O，延长AO，BO，CO分别交对边于D，E，F，则．数学意义：使用塞瓦定理可以进行直线形中线段长度比例的计算，其逆定理还可以用来进行三点共线、三线共点等问题的判定方法，是平面几何学以及射影几何学中的一项基本定理，具有重要的作用．任务解决：（1）如图2，当点D，E分别为边BC，AC的中点时，求证：点F为AB的中点；（2）若△ABC为等边三角形（如图3），AB＝12，AE＝4，点D是BC边的中点，求BF 的长，并直接写出△BOF的面积．（1）证明：∵点D，E分别为边BC，AC的中点，∴BD＝CD，CE＝AE，由赛瓦定理可得：，∴，∴AF＝BF，即点F为AB的中点；（2）∵△ABC为等边三角形，AB＝12，∴BC＝AC＝12，∵点D是BC边的中点，∴BD＝DC＝6，∵AE＝4，∴CE＝8，由赛瓦定理可得：BF＝8；△BOF的面积为．1．如图，在△ABC中，M是AC的中点，E是AB上一点，AE＝AB，连接EM并延长，交BC的延长线于D，则＝（）A．B．2C．D．解：如图，过C点作CP∥AB，交DE于P，∵PC∥AE，∴△AEM∽△CPM，∴＝，∵M是AC的中点，∴AM＝CM，∴PC＝AE，∵AE＝AB，∴CP＝AB，∴CP＝BE，∵CP∥BE，∴△DCP∽△DBE，∴＝＝，∴BD＝3CD，∴BC＝2CD，即＝2．故选：B．2．如图，在△ABC中，D、E分别是BC、AC上的点，AD与BE相交于点G，若AG：GD ＝4：1，BD：DC＝2：3，则AE：EC的值是（）A．B．C．D．解：过D作DH∥AC交BE于H，∴△DHG∽△AEG，△BDH∽△CBE，∴，，∴AE＝4DH，CE＝DH，∴，故选：B．3．如图，在△ABC中，AD是BC边上的中线，F是AD边上一点．射线CF交AB于点E，且，则等于．解：如图：过点D作DG∥EC交AB于G，∵AD是BC边上的中线，∴GD是△BEC的中位线，∴BD＝CD，BG＝GE．∵＝，∴＝∵DG∥EC，∴＝＝．故答案是：．4．如图，在△ABC中，点D是AB边上的一点，且AD＝3BD，连接CD并取CD的中点E，连接BE，若∠ACD＝∠BED＝45°，且CD＝6，则AB的长为4．解：如图，取AD中点F EF，过点D作DG⊥EF于G，DH⊥BE于H，设BD＝a，∴AD＝3BD＝3a，AB＝4a，∵点E为CD中点，点F为AD中点，CD＝6，∴DF＝a，EF∥AC，DE＝3，∴∠FED＝∠ACD＝45°，∵∠BED＝45°，∴∠FED＝∠BED，∠FEB＝90°，∵DG⊥EF，DH⊥BE，∴四边形EHDG是矩形，DG＝DH，∴四边形DGEH是正方形，∴DE＝DG＝3，DH∥EF，∴DG＝DH＝3，∵DH∥EF，∴∠BDH＝∠DFG，∴△BDH∽△DFG，∴，∴＝，∴BH＝2，∴BD＝＝＝，∴AB＝4，故答案为：4．5．如图，在△ABC中，∠ACB＝90°，AC＝8，BC＝16，AD是边BC的中线，过点C 作CE⊥AD于点E，连接BE并延长交AC于点F，则AD的长是16，EF的长是．解：过点G作DG∥AC，交BF于点G，∵D为BC的中点，BC＝16，∴CD＝BD＝8，∵∠ACB＝90°，AC＝8，∴AD＝＝16，∴sin∠CAD＝，∴CE＝＝，∴AE＝，∴DE＝AD﹣AE＝4，∵DG∥AC，∴，设DG＝x，则CF＝2x，AF＝，∵DG∥AC，∴∠DGE＝∠AFE，∠EDG＝∠EAF，∴△DEG∽△AEF，∴，即，解得：x＝，∴CF＝2x＝∴BF＝∵，∴，∵，∴EF＝＝．故答案为：16，．6．如图，△ABC中，D、E是BC边上的点，BD：DE：EC＝3：2：1，M在AC边上，CM：MA＝1：2，BM交AD、AE于H、G，则BH：HG：GM等于51：24：10．解：过M作MQ∥BC交AE于N，交AD于F，交AB于Q，∵BD：DE：EC＝3：2：1，∴设EC＝a，DE＝2a，BD＝3a，∵MQ∥BC，∴△AMN∞△ACE，∵CM：MA＝1：2，∴＝＝，∴MN＝a，同理MF＝2a，MQ＝4a，∵MQ∥BC，∴△MNG∽△BEG，∴＝，∴＝＝，∴＝＝同理＝＝＝，＝＝，∴＝，＝＝∴BH：HG：GM＝51：24：10，故答案为：51：24：10．7．如图，▱ABCD的对角线相交于点O，在AB的延长线上任取一点E，连接OE交BC于点F．若AB＝a，AD＝c，BE＝b，则BF＝．解：取AB的中点M，连接OM，∵四边形ABCD是平行四边形，∴AD∥BC，OB＝OD，∴OM∥AD∥BC，OM＝AD＝c，∴△EFB∽△EOM，∴，∵AB＝a，AD＝c，BE＝b，∴ME＝MB+BE＝AB+BE＝a+b，∴，∴BF＝．故答案为：．8．在△ABC中，∠ACB＝90°，AC＝BC，AM为BC边上的中线，CD⊥AM于点D，CD 的延长线交于点，求的值．解：过点B作BF⊥BC，交EC的延长线于点F，∵∠ACB＝90°，AC＝BC，∴∠BCF+∠ACD＝90°，又∵BF⊥BC，CD⊥AM，∴∠BCF+∠F＝90°，∠CAD+∠ACD＝90°，∴∠ACD＝∠F，∠BCF＝∠CAD，∴△ACM≌△CBF（AAS），∴BF＝CM，又∵AM为BC边上的中线，∴BF＝CM＝BC，∵∠AEC＝∠BEF，∴△ACE∽△BFE，∴＝2．9．如图，在△ABC中，M是AC的中点，E、F是BC上的两点，且BE＝EF＝FC，求BN：NQ：QM的值．解：连接MF，如图，∵M是AC的中点，EF＝FC，∴MF为△CEA的中位线，∴AE＝2MF，AE∥MF，∵NE∥MF，∴＝＝1，＝＝，∴BN＝NM，MF＝2NF，设BN＝a，NE＝b，则NM＝a，MF＝2b，AE＝4b，∵AN∥MF，∴＝＝＝，∴NQ＝a，QM＝a，∴BN：NQ：QM＝a：a：a＝5：3：2．10．如图，△ABC中，∠ACB＝90°，CD⊥AB于点D，E为BC上一点，AE交CD于点F，EH⊥AB于点H，若CF＝2FD，EH＝，求CE•BE的值．解：对于△CBD和截线AFE，由梅涅劳斯定理可知：，∵CF＝2FD，∴，∴，易知△ADC∽△EHB，∴，∴，由射影定理可知AC2＝AD•AB，∴BE•CE＝＝＝，∴BE•CE＝4．11．如图，△ABC中，AD⊥BC于点D，E是AB上一点，连接DE，2∠C+∠BDE＝180°．（1）求证：∠BDE＝2∠CAD；（2）若AC＝BD，∠AED＝∠ACB，求证BE＝2CD；（3）若AE＝kBE，BD＝mCD，则的值为．（用含m，k的式子表示）．（1）证明：∵2∠C+∠BDE＝180°，∴∠C+∠BDE＝90°，∵AD⊥BC，∴∠C+∠CAD＝90°，∴∠CAD＝∠BDE，∴∠BDE＝2∠CAD；（2）证明：如图，延长DE至F，使DF＝BD，连接BF，在DB上截取DG＝CD，连接AG，∵AD⊥BC，∴∠ADC＝∠ADG＝90°，在△ADC和△ADG中，，∴△ADC≌△ADG（SAS），∴AG＝AC，∠GAD＝∠CAD，∠AGC＝∠ACB，∴∠CAG＝2∠CAD，∵∠BDF＝2∠CAD，∴∠BDF＝∠CAG，∵AC＝BD，∴AC＝BD＝AG＝DF，∴△BDF≌△CAG（SAS），∴BF＝CG，∠DFB＝∠AGC＝∠ACB，∵∠AED＝∠ACB，∠AED＝∠BEF，∴∠DFB＝∠BEF，∴BF＝BE，∴BE＝CG，∵CG＝2CD，∴BE＝2CD；（3）解：如图，记AG与DE的交点为H，设CD＝y，则BD＝my，延长DE至F，使DF＝BD＝my，连接BF，在DB上截取DG＝CD＝y，连接AG，则CG＝CD＝2y，由（2）知，△ADC≌△ADG，∴AC＝AG，∠CAD＝∠GAD，∴∠CAG＝2∠CAD，由（1）知，∠BDE＝2∠CAD，∴∠BDE＝∠CAG，∵DF＝BD，AC＝AG，∴，∵△DBF∽△ACG，∴∠DBF＝∠AGC，∴AG∥BF，∴△DHG∽△DFB，∴，∴DH＝DG＝y，∵AG∥BF，∴△BEF∽△AEH，∴，∵AE＝kBE，∴＝＝，∴EH＝kEF，∵DF＝DH+EH+EF＝y+kEF+EF＝my，∴EF＝，∴EH＝，∴DE＝EH+DH＝+y＝，∴＝＝，故答案为：．12．如图1，Rt△ABC中，∠BAC＝90°，AD是中线，BE⊥AD，垂足为E，点F在AD上，∠ACF＝∠DBE．（1）求证：∠ABD＝∠CFD；（2）探究线段AF，DE的数量关系，并证明你的结论；（3）如图2，延长BE交CF于点P，AB＝AF，求的值．（1）证明：设∠DBE＝∠CFD＝α，∵BE⊥AD，∴∠BED＝90°，∴∠ADB+α＝90°，又∵∠BAC＝90°，AD是中线，∴AD＝BD＝CD，∴∠BAD＝∠ABD，∴∠ADB+2∠BAD＝180°，∴2∠BAD＝90°+α，又∵∠CFD＝∠DAC+∠ACF＝∠DAC+α＝90°﹣∠BAD+α＝2∠BAD﹣∠BAD＝∠BAD，∵∠ABD＝∠BAD，∴∠ABD＝∠CFD；（2）解：AF＝2DE．理由：过点C作CM⊥AD交AD的延长线于点M，∵AD是中线，∴BD＝CD，∵∠CMD＝∠BED＝90°，∠CDM＝∠BDE，∴△CDM≌△BDE（AAS），∴DM＝DE，CM＝BE，又∵∠BAD＝∠CFM，∠AEB＝∠CMF，∴△CMF≌△BEA（AAS），∴AE＝MF，∴AE﹣EF＝MF﹣EF，∴AF＝EM，又∵EM＝2DE，∴AF＝2DE；（3）解：过点C作CM⊥AD交AD的延长线于点M，由（2）可知，AF＝2DE，AD＝CD，设DE＝x，则AF＝2x，∵AB＝AF，∴AB＝2x，∴AB＝2x，设EF＝y，∴AE＝y+2x，AD＝CD＝y+3x，由（2）可知，BE＝CM，∴AB2﹣AE2＝CD2﹣DM2，∴＝（y+3x）2﹣x2，解得y＝3x，y＝﹣8x（舍去），∴AE＝5x，∵∠BDE＝∠CFE，∠AEB＝∠PEF，∴△BEA∽△PEF，∴．13．如图1，△ABC中，AB＝AC，点D在BA的延长线上，点E在BC上，DE＝DC，点F 是DE与AC的交点，且DF＝FE．（1）图1中是否存在与∠BDE相等的角？若存在，请找出，并加以证明，若不存在，说明理由；（2）求证：BE＝EC；（3）若将“点D在BA的延长线上，点E在BC上”和“点F是DE与AC的交点，且DF＝FE”分别改为“点D在AB上，点E在CB的延长线上”和“点F是ED的延长线与AC的交点，且DF＝kFE”，其他条件不变（如图2）．当AB＝1，∠ABC＝a时，求BE的长（用含k、a的式子表示）．解：（1）∠DCA＝∠BDE．证明：∵AB＝AC，DC＝DE，∴∠ABC＝∠ACB，∠DEC＝∠DCE．∴∠BDE＝∠DEC﹣∠DBC＝∠DCE﹣∠ACB＝∠DCA．（2）过点E作EG∥AC，交AB于点G，如图1，则有∠DAC＝∠DGE．在△DCA和△EDG中，∴△DCA≌△EDG（AAS）．∴DA＝EG，CA＝DG．∴DG＝AB．∴DA＝BG．∵AF∥EG，DF＝EF，∴DA＝AG．∴AG＝BG．∵EG∥AC，∴BE＝EC．（3）过点E作EG∥AC，交AB的延长线于点G，如图2，∵AB＝AC，DC＝DE，∴∠ABC＝∠ACB，∠DEC＝∠DCE．∴∠BDE＝∠DBC﹣∠DEC＝∠ACB﹣∠DCE＝∠DCA．∵AC∥EG，∴∠DAC＝∠DGE．在△DCA和△EDG中，∴△DCA≌△EDG（AAS）．∴DA＝EG，CA＝DG∴DG＝AB＝1．∵AF∥EG，∴△ADF∽△GDE．∴．∵DF＝kFE，∴DE＝EF﹣DF＝（1﹣k）EF．∴．∴AD＝．∴GE＝AD＝．过点A作AH⊥BC，垂足为H，如图2，∵AB＝AC，AH⊥BC，∴BH＝CH．∴BC＝2BH．∵AB＝1，∠ABC＝α，∴BH＝AB•cos∠ABH＝cosα．∴BC＝2cosα．∵AC∥EG，∴△ABC∽△GBE．∴．∴．∴BE＝．∴BE的长为．14．阅读以下材料，并按要求完成相应的任务．塞瓦（GiovanniCeva，1648～1734）意大利水利工程师，数学家，塞瓦定理载于1678年发表的《直线论》一书，塞瓦定理是指如图1，在△ABC内任取一点O，延长AO，BO，CO分别交对边于D，F，E，则．下面是该定理的部分证明过程：如图2，过点A作BC的平行线分别交BE，CF的延长线于点M，N．则∠N＝∠FCB，∠NAF＝∠FBC．∴△NAF∽△CBF．∴①．同理可得△NOA∽△COD．∴②．任务一：（1）请分别写出与△MOA，△MEA相似的三角形；（2）写出由（1）得到的比例线段；任务二：结合①②和（2），完成该定理的证明；任务三：如图3，△ABC中，∠ACB＝90°，AC＝4，BC＝3，CD⊥AB，垂足为D，点E 为DC的中点，连接AE并延长，交BC于点F，连接BE并延长，交AC于点G．小明同学自学了上面定理之后解决了如图3所示的问题，并且他用所学知识已经求出了BF与FC的比是25：16，请你直接写出△ECG与△EAG面积的比．解：任务一：（1）△MOA∽△BOD；△MEA∽△BEC；（2）；；任务二：证明：如图所示：由任务一可得：；；同理可得△OAN∽△ODC；△AFN∽△BFC；∴；；∴；∴．任务三：由任务一和任务二可得：在△ABC中，＝；∵Rt△ABC中，AC＝4，BC＝3，∴AB＝；∴cos∠BAC＝；∴；∴AD＝；∴BD＝AB﹣AD＝；∵＝1；∴＝1；解得＝；过点E作EH⊥AC于H；∴＝＝＝．15．问题提出如图（1），在△ABC中，AB＝AC，D是AC的中点，延长BC至点E，使DE＝DB，延长ED交AB于点F，探究的值．问题探究（1）先将问题特殊化．如图（2），当∠BAC＝60°时，直接写出的值；（2）再探究一般情形．如图（1），证明（1）中的结论仍然成立．问题拓展如图（3），在△ABC中，AB＝AC，D是AC的中点，G是边BC上一点，＝（n＜2），延长BC至点E，使DE＝DG，延长ED交AB于点F．直接写出的值（用含n的式子表示）．解：（1）如图，取AB的中点G，连接DG，∵点D是AC的中点，∴DG是△ABC的中位线，∴DG∥BC，∵AB＝AC，∠BAC＝60°，∴△ABC是等边三角形，∵点D是AC的中点，∴∠DBC＝30°，∵BD＝ED，∴∠E＝∠DBC＝30°，∴DF⊥AB，∵∠AGD＝∠ADG＝60°，∴△ADG是等边三角形，∴AF＝AG，∵AG＝AB，∴AF＝AB，∴；（2）取BC的中点H，连接DH，∵点D为AC的中点，∴DH∥AB，DH＝AB，∵AB＝AC，∴DH＝DC，∴∠DHC＝∠DCH，∵BD＝DE，∴∠DBH＝∠DEC，∴∠BDH＝∠EDC，∴△DBH≌△DEC（ASA），∴BH＝EC，∴，∵DH∥AB，∴△EDH∽△EFB，∴，∴，∴；问题拓展取BC的中点H，连接DH，由（2）同理可证明△DGH≌△DEC（ASA），∴GH＝CE，∴HE＝CG，∵＝，∴，∴，∴，∵DH∥BF，∴△EDH∽△EFB，∴，∵DH＝AB，∴，∴．16．阅读下面材料，完成（1）﹣（3）题数学课上，老师出示了这样一道题：如图1，△ABC中，∠BAC＝90°，点D、E在BC上，AD＝AB，AB＝kBD（其中＜k＜1）∠ABC＝∠ACB+∠BAE，∠EAC的平分线与BC相交于点F，BG⊥AF，垂足为G，探究线段BG与AC的数量关系，并证明．同学们经过思考后，交流了自己的想法：小明：“通过观察和度量，发现∠BAE与∠DAC相等．”小伟：“通过构造全等三角形，经过进一步推理，可以得到线段BG与AC的数量关系．”……老师：“保留原题条件，延长图中的BG，与AC相交于点H（如图2），可以求出的值．”（1）求证：∠BAE＝∠DAC；（2）探究线段BG与AC的数量关系（用含k的代数式表示），并证明；（3）直接写出的值（用含k的代数式表示）．证明：（1）∵AB＝AD，∴∠ABD＝∠ADB，∵∠ADB＝∠ACB+∠DAC，∠ABD＝∠ABC＝∠ACB+∠BAE，∴∠BAE＝∠DAC，（2）设∠DAC＝α＝∠BAE，∠C＝β，∴∠ABC＝∠ADB＝α+β，∵∠ABC+∠C＝α+β+β＝α+2β＝90°，∠BAE+∠EAC＝90°＝α+∠EAC，∴∠EAC＝2β，∵AF平分∠EAC，∴∠FAC＝∠EAF＝β，∴∠FAC＝∠C，∠ABE＝∠BAF＝α+β，∴AF＝FC，AF＝BF，∴AF＝BC＝BF，∵∠ABE＝∠BAF，∠BGA＝∠BAC＝90°，∴△ABG∽△BCA，∴∵∠ABE＝∠BAF，∠ABE＝∠ADB，∴△ABF∽△DBA，∴，且AB＝kBD，AF＝BC＝BF，∴k＝，即，∴（3）∵∠ABE＝∠BAF，∠BAC＝∠AGB＝90°，∴∠ABH＝∠C，且∠BAC＝∠BAC，∴△ABH∽△ACB，∴，∴AB2＝AC×AH设BD＝m，AB＝km，∵，∴BC＝2k2m，∴AC＝＝km，∴AB2＝AC×AH，（km）2＝km×AH，∴AH＝，∴HC＝AC﹣AH＝km﹣＝，∴。

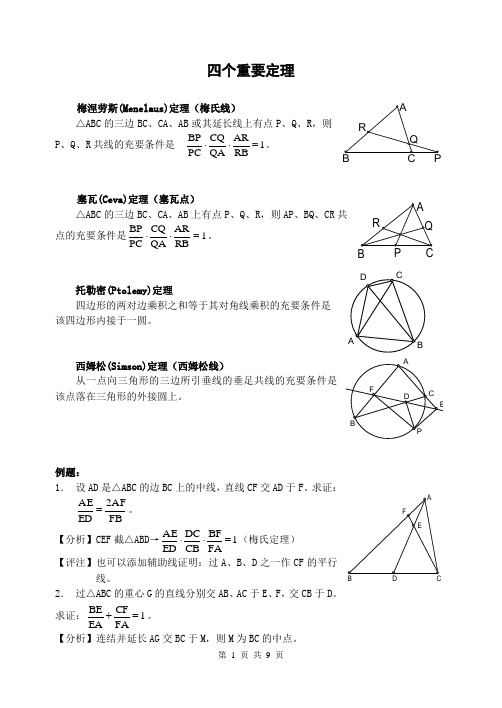
四个重要定理梅涅劳斯(Menelaus)定理（梅氏线）△ABC 的三边BC 、CA 、AB 或其延长线上有点P 、Q 、R ，则P 、Q 、R 共线的充要条件是 1RBARQA CQ PC BP =⋅⋅。

塞瓦(Ceva)定理（塞瓦点）△ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ，则AP 、BQ 、CR 共点的充要条件是1RBARQA CQ PC BP =⋅⋅。

托勒密(Ptolemy)定理四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。

西姆松(Simson)定理（西姆松线）该点落在三角形的外接圆上。

例题：1． 设AD 是△ABC 的边BC 上的中线，直线CF 交AD 于F 。

求证：FBAF2ED AE =。

【分析】CEF 截△ABD →1FABFCB DC ED AE =⋅⋅（梅氏定理） 【评注】也可以添加辅助线证明：过A 、B 、D 之一作CF 的平行线。

2． 过△ABC 的重心G 的直线分别交AB 、AC 于E 、F ，交CB 于D 。

求证：1FACFEA BE =+。

【分析】连结并延长AG 交BC 于M ，则M 为BC 的中点。

DEG 截△ABM →1DB MDGM AG EA BE =⋅⋅（梅氏定理） DGF 截△ACM →1DCMDGM AG FA CF =⋅⋅（梅氏定理）∴FA CF EA BE +=MDAG )DC DB (GM ⋅+⋅=MD GM 2MD 2GM ⋅⋅=1【评注】梅氏定理3． D 、E 、F 分别在△ABC 的BC 、CA 、AB 边上，λ===EACEFB AF DC BD ，AD 、BE 、CF 交成△LMN 。

求S △LMN 。

【分析】【评注】梅氏定理4． 以△ABC 各边为底边向外作相似的等腰△BCE 、△CAF 、△ABG 。

求证：AE 、BF 、CG 相交于一点。

【分析】【评注】塞瓦定理5． 已知△ABC 中，∠B=2∠C 。

梅涅劳斯定理：如果一条直线与ABC △的三边AB 、BC 、CA 或其延长线交于F 、D 、E 点，那么1AF BD CE FB DC EA⋅⋅=．这条直线叫ABC △的梅氏线，ABC △叫梅氏三角形．证法一：如左图，过C 作CG ∥DF ∵DB FB DC FG =，EC FG AE AF =∴1AF BD CE AF FB FG FB DC EA FB FG AF⋅⋅=⋅⋅=．证法二：如中图，过A 作AG BD ∥交DF 的延长线于G ∴AF AG FB BD =，BD BD DC DC =，CE DC EA AG=三式相乘即得：1AF BD CE AG BD DC FB DC EA BD DC AG ⋅⋅=⋅⋅=．证法三：如右图，分别过A B C 、、作DE 的垂线，分别交于123H H H 、、．则有123AH BH CH ∥∥，所以3122311CH AH BH AF BD CE FB DC EA BH CH AH ⋅⋅=⋅⋅=．梅涅劳斯定理的逆定理：若F 、D 、E 分别是ABC △的三边AB 、BC 、CA 或其延长线的三点，如果1AF BD CE FB DC EA⋅⋅=，则F 、D 、E 三点共线．知识点睛模块一梅涅劳斯定理和逆定理相似——塞瓦定理、梅涅劳斯定理【例1】如图，在△ABC 中，D 为BC 的中点，AE ：EF ：FD=4：3：1．求AG ：GH ：AB．【例2】如图，在△ABC 中，∠A 的外角平分线与边BC 的延长线交于点P ，∠B 的平分线与边CA 交于点Q ，∠C 的平分线与边AB 交于点R ，求证：P 、Q 、R三点共线．【巩固】过△ABC 的重心G 的直线分别交AB 、AC 于点E 、F ，交CB 的延长线于点D ．求证：1=+F A CF EA BE。

典型例题塞瓦定理：如果ABC △的三个顶点与一点P 的连线AP 、BP 、CP 交对边或其延长线于点D 、E 、F ，如图，那么1BD CE AF DC EA FB⋅⋅=．通常称点P 为ABC △的塞瓦点．证明：∵直线FPC 、EPB 分别是ABD △、ACD △的梅氏线，∴1BC DP AF CD PA FB ⋅⋅=，1DB CE AP BC EA PD ⋅⋅=．两式相乘即可得：1BD CE AF DC EA FB⋅⋅=．塞瓦定理的逆定理：如果点D 、E 、F 分别在ABC △的边BC 、CA 、AB 上或其延长线上，并且1BD CE AF DC EA FB⋅⋅=，那么AD 、BE 、CF相交于一点（或平行）．证明：⑴若AD 与BE 相交于一点P 时，如图，作直线CP 交AB 于'F ．由塞瓦定理得：'1BD CE AF DC EA F B ⋅⋅='，又已知1BD CE AF DC EA FB ⋅⋅=，∴AF AF FB F B '='，∴AB AB FB F B='，∴FB F B '=．∴'F 与F 重合∴'CF 与CF ∴AD 、BE 、CF 相交于一点．⑵若AD 与BE 所在直线不相交，则AD ∥BE ，如图．∴BD EA DC AC =，又已知1BD CE AF DC EA FB ⋅⋅=，∴1EA CE AF AC EA FB ⋅⋅=，即CE FB AC AF=．∴//BE FC ，∴AD BE FC ∥∥．说明：三线平行的情况在实际题目中很少见．知识点睛模块二塞瓦定理及其逆定理【例3】如果梯形ABCD 的两腰AD 、BC 的延长线交于M ，两条对角线交于N ．求证：直线MN 必平分梯形的两底．【例4】（1）设AX BY CZ ，，是ABC △的三条中线，求证：AX BY CZ ，，三线共点．（2）若AX BY CZ ，，为ABC △的三条内角平分线．求证：AX BY CZ ，，三线共点．【巩固】如图，M 为△ABC 内的一点，BM 与AC 交于点E ，CM 与AB 交于点F ，若AM 通过BC 的中点D ，求证：EF//BC．典型例题【例5】（1）如图1，若O 是△ABC 的重心（），连结AO 并延长交BC 于D ，证明：21=AD AO （2）如图2，若O 是△ABC 的重心，若AB ＝5，点G 从A 出发，在AB 边上以每秒一个单位的速度向B 运动，运动时间为t 秒，连GO ，直线GO 交直线AC 与H 点（G 、H 均不与△ABC 的顶点重合）.求OHGO （用含有t的式子表示）【例6】△ABC 中，D 、E 分别为BC 、AC 边上的动点，BD=mCD ，AE=nEC ，AD 与BE 相交于点O ．（1）如图1，当m=2，n=1时，BE OB =___________，CDOES AOE S 四△=___________；（2）当m=1.5时，求证：CEAE OD OA 35=；（3）如图2，若CO 的延长线交AGB 于点F ，当m 、n 之间满足关系式时，AF=2BF ．（直接填写结果，不要求证明）能力提升【例7】已知：线段OA ⊥OB ，点C 为OB 中点，D 为线段OA 上一点．连接AC ，BD 交于点P ．（1）如图1，当OA=OB ，且D 为OA 中点时，求PCAP 的值；（2）如图2，当OA=OB ，且41=AO AD 时，求APAD 的值．（3）如图3，当AD ：AO ：OB=1：n ：n 2时，直接写出AP AD 的值．【习题1】在△ABC 中，AD ：BD=1：1，AE ：CE=1：2，BE 与CD 交于点P ，则BP ：PE=（）A ．2：1B ．1：2C ．2：3D ．3：2【习题2】如图，已知ABC ∆中，:1:3AE EB =，:2:1BD DC =，AD 与CE 相交于F ，则EF AF FC FD +的值为（）A.52 B.1 C.32D.2真题赏析课后作业【习题3】如图，△ABC 中，D 为BC 的中点，E 为AC 上任意一点，BE 交AD 于O ．某同学在研究这一问题时，发现了如下事实：①当11121+==AC AE 时，有21232+==AD AO ；②当21131+==AC AE 时，有222+=AD AO ；③当31141+==AC AE 时，有322+=AD AO ；…；则当111=AC AE 时，AD AO =（）A ．51B ．112C ．61D ．132【习题4】如图，点D 、E 分别在ABC △的边AC 、AB 上，AE EB =，23AD DC =，BD 与CE 交于点F ，40ABC S =△．求AEFD S ．【习题5】若AX BY CZ ，，分别为锐角ABC △的三条高线，求证：AX BY CZ ，，三线共点．【习题6】在直角梯形ABCD中，AD∥BC，∠ABC=90°，AD+BC=CD，E为CD上一点，且DE=DA．（1）如图1，作EF⊥AB于F，交AC于M试说明ME，MF的数量关系并说明理由；（2）如图2，连接DF、CF，求证：∠DFE=∠CFE;（3）如图3，连接BE延长交AD的延长线于G，若E点到AB的距离为85，则1BC+1DG的值为____（直接写出结果，不解答）．。

第 1 页板块一 梅涅劳斯定理及其逆定理梅涅劳斯定理：如果一条直线与ABC △的三边AB 、BC 、CA 或其延长线交于F 、D 、E 点，那么1AF BD CE FB DC EA⋅⋅=．这条直线叫ABC △的梅氏线，ABC △叫梅氏三角形．证法一：如左图，过C 作CG ∥DF证法二：如中图，过A 作AG BD ∥交DF 的延长线于G三式相乘即得：1AF BD CE AG BD DCFB DC EA BD DC AG⋅⋅=⋅⋅=．证法三：如右图，分别过A B C 、、作DE 的垂线，分别交于123H H H 、、． 则有123AH BH CH ∥∥，所以3122311CH AH BH AF BD CE FB DC EA BH CH AH ⋅⋅=⋅⋅=．梅涅劳斯定理的逆定理：若F 、D 、E 分别是ABC △的三边AB 、BC 、CA 或其延长线的三点，如果1AF BD CE FB DC EA⋅⋅=，则F 、D 、E 三点共线．【例1】 如图，在ABC △中，AD 为中线，过点C 任作一直线交AB 于点F ，交AD 于点E ，求证：:2:AE ED AF FB =．【解析】 ∵直线FEC 是ABD △的梅氏线，∴1AE DC BF ED BC FA ⋅⋅=． 而12DC BC =，∴112AE BF ED FA ⋅⋅=，即2AE AF ED BF=． 习题1. 在△ABC 中，D 是BC 的中点，经过点D 的直线交AB 于点E ，交CA 的延长线于点F ．求证：FA EAFC EB=． 【解析】 直线截ABC △三边于D 、E 、F 三点，应用梅氏定理，知1CD BE AFDB EA FC⋅⋅=，又因为BD BC =，所以1BE AF EA FC ⋅=，即FA EAFC EB=． 习题2. 如图，在△ABC 中， 90ACB ∠=︒，AC BC =．AM 为BC 边上的中线，CD AM ⊥于点D ，CD 的延长线交AB 于点E ．求AEEB． 【解析】 由题设，在Rt AMC △中，CD AM ⊥，2AC CM =，由射影定理224AD AD AM AC DM DM AM CM⋅===⋅． 对ABM △和截线EDC ，由梅涅劳斯定理，1AE BC MD EB CM DA ⋅⋅=，即21114AE EB ⋅⋅=．所以2AE EB=．知识导航夯实基础梅涅劳斯定理与塞瓦定理【例2】 如图，在ABC △中，D 为AC 中点，BE EF FC ==，求证：::5:3:2BM MN ND =． 【解析】 ∵直线AE 是BCD △的梅氏线，∵直线AF 是BCD △的梅氏线，习题3. 如图，在ABC △中，D 为BC 的中点，::4:3:1AE EF FD =．求::AG GH AB ． 【解析】 ∵HFC 是ABD △的梅氏线，∵D 为BC 的中点，::4:3:1AE EF FD =， ∵GEC 是ABD △的梅氏线，【例3】 过ABC △的重心G 的直线分别交AB 、AC 于点E 、F ，交CB 的延长线于点D ．求证：1BE CFEA FA+=． 【解析】 作直线AG 交BC 于M ，同理，2CF DCFA DM=， 而2BD DC BD BD BM +=++2()2BD BM DM =+=【例4】 如图，点D 、E 分别在ABC △的边AC 、AB 上， AE EB =，23AD DC =，BD 与CE 交于点F ，40ABC S =△．求AEFD S ．【解析】 对ECA △和截线BFD ，由梅氏定理得：1EF CD AB FC DA BE ⋅⋅=，即32121EF FC ⋅⋅=，所以13EF FC =．所以1148BFE BEC ABC S S S ==△△△，进而211140115840AEFD ABD BEF ABC S S S S ⎛⎫=-=-=⋅= ⎪⎝⎭△△△． 习题4. 如图，在ABC △中，三个三角形面积分别为5，8，10．四边形AEFD 的面积为x ，求x的值．【解析】 对ECA △和截线BFD ，由梅氏定理得：1CD AB EF DA BE FC ⋅⋅=，即1823115152x x +⋅⋅=+，解得22x =．【备选】如图，ABC △被通过它的三个顶点与一个内点O 的三条直线分为6个小三角形，其中三个小三角形的面积如图所示，求ABC △的面积．【解析】 对ABD △和截线COF ，由梅氏定理得：1AF BC DO FB CD OA ⋅⋅=，即41132BC CD ⋅⋅=，所以32BC CD =，所以3BCBD=．所以33105315ABC ABD S S ==⨯=△△．【例5】 如图， 在ABC △中，A ∠的外角平分线与边BC 的延长线交于点P ，B ∠的平分线与边CA 交于点Q ，C ∠的平分线与边AB 交于点R ，求证：P 、Q 、R 三点共线．【解析】 AP 是BAC ∠的外角平分线，则BQ 是ABC ∠的平分线，则 CR 是ACB ∠的平分线，则 ⨯⨯①②③得非常挑战探索提升第 3 页因R 在AB 上，Q 在CA 上，P 在BC 的延长线上，则根据梅涅劳斯定理的逆定理得：P 、Q 、R 三点共线．习题5. 证明：不等边三角形的三个角的外角平分线与对边的交点是共线的三个点． 【解析】 如图，CD BE AF 、、分别为三角形ABC 的三个外角平分线，分别交AB AC BC 、、于D E F 、、．过C 作BE 的平行线，则BCP CBE EBD CPB ∠=∠=∠=∠， 所以BPC △是等腰三角形．则PB CB =．则有：CE PB CBEA BA BA ==． 同理AD AC DB CB =；BF BA FC AC=． 所以1CE AD BF CB AC BA EA DB FC BA CB AC ⋅⋅=⋅⋅=．所以D E F 、、共线．板块二 塞瓦定理及其逆定理塞瓦定理：如果ABC △的三个顶点与一点P 的连线AP 、BP 、CP 交对边或其延长线于点D 、E 、F ，如图，那么1BD CE AFDC EA FB⋅⋅=．通常称点P 为ABC △的塞瓦点． 证明： ∵直线FPC 、EPB 分别是ABD △、ACD △的梅氏线，两式相乘即可得：1BD CE AFDC EA FB⋅⋅=．塞瓦定理的逆定理：如果点D 、E 、F 分别在ABC △的边BC 、CA 、AB 上或其延长线上，并且1BD CE AF DC EA FB⋅⋅=，那么AD 、BE 、CF 相交于一点（或平行）． 证明： ⑴ 若AD 与BE 相交于一点P 时，如图，作直线CP 交AB 于'F ．由塞瓦定理得：'1BD CE AF DC EA F B⋅⋅='，又已知1BD CE AF DC EA FB ⋅⋅=，∴AF AF FB F B'='， ∴'F 与F 重合 ∴'CF 与CF 重合∴AD 、BE 、CF 相交于一点．⑵ 若AD 与BE 所在直线不相交，则AD ∥BE ，如图． ∴BD EA DC AC=，又已知1BD CE AF DC EA FB ⋅⋅=， ∴1EA CE AF AC EA FB ⋅⋅=，即CE FB AC AF=． 说明：三线平行的情况在实际题目中很少见．【例6】 （1）设AX BY CZ ，，是ABC △的三条中线，求证：AX BY CZ ，，三线共点．探索提升知识导航（2）若AX BY CZ ，，为ABC △的三条内角平分线．求证：AX BY CZ ，，三线共点．【解析】 （1）由条件知，BX XC YC YA ZA ZB ===，，．∴1BX CY AZXC YA ZB⋅⋅=，根据塞瓦定理的逆定理可得三条中线AX BY CZ ，，共点． 这个点称为这个三角形的重心．（2）由三角形内角平分线定理得：BX AB CY BC AZ ACXC AC YA BA ZB BC===，，． 三式分别相乘，得：1BX CY AZ AB BC ACXC YA ZB AC AB BC⋅⋅=⋅⋅=．根据塞瓦定理的逆定理可得三角形三内角平分线AX BY CZ ，，共点， 这个点称为这个三角形的内心．习题6. 若AX BY CZ ，，分别为锐角ABC △的三条高线，求证：AX BY CZ ，，三线共点．【解析】 由ABX CBZ △∽△得：BX AB BZ BC =；由BYA CZA △∽△得：AZ ACAY AB =； 由AXC BYC △∽△可得：YC BC CX AC =．所以1BX AZ YC AB AC BCBZ AY CX BC AB AC⋅⋅=⋅⋅=．根据塞瓦定理的逆定理可得三条高线AX BY CZ ，，共点．对直角三角形、钝角三角形，同样也可以证得三条高线共点．我们把一个三角形三条高线所在直线的交点叫做这个三角形的垂心．【例7】 如图， M 为ABC △内的一点，BM 与AC 交于点E ，CM 与AB 交于点F ，若AM 通过BC 的中点D ，求证：EF BC ∥．【解析】 对ABC △和点M 应用塞瓦定理可得：1AF BD CEFB DC EA⋅⋅=．又因为BD DC =，所以1AF CE FB EA ⋅=．进而AF AEFB EC=，所以EF BC ∥． 习题7. 如果梯形ABCD 的两腰AD 、BC 的延长线交于M ，两条对角线交于N ．求证：直线MN必平分梯形的两底． ∵1MD AQ BC DA QB CM⋅⋅=（由塞瓦定理得） 板块三 梅涅劳斯定理、塞瓦定理综合【备选】如图，E 、F 分别为ABC △的AC 、AB 边上的点，且3AE EC =，3BF FA =，BE 、CF 交于点P ，AP 的延长线交BC 于点D ．求:AP PD 的值．【解析】 ∵P 为ABC △的塞瓦点．∵EPB 为ACD △的梅氏线，【备选】如图，四边形ABCD 的对边AB 和DC ，DA 和CB 分别相交于点L K ，，对角线AC 与BD 交于点M ．直线KL 与BD 、AC 分别交于点F G 、．求证：KF KGLF LG=． 【解析】 对DKL △与点B 应用塞瓦定理得：1DA KF LCAK FL CD⋅⋅=．对DKL △和截线ACG 应用梅涅劳斯定理可得：1DA KG LCAK GL CD⋅⋅=．非常挑战进而可得KF KGLF LG．第 5 页。

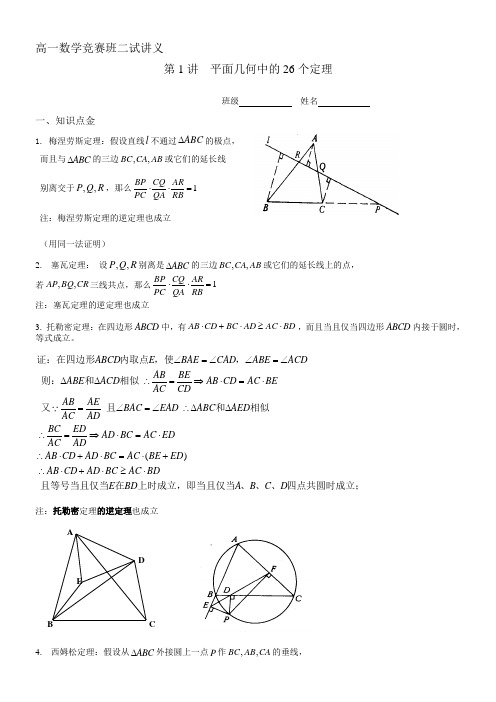
ED C B A 高一数学竞赛班二试讲义第1讲 平面几何中的26个定理班级 姓名一、知识点金1. 梅涅劳斯定理：假设直线l 不通过ABC ∆的极点，而且与ABC ∆的三边,,BC CA AB 或它们的延长线别离交于,,P Q R ，那么1BP CQ AR PC QA RB⋅⋅= 注：梅涅劳斯定理的逆定理也成立（用同一法证明）2. 塞瓦定理： 设,,P Q R 别离是ABC ∆的三边,,BC CA AB 或它们的延长线上的点，若,,AP BQ CR 三线共点，那么1BP CQ AR PC QA RB⋅⋅= 注：塞瓦定理的逆定理也成立3. 托勒密定理：在四边形ABCD 中，有AB CD BC AD AC BD ⋅+⋅≥⋅，而且当且仅当四边形ABCD 内接于圆时，等式成立。

()ABCD E BAE CAD ABE ACDAB BE ABE ACD AB CD AC BE AC CD AB AE BAC EAD ABC AED AC ADBC ED AD BC AC ED AC ADAB CD AD BC AC BE ED AB CD AD BC AC BD E BD A B C D ∠=∠∠=∠∆∆∴=⇒⋅=⋅=∠=∠∴∆∆∴=⇒⋅=⋅∴⋅+⋅=⋅+∴⋅+⋅≥⋅证：在四边形内取点，使，则：和相似又且和相似且等号当且仅当在上时成立，即当且仅当、、、四点共圆时成立；注：托勒密定理的逆定理也成立4. 西姆松定理：假设从ABC ∆外接圆上一点P 作,,BC AB CA 的垂线，垂足别离为,,D E F ，那么,,D E F 三点共线。

西姆松定理的逆定理：从一点P 作,,BC AB CA 的垂线，垂足别离为,,D E F 。

假设,,D E F 三点共线，那么点P 在ABC ∆的外接圆上。

5． 蝴蝶定理：圆O 中的弦PQ 的中点M ，过点M 任作两弦AB ，CD ，弦AD 与BC 别离交PQ 于X ，Y ，那么M 为XY 当中点。

塞瓦定理和梅涅劳斯定理的一种向量证法塞瓦定理和梅涅劳斯定理是初等几何中非常重要的定理，它们分别描述了三角形内部一点与三边的关系和两个三角形内部对应线段的关系。

虽然它们的证明有很多种不同的方法，但本文将介绍一种基于向量的证明方法，以期拓展读者对几何证明方法的认识。

塞瓦定理：三角形ABC内部一点D，BD与AC交于E，CE与AB交于F，则有AD/DB· BE/EC· CF/FA = 1。

我们首先将向量法中的一些重要定义列举如下：· 向量的加减法：若有向量a和向量b，则它们的和定义为a+b，差定义为a-b。

若有向量a和向量b，则它们的数量积定义为a·b=|a||b|cosθ，其中θ为a与b之间的夹角，|a|和|b|分别为它们的模长。

接下来，我们对塞瓦定理进行证明。

证明过程如下：设向量AD为a，向量BD为b，向量BE为c，向量CE为d，向量CF为e，向量AF为f。

则有：a=b+cc=d+ee=f+a将三个等式代入AD/DB· BE/EC· CF/FA = 1中，得：（b+c)/b· c/(d+e)· f/(c+a) = 1移项化简，得：将向量的数量积和叉积运算带入上式，得：由向量的分配律和叉积的结合律，得：(b×c + c×c)×f = b×d×c + b×e×c + c×c×a由向量的叉积运算，可将左边化简为：(b×c)×f+c×(c×f)由于向量的叉积满足a×b=-b×a，因此有：所以，左边可以进一步化简为：将右边的三项分别化简为：b×d×c = -b×c×d因此，右边可化为：通过化简，可以得到：再运用三角形相似的性质，即在三角形ABD和三角形EFC中可知，有：DB / AD = EC / EF由于有d+e=DC，DF+EF=FC，因此可以进一步化简为：根据相似三角形的性质，可知：合并式子，得：以上证明中，我们使用了向量的加减法、数量积和叉积，运用向量的运算性质和三角形的相似性质推导出了塞瓦定理。

第十讲：梅涅劳斯定理和塞瓦定理一、梅涅劳斯定理定理1若直线l不经过ABC的顶点,并且与ABC的三边BC、CA、AB或它们的延长线分别交于P 、Q、R,则BPPC CQQAARRB=1证明：设ℎA、ℎB、ℎC分别是A、B、C到直线l的垂线的长度,则：BPPC CQQAARRB=ℎBℎCℎCℎAℎAℎB=1;注：此定理常运用求证三角形相似的过程中的线段成比例的条件;例1若直角ABC中,CK是斜边上的高,CE是∠ACK的平分线,E点在AK上,D是AC的中点,F是DE与CK的交点,证明：BF∥CE;解析因为在EBC中,作∠B的平分线BH,则：∠EBC=∠ACK，∠HBC=∠ACE,∠HBC+∠HCB=∠ACK+∠HCB=90°,即BH⊥CE,所以EBC为等腰三角形,作BC上的高EP,则：CK=EP,对于ACK和三点D、E、F根据梅涅劳斯定理有：CDDA AEEKKFFC=1,于是KFFC=EKAE=CKAC=EPAC=BPBC=BKBE,即KFFC =BKBE,根据分比定理有：KFKC=BKKE,所以FKBCKE,所以BF∥CE;例2从点K引四条直线,另两条直线分别交直线与A、B、C、D和A1，B1，C1，D1,试证：AC BC :ADBD=A1C1B1C1:A1D1B1D1;解析若AD∥A1D1,结论显然成立；若AD与A1D1相交于点L,则把梅涅劳斯定理分别用于A1AL和B1BL可得：ADLDLD1A1D1A1KAK=1,LCACAKA1KA1C1LC1=1,BCLCLC1B1C1B1KBK=1,LDBDBKB1KB1D1LD1=1,将上面四个式子相乘,可得：ADAC BCBDA1C1A1D1B1D1B1C1=1,即：ACBC:ADBD=A1C1B1C1:B1D1B1C1定理2设P、Q、R 分别是ABC的三边BC、CA、AB上或它们延长线上的三点,并且P、Q、R三点中,位于ABC边上的点的个数为0或2,这时若BPPC CQQAARRB=1,求证P、Q、R三点共线;证明：设直线PQ与直线AB交于R’,于是由定理1得：BPPC CQQAAR‘R’B=1,又因为BPPCCQQAARRB=1,则AR‘R’B=ARRB,由于在同一直线上P、Q、R三点中,位于ABC边上的点的个数也为0或2,因此R与R‘或者同在AB线段上,或者同在AB的延长线上；若R与R‘同在AB线段上,则R与R‘必定重合,不然的话,设AR>AR‘,这时AB−AR<AB−AR‘,即BR<BR‘,于是可得ARBR >AR‘BR‘,这与AR BR =AR‘BR‘矛盾,类似地可证得当R与R‘同在AB的延长线上时,R与R‘也重合,综上可得：P、Q、R三点共线;注：此定理常用于证明三点共线的问题,且常需要多次使用再相乘；例3点P位于ABC的外接圆上；A1、B1、C1是从点P向BC、CA、AB引的垂线的垂足,证明点A1、B1、C1共线;解析易得：BA1CA1=−BP?cos∠PBCCP?cos∠PCB,CB1AB1=−CP?cos∠PCAAP?cos∠PAC,AC1BC1=−AP?cos∠PABBP?cos∠PBA,将上面三个式子相乘,且因为∠PCA=∠PBC,∠PAB=∠PCB,∠PCA+∠PBA=180°,可得BA1CA1CB1AB1AC1BC1=1,根据梅涅劳斯定理可知A1、B1、C1三点共线;例4 设不等腰ABC的内切圆在三边BC、CA、AB上的切点分别为D、E、F,则EF与BC,FD 与CA,DE与AB的交点X、Y、Z在同一条直线上;解析ABC被直线XFE所截,由定理1可得：BXXC CEEAAFFB=1,又因为AE=AF,代入上式可得BXXC =FBCE,同理可得CYYA=DCAF,AZZB=EABD,将上面的式子相乘可得：BXXC CYYAAZZB=1,又因为X、Y、Z丢不在ABC的边上,由定理2可得X、Y、Z三点共线;例5已知直线AA1,BB1,CC1相交于O,直线AB和A1B1的交点为C2,直线BC和B1C1的交点为A2,直线AC和A1C1的交点为B2,试证A2、B2、C2三点共线;解析设A2、B2、C2分别是直线BC和B1C1,AC和A1C1,AB和A1B1的交点,对所得的三角形和它们边上的点：OAB和A1，B1，C2,OBC和B1，C1，A2,OAC和A1，C1,B2应用梅涅劳斯定理有：AA1OA1OB1BB1BC2AC2=1,OC1CC1BB1OB1CA2BA2=1,OA1AA1CC1OC1AB2CB2=1,将上面的三个式子相乘,可得：BC2 AC2AB2CB2CA2BA2=1,由梅涅劳斯定理可知A2、B2、C2共线;例6在一条直线上取点E、C、A,在另一条上取点B、F、D,记直线AB和ED,CD和AF,EF和BC的交点依次为L、M、N,证明：L、M、N共线;解析记直线EF和CD,EF和AB,AB和CD的交点分别为U、V、W,对UVW,应用梅涅劳斯定理于五组三元点(L,D,E),(A,M,F),(B,C,N),(A,C,E),(B,D,F),则有UEVE VLWLWDUD=1,VAWAUFVFWMYM=1,UN VN WCUCVBWB=1,WAVAUCWCVEUE=1,WBVBUDWDVFUF=1,将上面五个式子相乘可得：VLWLWMUMUNVN=1,点L、M、N共线;二、塞瓦定理定理：设P、Q、R分别是ABC的BC、CA、AB边上的点,则AP、BQ、CR三线共点的充要条件是：BPPC CQQAARRB=1;证明：先证必要性：设AP、BQ、CR相交于点M,则BPPC =S ABPS ACP=S BMP S CMP =S ABMS ACM,同理CQQA=S BCMS ABM,ARRB=S ACMS BCM,以上三式相乘,得：CBA1A1B1CM QRACPBBP PC CQQAARRB=1,再证充分性：若BPPCCQQAARRB=1,设AP与BQ相交于M,且直线CM交AB于R’,由塞瓦定理有：BPPC CQQAAR’R’B=1,约翰斯：AR’R’B=ARRB,因为R和R’都在线段AB上,所以R’必与R重合,故AP、BQ、CR相交于一点M;例7证明：三角形的中线交于一点;解析记ABC的中线AA1,BB1,CC1,我们只须证明AC1C1B BA1A1CCB1B1A=1,而显然有：AC1=C1B,BA1=A1C,CB1=B1A,即AC1C1B BA1A1CCB1B1A=1成立,所以,ABC交于一点,例8在锐角ABC中,∠C的角平分线交AB于L,从L做边AC和BC的垂线,垂足分别是M和N,设AN和BM的交点是P,证明：CP⊥AB;解析作CK⊥AB,下证CK、BM、AN三线共点,且为P点,要证CK、BM、AN三线共点,根据塞瓦定理即要证：AM MC CNNBBKAK=1,又因为MC=CN,即要证明：AMAKBKNB=1,因为AMLAKC AMAK =ALAC,BNLBKC BKNB=BCBL,即要证ALACBCBL=1,根据三角形的角平分线定理可知：ALAC BCBL=1,所以CK、BM、AN三线共点,且为P点,所以CP⊥AB;例9设AD是ABC的高,且D在BC边上,若P是AD上任一点,BP、CP分别与AC、AB交于E和F,则∠EDA=∠FDA;解析过A作AD的垂线,与DE、DF的延长线分别交于M、N;欲证∠EDA=∠FDA,可以转化为证明AM=AN,因为AD⊥BC,故MN∥BC,可得AMECDE，ANFBDF,所以AMCD =AECE，ANBD=AFBF,于是AM=AE?CD CE ，AN=AF?BDBF,因为AD、BE、CF共点与P,根据塞瓦定理可得：BD DC CEEAAFFB=1,所以AE?CDCE=AF?BDBF,所以AM=AN，所以∠EDA=∠FDA例10在ABC的边BC、CA、AB上取点A1、B1、C1,证明AC1 C1B BA1A1CCB1B1A=sin∠ACC1sin∠C1CBsin∠BAA1sin∠A1ACsin∠CBB1sin∠B1BA解析如图对ACC1和BCC1应用正弦定理,可得AC1C1C=sin∠ACC1 sin∠A ,CC1C1B=sin∠Bsin∠C1CB,即AC1C1B=sin∠ACC1sin∠C1CBsin∠Bsin∠A,同理：BA1A1C=sin∠BAA1sin∠A1ACsin∠Csin∠B,CB1B1A=sin∠CBB1sin∠B1BAsin∠Asin∠C,从而AC1C1B BA1A1CCB1B1A=sin∠ACC1sin∠C1CBsin∠BAA1sin∠A1ACsin∠CBB1sin∠B1BA;CBA1A1B1CK LNMCBA。

一道初三课外练习的证明——梅涅劳斯定理和塞瓦定
理的应用
梅涅劳斯定理：梅涅劳斯定理是一个关于圆的定理，它告诉我们，如果一个圆的外接的正多边形的各个角度都是相等的，那么，这个正多边形的每条边都是等边的。

塞瓦定理：塞瓦定理是一个关于圆的定理，它告诉我们，如果一个圆的内接正多边形的每条边都是等边的，那么，这个正多边形的每个角度也是相等的。

证明：为了证明梅涅劳斯定理和塞瓦定理之间的关系，我们使用反证法。

假设正多边形的每个角度都是相等的，而它的每条边不是等边的。

根据梅涅劳斯定理，我们知道这个正多边形的每条边都是等边的，而这与我们的假设矛盾，因此该假设是错误的。

反之，假设正多边形的每条边都是等边的，而它的每个角度不是相等的。

根据塞瓦定理，我们知道这个正多边形的每个角度都是相等的，而这与我们的假设矛盾，因此该假设也是错误的。

由此可见，梅涅劳斯定理和塞瓦定理之间有着密切的联系。

即正多边形的每个角度都是相等的，那么它的每条边也都是等边的；反之，正多边形的每条边都是等边的，那么它的每个角度也都是相等的。

综上所述，梅涅劳斯定理和塞瓦定理之间是成立的。