五年级奥数页码问题讲座及练习答案(最新整理)
- 格式:pdf
- 大小:154.53 KB
- 文档页数:7

小学奥数-页码问题页码问题就是根据书的页码而编制出来的一类应用题.编一本书的页码,一共需要多少个数码呢?反过来,知道编一本书的页码所需的数码数量,求这本书的页数.这是页码问题中的两个基本内容。
页码问题实际上是数论的问题。
一、页码问题的几种题型:(1)已知页码数,要求考生求出书中一共含有多少个数码。
(2)已知页码数,要求考生求此书中某个数码出现的次数。
(3)已知书中包含的数码数,要求考生求出该书的页码数。
(4)已知书中某个数码出现的次数,要求考生求出该书的页码数。
二、页码问题解题基本原理要想要想顺利解答页码问题,首先要弄明白“页码”与“组成它的数码个数”之间的关系。
1.一位数组成的页码共有9个(从1~9),组成所有的一位数需要:(9-1+1)×1=9×1=9(个)数码。
2.两位数共有90个(从10~99),组成所有的两位数需要:2×(99-10+1)=180(个)数码。
3.三位数共有900个(从100~999),组成所有的三位数需要:3×(999-100+1)=2700(个)数码。
4.四位数共有9000个(从1000~9999),组成所有四位数需要:4×(9999-1000+1)=36000(个)数码。
5.9页的书共有:9个数码组成。
6.99页的书共有:9+180=189个数码组成。
7.999页的书共有:2700+180+9=2889个数码组成。
8.9999页的书共有:36000+2700+180+9=38889个数码组成。
三.例题:例1 一本书共204页,需多少个数码编页码?分析与解:1~9页每页上的页码是一位数,共需数码1×9=9(个);10~99页每页上的页码是两位数,共需数码2×90=180(个);100~204页每页上的页码是三位数,共需数码:(204-100+1)×3=105×3=315(个).综上所述,这本书共需数码:9+180+315=504(个).例2 一本小说的页码,在排版时必须用2211个数码.问:这本书共有多少页?分析:因为189<2211<2889,所以这本书有几百页.由前面的分析知道,这本书在排三位数的页码时用了数码(2211-189)个,所以三位数的页数有(2211-189)÷3=674(页).因为不到三位的页数有99页,所以这本书共有:99+674=773(页).解:99+(2211-189)÷3=773(页).答:这本书共有773页.例3 一本书的页码从1至62,即共有62页.在把这本书的各页的页码累加起来时,有一个页码被错误地多加了一次.结果,得到的和数为2000.问:这个被多加了一次的页码是几?分析与解:因为这本书的页码从1至62,所以这本书的全书页码之和为1+2+…+61+62=62×(62+1)÷2=31×63=1953.由于多加了一个页码之后,所得到的和数为2000,所以2000减去1953就是多加了一次的那个页码,是2000-1953=47.例4 有一本48页的书,中间缺了一张,小明将残书的页码相加,得到1131.老师说小明计算错了,你知道为什么吗?分析与解:48页书的所有页码数之和为1+2+…+48=48×(48+1)÷2=1176.按照小明的计算,中间缺的这一张上的两个页码之和为1176-1131=45.这两个页码应该是22页和23页.但是按照印刷的规定,书的正文从第1页起,即单数页印在正面,偶数页印在反面,所以任何一张上的两个页码,都是奇数在前,偶数在后,也就是说奇数小偶数大.小明计算出来的是缺22页和23页,这是不可能的.例5 将自然数按从小到大的顺序无间隔地排成一个大数:123456789101112…问:左起第2000位上的数字是多少?分析与解:本题类似于“用2000个数码能排多少页的页码?”因为(2000-189)÷3=603……2,所以2000个数码排到第99+603+1=703(页)的第2个数码“0”.所以本题的第2000位数是0.例6 排一本400页的书的页码,共需要多少个数码“0”?分析与解:将1~400分为四组:1~100,101~200,201~300,301~400.在1~100中共出现11次0,其余各组每组都比1~100多出现9次0,即每组出现20次0.所以共需要数码“0”例6、13/1995 化成小数后是一个无限小数,问在这个无限小数的小数点后面,从第一位到1995位,在这1995个数中,数字6共出现了多少次?解答:这是一个关于循环小数的周期问题。

奥数:页码问题(数论问题)页码问题编一本书的页码,一共需要多少个数码呢?反过来,知道编一本书的页码所需的数码数量,求这本书的页数.这是页码问题中的两个基本内容。
我们先看一下“数”与“组成它的数码个数”之间的关系.1、一位数的页码有9页,共1×9=9个数字;组成所有的一位数需要9个数码;2、两位数的页码有90页,共90×2=180个数字;需要180个数码3、三位数有900个,全部编上共用900×3=2700个数字,需要3×900=2700(个)数码。
题目会出1、一本书有N页,求排版时用了多少个数字;或者反过来,一本书排版时用了N个数字,求这本书有多少页;2、已知一本N页的书中,求某个数字出现多少次;3、已知一本N页的书中,求含有某个数字的页码有多少页一本书排版时用了N个数字,求这本书有多少页,数字数<2889时,用公式:页码数=数字数/3+36;数字数>2889时,用添加0计算。
例1 一本书共204页,需多少个数码编页码?2.编一本书的书页,用了270个数字(重复的也算,如页码115 用了2个1 和1个5共3个数字),问这本书一共有多少页?N/3+36。
270/3 +36=126。
2.一本小说的页码,在排版时必须用2211 个数码。
问这本书共有多少页?A.773 B.774 C .775 D.7763 .王先生在编一本书,其页数需要用6869 个字,问这本书具体是多少页?A.1999B.9999C.1994D.1995方法一:假设这个页数是A页,则:A+(A-9)+(A-99)+(A-999)=6869 ,求出A=1994方法二:6869>2889,所以,把所有的数字看作是4位数字,不足4位的添O补足4位,l , 2 , 3 , …9 记为0001 , 0002 , 0003 , ..0009 这样增加了3 * 9 = 27 个010 , 11 , 12 , …99 记为0010 , 0011 , 0012 ,..0099 增加了180 个0100 , 101 ,…999 记为0100 , 0101 ,…0999 增加了900 个O (6869+27+180+900)/4 =1994关于含“1”出现过多少次的问题,总结出的公式就是:总页数的1/10 乘以(数字位-1 ),再加上10 的(数字位数-l)次方。

第 2 4名思,与的有亲密系。
事上,就是依据的而制出来的一用。
一本的,一共需要多少个数呢?反来,知道一本的所需的数数目,求本的数。
是中的两个基本内容。
了利地解答,我先看一下“数”与“成它的数个数”之的关系。
一位数共有9个,成全部的一位数需要 9个数;两位数共有90个,成全部的两位数需要2×90=180(个)数;三位数共有900个,成全部的三位数需要3×900=2700(个)数⋯⋯了清楚起,我将n位数的个数、成全部n位数需要的数个数、成全部不大于n位的数需要的数个数之的关系列表以下:个数所用数字的个数1到最大所用数字的个数一位数91×9=99两位数902×90=180180+9=189三位数9003×900=2700189+2700=2889四位数90004×9000=3600002889+36000=38889例1一本共204,需多少个数?剖析与解:1~9每上的是一位数,共需数1×9=9(个);10~99每上的是两位数,共需数2×90=180(个);100~204每上的是三位数,共需数(204-100+1)×3=105×3=315(个).上所述,本共需数9+180+315=504(个).例2 一本小的,在排版必用2211个数.:本共有多少?剖析:因189<2211<2889,因此本有几百.由前方的剖析知道,本在排三位数的用了数(2211-189)个,因此三位数的数有(2211-189)÷3=674( ).因不到三位的数有99,因此本共有:99+674=773( ).解:99+(2211-189)÷3=773( ).答:本共有773.例3 一本的从 1至62,即共有62.在把本的各的累加起来,有一个被=地多加了一次.果,获得的和数2000.:个被多加了一次的是几?=剖析与解:因本的从1至62,因此本的全之和=1+2+⋯+61+62=62×(62+1)÷2=31×63=1953.因为多加了一个以后,所获得的和数2000,因此2000减去1953就是多加了一次的那个,是2000-1953=47.例4 有一本48的,中缺了一,小明将残的相加,获得1131.老少明算了,你知道什么?剖析与解:48的全部数之和1+2+⋯+4848×(48+1)÷21176.依据小明的算,中缺的一上的两个之和1176-1131=45.两个是22和23.可是依据印刷的定,的正文从第1起,即数印在正面,偶数印在反面,因此任何一上的两个,都是奇数在前,偶数在后,也就是奇数小偶数大.小明算出来的是缺22和23,是不行能的.⋯:左起第2000位上的数字是多少?剖析与解:本似于“用2000个数能排多少的?”因(2000-189)÷3=603⋯⋯2,所以2000个数排到第99+603+1=703( )的第2个数“0”.因此本的第2000位数是0.例6排一本400的的,共需要多少个数“0”?剖析与解:将1~400分四:1~100,101~200,201~300,301~400.在1~100中共出11次0,其他各每都比1~100多出9次0,即每出20次0.因此共需要数“0”典型例:例1、13/1995 化成小数后是一个无穷小数,在个无穷小数的小数点后边,从第一位到1995位,在1995个数中,数字6共出了多少次?解答:是一个对于循小数的周期。

五年级数学思维《页码问题》专题训练一、填空题(每小题6分,共60分)1 一本120页的《奥数教程》,小明把每页的页码加起来,所得的结来是.2 一本《漫画世界》共有180页,一共需要个数字来编页码.3 一本书的页码从1~60页,小军把每页的页码加起来时,有一个页码被重复加了一次,结果得到的和为1845,这个被重复加了一次的页码是.4 一本书的页码从1 ~55页,小红把每页的页码加起来时,由于粗心少加了一个页码,结果得到的和为1500,这个被遗漏的页码是.5 《蓝猫传奇》这本童话书共有96页,在印刷页码时,数字4一共出现了次.6 在1~750这750个连续的自然数中,各个数中的数字1一共有个.7 在2468101214…20082010中,一共有个数字.8 有一本故事书,中间缺了一张,缺的页数和是95,这木书缺的那一张正面是页.9 一本图书除封面和封底外的每张纸的两面都标有页码,若中央一张纸两面的页码之积是2450,则这本书的所有页码之和是 .10 如图是某年2月的日历,图中用一个方框框住的四个日期的数码之和是4+5+1+1+1+2=14,则在所有可能框住的四个日期中,数码之和最大是 .二、解答题(每小题15分,共60分)11 有一本300页的书,被人从中撕掉了15张纸,如果将这15张纸上的所有页码相加,那么所加的结果能不能等于2014?请说明理由.12 有本90页的书被人撕掉一张,结果书上页码加起来和4012,问:撕掉的是哪一张?13 一木科幻小说,编页码时一共用了2049个数字,这木书有多少页?14小数A=0.1234567891011121314…,在小数点后面第2016 位上的数字是几?。
奥数:页码问题(数论问题)页码问题与图书的页码有亲密联系.事实上,页码问题就是依据书的页码而编制出来的一类应用题.编一本书的页码,一共需要多少个数码呢?反过来,知道编一本书的页码所需的数码数目,求这本书的页数.这是页码问题中的两个基本内容。
页码问题是此刻的奥数比赛以及公事员考试中常有的、常常考试的知识点。
页码问题其实是数论的问题。
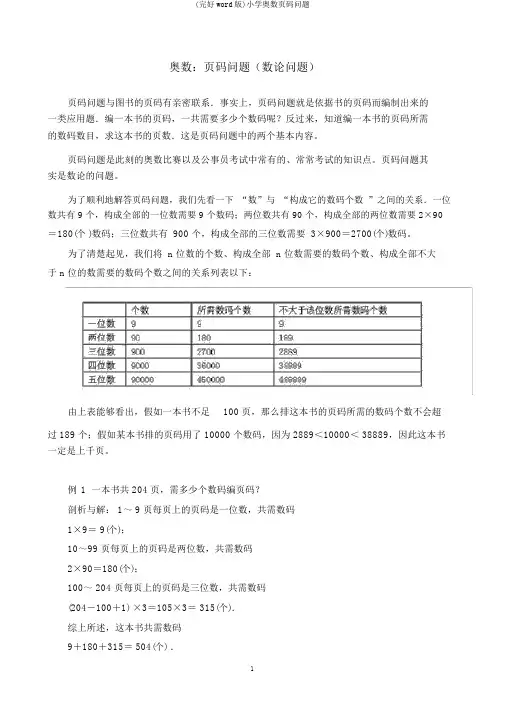
为了顺利地解答页码问题,我们先看一下“数”与“构成它的数码个数”之间的关系.一位数共有 9 个,构成全部的一位数需要 9 个数码;两位数共有 90 个,构成全部的两位数需要 2×90=180(个 )数码;三位数共有 900 个,构成全部的三位数需要 3×900=2700(个)数码。
为了清楚起见,我们将 n 位数的个数、构成全部 n 位数需要的数码个数、构成全部不大于 n 位的数需要的数码个数之间的关系列表以下:由上表能够看出,假如一本书不足100 页,那么排这本书的页码所需的数码个数不会超过 189 个;假如某本书排的页码用了 10000 个数码,因为 2889<10000< 38889,因此这本书一定是上千页。
例1 一本书共 204 页,需多少个数码编页码?剖析与解: 1~ 9 页每页上的页码是一位数,共需数码1×9= 9(个);10~99 页每页上的页码是两位数,共需数码2×90=180(个);100~ 204 页每页上的页码是三位数,共需数码(204-100+1) ×3=105×3= 315(个).综上所述,这本书共需数码9+180+315= 504(个) .例2 一本小的,在排版必用 2211 个数.:本共有多少?剖析:因 189< 2211< 2889,因此本有几百.由前面的剖析知道,本在排三位数的用了数(2211-189)个,因此三位数的数有(2211-189) ÷3= 674( ).因不到三位的数有99 ,因此本共有: 99+674=773( ).解: 99+(2211-189) ÷3=773( ).答:本共有773 .例 3 一本的从 1 至 62,即共有 62 .在把本的各的累加起来,有一个被地多加了一次.果,获得的和数 2000.:个被多加了一次的是几?剖析与解:因本的从 1 至 62,因此本的全之和1+2+⋯+ 61+62= 62×(62+ 1) ÷2= 31×63= 1953.因为多加了一个以后,所获得的和数2000,因此 2000 减去 1953 就是多加了一次的那个,是2000-1953=47.例 4有一本48的,中缺了一,小明将残的相加,获得1131.老小明算了,你知道什么?剖析与解: 48 的全部数之和1+2+⋯+ 48=48×(48+ 1) ÷2=1176.依据小明的算,中缺的一上的两个之和1176-1131= 45.两个是 22 和 23 .可是依据印刷的定,的正文从第 1 起,即数印在正面,偶数印在反面,因此任何一上的两个,都是奇数在前,偶数在后,也就是奇数小偶数大.小明算出来的是缺22 和 23 ,是不行能的.第2000 位上的数字是多少?剖析与解:本似于“用2000 个数能排多少的?”因(2000-189) ÷3=603⋯⋯2,因此2000 个数排到第 99+603+1=703( )的第 2 个数“ 0.”因此本的第 2000 位数是 0.例6 排一本 400 的的,共需要多少个数“0?”剖析与解:将1~400 分四:1~100,101~ 200,201~300, 301~400.在 1~100 中共出 11 次 0,其他各每都比 1~ 100 多出 9 次 0,即每出 20 次0.因此共需要数“ 0”典型例:例 1、13/1995 化成小数后是一个无穷小数,在个无穷小数的小数点后边,从第一位到1995 位,在 1995 个数中,数字 6 共出了多少次?解答:是一个对于循小数的周期。

奥数:页码问题(数论问题)页码问题与图书的页码有密切联系.事实上,页码问题就是根据书的页码而编制出来的一类应用题.编一本书的页码,一共需要多少个数码呢?反过来,知道编一本书的页码所需的数码数量,求这本书的页数.这是页码问题中的两个基本内容。
页码问题是现在的奥数竞赛以及公务员考试中常见的、经常考试的知识点.页码问题实际上是数论的问题。
为了顺利地解答页码问题,我们先看一下“数”与“组成它的数码个数”之间的关系.一位数共有9个,组成所有的一位数需要9个数码;两位数共有90个,组成所有的两位数需要2×90=180(个)数码;三位数共有900个,组成所有的三位数需要3×900=2700(个)数码。
现在我们来看几道例题.例1 一本书共204页,需多少个数码编页码?分析与解:1~9页每页上的页码是一位数,共需数码1×9=9(个);10~99页每页上的页码是两位数,共需数码2×90=180(个);100~204页每页上的页码是三位数,共需数码(204-100+1)×3=105×3=315(个).综上所述,这本书共需数码9+180+315=504(个).例2 一本小说的页码,在排版时必须用2211个数码.问:这本书共有多少页?分析:因为189<2211<2889,所以这本书有几百页.由前面的分析知道,这本书在排三位数的页码时用了数码(2211-189)个,所以三位数的页数有(2211-189)÷3=674(页).因为不到三位的页数有99页,所以这本书共有:99+674=773(页).解:99+(2211-189)÷3=773(页).答:这本书共有773页.例3 一本书的页码从1至62,即共有62页.在把这本书的各页的页码累加起来时,有一个页码被错误地多加了一次.结果,得到的和数为2000.问:这个被多加了一次的页码是几?分析与解:因为这本书的页码从1至62,所以这本书的全书页码之和为1+2+…+61+62=62×(62+1)÷2=31×63=1953.由于多加了一个页码之后,所得到的和数为2000,所以2000减去1953就是多加了一次的那个页码,是2000-1953=47.例4 有一本48页的书,中间缺了一张,小明将残书的页码相加,得到1131.老师说小明计算错了,你知道为什么吗?分析与解:48页书的所有页码数之和为1+2+…+48=48×(48+1)÷2=1176.按照小明的计算,中间缺的这一张上的两个页码之和为1176-1131=45.这两个页码应该是22页和23页.但是按照印刷的规定,书的正文从第1页起,即单数页印在正面,偶数页印在反面,所以任何一张上的两个页码,都是奇数在前,偶数在后,也就是说奇数小偶数大.小明计算出来的是缺22页和23页,这是不可能的.例5 将自然数按从小到大的顺序无间隔地排成一个大数:123456789101112…问:左起第2000位上的数字是多少?分析与解:本题类似于“用2000个数码能排多少页的页码?”因为(2000-189)÷3=603……2,所以2000个数码排到第99+603+1=703(页)的第2个数码“0”.所以本题的第2000位数是0.例6 排一本400页的书的页码,共需要多少个数码“0”?分析与解:将1~400分为四组:1~100,101~200,201~300,301~400.在1~100中共出现11次0,其余各组每组都比1~100多出现9次0,即每组出现20次0.所以共需要数码“0”典型例题:例1、13/1995 化成小数后是一个无限小数,问在这个无限小数的小数点后面,从第一位到1995位,在这1995个数中,数字6共出现了多少次?解答:这是一个关于循环小数的周期问题。
第24讲页码问题顾名思义,页码问题与图书的页码有密切联系。
事实上,页码问题就是根据书的页码而编制出来的一类应用题。
编一本书的页码,一共需要多少个数码呢?反过来,知道编一本书的页码所需的数码数量,求这本书的页数。
这是页码问题中的两个基本内容。
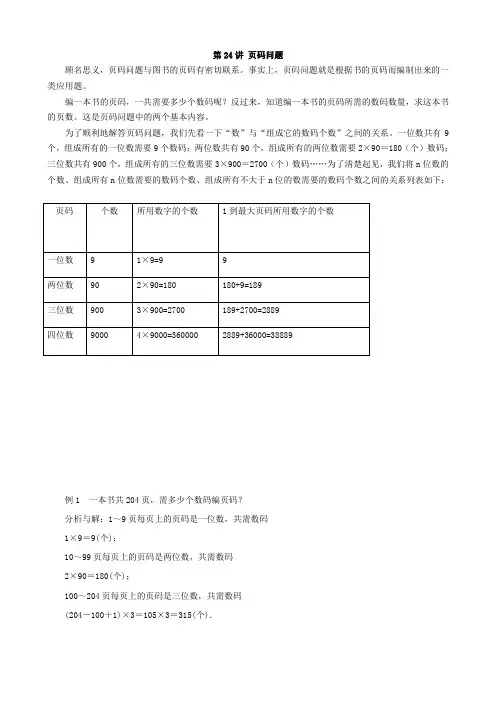
为了顺利地解答页码问题,我们先看一下“数”与“组成它的数码个数”之间的关系。
一位数共有9个,组成所有的一位数需要9个数码;两位数共有90个,组成所有的两位数需要2×90=180(个)数码;三位数共有900个,组成所有的三位数需要3×900=2700(个)数码……为了清楚起见,我们将n位数的个数、组成所有n位数需要的数码个数、组成所有不大于n位的数需要的数码个数之间的关系列表如下:例1 一本书共204页,需多少个数码编页码?分析与解:1~9页每页上的页码是一位数,共需数码1×9=9(个);10~99页每页上的页码是两位数,共需数码2×90=180(个);100~204页每页上的页码是三位数,共需数码(204-100+1)×3=105×3=315(个).综上所述,这本书共需数码9+180+315=504(个).例2 一本小说的页码,在排版时必须用2211个数码.问:这本书共有多少页?分析:因为189<2211<2889,所以这本书有几百页.由前面的分析知道,这本书在排三位数的页码时用了数码(2211-189)个,所以三位数的页数有 (2211-189)÷3=674(页).因为不到三位的页数有99页,所以这本书共有:99+674=773(页).解:99+(2211-189)÷3=773(页).答:这本书共有773页.例3 一本书的页码从1至62,即共有62页.在把这本书的各页的页码累加起来时,有一个页码被错误地多加了一次.结果,得到的和数为2000.问:这个被多加了一次的页码是几?分析与解:因为这本书的页码从1至62,所以这本书的全书页码之和为1+2+…+61+62=62×(62+1)÷2=31×63=1953.由于多加了一个页码之后,所得到的和数为2000,所以2000减去1953就是多加了一次的那个页码,是2000-1953=47.例4 有一本48页的书,中间缺了一张,小明将残书的页码相加,得到1131.老师说小明计算错了,你知道为什么吗?分析与解:48页书的所有页码数之和为1+2+…+48=48×(48+1)÷2=1176.按照小明的计算,中间缺的这一张上的两个页码之和为1176-1131=45.这两个页码应该是22页和23页.但是按照印刷的规定,书的正文从第1页起,即单数页印在正面,偶数页印在反面,所以任何一张上的两个页码,都是奇数在前,偶数在后,也就是说奇数小偶数大.小明计算出来的是缺22页和23页,这是不可能的.例5 将自然数按从小到大的顺序无间隔地排成一个大数:123456789101112…问:左起第2000位上的数字是多少?分析与解:本题类似于“用2000个数码能排多少页的页码?”因为(2000-189)÷3=603……2,所以2000个数码排到第99+603+1=703(页)的第2个数码“0”.所以本题的第2000位数是0.例6 排一本400页的书的页码,共需要多少个数码“0”?分析与解:将1~400分为四组:1~100,101~200,201~300,301~400.在1~100中共出现11次0,其余各组每组都比1~100多出现9次0,即每组出现20次0.所以共需要数码“0”典型例题:例1、13/1995 化成小数后是一个无限小数,问在这个无限小数的小数点后面,从第一位到1995位,在这1995个数中,数字6共出现了多少次?解答:这是一个关于循环小数的周期问题。

页码问题顾名思义,页码问题与图书的页码有密切联系。
事实上,页码问题就是根据书的页码而编制出来的一类应用题。
编一本书的页码,一共需要多少个数码呢?反过来,知道编一本书的页码所需的数码数量,求这本书的页数。
这是页码问题中的两个基本内容。
为了顺利地解答页码问题,我们先看一下“数”与“组成它的数码个数”之间的关系。
一位数共有9个,组成所有的一位数需要9个数码(数字);两位数共有90个,组成所有的两位数需要2×90=180(个)数码(数字);三位数共有900个,组成所有的三位数需要3×900=2700(个)数码(数字)……即:一位数(1—9):1x9=9(个)两位数(10—99):2x(90-10+1)=180个三位数(100—999):3x(999-100+1)=2700个……依次类推由上表看出,如果一本书不足100页,那么排这本书的页码所需的数码个数不会超过189个;如果某本书排的页码用了10000个数码,因为2889<10000<38889,所以这本书肯定是上千页。
下面,我们看几道例题。
例1一本书共204页,需多少个数码编页码?分析与解:1~9页每页上的页码是一位数,共需数码1×9=9(个);10~99页每页上的页码是两位数,共需数码2×90=180(个);100~204页每页上的页码是三位数,共需数码(204-100+1)×3=105×3=315(个)。
综上所述,这本书共需数码9+180+315=504(个)。
例2一本小说的页码,在排版时必须用2211个数码。
问:这本书共有多少页?分析:因为189<2211<2889,所以这本书有几百页。
由前面的分析知道,这本书在排三位数的页码时用了数码(2211-189)个,所以三位数的页数有(2211-189)÷3=674(页)。
因为不到三位的页数有99页,所以这本书共有99+674=773(页)。

小学奥数之页码问题页码问题一般要求计算出一本图书要多少个数码来编页码。
慢慢来,先说啥叫页码简单!咱们看书的时候,每一页下面都有一个数字代表这是第几页,这就是页码。
一本书有256页,就有256个页码。
啥叫数码数码就是组成一个数的各个数位上的数字。
问一个5位数有多少个数码,答案就是5,因为它是5位数,有5个数码组成。
消化了吧那就先举例做做看。
1、说一本书有204页,需要多少个数码编页码解题分析:实际上就是问你从1到204,一共需要多少个数字这就要分类型来看了,一位数的,两位数的,三位数的,要分别考虑:一位数的有1-9,那么需要9个数码;二位数的有10-99,有90个数,每个数都是两位数,所以数码需要90*2=180个数码;三位数的有100-204,有204-100+1=105个数,每个数都是三位数,所以数码需要105*3=315个数码。
上面统统加起来,9+180+315=504个数码。
下面我们反着来做做题目。
告诉你有多少数码,问一本书有多少页2、一本小说,在排版时用了2211个数码,问这本书有多少页解题分析:从第一题,我们可以看到,如果一本书有上百页,它至少需要189个数码。
那这题中的小说,肯定至少有几百页了。
好,先去除这本小说1-99页的数码个数,用2211-189=2022。
2022就是从100页开始的数码个数,还要除以3哦,才能算出三位数的页数有多少,就是2022/3=674。
那么这本书就是99+674=773页。
3、一本书的页码,从1到62页,把这本书的所有页码都加起来,有一个页码被多加了一次,计算结果是2000。
问多算了一次的页码是多少解题分析:按照正确的,从1到62,全部加起来,是(1+62)*62/2=1953(这里的计算公式是用到等差数列之和的公式哦)。
那么多算了一次的页码就是2000-1953=47。
1。

页码问题顾名思义,页码问题与图书的页码有密切联系。
事实上,页码问题就是根据书的页码而编制出来的一类应用题。
编一本书的页码,一共需要多少个数码呢?反过来,知道编一本书的页码所需的数码数量,求这本书的页数。
这是页码问题中的两个基本内容。
为了顺利地解答页码问题,我们先看一下“数”与“组成它的数码个数”之间的关系。
一位数共有9个,组成所有的一位数需要9个数码(数字);两位数共有90个,组成所有的两位数需要2×90=180(个)数码(数字);三位数共有900个,组成所有的三位数需要3×900=2700(个)数码(数字)……即:一位数(1—9):1x9=9(个)两位数(10—99):2x(90-10+1)=180个三位数(100—999):3x(999-100+1)=2700个……依次类推由上表看出,如果一本书不足100页,那么排这本书的页码所需的数码个数不会超过189个;如果某本书排的页码用了10000个数码,因为2889<10000<38889,所以这本书肯定是上千页。
下面,我们看几道例题。
例1一本书共204页,需多少个数码编页码?分析与解:1~9页每页上的页码是一位数,共需数码1×9=9(个);10~99页每页上的页码是两位数,共需数码2×90=180(个);100~204页每页上的页码是三位数,共需数码(204-100+1)×3=105×3=315(个)。
综上所述,这本书共需数码9+180+315=504(个)。
例2一本小说的页码,在排版时必须用2211个数码。
问:这本书共有多少页?分析:因为189<2211<2889,所以这本书有几百页。
由前面的分析知道,这本书在排三位数的页码时用了数码(2211-189)个,所以三位数的页数有(2211-189)÷3=674(页)。
因为不到三位的页数有99页,所以这本书共有99+674=773(页)。

页码问题(二)【例题1】一本小说的页码,在排版时须用2211个数码。
问:这本书共有多少页?1、给一本书编码,用了2049个数码,这本书有多少页?2、给一把长篇小说编页码,共用3005个数字,这本书有多少页?【例题2】在1~200这200个自然数中,数字“0”出现了多少次?1、一本400页的书,数码0、1在页码中分别出现多少次?2、一本书有608页,页码编号为1、2、3、...608.问:数字“3”在页码中出现多少次?3、一本400页的书,数码2在页码中出现多少次?【例题3】一本故事书中数字0出现了65次,这本书至少有多少页?1、一本故事书的页码共用了18个“0”这本书一共有多少页?2、一本故事书的页码共用了31个“0”这本书一共有多少页?【例题4】将自然数按从小到大的顺序无间隔地排成一个大数:123456789101112...问:左起第2018位上的数字是多少?1、《现代汉语词典》共有1772页,如果把它的页码按从小到大的顺序无间隔地排成一个大数:1234567891011121314151617181920...,请问左起第2020位上的数字是多少?2、将自然数按从小到大的顺序不间断地排成一个大数:12345678910111213...,这个大数左起第1000位是几?课堂巩固练习1、一本故事书的页码共用了38个“0”这本书共有多少页?2、排一本书,它的页码中共出现了71个零,问这本书共有多少页?3、今年是2018年,如果把公元1年到今年的所有年份连续放在一起,组成一个很大的数:1234567891011121314......2018。
这个很大的数是几位数?4、一本小学生作文选有320页。
问:(1)编这本书要用多少个数码?(2)数字2在页码中出现几次?5、将自然数按从1到460不间断地排成一个大数:12345678910111213...459460这个大数是几位数?第300个数字是几?6、在1984后面接着写一个数字,写下的每一个数字都是他前面的两个数的乘积的个位数,如:8×4=32,就在4后面写2 ,4×2=8,就在2后面写8,在1984286......这个数字中:①第2018位上的数它是多少?②这2018个数的和是多少?7、将自然数按从小到大的顺序无间隔地排成一个大数:123456789101112...问:左起第 2000位上的数字是多少?8、一本书的页码为1至62,即共有62页。
小学奥数页码问题1.从“1”一直写到“701”:12345678910111213…699700701。
共有多少个阿拉伯数字?2.一本书共399页,编上页码:1、2、3、4、…、398、399。
数字“2”在页码中共有多少个?3.一本故事书,仅排版页码就用去1392个铅字(数字)。
这本书有多少页?4.自然数的平方按从小到大排成一行:14916253649…,那么第112个位置上的数字是多少?5.设小数A=0.123456789101213…998999,试问,小数点右边第1998位上的数字是几?6.有一本书中间被撕掉一张,余下各页的页码数之和正好是1145。
那么,被撕掉那一张的页码数是?例1一本书共204页,需多少个数码编页码?例2一本小说的页码,在排版时必须用2211个数码.问:这本书共有多少页?例3一本书的页码从1至62,即共有62页.在把这本书的各页的页码累加起来时,有一个页码被错误地多加了一次.结果,得到的和数为2000.问:这个被多加了一次的页码是几?例4有一本48页的书,中间缺了一张,小明将残书的页码相加,得到1131.老师说小明计算错了,你知道为什么吗?例5将自然数按从小到大的顺序无间隔地排成一个大数:123456789101112…问:左起第2000位上的数字是多少?例6排一本400页的书的页码,共需要多少个数码“0”?例1求1~999的999个连续自然数的所有数字之和。
例2求1~xx连续自然数的全部数字之和。
例3求连续自然数2000~5000的全部数字之和. 例4求1~129的连续自然数全部数字之和。
练习:1.求1~899连续自然数所有数字之和。
2.求1~3000连续自然数所有数字之和。
3.求400~4000连续自然数所有数字之和。
4.求1~1500连续自然数所有数字之和。
5.求180~1800连续自然数所有数字之和。
1. 一本书共有112 页,请问页码中共有几个“ 1”?
2. 一本书共有500 页,1—500页的页码中,一共用了多少
个数字“ 1”?
3. 给一本书编码时,一共用了11 个数字“ 7”,请问这本书
共有几页?
4. 一本漫画书的页码共有16 个数字“ 0”,请问这本漫画书
有几页?
5. 编一本书的页码总共用了270 个数字,问这本书一共有几页?
6. 排一本学生字典用了2925 个数字,问这本字典共有多少页?
7. 一本书的页码为1至62,即共有62 页。
在把这本书的各
页的页码累加起来时,有一个页码漏加了,结果得到的和数为1939,问:这个被漏加的页码是几?
下面图范的井列有什么规律呢?问号处应该iB什么?诡逵择.
A B C I)
△ O △ △
E F G H
下ID各种各样的赠竝头好■网?找3WE们排刃的規悴吗?《tH规悴把嚴后f雉堆头as在横找上.
数一数,下国中共有多少个长方形?
数一数.下图中共有多少个三角形?。
五年级奥数题及答案-奇数页码篇数
【题目】小明的妈妈是图书编辑,最近她收到15篇文章,每篇文章的页数分别是1、2、3……14……15页,小明妈妈想讲这些文章按照某种次序装订成册,并统一编上页码,那么,每篇文章的第一页是奇数页码的文章最多能有多少篇?
【解析】
我们先来把偶数页的文章挑出来编排,即2(1)、4(3)、6(7)、8(13)、10(21)、12(33)、14(45),括号中是它们第一页所在的页码,这样就有7篇文章的第一页是奇数页码。
然后我们再来排奇数页的文章,即1(59)、3(60)、5(63)、7(68)、9(75)、11(84)、13(95)、15(108),但只有页数为1、5、9、13的文章第一页是奇数页码。
因此,每篇文章第一页是奇数页码的文章最多是7+4=11(篇)。
第24讲页码问题顾名思义,页码问题与图书的页码有密切联系。
事实上,页码问题就是根据书的页码而编制出来的一类应用题。
编一本书的页码,一共需要多少个数码呢?反过来,知道编一本书的页码所需的数码数量,求这本书的页数。
这是页码问题中的两个基本内容。
为了顺利地解答页码问题,我们先看一下“数”与“组成它的数码个数”之间的关系。
一位数共有9个,组成所有的一位数需要9个数码;两位数共有90个,组成所有的两位数需要2×90=180(个)数码;三位数共有900个,组成所有的三位数需要3×900=2700(个)数码……为了清楚起见,我们将n位数的个数、组成所有n位数需要的数码个数、组成所有不大于n位的数需要的数码个数之间的关系列表如下:例1 一本书共204页,需多少个数码编页码?分析与解:1~9页每页上的页码是一位数,共需数码1×9=9(个);10~99页每页上的页码是两位数,共需数码2×90=180(个);100~204页每页上的页码是三位数,共需数码(204-100+1)×3=105×3=315(个).综上所述,这本书共需数码9+180+315=504(个).例2 一本小说的页码,在排版时必须用2211个数码.问:这本书共有多少页?分析:因为189<2211<2889,所以这本书有几百页.由前面的分析知道,这本书在排三位数的页码时用了数码(2211-189)个,所以三位数的页数有 (2211-189)÷3=674(页).因为不到三位的页数有99页,所以这本书共有:99+674=773(页).解:99+(2211-189)÷3=773(页).答:这本书共有773页.例3 一本书的页码从1至62,即共有62页.在把这本书的各页的页码累加起来时,有一个页码被错误地多加了一次.结果,得到的和数为2000.问:这个被多加了一次的页码是几?分析与解:因为这本书的页码从1至62,所以这本书的全书页码之和为1+2+…+61+62=62×(62+1)÷2=31×63=1953.由于多加了一个页码之后,所得到的和数为2000,所以2000减去1953就是多加了一次的那个页码,是2000-1953=47.例4 有一本48页的书,中间缺了一张,小明将残书的页码相加,得到1131.老师说小明计算错了,你知道为什么吗?分析与解:48页书的所有页码数之和为1+2+…+48=48×(48+1)÷2=1176.按照小明的计算,中间缺的这一张上的两个页码之和为1176-1131=45.这两个页码应该是22页和23页.但是按照印刷的规定,书的正文从第1页起,即单数页印在正面,偶数页印在反面,所以任何一张上的两个页码,都是奇数在前,偶数在后,也就是说奇数小偶数大.小明计算出来的是缺22页和23页,这是不可能的.例5 将自然数按从小到大的顺序无间隔地排成一个大数:123456789101112…问:左起第2000位上的数字是多少?分析与解:本题类似于“用2000个数码能排多少页的页码?”因为(2000-189)÷3=603……2,所以2000个数码排到第99+603+1=703(页)的第2个数码“0”.所以本题的第2000位数是0.例6 排一本400页的书的页码,共需要多少个数码“0”?分析与解:将1~400分为四组:1~100,101~200,201~300,301~400.在1~100中共出现11次0,其余各组每组都比1~100多出现9次0,即每组出现20次0.所以共需要数码“0”典型例题:例1、13/1995 化成小数后是一个无限小数,问在这个无限小数的小数点后面,从第一位到1995位,在这1995个数中,数字6共出现了多少次?解答:这是一个关于循环小数的周期问题。
页码问题 顾名思义,页码问题与图书的页码有密切联系。
事实上,页码问题就是根据书的页码而编制出来的一类应用题。
编一本书的页码,一共需要多少个数码呢?反过来,知道编一本书的页码所需的数码数量,求这本书的页数。
这是页码问题中的两个基本内容。
为了顺利地解答页码问题,我们先看一下“数”与“组成它的数码个数”之间的关系。
一位数共有9个,组成所有的一位数需要9个数码(数字);两位数共有90个,组成所有的两位数需要2×90=180(个)数码(数字);三位数共有900个,组成所有的三位数需要3×900=2700(个)数码(数字)……即: 一位数(1—9): 1x9=9(个)两位数(10—99): 2x(90-10+1)=180个三位数(100—999): 3x(999-100+1)=2700个……依次类推 由上表看出,如果一本书不足100页,那么排这本书的页码所需的数码个数不会超过189个;如果某本书排的页码用了10000个数码,因为 2889<10000<38889,所以这本书肯定是上千页。
下面,我们看几道例题。
例1一本书共204页,需多少个数码编页码?分析与解:1~9页每页上的页码是一位数,共需数码 1×9=9(个); 10~99页每页上的页码是两位数,共需数码 2×90=180(个); 100~204页每页上的页码是三位数,共需数码 (204-100+1)×3=105×3=315(个)。
综上所述,这本书共需数码 9+180+315=504(个)。
例2一本小说的页码,在排版时必须用2211个数码。
问:这本书共有多少页? 分析:因为189<2211<2889,所以这本书有几百页。
由前面的分析知道,这本书在排三位数的页码时用了数码(2211-189)个,所以三位数的页数有 (2211-189)÷3=674(页)。
因为不到三位的页数有99页,所以这本书共有 99+674=773(页)。
解:99+(2211——189)÷3=773(页)。
答:这本书共有773页。
例3一本书的页码从1至62、即共有62页。
在把这本书的各页的页码累加起来时,有一个页码被错误地多加了一次。
结果,得到的和数为2000。
问:这个被多加了一次的页码是几?分析与解:因为这本书的页码从1至62,所以这本书的全书页码之和为 1+2+…+61+62 =62×(62+1)÷2 =31×63 =1953。
由于多加了一个页码之后,所得到的和数为2000,所以2000减去1953就是多加了一次的那个页码,是 2000——1953=47。
例4有一本48页的书,中间缺了一张,小明将残书的页码相加,得到1131。
老师说小明计算错了,你知道为什么吗?分析与解:48页书的所有页码数之和为 1+2+…+48 =48×(48+1)÷2 =1176。
按照小明的计算,中间缺的这一张上的两个页码之和为1176——1131=45。
这两个页码应该是22页和23页。
但是按照印刷的规定,书的正文从第1页起,即单数页印在正面,偶数页印在反面,所以任何一张上的两个页码,都是奇数在前,偶数在后,也就是说奇数小偶数大。
小明计算出来的是缺22页和23页,这是不可能的。
例5将自然数按从小到大的顺序无间隔地排成一个大数:1234567891011l2…问:左起第2000位上的数字是多少?分析与解:本题类似于“用2000个数码能排多少页的页码?”因为(2000-189)÷3=603……2,所以2000个数码排到第99+603+1=703(页)的第2个数码“0”。
所以本题的第2000位数是0。
例6排一本400页的书的页码,共需要多少个数码“0”?分析与解:将1~400分为四组: 1~100,101~200,201~300,301~400。
在1~100中共出现11次0,其余各组每组都比1~100多出现9次0,即每组出现20次0。
所以共需要数码“0”11+20×3=71(个)。
练习1、一本书共有40页,那么共需要多少个数码编页码?解:一位数的编码有:1 ×9=9(个)二位数编码有:2×(40-10+1)或2×(40-9)=2×31=62(个)62+9=71(个)2、一本书共有200页,那么共需要多少个数码编页码?解:一位数的编码:1-9页,共9页,每个页码用1个数字,共9个数字二位数的编码 10-99页,共90页,每个页码用2个数字,共180个数字100-200页,共101页,每个页码用3个数字,共303个数字总共=9+180+303=492个数字3、排一本小说的页码,需要用2202个数码,这本书共有多少页?99+(2202-189)÷3=770(页)。
2202>1*(9-0)=92202-9=2193>2*(99-9)=1802193-180=2013<3*(999-99)=27002013/3=671671+90+9=770(页)4、一本书的页码从1~62,共有62页.小丽在吧这本书的所有页码数累加起来的时候,发现这本书有一张纸被撕掉了,她把其他页码加起来的和是1858.问被撕掉的这张纸上的页码是多少?解:假设没有撕掉,则所有页码的和(1+62)62÷2=1953.故撕掉的页码和为1953-1858=95.(95-1)÷ 2=47故撕掉的页码为47,485、有一本96页的书,中间缺了一张。
如果将残书的所有页码相加,那么可能得到偶数吗?(1+96)*96/5=4656残书偶+奇=奇4656-奇=奇不能6、将自然数按从小到大的顺序无间隔地排成一个大数: 1234567891011121314…问:左起第1000位数是几?(1)1-9:每个数占1位,共占9位;10-99:每个数占2位,共占180位;100-999:每个数占3位;1000-9-180=811811÷3=270 (1)100+270-1=369左起第1000位数是3.(2)一位数9两位数10-99为90×2=180三位数100-999占位1000×3=3000(1000-180-9)÷3=270 (1)所以第1000个数字为第270个三位数369的第1个数即3 7.有一本科幻故事书,每四页中,有一页为文字,其余三页为图画。
如果第一页为图画,那么第二、三页也是图画,第四页为文字,第五、六、七页又为图画,依此类推。
如果第一页为文字,那么第二、三、四页为图画,第五页为文字,第六、七、八页又为图画,依此类推。
试问:(1)假如这本书有96页,且第一页是图画,那么这本书多少页有图画?99÷3=33(页)33*2=66(页)答:那么共有( 66 )页图画(2)假如这本书有99页,那么多少页有图画?89÷3=29(页)余2(页)29*1=29(页)答:那么共有( 29 )页文字8、一本故事书有400页,页码中数字4出现了多少次.个位数上每10数出现一次,出现的次数少400÷ 10=40次十位数上每100数出现10次,出现的次数少400÷ 10=40次百位是400个出现一次,只有一次所以页码中数字4出现的次数是40+40+1=81次9、一本书的中间被撕掉了一张,余下的各页码数和正好是1200页,这本书有多少页,撕掉的一张上的页码是_____和_____.肯定是1页开始,到最后x页合起来是1200‘从1加到50 可以算出来=(1+50)*50/2=1275,可以看出在1200附近所以尝试一下共有49页算出来所有页码数的和为1275-50=1225 所以满足条件只要第25页被撕掉,就正好和是1200,10、给一本书编页码,从第1页到第119页,一共用多少个数字.从第1页到第119页,一位数页码:9个,两位数页码:2×90=180(个),三位数页码:(119-100+1)×3=20×3=60(个).9共有:9+180+60=249(个).故答案为:249.11、从一本有200页书中撕下22张纸,这22张纸的页码之和是否可能是1000?为什么?如果撕下这本书的前22张纸,则被撕下的页码为1~44,则其和为:(1+44)×44÷2=45×22,=990.这22张纸的页码之和最小为990,1000-900=10,又因为相临两张纸页码之和最小相差4,如用第23张纸换下第22张纸,其和为994;用第24张纸换下第22张纸,其和为998;用第25张纸换下第22张纸其和为1002,再用用剩下的任何一张纸中的页码换下前22张中一张的页码其和会大于1000,所以任意22张纸的页码之和不可能是1000.所以22张纸的页码之和不可能是1000.12、一本书的各页上标着页码,共用了495个数字(如第36页用3、6两个数字).这本书共有多少页?一位数页码1~9共用9个数字;两位数页码10~99共用2×90=180个数字;则此时还剩下495-180-9=306个数,由于从100开始是3位数.306÷3=102.则这本书共有99+102=201页.答:在这本书共有201页13、一年级的小朋友练习写数,那么他从1写到100,在这100个数中,共写了多少个1.解:1~9,“2”共出了1次,10~20共出现了11次,20~99共出现了8次,100共出现了1次,所以,在这100个数中,共写了1+11+8+1=21(个).故答案为:21.14、一套数学分上下两册,编页码时共用了2010个数码.又知上册比下册多28页,那么上册有多少页.1~9页共9页用1位编码:共9个数码;10~99页共90页使用2位编码:共90×2=180个数码;100~999需要3位编码,三位共用了:2010-180-9=1821个数码;即1821÷3=607(页),书共607+90+9=706(页)则上册有:(706+28)÷2=367页.答:上册有367页.故答案为:367.15、奇奇正在读一本196页的故事书,不小心合上了,他记得刚读完的相邻两页页码之和是81.(1)奇奇刚读完的两页页码各是多少?(2)这本故事书还剩多少页没读?(3)如果奇奇每天读30页,剩下的几天读完?(1)81=40+41,答:这两页页码分别是40页、41页.(2)196-41=155(页),答:还剩下155页.(3)155÷30=5天(天)…5页,5+1=6(天),答:剩下的还要6天读完.16、一本法律书页码用了2862个数字,这本书共多少页?一位数1--9共用了9个数字,两位数10--99共用了90×2=180个数字,此时还剩下2862-9-180=2763个数字.2763÷3=921,即共用了921个三位数.则这本书共有9+90+921-1=919(页)答:这本书共有919页.17、一本小说的页码,在印刷时必须用1989个铅字,在这一本书的页码中数字1出现多少次?首先,1-9,九个铅字,有1个一其次,10-99,一百八十个铅字(=2×10×9),分两部分,10-19,有10+1个一20-99,有8个一然后,100-999,二千七百个铅字(=3×100×9),综上推出第1989个铅字是699的9.即需计算从1-699中,1出现的次数。