两圆的公切线

公切线定理
几何学中，公切线定理是非常重要和有用的一个定理。

它规定，如果一条直线在两个不
同的圆上有相交，那么这条直线既是这两个圆的公切线，即这两个圆的半径有着相等的距离。

考虑两个不同大小的圆C1和C2。

如果存在一条直线L，它分别从圆C1和C2的圆心出发，且相交在圆C1和C2的某点P处，那么该直线L就是这两个圆的公切线。

要证明该公切线定理，可以先设空间中有三点O1，O2和P，其中O1和O2分别为圆C1和
C2的圆心，P为圆C1和C2的公共交点。

根据三角形的勾股定理可知，
(1)PO1^2+PO2^2=2*OP^2
将两个式子代入到一起，得出：
(2)PO1^2-2*OP^2+PO2^2=0
根据二次多项式的相关知识，式子(2)构成了一个二次多项式a*x2+2b*x+c，其中a、b、c
均为实数，此时a、b、c分别等于1、−2、1，求x的根可得：
x^2-2x+1=0
因此，有x1=1，x2=1，可知PO1和PO2均为1，证明了直线L是圆C1和C2的公切线。

综上所述，公切线定理为：如果一条直线在两个不同大小的圆上有相交，那么该直线就是
这两个圆的公切线，即这两个圆的半径有着相等的距离。

该定理在几何学中有着非常重
要的地位和作用。

除了几何学研究，它还可以应用在其他领域中，如机械设计与波特参
数计算等。

初中数学公切线与圆的位置关系是什么
公切线与圆的位置关系主要有三种情况：外公切线、内公切线和不相交。

1. 外公切线：
-外公切线是指一条直线与圆相切，且位于圆的外部。

-外公切线与圆的切点位于圆上，且与切点连线垂直于圆的半径。

-外公切线与圆的切点构成的线段与圆的半径之差相等。

-外公切线与圆的位置关系是切点位于圆的外部，切线与圆的位置关系是切线与圆只有一个切点。

2. 内公切线：
-内公切线是指一条直线与圆相切，且位于圆的内部。

-内公切线与圆的切点位于圆上，且与切点连线垂直于圆的半径。

-内公切线与圆的切点构成的线段与圆的半径之和相等。

-内公切线与圆的位置关系是切点位于圆的内部，切线与圆的位置关系是切线与圆只有一个切点。

3. 不相交：
-当两个圆之间的距离大于两个圆的半径之和时，它们没有公共切点，也就是不存在公切线。

-不相交的圆之间有两种情况：一个圆在另一个圆的内部或两个圆完全分离。

需要注意的是，公切线与圆的位置关系是由两个因素决定的：切点的位置和切线与圆的关系。

公切线的切点位于圆上，且与切点连线垂直于圆的半径。

切线与圆的位置关系是切线与圆只有一个切点。

希望以上内容能够满足你对公切线与圆的位置关系的了解。

两个圆的公切线两个圆的公切线圆上任意⼀点拥有唯⼀的圆⼼⾓根据两个圆的位置关系来确定情况1. 两个圆内含，没有公共点，没有公切线2. 两圆内切，有⼀个条公切线3. 两圆完全重合，有⽆数条公切线4. 两圆相交。

有2条公切线5. 两圆外切，有3条公切线6. 两圆相离，有4条公切线1 与 3 什么都不求，情况2 可以直接求出直线AB的极⾓进⽽转换为圆⼼⾓来求切点，连接切点和圆⼼，旋转90度即可得到切线。

情况 4 有两条外公切线，求出圆⼼距d以及|AG| 即可求出α的⼤⼩，根据→AB的极⾓进⾏旋转即可求出切点，进⽽得到切线情况 5 的内切线类似情况2情况 6 的外公切线与情况4完全⼀样情况 6 的内切线也是先求出圆⼼⾓α，如何求？cosα=A r+B r |AB|struct circle{Point p;double r;// 通过圆⼼⾓求圆上某⼀点Point point(double a){return Point(p.x + cos(a) * r, c.y + sin(a) * r);}}// a[i] 存放第 i 条公切线与圆A 的交点int getTangents(circle A, circle B, Point*a, Point *b){int cnt = 0;// 以A为半径更⼤的那个圆进⾏计算if(A.r < B.r) return getTangents(B, A, b, a);db d2 = (A.p-B.p).len2(); // 圆⼼距平⽅db rdiff = A.r - B.r; // 半径差db rsum = A.r + B.r; //半径和if(d2 < rdiff * rdiff) return 0; // 情况1，内含,没有公切线Vector AB = B.p - A.p; // 向量AB，其模对应圆⼼距db base = atan2(AB.y, AB.x); // 求出向量AB对应的极⾓if(d2 == 0 && A.r == B.r) return -1;// 情况3，两个圆重合，⽆限多切线 if(d2 == rdiff * rdiff){ // 情况2，内切，有⼀条公切线a[cnt] = A.point(base);b[cnt] = B.point(base);cnt++;return 1;}// 求外公切线db ang = acos((A.r - B.r) / sqrt(d2)); //求阿尔法// 两条外公切线a[cnt] = A.point(base+ang); b[cnt] = B.point(base+ang); cnt++;a[cnt] = A.point(base-ang); b[cnt] = B.point(base-ang); cnt++;if(d2 == rsum * rsum){ // 情况5，外切，if⾥⾯求出内公切线a[cnt] = A.point(base); b[cnt] = B.point(pi+base); cnt++;}else if(d2 > rsum * rsum){ //情况6，相离，再求出内公切线db ang = acos((A.r + B.r) / sqrt(d2));a[cnt] = A.point(base + ang); b[cnt] = B.point(pi+base+ang);cnt++; a[cnt] = A.point(base - ang); b[cnt] = B.point(pi+base-ang);cnt++; }// 此时，d2 < rsum * rsum 代表情况 4 只有两条外公切线return cnt;}Processing math: 100%。

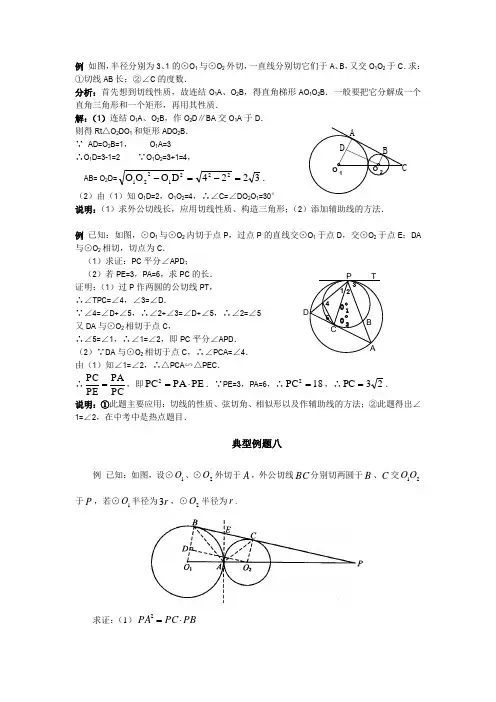
例 如图，半径分别为3、1的⊙O 1与⊙O 2外切，一直线分别切它们于A 、B ，又交O 1O 2于C ．求：①切线AB 长；②∠C 的度数．分析：首先想到切线性质，故连结O 1A 、O 2B ，得直角梯形AO 1O 2B ．一般要把它分解成一个直角三角形和一个矩形，再用其性质． 解：（1）连结O 1A 、O 2B ，作O 2D ∥BA 交O 1A 于D ． 则得Rt △O 2DO 1和矩形ADO 2B ． ∵ AD=O 2B=1， O 1A=3 ∴O 1D=3-1=2 ∵O 1O 2=3+1=4， AB= O 2D=3224D O O O 2221221=-=-．（2）由（1）知O 1D=2，O 1O 2=4，∴∠C=∠DO 2O 1=30° 说明：（1）求外公切线长，应用切线性质、构造三角形；（2）添加辅助线的方法．例 已知：如图，⊙O 1与⊙O 2内切于点P ，过点P 的直线交⊙O 1于点D ，交⊙O 2于点E ；DA 与⊙O 2相切，切点为C ．（1）求证：PC 平分∠APD ；（2）若PE=3，PA=6，求PC 的长． 证明：（1）过P 作两圆的公切线PT ， ∴∠TPC=∠4，∠3=∠D ． ∵∠4=∠D+∠5，∴∠2+∠3=∠D+∠5，∴∠2=∠5 又DA 与⊙O 2相切于点C ， ∴∠5=∠1，∴∠1=∠2，即PC 平分∠APD ．（2）∵DA 与⊙O 2相切于点C ，∴∠PCA=∠4．由（1）知∠1=∠2，∴△PCA ∽△PEC ． ∴PCPA PE PC =，即PE PA PC 2⋅=．∵PE=3，PA=6，∴18PC 2=，∴23PC =． 说明：①此题主要应用：切线的性质、弦切角、相似形以及作辅助线的方法；②此题得出∠1=∠2，在中考中是热点题目．典型例题八例 已知：如图，设⊙1O 、⊙2O 外切于A ，外公切线BC 分别切两圆于B 、C 交21O O 于P ，若⊙1O 半径为r 3，⊙2O 半径为r .求证：（1）PB PC PA ⋅=2O 1O 2A B CD O 1O 2A C BTP 12345（2）求P cos 的值。

怎样确定两圆的内公切线和外公切线答：首先应弄清公切线、内公切线和外公切线等概念．和两个圆都相切的直线，叫做两圆的公切线．两个圆在公切线同旁时，这样的公切线叫做外公切线图1(1)．两个圆在公切线6d22aeae8db846b70d2b475bba1b063c两旁时，这样的公切线叫做内公切线图1(2)．根据定义可以分清什么是两圆的内公切线，什么是两圆的外公切线．由于两圆的位置不同，这两圆的公切线条数也不相同．下面分别讨论．(1)当两圆外离时，可以作两条外公切线和两条内公切线，故共有4条公切线；(2)当两圆外切时，可以作两条外公切线和1条内公切线，故共有3条公切线；(3)当两圆相交时，可以作两条外公切线，而无法作出内公切线，故共有2条公切线；(4)当两圆内切时，只可作1条外公切线，而无法作两圆的内公切线，故共有1条公切线；(5)当两圆内含时，没有公切线．反过来，若两圆有4条、3条、2条、1条、没有公切线时，也可判定两圆的位置关系分别是外离、外切、相交、内切、内含．介绍两圆相外离时公切线的作法如下．作两圆的公切线，关键是作出切点，解决问题的方法是把它转化为过一点作圆的切线问题．可以想像把两圆中较小的一个圆的半径逐渐变小，最后成为一个点的情况；与小圆半径变小的同时，大圆的半径也相应地变小相等的长度，可结合画图，得到作相离两圆的外公切线转化为过圆外一点作圆(辅助圆)的切线．所以得出要先作出和大圆同心，并且半径等于两半径之差的辅助圆．如图2所示，画两个圆的公切线时，总是以较大的圆的圆心为圆心，先画一个辅助圆．如果是画外公切线．那么辅助圆的半径等于两圆半径的差；如果要画的是内公切线，那么辅助圆的半径等于两圆半径的和．辅助圆画好后，再从较小的圆的圆心作辅助圆的切线，连结切点和较大圆的圆心的线段，使之与较大圆相交于一点(画外公切线时要延长)，然后过这交点画辅助圆的切线的平行线，就得到要画的公切线．总之，画外公切线和画内公切线的方法是一样的，只是辅助圆的半径不同．当两圆外切、两圆相交时两圆外公切线的作法与两圆外离时的作法基本相同．想一想两圆外切时内公切线的作法(过切点作两圆连心线的垂线)．1421-1638-9529-3184。

计算圆的公切线一、引言圆是一种基本的几何图形，其在现实生活和科学研究中具有广泛的应用。

圆的公切线是与一个或多个圆相切的直线，其计算和求取对于许多领域如几何学、工程学和物理学等都有着重要的意义。

了解如何计算圆的公切线对于深入理解几何学基本概念和解决实际问题都具有不可或缺的作用。

二、公切线的定义与性质三、计算公切线的步骤与方法四、实例分析以两个相切的圆为例，说明如何计算它们的公切线。

假设两个相切圆的圆心分别为(h 1,k 1)和(h 2,k 2)，半径分别为r 1和r 2。

首先判断两圆的位置关系，由于是相切圆，所以两圆心距等于两圆半径之和或差。

然后使用公式求取公切线的方程：x −h 1D 1=y −k 1E 1=z −f 1F 1和x −h 2D 2=y −k 2E 2=z −f 2F 2其中D 1,E 1,F 1,D 2,E 2,F 2是与两圆相切的直线系参数。

通过解这两个方程组，可以求得公切线的参数和方程。

最后将求得的公切线方程应用于实际问题中，如机械零件的设计、建筑结构的分析等。

五、结论计算圆的公切线是几何学中的一个重要问题，对于解决实际问题具有重要的意义。

通过了解公切线的定义与性质、掌握计算公切线的步骤与方法以及实例分析，可以深入理解几何学的基本概念并提高解决实际问题的能力。

在未来的学习和工作中，可以进一步探索如何将计算圆的公切线的方法应用于更多领域中，发挥其在实际问题解决中的作用。

同时，可以深入研究其他类型的几何图形如椭圆、抛物线等的公切线计算方法，以丰富自己的几何学知识体系。

此外，随着计算机技术的发展，可以利用计算机编程语言和数学软件实现自动计算公切线的程序，以提高计算的准确性和效率。

1. 定义：公切线是与一个或多个圆在某点相切的直线。

对于两个相切的圆，公切线是它们唯一的一条共同切线，而与这两个圆相切的该公切线只有一个公共点（切点）。

2. 性质：公切线具有一些重要的性质，包括：公切线的长度等于两个相切圆的半径之和或差（根据两圆的位置关系而定）。

公切线的条数怎么看
公切线的条数怎么看的方法如下：
若两圆相离，则有4条公切线。

若两圆外切，则有3条公切线（两外切，一内切）。

两圆相交，则有2条公切线（外切）。

若两圆内切，则有1条公切线。

若两圆内含，则有0条公切线。

公切线是指同时相切于两条或两条以上的曲线的直线，例如和两个圆相切的直线叫做这两个圆的公切线。

公切线是指同时相切于两条或两条以上的曲线的直线，例如和两个圆相切的直线叫做这两个圆的公切线。

如果两个圆在公切线的同侧，则这公切线叫外公切线；如果两个圆在公切线的异侧，则叫内公切线。

公切线的条数与两圆的位置关系如下：若两圆相离，则有4条公切线；若两圆外切，则有3条公切线（两外切，一内切）；两圆相交，则有2条公切线（外切）；若两圆内切，则有1条公切线；若两圆内含，则有0条公切线。

两圆的公切线简介在几何学中，当两个圆相交或者相离时，我们可以找到连接两个圆的一条或多条切线。

当两个圆相交时，称为内公切线；当两个圆相离时，称为外公切线。

公切线是指切线同时接触两个圆的一条线段。

本文将介绍两个圆的公切线的性质和求解方法。

公切线的性质内公切线内公切线有以下几个性质：1.内公切线的切点在两个圆的连线上。

2.内公切线垂直于两个圆的连线。

3.两个圆心与内公切线的交点三者共线。

外公切线外公切线有以下几个性质：1.外公切线的切点不在两个圆的内部。

2.外公切线垂直于两个圆的连线。

3.两个圆心与外公切线的交点三者共线。

求解两圆的公切线内公切线的求解求解两个圆的内公切线的步骤如下：1.根据两个圆的半径和圆心之间的距离，判断两个圆的位置关系。

如果两个圆相离，则不存在内公切线；如果两个圆相交，可以继续下一步求解。

2.连接两个圆心，得到两个圆心连线。

3.在圆心连线上选择一个点，作为内公切线的切点。

4.通过切点，作出与两个圆相切的切线。

5.内公切线即为连接两个切点的线段。

外公切线的求解求解两个圆的外公切线的步骤如下：1.根据两个圆的半径和圆心之间的距离，判断两个圆的位置关系。

如果两个圆相交，则不存在外公切线；如果两个圆相离，可以继续下一步求解。

2.连接两个圆心，得到两个圆心连线。

3.在圆心连线上选择一个点，作为外公切线的切点。

4.通过切点，作出与两个圆相切的切线。

5.外公切线即为连接两个切点的线段。

总结两个圆的公切线是连接两个圆的一条线段，且同时接触两个圆。

内公切线和外公切线有着不同的性质和求解方法。

通过本文的介绍，我们了解到了两个圆的公切线的性质和求解方法，这对于几何学的学习和应用都具有重要意义。

希望本文能为读者提供清晰的思路和方法，帮助读者更好地理解和应用两个圆的公切线的知识。

两圆的公切线(二)引言在上一篇文章中，我们讨论了两个圆的公切线的概念以及求解公切线的方法。

本文将进一步探讨两个圆的公切线，并介绍几个实际问题中的应用。

求解两个圆的公切线假设有两个圆C1和C2，它们的圆心分别为O1和O2，半径分别为r1和r2。

我们的目标是求解这两个圆的公切线。

情况一：两个圆相交当两个圆相交时，存在两条内公切线和两条外公切线。

内公切线内公切线示意图内公切线示意图如图所示，设两个圆的半径分别为r1和r2，圆心之间的距离为d。

对于内公切线，设切点分别为A和B。

根据几何性质可知，AO1、BO1是两个圆的半径，且垂直于相应的切线。

因此，我们可以得到以下等式：(O1A)^2 + (O1O2)^2 = r1^2 —-(1)(O2B)^2 + (O1O2)^2 = r2^2 —-(2)将公式(1)和(2)相减，可以消去O1O2：(O1A)^2 - (O2B)^2 = r1^2 - r2^2根据O1A和AO2的互为相反数的关系，可得：(O1A + O2B)(O1A - O2B) = r1^2 - r2^2由于O1A + O2B = AB，我们可以得到：AB(O1A - O2B) = r1^2 - r2^2由于AB是切线的长度，而O1A - O2B是两个圆心之间的距离，即d。

因此，我们可以得到： AB = (r1^2 - r2^2) / d外公切线外公切线示意图外公切线示意图对于外公切线，同样设切点为A和B。

根据几何性质可知，AO1、BO1是两个圆的半径，且垂直于相应的切线。

因此，我们可以得到以下等式：(O1A)^2 - (O1O2)^2 = r1^2 —-(3)(O2B)^2 - (O1O2)^2 = r2^2 —-(4)将公式(3)和(4)相减，可以消去O1O2：(O1A)^2 - (O2B)^2 = r1^2 - r2^2同样由于O1A + O2B = AB，我们可以得到： AB = (r1^2 - r2^2) / d情况二：两个圆外切当两个圆外切时，存在两条内公切线和两条外公切线。

揭开圆与圆的公切线之谜圆与圆的公切线一直以来都是几何学中的研究热点之一。

公切线不仅仅是几何图形之间的触点，更是连接着不同圆之间的关系和相互作用。

本文将深入探讨圆与圆的公切线问题，揭开其中的谜团。

1. 公切线的定义与性质公切线是指两个几何图形（圆与圆或圆与直线）之间触点处的切线。

对于两个圆，公切线有两条，分别为内公切线和外公切线。

根据定义，公切线有以下性质：- 公切线与半径的关系：公切线与连接两圆心的半径相垂直。

- 动线：两圆的相对位置将决定公切线的动线。

当两圆相交时，公切线不存在；当两圆相离时，公切线只存在于两圆之间；当两圆内切或外切时，公切线则存在于两圆外或内。

- 角度：内公切线和外公切线的夹角恒为180度。

这意味着内公切线与外公切线互为补角。

2. 圆与圆的内公切线内公切线是指两个圆内部的公切线。

以圆A和圆B为例，描绘内公切线的步骤如下：步骤一：连接两圆心，得到连线CD。

步骤二：从圆A和圆B的圆心分别画出半径AE和BF。

步骤三：以AE和BF为直径，作两个新圆。

分别记作圆A'和圆B'。

步骤四：连接新圆A'与新圆B'的圆心，得到连线A'B'。

步骤五：连线A'B'即为圆A与圆B的内公切线。

3. 圆与圆的外公切线外公切线是指两个圆外部的公切线。

以圆A和圆B为例，描绘外公切线的步骤如下：步骤一：连接两圆心，得到连线CD。

步骤二：从圆A和圆B的圆心分别画出半径AE和BF。

步骤三：以AE和BF为直径，作两个新圆。

分别记作圆A'和圆B'。

步骤四：连接圆A'和圆B'的圆心，得到连线A'B'。

步骤五：连线A'B'即为圆A与圆B的外公切线。

4. 圆与圆的特殊情况除了一般情况下的内公切线和外公切线，圆与圆之间还存在一些特殊情况。

- 当两个圆相交时，它们之间没有公切线。

- 当两个圆相切时，它们有两条公切线，且这两条公切线相互垂直。

初中数学公切线的性质有哪些
公切线是两个圆或两个球体之间的一条直线，具有以下性质：
1. 公切线与两个圆或两个球体的切点构成等腰三角形：
公切线与两个圆或两个球体的切点，以及连接两个切点的直线构成一个等腰三角形。

在这个等腰三角形中，两个切点与切点直线的中点连线相等。

2. 公切线在切点处与切线相切：
公切线在两个圆或两个球体的切点处与切线相切。

切点的切线方向相反且互相垂直。

3. 公切线与切点连线互相垂直：
公切线与两个圆或两个球体的切点连线在切点处互相垂直，即两个切点与切点连线互相垂直。

4. 公切线在切点处的切线长度相等：
公切线在两个圆或两个球体的切点处的切线长度相等，即两个切点与切点连线的长度相等。

5. 外公切线与内公切线：
如果两个圆或两个球体相离，它们之间的公切线是外公切线。

外公切线与两个圆或两个球体的切点在同一侧。

如果两个圆或两个球体内切或相交，它们之间的公切线是内公切线。

内公切线与两个圆或两个球体的切点在不同侧。

6. 公切线上的切点坐标关系：
如果已知两个圆或两个球体的半径和圆心坐标，可以通过求解公切线上的切点坐标来确定公切线的方程。

7. 公切线的应用：
公切线在几何问题中有广泛的应用。

例如，可以利用公切线的性质来求解两个圆或两个球体之间的距离、判断两个圆或两个球体的位置关系、构造切线等。

以上是公切线的一些基本性质。

在实际问题中，还可以通过引入向量、三角函数等概念来更深入地研究公切线的性质和应用。

希望以上内容能够满足你对公切线性质的了解。