《计算机算法》课程实验指导书

《算法分析与设计》实验指导书《算法分析与设计》课程是计算机专业的一门必修课程。

开设算法分析与设计实验，目的就是为了使学生消化理论知识，加深对讲授内容的理解，尤其是一些算法的实现及其应用，培养学生独立编程和调试程序的能力，使学生对算法的分析与设计有更深刻的认识。

《算法分析与设计》课程实验的目的：是为了使学生在课程学习的同时，通过实验环境中的实际操作，对部分算法的具体应用有一个初步的了解，使学生加深了解和更好地掌握《算法分析与设计》课程教学大纲要求的内容。

《算法分析与设计》课程实验的注意事项：在《算法分析与设计》的课程实验过程中，要求学生做到：(1)预习实验指导书有关部分，认真做好实验内容的准备，就实验可能出现的情况提前作出思考和分析。

(2)认真书写实验报告。

实验报告包括实验目的和要求，实验情况及其分析。

(3)遵守机房纪律，服从辅导教师指挥，爱护实验设备。

(4)实验课程不迟到。

如有事不能出席，所缺实验一般不补。

《算法分析与设计》课程实验的验收：实验的验收将分为两个部分。

第一部分是上机操作，包括检查程序运行和即时提问。

第二部分是提交电子的实验报告。

实验一算法实现一一、实验目的与要求熟悉C/C++语言的集成开发环境；通过本实验加深对分治法、贪心算法的理解。

二、实验内容:掌握分治法、贪心算法的概念和基本思想，并结合具体的问题学习如何用相应策略进行求解的方法。

三、实验题1. 【伪造硬币问题】给你一个装有n个硬币的袋子。

n个硬币中有一个是伪造的。

你的任务是找出这个伪造的硬币。

为了帮助你完成这一任务，将提供一台可用来比较两组硬币重量的仪器，利用这台仪器，可以知道两组硬币的重量是否相同。

试用分治法的思想写出解决问题的算法，并计算其时间复杂度。

2.【找零钱问题】一个小孩买了价值为33美分的糖，并将1美元的钱交给售货员。

售货员希望用数目最少的硬币找给小孩。

假设提供了数目有限的面值为25美分、10美分、5美分、及1美分的硬币。

第一章 绪论一、主要要求通过实验，认真理解和体会数值计算的稳定性、精确性与步长的关系。

二、主要结果回顾：1、算法：电子计算机实质上只会做加、减、乘、除等算术运算和一些逻辑运算，由这些基本运算及运算顺序规定构成的解题步骤，称为算法．它可以用框图、算法语言、数学语言或自然语言来描述。

用计算机算法语言描述的算法称为计算机程序。

（如c —语言程序，c++语言程序，Matlab 语言程序等）。

2、最有效的算法：应该运算量少，应用范围广，需用存储单元少，逻辑结构简单，便于编写计算机程序，而且计算结果可靠。

3、算法的稳定性：一个算法如果输入数据有误差，而在计算过程中舍入误差不增长，则称此算法是数值稳定的，否则称此算法为不稳定的。

换句话说：若误差传播是可控制的,则称此算法是数值稳定的,否则称此算法为不稳定的。

4、控制误差传播的几个原则： 1）防止相近的两数相减； 2）防止大数吃小数；3）防止接近零的数做除数；4）要控制舍入误差的累积和传播；5）简化计算步骤,减小运算次数,避免误差积累。

三、数值计算实验（以下实验都需利用Matlab 软件来完成） 实验1.1（体会数值计算精度与步长关系的实验）实验目的：数值计算中误差是不可避免的，要求通过本实验初步认识数值分析中两个重要概念：截断误差和舍入误差，并认真体会误差对计算结果的影响。

问题提出：设一元函数f :R →R ，则f 在x 0的导数定义为：hx f h x f x f h )()(lim)('0000-+=→实验内容:根据不同的步长可设计两种算法,计算f 在x 0处的导数。

计算一阶导数的算法有两种：hx f h x f x f )()()('000-+≈（1）hh x f h x f x f 2)()()('000--+≈（2）请给出几个计算高阶导数的近似算法，并完成如下工作： 1、对同样的h ，比较(1)式和(2)式的计算结果；2、针对计算高阶导数的算法，比较h 取不同值时(1)式和(2)式的计算结果。

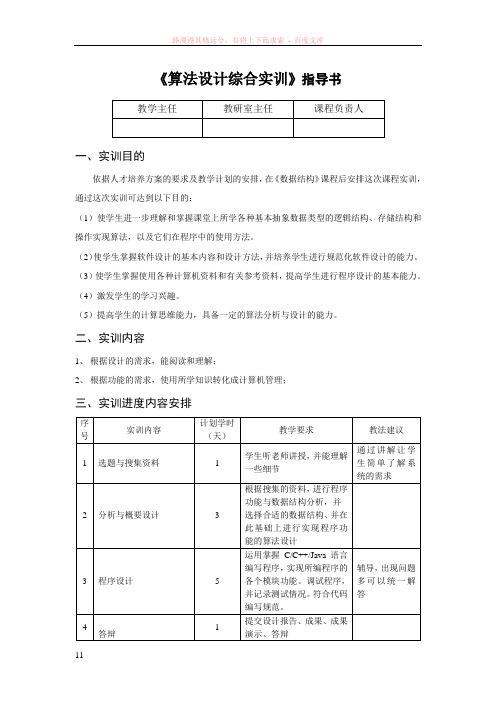
《算法设计综合实训》指导书一、实训目的依据人才培养方案的要求及教学计划的安排，在《数据结构》课程后安排这次课程实训，通过这次实训可达到以下目的：（1）使学生进一步理解和掌握课堂上所学各种基本抽象数据类型的逻辑结构、存储结构和操作实现算法，以及它们在程序中的使用方法。

（2）使学生掌握软件设计的基本内容和设计方法，并培养学生进行规范化软件设计的能力。

（3）使学生掌握使用各种计算机资料和有关参考资料，提高学生进行程序设计的基本能力。

（4）激发学生的学习兴趣。

（5）提高学生的计算思维能力，具备一定的算法分析与设计的能力。

二、实训内容1、根据设计的需求，能阅读和理解；2、根据功能的需求，使用所学知识转化成计算机管理；三、实训进度内容安排序号实训内容计划学时（天）教学要求教法建议1 选题与搜集资料 1 学生听老师讲授，并能理解一些细节通过讲解让学生简单了解系统的需求2 分析与概要设计3 根据搜集的资料，进行程序功能与数据结构分析，并选择合适的数据结构、并在此基础上进行实现程序功能的算法设计3 程序设计 5 运用掌握C/C++/Java语言编写程序，实现所编程序的各个模块功能。

调试程序，并记录测试情况。

符合代码编写规范。

辅导，出现问题多可以统一解答4答辩1提交设计报告、成果、成果演示、答辩教学主任教研室主任课程负责人合计10四、基本要求（一）设计要求（1）所有学生统一在机房进行设计；（2）听从指导老师的统一安排；（3）严格遵守作息时间、不迟到、不早退，病、事假必须向指导老师请假；（4）使用C/C++/JA V A进行开发；（5）满足编程规范；（6）设计结构清晰（模块化开发）。

（7) 根据任务书的要求选择设计题目，针对线性表、栈、队列与递归、字符串算法设计至少选作2个题目，树、图至少选作1个题目，查找与排序至少选作1个题目。

根据题目难易程度进行综合评分。

（8）抄袭他人程序者记零分。

（二）报告要求（1）问题描述：描述要求编程解决的问题。

计 算 方 法实 验 指 导 书彭彬计算机技术实验中心2012年3月· 实验环境： VC++ 6.0· 实验要求：在机房做实验只是对准备好的实验方案进行验证，因此上机前要检查实验准备情况，通过检查后方可上机。

没有认真准备的学生不能上机，本次实验没有分数。

实验中要注意考察和体会数值计算中出现的一些问题和现象：误差的估计,算法的稳定性、收敛性、收敛速度以及迭代初值对收敛的影响等。

· 关于计算精度：如果没有特别说明，在计算的过程中，小数点后保留5位数字，最后四舍五入到小数点后四位数字。

迭代运算的结束条件统一为51102-⨯。

在VC++ 6.0中，可使用setprecision 在流的输出中控制浮点数的显示（缺省显示6位）。

演示如下： # include<iostream.h> # include<math.h> # include<iomanip.h>//输出6位精度，输出左对齐cout<<setprecision(6)<<setiosflags(ios::left); //设置输出宽度为12（不够将补充0） cout<<setw(12)<<coeff[i];· 关于图形绘制本课程个别实验要求画出函数的曲线，所有画图题目均要求用MFC 完成。

利用VC++6.0的MFC 画图，先要建立一个工程，然后在***View 中加入自定义变量、自定义函数等，最后在OnDraw （）方法中调用自定义函数。

也可以把代码直接写入OnDraw （）方法中。

画曲线有两种方法，（一）一句坐标逐个打点（用SetPixel()函数），（二）先把当前光标移动（MoveTo（）函数）到曲线的始点，再用LineTo （）函数画线。

线的样式由画笔决定。

对封闭区域可以填充，填充的样式由画刷决定。

在VC++6.0中,先新建一个MFC AppWizard(exe)类型的工程(建立工程时，“应用程序类型”选择“单文档”；“是否包含数据库”选择“不包含数据库”；其它选择缺省),然后在“ClassView ”中选择XXView 类文件加以操作。

算法设计与分析实验指导书信电工程学院2015.7算法设计与分析一.实验目的算法设计与分析是计算机相关专业的核心课程之一。

本实验加深学生对算法设计的基本策略、主要方法及实验过程的理解；培养学生针对具体的问题，选择合适的数据结构和设计结构清晰、正确有效的算法的能力。

二.实验内容E05210801 算法概述E05210802 分治法E05210803 动态规划E05210804 贪心法E05210805 回溯法E05210806 分支限界法E05210807 NP完全问题E05210808 近似算法三.实验方法本课程所有实验均需上机进行，每个实验都有明确的实验目的，并根据实验要求提供实验题。

每位同学通过独立思考、与同学讨论、老师辅导答疑相结合的方法完成相应的实验题，在对题目进行分析、选择有效的方法、编程及测试的过程中，将达到加深学生印象、锻炼学生运用书本知识实际解决问题的能力。

四. 实验要求学生按照实验要求，上机前写好上机实验预习报告。

上机实验时按实验要求完成每一个实验的内容。

认真书写实验报告，内容包括：实验的目的、实验原理、实验内容、实验步骤、实验结果等。

实验一算法概述1. 实验目的(1) 复习数据结构课程的相关知识，实现课程间的平滑过渡；(2) 掌握并应用算法的数学分析和后验分析方法；(3) 理解这样一个观点：不同的算法能够解决相同的问题，这些算法的解题思路不同，复杂程度不同，解题效率也不同。

2. 实验内容求两个自然数m和n的最大公约数。

3. 实验要求(1) 至少设计出三个版本的求最大公约数算法；(2) 对所设计的算法采用大O符号进行时间复杂性分析；(3) 上机实现算法，并用计数法和计时法分别测算算法的运行时间；(4) 通过分析对比，得出自己的结论。

实验二分治法1. 实验目的(1) 进一步掌握递归算法的设计思想以及递归程序的调试技术；(2) 理解这样一个观点：分治与递归经常同时应用在算法设计之中。

武汉轻工大学数学与计算机学院计算机算法基础实验报告学校：武汉轻工大学院系：数学与计算机学院班级：软件工程1303班姓名：刘敏学号：1305110145指导老师：李诗高2015年11月8日星期天实验一、递归与分治算法实验实验目的掌握用递归和分治法的基本思想解决实际问题。

实验环境Windows系统, VC6.0实验题目1、编写一个在1，2，…，9（顺序不能变）数字之间插入+或-或什么都不插入，使得计算结果总是100的程序，并输出所有的可能性。

例如：1 + 2 + 34–5 + 67–8 + 9 = 100。

2、编写一个求无括号的四则运算式子的程序。

例如：输入1 + 2 *3-5 返回结果2。

3、问题描述：大于1的正整数n可以分解为n=x1*x2*…*x n。

例如，当n=12时，共有8种不同的分解式：12=12 12=6*2 12=4*3 12=3*412=3*2*2 12=2*6 12=2*3*2 12=2*2*3对于给定的正整数n，设计一个算法输出n的所有不同的分解形式。

对于整数因子分解问题，先从2到n先找到一个能被n整除的整数x1(即n%x1==0)，显然x1是n的一个因子。

因为n=x1*( n/x1)，只要找到( n/x1)因子分解，就找到了n的一个因子分解形式，所以问题被简化为对n/x1进行因子分解。

采用递归方法对n/x1求因子x2，持续递归迭代直到问题简化为对1求因子时，就找到了n的一个因子分解形式x1,x2,…提示：采用递归方法解决问题，重点是找到怎么将问题简化为一个比原问题规模小的同样的问题。

小的问题被简化为更小的问题，直到可以直接求解，最终小的问题被解决，同样地，大的问题也被解决。

实验要求1三个题目可任选一题实现，也可以完成多个。

2设计递归算法，并在vc6下编译和调试通过，通过具体的输入来测试程序并输出结果。

实验代码：题目一：#include<stdio.h>#include<stdlib.h>#include<string.h>const int N =9;void func(char op[],int sum,int prevadd,int a[],int i); int calcexp(const char *pexp);int main(const char *argv[], int argc){int a[N];char op[N]="+";for(int i = 0 ; i<N ; i++)a[i]=i+1;func(op , a[0] , a[0] , a , 1);return 0;}void func(char op[],int sum,int prevadd,int a[],int i){ if (i==N){if (sum==100){int j;printf("%d",a[0]);for (j=1 ; j<N ; j++){if (op[j]!=' ')printf("%c",op[j]);printf("%d",a[j]);}printf("\n",a[j]);}return;}//+op[i] = '+';sum += a[i];func(op , sum , a[i] , a , i+1);sum -= a[i];// -op[i] = '-';sum -= a[i];func(op , sum , -a[i] , a , i+1);sum += a[i];//无op[i] = ' ';sum -= prevadd;int tmp = prevadd >0 ? prevadd*10 + a[i] : prevadd*10 - a[i];sum += tmp;func(op,sum,tmp,a,i+1);sum -= tmp;sum +=prevadd;}题目二：#include<stdio.h>#include<stdlib.h>#include<string.h>int calcexp(const char *pexp);void main(){char *c = (char*)malloc(100);printf("请输入表达式：");scanf("%s",c);int val= calcexp(c);printf("%d\n",val);}int calcexp(const char *pexp){char newexp[1024];int opd1 = atoi(pexp);pexp = pexp + strlen(itoa(opd1 , newexp , 10));if (pexp[0] == '\0')return opd1;char op = *pexp++;if (op == '+')return opd1 + calcexp(pexp);else if(op == '-')return opd1 - calcexp(pexp);else{int opd2 = atoi(pexp);pexp = pexp +strlen(itoa(opd2 , newexp , 10));sprintf(newexp , "%d", op == '*' ? opd1*opd2 :opd1/opd2);strcat(newexp , pexp);return calcexp(newexp);}}题目三：#include<stdio.h>int k = 0;void func(int n){int i;if(n==1){k++;}else{for (i = 2;i<=n;i++){if (n%i==0){func(n/i);}}}}void main(){int a ;printf("请输入正整数：");scanf("%d",&a);func(a);printf("%d\n",k);}运行结果：题目一：题目二：题目三：。

实验三动态规划算法（2学时）一、实验目的与要求1、熟悉最长公共子序列问题的算法；2、初步掌握动态规划算法；二、实验题若给定序列X={x1,x2,…,xm}，则另一序列Z={z1,z2,…,zk}，是X的子序列是指存在一个严格递增下标序列{i1,i2,…,ik}使得对于所有j=1,2,…,k有：zj=xij。

例如，序列Z={B，C，D，B}是序列X={A，B，C，B，D，A，B}的子序列，相应的递增下标序列为{2，3，5，7}。

给定2个序列X和Y，当另一序列Z既是X的子序列又是Y的子序列时，称Z是序列X和Y 的公共子序列。

给定2个序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}，找出X和Y的最长公共子序列。

改进LCS 函数，不使用数组b而仅借助数组c本身在O(m+n)时间内构造最长公共子序列。

三、实验提示#include "stdlib.h"#include "string.h"void LCSLength(char *x ,char *y,int m,int n, int **c, int **b){int i ,j;for (i = 1; i <= m; i++) c[i][0] = 0;for (i = 1; i <= n; i++) c[0][i] = 0;for (i = 1; i <= m; i++)for (j = 1; j <= n; j++){if (x[i]==y[j]){c[i][j]=c[i-1][j-1]+1;b[i][j]=1;}else if (c[i-1][j]>=c[i][j-1]){c[i][j]=c[i-1][j];b[i][j]=2;}else{ c[i][j]=c[i][j-1];b[i][j]=3;}}}void LCS(int i ,int j, char *x ,int **b) {if (i ==0 || j==0) return;if (b[i][j]== 1){LCS(i-1,j-1,x,b);printf("%c",x[i]);}else if (b[i][j]== 2)LCS(i-1,j,x,b);else LCS(i,j-1,x,b);}。

第1篇第一章引言随着信息技术的飞速发展，计算机已经成为现代社会不可或缺的一部分。

为了培养适应新时代要求的计算机专业人才，实践教学在计算机教育中占据了越来越重要的地位。

本手册旨在为计算机实践教学提供全面、系统的指导，帮助教师和学生更好地开展实践环节，提高实践教学质量。

第二章实践教学目标与原则一、实践教学目标1. 培养学生的动手能力：通过实践，使学生掌握计算机的基本操作和编程技能，提高学生的动手能力。

2. 培养学生的创新意识：鼓励学生在实践中探索、创新，培养其创新精神和实践能力。

3. 培养学生的团队协作能力：通过实践项目，让学生学会与他人合作，提高团队协作能力。

4. 培养学生的综合素质：使学生在实践中锻炼自己的沟通能力、组织能力、解决问题的能力等。

二、实践教学原则1. 实践性原则：实践教学应以培养学生的实践能力为核心，注重理论知识与实践操作的紧密结合。

2. 逐步性原则：实践教学应遵循学生的认知规律，由浅入深、循序渐进地进行。

3. 个性化原则：根据学生的兴趣、特长和需求，开展个性化的实践教学。

4. 可持续发展原则：实践教学应关注学生的长远发展，培养学生的终身学习能力。

第三章实践教学内容与方法一、实践教学内容1. 计算机基础操作与维护2. 编程语言与程序设计3. 数据结构与算法4. 操作系统5. 计算机网络6. 数据库技术7. 软件工程8. 计算机安全9. 计算机应用技术10. 项目实践与毕业设计二、实践教学方法1. 实验教学：通过实验课程，让学生掌握计算机基本操作和编程技能。

2. 课程设计：以课程设计为载体，培养学生综合运用所学知识解决实际问题的能力。

3. 毕业设计：通过毕业设计，让学生将所学知识应用于实际项目，提高其创新能力。

4. 课外实践：鼓励学生参加各类竞赛、实践活动，拓宽知识面，提高实践能力。

5. 顶岗实习：让学生在企业或研究机构进行实习，了解行业动态，提高就业竞争力。

第四章实践教学评价一、评价体系1. 实验报告：评价学生在实验过程中的操作规范、实验结果和实验心得。

《算法设计与分析》实验指导书《算法设计与分析》实验指导书本文档主要用于《算法设计与分析》课程的实验指导。

《算法设计与分析》旨在教会学生处理各种问题的方法，通过实验，使学生能够把所学的方法用于具体的问题，并对所用算法进行比较分析，从而提高学生分析问题、解决问题的能力。

通过该课程的实验，使学生对课堂中所讲述的内容有一个直观的认识，更好地掌握所学的知识，培养学生的实际动手能力，加强学生创新思维能力的培养。

本课程设计了7个设计型实验。

实验内容包括用分治法、动态规划、贪心法、回溯法以及分支限界法求解问题。

一、实验内容安排二、实验基本要求实验前要求学生一定要先了解实验目的、内容、要求以及注意事项，要求学生熟悉实验对象，设计并编写相应的算法。

学生应独立完成所布置实验内容，编写代码，运行程序，记录结果并撰写实验报告。

三、实验报告要求实验结束后，应及时整理出实验报告，实验报告提交书面文档。

四、考核方式理论考试（60％）＋实验（30％）+作业（10%）五、实验内容与指导实验一快速排序问题1．实验目的(1) 用分治法求解该问题。

2．实验环境PC机，要求安装Eclipse软件或VC++软件供学生实验。

3．实验内容有n个无序的数值数据，现要求将其排列成一个有序的序列。

4. 实验步骤(1) 输入实现该问题的源代码；(2) 输入测试数据，验证代码的正确性。

5.实验要求(1)做好实验预习，熟悉本实验中所使用的开发环境。

(2)写出实验报告①实验目的②实验内容③出错信息及处理方法④实验结果实验二最少硬币问题1．实验目的(1) 用动态规划求解该问题。

2．实验环境PC机，要求安装Eclipse软件或VC++软件供学生实验。

3．实验内容有n种不同面值的硬币，各硬币面值存于数组T[1:n]；现用这些面值的钱来找钱；各面值的个数存在数组Num[1:n]中。

对于给定的1≤n≤10，硬币面值数组、各面值的个数及钱数m，0<=m<=2001，设计一个算法，计算找钱m的最少硬币数。

算法实验指导书12级《算法设计与分析》实验指导书本实验指导书是为配合《算法设计与分析》课程实验而编写的，其目的是使学生消化算法理论知识，加深对课堂讲授内容的理解，尤其是一些典型算法的实现及其应用，培养学生独立编程和调试程序的能力，使学生对算法的设计与分析有更深刻的认识。

一、上机实验应遵循以下步骤：（1）实验前，先准备好上机所需的程序。

手编程序应书写整齐，并经自我检查无误后才能上机。

（2）实验时，输入并调试自己所编的程序，独立上机调试，上机时出现的问题，最好能自己独立解决。

（3）实验结束后，按照规定整理出实验报告，并在规定时间内提交。

二、实验报告的内容：实验报告应该包括：实验名称、实验目的、实验题目、问题分析、程序清单、运行结果、实验结论（即算法的时间空间分析与改进建议）。

三、需写出实验报告的实验：实验一、实验四、实验五。

实验一递归与迭代算法一、实验目的与要求1、通过本实验掌握迭代算法和递归算法的基本思想及设计工作的主要步骤。

2、通过本实验加深对循环和递归过程的理解。

3、通过本实验加深对迭代过程的理解。

4、掌握两种算法策略的主要适用范围。

二、实验题目：1、求2+22+222+……+22……22（精确计算）n个22、从键盘输入任一正整数n（n>=3），打印如下图所示的n×n 方阵（下图中n=7）。

1 2 3 4 5 6 724 25 26 27 28 29 823 40 41 42 43 30 922 39 48 49 44 31 1021 38 47 46 45 32 1120 37 36 35 34 33 1219 18 17 16 15 14 133、完成给“余”猜数的游戏：心里先想好一个1~100之间的整数x，然后输入3个除数a、b、c，再输入x分别除以a、b、c后所得到的余数ra、rb、rc，计算机能求出这个数x并输出x。

4、用递归函数判断字符串str是否为“回文”。

三、实验步骤1、理解算法思想和问题要求。