数学与应用数学专业培养方案-同济大学数学系

数学与应用数学专业培养方案
数学与应用数学专业培养方案
一、专业历史沿革
同济大学数学系始建于1945年，程其襄、杨武之、朱言钧、樊映川、张国隆、陆振邦等一大批知名专家曾在此任教。

解放后，几经国家调整，本系时有间断。

于1980年，（应用）数学系正式恢复，陆续引进一批国内外培养的具有博士学位的青年教师，原有师资队伍的结构有了变化，充实了教学与科研力量。

从20世纪90年代开始，学校又先后引进国内知名数学家、博土生导师陈志华、陆洪文、姜礼尚教授等来数学系工作，教学和科研整体实力有很大提高。

数学与应用数学专业在建系后就已设立，文革期间中断了招生，1978年恢复高考后数学与应用数学专业也随之恢复了招生。

至今本专业已培养了毕业生3000多人，数学系的学生遍布国内外的许多国家,有的继续从事做数学的教学及科学研究工作，有的在大型国企和外企，特别是银行、金融、计算机等行业工作，很多毕业生已成为杰出科学家和行业精英。

二、学制与授予学位
四年制本科。

本专业所授学位为理学学士。

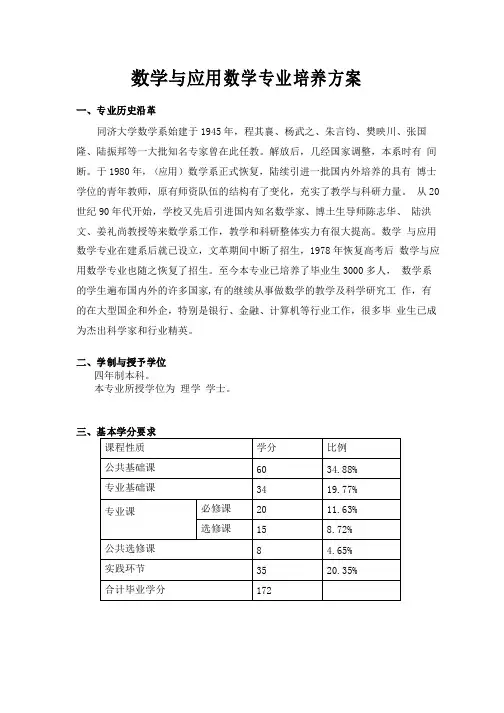
三、基本学分要求
四、专业培养目标
本专业培养具备扎实数学基础，并具备运用数学知识和计算机解决实际问题的能力，受到科学研究的初步训练，能在科技、教育、信息、金融保险等部门及企事业单位从事研究、教学、管理及计算机软件开发等具有国际视野的复合型高级专门人才，或能继续在国内外攻读研究生学位的高级专门人才。

五、专业培养标准
表 1 ：专业标准。

数学科学系数学与应用数学专业第二学士学位培养方案一、培养目标本着通识教育基础上的“厚基础，宽专业”的办学理念，培养具有扎实的数学基础知识和较强的数学应用能力的复合型人才。

使学生受到严格的科学思维训练，掌握数学学科的基本思想方法并有敏锐的应用意识。

二、基本要求数学与应用数学专业本科二学位毕业生应达到如下知识、能力和素质的要求：在学习并掌握微分方程、测度与积分、复分析、概率论(1)四门核心基础课程后，选修数学与应用数学方向的其他核心课程，参加相应的科研训练。

要求初步了解数学与应用数学方向基础知识和发展状况，具备开展自学、文献调研、论文写作、学术报告等各方面的综合能力。

三、学制与学位授予学制：第二学士学位学制二年，按学分制管理。

授予学位：理学第二学士学位。

四、学分要求选本专业为第二学位的学生必须修满培养方案规定的40学分，其中课程30学分，综合论文训练10学分。

五、课程设置1.专业必修课程 16学分微分方程(1) 4学分30420334 测度与积分4学分40420624 概率论(1) 4学分先修测度与积分30420464 复分析4学分2.专业选修课 14学分30420384 抽象代数4学分40420614 泛函分析(1) 4学分40420664 偏微分方程4学分先修微分方程(1) 40420644 微分几何4学分30420444 统计推断4学分先修概率论(1)30420433 线性回归3学分40420054 数值分析4学分40420534 数学规划4学分以上数学课程一般需要较为严格的数学论证，有些内容以数学分析课程的内容为基础，建议同学自行补习相关部分。

在选修以上课程时应综合考虑课程内容应用性与数学理论系统性间的平衡。

3．综合论文训练 10学分综合论文训练10学分选取有实际背景的课题，应用学生所掌握的数学方法，重在建立数学模型，与第一学位论文不能雷同。

在做双学位毕业论文的前一学期，学生需主动联系数学系老师做毕设指导老师，并在数学系教务科登记。

教案标题：同济大学高等数学教学计划一、教学目标本课程旨在帮助学生掌握高等数学的基本概念、理论和方法，培养学生的逻辑思维能力、创新意识和实际应用能力。

通过本课程的学习，学生应能熟练运用高等数学知识解决实际问题，为后续专业课程的学习和科学研究打下坚实的基础。

二、教学内容1. 函数与极限1.1 函数的概念、性质和图像1.2 极限的定义和性质1.3 无穷小和无穷大1.4 极限的运算法则1.5 极限的存在性判断2. 导数与微分2.1 导数的定义和性质2.2 导数的运算法则2.3 高阶导数2.4 隐函数和参数方程函数的导数2.5 微分及其应用3. 微分中值定理与导数的应用3.1 罗尔定理3.2 拉格朗日中值定理3.3 柯西中值定理3.4 泰勒公式3.5 导数在函数性质分析中的应用4. 不定积分4.1 不定积分的概念和性质4.2 基本积分公式4.3 换元积分法4.4 分部积分法4.5 不定积分在实际问题中的应用5. 定积分及其应用5.1 定积分的概念和性质5.2 定积分的运算法则5.3 定积分的换元法和分部法5.4 定积分的应用（如面积、体积、弧长等）6. 微分方程6.1 微分方程的概念和分类6.2 线性微分方程6.3 非线性微分方程6.4 微分方程的求解方法6.5 微分方程在实际问题中的应用三、教学方法1. 讲授法：通过系统、生动的讲解，使学生掌握高等数学的基本概念、理论和方法。

2. 案例分析法：结合具体实例，让学生了解高等数学在实际问题中的应用。

3. 练习法：布置适量的课后习题，巩固所学知识，提高学生的解题能力。

4. 讨论法：组织学生进行课堂讨论，培养学生的逻辑思维能力和创新意识。

5. 实验法：结合数学软件，让学生亲身体验高等数学的实践操作。

四、教学安排1. 授课时间：共计16周，每周2课时。

2. 课后习题：每节课后布置相应的习题，要求学生独立完成。

3. 课堂讨论：每学期组织2-3次课堂讨论，学生可就所学内容提出疑问或分享自己的见解。

数学与应用数学专业本科生培养方案一、培养目标本专业培养掌握数学科学的基本理论与基本方法、具有运用数学知识和使用计算机解决实际问题的能力、接受科学研究的初步训练，能在科技、教育、经济和金融等部门从事研究和教学工作，在生产、经营及管理部门从事实际应用、开发研究和管理工作，或继续攻读研究生学位的创新型人才。

二、培养要求本专业学生主要学习数学和应用数学的基本理论、基本方法并接受数学建模、计算机和数学软件方面的基本训练，在数学理论和应用两方面受到良好的教育，具有较高的科学素养和创新意识，具备科学研究、教学、解决实际问题及软件开发等方面的基本能力和较强的更新知识的能力。

毕业生应获得以下几方面的知识和能力：1.具有比较扎实的数学基础，接受严格的科学思维训练，初步掌握数学科学的思想方法, 为本硕连读的硕士阶段学习打下数学基础；2.具有运用数学知识建立数学模型以解决实际问题的初步能力和进行数学教学的能力；3.了解数学科学发展的历史概括以及当代数学的某些新发展和应用前景，4.能熟练使用计算机（包括常用语言、工具软件及数学软件），具有编写简单程序的能力, 为本硕连读的硕士阶段打下科研基础；5.有较强的语言表达能力，掌握资料查询、信息检索基础以及运用现代信息技术获取相关信息基本方法，具有一定的科学研究能力,为硕士阶段打下交流沟通基础。

三、主干学科数学四、专业主干课程数学分析、高等代数、解析几何、概率论、数理统计、实变函数、复变函数、常微分方程、数学物理方程、泛函分析初步、近世代数、点集拓扑学、数值分析、偏微分方程数值方法、微分几何、理论力学。

五、学制修业年限、授予学位及毕业学分要求修业年限：四年。

授予学位：理学学士。

毕业要求：达到培养方案全部要求，修满176.5学分，其中通识教育43学分（含人文社科类限选课和全校任选课8学分）、专业教育98.5学分、实践环节35学分（含文化素质教育系列讲座8次，累计1学分），毕业论文答辩合格，方可准予毕业。

数学与应用数学（普通类）专业本科人才培养方案本专业所在的数学系有七十多年的悠久办学历史，为湖北省专业综合改革试点专业及湖北大学品牌专业。

数学与应用数学分为普通类专业和师范类专业，学生可以在二年级初自主选择专业分流。

普通类专业主又主要包含数学、数学应用、金融数学和信息安全四个方向，为学生宽口径的发展奠定坚实的基础。

本专业旨在培养运用数学、计算机及金融理论等工具解决相关实际问题的专门人才。

拥有数学一级学科博士后流动站，数学一级学科博士学位授予权，数学一级学科硕士学位授予权。

其中，数学一级学科为湖北省重点学科，基础数学为湖北省优势学科。

专任教师中有博士生导师十余人，硕士生导师二十余人，约百分之九十的教师具有博士学位，拥有国家级专家、国家“百千万”人才工程一、二层次入选者、全国“五一”劳动奖章获得者、全国优秀留学回国人员、国务院政府特殊津贴、湖北省政府专项津贴、湖北省杰出青年基金获得者、楚天学子等人才。

专业代码：070101一、培养目标本专业培养具有良好的道德、科学与文化素养，具有良好的数学基础和数学思维能力，牢固掌握数学与应用数学的基本理论、方法和技能，能够应用数学知识和数学技术解决实际问题，适应数学与科技发展需求进行知识更新，能够在数学及相关领域从事研究、应用开发和管理等工作的拔尖创新型及交叉复合型人才。

二、毕业要求1.知识要求：掌握数学科学的基本理论知识和思想方法，了解其历史、方向的新发展及应用前景；能够熟练使用常用计算机语言及数学软件；掌握资料查询、文献检索以及运用现代技术获取信息的基本方法；熟练掌握英语，具有较强的听、说、写、译能力；掌握体育运动的一般知识和基本方法，形成良好的体育锻炼和卫生习惯。

2.能力要求：具备扎实宽广的数学理论基础、较强的逻辑推理能力、空间想象能力及数学语言表达能力；具备数学研究或运用数学知识解决实际问题的能力，特别是建立数学模型的初步能力；具备编写简单的应用程序的能力。

数学与应用数学〔师范〕专业本科教学方案专业代码 070101〔国家〕 0401〔学校〕一、培养目标与规格〔一〕培养目标本专业培养德、智、体、美、劳全面开展，掌握数学科学的根本理论、根底知识与根本方法，能够运用数学知识和使用计算机解决实际问题，具备在中等学校从事数学教学的教师、教学研究人员及其它教育工作者。

〔二〕培养规格1、热爱中国共产党，热爱社会主义祖国，掌握马克思主义、毛泽东思想、邓小平理论和三个代表的重要思想；坚持党的根本路线，坚持四项根本原则，坚持建立有中国特色的社会主义；具有科学的世界观、正确的人生观和高尚的道德品质。

2、具有扎实的数学根底和较宽的数学知识面，掌握数学专业的根本理论、根本知识和根本技能，了解数学科学开展的趋势，具有良好的数学思维素质，获取创新和科研的初步能力；掌握计算机的根本知识，并具有较强的应用能力，掌握应用数学建模、数学计算，解决实际问题的能力；英语水平到达国家规定的等级要求。

3、具有获得知识的能力、分析问题和解决问题的能力、创新意识和创新能力以及团队精神；具有科学合理的知识、能力和素质构造，有鲜明的个性特征。

4、热爱教育事业，为人师表，懂得教育根本理论，掌握现代教育技术，具备教师的根本素质和根本技能，到达国家语委规定的普通话标准，具有一定的语言和文字表达能力。

尤其是具备施行素质教育的意识和能力以及培育中学生创新意识和创造力的能力。

5、树立开拓创新、自主创业的思想，要努力提高就业竞争能力。

6、具有安康的体魄和一定的军事根本知识和根本技能，到达国家规定的体质安康和军事训练标准；养成终生锻炼身体的习惯。

7、有健全的人格、良好的心理素质和审美素质。

二、学制：四年，授予理学学士学位。

三、四年教育时间活动周数分配表，见附表一。

四、课程设置及学时学分安排〔一〕课程设置：本专业设有公共根底课程〔包括政治理论课程、通识文化课程、教师教育课程〕、学科与专业根底课程〔包括学科根底课程、专业根底课程〕、专业模块课程〔分理论研究方向、应用方向与数学教学研究方向〕、专业任意选修课程和公共选修课程。

本科高等数学教材推荐书目随着数学的发展，本科高等数学教材的选择变得越来越重要。

一本好的教材可以帮助学生更好地理解和应用数学知识，提高他们的学习效果。

下面是几本推荐的本科高等数学教材：1.《高等数学》（第七版）- 同济大学数学系作者：郭庆林、钱泳帆出版社：高等教育出版社2.《高等数学》（第六版）- 北京大学数学系作者：李建国、杜应奎出版社：高等教育出版社3.《高等数学》（上、下册）- 李建国版作者：李建国出版社：清华大学出版社4.《数学分析教程》(第二版) - 同济大学数学系作者：赵毅、李涛出版社：高等教育出版社5.《数学分析习题课程辅导》- 黄春来、郑晨编著出版社：高等教育出版社这些教材在本科高等数学教学中都有着很高的声誉和影响力。

它们以其全面、系统和详细的内容介绍、清晰易懂的表达方式以及丰富的例题和习题而闻名。

以下简要介绍每本教材的特点：《高等数学》（第七版）是同济大学数学系推荐使用的教材，由郭庆林教授和钱泳帆教授合著。

它以全面、详尽而又具有一定难度的内容，适合那些希望深入学习高等数学的学生。

《高等数学》（第六版）是北京大学数学系所编写的教材，被广大数学专业及相关专业的学生所使用。

该教材在内容上既保留了高等数学的经典部分，又增加了许多前沿的数学知识。

《高等数学》（上、下册）是李建国教授编写的教材，由清华大学出版社出版。

它以理论与实际相结合的方式，能够帮助学生更好地理解高等数学的概念与方法。

《数学分析教程》是由同济大学数学系赵毅教授和李涛教授合著的教材，该教材系统地介绍了数学分析的基本概念、定理和方法，并包含大量的例题和习题，有助于学生巩固所学知识。

《数学分析习题课程辅导》则侧重于提供一系列与教材对应的习题以供学生练习，由黄春来教授和郑晨编著，适合那些希望加强数学分析习题应用能力的学生。

总之，选择一本适合自己的本科高等数学教材是非常重要的。

这些推荐的教材都具备了全面、详细和易懂的特点，可以帮助学生更好地掌握数学知识，提高学习成效。

数学与应用数学专业培养方案一、专业历史沿革同济大学数学系始建于1945年，程其襄、杨武之、朱言钧、樊映川、张国隆、陆振邦等一大批知名专家曾在此任教。

解放后，几经国家调整，本系时有间断。

于1980年，（应用）数学系正式恢复，陆续引进一批国内外培养的具有博士学位的青年教师，原有师资队伍的结构有了变化，充实了教学与科研力量。

从20世纪90年代开始，学校又先后引进国内知名数学家、博土生导师陈志华、陆洪文、姜礼尚教授等来数学系工作，教学和科研整体实力有很大提高。

数学与应用数学专业在建系后就已设立，文革期间中断了招生，1978年恢复高考后数学与应用数学专业也随之恢复了招生。

至今本专业已培养了毕业生3000多人，数学系的学生遍布国内外的许多国家,有的继续从事做数学的教学及科学研究工作，有的在大型国企和外企，特别是银行、金融、计算机等行业工作，很多毕业生已成为杰出科学家和行业精英。

二、学制与授予学位四年制本科。

本专业所授学位为理学学士。

三、四、专业培养目标本专业培养具备扎实数学基础，并具备运用数学知识和计算机解决实际问题的能力，受到科学研究的初步训练，能在科技、教育、信息、金融保险等部门及企事业单位从事研究、教学、管理及计算机软件开发等具有国际视野的复合型高级专门人才，或能继续在国内外攻读研究生学位的高级专门人才。

五、专业培养标准座来增强，也鼓励学生与国外院校进行交流。

六、主干学科数学。

七、核心课程数学分析、高等代数、解析几何、常微分方程、复变函数、实变函数、概率论(理)、数值分析(理)、数理方程(理)等。

八、教学安排一览表见附表一。

九、实践环节安排表见附表二。

十、课外安排一览表见附表三。

十一、有关说明1. 公共基础课中的有3门计算机课程，其中在硬件技术基础、数据库技术基础、多媒体技术基础、Web技术基础和软件开发技术基础5门课程中应至少选修1门。

2.培养方案中打*的课程为研究生阶段设置的课程，供要求较高的学生选修。

数学与应用数学专业本科培养方案一、专业介绍数学与应用数学是一门以数学基础理论和应用为主要学科内容的本科专业。

该专业旨在培养掌握数学基本理论和数学方法，具备数理思维和逻辑推理能力，具备科学研究和实际问题分析解决的能力，具备在数学及其应用领域从事科研、教学、技术开发和管理工作的人才。

二、培养目标1.掌握坚实的数学基础理论，建立较好的数学基本功；2.熟悉数学应用领域的基本理论和方法，为将来的研究和实际问题解决提供基础；3.培养创新能力和实践能力，能够独立进行科学研究和技术开发；4.具备良好的团队合作精神和跨学科交流能力；5.具备良好的英语读写能力，能够阅读相关学术文献。

三、课程设置1.数学基础理论高等数学、线性代数、概率论与数理统计、数学分析、微分方程等。

2.数学应用领域数学物理方程、最优化理论与方法、数值计算、金融数学、统计建模、数据分析等。

3.计算机科学计算机基础、程序设计、数据结构与算法、计算方法等。

4.专业选修课程现代代数学、拓扑学、泛函分析、非线性优化、运筹学、数学建模等。

5.实践环节科研训练、实验课程、实践实习、毕业设计等。

四、培养方案1.学科基础培养阶段（大一-大二）主要培养学生的数学基础理论和计算机科学基础，包括高等数学、线性代数、计算机基础、程序设计等课程。

2.专业核心课程培养阶段（大三-大四上学期）主要培养学生的数学应用领域的基本理论和方法，包括最优化理论与方法、金融数学、数学物理方程、统计建模等课程。

3.专业选修课程培养阶段（大四下学期）根据学生的兴趣和发展方向，选择相应的专业选修课程，如现代代数学、泛函分析、运筹学等课程。

4.实践环节学生在大三下学期至大四上学期期间进行科研训练，包括参与导师的科研项目、参与学术讨论等。

大四下学期进行毕业设计，完成一定的科研或应用课题。

五、培养特色1.实践能力培养：强调实践课程和实践环节的重要性，培养学生实际问题解决的能力。

2.科研训练：提供机会参与科研项目，培养科研能力和创新能力。

数学及应用数学本科专业培养方案数学及应用数学本科专业培养方案是为了培养学生在数学及其应用领域具备扎实的理论基础和创新能力的专业人才。

该专业培养方案包括基础课程、专业核心课程、选修课程以及实践教学等环节的设置，旨在全面提高学生的数学素养和实践能力。

一、基础课程基础课程是学生进入数学及应用数学专业的第一步，旨在为学生打下数学基础。

基础课程主要包括高等数学、线性代数、概率论与数理统计、数学分析等。

通过学习这些基础课程，学生将掌握运算符号、基本运算法则、函数与方程的基本性质，并具备相关的计算能力和数学分析能力。

二、专业核心课程专业核心课程是数学及应用数学本科专业的重要环节，它包括数理方程、数值计算方法、数学建模、复变函数与积分变换等。

通过学习这些课程，学生将深入了解数学的基本原理和理论，并掌握其在实际问题中的应用方法。

同时，还将培养学生的创新意识和解决问题的能力，为将来的研究和应用工作打下坚实的基础。

三、选修课程选修课程是数学及应用数学专业培养方案的灵活组成部分，它为学生提供了更多的选择空间。

选修课程的设置可以根据学生的兴趣和发展方向进行调整，如偏向应用数学的学生可以选择金融数学、统计学等课程，偏向纯数学的学生可以选择拓扑学、群论等课程。

通过选修课程的学习，学生可以进一步丰富自己的知识广度和深度，拓展学科视野。

四、实践教学实践教学是数学及应用数学本科专业培养方案的重要环节，它包括实验课、实习和毕业设计等。

实验课通过实践操作和数据分析，帮助学生巩固理论知识，并培养实际问题的解决能力。

实习将学生引导到企业、研究机构等实际场景中，让他们对数学在实际应用中的角色和价值有更深刻的认识。

毕业设计要求学生在指导老师的指导下，独立完成一个具体的数学问题，并撰写相关的论文。

综上所述，数学及应用数学本科专业培养方案着重培养学生的数学基本功和创新能力，注重理论与实践的结合。

通过系统的课程设置和实践教学环节，帮助学生全面发展能力，成为既懂理论又擅长实践的专业人才。

数学与信息学院数学与应用数学专业本科培养方案(一) 专业培养目标本专业培养具有良好的政治思想素质，掌握数学科学基本理论、基础知识与基本方法，能运用数学知识和使用计算机解决若干实际数学问题，能在中等学校进行数学教学的教师、教学研究人员及其他教育工作者。

(二) 专业培养规格和要求本专业学生，应热爱祖国，拥护中国共产党的领导；掌握马列主义、毛泽东思想和邓小平理论的基本原理；树立正确的情感、态度和价值观。

具有敬业爱岗、艰苦奋斗、热爱劳动、遵纪守法、团结合作的品质；具有良好的思想品德、社会公德和职业道德。

本专业学生主要学习数学和应用数学的基本理论和方法，受到严格的数学思维训练，掌握计算机的基本原理和运用手段，并通过教育理论课程和教学实践环节，形成良好的教师素养，培养从事数学教学的基本能力和数学教育研究、数学科学研究、数学实际应用等基本能力。

毕业生应获得以下几方面的知识和能力：1．具有扎实的数学基础，初步掌握数学科学的基本思想方法，其中包括数学建模、数学计算、解决实际问题等基本能力；2．有良好的使用计算机的能力，能够进行简单的程序编写，掌握数学软件开发和计算机多媒体技术，能够对教学软件进行简单的二次开发；3．具备良好的教师职业素养和从事数学教学的基本能力，熟悉教育法规，掌握并初步运用教育学、心理学基本理论以及数学教学理论；4．了解近代数学的发展概貌及其在社会发展中的作用，了解数学科学的若干最新发展，数学教学领域的一些最新研究成果和教学方法，了解相近专业的一般原理和知识，学习文理渗透的课程，获得广泛的人文和科学修养；5．较强的语言表达能力和班级管理能力；6．掌握资料查询、文献检索及运用现代信息技术获得相关信息的基本方法，并有一定的科研能力；7．掌握一门外国语，能借助工具书阅读本学科和专业的外文书刊，具有一定的听、说、读、译的能力。

(三) 专业人才的知识、素质和能力发展要求表1 数学与应用数学本科专业人才知识、素质和能力发展细目表附图1：数学与应用数学专业知识、素质、能力结构图(四) 主干学科：数学(五) 专业主要课程数学分析、几何学、代数学、物理学、概率论与数理统计、微分方程、函数论、离散数学、数学史、数值方法与计算机技术、数学模型、数学实验、教育学与心理学基础、数学教学论、人文社会科学基础。

数学与应用数学专业主要课程简介（一）供外系学生修读的课程高等数学A（Higher Mathematics）课程类别：专业必修总学时：160-180 总学分：10 考核方式：闭卷课程编号：Z1101111高等数学A（一），学时：80-90 学分：5 考核方式：闭卷课程编号：Z1101112高等数学A（二），学时：80-90 学分：5 考核方式：闭卷课程目的：通过本课程的学习，使计算机科学与应用、物理学、应用电子、教育技术专业的相关专业的学生熟练掌握高等数学的基础理论，能运用各种基本理论解决实际工作中的专业问题。

课程内容:本课程分二学期讲授，第一学期主要讲授：函数、极限与连续、导数与微分、微分中值定理与导数的应用、不定积分、定积分、定积分的应用。

第二学期主要讲授：空间解析几何与向量代数、多元函数微分法及其应用、重积分、曲线积与曲面积分、无穷级数、微分方程等。

教材：同济大学数学教研室. 《高等数学》(上、下册), 第六版. 北京: 高等教育出版社，2002年.高等数学B（Higher Mathematics）课程类别：专业必修学时：142-147 学分：8 考核方式：闭卷课程编号：Z1101113高等数学B（一），学时：75 学分：4 考核方式：闭卷课程编号：Z1101114高等数学B（二），学时：72 学分：4 考核方式：闭卷课程目的：通过本课程的学习，使理工类相关专业专科学生全面掌握高等数学的基础理论，能利用微积分的理论解决实际问题。

课程内容：本课程分二学期讲授，第一学期主要讲授，函数、极限与连续、导数与微分、微分中值定理与导数的应用、不定积分、定积分。

第二学期主要讲授无穷级数、空间解析几何、多元函数微分法及其应用、定积分及其应用、曲线积分与曲面积分、常微分方程等。

教材：陈誌敏. 《高等数学》（上、下册），上海：复旦大学出版社，第二版，2005年.课程编号：Z1101115 高等数学C（Higher Mathematics）课程类别：专业必修总学时：90 总学分：5 考核方式：闭卷课程目的：通过本课程的学习，使化学、生物、农、林等相关专业学生掌握高等数学的基础知识，运用基本理论解决一些实际问题。

数学与应用数学专业培养方案一、专业概述二、培养目标1.培养学生扎实的数学基础知识，掌握数学分析、代数、几何等核心理论。

2.培养学生良好的数学建模和问题解决能力。

3.培养学生创新思维和科学研究能力，具备从事数学科研和教育工作的基础。

4.培养学生高度的责任心和团队协作精神，培养学生具备良好的职业道德和社会责任感。

三、培养要求1.课程设置方面，学生需要学习数学分析、高等代数、数学物理方程、数学建模等核心专业课程。

此外，还需学习计算机编程、统计分析、运筹学等跨学科课程。

2.实践环节方面，学生需要参加数学建模竞赛、实践教育、科研项目等实践活动，锻炼自己的问题解决能力和科学研究能力。

3.实习实训方面，学生需要参加一定的实习实训，与实际工作相结合，了解实际问题，并解决实际问题，为将来的就业或科研打下基础。

4.学术创新方面，学生需要参加学术研讨会、论文写作等活动，培养科研能力和创新思维。

5.学风建设方面，学生需要遵守学校的学术规范和诚信道德，保持良好的学风和学术道德。

四、培养模式1.专业课程教学：对核心专业课程进行系统的讲授，帮助学生掌握数学基本理论和应用能力。

2.实践教育：开展数学建模竞赛、实验课程等实践活动，培养学生问题解决能力和实际应用能力。

3.科研训练：开展科研项目、科研讨论等科研活动，培养学生科研能力和创新思维。

4.实习实训：提供实习实训机会，与实际工作相结合，为学生将来的就业或科研打下基础。

5.综合评价：采用多种评价方式，包括考试、论文、实践报告等，全面评估学生的学习成果和综合能力。

五、培养方案1.学科基础课程：数学分析、高等代数、几何学、常微分方程、数学物理方法、概率与统计、数学建模等。

2.专业核心课程：数学分析进阶、复变函数、实变函数与泛函分析、代数学、微分几何、偏微分方程、数论、运筹学、最优化方法等。

3.跨学科课程：计算机编程、统计分析、数值计算方法、金融数学、生物数学等。

4.实践教育：数学建模竞赛、科研实训、实验课程等。

数学与应用数学（师范）专业四年制本科培养方案一、培养目标与人才规格本专业培养德智体全面发展，具有较扎实的专业基础理论、基本知识和基本技能，能适应21世纪发达地区较高的教育要求，胜任基础教育由应试教育向素质教育转轨任务的高素质的中等学校数学教师和教育类人才。

同时为更高层次的学历教育输送合格的生源。

本专业的人才规格：1. 具有健康的身心素质，具有良好的政治品质、思想文化修养和职业道德，热爱教育事业；2. 掌握本专业所必需的基本理论、基本知识和基本技能，在数学、计算机应用等方面有较扎实的基础、较宽的知识面和修养；受到严格的科学思维训练，初步掌握数学科学的思想方法；具有一定的更新知识、继续学习的能力和应用数学解决实际问题的能力；3. 能较熟练使用计算机，掌握一些常用计算机语言和数学软件；4. 具有一定的教学能力和参与社会活动的能力，具备本专业领域初步的科研能力；5. 具有较好的外语水平，在听、说、读、写四个方面全面发展；掌握文献检索、资料查询的基本方法，能运用一种外语阅读专业文献；6. 具有一定的体育和军事基本知识，掌握科学锻炼身体的基本技能，养成良好的体育锻炼和卫生习惯，受到必要的军事训练，达到国家规定的大学生体育和军事训练合格标准，具备健全的心理和健康的体魄，能够履行建设祖国和保卫祖国的神圣义务。

二、学制标准学制为四年，可在三至六年内完成。

三、学分要求本专业总学时数为2826，总学分数为166，其中专业必修课中的学位课程为46学分。

四、本专业课程结构特点说明1．数学基础课程本部分课程是本专业学生所必须具备的知识，主干课程为：数学分析、高等代数、解析几何、概率论、数学建模等。

2．专业基础课程本部分课程是本专业学生为胜任中等学校数学教学工作必须具备的知识，主干课程为：初等数学研究（代数、几何）、数学教育学等。

3. 计算机软件类课程这部分课程使学生开拓知识面，培养学生具有一定的教学研究能力，主要课程为：C++程序设计，数学试验与数学软件选讲、计算机辅助教育等。