第3讲.初一预科班.教师版

有理数和实数第一部分第一讲有理数的基本概念1、正数像 3、1、+0.33 等的数，叫做正数。

在小学过的数，除 0 外都是正数。

正数都大于 0。

2、负数像−1、−3.12、−175 、−2012等在正数前加上“−”(读作负)号的数，叫做负数。

负数都小于 0。

0既不是正数，也不是负数。

3、相反意义的量如果正数表示某种意义，那么负数表示它的相反的意义。

“相反意义的量”的含义包含两部分：相反意义，在相反意义的基础上有数量。

如：南为正方向，向南 1km 表示为+1km ，那么向北 3km 表示为−3km 。

若向东走3km 如何表示？4、有理数整数与分数统称为有理数。

凡是可以化成分数形式的数，都是有理数。

否则，不是有理数。

150.5 1.3 0.1▪23▪ 0.12▪3▪ 0.123▪3.1415926 π5、无理数无限不循环小数，如 π。

有理数分类标准：①性质 、②正负⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数正分数分数零正整数整数有理数：先性质后正负 ⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数非正数非负数零正分数正整数正有理数有理数：先正负后性质)(⎪⎩⎪⎨⎧小数是有理数不可化成分数形式，不—无限不循环小数理数可化为分数形式，是有无限循环小数有限小数⎭⎬⎫注意：⑴正数和零统称为非负数；⑵负数和零统称为非正数；⑶正整数和零统称为非负整数；⑷负整数和零统称为非正整数。

例 1：⑴下列各组量中，具有相反意义的量是( )A. 节约汽油 10升和浪费粮食B. 向东走 8 公里和向北走 8公里C. 收入 300元和支出 100元D. 身高 1.8米和身高 0.9米⑵如果零上5 ℃记作+5 ℃，那么零下5 ℃记作( )A. −5B. −10C. −5 ℃D. −10 ℃⑶如果水位升高 4m时水位变化记为+4m，那么水位下降 3m记作___，水位不升不降时水位变化记为____m⑷甲乙两地的海拔高度分别为 200米，−150米，那么甲地比乙地高出( )A. 200米B. 50米C. 300米D. 350米⑸饮料公司生产的一种瓶装饮料外包装上印有“600 ± 30(ml) ”字样。

第一章 有理数1.1 具有相反意义的量学习目标： 1.用正数和负数表示生活中一对具有相反意义量；2.从具体情境中，体会引入正数、负数的必要性和合理性；3.理解有理数的意义，会对有理数进行分类.学习重点： 用正数和负数表示一对具有相反意义量.学习难点：负数概念的建立.一：用正数、负数表示具有相反意义的量为了便于区分相反意义的量，我们把其中一种量用 表示，例如：我们小学学过的3、125、10.5、32等大于0的自然数和分数（或小数）就是正数，而另一种量就用 表示，它是在正数前面加上“-”（读做负）号.例如：3、-1、-0.618、-32等就是负数. （1）0既不是 ，也不是 .（2）正数和零统称为 ，负数和零统称为 .（3）通常把水结冰时的温度规定为0℃，那么比水结冰时的温度低5℃应该记作（4）如果在东西向的马路上把出发点记为0，把向东走的路程记做正数，那么走-50m 表示 点拨：（1）在具有相反意义的一对量中，谁用正数表示，谁用负数表示是人为地规定的.如：向东走100米记为+100米，则向西走80米记作-80米，也可以向东走100米记为-100米，则向西走80米记作+80米.（2）有的时候在正数前面加上“+”（读作正），以强调它是正数.例如正数5写作+5，但通常把“+”号省略不写.（3）判断一个数是正数还是负数，不能简单地认为带有正号的数就是正数，带有负号的数就是负数.（4）0既不是正数，也不是负数，正数都大于0，负数都小于0.典例分析例1、 在一次体育课上，体育老师让同学们练习踢毽子，以踢7个为标准，超过的个数用正数表示，不足的个数用负数表示，其中8名同学的成绩分别为-1、0、3、4、-2、0、1、2.（1）这8名同学的实际成绩分别是多少？（2）这8名同学中有几个人达标（即踢7个或7个以上）解：（1）这8名同学的实际成绩分别是6个、7个、10个、11个、5个、7个、8个、9个.(2)这8名同学中有6人达标.二：有理数的分类(1)有理数的分类(2)有下列数：3.6、-53、78、0、-0.37、9、-5.14、-1，其中整数：分数：(3)下列有理数中，哪些是非负数，哪些是负数？-0.414、-7、2.7、-31、2010、0、41、-10.3、 2点拨（1）对有理数进行分类时，分类标准不同，分类结果也不同，其中整数与分数相应，正数与负数对应，要特别注意0既不是正数，也不是负数，零是整数，也是有理数.（2）正数和零统称为非负数，负数和零统称为非正数，正整数和0统称为非负整数.（即自然数）例2、把下列各数填入相应的大括号内-24、2.8、49、-5.3、21、-43、0、-（-121）、-5.4（1）正整数集合：｛｝（2）负整数集合：｛｝（3）正分数集合：｛｝（4）负分数集合：｛｝（5）非负数集合：｛｝达标检测1、面粉厂运进200吨面粉记做+200吨，那么运出50吨面粉记作吨.非负数非正数正整数正分数有理数负整数负分数2、若买进20件衣服记为+20件，那么-30件表示 .3、一艘潜艇在水面下-50米执行任务，其正上方10米处有一条鲨鱼在游弋，则鲨鱼所处高度为 米.4、一种红富士苹果箱上标明苹果质量为15kg +0.02kg ，若某箱苹果重14.95kg ,则这箱苹果 标准.（填“符合”或“不符合”）5、下列关于0的说法中正确的有（ ）①0是整数，0是有理数 ②0既不是正数，也不是负数③0不是整数，是有理数 ④0是整数，不是自然数A 、4个B 、3个C 、2个D 、1个6、某班数学平均成绩为87分，若90分记为+3分，则85分记为（ ）7、某种药品的说明书上标明保存温度是（20+28、有一列数：-21、52、-103、174……那么第7个数是 . 9、有一列数：1、2、-3、-4、5、6、--7、-8……，则这列数的第100个和第2005个数分别是1.2 数轴 相反数与绝对值1.2.1 数轴学习目标： 1. 理解数轴的概念，掌握数轴的三个要素，能正确地画数轴.2.能在数轴上标出表示已知有理数的点，能写出数轴上的某些点所表示的有理数.3.通过理解数轴上的点与有理数之间的关系，渗透数形结合的数学思想.学习重点：正确画数轴；在数轴上标出表示已知有理数的点；写出数轴上的某些点所表示的有理数. 学习难点： 数轴上的点与有理数之间的关系.一、概念点拨（1）数轴是一条规定了原点、正方向、单位长度的直线。

冀教版七年级整式预科专题讲义例3. 当x=1时，代数式13++qx px 的值为2005，求x=－1时，代数式13++qx px 的值.例2. 如果,0)1(22=-++b a 那么代数式(a+b)2005的值为（ ） A. –2005 B. 2005 C. -1 D. 1例3． 某品牌的彩电降价30%以后，每台售价为a 元，则该品牌彩电每台原价为（ ） A. 0.7a 元 B.0.3a 元 C.a 310 元 D. a 710元 几个重要的代数式（m 、n 表示整数）（1）a 与b 的平方差是： ； a 与b 差的平方是： ；（2）若a 、b 、c 是正整数，则两位整数是： ,则三位整数是： ； （3）若m 、n 是整数，则被5除商m 余n 的数是： ；偶数是： ，奇数是： ；三个连续整数是： ；（4）若b ＞0，则正数是: ，负数是： ，非负数是： ，非正数是： . 归纳法在代数式中的体现（1）观察下列各式：12+1=1×2，22+2=2×3，32+3=3×4------请你将猜想到的规律用自然数n(n ≥1)表示出来______________________.（2）如图，图1是个正五边形，分别连接这个正五边形各边中点得到图2，再分别连接图2小正五边形各边中点得到图3：图１ 图2 图31、填写下表：23、能否分出246个三角形？简述你的理由。

达标练习1. 某机关原有工作人员m 人，现精简机构，减少20%的工作人员，则剩下_____人.2. 甲以a 千米/小时、乙以b 千米/小时（a ＞b ）的速度沿同一方向前进，甲在乙的后面8千米处开始追乙，则甲追上乙需_____________小时.3. 某工厂有煤m 吨，计划每天用煤n 吨，实际每天节约用煤b 吨，节约后可以多用（ ） A 、⎪⎭⎫⎝⎛-+n m b n m 天 B 、⎪⎭⎫ ⎝⎛--b n m n m 天 C,⎪⎭⎫⎝⎛+-b n m n m 天 D ⎪⎭⎫ ⎝⎛--n m b n m天 4. 一艘轮船从A 港顺水航行到B 港的速度为a ，从B 港逆水航行到A 港的速度为b ，则此轮船从A港出发到B 港后再回到A 港的平均速度为（ ） A 、ba ab+B 、ba ab+2 C 、2ba + D 、abba 2+ 5. 某校学生中男生人数为x ，女生人数为y ，教师人数与全校师生人数的比为1:11，则教师人数为（ ） A 、11yx + B 、12yx + C 、10yx + D 、6yx + 6. 某餐饮公司为大庆路沿街20户居民提供早餐方便，决定在路旁建立一个快餐店P ，点P 选在何处，才能使这20户居民到P 点的距离总和最小？7. 某市出租车收费标准是：起步价10元，可乘3千米；3千米到5千米，每千米价1.3元；超过5千米，每千米价2.4元。

有理数第一章具有相反意义的量1.1学习目标：用正数和负数表示生活中一对具有相反意义量； 1. 从具体情境中，体会引入正数、负数的必要性和合理性； 2..理解有理数的意义，会对有理数进行分类 3.学习重点：.用正数和负数表示一对具有相反意义量学习难点：.负数概念的建立用正数、负数表示具有相反意义的量一：、10.5、125、为了便于区分相反意义的量，我们把其中一种量用表示，例如：我们小学学过的32”-的自然数和分数（或小数）就是正数，而另一种量就用表示，它是在正数前面加上“等大于0 32.、-等就是负数、.例如：3-1、-0.618（读做负）号3 .既不是，也不是（1）0 .）正数和零统称为，负数和零统称为（2（3）通常把水结冰时的温度规定为0℃，那么比水结冰时的温度低5℃应该记作（4）如果在东西向的马路上把出发点记为0，把向东走的路程记做正数，那么走-50m表示点拨：（1）在具有相反意义的一对量中，谁用正数表示，谁用负数表示是人为地规定的.如：向东走100米记为+100米，则向西走80米记作-80米，也可以向东走100米记为-100米，则向西走80米记作+80米.（2）有的时候在正数前面加上“+”（读作正），以强调它是正数.例如正数5写作+5，但通常把“+”号省略不写.（3）判断一个数是正数还是负数，不能简单地认为带有正号的数就是正数，带有负号的数就是负数.（4）0既不是正数，也不是负数，正数都大于0，负数都小于0.典例分析例1、在一次体育课上，体育老师让同学们练习踢毽子，以踢7个为标准，超过的个数用正数表示，不足的个数用负数表示，其中8名同学的成绩分别为-1、0、3、4、-2、0、1、2. （1）这8名同学的实际成绩分别是多少？（2）这8名同学中有几个人达标（即踢7个或7个以上）解：（1）这8名同学的实际成绩分别是6个、7个、10个、11个、5个、7个、8个、9个.(2)这8名同学中有6人达标.二：有理数的分类有理数的分类(1)．正整数非负数有理数正分数有理数负整数非正数有理数负分数3-0.37、9、-5.14、-1、78(2)有下列数：3.6、-，其中、0、5整数：分数：(3)下列有理数中，哪些是非负数，哪些是负数？11、2010、0、-、2.7、、-10.3、 2 -0.414、-734点拨）对有理数进行分类时，分类标准不同，分类结果也不同，其中整数与分数相应，正数与负数对应，（1.要特别注意0既不是正数，也不是负数，零是整数，也是有理数 .（即自然数））正数和零统称为非负数，负数和零统称为非正数，正整数和0统称为非负整数（2 、把下列各数填入相应的大括号内例2131、-、0、-5.32.8 -24、、49、、-（-1）、-5.4 242（1）正整数集合：｛｝（2）负整数集合：｛｝（3）正分数集合：｛｝（4）负分数集合：｛｝（5）非负数集合：｛｝达标检测.吨吨面粉记作50吨，那么运出+200吨面粉记做200、面粉厂运进12、若买进20件衣服记为+20件，那么-30件表示 .3、一艘潜艇在水面下-50米执行任务，其正上方10米处有一条鲨鱼在游弋，则鲨鱼所处高度为米.?0.02kg，若某箱苹果重14.95kg ,则这箱苹果、一种红富士苹果箱上标明苹果质量为15kg 标准.4（填“符合”或“不符合”）5、下列关于0的说法中正确的有（）①0是整数，0是有理数②0既不是正数，也不是负数③0不是整数，是有理数④0是整数，不是自然数A、4个B、3个C、2个D、1个6、某班数学平均成绩为87分，若90分记为+3分，则85分记为（）?）℃，请你写出适合药品保存的温度2、某种药品的说明书上标明保存温度是（720 . 1234、、-、……那么第8、有一列数：-7个数是 .5210179、有一列数：1、2、-3、-4、5、6、--7、-8……，则这列数的第100个和第2005个数分别是相反数与绝对值数轴1.2数轴1.2.1学习目标：能在数轴上标出表示已知有.2. 1. 理解数轴的概念，掌握数轴的三个要素，能正确地画数轴通过理解数轴上的点与有理数之间的关系，渗透数.3.理数的点，能写出数轴上的某些点所表示的有理数.形结合的数学思想学习重点：. 正确画数轴；在数轴上标出表示已知有理数的点；写出数轴上的某些点所表示的有理数学习难点：.数轴上的点与有理数之间的关系一、概念点拨）数轴是一条规定了原点、正方向、单位长度的直线。

1第一讲 二元一次方程组有关概念及代入消元法一、课标要求认识二元一次方程和二元一次方程组.了解二元一次方程和二元一次方程组的解，会求二元一次方程的正整数解. 用代入法解二元一次方程组.了解解二元一次方程组时的“消元思想”,“化未知为已知”的化归思想.二、知识疏理 1、温故知新1. 下面两个方程中，每个方程都含有 未知数（x 和y ），并且未知数的指数都是 ，像这样的方程叫做二元一次方程. 把两个方程合在一起，写成x ＋y ＝222x ＋y ＝40像这样，把两个二元一次方程合在一起，就组成了一个二元一次方程组.2. 一般地，使二元一次方程两边的值相等的两个未知数的值，叫做 . 二元一次方程组的两个方程的 ，叫做二元一次方程组的解.2、教材解读1．二元一次方程2x －3y ＝4的解是 （ ）A 、任何一个有理数对B 、无穷多个数对，但不是任何一个有理数对C 、仅有一个有理数对D 、有限个有理数对2.已知方程：①2x －y ＝3；②x ＋1＝2；③x 3＋3y ＝5；④x －xy ＝10；⑤x ＋y ＋z ＝6.其中是二元一次方程的有______________（填序号即可）3．下列方程中，属于二元一次方程组的是（ ）A ．22816581 (35927)23x y x y x y y B C D xxxy y x y x y -=⎧⎧-=+=⎧+=⎧⎪⎪⎨⎨⎨⎨=+=+=⎩⎩⎪⎪-=⎩⎩ 4．2x 与8y 的和的2倍是10，则可用方程表示为______________. 5．若方程2x2m ＋3＋3y5n －9＝4是关于x ，y 的二元一次方程，求m 2＋n 2的值.6．若方程ax －2y ＝4的一个解是 则a 的值是（ ）A 、－1B 、3C 、1D 、－37．方程组 的解是（ ）A 、B 、C 、D 、x －2y ＝3 x ＋2y ＝5x ＝4 y ＝3x ＝4 y ＝－4x ＝4 y ＝0.5x ＝3 y ＝2x ＝2y ＝1⎩⎨⎧-=+=-632953 )2(y x y x8．已知2x －y ＝1，则当x ＝3时，y ＝______；当y ＝3时，x ＝______.9．试写出一个二元一次方程组，使它的解是 ，这个方程组可以是________.10．判断 是否是方程组 的解.11．已知 是关于x 、y 的方程组 的解，求5m －2n 的值.三、典型例题解析例1．把下列方程写成用含x 的代数式表示y 的形式： ①3x+5y=21 ②2x-3y=-11; ③4x+3y=x-y+1练一练： 1.把方程3x-2y=1变形： （1）用含x 的代数式表示y ，得y=_______． （2）用含y 的代数式表示x ，得x=_______． 2.方程-x+4y=-15用含y 的代数式表示，x 是（ ）A ．-x=4y-15B ．x=-15+4yC ．x=4y+15D ．x=-4y+15 3．判断正误：（1）方程32x+2y=2变形得y=1-3x （ ） （2）方程x-3y=12x -写成含y 的代数式表示x 的形式是x=3y+12x- （ ）例2、用代入法解二元一次方程组（1）242231(2)(3)13211498x y y x s t x y x y s t +==-+=-⎧⎧⎧⎨⎨⎨-=+=-=⎩⎩⎩练一练：x ＝－1 y ＝32x －my ＝7 nx ＋3y ＝－4 x ＝2 y ＝13x －y ＝5 2x ＋5y ＝7x ＝－1 y ＝3⎩⎨⎧=+=-74823x y y x （1）总结：用代入法解二元一次方程组的步骤是：（1）把方程组中的一个方程变形，写出_________的形式； （2）把它_________中，得到一个一元一次方程； （3）解这个__________；（4）把求得的值代入到_________，从而得到原方程组的解．例3、已知 x=1 是方程组 ax+by=2 的解，则a 、b 的值是多少？y=1 x-by=3 练一练：1、若方程组 4x+3y=1 的解x 与y 相等，则a 的值是多少？ax+(a-1)y=32、甲、乙两个小马虎，在练习解方程组 时，由于粗心，甲看错了方程组中的a ，得到方程组的解为 ；乙看错了方程组中的b ，得到方程组的解为 问原方程组的解为多少？3．已知方程组25264x y ax by +=-⎧⎨-=-⎩和方程组35368x y bx ay -=⎧⎨+=-⎩的解相同，求(2a +b )2005的值．四、实战演练ax ＋y ＝10 x ＋by ＝7x ＝1 y ＝6x ＝－1 y ＝121．已知方程组23421x y y x -=⎧⎨=-⎩，把②代入①，正确的是（ ）A ．4y-2-3y=4B ．2x-6x-1=4 D ．2x-6x+3=42．用代入法解方程组34225x y x y +=⎧⎨-=⎩ ）A ．由①得x=243y - B ．由①得y=234x- C ．由②得x=52y + D ．由②得y=2x-53．将y=-2x-4代入3x-y=5可得（ ） A ．3x-2x+4=5 B ．3x+2x+4=5 C ．3x+2x-4=5D ．3x-2x-4=54．将y=12x+3代入2x+4y=-1后，化简的结果是________，从而求得x 的值是_____． 5．当a=3时，方程组122ax y x y +=⎧⎨+=⎩的解是_________．6．把方程7x-2y=15写成用含x 的代数式表示y 的形式，得（ ）A ．x=215152715157 (7)722x x y x xB xC yD y ----===7．用代入法解方程组252138x y x y +=-⎧⎨+=⎩较为简便的方法是（ ）A ．先把①变形B ．先把②变形C ．可先把①变形，也可先把②变形D ．把①、②同时变形8．已知方程2x+3y=2，当x 与y 互为相反数时，x=______，y=_______． 9．若方程组431(1)3x y kx k y +=⎧⎨+-=⎩的解x 和y 的值相等，则k=________．10、已知x+2y+3z=54，3x+y+2z=47，2x+3y+z=31，那么代数式x+y+z 的值是（ ）A 、132B 、32C 、22D 、17 11、若方程组⎩⎨⎧=--=+8)1(534y k kx y x 的解中的x 值比y 的值的相反数大1，则k 为（ ）A 、3B 、－3C 、2D 、－2 12、若3243y x b a +与b a y x -634是同类项，则=+b a（ ）A 、-3B 、0C 、3D 、613、某校运动员分组训练，若每组7人，余3人；若每组8人，则缺5人；设运动员人数为x 人，组数为y 组，则列方程组为 （ ）A 、⎩⎨⎧=++=x y x y 5837B 、⎩⎨⎧=-+=x y x y 5837C 、⎩⎨⎧+=-=5837x y x yD 、⎩⎨⎧+=+=5837x y x y14．在y=kx+b 中，当x=1时，y=2；当x=2时，y=4，那么k=_______，b=_______．15．若│x+y-2│+（x-y ）2=0，那么x=________，y=________．16．已知1331024x ax yy x by=--=⎧⎧⎨⎨=+=⎩⎩是方程组的解，求a、b的值．17．如果2151x xy y==⎧⎧⎨⎨=-=-⎩⎩和是方程mx+ny=15的两个解，求m，n的值．18．已知│4x+3y-5│+│x-2y-4│=0，求x，y的值．19．请用整体代入法解方程组：22(1)2(2)(1)5 x yx y-=-⎧⎨-+-=⎩20．已知方程组31242x yx ay+=⎧⎨+=⎩有正整数解（a为整数），求a的值．第二讲 二元一次方程组的解法一、课标要求用代入法.加减法解二元一次方程组.了解解二元一次方程组时的“消元思想”,“化未知为已知”的化归思想.会用二元一次方程组解决实际问题.在列方程组的建模过程中,强化方程的模型思想,培养学生列方程解决实际问题的意识和能力.将解方程组的技能训练与实际问题的解决融为一体,•进一步提高解方程组的技能.二、温故知新1、已知方程23x y -=，用含x 的式子表示y 的式子是____，用含y 的式子表示x 的式子是___________.2、将方程31x ＋2y ＝1中的x 项的系数化为2，则下列结果中正确的是（ ） A 、2x ＋6y ＝1B 、2x ＋2y ＝6C 、2x ＋6y ＝3D 、2x ＋12y ＝63.（2010年江苏盐城）若一个二元一次方程的一个解为21x y =⎧⎨=-⎩，则这个方程可以是_______________（只要求写出一个）4.等式的基本性质有哪些？ 5．用代入法解下列方程组：（1） （2）三、典型例题精讲例1：解方程组 x —y ＝23 2x ＋y ＝40这个方程组的两个方程中，y 的系数有什么关系？•利用这种关系你能发现新的消元方法吗？从上面的方程组的解法可以发现，把两个二元一次方程的两边分别进行相加减，就可以消去一个未知数，得到一个一元一次方程。

前言你喜欢数学吗你渴望考试取得高分吗你渴望你的数学成绩得到父母的肯定、同学的赞赏、老师的表扬吗相信你知道学习数学最好的方法就是勤奋练习、熟能生巧。

相信本书能给你带来帮助。

本资料的编写以《新课程标准》为指南，以知识与技能、过程与方法为指导思想，通过基础、提高、综合的三级训练，每一套资料都是从近几年来新课程教学中和各地区重点中学的试题中提炼出来，既有基础题，也有能力题、综合题、发散题、探究题和开放题，及具代表性，形成有特色的培训资料。

所有资料对疑难问题点拨到位，是学生正确掌握解题方法、避开思维误区，切实能够提高学生的成绩。

学生在老师的辅导下，复习旧知识、巩固新知识，学生对知识的掌握和灵活运用能力、综合运用能力有很大的提高。

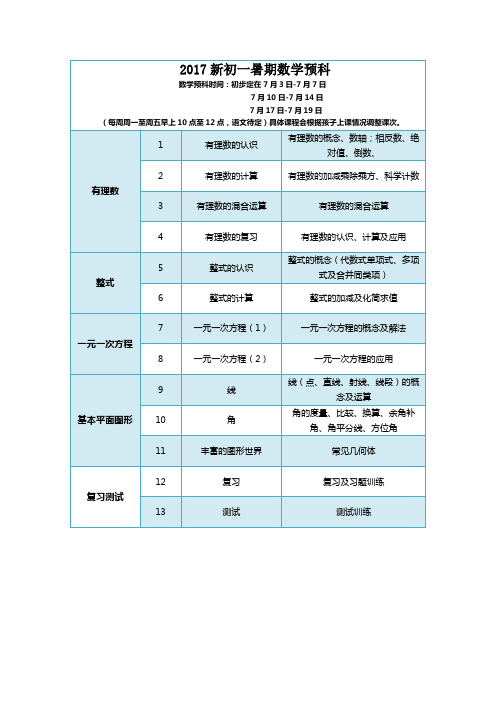
教学进度安排如下：￥七年级上册共有四章，分13次上完，第12次综合复习，第13次考试，第14次试卷简评和50分钟新课。

（每次内容都有120分钟的题量）第一次正数和负数、有理数、数轴、相反数、绝对值第二次有理数的加减法、有理数的乘法、除法及乘方运算第三次科学记数法、近似数、有效数字及有理数的章节复习第四次整式第五次整式的加减第六次一元一次方程和等式的性质第七次一元一次方程解法)第八次希望杯全国联赛试题选讲第九次列方程解应用题第十次一元一次方程的章节复习第十一次图形的认识初步，角的度量与比较第十二次余角和补角第十三次复习四章知识（40分钟），期末考试（40分钟）第十四次列方程解应用题（40分钟新课）试卷讲评（35分钟）附录：2011年第二十二届希望杯数学竞赛第一试试题|说明：1. 老师在教学的过程中，根据学生的具体情况和教学进度灵活的处理资料，要求讲清讲透，不能盲目内容，绝大部分资料按120分钟／次编排，老师可以根据学生实际从中选取80分钟内容讲授，余下的部分作为同学们自由练习用。

的赶资料的进度。

第一讲 正数和负数、有理数、数轴、相反数、绝对值一、课标要求 $通过本节课的学习，你将对有理数有进一步的认识，更好地理解正数、负数、有理数的分类、数轴、相反数、倒数、绝对值的概念，并能运用相关的知识解决一些实际问题二、知识疏理 1、温故知新（1） 有理数的分类：⎧⎧⎪⎪⎨⎪⎪⎪⎨⎩⎪⎧⎪⎨⎪⎩⎩正整数整数零自然数负整数有理数正分数分数负分数 ⎧⎧⎨⎪⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩正整数正有理数正分数有理数零负整数负有理数负分数 （2） 什么叫做数轴数轴的三要素是 、 、（3） 什么叫做相反数相反数具有什么性质相反数等于它本身的数是： . （4） 什么叫做倒数倒数具有什么性质零 （添有或没有）倒数，倒数等于它本身的数是 . （5） ！ （6） 什么叫做绝对值绝对值具有什么性质如何去绝对值的符号绝对值等于它本身的数是： . 几何意义表述：一个数的绝对值就是表示这个数的对应点离开原点的距离.（7） 有理数大小的比较 ①、所有的有理数都可以用数轴上的点表示，在数轴上表示的两个数，右边的点所表示的 数总是比左边的点所表示的数大． ②、正数大于0，负数小于0，正数大于一切负数，两个负数绝对值大的反而小2、教材解读 1、 521,76,106,14.3,732.1,34,5.2,0,1----+-中，正数有 ，负数有 。

|初一预科班·第4讲·教师版| 1一、整式Ⅰ：代数式代数式的定义：用基本的运算符号（加、减、乘、除、乘方等）把数或表示数的字母连结而成的式子叫做代数式．单独的一个数或字母也是代数式． Ⅱ：单项式单项式：像2a −，2r π，213x y −，abc −，237x yz ，……，这些代数式中，都是数字与字母的积，这样的代数式称为单项式．也就是说单项式中不存在数字与字母或字母与字母的加、减的关系，且单项式的分母中不含字母．单独的一个字母或数也叫做单项式，例如：a 、3−．单项式的次数：是指单项式中所有字母的指数和．例如：单项式212ab c −，它的指数为1214++=，是四次单项式．单独的一个数（零除外），它们的次数规定为零，叫做零次单项式．单项式的系数：单项式中的数字因数叫做单项数的系数．例如：我们把47叫做单项式247x y的系数．易错点：①单项式的系数包括单项式前面的符号；②π是一个数，不要将它当作字母． 同类项：所含字母相同，并且相同字母的指数也分别相同的单项式叫做同类项． Ⅲ：多项式多项式：几个单项式的和叫做多项式．例如：27319x x −+是多项式．多项式的项：其中每个单项式都是该多项式的一个项．多项式中的各项包括它前面的符号．多项式中不含字母的项叫做常数项．多项式的次数：多项式里，次数最高项的次数就是这个多项式的次数． 整式：单项式和多项式统称为整式．二、整式运算合并同类项：把多项式中同类项合并成一项，叫做合并同类项． 合并同类项时，只需把系数相加，所含字母和字母指数不变．知识点睛第四讲 整式概念及加减法|初一预科班·第4讲·教师版| 2【例1【例2】 ⑴6； ⑵B ； ⑶2；⑷ 2x y −等； B ⑸； B ⑹；⑺ 1或3；⑻ D ；⑼ 322πx y 【例3】 ⑴六，335x y −； C ⑵【例4】 ⑴六，四，4232310.10.013x y x y x y xy −−+−，0.01−，313xy −； 2⑵，12−【例5】D【例6】 ⑴24x −； ⑵10.80.2n n x x ++【例7】 ⑴26911x x −+−； ⑵2312x −+； 5⑶； ⑷42242b a b a −+ 算一算：26 【例8】C【例9】化简为()()222242374x x x x x =−+−−−2824x x =−−−181454=−×+−=−【例10】 原式22461261x y xy xy x y =−+−++ 2565x y xy =+−15465212⎛⎞=××−−−=−⎜⎟⎝⎠【例11】 ⑴2a =−，14b =，原式224148a b ab =−+=；⑵原式()()()()22119542a b a b a b a b =−−−−−+−()()211416444162044a b a b =−−−−=−×−×=−−=−【例12】8 【例13】A演练1 223xy ，a −，572t ，233a b c −，πx−是单项式．演练答案例题答案|初一预科班·第4讲·教师版| 3223xy 的系数是23，次数是3；a −的系数是1−，次数是1；572t 的系数是52（注意有些学校要求写成32），次数是7；233a b c −的系数是3−，次数是6；πx −的系数为1π−，次数为1．演练2 ⑴ C ；⑵ A ；⑶ 6m =，1n =；⑷ 1m =，2n =，()2009121−=−； ⑸3x =±，2y =±； ⑹4m =，14n =−演练3 ⑴C ； B ⑵； ⑶六，四，428x y −； ⑷9−，3，三，三； ⑸213m −=，24m =，2m =± 演练4 ⑴322187213x y x y xy y −−−+，四次四项式，318x y −； ⑵3225321x y x y xy y −−−+−，四次五项式，25x y −演练5 A 演练6 221132x xy y −− 演练7 A演练8 C演练9 ⑴()()32323322951782A B a b b a b b +=−−+−++32323318102782a b b a b b =−−−++ 322331872a b a b b =−−⑵ ()()2333233782951a b b a b b −++−−−23332321246951a b b a b b =−++−++ 23323219297a b a b b =−−++演练10 43642x x −+ 演练11 1010a b +演练12 7−演练13 原式29453944x y =−+=+=演练14 332x a a b =−−+223a b =+− ()23a b =+−3=−()222y c d d c =+−+−2= 原式116=−演练15 4挑战1 ()223347333A B x y xy x x y xy x −=++−−+−22347399x y xy x x y xy x =++−−−+ 5107xy x =−+− 因为3A B −与x 无关，大比拼答案|初一预科班·第4讲·教师版| 4所以5100xy x −+= 2y =37A B −=−挑战2 有道理，()22222222222233223A B C a b c a b c c a b a −+=+−−−−++−= 因为1a =所以1A B C −+=。

第一章 有理数及其运算 §1.1 数怎么不够用了【知识梳理】一、有理数的分类有理数⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数 或有理数⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数 二、数轴定义：规定了原点、正方向和单位长度的直线叫做数轴.三、求一个相反数的方法要求一个数的相反数，只要在这个数前面添上“-”，新的数就表示原数的相反数。

四、相反数的性质1、互为相反数的两个数的和为零，即如果b a 、互为相反数，则有0=+b a ；反之，如果两个数的和等于0，那么这两个数互为相反数，即若0=+b a ，则b a 、互为相反数2、相反数是本身的数只有一个，是03、1和-1互为相反数，也是互为负倒数。

4、互为相反数的两个数绝对值相等，但绝对值相等的两个数并不一定互为相反数 〖经典例题〗 例1.将下列具有相反意义的量用线连接起来向南走6米 失球2个 进球5个 亏损500元高于海平面960米 运出200吨粮食 盈利1000元 向北走30米运进500吨粮食 低于海平面300米 例2.把下列各数分别填在相应的大括号内.2.4,413,8.0,0,722,6,2,13,21-+-- 正数{ }负数{ } 正整数{ } 正分数{ } 负分数{ }例3.三峡大坝从6月1日开始下闸蓄水，下表是工作人员连续5天的水位记录（如果规定蓄水位为135米）情况，记录如下：（单位：米）6月1日6月2日6月3日6月4日6月5日-5 +2 -1 +3 +2 问：（1）这5天中每天的水位各是多少米？（2）总的来说，水位是高了，还是低了？若高，高了多少？若低，低了多少？例4.如图，数轴上点A 、B 、C 、D 、E 各表示什么数？ 例5.下列说法中正确的是（ ）2332和互为相反数 B.125.0-81和互为相反数 C.a -的相反数是正数 D.两个表示相反意义的量互为相反数例6.比较大小 （1）0 -3 (2) 21--2 (3)7 -10 〖变式练习〗1.指出下列语句的实际意义（1）温度下降了-9℃； （2）收入了-4000元2.将下列各数分别填入相应的集合里 431,01.14,0,07.0,7.5,2,21,1---正数集合{ }负分数集合{ } 整数集合{ }3.体育课上老师对九年级男生进行了引体向上的测试，以能做7个为标准，超过的个数用正数来表示，不足的个数用负数来表示，其中8名男生的成绩如下： 2，-1, 0, 3，-2，-3, 1, 0 这8男生有百分之几达到标准？ 他们共做了多少个引体向上？4.在数轴上画出表示下列各数的点 3， -1， 0，-221，3.5，-55.说出下列各数的相反数：5，-10，-3.9，.0,20042003,53-6.如图，数轴上的点A 、B 、C 、D 表示的数分别为-1.5，-3,2,3.5.回答下列问题：将A 、B 、C 、D 表示的数按从小到大的顺序用“<”连接。

目录第一讲数系的第一次扩充有理数概念 (4)有理数的表示----数轴 (9)第二讲相反数与绝对值相反数 (14)绝对值 (16)第三讲有理数的加减有理数的加法 (21)有理数的减法及加减混合运算 (25)第四讲有理数的乘除有理数的乘法 (30)有理数的除法 (32)第五讲有理数的乘方 (34)第六讲有理数的混合运算 (38)第七讲整式的概念及加减运算代数式及其运算 (41)单项式 (45)多项式 (47)第八讲整式的加减运算同类项及加减运算 (50)第九讲一元一次方程（一） (55)第十讲一元一次方程（二） (60)七年级数学单元检测题 (63)第十一讲 丰富的图形世界………………………………………… 67 第十二讲 平面图形及其位置关系………………………………… 78 第一讲 数系的第一次扩充学习目标1.认识负数，理解有理数的定义、分类2.通过反复对比练习掌握正数，负数，数轴的概念，并能解决实际问题。

学习重点1.与有理数有关概念的区分认识。

2.数轴的认识与应用。

知识框架图（你会画吗？）专题一 有理数概念整数、小数加减乘除的估算；会使用学过的简便算法，合理、灵活地进行计算)提问：生活中具有相反意义的量怎么表示？下面的问题该如何解决？（1） 温度：零上8度，零下8度，在数学中怎么表示？（2） 海拔高度：+25，-25分别表示什么意思？（3） 生活中常说负债800元，在数学中又是什么意思？2、 教材知识梳理负数的产生：我们把其中一种意义的量规定为正，把另一种和它意义相反的量规定为负，这样就产生了负数【知识点1】正数与负数的概念（一）正数：像5，1.2，13....这样的数叫做正数。

为了强调正数，前面加上“+”号，也可以省略不写。

按符号分类：0, 5.2⎪⎨⎪⎧⎪⎪⎪⎨-⎪⎪⎩⎩有理数负整数：如-1，-2,- 3，…负有理数11负分数：如-，-，…23 按定义分类：,5.2, 5.2⎧⎧⎪⎪⎪⎨⎪⎪⎪⎩⎪⎨⎪⎧⎪⎪⎪⎪⎨⎪⎪-⎪⎪⎩⎩正整数：如1，2, 3，…整数0负整数：如-1，-2,- 3，…有理数11正分数：如，，…23分数11负分数：如-，-，…23 【例1】把下列各数填在相应的集合内，－23，0.5，－32, 28, 0, 4, 513, －5.2. 整数集合 { }负数集合 { }负分数集合 { }非负正数数集合{ }【基础练习】1、零下30C 记作（ ）0C ；（ ）既不是正数，也不是负数。

|初一预科班·第8讲·教师版| 1直线、射线、线段的概念：① 在直线的基础上定义射线、线段：直线上的一点和这点一旁的部分叫射线，这个点叫做射线的端点． 直线上两点和中间的部分叫线段，这两个点叫线段的端点． ② 在线段的基础上定义直线、射线：把线段向一方无限延伸所形成的图形叫射线， 把线段向两方无限延伸所形成的图形是直线．两个重要公理：① 经过两点有且只有一条直线，也称为“两点确定一条直线”． ② 两点之间的连线中，线段最短，简称“两点之间，线段最短”． 两点之间的距离：两点确定的线段的长度．点、直线、射线、线段的表示方法⑴ 点的表示方法：我们经常用一个大写的英文字母表示点：A ，B ，C ，D ，…… ⑵ 直线的表示方法：① 用两个大写字母来表示，这两个大写字母表示直线上的点，不分先后顺序，如直线AB ，如下图⑴也可以写作直线BA ．(1) (2)l② 用一个小写字母来表示，如直线l ，如上图⑵．⑶ 射线的表示方法：① 用两个大写字母来表示．第一个大写字母表示射线的端点，第二个大写字母表示射线上的点．如射线OA ，如图⑶，但不能写作射线AO ． ② 用一个小写字母来表示，如射线l ，如图⑷．(3) (4)lA O⑷ 线段的表示方法：① 用两个大写字母来表示，这两个大写字母表示线段的两个端点，无先后顺序之分，如线段AB ，如图⑸，也可以写作线段BA ．② 也可以用一个小写字母来表示：如线段l ，如图⑹．l A B知识点睛第 八 讲线与角的相关概念及运算|初一预科班·第8讲·教师版| 2直线、射线、线段的主要区别：类型 端点 延长线及反向延长线用两个大写字母表示直线 0个无无顺序 射线 1个 有反向延长线 第一个表示端点线段2个两者都有无顺序中点：把线段分成两条相等的线段的点叫做这条线段的中点．（知识点仅供教学参考）角的定义：定义1：有公共端点的两条射线组成的图形叫角，这个公共端点是角的顶点，这两条射线是角的两条边． 定义2：角由一条射线绕着它的端点旋转到另一个位置所成的图形，处于初始位置的那条射线叫做角的始边，终止位置的那条射线叫做角的终边．注意点：角的两条边是射线，是无限延伸的．角的表示方法：① 用三个大写字母来表示，顶点一定要写在中间，如图⑴．也可记为BOA ∠，但不能写成BAO ∠或 ABO ∠等．② 用一个大写字母来表示，这个大写字母一定要表示角的顶点，而且以它为顶点的角有且只有一个．如图⑵．③ 用数字来表示角，如图⑶． ④ 用希腊字母来表示角，如图⑷．(1) (2) (3) (4)∠ a∠ 1∠A ∠AOBa1A角的相关计算1周角360=° 1平角180=° 1直角90=° 1周角2=平角 1平角2=直角 1度60=分（160′°=） 1分60=秒（160′′′=）角平分线：从一个角的顶点引出的一条射线，把这个角分成相等的两个角，这条射线叫做这个角的平分线.余角和补角余角：如果两个角的和等于90°．就说这两个角互为余角，即其中一个角是另一个角的余角． 补角：如果两个角的和等于180°，就说这两个角互为补角，即其中一个角是另一个角的补角． 两个基本定理：① 同角（或等角）的余角相等． ②同角（或等角）的补角相等．|初一预科班·第8讲·教师版| 3【例1】 ⑴选择B ； ⑵应选择②，根据：两点之间，线段最短． ⑶两点确定一条直线．【例2】 ⑴M 即为所求．⑵直线AC 即为所求． ⑶O 即为所求．【例3】如图，连接A ，B ，AB 与m 的交点即为所求的O 点，利用“两点之间线段最短”，可在m 上取O ′， 显然AO BO AB ′′+>【例4】解决本题时需要注意分类：如图⑴，第一种情况，当四点在同一条直线上的时候，显然只能画一条直线．如图⑵，第二种情况，当三点在同一条直线上的时候，而另一点却不在这条直线上，则可以 画四条直线．如图⑶【例5】选择B ；【例6】 ⑴同一直线上的线段才可加减，MP NP MN MB BP =+=−，NP NB BP MP MN =−=−． C ⑵【例7】 B ⑴； ⑵本道题目培养学生“画图做题”的好习惯，易求得254PQ =厘米．【例8】22210cm 333DE AC BC AB =+==，15cm AB =．【例9】此题培养学生根据题意画图解题的能力，易得35cm DC =． 【例10】B ．【例11】⑴ 首先在第一个空上填上20，然后计算(20.320)0.3°−°=°，0.30.36018′′°=×=，20.32018′°=° ⑵ 32.43322548′′′°=°⑶ 这是如何把度分秒形式的度数转化成小数的形式，12600.2′′′÷=，430.243.2′′′+=，43.2600.72′÷=°，65431265.72′′′°=°．【例12】 ⑴5149242175707610′′′′°+°=°=°； ⑵394124453810124451456′′′′′°−°=°−°=°；⑶231342369416′′′′′′°×=°； ⑷121343315′′′′°÷=°． ⑸4537291123263112711′′′′′′′′′°−°×=° 【例13】 B ⑴⑵150° ⑶90° ⑷149937′′′°【例14】11190222DOE AOC BOC AOB ∠=∠+∠=∠=°．互余的角有4对：AOD ∠与BOE ∠，AOD ∠与COE ∠，COD ∠与BOE ∠，COD ∠与COE ∠．例题答案O ′mOB AOMABCD|初一预科班·第8讲·教师版| 4演练1 C ⑴； ⑵B 演练2 1条或3条．演练3 应该建在AC ，BD 的交点P 上，如图所示．首先我们使购物中心到A 和C 的距离之和最小，那么购物中心就应该建在线段AC 的某点处．这是因为如果点P 不在AC 上，根据两点之间，线段最短，可以知道P A P C AC ′′+>．同时我们也能看出，购物中心建在线段AC 上的任意一点，都可以保证购物中心到A ，C 距离之和最小．同理，购物中心若到B ，D 之和距离最小，也必须建在线段BD 上，这样购物中心就必须建在AC ，BD 的交点P 上．演练4 C演练5 2，4，BC ，6演练6 ∵C 为线段AB 上一点，∴AC CB AB +=又∵10cm AB =，3cm BC = ∴7cm AC =又∵D 为AC 的中点∴13.5cm 2AD AC ==∴ 6.5cm DB AB AD =−=演练7 28cm AB =． 演练8 C ． 演练9 B 演练10 ⑴57.3257 19 12′′′°=°； ⑵12234212.395′′′°=°演练11 ⑴7742344511227′′′°+°=°； ⑵；180(34542133)12333′′′°−°+°=°⑶ 13533157435731136′′′′′°×+°÷=°．演练12 22()2(7045)50BOC BOD EOD EOB ∠=∠=∠−∠=×°−°=°．挑战1 0.5cm 或5.5cm挑战2 注意分情况讨论，容易的到答案：4324′°或12636′°．挑战3 根据题意可得：190(180)3αβ°−=×°−，1303αβ−=°，且32βα=，60,90,150αβαβ=°=°+=°．挑战4 已知每个角有两条边，从图中看任意两条射线都能组成一个角，如果学生会组合直接写2615C =；假如学生不会组合也没关系，分类讨论：OA 为角的始边，逆时针选择另一边，可选择5个这样的角；接下来以OB 为始边，逆时针选择另一边，可选择4个这样的角（有必要顺时针吗？根本不需要，那样会重复）；类似以OC 为始边，逆时针选择另一边，可选择3个这样的角； 类似以OD 为始边，逆时针选择另一边，可选择2个这样的角； 类似以OE 为始边，逆时针选择另一边，可选择1个这样的角；共有1234515++++=个．大比拼答案演练答案A C D|初一预科班·第8讲·教师版| 5【教师备选1】 ⑴108185623_______′′°−°=；⑵25152_________′′′′°÷=°；⑶ 23295837______′′′°+°=； ⑷513932532______′′′′°−°=；【解析】 ⑴1081856235155′′′°−°=° ⑵2515212.57.5123730′′′′′°÷=°=°；⑶23295837812937′′′′′′°+°=°； ⑷513932532193328′′′′′′′°−°=°【教师备选2】 一条射线OA ，从点O 再引两条射线OB 与OC ，使40AOB ∠=°，20BOC ∠=°，AOC ∠= ． 【解析】 60°或20°【教师备选3】 如图，O 是直线AB 上的一点，120AOD ∠=°，90AOC ∠=°，OE 平分BOD ∠，则图中彼此互补的角共有______对． 【解析】 根据题意可得：30BOE EOD DOC ∠=∠=∠=°，60BOD EOC ∠=∠=°等，互补的角只满足和为180°这个数量关系即可，与位置无关． 所以共有6对：AOE ∠与BOE ∠，AOE ∠与EOD ∠，AOE ∠与DOC ∠， AOD ∠与BOD ∠，AOD ∠与EOC ∠，AOC ∠与BOC ∠．ABC DE O。

目录第一讲数系的第一次扩充有理数概念 (4)有理数的表示----数轴 (9)第二讲相反数与绝对值相反数 (14)绝对值 (16)第三讲有理数的加减有理数的加法 (21)有理数的减法及加减混合运算 (25)第四讲有理数的乘除有理数的乘法 (30)有理数的除法 (32)第五讲有理数的乘方 (34)第六讲有理数的混合运算 (38)第七讲整式的概念及加减运算代数式及其运算 (41)单项式 (45)多项式 (47)第八讲整式的加减运算同类项及加减运算 (50)第九讲一元一次方程（一） (55)第十讲一元一次方程（二） (60)七年级数学单元检测题 (63)第十一讲丰富的图形世界 (67)第十二讲平面图形及其位置关系 (78)第一讲数系的第一次扩充学习目标1.认识负数，理解有理数的定义、分类2.通过反复对比练习掌握正数，负数，数轴的概念，并能解决实际问题。

学习重点1.与有理数有关概念的区分认识。

2.数轴的认识与应用。

知识框架图（你会画吗？）专题一有理数概念1、相关知识链接小学学过的数：（1）整数（自然数）：0，1，2，3…………（2）分数：1131,,,1,2342……………（3）小数：，，…………整数、小数、分数和百分数、负数(比较熟练地进行整数、小数、分数的四则运算，能进行整数、小数加减乘除的估算；会使用学过的简便算法，合理、灵活地进行计算)提问：生活中具有相反意义的量怎么表示？下面的问题该如何解决？（1）温度：零上8度，零下8度，在数学中怎么表示？（2）海拔高度：+25，-25分别表示什么意思？（3）生活中常说负债800元，在数学中又是什么意思？2、教材知识梳理负数的产生：我们把其中一种意义的量规定为正，把另一种和它意义相反的量规定为负，这样就产生了负数【知识点1】正数与负数的概念（一）正数：像5，，13....这样的数叫做正数。

为了强调正数，前面加上“+”号，也可以省略不写。

（二）负数：像-5，，-13等在正数前面加上“-”号的数叫做负数“—”不能省略。

七年级寒假衔接班讲义第三讲编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（七年级寒假衔接班讲义第三讲）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为七年级寒假衔接班讲义第三讲的全部内容。

七年级寒假衔接班讲义第三讲平行线的性质平行线的性质：(1）两条平行线被第三条直线所截，同位角相等.简记：两直线平行，同位角相等。

（2）两条平行线被第三条直线所截，内错角相等.简记：两直线平行，内错角相等。

（3）两条平行线被第三条直线所截，同旁内角互补。

简记:两直线平行,同旁内角互补。

例1.已知：如图，请分别根据已知条件进行推理，得出结论，并在括号内注明理由．(1）如果AB∥EF,那么∠2=______，理由是___________________________.(2）如果AB∥DC，那么∠3=______，理由是____________________________________.(3）如果AF∥BE，那么∠1+∠2=______,理由是_______________________________.(4）如果AF∥BE，∠4=120°,那么∠5=______,理由是________________________。

例2。

已知：如图，DE∥AB．请根据已知条件进行推理，分别得出结论，并在括号内注明理由．(1）∵DE∥AB，( ）∴∠2=______。

( , )(2）∵DE∥AB，( ）∴∠3=______.（， )(3)∵DE∥AB( ),∴∠1＋______=180°．（ , ）例3。

如图，若AB∥DE，∠B=1350,∠D=1450，你能求出∠C的度数吗?在AB∥DE的条件下，你能得出∠B、∠C、∠D之间的数量关系吗?并说明理由．例4.如图所示，AB//CD,∠A=1350，∠E=800，求∠CDE的度数。

第一篇积累与运用专题一汉字造字法及演变【知识聚焦】一、汉字的造字法1、一般说来汉字的造字方法有以下四种：(1) 象形象形是用描摹实物形状来造字的一种方法。

用这种方法造的字叫象形字，如：日、月、山、云、人、手、牛、爪、衣、卉、行、泉等。

(2) 指事指事是用抽象的符号或在象形字的基础上加指示性符号表示意义的一种造字法。

用这种方法造的字叫指事字，如：上、下、寸、刃、本、未、甘、亦等。

(3) 会意会意是把意义上可能发生关联的两个或两个以上的字组合在一起表示一个新的意思的一种造字法。

用这种方法造的字叫会意字，如：兵、北、从、步、采、牧、莫、暮、休、苗、开、伐、明、林、炎、磊等。

(4) 形声形声是用形和声两部分拼合在一起来造字的一种方法。

形，即形旁、形符，表示这个字的意义；声，即声旁、声符，表示这个字的读音。

用这种方法造的字叫形声字，如：恭、慕、灸、忽、超、钢、雾、梨、湖、忠、泳、鹅、珠、描等。

汉字中绝大多数是形声字。

据统计，在现代汉字中，形声字占百分之九十以上。

我们学习汉字，主要是学形声字。

形声字的形旁和声旁排列的位置是多种多样的：①左形右声——江、村、情②右形左声——飘、攻、③上形下声——箕、宇、④下形上声——货、烈、辜、⑤内形外声——问、闻、辩⑥外形内声——房、阅、店以上六种形式可概括为左右、上下、内外三种关系，其中以“左形右声”的形式占多数，以“上形下声”的形式比较常见。

我国古代所谓“六书”(汉代许慎的《说文解字》把汉字造字方法归纳为六种，叫“六书”)的说法，除了上面提到的“四书”以外，还有“转注”和“假借”。

转注”，就是用同一部首内读音相近、字义相通的字互相解释。

如“颠”、“顶”是一对转注字。

“假借”，就是借用已有的同音字来表示语言中的某个词。

如“豆”，原指食肉用具，后来借作豆子的“豆”，本义消失。

这种情况一开始也可以说写了一个“别字”，但流行开来，久而久之，约定俗成，这个“别字”就成了代表这个词的假借字。

初一预科班英语讲义(一)1、明确学习目标：（五级的目标）a.语音：日常会话中做到语音、语调正确、自然、流畅，能根据读音拼写单词b.词汇：学会使用1500~1600个单词和200~300个短语或固定搭配c.语法：强调语法的功能而不是语法形式d.功能：即交际功能2、掌握正确的学习方法、培养良好的学习习惯◆兴趣是最好的老师，兴趣是产生学习的动力；◆专心听讲，积极发言，做好笔记；◆课后仔细听录音，认真模仿，补充适当的口笔头练习；◆不耻下问，及时总结；◆诵读、熟读少不了，在北京四中，一所每年向清华、北大输送１００多名学生的名牌中学，他们的老师要求学生在高中３年将《新概念英语》第二册的所有文章背诵下来。

３年下来，他们的学生不仅英文成绩好，写出来的英文短文还十分地道；◆扩大阅读量，从而使课外知识成为课内知识的有益补充；养成猜测词义的习惯；◆动眼还要动手，做好课外阅读笔记，坚持做一些摘要、札记，记录一些优美词句；◆掌握记单词的方法：①按开、闭音节记忆：bag-cake②按字母组合记忆：beef, elephant, picture③分音节记忆：information，basketball④音、形、义结合法记忆：sometimes, sometime, some times和some time⑤归类记忆：服装类coat, shirt, skirt, sweater, 食品类cake, rice, dumpling, noodle⑥构词联想记忆：care→careful→carefully→careless, like→dislike→unlike→alikemoonlight, brunch,⑦对比联想记忆：big→small , right→write⑧搭配联想记忆：如含有get的短语有：get ready for，get up，get on with，get down，get back，got on，get off，get to，get out of, get lost前元音中元音后元音1. Who knows!2. That’s a deal!3. How come？=Why?4. Got it? = Understand?5. Don’t push me.6. Come on!7. Enjoy yourself.8. He has gone bananas.9. Wood head!1) --Hello, Helen.--Hi, Steven.--How are you today?--I’m very well, thank you. And you?--I’m fine, thanks.--How is Tony?--He’s fine, thanks.--How is Emma?--She’s very we ll, too, Helen. Goodbye, Helen. Nice to see you.--Nice to see you, too, Steven. Goodbye.2) -- Hi. My name is Mike Parker.-- I’m Jennifer Green.-- It’s nice to meet you, Jennifer.-- Nice to meet you, too.-- I’m sorry. What’s your last name again?①一般是直接加-s, 如: pen, chair规则变化②以s, x, sh, ch, 辅音加o结尾的名词加-es,如: bus，box, fish，watch，tomato名词的数③以辅音字母y结尾的名词变y为i, 加-es, 如: baby, city④以f或fe结尾的名词变f或fe为v, 加-es, 如: knife, life①元音发生变化, 如: man, foot不规则变化②词尾发生变化,如: child③词形不变,如: Chinese, sheep动词单三形式词尾加-s / -es的发音①一般情况下,在词尾加-s, 清辅音后读/s/; 浊辅音和元音后读/z/; 在t后面读/ts/;在d后面读/dz/。

初一英语预科教案设计初一英语预科教案1教学目标：1、语言目标(Language skills)巩固和强化上节课的学问： can I have ? Yes, you can./ No, you cant.能在图片的提示下听懂、认读、说出新单词：computer game、jipsaw puzzel、careful、fix,并懂得其意。

学会表达某人拥有某物的功能句型“I’ve got 。

He’s got。

She’s got。

It’s got。

”来进行沟通。

2、技能目标(Objectives of skills)学会运用have got 表述拥有某物3、情感目标(Objectives of emotion and attitude)让同学通过自由对话沟通自己拥有的东西，达到让其开口说英语的目的，从而激发他们学习英语的爱好及运用英语沟通的热忱。

重点难点：能正确拼读新单词：computer game、jipsaw puzzel、careful、fix; 理解本课句型：I have got。

并能够运用此句型和别人沟通自己拥有的东西。

教学过程：Step1、Warming up:Greeting. T: Hello, boys and girls!S: Hello, teacher!T: How are you, today?S: Fine, thank you.T:What’s the weather like today?S:It’s sunny day.设计意图：以简洁轻松的问候进入一个比较愉悦的课堂教学。

Step 2、Lead-in:老师指自己的物品，如课本、衣服等问。

T：what’s this ? S:This is a book;This is a coat. T：This is my book. I’ve got a book. This is my coat. I’ve got a coat. (板书并做动作让同学理解意思I’ve got )让同学运用I’ve got——像老师一样描述自己拥有的东西。