人教版高一物理必修2 6.4万有引力定律的成就 导学案设计(无答案)

人教版普通高中课程标准试验教科书物理必修2第六章第4节《万有引力理论的成就》教学设计一、教学分析1.教材分析本节课是《万有引力定律》之后的一节，内容是万有引力在天文学上的应用。

教材主要安排了“科学真是迷人”、“计算天体质量”和“发现未知天体”三个标题性内容。

学生通过这一节课的学习，一方面对万有引力的应用有所熟悉，另一方面通过卡文迪许“称量地球的质量”和海王星的发现，促进学生对物理学史的学习，并借此对学生进行情感、态度、价值观的学习。

2．教学过程概述本节课从宇宙中具有共同特点的几幅图片入手，对万有引力提供天体圆周运动的向心力进行了复习引入万有引力在天体运动中有什么应用呢？接下来，通过“假设你成为了一名宇航员，驾驶宇宙飞船……发现前方未知天体”，围绕“你有什么办法可以测出该天体的质量吗”全面展开教学。

密度的计算以及海王星的发现自然过渡和涉及。

在教材的处理上，既立足于教材，但不被教科书所限制，除了介绍教科书中重要的基本内容外，关注科技新进展和我国天文观测技术的发展，时代气息浓厚，反映课改精神，着力于培养学生的科学素养。

二、教学目标1.知识与技能（1）通过“计算天体质量”的学习，学会估算中数据的近似处理办法，学会运用万有引力定律计算天体的质量；（2）通过“发现未知天体”，“成功预测彗星的回归”等内容的学习，了解万有引力定律在天文学上的重要应用。

2.过程与方法运用万有引力定律计算天体质量，体验运用万有引力解决问题的基本思路和方法。

3.情感、态度、价值观（1）通过“发现未知天体”、“成功预测彗星的回归”的学习，体会科学定律在人类探索未知世界的作用；（2）通过了解我国天文观测技术的发展，激发学习的兴趣，养成热爱科学的情感。

三、教学重点1.中心天体质量的计算；2. “称量地球的质量”和海王星的发现，加强物理学史的教学。

四、教学准备实验器材、PPT课件等多媒体教学设备五、教学过程（一）、图片欣赏复习引入问题一：已知地球的质量M =6.0×1024kg,地球半径R =6.4×103km.请根据以上数据计算:(1)在赤道表面上质量为60 kg 的物体所受的重力及万有引力(2)该物体随地球自转所需的向心力.根据以上计算结果，在忽略地球自转的影响的情况下，你能得出什么结论？设计思想:学生通过计算比较既巩固了已学的知识,又理解了为什么可以忽略地球自转的影响。

《6.3万有引力定律》基础导学姓名 班级 组别 使用时间【学习目标】1．理解万有引力定律及使用条件；2．学会使用万有引力定律进行计算。

【学习重点】对万有引力定律的理解及应用【学习难点】万有引力定律的使用条件的理解．【自主学习】先阅读课本，再回答问题1、万有引力定律：自然界中任何两个物体都 ，引力的大小与 成正比，与 成反比。

用公式表示为 ，其中G 叫做 ，数值为 。

2、万有引力适用的条件： 万有引力公式中，对于距离较远的可以看做质点的物体来说，r 是指 的距离，对于均匀球体，指的是 。

3、万有引力定律的适用条件（1）万有引力定律适用于 间的相互作用；（2）质量分布均匀形状规则的物体间，距离r 为两物体 间的距离；4、小计算：我们粗略的来计算一下两个质量为50kg ，相距0.5m 的人之间的引力。

并思考：为什么我们只能粗略的计算．．．．．．？【合作探究】探究一： 月－地检验（阅读教材38页“月－地检验”部分的内容，完成下列问题）地面附近的重力加速度g=9.8m/s 2，月球绕地球运动的周期为27.3天，地球半径为R =6.4×106m ，轨道半径为地球半径的60倍。

设质量为m 的物体在月球的轨道上运动的加速度（月球公转的向心加速度）为a ，则r a 2ω=，Tπω2=，r =60R ， 运动学角度得 R T r a 604222⨯==πω， 代入数据解得 g a 26013600180.9=⨯=。

从引力角度得 月球位置物体受到地球引力2)60(R Mm G ma =， 地球表面物体满足2RMm G mg =，两式相比得g g 2601= 试通过上面计算结果，结合教材39页最上方的内容，你能得出什么结论？探究二： 两个物体的质量分别是m 1和m 2，当它们相距为r 时，它们之间的引力是F=__________。

(1) 若把m 1改为2m 1，其他条件不变，则引力为______F 。

(2)若把m 1改为2m 1，m 2改为3m 2，r 不变，则引力为 F 。

高中物理6.4万有引力理论的成就导学案新人教版必修6、4万有引力理论的成就导学案新人教版必修2学习目标：1、了解万有引力定律在天文学上的应用2、会用万有引力定律计算天体的质量和密度3、掌握综合运用万有引力定律和圆周运动学知识分析具体问题的方法自主学习：自学课本P41-43（一）基本思路：1、将行星（或卫星）的运动看成是运动、2、万有引力充当向心力F引=F向、或在球体表面附近F引=G重即：= = = = (提示：分别用线速度、角速度、周期、向心加速度、重力表示)（二）明确各物理量的含义：M表示，m表示，r表示。

（三）天体质量的计算：1、方法一、：已知天体的球体半径R和球体表面重力加速度g、求天体的质量。

基本思路：mg 得 M=2、方法二、：已知行星（或卫星）的公转周期T、轨道半径r，可求出中心天体的质量M（但不能求出行星或卫星的质量m）基本思路：得 M= 温馨提示：（1）计算天体质量的方法不仅适用于地球，也适用于其它任何天体。

（2）计算天体质量的方法只能计算中央天体的质量，而不能求环绕天体的质量。

（3）GM=gR2在有关计算中，是一个经常用到的替换关系，被称为“黄金代换”。

（四）天体密度的计算:1、基本思路：根据上面两种方式算出中心天体的质量M，结合球体体积计算公式 (式中R为星球的半径)物体的密度计算公式求出中心天体的密度。

2、由上面(三)中的方法一求得的质量算出的密度ρ= ; 由上面(三)中的方法二求得的质量算出的密度ρ= ;当r≈R时ρ= 、(五)发现未知天体:基本思路：当一个已知行星的实际轨道和理论计算的轨道之间有较大的误差时，说明还有未知的天体给这个行星施加引力、合作探究：1、某宇航员驾驶航天飞机到某一星球，他使航天飞机贴近该星球附近飞行一周，测出飞行时间为4、5103s，则该星球的平均密度是多少？2、一宇航员为了估测一星球的质量，他在该星球的表面做自由落体实验：让小球在离地面h高处自由下落，他测出经时间t 小球落地，又已知该星球的半径为R，试估算该星球的质量。

物理必修2§6.3《万有引力定律》导学案编制人： 审核人： 班级： 组名： 学生姓名： 学习目标1. 体会物理研究中猜想与验证的魅力，能够踏着牛顿的足迹了解月地检验。

2. 进一步大胆地推导得出万有引力定律。

3. 了解引力常量的测量及意义。

重点难点1.万有引力推导的过程。

2.万有引力公式的体会及应用。

3.引力常量的有关知识。

知识链接1．行星绕太阳的运动如何处理？行星为什么能够绕太阳运动？3．太阳与行星间的引力的公式？学习过程要点1.月—地检测探究：请举例说明一下生活中的物体受万有引力的情况？（联想一下天体绕地球转的受力情况）牛顿猜想：地球对苹果的力、地球对月球的力及太阳对行星的力可能是同一种性质的力，它们可能遵循相同的规律。

牛顿时代已经能够精确测定地球表面的重力加速度g=9.8m/s 2，也能比较精确地测定月球与地球的距离r 地月为地球半径r 地60倍，r=3.8×108m ；月球公转的周期为27.3天。

试用这些已知条件验证牛顿猜想。

（由牛顿第二定律可知F=m α）验证猜想：1、 地球对月球的引力为：月月地月地月a m r M m G F ==22、 地球对苹果的引力为：mg ma r mM G F ===2地地3、 得出月a 与g 的关系为 （提示：分别用含半径的表达式表示出月a 与g ，再计算两者关系）4、 由a n =r ω2，ω=2π/T ，得出月a =结论： ，我们再大胆猜测一下，是否任意两个物体之间都存在这样的引力呢？思考：月-地检验的目的是什么？要点2.万有引力定律（一）万有引力定律1、内容：自然界中 两个物体都相互 ，引力的方向 ，引力的大小与物体的 成正比，与它们之间的 成反比。

2、公式：3、公式中物理量的单位：m 1、m 2的单位 ，力的单位 ，距离的单位4、G 是比例系数，叫做 ，适用于 两个物体之间。

例1、某物体在地面上受到地球对它的万有引力为F ，为使此物体受到的引力减小到F/4，应把此物体置于距地面的高度为（R 为地球半径）（ ）A 、RB 、2RC 、3RD 、4R例2、估算两个质量为50Kg 的同学相距0.5m 时之间的万有引力是多大？地球质量为6.0×1024Kg ，太阳的质量为2.0×1030Kg ，地球距太阳距离1.5×1011m ，求太阳对地球的引力？（二）对万有引力定律中距离的理解1、物体相距很远，可以看做质点，r 为 的距离；2、物体相距较近不能看作质点时，若物体为质量均匀形状规则的球体，r 为 的距离；（如甲图）总结：万有引力定律公式的适用条件思考：1、当r趋于0时，万有引力能否用万有引力公式？2、太阳对地球的吸引力与地球对太阳的吸引力哪个大？3、牛顿得出了万有引力定律，但他却无法用这个公式来计算天体间的引力，为什么？知识了解-------引力常量现在我们通常取G= ，单位，引力常量是自然界中少数几个最重要的物理量之一。

1 / 2课题：§6-4 万有引力定律的成就第4课时（总12课时） 课型：新授【目标要求】 [学习目标](1)了解万有引力定律在天文学上的重要应用。

(2)会用万有引力定律计算天体质量，了解“称量地球质量”“计算太阳质量”的基本思路。

(3)认识万有引力定律的科学成就，体会科学思想方法。

[学习重点]▲ 会用万有引力定律计算天体的质量。

▲ 掌握运用万有引力定律处理天体问题的思路和方法。

[学习难点]万有引力定律处理天体问题的思路和方法。

【过程方法】 [自学提要]1.为什么说卡文迪许是称出地球质量的人？2.如何应用万有引力定律求解中心天体的质量？应用此方法能否求出环绕天体的质量？3.万有引力定律除了可以估算质量外，还在天文学上发现哪些行星？[自学反馈][探究释疑]例1. 已知月球绕地球运动周期T 和轨道半径r ，地球半径为R 求： （1）地球的质量？（2）地球的平均密度？例2．为了研究太阳的演化过程，需知道目前太阳的质量M ．已知地球半径R=6.4×106m ，地球质量m=6×1024kg ，日地中心的距离r=1.5×1011m ，地球表面处的重力加速度g 取10m/s 2，1年约为3.2×107s ，试估算目前太阳的质量M ．（保留一位有效数字，引力常量未知）[精练拓展]1．已知引力常数G 、月球中心到地球中心的距离R 和月球绕地球运行的周期T ，利用这三个数据，可以估算出的物理量有：（ ）A 、月球的质量B 、地球的质量C 、地球的半径D 、月球绕地球运行速度的大小 2.在圆轨道上运动的质量为m 的人造地球卫星，它到地面的距离等于地球半径R ，地面上的重力加速度为g ，则：（ ）A 、卫星运动的速度为gR 2 B 、卫星运动的周期为T=g R24πC 、卫星运动的加速度为g/2D 、卫星的角速度是g/4 3.下列有关行星运动的说法中，正确的是：（ ）A 、由r v=ω，行星轨道半径越大，角速度越小B 、由2ωr a =，行星轨道半径越大，行星的加速度越大C 、由r v a 2=，行星轨道半径越大，行星的加速度越小 D 、由r GMv =，行星轨道半径越大，线速度越小4. 某行星的卫星，在靠近行星的轨道上运行，若要计算行星的密度，惟一要测量的物理量是：（ ）A 、行星的半径B 、卫星的半径C 、卫星运行的线速度D 、卫星运行的周期o ---------------------------------------------------------高一年 部 班 学生姓名 ---------------------------------------------------o5.若人造卫星绕地球做匀速圆周运动，则下列说法正确的是：（）A、卫星的轨道半径越大，它的运行速度越大B、卫星的轨道半径越大，它的运行速度越小C、卫星的质量一定时，轨道半径越大，它需要的向心力越大D、卫星的质量一定时，轨道半径越大，它需要的向心力越小6.已知下面的哪组数据，可以算出地球的质量M（引力常量G已知）（）A、月球绕地球运动的周期T及月球到地球的中心的距离RB、地球绕太阳运行周期T及地球到太阳中心的距离RC、人造卫星在地面附近的运行速度v和运行周期TD、地球绕太阳的运行的速度v及地球到太阳中心的距离R7.有一星球的密度与地球的密度相同，但它表面处的重力加速度是地面上的重力加速度的4倍，则该星球的质量将是地球质量的：（）A、1/4B、4倍C、16倍D、64倍8.设士星绕太阳的运动为匀速圆周运动，若测得土星到太阳的距离为R，土星绕太阳运动的周期为T，万有引力常量为G，根据这些数据，能够求出的量有：（）A、土星线速度的大小B、土星加速度的大小C、土星的质量D、太阳的质量9.设火星和地球都是球体，火星质量和地球质量之比为p，火星半径和地球半径之比为q，则火星表面重力加速度和地面重力加速度之比等于：（）A、p/q2B、pq2C、p/qD、pq10.设行星A、B是两个均匀球体，A与B的质量比mA：mB=2：1，A与B的半径之比R A：R B=1：2，行星A的卫星a沿圆周轨道运行的周期为Ta，行星B的卫星b沿圆轨道运动的周期为Tb，两卫星的圆轨道都非常接近各自的行星表面，它们运行的周期之比为：（）A、Ta：Tb=1：4B、Ta：Tb=1：2C、Ta：Tb=2：1D、Ta：Tb=4：111.万有引力定律首次揭示了自然界中物体间一种基本相互作用的规律，以下说法正确的是：（）A、物体的重力不是地球对物体的万有引力引起的B、人造地球卫星离地球越远，受到的万有引力越大C、人造地球卫星绕地球运动的向心力由地球对它的万有引力提供D、宇宙飞船内的宇航员处于失重状态是由于没有受到万有引力的作用12. 最近科学家在望远镜中看到太阳系外某一恒星有一行星，并测得它围绕该恒星运动一周所用时间为1200年，它与该恒星的距离为地球到太阳距离的100倍，假定行星绕恒星运行的轨道和地球绕太阳运行的轨道都是圆周，仅利用以上两个数据可以求出的量有：（）A、恒星质量与太阳质量之比B、恒星密度与太阳密度之比C、行星质量与地球质量之比D、行星运行速度与地球公转速度之比13.已知地球质量大约是月球质量的81倍，地球半径大约是月球半径的4倍，不考虑地球月球自转的影响，由以上数据可推算出：（）A、地球的平均密度与月球的平均密度之比约为9：8B、地球表面重力加速度与月球表面重力加速度之比约为9：4C、靠近地球表面沿圆轨道运行的航天器的周期与靠近月球表面轨道运行的航天器的周期之比约为8：9D、靠近地球表面沿圆轨道运行的航天器的线速度与靠近月球表面轨道运行的航天器的线速度之比约为81：414.人类发射的空间探测器进入某行星的引力范围后，绕该行星做匀速圆周运动，已知该行星的半径为R，探测器运行轨道在其表面上空高为h处，运行周期为T。

4、 万有引力理论的成就学习目标：1.了解万有引力定律在天文学上的重要应用。

2.会用万有引力定律计算天体质量。

3.理解并总结万有引力定律处理天体问题的思路和方法。

学习重点：地球质量的计算、太阳等中心天体质量的计算 学习难点：根据已有条件求中心天体的质量；构建运动图景主要内容复习：发现万有引力定律的过程：新课探究：一. “科学真是迷人” ——测量地球的质量（1）若不考虑（忽略）地球 ，地面上质量为m 的物体所受的重力 万有引力。

表达式：（2）地球质量：（1）行星受到的引力 （2）太阳受到的引力 （3）行星和太阳间的引力 月-地检验 万有引力定律推广注：G 是引力常量，g 是地面的重力加速度，R 是地球半径。

例1.已知地面的重力加速度g=10m/s 2,地球半径R=6400km,卡文迪许通过扭秤实验“2次放大”测出了11226.6710/G N m kg -=⨯⋅,请你“称量地球的质量”。

二．计算天体的质量（1）测量太阳的质量 太阳质量远大于各个行星质量，高中阶段粗略计算，不考虑行星之间的万有引力。

设中心天体太阳质量M ，行星质量m ，轨道半径r ——也是行星与太阳的距离，公转周期T ，则由F F =万向有：太阳质量例2．把地球绕太阳公转看做是匀速圆周运动，平均半径为1.5×1011 m ，已知引力常量为G=6.67×10-11 N ·m 2/kg 2，则可估算出太阳的质量大约是多少千克?（结果取一位有效数字）太阳—行星模型：中心天体是行星—卫星模型：中心天体是（2）计算中心天体的质量围绕天体做圆周运动的向心力就是中心天体对围绕天体的万有引力，通过围绕天体的运动半径和周期求中心天体的质量。

表达式：中心天体质量例3．地球绕太阳公转，轨道半径为R ，周期为T 。

月球绕地球运行轨道半径为r ，周期为t ，则太阳与地球质量之比为多少？例4.一艘宇宙飞船绕一个不知名的、半径为R的行星表面飞行，环绕一周飞行时间为T。

6.4 万有引力理论的成就学习目标1．了解万有引力定律在天文学上的重要应用。

2．会用万有引力定律计算天体的质量、密度。

3．掌握综合运用万有引力定律和圆周运动学知识分析具体问题的基本方法。

学习方法通过万有引力定律在实际中的应用，培养理论联系实际的能力。

情感、态度与价值观利用万有引力定律可以发现求知天体，懂得理论来源于实践，反过来又可以指导实践的辩证唯物主义观点。

学习重点求中心天体的质量、密度。

学习难点应用万有引力定律解决实际问题预习案1，在处理天体运动的许多题目中，若不考虑天体自转的影响，天体表面上质量为m 的物体所受的重力等于天体对物体的万有引力，即。

其中g为天体表面的重力加速度，M为天体的质量，R为天体的半径。

在处理天体运动的许多题目中，这个关系是我们解决问题的重要关系之一，这个关系也常被称为“黄金代换”。

在不考虑地球自转的影响时，地面上物体受到的万有引力大小等于物体的重力。

所以有：，解得M=。

2，行星绕太阳做匀速圆周运动的向心力是由它们之间的万有引力提供的，设太阳的质量为M，m是某个行星的质量，r是它们之间的距离，ω是行星公转的角速度。

可列出方程，ω不能直接测出，但可以测出它的公转周期T，ω和T的关系为，联立得：，从而求出太阳的质量：，可见，只要测出行星的，和，就可算出太阳的质量。

同理，只要能测出环绕天体的公转周期和轨道半径，就能算出中心天Mm rG m r T π=2224体的质量。

3，发现未知天体等： 天文学家在用牛顿的引力理论分析天王星运动时，发现用万有引力定律计算出来的天王星的轨道与实际观测到的结果发生了偏差。

至此出现了两种观点：一是万有引力定律不准确；二是万有引力定律没有问题，只是天王星轨道外有未知的行星吸引天王星，使其轨道发生偏离。

英国剑桥大学的学生 和法国的 相信未知行星的存在。

他们根据天王星的观测资料，各自独立地利用万有引力定律计算出这颗“新”行星的轨道。

1846年，德国科学家 在勒维耶预言的位置附近发现了海王星。

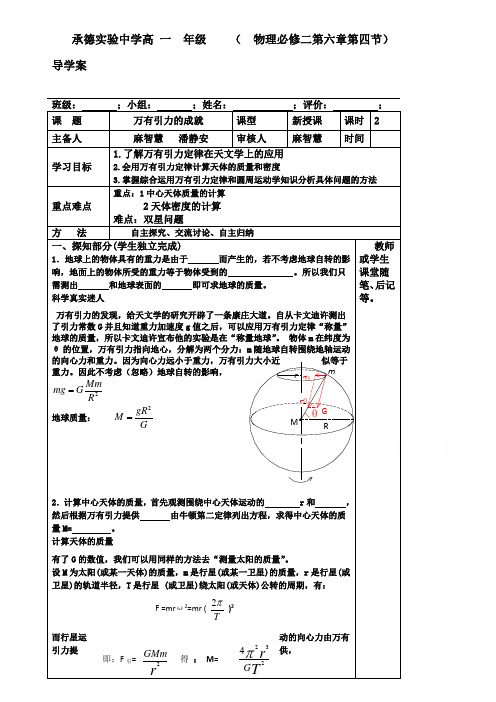
RMGθmwr F向F引承德实验中学高一年级（物理必修二第六章第四节）导学案班级：；小组：；姓名：；评价：；课题万有引力的成就课型新授课课时 2 主备人麻智慧潘静安审核人麻智慧时间学习目标1.了解万有引力定律在天文学上的应用2.会用万有引力定律计算天体的质量和密度3.掌握综合运用万有引力定律和圆周运动学知识分析具体问题的方法重点难点重点：1中心天体质量的计算2天体密度的计算难点：双星问题方法自主探究、交流讨论、自主归纳一、探知部分(学生独立完成)1．地球上的物体具有的重力是由于而产生的，若不考虑地球自转的影响，地面上的物体所受的重力等于物体受到的。

所以我们只需测出和地球表面的即可求地球的质量。

科学真实迷人万有引力的发现，给天文学的研究开辟了一条康庄大道。

自从卡文迪许测出了引力常数G并且知道重力加速度g值之后，可以应用万有引力定律“称量”地球的质量，所以卡文迪许宣布他的实验是在“称量地球”。

物体m在纬度为θ的位置，万有引力指向地心，分解为两个分力：m随地球自转围绕地轴运动的向心力和重力。

因为向心力远小于重力，万有引力大小近似等于重力。

因此不考虑（忽略）地球自转的影响，2RMmGmg=地球质量：GgRM2=2．计算中心天体的质量，首先观测围绕中心天体运动的 r和，然后根据万有引力提供由牛顿第二定律列出方程，求得中心天体的质量M= 。

计算天体的质量有了G的数值，我们可以用同样的方法去“测量太阳的质量”。

设M为太阳(或某一天体)的质量，m是行星(或某一卫星)的质量，r是行星(或卫星)的轨道半径，T是行星 (或卫星)绕太阳(或天体)公转的周期，有：而行星运动的向心力由万有引力提供，教师或学生课堂随笔、后记等。

Tπ2F =mrω2=mr ()2rGMm2TrG2324π即：F引= 得：M=3．海王星是在 年 月 日德国的伽勒在勒维耶预言的位置附近发现的，发现的过程是：发现 的实际运动轨道与 的轨道总有一些偏差，根据观察到的偏差数据和万有引力定律计算出 ，并预测可能出现的时刻和位置；在预测的时间去观察预测的位置。

万有引力专题复习导学案万有引力定律揭示了自然界中物体间普遍存在的一种基本相互作用规律和行星运动的本质原因，并且把地上的运动和天上的运动统一起来。

万有引力定律的具体应用有：发现新的天体，测天体质量，计算天体密度，研究天体的运动规律等.这一部分内容公式变化多，各种关系复杂，是高考的热点，也是学习的难点。

在复习过程中，要深刻理解万有引力定律的内容和应用，重点是要弄清以下几个问题。

（一）不同公式和问题中的r 含义不同万有引力定律公式221r m Gm F ⋅=中的r 指的是两个 间的距离，在实际问题当中，只有当两物体间的距离 物体本身的大小时，定律才适用，此时r 指的是这两个物体间的距离；定律也可适用于两个质量分布均匀的球体之间，此时r 指的是这两个球心的距离。

而向心力公式rv m F 2⋅=中的r ，对于椭圆轨道指的是曲率半径，对于圆轨道指的是 ，开普勒第三定律k Tr =23中的r 同一个r 在不同公式中所具有的含义迥异。

[例1] 飞船沿半径为R 某一点A 处将速率降低到适当数值，地球表面在B 点相切，如图所示，求飞船由A 径为0R ）当飞船在圆周上绕地球运动时，有 =当飞船进入椭圆轨道运动时，有 k =联立①②式得，T /=故解得飞船由A 运动到B 点所需的时间为T t '=21[例2] 力常量为G ，求：（1）双星转动的中心位置； （2）转动周期。

解：（1）设双星转动的中心位置O 距离1m 为r 角速度为ω对m 1有1向引F F = 即： ① 对m 2有2向引F F = 即： ② 解得=r （2）设双星转动周期为T对恒星1m ，有1向引F F = 即：得转动周期为=T （二）自转周期和公转周期的区别自转周期是天体绕自身轴线转动一周的时间，公转周期是卫星绕中心天体公转一周的时间。

这两个周期一般不相等，如地球自转周期为24小时，公转周期为365天。

但也有特殊情况，如月球的自转周期等于公转周期，所以它总是以相同的一面朝向地球。

例5．地球质量大约是月球质量的81倍,在登月飞船通过月、地之间的某一位置时，月球和地球对它的引力大小相等，该位置到月球中心和地球中心的距离之比为（）A．1:27 B. 1:9 C. 1:3 D. 9：1
例6.设想把一质量为m的物体放在地球的中心，这时它受到地球的万有引力是（）
A. 0
B. mg (g=9.8m/s2)
C. ∞
D. 无法确定
课后巩固案
1．下列关于陨石坠向地球的解释中，正确的是（）
A．陨石对地球的吸引力远小于地球对陨石的吸引力
B．陨石对地球的吸引力和地球对陨石的吸引力大小相等，但陨石的质量小，加速度大，所以改变运动方向落向地面
C．太阳不再吸引陨石，所以陨石落向地球
D．陨石受到其它星球的斥力而落向地球
2．如图在半径为R，质量M的匀质铜球中，挖一半径为R/2的球形空穴，空穴跟铜球相切。

质量为m的匀质小球位于铜球球心与空穴中心的连线上，离球心距离d。

试求这两个球之间的万有引力。

6.4万有引力成就课前复习1．向心力的表达式n F = = = （n F 与v T ω、、关系） 2．万有引力定律表达式F =万 适用条件： 一、计算天体的质量1．在实验室“称量”地球的质量：（阅读教材“科学真是迷人”部分的内容，同时考虑下列问题） “称量”地球质量的原理公式是 ，需知的条件有 、 、 ，地球质量的表达式为M= .2．估算太阳的质量：（阅读教材“天体质量的计算”部分的内容，同时考虑下列问题） 计算太阳质量的原理公式是2MmGr= ，需知的条件 、 、 ，太阳质量的表达式为M= 。

[想一想]：通过教材以上两部分内容的学习，你可否得出估算天体质量的方法？主要有几种？基本思路是什么？ 二、估算天体密度如果把天体看作质量分布均匀的球体，怎样估算天体的密度ρ？（=M V ρ，M 、V 是天体的质量和体积，其中34=3V R π球）三、发现未知天体[说一说]：根据万有引力定律，人们发现了太阳的行星 、 ，还计算了一颗著名慧星 慧星的轨道并正确预言了它的回归。

〖例1〗某星球它表面的重力加速度是地球表面重力加速度的2倍，星球半径是地球半径的2倍，则该星球质量是地球质量的 （ ）A 、0.5倍B 、2倍C 、4倍D 、8倍 〖针对训练〗1.火星的质量和半径分别约为地球的101和21，地球表面的重力加速度为g ，则火星表面的重力加速度约为（ ）A ．0.2gB ．0.4gC ．2.5gD ．5g 〖例2〗已知地球表面重力加速度为g ，地球半径为R ，万有引力常量为G ，用以上各量表示估算地球 的密度？ 〖例3〗（多选）利用下列哪组数据，可以计算出地球质量（ ）A ．已知地球绕太阳做匀速圆周运动的轨道半径和周期B ．已知月球绕地球做匀速圆周运动的轨道半径和周期C ．已知月球绕地球做匀速圆周运动的轨道半径和角速度D ．已知地球半径和地球表面重力加速度 〖针对训练〗2.一颗贴着木星表面运行的探测器，已知其运行周期为T ，木星的半径为R ，则估算木星的质量为质量为〖例4〗已知月球绕地球运动周期T 和轨道半径r ，地球半径为R ，估算地球的平均密度？3.若有一艘宇宙飞船在某一行星表面．．做匀速圆周运动，设其周期为T ，引力常量为G ，那么该行星的平均密度为（ ）A 、π32GTB 、23GT π C 、π42GT D 、24GT π4.有一星球的密度与地球的密度相同，但它表面处的重力加速度是地面上的重力加速度的4倍，则该星球的质量将是地球质量的：( ) A 、1/4 B 、4倍 C 、16倍 D 、64倍 5．已知引力常量G ＝6.67×10－11N ·m 2/kg 2，重力加速度g ＝9.8 m /s 2，地球半径R ＝6.4×106m ，则可知地球质量的数量级是( ) A ．1018 kg B ．1020 kg C ．1022 kgD ．1024 kg3．一飞船在某行星表面附近沿圆轨道绕该行星飞行，若认为行星是密度均匀的球体，那 么要确定该行星的密度，只需要测量( )A ．飞船的轨道半径B ．飞船的运行速度C ．飞船的运行周期D ．行星的质量 【小组总结】1．应用万有引力定律求解天体质量的基本思路是什么?2．求解天体质量的方程依据是什么?【达标检测】1．（多选）已知万有引力常量G 和下列各组数据，能计算出地球质量的是( ) A.月球绕地球运行的周期及月球距地球的距离B.地球绕太阳运行的周期及地球离太阳的距离C.人造卫星在地面附近运行的速度和运行周期D.若不考虑地球自转，已知地球的半径及地表重力加速度2．科学家们推测，太阳系的第九大行星就在地球的轨道上，从地球上看，它永远在太阳 的背面，人类一直未能发现它，可以说是“隐居”着的地球的“孪生兄弟”．由以上信息我们可以推知( )A ．这颗行星的公转周期与地球相等B ．这颗行星的自转周期与地球相等C ．这颗行星的质量与地球相等D ．这颗行星的密度与地球相等3.一艘宇宙飞船绕一个不知名的行星表面飞行，要测定该行星的密度，只需要（ ）A ．测定飞船的运行周期B ．测定飞船的环绕半径C ．测定行星的体积D ．测定飞船的运动速度5．已知地球半径R ＝6.4×106 m ，地面附近重力加速度g ＝9.8 m /s 2.计算在距离地面高为 h ＝2×106 m 的圆形轨道上的卫星做匀速圆周运动的线速度v 和周期T.4．某天体的质量约是地球质量的32倍，半径约是地球半径的2倍，已知地球表面的重力加速度为10m/s 2，求：（1）该天体表面的重力加速度为多大？（2）如果分别在该天体表面和地球表面以同样的初速度竖直上抛一物体，物体在该天体上上升的最大高度与在地球上上升的最大高度之比是多少？。

§6、4万有引力理论的成就【学习目标】1、了解万有引力定律在天文学上的重要应用2、会用万有引力定律计算天体的质量和密度3、理解并运用万有引力定律处理天体问题的思路、方法【重难点】重点：万有引力定律和圆周运动知识在天体运动中的应用难点：应用万有引力定律解决实际问题预习案【自主学习】------大胆试1、科学真是迷人如果______________的影响，地面上质量为m的物体受到重力等于__________，即mg=______________，由此得地球的质量表达式为______________。

已知g=10 m/s2, R=6371km, G=6.67×10-11N·m2/Kg2,则地球的质量约为______________kg。

2、计算天体的质量（1）计算太阳的质量：将_______的运动近似看作匀速圆周运动，向心力由___________提供，其牛顿第二定律方程是______________，由此得太阳的质量为______________。

（2）测量天体质量的主要方法是______________。

3、发现未知天体海王星是在______年____月____日发现的，发现过程是：发现________的实际运动轨道与______________的轨道总有一些偏差，根据观察到的偏差数据和万有引力定律计算出______________，并预测可能出现的时刻和位置；在预测的时间去观察预测的位置。

课堂探究案【合作探究】------我参与探究点一、地球自转对地表物体重力的影响如图所示，在纬度为 的地表处，物体所受的万有引力为F=_________，方向指向________，而物体随地球一起绕地轴自转所需的向心力为F向=___________，方向垂直于____________，这是物体所受到的万有引力的一个分力充当的，而万有引力的另一个分力就是通常所说的重力mg，严格地说：除了在地球的两个极点处，地球表面处的物体所受的重力并不等于万有引力，而只是万有引力的听得懂 会做题 想明白 讲清楚 能命题 - 2 -8 一题多解 一题多变 多题一解 一个分力。

6.4万有引力理论的成就 导纲编写：鲁江涛 审核：李长有【科学真迷人】若不考虑地球自转的影响，地面附近的重力与万有引力实质___________，即重力______引力。

卡文迪许把他自己的实验说成是“称量地球的重量（质量）”，那他是如何称得地球的质量的呢？一、计算天体质量其实当我们知道引力常量后我们就能计算天体的质量，方法主要有两种：方法一：根据天体的圆周运动，即其向心力由万有引力提供G Mm r 2﹦4π2mr T 2 方法二：根据重力加速度求天体质量，即引力=重力，表达式：G Mm R 2﹦mg 例1．某行星的一颗小卫星在半径为r 的圆轨道上绕行星运行，运行的周期是T 。

已知引力常量为G ，求这个行星的质量。

例2．已知地球表面的重力加速度为g ，引力常量为G ，地球半径为R ，求地球质量。

总结：在任何星球表面，g 和R 比较容易测量，当用到GM 时，可用GM ﹦gR 2换算，因此，该公式又称“黄金代换”。

【课内探究1】据报道，科学家最近在太阳系外发现了首颗“宜居”行星，其质量约为地球质量的 6.4倍，一个在地球表面重量为600N 的人在这个行星表面的重量将变为900N 。

由此可推知，该行星的半径与地球半径之比约为多少？思考与讨论：（1）前面“计算天体的质量”求的是“中心天体”的质量还是“环绕天体”的质量？（2）“计算天体的质量”为什么常常用周期表达式？总结：计算中心天体质量的周期表达式M =_____________。

指出各量表示的意义T_______________，r______________。

（3）“计算中心天体的质量”总结！I、若已知月球绕地球做匀速圆周运动的半径为r，周期为T，则地球质量的表达式为：II、若已知月球绕地球做匀速圆周运动的半径为r，线速度为v，则地球质量的表达式为：III、若已知月球绕地球做匀速圆周运动的半径为r，角速度为ω，则地球质量的表达式为：IV、若已知地球的半径R和地球表面的重力加速度g，地球表面物体的重力近似等于地球对物体的引力，可得地球质量的表达式为：二、计算天体密度：（1）利用绕行天体运动参量求中心天体的密度【课内探究2】设绕行天体的轨道半径为r，周期为T，中心天体半径为R，试列出中心天体密度的表达式：【课内探究3】当绕行天体绕中心天体表面运动时，其轨道半径r可认为等于中心天体半径R，则中心天体密度的表达式可变为：（2）利用天体表面的重力加速度求天体自身的密度例3、已知地球的半径为R，地面的重力加速度为g，引力常量为G，如果不考虑地球自转的影响，那么地球的平均密度的表达式为______________。