数学模型经典题目及答案
- 格式:docx
- 大小:311.20 KB
- 文档页数:10

初中数学几何模型大全+经典题型(含答案)全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生了解。
垂直也可以做为轴进行对称全等。
说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
对称最值(两点间线段最短)说明:通过对称进行等量代换,转换成两点间距离及点到直线距离。
说明:找到与所要求最值相关成三角形的两个定长线段,定长线段的和为最大值,定长线段的差为最小值。

完整版)初中数学几何模型大全+经典题型(含答案)通过将倍长中点相关线段进行旋转变换,可以构造出旋转全等模型。
这种模型的特点是,将相邻等线段所成角的一半旋转后拼接在一起,形成对称全等。
同时,也可以通过将两个等腰三角形或正多边形的夹角进行变化,来构造出模型变形。
如果遇到复杂图形找不到旋转全等,可以先找到两个正多边形或等腰三角形的公共极点,然后围绕公共极点找到两组相邻等线段,分组组成三角形证全等。
幂定理可以用等线段、等比值、等乘积进行代换,从而将两个数之间的比值转换成乘积。
在相似证明中,常用的辅助线是平行线,根据题目条件来确定比值并做出相应的平行线。
题目一:在半圆中,圆心为O,圆上有点C、E,CD垂直于AB,EF垂直于AB,EG垂直于CO。
证明CD等于GF。
题目二:在正方形ABCD内部,点P满足∠PAD=∠PDA=15度。
证明△PBC是正三角形。
题目三:在图中,ABCD、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点。
证明A2B2C2D2是正方形。
题目四:在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F。
证明∠DEN=∠F。
题目五:在△ABC中,H为垂心,O为外心,且OM垂直于BC于M。
1)证明AH等于2OM;2)如果∠BAC等于60度,证明AH等于AO。
1.设P为正三角形ABC内任意一点,连接PA,PB,PC,由三角形不等式可得PA+PB>AB。
PB+PC>BC。
PC+PA>CA。
将三式相加得到2PA+2PB+2PC>AB+BC+CA=3,即PA+PB+PC>3/2.又由于P到三角形三边的距离不超过1,所以PA+PB+PC<3,综上可得1.5≤PA+PB+PC<3,即所求不等式成立。
2.设P为正方形ABCD内任意一点,连接PA,PB,PC,PD。
由于正方形四边相等,所以PA+PC=2,PB+PD=2.又由于P到四边的距离不超过1,所以PA+PB+PC+PD<4.将前两式相加得到PA+PB+PC+PD=2(PA+PB)/2+2(PC+PD)/2≥2√(PA·PB)+2√(PC·P D)。

初中数学几何模型大全+ 经典题型(含答案)全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是 45 °、30 °、22.5 °、15 °及有一个角是 30 °直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含1/2 角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇60 度旋 60 度,造等边三角形遇90 度旋 90 度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋 180 度,造中心对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“ 8”字模型可以证明。
模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
中点旋转:说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
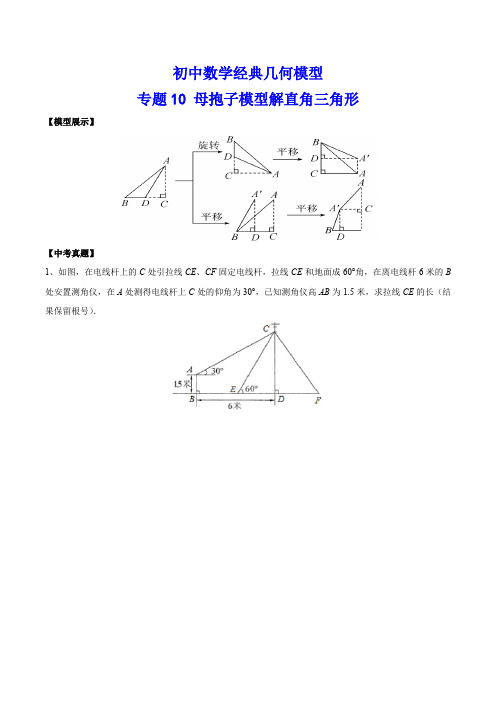
初中数学经典几何模型专题10 母抱子模型解直角三角形【模型展示】【中考真题】1、如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B 处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).2、如图,一垂直于地面的灯柱AB被一钢筋CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方2米处加固另一条钢线E D,ED与地面成53°夹角(∠EDB=53°),那么钢线ED的长度约为多少米?(结果精确到1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)【精典例题】1、如图,一艘轮船在A处时观测得小岛C在船的北偏东60°方向,轮船以40海里/时的速度向正东方向航行1.5小时到达B处,这时小岛C在船的北偏东30°方向.已知小岛C周围50海里范围内是暗礁区.(1)求B处到小岛C的距离(2)若轮船从B处继续向东方向航行,有无触礁危险?请说明理由.(参考数据:≈1.73)2、金桥学校“科技体艺节”期间,八年级数学活动小组的任务是测量学校旗杆AB的高,他们在旗杆正前方台阶上的点C处,测得旗杆顶端A的仰角为45°,朝着旗杆的方向走到台阶下的点F处,测得旗杆顶端A的仰角为60°,已知升旗台的高度BE为1米,点C距地面的高度CD为3米,台阶CF的坡角为30°,且点E、F、D在同一条直线上,求旗杆AB的高度(计算结果精确到0.1米,参考数据:≈1.41,≈1.73)3、如图,为了测得电视塔AB的高度,在D处用高为1 m的测角仪CD测得电视塔顶端A的仰角为30°,再向电视塔方向前进100 m到达F处,又测得电视塔顶端A的仰角为60°,则这个电视塔AB的高度(单位:m)为(C)A.50 3 B.51 C.503+1 D.1014、如图,小明在热气球A上看到横跨河流两岸的大桥BC,测得B,C两点的俯角分别为60°和45°,已知热气球离地面的高度为120 m,且大桥与地面在同一水平面上,求大桥BC的长度.(结果保留整数,3≈1.73)5、某数学兴趣小组为测量河对岸树AB的高,在河岸边选择一点C.从C处测得树梢A的仰角为45°,沿BC方向后退10米到点D,再次测得树梢A的仰角为30°,则树高为米.(结果精确到0.1米,参考数据:≈1.414,≈1.732)6、某矩形交通指示牌CDEF如图所示,AB的距离为5m,从A点测得指示牌顶端D点和底端C点的仰角分别是60°和45°,则指示牌的高度CD约为m.(精确到0.1m.参考数据:≈1.414,≈1.732)7、为做好疫情宣传巡查工作,各地积极借助科技手段加大防控力度.如图,亮亮在外出期间被无人机隔空喊话“戴上口罩,赶紧回家”.据测量,无人机与亮亮的水平距离是15米,当他抬头仰视无人机时,仰角恰好为30°,若亮亮身高1.70米,则无人机距离地面的高度约为米.(结果精确到0.1米,参考数据:≈1.732,≈1.414)8、广州塔又称广州新电视塔,昵称小蛮腰,位于广州市海珠区赤岗塔附近,是中国第一高塔,世界第四高塔.如图,广州塔BD附近有一大厦AC高150米,张强在楼底A处测得塔顶D的仰角为45°,上到大厦顶C处测得塔顶D的仰角为37°,求广州塔BD的高.(参考数据:s i n37°≈0.60,c o s37°≈0.80,tan37°≈0.75)9、如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角为45°,沿斜坡走3米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1:2.求大树BC的高度约为多少米?(≈1.732,结果精确到0.1)专题10 母抱子模型解直角三角形答案【模型展示】【中考真题】1、如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B 处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).解析:过点A作AH⊥CD,垂足为H,由题意可知四边形ABDH为矩形,∠CAH=30°,∴AB=DH=1.5,BD=AH=6,在R t△ACH中,tan∠CAH=,∴CH=AH•tan∠CAH,∴CH=AH•tan∠CAH=6tan30°=6×(米),又∵DH=1.5,∴CD=2+1.5,在R t△CDE中,∵∠CED=60°,s i n∠CED=,∴CE==(4+)(米),答:拉线CE的长为(4+)米.2、如图,一垂直于地面的灯柱AB被一钢筋CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方2米处加固另一条钢线E D,ED与地面成53°夹角(∠EDB=53°),那么钢线ED的长度约为多少米?(结果精确到1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)【精典例题】1、如图,一艘轮船在A处时观测得小岛C在船的北偏东60°方向,轮船以40海里/时的速度向正东方向航行1.5小时到达B处,这时小岛C在船的北偏东30°方向.已知小岛C周围50海里范围内是暗礁区.(1)求B处到小岛C的距离(2)若轮船从B处继续向东方向航行,有无触礁危险?请说明理由.(参考数据:≈1.73)解析:(1)由题意得∠CBD=60°,∠CAB=30°,∴∠ACB=30°,∴∠CAB=∠ACB,∴CB=AB=40×1.5=60(海里),∴B处到小岛C的距离为60海里;(2)过点C作CE⊥AD,垂足为点E,∵CE=CB×s i n∠CBE=60×s i n60°=30≈51.96海里,∴CE>50,∴轮船从B处继续向正东方向航行,没有触礁危险.2、金桥学校“科技体艺节”期间,八年级数学活动小组的任务是测量学校旗杆AB的高,他们在旗杆正前方台阶上的点C处,测得旗杆顶端A的仰角为45°,朝着旗杆的方向走到台阶下的点F处,测得旗杆顶端A的仰角为60°,已知升旗台的高度BE为1米,点C距地面的高度CD为3米,台阶CF的坡角为30°,且点E、F、D在同一条直线上,求旗杆AB的高度(计算结果精确到0.1米,参考数据:≈1.41,≈1.73)解析:过点C作CM⊥AB于M.则四边形MEDC是矩形,∴ME=DC=3.CM=ED,在R t△AEF中,∠AFE=60°,设EF=x,则AF=2x,AE=x,在R t△FCD中,CD=3,∠CFD=30°,∴DF=3,在R t△AMC中,∠ACM=45°,∴∠MAC=∠ACM=45°,∴MA=MC,∵ED=CM,∴AM=ED,∵AM=AE﹣ME,ED=EF+DF,∴x﹣3=x+3,∴x=6+3,∴AE=(6+3)=6+9,∴AB=AE﹣BE=9+6﹣1≈18.4米.答:旗杆AB的高度约为18.4米.3、如图,为了测得电视塔AB 的高度,在D 处用高为1 m 的测角仪CD 测得电视塔顶端A 的仰角为30°,再向电视塔方向前进100 m 到达F 处,又测得电视塔顶端A 的仰角为60°,则这个电视塔AB 的高度(单位:m )为( C )A .50 3B .51C .503+1D .1014、(2019·山东菏泽定陶三模)如图,小明在热气球A 上看到横跨河流两岸的大桥BC ,测得B ,C 两点的俯角分别为60°和45°,已知热气球离地面的高度为120 m ,且大桥与地面在同一水平面上,求大桥BC 的长度.(结果保留整数,3≈1.73)解析:如图,作AD ⊥CB 交CB 所在直线于点D .由题意知,∠ACD =45°,∠ABD =60°.在R t △ACD 中,∠ACD =45°,∴CD =AD =120 m . 在R t △ABD 中,∠ABD =60°,∴tan 60°=AD BD ,∴BD =33AD =40 3 m ,∴BC =CD -BD =120-403≈51(m ). 答:大桥BC 的长度约为51 m .5、某数学兴趣小组为测量河对岸树AB的高,在河岸边选择一点C.从C处测得树梢A的仰角为45°,沿BC方向后退10米到点D,再次测得树梢A的仰角为30°,则树高为米.(结果精确到0.1米,参考数据:≈1.414,≈1.732)解析:根据题意可知:∠ABC=90°,CD=10,在R t△ABC中,∠ACB=45°,∴AB=CB,在R t△ABD中,∠ADB=30°,BD=CD+BC=10+AB,∴tan30°=,即=,解得AB≈13.7(米).答:树高约为13.7米.6、某矩形交通指示牌CDEF如图所示,AB的距离为5m,从A点测得指示牌顶端D点和底端C点的仰角分别是60°和45°,则指示牌的高度CD约为m.(精确到0.1m.参考数据:≈1.414,≈1.732)解析:在R t△ADB中,∠DAB=60°,AB=5,∵tan∠DAB=,∴BD=5•tan60°=5,在R t△BAC中,∵∠CAB=45°,∴AB=BC=5,∴CD=BD﹣BC=(5﹣5)m≈3.7(m).故答案为:3.7.7、为做好疫情宣传巡查工作,各地积极借助科技手段加大防控力度.如图,亮亮在外出期间被无人机隔空喊话“戴上口罩,赶紧回家”.据测量,无人机与亮亮的水平距离是15米,当他抬头仰视无人机时,仰角恰好为30°,若亮亮身高1.70米,则无人机距离地面的高度约为米.(结果精确到0.1米,参考数据:≈1.732,≈1.414)解析:如图,根据题意可知:DE⊥BE,AB⊥BE,过点D作DC⊥AB于点C,所以四边形DEBC是矩形,∴BC=ED=1.70,DC=EB=15,在R t△ACD中,∠ADC=30°,∴tan30°=,即=,解得AC=5,∴AB=AC+CB=5+1.70≈10.4(米).答:无人机距离地面的高度约为10.4米.8、广州塔又称广州新电视塔,昵称小蛮腰,位于广州市海珠区赤岗塔附近,是中国第一高塔,世界第四高塔.如图,广州塔BD附近有一大厦AC高150米,张强在楼底A处测得塔顶D的仰角为45°,上到大厦顶C处测得塔顶D的仰角为37°,求广州塔BD的高.(参考数据:s i n37°≈0.60,c o s37°≈0.80,tan37°≈0.75)解析:如图,过点C作CE⊥BD于点E,即四边形ACEB是矩形∴BE=AC=150,CE=AB,根据题意可知:∠DAB=45°,∴DB=AB=CE,∴DE=DB﹣BE=DB﹣150,在R t△CDE中,∠DCE=37°,∴DE=CE•tan37°,即DB﹣150≈0.75DB,解得DB≈600(米).答:广州塔BD的高约为600米.9、如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角为45°,沿斜坡走3米到达斜坡上点D,在此处测得树顶端点B的仰角为30°,且斜坡AF的坡比为1:2.求大树BC的高度约为多少米?(≈1.732,结果精确到0.1)解析:作DH⊥AE于点H,作DG⊥BC于点G,如图,则四边形DGCH为矩形,在R t△ADH中,∵,∴AH=2DH,∵AH2+DH2=AD2,∴.∴DH=CG=3m,∴AH=2DH=6m,设BC=xm,则BG=(x﹣3)m,在R t△BAC中,∠BAC=45°,∴AC=BC=xm,∴CH=DG=(x+6)m,在R t△BDG中,∠BDG=30°∵tan30°=,∴,解得,x=≈15.3.答:大树BC的高度约为15.3米.。

半角模型经典例题初二数学以下是3个关于半角模型的初二数学经典例题及其答案:例题1:已知等腰三角形ABC中,AB=AC,∠BAC=120°,D是BC上一点,且∠BAD=30°,E在AB上,AD=AE,求∠EDC的度数。
答案:由题意知,∠BAC=120°,AB=AC,所以∠B=∠C=30°。
又因为∠BAD=30°,所以∠ADC=∠B+∠BAD=60°。
又因为AD=AE,所以∠ADE=∠AED。
设∠ADE=∠AED=x°,则∠EDC=∠ADC-∠ADE=(60-x)°。
由三角形外角等于不相邻的两个内角之和,得∠AED=∠EDC+∠C,即x=60-x+30,解得x=45。
所以,∠EDC=(60-x)°=15°。
例题2:在正方形ABCD中,E是BC上一点,且BE=2CE,F是CD上一点,且DF=CF,连接AE、AF、EF。
若∠EAF=45°,求∠EFC的度数。
答案:由题意知,∠B=∠C=∠D=90°,AB=BC=CD=DA。
又因为BE=2CE,DF=CF,所以EC:BE=FC:DF=1:2。
又因为∠B=∠D=90°,所以△ABE∽△ADF。
所以,∠BAE=∠DAF。
又因为∠EAF=45°,所以∠BAE+∠CAF=∠EAF=45°。
所以,∠CAF+∠DAF=∠BAD-∠EAF=90°-45°=45°。
在△AEF中,∠AEF+∠AFE+∠EAF=180°,所以∠AFE=(180°-45°)/2=67.5°。
又因为∠AFC=∠AFE-∠EFC,所以∠EFC=∠AFE-∠AFC=67.5°-45°=22.5°。
例题3:在△ABC中,∠BAC=90°,AB=AC,D是BC上一点,且BD=BA,E在BC的延长线上,且CE=CA。

初中数学几何模型大全+ 经典题型(含答案)全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是 45°、 30°、°、 15°及有一个角是 30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含1/2 角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇60 度旋 60 度,造等边三角形遇90 度旋 90 度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋 180 度,造中心对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“ 8”字模型可以证明。
模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
中点旋转:说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
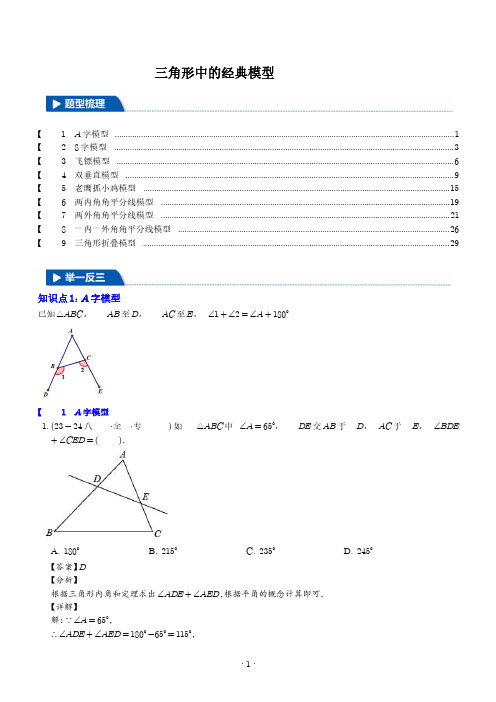
三角形中的经典模型【1A字模型 1【28字模型 3【3飞镖模型 6【4双垂直模型 9【5老鹰抓小鸡模型 15【6两内角角平分线模型 19【7两外角角平分线模型 21【8一内一外角角平分线模型 26【9三角形折叠模型 29知识点1:A字模型已知△ABC,AB至D,AC至E,∠1+∠2=∠A+180°【1A字模型1.(23-24八·全·专)如△ABC中∠A=65°,DE交AB于D,AC于E,∠BDE+∠CED=( ).A.180°B.215°C.235°D.245°【答案】D【分析】根据三角形内角和定理求出∠ADE+∠AED,根据平角的概念计算即可.【详解】解:∵∠A=65°,∴∠ADE+∠AED=180°-65°=115°,∴∠BDE+∠CED=360°-115°=245°,故选:D.【点睛】本题考查的是三角形内角和定理的应用,掌握三角形内角和等于180°是解题的关键.2.(23-24八年级·全国·专题练习)如图是某建筑工地上的人字架,若∠1=120°,那么∠3-∠2的度数为.【答案】60°【分析】根据平角的定义求出∠4,再利用三角形的外角的性质即可解决问题.【详解】解:如图∵∠1+∠4=180°,∠1=120°,∴∠4=60°,∵∠3=∠2+∠4,∴∠3-∠2=∠4=60°,故答案为:60°.【点睛】本题考查三角形外角的性质、平角的性质等知识,解题的关键是熟练掌握基本知识,属于中考基础题.3.(23-24八年级·河北沧州·期中)琪琪在操作课上将三角形剪掉一个角后得到四边形ABCD,则下列判断错误的是()A.变成四边形后对角线增加了两条B.变成四边形后内角和增加了360°C.外角和没有发生变化D.若剪掉的角的度数是60°,则∠1+∠2=240°【答案】B【分析】本题考查了多边形的对角线,内角和与外角和,三角形内角和定理,解题的关键是【详解】解:A、三角形没有对角线,变成四边形后对角线为两条,即增加了两条,故正确,不合题意;B、三角形内角和为180°,变成四边形后内角和为360°,增加了180°,故错误,不合题意;C、任意多边形的外角和是360°,故正确,不合题意;D、若剪掉的角的度数是60°,则∠A+∠B=120°,则∠1+∠2=360°-120°=240°,故正确,不合题意;故选:B.4.(23-24·浙江杭州·二模)将一把直尺与一块三角板在同一平面内按如图所示的方式放置,若∠1=130°,则∠2的度数为.【答案】40°/40度【分析】本题考查了平行线的性质,三角形的外角的性质,熟练掌握平行线的性质是解题的关键,根据平行线的性质可得∠FGH=∠1=130°,然后利用三角形外角的性质进行计算即可解答.【详解】解:如图:由题意得:AD∥BC,∴∠FGH=∠1=130°,∵∠FGH是△EFG的一个外角,∴∠FGH=∠2+∠E,∵∠E=90°,∴∠2=130°-90°=40°,故答案为:40°.知识点2:8字模型①已知AD,BC相交于O,则∠A+∠B=∠C+∠D②已知线段AP平分∠BAD,线段CP平分∠BCD,则∠P=12(∠B+∠D)【题型28字模型】5.(23-24八年级·浙江金华·期末)如图,BP平分∠ABC,交CD于点F,DP平分∠ADC交AB于点E,AB与CD相交于点G,∠A=42°.(1)若∠ADC=60°,求∠AEP的度数;(2)若∠C=38°,求∠P的度数.【答案】(1)72°;(2)40°.【分析】(1)根据角平分线的定义可得∠ADP=12∠ADC,然后利用三角形外角的性质即可得解;(2)根据角平分线的定义可得∠ADP=∠PDF,∠CBP=∠PBA,再根据三角形的内角和定理可得∠A+∠ADP=∠P+∠ABP,∠C+∠CBP=∠P+∠PDF,所以∠A+∠C=2∠P,即可得解.【详解】解:(1)∵DP平分∠ADC,∴∠ADP=∠PDF=12∠ADC,∵∠ADC=60°,∴∠ADP=30°,∴∠AEP=∠ADP+∠A=30°+42°=72°;(2)∵BP平分∠ABC,DP平分∠ADC,∴∠ADP=∠PDF,∠CBP=∠PBA,∵∠A+∠ADP=∠P+∠ABP,∠C+∠CBP=∠P+∠PDF,∴∠A+∠C=2∠P,∵∠A=42°,∠C=38°,∴∠P=12(38°+42°)=40°.【点睛】本题考查了三角形的内角和定理及三角形外角的性质,角平分线的定义,熟记定理并理解“8字形”的等式是解题的关键.6.(23-24八年级·河南漯河·期末)如图,AB和CD相交于点O,∠A=∠C,则下列结论中不能完全确定正确的是()A.∠B=∠DB.∠1=∠A+∠DC.∠2>∠DD.∠C=∠D【答案】D【分析】利用三角形的外角性质,对顶角相等逐一判断即可.【详解】∵∠A+∠AOD+∠D=180°,∠C+∠COB+∠B=180°,∠A=∠C,∠AOD=∠BOC,∴∠B=∠D,∵∠1=∠2=∠A+∠D,∴∠2>∠D,故选项A,B,C正确,故选D.【点睛】本题考查了对顶角的性质,三角形外角的性质,熟练掌握并运用两条性质是解题的关键.7.(23-24八年级·北京怀柔·期末)如图,在由线段AB,CD,DF,BF,CA组成的平面图形中,∠D=28°,则∠A+∠B+∠C+∠F的度数为( ).A.262°B.152°C.208°D.236°【答案】C【分析】如图标记∠1,∠2,∠3,然后利用三角形的外角性质得∠1=∠B+∠F=∠D+∠3,∠2=∠A+∠C,再利用∠2,∠3互为邻补角,即可得答案.【详解】解:如下图标记∠1,∠2,∠3,∵∠1=∠B+∠F=∠D+∠3,∵∠D=28°,∴∠3=∠B+∠F-28°,又∵∠2=∠A+∠C,∴∠2+∠3=∠A+∠C+∠B+∠F-28°,∵∠2+∠3=180°∴180°=∠A+∠C+∠B+∠F-28°,∴∠A+∠C+∠B+∠F=180°+28°=208°,故选C.【点睛】此题考查了三角形的外角性质与邻补角的意义,熟练掌握并灵活运用三角形的外角性质与邻补角的意义是解答此题的关键.8.(23-24八年级·全国·专题练习)如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H六个角的和.【答案】360°【分析】根据三角形内角和外角的性质可得:∠G+∠D=∠3,∠F+∠C=∠4,∠E+∠H=∠2,再根据三角形内角和定理可得答案.【详解】解:∵∠G+∠D=∠3,∠F+∠C=∠4,∠E+∠H=∠2,∴∠G+∠D+∠F+∠C+∠E+∠H=∠3+∠4+∠2,∵∠B+∠2+∠1=180°,∠3+∠5+∠A=180°,∴∠A+∠B+∠2+∠4+∠3=360°,∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=360°.【点睛】此题主要考查了三角形内角与外角的性质,关键是掌握三角形的一个外角等于和它不相邻的两个内角的和.知识点3:飞镖模型①已知四边形ABCD,则∠C=∠A+∠B+∠D②已知四边形ABCD,线段BO平分∠ABC,线段OD平分∠ADC,则∠O=12(∠A+∠C)【题型3飞镖模型】9.(23-24·河北秦皇岛·一模)如图,用铁丝折成一个四边形ABCD(点C在直线BD的上方),且∠A=70°,∠BCD=120°,若使∠ABC、∠ADC平分线的夹角∠E的度数为100°,可保持∠A不变,将∠BCD(填“增大”或“减小”)°.【答案】增大10【分析】利用三角形的外角性质先求得∠ABE+∠ADE=30°,根据角平分线的定义得到∠ABC+∠ADC= 60°,再利用三角形的外角性质求解即可.【详解】解:如图,连接AE并延长,连接AC并延长,∠BED=∠BEF+∠DEF=∠ABE+∠BAD+∠ADE=100°,∵∠BAD=70°,∴∠ABE+∠ADE=30°,∵BE,DE分别是∠ABC、∠ADC平分线,∴∠ABC+∠ADC=2(∠ABE+∠ADE)=60°,同上可得,∠BCD=∠BAD+∠ABC+∠ADC=130°,130°-120°=10°,∴∠BCD增大了10°.故答案为:增大,10.【点睛】本题考查了三角形的外角性质,三角形的内角和定理,角平分线的定义等知识,熟练运用题目中所给的结论是解题的关键.10.(23-24八年级·江苏苏州·阶段练习)在社会实践手工课上,小茗同学设计了如上图这样一个零件,如果∠A=52°,∠B=25°,∠C=30°,∠D=35°,∠E=72°,那么∠F=°.【答案】70【分析】延长BE、CF,交于点G,连接AG,根据三角形内角和定理和四边形的内角和为360°即可求解.【详解】解:延长BE、CF,交于点G,连接AG,如图,∴∠AGB=180°-∠B-∠BAG,∠AGC=180°-∠C-∠CAG,∴∠AGB+∠AGC=180°-∠B-∠BAG+180°-∠C-∠CAG=360°-∠B-∠C-∠BAC=253°,∴∠CGB=360°-∠AGB+∠AGC=107°.∵∠BED=72°,∴∠GED=108°,∴∠GFD=360°-∠GED-∠D-∠CGB=110°,∴∠CFD=70°.故答案为:70.【点睛】本题主要考查三角形内角和定理.正确的作出辅助线是解题关键.11.(23-24八年级·全国·专题练习)如图,若∠EOC=115°,则∠A+∠B+∠C+∠D+∠E+∠F=.【答案】230°【分析】根据三角形外角的性质,得到∠EOC=∠E+∠2=115°,∠2=∠D+∠C,∠EOC=∠1+∠F=115°,∠1=∠A+∠B,即可得到结论.【详解】解:如图∵∠EOC=∠E+∠2=115°,∠2=∠D+∠C,∴∠E+∠D+∠C=115°,∵∠EOC=∠1+∠F=115°,∠1=∠A+∠B,∴∠A+∠B+∠F=115°,∴∠A+∠B+∠C+∠D+∠E+∠F=230°,故答案为:230°.【点睛】本题主要考查三角形内角和定理和三角形外角的性质,解决本题的关键是要熟练掌握三角形外角性质.12.(23-24·河北邯郸·一模)嘉嘉在作业本上画了一个四边形,并标出部分数据(如图),淇淇说,这四个数据中有一个是标错的;嘉嘉经过认真思考后,进行如下修改:若∠A,∠B,∠BCD保持不变,则将图中∠D(填“增大”或“减小”)度,淇淇说,“改得不错”.【答案】增大5【分析】连接BD,利用三角形的内角和计算即可.【详解】解:连接BD,∵∠CDB+∠CBD=180°-∠A-∠ABC-∠ADC∠CDB +∠CBD =180°-∠BCD∴∠A +∠ABC +∠ADC =∠BCD∵∠A =90°,∠ABC =25°,∠BCD =145°∴∠ADC =145°-25°-90°=30°∴30°-25°=5°故答案为:增大,5【点睛】本题主要考查三角形的内角和,添加辅助线利用三角形内角和计算是解决本题的关键.知识点4:双垂直模型已知∠B =∠D =∠ACE =90°.则∠BAC =∠DCE ,∠ACB =∠CED .【证明】∵∠B =∠D =∠ACE =90°;∴∠BAC +∠ACB =90°;又∠ECD +∠ACB =90°;∴∠BAC =∠DCE 同理,∠ACB +∠DCE =90°,且∠CED +∠DCE =90°;∴∠ACB =∠CED ,得证.【题型4双垂直模型】13.(23-24八年级·广东珠海·期末)如图1,AB ⊥BC 于点B ,CD ⊥BC 于点C ,点E 在线段BC 上,且AE ⊥DE .(1)求证:∠EAB =∠CED ;(2)如图2,AF 、DF 分别平分∠BAE 和∠CDE ,则∠F 的度数是(直接写出答案即可);(3)如图3,EH 平分∠CED ,EH 的反向延长线交∠BAE 的平分线AF 于点G .求证:EG ⊥AF .(提示:三角形内角和等于180°)【答案】(1)见解析;(2)45°;(3)见解析【分析】(1)利用同角的余角相等即可证明;(2)过点F 作FM ∥AB ,利用∠DFA =∠DFM +∠AFM =12∠CDE +12∠EAB =12(∠CDE +∠EAB )即可解决问题;(3)想办法证明∠EAG +∠AEG =90°即可解决问题.【详解】解:(1)∵AB ⊥BC ,CD ⊥BC ,∴∠B =∠C =90°,∴∠BAE +∠AEB =90°,∵AE ⊥DE ,∴∠AED =90°,∴∠AEB +∠CED =90°,∴∠BAE =∠CED .(2)解:答案为45°;过点F 作FM ∥AB ,如图,∵AB ⊥BC ,CD ⊥BC ,∴∠B =∠C =90°,∴AB ∥CD ,∵∠C =90°,∴∠CED +∠CDE =90°,∵∠BAE =∠CED ,∴∠BAE +∠CDE =90°,∵AF 、DF 分别平分∠BAE 和∠CDE ,∴∠CDF =12∠CDE ,∠BAF =12∠BAE ,∴∠CDF +∠BAF =12(∠BAE +∠CDE )=45°,∵FM ∥AB ∥CD ,∴∠CDF =∠DFM ,∠BAF =∠AFM ,∴∠AFD =∠CDF +∠BAF =45°.(3)∵EH 平分∠CED ,∴∠CEH =12∠CED ,∴∠BEG =12∠CED ,∵AF 平分∠BAE ,∴∠BAG =12∠BAE ,∵∠BAE =∠CED ,∴∠BAG =∠BEG ,∵∠BAE +∠BEA =90°,∴∠BAG +∠GAE +∠AEB =90°,即∠GAE +∠AEB +∠BEG =90°,∴∠AGE =90°,∴EG ⊥AF .【点睛】本题考查三角形内角和定理、平行线的性质、角平分线的定义等知识,解题的关键是学会添加常用辅助线,构造平行线解决问题,属于中考常考题型.14.(23-24八年级·陕西西安·期末)如图,在等腰Rt △ABC 中,∠ACB =90°,D 为BC 的中点,DE ⊥AB ,垂足为E ,过点B 作BF ∥AC 交DE 的延长线于点F ,连接CF .(1)求证:AD⊥CF.(2)连接AF,试判断△ACF的形状,并说明理由.【答案】(1)见解析(2)△ACF为等腰直角三角形;理由见解析【分析】本题考查了全等三角形的判定和性质及等腰三角形性质和判定.(1)欲求证AD⊥CF,先证明∠CAG+∠ACG=90°,需证明∠CAG=∠BCF,利用三角形全等,易证.(2)要判断△ACF的形状,看其边有无关系.根据(1)的推导,易证CF=AF,从而判断其形状.【详解】(1)证明:在等腰直角△ABC中,∵∠ACB=90°,∴∠CBA=∠CAB=45°,∵DE⊥AB,∴∠DEB=90°,∴∠BDE=45°,∵BF∥AC,∴∠CBF=180°-∠ACB=90°,∴∠BFD=45°=∠BDE,∴BF=DB,又∵D为BC的中点,∴CD=DB,即BF=CD,在△CBF和△ACD中,BF=CD∠CBF=∠ACD=90°CB=AC,∴△CBF≌△ACD(SAS).∴∠BCF=∠CAD.∵∠BCF+∠GCA=90°,∴∠CAD+∠GCA=90°,即AD⊥CF.(2)解:△ACF是等腰三角形,理由为:连接AF,如图所示,由(1)知:△CBF≌△ACD,∴CF=AD,∵△DBF是等腰直角三角形,且BE是∠DBF的平分线,∴BE垂直平分DF,∴AF=AD,∵CF=AD,∴CF=AF,∴△ACF是等腰三角形.15.(23-24八年级·山西晋中·期中)请把下面的证明过程补充完整如图,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F,求证:CF=CE.证明:∵AE平分∠CAB(已知),∴∠CAE=∠FAB(①),∵∠ACE=90°(已知),∴∠CAE+∠CEF=90°(②),∵CD是△ABC的高(已知),∴∠CDA=90°(三角形高的定义),∴(③),(直角三角形的两个锐角互余),∴∠CEF=∠AFD(④),∵∠CFE=∠AFD(⑤),∴∠CFE=∠CEF(⑥),∴CF=CE(⑦).【答案】①角平分线的定义;②直角三角形的两锐角互余;③∠FAD+∠AFD=90°;④等角的余角相等;⑤对顶角相等;⑥等量代换;⑦等角对等边【分析】本题考查的是直角三角形的性质、角平分线的定义,等腰三角形的判定,掌握直角三角形的两锐角互余是解题的关键.根据角平分线的定义、直角三角形的性质、对顶角相等、等角对等边解答即可.【详解】证明:∵AE平分∠CAB(已知),∴∠CAE=∠FAB(角平分线的定义),∵∠ACE=90°(已知),∴∠CAE+∠CEF=90°(直角三角形的两锐角互余),∵CD是△ABC的高(已知),∴∠CDA=90°(三角形高的定义),∴∠FAD+∠AFD=90°(直角三角形的两锐角互余),∴∠CEF=∠AFD(等角的余角相等),∵∠CFE=∠AFD(对顶角相等),∴∠CFE=∠CEF(等量代换),∴CF=CE(等角对等边).故答案为:角平分线的定义;直角三角形的两锐角互余;∠FAD+∠AFD=90°;等角的余角相等;对顶角相等;等量代换;等角对等边.16.(23-24八年级·江苏扬州·阶段练习)在Rt △ABC 中,∠CAB =90°,AB =AC ,点O 是BC 的中点,点P 是射线CB 上的一个动点(点P 不与点C 、O 、B 重合),过点C 作CE ⊥AP 于点E ,过点B 作BF ⊥AP 于点F ,连接EO ,OF.(问题探究)如图1,当P 点在线段CO 上运动时,延长EO 交BF 于点G .(1)求证:△AEC ≌△BFA ;(2)BG 与AF 的数量关系为:(直接写结论,不需说明理由);(拓展延伸)(3)①如图2,当P 点在线段OB 上运动,EO 的延长线与BF 的延长线交于点G ,∠OFE 的大小是否变化?若不变,求出∠OFE 的度数;若变化,请说明理由;②当P 点在射线OB 上运动时,若AE =2,CE =6,直接写出△OEF 的面积,不需证明.【答案】(1)见解析;(2)BG =AF ;(3)①∠OFE 的大小不变,∠OFE =45°;②满足条件的△OEF 的面积为8或16【分析】(1)根据等角的余角相等得出∠CAE =∠ABF ,证明△AEC ≌△BFA AAS ;(2)证明△COE ≌△BOG AAS 得出CE =BG ,则CE =AF ,等量代换可得AF =BG ;(3)①证明△AEC ≌△BFA AAS ,进而证明∠CEO =∠BGO 证明△COE ≌△BOG AAS 得出∠EFO =12∠EFG =45°;②根据题意画出图形,分类讨论,根据三角形的面积公式,即可求解.【详解】(1)证明:如图1中,∵CE ⊥AE ,BF ⊥AE ,∴∠AEC =∠BFA =∠CAB =90°,∴∠CAE +∠BAF =90°,∠BAF +∠ABF =90°,∴∠CAE =∠ABF ,在△AEC 和△BFA 中,∠AEC =∠BFA∠CAE =∠ABF AC =BA,∴△AEC ≌△BFA AAS ;(2)解:结论:BG =AF .理由:∵CE ⊥AE ,BF ⊥AE ,∴CE ∥BG ,∴∠CEO =∠BGO ,∵O 是BC 的中点,∴OC =OB ,在△COE 和△BOG 中,∠CEO =∠BGO∠AOE =∠BOG OC =OB,∴△COE ≌△BOG AAS ,∴CE =BG ,∵△AEC ≌△BFA ,∴CE =AF ,∴AF =BG .故答案为:BG =AF .(3)解:①如图2中,结论:∠OFE 的大小不变,∠OFE =45°.理由:∵CE ⊥AE ,BF ⊥AE ,∴∠AEC =∠BFA =∠CAB =90°,∴∠CAE +∠BAF =90°,∠BAF +∠ABF =90°,∴∠CAE =∠ABF ,在△AEC 和△BFA 中,∠AEC =∠BFA∠CAE =∠ABF AC =BA,∴△AEC ≌△BFA AAS ;∴CE =AF ,AE =BF ,∵CE ⊥AE ,BF ⊥AE ,∴CE ∥BG ,∴∠CEO =∠BGO ,∵O 是BC 的中点,∴OC =OB ,在△COE 和△BOG 中,∠CEO =∠BGO∠AOE =∠BOG OC =OB,∴△COE ≌△BOG AAS ,∴CE =BG ,OE =OG ,∴AF =BG ,∴EF =FG ,根据△EFO ≌△GFO SSS 可得:∠EFO =∠GFO∴∠EFO =12∠EFG =45°;②如图2中,当AE =2,CE=6时,EF =FG =6-2=4,∴S △EOF =12S △EFC =12×12×4×4=4如图3中,当AE =2,CE =6时,EF =FG =6+2=8,∴S △EOF =12S △EFG =12×12×8×8=16综上所述,满足条件的△OEF 的面积为8或16.【点睛】本题考查了全等三角形的证明与性质,等腰三角形的判定和性质,三角形的动点问题以及三角形求面积的问题,正确掌握知识点是解题的关键.知识点5:老鹰抓小鸡模型如图,∠A+∠O=∠1+∠2;口诀:腋下两角之和等于上下两角之和【题型5老鹰抓小鸡模型】17.(23-24八年级·江苏扬州·阶段练习)如图,把△ABC沿EF对折,叠合后的图形如图所示.若∠A=60°,∠1=95°,则∠2的度数为()A.24°B.35°C.30°D.25°【答案】D【分析】根据三角形内角和定理可得∠AEF+∠AFE=120°,再根据邻补角的性质可得∠FEB+∠EFC= 360°-120°=240°,再根据由折叠可得:∠B′EF+∠EFC′=∠FEB+∠EFC=240°,然后计算出∠1+∠2的度数,即可求得∠2的度数.【详解】∵∠A=60°,∴∠AEF+∠AFE=180°-60°=120°,∴∠FEB+∠EFC=360°-120°=240°,∵由折叠可得:∠B′EF+∠EFC′=∠FEB+∠EFC=240°,∴∠1+∠2=240°-120°=120°,∵∠1=95°,∴∠2=120°-95°=25°,故选D.【点睛】本题考查了三角形的内角和定理,翻折变换的性质,熟记定理及性质并准确识图是解题的关键.18.(23-24八年级·重庆渝北·阶段练习)如图,将△ABC沿着DE翻折,使B点与B 点重合,若∠1+∠2=80°,则∠B的度数为.【答案】40°/40度【分析】由翻折的性质可知,∠B=∠B ,∠BED=∠B ED,∠BDE=∠B DE,由∠BED+∠B ED+∠1= 180°,∠BDE+∠B DE+∠2=180°,∠1+∠2=80°,可得∠BED+∠BDE=140°,根据∠B=180°-∠BED+∠BDE,计算求解即可.【详解】解:由翻折的性质可知,∠B=∠B ,∠BED=∠B ED,∠BDE=∠B DE,∵∠BED+∠B ED+∠1=180°,∠BDE+∠B DE+∠2=180°,∠1+∠2=80°,∴∠BED+∠BDE=140°,∴∠B=180°-∠BED+∠BDE=40°,故答案为:40°.【点睛】本题考查了翻折的性质,三角形内角和定理.解题的关键在于对知识的熟练掌握与灵活运用.19.(23-24八年级·安徽铜陵·期中)如图,将△ABC纸片沿DE折叠,使点A落在点A′处,且A′B平分∠ABC,A′C平分∠ACB,若∠1+∠2=120°,则∠BA′C的度数为()A.120°B.110°C.100°D.90°【答案】A【详解】由∠BDE、∠CED是△ADE的两个外角知∠BDE=∠A+∠AED、∠CED=∠A+∠ADE,据此得∠BDE+∠CED=∠A+∠AED+∠A+∠ADE,推出∠1+∠2=2∠A得到∠A=60°,根据BA'平分∠ABC,CA'平分∠ACB知∠A'BC+∠A'CB=12(∠ABC+∠ACB)=90°-12∠A.利用∠BA'C=180°-(∠A'BC+∠A'CB)可得答案.解:∵∠BDE、∠CED是△ADE的两个外角,∴∠BDE=∠A+∠AED,∠CED=∠A+∠ADE,∴∠BDE+∠CED=∠A+∠AED+∠A+∠ADE,∴∠1+∠ADE+∠2+∠AED=2∠A+∠AED+∠ADE,即∠1+∠2=2∠A,∵∠1+∠2=120°,∴∠A=60°,∵BA'平分∠ABC,CA'平分∠ACB,∴∠A'BC+∠A'CB=12(∠ABC+∠ACB)=12(180°-∠A )=90°-12∠A .∴∠BA 'C =180°-(∠A 'BC +∠A 'CB ),=180°-90°-12∠A =90°+12∠A =90°+12×60°=120°.故选:A .【点睛】本题考查三角形的内角和定理、角平分线的定义、三角形的外角的性质等知识,解题的关键是灵活运用所学知识,属于中考常考题型.20.(23-24八年级·山东烟台·期中)折纸是我国一项古老的传统民间艺术,这项具有中国特色的传统文化在几何中可以得到新的解读.已知在△ABC 中,请根据题意,探索不同情境中∠1+∠2(或∠1-∠2)与∠A 的数量关系.(1)如图①,若∠A =80°,沿图中虚线DE 截去∠A ,则∠1+∠2=.(2)如图②,若∠A =80°,沿图中虚线DE 将∠A 翻折,使点A 落在BC 上的点A '处,则∠1+∠2=.(3)如图③,翻折后,点A 落在点A '处,若∠1+∠2=80°,求∠B +∠C 的度数(4)如图④,△ABC 纸片沿DE 折叠,使点A 落在点A '处,若∠1=80°,∠2=24°,求∠A 的度数.【答案】(1)260°(2)160°(3)∠B +∠C =140°(4)∠A =28°【分析】(1)根据三角形内角和定理得出∠B +∠C =180°-80°=100°,再由平角进行求解即可;(2)利用翻折的性质得出∠EDA '=∠ADE ,∠AED =∠DEA ',根据三角形内角和定理得出∠ADE +∠AED =100°,结合图形,由平角及各角之间的关系进行计算即可‘(3)连接AA .根据三角形外角的性质得出∠1=∠DAA '+∠DA 'A ,∠2=∠EAA '+∠EA 'A ,然后利用各角之间的数量关系得出∠EAD =40°,再由三角形内角和定理即可求解;(4)设AB 与DA 交于点F ,根据三角形外角得出∠1=∠DFA +∠A ,∠DFA =∠A +∠2,再由折叠的性质得出∠A =∠A ,结合图形及各角之间的数量关系进行求解即可【详解】(1)解:∵∠A=80°,∴∠ADE+∠AED=180°-80°=100°,∴∠1+∠2=360°-∠ADE-∠AED=260°,故答案为:260°;(2)∵∠A=80°,∴∠ADE+∠AED=180°-80°=100°,∵翻折,∴∠EDA'=∠ADE,∠AED=∠DEA',∴∠ADA'+∠AEA'=2(∠ADE+∠AED)=200°,∴∠1+∠2=360°-(∠ADA'+∠AEA')=160°,故答案为:160°;(3)解:连接AA .如图所示:∵∠1=∠DAA'+∠DA'A,∠2=∠EAA'+∠EA'A,∴∠1+∠2=∠DAA'+∠DA'A+∠EAA'+∠EA'A=∠EAD+∠EA'D,∵∠EAD=∠EA D,∴∠1+∠2=2∠EAD=80°,∴∠EAD=40°,∴∠B+∠C=180°-40°=140°.(4)解:如图,设AB与DA 交于点F,∵∠1=∠DFA+∠A,∠DFA=∠A +∠2,由折叠可得,∠A=∠A ,∴∠1=∠A+∠A +∠2=2∠A+∠2,又∵∠1=80°,∠2=24°,∴80°=2∠A+24°,∴∠A=28°.【点睛】题目主要考查三角形内角和定理及三角形外角的性质,平角的定义等,理解题意,作出相应辅助线求解是解题关键.知识点6:两内角角平分线模型在△ABC 中,BI 、CI 分别是∠ABC 和∠ACB 的角平分线,且相交于点I .则∠I =90°+12∠A【题型6两内角角平分线模型】21.(23-24八年级·河南信阳·开学考试)如图,AD ,CE 都是△ABC 的角平分线,且交于点O ,∠DAC =30°,∠ECA =35°,则∠ABO 的度数为.【答案】25°/25度【分析】本题考查了三角形内角和定理、角平分线,利用角平分线的定义结合三角形内角和定理找出∠ABO 的度数是解题的关键.根据角平分线的定义可得出∠BAC =60°、∠ACB =70°,结合三角形内角和可得出∠ABC =50°,由三角形的三条角平分线交于一点,可得出BO 平分∠ABC ,进而可得出∠ABO 的度数,此题得解.【详解】解:∵AD 平分∠BAC ,CE 平分∠ACB ,∠DAC =30°,∠ECA =35°,∴∠BAC =2∠DAC =60°,∠ACB =2∠ECA =70°,∴∠ABC =180°-∠BAC -∠ACB =50°.∵△ABC 的三条角平分线交于一点,∴BO 平分∠ABC ,∴∠ABO =12∠ABC =25°.故答案为:25°.22.(23-24八年级·全国·课后作业)如图,在△ABC 中,∠ABC 和∠ACB 的平分线BE ,CF 相交于点G ,若∠A =66°,则∠BGC 的度数为.【答案】123°/123度【分析】本题考查角平分线和三角形内角和定理,熟练利用角平分线的性质和三角形内角和定理找出题目中角的等量关系是解答本题的关键.由角平分线的性质可知∠GBC =12∠ABC ,∠GCB =12∠ACB ,再由三角形内角和定理可知∠BGC =180°-∠GBC +∠GCB ,即可求解.【详解】∵∠A =66°,∴∠ABC +∠ACB =180°-∠A =114°,∵BE 和CF 分别是∠ABC 和∠ACB 的平分线,∴∠GBC =12∠ABC ,∠GCB =12∠ACB ,∴∠BGC =180°-∠GBC +∠GCB =180°-12∠ABC +∠ACB =123°,故答案为:123°.23.(23-24八年级·河南信阳·开学考试)如图,在△ABC 中,AD 是BC 边上的高,AE ,BF 分别是∠BAC 和∠ABC 的角平分线,它们相交于点O ,∠AOB =125°.求∠CAD 的度数.【答案】∠CAD =20°.【分析】本题考查了角平分线的性质,三角形的内角和定理,以及余角的性质,解题的关键是熟练掌握所学的知识,正确求出∠C =70°,从而求出答案.根据角平分线的性质,由∠AOB =125°,得到∠CAB +∠CBA =110°,然后得到∠C ,由余角的性质,即可求出答案.【详解】解:∵AE ,BF 分别是∠BAC 和∠ABC 的角平分线,∴∠OAB =12∠BAC ,∠OBA =12∠ABC .∴∠CAB +∠CBA =2(∠OAB +∠OBA )=2180°-∠AOB∵∠AOB =125°,∴∠CAB +∠CBA =110°,∴∠C =70°.∵AD 是BC 边上的高∴∠ADC =90°,∴∠CAD =20°.24.(23-24八年级·山东烟台·期末)如图,在△ABC 中,∠A =90°,BE ,CD 分别平分∠ABC 和∠ACB ,且相交于F ,EG ∥BC ,CG ⊥EG 于点G ,则下列结论:①∠CEG =2∠DCA ;②∠DFE =130°;③∠EFC =12∠G :④∠ADC =∠GCD ;⑤△EGC 是等腰直角三角形,其中正确的结论是()A.①③④⑤B.①②③④C.①②③D.①③④【答案】D 【分析】本题主要考查了平行线的性质,角平分线的定义,三角形内角和定理,熟知平行线的性质,角平分线的定义是解题的关键.根据平行线的性质与角平分线的定义即可判断①;只需要证明∠ADC +∠ACD =90°,∠GCD +∠BCD =90°,即可判断④;根据角平分线的定义和三角形内角和定理先推出∠BFC=135°,即可判断②③;根据现有条件无法推出⑤.【详解】解:∵CD平分∠ACB,∴∠ACB=2∠DCA,∠ACD=∠BCD∵EG∥BC,∴∠CEG=∠ACB=2∠DCA,故①正确;∵∠A=90°,CG⊥EG,EG∥BC,∴∠ADC+∠ACD=90°,CG⊥BC,即∠BCG=90°,∴∠GCD+∠BCD=90°,又∵∠BCD=∠ACD,∴∠ADC=∠GDC,故④正确;∵∠A=90°,∴∠ABC+∠ACB=90°,∵BE,CD分别平分∠ABC,∠ACB,∴∠FBC=12∠ABC,∠FCB=12∠ACB,∴∠BFC=180°-∠FBC-∠FCB=180°-12(∠ACB+∠ABC)=135°,∴∠EFC=180°-∠BFC=45°,∵CG⊥EG∴∠G=90°,∴∠EFC=12∠G,故③正确;∵∠BFC=135°,∴∠DFE=∠BFC=135°,故②错误;∵∠G=90°∴△EGC是直角三角形,根据现有条件,无法推出CG=CE,即无法得到△EGC是等腰直角三角形,故⑤错误;∴正确的有①③④,故选:D.知识点7:两外角角平分线模型在△ABC中,BI、CI分别是△ABC的外角的角平分线,且相交于点O.则∠O=90°-12∠A.【证明】∵BO是∠EBC平分线,∴∠2=12∠EBC,∵CO是∠FCB平分线,∴∠5=12∠FCB由△BCO中内角和定理可知:∠O=180°-∠2-∠5=180°-12∠EBC-12∠FCB=180°-12(180°-∠ABC)-12(180°-∠ACB)=12(∠ABC+∠ACB)=12(180°-∠A)=∠O=90°-12∠A【题型7两外角角平分线模型】25.(23-24八年级·全国·专题练习)如图,在△ABC中,∠B=58°,三角形两外角的角平分线交于点E,则∠AEC=.【答案】61°【分析】先根据三角形的内角和定理和平角定义求得∠DAC+∠ACF的度数,再根据角平分线的定义求得∠EAC+∠ECA的度数,即可解答.【详解】解:∵∠B+∠BAC+∠BCA=180°,∠B=58°,∴∠BAC+∠BCA=180°-∠B=180°-58°=122°,∵∠BAC+∠DAC=180°,∠BCA+∠ACF=180°,∴∠DAC+∠ACF=360°-(∠BAC+∠BCA)=360°-122°=238°,∵AE平分∠DAC,CE平分∠ACF,∴∠EAC=12∠DAC,∠ECA=12∠ACF,∴∠EAC+∠ECA=12(∠DAC+∠ACF)=119°,∵∠EAC+∠ECA+∠AEC=180°,∴∠AEC=180°-(∠EAC+∠ECA)=180°-119°=61°,故答案为:61°.【点睛】本题考查三角形的内角和定理、角平分线的定义、平角定义,熟练掌握三角形的内角和定理和角平分线的定义是解答的关键.26.(23-24八年级·河南郑州·阶段练习)如图,G是ΔAFE两外角平分线的交点,P是ΔABC的两外角平分线的交点,F,C在AN上,又B,E在AM上;如果∠FGE=66°,那么∠P=度.【答案】66【分析】利用角平分线的定义和三角形、四边形的内角和可求得:∠G=180°-12×[360°-(180°-∠A)]=90°-1 2∠A,∠P=180°-12×[360°-(180°-∠A)]=90°-12∠A,所以∠P=∠FGE=66°.【详解】解:因为G是△AFE两外角平分线的交点,∴∠FGE=180°-12×[360°-(180°-∠A)]=90°-12∠A,∵P是△ABC两外角平分线的交点,∴∠P=180°-12×[360°-(180°-∠A)]=90°-12∠A,∴∠P=∠FGE=66°.故答案为:66.【点睛】本题考查了三角形内角和定理、角平分线的性质和三角形外角的性质,结合图形熟练运用定理和性质进行求解是解题的关键.27.(23-24八年级·山东聊城·期末)如图,在△ABC中,∠ABC,∠ACB的平分线交于点O,D是∠ACF与∠ABC平分线的交点,E是△ABC的两外角平分线的交点,若∠BOC=130°,则∠D的度数为()A.25°B.30°C.40°D.50°【答案】C【分析】根据角平分线的定义和平角定义可得∠OCD=∠ACO+∠ACD=90°,根据外角的性质可得∠BOC =∠OCD+∠D,继而即可求解.【详解】解:∵CO平分∠ACB,CD平分∠ABC的外角,∴∠ACO=12∠ACB,∠ACD=12∠ACF,∵∠ACB+∠ACF=180°,∴∠OCD=∠ACO+∠ACD=12∠ACB+∠ACF=90°,∴∠BOC=∠OCD+∠D,∴∠D=∠BOC-∠OCD=130°-90°=40°,故选择C.【点睛】本题考查角平分线的定义,平角定义,三角形的外角性质,解题的关键是根据角平分线定义和平角定义可得∠OCD=90°,根据外角的性质求得∠BOC=∠OCD+∠D.28.(23-24八年级·全国·课后作业)(分类讨论思想)△ABC的两外角平分线交于点F.(1)如图1,若∠A=30°,则∠BFC的度数为.(2)如图2,过点F作直线MN∥BC,分别交射线AB,AC于点M,N,若设∠MFB=α,∠NFC=β,则∠A与α+β的数量关系是.(3)在(2)的条件下,将直线MN绕点F转动.①如图3,当直线MN与线段BC没有交点时,试探索∠A与α,β之间的数量关系,并说明理由.②当直线MN 与线段BC 有交点时,试问①中∠A 与α,β之间的数量关系是否仍然成立?若成立,请说明理由;若不成立,请给出三者之间的数量关系.【答案】(1)75°(2)α+β-12∠A =90°(3)①α+β-12∠A =90°,见解析;②不成立,β-α-12∠A =90°或α-β-12∠A =90°【分析】(1)由三角形内角和定理可得∠ACB +∠ABC =180°-∠A ,从而可得∠CBD +∠BCE =180°+∠A ,再由角平分线的定义可得∠CBF +∠BCF =90°+12∠A ,最后由三角形内角和定理可得∠BFC =90°-12∠A ,进行计算即可;(2)由(1)可得由(1)可得∠BFC =90°-12∠A ,再由α+∠BFC +β=180°代入进行计算即可;(3)①根据(1)中的结论∠BFC =90°-12∠A ,以及平角的定义,即可得到答案;②分两种情况进行讨论:根据(1)中的结论∠BFC =90°-12∠A ,以及平角的定义,即可得到答案.【详解】(1)解:∵∠A +∠ACB +∠ABC =180°,∴∠ACB +∠ABC =180°-∠A ,∵∠ACB +∠BCE =180°,∠ABC +∠CBD =180°,∴∠CBD +∠BCE=180°-∠ABC +180-∠ACB=360°-∠ABC +∠ACB=360°-180°-∠A=180°+∠A ,∵BF 和CF 分别是∠DBC 和∠BCE 的平分线,∴∠CBF =12∠CBD ,∠BCF =12∠BCE ,∴∠CBF +∠BCF ,=12∠CBD +12∠BCE =12∠CBD +∠BCE =12×180°+∠A =90°+12∠A ,∵∠BFC +∠CBF +∠BCF =180°,∴∠BFC =180°-∠CBF +∠BCF =180°-90°+12∠A =90°-12∠A =75°,故答案为:75°;(2)解:α+β-12∠A =90°,由(1)可得∠BFC =90°-12∠A ,∵α+∠BFC +β=180°,∴α+β+90°-12∠A =180°,即α+β-12∠A =90°.(3)解:①当直线MN 与线段BC 没有交点时,α+β-12∠A =90°,理由如下:∵∠BFC =90°-12∠A ,∠MFB +∠NFC +∠BFC =180°,∴α+β+90°-12∠A =180°,即α+β-12∠A =90°;②当直线MN 与线段BC 有交点时,①中∠A 与α,β之间的数量关系不成立,需分两种情况讨论:a .如图1,当M 在线段AB 上,N 在射线AC 上时,β-α-12∠A =90°,,∵∠BFC =90°-12∠A ,∠BFC -∠MFB +∠NFC =180°,∴90°-12∠A -α+β=180°,即β-α-12∠A =90°,b .如图2,当M 在射线AB 上,N 在线段AC 上时,α-β-12∠A =90°,,∵∠BFC =90°-12∠A ,∠BFC -∠NFC +∠MFB =180°,∴90°-12∠A -β+α=180°,即α-β-12∠A =90°.【点睛】本题考查了三角形内角和定理、角平分线的定义、平角的定义等知识,熟练掌握以上知识点,采用分类讨论的思想解题,是解此题的关键.知识点8:一内一外角角平分线模型已知△ABC 中,BP 、CP 分别是△ABC 的内角和外角的角平分线,且相交于点P .则∠P =12∠A【证明】∵BP 是∠ABC 平分线,∴∠3=12∠ABC ∵CP 是∠ACE 平分线,∴∠1=12∠ACE 由△ABC 外角定理可知:∠ACE =∠ABC +∠A 即:2∠1=2∠3+∠A ⋯⋯①对①式两边同时除以2,得:∠1=∠3+12∠A⋯⋯②又在△BPC中由外角定理可知:∠1=∠3+∠P⋯⋯③比较②③式子可知:∠P=12∠A.【题型8一内一外角角平分线模型】29.(23-24八年级·江苏泰州·期末)如图,点B、C分别在AM、AN上运动(不与A重合),CD是∠BCN的平分线,CD的反向延长线交∠ABC的平分线于点P.知道下列哪个条件①∠ABC+∠ACB;②∠A;③∠NCD -∠ABP;④∠ABC的值,不能求∠P大小的是()A.①B.②C.③D.④【答案】D【分析】本题考查三角形外角的性质与内角和定理,根据三角形外角的性质及角平分线的定义可得∠P=∠NCD-∠ABP,可判断③,再利用三角形外角的性质得到∠A=∠NCB-∠ABC,等量代换可判断②,根据三角形内角和定理及等量代换可判断①和④,即可求解.【详解】解:∵CD是∠BCN的平分线,CD的反向延长线交∠ABC的平分线于点P,∴∠NCD=∠BCD,∠ABP=∠CBP,∵∠P=∠DCB-∠CBP,∴∠P=∠NCD-∠ABP,∴③能求出∠P的大小;∵∠A=∠NCB-∠ABC=2∠NCD-∠ABP,∠P=∠NCD-∠ABP∴∠P=12∠A,∴②能求出∠P的大小;∵∠ABC+∠ACB=180°-∠A,∴∠A=180°-∠ABC+∠ACB∵∠P=12∠A,∴∠P=12180°-∠ABC+∠ACB=90°-12∠ABC+∠ACB,∴①能求出∠P的大小,④不能求出∠P的大小;故选:D.30.(23-24八年级·四川遂宁·开学考试)如图,点D为△ABC边BC的延长线上一点,若∠A:∠ABC=3:4,∠ACD=140°,∠ABC的角平分线与∠ACD的角平分线交于点M,则∠M=度.【答案】30【分析】本题考查了三角形的外角定理,与角平分线有关的计算.解题的关键是掌握三角形的一个外角等于与它不相邻的两个内角之和,以及角平分线的定义.先根据∠A:∠ABC=3:4,∠ACD=140°,求出∠ABC=80°,进而得出∠CBM=12∠ABC=40°,∠CDM=12∠ACD=70°,最后根据三角形的外角定理即可解答.【详解】解:∵∠ACD=140°,∴∠A+∠ABC=140°∵∠A:∠ABC=3:4,∴∠ABC=140°×43+4=80°,∵BM平分∠ABC,CM平分∠ACD,∴∠CBM=12∠ABC=40°,∠CDM=12∠ACD=70°,∴∠M=∠DCM-∠CBM=30°,故答案为:30.31.(23-24八年级·四川眉山·开学考试)如图,∠ABC=∠ACB,AD、BD、CD分别平分∠EAC、∠ABC和∠ACF.以下结论:①AD∥BC;②∠ACB=2∠ADB;③DB平分∠ADC;④∠ADC=90°-∠ABD.其中正确的结论有.(填序号)【答案】①②④【分析】证明∠EAD=∠DAC,由三角形外角得∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,得出∠EAD =∠ABC,再由平行线的判定即可判断出①是否正确;由AD∥BC,得出∠ADB=∠DBC,再由BD平分∠ABC,所以∠ABD=∠DBC,∠ABC=2∠ADB,进而可判断出②是否正确;假设DB平分∠ADC,推出与题干不符的结论,进而可判断出③是否正确,由∠ADC+∠CAD+∠ACD=180°,利用角的关系得∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,进而可判断出④是否正确;【详解】解:①∵AD平分△ABC的外角∠EAC,∴∠EAD=∠DAC,∵∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,∴∠EAD=∠ABC,∴AD∥BC,故①正确;②由(1)可知AD∥BC,∴∠ADB=∠DBC,∵BD平分∠ABC,∴∠ABD=∠DBC,∴∠ABC=2∠ADB,∵∠ABC=∠ACB,∴∠ACB=2∠ADB,故②正确;③若DB 平分∠ADC ,∴∠ADB =∠CDB ,∵∠ADB =∠DBC =∠ABD ,∴∠ADB =∠DBC =∠ABD =∠CDB ,∴∠ABC =∠ADC ,与题干条件矛盾.故③错误.④在△ADC 中,∠ADC +∠CAD +∠ACD =180°,∵CD 平分△ABC 的外角∠ACF ,∴∠ACD =∠DCF ,∵AD ∥BC ,∴∠ADC =∠DCF ,∠ADB =∠DBC ,∠CAD =∠ACB ,∴∠ACD =∠ADC ,∠CAD =∠ACB =∠ABC =2∠ABD ,∴∠ADC +∠CAD +∠ACD =∠ADC +2∠ABD +∠ADC =2∠ADC +2∠ABD =180°,∴∠ADC +∠ABD =90°,∴∠ADC =90°-∠ABD ,故④正确;故答案为:①②④【点睛】此题考查三角形的外角性质,平行线的判定与性质,三角形的内角和定理的应用,解题关键在于掌握外角性质.32.(23-24八年级·河南开封·期末)如图,在△ABC 中,∠A =48°,△ABC 的内角∠ABC 与外角∠ACD 的平分线相交于点A 1,得到∠A 1;∠A 1BC 与∠A 1CD 的平分线相交于点A 2,得到∠A 2;⋯⋯按此规律继续下去,∠A n -1BC 与∠A n -1CD 的平分线相交于点A n ,要使∠A n 的度数为整数,则n 的最大值为()A.3B.4C.5D.6【答案】B 【分析】本题主要考查了三角形的内角和,三角形的外角定理,角平分线的定义,熟练掌握三角形内角和是解题的关键.先根据外角和定理得出∠ACD =∠ABC +∠A ,再根据题意总结出规律,∠A n =12n ∠A 即可得到答案.【详解】解:∵∠ACD 是△ABC 的一个外角,∴∠ACD =∠ABC +∠A ,∵△ABC 的内角∠ABC 与外角∠ACD 的平分线相交于点A 1,得到∠A 1;∠A 1BC 与∠A 1CD 的平分线相交于点A 2,∴∠A 1BC =12∠ABC ,∠A 1CA =12∠ACD ,∴∠A 1=180°-∠A 1BC -∠A 1CB=180°-12∠ABC -(∠ACB +∠A 1CA )=180°-12∠ABC -∠ACB -12∠ACD =180°-12∠ABC -∠ACB -12(∠ABC +∠A )。


初中数学几何模型大全+经典题型(含答案)全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
几何最值模型对称最值(两点间线段最短)对称最值(点到直线垂线段最短)说明:通过对称进行等量代换,转换成两点间距离及点到直线距离。

角度计算的经典模型(八大题型)【题型01:双垂直模型】【题型02:A字模型】【题型03:8字模型】【题型04:飞镖模型】【题型05:风筝模型】【题型06:两内角角平分线模型】【题型07:两外角角平分线模型】【题型08:内外角平分线模型】【题型01:双垂直模型】【条件】∠B=∠D=∠ACE=90°.【结论】∠BAC=∠DCE,∠ACB=∠CED.1.AD、BE为△ABC的高,AD、BE相交于H点,∠C=50°,求∠BHD.2.如图,在△ABC中,∠BAC=80°,∠B=60°,AD是BC边上的高,∠ACB的平分线CF交AD于点E.求∠AEC的度数.3.如图,在△ABC中,AD⊥BC,垂足为D,E是AC边上一点,BE与AD交于点F,若∠ABC=45°,∠BAC=75°,∠BFD=60°,求∠BEC的度数.【题型02:A字模型】图1【条件】图1中三种情况【结论】∠1=∠2【证明】略图2【结论】∠1+∠2=∠3+∠4【证明】根据内角和定理,∠1+∠2+∠A=∠3+∠4+∠A=180°∴∠1+∠2=∠3+∠4图3【结论】∠1+∠2=180°+∠A【证明】∠1+∠2=(∠AED+∠A)+(∠ADE+∠A)=180°+∠A4.探索归纳:(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2=.(2)如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=.(3)如图2,根据(1)与(2)的求解过程,你归纳猜想∠1+∠2与∠A的关系是.(4)如图3,若没有剪掉∠A,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系,并说明理由.5.如图,在△ABC中,BD平分∠ABC,DE∥BC交AB于点E.若∠A=70°,∠BDC=100°,则∠BED的度数为()A.120°B.130°C.140°D.150°6.如图,已知:AD∥EF,∠CAD+∠DEF=180°.(1)证明:AC∥DE;(2)若AC平分∠BAD,∠ADC=35°,∠ACD=∠ADE+45°.求∠G的度数.7.在△ABC中,已知∠A=80°,∠C=30°,现把△CDE沿DE进行不同的折叠得△C DE,对折叠后产生的夹角进行探究:(1)如图(1)把△CDE沿DE折叠在四边形ADEB内,则求∠1+∠2的和;(2)如图(2)把△CDE沿DE折叠覆盖∠A,则求∠1+∠2的和;(3)如图(3)把△CDE沿DE斜向上折叠,探求∠1、∠2、∠C的关系.【题型03:8字模型】【条件】AE、BD相交于点C【结论】∠A+∠B=∠D+∠E.8.(1)已知:如图(1)的图形我们把它称为“8字形”,试说明:∠A+∠B=∠C+∠D.(2)如图(2),AP,CP分别平分∠BAD,∠BCD,若∠ABC=36°,∠ADC=16°.求∠P的度数.(3)如图(3),直线AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是;(4)如图(4),直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D的数量关系是.9.如图,∠1=60°,则∠A+∠B+∠C+∠D+∠E+∠F=()A.240°B.280°C.360°D.540°10.如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=.11.如图,已知AB∥CD,∠B=∠D,CD与AE相交于F.(1)求证:AD∥BC;(2)若∠B=50°,AE平分∠BAD,求∠DFE的度数.12.已知:如图,FE∥OC,AC和BD相交于点O,F是OD上一点,且∠1=∠A.(1)求证:AB∥DC;(2)若∠B=30°,∠1=65°,求∠OFE的度数.13.如图,BP平分∠ABC,交CD于点F,DP平分∠ADC交AB于点E,AB与CD相交于点G,∠A=42°.(1)若∠ADC=60°,求∠AEP的度数;(2)若∠C=38°,求∠P的度数.【题型04:飞镖模型】图1图2图3【条件】四边形ABPC如图1所示【结论】∠BPC=∠A+∠B+∠C.14.探究与发现:如图(1)所示的图形,像我们常见的学习用品一圆规,我们,不妨把这样图形叫做“规形图(1)观察“规形图(1)”,试探究∠BDC与∠A、∠B、∠C之间的数量关系,并说明理由;(2)请你直接利用以上结论,解决以下问题:①如图(2),把一块三角尺XYZ放置在△AC上使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=40°,则∠ABX+∠ACX=°.②如图(3),DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数.15.一个零件的形状如图,按要求∠A=90°,∠B=32°,∠C=21°,检验工人量得∠CDB=148°,就断定这个零件不合格,运用三角形的有关知识说明零件不合格的理由.16.附加题:如图,试说明:①∠BDC>∠A;②∠BDC=∠B+∠C+∠A.如果点D在线段BC的另一侧,结论会怎样?17.如图,△ABC中,∠A=30°,D为CB延长线上的一点,DE⊥AB于点E,∠D=40°,则∠C为()A.20°B.15°C.30°D.25°18.如图,点E在BC上,ED⊥AC于F,交BA的延长线于D,已知∠D=30°,∠C=20°,则∠B的度数是()A.20°B.30°C.40°D.50°19.如图,已知在△ABC中,∠A=40°,现将一块直角三角板放在△ABC上,使三角板的两条直角边分别经过点B,C,直角顶点D落在△ABC的内部,则∠ABD+∠ACD=( ).A.90°B.60°C.50°D.40°20.如图,若∠EOC=115°,则∠A+∠B+∠C+∠D+∠E+∠F=.【题型05:风筝模型】21.如图1和图2,在三角形纸片ABC中,点D,E分别在边AC,AB上,沿DE折叠,点A落在点A'的位置.(1)如图1,当点A′落在CD边上时,∠DAE与∠1之间的数量关系为(只填序号),并说明理由;①∠DAE=∠1②∠DAE=2∠1③∠1=2∠DAE(2)如图2,当点A落在△ABC内部时,直接写出∠DAE与∠1,∠2之间的数量关系.22.如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是()A.40°B.80°C.90°D.140°23.将纸片△ABC沿DE折叠使点A落在A′处的位置.(1)如果A′落在四边形BCDE的内部(如图1),∠A′与∠1+∠2之间存在怎样的数量关系?并说明理由.(2)如果A′落在四边形BCDE的BE边上,这时图1中的∠1变为0°角,则∠A′与∠2之间的关系是.(3)如果A′落在四边形BCDE的外部(如图2),这时∠A′与∠1、∠2之间又存在怎样的数量关系?并说明理由.【题型06:两内角角平分线模型】双内角平分线模型【条件】BP 、CP 分别为∠ABC 、∠ACB 的角平分线.【结论】∠P =90°+12∠A .24.如图1,点A 、B 分别在射线OM 、ON 上运动(不与点O 重合),AC 、BC 分别是∠BAO 和∠ABO 的角平分线,BC 延长线交OM 于点G .(1)若∠MON =60°,则∠ACG =;(直接写出答案)(2)若∠MON =n °,求出∠ACG 的度数;(用含n 的代数式表示)(3)如图2,若∠MON =80°,过点C 作CF ∥OA 交AB 于点F ,求∠BGO 与∠ACF 的数量关系.25.如图,BE 平分∠ABD ,CF 平分∠ACD ,BE 与CF 交于点G ,若∠BDC =140°,∠BGC =100°,则∠A =()A.80°B.75°C.60°D.45°26.如图,在△ABC 中,已知∠A =70°,∠ABC 、∠ACB 的平分线OB 、OC 相交于点O ,则∠BOC 的度数为.27.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点P.(1)若∠ABC+∠ACB=130°,求∠BPC的度数.(2)当∠A为多少度时,∠BPC=3∠A?【题型07:两外角角平分线模型】双外角平分线模型【条件】BP、CP分别为∠EBC、∠BCF的角平分线.【结论】∠P=90°-12∠A.28.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.(1)如果∠A=70°,求∠BPC的度数;(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q,∠A之间的数量关系.(3)如图③,延长线段BP,QC交于点E,在△BQE中,存在一个内角等于另一个内角的3倍,求∠A的度数.29.如图,在△ABC中,∠B=58°,三角形两外角的角平分线交于点E,则∠AEC=.30.如图,△ABC两个外角∠CBD、∠BCE的平分线相交于点O,∠A=40°,求∠BOC的度数.31.如图,在△ABC中,BO、CO分别平分∠ABC,∠ACB,BO的延长线交外角∠ACD的角平分线于点E.以下结论:①∠1=2∠2;②∠BOC=3∠2;③∠BOC=90°+∠2;④∠BOC=90°+∠1.其中正确的结论有(填序号).32.如图,在△ABC中,∠A=α,∠ABC与∠ACD的平分线交于点A1,得∠A1;∠A1BC与∠A1CD的平分线相交于点A2,得A2;⋯;∠A2019BC与∠A2019CD的平分线相交于点A2020,得∠A2020,则∠A2020=.33.【初步认识】(1)如图1,BM平分∠ABC,CM平分外角∠ACD,若∠A=80°,则∠M=°.【变式探究】(2)已知ABCD为四边形,E为边AB延长线上一点,如图2,∠ADC=110°,∠BCD=120°,∠DAB和∠CBE的平分线交于点F,则∠F=°.【继续探索】(3)已知ABCD为四边形,E为边AB延长线上一点,如图3,∠ADC=α,∠BCD=β,且α+β>180°,∠DAB和∠CBE的平分线交于点F,求∠F与α、β之间的数量关系,并说明理由;【终极挑战】(4)如果将(3)中的条件α+β>180°改为α+β<180°,再分别作∠DAB和∠CBE的平分线,且两平分线所在的直线交于点F,那么∠F与α、β又有怎样的数量关系?请直接写出结论.(不用说明理由)角度计算的经典模型(八大题型)【题型01:双垂直模型】【题型02:A字模型】【题型03:8字模型】【题型04:飞镖模型】【题型05:风筝模型】【题型06:两内角角平分线模型】【题型07:两外角角平分线模型】【题型08:内外角平分线模型】【题型01:双垂直模型】【条件】∠B=∠D=∠ACE=90°.【结论】∠BAC=∠DCE,∠ACB=∠CED.1.AD、BE为△ABC的高,AD、BE相交于H点,∠C=50°,求∠BHD.【答案】见试题解答内容【解答】解:∵AD是△ABC的高,∴∠BHD+∠HBD=90°,∵BE是△ABC的高,∴∠HBD+∠C=90°,∴∠BHD=∠C,∵∠C=50°,∴∠BHD=50°.2.如图,在△ABC中,∠BAC=80°,∠B=60°,AD是BC边上的高,∠ACB的平分线CF交AD于点E.求∠AEC的度数.【答案】110°【分析】本题考查三角形的内角和定理,角平分线的定义,三角形外角的性质.先根据三角形的内角和定理得到∠ACB 的度数,然后根据角平分线的定义得到∠ECD 的值,然后利用三角形的外角等于与它不相邻的两个内角的和解题即可.【详解】解:∵在△ABC 中,∠BAC =80°,∠B =60°,∴∠ACB =180°-∠CAB =∠B =180°-80°-60°=40°,∵CF 是∠ACB 的平分线,∴∠ECD =12∠ACD =12×40°=20°,∵AD 是BC 边上的高,∴∠ADC =90°,∴∠AEC =∠ADC +∠ECD =90°+20°=110°.3.如图,在△ABC 中,AD ⊥BC ,垂足为D ,E 是AC 边上一点,BE 与AD 交于点F ,若∠ABC =45°,∠BAC =75°,∠BFD =60°,求∠BEC 的度数.【答案】90°【分析】本题主要考查了三角形内角和定理,先根据三角形内角和定理求出∠C ,然后求出∠DBF ,进而得出答案.【详解】∵∠ABC =45°,∠BAC =75°,∴∠C =180°-45°-75°=60°.∵AD ⊥BC ,∴∠ADB =90°.∵∠BFD =60°,∴∠DBF =90°-60°=30°,∴∠BEC =180°-∠EBC -∠C =180°-60°-30°=90°.【题型02:A 字模型】图1【条件】图1中三种情况【结论】∠1=∠2【证明】略图2【结论】∠1+∠2=∠3+∠4【证明】根据内角和定理,∠1+∠2+∠A=∠3+∠4+∠A=180°∴∠1+∠2=∠3+∠4图3【结论】∠1+∠2=180°+∠A【证明】∠1+∠2=(∠AED+∠A)+(∠ADE+∠A)=180°+∠A4.探索归纳:(1)如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2=270°.(2)如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=220°.(3)如图2,根据(1)与(2)的求解过程,你归纳猜想∠1+∠2与∠A的关系是180°+∠A.(4)如图3,若没有剪掉∠A,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系,并说明理由.【答案】见试题解答内容【解答】解:(1):∵四边形的内角和为360°,直角三角形中两个锐角和为90°∴∠1+∠2=360°-(∠A+∠B)=360°-90°=270°.∴∠1+∠2等于270°.故答案为:270°;(2)∠1+∠2=180°+40°=220°,故答案是:220°;(3)∠1+∠2与∠A的关系是:∠1+∠2=180°+∠A;故答案为:180°+∠A;(4)∵△EFP是由△EFA折叠得到的,∴∠AFE=∠PFE,∠AEF=∠PEF∴∠1=180°-2∠AFE,∠2=180°-2∠AEF∴∠1+∠2=360°-2(∠AFE+∠AEF)又∵∠AFE+∠AEF=180°-∠A,∴∠1+∠2=360°-2(180°-∠A)=2∠A.5.如图,在△ABC中,BD平分∠ABC,DE∥BC交AB于点E.若∠A=70°,∠BDC=100°,则∠BED的度数为()A.120°B.130°C.140°D.150°【答案】A【分析】本题考查三角形内角和定理,角平分线的定义,平行线的性质等知识.求出∠EBD,∠EDB,再利用三角形内角和定理即可解决问题.【详解】解:∵∠A+∠ABD=∠BDC,∠A=70°,∠BDC=100°,∴∠ABD=30°,∵BD平分∠ABC,∴∠ABD=∠CBD=30°,又∵DE∥BC,∴∠BDE=∠CBD=30°,∴∠BED=180°-∠ABD-∠BDE=120°.故选:A.6.如图,已知:AD∥EF,∠CAD+∠DEF=180°.(1)证明:AC∥DE;(2)若AC平分∠BAD,∠ADC=35°,∠ACD=∠ADE+45°.求∠G的度数.【答案】(1)见解析(2)∠G=50°【分析】本题考查平行线的判定与性质,三角形内角和定理,角平分线的定义等知识点,解题的关键是熟练掌握平行线的判定与性质.(1)由平行线的性质可得∠DEF+∠ADG=180°,由∠CAD+∠DEF=180°可得∠CAD=∠ADG,即可证明;(2)首先利用已知条件可以去求出∠BAC=∠ADE=50°,然后利用三角形的外角求出∠BDG,解答即可.【详解】(1)证明:∵AD∥EF,∴∠DEF+∠ADG=180°.∵∠CAD+∠DEF=180°.∴∠CAD=∠ADG.∴AC∥DE;(2)解:∵AC是∠BAD的平分线,且AC∥DE,∴∠BAC=∠CAD,∠CAD=∠ADE,∴∠BAC=∠ADE,∵∠ACD=∠ADE+45°,∠ACD=∠B+∠BAC,∴∠B=45°,∵∠ADC=35°,∴∠BAD=180°-∠B-∠ADC=180°-45°-35°=100°.∵AC是∠BAD的平分线,∠BAD=50°,∴∠CAD=∠ADE=12∴∠G=∠BAD-∠ADE=100°-50°=50°.7.在△ABC中,已知∠A=80°,∠C=30°,现把△CDE沿DE进行不同的折叠得△C DE,对折叠后产生的夹角进行探究:(1)如图(1)把△CDE沿DE折叠在四边形ADEB内,则求∠1+∠2的和;(2)如图(2)把△CDE沿DE折叠覆盖∠A,则求∠1+∠2的和;(3)如图(3)把△CDE沿DE斜向上折叠,探求∠1、∠2、∠C的关系.【答案】(1)60°(2)50°(3)∠2-∠1=2∠C【分析】本题考查折叠性质,三角形内角和定理,解答此题时要充分利用折叠部分折叠前后形成的图形为全等形的性质,并且解答该题时要充分利用三角形的性质.(1)根据折叠前后的图象全等可知,∠1=180°-2∠CDE,∠2=180°-2∠CED,再根据三角形内角和定理比可求出答案;(2)连接DG,将∠ADG+∠AGD作为一个整体,根据三角形内角和定理来求;(3)将∠2看作180°-2∠CED,∠1看作2∠CDE-180°,再根据三角形内角和定理求解,即可解题.【详解】(1)解:由折叠性质可知:∠CDC =2∠CDE,∠CEC =2∠CED,∵∠C=30°,∴∠1+∠2=180°-2∠CDE+180°-2∠CED=360°-2∠CDE+∠CED=360°-2180°-∠C=2∠C=60°;(2)解:连接DG,∵∠A=80°,∴∠1+∠2=180°-∠C -∠ADG+∠AGD=180°-30°-180°-80°=50°;(3)解:∠2-∠1=180°【题型03:8字模型】【条件】AE、BD相交于点C【结论】∠A +∠B =∠D +∠E .8.(1)已知:如图(1)的图形我们把它称为“8字形”,试说明:∠A +∠B =∠C +∠D .(2)如图(2),AP ,CP 分别平分∠BAD ,∠BCD ,若∠ABC =36°,∠ADC =16°.求∠P 的度数.(3)如图(3),直线AP 平分∠BAD ,CP 平分∠BCD 的外角∠BCE ,猜想∠P 与∠B 、∠D 的数量关系是;(4)如图(4),直线AP 平分∠BAD 的外角∠FAD ,CP 平分∠BCD 的外角∠BCE ,猜想∠P 与∠B 、∠D 的数量关系是.【答案】(1)见解析;(2)26°;(3)∠P =90°+12∠B +∠D ;(4)∠P =180°-12∠B +∠D 【分析】(1)根据三角形的内角和等于180°和对顶角的性质即可得证;(2)设∠BAP =∠P AD =x ,∠BCP =∠PCD =y ,x +∠ABC =y +∠P x +∠P =y +∠ADC 解方程即可得到答案;(3)根据直线AP 平分∠BAD ,CP 平分∠BCD 的外角∠BCE ,得到∠P AB =∠P AD =12∠BAD ,∠PCB =∠PCE =12∠PCD 从而可以得到180°-2∠P AB +∠PCB +∠D =∠B ,再根据∠P +∠P AD =∠PCD +∠D ,∠BAD +∠B =∠BCD +∠D 得到∠P -∠B =∠P AD +∠PCB =∠P AB +∠PCB 即可求解;(4)连接PB ,PD ,求得∠APC +∠ABC +∠PCB +∠P AB =360°,∠APC +∠ADC +∠PCD +∠P AD =360°,再根据∠PCE +∠PCD =180°,∠P AB +∠P AF =180°,∠FAP =∠P AO ,∠PCE =∠PCB ,即可求解.【详解】解:(1)如图.∵∠A +∠B +∠AOB =180°,∠C +∠D +∠COD =180°,∴∠A +∠B +∠AOB =∠C +∠D +∠COD .∵∠AOB =∠COD ,∴∠A +∠B =∠C +∠D ;(2)如图.∵AP ,CP 分别平分∠BAD ,∠BCD ,设∠BAP =∠P AD =x ,∠BCP =∠PCD =y ,则有x +∠ABC =y +∠P x +∠P =y +∠ADC ,∴∠ABC -∠P =∠P -∠ADC ,∴∠P =12∠ABC +∠ADC =1236°+16° =26°(3)如图.∵直线AP 平分∠BAD ,CP 平分∠BCD 的外角∠BCE ,∴∠P AB =∠P AD =12∠BAD ,∠PCB =∠PCE =12∠BCE ,∴2∠P AB +∠B =180°-2∠PCB +∠D ,∴180°-2∠P AB +∠PCB +∠D =∠B∵∠P +∠P AD =∠PCD +∠D ,∠BAD +∠B =∠BCD +∠D∴∠P +∠P AD -∠BAD -∠B =∠PCD -∠BCD∴∠P -∠P AB -∠B =∠PCB ,∴∠P -∠B =∠P AB +∠PCB∴180°-2∠P -∠B +∠D =∠B ,即∠P =90°+12∠B +∠D .(4)连接PB ,PD∵直线AP 平分∠BAD 的外角∠FAD ,CP 平分∠BCD 的外角∠BCE ,∴∠FAP =∠P AO ,∠PCE =∠PCB ,∵∠APB +∠PBA +∠P AB =180°,∠PCB +∠PBC +∠BPC =180°∴∠APC +∠ABC +∠PCB +∠P AB =360°同理得到:∠APC +∠ADC +∠PCD +∠P AD =360°∴2∠APC +∠ABC +∠ADC +∠PCB +∠P AB +∠PCD +∠P AD =720°∴2∠APC +∠ABC +∠ADC +∠PCE +∠P AB +∠PCD +∠P AF =720°∵∠PCE +∠PCD =180°,∠P AB +∠P AF =180°∴2∠APC +∠ABC +∠ADC =360°,∴∠APC =180°-12∠ABC +∠ADC 【点睛】本题主要考查了角平分线的定义,三角形内角和定理,解题的关键在于能够熟练掌握相关知识进行求解.9.如图,∠1=60°,则∠A +∠B +∠C +∠D +∠E +∠F =()A.240°B.280°C.360°D.540°【答案】A 【分析】根据三角形内角和定理得到∠B 与∠C 的和,然后在五星中求得∠1与另外四个角的和,加在一起即可.【详解】解:由三角形外角的性质得:∠3=∠A +∠E ,∠2=∠F +∠D ,∵∠1+∠2+∠3=180°,∠1=60°,∴∠2+∠3=120°,即:∠A+∠E+∠F+∠D=120°,∵∠B+∠C=120°,∴∠A+∠B+∠C+∠D+∠E+∠F=240°.故选A.【点睛】本题考查了三角形的外角和三角形的内角和的相关知识,解决本题的关键是将题目中的六个角分成两部分来分别求出来,然后再加在一起.10.如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=.【答案】900°【分析】根据多边形的内角和,可得答案.【详解】解:连EF,GI,如图∵6边形ABCDEFK的内角和=(6-2)×180°=720°,∴∠A+∠B+∠C+∠D+∠E+∠F=720°-(∠1+∠2),即∠A+∠B+∠C+∠D+∠E+∠F+(∠1+∠2)=720°,∵∠1+∠2=∠3+∠4,∠5+∠6+∠H=180°,∴∠A+∠B+∠C+∠D+∠E+∠F∠H+(∠3+∠4)=900°,∴∠A+∠B+∠C+∠D+∠E+∠F(∠3+∠4)+∠5+∠6+∠H=720°+180°,∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=900°,故答案为:900°.【点睛】本题考查了n边形的内角和定理:n边形的内角和为(n-2)×180°(n≥3的整数).11.如图,已知AB∥CD,∠B=∠D,CD与AE相交于F.(1)求证:AD∥BC;(2)若∠B=50°,AE平分∠BAD,求∠DFE的度数.【答案】(1)见解析;(2)115°.【分析】本题考查平行线的判定和性质,与角平分线有关的计算:(1)AB∥CD,得到∠B=∠DCE,推出∠D=∠DCE,即可得证;(2)平行线的性质求出∠BAD的度数,角平分线求出∠DAE=65°,再利用三角形的外角求解即可.【详解】(1)证明:∵AB∥CD,∴∠B=∠DCE,∵∠B=∠D,∴∠D=∠DCE,∴AD∥BC,(2)∵AD∥BC,∴∠BAD=180°-∠B=180°-50°=130°,∵AE平分∠BAD,∴∠DAE=65°,∵∠D=∠B=50°,∴∠DFE=∠D+∠EAD=50°+65°=115°.12.已知:如图,FE∥OC,AC和BD相交于点O,F是OD上一点,且∠1=∠A.(1)求证:AB∥DC;(2)若∠B=30°,∠1=65°,求∠OFE的度数.【答案】(1)见解析(2)95°【分析】本题考查了平行线的性质和判定,三角形外角的性质的应用:(1)根据平行线的性质和已知得出∠A=∠C,根据平行线的判定推出即可;(2)根据平行线的性质求出∠D,根据三角形的外角性质推出即可.【详解】(1)证明:∵FE∥OC,∴∠1=∠C,∵∠1=∠A,∴∠A=∠C,∴AB∥DC;(2)解:∵AB∥DC,∴∠D=∠B,∵∠B=30°,∴∠D=30°,∵∠OFE是△DEF的外角,∴∠OFE=∠D+∠2,∵∠1=65°,∴∠OFE=30°+65°=95°.13.如图,BP平分∠ABC,交CD于点F,DP平分∠ADC交AB于点E,AB与CD相交于点G,∠A=42°.(1)若∠ADC=60°,求∠AEP的度数;(2)若∠C=38°,求∠P的度数.【答案】(1)72°;(2)40°.【分析】(1)根据角平分线的定义可得∠ADP=12∠ADC,然后利用三角形外角的性质即可得解;(2)根据角平分线的定义可得∠ADP=∠PDF,∠CBP=∠PBA,再根据三角形的内角和定理可得∠A+∠ADP=∠P+∠ABP,∠C+∠CBP=∠P+∠PDF,所以∠A+∠C=2∠P,即可得解.【详解】解:(1)∵DP平分∠ADC,∴∠ADP=∠PDF=12∠ADC,∵∠ADC=60°,∴∠ADP=30°,∴∠AEP=∠ADP+∠A=30°+42°=72°;(2)∵BP平分∠ABC,DP平分∠ADC,∴∠ADP=∠PDF,∠CBP=∠PBA,∵∠A+∠ADP=∠P+∠ABP,∠C+∠CBP=∠P+∠PDF,∴∠A+∠C=2∠P,∵∠A=42°,∠C=38°,∴∠P=12(38°+42°)=40°.【点睛】本题考查了三角形的内角和定理及三角形外角的性质,角平分线的定义,熟记定理并理解“8字形”的等式是解题的关键.【题型04:飞镖模型】图1图2图3【条件】四边形ABPC如图1所示【结论】∠BPC=∠A+∠B+∠C.14.探究与发现:如图(1)所示的图形,像我们常见的学习用品一圆规,我们,不妨把这样图形叫做“规形图(1)观察“规形图(1)”,试探究∠BDC与∠A、∠B、∠C之间的数量关系,并说明理由;(2)请你直接利用以上结论,解决以下问题:①如图(2),把一块三角尺XYZ放置在△AC上使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=40°,则∠ABX+∠ACX=50°.②如图(3),DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数.【答案】见试题解答内容【解答】解:(1)如图(1),∠BDC=∠BAC+∠B+∠C,理由是:过点A、D作射线AF,∵∠FDC=∠DAC+∠C,∠BDF=∠B+∠BAD,∴∠FDC+∠BDF=∠DAC+∠BAD+∠C+∠B,即∠BDC=∠BAC+∠B+∠C;(2)①如图(2),∵∠X=90°,由(1)知:∠A+∠ABX+∠ACX=∠X=90°,∵∠A=40°,∴∠ABX+∠ACX=50°,故答案为:50;②如图(3),∵∠A=40°,∠DBE=130°,∴∠ADE+∠AEB=130°-40°=90°,∵DC平分∠ADB,EC平分∠AEB,∴∠ADC=12∠ADB,∠AEC=12∠AEB,∴∠ADC+∠AEC=12∠ADB+∠AEB=45°,∴∠DCE=∠A+∠ADC+∠AEC=40°+45°=85°.15.一个零件的形状如图,按要求∠A=90°,∠B=32°,∠C=21°,检验工人量得∠CDB=148°,就断定这个零件不合格,运用三角形的有关知识说明零件不合格的理由.【答案】见试题解答内容【解答】解:如图,延长CD交AB于E,∵∠A=90°,∠C=21°,∴∠1=∠A+∠C=90°+21°=111°,∵∠B=32°,∴∠BDC=∠B+∠1=32°+111°=143°.又∵∠BDC=148°,∴这个零件不合格.16.附加题:如图,试说明:①∠BDC>∠A;②∠BDC=∠B+∠C+∠A.如果点D在线段BC的另一侧,结论会怎样?【答案】见试题解答内容【解答】解:①延长BD交AC于E,则∠BDC>∠DEC,而∠DEC>∠A,所以∠BDC>∠A;②由∠BDC=∠C+∠DEC,而∠DEC=∠A+∠B,所以∠BDC=∠A+∠B+∠C.如果点D在线段BC的另一侧,如图所示:结论:①∠BDC与∠A无法比较大小;②∠BDC=360°-(∠A+∠B+∠C),17.如图,△ABC中,∠A=30°,D为CB延长线上的一点,DE⊥AB于点E,∠D=40°,则∠C为()A.20°B.15°C.30°D.25°【答案】A【解答】解:∵DE⊥AB,∴∠DEB=90°,∵∠D=40°,∴∠ABD=180°-∠D-∠DEB=50°,∵∠ABD=∠A+∠C,∠A=30°,∴∠C=∠ABD-∠A=50°-30°=20°.故选:A.18.如图,点E在BC上,ED⊥AC于F,交BA的延长线于D,已知∠D=30°,∠C=20°,则∠B的度数是()A.20°B.30°C.40°D.50°【答案】C【解答】解:∵ED⊥AC,∠D=30°,∠C=20°,又∵∠DEC=∠B+∠D,∴∠C+∠DEC=∠C+∠D+∠B=90°,∴∠B=40°.故选:C.19.如图,已知在△ABC中,∠A=40°,现将一块直角三角板放在△ABC上,使三角板的两条直角边分别经过点B,C,直角顶点D落在△ABC的内部,则∠ABD+∠ACD=( ).A.90°B.60°C.50°D.40°【答案】C【分析】由三角形内角和定理可得∠ABC+∠ACB+∠A=180°,即∠ABC+∠ACB=180-∠A=140°,再说明∠DBC+∠DCB=90°,进而完成解答.【详解】解:∵在△ABC中,∠A=40°∴∠ABC+∠ACB=180-∠A=140°∵在△DBC中,∠BDC=90°∴∠DBC+∠DCB=180°-90°=90°∴∠ABD+∠ACD=40°-90°=50°故选C.【点睛】本题主要考查三角形内角和定理,灵活运用三角形内角和定理成为解答本题的关键.20.如图,若∠EOC=115°,则∠A+∠B+∠C+∠D+∠E+∠F=.【答案】230°【分析】根据三角形外角的性质,得到∠EOC=∠E+∠2=115°,∠2=∠D+∠C,∠EOC=∠1+∠F=115°,∠1=∠A+∠B,即可得到结论.【详解】解:如图∵∠EOC=∠E+∠2=115°,∠2=∠D+∠C,∴∠E+∠D+∠C=115°,∵∠EOC=∠1+∠F=115°,∠1=∠A+∠B,∴∠A+∠B+∠F=115°,∴∠A+∠B+∠C+∠D+∠E+∠F=230°,故答案为:230°.【点睛】本题主要考查三角形内角和定理和三角形外角的性质,解决本题的关键是要熟练掌握三角形外角性质.【题型05:风筝模型】21.如图1和图2,在三角形纸片ABC中,点D,E分别在边AC,AB上,沿DE折叠,点A落在点A'的位置.(1)如图1,当点A′落在CD边上时,∠DAE与∠1之间的数量关系为③(只填序号),并说明理由;①∠DAE=∠1②∠DAE=2∠1③∠1=2∠DAE(2)如图2,当点A落在△ABC内部时,直接写出∠DAE与∠1,∠2之间的数量关系.【答案】(1)③,理由详见解答过程.(2)∠1+∠2=2∠DAE.【解答】解:(1)由题意得:∠DAE=∠DA′E.∵∠1=∠EAD+∠EA′D=2∠DAE.故答案为:③.(2)∠1+∠2=2∠DAE,理由如下:如图2,连接AA′.由题意知:∠EAD=∠EA′D.∵∠1=∠A′AE+∠AA′E,∠2=∠A′AD+∠AA′D,∴∠1+∠2=∠EAA′+∠A′AD+∠EA′A+∠AA′D=∠EAD+∠EA′D=2∠EAD.22.如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是()A.40°B.80°C.90°D.140°【答案】B【解答】解:由折叠的性质得:∠D=∠C=40°,根据外角性质得:∠1=∠3+∠C,∠3=∠2+∠D,则∠1=∠2+∠C+∠D=∠2+2∠C=∠2+80°,则∠1-∠2=80°.故选:B.23.将纸片△ABC沿DE折叠使点A落在A′处的位置.(1)如果A′落在四边形BCDE的内部(如图1),∠A′与∠1+∠2之间存在怎样的数量关系?并说明理由.(2)如果A′落在四边形BCDE的BE边上,这时图1中的∠1变为0°角,则∠A′与∠2之间的关系是2∠A=∠2.(3)如果A′落在四边形BCDE的外部(如图2),这时∠A′与∠1、∠2之间又存在怎样的数量关系?并说明理由.【答案】见试题解答内容【解答】解:(1)图1中,2∠A=∠1+∠2,理由是:∵延DE折叠A和A′重合,∴∠AED=∠A′ED,∠ADE=∠A′DE,∵∠AED+∠ADE=180°-∠A,∠1+∠2=180°+180°-2(∠AED+∠ADE),∴∠1+∠2=360°-2(180°-∠A)=2∠A;(2)2∠A=∠2,如图∠2=∠A+∠EA′D=2∠A,故答案为:2∠A=∠2;(3)如图2,2∠A=∠2-∠1,理由是:∵延DE折叠A和A′重合,∴∠A=∠A′,∵∠DME=∠A′+∠1,∠2=∠A+∠DME,∴∠2=∠A+∠A′+∠1,即2∠A=∠2-∠1.【题型06:两内角角平分线模型】双内角平分线模型【条件】BP 、CP 分别为∠ABC 、∠ACB 的角平分线.【结论】∠P =90°+12∠A .24.如图1,点A 、B 分别在射线OM 、ON 上运动(不与点O 重合),AC 、BC 分别是∠BAO 和∠ABO 的角平分线,BC 延长线交OM 于点G .(1)若∠MON =60°,则∠ACG =;(直接写出答案)(2)若∠MON =n °,求出∠ACG 的度数;(用含n 的代数式表示)(3)如图2,若∠MON =80°,过点C 作CF ∥OA 交AB 于点F ,求∠BGO 与∠ACF 的数量关系.【答案】(1)60°;(2)90°-12n °;(3)∠BGO -∠ACF =50°【分析】(1)根据三角形内角和定理求出∠BAO +∠ABO ,根据角平分线的定义、三角形的外角性质计算,得到答案;(2)仿照(1)的解法解答;(3)根据平行线的性质得到∠ACF =∠CAG ,根据(2)的结论解答.【详解】解:(1)∵∠MON =60°,∴∠BAO +∠ABO =120°,∵AC 、BC 分别是∠BAO 和∠ABO 的角平分线,∴∠CBA =12∠ABO ,∠CAB =12∠BAO ,∴∠CBA +∠CAB =12(∠ABO +∠BAO )=60°,∴∠ACG =∠CBA +∠CAB =60°,故答案为:60°;(2)∵∠MON =n °,∴∠BAO +∠ABO =180°-n °,∵AC 、BC 分别是∠BAO 和∠ABO 的角平分线,∴∠CBA =12∠ABO ,∠CAB =12∠BAO ,∴∠CBA+∠CAB=12(∠ABO+∠BAO)=90°-12n°,∴∠ACG=∠CBA+∠CAB=90°-12n°;(3)∵CF∥OA,∴∠ACF=∠CAG,∴∠BGO-∠ACF=∠BGO-∠CAG=∠ACG,由(2)得:∠ACG=90°-12×80°=50°.∴∠BGO-∠ACF=50°.【点睛】本题考查的是角平分线的定义、平行线的性质、三角形的外角性质,掌握两直线平行、内错角相等是解题的关键.25.如图,BE平分∠ABD,CF平分∠ACD,BE与CF交于点G,若∠BDC=140°,∠BGC=100°,则∠A=()A.80°B.75°C.60°D.45°【答案】C【分析】连接BC,先求解∠DBC+∠DCB,再求解∠GBC+∠GCB,可得∠GBD+∠GCD,再利用角平分线的定义可得:∠ABD+∠ACD,从而可得:∠ABC+∠ACB,再利用三角形的内角和定理可得∠A的大小.【详解】解:连接BC,∵∠BDC=140°,∴∠DBC+∠DCB=180°-140°=40°,∵∠BGC=100°,∴∠GBC+∠GCB=180°-100°=80°,∴∠GBD+∠GCD=∠GBC+∠GCB-∠DBC-∠DCB=40°,∵BE平分∠ABD,CF平分∠ACD,∴∠ABD+∠ACD=2(∠GBD+∠GCD)=80°,∴∠ABC+∠ACB=∠ABD+∠ACD+∠DBC+∠DCB=80°+40°=120°,∴∠A=180°-(∠ABC+∠ACB)=60°.故选:C.【点睛】本题考查的是三角形的内角和定理的应用,角平分线的定义,熟练利用三角形的内角和定理求解与之相关的角的大小是解题的关键.26.如图,在△ABC中,已知∠A=70°,∠ABC、∠ACB的平分线OB、OC相交于点O,则∠BOC的度数为.【答案】125°【分析】根据三角形的内角和定理求出∠ABC +∠ACB ,再根据角平分线的定义求出∠OBC +∠OCB ,然后利用三角形的内角和定理列式计算即可得解.【详解】在△ABC 中,∠ABC +∠ACB =180°-∠A =180°-70°=110°,∵∠ABC 与∠ACB 的角平分线BO ,CO 相交于点O ,∴∠OBC +∠OCB =12∠ABC +∠ACB =12×110°=55°,在△BOC 中,∠BOC =180°-(∠OBC +∠OCB )=180°-55°=125°,故答案为:125°.【点睛】本题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.27.如图,在△ABC 中,∠ABC 和∠ACB 的平分线相交于点P .(1)若∠ABC +∠ACB =130°,求∠BPC 的度数.(2)当∠A 为多少度时,∠BPC =3∠A ?【答案】(1)115°;(2)∠A =36°【分析】(1)根据角平分线的定义,求得∠PBC ,∠PCB ,再根据三角形内角和定理即可求得∠BPC ;(2)根据(1)的方法求得∠BPC ,再结合条件∠BPC =3∠A ,解方程即可求得∠A .【详解】(1)∵PB 平分∠ABC ,PC 平分∠ACB ,∴∠PBC =12∠ABC ,∠PCB =12∠ACB ,∵∠ABC +∠ACB =130°,∴∠PBC +∠PCB =12(∠ABC +∠ACB )=65°,∴∠BPC =180°-(∠PBC +∠PCB )=180°-65°=115°,(2)∵PB 平分∠ABC ,PC 平分∠ACB ,∴∠PBC =12∠ABC ,∠PCB =12∠ACB ,∴∠PBC+∠PCB=12(∠ABC+∠ACB),∵∠ABC+∠ACB=180°-∠A,∴∠PBC+∠PCB=90°-12∠A,∠BPC=180°-(∠PBC+∠PCB)=180°-90°-12∠A=90°+12∠A∵∠BPC=3∠A∴3∠A=90°+12∠A,∴∠A=36°.【点睛】本题考查了与角平分线有关的角度计算,三角形内角和定理,掌握三角形内角和定理是解题的关键.【题型07:两外角角平分线模型】双外角平分线模型【条件】BP、CP分别为∠EBC、∠BCF的角平分线.【结论】∠P=90°-12∠A.28.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.(1)如果∠A=70°,求∠BPC的度数;(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q,∠A之间的数量关系.(3)如图③,延长线段BP,QC交于点E,在△BQE中,存在一个内角等于另一个内角的3倍,求∠A的度数.【答案】(1)125°(2)∠Q=90°-12∠A(3)∠A的度数是45°或60°或120°或135°【分析】(1)在△ABC中,根据三角形内角和定理求出∠ABC+∠ACB=110°,根据角平分线的定义得出∠PBC=12∠ABC,∠PCB=12∠ACB,求出∠PBC+∠PCB=55°,再在△BPC中,根据三角形内角和定理求出即可;(2)根据三角形外角性质得出∠MBC=∠ACB+∠A,∠NCB=∠ABC+∠A,求出∠MBC+∠NCB=∠ACB+∠A+∠ABC+∠A=180°+∠A,根据角平分线的定义得出QBC=12∠MBC,∠QCB=12∠NCB,求出∠QBC+∠QCB=90°+12∠A,根据三角形内角和定理求出即可;(3)根据角平分线的定义得出∠ACF=2∠BCF,∠ABC=2∠EBC,根据三角形外角性质得出∠ECF=∠EBC+∠E,求出∠A=2∠E,求出∠EBQ=90°,分为四种情况:①∠EBQ=3∠E=90°,②∠EBQ=3∠Q,③∠Q=3∠E,④∠E=3∠Q,再求出答案即可【详解】(1)∵∠A=70°,∴∠ABC+∠ACB=180°-∠A=110°,∵点P是∠ABC和∠ACB的角平分线的交点,∴∠PBC=12∠ABC,∠PCB=12∠ACB,∴∠PBC+∠PCB=55°,∴∠BPC=180°-(∠PBC+∠PCB)=125°;(2)∵∠MBC=∠ACB+∠A,∠NCB=∠ABC+∠A,∴∠MBC+∠NCB=∠ACB+∠A+∠ABC+∠A=180°+∠A,∵点Q是∠MBC和∠NCB的角平分线的交点,∴∠QBC=12∠MBC,∠QCB=12∠NCB,∴∠QBC+∠QCB=12(∠MBC+∠NCB)=12(180°+∠A)=90°+12∠A,∴∠Q=180°-(∠QBC+∠QCB)=180°-90°+12∠A=90°-12∠A;(3)∵CQ为△ABC的外角∠NCB的角平分线,∴CE是△ABC的外角∠ACF的平分线,∴∠ACF=2∠BCF,∵BE平分∠ABC,∴∠ABC=2∠EBC,∵∠ECF=∠EBC+∠E,∴2∠ECF=2∠EBC+2∠E,即∠ACF=∠BC+2∠E,∵∠ACF=∠ABC+∠A,∴∠A=2∠E,即∠E=12∠A,∵∠EBQ=∠EBC+∠CBQ=12∠ABC+12∠MBC=12(∠ABC+∠A+∠ACB) =90°,如果△BQE中,存在一个内角等于另一个内角的3倍,那么分为四种情况:①∠EBQ=3∠E=90°,则∠E=30°,∠A=2∠E=60°;②∠EBQ=3∠Q,则∠Q=30°,∠E=60°,∠A=2∠E=120°;③∠Q=3∠E,则∠E=22.5°,∠A=2∠E=45°;④∠E=3∠Q,则∠E=67.5°,∠A=2∠E=135°,综合上述,∠A的度数是45°或60°或120°或135°.【点睛】本题考查了三角形的外角性质,三角形内角和定理,角平分线的定义等知识点,熟练掌握知识点及运用分类讨论思想是解题的关键.29.如图,在△ABC中,∠B=58°,三角形两外角的角平分线交于点E,则∠AEC=.【答案】61°【分析】先根据三角形的内角和定理和平角定义求得∠DAC+∠ACF的度数,再根据角平分线的定义求得∠EAC+∠ECA的度数,即可解答.【详解】解:∵∠B+∠BAC+∠BCA=180°,∠B=58°,∴∠BAC+∠BCA=180°-∠B=180°-58°=122°,∵∠BAC+∠DAC=180°,∠BCA+∠ACF=180°,∴∠DAC+∠ACF=360°-(∠BAC+∠BCA)=360°-122°=238°,∵AE平分∠DAC,CE平分∠ACF,∴∠EAC=12∠DAC,∠ECA=12∠ACF,∴∠EAC+∠ECA=12(∠DAC+∠ACF)=119°,∵∠EAC+∠ECA+∠AEC=180°,∴∠AEC=180°-(∠EAC+∠ECA)=180°-119°=61°,故答案为:61°.【点睛】本题考查三角形的内角和定理、角平分线的定义、平角定义,熟练掌握三角形的内角和定理和角平分线的定义是解答的关键.30.如图,△ABC两个外角∠CBD、∠BCE的平分线相交于点O,∠A=40°,求∠BOC的度数.【答案】见试题解答内容【解答】解:∵∠CBD、∠BCE的平分线相交于点O,∴∠OBC=12(∠A+∠ACB),∠OCB=12(∠A+∠ABC),∴∠OBC +∠OCB =12(∠A +∠ACB +∠ABC +∠A ),∵∠A +∠ACB +∠ABC =180°,∴∠OBC +∠OCB =90°+12∠A ,在△OBC 中,∠BOC =180°-(∠OBC +∠OCB )=180°-(90°+12∠A )=90°-12∠A ,∵∠A =40°,∴∠BOC =90°-12×40°=90°-20°=70°.【题型08:内外角平分线模型】内外角平分线模型【条件】BP 、CP 分别为∠ABC 、∠ACE 的角平分线【结论】∠P =12∠A 【典例8】(1)如图1,在△ABC 中,BP 平分∠ABC ,CP 平分∠ACB ,求证:∠P =90°+12∠A ;(2)如图2,在△ABC 中,BP 平分∠ABC ,CP 平分外角∠ACE ,猜想∠P 和∠A 有何数量关系,并证明你的结论.【答案】(1)证明过程见解答;(2)∠P =12∠A .【解答】(1)证明:∵A +∠ABC +∠ACB =180°,∴∠ABC +∠ACB =180°-∠A ,∵BP 平分∠ABC ,CP 平分∠ACB ,∴∠PCB =12∠ACB ,∠PBC =12∠ABC ,∴∠P =180°-(∠PCB +∠PBC )=180°-12(∠ACB +∠ABC )=180°-12(180°-∠A )=90°+12∠A ;(2)猜想:∠P=12∠A证明:∵∠ACE=∠A+∠ABC,∴∠A=∠ACE-∠ABC,∵∠PCE=∠P+∠PBC,∴∠P=∠PCE-∠PBC,又∵BP平分∠ABC,CP平分∠ACE,∴∠PBC=12∠ABC,∠PCE=12∠ACE,∴∠P=12∠ACE-12∠ABC=12(∠ACE-∠ABC)=12∠A.31.如图,在△ABC中,BO、CO分别平分∠ABC,∠ACB,BO的延长线交外角∠ACD的角平分线于点E.以下结论:①∠1=2∠2;②∠BOC=3∠2;③∠BOC=90°+∠2;④∠BOC=90°+∠1.其中正确的结论有(填序号).【答案】①③/③①【分析】依据角平分线的性质以及三角形外角性质,即可得到∠1=2∠2,∠BOC=90°+12∠1,∠BOC=90°+∠2,即可得出答案.【详解】解:∵CE为外角∠ACD的平分线,BE平分∠ABC,∴∠DCE=12∠ACD,∠DBE=12∠ABC,又∵∠DCE是△BCE的外角,∴∠2=∠DCE-∠DBE=12∠ACD-∠ABC=12∠1,即∠1=2∠2,故①正确;∵BO、CO分别平分∠ABC,∠ACB,∴∠OBC=12∠ABC,∠OCB=12∠ACB,∴∠BOC=180°-∠OBC+∠OCB=180°-12∠ABC+∠ACB=180°-12180°-∠1=90°+12∠1,故④错误;∵CO平分∠ACB,CE平分∠ACD,∴∠ACO=12∠ACB,∠ACE=12ACD,∴∠OCE =12∠ACB +∠ACD =12×180°=90°,∵∠BOC 是△COE 的外角,∴∠BOC =∠OCE +∠2=90°+∠2,故②错误、③正确;综上,正确的有①③.故答案为:①③.【点睛】本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,以及角平分线的定义.32.如图,在△ABC 中,∠A =α,∠ABC 与∠ACD 的平分线交于点A 1,得∠A 1;∠A 1BC 与∠A 1CD 的平分线相交于点A 2,得A 2;⋯;∠A 2019BC 与∠A 2019CD 的平分线相交于点A 2020,得∠A 2020,则∠A 2020=.【答案】α22020【分析】结合题意,根据角平分线、三角形外角、三角形内角和的性质,得∠A 1=12∠A ,同理得∠A 2=12∠A 1=α22;再根据数字规律的性质分析,即可得到答案.【详解】根据题意,∠A =α,∠ABC 与∠ACD 的平分线交于点A 1∴∠A 1=180°-12∠ABC -∠ACB -12∠ACD ∵∠ACD =∠A +∠ABC∴∠A 1=180°-∠ABC -∠ACB -12∠A ∵∠A +∠ABC +∠ACB =180°∴∠A 1=12∠A 同理,得∠A 2=12∠A 1=12×12∠A =α22;∠A 3=12∠A 2=12×12×12∠A =α23;∠A 4=12∠A 3=12×12×12×12∠A =α24;⋯∠A n =12∠A n -1=α2n ∴∠A 2020=α22020故答案为:α22020.【点睛】本题考查了三角形和数字规律的知识;解题的关键是熟练掌握三角形内角和、三角形外角、角平分线、数字规律的性质,从而完成求解.33.【初步认识】(1)如图1,BM 平分∠ABC ,CM 平分外角∠ACD ,若∠A =80°,则∠M =°.【变式探究】(2)已知ABCD 为四边形,E 为边AB 延长线上一点,如图2,∠ADC =110°,∠BCD =120°,∠DAB 和∠CBE 的平分线交于点F ,则∠F =°.【继续探索】(3)已知ABCD 为四边形,E 为边AB 延长线上一点,如图3,∠ADC =α,∠BCD =β,且α+β>180°,∠DAB 和∠CBE 的平分线交于点F ,求∠F 与α、β之间的数量关系,并说明理由;【终极挑战】(4)如果将(3)中的条件α+β>180°改为α+β<180°,再分别作∠DAB 和∠CBE 的平分线,且两平分线所在的直线交于点F ,那么∠F 与α、β又有怎样的数量关系?请直接写出结论.(不用说明理由)【答案】(1)40;(2)25;(3)∠F =12α+12β-90°,理由见解析;(4)∠F =90°-12α-12β【分析】本题考查了角平分线的定义,三角形外角的性质,三角形内角和定理等知识,解题的关键是:(1)利用角平分线定义和三角形外交的性质可探究出∠M =12∠A ,即可求解;(2)延长AD 、BC 相交于G ,先求出∠G 的度数,然后同(1)得出∠F =12∠G ,即可求解;(3)类似(2)探究即可;(4)延长DA ,CB 相交于G ,延长BA ,先求出∠G =180°-α-β,再判断AF 平分∠NAG ,FB 平分∠ABG ,然后同(1)得出∠F =12∠G ,即可求解.【详解】解:∵BM 平分∠ABC ,CM 平分外角∠ACD ,∴∠MBC =12∠ABC ,∠MCD =12∠ACD ,∵∠A =∠ACD -∠ABC ,∠M =∠MCD -∠MBD ,∴∠M =12∠ACD -12∠ABC =12∠A ,∵∠A =80°,∴∠M =40°,故答案为:40;(2)延长AD 、BC 相交于G ,∵∠ADC =110°,∠BCD =120°,∴∠GDC =70°,∠GCD =60°,∴∠G =50°,同(1)可证∠F =12∠G ,∴∠F =25°,故答案为:25;(3)∠F =12α+12β-90°理由:延长AD 、BC 相交于G ,∵∠ADC =α,∠BCD =β,。

数学模型试题及答案初中一、选择题(每题3分,共30分)1. 已知函数\( y = 3x + 2 \),当\( x = 1 \)时,\( y \)的值为:A. 5B. 4C. 3D. 2答案:A2. 下列哪个选项不是一次函数的图象?A. 直线B. 曲线C. 射线D. 线段答案:B3. 一个数的平方是16,这个数是:A. 4B. -4C. 4或-4D. 以上都不对答案:C4. 如果一个角的补角是它的两倍,则这个角的度数是:A. 30°B. 60°C. 90°D. 120°答案:A5. 一个等腰三角形的两边长分别为3和4,那么它的周长是:A. 10B. 11C. 12D. 13答案:C6. 一个圆的直径是10厘米,那么它的半径是:A. 5厘米B. 10厘米C. 15厘米D. 20厘米答案:A7. 一个数的倒数是它本身,这个数是:A. 0B. 1C. -1D. 以上都不对答案:B8. 一个数的绝对值是它本身,这个数是:A. 正数B. 负数C. 非负数D. 非正数答案:C9. 一个数的平方根是它本身,这个数是:A. 0B. 1C. 0或1D. 以上都不对答案:C10. 一个数的立方根是它本身,这个数是:A. 0B. 1C. -1D. 0, 1, 或 -1答案:D二、填空题(每题4分,共20分)1. 一个数的平方是25,这个数是______。
答案:±52. 一个角的补角是100°,那么这个角的度数是______。
答案:80°3. 一个等腰三角形的两边长分别为5和8,那么它的周长是______。
答案:184. 一个圆的半径是5厘米,那么它的直径是______。
答案:10厘米5. 一个数的倒数是\( \frac{1}{2} \),这个数是______。
答案:2三、解答题(每题10分,共50分)1. 已知函数\( y = 2x - 3 \),求当\( x = 4 \)时,\( y \)的值。

一、把椅子往地面一放,通常只有三只脚着地,放不稳,然而只需稍挪动几次,就可以使四只脚同时着地放稳了,就四脚连线成长方形的情形建模并加以说明。
(15分) 解:一、模型假设:1. 椅子四只脚一样长,椅脚与地面的接触可以看作一个点,四脚连线呈长方形。
2. 地面高度是连续变化的,沿任何方向都不会出现间断,地面可以看成一张光滑曲面。
3. 地面是相对平坦的,使椅子在任何位置至少有三只脚同时着地。
(3分) 二、建立模型:以初始位置的中位线为坐标轴建立直角坐标系,用θ表示椅子绕中心O 旋转的角度,椅子的位置可以用θ确定:()f θ记为A 、B 两点与地面的距离之和 ()g θ记为C 、D 两点与地面的距离之和由假设3可得,()f θ、()g θ中至少有一个为0。
由假设2知()f θ、()g θ是θ的连续函数。
(3分) 问题归结为:已知()f θ和()g θ是θ的连续函数,对任意θ,()()0f g θθ=,且设()()00,00g f =>。
证明存在0θ, 使得()()000f g θθ== (3分) 三、模型求解: 令()()()h f θθθ=-g 若()()000f g =,结论成立若()()000f g 、不同时为,不妨设()()00,00g f =>,椅子旋转()180π或后,AB 与CD 互换,即()()0,0g f ππ>=,则()(0)0,0h h π><。
(3分)由f g 和的连续性知h 也是连续函数。
根据连续函数的基本性质,必存在()000θθπ<<使000()0,()()h f g θθθ==即。
最后,因为00()()0f g θθ=,所以00()()0f g θθ==。
(3分)图 5二、给出7支队参加比赛的循环比赛赛程安排,要求各参赛队的每两场比赛之间的休息场次尽可能均衡,并列出表格说明。
解:设(1,2,7)i A i =表示7支参赛队。

初中数学几何模型大全+经典题型(含答案)全等变换平移:平行等线段(平行四边形)对称:角平分线或垂直或半角旋转:相邻等线段绕公共顶点旋转对称全等模型说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
对称半角模型说明:上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型半角:有一个角含1/2角及相邻线段自旋转:有一对相邻等线段,需要构造旋转全等共旋转:有两对相邻等线段,直接寻找旋转全等中点旋转:倍长中点相关线段转换成旋转全等问题旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
中点旋转:说明:两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。
证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
几何最值模型对称最值(两点间线段最短)对称最值(点到直线垂线段最短)说明:通过对称进行等量代换,转换成两点间距离及点到直线距离。

数学模型习题答案数学模型习题答案数学模型是一门应用数学的学科,它通过建立数学模型来解决实际问题。
数学模型习题是数学模型课程中重要的一环,通过解答这些习题,我们可以更好地理解和应用数学模型的知识。
在本文中,我将为大家提供一些数学模型习题的答案,希望能对大家的学习有所帮助。
1. 一辆汽车以每小时60公里的速度匀速行驶,行驶了4小时后,行驶的总里程是多少?解答:根据题意,汽车的速度是每小时60公里,行驶了4小时,所以行驶的总里程为60公里/小时× 4小时 = 240公里。
2. 一个球从高度为10米的地方自由落下,每次落地后反弹的高度是前一次高度的一半,求球在第5次落地时的总共运动距离。
解答:球第一次落地时的高度为10米,第二次落地时的高度为10米的一半,即5米,第三次落地时的高度为5米的一半,即2.5米,以此类推,第五次落地时的高度为10米× (1/2)^4 = 0.625米。
球在每次落地前的运动距离为高度的两倍,所以总共运动距离为10米 + 5米 + 2.5米 + 1.25米 + 0.625米 = 19.375米。
3. 一个水桶的容量为10升,水龙头每分钟可以注满3升的水,水桶中原有4升的水,问需要多少时间才能将水桶注满?解答:水龙头每分钟可以注满3升的水,所以注满10升的水需要10升÷ 3升/分钟 = 3.33分钟。
水桶中原有4升的水,所以需要的时间为3.33分钟 - 4升÷ 3升/分钟 = 2.33分钟。
4. 一个人每天早上骑自行车上班,速度为每小时15公里,下班时因为疲劳速度减半,求他每天上下班总共需要多长时间?解答:上班的路程和下班的路程是一样的,所以只需要考虑一段路程的时间。
上班时速度为每小时15公里,所以上班需要的时间为路程÷ 速度 = 路程÷ 15公里/小时。
下班时速度减半,所以下班需要的时间为路程÷ (15公里/小时× 1/2) = 路程÷ 7.5公里/小时。
模型与算法四道题及“跳棋”思考题1、找零钱思想:先找零25分的,然后再依次满足10分、5、1.算法:符号说明:Sum1:消费金额。
Sleft2:找零金额。
X1、X2、X3、X4:需要找零25分、10分、5分和1分的数量。
S1:请输入小于100分的消费金额:Sum1。
S2:需要找零的金额为:Sleft2=100- Sum1。
S3:计算与赋值:X1=[Sleft2/25]、X2=[(Sleft2-25*X1)/10]、X3=[(Sleft2-25* X1-10*X2)/5]、X4=Sleft2-25*X1-10*X2-5*X3.S4:输出X1、X2、X3、X4。
2、带有时间窗的任务分配算法S未:还未被分配的任务集合。
S已:已经被分配的任务集合。
A:临时集合。
S1:赋值k=1。
S2:从S未中找出一个开始时间最小的任务i,并输出:“任务i分配到第k个机器“,并且 S已=S已∪{ i },S未=S未−{ i }。
S3:判断A={i∈S未|s i≥f j∀ j∈S已}是否为空集,若A为空集,则此机器已经满了,k=k+1, S已=∅,进入S4;否则从A中选出一个开始时间最小的任务i,并输出:“任务i分配到第k个机器“,并S已=S已∪{ i },S未=S未−{ i },进入S3。
S4:判断S未是否为空集,若是,程序结束;否则进入S3。
#include<stdio.h>void main(){char a[7]={'a','b','c','d','e','f','g'};char b;char x[7];int s[7]={0,3,4,9,7,1,6};int f[8]={2,7,7,11,10,5,8,0};int i,j,k,n,m,c,d,x1,x2,x3,x4;bool y1,y2;k=0;m=1;for(i=0;i<7;i++) // 将任务按开始时间从小到大排序。
{for(j=i;j<7;j++){if(s[i]>s[j]){c=s[i];s[i]=s[j];s[j]=c;d=f[i];f[i]=f[j];f[j]=d;b=a[i];a[i]=a[j];a[j]=b;}}}x[0]=0;n=0;do{printf("安排在第%d台机器上的任务有:",m);if(m==1) printf(" %c",a[0]);for(i=1;i<7;i++){y2=1;for(j=0;j<k;j++){y1=(i!=x[j])&&y2; // 保证即将安排的任务是未被分配的。
y2=y1;}if(y1){if((s[i]>=f[n])) // 保证即将安排的任务开始时间不得小于前一个任务的结束时间。
{k=k+1;x[k]=i;n=x[k];printf(" %c",a[i]);}}if(i==6) n=8;}printf("\n");++m;}while(k<6);}3、0—1背包问题启发式算法(回溯法):给定n中物品和一个背包,假设物品i的重量w i,其价值为v i,背包容量为C。
物品i有两种状态,装入背包或者不装入背包。
X i=0时表示物品i不装入背包,X i=1时表示物品装入背包,则决策物品是否装入背包的问题转化为一个二叉树搜索问题,根据约束条件进行剪枝,然后结合回溯法求出解。
所给物品按照单位价值量进行非增排序,解空间表示为集合S={X1,X2,…..X n|X i∈{0,1},i=1,2….n},如何选择物品装入背包,使得包内物品的总价值最大的算法如下:Step1:从根节点开始,计算此时背包的剩余容量和背包中物品的价值;此时根节点为活结点,也是当前的扩展结点。
Step2:以深度优先方式搜索,从当前的一个扩展结点向纵深方向移至一个新的结点,此时这根结点成为活结点并成为当前扩展结点。
计算此时背包的剩余容量,并计算背包中物品的价值;Step3:根据约束条件判断当前的扩展结点是否可以再向纵深方向移动;Step4:如果满足约束条件则向纵深方向移至新节点,否则回溯至最近的活结点,使其成为当前扩展结点;Step5:转step2,直到找出最优解或者解空间中没有活结点;Step6:算法结束。
0—1背包问题的邻域搜索算法:Step1:根据约束条件给出一个可行解S0,并计算初始可行解时装入背包中物品的价值V0;Step2:利用贪心算法构造领域函数,将单位价值量大的物品替换初始可行解中的单位价值量小的物品;Step3:计算新解S1时,背包中物品的价值V1,若V1>V0,则S0=S1,V0=V1;Step4:转Step1,直到算出最优解或者满意解为止;Step5:算法结束。
例子:假设n=6,i=1,2…..6,W={9,7,5,13,8,6},V={4,3,2,5,3,2},C=24;利用邻域搜索算算法求解时:Step1:首先给出初始可行解S0={1,1,1,0,0,0},此时V0=9;Step2:通过邻域搜索用S1={1,1,0,0,1,0}替换S0。
Step3:计算V1=10,V1>V0,则S0=S1,V0=V1;Step4:转Step1,直到算出最优解或者满意解为止;Step5:算法结束。
4、写出网络图中寻找V1至Vn的路径的算法Step1:用W ij表示图中两点V i与V j之间的距离,若V i与V j之间没有连线,W ij=+∞。
显然可令图中每个顶点W ii=0。
Step2:给起点V i标上固定的标号P(v1)=0,并打上*号。
给其它各点标上临时标号,如起点到该点有边直接相连,就标T(v j)=w1j,否则T(v j)=+∞。
Step3:在所有T标号中选取最小的,将其改为P标号,并重新计算有T标号的其它各点的T标号。
Step4:转step3,直至所有的顶点得到P标号为止。
Step5:算法结束。
5、独立砖石跳棋问题题目:图中33个顶点摆着32枚棋子,仅中央的顶点空着未摆放棋子。
下棋的规则是任一棋子可以沿水平或垂直方向跳过与其相邻的棋子,进入空着的顶点并吃掉被跳过的棋子。
试设计一个算法找出一种下棋方法,使得最终棋盘上只剩下一个棋子在棋盘中央。
解:回溯法的基本思想是:在问题的解空间树中,按深度优先策略,从根结点出发搜索解空间树,算法搜索至解空间树的任意一点时,先判断该结点是否包含问题的解,如果肯定不包含,跳过对该结点为根的子树的搜索,逐层向其祖先结点回溯;否则,进入该子树,继续按深度优先策略搜索。
简而言之就是从某一可行解开始进行,能进则进,不进则退至上一步,换一可行路径再试。
本题中用回溯的思想,如果两个子之间能跳,那么跳了之后记录其新的位置,因为跳的前后都是一个问题,所以我们能用递归分治,跳了一次之后棋子数减一,并把跳过的棋子和编号最后的棋子交换,这样就达到了把棋子去掉的目的,并把最优解保存。
把棋盘上的位置规定成一个二维数组,如图所示:#include <iostream>#include <fstream>using namespace std;struct step //记录移动棋子的信息{int sx, sy; // 记录移动棋子前棋子的位置int tx, ty; // 记录移动棋子后棋子的位置int dir; // dir值代表移动棋子的方向}struct step mystack[100], last_step;char diamond[7][7];int Left_diamond = 32;int x, y, nx, ny, ndir, top; //ndir值代表方向, 0向右, 1向下, 2向左, 3向上int flag=1; // 是否成功找到解的标志//初始化棋盘void Init_diamond(){for(int i=0; i<7; i++){for(int j=0; j<7; j++){if((i<2 || i>4) && (j<2 || j>4));else{diamond[i][j] = '*';}}}diamond[3][3] = '.';}//移动棋子int Move_diamond(int y, int x, int dir){if(diamond[y][x] != '*'){ return 0; }struct step temp;switch(dir){case 0:{if(x+2>6 || diamond[y][x+1]!='*' || diamond[y][x+2]!='.') { return 0; }diamond[y][x] = diamond[y][x+1] = '.';diamond[y][x+2] = '*';temp.sx = x;temp.sy = y;temp.tx = x+2;temp.ty = y;temp.dir = dir;mystack[top++] = temp;return 1;}break;case 1:{if(y+2>6 || diamond[y+1][x]!='*' || diamond[y+2][x]!='.'){ return 0; }diamond[y][x] = diamond[y+1][x] = '.';diamond[y+2][x] = '*';temp.sx = x;temp.sy = y;temp.tx = x;temp.ty = y+2;temp.dir = dir;mystack[top++] = temp;return 1;}break;case 2:{if(x-2<0 || diamond[y][x-1]!='*' || diamond[y][x-2]!='.'){ return 0; }diamond[y][x] = diamond[y][x-1] = '.';diamond[y][x-2] = '*';temp.sx = x;temp.sy = y;temp.tx = x-2;temp.ty = y;temp.dir = dir;mystack[top++] = temp;return 1;}break;case 3:{if(y-2<0 || diamond[y-1][x]!='*' || diamond[y-2][x]!='.'){ return 0; }diamond[y][x] = diamond[y-1][x] = '.';diamond[y-2][x] = '*';temp.sx = x;temp.sy = y;temp.tx = x;temp.ty = y-2;temp.dir = dir;mystack[top++] = temp;return 1;}break;default:break;}return 0;}//主函数void main(){answer.txt // 输出一个解到文本文件ofstream answer("answer.txt");Init_diamond();top = nx = ny = ndir = 0;while(1) // 回溯遍历,直到找到一个解{if(Left_diamond == 1 && diamond[3][3] == '*'){ break; }for(y=ny; y<7; y++,nx=0){for(x=nx; x<7; x++,ndir=0){for(int dir=ndir; dir<4; dir++){if(Move_diamond(y, x, dir)){Left_diamond--;nx = ny = ndir = 0;goto nextstep;}}}}nextstep:if(y == 7){top--;if(top >= 0) // 回到上一步,并改变方向{last_step = mystack[top];diamond[(last_step.sy + last_step.ty)/2][(last_step.sx + last_step.tx)/2] = '*'; diamond[last_step.sy][last_step.sx] = '*';diamond[last_step.ty][last_step.tx] = '.';nx = last_step.sx;ny = last_step.sy;ndir = last_step.dir + 1;Left_diamond++;}else{answer<<"Can't find any answer, I am sorry."<<endl;cout<<"Can't find any answer, I am sorry."<<endl;flag=0;break;}}}Init_diamond();answer<<"The initialization diamond states:"<<endl;for(int i=0; i<7; i++){for(int j=0; j<7; j++){ answer<<diamond[i][j]<<' '; }answer<<endl;}answer<<endl<<endl; for(int n=0; n<top; n++) // 输出解{answer<<"step "<<n+1<<": Move diamond ("<<mystack[n].sy+1<<","<<mystack[n].sx+1<<")--->("<<mystack[n].ty+1<<","<<mystack[n].tx+1<<")"<<endl;diamond[mystack[n].sy][mystack[n].sx] = '.';diamond[(mystack[n].sy+mystack[n].ty)/2][(mystack[n].sx+mystack[n].tx)/2] = '.'; diamond[mystack[n].ty][mystack[n].tx] = '*';answer<<"Left diamonds : "<<top-n<<endl;for(int k=0; k<7; k++){for(int j=0; j<7; j++){ answer<<diamond[k][j]<<' '; }answer<<endl;}answer<<endl<<endl;}if(flag){cout<<"The answer has been exported to file \"answer.txt\" in the same directory.Welcome to see!"<<endl;}}。