高中数学三视图2

高中数学空间几何体的三视图和直观图知识点1.多面体的结构特征(1)棱柱有两个面相互平行，其余各面都是平行四边形，每相邻两个四边形的公共边平行。

正棱柱：侧棱垂直于底面的棱柱叫做直棱柱，底面是正多边形的直棱柱叫做正棱柱.反之，正棱柱的底面是正多边形，侧棱垂直于底面，侧面是矩形.(2)棱锥的底面是任意多边形，侧面是有一个公共顶点的三角形.正棱锥：底面是正多边形，顶点在底面的射影是底面正多边形的中心的棱锥叫做正棱锥.特别地，各棱均相等的正三棱锥叫正四面体.反过来，正棱锥的底面是正多边形，且顶点在底面的射影是底面正多边形的中心.(3)棱台可由平行于底面的平面截棱锥得到，其上下底面是相似多边形.2.旋转体的结构特征(1)圆柱可以由矩形绕一边所在直线旋转一周得到.(2)圆锥可以由直角三角形绕一条直角边所在直线旋转一周得到.(3)圆台可以由直角梯形绕直角腰所在直线旋转一周或等腰梯形绕上下底面中心所在直线旋转半周得到，也可由平行于底面的平面截圆锥得到.(4)球可以由半圆面绕直径旋转一周或圆面绕直径旋转半周得到.3.空间几何体的三视图空间几何体的三视图是用平行投影得到，这种投影下，与投影面平行的平面图形留下的影子，与平面图形的形状和大小是全等和相等的，三视图包括正视图、侧视图、俯视图.三视图的长度特征：“长对正，宽相等，高平齐”，即正视图和侧视图一样高，正视图和俯视图一样长，侧视图和俯视图一样宽.若相邻两物体的表面相交，表面的交线是它们的分界线，在三视图中，要注意实、虚线的画法.4.空间几何体的直观图空间几何体的直观图常用斜二测画法来画，基本步骤是：(1)画几何体的底面在已知图形中取互相垂直的x轴、y轴，两轴相交于点O，画直观图时，把它们画成对应的x′轴、y′轴，两轴相交于点O′，且使∠x′O′y′=45°或135°，已知图形中平行于x轴、y轴的线段，在直观图中平行于x′轴、y′轴.已知图形中平行于x轴的线段，在直观图中长度不变，平行于y轴的线段，长度变为原来的一半.(2)画几何体的高在已知图形中过O点作z轴垂直于xOy平面，在直观图中对应的z′轴，也垂直于x′O′y′平面，已知图形中平行于z轴的线段，在直观图中仍平行于z′轴且长度不变.。

重难点展示：一．多面体1、棱柱特征：（1）有两个底面相互平行；（2）其余各面每相邻两个四边形的公共边都互相平行。

性质：（1）侧棱都相等，侧面是平行四边形；（2）两个底面与平行于底面的截面是全等的多边形；（3）过不相邻的两条侧棱的截面是平行四边形。

分类：（1）按底面多边形的边数分为：三棱柱、四棱柱等；（2）按侧棱与底面的位置关系分为：⎧⎪⎧⎨⎨⎪⎩⎩斜棱柱正棱柱直棱柱一般棱柱 说明：深刻理解棱柱的特征及性质，才能准确地应对概念题，才能准确地判断棱柱中的线线、线面、面面关系。

2、棱锥特征：（1）有一个面是多边形；（2）其余各面是有一个公共顶点的三角形。

一般棱锥的截面性质：如果棱锥被平行于底面的平面所截，那么截面和底面相似，并且它们的面积比等于截得的棱锥的高与已知棱锥的高的平方比。

如果一个棱锥的底面是正多边形，并且水平放置，它的顶点又在多边形中心的铅垂线上，则这个棱锥叫做正棱锥。

正棱锥的性质：（1）各侧棱相等，各侧面都是全等的等腰三角形；（2）棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形；（3）棱锥的高、侧棱和侧棱在底面内的射影也组成一个直角三角形。

掌握正棱锥的概念，特别是其中的几个直角三角形，可求高、斜高、侧棱长等；另外，还要熟悉一条侧棱垂直底面的棱锥，此两点是高考中常见考点。

3、棱台特征：（1）圆棱锥的底面和与其平行的截面分别叫做棱台的下底面、上底面；（2）其他各面叫做棱台的侧面；（3）相邻两侧面的公共边叫做棱台的侧棱；（4）当棱台的底面水平放置时，铅垂线与两底面交点间的线段或距离叫做棱台的高；由正棱锥截得的棱台叫做正棱台。

正棱台的性质：（1）各侧棱相等，侧面是全等的等腰梯形；（2）两底面以及平行于底面的截面是相似多边形；（3）两底面中心两线、相应的边心距和斜高组成一个直角梯形；（4）正棱台的上下底面中心的连线是棱台的高；（5）正棱台各侧面都是全等的等腰梯形，这些等腰梯形的高叫做棱台的斜高。

高中数学三视图绘制与构造方法解析在高中数学中，三视图绘制是一个重要的内容，它与几何图形的认识、空间想象力以及工程制图等领域密切相关。

本文将对高中数学三视图绘制的基本概念、构造方法和解题技巧进行详细解析，帮助高中学生和他们的父母更好地理解和掌握这一知识点。

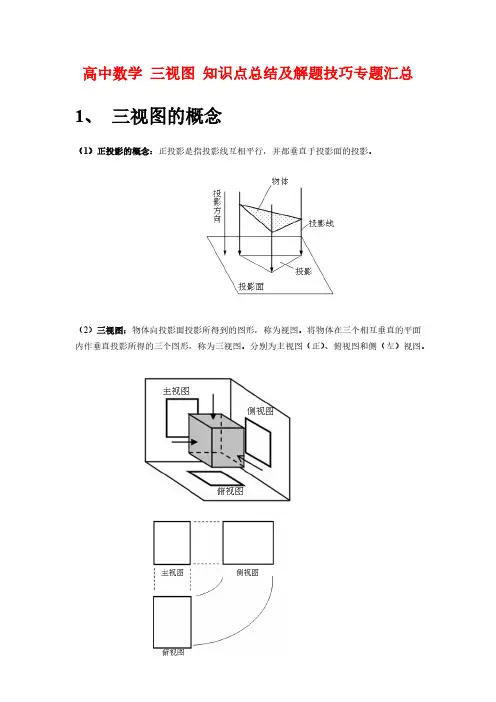
一、基本概念三视图是指一个立体图形在三个相互垂直的平面上的投影图。

通常将这三个平面分别称为主视图、俯视图和左视图。

主视图是从正面观察立体图形，俯视图是从上方观察立体图形，左视图是从左侧观察立体图形。

通过绘制这三个视图，我们可以全面地了解一个立体图形的形状和结构。

二、构造方法1. 主视图的绘制主视图是从正面观察立体图形，因此我们需要找到一个与主视图垂直的平面。

一种常用的方法是将立体图形放置在一个透明的立方体中，然后在透明立方体的正面上绘制主视图。

例如，我们考虑一个正方体，边长为a，我们可以在一个平面上绘制一个边长为a的正方形作为主视图。

2. 俯视图的绘制俯视图是从上方观察立体图形，因此我们需要找到一个与俯视图垂直的平面。

一种常用的方法是将立体图形放置在一个透明的立方体中，然后在透明立方体的上方绘制俯视图。

例如，我们考虑一个长方体，长为a，宽为b，高为c，我们可以在一个平面上绘制一个长为a，宽为b的长方形作为俯视图。

3. 左视图的绘制左视图是从左侧观察立体图形，因此我们需要找到一个与左视图垂直的平面。

一种常用的方法是将立体图形放置在一个透明的立方体中，然后在透明立方体的左侧绘制左视图。

例如，我们考虑一个长方体，长为a，宽为b，高为c，我们可以在一个平面上绘制一个长为c，宽为b的长方形作为左视图。

三、解题技巧1. 利用已知条件确定立体图形的形状和尺寸在解题过程中，我们通常会给出一些已知条件，如立体图形的体积、表面积或者某些边长、角度等信息。

我们可以利用这些已知条件来确定立体图形的形状和尺寸，从而更好地进行三视图的绘制。

2. 利用投影关系确定三视图之间的位置关系在绘制三视图时，我们需要注意不同视图之间的位置关系。