附录A 拉普拉斯变换及反变换
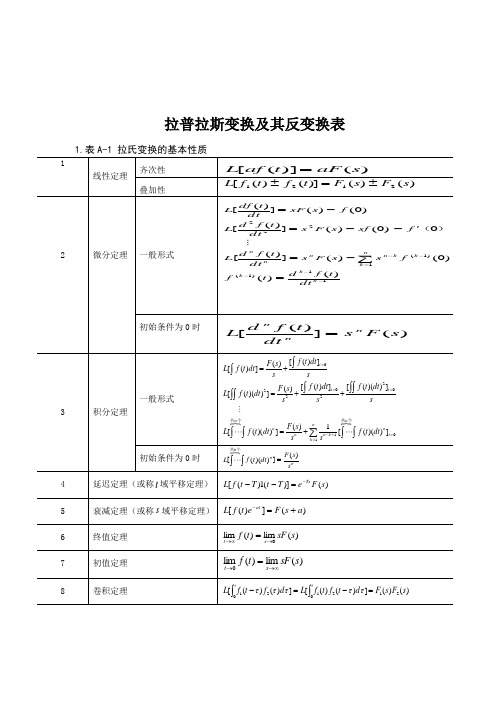
1.拉氏变换的基本性质
附表A-1 拉氏变换的基本性质
1()1
()([n n k F s f t dt s s
-+=
+∑⎰个
[f L
2．常用函数的拉氏变换和z变换表
附表A-2 常用函数的拉氏变换和z变换表
3． 用查表法进行拉氏反变换
用查表法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。设)(s F 是s 的有理真分式，即
11
10
111)()()(a s a s a s a b s b s b s b s A s B s F n n n n m m m m ++++++++==---- （m n >） 式中，系数n n a a a a ,,...,,110-和011,,
,,m m b b b b -都是实常数；n m ,是正整数。按代数定理
可将)(s F 展开为部分分式。分以下两种情况讨论。
（1）0)(=s A 无重根：这时，F(s)可展开为n 个简单的部分分式之和的形式，即
∑=-=-++-++-+-=n
i i
i n n i i s s c s s c s s c s s c s s c s F 122
11)( （F-1）
式中，n s s s ,,,21 是特征方程A(s)＝0的根；i c 为待定常数，称为()F s 在i s 处的留数，可按下列两式计算：lim()()i
i i s s c s s F s →=- （F-2）
或
i
s
s i
s A s B c ='=
)()
( （F-3）
式中，)(s A '为)(s A 对s 的一阶导数。根据拉氏变换的性质，从式（F-1）可求得原函数为
[]⎥⎦⎤⎢⎣⎡-==∑=--n i i i s s c L s F L t f 11
1
)()(＝1
i
n s t
i i c e =∑ (F-4)
（2）0)(=s A 有重根：设0)(=s A 有r 重根1s ，F(s)可写为
())
()()()
(11n r r
s s s s s s s B s F ---=
+ =
n
n i i r r r r r r s s c s s c s s c s s c s s c s s c -++-++-+-++-+-++-- 11
111
111)()()( 式中，1s 为F(s)的r 重根，1+r s ，…，n s 为F(s)的n r -个单根；其中，1+r c ，…，n c 仍按式(F-2)或式(F-3)计算，r c ，1-r c ，…，1c 则按下式计算：
)()(lim 11
s F s s c r s s r -=→
11lim
[()()]i
r r s s d
c s s F s ds
-→=-
)()(lim !11)()
(1s F s s ds
d j c r j j s s j
r -=→- (F-5)
)()(lim )!1(11)1()
1(11s F s s ds
d r c r r r s s --=--→
原函数)(t f 为 [])()(1
s F L
t f -=
⎥⎦⎤⎢⎣⎡-++-++-+-++-+-=++---n n i i r r r r r r s s c s s c s s c s s c s s c s s c L 11
111
1111)()()
( t s n
r i i t s r r r r i
e c e c t c t r c t r c ∑+=---+⎥⎦
⎤⎢⎣⎡+++-+-=112211
1
)!2()!1( （F-6）
