土力学课后习题答案.doc
- 格式:doc
- 大小:970.00 KB
- 文档页数:21

第一章 土的组成和物理分析1.1 已知土样试验数据为:土的重度19.03/kN m ,土粒密度2.713/g cm ,土的干重度为14.53/kN m ,求土样的含水率、孔隙比、孔隙率和饱和度。
解:(1) 含水率()()(19.014.5)100%100%100%100%31.03%14.5w d d s d dm V w m V γγγγγγ−−−=×=×=×=×= (2) 孔隙比(1) 2.71(131.03%)10110.86919.0s w g e ργ+×+×=−=−=(3) 孔隙率19.0110.46(1)2.7110(131.03%)s n g w γρ=−=−=+××+(4) 饱和度31.03% 2.71100.9680.86910.0s r ww g s e ργ××===×1.2某土样采用体积为1003cm 的环刀取样试验,用天平测得环刀加湿土的质量为241.0g ,环刀质量为55.0g ,烘干后土样质量为162.0g ,土粒比重为2.70,。
计算该土样的含水率w ,饱和度r S ,孔隙比e ,孔隙率n 及天然密度,饱和密度sat ρ,有效密度'ρ和干密度d ρ,并比较各种密度的大小。
解:湿土质量:241.055.0186.0m g =−= 土的湿重度:3186.21018.6/100mg kN m V γ×=== 含水率:186.0162.0100%100%100%14.8%162.0w s s s m m m w m m −−=×=×=×= 饱和度:[][]18.6 2.701014.8%60.0%(1)10 2.710(114.8%)18.6s r w s gwS g w γργργ×××===+−×××+−孔隙比:14.8% 2.70100.66660.0%10.0s r ww g e S ργ××===×孔隙率:0.6660.40110.666e n e ===++ 天然密度:3186.01.86/100m g cm V ρ===饱和密度:30.6661.010*******.666 2.02/100w s w v s sat e V m V m e g cm V Vρρρ+××++++====有效密度:'32.02 1.0 1.02/sat w g cm ρρρ=−=−=干密度:3162.01.62/100s d m g cm Vρ=== 比较各种密度的大小:'sat d ρρρρ>>>1.3土样试验数据见表1-16,求表内空白项的数值。

第三章 土中应力和地基应力分布3-1 取一均匀土样,置于 x 、y 、z 直角坐标中,在外力作用下测得应力为: x σ=10kPa ,y σ=10kPa ,z σ=40kPa ,xy τ=12kPa 。
试求算:① 最大主应力 ,最小主应力 ,以及最大剪应力τmax ?② 求最大主应力作用面与 x 轴的夹角θ? ③根据1σ和3σ绘出相应的摩尔应力圆,并在圆上标出大小主应力及最大剪应力作用面的相对位置? 3-1 分析:因为0==yz xz ττ,所以z σ为主应力。
解:由公式(3-3),在xoy 平面内,有:kPa 222121012)21010()1010(5.0)2()(215.0222/12231-=±=⎥⎦⎤⎢⎣⎡+-±+⨯=⎥⎦⎤⎢⎣⎡+-±+='xy y x y x τσσσσσσ 比较知,kPa 2kPa 22kPa403121-=='===σσσσσz ,于是:应力圆的半径: kPa 21))2(40(5.0)(2131=--⨯=-=σσR圆心坐标为: kPa 19))2(40(5.0)(2131=-+⨯=+σσ由此可以画出应力圆并表示出各面之间的夹角。
易知大主应力面与x 轴的夹角为90︒。
注意,因为x 轴不是主应力轴,故除大主应力面的方位可直接判断外,其余各面的方位须经计算确定。
有同学还按材料力学的正负号规定进行计算。
3-2 抽取一饱和黏土样,置于密封压力室中,不排水施加围压30kPa (相当于球形压力),并测得孔隙压为30 kPa ,另在土样的垂直中心轴线上施加轴压Δ1σ=70 kPa (相当于土样受到∆1σ—∆3σ 压力),同时测得孔隙压为60 kPa ,求算孔隙压力系数 A 和B ?3-3 砂样置于一容器中的铜丝网上,砂样厚25cm ,由容器底导出一水压管,使管中水面高出容器溢水面 。
若砂样孔隙比e =0.7,颗粒重度s γ=26.5 kN/m 3 ,如图3-42所示。

第一章:土的物理性质及工程分类名词解释1、土粒级配:是指土中各粒组的相对百分含量,或土中中各粒组占总质量的百分数。
2、不均匀系数:用来描述土粒的不均匀性大小的指标。
用公式表示 1060d d C u =3、曲率系数:用来反映颗分曲线的整体形状和细粒含量多少的指标。
用公式表示1060230)(d d d C c =4、液限:是指土体处于可塑态和流动态的界限含水率,用w l 表示。
5、塑限:是指土体处于可塑态和半固态的界限含水率。
用w p 表示。
6、塑性指数:表示粘性土呈可塑状态的含水率的变化范围,其大小等于液限与塑限的差值(去百分号)。
用公式表示100)(⨯-=p l p w w I7、液性指数:表征了粘性土的天然含水率和界限含水率之间的相对关系,用来区分天然土所处的状态。
用公式表示pppl p l I w w w w w w I -=--=8、最大干密度:在击实曲线中,当土的含水率增加到某一值时,干密度可以达到了最大值,这一干密度称为最大干密度,用ρdmax 表示。
9、最优含水率:在击实曲线中,当土的含水率增加到某一值时,干密度可以达到了最大值,这一含水率称为最优含水率,用w op 表示。
10、灵敏度:原状土的单轴抗压强度与重塑土的单轴抗压强度之比。
用公式表示uu t q q S =简答1、A 土样的孔隙比小于B 土样的孔隙比,那么A 土样一定比B 土样密实么?为什么? 答:不一定;如果对于同一种土来说,孔隙比的大小可以反映出土的密实程度;而对于不同土来说,仅仅用孔隙比是无法判断土的密实程度的,还与土样的物理性质有关。
2、什么是颗分试验?有几种方法?适用范围是什么?答:测定土体中各粒组的质量占总土重百分数,确定各粒径分布范围的试验。
常用方法有:筛分法,适用于粒径d ≥0.075mm 且P ≥90%的粗粒土;密度计法,适用于粒径d ≤0.075mm 且P ≥90%的细粒土。
对于粗细混合土可采用联合测定法。

《土力学》课后习题答案第一章1-1:已知:V=72cm3m=129.1g m s=121.5g G s=2.70则:129.1121.56.3%121.5ssm mwm--===3333 129.1*1017.9/72121.5452.77245271.0*27121.5*1020.6/72sssV ssat w V ssat satmg g KN mvmV cmV V V cmm V mg g g KN mV Vγρρργρ========-=-=++=====3320.61010.6/121.5*1016.9/72sat wsdsat dKN mmg KN mVγγγγγγγγ'=-=-===='>>>则1-2:已知:G s=2.72 设V s=1cm3则33332.72/2.722.72*1016/1.72.720.7*1*1020.1/1.720.11010.1/75%1.0*0.7*75%0.5250.52519.3%2.720.525 2.721.sssd ds V wwrw w V rwsw sg cmm gmg g KN mVm Vg g KN mVKN mm V S gmwmm mg gVργρργργγγργρ======++===='=-=-========++===当S时,3*1019.1/7KN m=1-3:3477777331.70*10*8*1013.6*1013.6*10*20%2.72*1013.6*10 2.72*10850001.92*10s d w s s wm V kg m m w kg m m V m ρρ======++==挖1-4: 甲:33334025151* 2.72.7*30%0.81100%0.812.70.811.94/10.8119.4/2.71.48/1.8114.8/0.81p L P s s s s w r wV ws w s w s d s w d d vsI w w V m V g m g S m V m m g cm V V g KN m m g cm V V g KN m V e V ρρργρργρ=-=-=======∴==++===++=====+====设则又因为乙:3333381 2.682.68*22%0.47960.47962.680.47962.14/10.47962.14*1021.4/2.681.84/1.47961.84*1018.4/0.4796p L p s s s s w s V s w s V s d s w d d VsI w w V m V g m m w g V cm m m g cm V V g KN m m g cm V V g KN m V e V ρργρργρ=-========++===++======+=====设则则γγ∴<乙甲 d d γγ<乙甲 e e >乙甲 p p I I >乙甲则(1)、(4)正确1-5:1s w d G eρρ=+ 则2.7*1110.591.7022%*2.7185%0.59s wds r G e wG S e ρρ=-=-====>所以该料场的土料不适合筑坝,建议翻晒,使其含水率降低。

2.21 某办公楼工程地质勘探中取原状土做试验。
用天平称50cm3湿土质量为95.15g.烘干后质量为75.05g.土粒比重为2.67。
计算此土样的天然密度、干密度、饱和密度、天然含水率、孔隙比、孔隙率以及饱和度。
【解】m= 95.15g.m s= 75.05g.m w= 95.15 - 75.05 = 20.1g.V= 50.0 cm3.d s = 2.67。
V= 75.05/(2.67 1.0) = 28.1 cm3s取g = 10 m/s2.则V w = 20.1 cm3V= 50.0 - 28.1 = 21.9 cm3vV= 50.0 – 28.1 – 20.1 = 1.8 cm3a于是.= m / V = 95.15 / 50 = 1.903g/ cm3= m s / V = 75.05 / 50 = 1.501g/ cm3d= (m s +w V v)/ V = (75.05 + 1.0 21.9) / 50 = 1.939g/ cm3 s a tw = m/ m s = 20.1 / 75.05 = 0.268 = 26.8%we = V/ V s = 21.9 / 28.1 = 0.779vn = V/ V = 21.9 / 50 = 0.438 = 43.8%vS= V w / V v = 20.1 / 21.9 = 0.918r2.22 一厂房地基表层为杂填土.厚1.2m.第二层为粘性土.厚5m.地下水位深1.8m。
在粘性土中部取土样做试验.测得天然密度 = 1.84g/ cm3.土粒比重为2.75。
计算此土样的天然含水率w、干密度d、孔隙比e和孔隙率n。
【解】依题意知.S r = 1.0.s a t= = 1.84g/ cm3。
由.得n = e /(1 + e) = 1.083 /(1 + 1.083) = 0.520g/cm3。
= 1.54g/ cm3.含水率2.23 某宾馆地基土的试验中.已测得土样的干密度dw = 19.3%.土粒比重为2.71。

土力学课后习题与答案思考题]1-1 什么叫土?土是怎样形成的?粗粒土和细粒土的组成有何不同?1-2什么叫残积土?什么叫运积土?他们各有什么特征?1-3何谓土的级配?土的粒径分布曲线是怎样绘制的?为什么粒径分布曲线用半对数坐标?1-4何谓土的结构?土的结构有哪几种类型?它们各有什么特征?1 -5 土的粒径分布曲线的特征可以用哪两个系数来表示?它们定义又如何?1 - 6如何利用土的粒径分布曲线来判断土的级配的好坏?1-7什么是吸着水?具有哪些特征?1-8什么叫自由水?自由水可以分为哪两种?1-9什么叫重力水?它有哪些特征?1-10 土中的气体以哪几种形式存在?它们对土的工程性质有何影响?1 -11什么叫的物理性质指标是怎样定义的?其中哪三个是基本指标?1-12什么叫砂土的相对密实度?有何用途?1-13何谓粘性土的稠度?粘性土随着含水率的不同可分为几种状态?各有何特性?1-14何谓塑性指数和液性指数?有何用途?1 -15何谓土的压实性?土压实的目的是什么?1-16 土的压实性与哪些因素有关?何谓土的最大干密度和最优含水率?1-17 土的工程分类的目的是什么?1-18什么是粗粒土?什么叫细粒土?思考题22- 1 土屮的应力按照其起因和传递方式分哪几种?怎么定义?2-2何谓自重应力,何谓静孔隙水应力?计算自重应力应注意些什么?2-3何谓附加应力,空间问题和平面问题各有几个附加应力分量?计算附加应力时对地基做了怎样的假定?2-4什么叫柔性基础?什么叫刚性基础?这两种基础的基底压力有何不同?2-5地基屮竖向附加应力的分布有什么规律?相邻两基础下附加应力是否会彼此影响?2-6附加应力的计算结果与地基中实际的附加应力能否一致,为什么?2-7什么是有效应力?什么是孔隙应力?其屮静孔隙应力如何计算?2-8你能熟练掌握角度法和叠加原理的应用吗?会计算各种荷载条件下地基中任意点的竖向附加应力吗?思考题33-1何谓达西定律,达西定律成立的条件有哪些?3-2实验室内测定渗透系数的方法有几种?它们之间又什么不同?3-3流网有什么特征?3-4渗透变形有几种形式?各有什么特征?3-5什么是临界水力梯度?如何对其进行计算?3-6孔隙水应力在静水条件下和在稳定渗流作用下有什么不同?如何利用流网确定渗流作用的孔隙水压力。


完美WORD 格式绪论答案:略第1章土的物理性质及工程一、填空题自由水;3、最松散,最密实;4、塑限,液限;5、单粒,蜂窝,絮状; 7、含水率,黏粒含量。
四、计算题156.6 —45 —82.335.6%1、w=「二1566 4510.0 =18.60kN/m 3 6082.3 3d10.0 =13.72kN/m60G s=2.73二涮- w =18.69-10.0 =8.69kN/m 3 土样 号 (kN/m 3) G s © (%) J (kN/m 3) e n S r (%) 体积 (cm 3) 土的重力(N ) 湿 干 1 18.96 2.72 34.0 14.17 0.92 0.48 100.0 一 一 一 2 17.3 2.74 9.1 15.84 0.73 0.42 34.2 一 一 一 3 19.02.7431.014.50.890.4795.710.0 0.190.145土样号I PI L 土的名称 土的状态 131 17 141.29低液限黏土流塑1、A,2、D ,三、证明题 G s v 1、 - w 1 esV v V s2、G s (1 -n)4、C,5、D,6、D ,二 V v V sV s mWG s (^V;) m sV V s sVV vm wm s 3— V vV v Sr1、固体颗粒,水;2、结合水, 6、土中水的质量,土粒质量;二、选择题 82.32.73 (1 0.356)1.86-1 =0.99S ^ —e sat0.99 1 0.99= 0.4970.356*2.73 0.99-0.982G s e _ 1 e2.73 0.991 0.99310 =18.69kN /m4、 e G (1 十⑷)?w e—12.68 (1 0.105)-1 =0.692Dr%x 「e = 0.941 -°692emax—為山 0.941 —°.46O氓0.5180.4811、蒙脱石,高岭土,伊利石;2、硅氧四面体,氢氧化铝八面体。

第一章 土的物理性质1-8 有一块体积为60 cm 3的原状土样,重1.05 N, 烘干后0.85 N 。
已只土粒比重(相对密度)s G =2.67。
求土的天然重度γ、天然含水量w 、干重度γd 、饱和重度γsat 、浮重度γ’、孔隙比e 及饱和度S r1-8 解:分析:由W 和V 可算得γ,由W s 和V 可算得γd ,加上G s ,共已知3个指标,故题目可解。
363kN/m 5.1710601005.1=⨯⨯==--V W γ 363s d kN/m 2.1410601085.0=⨯⨯==--V W γ 3w sw s kN/m 7.261067.2=⨯===∴γγγγs sG G %5.2385.085.005.1s w =-==W W w 884.015.17)235.01(7.261)1(s =-+=-+=γγw e (1-12) %71884.06.2235.0s =⨯=⋅=e G w S r (1-14) 注意:1.使用国际单位制;2.γw 为已知条件,γw =10kN/m 3;3.注意求解顺序,条件具备这先做;4.注意各γ的取值范围。
1-9 根据式(1—12)的推导方法用土的单元三相简图证明式(1-14)、(1-15)、(1-17)。
1-10 某工地在填土施工中所用土料的含水量为5%,为便于夯实需在土料中加水,使其含水量增至15%,试问每1000 kg 质量的土料应加多少水1-10 解:分析:加水前后M s 不变。
于是:加水前: 1000%5s s =⨯+M M (1) 加水后: w s s 1000%15M M M ∆+=⨯+ (2) 由(1)得:kg 952s =M ,代入(2)得: kg 2.95w =∆M注意:土料中包含了水和土颗粒,共为1000kg ,另外,sw M M w =。
1-11 用某种土筑堤,土的含水量w =15%,土粒比重G s =2.67。
分层夯实,每层先填0.5m ,其重度等γ=16kN/ m 3,夯实达到饱和度r S =85%后再填下一层,如夯实时水没有流失,求每层夯实后的厚度。

土力学基础课后习题答案
1、土由哪几部分组成?土中水分为哪几类?其特征如何?对土的工程性质影响如何?
答:土体一般由固相、液相和气相三部分组成(即土的三相)。
土中水按存在形态分为:液态水、固态水和气态水(液态水分为自由水和结合水,结合水分为强结合水和弱结合水,自由水又分为重力水和毛细水)
特征:固态水是指存在于颗粒矿物的晶体格架内部或是参与矿物构造的水,液态水是人们日常生活中不可缺少的物质,气态水是土中气的一部分。
影响:土中水并非处于静止状态,而是运动着的。
工程实践中的流沙、管涌、冻胀、渗透固结、渗流时的边坡稳定问题都与土中水的运用有关。
2、土的不均匀系数cu及曲率系数cc的定义是什么?如何从土的颗粒级配曲线形态上,cu和cc数值上评价土的工程性质。
答:不均匀系数cu反映了大小不同粒组的分布情况。
曲率系数CC 描述了级配曲线分布的整体形态,表示是否有某粒组缺失的情况。
评价:(1)对于级配连续的土:cu5,级配良好;cu5,级配不良。
(2)对于级配不连续的土:同时满足cu5和cc=1~3,级配良好,反之则级配不良。
3、说明土的天然重度、饱和重度、浮重度和干重度的物理概念和相互联系,比较同一种土各重度数值的大小。
答:天然重度、饱和重度、浮重度和干重度分别表示单位体积的土分别在天然、饱和、湿润、干燥状态下的重量,它们反映了土在不同状态下质量的差异。
饱和重度天然重度干重度浮重度。

土力学 第二章2-2、有一饱和的原状土样切满于容积为21.7cm 3的环刀内,称得总质量为72.49g ,经105℃烘干至恒重为61.28g ,已知环刀质量为32.54g ,土粒比重为2.74,试求该土样的湿密度、含水量、干密度及孔隙比(要求汇出土的三相比例示意图,按三相比例指标的定义求解)。
解:3/84.17.2154.3249.72cm g V m =-==ρ %3954.3228.6128.6149.72=--==S W m m ω 3/32.17.2154.3228.61cm g V m S d =-==ρ 069.149.1021.11===S V V V e 2-3、某原状土样的密度为1.85g/cm 3,含水量为34%,土粒相对密度为2.71,试求该土样的饱和密度、有效密度和有效重度(先推导公式然后求解)。
解:(1)VV m WV s sat ρρ⋅+=W S m m m += SW m m =ω 设1=S m ρω+=∴1VWS S S V m d ρ=W S W S S S d d m V ρρ⋅=⋅=∴1()()()()()()3W S S W S S W W satcm /87g .1171.20.341171.285.1d 11d 11d 111d 11111=+⨯+-⨯=++-=+++⎪⎪⎭⎫⎝⎛-=+-++=+⎪⎪⎭⎫ ⎝⎛⋅-++=∴ρωρωρωρωρρωρρωρρρωρW S d 有(2)()3'/87.0187.1cm g VV V V V V V m V V m W sat W V Ssat WV W V W S S W S S =-=-=+-=-+-=-=ρρρρρρρρρ (3)3''/7.81087.0cm kN g =⨯=⋅=ργ 或3'3/7.8107.18/7.181087.1cmkN cm kN g W sat sat sat =-=-==⨯=⋅=γγγργ2-4、某砂土土样的密度为1.77g/cm 3,含水量9.8%,土粒相对密度为2.67,烘干后测定最小孔隙比为0.461,最大孔隙比为0.943,试求孔隙比e 和相对密实度Dr ,并评定该砂土的密实度。

土力学(第三版)中国建筑工业出版社课后题答案(全)(完整资料).doc第 3 页共 4 页【最新整理,下载后即可编辑】2-10章第二章2-2、有一饱和的原状土样切满于容积为21.7cm 3的环刀内,称得总质量为72.49g ,经105℃烘干至恒重为61.28g ,已知环刀质量为32.54g ,土粒比重为2.74,试求该土样的湿密度、含水量、干密度及孔隙比(要求汇出土的三相比例示意图,按三相比例指标的定义求解)。
解:3/84.17.2154.3249.72cm g V m =-==ρ%3954.3228.6128.6149.72=--==S W m m ω3/32.17.2154.3228.61cm g V m S d =-==ρ 069.149.1021.11===S V V V e 2-3、某原状土样的密度为1.85g/cm 3,含水量为34%,土粒相对密度为2.71,试求该土样的饱和密度、有效密度和有效重度(先推导公式然后求解)。
解:(1)V V m WV s sat ρρ?+=W S m m m += SW m m =ω 设1=S m ρω+=∴1VW S S S V m d ρ= WS W S S S d d m V ρρ?=?=∴1()()()()()()3W S S WS SW W satcm /87g .1171.20.341171.285.1d 11d 11d 111d 11111=+?+-?=++-=+++???? ?-=+-++=+???? ???-++=∴ρωρωρωρωρρωρρωρρρωρW S d 有(2)()3'/87.0187.1cm g VV V V V V V m V V m W sat W V Ssat WV W V W S S W S S =-=-=+-=-+-=-=ρρρρρρρρρ (3)3''/7.81087.0cm kN g =?=?=ργ 或3'3/7.8107.18/7.181087.1cmkN cm kN g W sat sat sat =-=-==?=?=γγγργ第 3 页共 4 页2-4、某砂土土样的密度为1.77g/cm 3,含水量9.8%,土粒相对密度为2.67,烘干后测定最小孔隙比为0.461,最大孔隙比为0.943,试求孔隙比e 和相对密实度Dr ,并评定该砂土的密实度。
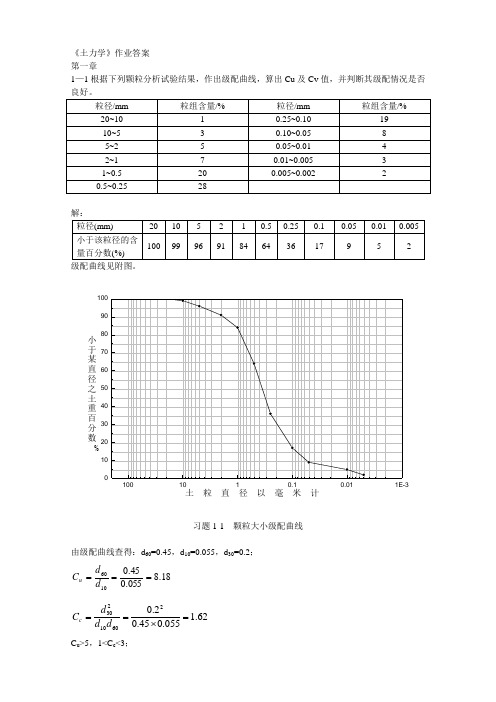
《土力学》作业答案 第一章1—1根据下列颗粒分析试验结果,作出级配曲线,算出Cu 及Cv 值,并判断其级配情况是否良好。
解: 级配曲线见附图。
小于某直径之土重百分数%土粒直径以毫米计习题1-1 颗粒大小级配曲线由级配曲线查得:d 60=0.45,d 10=0.055,d 30=0.2;18.8055.045.01060===d d C u 62.1055.045.02.026010230=⨯==d d d C cC u >5,1<C c <3;故,为级配良好的土。
(2)确定不均匀系数Cu 及曲率系数Cv ,并由Cu 、Cv 判断级配情况。
解:土粒直径以毫米计小于某直径之土重百分数%习题1-2 颗粒大小级配曲线1—3某土样孔隙体积等于颗粒体积,求孔隙比e 为若干? 若Gs=2.66,求ρd =? 若孔隙为水所充满求其密度ρ和含水量W 。
解:111===s v V V e ; /33.1266.2g V M s d ===ρ.12166.2V M M w s =+=+=ρ%6.3766.21===s w M M ω。
1—4在某一层土中,用容积为72cm 3的环刀取样,经测定,土样质量129.1g ,烘干后质量121.5g ,土粒比重为2.70,问该土样的含水量、密度、饱和密度、浮密度、干密度各是多少?解:3457.25.121cm G MV s ss ===;✞3274572cm V V V s V =-=-=;%26.60626.05.1215.1211.129==-==s w M M ω; 3/79.1721.129cm g V M ===ρ; 3/06.2722715.121cm g V V M v w s sat =⨯+=+=ρρ;3/06.1724515.121'cm g V V M s w s =⨯-=-=ρρ;[或3/06.1106.2'cm g w sat =-=-=ρρρ];3/69.1725.121cm g V M s d ===ρ。

土力学课后习题答案(清华大学出版社)第一章1-1:未知:v=72cm3m=129.1gms=121.5ggs=2.70则:w?m?ms129.1?121.5??6.3%ms121.5m129.1g?*10?17.9kn/m3v72m121.5vs?s??45cm3?s2.7g?vv?v?vs?72?45?27cm3?sat??satg?msat?v?ms1.0*27?121.5g?wvg?*10?20.6kn/m3vv72 sat??w?20.6?10?10.6kn/m3ms121.5g?*10?16.9kn/m3v72则?satdd?1-2:未知:gs=2.72设vs=1cm3s2.72g/cm3ms2.72gms2.72g*1016kn/m3v1.7mv2.720.7*1gsvwg*1020. 1kn/m3v1.7则w?20.1?10?10.1kn/m3ddg当sr?75%时,mw??wvvsr?1.0*0.7*75%?0.525gw?mw0.525??19.3%ms2.72mw?ms0.525?2.72g?*10?19.1kn/ m3v1.7g?1-3:ms??dv?1.70*103*8*104?13.6*107kgmw?msw?13.6*107*20%?2.72*107kgv挖出?ms?mw13.6*1072.72*10785000m331.92*101-4:甲:ip?wl?wp?40?25?15设vs?1则ms??s*vs?2.7gmw?2.7*30%?0.81g又因为sr?100%?vv?mw?0.81?w??ms?mw2.7?0.81??1.94g/cm3vs?vw1?0.81ms2.7??1.48g/cm3vs?vw 1.81g?19.4kn/m3?d??d??dg?14.8kn/m3e?vv?0.81vs乙:ip?wl?wp?8设vs?1则ms??svs?2.68gmw?msw?2.68*22%?0.4796g则vv?0.4796cm3ms?mw2.68?0.4796??2.14g/cm3vs?vv1?0.4796ms2.68??1.84g/cm3vs?vw1.4796g?2.14*10?21.4kn/m3?d??d??dg?1.8 4*10?18.4kn/m3e?vv?0.4796vs??甲??乙?d甲??d乙e甲?e乙ip甲?ip乙则(1)、(4)正确1-5:g??d?sw则1?ee?gs?wd1?2.7*1?1?0.591.70wgs22%*2.7sr1?85à.59所以该料场的土料不适宜堤坝,建议翻晒,并使其含水率减少。

土力学课后习题与答案思考题11-1 什么叫土?土是怎样形成的?粗粒土和细粒土的组成有何不同?1-2 什么叫残积土?什么叫运积土?他们各有什么特征?1-3 何谓土的级配?土的粒径分布曲线是怎样绘制的?为什么粒径分布曲线用半对数坐标?1-4 何谓土的结构?土的结构有哪几种类型?它们各有什么特征?1-5 土的粒径分布曲线的特征可以用哪两个系数来表示?它们定义又如何?1-6 如何利用土的粒径分布曲线来判断土的级配的好坏?1-7 什么是吸着水?具有哪些特征?1-8 什么叫自由水?自由水可以分为哪两种?1-9 什么叫重力水?它有哪些特征?1-10 土中的气体以哪几种形式存在?它们对土的工程性质有何影响?1-11 什么叫的物理性质指标 是怎样定义的?其中哪三个是基本指标?1-12 什么叫砂土的相对密实度?有何用途?1-13 何谓粘性土的稠度?粘性土随着含水率的不同可分为几种状态?各有何特性?1-14 何谓塑性指数和液性指数?有何用途?1-15 何谓土的压实性?土压实的目的是什么?1-16 土的压实性与哪些因素有关?何谓土的最大干密度和最优含水率?1-17 土的工程分类的目的是什么?1-18 什么是粗粒土?什么叫细粒土? 思考题22-1 土中的应力按照其起因和传递方式分哪几种?怎么定义?2-2 何谓自重应力,何谓静孔隙水应力?计算自重应力应注意些什么?2-3 何谓附加应力,空间问题和平面问题各有几个附加应力分量?计算附加应力时对地基做了怎样的假定?2-4 什么叫柔性基础?什么叫刚性基础?这两种基础的基底压力有何不同?2-5 地基中竖向附加应力的分布有什么规律?相邻两基础下附加应力是否会彼此影响?2-6 附加应力的计算结果与地基中实际的附加应力能否一致,为什么?2-7 什么是有效应力?什么是孔隙应力?其中静孔隙应力如何计算?2-8 你能熟练掌握角度法和叠加原理的应用吗?会计算各种荷载条件下地基中任意点的竖向附加应力吗?思考题33-1 何谓达西定律,达西定律成立的条件有哪些?3-2 实验室内测定渗透系数的方法有几种?它们之间又什么不同?3-3 流网有什么特征?3-4 渗透变形有几种形式?各有什么特征?3-5 什么是临界水力梯度?如何对其进行计算?3-6 孔隙水应力在静水条件下和在稳定渗流作用下有什么不同?如何利用流网确定渗流作用的孔隙水压力。
1-8 有一块体积为60 cm 3的原状土样,重1.05 N, 烘干后0.85 N 。
已只土粒比重(相对密度)s G =2.67。
求土的天然重度γ、天然含水量w 、干重度γd 、饱和重度γsat 、浮重度γ’、孔隙比e 及饱和度S r解:分析:由W 和V 可算得γ,由W s 和V 可算得γd ,加上G s ,共已知3个指标,故题目可解。
363kN/m 5.1710601005.1=⨯⨯==--V W γ 363s d kN/m 2.1410601085.0=⨯⨯==--V W γ 3w sw s kN/m 7.261067.2=⨯===∴γγγγs sG G Θ %5.2385.085.005.1s w =-==W W w 884.015.17)235.01(7.261)1(s =-+=-+=γγw e (1-12) %71884.06.2235.0s =⨯=⋅=e G w S r (1-14) 注意:1.使用国际单位制;2.γw 为已知条件,γw =10kN/m 3;3.注意求解顺序,条件具备这先做;4.注意各γ的取值范围。
1-10 某工地在填土施工中所用土料的含水量为5%,为便于夯实需在土料中加水,使其含水量增至15%,试问每1000 kg 质量的土料应加多少水解:分析:加水前后M s 不变。
于是:加水前: 1000%5s s =⨯+M M (1) 加水后: w s s 1000%15M M M ∆+=⨯+ (2) 由(1)得:kg 952s =M ,代入(2)得: kg 2.95w =∆M注意:土料中包含了水和土颗粒,共为1000kg ,另外,sw M M w =。
1-11 用某种土筑堤,土的含水量w =15%,土粒比重G s =2.67。
分层夯实,每层先填0.5m ,其重度等γ=16kN/ m 3,夯实达到饱和度r S =85%后再填下一层,如夯实时水没有流失,求每层夯实后的厚度。
解:分析:压实前后W s 、V s 、w 不变,如设每层填土的土颗粒所占的高度为h s ,则压实前后h s 不变,于是有:2211s 11e h e h h +=+= (1) 由题给关系,求出:919.0116)15.01(1067.21)1(s 1=-+⨯⨯=-+=γγw e 471.085.015.067.2s 2=⨯==r S w G e 代入(1)式,得: m 383.05.0919.01471.011)1(1122=⨯++=++=e h e h 1-9 根据式(1—12)的推导方法用土的单元三相简图证明式(1-14)、(1-15)、(1-17)。
)1()1()1()1()1(1)1()(1)1(1)1()1(1)1(1)1(1)1(11)1(1)1()1(/)1(1ωγγγγγωγγωγγγωγγγγωγγωγγγγωγωωγγγωγγωγγωγγωγγωγγωγγγωγωγγωωωγγ+-=-='++-=+⎪⎭⎫ ⎝⎛-++=+=+=+==-+==+-=+⎪⎭⎫ ⎝⎛-+==-+=⎪⎭⎫ ⎝⎛-+==-+=-=+==⇒===+=+===⇒===⇒==s s w sat w s s w s w w s w s w v s sat w s w s s d w s s v w r w s w s w s v w s w s s v w s s v w s sw w w w s w s ws s w s w s w w s s ws s s s d d d d d d d V V W d d V W d d V V S d d d V V n d d V V e d V V V d W V V W d W V d W W W d W W W W m m d W V W d V 根据各指标定义:三相草图各量已填满,设1-14 某砂土的重度s γ=17 kN/ m 3,含水量w =8.6%,土粒重度s γ=26.5 kN/ m 3。
其最大孔隙比和最小孔隙比分别为0.842和0.562求该沙土的孔隙比e 及相对密实度Dr ,并按规范定其密实度。
1-14 已知:s γ=17kN/m 3,w =8.6%,γs =26.5kN/m 3,故有:693.0117)086.01(5.261)1(s =-+⨯=-+=γγw e 又由给出的最大最小孔隙比求得D r =0.532,所以由桥规确定该砂土为中密。
1-15 试证明。
试中m ax d γ、d γ、m in d γ分别相应于e max 、e 、e min 的干容重证:关键是e 和γd 之间的对应关系: 由111dmaxs min dmin s max d s -=-=-=γγγγγγe e e 和,可以得到,需要注意的是公式中的e max 和γdmin 是对应的,而e min 和γdmax 是对应的。
2-3 如图2-16所示,在恒定的总水头差之下水自下而上透过两个土样,从土样1顶面溢出。
(1) 已土样2底面c -c 为基准面,求该面的总水头和静水头;(2) 已知水流经土样2的水头损失为总水头差的30%,求 b -b 面的总水头和静水头;(3) 已知土样2的渗透系数为0.05cm/s ,求单位时间内土样横截面单位面积的流量; ( 4 ) 求土样1的渗透系数。
图2-16 习题2-3图 (单位:cm )2-3 如图2-16,本题为定水头实验,水自下而上流过两个土样,相关几何参数列于图中。
解:(1)以c-c 为基准面,则有:z c =0,h wc =90cm ,h c =90cm(2)已知∆h bc =30%⨯∆h ac ,而∆h ac 由图2-16知,为30cm ,所以:∆h bc =30%⨯∆h ac =0.3⨯30=9cm∴ h b =h c -∆h bc =90-9=81cm又∵ z b =30cm ,故 h wb =h b - z b =81-30=51cm(3)已知k 2=0.05cm/s ,q/A=k 2i 2= k 2⨯∆h bc /L 2=0.05⨯9/30=0.015cm 3/s/cm 2=0.015cm/s(4)∵ i 1=∆h ab /L 1=(∆h ac -∆h bc )/L 1=(30-9)/30=0.7,而且由连续性条件,q/A=k 1i 1=k 2i 2 ∴ k 1=k 2i 2/i 1=0.015/0.7=0.021cm/s2-5 如图2-17所示,在5.0m 厚的黏土层下有一砂土层厚6.0 m ,其下为基岩(不透水)。
为测定该沙土的渗透系数,打一钻孔到基岩顶面并以10-2m 3/s 的速率从孔中抽水。
在距抽水孔15m 和30m 处各打一观测孔穿过黏土层进入砂土层,测得孔内稳定水位分别在地面以下3.0m 和2.5m ,试求该砂土的渗透系数。
图2-17 习题2-5图 (单位:m )2-5 分析:如图2-17,砂土为透水土层,厚6m ,上覆粘土为不透水土层,厚5m ,因为粘土层不透水,所以任意位置处的过水断面的高度均为砂土层的厚度,即6m 。
题目又给出了r 1=15m ,r 2=30m ,h 1=8m ,h 2=8.5m 。
解:由达西定律(2-6),drdh r k dr dh r k kAi q ππ1262=⋅⋅==,可改写为: )(12ln ,121212h h k r r q dh k r dr q -=⋅=ππ积分后得到: 带入已知条件,得到:cm/s 103.68m/s 1068.31530ln )85.8(1201.0ln )(123-41212⨯=⨯=-=-=-ππr r h h q k 本题的要点在于对过水断面的理解。
另外,还有个别同学将ln 当作了lg 。
2-6 如图2-18,其中土层渗透系数为5.0×10-2 m 3/s ,其下为不透水层。
在该土层内打一半径为0.12m 的钻孔至不透水层,并从孔内抽水。
已知抽水前地下水位在不透水层以上10.0m ,测得抽水后孔内水位降低了2.0m ,抽水的影响半径为70.0m ,试问:(1) 单位时间的抽水量是多少?(2) 若抽水孔水位仍降低2.0 ,但要求扩大影响,半径应加大还是减小抽水速率?图2-18 习题2-6图 (单位:m )2-6 分析:本题只给出了一个抽水孔,但给出了影响半径和水位的降低幅度,所以仍然可以求解。
另外,由于地下水位就在透水土层内,所以可以直接应用公式(2-18)。
解:(1)改写公式(2-18),得到:s /m 1088.8)12.0/70ln()810(105)/ln()(33224122122--⨯=-⨯=-=ππr r h h k q (2)由上式看出,当k 、r 1、h 1、h 2均为定值时,q 与r 2成负相关,所以欲扩大影响半径,应该降低抽水速率。
注意:本题中,影响半径相当于r 2,井孔的半径相当于r 1。
2-9 试验装置如图2-20所示,土样横截面积为30cm 2,测得10min 内透过土样渗入其下容器的水重0.018N ,求土样的渗透系数及其所受的渗透力。
图2-20 习题2-9图 (单位:cm )2-9 分析:本题可看成为定水头渗透试验,关键是确定水头损失。
解:以土样下表面为基准面,则上表面的总水头为:cm 1008020=+=上h下表面直接与空气接触,故压力水头为零,又因势水头也为零,故总水头为:cm 000=+=下h所以渗流流经土样产生的水头损失为100cm ,由此得水力梯度为:520100==∆=L h i 渗流速度为:cm/s 101m/s 101103060101010018.04-643⨯=⨯=⨯⨯⨯⨯⨯==---tA W v w w γ cm /s 102510154--⨯=⨯==∴i v k 30NkN 03.02.0103050kN/m505104==⨯⨯⨯===⨯==-jV J i j w γ注意:1.∆h 的计算;2.单位的换算与统一。
3-1 取一均匀土样,置于 x 、y 、z 直角坐标中,在外力作用下测得应力为: x σ=10kPa ,yσ=10kPa ,z σ=40kPa ,xy τ=12kPa 。
试求算:① 最大主应力 ,最小主应力 ,以及最大剪应力τmax ?② 求最大主应力作用面与 x 轴的夹角θ? ③根据1σ和3σ绘出相应的摩尔应力圆,并在圆上标出大小主应力及最大剪应力作用面的相对位置?3-1 分析:因为0==yz xz ττ,所以z σ为主应力。
解:由公式(3-3),在xoy 平面内,有:kPa 222121012)21010()1010(5.0)2()(215.0222/12231-=±=⎥⎦⎤⎢⎣⎡+-±+⨯=⎥⎦⎤⎢⎣⎡+-±+='xy y x y x τσσσσσσ 比较知,kPa 2kPa 22kPa 403121-=='===σσσσσz ,于是:应力圆的半径: kPa 21))2(40(5.0)(2131=--⨯=-=σσR 圆心坐标为: kPa 19))2(40(5.0)(2131=-+⨯=+σσ 由此可以画出应力圆并表示出各面之间的夹角。