15.3.5 卡诺图化简逻辑函数练习题

Made by 遇见 第一套一．选择题（18分）1．以下式子中不正确的是（ ） a ．1•A ＝A b ．A ＋A=A c ．B A B A +=+ d ．1＋A ＝12．已知B A B B A Y ++=下列结果中正确的是（ ）a ．Y ＝Ab ．Y ＝Bc ．Y ＝A ＋Bd ．B A Y +=3．TTL 反相器输入为低电平时其静态输入电流为（ ） a ．－3mA b ．＋5mA c ．－1mA d ．－7mA4．下列说法不正确的是（ ） a ．集电极开路的门称为OC 门b ．三态门输出端有可能出现三种状态（高阻态、高电平、低电平）c ．OC 门输出端直接连接可以实现正逻辑的线或运算d 利用三态门电路可实现双向传输 5．以下错误的是（ ）a ．数字比较器可以比较数字大小b ．实现两个一位二进制数相加的电路叫全加器c ．实现两个一位二进制数和来自低位的进位相加的电路叫全加器d ．编码器可分为普通全加器和优先编码器 6．下列描述不正确的是（ ）a ．触发器具有两种状态，当Q=1时触发器处于1态b ．时序电路必然存在状态循环c ．异步时序电路的响应速度要比同步时序电路的响应速度慢d ．边沿触发器具有前沿触发和后沿触发两种方式，能有效克服同步触发器的空翻现象 7．电路如下图（图中为下降沿Jk 触发器），触发器当前状态Q 3 Q 2 Q 1为“011”，请问时钟作用下，触发器下一状态为（ ）a ．“110”b ．“100”c ．“010”d ．“000”8、下列描述不正确的是（ ）a ．时序逻辑电路某一时刻的电路状态取决于电路进入该时刻前所处的状态。

b ．寄存器只能存储小量数据，存储器可存储大量数据。

c ．主从JK 触发器主触发器具有一次翻转性d ．上面描述至少有一个不正确 9．下列描述不正确的是（ ）a ．EEPROM 具有数据长期保存的功能且比EPROM 使用方便b ．集成二—十进制计数器和集成二进制计数器均可方便扩展。

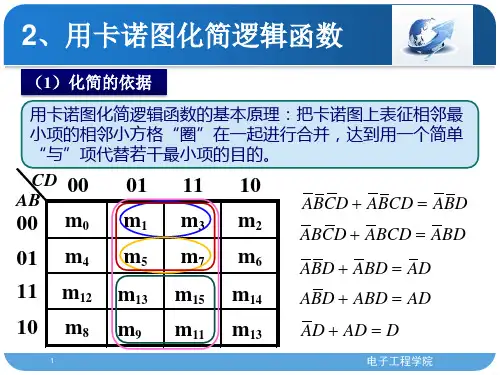
数字电路证明化简题练习与复习题证明化简题1（1）证明下列恒等式：B A C AB B A A +=++ （2）用代数法化简函数： )(A B C A B Y +=（3）用卡诺图法化简函数：D C A D C A C B A D C ABD ABC L +++++=证明化简题1参考答案（1）证明：右边）（左边=+=+=++=++=B A B A A B A C AB A C AB B A A 。

（2）AB （BC +A ）= ABC+AB=AB （3）∴D A L +=证明化简题2（1）证明下列恒等式：（2）用代数法化简下列各式：)(C B BC A Y += （3）用卡诺图法化简：C B C B C A C A L +++=证明化简题参考答案 1． 证明： 左边==右边2．答案：C AB C C B C B C A AB C B C B BC A Y +=++++=+++=+=）（)C B (A )( 3．∴B A C B C A L ++=化简题31 、 B A B A B A AB Y +++=12、))((Y 2C B A C B A ++++=3、C AB C B BC A AC Y +++=3化简题3参考答案BA AB B A B A ⋅+=+B A AB B A B A B A B A B A B A +=++=∙=+))((（1）B A B A B A AB Y +++=1=0 （2）))((Y 2C B A C B A ++++== A +B（3）C Y =34化简题4（1）C B AC BC A L++=（2）C AB C B BC A AC Y +++=（3）L （A,B,C,D ）=∑m （3,4,5,6,9,10,12,13,14,15） 化简题4参考答案 （1）CC AC C B B AC C B BC AC C B C B A C B C A B A C B AC BC A L =+=++=++=++=++=++=)()()(（2）C AB C B BC A AC +++=C AB C B BC A AC ++⋅(摩根定律)=C AB C B C B A C A ++++⋅+)()((摩根定律) =C AB C B C C B C A C A B A ++++++（分配律） =C B C B A ++（吸收律） =B C B A ++（吸收律） =B C +（吸收律）=BC (摩根定律)（3）L （A ,B ,C ,D ）=∑m （3,4,5,6,9,10,12,13,14,15）将逻辑函数填入卡诺图并圈“1”，如下图所示。

公式化简习题：1、用公式化简法将C B BC BC A ABC A ++++=F 化为最简与或式。

(要求化简过程)解：F=A +ABC +ABC̅̅̅̅+BC +B ̅C =A (1+BC )+ABC̅̅̅̅+BC +B ̅C =A+A BC̅̅̅̅+BC +B ̅C =A(1+BC̅̅̅̅)+BC+B ̅C =A+C(B+B̅) =A+C2、用公式化简法将AB B A B A C B A Y ++=),,(化为最简与或式(要求写出过程)。

解：Y (A,B,C )=AB̅+A ̅B +AB =A (B +B̅)+A ̅B =A +A̅B =A +B3、用公式化简法将)(),,(C A B B A C B A Y +++=化为最简与或式(要求写出过程)。

解：Y (A,B,C )=AB ̅+B +(A +C̅)̅̅̅̅̅̅̅̅̅̅ =AB̅+B +A ̅C =A +B +C4、用公式化简法将BD A CD B A D C B A Y ++=),,,(化为最简与或式(要求写出过程)。

解：Y (A,B,C,D )=A +B̅CD +A ̅BD =A +BD +B̅CD =A +D (B +B̅C ) =A +D (B +C )=A +BD +CD5、用公式化简法将D C A ABD CD B A D C B A Y ++=),,,(化为最简与或式(要求写出过程)。

解：Y (A,B,C,D )=AB̅CD +ABD +AC ̅D =AD(B̅C +B +C ̅) =AD(B +C +C̅) =AD (B +1)=AD卡诺图化简习题：1. 用卡诺图法化简函数Y(A 、B 、C 、D)= ∑m(1,2,5,6,9)+ ∑d(10,11,12,13,14,15)。

式中d 表示无关项，求其最简与或表达式。

(要求圈出过程)卡诺图如下：2. 用卡诺图法化简函数Y(A 、B 、C 、D)=，求其最简与或表达式(要求圈出过程)。

第三章逻辑代数基础（Basis of Logic Algebra）1．知识要点逻辑代数（Logic Algebra）的公理、定理及其在逻辑代数化简时的作用；逻辑函数的表达形式及相互转换；最小项（Minterm）和最大项（Maxterm）的基本概念和性质；利用卡诺图（Karnaugh Maps）化简逻辑函数的方法。

重点：1．逻辑代数的公理（Axioms）、定理（Theorems），正负逻辑（Positive Logic, Negative Logic）的概念与对偶关系（Duality Theorems）、反演关系（Complement Theorems）、香农展开定理，及其在逻辑代数化简时的作用；2．逻辑函数的表达形式：积之和与和之积标准型、真值表（Truth Table）、卡诺图（Karnaugh Maps）、最小逻辑表达式之间的关系及相互转换；3．最小项（Minterm）和最大项（Maxterm）的基本概念和性质；4．利用卡诺图化简逻辑函数的方法。

难点：利用卡诺图对逻辑函数进行化简与运算的方法（1）正逻辑（Positive Logic）、负逻辑（Negative Logic）的概念以及两者之间的关系。

数字电路中用电压的高低表示逻辑值1和0，将代数中低电压（一般为参考地0V）附近的信号称为低电平，将代数中高电压（一般为电源电压）附近的信号称为高电平。

以高电平表示1，低电平表示0，实现的逻辑关系称为正逻辑（Positive Logic），相反，以高电平表示0，低电平表示1，实现的逻辑关系称为负逻辑（Negative Logic），两者之间的逻辑关系为对偶关系。

（2）逻辑函数的标准表达式积之和标准形式（又称为标准和、最小项和式）：每个与项都是最小项的与或表达式。

和之积标准形式（又称为标准积、最大项积式）：每个或项都是最大项的或与表达式。

逻辑函数的表达形式具有多样性，但标准形式是唯一的，它们和真值表之间有严格的对应关系。

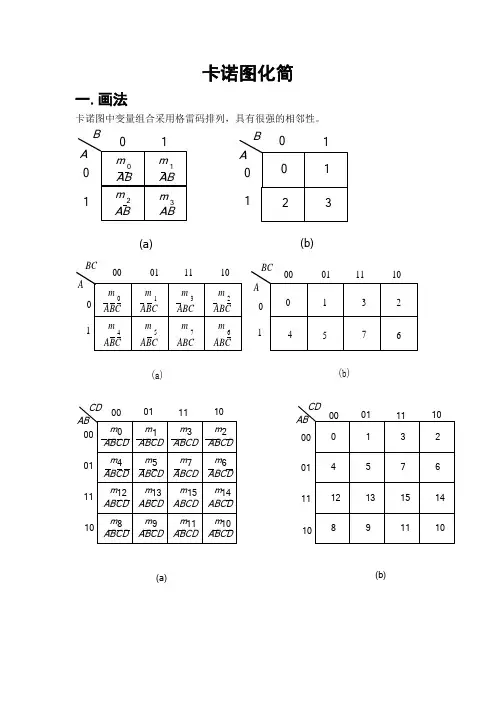
卡诺图化简一.画法卡诺图中变量组合采用格雷码排列，具有很强的相邻性。

0110m AB m AB1m 03m AB AB2(a)0132B (b)B A0101A0m ABC m ABC 1m 3m ABC ABC 265m ABC74ABCm m m ABCABC 0(a)(b)132457610011100BC A01BC A 1001110001m 0ABCD ABCD m 1ABCD m 3m ABCD 2m 567m m ABCD ABCD m ABCD 4ABCD ABCD m m 13ABCDABCD 1412m 15m ABCDABCDABCDm ABCD8m 1011m 9m ABCD 0132765413141512981110ABCD0000010*******10(a)(b)ABCD 0000010111111010二．步骤1．逻辑函数化为最小项表达式；写出最小项之和的形式、标准与或式2．根据变量的个数画出相应的卡诺图。

3．画卡诺圈并检查；填卡诺图（Y中包含的最小项填1），画包围圈（2n个相邻方格组，n=1，2，…4．将各卡诺圈合并为与项；各包围圈合并为一个与项（消去形式不同的变量，保留形式相同的变量5．将所有与项相加写出最简与或表达式合并后的各与项相加即为化简的逻辑函数三．注意：1．卡诺圈的面积要尽可能大，这样消去的变量就多，可保证与项中变量最少。

2．卡诺圈的个数要尽可能少，每个卡诺圈合并后代表一个与项，这样可保证与项最少。

3．每个卡诺圈内方格数为2n（n=0，1，2…），根据“去异留同”的原理将这2n个相邻的最小项结合，可以消去n个共有并且互补的变量而合并为一项。

4. 卡诺图中所有取值为1的方格均要被圈过，不能漏下。

5．取值为1的同一方格可被不同卡诺圈重复包围，但新增卡诺圈要有新方格。

6. 相邻方格包括上下相邻、左右相邻、四角相邻（注意对角不相邻）。

综上所述，画卡诺圈时应遵循先画大圈后画小圈的顺序，同时要保证圈内方格数为2n且不能漏下任何1方格。

第三章逻辑代数基础（Basis of Logic Algebra）1．知识要点逻辑代数（Logic Algebra）的公理、定理及其在逻辑代数化简时的作用；逻辑函数的表达形式及相互转换；最小项（Minterm）和最大项（Maxterm）的基本概念和性质；利用卡诺图（Karnaugh Maps）化简逻辑函数的方法。

重点：1．逻辑代数的公理（Axioms）、定理（Theorems），正负逻辑（Positive Logic, Negative Logic）的概念与对偶关系（Duality Theorems）、反演关系（Complement Theorems）、香农展开定理，及其在逻辑代数化简时的作用；2．逻辑函数的表达形式：积之和与和之积标准型、真值表（Truth Table）、卡诺图（Karnaugh Maps）、最小逻辑表达式之间的关系及相互转换；3．最小项（Minterm）和最大项（Maxterm）的基本概念和性质；4．利用卡诺图化简逻辑函数的方法。

难点：利用卡诺图对逻辑函数进行化简与运算的方法（1）正逻辑（Positive Logic）、负逻辑（Negative Logic）的概念以及两者之间的关系。

数字电路中用电压的高低表示逻辑值1和0，将代数中低电压（一般为参考地0V）附近的信号称为低电平，将代数中高电压（一般为电源电压）附近的信号称为高电平。

以高电平表示1，低电平表示0，实现的逻辑关系称为正逻辑（Positive Logic），相反，以高电平表示0，低电平表示1，实现的逻辑关系称为负逻辑（Negative Logic），两者之间的逻辑关系为对偶关系。

（2）逻辑函数的标准表达式积之和标准形式（又称为标准和、最小项和式）：每个与项都是最小项的与或表达式。

和之积标准形式（又称为标准积、最大项积式）：每个或项都是最大项的或与表达式。

逻辑函数的表达形式具有多样性，但标准形式是唯一的，它们和真值表之间有严格的对应关系。

§8-6 卡诺图化简逻辑函数练习题
一、将下列卡诺图表示的函数，化简为最简“与或”式
1、2、3、
4、5、
6、
10、11、12、
13、14、15、
二、用卡诺图化简下列逻辑函数 1、108753210m m m m m m m m +++++++=）（ABCD Y 2、C B A ABC BC A Y ++= 3、C B A BC C A Y ++= 4、∑=），（）（7,5,21,0m ABC Y 5、A AB Y +=
6、C B C B C A Y ++=
7、BC D B C B Y ++=
8、D BC A C B A D C A C B CD B Y ++++= 9、∑=），，，（）（7654m ABC Y 10、∑=），，，，，（）（753210m ABC Y 11、∑=），，，，，，，，（）（11108543210m ABCD Y 12、∑=），，，，，，，，，（）（151413111098762m ABCD Y
三、根据要求设计逻辑电路
1、某剧团选舞蹈演员，有四个评委，每个评委桌上有一按键，2个以上评委亮灯，表示选手通过初选（选
手身后灯亮，）否则未通过（灯不亮）。

2、某剧团选舞蹈演员，三位评委（一名主评委，两名副评委），选拔规则：主评委和一名副
评委按键说明初选通过，否则表演不成功未通过。

每个评委桌上有一按键，演员身后有一心形红灯。

逻辑“1”表示评委按下按键，逻辑“0”表示未按按键；Y=1表示表演成功（舞台灯光亮、音乐响起），Y=0表示表演失败（舞台灯光不亮、无音乐）。

设计逻辑电路，实现此功能。