2015—2016学年高二培优材料-----圆锥曲线(2)

高二数学圆锥曲线试题答案及解析1.已知椭圆的离心率，右焦点为，方程的两个实根，，则点（）A．必在圆内B．必在圆上C．必在圆外D．以上三种情况都有可能【答案】A【解析】本题只要判断与2的大小，时，点在圆上；时，点在圆内；时，点在圆外.由已知，，椭圆离心率为，从而，点在圆内，故选A.【考点】1.点与圆的位置关系；2.二次方程根与系数的关系.2.若抛物线y2＝4x上的点A到其焦点的距离是6，则点A的横坐标是( )A．5B．6C．7D．8【答案】A【解析】由抛物线的方程可知抛物线的准线为，根据抛物线的定义可知点到其准线的距离也为6，即，所以。

故A正确。

【考点】抛物线的定义。

3.设一个焦点为,且离心率的椭圆上下两顶点分别为,直线交椭圆于两点,直线与直线交于点.(1)求椭圆的方程；(2)求证：三点共线.【答案】(1)(2)详见解析.【解析】(1)利用椭圆的定义和几何性质；(2)直线与圆锥曲线相交问题，可以设而不求，联立直线与椭圆方程，利用韦达定理结合题目条件来证明.试题解析：(1)由题知，，∴，3分∴椭圆.4分(2) 设点，由(1)知∴直线的方程为，∴.5分∴，，8分由方程组化简得:,,.10分∴,∴三点共线.12分【考点】1.椭圆的标准方程；2.直线与圆锥曲线相交问题；3.韦达定理.4.已知双曲线的右焦点为，若过且倾斜角为的直线与双曲线的右支有且只有一个交点，则双曲线离心率的取值范围是( )A．B．C．D．【答案】A【解析】由渐进线的斜率.又因为过且倾斜角为的直线与双曲线的右支有且只有一个交点，所以.所以.故选A.本小题关键是对比渐近线与过焦点的直线的斜率的大小.【考点】1.双曲线的渐近线.2.离心率.3.双曲线中量的关系.5.点P是抛物线y2 = 4x上一动点，则点P到点（0，－1）的距离与到抛物线准线的距离之和的最小值是 .【答案】【解析】抛物线y2 = 4x的焦点，点P到准线的距离与点P到点F的距离相等，本题即求点P到点的距离与到点的距离之和的最小值，画图可知最小值即为点与点间的距离，最小值为.【考点】抛物线的定义.6.准线方程为x=1的抛物线的标准方程是（）A．B．C．D．【答案】A【解析】由题意可知：=1，∴p=2且抛物线的标准方程的焦点在x轴的负半轴上故可设抛物线的标准方程为：y2=-2px,将p代入可得y2=-4x．选A.【考点】抛物线的性质点评：本题主要考查抛物线的基本性质以及计算能力．在涉及到求抛物线的标准方程问题时，一定要先判断出焦点所在位置，避免出错．7.动点到两定点,连线的斜率的乘积为（）,则动点P在以下哪些曲线上（）（写出所有可能的序号）①直线②椭圆③双曲线④抛物线⑤圆A．①⑤B．③④⑤C．①②③⑤D．①②③④⑤【答案】C【解析】由题设知直线PA与PB的斜率存在且均不为零所以kPA •kPB=，整理得，点P的轨迹方程为kx2-y2=ka2（x≠±a）；①当k＞0，点P的轨迹是焦点在x轴上的双曲线（除去A，B两点）②当k=0，点P的轨迹是x轴（除去A，B两点）③当-1＜k＜0时，点P的轨迹是焦点在x轴上的椭圆（除去A，B两点）④当k=-1时，点P的轨迹是圆（除去A，B两点）⑤当k＜-1时，点P的轨迹是焦点在y轴上的椭圆（除去A，B两点）.故选C.【考点】圆锥曲线的轨迹问题．点评：本题考查圆锥曲线的轨迹问题，解题时要认真审题，注意分类讨论思想的合理运用．8.已知F1，F2是椭圆 (a＞b＞0)的左，右焦点，点P是椭圆在y轴右侧上的点，且∠F1PF2＝，记线段PF1与y轴的交点为Q，O为坐标原点，若△F1OQ与四边形OF2PQ的面积之比为1∶2，则该椭圆的离心率等于【答案】－1【解析】根据题意，由于F1，F2是椭圆 (a＞b＞0)的左，右焦点，点P是椭圆在y轴右侧上的点，且∠F1PF2＝，且有△F1OQ与四边形OF2PQ的面积之比为1∶2，则可知为点P到x轴的距离是Q到x轴距离的3：2倍，那么结合勾股定理可知该椭圆的离心率等于－1 ，故答案为－1 。

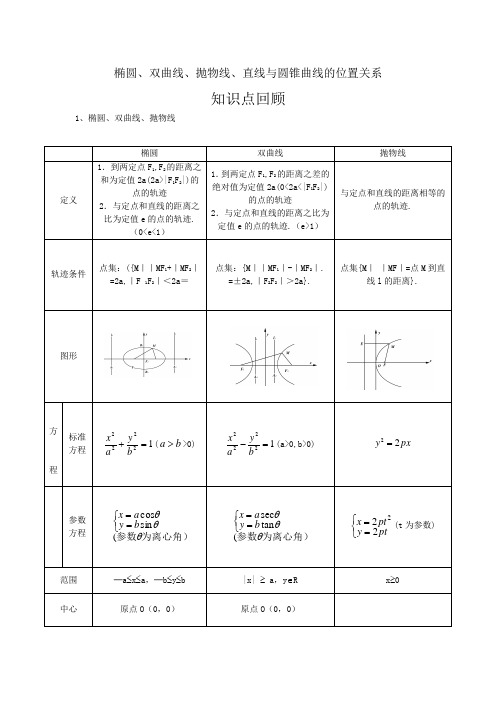
椭圆、双曲线、抛物线、直线与圆锥曲线的位置关系知识点回顾1、椭圆、双曲线、抛物线椭圆双曲线抛物线定义1．到两定点F1,F2的距离之和为定值2a(2a>|F1F2|)的点的轨迹2．与定点和直线的距离之比为定值e的点的轨迹.（0<e<1）1．到两定点F1,F2的距离之差的绝对值为定值2a(0<2a<|F1F2|)的点的轨迹2．与定点和直线的距离之比为定值e的点的轨迹.（e>1）与定点和直线的距离相等的点的轨迹.轨迹条件点集：({M｜｜MF1+｜MF2｜=2a,｜F 1F2｜＜2a＝点集：{M｜｜MF1｜-｜MF2｜.=±2a,｜F2F2｜＞2a}.点集{M｜｜MF｜=点M到直线l的距离}.图形方程标准方程12222=+byax(ba>>0) 12222=-byax(a>0,b>0) pxy22=参数方程为离心角）参数θθθ(sincos⎩⎨⎧==byax为离心角）参数θθθ(tansec⎩⎨⎧==byax⎩⎨⎧==ptyptx222(t为参数)范围─a≤x≤a，─b≤y≤b |x| ≥ a，y∈R x≥0中心原点O（0，0）原点O（0，0）补充： 双曲线：(1)等轴双曲线：双曲线222a y x ±=-称为等轴双曲线，其渐近线方程为x y ±=，离心率2=e .(2)共轭双曲线：以已知双曲线的虚轴为实轴，实轴为虚轴的双曲线，叫做已知双曲线的共轭双曲线.λ=-2222b y a x 与λ-=-2222by a x 互为共轭双曲线，它们具有共同的渐近线：02222=-b y a x .抛物线：（1）抛物线2y =2px(p>0)的焦点坐标是(2p ,0)，准线方程x=-2p，开口向右；抛物线2y =-2px(p>0)的焦点坐标是(-2p ,0)，准线方程x=2p，开口向左；抛物线2x =2py(p>0)的焦点坐标是(0,2p )，准线方程y=-2p ，开口向上；抛物线2x =-2py （p>0）的焦点坐标是（0,-2p ），准线方程y=2p ，开口向下.（2）抛物线2y =2px(p>0)上的点M(x0,y0)与焦点F 的距离20p x MF +=；抛物线2y =-2px(p>0)上的点M(x0,y0)与焦点F 的距离02x pMF -=（3）设抛物线的标准方程为2y =2px(p>0)，则抛物线的焦点到其顶点的距离为2p ，顶点到顶点(a,0), (─a,0), (0,b) , (0,─b) (a,0), (─a,0) (0,0)对称轴 x 轴，y 轴； 长轴长2a,短轴长2bx 轴，y 轴;实轴长2a, 虚轴长2b.x 轴焦点 F 1(c,0), F 2(─c,0) F 1(c,0), F 2(─c,0))0,2(p F 准 线x=±ca 2准线垂直于长轴，且在椭圆外.x=±ca 2准线垂直于实轴，且在两顶点的内侧.x=-2p 准线与焦点位于顶点两侧，且到顶点的距离相等.焦距2c （c=22b a -）2c （c=22b a +）离心率)10(<<=e ace )1(>=e ace e=1准线的距离2p，焦点到准线的距离为p. （4）已知过抛物线2y =2px(p>0)焦点的直线交抛物线于A 、B 两点，则线段AB 称为焦点弦，设A(x1,y1),B(x2,y2)，则弦长AB =21x x ++p ，12pAF x =+(AF 叫做焦半径). 2、直线与圆锥曲线的位置关系 （1）、相切、相交、相离（2）、弦长公式：斜率为k 的直线l 与圆锥曲线C 相交于A ()11,x y B ()22,x y ，两个不同的点()22221212121221()11AB x x y y k x x y y k =-+-=+-=+-3、常用方法（1）巧用椭圆、双曲线的第二定义（2）解圆锥曲线经常用“设而不求”的方法，设而不求法对于直线与圆锥曲线相交而产生的弦中点问题，常用“点差法”，即设弦的两个端点A(x1,y1),B(x2,y2),弦AB 中点为M(x0,y0)，将点A 、B 坐标代入圆锥曲线方程，作差后，产生弦中点与弦斜率的关系，这是一种常见的“设而不求”法（3）巧用韦达定理，直线与圆锥曲线的问题常转化为方程组关系问题，最终转化为一元二次方程问题，最好用韦达定理及判别式是解决圆锥曲线问题，尤其在弦中点问题，弦长问题，可用韦达定理直接解决经典练习：一、选择题1、设12F F 是椭圆2222:1(0)x y E a b a b+=>>的左、右焦点，P 为直线32ax =上一点，12PF F ∆是底角为30的等腰三角形，则E 的离心率为（ ）()A 12 ()B 23 ()C 34()D 452、等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线x y 162=的准线交于,A B 两点，43AB =；则C 的实轴长为（ ）()A 2 ()B 2 ()C 4 ()D 83、已知双曲线1C ：22221(0,0)x y a b a b -=>>的离心率为2.若抛物线22:2(0)C x py p =>的焦点到双曲线1C 的渐近线的距离为2，则抛物线2C 的方程为（ ） (A) 2833x y =(B) 21633x y = (C)28x y = (D)216x y = 4、椭圆的中心在原点，焦距为4，一条准线为4x =-，则该椭圆的方程为（A ）2211612x y += （B ）221128x y += （C ）22184x y += （D ）221124x y +=5、已知1F 、2F 为双曲线22:2C x y -=的左、右焦点，点P 在C 上，12||2||PF PF =，则12cos F PF ∠= （A ）14 （B ）35 （C ）34 （D ）456、 如图，中心均为原点O 的双曲线与椭圆有公共焦点，M ，N 是双曲线的两顶点。

2015—2016学年高二培优材料-----圆锥曲线（3）------------ 直线与圆锥曲线的综合应用(2) 题型1 最值问题【例1】(文)(2014·南京、盐城一模)在平面直角坐标系xOy 中，已知椭圆C ：x 2a 2＋y 2b2＝1(a ＞b ＞0)的左、右焦点分别为F 1、F 2，焦距为2，一条准线方程为x ＝2.P 为椭圆C 上一点，直线PF 1交椭圆C 于另一点Q.(1) 求椭圆C 的方程；(2) 若点P 的坐标为(0，b)，求过P 、Q 、F 2三点的圆的方程；(3) 若F 1P →＝λQF 1→，且λ∈⎣⎡⎦⎤12，2，求OP →·OQ →的最大值． 解：(1) 由题意得⎩⎪⎨⎪⎧2c ＝2，a 2c ＝2，解得c ＝1，a 2＝2，所以b 2＝a 2－c 2＝1.所以椭圆的方程为x 22＋y 2＝1.(2) 因为P(0，1)，F 1(－1，0)， 所以PF 1的方程为x －y ＋1＝0.由⎩⎪⎨⎪⎧x －y ＋1＝0，x 22＋y 2＝1，解得⎩⎪⎨⎪⎧x ＝0，y ＝1，或⎩⎨⎧x ＝－43，y ＝－13， 所以点Q 的坐标为⎝⎛⎭⎫－43，－13. (解法1)因为kPF 1·kPF 2＝－1，所以△PQF 2为直角三角形．因为QF 2的中点为⎝⎛⎭⎫－16，－16，QF 2＝523， 所以圆的方程为⎝⎛⎭⎫x ＋162＋⎝⎛⎭⎫y ＋162＝2518.(解法2)设过P 、Q 、F 2三点的圆为x 2＋y 2＋Dx ＋Ey ＋F ＝0，则⎩⎪⎨⎪⎧1＋E ＋F ＝0，1＋D ＋F ＝0，179－43D －13E ＋F ＝0，解得⎩⎪⎨⎪⎧D ＝13，E ＝13，F ＝－43.所以圆的方程为x 2＋y 2＋13x ＋13y －43＝0.(3) 设P(x 1，y 1)，Q(x 2，y 2)，则F 1P →＝(x 1＋1，y 1)，QF 1→＝(－1－x 2，－y 2)．因为F 1P →＝λQF 1→，所以⎩⎪⎨⎪⎧x 1＋1＝λ（－1－x 2），y 1＝－λy 2，即⎩⎪⎨⎪⎧x 1＝－1－λ－λx 2，y 1＝－λy 2， 所以⎩⎨⎧（－1－λ－λx 2）22＋λ2y 22＝1，x 222＋y 22＝1，解得x 2＝1－3λ2λ.所以OP →·OQ →＝x 1x 2＋y 1y 2＝x 2(－1－λ－λx 2)－λy 22＝－λ2x 22－(1＋λ)x 2－λ＝－λ2⎝⎛⎭⎫1－3λ2λ2－(1＋λ)·1－3λ2λ－λ＝74－58⎝⎛⎭⎫λ＋1.因为λ∈⎣⎡⎦⎤12，2，所以λ＋1λ≥2λ·1λ＝2，当且仅当λ＝1λ，即λ＝1时取等号． 所以OP →·OQ →≤12，即OP →·OQ →的最大值为12.(理)如图，椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的离心率为12，其左焦点到点P(2，1)的距离为10.不过原点O 的直线l 与C 相交于A 、B 两点，且线段AB 被直线OP 平分．(1) 求椭圆C 的方程；(2) 求△ABP 面积取最大值时直线l 的方程．解：(1) 设椭圆左焦点为F(－c ，0)，则由题意得⎩⎪⎨⎪⎧（2＋c ）2＋1＝10，c a ＝12，得⎩⎪⎨⎪⎧c ＝1，a ＝2.所以椭圆方程为x 24＋y 23＝1.(2) 设A(x 1，y 1)，B(x 2，y 2)，线段AB 的中点为M.当直线AB 与x 轴垂直时，直线AB 的方程为x ＝0，与不过原点的条件不符，舍去．故可设直线AB 的方程为y ＝kx ＋m(m ≠0)，由⎩⎪⎨⎪⎧y ＝kx ＋m ，3x 2＋4y 2＝12消去y ，整理得(3＋4k 2)x 2＋8kmx ＋4m 2－12＝0，① 则Δ＝64k 2m 2－4(3＋4k 2)(4m 2－12)＞0，⎩⎪⎨⎪⎧x 1＋x 2＝－8km3＋4k 2，x 1x 2＝4m 2－123＋4k 2，所以线段AB 的中点为M ⎝⎛⎭⎫－4km 3＋4k 2，3m3＋4k 2.因为M 在直线OP ：y ＝12x 上，所以3m 3＋4k 2＝－2km 3＋4k2，得m ＝0(舍去)或k ＝－32. 此时方程①为3x 2－3mx ＋m 2－3＝0，则Δ＝3(12－m 2)＞0，⎩⎪⎨⎪⎧x 1＋x 2＝m ，x 1x 2＝m 2－33.所以AB ＝1＋k 2·|x 1－x 2|＝396·12－m 2，设点P 到直线AB 的距离为d ，则d ＝|8－2m|32＋22＝2|m －4|13.设△ABP 的面积为S ，则S ＝12AB ·d ＝36·（m －4）2·（12－m 2）.其中m ∈(－23，0)∪(0，23)．令u(m)＝(12－m 2)(m －4)2，m ∈[－23，23]， u ′(m)＝－4(m －4)(m 2－2m －6)＝－4(m －4)·(m －1－7)(m －1＋7)．所以当且仅当m ＝1－7时，u(m)取到最大值．故当且仅当m ＝1－7时，S 取到最大值．综上，所求直线l 的方程为3x ＋2y ＋27－2＝0. 变式训练(文)(2014·泰州期末)已知椭圆C ：x 2a 2＋y 2b2＝1(a>b>0)和圆O ：x 2＋y 2＝a 2，F 1(－1，0)、F 2(1，0)分别是椭圆的左、右两焦点，过F 1且倾斜角为α⎝⎛⎭⎫α∈⎝⎛⎦⎤0，π2的动直线l 交椭圆C 于A 、B 两点，交圆O 于P 、Q 两点(如图所示，点A 在x 轴上方)．当α＝π4时，弦PQ 的长为14.(1) 求圆O 与椭圆C 的方程；(2) 若点M 是椭圆C 上一点，求当AF 2、BF 2、AB 成等差数列时，△MPQ 面积的最大值．解：(1) 取PQ 的中点D ，连结OD 、OP.由α＝π4，c ＝1，知OD ＝22，∵ PQ ＝14，∴ OP 2＝PQ 24＋OD 2＝4，∴ a 2＝4，b 2＝3，∴ 椭圆C 的方程为x 24＋y23＝1，圆O 为x 2＋y 2＝4.(2) 设AF 2＝s ，BF 2＝t ，∵ AF 1＋AF 2＝2a ＝4，BF 1＋BF 2＝2a ＝4，∵ AF 2、BF 2、AB的长成等差数列，∴ 2t ＝s ＋8－s －t ，∴ t ＝83.设B(x 0，y 0)，由⎩⎨⎧（x 0－1）2＋y 20＝649，x 204＋y 203＝1，得B(－43，－153)，∴ k ＝15，∴ PQ ：y ＝15(x ＋1)，∴ PQ ＝72.易求得椭圆上一点到直线PQ 的距离的最大值是37＋154，∴ △MPQ 的面积的最大值是217＋71516.(理)如图，在平面直角坐标系xOy 中，椭圆的中心在原点O ，右焦点F 在x 轴上，椭圆与y 轴交于A 、B 两点，其右准线l 与x 轴交于T 点，直线BF 交椭圆于C 点，P 为椭圆上弧AC 上的一点．(1) 求证：A 、C 、T 三点共线；(2) 如果BF →＝3FC →，四边形APCB 的面积最大值为6＋23，求此时椭圆的方程和P 点坐标．(1) 证明：设椭圆方程为x 2a 2＋y 2b2＝1(a ＞b ＞0) ①，则A(0，b)，B(0，－b)，T ⎝⎛⎭⎫a 2c ，0.AT ：x a 2c ＋y b ＝1 ②，BF ：x c ＋y －b ＝1 ③，解得交点C(2a 2c a 2＋c 2，b 3a 2＋c 2)，代入①得⎝⎛⎭⎫2a 2c a 2＋c 22a 2＋⎝⎛⎭⎫b 3a 2＋c 22b 2＝4a 2c 2（a 2－c 2）2（a 2＋c 2）2＝1，满足①式，则C 点在椭圆上，即A 、C 、T 三点共线．(2) 解：过C 作CE ⊥x 轴，垂足为E ，则△OBF ∽△ECF.∵ BF →＝3FC →，CE ＝13b ，EF ＝13c ，则C ⎝⎛⎭⎫4c 3，b 3，代入①得⎝⎛⎭⎫43c 2a 2＋⎝⎛⎭⎫b 32b2＝1，∴ a 2＝2c 2，b 2＝c 2.设P(x 0，y 0)，则x 0＋2y 20＝2c 2.此时C ⎝⎛⎭⎫4c 3，c 3，AC ＝23 5c ，S △ABC ＝12·2c ·4c 3＝43c 2，直线AC 的方程为x ＋2y －2c ＝0，P 到直线AC 的距离为d ＝|x 0＋2y 0－2c|5＝x 0＋2y 0－2c5，S△APC ＝12d ·AC ＝12·x 0＋2y 0－2c 5·23 5c ＝x 0＋2y 0－2c 3·c ，只须求x 0＋2y 0的最大值． (解法1)∵ (x 0＋2y 0)＝x 20＋4y 20＋2·2x 0y 0≤x 20＋4y 20＋2(x 20＋y 20)＝3(x 20＋2y 20)＝6c 2，∴ x 0＋2y 0≤6c.当且仅当x 0＝y 0＝63c 时，(x 0＋2y 0)max ＝6c.(解法2)令x 0＋2y 0＝t ，代入x 20＋2y 20＝2c 2得(t －2y 0)2＋2y 20－2c 2＝0，即6y 20－4ty 0＋t 2－2c 2＝0.Δ＝(－4t)2－24(t 2－2c 2)≥0，得t ≤6c.当t ＝6c ，代入原方程解得x 0＝y 0＝63c.∴ 四边形的面积最大值为6－23c 2＋43c 2＝6＋23c 2＝6＋23，∴ c 2＝1，a 2＝2，b 2＝1，此时椭圆方程为x 22＋y 2＝1.P 点坐标为⎝⎛⎭⎫63，63.题型2 定值问题【例2】(文)如图，在直角坐标系xOy 中，椭圆E ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的焦距为2，且过点⎝⎛⎭⎫2，62.(1) 求椭圆E 的方程；(2) 若点A 、B 分别是椭圆E 的左、右顶点，直线l 经过点B 且垂直于x 轴，点P 是椭圆上异于A 、B 的任意一点，直线AP 交l 于点M.① 设直线OM 的斜率为k 1，直线BP 的斜率为k 2，求证：k 1k 2为定值；② 设过点M 垂直于PB 的直线为m.求证：直线m 过定点，并求出定点的坐标．(1) 解：由题意得2c ＝2 ，所以c ＝1.又2a 2＋32b2＝1，消去a 可得2b 4－5b 2－3＝0，解得b 2＝3或b 2＝－12(舍去)，则a 2＝4，所以椭圆E 的方程为x 24＋y 23＝1.(2) 证明：① 设P(x 1，y 1)(y 1≠0)，M(2，y 0)，则k 1＝y 02，k 2＝y 1x 1－2，因为A 、P 、M 三点共线，所以y 0＝4y 1x 1＋2， 则k 1k 2＝4y 212（x 21－4）.因为P(x 1，y 1)在椭圆上，所以y 21＝34(4－x 21)，则k 1k 2＝4y 212（x 21－4）＝－32为定值．② (方法1)直线BP 的斜率为k 2＝y 1x 1－2，直线m 的斜率为k m ＝2－x 1y 1，则直线m 的方程为y －y 0＝2－x 1y 1(x －2)，即y ＝2－x 1y 1(x －2)＋y 0＝2－x 1y 1(x －2)＋4y 1x 1＋2＝2－x 1y 1[(x －2)＋4y 214－x 21]＝2－x 1y 1⎣⎢⎡⎦⎥⎤（x －2）＋12－3x 214－x 21＝2－x 1y 1(x ＋1)，所以直线m 过定点(－1，0)． (方法2)直线BP 的斜率为k 2＝y 1x 1－2，直线m 的斜率为k m ＝2－x 1y 1，则直线m 的方程为y －4y 1x 1＋2＝2－x 1y 1(x －2)，若P 为(0，3)，则m 的方程为y ＝233x ＋233，若P 为(0，－3)，则m 的方程为y ＝－233x －233，两直线方程联立解得Q(－1，0)．因为k MQ ·k 2＝4y 13（x 1＋2）·y 1x 1－2＝4y 213（x 21－4）＝12－3x 213（x 21－4）＝－1，所以Q 在过M 且与BP 垂直的直线上，所以直线m 过定点(－1，0)．(理)如图，椭圆C 0：x 2a 2＋y 2b2＝1(a>b>0，a 、b 为常数)，动圆C 1：x 2＋y 2＝t 21，b<t 1<a.点A 1、A 2分别为C 0的左、右顶点，C 1与C 0相交于A 、B 、C 、D 四点．(1) 求直线AA 1与直线A 2B 交点M 的轨迹方程； (2) 设动圆C 2：x 2＋y 2＝t 22与C 0相交于A′，B ′，C ′，D ′四点，其中b<t 2<a ，t 1≠t 2.若矩形ABCD 与矩形A′B′C′D′的面积相等，证明：t 21＋t 22为定值．(1) 解：设A(x 1，y 1)，B(x 1，－y 1)，又知A 1(－a ，0)，A 2(a ，0)，则直线A 1A 的方程为y ＝y 1x 1＋a (x ＋a)，①直线A 2B 的方程为y ＝－y 1x 1－a(x －a)，②由①②得y 2＝－y 21x 21－a2(x 2－a 2)．③由点A(x 1，y 1)在椭圆C 0上，故x 21a 2＋y 21b2＝1.从而y 21＝b 2⎝⎛⎭⎫1－x 21a 2，代入③得x 2a 2－y 2b2＝1(x<－a ，y<0)．(2) 证明：设A′(x 2，y 2)，由矩形ABCD 与矩形A ′B ′C ′D ′的面积相等，得4|x 1||y 1|＝4|x 2||y 2|，故x 21y 21＝x 22y 22.因为点A ，A ′均在椭圆上，所以b 2x 21⎝⎛⎭⎫1－x 21a 2＝b 2x 22⎝⎛⎭⎫1－x 22a 2.由t 1≠t 2，知x 1≠x 2，所以x 21＋x 22＝a 2，从而y 21＋y 22＝b 2，因此t 21＋t 22＝a 2＋b 2为定值．变式训练(2014·苏锡常镇一模)如图，在平面直角坐标系xOy 中，已知A 、B 、C 是椭圆x 2a 2＋y 2b2＝1(a ＞b ＞0)上不同的三点，A ⎝⎛⎭⎫32，322，B(－3，－3)，C 在第三象限，线段BC 的中点在直线OA 上．(1) 求椭圆的标准方程； (2) 求点C 的坐标；(3) 设动点P 在椭圆上(异于点A 、B 、C)且直线PB 、PC 分别交直线OA 于M 、N 两点，证明：OM →·ON →为定值，并求出该定值．解：(1) 由已知，得⎩⎪⎨⎪⎧18a 2＋92b 2＝1，9a 2＋9b 2＝1，解得⎩⎪⎨⎪⎧a 2＝27，b 2＝272.∴ 椭圆的标准方程为x 227＋y 2272＝1.(2) 设点C(m ，n)(m ＜0，n ＜0)，则BC 中点为⎝⎛⎭⎫m －32，n －32.由已知，求得直线OA 的方程为x －2y ＝0，从而m ＝2n －3. ①∵ 点C 在椭圆上，∴ m 2＋2n 2＝27. ②由①②，解得n ＝3(舍)，n ＝－1，从而m ＝－5. ∴ 点C 的坐标为(－5，－1)．(3) 设P(x 0，y 0)，M(2y 1，y 1)，N(2y 2，y 2)． ∵ P 、B 、M 三点共线，∴ y 1＋32y 1＋3＝y 0＋3x 0＋3，整理，得y 1＝3（y 0－x 0）x 0－2y 0－3. ∵ P 、C 、N 三点共线，∴ y 2＋12y 2＋5＝y 0＋1x 0＋5，整理，得y 2＝5y 0－x 0x 0－2y 0＋3. ∵ 点P 在椭圆上，∴ x 20＋2y 20＝27，x 20＝27－2y 20.从而y 1y 2＝3（x 20＋5y 20－6x 0y 0）x 20＋4y 20－4x 0y 0－9＝3（3y 20－6x 0y 0＋27）2y 20－4x 0y 0＋18＝3×32＝92.∴ OM →·ON →＝5y 1y 2＝452. ∴ OM →·ON →为定值，定值为452.题型3 定点问题【例3】(文)(2014·南通一模)在平面直角坐标系xOy 中，设曲线C 1：|x|a ＋|y|b ＝1(a ＞b＞0)所围成的封闭图形的面积为4 2.曲线C 1上的点到原点O 的最短距离为223，以曲线C 1与坐标轴的交点为顶点的椭圆记为C 2.(1) 求椭圆C 2的标准方程；(2) 设AB 是过椭圆C 2中心O 的任意弦，l 是线段AB 的垂直平分线，M 是l 上的点(与O 不重合)．① 若MO ＝2OA ，当点A 在椭圆C 2上运动时，求点M 的轨迹方程； ② 若M 是l 与椭圆C 2的交点，求△AMB 面积的最小值．解：(1) 由题意得⎩⎪⎨⎪⎧2ab ＝42，ab a 2＋b2＝223.又a ＞b ＞0，解得a 2＝8，b 2＝1.因此所求椭圆的标准方程为x 28＋y 2＝1.(2) ① 设M(x ，y)，A(m ，n)，则由题设知：|OM →|＝2|OA →|，OA →·OM →＝0.即⎩⎪⎨⎪⎧x 2＋y 2＝4（m 2＋n 2），mx ＋ny ＝0，解得⎩⎨⎧m 2＝14y 2，n 2＝14x 2.因为点A(m ，n)在椭圆C 2上，所以m28＋n 2＝1，即⎝⎛⎭⎫y 228＋⎝⎛⎭⎫x 22＝1，亦即x 24＋y 232＝1.所以点M 的轨迹方程为x 24＋y 232＝1.② (解法1)设M(x ，y)，则A(λy ，－λx )(λ∈R ，λ≠0)，因为点A 在椭圆C 2上，所以λ2(y 2＋8x 2)＝8，即y 2＋8x 2＝8λ2.①又x 2＋8y 2＝8，②①＋②，得x 2＋y 2＝89⎝⎛⎭⎫1＋1λ2， 所以S △AMB ＝OM·OA ＝|λ|(x 2＋y 2)＝89⎝⎛⎭⎫|λ|＋1|λ|≥169. 当且仅当λ＝±1(即k AB ＝±1)时，(S △AMB )min ＝169.(解法2)假设AB 所在的直线斜率存在且不为零，设AB 所在直线方程为y ＝kx(k ≠0)，解方程组⎩⎪⎨⎪⎧x 28＋y 2＝1，y ＝kx ，得x 2A ＝81＋8k 2，y 2A ＝8k 21＋8k 2，所以OA 2＝x 2A ＋y 2A ＝81＋8k 2＋8k 21＋8k 2＝8（1＋k 2）1＋8k 2，AB 2＝4OA 2＝32（1＋k 2）1＋8k 2.又⎩⎨⎧x 28＋y 2＝1，y ＝－1kx ，解得x 2M ＝8k 2k 2＋8，y 2M ＝8k 2＋8，所以OM 2＝8（1＋k 2）k 2＋8.求△AMB 面积的最小值又有如下两种方法：(方法1)由于S 2△AMB ＝14AB 2·OM 2＝14×32（1＋k 2）1＋8k 2×8（1＋k 2）k 2＋8＝64（1＋k 2）2（1＋8k 2）（k 2＋8）≥64（1＋k 2）2⎝⎛⎭⎫1＋8k 2＋k 2＋822＝64（1＋k 2）2814（1＋k 2）2＝25681， 当且仅当1＋8k 2＝k 2＋8时等号成立，即k ＝±1时等号成立，此时△AMB 面积的最小值是S △AMB ＝169.当k ＝0时，S △AMB ＝12×42×1＝22＞169；当k 不存在时，S △AMB ＝12×22×2＝22＞169.综上所述，△AMB 面积的最小值为169.(方法2)因为1OA 2＋1OM 2＝18（1＋k 2）1＋8k 2＋18（1＋k 2）k 2＋8＝1＋8k 2＋k 2＋88（1＋k 2）＝98，又1OA 2＋1OM 2≥2OA·OM ，于是OA·OM ≥169， 当且仅当1＋8k 2＝k 2＋8时等号成立，即k ＝±1时等号成立．(以下同方法1)(理)在平面直角坐标系xOy 中，已知圆C 1：(x ＋3)2＋(y －1)2＝4和圆C 2：(x －4)2＋(y －5)2＝4.(1) 若直线l 过点A(4，0)，且被圆C 1截得的弦长为23，求直线l 的方程；(2) 设P 为平面上的点，满足：存在过点P 的无穷多对互相垂直的直线l 1和l 2，它们分别与圆C 1和圆C 2相交，且直线l 1被圆C 1截得的弦长与直线l 2被圆C 2截得的弦长相等，试求所有满足条件的点P 的坐标．解：(1) 设直线l 的方程为y ＝k(x －4)，即kx －y －4k ＝0.由垂径定理，得圆心C 1到直线l 的距离d ＝22－⎝⎛⎭⎫2 322＝1，结合点到直线距离公式，得|－3k －1－4k|k 2＋1＝1，化简得24k 2＋7k ＝0，解得k ＝0或k ＝－724.所求直线l 的方程为y ＝0或y ＝－724(x －4)，即y ＝0或7x ＋24y －28＝0.(2) 设点P 坐标为(m ，n)，直线l 1、l 2的方程分别为y －n ＝k(x －m)，y －n ＝－1k(x －m)，即kx －y ＋n －km ＝0，－1k x －y ＋n ＋1km ＝0.因为直线l 1被圆C 1截得的弦长与直线l 2被圆C 2截得的弦长相等，两圆半径相等．由垂径定理，得圆心C 1到直线l 1与圆心C 2到直线l 2的距离相等．故有|－3k －1＋n －km|k 2＋1＝⎪⎪⎪⎪－4k－5＋n ＋1k m 1k 2＋1，化简得(2－m －n)k ＝m －n －3或(m －n ＋8)k ＝m ＋n －5.因为关于k 的方程有无穷多解，所以有⎩⎪⎨⎪⎧2－m －n ＝0，m －n －3＝0或⎩⎪⎨⎪⎧m －n ＋8＝0，m ＋n －5＝0，解得点P 坐标为⎝⎛⎭⎫－32，132或⎝⎛⎭⎫52，－12. 变式训练(2014·湖南)如图，O 为坐标原点，椭圆C 1：x 2a 2＋y 2b2＝1(a ＞b ＞0)的左、右焦点分别为F 1、F 2，离心率为e 1；双曲线C 2：x 2a 2－y2b2＝1的左、右焦点分别为F 3、F 4，离心率为e 2.已知e 1e 2＝32，且|F 2F 4|＝3－1.(1) 求C 1，C 2的方程；(2) 过F 1作C 1的不垂直于y 轴的弦AB ，M 为AB 的中点．当直线OM 与C 2交于P 、Q 两点时，求四边形APBQ 面积的最小值．解： (1) 因为e 1e 2＝32，所以a 2－b 2a ·a 2＋b 2a ＝32，即a 4－b 4＝34a 4，因此a 2＝2b 2，从而F 2(b ，0)，F 4(3b ，0)，于是3b －b ＝|F 2F 4|＝3－1，所以b ＝1，a 2＝2.故C 1、C 2的方程分别为x 22＋y 2＝1，x 22－y 2＝1.(2) 因AB 不垂直于y 轴，且过点F 1(－1，0)，故可设直线AB 的方程为x ＝my －1，由⎩⎪⎨⎪⎧x ＝my －1，x 22＋y 2＝1得(m 2＋2)y 2－2my －1＝0.易知此方程的判别式大于0. 设A(x 1，y 1)，B(x 2，y 2)，则y 1、y 2是上述方程的两个实根，所以y 1＋y 2＝2mm 2＋2，y 1y 2＝－1m 2＋2.因此x 1＋x 2＝m(y 1＋y 2)－2＝－4m 2＋2，于是AB 的中点为M ⎝ ⎛⎭⎪⎫－2m 2＋2，m m 2＋2，故直线PQ的斜率为－m 2，PQ 的方程为y ＝－m2x.由⎩⎨⎧y ＝－m 2x ，x22－y 2＝1得(2－m 2)x 2＝4，所以2－m 2>0，且x 2＝42－m 2，y 2＝m 22－m 2，从而|PQ|＝2x 2＋y 2＝2m 2＋42－m 2.设点A 到直线PQ 的距离为d ，则点B 到直线PQ 的距离也为d ，所以2d ＝|mx 1＋2y 1|＋|mx 2＋2y 2|m 2＋4.因为点A 、B 在直线mx ＋2y ＝0的异侧，所以(mx 1＋2y 1)(mx 2＋2y 2)<0，于是|mx 1＋2y 1|＋|mx 2＋2y 2|＝|mx 1＋2y 1－mx 2－2y 2|，从而2d ＝（m 2＋2）|y 1－y 2|m 2＋4.因为|y 1－y 2|＝（y 1＋y 2）2－4y 1y 2＝22·1＋m 2m 2＋2，所以2d ＝22·1＋m 2m 2＋4.故四边形APBQ 的面积S ＝12|PQ|·2d ＝22·1＋m 22－m 2＝22·－1＋32－m 2. 而0<2－m 2≤2，故当m ＝0时，S 取最小值2. 综上所述，四边形APBQ 面积的最小值为2.题型4 轨迹问题【例4】(理)(2014·广东)已知椭圆C ：x 2a 2＋y 2b 2＝1(a>b>0)的一个焦点为(5，0)，离心率为53. (1) 求椭圆C 的标准方程；(2) 若动点P(x 0，y 0)为椭圆C 外一点，且点P 到椭圆C 的两条切线相互垂直，求点P 的轨迹方程．解：(1) 依题意有c ＝5，a ＝3，b ＝2，故所求椭圆C 的标准方程为x 29＋y 24＝1.(2) 当两条切线的斜率存在时，设过P(x 0，y 0)点的切线为y －y 0＝k(x －x 0)，联立⎩⎪⎨⎪⎧y －y 0＝k （x －x 0），x 29＋y 24＝1，消去y 得(4＋9k 2)x 2＋18k(y 0－kx 0)x ＋9(y 0－kx 0)2－36＝0，判别式Δ＝182k 2(y 0－kx 0)2－36(4＋9k 2)[(y 0－kx 0)2－4]＝0，化简得(y 0－kx 0)2－9k 2－4＝0，即(x 20－9)k2－2x 0y 0k ＋y 20－4，依题意得k 1·k 2＝y 20－4x 20－9＝－1，即x 20＋y 20＝13，当两条切线的斜率有一条不存在时，结合图象得P 是直线x ＝－3，x ＝3，y ＝2，y ＝－2的四个交点，也满足x 20＋y 20＝13，故点P 的轨迹方程x 2＋y 2＝13.变式训练已知动点M(x ，y)到直线l ：x ＝4的距离是它到点N(1，0)的距离的2倍．(1) 求动点M 的轨迹C 的方程；(2) 过点P(0，3)的直线m 与轨迹C 交于A 、B 两点，若A 是PB 的中点，求直线m 的斜率．图1图2解：(1) 如图1，设点M 到直线l 的距离为d ，根据题意，d ＝2|MN|，由此得|4－x|＝2（x －1）2＋y 2，化简得x 24＋y 23＝1，∴ 动点M 的轨迹C 的方程为x 24＋y 23＝1.(2) (解法1)由题意，设直线m 的方程为y ＝kx ＋3，A(x 1，y 1)，B(x 2，y 2)，如图2，将y ＝kx ＋3代入x 24＋y 23＝1中，有(3＋4k 2)x 2＋24kx ＋24＝0.其中Δ＝(24k)2－4×24(3＋4k 2)＝4(2k 2－3)>0，由根与系数的关系，得x 1＋x 2＝－24k3＋4k 2，①x 1x 2＝243＋4k 2.②又A 是PB 的中点，故x 2＝2x 1.③11 将③代入①②，得x 1＝－8k 3＋4k 2，x 21＝123＋4k 2， 可得⎝ ⎛⎭⎪⎫－8k 3＋4k 22＝123＋4k 2，且k 2>32，解得k ＝－32或k ＝32， ∴ 直线m 的斜率为－32或32. (解法2)由题意，设直线m 的方程为y ＝kx ＋3，A(x 1，y 1)，B(x 2，y 2)，如图2.∵ A 是PB 的中点，∴ x 1＝x 22，① y 1＝3＋y 22，② 又x 214＋y 213＝1，③ x 224＋y 223＝1，④ 联立①②③④，解得⎩⎪⎨⎪⎧x 2＝2，y 2＝0或⎩⎪⎨⎪⎧x 2＝－2，y 2＝0， 即点B 的坐标为(2，0)或(－2，0)，∴ 直线m 的斜率为－32或32.。

高二数学培优秘籍10-----圆锥曲线题型总结2 题型七弦或弦长为定值、最值问题
题型八直线问题
题型九轨迹问题
1、直接法
如果动点运动的条件就是一些几何量的等量关系，这些条件简单明确，不需要特殊的技巧，易于表述成含x，y的等式，就得到轨迹方程，这种方法称之为直接法。

用直接法求动点轨迹一般有建系，设点，列式，化简，证明五个步骤，最后的证明可以省略，但要注意“挖”与“补”。

求轨迹方程一般只要求出方程即可，求轨迹却不仅要求出方程而且要说明轨迹是什么。

2、定义法：运用解析几何中一些常用定义（例如圆锥曲线的定义），可从曲线定义出发直接写出轨迹方程，或从曲线定义出发建立关系式，从而求出轨迹方程。

3相关点法：动点所满足的条件不易表述或求出，但形成轨迹的动点P(x，y)却随另一动点Q(x’，y’)的运动而有规律的运动，且动点Q的轨迹为给定或容易求得，则可先将x’，y’表示为x，y的式子，再代入Q的轨迹方程，然而整理得P的轨迹方程，代入法也称相关点法。

3-1几何法：利用平面几何或解析几何的知识分析图形性质，发现动点运动规律和动点满足的条件，然而得出动点的轨迹方程。

一般地，定比分点问题，对称问题或能转化为这两类的轨迹问题，都可用相关点法。

4直接法
求轨迹方程有时很难直接找到动点的横坐标、纵坐标之间的关系，则可借助中间变量（参数），使x，y之间建立起联系，然而再从所求式子中消去参数，得出动点的轨迹方程。

5、交轨法。

高二数学圆锥曲线试题答案及解析1.设函数分别在、处取得极小值、极大值．平面上点、的坐标分别为、，该平面上动点满足，点是点关于直线的对称点．（Ⅰ）求点、的坐标；（Ⅱ）求动点的轨迹方程．【答案】（1）；（2）.【解析】（1）解决类似的问题时，要先求函数在区间内使的点，再判断导函数在各区间上的正负，由此得出函数的极大值和极小值.（2）第二问关键是理清思路，要求谁的方程，那就在这个曲线上任意选取一个点设为，然后根据条件寻找X与Y间的关系式即可. 试题解析：（Ⅰ）令解得当x＜﹣1时，，当﹣1＜x＜1时，，当x＞1时，所以，函数在处取得极小值，在取得极大值，故所以，点A、B的坐标为．（Ⅱ）设Q（x，y），①又点Q是点P关于直线y=x的对称点代入①得：，即为Q的轨迹方程【考点】（1）函数导数以及极值问题；（2）求点的轨迹方程问题.2.若抛物线的焦点与椭圆的右焦点重合，则的值为（）A．B．C．D．【答案】D【解析】抛物线的焦点坐标为，而椭圆的右焦点坐标为即，依题意可得，故选D.【考点】1.椭圆的几何性质；2.抛物线的几何性质.3.已知离心率的椭圆一个焦点为.(1)求椭圆的方程；(2) 若斜率为1的直线交椭圆于两点,且，求直线方程.【答案】(1)；【解析】(2) 或.(1)由焦点坐标、离心率及解方程即可；(2)可以联立直线L与椭圆方程消去y，得到关于x的一元二次方程，然后利用弦长公式建立方程求出斜率截距m即可.试题解析：解：(1)由题知，，∴，3分∴椭圆.4分(2) 设直线方程为，点，由方程组6分化简得:,.8分∴,9分，解得.11分∴直线方程或.12分【考点】1.椭圆的标准方程；2.直线与圆锥曲线相交；3.弦长公式.4.（1）已知点和，过点的直线与过点的直线相交于点，设直线的斜率为，直线的斜率为，如果，求点的轨迹；（2）用正弦定理证明三角形外角平分线定理：如果在中，的外角平分线与边的延长线相交于点，则.【答案】（1）的轨迹是以为顶点，焦点在轴的椭圆（除长轴端点）；（2）证明详见解析.【解析】（1）本题属直接法求轨迹方程，即根据题意设动点的坐标，求出，列出方程，化简整理即可；（2）设，在中，由正弦定理得，同时在在中，由正弦定理得，然后根据，进而得到，最后将得到的两等式相除即可证明.试题解析：（1）设点坐标为，则 2分整理得 4分所以点的轨迹是以为顶点，焦点在轴的椭圆（除长轴端点） 6分（2）证明：设在中，由正弦定理得① 8分在中，由正弦定理得，而所以② 10分①②两式相比得 12分.【考点】1.轨迹方程的求法；2.正弦定理的应用.5.如图，已知椭圆：的离心率为，点为其下焦点，点为坐标原点，过的直线：（其中）与椭圆相交于两点，且满足：.（1）试用表示；（2）求的最大值；（3）若，求的取值范围.【答案】（1）；（2）离心率的最大值为；（3）的取值范围是.【解析】（1）设，联立椭圆与直线的方程，消去得到，应用二次方程根与系数的关系得到，，然后计算得，将其代入化简即可得到；（2）利用（1）中得到的，即（注意），结合，化简求解即可得出的最大值；（3）利用与先求出的取值范围，最后根据（1）中，求出的取值范围即可.试题解析：（1）联立方程消去，化简得 1分设，则有， 3分∵∴ 5分∴即 6分（2）由（1）知∴，∴ 8分∴∴离心率的最大值为 10分(3)∵∴∴ 12分解得∴即∴的取值范围是 14分【考点】1.椭圆的标准方程及其性质；2.二次方程根与系数的关系.6.已知椭圆的一个焦点为，过点且垂直于长轴的直线被椭圆截得的弦长为；为椭圆上的四个点。

高二数学圆锥曲线试题答案及解析1.已知点的坐标为，点为轴负半轴上的动点，以线段为边作菱形，使其两对角线的交点恰好在轴上,则动点的轨迹E 的方程 .【答案】【解析】试题解析：依题意，设对角线的交点为，因为在轴上，又顶点与关于对称，所以始终在直线上，根据菱形的特点，亦即轴，有到定点的距离与到定直线的距离相等，显然，的轨迹是以为焦点，直线为准线的抛物线即，所以，抛物线方程为：，动点D的轨迹E 的方程为：.【考点】动点的轨迹方程.2.已知实数1，m，9构成一个等比数列，则圆锥曲线+y2=1的离心率为_________．【答案】或2【解析】因为实数1，m ，9构成一个等比数列，所以即m=3或m=-3，当m=3时，曲线为焦点在x轴的椭圆，离心率为；当m=-3时，曲线为焦点在y轴的双曲线，离心率为2，答案为或2.【考点】1.等比数列的性质；2.圆锥曲线的性质3.在中，，给出满足的条件，就能得到动点的轨迹方程，下表给出了一些条件及方程：条件方程①周长为10②面积为10③中，则满足条件①、②、③的点轨迹方程按顺序分别是A. 、、B. 、、C. 、、D. 、、【答案】A【解析】①周长为10，即，轨迹为椭圆；②面积为10，即，∴所以轨迹为；③中，，即为圆周上一点，所以轨迹为圆.【考点】圆锥曲线问题、轨迹问题.4.若抛物线y2＝4x上的点A到其焦点的距离是6，则点A的横坐标是( )A．5B．6C．7D．8【答案】A【解析】由抛物线的方程可知抛物线的准线为，根据抛物线的定义可知点到其准线的距离也为6，即，所以。

故A正确。

【考点】抛物线的定义。

5.若一个动点到两个定点的距离之差的绝对值等于8，则动点M的轨迹方程为 ( )A．B．C．D．【答案】C【解析】因为，由双曲线的定义可知，点的轨迹是以为焦点的双曲线。

此时，即，，所以点的轨迹方程是。

故C正确。

【考点】双曲线的定义。

6.设椭圆的方程为，斜率为1的直线不经过原点，而且与椭圆相交于两点，为线段的中点.（1）问：直线与能否垂直？若能，之间满足什么关系；若不能，说明理由；（2）已知为的中点，且点在椭圆上.若，求椭圆的离心率.【答案】（1）直线与不能垂直；（2）【解析】（1）设直线的方程为，与椭圆方程联立，消去整理为关于的一元二次方程，因为有两个交点则判别式应大于0，由韦达定理可得根与系数的关系，用中点坐标公式求点的坐标。

（数学选修 1-1 ）第二章圆锥曲线 [ 提高训练 C 组] 及答案一、选择题1．若抛物线y 2x 上一点 P 到准线的距离等于它到顶点的距离，则点P 的坐标为（）1 2 1 2 ) 121 2A ．( , 4 )B ．( ,4 C ． (,) D ．(,4)484 4 82．椭圆x 2y 21上一点 P 与椭圆的两个焦点F 1 、 F 2 的连线互相垂直，49 24则△ PF 1F 2 的面积为（）A ． 20B ． 22C ． 28D ． 243．若点 A 的坐标为 (3, 2) ， F 是抛物线 y 2 2x 的焦点，点 M 在抛物线上移动时，使MFMA 取得最小值的 M 的坐标为（）A ．0,0B ．1 ． 1, 2D ．2,2,1C24．与椭圆x 2 y 2 1共焦点且过点 Q (2,1) 的双曲线方程是（ ）4A ． x 2 y 21 B ．x 2y21 C ． x 2y 21D ． x 2y 21243325．若直线 ykx 2 与双曲线 x 2 y 26 的右支交于不同的两点，那么 k 的取值范围是（ ）A ．（ 1515 B ．（ 0,15 C ．（15D ．（15 ）3,3 ））,0 ） , 13336．抛物线 y2x 2 上两点 A( x 1 , y 1 ) 、 B( x 2 , y 2 ) 关于直线yx m 对称，且x 1 x 21，则 m 等于（ ）235A ．B ． 2D ． 32C ．2二、填空题x2y21的焦点 F1、 F2，点P为其上的动点，当∠F1P F2为钝角时,点P横坐标的取值1．椭圆49范围是。

2．双曲线tx2y2 1 的一条渐近线与直线2x y 1 0 垂直，则这双曲线的离心率为___。

3．若直线y kx2与抛物线 y28x 交于A、B两点，若线段AB 的中点的横坐标是 2 ，则AB ______。

4．若直线y kx1与双曲线 x2y24始终有公共点，则 k 取值范围是。

高二数学训练题：圆锥曲线(2)高二数学训练题：圆锥曲线（二）安徽省福山中学方龙翔一、选择题：2.X21。

已知椭圆C:？Y1的右焦点是f，右引导线是l，点a？l、线段AF与椭圆C在B中相交，如果fa？f3b2则|af|等于（）a、二,b．2二二c．3d．3X22。

如果直线MX+NY=4和圆O:x+y=4没有交点，则通过（m，n）和椭圆（）w_wwk#s5_uo*m9?y24?1的交点a、最多一个B.2 C.1 d.03、设斜率为2的直线l过抛物线y2?ax(a?0)的焦点f，且和y轴交于点a，若△oaf （o为坐标原点）的面积为4，则抛物线方程为（）（a） y2？4x4，双曲线以上xa2222（b）y2？8x（c）y2？？4x（d）y2？？8xyb1(a0,b0)的左顶点a作斜率为1的直线，该直线与双曲线的两条渐进线1.的交点分别是B和C。

如果AB？那么双曲线的偏心率是（）2a.3b.2c.10d.525、已知两点a(?1,0),b(1,0),且点c(x,y)满足a.6x?x?1?2?yx?4?12,则ac?bc?（）w_wk#5_uo*mb。

22摄氏度。

4y2d。

不确定6、曲线25?9?1x2与曲线25?k?y29?k?1(k?9)的（）a、等焦距B.等长轴和短轴C.等偏心率D.相同的准直3，则7.已知双曲线的中心在原点，焦点在x轴上，其一条渐近线与x轴之间的夹角为？，4双曲线的偏心率取值范围为（）w_wwk#5_uo*m第1页共9页答。

1,2b．?22,2?c．?1,2?d．?2,22?8.方程式2x？5倍？2.0的两个根可用作（）A.椭圆和双曲线的偏心率B.两条抛物线的偏心率C.椭圆和抛物线的偏心率D.两个椭圆的偏心率x229、双曲线aahof?yb22?1(a?0,b?0)的中心、右焦点、右顶点、右准线与x轴的交点依次为o,f,a,h,则的最大值为（）11w_wk#s5_uo*m1a。

2b。

高二数学培优秘籍8-----圆锥曲线题型一数形结合：确定直线和圆锥曲线的位置关系
简单题型未总结。

题型二弦的垂直平分线问题
【涉及到弦的垂直平分线问题】
这种问题主要是需要用到弦AB的垂直平分线L的方程，往往是利用点差或者韦达定理产生弦AB的中点坐标M，结合弦AB与它的垂直平分线L的斜率互为负倒数，写出弦的垂直平分线L的方程，然后解决相关问题，比如：求L在x轴y轴上的截距的取值范围，求L过某定点等等。

有时候题目的条件比较隐蔽，要分析后才能判定是有关弦AB的中点问题，比如：弦与某定点D构成以D为顶点的等腰三角形（即D在AB的垂直平分线上）、曲线上存在两点AB关于直线m对称等等。

题型三动弦过定点的问题
题型四过已知曲线上定点的弦的问题
题型五共线向量问题
类型一求待定字母的值
类型二
求动点的轨迹
类型三
证明定值问题
类型四探索点、线的存在性
类型五求相关量的取值范围
存在、向量。

2015—2016学年度高二（上）寒假作业（3）——圆锥曲线综合一、填空题：1．)∪(02．3． 44． 12-5．6．分析：椭圆的右顶点为(),0a ，所以直线方程为)00y x a y -=---=，2222134442c b a b a c e a =∴==-∴== 7． 3π 8．解：设A (x 1，y 1)，B (x 2，y 2)，因为A 、B 两点在抛物线上，∴⎩⎪⎨⎪⎧y 21＝2px 1， ①y 22＝2px 2， ②①－②得(y 1－y 2)(y 1＋y 2)＝2p (x 1－x 2)，又线段AB 的中点的纵坐标为2，∴y 1＋y 2＝4，又直线的斜率为1，∴y 1－y 2x 1－x 2＝1，∴ 2p ＝4，p ＝2，∴抛物线的准线方程x ＝－1．9． 10． 11,22k ⎡⎤∈-⎢⎥⎣⎦11．12． 91613．解：由点在半圆上，所以1b =，而当点M 位于 点时，AGM ∆的面积最大可知，OM ⊥AG ，即1OM AG k k ⋅=-，a =∴半椭圆的方程为2212y x +=（y ≥0）14．分析：设出M ，N 的坐标分别为()()1122,,,x y x y ∵M ，N 在抛物线22(0)y px p =>∴2112y px =①2222y px =②，①-②知()()2212122yy p x x -=-12121212y y y y kp x x k -=-∴+=--∵M ，N 在直线2l ：()1y x p k=--上()21221x x p k ∴+=+即弦MN 的中点坐标为()()21,p k kp +-∵过定点（p ，0）作两条互相垂直的直线12,l l ，1l 与抛物线交于P ，Q 两点，2l 与抛物线交于M ，N 两点，设1l 的斜率为k ∴1mn k k=-∴弦MN 的中垂线的斜率为k ，∴弦MN的中垂线的方程为：()()21y kp k x p k +=-+令x =0得y =32pk pk --． 二、解答题： 15．解析：（1）设直线l 的方程为y=kx+b ；由条件知112c a a ==，∴a =2，b 2=4﹣1=3；∴椭圆C 的方程为22143x y +=；将直线l 的方程带入椭圆C 的方程并整理得：（3+4k 2）x 2+8kbx +4b 2﹣12=0；若设A (x 1，y 1)，B (x 2，y 2)，则：122834kbx x k -+=+，21228234k b y y b k -+=++；根据AB 的中点坐标，所以：222413424134kb k k b b k -⎧=⎪⎪+⎨-⎪+=⎪+⎩；解得319,816k b =-=；∴直线l 的方程为319816y x =-+； （2）由条件知b =1，a 2=2，椭圆方程为；直线l 过F 2（1，0），方程可设为：y =k （x ﹣1）；∴代入椭圆方程并整理得：（1+2k 2）x 2﹣4k 2x +2k 2﹣2=0； 若设P （x 1，y 1），Q （x 2，y 2），则：222121212222422,.11212k k k x x x x y y k --+===+++，由条件11F P F Q ⊥得211271012k F P FQ k -⋅==+ ∴解得7k =；∴直线l 的方程为71)y x =-16．解：（1）由已知5|||AB BF 225a b +，222445a b a +=，222244()5a a c a +-=，∴ 3c e a == （2）由（1）知224a b =，∴ 椭圆C ：222214x y b b+=．设11(,)P x y ，22(,)Q x y ，直线l 的方程为22(0)y x -=-，即220x y -+=．由22222222204(22)4014x y x x b x y bb -+=⎧⎪⇒++-=⎨+=⎪⎩， 即2217321640x x b ++-=．22217321617(4)0b b ∆=+⨯->⇔>123217x x +=-，21216417b x x -=．∵ OP OQ ⊥，∴ 0OP OQ ⋅=， 即12120x x y y +=，1212(22)(22)0x x x x +++=，121254()40x x x x +++=． 从而25(164)128401717b --+=，解得1b =，∴ 椭圆C 的方程为2214x y +=．17．解：（1）将直线1x y +=代入椭圆方程，因为直线与椭圆交于两点，故0∆>，解得3b >，所以b 的范围为36(． yxB A O F（2）将直线1x y +=代入椭圆方程，可得：2222121222222,a a a b x x x x a b a-+==++ 由OA OB ⊥可得12120x x y y +=，解得22222a b a b +=即2211122a b+=，代2到椭圆方程得2022112y a b +=即212y =，所以点P 的纵坐标为 . （3）设直线1x y+=与坐标轴交于C D 、，则12COD CD S ∆==又,AOB COD ∆∆两个三角形等高，故54AOB COD S AB CD S ∆∆==所以12|AB x x ==-，求得22167a b =所以2244,7a b ==，所以椭圆方程为227144x y +=.18．解析：（1）焦点(1,0)F ．∵直线l 的斜率不为0，所以设:1l x my =+，11(,)A x y ，22(,)B x y 由214x my y x=+⎧⎨=⎩得2440y my --=， 124y y m +=，124y y =-，21212()242x x m y y m +=++=+，2221212(4)14416y y x x -=⋅==，∴212||2445AB x x m =++=+=， ∴214m =． ∴直线l 的斜率24k =，∵0k >，∴2k =． ∴直线l 的方程为220x y --=． （2）设2(,2)M a a ，1122211122424MAy a y a k y x a y a a --===-+-，同理242MBk y a=+，2221MD a m k a +=+， ∵直线MA ，MD ，MB 的斜率始终成等差数列，∴2MD MA MB k k k =+恒成立，即2124444122a m a y a y a +=++++恒成立．∴212111122a m a y a y a +=++++122212121412()4a y y a m a y y a y y a +++⇒=++++，把124y y m +=，124y y =-代入上式，得21(1)()0a m m-+=恒成立，1a ∴=±．∴存在点M (1，2)或M (1，－2)使得对任意直线l ，直线MA ，MD ，MB 的斜率始终成等差数列． 19．解：（1）由题意可得11,22c bc a =，解得1b =，a 2212x y +=．（2）假设存在直线l 交椭圆于P ，Q 两点，且F 为△PQM 的垂心，设11(,)P x y ，22(,),Q x y 因为(0,1)M ，(1,0)F ，故1PQ k =．于是设直线l 的方程为y x m =+， 由22,22,y x m x y =+⎧⎨+=⎩得2234220x mx m ++-=． 由0∆>，得23m <， 且1243m x x +=-,212223m x x -=．由题意应有0MP FQ ⋅=，又1122(,1),(1,)MP x y FQ x y =-=-，故1221(1)(1)0x x y y -+-=，得1221(1)()(1)0x x x m x m -+++-=．即212122()(1)0x x x x m m m ++-+-=． 整理得222242(1)033m m m m m -⨯--+-=．解得43m =-或1m =．经检验，当1m =时，△PQM 不存在，故舍去1m =．∴当43m =-时，所求直线l 存在，且直线l 的方程为43y x =-．20．解析：（1）椭圆C 的标准方程为2213x y +=．所以a =1b =，cc e a ==（2）因为AB 过点(1,0)D 且垂直于x 轴，所以可设1(1,)A y ，1(1,)B y -．直线AE 的方程为11(1)(2)y y x -=--．令3x =，得1(3,2)M y -．所以112131BM y y k -+==-．（3）直线BM 与直线DE 平行．证明如下：当直线AB 的斜率不存在时，由（2）可知1BM k =．又因为直线DE 的斜率10121DE k -==-，所以//BM DE ．当直线AB 的斜率存在时，设其方程为(1)(1)y k x k =-≠．设11(,)A x y ，22(,)B x y ，则直线AE 的方程为1111(2)2y y x x --=--．令3x =，得点1113(3,)2y x M x +--．由2233(1)x y y k x ⎧+=⎨=-⎩，得2222(13)6330k x k x k +-+-=． 所以2122613k x x k +=+，21223313k x x k -=+．直线BM 的斜率11212323BM y x y x k x +---=-．因为11112121(1)3(1)(2)(3)(2)1(3)(2)BM k x x k x x x x k x x -+--------=--121221(1)[2()3)(3)(2)k x x x x x x --++-=--2222213312(1)[3)1313(3)(2)k k k k k x x -+-+-++=--0=，所以1BM DE k k ==．所以//BM DE ．综上可知，直线BM 与直线DE 平行．。

一 原点三角形面积公式 1. 已知椭圆的离心率为，且过点．若点M （x 0，y 0）在椭圆C 上，则点称为点M 的一个“椭点”．（1）求椭圆C 的标准方程；（2）若直线l ：y=kx+m 与椭圆C 相交于A ，B 两点，且A ，B 两点的“椭点”分别为P ，Q ，以PQ 为直径的圆经过坐标原点，试求△AOB 的面积．2. 己知椭圆 x 2+2y 2=1，过原点的两条直线 l 1 和 l 2 分别与椭圆交于点 A ，B 和C ，D ．记 △AOC 的面积为 S ．（1）设 A (x 1,y 1)，C (x 2,y 2)．用 A ，C 的坐标表示点 C 到直线 l 1 的距离，并证明 S =12∣x 1y 2−x 2y 1∣； （2）设 l 1:y =kx ，C (√33,√33)，S =13，求 k 的值．（3）设 l 1 与 l 2 的斜率之积为 m ，求 m 的值，使得无论 l 1 与 l 2 如何变动，面积 S 保持不变．3. 已知椭圆()0,01:2222>>=+b by x C αα的左、右两焦点分别为()()0,1,0,121F F -,椭圆上有一点A 与两焦点的连线构成的21F AF ∆中，满足.127,121221ππ=∠=∠F AF F AF （1）求椭圆C 的方程；（2）设点D C B ,,是椭圆上不同于椭圆顶点的三点，点B 与点D 关于原点O 对称，设直线OC OB CD BC ,,,的斜率分别为4321,,,k k k k ，且4321k k k k ⋅=⋅，求22OC OB +的值.4. 在平面直角坐标系内，动点与两定点，连线的斜率之积为(1)求动点的轨迹的方程；(2)设点是轨迹上相异的两点．(I)过点A ，B 分别作抛物线的切线、，与两条切线相交于点，证明：；xoy (,)M x y (2,0),(2,0)-14-M C 1122(,),(,)A x y B x yC 2y =1l 2l 1l 2l ()N t 0NA NB =u u u r u u u rg(Ⅱ)若直线OA 与直线OB 的斜率之积为，证明：为定值，并求出这个定值·5. 已知 A 、 B 分别是 x 轴和 y 轴上的两个动点，满足 ∣AB∣=2，点 P 在线段 AB 上，且 AP ⃗⃗⃗⃗⃗ =tPB ⃗⃗⃗⃗⃗ （t 是不为 0 的常数），设点 P 的轨迹方程为 C ．（1）求点 P 的轨迹方程 C ；（2）若曲线 C 为焦点在 x 轴上的椭圆，试求实数 t 的取值范围； （3）若 t =2，点 M ，N 是曲线 C 上关于原点对称的两个动点，点 Q 的坐标为 (32,3)，求 △QMN 的面积 S 的最大值．6. 已知椭圆 C 1 的焦点在 x 轴上，中心在坐标原点；抛物线 C 2 的焦点在 y轴上，顶点在坐标原点．在 C 1，C 2 上各取两个点，将其坐标记录于表格中： x3−24√2y908√2（1）求 C 1，C 2 的标准方程；（2）已知定点 C (0,18)，P 为抛物线 C 2 上一动点，过点 P 作抛物线 C 2的切线交椭圆 C 1 于 A ，B 两点，求 △ABC 面积的最大值．7. 已知抛物线 y 2=4x 的焦点为 F ，过点 F 的直线交抛物线于 A ，B 两点．（1）若 AF⃗⃗⃗⃗⃗ =2FB ⃗⃗⃗⃗⃗ ，求直线 AB 的斜率； （2）设点 M 在线段 AB 上运动，原点 O 关于点 M 的对称点为 C ，求四边形 OACB 面积的最小值．8. 设椭圆 C 1：x 2a +y 2b =1 (a >b >0) 的左、右焦点分别是 F 1 、 F 2，下顶点为 A ，线段 OA 的中点为 B （O 为坐标原点），如图．若抛物线 C 2：y =x 2−1 与 y 轴的交点为 B ，且经过 F 1，F 2 点．（1）求椭圆 C 1 的方程；14-AOB S∆（2）设 M (0,−45)，N 为抛物线 C 2 上的一动点，过点 N 作抛物线 C 2 的切线交椭圆 C 1 于 P 、 Q 两点，求 △MPQ 面积的最大值．二 定点定值问题9. 动点P 在圆E ：22(1)16x y ++=上运动，定点(1,0)F ，线段PF 的垂直平分线与直线PE 的交点为Q ． （Ⅰ）求Q 的轨迹T 的方程；（Ⅱ）过点F 的直线1l ，2l 分别交轨迹E 于A ，B 两点和C ，D 两点，且12l l ⊥．证明：过AB 和CD 中点的直线过定点．10. 在直角坐标系xOy 中，抛物线C 的顶点是双曲线D 抛物线C 的焦点与双曲线D 的焦点相同． （Ⅰ）求抛物线C 的方程；（Ⅱ）若点(,1)P t (0)t >为抛物线C 上的定点，A ，B 为抛物线C 上两个动点．且PA⊥PB ，问直线AB 是否经过定点？若是，求出该定点，若不是，说明理由．11. 如图，在平面直角坐标系 xOy 中，椭圆 C:x 2a 2+y 2b 2=1(a >b >0) 的离心率为 √63，直线 l 与 x 轴交于点 E ，与椭圆 C 交于 A,B 两点．当直线 l 垂直于 x 轴且点 E 为椭圆 C 的右焦点时，弦 AB 的长为2√63．（1）求椭圆 C 的方程；（2）若点 E 的坐标为 (√32,0)，点 A 在第一象限且横坐标为 √3，连接点 A 与原点 O 的直线交椭圆 C 于另一点 P ，求 △PAB 的面积； （3）是否存在点 E ，使得 1EA 2+1EB 2 为定值?若存在，请指出点 E 的坐标，并求出该定值；若不存在，请说明理由．12. 已知椭圆的左焦点为F ，不垂直于x 轴且不过F 点的直线l 与椭圆C 相交于A ，B 两点．（1）如果直线FA ，FB 的斜率之和为0，则动直线l 是否一定经过一定点？若过一定点，则求出该定点的坐标；若不过定点，请说明理由． （2）如果FA ⊥FB ，原点到直线l 的距离为d ，求d 的取值范围．13. 如图，已知直线:1(0)l y kx k =+>关于直线1y x =+对称的直线为1l ，直线1,l l 与椭圆22:14x E y +=分别交于点A 、M 和A 、N ，记直线l 的斜率为k . （Ⅰ）求1k k ⋅的值；（Ⅱ）当k 变化时，试问直线MN 是否恒过定点恒过定点，请说明理由.14. 如图，椭圆 E:x 2a 2+y 2b 2=1（a >b >0）的离心率是 √22，过点 P (0,1) 的动直线 l 与椭圆相交于 A ，B 两点．当直线 l 平行于x 轴时，直线 l 被椭圆 E 截得的线段长为 2√2．（1）求椭圆 E 的方程；（2）在平面直角坐标系 xOy 中，是否存在与点 P 不同的定点 Q ，使得∣QA∣∣QB∣=∣PA∣∣PB∣ 恒成立? 若存在，求出点 Q 的坐标；若不存在，请说明理由．15. 已知动圆过定点 (p2,0)，且与直线 x =−p2 相切，其中 p >0．（1）求动圆圆心 C 的轨迹的方程；（2）设 A 、 B 是轨迹 C 上异于原点 O 的两个不同点，直线 OA 和 OB的倾斜角分别为 α 和 β，当 α，β 变化且 α+β 为定值 θ(0<θ<π) 时，证明直线 AB 恒过定点，并求出该定点的坐标．16. 已知抛物线 E:y 2=2px (p >0) 的准线与 x 轴交于点 K ，过点 K 做圆C:(x −5)2+y 2=9 的两条切线，切点为 M ，N ，|MN|=3√3． （1）求抛物线 E 的方程；（2）设 A ，B 是抛物线 E 上分别位于 x 轴两侧的两个动点，且 OA ⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗ =94（ 其中 O 为坐标原点）． ①求证：直线 AB 必过定点，并求出该定点 Q 的坐标；②过点 Q 作 AB 的垂线与抛物线交于 G ，D 两点，求四边形 AGBD面积的最小值．17.18. 如图，在平面直角坐标系xOy 中，设点M(x0，y0)是椭圆C ：2212x y +=上一点，从原点O 向圆M:22002()()3x x y y -+-=作两条切线分别与椭圆C 交于点P 、Q ，直线OP 、OQ 的斜率分别记为k1，k2 (1)求证：k1k2为定值;(2)求四边形OPMQ 面积的最大值.19. 如图，在平面直角坐标系xOy 中，已知()00 R x y ，是椭圆22:12412x y C +=上的一点，从原点O 向圆()()2200:8R x x y y -+-=作两条切线，分别交椭圆于P ，Q .（1）若R 点在第一象限，且直线OP ，OQ 互相垂直，求圆R 的方程； （2）若直线OP ，OQ 的斜率存在，并记为12 k k ，，求12 k k ，的值； （3）试问22OP OQ +是否为定值？若是，求出该值；若不是，说明理由.三 中点弦问题20. 椭圆()2222:10x y C a b a b+=>>的长轴长为P 为椭圆C 上异于顶点的一个动点，O 为坐标原点，2A 为椭圆C 的右顶点，点M 为线段2PA 的中点，且直线2PA 与直线OM 的斜率之积为12-. （1）求椭圆C 的方程；（2）过椭圆C 的左焦点1F 且不与坐标轴垂直的直线l 交椭圆C 于两点,A B ，线段AB 的垂直平分线与x 轴交于点N ，N 点的横坐标的取值范围是1,04⎛⎫- ⎪⎝⎭，求线段AB 的长的取值范围.21. 在平面直角坐标系xoy 中，过椭圆2222:1(0)x y C a b a b+=>>右焦点的直线20x y +-=交椭圆C 于,M N 两点，P 为,M N 的中点，且直线OP 的斜率为13． （Ⅰ）求椭圆C 的方程；（Ⅱ）设另一直线l 与椭圆C 交于,A B 两点，原点O 到直线l AOB ∆面积的最大值．22. 如图，椭圆2222:1(0)x y E a b a b+=>>左右顶点为A 、B ，左右焦点为1212,,4,23F F AB F F ==，直线(0)y kx m k =+>交椭圆E 于点C 、D 两点，与线段12F F 椭圆短轴分别交于M 、N 两点（M 、N 不重合），且CM DN =.（1）求椭圆E 的方程；（2）设直线,AD BC 的斜率分别为12,k k ，求12k k 的取值范围.23. 如图，在平面直角坐标系xoy 中，已知椭圆C ：)0(12222>>=+b a bya x 的离心率21=e ，左顶点为)0,4(-A ，过点A 作斜率为)0(≠k k 的直线l 交椭圆C 于点D ，交y 轴于点E . （Ⅰ）求椭圆C 的方程;（Ⅱ）已知P 为AD 的中点，是否存在定点Q ，对于任意的)0(≠k k 都有EQ OP ⊥，若存在，求出点Q 的坐标；若不存在说明理由;（Ⅲ）若过O 点作直线l 的平行线交椭圆C 于点M ，求||||||OM AE AD +的最小值.24. 已知椭圆 M:x 2a 2+y 2b 2=1(a >b >0) 过点 A (0,−1)，且离心率 e =√32． （1）求椭圆 M 的方程；（2）若椭圆 M 上存在点 B,C 关于直线 y =kx −1 对称，求 k 的所有取值构成的集合 S ，并证明对于 ∀k ∈S ，BC 的中点恒在一条定直线上．P DMA Oxy E25. 如图，在直角坐标系 xOy 中，点 P (1,12) 到抛物线 C:y 2=2px (p >0) 的准线的距离为 54．点 M (t,1) 是 C 上的定点，A ，B 是 C 上的两动点，且线段 AB 被直线 OM 平分．（1）求 p ，t 的值；（2）求 △ABP 面积的最大值．26. 已知抛物线 C:y 2=4x ，过其焦点 F 作两条相互垂直且不平行于 x 轴的直线，分别交抛物线 C 于点 P 1，P 2 和点 P 3，P 4，线段 P 1P 2，P 3P 4 的中点分别记为 M 1，M 2．（1）求 △FM 1M 2 面积的最小值；（2）求线段 M 1M 2 的中点 P 满足的方程．27. 平面直角坐标系xOy 中，椭圆C ：22221x y a b+=（0a b >>）的离心率是32，抛物线E ：22x y =的焦点F 是C 的一个顶点．（1）求椭圆C 的方程；（2）设P 是E 上动点，且位于第一象限，E 在点P 处的切线l 与C 交于不同的两点A ，B ，线段AB 的中点为D ，直线OD 与过P 且垂直于x 轴的直线交于点M ． （i ）求证：点M 在定直线上；（ii ）直线l 与y 轴交于点G ，记PFG ∆的面积为1S ，PDM ∆的面积为2S ，求12S S 的最大值及取得最大值时点P 的坐标．四 定比分点28. 已知点)0,2(-E ，点P 是椭圆F ：36)2(22=+-y x 上任意一点，线段EP 的垂直平分线FP 交于点M ，点M 的轨迹记为曲线C . （Ⅰ）求曲线C 的方程；（Ⅱ）过F 的直线交曲线C 于不同的A ，B 两点,交y 轴于点N ，已知m =，BF n NB =，求n m +的值.29. 在直角坐标系xOy 上取两个定点12(A A 再取两个动点1(0 , )N m ，2(0 , )N n ，且2mn =．（Ⅰ）求直线11A N 与22A N 交点M 的轨迹C 的方程；（Ⅱ）过(3 , 0)R 的直线与轨迹C 交于P ,Q ，过P 作PN x ⊥轴且与轨迹C 交于另一点N ，F 为轨迹C 的右焦点，若(1)RP RQ λλ=>u u u r u u u r ，求证：NF FQ λ=u u u r u u u r.30. 如图，在平面直角坐标系xOy 中，椭圆C ：22221x y a b+=()0a b ＞＞的左、右焦点分别为1F ，2F ，P 为椭圆上一点（在x 轴上方），连结1PF 并延长交椭圆于另一点Q ，设11PF FQ λ=u u u r u u u r． （1）若点P 的坐标为3(1,)2，且2PQF △的周长为8，求椭圆C 的方程；（2）若2PF 垂直于x 轴，且椭圆C 的离心率1,2e ∈⎡⎢⎣，求实数λ的取值范围．五 结论31. 已知椭圆 20.已知椭圆()2222:10x y C a b a b+=>>经过点(2，点 A B ，分别为椭圆C 的左右顶点，点P 在椭圆C 上. （1）求椭圆C 的方程；（2） M N ，是椭圆C 上非顶点的两点，满足 OM AP ON BP ∥，∥，求证：三角形MON 的面积是定值.32. 过点 (1,√32)，离心率为 √32．过椭圆右顶点 A 的两条斜率乘积为 −14的直线分别交椭圆 C 于 M ，N 两点． （1）求椭圆 C 的标准方程；（2）直线 MN 是否过定点 D ?若过定点 D ，求出点 D 的坐标，若不过点 D ，请说明理由．33. 已知椭圆的两个焦点为，，是椭圆上一点，若，（1）求椭圆的方程；（2）点是椭圆上任意一点，分别是椭圆的左、右顶点，直线与直线分别交于两点，试证：以为直径的圆交轴于定点，并求该定点的坐标.34. 已知抛物线()220x py p =>的焦点为F ，直线4x =与x 轴的交点为P ，与抛物线的()1F )2F M 120MF MF ⋅=u u u u r u u u u rP 12A A 、12PA PA ，2x =,E F EF x交点为Q,且5.4QF PQ = （1）求抛物线的方程； （2）如图所示，过F 的直线l 与抛物线相交于A,D 两点，与圆()2211x y +-=相交于B,C 两点（A ，B 两点相邻），过A,D 两点分别作我校的切线，两条切线相交于点M,求ABM ∆与CDM ∆的面积之积的最小值.35. 已知椭圆 x 2a 2+y 2b 2=1(a >b >0)，其右准线 l 与 x轴交于点 A ，椭圆的上顶点为 B ，过它的右焦点 F且垂直于长轴的直线交椭圆于点 P ，直线 AB 恰经过线段 FP 的中点 D ．（1）求椭圆的离心率；（2）设椭圆的左、右顶点分别是 A 1 、 A 2，且 BA 1⃗⃗⃗⃗⃗⃗⃗⃗ ⋅BA 2⃗⃗⃗⃗⃗⃗⃗⃗ =−3，求椭圆的方程；（3）在（2）的条件下，设 Q 是椭圆右准线 l 上异于 A 的任意一点，直线 QA 1，QA 2 与椭圆的另一个交点分别为 M 、 N ，求证：直线 MN 与 x 轴交于定点．36. 已知点(1,0)A -，(1,0)B ，直线AM 与直线BM 相交于点M ，直线AM 与直线BM的斜率分别记为AM k 与BM k ，且2AM BM k k ⋅=-．（Ⅰ）求点M 的轨迹C 的方程；（Ⅱ）过定点(0,1)F 作直线PQ 与曲线C 交于,P Q 两点，OPQ ∆的面积是否存在最大值？若存在，求出OPQ ∆面积的最大值；若不存在，请说明理由．37. 已知一个动圆与两个定圆41)2(22=+-y x 和449)2(22=++y x 均相切,其圆心的轨迹为曲线C.(1) 求曲线C 的方程；(2) 过点F （0,2)做两条可相垂直的直线21,l l ，设1l 与曲线C 交于A,B 两点, 2l 与曲线 C交于C,D 两点，线段AC ，BD 分别与直线2=x 交于M ，M,N 两点。

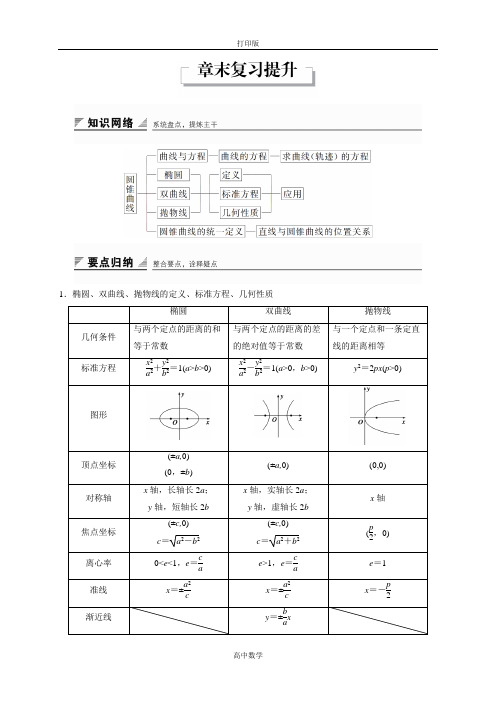
1．椭圆、双曲线、抛物线的定义、标准方程、几何性质椭圆双曲线抛物线几何条件与两个定点的距离的和等于常数与两个定点的距离的差的绝对值等于常数 与一个定点和一条定直线的距离相等标准方程x 2a 2＋y 2b 2＝1(a >b >0) x 2a 2－y 2b 2＝1(a >0，b >0) y 2＝2px (p >0)图形顶点坐标(±a,0) (0，±b ) (±a,0) (0,0)对称轴 x 轴，长轴长2a ； y 轴，短轴长2bx 轴，实轴长2a ； y 轴，虚轴长2bx 轴 焦点坐标 (±c,0) c ＝a 2－b 2 (±c,0) c ＝a 2＋b 2 (p2，0) 离心率 0<e <1，e ＝c ae >1，e ＝c ae ＝1 准线 x ＝±a 2cx ＝±a 2cx ＝－p 2渐近线y ＝±b ax2.曲线与方程(1)曲线与方程：如果曲线C 上的点与一个二元方程的实数解建立了如下的关系：①曲线上点的坐标都是这个方程的解；②以这个方程的解为坐标的点都在曲线上，那么，这条曲线叫做方程的曲线，这个方程叫做曲线的方程．(2)圆锥曲线的共同特征：圆锥曲线上的点到一个定点的距离与它到一条定直线的距离之比是定值e ；当0<e <1时，圆锥曲线是椭圆；当e >1时，圆锥曲线是双曲线；当e ＝1时，圆锥曲线是抛物线． 3．直线与圆锥曲线的位置关系直线和圆锥曲线的位置关系有三种：相离、相切、相交．设直线l 的方程为Ax ＋By ＋C ＝0，与圆锥曲线D 的方程联立⎩⎪⎨⎪⎧Ax ＋By ＋C ＝0，f (x ，y )＝0，可得(消去y )ax 2＋bx ＋c ＝0(*)．(1)当a ≠0时，若关于x 的方程(*)的判别式Δ>0，则直线与圆锥曲线有两个不同交点；若Δ<0，则直线与圆锥曲线没有交点；若Δ＝0，则直线与圆锥曲线相切． (2)当a ＝0时，若方程(*)有解，则直线与圆锥曲线有一个交点．题型一 圆锥曲线定义与几何性质的应用椭圆、双曲线、抛物线的定义是经常考查的内容，往往体现在数学上的转化与化归思想．圆锥曲线的几何性质包括椭圆、双曲线、抛物线的对称性、顶点坐标、离心率，双曲线的渐近线，抛物线的准线等内容，主要考查这些性质的理解记忆．例1 如图，已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)的离心率为22，以该椭圆上的点和椭圆的左，右焦点F 1，F 2为顶点的三角形的周长为4(2＋1)；一等轴双曲线的顶点是该椭圆的焦点，设P 为该双曲线上异于顶点的任一点，直线PF 1和PF 2与椭圆的交点分别为A 、B 和C 、D . (1)求椭圆和双曲线的标准方程；(2)设直线PF 1、PF 2的斜率分别为k 1、k 2，证明k 1·k 2＝1.(1)解 由题意知，椭圆离心率为c a ＝22，得a ＝2c ，又由以椭圆上的点和椭圆的左，右焦点F 1，F 2为顶点的三角形的周长为4(2＋1)，结合椭圆定义得2a ＋2c ＝4(2＋1)，所以可解得a ＝22，c ＝2，故b 2＝a 2－c 2＝4，所以椭圆的标准方程为x 28＋y 24＝1.易得椭圆的焦点坐标为(±2,0)，因为双曲线为等轴双曲线，且顶点是该椭圆的焦点，所以该双曲线的标准方程为x 24－y 24＝1.(2)证明 设点P (x 0，y 0)，则k 1＝y 0x 0＋2，k 2＝y 0x 0－2，所以k 1·k 2＝y 0x 0＋2·y 0x 0－2＝y 20x 20－4，又点P (x 0，y 0)在双曲线上，所以有x 204－y 204＝1，即y 20＝x 20－4，所以k 1·k 2＝y 20x 20－4＝1.跟踪演练1 已知椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左焦点为F ，左、右顶点分别为A 、C ，上顶点为B ，O为原点，P 为椭圆上任意一点．过F 、B 、C 三点的圆的圆心坐标为(m ，n )． (1)当m ＋n ≤0时，求椭圆的离心率的取值范围；(2)当(1)的条件下，椭圆的离心率最小时，若点D (b ＋1,0)，(PF →＋OD →)·PO →的最小值为72，求椭圆的方程．解 (1)设半焦距为c .由题意得FC 、BC 的中垂线方程分别为x ＝a －c 2、y －b 2＝ab ⎝⎛⎭⎫x －a 2， 于是圆心坐标为⎝ ⎛⎭⎪⎫a －c 2，b 2－ac 2b .所以m ＋n ＝a －c 2＋b 2－ac2b ≤0，即ab －bc ＋b 2－ac ≤0，即(a ＋b )(b －c )≤0，所以b ≤c ， 于是b 2≤c 2，即a 2＝b 2＋c 2≤2c 2， 所以e 2＝c 2a 2≥12，即22≤e ＜1. (2)由(1)知e min ＝22，a ＝2b ＝2c ， 此时椭圆的方程为x 22c 2＋y 2c 2＝1，设P (x ，y )，则－ 2c ≤x ≤2c ，所以(PF →＋OD →)·PO →＝12x 2－x ＋c 2＝12(x －1)2＋c 2－12.当c ≥22时，上式的最小值为c 2－12，即c 2－12＝72，得c ＝2； 当0＜c ＜22时，上式的最小值为12(2c )2－2c ＋c 2，即12(2c )2－2c ＋c 2＝72， 解得c ＝2＋304，与0＜c ＜22矛盾，舍去． 综上所述，椭圆的方程为x 28＋y 24＝1.题型二与圆锥曲线有关的轨迹问题轨迹是动点按一定规律运动而形成的，轨迹的条件可以用动点坐标表示出来．求轨迹方程的基本方法是(1)直接法求轨迹方程：建立适当的直角坐标系，根据条件列出方程；(2)待定系数法求轨迹方程：根据曲线的标准方程；(3)定义法求轨迹方程：动点的轨迹满足圆锥曲线的定义；(4)代入法求轨迹方程：动点M(x，y)取决于已知曲线C上的点(x0，y0)的坐标变化，根据两者关系，得到x，y，x0，y0的关系式，用x，y表示x0，y0，代入曲线C的方程．例2如图，已知线段AB＝4，动圆O1与线段AB切于点C，且AC－BC＝22，过点A、B分别作圆O1的切线，两切线交于点P，且P、O1均在AB的同侧，求动点P的轨迹方程．解建立如图所示的直角坐标系，则A(－2,0)，B(2,0)，由切线长定理得AC－BC＝PA－PB＝22<4，∴点P的轨迹是以点A、B为焦点的双曲线的右支(不包括顶点)．∵a＝2，c＝2，∴b2＝2.∴动点P的轨迹方程是x2－y2＝2 (x>2)．跟踪演练2若动圆P过点N(－2,0)，且与另一圆M：(x－2)2＋y2＝8相外切，求动圆P的圆心的轨迹方程．解设P(x，y)，因为动圆P过点N，所以PN是该圆的半径，又因为动圆P与圆M外切，所以有PM＝PN＋22，即PM－PN＝22，故点P的轨迹是以M、N为焦点，实轴长为22，焦距MN为4的双曲线的左支，即a＝2，c＝2，所以b＝c2－a2＝2，从而动圆P的圆心的轨迹方程为x22－y22＝1 (x≤－2)．题型三圆锥曲线的综合问题圆锥曲线中定点、定值、最值、范围问题是圆锥曲线的综合问题，它是解析法的应用，它涉及数形结合的数学思想，圆锥曲线与圆锥曲线的位置关系，圆锥曲线知识的纵向联系，圆锥曲线知识与三角、函数、不等式、方程、平面向量等代数知识的横向联系．解这类问题的分析思想与方法是可循的，重要的是要善于掌握圆锥曲线知识纵向、横向的联系，努力提高解题能力．例3 如图，设A (a,0) (a >0)，B 、C 分别为x 轴、y 轴上的点，非零向量BP →满足：BP →＝2BC →，BP →⊥AC →.(1)当点B 在x 轴上运动时，求点P 的轨迹E 的方程；(2)设Q 是曲线E 上异于P 的点，且OP →·OQ →＝0，求证：直线PQ 过定点． (1)解 设B (x 0,0)，C (0，y 0)，P (x ，y )． ∵BP →＝2BC →，∴C 是BP 的中点，∴⎩⎪⎨⎪⎧x 0＝－x ，y 0＝12y .易知BC →＝(－x 0，y 0)，AC →＝(－a ，y 0)， 由BP →⊥AC →，即BC →⊥AC →，得ax 0＋y 20＝0， ∴－ax ＋14y 2＝0，即y 2＝4ax .又BP →＝(2x ，y )≠0，∴P 点的轨迹方程是y 2＝4ax (a >0，x ≠0)． (2)证明 ∵OP →·OQ →＝0，∴OP ⊥OQ ， 显然直线OP 的斜率存在，且不为0，∴可设直线OP ：y ＝kx ，则直线OQ ：y ＝－1kx ，由⎩⎪⎨⎪⎧y 2＝4ax ，y ＝kx ，得P ⎝⎛⎭⎫4a k 2，4a k ； 由⎩⎪⎨⎪⎧y 2＝4ax ，y ＝－1k x ，得Q ＝(4ak 2，－4ak )． 当k ＝±1时，直线PQ 的方程为x ＝4a ，过定点(4a,0)； 当k ≠±1时，直线PQ 的方程为y －4a k－4ak －4a k ＝x －4ak24ak 2－4ak 2，整理得k (x －4a )＋(k 2－1)y ＝0，∵k ≠0，∴过定点(4a,0)． 综上，直线PQ 必过定点(4a,0)．跟踪演练3 如图，已知A (－3p,0) (p >0)，B 、C 两点分别在y 轴和x 轴上运动，并且满足AB →·BQ →＝0，BC →＝12CQ →.(1)求动点Q 的轨迹方程；(2)设过点A 的直线与Q 的轨迹交于E 、F 两点，A ′(3p,0)，求直线A ′E ，A ′F 的斜率之和．解 (1)设Q (x ，y )，B (0，y 0)，C (x 0,0)， 则BC →＝(x 0，－y 0)，CQ →＝(x －x 0，y )， ∵BC →＝12CQ →，∴(x 0，－y 0)＝12(x －x 0，y )，即x 0＝x 3，y 0＝－y2.∴B ⎝⎛⎭⎫0，－y 2，C ⎝⎛⎭⎫x 3，0. 又A (－3p,0)，∴AB →＝⎝⎛⎭⎫3p ，－y 2，BQ →＝⎝⎛⎭⎫x ，32y ， 由AB →·BQ →＝0，得3px －34y 2＝0，即y 2＝4px .∴Q 点的轨迹方程为y 2＝4px (p >0)．(2)设过点A 的直线方程为y ＝k (x ＋3p ) (k ≠0)，E (x 1，y 1)，F (x 2，y 2)．联立方程组⎩⎪⎨⎪⎧y ＝k (x ＋3p )，y 2＝4px消去x ，得k4p y 2－y ＋3kp ＝0.∴y 1y 2＝12p 2， k A ′E ＋k A ′F ＝y 1x 1－3p ＋y 2x 2－3p＝y 1x 2－3py 1＋y 2x 1－3py 2(x 1－3p )(x 2－3p )，又y 21＝4px 1，y 22＝4px 2，∴k A ′E ＋k A ′F ＝y 1y 224p －3py 1＋y 2y 214p－3py 2(x 1－3p )(x 2－3p ).由y 1y 2＝12p 2，得k A ′E ＋k A ′F ＝0.1．圆锥曲线的定义是圆锥曲线问题的根本，利用圆锥曲线的定义解题是高考考查圆锥曲线的一个重要命题点，在历年的高考试题中曾多次出现．2．圆锥曲线的标准方程是用代数方法研究圆锥曲线的几何性质的基础，高考对圆锥曲线标准方程的考查方式有两种：一个是在解答题中作为试题的入口进行考查；二是在填空题中结合圆锥曲线的简单几何性质进行考查．3．圆锥曲线的简单几何性质是圆锥曲线的重点内容，高考对此进行重点考查，主要考查椭圆与双曲线的离心率的求解、双曲线的渐近线方程的求解，试题一般以圆锥曲线的标准方程、直线与圆锥曲线的位置关系等为主进行交汇命题．4．虽然考纲中没有直接要求关于直线与圆锥曲线相结合的知识，但直线与圆锥曲线是密不可分的，如双曲线的渐近线、抛物线的准线，圆锥曲线的对称轴等都是直线．高考不但不回避直线与圆锥曲线，而且在试题中进行重点考查，考查方式既可以是填空题，也可以是解答题．5．考纲对曲线与方程的要求是“了解方程的曲线与曲线的方程的对应关系”，高考对曲线与方程的考查主要体现在以利用圆锥曲线的定义和待定系数法求圆锥曲线的方程，以直接法、代入法等方法求圆锥曲线的方程．6．高考对圆锥曲线的考查是综合性的，这种综合性体现在圆锥曲线、直线、圆、平面向量、不等式等知识的相互交汇，高考对圆锥曲线的综合考查主要是在解答题中进行，一般以椭圆或者抛物线为依托，全面考查圆锥曲线与方程的求法、直线与圆锥曲线的位置关系，考查函数、方程、不等式、平面向量等在解决问题中的综合运用．。

卜人入州八九几市潮王学校第十一讲圆锥曲线知识整理1、 圆锥曲线的定义、HY 方程、图象、几何性质由双曲线求渐进线：x a by a x b y a x b y b y a x b y a x ±=⇒±=⇒=⇒=-⇒=-22222222222201由双曲线求渐进线：λ=-⇒=-⇒=⇒±=⇒±=2222222222220by a x b y a x a x b y a x b y x a b y2、直线和圆锥曲线的位置关系：〔1〕、判断直线与圆锥曲线的位置关系的方法〔根本思路〕→消元→一元二次方程→判别式Δ〔方程的思想〕〔2〕、求弦长的方法：①求交点，利用两点间间隔公式求弦长； ②弦长公式 练习训练1、椭圆5x 2+9y 2=45的离心率是〔〕A.143B.2149C.23D.322、在双曲线的实轴在y 轴上，它的两条渐近线方程分别是2x 3y=0，实轴长为12，那么它的方程是〔〕A.x y 2236161-= B.y x 221443241-= C.y x 2236811-= D.y x 2212271-= 3、以原点为中心，实轴在x 轴上的双曲线，一条渐近线为y x =34，焦点到渐近线的间隔为6，那么它的方程是〔〕A.x y 221691-= B.x y 229161-= C.x y 2236641-= D.x y 2264361-= 4、假设方程222212m y m x --+=1表示双曲线，那么其焦距为()(A)3(B)3 (C)23(D)65、方程y 2=2px (p >0)中的字母p 表示() A ．顶点、准线间的间隔B ．焦点、准线间的间隔⎩⎨⎧圆锥曲线方程直线方程联立） （消　） （消x y y y y ky y k y x x x x k x x k l ]4))[(11(||11]4))[(1(1212212212212212212-++=-+=-++=-+=C ．原点、焦点间间隔D ．以上都不对6、顶点为原点，焦点为F(0，－1)的抛物线方程是〔〕2=－2x 2=－4x 2=－2y 2=－4y7、如图，抛物线形拱桥的顶点距水面2米时，测得拱桥内水面宽为12米，当水面升高1米后，拱桥内水面宽度是()(A)62米(B)66米 (C)32米(D)36米8、〔1〕椭圆的方程为116922=+x y ，那么它的长轴长为______，短轴长为______，焦距为_____，焦点坐标为________________，离心率为________.〔2〕双曲线的方程为116922=-y x ，那么它的实轴长为______，虚轴长为_____，焦距为_____，焦点坐标为_________________，离心率为_______， 渐近线方程为_________________.〔3〕抛物线22x y -=的焦点坐标为__________，准线方程为____________.9、〔1〕短轴长为16，离心率为53，焦点在y 轴上的椭圆方程为__________. 〔2〕焦距为10，离心率为35，焦点在x 轴上的双曲线的方程为__________. 10、一等轴双曲线的焦距为4，那么它的HY 方程为____________________.11、与椭圆1492422=+y x 有公一共焦点，且离心率为45的双曲线方程为________________12、(1)顶点在原点，对称轴为坐标轴，焦点为)0,2(-的抛物线方程为_____________.(2)顶点在原点，对称轴为坐标轴，准线方程为81-=y 的抛物线方程为______________ 13、假设抛物线y 2=2px 上一点横坐标为6，这个点与焦点的间隔为10，那么p=14、抛物线顶点在原点，对称轴是坐标轴，焦点在直线02=+-y x 上，那么抛物线的方程为______15、〔1〕椭圆的方程为16422=+y x ，假设P 是椭圆上一点，且,7||1=PF 那么________||2=PF .〔2〕双曲线方程为14491622-=-y x ，假设P 是双曲线上一点，且,7||1=PF 那么________||2=PF .16、曲线方程为14922=-+-k y k x ，(1)当曲线为椭圆时，k 的取值范围是______________. (2)当曲线为双曲线时，k 的取值范围是______________.。

第3讲圆锥曲线中的热点问题考情解读 1.本部分主要以解答题形式考查，往往是试卷的压轴题之一，一般以椭圆或抛物线为背景，考查弦长、定点、定值、最值、范围问题或探索性问题，试题难度较大.2.求轨迹方程也是高考的热点与重点，若在客观题中出现通常用定义法，若在解答题中出现一般用直接法、代入法、参数法或待定系数法，往往出现在解答题的第(1)问中．1．直线与圆锥曲线的位置关系(1)直线与椭圆的位置关系的判定方法：将直线方程与椭圆方程联立，消去一个未知数，得到一个一元二次方程．若Δ>0，则直线与椭圆相交；若Δ＝0，则直线与椭圆相切；若Δ<0，则直线与椭圆相离．(2)直线与双曲线的位置关系的判定方法：将直线方程与双曲线方程联立，消去y(或x)，得到一个一元方程ax2＋bx＋c＝0(或ay2＋by ＋c＝0)．①若a≠0，当Δ>0时，直线与双曲线相交；当Δ＝0时，直线与双曲线相切；当Δ<0时，直线与双曲线相离．②若a＝0时，直线与渐近线平行，与双曲线有一个交点．(3)直线与抛物线的位置关系的判定方法：将直线方程与抛物线方程联立，消去y(或x)，得到一个一元方程ax2＋bx＋c＝0(或ay2＋by ＋c＝0)．①当a≠0时，用Δ判定，方法同上．②当a＝0时，直线与抛物线的对称轴平行，只有一个交点．2．有关弦长问题有关弦长问题，应注意运用弦长公式及根与系数的关系，“设而不求”；有关焦点弦长问题，要重视圆锥曲线定义的运用，以简化运算．(1)斜率为k的直线与圆锥曲线交于两点P1(x1，y1)，P2(x2，y2)，则所得弦长|P1P2|＝1＋k2|x2－x1|或|P1P2|＝1＋1k2|y2－y1|，其中求|x2－x1|与|y2－y1|时通常使用根与系数的关系，即作如下变形：|x2－x1|＝(x1＋x2)2－4x1x2，|y2－y1|＝(y1＋y2)2－4y1y2.(2)当斜率k 不存在时，可求出交点坐标，直接运算(利用两点间距离公式)． 3．弦的中点问题有关弦的中点问题，应灵活运用“点差法”，“设而不求法”来简化运算． 4．轨迹方程问题(1)求轨迹方程的基本步骤：①建立适当的平面直角坐标系，设出轨迹上任一点的坐标——解析法(坐标法)． ②寻找动点与已知点满足的关系式——几何关系． ③将动点与已知点的坐标代入——几何关系代数化． ④化简整理方程——简化．⑤证明所得方程为所求的轨迹方程——完成其充要性． (2)求轨迹方程的常用方法：①直接法：将几何关系直接翻译成代数方程；②定义法：满足的条件恰适合某已知曲线的定义，用待定系数法求方程； ③代入法：把所求动点的坐标与已知动点的坐标建立联系；④交轨法：写出两条动直线的方程直接消参，求得两条动直线交点的轨迹；(3)注意①建系要符合最优化原则；②求轨迹与“求轨迹方程”不同，轨迹通常指的是图形，而轨迹方程则是代数表达式．步骤②⑤省略后，验证时常用途径：化简是否同解变形，是否满足题意，验证特殊点是否成立等.热点一 圆锥曲线中的范围、最值问题例1 (2013·浙江)如图，点P (0，－1)是椭圆C 1：x 2a 2＋y 2b 2＝1(a >b >0)的一个顶点，C 1的长轴是圆C 2：x 2＋y 2＝4的直径．l 1，l 2是过点P 且互相垂直的两条直线，其中l 1交圆C 2于A ，B 两点，l 2交椭圆C 1于另一点D .(1)求椭圆C 1的方程；(2)求△ABD 面积取最大值时直线l 1的方程．思维启迪 (1)P 点是椭圆上顶点，圆C 2的直径等于椭圆长轴长；(2)设直线l 1的斜率为k ，将△ABD 的面积表示为关于k 的函数．解 (1)由题意得⎩⎪⎨⎪⎧b ＝1，a ＝2.所以椭圆C 1的方程为x 24＋y 2＝1.(2)设A (x 1，y 1)，B (x 2，y 2)，D (x 0，y 0)． 由题意知直线l 1的斜率存在，不妨设其为k ， 则直线l 1的方程为y ＝kx －1. 又圆C 2：x 2＋y 2＝4， 故点O 到直线l 1的距离 d ＝1k 2＋1，所以|AB |＝24－d 2＝24k 2＋3k 2＋1. 又l 2⊥l 1，故直线l 2的方程为x ＋ky ＋k ＝0.由⎩⎪⎨⎪⎧x ＋ky ＋k ＝0，x 2＋4y 2＝4.消去y ，整理得(4＋k 2)x 2＋8kx ＝0， 故x 0＝－8k 4＋k 2.所以|PD |＝8k 2＋14＋k2. 设△ABD 的面积为S ， 则S ＝12|AB |·|PD |＝84k 2＋34＋k 2，所以S ＝324k 2＋3＋134k 2＋3≤3224k 2＋3·134k 2＋3＝161313，当且仅当k ＝±102时取等号． 所以所求直线l 1的方程为y ＝±102x －1. 思维升华 求最值及参数范围的方法有两种：①根据题目给出的已知条件或图形特征列出一个关于参数的函数关系式，将其代入由题目列出的不等式(即为消元)，然后求解不等式；②由题目条件和结论建立目标函数，进而转化为求函数的值域．已知椭圆C 的左，右焦点分别为F 1，F 2，椭圆的离心率为12，且椭圆经过点P (1，32)． (1)求椭圆C 的标准方程；(2)线段PQ 是椭圆过点F 2的弦，且PF 2→＝λF 2Q →，求△PF 1Q 内切圆面积最大时实数λ的值． 解 (1)e ＝c a ＝12，P (1，32)满足1a 2＋(32)2b 2＝1，又a 2＝b 2＋c 2，∵a 2＝4，b 2＝3， ∴椭圆标准方程为x 24＋y 23＝1.(2)显然直线PQ 不与x 轴重合，当直线PQ 与x 轴垂直时，|PQ |＝3，|F 1F 2|＝2， S △PF 1Q ＝3；当直线PQ 不与x 轴垂直时，设直线PQ ：y ＝k (x －1)，k ≠0代入椭圆C 的标准方程， 整理，得(3＋4k 2)y 2＋6ky －9k 2＝0， Δ>0，y 1＋y 2＝－6k3＋4k 2，y 1·y 2＝－9k 23＋4k 2.S △PF 1Q ＝12×|F 1F 2|×|y 1－y 2|＝12k 2＋k 4(3＋4k 2)2，令t ＝3＋4k 2，∴t >3，k 2＝t －34，∴S △PF 1Q ＝3－3(1t ＋13)2＋43，∵0<1t <13，∴S △PF 1Q ∈(0,3)，∴当直线PQ 与x 轴垂直时S △PF 1Q 最大，且最大面积为3. 设△PF 1Q 内切圆半径为r ，则S △PF 1Q ＝12(|PF 1|＋|QF 1|＋|PQ |)·r ＝4r ≤3.即r max ＝34，此时直线PQ 与x 轴垂直，△PF 1Q 内切圆面积最大，∴PF 2→＝F 2Q →，∴λ＝1.热点二 圆锥曲线中的定值、定点问题例2 (2013·陕西)已知动圆过定点A (4,0)，且在y 轴上截得弦MN 的长为8. (1)求动圆圆心的轨迹C 的方程；(2)已知点B (－1,0)，设不垂直于x 轴的直线l 与轨迹C 交于不同的两点P ，Q ，若x 轴是∠PBQ 的角平分线，证明：直线l 过定点．思维启迪 (1)设动圆圆心坐标，利用圆的半径、半弦长和弦心距组成的直角三角形求解；(2)设直线方程y ＝kx ＋b ，将其和轨迹C 的方程联立，再设两个交点坐标，由题意知直线BP 和BQ 的斜率互为相反数，推出k 和b 的关系，最后证明直线过定点．(1)解 如图，设动圆圆心为O 1(x ，y )，由题意，得|O 1A |＝|O 1M |，当O 1不在y 轴上时，过O 1作O 1H ⊥MN 交MN 于H ，则H 是MN 的中点， ∴|O 1M |＝x 2＋42， 又|O 1A |＝(x －4)2＋y 2，∴(x －4)2＋y 2＝x 2＋42，化简得y 2＝8x (x ≠0)．又当O 1在y 轴上时，O 1与O 重合，点O 1的坐标为(0,0)也满足方程y 2＝8x ， ∴动圆圆心的轨迹C 的方程为y 2＝8x .(2)证明 如图由题意，设直线l 的方程为y ＝kx ＋b (k ≠0)， P (x 1，y 1)，Q (x 2，y 2)， 将y ＝kx ＋b 代入y 2＝8x 中， 得k 2x 2＋(2bk －8)x ＋b 2＝0. 其中Δ＝－32kb ＋64>0.由根与系数的关系得，x 1＋x 2＝8－2bk k 2，①x 1x 2＝b 2k2，②∵x 轴是∠PBQ 的角平分线， ∴y 1x 1＋1＝－y 2x 2＋1， 即y 1(x 2＋1)＋y 2(x 1＋1)＝0， (kx 1＋b )(x 2＋1)＋(kx 2＋b )(x 1＋1)＝0， 2kx 1x 2＋(b ＋k )(x 1＋x 2)＋2b ＝0③将①②代入③得2kb 2＋(k ＋b )(8－2bk )＋2k 2b ＝0， ∴k ＝－b ，此时Δ>0，∴直线l 的方程为y ＝k (x －1)，即直线l 过定点(1,0)．思维升华 (1)定值问题就是在运动变化中寻找不变量的问题，基本思想是使用参数表示要解决的问题，证明要解决的问题与参数无关．在这类试题中选择消元的方向是非常关键的． (2)由直线方程确定定点，若得到了直线方程的点斜式：y －y 0＝k (x －x 0)，则直线必过定点(x 0，y 0)；若得到了直线方程的斜截式：y ＝kx ＋m ，则直线必过定点(0，m )．已知椭圆C 的中点在原点，焦点在x 轴上，离心率等于12，它的一个顶点恰好是抛物线x 2＝83y 的焦点． (1)求椭圆C 的方程；(2)已知点P (2,3)，Q (2，－3)在椭圆上，点A 、B 是椭圆上不同的两个动点，且满足∠APQ ＝∠BPQ ，试问直线AB 的斜率是否为定值，请说明理由．解 (1)设椭圆C 的方程为x 2a 2＋y 2b 2＝1(a >b >0)，则b ＝2 3.由c a ＝12，a 2＝c 2＋b 2，得a ＝4，∴椭圆C 的方程为x 216＋y 212＝1.(2)当∠APQ ＝∠BPQ 时，P A 、PB 的斜率之和为0，设直线P A 的斜率为k ，则PB 的斜率为－k ，P A 的直线方程为y －3＝k (x －2)，由⎩⎪⎨⎪⎧y －3＝k (x －2)，x 216＋y 212＝1，整理得 (3＋4k 2)x 2＋8(3－2k )kx ＋4(3－2k )2－48＝0， x 1＋2＝8(2k －3)k 3＋4k 2，同理PB 的直线方程为y －3＝－k (x －2)， 可得x 2＋2＝－8k (－2k －3)3＋4k 2＝8k (2k ＋3)3＋4k 2.∴x 1＋x 2＝16k 2－123＋4k 2，x 1－x 2＝－48k3＋4k 2， k AB ＝y 1－y 2x 1－x 2＝k (x 1－2)＋3＋k (x 2－2)－3x 1－x 2＝k (x 1＋x 2)－4k x 1－x 2＝12， ∴直线AB 的斜率为定值12.热点三 圆锥曲线中的探索性问题例3 已知椭圆C 1、抛物线C 2的焦点均在x 轴上，C 1的中心和C 2的顶点均为原点O ，从每条曲线上各取两个点，将其坐标记录于下表中：x 3 －2 4 2 y－23－422(1)求C 1，C 2的标准方程；(2)是否存在直线l 满足条件：①过C 2的焦点F ；②与C 1交于不同的两点M ，N ，且满足OM →⊥ON →？若存在，求出直线l 的方程；若不存在，说明理由．思维启迪 (1)比较椭圆及抛物线方程可知，C 2的方程易求，确定其上两点，剩余两点，利用待定系数法求C 1方程.(2) 联立方程，转化已知条件进行求解. 解 (1)设抛物线C 2：y 2＝2px (p ≠0)， 则有y 2x＝2p (x ≠0)，据此验证四个点知(3，－23)，(4，－4)在C 2上， 易求得C 2的标准方程为y 2＝4x . 设椭圆C 1：x 2a 2＋y 2b2＝1(a >b >0)，把点(－2,0)，(2，22)代入得⎩⎨⎧4a 2＝12a 2＋12b2＝1，解得⎩⎪⎨⎪⎧a 2＝4b 2＝1，所以C 1的标准方程为x 24＋y 2＝1.(2)容易验证当直线l 的斜率不存在时，不满足题意． 当直线l 的斜率存在时，设其方程为y ＝k (x －1)， 与C 1的交点为M (x 1，y 1)，N (x 2，y 2)． 由⎩⎪⎨⎪⎧x 24＋y 2＝1y ＝k (x －1)消去y 并整理得(1＋4k 2)x 2－8k 2x ＋4(k 2－1)＝0， 于是x 1＋x 2＝8k 21＋4k 2，① x 1x 2＝4(k 2－1)1＋4k 2.②所以y 1y 2＝k 2(x 1－1)(x 2－1) ＝k 2[x 1x 2－(x 1＋x 2)＋1]＝k 2[4k 2－11＋4k 2－8k 21＋4k 2＋1]＝－3k 21＋4k 2.③由OM →⊥ON →，即OM →·ON →＝0，得x 1x 2＋y 1y 2＝0.(*)将②③代入(*)式，得4(k 2－1)1＋4k 2－3k 21＋4k 2＝k 2－41＋4k 2＝0，解得k ＝±2，所以存在直线l 满足条件， 且直线l 的方程为2x －y －2＝0或2x ＋y －2＝0.思维升华 解析几何中的探索性问题，从类型上看，主要是存在类型的相关题型．解决问题的一般策略是先假设结论成立，然后进行演绎推理或导出矛盾，即可否定假设或推出合理结论，验证后肯定结论，对于“存在”或“不存在”的问题，直接用条件证明或采用反证法证明．解答时，不但需要熟练掌握圆锥曲线的概念、性质、方程及不等式、判别式等知识，还要具备较强的审题能力、逻辑思维能力以及运用数形结合的思想分析问题和解决问题的能力．如图，抛物线C ：y 2＝2px 的焦点为F ，抛物线上一定点Q (1,2)．(1)求抛物线C 的方程及准线l 的方程．(2)过焦点F 的直线(不经过Q 点)与抛物线交于A ，B 两点，与准线l 交于点M ，记QA ，QB ，QM 的斜率分别为k 1，k 2，k 3，问是否存在常数λ，使得k 1＋k 2＝λk 3成立，若存在λ，求出λ的值；若不存在，说明理由． 解 (1)把Q (1,2)代入y 2＝2px ，得2p ＝4， 所以抛物线方程为y 2＝4x ，准线l 的方程：x ＝－1. (2)由条件可设直线AB 的方程为y ＝k (x －1)，k ≠0. 由抛物线准线l ：x ＝－1，可知M (－1，－2k )． 又Q (1,2)，所以k 3＝2＋2k 1＋1＝k ＋1，即k 3＝k ＋1.把直线AB 的方程y ＝k (x －1)，代入抛物线方程y 2＝4x ，并整理，可得k 2x 2－2(k 2＋2)x ＋k 2＝0.设A (x 1，y 1)，B (x 2，y 2)，由根与系数的关系，知 x 1＋x 2＝2k 2＋4k2，x 1x 2＝1.又Q (1,2)，则k 1＝2－y 11－x 1，k 2＝2－y 21－x 2.因为A ，F ，B 共线，所以k AF ＝k BF ＝k ， 即y 1x 1－1＝y 2x 2－1＝k . 所以k 1＋k 2＝2－y 11－x 1＋2－y 21－x 2＝y 1x 1－1＋y 2x 2－1－2(x 1＋x 2－2)x 1x 2－(x 1＋x 2)＋1＝2k －2(2k 2＋4k2－2)1－2k 2＋4k 2＋1＝2k ＋2， 即k 1＋k 2＝2k ＋2.又k 3＝k ＋1，可得k 1＋k 2＝2k 3.即存在常数λ＝2，使得k 1＋k 2＝λk 3成立．1．圆锥曲线的最值与范围问题的常见求法(1)几何法：若题目的条件和结论能明显体现几何特征和意义，则考虑利用图形性质来解决； (2)代数法：若题目的条件和结论能体现一种明确的函数关系，则可首先建立起目标函数，再求这个函数的最值，在利用代数法解决最值与范围问题时常从以下五个方面考虑： ①利用判别式来构造不等关系，从而确定参数的取值范围；②利用已知参数的范围，求新参数的范围，解这类问题的核心是在两个参数之间建立等量关系；③利用隐含或已知的不等关系建立不等式，从而求出参数的取值范围； ④利用基本不等式求出参数的取值范围； ⑤利用函数的值域的求法，确定参数的取值范围． 2．定点、定值问题的处理方法定值包括几何量的定值或曲线过定点等问题，处理时可以直接推理求出定值，也可以先通过特定位置猜测结论后进行一般性证明．对于客观题，通过特殊值法探求定点、定值能达到事半功倍的效果． 3．探索性问题的解法探索是否存在的问题，一般是先假设存在，然后寻找理由去确定结论，如果真的存在，则可以得出相应存在的结论；若不存在，则会由条件得出矛盾，再下结论不存在即可.真题感悟(2014·北京)已知椭圆C ：x 2＋2y 2＝4.(1)求椭圆C 的离心率；(2)设O 为原点，若点A 在椭圆C 上，点B 在直线y ＝2上，且OA ⊥OB ，试判断直线AB 与圆x 2＋y 2＝2的位置关系，并证明你的结论．解 (1)由题意，得椭圆C 的标准方程为x 24＋y 22＝1， 所以a 2＝4，b 2＝2，从而c 2＝a 2－b 2＝2.因此a ＝2，c ＝ 2.故椭圆C 的离心率e ＝c a ＝22. (2)直线AB 与圆x 2＋y 2＝2相切．证明如下：设点A ，B 的坐标分别为(x 0，y 0)，(t,2)，其中x 0≠0.因为OA ⊥OB ，所以OA →·OB →＝0，即tx 0＋2y 0＝0，解得t ＝－2y 0x 0. 当x 0＝t 时，y 0＝－t 22，代入椭圆C 的方程，得t ＝±2， 故直线AB 的方程为x ＝±2，圆心O 到直线AB 的距离d ＝ 2.此时直线AB 与圆x 2＋y 2＝2相切．当x 0≠t 时，直线AB 的方程为y －2＝y 0－2x 0－t(x －t )． 即(y 0－2)x －(x 0－t )y ＋2x 0－ty 0＝0.圆心O 到直线AB 的距离d ＝|2x 0－ty 0|(y 0－2)2＋(x 0－t )2.又x 20＋2y 20＝4，t ＝－2y 0x 0， 故d ＝⎪⎪⎪⎪2x 0＋2y 20x 0x 20＋y 20＋4y 20x 20＋4＝⎪⎪⎪⎪⎪⎪4＋x 20x 0x 40＋8x 20＋162x 20＝ 2.此时直线AB 与圆x 2＋y 2＝2相切． 押题精练已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为22，其左、右焦点分别是F 1、F 2，过点F 1的直线l 交椭圆C 于E 、G 两点，且△EGF 2的周长为4 2.(1)求椭圆C 的方程；(2)若过点M (2,0)的直线与椭圆C 相交于两点A 、B ，设P 为椭圆上一点，且满足OA →＋OB →＝tOP→(O 为坐标原点)，当|P A →－PB →|<253时，求实数t 的取值范围．解 (1)由题意知椭圆的离心率e ＝c a ＝22，∴e 2＝c 2a 2＝a 2－b 2a 2＝12，即a 2＝2b 2.又△EGF 2的周长为42，即4a ＝42，∴a 2＝2，b 2＝1.∴椭圆C 的方程为x 22＋y 2＝1.(2)由题意知直线AB 的斜率存在，即t ≠0.设直线AB 的方程为y ＝k (x －2)，A (x 1，y 1)，B (x 2，y 2)，P (x ，y )，由⎩⎪⎨⎪⎧ y ＝k (x －2)，x 22＋y 2＝1，得(1＋2k 2)x 2－8k 2x ＋8k 2－2＝0.由Δ＝64k 4－4(2k 2＋1)(8k 2－2)>0，得k 2<12.x 1＋x 2＝8k 21＋2k 2，x 1x 2＝8k 2－21＋2k 2，∵OA →＋OB →＝tOP →，∴(x 1＋x 2，y 1＋y 2)＝t (x ，y )，x ＝x 1＋x 2t ＝8k 2t (1＋2k 2)，y ＝y 1＋y 2t ＝1t [k (x 1＋x 2)－4k ]＝－4kt (1＋2k 2).∵点P 在椭圆C 上，∴(8k 2)2[t (1＋2k 2)]2＋2(－4k )2[t (1＋2k 2)]2＝2， ∴16k 2＝t 2(1＋2k 2)．∵|P A →－PB →|<253，∴1＋k 2|x 1－x 2|<253， ∴(1＋k 2)[(x 1＋x 2)2－4x 1x 2]<209， ∴(1＋k 2)[64k 4(1＋2k 2)2－4·8k 2－21＋2k 2]<209， ∴(4k 2－1)(14k 2＋13)>0，∴k 2>14.∴14<k 2<12. ∵16k 2＝t 2(1＋2k 2)，∴t 2＝16k 21＋2k 2＝8－81＋2k 2， 又32<1＋2k 2<2，∴83<t 2＝8－81＋2k 2<4， ∴－2<t <－263或263<t <2， ∴实数t 的取值范围为(－2，－263)∪(263，2)．(推荐时间：50分钟)一、选择题1．已知点M 与双曲线x 216－y 29＝1的左、右焦点的距离之比为2∶3，则点M 的轨迹方程为( ) A ．x 2－y 2＋26x ＋25＝0B ．x 2＋y 2＋16x ＋81＝0C ．x 2＋y 2＋26x ＋25＝0D ．x 2＋y 2＋16x －81＝0答案 C解析 设点M (x ，y )，F 1(－5,0)，F 2(5,0)，则由题意得|MF 1||MF 2|＝23，将坐标代入，得(x ＋5)2＋y 2(x －5)2＋y 2＝49， 化简，得x 2＋y 2＋26x ＋25＝0.2．已知椭圆E 的左、右焦点分别为F 1、F 2，过F 1且斜率为2的直线交椭圆E 于P 、Q 两点，若△PF 1F 2为直角三角形，则椭圆E 的离心率为( ) A.53 B.23 C.23 D.13答案 A解析 由题意可知，∠F 1PF 2是直角，且tan ∠PF 1F 2＝2，∴|PF 2||PF 1|＝2，又|PF 1|＋|PF 2|＝2a ， ∴|PF 1|＝2a 3，|PF 2|＝4a 3. 根据勾股定理得⎝⎛⎭⎫2a 32＋⎝⎛⎭⎫4a 32＝(2c )2，所以离心率e ＝c a ＝53. 3．已知抛物线y 2＝8x 的焦点F 到双曲线C ：y 2a 2－x 2b 2＝1(a >0，b >0)渐近线的距离为455，点P 是抛物线y 2＝8x 上的一动点，P 到双曲线C 的上焦点F 1(0，c )的距离与到直线x ＝－2的距离之和的最小值为3，则该双曲线的方程为( )A.y 22－x 23＝1 B ．y 2－x 24＝1 C.y 24－x 2＝1 D.y 23－x 22＝1 答案 C解析 由题意得，抛物线y 2＝8x 的焦点F (2,0)，双曲线C ：y 2a 2－x 2b2＝1(a >0，b >0)的一条渐近线的方程为ax －by ＝0， ∵抛物线y 2＝8x 的焦点F 到双曲线C ：y 2a 2－x 2b 2＝1(a >0，b >0)渐近线的距离为455， ∴2aa 2＋b 2＝455， ∴a ＝2b .∵P 到双曲线C 的上焦点F 1(0，c )的距离与到直线x ＝－2的距离之和的最小值为3， ∴|FF 1|＝3，∴c 2＋4＝9，∴c ＝5，∵c 2＝a 2＋b 2，a ＝2b ，∴a ＝2，b ＝1.∴双曲线的方程为y 24－x 2＝1，故选C. 4．若点O 和点F 分别为椭圆x 24＋y 23＝1的中心和左焦点，点P 为椭圆上的任意一点，则OP →·FP →的最大值为( )A ．2B ．3C ．6D ．8答案 C解析 设P (x 0，y 0)，则x 204＋y 203＝1，即y 20＝3－3x 204， 又因为F (－1,0)，所以OP →·FP →＝x 0·(x 0＋1)＋y 20＝14x 20＋x 0＋3 ＝14(x 0＋2)2＋2， 又x 0∈[－2,2]，即OP →·FP →∈[2,6]，所以(OP →·FP →)max ＝6.5．设M (x 0，y 0)为抛物线C ：x 2＝8y 上一点，F 为抛物线C 的焦点，以F 为圆心，|FM |为半径的圆和抛物线的准线相交，则y 0的取值范围是( )A ．(0,2)B ．[0,2]C ．(2，＋∞)D ．[2，＋∞)答案 C解析 依题意得F (0,2)，准线方程为y ＝－2，又∵以F 为圆心，|FM |为半径的圆和抛物线的准线相交，且|FM |＝|y 0＋2|，∴|FM |>4，即|y 0＋2|>4，又y 0≥0，∴y 0>2.6．已知双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的左，右焦点分别为F 1(－c,0)，F 2(c,0)，若双曲线上存在点P 满足a sin ∠PF 1F 2＝c sin ∠PF 2F 1，则该双曲线的离心率的取值范围为( ) A ．(1，2＋1) B ．(1，3)C ．(3，＋∞)D ．(2＋1，＋∞) 答案 A解析 根据正弦定理得|PF 2|sin ∠PF 1F 2＝|PF 1|sin ∠PF 2F 1， 所以由a sin ∠PF 1F 2＝c sin ∠PF 2F 1可得a |PF 2|＝c |PF 1|， 即|PF 1||PF 2|＝c a＝e ， 所以|PF 1|＝e |PF 2|.因为e >1，所以|PF 1|>|PF 2|，点P 在双曲线的右支上．又|PF 1|－|PF 2|＝e |PF 2|－|PF 2|＝|PF 2|(e －1)＝2a ，解得|PF 2|＝2ae －1， 因为|PF 2|>c －a ，所以2a e －1>c －a ，即2e －1>e －1， 即(e －1)2<2，解得1－2<e <2＋1.又e >1，所以e ∈(1，2＋1)，故选A.二、填空题7．直线y ＝kx ＋1与椭圆x 25＋y 2m＝1恒有公共点，则m 的取值范围是________． 答案 m ≥1且m ≠5解析 ∵方程x 25＋y 2m＝1表示椭圆， ∴m >0且m ≠5.∵直线y ＝kx ＋1恒过(0,1)点，∴要使直线与椭圆总有公共点，应有：025＋12m≤1，m ≥1， ∴m 的取值范围是m ≥1且m ≠5.8．在直线y ＝－2上任取一点Q ，过Q 作抛物线x 2＝4y 的切线，切点分别为A 、B ，则直线AB 恒过定点________．答案 (0,2)解析 设Q (t ，－2)，A (x 1，y 1)，B (x 2，y 2)，抛物线方程变为y ＝14x 2，则y ′＝12x ，则在点A 处的切线方程为y －y 1＝12x 1(x －x 1)，化简得，y ＝12x 1x －y 1，同理，在点B 处的切线方程为y ＝12x 2x －y 2.又点Q (t ，－2)的坐标满足这两个方程，代入得：－2＝12x 1t －y 1，－2＝12x 2t －y 2，则说明A (x 1，y 1)，B (x 2，y 2)都满足方程－2＝12xt －y ，即直线AB 的方程为：y －2＝12tx ，因此直线AB 恒过定点(0,2)．9．(2014·辽宁)已知椭圆C ：x 29＋y 24＝1，点M 与C 的焦点不重合．若M 关于C 的焦点的对称点分别为A ，B ，线段MN 的中点在C 上，则|AN |＋|BN |＝________.答案 12解析 椭圆x 29＋y 24＝1中，a ＝3.如图，设MN 的中点为D ，则|DF 1|＋|DF 2|＝2a ＝6.∵D ，F 1，F 2分别为MN ，AM ，BM 的中点，∴|BN |＝2|DF 2|，|AN |＝2|DF 1|，∴|AN |＋|BN |＝2(|DF 1|＋|DF 2|)＝12.10．(2013·安徽)已知直线y ＝a 交抛物线y ＝x 2于A ，B 两点．若该抛物线上存在点C ，使得∠ACB 为直角，则a 的取值范围为________．答案 [1，＋∞)解析 以AB 为直径的圆的方程为x 2＋(y －a )2＝a ，由⎩⎪⎨⎪⎧y ＝x2x 2＋(y －a )2＝a ， 得y 2＋(1－2a )y ＋a 2－a ＝0.即(y －a )[y －(a －1)]＝0，由已知⎩⎪⎨⎪⎧a >0，a －1≥0，解得a ≥1. 三、解答题11.如图所示，椭圆C 1：x 2a 2＋y 2b 2＝1(a >b >0)的离心率为22，x 轴被曲线C 2：y ＝x 2－b 截得的线段长等于C 1的短轴长．C 2与y 轴的交点为M ，过坐标原点O 的直线l 与C 2相交于点A ，B ，直线MA ，MB 分别与C 1相交于点D ，E .(1)求C 1，C 2的方程；(2)求证：MA ⊥MB ；(3)记△MAB ，△MDE 的面积分别为S 1，S 2，若S 1S 2＝λ，求λ的取值范围． (1)解 由题意，知c a ＝22， 所以a 2＝2b 2. 又2b ＝2b ，得b ＝1.所以曲线C 2的方程y ＝x 2－1，椭圆C 1的方程x 22＋y 2＝1. (2)证明 设直线AB ：y ＝kx ，A (x 1，y 1)，B (x 2，y 2)，由题意，知M (0，－1)．则⎩⎪⎨⎪⎧y ＝kx ，y ＝x 2－1⇒x 2－kx －1＝0， MA →·MB →＝(x 1，y 1＋1)·(x 2，y 2＋1)＝(k 2＋1)x 1x 2＋k (x 1＋x 2)＋1＝－(1＋k 2)＋k 2＋1＝0，所以MA ⊥MB .(3)解 设直线MA ：y ＝k 1x －1，MB ：y ＝k 2x －1，k 1k 2＝－1，M (0，－1)，由⎩⎪⎨⎪⎧ y ＝k 1x －1，y ＝x 2－1，解得⎩⎪⎨⎪⎧ x ＝0，y ＝－1或⎩⎪⎨⎪⎧x ＝k 1，y ＝k 21－1， 所以A (k 1，k 21－1)．同理，可得B (k 2，k 22－1)．故S 1＝12|MA |·|MB |＝121＋k 21·1＋k 22|k 1||k 2|. 由⎩⎪⎨⎪⎧ y ＝k 1x －1，x 22＋y 2＝1，解得⎩⎪⎨⎪⎧ x ＝0，y ＝－1或⎩⎨⎧ x ＝4k 11＋2k 21，y ＝2k 21－11＋2k 21，所以D (4k 11＋2k 21，2k 21－11＋2k 21)． 同理，可得E (4k 21＋2k 22，2k 22－11＋2k 22)． 故S 2＝12|MD |·|ME | ＝121＋k 21·1＋k 22|16k 1k 2|(1＋2k 21)(1＋2k 22)， S 1S 2＝λ＝(1＋2k 21)(1＋2k 22)16＝5＋2(1k 21＋k 21)16≥916， 则λ的取值范围是[916，＋∞)． 12．已知双曲线C ：x 2a 2－y 2b2＝1(a >0，b >0)的焦距为27，其一条渐近线的倾斜角为θ，且tan θ＝32.以双曲线C 的实轴为长轴，虚轴为短轴的椭圆记为E . (1)求椭圆E 的方程；(2)设点A 是椭圆E 的左顶点，P 、Q 为椭圆E 上异于点A 的两动点，若直线AP 、AQ 的斜率之积为－14，问直线PQ 是否恒过定点？若恒过定点，求出该点坐标；若不恒过定点，说明理由．解 (1)双曲线x 2a 2－y 2b2＝1的焦距2c ＝27， 则c ＝7，∴a 2＋b 2＝7.①渐近线方程y ＝±b ax ， 由题意知tan θ＝b a ＝32.② 由①②得a 2＝4，b 2＝3，所以椭圆E 的方程为x 24＋y 23＝1. (2)在(1)的条件下，当直线PQ 的斜率存在时，设直线PQ 的方程为y ＝kx ＋m ，由⎩⎪⎨⎪⎧ x 24＋y 23＝1y ＝kx ＋m，消去y 得 (3＋4k 2)x 2＋8kmx ＋4m 2－12＝0.设P (x 1，y 1)，Q (x 2，y 2)，则x 1＋x 2＝－8km3＋4k 2，x 1x 2＝4m 2－123＋4k 2， 又A (－2,0)，由题意知k AP ·k AQ ＝y 1x 1＋2·y 2x 2＋2＝－14， 则(x 1＋2)(x 2＋2)＋4y 1y 2＝0，且x 1x 2≠－2.则x 1x 2＋2(x 1＋x 2)＋4＋4(kx 1＋m )(kx 2＋m )＝(1＋4k 2)x 1x 2＋(2＋4km )(x 1＋x 2)＋4m 2＋4＝0.则m 2－km －2k 2＝0.∴(m －2k )(m ＋k )＝0.∴m ＝2k 或m ＝－k .当m ＝2k 时，直线PQ 的方程是y ＝kx ＋2k .此时直线PQ 过定点(－2,0)，显然不符合题意．当m ＝－k 时，直线PQ 的方程为y ＝kx －k ，此时直线PQ 过定点(1,0)． 当直线PQ 的斜率不存在时，若直线PQ 过定点，P ，Q 点的坐标分别是(1，32)，(1，－32)，满足k AP·k AQ＝－1 4.综上，直线PQ恒过定点(1,0)．。

2016圆锥曲线填空选择汇编1（2016全国高考新课标Ⅰ卷· 文数）直线l 经过椭圆的一个顶点和一个焦点，若椭圆中心到l 的距离为其短轴长的14，则该椭圆的离心率为（ ） A ．13 B ．12 C ．23 D ．34【答案】B 【解析】如图，由题意得在椭圆中，11,,242OF c OB b OD b b ===⨯=⨯在Rt OFB ∆中，OF OB BF OD ⨯=⨯，且222a b c =+，代入解得224a c =，所以椭圆得离心率得：12e =，故选B.2（2016全国高考新课标Ⅲ卷· 文数12）已知O 为坐标原点，F 是椭圆C ：22221(0)x y a b a b+=>>的左焦点，A ，B 分别为C 的左，右顶点.P 为C 上一点，且PF ⊥x 轴.过点A 的直线l 与线段PF 交于点M ，与y 轴交于点E . 若直线BM 经过OE 的中点，则C 的离心率为 （ ）A ．13 B ．12 C ．23 D ．34【答案】A 【解析】由题意得，(,0)A a -，(,0)B a ，根据对称性，不妨2(,)b P c a -，设:l x my a =-，∴(,)a c M c m --，(0,)a E m ，∴直线BM ：()()a cy x a m a c -=--+，又∵直线BM 经过OE 中点，∴()1()23a c a a c e a c m m a -=⇒==+，故选A.3（2016全国高考新课标Ⅲ卷· 理数）已知O 为坐标原点，F 是椭圆C ：22221(0)x y a b a b+=>>的左焦点，A ，B 分别为C 的左，右顶点.P 为C 上一点，且PF x ⊥轴.过点A 的直线l 与线段PF 交于点M ，与y 轴交于点E .若直线BM 经过OE 的中点，则C 的离心率为A ．13B ．12C ．23D ．34【答案】A 【解析】由题意设直线l 的方程为(),y k x a =+分别令x c =与0x =得点(),FM k a c =-,OE ka =由,OBECBM ∆∆得12OE OB FM BC =，即2()ka a k a c a c =-+，整理得13c a =，所以椭圆的离心率为13e = 4（2016全国高考新课标Ⅰ卷· 理数）已知方程222213-x y m n m n-=+表示双曲线，且该双曲线两焦点间的距离为4，则n 的取值范围是（ ）A ．(–1，3)B ．(–1，3)C ．(0，3)D ．(0，3)【答案】A 【解析】由题意知：双曲线的焦点在x 轴上，所以2234m n m n ++-=，解得：21m =，因为方程22113x y n n -=+-表示双曲线，所以1030n n +>⎧⎨->⎩，解得13n n >-⎧⎨<⎩，所以n 的取值范围是()1,3-，5（2016全国高考新课标Ⅱ卷· 理数）已知12,F F ，是双曲线E ：的左，右焦点，点M 在E 上，1MF 与x 轴垂直，121sin 3MF F ∠= ,则E 的离心率为A ．B ．32CD ．2 【答案】A 【解析】离心率1221F F e MF MF =-，由正弦定理得122112sin 31sin sin 13F F Me MF MF F F ====--- 6（2016年天津高考）已知双曲线2224=1x y b-（b >0），以原点为圆心，双曲线的实半轴长为半径长的圆与双曲线的两条渐近线相交于A 、B 、C 、D 四点，四边形的ABCD 的面积为2b ，则双曲线的方程为（ ）A ．22443=1y x -B ． 22344=1y x -C ．2234=1y x - D ．2224=11x y - 【答案】D 【解析】根据对称性不妨设A 在第一象限，(,)A x y ，所以由22=4x y +和=2by x 得: x,2b y 所以2216=12422b b xy b b ⋅=⇒=+，故双曲线的方程为2224=11x y - 考点：双曲线渐近线7（2016年北京高考）双曲线22221x y a b-=（0a >，0b >）的渐近线为正方形OABC 的边OA ，OC 所在的直线，点B 为该双曲线的焦点，若正方形OABC 的边长为2，则a =_______________.22221x y a b-=【答案】2【解析】∵双曲线的渐近线为正方形OABC 的边OA ，OC 所在的直线，∴渐近线互相垂直，则双曲线为等轴双曲线，即渐近线方程为y =±x ，即a=b ， ∵正方形OABC 的边长为2，∴22OB =，即22c =，则2228a b c +==，即228a =，则242a a ==，，8（2016年山东高考）已知双曲线E ：22221x y a b-= （a ＞0，b ＞0），若矩形ABCD 的四个顶点在E 上，AB ，CD 的中点为E 的两个焦点，且2|AB |=3|BC |，则E 的离心率是_______. 【答案】2 【解析】由题意2BC c =，所以3AB c =，于是点),23（c c 在双曲线E 上，代入方程，得1492222=bc －a c ， 在由2c b a =+22得E 的离心率为2==ace ，9（2016全国高考新课标Ⅱ卷· 文数）设F 为抛物线2:4C y x =的焦点，曲线(0)ky k x =>与C 交于点P ，PF x ⊥轴，则k =A ．12 B ．1 C ．32D ．2 【答案】D 【解析】因为F 是抛物线24y x =的焦点，所以(1,0)F又因为曲线(0)k y k x =>与C 交与点P ，PF x ⊥轴，所以21k=，所以2k =，选D10（2016年四川高考）设O 为坐标原点，P 是以F 为焦点的抛物线22(0)y px p => 上任意一点，M 是线段PF 上的点，且PM =2MF ,则直线OM 的斜率的最大值为A ．3 B ．23 C ．2 D ．1【答案】C 【解析】如图，由题可知,02p F ⎛⎫⎪⎝⎭，设P 点坐标为200,2y y p ⎛⎫⎪⎝⎭yx OFP M显然，当00y <时，0OM k <；00y >时，0OM k >，要求OM k 最大值，不妨设00y >.则()2001112,3333633y y p OM OF FM OF FP OF OP OF OP OF p ⎛⎫=+=+=+-=+=+⎪⎝⎭20002223222263OM y k y p y p p y p ===++≤，当且仅当2202y p =等号成立，故选C11（2016全国高考新课标Ⅰ卷· 理数）以抛物线C 的顶点为圆心的圆交C 于A,B 两点，交C 的准线于D,E 两点．已知|AB |=42，|DE|=25，则C 的焦点到准线的距离为（ ）A ．2B ．4C ．6D ．8【答案】B 【解析】如图，设抛物线方程为22y px =，,AB DE 交x 轴于,C F 点，则22AC =，即A 点纵坐标为22，则A 点横坐标为4p ，即4OC p=， 由勾股定理知2222DF OF DO r +==，2222AC OC AO r +==，即22224(5)()(22)()2p p+=+，解得4p =，即C 的焦点到准线的距离为4，故选B.12（2016年浙江高考）若抛物线y 2=4x 上的点M 到焦点的距离为10，则M 到y 轴的距离是_______． 【答案】9 【解析】1109M M x x +=⇒=2015圆锥曲线填空选择汇编1（2015北京文数）已知()2,0是双曲线()22210y x b b-=>的一个焦点，则b =解析依题意，由()2,0是双曲线()22210y x b b-=>的一个焦点，得214b +=，即23b =，又0b >，得b =2（2015福建理数）若双曲线22:1916x y E -=的左、右焦点分别为12,F F ，点P 在双曲线E 上，且13PF =，则2PF =（ ）A ．11B ．9C ．5D ．3解析由双曲线定义得1226PF PF a -==，即236PF -=，解得29PF =． 故选B ．3（2015北京理数）已知双曲线()22210x y a a-=>0y +=，则a =解析 依题意，双曲线()22210x y a a-=>的渐近线方程为x y a =±，则1a -=得a =4（2015广东理数）已知双曲线C :22221x y a b-=的离心率54e =，且其右焦点为()25,0F ，则双曲线C 的方程为（ ）A ．22143x y -=B ．221916x y -=C ．221169x y -=D ．22134x y -= 解析因为所求双曲线的右焦点为()25,0F 且离心率为54c e a ==，所以5c =，4a =，2229b c a =-=所以所求双曲线方程为221169x y -=，故选C 。