人教版九年级数学26.1.2_二次函数图象(1)
- 格式:ppt
- 大小:858.50 KB
- 文档页数:15


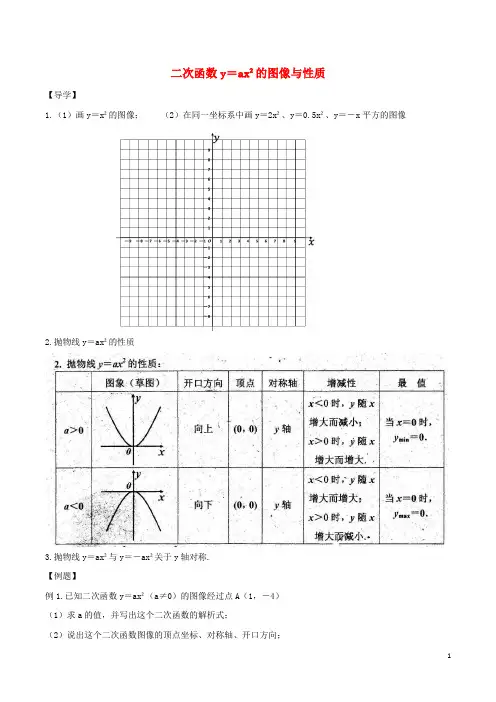
二次函数y=ax²的图像与性质【导学】1.(1)画y=x²的图像;(2)在同一坐标系中画y=2x²、y=0.5x²、y=-x平方的图像2.抛物线y=ax²的性质3.抛物线y=ax²与y=-ax²关于y轴对称.【例题】例1.已知二次函数y=ax²(a≠0)的图像经过点A(1,-4)(1)求a的值,并写出这个二次函数的解析式;(2)说出这个二次函数图像的顶点坐标、对称轴、开口方向;(3)判断点B(-0.5,-2)是否在此抛物线上;(4)求出抛物线上纵坐标为﹣8的点的坐标.例2.已知y=(k+2)是关于x的二次函数,且当x>0时,y随x的增大而减小。
求k的值.【练习】1.函数y=3x²的图像是,对称轴是;开口向;顶点是;顶点是图像的最点.2.抛物线y=(a-2)x²经过点(1,3),则a= .3.二次函数y=ax²,当x=1时,y=4,则y=8时,x= .4.函数y=m时二次函数,当m=时,其图像开口向上;当m=时。
其图像开口向下.5.若点A(2,n)在抛物线y=-x²,则点A关于y轴对称点的坐标是6.对于函数y=x²,当-1≤x≤2时,y的取值范围是 .7.抛物线y=-2x²不具有的性质是()A.开口向下B.对称轴是y轴C.与y轴不相交D.最高点是原点8.下列关于抛物线y=x²和y=-x²的关系的说法错误的是()A.它们有共同的顶点和对称轴B.它们都关于y轴对称C.它们的形状相同,开口方向相反D.点A(-2,4)在抛物线y=x²上也在y=-x平方上9.下列抛物线中,开口向下且开口最大的是()A.y=-x²B.y=-x²C. y=x²D.y=x²10.已知函数y=ax²的图像过点(1,2)和点(4,m)(1)求a和m的值;(2)点(-1,2)在函数y=ax²的图像上吗?为什么?。





《26.1.2反比例函数的图象和性质(1)》 教学模式介绍:数学的核心素养包括数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析。
这些数学学科素养既相对独立,又互相交融,是一个有机的整体。
核心素养下的教学设计是利用设计好的核心问题在课堂中培养学生的数学核心素质,重视学生在学习活动中的主体地位,让学生在积极参与学习活动的过程中得到发展。
教师创设情境设计问题,或通过富有启发性的讲授,或引导学生独立思考、自主探索、合作交流,组织学生操作实验、观察现象、提出猜想、推理论证等,有效地启发学生思考,使学生成为学习的主体,学会学习。
课堂教学中,要注重让学生理解和掌握数学的基础知识和基本技能,让学生感悟数学思想,积累数学活动经验,在学习数学和应用数学的过程中,发展数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析等数学学科核心素养,让学生能与他人建立良好关系,有效地管理自己的学习、生活,能够发掘自身潜力,战胜学习数学中的困难,让学生能够适应未来社会、进行终身学习,实现全面发展。
设计思路说明:“反比例函数的图象和性质”是在学习了一次函数,二次函数的有关内容以及反比例函数概念的基础上的进一步研究。
这节课从复习旧知入手,类比研究二次函数20y ax a =≠,图象和性质的过程,自然的过渡到反比例函数的图象。
在前面学习一次函数和二次函数的时候,学生已经经历过观察、分析图象特征,抽象、概括函数性质的过程,对研究函数性质的方法也有一定的了解。
因此,通过类比方法,探究反比例函数的图象性质,从方法上不会存在障碍。
但对于反比例函数的图象是两条曲线,函数图象的变化趋势只在每个象限内成立,学生在前面的学习中并未遇到,所以无论是总结还是应用变化趋势这条性质对学生来说都比较困难,第二个环节是师生共同完成6y x=的图象,教师在学生完成作图后找出典型的错误集体订正,这样设计有效的降低了学生画反比例函数图象这个难点,再由学生独立完成12y x= 的图象来巩固,第三个环节步归纳k >0时,函数的图象特征和性质;第四个环节就是完全类比k >0时的研究,我们研究k <0时的情况,同样遵循从特殊到一般的过程,再通过对图象的探究,归纳得出反比例函数的性质,并加以应用,发展学生的数学核心素养。
§26.1.1 二次函数的图像(1)____月____日星期_____姓名:________学习目标:掌握二次函数2y ax=的图像及其性质重点难点:正确理解研究二次函数2y ax=的图像及其性质学习过程一、课前准备1、一般地,我把自变量x的指数是_____的函数y叫“________函数”它的一般形式(通式)为:_____________(_________)其中_______,_______和_______。
分别作为点的____坐标和__________。
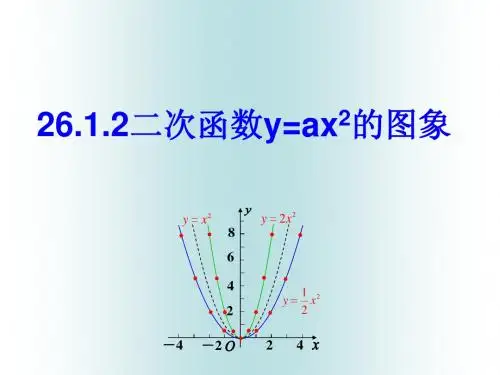
二、新课导学问题1:研究二次函数212y x=,2y x=和22y x=的图象特点,第三步,描点,连线。
(1)二次函数212y x=,2y x=和22y x=的二次项系数a分别是_____________(2)观察上面三个函数的图象,发现它们的图象的“开口方向”指向______,其中二次函数______________的图象“开口”打开较大;(3)归纳:二次函数的图象的开口大小的研究:当a>0时,a越大,二次函数的图象的开口越_____;问题2:研究二次函数212y x=-,2y x=-和22y x=-的图象特点,第一步,列表:月 日 姓名: 编写: 校审:2第三步,描点,连线。
(1) 二次函数212y x =-,2y x =-和22y x =-的二次项系数a 分别是_____________ (2)观察上面三个函数的图象,发现它们的图象的“开口方向”指向______,其中二次函数______________的图象“开口”打开较大; (3)归纳:二次函数的图象的开口大小的研究: 当a<0时,a 越大,二次函数的图象的开口越_____; (4) 问题4:二次函数的图象的开口大小的研究:当a>0时,a 越大,二次函数的图象的开口越_____; 当a<0时,a 越大,二次函数的图象的开口越_____;综合,即a 越大,二次函数的图象开口越_____;问题2:研究二次函数2y x =-和22y x =的图象特点,回答下列问题: 第一步,列表:第三步,描点,连线。