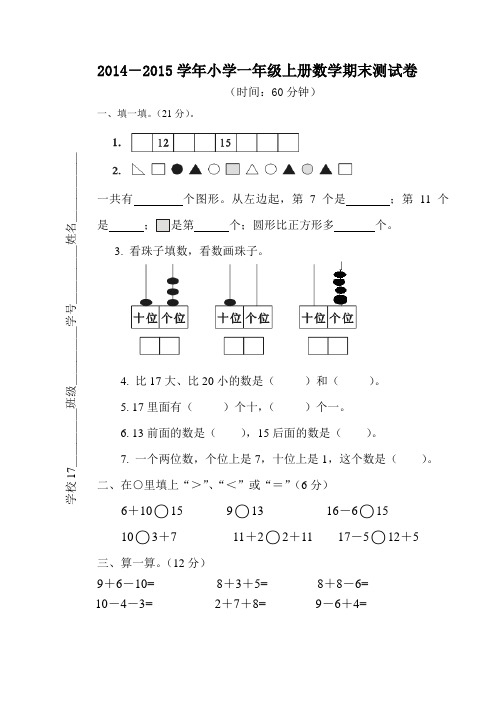
白鹤各校学生数 2013学年第二学期
- 格式:xls
- 大小:38.00 KB
- 文档页数:1

伊吾高级中学高中体育工作计划(下学期)教学工作计划一、学生情况分析:高一年的学生选项为武术教学班人数较多,高二年选项出现一些人数参差不齐的现象,但也基本上是上个学分选项时的基本情况,对于学习时起到这个项目的连续性有一定的帮助。
学习时也能了解到教师的教学意图,这样方便教学的总体安排,也可在一定程度上增加一些技术难度与要求。
二、教材与教辅分析:①分析教材与教辅的内容与结构:这个学期采用2个学分同时选项,这样有利于全学期的学习计划与安排,不用再教基本功,本学期我安排了校本课程永春白鹤拳里的两个套路进行教学,采用一套拳,一套器械的方式配合实用技能进行教学,这样有利于学生的学习兴趣,从内容与结构上的安排是注重学生的学习过程,特别是动作的到位,学不在多,而在精。
②分析教材的特点与重点、难点:教材的特点为有利于学生的学习,兴趣比较浓,对于学习过程比较注重,方便学生的素质不同者的学习;重点在于武德,这是本个项目开设的重点,也是教学过程中最重最重的重点,让学生知道学习的基本意图,也让学生能自我控制;难点在于如何去掌握套路的实用技能,提高学以致用,能有防身的本领。
③提出教学任务:在全面发展体能的基础上,进一步发展灵敏、力量,速度和有氧耐力,武德的培养;引导学生学会合理掌握练习与讨论的时间,了解实现目标时可能遇到的困难。
在不断体验进步和成功的过程中,表现出适宜的自信心,形成勇于克服困难积极向上,乐观开朗的优良品质;认识现代社会所必需的合作和竞争意识,在武术学习过程中学会尊重和关心他人,将自身健康与社会需要相联系,表现出良好的体育道德品质,结合本身项目去了解一些武术名人并能对他们进行简单的评价;加强研究性的学习,去讨论与研究技能的实用性,加强同学之间的讨论交流的环节。
三、教学目标:①总体目标:建立健康第一的理念,培养学生的健康意识和体魄,进一步激发学生的学习永春白鹤拳兴趣,培养学生的终身体育意识,以学生身心健康发展为中心,重视学生主体地位的同时关注学生的个体差异与不同需求,确保每一个学生都受益,以及多样性和选择性的教学理念,结合学校的实际情况,设计本教学工作计划,以满足学生选项学生的需求,加深学生的运动体验和理解,保证学生在本永春白鹤拳选项课的学习中修满2学分。



南京市第九中学、第十三中学2024-2025学年高二年级第一次质量调研数学(时间:120分钟 满分:150分)2024年10月11日一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是正确的,请把正确的选项填涂在答题卡相应的位置上.1.若1i 1zz =+-,则z =( )A .i 1--B .i 1-+C .1i -D .1i +2.已知一组数据:3,5,7,x ,9的平均数为6.则该组数据的40百分位数为( ) A .6B .5.5C .5D .4.53.已知三个单位向量a ,b ,c 满足a b c =+,则向量b ,c 的夹角为( ) A .π6B .π3C .2π3D .5π64.“太极图”因其形状如对称的阴阳两鱼互抱在一起,故也被称为“阴阳鱼太极图”.如图是放在平面直角坐标系中的“太极图”,图中曲线为圆或半圆,已知点(),P x y 是阴影部分(包括边界)的动点,则2y x -的最小值为( )A .23-B .32-C .43-D .235.已知两直线1110a x b y +-=和2210a x b y +-=的交点为()1,2P ,则过()111,Q a b ,()222,Q a b 两点的直线方程为( ) A .210x y +-=B .210x y --=C .210x y --=D .210x y +-=6.设直线l 的方程为()cos 3x y θθθ++=∈R ,则直线l 的倾斜角α的取值范围为( ) A .[)0,πB .ππ,42⎡⎫⎪⎢⎣⎭C .πππ3π,,4224⎡⎫⎛⎤⎪ ⎢⎥⎣⎭⎝⎦D .,π3π,44⎡⎤⎢⎥⎣⎦7.在三棱柱111ABC A B C -中,1AA ⊥平面ABC ,2AB AC ==,120BAC ∠=︒,D 是棱BC 上的动点,直线1A D 与平面ABC 所成角的最大值是45°,点P 在底面ABC 内,且1A P =则点P 的轨迹长为( )A .π3B .2π3C .4π3D .2π8.已知圆221:220C x y x y +--=,设其与x 轴正半轴、y 轴正半轴分别交于M ,N 两点.已知另一圆2C的半径为1C 相外切,则22C M C N ⋅的最大值为( )A .20B .C .10D .二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对得6分,部分选对的得部分分,选对但不全的得部分分,有选错的得0分.9.设A ,B 为两个随机事件,以下命题正确的有( ) A .若A 与B 对位,则()1P AB =B .若A 与B 互斥,()13P A =,()12P B =,则()56P A B += C .若()13P A =,()12P B =,且()16P AB =,则A 与B 相互独立D .若A 与B 相互独立,()13P A =,()23P B =,则()19P AB =10.已知点A ,B 在圆22:4O x y +=上,点P 在直线:250l x y +-=上,则( ) A .直线l 与圆O 相离B .当AB =PA PB +的最小值是1C .当P A 、PB 为圆O 的两条切线时,()OA OB OP +⋅为定值 D .当P A 、PB 为圆O 的两条切线时,直线AB 过定点84,55⎛⎫⎪⎝⎭11.数学美的表现形式不同于自然美或艺术美那样直观,它藴藏于特有的抽象概念、公式符号、推理论证、思维方法等之中,揭示了规律性,是一种科学的真实美,曲线()()22:118C x y -+-=就是一条形状优美的曲线,则( )A .曲线C 上两点间距离的最大值为B .若点(),P a a 在曲线C 内部(不含边界),则33a -<<C .若曲线C 与直线y x m =+有公共点,则66m -≤≤D .若曲线C 与圆()2220x y rr +=>有公共点,则72r ≤≤三、填空题:本题共3小题,每小题5分,共15分.12.已知4sin 25a =-,则tan 2πtan 4aa =⎛⎫+ ⎪⎝⎭______. 13.若直线2y x a =+和直线12y x b =-+将圆()()22111x y -+-=的周长四等分,则a b +=______. 14.“曼哈顿距离”是十九世纪的赫尔曼可夫斯基所创词汇,定义如下:在直角坐标平面上任意两点()11,A x y ,()22,B x y 的曼哈顿距离为:()1212,d x x A B y y =-+-.己知点M 在圆22:1O x y +=上,点N 在直线:390l x y +-=上,则(),d M N 的最小值为______.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(本题满分13分)已知直线()()1:31410l x y -+-=,()2:3420l x y ++=,点A 和点B 分別是直线1l ,2l 上一动点. (1)若直线AB 经过原点O ,且3AB =,求直线AB 的方程; (2)设线段AB 的中点为P ,求点P 到原点O 的最短距离. 16.(本题满分15分)记ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,已知πsin sin 3c B b C =+⎛⎫ ⎪⎝⎭. (1)求C ;(2)若6b =,且ABC △的面积为ABC △的周长. 17.(本题满分15分)在四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,AB CD ∥,AB BC ⊥,4DC BC ==,8AB =,AD =(1)证明:BD PA ⊥;(2)若PAD △为等边三角形,求点C 到平面PBD 的距离. 18.(本题满分17分) 己知以点()2,0C t t t ⎛⎫> ⎪⎝⎭为圆心的圆经过原点O ,且与x 轴交于另一点A ,与y 轴交于另一点B . (1)求证:AO BO ⋅为定值(2)设直线240x y +-=与圆C 交于点M ,N ,若OM ON =,求圆C 的方程.(3)在(2)的条件下,设P ,Q 分別是直线:20l x y ++=和圆C 上的动点,求PB PQ +的最小值及此时点P 的坐标. 19.(本题满分17分)已知圆()22:1C x a y -+=与直线1y x =--交于M 、N 两点,点P 为线段MN 的中点,O 为坐标原点,直线OP 的斜率为13-. (1)求a 的值;(2)求MON △的面积;(3)若圆C 与x 轴交于A ,B 两点,点Q 是圆C 上异于A ,B 的任意一点,直线QA 、QB 分别交:4l x =-于R 、S 两点,当点Q 变化时,以RS 为直径的圆是否过圆C 内的一定点,若过定点,请求出定点;若不过定点,请说明理由.参考答案12.-4 13.12 14.3-103 15.(本题满分13分)已知直线l 1:3(x -1)+4(y -1)=0,l 2:3x +4(y +2)=0,点A 和点B分别是直线l 1,l 2上一动点. (1)若直线AB 经过原点O ,且|AB |=3,求直线AB 的方程; (2)设线段AB 的中点为P ,求点P 到原点O 的最短距离. 【答案】(1)43y x =;(2)110. 【解析】(1)将()()()12:31410,:3420l x y l x y -+-=++=化为一般式方程,得,12:3470,:3480l x y l x y +-=++=,则两直线平行,故两直线的距离为3d AB ===. . . . . . . 3分因为3AB =,所以AB 和两直线垂直. 因为12,l l的斜率为34-,所以43AB k =. 又因为直线AB 经过原点O ,所以直线AB 的方程为43y x =. . . . . . .6分 (2)因为12,l l 互相平行,所以线段AB 的中点P 的轨迹为873402x y -++=,即13402x y ++=, 所以点P 到原点O 的最短距离即点O 到直线13402x y ++=的距离. . . . . . .10分因为点O 到直线13402x y ++=110=. 所以点P 到原点O 的最短距离为110. . . . . . .13分16.(本题满分15分)记△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知c sin B =b sin(C +π3).(1)求C ;(2)若b =6,且△ABC 的面积为63,求△ABC 的周长.【答案】(1)π3C =;(2)10+ 【解析】(1)在△ABC 中,由πsin sin()3c B b C =+及正弦定理,得πsin sin sin sin()3C B B C =+, . . . . . .2分而B ∈(0,π),所以sin 0B >,所以sin()sin 3C C π+=,即1sin sin 2C C C +=,sin C C =,又()0,C π∈,所以sin C ≠0,从而cos C ≠0,因此tan C =π3C =. . . . . . .6分(2)由(1)及三角形面积公式,得1sin 2ab C ==4a =, . . .10分由余弦定理得c === . . .14分所以△ABC 的周长为10a b c ++=+ . . . . . .15分 17.(本题满分15分)在四棱锥P -ABCD 中,平面PAD ⊥平面ABCD ,AB ∥CD ,AB ⊥BC ,DC =BC =4,AB =8,AD =42.(1)证明:BD ⊥PA ;(2)若△PAD 为等边三角形,求点C 到平面PBD 的距离.【答案】(1)证明见解析;.【解析】(1)因为//4AB BC AB CD DC BC ⊥==,,,所以BD =,又因为8AD AB ==,所以222AD BD AB +=,则AD BD ⊥. . . . . . .2分 因为平面PAD ⊥平面ABCD ,且平面PAD ⋂平面ABCD AD =,BD ⊂平面ABCD , 所以BD ⊥平面PAD . . . . . . .5分因为PA ⊂平面PAD ,所以BD ⊥PA . . . . . . .6分(2)取AD 中点O ,连结PO ,因为△PAD 为等边三角形,所以PO AD ⊥.因为平面PAD ⊥平面ABCD ,且平面PAD ⋂平面ABCD AD =,PO ⊂平面PAD , 所以PO ⊥平面ABCD ,如图所示. . . . . . .9分因为PA AD PD PO =====由(1)知BD ⊥平面PAD ,由PD ⊂面PAD 可得BD PD ⊥,在Rt PBD △中,1162PBD S =⨯=△,而14482BCD S =⨯⨯=△,11833P BCD BCDV PO S-=⋅=⨯=. . . . . . .12分 设点C 到平面PBD 的距离为h ,由P BCD C PBD V V --=得1163h ⨯=,解得h =,所以点C 到平面PBD . . . . . .15分 18.(本题满分17分)已知以点C (t ,2t )(t >0)为圆心的圆经过原点O ,且与x 轴交于另一点A ,与y 轴交于另一点B . (1)求证:|AO|·|BO|为定值.(2)设直线2x +y -4=0与圆C 交于点M ,N ,若|OM |=|ON |,求圆C 的方程.(3)在(2)的条件下,设P ,Q 分别是直线l :x +y +2=0和圆C 上的动点,求|PB |+|PQ |的最小值及此时点P 的坐标.【解析】(1)由题意可得圆的方程为:()222224x t y t t t ⎛⎫-+-=+ ⎪⎝⎭,化简可得22402x tx y y t--=+, . . . . . .2分 分别令y =0和x =0,可得与坐标轴的交点分别为:()2,0A t ,40,B t ⎛⎫ ⎪⎝⎭,所以|AO|·|BO|=428t t⋅=为定值. . . . . . .4分(2)如图所示,OM ON =,∴原点O 在线段MN 的垂直平分线上,设线段MN 的中点为H ,则C ,H ,O 三点共线, . . . . . .6分 又OC 的斜率22k t=, ()2221t ⎛⎫∴⨯-=- ⎪⎝⎭, 解得2t =±, 又0t >,所以2t =, 可得圆心()2,1C ,∴圆C 的方程为:()()22215x y -+-=. . . . . . .10分(3)如图所示,由(2)可知:圆心()2,1C ,半径r =,()0,2B , 设点B 关于直线20x y ++=的对称点为(),B x y ', 则BB '中点为2,22x y +⎛⎫⎪⎝⎭,且()21122022y xx y -⎧⋅-=-⎪⎪⎨+⎪++=⎪⎩,解得42x y =-⎧⎨=-⎩,即()4,2B '--, . . . . . .13分则PB PQ PB PQ B Q ++≥''=, 又点B '到圆上点Q 的最短距离为B C r -=='则PB PQ +的最小值为 . . . . . .15分 此时直线B C '的方程为:2xy =, 点P 为直线B C '与直线l 的交点,则220x y x y ⎧=⎪⎨⎪++=⎩,解得4323x y ⎧=-⎪⎪⎨⎪=-⎪⎩,即点42,33P ⎛⎫-- ⎪⎝⎭. . . . . . .17分19.(本题满分17分)已知圆C :(x -a )2+y 2=1与直线y =-x -1交于M 、N 两点,点P 为线段MN 的中点,O 为坐标原点,直线OP 的斜率为-13.(1)求a 的值; (2)求△MON 的面积;(3)若圆C 与x 轴交于A ,B 两点,点Q 是圆C 上异于A ,B 的任意一点,直线QA 、QB 分别交l :x =-4于R 、S 两点.当点Q 变化时,以RS 为直径的圆是否过圆C 内的一定点,若过定点,请求出定点;若不过定点,请说明理由.【答案】(1)2a =-;(2)12MONS=;(3)过定点,()4-. 【解析】(1)由题知:直线OP 方程为13y x =-,则由113y x y x =--⎧⎪⎨=-⎪⎩,得到3212x y ⎧=-⎪⎪⎨⎪=⎪⎩,即31,22P ⎛⎫- ⎪⎝⎭. . . . . . .2分 点P 为线段MN 的中点,MN PC ∴⊥,即1021132MN PCk k a -⋅=-⨯=-+,2a ∴=-. . . . . . .4分(2)由2a =-,则圆心()2,0C -,C ∴到直线=1y x --距离为2d ==, . . . . . .6分MN ∴== . . . . . .8分又O 到直线=1y x --的距离为2,MN 边上的高为2.11222MONS∴=⨯=. . . . . . .10分 (3)由圆C 与x 轴交于,A B 两点,得()()3,0,1,0B --, 不妨设直线QA 的方程为()3y k x =+,其中0k ≠, 在直线QA 的方程中,令4x =-,可得()4,R k --, 因为QA QB ⊥,则直线QB 的方程为()11y x k=-+, 在直线QB 的方程中,令4x =-,可得3y k =,即点34,S k ⎛⎫- ⎪⎝⎭, . . . . . .12分则线段RS 的中点为234,2k F k ⎛⎫-- ⎪⎝⎭,圆的半径平方为2232k k ⎛⎫+⎪⎝⎭, 所以,以线段RS 为直径的圆的方程为()2222233422k k x y k k ⎛⎫⎛⎫-+++-= ⎪ ⎪⎝⎭⎝⎭,即()2223430k x y y k-++--=, . . . . . .14分由()243031xyx⎧+-=⎪=⎨⎪-<<-⎩,解得4xy⎧=-+⎪⎨=⎪⎩因此,当点Q变化时,以RS为直径的圆恒过圆C内的定点()4-. . . . . . .17分。




白鹤镇小学2013学年第二学期教学质量评价实施安排评价科目:三至五年级语文、数学、英语、科学一、评价机构1、教学质量评价领导小组组长:陆修焕副组长:施自强姜中帅陈家富夏建阳成员:王叶卫、王良峰、王平西、庞宪卫范琳燕、姜丽华、卢丽君、陈晓红2、考务组组长:姜丽华成员:教导处全体成员二、评价时间、科目、学校统一信号三、主考、巡视员及监考教师安排表(见附表一)四、主考工作要求1、全面负责本考点工作,处理考点发生的一切事项;难以处理的重大事情,请与“评价领导小组”联系。
2、6月26日各校召开考务会议。
3、各校各年级按编号“S”形安排、布置好试场,所有考生一人一桌,每个试场30人(最多不超过35人,鹤楼五年级36人除外),下庄小学三四年级合并为一个考场,各校考场分四排,各排之间要分开,两边靠墙,考号统一贴桌上左上角。
4、保证本考点所有学生参加评估,上送所有考生试卷。
5、各考点主考在开考前要对试卷袋进行验封,考试后,要密封试卷,盖上校印。
交巡视员带回白鹤中心小学教导处。
5、准备好数学草稿纸,胶水及播放英语听力CD的电教器材等。
五、监考教师工作1、各监考教师必须在提前30分钟(上午7:30前;下午1:00前)到达监考学校。
2、各考点监考教师提前20分钟领卷,提前10分钟发卷,早5分钟学生进场(填写校名、班级、姓名、编号),监考教师要逐一检查。
各科考试结束前15分钟口头提醒学生一次。
3、考试结束后,将各年级试卷按编号从小到大整理好放回密封袋交给巡视员。
4、各监考教师必须认真负责,履行好职责,发现问题,及时处理,并马上向评价领导小组汇报,因玩忽职守而延误工作的,要追究责任,严肃处理。
六、巡视员工作1、6月27日上午7:00前到中心校教导处姜丽华处领取试卷, 7:30前到达巡视学校。
2、检查考点试场课桌安排情况。
3、对监考教师进行点名,明白考点铃声,同时做好监考老师与学校时间核对工作。
4、试卷在当天下午4:10前送交白鹤中心小学教导处姜丽华老师。


2012-2013学年度湖南省初中省级三好学生名单长沙苏宇轩男湖南师大附中博才实验中学苏琪女青竹湖湘一外国语学校王思滔男雅礼雨花中学杨诗宇男湖南师大附中星城实验中学童思艺女长沙县星沙中学郝拓帆男浏阳市浏阳河中学周瑾葳女宁乡玉潭城北中学吴浅浅女麓山国际实验学校李妍舒女南雅中学衡阳廖国梁男衡南县星火实验中学曹向东男衡阳县蒸阳中学宗志轩男衡山县实验中学刘洋洋男衡东县第六中学黄思超男耒阳县第三中学蒋奕昕男蒸湘区蒸湘中学左珊女衡阳市第三中学赵逸乐男衡阳市外国语学校肖亚卿女衡阳市逸夫中学陈紫嫣女衡阳市第二十三中学凌骏达男船山实验中学文振东男成章实验中学株洲肖懿嘉女株洲景炎学校钟嘉怡女株洲县渌口镇中学贺思敏女醴陵泗汾中学刘淮齐女攸县第五中学罗子怡女茶陵云阳中学湘潭彭茁峻男湘潭市第十六中学王婷玉女韶山市实验中学崔嘉懿男湘潭县江声实验学校周寅男湘乡市第二中学邵阳华凤林女邵阳市第十中学刘钰琪女新宁县黄龙中学蒋心健女邵东县塘渡口镇中学黄明远男绥宁县民族中学肖雨茜女洞口县石江镇中学刘兴隆男武冈第三中学刘陈喆女新邵县酿溪镇中学葛畅男邵东县两市镇二中申缙男邵东县两市镇四中廖丽蓉女隆回县司门前中学龙 男隆回县城西中学付娅玙女姚喆中学岳阳张越女岳阳市十二中向争女汨罗市红花初级中学兰天纬男岳阳县第八中学徐紫东男华容县实验初中唐泳麟男平江县安定中学姜浩东男湘阴县樟树中学刘方冕女临湘市成大实验学校常德丁若桐女常德市第十一中学陈炳安男鼎城区善卷中学刘洋女汉寿县詹乐贫中学陈子威男桃源县漳江中学岳美君女石门县澧斓实验完中张益聪女澧县城关中学赵辞放女安乡县城北中学益阳陈佳龙男梅城镇中学胡玉琴女三堂街镇中学黄琦雯女赫山实验学校陈思俭女城西中学张康乐男南大膳镇学校郴州梁栎鹏女郴州市第六中学何恒黎女苏仙中学吴瑶琴女桂阳县蒙泉学校张真女宜章县第八中学罗家琪男嘉禾县第五中学侯倩怡女安仁县宜溪学校张家界卢润凡女市民族中学杨炎男武陵源第一中学娄底吴鑫焯女娄底市第一中学谢灿男小碧中学刘夥男冷水江第二中学沈宇君女涟源市第七中学凌汞男双峰县走马龙田中学卿悦女新化县上渡中心学校怀化周玥女怀化第四中学李修杰男沅陵县第一中学艾曦子女溆浦县卢峰镇中学钟朦女新晃县第二中学吴星宇女靖州县第一中学周优女怀化铁路第二中学戴洁女怀化第三中学永州唐银芳女黎家坪一中邓旻女双牌县第一中学唐真茹女新田县瑞华实验学校黄建男岚角山中学唐炯女江华县创新实验学校叶佳丽女江永县源口瑶族乡学校邓怡航男东安县澄江实验中学赵丹女永州市第九中学湘西自治州陈蕾宇男吉首第一中学田思敏女泸溪县第一中学田萌女凤凰县第一中学田邵君女永顺县民族实验学校黄方全男龙山县第二中学。

江苏省盐城市2023-2024学年五年级上学期语文期中试卷姓名:__________ 班级:__________考号:__________1.看拼音,写词语。
huī huánɡxī hɑn bēnɡ tālǎn duòyǐn bìshānɡ yì2.默写(1),忽然闭口立。
(2),非是藉秋风。
(3)王师北定中原日,。
(4)天戴其苍,。
,横有八荒。
(5)不饱食以终日,。
3.下题中,都有一项加点字的读音是错误的。
(1)A.眼睑.(jiǎn)B.嗜.好(sì)C.嵌.入(qiàn)D.允诺.(nuò)(2)A.画框.(kuànɡ)B.冠.军(ɡuàn)C.缠.绕(chán)D.垂蔓.(wàn)(3)A.上卿.(qīn)B.强.逼(qiǎng)C.搁.置(ɡē)D.浸.透(jìn)4.下题中,都有一项有错别字。
把它找出来。
(1)A.糕饼B.恩慧C.平衡D.同心协力(2)A.赤道B.修筑C.迟延D.不记其数5.选出加点字的解释是错误的。
(1)A.干将发硎.(磨刀石)B.完.璧归赵(完美)C.万马齐喑.(沉默)D.民不聊.生(依赖)(2)A.铿锵..(声音响亮有力)B.难以置.信(使得、让)C.伏.案(趴)D.人影绰绰..(模糊不清)()6.下列句子中,加点的成语使用有误..的一项是()。
A.尽管小明有些喋喋不休....,但说的还是有些道理的。
B.蔺相如诡计多端....,一心守护着和氏璧,生怕被秦王骗去。
C.厂长直言不讳....地指出车间里存在的安全问题。
D.马上就要比赛了,别人都很紧张,小明却悠然自得....地看着闲书。
7.下列句子中,没有语病....的一句是()。
A.凛冽的寒风中,那个老奶奶只穿着薄薄的外套和破手套。
B.春天的江南,是人们旅游观光的好时节。
C.每个人的脸上都洋溢着澎湃的激情、胜利的喜悦和无限的自豪。

赞美丹顶鹤的唯美句子8篇以下是网友分享的关于赞美丹顶鹤的唯美句子的资料8篇,希望对您有所帮助,就爱阅读感谢您的支持。
第一篇1. 湖中心有一只丹顶鹤站立在荷花上。
它张开翅膀,伸长脖子,昂起头喷水,喷出一条条水柱,水花落在平静的湖面上,出现了一个个小圆晕,还可以看见丹顶鹤的倒影呢,真漂亮!2. 当丹顶鹤正要展翅飞翔的时候,那双美丽的翅膀,翩翩起舞,那修长的双腿,就像优雅的舞姿多么杰出,多么美丽。
这种情景便让我想起了刘禹锡的诗句:晴空一鹤排云上,便引诗情到碧霄。
3. 在潮湿的芦苇丛中,是一只只亭亭玉立的丹顶鹤。
有的单腿站立不动,正凝视着远方;有的微微张开翅膀,美滋滋地对着湖面照镜子;有的用它那又尖又长的细嘴在湖中捕鱼;有的在天空中自由飞翔,仿佛正在欣赏这美丽的风景4. 看哪!一只美丽的丹顶鹤,他灰白色的羽毛,纤细的长腿,褐黄色的嘴,正在捉鱼。
5. 一只丹顶鹤站立在湖边,像一位亭亭玉立的少女在展现着自己的风姿。
湖上飞着一群雪白的天鹅,它们伸长脖颈,扇动着洁白的翅膀,宛如仙女在飘动着长袖飞翔。
那高傲的身姿美丽动人,使人陶醉。
6. 丹顶鹤亭亭玉立的身姿,天鹅飞翔的美丽姿态,再加上湖水的衬映,让仙鹤湖更加美丽动人。
7. 水池中央还有2只丹顶鹤,长长的嘴巴,穿着雪白的衣服。
有一只在叼荷叶,另一只在梳理自己的羽毛,可爱极了!8. 丹顶鹤头上有一片红色的羽毛,就像一块红色的玛瑙,真的是华丽高贵,光彩照人。
9. 丹顶鹤是天生的舞蹈家。
它们头顶鲜红,脖颈修长,羽毛洁白,双腿纤细,真个是形体秀丽,举止潇洒,神采飘逸。
10. 丹顶鹤羽色素朴纯洁,体态飘逸雅致,鸣声超凡不俗,在《涛经鹤鸣》中就有鹤鸣于九皋,声闻于野的精彩描述。
在中国古代神话和民间传说中被誉为仙鹤,成为高雅、长寿的象征。
11. 仙鹤头上有一片红色的羽毛,就像戴着一顶红色的帽子;长长的脖子上有一圈黑色的羽毛,像围着黑围巾。
12. 丹顶鹤常常飞行在蔚蓝晴朗的天空之中,你回归的钟声刚一敲响,它们就一飞冲天,用翅膀拍开乌云,在天地之间,昂然长嘶,是母亲曾经的哀号,响砌在云霄。

2023-2024学年度第二学期小学期末学业质量监测四年级语文试题(时间:90分钟 满分100分)深深浅浅的脚印,写满成长的故事。
四年级围绕“畅享童年”开展了系列活动,让我们一起参与吧。
活动一 开启童年的门扉一、请完成下列选择题,赢取开启童年大门的钥匙吧。
1. 下面读音完全正确的一项是( )A. 呛(qiāng )水 祈求(qí) 逃窜(cuàn )B. 旋涡(xuàn ) 黝黑(yǒu ) 刹(chà)那C. 徜徉(yáng ) 胆怯(què) 开辟(pì)D. 松脂(zhī) 慰藉 (jí) 挣扎(zhá)2. 下列书写完全正确的一项是( )A. 遗憾 拂试 分辨 一丝不苟B. 撕鸣 俱备 怒吼 无能为力C. 即将 慌忙 冲刷 惊天动地D. 晌午 教练 警诫 空空如也3. “我家洗砚池头树”中的“洗砚池”用了( )的典故A 孔子“韦编三绝” B. 王羲之“墨池”C. 左思“洛阳纸贵”D. 赵长卿“磨穿枯砚,生涯微薄”4. 亮亮在读课外书时读到一个成语“睚眦必报”,其中“睚眦”这个词不理解,于是就有了以下的猜测,你认为哪一项是正确的?( )A. 读音是yá zì,意思是发怒时瞪眼。
B. 读音是yā zhì,意思是发怒时瞪眼。
C. 读音是yá zì,意思是发怒时张大嘴。
D. 读音是yà zhì,意思是发怒时张大嘴。
5. 下面各项中,加点字意思相同的一项是( )A. 是否 过是溪B. 照例 盛数十萤火以照书C. 如梦如幻 洛阳亲友如相问D. 兔走触株 儿童急走追黄蝶6. 下列与诗句“粉骨碎身浑不怕,要留清白在人间。
”表现的精神品格最相近的一项是( )A. 欲穷千里目,更上一层楼。
B. 至今思项羽,不肯过江东。
.C. 不要人夸颜色好,只留清气满乾坤。

2023—2024学年江西省九江市十校高三第二次联考数学试卷一、单选题(★) 1. 已知集合,,则()A.B.C.D.(★★) 2. 已知复数满足,其中为虚数单位,则()A.B.C.D.(★★) 3. 的展开式中常数项为()A.B.160C.80D.(★★) 4. 已知火箭在时刻的速度为(单位:千米/秒),质量为(单位:千克),满足(为常数),、分别为火箭初始速度和质量.假设一小型火箭初始质量千克,其中包含燃料质量为500千克,初始速度为,经过秒后的速度千米/秒,此时火箭质量千克,当火箭燃料耗尽时的速度大约为()(,).A.4B.5C.6D.7(★★) 5. 已知抛物线过点,为的焦点,点为上一点,为坐标原点,则()A.的准线方程为B.的面积为1C.不存在点,使得点到的焦点的距离为2D.存在点,使得为等边三角形(★★★) 6. 已知在四边形中,,,,则的长为()A.B.C.D.(★★★) 7. 已知椭圆的上顶点为,离心率为,过其左焦点倾斜角为30°的直线交椭圆于,两点,若的周长为16,则的方程为()A.B.C.D.(★★★) 8. 已知函数,若方程的实根个数为()A.B.C.D.二、多选题(★★) 9. 已知且,满足,,则()A.若,则B.若,则C.若,则D.若,则(★★★) 10. 已知,,若函数的图象关于对称,且函数在上单调,则()A.的最小正周期为B.C.为偶函数D.(★★★) 11. 已知数列的前项和为,且,若,则()A.是等比数列B.是等比数列C.是等差数列D.是等差数列三、填空题(★★) 12. 已知锐角满足,则 ______ .(★★) 13. 将甲,乙,丙三名志愿者分配到,,三个社区服务,每人分配到一个社区且每个社区至多分配一人,则在乙分配到社区的条件下,甲分配到社区的概率为 ______ .(★★★★) 14. 将两个观赏球体封闭在一个正方体容器内,设正方体棱长为1,则两个球体体积之和的最大值为 ___________ .四、解答题(★★★) 15. 据统计,截止2023年十月底,中国网络购物用户规模近8亿人.据统计社区100户居民的网上购物情况如下图表所示:(1)是否有的把握认为社区的居民是否喜欢网上购物与年龄有关?(2)用频率估计概率,现从社区居民中随机抽取20位,记其中喜欢网上购物的居民人数为,表示20位居民中有位居民喜欢网上购物的概率,当取得最大值时,求的值.附:.0.0500.0100.0013.841(★★★) 16. 在三棱柱中,,,,分别为,的中点,.(1)求证:;(2)若,求二面角的正弦值.(★★★) 17. 已知双曲线的离心率为,点在上.(1)求双曲线的方程;(2)直线与双曲线交于不同的两点,,若直线,的斜率互为倒数,证明:直线过定点.(★★★★) 18. 已知函数,直线与曲线相切.(1)求实数的值;(2)若函数有三个极值点,,,求实数的取值范围.(★★★) 19. 已知无穷数列中,,记,,.(1)若为2,0,2,4,2,0,2,4,…,是一个周期为4的数列(即,),直接写出,,,的值;(2)若为周期数列,证明:,使得当时,是常数;(3)设是非负整数,证明:的充分必要条件为为公差为的等差数列.。