工程力学实验报告标准答案

第一章静力学的基本概念受力图第二章 平面汇交力系2-1解：由解析法，23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故：22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故： 223R RX RY F F F KN=+= 方向沿OB 。

2-3 解：所有杆件均为二力杆件，受力沿直杆轴线。

（a ） 由平衡方程有：0X =∑sin 300AC AB F F -=0Y =∑cos300AC F W -=0.577AB F W=（拉力）1.155AC F W=（压力）（b ） 由平衡方程有：0X =∑ cos 700AC AB F F -=0Y =∑sin 700AB F W -=1.064AB F W=（拉力）0.364AC F W=（压力）（c ） 由平衡方程有：0X =∑cos 60cos300AC AB F F -=0Y =∑sin 30sin 600AB AC F F W +-=0.5AB F W= (拉力)0.866AC F W=（压力）（d ） 由平衡方程有：0X =∑sin 30sin 300AB AC F F -=0Y =∑cos30cos300AB AC F F W +-=0.577AB F W= (拉力)0.577AC F W= (拉力)2-4 解：（a ）受力分析如图所示：由x =∑ 22cos 45042RA F P -=+15.8RA F KN∴=由Y =∑ 22sin 45042RA RB F F P +-=+7.1RB F KN∴=(b)解：受力分析如图所示：由x =∑3cos 45cos 45010RA RB F F P ⋅--=0Y =∑1sin 45sin 45010RA RB F F P ⋅+-=联立上二式，得：22.410RA RB F KN F KN==2-5解：几何法：系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以：5RA F KN= （压力）5RB F KN=（与X 轴正向夹150度）2-6解：受力如图所示：已知，1R F G = ，2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解：受力分析如图所示，取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后，解得：0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式，解得：7.32AB F KN=-（受压）27.3AC F KN=（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==（2）取B 点列平衡方程：由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解：取B 为研究对象：由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象：由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BCBC F F '= 解得：2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象：由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有：22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解：取A 点平衡：x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得： 2cos 75AD AB PF F ==取D 点平衡，取如图坐标系：x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD P F F F KN'∴===⋅=2-12解：整体受力交于O 点，列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得：2.92RA F KN=1.33DC F KN=（压力）列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得： 1.67AC F KN=（拉力）1.0BC F KN=-（压力）2-13解：（1）取DEH 部分，对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q =联立方程后解得： 5RD F Q =2REF Q '=（2）取ABCE 部分，对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得： 22RA F Q =2RB F Q P=+（3）取BCE 部分。

大学《工程力学》课后习题解答-精品2020-12-12【关键字】情况、条件、动力、空间、主动、整体、平衡、建立、研究、合力、位置、安全、工程、方式、作用、结构、水平、关系、分析、简化、倾斜、支持、方向、协调、推动(e)(c)(d)(e)’CD2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。

解：(1) 取节点(2) AC 与BC 2-3 水平力F A 和D 处的约束力。

解：(1) 取整体(2) 2-4 在简支梁，力的大小等于20KN ，如图所示。

若解：(1)(2)求出约束反力：2-6 如图所示结构由两弯杆ABC 和DE 构成。

构件重量不计，图中的长度单位为cm 。

已知F =200 N ，试求支座A 和E 的约束力。

解：(1) 取DE (2) 取ABC2-7 在四连杆机构ABCD 试求平衡时力F 1和F 2解：（1）取铰链B (2) 取铰链C 由前二式可得：F FF ADF2-9 三根不计重量的杆AB，AC，AD在A点用铰链连接，各杆与水平面的夹角分别为450，，450和600，如图所示。

试求在与O D平行的力F作用下，各杆所受的力。

已知F=0.6 kN。

解：(1)间汇交力系；(2)解得：AB、AC3-1 已知梁AB 上作用一力偶，力偶矩为M ，梁长为l ，梁重不计。

求在图a ，b ，c 三种情况下，支座A 和B 的约束力解：(a) (b) (c) 3-2 M ，试求A 和C解：(1) 取 (2) 取 3-3 Nm ，M 2解：(1)(2) 3-5 大小为AB 。

各杆 解：(1)(2)可知：(3) 研究OA 杆，受力分析，画受力图：列平衡方程：AB A3-7 O1和O2圆盘与水平轴AB固连，O1盘垂直z轴，O2盘垂直x轴，盘面上分别作用力偶（F1，F’1），（F2，F’2）如题图所示。

第一章静力学的基本概念受力图第二章 平面汇交力系2-1解：由解析法，23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故：22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故： 223R RX RY F F F KN=+= 方向沿OB 。

2-3 解：所有杆件均为二力杆件，受力沿直杆轴线。

（a ） 由平衡方程有：0X =∑sin 300AC AB F F -=0Y =∑cos300AC F W -=0.577AB F W=（拉力）1.155AC F W=（压力）（b ） 由平衡方程有：0X =∑ cos 700AC AB F F -=0Y =∑sin 700AB F W -=1.064AB F W=（拉力）0.364AC F W=（压力）（c ） 由平衡方程有：0X =∑cos 60cos300AC AB F F -=0Y =∑sin 30sin 600AB AC F F W +-=0.5AB F W= (拉力)0.866AC F W=（压力）（d ） 由平衡方程有：0X =∑sin 30sin 300AB AC F F -=0Y =∑cos30cos300AB AC F F W +-=0.577AB F W= (拉力)0.577AC F W= (拉力)2-4 解：（a ）受力分析如图所示：由x =∑ 22cos 45042RA F P -=+15.8RA F KN∴=由Y =∑ 22sin 45042RA RB F F P +-=+7.1RB F KN∴=(b)解：受力分析如图所示：由x =∑3cos 45cos 45010RA RB F F P ⋅--=0Y =∑1sin 45sin 45010RA RB F F P ⋅+-=联立上二式，得：22.410RA RB F KN F KN==2-5解：几何法：系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以：5RA F KN= （压力）5RB F KN=（与X 轴正向夹150度）2-6解：受力如图所示：已知，1R F G = ，2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解：受力分析如图所示，取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后，解得：0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式，解得：7.32AB F KN=-（受压）27.3AC F KN=（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==（2）取B 点列平衡方程：由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解：取B 为研究对象：由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象：由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BCBC F F '= 解得：2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象：由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有：22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解：取A 点平衡：x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得： 2cos 75AD AB PF F ==取D 点平衡，取如图坐标系：x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD P F F F KN'∴===⋅=2-12解：整体受力交于O 点，列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得：2.92RA F KN=1.33DC F KN=（压力）列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得： 1.67AC F KN=（拉力）1.0BC F KN=-（压力）2-13解：（1）取DEH 部分，对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q =联立方程后解得： 5RD F Q =2REF Q '=（2）取ABCE 部分，对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得： 22RA F Q =2RB F Q P=+（3）取BCE 部分。

报告编号：YT-FS-3164-69工程力学实验报告(完整版)After Completing The T ask According To The Original Plan, A Report Will Be Formed T o Reflect The Basic Situation Encountered, Reveal The Existing Problems And Put Forward Future Ideas.互惠互利共同繁荣Mutual Benefit And Common Prosperity工程力学实验报告(完整版)备注：该报告书文本主要按照原定计划完成任务后形成报告，并反映遇到的基本情况、实际取得的成功和过程中取得的经验教训、揭露存在的问题以及提出今后设想。

文档可根据实际情况进行修改和使用。

拉伸实验是测定材料在常温静载下机械性能的最基本和重要的实验之一。

这不仅因为拉伸实验简便易行，便于分析，且测试技术较为成熟。

更重要的是，工程设计中所选用的材料的强度、塑形和弹性模量等机械指标，大多数是以拉伸实验为主要依据。

实验目的（二级标题左起空两格，四号黑体，题后为句号）1、验证胡可定律，测定低碳钢的E。

2、测定低碳钢拉伸时的强度性能指标：屈服应力Rel和抗拉强度Rm。

3、测定低碳钢拉伸时的塑性性能指标：伸长率A 和断面收缩率Z4、测定灰铸铁拉伸时的强度性能指标：抗拉强度Rm5、绘制低碳钢和灰铸铁拉伸图，比较低碳钢与灰铸铁在拉伸树的力学性能和破坏形式。

实验设备和仪器万能试验机、游标卡尺，引伸仪实验试样实验原理按我国目前执行的国家GB/T 228—20xx标准——《金属材料室温拉伸试验方法》的规定，在室温10℃～35℃的范围内进行试验。

将试样安装在试验机的夹头中，固定引伸仪，然后开动试验机，使试样受到缓慢增加的拉力（应根据材料性能和试验目的确定拉伸速度），直到拉断为止，并利用试验机的自动绘图装置绘出材料的拉伸图（图2－2所示）。

一、实验目的1. 了解工程力学实验的基本方法和步骤。

2. 通过实验，掌握力学基本理论在工程实际中的应用。

3. 培养实验操作技能，提高实验数据分析能力。

二、实验内容1. 材料力学实验：拉伸试验、压缩试验、弯曲试验。

2. 建筑力学实验：静力平衡实验、超静定结构受力分析实验。

三、实验步骤1. 实验一：拉伸试验（1）将试样固定在拉伸试验机上，调整试验机至预定位置。

（2）缓慢加载，记录加载过程中的力值和位移值。

（3）观察试样变形情况，记录断裂位置。

（4）分析试验数据，绘制拉伸曲线，计算弹性模量、屈服强度等指标。

2. 实验二：压缩试验（1）将试样固定在压缩试验机上，调整试验机至预定位置。

（2）缓慢加载，记录加载过程中的力值和位移值。

（3）观察试样变形情况，记录断裂位置。

（4）分析试验数据，绘制压缩曲线，计算抗压强度、弹性模量等指标。

3. 实验三：弯曲试验（1）将试样固定在弯曲试验机上，调整试验机至预定位置。

（2）缓慢加载，记录加载过程中的力值和位移值。

（3）观察试样变形情况，记录断裂位置。

（4）分析试验数据，绘制弯曲曲线，计算抗弯强度、弹性模量等指标。

4. 实验四：静力平衡实验（1）搭建静力平衡实验装置，调整实验参数。

（2）观察实验现象，记录实验数据。

（3）分析实验数据，验证静力平衡原理。

5. 实验五：超静定结构受力分析实验（1）搭建超静定结构实验装置，调整实验参数。

（2）观察实验现象，记录实验数据。

（3）分析实验数据，验证超静定结构受力分析原理。

四、实验结果与分析1. 拉伸试验根据实验数据，绘制拉伸曲线，计算弹性模量E=...（单位：MPa），屈服强度σs=...（单位：MPa），抗拉强度σb=...（单位：MPa）。

2. 压缩试验根据实验数据，绘制压缩曲线，计算抗压强度σc=...（单位：MPa），弹性模量E=...（单位：MPa）。

3. 弯曲试验根据实验数据，绘制弯曲曲线，计算抗弯强度σb=...（单位：MPa），弹性模量E=...（单位：MPa）。

工程力学实验报告学生姓名：学号：专业班级：南昌大学工程力学实验中心目录实验一金属材料的拉伸及弹性模量测定试验 2 实验二金属材料的压缩试验 6 实验三复合材料拉伸实验9 实验四金属扭转破坏实验、剪切弹性模量测定12 实验五电阻应变片的粘贴技术及测试桥路变换实验16 实验六弯曲正应力电测实验19 实验七叠（组）合梁弯曲的应力分析实验23 实验八弯扭组合变形的主应力测定32实验九偏心拉伸实验37 实验十偏心压缩实验41 实验十二金属轴件的高低周拉、扭疲劳演示实验45 实验十三冲击实验47 实验十四压杆稳定实验49 实验十五组合压杆的稳定性分析实验53 实验十六光弹性实验59 实验十七单转子动力学实验62 实验十八单自由度系统固有频率和阻尼比实验65实验一金属材料的拉伸及弹性模量测定试验实验时间：设备编号：温度：湿度：一、实验目的二、实验设备和仪器三、实验数据及处理引伸仪标距l = mm实验前低碳钢弹性模量测定()F lE l Aδ∆⋅=∆⋅ =实验后屈服载荷和强度极限载荷载荷―变形曲线(F―Δl曲线)及结果四、问题讨论（1）比较低碳钢与铸铁在拉伸时的力学性能；（2）试从不同的断口特征说明金属的两种基本破坏形式。

金属材料的拉伸及弹性模量测定原始试验数据记录实验二金属材料的压缩试验实验时间：设备编号：温度：湿度：一、实验目的二、实验设备和仪器三、实验数据及处理载荷―变形曲线(F―Δl曲线)及结果四、问题讨论（1）观察铸铁试样的破坏断口，分析破坏原因；（2）分析比较两种材料拉伸和压缩性质的异同。

金属材料的压缩试验原始试验数据记录实验三复合材料拉伸实验实验时间：设备编号：温度：湿度：一、实验目的二、实验设备和仪器三、实验数据及处理试件尺寸电阻应变片数据载荷和应变四、问题讨论复合材料拉伸实验原始试验数据记录实验四金属扭转破坏实验、剪切弹性模量测定实验时间：设备编号：温度：湿度：一、实验目的二、实验设备和仪器三、实验数据及处理弹性模量E= 泊松比 =实验前低碳钢剪切弹性模量测定PI l T G ⋅⋅=ϕ∆∆0=理论值)1(2μ+=EG = ；相对误差（%）==⨯-%100理实理G G G 载荷―变形曲线(F ―Δl 曲线)及结果四、问题讨论（1）为什么低碳钢试样扭转破坏断面与横截面重合，而铸铁试样是与试样轴线成45o 螺旋断裂面？（2）根据低碳钢和铸铁拉伸、压缩、扭转试验的强度指标和断口形貌，分析总结两类材料的抗拉、抗压、抗剪能力。

工程力学课后习题答案1. 弹簧的力学行为问题描述一根长度为L，截面形状为圆形的弹簧，其材料为线性弹性材料，弹性模量为L，初始长度为L0。

当对该弹簧施加一个轴向拉力L时，弹簧的长度变为L′，求解弹簧的伸长量$\\DeltaL$。

解答我们可以利用胡克定律来求解弹簧的伸长量。

根据胡克定律，弹簧的伸长量与施加在其上的拉力成正比，即$\\Delta L = \\frac{FL'}{EA}$，其中L为弹簧的横截面积。

根据几何关系，弹簧的横截面积可以表示为$A = \\pi r^2$，其中L为弹簧的半径。

因此，弹簧的伸长量可以表示为$\\Delta L = \\frac{FL'}{E\\pi r^2}$。

2. 牛顿第二定律应用问题描述一辆质量为L的汽车以速度L0匀速行驶，当司机踩下刹车后，汽车在L秒内减速L。

求解汽车行驶的距离L。

解答首先，根据牛顿第二定律L=LL，可以得到刹车时汽车受到的减速度$a = \\frac{F}{m}$。

其次，根据运动学关系L2=L2+2LL，其中L为刹车前的速度，L为刹车后的速度，L为刹车行驶的距离。

由于时间L内汽车的速度从L0减速到0，因此L=0，L=L0。

将上述关系代入运动学公式中，可以得到0=L02+2LL。

解方程可得刹车行驶的距离$s = \\frac{-v_0^2}{2a}$。

3. 动量守恒定律问题描述在一次碰撞实验中，一个质量为L1的小球以速度L1沿着一条直线运动，与一个质量为L2的小球发生完全弹性碰撞，求解碰撞后两个小球的速度L1′和L2′。

解答根据动量守恒定律，碰撞前后系统的总动量保持不变，即L1L1+L2L2=L1L1′+L2L2′。

根据动能守恒定律，碰撞前后系统的总动能保持不变，即$\\frac{1}{2}m_1v_1^2 + \\frac{1}{2}m_2v_2^2 =\\frac{1}{2}m_1v_1'^2 + \\frac{1}{2}m_2v_2'^2$。

力学实验报告答案力学实验报告答案引言：力学是物理学的一个重要分支，研究物体的运动和相互作用。

在力学实验中，通过设计合适的实验装置和进行精确的测量，可以验证力学理论，并获得一些有价值的实验数据。

本文将就几个力学实验的结果和分析进行讨论，以加深对力学知识的理解。

实验一：简谐振动简谐振动是力学中的重要概念，指的是振动系统在无阻尼和无外力的情况下，受到恢复力作用而产生的振动。

我们通过实验装置模拟了简谐振动，并测量了振动周期与振幅的关系。

实验结果显示，振动周期与振幅的平方成正比。

这符合简谐振动的特性，即振动周期与振幅无关，只与振动系统的特性有关。

通过分析实验数据，我们可以得出简谐振动的周期公式：T=2π√(m/k)，其中T为振动周期，m为振动系统的质量，k为恢复力系数。

实验二：牛顿第二定律牛顿第二定律是力学中的重要定律，描述了物体的加速度与作用在物体上的合力之间的关系。

我们通过实验验证了牛顿第二定律，并测量了物体的加速度与施加在物体上的力的关系。

实验结果显示，物体的加速度与施加在物体上的力成正比。

这符合牛顿第二定律的表述：F=ma，其中F为合力，m为物体的质量，a为物体的加速度。

通过分析实验数据，我们可以得出物体的加速度与施加在物体上的力的关系为：a=F/m。

实验三：动量守恒定律动量守恒定律是力学中的重要定律，描述了一个封闭系统中物体的总动量保持不变。

我们通过实验验证了动量守恒定律，并测量了碰撞前后物体的动量之和。

实验结果显示，碰撞前后物体的动量之和保持不变。

这符合动量守恒定律的表述：m1v1 + m2v2 = m1v1' + m2v2'，其中m1和m2分别为两个物体的质量，v1和v2分别为碰撞前两个物体的速度，v1'和v2'分别为碰撞后两个物体的速度。

通过分析实验数据，我们可以验证动量守恒定律的成立。

结论：通过以上实验的结果和分析，我们验证了简谐振动、牛顿第二定律和动量守恒定律这几个力学理论。

1－1五个力作用于一点O，如图示。

图中方格的边长为10mm 。

试求此力系的合力。

解题思路：（1）由式（1－13）求合力在直角坐标轴上的投影；（2）由式（1－14）求合力的大小；（3）由式（1－15）求合力的方向。

答案：F R ＝669.5N , ∠(F R，i )＝34.901－2如图示平面上的三个力F1＝100N，F2＝50N，F3＝50N，三力作用线均过A点，尺寸如图。

试求此力系的合力。

解题思路：（1）由式（1－13）求合力在直角坐标轴上的投影；（2）由式（1－14）求合力的大小；（3）由式（1－15）求合力的方向。

答案：F R ＝161.2N , ∠(F R，F i)＝29.701－3试计算下列各图中的力F对点O之矩。

解题思路：各小题均由式（1－16）求力矩。

答案：略1－4如图所示的挡土墙重G 1＝75 kN ，铅直土压力G 2＝120 kN ，水平土压力F p ＝90 kN 。

试求三力对前趾A 点之矩的和，并判断挡土墙是否会倾倒。

解题思路：（1）由式（1－16）求三力对前趾A 点之矩的代数和； （2）若其值为负（顺时针转），则挡土墙不会翻倒。

答案：∑M A ＝－180kN.m ，不会倾倒。

1－5如图所示，边长为a 的正六面体上沿对角线AH 作用一力F 。

试求力F 在三个坐标轴上的投影，力F 对三个坐标轴之矩以及对点O 之矩矢。

解题思路：（1）由式（1－13）、（1－14）、（1－15）求合力的大小和方向； （2）由式（1－25）求力对三个坐标轴之矩； （3）由式（1－26）求力对坐标原点之矩。

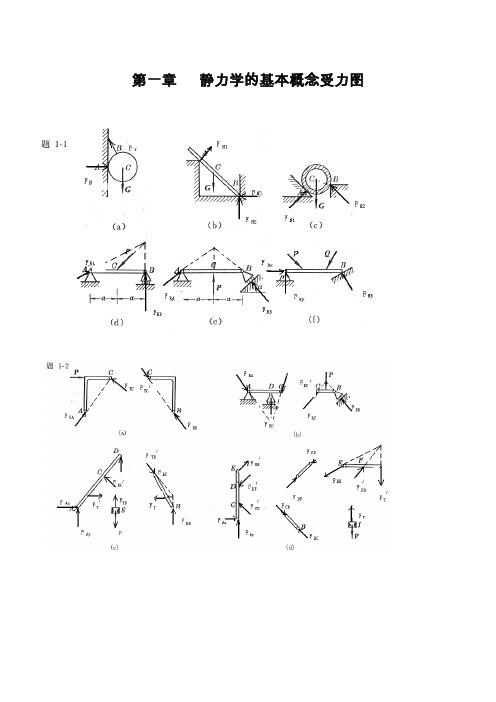
答案：M x ＝0，Fa M y 33＝，Fa M 33z ＝－, k Fa j Fa M O 3333-＝1－7试画出下列各图中物体A ，构件AB 的受力图。

未画重力的物体重量不计，所有接触面均为光滑接触。

解题思路：（1）画出研究对象的轮廓形状； （2）画出已知的主动力；（3）在解除约束处按约束的性质画出约束力。

试验目的：1. 测定低碳钢（塑性材料）的弹性摸量E；屈服极限σs 等机械性能。

2．测定灰铸铁（脆性材料）的强度极限σb3．了解塑性材料和脆性材料压缩时的力学性能。

材料拉伸与压缩实验指导书低碳钢拉伸试验拉伸试验的意义: 单向拉伸试验是在常温下以缓慢均匀的速度对专门制备的试件施加轴向载荷，在试件加载过程中观测载荷与变形的关系，从而决定材料有关力学性能。

通过拉伸试验可以测定材料在单向拉应力作用下的弹性模量及屈服强度、抗拉强度、延伸率、截面收缩率等指标。

其试验方法简单且易于得到较可靠的试验数据，所以是研究材料力学性能最基本、应用最广泛的试验。

操作步骤：1．试验设备：WDW－3050电子万能试验机2．试件准备：用游标卡尺测量试件试验段长度l0和截面直径d0，并作记录。

3．打开试验机主机及计算机等相关设备。

4．试件安装（详见WDW3050电子万能试验机使用与操作三．拉伸试件的安装）。

5．引伸计安装（用于测量E, 详见WDW3050电子万能试验机使用与操作四．引伸计安装）。

6．测量参数的设定:7．再认真检查一遍试件安装等试验准备工作。

8．负荷清零，轴向变形清零，位移清零。

9．开始进行试验，点击试验开始。

10．根据提示摘除引伸计。

11．进入强化阶段以后，进行冷作硬化试验，按主机控制面板停止，再按▼，先卸载到10kN，再加载，按▲，接下来计算机控制，一直到试件断裂（此过程中计算机一直工作，注意观察负荷位移曲线所显示的冷作硬化现象．）．12．断裂以后记录力峰值。

13．点击试验结束（不要点击停止）。

14．材料刚度特征值中的弹性模量E的测定试验结束后，在试验程序界面选定本试验的试验编号，并选择应力─应变曲线。

在曲线上较均匀地选择若干点，记录各点的值，分别为及(如i =0,1,2,3,4),并计算出相应的计算E i的平均值，得到该材料的弹性模量E的值。

15．材料强度特征值屈服极限和强度极限的测定试验结束后，在试验程序界面选定本试验的试验编号，并选择负荷─位移曲线，找到的曲线屈服阶段的下屈服点，即为屈服载荷F s, 找到的曲线上最大载荷值，即为极限载荷P b.计算屈服极限：；计算强度极限：；16．材料的塑性特征值延伸率及截面收缩率的测定试件拉断后，取下试件，沿断裂面拼合，用游标卡尺测定试验段长度，和颈缩断裂处截面直径。

工程力学实验报告引言工程力学是工程学中的基础课程，通过实验可以直观地展示其中一些重要原理和理论，并帮助学生巩固和加深对这些知识的理解。

本次实验主要涉及杆件的静力学分析和材料力学。

1. 实验背景工程力学实验是为了让学生更好地理解力学原理和应用，以及在工程实践中如何利用这些原理解决问题。

本次实验中，我们将使用静力学和材料力学的原理来分析和测试杆件的性能。

2. 实验材料和设备本次实验所用的杆件是一根钢杆，长约1米，直径约2厘米。

实验室中还准备了支撑架、测力计、游标卡尺、千分表等测量设备。

3. 静力学分析3.1 杆件在自重下的变形首先，我们将测量钢杆的质量，并把它悬挂在支撑架上。

然后使用测力计在不同位置测量钢杆的变形。

通过对测量结果的分析，我们可以计算出钢杆在自重下的应变和变形。

3.2 杆件在外力作用下的变形接着，我们将在钢杆上施加不同的力，并使用测力计测量其变形。

通过分析测量结果，可以计算出钢杆在外力作用下的应力分布和变形。

4. 材料力学分析4.1 杨氏模量的测量杨氏模量是衡量材料刚度的重要参数，可以通过实验来测量得到。

在本次实验中，我们将使用弹性极限方法来测量钢杆的杨氏模量。

通过测量钢杆在不同受力状态下的应力和应变，然后绘制应力与应变的线性关系图，可以计算出杨氏模量。

4.2 断裂强度的测量断裂强度是材料的抗拉能力，通过实验可以测量得到。

我们将在钢杆上逐渐增加外力，直到钢杆发生断裂。

根据实验过程中测得的最大施加力和钢杆的横截面积，可以计算出断裂强度。

5. 结果和讨论在本次实验中，我们用测力计记录了钢杆在不同受力状态下的变形和力的大小，并用测量设备记录了钢杆的直径和长度。

通过静力学和材料力学的分析，我们得到了钢杆的应力、应变、变形、杨氏模量和断裂强度的数值。

结论通过本次实验，我们深入地了解了工程力学的理论和原理，并通过实际操作加深了对杆件静力学和材料力学的理解。

我们还学到了如何利用测力计等仪器来测试和测量受力物体的性能，为工程实践提供了基础知识和实验技能。

第一章静力学基本概念与物体的受力分析下列习题中，未画出重力的各物体的自重不计，所有接触面均为光滑接触。

1.1试画出下列各物体（不包括销钉与支座）的受力图。

解：如图1.2画出下列各物体系统中各物体（不包括销钉与支座）以及物体系统整体受力图。

解：如图1.3铰链支架由两根杆AB、CD和滑轮、绳索等组成，如题1.3图所示。

在定滑轮上吊有重为W的物体H。

试分别画出定滑轮、杆CD、杆AB和整个支架的受力图。

解：如图1.4题1.4图示齿轮传动系统，O1为主动轮，旋转方向如图所示。

试分别画出两齿轮的受力图。

解：1.5结构如题1.5图所示，试画出各个部分的受力图。

解：第二章汇交力系2.1在刚体的A点作用有四个平面汇交力。

其中F1＝2kN，F2=3kN，F3=lkN，F4=2.5kN，方向如题2.1图所示。

用解读法求该力系的合成结果。

解2.2 题2.2图所示固定环受三条绳的作用，已知F1＝1kN，F2=2kN，F3=l.5kN。

求该力系的合成结果。

解：2.2图示可简化为如右图所示2.3 力系如题2.3图所示。

已知：F 1＝100N ，F 2=50N ，F 3=50N ，求力系的合力。

解：2.3图示可简化为如右图所示2.4 球重为W ＝100N ，悬挂于绳上，并与光滑墙相接触，如题2.4图所示。

已知，试求绳所受的拉力及墙所受的压力。

解：2.4图示可简化为如右图所示墙所受的压力F=57.74N2.5 均质杆AB 重为W 、长为 l ，两端置于相互垂直的两光滑斜面上，如题2.5图所示。

己知一斜面与水平成角，求平衡时杆与水平所成的角及距离OA 。

解：取 AB 杆为研究对象，受力如图所示由于杆件再三力作用下保持平衡，故三力应汇交于C 点。

AB 杆为均质杆，重力作用在杆的中点，则W 作用线为矩形ACBO 的对角线。

由几何关系得 所以 又因为 所以2.6 一重物重为20kN ，用不可伸长的柔索AB 及BC悬挂于题2.6图所示的平衡位置。

《工程力学实验》标准答案（2006-2007学年第1学期）2007.1.12A 卷1 【单自由度系统自由振动】（15分）(1)简支梁单自由度系统的力学模型(3分)(2) 简支梁自由振动的有阻尼固有频率(3分)02375.0415=−=ΔT T T s 11.421=Δ=Tf d Hz (3) 简支梁的阻尼比(3分)029022025.0ln4151==A A δ 31062.42−×==πδς (4) 简支梁中点处的等效质量(3分)026.04'1'5'=−=ΔT T T s46.381'=Δ=ΔTf d Hz 504.0122=−Δ=Δd d f f m m kg(5) 简支梁中点处的等效刚度(3分)35268)2(222==≈=d d n f m m m k πωωN/m2 【单自由度系统强迫振动】（10分）（1）（6分） 答：单自由度系统强迫振动力学模型由质量、弹簧、阻尼和外部激振力组成，其基本方程为：t F kx x c xm ωsin 0=++&&&。

如右图所示。

（2）（4分）答：归一化的幅频特性曲线为mB B，由于0F B =，则 ()22222020244ωδωωωδ+−=mB B可见mB B跟外部激励力没有关系，只跟外部的激励频率，以及系统的固有频率0ω、阻尼系数δ有关，所以说归一化的幅频特性曲线为系统的固有特性曲线。

（注：答出其结果可得4分）在实验中测试得电压：B K K U 21=，1K 为传感器灵敏系数，2K 为放大器的灵敏系数 课件mm U UB B =与1K 、2K 都没有关系，即归一化的幅频特性曲线与测量仪器无关，是系统的固有特性曲线（注：答出其结果可得2分）。

3 【连杆质心与转动惯量测量】（15分）（1）秒表的读数误差;->提高秒表读数 （2）电子秤的精度误差;->提高电子秤精度（3）空气阻力;->尽量在空气流动少的地方做实验;甚至真空中 （4）质心对准误差;->用激光对准等. （5）g 值取舍误差（6）调节水平的误差;->用高精度的倾角仪校正 （7）水平晃动引起的误差;->该进晃动形式（8）测量绳子长度引起的误差;->应用没有伸缩性的绳子（9）周期计时的开始与结束误差;->应用秒表触发计时;取代人工 （10）线性化误差（11）连杆非对称性误差4 【拉伸与压缩】（10分）如断口到最近的标距端点的距离小于l0/3。