江苏省盐城市东台第一教研片2014-2015学年八年级数学下学期第一次阶段检测试题及答案

江苏省盐城市东台市2013-2014学年八年级下学期第一次月考语文试题一、选择题（10分）1、选出加粗字注音全对的一项（）A．呻吟（shēng xíng）蜿蜒（yán）掠起（luè）秀颀（qí）B．晕圈（yùn）纵横决荡（hèng）外壳（ké）奇崛（jué）C．琢磨（zhuó）盎然（àng）秀颀（xiù）伫立（zhù）D．酒酿（niàng）迸溅（bìng）犀利（xī）丰腴（yú）3、下列语句中标点符号使用正确的一项是（）A、这是一颗怎样固执而又简单的心啊？B、你让我谈谈怎么回事？我也不知道怎么谈才好。

C、《敬业与乐业》是近代著名学者梁启超的作品，文章告诉读者对待“业”必须保持“趣味”和“责任心”。

D、有人以为学问就是智慧，其实有学问的人，何曾都有智慧。

4．下列句子没有语病的一句是（）A．通过阅读这几篇文章，使我认识到人类要与动物、环境和谐相处。

B．听到马航飞机失联的消息，我的心长时间久久不能平静。

C．伊拉克局势能不能稳定下来，是联合国工作人员返回巴格达的基本条件。

D．“神舟”五号载人飞船的成功发射和顺利返回，是载入中华民族史册的不朽盛事。

5．“只要老老实实扪心自问，我们都可以找到出现警报的地方”这句话放置在下面文段中，最合适的一处是（）①人生就是如此。

②被小石子打中，如果不能及时醒悟，一味置之不理，就会被砖块打中。

③如果仍然执迷不悟，就会被大石头狠狠击中。

④但我们还是会厚着脸皮说：“为什么老是我遭殃？”A．①②句间 B．②③句间 C．③④句间 D．④句后二、积累与运用（22分）6、下列词语中共有四个错别字，一一找出，然后按顺序改正。

（4分）无边无垠潜滋按长发奋忘食失之交臂狼籍旁逸斜出7、默写。

（共8分）（1） ,泥香带落花。

（2）临风一唳思何事，。

( 卷面总分：100分考试时间：100分钟命题学校：后港中学)一．听力（共20小题，每小题1分，记20分）第一部分听对话回答问题（计10分）本部分共有10道小题，每道小题你将听到一段对话，每段对话听两遍。

1.Where has the woman been in China?A. B. C.2.Where would the man like to go?A. B. C.3.What did Henry do last night?A. B. C.4.Where did Lucy stay yesterday?A. B. C.5.What happened to Lucy?A .She had a traffic accident. B. Her bike didn't work. C. She lost her car.6.What time will they meet?A.1:15.B.1:30.C.1:45.7.Who is Lucy waiting for?A. Mr. Smith.B. Mrs. Smith.C. Mr. and Mrs. Smith.8.Why can't she go out for a walk?A. Because she is ill.B. Because she has some homework to do.C. Because she doesn't like walking.9.How old is Peter?A. He is twelve.B. He is five.C. He is seventeen.10.Does Mrs. Green like pork better than beef?A. Mrs. Green likes beef better than pork.B. Yes, she does.C. No, she doesn't.第二部分听对话和短文答题（计10分）你将听到一段对话和两篇短文，各听两遍。

江苏省盐城市东台市第一教研片2015-2016学年八年级数学下学期期中试题一、选择题：（每题2分，共16分）1．在，，中，是分式的有（）A．0个B．1个C．2个D．3个2．如图所示的几何图形中，既是轴对称图形又是中心对称图形的个数是（）A．4 B．3 C．2 D．13．若分式有意义，则x的取值范围是（）A．x≠1 B．x＞1 C．x=1 D．x＜14．如果把分式中的x和y都扩大5倍，那么分式的值（）A．扩大5倍 B．不变 C．扩大10倍D．缩小5．若反比例函数y=的图象经过点（﹣1，2），则这个函数的图象一定经过点（）A．（﹣2，﹣1）B．（﹣，2）C．（2，﹣1）D．（，2）6．在下列性质中，矩形具有而菱形不一定有的是（）A．对角线互相垂直B．对角线互相平分C．四个角是直角 D．四条边相等7．解分式方程﹣=1时，去分母后可得到（）A．x（2+x）﹣2（ 3+x）=1 B．x（2+x）﹣2=2+xC．x（2+x）﹣2（ 3+x）=（2+x）（3+x）D．x﹣2（ 3+x）=3+x8．如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF 于G，下列结论：①BE=DF，②∠DAF=15°，③AC垂直平分EF，④BE+DF=EF，⑤S△CEF=2S△ABE．其中正确结论有（）个．A．4 B．3 C．2 D．1二、填空题（每空2分，共16分）9．请写出一个是中心对称图形的几何图形的名称：．10．如果反比例函数的图象在二、四象限内，则m的取值范围是．11．如图，为测量位于一水塘旁的两点A、B间的距离，在地面上确定点O，分别取OA、OB 的中点C、D，量得CD=20m，则A、B之间的距离是m．12．如图，在四边形ABCD中，AB∥CD，请你添加一个条件，使得四边形ABCD成为平行四边形，你添加的条件是．13．菱形的两条对角线分别为3cm和4cm，则菱形的面积为cm．14．如图，P是矩形ABCD的边AD上一个动点，矩形的两条边AB、BC的长分别为6和8，那么点P到矩形的两条对角线AC和BD的距离之和是．15．关于x的分式方程=﹣2解为正数，则m的取值范围是．16．如图，平行四边形ABCD中，AC与BD相交于点E，∠AEB=45°，BD=2，将△ABC沿AC 所在直线翻折到同一平面内，若点B的落点记为B′，则DB′的长为．三、解答题（共68分）17．△ABC在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位长度．按要求作图：①画出△ABC关于原点O的中心对称图形△A1B1C1；②画出将△ABC绕点C顺时针旋转90°得到△A2B2C．18．计算．（1）（2）．19．先化简代数式（1﹣）÷，再从0，﹣2，2，﹣1，1中选取一个恰当的数作为a的值代入求值．20．解方程：（1）=（2）=1+．21．制作一种产品，需先将材料加热达到60℃后，再进行操作．设该材料温度为y（℃），从加热开始计算的时间为x（分钟）．据了解，该材料加热时，温度y与时间x成一次函数关系；停止加热进行操作时，温度y与时间x成反比例关系（如图）．已知该材料在操作加工前的温度为15℃，加热5分钟后温度达到60℃．（1）分别求出将材料加热和停止加热进行操作时，y与x的函数关系式；（2）根据工艺要求，当材料的温度低于15℃时，须停止操作，那么从开始加热到停止操作，共经历了多少时间？22．已知：如图，四边形ABCD四条边上的中点分别为E、F、G、H，顺次连接EF、FG、GH、HE，得到四边形EFGH（即四边形ABCD的中点四边形）．（1）四边形EFGH的形状是，证明你的结论．（2）当四边形ABCD的对角线满足条件时，四边形EFGH是矩形．（3）你学过的哪种特殊四边形的中点四边形是菱形？．23．某市为进一步缓解交通拥堵现象，决定修建一条从市中心到飞机场的轻轨铁路．实际施工时，每月的工效比原计划提高了20%，结果提前5个月完成这一工程．求原计划完成这一工程的时间是多少月？24．如图，点A是反比例函数y=﹣在第二象限内图象上一点，点B是反比例函数y=在第一象限内图象上一点，直线AB与y轴交于点C，且AC=BC，连接OA、OB，求△AOB的面积．25．在△ABC中，AB=AC，点D在边BC所在的直线上，过点D作DF∥AC交直线AB于点F，DE∥AB交直线AC于点E．（1）当点D在边BC上时，如图①，求证：DE+DF=AC．（2）当点D在边BC的延长线上时，如图②；当点D在边BC的反向延长线上时，如图③，请分别写出图②、图③中DE，DF，AC之间的数量关系，不需要证明．（3）若AC=6，DE=4，则DF= ．2015-2016学年江苏省盐城市东台市第一教研片八年级（下）期中数学试卷参考答案与试题解析一、选择题：（每题2分，共16分）1．在，，中，是分式的有（）A．0个B．1个C．2个D．3个【考点】分式的定义．【分析】判断分式的依据是看分母中是否含有字母，如果含有字母则是分式，如果不含有字母则不是分式．【解答】解：的分母中不含有字母，因此它们是整式，而不是分式．，的中分母中含有字母，因此是分式．故选：才．2．如图所示的几何图形中，既是轴对称图形又是中心对称图形的个数是（）A．4 B．3 C．2 D．1【考点】中心对称图形；轴对称图形．【分析】根据轴对称图形与中心对称图形的概念对各图形分析判断后解答即可．【解答】解：第一个图形是轴对称图形，不是中心对称图形；第二个图形是轴对称图形，不是中心对称图形；第三个图形是轴对称图形，也是中心对称图形；第四个图形是轴对称图形，不是中心对称图形；第五个图形是轴对称图形，也是中心对称图形；综上所述，第三个和第五个图形既是中心对称图形又是轴对称图形，共2个．故选C．3．若分式有意义，则x的取值范围是（）A．x≠1 B．x＞1 C．x=1 D．x＜1【考点】分式有意义的条件．【分析】本题主要考查分式有意义的条件：分母不等于0．【解答】解：∵x﹣1≠0，∴x≠1．故选：A．4．如果把分式中的x和y都扩大5倍，那么分式的值（）A．扩大5倍 B．不变 C．扩大10倍D．缩小【考点】分式的基本性质．【分析】根据分式的分子分母都乘以或除以同一个数（或整式），结果不变，可得答案．【解答】解：把分式的x和y的值都扩大5倍，那么分式的值不变，故选：B．5．若反比例函数y=的图象经过点（﹣1，2），则这个函数的图象一定经过点（）A．（﹣2，﹣1）B．（﹣，2）C．（2，﹣1）D．（，2）【考点】反比例函数图象上点的坐标特征．【分析】将（﹣1，2）代入y=即可求出k的值，再根据k=xy解答即可．【解答】解：∵反比例函数y=的图象经过点（﹣1，2），∴k=﹣1×2=﹣2，只需把所给点的横纵坐标相乘，结果是﹣2的，就在此函数图象上；四个选项中只有C：2×（﹣1）=﹣2符合．故选C．6．在下列性质中，矩形具有而菱形不一定有的是（）A．对角线互相垂直B．对角线互相平分C．四个角是直角 D．四条边相等【考点】矩形的性质；菱形的性质．【分析】由矩形的性质和菱形的性质，容易得出结论．【解答】解：矩形的性质有：四个角都是直角；对角线互相平分且相等；菱形的性质有：四条边相等；对角线互相垂直平分；矩形具有而菱形不一定有的是：四个角都是直角．故选：C．7．解分式方程﹣=1时，去分母后可得到（）A．x（2+x）﹣2（ 3+x）=1 B．x（2+x）﹣2=2+xC．x（2+x）﹣2（ 3+x）=（2+x）（3+x）D．x﹣2（ 3+x）=3+x【考点】解分式方程．【分析】等式两边同时乘以（3+x）（2+x），进行去分母．【解答】解：去分母得：x（2+x）﹣2（3+x）=（3+x）（2+x）．故选C．8．如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF 于G，下列结论：①BE=DF，②∠DAF=15°，③AC垂直平分EF，④BE+DF=EF，⑤S△CEF=2S△ABE．其中正确结论有（）个．A．4 B．3 C．2 D．1【考点】正方形的性质；全等三角形的判定与性质；线段垂直平分线的性质；等边三角形的性质．【分析】通过条件可以得出△ABE≌△ADF，从而得出∠BAE=∠DAF，BE=DF，由正方形的性质就可以得出EC=FC，就可以得出AC垂直平分EF，设EC=x，BE=y，由勾股定理就可以得出x 与y的关系，表示出BE与EF，利用三角形的面积公式分别表示出S△CEF和2S△ABE，再通过比较大小就可以得出结论．【解答】解：∵四边形ABCD是正方形，∴AB=BC=CD=AD，∠B=∠BCD=∠D=∠BAD=90°．∵△AEF等边三角形，∴AE=EF=AF，∠EAF=60°．∴∠BAE+∠DAF=30°．在Rt△ABE和Rt△ADF中，，Rt△ABE≌Rt△ADF（HL），∴BE=DF（故①正确）．∠BAE=∠DAF，∴∠DAF+∠DAF=30°，即∠DAF=15°（故②正确），∵BC=CD，∴BC﹣BE=CD﹣DF，即CE=CF，∵AE=AF，∴AC垂直平分EF．（故③正确）．设EC=x，由勾股定理，得EF=x，CG=x，AG=AEsin60°=EFsin60°=2×CGsin60°=x，∴AC=，∴AB=，∴BE=﹣x=，∴BE+DF=x﹣x≠x，（故④错误），∵S△CEF=，S△ABE==，∴2S△ABE==S△CEF，（故⑤正确）．综上所述，正确的有4个，故选：A．二、填空题（每空2分，共16分）9．请写出一个是中心对称图形的几何图形的名称：平行四边形．【考点】中心对称图形．【分析】常见的中心对称图形有：平行四边形、正方形、圆、菱形，写出一个即可．【解答】解：平行四边形是中心对称图形．故答案可为：平行四边形．10．如果反比例函数的图象在二、四象限内，则m的取值范围是m＜4 ．【考点】反比例函数的性质．【分析】根据反比例函数的性质可得m﹣4＜0，再解不等式即可．【解答】解：∵反比例函数的图象在二、四象限内，∴m﹣4＜0，解得m＜4．故答案为：m＜4．11．如图，为测量位于一水塘旁的两点A、B间的距离，在地面上确定点O，分别取OA、OB 的中点C、D，量得CD=20m，则A、B之间的距离是40 m．【考点】三角形中位线定理．【分析】根据三角形的中位线平行于第三边并且等于第三边的一半解答即可．【解答】解：∵C、D分别是OA、OB的中点，∴CD是△OAB的中位线，∵CD=20m，∴AB=2CD=2×20=40m．故答案为：40．12．如图，在四边形ABCD中，AB∥CD，请你添加一个条件，使得四边形ABCD成为平行四边形，你添加的条件是答案不唯一，如：AB=CD或AD∥BC或∠A=∠C或∠B=∠D或∠A+∠B=180°或∠C+∠D=180°等．【考点】平行四边形的判定．【分析】已知AB∥CD，可根据有一组边平行且相等的四边形是平行四边形来判定，也可根据两组分别平行的四边形是平行四边形来判定．【解答】解：∵在四边形ABCD中，AB∥CD，∴可添加的条件是：AB=DC，∴四边形ABCD是平行四边形（一组对边平行且相等的四边形是平行四边形）故答案为：AB=CD或AD∥BC或∠A=∠C或∠B=∠D或∠A+∠B=180°或∠C+∠D=180°等．13．菱形的两条对角线分别为3cm和4cm，则菱形的面积为 6 cm．【考点】菱形的性质．【分析】根据菱形的面积等于两对角线乘积的一半求得其面积即可．【解答】解：根据菱形的面积等于两对角线乘积的一半得，菱形的面积为3×4÷2=6cm2．故答案为6．14．如图，P是矩形ABCD的边AD上一个动点，矩形的两条边AB、BC的长分别为6和8，那么点P到矩形的两条对角线AC和BD的距离之和是 4.8 ．【考点】矩形的性质．【分析】首先连接OP，由矩形的两条边AB、BC的长分别为6和8，可求得OA=OD=5，△AOD的面积，然后由S△AOD=S△AOP+S△DOP=OA•PE+OD•PF求得答案．【解答】解：连接OP，∵矩形的两条边AB、BC的长分别为6和8，∴S矩形ABCD=AB•BC=48，OA=OC，OB=OD，AC=BD==10，∴OA=OD=5，∴S△ACD=S矩形ABCD=24，∴S△AOD=S△ACD=12，∵S△AOD=S△AOP+S△DOP=OA•PE+OD•PF=×5×PE+×5×PF=（PE+PF）=12，解得：PE+PF=4.8．故答案为：4.8．15．关于x的分式方程=﹣2解为正数，则m的取值范围是m＜6且m≠﹣6 ．【考点】分式方程的解．【分析】先去分母，用m表示x，求出m的范围【解答】解：去分母得，2x+m=﹣2x+6，∴x=，∵分式方程的解为正数，∴＞0且≠3∴m＜6且m≠﹣6，故答案为：m＜6且m≠﹣6．16．如图，平行四边形ABCD中，AC与BD相交于点E，∠AEB=45°，BD=2，将△ABC沿AC所在直线翻折到同一平面内，若点B的落点记为B′，则DB′的长为．【考点】翻折变换（折叠问题）；平行四边形的性质．【分析】首先连接B′E，由折叠的性质，即可得B′E=BE，∠B′EA=∠BEA=45°，可得∠B′ED=90°，然后由四边形ABCD是平行四边形，求得B′E=BE=DE=1，在Rt△B′ED中利用勾股定理即可求得DB′的长．【解答】解：连接B′E，∵将△ABC沿AC所在直线翻折到同一平面内，若点B的落点记为B′，∴B′E=BE，∠B′EA=∠BEA=45°，∴∠B′EB=90°，∴∠B′ED=180°﹣∠BEB′=90°，∵四边形ABCD是平行四边形，∴BE=DE=BD=×2=1，∴B′E=BE=DE=1，∴在Rt△B′ED中，DB′==．故答案为：．三、解答题（共68分）17．△ABC在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位长度．按要求作图：①画出△ABC关于原点O的中心对称图形△A1B1C1；②画出将△ABC绕点C顺时针旋转90°得到△A2B2C．【考点】作图-旋转变换．【分析】①根据关于原点中心对称的点的坐标特征，分别描出点A、B、C的对应点A1、B1、C1，即可得到△A1B1C1；②利用网格特点，根据旋转的性质画出点A、B旋转后的对应点A2、B2，即可得到△A2B2C．【解答】解：①如图，△A1B1C1为所作；②如图，△A2B2C为所作．18．计算．（1）（2）．【考点】分式的混合运算．【分析】（1）先把括号内的分式通分，括号外面的分式分子分母因式分解，再把加减的结果和外面的分式约分，从而到问题的答案；（2）此题要把a﹣1，看作分母为1的分数，再和分式通分即可．【解答】解：（1）原式=×，=x+9；（2）原式=﹣，=．19．先化简代数式（1﹣）÷，再从0，﹣2，2，﹣1，1中选取一个恰当的数作为a的值代入求值．【考点】分式的化简求值．【分析】先对原式化简，然后从0，﹣2，2，﹣1，1中选取一个使得原分式有意义的x的值代入化简后的式子即可解答本题．【解答】解：（1﹣）÷=×==，当a=0时，原式==﹣2．20．解方程：（1）=（2）=1+．【考点】解分式方程．【分析】两分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．【解答】解：（1）去分母得：4x2﹣9=4x2﹣5x+1，解得：x=2，经检验x=2是分式方程的解；（2）去分母得：x2﹣x=x2+2x﹣3+2x+6，解得：x=﹣，经检验x=﹣是分式方程的解．21．制作一种产品，需先将材料加热达到60℃后，再进行操作．设该材料温度为y（℃），从加热开始计算的时间为x（分钟）．据了解，该材料加热时，温度y与时间x成一次函数关系；停止加热进行操作时，温度y与时间x成反比例关系（如图）．已知该材料在操作加工前的温度为15℃，加热5分钟后温度达到60℃．（1）分别求出将材料加热和停止加热进行操作时，y与x的函数关系式；（2）根据工艺要求，当材料的温度低于15℃时，须停止操作，那么从开始加热到停止操作，共经历了多少时间？【考点】反比例函数的应用；一次函数的应用．【分析】（1）首先根据题意，材料加热时，温度y与时间x成一次函数关系；停止加热进行操作时，温度y与时间x成反比例关系；将题中数据代入用待定系数法可得两个函数的关系式；（2）把y=15代入y=中，进一步求解可得答案．【解答】解：（1）材料加热时，设y=ax+15（a≠0），由题意得60=5a+15，解得a=9，则材料加热时，y与x的函数关系式为y=9x+15（0≤x≤5）．停止加热时，设y=（k≠0），由题意得60=，解得k=300，则停止加热进行操作时y与x的函数关系式为y=（x≥5）；（2）把y=15代入y=，得x=20，因此从开始加热到停止操作，共经历了20分钟．答：从开始加热到停止操作，共经历了20分钟．22．已知：如图，四边形ABCD四条边上的中点分别为E、F、G、H，顺次连接EF、FG、GH、HE，得到四边形EFGH（即四边形ABCD的中点四边形）．（1）四边形EFGH的形状是平行四边形，证明你的结论．（2）当四边形ABCD的对角线满足AC⊥BD 条件时，四边形EFGH是矩形．（3）你学过的哪种特殊四边形的中点四边形是菱形？矩形．【考点】中点四边形．【分析】（1）连接BD，根据三角形的中位线定理得到EH∥BD，EH=BD，FG∥BD，FG═BD，推出，EH∥FG，EH=FG，根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH 是平行四边形；（2）根据有一个角是直角的平行四边形是矩形，可知当四边形ABCD的对角线满足AC⊥BD 的条件时，四边形EFGH是矩形；（3）根据三角形的中位线定理和矩形的性质得出EF=FG=GH=EH即可得出结论．【解答】解：（1）四边形EFGH的形状是平行四边形．理由如下：如图1，连结BD．∵E、H分别是AB、AD中点，∴EH∥BD，EH=BD，同理FG∥BD，FG=BD，∴EH∥FG，EH=FG，∴四边形EFGH是平行四边形；故答案为：平行四边形；（2）当四边形ABCD的对角线满足互相垂直的条件时，四边形EFGH是矩形．理由如下：如图2，连结AC、BD．∵E、F、G、H分别为四边形ABCD四条边上的中点，∴EH∥BD，HG∥AC，∵AC⊥BD，∴EH⊥HG，又∵四边形EFGH是平行四边形，∴平行四边形EFGH是矩形；故答案为：AC⊥BD；（3）矩形的中点四边形是菱形．理由如下：如图3，连结AC、BD．∵E、F、G、H分别为四边形ABCD四条边上的中点，∴EH=BD，FG=BD，EF=AC，GH=AC，∵四边形ABCD是矩形，∴AC=BD，∴EF=FG=GH=EH，∴四边形EFGH是菱形．23．某市为进一步缓解交通拥堵现象，决定修建一条从市中心到飞机场的轻轨铁路．实际施工时，每月的工效比原计划提高了20%，结果提前5个月完成这一工程．求原计划完成这一工程的时间是多少月？【考点】分式方程的应用．【分析】设原来计划完成这一工程的时间为x个月，根据工程问题的数量关系建立方程求出其解即可．【解答】解：设原来计划完成这一工程的时间为x个月，由题意，得，解得：x=30．经检验，x=30是原方程的解．答：原计划完成这一工程的时间是30个月．24．如图，点A是反比例函数y=﹣在第二象限内图象上一点，点B是反比例函数y=在第一象限内图象上一点，直线AB与y轴交于点C，且AC=BC，连接OA、OB，求△AOB的面积．【考点】反比例函数与一次函数的交点问题．【分析】分别过A、B两点作x轴的垂线，构成直角梯形，根据AC=BC，判断OC为直角梯形的中位线，得出OD=OE=a，根据双曲线解析式确定A、B两点的坐标及AD、BE的长，根据S△AOB=S 梯形ADBE﹣S△AOD﹣S△BOE求解．【解答】解：分别过A、B两点作AD⊥x轴，BE⊥x轴，垂足为D、E，∵AC=CB，∴OD=OE，设A（﹣a，），则B（a，），故S△AOB=S梯形ADBE﹣S△AOD﹣S△BOE=（+）×2a﹣a×﹣a×=3．25．在△ABC中，AB=AC，点D在边BC所在的直线上，过点D作DF∥AC交直线AB于点F，DE∥AB交直线AC于点E．（1）当点D在边BC上时，如图①，求证：DE+DF=AC．（2）当点D在边BC的延长线上时，如图②；当点D在边BC的反向延长线上时，如图③，请分别写出图②、图③中DE，DF，AC之间的数量关系，不需要证明．（3）若AC=6，DE=4，则DF= 2或10 ．【考点】平行四边形的判定与性质；全等三角形的判定与性质；等腰三角形的性质．【分析】（1）证明四边形AFDE是平行四边形，且△DEC和△BDF是等腰三角形即可证得；（2）与（1）的证明方法相同；（3）根据（1）（2）中的结论直接求解．【解答】解：（1）证明：∵DF∥AC，DE∥AB，∴四边形AFDE是平行四边形．∴AF=DE，∵DF∥AC，∴∠FDB=∠C又∵AB=AC，∴∠B=∠C，∴∠FDB=∠B∴DF=BF∴DE+DF=AB=AC；（2）图②中：AC+DE=DF．图③中：AC+DF=DE．（3）当如图①的情况，DF=AC﹣DE=6﹣4=2；当如图②的情况，DF=AC+DE=6+4=10．故答案是：2或10．。

2014～2015学年度第一学期第一次质量检测八年级数学试题（满分：120分 考试时间：100分钟）一、选择题：（每题3分，共24分）1.下列图形中，不是轴对称图形的是（ ）2.以下列各组数为边长，不能构成直角三角形的是（ ）A. 1，5,2,3B.7,24,25C.6,8,10D. 9,12,15 3.到三角形的三个顶点距离相等的点是（ ）A.三条角平分线的交点B.三条中线的交点C.三条高的交点D.三条边的垂直平分线的交点 4.如图，点A 、B 、C 、D 、O 都在方格纸的格点上，若△COD 是由△AOB 绕点O 按逆时针方向旋转而得，则旋转的角度为（ ）A. 30B. 45C. 90D. 60° 5.如图，在△ABC 中，BC =8cm ，AB 的垂直平分线交AB 于点D ，交边AC 点E ，AC 的长为12cm ，则△BCE 的周长等于（ ）A.16cmB.20cmC.24cmD.26cm6.如图，等腰三角形ABC 中，AB =AC ，∠A = 46，CD ⊥AB 于D ，则 ∠DCB 等于（ ） A. 30 B. 26 C. 23 D. 20O ABCD 第6题ABCD CDEBA第5题第4题7．已知等腰三角形的腰长为10，一腰上的高为6，则以底边为边长的正方形的面积为（ ）A ．40B ．80C ．40或360D ．80或360 8.将一正方形纸片按下面图（1）、（2）的方式依次对折后，再沿（3）中的虚线裁剪，最后将（4）中的纸片打开铺平，所得图案应该是下面图案中的（ ）二、填空题：（每空3分，共30分）9．若等腰三角形的底角为70度，则它的顶角为 度．10．已知三角形ABC 中∠C=90°,AC=3,BC=4,则斜边AB 上的高为 11．若直角三角形两直角边的比为3：4，斜边长为20，则此直角三角形的周长为 。

12．已知ΔABC ≌ΔDEF ，点A 与点D.点B 与点E 分别是对应顶点， （1）若ΔABC 的周长为32，AB=10，BC=14，则DF= （2）∠A=48°，∠B =53°，则∠F= 。

第7题2016/2017学年度春学期期初调研考试八年级数学试题（满分150分，时间120分钟）一、选择题（24分）1、下列四个数中，最小的数是（ ） A 、1 B 、0 C 、－3 D 、－52、为了了解射阳县2015年中考数学学科各分数段成绩分布情况，从中抽取150名考生的中考数学成绩进行统计分析。

在这个问题中，样本是指 （ ）A 、150B 、被抽取的150名考生C 、被抽取的150名考生的中考数学成绩 D 、射阳县2015年中考数学成绩3、下列图形中，既是轴对称图形又是中心对称图形的是（ ） A 、正三角形 B 、正方形 C 、等腰三角形 D 、平行四边形4、在平面直角坐标系中，点P （1，－3）在（ ）A 、第一象限B 、第二象限C 、第三象限D 、第四象限 5、在反比例函数xk y 1-=的图象的每一条曲线上，y 都随x 的增大而减小，则k 的取值范围是（ ）A 、k ＞1B 、k ＞0C 、k≥1D 、k ＜1 6、下列说法中不正确的是（ ）A 、一组邻边相等的矩形是正方形B 、一组邻边相等的平行四边形是菱形C 、一组对边相等且有一个角是直角的四边形是矩形D 、一组对边平行且相等的四边形是平行四边形7、如图，在□ABCD 中，∠ODA ＝ 90°，AC ＝10 cm ，BD ＝6 cm ，则AD 的长为（ ） A 、4 cm B 、5 cm C 、6 cm D 、8 cm8、已知A 、B 两地相距120千米，甲骑自行车以20千米/时的速度由起点A 前往终点B ，乙骑摩托车以40千米/时的速度由起点B 前往终点A ．两人同时出发，各自到达终点后停止．设两人之间的距离为s （千米），甲行驶的时间为t （小时），则下图中正确反映s 与t 之间函数关系的是（ ）A B C D第17题第18题二、填空题（30分）9、若分式51-x 有意义，则x 的取值范围是__________________． 10、计算(508)2-÷的结果是 ．11、在一个不透明的袋子中有10个除颜色外其余均相同的小球，通过多次摸球实验后，发现摸到白球的频率约为40%，估计袋子中白球有 个.12、 一个反比例函数y=kx（k ≠0）的图象经过点P （-2，-3），则该反比例函数的解析式是 ．13、已知3=x 是方程260x x k -+=的一个根，则k = 14、若433+-+-=x x y ，则xy = ．15、若关于x 的一元二次方程kx 2－2x －1＝0有两个不相等的实数根，则实数k 的取值范围是＿＿＿＿＿16、若分式方程0414=----xxx m 有增根，则m 的值是____________ 17、如图，△ABC 中，D 、E 分别是BC 、AC 的中点，BF 平分∠ABC ，交DE 于点F ，若BC ＝6，则DF 的长是＿＿＿＿＿18、如图，已知在平面直角坐标系xOy 中，O 是坐标原点，点A 是函数xy 1=(x<0)图象上一点，AO 的延长线交函数xk y 2= (x ＞0，k ＞0的常数)的图象于点C ，点A关于y 轴的对称点为A′，点C 关于x 轴的对称点为C′且点O 、A′、C′在同一条直线上，连接CC′，交x 轴于点B ，连接AB ，AA′，A′C′，若△ABC 的面积等于6，则由线段AC ，CC′，C′A′，A′A 所围成的图形的面积等于＿＿＿＿＿ 三、解答题19、（8分）计算（1）18－22＋|1－2|化简（2）1－x 2－9x 2－6x ＋9÷x ＋3x ＋4AE FB CD20、（8分）解方程：（1）3x －1－1＝11－x（2）x (x －2)＝3x －621、（8分）化简、求值：01,121)231(22=--+-+-÷+-x x x x xx x x x 满足其中.22、（8分）随着车辆的增加，交通违规的现象越来越严重，交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30﹣40含起点值30，不含终点值40)，得到其频数及频率如表：数据段 频数 频率 30﹣40 10 0.05 40﹣50 36 c50﹣60 a 0.39 60﹣70 b d70﹣80 20 0.10 总计2001（1）表中a 、b 、c 、d 分别为:a ＝＿＿＿＿; b ＝＿＿＿＿; c ＝＿＿＿＿; d ＝＿＿＿＿. （2）补全频数分布直方图；（3）如果某天该路段约有1500辆通过，汽车时速不低于60千米即为违章，通过该统计数据估计当天违章车辆约有多少辆？23、（10分）如图，E 、F 分别是□ABCD 的边B C 、AD 上的点，且BE ＝DF ． （1）求证：四边形AECF 是平行四边形；（2）若BC ＝10，∠BAC ＝90°，且四边形AECF 是菱形，求BE 的长．24、（10分）某市从今年1月1日起调整水价，每立方米水费上涨了原价的31．据了解，某校去年11月份的水费是1800元，而今年1月份的水费是3600元．如果该校今年1月份的用水量比去年11月份的用水量多600m 3．（1）该市原来每立方米水价是多少元？（2）该校开展了“节约每一滴水”的主题活动，采取了有效的节约用水措施，计划今年5月份的用水量较1月份降低20%，那么该校今年5月份应交的水费是多少？25、（10分）如图，一次函数y =﹣x +5的图象与反比例函数xky （k ≠0）在第一象限的图象交于A （1，n ）和B 两点．ABFDC（1）求反比例函数的解析式及点B 坐标；（2）在第一象限内，当一次函数y ＝－x ＋5的值大于反比例函数xky （k ≠0）的值时，写出自变量x 的取值范围．26、（10分）如图1所示，在A ，B 两地之间有汽车站C 站，客车由A 地驶往C 站，货车由B 地驶往A 地．两车同时出发，匀速行驶．图2是客车、货车离C 站的路程y 1，y 2（千米）与行驶时间x （小时）之间的函数关系图象．（1）填空：A ，B 两地相距＿＿＿＿＿千米；（2）求两小时后，货车离C 站的路程y 2与行驶时间x 之间的函数关系式； （3）当客车行驶多长时间．．．．．．．．，客、货两车相距150千米.27、（12分）在△ABC 和△DEC 中，AC =BC ，DC =EC ，∠ACB =∠ECD =90°． （1）如图1，当点A 、C 、D 在同一条直线上时，AC =12，EC =5． ①求证：AF ⊥BD ， ②求AF 的长度；（2）如图2，当点A 、C 、D 不在同一条直线上时．求证：AF ⊥BD ；（3）如图3，在（2）的条件下，连接CF 并延长CF 交AD 于点G ，∠AFG 是一个固定的值吗？若是，求出∠AFG 的度数，若不是，请说明理由．GF EDCBAABCDEFFEDCBA图1 图2 图328、（12分）如图，直线y ＝－x ＋4与x 轴、y 轴分别交于A 、B 两点，直线BC 与x 轴、y 轴分别交于C 、B 两点，连接BC ，且OB OC43． （1）求点A 的坐标及直线BC 的函数关系式；（2）点M 在x 轴上，连接MB ，当∠MBA+∠CBO=45°时，求点M 的坐标；（3）若点P 在x 轴上，平面内是否存在点Q ，使点B 、C 、P 、Q 为顶点的四边形是菱形？若存在，请直接写出点Q 的坐标；若不存在，请说明理由．备用图 备用图2016/2017学年度春学期期初调研考试八年级数学参考答案一、选择题（24分） 1－8 CCBD ACAA 二、填空题（30分） 9、x ≠510、311、4 12、xy 6=13、9 14、2315、k ＞－1且k ≠016、317、318、10三、解答题19、（8分）（1）123- （2）－37-x20、（8分）（1）解：x ＝5 （2）x 1＝2，x 2＝3检验：x ＝5是原方程的解21、（8分）解：原式＝12+x x 当x 2＝x ＋1时 原式＝122、（8分）（1）a ＝78 b ＝56 c ＝0.18 d ＝0.28 （2）略 （3）570 23、（10分）（1）证明：∵四边形ABCD 是平行四边形∴AD ＝BC ，AD ∥BC∵BE ＝DF ∴AF ＝CE ，且AF ∥CE ∴四边形AECF 是平行四边形（2）∵四边形A ECF 是菱形∴AE ＝CE ∴∠EAC ＝∠ECA∵∠BAE ＋∠EAC ＝90°，∠ECA ＋∠B ＝90°∴∠B ＝∠BAE ∴AE ＝BE ∵AE ＝CE ∴BE ＝CE ＝21BC ＝5 24、（10分）（1）原来每立方米水价是1.5元（需检验）（2）2880元 25、（10分） （1）xy 4=B （4，1） （2）1＜x ＜4 26、（10分）（1）420 （2）y 2＝30x －60 （3）t ＝3（小时） （多一解扣2分） 27、（12分）①证明：如图3，∵AC =BC ，∠ACB =∠ECD =90°，EC =DC ，∴△ACE ≌△BCD ， ∴∠1=∠2，∵∠3=∠4，∴∠BFE =∠ACE =90°，∴AF ⊥BD ．②∵∠ECD =90°，BC = AC =12，DC = EC =5，∴BD =13， ∵S △ABD =12 AD ·BC =12 BD ·AF ，∴AF =20413．（法2：∵∠ECD =90°，BC = AC =12，DC = EC =5，∴AE =BD =13，BE =7， 设EF =x ， ∵∠BFE =90°，∴BF 2=BE 2-EF 2，BF 2=AB 2-AF 2，∴72-x 2=288-（13+x ）2， ∴x =3513 ，∴AF =13+3513 =20413．）（2）证明：如图4，∵∠ACB =∠ECD ，∴∠ACB +∠ACD =∠ECD +∠ACD ，∴∠BCD =∠ACE ， ∵AC =BC ，∠ACE =∠BCD ，EC =DC ，∴△ACE ≌△BCD ，∴∠1=∠2， ∵∠3=∠4，∴∠BFA =∠BCA =90°，∴AF ⊥BD ． （3）∠AFG =45°．如图4，过点C 作CM ⊥BD ，CN ⊥AE ，垂足分别为M 、N ， ∵△ACE ≌△BCD ，∴S △ACE =S △BCD ，AE =BD ，∵S △ACE =12 AE ·CN ，S △BCD =12BD ·CM ，∴CM =CN ，∵CM ⊥BD ，CN ⊥AE ，∴CF 平分∠BFE ，∵AF ⊥BD ，∴∠BFE =90°，∴∠EFC =45°，∴∠AFG =45°．（法2：过点C 作CM ⊥BD ，CN ⊥AE ，垂足分别为M 、N ，∵CM ⊥BD ，CN ⊥AE ， ∴∠BMC =∠ANC =90°，∵△ACE ≌△BCD ，∴∠1=∠2， ∵∠BMC =∠ANC =90°，∠1=∠2，AC =BC ，∴△BCM ≌△ACN ，∴CM =CN ，∵CM ⊥BD ，CN ⊥AE ，∴CF 平分∠BFE ，∵AF ⊥BD ，∴∠BFE =90°，∴∠EFC =45°，∴∠AFG =45°．） 28、（12分）（1）A （4，0） l BC ：434+=x y （2）M 1（3，0） ⎪⎭⎫⎝⎛0,3162M （3）Q 1（－5，4） Q 2（5，4） Q 3（0，－4） Q 4⎪⎭⎫⎝⎛-4,625 图41243N M ABCD EF G。

江苏省盐城市东台第一教研片2014-2015学年八年级生物下学期第一次阶段检测试题（满分30分）一、选择题（每小题1分计20分）1、下列常用芽接的方法进行繁殖的果树是：( )A、柑B、桃C、橘D、葡萄2、下列昆虫发育过程为不完全变态发育的是：( )A、蚕B、蚊C、菜粉蝶D、蟋蟀3、根据发育方式，请找出与其他三个不同类的：( )A、蝇B、蝗虫C、蟑螂D、蝼蛄4、从蝌蚪发育为成蛙，其呼吸器官的变化为：( )A、外鳃→内鳃→肺B、内鳃→外鳃→肺C、外鳃→肺D、内鳃→肺5、下列与娃娃鱼生殖和发育方式一样的动物是：( )A、鲍鱼B、鲸C、蝾螈D、鳝6、下列哪项是早成鸟具有的特点：( )A、腿足无力B、腿足有力C、不能自行觅食D、绒羽很少7、绿色开花植物受精卵发育的部位是：( )A、柱头B、子房C、花D、胚珠8、家蚕一生中吐丝的阶段是：( )A、受精卵B、幼虫C、蛹D、成虫9、受精的鸟卵在雌鸟体内开始发育，但鸟卵产出后就停止发育，原因是外界：( )A、具有阳光B、具有空气C、温度太高D、温度太低10.下列有关人类生殖细胞的叙述，错误的一项是( )A.精子有两种，一种含X染色体，一种含Y染色体，比例相等B.卵细胞只有一种，每个卵细胞都只含有一条X染色体C.人的精子中的染色体数可表示为23+X或23+YD.男性一次所排的精液中，都含有上亿个精子，而女性一次排卵一般只有一个卵细胞11.人类和其他高等动物的性别决定是在( )A.新生个体出生时B.受精卵发育成新个体时C.精子与卵细胞结合时D.形成生殖细胞时12.近亲结婚后代患遗传病的可能性增大的原因是，血缘关系越近( )A.生活环境越相同B.染色体数目越相同C.生活习性越相同D.遗传基因也越相似13.显性基因R控制豌豆开红花，隐性基因R控制豌豆开白花。

一株基因组成为RR的豌豆植株，自花受粉以后所结的种子播种后所长出的植株开花的情况是( )A.全部开红花B.全部开白花C.全部开粉红色花D.一部分开红花，一部分开白花14.有关遗传的变异的正确叙述是( )A.遗传物质没有发生变化的变异B.不能传递给后代的变异C.遗传物质发生了变化而引起的变异D.环境条件的改变而引起的变异15.下列哪一种现象不能作为变异的实例( )A.羊有角，马没有角B.月季花的颜色有红色、白色等C.奶牛产奶量高，役用牛产奶量低D.人的视觉有正常、色盲之分16、下列能使牛奶变成酸奶，使蔬菜变成有酸味的泡菜的是（）。

2014-2015学年江苏省盐城市东台市第一教研片八年级（上）第一次月考数学试卷一、选择题（本大题共有8小题，每小题3分，共24分．在每小题所给出的四个选项中，只有一项是符合题目要求的，请将正确选项的字母代号填写在表格相应的位置） B2．（3分）（2014•黔西南州）如图，已知AB=AD ，那么添加下列一个条件后，仍无法判定△ABC ≌△ADC的是（ ）3．（3分）（2010秋•西林区期末）如图所示，某同学把一块三角形的玻璃不小心打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带（ ）去．4．（3分）（2008秋•自贡期末）如图，△ABC ≌△DEF ，则此图中相等的线段有（ ）5．（3分）（2014秋•新泰市期末）如图，△ABC ≌△CDA ，并且AB=CD ，那么下列结论错误的是（ ）6．（3分）（2014秋•射阳县校级月考）如图，AD=BC，AC=BD，则下列结论中，不正确的是（）7．（3分）（2014秋•射阳县校级月考）如图，已知△ABC≌△CDA，A和C，D和B分别是对应点，如果AB=7cm，AD=6cm，AC=4cm，则DC的长为（）8．（3分）（2011•梧州）如图，点B、C、E在同一条直线上，△ABC与△CDE都是等边三角形，则下列结论不一定成立的是（）二、填空题（本大题共有8小题，每小题3分，共24分．不需写出解答过程，请将答案直接写在横线上）9．（3分）（2014秋•射阳县校级月考）如果△ABC≌△DEC，∠B=60度，那么∠E=度．10．（3分）（2011•浦东新区模拟）角是轴对称图形，则对称轴是．11．（3分）（2014•淮安）如图，△ABD≌△CBD，若∠A=80°，∠ABC=70°，则∠ADC的度数为．12．（3分）（2006•襄阳）如图所示，AB=AD，∠1=∠2，添加一个适当的条件，使△ABC≌△ADE，则需要添加的条件是．13．（3分）（2012秋•庐江县期末）如图，△ABC中，AD⊥BC于D，要使△ABD≌△ACD，若根据“HL”判定，还需要加条件，若加条件∠B=∠C，则可用判定．14．（3分）（2008•贵阳）如图，正方形ABCD的边长为4cm，则图中阴影部分的面积为cm2．15．（3分）（2013秋•五华区校级期中）如图，把两根钢条AA′、BB′的中点连在一起，可以做成一个测量工件内槽宽的工具（卡钳），若测得AB=5米，则槽宽为米．16．（3分）（2011春•兰州期末）AD是△ABC的边BC上的中线，AB=12，AC=8，则边BC的取值范围是；中线AD的取值范围是．三、作图题（本大题共2小题，共14分）17．（8分）（2014秋•射阳县校级月考）按下列要求作图：（1）图1，用直尺和圆规作线段BC的垂直平分线；（2）在图2中画△ABC出关于L的对称图形（不写作法，保留作图痕迹）18．（6分）（2014秋•射阳县校级月考）请用三种不同的方法把一个平行四边形分割成四个全等的图形．四、解答题（本大题共有7小题，共58分，解答时应写出文字说明、推理过程或演算步骤）19．（7分）（2012•东城区二模）已知：如图，∠ABC=∠DCB，BD、CA分别是∠ABC、∠DCB 的平分线．求证：AB=DC．20．（8分）（2010秋•河南校级期中）如图，∠DCE=90°，CD=CE，AD⊥AC，BE⊥AC，垂足分别为A、B．试说明AD+AB=BE．21．（9分）（2014秋•射阳县校级月考）如图，在图中的两个三角形是全等三角形，其中A 和D、B和E是对应点．（1）用符号“≌“表示这两个三角形全等（要求对应顶点写在对应位置上）；（2）写出图中相等的线段和相等的角；（3）写出图中互相平行的线段，并说明理由．22．（8分）（2009春•宿迁期末）如图：在△ABC中，AD⊥BC，AE平分∠BAC，∠B=70°，∠C=34°．求∠DAE的度数．23．（8分）（2008•温州）文文和彬彬在证明“有两个角相等的三角形是等腰三角形”这一命题时，画出图形，写出“已知”，“求证”（如图），她们对各自所作的辅助线描述如下：文文：“过点A作BC的中垂线AD，垂足为D”；彬彬：“作△ABC的角平分线AD”．数学老师看了两位同学的辅助线作法后，说：“彬彬的作法是正确的，而文文的作法需要订正．”（1）请你简要说明文文的辅助线作法错在哪里；（2）根据彬彬的辅助线作法，完成证明过程．24．（9分）（2014秋•句容市校级期末）已知：如图①，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=50°（1）求证：①AC=BD；②∠APB=50°；（2）如图②，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD=α，则AC与BD间的等量关系为，∠APB的大小为25．（9分）（2014秋•东台市期中）如图①A、E、F、C在一条直线上，AE=CF，过E、F 分别作DE⊥AC，B F⊥AC，若AB=CD．（1）图①中有对全等三角形，并把它们写出来；（2）求证：BD与EF互相平分于G；（3）若将△ABF的边AF沿GA方向移动变为图②时，其余条件不变，第（2）题中的结论是否成立，如果成立，请予证明．。

江苏省盐城市东台第一教研片2014-2015学年八年级历史下学期第一次阶段检测试题（本试卷分值：５０分 考试形式：闭卷 ）一、选择题（本大题共30小题，每小题1分，共30分。

在每小题所列出的四个选项中，只有一项是最符合题目要求的）1、1949年春七届二中全会后，毛泽东对其他中共领导人说：“我们要去北平赶考了。

”这指的是（ ）A ．建立和巩固新政权 B ．与国民党反动势力进行决战C ．要和平解放西藏D ．采取公务员考试办法，选拔优秀干部人才2、1949年召开的中国人民政治协商会议的中心议题是（ ）A 、选举第一届全国政协委员会B 、讨论通过“共同纲领”C 、选举中央人民政府委员会D 、讨论新中国成立的问题3、一首歌中唱道“让我告诉世界，中国命运自己主宰，让我告诉未来，中国进行着接力赛……” 你知道中国人民“命运自己主宰”开始于（ ）A ．1949年9月B ．1949年10月1日C ．1950年10月1日D ．1953年7月4、中华人民共和国的成立开辟了中国历史新纪元，“新”在（ ）A ．中国真正是一个独立自主的国家了B ．推翻了两千多年的封建君主专制C ．中国开始了社会主义建设新时期D ．社会主义制度由此建立5、中国人深知“户破堂危，唇亡齿寒”、“救邻自救”的道理，当朝鲜民主主义人民共和国请求中国政府派兵援助时，为了抗美援朝，保家卫国，中央政府便派谁为司令员率军队入朝作战（ ）A 、彭德怀B 、林彪C 、邓小平D 、刘伯承6、“他的名字及英雄事迹被镌刻在上甘岭北面的五圣山石壁上。

”他是 （ ）A 、董存瑞B 、黄继光C 、邱少云D 、刘胡兰7、右图农民所作所为的依据是 （ ）A 、《中国人民政治协商会议共同纲领》B 、《中华人民共和国宪法》C 、《中华人民共和国土地改革法》D 、中共“八大”决议8、某中学历史小组要完成一个关于“农业、农村、农民”的社会调查报告，准备在今年暑假采访一位经历过“土地改革”的人物，下列采访对象中最合适的是 （ ）A 、52岁的李伯伯B 、83岁的张大爷C 、35岁的方叔叔D 、46岁的杨阿姨9由此可见，我国当时 （ ）A 、农轻重三业均衡发展B 、优先发展重工业C 、优先发展运输交通业D 、已进入社会主义初级阶段10、在第一届全国人民代表大会上，毛泽东说：“这次会议是标志着我国人民从1949年建国以来的新胜利和新发展的里程碑……”这次会议被称为“里程碑”的理由是 ( )A 、通过了《共同纲领》B 、确立了土地改革的路线C 、公布了“一五”计划D 、通过了第一部《中华人民共和国宪法》 11、1953—1956年我国进行了社会主义改造，下面不能反映这一历史事件的词汇是( )A 、生产合作社B 、赎买C 、集体化D 、大包干12、1953-1956年我国农业经济发展快速上升的主要原因是 (四川金堂县贫农分)A、土地改革运动B、农业合作化运动C、“大跃进”运动D、人民公社化运动13、下图反映的是新中国在20世纪五六十年代的农业经济发展状况，出现图中B点到C点这一变化的主要原因是A、经济建设没有计划性B、自然灾害迅速蔓延C、“左”倾错误严重泛滥D、“文革”扩展到经济领14、“稻堆脚儿摆得圆，社员堆稻上了天。

2015-2016学年江苏省盐城市东台市第一教研片八年级（下）期中数学试卷一、选择题：（每题2分，共16分）1．（2分）在，，中，是分式的有（）A．0个B．1个C．2个D．3个2．（2分）如图所示的几何图形中，既是轴对称图形又是中心对称图形的个数是（）A．4B．3C．2D．13．（2分）若分式有意义，则x的取值范围是（）A．x≠1B．x＞1C．x=1D．x＜14．（2分）如果把分式中的x和y都扩大5倍，那么分式的值（）A．扩大5倍B．不变C．扩大10倍D．缩小5．（2分）若反比例函数y=的图象经过点（﹣1，2），则这个函数的图象一定经过点（）A．（﹣2，﹣1）B．（﹣，2）C．（2，﹣1）D．（，2）6．（2分）在下列性质中，矩形具有而菱形不一定有的是（）A．对角线互相垂直B．对角线互相平分C．四个角是直角D．四条边相等7．（2分）解分式方程﹣=1时，去分母后可得到（）A．x（2+x）﹣2（3+x）=1B．x（2+x）﹣2=2+xC．x（2+x）﹣2（3+x）=（2+x）（3+x）D．x﹣2（3+x）=3+x8．（2分）如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于G，下列结论：①BE=DF，②∠DAF=15°，③AC垂直平分EF，④BE+DF=EF，⑤S=2S△ABE．△CEF其中正确结论有（）个．A．4B．3C．2D．1二、填空题（每空2分，共16分）9．（2分）请写出一个是中心对称图形的几何图形的名称：．10．（2分）如果反比例函数的图象在二、四象限内，则m的取值范围是．11．（2分）如图，为测量位于一水塘旁的两点A、B间的距离，在地面上确定点O，分别取OA、OB的中点C、D，量得CD=20m，则A、B之间的距离是m．12．（4分）如图，在四边形ABCD中，AB∥CD，请你添加一个条件，使得四边形ABCD成为平行四边形，你添加的条件是．13．（2分）菱形的两条对角线分别为3cm和4cm，则菱形的面积为cm．14．（2分）如图，P是矩形ABCD的边AD上一个动点，矩形的两条边AB、BC 的长分别为6和8，那么点P到矩形的两条对角线AC和BD的距离之和是．15．（2分）关于x的分式方程=﹣2解为正数，则m的取值范围是．16．（2分）如图，平行四边形ABCD中，AC与BD相交于点E，∠AEB=45°，BD=2，将△ABC沿AC所在直线翻折到同一平面内，若点B的落点记为B′，则DB′的长为．三、解答题（共68分）17．（6分）△ABC在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位长度．按要求作图：①画出△ABC关于原点O的中心对称图形△A1B1C1；②画出将△ABC绕点C顺时针旋转90°得到△A2B2C．18．（8分）计算．（1）（2）．19．（6分）先化简代数式（1﹣）÷，再从0，﹣2，2，﹣1，1中选取一个恰当的数作为a的值代入求值．20．（10分）解方程：（1）=（2）=1+．21．（6分）制作一种产品，需先将材料加热达到60℃后，再进行操作．设该材料温度为y（℃），从加热开始计算的时间为x（分钟）．据了解，该材料加热时，温度y与时间x成一次函数关系；停止加热进行操作时，温度y与时间x 成反比例关系（如图）．已知该材料在操作加工前的温度为15℃，加热5分钟后温度达到60℃．（1）分别求出将材料加热和停止加热进行操作时，y与x的函数关系式；（2）根据工艺要求，当材料的温度低于15℃时，须停止操作，那么从开始加热到停止操作，共经历了多少时间？22．（6分）已知：如图，四边形ABCD四条边上的中点分别为E、F、G、H，顺次连接EF、FG、GH、HE，得到四边形EFGH（即四边形ABCD的中点四边形）．（1）四边形EFGH的形状是，证明你的结论．（2）当四边形ABCD的对角线满足条件时，四边形EFGH是矩形．（3）你学过的哪种特殊四边形的中点四边形是菱形？．23．（8分）某市为进一步缓解交通拥堵现象，决定修建一条从市中心到飞机场的轻轨铁路．实际施工时，每月的工效比原计划提高了20%，结果提前5个月完成这一工程．求原计划完成这一工程的时间是多少月？24．（8分）如图，点A是反比例函数y=﹣在第二象限内图象上一点，点B是反比例函数y=在第一象限内图象上一点，直线AB与y轴交于点C，且AC=BC，连接OA、OB，求△AOB的面积．25．（8分）在△ABC中，AB=AC，点D在边BC所在的直线上，过点D作DF∥AC 交直线AB于点F，DE∥AB交直线AC于点E．（1）当点D在边BC上时，如图①，求证：DE+DF=AC．（2）当点D在边BC的延长线上时，如图②；当点D在边BC的反向延长线上时，如图③，请分别写出图②、图③中DE，DF，AC之间的数量关系，不需要证明．（3）若AC=6，DE=4，则DF=．2015-2016学年江苏省盐城市东台市第一教研片八年级（下）期中数学试卷参考答案与试题解析一、选择题：（每题2分，共16分）1．（2分）在，，中，是分式的有（）A．0个B．1个C．2个D．3个【解答】解：的分母中不含有字母，因此它们是整式，而不是分式．，的中分母中含有字母，因此是分式．故选：C．2．（2分）如图所示的几何图形中，既是轴对称图形又是中心对称图形的个数是（）A．4B．3C．2D．1【解答】解：第一个图形是轴对称图形，不是中心对称图形；第二个图形是轴对称图形，不是中心对称图形；第三个图形是轴对称图形，也是中心对称图形；第四个图形是轴对称图形，不是中心对称图形；第五个图形是轴对称图形，也是中心对称图形；综上所述，第三个和第五个图形既是中心对称图形又是轴对称图形，共2个．故选：C．3．（2分）若分式有意义，则x的取值范围是（）A．x≠1B．x＞1C．x=1D．x＜1【解答】解：∵x﹣1≠0，∴x≠1．故选：A．4．（2分）如果把分式中的x和y都扩大5倍，那么分式的值（）A．扩大5倍B．不变C．扩大10倍D．缩小【解答】解：把分式的x和y的值都扩大5倍，那么分式的值不变，故选：B．5．（2分）若反比例函数y=的图象经过点（﹣1，2），则这个函数的图象一定经过点（）A．（﹣2，﹣1）B．（﹣，2）C．（2，﹣1）D．（，2）【解答】解：∵反比例函数y=的图象经过点（﹣1，2），∴k=﹣1×2=﹣2，只需把所给点的横纵坐标相乘，结果是﹣2的，就在此函数图象上；四个选项中只有C：2×（﹣1）=﹣2符合．故选：C．6．（2分）在下列性质中，矩形具有而菱形不一定有的是（）A．对角线互相垂直B．对角线互相平分C．四个角是直角D．四条边相等【解答】解：矩形的性质有：四个角都是直角；对角线互相平分且相等；菱形的性质有：四条边相等；对角线互相垂直平分；矩形具有而菱形不一定有的是：四个角都是直角．故选：C．7．（2分）解分式方程﹣=1时，去分母后可得到（）A．x（2+x）﹣2（3+x）=1B．x（2+x）﹣2=2+xC．x（2+x）﹣2（3+x）=（2+x）（3+x）D．x﹣2（3+x）=3+x【解答】解：去分母得：x（2+x）﹣2（3+x）=（3+x）（2+x）．故选：C．8．（2分）如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于G，下列结论：①BE=DF，②∠DAF=15°，③AC垂直平分EF，④BE+DF=EF，⑤S=2S△ABE．△CEF其中正确结论有（）个．A．4B．3C．2D．1【解答】解：∵四边形ABCD是正方形，∴AB=BC=CD=AD，∠B=∠BCD=∠D=∠BAD=90°．∵△AEF等边三角形，∴AE=EF=AF，∠EAF=60°．∴∠BAE+∠DAF=30°．在Rt△ABE和Rt△ADF中，，Rt△ABE≌Rt△ADF（HL），∴BE=DF（故①正确）．∠BAE=∠DAF，∴∠DAF+∠DAF=30°，即∠DAF=15°（故②正确），∵BC=CD，∴BC﹣BE=CD﹣DF，即CE=CF，∵AE=AF，∴AC垂直平分EF．（故③正确）．设EC=x，由勾股定理，得EF=x，CG=x，AG=AEsin60°=EFsin60°=2×CGsin60°=x，∴AC=，∴AB=，∴BE=﹣x=，∴BE+DF=x﹣x≠x，（故④错误），=，∵S△CEFS△ABE==，==S△CEF，（故⑤正确）．∴2S△ABE综上所述，正确的有4个，故选：A．二、填空题（每空2分，共16分）9．（2分）请写出一个是中心对称图形的几何图形的名称：平行四边形．【解答】解：平行四边形是中心对称图形．故答案可为：平行四边形．10．（2分）如果反比例函数的图象在二、四象限内，则m的取值范围是m＜4．【解答】解：∵反比例函数的图象在二、四象限内，∴m﹣4＜0，解得m＜4．故答案为：m＜4．11．（2分）如图，为测量位于一水塘旁的两点A、B间的距离，在地面上确定点O，分别取OA、OB的中点C、D，量得CD=20m，则A、B之间的距离是40 m．【解答】解：∵C、D分别是OA、OB的中点，∴CD是△OAB的中位线，∵CD=20m，∴AB=2CD=2×20=40m．故答案为：40．12．（4分）如图，在四边形ABCD中，AB∥CD，请你添加一个条件，使得四边形ABCD成为平行四边形，你添加的条件是答案不唯一，如：AB=CD或AD ∥BC或∠A=∠C或∠B=∠D或∠A+∠B=180°或∠C+∠D=180°等．【解答】解：∵在四边形ABCD中，AB∥CD，∴可添加的条件是：AB=DC，∴四边形ABCD是平行四边形（一组对边平行且相等的四边形是平行四边形）故答案为：AB=CD或AD∥BC或∠A=∠C或∠B=∠D或∠A+∠B=180°或∠C+∠D=180°等．13．（2分）菱形的两条对角线分别为3cm和4cm，则菱形的面积为6cm．【解答】解：根据菱形的面积等于两对角线乘积的一半得，菱形的面积为3×4÷2=6cm2．故答案为6．14．（2分）如图，P是矩形ABCD的边AD上一个动点，矩形的两条边AB、BC 的长分别为6和8，那么点P到矩形的两条对角线AC和BD的距离之和是4.8．【解答】解：连接OP，∵矩形的两条边AB、BC的长分别为6和8，=AB•BC=48，OA=OC，OB=OD，AC=BD==10，∴S矩形ABCD∴OA=OD=5，=S矩形ABCD=24，∴S△ACD=S△ACD=12，∴S△AOD=S△AOP+S△DOP=OA•PE+OD•PF=×5×PE+×5×PF=（PE+PF）=12，∵S△AOD解得：PE+PF=4.8．故答案为：4.8．15．（2分）关于x的分式方程=﹣2解为正数，则m的取值范围是m＜6且m≠﹣6．【解答】解：去分母得，2x+m=﹣2x+6，∴x=，∵分式方程的解为正数，∴＞0且≠3∴m＜6且m≠﹣6，故答案为：m＜6且m≠﹣6．16．（2分）如图，平行四边形ABCD中，AC与BD相交于点E，∠AEB=45°，BD=2，将△ABC沿AC所在直线翻折到同一平面内，若点B的落点记为B′，则DB′的长为．【解答】解：连接B′E，∵将△ABC沿AC所在直线翻折到同一平面内，若点B的落点记为B′，∴B′E=BE，∠B′EA=∠BEA=45°，∴∠B′EB=90°，∴∠B′ED=180°﹣∠BEB′=90°，∵四边形ABCD是平行四边形，∴BE=DE=BD=×2=1，∴B′E=BE=DE=1，∴在Rt△B′ED中，DB′==．故答案为：．三、解答题（共68分）17．（6分）△ABC在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位长度．按要求作图：①画出△ABC关于原点O的中心对称图形△A1B1C1；②画出将△ABC绕点C顺时针旋转90°得到△A2B2C．【解答】解：①如图，△A1B1C1为所作；②如图，△A2B2C为所作．18．（8分）计算．（1）（2）．【解答】解：（1）原式=×，=x+9；（2）原式=﹣，=．19．（6分）先化简代数式（1﹣）÷，再从0，﹣2，2，﹣1，1中选取一个恰当的数作为a的值代入求值．【解答】解：（1﹣）÷=×==，当a=0时，原式==﹣2．20．（10分）解方程：（1）=（2）=1+．【解答】解：（1）去分母得：4x2﹣9=4x2﹣5x+1，解得：x=2，经检验x=2是分式方程的解；（2）去分母得：x2﹣x=x2+2x﹣3+2x+6，解得：x=﹣，经检验x=﹣是分式方程的解．21．（6分）制作一种产品，需先将材料加热达到60℃后，再进行操作．设该材料温度为y（℃），从加热开始计算的时间为x（分钟）．据了解，该材料加热时，温度y与时间x成一次函数关系；停止加热进行操作时，温度y与时间x 成反比例关系（如图）．已知该材料在操作加工前的温度为15℃，加热5分钟后温度达到60℃．（1）分别求出将材料加热和停止加热进行操作时，y与x的函数关系式；（2）根据工艺要求，当材料的温度低于15℃时，须停止操作，那么从开始加热到停止操作，共经历了多少时间？【解答】解：（1）材料加热时，设y=ax+15（a≠0），由题意得60=5a+15，解得a=9，则材料加热时，y与x的函数关系式为y=9x+15（0≤x≤5）．停止加热时，设y=（k≠0），由题意得60=，解得k=300，则停止加热进行操作时y与x的函数关系式为y=（x≥5）；（2）把y=15代入y=，得x=20，因此从开始加热到停止操作，共经历了20分钟．答：从开始加热到停止操作，共经历了20分钟．22．（6分）已知：如图，四边形ABCD四条边上的中点分别为E、F、G、H，顺次连接EF、FG、GH、HE，得到四边形EFGH（即四边形ABCD的中点四边形）．（1）四边形EFGH的形状是平行四边形，证明你的结论．（2）当四边形ABCD的对角线满足AC⊥BD条件时，四边形EFGH是矩形．（3）你学过的哪种特殊四边形的中点四边形是菱形？矩形．【解答】解：（1）四边形EFGH的形状是平行四边形．理由如下：如图1，连结BD．∵E、H分别是AB、AD中点，∴EH∥BD，EH=BD，同理FG∥BD，FG=BD，∴EH∥FG，EH=FG，∴四边形EFGH是平行四边形；故答案为：平行四边形；（2）当四边形ABCD的对角线满足互相垂直的条件时，四边形EFGH是矩形．理由如下：如图2，连结AC、BD．∵E、F、G、H分别为四边形ABCD四条边上的中点，∴EH∥BD，HG∥AC，∵AC⊥BD，∴EH⊥HG，又∵四边形EFGH是平行四边形，∴平行四边形EFGH是矩形；故答案为：AC⊥BD；（3）矩形的中点四边形是菱形．理由如下：如图3，连结AC、BD．∵E、F、G、H分别为四边形ABCD四条边上的中点，∴EH=BD，FG=BD，EF=AC，GH=AC，∵四边形ABCD是矩形，∴AC=BD，∴EF=FG=GH=EH，∴四边形EFGH是菱形．23．（8分）某市为进一步缓解交通拥堵现象，决定修建一条从市中心到飞机场的轻轨铁路．实际施工时，每月的工效比原计划提高了20%，结果提前5个月完成这一工程．求原计划完成这一工程的时间是多少月？【解答】解：设原来计划完成这一工程的时间为x个月，由题意，得，解得：x=30．经检验，x=30是原方程的解．答：原计划完成这一工程的时间是30个月．24．（8分）如图，点A是反比例函数y=﹣在第二象限内图象上一点，点B是反比例函数y=在第一象限内图象上一点，直线AB与y轴交于点C，且AC=BC，连接OA、OB，求△AOB的面积．【解答】解：分别过A、B两点作AD⊥x轴，BE⊥x轴，垂足为D、E，∵AC=CB，∴OD=OE，设A（﹣a，），则B（a，），=S梯形ADBE﹣S△AOD﹣S△BOE故S△AOB=（+）×2a﹣a×﹣a×=3．25．（8分）在△ABC中，AB=AC，点D在边BC所在的直线上，过点D作DF∥AC 交直线AB于点F，DE∥AB交直线AC于点E．（1）当点D在边BC上时，如图①，求证：DE+DF=AC．（2）当点D在边BC的延长线上时，如图②；当点D在边BC的反向延长线上时，如图③，请分别写出图②、图③中DE，DF，AC之间的数量关系，不需要证明．（3）若AC=6，DE=4，则DF=2或10．【解答】解：（1）证明：∵DF∥AC，DE∥AB，∴四边形AFDE是平行四边形．∴AF=DE，∵DF∥AC，∴∠FDB=∠C又∵AB=AC，∴∠B=∠C，∴∠FDB=∠B∴DF=BF∴DE+DF=AB=AC；（2）图②中：AC+DE=DF．图③中：AC+DF=DE．（3）当如图①的情况，DF=AC﹣DE=6﹣4=2；当如图②的情况，DF=AC+DE=6+4=10．故答案是：2或10．。

2024届江苏省盐城市东台市第一教育集团八年级数学第二学期期末复习检测模拟试题考生须知：1．全卷分选择题和非选择题两部分，全部在答题纸上作答。

选择题必须用2B铅笔填涂；非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。

2．请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。

3．保持卡面清洁，不要折叠，不要弄破、弄皱，在草稿纸、试题卷上答题无效。

一、选择题(每小题3分,共30分)1．矩形是轴对称图形，对称轴可以是（）A．1l B．2l C．3l D．4l2．甲，乙两个样本的容量相同，甲样本的方差为0.102，乙样本的方差是0.06，那么（）A．甲的波动比乙的波动大B．乙的波动比甲的波动大C．甲，乙的波动大小一样D．甲，乙的波动大小无法确定3．如图，有一个水池，其底面是边长为16尺的正方形，一根芦苇AB生长在它的正中央，高出水面部分BC的长为2尺，如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B恰好碰到岸边的B′，则这根芦苇AB的长是（）A．15尺B．16尺C．17尺D．18尺4．某烟花爆竹厂从20万件同类产品中随机抽取了100件进行质检，发现其中有5件不合格，那么请你估计该厂这20万件产品中合格产品约有（）A．1万件B．18万件C．19万件D．20万件5．下列手机软件图标中，是轴对称图形的是（）A．B．C．D．6．下列式子是分式的是（）A ．2019xB ．2019xC ．2019x πD ．2019x y + 7．如图，平行四边形ABCD 的对角线AC 与BD 相交于点O ，AE ⊥BC 于E ，AB ＝3，AC ＝2，BD ＝4，则AE 的长为（ ）A ．32B ．32C ．217D ．22178．如图，直线y ax b =+过点()0,3A 和点()2,0B -，则方程0ax b +=的解是（）A ．3x =B ．2x =-C ．0x =D ．3x =-9．如图，在矩形ABCD 中，AB=4，BC=8，对角线AC 、BD 相交于点O ，过点O 作OE 垂直AC 交AD 于点E ，则AE 的长是（ ）A ．5B ．3C ．2.4D ．2.510．如图，菱形ABCD 的对角线AC 、BD 相交于点O ，过点C 作CE ⊥AD 于点E ，连接OE ，若OB ＝8，S 菱形ABCD ＝96，则OE 的长为（ ）A ．23B ．25C ．6D ．8二、填空题(每小题3分,共24分)11．如图，已知菱形OABC 的顶点O(0，0)，B(2，2)，则菱形的对角线交点D 的坐标为____；若菱形绕点O 逆时针旋转，每秒旋转45°，则第60秒时，点D 的坐标为_____．12．已知一次函数y =2x 与y =-x +b 的交点为（1，a ），则方程组200x y x y b -=⎧⎨+-=⎩的解为______． 13．已知a 为实数，若有正数b ，m ，满足()()2a b a b m +-=，则称a 是b ，m 的弦数．若15a <且a 为正数，请写出一组a ，b, m 使得a 是b ，m 的弦数：_____________．14．如图，某小区有一块直角三角形绿地，量得直角边AC=4m ，BC=3m ，考虑到这块绿地周围还有足够多的空余部分，于是打算将这块绿地扩充成等腰三角形，且扩充部分是以AC 为一条直角边的直角三角形，则扩充的方案共有_____种．15．169的算术平方根是______．16．方程22150x x --=的解为_________．17．根据《中华人民共和国2017年国民经济和社会发展统计公报》，我国20132017-年农村贫困人口统计如图所示.根据统计图中提供的信息，预估2018年年末全国农村贫困人口约为______万人，你的预估理由是______．18．若关于x 的一元一次不等式组23x x x a ->⎧⎨<⎩的的解集为1x <-，则a 的取值范围是___________．三、解答题(共66分)19．（10分）已知Rt ABC ∆中，其中两边的长分别是3，5，求第三边的长．20．（6分）（定义学习）定义:如果四边形有一组对角为直角，那么我们称这样的四边形为“对直四边形”（判断尝试）在①梯形;②矩形:③菱形中，是“对直四边形”的是哪一个. (填序号)（操作探究）在菱形ABCD 中，2,60,AB B AE BC ︒=∠=⊥于点E,请在边AD 和CD 上各找一点F,使得以点A 、E 、C 、F 组成的四边形为“对直四边形”，画出示意图，并直接写出EF 的长，（实践应用）某加工厂有一批四边形板材，形状如图所示，若AB=3米，AD=1米，4590C A B ︒︒∠=∠=∠=.现根据客户要求，需将每张四边形板材进一步分割成两个等腰三角形板材和一个“对直四边形"板材，且这两个等腰三角形的腰长相等，要求材料充分利用无剩余.求分割后得到的等腰三角形的腰长，21．（6分）在坐标系下画出函数1|4|y x =-的图象，（1）正比例函数212y x =的图象与1y 图象交于A ，B 两点，A 在B 的左侧，画出2y 的图象并求A ，B 两点坐标 （2）根据图象直接写出21y y ≤时自变量x 的取值范围 （3）1y 与x 轴交点为C ，求ABC 的面积22．（8分）如图，在正方形网格中，△TAB 的顶点坐标分别为 T(1，1)、A(2，3)、B(4，2)．(1)以点 T(1，1)为位似中心，在位似中心的 同侧将△TAB 放大为原来的 3 倍，放大 后点 A 、B 的对应点分别为 A'、B'，画出△TA'B'：(2)写出点 A'、B'的坐标：A'( )、B'（ ）；(3)在(1)中，若 C(a ，b)为线段 AB 上任一 点，则变化后点 C 的对应点 C'的坐标为 ( )．23．（8分）下面的图象反映的过程是：张强从家跑步去体育场，在那里锻炼了一阵后又原路返回，顺路到文具店去买笔，然后散步回家.其中x 表示时间，y 表示张强离家的距离.根据图象回答：（1）体育场离张强家的多远？张强从家到体育场用了多长时间？（2）体育场离文具店多远？（3）张强在文具店逗留了多久？（4）计算张强从文具店回家的平均速度.24．（8分）如图，折叠长方形一边AD ，点D 落在BC 边的点F 处，BC =10cm ，AB =8cm ．求：（1）FC 的长；（2）EF 的长．25．（10分）如图，在ABC 中，AD 是BC 边上的中线，E 是AD 的中点，延长BE 到F ，使BE EF =，连接AF 、CF 、DF ．()1求证：AF BD =；()2若AB AC ⊥，试判断四边形ADCF 的形状，并证明你的结论．26．（10分）如图，ABC ∆，D 、E 分别是AB 、AC 的中点，图①是沿DE 将ADE ∆折叠，点A '落在BC 上，图②是绕点E 将ADE ∆顺时针旋转180︒.（1）在图①中，判断DBA '∆和ECA '∆形状.（填空）_______________________________________（2）在图②中，判断四边形DBA D ''的形状，并说明理由.参考答案一、选择题(每小题3分,共30分)1、D【解题分析】根据轴对称图形的概念求解．矩形是轴对称图形，可以左右重合和上下重合．【题目详解】解：矩形是轴对称图形，可以左右重合和上下重合，故4l可以是矩形的对称轴，故选：D.【题目点拨】此题主要考查了轴对称的概念，轴对称的关键是寻找对称轴，两边图象折叠后可重合．2、A【解题分析】根据方差的定义，方差越小数据越稳定，故可选出正确选项．【题目详解】解：根据方差的意义，甲样本的方差大于乙样本的方差，故甲的波动比乙的波动大．故选A．【题目点拨】本题考查方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．3、C【解题分析】我们可以将其转化为数学几何图形，如图所示，根据题意，可知EB'的长为16尺，则B'C=8尺，设出AB=AB'=x尺，表示出水深AC，根据勾股定理建立方程，求出的方程的解即可得到芦苇的长．【题目详解】解：依题意画出图形，设芦苇长AB=AB′=x尺，则水深AC=（x-2）尺，因为B'E=16尺，所以B'C=8尺在Rt△AB'C中，82+（x-2）2=x2，解之得：x=17，即芦苇长17尺．故选C．【题目点拨】本题主要考查勾股定理的应用，熟悉数形结合的解题思想是解题关键．4、C【解题分析】抽取的100件进行质检，发现其中有5件不合格，那么合格的有95件，由此即可求出这类产品的合格率是95%，然后利用样本估计总体的思想，即可知道合格率是95%，即可求出该厂这20万件产品中合格品的件数．【题目详解】∵某烟花爆竹厂从20万件同类产品中随机抽取了100件进行质检，发现其中有5件不合格，∴合格的有95件，∴合格率为95÷100=95%，∴估计该厂这20万件产品中合格品约为20×95%=19万件，故选C.【题目点拨】此题主要考查了样本估计总体的思想，此题利用样本的合格率去估计总体的合格率．5、C【解题分析】根据轴对称图形的概念求解．【题目详解】A、不是轴对称图形，故错误；B、不是轴对称图形，故错误；C、是轴对称图形，故正确；D、不是轴对称图形，故错误．故选C．【题目点拨】本题考查了轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合．6、B【解题分析】根据分母中含有字母的式子是分式，可得答案．【题目详解】解：2019x是分式，故选：B.【题目点拨】本题考查了分式的定义，分母中含有字母的式子是分式，否则是整式.7、D【解题分析】由勾股定理的逆定理可判定△BAC是直角三角形，继而根据求出平行四边形ABCD的面积即可求解．【题目详解】解：∵AC＝2，BD＝4，四边形ABCD是平行四边形，∴AO＝12AC＝1，BO＝12BD＝2，∵AB，∴AB2+AO2＝BO2，∴∠BAC＝90°，∵在Rt△BAC中，BC==S△BAC＝12×AB×AC＝12×BC×AE，2，∴AE，故选：D．【题目点拨】本题考查了勾股定理的逆定理和平行四边形的性质，能得出△BAC是直角三角形是解此题的关键．8、B【解题分析】一次函数y＝kx＋b的图象与x轴的交点横坐标就是kx＋b＝0的解．【题目详解】解：∵直线y＝ax＋b过点B（−2，0），∴方程ax＋b＝0的解是x＝−2，故选：B．【题目点拨】此题主要考查了一次函数与一元一次方程，关键是掌握任何一元一次方程都可以转化为ax＋b＝0 （a，b为常数，a≠0）的形式，所以解一元一次方程可以转化为：当某个一次函数的值为0时，求相应的自变量的值．从图象上看，相当于确定已知直线y＝ax＋b与x轴的交点的横坐标的值．9、A【解题分析】根据矩形的性质得出∠CDE=90°，AD=BC=8，AB=DC=4，AO=OC，根据线段垂直平分线性质得出AE=CE，在Rt△CDE 中，由勾股定理得出CE=CD+DE，代入求出即可．【题目详解】如图，连接EC，∵在矩形ABCD中，AB=4，BC=8，∴∠CDE=90°，AD=BC=8，AB=DC=4，AO=OC，∵OE⊥AC，∴AE=CE，在Rt△CDE中，由勾股定理得：CE=CD+DE，即AE=4+(8−AE) ，解得：AE=5，故选A.【题目点拨】此题考查线段垂直平分线的性质，解题关键在于作辅助线.10、C【解题分析】由菱形的性质得出BD=16，由菱形的面积得出AC=12，再由直角三角形斜边上的中线性质即可得出结果．【题目详解】∵四边形ABCD是菱形，∴OA＝OC，OB＝OD＝12BD，BD⊥AC，∴BD＝16，∵S菱形ABCD═12AC×BD＝96，∴AC＝12，∵CE⊥AD，∴∠AEC＝90°，∴OE＝12AC＝6，故选C．【题目点拨】此题主要考查了菱形的性质、直角三角形斜边上的中线性质；熟练掌握菱形的性质是解题的关键．二、填空题(每小题3分,共24分)11、 (1，1)(－1，－1)．【解题分析】根据菱形的性质，可得D点坐标，根据旋转的性质，可得D点旋转后的坐标．【题目详解】∵菱形OABC的顶点O（0，0），B（2，2），得∴D点坐标为（1，1）．∵每秒旋转45°，∴第60秒旋转45°×60=2700°，2700°÷360°=7.5周，即OD旋转了7周半，∴菱形的对角线交点D的坐标为（-1，-1），故答案为：（1，1）；（-1，-1）【题目点拨】本题考查了旋转的性质及菱形的性质，利用旋转的性质得出OD旋转的周数是解题关键．12、12 xy=⎧⎨=⎩【解题分析】把（1，a）代入y=2x可确定交点坐标，然后根据方程组的解就是两个相应的一次函数图象的交点坐标的横纵坐标，由此即可求解．解：把（1，a ）代入y=2x 得a=2，所以方程组200x y x y b -=⎧⎨+-=⎩的解为12x y =⎧⎨=⎩． 故答案为：12x y =⎧⎨=⎩． 【题目点拨】本题考查了一次函数与二元一次方程（组）的关系，方程组的解就是使方程组中两个方程同时成立的一对未知数的值，而这一对未知数的值也同时满足两个相应的一次函数式，因此方程组的解就是两个相应的一次函数图象的交点坐标．13、5,4,3a b m ===（答案不唯一）【解题分析】根据题中提供的弦数的定义判断即可．【题目详解】解：2(54)(54)913+⨯-=⨯=，5∴是4，3的弦数，故答案为：5,4,3a b m ===（答案不唯一）【题目点拨】本题考查了平方差公式，正确理解题中的新定义是解本题的关键．14、1【解题分析】由于扩充所得的等腰三角形腰和底不确定，若设扩充所得的三角形是△ABD ，则应分为①AB=AD ，②AB=BD ，③AD=BD ，1种情况进行讨论．【题目详解】解：如图所示：故答案是：1．本题考查了等腰三角形的性质以及勾股定理的应用，关键是正确进行分类讨论．15、1【解题分析】根据算术平方根的定义解答即可．【题目详解】．故答案为：1．【题目点拨】此题主要考查了算术平方根的定义：如果一个数的平方等于A ，那么这个数就叫做A 的平方根，其中非负的平方根叫做这个数的算术平方根．16、125,3x x ==-【解题分析】此题采用因式分解法最简单，解题时首先要观察，然后再选择解题方法．配方法与公式法适用于所用的一元二次方程，因式分解法虽有限制，却最简单．【题目详解】∵2215x x -=∴22+115+1x x -=∴()2116x -=∴14x -=±∴125,3x x ==-故答案为：125,3x x ==-.【题目点拨】此题考查解一元二次方程-配方法，解题关键在于掌握运算法则.17、1700 由统计图可知，2016～2017减少约1300万，则2017～2018减少约为1300万，故2018年农村贫困人口约为1700万．【解题分析】根据统计图可以得到得到各年相对去年减少的人数，从而可以预估2018年年末全国农村贫困人口约为多少万人，并说明理由．解：2018年年末全国农村贫困人口约为1700万人，预估理由：由统计图可知，2016～2017减少约1300万，则2017～2018减少约为1300万，故2018年农村贫困人口约为1700万，故答案为1700、由统计图可知，2016～2017减少约1300万，则2017～2018减少约为1300万，故2018年农村贫困人口约为1700万．【题目点拨】本题考查用样本估计总体、条形统计图，解题的关键是明确条形统计图的特点，从中得到必要的解题信息． 18、1a ≥-.【解题分析】不等式待定系数的取值范围就是已知不等式或不等式组的解集或特殊解，确定不等式中未知数的系数的取值范围.【题目详解】由23x x x a ->⎧⎨<⎩得 1 x x a <-⎧⎨<⎩因为解集为1x <-所以1a ≥-故答案为：1a ≥-【题目点拨】考核知识点：不等式组解集.会解不等式组是关键.三、解答题(共66分)19、4【解题分析】分5是斜边长、5是直角边长两种情况，根据勾股定理计算即可．【题目详解】解：当5是斜边长时，第三边长4==，当5是直角边长时，第三边长=则第三边长为4本题考查的是勾股定理，如果直角三角形的两条直角边长分别是a ，b ，斜边长为c ，那么222+=a b c ．20、【判断尝试】②；【操作探究】EF 的长为2，EF 的长为3；【实践应用】方案1：两个等腰三角形的腰长都为322米．理由见解析，方案2：两个等腰三角形的腰长都为2米．理由见解析，方案3：两个等腰三角形的腰长都为5米，理由见解析．方案4：两个等腰三角形的腰长都为22米，理由见解析． 【解题分析】 [判断尝试]根据“对直四边形”定义和①梯形;②矩形:③菱形的性质逐一分析即可解答.[操作探究]由菱形性质和30°直角三角形性质即可求得EF 的长.[实践应用]先作出“对直四边形”，容易得到另两个等腰三角形，再利用等腰三角形性质和勾股定理即可求出腰长.【题目详解】解： [判断尝试]①梯形不可能一组对角为直角;③菱形中只有正方形的一组对角为直角，②矩形四个角都是直角，故矩形有一组对角为直角，为“对直四边形”，故答案为② ，[操作探究]F 在边AD 上时，如图：∴四边形AECF 是矩形，∴AE=CE ，又∵2,60,AB B AE BC ︒=∠=⊥，∴BE=1，3CE=AF=1，∴在Rt △AEF 中，22AE AF +EF 的长为2.F 在边CD 上时，AF ⊥CD ，∵四边形ABCD是菱形，∴AB=AD=2，∠B=∠D=60°，又∵AE⊥BC，∴∠BAE=∠BAF=30°，∴AE=AF=3，∵∠BAD=120°，∴∠EAF=60°，∴△AEF为等边三角形，∴EF=AF=AE=3即：EF的长为3；故答案为2，3.[实践应用]方案1：如图①，作DE BC,EF CD⊥⊥，则四边形ABCD分为等腰FED、等腰FEC、“对直四边形”ABED，其中两个等腰三角形的腰长都为322米．理由：∵A B90︒∠=∠=，∴四边形ABED为矩形，∴DE AB==3米，∵C45︒∠=，∴△DEC为等腰直角三角形，∴DE=EC=3米，∴DC=32米， ∵EF CD ⊥，∴FD FE FC ===12DC=322米． 方案2：如图②，作BE DC,EF BC ⊥⊥，则四边形ABCD 分为等腰△FEB 、等腰△FEC 、“对直四边形”ABED ，其中两个等腰三角形的腰长都为2米．理由：作DG BC ⊥，由（1）可知DG AB GC ===3米，BG=AD=1米，∴BC=1+3=4米，∵C 45,BE DC ︒∠=⊥，∴△BEC 为等腰直角三角形，∵EF BC ⊥，∴FE FB FC ===12BC=2米． 方案3：如图③，作CD 、BC 的垂直平分线交于点E ，连接ED 、EB ，则四边形ABCD 分为等腰△CED 、等腰△CEB 、“对直四边形”ABED ，其中两个等腰三角形的腰长都为5米．理由：连接CE ，并延长交AB 于点F ，∵CD 、BC 的垂直平分线交于点E ，∴ED EC EB ==，∴12,34∠=∠∠=∠，∴DEB 65123421232(13)∠=∠+∠=∠+∠+∠+∠=∠+∠=∠+∠2DCB 24590︒︒=-∠=-⨯=-．连接DB ， DB=22AD AB +=10，∵ED=EB ，∴△BED 为等腰直角三角形， ∴ED=5米，∴ED EC EB ===5米．方案4：如图④，作DE DC ⊥，交AB 于点E ，AF DE ⊥，则四边形ABCD 分为等腰△AFE 、等腰△AFD 、“对直四边形”BEDC ，其中两个等腰三角形的腰长都为22米． 理由：作DE DC ⊥，交AB 于点E ，可证∠ADE =45°，∵DAE 90︒∠=，∴△ADE 为等腰直角三角形，∴2米， 作AF DE ⊥，∴FE FD FA ===12DE=22米． 【题目点拨】 此题是四边形综合题，主要考查了新定义“对直四边形”的理解和应用，矩形的判定和性质，勾股定理，正确作出图形是解本题的关键．21、（1）图象详见解析，A （83，43），B （8，4）；（2）x ≤83或x ＞8；（3）163． 【解题分析】（1）用描点法画出1|4|y x =-和212y x =的图象，再解方程组求得点A 、B 的坐标即可；（2）观察图象，结合点A 、B 的坐标即可求解；（3）先求得点C 的坐标，再利用S △ABC ＝S △OBC ﹣S △OAC 即可求得△ABC 的面积.【题目详解】（1）画出函数y1＝|x﹣4|的图象如图：∵y＝|x﹣4|∴4(4)4(4) y x xy x x=-≥⎧⎨=-+<⎩，解412y xy x=-+⎧⎪⎨=⎪⎩得8343xy⎧=⎪⎪⎨⎪=⎪⎩，∴A（83，43），解412y xy x=-⎧⎪⎨=⎪⎩得84xy=⎧⎨=⎩，∴B（8，4）；（2）y2≤y1时自变量x的取值范围是：x≤83或x≥8；（3）令y＝0则0＝|x﹣4|，解得x＝4，∴C（0，4），∴S△ABC＝S△OBC﹣S△OAC＝12×4×4﹣14423⨯⨯＝163．【题目点拨】本题考查了函数图象的画法及函数的交点坐标问题，正确求得两个函数的交点坐标是解决问题的关键.22、（1）详见解析；（1）A′（4，7），B′（10，4）（3）(3a-1,3b-1)【解题分析】（1）根据题目的叙述，在位似中心的同侧将△TAB放大为原来的3倍，得到对应点坐标，正确地作出图形即可，（1）根据图象确定各点的坐标即可．（3）根据（1）中变换的规律，即可写出变化后点C的对应点C′的坐标．【题目详解】解：（1）如图所示：（1）点A′，B′的坐标分别为：A′（4，7），B′（10，4）；故答案为：(4，7)；(10，4)；（3）变化后点C的对应点C′的坐标为：C′（3a-1，3b-1）故答案为：3a-1，3b-1．【题目点拨】本题考查了位似变换作图的问题，正确理解位似变换的定义，会进行位似变换的作图是解题的关键．23、（1）体育场离张强家2.5km，张强从家到体育场用了15min；（2）体育场离文具店1km；(3) 张强在文具店逗留了20min；（4）张强从文具店回家的平均速度为370km/min【解题分析】（1）根据张强锻炼时时间增加，路程没有增加，表现在函数图象上就出现第一次与x轴平行的图象；（2）由图中可以看出，体育场离张强家2.5千米，文具店离张强家1.5千米，得出体育场离文具店距离即可；（3）张强在文具店逗留，第二次出现时间增加，路程没有增加，时间为：65-1．（4）根据观察函数图象的纵坐标，可得路程，根据观察函数图象的横坐标，可得回家的时间，根据路程与时间的关系，可得答案．【题目详解】解：（1）从图象上看，体育场离张强家2.5km，张强从家到体育场用了15min.（2）2.5-1.5=1（km），所以体育场离文具店1km.（3）65-1=20（min ），所以张强在文具店逗留了20min.（4）1.5÷(100-65)= 370（km/min ）， 张强从文具店回家的平均速度为370km/min. 【题目点拨】此题主要考查了函数图象，正确理解函数图象横纵坐标表示的意义是解答此题的关键，需注意理解时间增多，路程没有变化的函数图象是与x 轴平行的一条线段．24、 (1)4cm ；(2)5cm.【解题分析】（1）由于△ADE 翻折得到△AEF ，所以可得AF =AD ，则在Rt △ABF 中，由勾股定理即可得出结论；（2）由于EF =DE ，可设EF 的长为x ．在Rt △EFC 中，利用勾股定理即可得出结论．【题目详解】（1）由题意可得：AF =AD =10cm ．在Rt △ABF 中，∵AB =8 cm ，∴BF =6cm ，∴FC =BC ﹣BF =10﹣6=4（cm ）．（2）由题意可得：EF =DE ，可设DE 的长为x ，则在Rt △EFC 中，（8﹣x ）2+42=x 2，解得：x =5，即EF 的长为5cm ．【题目点拨】本题考查了矩形的性质以及翻折的问题，能够熟练运用矩形的性质求解一些简答的问题．25、（1）证明见解析（2）四边形AFCD 是菱形【解题分析】(1)只要证明四边形ABDF 是平行四边形即可；(2)结论：四边形AFCD 是菱形.首先证明四边形ADCD 是平行四边形，再证明DA=DC 即可.【题目详解】（1）AE ED =，BE EF =，∴四边形ABDF 是平行四边形，AF BD ∴=；()2结论：四边形ADCF 是菱形，理由如下：AB AC ⊥，CAB 90∠∴=，CD DB =，1AD BC DC 2∴==，四边形ABDF 是平行四边形，AF//CD ∴，AF BD =，AF CD ∴=，∴四边形AFCD 是平行四边形，DA DC =，∴四边形AFCD 是菱形．【题目点拨】本题考查了平行四边形的判定与性质、菱形的判定、直角三角形斜边中线等，熟练掌握相关的性质与定理是解题的关键.26、（1）DBA '∆和ECA '∆均为等腰三角形；（2）四边形DBA D ''为平行四边形，证明详见解析.【解题分析】根据平行线的性质和折叠的性质解答即可；（2）由三角形中位线的性质可证//DE BC ，12DE BC =，由旋转的性质可知ED DE '=，从而DD BA ''=，然后根据平行四边形的判定方法可证四边形DBA D ''是平行四边形.【题目详解】解：（1）DBA '∆和ECA '∆均为等腰三角形.∵DE ∥BC,∴∠A ′DE=∠BA ′D, ∠B=∠ADE,∵∠ADE=∠A ′DE,∴∠B=∠BA ′D,∴BD=A ′D ，∴DBA '∆为等腰三角形；同理可证CE=A ′E ，即ECA '∆为等腰三角形.（2）四边形DBA D ''为平行四边形. 理由：D 、E 分别是AB 、AC 的中点，∴//DE BC ，12DE BC =. 由旋转的性质可知ED DE '=，∴DD BA ''=，∴四边形DBA D ''是平行四边形.【题目点拨】本题考查了折叠的性质，旋转的性质，三角形的中位线，平行线的性质，等腰三角形的判定，以及平行四边形的判定等知识，熟练掌握折叠的性质及旋转的性质是解答本题的关键.。

2014-2015学年度第二学期第一次阶段检测八年级语文试题（满分100分 时间120分钟）一、语言积累与运用。

（23分） 1.古诗文默写。

（6分）（1）世有伯乐， 。

（韩愈《马说》） （2）管中窥豹， 。

（《晋书·王献之传》） （3） ，无欲则刚。

（清，林则徐）（4） ，小桥流水人家。

（5）李白的《宣州谢眺楼饯别校书叔云》中最能表现他面对挫折积极向上，对理想执着追求的诗句是： __ ，_______ __________ 。

2.根据汉语拼音写出汉字，或给加粗字注音（4分）无私，敬业，诚信，友善，谦和，宽容……是我们中国人提倡和追求的精神境界。

对人民无比热忱． ，对工作无比负责的白求恩以身殉职于中国的抗日前线，忠实的践行了一个国际主义战士的崇高境界 ；梁启超先生认为心无旁w ù ,专心忠实与自己所从事的职业便是敬业，否则便是xi è 渎圣神的职业，宽广的胸襟． 是建立和谐人际关系的前提……学习这些优美的篇章，你会自觉的追求道德修养的更高境界。

，那就会贻误战机，造成严重的损失。

4.下列对病句的修改不正确的一项是（2分） （ ） A ．中学生之所以喜欢网络小说的原因，在于这些作品大多思想感情丰富细腻，而且叙述方法自由活泼。

（语意重复，“之所以”和“的原因”去掉其中之一。

）B ．我认为，应该尽可能使用简化字，不要滥用繁体字，这样会给汉字规范化和青少年的学习增加困难。

（表意不清，“这样”一词指代不明，应该改为“滥用繁体字”。

）C ．望着白云缭绕的五皇山，无不使游览者感受到了大自然的壮美雄奇和神功伟力。

（缺学校： 班级： 姓名： 读卡号 座位号：装订线内请勿答题主语，去掉“无不使”。

）D．他们在遇到困难的时候，并没有消沉，而是在大家的依赖和关怀中得到了力量，树立了克服困难的信心。

（用词不当，将“依赖”改为“依靠”。

）5．专题与语文实践活动。

（4分）学习了“鸟”专题后，班级开展“鸟”专题研究活动。

2014～2015学年度第二学期期中考试八年级数学试题（满分：120分 考试时间：100分钟）一、选择题（本大题共8小题，每小题3分，共24分，每小题仅有一个答案正确 ） 1．下列事件中，是不可能事件的是‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥（ ） A ．买一张电影票，座位号是奇数 B ．射击运动员射击一次，命中9环C ．明天会下雨D ．度量三角形的内角和，结果是360º2．若分式242x x -+的值为0，则x 的值为‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥（ ）A ．±2B ．2C ．－2D ．03．在反比例函数1k y x-=的图象的每个象限内，y 随x 的增大而增大，则k 值可以是（ ） A ．－1B ．1C ．2D ．34．下列命题中，正确的是‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥（ ）A ．两条对角线相等的四边形是平行四边形B ．两条对角线相等且互相垂直的四边形是矩形C ．两条对角线互相垂直平分的四边形是菱形D ．两条对角线互相平分且相等的四边形是正方形5．下列运算正确的是‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥( )A ．a b ab =22 B ．a bc a c b =++ C ．a db a d a b 2+=+ D ．1-=+--y x y x 6．顺次连接四边形ABCD 四条边的中点所得的四边形是菱形，则四边形ABCD 是‥‥‥ ( ）A ．矩形B ．等腰梯形C ．对角线相互垂直的四边形D ．对角线相等的四边形7．如图，E 、F 分别是正方形ABCD 的边CD 、AD 上的点，且CE =DF ，AE 、BF 相交于点O ，下列结论：（1）AE =BF ；（2）AE ⊥BF ；（3）AO =OE ；（4）AOB DEOF S S ∆=四边形中一定正确的有‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥（ ）A ．4个B ．3个C ．2个D ．1个8．如图，菱形OABC 的顶点C 的坐标为（3，4），顶点A 在x 轴的正半轴上，反比例函数(0)ky x x=>的图像经过顶点B ，则k 的值为‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥‥（ ）.A 32 B ． 24 C ．20 D ．12二、填空题（本大题共10小题，每小题3分，共30分）9．一个布袋中装有3个红球和4个白球，这些除颜色外其它都相同．从袋子中随机摸出一个球，这个球是白球的概率为 ．10．如图，A 、B 两地间有一池塘阻隔，为测量A 、B 两地的距离，在地面上选一点C ，连接CA 、CB 的中点D 、E ．若DE 的长度为30m ，则A 、B 两地的距离为 m ． 11．已知a b =135，则b a b a +-的值是 ．12．已知a 、b为两个连续的整数，且a b <，则________=+b a ． 13．若菱形的两条对角线分别为2和3，则此菱形的面积是14．如图，平行四边形ABCD 的周长为36．对角线AC ，BD 相交于点O ．点E 是CD 的中点．BD =12．则△DOE 的周长为_______． 15．如图，直线x =2与反比例函数x y 2=， xy 1-=的图象分别交于A ，B 两点，若点P 是y 轴上任意一点，则△P AB 的面积是 ．16．如图，将矩形ABCD 绕点A 顺时针旋转到矩形D C B A ''''的位置，旋转角为α (0︒<α<90︒)。

江苏省盐城市东台第一教研片2017-2018学年八年级数学下学期第一次阶段检测试题（考试时间：100分钟， 满分：120分 ）一、选择题（本大题共有10小题，每小题3分，共30分）1．下列说法正确的是 （ ）A ．为了了解某中学800名学生的视力情况，从中随机抽取了50名学生进行调查，在此次调查中，样本容量为50名学生的视力B ．了解常州市每天的流动人口数，采用抽查方式C ．若一个游戏的中奖率是1%，则做100次这样的游戏一定会中奖D ．“掷一枚硬币，正面朝上”是必然事件2．十字路口的交通信号灯每分钟红灯亮30秒，绿灯亮25秒，黄灯亮5秒，当你抬头看信号灯时，是黄灯的概率是（ ） A ．121 B ．13 C ．125 D ．123．下列图形中，既是轴对称图形又是中心对称图形的是 （ ）4．对于下列图形：①平行四边形；②矩形；③菱形；④正方形；⑤等腰三角形；⑥等边三角形．其中可以用任意两个全等的直角三角形拼成的图形有 （ ） A ．①④⑥ B ．①②⑤ C ．①③⑤ D ．②⑤⑥5．以长为5cm ，4cm ，7cm 的三条线段中的两条为边，另一条为了对角线画平行四边形，可以画出形状不同的平行四边形的个数有 （ ）A ．1个B ．2个C ．3个D ．4个6．不论x 取何值，下列分式中一定有意义的是 （ ）A ．B ．C ．D ．7.如上图，在矩形ABCD 中，R是C D 边上的定点，P 是BC 边上的动点，E 、F 分别是PA 、PR 的中点，当P 点从B 向C 移动时，线段EF 的长度（ ）A ．保持不变B ．逐渐减少C ．逐渐增大D ．先减小后增大 8.把分式 中的x 和y 都扩大为原来的5倍，那么这个分式的值（ ）A ．扩大为原来的5倍；B ．不变C ．缩小到原来的 ；D ．扩大为原来的 倍9. 顺次连接矩形四边中点所得的四边形一定是 （ ）A.平行四边形B.矩形C.菱形D.正方形10.已知菱形的周长为40 cm ，两对角线长度比为3：4，则对角线长分别为 （ ） A ．12 cm ．16 cm B ．6 cm ，8 cm C ．3 cm ，4 cm D ．24 cm ，32 cm11-+x x 11-+x x 11+-x x x+y xy1552x -1x 2二、填空题（本大题共10小题，每小题3分，共30分）11. 在条形统计图中，若各个小长方形的面积比为1: 6:3:5，则用扇形统计图表示时，各扇形的圆心角度数分别为 . 12．某学校的八（2）班，有男生20人，女生24人，其中男生有18人住宿，女生有20人住宿。

东台市第一教研片初二下学期第一次月考数学试卷及答案八年级数学考试时刻100分钟，试卷满分100分。

考试形式闭卷 命题：后港中学一、选择题（本大题共有8小题，每小题3分，共24分。

在每小题所给出的四个选项中，只有一项是符合题目要求的，请将正确选项的字母代号填写在相应的位置）1、下列图形中，中心对称图形有 （ ）A ．1个B ．2个C ．3个D ．4个2．若分式21x 有意义，则x 的取值范畴是 ( ) A ．x ≠1 B ．x ＞1 C ．x=1 D ．x ＜13．下列性质中，正方形具有而菱形不一定具有的性质是 ( ) A ．四条边相等 B ．对角线相等 C ．对角线互相平分 D ．对角线互相垂直4. 如图，矩形ABCD 的对角线AC 、BD 相交于点O ，CE ∥BD ，DE ∥AC ，若AC =4，则四边形CODE 的周长为 （ ） A ． 4 B ． 6C ． 8D ． 105. 如图，ABCD 是正方形，G 是BC 上（除端点外）的任意一点，DE ⊥AG 于点E ，BF ∥DE ，交AG 于点F ．下列结论不一定成立的是 ( )A ．△AED ≌△BF AB ．DE －BF ＝EFC ．AF －BF ＝EFD ．DE －BG ＝FG第4题图第5题图 第6题图 第8题图6、如图，在平行四边形ABCD 中，AB =3cm ，BC =5cm ，对角线AC ，BD 相交于点O ，则OA 的取值范畴是 （ ）A ．1cm ＜OA ＜4cmB ．2cm ＜OA ＜8cmC ．2cm ＜OA ＜5cmD ．3cm ＜OA ＜8cm 7、已知四边形ABCD 是平行四边形，下列结论中不正确的是 （ ）A ．当AB =AD 时，它是菱形 B ．当AC =BD 时，它是正方形 C ．当∠ABC =90°时，它是矩形 D ．当AC ⊥BD 时，它是菱形 8. 如图，E 、F 分别是正方形ABCD 的边CD 、AD 上的点，且CE =DF ，AE 、BF 相交于点O ，下列结论：⑴ AE ＝BF ⑵ AE ⊥BF ⑶ AO =OE ⑷ S △AOB =S 四边形DEOF 中，正确的有 （ ） A 、1个 B 、2个 C 、3个 D 、4个ABC DOFE二、填空题（本大题共有10小题，每小题2分，共20分。

江苏省东台市第一教育联盟2016-2017学年八年级数学下学期第一次月考试题一选择题（本大题共有8小题，每小题3分，共24分．在每小题所给出的四个选项中，只有一项是符合题目要求的，请将正确选项的字母代号填写在相应的位置）1．下列图形中，既是轴对称图形，又是中心对称图形的是（）A． B． C． D．2．某市决定从桂花、菊花、杜鹃花中随机选取一种作为市花，选到杜鹃花的概率是（）A．1 B． C． D．03. 2015年我市有1.6万名初中毕业生参加升学考试，为了了解这1.6万名考生的数学成绩，从中抽取2000名考生的数学成绩进行统计，在这个问题中样本是（）A．1.6万名考生 B．2000名考生C．1.6万名考生的数学成绩 D．2000名考生的数学成绩4．下列事件中，属于必然事件的是（）A．抛掷1个均匀的骰子，出现4点向上 B．任意数的绝对值都是正数C．两直线被第三条直线所截，内错角相等 D．13人中至少有2人的生日在同一个月5．如图，在△ABC中，∠CAB=65°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为（）A．35°B．40°C．50°D．65°第5题图第7题图第8题图6．矩形具有而平行四边形不一定具有的性质是（）A．对角线互相平分 B．两组对角相等C．对角线相等 D．两组对边相等7．如图，四边形ABCD中，点E、F、G、H分别是边AB、BC、CD、DA的中点．若四边形EFGH为菱形，则对角线AC 、BD 应满足条件是（ ）A ．AC ⊥BDB ．AC=BDC ．AC ⊥BD 且AC=BD D ．不确定8．ABCD 是边长为1的正方形，△BPC 是等边三角形，则△BPD 的面积为（ ）A． B． C． D．二、填空题（本大题共有10小题，每小题2分，共20分．不需写出解答过程，请将答案直接写在横线上）9．调查神舟九号宇宙飞船各部件功能是否符合要求，这种调查适合用 （填“普查”或“抽样调查”）．10．对某班组织的一次考试成绩进行统计，已知80.5～90.5分这一组的频数是7，频率是0.2，那么该班级的人数是 人．11.如图，在▱ABCD 中，BE 平分∠ABC ，BC=6，DE=2，则▱ABCD 的周长等于 ．12.在▱ABCD 中，AB ：BC=4：3，周长为28cm ，则AD= cm ．13平行四边形的两条对角线长分别为8和10，则其中每一边长x 的取值范围是。

2016-2017学年度第二学期第一次月考八年级数学试题（满分：100分考试时间:100分钟）一、选择题：(每题3分，共24分）1．下列四个图形中,既是轴对称图形又是中心对称图形的有( ）A．4个B．3个C．2个D．1个2．下列调查适合做普查的是（)A．了解全球人类男女比例情况B．了解一批灯泡的平均使用寿命C．调查20～25岁年轻人最崇拜的偶像D．对患甲型H7N9的流感患者同一车厢的乘客进行医学检查3、在某校艺体节的乒乓球比赛中，李东同学顺利进入总决赛，且个人技艺高超,有同学预测“李东夺冠的可能性是80％”，对该同学的说法理解正确的是 ( ）A．李东夺冠的可能性较小 B．李东和他的对手比赛10局时,他一定会赢8局C．李东夺冠的可能性较大 D．李东肯定会赢4．已知样本数据个数为30,且被分成4组，各组数据个数之比为2：4：3:1，则第二小组和第三小组的频率分别为（）A．0.4和0。

3 B．0。

4和9 C．12和0。

3 D．12和95．在矩形ABCD中，AB=3，AD=4，P是AD上的动点，PE⊥AC于E，PF⊥BD于F，则PE+PF的值为（)A．B．2 C．D．16．如图，菱形ABCD中，∠B=60°，AB=2cm，E、F分别是BC 、CD 的中点，连接AE 、EF 、AF ， 则△AEF 的周长为( ) A ．2cm B ． 3 cm C ．4cm D ．3cm7．如图，正方形ABCD 中,点E 、F 分别在BC 、CD 上， △AEF 是等边三角形，连接AC 交EF 于G ，下列结论： ①BE=DF，②∠DAF=15°，③AC 垂直平分EF,④BE+DF=E F ， ⑤S △CEF =2S △ABE ．其中正确结论有（ ）个． A ．4B ．3C ．2D ．18．下列从左到右的变形中，正确的是 ( ）①b ab a 212=②ac bc a b 3434=③ba b a b a 214222+=--④c c a a 1=+ A ．①和② B ．①和③ C ．②和③ D ．②和④二、填空题： （每题2 分，共20分)9．在平行四边形ABCD 中,已知∠A=60°，则∠C= 度．10．平行四边形的周长为24 cm ，相邻两边长的比为3：1，那么这个平行四边形较短的边长为___________cm ．11。

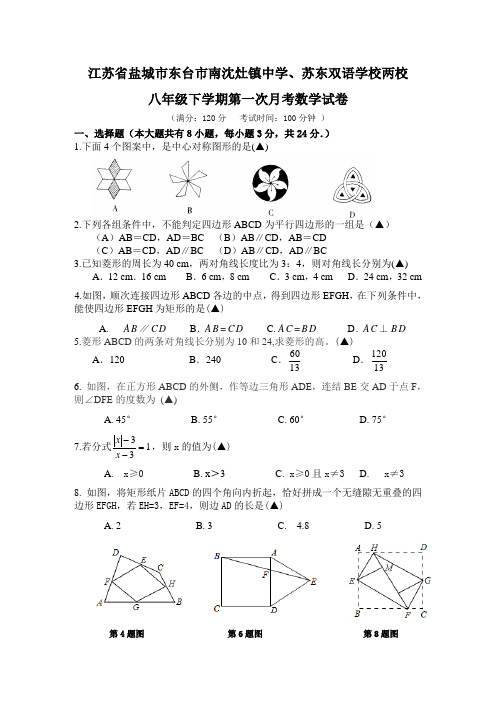
江苏省盐城市东台市南沈灶镇中学、苏东双语学校两校八年级下学期第一次月考数学试卷（满分：120分 考试时间：100分钟 ）一、选择题（本大题共有８小题，每小题3分，共24分．） 1.下面4个图案中，是中心对称图形的是(▲)2.下列各组条件中，不能判定四边形ABCD 为平行四边形的一组是（▲） （A ）AB ＝CD ，AD ＝BC （B ）AB ∥CD ，AB ＝CD （C ）AB ＝CD ，AD ∥BC （D ）AB ∥CD ，AD ∥BC3.已知菱形的周长为40 cm ，两对角线长度比为3：4，则对角线长分别为(▲)A ．12 cm ．16 cmB ．6 cm ，8 cmC ．3 cm ，4 cmD ．24 cm ，32 cm 4.如图，顺次连接四边形ABCD 各边的中点，得到四边形EFGH ，在下列条件中，能使四边形EFGH 为矩形的是(▲)A. AB ∥C D B . A B =C D C. A C =B D D. AC ⊥B D 5.菱形ABCD 的两条对角线长分别为10和24,求菱形的高。

(▲)A ．120B ．240C ．1360D ．131206. 如图，在正方形ABCD 的外侧，作等边三角形ADE ，连结BE 交AD 于点F ，则∠DFE 的度数为 (▲)A. 45°B. 55°C. 60°D. 75° 7.若分式133=--x x ，则x 的值为(▲)A. x ≥0B. x ＞3C. x ≥0且x ≠3D. x ≠3 8. 如图，将矩形纸片ABCD 的四个角向内折起，恰好拼成一个无缝隙无重叠的四边形EFGH ，若EH=3，EF=4，则边AD 的长是(▲)A. 2B. 3C. 4.8D. 5第4题图 第6题图 第8题图二、填空题（本大题共有10小题，每小题3分，共30分．）9. 不改变分式 2-x2-1-x的值，使分式的分子和分母的最高次项的系数是正数：▲ 。

一、单选题2014-2015学年江苏东台第一教研片八年级下第一次月考英语试卷江苏初二月考2015-05-20149次1. —Who will go to the airport to meet Mary?—I will. I her several times. I can find her easily.A．met B．have met C．had met D．will meet2. We each other since I left school.A．don’t see B．didn’t see C．haven’t see D．haven’t seen3. —Where have you _________? —I’ve ________ the supermarket.A．gone, gone to B．been, been to C．gone, been at D．been, gone to4. It's very to play chess with old friends at home.A．pleasant; /B．interesting; the C．pleasant; the D．interested;5. --- ________ did your uncle leave his home town?.--- Let me see. He _______ for nearly twenty years.A．When; has left B．When; has been awayC．How long; has left D．How long; has been away6. There __________great changes in our hometown in the past fifteen years.A．has been B．have beenC．was D．were7. -- Has your sister come back? --Yes, she has. She______ back two days ago.A．came B．has cameC．has come D．has been8. ---Have you seen Dr. Adams recently?---No. He __________ Hong Kong for an important meeting. He’ll come back tomorrow.A．has gone in B．has been in C．has gone to D．has been to9. Since few years ago, all the supermarkets have ________ free plastic bags.A．to stop to provide B．to stop providingC．stopped to provide D．stopped providing10. How much time did you spend the new words in Unit 10?A．to learn B．learning C．learned D．learn 二、完型填空11. A rich man wanted to go____a trip to another town．He wanted to take things to____and also wanted to buy things．He decided to take ten servants(仆人)____him．They would carry the things to sell and also food____on the way．He said to one of his servants，‘You are the youngest and the thinnest of all my servants，so you can't carry a heavy load(担)．You must choose the lightes t load to carry．’The servant pointed(指)to the biggest load which was bread to eat on the way．The rich man said，‘You are foolish．That is the heaviest load．’____the s ervant lifted up the load gladly and they started their trip．They walked____four hours，then they stopped____a rest．They all ate some of the bread．Now there was less bread for the servant to carry．Every day they____more bread and there was less to carry．His load grew(变得)smaller and fighter every day．At the end the clever servant____nothing____．【小题1】A．in B．at C．to D．on【小题2】A．buy B．use C．see D．sell【小题3】A．on B．with C．in D．without【小题4】A．to look B．use C．to eat D．throw【小题5】A．But B．And C．So D．For【小题6】A．at B．since C．for D．on【小题7】A．to B．for C．in D．on【小题8】A．eat B．eating C．ate D．use【小题9】A．didn't B．can’t C．buy D．had【小题10】A．buy B．to eat C．to carry D．carry三、阅读单选12. It’s Really a Miracle (奇迹)Mr. Clarke works in New York and he brought his family to China last summer. They visited many places of interest and had a good time here. Before they l eft for New York, the Clarkes climbed the Great Wall. It was the greatest project over two thousand years ago. They took a lot of photos there and then they had a picnic under a big tree. Suddenly it began to rain and they hurried to the car. And when they returned to the hotel, they couldn’t find the bag in which t heir expensive camera was. They were all sorry for it. They could buy another camera but had no time to go to the Great Wall again. They could not miss th e plane!That evening they didn’t have supper. Mr. Clarke hoped to make them happy, so he said, “Well, let me tell you a story. An old man lived in a sixty-storey bui lding. One day he fell down from it when he was cleaning the window. But he didn’t hurt himself.”“It was a miracle!” called out his children, “Why?”“Because he lived on the first floor!”They all began to laugh while two policemen with a bag came in. They said a Chinese boy found it under a big tree and he asked them to find out who lost i t.“It’s really a miracle!” the Clarkes said happily.【小题1】Where did the Clarkes enjoy themselves before they left for New York?A．In London.B．In Beijing.C．In Shanghai.D．In Hong Kong.【小题2】Where did the Clarkes left their bag?A．They left their bag on the Great Wall.B．They left their bag in the car.C．They left their bag under a big tree.D．They left their bag in the plane.【小题3】Why didn’t they have anything that evening?A．Because they were sorry for losing the camera.B．Because they were not hungry.C．Because they had no time to have supper.D．Because they had nothing to eat.【小题4】What did Mr. Clarke tell a story to his family for?A．His children asked him to do so.B．He wanted to make his family happy.C．He wanted to tell them a miracle.D．He liked telling stories.【小题5】Who found the bag?A．Two policemen.B．A Chinese boy.C．A Chinese girl.D．An American boy.13. Every year thousands of young people in England finish school and then take a year off before they start work or go to university. Some young people g o to other countries and work as volunteers (志愿者). V olunteers give their time to help people. For example, they work in schools or hospitals, or they do s omething helpful for the environment.Pauline Jones, 18, lives in Cardiff, Wales. Next year she is going to university to study Chinese, but now she’s living in Belize. Pauline says, “I’m working with other people here to save the coral reefs (珊瑚礁) in the sea near Belize. The reefs here are beautiful, but if the sea water is very polluted, the coral will die. I’m helping to do research on the coral and the fish that live around the reefs. All over the world, coral reefs are dying. We need to do something about t he problem before it’s too late.”“I’m staying with a family here and I help do some housework. I don’t get any money, butthat’s OK. I love my work here, and I’m learning a lot about the people of Belize—and myself!After I finish my work, I want to stay here for another three months. I want to travel aroundBelize and Central America.”【小题1】Some young people from England _______ after they finish school.A．go to university abroadB．spend one year abroad as volunteersC．go to work for money四、填空A ．EnglandB ．ChinaC ．BelizeD ．Cardiff【小题3】 Pauline Jones is _______ with other people.A ．studying Chinese in a university B ．working to save the coral reefs C ．helping do some housework D ．doing some research in Wales【小题4】From the passage, we know that the coral reefs ______.A ．will die because of the pollution B ．are not as beautiful as before C ．cannot live without fish in the sea D ．will probably be sold for money【小题5】 Pauline Jones wants to after she finishes her work as a volunteer.A ．stay there for another year B ．go back home to start work C ．learn about the people home D ．travel around Central America14. Do you go to school by bus ？It is very important for you to know how to be safe when taking a bus ，no matter whether you like it or not.First ，don't run to the bus stop ，but walk. While you are at the bus stop ，you should wait in a safe place. Do not run or play while waiting. And never get into a car with a stranger.Second ，don't talk in a loud voice when you are on the bus ，so the driver will not be disturbed （打扰）.If you need to talk with the bus driver ，yo u'd better wait until the bus stop. Never throw things on the bus or out of the windows. Never play near the emergency exit （紧急出口）.When there is a fi re ，the most important thing is to break the window with a hammer or any sharp things and then jump out.Third ，when you are getting off the bus ，make sure you walk （not run ）three more steps away from the door. This is the best place to be around a bu s. Stay away from the bus wheels and watch out for moving cars ！Last ，if you leave something on the bus ，never return （回到）to the bus to get it. The driver may not see you come back and he may begin moving t he bus. Also ，if you drop something near the bus ，tell the driver before you try to pick it up ，so he will know where you are.【小题1】 to be safe when taking a bus?Before getting on a bus【小题2】 to the bus stop. Wait in a safe place.Never get into a car with a 【小题3】 .【小题2】Pauline Jones, an eighteen-year-old girl, is living in _______ now.D ．start work in schools or hospitals五、根据句意填空On the bus【小题7】 getting off the bus15. Now there is a family problem. Nearly every parent says that we never grow up. In fact we are probably 16 or 17 years old. In their eyes, we are always l ittle ones and often do wrong things. For example, when I need to stay at home alone, they always worry about me and my life without them.Most parents always think that they have offered the best things they can to make their children live in a comfortable world. They buy their children pretty c lothes, cool shoes, everything that they can for their dear children. In return, they only want their children to get good results in the exams.But why still can’t their children understand them? Does it mean that we still want more material(物质) things? No. As a matter of fact, what we want is a tr ue family. What does a true family mean”? I think it means a place where we can hide ourselves from the cold world outside. From here, we can get warmth,we can get consolation(安慰), and we can get happiness. And one important thing is that we should be stronger and more confident(自信的) in the outside world because we know that we have a true family.So I think that parents should sit down to talk with their children to let them know that they have a true family, so the children and their parents could unders tand each other more and more. Then, parents will not treat their children as little ones.【小题1】In whose eyes are we little children?【小题2】What do most parents want to get from their children?【小题3】What do the children really want?【小题4】What can we get from a true family?【小题5】What do you think parents should do to make their children understand them more? (自拟一句作答)16. 根据句意、首字母或汉语意思完成单词【小题1】When you smile or laugh, your body ____________ (放松).【小题2】We can usually type （打字）words into the computer with a_______（键盘）．【小题3】The frog was too tired and it rested at the_______（底部）of the well.k up the things near the bus.bus to get the things that you leave. Tell the bus driver before you 【小题10】to pic Walk three more 【小题8】away from the door.Don't 【小题9】back to the 【小题6】the window when there is a fire.s.Don't talk 【小题4】.Don't throw 【小题5】on the bus or out of the window六、看图作文17. 用所给词的适当形式填空。