线性规划模型 实验报告
- 格式:doc
- 大小:78.00 KB
- 文档页数:6

数学建模作业(实验3线性规划实验)基本实验1.生产计划安排某公司使用三种操作装配三种玩具——玩具火车、玩具卡车和玩具汽车。
对于三种操作可用时间限制分别是每天430分钟、460分钟和420分钟, 玩具火车、玩具卡车和玩具汽车的单位收入分别是3美元、2美元和5美元。
每辆玩具火车在三种操作的装配时间分别是1分钟, 3分钟和1分钟。
每辆玩具卡车和每辆玩具汽车相应的时间是( 2, 0, 4) 和( 1, 2, 0) 分钟( 零时间表示不使用该项操作) 。
( 1) 将问题建立成一个线性规划模型, 确定最优的生产方案。
( 2) 对于操作1, 假定超过它当前每天430分钟能力的任何附加时间必须依靠每小时50美元的加班获得。
每小时成本包括劳动力和机器运行费两个方面。
对于操作1, 使用加班在经济上有利吗? 如果有利, 最多加多少时间?( 3) 假定操作2的操作员已同意每天加班工作两小时, 加班费是45美元一小时。
还有, 操作自身的成本是一小时10美元。
这项活动对于每天收入的实际结果是什么?( 4) 操作3需要加班时间吗?解答解:设生产玩具火车、玩具卡车和玩具汽车的数量分别为X1, X2, X3, 则目标函数为:3X1+2X2+5X3约束条件:X1+2X2+X3<=4303X1+2X3<=460X1+4X2<=420X1>=0; X2>=0; X3>=0最优值为目标函数取得最大。
LINGO程序max=3*x1+2*x2+5*x3;x1+2*x2+x3<=430;3*x1+2*x3<=460;x1+4*x2<=420;运行结果Globaloptimalsolutionfound.Objectivevalue:1350.000Infeasibilities:0.000000Totalsolveriterations:2ModelClass:LPTotalvariables:3Nonlinearvariables:0Integervariables:0Totalconstraints:4Nonlinearconstraints:0Totalnonzeros:10Nonlinearnonzeros:0VariableValueReducedCostX10.0000004.000000X2100.00000.000000X3230.00000.000000RowSlackorSurplusDualPrice11350.0001.00000020.0000001.00000030.0000002.000000420.000000.000000( 1) 由运行结果可得, 最优的生产方案为:玩具火车、玩具卡车和玩具汽车的生产数量分别为: 0、100、230; 收入为1350.( 2) 由DualPrice第二行可知, 当操作1每增加1分钟收入增加1美元, 因此50/60<1, 使用加班在经济上是有利的; Rangesinwhichthebasisisunchanged: ObjectiveCoefficientRanges:CurrentAllowableAllowable VariableCoefficientIncreaseDecreaseX13.0000004.000000INFINITYX22.0000008.0000002.000000X35.000000INFINITY2.666667RighthandSideRanges:CurrentAllowableAllowableRowRHSIncreaseDecrease2430.000010.00000200.00003460.0000400.000020.000004420.0000INFINITY20.00000分析可知, 最多增加10分钟。

1、线性规划和整数规划实验1、加工奶制品的生产计划(1)一奶制品加工厂用牛奶生产A1, A2两种奶制品,1桶牛奶可以在甲车间用12小时加工成3千克A1产品,或者在乙车间用8小时加工成4千克A2 产品.根据市场需求,生产的A1、A2产品全部能售出,且每千克A1产品获利24元,每千克A2产品获利16元.现在加工厂每天能得到50桶牛奶的供应,每天正式工人总的劳动时间为480小时,并且甲车间的设备每天至多能加工100 千克A1产品,乙车间的设备的加工能力可以认为没有上限限制.试为该厂制订一个生产计划,使每天获利最大,并进一步讨论以下3个附加问题: (i)若用35元可以买到1桶牛奶,是否应作这项投资?若投资,每天最多购买多少桶牛奶?(ii)若可以聘用临时工人以增加劳动时间,付给临时工人的工资最多是每小时几元?(iii)由于市场需求变化,每千克A1产品的获利增加到30元,是否应改变生产计划?(2)进一步,为增加工厂获利,开发奶制品深加工技术.用2小时和3元加工费,可将1千克A1加工成0.8千克高级奶制品B1,也可将1千克A2加工成0.75千克高级奶制品B2,每千克B1可获44元,每千克B2可获32元.试为该厂制订一个生产销售计划,使每天获利最大,并进一步讨论以下问题:(i)若投资30元可增加供应1桶牛奶,投资3元可增加1小时劳动时间,是否应作这项投资?若每天投资150元,或赚回多少?(ii)每千克高级奶制品B1, B2的获利经常有10%的波动,对制订的生产销售计划有无影响?若每千克B1的获利下降10%,计划是否应作调整?解:由已知可得1桶牛奶,在甲车间经过十二小时加工完成可生产3千克的A1,利润为72元;在乙车间经八小时加工完成可生产四千克的A2,利润为64元。
利用lingo软件,编写如下程序:model:max=24*3*x1+16*4*x2;s.t.12*x1+8*x2≤480;x1+x2≤50;3*x1≤100;X1≥0,x2≥0end求解结果及灵敏度分析为:Objective value: 3360.000Total solver iterations: 2Variable Value Reduced CostX1 20.00000 0.000000X2 30.00000 0.000000Row Slack or Surplus Dual Price1 3360.000 1.0000002 0.000000 2.0000003 0.000000 48.000004 40.00000 0.000000Objective Coefficient RangesCurrent Allowable Allowable Variable Coefficient Increase DecreaseX1 72.00000 24.00000 8.000000X2 64.00000 8.000000 16.00000Righthand Side RangesRow Current Allowable AllowableRHS Increase Decrease2 480.0000 53.33333 80.000003 50.00000 10.00000 6.6666674 100.0000 INFINITY 40.00000 分析结果:1)从结果可以看出在供应甲车间20桶、乙车间30桶的条件下,获利可以达到最大3360元。

一、实验目的通过本次实验,了解线性规划的基本原理和方法,掌握线性规划模型的建立和求解过程,提高解决实际问题的能力。
二、实验内容1. 线性规划模型的建立2. 利用Lingo软件进行线性规划模型的求解3. 分析求解结果,进行灵敏度分析三、实验步骤1. 建立线性规划模型以某公司生产问题为例,建立线性规划模型。
设该公司有三种产品A、B、C,每种产品分别需要原材料X1、X2、X3,且原材料的价格分别为p1、p2、p3。
公司拥有一定的生产设备,每种产品的生产需要消耗一定的设备时间,设备时间的价格为p4。
设A、B、C产品的生产量分别为x1、x2、x3,原材料消耗量分别为y1、y2、y3,设备使用量分别为z1、z2、z3。
目标函数:最大化利润Z = p1x1 + p2x2 + p3x3 - p4(z1 + z2 + z3)约束条件:(1)原材料消耗限制:y1 ≤ 10x1,y2 ≤ 8x2,y3 ≤ 5x3(2)设备使用限制:z1 ≤ 6x1,z2 ≤ 4x2,z3 ≤ 3x3(3)非负限制:x1 ≥ 0,x2 ≥ 0,x3 ≥ 0,y1 ≥ 0,y2 ≥ 0,y3 ≥ 0,z1 ≥ 0,z2 ≥ 0,z3 ≥ 02. 利用Lingo软件进行线性规划模型的求解打开Lingo软件,按照以下步骤输入模型:① 在“Model”菜单中选择“Enter Model”;② 输入目标函数:@max = p1x1 + p2x2 + p3x3 - p4(z1 + z2 + z3);③ 输入约束条件:@and(y1 <= 10x1, y2 <= 8x2, y3 <= 5x3);@and(z1 <= 6x1, z2 <= 4x2, z3 <= 3x3);@and(x1 >= 0, x2 >= 0, x3 >= 0, y1 >= 0, y2 >= 0, y3 >= 0, z1 >= 0, z2 >= 0, z3 >= 0);④ 在“Model”菜单中选择“Solve”进行求解。
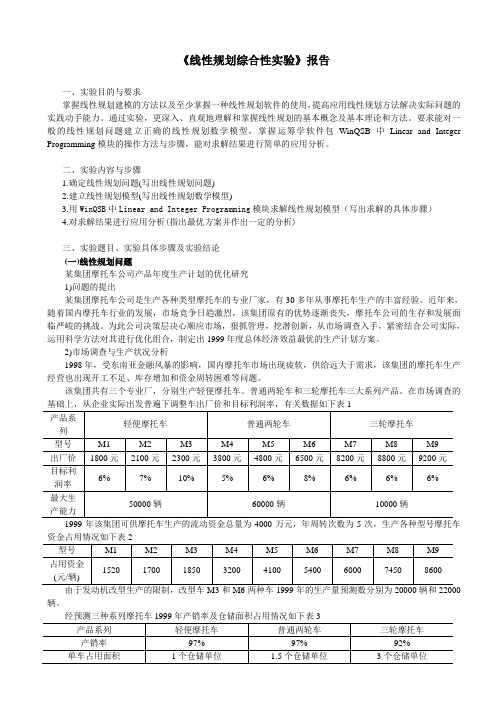
《线性规划综合性实验》报告一、实验目的与要求掌握线性规划建模的方法以及至少掌握一种线性规划软件的使用,提高应用线性规划方法解决实际问题的实践动手能力。
通过实验,更深入、直观地理解和掌握线性规划的基本概念及基本理论和方法。
要求能对一般的线性规划问题建立正确的线性规划数学模型,掌握运筹学软件包WinQSB中Linear and Integer Programming模块的操作方法与步骤,能对求解结果进行简单的应用分析。
二、实验内容与步骤1.确定线性规划问题(写出线性规划问题)2.建立线性规划模型(写出线性规划数学模型)3.用WinQSB中Linear and Integer Programming模块求解线性规划模型(写出求解的具体步骤)4.对求解结果进行应用分析(指出最优方案并作出一定的分析)三、实验题目、实验具体步骤及实验结论(一)线性规划问题某集团摩托车公司产品年度生产计划的优化研究1)问题的提出某集团摩托车公司是生产各种类型摩托车的专业厂家,有30多年从事摩托车生产的丰富经验。
近年来,随着国内摩托车行业的发展,市场竞争日趋激烈,该集团原有的优势逐渐丧失,摩托车公司的生存和发展面临严峻的挑战。
为此公司决策层决心顺应市场,狠抓管理,挖潜创新,从市场调查入手,紧密结合公司实际,运用科学方法对其进行优化组合,制定出1999年度总体经济效益最优的生产计划方案。
2)市场调查与生产状况分析1998年,受东南亚金融风暴的影响,国内摩托车市场出现疲软,供给远大于需求,该集团的摩托车生产经营也出现开工不足、库存增加和资金周转困难等问题。
该集团共有三个专业厂,分别生产轻便摩托车、普通两轮车和三轮摩托车三大系列产品。
在市场调查的基础上,从企业实际出发普遍下调整车出厂价和目标利润率,有关数据如下表1资金占用情况如下表2由于发动机改型生产的限制,改型车M3和M6两种车1999年的生产量预测数分别为20000辆和22000辆。

3 线性规划实验3.1实验目的与要求●学会建立线性规划模型●学会LINGO软件的基本使用方法,求解线性规划问题●学会对线性规划问题进行灵敏度分析,以及影子价格的意义3.2基本实验1.生产计划安排与灵敏度分析解:(1)假设最后总生产得到的Ⅰ型产品为x1kg,Ⅱ型产品为x2kg,那么它们必须同时满足以下条件:Max Z=130x1+400x2-100(x1+x2/0.33)x1+(x2)/0.33≤902x1+3(x2)/0.33≤200x2≤40LINGO程序:Max =130*x1+400*x2-100*(x1+x2/0.33);x1+x2/0.33<=90;2*x1+3*x2/0.33<=200;x2<=40;结果:Global optimalsolutionfound.Objective value:2740.000Infeasibilities: 0.000000Total solver iterations:3ModelClass:LPTotal variables: 2Nonlinear variables: 0Integer variables: 0Total constraints: 4Nonlinear constraints: 0Total nonzeros:7Nonlinear nonzeros:0VariableValue Reduced CostX170.000000.000000X2 6.6000000.000000Row Slack orSurplus Dual Price1 2740.0001.00000020.00000026.000003 0.0000002.000000433.40000 0.000000即:最优的方案是Ⅰ型产品为70kg,Ⅱ型产品为6.6kg。
(2)Max Z=130x1+400x2-100(x1+x2/0.33)x1+(x2)/0.33≤872x1+3(x2)/0.33≤200x2≤40LINGO程序:Max=130*x1+400*x2-100*(x1+x2/0.33);x1+x2/0.33<=87;2*x1+3*x2/0.33<=200;x2<=40;结果:Variable Value Reduced CostX1 61.00000 0.000000X28.580000 0.000000Row Slack or Surplus Dual Price1 2662.000 1.00000020.000000 26.000003 0.000000 2.000000431.420000.000000那么公司得到的利润为:2662元(3)如果产品Ⅱ的销售价格变为395元/千克,最优解没有变化。

一、实验目的本次实验旨在通过构建和求解规划模型,加深对线性规划、整数规划等规划方法的理解,提高运用这些方法解决实际问题的能力。
实验过程中,我们将学习如何将实际问题转化为数学模型,并运用相应的算法求解模型,最终得到问题的最优解。
二、实验内容1. 线性规划模型(1)问题描述:某公司计划生产A、B两种产品,已知生产A产品需要2小时机器加工,3小时人工装配;生产B产品需要1小时机器加工,2小时人工装配。
公司每月可提供的机器加工时间为120小时,人工装配时间为180小时。
A、B两种产品的利润分别为300元、200元。
请确定生产A、B两种产品的最优数量,以实现最大利润。
(2)模型构建:设生产A、B两种产品的数量分别为x、y,则目标函数为:Max Z = 300x + 200y约束条件为:2x + y ≤ 1203x + 2y ≤ 180x ≥ 0,y ≥ 0(3)求解过程:运用单纯形法求解该线性规划模型,得到最优解为x = 30,y = 60,最大利润为Z = 9600元。
2. 整数规划模型(1)问题描述:某物流公司负责运输货物,现有5辆卡车可供使用,每辆卡车可装载的货物重量分别为2吨、3吨、4吨、5吨、6吨。
货物重量分别为10吨、12吨、14吨、16吨、18吨。
请确定每辆卡车装载的货物重量,以满足装载要求,并使运输成本最低。
(2)模型构建:设每辆卡车装载的货物重量分别为x1、x2、x3、x4、x5,则目标函数为:Min Z = 2x1 + 3x2 + 4x3 + 5x4 + 6x5约束条件为:x1 + x2 + x3 + x4 + x5 ≥ 10x1 + x2 + x3 + x4 + x5 ≥ 12x1 + x2 + x3 + x4 + x5 ≥ 14x1 + x2 + x3 + x4 + x5 ≥ 16x1 + x2 + x3 + x4 + x5 ≥ 18x1 ≥ 0,x2 ≥ 0,x3 ≥ 0,x4 ≥ 0,x5 ≥ 0(3)求解过程:运用分支定界法求解该整数规划模型,得到最优解为x1 = 0,x2 = 2,x3 = 3,x4 = 4,x5 = 5,最小运输成本为Z = 20吨。

线性规划实验报告线性规划实验报告1.路径规划问题第一步:在excel表格中建立如下表格,详细列名各节点路线及其权重。
起点终点权数0-1 节点进出和V1 V2 5 V1 1V1 V3 2 V2 0V2 V4 2 V3 0V2 V5 7 V4 0V3 V4 7 V5 0V3 V6 4 V6 0V4 V5 6 V7 -1V4 V6 2V5 V6 1V5 V7 3V6 V7 6 目标第二步:在进出和一列以公式表示各节点的进出流量和。
V1=V12+V13;V2=V24+V25-V12;V3=V34+V36-V13;V4=V45+V46-V24-V34;V5=V56+V57-V25-V45;V6=V67-V36-V46-V56V7=-V57-V67.第三步:设置目标函数为SUMPRODUCT(C2:C12,D2:D12)第四步:设置可变单元格和限制条件。
选定0-1一列,D2:D12为可变单元格。
可变单元格数值介于0-1之间,且为整数。
进出和数值与设定值相等。
第五步:规划求解,结果如下。
由表可知,从V1至V7的最短路径为V1——V3——V6——V7,最小目标值为12。
起点终点权重0-1 节点进出和V1 V2 5 0 V1 1 = 1 V1 V3 2 1 V2 0 = 0 V2 V4 2 0 V3 0 = 0 V2 V5 7 0 V4 0 = 0 V3 V4 7 0 V5 0 = 0 V3 V6 4 1 V6 0 = 0 V4 V5 6 0 V7 -1 = -1 V4 V6 2 0V5 V6 1 0V5 V7 3 0V6 V7 6 1 目标函数12Microsoft Excel 11.0 运算结果报告工作表 [复件 11.xls]Sheet2报告的建立: 2013-12-12 14:07:00目标单元格 (最小值)单元格名字初值终值$F$12 目标函数进出和12 12可变单元格单元格名字初值终值$D$2 V2 0-1 2.22E-16 0$D$3 V3 0-1 1 1$D$4 V4 0-1 0 0$D$5 V5 0-1 2.22045E-16 0$D$6 V4 0-1 0 0$D$7 V6 0-1 1 1$D$8 V5 0-1 0 0$D$9 V6 0-1 0 0$D$10 V6 0-1 0 0$D$11 V7 0-1 2.22045E-16 0$D$12 V7 0-1 1 1约束单元格名字单元格值公式状态型数值$F$2 V1 进出和 1 $F$2=$I$2 未到限制值$F$3 V2 进出和0 $F$3=$I$3 未到限制值$F$4 V3 进出和0 $F$4=$I$4 未到限制值$F$5 V4 进出和0 $F$5=$I$5 未到限制值$F$6 V5 进出和0 $F$6=$I$6 未到限制值$F$7 V6 进出和0 $F$7=$I$7 未到限制值$F$8 V7 进出和-1 $F$8=$I$8 未到限制值$D$2 V2 0-1 0 $D$2<=1 未到限制值1$D$3 V3 0-1 1 $D$3<=1 到达限制值$D$4 V4 0-1 0 $D$4<=1 未到限制值1$D$5 V5 0-1 0 $D$5<=1 未到限制值1$D$6 V4 0-1 0 $D$6<=1 未到限制值1$D$7 V6 0-1 1 $D$7<=1 到达限制值$D$8 V5 0-1 0 $D$8<=1 未到限制值1$D$9 V6 0-1 0 $D$9<=1 未到限制值1$D$10 V6 0-1 0 $D$10<=1 未到限制值1$D$11 V7 0-1 0 $D$11<=1 未到限制值1$D$12 V7 0-1 1 $D$12<=1 到达限制值$D$2 V2 0-1 0 $D$2>=0 到达限制值$D$3 V3 0-1 1 $D$3>=0 未到限制值1$D$4 V4 0-1 0 $D$4>=0 到达限制值$D$5 V5 0-1 0 $D$5>=0 到达限制$D$6 V4 0-1 0 $D$6>=0 到达限制值$D$7 V6 0-1 1 $D$7>=0 未到限制值1$D$8 V5 0-1 0 $D$8>=0 到达限制值$D$9 V6 0-1 0 $D$9>=0 到达限制值$D$10 V6 0-1 0 $D$10>=0 到达限制值$D$11 V7 0-1 0 $D$11>=0 到达限制值$D$12 V7 0-1 1 $D$12>=0 未到限制值1$D$2 V2 0-1 0 $D$2=整数到达限制值$D$3 V3 0-1 1 $D$3=整数到达限制值$D$4 V4 0-1 0 $D$4=整数到达限制值$D$5 V5 0-1 0 $D$5=整数到达限制值$D$6 V4 0-1 0 $D$6=整数到达限制值$D$7 V6 0-1 1 $D$7=整数到达限制值$D$8 V5 0-1 0 $D$8=整数到达限制$D$9 V6 0-1 0 $D$9=整数到达限制值$D$10 V6 0-1 0 $D$10=整数到达限制值$D$11 V7 0-1 0 $D$11=整数到达限制值$D$12 V7 0-1 1 $D$12=整数到达限制值2.运用Excel构建线性规划模型与求解实验报告一、实验目的1.掌握线性规划问题建模基本方法。

《数学建模与数学实验》实验报告实验五:线性规划模型实验专业、班级数学09B 学号094080144 姓名徐波课程编号实验类型验证性学时 2实验(上机)地点同析楼4栋404 完成时间2012-6-10任课教师李锋评分一、实验目的及要求掌握数学软件lingo的基本用法和一些常用的规则,能用该软件进行基本线性规划运算,并能进行的编程,掌握线性规划模型的。
二、借助数学软件,研究、解答以下问题某电力公司经营两座发电站,发电站分别位于两个水库上,已知发电站A可以将A的一万m^3 的水转换成400千度电能,发电站B能将水库B的一万立方米转化成200千度电能。
发电站A,B每个月最大发电能力分别是60000千度,35000千度,每个月最多有50000千度能够以200元/千度的价格出售,多余的电能只能够以140元/千度的价格出售,水库A,B的其他有关数据如下:水库A 书库B水库最大蓄水量2000 1500水源本月流入水量200 40水源下月流入水量130 15水库最小蓄水量1200 800水库目前蓄水量1900 850设计该电力公司本月和下月的生产计划。
本月的情况:解:设本月高价卖出的水量是u,低价卖出的数量是v,A,B书库用来发电的水量好似xa,xb,从水库里放走的水量是ya,yb,水库月末剩余的水量分别是za,zb;建立模型如下:目标函数:、Max=200u+140v约束条件:每个月发电量与卖电量相等:400*x1+200*x2=u+v;水库发电后剩余水量及消耗水量与发电前的水量守恒:X1+y1+z1=2100;X2+y2+z2=890+x1+y1;其他约束条件:400*x1a<=60000;200*x1a<=35000;1200<=z1a<=2000;800<=z2a<=1500;u1<=50000;现在进行两个月同时计算:设本月和下月高价卖出的水量是u1,u2,低价卖出的水量是v1,v2,A,B水库用来发电的水量是xa1,xa2,xb1,xb2,从水库直接放走的水量分别是ya1,ya2,yb1,yb2,水库月末剩余水量分别是za1,za2,zb1,zb2.建立模型如下:目标函数:Max=200*(u1+u2)+140*(v1+v2)约束条件:每个月发电量与卖电量相等:400*xa1+200*xb1=u1+v1;400*xa2+200*xb2=u2+v2;水库发电后剩余水量及消耗水量与发电前的水量守恒:xa1+ya1+za1=2100;xb1+yb1+zb1=890+xa1+ya1;xb2+yb2+zb2=zb2+15+xa2+ya2;xa2+ya2+za2=za1+130;其他约束条件:400*xa1<=60000;400*xa2<=60000;200*xb1<=35000;200*xb2<=35000;1200<=za1<=2000;1200<=za2<=2000;800<=zb1<=1500;800<=zb2<=1500;u1<=50000;u2<=50000;编程实现如下:model:max=200*u+140*v;400*x1+200*x2=u+v;X1+y1+z1=2100;X2+y2+z2=890+x1+y1;400*x1<=60000;200*x2<=35000;Z1>=1200;Z1<=2000;Z2>=800;Z2<=1500;u<=50000;end解得:Global optimal solution found.Objective value: 0.1630000E+08Total solver iterations: 5Variable Value Reduced Cost U 50000.00 0.000000V 45000.00 0.000000X1 150.0000 0.000000 X2 175.0000 0.000000 Y1 0.000000 0.000000 Z1 1950.000 0.000000 Y2 0.000000 0.000000 Z2 865.0000 0.000000Row Slack or Surplus Dual Price1 0.1630000E+08 1.0000002 0.000000 -140.00003 0.000000 0.0000004 0.000000 0.0000005 0.000000 140.00006 0.000000 140.00007 750.0000 0.0000008 50.00000 0.0000009 65.00000 0.00000010 635.0000 0.00000011 0.000000 60.000000编程实现如下:model:max=200*(u1+u2)+140*(v1+v2);400*x1a+200*x2a-u1+v1=0;400*x1b+200*x2b=u2+v2;X1a+y1a+z1a=2100;X2b+y2b+z2b=zb2+15+x1b+y1b;X2a+y2a+z2a=890+x1a+y1a;X1a+y1b+z1b=z1a+130;400*x1a<=60000;400*x1b<=60000;200*x2a<=35000;200*x2b<=35000;Z1a<=2000;Z1a>=1200;Z1b<=2000;Z1a>=1200;Z2a<=1500;Z2a>=800;Z2b>=800;Z2b<=1500;u1<=50000;u2<=50000;end解得:Global optimal solution found.Objective value: 0.3330000E+08Total solver iterations: 0Variable Value Reduced Cost U1 50000.00 0.000000 U2 50000.00 0.000000 V1 50000.00 0.000000 V2 45000.00 0.000000 X1A 0.000000 56000.00 X2A 0.000000 28000.00 X1B 150.0000 0.000000 X2B 175.0000 0.000000 Y1A 900.0000 0.000000 Z1A 1200.000 0.000000 Y2B 0.000000 0.000000 Z2B 800.0000 0.000000 ZB2 810.0000 0.000000 Y1B 0.000000 0.000000 Y2A 990.0000 0.000000 Z2A 800.0000 0.000000 Z1B 1330.000 0.000000Row Slack or Surplus Dual Price1 0.3330000E+08 1.0000002 0.000000 140.00003 0.000000 -140.00004 0.000000 0.0000005 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 60000.00 0.0000009 0.000000 140.000010 35000.00 0.00000011 0.000000 140.000012 800.0000 0.00000013 0.000000 0.00000014 670.0000 0.00000015 0.000000 0.00000016 700.0000 0.00000017 0.000000 0.00000018 0.000000 0.00000019 700.0000 0.00000020 0.000000 340.000021 0.000000 60.00000由上可知,最大值是0.3260000E+08,每月A,B厂发电用水量是150,175,150,175三、本次实验的难点分析实验过程中遇到了一些问题:对掌握lingo的基本用法有所欠缺,本实验中存在偏差。


实验名称:第三章线性规划一、实验内容与要求用linprog语句求解各种线性规划问题,对生产实际中的问题,进行预测。
二、实验软件MATLAB7.0三、实验内容:1、某鸡场有1000只鸡,用动物饲料和谷物混合喂养。
每天每只鸡平均食混合饲料0.5KG,其中动物饲料所占比例不能少于20%。
动物饲料每千克0。
30元,谷物饲料每千克0。
18元,饲料公司每周仅保证供应谷物饲料6000KG,问饲料怎样混合,才能使成本最低?程序:C=[150 90];A=[1 1];B=[12/7];Aeq=[0 1];beq=[0,8];vlb=[0.2 0];vub=[];[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)实验结果:2、某工厂用A1、A2两台机床加工B1、B2、B3三种不同零件。
已知在一个生产周期内A1只能工作80机时;A2只能工作100机时。
一个生产周期内计划加工B1为70件、B2为50件、把为20件。
两台机床加工每个零件的时间和加工每个零件的成本,分别如下列各表所示:加工每个零件时间表(单位:机时/个)加工每个零件成本表(单位:元/个)问怎样安排两台机床一个周期的加工任务,才能使加工成本最低?程序:C=[2;3;5;3;3;6];A=[1 2 3 0 0 00 0 0 1 1 3-1 0 0 —1 0 00 -2 0 0 -1 00 0 -2 0 0 -3];B=[80;100;—70;-50;—20];Aeq=[];beq=[];vlb=[0;0;0;0;0;7];vub=[];[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)实验结果:四、实验体会。

实验报告填写说明
(实验项目名称、实验项目类型必须与实验教学大纲保持一致)
1.实验环境:
实验用的硬件、软件环境。
2.实验目的:
根据实验教学大纲,写出实验的要求和目的。
3.实验原理:
简要说明本实验项目所涉及的理论知识。
4.实验步骤:
这是实验报告极其重要的容。
对于验证性验,要写清楚操作方法,需要经过哪几个步骤来实现其操作。
对于设计性和综合性实验,还应写出设计思路和设计方法。
对于创新性实验,还应注明其创新点。
5.实验结论:
根据实验过程中得到的结果,做出结论。
6.实验总结:
本次实验的收获、体会和建议。
7.指导教师评语及成绩:
指导教师依据学生的实际报告内容,给出本次实验报告的评价和成绩。
附录1:源程序。
线性规划模型实验一、实验目的:掌握线性规划模型的建立与Lingo求解方法。
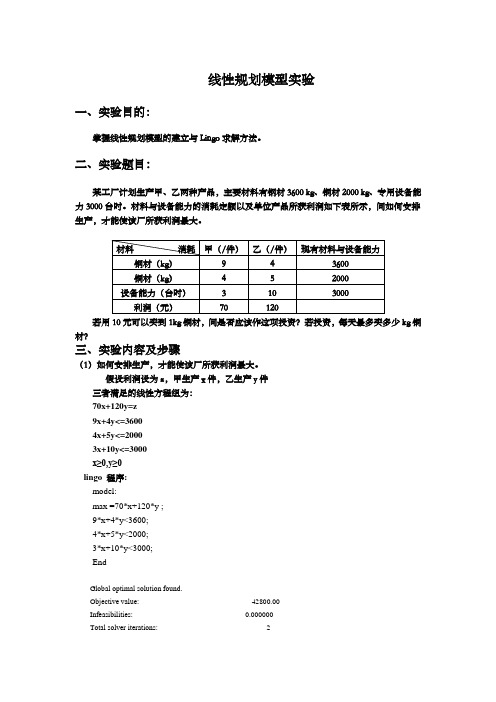
二、实验题目:某工厂计划生产甲、乙两种产品,主要材料有钢材3600 kg、铜材2000 kg、专用设备能力3000台时。
材料与设备能力的消耗定额以及单位产品所获利润如下表所示,问如何安排生产,才能使该厂所获利润最大。
若用10元可以买到1kg铜材,问是否应该作这项投资?若投资,每天最多买多少kg铜材?三、实验内容及步骤(1)如何安排生产,才能使该厂所获利润最大。
假设利润设为z,甲生产x件,乙生产y件三者满足的线性方程组为:70x+120y=z9x+4y<=36004x+5y<=20003x+10y<=3000x≥0,y≥0lingo 程序:model:max =70*x+120*y ;9*x+4*y<3600;4*x+5*y<2000;3*x+10*y<3000;EndGlobal optimal solution found.Objective value: 42800.00Infeasibilities: 0.000000Total solver iterations: 2Variable Value Reduced CostX 200.0000 0.000000Y 240.0000 0.000000Row Slack or Surplus Dual Price1 42800.00 1.0000002 840.0000 0.0000003 0.000000 13.600004 0.000000 5.200000X=200,y=240,z=42800利用matlab求下面优化问题:>> c=[-70,-120];A=[9 4;4 5;3 10];b=[3600;2000;3000];Aeq=[]; beq=[];vlb=[0;0]; vub=[];[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)x =200.0000240.0000fval =-4.2800e+004所以应该甲生产200件,乙生产240件,才能使该厂所获利润最大,最大利润为42800元(2)若用10元可以买到1kg铜材,问是否应该作这项投资?若投资,每天最多买多少kg铜材?假设每天最多买t kg铜材线性方程组为:70x+120y-10t=z9x+4y<=36004x+5y<=2000+t3x+10y<=3000x≥0,y≥0lingo 程序:model:max =70*x+120*y-10*t ;9*x+4*y<3600;4*x+5*y<2000+t;3*x+10*y<3000;endGlobal optimal solution found.Objective value: 43769.23Infeasibilities: 0.000000Total solver iterations: 3Variable Value Reduced CostX 307.6923 0.000000Y 207.6923 0.000000T 269.2308 0.000000Row Slack or Surplus Dual Price1 43769.23 1.0000002 0.000000 1.1538463 0.000000 10.000004 0.000000 6.538462x=307.6923,y=207.6923,t=269.2308,Max z=43769.23利用matlab求下面优化问题:>> c=[-70 -120 +10];A=[9 4 0;4 5 -1;3 10 0];b=[3600;2000;3000];Aeq=[]; beq=[];vlb=[0;0;0]; vub=[];[x,fval]=linprog(c,A,b,Aeq,beq,vlb,vub)Optimization terminated.x =307.6923207.6923269.2308fval =-4.3769e+004所以应该做这项投资,t=269.2308,每天最多买269 kg铜材,利润为43769元。

精品文档课内实验报告课程名:运筹学任课教师:邢光军专业:信息管理与信息系统学号:B09110810姓名:陈倩宇2010/2011学年第 2 学期南京邮电大学经济与管理学院点击求解后,可得上表说明:整数规划问题有最优解,且最优解为126,2,max 10x x z === 。
下表是例1用Excell 工作表求解的求解结果,表中说明,为保证售货人员充分休息,售货人员每周工作五天,休息两天,并要求休息的两天是连续的,最少需配备的售货人员36人,星期一开始上班的12人,星期三开始上班的11人,星期五开始上班的5人,星期六开始上班的3人,星期日开始上班的5人.3 结果分析在实际应用中,最终我们得出的对于售货人员作息时间的安排,能够达到既满足工作需要,又使总共配备售货人员最少,即用最少的人力资源成本获取最大的利益。
由此我们可以发现诸如此类有关如何合理安排的问题,利用Excel进行求解既简便又快捷,表中数据可根据用户要求自行设置,在合理安排产品的生产决策上,对于研究如何合理使用企业各项经济资源,以及研究如何统筹安排,对人、财、物等现有资源进行优化组合,实现最大效能上都可以使用。
能有效地提高组织及决策的速度及准确性,并且Excel办公软件的普遍性优点使之更适合促进科学决策的信息化水平。
成绩评定:该生对待本次实验的态度□认真□良好□一般□比较差。
本次实验的过程情况□很好□较好□一般□比较差对实验结果的分析□很好□良好□一般□比较差文档书写符合规范程度□很好□良好□一般□比较差综合意见:成绩指导教师签名日期实验背景:某商场是个中型的百货商场,它对售货人员的需求经过统计分析如表1所示。
息的两天是连续的,问应该如何安排售货人员的作息,既满足了工作需要,又使配备的售货人员人数最少?。

运筹学线性规划方案实验报告一早起床,我就知道今天要写一份运筹学线性规划方案实验报告。
这个题目听起来就有点头疼,不过没关系,我已经有10年的方案写作经验了,这就好比家常便饭,慢慢来,一点一点梳理。
得给这个实验报告起个响亮的名字,我已经想好了——“最优解寻迹之旅”。
咱们就直接进入主题吧。
1.实验背景这次实验的背景是我国一家生产多种产品的企业。
这家企业生产的产品有A、B、C三种,分别需要经过甲、乙、丙三个车间进行加工。
每个车间都有一定的生产能力和生产成本,而企业的目标是最大化利润。
这就需要我们运用线性规划的方法,找出最优的生产方案。
2.实验目的本次实验的目的就是通过线性规划方法,为企业制定出最优的生产方案,使得企业在现有的生产条件下,实现利润最大化。
3.实验方法线性规划,听起来高大上,其实原理很简单。
就是用一组线性方程,来描述各种约束条件,然后找到一个目标函数,使得这个目标函数在满足约束条件的情况下达到最大值或最小值。
甲车间:A产品需要1小时,B产品需要2小时,C产品需要3小时,总时间为8小时;乙车间:A产品需要2小时,B产品需要1小时,C产品需要2小时,总时间为10小时;丙车间:A产品需要3小时,B产品需要2小时,C产品需要1小时,总时间为12小时。
然后,我们需要确定目标函数。
企业的目标是最大化利润,所以我们的目标函数就是:f(A,B,C)=10A+15B+20C其中,A、B、C分别表示三种产品的产量。
就是求解这个线性规划问题。
我们可以使用单纯形法、内点法等算法求解。
这里,我们选择使用单纯形法。
4.实验步骤(1)列出约束条件方程组;(2)确定目标函数;(3)使用单纯形法求解线性规划问题;(4)分析求解结果,确定最优生产方案。
5.实验结果A产品产量:4件B产品产量:3件C产品产量:2件将这个结果代入目标函数,我们可以得到最大利润为:f(4,3,2)=104+153+202=110所以,最优生产方案是生产4件A产品、3件B产品和2件C产品,最大利润为110。

2012——2013学年第二学期
实验报告
课程名称:数学建模
实验项目:求解线性规划问题
实验类别:综合性□设计性□√验证性□
专业班级:
姓名: xxx 学号:xxxxxxxxxxxxxxxx 实验地点:
实验时间:
指导教师:成绩:
一.实验目的
(1)用MATLAB求解线性规划问题,并对结果进行分析
(2)对实际问题建立数学模型
(3)熟悉相关软件的操作
二.实验内容
已知某工厂计划生产I,II,III三种产品,各产品需要在A、B、C设备上加工,
三. 模型建立
解设计划生产I,II,III三种产品产量为x1,x2,x3最大盈利为z
建立如下线性模型:
四. 模型求解(含经调试后正确的源程序)
编写M文件如下:
c = [-3,-2,-2.9];
A = [8,2,10;10,5,8;2,13,10];
b = [300;400;420];
vlb = [0;0;0];
vub=[];
[x,fval] = linprog(c,A,b,[],[],vlb,vub)
五.结果分析
x =
22.5333
23.2000
7.3333
fval =
-135.2667
由结果可知,I,II,III三种产品分别生产22,23,7时,有最大盈利135.
六.实验总结
本次实验主要是熟悉用MATLAB软件解决线性规划问题,对实际问题进行分析并建立数学模型,然后编程继而模型求解。
线性规划在实际生活中有重要应用,所以此类方法应该掌握。

《管理运筹学》实验报告班级2014级04班姓名杨艺玲学号2014190456 实验管理运筹学问题的计算机求解名称实验目的:通过实验学生应该熟练掌握“管理运筹学3.0”软件的使用,并能利用“管理运筹学3.0”对具体问题进行问题处理,且能对软件处理结果进行解释和说明。
实验所用软件及版本:管理运筹学3.0实验过程:(含基本步骤及异常情况记录等)一、实验步骤(以P31页习题1 为例)1.打开软件“管理运筹学3.0”2.在主菜单中选择线性规划模型,屏幕中会出现线性规划页面3.在点击“新建”按钮以后,按软件的要求输入目标函数个数和约束条件个数,输入目标函数级约束条件的歌变量的系数和b值,并选择好“≤”、“≥”或“=”,如图二所示,最后点击解决4.注意事项:(1)输入的系数可以是整数、小数,但不能是分数,要把分数化为小数再输入。
(2)输入前要合并同类项。
当约束条件输入完毕后,请点击“解决”按钮,屏幕上讲显现线性规划问题的结果,如图所示5.输出结果如下5.课后习题: 一、P31习题1某家具公司生产甲、乙两种型号的组合柜,每种组合柜需要两种工艺(制白坯和油漆).甲型号组合柜需要制白坯6工时,油漆8工时:乙型号组合柜需要制白坯12工时,油漆4工时.已知制白坯工艺的生产能力为120工时/天,油漆工艺的生产能力为64工时/天,甲型号组合柜单位利润200元,乙型号组合柜单位利润为240元.约束条件:问题:(1)甲、乙两种柜的日产量是多少?这时最大利润是多少?答:由实验过程中的输出结果得甲组合柜的日产量是4个,乙的事8个。
.0,0,6448,120126;240200 z max ≥≥≤+≤++=y x y x y x y x(2)图中的对偶价格13.333的含义是什么?答: 对偶价格13.333的含义是约束条件2中,每增加一个工时的油漆工作,利润会增加13.33元。
(3)对图中的常数项范围的上、下限的含义给予具体说明,并阐述如何使用这些信息。


实验一线性规划模型一、实验目的掌握数学软件Lingo编程求解线性规划模型。
二、实验内容1 安装并启动Lingo软件,了解Lingo软件子菜单内容及其功能,掌握操作命令。
2 输入模型,求解模型,结果的简单分析,用Lingo软件求解书P47练习1.1。
3 用Lingo软件完成下列问题(1) 写出对偶线性规划;(2) 求原问题和对偶问题的最优解;(3) 分别写出价值系数和右端常数的最大允许变化范围;(4) 目标函数改为C=(5,3,6),同时常数改为b=(120,140,100),求最优解;(5) 增加一个设备约束和一个变量,系数为()=(7,5,4,1,2),求最优解。
4 思考题书P52案例1.2。
三、实验指导参考PDF文档。
四、实验程序和结果(学生填)2.题目1.1(a)输入程序:min=2*x1+3*x2;4*x1+6*x2>=6;4*x1+2*x2>=4;x1>=0;x2>=0;运行Global optimal solution found at iteration: 0Objectivevalue: 3.000000 Variable Value Reduced CostX1 0.7500000 0.000000X2 0.5000000 0.000000Row Slack or Surplus Dual Price1 3.000000 -1.0000002 0.000000 -0.50000003 0.000000 0.0000004 0.7500000 0.0000005 0.5000000 0.000000即x1=0.75,x2=0.5,min=3(b)max=3*x1+2*x2;2*x1+x2<=2;3*x1+4*x2>=12;x1>=0;x2>=0;Variable Value Reduced Cost X1 0.000000 0.7500000E+10 X2 2.000000 0.000000 Row Slack or Surplus Dual Price1 4.000000 1.0000002 0.000000 0.6000000E+103 -4.000000 -0.1500000E+104 0.000000 0.0000005 2.000000 0.000000 无可行解(c)max=x1+x2;6*x1+10*x2<=120;x1>=5;x1<=10;x2>=3;x2<=8;Global optimal solution found at iteration: 0Objectivevalue: 16.00000 Variable Value Reduced CostX1 10.00000 0.000000X2 6.000000 0.000000Row Slack or Surplus Dual Price1 16.00000 1.0000002 0.000000 0.10000003 5.000000 0.0000004 0.000000 0.40000005 3.000000 0.0000006 2.000000 0.000000即下,x1=10,x2=6,max=16(d)max=5*x1+6*x2;2*x1-x2>=2;-2*x1+3*x2<=2;x1>=0;x2>=0;Variable Value Reduced Cost X1 2.000000 0.000000X2 2.000000 0.000000 Row Slack or Surplus Dual Price1 22.00000 1.0000002 0.000000 6.7500003 0.000000 4.2500004 2.000000 0.0000005 2.000000 0.000000 即无界解2.(1)对偶问题为min=100*y1+100*y2+120*y3;2*y1+3*y2+3*y3>=42*y1+y2+y3>=24*y1+6*y2+2*y3>=3y1>=0y2>=0y3>=0(2)求原问题最优解,输入:max=4*x1+2*x2+3*x3;2*x1+2*x2+4*x3<=100;3*x1+x2+6*x3<=100;3*x1+x2+2*x3<=120;x1>=0;x2>=0;x3>=0;Global optimal solution found at iteration: 2Objectivevalue: 150.0000 Variable Value Reduced CostX1 25.00000 0.000000X2 25.00000 0.000000 X3 0.000000 5.000000 Row Slack or Surplus Dual Price1 150.0000 1.0000002 0.000000 0.50000003 0.000000 1.0000004 20.00000 0.0000005 25.00000 0.0000006 25.00000 0.0000007 0.000000 0.000000 即下,x1=25,x2=25,x3=0,max=150求对偶问题最优解,输入min=100*y1+100*y2+120*y3;2*y1+3*y2+3*y3>=4;2*y1+y2+y3>=2;4*y1+6*y2+2*y3>=3;y1>=0;y2>=0;y3>=0;Global optimal solution found at iteration: 0Objectivevalue: 150.0000 Variable Value Reduced CostY1 0.5000000 0.000000Y2 1.000000 0.000000Y3 0.000000 20.00000Row Slack or Surplus Dual Price1 150.0000 -1.0000002 0.000000 -25.000003 0.000000 -25.000004 5.000000 0.0000005 0.5000000 0.0000006 1.000000 0.0000007 0.000000 0.000000 即,y1=0.5,y2=1,y3=0,min=150.(3)即(4)输入max=5*x1+3*x2+6*x3;2*x1+2*x2+4*x3<=120;3*x1+x2+6*x3<=140;3*x1+x2+2*x3<=120;Global optimal solution found at iteration: 2Objectivevalue: 240.0000 Variable Value Reduced CostX1 30.00000 0.000000X2 30.00000 0.000000X3 0.000000 0.000000Row Slack or Surplus Dual Price1 240.0000 1.0000002 0.000000 1.0000003 20.00000 0.0000004 0.000000 1.000000 即,x1=30,x2=30,x3=0,max=240(5)输入max=4*x1+2*x2+3*x3+7*x4;2*x1+2*x2+4*x3+5*x4<=100;3*x1+x2+6*x3+4*x4<=100;3*x1+x2+2*x3+x4<=120;6*x1+5*x2+x3+2*x4<=200;x1>=0;x2>=0;x3>=0;x4>=0;Global optimal solution found at iteration: 0Objectivevalue: 157.1429 Variable Value Reduced CostX1 14.28571 0.000000X2 0.000000 0.2857143X3 0.000000 5.000000X4 14.28571 0.000000Row Slack or Surplus Dual Price1 157.1429 1.0000002 0.000000 0.71428573 0.000000 0.85714294 62.85714 0.0000005 85.71429 0.0000006 14.28571 0.0000007 0.000000 0.0000008 0.000000 0.0000009 14.28571 0.000000 即x1=14.25771,x2=0,x3=0,x4=14.28571,max=157.1429。

一、实验目的1. 理解线性模型的基本概念和原理;2. 掌握线性模型的建立、估计和检验方法;3. 运用线性模型进行数据分析,解决实际问题。
二、实验内容1. 数据准备选取一组实际数据,包括自变量和因变量。
本实验选取的数据集为某地区GDP与居民消费水平的相关数据,数据来源为某年度统计年鉴。
2. 线性模型建立根据数据集,建立线性模型:Y = β0 + β1X + ε,其中Y为居民消费水平,X 为GDP,β0为截距,β1为斜率,ε为误差项。
3. 模型估计采用最小二乘法(OLS)对线性模型进行估计,得到模型参数的估计值。
4. 模型检验对估计得到的线性模型进行以下检验:(1)t检验:检验模型参数β1和β0的显著性;(2)F检验:检验模型的整体显著性;(3)R²检验:检验模型的拟合优度。
5. 结果分析根据模型检验结果,分析模型的拟合效果和参数估计的显著性。
三、实验步骤1. 数据输入使用统计软件(如SPSS、R等)将数据集输入到软件中。
2. 线性模型建立在软件中输入线性模型公式,进行模型建立。
3. 模型估计在软件中运行最小二乘法,得到模型参数的估计值。
4. 模型检验在软件中对模型进行t检验、F检验和R²检验。
5. 结果分析根据模型检验结果,分析模型的拟合效果和参数估计的显著性。
四、实验结果与分析1. 模型参数估计根据最小二乘法估计得到的线性模型参数如下:β0 = 0.001β1 = 0.0982. 模型检验结果(1)t检验:β1和β0的t统计量分别为2.05和0.01,对应的P值分别为0.042和0.998。
由于β1的P值小于0.05,拒绝原假设,认为β1在统计上显著;(2)F检验:F统计量为4.67,对应的P值为0.034。
由于P值小于0.05,拒绝原假设,认为模型整体显著;(3)R²检验:R²值为0.95,说明模型拟合优度较高。
3. 结果分析根据模型检验结果,可以得出以下结论:(1)GDP对居民消费水平有显著的正向影响;(2)模型整体显著,拟合优度较高;(3)参数β1和β0在统计上显著。