最新西师版数学五年级上册重点知识复习

最新】西师版五年级数学上册(全册)知识点汇总(预习复习必背)西师大版五年级数学上册知识点总结课本目录一、小数乘法1.小数乘整数2.小数乘小数3.积的近似值二、图形的平移、旋转与对称1.图形的平移描述平移路线时要说明方向和距离平移后的图形要保证大小和形状不变2.图形的旋转顺时针和逆时针方向的区别绕固定点旋转三、小数除法1.除数是整数的除法2.除数是小数的除法3.商的近似值4.循环小数四、小数混合运算五、多边形面积的计算1.平行四边形的面积2.三角形的面积3.梯形的面积4.不规则图形的面积5.认识平方千米和公顷六、可能性知识点总结：第一单元：小数乘法1.计算小数乘法的方法是先按整数乘法计算积，再点小数点2.两个不同的数相乘，当一个因数比1小，积比另一个因数小；当一个因数比1大，积比另一个因数大；当一个因数等于1，积等于另一个因数3.估算乘法时，将不是整十或整百的数看成与其接近的整数，化繁为简4.求积的近似值，根据需要保留一定的小数位数，用四舍五入法5.解决问题，分析数量关系，列算式计算第二单元：图形的平移、旋转与对称1.图形平移后大小和形状不变，只是位置改变2.描述平移路线时，说明方向和距离，保证格数正确3.图形旋转时，绕固定点旋转，顺时针和逆时针方向不同描述图形的旋转路线时，需要明确说明图形是绕哪个点，沿哪个方向旋转了多少度。

在画出旋转后的图形之前，需要先确定一条关键的线段，用这条线段的旋转来判断整个图形的旋转。

轴对称图形是指沿一条直线对折后，两部分能完全重合的图形，对称轴是指折痕所在的直线。

不同的轴对称图形有不同数量的对称轴，如长方形有2条对称轴，正方形有4条对称轴，等腰三角形有1条对称轴，等边三角形有3条对称轴，等腰梯形有1条对称轴，而圆则有无数条对称轴。

需要注意的是，平行四边形不是轴对称图形。

在画轴对称图形的另一半时，需要注意两点：一是对称轴两边图形所对应的方格数要相同，二是左边部分的图形要和右边部分的图形相同。

西师大版五年级数学上册知识点总结课本目录小数乘小数积的近似值二图形的平移、旋转与对称图形的平移图形的旋转轴对称图形设计图案除数是小数的除法四小数混合运算小数混合运算五多边形面积的计算六可能性知识点总结第一单元小数乘法1、计算小数乘法的方法，先按照整数乘法的计算方法算出积，再看因数中一共有几位小数，就从积的右边起数出几位，点上小数点。

当积的位数不够时，用0补位，再点小数点。

2、两个不为0的数相乘，当一个因数比1小，它们的积比另一个因数小；当一个因数比1大，它们的积比另一个因数大；当一个因数等于1，它们的积等于另一个因数。

3、做乘法的估算，通常是把不是整个、整十、整百的数看成与它接近的整个、整十、整百的数后再估算。

关键是化繁为简。

4、求积的近似值，通常是根据实际需要，确定应该保留几位小数，用“四舍五入”法保留一定的小数位数，求出积的近似值。

5、解决问题：分析题中的数量关系，根据数量关系列出算式，再算出结果。

如本单元典型数量关系：（1）读天然气表，电表或水表，算本月的费用通常是本月读数-上月读数=实际用量单价×实际用量= 本月费用（2）出租车计费，通常有起步价+规定路程外按一定单价计价的出租车费=一共要付的费用演变一：（一共要付的费用-起步价）÷起步价规定路程外的单价+起步价包括的路程=总路程上网费、停车费与出租车费道理相通。

（3）工程问题中，通常有：工作效率×工作时间=工作总量演变一：工作效率×工作时间×工作队伍数=工作总量演变二：工作总量÷工作时间÷工作队伍数=工作效率每一个基本的数量关系都可以有很多不同的演变。

第二单元图形的平移、旋转与对称1、图形平移后形状、大小都不变，只是位置发生了变化。

描述图形的平移路线时要说清楚图形平移的方向和平移的距离。

画平移后的图形的方法：平移前，先确定一个点，看这个点会平移到哪儿，保证平移的格数正确；二是注意看原来的图中的每条线段各占几格，保证图形和原来一样。

西师版数学五年级上册知识要点一、小数乘法1、计算小数乘法时，先按整数乘法的计算方法算出积，再看因数中一共有几位小数，就从积的右边起数出几位，点上小数点。

当积的位数不够时，用0补足，再点小数点。

2、两个不为0的数相乘，其中一个因数比1小，它们的积比另一个因数小；其中一个因数比1大，它们的积比另一个因数大；其中一个因数等于1，它们的积等于另一个因数。

3、小数乘法的估算，把小数看成跟它最接近的整个、整十、整百……，再计算。

4、求积的近似值，先算出积，再根据实际需要，确定保留几位小数，用“四舍五入”法取近似值。

5、解决问题: ⑴水费、电费、气费的计算方法：实际用量=本月读数—上月读数费用=实际用量×单价⑵出租车计费：总价=起步价+（总路程—起步路程）×每公里单价（上网费、停车费与出租车费道理相同）⑶工作总量=工作效率×工作时间工作时间=工作总量÷工作效率工作效率=工作总量÷工作时间二、图形的平移、旋转、轴对称1、图形平移后，形状、大小都不变，只是位置发生了变化。

2、描述图形的平移路线时要说清楚图形平移的方向和平移的距离。

3、画平移后的图形的方法：（1）平移前，先确定一个点，再数格子，看这个点平移到哪儿，注意格数正确。

（2）注意看原来图中的每条线段各占几格，确保图和原来的一样。

4、与时针旋转方向相同，叫顺时针旋转；与时针旋转方向相反，叫逆时针旋转。

5、图形旋转总是绕着一个固定的点转动。

描述图形的旋转要说清楚旋转的中心点、方向、度数、起止位置。

6、画旋转后的图形的方法：旋转前，先确定一条线段用这条关键线段的旋转来判断整个图形的旋转。

7、沿一条直线对折后，两部分能完全重合的图形叫轴对称图形，折痕所在的直线叫对称轴。

8、长方形有2 条对称轴，正方形有4条对称轴，等腰三角形有1条对称轴，等边三条形有3条对称轴，等腰梯形有1 条对称轴，圆有无数条对称轴。

平行四边形不是轴对称图形。

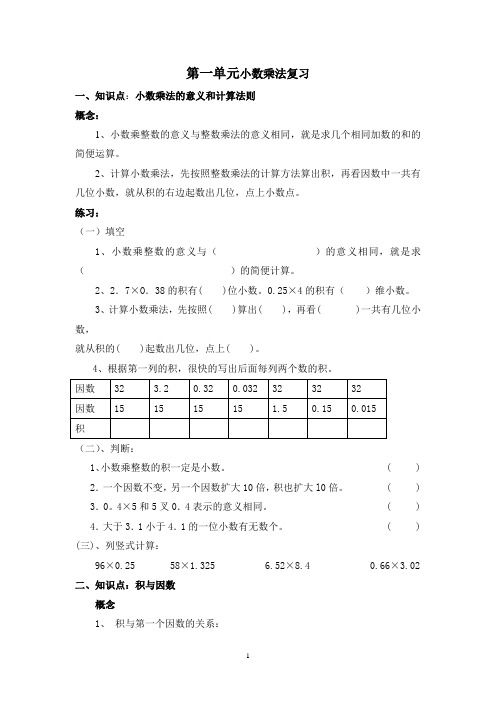
第一单元小数乘法复习一、知识点：小数乘法的意义和计算法则概念：1、小数乘整数的意义与整数乘法的意义相同，就是求几个相同加数的和的简便运算。

2、计算小数乘法，先按照整数乘法的计算方法算出积，再看因数中一共有几位小数，就从积的右边起数出几位，点上小数点。

练习：（一）填空1、小数乘整数的意义与（）的意义相同，就是求（）的简便计算。

2、2．7×O．38的积有( )位小数。

0.25×4的积有（）维小数。

3、计算小数乘法，先按照( )算出( )，再看( )一共有几位小数，就从积的( )起数出几位，点上( )。

4、根据第一列的积，很快的写出后面每列两个数的积。

（二）、判断：1、小数乘整数的积一定是小数。

( ) 2．一个因数不变，另一个因数扩大10倍，积也扩大l0倍。

( ) 3．0。

4×5和5叉0．4表示的意义相同。

( ) 4．大于3．1小于4．1的一位小数有无数个。

( ) (三)、列竖式计算：96×0.25 58×1.325 6.52×8.4 0.66×3.02 二、知识点：积与因数概念1、积与第一个因数的关系：一个数（0除外）乘大于1的数，积比原数大；一个数（0除外）乘小于1的数，积比原数小。

2、积与因数的关系：①.当两个因数都小于1时，积一定小于其中任何一个因数；②.当一个因数大于1，另一个因数小于1，那么积应该比小的因数大，比大的因数小；③.当两个因数都大于1时，积比其中任何一个因数都大练习：（一）、在下面的○里填上“＞”、“＜”或“=”符号。

5.8×1.1○5.8 0.54×9○9 4.6×0.99○4.6 0.25×4○2.5×0.40.1×0.1○0.2 0.39×1.4○3.9×0.14 1.6×1.09○1.59(二).填空。

算式2.5×A,当A（）1时，乘积大于2.5，当A（）1时，乘积小于2.5，当A（）1时，乘积等于2.5.三、知识点：估算。

五年级上册数学知识点西师版以下是五年级上册数学知识点（西师版）：1. 数的认识与比较- 数的认识：个位数、十位数、百位数、千位数- 数的比较：大于、小于、等于- 恒等式、方程和算式的关系2. 数的运算- 加法、减法、乘法、除法- 两个数的运算：加减乘除的结合律、交换律、分配律- 三个数的运算：加法与减法的运算顺序，加减法与乘除法的运算顺序3. 数量关系和代数式- 基本数量关系的表示：比例、相等、数列- 数字与字母的关系：代数式、字母代数式、变量、常量4. 小数- 小数的表示：小数点后的数字、百分数- 小数的读法、写法和大小比较- 小数与分数的关系5. 分数- 分数的认识：分子、分母、假分数、带分数- 分数的大小比较- 分数的运算：加法、减法、乘法、除法- 分数与小数的关系6. 四则运算- 加法、减法：进位、退位- 乘法：整数与整数相乘、整数与小数相乘、分数与分数相乘、小数与小数相乘- 除法：整数与整数相除、整数与小数相除、分数与分数相除、小数与小数相除7. 尺度和单位- 米、分米、厘米、毫米的换算- 千克、克、毫克的换算- 吨、升、分升、毫升的换算8. 三角形和四边形- 三角形的边和角：等边三角形、等腰三角形、直角三角形、锐角三角形、钝角三角形- 四边形的边和角：矩形、正方形、平行四边形、菱形、梯形、不规则四边形9. 直角坐标系- 横坐标和纵坐标的认识：横轴和纵轴- 点在直角坐标系中的位置- 图形在直角坐标系中的位置与移动：平移、旋转、翻转以上是五年级上册数学知识点（西师版）的大致内容，具体的内容和深度可能会有所不同，建议您参考教材或联系老师获取详细的信息。

第一单元小数乘法1.小数乘整数1、意义——求几个相同加数的和的简便运算。

如：1.5×3表示求3个1.5的和的简便运算（或1.5的3倍是多少）。

2、计算方法：先把小数扩大成整数；按整数乘法的法则算出积；再看因数中一共有几位小数，就从积的右边起（向左）数出几位点上小数点。

2.小数乘小数1、意义——就是求这个数的几分之几是多少。

如：1.5×0.8就是求1.5的十分之八是多少（或求1.5的1.8倍是多少）。

2、计算方法：先把小数扩大成整数；按整数乘法的法则算出积；再看因数中一共有几位小数，就从积的右边起（向左）数出几位，点上小数点。

3、注意：按整数算出积后，小数末尾的0要去掉，也就是把小数化简。

3.规律：一个数（0除外）乘一个大于1的数，积比原来的数大；一个数（0除外）乘一个小于1的数，积比原来的数小。

4.求近似数的方法一般有三种：1、四舍五入法；2、进一法；3、去尾法5、计算钱数的时候，保留两位小数，表示计算到分；保留一位小数，表示计算到角。

与钱数有关的题，如果题目没有特别要求，一般保留两位小数6、小数四则运算顺序和运算定律跟整数是一样的。

第二单元图形的平移、旋转与轴对称1.图形的平移1、平移的定义：在平面内，将一个图形沿某个方向平行移动一定的距离，这样的图形运动称为平移。

2.平移的特点：经平移运动后的图形: 形状和大小不变，图形的位置发生变化。

2.图形的旋转1、旋转的定义：在平面内，将一个图形绕着一个定点沿着某个方向转动一个角度，这样的图形运动称为旋转。

2、旋转由三个要素所决定:旋转中心、旋转方向和旋转的角度3、旋转的基本性质：（1）旋转不改变图形的形状和大小。

（2）图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度。

（3）任意一组对应点与旋转中心的连线所成的角叫做旋转角。

（4）对应点到旋转中心的距离相等。

（5）对应线段相等,对应角相等。

3.轴对称将图形沿着一条直线对折，如果直线两侧的部分能够完全重合，这样的图形叫做轴对称图形。

复习知识点第一单元小数乘法1、计算小数乘法的方法：先按照整数乘法的计算方法算出积，再看因数中一共有几位小数，就从积的右边起数出几位，点上小数点。

当积的位数不够时，用0补位，再点小数点。

当得数的小数部分末尾有0，一般要把0去掉，进行化简。

整数乘法的计算方法：1）从右边起，依次用第二个因数每位上的数去乘第一个因数，乘到哪一位，得数的末尾就和第二个因数的哪一位对齐；2）然后把几次乘得的数加起来。

（整数末尾有0的乘法：可以先把0前面的数相乘，然后看各因数的末尾一共有几个0，就在乘得的数的末尾添写几个0。

）2、两个不为0的数相乘，当一个因数比1小，它们的积比另一个因数小；当一个因数比1大，它们的积比另一个因数大；当一个因数等于1，它们的积等于另一个因数。

3、做乘法的估算，通常是把不是整个、整十、整百的数看成与它接近的整个、整十、整百的数后再估算。

关键是化繁为简。

4、求积的近似值，通常是根据实际需要，确定应该保留几位小数，用“四舍五入”法保留一定的小数位数，求出积的近似值。

“四舍五入法”：在取小数近似数的时候，如果尾数的最高位数字是4或者比4小，就把尾数去掉。

如果尾数的最高位数是5或者比5大，就把尾数舍去并且在它的前一位进"1",这种取近似数的方法叫做四舍五入法。

5、解决问题：分析题中的数量关系，根据数量关系列出算式，再算出结果。

如本单元典型数量关系：（1）读天然气表，电表或水表，算本月的费用通常是本月读数-上月读数=实际用量单价×实际用量= 本月费用（2）出租车计费，通常有起步价+规定路程外按一定单价计价的出租车费 = 一共要付的费用演变一：（一共要付的费用-起步价）÷起步价规定路程外的单价+起步价包括的路程=总路程上网费、停车费与出租车费道理相通。

（3）工程问题中，通常有：工作效率×工作时间=工作总量演变一：工作效率×工作时间×工作队伍数=工作总量演变二：工作总量÷工作时间÷工作队伍数=工作效率每一个基本的数量关系都可以有很多不同的演变。

五年级上册数学知识点西师版
1. 数的大小比较：使用不等号（>、<、≥、≤）来表示数的大小关系。

2. 除法运算：掌握除法的概念和运算方法，包括带余数的除法和整除。

3. 分数的概念：了解分数的含义和表示方法，包括真分数和假分数。

4. 分数的加减运算：掌握相同分母的分数相加减的方法，学会化简分数。

5. 分数的乘法和除法：掌握分数的乘法和除法的运算方法。

6. 数字的应用问题：通过实际应用问题来理解数学运算的意义和解决问题的方法。

7. 三角形和四边形：了解三角形和四边形的概念和性质，学会计算和测量线段和角度。

8. 图形的类比和相似：通过观察图形的相似性质来解决一些问题。

9. 规律和综合运算：通过观察和探索数学问题中的规律来解决问题。

10. 单位换算：学会常用长度、容量和质量单位之间的换算和计算。

11. 时、分和秒的认识和换算：学会用时针和分钟表示时间，并能进行简单的时间换算。

五年级数学上册知识点复习第一单元小数乘法1、小数乘整数：意义——求几个相同加数的和的简便运算。

如：1.5×3表示1.5的3倍是多少或3个1.5是多少。

计算方法：先把小数扩大成整数；按整数乘法的法则算出积；再看因数中一共有几位小数，就从积的右边起数出几位点上小数点。

2、小数乘小数：意义——就是求这个数的几分之几是多少。

如：1.5×0.8（整数部分是0）就是求1.5的十分之八是多少。

1.5×1.8（整数部分不是0）就是求1.5的1.8倍是多少。

3、小数乘法的计算方法：先按整数乘法算出积、在数出因数中一共有几位小数，点上小数点，位数不够添上0。

小数末尾的0要去掉。

例如： 4.25×0.108= （1）、一个数（0除外）乘以小于1的数，积比这个数小。

如：3.2×0.88﹤3.2 0.13×4.76﹤4.76（2）一个数（0除外）乘以大于1的数，积比这个数大。

如：0.23×1.04﹥0.23 3.5×7.3﹥7.34、求近似数的方法一般有三种：⑴四舍五入法；⑵进一法；⑶去尾法5、小数四则运算顺序跟整数是一样的。

先乘除，后加减，有括号先算小括号。

6、运算定律和性质：加法：加法交换律：a+b=b+a 加法结合律:(a+b)+c=a+(b+c)※一个数连续的减去几个数，可以把后面的所有减数相加，再和被减数相减：a –b-c=a-(b+c)乘法：乘法交换律：a×b=b×a乘法结合律：(a×b)×c=a×(b×c)见2.5找4或0.4，见1.25找8或0.8 乘法分配律：(a+b)×c=a×c+b×c或a×c+b×c=(a+b)×c（b=1时，省略b）变式： (a-b)×c=a×c-b×c或a×c-b×c=(a-b)×c练习：下列各题怎样简便就怎样算。

小学数学五年级上册基本知识点第一单元小数乘法1、计算小数乘法的方法，先按照整数乘法的计算方法算出积，再看因数中一共有几位小数，就从积的右边起数出几位，点上小数点。

当积的位数不够时，用0补位，再点小数点。

（解决中间有0、末尾有0的乘法）2、两个不为0的数相乘，当一个因数比1小，它们的积比另一个因数小；当一个因数比1大，它们的积比另一个因数大；当一个因数等于1，它们的积等于另一个因数。

(填空、判断、选择)3、做乘法的估算，通常是把不是整个、整十、整百的数看成与它接近的整个、整十、整百的数后再估算。

关键是化繁为简。

4、求积的近似值，通常是根据实际需要，确定应该保留几位小数，用“四舍五入”法保留一定的小数位数，求出积的近似值。

5、解决问题：分析题中的数量关系，根据数量关系列出算式，再算出结果。

如本单元典型数量关系：（1）读天然气表，电表或水表，算本月的费用通常是本月读数－上月读数=实际用量单价×实际用量= 本月费用（2）出租车计费，通常有起步价+规定路程外按一定单价计价的出租车费=一共要付的费用演变一：（一共要付的费用-起步价）÷起步价规定路程外的单价+起步价包括的路程=总路程上网费、停车费与出租车费道理相通。

（3）工程问题中，通常有：工作效率×工作时间=工作总量演变一：工作效率×工作时间×工作队伍数=工作总量演变二：工作总量÷工作时间÷工作队伍数=工作效率每一个基本的数量关系都可以有很多不同的演变。

第二单元图形的平移、旋转与对称1、图形平移后形状、大小都不变，只是位置发生了变化。

描述图形的平移路线时要说清楚图形平移的方向和平移的距离。

画平移后的图形的方法：平移前，先确定一个点，看这个点会平移到哪儿，保证平移的格数正确；二是注意看原来的图中的每条线段各占几格，保证图形和原来一样。

2、与时针旋转的方向相同，通常叫顺时针方向旋转。

与时针旋转方向相反，通常叫逆时针方向旋转。

西师版五年级上册数学知识点西师版五年级上册数学知识点1、用字母表运算定律。

加法交换律： a+b=b+a 加法结合律： a+b+c=a+(b+c)乘法交换律： a×b=b×a 乘法结合律：a×b×c=a×(b×c) 乘法分配律： (a±b)×c=a×c±b×c2、用字母表示计算公式。

长方形的周长公式： c=(a+b)×2 长方形的面积公式： s=ab 正方形的周长公式： c=4a 正方形的面积公式： s=3、读作：x的平方，表示：两个x相乘。

2x表示：两个x相加，或者是2乘x。

4、①含有未知数的等式称为方程。

②使方程左右两边相等的未知数的值叫做方程的解。

③求方程的解的过程叫做解方程。

5、把下面的数量关系补充完整。

路程=(速度)×(时间) 速度=(路程)÷(时间) 时间=(路程)÷(速度)总价=(单价)×(数量) 单价=(总价)÷(数量) 数量=(总价)÷(单价)总产量=(单产量)×(数量) 单产量=(总产量)÷(数量)数量=(总产量)÷(单价 )工作总量=(工作效率)×(工作时间)工作效率=(工作总量)÷(工作时间)工作时间=(工作总量)÷(工作效率)大数-小数=相差数大数-相差数=小数小数+相差数=大数一倍量×倍数=几倍量几倍量÷倍数=一倍量几倍量÷一倍量=倍数被减数=减数+差减数=被减数-差加数=和-另一个加数被除数=除数×商除数=被除数÷商因数=积÷另一个因数小学数学四边形知识点1、有4条直的边和4个角封闭图形我们叫它四边形。

2、四边形的特点：有四条直的边，有四个角。

3、长方形的特点：长方形有两条长,两条宽，四个直角，对边相等。

西师大版五年级数学上册知识点总结课本目录小数乘小数积的近似值二图形的平移、旋转与对称图形的平移图形的旋转轴对称图形设计图案除数是小数的除法四小数混合运算小数混合运算五多边形面积的计算六可能性知识点总结第一单元小数乘法1、计算小数乘法的方法，先按照整数乘法的计算方法算出积，再看因数中一共有几位小数，就从积的右边起数出几位，点上小数点。

当积的位数不够时，用0补位，再点小数点。

2、两个不为0的数相乘，当一个因数比1小，它们的积比另一个因数小；当一个因数比1大，它们的积比另一个因数大；当一个因数等于1，它们的积等于另一个因数。

3、做乘法的估算，通常是把不是整个、整十、整百的数看成与它接近的整个、整十、整百的数后再估算。

关键是化繁为简。

4、求积的近似值，通常是根据实际需要，确定应该保留几位小数，用“四舍五入”法保留一定的小数位数，求出积的近似值。

5、解决问题：分析题中的数量关系，根据数量关系列出算式，再算出结果。

如本单元典型数量关系：（1）读天然气表，电表或水表，算本月的费用通常是本月读数-上月读数=实际用量单价×实际用量= 本月费用（2）出租车计费，通常有起步价+规定路程外按一定单价计价的出租车费=一共要付的费用演变一：（一共要付的费用-起步价）÷起步价规定路程外的单价+起步价包括的路程=总路程上网费、停车费与出租车费道理相通。

（3）工程问题中，通常有：工作效率×工作时间=工作总量演变一：工作效率×工作时间×工作队伍数=工作总量演变二：工作总量÷工作时间÷工作队伍数=工作效率每一个基本的数量关系都可以有很多不同的演变。

第二单元图形的平移、旋转与对称1、图形平移后形状、大小都不变，只是位置发生了变化。

描述图形的平移路线时要说清楚图形平移的方向和平移的距离。

画平移后的图形的方法：平移前，先确定一个点，看这个点会平移到哪儿，保证平移的格数正确；二是注意看原来的图中的每条线段各占几格，保证图形和原来一样。

五年级数学上册复习知识点第一单元小数乘法1、计算小数乘法的方法：先按照整数乘法的计算方法算出积，再看因数中一共有几位小数，就从积的右边起数出几位，点上小数点。

当积的位数不够时，用0补位，再点小数点。

当得数的小数部分末尾有0，一般要把0去掉，进行化简。

整数乘法的计算方法：1）从右边起，依次用第二个因数每位上的数去乘第一个因数，乘到哪一位，得数的末尾就和第二个因数的哪一位对齐；2）然后把几次乘得的数加起来。

（整数末尾有0的乘法：可以先把0前面的数相乘，然后看各因数的末尾一共有几个0，就在乘得的数的末尾添写几个0。

）2、两个不为0的数相乘，当一个因数比1小，它们的积比另一个因数小；当一个因数比1大，它们的积比另一个因数大；当一个因数等于1，它们的积等于另一个因数。

3、做乘法的估算，通常是把不是整个、整十、整百的数看成与它接近的整个、整十、整百的数后再估算。

关键是化繁为简。

4、求积的近似值，通常是根据实际需要，确定应该保留几位小数，用“四舍五入”法保留一定的小数位数，求出积的近似值。

“四舍五入法”尾数去掉。

如果尾数的最高位数是5或者比5大，就把尾数舍去并且在它的前一位进"1",这种取近似数的方法叫做四舍五入法。

5、解决问题：分析题中的数量关系，根据数量关系列出算式，再算出结果。

如本单元典型数量关系：（1）读天然气表，电表或水表，算本月的费用通常是本月读数-上月读数=实际用量单价×实际用量= 本月费用（2）出租车计费，通常有起步价+规定路程外按一定单价计价的出租车费= 一共要付的费用演变一：（一共要付的费用-起步价）÷起步价规定路程外的单价+起步价包括的路程=总路程上网费、停车费与出租车费道理相通。

（3）工程问题中，通常有：工作效率×工作时间=工作总量演变一：工作效率×工作时间×工作队伍数=工作总量演变二：工作总量÷工作时间÷工作队伍数=工作效率每一个基本的数量关系都可以有很多不同的演变。

西师版小学数学五年级上册知识点五年级数学上册复知识点第一单元：小数乘法小数乘法的计算方法是先按照整数乘法的计算方法算出积，再看因数中一共有几位小数，就从积的右边起数出几位，点上小数点。

当积的位数不够时，用补位，再点小数点。

当得数的小数部分末尾有，一般要把去掉，进行化简。

整数乘法的计算方法是从右边起，依次用第二个因数每位上的数去乘第一个因数，乘到哪一位，得数的末尾就和第二个因数的哪一位对齐，然后把几次乘得的数加起来。

对于整数末尾有的乘法，可以先把前面的数相乘，然后看各因数的末尾一共有几个，就在乘得的数的末尾添写几个。

两个不为的数相乘，当一个因数比1小，它们的积比另一个因数小；当一个因数比1大，它们的积比另一个因数大；当一个因数等于1，它们的积等于另一个因数。

做乘法的估算，通常是把不是整个、整十、整百的数看成与它接近的整个、整十、整百的数后再估算。

关键是化繁为简。

求积的近似值，通常是根据实际需要，确定应该保留几位小数，用“四舍五入”法保留一定的小数位数，求出积的近似值。

四舍五入法是在取小数近似数的时候，如果尾数的最高位数字是4或者比4小，就把尾数去掉。

如果尾数的最高位数是5或者比5大，就把尾数舍去并且在它的前一位进"1"，这种取近似数的方法叫做四舍五入法。

解决问题的关键是分析题中的数量关系，根据数量关系列出算式，再算出结果。

本单元的典型数量关系有：读天然气表、电表或水表，算本月的费用；出租车计费；上网费、停车费与出租车费；工程问题中的工作效率、工作时间和工作总量。

第二单元：图形的平移、旋转与对称图形平移后形状、大小都不变，只是位置发生了变化。

描述图形的平移路线时要说清楚图形平移的方向和平移的距离。

画平移后的图形的方法是平移前，先确定一个点，看这个点会平移到哪里，保证平移的格数正确；二是注意看原来的图中的每条线段各占几格，保证图形和原来一样。

2、顺时针方向旋转是指与时针旋转方向相同，逆时针方向旋转是指与时针旋转方向相反。

学习必备欢迎下载小学数学五年级上册基本知识点一、小数乘法1、计算小数乘法的方法，先按照整数乘法的计算方法算出积，再看因数中一共有几位小数，就从积的右边起数出几位，点上小数点。

当积的位数不够时，用0补位，再点小数点。

2、两个不为0的数相乘，当一个因数比1小，它们的积比另一个因数小；当一个因数比1大，它们的积比另一个因数大；当一个因数等于1，它们的积等于另一个因数。

3、做乘法的估算，通常是把不是整个、整十、整百的数看成与它接近的整个、整十、整百的数后再估算。

关键是化繁为简。

4、求积的近似值，通常是根据实际需要，确定应该保留几位小数，用“四舍五入”法保留一定的小数位数，求出积的近似值。

5、解决问题：分析题中的数量关系，根据数量关系列出算式，再算出结果。

如本单元典型数量关系：（1）读天然气表，电表或水表，算本月的费用通常是本月读数-上月读数=实际用量单价×实际用量= 本月费用（2）出租车计费，通常有：起步价+规定路程外按一定单价计价的出租车费=一共要付的费用演变一：（一共要付的费用-起步价）÷起步价规定路程外的单价+起步价包括的路程=总路程上网费、停车费与出租车费道理相通。

（3）工程问题中，通常有：工作效率×工作时间=工作总量演变一：工作效率×工作时间×工作队伍数=工作总量演变二：工作总量÷工作时间÷工作队伍数=工作效率每一个基本的数量关系都可以有很多不同的演变。

二、图像平移与旋转1、图形平移后形状、大小都不变，只是位置发生了变化。

描述图形的平移路线时要说清楚图形平移的方向和平移的距离。

画平移后的图形的方法：平移前，先确定一个点，看这个点会平移到哪儿，保证平移的格数正确；二是注意看原来的图中的每条线段各占几格，保证图形和原来一样。

2、与时针旋转的方向相同，通常叫顺时针方向旋转。

与时针旋转方向相反，通常叫逆时针方向旋转。

3、图形旋转时总是绕着一个固定的点转动的。