人教版五年级数学下册长方体的表面积

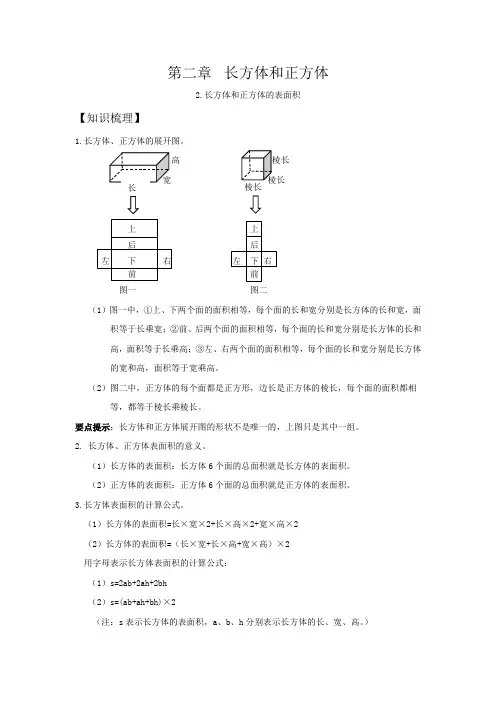
第二章 长方体和正方体2.长方体和正方体的表面积【知识梳理】1.长方体、正方体的展开图。

高图一 图二（1）图一中，①上、下两个面的面积相等，每个面的长和宽分别是长方体的长和宽，面 积等于长乘宽；②前、后两个面的面积相等，每个面的长和宽分别是长方体的长和 高，面积等于长乘高；③左、右两个面的面积相等，每个面的长和宽分别是长方体 的宽和高，面积等于宽乘高。

（2）图二中，正方体的每个面都是正方形，边长是正方体的棱长，每个面的面积都相等，都等于棱长乘棱长。

要点提示：长方体和正方体展开图的形状不是唯一的，上图只是其中一组。

2. 长方体、正方体表面积的意义。

（1）长方体的表面积：长方体6个面的总面积就是长方体的表面积。

（2）正方体的表面积：正方体6个面的总面积就是正方体的表面积。

3.长方体表面积的计算公式。

（1）长方体的表面积=长×宽×2+长×高×2+宽×高×2（2）长方体的表面积=（长×宽+长×高+宽×高）×2用字母表示长方体表面积的计算公式：（1）s=2ab+2ah+2bh（2）s=(ab+ah+bh)×2（注：s 表示长方体的表面积，a 、b 、h 分别表示长方体的长、宽、高。

）4.长方体表面积的计算公式。

正方体的表面积=棱长×棱长×6用字母表示正方体表面积的计算：s=6a2。

（注：s表示正方体的表面积，a表示正方体的棱长。

）5.拓展提高。

如果正方体的棱长扩大到原来的n倍，它的表面积就扩大到原来的n2倍。

如正方体的棱长扩大到原来的3倍，它的表面积就扩大到原来的9倍。

6.温馨提示：在实际生活中，并不是所有的长方体形状的物体都有6个面，如长方体形状的鱼缸、游泳池等只有5个面，长方体形状的烟囱、通风管等只有4个面。

【诊断自测】1.填空。

（1）一个长方体的长是15cm，宽是4cm，高是6cm，这个长方体的表面积是（）cm2。

人教版小学数学五年级下册学情分析汶上县实验小学渠冠军学情分析一、学生具体情况五年级三班共有学生 71 名。

总体来看，绝大部分同学学习习惯良好，学习积极性高，能较好地完成学习任务，为了更有针对性地去开展教育教学活动，提高数学课堂教学质量，真正做到既备教材，又备学生。

现对学生的学情做以下分析，希望能做到有的放矢，因材施教。

二、学生基本学习状态从大的方面来说，五年级的同学整体水平比较平均，课堂纪律以及作业质量相对较好，思维整体来说比较活跃，在数学课堂上能主动提出有价值的数学问题。

基本上都能积极参加数学教学活动，学习气氛浓厚，作业书写规范整齐。

但不足的地方就是一小部分学生的数学学习显得比较浮躁，这主要表现在课堂纪律和作业质量方面，同时学习困难成绩差的学生有十几个，还有十几个学生放学后依靠小饭桌，这部分学生学习习惯不好作业不能及时上交。

三、教材分析：人教版小学数学五年级下册第三单元《长方体和正方体的表面积》是本单元的第二课时。

"长方体和正方体"这一单元是学生系统学习立体图形知识的开始，本课时主要教学长方体、正方体表面积的概念和计算方法。

教材先通过把一个长方体或正方体纸盒的6个面展开，帮助学生认识表面积的概念。

这样可以把表面积的概念与刚刚建立起来的长方体和正方体的特征很好的联系起来，为下面学习计算表面积做好准备。

接着，通过例1教学长方体表面积的计算方法。

然后安排"试一试"学习立方体表面积的计算方法。

关于长方体表面积的计算，教材中没有给出计算公式，而是启发学生用不同的方法列式计算，这样安排有利于他们更好的掌握表面积的概念及有关计算，有利于更好的发展学生的空间观念。

四、学习者分析：长方体和正方体的表面积这部分知识是在学生掌握了长方形与正方形的面积计算，并对长方体与正方体的特征有了初步认识的基础上进行教学的，即学生已经明确了长方体与正方体都有6个面，而且长方体相对的面的面积相等，正方体6个面的面积都相等的基础上教学的。

《长方体和正方体的表面积》说课稿尊敬的各位评委、老师：大家好！在这秋高气爽、景色宜人的季节里，有机会和各位同仁一起探讨数学的教学教法，心中特别开心。

《数学课程标准》指出：数学教学，要让学生亲身经历数学知识的形成过程，也就是经历一个丰富、生动的思维过程，使学生通过数学活动，掌握基本的数学知识和技能，激发学生对数学学习的兴趣。

因此，让每一个学生愉快地、自信地走进我的数学课堂，从中感受快乐、体验成功是我孜孜以求的目标。

今天，我说课的内容是九年制义务教育人教版小学数学五年级下册第三单元33-34页的《长方体和正方体的表面积》。

我将从教材分析、学情分析、教学目标、教学重难点、教法与学法、教具准备、教学过程、作业设计以及板书设计几方面来展开我的说课。

一、说教材分析本节课是在学生认识并掌握了长方体和正方体的基本特征的基础上进行教学的。

通过学习，有助于学生解决生活中的实际问题，切身感受数学的价值。

同时，还可以使学生形成初步的空间观念，是进一步学习其他立体几何图形的基础。

二、说学情分析五年级学生已经掌握了长方形、正方形面积的计算方法，表面积对于他们来说，是一个全新的概念，显得有点抽象。

虽然五年级学生的抽象思维有了一定的发展，但仍以形象思维为主，分析、归纳、概括的能力有待进一步加强。

为此，我在教学中加强了学生的动手操作，并利用多媒体课件辅助教学，突破难点。

三、说教学目标遵照“新课标”的基本理念，结合本课的教材内容和学生实际情况，我确立了如下教学目标：1.使学生理解长方体表面积的意义，掌握长方体表面积的计算方法。

2.提高学生运用新知灵活解题的能力，发展学生的思维，培养学生分析、归纳、推理的能力。

3.培养学生互助、合作的精神，促进学生在态度、情感等方面的健康发展。

四、教学重点、难点根据这节课的教学内容，我把建立表面积的概念以及理解并掌握长方体表面积的计算方法作为本节课的重点，由于学生刚刚深入学习空间立体图形，空间想象能力较弱，因此我把根据给出的长方体的长、宽、高，想象出每个面的长和宽各是多少，作为本节课的难点。

人教版数学五年级下册《长方体和正方体的表面积》教学设计一. 教材分析人教版数学五年级下册《长方体和正方体的表面积》是本册教材中的一个重要内容。

通过学习，学生能够理解长方体和正方体的表面积的概念，掌握计算长方体和正方体表面积的方法，并能运用所学知识解决实际问题。

本节课的内容为后续学习体积和表面积的计算打下基础。

二. 学情分析五年级的学生已经掌握了平面图形的面积计算方法，具备了一定的空间观念。

但在计算三维图形的表面积时，还需要进一步引导和培养。

此外，学生对实际问题的解决能力有待提高，需要通过实例演示和练习，使学生能够将所学知识应用于实际问题中。

三. 教学目标1.知识与技能：学生能够理解长方体和正方体的表面积的概念，掌握计算长方体和正方体表面积的方法，并能运用所学知识解决实际问题。

2.过程与方法：通过观察、操作、交流等活动，学生能够培养空间观念，提高动手操作和解决问题的能力。

3.情感态度与价值观：学生能够积极参与课堂活动，克服困难，增强自信心，培养合作意识和创新精神。

四. 教学重难点1.重点：学生能够掌握计算长方体和正方体表面积的方法。

2.难点：学生能够运用所学知识解决实际问题，并灵活运用表面积公式。

五. 教学方法1.情境教学法：通过实物展示、模型演示等手段，创设情境，引导学生观察、思考、操作。

2.启发式教学法：教师提出问题，引导学生主动探究，培养学生解决问题的能力。

3.合作学习法：学生分组讨论、合作解决问题，培养团队协作精神。

4.反馈评价法：教师及时给予学生反馈，鼓励学生积极改正，提高学习效果。

六. 教学准备1.教具：长方体和正方体模型、卡片、课件等。

2.学具：学生每人一份长方体和正方体模型、练习纸等。

七. 教学过程1.导入（5分钟）教师通过展示长方体和正方体模型，引导学生观察其特征，并提出问题：“同学们，你们能找出长方体和正方体的特点吗？它们有什么共同之处和不同之处？”学生积极思考、回答问题，从而引出本节课的内容。

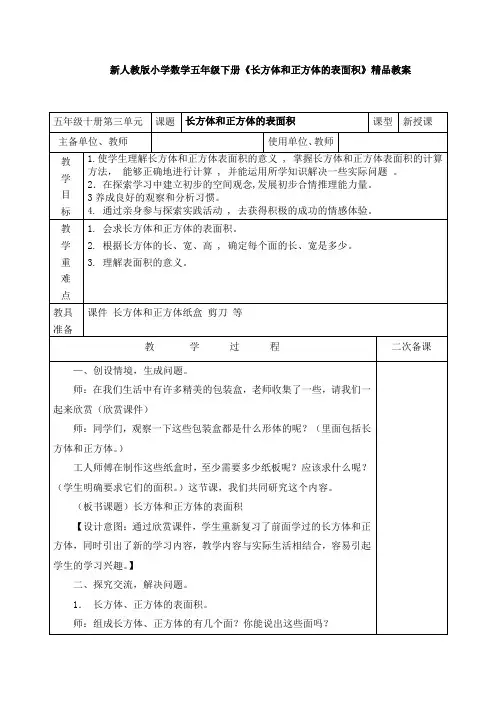
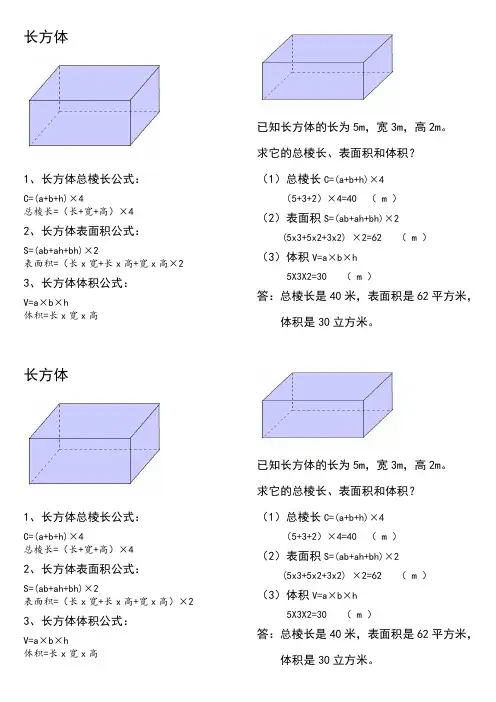
1、长方体总棱长公式：C=(a+b+h)×4总棱长=（长+宽+高）×42、长方体表面积公式：S=(ab+ah+bh)×2表面积=（长x宽+长x高+宽x高×2 3、长方体体积公式：V=a×b×h体积=长x宽x高长方体1、长方体总棱长公式：C=(a+b+h)×4总棱长=（长+宽+高）×42、长方体表面积公式：S=(ab+ah+bh)×2表面积=（长x宽+长x高+宽x高）×2 3、长方体体积公式：V=a×b×h体积=长x宽x高已知长方体的长为5m，宽3m，高2m。

求它的总棱长、表面积和体积？（1）总棱长C=(a+b+h)×4（5+3+2）×4=40 （ m ）（2）表面积S=(ab+ah+bh)×2(5x3+5x2+3x2) ×2=62 （ m ）（3）体积V=a×b×h5X3X2=30 （ m ）答：总棱长是40米，表面积是62平方米，体积是30立方米。

已知长方体的长为5m，宽3m，高2m。

求它的总棱长、表面积和体积？（1）总棱长C=(a+b+h)×4（5+3+2）×4=40 （ m ）（2）表面积S=(ab+ah+bh)×2(5x3+5x2+3x2) ×2=62 （ m ）（3）体积V=a×b×h5X3X2=30 （ m ）答：总棱长是40米，表面积是62平方米，体积是30立方米。

1、正方体总棱长公式：C=a×12总棱长=棱长×122、正方体表面积公式：S=a×a×6表面积=棱长×棱长×6 3、正方体体积公式：V=a×a×a体积=棱长x棱长x棱长正方体1、正方体总棱长公式：C=a×12总棱长=棱长×122、正方体表面积公式：S=a×a×6表面积=棱长×棱长×6 3、正方体体积公式：V=a×a×a体积=棱长x棱长x棱长已知正方体的棱长为5m。

第三单元《长方体和正方体》1.长方体：由六个长方形（特殊情况有两个相对的面是正方形）围成的立体图形叫长方体.长方体的任意一个面的对面都与它完全相同。

2.长、宽、高：长方体的每一个矩形都叫做长方体的面，面与面相交的线叫做长方体的棱，三条棱相交的点叫做长方体的顶点，相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。

3.长方体的特征(1)长方体有6个面,每个面都是长方形,至少有两个相对的两个面完全相同。

特殊情况时有两个面是正方形，其他四个面都是长方形，并且完全相同。

(3)长方体有12条棱，相对的棱长度相等。

可分为三组，每一组有4条棱。

还可分为四组，每一组有3条棱。

(3)长方体有8个顶点。

每个顶点连接三条棱。

(4) 长方体相邻的两条棱互相（相互）垂直。

长方体是由6个长方形（特殊情况有两个相对的面是正方形）围成的立体图形。

在一个长方体中，相对的面完全相同，相对的棱长度相等。

顶点个数面棱个数大小关系条数长度关系8 6 相对的面相等12 平行的棱长相等4.棱长总和公式：长方体棱长总和=4条长+4条宽+4条高＝（长+高+宽）×4宽=棱长之和÷4－长－高长＝棱长之和÷4－宽－高高＝棱长之和÷4－宽－长二、正方体的认识：1. 正方体的认识：正方体是由6个完全相同的正方形围成的立体图形。

正方体有6个面，12条棱，8个顶点，每个面都是正方形，面积都相等。

每条棱的长度都相等。

正方体的长、宽、高都相等，统称棱长。

2.长方体和正方体的关系：正方体是一种特殊的长方体。

3．正方体棱长之和：棱长×１２=棱长之和棱长之和÷１２＝棱长4.长方体的表面积（1）长方体和正方体6个面的总面积，叫做它的表面积。

（2）表面积计算公式①.因为长方体有“上”、“下”、“前”、“后”、“左”、“右”6个面,相对的2个面相等，所以先算上下两个面，再算前后两个面，最后算左右两个面。

②长方体的表面积=（长×宽＋长×高＋宽×高）×2用字母表示： S=（ab＋ah＋bh）×2长方体表面积＝（长×宽＋长×高＋宽×高）×2设一个长方体的长、宽、高分别为a、b、c，则它的表面积S：S = 2ab + 2bc+ 2ca= 2 ( ab + bc + ca)长方体没盖的表面积＝长×宽＋长×高×2 ＋宽×高×2③特殊长方体的表面积（有两个面是正方形）正方形的两个面完全相同，其余四个面完全相同。

2、一个长方体的长是 15 厘米，宽是 12 厘米，高是 8 厘米，这 个长方体的表面积是平方厘米。

3、一个正方体的棱长是８分米，它的棱长总和是，表面积是。

4、用 60 厘米长的铁丝焊接成一个正方体的框架，这个正方体的 表面积是平方厘米。

5、用铁丝焊接成一个长 12 厘米，宽 10 厘米，高 5 厘米的长方 体的框架，至少需要铁丝厘米 6、一个长方体的长是 25 厘米，宽是 20 厘米，高是 18 厘米，的 面的长是厘米，宽是厘米，一个这样的面的面积是平方厘米；最小的 面长是厘米，宽是厘米，一个这样的面的面积是平方厘米。

7、一个长方体的长是 1 米 4 分米，宽是 5 分米，高是 5 分米， 这个长方体有个面是正方形，每个面的面积是平方分米；其余四个面 是长方形的面积大小，每个面的面积是平方分米；这个长方体的表面 积是平方分米。

8、一个长方体的金鱼缸，长是 8 分米，宽是 5 分米，高是 6 分 米，不小心前面的玻璃被打坏了，修理时配上的玻璃的面积是。

9、一个正方体的棱长总和是 72 厘米，它的一个面是边长厘米的 正方形，它的表面积是平方厘米。

二、应用题。

1、一个通风管的横截面是边长是 05 米的正方形，长 25 米。

如果用铁皮做这样的通风管 50 只，需要多少平方米的铁皮？ _____________________________________2、一个长方体的游泳池，长 20 米，宽 18 米，水深 25 米，如在 四壁和底面抹水泥，求抹水泥的面积是多少平方米？_____________________________________ 3、做一个长方体的浴缸无盖，长 8 分米，宽 4 分米，高 6 分米， 至少需要多少平方分米的玻璃？如果每平方分米玻璃 4 元钱，至少需 要多少钱买玻璃？ _____________________________________ 4、一个房间的长 6 米，宽 35 米，高 3 米，门窗面积是 8 平方米。

长方体和正方体二、内容讲解：知识点一：长方体和正方体的特征(1)长方体：由6个长方形围成的立体图形。

(2)正方体：由6个完全相同的正方形围成的立体图形叫做正方体（也叫做立方体）。

它是一种特殊的长方体。

(3)两个面相交的边叫做棱。

三条棱相交的点叫做顶点。

相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。

特征：①有几个面？面的位置和大小有什么关系？②有多少条棱？棱的位置、长短有什么关系？③有多少个顶点？例一：1、（a）图是（）体，它的6个面是（）形。

（b）图是（）体，它的6个面是（）形。

2、长方体有（）个面，（）条棱，（）个顶点。

相对的棱的长度（），相对的面完全（）。

3、正方体所有的面都（），（）条棱都（）。

4、长、宽、高相等的长方体叫做（）。

知识点二：长方体、正方体棱长的计算（1）各棱长之间的关系及棱长的计算方法长方体的棱长总和=（长+宽+高）×4 L=（a＋b＋h）×4 长=棱长总和÷4－宽－高a=L÷4－b－h宽=棱长总和÷4－长－高b=L÷4－a－h高=棱长总和÷4－长－宽h=L÷4－a－b正方体的棱长总和=棱长×12 L=a×12正方体的棱长=棱长总和÷12 a=L÷12例二：1、一个长方体的长8厘米，宽7厘米，高6厘米，棱长和是多少厘米？2、如果用一根长72厘米的铁丝做一个宽4厘米，高6厘米的长方体框架，长是多少厘米？知识点三：长方体、正方体的表面积表面积：长方体或正方体6个面的总面积，叫做它的表面积已知长、宽、高，求面积S=(ɑb+bc+ɑc)×2长方体的表面积= ( 长×宽+ 长×高+ 宽×高) × 2正方体的表面积=（长×宽）×6例三：1、一个长方体油箱，从里面量长是70厘米，宽是30厘米，高是85厘米，如果每升汽油重约0. 73千克，这个油箱最多能装多重的汽油？（一）已知棱长和求面积长方体棱长和=（长+宽+高）×4正方体棱长和=棱长×12例四：1、一个正方体框架是用一根长48分米的铁丝焊接成的，如果给这个正方体粘上一层塑料，至少需要多少平方分米的塑料？（二）已知长、宽、高的关系求面积例五：1、已知一个长方体的长是20分米，这个长方体的宽是长的4/5，高是宽的一半，求这个长方体的面积？2、一个长方体房间，长8米，宽比长短1/4，高比宽短1/3，这个房间的表面积是多少？（三）已知棱长和，求转换后图形面积例六：1、一根铁丝可以围成一个长6分米、宽4.5分米、高2.5分米长方体框架，现在想将其围成一个正方体，这个正方体的表面积是多少？（四）求面不全的长方体（正方体）表面积柱子：求四个面的面积，不算上下两面（长×宽）鱼缸：正面是玻璃，1、求其他五个面的面积，不算正面（长×高）2、前面的玻璃坏了，若求配上的玻璃面积，则只求正面的面积。

（人教版）五年级数学下册长方体和正方体的表面积和体积（人教版）五年级数学下册长方体和正方体的表面积和体积班级姓名分数一、填空题。

1.一个长方体框架长8厘米，宽6厘米，高4厘米，做这个框架共要（）厘米铁丝，是求长方体（），在表面贴上塑料板，是求长方体（），在里面能盛（）升水是求（），这个盒子有（）立方米是求（）。

长方体的短就是6厘米，阔就是4厘米，低就是4厘米，它的棱长总和就是（）厘米，六个面中最小的面积就是（）平方厘米，表面积就是（）平方厘米，体积就是（）立方厘米，（）条棱成正比。

2.一瓶可乐的容积大约是230（）；一个雪糕的体积是20（）；一台冰箱的容积大约是180（）；一瓶眼药水约有12（）。

3.1立方分米的1个正方体可以分为（）个1立方厘米的小正方体，如果把这些大正方体排在一排，一共短（）分后米。

4.用长2厘米、宽1厘米、高1厘米的长方体木块拼成一个正方体，至少用（）个这样的长方体。

拼成的正方体的表面积是（）平方厘米。

5.搞一个长6分米，阔4分米，低1.5分米的抽屉，至少须要木板（）。

6．一根铁丝长36厘米，如果搞一个正方体框架，棱长就是（）厘米；如果搞一个低和阔都就是2厘米的长方体框架，短就是（）厘米。

7．一个长方体水池占地6平方米，他深1.5米，池内最多能容水（）升。

8．把一个棱长2分米的正方体，切成两个相等的长方体，表面积增加了（）。

9．至少（）个棱长2厘米的小正方体可以拼成一个大正方体。

10．一个长方体的长、阔、低各不断扩大了3倍，它的体积不断扩大了（）倍。

11．把5个棱长1厘米的小正方体拆成长方体，这个长方体的表面积就是（）。

12．一个长方体的玻璃缸，长4分米、宽3分米、高5分米，倒入水后量得水深3.5分米，倒入的水有（）升。

13.用两个长6厘米，阔3厘米，低1厘米的长方体拆成一个表面积尽可能大的正方体，这个拆成的长方体的表面积就是（）平方厘米。

14.一个长方体的体积是30立方厘米，长是5厘米，高是3厘米，宽是（）。