高二数学培优题组一

高二数学人教版选择性必修第一册全册考试复习必刷检测卷（培优版）一、单项选择题：本题共8小题，每小题满分5分，共40分．在每小题给出的四个选项中，只有一项符合题目要求，选对得5分，选错得0分．1．（2021·全国高二课时练习）已知M 、N 分别是四面体OABC 的棱OA ，BC 的中点，点P 在线段MN 上，且MP =2PN ，设向量OA a =，OB b =，OC c =，则OP =（）A ．111666a b c++B ．111333a b c++C ．111633a b c++D ．111366a b c++2．（2021·重庆市清华中学校高二月考）在棱长为1的正方体1111ABCD A B C D -中，点E 为底面1111D C B A 内一动点，则EA EC ⋅的取值范围是（）A ．1,12⎡⎤⎢⎥⎣⎦B ．[]0,1C ．[]1,0-D ．1,02⎡⎤-⎢⎥⎣⎦3．（2021·四川仁寿一中高二月考）已知点P 为直线1y x =+上的一点，,M N 分别为圆221:(4)(1)4C x y -+-=与圆222:(4)1C x y +-=上的点，则||||PM PN +的最小值为（）A ．5B ．6C ．2D ．14．（2021·黑龙江让胡路·大庆中学高二月考）已知圆O 的圆心在坐标原点，且与直线22y x =+相切，点P 为直线290x y +-=上一动点，过点P 向圆O 引两条切线PA ，PB ，A 、B 为切点，则直线AB 经过定点（）A ．48,99⎛⎫ ⎪⎝⎭B ．24,99⎛⎫ ⎪⎝⎭C ．()2,0D ．()9,05．（2021·怀仁市大地学校高中部高二月考）已知曲线C ：221mx ny +=（）A ．若m >n >0，则C 是椭圆，其焦点在x 轴上B ．若m =n >0，则C 是圆，其半径为r =1C ．若mn <0，则C 是双曲线，其渐近线方程为n y x m=±D ．若m =0，n >0，则C 是两条直线6．（2021·全国高二单元测试）已知O 为坐标原点，F 是椭圆C ：22221x y a b+=（0a b >>）的左焦点，,A B 分别为椭圆C 的左、右顶点，P 为椭圆C 上一点，且PF x ⊥轴.过点A 的直线l 与线段PF 交于点M ，与y 轴交于点E .若直线BM 经过OE 的中点，则椭圆C 的离心率为（）A ．13B ．12C ．23D ．347．（2021·浙江温州·高二期中）古希腊数学家阿波罗尼奥斯（约公元首262～公元前190年）的著作《圆锥曲线论》是古代世界光辉的科学成果，著作中有这样一个命题：平面内与两定点距离的比为常数k （0k >且1k ≠）的点的轨迹是圆，后人将这个圆称为阿波罗尼期圆．已知(0,0)O ，(3,0)A ，圆222:(2)(0)C x y r r -+=>上有且仅有一个点P 满足||2||PA PO =，则r 的取值可以为（）A ．1B ．2C ．3D ．48．（2021·全国高二课时练习）如图，设1F ，2F 是双曲线()22210xy a a-=>的左、右焦点，过点2F 作渐近线的平行线交另外一条渐近线于点A ，若12AF F △的面积为54，离心率满足12e <<，则双曲线的方程为（）A ．2215x y -=B ．2214x y -=C ．2213x y -=D ．2212x y -=二、三、多项选择题：本题共4小题，每小题满分5分，共20分．在每小题给出的四个选项中，有多项符合题目要求。

第一章 空间向量与立体几何本卷满分150分，考试时间120分钟。

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符合题目要求的． 1．下列四个结论正确的是 （ ）A ．任意向量,a b ，若0a b ⋅=，则0a =或0b =B ．若空间中点O ，A ，B ，C 满足1233OC OA OB =+，则A ，B ，C 三点共线C ．空间中任意向量,,a b c 都满足()()a b c a b c ⋅⋅=⋅⋅ D ．已知向量()()1,1,,2,,4a x b x ==-，若25x <，则,a b 为钝角 【答案】B【解析】0a b ⋅=则0a =或0b =或0,0a b ≠≠，a b ⊥，故A 错误； 若空间中点O ，A ，B ，C 满足1233OC OA OB =+，即()()1233OC OA OB OC -=-， 所以1233AC CB =，化简得：2AC CB =，则A ，B ，C 三点共线，B 正确；设()()()1,1,1,2,2,1a b c ===。

则不满足()()a b c a b c ⋅⋅=⋅⋅，C 错误；()()1,1,,2,,4a x b x ==-，则()()1,1,2,,42452a b x x x x x ⋅=⋅-=-++=-，令520x -<得：25x <，当1124xx ==-时，2x =-，此时,a b 反向， 要想,a b 为钝角，则25x <且2x ≠-，故D 错误. 故选：B2．直角梯形ABCD 中，,4,2,,AB DC AB CD AD BC AB E ===⊥∥是边AB 的中点，将三角形ADE 沿DE 折叠到1A DE 位置，使得二面角1A DE B --的大小为120，则异面直线1A D 与CE 所成角的余弦值为（ ）A ．14B C D ．34【答案】D建如图所示空间直角坐标系，得)11,0A -，()()()0,0,2,0,0,0,0,2,2D E C ，所以()()13,1,2,0,2,2A D EC =-=，所以11123cos ,48A D EC A D EC A D EC⋅+===. 故选：D3．如图，空间四边形OABC 中，OA a =，OB b =，OC c =，点M 在OA 上，且满足2OM MA =，点N 为BC 的中点，则MN =（ ）A ．121232a b c -+B ．211322a b c -++C ．111222a b c +-D ．221332a b c +-【答案】B【解析】1121132322MN MA AB BN OA OB OA BC OA OB OC OB =++=+-+=-++-211322OA OB OC =-++，又OA a =，OB b =，OC c =，∴211322MN a b c =-++,故选：B ．4．以下四组向量在同一平面的是（ ） A ．()1,1,0、()0,1,1、()1,0,1B ．()3,0,0、()1,1,2、()2,2,4C ．()1,2,3、()1,3,2、()2,3,1D ．()1,0,0、()0,0,2、()0,3,0【答案】B对于A 选项，设()()()1,1,00,1,11,0,1m n =+，所以，110n m m n =⎧⎪=⎨⎪+=⎩，无解；对于B 选项，因为()()()2,2,403,0,021,1,2=⋅+，故B 选项中的三个向量共面； 对于C 选项，设()()()1,2,31,3,22,3,1x y =+，所以，2133223x y x y x y +=⎧⎪+=⎨⎪+=⎩，无解；对于D 选项，设()()()1,0,00,0,20,3,0a b =+，所以，013020b a =⎧⎪=⎨⎪=⎩，矛盾.故选：B.5．如图，OABC 是四面体，G 是ABC 的重心，1G 是OG 上一点，且14OG OG =，则（ ）A ．1111666OG OA OB OC =++B ．1OG =111121212OA OB OC ++ C ．1OG =111181818OA OB OC ++ D ．1OG =111888OA OB OC ++【答案】B【解析】连接AG 并延长交BC 于N ，连接ON ，由G 是ABC 的重心，可得23AG AN =，()12ON OB OC =+则()()2221112=3332333AG AN ON OA OB OC OA OB OC OA ⎡⎤=-=+-=+-⎢⎥⎣⎦ 则()1111112444333OG OG OA AG OA OB OC OA ⎛⎫==+=++- ⎪⎝⎭111121212OA OB OC =++故选：B6．设P ABC -是正三棱锥，G 是ABC 的重心，D 是PG 上的一点，且PD DG =，若PD x yPB z PA PC =++，则(),,x y z 为（ ）A ．512,,633⎛⎫ ⎪⎝⎭B ．111,,666⎛⎫ ⎪⎝⎭C ．111,,633⎛⎫ ⎪⎝⎭D ．111,,363⎛⎫ ⎪⎝⎭【答案】B【解析】因为三棱锥P ABC -是正三棱锥，G 是ABC 的重心， 所以1111112()()3333333AG AB AC PB PA PC PA PB PC PA =+=-+-=+-， 因为D 是PG 上的一点，且PD DG =， 所以12PD PG =， 因为PG PA AG =+， 所以111222PD PG PA AG ==+ 1111222333PA PB PC PA ⎛⎫=++- ⎪⎝⎭11112663PA PB PC PA =++-111666PA PB PC =++, 因为PD x yPB z PA PC =++，所以16x y z ===，所以(),,x y z 为111,,666⎛⎫ ⎪⎝⎭，故选：B7．已知正方形ABCD 的边长为2，E ，F 分别为CD ，CB 的中点，分别沿AE ，AF 将三角形ADE ，ABF 折起，使得点B ，D 恰好重合，记为点P ，则AC 与平面PCE 所成角等于（ ）A ．6πB ．4π C ．3πD ．512π 【答案】A【解析】由题意得,PA PF PA PE ⊥⊥，因为正方形ABCD 的边长为2，E ，F 分别为CD ，CB 的中点， 所以1PE PF CE CF ====，所以222222EF CE CF PE PF =+==+， 所以PE PF ⊥所以P A ，PE ，PF 三线互相垂直，故以PE ，PF ，P A 分别为x ，y ，z 轴建立空间直角坐标系，则()0,0,0P ，()1,0,0E ，()0,0,2A ，()0,1,0F ，设(),,C x y z ，则(,,2),(1,,),(,1,)AC x y z EC x y z FC x y z =-=-=-由AC =1EC =，1FC =，得222222222(2)8,(1)1,(1)1x y z x y z x y z ++-=-++=+-+=，解得222,,333C ⎛⎫- ⎪⎝⎭，则222,,,(1,0,0)333PC PE ⎛⎫=-= ⎪⎝⎭设平面PCE 的法向量为(,,)n x y z =，则22203330n PC x y z n PE x ⎧⋅=+-=⎪⎨⎪⋅==⎩，令1z =，则()0,1,1n =， 因为228,,333AC ⎛⎫=- ⎪⎝⎭，所以AC 与平面PCE 所成角的正弦值1cos ,22n AC n AC n AC⋅===，因为AC 与平面PCE 所成角为锐角， 所以AC 与平面PCE 所成角为6π， 故选：A8．在中国古代数学著作《九章算术》中记载了一种称为“曲池”的几何体，该几何体的上､下底面平行，且均为扇环形（扇环是指圆环被扇形截得的部分）.现有一个如图所示的曲池，它的高为2，1AA ，1BB ，1CC ，1DD 均与曲池的底面垂直，底面扇环对应的两个圆的半径分别为1和2，对应的圆心角为90°，则图中异面直线1AB 与1CD 所成角的余弦值为（ ）A ．45B ．35C ．34D ．23【答案】A【解析】设上底面圆心为1O ，下底面圆心为O ，连接1,,OO OC OB 以O 为原点，分别以1,,OC OB OO 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系 则11(1,0,0),(0,2,0),(0,1,2),(2,0,2),C A B D 则11(1,0,2),(0,1,2)CD AB ==- 1111114cos ,55CD AB CD AB CD AB ⋅===⋅又异面直线所成角的范围为π(0,2⎤⎥⎦故异面直线1AB 与1CD 所成角的余弦值为45故选：A一、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分．9．在长方体1111ABCD A B C D -中，1AB AD ==，12AA =，动点P 在体对角线1BD 上（含端点），则下列结论正确的有（ ）A ．当P 为1BD中点时，APC ∠为锐角B ．存在点P ，使得1BD ⊥平面APCC ．AP PC +的最小值D ．顶点B 到平面APC 【答案】ABD【解析】：如图，以点D 为原点建立空间直角坐标系， 设()101BP BD λλ=≤≤，则()()()()11,0,0,1,1,0,0,1,0,0,0,2A B C D ， 则()11,1,2BD =--，故()1,,2BP BD λλλλ==--， 则()()()0,1,0,,2,1,2AP AB BP λλλλλλ=+=+--=--，()()()1,0,0,,21,,2CP CB BP λλλλλλ=+=+--=--，对于A ，当P 为1BD 中点时，则11,,122AP ⎛⎫=- ⎪⎝⎭，11,,122CP ⎛⎫=- ⎪⎝⎭，则11,,122PA ⎛⎫=-- ⎪⎝⎭，11,,122PC ⎛⎫=-- ⎪⎝⎭，所以1cos 03PA PC APC PA PC⋅∠==>⋅， 所以APC ∠为锐角，故A 正确； 当1BD ⊥平面APC ，因为,AP CP ⊂平面APC ，所以11,BD AP BD CP ⊥⊥， 则11140140BD AP BD CP λλλλλλ⎧⋅=+-+=⎪⎨⋅=-++=⎪⎩，解得16λ=，故存在点P ，使得1BD ⊥平面APC ，故B 正确；对于C ，当11,BD AP BD CP ⊥⊥时，AP PC +取得最小值， 由B 得，此时16λ=， 则151,,663AP ⎛⎫=- ⎪⎝⎭，511,,663CP ⎛⎫=- ⎪⎝⎭，所以306AP CP ==即AP PC +C 错误； 对于D ，()()0,1,0,1,1,0AB AC =-， 设平面APC 的法向量(),,n x y z =， 则有()0120n AC x y n AP x z λλλ⎧⋅=-+=⎪⎨⋅=-+-+=⎪⎩，可取()2,2,21n λλλ-，则点B 到平面APC 的距离为cos ,12AB n AB AB n nλ⋅⋅==当0λ=时，点B 到平面APC 的距离为0，当01λ<≤时，==≤，当且仅当12λ=时，取等号，所以点B 到平面APC，故D 正确. 故选：ABD.10．如图，已知正方体1111ABCD A B C D -中，E ，F ，M ，N 分别是CD ，11A B ，1DD ，BC 的中点，则下列说法正确的有（ ）A ．E ，F ，M ，N 四点共面B ．BD 与EF 所成的角为3πC ．在线段BD 上存在点P ，使1PC ⊥平面EFMD ．在线段1A B 上任取点Q ，三棱锥Q EFM -的体积不变 【答案】ABD【解析】以D 为原点，以DA ，DC ，1DD 所在直线分别为x 轴、 y 轴、z 轴，建立如图所示的空间直角坐标系．设2AB =，则()0,0,0D ，()2,0,0A ，()2,2,0B ，()0,2,0C ，()12,0,2A ，()10,2,2C ，()0,1,0E ，()2,1,2F ，()0,0,1M ，()1,2,0N ，设DE xDF yDM zDN =++，则()()()()0,1,02,1,20,0,11,2,0x y z =++，所以20,21,20,x z x z x y +=⎧⎪+=⎨⎪+=⎩，解得1,32,32,3x y z ⎧=-⎪⎪⎪=⎨⎪⎪=⎪⎩故1x y z ++=，即E ，F ，M ，N 四点共面，选项A 正确；因为()2,2,0DB =．()2,0,2EF =，所以1cos ,28DB EF DB EF DB EF⋅===⋅， 所以BD 与EF 所成的角为3π，选项B 正确； 假设在线段BD 上存在点P ，符合题意.设()01DP DB λλ=≤≤，则()1112,22,2PC DC DP DC DB λλλ=-=-=--，若1PC ⊥平面EFM ，则10PC ME ⋅=，10PC MF ⋅=．因为()0,1,1ME =-，()2,1,1MF =，所以2220,42220,λλλ--=⎧⎨-+-+=⎩，此方程组无解，所以在线段BD 上不存在点P ，使1PC ⊥平面EFM ，选项C 错误； 因为()10,2,22A B ME =-=，所以1A B ME ∥，又1A B ⊄平面EFM ，ME ⊂平面EFM ，所以1A B ∥平面EFM ，故1A B 上的所有点到平面EFM 的距离均相等，即在线段1A B 上任取点Q ， 三棱锥Q EFM -的体积不变，选项D 正确． 故选：ABD11．关于空间向量，下列说法正确的是（ ）A ．直线l 的方向向量为()1,1,2a =-，直线m 的方向向量12,1,2b ⎛⎫=- ⎪⎝⎭，则l m ⊥B ．直线l 的方向向量为()0,1,1a =--，平面α的法向量为()0,1,1b =，则l α∥C ．平面α，β的法向量分别为()1,1,2a =-，11,0,2b ⎛⎫= ⎪⎝⎭，则αβ∥D ．若对空间内任意一点O ，都有111236OP OA OB OC =++，则P ，A ，B ，C 四点共面【答案】AD【解析】对于A ，直线l 的方向向量为()1,1,2a =-，直线m 的方向向量12,1,2b ⎛⎫=- ⎪⎝⎭，由2110a b ⋅=--=，则l m ⊥，故正确对于B ，直线l 的方向向量为()0,1,1a =--，平面α的法向量为()0,1,1b =， 所以a b =-，则l α⊥，故错误；对于C ，平面α，β的法向量分别为()1,1,2a =-，11,0,2b ⎛⎫= ⎪⎝⎭，所以()11,0,1,1,21102⎛⎫⋅=⨯-=-+= ⎪⎝⎭a b ，a b ⊥，则αβ⊥，故错误；对于D ，111236OP OA OB OC =++，得1111236++=，则P ，A ，B ，C 四点共面，故正确.故选：AD.12．已知点P 为正方体1111ABCD A B C D -内及表面一点，若AP BD ⊥，则（ ） A ．若//DP 平面1AB C 时，则点P 位于正方体的表面 B ．若点P 位于正方体的表面，则三棱锥C APD -的体积不变 C ．存在点P ，使得BP ⊥平面11B CDD ．AP ，CD 的夹角π3π,24⎡⎤∈⎢⎥⎣⎦【答案】AD【解析】：在正方体1111ABCD A B C D -中，AC BD ⊥，1AA ⊥平面ABCD ，BD ⊂平面ABCD ， 所以1AA BD ⊥，又1AC AA A =∩，1,AC AA ⊂平面11ACC A ， 所以BD ⊥平面11ACC A ，又AP BD ⊥，所以点P 在平面11ACC A 上（包括边界），又11//DA CB ，1DA ⊄平面1AB C ，1CB ⊂平面1AB C ，所以1//DA 平面1AB C ， 同理可得11//A C 平面1AB C ，1111AC A D A ⋂=，111,A C A D ⊂平面11AC D ， 所以平面11//AC D 平面1AB C ，因为//DP 平面1AB C ，D ∈平面11AC D ，所以DP ⊂平面11AC D ，又平面11AC D ⋂平面1111ACC A C A =，所以11P C A ∈，即P 位于正方体的表面，故A 正确； 对于B ，设P 到平面ADC 的距离为h ，则13C APD P ACD ADCV V Sh --==⋅显然当11P C A ∈和1P AA ∈（不包括1A 点）时h 不一样，则三棱锥C APD -的体积不一样，故B 错误；如图建立空间直角坐标系，令正方体的棱长为1，则()1,0,0A ，()0,1,0C ，()10,0,1D ，()11,1,1B ，()10,1,1C ，所以()11,1,1AC =-，()10,1,1CD =-，()11,0,1CB =，所以110AC CD ⋅=，110AC CB ⋅=，即11AC CD ⊥，11AC CB ⊥， 11CD CB C ⋂=，11,CD CB ⊂平面11B CD ，所以1AC ⊥平面11B CD ，若BP ⊥平面11B CD ，则1//BP AC ，显然在平面11ACC A 上（包括边界）不存在点P ，使得1//BP AC ，故C 错误；因为设(),,P x y z ，()1,,AP x y z =-，()1,1,0DB =，所以10AP DB x y ⋅=-+=，即1y x =-， 又()0,1,0CD =-，所以AP CD y ⋅=-，1CD =，(AP x =，设所以AP，CD的夹角为θ，则cos θ==当0y =时cos 0θ=，2πθ=，当0y ≠时cos θ=222z y⎛⎫+≥ ⎪⎝⎭≥ 所以0<≤，所以cos 0θ≤<，因为[]0,θπ∈，所以3,24ππθ⎛⎤∈ ⎥⎝⎦，综上可得3,24ππθ⎡⎤∈⎢⎥⎣⎦，故D 正确；故选：AD三 填空题：本题共4小题，每小题5分，共20分．13．已知梯形ABCD 和矩形CDEF ．在平面图形中，112AB AD DE CD ====，CD AE ⊥．现将矩形CDEF 沿CD 进行如图所示的翻折，满足面ABCD 垂直于面CDEF ．设2EN NC =，EP PB μ=，若AP ∥面DBN ，则实数μ的值为______．【答案】3【解析】易得,CD DE CD DA ⊥⊥，又面ABCD ⊥面CDEF ，面ABCD面CDEF EF =，又AD ⊂面ABCD ，则AD ⊥面CDEF ，又DE ⊂面CDEF ，则AD DE ⊥，以D 为原点建立如图所示空间直角坐标系，则()()()()()0,0,0,1,1,0,1,0,0,0,0,10,2,0D B A E C ，又()2212410,,333333DN DE EN DE EC DE DC DE DE DC ⎛⎫=+=+=+-=+= ⎪⎝⎭，同理可得11,,111111DP DE EP DE EB DE DB μμμμμμμμμμ⎛⎫=+=+=+= ⎪++++++⎝⎭，设面DBN 的法向量为(),,n x y z =，则041033n DB x y n DN y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩，令1y =，则()1,1,4n =--，又11,,111AP AD DP μμμμ⎛⎫=+=- ⎪+++⎝⎭， 又AP ∥面DBN ，则140111AP n μμμμ⋅=+-=+++，解得3μ=. 故答案为：3.14．正四棱柱1111ABCD A B C D -中，14AA =，AB =N 为侧面11BCC B 上一动点（不含边界），且满足1D N CN ⊥.记直线1D N 与平面11BCC B 所成的角为θ，则tan θ的取值范围为_________.【答案】13,22⎫⎛⎫+∞⎪ ⎪⎪ ⎪⎝⎭⎝⎭【解析：建立如图所示空间直角坐标系：则()()10,0,4,0,3,0D C ，设(),3,N x z ，所以()()1,3,4,,0,D N x z CN x z =-=，因为1D N CN ⊥，所以22140D N CN x z z ⋅=+-=， 则224x z z =-+，因为0x <2043z z <-+<， 解得01z <<或34z <<，易知平面11BCC B 的一个法向量为()0,1,0n =， 所以11sin D N n D N nx θ⋅===⋅则cos ,tan θθ==所以tan θ=∈13,22⎫⎛⎫+∞⎪ ⎪⎪ ⎪⎝⎭⎝⎭，故答案为：13,22⎫⎛⎫+∞⎪ ⎪⎪ ⎪⎝⎭⎝⎭.15．如图，锐二面角l αβ--的棱上有A ，B 两点，直线AC ，BD 分别在这个二面角的两个半平面内，且都垂直于AB .已知4AB =，6AC BD ==，CD =则锐二面角l αβ--的平面角的余弦值是___________.【答案】23【解析】设锐二面角l αβ--的平面角为θ，AC CD B A BD =-++，则2222222=36+16+3672cos =40AC AB BD AC AB AC BD A C B D D B θ=++-⋅-⋅+⋅-，则2cos 3θ=.故答案为：2316．如图，棱长为1的正方体ABCD -A 1B 1C 1D 1中，P 为线段A 1B 上的动点(不含端点)，有下列结论：∴平面A 1D 1P ∴平面A 1AP ；∴多面体1D CDP -的体积为定值； ∴直线D 1P 与BC 所成的角可能为3π； ∴APD 1能是钝角三角形.其中结论正确的序号是___________(填上所有序号). 【答案】∴∴∴【解析】对于∴，正方体1111ABCD A B C D -中，111A D AA ⊥，11A D AB ⊥，1AA AB A =，11A D ∴⊥平面1A AP ，11A D ⊥平面11D A P ，∴平面11D A P ⊥平面1A AP ，故∴正确；对于∴，1111122CDD S=⨯⨯=，P 到平面1CDD 的距离1BC =， ∴三棱锥1D CDP -的体积：111111326D CDP P CDD V V --==⨯⨯=，为定值，故∴正确；对于∴，以D 为原点，DA 为x 轴，DC 为y 轴，1DD 为z 轴，建立空间直角坐标系，1(0D ，0，1)，(1,1,0)B ，(0C ，1，0)，设(1P ，a ，)b ，(01,01)a b <<<<，1(1D P =，a ，1)b -，(1,0,0)BC =-，1cos D P <，110||||1D P BC BC D P BC >==<，12=-，所以22(1)3a b +-=， 01a <<，01b <<，所以22(1)3a b +-<，所以假设不成立，故∴错误；对于∴，见上图，由题得1(1,0,0),(0,0,1)A D ,设(1,,1),(01)P y y y -<<， 所以1(0,,1),(1,,)PA y y PD y y =--+=--，所以21112(21)cos ,||||||||y y y yPA PD PA PD PA PD --<>==，当102y <<时，1cos ,0PA PD <><，即1APD ∠是钝角.此时APD 1是钝角三角形. 故∴正确. 故答案为：∴∴∴四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤． 17．（10分）如图，在圆锥PO 中，已知2,PO O =的直径2AB =，点C 是AB 的中点，点D 为AC 中点.(1)证明：AC ⊥平面POD ；(2)求二面角A PC B --的正弦值. 【答案】(1)证明见解析【解析】(1)连接OC ，如图所示：因为,OA OC D =为AC 的中点，所以AC OD ⊥. 又PO ⊥底面,O AC ⊂底面O ，所以AC PO ⊥.因为,OD PO 是平面POD 内的两条相交直线，所以AC ⊥平面POD (2)以O 为坐标原点，,,OB OC OP 所在的直线分别为x 轴，y 轴，z 轴， 建立空间直角坐标系，如图所示：则()()()()1,0,0,1,0,0,0,1,0,0,0,2A B C P -.()()()1,0,2,0,1,2,1,1,0AP CP BC ==-=-设平面APC 的一个法向量为()1111,,x n y z =，则有1100n AP n CP ⎧⋅=⎪⎨⋅=⎪⎩，即11112020x z y z +=⎧⎨-+=⎩， 令11z =，则112,2x y =-=，所以()12,2,1n =-设平面BPC 的一个法向量为()2222,,n x y z =，则有2200n BC n CP ⎧⋅=⎪⎨⋅=⎪⎩，即2222020x y y z -+=⎧⎨-+=⎩，令22y =，则222,1x z ==，所以()22,2,1n = 所以1212121cos ,94n n n nn n ⋅===.所以12sin ,1n n =故二面角A PC B -- 18（12分）如图所示，1111ABCD A B C D -是棱长为1的正方体.(1)设11BAC △的重心为O ，求证：直线OD ⊥平面11BA C ；(2)设E ､F 分别是棱AD ､11D C 上的点，且1DED F a ==，M 为棱AB 的中点，若异面直线DM 与EF a 的值. 【答案】(1)证明见解析；． 【解析】【分析】 (1)设1111AC B D N =，连接1DB ，首先1DD ⊥平面1111D C B A ，11A C ⊂平面1111D C B A ，则111DD AC ⊥， 又1111B D A C ⊥，1111DD B D D =，111,DD B D ⊂平面11BDD B ，所以11A C ⊥平面11BDD B ，而1B D ⊂平面11BDD B ，所以111AC B D ⊥， 同理11A B B D ⊥，1111A C A B A =，111,A C A B ⊂平面11A BC ，所以1B D ⊥平面11A BC ， 连接BN 交1B D 于O ，因为11DA DB DC ==，所以O 是等边11A BC 的中心也是重心， 所以DO ⊥平面11A BC ，(2)如图，以1,,DA DC DD 为,,x y z 轴建立空间直角坐标系，则(,0,0)E a ，1(1,,0)2M ，(0,,1)F a ，1(1,,0)2DM =，(,,1)EF a a =-，由题意cos ,1DM EF DM EF DM EF⋅<>===解得：a =． 19（12分）如图，在四棱锥P −ABCD 中，平面P AD ∴平面ABCD ，点E 为PC 的中点，AB ∴CD ，CD ∴AD ，CD ＝2AB ＝2，P A ＝AD ＝1，P A ∴AD ．(1)证明：BE ∴平面PCD ；(2)求二面角P −BD −E 的余弦值． 【答案】(1)证明见解析(2)13【解析】(1)证明：取PD 的中点F ，连接AF ，EF ，则//EF CD ，12EF CD =．又//AB CD ，12AB CD =，所以//EF AB ，EF AB =，所以四边形ABEF 为平行四边形，所以//AF BE ． 因为1PA AD ==，PF FD =，所以AF PD ⊥． 所以BE PD ⊥．．．．．．因为平面P AD ∴平面ABCD ，PA AD ⊥， 所以P A ∴平面ABCD ，所以PA AB ⊥，．．．．．．所以PB BC ==又点E 为PC 的中点，所以BE PC ⊥．．．．． 又PC PD D ⋂=，所以BE ∴平面PCD ． (2)以A 为原点建立如图所示的空间直角坐标系，则A （0，0，0），P （0，0，1），B （1，0，0），D （0，1，0），C （2，1，0），E （1，12，12）． ．．．．． 于是()()111,0,1,1,1,0,0,,22PB BD BE ⎛⎫=-=-= ⎪⎝⎭设平面PBD 的法向量为()1111,,n x y z =，则110n PB n BD ⎧⋅=⎪⎨⋅=⎪⎩ 得11110x z x y -=⎧⎨-+=⎩．取11x =．得()11,1,1n =…………设平面EBD 的法向量为()2222,n x y z =，则2200n BE n BD ⎧⋅=⎪⎨⋅=⎪⎩，得2222110220y z x y ⎧+=⎪⎨⎪-+=⎩取21x =．得()21,1,1n =-．…………所以1212121cos ,3n n n n n n ⋅〈==〉， 所以二面角P −BD −E 的余弦值为13.20（12分）如图（1），在直角梯形ABCD 中，//AB CD ，AB BC⊥，且122BC CD AB ===，取AB 的中点O ，连结OD ，并将AOD △沿着OD 翻折，翻折后AC =,M N 分别是线段,ADAB 的中点，如图（2）.(1)求证：AC OM ⊥；(2)求平面OMN 与平面OBCD 夹角的余弦值. 【答案】(1)证明见解析【解析】(1)连接OC ，//ABCD ，AB BC ⊥，122BC CD AB ===，O 为AB 中点， ∴四边形ODCB 为正方形，OC ∴=，翻折后，AC =((2222222OA OC AC ∴+=+==，OA OC ∴⊥；又OA OD ⊥，OC OD O =，,OC OD ⊂平面OCD ，OA ∴⊥平面OCD ，CD ⊂平面OCD ，OA CD ∴⊥，又CD OD ⊥，OA OD O =，,OA OD ⊂平面OAD ，CD平面OAD ，OM ⊂平面OAD ，CD OM ∴⊥；OA OD =，M 为AD 中点，OM AD ∴⊥，又CDAD D =，,CD AD ⊂平面ACD ，OM ∴⊥平面ACD ，AC ⊂平面ACD ，AC OM ∴⊥. (2)以O 为坐标原点，,,OD OB OA 正方向为,,x y z 轴，可建立如图所示空间直角坐标系，则()0,0,0O ，()1,0,1M ，()0,1,1N ，()1,0,1OM ∴=，()0,1,1ON =；z 轴⊥平面OBCD ，∴平面OBCD 的一个法向量()0,0,1m =； 设平面OMN 的法向量(),,n x y z =，则00OM n x z ON n y z ⎧⋅=+=⎨⋅=+=⎩，令1x =，解得：1y =，1z =-，()1,1,1n ∴=-；1cos ,3m n m n m n⋅∴<>==⋅即平面OMN 与平面OBCD 21（12分）在四棱锥P ABCD -中，已知侧面PCD 为正三角形，底面ABCD 为直角梯形，AB CD ，90ADC ∠=︒，3AB AD ==，4CD =，点M ，N 分别在线段AB 和PD 上，且2AM DNMB NP==． (1)求证：//PM 平面ACN ；(2)设二面角P CD A --大小为θ，若cos 3θ=，求直线AC 和平面PAB 所成角的正弦值．【答案】(1)证明见解析(2)5 【解析】(1)连接MD ，交AC 于点E ，连接NE ；2AM MB =，223AM AB ∴==，//AB CD ，12AM ME CD DE ∴==， 又2DN NP =，ME PN DE DN ∴=，//NE PM ∴， 又NE ⊂平面ACN ，PM ⊄平面ACN ，//PM ∴平面ACN .(2)取CD 中点F ，连接,PF MF ；作PO MF ⊥，垂足为O ；PCD 为正三角形，PF CD ∴⊥；2AM DF ==，//AM DF ，∴四边形AMFD 为平行四边形，//AD FM ∴， 又90ADC ∠=，CD FM ∴⊥，又PF FM F =，,PF FM ⊂平面PFM ， CD 平面PFM ；PO ⊂平面PFM ，CD PO ∴⊥，又PO FM ⊥，CD FM F =，,CD FM ⊂平面ABCD ，PO ∴⊥平面ABCD ； 作//OG CD ，交BC 于点G ，则OG FM ⊥，以O 为坐标原点，,,OM OG OP 正方向为,,x y z 轴，可建立如下图所示空间直角坐标系，PF CD ⊥，MF CD ⊥，PFO ∴∠即为二面角P CD A --的平面角，又PF =cos PFO ∠=cos 2OF PF PFO ∴=∠=，OP ∴=则(P ，()2,2,0C -，()1,2,0A -，()1,1,0B ，()3,4,0AC ∴=-，(AP =-，(1,BP =--， 设平面PAB 的法向量(),,n x y z =，则200AP n x y BP n x y ⎧⋅=-++=⎪⎨⋅=--+=⎪⎩，令1z =，解得：x =0y =，()22,0,1n ∴=；设直线AC 和平面PAB 所成角为θ，62sin cos ,535AC n AC n AC n θ⋅∴=<>===⨯⋅，故直线AC 和平面PAB 22．（12分） 如图，四棱锥P ABCD -中，四边形ABCD 是矩形，DA ⊥平面PAB ，E 是DA 的中点．(1)若PB 的中点是M ，求证：//EM 平面PCD ；(2)若,2,⊥===PA PB PA AD AB PCE 与平面PAB 所成二面角的正弦值．【答案】(1)证明见解析【解析】(1)如图所示： 取PC 的中点F ，连接EM ，DF ，FM ，因为四边形ABCD 为矩形，E 是AD 的中点，所以1,//2DE BC DE BC =，1,//2=FM BC FM BC ，所以,//DE FM DE FM =， 所以四边形DEMF 是平行四边形，所以//EM DF ，又EM ⊄平面PCD ，DF ⊂平面PCD ，所以//EM 平面PCD .(2)由AD ⊥平面PAB ，PA PB ⊥，建立如图所示空间直角坐标系，则()()()0,0,0,0,2,1,2,0,2P E C ，所以 ()()0,2,1,2,0,2PE PC ==，设平面PCE 的一个法向量为 (),,n x y z =， 则00⎧⋅=⎪⎨⋅=⎪⎩P P n n E C ，即 20220y z x z +=⎧⎨+=⎩， 令 1z =，得11,,12n ⎫⎛=-- ⎪⎝⎭， 易知平面P AB 的一个法向量为 ()0,0,1m =， 则 12cos ,31⋅==⋅+n mn m n m ，设平面PCE 与平面PAB 所成二面角为()0,πθθ⎡⎤∈⎣⎦， 所以5sin ,3n m θ==.。

一、选择题1．已知函数()()sin f x A x ωϕ=+(A 、ω、ϕ均为正的常数)的最小正周期为π，当23x π=时，函数()f x 取得最小值，则下列结论正确的是（ ）A ．()()()220f f f -<<B ．()()()220f f f <-<C ．()()()202f f f -<<D ．()()()022f f f <-<2．已知向量a 、b 、c 满足a b c +=，且::1:1:2a b c =a 、b 夹角为（ ） A ．4π B ．34π C ．2π D ．23π 3．将函数sin()cos()22y x x ϕϕ=++的图象沿x 轴向右平移8π个单位后，得到一个偶函数的图象，则ϕ的取值不可能是（ ）A ．54π-B ．4π-C ．4π D ．34π 4．非零向量a b ，满足：a b a -=，()0a a b ⋅-=，则a b -与b 夹角的大小为 A ．135° B ．120° C ．60° D ．45°5．已知P （14，1），Q （54，－1）分别是函数()()cos f x x ωϕ=＋0,2πωϕ⎛⎫>< ⎪⎝⎭的图象上相邻的最高点和最低点，则ωϕ-=（ ） A ．54π-B ．54πC ．－34π D ．34π 6．已知a R ∈，则“cos 02πα⎛⎫+> ⎪⎝⎭”是“α是第三象限角”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件7．函数()sin()A f x x ωϕ=+(0,)2πωϕ><的部分图象如图所示，则()f π=（ ）A ．4B ．23C ．2D ．38．已知函数()(0,0)y sin x ωθθπω=+<为偶函数，其图象与直线1y =的某两个交点横坐标为1x 、2x ，若21x x -的最小值为π，则（ ） A ．2,2πωθ==B ．1,22==πωθ C ．1,24==πωθ D ．2,4==πωθ9．将函数y =2sin （ωx +π6）（ω>0）的图象向右移2π3个单位后，所得图象关于y 轴对称，则ω的最小值为 A ．2 B ．1 C ．12 D ．1410．已知a ，b 是平面内两个互相垂直的单位向量，若向量c 满足()()0a c b c -⋅-=，则c 的最大值是( ) A ．1B ．2C ．D ．11．已知角6πα-的顶点在原点，始边与x 轴正半轴重合，终边过点()5,12P -， 则7cos 12πα⎛⎫+= ⎪⎝⎭( ) A ．17226-B ．7226-C ．226D ．22612．已知4sin 5α，并且α是第二象限的角，那么tan()απ+的值等于 A ．43-B ．34-C ．34D ．4313．已知f (x )=A sin(ωx+θ)(ω>0),若两个不等的实数x 1,x 2∈()2A x f x ⎧⎫=⎨⎬⎩⎭,且|x 1-x 2|min =π,则f (x )的最小正周期是( ) A ．3πB ．2πC ．πD ．π214．已知tan 3a =，则21cos sin 22a a +=（） A ．25-B ．3C ．3-D ．2515．设0002012tan15cos 22,,21tan 15a b c ===+，则有（ ） A ．c a b <<B ．a b c <<C ．b c a <<D ．a c b <<二、填空题16．已知24sin 225θ=，02πθ⎛⎫<< ⎪⎝⎭4πθ⎛⎫- ⎪⎝⎭的值为_______________.17．已知向量a ，b 满足1a =，且()2a a b b -==，则向量a 与b 的夹角是__________．18．已知角θ的终边上的一点P 的坐标为()3,4，则cos 21sin 2θθ=+________________．19．函数()211sinsin (0)222x f x x ωωω=+->，若函数()f x 在区间x ∈(),2ππ内没有零点，则实数ω的取值范围是_____20．三棱锥V-ABC 的底面ABC 与侧面VAB 都是边长为a 的正三角形，则棱VC 的长度的取值范围是_________.21．在矩形ABCD 中， 3AB =， 1AD =，若M ， N 分别在边BC ， CD 上运动（包括端点，且满足BM CN BCCD=，则AM AN ⋅的取值范围是__________．22．设(1,3,2)a =-，(2,+1,1)b m n =-，且a //b ，则实数m n -=_____．23．为得到函数2y sin x =的图象,要将函数24y sin x π⎛⎫=+ ⎪⎝⎭的图象向右平移至少__________个单位. 24．已知已知sin π3()25α+=，α∈π(0,)2，则sin(π＋α)等于__________25．已知向量()()121a b m =-=，，，，若向量a b +与a 垂直，则m =______． 三、解答题26．已知点(2,0)A -,(1,9)B ,(,)C m n ，O 是原点. （1）若点,,A B C 三点共线，求m 与n 满足的关系式； （2）若AOC ∆的面积等于3，且AC BC ⊥,求向量OC . 27．已知4a =，3b =，()()23261a b a b -⋅+=. （1）求向量a 与b 的夹角θ；（2）若()1c ta t b =+-，且0b c ⋅=，求实数t 的值及c . 28．已知函数()2sin 22cos 6f x x x π⎛⎫=-- ⎪⎝⎭. （1）求函数()f x 的单调增区间； （2）求函数()f x 在0,2π⎡⎤⎢⎥⎣⎦上的值域. 29．已知圆．（1）求过点(3,0)Q 的圆C 的切线l 的方程；（2）如图，(1,0),A M 定点为圆C 上一动点，点P 在AM 上，点N 在CM 上，且满足2,0,AM AP NP AM =⋅=求N 点的轨迹．30．如图所示,函数()2cos (,0.0)2y x x R πωθωθ=+∈>≤≤的图象与y 轴交于点()0,3,且该函数的最小正周期为π.(1)求θ和ω的值； (2)已知点πA ,02⎛⎫⎪⎝⎭,点P 是该函数图象上一点,点00(,)Q x y 是PA 的中点,当003,,22y x ππ⎡⎤=∈⎢⎥⎣⎦时，求0x 的值.【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题1．B2．C3．C4．A5．B6．B7．A8．A9．B10．C11．B12．A13．A14．D15．A二、填空题16．【解析】【分析】由三角函数的基本关系式和正弦的倍角公式求得再由两角差的余弦函数的公式即可求解【详解】由即则又由所以又由【点睛】本题主要考查了三角函数的基本关系式以及正弦的倍角公式和两角差的余弦公式的17．【解析】【分析】先根据条件得再根据向量夹角公式求结果【详解】因为且所以因此【点睛】求平面向量夹角方法：一是夹角公式；二是坐标公式；三是几何方法从图形判断角的大小18．【解析】分析：由角的终边上的一点的坐标为求出的值利用将的值代入即可得结果详解：角的终边上的一点的坐标为那么故答案为点睛：本题主要考查三角函数的定义及二倍角的正弦公式与余弦公式属于中档题给值求值问题求19．【解析】分析：先化简函数f(x)再求得再根据函数在区间内没有零点得到不等式组最后解不等式组即得w的范围详解：由题得f(x)=因为所以当或时f(x)在内无零点由前一式得即由k=0得K取其它整数时无解同20．【解析】分析：设的中点为连接由余弦定理可得利用三角函数的有界性可得结果详解：设的中点为连接则是二面角的平面角可得在三角形中由余弦定理可得即的取值范围是为故答案为点睛：本题主要考查空间两点的距离余弦定21．19【解析】设则也即是化简得到其中故填点睛：向量数量积的计算有3个基本的思路：（1）基底法：如果题设中有一组不共线的向量它们的模长和夹角已知则其余的向量可以用基底向量去表示数量积也就可以通过基底向量22．8【解析】由题意得23．【解析】函数的解析式：则要将函数的图象向右平移至少个单位点睛：由y＝sinx的图象利用图象变换作函数y＝Asin(ωx＋φ)(A＞0ω＞0)(x∈R)的图象要特别注意：当周期变换和相位变换的先后顺序24．【解析】由题意得25．【解析】利用平面向量的加法公式可得：由平面向量垂直的充要条件可得：解方程可得：三、解答题26．27．28．29．30．2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题 1．B 解析：B 【解析】依题意得，函数f （x ）的周期为π， ∵ω＞0，∴ω=2ππ=2．又∵当x=23π 时，函数f （x ）取得最小值， ∴2×23π +φ=2kπ+32π ，k ∈Z ，可解得：φ=2kπ+6π，k ∈Z ， ∴f （x ）=Asin （2x+2kπ+6π）=Asin （2x+6π）． ∴f （﹣2）=Asin （﹣4+6π）=Asin （6π﹣4+2π）＞0． f （2）=Asin （4+6π）＜0， f （0）=Asin 6π=Asin 56π＞0， 又∵32π＞6π﹣4+2π＞56π＞2π，而f （x ）=Asinx 在区间（2π，32π）是单调递减的，∴f （2）＜f （﹣2）＜f （0）． 故选：B ．2．C解析：C 【解析】 【分析】对等式a b c +=两边平方，利用平面向量数量积的运算律和定义得出0a b ⋅=，由此可求出a 、b 的夹角. 【详解】等式a b c +=两边平方得2222a a b b c +⋅+=，即2222cos a b b c a θ+⋅+=，又::1:1:a b c =0a b ⋅=，a b ∴⊥，因此，a 、b 夹角为2π，故选：C. 【点睛】本题考查平面向量夹角的计算，同时也考查平面向量数量积的运算律以及平面向量数量积的定义，考查计算能力，属于中等题.3．C解析：C 【解析】试题分析：()1sin()cos()sin 2222y x x x ϕϕϕ=++=+将其向右平移8π个单位后得到：11sin 2sin 22824y x x ππϕϕ⎛⎫⎛⎫⎛⎫=-+=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，若为偶函数必有：()42k k Z ππϕπ-=+∈，解得：()34k k Z πϕπ=+∈，当0k =时，D 正确，1k =-时，B 正确，当2k =-时，A 正确，综上，C 错误. 考点：1.函数的图像变换；2.函数的奇偶性.4．A解析：A 【解析】 【分析】先化简()0a a b ⋅-=得2=a a b ⋅，再化简a b a -=得2b a =，最后求a b -与b 的夹角. 【详解】因为()0a a b ⋅-=，所以220=a a b a a b -⋅=∴⋅，，因为a b a -=，所以2222a a a b b =-⋅+， 整理可得22b a b =⋅， 所以有2b a =，设a b -与b 的夹角为θ，则()2cos a b b a b b a b ba bθ-⋅⋅-===-222222||a a =-， 又0180θ︒≤≤︒，所以135θ=︒， 故选A ． 【点睛】本题主要考查数量积的运算和向量夹角的计算，意在考查学生对这些知识的理解掌握水平和分析推理能力.5．B解析：B 【解析】【分析】由点P,Q 两点可以求出函数的周期，进而求出ω，再将点P 或点Q 的坐标代入，求得ϕ，即求出ωϕ-． 【详解】 因为512244πω⎛⎫-=⎪⎝⎭，所以ωπ=，把1,14P ⎛⎫ ⎪⎝⎭的坐标代入方程()cos y x πϕ=+，得 ()24k k Z ϕππ=-+∈，因为2πϕ<，所以5,44ππϕωϕ=--=，故选B ． 【点睛】本题主要考查利用三角函数的性质求其解析式．6．B解析：B 【解析】 【分析】 先化简“cos 02πα⎛⎫+> ⎪⎝⎭”，再利用充要条件的定义判断. 【详解】 因为cos 02πα⎛⎫+> ⎪⎝⎭，所以-sin 0,sin 0,ααα>∴<∴是第三、四象限和y 轴负半轴上的角.α是第三、四象限和y 轴负半轴上的角不能推出α是第三象限角，α是第三象限角一定能推出α是第三、四象限和y 轴负半轴上的角，所以“cos 02πα⎛⎫+>⎪⎝⎭”是“α是第三象限角”的必要非充分条件. 故答案为：B. 【点睛】(1)本题主要考查充要条件的判断和诱导公式，考查三角函数的值的符号，意在考查学生对这些知识的掌握水平和分析推理能力.(2) 判定充要条件常用的方法有定义法、集合法、转化法.7．A解析：A 【解析】试题分析：根据题意，由于函数()sin()A f x x ωϕ=+(0,)2πωϕ><，那么根据图像可知周期为2π，w=4，然后当x=6π,y=2，代入解析式中得到22sin(4)6πϕ=⨯+，6πϕ=-，则可知()f π=4，故答案为A.考点：三角函数图像点评：主要是考查了根据图像求解析式，然后得到函数值的求解，属于基础题．8．A解析：A 【解析】分析：首先根据12x x -的最小值是函数的最小正周期，求得ω的值，根据函数是偶函数，求得θ的值，从而求得正确的选项.详解：由已知函数sin()(0)y x ωθθπ=+<<为偶函数，可得2πθ=，因为函数sin()(0)y x ωθθπ=+<<的最大值为1，所以21x x -的最小值为函数的一个周期，所以其周期为T π=，即2=ππω，所以=2ω，故选A.点睛：该题考查的是有关三角函数的有关问题，涉及到的知识点有函数的最小正周期的求法，偶函数的定义，诱导公式的应用，正确使用公式是解题的关键，属于简单题目.9．B解析：B 【解析】 将函数y =2sin （ωx +π6）（ω>0）的图象向右移2π3个单位后，可得y =2sin （ωx –2π3ω+π6）的图象，再根据所得图象关于y 轴对称，∴–2π3ω+π6=kπ+π2，k ∈Z ，即ω=–31–22k ，∴当k =–1时，ω取得最小值为1，故选B ． 10．C解析：C 【解析】 【分析】 【详解】 试题分析：由于垂直，不妨设，，，则，，表示到原点的距离，表示圆心，为半径的圆，因此的最大值，故答案为C ．考点：平面向量数量积的运算．11．B解析：B【解析】分析：利用三角函数的定义求得66cos sin ππαα⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭， 结果，进而利用两角和的余弦函数公式即可计算得解．详解：由三角函数的定义可得512,613613cos sin ππαα⎛⎫⎛⎫-=--= ⎪ ⎪⎝⎭⎝⎭， 则773cos cos cos 12661264ππππππααα⎛⎫⎛⎫⎛⎫+=-++=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭33=cos cos sin sin 6464ππππαα⎛⎫⎛⎫⎛⎫⎛⎫--- ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭512=1313⎛⎛⎫--= ⎪ ⎝⎭⎝⎭ 点睛：本题考查任意角的三角函数的定义，两角和与差的余弦函数公式，考查了计算能力和转化思想，属于基础题．12．A解析：A 【解析】 【分析】由诱导公式可得()tan tan παα+=，由角的正弦值和角所在的象限，求出角的余弦值，然后，正弦值除以余弦值得正切值．即可得到答案 【详解】 ∵4sin 5α=，并且α是第二象限的角，，35cos α∴-＝ ， ∴tanα＝43-，则么()4tan tan 3παα+==-. 故选A ． 【点睛】本题考查给值求值问题．掌握同角三角函数的基本关系式和诱导公式，并会运用它们进行简单的三角函数式的化简、求值及恒等式证明．13．A解析：A 【解析】 【分析】 由题意可得123ππω⨯=，求得ω的值，可得()f x 的最小正周期是2πω的值 【详解】由题意可得()1sin 2x ωθ+=的解为两个不等的实数1x ，2x且123ππω⨯=，求得23ω= 故()f x 的最小正周期是23ππω=故选A 【点睛】本题主要考查了的是三角函数的周期性及其图象，解题的关键根据正弦函数的图象求出ω的值，属于基础题14．D解析：D 【解析】 【分析】根据正弦的倍角公式和三角函数的基本关系式，化为齐次式，即可求解，得到答案． 【详解】由题意，可得222221cos sin cos cos sin 2cos sin cos 2cos sin a a a a a a a a a a++=+=+221tan 1321tan 135a a ++===++，故选D ．【点睛】 本题主要考查了正弦的倍角公式，以及三角函数的基本关系式的化简、求值，着重考查了推理与运算能力，属于基础题．15．A解析：A 【解析】 【分析】利用两角差的正弦公式化简a ，分子分母同乘以2cos 15结合二倍角的正弦公式化简b ，利用降幂公式化简c ，从而可得结果. 【详解】()sin 302sin28a =︒-︒=︒ ，222sin15cos15sin 30cos 15cos 15b ==+sin28a >=sin25sin28,c a b a c ==︒<︒=∴>>，故选A.【点睛】本题主要考查二倍角的正弦公式、二倍角的余弦公式，两角差的正弦公式，意在考查综合运用所学知识解答问题的能力，属于中档题.二、填空题16．【解析】【分析】由三角函数的基本关系式和正弦的倍角公式求得再由两角差的余弦函数的公式即可求解【详解】由即则又由所以又由【点睛】本题主要考查了三角函数的基本关系式以及正弦的倍角公式和两角差的余弦公式的解析：75【解析】 【分析】由三角函数的基本关系式和正弦的倍角公式，求得249(cos sin )25θθ+=，再由两角差的余弦函数的公式，即可求解． 【详解】 由24sin 225θ=，即242sin cos 25θθ=， 则2222449(cos sin )cos 2sin cos sin 12525θθθθθθ+=++=+=， 又由02πθ<<，所以cos 0,sin 0θθ>>，7cos()cos sin 45πθθθ-=+=．【点睛】本题主要考查了三角函数的基本关系式，以及正弦的倍角公式和两角差的余弦公式的化简、求值，着重考查了推理与运算能力，属于基础题．17．【解析】【分析】先根据条件得再根据向量夹角公式求结果【详解】因为且所以因此【点睛】求平面向量夹角方法：一是夹角公式；二是坐标公式；三是几何方法从图形判断角的大小 解析：120︒【解析】 【分析】先根据条件得a b ⋅，再根据向量夹角公式求结果. 【详解】因为1a =，且()2a a b ⋅-=，所以2-2,121,a a b a b ⋅=∴⋅=-=- 因此112πcos ,,1223a b a b a b a b⋅-===-∴=⨯⋅. 【点睛】求平面向量夹角方法：一是夹角公式cos a b a bθ⋅=⋅；二是坐标公式cos θ=；三是几何方法，从图形判断角的大小.18．【解析】分析：由角的终边上的一点的坐标为求出的值利用将的值代入即可得结果详解：角的终边上的一点的坐标为那么故答案为点睛：本题主要考查三角函数的定义及二倍角的正弦公式与余弦公式属于中档题给值求值问题求解析：17-【解析】分析：由角θ的终边上的一点P 的坐标为()3,4，求出,cos sin θθ的值，利用2cos 212sin 1212cos sin sin θθθθθ-=++，将,cos sin θθ的值代入即可得结果. 详解：角θ的终边上的一点P 的坐标为()3,4，43,cos 55y x sin r r θθ∴====， 那么216712cos 212sin 1252543491212cos 7125525sin sin θθθθθ-⨯--====-+++⨯⨯，故答案为17-. 点睛：本题主要考查三角函数的定义及二倍角的正弦公式与余弦公式，属于中档题.给值求值问题，求值时要注意：(1)观察角，分析角与角之间的差异以及角与角之间的和、差、倍的关系，巧用诱导公式或拆分技巧；(2)观察名，尽可能使三角函数统一名称；(3)观察结构，以便合理利用公式，整体化简求值.19．【解析】分析：先化简函数f(x)再求得再根据函数在区间内没有零点得到不等式组最后解不等式组即得w 的范围详解：由题得f(x)=因为所以当或时f(x)在内无零点由前一式得即由k=0得K 取其它整数时无解同解析：][1150,,848⎛⎤⋃ ⎥⎝⎦【解析】分析：先化简函数f(x) )24wx π=-,再求得(,2),444wx w w πππππ-∈--再根据函数()f x 在区间x ∈ (),2ππ内没有零点得到不等式组，最后解不等式组即得w 的范围. 详解：由题得f(x)=1cos 1111sin sin cos )222224wx wx wx wx wx π-+-=-=-, 因为x ∈ (),2ππ，所以(,2),444wx w w πππππ-∈--当(,2)(2,2),44w w k k k z πππππππ--⊆+∈或(,2)(2,2),44w w k k k z πππππππ--⊆-∈时，f(x)在(),2ππ内无零点，由前一式得24,224k w w k πππππππ⎧≤-⎪⎪⎨⎪-≤+⎪⎩即152,48k w k +≤≤+由k=0得1548w ≤≤， K 取其它整数时无解，同理，由后一式，解得1(0,]8w ∈， 综上，w 的取值范围是][1150,,848⎛⎤⋃ ⎥⎝⎦. 点睛：（1）本题主要考查三角恒等变换，考查三角函数的图像和性质，考查三角函数的零点问题，意在考查学生对这些知识的掌握水平和分析推理能力数形结合的思想方法.(2)解答本题的关键有两点，其一是分析得到当(,2)(2,2),44w w k k k z πππππππ--⊆+∈或(,2)(2,2),44w w k k k z πππππππ--⊆-∈时，f(x)在(),2ππ内无零点，其二是进一步转化得到不等式组解不等式组. 20．【解析】分析：设的中点为连接由余弦定理可得利用三角函数的有界性可得结果详解：设的中点为连接则是二面角的平面角可得在三角形中由余弦定理可得即的取值范围是为故答案为点睛：本题主要考查空间两点的距离余弦定解析：)【解析】分析：设AB 的中点为D ，连接,,VD CD VC ，由余弦定理可得22233cos 22VC a a VDC =-∠，利用三角函数的有界性可得结果. 详解：设AB 的中点为D ， 连接,,VD CD VC，则VD VC ==VDC ∠是二面角V AB C --的平面角， 可得0,1cos 1VDC VDC π<∠<-<∠<，在三角形VDC 中由余弦定理可得，2222cos VC VDC ⎫⎫=+-∠⎪⎪⎪⎪⎝⎭⎝⎭ 2233cos 22a a VDC =-∠22030VC a VC <<⇒<<，即VC的取值范围是()，为故答案为().点睛：本题主要考查空间两点的距离、余弦定理的应用，意在考查空间想象能力、数形结合思想的应用，属于中档题.21．19【解析】设则也即是化简得到其中故填点睛：向量数量积的计算有3个基本的思路：（1）基底法：如果题设中有一组不共线的向量它们的模长和夹角已知则其余的向量可以用基底向量去表示数量积也就可以通过基底向量解析：[1,9] 【解析】设,BM BC CN CD λλ==，则()()··AM AN AB BM AD DN =++，也即是()()··1AM AN AB BC AD DC λλ⎡⎤=++-⎣⎦，化简得到·98AM AN λ=-，其中[]0,1λ∈，故[]·1,9AM AN ∈，填[]1,9．点睛：向量数量积的计算有3个基本的思路：（1）基底法：如果题设中有一组不共线的向量，它们的模长和夹角已知，则其余的向量可以用基底向量去表示，数量积也就可以通过基底向量间的运算去考虑；（2）坐标法：建立合适的坐标系，把数量积的计算归结为坐标的运算；（2）靠边靠角转化：如果已知某些边和角，那么我们在计算数量积时尽量往这些已知的边和角去转化．22．8【解析】由题意得解析：8 【解析】 由题意得2115,3,8132m n m n m n +-==∴==--=- 23．【解析】函数的解析式：则要将函数的图象向右平移至少个单位点睛：由y ＝sinx 的图象利用图象变换作函数y ＝Asin(ωx ＋φ)(A ＞0ω＞0)(x ∈R)的图象要特别注意：当周期变换和相位变换的先后顺序解析：8π 【解析】 函数的解析式：sin 2sin 248y x x ππ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭. 则要将函数24y sin x π⎛⎫=+ ⎪⎝⎭的图象向右平移至少8π个单位. 点睛：由y ＝sin x 的图象，利用图象变换作函数y ＝A sin(ωx ＋φ)(A ＞0，ω＞0)(x ∈R)的图象，要特别注意：当周期变换和相位变换的先后顺序不同时，原图象沿x 轴的伸缩量的区别．先平移变换再周期变换(伸缩变换)，平移的量是|φ|个单位；而先周期变换(伸缩变换)再平移变换，平移的量是ϕω个单位．24．【解析】由题意得解析：4-5【解析】 由题意得3π44cos ,(0,)sin ,sin(π)sin 5255ααααα=∈∴=+=-=- 25．【解析】利用平面向量的加法公式可得：由平面向量垂直的充要条件可得：解方程可得： 解析：7【解析】利用平面向量的加法公式可得：()1,3a b m +=-+，由平面向量垂直的充要条件可得：()()()()1,31,2160a b a m m +⋅=-+⋅-=--++=， 解方程可得：7m =.三、解答题 26．（1）360n m --=（2）()4,3OC =或()5,3OC =- 【解析】 【分析】(1)由题意结合三点共线的充分必要条件确定m ,n 满足的关系式即可； (2)由题意首先求得n 的值，然后求解m 的值即可确定向量的坐标. 【详解】（1）()3,9AB =，()2,AC m n =+， 由点A ，B ，C 三点共线，知AB ∥AC ， 所以()3920n m -+=，即360n m --=； （2）由△AOC 的面积是3，得1232n ⨯⨯=，3n =±， 由AC BC ⊥，得0AC BC ⋅=，所以()()2,1,90m n m n +⋅--=，即22920m n m n ++--=, 当3n =时，2200m m +-=， 解得4m =或5m =-， 当3n =-时，2340m m ++=，方程没有实数根， 所以()4,3OC =或()5,3OC =-． 【点睛】本题主要考查三点共线的充分必要条件，向量垂直的充分必要条件等知识，意在考查学生的转化能力和计算求解能力.27．（1）23πθ=；（2）35t =，c =63. 【解析】 【分析】（1）由向量的数量积，代值计算即可； （2）由数量积为0，代入计算即可. 【详解】（1）因为()()23261a b a b -⋅+= 故2244361a a b cos b θ-⋅-=解得：12cos θ=-因为[]0,θπ∈，所以23πθ=. （2）0b c ⋅= 则()()10b ta t b ⋅+-=()210ta b t b ⋅+-=化简得：159t = 解得：35t = 此时3255c a b =+ 23255a b ⎫+⎪⎭ 224122525a b a b ++⋅【点睛】本题考查向量数量积的运算，属基础题.28．（1）()π5ππ,π1212k k k Z ⎡⎤-+∈⎢⎥⎣⎦；（2）512⎡⎤-⎢⎥⎣⎦.【解析】 【分析】 化简()f x 解析式.（1）根据三角函数单调区间的求法，求得函数()f x 的单调增区间；（2）根据三角函数值域的求法，求得函数()f x 在0,2π⎡⎤⎢⎥⎣⎦上的值域.【详解】 依题意()()ππsin 2cos cos 2sin 1cos 266f x x x x =--+33sin 2cos 2122x x =--π3sin 213x ⎛⎫=-- ⎪⎝⎭.（1）由πππ2π22π232k x k -+≤-≤+，解得π5πππ1212k x k -≤≤+，所以()f x 的单调增区间为()π5ππ,π1212k k k Z ⎡⎤-+∈⎢⎥⎣⎦. （2）由于π02x ≤≤，所以ππ2π2333x -≤-≤，所以π53sin 21,3132x ⎛⎫⎡⎤--∈-- ⎪⎢⎥⎝⎭⎣⎦.所以()f x 在0,2π⎡⎤⎢⎥⎣⎦上的值域为5,312⎡⎤--⎢⎥⎣⎦. 【点睛】本小题主要考查三角恒等变换，考查三角函数单调区间的求法，考查三角函数值域的求法，考查运算求解能力，属于基础题.29．（1），（2）【解析】 【分析】 【详解】（1）由题意知所求的切线斜率存在，设其方程为，即； 由得，解得， 从而所求的切线方程为，．（2）∴NP 为AM 的垂直平分线，∴|NA|=|NM|． 又∴动点N 的轨迹是以点C （－1，0），A （1，0）为焦点的椭圆． 且椭圆长轴长为焦距2c=2．∴点N 的轨迹是方程为30．(1)πθ6=.ω2=.(2)023x π=，或034x π=. 【解析】试题分析：(1)由三角函数图象与y 轴交于点(3可得3cos 2θ=，则6πθ=.由最小正周期公式可得2ω=.(2)由题意结合中点坐标公式可得点P 的坐标为0232x π⎛-⎝.代入三角函数式可得053cos 46x π⎛⎫-= ⎪⎝⎭，结合角的范围求解三角方程可得023x π=，或034x π=. 试题解析：(1)将0,3x y ==()2cos y x ωθ=+中，得3cos θ=， 因为02πθ≤≤，所以6πθ=.由已知T π=，且0ω>，得222T ππωπ===. (2)因为点()00,0,,2A Q x y π⎛⎫⎪⎝⎭是PA 的中点， 03y =P 的坐标为0232x π⎛- ⎝.又因为点P 在2cos 26y x π⎛⎫=+ ⎪⎝⎭的图象上，且02x ππ≤≤，所以053cos 462x π⎛⎫-= ⎪⎝⎭，且075194666x πππ≤-≤， 从而得0511466x ππ-=，或0513466x ππ-=，即023x π=，或034x π=.。

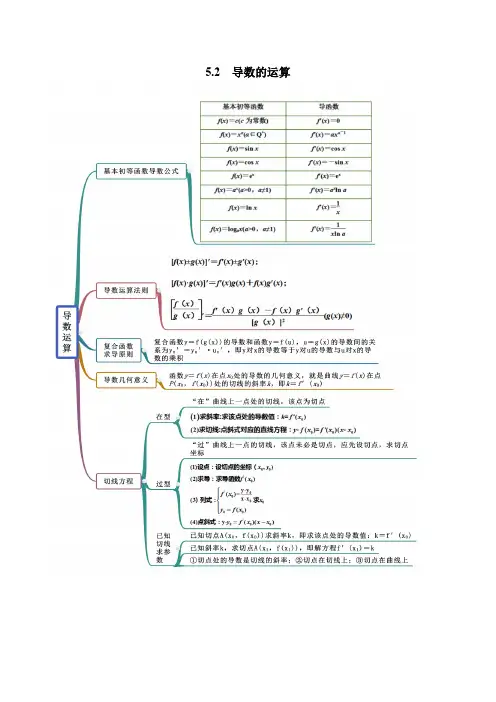
5.2 导数的运算考点一 初等函数求导【例1】（2020·林芝市第二高级中学高二期末（文））求下列函数的导函数.（1）()3224f x x x =-+（2）()32113f x x x ax =-++（3）()cos ,(0,1)f x x x x =+∈ （4）2()3ln f x x x x =-+-（5）sin y x = （6）11x y x +=-【答案】(1)2()68f x x x =-+ (2)2()2f x x x a '=-+ (3)()sin 1f x x '=-+ (4)1()23f x x x'=--+ (5)cos y x '= (6)22(1)y x '=--【解析】（1）由()3224f x x x =-+，则()'268f x x x =-+；（2）由()32113f x x x ax =-++，则()'22f x x x a =-+；（3）由()cos ,(0,1)f x x x x =+∈ ，则()1sin ,(0,1)f x x x =-∈；（4）由2()3ln f x x x x =-+-，则'1()23f x x x=-+-；（5）由sin y x =，则 'cos y x =；（6）由11x y x +=-，则'''22(1)(1)(1)(1)2(1)(1)x x x x y x x +⨯--+⨯-==---.【一隅三反】1．（2020·西藏高二期末（文））求下列函数的导数.（1）2sin y x x =；（2）n 1l y x x=+；（3）322354y x x x =-+-.【答案】（1）22sin cos y x x x x '=+（2）211y x x'=-（3）2665y x x '=-+【解析】（1）2sin y x x =22sin cos y x x x x '=+（2）n 1l y x x =+211y x x'=-（3）322354y x x x x =-+-2665y x x '=-+2．（2020·通榆县第一中学校高二月考（理））求下列函数的导数：（Ⅰ）22ln cos y x x x =++；（Ⅱ）3e x y x =.【答案】（Ⅰ）14sin x x x+-；（Ⅱ）()233e xx x +.【解析】（Ⅰ）由导数的计算公式，可得()212(ln )(cos )4sin y x x x x x x'=++=+-'''.（Ⅱ）由导数的乘法法则，可得()()()3323e e 3e x xx y x x xx ''=+=+'.3．（2020·山东师范大学附中高二期中）求下列函数在指定点的导数：（1）4ln(31)y x =++ ，1x =； （2）2cos 1sin x y x=+，π2x =．【答案】（1）12x y ='=（2）21ln 2x y π==+'【解析】（1）321231y x x -'=-++，12x y ='=（2）21sin y x+'=，21ln2x y π==+'考点二 复合函数求导【例2】．（2020·凤阳县第二中学高二期末（理））求下列函数的导数：（1）2=e x y ；（2）()313y x =-.【答案】（1）22x e ；（2）29(13)x --或281549y x x '=-+-．【解析】（1）2'22e (2)e 22e x x x y x =⋅=⋅='；（2）()()22'313(13)913y x x x =--=--'．或281549y x x '=-+-． 【一隅三反】1．（2020·陕西碑林·西北工业大学附属中学高二月考（理））求下列函数的导数：(1)()*()2+1ny x n N ∈＝，；(2)(ln y x =+；(3)11x x e y e +=-；(4)2)2(+5y xsin x ＝．【答案】（1）()1'221n y n x -=+；（2）'y =；（3）()221xxe y e-'=-；（4）2sin(25)4cos(25)y x x x '=+++.【解析】(1)()()()11'2121'221n n y n x x n x ⋅－－＝＋＋＝＋；（2）1y ⎛=+= ⎝'（3）∵12111xx xe y e e +==+--∴()()222211xxx xe e y e e'-=-=--；（4）()()2sin 254cos 25y x x x =+'++.2．（2020·横峰中学高二开学考试（文））求下列各函数的导数：（1）ln(32)y x =-；（2）()212x x f x ee e -+=++（3）y【答案】（1）332y x '=-；（2）21()2x x f x e e -+'=-+.（3）y '=【解析】（1）因为ln(32)y x =-令32t x =-，ln y t =所以()()1332ln 332y x t t x '''=-⋅=⋅=-（2）()21221,()2x x x x f x e f x ee e e -+-+∴'=-+++= .（3）令212t x =-，则12y t =，所以112211()(4)22y t t t x -'''==⋅=-=；考点三 求导数值【例3】．（2020·甘肃城关·兰州一中高二期中（理））已知函数()f x 的导函数为()'f x ，且满足()3(1)ln f x xf x '=+，则(1)f '=A ．12-B ．12C ．1-D ．e【答案】A【解析】()()31ln f x xf x '=+ ，求导得()()131f x f x''=+，则()()1311f f ''=+，解得()112f '=-.故选：A.【一隅三反】1．（2020·广东湛江·高二期末（文））已知函数()cos x f x x =，则2f π⎛⎫= ⎪⎝⎭'（ ）A ．2π-B ．2πC ．3πD ．3π-【答案】A【解析】()cos x f x x = ，()2sin cos x x x f x x --'∴=，因此，2sin 22222f πππππ⎛⎫⎛⎫--- ⎪ ⎪⎛⎫⎝⎭⎝⎭'-==- ⎪⎝⎭⎛⎫- ⎪⎝⎭.故选：A.2．（2020·四川高二期中（理））若函数()()22co 102s x f x x f x '=++，则6f π⎛⎫' ⎪⎝⎭的值为（ ）A ．0B ．6πC ．3πD ．π【答案】B【解析】因为()()20sin 1f x x f x ''=-+，所以令0x =，则()01f '=，所以()2sin 1f x x x '=-+，则66f ππ⎛⎫'=⎪⎝⎭，故选： B.3．（2020·广西桂林·高二期末（文））已知函数2()f x x x =+，则()1f '=（ ）A ．3B ．0C ．2D ．1【答案】A【解析】由题得()21(1)3f x x f ''=+∴=，.故选：A 考点四 求切线方程【例4】．（2020·郸城县实验高中高二月考（理））已知曲线31433y x =+（1）求曲线在点(2,4)P 处的切线方程；（2）求曲线过点(2,4)P 的切线方程【答案】（1）440x y --=；（2）20x y -+=或440x y --=．【解析】（1）∵2y x '=，∴在点()2,4P 处的切线的斜率2|4x k y ='==，∴曲线在点()2,4P 处的切线方程为()442y x -=-，即440x y --=．（2）设曲线31433y x =+与过点()2,4P 的切线相切于点30014,33A x x ⎛⎫+ ⎪⎝⎭，则切线的斜率020|x x k y x =='=，∴切线方程为()320001433y x x x x ⎛⎫-+=-⎪⎝⎭，即23002433y x x x =⋅-+．∵点()2,4P 在该切线上，∴2300244233x x =-+，即320340x x -+=，∴322000440x x x +-+=，∴()()()2000014110x x x x +-+-=，∴()()200120x x +-=，解得01x =-或02x =．故所求切线方程为440x y --=或20x y -+=．【一隅三反】1．（2020·黑龙江大庆实验中学高三月考（文））曲线2xy x =-在点()1,1-处的切线方程为A ．21y x =-+B ．32y x =-+C ．23y x =-D ．2y x =-【答案】A【解析】2xy x =-的导数为22'(2)y x =--，可得曲线22y x =-在点()1,1-处的切线斜率为1'|2x k y ===-，所以曲线2xy x =-在点()1,1-处的切线方程为12(1)y x +=--，即21y x =-+，故选A.2．（2020·河南高三其他（理））曲线()21ln 22y x x =-在某点处的切线的斜率为32-，则该切线的方程为（）A ．3210x y +-=B ．3210x y ++=C ．6450x y +-=D ．12870x y +-=【答案】D【解析】求导得1y x x '=-，根据题意得132y x x '=-=-，解得2x =-（舍去）或12x =，可得切点的坐标为11,28⎛⎫⎪⎝⎭，所以该切线的方程为131822y x ⎛⎫-=-- ⎪⎝⎭，整理得12870x y +-=.故选：D.3．（2020·北京高二期末）过点P （0，2）作曲线y ＝1x 的切线，则切点坐标为（ ）A ．（1，1）B ．（2，12）C ．（3，13）D ．（0，1）【答案】A【解析】设切点001(,)x x ,022001112(0)y x x x x '=-∴-=--Q 01x ∴=,即切点(1,1)故选：A4．（2020·吉林洮北·白城一中高二月考（理））已知函数f(x)＝x 3－4x 2＋5x －4．(1)求曲线f(x)在点(2，f(2))处的切线方程；(2)求经过点A(2，－2)的曲线f(x)的切线方程．【答案】（1）x －y －4＝0（2）x －y －4＝0或y ＋2＝0【解析】(1)∵f′(x)＝3x 2－8x ＋5，∴f′(2)＝1，又f(2)＝－2，∴曲线f(x)在点(2，f(2))处的切线方程为y －(－2)＝x －2，即x －y －4＝0．(2)设切点坐标为(x 0，x 03－4x 02＋5x 0－4)，∵f′(x 0)＝3x 02－8x 0＋5，∴切线方程为y －(－2)＝(3x 02－8x 0＋5)(x －2)，又切线过点(x 0，x 03－4x 02＋5x 0－4)，∴x 03－4x 02＋5x 0－2＝(3x 02－8x 0＋5)(x 0－2)，整理得(x 0－2)2(x 0－1)＝0，解得x 0＝2或x 0＝1，∴经过A(2，－2)的曲线f(x)的切线方程为x －y －4＝0或y ＋2＝0．考点五 利用切线求参数【例5】．（2020·全国高三其他（理））已知曲线()ln xy e ax x =-在点()1,ae 处的切线方程为y kx =，则k =（）A ．1-B ．0C ．1D ．e【答案】D【解析】令()()ln xy f x eax x ==-，则()()1ln x xf x e ax x e a x'=-+-（，所以()12f ea e ='-，因为曲线()ln xy eax x =-在点()1,ae 处的切线方程为y kx =，所以该切线过原点，所以()12f ea e ae ='-=，解得1a =，即k e =.故选：D.【一隅三反】1．（2020·岳麓·湖南师大附中月考）已知函数()2ln xf x ax x=-，若曲线()y f x =在()()1,1f 处的切线与直线210x y -+=平行，则a =______.【答案】12-【解析】因为函数()2ln x f x ax x =-，所以()21ln 2xf x ax x-'=-，又因为曲线()y f x =在()()1,1f 处的切线与直线210x y -+=平行，所以()1122f a '=-=，解得12a =-，故答案为：12-2．（2020·安徽庐阳·合肥一中高三月考（文））曲线(1)x y ax e =+在点（0，1）处的切线的斜率为2，则a ＝_____.【答案】1【解析】 (1)x y ax e =+，∴(1)x y ax a e '=++ 012x y a =∴=+='，1a \=.故答案为：1.3．（2020·山东莱州一中高二月考）已知直线y x b =+是曲线3x y e =+的一条切线，则b =________.【答案】4【解析】设()3xf x e =+，切点为()00,+3xx e ，因为()xf x e '=，所以01x e =，解得00x =，所以0034y e =+=，故切点为(0,4)，又切点在切线y x b =+上，故4b =.故答案为：4。

1、 如图A 、B 、C 、D 为四个村庄,要修筑三条公路,将这四个村庄连接起来,则不同的修筑方案共有( )A. 8种B. 12种C. 16种D. 20种2、 一圆周上有9个点,以这9个点为顶点作三个三角形,当这三个三角形的边互不相交时,我们把它称为一种构图．则满足这样条件的构图共有 ( )A. 3种B. 6种C. 9种D. 12种3、从1，2，3…，100这100个数中，任取两个数，使它们的乘积能被7整除，这两个数的取法（不计顺序）共有多少种？4、从10,,4,3,2,1 这10个自然数中，每次取出不同的两个，使它们乘积是6的倍数，则不同的取法有__________种。

排列组合问题-思维方法5、设4321,,,x x x x 为自然数1，2，3，4的一个全排列，且满足643214321=-+-+-+-x x x x ，则这样的排列有 个.6、 某年数学竞赛邀请了一位来自X 星球的选手参加填空题比赛，共10道题目，这位选手做题有一个古怪的习惯：先从最后一题（第10题）开始往前看，凡是遇到会的题目就作答，遇到不会的题目先跳过（允许跳过所有的题目），一直看到第1题：然后从第1题开始往后看，凡是遇到先前未答的题目就随便写个答案，遇到先前已答的题目则跳过（例如，他可以按照9、8、7、4、3、2、1、5、6、10的次序答题），这样所有题目均有作答，设这位选手可能的答题次序有n 种，则n 的值为（ ）A. 512B. 511C. 1024D. 10237、（2010理14）以集合{},,,U a b c d =的子集中选出4个不同的子集，需同时满足以下两个条件：(1),U ∅都要选出；（2）对选出的任意两个子集A 和B ，必有A B ⊆或B A ⊆，那么共有_________种不同的选法8、如图，甲从A 到B ，乙从C 到D ，两人每次都只能向上或者向右走一格. 如果两个人的线路不相交，则称这两个人的路径为一对孤立路，那么不同的孤立路一共有_____对.（用数字作答）9、将前12个正整数构成的集合{}1,2,,12M =中的元素分成1234,,,M M M M 四个三元子集，使得每个三元子集中的三个数都满足：其中一个数等于另外两数之和，试求不同的分法种数.10、四棱锥的8条棱代表8种不同的化工产品,有公共点的两条棱代表的化工产品放在同一仓库是危险的,没有公共顶点的两条棱多代表的化工产品放在同一仓库是安全的,现打算用编号为①、②、③、④的4个仓库存放这8种化工产品,那么有____种不同的安全存放的方法．10、如图，用四种不同颜色给图中的,,,,,A B C D E F 六个点涂色，要求每个点涂一种颜色，且图中每条线段的两个端点涂不同颜色，则不同的涂色方法共有（ ）种 DAC BA、288种B、264种C、240种D、168种。

八 等比数列的性质及应用(30分钟 60分)一、选择题(每小题5分，共30分)1．已知等比数列{a n }中，a 3a 13＝16，则a 8的值等于( ) A ．4 B ．8 C ．±4 D ．±8【解析】选C.因为a 28 ＝a 3a 13＝16，所以a 8＝±4. 2．已知等比数列{}a n 满足a 5＋a 8＝2，a 6·a 7＝－8，则q 3＝( ) A ．－12 B ．－2 C ．－12 或－2 D ．2【解析】选C.由等比数列的性质可知，a 5·a 8＝a 6·a 7＝－8，又因为a 5＋a 8＝2，所以a 5＝4，a 8＝－2，或a 5＝－2，a 8＝4，所以q 3＝a 8a 5＝－2或－12 .3．(2020·全国Ⅰ卷)设{a n }是等比数列，且a 1＋a 2＋a 3＝1，a 2＋a 3＋a 4＝2，则a 6＋a 7＋a 8＝( )A ．12B ．24C ．30D ．32 【解析】选D.设等比数列{}a n 的公比为q ，则a 1＋a 2＋a 3＝a 1⎝⎛⎭⎫1＋q ＋q 2 ＝1，a 2＋a 3＋a 4＝a 1q ＋a 1q 2＋a 1q 3＝a 1q ⎝⎛⎭⎫1＋q ＋q 2 ＝q ＝2，因此，a 6＋a 7＋a 8＝a 1q 5＋a 1q 6＋a 1q 7＝a 1q 5⎝⎛⎭⎫1＋q ＋q 2 ＝q 5＝32. 4．设{a n }是由正数组成的等比数列，公比q ＝2，且a 1·a 2·a 3·…·a 30＝230，那么a 3·a 6·a 9·…·a 30等于( )A ．210B ．220C ．216D ．215 【解析】选B.设A ＝a 1a 4a 7…a 28，B ＝a 2a 5a 8…a 29， C ＝a 3a 6a 9…a 30，则A ，B ，C 成等比数列， 公比为q 10＝210，由条件得A·B·C ＝230， 所以B ＝210，所以C ＝B·210＝220.5．若1，a ，3成等差数列，1，b ，4成等比数列，则ab 的值为( ) A ．±12 B ．12 C ．1 D ．±1 【解析】选D.由题知2a ＝1＋3， 所以a ＝2.由b 2＝4得b ＝±2，所以a b ＝±1.6．某家庭决定要进行一项投资活动，预计每年收益5%.该家庭2020年1月1日投入10万元，按照复利(复利是指在每经过一个计息期后，都将所得利息加入本金，以计算下期的利息)计算，到2030年1月1日，该家庭在此项投资活动的资产总额大约为( )参考数据：1.058≈1.48，1.059≈1.55，1.0510≈1.63，1.0511≈1.71 A ．14.8万元 B ．15.5万元 C ．16.3万元 D ．17.1万元【解析】选C.由题意知，该家庭2021年1月1日本金加收益和为10·(1＋5%)＝10×1.05，2022年1月1日本金加收益和为10×1.052，2023年1月1日本金加收益和为10×1.053……2030年1月1日本金加收益和为10×1.0510≈10×1.63＝16.3.所以到2030年1月1日，该家庭在此项投资活动的资产总额大约为16.3万元． 二、填空题(每小题5分，共10分)7．等比数列{a n }中，a 1＝3，q ＝2，则a 4＝________，a n ＝________． 【解析】a 4＝a 1q 3＝3×23＝24，a n ＝a 1q n －1＝3×2n －1. 答案：24 3×2n －18．若等差数列{}a n 和等比数列{}b n 满足a 1＝b 1＝1，a 2＝b 2＝2，则a 5b 5＝________.【解析】设等差数列的公差为d ，等比数列的公比为q ，则d ＝2－1＝1，q ＝21 ＝2，所以a 5＝a 1＋4d ＝5，b 5＝b 1×q 4＝16，故a 5b 5＝80. 答案：80三、解答题(每小题10分，共20分)9．已知{a n }是各项均为正数的等比数列，且a 1＋a 2＝2⎝⎛⎭⎪⎫1a 1＋1a 2 ，a 3＋a 4＋a 5＝64⎝ ⎛⎭⎪⎫1a 3＋1a 4＋1a 5 ，求{a n }的通项公式． 【解析】设数列{a n }的公比为q(q>0).因为a 1＋a 2＝2·⎝ ⎛⎭⎪⎫1a 1＋1a 2 ， 所以a 1＋a 1q ＝2·1＋q a 1q ，即a 1＝2a 1q .①又因为a 3＋a 4＋a 5＝64⎝⎛⎭⎪⎫1a 3＋1a 4＋1a 5 ，所以a 3(1＋q ＋q 2)＝64·q 2＋q ＋1a 3q 2 ，即a 3＝64a 3q 2 .②联立①②，解得q ＝2，a 1＝1，故a n ＝2n －1(n ∈N *).10．在等比数列{a n }(n ∈N *)中，a 1＞1，公比q ＞0.设b n ＝log 2a n ，且b 1＋b 3＋b 5＝6，b 1b 3b 5＝0.(1)求证：数列{b n }是等差数列；(2)求{b n }的前n 项和S n 及{a n }的通项a n ； (3)试比较a n 与S n 的大小． 【解析】(1)因为b n ＝log 2a n ，所以b n ＋1－b n ＝log 2a n ＋1－log 2a n ＝log 2 a n ＋1a n＝log 2q(q ＞0)为常数，所以数列{b n }为等差数列且公差d ＝log 2q. (2)因为b 1＋b 3＋b 5＝6，所以(b 1＋b 5)＋b 3＝2b 3＋b 3＝3b 3＝6，即b 3＝2. 又因为a 1＞1，所以b 1＝log 2a 1＞0， 又因为b 1·b 3·b 5＝0，所以b 5＝0，即⎩⎨⎧b 3＝2，b 5＝0， 即⎩⎨⎧b 1＋2d ＝2，b 1＋4d ＝0， 解得⎩⎨⎧b 1＝4，d ＝－1，因此S n ＝4n ＋(－1)n （n －1）2＝9n －n 22 . 又因为d ＝log 2q ＝－1，所以q ＝12 ，b 1＝log 2a 1＝4， 即a 1＝16，所以a n ＝25－n (n ∈N *). (3)由(2)知，a n ＝25－n ＞0， 当n≥9时，S n ＝n （9－n ）2 ≤0， 所以当n≥9时，a n ＞S n .又因为a 1＝16，a 2＝8，a 3＝4，a 4＝2，a 5＝1，a 6＝12 ，a 7＝14 ，a 8＝18 ，S 1＝4，S 2＝7，S 3＝9，S 4＝10， S 5＝10，S 6＝9，S 7＝7，S 8＝4，所以当n ＝3，4，5，6，7，8时，a n <S n ； 当n ＝1，2或n≥9，n ∈N *时，a n ＞S n .(35分钟 70分)一、选择题(每小题5分，共20分)1．已知数列{}a n 中，a 1＝1，a n ＋1＝2a n ＋3，则a 10＝( ) A ．2 045 B ．1 021 C ．1 027 D ．2 051【解析】选A.因为a n ＋1＝2a n ＋3，变形为a n ＋1＋x ＝2(a n ＋x)⇒a n ＋1＝2a n ＋x ⇒x ＝3，即a n ＋1＋3＝2(a n ＋3)，故数列⎩⎨⎧⎭⎬⎫a n ＋3 为等比数列，首项为4，公比为2. 所以a n ＋3＝4·2n －1所以a n ＝4·2n －1－3＝2n ＋1－3， 所以a 10＝2 045.2．若方程x 2－5x ＋m ＝0与x 2－10x ＋n ＝0的四个根适当排列后，恰好组成一个首项为1的等比数列，则mn 的值是( ) A ．4 B ．2 C ．12 D ．14【解析】选D.由题意可知1是方程的1个根，若1是方程x 2－5x ＋m ＝0的根，则m ＝4，另一根为4，设x 3，x 4是方程x 2－10x ＋n ＝0的根，则x 3＋x 4＝10，这四个数的排列顺序只能为1，x 3，4，x 4，公比为2，x 3＝2，x 4＝8，n ＝16，mn ＝14 ；若1是方程x 2－10x ＋n ＝0的根，另一根为9，则n ＝9，设x 2－5x ＋m ＝0的两个根为x 1，x 2，则x 1＋x 2＝5，无论什么顺序均不合题意．3．已知等比数列{a n }满足a n >0，且a 5·a 2n －5＝22n (n≥3)，则当n≥3时，log 2a 1＋log 2a 3＋…＋log 2a 2n －1等于( )A ．2nB ．2n 2C ．n 2D ．n【解析】选C.log 2a 1＋log 2a 3＋…＋log 2a 2n －1＝log 2(a 1a 3·…·a 2n －1) ＝log 2(a 1a 2n －1)n2＝log 2(a 5a 2n －5)n 2＝log 2(22n )n 2＝log 22n 2＝n 2.4．等比数列{a n }的各项均为正数，已知向量a ＝(a 4，a 5)，b ＝(a 7，a 6)，且a ·b ＝4，则log 2a 1＋log 2a 2＋…＋log 2a 10＝( ) A ．12 B ．10 C ．5 D ．2＋log 25【解析】选C.向量a ＝(a 4，a 5)，b ＝(a 7，a 6)，且a ·b ＝4，所以a 4a 7＋a 5a 6＝4， 由等比数列的性质可得：a 1a 10＝…＝a 4a 7＝a 5a 6＝2，则log 2a 1＋log 2a 2＋…＋log 2a 10＝log 2(a 1a 2·a 10)＝log 2(a 1a 10)5＝log 225＝5. 二、填空题(每小题5分，共20分)5．在3和一个未知数间填上一个数，使这三个数成等差数列，若中间项减去6则成等比数列，则此未知数是________．【解析】设此三数为3，a ，b ，则⎩⎨⎧2a ＝3＋b ，（a －6）2＝3b ，解得⎩⎨⎧a ＝3，b ＝3或⎩⎨⎧a ＝15，b ＝27，所以这个未知数为3或27.答案：3或276．在12 和8之间插入3个数，使它们与这两个数依次构成等比数列，则这3个数的积为________．【解析】设插入的3个数依次为a ，b ，c ，即12 ，a ，b ，c ，8成等比数列，由等比数列的性质可得b 2＝ac ＝12 ×8＝4，因为a 2＝12 b>0，所以b ＝2(负值舍去).所以这3个数的积为abc ＝4×2＝8. 答案：87．数列{a n }的首项为1，数列{b n }为等比数列且b n ＝a n ＋1a n，若b 10·b 11＝2，则a 21＝__________．【解题指南】解答本题首先要注意b 1·b 2·b 3·…·b 20＝a 2a 1 ·a 3a 2 ·a 4a 3 ·…·a 21a 20 ＝a 21a 1 ＝a 21，另外要注意根据b 10·b 11＝2用等比数列性质求b 1·b 2·b 3·…·b 20. 【解析】因为b n ＝a n ＋1a n，所以b 1＝a 2a 1，b 2＝a 3a 2，b 3＝a 4a 3 ，…，b 20＝a 21a 20.以上各式相乘，得b 1·b 2·b 3·…·b 20＝a 2a 1·a 3a 2·a 4a 3·…·a 21a 20＝a 21a 1＝a 21，因为数列{b n }为等比数列，所以b 1·b 20＝b 2·b 19＝b 3·b 18＝…＝b 10·b 11＝2， 所以a 21＝b 1·b 2·b 3·…·b 20＝210＝1 024. 答案：1 0248．在等比数列{a n }中，若a 7＋a 8＋a 9＋a 10＝158 ，a 8a 9＝－98 ，则1a 7 ＋1a 8 ＋1a 9 ＋1a 10 ＝________.【解析】因为a 7＋a 8＋a 9＋a 10＝158 ，a 8·a 9＝a 7·a 10＝－98 ， 所以1a 7 ＋1a 8 ＋1a 9 ＋1a 10＝a 8a 9a 10＋a 7a 9a 10＋a 7a 8a 10＋a 7a 8a 9a 7a 8a 9a 10 ＝a 8a 9（a 10＋a 9＋a 8＋a 7）a 7a 8a 9a 10＝a 7＋a 8＋a 9＋a 10a 7a 10＝158－98 ＝－53 . 答案：－53【一题多解】因为a 7＋a 8＋a 9＋a 10＝158 ，a 8a 9＝－98 ，所以a 7＋a 8＋a 9＋a 10a 8a9＝－53 ， 即a 7a 8a 9 ＋1a 9 ＋1a 8 ＋a 10a 8a 9 ＝－53 . 又a 7a 10＝a 8a 9，所以a 7a 7a 10 ＋1a 9 ＋1a 8 ＋a 10a 7a 10 ＝－53 .所以1a 7 ＋1a 8 ＋1a 9 ＋1a 10 ＝－53 .答案：－53三、解答题(每小题10分，共30分)9．已知数列{a n }的前n 项和为S n ，且S n ＝2a n －3n(n ∈N *).(1)求a 1，a 2，a 3的值．(2)设b n ＝a n ＋3，证明数列{b n }为等比数列，并求通项公式a n . 【解析】(1)由已知，当n ＝1时，a 1＝S 1＝2a 1－3×1，解得a 1＝3， 当n ＝2时，S 2＝2a 2－3×2＝a 1＋a 2，解得a 2＝9， 当n ＝3时，S 3＝2a 3－3×3＝a 1＋a 2＋a 3，解得a 3＝21. (2)因为S n ＝2a n －3×n ， 所以S n ＋1＝2a n ＋1－3×(n ＋1)， 两式相减得a n ＋1＝2a n ＋3，所以b n ＋1b n ＝a n ＋1＋3a n ＋3 ＝（2a n ＋3）＋3a n ＋3 ＝2，又因为b 1＝a 1＋3＝6，所以{b n }是首项为6，公比为2的等比数列， b n ＝6×2n －1，所以a n ＝b n －3＝6×2n －1－3＝3(2n －1).【补偿训练】设S n 为数列{a n }的前n 项和，S n ＝kn 2＋n ，n ∈N *，其中k 是常数． (1)求a 1及a n ；(2)若对于任意的m ∈N *，a m ，a 2m ，a 4m 成等比数列，求k 的值． 【解析】(1)由S n ＝kn 2＋n ，得a 1＝S 1＝k ＋1. 当n≥2时，a n ＝S n －S n －1＝2kn －k ＋1. 经验证，n ＝1时，上式也成立，所以a n ＝2kn －k ＋1.(2)因为a m ，a 2m ，a 4m 成等比数列，所以a 22m ＝a m ·a 4m ，即(4mk －k ＋1)2＝(2km －k ＋1)(8km －k ＋1)，整理得mk(k －1)＝0.因为对任意的m ∈N *成立，所以k ＝0或k ＝1.10．已知数列{}a n 的通项公式a n ＝2n －6⎝⎛⎭⎫n ∈N * .(1)求a 2，a 5；(2)若a 2，a 5分别是等比数列{}b n 的第1项和第2项，求数列{}b n 的通项公式．【解析】(1)因为a n ＝2n －6⎝⎛⎭⎫n ∈N * ，所以a 2＝－2，a 5＝4，(2)由题意知：等比数列{}b n 中，b 1＝a 2＝－2，b 2＝a 5＝4，公比q ＝b 2b 1 ＝－2，等比数列{}b n 的通项公式b n ＝b 1·q n －1＝(－2)·(－2)n －1＝(－2)n .11．已知数列{a n }的前n 项和S n ＝3n 2＋5n ，数列{b n }中，b 1＝8，64b n ＋1－b n ＝0，问是否存在常数c ，使得对任意的正整数n(n ∈N *)，a n ＋log c b n 恒为常数m ？若存在，求出常数c 和m 的值；若不存在，请说明理由．【解题指南】先求出a n 与b n ，假设存在c 与m ，利用n 的任意性建立c ，m 的方程，判断解是否存在． 【解析】因为S n ＝3n 2＋5n ，所以当n≥2时，a n ＝S n －S n －1＝6n ＋2， 而a 1＝S 1＝8适合上式．所以a n ＝6n ＋2， 由64b n ＋1－b n ＝0得b n ＋1b n＝164 ，所以{b n }是首项为8，公比为8－2的等比数列． 所以b n ＝8×(8－2)n －1＝83－2n . 假设存在常数c 和m ，使a n ＋log c b n ＝m 恒成立， 则6n ＋2＋log c 83－2n ＝m ，即(6－2log c 8)n ＋(2＋3log c 8)＝m ，对任意n ∈N *恒成立．所以⎩⎨⎧6－2log c 8＝0，2＋3log c 8＝m ， 解得⎩⎨⎧c ＝2，m ＝11. 所以存在常数c ＝2，使得对任意n ∈N *，恒有a n ＋log c b n ＝11.【补偿训练】设关于x 的二次方程a n x 2－a n ＋1x ＋1＝0(n ＝1，2，3，…)有两根α和β，且满足6α－2αβ＋6β＝3.(1)试用a n 表示a n ＋1.(2)求证：⎩⎨⎧⎭⎬⎫a n －23 是等比数列． (3)当a 1＝76 时，求数列{a n }的通项公式及项的最值．【解析】(1)由根与系数的关系得⎩⎪⎨⎪⎧α＋β＝a n ＋1a n ，αβ＝1a n ．代入6(α＋β)－2αβ＝3得6a n ＋1a n －2a n＝3， 所以a n ＋1＝12 a n ＋13 .(2)因为a n ＋1＝12 a n ＋13 ，所以a n ＋1－23 ＝12 ⎝ ⎛⎭⎪⎫a n －23 . 若a n ＝23 ，则方程a n x 2－a n ＋1x ＋1＝0可化为 23 x 2－23x ＋1＝0，即2x 2－2x ＋3＝0， 此时Δ＝(－2)2－4×2×3＜0，所以a n ≠23 ，即a n －23 ≠0， 所以⎩⎨⎧⎭⎬⎫a n －23 是公比为12 的等比数列． (3)当a 1＝76 时，a 1－23 ＝12 ， 所以⎩⎨⎧⎭⎬⎫a n －23 是首项为12 ， 公比为12 的等比数列， 所以a n －23 ＝12 ×⎝ ⎛⎭⎪⎫12 n －1 ＝⎝ ⎛⎭⎪⎫12 n ， 所以{a n }的通项公式为a n ＝23 ＋⎝ ⎛⎭⎪⎫12 n ， n ＝1，2，3，….由函数y ＝⎝ ⎛⎭⎪⎫12 x 在(0，＋∞)上单调递减知 当n ＝1时，a n 的值最大，最大值为a 1＝76 .。

教师姓名学生姓名年级高二上课时间学科数学课题名称排列组合问题-思维方法排列组合问题-思维方式思维方法一、正难则反----总体淘汰策略例1、从0,1,2,3,4,5,6,7,8,9这十个数字中取出三个数，使其和为不小于10的偶数,不同的取法有多少种？有些排列组合问题,正面直接考虑比较复杂,而它的反面往往比较简捷,可以先求出它的反面,再从整体中淘汰.尤其含“至多”或“至少”的排列组合问题，多使用总体淘汰法试一试、1、从4台甲型和5台乙型电视机中任意取出3台，其中至少要甲型与乙型电视机各一台，则不同的取法共有( )种．A．140种B．80种C．70种D．35种2、.正六边形的中心和顶点共7个点，以其中3个点为顶点的三角形共有多少个.共有，其中满足“对所有”都的不同排列有．,n n (),2,n a n n *≥∈,n,,a中0k2、中日围棋擂台赛中，双方都出4名队员，按事先安排好的顺序出场，双方先由1号队员比赛，负者淘汰，直到某一方获胜为止。

问：中方获胜的所有可能出现的比赛过程有__________种。

思维方法六、条件复杂穷举策略例9、奥运火炬传递在A 、B 、C 、D 、E 五个城市之间进行，各城市之间的路线距离（单位：百公里）见下表.若以A 为起点，E 为终点，每个城市经过且只经过一次，那么火炬传递的最短路线距离是_________A. B.21 C.22 D.23试一试、将1,2,3,4,5,6,7,8,9这9个数随机分给甲、乙、丙三人，每人三个数，则每个人手中的三个数都能构成等差数列的分法为_______________树图策略例10．人相互传球,由甲开始发球,并作为第一次传球,经过4次传球后,球仍回到甲的手中,则不同的传球方式有______20.63对于条件比较复杂的排列组合问题，不易用公式进行运算，往往利用穷举法或画出树状图，表格会收到意想不到的结果一些不易理解的排列组合题如果能转化为非常熟悉的模型，如占位填空模型，排队模型，装盒模型等，可使问题直观解决,n 呢？}{}{}1212,,,,,,,,,n n n a B b b b C c c c ==，若C 中的元素满足条件：n c <，)1,2,3,,n =，则称M 为“完并集合”，对于“完并集合”1,2,3,4,5,6,7,8,9,10,11,12在所有符合条件的集合C 中，其元素乘积最小的集合是___________2、（2016文11）某食堂规定，每份午餐可以在四种水果中任选两种，则甲、乙两同学各自所选的两种水果相同的概率为_____1、5位好朋友相约乘坐迪士尼乐园的小火车，小火车的车厢共有4节，设每一位乘客进入每节车厢是等可能的，则这5位好朋友无人落单（即一节车厢内，至少有5人中的2人）的有________种情形2、从中随机选取一个数为，从中随机选取一个数为，则的选法有____种3、从六个字母A B C D E F 、、、、、中任取4个作排列，其中A 在B 前的排法共有多少种？4、一条长椅上有9个座位,3个人坐,若相邻2个人之间至少有2个空位,共有 种不同的坐法.5、如下图所示，平面被分成六个区域，进行六染色，旋转后重合视为同一种，求染法总数．{}1,2,3,4,5a {}1,2,3b b a >分解与合成策略是排列组合问题的一种最基本的解题策略,把一个复杂问题分解成几个小问题逐一解决,然后依据问题分解后的结构,用分类计数原理和分步计数原理将问题合成,从而得到问题的答案 ,每个比较复杂的问题都要用到这种解题策略。

高二数学人教版选择性必修第一册全册考试复习必刷检测卷（培优版）全解全析1．C 由题意，22()33OM MP OM MN O OM ON OM P =+=+=+-=23ON +13OM =23×12(OB +OC )+13×12OA =111633a b c++故选：C 2．A解：如图建立空间直角坐标系，则()1,0,0A ，()0,1,0C ，设(),,1E x y 则[]0,1x ∈，[]0,1y ∈，所以()1,,1EA x y =---，(),1,1EC x y =---，所以()()22221111111222EA EC x x y y x x y y x y ⎛⎫⎛⎫⋅=----+=-+-+=-+-+ ⎪ ⎪⎝⎭⎝⎭，因为[]0,1x ∈，[]0,1y ∈，所以211024x ⎛⎫≤-≤ ⎪⎝⎭，211024y ⎛⎫≤-≤ ⎪⎝⎭，所以1,12EA EC ⎡⎤⋅∈⎢⎥⎣⎦，故选：A3．C如图所示，由圆221:(4)(1)4C x y -+-=，可得圆心1(4,1)C ，半径为12r =，圆222:(4)1C x y +-=，可得圆心2(0,4)C ，半径为21r =，可得圆心距125C C ==，所以12||||52PM PN r r +≥--=，当12,,,,M N C C P 共线时，取得最小值，故||||PM PN +的最小值为2.故选：C.4．A由点P 是直线290x y +-=上的任一点，所以设()92P m m -,，因为圆22:4O x y +=的两条切线PA 、PB ，切点分别为A 、B ，所以OA PA ⊥，OB PB ⊥，则点A 、B 在以OP 为直径的圆C 上，即AB 是圆O 和圆C 的公共弦，则圆心C 的坐标是92,22m m -⎛⎫ ⎪⎝⎭，且半径的平方是()222924m m r -+=，所以圆C 的方程是()22229292224m m m m x y -+-⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭，又由224x y +=，两式相减，可得()9240m x my -+-=，即公共弦AB 所在的直线方程是()9240m x my -+-=，即()() 2940m y x x -+-=，由20940y x x -=⎧⎨-=⎩，解得48,99x y ==，所以直线AB 恒过定点48,99⎛⎫⎪⎝⎭.故选： A.5．D 【详解】对于A ，若0m n >>，则221mx ny +=可化为22111x y m n+=，因为0m n >>，所以11m n<，即曲线C 表示焦点在y 轴上的椭圆，故A 错误；对于B ，若0m n =>，则221mx ny +=可化为221x y n+=，此时曲线C 表示圆心在原点，半径为n的圆，故B 错误；对于C ，若0mn <，则221mx ny +=可化为22111x y m n+=，此时曲线C 表示双曲线，由220mx ny +=可得y =，故C 错误；对于D ，若0,0m n =>，则221mx ny +=可化为21y n=，y =C 表示平行于x 轴的两条直线，故D 正确.故选： D.6．A 【详解】作图，由题意得(),0A a -、(),0B a 、(),0F c -，设()0,E m ，由//PF OE 得MF AF OEAO=，则()m a c MF a-=①，又由//OE MF ，得12OE BO MF BF=，则()2m a c MF a +=②，由①②得1()2a c a c -=+，即3a c =，则13c e a ==，故选：A.7．A 【详解】设动点(),P x y ，由2PA PO =，得()2222344x y x y -+=+，整理得()2214x y ++=，又点P 是圆C ：()()22220y x r r +=->上有且仅有的一点，所以两圆相切.圆()2214x y ++=的圆心坐标为()1,0-，半径为2，圆C ：()()22220y x r r +=->的圆心坐标为()20,，半径为r ，两圆的圆心距为3，当两圆外切时，23r +=，得1r =，当两圆内切时，23r -=，0r >，得=5r ．故选：A.8．B设双曲线的渐近线OA 的倾斜角为π0,2θ⎛⎫∈ ⎪⎝⎭，则1tan a θ=，在等腰三角形2AOF 中，根据正弦定理可得：2sin sin 2OA OF θθ=，得2cos cOA θ=，所以122221tan 152sin 2224AF F c a SOA OF a θθ+=⨯⨯⨯⨯===，解得2a =或12，又1e <<e 1a >，从而2a =，所以双曲的方程为2214xy -=，故选：B ．【点睛】本题目比较巧妙的地方在于借助渐近线的倾斜角，得到倾斜角与a 的关系，结合解三角形的方法来表示三角形的面积，求出a 的值；题目也可以用渐近线方程直接求解9．AB对于A ：向量,a b 同向时，a b a b -≠+，故A 错误；对于B ：需要强调0b ≠r r，故B 错误；对于C ：因为2231+-=，则由共面定理知P ，A ，B ，C 四点共面，故C 正确；对于D ：{},,a b c 为空间的一个基底，则,,a b c 不共面，故,,a b b c c a +++也不共面，所以{},,a b b c c a +++构成空间的另一个基底，故D 正确；故选：AB 10．BCD对于A 中，当直线过原点时，此时直线在坐标轴上的截距相等，但不能用方程1x ya a+=表示，所以A 不正确；对于B 中，由圆224x y +=，可得圆心坐标为(0,0)C ，半径为2r =，则圆心C到直线:0l x y -=的距离为1d =，所以圆C 上有且仅有3个点到直线l 的距离都等于1，所以B 正确；对于C 中，由圆22120C :x y x ++=，可得圆心坐标为1(1,0)C -，半径为11r =，由圆222480C :x y x y m +--+=，可得圆心坐标为2(2,4)C，半径为2r =可得圆心距125C C =，要使得圆1C 与2C 恰有三条公切线，则15=且200m ->，解得4m =，所以C 正确；对于D 中，设(,)P m n ，可得142m n+=，以OP 为直径的圆的方程为220x y mx ny +--=，两圆的方程作差，可得直线AB 的方程为1mx ny +=，消去n 可得()2102y m x y -+-=，令0,2102yx y -=-=，解得11,42x y ==，即直线AB 经过定点11(,42，所以D 正确.故选：BCD 11．AD 【详解】设,AB n →→的夹角为()0πθθ≤≤，由题意得11cos 3||||||AB nAB n AB n n ABθ→→→→→→→→⋅⋅==⋅=-⋅，∴sin 3θ=，①当双曲线的焦点在x 轴上时，其渐近线方程为by x a=±，即0bx ay ±=，∴点(0)2，到渐近线的距离为sin ||n d θ→==⋅，整理得2218b a =，∴c e a ==②当双曲线的焦点在y 轴上时，其渐近线方程为ay x b=±，即0ax by ±=，∴点(0)2，到渐近线的距离为42sin 3||n d θ→==⋅=，整理得228b a =，∴3c e a ==，综上双曲线的离心率为324或3.故选：AD.12．BCD 【详解】12OF F P c O O ===，12PF PF ∴⊥124cos 5F QF ∠=,设1||4,||5PQ m FQ m ==则1||3PF m =又11||||||4PQ FQ PF a ++=，12m =3m ∴=12|||PF PF ∴==12||2F F ∴=，即1,c e ==A 不正确；当点M 在y 轴上时三角形12MF F 面积的最大，此时1211222S F F OM ==⨯=,所以B 正确；因为12|||PF PF ==所以22124PF PF +=，故C 正确；圆228:9G x y +=，13r b =<=，圆在椭圆内部，所以点M 在椭圆内部，所以D 正确.故选：BCD 13．32解：由题意，翻折后1AD AB BC CD ====，BD =在翻折后的图形中，取BD 的中点O ，连接,AO CO ，则2AO CO ==则,AO BD CO BD ⊥⊥，所以AOC ∠即为二面角A BD C --的平面角，所以2AOC π∠=，即AO CO ⊥，所以1AC =，又因AO CO O =，所以BD ⊥平面AOC ，因为AC ⊂平面AOC ，所以AC BD ⊥，则22||BP BP =211()22BA BC BD =-+21()2CA BD =+221||||4CA BD CA BD =++⋅94=，所以32BP =.故答案为：32.14．[)4,+∞解：设|34||349|z x y a x y =-++--=，故|34||349|x y a x y -++--可以看作点(,)P x y 到直线:340m x y a -+=与直线:3490l x y --=距离之和的5倍，|34||349|x y a x y -++--的取值与x ，y 无关，∴这个距离之和与点P 在圆上的位置无关，如图所示：可知直线m 平移时，P 点与直线m ，l 的距离之和均为m ，l 的距离，即此时圆在两直线内部，当直线m 与圆()()22321x y -+-=1，化简得|1|5a +=，解得4a =或6a =-（舍去），4a ∴≥，即[)4,a ∈+∞．故答案为：[)4,+∞．15．①③④解：(4,0)A ，(0,2)B ，∴过A 、B 的直线方程为142xy+=，即240x y +-=，圆22(5)(5)16x y -+-=的圆心坐标为(5,5)，圆心到直线240x y +-=的距离4d ，∴点P 到直线AB 的距离的范围为44]+，5<，∴41<，4105+<，∴点P 到直线AB 的距离小于10，但不一定大于2，故①正确，②错误；如图，当过B 的直线与圆相切时，满足PBA ∠最小或最大(P 点位于1P 时PBA ∠最小，位于2P 时PBA ∠最大），此时||BC ==||PB ∴==，故③④正确．故选：①③④．16【详解】由22CBF CF B ∠∠=，设2CB CF m ==，由双曲线的定义得122CF CF a -=，所以12BF a =，24BF a =，又因为过1F 的直线与by x a=-垂直，所以112tan F C a k BF F b=∠=，则12cos bBF F c∠=，在12BF F △中，由余弦定理得222222121212124416cos 28BF BF F F a c a b BF F BF BF ac c+-+-∠===⋅，令1a =，则2220b b --=，解得1b =所以c =则e =，17．（1）证明：把直线l 的方程改写成：()()72100x y m x y +-++-=，由方程组702100x y x y +-=⎧⎨+-=⎩，解得：34x y =⎧⎨=⎩，所以直线l 总过定点(3，4).圆C 的方程可写成()()221225x y -+-=，所以圆C 的圆心为(1，2)，半径为5.因为定点(3，4)到圆心(1，2)5=<，即点(3，4)在圆内，所以过点(3，4)的直线l 总与圆相交，即不论m 取什么实数，直线l 与圆C 总相交（2）设直线l 与圆交于A 、B 两点.当直线l 过定点M (3，4)且垂直于过点M 的圆C 的半径时，l 被截得的弦长|AB|最短.因为2AB =此时1114231AB CMk k =-=-=---，所以直线AB 的方程为()413y x -=--，即70x y +-=.故直线l 被圆C 截得的弦长最小值为l 的方程为70x y +-=.18．（1）因为平面PAD ⊥平面ABCD ，平面PAD 平面ABCD AD =，AB AD ⊥，AB Ì平面ABCD ，所以AB ⊥平面PAD ，PD ⊂Q 平面PAD ，所以AB PD ⊥.又因为PA PD ⊥，AB PA A ⋂=，所以PD ⊥平面PAB .因为PD ⊂平面PDC ，所以平面PDC ⊥平面PAB ；（2）取AD 的中点O ，连接PO 、CO ，因为PA PD =，所以PO AD ⊥.又因为PO ⊂平面PAD ，平面PAD ⊥平面ABCD ，平面PAD 平面ABCD AD =，所以PO ⊥平面ABCD .因为CO ⊂平面ABCD ，所以PO CO ⊥.因为AC CD =，所以CO AD ⊥.以点O 为坐标原点，OC 、OA 、OP 所在直线分别为x 、y 、z 轴建立空间直角坐标系，由题意得()0,1,0A 、,1,02B ⎛⎫⎪ ⎪⎝⎭、)C 、()0,1,0D -、()0,0,1P ，所以()0,1,1PA =-，)1PC =-uu u r，1PB ⎫=-⎪⎪⎝⎭uu r .设平面PBC 的法向量为(),,n x y z =，则00n PB n PC ⎧⋅=⎨⋅=⎩，即30230x y z z +-=⎪⎪-=⎩，令2x =，则23z =3y =，所以(3,3n =.所以，3114cos ,38192n PA n PA n PA⋅<>==-=-⨯⋅，则直线PA 与平面PBC 11419．（1）圆222x y r +=与直线380x -=相切，∴圆心O 到直线的距离为22841(3)d r -==+-，∴圆O 的方程为：2216x y +=．若直线l 的斜率不存在，直线l 为2x =-，此时直线l 截圆所得弦长为43若直线l 的斜率存在，设直线l 为：()62y k x =+，则有2226431621k ⎛⎫⎛⎫+=⎪ ⎪⎪ ⎪+⎭⎝⎭，解得：612k =此时直线l 为26100x +-=，则所求的直线l 为2x =-或26100x +-=．（2）证明：由题意知，()40M ，，设直线MA ：()14y k x =-，与圆方程联立得：()122416y k x x y ⎧=⋅-⎨+=⎩，消去y 得：()()2222111181610k x k x k +-+-=，()21211611M A k x x k -∴=+，()2121411A k x k -∴=+，12181A k y k -=+，因为123k k ⋅=-，用13k -换掉1k 得到B 点坐标，21213649B k x k -∴=+，121249B k y k =+，则()1122111222111221124891434136491AB k k k k k k k k k k k +++==----++，∴直线AB 的方程为21112221118444131k k k y x k k k ⎛⎫-+=- ⎪+-+⎝⎭，整理得：()121423k y x k =--，则直线AB 恒过定点为()20，．20．（1）由题意知22222191,41,2,a b c a a b c ⎧+=⎪⎪⎪=⎨⎪=+⎪⎪⎩解得2,1,a b c =⎧⎪=⎨⎪=⎩故椭圆C 的方程为22143x y +=.（2）证明：设()00,M x y ，()11,A x y ，()22,B x y ，由于A ，B 为椭圆C 上的点，所以2211143x y +=，2222143x y +=，两式相减得()()()()1212121243x x x x y y y y +-+-=-，所以()()120121*********x x x y y k x x y y y +-==-=--+.又00k y x =，故134k k =-，为定值.21．（1）抛物线C 的方程为28y x =，准线方程为2x =-；（2）存在直线1)y x =+或1)3y x =-+．【详解】（1）因为横坐标为1的点到焦点的距离为3,所以132p +=,解得4p =,所以28y x =，即准线方程为2x =-.（2）显然直线l 的斜率存在,设直线l 的方程为(1)y k x =+(0)k ≠,1122(,),(,)A x y B x y .联立得28(1)y x y k x ⎧=⎨=+⎩，消去y 得2222(28)0k x k x k +-+=.由224(28)40k k ∆=-->,解得k <.所以k <且0k ≠.由韦达定理得212282k x x k -+=,121=x x .直线BF 的方程为22(2)2y y x x =--,又1D x =-,所以2232D y y x -=-,所以223(1,)2y D x ---,因为//DE AF ,所以直线DE 与直线AF 的斜率相等又(4,3)E k --,所以221133232y k x y x -+-=--.整理得121222y y k x x =+--,即1212(1)(1)22k x k x k x x ++=+--,化简得121211122x x x x ++=+--,121212122()412()4x x x x x x x x -+-=-++,即12+7x x =.所以2282=7k k -,整理得289k =,解得3k =±.经检验,3k =±符合题意.所以存在这样的直线l ,直线l的方程为1)y x =+或1)y x =+．22．（1）2214x y +=；（2）是，()T .（1）由△12F PF3450x y -+=相切.∴121221PF F S c b b ⎧=⋅⋅=⎪⎪⎨⎪==⎪⎩，解得1b =，c =2a =，则椭圆C 的方程是2214x y +=.（2）以线段PQ 为直径的圆过x 轴上的定点.法一：当直线l 斜率不存在时，以PQ 为直径的圆的方程为：223x y +=，恒过定点()0.当直线l 斜率存在时，设()1y k x =-，()0k ≠.由()22114y k x x y ⎧=-⎪⎨+=⎪⎩得：()2222148440k x k x k +-+-=.设()11,A x y ，()22,B x y ，则有2122814k x x k +=+，21224414k x x k -=+.又M 是椭圆C 的右顶点，则()2,0M .由题意知：直线AM 为()1122y y x x =--，故11(0,22y x P --.直线BM 为：()2222y y x x =--，故2220,2y Q x ⎛⎫- ⎪-⎝⎭.若以PQ 为直径的圆过x 轴上的定点()0,0N x ，则等价于0PN QN ⋅=恒成立.又1012,2y PN x x ⎛⎫= ⎪-⎝⎭，2022,2y QN x x ⎛⎫= ⎪-⎝⎭，∴21201222022y y PN QN x x x ⋅=+⋅=--恒成立.又()()()2221212122224484222424141414k k k x x x x x x k k k ---=-++=-⨯+=+++()()()222221212121222244831111141414k k k y y k x k x k x x x x k k k k ⎛⎫--=--=-++=-+= ⎪+++⎝⎭.∴()()22222120002122124143042214k y y k x x x k x x k -++=+=-=--+，解得0x =故以PQ 为直径的圆过x轴上的定点()0.法二：设1x my =+，代入2214x y +=得()224230m y my ++-=.12224m y y m +=-+，12234y y m =-+直线AM ：()1122y y x x =--，令0x =得11112221y y y x my --==+-，即1120,1y P my ⎛⎫- ⎪-⎝⎭，同理得2220,1y Q my ⎛⎫- ⎪-⎝⎭设以线段PQ 为直径的圆过x 轴上的定点(),0T t ，有PT QT ⊥，即0PT QT ⋅=，则()21221212401y y t m y y m y y +=-++，将12y y +、12y y 代入得230t -=，t =()T .。

高二数学培优直线与圆综合一、填空题1．对于直线l 上任意一点),(y x A ，点)3,24(y x y x B ++仍在直线l 上，则直线l 的方程为 ．2.若方程0lg 6=++-+m y x y x 表示一条直线，则实数m 的取值范是 ．3.直线2:-=x y l ，点)1,1(-A 和点)1,1(B ，在直线l 上的点P ，使得APB ∠最大，则P 点的坐标为 ．4.1122(,),(,)M x y N x y 不同两点，直线:0++=l ax by c ，1122ε++=++ax by c ax by c，以下命题中正确的序号为_________。

（1）不论ε为何值时，点N 都不在直线l 上；（2）若ε=1，则直线MN 与直线l 平行；（3）若1ε=-，则直线l 经过MN 的中点；（4）1ε>，则点M 、N 在直线l 的同色且直线l 与线段MN 的延长线相交。

5.（1）22(4cos 32)(3sin 132)t t θθ+-+++的最小值为 。

（2的最小值为 ．6.已知长方形的四个顶点)1,0(),1,2(),0,2(),0,0(D C B A ，一质点从AB 的中点0P 沿与AB 夹角为θ的方向射到BC 上的点1P 后，依次反射到AB DA CD ,,上的点432,,P P P .若4P 与0P 重合，则θtan = ．7.已知圆()()221:231C x y -+-=，圆()()222:349C x y -+-=，,M N 分别是圆12,C C 上的动点，P 为x 轴上的动点，则PM PN +的最小值为（ ）A 、4- B1C、6- D8.（1）已知圆122=+y x 和直线m x y +=2相交于B A ,且OB OA ,与x 轴正方向所成的角是α和β，则=+)sin(βα ．（2）直线a y x 1=+与圆a ay x 21222+-=+有公共点),(n m ，且mn t =，则t 的取值范围是二、解答题1.已知圆C ：x 2+y 2+2x -3=0．（1）求圆的圆心C 的坐标和半径长；（2）直线l 经过坐标原点且不与y 轴重合，l 与圆C 相交于A （x 1，y 1）、B （x 2，y 2）两点，求证：2111x x +为定值；（3）斜率为1的直线m 与圆C 相交于D 、E 两点，求直线m 的方程，使△CDE 的面积最大．2.已知点G （5，4），圆C 1：（x -1）2+（x -4）2=25，过点G 的动直线l 与圆C 1相交于E 、F 两点，线段EF 的中点为C ．（1）求点C 的轨迹C 2的方程；（2）若过点A （1，0）的直线l 1与C 2相交于P 、Q 两点，线段PQ 的中点为M ；又l 1与l 2：x +2y +2=0的交点为N ，求证|AM|•|AN|为定值．3.已知点C （1，0），点A ，B 是⊙O ：x2+y2=9上任意两个不同的点，且满足0=⋅，设M 为弦AB 的中点．求点M 的轨迹T 的方程；4.已知平面直角坐标系上一动点(,)P x y 到点(2,0)A -的距离是点P 到点(1,0)B 的距离的2倍。

单元素养检测(一)(第四章)(120分钟 150分)一、选择题(本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知等差数列{a n }的前n 项和为S n ，且a 4＝52 ，S 10＝15，则a 7＝( ) A ．12 B ．1 C ．32 D ．2【解析】选 A.方法一：设等差数列{a n }的公差为d ，则由题设得⎩⎪⎨⎪⎧a 4＝a 1＋3d ＝52，S 10＝10a 1＋10×92d ＝15，解得⎩⎪⎨⎪⎧a 1＝92，d ＝－23，所以a 7＝a 1＋6d ＝92 ＋6×⎝ ⎛⎭⎪⎫－23 ＝12 . 方法二：因为S 10＝10（a 1＋a 10）2 ＝15，所以a 1＋a 10＝3， 又a 4＋a 7＝a 1＋a 10，a 4＝52 ，所以52 ＋a 7＝3，解得a 7＝12 .2．在等比数列{a n }中，若a 4，a 3，a 5成等差数列，则数列{a n }的公比为( ) A ．0或1或－2 B ．1或2 C ．1或－2D ．－2【解析】选C.因为a 4，a 3，a 5成等差数列， 所以2a 3＝a 4＋a 5，又因为等比数列{a n }， 即2＝q ＋q 2，解得q ＝1或q ＝－2.3．(2020·全国Ⅱ卷)数列{}a n 中，a 1＝2，a m ＋n ＝a m a n ，若a k ＋1＋a k ＋2＋…＋a k ＋10＝215－25，则k ＝( )A ．2B ．3C ．4D ．5【解析】选C.取m ＝1，则a n ＋1＝a 1a n ，又a 1＝2， 所以a n ＋1a n＝2，所以{}a n 是等比数列，则a n ＝2n ，所以a k ＋1＋a k ＋2＋…＋a k ＋10＝2k ＋1⎝⎛⎭⎫1－2101－2＝2k ＋11－2k ＋1＝215－25，所以k ＝4.4．等比数列{a n }的前n 项和为S n ，若a 1＋a 2＋a 3＝3，a 4＋a 5＋a 6＝6，则S 12＝( ) A ．15 B ．30 C ．45 D ．60【解析】选C.由题意，等比数列{a n }的前n 项和为S n ，满足a 1＋a 2＋a 3＝3，a 4＋a 5＋a 6＝6，则a 4＋a 5＋a 6a 1＋a 2＋a 3 ＝63 ＝2，所以a 7＋a 8＋a 9＝12，a 10＋a 11＋a 12＝24，则S 12＝a 1＋a 2＋a 3＋…＋a 10＋a 11＋a 12＝45. 5．在数列{}a n 中，若a 1＝1，a 2＝12 ，2a n ＋1 ＝1a n ＋1a n ＋2 (n ∈N *)，则该数列的通项为( ) A ．a n ＝1nB ．a n ＝2n ＋1C ．a n ＝2n ＋2D ．a n ＝3n【解析】选A.因为2a n ＋1 ＝1a n ＋1a n ＋2⎝⎛⎭⎫n ∈N * ，所以数列⎩⎨⎧⎭⎬⎫1a n 是等差数列，又1a 2 －1a 1＝2－1＝1，所以1a n ＝1＋(n －1)＝n ，所以a n ＝1n .【补偿训练】1.在a 和b 两数之间插入5个数，使它们与a ，b 组成等差数列，则该数列的公差为( ) A ．b －a5 B ．b －a6 C ．a －b6D ．b －a 7【解析】选B.在a 和b 两数之间插入5个数，使它们与a ，b 组成等差数列，则这个数列共有7项，所以d ＝b －a7－1＝b －a6 .2．在等比数列{}a n 中，a 3，a 15是方程x 2－6x ＋8＝0的根，则a 1a17a 9的值为( )A ．2 2B ．4C ．±2 2D ．±4【解析】选A.a 3·a 15＝8，a 3＋a 15＝6， 故a 1a 17a 9 ＝a 3·a 15a 3·a 15＝a 3·a 15 ＝8 ＝2 2 .6．已知在各项为正数的等比数列{}a n 中，a 2与a 8的等比中项为8，则4a 3＋a 7取最小值时，首项a 1＝( ) A ．8 B ．4 C ．2 D ．1【解析】选C.因为a 2a 8＝82＝a 25 ⇒a 5＝8，设公比为q(q>0)，所以4a 3＋a 7＝4a 5q 2 ＋a 5q 2＝32q 2 ＋8q 2≥232q2×8q 2＝32， 当且仅当32q 2 ＝8q 2，即q 2＝2时取等号， 此时a 1＝a 5q 4 ＝2.7．在正项等比数列{a n }中，若a 6，3a 5，a 7依次成等差数列，则{a n }的公比为( ) A ．2 B ．12 C ．3 D ．13 【解析】选A.由题意知2×3a 5＝a 6＋a 7， 又{a n }为正项等比数列，所以6a 1q 4＝a 1q 5＋a 1q 6， 且q>0，所以q 2＋q －6＝0， 所以q ＝2或q ＝－3(舍).8．已知数列{a n }，{b n }满足a 1＝1，且a n ，a n ＋1是方程x 2－b n x ＋2n ＝0的两根，则b 10等于( )A ．24B ．32C ．48D ．64【解析】选D.由已知有a n a n ＋1＝2n，所以a n ＋1a n ＋2＝2n ＋1，则a n ＋2a n＝2，所以数列{a n }的奇数项、偶数项均是公比为2的等比数列，由a 1a 2＝2可以求出a 2＝2，所以数列{a n }的项分别为1，2，2，4，4，8，8，16，16，32，32，…，而b n ＝a n ＋a n ＋1，所以b 10＝a 10＋a 11＝32＋32＝64.二、选择题(本大题共4小题，每小题5分，共20分，在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，选对但不全的得2分，有选错的得0分)9．在数列{a n}中，n∈N*，若a n＋2－a n＋1a n＋1－a n＝k(k为常数)，则称{a n}为“等差比数列”，下列对“等差比数列”的判断正确的为()A．k不可能为0B．等差数列一定是“等差比数列”C．等比数列一定是“等差比数列”D．“等差比数列”中可以有无数项为0【解析】选AD.由等差比数列的定义可知，等差比数列的公比不为0，所以A 正确；当等差数列的公差为0即等差数列为常数列时，等差数列不是等差比数列，所以选项B不正确；当{a n}是等比数列时，当公比q＝1时，{a n}不是等差比数列，所以选项C不正确；数列0，1，0，1，…是公比为－1的等差比数列，该数列中有无数多个0，所以选项D正确．10．已知等比数列{a n}的各项均为正数，公比为q，且a1>1，a6＋a7>a6a7＋1>2，记{a n}的前n项积为T n，则下列选项中正确的选项是()A．0<q<1 B．a6>1C．T12>1 D．T13>1【解析】选ABC.由于等比数列{a n}的各项均为正数，公比为q，且a1>1，a6＋a7>a6a7＋1>2，所以(a6－1)(a7－1)<0，由题意得a6>1，a7<1，所以0<q<1.因为a6a7＋1>2，所以a6a7>1，T12＝a1·a2·…·a11·a12＝(a6a7)6>1，T13＝a137<1.11．已知{a n}为等差数列，其前n项和为S n，且2a1＋3a3＝S6，则以下结论正确的是()A ．a 10＝0B ．S 10最小C ．S 7＝S 12D ．S 19＝0【解析】选ACD.2a 1＋3a 3＝S 6，所以2a 1＋3a 1＋6d ＝6a 1＋15d ，所以a 1＋9d ＝0，即a 10＝0，A 正确；当d<0时，S n 没有最小值，B 错误； S 12－S 7＝a 8＋a 9＋a 10＋a 11＋a 12＝5a 10＝0， 所以S 12＝S 7，C 正确；S 19＝（a 1＋a 19）×192 ＝19a 10＝0，D 正确．【补偿训练】已知等比数列{a n }中，满足a 1＝1，q ＝2，则( )A ．数列⎩⎨⎧⎭⎬⎫1a n 是等差数列B ．数列⎩⎨⎧⎭⎬⎫1a n 是递减数列C ．数列{log 2a n }是等差数列D ．数列{log 2a n }是递减数列【解析】选BC.a n ＝2n －1，A.1a n ＝12n －1 ，1a n ＋11a n ＝2n －12n ＝12 ，所以⎩⎨⎧⎭⎬⎫1a n 是公比为12 的等比数列，不是等差数列，故不正确；B ．由A 可知，数列⎩⎨⎧⎭⎬⎫1a n 是首项为1，公比为12 的等比数列，所以是递减数列，故正确；C ．log 2a n ＝n －1，log 2a n ＋1－log 2a n ＝n －(n －1)＝1，所以{log 2a n }是等差数列，故正确；D.由C 可知{log 2a n }是公差为1的等差数列，所以是递增数列，故D 不正确．12．已知各项均为正项的等比数列{a n }，a 1>1，0<q<1，其前n 项和为S n ，下列说明正确的是( ) A ．数列{ln a n }为等差数列 B ．若S n ＝Aq n ＋B ，则A ＋B ＝0C ．S n ·S 3n ＝S 22nD ．记T n ＝a 1·a 2·…·a n ，则数列{T n }有最大值【解析】选ABD.由题可知，a n ＝a 1q n －1，S n ＝a 1（1－q n ）1－q；对A ，ln a n ＝ln a 1q n －1＝ln a 1＋(n －1)ln q ，ln a n ＋1＝ln a 1q n ＝ln a 1＋n ln q ，ln a n ＋1－ln a n ＝ln q ，A 对；对B ，S n ＝a 1（1－q n ）1－q ＝－a 11－q q n＋a 11－q，又S n ＝Aq n＋B ，则A ＋B ＝－a 11－q ＋a 11－q＝0，B 对；对C ，S n ＝a 1（1－q n ）1－q ，S 3n ＝a 1（1－q 3n ）1－q，S n ·S 3n ＝a 21 （1－q n ）（1－q 3n）（1－q ）2， S 2n ＝a 1（1－q 2n ）1－q ，S 22n ＝a 21 （1－q 2n ）2（1－q ）2，很明显S n ·S 3n ≠S 22n ，C 错误；对D ，T n ＝a 1·a 2·…·a n ，由于数列a 1>1，0<q<1，故数列为单调递减数列，总存在从某一项开始使得a k ＝a 1q k －1∈(0，1)，故T k －1＝a 1·a 2·…·a k －1有最大值，故D 正确．三、填空题(本大题共4小题，每小题5分，共20分．请把正确答案填在题中横线上)13．若等差数列{a n }和等比数列{b n }满足a 1＝b 1＝1，a 4＝b 4＝8，则a 3＋b 3＝________.【解析】设等差数列{a n }的公差为d ，等比数列的公比为q ， 由a 4－a 1＝3d ＝7⇒d ＝73 ⇒a 3＝173 ，q 3＝b 4b 1＝8⇒q ＝2，b 3＝4，则a 3＋b 3＝173 ＋4＝293 . 答案：29314．数列{a n }的前n 项和S n ＝An 2＋Bn(A≠0)，若a 1＝1，a 1，a 2，a 5成等比数列，则a 3＝________.【解析】由S n 的解析式知，{a n }为等差数列，设公差为d ，则1，1＋d ，1＋4d 成等比数列，故(1＋d)2＝1＋4d ，即d 2－2d ＝0，解得d ＝0或d ＝2，若d ＝0，a n ＝1，S n ＝n ，与A≠0矛盾，故d ＝2，a 3＝1＋2d ＝5. 答案：515．已知F(x)＝f ⎝ ⎛⎭⎪⎫x ＋12 －1是R 上的奇函数．a n ＝f(0)＋f ⎝ ⎛⎭⎪⎫1n ＋…＋f ⎝ ⎛⎭⎪⎪⎫n －1n ＋f(1)(n ∈N *)，则数列{a n }的通项公式为________．【解析】因为F(x)＋F(－x)＝0，所以f ⎝ ⎛⎭⎪⎫x ＋12 ＋f ⎝ ⎛⎭⎪⎫－x ＋12 ＝2，即若a ＋b ＝1，则f(a)＋f(b)＝2.于是由a n ＝f(0)＋f ⎝ ⎛⎭⎪⎫1n ＋…＋f ⎝ ⎛⎭⎪⎪⎫n －1n ＋f(1)(n ∈N *)，得2a n ＝[f(0)＋f(1)]＋[f ⎝ ⎛⎭⎪⎫1n ＋f ⎝ ⎛⎭⎪⎪⎫n －1n ]＋…＋⎣⎢⎢⎡⎦⎥⎥⎤f ⎝ ⎛⎭⎪⎪⎫n －1n ＋f ⎝ ⎛⎭⎪⎫1n ＋[f(1)＋f(0)]＝2n ＋2，所以a n ＝n ＋1. 答案：a n ＝n ＋116．已知数列{a n }的通项公式是a n ＝⎩⎪⎨⎪⎧2－n （n 是奇数），12n ＋n 2（n 是偶数）， 则它的前4项和为________．【解析】S 4＝a 1＋a 2＋a 3＋a 4＝12 ＋12×2＋22 ＋123 ＋12×4＋42 ＝1924 . 答案：1924四、解答题(本大题共6个小题，共70分，解答时应写出必要的文字说明、证明过程或演算步骤)17．(10分)已知等差数列{a n }前三项的和为－9，前三项的积为－15. (1)求等差数列{a n }的通项公式；(2)若{a n }为递增数列，求数列{|a n |}的前n 项和S n .【解析】(1)设公差为d ，则依题意得a 2＝－3，则a 1＝－3－d ，a 3＝－3＋d ， 所以(－3－d)(－3)(－3＋d)＝－15，得d 2＝4，d ＝±2. 所以a n ＝－2n ＋1或a n ＝2n －7.(2)由题意得a n ＝2n －7，所以|a n |＝⎩⎨⎧7－2n ，n≤3，2n －7，n≥4，①n≤3时，S n ＝－(a 1＋a 2＋…＋a n )＝5＋（7－2n ）2n ＝6n －n 2； ②n≥4时，S n ＝－a 1－a 2－a 3＋a 4＋…＋a n ＝－2(a 1＋a 2＋a 3)＋(a 1＋a 2＋…＋a n )＝18－6n ＋n 2.综上，数列{|a n |}的前n 项和S n ＝⎩⎨⎧－n 2＋6n ，n≤3，n 2－6n ＋18，n≥4.18．(12分)在数列{a n }中，a 1＝1，数列{a n ＋1－3a n }是首项为9，公比为3的等比数列． (1)求a 2，a 3.(2)求数列⎩⎨⎧⎭⎬⎫a n 3n 的前n 项和S n .【解析】(1)因为数列{a n ＋1－3a n }是首项为9，公比为3的等比数列，所以a n ＋1－3a n ＝9×3n －1＝3n ＋1，所以a 2－3a 1＝9，a 3－3a 2＝27，所以a 2＝12，a 3＝63. (2)因为a n ＋1－3a n ＝3n ＋1，所以a n ＋13n ＋1 －a n3n ＝1，所以数列⎩⎨⎧⎭⎬⎫a n 3n 是首项为13 ，公差为1的等差数列， 所以数列⎩⎨⎧⎭⎬⎫a n 3n 的前n 项和S n ＝n 3 ＋n （n －1）2 ＝3n 2－n6 . 19．(12分)(2021·全国乙卷)记S n 为数列{a n }的前n 项和，b n 为数列{S n }的前n 项积，已知2S n ＋1b n＝2.(1)证明：数列{b n }是等差数列；(2)求{a n }的通项公式．【解析】(1)由已知可得2S n ＋1b n＝2， b n b n －1＝S n (n≥2)⇒2b n －1b n ＋1b n ＝2(n≥2)⇒2b n －1＋1＝2b n (n≥2)⇒b n －b n －1＝12 (n≥2)，b 1＝32 .故{b n }是以32 为首项，12 为公差的等差数列．(2)由(1)知b n ＝32 ＋12 (n －1)＝n ＋22 ，则2S n ＋2n ＋2 ＝2⇒S n ＝n ＋2n ＋1. n ＝1时，a 1＝S 1＝32 .n≥2时，a n ＝S n －S n －1＝n ＋2n ＋1 －n ＋1n ＝－1n （n ＋1）. 故a n ＝⎩⎪⎨⎪⎧32，n ＝1，－1n （n ＋1），n≥2. 20．(12分)已知数列{a n }的前n 项和S n ＝n 2＋n 2 ，n ∈N *.(1)求数列{a n }的通项公式；(2)设b n ＝2a n ＋(－1)n a n ，求数列{b n }的前2n 项和．【解析】(1)①若n ＝1，a 1＝S 1＝1，②若n≥2，a n ＝S n －S n －1＝n 2＋n 2 －（n －1）2＋（n －1）2＝n ， 综上，{a n }的通项公式为a n ＝n ，n ∈N *.(2)由(1)及已知，b n ＝2a n ＋(－1)n a n ＝2n ＋(－1)n n ，记数列{b n }的前2n 项和为T 2n ， 所以T 2n ＝b 1＋b 2＋b 3＋b 4＋…＋b 2n －1＋b 2n＝(21－1)＋(22＋2)＋(23－3)＋(24＋4)＋…＋[22n －1－(2n －1)]＋(22n ＋2n) ＝(21＋22＋23＋24＋…＋22n －1＋22n )＋(－1＋2)＋(－3＋4)＋…＋[－(2n －1)＋2n] ＝21－22n ×21－2＋n ＝22n ＋1＋n －2，所以{b n }的前2n 项和为T 2n ＝22n ＋1＋n －2，n ∈N *.21．(12分)已知等比数列{a n }的前n 项和是S n ，S 18∶S 9＝7∶8.(1)求证：S 3，S 9，S 6依次成等差数列；(2)a 7与a 10的等差中项是否是数列{a n }中的项？如果是，是{a n }中的第几项？如果不是，请说明理由．【解析】(1)设等比数列{a n }的公比为q ，若q ＝1， 则S 18＝18a 1，S 9＝9a 1，S 18∶S 9＝2∶1≠7∶8.所以q≠1.所以S 18＝a 11－q (1－q 18)，S 9＝a 11－q(1－q 9)， S 18∶S 9＝1＋q 9.所以1＋q 9＝78 ，解得q 3＝－12 ，q ＝⎝ ⎛⎭⎪⎫－12 13 . 所以S 3＝a 1（1－q 3）1－q ＝32 ×a 11－q， S 6＝a 1（1－q 6）1－q ＝34 ×a 11－q. S 9＝a 11－q (1－q 9)＝98 ×a 11－q. 因为S 9－S 3＝－38 ×a 11－q ，S 6－S 9＝－38 ×a 11－q， 所以S 9－S 3＝S 6－S 9.所以S 3，S 9，S 6依次成等差数列．(2)a 7与a 10的等差中项等于a 7＋a 102 ＝14a 1－18a 12＝a 116 . 设a 7与a 10的等差中项是数列{a n }中的第n 项，则a 1⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫－1213 n －1 ＝a 116 ， 化简得(－2)－n －13 ＝(－2)－4，则－n －13 ＝－4，解得n ＝13.所以a 7与a 10的等差中项在数列{a n }中是第13项．22．(12分)已知等比数列{a n }的前n 项和为S n ，S n ＝2a n －2，{b n }为等差数列，b 3＝a 2，b 2＋b 6＝10.(1)求数列{a n }，{b n }的通项公式；(2)求数列{a n (2b n －3)}的前n 项和T n .【解析】(1)当n ＝1时，S 1＝2a 1－2＝a 1， 解得a 1＝2，当n≥2时，a n ＝S n －S n －1＝(2a n －2)－(2a n －1－2)， 变形得a n ＝2a n －1，所以等比数列{a n }的a 1＝2，公比q ＝2， 通项公式a n ＝2×2n －1＝2n ，对于{b n }，b 3＝a 2＝4，b 2＋b 6＝2b 4＝10， 即b 4＝5，公差d ＝b 4－b 3＝1，通项公式b n ＝b 3＋(n －3)×d ＝n ＋1，(2)由(1)知，a n ＝2n ，b n ＝n ＋1， a n (2b n －3)＝(2n －1)·2n ，所以T n ＝1×2＋3×22＋5×23＋…＋(2n －1)×2n ，① 2T n ＝1×22＋3×23＋5×24＋…＋(2n －1)×2n ＋1，② ①－②得－T n ＝2＋2(22＋23＋…＋2n )－(2n －1)×2n ＋1， 所以T n ＝(2n －3)·2n ＋1＋6.【补偿训练】已知数列{a n }是首项为正数的等差数列，数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n ·a n ＋1 的前n 项和为n 2n ＋1 .(1)求数列{a n }的通项公式．(2)设b n ＝(a n ＋1)·2a n ，求数列{b n }的前n 项和T n .【解析】(1)由题意设a n ＝a 1＋(n －1)d ，a 1>0，数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n ·a n ＋1 的前n 项和为S n ， 因为1a n ·a n ＋1 ＝1d ⎝⎛⎭⎪⎪⎫1a n －1a n ＋1 ， S n ＝1d [⎝ ⎛⎭⎪⎫1a 1－1a 2 ＋⎝ ⎛⎭⎪⎫1a 2－1a 3 ＋…＋ ⎝ ⎛⎭⎪⎪⎫1a n －1a n ＋1 ] ＝1d ⎝ ⎛⎭⎪⎪⎫1a 1 －1a n ＋ 1 ＝n a 21 ＋ a 1 dn＝n 2n ＋ 1， 解得⎩⎨⎧a 1＝1，d ＝2.所以a n ＝2n －1.(2)b n ＝(a n ＋1)·2a n ＝n×4n .T n ＝b 1＋b 2＋b 3＋…＋b n ＝1×41＋2×42＋3×43＋…＋n×4n ， 则4T n ＝1×42＋2×43＋3×44＋…＋n×4n ＋1， 两式相减得－3T n ＝4＋42＋43＋…＋4n －n×4n ＋1 ＝4（1－4n ）1－4－n×4n ＋1＝1－3n 3 ×4n ＋1－43 ，3n－19×4n＋1＋49.所以T n＝。

浙江强基（培优）联盟2024年7月学考联考高二数学试题卷浙江强基（培优）联盟研究院命题（时间80分钟 总分100分）选择题部分一、单项选择题（本大题共12小题，每小题3分，共36分．每小题列出的四个备选项中只有一个是符合题目要求的，不选、多选、错选均不得分）1．函数()f x = ）A ．[)1,+∞B ．[)1,−+∞C ．(],1−∞D ．(],1−∞−2．已知集合{}{}21,2,3,4,20AB x xx ==−−=，则A B = （）A ．{}1,1,2,3,4−B ．{}1,2,3,4C ．{}1,0,1,2,3,4−D ．{}2,1,2,3,4−3．在ABC △中，D 为边AB 的中点，则（ ）A ．0AD BD −=B ．0AD DB +=C ．CB CD BD−=D ．2CA CB CD+=4．数据1，2，3，4，5，6，7，7的第25百分位数是（ ）A ．2B ．2.5C ．3D ．3.55．从第4题所给的数据中随机选择一个数，则这个数平方的个位数是6或9的概率为（ ）A ．14B ．38C ．12D ．586．已知空间中两个不重合的平面α和平面β，直线l ⊂平面α，则“l β∥”是“αβ∥”的（ ）A ．充分不必要条件 B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件7．不等式1101x +≤−的解集是（）A ．[)0,1B ．(]0,1C ．[]1,2D ．(]1,28．近年，“人工智能”相关软件以其极高的智能化水平引起国内关注，深度学习是人工智能的一种具有代表性的实现方法，它是以神经网络为出发点的．在神经网络优化中，指数衰减的学习率模型为181425G L=×，其中L 表示每一轮优化时使用的学习率，G 表示训练迭代轮数，则学习率衰减到0.2及以下所需的训练迭代轮数至少为（参考数据：lg20.301≈）（ ） A ．16B ．72C ．74D ．909．在ABC △中，已知角,,A B C 所对的边分别是,,a b c ，已知45,75a B C ==°=°，则b 等于（ ）A ．2B ．CD ．10．已知函数()222x x f x =−，则其图象一定不过（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限11．已知α为锐角，且22sin cos cos sin 55ππαα=，则sin2α的值为（ ） A ．45 B ．513C ．2425D ．91612．已知正方体1111ABCD A B C D −，点M 在1B C 上运动（不含端点），点N 在11B D 上运动（不含端点），直线MN 与直线AC 所成的角为α，直线MN 与平面1ACB 所成的角为β，则下列关于,αβ的取值可能正确的是（ ） A ．30α=°B ．45α=°C ．60β=°D ．75β=°二、多项选择题（本大题共4小题，每小题4分，共16分．每小题列出的四个备选项中有多个是符合题目要求的，全部选对得4分，部分选对且没有错选得2分，不选、错选得0分）13．民营经济是推进中国式现代化的生力军，是浙江的最大特色、最大资源和最大优势．为了更好地支持民营企业的发展，我省某市决定对部分企业的税收进行适当的减免．某机构调查了当地的中小型民营企业年收入情况，并根据所得数据画出了样本的频率分布直方图，则下列结论正确的是（ ）A ．样本数据落在区间[)300,500内的频率为0.45B ．若规定年收人在500万元以内的民营企业才能享受减免税政策，估计有55%的当地中小型民营企业能享受到减免税政策C ．若该调查机构调查了100家民营企业，则年收人不少于400万元的有80家D ．估计样本的中位数为480万元14．已知复数12,z z ，则下列结论正确的有（ ） A ．2211z z = B ．1212z z z z +=+ C ．1212z z z z =⋅D ．1212z z z z +=+15．已知平面向量12,e e 的夹角为π3，且121e e == ，若12122,a e e b e e =−=+ ，则下列结论正确的是（ ）A ．a b ⊥B ．a =C ．a b a +=D ．a 在b 上的投影向量为12b −16．我们知道，函数()y f x =的图象关于坐标原点成中心对称图形的充要条件是函数()y f x =为奇函数，有同学发现可以将其推广为函数()y f x =的图象关于点(),P a b 成中心对称图形的充要条件是函数()y f x a b =+−为奇函数．此结论与必修一教材上的结论相吻合，则下列结论正确的是（ ）A ．函数()211x f x x +=−的图象关于点()1,2成中心对称图形 B ．若定义在R 上的函数()f x 对任意的x 都有()()22f x f x ++−=，则函数()f x 图象的对称中心为()2,2C ．若()yf x a =+是偶函数，则()f x 的图象关于直线x a =成轴对称D ．若函数()f x 满足()11y f x =+−为奇函数，且其图象与函数()422xg x =+的图象有2024个交点，记为()(),1,2,,2024i i i A x y i = ，则()202414048ii i xy =+=∑非选择题部分三、填空题（本大题共4小题，每空3分，共15分）17．已知一圆锥的母线长为2，底面半径为1，则该圆锥的侧面积为________；体积为________． 18．在中国古代数学著作《九章算术》中，鳖懦是指四个面都是直角三角形的四面体．如图，在直角ABC △中，AD 为斜边BC 上的高，3,4AB AC ==，现将ABD △沿AD 翻折成AB D ′△，使得四面体AB CD ′为一个鳖臑，则该鳖臑外接球的表面积为________19．设,A B 是一个随机试验中的两个事件，且()()()121,,234P A P B P AB ===，则()P A B = ________． 20．若函数()20(1)f x x ax b a =++=>的值域为[)0,+∞，则11a b a ++−的最小值为________． 四、解答题（本大题共3小题，共33分）21．已知函数()πsin2sin 23f x x x=−+．（1）求函数()f x 的最小正周期；（2）已知锐角ABC △三个内角,,A B C 所对的边分别为,,a b c ，且2,3b c ==，若()f A =，求ABC △的面积．22．如图，在三棱台111ABC A B C −中，1111124,AA AC AC BC CC AA =====⊥平面,,ABC AB BC D ⊥为AB 的中点．（1）证明：111A B DC ⊥．（2）过11,,A D C 的平面把三棱台111ABC A B C −分成两部分，体积分别是1V 和()212V V V <，求12V V 的值． （3）求平面1CC D 和平面1ABB 所成锐二面角的正切值．23．已知函数()()21,0,2,0,x x f x g x x x −≥== −< ． （1）若()()f x g x ≤，求x 的取值范围． （2）记{}(),max ,(),a ab a b b a b ≥=< 已知函数()(){}max ,2yf xg x ax −−有k 个不同的零点．（ⅰ）若2k =，求a 的取值范围；（ⅱ）若3k =，且,αβ是其中两个非零的零点，求11αβ+的取值范围．浙江强基（培优）联盟2024年7月学考联考高二数学参考答案一、单项选择题（本大题共12小题，每小题3分，共36分．每小题列出的四个备选项中只有一个是符合题目要求的，不选、多选、错选均不得分）1 2 3 4 5 6 7 8 9 10 11 12 C A D B D B A C A BDC1．解：要使函数有意义，则10x −≥，得1x ≤，所以函数的定义域为(],1−∞．故选C ． 2．解：因为{}{}1,2,3,4,1,2A B ==−，所以{}1,1,2,3,4A B− ．故选A ．3．解：由平行四边形法则可知2CA CB CE CD +==．故选D ．4．解：因为825%2×=，所以第25百分位数为2和3的平均数，即为2.5．故选B ．5．解：样本空间的样本点总数为8，事件A （这个数平方的个位数是6或9）的样本点为4，6，3，7，7，共5个，所以概率58P =．故选D ． 6．解：当l β∥时，α与β可能相交也可能平行，故l β∥不能推出αβ∥；反之，αβ∥可以推出l β∥．故“l β∥”是“αβ∥”的必要不充分条件．故选B ．7．解：不等式可化为1101x +=≤−，等价于()10,10,x x x−≤ −≠ 解得01x ≤<，所以不等式的解集为[)0,1．故选A ．8．解：由题意知，只要解不等式18141255G×≤ ，化简得42lg lg 1855G ≤．因为4lg 05<，所以lg2lg52lg214.118lg4lg53lg21G −−≥=≈−−，所以18 4.173.8G ≥×=．故选C ． 9．解：由三角形内角和定理得60A =°sin 45b=°，解得2b =．故选A ． 10．解：因为1x ≠，取2x =，得()22f =，所以()f x 在第一象限有图象，取12x =，得102f=<，所以()f x 在第四象限有图象，取1x =−，得()21(1)1022f −−−=<−，所以()f x 在第三象限有图象．由排除法知图象不过第二象限．故选B ．11．解：因为α是锐角，所以2π2ππ2π2ππ0cos ,0sin 552552αα<<<<<<， 所以2ππ2πcos sin 525αα=−，化简得5cos sin 4αα+=，平方得251sin216α+=， 所以9sin216α=．故选D ．12．解：由题意可知，四面体11D AB C 为正四面体，设直线AC 与平面11B D C 所成的角为1θ，易知1cos θ=由最小角定理得11,cos cos αθαθ><，故A ，B 错误．再设平面11B D C 与平面1ACB 所成的角为2θ，易知21cos 3θ=，由最大角定理得22,cos cos θβθβ><，代入选项得C 可能正确．故选C ．二、多项选择题（本大题共4小题，每小题4分，共16分．每小题列出的四个备选项中有多个是符合题目要求的，全部选对得4分，部分选对且没有错选得2分，不选、错选得0分）13141516ABD BC BCD ACD13．解：由()0.0010.00150.0020.000521001a ++++×=，得0.0025a =， 所以数据落在区间[)300,500内的频率为()0.0020.00251000.45+×=，A 正确； 数据落在区间[)200,500内的频率为()0.0010.0020.00251000.55++×=，B 正确；100n =，年收入大于或等于400万元的有四组，其频率和是()1000.00250.00250.00150.7×+++=，所以符合条件的民营企业有0.710070×=家，C 错误； 数据落在区间[)200,400内的频率为0.3，数据落在区间[)200,500内的频率为0.55，估计中位数为0.50.34001004800.25−+×=，D 正确．故选ABD ．14．解：对于A ，若1i z =，则22111,1z z =−=，故A 错误； 对于B，设12i,iz a b z c d =+=+，则()()()()1212i,i i i z z a c b d z z a b c d a c b d +=+−++=−+−=+−+，故B 正确；对于C ，设12i,i z a b z c d =+=+，则()()12i z z ac bd ad bc =−++==，2212z z ⋅=故C 正确；对于D ，若121i,i z z =+=，则121z z +=+，故D 错误．故选BC ．15．解：由题意得22121211,2e e e e ==⋅= ．对于A ，()()2212121122132212022a b e e e e e e e e ⋅=−⋅+=−⋅−=−−=−≠ ，故A 错误； 对于B，a =B 正确； 对于C ，方法同B ，故C 正确；对于D，易得b = a 在b 上的投影向量为31232a bb b b b b⋅⋅=−⋅=−，故D 正确．故选BCD ． 16．解：对于A ，因为()312f x x+−=为奇函数，所以()f x 的图象关于点()1,2成中心对称图形，故A 正确； 对于B，设()()g x f x a b=+−，若()g x 是奇函数，则()()()()0g x g x f x a b f x a b +−=+−+−+−=，所以()()2f x a f x a b ++−+=，因为()()22f x f x ++−=，所以()1f x +−1为奇函数，所以()f x 图象的对称中心为()1,1，故B 错误；对于C ，设()()g x f x a =+，因为()g x 是偶函数，所以()()g x g x =−，则()()f x a f x a +=−+，所以()f x 的图象关于直线x a =成轴对称，故C 正确；对于D ，显然()f x 的图象关于点()1,1成中心对称图形，再考虑()422x g x =+的对称性， ()422x g x =+可化为()()()4,22x a h x g x a b b h x +=+−=−+为奇函数， 则()()()00,11,h h h =−=− 即1140,2244,2222a a ab b −+ − + −=−+ ++即11448222222a a a−++=+++， 令2at =，则2124222t t t +=+++，即220t t −=，解得2t =或0t =（舍去）， 所以22a =，则1,1a b ==，因为()h x 为奇函数，所以()422xg x =+图象的对称中心为()1,1． ()f x 与()g x 有相同的对称中心，所以2024个交点每两个一组关于点()1,1中心对称，()()()2024123202412320241202420244048iii x y xx x x y y y y =+=+++++++++=+=∑ ，故D 正确．故选ACD ．三、填空题（本大题共4小题，每空3分，共15分）17．2π 18．16π19．71220．317．解：由题意得圆锥的高h =，所以21π2π,π3S rl V r h ====侧． 18．解：由题意得AC 的中点是外接球的球心，所以22,4π16πR S R ===． 19．解：由概率的性质得()()()P A P AB AB P =+，所以()()()111244P AB P A P AB =−=−=，所以()()()()1217123412P A B P A P B P AB =+−=+−= ． 20．解：由题意得2Δ40a b =−=，所以()()2221144(2)4114141a a a b a a a a a a a +++++++====−−−−()()()22(1)6191(13)119116634141414a a a a a a a −+−+−+ ⋅=⋅=−++≥+= −−− ，当且仅当4a =时，等号成立，则最小值为3．四、解答题（本大题共3小题，共33分）21．解：（1）()πππsin 2sin 2sin 2sin 2cos cos2sin 333f x x x x x x=−+=−−1πsin 2sin 223x x x=−=−， 所以2ππ2T ==． （2）因为()πsin 23f x x =−，所以()πsin 23f A A=−=． 因为A 是锐角三角形的内角，所以ππ233A −=或π2π233A −=（舍去）， 所以π3A =．又2,3b c ==， 所以ABC △的面积1π23sin 23S =×××=． 22．（1）证明：如图1，连接1AC，得1AC =1BC ．因为1AA ⊥平面ABC ，所以1AA BC ⊥． 又BC AB ⊥，所以BC ⊥平面11ABB A ， 所以在直角梯形11BCC B中，1111BC B C BB A D====，所以1BC =，即1ABC 是以AB 为底边的等腰三角形，D 是AB 的中点，所以1AB DC ⊥．又11AB A B ∥，所以111A B DC ⊥．（2）解：如图2，取BC 的中点E ，连接1,DE C E ，可得11AC DE ∥． 所以过11,,A C D 的平面把棱台分成斜棱柱111DBE A B C −和几何体11ADECC A 由题意得()11112841233ABCA B C V =××++=棱台，111DBE-1442A B C V =××=棱柱． 因为1128164433ADECA C V =−=>几何体， 所以12164,3V V ==，故12431643V V ==．（3）解：如图3，取11A B 的中点F ，连接1,C F DF ，则DF 是平面1DCC 和平面11ABB A 所成二面角的棱，由于BC ⊥平面11ABB A ，过B 作FD 延长线的垂线，垂足为G ，连接CG ，易证得BGC ∠为所求的角．延长1AA 和1BB 交于点O ，过A 作FD 的垂线，垂足为H （如图4），易得8,AO AD ==，GB AH ==，所以tan BGC ∠==． 即平面1CC D 和平面11ABB A．23．解：（1）由题意得函数()g x 的定义域为[]1,1−．当[]0,1x ∈时，不等式()()f x g x ≤等价于21x −≤当[)1,0x ∈−时，不等式())f x g x ≤等价于2x −≤，即221x ≤，解得0x ≤<． 综上，()()f x g x ≤的解集为， 即当x的取值范围为时，()()f x g x ≤成立． （2）（ⅰ）令()()(){}()(),1max ,,1,f x x h x f x g x g x x −≤< ==≤≤ 原题可转化为()2h x ax =+的实根个数问题（二重根为一个零点）．当1x −≤≤时，即为()2f x ax =+，所以22x ax −=+至多一个实根①；当1x ≤≤时，即为()2g x ax =+，所以2ax =+至多两个实根②．由①知，21,2x a −=∈− + ，所以02a ≤<−，由②知，2ax =+，所以0x =或244a x a =−∈ +，所以2a ≤−或2a ≥+，且0a ≠．当2k =时，若0a =，则有两个零点0和-1，符合题意．当0a <时，①无实根，对于②，只要2414a x a =−≤+，化简得2(2)0a +≥，则20a −≤<，符合题意．当0a >时，若02a <<−，则有三个不等实根，不符合题意．若2a =−，则有两个零点0和，符合题意．若2a >−，则仅有一个零点0，不符合题意．综上所述，当2k =时，a 的取值范围为[]{}2,02−∪−．7分（ⅱ）由（ⅰ）得当3k =时，02a <<−，且三个零点分别为224,,024a a a −−++，显然,0αβ≠，所以()11311,24a a a αβ+=++∈．9分易得函数3114y a a =++在()2−上单调递减，所以3114y a a =++>所以()11αβ+∈+∞．。

高中数学冲刺培优
1
1、有6个不同的小球,装入4个不同的盒内,每盒至少装一个球,共有多少不同的装法. 答案：3422464644
115602C P C C P += 2、有两排座位，前排11个座位，后排12个座位，现安排2人就座，并且这2人不相邻，那么不同排法的种数是__________
答案：222
2464P += 题型：多排问题：不相邻问题：
3、9人参加会议，每一个人和其他两人握手，求共有_________种可能发生的握手方式.
答案：1298843
P C = 解析：第一步，从9个人中选出1个人，第二步，从剩余8个人中选出两个人，最后将
含有的序去掉，共有12983
P C 种 4、现安排7名同学去参加5个运动项目，要求甲、乙两同学不能参加同一个项目，每个项目都有人参加，每人只参加一个项目，则满足上述要求的不同安排方案数为_______
答案：15000
解析：满足条件的方案有两种情形：
①有一个项目有3人参加，共有35157
5553600C P C P -=， ②有两个项目各有2人参加，共有()
11400215525552527=⋅-⋅P C P C C ， 所以满足条件的方案数为：3600+11400=15000；
排列组合-易错分析。

一、选择题1．(0分)[ID：13322]如图，一个边长为2的正方形里有一个月牙形的图案，为了估算这个月牙形图案的面积，向这个正方形里随机投入500粒芝麻，经过统计，落在月牙形图案内的芝麻有150粒，则这个月牙图案的面积约为（）A．35B．45C．1D．652．(0分)[ID：13312]将A，B，C，D，E，F这6个字母随机排成一排组成一个信息码，则所得信息码恰好满足A，B，C三个字母连在一起，且B在A与C之间的概率为（）A．112B．15C．115D．2153．(0分)[ID：13306]如图，矩形ABCD中，点E为边CD的中点，若在矩形ABCD内部随机取一个点Q，则点Q取自△ABE内部的概率等于A．14B．13C．12D．234．(0分)[ID：13302]大学生小明与另外3名大学生一起分配到某乡镇甲、乙丙3个村小学进行支教，若每个村小学至少分配1名大学生，则小明恰好分配到甲村小学的概率为（）A．112B．12C．13D．165．(0分)[ID：13300]学校为了解新课程标准提升阅读要求对学生阅读兴趣的影响情况，随机抽取了100名学生进行调查.根据调查结果绘制学生周末阅读时间的频率分布直方图如图所示：将阅读时间不低于30分钟的观众称为“阅读霸”，则下列命题正确的是（ ） A ．抽样表明，该校有一半学生为阅读霸 B ．该校只有50名学生不喜欢阅读 C ．该校只有50名学生喜欢阅读 D ．抽样表明，该校有50名学生为阅读霸6．(0分)[ID ：13272]公元263年左右，我国魏晋时期的数学家刘徽首创割圆术，为计算圆周率建立了严密的理论和完善的算法，所谓割圆术，就是不断倍增圆内接正多边形的边数求出圆周率近似值的方法.如图是利用刘徽的割圆术”思想设汁的一个程序框图，若输出n 的值为24，则判断框中填入的条件可以为（ ）(参考数据：3 1.732,sin150.2588,sin 7.50.1305≈︒≈︒≈)A ． 3.10?S ≤B ． 3.11?S ≤C ． 3.10?S ≥D ． 3.11?S ≥7．(0分)[ID ：13268]执行如图所示的程序框图，如果输入的1a =-，则输出的S =A ．2B ．3C ．4D ．58．(0分)[ID ：13260]要从其中有50个红球的1000个形状相同的球中，采用按颜色分层抽样的方法抽取100个进行分析，则应抽取红球的个数为（ ） A ．5个B ．10个C ．20个D ．45个9．(0分)[ID ：13255]类比“赵爽弦图”，可类似地构造如图所示的图形，它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形，设D 为BE 中点，若在大等边三角形中随机取一点，则此点取自小等边三角形的概率是（ ）A ．17B ．14C ．13D ．41310．(0分)[ID ：13239]甲、乙两位同学在高一年级的5次考试中，数学成绩统计如茎叶图所示，若甲、乙两人的平均成绩分别是12,x x ，则下列叙述正确的是（ ）A ．12x x >，乙比甲成绩稳定B ．12x x >，甲比乙成绩稳定C ．12x x <，乙比甲成绩稳定D ．12x x <，甲比乙成绩稳定11．(0分)[ID ：13234]执行如图所示的程序框图，若输入x =9，则循环体执行的次数为（ ）A ．1次B ．2次C ．3次D ．4次12．(0分)[ID ：13320]一块各面均涂有油漆的正方体被锯成27个大小相同的小正方体，若将这些小正方体均匀地搅混在一起，从中任意取出一个，则取出的小正方体两面涂有油漆的概率是( ) A ．127B ．29C ．49D ．82713．(0分)[ID ：13317]将1000名学生的编号如下：0001，0002，0003，…，1000，若从中抽取50个学生，用系统抽样的方法从第一部分0001，0002，…，0020中抽取的号码为0015时，抽取的第40个号码为（ ） A ．0795B ．0780C ．0810D ．081514．(0分)[ID ：13282]预测人口的变化趋势有多种方法，“直接推算法”使用的公式是()0 1nn P P k =+（1k >-），n P 为预测人口数，0P 为初期人口数，k 为预测期内年增长率，n 为预测期间隔年数．如果在某一时期有10k -<<，那么在这期间人口数 A ．呈下降趋势B ．呈上升趋势C ．摆动变化D ．不变15．(0分)[ID ：13229]2路公共汽车每5分钟发车一次，小明到乘车点的时刻是随机的，则他候车时间不超过两分钟的概率是（ ） A ．25B ．35C ．23D ．15二、填空题16．(0分)[ID ：13405]执行如图所示的伪代码，若输出的y 的值为10，则输入的x 的值是________．17．(0分)[ID ：13396]为调查某校学生每天用于课外阅读的时间，现从该校3000名学生中随机抽取100名学生进行问卷调查，所得数据均在区间[50,100]上，其频率分布直方图如图所示，则估计该校学生中每天用于阅读的时间在[70,80)(单位：分钟)内的学生人数为____．18．(0分)[ID ：13389]玉林市有一学校为了从254名学生选取部分学生参加某次南宁研学活动，决定采用系统抽样的方法抽取一个容量为42的样本，那么从总体中应随机剔除的个体数目为__________．19．(0分)[ID ：13387]下图是华师一附中数学讲故事大赛7位评委给某位学生的表演打出的分数的茎叶图.记分员在去掉一个最高分和一个最低分后，算得平均分为91分，复核员在复核时，发现有一个数字(茎叶图中的x )无法看清，若记分员计算无误，则数字x 应该是____________.20．(0分)[ID ：13372]在[0,1]上随机取两个实数,a b ，则,a b 满足不等式221a b +≤的概率为________．21．(0分)[ID ：13371]执行如图所示的程序框图，输出的值为__________．22．(0分)[ID：13367]变量X与Y相对应的5组数据和变量U与V相对应的5组数据统计如表：X1011.311.812.513U1011.311.812.513 Y12345V54321用b1表示变量Y与X之间的回归系数，b2表示变量V与U之间的回归系数，则b1与b2的大小关系是___．23．(0分)[ID：13343]使用如图所示算法对下面一组数据进行统计处理，则输出的结果为__________．数据：19.3a =，29.6a =，39.3a = 49.4a =，59.4a =，69.3a = 79.3a =，89.7a =，99.2a = 109.5a =，119.3a =，129.6a =24．(0分)[ID ：13339]父亲节小明给爸爸从网上购买了一双运动鞋，就在父亲节的当天，快递公司给小明打电话话说鞋子已经到达快递公司了，马上可以送到小明家，到达时间为晚上6点到7点之间，小明的爸爸晚上5点下班之后需要坐公共汽车回家，到家的时间在晚上5点半到6点半之间．求小明的爸爸到家之后就能收到鞋子的概率（快递员把鞋子送到小明家的时候，会把鞋子放在小明家门口的“丰巢”中）为 __________．25．(0分)[ID ：13340]一组样本数据按从小到大的顺序排列为：1-，0，4，x ，y ，14，已知这组数据的平均数与中位数均为5，则其方差为__________． 三、解答题26．(0分)[ID ：13499]“绿水青山就是金山银山”，“建设美丽中国”已成为新时代中国特色社会主义生态文明建设的重要内容，某班在一次研学旅行活动中，为了解某苗圃基地的柏树幼苗生长情况，在这些树苗中随机抽取了120株测量高度（单位：cm），经统计，树苗的高度均在区间[19,31]内，将其按[19,21)，[21,23)，[23,25)，[25,27)，[27,29)，[29,31]分成6组，制成如图所示的频率分布直方图.据当地柏树苗生长规律，高度不低于27cm的为优质树苗.（1）求图中a的值；（2）已知所抽取的这120株树苗来自于A，B两个试验区，部分数据如列联表：A试验区B试验区合计优质树苗20非优质树苗60合计将列联表补充完整，并判断是否有99.9%的把握认为优质树苗与A，B两个试验区有关系，并说明理由；（3）用样本估计总体，若从这批树苗中随机抽取4株，其中优质树苗的株数为X，求X 的分布列和数学期望EX.附：参考公式与参考数据：22()()()()()n ad bcKa b c d a c b d-=++++，其中n a b c d=+++()2P K k0.0100.0050.001k 6.6357.87910.82827．(0分)[ID：13494]甲、乙两个篮球运动员互不影响地在同一位置投球，命中率分别为与，且乙投球2次均未命中的概率为.（Ⅰ）求乙投球的命中率；（Ⅱ）若甲投球1次，乙投球2次，两人共命中的次数记为，求的分布列和数学期望. 28．(0分)[ID ：13455]为研究女高中生身高与体重之间的关系，一调查机构从某中学中随机选取8名女高中生，其身高()x cm 和体重()y kg 数据如下表所示： 编号 1 2 3 4 5 6 7 8 身高/x cm164160158172162164174166体重/y kg60 46 43 48 48 50 61 52该调查机构绘制出该组数据的散点图后分析发现，女高中生的身高与体重之间有较强的线性相关关系.（1）调查员甲计算得出该组数据的线性回归方程为ˆˆ0.7yx a =+，请你据此预报一名身高为176cm 的女高中生的体重；（2）调查员乙仔细观察散点图发现，这8名同学中，编号为1和4的两名同学对应的点与其他同学对应的点偏差太大，于是提出这样的数据应剔除，请你按照这名调查人员的想法重新计算线性回归话中，并据此预报一名身高为176cm 的女高中生的体重； （3）请你分析一下，甲和乙谁的模型得到的预测值更可靠？说明理由. 附：对于一组数据()()()1122,,,,,,n n x y x y x y ，其回归方程ˆˆˆy bx a =+的斜率和截距的最小二乘法估计分别为：()()()121ˆˆ,niii ni i x x y y b ay bx x x==--==--∑∑. 29．(0分)[ID ：13430]某学校高一、高二、高三的三个年级学生人数如下表高三高二高一女生100150z男生300450600按年级分层抽样的方法评选优秀学生50人，其中高三有10人．（1）求z的值；（2）用分层抽样的方法在高一中抽取一个容量为5的样本，将该样本看成一个总体，从中任取2人，求至少有1名女生的概率；（3）用随机抽样的方法从高二女生中抽取8人,经检测她们的得分如下：9．4，8．6，9．2， 9．6，8．7，9．3，9．0，8．2，把这8人的得分看作一个总体，从中任取一个数，求该数与样本平均数之差的绝对值不超过0．5的概率．30．(0分)[ID：13504]某县一中学的同学为了解本县成年人的交通安全意识情况，利用假期进行了一次全县成年人安全知识抽样调查.已知该县成年人中40%的拥有驾驶证，先根据是否拥有驾驶证，用分层抽样的方法抽取了100名成年人，然后对这100人进行问卷调查，所得分数的频率分布直方图如下图所示.规定分数在80以上（含80）的为“安全意识优秀”.拥有驾驶证没有驾驶证合计得分优秀得分不优秀25合计100（1）补全上面22的列联表，并判断能否有超过99%的把握认为“安全意识优秀与是否拥有驾驶证”有关？（2）若规定参加调查的100人中分数在70以上（含70）的为“安全意识优良”，从参加调查的100人中根据安全意识是否优良，按分层抽样的方法抽出5人，再从5人中随机抽取3人，试求抽取的3人中恰有一人为“安全意识优良”的概率.附表及公式：()()()()()22n ad bcKa b c d a c b d-=++++，其中n a b c d=+++.【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、选择题1．D2．C3．C4．C5．A6．C7．B8．A9．A10．C11．C12．C13．A14．A15．A二、填空题16．3【解析】【分析】分析出算法的功能是求分段函数的值根据输出的值为10分别求出当时和当时的值即可【详解】由程序语句知：算法的功能是求的值当时解得(或不合題意舍去)；当时解得舍去综上的值为3故答案为3【17．900【解析】【分析】利用频率分布直方图中频率和为1求a值根据7080）的频率求出在此区间的人数即可【详解】由1﹣005﹣035﹣02﹣01＝03故a＝003故阅读的时间在7080）（单位：分钟）内18．2【解析】【分析】根据系统抽样的概念结合可得最后结果为2【详解】学生总数不能被容量整除根据系统抽样的方法应从总体中随机剔除个体保证整除∵故应从总体中随机剔除个体的数目是2故答案为2【点睛】本题主要考19．1【解析】【分析】因为题目中要去掉一个最高分所以对进行分类讨论然后结合平均数的计算公式求出结果【详解】若去掉一个最高分和一个最低分86分后平均分为不符合题意故最高分为94分去掉一个最高分94分去掉一20．【解析】【分析】画出不等式组表示的平面区域结合图形利用几何概型的概率公式可求得对应的概率【详解】根据题意画出不等式组表示的平面区域如图所示在上随机取两个实数则满足不等式的概率为故答案为【点睛】本题主21．【解析】【分析】模拟执行程序框图只要按照程序框图规定的运算方法逐次计算直到达到输出条件即可得到输出的的值【详解】输入第一次循环；第二次循环；第三次循环；第四次循环；第五次循环；第六次循环退出循环输出22．【解析】分析：根据回归系数几何意义得详解：因为Y与X之间正增长所以因为V与U之间负增长所以因此点睛：函数关系是一种确定的关系相关关系是一种非确定的关系事实上函数关系是两个非随机变量的关系而相关关系是23．【解析】【分析】分析程序框图的功能在于寻找和输出一组数据的最大值观察该题所给的数据可知其最大值为M的值即为取最大时对应的脚码从而求得结果【详解】仔细分析程序框图的作用和功能所解决的问题是找出一组数据24．【解析】分析：设爸爸到家时间为快递员到达时间为则可以看作平面中的点分析可得全部结果所构成的区域及其面积所求事件所构成的区域及其面积由几何概型公式计算可得答案详解：设爸爸到家时间为快递员到达时间为以横25．【解析】分析：根据中位数为求出是代入平均数公式可求出从而可得出平均数代入方差公式得到方差详解中位数为这组数据的平均数是可得这组数据的方差是故答案为点睛：本题主要考查平均数与方差属于中档题样本数据的算三、解答题 26． 27． 28． 29． 30．2016-2017年度第*次考试试卷 参考解析【参考解析】**科目模拟测试一、选择题 1．D 解析：D 【解析】 【分析】利用与面积有关的几何概型概率计算公式求解即可. 【详解】由题可知,正方形的面积为=22=4S ⨯正,设这个月牙图案的面积为S , 由与面积有关的几何概型概率计算公式可得,向这个正方形里随机投入芝麻,落在月牙形图案内的概率为150=4500S S P S ==正,解得65S =. 故选:D 【点睛】本题考查与面积有关的几何概型概率计算公式;属于基础题、常考题型.2．C解析：C 【解析】 【分析】将A ，B ，C 三个字捆在一起，利用捆绑法得到答案. 【详解】由捆绑法可得所求概率为242466A A 1A 15P ==. 故答案为C 【点睛】本题考查了概率的计算，利用捆绑法可以简化运算.3．C解析：C 【解析】 【分析】利用几何概型的计算概率的方法解决本题，关键要弄准所求的随机事件发生的区域的面积和事件总体的区域面积，通过相除的方法完成本题的解答． 【详解】解：由几何概型的计算方法，可以得出所求事件的概率为P=．故选C ． 【点评】本题考查概率的计算，考查几何概型的辨别，考查学生通过比例的方法计算概率的问题，考查学生分析问题解决问题的能力，考查学生几何图形面积的计算方法，属于基本题型．4．C解析：C 【解析】 【分析】基本事件总数n 2343C A ==36，小明恰好分配到甲村小学包含的基本事件个数m 322332A C A =+=12，由此能求出小明恰好分配到甲村小学的概率．【详解】解：大学生小明与另外3名大学生一起分配到某乡镇甲、乙、丙3个村小学进行支教， 每个村小学至少分配1名大学生，基本事件总数n 2343C A ==36，小明恰好分配到甲村小学包含的基本事件个数m 322332A C A =+=12，∴小明恰好分配到甲村小学的概率为p 121363m n ===． 故选C ． 【点睛】本题考查概率的求法，考查古典概率、排列组合等基础知识，考查运算求解能力，是基础题．5．A解析：A 【解析】 【分析】根据频率分布直方图得到各个时间段的人数，进而得到结果. 【详解】根据频率分布直方图可列下表：故选A. 【点睛】这个题目考查了频率分布直方图的实际应用，以及样本体现整体的特征的应用，属于基础题.6．C解析：C 【解析】模拟执行程序可得：6n =，3sin 60S =⨯︒=，不满足条件，12n =，6sin303S =⨯︒=，不满足条件，24n =，12sin15120.2588 3.1056S =⨯︒≈⨯=，因为输出n 的值为24，则满足条件，退出循环，故判断框中填入的条件为 3.10S ≥. 故选C. 7．B 解析：B 【解析】 【详解】阅读流程图，初始化数值1,1,0a k S =-==. 循环结果执行如下：第一次：011,1,2S a k =-=-==；第二次：121,1,3S a k =-+==-=； 第三次：132,1,4S a k =-=-==； 第四次：242,1,5S a k =-+==-=； 第五次：253,1,6S a k =-=-==； 第六次：363,1,7S a k =-+==-=， 结束循环，输出3S =.故选B.点睛:算法与流程图的考查，侧重于对流程图循环结构的考查.求解时，先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，如：是求和还是求项.8．A解析：A 【解析】应抽取红球的个数为5010051000⨯= ，选A. 点睛：在分层抽样的过程中，为了保证每个个体被抽到的可能性是相同的，这就要求各层所抽取的个体数与该层所包含的个体数之比等于样本容量与总体的个体数之比，即n i ∶N i ＝n ∶N .9．A解析：A 【解析】 【分析】根据几何概型的概率计算公式，求出中间小三角形的面积与大三角形的面积的比值即可 【详解】设DE x =，因为D 为BE 中点，且图形是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形 所以2BE x =，CE x =，120CEB ∠=︒所以由余弦定理得：2222cos BC BE CE BE CE CEB =+-⋅⋅∠222142272x x x x x ⎛⎫=+-⨯⨯⨯-= ⎪⎝⎭即BC =，设DEF 的面积为1S ，ABC 的面积为2S因为DEF 与ABC 相似所以21217S DE P S BC ⎛⎫=== ⎪⎝⎭故选：A10．C解析：C【解析】 甲的平均成绩11(7378798793)825x =++++=，甲的成绩的方差22222211[(7382)(7882)(7982)(8782)(9382)]50.45s =-+-+-+-+-=；乙的平均成绩21(7989899291)885x =++++=，乙的成绩的方差22222221[(7988)(8988)(8988)(9288)(9188)]21.65s =-+-+-+-+-=.∴12x x <，乙比甲成绩稳定. 故选C .11．C解析：C 【解析】 【分析】根据程序框图依次计算得到答案. 【详解】9,5x y ==，41y x -=>；115,3x y ==，413y x -=>； 1129,39x y ==，419y x -=<；结束. 故选：C . 【点睛】本题考查了程序框图的循环次数，意在考查学生的理解能力和计算能力.12．C解析：C 【解析】 【分析】先求出基本事件总数n ＝27，在得到的27个小正方体中，若其两面涂有油漆，则这个小正方体必在原正方体的某一条棱上，且原正方体的一条棱上只有一个两面涂有油漆的小正方体，则两面涂有油漆的小正方体共有12个，由此能求出在27个小正方体中，任取一个其两面涂有油漆的概率． 【详解】∵一块各面均涂有油漆的正方体被锯成27个大小相同的小正方体， ∴基本事件总数n ＝27， 在得到的27个小正方体中，若其两面涂有油漆，则这个小正方体必在原正方体的某一条棱上， 且原正方体的一条棱上只有一个两面涂有油漆的小正方体，则两面涂有油漆的小正方体共有12个，则在27个小正方体中，任取一个其两面涂有油漆的概率P =1227=49故选：C 【点睛】本题考查概率的求法，考查古典概型、正方体性质等基础知识，考查推理论证能力、空间想象能力，考查函数与方程思想，是基础题．13．A解析：A 【解析】分析：先确定间距，再根据等差数列通项公式求结果.详解：因为系统抽样的方法抽签，所以间距为10002050= 所以抽取的第40个数为1520(401)795+⨯-=选A.点睛：本题考查系统抽样概念，考查基本求解能力.14．A解析：A 【解析】 【分析】可以通过n P 与0P 之间的大小关系进行判断． 【详解】当10k -<<时，()011011nk k <+<<+<，， 所以()001nn P P k P =+<，呈下降趋势． 【点睛】判断变化率可以通过比较初始值与变化之后的数值之间的大小来判断．15．A解析：A 【解析】分析：根据已知中某公共汽车站每隔5分钟有一辆车通过，我们可以计算出两辆车间隔的时间对应的几何量长度为5，然后再计算出乘客候车时间不超过2分钟的几何量的长度，然后代入几何概型公式，即可得到答案 详解：：∵公共汽车站每隔5分钟有一辆车通过当乘客在上一辆车开走后3分钟内到达候车时间会超过2分钟 ∴乘客候车时间不超过2分钟的概率为53255P -=＝ ． 故选A .点睛：本题考查的知识点是几何概型，其中计算出所有事件和满足条件的事件对应的几何量的值是解答此类问题的关键二、填空题16．3【解析】【分析】分析出算法的功能是求分段函数的值根据输出的值为10分别求出当时和当时的值即可【详解】由程序语句知：算法的功能是求的值当时解得(或不合題意舍去)；当时解得舍去综上的值为3故答案为3【 解析：3 【解析】 【分析】分析出算法的功能是求分段函数22,31,3x x y x x <⎧=⎨+≥⎩的值，根据输出的值为10 ,分别求出当3x <时和当3x ≥时的x 值即可. 【详解】由程序语句知：算法的功能是求22,31,3x x y x x <⎧=⎨+≥⎩的值， 当3x ≥时，2110y x =+=，解得3x =(或3- ,不合題意舍去)； 当3x <时，210y x ==,解得5x = ,舍去， 综上，x 的值为3，故答案为3 . 【点睛】本题主要考查条件语句以及算法的应用，属于中档题 .算法是新课标高考的一大热点，其中算法的交汇性问题已成为高考的一大亮，这类问题常常与函数、数列、不等式等交汇自然，很好地考查考生的信息处理能力及综合运用知识解决问題的能力，解决算法的交汇性问题的方：（1）读懂程序框图、明确交汇知识，(2）根据给出问题与程序框图处理问题即可.17．900【解析】【分析】利用频率分布直方图中频率和为1求a 值根据7080）的频率求出在此区间的人数即可【详解】由1﹣005﹣035﹣02﹣01＝03故a ＝003故阅读的时间在7080）（单位：分钟）内 解析：900【解析】 【分析】利用频率分布直方图中频率和为1求a 值，根据[70，80）的频率求出在此区间的人数即可． 【详解】由1﹣0.05﹣0.35﹣0.2﹣0.1＝0.3， 故a ＝0.03，故阅读的时间在[70，80）（单位：分钟）内的学生人数为：0.3×3000＝900， 故答案为：900． 【点睛】本题考查频率分布直方图中的有关性质的应用，考查直方图中频率和频数的求法.18．2【解析】【分析】根据系统抽样的概念结合可得最后结果为2【详解】学生总数不能被容量整除根据系统抽样的方法应从总体中随机剔除个体保证整除∵故应从总体中随机剔除个体的数目是2故答案为2【点睛】本题主要考解析：2 【解析】 【分析】根据系统抽样的概念结合2544262=⨯+，可得最后结果为2. 【详解】学生总数不能被容量整除，根据系统抽样的方法，应从总体中随机剔除个体，保证整除. ∵2544262=⨯+，故应从总体中随机剔除个体的数目是2，故答案为2. 【点睛】本题主要考查系统抽样，属于基础题；从容量为N 的总体中抽取容量为n 的样本，系统抽样的前面两个步骤是：（1）将总体中的N 个个体进行编号；（2）当Nn为整数时，抽样距即为N n ；当N n 不是整数时，从总体中剔除一些个体，使剩下的总体中的个体的个数N '能被n 整除．19．1【解析】【分析】因为题目中要去掉一个最高分所以对进行分类讨论然后结合平均数的计算公式求出结果【详解】若去掉一个最高分和一个最低分86分后平均分为不符合题意故最高分为94分去掉一个最高分94分去掉一解析：1 【解析】 【分析】因为题目中要去掉一个最高分，所以对x 进行分类讨论，然后结合平均数的计算公式求出结果 【详解】若4x >，去掉一个最高分()90x +和一个最低分86分后，平均分为()1899291949291.65++++=，不符合题意，故4x ≤，最高分为94分，去掉一个最高分94分，去掉一个最低分86分后，平均分()18992909192915x +++++=，解得1x =，故数字x 为1 【点睛】本题考查了由茎叶图求平均值，理解题目意思运用平均数计算公式即可求出结果，注意分类讨论20．【解析】【分析】画出不等式组表示的平面区域结合图形利用几何概型的概率公式可求得对应的概率【详解】根据题意画出不等式组表示的平面区域如图所示在上随机取两个实数则满足不等式的概率为故答案为【点睛】本题主解析：4π【解析】 【分析】画出不等式组2201011a b a b ≤≤⎧⎪≤≤⎨⎪+≤⎩表示的平面区域，结合图形利用几何概型的概率公式可求得对应的概率. 【详解】根据题意，画出不等式组2201011a b a b ≤≤⎧⎪≤≤⎨⎪+≤⎩表示的平面区域，如图所示，在[]0,1上随机取两个实数,a b ，则,a b 满足不等式221a b +≤的概率为2211414P ππ⨯==，故答案为4π. 【点睛】本题主要考查“面积型”的几何概型，属于中档题. 解决几何概型问题常见类型有：长度型、角度型、面积型、体积型，求与面积有关的几何概型问题关鍵是计算问题的总面积以及事件的面积；几何概型问题还有以下几点容易造成失分，在备考时要高度关注：（1）不能正确判断事件是古典概型还是几何概型导致错误；（2）基本事件对应的区域测度把握不准导致错误 ；（3）利用几何概型的概率公式时 , 忽视验证事件是否等可能性导致错误.21．【解析】【分析】模拟执行程序框图只要按照程序框图规定的运算方法逐次计算直到达到输出条件即可得到输出的的值【详解】输入第一次循环；第二次循环；第三次循环；第四次循环；第五次循环；第六次循环退出循环输出 解析：42【解析】 【分析】模拟执行程序框图，只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可得到输出的S 的值。

一、选择题1．(0分)[ID ：13605]O 是平面上的一定点，,,A B C 是平面上不共线的三点，动点P 满足+OP OA λ= ()·cos ?cos AB AC AB B AC C+，(0,)λ∈∞，则动点P 的轨迹一定经过ABC ∆的（ ） A ．重心 B ．垂心 C ．外心 D ．内心 2．(0分)[ID ：13601]若sin 0α<，且tan 0α>，则α是（ ）A ．第一象限角B ．第二象限角C ．第三象限角D ．第四象限角3．(0分)[ID ：13576]若x 1=4π，x 2=34π是函数f (x )=sin x ω(ω>0)两个相邻的极值点，则ω=A ．2B ．32C ．1D ．124．(0分)[ID ：13622]函数()()sin (0,0,)2f x A x A πωϕωϕ=+>><的部分图象如图所示，为了得到sin2y x =的图象，只需将()f x 的图象( )A ．向右平移3π个单位 B ．向右平移6π个单位 C ．向左平移3π个单位D ．向左平移6π个单位5．(0分)[ID ：13616]已知函数()sin(),f x x ϕ=-且23()0,f x dx π=⎰则函数()f x 的图象的一条对称轴是( ) A ．56x π=B ．712x π=C ．3x π=D ．6x π=6．(0分)[ID ：13614]已知函数()()2cos 23042x f x x πωωω⎛⎫=-->⎪⎝⎭在区间0,2π⎡⎤⎢⎥⎣⎦上单调递减，则ω的最大值为（ ）.A ．1B ．65C ．43D ．327．(0分)[ID ：13594]已知向量()()2,1,,2a b x ==-，若//a b ，则a b +=（ ） A ．()2,1--B ．()2,1C ．()3,1-D ．()3,1-8．(0分)[ID ：13591]在ABC ∆中，已知向量AB 与AC 满足()AB AC BC ABAC+⊥且1•2AB AC ABAC=，则ABC ∆是( ) A ．三边均不相同的三角形 B ．直角三角形 C ．等腰非等边三角形D ．等边三角形9．(0分)[ID ：13589]已知AB AC ⊥，1AB t=，AC t =，若P 点是ABC 所在平面内一点，且4AB AC AP ABAC=+，则·PB PC 的最大值等于（ ）.A ．13B ．15C ．19D ．2110．(0分)[ID ：13586]若1tan 3θ= ，则cos2θ=( ) A ．45-B ．15-C ．15D ．4511．(0分)[ID ：13569]已知0w >,0φπ<<，直线4x π=和54=x π是函数()sin()f x wx φ=+图像的两条相邻的对称轴，则φ=（ ）A ．π4B ．π3C ．π2D ．3π412．(0分)[ID ：13562]函数()()2sin 3f x x ϕ=+的图象向右平移动12π个单位，得到的图象关于y 轴对称，则ϕ的最小值为（ ） A ．12πB ．4π C ．3π D ．512π 13．(0分)[ID ：13539]设,a b 是两个非零向量，则下列命题为真命题的是 A ．若a b a b a b +=-⊥，则 B ．若,a b a b a b ⊥+=-则C ．若a b a b +=-，则存在实数λ，使得a b λ=D ．若存在实数λ，使得a b λ=，则a b a b +=-14．(0分)[ID ：13538]3cos()45x π-=，那么sin 2x =（ ） A ．1825B ．2425±C ．725-D ．72515．(0分)[ID ：13531]ABC 中，点D 在AB 上，CD 平分ACB ∠．若CB a =，CA b =，1a =，2b =，则CD =A ．1233a b +B ．2133a b + C ．3455a b + D ．4355a b + 二、填空题16．(0分)[ID ：13705]在各棱长都等于1的正四面体O ABC -中，若点P 满足1)(OP xOA yOB zOC x y z =++++=,则OP 的最小值为_____________.17．(0分)[ID ：13701]已知P 是ABC 内部一点230PA PB PC ++=，记PBC 、PAC 、PAB △的面积分别为1S 、2S 、3S ，则::123S S S =________.18．(0分)[ID ：13698]若1e ，2e 是两个不共线的向量，已知12AB 2e ke =+，12CB e 3e =+，12CD 2e e =-，若A ，B ，D 三点共线，则k =________.19．(0分)[ID ：13690]已知A 、B 、C 为直线l 上不同的三点，点O 在直线l 外，若实数220x OA xOB OC -+=，则x =_____.20．(0分)[ID ：13676]已知向量a 在向量b 方向上的投影为2-，且3b =，则a b ⋅=_______．(结果用数值表示)21．(0分)[ID ：13671]已知ABC ∆的外接圆的圆心为O ，半径为2，若2AO AB AC =+，且AO AB =，则向量BA 在向量CB 上的投影为_____22．(0分)[ID ：13667]在ABC ∆中，sin 2cos sin A B C =，则ABC ∆为_____三角形． 23．(0分)[ID ：13655]在平面直角坐标系中，已知向量(2,1)a =，O 是坐标原点，M 是曲线||2||2x y +=上的动点，则a OM --→⋅的取值范围为__________. 24．(0分)[ID ：13653]已知3cos 63πα⎛⎫-=⎪⎝⎭，则25sin cos 66παπα⎛⎫⎛⎫--+ ⎪ ⎪⎝⎭⎝⎭的值为__________ .25．(0分)[ID ：13635]已知D 是ABC ∆中AC 所在边上的一点，，则DB 在AC 上投影的最小值是_____．三、解答题26．(0分)[ID ：13812]已知()1,2a =，()3,2b =-. （1）当k 为何值时，ka b +与3a b -垂直？ （2）当k 为何值时，ka b +与3a b -平行？27．(0分)[ID ：13795]平面内给定三个向量()1,3a =，()1,2b =-，()4,3c =-，回答下列问题：（1）求满足a mb nc =+的实数m ，n（2）若a kc +与2b c +的夹角为锐角，求出实数k 的取值范围28．(0分)[ID ：13732]（本小题满分12分）已知A 、B 、C 为△ABC 的内角，tanA 、tanB 是关于方程x 2＋√3px －p ＋1＝0（p ∈R ）两个实根. （Ⅰ）求C 的大小（Ⅱ）若AB ＝3，AC ＝√6，求p 的值29．(0分)[ID ：13808]已知向量(,)u x y =与向量(,)v x y x y =-+的对应关系用()v f u =表示.(1) 证明：对于任意向量a 、b 及常数m 、n ，恒有()()()f ma nb mf a nf b +=+； (2) 证明：对于任意向量a ，()2f a a =；(3) 证明：对于任意向量a 、b ，若a b ⊥，则()()f a f b ⊥.30．(0分)[ID ：13806]已知函数44()cos 2sin cos sin f x x x x x =--. （1）求()f x 的最小正周期； （2）当0,2x π⎡⎤∈⎢⎥⎣⎦时，求()f x 的最小值以及取得最小值是x 的值.【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题 1．B 2．C 3．A 4．B 5．A6．C7．A8．D9．A10．D11．A12．B13．C14．C15．B二、填空题16．【解析】根据题意可得∵点P满足可得∴点P是平面ABC内的一点又∵正四面体O﹣ABC是各棱长都等于1∴当点P与O在ABC上的射影重合时等于正四面体的高此时=且达到最小值故答案为17．【解析】【分析】延长到使得;延长到使得构造出根据线段关系及三角形面积公式即可求得面积比【详解】延长到使得;延长到使得如下图所示:则可化为所以为的重心设则所以故答案为:【点睛】本题考查了向量加法法则的18．-8【解析】【分析】计算得到根据共线得到代入计算得到答案【详解】则；ABD三点共线故即解得故答案为：【点睛】本题考查了根据向量共线计算参数意在考查学生的计算能力19．【解析】【分析】变换得到根据三点共线得到计算得到答案【详解】为直线上不同的三点则故答案为：【点睛】本题考查了向量三点共线问题意在考查学生的计算能力20．【解析】由题向量在向量方向上的投影为即即答案为-621．－1【解析】【分析】因为可知为直角三角形又可知为等边三角形故所求投影为＝【详解】因为所以为的中点即为直角三角形又可知为边长为2的等边三角形故向量在向量上的投影为＝故答案为：-1【点睛】本题主要考查向22．等腰【解析】【分析】利用内角和定理以及诱导公式得出然后利用两角差的正弦公式得出由此可判断出的形状【详解】因为所以即所以即所以因为所以因此是等腰三角形故答案为等腰【点睛】本题考查利用内角和定理诱导公式23．【解析】【分析】先作出曲线对应的图像再结合简单的线性规划问题观察图像即可得解【详解】解：曲线对应的图像为如图所示的菱形设则因为是曲线上的动点则又向量则由图可知：目标函数过点时函数取最小值过点时函数取24．【解析】分析：由同角三角函数关系得诱导公式得进而得解详解：由得所以故答案为：点睛：本题主要考查了同角三角函数的关系和诱导公式属于基础题25．【解析】【分析】依题意设然后根据数量积可以求出的最小值从而可求出在上投影的最小值【详解】依题意设∵（时取等此时与重合）∴在上投影为故答案为【点睛】本题考查了平面向量数量积的性质及其运算属中档题三、解答题26．27．28．29．30．2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1．B解析：B【解析】【分析】解出AP，计算AP BC并化简可得出结论．【详解】AP OP OA =-=λ（AB AC AB cosBAC cosC+⋅⋅），∴()...0AB BC AC BC AP BC BC BC AB cosB AC cosC λλ⎛⎫⎪=+=-+= ⎪⋅⋅⎝⎭， ∴AP BC ⊥，即点P 在BC 边的高上，即点P 的轨迹经过△ABC 的垂心． 故选B ． 【点睛】本题考查了平面向量的数量积运算在几何中的应用，根据条件中的角计算AP BC ⋅是关键．2．C解析：C 【解析】sin 0α<，则α的终边在三、四象限；tan 0α>则α的终边在三、一象限，sin 0α<，tan 0α>，同时满足，则α的终边在三象限． 3．A解析：A 【解析】 【分析】从极值点可得函数的周期，结合周期公式可得ω. 【详解】由题意知，()sin f x x ω=的周期232()44T ωπππ==-=π，得2ω=．故选A ． 【点睛】本题考查三角函数的极值、最值和周期，渗透了直观想象、逻辑推理和数学运算素养．采取公式法，利用方程思想解题．4．B解析：B 【解析】试题分析：由图象知1A =，74123T T πππ=-⇒=，22ππωω=⇒=，7()112f π=-7322122k ππϕπ⇒⋅+=+，2πϕ<，得3πϕ=，所以()sin(2)3f x x π=+，为了得到()sin 2g x x =的图象，所以只需将()f x 的图象向右平移6π个长度单位即可，故选D ． 考点：三角函数图象.5．A解析：A 【解析】 【分析】 【详解】函数()f x 的对称轴为12x k πϕπ-=+12x k πϕπ⇒=++,因为()232sin 0cos cos 03x dx ππϕϕϕ⎛⎫-=⇒--+= ⎪⎝⎭⎰sin 03πϕ⎛⎫⇒-= ⎪⎝⎭, 所以23k πϕπ-=23k πϕπ⇒=-,即对称轴121526x k k k ππϕπππ=++=-+(12,k k N ∈) 则56x π=是其中一条对称轴,故选A. 6．C解析：C 【解析】 【分析】首先化简函数()2cos 3f x x πω⎛⎫=+ ⎪⎝⎭，需满足22T π≥，根据函数在区间0,2π⎡⎤⎢⎥⎣⎦单调递减，所以求3x πω+的范围，且是[]0,π的子集，最后求ω的范围.【详解】()cos 1cos 2f x x x πωω⎫⎛⎫=+- ⎪⎪⎝⎭⎭cos x x ωω=2cos 3x πω⎛⎫=+- ⎪⎝⎭()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上单调递减，22T π∴≥ ,即2ππω≥ 02ω∴<≤ ，当[0,]2x π∈时，[,]3323x ππωπωπ+∈+， ∴ [,][0,]323πωπππ+⊆ ∴23ωπππ+≤，403ω∴<≤， 综上可知403ω<≤. 故选C 【点睛】本题考查三角函数的恒等变形，以及根据区间的单调性求参数的取值范围，属于中档题型，利用三角函数的奇偶性，周期性，对称性求解参数的值或范围是一个重点题型，首先将三角函数写成形如()sin y A x b ωϕ=++，或()cos y A x b ωϕ=++，()tan y A x b ωϕ=++的形式，然后利用三角函数的性质，借助公式，区间范围关系等将参数表示出来，得到函数参数的等式或不等式，求解.7．A解析：A 【解析】 【分析】先根据向量的平行求出x 的值，再根据向量的加法运算求出答案． 【详解】向量()()2,1,,2a b x ==-， //a b ， 22x ∴⨯-=（），解得4x =-， ∴214221a b +=+--=--（，）（，）（，）， 故选A ． 【点睛】本题考查了向量的平行和向量的坐标运算，属于基础题．8．D解析：D 【解析】 【分析】AB AB和AC AC是两个单位向量，设AB AC ABAC+＝AD ，则AD 是BAC ∠的平分线，由此可得AD BC ⊥，从而确定三角形是等腰三角形，再由1•2AB AC ABAC=，求出BAC ∠即可判断． 【详解】 设AB AC ABAC+＝AD ，∵AB AB和AC AC是两个单位向量，∴AD 是BAC ∠的平分线，由题意AD BC ⊥，∴ABC ∆是等腰三角形，•AB AC ABAC111cos 2BAC ⨯⨯∠=，即1cos 2BAC ∠=，∴3BAC π∠=， ∴ABC ∆是等边三角形， 故选：D ． 【点睛】本题考查向量的数量积，考查向量加法的平行四边形法则．解题关键是由向量垢平行四边形法则得出设AB AC ABAC+＝AD ，则AD 是BAC ∠的平分线．9．A解析：A 【解析】以A 为坐标原点，建立平面直角坐标系，如图所示，则1(,0)B t，(0,)C t ，10)4(0,1)(1,4)AP =+=（，，即14)P （，，所以114)PB t=--（，，14)PC t =--（，，因此PB PC ⋅11416t t =--+117(4)t t =-+，因为114244t t t t+≥⋅=，所以PB PC ⋅的最大值等于13，当14t t =，即12t =时取等号．考点：1、平面向量数量积；2、基本不等式．10．D解析：D 【解析】222222cos cos2cos cos sin sin sin θθθθθθθ-=-=+. 分子分母同时除以2cos θ，即得：2211149cos211519tan tan θθθ--===++. 故选D.11．A解析：A 【解析】 因为直线4x π=和54x π=是函数()()sin f x wx φ=+图像的两条相邻的对称轴， 所以T=522π44ππ⎛⎫⨯-=⎪⎝⎭．所以ω=1，并且sin （4π+φ）与sin （54π+φ）分别是最大值与最小值，0＜φ＜π，所以φ=4π． 故选：A ． 12．B 解析：B 【解析】函数()()2sin 3f x x ϕ=+的图象向右平移动12π个单位得到：()2sin(3)4f x x πϕ=+-图象关于y 轴对称，即函数为偶函数，故424k k πππϕπϕπ-=-⇒=-，所以ϕ的最小值为4π 13．C 解析：C 【解析】试题分析：对于A 若a b a b +=-，则2222a b ab a b a b ++=+-，得0ab a b =-≠，则a b ⊥不成立，所以A 不正确．对于B ，由A 解析可知，0ab a b =-≠，所以B 不正确．对于C a b a b +=-，则2222a b ab a b a b ++=+-，得0ab a b =-≠，则cos 1θ=-，则a 与b 反向，因此 存在实数λ，使得a b λ=，所以C 正确．对于D ，若存在实数λ,使得a b λ=，则22,a b a a b a λλ⋅=-⋅=-，由于λ不能等于0，因此ab a b ≠-，则a b a b +≠-，所以D 不正确．故选C ．考点：平面向量的综合题14．C解析：C 【解析】 【分析】由3cos 45x π⎛⎫-= ⎪⎝⎭，利用二倍角的余弦公式求得sin2cos 22x x π⎛⎫=- ⎪⎝⎭的值． 【详解】 由题意可得3cos 45x π⎛⎫-= ⎪⎝⎭， ∴sin2cos 2cos 224x x x ππ⎡⎤⎛⎫⎛⎫=-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ 2972cos 12142525x π⎛⎫=--=⨯-=- ⎪⎝⎭，故选C ． 【点睛】本题主要考查二倍角的余弦公式的应用，属于基本知识的考查．15．B解析：B 【解析】 【分析】 【详解】如图所示，由题设条件知∠1＝∠2，∴BD DA＝CB CA＝12， ∴BD ＝13BA＝13(CA －CB )＝13b －13a ， ∴CD ＝CB ＋BD ＝a ＋13b －13a ＝23a ＋13b .二、填空题16．【解析】根据题意可得∵点P 满足可得∴点P 是平面ABC 内的一点又∵正四面体O ﹣ABC是各棱长都等于1∴当点P 与O 在ABC 上的射影重合时等于正四面体的高此时=且达到最小值故答案为解析：63【解析】根据题意，可得∵点P 满足()1OP xOA yOB zOC x y z =++++=，()()AP OP OA y OA OB z OA OC =-=----可得AP yBA zCA =-- ∴点P 是平面ABC 内的一点．又∵正四面体O ﹣ABC 是各棱长都等于1，∴当点P 与O 在ABC 上的射影重合时，OP 等于正四面体的高， 此时OP =63且OP 达到最小值． 故答案为63. 17．【解析】【分析】延长到使得;延长到使得构造出根据线段关系及三角形面积公式即可求得面积比【详解】延长到使得;延长到使得如下图所示:则可化为所以为的重心设则所以故答案为:【点睛】本题考查了向量加法法则的 解析：1:2:3【解析】 【分析】延长PB 到'B ,使得'2PB PB =;延长PC 到'C,使得'3PC PC =,构造出''AB C∆,根据线段关系及三角形面积公式即可求得面积比.【详解】延长PB 到'B ,使得'2PB PB =;延长PC 到'C,使得'3PC PC =,如下图所示:则230PA PB PC ++=可化为''0PA PB PC ++=所以P 为''AB C ∆的重心设''''PAB PAC PB C S S S k ∆∆∆=== 则3'1122PAB PAB S S S k ∆∆=== 3'1122PAB PAB S S S k ∆∆=== 2'1133PAC PAC S S S k ∆∆=== ''11111sin sin 2223PBC S S PB PC BPC PB PC BPC ∆⎛⎫⎛⎫==⨯⨯∠=⨯⨯∠ ⎪ ⎪⎝⎭⎝⎭''''1111sin 6266PB C PB PC BPC S k ∆⎛⎫=⨯⨯⨯∠== ⎪⎝⎭ 所以123111::::1:2:3632S S S k k k ⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭故答案为: 1:2:3 【点睛】本题考查了向量加法法则的应用,三角形面积的表示方法,需要构造三角形解决问题,属于中档题.18．-8【解析】【分析】计算得到根据共线得到代入计算得到答案【详解】则；ABD 三点共线故即解得故答案为：【点睛】本题考查了根据向量共线计算参数意在考查学生的计算能力解析：-8 【解析】 【分析】计算得到12e 4e BD CD CB =-=-，根据共线得到AB BD λ=，代入计算得到答案. 【详解】123CB e e =+，122CD e e =-，则12e 4e BD CD CB =-=-；A ，B ，D 三点共线，故AB BD λ=，即()121224e ke e e λ+=-解得2,8k λ==- 故答案为：8- 【点睛】本题考查了根据向量共线计算参数，意在考查学生的计算能力.19．【解析】【分析】变换得到根据三点共线得到计算得到答案【详解】为直线上不同的三点则故答案为：【点睛】本题考查了向量三点共线问题意在考查学生的计算能力解析：1【解析】 【分析】变换得到22OC xOB x OA =-，根据三点共线得到221x x -=，计算得到答案. 【详解】22202x xOB OC OC xOB OA OA x -+=∴=-，A 、B 、C 为直线l 上不同的三点则2211x x x -=∴= 故答案为：1 【点睛】本题考查了向量三点共线问题，意在考查学生的计算能力.20．【解析】由题向量在向量方向上的投影为即即答案为-6 解析：6-【解析】由题向量a 在向量b 方向上的投影为2-，即cos ,2,3, 6.a b a ba ab ab a b a b b⋅⋅===-=∴⋅=-⋅即答案为-6.21．－1【解析】【分析】因为可知为直角三角形又可知为等边三角形故所求投影为＝【详解】因为所以为的中点即为直角三角形又可知为边长为2的等边三角形故向量在向量上的投影为＝故答案为：-1【点睛】本题主要考查向解析：－1 【解析】 【分析】因为2AO AB AC =+可知，ABC ∆为直角三角形，又AO AB =可知，ABO ∆为等边三角形，故所求投影为cos120BA ＝1-． 【详解】因为2AO AB AC =+，所以O 为BC 的中点，即ABC ∆为直角三角形，又AO AB =可知，ABO ∆为边长为2的等边三角形，故向量BA 在向量CB 上的投影为cos120BA ＝1-．故答案为：-1．【点睛】本题主要考查向量中点公式的应用以及向量投影的求法．22．等腰【解析】【分析】利用内角和定理以及诱导公式得出然后利用两角差的正弦公式得出由此可判断出的形状【详解】因为所以即所以即所以因为所以因此是等腰三角形故答案为等腰【点睛】本题考查利用内角和定理诱导公式解析：等腰 【解析】 【分析】利用内角和定理以及诱导公式得出()sin sin A B C =+，然后利用两角差的正弦公式得出B C =，由此可判断出ABC ∆的形状.【详解】因为()A B C π=-+，所以()sin 2cos sin B C B C π⎡⎤-+=⎣⎦，即()sin 2cos sin B C B C +=，所以sin cos cos sin 2cos sin B C B C B C +=， 即sin cos cos sin 0B C B C -=，所以()sin 0B C -=，因为B 、()0,C π∈，(),B C ππ-∈-，所以B C =，因此，ABC ∆是等腰三角形． 故答案为等腰. 【点睛】本题考查利用内角和定理、诱导公式以及三角恒等变换思想来判断三角形的形状，考查推理能力，属于中等题.23．【解析】【分析】先作出曲线对应的图像再结合简单的线性规划问题观察图像即可得解【详解】解：曲线对应的图像为如图所示的菱形设则因为是曲线上的动点则又向量则由图可知：目标函数过点时函数取最小值过点时函数取 解析：[]4,4-【解析】 【分析】先作出曲线||2||2x y +=对应的图像，再结合简单的线性规划问题，观察图像即可得解. 【详解】解：曲线||2||2x y +=对应的图像为如图所示的菱形ABCD ，设00()M x y ，则()00,OM x y =，因为M 是曲线||2||2x y +=上的动点， 则00||2||2x y +=，又向量(2,1)a =，则002z a OM x y --→=⋅+=，由图可知：目标函数2z x y =+过点(2,0)A -时，函数取最小值2(2)104⨯-+⨯=-， 过点(2,0)C 时，函数取最大值22104⨯+⨯=， 即a OM --→⋅的取值范围为[]4,4-，故答案为：[]4,4-.【点睛】本题考查了简单的线性规划问题，重点考查了数形结合的数学思想方法，属中档题.24．【解析】分析：由同角三角函数关系得诱导公式得进而得解详解：由得所以故答案为：点睛：本题主要考查了同角三角函数的关系和诱导公式属于基础题 解析：233+ 【解析】分析：由同角三角函数关系得222sin 11666cos cos πππααα⎛⎫⎛⎫⎛⎫-=--=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，诱导公式得5cos cos π cos 666πππααα⎡⎤⎛⎫⎛⎫⎛⎫+=--=-- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦，进而得解. 详解：由3cos 63πα⎛⎫-=⎪⎝⎭，得22212sin 11166633cos cos πππααα⎛⎫⎛⎫⎛⎫-=--=--=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.53cos cos π cos 6663πππααα⎡⎤⎛⎫⎛⎫⎛⎫+=--=--=-⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦. 所以2523sin cos 66παπα+⎛⎫⎛⎫--+=⎪ ⎪⎝⎭⎝⎭23+ 点睛：本题主要考查了同角三角函数的关系和诱导公式，属于基础题.25．【解析】【分析】依题意设然后根据数量积可以求出的最小值从而可求出在上投影的最小值【详解】依题意设∵（时取等此时与重合）∴在上投影为故答案为【点睛】本题考查了平面向量数量积的性质及其运算属中档题 解析：2912-【解析】 【分析】依题意6AC =，设(),06CD t t =≤≤，然后根据数量积可以求出DB AC ⋅的最小值，从而可求出DB 在AC 上投影的最小值 【详解】依题意6AC =，设(),06CD t t =≤≤∵()DB AC AB AD AC AB AC AD AC ⋅=-⋅=⋅-⋅()22246329294666624622t t +-=⨯⨯--=-≥-⨯⨯ （0t =时取等，此时D 与C 重合）， ∴DB 在AC 上投影为29292=6612DB AC DB AC AC⋅⋅≥-=-．故答案为2912-．【点睛】本题考查了平面向量数量积的性质及其运算，属中档题．三、解答题 26．（1）19k =（2）13k =- 【解析】 【分析】（1）由向量垂直的坐标公式得k 的方程，求解即可； （2）由向量平行的坐标公式得k 的方程，求解即可； 【详解】（1）()13221a b ⋅=⋅-+⋅=，()()3ka b a b +⋅-()22133238=0ka k a b b k =+-⋅-=-, 故19k =（2）因为()=3,22ka b k k +-+，()3=104a b --，若ka b +与3a b -平行，则()()14310222483k k k k --=+⇒=-∴=-【点睛】本题考查向量垂直与平行的坐标运算，是基础题27．（1）1m =，3n =；（2）1k >-且12k ≠ 【解析】 【分析】(1)根据向量的坐标运算求解即可.(2)利用()()20b c a kc +⋅>+且a kc +与2b c +不同向即可. 【详解】(1)因为a mb nc =+,故()()()()1,21,34,34,23m n m m n n -=-++-=-.故4132331m n m m n n -+==⎧⎧⇒⎨⎨-==⎩⎩.(2)由题()()20b c a kc +⋅>+且a kc +与2b c +不同向,则()()14,3324,430k k +-⋅-+->. 即283301k k k ++->⇒>-.当a kc +与2b c +同向,即()14,33k k +-与()2,1同向时, 此时()14233k k +=-,解得12k =.代入可得此时a kc +与2b c +同向. 故若a kc +与2b c +的夹角为锐角,则1k >-且12k ≠ 【点睛】本题主要考查了平面向量的坐标运算以及夹角的表示方法等,需要根据题意列出对应的表达式,注意向量数量积大于0包括同向的情况.属于中等题型.28．（Ⅰ）C ＝60°；（Ⅱ）－1－√3 【解析】（Ⅰ）由已知，方程x 2＋√3px －p ＋1＝0的判别式 △＝（√3p ）2－4（－p ＋1）＝3p 2＋4p －4≥0 所以p≤－2或p≥23由韦达定理，有tanA ＋tanB ＝－√3p ，tanAtanB ＝1－p 于是1－tanAtanB ＝1－（1－p ）＝p≠0 从而tan （A ＋B ）＝tanA+tanB 1−tanAtanB=−√3p p=−√3所以tanC ＝－tan （A ＋B ）＝√3所以C ＝60°（Ⅱ）由正弦定理，得 sinB ＝ACsinC AB=√6sin6003=√22解得B ＝45°或B ＝135°（舍去） 于是A ＝180°－B －C ＝75° 则tanA ＝tan75°＝tan （45°＋30°）＝tan450+tan3001−tan450tan30=1+√331−√33=2+√3所以p ＝－√3（tanA ＋tanB ）＝－√3（2＋√3＋1）＝－1－√3考点：本题主要考查和角公式、诱导公式、正弦定理、一元二次方程根与系数关系等基础知识，考查运算求解能力，考查函数与方程、化归与转化等数学思想.29．(1) 证明见解析；(2) 证明见解析；(3) 证明见解析 【解析】 【分析】 (1)设向量11(,)a x y ，22(,)b x y ，然后利用题中关系式即可推导出所证恒等式； (2)设向量11(,)a x y ，则利用题中关系以及向量模的求解即可证明等式；(3)设向量11(,)ax y ，22(,)b x y ，由a b ⊥可得出12120x x y y +=,然后利用题中关系式可推导出()()0f a f b ⋅=，即可证明()()f a f b ⊥成立. 【详解】 证：(1)设向量11(,)ax y ，22(,)b x y ，则11221212(,)(,)(,)ma nb m x y n x y mx nx my ny +=+=++由题中关系式可得：12121212()(,)f ma nb mx nx my ny mx nx my ny +=+--+++，11112222()()(,)(,)mf a nf b m x y x y n x y x y +=-++-+1122112212121212(,)(,)mx my nx ny mx my nx ny mx nx my ny mx nx my ny =-+-+++=+--+++∴()()()f ma nb mf a nf b +=+，对于任意向量a 、b 及常数,m n 恒成立；(2)设向量11(,)ax y ，则由题中关系可得1111()(,)f a x y x y =-+，则2222221111111111()|(,)|()()2()f a x y x y x y x y x y =-+=-++=+， 即得()2f a x =，因为21a x y =+∴()2f a a =成立，命题得证；(3)设向量11(,)ax y ，22(,)b x y ， 由a b ⊥，可得0a b ⋅=，即得12120x x y y +=由题中关系式可得：1111()(,)f a x y x y =-+，2222()(,)f b x y x y =-+ 则由()()()()1111111222222212()()(,)(,)f a f b x y x y x y x y x y x y x y x y ⋅=-+⋅-+=--+++ ()121220x x y y =+=，即()()0f a f b ⋅=，所以()()f a f b ⊥成立.【点睛】本题着重考查了对题意的理解，利用题中关系式结合向量的坐标运算、向量模的表达式以及向量垂直的性质来推导所证命题结果，属于一般难度的题.30．(Ⅰ)π；(Ⅱ)答案见解析.【解析】【分析】（1）利用倍角公式化简整理函数()f x 的表达式，由周期2T πω=． （2）先求解52,444x πππ⎡⎤+∈⎢⎥⎣⎦，由正弦函数图像求解最值． 【详解】：()()()442222cos 2sin cos sin cos sin cos sin 2sin cos f x x x x x x x x x x x =--=+--cos2sin224x x x π⎛⎫=-=+ ⎪⎝⎭ (1)最小正周期为π(2)由0,2x π⎡⎤∈⎢⎥⎣⎦得52,444x πππ⎡⎤+∈⎢⎥⎣⎦，所以当32,,48x x πππ+==即时 ()f x 的最小值为. ()f x 取最小值时x 的集合为3.8π⎧⎫⎨⎬⎩⎭ 【点睛】：三角函数()y Asin φx ω=+在闭区间内[]a,b 上的最值问题的步骤：（1）换元，令t φx ω=+，其中[]12t t t ∈，（2）画出三角函数y Asint =的函数图像．（3）由图像得出最值．。

一、选择题1．(0分)[ID ：13606]函数()()()sin 0,0f x A x A ωϕω=+>>在区间[],m n 上是增函数，且()f m A =-，()f n A =，则函数()()()cos 0,0g x A x A ωϕω=+>>在区间[],m n 上（ ）A ．是增函数B ．是减函数C ．可以取到最大值AD ．可以取到最小值A -2．(0分)[ID ：13600]函数()()sin 02f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭，的最小正周期是π，若其图象向左平移3π个单位后得到的函数为偶函数，则函数()f x 的图象（ ） A ．关于点012π⎛⎫⎪⎝⎭，对称 B ．关于直线12x π=对称 C ．关于点06π⎛⎫⎪⎝⎭，对称 D ．关于直线6x π=对称3．(0分)[ID ：13598]已知函数()sin()(0,0,||)2f x A x A πωϕωϕ=+>><的部分图象如下图所示，则函数()f x 的解析式（ ）A ．1()2sin()26f x x π=+ B ．1()2sin()26f x x π=-C ．()2sin(2)6f x x π=-D ．()2sin(2)6f x x π=+ 4．(0分)[ID ：13584]若4sin()65x π-=，则sin(2)6x π+的值为（ ） A ．725B ．725-C ．2425D ．2425-5．(0分)[ID ：13574]如图，在ΔABC 中，AN ⃑⃑⃑⃑⃑ =12AC ⃑⃑⃑⃑ ，P 是BN 的中点，若AP⃑⃑⃑⃑⃑ =mAB ⃑⃑⃑⃑⃑ +14AC ⃑⃑⃑⃑ ，则实数m 的值是（ ）A ．14B ．1C ．12D ．326．(0分)[ID ：13558]已知tan 3α=，0,2πα⎛⎫∈ ⎪⎝⎭，则()sin2cos απα+-的值为()A 610- B 610+ C 510-D 510+ 7．(0分)[ID ：13554]设函数()2sin()f x x ωϕ=+，x ∈R ，其中0>ω，||ϕπ<.若5()28f π=，()08f 11π=，且()f x 的最小正周期大于2π，则 A ．23ω=，12πϕ= B ．23ω=，12ϕ11π=- C ．13ω=，24ϕ11π=- D ．13ω=，724πϕ=8．(0分)[ID ：13611]若1sin 24α=，42ππα<<，则cos sin αα-的值是（ ）A 3B ．3C ．34D ．34-9．(0分)[ID ：13594]已知向量()()2,1,,2a b x ==-，若//a b ，则a b +=（ ） A ．()2,1--B ．()2,1C ．()3,1-D ．()3,1-10．(0分)[ID ：13587]角θ的终边经过点(,)P y 4，且sin θ=35，则θtan = A ．43-B ．43C ．34-D ．3411．(0分)[ID ：13573]已知1sin cos 2αα-=，且()0,απ∈，则sin cos αα+=（ ） A 7 B ．7C ．7D ．12±12．(0分)[ID ：13567]把函数y ＝sin(x ＋π6)图象上各点的横坐标缩短到原来的12(纵坐标不变)，再将图象向右平移π3个单位长度，那么所得图象的一条对称轴方程为( )A ．x ＝－π2B ．x ＝－π4C ．x ＝π8D ．x ＝π413．(0分)[ID ：13549]将函数3cos sin ()y x x x R =+∈的图象向左平移()0m m >个长度单位后，所得到的图象关于y 轴对称，则m 的最小值是（ ） A ．12π B ．6π C ．3π D ．56π 14．(0分)[ID ：13545]下列函数中，在区间(1,1)-上为减函数的是 A ．11y x=- B ．cos y x =C ．ln(1)y x =+D ．2x y -=15．(0分)[ID ：13533]下列命题中，真命题是（ ） A ．若a 与b 互为相反向量，则0a b += B ．若0a b ⋅=，则0a =或0b = C ．若a 与b 都是单位向量，则1a b ⋅=D ．若k 为实数且0ka =，则0k =或0a =二、填空题16．(0分)[ID ：13724]若函数sin()(0)y x ωϕω=+>的部分图象如图所示，则ω的值为_______________．17．(0分)[ID ：13723]已知向量a ()2,3=，b ()2,1=-，则a 在b 方向上的投影等于______．18．(0分)[ID ：13714]已知||2,||3a b ==，且a 与b 的夹角是60︒，则|32|a b -=______19．(0分)[ID ：13713]若向量a 、b 满足a ＝1，b ＝2，且a 与b 的夹角为3π，则a b +＝_________.20．(0分)[ID ：13691]已知α为锐角，5cos 5α=，则tan 4πα⎛⎫+= ⎪⎝⎭__________． 21．(0分)[ID ：13689]已知平面内两点P 、Q 的坐标分别为（-2，4）、（2，1），则PQ 的单位向量0a =_____22．(0分)[ID ：13676]已知向量a 在向量b 方向上的投影为2-，且3b =，则a b ⋅=_______．(结果用数值表示)23．(0分)[ID ：13664]已知向量a 、b ，满足1a =，()(2)0a b a b +⋅-=，则b 的最小值为_________．24．(0分)[ID ：13645]如图，在平面四边形ABCD 中，AB BC ⊥，AD CD ⊥，120BAD ∠=︒，1AB AD ==．若点E 为边CD 上的动点，当AE BE ⋅取到最小值时，DE 的长为______．25．(0分)[ID ：13640]已知12(1,1),(2,3)P P =-=，若P 在12PP 的长线上，且1222PP P P =，则点P 的坐标为______．三、解答题26．(0分)[ID ：13813]某同学用“五点法”画函数π()sin()(0,)2f x A x ωϕωϕ=+><在某一个周期内的图象时，列表并填入了部分数据，如下表：x ωϕ+π2π3π22π xπ35π6sin()A x ωϕ+0 55-（Ⅰ）请将上表数据补充完整，填写在答题卡上相应位置，并直接写出函数()f x 的解析式；（Ⅱ）将()y f x =图象上所有点向左平行移动θ(0)θ>个单位长度，得到()y g x =的图象．若()y g x =图象的一个对称中心为5π(,0)12，求θ的最小值．27．(0分)[ID ：13767]已知O 为坐标原点，()()()34,63,5,3OA OB OC m m =-=-=---，，（1）若ABC ∠为锐角，求实数m 的取值范围；（2）若ABC ∆是以B 为直角的直角三角形，求实数m 的值并求ABC ∆的面积. 28．(0分)[ID ：13760]已知函数()()2cos 23sin cos sin (0)f x x x x x ωωωωω=-+>的最小正周期为2π．()1求ω的值；()2ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，()2f B =，3a =，ABC 面积334S =，求b ． 29．(0分)[ID ：13752]边长为1的正三角形ABC ，E 、F 分别是边AB 、AC 上的点，若AE mAB =，AF nAC =，其中,(0,1)m n ∈，设EF 的中点为M ，BC 中点为N .（1）若A 、M 、N 三点共线，求证：m n =； （2）若1m n +=，求||MN 的最小值.30．(0分)[ID ：13787]M 为ABC ∆的中线AD 的中点，过点M 的直线分别交两边,AB AC 于点,P Q ，设,AP xAB AQ y AC ==，记()y f x =.（1）求函数()y f x =的表达式； （2）求APQ ABCS S ∆∆的取值范围.【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题 1．C2．A3．D4．B5．C6．A7．A8．B9．A10．C11．A12．A13．B14．D15．D二、填空题16．【解析】【分析】由所给函数图像过点列式利用诱导公式可得【详解】由函数图像过点得所以又两点在同一周期所以故答案为4【点睛】本题考查三角函数的图像与性质考查简单三角方程的解考查图形识别与运算求解能力属于17．【解析】【分析】根据投影的定义得到在方向上的投影为利用公式求解即可得到答案【详解】根据投影的定义可得：在方向上的投影为故答案为：【点睛】本题主要考查了向量在方向上的投影其中熟记向量的投影的定义和向量18．6【解析】【分析】由计算【详解】∴＝6故答案为：6【点睛】本题考查向量的模的运算解题时求向量的模一般都是转化为向量的数量积即由转化19．【解析】【分析】由夹角为利用平面向量数量积公式求得平方的值从而可得结果【详解】夹角为所以所以故答案为20．【解析】【分析】先利用同角三角函数关系计算sinαtanα再利用两角和的正切即可求得结论【详解】∵α为锐角∴∴tanα2∴tan故答案为【点睛】本题考查同角三角函数关系考查两角和的正切公式考查学生的21．【解析】【分析】利用向量的单位向量的计算公式即可求解【详解】由题意两点的坐标分别为可得向量所以向量的单位向量故答案为：【点睛】本题主要考查了单位向量的计算与求解其中解答中熟记向量的单位向量的计算公式22．【解析】由题向量在向量方向上的投影为即即答案为-623．【解析】试题分析：由得所以解得所以的最小值为考点：向量的数量积运算及其性质【方法点晴】要求的最小值可以考虑建立关于的不等式或不等式组已知由结合向量数量积的运算律可得关于及的关系式根据向量数量积的定义24．【解析】【分析】设由已知结合余弦定理可求而展开结合向量的数量积的运算及二次函数的性质即可求出结果【详解】设中由余弦定理可得中此时故答案为：【点睛】本题以向量的基本运算为载体主要考查了向量的数量积的定25．【解析】【分析】首先利用线段的比值求出λ进一步利用分点坐标公式即可求出结果【详解】由题意因为点P在的延长线上且所以可得又由设可得所以点的坐标为故答案为：【点睛】本题主要考查了定比分点的坐标公式的应用三、解答题26．27．28．29．30．2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1．C解析：C【解析】【分析】根据题意计算出当[],x m n ∈时，x ωϕ+的取值范围，结合余弦函数的单调性可得出结论. 【详解】函数()()()sin 0,0f x A x A ωϕω=+>>在区间[],m n 上是增函数，且()f m A =-，()f n A =，则当[],x m n ∈时，()2,222x k k k Z ππωϕππ⎡⎤+∈-++∈⎢⎥⎣⎦，而函数cos y x =在区间()2,222k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦上先增后减，所以，函数()()cos g x A x ωϕ=+在区间[],m n 上先增后减，当()2x k k Z ωϕπ+=∈，该函数取到最大值A . 故选：C. 【点睛】本题考查余弦型函数单调性的判断与应用，求出x ωϕ+的取值范围是解答的关键，考查推理能力，属于中等题.2．A解析：A 【解析】 【分析】根据函数()f x 的最小正周期是π，求得2w =，即()()sin 2f x x ϕ=+，再根据三角函数的图象变换求得2()sin(2)3g x x πϕ=++，利用三角函数的对称性，求得6πϕ=-，得到函数()sin 26f x x π⎛⎫=- ⎪⎝⎭，再利用三角函数的性质，即可求解.【详解】由题意，函数()()sin f x x ωϕ=+的最小正周期是π，即2wππ=，解得2w =， 所以()()sin 2f x x ϕ=+， 将函数()f x 的向左平移3π个单位后得到函数2()sin[2()]sin(2)33g x x x ππϕϕ=++=++ 因为()g x 为偶函数，所以2(0)sin()13g πϕ=+=±，即2,32k k Z ππϕπ+=+∈， 解得,6k k Z πϕπ=-+∈，因为2πϕ<，所以6πϕ=-，所以()sin 26f x x π⎛⎫=- ⎪⎝⎭，令2,6x k k Z ππ-=∈，解得,122k x k Z ππ=+∈， 令0k =，则12x π=，所以函数()f x 关于012π⎛⎫⎪⎝⎭，对称，故选A. 【点睛】本题主要考查了三角函数的图象变换，以及三角函数的图象与性质的应用，其中解答中熟练应用三角函数的图象变换求得函数的解析式，再利用三角函数的图象与性质求解是解答的关键，着重考查了推理与运算能力，属于基础题.3．D解析：D 【解析】 【分析】根据函数的图象求出A ，ω 和φ的值即可． 【详解】由函数的图象得524126A T πππ==⨯-=，（）， 即2 ππω=， 则2ω=，则22f x sin x ϕ=+（）（） ，22266f sin ππϕ=⨯+=（）（），则13sinπϕ+=（）， 则 232k ππϕπ+=+，则26k k Z ，，πϕπ=+∈∵2πϕ<，∴当k=0时，6，πϕ=则函数()2sin 26f x x π⎛⎫=+ ⎪⎝⎭． 故选D. 【点睛】本题主要考查三角函数的图象和性质，根据图象求出A ，ω和φ的值是解决本题的关键．4．B解析：B 【解析】 【分析】先根据诱导公式化简sin(2)6x π+，再根据二倍角余弦公式得结果.【详解】 ∵4sin()65x π-=，∴2327sin(2)cos 212sin 16362525x x x πππ-⎛⎫⎛⎫+=-=--=-= ⎪ ⎪⎝⎭⎝⎭，故选B. 【点睛】本题考查诱导公式以及二倍角余弦公式，考查基本分析求解能力,属基础题.5．C解析：C 【解析】 【分析】以AB⃑⃑⃑⃑⃑ ,AC ⃑⃑⃑⃑ 作为基底表示出AP ⃑⃑⃑⃑⃑ ，利用平面向量基本定理，即可求出． 【详解】∵P ，N 分别是BN ，AC 的中点，∴AP ⃑⃑⃑⃑⃑ =AB ⃑⃑⃑⃑⃑ +BP ⃑⃑⃑⃑⃑ =AB ⃑⃑⃑⃑⃑ +12BN ⃑⃑⃑⃑⃑ =AB ⃑⃑⃑⃑⃑ +12(AN ⃑⃑⃑⃑⃑ −AB ⃑⃑⃑⃑⃑ )=12AB ⃑⃑⃑⃑⃑ +12AN ⃑⃑⃑⃑⃑ =12AB ⃑⃑⃑⃑⃑ +14AC ⃑⃑⃑⃑ .又AP ⃑⃑⃑⃑⃑ =mAB ⃑⃑⃑⃑⃑ +14AC ⃑⃑⃑⃑ ，∴m =12.故选C.【点睛】本题主要考查平面向量基本定理以及向量的线性运算，意在考查学生的逻辑推理能力．6．A解析：A 【解析】 【分析】先利用正切值求得余弦值，再利用诱导公式、二倍角公式以及弦切互化公式求得表达式的值. 【详解】tan 3α=，0,2πα⎛⎫∈ ⎪⎝⎭得cos αα==， 而()6sin2cos 2sin cos cos 210101010απαααα+-=-=⨯-=. 故选A. 【点睛】本小题主要考查已知正切值求两弦值的方法，考查三角函数诱导公式、二倍角公式，属于基础题.7．A解析：A 【解析】由题意125282118k k ωππϕπωπϕπ⎧+=+⎪⎪⎨⎪+=⎪⎩，其中12,k k Z ∈，所以2142(2)33k k ω=--，又22T ππω=>，所以01ω<<，所以23ω=，11212k ϕππ=+，由ϕπ<得12πϕ=，故选A ．【考点】求三角函数的解析式【名师点睛】有关sin()y A x ωϕ=+问题，一种为提供函数图象求解析式或某参数的范围，一般先根据图象的最高点或最低点确定A ，再根据周期或12周期或14周期求出ω，最后再利用最高点或最低点坐标满足解析式，求出满足条件的ϕ值，另一种时根据题目用文字形容的函数图象特点，如对称轴或曲线经过的点的坐标，根据题意自己画出图象，再寻求待定的参变量，题型很活，求ω或ϕ的值或最值或范围等.8．B解析：B 【解析】22122cos ,sin cos 14sin sin ααααα==+=，()213cos 144sin αα∴-=-=，,cos sin 42ππααα<<∴-= B. 9．A解析：A 【解析】 【分析】先根据向量的平行求出x 的值，再根据向量的加法运算求出答案． 【详解】向量()()2,1,,2a b x ==-， //a b ， 22x ∴⨯-=（），解得4x =-， ∴214221a b +=+--=--（，）（，）（，）， 故选A ． 【点睛】本题考查了向量的平行和向量的坐标运算，属于基础题．10．C解析：C 【解析】 【分析】由题意利用任意角的正弦函数的定义可求得3y =-，再根据正切函数的定义即可求得结果． 【详解】∵角θ的终边经过点()4,P y ，且35sin θ=-=，∴3y =-，则3tan 44y θ==-，故选C ． 【点睛】本题主要考查任意角的三角函数的定义，属于基础题，若角α的终边经过点(),x y （异与原点），则sin α=cos α=，()tan 0yx xα=≠. 11．A解析：A 【解析】 【分析】根据sin cos ,sin cos ,sin cos αααααα+-间的关系求解可得答案． 【详解】 ∵12sin cos αα-=， ∴21(sin cos )12sin cos 4αααα-=-=, ∴3sin cos 08αα=>， ∴02πα<<， ∴sin 0,cos 0αα>>， ∴sin cos 0αα+>，∴sin cos αα+====故选A ． 【点睛】解答本题时注意灵活运用sin cos ,sin cos ,sin cos αααααα+-间的关系，即知道其中的一个可求另外的两个，解题中容易出现的错误是忽视所求值的符号．12．A解析：A 【解析】 把函数y ＝sin(x ＋π6)图象上各点的横坐标缩短到原来的12(纵坐标不变)得πsin(2)6y x =+ ，再将图象向右平移π3个单位长度得πππsin(2())sin(2)cos 2362y x x x =-+=-=-，一条对称轴方程为x ＝－π2，选A.点睛：三角函数的图象变换，提倡“先平移，后伸缩”，但“先伸缩，后平移”也常出现在题目中，所以也必须熟练掌握.无论是哪种变形，切记每一个变换总是对字母x 而言. 函数sin()()y A x x R ωϕ=+∈是奇函数π()k k Z ϕ⇔=∈；函数sin()()y A x x R ωϕ=+∈是偶函数ππ+()2k k Z ϕ⇔=∈；函数cos()()y A x x R ωϕ=+∈是奇函数ππ+()2k k Z ϕ⇔=∈；函数cos()()y A x x R ωϕ=+∈是偶函数π()k k Z ϕ⇔=∈.13．B解析：B 【解析】 【分析】 【详解】试题分析：由题意得，3cos sin 2sin()3yx x x，令,32x k k Z πππ+=+∈，可得函数的图象对称轴方程为,6x k k Z ππ=+∈，取0k =是y 轴右侧且距离y 轴最近的对称轴，因为将函数的图象向左平移()0m m >个长度单位后得到的图象关于y 轴对称，m 的最小值为6π，故选B ．考点：两角和与差的正弦函数及三角函数的图象与性质． 【方法点晴】本题主要考查了两角和与差的正弦函数及三角函数的图象与性质，将三角函数图象向左平移m 个单位，所得图象关于y 轴对称，求m 的最小值，着重考查了三角函数的化简、三角函数图象的对称性等知识的灵活应用，本题的解答中利用辅助角公式，化简得到函数2sin()3y x π=+,可取出函数的对称轴，确定距离y 最近的点，即可得到结论．14．D解析：D 【解析】 试题分析：11y x=-在区间()1,1-上为增函数；cos y x =在区间()1,1-上先增后减；()ln 1y x =+在区间()1,1-上为增函数；2x y -=在区间()1,1-上为减函数，选D.考点：函数增减性15．D解析：D 【解析】 【分析】根据两个向量和仍然是一个向量，可以判断A 的真假；根据向量数量积为0，两个向量可能垂直，可以判断B 的真假；根据向量数量积公式，我们可以判断C 的真假；根据数乘向量及其几何意义，可以判断D 的真假；进而得到答案． 【详解】对A ，若a 与b 互为相反向量，则0a b +=，故A 为假命题； 对B ，若0a b ⋅=，则0a =或0b =或a b ⊥，故B 为假命题；对C ，若a ，b 都是单位向量，则11a b -⋅，故C 为假命题； 对D ，若k 为实数且0ka =，则0k =或0a =，故D 为真命题； 故选：D ． 【点睛】本题考查向量的加法及其几何意义、向量的数乘运算及其几何意义、面向量的数量积的运算，其中熟练掌握平面向量的基本定义，基本概念，是解答本题的关键．二、填空题16．【解析】【分析】由所给函数图像过点列式利用诱导公式可得【详解】由函数图像过点得所以又两点在同一周期所以故答案为4【点睛】本题考查三角函数的图像与性质考查简单三角方程的解考查图形识别与运算求解能力属于 解析：=4ω. 【解析】 【分析】由所给函数图像 过点05(,)24y π,011(,)24y π-，列式115sin()sin()2424ππωϕωϕ+=-+，利用诱导公式可得.【详解】由函数图像过点05(,)24y π,011(,)24y π-,得05sin()24y πωϕ=+，011sin()24y πωϕ-=+，所以115sin()sin()2424ππωϕωϕ+=-+，又两点在同一周期，所以115()2424ππωϕπωϕ+=++，4ω=.故答案为4. 【点睛】本题考查三角函数的图像与性质，考查简单三角方程的解，考查图形识别与运算求解能力，属于基础题.17．【解析】【分析】根据投影的定义得到在方向上的投影为利用公式求解即可得到答案【详解】根据投影的定义可得：在方向上的投影为故答案为：【点睛】本题主要考查了向量在方向上的投影其中熟记向量的投影的定义和向量解析：【解析】 【分析】根据投影的定义得到a 在b 方向上的投影为cos ,a ba ab b⋅=，利用公式求解，即可得到答案．【详解】根据投影的定义可得：a 在b 方向上的投影为a b 5a cosa,b 5b⋅==-.故答案为： 【点睛】本题主要考查了向量a 在b 方向上的投影，其中熟记向量的投影的定义和向量a 在b 方向上的投影的计算公式是解答的关键，着重考查了推理与运算能力．18．6【解析】【分析】由计算【详解】∴＝6故答案为：6【点睛】本题考查向量的模的运算解题时求向量的模一般都是转化为向量的数量积即由转化解析：6 【解析】 【分析】 由2232(32)a b a b -=-计算。

2022-2023学年安徽省示范高中培优联盟高二下学期春季联赛数学试题一、单选题1．已知集合(){}(){}2,,,P x y y x Q x y y x ====∣∣，则P Q = （）A ．{}0B ．{}0,1C ．(){}0,0D ．()(){}0,0,1,1【答案】D【分析】根据集合的含义，结合解方程组，即可求得两集合的交集.【详解】由题意集合(){}(){}2,,,P x y y x Q x y y x ====∣∣表示点集，解方程组2y xy x ⎧=⎪⎨=⎪⎩，得00x y =⎧⎨=⎩或11x y =⎧⎨=⎩，故()(){}0,0,1,1P Q = ，故选：D2．若13i +是关于x 的实系数方程210ax bx ++=的一个复数根，则（）A ．14a =，12b =B ．14a =，12b =-C ．14a =-，12b =D ．14a =-，12b =-【答案】B【分析】根据一元二次方程复数根的特点及韦达定理即可求出答案.【详解】根据一元二次方程复数根成共轭复数形式出现，则另一个复数根为13i -，根据两根之积得()()113i 13i 4a+-==，则14a =，根据两根之和有214b ba=-=-，解得12b =-，故选：B.3．已知,αβ是空间两个不同的平面，,m n 是空间两条不同的直线，则下列命题为真命题的是（）A ．若,m n αα∥∥，则m n ∥B ．若,m m n α∥∥，则n α∥C ．若,m n αβ⊥∥，且m n ⊥，则αβ⊥D ．若,m n αβ⊥⊥，且αβ∥，则m n ∥【答案】D【分析】根据线面之间的位置关系判定即可.【详解】对于A 项，,m n 可能相交，如图所示正方体中，若,m n 分别为直线AB BC 、，α为平面1111D C B A ，此时符合条件，但结论不成立，故A 错误；对于B 项，有n ⊂α的可能，如图所示正方体中，若,m n 分别为直线11AB A B 、，α为平面1111D C B A ，此时符合条件，但结论不成立，故B 错误；对于C 项，如图所示正方体中，若,m n 分别为直线111AA B C 、，α为平面1111D C B A ，β为平面ABCD ，此时符合条件，但结论不成立，故C 错误；对于D 项，因为αβ∥，,m m αβ⊥⇒⊥又n β⊥，所以m n ∥，故D 正确；故选：D4．某公司将包括2名女员工在内的5名员工派往3个不同的地方学习，要求每人去一个地方，每个地方至少去一人，则2名女员工必须在一起学习的不同的分配方案有（）A ．24B ．32C ．36D ．48【答案】C【分析】分1,1,3三组，1,2,2三组讨论，并利用排列组合公式即可得到答案.【详解】如果5人分成1,1,3三组，则分配方法有：213233C C A 种，如果5人分成1,2,2三组，则分配方法有：223233C C A 种，由加法原理可得：不同分配方法数为213223233233C C A C C A 36+=种.故选：C5．著名的天文学家拉普拉斯曾经说过“对数的发明以其节省劳力而延长了天文学家的寿命”，对数可以将乘除运算转化为加减运算，从而简化运算过程.在一次趣味表演中，主持人出题：一个35位整数的31次方根仍是一个整数，下面我报出这个35位数，请说出它的31次方根.还未等主持人报出第一个数字，速算专家已经写出了答案：这个数的31次方根是13，他的秘诀就是：他心中记住了下面的表（表中常用对数为近似值），请你也试一试，一个20位整数的32次方根仍是一个整数，这个32次方根是多少？（）真数常用对数真数常用对数20.3090.9530.4810 1.0040.6011 1.0450.7012 1.0860.7813 1.1170.8514 1.1580.90151.18A ．3B ．4C ．5D ．6【答案】B【分析】设这个数为x ，则可得32x N =，利用对数运算并结合已知图表可求得lg 0.60x =，即可求得x 的值，即得答案.【详解】设所求这个数为x ，则32x N =，N 为20位整数，则321lg lg ,lg lg 32x N x N =∴=，因为20191010N <<，故19lg 20N <<，所以10.5938lg 0.62532N <<，由表可知lg 0.60x =，即4x =，故这个32次方根是4，故选：B6．已知函数()32f x x ax bx =++有两个极值点12,x x ，且()12f x x =，()21f x x =，那么关于x 的方程()()2320f x af x b ⎡⎤++=⎣⎦的不同实根的个数是（）A ．6个B ．4个C ．2个D ．1个【答案】B【分析】首先利用导数得到函数单调性，再作出图象，而由方程可知()()12,f x x f x x ==，再利用图象即可得到根的个数.【详解】()232f x x ax b '=++，令()0f x '=得12,x x x x ==，不妨令12x x <，故()f x 在()()12,,x x -∞+∞,上单调递增，在()12,x x 上单调递减，方程()()23[]20f x af x b ++=可得()()12,f x x f x x ==，而()12f x x =，()21f x x =，由()f x 的单调性并作出图象可知直线12,y x y x ==分别过点2112(,()),(,())x f x x f x ，与函数()f x 图象均有两个交点，故方程()()23[]20f x af x b ++=的根的个数是4个.故选：B.二、解答题7．已知()()()ln 1R f x x ax a =-+∈(1)讨论函数()f x 的单调性；(2)当1a =时，()e ln 1xb b x f x +++≥恒成立，求b 的取值范围.【答案】(1)答案见解析(2))2e ,∞-⎡+⎣【分析】（1）求得()()11ax a f x x --'=-，分0a =、0a >和a<0，三种情况讨论，结合()f x '的符号，即可求解.（2）解法1：转化为()e ln 1ln 10xb b x ++--≥恒成立，设()()e ln 1ln 1x g x b b x =++--，求得()1e 1x g x b x ='--，得到()g x '存在唯一的实数()1,t ∈+∞，使得1e 01tb t -=-，得出函数()g x 的单调性与最小值()()12ln 111g t t t t =---+-，进而转化为()1e 1t b t =-在(]1,2t ∈时的取值范围，设()()1e 1t h t t =-，利用导数求得其最小值，即可求解；解法2：由题意转化为()()ln e ln ln 11x bx b x x +++≥-+-，构造函数()e t h t t =+，转化为证明()ln ln 1b x x ≥--，设()()ln 1g x x x =--，利用导数求得单调性与最值，即可求解.【详解】（1）解：由题意，函数()()ln 1f x x ax =-+的定义域为{1}x x >∣，可得()()1111ax a f x a x x --=+=--'.当0a =时，()101f x x -'=>，()f x 在()1,+∞单调递增；当0a >时，()()11011a a x ax a a f x x x -⎛⎫- ⎪--⎭-'⎝==>-，()f x 在()1,+∞单调递增；当a<0时，令()0f x '=，得11x a=-，故()f x 在11,1a ⎛⎫- ⎪⎝⎭单调递增，在11,a ⎛⎫-+∞ ⎪⎝⎭上单调递减.综上所述，当0a ≥时，()f x 在()1,+∞单调递增；当a<0时，()f x 在11,1a ⎛⎫- ⎪⎝⎭单调递增，在11,a ⎛⎫-+∞ ⎪⎝⎭上单调递减.（2）解法1：只要证明()e ln 1ln 1xb b x ++≥-恒成立即可，即证明()e ln 1ln 10xb b x ++--≥恒成立即可，设()()e ln 1ln 1xg x b b x =++--，其中0b >，函数()g x 的定义域为{1}x x >∣且()1e 1xg x b x ='--，令()1e 1xx b x ϕ=--，可得()21e 0(1)x x b x ϕ'=+>-，所以()g x 为单调递增函数，可得存在唯一的实数()1,t ∈+∞，使得1e 01tb t -=-，即()ln e ln 1b t t +=--当()1,x t ∈时，()0g x '<，当(),x t ∈+∞时，()0g x '>.故()g x 的最小值为()()()1ln ln 112ln 111tg t be b t t t t =+--+=---+-，又由()()2111011g t t t '=---<--，所以()g t 在()1,+∞是减函数，且()20g =.要使()0g t ≥恒成立，只需(]1,2t ∈即可，即求()1e 1t b t =-在(]1,2t ∈时的取值范围.，设()()(]1,1,2e 1t h t t t =∈-，可得()2e [e (1)0]t t t h t t '=--⋅<，所以()h t 在定义域内为减函数，故()()22e h t h -≥=.所以b 的取值范围为)2e ,∞-⎡+⎣.解法2：只要证明()e ln 1ln 1xb b x x x +++≥-+恒成立即可，即证明()()ln eln ln 11x bx b x x +++≥-+-构造函数()e th t t =+，易知()h t 为增函数，原式等价于证明()()()ln ln 1h x b h x +≥-即证明()ln ln 1x b x +≥-，得()ln ln 1b x x ≥--.设()()ln 1g x x x =--，则()12111-'=-=--x g x x x ，所以()g x 在()1,2单调递增，在()2,+∞上单调递减.()max ln ()22b g x g ≥==-，所以b 的取值范围为)2e ,∞-⎡+⎣.【点睛】方法技巧：对于利用导数研究不等式的恒成立与有解问题的求解策略：1、通常要构造新函数，利用导数研究函数的单调性，求出最值，从而求出参数的取值范围；2、利用可分离变量，构造新函数，直接把问题转化为函数的最值问题．3、根据恒成立或有解求解参数的取值时，一般涉及分离参数法，但压轴试题中很少碰到分离参数后构造的新函数能直接求出最值点的情况，进行求解，若参变分离不易求解问题，就要考虑利用分类讨论法和放缩法，注意恒成立与存在性问题的区别．8．已知双曲线的标准方程为22221(0,0)x y a b a b-=>>，其中点F 为右焦点，过点F 作垂直于x 轴的垂线，在第一象限与双曲线相交于点A ，过点F 作双曲线渐近线的垂线，垂足为M ，若6AF =，23MF =.(1)求双曲线的标准方程；(2)过点M 作AF 的平行线l ，在直线l 上任取一点P ，连接PA 与双曲线相交于点B ，求证点P 到直线BF 的距离是定值.【答案】(1)221412x y -=(2)证明见解析【分析】（1）根据焦点(),0F c 到渐近线的距离为23，列出方程求得b ，再由26bAF a==，求得2a =，即可求得双曲线的方程；（2）设点()00,B x y ，得到直线BF 的方程()000440y x x y y ---=，设直线l 的方程为x m =，点(),3M m m ，根据FM l ⊥，取得1m =，得到直线l 的方程为1x =，设()1,P t ，根据,,P B A 共线，求得()00361,64y P x ⎛⎫--+ ⎪-⎝⎭，结合点到直线的距离公式，即可求解.【详解】（1）解：由双曲线22221(0,0)x y a b a b -=>>，可得焦点(),0F c ，其中一条渐近线方程为b y x a=，则点(),0F c 到渐近线的距离为2223()bc d b a ==+-，解得23b =，又由2,b A c a ⎛⎫ ⎪⎝⎭，可得26b AF a ==，解得2a =，故双曲线的标准方程为221412x y -=.（2）解：由双曲线221412x y -=，可得()()4,0,4,6F A ，设点()00,B x y ，则直线BF 的方程为()0044=--y y x x ，即()000440y x x y y ---=，由题意，设直线l 的方程为x m =，由点M 在直线l 上，可设点(),3M m m ，又由FM l ⊥，可得3343m m =--，解得1m =，即直线l 的方程为1x =，设()1,P t ，由点,,P B A 共线，可得AP AB k k =，即006634y t x --=--，得()003664y t x -=-+-，即点()00361,64y P x ⎛⎫--+⎪-⎝⎭，则点P 到直线BF 的距离为()()()()00000022220000036644666132143412y y x y x x d x y x x x +-----+-====-+-+--.即点P 到直线BF 的距离为定值.9．如图所示，在四棱锥S ABCD -中，侧面SAB 为边长为2的等边三角形，底面ABCD 为等腰梯形，//AB CD ，1CD =，底面梯形的两条对角线AC 和BD 互相垂直，垂足为O ，2SO =，点M 为棱SB上的任意一点.(1)求证：AC DM ⊥；(2)是否存在点M 使得二面角M AD C --的余弦值为7618，若存在求出点M 的位置；若不存在请说明理由.【答案】(1)证明见解析(2)存在，点M 为靠近B 的三等分点【分析】（1）由222SA SO OA =+，证得SO AO ⊥，得到SO AC ⊥，又由AC BD ⊥，利用线面垂直的判定定理，证得AC ⊥平面SBD ，进而证得AC DM ⊥.（2）以O 为原点，建立空间直角坐标系，设棱SB 上存在一点M ，设[],0,1SM SB λλ=∈，得到20,2,222DM λλ⎛⎫=+- ⎪ ⎪⎝⎭，分别求得平面ADM 和平面ACD 的一个法向量，利用向量的夹角公式，列出方程，求得λ的值，即可求解.【详解】（1）证明：因为四边形ABCD 为等腰梯形，且AC BD ⊥，所以OAB 为等腰直角三角形，因为2AB =，所以2OA OB ==，因为2,2SA SO ==，所以222SA SO OA =+，所以SO AO ⊥，即SO AC ⊥，又因为BD ⊂平面SBD ，SO ⊂平面SBD ，且BD SO O ⋂=，所以AC ⊥平面SBD ，因为DM ⊂平面SBD ，所以AC DM ⊥.（2）解：如图所示，以O 为原点，,,OA OB OS 分别为,,x y z ，轴建立空间直角坐标系，由（1）知22OA OB OS OD ====，故()()()()20,0,0,2,0,0,0,2,0,0,,0,0,0,22O AB D S ⎛⎫- ⎪ ⎪⎝⎭，故()()220,,2,2,0,2,0,2,2,2,,022DS AS SB AD ⎛⎫⎛⎫==-=-=-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭假设在棱SB 上存在一点M 满足题意，设,[0,1)SM SB λλ=∈.所以20,2,222DM DS SM DS SB λλλ⎛⎫=+=+=+-⎪ ⎪⎝⎭设平面ADM 的法向量为(),,m x y z = ，则()2202222202m AD x y m DM y z λλ⎧⋅=+=⎪⎪⎨⎛⎫⎪⋅=++-= ⎪ ⎪⎪⎝⎭⎩ ，易令2y =，可得121,1x z λλ+=-=-，所以121,2,1m λλ+⎛⎫=- ⎪-⎝⎭又由平面ACD 的一个法向量为()0,0,1n =设二面角M AD C --为θ，可知二面角为锐二面角则212761cos cos ,181251m n m n m nλλθλλ+⋅-====+⎛⎫+ ⎪-⎝⎭，整理得2127618966λλλ+=-+，即21534160λλ-+=，解得23λ=或85λ=（舍去），所以，存在点M 为靠近B 的三等分点.10．“十三五”时期，在党中央､国务院坚强领导下，全民健身国家战略深入实施，全民健身公共服务水平显著提升，全民健身场地设施逐步增多，人民群众通过健身促进健康的热情日益高涨，经常参加体育锻炼人数和参加锻炼的时间都在明显增加.某城市为了调查该市市民积极参加体育锻炼的情况，从市民中随机抽取了50人，结果是他们参加锻炼的时间都在区间[50,100]内，锻炼时间的频率分布直方图如下：(1)如果锻炼时间的中位数的估计值大于或者等于平均数的估计值，则说明该城市市民积极参加锻炼的意识很强，否则说明该城市市民积极参加锻炼的意识不强，请你根据直方图对他们积极参加锻炼的意识强与不强做出判断；(2)假如根据调查统计结果规定：锻炼时间在[80,100]的市民为优秀层次，时间在[50,80)的为非优秀层次，（ⅰ）从被调查的50人中按分层抽样的方法抽取10人，再从这10人中随机抽取5人，求这5人中优秀层次的人数大于非优秀层次的人数的概率；（ⅱ）用频率作为概率，现从该城市所有市民中随机抽取3人，这3人中锻炼时间为优秀层次的人数为X ，求随机变量X 的分布列和数学期望.【答案】(1)该市市民积极参加体育钗炼的意识很强(2)（ⅰ）3142；（ⅱ）分布列见解析，()95E X =【分析】（1）分别利用频率分布直方图估计中位数和平均数，即可得答案；（2）（ⅰ）由题可得10人中，优秀6人，非优秀4人，则5人中优秀层次的人数大于非优秀层次的人数的情况有优秀5人，优秀4人非优秀1人，优秀3人非优秀2人三种情况，即可得概率；（ⅱ）由题可知33,5X B ⎛⎫⎪⎝⎭，即可得随机变量X 的分布列和数学期望.【详解】（1）锻炼时长中位数的估计值为直方图中等分面积的线对应的值，设为x ，0.01100.01100.02100.5⨯+⨯+⨯< .0.01100.01100.02100.03100.5⨯+⨯+⨯+⨯>，则x 在[)80,90之间.()0.01100.01100.02100.03800.5x ∴⨯+⨯+⨯+⨯-=解得2503x =，即中位数的故计值2503分钟.又锻炼时长平均数估计值为:0.0110550.0110650.0210750.0310850.03109581⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯=.因为中位数的估计值2503分钟大于平均数估计值81分钟，所以，根据这次调查，该市市民积极参加体育钗炼的意识很强.（2）（ⅰ）由题可得10人中，优秀6人，非优秀4人，则5人中优秀层次的人数大于非优秀层次的人数的情况有优秀5人，优秀4人非优秀1人，优秀3人非优秀2人三种情况，则5人中优秀层次的人数大于非优秀层次的人数的概率5413266464510C C C C C 31C 42P +⋅+⋅==；（ⅱ）根据频率，不难得到从该城市市民中随机抽取一人，锻炼时间为优秀层次的概率为35，人数X服从二项分布33,5B ⎛⎫⎪⎝⎭，故X 的分布列为X0123P8125361255412527125数学期望()39355E X =⨯=.11．如下图，已知有()24n n ≥个正数排成n 行n 列：其中每一行都成等差数列，每一列都成等比数列，且所有的公比相等，已知121a =，142a =，428a =.(1)求34a 和44a 的值；(2)求1122nn S a a a =+++ （用含n 的式子表达）.【答案】(1)348a =，4416a =；(2)()11212n S n -=-+.【分析】（1）设第n 行的公差为n d ，公比为q ，根据12a ，14a 及等差数列的通项公式求解1d ，根据12a ，42a 及等比数列的通项公式求出q ，再由等差数列的通项公式求出14a ，最后由等比数列的通项公式求34a 和44a 的值；（2）先根据等差数列的通项公式求出1k a ，再根据等比数列的通项公式求出kk a ，最后由错位相减法求和.【详解】（1）设第n 行的公差为n d ，公比为q ，因为121a =，142a =，428a =，所以141212114222a a d --===-，342128a q a ==,解得2q =.所以223414228a a q ==⨯=，44348216a a q ==⨯=.（2）()()11211121222k a a k d k k =+-=+-=，11211222k k k kk k a a q k k ---==⋅=⋅()1,2,,k n =L ，所以210121122121222322nk n nn k S a a a k n ---==+++=⋅=⋅+⋅+⋅++⋅∑ ，012121222322n S n -=⋅+⋅+⋅+⋅ ，作差可得()111012111221222222221122n n n n n S S S n n n ---------=-=++++-⋅=-⋅=--- ，所以()11212n S n -=-+.12．已知ABC 的三个内角,,A B C 所对的边分别为,,a b c ，且π3A =，22cos cos 3222C B b c b c ++=+，设B x =，ABC 的周长为y .(1)当π4x =时，求y 的值；(2)求函数()y f x =的解析式及最大值.【答案】(1)32236++(2)()π43sin 236f x x ⎛⎫=++ ⎪⎝⎭，其中2π03x <<；最大值为63【分析】（1）根据题意，由正弦定理得()2sin sin sin sin 2sin 23R B C C B R A +==，求得2R =，进而求得,,a b c 的长，得到三角形的周长；（2）由B x =，根据正弦定理得到243sin 23,06ππ3y x x ⎛⎫⎛⎫=++<< ⎪ ⎪⎝⎭⎝⎭，结合三角函数的性质，即可求解.【详解】（1）解：由22cos cos 3222C B b cb c ++=+，可得1cos 1cos 3222C B b cb c +++⋅+⋅=+，即cos cos 23b C c B ⋅+⋅=，设三角形ABC 的外接圆半径是R ，由正弦定理得()2sin cos sin cos 2sin()2sin 23R B C C B R B C R A +=+==，因为3sin 2A =，所以2R =，又62sin sin 344C ππ+⎛⎫=+=⎪⎝⎭又由43262224a b c ===+，解得23,22,62a b c ===+，所以三角形ABC 的周长为22232632236y =+++=++.（2）解：由B x =，且π3A =，可得π2ππ33C x x =--=-，可得2π4sin ,4sin()3b xc x ==-，所以()2314sin 4sin 234sin 4(cos sin )233π22y f x x x x x x ⎛⎫==+-+=+++ ⎪⎝⎭ππ26sin 23cos 43sin 23,063x x x x ⎛⎫⎛⎫=+=++<< ⎪ ⎪⎝⎭⎝⎭，由ππ25(0,)(,)366ππ6x x ∈+∈，所以当ππ62x +=，即π3x =时，()y f x =取到最大值63.三、填空题13．已知双曲线()2222:10,0x y C a b a b-=>>的右焦点为F ，在双曲线左支上取一点M ，若直线MF 与以双曲线实轴为直径的圆相切于N ，若向量2MN NF =，则双曲线C 的离心率为__________.【答案】132【分析】连接ON ，取双曲线的左焦点为1F ，连接1MF ，过1F 作MF 的垂线，垂足为G ，可得FNO △相似于1FGF ，且相似比为1:2，结合双曲线的定义可得1MF ，在直角1F MG △中，由勾股定理得出,a b 的等量关系，再由双曲线的离心率公式即可求解.【详解】连接ON ，取双曲线的左焦点为1F ，连接1MF ，过1F 作MF 的垂线，垂足为G ，直线MF 与圆222x y a +=相切,,ON MF ON a ∴⊥=，,OF c NF b =∴= ，O 为1F F 的中点，1//F G ON ，FNO ∴ 相似于1FGF ，且相似比为1:2，故12,F G a NG b ==.22,,,3MN NF MN b MG b MF b =∴=∴==.在双曲线()222210,0x y a b a b -=>>中，由双曲线定义知12MF MF a -=，132MF b a ∴=-.11,//,ON MF F G ON F MG ⊥∴ △为直角三角形，22211||F G MG MF ∴+=，即222(2)(32)a b b a +=-，解得23b a =，故双曲线的离心率为21312b e a ⎛⎫=+= ⎪⎝⎭.故答案为:132.14．已知函数()y f x =定义域为R 且满足①()2y f x =+为偶函数；②任意2,2x y ≥≥都有()()()1f x y f x f y +-=+成立；③[)1212,2,,x x x x ∀∈+∞≠，都有()()12120f x f x x x ->-，请给出满足上述三个性质的一个函数为__________.【答案】()122f x x =-（答案不唯一）【分析】由三个条件依次分析出函数具有对称性、单调性等性质，可从熟悉的函数中找到符合条件的函数.【详解】由性质①()2y f x =+为偶函数知，函数()y f x =关于直线2x =对称；由性质②任意2,2x y ≥≥都有()()()1f x y f x f y +-=+成立，可设()f x kx b =+，待定系数可得当2x ≥时，()1f x kx =-；由性质成立③[)1212,2,,x x x x ∀∈+∞≠，都有()()1212f x f x x x ->-可知函数()y f x =在[)2,+∞上单调递增，因此可写出满足上述三个性质的一个函数为()122f x x =-.故答案为：()122f x x =-（答案不唯一）15．若33223(106)x y ax bx y cxy dy +=+++，则248a b c d -+-+=__________.【答案】8【分析】令1,2x y =-=，可得答案.【详解】注意到()()()()3232248112122a b c d a b c d -+-+=⋅-+⋅-⨯+⋅-⨯+⋅.又33223(106)x y ax bx y cxy dy +=+++，则248a b c d -+-+=()3101628⎡⎤⨯-+⨯=⎣⎦.故答案为：816．已知2286160x y x y +--+=，则yx的最小值为__________.【答案】0【分析】设yk x=，根据圆心到直线的距离小于等于半径列式可求出结果.【详解】由2286160x y x y +--+=可得圆心为(4,3)，半径为3，设yk x=，即0kx y -=，依题意得2|43|31k k -≤+，解得2407k ≤≤，所以yx的最小值为0.故答案为：0.四、多选题17．已知正方形ABCD 的边长为2，点,M N 分别是线段,CD BC 上的动点，若满足AC x AM y AN =+，则下列说法正确的是（）A ．当1x =时，则1y =B ．当23x y ==时，点,M N 分别是线段,CD BC 的中点C ．当23x y ==时，0AC MN ⋅= D ．当22111CM CN +=时，x y +的最小值为8227+【答案】BCD【分析】建立平面直角坐标系，设出,M N 的坐标，利用向量的坐标运算逐一判断各个选项作答.【详解】以点A 为坐标原点，,AB AD 分别为x 轴，y轴建立平面直角坐标系，如图，设(,2),(2,)M a N b ，02,02a b ≤≤≤≤，(,2),(2,)AM a AN b == ，由AC x AM y AN =+ ，得(2,2)(2,2)ax y x by ++=，则2222ax y x by +=⎧⎨+=⎩，对于A ，当1x =时，得220a y by +=⎧⎨=⎩，不能得1y =，如取0b =，11,2a y ==，满足条件，A 错误；对于B ，当23x y ==时，得1a b ==，此时点,M N 分别是线段,CD BC 的中点，B 正确；选项C ，由选项B 知，(1,2),(2,1)M N ，(1,1)MN =-，而(2,2)AC = ，212(1)0AC MN ⋅=⨯+⨯-= ，C 正确；选项D ，当22111CM CN+=时，显然2a ≠且2b ≠，此时0xy ≠，否则2a =或2b =，矛盾，即有22111(2)(2)a b +=--，而2222y a x x b y -⎧=⎪⎪⎨-⎪=⎪⎩，因此22224(1)(1)x y x y x y +=+-+-，整理得2224(1),0,0x y x y x y +=+->>，而22222()()()22x y x y x y x y ++-++=≥，于是22()24(1)x y x y ++≥-，当且仅当x y =时取等号，整理得27()16()80x y x y +-++≥，令AC 交MN 于E ，显然E 与C 不重合，AE AC xAM y AN λλλ==+，01λ<<，由,,M E N 共线，得1x y λλ+=，即11x y λ+=>，解得8227x y ++≥，即，x y +的最小值为8227+，D 正确.故选：BCD18．如图所示，已知()0,0O ，()2,0A ，()11,1B ，作以1B 为直角顶点的等腰直角1OAB ，作点A 和点1B 的中点1C ，继续作以1C 为直角顶点的等腰直角121,B B C ，如此继续作中点，作等腰直角三角形.这样会得到一组分别以1122,,,,B C B C 为直角顶点的等腰直角三角形.下列说法正确的是（）A ．所作的等腰直角三角形的边长构成公比为12的等比数列B ．第4个等腰直角三角形的不在第3个等腰直角三角形边上的顶点坐标为39,14B ⎛⎫⎪⎝⎭C ．点4C 的纵坐标为511512D ．若记第n 个等腰直角三角形的面积为n S ，则14lim 3ni n i S →∞==∑【答案】ABD【分析】由题意分析逐项判断即可.【详解】由图易知，所作的等腰直角三角形的边长构成公比为12的等比数列，故选项A 正确；选项B ，()()12311,1,11,1,11,14B B B ⎛⎫+++ ⎪⎝⎭，故选项B 正确；选项C ，点1C 的纵坐标为112-，点2C 的纵坐标为3112-，点3C 的纵坐标为5112-，点4C 的纵坐标为7112-，点5C 的纵坐标为9112-，故选项C 错误；选项D ，121111111141441,,lim lim 1lim lim 114416434314nni n n n n n ni S S S -→∞→∞→∞→∞=⎛⎫- ⎪⎛⎫⎛⎫===++++==-= ⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪-⎝⎭∑ ，故选项D 正确.故选：ABD.五、单选题19．已知函数()ππ3cos cos (0)44f x x x ωωω⎛⎫⎛⎫=++-> ⎪ ⎪⎝⎭⎝⎭，当π0,2x ⎡⎤∈⎢⎥⎣⎦时函数恰有3个零点，则正整数ω的取值可以是（）A ．5B ．6C ．7D ．8【答案】AB【分析】化简()72sin 12f x x πω⎛⎫=+⎪⎝⎭，根据题意，结合正弦函数的图象，得到，734212ωππππ≤+<，求得ω的范围，结合选项，即可求解.【详解】由函数()3cos cos 3cos sin 4444f x x x x x ππππωωωω⎛⎫⎛⎫⎛⎫⎛⎫=++-=+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭72sin 2sin 4312x x πππωω⎛⎫⎛⎫=++=+ ⎪ ⎪⎝⎭⎝⎭，当0,2x π⎡⎤∈⎢⎥⎣⎦时，可得777,1212212x ππωππω⎡⎤+∈+⎢⎥⎣⎦，因为()f x 在π0,2x ⎡⎤∈⎢⎥⎣⎦上有3个零点，结合正弦函数的图象可知，734212ωππππ≤+<，解出293966ω≤<，所以正整数ω的取值可以是5或6.故选：AB.六、多选题20．我们可以用统计图表表示数据，对获得数据进行统计分析.据《中国统计年鉴（2022）》可知，2016~2021年我国人口年龄分布情况（百分比）如表所示.（已知少儿抚养比()014%100%1564~=⨯~岁人数岁人数，老年抚养比()65%100%1564=⨯~岁及以上人数岁人数，总抚养比（%）=少儿抚养比（%）+老年抚养比（%））根据图表，下列说法正确的有（）A ．从2016年到2021年期间，0~14岁人口比重在逐年上升B ．从2016年到2021年期间，15~64岁人口比重在逐年下降C ．2021赡养老人的压力比2020年更重D ．2021年总抚养比大于2020年总抚养比【答案】BCD【分析】根据图表，逐项分析每个选项中的数据，可得答案.【详解】对于A ，由图表可知2018年到2019年间以及2020年到2021年间0~14岁人口比重在降低，A 错误；对于B ，从2016年到2021年期间，15~64岁人口比重在逐年下降，正确；对于C ，2021年65岁以及以上老年人抚养比为14.220.8%68.3≈，2020年65岁以及以上老年人抚养比为13.520.7%68.6≈，故2021赡养老人的压力比2020年更重，C 正确；对于D ，2021年总抚养比为14.217.546.4%68.3+≈，2020年总抚养比为13.517.945.8%68.6+≈，故2021年总抚养比大于2020年总抚养比，D 正确，故选：BCD七、单选题21．已知矩形ABCD 中，2,1AB AD ==，沿着对角线AC 将ACD 折起，使得点D 不在平面ABC 内，当AD BC ⊥时，求该四面体ABCD 的内切球和外接球的表面积比值为（）A ．18935-B ．19935-C ．211235-D ．241235-【答案】C【分析】根据题意分析可得四面体的外接球的球心为AC 的中点O ，再利用等体积法求内切球的半径，进而可得结果.【详解】取AC 中点O ，由矩形的性质可知OA OB OC OD ===，即O 为该四面体的外接球的球心，故外接球的半径1522R AC ==；因为,AD BC AD DC ⊥⊥，BC DC C = ，,BC DC ⊂平面BCD ，可得AD ⊥平面BCD ，DC ⊂平面BCD ，则AD DC ⊥，且,AD BC BC AB ⊥⊥，AD AB A ⋂=，,AD AB ⊂平面ABD ，可得BC ⊥平面ABD ，BD ⊂平面ABD ，则BC BD ⊥，故该四面体ABCD 的四个面都是直角三角形，设四面体的内切球的半径为r ，因为内切球与四面体的四个面都相切，故r 满足13V rS =四面体表，则1112122133211113223r ⨯⨯⎛⎫=⨯⨯⨯⨯⨯⨯+⨯⨯⨯ ⎪⎝⎭，解得32332423r -==+；因此该四面体的内切球和外接球的表面积的比值为22222223324π211234π552S r r S R R ⎛⎫-⎪-⎝⎭====⎛⎫ ⎪⎝⎭内外.故选：C.22．我们知道立体图形上的最短路径问题通常是把立体图形展开成平面图形，连接两点，根据两点之间线段最短确定最短路线.请根据此方法求函数()2222,31313(0,0)f x y x x y y x xy y x y =-++-++-+>>的最小值（）A ．2B ．3C ．6D ．23【答案】A【分析】构造合适的三棱锥模型-P ABC ，其中1,,PA PB x PC y ===，，利用余弦定理证明(),f x y 即为底面周长，最后将其展开即可得到最小值.【详解】根据函数(),f x y 的表达式可知，构造三棱锥-P ABC ，其中1,,PA PB x PC y ===，且30,30,30APB BPC APC ∠∠∠=== ，由余弦定理可得，2231,31AB x x AC y y =-+=-+，223BC x xy y =-+，(),f x y 的最小值即为AB AC BC ++的最小值，将三棱锥-P ABC 按照PA 展开可得展开图，且90,2APA AA ∠'='= ，故(),f x y 的最小值为2.故选：A.。