高二数学培优测试

25深圳实验学校高中部高二上第二次培优数学试卷10月一.单选题:每小题5分1.直线√3x-3y-1=0的倾斜角为( ). A. 30o B. 135o C. 60o D. 150o2.已知直线ax+2ay+1=0与(a-1)x-(a+1)y-1=0垂直,则实数a 的值是( ). A. 0或3 B. 3 C. 0或-3 D. -33.已知A(-1,0)、B(3,6),则以AB 为直径的圆的一般方程为( ).A.x 2+y 2-2x-6y+3=0B.x 2+y 2-2x-6y-3=0C.x 2+y 2+2x-6y+3=0D.x 2+y 2+2x-6y-3=04.如图,直线l 1:ax+y+b=0与l 2:bx-y+a=0(ab ≠0,a ≠b)的图象可能是( ). A B C D5.直线x+y+2=0分别与x 轴,y 轴交于A,B 两点,点P 在圆(x-2)2+y 2=2上,则△ABP 面积的取值范围是( ).A. [2,6]B. [4,8]C. [√2,3√2]D. [2√2,3√2]6. M,N 分别为直线3x-4y-12=0与6x-8y+5=0上任意一点,则|MN|最小值为( ). A. 2910 B. 295 C. 175 D. 17107.直线l 1:x+(m+1)y-2m-2=0与直线l 2:(m+1)x-y-2m-2=0相交于点P,对任意实数m,直线l 1,l 2分别恒过定点A,B,则|PA|+|PB|的最大值为( ).A. 4B. 8C. 2√2D. 4√28.在长方体ABCD-A 1B 1C 1D 1中,AB=AD=2,AA 1=1,0是AC 的中点,点P 在线段A 1C 1上,若直线OP 与平面ACD 1所成的角为θ,则sin θ的取值范围是( ).A. [√23,√33]B. [√23,√63]C. [√33,√73]D. [√34,√33]二.多选题:9.下面四个结论正确的是( ).A. 已知向量a ⃗ =(1,1,x),b ⃗ =(-3,x,9),若x<310,则<a ⃗ ,b ⃗ >为钝角B. 已知a ⃗ =(2,0,-1),b ⃗ =(3,-2,5),则向量b ⃗ 在向量a ⃗ 上的投影向量是15(2,0,-1)C.若直线ax+by+c=0经过第三象限,则ab>0,bc<0D.已知A,B,C 三点不共线,对于空间任意一点O,若OP ⃗⃗⃗⃗⃗ =25OA ⃗⃗⃗⃗⃗ +15OB ⃗⃗⃗⃗⃗ +25OC ⃗⃗⃗⃗⃗ ,则P,A,B,C 四点共面 10.下述四个结论,正确的是( ).A. 过点A(1,1)在x 轴,y 轴上截距都相等的直线方程为x+y-2=0B. 直线x-y+k=0与圆x 2+y 2=1相交的充分不必要条件是k=1C. 直线ax+y+1=0表示过点(0,-1)的所有直线D. 过点B(1,√3)与圆x 2+y 2=4相切的直线方程为x+√3y-4=011.已知点A(3,3)和B(4,-2),P 是直线l:x+y+2=0上的动点,则( ).A. 存在P(1,-3),使|PA|+|PB|最小B. 存在P(-1,-1),使||PA|-|PB||最小C. 存在P(5,-7),使||PA|-|PB||最大D. 存在P(12,-52),使|PA|2+|PB|2最小 三.填空题:每小题5分.12.已知x 、y 满足x 2+y 2-4x-2y+4=0,则x 2+y 2的最大值为______.13.已知从点(-5,3)发出的光线,经x 轴反射后,反射光线恰好平分圆:x 2+y 2-2x-2y-3=0的圆周,则反射光线所在的直线方程为______.14.阅读下面材料:在空间直角坐标系Oxyz 中,过点P(x 0,y 0,z 0)且一个法向量为m ⃗⃗⃗ =(a,b,c)的平面α的方程为a(x-x 0)+b(y-y 0)+c(z-z 0)=0,过点P(x 0,y 0,z 0)且方向向量为n ⃗ =(u,v,w)(uvw ≠0)的直线1的方程为x−x 0u =y−y 0v =z−z 0w =3.根据上述材料,解决下面问题:已知平面α的方程为2x-y+z-7=0,直线l 是两个平面x-y+2=0与2x-z+1=0的交线,则直线l 与平面α所成角的余弦值为______.四.解答题:解答应写出文字说明,证明过程或演算步骤。

高二数学培优（三）班级： 姓名：1. △ABC 中，sin 2A =sin 2B +sin 2C ，则△ABC 为 ( )ABC 等边三角形 D2. 在△ABC 中，b=c=3，B=300，则a 等于（ ）A ．B ．12CD ．2 3. 不解三角形，下列判断中正确的是（ ）A ．a=7，b=14，A=300有两解 B ．a=30，b=25，A=1500有一解C ．a=6，b=9，A=450有两解D ．a=9，c=10，B=600无解4. 在△ABC 中，角A ，B ，C 所对的边长分别为a ，b ，c ，若∠C=120°，a ，则 A.a ＞b B.a ＜b C. a ＝b D.a 与b 的大小关系不能确定5. 在△ABC 中，A ＝60°，b ＝1，其面积为3，则CB A cb a sin sin sin ++++等于( )A ．33B ．3392 C ．338D ．2396. 在△ABC 中，AB ＝5，BC ＝7，AC ＝8，则BC AB ⋅的值为( ) A ．79 B ．69 C ．5 D ．-57.关于x 的方程02cos cos cos 22=-⋅⋅-CB A x x 有一个根为1，则△ABC 一定是（ ）A ．等腰三角形B ．直角三角形C ．锐角三角形D ．钝角三角形8. 设m 、m+1、m+2是钝角三角形的三边长，则实数m 的取值范围是( ) A.0＜m ＜3 B.1＜m ＜3 C.3＜m ＜4 D.4＜m ＜6 9在锐角ABC ∆中，1,2,BC B A ==则cos ACA的值等于 ________ ，AC 的取值范围 为_______________.10.在△ABC 中，有等式：①asinA=bsinB ；②asinB=bsinA ；③acosB=bcosA ；④sin sin sin a b cA B C+=+. 其中恒成立的等式序号为______________ 11在等腰三角形 ABC 中，已知sinA ∶sinB=1∶2，底边BC=10，则△ABC 的周长是 。

浙江强基（培优）联盟2024年7月学考联考高二数学试题（时间80分钟总分100分）一、单项选择题（本大题共12小题，每小题3分，共36分．每小题列出的四个备选项中只有一个是符合题目要求的，不选、多选、错选均不得分）1．函数()f x =）A ．[)1,+∞B ．[)1,-+∞C ．(],1-∞D ．(],1-∞-2．已知集合{}{}21,2,3,4,20A B x x x ==--=，则A B = （）A ．{}1,1,2,3,4-B ．{}1,2,3,4C ．{}1,0,1,2,3,4-D ．{}2,1,2,3,4-3．在ABC △中，D 为边AB 的中点，则（）A ．0AD BD -= B ．0AD DB += C ．CB CD BD-= D ．2CA CB CD+= 4．数据1，2，3，4，5，6，7，7的第25百分位数是（）A ．2B ．2.5C ．3D ．3.55．从第4题所给的数据中随机选择一个数，则这个数平方的个位数是6或9的概率为（）A ．14B ．38C ．12D ．586．已知空间中两个不重合的平面α和平面β，直线l ⊂平面α，则“l β∥”是“αβ∥”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件7．不等式1101x +≤-的解集是（）A ．[)0,1B ．(]0,1C ．[]1,2D ．(]1,28．近年，“人工智能”相关软件以其极高的智能化水平引起国内关注，深度学习是人工智能的一种具有代表性的实现方法，它是以神经网络为出发点的．在神经网络优化中，指数衰减的学习率模型为181425G L ⎛⎫=⨯ ⎪⎝⎭，其中L 表示每一轮优化时使用的学习率，G 表示训练迭代轮数，则学习率衰减到0.2及以下所需的训练迭代轮数至少为（参考数据：lg20.301≈）（）A ．16B ．72C ．74D ．909．在ABC △中，已知角,,A B C 所对的边分别是,,a b c ，已知45,75a B C ==︒=︒，则b 等于（）A ．2B．C．D．10．已知函数()222x x f x =-，则其图象一定不过（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限11．已知α为锐角，且22sin cos cos sin 55ππαα⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，则sin2α的值为（）A ．45B ．513C ．2425D ．91612．已知正方体1111ABCD A B C D -，点M 在1B C 上运动（不含端点），点N 在11B D 上运动（不含端点），直线MN 与直线AC 所成的角为α，直线MN 与平面1ACB 所成的角为β，则下列关于,αβ的取值可能正确的是（）A ．30α=︒B ．45α=︒C ．60β=︒D ．75β=︒二、多项选择题（本大题共4小题，每小题4分，共16分．每小题列出的四个备选项中有多个是符合题目要求的，全部选对得4分，部分选对且没有错选得2分，不选、错选得0分）13．民营经济是推进中国式现代化的生力军，是浙江的最大特色、最大资源和最大优势．为了更好地支持民营企业的发展，我省某市决定对部分企业的税收进行适当的减免．某机构调查了当地的中小型民营企业年收入情况，并根据所得数据画出了样本的频率分布直方图，则下列结论正确的是（）A ．样本数据落在区间[)300,500内的频率为0.45B ．若规定年收人在500万元以内的民营企业才能享受减免税政策，估计有55%的当地中小型民营企业能享受到减免税政策C ．若该调查机构调查了100家民营企业，则年收人不少于400万元的有80家D ．估计样本的中位数为480万元14．已知复数12,z z ，则下列结论正确的有（）A ．2211z z =B ．1212z z z z +=+C ．1212z z z z =⋅D ．1212z z z z +=+15．已知平面向量12,e e 的夹角为π3，且121e e == ，若12122,a e e b e e =-=+ ，则下列结论正确的是（）A ．a b ⊥B ．a =C ．a b a+= D ．a 在b 上的投影向量为12b- 16．我们知道，函数()y f x =的图象关于坐标原点成中心对称图形的充要条件是函数()y f x =为奇函数，有同学发现可以将其推广为函数()y f x =的图象关于点(),P a b 成中心对称图形的充要条件是函数()y f x a b =+-为奇函数．此结论与必修一教材上的结论相吻合，则下列结论正确的是（）A ．函数()211x f x x +=-的图象关于点()1,2成中心对称图形B ．若定义在R 上的函数()f x 对任意的x 都有()()22f x f x ++-=，则函数()f x 图象的对称中心为()2,2C ．若()y f x a =+是偶函数，则()f x 的图象关于直线x a =成轴对称D ．若函数()f x 满足()11y f x =+-为奇函数，且其图象与函数()422xg x =+的图象有2024个交点，记为()(),1,2,,2024i i i A x y i = ，则()202414048ii i xy =+=∑三、填空题（本大题共4小题，每空3分，共15分）17．已知一圆锥的母线长为2，底面半径为1，则该圆锥的侧面积为________；体积为________．18．在中国古代数学著作《九章算术》中，鳖懦是指四个面都是直角三角形的四面体．如图，在直角ABC △中，AD 为斜边BC 上的高，3,4AB AC ==，现将ABD △沿AD 翻折成AB D '△，使得四面体AB CD '为一个鳖臑，则该鳖臑外接球的表面积为________19．设,A B 是一个随机试验中的两个事件，且()()()121,,234P A P B P AB ===，则()P A B = ________．20．若函数()20(1)f x x ax b a =++=>的值域为[)0,+∞，则11a b a ++-的最小值为________．四、解答题（本大题共3小题，共33分）21．已知函数()πsin2sin 23f x x x ⎫⎛=-+ ⎪⎝⎭．（1）求函数()f x 的最小正周期；（2）已知锐角ABC △三个内角,,A B C 所对的边分别为,,a b c ，且2,3b c ==，若()f A =，求ABC △的面积．22．如图，在三棱台111ABC A B C -中，1111124,AA AC AC BC CC AA =====⊥平面,,ABC AB BC D ⊥为AB的中点．（1）证明：111A B DC ⊥．（2）过11,,A D C 的平面把三棱台111ABC A B C -分成两部分，体积分别是1V 和()212V V V <，求12V V 的值．（3）求平面1CC D 和平面11ABB A 所成锐二面角的正切值．23．已知函数()()21,0,2,0,x x f x g x x x ⎧-≥==⎨-<⎩．（1）若()()f x g x ≤，求x 的取值范围．（2）记{}(),max ,(),a ab a b b a b ⎧≥=⎨<⎩已知函数()(){}max ,2y f x g x ax =--有k 个不同的零点．（ⅰ）若2k =，求a 的取值范围；（ⅱ）若3k =，且,αβ是其中两个非零的零点，求11αβ+的取值范围．浙江强基（培优）联盟2024年7月学考联考高二数学试题答案一、单项选择题（本大题共12小题，每小题3分，共36分．每小题列出的四个备选项中只有一个是符合题目要求的，不选、多选、错选均不得分）123456789101112CADBDBACABDC1．解：要使函数有意义，则10x -≥，得1x ≤，所以函数的定义域为(],1-∞．故选C ．2．解：因为{}{}1,2,3,4,1,2A B ==-，所以{}1,1,2,3,4A B =- ．故选A ．3．解：由平行四边形法则可知2CA CB CE CD +==．故选D ．4．解：因为825%2⨯=，所以第25百分位数为2和3的平均数，即为2.5．故选B ．5．解：样本空间的样本点总数为8，事件A （这个数平方的个位数是6或9）的样本点为4，6，3，7，7，共5个，所以概率58P =．故选D ．6．解：当l β∥时，α与β可能相交也可能平行，故l β∥不能推出αβ∥；反之，αβ∥可以推出l β∥．故“l β∥”是“αβ∥”的必要不充分条件．故选B ．7．解：不等式可化为11011xx x +=≤--，等价于()10,10,x x x ⎧-≤⎨-≠⎩解得01x ≤<，所以不等式的解集为[)0,1．故选A ．8．解：由题意知，只要解不等式18141255G⎛⎫⨯≤ ⎪⎝⎭，化简得42lg lg 1855G ≤．因为4lg 05<，所以lg2lg52lg21 4.118lg4lg53lg21G --≥=≈--，所以18 4.173.8G ≥⨯=．故选C ．9．解：由三角形内角和定理得60A =︒，由正弦定理得sin 60sin 45b=︒︒，解得2b =．故选A ．10．解：因为1x ≠，取2x =，得()22f =，所以()f x 在第一象限有图象，取12x =，得2102f ⎛⎫=< ⎪⎝⎭，所以()f x 在第四象限有图象，取1x =-，得()21(1)1022f ---=<-，所以()f x 在第三象限有图象．由排除法知图象不过第二象限．故选B ．11．解：因为α是锐角，所以2π2ππ2π2ππ0cos ,0sin 552552αα<<<<<<，所以2ππ2πcos sin 525αα=-，化简得5cos sin 4αα+=，平方得251sin216α+=，所以9sin216α=．故选D ．12．解：由题意可知，四面体11D AB C 为正四面体，设直线AC 与平面11B D C 所成的角为1θ，易知13cos 3θ=，由最小角定理得11,cos cos αθαθ><，故A ，B 错误．再设平面11B D C 与平面1ACB 所成的角为2θ，易知21cos 3θ=，由最大角定理得22,cos cos θβθβ><，代入选项得C 可能正确．故选C ．二、多项选择题（本大题共4小题，每小题4分，共16分．每小题列出的四个备选项中有多个是符合题目要求的，全部选对得4分，部分选对且没有错选得2分，不选、错选得0分）13141516ABDBCBCDACD13．解：由()0.0010.00150.0020.000521001a ++++⨯=，得0.0025a =，所以数据落在区间[)300,500内的频率为()0.0020.00251000.45+⨯=，A 正确；数据落在区间[)200,500内的频率为()0.0010.0020.00251000.55++⨯=，B 正确；100n =，年收入大于或等于400万元的有四组，其频率和是()1000.00250.00250.00150.00050.7⨯+++=，所以符合条件的民营企业有0.710070⨯=家，C 错误；数据落在区间[)200,400内的频率为0.3，数据落在区间[)200,500内的频率为0.55，估计中位数为0.50.34001004800.25-+⨯=，D 正确．故选ABD ．14．解：对于A ，若1i z =，则22111,1z z =-=，故A 错误；对于B ，设12i,i z a b z c d =+=+，则()()()()1212i,i i i z z a c b d z z a b c d a c b d +=+-++=-+-=+-+，故B 正确；对于C ，设12i,i z a b z c d =+=+，则()()12i z z ac bd ad bc =-++==，2212z z ⋅==C 正确；对于D ，若121i,i z z =+=，则12121z z z z +=+=，故D 错误．故选BC ．15．解：由题意得22121211,2e e e e ==⋅= ．对于A ，()()2212121122132212022a b e e e e e e e e ⋅=-⋅+=-⋅-=--=-≠ ，故A 错误；对于B，a == B 正确；对于C ，方法同B ，故C 正确；对于D，易得b = a 在b 上的投影向量为31232a bb b b bb⋅⋅=-⋅=-，故D 正确．故选BCD ．16．解：对于A ，因为()312f x x+-=为奇函数，所以()f x 的图象关于点()1,2成中心对称图形，故A 正确；对于B ，设()()g x f x a b =+-，若()g x 是奇函数，则()()()()0g x g x f x a b f x a b +-=+-+-+-=，所以()()2f x a f x a b ++-+=，因为()()22f x f x ++-=，所以()1f x +-1为奇函数，所以()f x 图象的对称中心为()1,1，故B 错误；对于C ，设()()g x f x a =+，因为()g x 是偶函数，所以()()g x g x =-，则()()f x a f x a +=-+，所以()f x 的图象关于直线x a =成轴对称，故C 正确；对于D ，显然()f x 的图象关于点()1,1成中心对称图形，再考虑()422x g x =+的对称性，()422x g x =+可化为()()()4,22x a h x g x a b b h x +=+-=-+为奇函数，则()()()00,11,h h h ⎧=⎪⎨-=-⎪⎩即1140,2244,2222a a ab b b -+⎧-=⎪⎪+⎨⎪-=-+⎪⎩++即11448222222a a a-++=+++，令2at =，则2124222t t t +=+++，即220t t -=，解得2t =或0t =（舍去），所以22a=，则1,1a b ==，因为()h x 为奇函数，所以()422x g x =+图象的对称中心为()1,1．()f x 与()g x 有相同的对称中心，所以2024个交点每两个一组关于点()1,1中心对称，()()()2024123202412320241202420244048ii i xy x x x x y y y y =+=+++++++++=+=∑ ，故D 正确．故选ACD ．三、填空题（本大题共4小题，每空3分，共15分）17．2π;π318．16π19．71220．317．解：由题意得圆锥的高h =，所以2 13π2π,ππ33S rl V r h ====侧．18．解：由题意得AC 的中点是外接球的球心，所以22,4π16πR S R ===．19．解：由概率的性质得()()()P A P AB AB P =+，所以()()()111244P AB P A P AB =-=-=，所以()()()()1217123412P A B P A P B P AB =+-=+-= ．20．解：由题意得2Δ40a b =-=，所以()()2221144(2)4114141a a a b a a a a a a a +++++++====----()()()22(1)6191(13)119116634141414a a a a a a a -+-+-+⎡⎤⋅=⋅=-+≥=⎢⎥---⎣⎦，当且仅当4a =时，等号成立，则最小值为3．四、解答题（本大题共3小题，共33分）21．解：（1）()πππsin 2sin 2sin 2sin 2cos cos2sin 333f x x x x x x ⎛⎫=-+=-- ⎪⎝⎭13πsin 2cos2sin 2223x x x ⎛⎫=-=- ⎪⎝⎭，所以2ππ2T ==．（2）因为()πsin 23f x x ⎛⎫=-⎪⎝⎭，所以()π3sin 232f A A ⎛⎫=-= ⎪⎝⎭．因为A 是锐角三角形的内角，所以ππ233A -=或π2π233A -=（舍去），所以π3A =．又2,3b c ==，所以ABC △的面积1π3323sin 232S =⨯⨯⨯=．22．（1）证明：如图1，连接1AC，得1AC =1BC ．因为1AA ⊥平面ABC ，所以1AA BC ⊥．又BC AB ⊥，所以BC ⊥平面11ABB A ，所以在直角梯形11BCC B 中，11112,2,2BC B C BB A D ====，所以15BC =，即1ABC 是以AB 为底边的等腰三角形，D 是AB 的中点，所以1AB DC ⊥．又11AB A B ∥，所以111A B DC ⊥．（2）解：如图2，取BC 的中点E ，连接1,DE C E ，可得11AC DE ∥．所以过11,,A C D 的平面把棱台分成斜棱柱111DBE A B C -和几何体11ADECC A 由题意得()111128414233ABCA B C V =⨯⨯++=棱台，111DBE-142242A B C V =⨯=棱柱．因为1128164433ADECA C V =-=>几何体，所以12164,3V V ==，故12431643V V ==．（3）解：如图3，取11A B 的中点F ，连接1,C F DF ，则DF 是平面1DCC 和平面11ABB A 所成二面角的棱，由于BC ⊥平面11ABB A ，过B 作FD 延长线的垂线，垂足为G ，连接CG ，易证得BGC ∠为所求的角．延长1AA 和1BB 交于点O ，过A 作FD 的垂线，垂足为H （如图4），易得8,AO AD ==，GB AH ==，所以66tan 4BGC ∠==．即平面1CC D 和平面11ABB A所成锐二面角的正切值为4．23．解：（1）由题意得函数()g x 的定义域为[]1,1-．当[]0,1x ∈时，不等式()()f x g x ≤等价于21x -≤当[)1,0x ∈-时，不等式()()f x g x ≤等价于2x -≤，即221x ≤，解得02x -≤<．综上，()()f x g x ≤的解集为,12⎡⎤-⎢⎥⎣⎦，即当x 的取值范围为2,12⎡⎤-⎢⎥⎣⎦时，()()f x g x ≤成立．（2）（ⅰ）令()()(){}()()2,1,2max ,,1,2f x x h x f xg x g x x ⎧-≤<-⎪⎪==⎨⎪-≤≤⎪⎩原题可转化为()2h x ax =+的实根个数问题（二重根为一个零点）．当12x -≤≤-时，即为()2f x ax =+，所以22x ax -=+至多一个实根①；当12x -≤≤时，即为()2g x ax =+，所以2ax =+至多两个实根②．由①知，221,22x a ⎡-=∈--⎢+⎣），所以02a ≤<-，由②知，2ax =+，所以0x =或242,142a x a ⎡⎤=-∈-⎢⎥+⎣⎦，所以2a ≤-或2a ≥+，且0a ≠．当2k =时，若0a =，则有两个零点0和-1，符合题意．当0a <时，①无实根，对于②，只要2414a x a =-≤+，化简得2(2)0a +≥，则20a -≤<，符合题意．当0a >时，若02a <<-，则有三个不等实根，不符合题意．若2a =-，则有两个零点0和22-，符合题意．若2a >-，则仅有一个零点0，不符合题意．综上所述，当2k =时，a 的取值范围为[]{}2,02-⋃-．7分（ⅱ）由（ⅰ）得当3k =时，02a <<-，且三个零点分别为224,,024a a a --++，显然,0αβ≠，所以()11311,24a a a αβ+=++∈．9分易得函数3114y a a =++在()2-上单调递减，所以3114y a a =++>所以()11αβ+∈+∞．。

培优联盟2024春季联赛高二数学参考答案1234567891011BBDCACDACDBCDAD一、选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．B【解析】取0a =，0b <，则可知由“0ab =”无法推出a b =+”．2．B【解析】(3,4)BC DA BA AC DA BA DC AB CD+=++=+=--=--．3．D【解析】两式作差得，cos sin 2024cos cos 2024sin sin 2024cos()2024cos A A B C B C B C A -=-=+=-，所以sin 2025cos A A =，即tan 2025A =．4．C【解析】若插入两个整数后众数不变，则插入的数可以是“两个都是3”，或是“一个为3，另一个不是3”，或是“两个不等的且不是8,11,28”。

①因为新的一组数极差加倍，所以插入的两个数不可能都是3；②因为中位数保持不变，若插入的数“一个为3，另一个不是3”，则一个为3，另一个数不小于8，又因为极差加倍，则另一个数为53，此时56m n +=；③若插入的两个数是不等的且不是3，8，11，28，且极差为50，则两个数可以为753m n ì=ïïíï=ïî，653m n ì=ïïíï=ïî，553m n ì=ïïíï=ïî，453m n ì=ïïíï=ïî，252m n ì=ïïíï=ïî，151m n ì=ïïíï=ïî，050m n ì=ïïíï=ïî，…所以，m n +的最大值为60．5．A【解析】()3sin 3cos 44cos3sin 4f x x x x x '=--，''()24sin 4sin 325cos3cos 4f x x x x x =-．6．C【解析】3334tan 4882a =>⋅=，422113log 7log 7log 8222b ==<=，2222274ln12ln 4(ln 7)(ln12ln 4)4(ln 7)(ln 49)4(ln 7)log 12log 70ln 7ln 44ln 7ln 44ln 7ln 4c b -+---=-=<<=，7．D【解析】记AB 与圆222:O x y b +=相切于点00(,)P x y ，则0c AP x a =，0cAF a x a=-，进一步有AP AF a +=，同理BP BF a +=，故ABF △的周长为2a ．8．A【解析】令0x y ==，则22(0)2[(0)]f f =，解得(0)0f =或(0)1f =令2t x y ==，则2()(0)2[()]2tf t f f +=，故()1f t ≥-．二、选择题：本题共3小题，每小题6分，共18分，在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分．9．CD【解析】选项A 取1p q ==，r =．选项B ，取1p =，i q =．选项C ，由“两个复数相除为实数”可知，实部与虚部比值相等，进而得到两点间的斜率相等，故P ，Q ，R 三点共线．选项D ，||||||||||||q r q r p q p q =⇒=，则||p ，||q ，||r 成等比数列．10．BCD【解析】选项A ：若PC BD ^，则BD ⊥平面PAC ，进一步有BD AC ⊥，而底面ABCD 是矩形，不能保证BD AC ⊥．选项B ：取PD 中点M ，则12EA CD FM ==，进一步有EF AM = ．选项C ：1()2EF AP BC =+．11．AD【解析】选项B ：取3a =，4b =，5c =，则222a b c +<；选项C ：取4a b ==，1c =，则sin sin 0sin a b c+<<选项D ：由2a a b c a b c <+++，2b b c a a b c <+++，2c c a b a b c <+++可得2a b cb c c a a b++<+++．三、填空题：本题共3小题，每小题5分，共15分．12．3【解析】根据余弦定理计算得BC =6，所以632BC e AC AB ===-.13．2e 【解析】ln 1a c -=，ln 1b d -=．由2ln ln 1ln 1a c d a b =+=-+-，即ln ln 2b a -=，即2e ba=。

高中数学培优试题及答案一、选择题（每题5分，共20分）1. 若函数f(x)=2x^2-4x+3，求f(2)的值为：A. 1B. 3C. 5D. 7答案：B2. 已知等差数列{an}的首项a1=3，公差d=2，求第10项a10的值：A. 23B. 27C. 29D. 31答案：A3. 计算下列定积分的值：∫(0,2) (x^2 - 3x + 2) dx：A. 0B. 4C. 6D. 8答案：C4. 若复数z满足|z-1|=2，则z的模长|z|的最小值为：A. 1B. √3C. 2D. √5答案：B二、填空题（每题5分，共20分）5. 函数y=x^3-3x^2+4x-5的极值点个数为_______。

答案：26. 一个圆的半径为5，圆心在原点，求该圆的面积为_______。

答案：25π7. 已知函数f(x)=x^2-2x+1，求f(x)的对称轴方程为_______。

答案：x=18. 若直线y=3x+2与抛物线y^2=4x相交于点A和B，求线段AB的中点坐标为_______。

答案：(1, 5/3)三、解答题（每题15分，共30分）9. 已知等比数列{bn}的前三项依次为b1=2，b2=4，b3=8，求该数列的通项公式。

答案：bn=2^n10. 已知函数f(x)=x^3-3x^2+2x+1，求函数f(x)的单调递增区间。

答案：(-∞, 1)和(2, +∞)四、证明题（每题15分，共15分）11. 证明：若a, b, c为实数，且满足a^2+b^2+c^2=1，则(a+b+c)^2≤3。

答案：证明如下：由柯西-施瓦茨不等式可知，对于任意实数a, b, c有(a^2+b^2+c^2)(1^2+1^2+1^2)≥(a+b+c)^2，即(a^2+b^2+c^2)(3)≥(a+b+c)^2。

又因为a^2+b^2+c^2=1，所以(a+b+c)^2≤3。

五、应用题（每题15分，共15分）12. 某商场进行促销活动，规定顾客每消费满100元即可获得一张优惠券，每张优惠券可以抵用10元。

2022-2023学年安徽省示范高中培优联盟高二下学期春季联赛数学试题一、单选题1．已知集合(){}(){}2,,,P x y y x Q x y y x ====∣∣，则P Q = （）A ．{}0B ．{}0,1C ．(){}0,0D ．()(){}0,0,1,1【答案】D【分析】根据集合的含义，结合解方程组，即可求得两集合的交集.【详解】由题意集合(){}(){}2,,,P x y y x Q x y y x ====∣∣表示点集，解方程组2y xy x ⎧=⎪⎨=⎪⎩，得00x y =⎧⎨=⎩或11x y =⎧⎨=⎩，故()(){}0,0,1,1P Q = ，故选：D2．若13i +是关于x 的实系数方程210ax bx ++=的一个复数根，则（）A ．14a =，12b =B ．14a =，12b =-C ．14a =-，12b =D ．14a =-，12b =-【答案】B【分析】根据一元二次方程复数根的特点及韦达定理即可求出答案.【详解】根据一元二次方程复数根成共轭复数形式出现，则另一个复数根为13i -，根据两根之积得()()113i 13i 4a+-==，则14a =，根据两根之和有214b ba=-=-，解得12b =-，故选：B.3．已知,αβ是空间两个不同的平面，,m n 是空间两条不同的直线，则下列命题为真命题的是（）A ．若,m n αα∥∥，则m n ∥B ．若,m m n α∥∥，则n α∥C ．若,m n αβ⊥∥，且m n ⊥，则αβ⊥D ．若,m n αβ⊥⊥，且αβ∥，则m n ∥【答案】D【分析】根据线面之间的位置关系判定即可.【详解】对于A 项，,m n 可能相交，如图所示正方体中，若,m n 分别为直线AB BC 、，α为平面1111D C B A ，此时符合条件，但结论不成立，故A 错误；对于B 项，有n ⊂α的可能，如图所示正方体中，若,m n 分别为直线11AB A B 、，α为平面1111D C B A ，此时符合条件，但结论不成立，故B 错误；对于C 项，如图所示正方体中，若,m n 分别为直线111AA B C 、，α为平面1111D C B A ，β为平面ABCD ，此时符合条件，但结论不成立，故C 错误；对于D 项，因为αβ∥，,m m αβ⊥⇒⊥又n β⊥，所以m n ∥，故D 正确；故选：D4．某公司将包括2名女员工在内的5名员工派往3个不同的地方学习，要求每人去一个地方，每个地方至少去一人，则2名女员工必须在一起学习的不同的分配方案有（）A ．24B ．32C ．36D ．48【答案】C【分析】分1,1,3三组，1,2,2三组讨论，并利用排列组合公式即可得到答案.【详解】如果5人分成1,1,3三组，则分配方法有：213233C C A 种，如果5人分成1,2,2三组，则分配方法有：223233C C A 种，由加法原理可得：不同分配方法数为213223233233C C A C C A 36+=种.故选：C5．著名的天文学家拉普拉斯曾经说过“对数的发明以其节省劳力而延长了天文学家的寿命”，对数可以将乘除运算转化为加减运算，从而简化运算过程.在一次趣味表演中，主持人出题：一个35位整数的31次方根仍是一个整数，下面我报出这个35位数，请说出它的31次方根.还未等主持人报出第一个数字，速算专家已经写出了答案：这个数的31次方根是13，他的秘诀就是：他心中记住了下面的表（表中常用对数为近似值），请你也试一试，一个20位整数的32次方根仍是一个整数，这个32次方根是多少？（）真数常用对数真数常用对数20.3090.9530.4810 1.0040.6011 1.0450.7012 1.0860.7813 1.1170.8514 1.1580.90151.18A ．3B ．4C ．5D ．6【答案】B【分析】设这个数为x ，则可得32x N =，利用对数运算并结合已知图表可求得lg 0.60x =，即可求得x 的值，即得答案.【详解】设所求这个数为x ，则32x N =，N 为20位整数，则321lg lg ,lg lg 32x N x N =∴=，因为20191010N <<，故19lg 20N <<，所以10.5938lg 0.62532N <<，由表可知lg 0.60x =，即4x =，故这个32次方根是4，故选：B6．已知函数()32f x x ax bx =++有两个极值点12,x x ，且()12f x x =，()21f x x =，那么关于x 的方程()()2320f x af x b ⎡⎤++=⎣⎦的不同实根的个数是（）A ．6个B ．4个C ．2个D ．1个【答案】B【分析】首先利用导数得到函数单调性，再作出图象，而由方程可知()()12,f x x f x x ==，再利用图象即可得到根的个数.【详解】()232f x x ax b '=++，令()0f x '=得12,x x x x ==，不妨令12x x <，故()f x 在()()12,,x x -∞+∞,上单调递增，在()12,x x 上单调递减，方程()()23[]20f x af x b ++=可得()()12,f x x f x x ==，而()12f x x =，()21f x x =，由()f x 的单调性并作出图象可知直线12,y x y x ==分别过点2112(,()),(,())x f x x f x ，与函数()f x 图象均有两个交点，故方程()()23[]20f x af x b ++=的根的个数是4个.故选：B.二、解答题7．已知()()()ln 1R f x x ax a =-+∈(1)讨论函数()f x 的单调性；(2)当1a =时，()e ln 1xb b x f x +++≥恒成立，求b 的取值范围.【答案】(1)答案见解析(2))2e ,∞-⎡+⎣【分析】（1）求得()()11ax a f x x --'=-，分0a =、0a >和a<0，三种情况讨论，结合()f x '的符号，即可求解.（2）解法1：转化为()e ln 1ln 10xb b x ++--≥恒成立，设()()e ln 1ln 1x g x b b x =++--，求得()1e 1x g x b x ='--，得到()g x '存在唯一的实数()1,t ∈+∞，使得1e 01tb t -=-，得出函数()g x 的单调性与最小值()()12ln 111g t t t t =---+-，进而转化为()1e 1t b t =-在(]1,2t ∈时的取值范围，设()()1e 1t h t t =-，利用导数求得其最小值，即可求解；解法2：由题意转化为()()ln e ln ln 11x bx b x x +++≥-+-，构造函数()e t h t t =+，转化为证明()ln ln 1b x x ≥--，设()()ln 1g x x x =--，利用导数求得单调性与最值，即可求解.【详解】（1）解：由题意，函数()()ln 1f x x ax =-+的定义域为{1}x x >∣，可得()()1111ax a f x a x x --=+=--'.当0a =时，()101f x x -'=>，()f x 在()1,+∞单调递增；当0a >时，()()11011a a x ax a a f x x x -⎛⎫- ⎪--⎭-'⎝==>-，()f x 在()1,+∞单调递增；当a<0时，令()0f x '=，得11x a=-，故()f x 在11,1a ⎛⎫- ⎪⎝⎭单调递增，在11,a ⎛⎫-+∞ ⎪⎝⎭上单调递减.综上所述，当0a ≥时，()f x 在()1,+∞单调递增；当a<0时，()f x 在11,1a ⎛⎫- ⎪⎝⎭单调递增，在11,a ⎛⎫-+∞ ⎪⎝⎭上单调递减.（2）解法1：只要证明()e ln 1ln 1xb b x ++≥-恒成立即可，即证明()e ln 1ln 10xb b x ++--≥恒成立即可，设()()e ln 1ln 1xg x b b x =++--，其中0b >，函数()g x 的定义域为{1}x x >∣且()1e 1xg x b x ='--，令()1e 1xx b x ϕ=--，可得()21e 0(1)x x b x ϕ'=+>-，所以()g x 为单调递增函数，可得存在唯一的实数()1,t ∈+∞，使得1e 01tb t -=-，即()ln e ln 1b t t +=--当()1,x t ∈时，()0g x '<，当(),x t ∈+∞时，()0g x '>.故()g x 的最小值为()()()1ln ln 112ln 111tg t be b t t t t =+--+=---+-，又由()()2111011g t t t '=---<--，所以()g t 在()1,+∞是减函数，且()20g =.要使()0g t ≥恒成立，只需(]1,2t ∈即可，即求()1e 1t b t =-在(]1,2t ∈时的取值范围.，设()()(]1,1,2e 1t h t t t =∈-，可得()2e [e (1)0]t t t h t t '=--⋅<，所以()h t 在定义域内为减函数，故()()22e h t h -≥=.所以b 的取值范围为)2e ,∞-⎡+⎣.解法2：只要证明()e ln 1ln 1xb b x x x +++≥-+恒成立即可，即证明()()ln eln ln 11x bx b x x +++≥-+-构造函数()e th t t =+，易知()h t 为增函数，原式等价于证明()()()ln ln 1h x b h x +≥-即证明()ln ln 1x b x +≥-，得()ln ln 1b x x ≥--.设()()ln 1g x x x =--，则()12111-'=-=--x g x x x ，所以()g x 在()1,2单调递增，在()2,+∞上单调递减.()max ln ()22b g x g ≥==-，所以b 的取值范围为)2e ,∞-⎡+⎣.【点睛】方法技巧：对于利用导数研究不等式的恒成立与有解问题的求解策略：1、通常要构造新函数，利用导数研究函数的单调性，求出最值，从而求出参数的取值范围；2、利用可分离变量，构造新函数，直接把问题转化为函数的最值问题．3、根据恒成立或有解求解参数的取值时，一般涉及分离参数法，但压轴试题中很少碰到分离参数后构造的新函数能直接求出最值点的情况，进行求解，若参变分离不易求解问题，就要考虑利用分类讨论法和放缩法，注意恒成立与存在性问题的区别．8．已知双曲线的标准方程为22221(0,0)x y a b a b-=>>，其中点F 为右焦点，过点F 作垂直于x 轴的垂线，在第一象限与双曲线相交于点A ，过点F 作双曲线渐近线的垂线，垂足为M ，若6AF =，23MF =.(1)求双曲线的标准方程；(2)过点M 作AF 的平行线l ，在直线l 上任取一点P ，连接PA 与双曲线相交于点B ，求证点P 到直线BF 的距离是定值.【答案】(1)221412x y -=(2)证明见解析【分析】（1）根据焦点(),0F c 到渐近线的距离为23，列出方程求得b ，再由26bAF a==，求得2a =，即可求得双曲线的方程；（2）设点()00,B x y ，得到直线BF 的方程()000440y x x y y ---=，设直线l 的方程为x m =，点(),3M m m ，根据FM l ⊥，取得1m =，得到直线l 的方程为1x =，设()1,P t ，根据,,P B A 共线，求得()00361,64y P x ⎛⎫--+ ⎪-⎝⎭，结合点到直线的距离公式，即可求解.【详解】（1）解：由双曲线22221(0,0)x y a b a b -=>>，可得焦点(),0F c ，其中一条渐近线方程为b y x a=，则点(),0F c 到渐近线的距离为2223()bc d b a ==+-，解得23b =，又由2,b A c a ⎛⎫ ⎪⎝⎭，可得26b AF a ==，解得2a =，故双曲线的标准方程为221412x y -=.（2）解：由双曲线221412x y -=，可得()()4,0,4,6F A ，设点()00,B x y ，则直线BF 的方程为()0044=--y y x x ，即()000440y x x y y ---=，由题意，设直线l 的方程为x m =，由点M 在直线l 上，可设点(),3M m m ，又由FM l ⊥，可得3343m m =--，解得1m =，即直线l 的方程为1x =，设()1,P t ，由点,,P B A 共线，可得AP AB k k =，即006634y t x --=--，得()003664y t x -=-+-，即点()00361,64y P x ⎛⎫--+⎪-⎝⎭，则点P 到直线BF 的距离为()()()()00000022220000036644666132143412y y x y x x d x y x x x +-----+-====-+-+--.即点P 到直线BF 的距离为定值.9．如图所示，在四棱锥S ABCD -中，侧面SAB 为边长为2的等边三角形，底面ABCD 为等腰梯形，//AB CD ，1CD =，底面梯形的两条对角线AC 和BD 互相垂直，垂足为O ，2SO =，点M 为棱SB上的任意一点.(1)求证：AC DM ⊥；(2)是否存在点M 使得二面角M AD C --的余弦值为7618，若存在求出点M 的位置；若不存在请说明理由.【答案】(1)证明见解析(2)存在，点M 为靠近B 的三等分点【分析】（1）由222SA SO OA =+，证得SO AO ⊥，得到SO AC ⊥，又由AC BD ⊥，利用线面垂直的判定定理，证得AC ⊥平面SBD ，进而证得AC DM ⊥.（2）以O 为原点，建立空间直角坐标系，设棱SB 上存在一点M ，设[],0,1SM SB λλ=∈，得到20,2,222DM λλ⎛⎫=+- ⎪ ⎪⎝⎭，分别求得平面ADM 和平面ACD 的一个法向量，利用向量的夹角公式，列出方程，求得λ的值，即可求解.【详解】（1）证明：因为四边形ABCD 为等腰梯形，且AC BD ⊥，所以OAB 为等腰直角三角形，因为2AB =，所以2OA OB ==，因为2,2SA SO ==，所以222SA SO OA =+，所以SO AO ⊥，即SO AC ⊥，又因为BD ⊂平面SBD ，SO ⊂平面SBD ，且BD SO O ⋂=，所以AC ⊥平面SBD ，因为DM ⊂平面SBD ，所以AC DM ⊥.（2）解：如图所示，以O 为原点，,,OA OB OS 分别为,,x y z ，轴建立空间直角坐标系，由（1）知22OA OB OS OD ====，故()()()()20,0,0,2,0,0,0,2,0,0,,0,0,0,22O AB D S ⎛⎫- ⎪ ⎪⎝⎭，故()()220,,2,2,0,2,0,2,2,2,,022DS AS SB AD ⎛⎫⎛⎫==-=-=-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭假设在棱SB 上存在一点M 满足题意，设,[0,1)SM SB λλ=∈.所以20,2,222DM DS SM DS SB λλλ⎛⎫=+=+=+-⎪ ⎪⎝⎭设平面ADM 的法向量为(),,m x y z = ，则()2202222202m AD x y m DM y z λλ⎧⋅=+=⎪⎪⎨⎛⎫⎪⋅=++-= ⎪ ⎪⎪⎝⎭⎩ ，易令2y =，可得121,1x z λλ+=-=-，所以121,2,1m λλ+⎛⎫=- ⎪-⎝⎭又由平面ACD 的一个法向量为()0,0,1n =设二面角M AD C --为θ，可知二面角为锐二面角则212761cos cos ,181251m n m n m nλλθλλ+⋅-====+⎛⎫+ ⎪-⎝⎭，整理得2127618966λλλ+=-+，即21534160λλ-+=，解得23λ=或85λ=（舍去），所以，存在点M 为靠近B 的三等分点.10．“十三五”时期，在党中央､国务院坚强领导下，全民健身国家战略深入实施，全民健身公共服务水平显著提升，全民健身场地设施逐步增多，人民群众通过健身促进健康的热情日益高涨，经常参加体育锻炼人数和参加锻炼的时间都在明显增加.某城市为了调查该市市民积极参加体育锻炼的情况，从市民中随机抽取了50人，结果是他们参加锻炼的时间都在区间[50,100]内，锻炼时间的频率分布直方图如下：(1)如果锻炼时间的中位数的估计值大于或者等于平均数的估计值，则说明该城市市民积极参加锻炼的意识很强，否则说明该城市市民积极参加锻炼的意识不强，请你根据直方图对他们积极参加锻炼的意识强与不强做出判断；(2)假如根据调查统计结果规定：锻炼时间在[80,100]的市民为优秀层次，时间在[50,80)的为非优秀层次，（ⅰ）从被调查的50人中按分层抽样的方法抽取10人，再从这10人中随机抽取5人，求这5人中优秀层次的人数大于非优秀层次的人数的概率；（ⅱ）用频率作为概率，现从该城市所有市民中随机抽取3人，这3人中锻炼时间为优秀层次的人数为X ，求随机变量X 的分布列和数学期望.【答案】(1)该市市民积极参加体育钗炼的意识很强(2)（ⅰ）3142；（ⅱ）分布列见解析，()95E X =【分析】（1）分别利用频率分布直方图估计中位数和平均数，即可得答案；（2）（ⅰ）由题可得10人中，优秀6人，非优秀4人，则5人中优秀层次的人数大于非优秀层次的人数的情况有优秀5人，优秀4人非优秀1人，优秀3人非优秀2人三种情况，即可得概率；（ⅱ）由题可知33,5X B ⎛⎫⎪⎝⎭，即可得随机变量X 的分布列和数学期望.【详解】（1）锻炼时长中位数的估计值为直方图中等分面积的线对应的值，设为x ，0.01100.01100.02100.5⨯+⨯+⨯< .0.01100.01100.02100.03100.5⨯+⨯+⨯+⨯>，则x 在[)80,90之间.()0.01100.01100.02100.03800.5x ∴⨯+⨯+⨯+⨯-=解得2503x =，即中位数的故计值2503分钟.又锻炼时长平均数估计值为:0.0110550.0110650.0210750.0310850.03109581⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯=.因为中位数的估计值2503分钟大于平均数估计值81分钟，所以，根据这次调查，该市市民积极参加体育钗炼的意识很强.（2）（ⅰ）由题可得10人中，优秀6人，非优秀4人，则5人中优秀层次的人数大于非优秀层次的人数的情况有优秀5人，优秀4人非优秀1人，优秀3人非优秀2人三种情况，则5人中优秀层次的人数大于非优秀层次的人数的概率5413266464510C C C C C 31C 42P +⋅+⋅==；（ⅱ）根据频率，不难得到从该城市市民中随机抽取一人，锻炼时间为优秀层次的概率为35，人数X服从二项分布33,5B ⎛⎫⎪⎝⎭，故X 的分布列为X0123P8125361255412527125数学期望()39355E X =⨯=.11．如下图，已知有()24n n ≥个正数排成n 行n 列：其中每一行都成等差数列，每一列都成等比数列，且所有的公比相等，已知121a =，142a =，428a =.(1)求34a 和44a 的值；(2)求1122nn S a a a =+++ （用含n 的式子表达）.【答案】(1)348a =，4416a =；(2)()11212n S n -=-+.【分析】（1）设第n 行的公差为n d ，公比为q ，根据12a ，14a 及等差数列的通项公式求解1d ，根据12a ，42a 及等比数列的通项公式求出q ，再由等差数列的通项公式求出14a ，最后由等比数列的通项公式求34a 和44a 的值；（2）先根据等差数列的通项公式求出1k a ，再根据等比数列的通项公式求出kk a ，最后由错位相减法求和.【详解】（1）设第n 行的公差为n d ，公比为q ，因为121a =，142a =，428a =，所以141212114222a a d --===-，342128a q a ==,解得2q =.所以223414228a a q ==⨯=，44348216a a q ==⨯=.（2）()()11211121222k a a k d k k =+-=+-=，11211222k k k kk k a a q k k ---==⋅=⋅()1,2,,k n =L ，所以210121122121222322nk n nn k S a a a k n ---==+++=⋅=⋅+⋅+⋅++⋅∑ ，012121222322n S n -=⋅+⋅+⋅+⋅ ，作差可得()111012111221222222221122n n n n n S S S n n n ---------=-=++++-⋅=-⋅=--- ，所以()11212n S n -=-+.12．已知ABC 的三个内角,,A B C 所对的边分别为,,a b c ，且π3A =，22cos cos 3222C B b c b c ++=+，设B x =，ABC 的周长为y .(1)当π4x =时，求y 的值；(2)求函数()y f x =的解析式及最大值.【答案】(1)32236++(2)()π43sin 236f x x ⎛⎫=++ ⎪⎝⎭，其中2π03x <<；最大值为63【分析】（1）根据题意，由正弦定理得()2sin sin sin sin 2sin 23R B C C B R A +==，求得2R =，进而求得,,a b c 的长，得到三角形的周长；（2）由B x =，根据正弦定理得到243sin 23,06ππ3y x x ⎛⎫⎛⎫=++<< ⎪ ⎪⎝⎭⎝⎭，结合三角函数的性质，即可求解.【详解】（1）解：由22cos cos 3222C B b cb c ++=+，可得1cos 1cos 3222C B b cb c +++⋅+⋅=+，即cos cos 23b C c B ⋅+⋅=，设三角形ABC 的外接圆半径是R ，由正弦定理得()2sin cos sin cos 2sin()2sin 23R B C C B R B C R A +=+==，因为3sin 2A =，所以2R =，又62sin sin 344C ππ+⎛⎫=+=⎪⎝⎭又由43262224a b c ===+，解得23,22,62a b c ===+，所以三角形ABC 的周长为22232632236y =+++=++.（2）解：由B x =，且π3A =，可得π2ππ33C x x =--=-，可得2π4sin ,4sin()3b xc x ==-，所以()2314sin 4sin 234sin 4(cos sin )233π22y f x x x x x x ⎛⎫==+-+=+++ ⎪⎝⎭ππ26sin 23cos 43sin 23,063x x x x ⎛⎫⎛⎫=+=++<< ⎪ ⎪⎝⎭⎝⎭，由ππ25(0,)(,)366ππ6x x ∈+∈，所以当ππ62x +=，即π3x =时，()y f x =取到最大值63.三、填空题13．已知双曲线()2222:10,0x y C a b a b-=>>的右焦点为F ，在双曲线左支上取一点M ，若直线MF 与以双曲线实轴为直径的圆相切于N ，若向量2MN NF =，则双曲线C 的离心率为__________.【答案】132【分析】连接ON ，取双曲线的左焦点为1F ，连接1MF ，过1F 作MF 的垂线，垂足为G ，可得FNO △相似于1FGF ，且相似比为1:2，结合双曲线的定义可得1MF ，在直角1F MG △中，由勾股定理得出,a b 的等量关系，再由双曲线的离心率公式即可求解.【详解】连接ON ，取双曲线的左焦点为1F ，连接1MF ，过1F 作MF 的垂线，垂足为G ，直线MF 与圆222x y a +=相切,,ON MF ON a ∴⊥=，,OF c NF b =∴= ，O 为1F F 的中点，1//F G ON ，FNO ∴ 相似于1FGF ，且相似比为1:2，故12,F G a NG b ==.22,,,3MN NF MN b MG b MF b =∴=∴==.在双曲线()222210,0x y a b a b -=>>中，由双曲线定义知12MF MF a -=，132MF b a ∴=-.11,//,ON MF F G ON F MG ⊥∴ △为直角三角形，22211||F G MG MF ∴+=，即222(2)(32)a b b a +=-，解得23b a =，故双曲线的离心率为21312b e a ⎛⎫=+= ⎪⎝⎭.故答案为:132.14．已知函数()y f x =定义域为R 且满足①()2y f x =+为偶函数；②任意2,2x y ≥≥都有()()()1f x y f x f y +-=+成立；③[)1212,2,,x x x x ∀∈+∞≠，都有()()12120f x f x x x ->-，请给出满足上述三个性质的一个函数为__________.【答案】()122f x x =-（答案不唯一）【分析】由三个条件依次分析出函数具有对称性、单调性等性质，可从熟悉的函数中找到符合条件的函数.【详解】由性质①()2y f x =+为偶函数知，函数()y f x =关于直线2x =对称；由性质②任意2,2x y ≥≥都有()()()1f x y f x f y +-=+成立，可设()f x kx b =+，待定系数可得当2x ≥时，()1f x kx =-；由性质成立③[)1212,2,,x x x x ∀∈+∞≠，都有()()1212f x f x x x ->-可知函数()y f x =在[)2,+∞上单调递增，因此可写出满足上述三个性质的一个函数为()122f x x =-.故答案为：()122f x x =-（答案不唯一）15．若33223(106)x y ax bx y cxy dy +=+++，则248a b c d -+-+=__________.【答案】8【分析】令1,2x y =-=，可得答案.【详解】注意到()()()()3232248112122a b c d a b c d -+-+=⋅-+⋅-⨯+⋅-⨯+⋅.又33223(106)x y ax bx y cxy dy +=+++，则248a b c d -+-+=()3101628⎡⎤⨯-+⨯=⎣⎦.故答案为：816．已知2286160x y x y +--+=，则yx的最小值为__________.【答案】0【分析】设yk x=，根据圆心到直线的距离小于等于半径列式可求出结果.【详解】由2286160x y x y +--+=可得圆心为(4,3)，半径为3，设yk x=，即0kx y -=，依题意得2|43|31k k -≤+，解得2407k ≤≤，所以yx的最小值为0.故答案为：0.四、多选题17．已知正方形ABCD 的边长为2，点,M N 分别是线段,CD BC 上的动点，若满足AC x AM y AN =+，则下列说法正确的是（）A ．当1x =时，则1y =B ．当23x y ==时，点,M N 分别是线段,CD BC 的中点C ．当23x y ==时，0AC MN ⋅= D ．当22111CM CN +=时，x y +的最小值为8227+【答案】BCD【分析】建立平面直角坐标系，设出,M N 的坐标，利用向量的坐标运算逐一判断各个选项作答.【详解】以点A 为坐标原点，,AB AD 分别为x 轴，y轴建立平面直角坐标系，如图，设(,2),(2,)M a N b ，02,02a b ≤≤≤≤，(,2),(2,)AM a AN b == ，由AC x AM y AN =+ ，得(2,2)(2,2)ax y x by ++=，则2222ax y x by +=⎧⎨+=⎩，对于A ，当1x =时，得220a y by +=⎧⎨=⎩，不能得1y =，如取0b =，11,2a y ==，满足条件，A 错误；对于B ，当23x y ==时，得1a b ==，此时点,M N 分别是线段,CD BC 的中点，B 正确；选项C ，由选项B 知，(1,2),(2,1)M N ，(1,1)MN =-，而(2,2)AC = ，212(1)0AC MN ⋅=⨯+⨯-= ，C 正确；选项D ，当22111CM CN+=时，显然2a ≠且2b ≠，此时0xy ≠，否则2a =或2b =，矛盾，即有22111(2)(2)a b +=--，而2222y a x x b y -⎧=⎪⎪⎨-⎪=⎪⎩，因此22224(1)(1)x y x y x y +=+-+-，整理得2224(1),0,0x y x y x y +=+->>，而22222()()()22x y x y x y x y ++-++=≥，于是22()24(1)x y x y ++≥-，当且仅当x y =时取等号，整理得27()16()80x y x y +-++≥，令AC 交MN 于E ，显然E 与C 不重合，AE AC xAM y AN λλλ==+，01λ<<，由,,M E N 共线，得1x y λλ+=，即11x y λ+=>，解得8227x y ++≥，即，x y +的最小值为8227+，D 正确.故选：BCD18．如图所示，已知()0,0O ，()2,0A ，()11,1B ，作以1B 为直角顶点的等腰直角1OAB ，作点A 和点1B 的中点1C ，继续作以1C 为直角顶点的等腰直角121,B B C ，如此继续作中点，作等腰直角三角形.这样会得到一组分别以1122,,,,B C B C 为直角顶点的等腰直角三角形.下列说法正确的是（）A ．所作的等腰直角三角形的边长构成公比为12的等比数列B ．第4个等腰直角三角形的不在第3个等腰直角三角形边上的顶点坐标为39,14B ⎛⎫⎪⎝⎭C ．点4C 的纵坐标为511512D ．若记第n 个等腰直角三角形的面积为n S ，则14lim 3ni n i S →∞==∑【答案】ABD【分析】由题意分析逐项判断即可.【详解】由图易知，所作的等腰直角三角形的边长构成公比为12的等比数列，故选项A 正确；选项B ，()()12311,1,11,1,11,14B B B ⎛⎫+++ ⎪⎝⎭，故选项B 正确；选项C ，点1C 的纵坐标为112-，点2C 的纵坐标为3112-，点3C 的纵坐标为5112-，点4C 的纵坐标为7112-，点5C 的纵坐标为9112-，故选项C 错误；选项D ，121111111141441,,lim lim 1lim lim 114416434314nni n n n n n ni S S S -→∞→∞→∞→∞=⎛⎫- ⎪⎛⎫⎛⎫===++++==-= ⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪-⎝⎭∑ ，故选项D 正确.故选：ABD.五、单选题19．已知函数()ππ3cos cos (0)44f x x x ωωω⎛⎫⎛⎫=++-> ⎪ ⎪⎝⎭⎝⎭，当π0,2x ⎡⎤∈⎢⎥⎣⎦时函数恰有3个零点，则正整数ω的取值可以是（）A ．5B ．6C ．7D ．8【答案】AB【分析】化简()72sin 12f x x πω⎛⎫=+⎪⎝⎭，根据题意，结合正弦函数的图象，得到，734212ωππππ≤+<，求得ω的范围，结合选项，即可求解.【详解】由函数()3cos cos 3cos sin 4444f x x x x x ππππωωωω⎛⎫⎛⎫⎛⎫⎛⎫=++-=+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭72sin 2sin 4312x x πππωω⎛⎫⎛⎫=++=+ ⎪ ⎪⎝⎭⎝⎭，当0,2x π⎡⎤∈⎢⎥⎣⎦时，可得777,1212212x ππωππω⎡⎤+∈+⎢⎥⎣⎦，因为()f x 在π0,2x ⎡⎤∈⎢⎥⎣⎦上有3个零点，结合正弦函数的图象可知，734212ωππππ≤+<，解出293966ω≤<，所以正整数ω的取值可以是5或6.故选：AB.六、多选题20．我们可以用统计图表表示数据，对获得数据进行统计分析.据《中国统计年鉴（2022）》可知，2016~2021年我国人口年龄分布情况（百分比）如表所示.（已知少儿抚养比()014%100%1564~=⨯~岁人数岁人数，老年抚养比()65%100%1564=⨯~岁及以上人数岁人数，总抚养比（%）=少儿抚养比（%）+老年抚养比（%））根据图表，下列说法正确的有（）A ．从2016年到2021年期间，0~14岁人口比重在逐年上升B ．从2016年到2021年期间，15~64岁人口比重在逐年下降C ．2021赡养老人的压力比2020年更重D ．2021年总抚养比大于2020年总抚养比【答案】BCD【分析】根据图表，逐项分析每个选项中的数据，可得答案.【详解】对于A ，由图表可知2018年到2019年间以及2020年到2021年间0~14岁人口比重在降低，A 错误；对于B ，从2016年到2021年期间，15~64岁人口比重在逐年下降，正确；对于C ，2021年65岁以及以上老年人抚养比为14.220.8%68.3≈，2020年65岁以及以上老年人抚养比为13.520.7%68.6≈，故2021赡养老人的压力比2020年更重，C 正确；对于D ，2021年总抚养比为14.217.546.4%68.3+≈，2020年总抚养比为13.517.945.8%68.6+≈，故2021年总抚养比大于2020年总抚养比，D 正确，故选：BCD七、单选题21．已知矩形ABCD 中，2,1AB AD ==，沿着对角线AC 将ACD 折起，使得点D 不在平面ABC 内，当AD BC ⊥时，求该四面体ABCD 的内切球和外接球的表面积比值为（）A ．18935-B ．19935-C ．211235-D ．241235-【答案】C【分析】根据题意分析可得四面体的外接球的球心为AC 的中点O ，再利用等体积法求内切球的半径，进而可得结果.【详解】取AC 中点O ，由矩形的性质可知OA OB OC OD ===，即O 为该四面体的外接球的球心，故外接球的半径1522R AC ==；因为,AD BC AD DC ⊥⊥，BC DC C = ，,BC DC ⊂平面BCD ，可得AD ⊥平面BCD ，DC ⊂平面BCD ，则AD DC ⊥，且,AD BC BC AB ⊥⊥，AD AB A ⋂=，,AD AB ⊂平面ABD ，可得BC ⊥平面ABD ，BD ⊂平面ABD ，则BC BD ⊥，故该四面体ABCD 的四个面都是直角三角形，设四面体的内切球的半径为r ，因为内切球与四面体的四个面都相切，故r 满足13V rS =四面体表，则1112122133211113223r ⨯⨯⎛⎫=⨯⨯⨯⨯⨯⨯+⨯⨯⨯ ⎪⎝⎭，解得32332423r -==+；因此该四面体的内切球和外接球的表面积的比值为22222223324π211234π552S r r S R R ⎛⎫-⎪-⎝⎭====⎛⎫ ⎪⎝⎭内外.故选：C.22．我们知道立体图形上的最短路径问题通常是把立体图形展开成平面图形，连接两点，根据两点之间线段最短确定最短路线.请根据此方法求函数()2222,31313(0,0)f x y x x y y x xy y x y =-++-++-+>>的最小值（）A ．2B ．3C ．6D ．23【答案】A【分析】构造合适的三棱锥模型-P ABC ，其中1,,PA PB x PC y ===，，利用余弦定理证明(),f x y 即为底面周长，最后将其展开即可得到最小值.【详解】根据函数(),f x y 的表达式可知，构造三棱锥-P ABC ，其中1,,PA PB x PC y ===，且30,30,30APB BPC APC ∠∠∠=== ，由余弦定理可得，2231,31AB x x AC y y =-+=-+，223BC x xy y =-+，(),f x y 的最小值即为AB AC BC ++的最小值，将三棱锥-P ABC 按照PA 展开可得展开图，且90,2APA AA ∠'='= ，故(),f x y 的最小值为2.故选：A.。

1、 如图A 、B 、C 、D 为四个村庄,要修筑三条公路,将这四个村庄连接起来,则不同的修筑方案共有( )A. 8种B. 12种C. 16种D. 20种2、 一圆周上有9个点,以这9个点为顶点作三个三角形,当这三个三角形的边互不相交时,我们把它称为一种构图．则满足这样条件的构图共有 ( )A. 3种B. 6种C. 9种D. 12种3、从1，2，3…，100这100个数中，任取两个数，使它们的乘积能被7整除，这两个数的取法（不计顺序）共有多少种？4、从10,,4,3,2,1 这10个自然数中，每次取出不同的两个，使它们乘积是6的倍数，则不同的取法有__________种。

排列组合问题-思维方法5、设4321,,,x x x x 为自然数1，2，3，4的一个全排列，且满足643214321=-+-+-+-x x x x ，则这样的排列有 个.6、 某年数学竞赛邀请了一位来自X 星球的选手参加填空题比赛，共10道题目，这位选手做题有一个古怪的习惯：先从最后一题（第10题）开始往前看，凡是遇到会的题目就作答，遇到不会的题目先跳过（允许跳过所有的题目），一直看到第1题：然后从第1题开始往后看，凡是遇到先前未答的题目就随便写个答案，遇到先前已答的题目则跳过（例如，他可以按照9、8、7、4、3、2、1、5、6、10的次序答题），这样所有题目均有作答，设这位选手可能的答题次序有n 种，则n 的值为（ ）A. 512B. 511C. 1024D. 10237、（2010理14）以集合{},,,U a b c d =的子集中选出4个不同的子集，需同时满足以下两个条件：(1),U ∅都要选出；（2）对选出的任意两个子集A 和B ，必有A B ⊆或B A ⊆，那么共有_________种不同的选法8、如图，甲从A 到B ，乙从C 到D ，两人每次都只能向上或者向右走一格. 如果两个人的线路不相交，则称这两个人的路径为一对孤立路，那么不同的孤立路一共有_____对.（用数字作答）9、将前12个正整数构成的集合{}1,2,,12M =中的元素分成1234,,,M M M M 四个三元子集，使得每个三元子集中的三个数都满足：其中一个数等于另外两数之和，试求不同的分法种数.10、四棱锥的8条棱代表8种不同的化工产品,有公共点的两条棱代表的化工产品放在同一仓库是危险的,没有公共顶点的两条棱多代表的化工产品放在同一仓库是安全的,现打算用编号为①、②、③、④的4个仓库存放这8种化工产品,那么有____种不同的安全存放的方法．10、如图，用四种不同颜色给图中的,,,,,A B C D E F 六个点涂色，要求每个点涂一种颜色，且图中每条线段的两个端点涂不同颜色，则不同的涂色方法共有（ ）种 DAC BA、288种B、264种C、240种D、168种。

智才艺州攀枝花市创界学校高二数学文科培优训练题二时量：120分钟总分值是：150分一、选择题：〔本大题一一共10个小题，每一小题5分，一共50分〕221mx y +=的虚轴长是实轴长的2倍，那么m =(A)A ．14-B ．4-C ．4D ．14【解析】代m =14-入双曲线方程知:双曲线实轴长为2,虚轴长为4,应选A.2．中心在原点,准线方程为x=±4,离心率为21的椭圆方程为(A)A ．13422=+y x B.14322=+y x C.42x ＋y 2=1D.x 2＋42y =1【解析】由2a c =4，12c a =，所以2222,1,3a c b a c ===-=,应选A.3．假设抛物线28y x =的焦点与椭圆22212x y a +=〔0a >〕的右焦点重合，那么a 的值是〔D 〕 A ．3B．6D【解析】抛物线28y x =的焦点为(2,0)，所以椭圆22212x y a +=的右焦点为(2,0)，那么224a -=，应选D.4．圆心在抛物线x y 42=上动圆，过点〔0，1〕且恒与定直线L 相切，那么直线L 的方程为〔C 〕A ．x=1B.x=161C.y=-1D.y=-161【解析】由点〔0，1〕为抛物线x y 42=的焦点，由抛物线的定义知直线L 即为抛物线的准线，应选C.5．双曲线22221(00)x y a b a b－＝＞，＞的右焦点为F ，右准线与一条渐近线交于点A ，△OAF的面积为O 为原点)，那么两条渐近线的夹角为〔C 〕 A ．30° B ．45° C ．60° D ．90°【解析】易知点A 〔2,a abc c ±〕,又OAF S ∆211222A OF y ab ===,故3b a =,应选C. 6.〕抛物线C ：842+-=x x y 作C 关于原点对称的曲线C 1，然后把1C 的图象沿着向量m ＝〔b a ,〕平移后就可得到抛物线2x y -=的图象，那么b a ,之值分别是〔〕 A ．2，3B.3，2C.2，4D.3，3【解析】曲线C 1的方程为248y x x =---，然后把1C 向右平移2个单位，再向上平移4个单位，就可得到抛物线2x y -=，应选C.2=14y 上的点到直线–4x+y+2=0的间隔的最小值是〔B 〕A.17 B．17C．17D ．0 【解析】由间隔公式知:d ===≥应选B ． 8．设11(,)A x y 9(4,),5B 22(,)C x y 是右焦点为F 的椭圆221259x y +=上三个不同的点，那么是“128x x +=〞的〔A 〕A.充分必要条件B ．必要不充分条件C ．充分不必要条件D ．既非充分也非必要条件【解析】由椭圆的焦半径公式知:|AF |=5－45x 1,|BF |=5–45×4,|CF |=5–45x 2,所以,AF ,BF CF 成等差数列2BF AF CF ⇔=+⇔x 1＋x 2=8,应选A.9.椭圆22a x +22by =1(a>b>0)上两点A ，B 与中心O 的连线互相垂直，那么21OA +21OB的值是(D) A ．221ba + B.221b a C.2222b a b a + D.2222ba b a + 【解析】恒成立问题特殊化,分别取A ，B 两点为(a,0)(0,b)即可知选D10.假设直线y=kx+2与双曲线x 2-y 2=6的右支点交于不同两点,那么k 的取值范围为(D)A.(,33-B.(0,3C.(3-D.(,1)3-- 【解析】画出图形,考察四个选项,A 、B 、C 三项明显错误.结合判别式,D 项确实正确.二．填空题〔本大题一一共5个小题，每一小题4分，一共20分〕11．假设圆锥曲线15222=++-k y k x 的焦距与k 无关，那么它的焦点坐标是)7,0(±． 【解析】由曲线为焦点在y 轴上的双曲线，其中C 2=(k ＋5)－(k －2)=7,故它的焦点坐标是)7,0(±．116922=-y x 的右焦点为F ，定点A 〔6，2〕，点P在双曲线右支上挪动，那么PF PA 53+的最小值为215【解析】设P 到双曲线准线的间隔为d ,由双曲线的第二定义知：PF PA 53+=PF d +≥215.28y x =的准线与x 轴交于点Q,假设过点Q 的直线l 与抛物线有公一共点,那么直线l 的斜率的取值范围为[-1,1]【解析】抛物线28y x =的准线与x 轴交于点Q(-2,0),设过点Q 的直线l :y -0=k (x +2),将直线方程代入28y x =整理得:222(48)k x k x +-240k +=,因为直线l 与抛物线有公一共点,所以2222(48)440k k k ∆=--⋅≥.解得:-1≤k ≤1.14．椭圆125922=+y x 上的一点P 到两焦点的间隔的乘积为m ，那么当m 取最大值时，点P 的坐标是()0,3-或者().0,3【解析】222PF PF PF PF a ⎛⎫+≤= ⎪ ⎪⎝⎭左右左右,等号当且仅当PF PF =左右时成立,此时点P 的坐标是()0,3-或者().0,3①设A 、B 为两个定点，k 为非零常数，||||PA PB k -=，那么动点P 的轨迹为双曲线；②过定圆C 上一定点A 作圆的动点弦AB ，O 为坐标原点，假设1()2OP OA OB =+,那么动为椭圆；③方程02522=+-x x 的两根可分别作为椭圆和双曲线的离心率；④双曲线13519252222=+=-y x y x 与椭圆有一样的焦点. ③④【解析】①与双曲线的定义不符,②由1()2OP OA OB =+知P 为弦AB 的中点,所以CP ⊥AB ,点P 的轨迹为以CA 为直径的圆(去掉点A),其它易知. 三、解答题16．等轴双曲线的中心在原点，焦点在y 轴上，它截2y x =得到的弦长AB ，求双曲线方程.解：设等轴双曲线方程为阶段222y x a -=， ……………………………………………〔2分〕 将2y x =代入等轴双曲线222y x a -=，得223,x a =即x =，……………〔6分〕 由双曲线的对称性知：AB ==2……………………………………〔8分〕解得294a =，……………………………〔10分〕∴双曲线方程为2294x y -=…………〔12分〕17.〔总分值是12分〕抛物线),0p (px 2y 2>= 过焦点F 的动直线l 交抛物线于A ，B 两点，O为坐标原点,求证:OB OA ⋅为定值;解:假设直线l 垂直于x 轴,那么)p ,2p (A ,)p ,2p(B - .=⋅OB OA .p 43p )2p (222-=- 假设直线l 不垂直于x 轴,设其方程为)2px (k y -=,)y ,x (A 11 )y ,x (B 22 .由0k 4p x )k 2(p x k px2y )2p x (k y 222222=++-⇒⎪⎩⎪⎨⎧=-=2212122(2), 4k p x x p x x k ++=⋅=.OB OA ⋅1212x x y y =+＝12x x 212()()22p p k x x +--4k p )x x (k 2p x x )k 1(22212212++-+=22222222p 434k p kp )k 2(k 2p 4p )k 1(-=++⋅-+=综上,OB OA ⋅2p 43-=为定值.18．焦点在x 轴上的双曲线C 的两条渐近线过坐标原点，且两条渐近线与以点)2,0(A 为圆心，1为半径为圆相切，又知C 的一个焦点与A 关于直线y=x 对称.〔Ⅰ〕求双曲线C 的方程；〔Ⅱ〕假设Q 是双曲线C 上的任一点，F 1、F 2为双曲线C 的左、右两个焦点，从F 1引∠F 1QF 2的平分线的垂线，垂足为N ，试求点N 的轨迹方程.解:〔Ⅰ〕设双曲线C 的渐近线方程为y=k x ，即k x －y=0∵该直线与圆1)2(22=-+y x 相切，∴双曲线C 的两条渐近线方程为x y ±=〔2分〕故设双曲线C 的方程为12222=-ay a x ，又∵双曲线C 的一个焦点为)0,2(∴222,a =∴21a =，∴双曲线C 的方程为122=-y x ………〔4分〕〔Ⅱ〕假设Q 在双曲线的右支上，那么延长QF 2到T ，使|QT|=|OF 1|,假设Q 在双曲线的左支上，那么在QF 2上取一点T ，使|QT|=|QF 1|根据双曲线的定义|TF 2|=2，所以点T 在以F 2)0,2(为圆心，2为半径的圆上，即点T 的轨迹方程是)0(4)2(22≠=+-x y x ①………〔8分〕由于点N 是线段F 1T 的中点，设N 〔x ，y 〕，T 〔T T y x ,〕那么⎩⎨⎧=+=⎪⎪⎩⎪⎪⎨⎧=-=yy x x y y x x T T T T 222,222即 代入①并整理得点N 的轨迹方程为)22(122≠=+x y x …………〔12分〕 19．两定点M 〔－2，0〕，N 〔2，0〕，动点P 在y 轴上的射影是H ，假设PH PH ⋅和PN PM ⋅分别是公比为2的等比数列的第三项，第四项. 〔I 〕求动点P 的轨迹方程C ；〔II 〕过点N 的直线l 交曲线C 于x 轴下方两个不同点A 、B ，R 为AB 的中点，定点Q 〔0，－2〕，求直线R Q 的横截距的取值范围．〔〕解：〔1〕设(,),(0,),P x y H y 则(,0),PH x =-(2,),PM x y =---(2,)PN x y =--∴2PH PH x ⋅=，224PM PN x y ⋅=-+ …………………………………………〔2分〕 ∴22224,x x y =-+P 点轨迹方程为)0(422≠=-x x y …………………〔5分〕〔2〕将(2)y k x =-代入224y x -=整理得:222(1)480k y ky k ---=,因为直线l 交曲线C 于x 轴下方两个不同点A 、B ，记11(,)A x y ，22(,)B x y ，那么12200121212<<⇒⎪⎪⎩⎪⎪⎨⎧><+>∆≠-k y y y y k ……………〔7分〕 那么AB 中点R 为)12,12(222--k kk k 可得直线QR 方程为x k k k y 2212-+=+……………〔9分〕令0=y 得45)211(220+--=k x ,其中)122(<<k …………………………〔12分〕∴022x <<…………………〔14分〕20．椭圆2212x y +=的左焦点为F ，O 为坐标原点。

高二数学人教版选择性必修第一册全册考试复习必刷检测卷（培优版）全解全析1．C 由题意，22()33OM MP OM MN O OM ON OM P =+=+=+-=23ON +13OM =23×12(OB +OC )+13×12OA =111633a b c++故选：C 2．A解：如图建立空间直角坐标系，则()1,0,0A ，()0,1,0C ，设(),,1E x y 则[]0,1x ∈，[]0,1y ∈，所以()1,,1EA x y =---，(),1,1EC x y =---，所以()()22221111111222EA EC x x y y x x y y x y ⎛⎫⎛⎫⋅=----+=-+-+=-+-+ ⎪ ⎪⎝⎭⎝⎭，因为[]0,1x ∈，[]0,1y ∈，所以211024x ⎛⎫≤-≤ ⎪⎝⎭，211024y ⎛⎫≤-≤ ⎪⎝⎭，所以1,12EA EC ⎡⎤⋅∈⎢⎥⎣⎦，故选：A3．C如图所示，由圆221:(4)(1)4C x y -+-=，可得圆心1(4,1)C ，半径为12r =，圆222:(4)1C x y +-=，可得圆心2(0,4)C ，半径为21r =，可得圆心距125C C ==，所以12||||52PM PN r r +≥--=，当12,,,,M N C C P 共线时，取得最小值，故||||PM PN +的最小值为2.故选：C.4．A由点P 是直线290x y +-=上的任一点，所以设()92P m m -,，因为圆22:4O x y +=的两条切线PA 、PB ，切点分别为A 、B ，所以OA PA ⊥，OB PB ⊥，则点A 、B 在以OP 为直径的圆C 上，即AB 是圆O 和圆C 的公共弦，则圆心C 的坐标是92,22m m -⎛⎫ ⎪⎝⎭，且半径的平方是()222924m m r -+=，所以圆C 的方程是()22229292224m m m m x y -+-⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭，又由224x y +=，两式相减，可得()9240m x my -+-=，即公共弦AB 所在的直线方程是()9240m x my -+-=，即()() 2940m y x x -+-=，由20940y x x -=⎧⎨-=⎩，解得48,99x y ==，所以直线AB 恒过定点48,99⎛⎫⎪⎝⎭.故选： A.5．D 【详解】对于A ，若0m n >>，则221mx ny +=可化为22111x y m n+=，因为0m n >>，所以11m n<，即曲线C 表示焦点在y 轴上的椭圆，故A 错误；对于B ，若0m n =>，则221mx ny +=可化为221x y n+=，此时曲线C 表示圆心在原点，半径为n的圆，故B 错误；对于C ，若0mn <，则221mx ny +=可化为22111x y m n+=，此时曲线C 表示双曲线，由220mx ny +=可得y =，故C 错误；对于D ，若0,0m n =>，则221mx ny +=可化为21y n=，y =C 表示平行于x 轴的两条直线，故D 正确.故选： D.6．A 【详解】作图，由题意得(),0A a -、(),0B a 、(),0F c -，设()0,E m ，由//PF OE 得MF AF OEAO=，则()m a c MF a-=①，又由//OE MF ，得12OE BO MF BF=，则()2m a c MF a +=②，由①②得1()2a c a c -=+，即3a c =，则13c e a ==，故选：A.7．A 【详解】设动点(),P x y ，由2PA PO =，得()2222344x y x y -+=+，整理得()2214x y ++=，又点P 是圆C ：()()22220y x r r +=->上有且仅有的一点，所以两圆相切.圆()2214x y ++=的圆心坐标为()1,0-，半径为2，圆C ：()()22220y x r r +=->的圆心坐标为()20,，半径为r ，两圆的圆心距为3，当两圆外切时，23r +=，得1r =，当两圆内切时，23r -=，0r >，得=5r ．故选：A.8．B设双曲线的渐近线OA 的倾斜角为π0,2θ⎛⎫∈ ⎪⎝⎭，则1tan a θ=，在等腰三角形2AOF 中，根据正弦定理可得：2sin sin 2OA OF θθ=，得2cos cOA θ=，所以122221tan 152sin 2224AF F c a SOA OF a θθ+=⨯⨯⨯⨯===，解得2a =或12，又1e <<e 1a >，从而2a =，所以双曲的方程为2214xy -=，故选：B ．【点睛】本题目比较巧妙的地方在于借助渐近线的倾斜角，得到倾斜角与a 的关系，结合解三角形的方法来表示三角形的面积，求出a 的值；题目也可以用渐近线方程直接求解9．AB对于A ：向量,a b 同向时，a b a b -≠+，故A 错误；对于B ：需要强调0b ≠r r，故B 错误；对于C ：因为2231+-=，则由共面定理知P ，A ，B ，C 四点共面，故C 正确；对于D ：{},,a b c 为空间的一个基底，则,,a b c 不共面，故,,a b b c c a +++也不共面，所以{},,a b b c c a +++构成空间的另一个基底，故D 正确；故选：AB 10．BCD对于A 中，当直线过原点时，此时直线在坐标轴上的截距相等，但不能用方程1x ya a+=表示，所以A 不正确；对于B 中，由圆224x y +=，可得圆心坐标为(0,0)C ，半径为2r =，则圆心C到直线:0l x y -=的距离为1d =，所以圆C 上有且仅有3个点到直线l 的距离都等于1，所以B 正确；对于C 中，由圆22120C :x y x ++=，可得圆心坐标为1(1,0)C -，半径为11r =，由圆222480C :x y x y m +--+=，可得圆心坐标为2(2,4)C，半径为2r =可得圆心距125C C =，要使得圆1C 与2C 恰有三条公切线，则15=且200m ->，解得4m =，所以C 正确；对于D 中，设(,)P m n ，可得142m n+=，以OP 为直径的圆的方程为220x y mx ny +--=，两圆的方程作差，可得直线AB 的方程为1mx ny +=，消去n 可得()2102y m x y -+-=，令0,2102yx y -=-=，解得11,42x y ==，即直线AB 经过定点11(,42，所以D 正确.故选：BCD 11．AD 【详解】设,AB n →→的夹角为()0πθθ≤≤，由题意得11cos 3||||||AB nAB n AB n n ABθ→→→→→→→→⋅⋅==⋅=-⋅，∴sin 3θ=，①当双曲线的焦点在x 轴上时，其渐近线方程为by x a=±，即0bx ay ±=，∴点(0)2，到渐近线的距离为sin ||n d θ→==⋅，整理得2218b a =，∴c e a ==②当双曲线的焦点在y 轴上时，其渐近线方程为ay x b=±，即0ax by ±=，∴点(0)2，到渐近线的距离为42sin 3||n d θ→==⋅=，整理得228b a =，∴3c e a ==，综上双曲线的离心率为324或3.故选：AD.12．BCD 【详解】12OF F P c O O ===，12PF PF ∴⊥124cos 5F QF ∠=,设1||4,||5PQ m FQ m ==则1||3PF m =又11||||||4PQ FQ PF a ++=，12m =3m ∴=12|||PF PF ∴==12||2F F ∴=，即1,c e ==A 不正确；当点M 在y 轴上时三角形12MF F 面积的最大，此时1211222S F F OM ==⨯=,所以B 正确；因为12|||PF PF ==所以22124PF PF +=，故C 正确；圆228:9G x y +=，13r b =<=，圆在椭圆内部，所以点M 在椭圆内部，所以D 正确.故选：BCD 13．32解：由题意，翻折后1AD AB BC CD ====，BD =在翻折后的图形中，取BD 的中点O ，连接,AO CO ，则2AO CO ==则,AO BD CO BD ⊥⊥，所以AOC ∠即为二面角A BD C --的平面角，所以2AOC π∠=，即AO CO ⊥，所以1AC =，又因AO CO O =，所以BD ⊥平面AOC ，因为AC ⊂平面AOC ，所以AC BD ⊥，则22||BP BP =211()22BA BC BD =-+21()2CA BD =+221||||4CA BD CA BD =++⋅94=，所以32BP =.故答案为：32.14．[)4,+∞解：设|34||349|z x y a x y =-++--=，故|34||349|x y a x y -++--可以看作点(,)P x y 到直线:340m x y a -+=与直线:3490l x y --=距离之和的5倍，|34||349|x y a x y -++--的取值与x ，y 无关，∴这个距离之和与点P 在圆上的位置无关，如图所示：可知直线m 平移时，P 点与直线m ，l 的距离之和均为m ，l 的距离，即此时圆在两直线内部，当直线m 与圆()()22321x y -+-=1，化简得|1|5a +=，解得4a =或6a =-（舍去），4a ∴≥，即[)4,a ∈+∞．故答案为：[)4,+∞．15．①③④解：(4,0)A ，(0,2)B ，∴过A 、B 的直线方程为142xy+=，即240x y +-=，圆22(5)(5)16x y -+-=的圆心坐标为(5,5)，圆心到直线240x y +-=的距离4d ，∴点P 到直线AB 的距离的范围为44]+，5<，∴41<，4105+<，∴点P 到直线AB 的距离小于10，但不一定大于2，故①正确，②错误；如图，当过B 的直线与圆相切时，满足PBA ∠最小或最大(P 点位于1P 时PBA ∠最小，位于2P 时PBA ∠最大），此时||BC ==||PB ∴==，故③④正确．故选：①③④．16【详解】由22CBF CF B ∠∠=，设2CB CF m ==，由双曲线的定义得122CF CF a -=，所以12BF a =，24BF a =，又因为过1F 的直线与by x a=-垂直，所以112tan F C a k BF F b=∠=，则12cos bBF F c∠=，在12BF F △中，由余弦定理得222222121212124416cos 28BF BF F F a c a b BF F BF BF ac c+-+-∠===⋅，令1a =，则2220b b --=，解得1b =所以c =则e =，17．（1）证明：把直线l 的方程改写成：()()72100x y m x y +-++-=，由方程组702100x y x y +-=⎧⎨+-=⎩，解得：34x y =⎧⎨=⎩，所以直线l 总过定点(3，4).圆C 的方程可写成()()221225x y -+-=，所以圆C 的圆心为(1，2)，半径为5.因为定点(3，4)到圆心(1，2)5=<，即点(3，4)在圆内，所以过点(3，4)的直线l 总与圆相交，即不论m 取什么实数，直线l 与圆C 总相交（2）设直线l 与圆交于A 、B 两点.当直线l 过定点M (3，4)且垂直于过点M 的圆C 的半径时，l 被截得的弦长|AB|最短.因为2AB =此时1114231AB CMk k =-=-=---，所以直线AB 的方程为()413y x -=--，即70x y +-=.故直线l 被圆C 截得的弦长最小值为l 的方程为70x y +-=.18．（1）因为平面PAD ⊥平面ABCD ，平面PAD 平面ABCD AD =，AB AD ⊥，AB Ì平面ABCD ，所以AB ⊥平面PAD ，PD ⊂Q 平面PAD ，所以AB PD ⊥.又因为PA PD ⊥，AB PA A ⋂=，所以PD ⊥平面PAB .因为PD ⊂平面PDC ，所以平面PDC ⊥平面PAB ；（2）取AD 的中点O ，连接PO 、CO ，因为PA PD =，所以PO AD ⊥.又因为PO ⊂平面PAD ，平面PAD ⊥平面ABCD ，平面PAD 平面ABCD AD =，所以PO ⊥平面ABCD .因为CO ⊂平面ABCD ，所以PO CO ⊥.因为AC CD =，所以CO AD ⊥.以点O 为坐标原点，OC 、OA 、OP 所在直线分别为x 、y 、z 轴建立空间直角坐标系，由题意得()0,1,0A 、,1,02B ⎛⎫⎪ ⎪⎝⎭、)C 、()0,1,0D -、()0,0,1P ，所以()0,1,1PA =-，)1PC =-uu u r，1PB ⎫=-⎪⎪⎝⎭uu r .设平面PBC 的法向量为(),,n x y z =，则00n PB n PC ⎧⋅=⎨⋅=⎩，即30230x y z z +-=⎪⎪-=⎩，令2x =，则23z =3y =，所以(3,3n =.所以，3114cos ,38192n PA n PA n PA⋅<>==-=-⨯⋅，则直线PA 与平面PBC 11419．（1）圆222x y r +=与直线380x -=相切，∴圆心O 到直线的距离为22841(3)d r -==+-，∴圆O 的方程为：2216x y +=．若直线l 的斜率不存在，直线l 为2x =-，此时直线l 截圆所得弦长为43若直线l 的斜率存在，设直线l 为：()62y k x =+，则有2226431621k ⎛⎫⎛⎫+=⎪ ⎪⎪ ⎪+⎭⎝⎭，解得：612k =此时直线l 为26100x +-=，则所求的直线l 为2x =-或26100x +-=．（2）证明：由题意知，()40M ，，设直线MA ：()14y k x =-，与圆方程联立得：()122416y k x x y ⎧=⋅-⎨+=⎩，消去y 得：()()2222111181610k x k x k +-+-=，()21211611M A k x x k -∴=+，()2121411A k x k -∴=+，12181A k y k -=+，因为123k k ⋅=-，用13k -换掉1k 得到B 点坐标，21213649B k x k -∴=+，121249B k y k =+，则()1122111222111221124891434136491AB k k k k k k k k k k k +++==----++，∴直线AB 的方程为21112221118444131k k k y x k k k ⎛⎫-+=- ⎪+-+⎝⎭，整理得：()121423k y x k =--，则直线AB 恒过定点为()20，．20．（1）由题意知22222191,41,2,a b c a a b c ⎧+=⎪⎪⎪=⎨⎪=+⎪⎪⎩解得2,1,a b c =⎧⎪=⎨⎪=⎩故椭圆C 的方程为22143x y +=.（2）证明：设()00,M x y ，()11,A x y ，()22,B x y ，由于A ，B 为椭圆C 上的点，所以2211143x y +=，2222143x y +=，两式相减得()()()()1212121243x x x x y y y y +-+-=-，所以()()120121*********x x x y y k x x y y y +-==-=--+.又00k y x =，故134k k =-，为定值.21．（1）抛物线C 的方程为28y x =，准线方程为2x =-；（2）存在直线1)y x =+或1)3y x =-+．【详解】（1）因为横坐标为1的点到焦点的距离为3,所以132p +=,解得4p =,所以28y x =，即准线方程为2x =-.（2）显然直线l 的斜率存在,设直线l 的方程为(1)y k x =+(0)k ≠,1122(,),(,)A x y B x y .联立得28(1)y x y k x ⎧=⎨=+⎩，消去y 得2222(28)0k x k x k +-+=.由224(28)40k k ∆=-->,解得k <.所以k <且0k ≠.由韦达定理得212282k x x k -+=,121=x x .直线BF 的方程为22(2)2y y x x =--,又1D x =-,所以2232D y y x -=-,所以223(1,)2y D x ---,因为//DE AF ,所以直线DE 与直线AF 的斜率相等又(4,3)E k --,所以221133232y k x y x -+-=--.整理得121222y y k x x =+--,即1212(1)(1)22k x k x k x x ++=+--,化简得121211122x x x x ++=+--,121212122()412()4x x x x x x x x -+-=-++,即12+7x x =.所以2282=7k k -,整理得289k =,解得3k =±.经检验,3k =±符合题意.所以存在这样的直线l ,直线l的方程为1)y x =+或1)y x =+．22．（1）2214x y +=；（2）是，()T .（1）由△12F PF3450x y -+=相切.∴121221PF F S c b b ⎧=⋅⋅=⎪⎪⎨⎪==⎪⎩，解得1b =，c =2a =，则椭圆C 的方程是2214x y +=.（2）以线段PQ 为直径的圆过x 轴上的定点.法一：当直线l 斜率不存在时，以PQ 为直径的圆的方程为：223x y +=，恒过定点()0.当直线l 斜率存在时，设()1y k x =-，()0k ≠.由()22114y k x x y ⎧=-⎪⎨+=⎪⎩得：()2222148440k x k x k +-+-=.设()11,A x y ，()22,B x y ，则有2122814k x x k +=+，21224414k x x k -=+.又M 是椭圆C 的右顶点，则()2,0M .由题意知：直线AM 为()1122y y x x =--，故11(0,22y x P --.直线BM 为：()2222y y x x =--，故2220,2y Q x ⎛⎫- ⎪-⎝⎭.若以PQ 为直径的圆过x 轴上的定点()0,0N x ，则等价于0PN QN ⋅=恒成立.又1012,2y PN x x ⎛⎫= ⎪-⎝⎭，2022,2y QN x x ⎛⎫= ⎪-⎝⎭，∴21201222022y y PN QN x x x ⋅=+⋅=--恒成立.又()()()2221212122224484222424141414k k k x x x x x x k k k ---=-++=-⨯+=+++()()()222221212121222244831111141414k k k y y k x k x k x x x x k k k k ⎛⎫--=--=-++=-+= ⎪+++⎝⎭.∴()()22222120002122124143042214k y y k x x x k x x k -++=+=-=--+，解得0x =故以PQ 为直径的圆过x轴上的定点()0.法二：设1x my =+，代入2214x y +=得()224230m y my ++-=.12224m y y m +=-+，12234y y m =-+直线AM ：()1122y y x x =--，令0x =得11112221y y y x my --==+-，即1120,1y P my ⎛⎫- ⎪-⎝⎭，同理得2220,1y Q my ⎛⎫- ⎪-⎝⎭设以线段PQ 为直径的圆过x 轴上的定点(),0T t ，有PT QT ⊥，即0PT QT ⋅=，则()21221212401y y t m y y m y y +=-++，将12y y +、12y y 代入得230t -=，t =()T .。

一、选择题1．如图，,,,A B C D 是平面上的任意四点，下列式子中正确的是（ ）A ．AB CD BC DA +=+ B ．AC BD BC AD +=+ C ．AC DB DC BA +=+D ．AB DA AC DB +=+2．已知,a b 是单位向量，且,a b 的夹角为3π，若向量c 满足22c a b -+=，则||c 的最大值为（ ） A ．23 B ．23C 72D 723．已知1sin()62πθ-=，且02πθ⎛⎫∈ ⎪⎝⎭，，则cos()3πθ-=( ) A ．0B ．12C ．1D 34．平面直角坐标系xOy 中，点()00,P x y 在单位圆O 上，设xOP α∠=，若3,44ππα⎛⎫∈ ⎪⎝⎭，且3sin 45πα⎛⎫+= ⎪⎝⎭，则0x 的值为( )A 3B 2C ．2D ．35．若将函数1()cos 22f x x =的图像向左平移6π个单位长度，则平移后图像的一个对称中心可以为（ ） A ．(,0)12πB ．(,0)6πC ．(,0)3πD ．(,0)2π6．已知关于x 的方程22cos cos 2sin 02Cx x A B -+=的两根之和等于两根之积的一半，则ABC 一定是( ) A ．直角三角形B ．等腰三角形C ．钝角三角形D ．等边三角形7．在三角形ABC 中,,CA a CB b ==，点P 在直线AB 上,且2AP PB =，则CP 可用,a b 表示为（ ）A ．2CP a b =+B ．CP a b =-C ．12CP a b =- D ．1233CP a b =+ 8．已知2tan θ＝ ，则222sin sin cos cos θθθθ＋－ 等于( ) A ．－43B ．－65C ．45D ．959．已知角α的终边经过点()2,1P -，则sin cos sin cos αααα-=+（ ）A ．4-B ．3-C ．12D ．3410．下列函数中，最小正周期为π且图象关于原点对称的函数是（ ） A ．cos 22y x π⎛⎫=+⎪⎝⎭B ．sin 22y x π⎛⎫=+⎪⎝⎭C ．sin2cos2y x x =+D ．sin cos y x x =+11．若O 为ABC ∆所在平面内一点，()()20OB OC OB OC OA -⋅+-=，则ABC ∆形状是（ ）． A ．等腰三角形 B ．直角三角形 C ．正三角形D ．以上答案均错12．已知函数()sin f x x x =，将函数()f x 的图象向左平移()0m m >个单位长度后，所得到的图象关于y 轴对称，则m 的最小值是（ ） A ．6πB ．4π C ．3π D ．2π13．已知sin α=，则44sin cos αα-的值为 A ．35B ．15-C ．15D ．3514．设sin1+=43πθ（），则sin 2θ=（ ） A ．79-B ．19-C ．19D ．7915．设0002012tan15cos 22,,21tan 15a b c ===+，则有（ ） A ．c a b <<B ．a b c <<C ．b c a <<D ．a c b <<二、填空题16．已知|a|=1，()b=13，，()b a a -⊥，则向量a 与向量b 的夹角为_______________. 17．函数()1sin cos 533f x x x ππ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭的最大值为________________.18．已知函数()cos()5f x x π=-的对称轴方程为__________．19．设向量(2,1)a =，(1,1)b =-，若a b -与ma b +垂直，则m 的值为_____ 20．设向量()sin ,2m θ=，()1,cos n θ=-，且m n ⊥，则tan 4πθ⎛⎫- ⎪⎝⎭的值为__________． 21．若()1sin 3πα-=，且2παπ≤≤，则cos α的值为__________． 22．已知向量a b ，均为单位向量，a 与b 夹角为3π，则|2|a b -=__________．23．若将函数sin y x x =的图象向右平移()0ϕϕ>个单位长度得到函数sin y x x =-的图象，则ϕ的最小值为________________.24．设G 是ABC ∆的重心（即三条中线的交点），AB a =，AC b =，试用a 、b 表示AG =________.25．已知1tan 2α=，则2(sin cos )cos 2ααα+=____________ .三、解答题26．在ABC ∆中，角,,A B C 的对边分别为,,a b c ，S 为ABC ∆的面积，若2cos 0S A =．（1）求cos A ；（2）若3a b c =-=，求,b c 的值．27．已知ABC ∆的三个内角A ，B ，C 的对边分别为a ，b ，c ，函数()()2sin cos sin f x x A x A =-+，且当512x π=时，()f x 取最大值. （1）若关于x 的方程()f x t =，0,2x π⎛⎫∈ ⎪⎝⎭有解，求实数t 的取值范围；（2）若5a =，且sin sin 5B C +=，求ABC ∆的面积. 28．如图，在ABC ∆中， 3B π∠=， 8AB =，点D 在BC 边上，且2CD =，1cos 7ADC ∠=. （1）求sin BAD ∠； （2）求,BD AC 的长.29．已知向量()1,3a =，(1,3b =-. （1）若a λb +与a b λ-垂直，求实数λ的值；（2）若对任意的实数m ，都有ma nb a b +≥+，求实数n 的取值范围； （3）设非零向量(,)c xa yb x y R =+∈，求x c的最大值.30．在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，已知向量(sin ,sin sin )A B C =-m ，n =(3,)a b b c +，且m n ⊥．（1）求角C 的值；（2）若ABC 为锐角三角形，且1c =3a b -的取值范围．【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题 1．B 2．B 3．C 4．C 5．A 6．B 7．D8．D9．B10．A11．A12．A13．A14．A15．A二、填空题16．【解析】【分析】由条件利用两个向量垂直的性质两个向量的数量积的定义求得向量与向量的夹角的余弦值可得向量与向量的夹角的值【详解】由题意可得即为向量与向量的夹角）求得故答案为【点睛】本题主要考查向量的模17．【解析】【分析】先利用两角和与差的正弦余弦公式将函数的解析式展开合并同类项后利用辅助角公式进行化简即可得出函数的最大值【详解】其中因此函数的最大值为故答案为【点睛】本题考查三角函数的最值解题的关键就18．【解析】分析：令解出即可详解：函数对称轴方程为故答案为：点睛：考查了余弦函数的图像的性质》19．【解析】与垂直20．【解析】分析：先根据向量垂直得再根据两角差正切公式求解详解：因为所以因此点睛：向量平行：向量垂直：向量加减：21．【解析】由题意得22．【解析】【分析】【详解】由已知得到向量的数量积为所以所以故答案为23．【解析】将函数的图象向右平移个单位长度后得到的图象而所以可得故答案为24．【解析】【分析】延长交于点利用重心的性质得出以及中线向量可求出的表达式【详解】延长交于点则点为线段的中点由平面向量加法的平行四边形法则可知则为的重心因此故答案为【点睛】本题考查向量的基底分解解题的关25．3【解析】【分析】由题意首先展开三角函数式然后结合同角三角函数基本关系转化为的式子最后求解三角函数式的值即可【详解】由题意可得：【点睛】本题主要考查三角函数式的化简求值问题三角函数齐次式的计算同角三三、解答题26．27．28．29．30．2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1．B解析：B【解析】【分析】用不同的方法表示出同一向量，然后对式子进行化简验证．【详解】=-，DC BC BD=-，DC AC AD∴AC AD BC BD-=-，∴AC BD BC AD+=+．故选：B．【点睛】本题主要考查了平面向量的加减法及其几何意义，属于容易题．2．B解析：B【解析】不妨设(1,0)a =，13(,22b =，(,)c x y =，则2(,c a b x y -+=+，所以22(2c a b x -+=+=，即22(4x y +=，点(,)x y 在以(0,为圆心，2为半径的圆上，所以2c x =+2+．故选B ．3．C解析：C 【解析】 【分析】解法一：由题意求出θ的值，然后代入求出结果；解法二：由两角差的余弦公式求出结果 【详解】 解法一：由π1sin 62θ⎛⎫-= ⎪⎝⎭，且π0,2θ⎛⎫∈ ⎪⎝⎭得，π3θ=，代入πcos 3θ⎛⎫- ⎪⎝⎭得， πcos 3θ⎛⎫- ⎪⎝⎭=cos01=，故选C ．解法二：由π1sin 62θ⎛⎫-= ⎪⎝⎭，且π0,2θ⎛⎫∈ ⎪⎝⎭得，πcos 62θ⎛⎫-= ⎪⎝⎭， 所以πππππππcos cos cos cos sin sin 13666666θθθθ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-=--=-+-= ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦，故选C ． 【点睛】本题考查了运用两角差的余弦公式来求出三角函数值，较为基础4．C解析：C 【解析】 【分析】利用两角和差的余弦公式以及三角函数的定义进行求解即可． 【详解】3,44ππα⎛⎫∈⎪⎝⎭， ,42ππαπ⎛⎫∴+∈ ⎪⎝⎭， 3sin 45πα⎛⎫+= ⎪⎝⎭，4cos 45πα⎛⎫∴+=- ⎪⎝⎭，则0cos cos cos cos sin sin 444444x ππππππαααα⎡⎤⎛⎫⎛⎫⎛⎫==+-=+++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦43525210=-⨯+⨯=-， 故选C ． 【点睛】本题主要考查两角和差的三角公式的应用，结合三角函数的定义是解决本题的关键．5．A解析：A 【解析】 【分析】 通过平移得到1cos(2)23y x π=+，即可求得函数的对称中心的坐标，得到答案. 【详解】向左平移6π个单位长度后得到1cos 223y x π⎛⎫=+ ⎪⎝⎭的图像，则其对称中心为(),0122k k Z ππ⎛⎫+∈ ⎪⎝⎭,或将选项进行逐个验证,选A. 【点睛】本题主要考查了三角函数的图象变换，以及三角函数的图象与性质的应用，其中解答中根据三角函数的图象变换，以及熟记三角函数的图象与性质是解答的关键，着重考查了推理与运算能力.6．B解析：B 【解析】分析：根据题意利用韦达定理列出关系式，利用两角和与差的余弦函数公式化简得到A=B ，即可确定出三角形形状． 详解：设已知方程的两根分别为x 1，x 2， 根据韦达定理得：x 1+x 2=cosAcosB ，x 1x 2=2sin 22C=1﹣cosC ， ∵x 1+x 2=12x 1x 2， ∴2cosAcosB=1﹣cosC ， ∵A+B+C=π，∴cosC=﹣cos （A+B ）=﹣cosAcosB+sinAsinB ， ∴cosAcosB+sinAsinB=1，即cos （A ﹣B ）=1， ∴A ﹣B=0，即A=B ， ∴△ABC 为等腰三角形． 故选B ．点睛：此题考查了三角形的形状判断，涉及的知识有：根与系数的关系，两角和与差的余弦函数公式，以及二倍角的余弦函数公式，熟练掌握公式是解本题的关键．解析：D 【解析】 【分析】利用向量三角形法则得到：1212++3333CP CA CB a b ==得到答案. 【详解】利用向量三角形法则得到：221212++()++333333CP CA AP CA AB CA CB CA CA CB a b =+==-==故选：D 【点睛】本题考查了向量的表示，也可以利用平行四边形法则得到答案.8．D解析：D 【解析】 ∵tanθ＝2，∴原式＝22222sin sin cos cos sin cos θθθθθθ＋－＋＝22211tan tan tan θθθ+－＋＝82141＋－＋＝95. 本题选择D 选项.点睛：关于sin α，cos α的齐次式，往往化为关于tan α的式子．9．B解析：B 【解析】 【分析】根据角的终边上一点的坐标，求得tan α的值，对所求表达式分子分母同时除以cos α，转化为只含tan α的形式，由此求得表达式的值. 【详解】依题意可知1tan 2α=-，11sin cos tan 1231sin sin tan 112αααααα----===-++-+．故选B. 【点睛】本小题主要考查三角函数的定义，考查齐次方程的计算，属于基础题. 10．A解析：A 【解析】 【分析】求出函数的周期，函数的奇偶性，判断求解即可．解：y ＝cos （2x 2π+）＝﹣sin2x ，是奇函数，函数的周期为：π，满足题意，所以A 正确 y ＝sin （2x 2π+）＝cos2x ，函数是偶函数，周期为：π，不满足题意，所以B 不正确；y ＝sin2x +cos2x =（2x 4π+），函数是非奇非偶函数，周期为π，所以C 不正确；y ＝sin x +cos x =（x 4π+），函数是非奇非偶函数，周期为2π，所以D 不正确；故选A ．考点：三角函数的性质. 11．A 解析：A 【解析】 【分析】根据向量的减法运算可化简已知等式为()0CB AB AC ⋅+=，从而得到三角形的中线和底边垂直，从而得到三角形形状. 【详解】()()()20OB OC OB OC OA CB AB AC -⋅+-=⋅+= ()CB AB AC ∴⊥+∴三角形的中线和底边垂直 ABC ∆∴是等腰三角形本题正确选项：A 【点睛】本题考查求解三角形形状的问题，关键是能够通过向量的线性运算得到数量积关系，根据数量积为零求得垂直关系.12．A解析：A 【解析】 【分析】利用函数的平移变换得π2sin 3y x m ⎛⎫=++ ⎪⎝⎭，再根所图象关于y 轴对称，得到角的终边落在y 轴上，即π2π3πm k +=+，k Z ∈，即可得答案. 【详解】()sin 2s πin 3f x x x x ⎛⎫=+=+ ⎪⎝⎭，将函数()f x 的图象向左平移m 个单位长度后，得到函数π2sin 3y x m ⎛⎫=++⎪⎝⎭的图象，又所得到的图象关于y 轴对称，所以π2π3πm k +=+，k Z ∈， 即ππ6m k =+，k Z ∈， 又0m >，所以当0k =时，m 的最小值为π6. 故选：A. 【点睛】本题考查三角函图象的变换、偶函数的性质，考查函数与方程思想、转化与化归思想，考查逻辑推理能力和运算求解能力.13．A解析：A 【解析】44sin cos αα-()()2222sin cos sin cos αααα=-+22sin cos αα=-22sin 1α=-35=-，故选A.点睛：已知一个角的某一个三角函数值，便可运用基本关系式求出其它三角函数值．在求值中，确定角的终边位置是关键和必要的，用平方差公式分解要求的算式，两个因式中一部分用同角的三角函数关系整理，另一部分把余弦变为正弦，代入题目的条件，得到结论.14．A解析：A 【解析】 试题分析：，两边平方后得，整理为，即，故选A.考点：三角函数15．A解析：A 【解析】 【分析】利用两角差的正弦公式化简a ，分子分母同乘以2cos 15结合二倍角的正弦公式化简b ，利用降幂公式化简c ，从而可得结果. 【详解】()sin 302sin28a =︒-︒=︒ ，222sin15cos15sin 30cos 15cos 15b ==+sin28a >=sin25sin28,c a b a c ==︒<︒=∴>>，故选A.【点睛】本题主要考查二倍角的正弦公式、二倍角的余弦公式，两角差的正弦公式，意在考查综合运用所学知识解答问题的能力，属于中档题.二、填空题16．【解析】【分析】由条件利用两个向量垂直的性质两个向量的数量积的定义求得向量与向量的夹角的余弦值可得向量与向量的夹角的值【详解】由题意可得即为向量与向量的夹角）求得故答案为【点睛】本题主要考查向量的模解析：3π【解析】 【分析】由条件利用两个向量垂直的性质,两个向量的数量积的定义，求得向量a 与向量b 的夹角的余弦值,可得向量a 与向量b 的夹角的值. 【详解】由题意可得()1,132,0a b b a a ==+=-⋅=，即2a b a ⋅=,12cos 1(θθ∴⨯⨯=为向量a 与向量b 的夹角），求得1cos ,23πθθ=∴=，故答案为3π.【点睛】本题主要考查向量的模、夹角及平面向量数量积公式，属于中档题.平面向量数量积公式有两种形式，一是cos a b a b θ⋅=，二是1212a b x x y y ⋅=+，主要应用以下几个方面:(1)求向量的夹角， cos a b a bθ=（此时a b 往往用坐标形式求解）；（2）求投影，a 在b上的投影是a b b⋅；（3）,a b 向量垂直则0a b ⋅=;(4)求向量ma nb + 的模（平方后需求a b ⋅）.17．【解析】【分析】先利用两角和与差的正弦余弦公式将函数的解析式展开合并同类项后利用辅助角公式进行化简即可得出函数的最大值【详解】其中因此函数的最大值为故答案为【点睛】本题考查三角函数的最值解题的关键就.【解析】 【分析】先利用两角和与差的正弦、余弦公式将函数()y f x =的解析式展开，合并同类项后利用辅助角公式进行化简，即可得出函数()y f x =的最大值. 【详解】()1111sin cos sin cos cos 53352222f x x x x x x x ππ⎛⎫⎛⎫⎛⎫⎛⎫=++-=+++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭()x x x ϕ==+，其中tan ϕ==，因此，函数()y f x =，.【点睛】本题考查三角函数的最值，解题的关键就是利用三角恒等变换思想将三角函数解析式进行化简，同时也考查了三角函数的基本性质，考查计算能力和转化思想，属于中等题.18．【解析】分析：令解出即可详解：函数对称轴方程为故答案为：点睛：考查了余弦函数的图像的性质》 解析：ππ,5x k k z =+∈【解析】 分析：令=,5x k k z ππ-∈，解出即可.详解：函数()cos 5f x x π⎛⎫=- ⎪⎝⎭，对称轴方程为=,5x k k z ππ-∈，,5x k k z ππ=+∈故答案为：ππ,5x k k z =+∈. 点睛：考查了余弦函数的图像的性质》19．【解析】与垂直 解析：14【解析】a b -与ma b +垂直1()()0(1,2)(21,1)0212204a b ma b m m m m m ⇒-⋅+=⇒⋅+-=⇒++-=⇒=20．【解析】分析：先根据向量垂直得再根据两角差正切公式求解详解：因为所以因此点睛：向量平行：向量垂直：向量加减：解析：13【解析】分析：先根据向量垂直得sin 2cos 0θθ-= ，再根据两角差正切公式求解.详解：因为m n ⊥ ，所以=0m n ⋅,sin 2cos 0tan 2,θθθ-==，因此tan 1211tan().41tan 123πθθθ---===++点睛：向量平行：1221//a y b x y x ⇒=，向量垂直：121200a b x x y y ⋅=⇒+=，向量加减： 1212(,).a b x x y y ±=±±21．【解析】由题意得 解析：223-【解析】由题意得()1122sin sin ,[,],cos 1.3293ππαααπα-==∈∴=--=- 22．【解析】【分析】【详解】由已知得到向量的数量积为所以所以故答案为 解析：3【解析】 【分析】 【详解】由已知得到向量a ，b 的数量积为1cos 32a b π⋅==，所以222|2|444213a b a a b b -=-⋅+=-+=，所以23a b -=，故答案为3.23．【解析】将函数的图象向右平移个单位长度后得到的图象而所以可得故答案为 解析：【解析】32cos cos 2333y sinx x sinx xsin sin x πππ⎛⎫⎛⎫=+=+=+ ⎪ ⎪⎝⎭⎝⎭ ，将函数的图象向右平移()0ϕϕ> 个单位长度后，得到()2233y sin x sin x ππϕϕ⎡⎤⎛⎫=-+=+- ⎪⎢⎥⎣⎦⎝⎭的图象，而sin y x x =-2sin 3x π⎛⎫=- ⎪⎝⎭，所以，33ππϕ-=- ，可得23ϕπ=，故答案为23π. 24．【解析】【分析】延长交于点利用重心的性质得出以及中线向量可求出的表达式【详解】延长交于点则点为线段的中点由平面向量加法的平行四边形法则可知则为的重心因此故答案为【点睛】本题考查向量的基底分解解题的关解析：1133a b +. 【解析】 【分析】延长AG 交BC 于点D ，利用重心的性质得出23AG AD =以及中线向量 ()12AD AB AC =+可求出AG 的表达式. 【详解】 延长AG 交BC 于点D ，则点D 为线段BC 的中点，由平面向量加法的平行四边形法则可知2AD AB AC a b =+=+，则1122AD a b =+， G 为ABC ∆的重心，因此，221111332233AG AD a b a b ⎛⎫==⨯+=+ ⎪⎝⎭， 故答案为1133a b +. 【点睛】本题考查向量的基底分解，解题的关键就是三角形重心的性质和中线向量的应用，考查分析问题和解决问题的能力，属于中等题.25．3【解析】【分析】由题意首先展开三角函数式然后结合同角三角函数基本关系转化为的式子最后求解三角函数式的值即可【详解】由题意可得：【点睛】本题主要考查三角函数式的化简求值问题三角函数齐次式的计算同角三解析：3 【解析】 【分析】由题意首先展开三角函数式，然后结合同角三角函数基本关系转化为tan α的式子，最后求解三角函数式的值即可. 【详解】由题意可得：22222(sin cos )sin 2sin cos cos cos 2cos sin ααααααααα+++=-22tan 2tan 11tan ααα++=-1114114++=-3=.【点睛】本题主要考查三角函数式的化简求值问题，三角函数齐次式的计算，同角三角函数基本关系等知识，意在考查学生的转化能力和计算求解能力.三、解答题 26． （1）12-；（2）52b c =⎧⎨=⎩ 【解析】【试题分析】（1）利用三角形的面积公式化简题目所给等式可求得A 的大小，进而求得cos A 的值.（2）结合（1）用A 的余弦定理，化简得出10bc =，结合3b c -=可求出,b c 点的值.【试题解析】（1）由1sin 2S bc A =有sin cos 0bc A A =，得tan A = 由0A π<<可得23A π=，故21cos cos32A π==-． （2）由余弦定理有：22222cos3a b c bc π=+-，得2239b c bc ++=，即()2339b c bc -+=，可得10bc =，由510b c bc -=⎧⎨=⎩，解得：52b c =⎧⎨=⎩．27．（1）(,1]2-；（2. 【解析】 【分析】（1）利用两角和差的正弦公式整理()f x 可得：()sin(2)A f x x =-，再利用已知可得：522122A k πππ⨯-=+（k Z ∈），结合已知可得：3A π=，求得：(0,)2x π∈时，sin(2)123x π-<-≤，问题得解.（2）利用正弦定理可得：sin sin )10+=+B C b c ，结合sin sin 5B C +=可得：8+=b c ，对a 边利用余弦定理可得：2222cos a b c bc A =+-，结合已知整理得：13=bc ，再利用三角形面积公式计算得解.【详解】解：（1）()2sin()cos sin f x x A x A =-+2sin()cos sin[()]x A x x x A =-+--2sin()cos sin cos()cos sin()x A x x x A x x A =-+--- sin cos()cos sin()x x A x x A =-+-sin(2)x A =-.因为()f x 在512x π=处取得最大值， 所以522122A k πππ⨯-=+，k Z ∈, 即2,3A k k Z ππ=-+∈. 因为(0,)A π∈，所以3A π=，所以()sin(2)3f x x π=-.因为(0,)2x π∈，所以22(,)333x πππ-∈-所以sin(2)13x π<-≤，因为关于x 的方程()f x t =有解，所以t 的取值范围为(2-．（2）因为5a =，3A π=，由正弦定理sin sin sin b c a B C A ==于是sin sin )+=+B C b c ．又sin sin B C +=，所以8+=b c . 由余弦定理得：2222cos a b c bc A =+-，整理得：2225=+-b c bc ，即225()3643=+-=-b c bc bc ， 所以13=bc ，所以1sin 2ABC S bc A ∆== 【点睛】本题主要考查了两角和、差的正弦公式应用，还考查了三角函数的性质及方程与函数的关系，还考查了正弦定理、余弦定理的应用及三角形面积公式，考查计算能力及转化能力，属于中档题．28．（12）7. 【解析】试题分析：（I ）在ABD ∆中，利用外角的性质，得()sin sin BAD ADC B ∠=∠-∠即可计算结果；（II ）由正弦定理，计算得3BD =，在ABC ∆中，由余弦定理，即可计算结果．试题解析：（I ）在ADC ∆中，∵1cos 7ADC ∠=，∴sin ADC ∠=∴()sin sin BAD ADC B ∠=∠-∠=（II ）在ABD ∆中，由正弦定理得：sin 3sin AB BADBD ADB⋅∠==∠在ABC ∆中，由余弦定理得：2222cos 49AC AB BC AB BC B =+-⋅⋅= ∴7AC =考点：正弦定理与余弦定理．29．（1）1λ=±（2）2n ≤-或2n ≥（3）3【解析】 【分析】（1）由向量垂直的坐标运算即可得解；（2）由向量模的运算可得2230m mn m ++-≥对任意实数m 都成立，再结合判别式()22430n n ∆=--≤求解即可；（3）由向量模的运算可得2222222224442x x x c x xy y x a xya b y b ⎛⎫== ⎪ ⎪+++⋅+⎝⎭，再分别讨论当0x =时，当0x ≠时，求解即可. 【详解】解：（1）由向量()1,3a =，(1,3b =-. 则2a b ==由a b λ+与a b λ-垂直，得()()0a b a b λλ+⋅-=， 即2220a b λ-=，从而2440λ-=，解得1λ=±；（2）由ma nb a b +≥+，将222222m a mna b n b a b +⋅+≥+， 即2244412m mn n ++≥，从而2230m mn m ++-≥对任意实数m 都成立， 于是()22430n n ∆=--≤，解得2n ≤-或2n ≥；（3）当0x =时，0x c=；当0x ≠时，2222222224442x x x c x xy y x a xya b y b ⎛⎫== ⎪ ⎪+++⋅+⎝⎭22111444432y y y x x x ==⎛⎫⎛⎫++++ ⎪ ⎪⎝⎭⎝⎭，故当12y x =-时，||||x c 有最大值综上可得||||x c有最大值3. 【点睛】本题考查了向量垂直的坐标运算，重点考查了向量模的运算，属中档题.30．（1）6C π=；（2）【解析】 【分析】（1）根据()sin ()(sin sin )0m n a A b c B C ⋅=-++-=和正弦定理余弦定理求得6C π=.(2)先利用正弦定理求出R=1,b -化成2sin()6A π-，再利用三角函数的图像和性质求解. 【详解】（1）因为m n ⊥，所以()sin ()(sin sin )0m n aA b cBC ⋅=-++-=，由正弦定理化角为边可得2220a b c +-=， 即222a b c +-=，由余弦定理可得cos C =，又0C π<<，所以6C π=．（2）由（1）可得56A Bπ+=，设ABC 的外接圆的半径为R ，因为6C π=，1c =，所以122sin sin30c R C ===︒， 则52sin 2sin 2sin )2sin()]6b R A R B R A B R A A π-=-=-=--= 2sin()2sin()66R A A ππ-=-，因为ABC 为锐角三角形，所以025062A A πππ⎧<<⎪⎪⎨⎪<-<⎪⎩，即32A ππ<<，所以663A πππ<-<，所以1sin()262A π<-<，所以12sin()6A π<-<b -的取值范围为．【点睛】(1)本题主要考查正弦定理余弦定理解三角形，考查三角函数的图像和性质，意在考查学生对这些知识的掌握水平和分析推理能力.(2) 对于复合函数的问题自然是利用复合函数的性质解答，求复合函数的最值，一般从复合函数的定义域入手，结合三角函数的图像一步一步地推出函数sin()y A wx h φ=++的最值.。

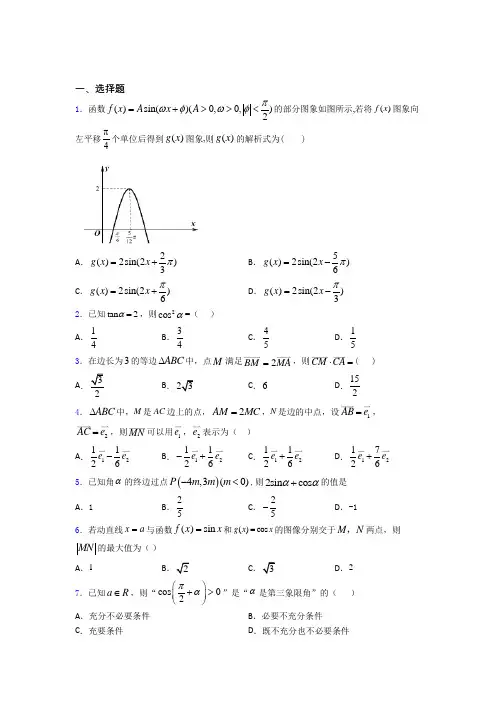
一、选择题1．函数()sin()(0,0,)2f x A x A πωφωφ=+>><的部分图象如图所示,若将()f x 图象向左平移4π个单位后得到()g x 图象,则()g x 的解析式为( )A ．2()2sin(2)3g x x π=+ B ．5()2sin(2)6g x x π=- C ．()2sin(2)6g x x π=+D ．()2sin(2)3g x x π=-2．已知tan 2α=，则2cos α=（ ） A ．14B ．34C ．45D ．153．在边长为3的等边ABC ∆中，点M 满足BM 2MA =，则CM CA ⋅=( ) A 3B ．3C ．6D ．1524．ABC ∆中，M 是AC 边上的点，2AM MC =，N 是边的中点，设1AB e =，2AC e =，则MN 可以用1e ，2e 表示为（ ）A ．121126e e - B ．121126e e -+ C ．121126e e + D ．121726e e + 5．已知角α的终边过点()4,3(0)P m m m -<,则2sin cos αα+的值是A ．1B ．25 C ．25- D ．-1 6．若动直线x a =与函数()sin f x x =和()cos g x x =的图像分别交于M N ，两点，则MN 的最大值为（ ）A ．1B 2C 3D ．27．已知a R ∈，则“cos 02πα⎛⎫+> ⎪⎝⎭”是“α是第三象限角”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件8．下列函数中，最小正周期为π且图象关于原点对称的函数是（ ） A ．cos 22y x π⎛⎫=+⎪⎝⎭B ．sin 22y x π⎛⎫=+⎪⎝⎭C ．sin2cos2y x x =+D ．sin cos y x x =+9．已知函数()2sin(2)(0)f x x ϕϕπ=+<<，若将函数()f x 的图象向右平移6π个单位后关于y 轴对称，则下列结论中不正确．．．的是 A ．56πϕ=B ．(,0)12π是()f x 图象的一个对称中心C ．()2f ϕ=-D ．6x π=-是()f x 图象的一条对称轴10．已知函数()()sin 0,0,2f x A x A πωϕωϕ=+>>≤⎛⎫⎪⎝⎭的部分图象如图所示，则函数()y f x =的表达式是（ ）A ．()2sin 12f x x π⎛⎫=+⎪⎝⎭ B ．()2sin 23f x x π⎛⎫=+ ⎪⎝⎭ C ．()22sin 23f x x π⎛⎫=- ⎪⎝⎭D ．()2sin 23f x x π⎛⎫=-⎪⎝⎭11．已知4sin 5α，并且α是第二象限的角，那么tan()απ+的值等于 A ．43-B ．34-C ．34D ．4312．已知函数2()3cos cos f x x x x =+，则（ ） A ．()f x 的图象关于直线6x π=对称B ．()f x 的最大值为2C ．()f x 的最小值为1-D ．()f x 的图象关于点(,0)12π-对称13．已知非零向量a ⃑ =(t,0),b ⃑ =(−1,√3)，若a ⃑ ⋅b ⃑ =−4，则a ⃑ +2b ⃑ 与b⃑ 的夹角（ ） A ．π3B ．π2C ．π6D ．2π314．设0002012tan15cos 2sin 2,,221tan 15a b c =-==+，则有（ ） A ．c a b <<B ．a b c <<C ．b c a <<D ．a c b <<15．已知函数()sin(2)3f x x π=+，将其图象向右平移(0)ϕϕ>个单位长度后得到函数()g x 的图象，若函数()g x 为偶函数，则ϕ的最小值为（ ）A ．12πB ．512π C ．6π D ．56π 二、填空题16．已知ABC ∆是顶点为A 腰长为2的等腰直角三角形，P 为平面ABC 内一点，则()PA PB PC ⋅+的最小值是__________．17．已知函数()sin()(,0,0,0)2f x A x x R A πωϕωϕ=+∈>><<的图象与x 轴的交点中，相邻两个交点之间的距离为2π，且图象上一个最低点为2(,2)3M π-.则()f x 的解析式为________．18．已知a ，b 是单位向量.若2a b b a +≥-，则向量a ，b 夹角的取值范围是_________.19．向量,a b 的夹角为60︒，且2,1a b ==则(2)a a b ⋅+=__________. 20．设向量(2,1)a =，(1,1)b =-，若a b -与ma b +垂直，则m 的值为_____ 21．在ABC ∆中，角,,A B C 所对的边分别为,,a b c ，1a =，3B π=，当ABC ∆的面积等tan C =__________．22．若向量(2,1)m =，(3,2)n λ=-，且(2)//(3)m n m n -+，则实数λ=__________． 23．已知0>ω，在函数sin y x ω=与cos y x ω=的图象的交点中，距离最短的两个交点，则ω值为__________．24．若将函数sin y x x =的图象向右平移()0ϕϕ>个单位长度得到函数sin y x x =-的图象，则ϕ的最小值为________________.25．在三角形ABC 所在平面内有一点H 满足222222HA BC HB CA HC AB +=+=+,则H 点是三角形ABC 的___________.三、解答题26．已知向量a 、b 的夹角为2,||1,||23a b π==.（1）求a ·b 的值（2）若2a b -和ta b +垂直，求实数t 的值.27．已知向量(1,2),(,1)a b x →→==（1）当(2)(2)a b a b +⊥-时,求x 的值；（2）若,a b <>为锐角,求x 的范围.28．已知平面上三个向量a ⃑ ,b ⃑ ,c ,的模均为1，它们相互之间的夹角均为1200．（I ）求证：(a ⃑ −b⃑ )⊥c ⃑ ； （II ）若|ka ⃑ +b ⃑ +c |>1 (k ∈R)，求k 的取值范围．29．已知数列{}n a 是公差不为零的等差数列，1a ＝1，且139,,a a a 成等比数列． (1)求数列{}n a 的通项；(2)设2n an b =，求数列{}n b 的前n 项和S n .30．已知(1,2)a =，(2,1)b =-，(2)m a t b =++，n ka tb =+（k ∈R ）. （1）若1t =，且m ∥n ，求k 的值； （2）若t ∈R ，且||5m n -≤，求k 的取值范围.【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题 1．C 2．D 3．D 4．A 5．C 6．B 7．B 8．A 9．C11．A12．A13．A14．A15．B二、填空题16．【解析】【分析】以所在直线为轴建立坐标系设运用向量的坐标运算和向量数量积的坐标表示得出关于的表达式配方即可得出结论【详解】以所在直线为轴以边上的高为轴建立坐标系是直角边为2的等腰直角三角形且为直角顶17．【解析】【分析】根据函数周期为求出再由图象的最低点得到振幅及【详解】因为图象与两个交点之间的距离为所以所以由于图象的最低点则所以当时因为所以故填：【点睛】本题考查正弦型函数的图象与性质考查数形结合思18．【解析】【分析】设向量的夹角为在不等式两边平方利用数量积的运算律和定义求出的取值范围于此可求出的取值范围【详解】设向量的夹角为两边平方得都是单位向量则有得因此向量的夹角的取值范围是故答案为【点睛】本19．6【解析】【分析】由题意利用向量的数量积的运算可得即可求解【详解】由题意可知向量的夹角为且则【点睛】本题主要考查了平面向量的数量积的运算其中解答中熟记平面向量的数量积的运算公式准确计算是解答的关键着20．【解析】与垂直21．【解析】由题意即则所以由余弦定理所以所以应填答案点睛：解答本题的思路是先借助三角形的面积公式求出边进而运用余弦定理求出边然后再运用余弦定理求出进而求出最后求出22．【解析】依题设由∥得解得23．【解析】由题意令则所以即当；当如图所示由勾股定理得解得24．【解析】将函数的图象向右平移个单位长度后得到的图象而所以可得故答案为25．垂心【解析】【分析】根据向量运算用表示出向量可得从而可得【详解】因为所以整理得即;同理可得所以可知为垂心【点睛】本题主要考查平面向量的运算三角形垂心的向量表示考查转化化归思想三、解答题27． 28． 29． 30．2016-2017年度第*次考试试卷 参考解析【参考解析】**科目模拟测试一、选择题 1．C 解析：C 【解析】 【分析】根据函数的图象求出函数()f x 的解析式，再根据图象的平移变换得到()g x 的解析式即可. 【详解】 由图象可知，A =2,541264T πππ=-=, 2T ππω∴==, 2ω∴=,又当512x π=时，52sin(2)212πφ⨯+=， 即5sin()16πφ+=， 2πφ<，3πφ∴=-，故()sin()f x x π=-223，将()f x 图象向左平移4π个单位后得到()g x ， ∴ ()2sin[2()]2sin(2)436g x x x πππ=+-=+，故选：C 【点睛】本题主要考查了正弦型函数的图象与性质，图象的变换，属于中档题.2．D解析：D 【解析】 【分析】根据同角三角函数的基本关系，由2222cos cos cos sin αααα=+，化为正切即可求解. 【详解】22222cos 1cos cos sin 1tan ααααα==++, 且tan 2α=，∴211cos 145α==+， 故选：D 【点睛】本题主要考查了同角三角函数的基本关系，弦化切的思想，属于中档题.3．D解析：D 【解析】 【分析】结合题意线性表示向量CM ，然后计算出结果 【详解】 依题意得：121211215)333333333232CM CA CB CA CA CB CA CA CA ⋅=+⋅=⋅+⋅=⨯⨯⨯+⨯⨯=（，故选D ．【点睛】本题考查了向量之间的线性表示，然后求向量点乘的结果，较为简单4．A解析：A【解析】 【分析】利用向量的线性运算求解即可. 【详解】由题, ()12111111322626MN MC CN AC AB AC AB AC e e =+=+-=-=-.故选：A 【点睛】本题主要考查了平面向量的线性运算,属于基础题型.5．C解析：C 【解析】因为角α的终边过点()4,3(0)P m m m -<，所以sin α=35-，4cos 5α=，所以2sin cos αα+=642555-+=-，故选C.6．B解析：B 【解析】 【分析】 【详解】 构造函数，根据辅助角公式，对函数的解析式进行化简，再根据正弦函数求出其最值，即可得到答案．则可知2()sin cos sin 4F x x x x π⎛⎫=-=- ⎪⎝⎭，F（x 2,故|MN|2,故选B7．B解析：B 【解析】 【分析】先化简“cos 02πα⎛⎫+> ⎪⎝⎭”，再利用充要条件的定义判断. 【详解】 因为cos 02πα⎛⎫+> ⎪⎝⎭，所以-sin 0,sin 0,ααα>∴<∴是第三、四象限和y 轴负半轴上的角.α是第三、四象限和y 轴负半轴上的角不能推出α是第三象限角，α是第三象限角一定能推出α是第三、四象限和y 轴负半轴上的角，所以“cos 02πα⎛⎫+>⎪⎝⎭”是“α是第三象限角”的必要非充分条件. 故答案为：B. 【点睛】(1)本题主要考查充要条件的判断和诱导公式，考查三角函数的值的符号，意在考查学生对这些知识的掌握水平和分析推理能力.(2) 判定充要条件常用的方法有定义法、集合法、转化法.8．A解析：A 【解析】 【分析】求出函数的周期，函数的奇偶性，判断求解即可． 【详解】 解：y ＝cos （2x 2π+）＝﹣sin2x ，是奇函数，函数的周期为：π，满足题意，所以A 正确 y ＝sin （2x 2π+）＝cos2x ，函数是偶函数，周期为：π，不满足题意，所以B 不正确；y ＝sin2x +cos2x =（2x 4π+），函数是非奇非偶函数，周期为π，所以C 不正确；y ＝sin x +cos x =（x 4π+），函数是非奇非偶函数，周期为2π，所以D 不正确；故选A ．考点：三角函数的性质. 9．C 解析：C 【解析】函数()()2sin 2f x x ϕ=+的图象向右平移6π个单位，可得()2sin 23g x x πϕ⎛⎫=-+ ⎪⎝⎭,() 2sin 23g x x πϕ⎛⎫=-+ ⎪⎝⎭的图象关于y 轴对称，所以32k ππϕπ-+=+, 0k =时可得5=6πϕ，故5()2sin(2)6f x x π=+，555()=2sin()2sin 2362f πππϕ+==，()2f ϕ=-不正确，故选C. 10．D解析：D 【解析】 【分析】根据函数的最值求得A ，根据函数的周期求得ω，根据函数图像上一点的坐标求得ϕ，由此求得函数的解析式. 【详解】由题图可知2A =，且11522122T πππ=-=即T π=，所以222T ππωπ===， 将点5,212π⎛⎫⎪⎝⎭的坐标代入函数()()2sin 2x x f ϕ=+， 得()5262k k ππϕπ+=+∈Z ，即()23k k πϕπ=-∈Z ， 因为2πϕ≤，所以3πϕ=-，所以函数()f x 的表达式为()2sin 23f x x π⎛⎫=- ⎪⎝⎭．故选D.【点睛】本小题主要考查根据三角函数图像求三角函数的解析式，属于基础题.11．A解析：A 【解析】 【分析】由诱导公式可得()tan tan παα+=，由角的正弦值和角所在的象限，求出角的余弦值，然后，正弦值除以余弦值得正切值．即可得到答案 【详解】 ∵4sin 5α=，并且α是第二象限的角，，35cos α∴-＝ ， ∴tanα＝43-，则么()4tan tan 3παα+==-. 故选A ． 【点睛】本题考查给值求值问题．掌握同角三角函数的基本关系式和诱导公式，并会运用它们进行简单的三角函数式的化简、求值及恒等式证明．12．A解析：A 【解析】 【分析】利用三角函数恒等变换的公式，化简求得函数的解析式，再根据三角函数的图象与性质，逐项判定，即可求解． 【详解】 由题意，函数2111()cos cos 2cos 2sin(2)22262f x x x x x x x π=+=++=++， 当6x π=时，113()sin(2)sin 6662222f ππππ=⨯++=+=，所以6x π=函数()f x 的对称轴，故A 正确；由sin(2)[1,1]6x π+∈-，所以函数()f x 的最大值为32，最小值为12-，所以B 、C 不正确；又由12x π=时，11()sin(2)6126222f πππ=⨯++=+，所以(,0)12π-不是函数()f x 的对称中心，故D 不正确， 故选A ． 【点睛】本题主要考查了三角恒等变换的公式的应用，以及函数sin()y A wx b ϕ=++的图象与性质的应用，着重考查了推理与运算能力，属于基础题．13．A解析：A 【解析】 【分析】根据条件容易求出t=4，从而得出a ⃑ =(4,0)，从而得出a ⃑ +2b ⃑ =(2,2√3)可设a ⃑ +2b ⃑ 与b⃑ 的夹角为θ，这样根据cosθ=(a ⃑ +2b ⃑ )·b ⃑ |a⃑ +2b ⃑ ||b ⃑ | 即可求出cosθ，进而得出θ的值．【详解】因a ⃑ ⋅b⃑ =−4=−t ∴t=4；∴a ⃑ =(4,0)，b ⃑ =(−1,√3)，a ⃑ +2b⃑ =(2,2√3) 设a ⃑ +2b ⃑ 与b ⃑ 的夹角为θ，则：cosθ=(a ⃑ +2b ⃑ )·b ⃑|a ⃑ +2b ⃑ ||b ⃑ |=-2+64×2=12，∴θ=π3 故答案为A ． 【点睛】本题主要考查向量的模及平面向量数量积公式、余弦定理的应用，属于中档题.平面向量数量积公式有两种形式，一是a ⃑ ⋅b ⃑ =|a ⃑ ||b ⃑ |cosθ，二是a ⃑ ⋅b ⃑ =x 1x 2+y 1y 2，主要应用以下几个方面:(1)求向量的夹角， cosθ=a⃑ ·b ⃑ |a⃑ |·|b ⃑ | （此时a⃑ ·b ⃑ 往往用坐标形式求解）；（2）求投影，a ⃑ 在b ⃑ 上的投影是a⃑ ⋅b ⃑ |b ⃑ |；（3）a ⃑ ,b ⃑ 向量垂直则a ⃑ ⋅b ⃑ =0;(4)求向量ma ⃑ +nb ⃑ 的模（平方后需求a ⃑ ⋅b ⃑ ）. 14．A解析：A 【解析】 【分析】利用两角差的正弦公式化简a ，分子分母同乘以2cos 15结合二倍角的正弦公式化简b ，利用降幂公式化简c ，从而可得结果. 【详解】()sin 302sin28a =︒-︒=︒ ，222sin15cos15sin 30cos 15cos 15b ==+sin28a >=sin25sin28,c a b a c ==︒<︒=∴>>，故选A.【点睛】本题主要考查二倍角的正弦公式、二倍角的余弦公式，两角差的正弦公式，意在考查综合运用所学知识解答问题的能力，属于中档题.15．B解析：B 【解析】 【分析】由平移变换得到()sin(22)3g x x πϕ=-+，由偶函数的性质得到sin(22)13x πϕ-+=±，从而求min 512πϕ=. 【详解】由题意得：()sin[2())]sin(22)33g x x x ππϕϕ=-+=-+， 因为()g x 为偶函数，所以函数()g x 的图象关于0x =对称，所以当0x =时，函数()g x 取得最大值或最小值，所以sin(2)13πϕ-+=±，所以2,32k k Z ππϕπ-+=+∈，解得：1,22k k Z ππϕ=--∈， 因为0ϕ>，所以当1k =-时，min 512πϕ=，故选B.【点睛】平移变换、伸缩变换都是针对自变量x 而言的，所以函数()f x 向右平移(0)ϕϕ>个单位长度后得到函数()g x ，不能错误地得到()sin (2)3g x x x πϕ=+-.二、填空题16．【解析】【分析】以所在直线为轴建立坐标系设运用向量的坐标运算和向量数量积的坐标表示得出关于的表达式配方即可得出结论【详解】以所在直线为轴以边上的高为轴建立坐标系是直角边为2的等腰直角三角形且为直角顶解析：1-【解析】 【分析】以BC 所在直线为x 轴建立坐标系，设P x y （，） ，运用向量的坐标运算和向量数量积的坐标表示，得出()PA PB PC ⋅+关于x y ， 的表达式，配方即可得出结论． 【详解】以BC 所在直线为x 轴，以BC 边上的高为y 轴建立坐标系，ABC ∆是直角边为2的等腰直角三角形，且A 为直角顶点，斜边22BC =，则022020A B C -（，），（，），（，），设P x y （，），则2222PB PC PO x y PA x y （，），（，），+==--=-∴()22222 2222221PA PB PC x y x y ⋅+=+-=+-（，∴当20x y ==，时，()PA PB PC ⋅+取得最小值-1． 故答案为：-1． 【点睛】本题考查了平面向量的数量积运算，运用坐标法解题是关键，属于中档题．17．【解析】【分析】根据函数周期为求出再由图象的最低点得到振幅及【详解】因为图象与两个交点之间的距离为所以所以由于图象的最低点则所以当时因为所以故填：【点睛】本题考查正弦型函数的图象与性质考查数形结合思解析：()2sin 26f x x π⎛⎫=+ ⎪⎝⎭【解析】 【分析】根据函数周期为π，求出2ω=，再由图象的最低点2(,2)3M π-，得到振幅2A =，及6π=ϕ.【详解】因为图象与x 两个交点之间的距离为2π，所以222T T ππππω=⇒=⇒=， 所以2ω=，由于图象的最低点2(,2)3M π-，则2A =， 所以()()2sin 2f x x ϕ=+，当23x π=时，4sin 13πϕ⎛⎫+=-⎪⎝⎭， 因为02πϕ<<，所以6π=ϕ，故填：()2sin 26f x x π⎛⎫=+ ⎪⎝⎭.【点睛】本题考查正弦型函数的图象与性质，考查数形结合思想的应用，注意02πϕ<<这一条件限制，从面得到ϕ值的唯一性.18．【解析】【分析】设向量的夹角为在不等式两边平方利用数量积的运算律和定义求出的取值范围于此可求出的取值范围【详解】设向量的夹角为两边平方得都是单位向量则有得因此向量的夹角的取值范围是故答案为【点睛】本解析：0,3π⎡⎤⎢⎥⎣⎦【解析】 【分析】设向量a 、b 的夹角为θ，在不等式2a b b a +≥-两边平方，利用数量积的运算律和定义求出cos θ的取值范围，于此可求出θ的取值范围． 【详解】设向量a 、b 的夹角为θ，2a b b a +≥-，两边平方得2222244a a b b a a b b +⋅+≥-⋅+，a 、b 都是单位向量，则有22cos 54cos θθ+≥-，得1cos 2θ≥， 0θπ≤≤，03πθ∴≤≤，因此，向量a 、b 的夹角的取值范围是0,3π⎡⎤⎢⎥⎣⎦， 故答案为0,3π⎡⎤⎢⎥⎣⎦．【点睛】本题考查平面数量积的运算，考查平面向量夹角的取值范围，在涉及平面向量模有关的计算时，常将等式或不等式进行平方，结合数量积的定义和运算律来进行计算，考查运算求解能力，属于中等题．19．6【解析】【分析】由题意利用向量的数量积的运算可得即可求解【详解】由题意可知向量的夹角为且则【点睛】本题主要考查了平面向量的数量积的运算其中解答中熟记平面向量的数量积的运算公式准确计算是解答的关键着解析：6 【解析】 【分析】由题意，利用向量的数量积的运算，可得2(2)2a a b a a b ⋅+=+⋅，即可求解.【详解】由题意，可知向量,a b 的夹角为060，且2,1a b ==则221(2)22cos60422162a ab a a b a a b ⋅+=+⋅=+⋅=+⨯⨯⨯=. 【点睛】本题主要考查了平面向量的数量积的运算，其中解答中熟记平面向量的数量积的运算公式，准确计算是解答的关键，着重考查了推理与运算能力.20．【解析】与垂直 解析：14【解析】a b -与ma b +垂直1()()0(1,2)(21,1)0212204a b ma b m m m m m ⇒-⋅+=⇒⋅+-=⇒++-=⇒=21．【解析】由题意即则所以由余弦定理所以所以应填答案点睛：解答本题的思路是先借助三角形的面积公式求出边进而运用余弦定理求出边然后再运用余弦定理求出进而求出最后求出解析：-【解析】由题意1sin 23ac π=4c =⇒=，则b ==，所以由余弦定理cosC ==sin C ==tan (C ==-- 点睛：解答本题的思路是先借助三角形的面积公式求出边4c =，进而运用余弦定理求出边1116214132b =+-⨯⨯⨯=，然后再运用余弦定理求出113161cos 211313C +-==-⨯⨯，进而求出112sin 11313C =-=，最后求出23tan (13)2313C =⨯-=-。

一、选择题1．在四边形ABCD 中，AB DC =，且AC ·BD ＝0，则四边形ABCD 是（ ）A ．菱形B ．矩形C ．直角梯形D ．等腰梯形2．化简12sin(2)cos(2)ππ+-⋅-得( ) A ．sin2cos2+ B ．cos2sin2- C ．sin2cos2- D ．cos2sin2±- 3．(1＋tan 17°)(1＋tan 28°)的值是( )A ．－1B ．0C ．1D ．24．平面向量(1,2)a =，(4,2)b =，c ma b =+（m R ∈），且c 与a 的夹角等于c 与b的夹角，则m =（ ） A ．2-B ．1-C ．1D ．25．已知函数()()π2cos 332f x x ϕϕ⎛⎫=++≤ ⎪⎝⎭，若ππ,612x ⎛⎫∀∈- ⎪⎝⎭，()f x 的图象恒在直线3y =的上方，则ϕ的取值范围是( ) A ．ππ,122⎛⎫⎪⎝⎭B ．ππ,63⎡⎤⎢⎥⎣⎦C ．π0,4⎡⎤⎢⎥⎣⎦D ．ππ,63⎛⎫-⎪⎝⎭6．将函数sin y x =图象上所有点的横坐标缩短到原来的12倍（纵坐标不变），再将所得图象上所有的点向左平移π4个单位长度，则所得图象对应的函数解析式为（ ） A ．sin(2)4y x π=+B ．sin()24x y π=+C ．cos 2x y =D ．cos 2y x =7．在锐角ABC 中，4sin 3cos 5,4cos 3sin 23A B A B +=+=，则角C 等于（ ）A ．150B ．120C ．60D ．308．若动直线x a =与函数()sin f x x =和()cos g x x =的图像分别交于M N ，两点，则MN 的最大值为（ ）A ．1B ．2C ．3D ．29．设奇函数()()()()sin 3cos 0f x x x ωφωφω=+-+>在[]1,1x ∈-内有9个零点，则ω的取值范围为( )A ．[)4,5ππ B ．[]4,5ππC ．11,54ππ⎡⎤⎢⎥⎣⎦D ．11,54ππ⎛⎤ ⎥⎝⎦10．在中，,,A B C ∠∠∠所对的边长分别是,,a b c ，若sin sin()sin 2C B A A +-=，则的形状为A ．等腰三角形B ．直角三角形C ．等腰直角三角形D ．等腰三角形或直角三角形11．下列函数中，最小正周期为π且图象关于原点对称的函数是（ ） A ．cos 22y x π⎛⎫=+⎪⎝⎭B ．sin 22y x π⎛⎫=+⎪⎝⎭C ．sin2cos2y x x =+D ．sin cos y x x =+12．已知函数()()sin 0,0,,2f x A x A x R πωϕωϕ⎛⎫=+>><∈ ⎪⎝⎭在一个周期内的图象如图所示.则()y f x =的图象，可由函数cos y x =的图象怎样变换而来（纵坐标不变）（ ）A ．先把各点的横坐标缩短到原来的12倍，再向左平移6π个单位B ．先把各点的横坐标缩短到原来的12倍，再向右平移12π个单位C ．先把各点的横坐标伸长到原来的2倍，再向左平移6π个单位 D ．先把各点的横坐标伸长到原来的2倍，再向右平移12π个单位13．已知函数()()sin 0,0,2f x A x A πωϕωϕ=+>>≤⎛⎫⎪⎝⎭的部分图象如图所示，则函数()y f x =的表达式是（ ）A ．()2sin 12f x x π⎛⎫=+⎪⎝⎭ B ．()2sin 23f x x π⎛⎫=+ ⎪⎝⎭C ．()22sin 23f x x π⎛⎫=- ⎪⎝⎭D ．()2sin 23f x x π⎛⎫=-⎪⎝⎭14．若02πα<<，02πβ-<<，1cos 43πα⎛⎫+= ⎪⎝⎭，3cos 423πβ⎛⎫-= ⎪⎝⎭，则cos 2βα⎛⎫+ ⎪⎝⎭等于（ ）A ．33B ．33-C ．539D ．69-15．如图，在ABC ∆中，23AD AC =，13BP BD =，若AP AB AC λμ=+，则=λμ( )A ．3-B ．3C ．2D ．2-二、填空题16．已知平面向量,,a b c 满足21a b a ⋅==，1b c -=，则a c ⋅的最大值是____． 17．已知C 是以AB 为直径的半圆弧上的动点，O 为圆心，P 为OC 中点，若4AB =，则()PA PB PC +⋅=__________．18．把单位向量OA 绕起点O 逆时针旋转120︒，再把模扩大为原来的3倍，得到向量OB ，点C 在线段AB 上，若12AC CB =，则OC BA ⋅的值为__________．19．将函数()2sin(2)6f x x π=-的图象向左平移(0)φφ>个单位，若所得到图象关于原点对称，则φ的最小值为__________．20．已知角θ的终边上的一点P 的坐标为()3,4，则cos 21sin 2θθ=+________________．21．将函数e x y =的图像上所有点的横坐标变为原来的一半，再向右平移2个单位，所得函数的解析式为__________． 22．已知()1sin 3x y +=，()sin 1x y -=，则tan 2tan x y +=__________． 23．为得到函数2y sin x =的图象,要将函数24y sin x π⎛⎫=+ ⎪⎝⎭的图象向右平移至少__________个单位.24．已知()1tan 2αβ+=，()tan 1αβ-=-，则sin 2sin 2αβ的值为__________．25．若将函数sin 3cos y x x =+的图象向右平移()0ϕϕ>个单位长度得到函数sin 3cos y x x =-的图象，则ϕ的最小值为________________.三、解答题26．已知函数π()sin()(0,0,)2f x A x B A ωϕωϕ=++>><的部分图象如图所示：（I ）求()f x 的解析式及对称中心坐标； （Ⅱ）将()f x 的图象向右平移6π个单位,再将横坐标伸长到原来的2倍,纵坐标不变,最后将图象向上平移1个单位,得到函数()g x 的图象,求函数()y g x =在7π0,6x ⎡⎤∈⎢⎥⎣⎦上的单调区间及最值．27．已知向量32a i j b i j =-=+，，其中,i j 是互相垂直的单位向量. (1) 求向量a 在向量b 方向上的投影；(2) 设向量,m a b n a b λ=-=+，若m n ⊥，求实数λ的值. 28．已知()1,2a =，()3,2b =-.（1）当k 为何值时，ka b +与3a b -垂直？ （2）当k 为何值时，ka b +与3a b -平行？29．在ABC ∆中，角A 、B 、C 所对的边分别为a 、b 、c ．且满足sin 33B B =1a =.（1）求角B 的大小；（2）若2b ac =，求ABC ∆的面积．30．如图，某污水处理厂要在一个矩形污水处理池ABCD 的池底水平铺设污水净化管道（Rt FHE ∆三条边，H 是直角顶点）来处理污水，管道越长，污水净化效果越好.要求管道的接口H 是AB 的中点，,E F 分别落在线段,BC AD 上，已知20AB =米，103AD =BHE θ∠=.∆的周长）表示为θ的函数，并求出定义(1)试将污水净化管道的总长度L（即Rt FHE域；(2)问θ取何值时，污水净化效果最好？并求出此时管道的总长度.【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、选择题1．A2．C3．D4．D5．C6．D7．D8．B9．A10．D11．A12．B13．D15．B二、填空题16．2【解析】【分析】根据已知条件可设出的坐标设利用向量数量积的坐标表示即求的最大值根据可得出的轨迹方程从而求出最大值【详解】设点是以为圆心1为半径的圆的最大值是2故填：2【点睛】本题考查了向量数量积的17．【解析】【分析】先用中点公式的向量式求出再用数量积的定义求出的值【详解】【点睛】本题主要考查向量中的中点公式应用以及数量积的定义18．【解析】【分析】由题意可得与夹角为先求得则再利用平面向量数量积的运算法则求解即可【详解】单位向量绕起点逆时针旋转再把模扩大为原来的3倍得到向量所以与夹角为因为所以所以故答案为【点睛】本题主要考查平面19．【解析】分析：先根据图像平移得解析式再根据图像性质求关系式解得最小值详解：因为函数的图象向左平移个单位得所以因为所以点睛：三角函数的图象变换提倡先平移后伸缩但先伸缩后平移也常出现在题目中所以也必须熟20．【解析】分析：由角的终边上的一点的坐标为求出的值利用将的值代入即可得结果详解：角的终边上的一点的坐标为那么故答案为点睛：本题主要考查三角函数的定义及二倍角的正弦公式与余弦公式属于中档题给值求值问题求21．【解析】分析：根据图像平移规律确定函数解析式详解：点睛：三角函数的图象变换提倡先平移后伸缩但先伸缩后平移也常出现在题目中所以也必须熟练掌握无论是哪种变形切记每一个变换总是对字母而言22．0【解析】分析：利用和差角的正弦公式可求及的值可得详解：联立可解得故即答案为0点睛：本题综合考查了三角函数公式灵活运用和差角公式和同角三角函数基本关系式是解题的关键属于中档题23．【解析】函数的解析式：则要将函数的图象向右平移至少个单位点睛：由y＝sinx的图象利用图象变换作函数y＝Asin(ωx＋φ)(A＞0ω＞0)(x∈R)的图象要特别注意：当周期变换和相位变换的先后顺序24．【解析】∵(α+β)+(α−β)=2α(α+β)−(α−β)=2β∴====故答案为：点睛：三角函数式的化简要遵循三看原则:一看角这是重要一环通过看角之间的差别与联系把角进行合理的拆分从而正确使用公25．【解析】将函数的图象向右平移个单位长度后得到的图象而所以可得故答案为三、解答题26．28．29．30．2016-2017年度第*次考试试卷参考解析【参考解析】**科目模拟测试一、选择题1．A解析：A【解析】【分析】由AB DC=可得四边形为平行四边形，由AC·BD＝0得四边形的对角线垂直，故可得四边形为菱形．【详解】∵AB DC=，∴AB与DC平行且相等，∴四边形ABCD为平行四边形．又0⋅=，AC BD⊥，∴AC BD即平行四边形ABCD的对角线互相垂直，∴平行四边形ABCD为菱形．故选A．【点睛】本题考查向量相等和向量数量积的的应用，解题的关键是正确理解有关的概念，属于基础题．2．C解析：C 【解析】 【分析】先利用诱导公式化简角，然后利用正弦的二倍角公式和完全平方式结合角在各个象限中的符号化简即可得到答案. 【详解】==，∵22ππ<<，∴sin2cos20->.∴原式sin2cos2=-. 故选C. 【点睛】本题考查诱导公式和二倍角公式以及三角函数在各个象限中的符号的应用，属于基础题.3．D解析：D 【解析】()()1tan171tan28++00000000001tan17tan 28tan17tan 281tan(1728)(1tan17tan 28)tan17tan 28=+++=++-+000001tan 45(1tan17tan 28)tan17tan 282=+-+=，选D.点睛：应用三角公式解决问题的三个变换角度(1)变角：目的是沟通题设条件与结论中所涉及的角，其手法通常是“配凑”.(2)变名：通过变换函数名称达到减少函数种类的目的，其手法通常有“切化弦”、“升幂与降幂”等.(3)变式：根据式子的结构特征进行变形，使其更贴近某个公式或某个期待的目标，其手法通常有：“常值代换”、“逆用变用公式”、“通分约分”、“分解与组合”、“配方与平方”等.4．D解析：D 【解析】 【分析】 【详解】()()4,22,422258c m m a c m m m =++⋅=+++=+,()()44222820b c m m m ⋅=+++=+,5,20a b ===c 与a 的夹角等于c 与b 的夹角 ,c a c b c a c b ⋅⋅=⋅⋅,=,解得2m =, 故选D. 【考点定位】向量的夹角及向量的坐标运算.5．C解析：C 【解析】分析：根据函数()f x 的解析式，利用x 的取值范围，结合题意求出ϕ的取值范围． 详解：函数函数()()π2cos 332f x x ϕϕ⎛⎫=++≤⎪⎝⎭，ππ,612x ⎛⎫∈- ⎪⎝⎭时，324x ππϕϕϕ+∈-++（，），又()f x 的图象恒在直线3y =的上方，2223333042cos x cos x ππϕϕϕππϕ⎧-+≥-⎪⎪∴++∴+∴⎨⎪+≤⎪⎩（）＞，（）＞，， 解得04πϕ≤≤；∴ϕ的取值范围是π0,4⎡⎤⎢⎥⎣⎦．故选C ．点睛：本题考查了三角函数的图象与性质的应用问题，是基础题．6．D解析：D 【解析】 【分析】由正弦函数的周期变换以及平移变换即可得出正确答案. 【详解】函数sin y x =图象上所有点的横坐标缩短到原来的12倍（纵坐标不变）得到sin 2y x =，再将所得图象上所有的点向左平移π4个单位长度，得到sin 2sin 2cos 242y x x x ππ⎛⎫⎛⎫=+=+= ⎪ ⎪⎝⎭⎝⎭故选：D 【点睛】本题主要考查了正弦函数的周期变换以及平移变换，属于中档题.7．D解析：D 【解析】 【分析】由题：()()224sin 3cos 25,4cos 3sin 12A B A B +=+=，两式相加即可求出sin()A B +，进而求出A B +，角C 得解.【详解】由题：()()224sin 3cos 25,4cos 3sin 12A B A B +=+=，2216sin 24sin cos 9cos 25A A B B ++=，2216cos 24cos sin 9sin 12A A B B ++=，两式相加得：()1624sin cos cos sin 937A B A B +++=，1sin()2A B +=，所以1sin sin(())2C A B π=-+=，且C 为锐角， 所以30C =. 故选：D 【点睛】此题考查同角三角函数基本关系与三角恒等变换综合应用，考查对基本公式的掌握和常见问题的处理方法.8．B解析：B 【解析】 【分析】 【详解】 构造函数，根据辅助角公式，对函数的解析式进行化简，再根据正弦函数求出其最值，即可得到答案．则可知2()sin cos sin 4F x x x x π⎛⎫=-=- ⎪⎝⎭，F（x 2,故|MN|2,故选B9．A解析：A 【解析】f （x ）=sin （ωx+φ3（ωx+φ）=2[12sin （ωx+φ）﹣32cos （ωx+φ）]=2[cos3πsin （ωx+φ）﹣sin 3πcos （ωx+φ）]=2sin （ωx+φ﹣3π） ∵函数f （x ）为奇函数，∴f （0）=2sin （φ﹣3π）=0，∴φ=3π+kπ，k ∈Z ∴f （x ）=2sin （ωx+kπ），f （x ）=0即sin （ωx+kπ）=0，ωx+kπ=mπ，m ∈Z ，解得，x=()m k πω-，设n=m ﹣k ，则n ∈Z ，∵A ∈[﹣1，1]，∴﹣1≤x≤1,[]1,1n πω∈-，∴n ωωππ-≤≤, ∵A ∈[﹣1，1]中有9个元素,4545.ωπωππ∴≤<⇒≤< 故答案为A.点睛：函数的零点或方程的根的问题，一般以含参数的三次式、分式、以e 为底的指数式或对数式及三角函数式结构的函数零点或方程根的形式出现，一般有下列两种考查形式：(1)确定函数零点、图象交点及方程根的个数问题；(2)应用函数零点、图象交点及方程解的存在情况，求参数的值或取值范围问题．研究方程根的情况，可以通过导数研究函数的单调性、最值、函数的变化趋势等，根据题目要求，通过数形结合的思想去分析问题，可以使得问题的求解有一个清晰、直观的整体展现.同时在解题过程中要注意转化与化归、函数与方程、分类讨论思想的应用．10．D解析：D 【解析】试题分析：由sinC ＋sin(B －A)＝sin2A再注意到：，所以有，故知△ABC 是等腰三角形或直角三角形，故选D. 考点：三角恒等变形公式.11．A解析：A 【解析】 【分析】求出函数的周期，函数的奇偶性，判断求解即可． 【详解】 解：y ＝cos （2x 2π+）＝﹣sin2x ，是奇函数，函数的周期为：π，满足题意，所以A 正确 y ＝sin （2x 2π+）＝cos2x ，函数是偶函数，周期为：π，不满足题意，所以B 不正确；y ＝sin2x +cos2x =（2x 4π+），函数是非奇非偶函数，周期为π，所以C 不正确；y ＝sin x +cos x =（x 4π+），函数是非奇非偶函数，周期为2π，所以D 不正确； 故选A ．考点：三角函数的性质.12．B解析：B 【解析】 【分析】根据图象可知1A =，根据周期为π知=2ω，过点(,1)12π求得3πϕ=，函数解析式()sin(2)3f x x π=+，比较解析式cos sin()2y x x π==+，根据图像变换规律即可求解.【详解】由()()sin 0,0,,2f x A x A x R πωϕωϕ⎛⎫=+>><∈ ⎪⎝⎭在一个周期内的图象可得1A =,11244126T πππω=⋅=+，解得=2ω，图象过点(,1)12π，代入解析式得1sin(2)12πϕ=⨯+，因为2πϕ<，所以3πϕ=，故()sin(2)3f x x π=+，因为cos sin()2y x x π==+，将函数图象上点的横坐标变为原来的12得sin 22y x π⎛⎫=+ ⎪⎝⎭，再向右平移12π个单位得sin[2()]sin(2)()1223y x x f x πππ=-+=+=的图象，故选B. 【点睛】本题主要考查了由sin()y A x ωϕ=+部分图像求解析式，图象变换规律，属于中档题.13．D解析：D 【解析】 【分析】根据函数的最值求得A ，根据函数的周期求得ω，根据函数图像上一点的坐标求得ϕ，由此求得函数的解析式. 【详解】由题图可知2A =，且11522122T πππ=-=即T π=，所以222T ππωπ===，将点5,212π⎛⎫⎪⎝⎭的坐标代入函数()()2sin 2x x f ϕ=+， 得()5262k k ππϕπ+=+∈Z ，即()23k k πϕπ=-∈Z ， 因为2πϕ≤，所以3πϕ=-，所以函数()f x 的表达式为()2sin 23f x x π⎛⎫=- ⎪⎝⎭．故选D. 【点睛】本小题主要考查根据三角函数图像求三角函数的解析式，属于基础题.14．C解析：C 【解析】 【分析】利用同角三角函数的基本关系求出sin 4πα⎛⎫+ ⎪⎝⎭与sin 42πβ⎛⎫-⎪⎝⎭，然后利用两角差的余弦公式求出cos cos 2442βππβαα⎡⎤⎛⎫⎛⎫⎛⎫+=+-- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦值． 【详解】02πα<<，3444πππα∴<+<，则sin 43πα⎛⎫+== ⎪⎝⎭，02πβ-<<，则4422ππβπ<-<，所以，sin 423πβ⎛⎫-==⎪⎝⎭， 因此，cos cos 2442βππβαα⎡⎤⎛⎫⎛⎫⎛⎫+=+-- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦1cos cos sin sin 44244233339ππβππβαα⎛⎫⎛⎫⎛⎫⎛⎫=+-++-=+⋅=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭， 故选C ． 【点睛】本题考查利用两角和的余弦公式求值，解决这类求值问题需要注意以下两点： ①利用同角三角平方关系求值时，要求对象角的范围，确定所求值的正负； ②利用已知角来配凑未知角，然后利用合适的公式求解．15．B解析：B 【解析】 ∵21,33AD AC BP BD =∴=121()393AD AB AC AB -=-∴2239AP AB BP AB AC =+=+ 又AP AB AC λμ=+，∴22,,339λλμμ=== 故选B.二、填空题16．2【解析】【分析】根据已知条件可设出的坐标设利用向量数量积的坐标表示即求的最大值根据可得出的轨迹方程从而求出最大值【详解】设点是以为圆心1为半径的圆的最大值是2故填：2【点睛】本题考查了向量数量积的 解析：2 【解析】 【分析】根据已知条件可设出,,a b c 的坐标，设()1,0a =，()1,b k =，(),c x y =，利用向量数量积的坐标表示a c x ⋅=，即求x 的最大值，根据1b c -=，可得出(),x y 的轨迹方程，从而求出最大值. 【详解】设()1,0a =，()1,b k =，(),c x y =()1,b c x k y -=-- ，1b c -=()()2211x y k ∴-+-=，∴点(),x y 是以()1,k 为圆心，1为半径的圆，02x ≤≤，a c x ⋅=，02x ≤≤a c ∴⋅的最大值是2. 故填：2. 【点睛】本题考查了向量数量积的应用，以及轨迹方程的综合考查，属于中档题型，本题的关键是根据条件设出坐标，转化为轨迹问题.17．【解析】【分析】先用中点公式的向量式求出再用数量积的定义求出的值【详解】【点睛】本题主要考查向量中的中点公式应用以及数量积的定义 解析：2-【解析】 【分析】先用中点公式的向量式求出PA PB +，再用数量积的定义求出()PA PB PC +⋅的值． 【详解】2PA PB PO +=，()2211cos1802PA PB PC PO PC ο∴+⋅=⋅=⨯⨯⨯=-【点睛】本题主要考查向量中的中点公式应用以及数量积的定义．18．【解析】【分析】由题意可得与夹角为先求得则再利用平面向量数量积的运算法则求解即可【详解】单位向量绕起点逆时针旋转再把模扩大为原来的3倍得到向量所以与夹角为因为所以所以故答案为【点睛】本题主要考查平面 解析：116-【解析】 【分析】由题意可得3OB =，OA 与OB 夹角为120︒，先求得1(2)3OC OA AC OA OB =+=+，则1(2)()3OC BA OA OB OA OB ⋅=+⋅-，再利用平面向量数量积的运算法则求解即可. 【详解】单位向量OA 绕起点O 逆时针旋转120︒，再把模扩大为原来的3倍，得到向量OB ， 所以3OB =，OA 与OB 夹角为120︒， 因为12AC CB =，所以111()(2)333OC OA AC OA AB OA OB OA OA OB =+=+=+-=+，所以()2211(2)()233OC BA OA OB OA OB OA OB OA OB ⋅=+⋅-=--⋅ 11291332⎡⎤⎛⎫=--⨯⨯- ⎪⎢⎥⎝⎭⎣⎦116=-，故答案为116-. 【点睛】 本题主要考查平面向量几何运算法则以及平面向量数量积的运算，属于中档题. 向量的运算有两种方法：（１）平行四边形法则（平行四边形的对角线分别是两向量的和与差；（２）三角形法则（两箭头间向量是差，箭头与箭尾间向量是和）．19．【解析】分析：先根据图像平移得解析式再根据图像性质求关系式解得最小值详解：因为函数的图象向左平移个单位得所以因为所以点睛：三角函数的图象变换提倡先平移后伸缩但先伸缩后平移也常出现在题目中所以也必须熟 解析：12π【解析】分析：先根据图像平移得解析式，再根据图像性质求φ关系式，解得最小值. 详解：因为函数()2sin 26f x x π⎛⎫=-⎪⎝⎭的图象向左平移(0)φφ>个单位得()2sin(2())6g x x πφ=+-，所以2()()6122k k k Z k Z πππφπφ-=∈∴=+∈因为0φ>，所以min .12πφ=点睛：三角函数的图象变换，提倡“先平移，后伸缩”，但“先伸缩，后平移”也常出现在题目中，所以也必须熟练掌握.无论是哪种变形，切记每一个变换总是对字母x 而言.20．【解析】分析：由角的终边上的一点的坐标为求出的值利用将的值代入即可得结果详解：角的终边上的一点的坐标为那么故答案为点睛：本题主要考查三角函数的定义及二倍角的正弦公式与余弦公式属于中档题给值求值问题求解析：17-【解析】分析：由角θ的终边上的一点P 的坐标为()3,4，求出,cos sin θθ的值，利用2cos 212sin 1212cos sin sin θθθθθ-=++，将,cos sin θθ的值代入即可得结果. 详解：角θ的终边上的一点P 的坐标为()3,4，43,cos 55y x sin r r θθ∴====， 那么216712cos 212sin 1252543491212cos 7125525sin sin θθθθθ-⨯--====-+++⨯⨯，故答案为17-. 点睛：本题主要考查三角函数的定义及二倍角的正弦公式与余弦公式，属于中档题.给值求值问题，求值时要注意：(1)观察角，分析角与角之间的差异以及角与角之间的和、差、倍的关系，巧用诱导公式或拆分技巧；(2)观察名，尽可能使三角函数统一名称；(3)观察结构，以便合理利用公式，整体化简求值.21．【解析】分析：根据图像平移规律确定函数解析式详解：点睛：三角函数的图象变换提倡先平移后伸缩但先伸缩后平移也常出现在题目中所以也必须熟练掌握无论是哪种变形切记每一个变换总是对字母而言 解析：24e x y -=【解析】分析：根据图像平移规律确定函数解析式. 详解：222(2)24e ee e xxx x y y y --=→=→==横坐标变为一半右移个单位点睛：三角函数的图象变换，提倡“先平移，后伸缩”，但“先伸缩，后平移”也常出现在题目中，所以也必须熟练掌握.无论是哪种变形，切记每一个变换总是对字母x 而言.22．0【解析】分析：利用和差角的正弦公式可求及的值可得详解：联立可解得故即答案为0点睛：本题综合考查了三角函数公式灵活运用和差角公式和同角三角函数基本关系式是解题的关键属于中档题解析：0 【解析】分析：利用和差角的正弦公式，可求sin cos x y 及cos sin x y 的值，可得tan 2.tan xy=- 详解：()1sin sin cos cos sin ,3x y x y x y +=+=()sin sin cos cos sin 1,x y x y x y -=-= 联立可解得21sin cos ,cos sin ,33x y x y ==-sin cos tan 2.cos sin tan x y x x y y∴==- 故tan 2tan 0.x y += 即答案为0.点睛：本题综合考查了三角函数公式，灵活运用和差角公式和同角三角函数基本关系式是解题的关键，属于中档题．23．【解析】函数的解析式：则要将函数的图象向右平移至少个单位点睛：由y ＝sinx 的图象利用图象变换作函数y ＝Asin(ωx＋φ)(A＞0ω＞0)(x∈R)的图象要特别注意：当周期变换和相位变换的先后顺序解析：8π 【解析】 函数的解析式：sin 2sin 248y x x ππ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭. 则要将函数24y sin x π⎛⎫=+ ⎪⎝⎭的图象向右平移至少8π个单位. 点睛：由y ＝sin x 的图象，利用图象变换作函数y ＝A sin(ωx ＋φ)(A ＞0，ω＞0)(x ∈R)的图象，要特别注意：当周期变换和相位变换的先后顺序不同时，原图象沿x 轴的伸缩量的区别．先平移变换再周期变换(伸缩变换)，平移的量是|φ|个单位；而先周期变换(伸缩变换)再平移变换，平移的量是ϕω个单位． 24．【解析】∵(α+β)+(α−β)=2α(α+β)−(α−β)=2β∴====故答案为：点睛：三角函数式的化简要遵循三看原则:一看角这是重要一环通过看角之间的差别与联系把角进行合理的拆分从而正确使用公解析：13-∵()1tan 2αβ+=，()tan 1αβ-=-， (α+β)+(α−β)=2α,(α+β)−(α−β)=2β，∴sin2sin2αβ=()()()()sin αβαβsin αβαβ⎡⎤++-⎣⎦⎡⎤+--⎣⎦=()()()()()()()()sin αβcos αβcos αβsin αβsin cos cos sin αβαβαβαβ+-++-+--+- =()()()()tan αβtan αβtan tan αβαβ++-+-- =13-.故答案为：13-.点睛：三角函数式的化简要遵循“三看”原则:一看角，这是重要一环，通过看角之间的差别与联系，把角进行合理的拆分，从而正确使用公式 ；二看函数名称，看函数名称之间的差异，从而确定使用的公式，常见的有切化弦；三看结构特征，分析结构特征，可以帮助我们找到变形的方向，如遇到分式要通分等.25．【解析】将函数的图象向右平移个单位长度后得到的图象而所以可得故答案为 解析：【解析】32cos cos 2333y sinx x sinx xsin sin x πππ⎛⎫⎛⎫=+=+=+ ⎪ ⎪⎝⎭⎝⎭ ，将函数的图象向右平移()0ϕϕ> 个单位长度后，得到()2233y sin x sin x ππϕϕ⎡⎤⎛⎫=-+=+- ⎪⎢⎥⎣⎦⎝⎭的图象，而sin 3cos y x x =-2sin 3x π⎛⎫=- ⎪⎝⎭，所以，33ππϕ-=- ，可得23ϕπ= ，故答案为23π.三、解答题 26．(Ⅰ) ()2sin(2)13f x x π=+-；对称中心的坐标为,126k ππ⎛⎫--⎪⎝⎭(k Z ∈) (Ⅱ)见解析 【解析】 【分析】（I ）先根据图像得到函数的最大值和最小值，由此列方程组求得,A B 的值，根据周期求得ω的值，根据图像上()112f π=求得ϕ的值，由此求得()f x 的解析式，进而求得()f x 的对称中心.（II ）求得图像变换之后的解析式()2sing x x =，通过求出()g x 的单调区间求得()g x 在区间7π0,6⎡⎤⎢⎥⎣⎦上的最大值和最小值.解：（I ）由图像可知：13A B A B +=⎧⎨-+=-⎩,可得：2,1A B ==-又由于721212T ππ=-,可得：T π=,所以22T πω==由图像知()112f π=,sin(2)112πϕ⨯+=,又因为2363πππϕ-<+<所以2122ππϕ⨯+=,3πϕ=.所以()2sin(2)13f x x π=+-令23x k ππ+=(k Z ∈),得：26k x ππ=-(k Z ∈) 所以()f x 的对称中心的坐标为,126k ππ⎛⎫--⎪⎝⎭(k Z ∈) （II ）由已知的图像变换过程可得：()2sin g x x = 由()2sin g x x =的图像知函数在7π0,6x ⎡⎤∈⎢⎥⎣⎦上的单调增区间为0,2π⎡⎤⎢⎥⎣⎦, 单调减区间7,26ππ⎡⎤⎢⎥⎣⎦当2x π=时,()g x 取得最大值2；当76x π=时,()g x 取得最小值1-． 【点睛】本小题主要考查根据三角函数图像求三角函数解析式，考查三角函数对称中心的求法，考查三角函数图像变换，考查三角函数的单调性和最值的求法，属于中档题.27．（12）0λ= 【解析】 【分析】（1）根据题中条件，结合向量投影的概念，即可得出结果； （2）根据m n ⊥，得到()()0a b a b λ-⋅+=，得出220λλ+⋅-⋅-=aa b a b b ，进而求解，即可得出结果. 【详解】（1）因为32,=-=+a i j b i j ，,i j 是互相垂直的单位向量， 所以()()32615⋅=-+=-=a b i ji j ，()23391===--+a i j i j ()2224=+=+=+=b i j i j所以向量a 在向量b 方向上的投影为5cos ,5⋅<>===a b a a b b（2）因为,m a b n a b λ=-=+，m n ⊥， 则()()0a b a b λ-⋅+=，即220λλ+⋅-⋅-=aa b a b b ，即105550λλ+--=，解得0λ=. 【点睛】本题主要考查求向量的投影，以及由向量垂直求参数，熟记向量数量积的运算法则即可，属于常考题型.28．（1）19k =（2）13k =- 【解析】 【分析】（1）由向量垂直的坐标公式得k 的方程，求解即可； （2）由向量平行的坐标公式得k 的方程，求解即可； 【详解】（1）()13221a b ⋅=⋅-+⋅=，()()3ka b a b +⋅-()22133238=0ka k a b b k =+-⋅-=-, 故19k =（2）因为()=3,22ka b k k +-+，()3=104a b --，若ka b +与3a b -平行，则()()14310222483k k k k --=+⇒=-∴=-【点睛】本题考查向量垂直与平行的坐标运算，是基础题29．（1）3π；（2）4. 【解析】 【分析】（1）由辅助角公式得出sin 32B π⎛⎫+= ⎪⎝⎭，结合角B 的取值范围可得出角B 的值； （2）由余弦定理结合条件2b ac =，可得出a c =，由此可知ABC ∆为等边三角形，再利用三角形的面积公式可求出ABC ∆的面积. 【详解】（1）由sin B B =2sin 3B π⎛⎫+= ⎪⎝⎭，sin 2B ∴=， 由()0,B π∈得4,333B πππ⎛⎫+∈ ⎪⎝⎭，故233B ππ+=，3B π∴=； （2）由2b ac =， 由余弦定理得22222222co 2s3cos a c b a c a ac c c a c a B π=+-⋅=+=--+⋅， 故22ac a c ac =+-，得()20a c -=，故ABC ∆为正三角形，1a c ∴==，因此，ABC ∆的面积为211sin 122ABC S ac B ∆==⨯=. 【点睛】本题考查利用三角恒等变换思想求角、以及余弦定理和三角形面积公式解三角形，解题时要根据三角形已知元素类型选择正弦定理或余弦定理解三角形，考查运算求解能力，属于中等题. 30．（1）sin θcos θ1L 10sin θcos θ++=⨯⋅，ππθ,.63⎡⎤∈⎢⎥⎣⎦； （2）πθ6=或πθ3=时，L 取得最大值为)201米．. 【解析】【分析】（1）解直角三角形求得得EH 、FH 、EF 的解析式，再由 L=EH +FH +EF 得到污水净化管道的长度L 的函数解析式，并注明θ的范围．（2）设sinθ+cosθ=t ，根据函数 L=201t - 在]上是单调减函数，可求得L 的最大值．所以当t =πθ6= 或πθ3= 时，L 取得最大值为)201米． 【详解】 ()1由题意可得10EH cos θ=，10FH sin θ=，10EF sin θcos θ=，由于 BE 10tan θ=≤10AF tan θ=≤，tan θ≤≤ππθ,63⎡⎤∈⎢⎥⎣⎦， 101010L cos θsin θsin θcos θ∴=++，ππθ,.63⎡⎤∈⎢⎥⎣⎦即sin θcos θ1L 10sin θcos θ++=⨯⋅，ππθ,.63⎡⎤∈⎢⎥⎣⎦()2设sin θcos θt +=，则2t 1sin θcos θ2-=，由于ππθ,63⎡⎤∈⎢⎥⎣⎦，π1sin θcos θt θ.42⎛⎫∴+==+∈ ⎪⎝⎭⎣由于20L t 1=-在⎣上是单调减函数，∴当t =πθ6=或πθ3=时，L 取得最大值为)201米．。

一、选择题1．(0分)[ID ：13327]在如图所示的算法框图中，若()321a x dx =-⎰，程序运行的结果S为二项式()52x +的展开式中3x 的系数的9倍，那么判断框中应填入的关于k 的判断条件是（ ）A ．3K <B ．3K >C ．2K <D ．2K >2．(0分)[ID ：13326]如图阴影部分为曲边梯形，其曲线对应函数为1xy e =-，在长方形内随机投掷一颗黄豆，则它落在阴影部分的概率是（ ）A ．23e - B ．13e - C ．43e- D ．53e- 3．(0分)[ID ：13311]我国古代数学著作《九章算术》中，其意是：“今有器中米，不知其数，前人取半，中人三分取一，后人四分取一，余米一斗五升．问：米几何？右图是源于其思想的一个程序框图，若输出的2S =（单位：升），则输入k 的值为A ．6B ．7C ．8D ．94．(0分)[ID ：13307]公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形面积可无限逼近圆的面积，并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14，这就是著名的“徽率”.小华同学利用刘徽的“割圆术”思想在半径为1的圆内作正n 边形求其面积，如图是其设计的一个程序框图，则框图中应填入、输出n 的值分别为（ ）（参考数据：020sin 200.3420,sin()0.11613≈≈）A ．01180sin ,242S n n =⨯⨯B ．01180sin ,182S n n =⨯⨯C ．01360sin ,542S n n=⨯⨯D ．01360sin ,182S n n=⨯⨯5．(0分)[ID ：13303]如果数据121x +、221x +、、21n x +的平均值为5，方差为16，则数据：153x -、253x -、、53n x -的平均值和方差分别为（ ）A ．1-，36B ．1-，41C ．1，72D ．10-，1446．(0分)[ID ：13298]若执行如图所示的程序框图，则输出S 的值为( )A．10072015B．10082017C．10092019D．101020217．(0分)[ID：13296]袋中装有红球3个、白球2个、黑球1个，从中随机摸出2个球，则与事件“至少有1个白球”互斥但不对立的事件是（）A．没有白球B．2个白球C．红、黑球各1个D．至少有1个红球8．(0分)[ID：13291]执行如图所示的程序框图，输出的S值为（）A．1B．-1C．0D．-29．(0分)[ID：13285]设A为定圆C圆周上一点，在圆周上等可能地任取一点与A连接，2倍的概率（）A．34B．35C．13D．1210．(0分)[ID：13276]在长为10cm的线段AB上任取一点C，作一矩形，邻边长分別等于线段AC、CB的长，则该矩形面积小于216cm的概率为（）A ．23B ．34C ．25D ．1311．(0分)[ID ：13257]我国古代数学著作《九章算术》中，有这样一道题目：“今有器中米，不知其数，前人取半，中人三分取一，后人四分取一，余米一斗五升.问：米几何？”下图是源于其思想的一个程序框图，若输出的3S =（单位：升），则输入的k =（ ）A ．9B ．10C ．11D ．1212．(0分)[ID ：13256]太极图是以黑白两个鱼形纹组成的图案，它形象化地表达了阴阳轮转、相反相成是万物生成变化根源的哲理，展现了一种相互转化、相对统一的形式美.按照太极图的构图方法，在平面直角坐标系中，圆O 被3sin6y x π=的图象分割为两个对称的鱼形图案，其中小圆的半径均为1，现在大圆内随机取一点，则此点取自阴影部分的概率为（ ）A ．136B ．118C ．112D ．1913．(0分)[ID ：13254]从0，1，2，3这四个数中任取两个不同的数组成一个两位数，则这个两位数是偶数的概率为（ ）A ．27 B ．57C ．29D ．5914．(0分)[ID ：13240]如图，在圆心角为直角的扇形OAB 中，分别以,OA OB 为直径作两个半圆，在扇形OAB 内随机取一点，则此点取自阴影部分的概率是（ ）A．21π-B．122π-C．2πD．1π15．(0分)[ID：13233]执行如图所示的程序框图，则输出s的值为（）A．10 B．17 C．19 D．36二、填空题16．(0分)[ID：13424]北京市某银行营业点在银行大厅悬挂着不同营业时间段服务窗口个数的提示牌，如图所示. 设某人到达银行的时间是随机的，记其到达银行时服务窗口的个数为X，则()E X=______________．17．(0分)[ID：13423]已知样本数据为40，42，40，a，43，44，且这个样本的平均数为43，则该样本的标准差为_________.18．(0分)[ID：13419]已知2件次品和3件正品放在一起，现需要通过检测将其区分，每次随机检测一件产品，检测后不放回，直到检测出2件次品或者检测出3件正品时检测结束，则恰好检测四次停止的概率为_____（用数字作答）．19．(0分)[ID：13411]如图，在半径为1的圆上随机地取两点,B E，连成一条弦BE，则∆边长的概率是__________．弦长超过圆内接正BCD20．(0分)[ID：13396]为调查某校学生每天用于课外阅读的时间，现从该校3000名学生中随机抽取100名学生进行问卷调查，所得数据均在区间[50,100]上，其频率分布直方图如图所示，则估计该校学生中每天用于阅读的时间在[70,80)(单位：分钟)内的学生人数为____．21．(0分)[ID：13392]如果执行如图的程序框图，那么输出的S=__________．22．(0分)[ID：13368]如图所示的程序框图，输出的S的值为()A ．12B ．2C ．1-D ．12-23．(0分)[ID ：13347]在区间[0,1]中随机地取出两个数，则两数之和大于45的概率是______.24．(0分)[ID ：13344]为了了解2100名学生早晨到校时间，计划采用系统抽样的方法从全体学生中抽取容量为100栋样本，则分段间隔为__________．25．(0分)[ID ：13337]已知AOB ∆中，60AOB ∠=，2OA =，5OB =，在线段OB 上任取一点C ，则AOC ∆为锐角三角形的概率_________．三、解答题26．(0分)[ID ：13524]从某居民区随机抽取10个家庭，获得第i 个家庭的月收入i x （单位：千元）与月储蓄i y ，（单位：千元）的数据资料，算出101010102111180,20184,720ii i i i i i i i xy x y x ========∑∑∑∑，，附：线性回归方程1221ˆˆˆˆˆˆ,,ni ii nii x y nxyybx a b ay bx xnx ==-=+==--∑∑，其中,x y 为样本平均值. （1）求家庭的月储蓄y 对月收入x 的线性回归方程ˆˆˆybx a =+ ； （2）若该居民区某家庭月收入为7千元，预测该家庭的月储蓄.27．(0分)[ID ：13512]A B 两个班共有65名学生，为调查他们的引体向上锻炼情况，通过分层抽样获得了部分学生引体向上的测试数据（单位：个），用茎叶图记录如下：(1)试估计B 班的学生人数；(2)从A 班和B 班抽出的学生中，各随机选取一人，A 班选出的人记为甲，B 班选出的人记为乙，假设所有学生的测试相对独立，比较甲、乙两人的测试数据得到随机变量X .规定：当甲的测试数据比乙的测试数据低时，记1X =-；当甲的测试数据与乙的测试数据相等时，记X 0=；当甲的测试数据比乙的测试数据高时，记1X =.求随机变量X 的分布列及数学期望.(3)再从A 、B 两个班中各随机抽取一名学生，他们引体向上的测试数据分别是10，8（单位：个），这2个新数据与表格中的数据构成的新样本的平均数记1μ，表格中数据的平均数记为0μ，试判断0μ和1μ的大小.（结论不要求证明）28．(0分)[ID ：13474]某校学生会开展了一次关于“垃圾分类”问卷调查的实践活动，组织部分学生干部在几个大型小区随机抽取了共50名居民进行问卷调查.调查结束后，学生会对问卷结果进行了统计，并将其中一个问题“是否知道垃圾分类方法（知道或不知道）”的调查结果统计如下表： 年龄（岁） [10,20)[20,30) [30,40) [40,50)[50,60)[60,70]频数 mn14 12 8 6 知道的人数348732（1）求上表中的,m n 的值，并补全右图所示的的频率直方图；（2）在被调查的居民中，若从年龄在[10,20),[20,30)的居民中各随机选取1人参加垃圾分类知识讲座，求选中的两人中仅有一人不知道垃圾分类方法的概率.29．(0分)[ID ：13439]设甲、乙、丙三个乒乓球协会分别选派3，1，2名运动员参加某次比赛，甲协会运动员编号分别为1A ，2A ，3A ，乙协会编号为4A ，丙协会编号分别为5A ，6A ，若从这6名运动员中随机抽取2名参加双打比赛.（1）用所给编号列出所有可能抽取的结果；（2）求丙协会至少有一名运动员参加双打比赛的概率；（3）求参加双打比赛的两名运动员来自同一协会的概率.30．(0分)[ID：13504]某县一中学的同学为了解本县成年人的交通安全意识情况，利用假期进行了一次全县成年人安全知识抽样调查.已知该县成年人中40%的拥有驾驶证，先根据是否拥有驾驶证，用分层抽样的方法抽取了100名成年人，然后对这100人进行问卷调查，所得分数的频率分布直方图如下图所示.规定分数在80以上（含80）的为“安全意识优秀”.拥有驾驶证没有驾驶证合计得分优秀得分不优秀25合计100（1）补全上面22⨯的列联表，并判断能否有超过99%的把握认为“安全意识优秀与是否拥有驾驶证”有关？（2）若规定参加调查的100人中分数在70以上（含70）的为“安全意识优良”，从参加调查的100人中根据安全意识是否优良，按分层抽样的方法抽出5人，再从5人中随机抽取3人，试求抽取的3人中恰有一人为“安全意识优良”的概率.附表及公式：()()()()()22n ad bcKa b c d a c b d-=++++，其中n a b c d=+++.()2P K k≥0.150.100.050.0250.0100.0050.001 k 2.072 2.706 3.841 5.024 6.6357.87910.828【参考答案】2016-2017年度第*次考试试卷参考答案**科目模拟测试一、选择题1．A2．D3．C4．C5．A6．C7．C8．B9．D10．C11．D12．B13．D14．A15．C二、填空题16．【解析】【分析】列出随机变量的分布列求解【详解】由题意知某人到达银行的概率为几何概型所以：其到达银行时服务窗口的个数为的分布列为：54342则【点睛】本题考查几何概型及随17．【解析】【分析】由平均数的公式求得再利用方差的计算公式求得即可求解【详解】由平均数的公式可得解得所以方差为所以样本的标准差为【点睛】本题主要考查了样本的平均数与方差标准差的计算着重考查了运算与求解能18．【解析】由题意可知2次检测结束的概率为3次检测结束的概率为则恰好检测四次停止的概率为19．【解析】【分析】取圆内接等边三角形的顶点为弦的一个端点当另一端点在劣弧上时求出劣弧的长度运用几何概型的计算公式即可得结果【详解】记事件{弦长超过圆内接等边三角形的边长}如图取圆内接等边三角形的顶点为20．900【解析】【分析】利用频率分布直方图中频率和为1求a值根据7080）的频率求出在此区间的人数即可【详解】由1﹣005﹣035﹣02﹣01＝03故a＝003故阅读的时间在7080）（单位：分钟）内21．42【解析】【分析】输入由循环语句依次执行即可计算出结果【详解】当时当时当时当时当时当时故答案为42【点睛】本题主要考查了程序框图中的循环语句的运算求出输出值较为基础22．A【解析】【分析】模拟执行程序框图依次写出每次循环得到的k的值当k=2012时不满足条件退出循环输出的值为【详解】模拟执行程序框图可得满足条件满足条件满足条件满足条件由此可见S的周期为3故当k=2023．【解析】分析：将原问题转化为几何概型的问题然后利用面积型几何概型公式整理计算即可求得最终结果详解：原问题即已知求的概率其中概率空间为如图所示的正方形满足题意的部分为图中的阴影部分所示其中结合面积型几24．【解析】【分析】根据系统抽样的特征求出分段间隔即可【详解】根据系统抽样的特征得：从2100名学生中抽取100个学生分段间隔为故答案是21【点睛】该题所考查的是有关系统抽样的组距问题应用总体除以样本容25．6【解析】如图过点作垂线垂足为在中故；过点作垂线与因则结合图形可知：当点位于线段上时为锐角三角形所以由几何概型的计算公式可得其概率应填答案点睛：本题的涉及到的知识点是几何概型的计算问题解答时充分借助三、解答题26．27．28．29．30．2016-2017年度第*次考试试卷 参考解析【参考解析】**科目模拟测试一、选择题 1．A 解析：A 【解析】 【分析】根据二项式5(2)x +展开式的通项公式，求出3x 的系数，由已知先求a 的值，模拟程序的运行，可得判断框内的条件． 【详解】解：由于32300(21)|6a x dx x x =-=-=⎰，二项式5(2)x -展开式的通项公式是5152r r r r T C x -+=⋅⋅，令3r =，3233152T C x +∴=⋅⋅；3x ∴的系数是32352140C ⋅⋅=．∴程序运行的结果S 为360，模拟程序的运行，可得6k =，1S = 不满足条件，执行循环体，6S =，5k = 不满足条件，执行循环体，30S =，4k = 不满足条件，执行循环体，120S =，3k = 不满足条件，执行循环体，360S =，2k =由题意，此时，应该满足条件，退出循环，输出S 的值为360． 则判断框中应填入的关于k 的判断条件是3k <？ 故选A ． 【点睛】本题考查程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．2．D解析：D 【解析】 【分析】通过定积分可求出空白部分面积，于是利用几何概型公式可得答案. 【详解】由题可知长方形面积为3，而长方形空白部分面积为：()()11001|2x x e dx e x e -=-=-⎰，故所求概率为25133e e---=，故选D. 【点睛】本题主要考查定积分求几何面积，几何概型的运算，难度中等.3．C解析：C 【解析】分析：执行程序框图，得到输出值4k S =，令24k=，可得8k . 详解：阅读程序框图，初始化数值1,n S k ==，循环结果执行如下：第一次：14n =<成立，2,22k k n S k ==-=； 第二次：24n =<成立，3,263k k k n S ==-=； 第三次：34n =<成立，4,3124k k k n S ==-=； 第四次：44n =<不成立，输出24kS ==，解得8k . 故选C.点睛：解决循环结构程序框图问题的核心在于：第一，要确定是利用当型还是直到型循环结构；第二，要准确表示累计变量；第三，要注意从哪一步开始循环，弄清进入或终止的循环条件、循环次数.4．C解析：C 【解析】分析：在半径为1的圆内作出正n 边形，分成n 个小的等腰三角形，可得正n 边形面积是13602S n sinn=⨯⨯，按照程序框图规定的运算方法逐次计算，直到达到输出条件即可的结果.详解：在半径为1的圆内作出正n 边形，分成n 个小的等腰三角形，每一个等腰三角形两腰是1，顶角是360n ⎛⎫ ⎪⎝⎭，所以正n 边形面积是13602S n sinn=⨯⨯， 当6n =时， 2.6S =≈； 当18n =时， 3.08S ≈；当54n =时， 3.13S ≈；符合 3.11S ≥，输出54n =，故选C.点睛：本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.5．A解析：A 【解析】 【分析】计算出数据1x 、2x 、、n x 的平均值x 和方差2s 的值，然后利用平均数和方差公式计算出数据153x -、253x -、、53n x -的平均值和方差.【详解】 设数据1x 、2x 、、n x 的平均值为x ，方差为2s ，由题意()()()()121221212121215n n x x x x x x x nn++++++++=+=+=，得2x =，由方差公式得()()()()()()22212212121212121n x x x x x x n⎡⎤⎡⎤⎡⎤+-+++-++++-+⎣⎦⎣⎦⎣⎦()()()2221224416n x x x x x x s n⎡⎤-+-++-⎢⎥⎣⎦===，24s ∴=. 所以，数据153x -、253x -、、53n x -的平均值为()()()12535353n x x x n-+-+-()1235535321n x x x x n+++=-=-=-⨯=-，方差为()()()()()()22212535353535353n x x x x x x n⎡⎤⎡⎤⎡⎤---+---++---⎣⎦⎣⎦⎣⎦()()()2221229936n x x x x x x s n⎡⎤-+-++-⎢⎥⎣⎦===.故选：A. 【点睛】本题考查平均数与方差的计算，熟练利用平均数与方差的公式计算是解题的关键，考查计算能力，属于中等题.6．C解析：C 【解析】 【分析】首先确定流程图的功能为计数111113355720172019S =++++⨯⨯⨯⨯的值，然后利用裂项求和的方法即可求得最终结果. 【详解】由题意结合流程图可知流程图输出结果为111113355720172019S =++++⨯⨯⨯⨯，11(2)111(2)2(2)22n n n n n n n n +-⎛⎫=⨯=- ⎪+++⎝⎭，111113355720172019S ∴=++++⨯⨯⨯⨯11111111123355720172019⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦1110091220192019⎛⎫=-=⎪⎝⎭. 本题选择C 选项. 【点睛】识别、运行程序框图和完善程序框图的思路： (1)要明确程序框图的顺序结构、条件结构和循环结构． (2)要识别、运行程序框图，理解框图所解决的实际问题． (3)按照题目的要求完成解答并验证．7．C解析：C 【解析】分析：写出从红球3个、白球2个、黑球1个中随机摸出2个球的取法情况，然后逐一核对四个选项即可得到答案详解：从红球3个、白球2个、黑球1个中随机摸出2个球的取法有：2个红球，2个白球，1红1黑，1红1白，1黑1白共五种情况则与事件“至少有1个白球”互斥但不对立的事件是红球，黑球各一个包括1红1白，1黑1白两种情况． 故选C点睛：本题主要考查了互斥事件和对立事件，是基础的概念题，只要理解其概念，结合本题列举出所有情况即可得出结果．8．B解析：B 【解析】 【分析】由题意结合流程图运行程序，考查5i >是否成立来决定输出的数值即可. 【详解】结合流程图可知程序运行过程如下： 首先初始化数据：1,2i S ==， 此时不满足5i >，执行循环：111,122S i i S =-==+=； 此时不满足5i >，执行循环：111,13S i i S=-=-=+=； 此时不满足5i >，执行循环：112,14S i i S=-==+=； 此时不满足5i >，执行循环：111,152S i i S =-==+=； 此时不满足5i >，执行循环：111,16S i i S=-=-=+=； 此时满足5i >，输出1S =-. 本题选择B 选项. 【点睛】本题主要考查循环结构流程图的识别与运行过程，属于中等题.9．D解析：D 【解析】 【分析】的图象的测度，再代入几何概型计算公式求解，即可得到答案． 【详解】对应的弧”， 其构成的区域为半圆NP ,倍的概率12NP P ==圆的周长，【点睛】本题主要考查了几何概型的概率计算中的“几何度量”，对于几何概型的“几何度量”可以线段的长度比、图形的面积比、几何体的体积比等，且这个“几何度量”只与“大小”有关，与形状和位置无关，着重考查了分析问题和解答问题的能力．10．C解析：C 【解析】 【分析】根据几何概型的概率公式，设AC ＝x ，则BC ＝10﹣x ，由矩形的面积S ＝x （10﹣x ）＜16可求x 的范围，利用几何概率的求解公式求解． 【详解】设线段AC 的长为xcm ，则线段CB 长为(10)cm x -， 那么矩形面积为(10)16x x -<，2x <或8x >，又010x <<， 所以该矩形面积小于216cm 的概率为42105=. 故选：C 【点睛】本题考查几何概型，考查了一元二次不等式的解法，明确测度比为长度比是关键，是中档题．11．D解析：D 【解析】 【分析】计算出每次循环时各变量的值并与3S =比较后可得对应的k 的值. 【详解】1n =，S k =； 2n =，22k k S k =-=； 3n =，263k k k S =-=； 4n =，33124k k kS =-==，所以12k =. 故选：Ｄ.【点睛】本题以数学文化为背景考虑流程图，此类问题应该根据流程图计算每次循环时各变量的值，从而可得程序终止的条件、输出的结果等，本题属于中档题.12．B解析：B 【解析】设大圆的半径为R ，则：126226T R ππ==⨯=， 则大圆面积为：2136S R ππ==，小圆面积为：22122S ππ=⨯⨯=，则满足题意的概率值为：213618p ππ==. 本题选择B 选项.点睛：数形结合为几何概型问题的解决提供了简捷直观的解法．用图解题的关键：用图形准确表示出试验的全部结果所构成的区域，由题意将已知条件转化为事件A 满足的不等式，在图形中画出事件A 发生的区域，据此求解几何概型即可.13．D解析：D 【解析】 【分析】由题意列出所有可能的结果，然后结合古典概型计算公式可得概率值. 【详解】能组成两位数有：10，12，13，20，21，23，30，31，32，总共有9种情况. 其中偶数有5种情况，故组成的两位数是偶数的概率为59p =. 故选：D . 【点睛】本题主要考查古典概型计算公式，属于中等题.14．A解析：A 【解析】试题分析：设扇形OAB 半径为，此点取自阴影部分的概率是112π-，故选B. 考点：几何概型.【方法点晴】本题主要考查几何概型，综合性较强，属于较难题型.本题的总体思路较为简单：所求概率值应为阴影部分的面积与扇形的面积之比．但是，本题的难点在于如何求阴影部分的面积，经分析可知阴影部分的面积可由扇形面积减去以为直径的圆的面积，再加上多扣一次的近似“椭圆”面积．求这类图形面积应注意切割分解，“多还少补”.15．C解析：C 【解析】试题分析：该程序框图所表示的算法功能为：235919S =+++=，故选C ． 考点：程序框图．二、填空题16．【解析】【分析】列出随机变量的分布列求解【详解】由题意知某人到达银行的概率为几何概型所以：其到达银行时服务窗口的个数为的分布列为：54342则【点睛】本题考查几何概型及随解析：3.5625【解析】 【分析】列出随机变量的分布列求解. 【详解】由题意知某人到达银行的概率为几何概型，所以： 其到达银行时服务窗口的个数为的分布列为：X5 4 3 4 2P18316 516 14 18则()54342 3.56258161648E X =⨯+⨯+⨯+⨯+⨯=. 【点睛】本题考查几何概型及随机变量的分布列.17．【解析】【分析】由平均数的公式求得再利用方差的计算公式求得即可求解【详解】由平均数的公式可得解得所以方差为所以样本的标准差为【点睛】本题主要考查了样本的平均数与方差标准差的计算着重考查了运算与求解能 解析：2213【解析】 【分析】由平均数的公式，求得49a =，再利用方差的计算公式，求得2283s =，即可求解. 【详解】由平均数的公式，可得1(4042404344)436a +++++=，解得49a =， 所以方差为2222222128[(4043)(4243)(4043)(4343)(4343)(4443)]63s =-+-+-+-+-+-=，所以样本的标准差为2213s =. 【点睛】本题主要考查了样本的平均数与方差、标准差的计算，着重考查了运算与求解能力，属于基础题.18．【解析】由题意可知2次检测结束的概率为3次检测结束的概率为则恰好检测四次停止的概率为解析：35【解析】由题意可知，2次检测结束的概率为22225110A p A ==，3次检测结束的概率为31123232335310A C C A p A +==， 则恰好检测四次停止的概率为231331110105p p p =--=--=. 19．【解析】【分析】取圆内接等边三角形的顶点为弦的一个端点当另一端点在劣弧上时求出劣弧的长度运用几何概型的计算公式即可得结果【详解】记事件{弦长超过圆内接等边三角形的边长}如图取圆内接等边三角形的顶点为解析：13【解析】 【分析】取圆内接等边三角形BCD 的顶点B 为弦的一个端点，当另一端点在劣弧CD 上时，BE BC >，求出劣弧CD 的长度，运用几何概型的计算公式，即可得结果.【详解】记事件A ={弦长超过圆内接等边三角形的边长}，如图，取圆内接等边三角形BCD 的顶点B 为弦的一个端点， 当另一端点在劣弧CD 上时，BE BC >， 设圆的半径为r ，劣弧CD 的长度是23rπ， 圆的周长为2r π，所以()21323rP A r ππ==，故答案为13. 【点睛】本题主要考查“长度型”的几何概型，属于中档题. 解决几何概型问题常见类型有：长度型、角度型、面积型、体积型，求与长度有关的几何概型问题关鍵是计算问题的总长度以及事件的长度；几何概型问题还有以下几点容易造成失分，在备考时要高度关注：（1）不能正确判断事件是古典概型还是几何概型导致错误；（2）基本事件对应的区域测度把握不准导致错误 ；（3）利用几何概型的概率公式时 , 忽视验证事件是否等可能性导致错误.20．900【解析】【分析】利用频率分布直方图中频率和为1求a 值根据7080）的频率求出在此区间的人数即可【详解】由1﹣005﹣035﹣02﹣01＝03故a ＝003故阅读的时间在7080）（单位：分钟）内 解析：900【解析】 【分析】利用频率分布直方图中频率和为1求a 值，根据[70，80）的频率求出在此区间的人数即可． 【详解】由1﹣0.05﹣0.35﹣0.2﹣0.1＝0.3， 故a ＝0.03，故阅读的时间在[70，80）（单位：分钟）内的学生人数为：0.3×3000＝900， 故答案为：900． 【点睛】本题考查频率分布直方图中的有关性质的应用，考查直方图中频率和频数的求法.21．42【解析】【分析】输入由循环语句依次执行即可计算出结果【详解】当时当时当时当时当时当时故答案为42【点睛】本题主要考查了程序框图中的循环语句的运算求出输出值较为基础解析：42 【解析】 【分析】输入1k =，由循环语句，依次执行，即可计算出结果 【详解】当1k =时，0212S =+⨯= 当2k =时，021226S =+⨯+⨯= 当3k =时，021222312S =+⨯+⨯+⨯= 当4k =时，021********S =+⨯+⨯+⨯+⨯= 当5k =时，0212223242530S =+⨯+⨯+⨯+⨯+⨯= 当6k =时，021222324252642S =+⨯+⨯+⨯+⨯+⨯+⨯= 故答案为42 【点睛】本题主要考查了程序框图中的循环语句的运算，求出输出值，较为基础22．A 【解析】【分析】模拟执行程序框图依次写出每次循环得到的k 的值当k=2012时不满足条件退出循环输出的值为【详解】模拟执行程序框图可得满足条件满足条件满足条件满足条件由此可见S 的周期为3故当k=20解析：A 【解析】 【分析】模拟执行程序框图，依次写出每次循环得到的k ，S 的值，当k=2012时不满足条件2011k ≤ ，退出循环，输出S 的值为12.【详解】模拟执行程序框图，可得 2,1S k ==满足条件2011k ≤，1,22S k ==， 满足条件2011k ≤，1,3S k =-=，满足条件2011k ≤，2,4S k ==，满足条件2011k ≤，1,52S k ，== 由此可见S 的周期为3，20113670...1,÷= 故当k=2012时不满足条件2011k ≤ ，退出循环，输出S 的值为12. 故选A. 【点睛】本题主要考查了循环结构的程序框图，属于基础题．23．【解析】分析：将原问题转化为几何概型的问题然后利用面积型几何概型公式整理计算即可求得最终结果详解：原问题即已知求的概率其中概率空间为如图所示的正方形满足题意的部分为图中的阴影部分所示其中结合面积型几 解析：1725【解析】分析：将原问题转化为几何概型的问题，然后利用面积型几何概型公式整理计算即可求得最终结果.详解：原问题即已知01,01x y ≤≤≤≤，求45x y +≥的概率， 其中概率空间为如图所示的正方形，满足题意的部分为图中的阴影部分所示， 其中4,05E ⎛⎫⎪⎝⎭，40,5F ⎛⎫ ⎪⎝⎭，结合面积型几何概型计算公式可得满足题意的概率值为：1441725511125p ⨯⨯=-=⨯.点睛：数形结合为几何概型问题的解决提供了简捷直观的解法．用图解题的关键：用图形准确表示出试验的全部结果所构成的区域，由题意将已知条件转化为事件A 满足的不等式，在图形中画出事件A 发生的区域，据此求解几何概型即可.24．【解析】【分析】根据系统抽样的特征求出分段间隔即可【详解】根据系统抽样的特征得：从2100名学生中抽取100个学生分段间隔为故答案是21【点睛】该题所考查的是有关系统抽样的组距问题应用总体除以样本容 解析：21【解析】 【分析】根据系统抽样的特征，求出分段间隔即可. 【详解】根据系统抽样的特征，得：从2100名学生中抽取100个学生，分段间隔为210021100=， 故答案是21. 【点睛】该题所考查的是有关系统抽样的组距问题，应用总体除以样本容量等于组距，得到结果，属于简单题目.。

一、选择题1．已知,a b 是单位向量，且,a b 的夹角为3π，若向量c 满足22c a b -+=，则||c 的最大值为（ ） A ．23- B ．23+ C ．72+ D ．72- 2．将函数()sin 3f x x πω⎛⎫=+ ⎪⎝⎭的图象向左平移(0)ϕϕ>个单位长度后得到函数()cos2g x x =的图象，则ϕ的最小值为（ ）A ．3πB ．6πC ．12πD ．24π3．已知sin cos 1sin cos 2αααα-=+，则cos2α的值为（ ） A ．45- B ．35 C ．35 D ．454．在边长为3的等边ABC ∆中，点M 满足BM 2MA =，则CM CA ⋅=( ) A ．32 B ．23 C ．6 D ．152 5．平面向量(1,2)a =，(4,2)b =，c ma b =+（m R ∈），且c 与a 的夹角等于c 与b 的夹角，则m =（ ）A ．2-B ．1-C ．1D ．26．已知2sin2α＝1＋cos2α，则tan2α＝（ ）A ．43-B ．43C ．43-或0D ．43或0 7．在平面直角坐标系中，角α的顶点与原点重合，始边与x 轴的非负半轴重合，终边过点(3,1)P --，则sin(2)2πα-=（ ） A ．32 B ．32- C ．12 D ．12- 8．已知2sin()3,且(,0)2απ∈-，则tan(2)πα-= （ ） A ．255 B ．255- C ．52 D ．52- 9．在中，,,A B C ∠∠∠所对的边长分别是,,a b c ，若sin sin()sin 2C B A A +-=，则的形状为 A ．等腰三角形B ．直角三角形C ．等腰直角三角形D ．等腰三角形或直角三角形10．延长正方形CD AB 的边CD 至E ，使得D CD E =．若动点P 从点A 出发，沿正方形的边按逆时针方向运动一周回到A 点，若λμAP =AB +AE ，下列判断正确的是（ ）A ．满足2λμ+=的点P 必为CB 的中点B ．满足1λμ+=的点P 有且只有一个C ．λμ+的最小值不存在D ．λμ+的最大值为311．已知函数()sin 3cos f x x x =+，将函数()f x 的图象向左平移()0m m >个单位长度后，所得到的图象关于y 轴对称，则m 的最小值是（ ）A ．6πB ．4πC ．3πD ．2π 12．已知角6πα-的顶点在原点，始边与x 轴正半轴重合，终边过点()5,12P -， 则7cos 12πα⎛⎫+= ⎪⎝⎭( ) A ．17226- B ．7226- C ．7226 D ．1722613．若向量a ，b 满足2a b ==，a 与b 的夹角为60，则a b +等于（ ） A ．223+ B ．23 C ．4 D ．1214．如图，在ABC ∆中，BE 是边AC 的中线，O 是BE 边的中点，若,AB a AC b ==,则AO =（ ）A ．1122a b +B ．1124a b +C ．1142a b +D ．1144a b + 15．已知A ，B 2的⊙O 上的两个点，OA ·OB ＝1，⊙O 所在平面上有一点C满足｜OA ＋CB ｜＝1，则｜AC ｜的最大值为（ ）A＋1 B1 C ．＋1 D+1二、填空题16．已知函数()sin()(,0,0,0)2f x A x x R A πωϕωϕ=+∈>><<的图象与x 轴的交点中，相邻两个交点之间的距离为2π，且图象上一个最低点为2(,2)3M π-.则()f x 的解析式为________．17．已知C 是以AB 为直径的半圆弧上的动点，O 为圆心，P 为OC 中点，若4AB =，则()PA PB PC +⋅=__________． 18．已知向量()()()12311a b c λ===，，，，，.若2a b -与c 共线，则a 在c 方向上的投影为 ________.19．在ABC ∆中，角,,A B C 所对的边分别边,,a b c ，若224a b ab ++=，2c =，则2a b +的取值范围是_____．20+_________.21．已知点1,0A ，M ，N 分别是x 轴、y 轴上的动点，且满足0AN MN ⋅=.若点P 满足2MP NP =，则点P 的轨迹方程是______.22．已知向量a ，b 满足1a =，且()2a a b b -==，则向量a 与b 的夹角是__________．23．已知1cos()63πα+=，则5sin(2)6πα+=________． 24．函数()211sin sin (0)222x f x x ωωω=+->，若函数()f x 在区间x ∈(),2ππ内没有零点，则实数ω的取值范围是_____ 25．计算：2tan81tan8ππ=- __________．三、解答题 26．已知函数() 22.3f x x sinxcosx π⎛⎫ -⎪⎝⎭=-（1）求()f x 的最小正周期；（2）求()f x 的单调递增区间. 27．如图，制图工程师要用两个同中心的边长均为4的正方形合成一个八角形图形，由对称性，图中8个三角形都是全等的三角形，设11AA H α∠=.(1)试用α表示11AA H ∆的面积；(2)求八角形所覆盖面积的最大值，并指出此时α的大小.28．已知平面上三个向量a ⃗ ,b ⃗ ,c ,的模均为1，它们相互之间的夹角均为1200．（I ）求证：(a ⃗ −b⃗ )⊥c ⃗ ； （II ）若|ka ⃗ +b ⃗ +c |>1 (k ∈R)，求k 的取值范围．29．已知函数()32f x x =.（Ⅰ）若α为锐角，且6cos 3α=，求()f α的值； （Ⅱ）若函数22()()cos sin g x f x x x =+-，当[0,]x π∈时，求()g x 的单调递减区间.30．已知A(1,2),B(a,1),C(2,3),D(-1,b)(a,b ∈R)是复平面上的四个点,且向量,AB CD 对应的复数分别为z 1,z 2.(1)若z 1+z 2=1+i,求z 1,z 2;(2)若|z 1+z 2|=2,z 1-z 2为实数,求a,b 的值.【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题1．B2．C3．A4．D5．D6．D7．D8．A9．D10．D11．A12．B13．B14．B15．A二、填空题16．【解析】【分析】根据函数周期为求出再由图象的最低点得到振幅及【详解】因为图象与两个交点之间的距离为所以所以由于图象的最低点则所以当时因为所以故填：【点睛】本题考查正弦型函数的图象与性质考查数形结合思17．【解析】【分析】先用中点公式的向量式求出再用数量积的定义求出的值【详解】【点睛】本题主要考查向量中的中点公式应用以及数量积的定义18．【解析】【分析】利用共线向量的坐标表示求出参数再依据投影的概念求出结果即可【详解】∵∴又∵与共线∴∴∴∴在方向上的投影为【点睛】本题主要考查共线向量的坐标表示以及向量投影的概念注意投影是个数量19．【解析】【分析】先根据余弦定理求C再根据正弦定理化为角的函数关系式最后根据正弦函数性质求结果【详解】又因此故答案为【点睛】本题考查余弦定理正弦定理以及正弦函数性质考查综合分析求解能力属中档题20．【解析】原式因为所以且所以原式21．【解析】【分析】设点MNP三点坐标根据平面向量垂直特性列出方程可得结果【详解】解：设点M坐标（a0）N坐标（0b）点P坐标（xy）则=（-1b）=（-ab）而==代入可得故答案为【点睛】本题考查了平22．【解析】【分析】先根据条件得再根据向量夹角公式求结果【详解】因为且所以因此【点睛】求平面向量夹角方法：一是夹角公式；二是坐标公式；三是几何方法从图形判断角的大小23．【解析】分析：由题意利用目标角和已知角之间的关系现利用诱导公式在结合二倍角公式即可求解详解：由题意又由所以点睛：本题主要考查了三角函数的化简求值问题其中解答中正确构造已知角与求解角之间的关系合理选择24．【解析】分析：先化简函数f(x)再求得再根据函数在区间内没有零点得到不等式组最后解不等式组即得w 的范围详解：由题得f(x)=因为所以当或时f(x)在内无零点由前一式得即由k=0得K 取其它整数时无解同25．【解析】根据正切公式的二倍角公式得到故答案为：三、解答题26．27．28．29．30．2016-2017年度第*次考试试卷 参考解析【参考解析】**科目模拟测试一、选择题1．B解析：B【解析】不妨设(1,0)a =，13(,22b =，(,)c x y =，则2(,c a b x y -+=+，所以22(2c a b x -+=+=，即22(4x y +=，点(,)x y 在以(0,为圆心，2为半径的圆上，所以2c x =+2+．故选B ．2．C解析：C【解析】【分析】根据题意得到变换后的函数解析式，利用诱导公式求得结果【详解】由题，向左平移(0)ϕϕ>不改变周期，故2ω=，∴平移得到()sin 2sin 22cos 233x x x ππϕϕ⎡⎤⎡⎤⎛⎫++=++= ⎪⎢⎥⎢⎥⎣⎦⎝⎭⎣⎦ 2+=+232k ππϕπ∴，12k πϕπ∴=+0ϕ>，∴当0k =时，min 12πϕ=，故选C【点睛】 本题考查函数()sin y A x ωϕ=+的图象变换规律，利用诱导公式完成正、余弦型函数的转化3．A解析：A【解析】∵sin cos 1sin cos 2αααα-=+，∴tan α11tan α3tan α12-==+，. ∴cos2α=222222cos sin 1tan 4cos sin 1tan 5αααααα--==-++ 故选A4．D解析：D【解析】【分析】 结合题意线性表示向量CM ，然后计算出结果 【详解】 依题意得：121211215)333333333232CM CA CB CA CA CB CA CA CA ⋅=+⋅=⋅+⋅=⨯⨯⨯+⨯⨯=（，故选D ． 【点睛】本题考查了向量之间的线性表示，然后求向量点乘的结果，较为简单5．D【解析】【分析】【详解】()()4,22,422258c m m a c m m m =++⋅=+++=+,()()44222820b c m m m ⋅=+++=+, 5,2025a b ===,c 与a 的夹角等于c 与b 的夹角 ,c a c b c a c b ⋅⋅=⋅⋅,58820525m m ++∴=,解得2m =, 故选D.【考点定位】向量的夹角及向量的坐标运算.6．D解析：D【解析】【分析】【详解】试题分析：把2sin 21cos2αα=+的两边平方得224sin 2(1cos 2)αα=+，整理可得2244cos 412cos 2cos 2ααα-=++，即25cos 22cos 230αα+-=，所以(5cos 23)(cos 21)0αα-+=，解得3cos 25α=或cos21α=-，当2312sin 5α-=时，1cos 244sin 2,tan 2253ααα+===；当cos21α=-时，1cos 2sin 20,tan 202ααα+===，所以4tan 23α=或0，故选D. 考点：三角函数的基本关系式及三角函数的化简求值.7．D解析：D【解析】试题分析：因,则,故sin(2)2πα-,选D ．考点：三角函数的定义． 8．A解析：A【解析】由三角函数的诱导公式，求得2sin 3，再由三角函数的基本关系式，求得5cos α3， 最后利用三角函数的基本关系式，即可求解tan(2)πα-的值，得到答案.【详解】由三角函数的诱导公式，可得2sin()sin 3παα-==-， 因为(,0)2απ∈-，所以25cos 1sin 3αα=-=， 又由sin 25tan(2)tan cos 5απααα-=-=-=，故选A. 【点睛】本题主要考查了三角函数的诱导公式和三角函数的基本关系式的化简、求值问题，其中解答中熟练应用三角函数的诱导公式和三角函数的基本关系式，准确计算是解答的关键，着重考查了推理与运算能力，属于基础题.9．D解析：D【解析】试题分析：由sinC ＋sin(B －A)＝sin2A再注意到：，所以有，故知△ABC 是等腰三角形或直角三角形，故选D.考点：三角恒等变形公式. 10．D解析：D【解析】试题分析：设正方形的边长为1，建立如图所示直角坐标系，则,,,,A B C D E 的坐标为(0,0),(1,0),(1,1),(0,1),(1,1)-，则(1,0),(1,1)AB AE ==-设(,)AP a b =，由λμAP =AB +AE 得(,)(,)a b λμμ=-，所以{a b λμμ=-=，当P 在线段AB 上时，01,0a b ≤≤=，此时0,a μλ==，此时a λμ+=，所以01λμ≤+≤；当P 在线段BC 上时，，此时,1b a b μλμ==+=+，此时12b λμ+=+，所以13λμ≤+≤；当P 在线段CD 上时，，此时1,1a a μλμ==+=+，此时2a λμ+=+，所以13λμ≤+≤；当P 在线段DA 上时，0,01,a b =≤≤，此时,b a b μλμ==+=，此时2b λμ+=，所以02λμ≤+≤；由以上讨论可知，当2λμ+=时，P 可为BC 的中点，也可以是点D ，所以A 错；使1λμ+=的点有两个，分别为点B 与AD 中点，所以B 错，当P 运动到点A 时，λμ+有最小值0，故C 错，当P 运动到点C 时，λμ+有最大值3，所以D 正确，故选D ．考点：向量的坐标运算．【名师点睛】本题考查平面向量线性运算，属中档题．平面向量是高考的必考内容，向量坐标化是联系图形与代数运算的渠道，通过构建直角坐标系，使得向量运算完全代数化，通过加、减、数乘的运算法则，实现了数形的紧密结合，同时将参数的取值范围问题转化为求目标函数的取值范围问题，在解题过程中，还常利用向量相等则坐标相同这一原则，通过列方程（组）求解，体现方程思想的应用．11．A解析：A【解析】【分析】 利用函数的平移变换得π2sin 3y x m ⎛⎫=++⎪⎝⎭，再根所图象关于y 轴对称，得到角的终边落在y 轴上，即π2π3πm k +=+，k Z ∈，即可得答案. 【详解】 ()sin 32s πin 3f x x x x ⎛⎫=+=+ ⎪⎝⎭， 将函数()f x 的图象向左平移m 个单位长度后， 得到函数π2sin 3y x m ⎛⎫=++ ⎪⎝⎭的图象， 又所得到的图象关于y 轴对称，所以π2π3πm k +=+，k Z ∈， 即ππ6m k =+，k Z ∈，又0m >，所以当0k =时，m 的最小值为π6. 故选：A. 【点睛】本题考查三角函图象的变换、偶函数的性质，考查函数与方程思想、转化与化归思想，考查逻辑推理能力和运算求解能力.12．B解析：B 【解析】分析：利用三角函数的定义求得66cos sin ππαα⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭， 结果，进而利用两角和的余弦函数公式即可计算得解．详解：由三角函数的定义可得512,613613cos sin ππαα⎛⎫⎛⎫-=--= ⎪ ⎪⎝⎭⎝⎭， 则773cos cos cos 12661264ππππππααα⎛⎫⎛⎫⎛⎫+=-++=-+ ⎪⎪⎪⎝⎭⎝⎭⎝⎭33=cos cos sin sin 6464ππππαα⎛⎫⎛⎫⎛⎫⎛⎫--- ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭512=1313⎛⎛⎫--= ⎪ ⎝⎭⎝⎭ 点睛：本题考查任意角的三角函数的定义，两角和与差的余弦函数公式，考查了计算能力和转化思想，属于基础题．13．B解析：B 【解析】 【分析】将a b +平方后再开方去计算模长，注意使用数量积公式. 【详解】因为2222cos 6044412a b a a b b +=+︒+=++=，所以23a b +=， 故选：B. 【点睛】本题考查向量的模长计算，难度一般.对于计算xa yb +这种形式的模长，可通过先平方再开方的方法去计算模长.14．B解析：B 【解析】【分析】 【详解】分析：利用向量的共线定理、平行四边形法则即可得出． 详解：∵在ABC ∆中，BE 是AC 边上的中线 ∴12AE AC =∵O 是BE 边的中点 ∴1()2AO AB AE =+ ∴1124AO AB AC =+ ∵,AB a AC b == ∴1124AO a b =+ 故选B.点睛：本题考查了平面向量的基本定理的应用.在解答此类问题时，熟练掌握向量的共线定理、平行四边形法则是解题的关键．15．A解析：A 【解析】 【分析】先由题意得到2==OA OB ，根据向量的数量积求出3AOB π∠=，以O 为原点建立平面直角坐标系，设A （2cos θ，2sin θ）得到点B 坐标，再设C （x ，y ），根据点B 的坐标，根据题中条件，即可求出结果. 【详解】依题意，得：2==OA OB ，因为cos OA OB OA OB AOB ⋅=⋅∠， 所以，22cos AOB ⨯∠＝1，得：3AOB π∠=，以O 为原点建立如下图所示的平面直角坐标系，设A （2cos θ，2sin θ），则B （2cos 3πθ⎛⎫+ ⎪⎝⎭，2sin 3πθ⎛⎫+⎪⎝⎭） 或B （2cos 3πθ⎛⎫- ⎪⎝⎭，2sin 3πθ⎛⎫-⎪⎝⎭） 设C （x ，y ）， 当B （2cos 3πθ⎛⎫+⎪⎝⎭，2sin 3πθ⎛⎫+⎪⎝⎭）时， 则OA CB +＝（2cos θ＋2cos 3πθ⎛⎫+ ⎪⎝⎭－x ，2sin θ＋2sin 3πθ⎛⎫+⎪⎝⎭－y ） 由｜OA ＋CB ｜＝1，得：222cos 2cos 2sin 2sin 33x y ππθθθθ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-+++-++⎢⎥⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦＝1，即点C 在1为半径的圆上，A （2cos θ，2sin θ）到圆心(2cos 2cos 2sin 2sin )33ππθθθθ⎛⎫⎛⎫++++ ⎪ ⎪⎝⎭⎝⎭，的距离为：22 2cos (2sin )33d ππθθ⎛⎫⎛⎫⎛⎫=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭＝2｜AC ｜的最大值为2＋1 当B （2cos 3πθ⎛⎫- ⎪⎝⎭，2sin 3πθ⎛⎫-⎪⎝⎭）时，结论一样． 故选A【点睛】本题主要考查向量模的计算，熟记向量的几何意义，以及向量模的计算公式，即可求解，属于常考题型.二、填空题16．【解析】【分析】根据函数周期为求出再由图象的最低点得到振幅及【详解】因为图象与两个交点之间的距离为所以所以由于图象的最低点则所以当时因为所以故填：【点睛】本题考查正弦型函数的图象与性质考查数形结合思解析：()2sin 26f x x π⎛⎫=+ ⎪⎝⎭【解析】 【分析】根据函数周期为π，求出2ω=，再由图象的最低点2(,2)3M π-，得到振幅2A =，及6π=ϕ.【详解】因为图象与x 两个交点之间的距离为2π，所以222T T ππππω=⇒=⇒=， 所以2ω=，由于图象的最低点2(,2)3M π-，则2A =， 所以()()2sin 2f x x ϕ=+，当23x π=时，4sin 13πϕ⎛⎫+=-⎪⎝⎭， 因为02πϕ<<，所以6π=ϕ，故填：()2sin 26f x x π⎛⎫=+ ⎪⎝⎭.【点睛】本题考查正弦型函数的图象与性质，考查数形结合思想的应用，注意02πϕ<<这一条件限制，从面得到ϕ值的唯一性.17．【解析】【分析】先用中点公式的向量式求出再用数量积的定义求出的值【详解】【点睛】本题主要考查向量中的中点公式应用以及数量积的定义 解析：2-【解析】 【分析】先用中点公式的向量式求出PA PB +，再用数量积的定义求出()PA PB PC +⋅的值． 【详解】2PA PB PO +=，()2211cos1802PA PB PC PO PC ο∴+⋅=⋅=⨯⨯⨯=-【点睛】本题主要考查向量中的中点公式应用以及数量积的定义．18．【解析】【分析】利用共线向量的坐标表示求出参数再依据投影的概念求出结果即可【详解】∵∴又∵与共线∴∴∴∴在方向上的投影为【点睛】本题主要考查共线向量的坐标表示以及向量投影的概念注意投影是个数量解析：【解析】 【分析】利用共线向量的坐标表示求出参数λ，再依据投影的概念求出结果即可． 【详解】∵()()123a b λ==，，，∴()()21222336a b λλ-=-⨯⋅-⨯=--，. 又∵2a b -与c 共线，∴36λ-=-，∴3λ=，∴()13a =，， ∴a 在c 方向上的投影为22a c c⋅=.【点睛】本题主要考查共线向量的坐标表示以及向量投影的概念，注意投影是个数量．19．【解析】【分析】先根据余弦定理求C 再根据正弦定理化为角的函数关系式最后根据正弦函数性质求结果【详解】又因此故答案为【点睛】本题考查余弦定理正弦定理以及正弦函数性质考查综合分析求解能力属中档题 解析：(2,4)【解析】 【分析】先根据余弦定理求C,再根据正弦定理化2a b +为角的函数关系式，最后根据正弦函数性质求结果. 【详解】224a b ab ++=，2c =， 222a b ab c ∴++=，∴ 222122a b c ab +-=-，1cos 2C ∴=-，又0C π<<，23C π∴=，因此)sin sin 222sin sin sin sin c A c B a b A B C C +=⨯+=+2sin sin ?4sin 36A A A ππ⎫⎛⎫⎛⎫=+-=+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭ 03A π<<，∴662A πππ<+<，∴1sin 126A π⎛⎫<+< ⎪⎝⎭， 224a b <+< 故答案为()2,4． 【点睛】本题考查余弦定理、正弦定理以及正弦函数性质，考查综合分析求解能力，属中档题.20．【解析】原式因为所以且所以原式 解析：2sin 4-【解析】原式2cos42sin4cos4==+-，因为53442ππ<<，所以cos40<，且sin4cos4<，所以原式()2cos42sin4cos42sin4=---=-．21．【解析】【分析】设点MNP 三点坐标根据平面向量垂直特性列出方程可得结果【详解】解：设点M 坐标（a0）N 坐标（0b ）点P 坐标（xy ）则=（-1b ）=（-ab ）而==代入可得故答案为【点睛】本题考查了平 解析：24y x =【解析】 【分析】设点M,N,P 三点坐标，根据平面向量垂直特性，列出方程可得结果. 【详解】解：设点M 坐标（a,0），N 坐标（0，b ），点P 坐标（x,y ）,则AN =（-1，b ），MN =（-a,b ），∴AN MN ⋅=20a b +=⇒2a b =-， 而MP =(),x a y -,NP =(),x y b -,2MP NP=⇒()22()x x a y b y⎧=-⎨-=⎩⇒2x a y b =-⎧⎨=⎩,代入2a b =-可得24y x =. 故答案为24y x =. 【点睛】本题考查了平面向量垂直的乘积和点的轨迹方程的求法，属于简单题.22．【解析】【分析】先根据条件得再根据向量夹角公式求结果【详解】因为且所以因此【点睛】求平面向量夹角方法：一是夹角公式；二是坐标公式；三是几何方法从图形判断角的大小 解析：120︒【解析】 【分析】先根据条件得a b ⋅，再根据向量夹角公式求结果. 【详解】因为1a =，且()2a a b ⋅-=，所以2-2,121,a a b a b ⋅=∴⋅=-=- 因此112πcos ,,1223a b a b a b a b⋅-===-∴=⨯⋅. 【点睛】求平面向量夹角方法：一是夹角公式cos a b a bθ⋅=⋅；二是坐标公式cos θ=；三是几何方法，从图形判断角的大小.23．【解析】分析：由题意利用目标角和已知角之间的关系现利用诱导公式在结合二倍角公式即可求解详解：由题意又由所以点睛：本题主要考查了三角函数的化简求值问题其中解答中正确构造已知角与求解角之间的关系合理选择解析：79- 【解析】分析：由题意，利用目标角和已知角之间的关系，现利用诱导公式，在结合二倍角公式，即可求解． 详解：由题意25sin(2)sin(2)cos(2)cos[2()]2cos ()1623366ππππππααααα+=++=+=+=+-， 又由1cos()63πα+=， 所以22517sin(2)2cos ()12()16639ππαα+=+-=⨯-=-． 点睛：本题主要考查了三角函数的化简求值问题，其中解答中正确构造已知角与求解角之间的关系，合理选择三角恒等变换的公式是解答的关键，着重考查了分析问题和解答问题的能力，以及推理与运算能力．24．【解析】分析：先化简函数f(x)再求得再根据函数在区间内没有零点得到不等式组最后解不等式组即得w 的范围详解：由题得f(x)=因为所以当或时f(x)在内无零点由前一式得即由k=0得K 取其它整数时无解同解析：][1150,,848⎛⎤⋃ ⎥⎝⎦【解析】分析：先化简函数f(x) )24wx π=-,再求得(,2),444wx w w πππππ-∈--再根据函数()f x 在区间x ∈ (),2ππ内没有零点得到不等式组，最后解不等式组即得w 的范围.详解：由题得f(x)=1cos 1111sin sin cos )2222224wx wx wx wx wx π-+-=-=-, 因为x ∈ (),2ππ，所以(,2),444wx w w πππππ-∈--当(,2)(2,2),44w w k k k z πππππππ--⊆+∈或(,2)(2,2),44w w k k k z πππππππ--⊆-∈时，f(x)在(),2ππ内无零点，由前一式得24,224k w w k πππππππ⎧≤-⎪⎪⎨⎪-≤+⎪⎩即152,48k w k +≤≤+由k=0得1548w ≤≤， K 取其它整数时无解，同理，由后一式，解得1(0,]8w ∈， 综上，w 的取值范围是][1150,,848⎛⎤⋃ ⎥⎝⎦. 点睛：（1）本题主要考查三角恒等变换，考查三角函数的图像和性质，考查三角函数的零点问题，意在考查学生对这些知识的掌握水平和分析推理能力数形结合的思想方法.(2)解答本题的关键有两点，其一是分析得到当(,2)(2,2),44w w k k k z πππππππ--⊆+∈或(,2)(2,2),44w w k k k z πππππππ--⊆-∈时，f(x)在(),2ππ内无零点，其二是进一步转化得到不等式组解不等式组. 25．【解析】根据正切公式的二倍角公式得到故答案为： 解析：12【解析】根据正切公式的二倍角公式得到22tan 8tantan 21481tan 8ππππ=⨯==-，2tan1821tan 8ππ=-. 故答案为：12.三、解答题 26．（1）π；（2）()5,1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦. 【解析】 【分析】（1）利用两角差公式、倍角公式和辅助角公式，把()f x 化为()sin 23f x x π⎛⎫=+ ⎪⎝⎭，从而求出最小正周期. （2）令222,232k x k k Z πππππ-≤+≤+∈，求出x 的范围，即得()f x 的单调递增区间. 【详解】（1）() 223f x x sinxcosx π⎛⎫⎪⎝-⎭=-1cos 2cos sin 2sin sin 2cos 22sin 2332x x x x x x ππ⎫⎫=+-=+-⎪⎪⎪⎭⎭12sin 2sin 223x x x π⎛⎫=+=+ ⎪⎝⎭. ()f x ∴的最小正周期为π.（2）由（1）知()sin 23f x x π⎛⎫=+ ⎪⎝⎭. 令222,232k x k k Z πππππ-≤+≤+∈，得51212k x k ππππ-≤≤+， ()f x ∴的单调递增区间为()5,1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦.【点睛】本题考查三角函数的性质和三角恒等变换，属于基础题.27．(1) 11212tan AA Hx S α∆=⋅=28sin cos (sin cos 1)αααα++，(0,)2πα∈.(2) 45α=时, 11AA H S ∆达到最大此时八角形所覆盖面积前最大值为64- 【解析】 【分析】（1）注意到1111,BA AA AH H H ==，从而11AA H ∆的周长为4，故14sin sin cos 1AH ααα=++，所以1128sin cos (sin cos 1)AA H S αααα∆=++，注意(0,)2πα∈.（2）令sin cos t αα=+，则11441AA H t S t ∆-=+，根据(t ∈可求最大值. 【详解】(1)设1AH 为x ,4sin tan x xx αα∴++=， 4sin sin cos 1x ααα=++，11212tan AA H x S α∆=⋅=28sin cos (sin cos 1)αααα++，(0,)2πα∈，(2)令sin cos t αα=+∈,只需考虑11AA H S ∆取到最大值的情况,即为2224(1)84+1(1)t S t t -==-+，当t =,即45α=时, 11AA H S ∆达到最大，此时八角形所覆盖面积为16+411AA H S ∆最大值为64-. 【点睛】如果三角函数式中仅含有sin cos x x 和sin cos x x +，则可令sin cos t x x =+后利用21sin cos 2t x x -=把三角函数式变成关于t 的函数，注意换元后t 的范围. 28．（Ⅰ）证明见解析；（II ）k >2或k <0 【解析】 【分析】 【详解】（I ）因为向量a ⃗ ,b ⃗ ,c ,的模均为1，它们相互之间的夹角均为1200 ∴(a ⃗ −b ⃗ )⋅c ⃗ =a ⃗ ⋅c ⃗ −b ⃗ ⋅c ⃗ =0， (a ⃗ −b ⃗ )⊥c⃗ . (II) 不等式|ka ⃗ +b ⃗ +c |>1⇔|ka ⃗ +b ⃗ +c |2>1⇔k 2a ⃗ 2+b ⃗ 2+c ⃗ 2+2ka ⃗ ⋅b⃗ +2ka ⃗ ⋅c ⃗ +2b ⃗ ⋅c ⃗ >1 ∵|a ⃗ |=|b ⃗ |=|c |=1,且a ⃗ ,b ⃗ ,c ,的夹角均为120°,∴a ⃗ 2=b ⃗ 2=c 2=1,a ⃗ ⋅b ⃗ =b ⃗ ⋅c =a ⃗ ⋅c =−12,∴k 2−2k >0,∴k >2或k <0.29．(Ⅱ) 2,63ππ⎛⎫ ⎪⎝⎭【解析】 【分析】（Ⅰ）由已知利用同角三角函数基本关系式可求sin α的值，进而根据二倍角的正弦函数公式即可计算得解；（Ⅱ）由已知利用三角函数恒等变换的应用可求g （x ）＝2sin （2x 6π+），根据正弦函数的单调性即可求解． 【详解】 （Ⅰ）α为锐角，cos α=sin α∴=, ()αααcos αf ====（Ⅱ） ()223sin2cos -sin 3sin2cos22sin 26g x x x x x x x π⎛⎫=+=+=+ ⎪⎝⎭3222,262k x k k Z πππππ+<+<+∈,263k x k ππππ+<<+, k Z ∈ []0,x π∈,所以单调递减区间是2,63ππ⎛⎫ ⎪⎝⎭【点睛】本题主要考查了同角三角函数基本关系式，二倍角的正弦函数公式，三角函数恒等变换的应用，正弦函数的单调性的综合应用，考查了数形结合思想和转化思想，属于基础题． 30．（1）124,32z i z i =-=-+；（2）4,2a b ==【解析】【分析】（1）向量()()1,1,3,3AB a CD b =--=--对应的复数分别为()11i z a =--， ()233i z b =-+-，利用()()1244i 1i z z a b +=-+-=+，即可得出,a b ；（2） 12122,z z z z +=-为实数，可得()()22442,20a b b -+-=-=，即可得出结论. 【详解】(1)∵=(a-1,-1),=(-3,b-3),∴z 1=(a-1)-i,z 2=-3+(b-3)i,∴z 1+z 2=(a-4)+(b-4)i=1+i,∴a-4=1,b-4=1,解得a=b=5,∴z 1=4-i,z 2=-3+2i.(2)∵|z 1+z 2|=2,z 1-z 2为实数,z 1+z 2=(a-4)+(b-4)i,z 1-z 2=(a+2)+(2-b)i,∴=2,2-b=0,∴a=4,b=2. 【点睛】本题主要考查复数的几何意义，复数的模以及复数与向量的综合应用，属于中档题. 复数的模的几何意义是复平面内两点间的距离，所以若z x yi =+，则z a bi -+表示点(),x y 与点(),a b 的距离.。

2019学年上期第一次阶段性考试高二（培优班）数学试卷（时间：120分钟 满分：150分）注意事项：1．答第I 卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上． 2．每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其它答案标号．不能答在试题卷上． 3．第II 卷答案要写在答题卷相应位置，写在试卷上无效．第Ⅰ卷（选择题 共60分）一、选择题（本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的，请将正确答案的选项涂在答题卡上．） 1．若命题“()p q ⌝∨”为假命题,则下列命题中正确的是A ．,p q 均为真命题B ．,p q 中至少有一个为真命题C ．,p q 均为假命题D ．,p q 中至多有一个为真命题2．由12,3a d ==确定的等差数列{}n a ,当98n a =时,序号n 等于A ．99B ．33C ．11D ．223．ABC ∆中,若sin sin sin cos cos sin cos cos 2A B A B A B A B +++=,则ABC ∆是A ．等边三角形B ．钝角三角形C ．等腰直角三角形D ．直角三角形4．已知各项均为正数的等比数列{}19,16n a a a ⋅=则258a a a ⋅⋅的值为A ．16B ．32C ．48D ．645．已知ABC ∆中,30,120AB A B =∠=∠=o o ,则ABC ∆的外接圆的面积为A ．9πBC ．12πD ．3π6．ABC ∆中,,,a b c 分别是内角,,A B C 所对的边,若,,a b c 成等比数列,且2c a =,则sin B =A ．35B ．4C ．34D ．457．设x R ∈,则“12x >”是“2210x x +->”的 A ．充分而不必要条件B ．必要而不充分条件C ．充要必要条件D ．既不充分也不必要条件8．设0,0a b >>是3a 与3b 的等比中项,则11a b+的最小值为 A ．3B ．4C ．1D ．149．已知p :函数12x y -=的图象关于直线x =1对称；q :函数1y x x=+在()0,+∞上是增函数．由它们组成的新命题“p q ∧”“p q ∨”“p ⌝”中,真命题的个数为 A ．0B ．1C ．2D ．310．不等式2313x x a a +--≤-对任意实数x 恒成立,则实数a 的取值范围为A ．(][),14,-∞-+∞UB ．(][),25,-∞-+∞UC ．[]1,2D ．(][),12,-∞+∞U11．已知每项均大于零的数列{}n a 中,首项11a =且前n 项和n S 满足n S S -=*n N ∈且2n ≥），则81a =A ． 638B ． 639C ． 640D ． 64112．设函数()()331f x x x =-+-，数列{}n a 是公差不为0的等差数列，()()()12714f a f a f a +++=L ，则127a a a +++=LA ． 0B ． 7C ． 14D ． 21第Ⅱ卷（非选择题 共90分）二、填空题（本大题共4小题，每小题5分，共20分．）13．已知数列{}n a 中,1111,12n na a a +==-,则2018a = ． 14． 设动点P 是抛物线221y x =+上任意一点,顶点()0,1A -,点M 使得2PM MA =u u u u r u u u r,则M 的轨迹方程是 ．15．如图,测量河对岸的塔高AB 时,可以选与塔底B 在同一水平面内的两个测点C 与D ．现测得,,634BCD BDC CD ππ∠=∠==,并在点C 测得塔顶A 的仰角为4π,则塔高AB 为 ． 16．在三角形ABC 中, a ，b ，c 分别是内角A ，B ，C 所对的边，b =c ,且满足cos cos b A a a B =-,若点O 是三角形ABC 外一点,()0AOB γγπ∠=<<,3,2OA OB ==,则平面四边形OACB 面积的最大值是 ．三、解答题（本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤） 17．（本题满分10分）在锐角ABC ∆中，a ，b ，c 分别为角A ，B ，C 所对的边,且32sin a c A =． （1）确定C 的大小; （2）若7c =,且ABC ∆的周长为57+,求ABC ∆的面积．18．（本题满分12分）已知命题2:450p x x --≤,命题()22:2100q x x m m -+-≤>（1）若p 是q 的充分条件,求实数m 的取值范围;（2）若5m =,p q ∨为真命题, p q ∧为假命题,求实数x 的取值范围．19．（本题满分12分）在ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c ，设S 为ABC ∆的面积，满足)222S a b c=+-．（1）求C的大小;（2）若tan21tanA cB b+=，且32BA BC⋅=u u u r u u u r,求c的值．20．（本题满分12分）某玩具生产公司计划每天生产卫兵、骑兵、伞兵这三种玩具共100个，生产一个卫兵需5分钟，生产一个骑兵需7分钟，生产一个伞兵需4分钟，已知总生产时间不超过10小时．若生产一个卫兵可获利润5元，生产一个骑兵可获利润6元，生产一个伞兵可获利润3元．（1）试用每天生产的卫兵个数x 与骑兵个数y ，表示每天的利润（元）； （2）怎样分配生产任务才能使每天的利润最大，最大利润是多少．21．（本题满分12分）已知各项均为正数的数列{}n a ,满足()221120*n n n n a a a a n N ++--=∈且12a =.（1）求数列{}n a 的通项公式； （2）设12log n n n b a a =⋅,若n b 的前n 项和为n S ,求nS ；（3）在（2）的条件下,求使1250n n S n ++⋅>成立的正整数n 的最小值．22．（本题满分12分）数列{}n a 中，11a =，{}n a 的前n 项和为n T ，且2(1)4n n a T +=．（1）求数列{}n a 的通项公式; （2）令11n n n b a a +=,数列n b 的前n 项和为n S ． （ⅰ）求n S ;（ⅱ）是否存在整数()0λλ≠,使得不等式()()141*2nn S n N λ+-<∈恒成立?若存在,求出λ的取值的集合;若不存在,请说明理由．辉县市一中2018——2019学年上期第一次阶段性考试高二（培优班）数学试卷 参考答案一、选择题1—12 BBCD DBAB BACD11.解析： 由n S S -=2=，所以是以1为首项，2为公差的等差数列，()221,21n n S n =-=-，所以22818180161159640a S S =-=-=，故选C.12.解析：()()()()()()33312711227731313114f a f a f a a a a a a a +++=-+-+-+-+-+-=L L ，即()()()3331122773333330a a a a a a -+-+-+-+-+-=L ，根据等差数列的性质得()()()()3334444333233730a d a d a d a --+--+-++-=L ，即()()()()()()33333444444333332323730a d a d a d a d a a --+-++--+--++-+-=L()()()()()()()()()22222244444423327233122333a a d a a d a a d ∴--++--++--+()()3443730a a +-+-=，即()()()22443738470a a d --++=，430a ∴-=，即43a =，1274721a a a a ∴+++==L ，故选D.二、填空题13．-1 14．2163y x =- 15．1)y = 16三、解答题17．解：（12sin c A =2sin sin A C A =，因为sin 0A ≠，所以sin 2C =. 所以3C π=或23C π=. 因为ABC ∆是锐角三角形， 所以3C π=.（2）因为c =ABC ∆的周长为5+，所以a +b =5 ①由余弦定理得222cos73a b ab π+-= ，即227a b ab +-= ②由②变形得()237a b ab +-=，所以ab =6，得1sin 232S ab π==. 18．解：（1）对于[]:1,5p A =-，对于[]:1,1q B m m =-+， 由已知， A B ⊆，∴1115m m -≤-⎧⎨+≥⎩∴[4,)m ∈+∞（2）若p 真: 15x -≤≤，若q 真: 46x -≤≤. 由已知,p q 一真一假.①若p 真q 假，则1546x x x -≤≤⎧⎨<->⎩或无解; ②若p 假q 真，则1546x x x <->⎧⎨-≤≤⎩或∴[)(]4,15,6x ∈--⋃19．解：（1）∵根据余弦定理得2222cos a b c ab C +-=，ABC ∆的面积1sin 2S ab C =；∴由)2224S a b c =+-得tan C =∵0C π<<，∴3C π=.（2）∵sin cos cos sin sin cos 21sin cos cos sin A B A B A B cB A A B b ++==，可得sin 2cos sin C c A B b =，即sin 2cos sin C cA B b=. ∴由正弦定理得sin 2sin cos sin sin C CA B B =，解得1cos 2A =.结合0A π<<，得3A π=.∵ABC ∆中，3C π=，∴()3B AC ππ=-+=，∵32BA BC ⋅=u u u r u u u r ， ∴21322c =，即8c =.20．解：（1）依据题意可得每天生产的伞兵个数为（100x y --）， ∴利润()56310023300x y x y x y ω=++--=++即23300x y ω=++. （2）根据题目信息可得：约束条件为：()5741060010000,0x y x y x y x y ++--≤⎧⎪--≥⎨⎪≥≥⎩整理可得32001000,0x y x y x y +≤⎧⎪+≤⎨⎪≥≥⎩目标函数为：23300x y ω=++. 作出可行域，如图所示.初始直线：230x y +=，平移初始直线经过点A 时，有最大值.由3200100x y x y +=⎧⎨+=⎩可得5050x y =⎧⎨=⎩，最优解为A （50，50），∴max 23300550x y ω=++=，即的最大值为550元.故每天生产卫兵50个，骑兵50个，伞兵0个时利润最大，最大利润为550元.21．解：（1）∵221120n n n n a a a a ++--=，()()1120n n n n a a a a ++∴+-=∵数列{}n a 的各项均为正数，∴10n n a a ++>， ∴120n n a a +-=，即()12*n n a a n N +=∈ 所以数列{}n a 是以2为公比的等比数列.∵12a =，∴数列{}n a 的通项公式2n n a =.（2）由（1）及12log n n n b a a =得，2n nb n =-⋅，∵12n n S b b b =+++L ，∴23422232422nn S n =--⋅-⋅-⋅--⋅L ①∴()2345122223242122nn n S n n +=--⋅-⋅-⋅---⋅-⋅L ②②-①得()()23451112122222222212212n n n n n n S n n n +++-=++++++-⋅=-⋅=-⋅--L********灿若寒星竭诚为您提供优质文档*********灿若寒星（3）要使1250nnS n++⋅>成立，只需12250n+->成立，即1252n+>，∴使1250nnS n++⋅>成立的正整数n的最小值为5.22．解：（1）21na n=-.（2）（ⅰ）()()()()111112121212122121 nbn n n n n n⎛⎫===-⎪-+-+-+⎝⎭111111123352121nSn n⎡⎤⎛⎫⎛⎫⎛⎫∴=-+-++-⎪ ⎪ ⎪⎢⎥-+⎝⎭⎝⎭⎝⎭⎣⎦L111221nSn⎛⎫∴=-⎪+⎝⎭11242nSn∴=-+（ⅱ）存在整数λ使得不等式()()141*2n nSn Nλ+-<∈恒成立.因为14312221nSn+=-+.要使得不等式()()311*221n n Nnλ-<-∈+恒成立，当n为奇数时，()311221nnλ-<-+，即31221nλ>-++.所以当1n=时，31221n-++的最大值为76-，所以只需76λ>-.当n为偶数时，31221nλ<-+，所以当2n=时，31221n-+的最小值为1310，所以只需1310λ<.可知存在713610λ-<<，且0λ≠.又λ为整数，所以λ取值集合为{}1,1-.。