船体梁纯弯曲实验

Page 1 of 10材料力学》课程实验报告纸实验二：梁的纯弯曲正应力试验实验目的1、 测定矩形截面梁在只受弯矩作用的条件下，横截面上正应力的大小随高 度变化的分布规律，并与理论值进行比较，以验证平面假设的正确性，即 横截面上正应力的大小沿高度线性分布。

2、 学习多点静态应变测量方法。

二：实验仪器与设备 :① 贴有电阻应变片的矩形截面钢梁实验装置 ② DH3818静态应变测试仪1三、实验原理（1）受力图主梁材料为钢梁，矩形截面，弹性模量 E=210GPa 高, 度 h=40.0mm ，宽度b=15.2mm 。

旋动转轮进行加载，压力器借助于下面辅助梁和拉杆（对称分布）的 传递，分解为大小相等的两个集中力分别作用于主梁的 C 、D 截面。

对主梁进行 受力分析，得到其受力简图，如图 1 所示。

（2）内力图分析主梁的受力特点，进行求解并画出其内力图，我们得到 CD 段上的剪力为零，而弯矩则为常值，因此主梁的 CD 段按理论描述，处于纯弯曲状态。

主梁 的内力简图，如图 2 所示。

材料力学》课程实验报告纸Page 2 of 10（4）理论正应力根据矩形截面梁受纯弯矩作用时， 对其变形效果所作的平面假设， 即横截面 上只有正应力，而没有切应力（或 0 ），得到主梁纯弯曲 CD 段横截面上任一 高度处正应力的理论计算公式为M y i i 理论 IIz其中， M 为 CD 段的截面弯矩（常值） ， I z 为惯性矩， y i 为所求点至中性轴的距 离。

（5）实测正应力测量时，在主梁的纯弯曲 CD 段上取 5 个不同的等分高度处（ 1、2、3、4、 5），沿着与梁的纵向轴线平行的方向粘贴 5 个电阻应变片，如图 4所示。

在矩形截面梁上粘贴上如图 5.3所示的 2组电阻应变片，应变片 1－5 分别贴在 横力弯曲区， 6－10 贴在纯弯曲区，同一组应变片之间的间隔距离相等。

3）弯曲变形效果图（纵向剖面）材料力学》课程实验报告纸Page 3 of 10根据应变电测法的基本原理， 电阻应变片粘贴到被测构件表面， 构件在受到 外载荷作用，发生变形，应变片因感受测点的应变，而同步发生变形，从而自身 的电阻发生变化。

梁的纯弯曲实验原理-回复
梁的纯弯曲实验是一种用来研究梁的弯曲特性的实验。

其原理基于以下几个假设：
1. 梁在受到外力作用时，内部各个截面上的纤维只发生纯弯曲，即纤维的伸长和压缩忽略不计，且梁材料具有良好的弹性行为。

2. 梁材料是均匀各向同性的，其性质在整个试验中保持不变。

基于以上假设，梁的纯弯曲实验采用以下步骤进行：
1. 在梁上施加一个或多个力，使其发生弯曲。

力的大小和位置视具体实验要求而定。

2. 在梁的中性轴上选取一个截面，测量该截面上的应力和应变。

可以通过张力计、应变计等设备进行测量。

3. 根据经典梁理论，计算出该截面上的弯矩和曲率。

4. 将所测得的数据绘制成应力-应变曲线、弯矩-曲率曲线等，以分析梁的弯曲性能，并得到梁的力学参数，如弹性模量、截面惯性矩等。

通过梁的纯弯曲实验，可以了解梁材料的弯曲刚度、变形特性以及承受弯曲载荷
的能力等。

这对于工程设计、材料选用等方面都有着重要的意义。

梁的纯弯曲正应力实验报告梁的纯弯曲正应力实验报告一、实验目的本实验旨在通过对实验材料进行纯弯曲加载，测量其正应力和弯曲角度，从而掌握材料在纯弯曲状态下的应力特性，并探究材料性能的影响因素。

二、实验原理当梁在纯弯曲时，受到的载荷可以分解为一个弯矩和一个剪力。

由于实验中去除了外部作用力，剪力为零，因此我们只需要考虑弯矩作用下的应力情况。

在梁的截面上，由于受到弯曲，不同位置的应变不同，因此会形成不同大小的应力。

在正常情况下，当梁未发生破坏时，梁的内部应力呈线性分布，即受到的弯矩越大，所受到的应力也会相应增大。

三、实验设备本实验所使用的设备包括：1.纯弯曲实验台2.测力仪3.梁材料（一定长度的圆形钢管或方管）四、实验步骤1. 选择一段合适材质的梁进行实验。

2. 将梁固定在纯弯曲实验台上。

3. 在梁的一端加上一定荷载。

4. 通过测力仪测量在梁部位不同位置受到的正应力。

5. 在梁的另一端加上一定数量的荷载，并重复步骤4，记录正应力。

6. 重复以上操作，直到梁发生破坏。

五、实验结果在实验过程中，我们记录了梁不同位置受到的正应力，并根据实验数据分析了不同弯矩下的应力分布曲线。

实验结果表明，在纯弯曲状态下，梁的内部应力呈线性分布，随着弯矩的增大，所受应力也会逐渐增大，直到梁发生破坏。

六、实验分析根据实验结果，我们可以发现梁的性能会受到材料的影响。

不同的材料具有不同的弯曲特性，不同的性能和抗断性能。

而在实验中，我们也可以通过调整材料的材质和长度来控制弯曲的程度，从而控制梁的应力分布和破坏点位置。

七、实验结论本实验通过纯弯曲实验台对梁进行弯曲测试，得到了不同弯矩下的应力分布曲线。

实验结论表明，梁在纯弯曲状态下，其内部应力呈线性分布，随着弯矩的增大，所受应力也会逐渐增大，直到梁发生破坏。

同时，不同材质和长度的材料在弯曲状态下具有不同的弯曲特性和抗断性能。

梁的弯曲变形测定实验一、预习要求1、复习材料力学有关弯曲变形内容和关于百分表的内容。

2、预习本节弄懂实验原理和测量方法。

二、实验目的1、测定钢梁在弯曲受力时的挠度f 和转角θ，并与理论计算值进行比较，以验证理论计算方法的正确性。

2、学习挠度和转角的测试方法。

三、实验装置和仪器1、弯曲梁实验装置如图1所示。

2、百分表2只、5N 砝码3块。

3、直尺、扳手等工具。

四、实验原理及方法1、实验原理弯曲梁实验装置简图如图2所示。

可以看出，钢梁AD （标号1）是外伸梁，A 、B 两处用铰链支承，载荷通过砝码2加在C 截面处，在C 、D 截面处沿位移方向安装两个百分表3和4，用以测量C 、D 两点的位移。

根据材料力学理论，钢梁1在△P 作用下，梁C 截面上的挠度f C 和B 截面转角θB 分别为图1 弯曲梁实验装置图2 弯曲梁实验装置简图EIL P f c 48)2(3∆=和 EIL P B 16)2(2∆=θ式中，123ba I =， 为对矩形梁横截面中性轴的惯性矩。

实验时，加载荷增量△P ，用百分表测出D 、C 截面处的位移增量△D 和△C ，则梁C 截面实测挠度和B 截面的实测转角分别为：C f C ∆=' ，1L D B∆='θ2、实验方法①将测量好数据的钢梁按图2所示位置要求安装在相应的卡具中，并记录有关数据，填入表1中；②将百分表3和4安装在指定位置，并检查和调整它们的工作情况。

检查时，用手轻轻下压钢梁，观察百分表上的读数是否稳定，指针走动是否均匀，能否复原；③加砝码进行实验。

载荷共分3级，每加一级后记下砝码重和百分表的读数。

实验数据按表2记录；④实验完后，卸去砝码。

表1 钢梁原始数据表表2 实验数据记录表五、实验结果处理和实验报告1、按表1和2记录实验原始数据。

2、按载荷△P 计算钢梁截面C 和截面B 上的理论挠度f C 和转角θB ，计算实测平均挠度C f '和平均转角Bθ'。

实验四 梁的弯曲实验一、实验目的掌握剪应力计算和平衡校核方法。

1、 作梁的整数级或半数级等差线图案；2、 根据所测定的等差线和等倾线数据，计算各测点的剪应力值；3、 与材料力学所计算出的理论结果比较。

二、实验设备偏光弹性仪三、实验模型及加载方式四、实验步骤1、测量模型尺寸用卡尺测量模型尺寸，做记录，同时检查刻线尺寸。

2、安装模型及调整仪器（1）调整仪器为正交圆偏振场，并调节杠杆平衡。

（2）调节下支座间距和位置，将模型置于二支座上，并在梁中点置一小钢柱，同时将杠杆压下并加少许载荷（10N ），调节夹头上下位置使其保持水平。

（3）开启白光光源（同时开启钠光灯预热），观察等差线图案是否对称；若不对称，需再调整直至对称为止，方可继续加载。

3、绘制等差线图案（1）用白光观察等差线图案，逐渐加载直至边界处最高条纹级数为4~5级左右。

弄清等差线图案的特点，找出0级位置及级数变化趋势，并用铅笔在模型上描出0级条纹，记录载荷数量。

（2）用单色光，描出整个等差线图案，标明级数，反复检查核对。

（3）卸除载荷，取下模型，用描图纸描摹出条纹图案，标明级数，注明载荷，最后从模型上擦掉等差线图案。

4、作等倾线图案，测量各测点的等倾线度数四点弯曲梁受力示意图三点弯曲梁受力示意图（1）调整仪器为正交平面偏振场，重新安装模型，施加适当载荷，按逆时针方向同步旋转偏振轴，仔细观察等倾线的特征，待摸清等倾线的变化规律后，将偏振轴恢复到00位置。

（2）按逆时针方向同步旋转偏振轴，依次描绘出00、150、300、450、600及750等倾线，标明度数，并反复检查核对。

（3）测量AB、CD截面上各测点的等倾线度数，并填入表格7-2中，分析判定σx方向。

（4）卸下模型，用描图纸描摹等倾线图案，标明度数。

5、补偿各测点的等差线条纹级数（1）擦去等倾线图案，重新安装模型，并施加作等差线时的相同载荷量。

（2）用单色光，以旋转分析镜补偿法确定各测点的非整数级等差线条纹级数，并填入记录表格。

实验七 纯弯曲梁的正应力实验一、实验目的1．测定梁纯弯曲时的正应力分布规律，并与理论计算结果进行比较，验证弯曲正应力公式。

2．掌握电测法的基本原理。

二、实验设备1．纯弯曲梁实验装置。

2．静态电阻应变仪。

三、实验原理已知梁受纯弯曲时的正应力公式为z I y M ⋅=σ 式中M 为纯弯曲梁横截面上的弯矩，z I 为横截面对中性轴Z 的惯性矩，y 为横截面中性轴到欲测点的距离。

本实验采用铝制的箱形梁，在梁承受纯弯曲段的侧面，沿轴向贴上五个电阻变应片，如图7－1所示，1R 和5R 分别贴在梁的顶部和低部，2R 、4R 贴在 4H y ±=的位置，3R 在中性层处。

当梁受弯曲时，即可测出各点处的轴向应变实i ε（i=1、2、3、4、5）。

由于梁的各层纤维之间无挤压，根据单向应力状态的胡克定律，求出各点的实验应力为：实i σ= ⋅E 实i ε（=i 1、2、3、4、5）式中，E 是梁材料的弹性模量。

这里采用的增量法加载，每增加等量的载荷△P ，测得各点相应的应变增量为△实i ε，求出△实i ε的平均值实i ε∆，依次求出各点的应力增量△实i σ为：△实i σ = ⋅E 实i ε∆ （7－1）把△实i σ与理论公式算出的应力增量：i σ∆理 = z i I y M ⋅∆ （7－2） 加以比较从而验证理论公式的正确性。

从图 7－l 的试验装置可知，a P M ⋅∆=∆21 （7－3）图7－1 纯弯曲梁装置四、实验步骤1．拟定加载方案。

在0～20kg 的范围内分4级进行加载，每级的载荷增量kg P 5=∆。

2． 接通应变仪电源，把测点1的应变片和温度补偿片按半桥接线法接通应变仪，具体做法是：将测点1的应变片接在应变仪的A 、B 接线柱上，将温度补偿片接在B 、C 接线柱上。

调整应变仪零点（或记录应变仪的初读数）。

3．每增加一级载荷（kg P 5=∆），记录引伸仪读数一次，直至加到20kg 。

注意观察各级应变增量情况。

纯弯曲梁的正应力实验报告纯弯曲梁的正应力实验报告引言：纯弯曲梁是一种常见的结构形式，它在工程中广泛应用于桥梁、建筑物以及机械设备等领域。

了解纯弯曲梁的正应力分布规律对于工程设计和结构安全至关重要。

本实验旨在通过实验方法测量纯弯曲梁的正应力分布，并对实验结果进行分析和讨论。

实验原理：纯弯曲梁在受力时，其截面上的纵向纤维会发生伸长或压缩，从而产生正应力和剪应力。

根据弯曲梁的理论，当弯矩作用于梁上时，梁截面上的正应力与截面距离中性轴的距离成正比。

实验步骤：1. 实验准备：选择一根长度适中的纯弯曲梁，清理梁的表面，并使用卡尺测量梁的几何参数，如宽度、高度和长度等。

2. 悬挂梁：在实验装置上悬挂梁，并调整悬挂点的位置，使梁能够自由弯曲。

3. 施加载荷：逐渐施加外力，使梁发生弯曲，同时记录外力大小和梁的挠度。

4. 测量应变：在梁的表面粘贴应变片，并使用应变仪测量不同位置的应变值。

5. 计算正应力：根据应变与正应力之间的线性关系，使用应变-应力关系计算不同位置的正应力。

6. 绘制应力分布曲线：将测得的正应力数据绘制成应力分布曲线，并进行分析和讨论。

实验结果与分析：通过实验测量和计算，得到了纯弯曲梁不同位置的正应力值，并绘制了应力分布曲线。

实验结果显示，在纯弯曲梁的中性轴附近，正应力较小；而在梁的顶部和底部，正应力较大。

这符合弯曲梁的理论，即正应力与截面距离中性轴的距离成正比。

进一步分析发现，纯弯曲梁的正应力分布呈现出一种对称性，即梁的上下两侧的正应力大小相等。

这是由于梁在弯曲过程中，上下两侧受到的外力大小和方向相反，从而使得正应力分布对称。

此外，实验结果还显示，纯弯曲梁的正应力在梁的中心位置达到最小值，这是由于中性轴处的纤维受力最小，所以正应力最小。

结论：通过本实验，我们成功测量和分析了纯弯曲梁的正应力分布规律。

实验结果表明，纯弯曲梁的正应力与截面距离中性轴的距离成正比，且呈现对称分布。

这对于工程设计和结构安全具有重要意义，能够帮助工程师更好地预测和评估梁的受力情况。

74实验四 纯弯曲梁正应力实验一、实验目的1、测定矩形截面梁在纯弯曲时的正应力分布规律，并验证弯曲正应力公式的正确性；2、学习多点静态应变测量方法。

二、仪器设备1、纯弯曲梁实验装置；2、YD-88型数字式电阻应变仪；3、游标卡尺。

三、试件制备与实验装置1、试件制备本实验采用金属材料矩形截面梁为实验对象。

为了测量梁横截面上正应力的大小和它沿梁高度的分布规律，在梁的纯弯段某一截面处，中性轴和以其为对称轴的上下1/4点、梁顶、梁底等5个测点沿高度方向均匀粘贴了五片轴向的应变计（如图4-4-1），梁弯曲后，其纵向应变可通过应变仪测定。

图4-4-12、实验装置如图4-4-2和图4-4-3所示，将矩形截面梁安装在纯弯曲梁实验装置上，逆时针转动实验装置前端的加载手轮，梁即产生弯曲变形。

从梁的内力图可以发现：梁的CD 段承受的剪力为0，弯矩为一常数，处于“纯弯曲”状态，且弯矩值M=21P •a ，弯曲正应力公式 σ=z yI ⋅M可变换为σ=y az⋅P ⋅I 2图4-4-2图4-4-37576四、实验原理实验时，通过转动手轮给梁施加载荷，各测点的应变值可由数字式电阻应变仪测量。

根据单向胡克定律即可求得σi 实=E ·εi 实(i=1,2,3,6,7)为了验证弯曲正应力公式σ=z y I ⋅M 或σ=y az⋅P ⋅I 2的正确性，首先要验证两个线性关系，即σ∝y 和σ∝P 是否成立:1、检查每级载荷下实测的应力分布曲线，如果正应力沿梁截面高度的分布是呈直线的，则说明σ∝y 成立；2、由于实验采用增量法加载，且载荷按等量逐级增加。

因此，每增加一级载荷，测量各测点相应的应变一次，并计算其应变增量，如果各测点的应变增量也大致相等，则说明σ∝P 成立。

最后，将实测值与理论值相比较，进一步可验证公式的正确性。

五、实验步骤1、试件准备用游标卡尺测量梁的截面尺寸（一般由实验室老师预先完成），记录其数值大小；将梁正确地放置在实验架上，保证其受力仅发生平面弯曲，注意将传感器下部的加力压杆对准加力点的缺口，然后打开实验架上测力仪背面的电源开关；2、应变仪的准备 a.测量电桥连接：图4-4-4如图4-4-4，为了简化测量电桥的连接，将梁上5个测点的应变计引出导线各取出其中一根并联成一根总的引出导线，并以不同于其他引出导线的颜色区别，所以，测量导线由原来的10根缩减为6根，连接测量电桥时，将颜色相同的具有编号1、2、3、6、7的五根线分别连接在仪器后面板上五个不同通道的A号接线孔内，并将具有特殊颜色的总引出导线连接在仪器后面板上的“公共补偿片BC”位置的B号接线孔内。

竭诚为您提供优质文档/双击可除梁的纯弯曲实验报告篇一：纯弯曲实验报告page1of10page2of10page3of10page4of10page5of10篇二：弯曲实验报告弯曲实验报告材成1105班3111605529张香陈一、实验目的测试和了解材料的弯曲角度、机械性能、相对弯曲半径及校正弯曲时的单位压力等因素对弯曲角的影响及规律。

二、实验原理坯料在模具内进行弯曲时，靠近凸模的内层金属和远离凸模的外层金属产生了弹—塑性变。

但板料中性层附近的一定范围内，却处于纯弹性变形阶段。

因此，弯曲变形一结束，弯曲件由模中取出的同时伴随着一定的内外层纤维的弹性恢复。

这一弹性恢复使它的弯曲角与弯曲半径发生了改变。

因此弯曲件的形状的尺寸和弯曲模的形状尺寸存在差异。

二者形状尺寸上的差异用回弹角来表示。

本实验主要研究影响回弹角大小的各因素。

三、实验设备及模具（1）工具：弯曲角为90度的压弯模一套，配有r=0.1、0.4、0.8、2、4五种不同半径的凸模各一个。

刚字头，万能角度尺，半径样板和尺卡。

（2）设备：曲柄压力机（3）试件：08钢板（不同厚度），铝板（不同厚度），尺寸规格为52x14mm，纤维方向不同四、实验步骤1.研究弯曲件材料的机械性能，弯曲角度和相对弯曲半径等回弹角度的影响。

实验时利用90度弯曲角度分别配有五种不同的弯曲半径的弯模，对尺寸规格相同的试件进行弯曲，并和不同的弯曲半径各压制多件。

对不同弯曲半径的试件压成后需要打上字头0.1、0.4、0.8、2、4等，以示区别。

最后，按下表要求测量和计算。

填写好各项内容。

五、数据处理（t/mm）试件尺寸：52x14mm弯曲后的试样如下图所示δθ=f(r凸/t)曲线如下图所示分析讨论：分析相对弯曲半径，弯曲角度及材料机械性能对回弹角的影响。

答：相对弯曲半径越小，弯曲的变形程度越大，塑性变形在总变形中所占比重越大，因此卸载后回弹随相对弯曲半径的减小而减小，因而回弹越小。

纯弯曲实验报告纯弯曲是一种力学试验方法，通常用于评估材料的弯曲刚度和弯曲强度。

本次实验旨在探究两种不同材料的弯曲性能，并分析其结果。

实验设计本次实验使用了两个不同材质的杆材进行测试。

第一个杆材采用了铝合金材料，长度为100cm，直径为1cm。

第二个杆材采用了无定形塑料材料，长度为100cm，直径为0.5cm。

在实验开始前，我们打开实验设备的电源并准备好测试仪器。

我们调整测试仪器的参数以适应我们所使用的材料，包括弯曲测试的速度和初始弯曲角度。

一切准备就绪后，我们将第一个杆材放入实验装置并进行第一轮弯曲测试。

我们记录了此次测试的弯曲载荷和弯曲程度。

接着，我们继续进行第二轮弯曲测试，直到达到极限载荷。

在此过程中，我们还记录了杆材的弯曲程度和载荷大小。

同样，我们对第二个杆材也进行了此次实验的全部步骤，并记录相应数据。

实验结果我们用实验数据绘制了载荷-弯曲变形曲线，并进行了一些计算。

首先，我们计算了弯曲刚度，即载荷与弯曲程度之比。

然后，我们计算了每个杆材的最大弯曲载荷和最大弯曲程度。

从实验数据和图表中可以看出，铝合金杆材的弯曲刚度远高于无定形塑料杆材。

这表明铝合金杆材在受到载荷时可以更好地保持强度和稳定性。

此外，铝合金杆材的最大弯曲载荷也比无定形塑料杆材高得多，即使受到相同的弯曲程度，铝合金杆材仍能够继续承受更大的载荷。

结论本次纯弯曲实验表明，铝合金杆材在弯曲测试中表现出更高的刚度和更高的弯曲载荷。

这意味着铝合金杆材对承受弯曲载荷时能够保持更好的形状和稳定性。

无定形塑料杆材的弯曲刚度较低，更容易形变，并且其弯曲载荷较小。

实验中采用的测试方法和参数可以用于评估各种材料的弯曲性能，并为材料选择和设计提供有用的指导。

最后，我们需要指出，本次实验并非杆材在实际应用中所处的环境，故实验结果所表现的杆材弯曲性能与实际环境可能会有所不同。

因此，在实际设计中，需要考虑到实际环境、应用载荷、材料因素等多方面因素。

梁的弯曲实验实验报告梁的弯曲实验实验报告摘要：梁的弯曲实验是一种常见的力学实验，通过对梁的施加不同的外力，观察梁的弯曲变形情况，探究梁在外力作用下的力学性质。

本实验通过设计不同材料和不同截面形状的梁，测量其弯曲变形与外力之间的关系，分析梁的强度和刚度。

引言：梁是工程中常见的结构元件，广泛应用于建筑、桥梁、机械等领域。

了解梁的力学性质对于设计和优化结构具有重要意义。

梁的弯曲实验是研究梁的力学性质的常用方法之一。

实验目的：1. 掌握梁的弯曲实验的基本原理和方法。

2. 通过实验测量和分析，了解梁的强度和刚度与外力之间的关系。

3. 通过对不同材料和截面形状的梁进行实验，比较不同梁的力学性质。

实验器材：1. 实验台2. 不同材料和截面形状的梁3. 弹簧测力计4. 支撑架5. 测量尺6. 实验记录表格实验步骤：1. 将实验台调整水平，确保实验的准确性。

2. 将梁放置在支撑架上，调整支撑点的位置，使梁的长度适当。

3. 在梁的中间位置放置弹簧测力计，记录其初始读数。

4. 通过调整弹簧测力计上的螺母，施加不同的外力到梁上。

5. 记录不同外力下梁的弯曲变形情况，并测量弹簧测力计的读数。

6. 将实验数据整理并分析，得出梁的弯曲性质。

实验结果：通过实验测量和数据分析，我们得到了不同外力下梁的弯曲变形情况和弹簧测力计的读数。

我们发现，随着外力的增加，梁的弯曲变形也增加，弹簧测力计的读数也相应增加。

这表明梁的弯曲变形与外力之间存在一定的线性关系。

同时，我们还比较了不同材料和截面形状的梁的弯曲性质。

实验结果显示，不同材料和截面形状的梁在相同外力下的弯曲变形和弹簧测力计的读数存在差异。

这说明梁的材料和截面形状对其弯曲性质有重要影响。

讨论与分析：根据实验结果，我们可以得出以下结论：1. 外力与梁的弯曲变形之间存在线性关系，外力越大，梁的弯曲变形越大。

2. 梁的材料和截面形状对其弯曲性质有重要影响，不同材料和截面形状的梁在相同外力下的弯曲变形存在差异。

梁的纯弯曲实验报告梁的纯弯曲实验报告摘要：本实验旨在研究梁在纯弯曲状态下的力学性质。

通过对不同材料和截面形状的梁进行纯弯曲实验，测量梁的位移和应力分布，分析梁的弯曲刚度和断裂强度，以及不同因素对梁的弯曲性能的影响。

实验结果表明，梁的纯弯曲性能与材料的弹性模量、截面形状和几何尺寸密切相关。

引言：梁是一种常见的结构元件，广泛应用于建筑、桥梁、机械等领域。

在实际工程中，梁常常承受弯曲载荷，因此研究梁在纯弯曲状态下的力学性质具有重要意义。

本实验通过纯弯曲实验，探究梁的弯曲刚度、应力分布和断裂强度，为工程设计和材料选择提供依据。

实验方法：本实验使用了不同材料和截面形状的梁进行纯弯曲实验。

首先，选择合适的试验材料，如钢材、铝材等，并根据实验要求制备不同截面形状的梁。

然后，在实验装置上将梁固定，施加纯弯曲载荷，通过位移传感器测量梁的变形情况。

同时，使用应变片测量梁的应变分布，进而计算出梁的应力分布。

最后，记录实验数据并进行分析。

实验结果：实验结果显示，不同材料和截面形状的梁在纯弯曲状态下表现出不同的力学性能。

首先，弯曲刚度是评价梁抗弯能力的重要指标。

实验发现，梁的弯曲刚度与材料的弹性模量密切相关，弹性模量越大，梁的弯曲刚度越高。

其次，应力分布是研究梁弯曲性能的重要参数。

实验结果表明，梁的应力分布呈现出高应力区和低应力区的分布特点，高应力区位于梁的上表面，低应力区位于梁的下表面。

最后，实验还发现，梁的断裂强度与材料的抗拉强度密切相关，抗拉强度越高，梁的断裂强度越大。

讨论：本实验结果表明，梁的纯弯曲性能受多个因素的影响，如材料的弹性模量、截面形状和几何尺寸等。

首先，材料的弹性模量决定了梁的弯曲刚度，弹性模量越大，梁的弯曲刚度越高。

因此，在工程设计中，应选择具有高弹性模量的材料来提高梁的弯曲刚度。

其次，截面形状对梁的弯曲性能也有显著影响。

不同截面形状的梁具有不同的惯性矩和截面模量，从而导致不同的应力分布和弯曲刚度。

实验二：纯弯曲梁实验
一、实验目的：
1、测定梁在纯弯曲时某一截面上的应力及其分布情况。

2、实验结果与理论值比较,验证弯曲正应力公式σ=My/I z 的正确性。

3、测定泊松比μ。

二、实验设备：
材料力学多功能实验台、纯弯曲梁 三、实验原理
本实验采用逐级等量加载的方法加载，每次增加等量的载荷⊿P ，测定各点
相应的应变增量一次，即：初载荷为零，最大载荷为4kN ，等量增加的载荷⊿P 为500N 。

分别取应变增量的平均值(修正后的值)，求出各点应力增量的平
均值。

四、实验内容与步骤
1. 确认纯弯梁截面宽度 b=20mm,高度 h=40mm,载荷作用点到梁两侧支点距离c=100mm 。

2. 将传感器连接到BZ 2208-A 测力部分的信号输入端，将梁上应变片的公共线接至应变仪任意通道的A 端子上，其它接至相应序号通道的B 端子上，公共补偿片接在公共补偿端子上。

检查并纪录各测点的顺序。

3. 打开仪器，设置仪器的参数，测力仪的量程和灵敏度设为传感器量程、灵敏度。

4. 本实验取初始载荷P 0=0.5KN （500N ），P max =2.5KN(2500N)，ΔP=0.5KN(500N)，以后每增加载荷500N ，记录应变读数εi ，共加载五级，然后卸载。

再重复测量，共测三次。

取数值较好的一组，记录到数据列表中。

5. 实验完毕，卸载。

实验台和仪器恢复原状。

五、 实验报告
实
ε∆实
σ∆
表1 测点位置
表2 实验记录
六、实验结论
的正确性实验结果与理论值比较,验证弯曲正应力公式σ=My/I
z。

第3期2021年3月机械设计与制造Machinery Design & Manufacture181船用管件弯曲成型的有限元建模与实验验证钱峰，潘笑誉，何亚伟，叶小奔(大连理工大学机械工程学院，辽宁大连116024)摘要:基于弯曲成型理论并结合船用管件弯曲成型的实际工况，采用A B A Q U S/C A E模块建立了 20钢管件的数控弯曲 成型有限元模型，对建模过程中的力学模型、几何模型、单元定义、网格划分及其敏感性分析和约束接触设置等步骤进行 了详细的说明。

通过提取弯曲段横截面的最小壁厚值，与变形前的截面壁厚相比，定义了弯管外侧壁厚的减薄率。

同时，通过提取畸变后的管件截面的椭圆长短轴，推导出了截面畸变程度质量指标的计算方法。

与实验结果比较，有限元模型 的计算结果与实验测量数据之间的相对误差较小，从而验证了有限元模型计算的精确度和可靠性，为管件的弯曲成型加 工提供了理论依据，可应用于加工后管件质量的评价。

关键词:数控弯管机;有限元;弯曲成型;约束条件;实验验证中图分类号:T H16;T P242文献标识码:A文章编号：100丨-3997(2021 )03-0181-04FEA Modeling and Experimental Validation of Marine Pipe in the Bending ProcessQIAN Feng, PAN Xiao-yu, HE Ya-wei, YE Xiao-ben(School of Mechanical Engineering, Dalian University of Technology,Liaoning Dalian 116024, China)Abstract on the theory o f bending f orming and the processing environment, a f inite element model o f the marine pipe made of 20# steel was built with the A B A Q U S/C A E package, wherein modeling procedure including the mechanical models geometric m odel，unit definition, grid meshing with sensitivity analysis y constraint and contact setting were described in detail. The relative error between the minimum thickness o f t he deformed pipe and the original thickness was adopted to define the wall thinning rate. Moreover, the performance indices,corresponding to cross-section distortion defined by the longer and shorter axes o f the ellipse formed by the deformed pipe cross-section y were introduced. The comparison between the F E A and experimental results shows that the relative errors between them are relatively small and acceptable to validate the F E A model, which can be applied f or evaluating the quality o f the pipe bending process.Key Words：CNC Pipe Bending Machine；Finite Element；Bending Forming Theory；Constraints；Experimental Val­idationi引言船舶在构建生产过程中，其管道配件的生产在占有极其重 要的地位。

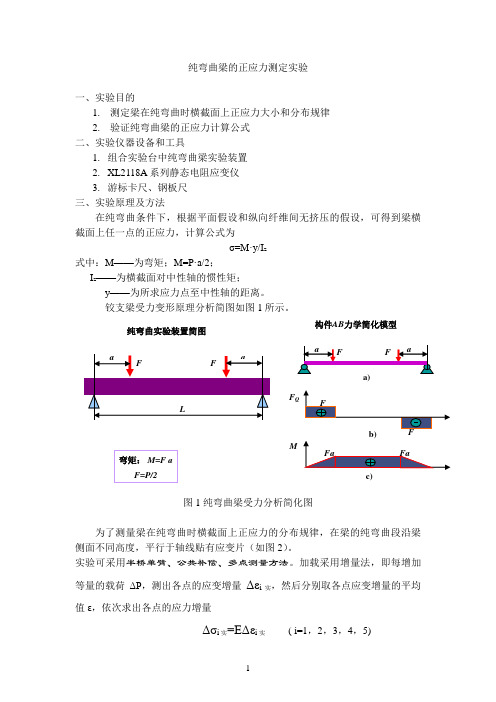
纯弯曲梁的正应力测定实验一、实验目的1. 测定梁在纯弯曲时横截面上正应力大小和分布规律2. 验证纯弯曲梁的正应力计算公式 二、实验仪器设备和工具1. 组合实验台中纯弯曲梁实验装置2. XL2118A 系列静态电阻应变仪3. 游标卡尺、钢板尺 三、实验原理及方法在纯弯曲条件下，根据平面假设和纵向纤维间无挤压的假设，可得到梁横截面上任一点的正应力，计算公式为σ=M·y/I z式中：M ——为弯矩；M=P·a/2；I z ——为横截面对中性轴的惯性矩；y ——为所求应力点至中性轴的距离。

铰支梁受力变形原理分析简图如图1所示。

图1 纯弯曲梁受力分析简化图为了测量梁在纯弯曲时横截面上正应力的分布规律，在梁的纯弯曲段沿梁侧面不同高度，平行于轴线贴有应变片（如图2）。

实验可采用半桥单臂、公共补偿、多点测量方法。

加载采用增量法，即每增加等量的载荷ΔP ，测出各点的应变增量Δεi 实，然后分别取各点应变增量的平均值ε，依次求出各点的应力增量Δσi 实=EΔεi 实 ( i=1，2，3，4，5)纯弯曲实验装置简图弯矩： M=F a F=P/2F QMc)构件AB 力学简化模型将实测应力值与理论应力值进行比较，以验证弯曲正应力公式。

图 2应变片在梁中的位置实验接线方法实验接桥采用1/4桥（半桥单臂）方式，应变片与应变仪组桥接线方法如图3所示。

使用弯曲梁上的应变片Ri（R1，R2，R3，R4，R5即工作应变片）分别连接到应变仪测点的A/B上，测点上的B和B1用短路片短接；温度补偿应变片Rt连接到桥路选择端的A/D上，桥路选择短接线将D1/D2短接，并将所有螺钉旋紧。

四、实验步骤1.设计好本实验所需的各类数据表格。

2.测量矩形截面梁的宽度b和高度h、载荷作用点到梁支点距离a及各应变片到中性层的距离y i。

见附表13.拟订加载方案。

可先选取适当的初载荷P0=200N，估算P max（该实验载荷范围P max≤2000N），分4级加载(300N，600N，900N，1200N)。

光测法梁的纯弯曲实验报告光测法
一、实验目的
说明本次实验的目的和意义。

二、实验原理
介绍光测法测量梁变形的原理，包括应变测量和位移测量两个方面的原理。

三、实验装置与仪器
描述实验用到的装置、仪器和材料，包括梁、支座、加载装置、光电仪器等等。

四、实验步骤与数据处理
依次介绍实验的具体步骤，包括加载、光电测量、数据记录等。

并详细描述如何进行数据处理，如何求得梁的瞬时弯矩、弯曲角、曲率半径等参数，并给出典型数据和图表。

五、实验结果分析
根据实验获得的数据，分析和讨论光测法测量精度的影响因素，比如光电测量误差、支座刚度、梁截面形状等，以及实验结果和理论计算结果的比较，分析误差及其原因。

六、结论
总结实验结果和分析，指出实验的优点、不足，及其工程应用的前景，并给出改进措施和建议。

七、参考文献
列出本实验中所参考的文献、资料与软件。

注：以上仅为一个写作思路示例，具体写作内容应根据实验条件、数据和要求进行具体调整和修改。

同时需要注意不能出现涉及政治敏感、敏感信息等问题。