纯弯曲正应力分布实验报告
- 格式:docx
- 大小:31.82 KB
- 文档页数:11

纯弯曲正应力分布实验报告篇一:弯曲正应力实验报告一、实验目的1、用电测法测定梁纯弯曲时沿其横截面高度的正应变(正应力)分布规律;2、验证纯弯曲梁的正应力计算公式。
3、初步掌握电测方法,掌握1/4桥,1/2桥,全桥的接线方法,并且对试验结果及误差进行比较。
二、实验仪器和设备1、多功能组合实验装置一台;2、TS3860型静态数字应变仪一台;3、纯弯曲实验梁一根。
4、温度补偿块一块。
三、实验原理和方法弯曲梁的材料为钢,其弹性模量E=210GPa,泊松比μ=。
用手转动实验装置上面的加力手轮,使四点弯上压头压住实验梁,则梁的中间段承受纯弯曲。
根据平面假设和纵向纤维间无挤压的假设,可得到纯弯曲正应力计算公式为:??My Ix式中:M为弯矩;Ix为横截面对中性轴的惯性矩;y为所求应力点至中性轴的距离。
由上式可知,沿横截面高度正应力按线性规律变化。
实验时采用螺旋推进和机械加载方法,可以连续加载,载荷大小由带拉压传感器的电子测力仪读出。
当增加压力?P时,梁的四个受力点处分别增加作用力?P/2,如下图所示。
为了测量梁纯弯曲时横截面上应变分布规律,在梁纯弯曲段的侧面各点沿轴线方向布置了3片应变片,各应变片的粘贴高度见弯曲梁上各点的标注。
此外,在梁的上表面和下表面也粘贴了应变片。
如果测得纯弯曲梁在纯弯曲时沿横截面高度各点的轴向应变,则由单向应力状态的虎克定律公式??E?,可求出各点处的应力实验值。
将应力实验值与应力理论值进行比较,以验证弯曲正应力公式。
σ实=Eε式中E是梁所用材料的弹性模量。
实图3-16为确定梁在载荷ΔP的作用下各点的应力,实验时,可采用“增量法”,即每增加等量的载荷ΔP测定各点相应的应变增量一次,取应变增量的平均值Δε 把Δσ实与理论公式算出的应力??式中的M应按下式计算:实来依次求出各点应力。
??比较,从而验证公式的正确性,上述理论公????四、实验步骤1?Pa (3.16) 21、检查矩形截面梁的宽度b和高度h、载荷作用点到梁支点距离a,及各应变片到中性层的距离yi。
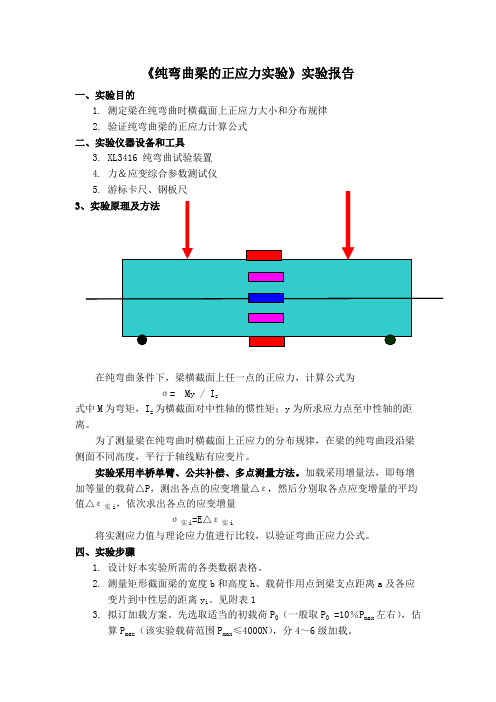
《纯弯曲梁的正应力实验》实验报告一、实验目的1.测定梁在纯弯曲时横截面上正应力大小和分布规律2.验证纯弯曲梁的正应力计算公式二、实验仪器设备和工具3.XL3416 纯弯曲试验装置4.力&应变综合参数测试仪5.游标卡尺、钢板尺3、实验原理及方法在纯弯曲条件下,梁横截面上任一点的正应力,计算公式为σ= My / I z式中M为弯矩,I z为横截面对中性轴的惯性矩;y为所求应力点至中性轴的距离。
为了测量梁在纯弯曲时横截面上正应力的分布规律,在梁的纯弯曲段沿梁侧面不同高度,平行于轴线贴有应变片。
实验采用半桥单臂、公共补偿、多点测量方法。
加载采用增量法,即每增加等量的载荷△P,测出各点的应变增量△ε,然后分别取各点应变增量的平均值△ε实i,依次求出各点的应变增量σ实i=E△ε实i将实测应力值与理论应力值进行比较,以验证弯曲正应力公式。
四、实验步骤1.设计好本实验所需的各类数据表格。
2.测量矩形截面梁的宽度b和高度h、载荷作用点到梁支点距离a及各应变片到中性层的距离y i。
见附表13.拟订加载方案。
先选取适当的初载荷P0(一般取P0 =10%P max左右),估算P max(该实验载荷范围P max≤4000N),分4~6级加载。
4.根据加载方案,调整好实验加载装置。
5. 按实验要求接好线,调整好仪器,检查整个测试系统是否处于正常工作状态。
6.加载。
均匀缓慢加载至初载荷P 0,记下各点应变的初始读数;然后分级等增量加载,每增加一级载荷,依次记录各点电阻应变片的应变值εi ,直到最终载荷。
实验至少重复两次。
见附表27.作完实验后,卸掉载荷,关闭电源,整理好所用仪器设备,清理实验现场,将所用仪器设备复原,实验资料交指导教师检查签字。
附表1 (试件相关数据)附表2 (实验数据)P 50010001500200025003000载荷N △P 500500500500500εP -33-66-99-133-166△εP -33-33-34-334平均值-33.25εP -16-33-50-67-83△εP -17-17-17-162平均值16.75εP 00000△εP 00001平均值0εP 1532476379△εP 171516163平均值16εP 326597130163△εP 33323333 各 测点电阻应变仪读数µε5平均值32.75五、实验结果处理1.实验值计算根据测得的各点应变值εi 求出应变增量平均值△εi ,代入胡克定律计算应变片至中性层距离(mm )梁的尺寸和有关参数Y 1-20宽 度 b = 20 mm Y 2-10高 度 h = 40 mm Y 30跨 度 L = 620mm (新700 mm )Y 410载荷距离 a = 150 mm Y 520弹性模量 E = 210 GPa ( 新206 GPa )泊 松 比 μ= 0.26惯性矩I z =bh 3/12=1.067×10-7m 4 =106667mm 4。

实验五弯曲正应力实验报告___________系____________专业__________班姓名____________ 学号_________ 1.实验目的:(1)测定梁在纯弯曲下的弯曲正应力大小及其分布规律。
(2)验证弯曲正应力计算公式。
(3)掌握电测方法。
2.实验设备:3.实验记录及计算结果:a.梁的已知数据试件材料:A3 钢弹性模量: E= GPa电阻片灵敏系数: K=试件尺寸电阻片到中性层的距离(mm)b = mm Y1= mmh = mm Y2= mmL = mm Y3= mma = mm Y4= mmI z= mm4Y5= mmb.实验记录:c.计 算:实验值计算:根据测得的应变增量平均值Δε平均,应用虎克定律算出各点对应的应力增量:平均实i i εσ∆•E =∆ (i=1,2,3,4,5)理论值计算:zii I y •∆M =∆理σ (i=1,2,3,4,5) 式中 : 123bh I z = ——惯性矩a 2∆P=∆M ——弯矩增量 y i ——各测点到中性层的距离d.正应力实验结果与理论计算值比较: 各测点正应力值(MPa )测点 1 2 3 4 5 实验值σ∆实 理论值σ∆理误差%100⨯∆∆-∆=理实理σσσe.按比例绘出(实测应力和理论计算应力)正应力分布图。
4.问题讨论:1)说明梁在纯弯曲时正应力沿梁高度的分布规律。
2)比较各测点的实测应力值与理论计算应力值,并分析产生误差的原因。
指导教师:________________________年_______月______日。

一、实验目的1. 通过实验,了解梁在弯曲状态下的应力分布规律;2. 验证梁的弯曲正应力计算公式的准确性;3. 掌握应变电测法的基本原理和操作方法;4. 培养学生严谨的实验态度和科学的研究方法。
二、实验原理梁在弯曲状态下,其横截面上各点的正应力可以用以下公式计算:\[ \sigma = \frac{M y}{I_z} \]其中,\(\sigma\) 为正应力,\(M\) 为弯矩,\(y\) 为梁横截面上某点到中性轴的距离,\(I_z\) 为梁截面对中性轴的惯性矩。
实验中,通过测量梁横截面上不同位置的应变,根据虎克定律,可计算出相应位置的应力。
实验装置主要包括梁、应变片、静态数字电阻应变仪等。
三、实验仪器与设备1. 梁材料:矩形截面试件,尺寸为 \(b \times h\);2. 应变片:电阻应变片,用于测量梁横截面上的应变;3. 静态数字电阻应变仪:用于测量应变片输出的电阻变化,从而计算出应变;4. 加载装置:用于对梁施加弯矩;5. 游标卡尺:用于测量梁的尺寸;6. 计算器:用于计算实验数据。
四、实验步骤1. 准备实验装置,包括梁、应变片、应变仪等;2. 将应变片粘贴在梁的预定位置,确保应变片与梁表面紧密贴合;3. 接通应变仪电源,调整应变仪的量程和灵敏度;4. 使用游标卡尺测量梁的尺寸,记录数据;5. 在梁上施加预定的弯矩,确保梁处于弯曲状态;6. 使用应变仪测量梁横截面上不同位置的应变,记录数据;7. 根据实验数据和应变片的位置,计算出梁横截面上不同位置的应力;8. 比较实验测得的应力与理论计算值,分析误差原因。
五、实验结果与分析1. 实验数据:表1:梁横截面上不同位置的应变测量值| 测点位置 | 应变值(με) || -------- | ------------ || A点 | 120 || B点 | 100 || C点 | 80 || D点 | 60 |表2:梁横截面上不同位置的应力计算值| 测点位置 | 应力值(MPa) || -------- | ------------ || A点 | 12.00 || B点 | 10.00 || C点 | 8.00 || D点 | 6.00 |2. 结果分析:通过实验数据与理论计算值的比较,可以看出,在梁的弯曲状态下,应力在梁横截面上呈线性分布。


纯-弯曲梁的正应力实验本实验旨在研究弯曲梁在受力时的正应力分布情况,通过实验数据的测量及分析,探讨影响梁正应力分布的因素,并对梁的强度进行评估。
1. 实验原理1.1 弯曲梁正应力分析弯曲梁是一种常用的结构元件,例如桥梁、楼层结构等,她受到外力的作用会发生弯曲形变,产生正应力和剪应力。
弯曲梁的正应力是沿着截面法向的应力,在梁的顶部为拉应力,底部为压应力。
正应力的计算公式如下:$$\sigma = \frac{My}{I}$$其中,$\sigma$为正应力,$M$为弯矩,$y$为受力点到截面重心的距离,$I$为截面惯性矩。
弯曲梁正应力的分布情况受到多种因素的影响,主要包括:① 梁材料的弹性模量:弹性模量越大,弯曲梁的刚度越大,相同外力作用下,梁的形变和正应力都会相应减小。
② 梁截面形状和尺寸:梁截面的惯性矩影响正应力的大小和分布情况。
截面抗弯性能越强,正应力越小。
③ 受力位置和方向:受力位置和作用方向是影响正应力大小和分布情况的重要因素。
不同位置和方向的外力作用会导致不同的正应力分布规律。
2. 实验设备和方法本实验采用的主要设备有:弯曲梁试验机、电子天平、千分尺等。
2.2 实验步骤1. 准备弯曲梁样品,将其加工成常用的矩形截面和半圆形截面,分别测量其截面形状和尺寸。
2. 调整弯曲梁试验机,设置好取样位置和取样方式。
3. 将弯曲梁放入试验机,设置试验参数,包括荷重大小、位移速率等。
4. 开始试验,记录每个荷载下的跨中挠度和荷载大小,并计算出弯矩大小。
5. 在试验过程中,用电子天平测量梁的重量,并用千分尺对梁的跨中直径和截面高度进行测量,计算出截面惯性矩。
6. 根据测量数据,计算出每个荷载下的正应力,并绘制出正应力分布图。
3. 结果分析3.1 实验数据记录本实验用常见的矩形和半圆形弯曲梁进行了试验,记录了不同工况下的荷载和跨中挠度等数据。
根据数据计算得出弯矩以及正应力等数据,具体数据结果如下表:1. 矩形截面弯曲梁(1)弯曲梁在起始荷载下出现了微小的振动,但并未发生失稳。

梁的纯弯曲正应力实验报告一、实验目的。
本实验旨在通过对梁的纯弯曲实验,了解在梁的弯曲变形中产生的正应力分布规律,并通过实验数据的处理和分析,验证梁的正应力分布与理论计算的结果是否一致。
二、实验原理。
梁的纯弯曲是指梁在外力作用下只产生弯曲变形,不产生轴向拉伸或压缩的情况。
在梁的弯曲变形中,梁的上表面产生拉应力,下表面产生压应力,且在梁的截面上,不同位置的应力大小不同。
根据梁的弯曲理论,梁在弯曲变形中的正应力分布规律可以通过理论计算得出。
三、实验装置和仪器。
本实验所使用的实验装置包括梁的支撑装置、加载装置、测力传感器、位移传感器等。
其中,测力传感器用于测量梁在加载过程中的受力情况,位移传感器用于测量梁在加载过程中的位移情况。
四、实验步骤。
1. 将梁放置在支撑装置上,并调整支撑装置,使梁能够自由地产生弯曲变形;2. 将加载装置与梁连接,并通过加载装置施加一定的加载力;3. 同时记录梁在加载过程中的受力情况和位移情况;4. 依据实验数据,计算梁在不同位置的正应力大小,并绘制出正应力分布图;5. 将实验数据与理论计算结果进行对比分析,验证梁的正应力分布规律。
五、实验数据处理和分析。
通过实验测得的数据,我们计算出了梁在不同位置的正应力大小,并绘制出了正应力分布图。
通过对比实验数据与理论计算结果,我们发现梁的正应力分布与理论计算的结果基本一致,验证了梁的正应力分布规律。
六、实验结论。
通过本次实验,我们了解了梁的纯弯曲正应力分布规律,并通过实验数据的处理和分析,验证了梁的正应力分布与理论计算的结果基本一致。
因此,本实验取得了预期的实验目的。
七、实验总结。
本次实验通过对梁的纯弯曲实验,加深了我们对梁的弯曲变形和正应力分布规律的理解,同时也提高了我们的实验操作能力和数据处理能力。
希望通过本次实验,能够对大家有所帮助。
八、参考文献。
[1] 《材料力学实验指导书》。
[2] 《材料力学实验讲义》。
以上为梁的纯弯曲正应力实验报告,谢谢阅读。

姓名: 班级: 学号:实验陈述 纯曲折梁的正应力实验一.实验目标:1.测定梁在纯曲折时横截面上正应力大小和散布纪律2.验证纯曲折梁的正应力公式 二.实验装备及对象:1.材料力学多功效实验台中的纯曲折梁实验装配2.数字测力仪.电阻应变仪 三.实验道理及办法:在纯曲折前提下,依据平面假设和纵向纤维间无挤压的假设,可得到梁横截面上随意率性一点的正应力,盘算公式:zM yI σ⋅=为测量梁横截面上的正应力散布纪律,在梁的曲折段沿梁正面不合高度,平行于轴线贴有应变片.贴法:中性层一片,中性层高低1/4梁高处各一片,梁高低两侧各一片,共计五片.采取增量法加载,每增长等量荷载△P (500N )测出各点的应变增量△ε,求的各点应变增量的平均值△ε实i ,从而求出应力增量:σ实i =E △ε实i将实验应力值与理论应力值进行比较,已验证曲折正应力公式. 四.原始数据:五.实验步调:1. 打开应变仪.测力仪电源开关2.连策应变仪上电桥的连线,肯定第一测点到第五测点在电桥通道上的序号.3. 检讨测力仪,选择力值加载单位N或kg,按动按键直至显示N 上的红灯亮起.按清零键,使测力计显示零.4.应变仪调零.按下“主动均衡”键,使应变仪显示为零.5.转着手轮,按铭牌指导加载,加力的学生要迟缓匀速加载,到测力计上显示500N,读数的学生读下5个测点的应变值,(留意记载下正.负号).用应变仪右下角的通道切换键来显示第5测点的读数.今后,加力每次500N,到3000N为止.6.读完3000N应变读数后,卸下载荷,封闭电源.六.实验成果及处理:1.各点实验应力值盘算依据上表数据求得应变增量平均值△εPi,带入胡克定律盘算各点实验值:σ实i=E△εPi×10-62.各点理论应力值盘算载荷增量△P = 500N弯矩增量△M = △P/2×L P应力理论值盘算(验证的就是它)3.绘出实验应力值和理论应力值的散布图以横坐标暗示各测点的应力σ实和σ理,以纵坐标暗示各测点距梁中性层的地位.将各点用直线衔接,实测用实线,理论用虚线.σy4.实验值与理论值比较,验证纯曲折梁的正应力公式。

30yp 应力分布曲线20 10 0 10 -20 -30应力b七、思考题1•为什么要把温度补偿片贴在与构件相同的材料上 ?答:应变片是比较高精度的传感元件,必须考虑温度的影响,所以需要把温度补 偿片贴在与构件相同的材料上,来消除温度带来的应变。
2•影响实验结果的主要因素是什么?答:影响本实验的主要因素:实验材料生锈,实验仪器精度以及操作的过程。
一、 实验目的和要求:1)2)用电测法测定纯弯曲梁受弯曲时(或 )截面各点的正应力值,与理论计算值进行比较。
了解电阻应变仪的基本原理和操作方法二、 实验设备CM-1C 型静态电阻应变仪,纯弯曲梁实验装置三、 弯曲梁简图:—0理 亠b 宝J/2 J/2| / [11 I 丄丄. ___ JULlllx|图5-1 已知:、 、、、c h 『6、I : 200GPa(或)截面处粘贴七片电阻片,即 R1、R2、R3、R4、R5、R6、在梁的纯弯曲段内R7。
R4贴在中性层处,实验时依次测出1、2、3、4、5、6、7点的应变,计算 出应力。
四、测量电桥原理 构件的应变值一般均很小,所以,应变片电阻变化率也很小,需用专门仪器进行 测量,测量应变片的电阻变化率的仪器称为电阻应变仪,其测量电路为惠斯顿电 桥,如图所示。
如图所示,电桥四个桥臂的电阻分别为 R1、R2、R3和R4,在设A 、C 端接电源,B 、D 端为输出端W-1ABL22fn/2A、B和B、C以上为全桥测量的读数,如果是半桥测量,则读数为半桥测量是将应变片R3和R4放入仪器内部,R1和R2测量片接入电桥,接入组成半桥测量。
五、理论和实验计算理论计算、扰I?实验值计算:AO _D二4JiD 门电桥,当构件受力后,设上述应变片感受到的应变分别为[、2、3、4相应的电阻改变量分别为、、和,应变仪的读数为d 4 U 1 2 34KU4 U 1 2KU:3.5bh2M cl 4 (JWZ l/.6bh3> 2.6M c2 1Z、d半所谓上式代表电桥的输出电压与各臂电阻改变量的一般关系。

纯弯曲正应力分布规律实验数据一、实验介绍本次实验旨在研究纯弯曲情况下的正应力分布规律,通过测量和分析实验数据,探究不同材料和不同截面形状的试件在纯弯曲条件下的应力分布情况,为工程设计提供参考。
二、实验原理1. 纯弯曲概念纯弯曲是指杆件在外力作用下只发生弯曲变形而不发生拉伸或压缩变形的情况。
在纯弯曲状态下,杆件内部产生的应力是沿截面法线方向分布的。
2. 弹性模量弹性模量是材料抵抗变形能力的一个物理量,表示单位应力作用下单位长度物体产生的相对变形。
它是描述材料刚度大小的重要参数。
3. 截面惯性矩截面惯性矩是描述截面形状对于扭转刚度影响大小的一个物理量。
它越大,则说明该截面形状对于扭转刚度影响越小。
4. 应力公式在纯弯曲情况下,试件内部产生的正应力可以通过以下公式计算:σ = M*y/I其中,σ为正应力,M为弯矩,y为距离中心轴线的距离,I为截面惯性矩。
三、实验步骤1. 制备试件:根据实验要求制备不同材料和不同截面形状的试件。
2. 安装测力传感器:将测力传感器安装在试件上,用以测量试件受到的弯曲力和弯矩。
3. 进行弯曲试验:在实验机上进行弯曲试验,并记录下每个角度下试件受到的弯矩和变形量数据。
4. 计算应力分布:根据公式计算出每个角度下试件内部产生的正应力,并绘制出应力分布图。
5. 数据分析:对实验数据进行分析,探究不同材料和不同截面形状对于应力分布规律的影响。
四、实验数据与结果以下是本次实验得到的部分数据和结果:1. 材料为钢板,截面形状为圆形:弹性模量E = 2.1×10^11 Pa截面惯性矩I = πr^4/4其中r为半径。
通过计算得到该试件在不同角度下产生的正应力分布图如下:(插入图片)从图中可以看出,在圆形截面试件的弯曲过程中,试件内部产生的正应力沿截面法线方向分布,且最大值出现在距离中心轴线最远的位置。
此外,正应力随着距离中心轴线的距离增加而逐渐减小。
2. 材料为铝合金,截面形状为矩形:弹性模量E = 7.0×10^10 Pa截面惯性矩I = bh^3/12其中b为宽度,h为高度。

纯弯曲梁正应力测定一、 实验目的1.测定梁在纯弯曲时横截面上的正应力分布,验证平面假设理论和弯曲正应力公式。
2.学习电测应力实验方法。
二、 实验设备1.简支梁及加载装置。
2.电阻应变仪。
3.直尺,游标卡尺。
三、 实验原理根据弯曲梁的平面假设沿着梁横截面高度的正应力分布规律应当是直线。
为了验证这一假设,我们在梁的纯弯曲段内粘贴7片电阻应变片:1#、2#、3#、4#、5#、6#、7#,见指导书中图,由应变仪测出读数即知道沿着梁横面高度的正应力分布规律。
四、 实验步骤1.用游标卡尺测量梁的尺寸b 和h ,用钢尺量梁的支点至力作用点的距离d 。
2.将各点的应变片和温度补偿片以半桥的形式接入应变仪。
被测应变片接在AB 上,补偿片接在BC 上。
仪器操作步骤:1)半桥测量时将D 1DD 2接线柱用连接片连接起来并旋紧。
2)将标准电阻分别与A 、B 、C 接线柱相连。
3)接通电源开关。
4)按下“基零”键仪表显示“0000”或“-0000”(仪表内部已调好)。
5)按下“测量”键,显示测量值,将测量值调到“0000”或“-0000”。
6)按下“标定”键仪表显示-10000附近值,按照所使用应变片灵敏度K=2.17,调节灵敏度使显示为-9221。
7)将“本机、切换”开关置“切换”状态。
主机的 A 、B 、C 接线柱上的标准电阻去掉,将各被测量应变片一端分别与左上对应的各A (A 1~A 7)接线柱相连,公共输出端与一B 接线柱相连,温度补偿片接在B 、C 之间。
被测点(应变片号) 6 4 2 1 3 5 7 接线端子(通道号) 1 2 3 4 5 6 78)切换开关, 按次序所有点的平衡都调节在0000或-0000值上。
9)转动手轮,使梁加载荷,逐点测量、记录应变值。
采用增量法加载,每次0.5kN 。
注意不能超载。
0.5 kN , 初载荷调零; 1.0 kN , 1.5 kN ,2.0 kN ,2.5 kN ,读出应变值10)实验结束。

纯弯曲梁正应力实验报告材料力学课程实验报告纯弯曲梁正应力实验报告学院系班级实验组别实验人员姓名实验日期年月日一、实验目的二、实验设备静态电阻应变仪型号实验装置名称型号量具名称精度㎜三、实验数据及处理梁试件的弹性模量梁试件的横截面尺寸h ㎜b ㎜支座到集中力作用点的距离d ㎜各测点到中性层的位置1y ㎜2y ㎜ 3y ㎜ 4y ㎜ 5y ㎜ 6y ㎜材料力学课程实验报告载荷N 静态电子应变仪读数106 1点 2点 3点 4点 5点 6点 F F 读数1 增量1 读数2 增量2 读数3 增量3 读数4 增量4 读数5 增量5 读数6 增量6 F 1 2 3 4 5 6 应变片位置 1点 2点 3点 4点 5点 6点实验应力值/MPa 理论应力值/MPa 相对误差/ 泊松比值注表中读数1、2、3、4、5、6为两次实验所得读数的平均值。
F为荷载增量的平均值。
1、2、3、4、5、6为各点应变增量的平均值材料力学课程实验报告四、应力分布图理论和实验的应力分布图画在同一图上五、思考题 1.为什么要把温度补偿片贴在与构件相同的材料上 2.影响实验结果的主要因素是什么材料力学课程实验报告测定材料E、实验报告学院系班级实验组别实验人员姓名实验日期年月日一、实验目的二、实验设备静态电阻应变仪型号实验装置名称型号量具名称精度㎜三、实验数据及处理板试件尺寸试件截面宽b ㎜高h ㎜截面积oA mm2 NF oAFMPa 纵向应变106 横向应变106 1r 2r 3r 1r 2r 3r 材料力学课程实验报告数据处理方法 1平均法均均oAFE 均均计算过程 2最小二乘法niiniiiE121niiniii121 计算过程材料力学课程实验报告四、画出关系图理论和实验的关系图画在同一图上平均法理论和实验的关系图最小二乘法理论和实验的关系图五、思考题 1.试件尺寸和形式对测定弹性模量E有无影响 2.影响实验结果的因素有那些为何要用等量增载法进行实验材料力学课程实验报告圆管扭转应力试验实验报告学院系班级实验组别实验人员姓名实验日期年月日一、实验目的二、实验设备静态电阻应变仪型号实验装置名称型号量具名称精度㎜三、实验数据及处理薄壁圆管尺寸外径D ㎜内径d ㎜加力臂长度L ㎜切变模量 Pa 弹性模量 Pa 泊松比电阻片号两次读数平均值两次读数平均值 1 2 3 4 5 6 注由于纯扭实验中004545故045采用1、4、3、6的绝对值加以平均表中电阻号1、4相对于45°应变片3、6相对于-45°应变片2、5相对于0°应变片材料力学课程实验报告四、计算B、D点实测时的主应力和主方向五、计算B、D点理论主应力和主方向六、思考题 1.求出实测主应力、主方向与理论主应力、主方向的相对误差。

纯弯曲梁正应力实验报告材料力学课程实验报告纯弯曲梁正应力实验报告学院系班级实验组别实验人员姓名实验日期年月日一、实验目的二、实验设备静态电阻应变仪型号实验装置名称型号量具名称精度㎜三、实验数据及处理梁试件的弹性模量11101.2EPa 梁试件的横截面尺寸h ㎜b ㎜支座到集中力作用点的距离d ㎜各测点到中性层的位置1y ㎜2y ㎜3y ㎜4y ㎜5y ㎜6y ㎜材料力学课程实验报告载荷N 静态电子应变仪读数106 1点2点3点4点5点6点F F 读数1 增量1 读数2 增量2 读数3 增量3 读数4 增量4 读数5 增量5 读数6 增量6 F 1 2 3 4 5 6 应变片位置1点2点3点4点5点6点实验应力值/MPa 理论应力值/MPa 相对误差/ 泊松比值注表中读数1、2、3、4、5、6为两次实验所得读数的平均值。
F为荷载增量的平均值。
1、2、3、4、5、6为各点应变增量的平均值材料力学课程实验报告四、应力分布图理论和实验的应力分布图画在同一图上五、思考题1.为什么要把温度补偿片贴在与构件相同的材料上2.影响实验结果的主要因素是什么材料力学课程实验报告测定材料E、实验报告学院系班级实验组别实验人员姓名实验日期年月日一、实验目的二、实验设备静态电阻应变仪型号实验装置名称型号量具名称精度㎜三、实验数据及处理板试件尺寸试件截面宽b ㎜高h ㎜截面积oA mm2 NF oAFMPa 纵向应变106 横向应变106 1r 2r 3r 1r 2r 3r 材料力学课程实验报告数据处理方法1平均法均均oAFE 均均计算过程2最小二乘法niiniiiE121 niiniii121 计算过程材料力学课程实验报告四、画出关系图理论和实验的关系图画在同一图上平均法理论和实验的关系图最小二乘法理论和实验的关系图五、思考题1.试件尺寸和形式对测定弹性模量E有无影响2.影响实验结果的因素有那些为何要用等量增载法进行实验材料力学课程实验报告圆管扭转应力试验实验报告学院系班级实验组别实验人员姓名实验日期年月日一、实验目的二、实验设备静态电阻应变仪型号实验装置名称型号量具名称精度㎜三、实验数据及处理薄壁圆管尺寸外径D ㎜内径d ㎜加力臂长度L ㎜切变模量111082.0G Pa 弹性模量11101.2E Pa 泊松比28.0 电阻片号kNPo1.0 kNPn1.1 两次读数平均值两次读数平均值1 2 3 4 5 6 注由于纯扭实验中004545故045采用1、4、3、6的绝对值加以平均表中电阻号1、4相对于45°应变片3、6相对于-45°应变片2、5相对于0°应变片材料力学课程实验报告四、计算B、D点实测时的主应力和主方向五、计算B、D点理论主应力和主方向六、思考题1.求出实测主应力、主方向与理论主应力、主方向的相对误差。


纯弯曲正应力实验报告一、实验目的1. 掌握纯弯曲正应力的基本原理和实验方法;2. 通过实验数据分析,了解梁在不同弯曲程度下的正应力分布情况;3. 培养实验操作能力,提高数据处理和分析水平。
二、实验原理纯弯曲正应力是指在受力构件的横截面上只有弯矩作用而无轴向力作用的情况下的正应力。
根据材料力学的基本理论,纯弯曲正应力可以用以下公式表示:σ=My/I其中,σ为正应力,M为弯矩,y为截面点到弯曲中心的距离,I为截面对弯曲中心的惯性矩。
三、实验步骤1. 准备实验器材:梁、砝码、测力计、测量尺、支撑架等;2. 将梁放在支撑架上,调整梁的位置,使其一端固定,另一端自由;3. 在梁上放置砝码,施加弯矩;4. 使用测力计测量梁上的作用力,记录数据;5. 使用测量尺测量梁的弯曲程度,记录数据;6. 改变砝码的数量和位置,重复步骤4和5,获取多组数据;7. 将实验数据整理成表格。
四、实验数据分析与结论通过实验数据,我们可以计算出梁在不同弯曲程度下的正应力值。
根据计算结果,我们可以得出以下结论:1. 随着弯矩的增大,梁的正应力值逐渐增大;2. 随着梁的弯曲程度的增加,正应力分布不均匀程度逐渐增大;3. 在实验条件下,纯弯曲正应力的计算公式适用。
五、实验总结与建议通过本次实验,我们掌握了纯弯曲正应力的基本原理和实验方法,了解了梁在不同弯曲程度下的正应力分布情况。
在实验过程中,我们需要注意以下几点:1. 确保梁的放置位置正确,避免支撑架的移动或倾斜对实验结果的影响;2. 在测量梁的弯曲程度时,要选择合适的测量点,避免误差的产生;3. 在计算正应力时,要确保数据的准确性和可靠性。

姓名:班级:学号:实验报告纯弯曲梁的正应力实验一、实验目的:1.测定梁在纯弯曲时横截面上正应力大小和分布规律2.验证纯弯曲梁的正应力公式二、实验设备及工具:1.材料力学多功能试验台中的纯弯曲梁实验装置2.数字测力仪、电阻应变仪三、实验原理及方法:在纯弯曲条件下,根据平面假设和纵向纤维间无挤压的假设,可得到梁横截面上任意一点的正应力,计算公式:σ=My/I z为测量梁横截面上的正应力分布规律,在梁的弯曲段沿梁侧面不同高度,平行于轴线贴有应变片。
贴法:中性层一片,中性层上下1/4梁高处各一片,梁上下两侧各一片,共计五片。
采用增量法加载,每增加等量荷载△P(500N)测出各点的应变增量△ε,求的各点应变增量的平均值△ε实i,从而求出应力增量:σ实i=E△ε实i将实验应力值与理论应力值进行比较,已验证弯曲正应力公式。
四、原始数据:五、实验步骤:1.打开应变仪、测力仪电源开关2.连接应变仪上电桥的连线,确定第一测点到第五测点在电桥通道上的序号。
3. 检查测力仪,选择力值加载单位N或kg,按动按键直至显示N上的红灯亮起。
按清零键,使测力计显示零。
4.应变仪调零。
按下“自动平衡”键,使应变仪显示为零。
5.转动手轮,按铭牌指示加载,加力的学生要缓慢匀速加载,到测力计上显示500N,读数的学生读下5个测点的应变值,(注意记录下正、负号)。
用应变仪右下角的通道切换键来显示第5测点的读数。
以后,加力每次500N,到3000N 为止。
6.读完3000N应变读数后,卸下载荷,关闭电源。
六、实验结果及处理:1.各点实验应力值计算根据上表数据求得应变增量平均值△εPi,带入胡克定律计算各点实验值:σ实i=E△εPi×10-62.各点理论应力值计算载荷增量△P=500N弯矩增量△M=△P/2×a应力理论值计算σ理i=∆M∙YiI z(验证的就是它)3.绘出实验应力值和理论应力值的分布图以横坐标表示各测点的应力σ实和σ理,以纵坐标表示各测点距梁中性层的位置。

纯弯曲梁正应力实验报告纯弯曲梁正应力实验报告引言:纯弯曲梁正应力实验是结构力学实验中的一项重要内容,通过对纯弯曲梁的加载和变形进行观察和测量,可以研究梁的正应力分布规律,探索材料的力学性质以及结构的强度和稳定性。
本实验旨在通过实际操作和数据分析,深入了解纯弯曲梁的正应力分布特点,并对实验结果进行讨论和总结。
实验目的:1. 了解纯弯曲梁的正应力分布规律;2. 掌握测量和计算纯弯曲梁的正应力的方法;3. 分析实验结果,验证理论计算和实验测量的一致性。
实验原理:纯弯曲梁在受到外力作用时,梁的上表面受到拉应力,下表面受到压应力,而中性轴上则不受应力。
根据梁的几何形状和材料特性,可以通过理论计算得到梁上各点的正应力大小。
实验装置:1. 纯弯曲梁实验台:用于支撑和加载梁;2. 弯曲梁加载装置:用于施加力矩,产生弯曲变形;3. 应变计:用于测量梁上各点的应变;4. 数据采集系统:用于记录和分析实验数据。
实验步骤:1. 将纯弯曲梁固定在实验台上,并调整加载装置,使其施加合适的力矩;2. 在梁上选择若干个测量点,安装应变计,并进行校准;3. 施加力矩后,使用数据采集系统实时记录梁上各点的应变数据;4. 停止加载后,记录应变计的读数,并进行数据处理和分析。
实验结果:通过实验测量和数据处理,得到了纯弯曲梁上各点的应变数据。
根据应变-应力关系,可以计算出相应点的正应力大小。
通过对实验结果的分析,可以得到纯弯曲梁的正应力分布规律,验证理论计算和实验测量的一致性。
讨论与分析:1. 实验结果与理论计算相比,是否存在较大的误差?如果有,可能的原因是什么?2. 实验中是否存在其他因素对结果产生影响?如温度变化、材料非均匀性等。
3. 在实际工程中,纯弯曲梁的正应力分布特点对结构设计和施工有何重要意义?结论:通过纯弯曲梁正应力实验,我们深入了解了纯弯曲梁的正应力分布规律,并通过实验结果的分析和讨论,对实验的准确性和可靠性进行了评估。

纯弯曲梁正应力电测实验报告一、实验目的本次实验旨在通过纯弯曲梁正应力电测实验,掌握梁的正应力计算方法以及电阻应变计的使用方法,并了解梁的受力特性和变形规律。
二、实验原理1.梁的受力特性当梁受到外力作用时,会产生内部应力和变形。
根据材料力学原理,内部应力可以分为正应力和剪应力。
在纯弯曲情况下,梁内部只存在正应力,且沿截面法线方向呈线性分布。
2.电阻应变计电阻应变计是一种常用的测量金属材料应变的仪器。
当金属材料发生形变时,其电阻值也会发生微小变化。
通过测量这种微小变化来计算金属材料的应变值。
3.纯弯曲梁正应力计算公式在纯弯曲情况下,梁内部只存在正应力。
根据受拉或受压状态下截面上某点处的正应力公式:σ = M*y/I其中,σ为该点处的正应力;M为作用于该点处剪跨截面上侧边缘的弯矩;y为该点到中性轴的距离;I为该截面的惯性矩。
三、实验器材和试件1.器材:纯弯曲梁实验台、电阻应变计、数字万用表等。
2.试件:长度为1.2m,宽度为20mm,厚度为2mm的钢板梁。
四、实验步骤1.将钢板梁放置在纯弯曲梁实验台上,并调整好实验台的支承距离。
2.将电阻应变计粘贴在梁上,保证其与梁表面紧密贴合,并接好电路。
3.通过旋钮调节实验台施加的力矩大小,使得钢板梁发生一定程度的弯曲变形,并记录下此时电阻应变计显示的电压值。
4.重复以上步骤,每次增加一定大小的力矩,直至达到最大载荷或者出现塑性变形等异常情况。
5.根据所得到的数据,计算出不同载荷下钢板梁各点处的正应力值,并绘制出正应力-距离曲线图和载荷-挠度曲线图。
五、实验结果分析1.正应力-距离曲线图通过计算所得到的正应力-距离曲线图,可以看出钢板梁内部正应力随着距离的增加而减小,且呈线性分布。
在最大载荷下,梁中心处的正应力最大,约为200MPa。
2.载荷-挠度曲线图通过实验数据计算得到的载荷-挠度曲线图,可以看出钢板梁的弯曲刚度随着载荷的增加而降低。
当达到最大载荷时,梁发生塑性变形并无法恢复原状。
竭诚为您提供优质文档/双击可除纯弯曲正应力分布实验报告
篇一:弯曲正应力实验报告
一、实验目的
1、用电测法测定梁纯弯曲时沿其横截面高度的正应变(正应力)分布规律;
2、验证纯弯曲梁的正应力计算公式。
3、初步掌握电测方法,掌握1/4桥,1/2桥,全桥的接线方法,并且对试验结果及误差进行比较。
二、实验仪器和设备
1、多功能组合实验装置一台;
2、Ts3860型静态数字应变仪一台;
3、纯弯曲实验梁一根。
4、温度补偿块一块。
三、实验原理和方法
弯曲梁的材料为钢,其弹性模量e=210gpa,泊松比μ
=0.29。
用手转动实验装置上面的加力手轮,使四点弯上压
头压住实验梁,则梁的中间段承受纯弯曲。
根据平面假设和纵向纤维间无挤压的假设,可得到纯弯曲正应力计算公式为:
??
m
yIx
式中:m为弯矩;Ix为横截面对中性轴的惯性矩;y为所求应力点至中性轴的距离。
由上式可知,沿横截面高度正应力按线性规律变化。
实验时采用螺旋推进和机械加载方法,可以连续加载,载荷大小由带拉压传感器的电子测力仪读出。
当增加压力?p 时,梁的四个受力点处分别增加作用力?p/2,如下图所示。
为了测量梁纯弯曲时横截面上应变分布规律,在梁纯弯曲段的侧面各点沿轴线方向布置了3片应变片,各应变片的粘贴高度见弯曲梁上各点的标注。
此外,在梁的上表面和下表面也粘贴了应变片。
如果测得纯弯曲梁在纯弯曲时沿横截面高度各点的轴
向应变,则由单向应力状态的虎克定律公式??e?,可求出各点处的应力实验值。
将应力实验值与应力理论值进行比较,以验证弯曲正应力公式。
σ实=eε
式中e是梁所用材料的弹性模量。
实
图3-16
为确定梁在载荷Δp的作用下各点的应力,实验时,可
采用“增量法”,即每增加等量的载荷Δp测定各点相应的应变增量一次,取应变增量的平均值Δε
把Δσ实与理论公式算出的应力??式中的m应按下式计算:
实
来依次求出各点应力。
??
比较,从而验证公式的正确性,上述理论公??
??
四、实验步骤
1
?pa(3.16)2
1、检查矩形截面梁的宽度b和高度h、载荷作用点到梁支点距离a,及各应变片到中性层的距离yi。
2、检查压力传感器的引出线和电子秤的连接是否良好,接通电子秤的电源线。
检查应变仪的工作状态是否良好。
分别采用1/4桥,1/2桥,全桥的接线方法进行测量,其中1/4桥需要接温度补偿片,1/2桥通过交换接线方式分别进行两次试验来比较试验结果。
?s确3、根据梁的材料、尺寸和受力形式,估计实验时的初始载荷p0(一般按p0?0.1
定)、最大载荷pmax(一般按pmax?0.7?s确定)和分级载
荷?p(一般按加载4~6级考虑)。
本实验中分四次加载。
实验时逐级加载,并记录各应变片在各级载荷作用下的读数应变。
4、实验完毕后将载荷卸掉,关上电阻应变仪电源开关,并请教师检查实验数据后,方可离开实验室。
五、数据处理
1、原始数据。
其中a=80mmb=19.62mmh=39.38mm
1/4桥
??实?e??实
??实?
??
n
i
bh3?m*y?p*a
Iz理?
?m?
Iz122
相对误差=|
??实理
??理
|×100%
在梁的中性层内,因??理?0,只需计算绝对误差,绝对误差=10.5Kpa。
i
??实
n
??实?e??实
bh3?m*y?p*a
Iz理?*2?m?
I
z122
相对误差=|
??实理
??理
|×100%
i
??实
n
??实?e??实
bh3?m*y?p*a
Iz理?*2?m?
I
z122
相对误差=|
??实理
??理
|×100%
篇二:纯弯曲正应力分布规律实验
纯弯曲正应力分布规律实验
一、实验目的
1、用电测法测定梁纯弯曲时沿其横截面高度的正应变(正应力)分布规律;
2、验证纯弯曲梁的正应力计算公式。
二、实验仪器和设备
1、多功能组合实验装置一台;
2、Ts3860型静态数字应变仪一台;
3、纯弯曲实验梁一根。
4、温度补偿块一块。
三、实验原理和方法
弯曲梁的材料为钢,其弹性模量e=210gpa,泊松比μ
=0.28。
用手转动实验装置上面的加力手轮,使四点弯上压
头压住实验梁,则梁的中间段承受纯弯曲。
根据平面假设和纵向纤维间无挤压的假设,可得到纯弯曲正应力计算公式为:??
m。